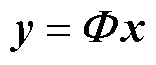（1）摘要 针对局部放电信号频域非带限且要求采样频率过高而引发的电路参数与性能矛盾，提出一种基于虚拟通道延拓的局部放电信号压缩采样方法，利用压缩感知并行测量来降低采样频率。通过在采样电路中实现虚拟通道延拓，降低了并行测量通道数，优化了压缩采样电路结构。为了使测量通道参数适合局部放电信号特征，提出了基于非相干性延拓的三值观测矩阵设计算法，包括引入自相干正则项和利用时序加窗差值的变步长梯度下降法来降低参数相干性。最后，将观测矩阵用于虚拟通道延拓电路，实现局部放电信号的压缩采样。结果表明，文中的压缩采样方法将采样频率降低至1.6 MHz，利用多通道测量将整体采样频率和数据量分别压缩至48%和14%，将实际并行测量通道数优化至12条。该文的压缩采样方法降低了传感设备的元器件参数要求和电路结构复杂度，达到了电力设备局部放电信号在线监测的需求。
关键词：局部放电 压缩感知 观测矩阵 非相干性 虚拟通道延拓
电力设备运行中绝缘劣化发展导致停机故障的主要原因是局部放电（Partial Discharge, PD），因此需要对电力设备PD信号实现在线监测[1-2]。然而PD信号在时域表现为短时脉冲，在频域上是非带限的，当前对其实现精准采样需要采用专业局部放电测量仪。在新型电力系统中，PD信号监测采用分布式传感与边缘计算相融合的方式。由于PD监测传感器部署量大，在传感器本身部署算力将大幅提高成本，限制其应用与推广，为此需要引入现场智能终端作为中心计算节点。传感器将原始采样数据传输至其所属现场智能终端进行特征提取。其中传感器理论上需要配备无限高采样频率的模数转换器（Analog-to-Digital Converter, ADC）[3-4]。但ADC由于受生产工艺限制，导致其成本随采样频率呈指数级上升[5]。高频模拟信号在电路中的串扰问题使得采样器板卡封装制作严重受限[6-7]。此外，高频采样还对采样器内存、通信接口、信号总线、对应接收终端的通信模块、系统级芯片（System on Chip, SoC）等元器件也提出了很高的要求。
以上对元器件参数的要求直接导致基于PD信号的在线监测成本高昂。而要实现PD信号在线监测在电网中部署应用，首先要保证信号的测量精度，需基于PD信号的数据特征选取采样方式；其次，要求传感器降低采样频率和电路板卡封装难度，以提高经济性和可推广性；最后，需降低测量信号的数据量，满足传感器实时监测数据在边缘侧的传输能力，降低数据服务成本。因此，实现PD在线监测的关键问题是如何在保证准确性的同时降低ADC采样频率。
压缩感知（Compressed Sensing, CS）理论证明，信号的实际有效“信息率”远低于信号的Nyquist频率[8]。文献[9-10]在图像处理领域成功地应用CS理论验证了数据的可压缩性。此外，已有相关研究将其应用于高频通信、水下声波、无线传感等一维模拟信号的数据压缩[11-13]。但以上研究是将Nyquist频率信号进行数据压缩，未涉及信号的低频率采样研究。当前对PD信号应用CS理论仍需获取高频测量信号（Nyquist网格点），无法解决传感器的电路与性能矛盾[14-15]。
文献[16]论证了CS理论可低于Nyquist频率采样并保证测量的准确性，即CS理论可用于降低PD信号在线监测的采样频率[17]。基于CS理论对模拟信号进行低频率采样并转化为数字信息的采样方法称为模拟信息转换器（Analog-to-Information Converter, AIC）[18]。设计适用于PD信号的AIC需要在采样的同时实现全局信息的调制与混叠[19]。当前已有随机解调和m序列调制的方法实现了对无线通信信号的压缩采样[20-21]。但以上研究需待测信号在频域稀疏。针对频域非稀疏信号，文献[22-23]提出了随机延时采样和延时触发的调制宽带转换器（Modulation Wideband Converter, MWC）改进方案，其利用随机性混叠全局信息，但要求信号具有严格的周期性；文献[24]基于频域非稀疏的声信号提出了二次观测思想，但信号测量精度低；文献[25]提出利用随机调制预积分电路实现对频域非稀疏信号的压缩采样，但电路实现需要大量并行测量通道，结构过于复杂、实用性较低。以上AIC方案受限于信号特征、测量精度和电路结构，不适用于PD信号的压缩采集。
为解决上述问题，实现电力设备PD信号的压缩采样，本文提出一种基于虚拟通道延拓的局部放电信号模拟信息转换器方案（Analog-to-Information Converter for PD signal based on Virtual Channel Extension, VCE-AIC）。为了优化电路结构，降低了测量通道数，利用虚拟通道延拓方法构建PD信号的AIC采集方案。为保证测量精度并贴合PD信号的自身特征，VCE-AIC提出基于非相干性延拓的三值观测矩阵设计算法，以此来获取适合其采样方案的观测矩阵。最后利用压缩采样算例，验证以上内容的正确性。
压缩感知理论的基本数学模型为
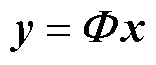（1）
式中，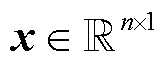
为原信号在Nyquist网格上的数据点；
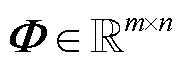为观测矩阵；
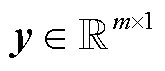为压缩测量信号，
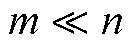。求解式（1）的欠定方程要求
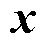在某个变换域
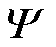内稀疏[26]，即有
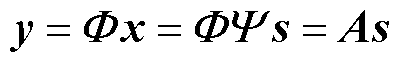（2）
式中，
为稀疏基；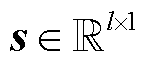
为稀疏系数，且
；
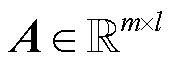为压缩传感算子。其中要求
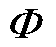的引入不能影响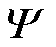中各向量间的相干性，需验证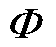与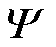的非相干性[27]。相干系数为
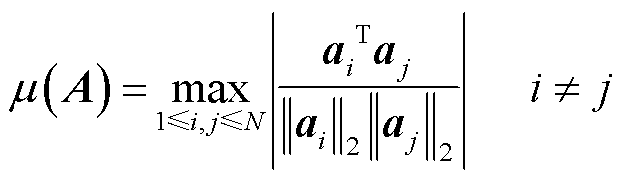（3）
式中，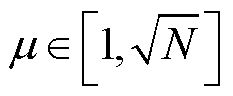
，
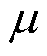越小压缩测量信号y携带的有效信息越多。
利用重构算法求解式（4）得到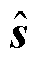
后，经稀疏反变换
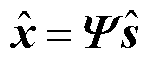，可得原始信号。CS原理如图1所示。
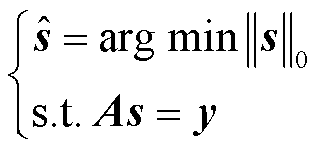（4）
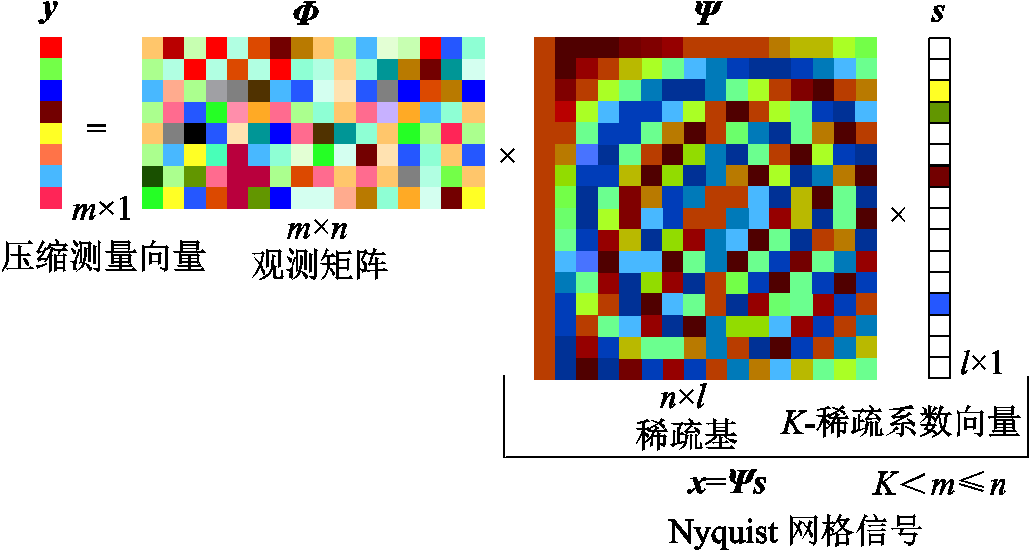
图1 压缩感知原理示意图
Fig.1 The schematic of compressed sensing principle
PD信号在频域无限连续且存在大量小数值点，局部放电信号频谱如图2所示。幅值较高的低频段主要是直流、工频及谐波分量，不能反映PD波形信息。因此无法忽略小数值点信息，即PD信号在频域非带限、非稀疏。
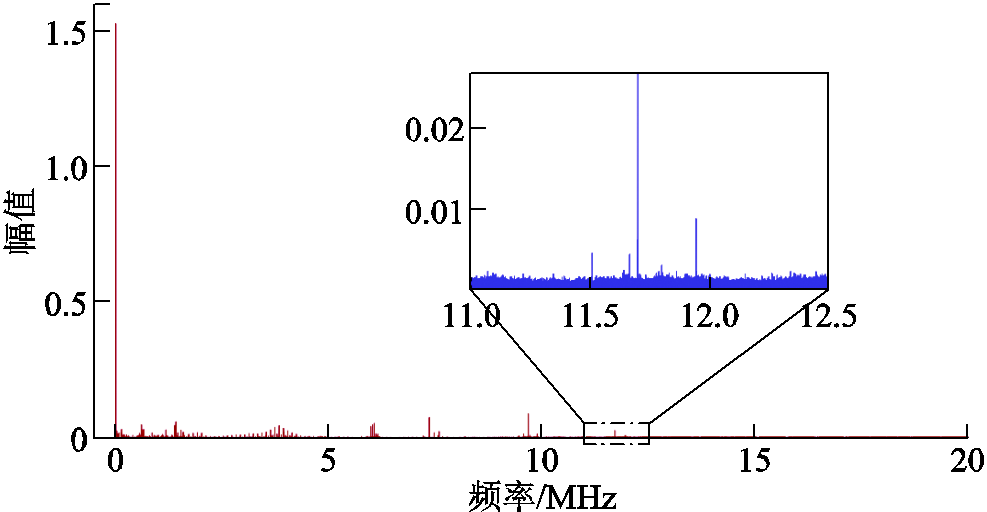
图2 局部放电信号频谱
Fig.2 The spectrum of partial discharge signal
当前适于频域非稀疏信号的AIC方案是将CS引入采样环节，利用乘法器与积分器将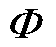中的参数硬件化，在采样电路中加入信号发生单元将观测矩阵作为固定周期的模拟信号输出。利用模拟乘法器将此信号与待测信号以相乘的方式调制。之后对调制后的模拟信号利用积分器进行积分输出，周期
(
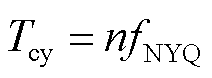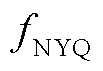为Nyquist采样频率)实现全局信息混叠，完成观测矩阵与原始信号的相乘。然后在对信号进行A-D采样之前进行抗混滤波，之后利用低频率ADC进行采样获取低频压缩测量信号y，在后期进行信号重构整体实现Sub-Nyquist采样。其中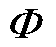，中的各调制向量需要在电路中配置对应的并行测量通道[25]。在AIC的应用场景下，PD监测设备的采样频率和可用性存在成本与性能矛盾。采样频率过高会首先导致AD芯片成本过高，其次造成在采样过程中信号高频串扰严重、通信速率不匹配、数据传输与存储成本大等问题，不利于PD信号在线监测的大规模应用；采样频率过低会导致并行测量通道过多、长时间积分造成积分器误差、降低信号精度等问题，同样不利于PD信号在线监测的应用。
本文结合PD信号特征提出了一种基于虚拟通道延拓的模拟信息转换器（VCE-AIC）方案，该方案利用并行测量降低采样频率，并基于子测量段非相干性延拓来建立虚拟测量通道，降低实际测量通道数。为此，需在根据通道延拓需求和稀疏字典的非相干性准则来设计相应的观测矩阵。之后基于观测矩阵参数产生调制信号与PD输入进行模拟域相乘，在积分与滤波后输出低频率的压缩测量信号，后期对其重构方可表达信号原始波形。因此VCE-AIC的研究重点在于观测矩阵的设计，整体流程如图3所示。
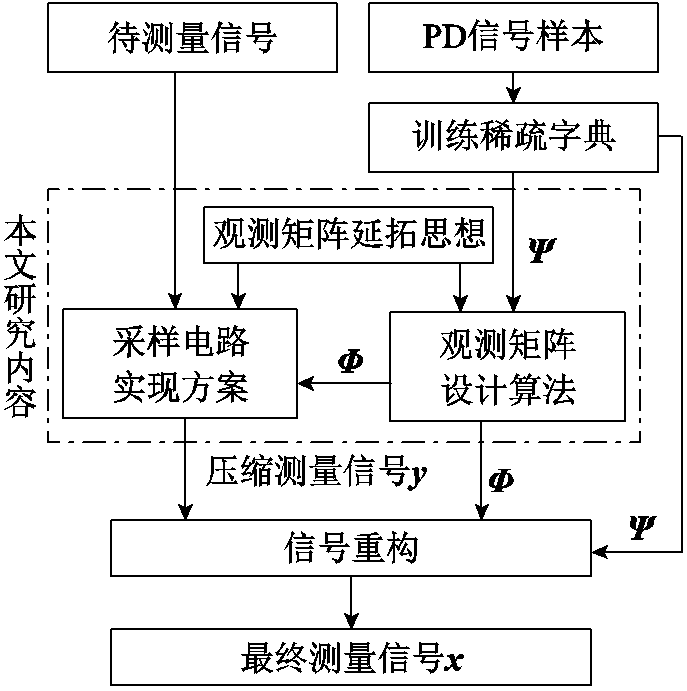
图3 PD信号压缩采样的整体流程
Fig.3 Overall flow of PD signal compressed sampling
为了减少对信号压缩采样时电路中的实际测量通道数，提出虚拟通道延拓方法。虚拟通道在实际通道的后端实现，基于实际采样通道输出的压缩信号进行非相干性重组（二次测量），构建新的信号输出通道。
定义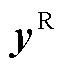
、
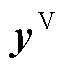分别是实际和虚拟测量通道输出。首先把积分周期
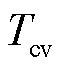分为p个子测量区间，则VCE-AIC通道i的测量向量
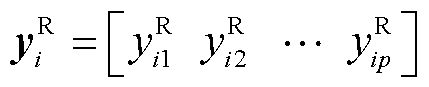。其中第j个子测量段
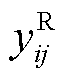的获取过程如下。
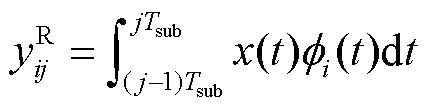（5）
式中，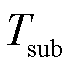
为子测量时间，
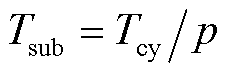；i为实际测量通道索引，
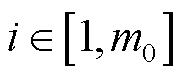；j为子测量段索引，
；
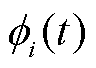为积分通道i的调制信号。为了在压缩测量时最大程度地保留有效信息，调制信号要与稀疏字典不相干，即各通道的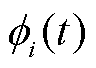要针对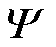进行优化设计。
积分通道i的完整周期输出为
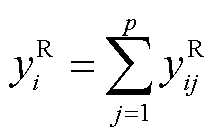（6）
单积分周期测量点数由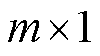
变为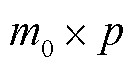
，通过特定组合子测量段构成虚拟测量点
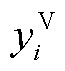，即
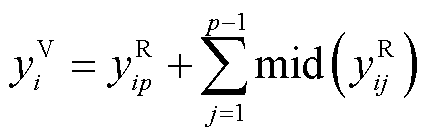（7）
式中，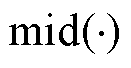
为基于相干性的子测量段选取算子，选取相干性最低的各子测量段；i为各并行通道数，
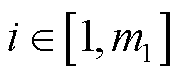。虚拟通道构建方式示意图如图4所示。
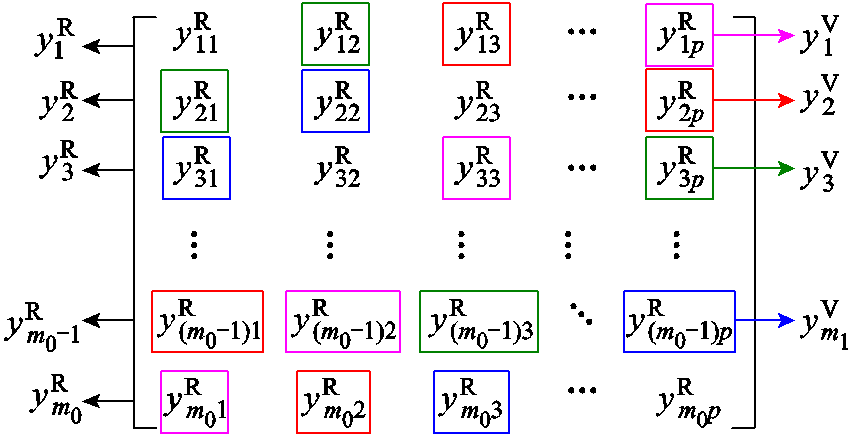
图4 实际和虚拟通道的测量点构建示意图
Fig.4 Construction schematic of the measurement value in actual and virtual channels
之后，根据PD信号与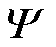构建最优的虚拟测量通道，利用
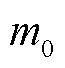条实际测量通道自适应延拓出
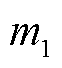条虚拟测量通道，建立
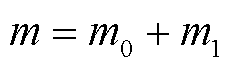条逻辑测量通道。在采样电路中由信号发生单元输出对应的模拟调制信号，采用模拟乘法器将其与原始PD信号相乘。此过程在电路中表现为信号调制，在数学中对应矩阵相乘中行向量与列向量逐个相乘的过程。之后采用积分器对调制信号进行积分累加，单次积分时间为Tsub，实现了数学上的求和过程，完成观测矩阵与PD信号的相乘。积分信号在AD采样之前需采用低通滤波器进行抗混滤波，防止出现信号中的高频分量折叠到低频段而出现频率混叠。VCE-AIC基本采样电路结构如图5所示。
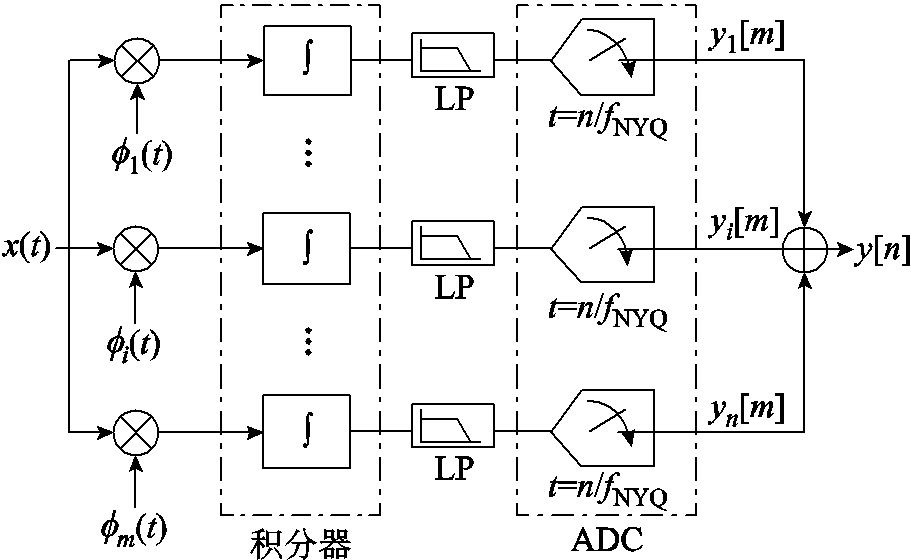
图5 VCE-AIC基本采样电路结构
Fig.5 The basic sampling circuit structure of VCE-AIC
VCE-AIC测量通道的调制信号是实现信息压缩采集的关键，需要利用模拟乘法器将调制信号在模拟域与原始局部放电信号相乘进行信息混叠。调制信号参数对应观测矩阵，则与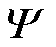之间需要具有低相干性。本节以PD信号的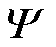、通道延拓需求和电路实现条件为约束，提出了基于非相干性延拓的三值观测矩阵设计算法，产生适用于VCE-AIC测量通道的调制信号。
当前通用观测矩阵有随机数和特定整数序列。随机数对应的调制信号需要增设专用数模转换器，经济性差；特定整数序列无法调参，不适于非正交基稀疏字典。因此，本文对观测矩阵的硬件化实现采用布尔型数值±1、0的逻辑电平实现，即采用三值序列（±1,0）并结合PD信号特征进行优化，其对应的调制信号在电路只需输出周期型的固定逻辑电平信号即可，兼具泛化性和实用性。
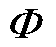的行数m即为测量通道数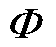，与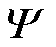高概率重构原始信号需满足低相干性，即
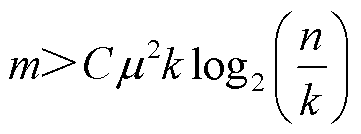（8）
式中，C为经验值1.7；n为字典原子长度；k为稀疏度（稀疏系数非零值数量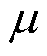）；为压缩传感算子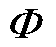与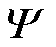的相干性，见式（3），
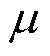的理想值为1。
为了最大程度地降低m并优化测量通道，本文以式（8）的理想取值建立初始伯努利分布矩阵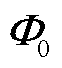
。优化时考虑自相干性并约束元素值为±1和0，建立基于时序加窗差值的变步长梯度下降的求解算法。之后通过对比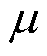和m，对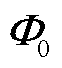进行逐行延拓。在延拓时最大化子测量段间的非相干性，确保以最少的延拓通道数m1达到式（8）的约束。即
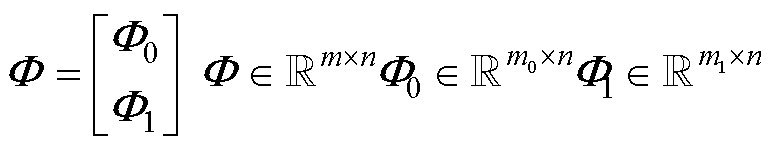（9）
整体观测矩阵设计算法框架如图6所示。
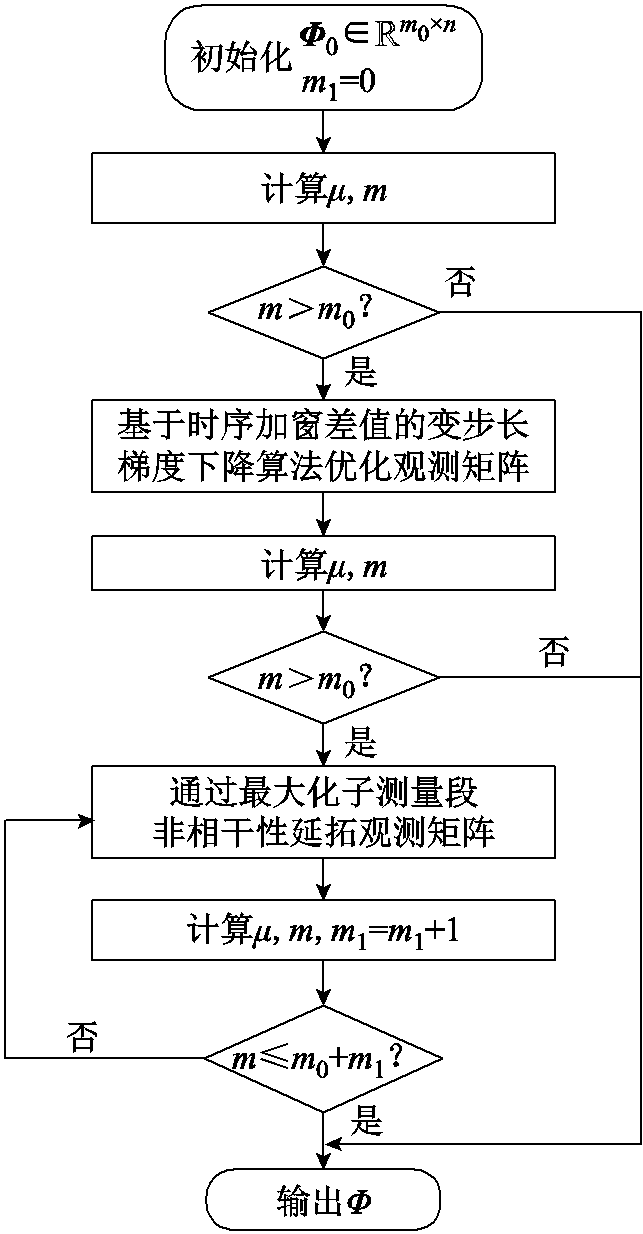
图6 基于非相干性延拓的三值观测矩阵设计算法
Fig.6 Three-valued measurement matrix design algorithm based on incoherent extension
观测矩阵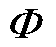的设计流程如下。
（1）建立观测矩阵优化目标函数
观测矩阵通用损失函数为
（10）
式中，I为单位阵，无法优化至正交基，此处采用正交基的推广形式等角紧框架。此外，引入正则项
保证行间相干性最低。式（10）变形为
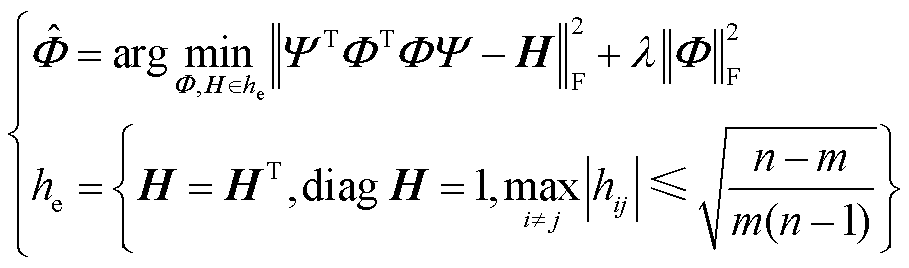（11）
式中，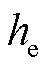
代表等角紧框架；
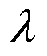为正则化因子。将式（11）前项变换为
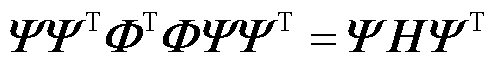（12）
式中，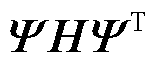
恒存在谱分解，即
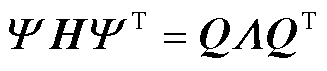。令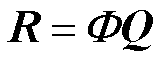
。式（11）转化为
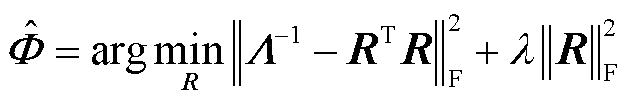（13）
（2）求解观测矩阵优化目标函数
采用梯度迭代思想求解式（13）的二次凸优化目标函数。在保持三值约束的基础上，为提高迭代速度和精度，建立了基于时序加窗差值的变步长梯度下降求解算法。通过增加变步长因子，提高迭代初期的计算速度。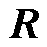
的梯度为
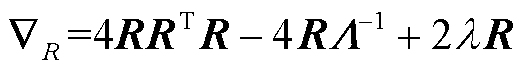（14）
引入全0、全1和全-1阵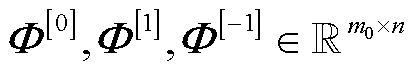
与迭代过程中
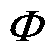进行三维差值计算，得到差值矩阵
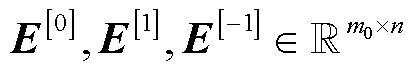。在控制窗口内比较迭代时序中各维度中元素。若窗口内差值矩阵中存在元素值和时序变化梯度趋近于0，则将其相应地置为0、1或-1，并固定。
（3）延拓观测矩阵
通过最大化子测量段非相干性进行观测矩阵延拓。首先构建子测量段群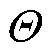
并加入基准子测量段，逐次从各行相应位置选取与群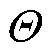内各段相干性均值最低的子测量段加入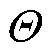。之后组合各子测量段延拓观测矩阵，并结合测量行数约束条件自适应完成整体延拓。算法伪代码内容如下。
基于非相干性延拓设计三值观测矩阵 输入：, k,, C, h, p,w,输出：1:初始化,,;2:生成以伯努利分布生成矩阵;3:4: for (g=1,g＜h&|E|＞ε,g++) do5: 6: ;7: ;8: if (9: ;10: end if11: end for12:将中分数值相似逼近为三值得;13:更新14:for (m1=1,m＞(m0+m1)&m1＜m0,m1++) do15: 16: 选取基准子测量段17: for (j=1, j＜p, j++) do18: 19: 20: end for21: 将组合为,22:end for23:
通过压缩采样获得的压缩测量信号y是经过调制后的随机混叠信号，需要信号重构才可获得最终的测量信号x，即对式（4）进行寻优。本文采用当前兼顾准确度和计算效率的正交匹配追踪算法进行重构，其通过增加正交分量删除环节，高效求得最优解。
找出重构残差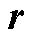
(
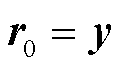)与
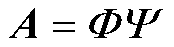中各列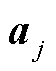
内积值最大时的列索引
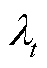为
（15）
更新索引集
，并级联重建原子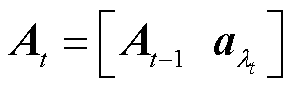
。通过最小二乘得到稀疏系数为
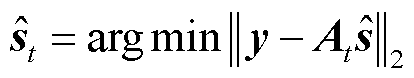（16）
更新残差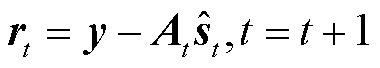
，以此迭代获取最优稀疏解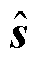。最后通过稀疏反变换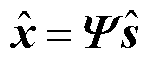即可重构原始信号
。
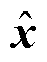测试信号采样方式为通过高频电流互感器（High Frequency Current Transducer, HFCT）耦合PD在设备本体产生的脉冲电流模拟信号，由采样频率为40 MHz的局部放电测试仪获取数字信号。从而得到10 kV设备不同故障类型的实际PD数据。工作温度35～40℃，带宽50 kHz～50 MHz，灵敏度小于1 pC。实验采用Proteus 8.10搭建电路模型作为压缩采样下位机，在自定义激励FILE中里导入测试信号作为PD信号源x(t)。上位机的语言环境为python 3.8.8，运行环境为spyder5，CPU采用AMD Ryzen 5 4600 H，内存配置为16 GB RAM。
采用K-SVD算法训练稀疏字典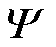，其中训练所用的数据集为实验室PD高频脉冲电流信号数据集，其内部数据样本丰富，包括不同故障类型、故障程度、信噪比的PD数据，在此基础上，可最大程度地提高PD信号稀疏字典的完备性和通用性[28]。VCE-AIC电路参数设定见表1。
表1 VCE-AIC的参数设定表
Tab.1 Parameter setting table of VCE-AIC
符号释义数值 n稀疏字典原子长度250 C相干性常数1.7 h迭代次数约束200 迭代误差约束0.05 w加窗宽度5
采用PD信号研究中通用的波形相似系数（Normalized Correlation Coefficient, NCC）、方均根误差（Root Mean Square Error, RMSE）等指标对各方法性能进行评价[14]。
本文以虚拟通道延拓的思想设计观测矩阵，其中采样频率、并行通道数等采样电路的核心参数便是子测量段长度p。该长度信号在采样前进行积分累加，后由AD芯片进行单次采样输出。为此，本节首先对参数p的设置进行定量分析。以延拓比和总采样压缩率为评价指标，定义为
子测量段长度影响曲线如图7所示。从图中可见，延拓比与p正相关，而采样压缩率与p负相关。原因是p越大，子测量段数量越少，难以找到最优的非相干性组合，且后期子测量段过长已不具备矩阵延拓能力，因此延拓比无后段数据。而采样压缩率、实际通道数和p直接相关，p越长采样压缩率越低。当p＜6时，由于单ADC采样频率降低倍数不多，反而增加了过多的并行通道，导致其采样压缩率大于1，不具备压缩能力。从图7可见，能将延拓行数最大化并实现最优采样压缩率的区间为[14, 33]。而要使压缩采样可以在覆盖调制全周期信号，则Nyquist网格数据量与子测量段的比值尽量取整由于信号网格数据量为8×107，为使相应采样频率的基础上尽可能地提高，40 MHz频率对应的Nyquist对应降低25倍，fc=1.6 MHz。
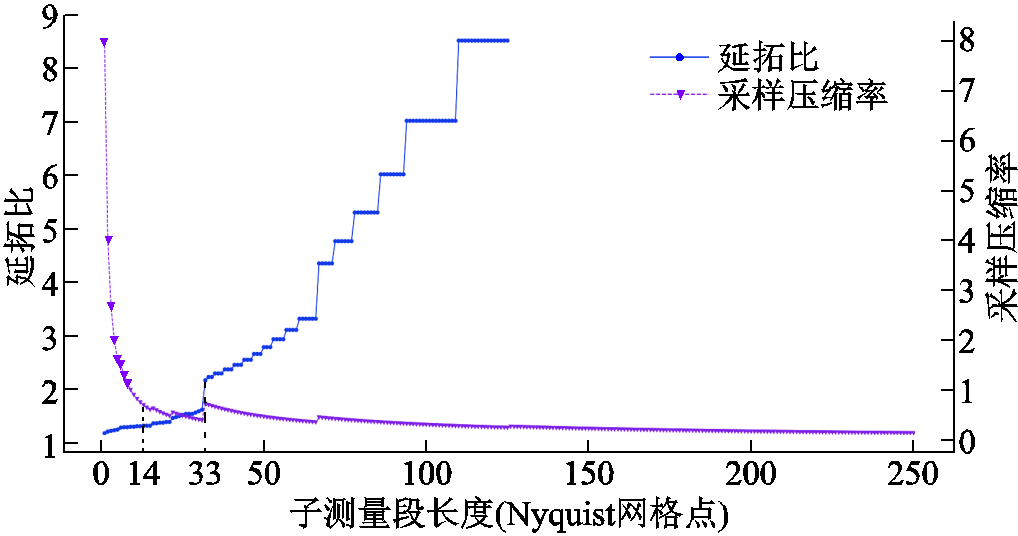
图7 子测量段长度影响曲线
Fig.7 The analysis diagram of sub-measurement section length influence
本节验证VCE-AIC中观测矩阵的优化效果，从以下两个角度展开分析：①相干系数分布；②对PD信号的测量效果。其中作为对照的观测矩阵是伯努利随机矩阵[18]与m序列矩阵[21]。伯努利和m序列均未针对稀疏字典进行矩阵优化；而VCE-AIC采用的是文中基于非相干性延拓设计的三值观测矩阵。
3.2.1 相干系数分布分析
实际测量通道的数量取决于观测矩阵的相干系数大小。因此本节统计了不同观测矩阵与PD信号稀疏字典的相干系数在不同区间的数量，如图8所示。
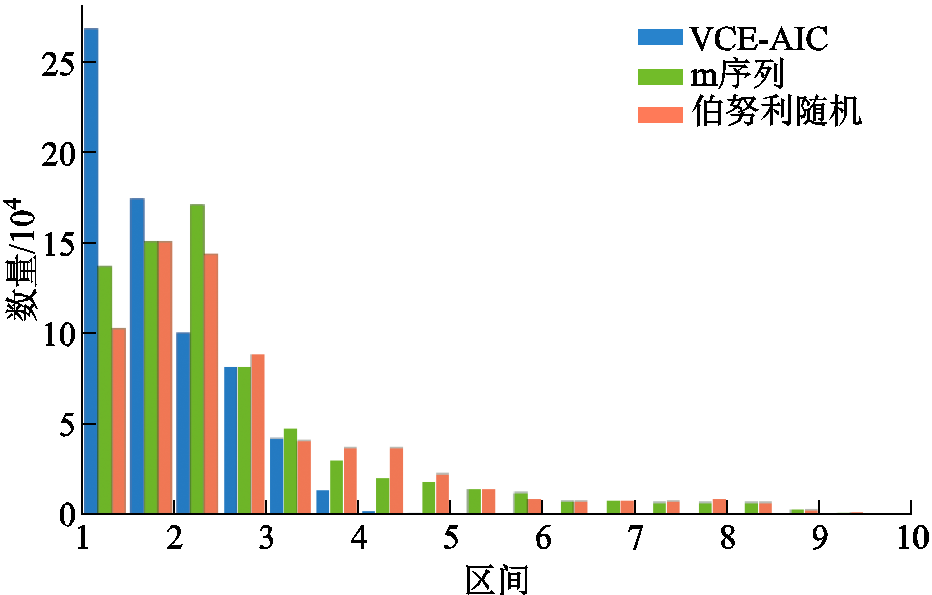
图8 不同观测矩阵相干系数分布
Fig.8 Coherence coefficient distribution of different measurement matrices
结果表明，未优化的观测矩阵中相干系数分布范围较宽，甚至存在大于8的系数。这说明未优化的观测矩阵与稀疏字典整体相干性较高，所需测量通道数多。而VCE-AIC中优化后的观测矩阵相干系数分布规律明显，不存在大于4的系数，且集中于[1, 3]区间。由于VCE-AIC还配置了虚拟通道延拓能力，由表2可见其实际测量通道数要远小于其他方法。此实验验证了VCE-AIC可以有效减少采样电路中的实际测量通道数。
表2 不同观测矩阵所需的实际测量通道数
Tab.2 The number of real measurement channels required for different measurement matrices
伯努利随机m序列VCE-AIC 实际测量通道数424512
3.2.2 PD信号的测量效果分析
以NCC和RMSE为指标评价PD信号的测量效果，进行20次重复测量实验，测量效果如图9所示。
结果表明，VCE-AIC的NCC远大于对照观测矩阵，而RMSE远小于对照观测矩阵，即通过VCE-AIC压缩采样后重构出的信号与原始信号波形更接近、误差更小。此实验验证了基于非相干性延拓的三值观测矩阵优化方法有效提升了VCE-AIC对PD信号有效信息的获取能力，对PD信号的测量效果明显优于未优化的观测矩阵。
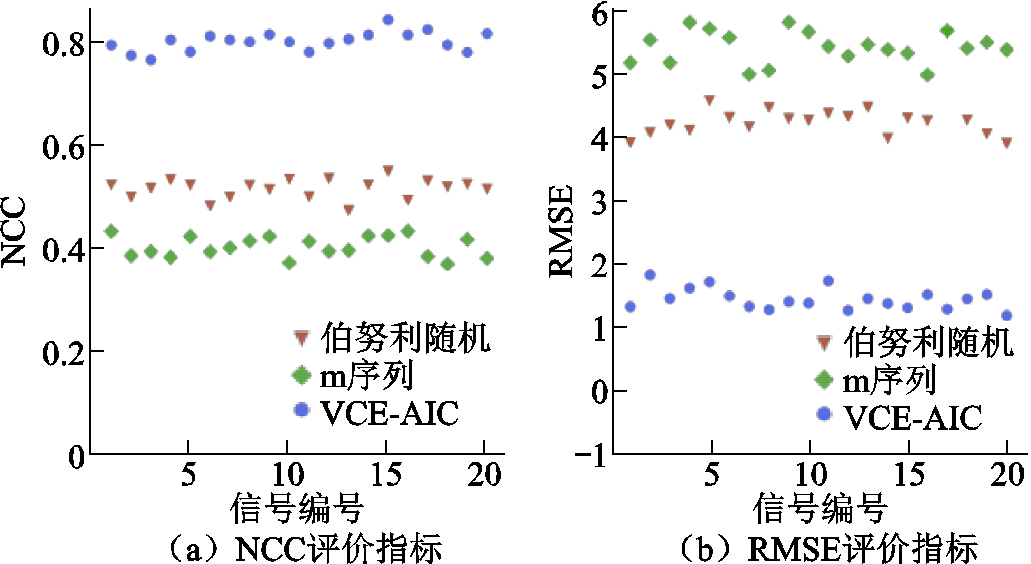
图9 各观测矩阵的测量效果
Fig.9 Measurement effects of measurement matrices
本节验证VCE-AIC对PD信号的整体采集效果，对比方法为RMPI[25]和理想数据压缩[28]。RMPI是观测矩阵未经过优化且无虚拟通道配置的一种AIC采样方案。理想数据压缩是对高频采集的数字信号基于高斯随机调制进行数据压缩与重构，但因受电路条件约束，其无法在采样中实现，本节将其用作理想波形对照。PD放电信号整体采集效果如图10所示。
由图10可见，RMPI采集波形中脉冲的幅值和数量已出现严重失真。VCE-AIC无明显波形畸变，仍可对PD信号波形进行高概率重构，尤其对于脉冲较为密集的信号中段位置，VCE-AIC的采集效果明显优于RMPI。
图10 局部放电信号采集效果对比
Fig.10 Comparison of the acquisition effect of PD signal
PD脉冲波形的局部放大对比如图11所示。从图11的局部放大图可见，RMPI压缩采样后的重构效果存在严重偏差，甚至出现幅值反相和相位延迟，对于幅值、相位无偏的脉冲波形也仅可表达最高极值点，无法重现波形振荡曲线；而VCE-AIC对实际信号的贴合度更高，准确表达出各脉冲的幅值与相位，实现了完整局部放电振荡波形的准确重构和实对波形的高精度压缩采样，可支撑后续对波形的研究工作。采集效果参数对比见表3。
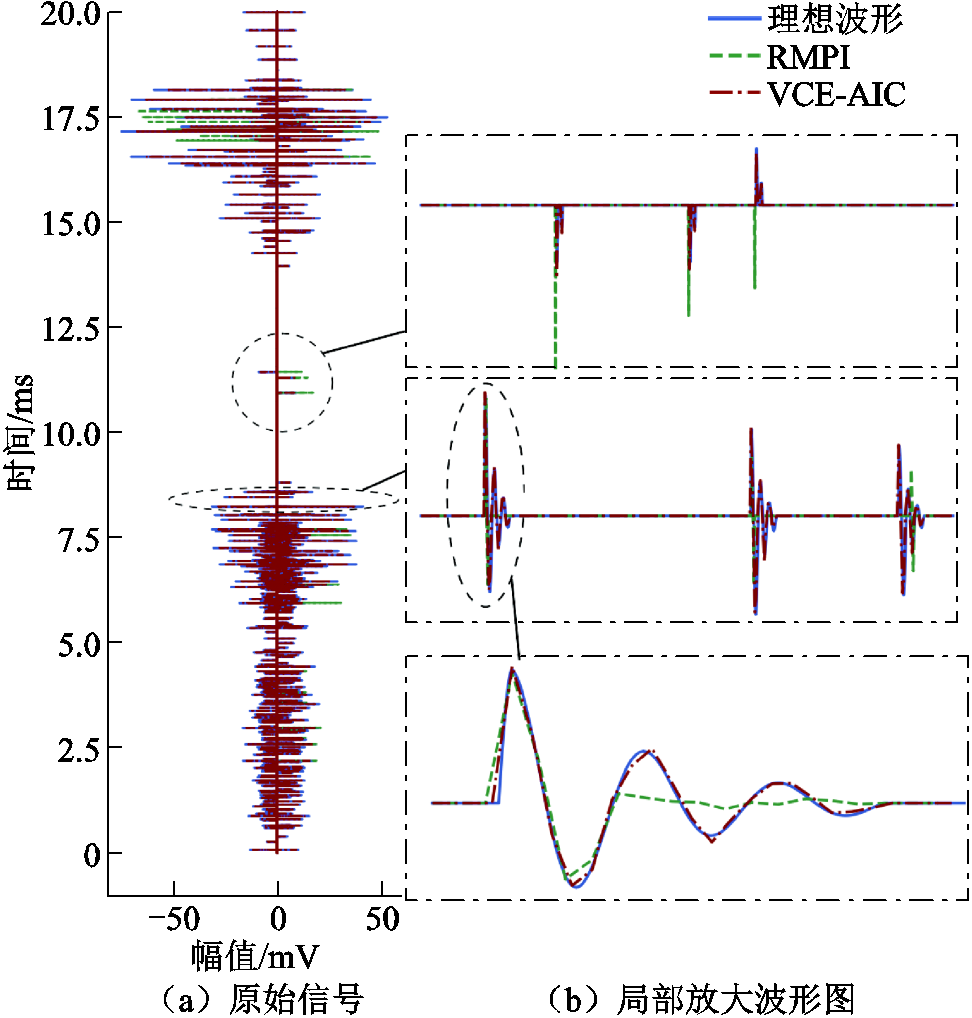
图11 局部波形放大对比
Fig.11 Magnified comparison of local waveforms
表3 各系统采集效果参数对比
Tab.3 Comparison table of the parameters of each compressed acquisition system
参数数值 数据压缩重构RMPIVCE-AIC 实际测量通道数—4512 虚拟测量通道数21—23 单ADC采样频率/MHz400.41.6 总采样压缩率（%）10025.0048.00
（续）
数据压缩重构RMPIVCE-AIC 数据压缩率（%）8.4018.0014.00 NCC0.9230.5020.853 RMSE（去噪前）2.477.933.54 RMSE（去噪后）0.956.431.30
表3中NCC和RMSE指标验证了对图10和图11的波形分析。原因分析：RMPI中的观测矩阵未进行优化限制了信息获取能力，且长时间积分会引起积分器误差。而VCE-AIC的观测矩阵基于信号特征进行了针对性的优化，且虚拟通道延拓方案的子测量段设置也避免了积分器误差。VCE-AIC中误差的原因是为了电路实现引入的矩阵数值约束。
VCE-AIC的重构准确性和电路可实现性都远高于RMPI，且大幅降低了采样频率。单个ADC的采样频率由40 MHz降低至1.6 MHz，利用多通道测量将整体采样频率压缩至48%。此外由于VCE-AIC采用虚拟通道延拓方法，并对
进行了非相干性优化，使得电路中的实际测量通道数由RMPI中的45通道降低至12通道，通道数减少至29%以下。从数据的整体压缩率来看，VCE-AIC将Nyquist网格点所需的通信数据量压缩至14%，由于对进行了非相干性优化，使其数据压缩能力优于RMPI。VCE-AIC有效解决了PD信号在线监测中的电路和数据难题。
本文通过测量PD信号的同一套设备采集现场噪声，并与实际PD信号进行分级放大混叠，构成现场实测不同信噪比（Signal-to-Noise Ratio, SNR）信号。经计算，其SNR分别为0.15 dB、-3.40 dB、-5.21 dB、-9.87 dB、-14.04 dB、-20.65 dB。为了定量分析SNR对PD信号压缩采样效果的影响，本文以NCC、RMSE、SNR和SNR提升幅度（SNR Improvement Amplitude, SNRIA）为指标与其对应染噪信号分别对比。结果见表4和如图12所示。
表4 不同信噪比信号的采样效果评价参数
Tab.4 Evaluation parameters of sampling effect of different signal-to-noise ratio signals
染噪信号/dBNCCRMSESNR/dBSNRIA/dB 0.150.791.779.869.71 -3.400.742.018.7812.18 -5.210.694.051.847.05 -9.870.593.58-4.635.24 -14.040.671.26-11.372.67 -20.650.740.88-18.941.71
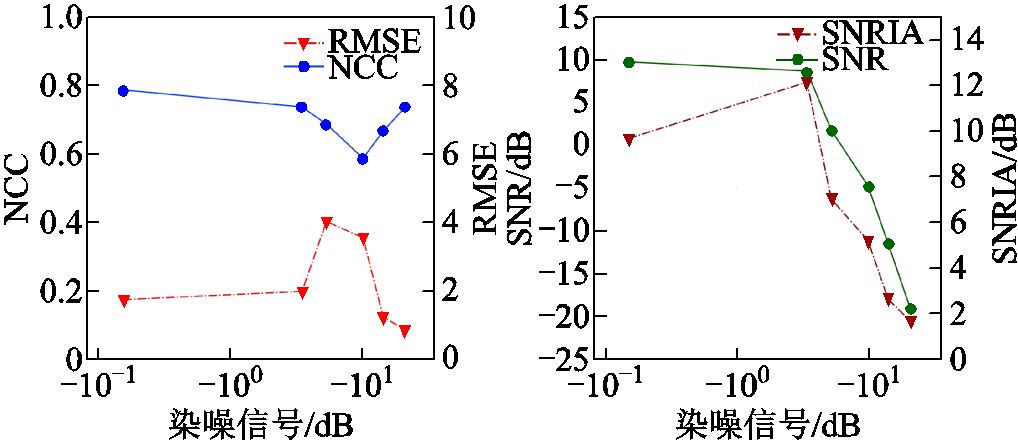
图12 不同信噪比信号的采样效果
Fig.12 Sampling effect of signals with different SNRs
基于表4和图12数据分析SNR对PD信号采样效果的影响。NCC指标随着SNR的降低呈现出先降低后升高的趋势。原因是VCE-AIC基于的CS理论本身存在对小幅值点的忽略，SNR较高的信号包含的噪声分量幅值低，在重构后与原始波形的相似度较高。随着噪声分量幅值增大，信号的相似度降低。当噪声提高到一定水平，VCE-AIC将其在稀疏字典中映射成为主成分参量，并重构出噪声波形。由于幅值越高波形重构越准确，呈现出随着SNR降低NCC指标增大的趋势。RMSE指标随着SNR的降低呈现出先升高后降低的趋势。原因与NCC指标的变化趋势相同。
SNR指标与染噪信号的SNR正相关。原因是VCE-AIC对信号的测量是基于波形向稀疏字典的映射，不对内部噪声分量进行提取分解，最大程度地重构原始信号。不同信号的SNRIA指标均大于0，原因是现场噪声表现为覆盖全波形周期的小幅值点，而VCE-AIC的测量与重构过程会忽略小幅值点，在客观上提升了PD信号的SNR。但SNRIA随着SNR的降低先升高后降低，原因是SNR较高时噪声分量较小，对SNR的提升程度有限。随着噪声分量的增大，VCE-AIC对SNR的提升效果凸显。当噪声分量幅值增大到在稀疏字典中映射为主要分量时，VCE-AIC在测量信号时也对幅值较大的噪声波形进行了重构，对SNR的提升幅度逐渐降低。
因此，原始信号的SNR对VCE-AIC的采样效果存在影响，但信号的测量和重构结果符合VCE-AIC的设计理论，其对染噪信号也具备较高的波形相似度，准确表达出了各脉冲的幅值与相位。VCE-AIC可以在数据量大幅降低的前提下对PD信号波形进行高概率重构，尤其对于SNR＞-10 dB的PD波形信号，可准确重构原始波形且有效去除噪声分量。
基于以上理论分析内容和参数设置依据，本节开展PD信号采集实验，验证VCE-AIC的有效性，以排除仿真中可能忽略的其他因素。
为了方便采样电路的通道控制与参数调试，采用多通道模拟采样器输入上位机进行软件实验。模拟采样电路参数如下：AC耦合输入，软件自动校准可编程采样，ADC位分辨率12 bit，采样率2 MHz，内设2 GB内存，测量带宽50 MHz，采集时钟、主卡同步10 M时钟。VCE-AIC的参数设定参照表3中提供的理论依据，设置12组并行采样通道，采样频率为1.6 MHz。同时单独设置一组并行信号支路以40 MHz采样频率同步采样，以其为参考样本对VCE-AIC的实验结果进行分析。两组采样方式输出的数据如图13所示。
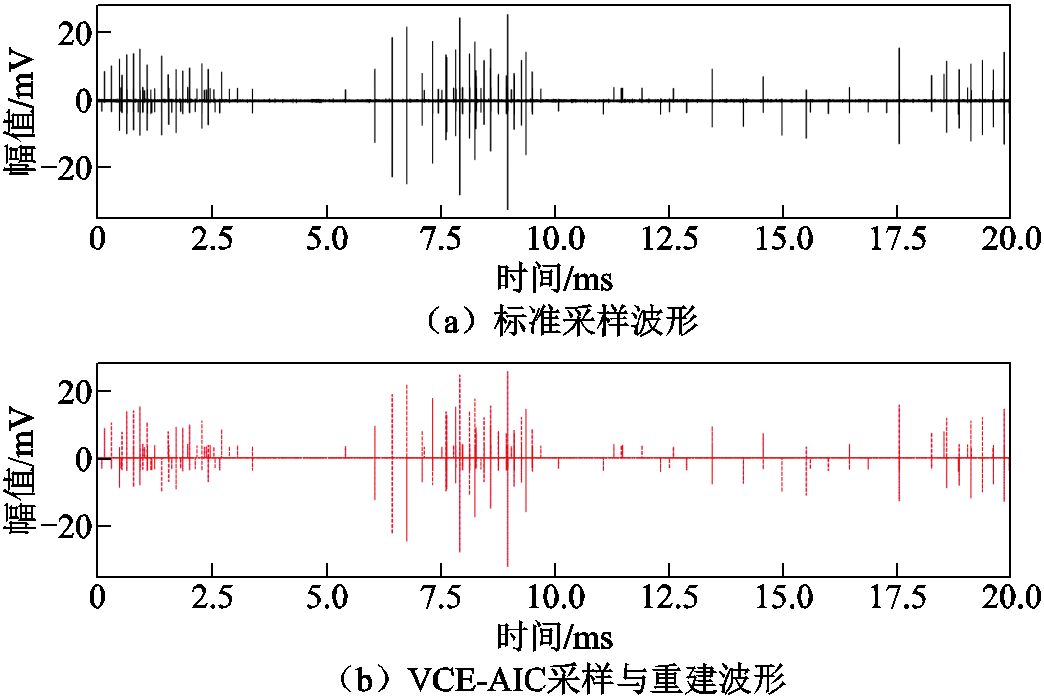
图13 PD信号实验采样数据
Fig.13 Experimental sampling data of PD signals
由图13可见，标准采样波形和VCE-AIC采样与重构波形的脉冲幅值、脉冲位置、脉冲数量基本保持一致。NCC和RMSE指标分别为0.73和2.04。波形呈现与评价指标和理论分析保持一致，验证了虚拟通道延拓和观测矩阵设计算法的有效性，即VCE-AIC可以实现对PD波形的精准压缩采集。因此，通过实验对比分析验证了VCE-AIC对PD波形压缩采集的有效性和精准度。
本节对PD信号与压缩测量信号进行对比，并分析VCE-AIC在电网PD监测中的应用方式。图14是一组原始PD信号和VCE-AIC部分压缩测量通道的信号输出。从图14中可见，各通道的输出数据量为3 200个点，远小于原始数据量的800 000个点，在包含PD波形信息的基础上极大地压缩了测量数据。
本文从以下六个方面保证了压缩测量信号重构的准确性：①观测矩阵的设计满足RIP准则，即观测矩阵与稀疏字典之间具有低相干性；②为VCE- AIC提出基于非相干性延拓的三值观测矩阵设计算法；③最大程度地提高PD信号稀疏字典的完备性和通用性；④采用正交匹配追踪算法进行信号重构；⑤选取普遍通用的PD信号波形评价指标；⑥对各项参数选取设置完备丰富的理论与实验分析。其中，①②③是信号重构准确性的前期基础，④是信号重构准确性的直接因素，⑤⑥是信号重构准确性的后期保证。
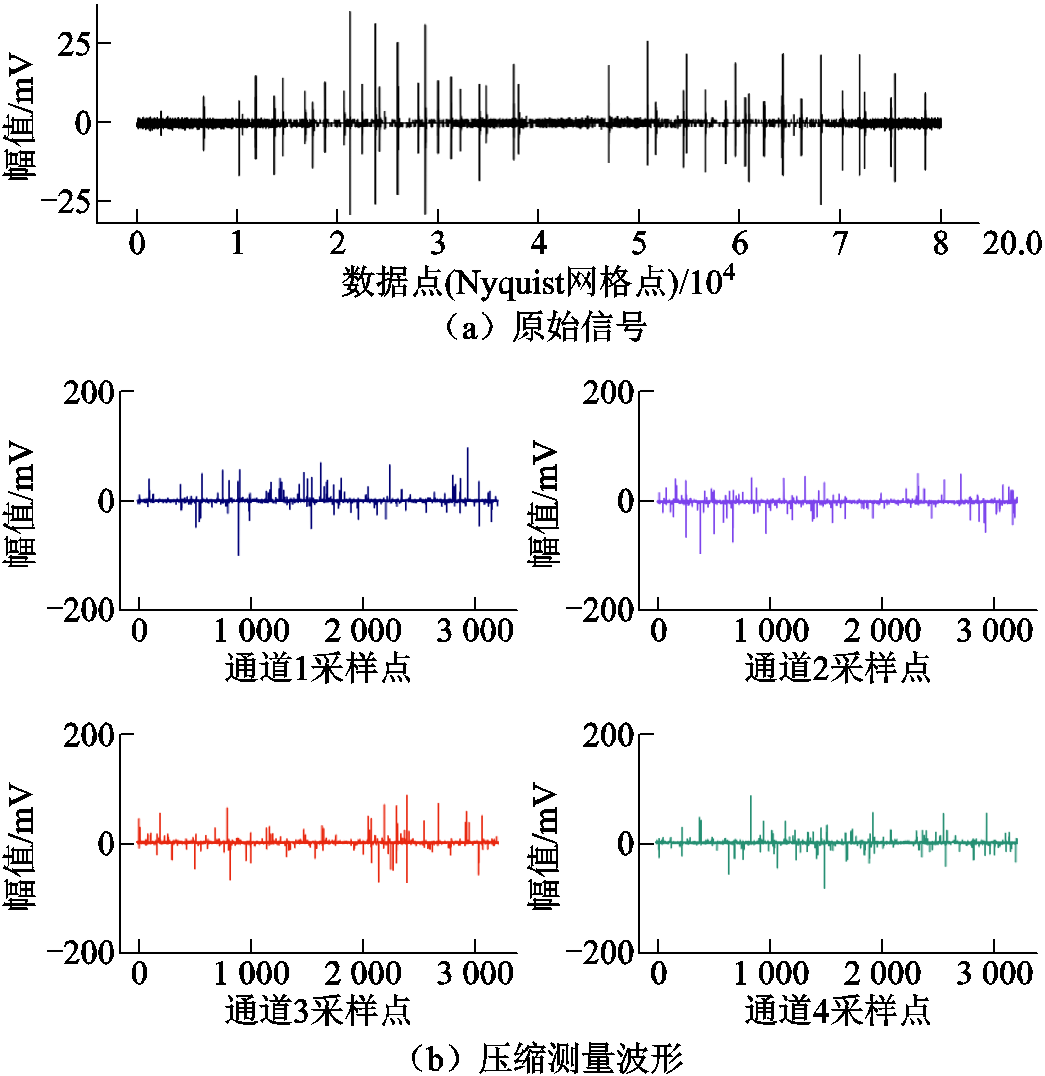
图14 原始PD信号与其压缩测量波形
Fig. 14 Original PD signal and its compression measurement waveform
此外，PD信号的压缩测量信号与原始波形不相似，原因在于压缩采样存在调制过程，必须已知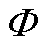
与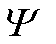
才可重构原始信号，即VCE-AIC天然具备极高的数据安全性。因此，VCE-AIC适合新型电力系统中分布式传感与边缘计算相融合的物联监测体系。部署于设备侧的VCE-AIC只需对PD信号进行压缩测量和低速率传输。现场智能终端作为中心计算节点对测量信号重构后进行PD特征提取与分类，以满足边缘侧传感网络的成本与算力限制。此外，VCE-AIC对PD信号的压缩采集可实现向后端服务器远程实时传输数据，利用其冗余算力进行字典训练和重构算法的优化。
其应用场景以PD信号模式识别为例，将VCE-AIC获取的50组压缩测量信号依次重构生成一组PRPD样本需303.50 s，单周期信号重构平均需要6.07 s。即生成一组连续PRPD样本的时间符合PD监测要求[29]。
综上所述，VCE-AIC利用虚拟通道延拓降低了传感设备的采样频率和采集数据量，进而降低了对采样电路、通信设备的硬件要求。在分布式传感与边缘计算相融合的监测体系下，VCE-AIC的应用可使现场实时分析设备PD特征，并满足运维中心对设备的长期监测与分析要求，兼具经济性和安全性，适用于电力设备PD信号在线监测的应用场景。
针对电力设备PD信号在线监测中存在的采样频率过高的问题，本文提出了基于虚拟通道延拓的模拟信息转换器（VCE-AIC）方案。可得如下结论：
1）VCE-AIC降低了ADC采样频率且优化了电路结构。VCE-AIC基于虚拟通道延拓的压缩采样可将采样频率降低至1.6 MHz，利用多通道测量将整体采样频率压缩至48%，将实际并行测量通道数优化至12条。VCE-AIC利用简单易实现的三值观测矩阵大幅提升了电路的可实现性。
2）VCE-AIC极大地降低了监测数据量，与传统采样方式相比其可将数据量压缩至14%，减轻了PD监测的数据通信量，提高了PD信号在线监测的工程应用性。
3）VCE-AIC因其多通道压缩采样和电路结构优化，有效解决了电网中PD信号在线监测所面临的电路与性能矛盾。此外，还兼具数据安全性和一定去除白噪声的效果。
下一步的研究方向是如何实现PD信号自适应确定稀疏基，增强压缩采样对PD信号有效信息的获取能力。
参考文献
[1] 马鑫, 尚毅梓, 胡昊, 等. 基于数据特征增强和残差收缩网络的变压器故障识别方法[J]. 电力系统自动化, 2022, 46(3): 175-183. Ma Xin, Shang Yizi, Hu Hao, et al. Identification method of transformer fault based on data feature enhancement and residual shrinkage network[J]. Automation of Electric Power Systems, 2022, 46(3): 175-183.
[2] 周利军, 刘聪, 权圣威, 等. 基于点对称变换的乙丙橡胶电缆终端缺陷诊断[J]. 电工技术学报, 2022, 37(9): 2388-2398. Zhou Lijun, Liu Cong, Quan Shengwei, et al. Defect diagnosis of EPR cable terminal based on symmetrized dot pattern[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2388-2398.
[3] Ghosh R, Chatterjee B, Dalai S. A method for the localization of partial discharge sources using partial discharge pulse information from acoustic emissions[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(1): 237-245.
[4] 单秉亮, 李舒宁, 杨霄, 等. XLPE配电电缆缺陷诊断与定位技术面临的关键问题[J]. 电工技术学报, 2021, 36(22): 4809-4819. Shan Bingliang, Li Shuning, Yang Xiao, et al. Key problems faced by defect diagnosis and location technologies for XLPE distribution cables[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4809-4819.
[5] Deng Rui, He Jing, Yu Jianjun, et al. Increasing data rate of an optical IMDD system using a cost-efficient dual-band transmission scheme based on RTZ DAC and sub-Nyquist sampling ADC[J]. Optics Express, 2018, 26(9): 11599-11607.
[6] 卿晓东, 苏玉刚. 电场耦合无线电能传输技术综述[J]. 电工技术学报, 2021, 36(17): 3649-3663. Qing Xiaodong, Su Yugang. An overview of electric-filed coupling wireless power transfer technology[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3649-3663.
[7] 王佩月, 左志平, 孙跃, 等. 基于双侧LCC的全双工无线电能传输能量信号并行传输系统[J]. 电工技术学报, 2021, 36(23): 4981-4991. Wang Peiyue, Zuo Zhiping, Sun Yue, et al. Full-duplex simultaneous wireless power and data transfer system based on double-sided LCC topology[J]. Transactions of China Electrotechnical Society, 2021, 36(23): 4981-4991.
[8] Song Shoupeng, Yu Jiahui, Shen Jingjing. Novel circuit implementation method for pulse signal finite rate of innovation sparse sampling based on an improved exponential reproducing kernel[J]. Circuits, Systems, and Signal Processing, 2019, 38(10): 4683-4699.
[9] Lissner I, Urban P. Toward a unified color space for perception-based image processing[J]. IEEE Transactions on Image Processing: A Publication of the IEEE Signal Processing Society, 2012, 21(3): 1153-1168.
[10] 于华楠, 武云瑞, 胡绪超. 基于压缩感知的电力设备视频图像去噪方法研究[J]. 电测与仪表, 2016, 53(18): 10-13, 40. Yu Huanan, Wu Yunrui, Hu Xuchao. The research of power equipment image de-noising algorithm based on compressed sensing[J]. Electrical Measurement & Instrumentation, 2016, 53(18): 10-13, 40.
[11] Shen Zhiyuan, Wang Qianqian. A high-precision spectrum-detection algorithm based on the normalized variance of nonreconstruction compression sensing[J]. Mathematical Problems in Engineering, 2020, 2020: 1-9.
[12] Wu Feiyun, Yang Kunde, Duan Rui, et al. Compressive sampling and reconstruction of acoustic signal in underwater wireless sensor networks[J]. IEEE Sensors Journal, 2018, 18(14): 5876-5884.
[13] Chen F, Chandrakasan A P, Stojanovic V M. Design and analysis of a hardware-efficient compressed sensing architecture for data compression in wireless sensors[J]. IEEE Journal of Solid-State Circuits, 2012, 47(3): 744-756.
[14] Majidi M, Fadali M S, Etezadi-Amoli M, et al. Partial discharge pattern recognition via sparse representation and ANN[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2015, 22(2): 1061-1070.
[15] 谢军, 刘云鹏, 刘磊, 等. 局放信号自适应加权分帧快速稀疏表示去噪方法[J]. 中国电机工程学报, 2019, 39(21): 6428-6439. Xie Jun, Liu Yunpeng, Liu Lei, et al. A partial discharge signal denoising method based on adaptive weighted framing fast sparse representation[J]. Proceedings of the CSEE, 2019, 39(21): 6428-6439.
[16] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.
[17] Mangia M, Pareschi F, Rovatti R, et al. Adapted compressed sensing: a game worth playing[J]. IEEE Circuits and Systems Magazine, 2020, 20(1): 40-60.
[18] Haque T, Yazicigil R T, Pan K J L, et al. Theory and design of a quadrature analog-to-information converter for energy-efficient wideband spectrum sensing[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2015, 62(2): 527-535.
[19] Rani M, Dhok S B, Deshmukh R B. A systematic review of compressive sensing: concepts, implementations and applications[J]. IEEE Access, 2018, 6: 4875-4894.
[20] Kirolos S, Laska J, Wakin M, et al. Analog-to-information conversion via random demodulation[C]//2006 IEEE Dallas/CAS Workshop on Design, Applications, Integration and Software, Richardson, TX, USA, 2007: 71-74.
[21] Mishali M, Eldar Y C. From theory to practice: sub-nyquist sampling of sparse wideband analog signals[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 375-391.
[22] Zhao Yijiu, Hu Yuhen, Wang Houjun. Enhanced random equivalent sampling based on compressed sensing[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(3): 579-586.
[23] Zhao Yijiu, Hu Yuhen, Liu Jingjing. Random triggering-based sub-nyquist sampling system for sparse multiband signal[J]. IEEE Transactions on Instrumentation and Measurement, 2017, 66(7): 1789-1797.
[24] 崔兴梅, 吴键, 徐云鹏. 基于改进m序列的压缩采样观测矩阵设计[J]. 振动测试与诊断, 2017, 37(6): 1163-1168, 1279. Cui Xingmei, Wu Jian, Xu Yunpeng. Design of compressed sampling observation matrix based on improved m sequence[J]. Journal of Vibration, Measurement & Diagnosis, 2017, 37(6): 1163-1168, 1279.
[25] 赵仕策, 赵洪山, 寿佩瑶. 智能电力设备关键技术及运维探讨[J]. 电力系统自动化, 2020, 44(20): 1-10. Zhao Shice, Zhao Hongshan, Shou Peiyao. Discussion on key technology and operation & maintenance of intelligent power equipment[J]. Automation of Electric Power Systems, 2020, 44(20): 1-10.
[26] 李庭, 陈杰, 于泓, 等. 压缩感知理论在IGBT状态监测中的应用[J]. 电工技术学报, 2022, 37(增刊1): 163-171. Li Ting, Chen Jie, Yu Hong, et al. Application of compressed sensing method in condition monitoring of insulated gate bipolar transistor[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 163-171.
[27] Candès E, Romberg J. Sparsity and incoherence in compressive sampling[J]. Inverse Problems, 2007, 23(3): 969-985.
[28] Shen Zhiyuan, Cheng Xinmiao, Wang Qianqian. A cooperative construction method for the measurement matrix and sensing dictionary used in compression sensing[J]. EURASIP Journal on Advances in Signal Processing, 2020(1): 1-8.
[29] 王刘旺, 朱永利, 贾亚飞, 等. 局部放电大数据的并行PRPD分析与模式识别[J]. 中国电机工程学报, 2016, 36(5): 1236-1244. Wang Liuwang, Zhu Yongli, Jia Yafei, et al. Parallel phase resolved partial discharge analysis for pattern recognition on massive PD data[J]. Proceedings of the CSEE, 2016, 36(5): 1236-1244.
Abstract Partial discharge (PD) is the important parameter to monitor the operating status of power equipment. However, PD signals are non-band-limited in the frequency domain, and the sensor theoretically needs to be equipped with the analog-to-digital converter (ADC) with infinitely high sampling frequency. The cost of ADCs increases exponentially with the sampling frequency due to production process limitations. Aiming at this circuit parameter and performance contradiction, the compressive sensing (CS) theory is introduced to achieve compressed sampling of PD signals from power equipment. A compressed sampling method for PD signals based on virtual channel delay topology is proposed to reduce the sampling frequency by using compressed sensing parallel measurement.
Firstly, Analog-to-information converter for PD signal based on virtual channel extension (VCE-AIC) is proposed in combination with PD signals characteristics. Parallel measurements are used to reduce the sampling frequency and to create virtual measurement channels based on non-coherent extension of submeasurement segments. The actual number of measurement channels is reduced, and the compressed sampling circuit structure is optimized. After that, according to the characteristics of PD signals, channel delay requirements and noncoherence criterion, a three-valued observation matrix design algorithm based on noncoherent delay is proposed. It includes the introduction of a self-consistent regular term and a variable-step gradient descent method using the time-series plus window difference to reduce the parameter coherence. Finally, the observation matrix is used in the virtual channel delay topology circuit to realize the compressed sampling of PD signals.
The reconstruction accuracy of the compressed measurement signal is guaranteed from the following six perspectives. (Ⅰ) The observation matrix is designed to satisfy the RIP criterion, i.e., the observation matrix has low coherence with the sparse dictionary. (Ⅱ) The proposed three-valued observation matrix design algorithm based on non-coherent extension for VCE-AIC. (Ⅲ) Maximize the completeness and generality of the sparse dictionary for PD signals. (Ⅳ) Adopting orthogonal matching tracking algorithm for signal reconstruction. (Ⅴ) The generally common PD signals waveform evaluation index is selected. (Ⅵ) The complete theoretical and experimental analysis is set up for the selection of each parameter.
Sampling analysis is performed based on the measured PD signals. The results show that the compressed sampling method reduces the sampling frequency to 1.6 MHz. The overall sampling frequency and data volume are compressed to 48% and 14%, respectively, using multi-channel measurements. The actual number of parallel measurement channels is optimized to 12.
The following conclusions can be drawn from the analysis of the experimental results. (Ⅰ) VCE-AIC reduces the ADC sampling frequency and optimizes the circuit structure. VCE-AIC uses multi-channel measurement to compress the overall sampling frequency to 48% and optimizes the actual number of parallel measurement channels to 12. VCE-AIC significantly improves the circuit implementability with an easy-to-implement three-value observation matrix. (Ⅱ) VCE-AIC can compress the data volume up to 14%, which greatly reduces the data communication volume of PD monitoring. (Ⅲ) VCE-AIC effectively solves the circuit and performance conflicts faced by online monitoring of PD signals due to its multi-channel compressed sampling and circuit structure optimization. In addition, it also has data security and limited denoising capability. The compressed sampling method in this paper reduces the component parameter requirements and circuit structure complexity of the sensing equipment and meets the demand for online monitoring of PD signals of power equipment.
keywords：Partial discharge, compressed sensing, measurement matrix, incoherence, virtual channel extension
DOI: 10.19595/j.cnki.1000-6753.tces.220372
中图分类号：TM935
收稿日期 2022-03-14
改稿日期 2022-10-01
赵仕策 男，1994年生，博士研究生，研究方向为配电设备的多参量传感与智能感知方法。E-mail：zscsysut@163.com
赵洪山 男，1965年生，教授，博士生导师，研究方向为电力设备的在线监测与态势感知、风电机组的故障预测与优化检修等。E-mail：zhaohshcn@126.com（通信作者）
（编辑 郭丽军）