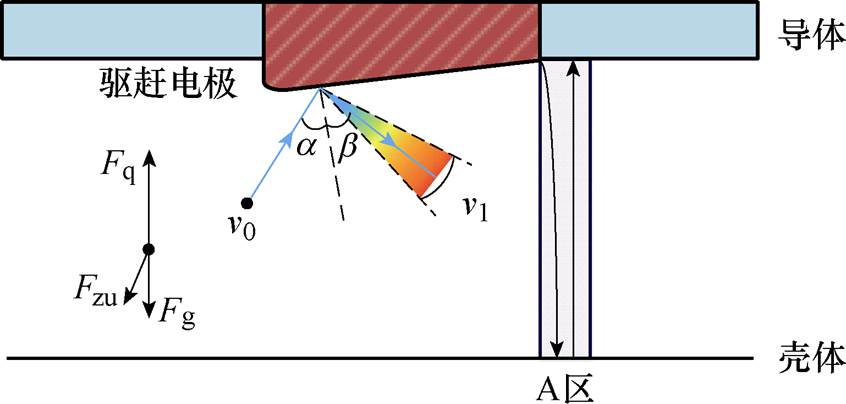
图1 金属微粒轴向平面运动模型
Fig.1 Axial plane motion model of metal particles
摘要 直流气体绝缘组合电器和封闭输电线路中的运动金属微粒是造成绝缘故障的重要原因，采用驱赶电极可使微粒朝远离绝缘子的方向运动，与微粒陷阱配合使用可显著提高微粒的捕获概率。该文首先建立微粒与驱赶电极的碰撞动力学模型，发现受驱赶电极作用的微粒落点具有强集中性，进而考虑电场畸变特性与微粒落点分布对驱赶电极的结构参数进行了优化设计。进一步以微粒陷阱的捕获概率优化为目标，提出驱赶电极与微粒陷阱的协同布置策略，相较于无驱赶电极时，陷阱布置在驱赶电极下微粒集中落点位置时的捕获概率提升了20 %。同时，考虑驱赶电极对陷阱中微粒入射角的影响，提出驱赶电极与微粒陷阱结构参数的协同优化方法，增加了微粒在陷阱内碰撞次数，提高了微粒陷阱的捕获概率。具体结果表明，当驱赶电极倾角为8 °、陷阱倾角为50 °时，微粒陷阱的捕获概率最高，可达69.8 %。通过搭建包含驱赶电极与微粒陷阱的实验平台，验证了协同布置策略与参数优化方法的有效性。所提出的驱赶电极与微粒陷阱的协同设计方法适用于不同尺寸的直流气体绝缘装备，可为实际工程的微粒有效抑制提供指导。
关键词：驱赶电极 微粒陷阱 协同抑制 优化设计方法
气体绝缘组合电器（Gas Insulated Switchgear, GIS）和气体绝缘输电线路（Gas Insulated trans- mission Lines, GIL）是构建新能源电力系统的物理支撑，应用前景广阔[1-2]。在GIS/GIL中，缘于机械碰撞、热伸缩摩擦等因素，会不可避免地产生金属微粒污染物，而金属微粒引起的绝缘故障是影响设备可靠性的主要因素之一[3-4]。相对于交流GIS/ GIL，直流电场下微粒带电量更高、运动更加活跃，易引起极间气隙击穿，或附着在绝缘子表面引发沿面闪络，因此，采取有效技术措施治理直流GIS/GIL内金属微粒显得十分迫切[5]。对此，国内外许多专家学者开展详细的研究，也提出了许多微粒治理方案，如加设驱赶电极、微粒陷阱等[6-8]。
设置驱赶电极可使微粒朝着远离绝缘子的方向运动，从而驱赶直流绝缘子附近可能引发闪络的危险微粒。国内外专家学者将驱赶电极设计为空心圆台状，从电场角度分析了同时布置驱赶电极与微粒陷阱时对运动微粒的抑制效果，但研究过程中并未考虑微粒的碰撞随机特性，对于驱赶电极的作用机制也未给出定量表征[9-11]。詹振宇等学者对交流GIL屏蔽罩下方启举微粒的运动状态进行研究，发现大部分微粒会聚集在远离绝缘子的位置，存在一个特征聚合区[12]。由此，若利用已有的屏蔽罩并将其设计为驱赶电极，将具有工程可实施性，而目前对于驱赶电极的优化设计尚缺少行之有效的方法。
微粒陷阱可在同轴圆柱结构间形成一个低电场区域，使微粒运动到该区域时所受电场力小于重力，从而实现微粒捕获[13-14]。目前存在条形、孔式、栅格式等众多的微粒陷阱设计方案[15-16]。而刘鹏等学者的研究表明，直流GIL内置的各类可拆卸微粒陷阱的捕获效率较低，不超过16 %，微粒有较大概率发生逃逸而造成绝缘子闪络[17]。为提高捕捉效率，王健等学者设计了一种楔形微粒陷阱，其侧壁与底部呈一定倾角，但楔形陷阱下微粒运动仍具有随机性，陷阱缺少主动捕获微粒的能力，可考虑楔形陷阱与驱赶电极配合以提高陷阱的捕获概率[18]。
驱赶电极可驱离绝缘子附近的危险金属微粒，但不能有效抑制微粒运动；微粒陷阱可捕获运动的微粒，但捕获概率低。倘将两者协同应用，理论上有望获得更理想的微粒治理效果。已有的屏蔽罩结构为设计驱赶电极提供了工程实施的可能性，但目前对驱赶电极与微粒陷阱的协同应用罕有研究，对其协同作用机制尚不清晰，这影响到微粒抑制措施的定量优化设计。
基于以上考虑，本文融合实验与仿真分析，研究了驱赶电极与微粒陷阱的协同作用机制，以及结构参数的优化设计方法。首先通过建立微粒与驱赶电极随机碰撞的动力学模型，分析了影响微粒驱赶效果的关键参数，获得微粒集中落点位置的分布特征。继而提出驱赶电极与微粒陷阱协同布置的优化设计方法，并搭建真型实验平台对优化设计结果进行了验证。文中提出的协同布置方案与优化设计方法，为当前工程中的微粒抑制技术提供了量化依据。
驱赶电极通常设计为呈一定倾角的空心圆台状，通过建立微粒与驱赶电极随机碰撞的动力学模型，可定量分析驱赶电极对微粒的驱赶效果。
为简化计算并不失一般性，此处主要考虑微粒轴向平面内的运动行为，金属微粒轴向平面运动模型如图1所示。半径为a的球形金属微粒在直流GIS/GIL中，所受的力主要包括重力、浮力、电场力和气体阻力，其受力解析式见表1。
图1 金属微粒轴向平面运动模型
Fig.1 Axial plane motion model of metal particles
表1中，rAl、rgas分别为微粒与空气的密度；g为重力加速度；q为金属微粒带电量；U为高压电极的施加电压；k为镜像修正系数，一般情况下取1，当微粒与电极接触或与同性电极接近时取0.832；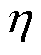
为气体黏性系数；v为微粒的运动速度。
表1 球形金属微粒受力解析式
Tab.1 The analytical formula for the force of spherical metal particles
受力类型受力幅值 重力 浮力 库仑力 气体阻力
根据已有研究，微粒与电极碰撞时刻介电区域内的静电场满足泊松方程，因此微粒与导体（高压电极）碰撞所带正电荷可表示为
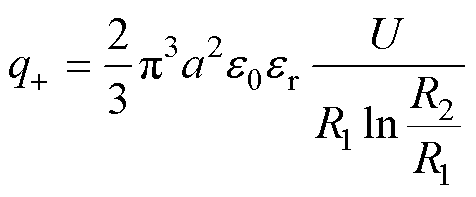（1）
微粒与壳体（地电极）碰撞所带负电荷为
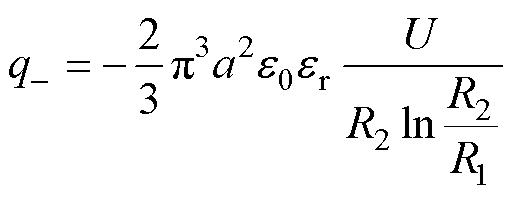（2）
式中，R1、R2分别为导体外径和外壳内径；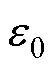
、
分别为真空介电常数和介质相对介电常数。
微粒与驱赶电极碰撞后会朝着驱赶电极斜面法向方向运动，但因粗糙电表面的存在，微粒碰撞电极后的反射角并不等于入射角，微粒的运动具有强随机性[19]。由文献[20]的研究可知，该反射角呈对数正态分布，可由式（3）～式（5）计算。
（3）
（4）
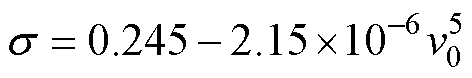（5）
式中，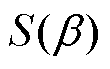
为反射角分布；v0为微粒入射速度。
经驱赶电极多次反射后，微粒将离开驱赶电极下方，在导体与壳体之间做“谐振运动”，此时微粒运动范围小，因此经驱赶的微粒有较大概率出现在图1所示的驱赶电极与导体结合处正下方A区范围内[21]。
金属微粒在碰撞电极时，存在一定的能量损失，假设某一金属微粒接近碰撞前的速度大小为v0，其碰撞之后的速度大小v1为
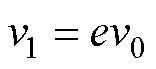（6）
式中，e为弹性力学中的恢复系数。
由文献[22]可知，恢复系数与材料系数及物体速度有关，微粒与电极或外壳碰撞的恢复系数可由式（7）经验公式得到。
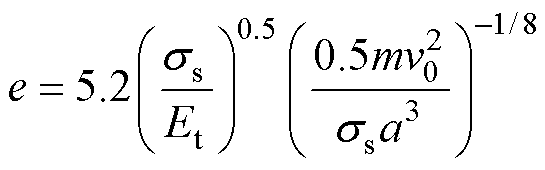（7）
式中，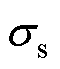
为碰撞材料屈服极限；Et为物体的弹性模量；m为微粒质量。
金属微粒未发生碰撞时，可列写运动方程为
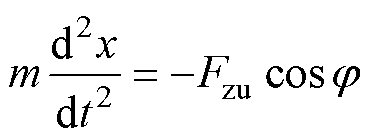（8）
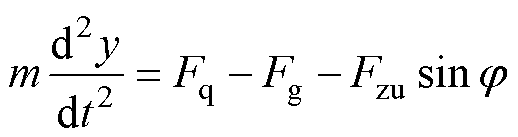（9）
式中，Fzu为气体阻力；Fq为电场力；Fg为金属微粒所受重力与浮力的合力；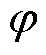
为微粒运动速度方向与轴向的夹角。
由于微粒在GIS/GIL中运动具有强随机性，本文基于蒙特卡洛思想计算微粒的运动路径，研究驱赶电极的作用机制。
参考实际直流气体绝缘设备比例，搭建驱赶电极模型：设置模型外壳内径为60 mm，导体外径为20 mm，球形微粒半径为0.1 mm，密度为2 700 kg/m3；驱赶电极材料设为铝；材料屈服极限为65 MPa，等效弹性模量为75 GPa，模型内部温度为27℃，普适气体常数为8.31 [J/(mol∙K)]，Sutherland常数为110.56 K。
设置驱赶电极长度为50 mm，凸起处长度为8 mm，分析该电极效果。为说明模型电场强度大小，与外壳内径为120 mm，导体外径为45 mm的100 kV直流GIS/GIL中电场强度进行对比，当模型外施38 kV电压时，电场强度和GIS/GIL外壳内表面一致；当施加48 kV电压时，电场强度和GIS/GIL导体表面一致。
计算流程如下：设定好模型参数，在导体处施加38 kV电压，微粒的轴向初始位置设置在驱赶电极正下方壳体上随机一处，微粒启举后通过判断微粒是否发生碰撞，由式（6）～式（9）求解相应运动方程，循环统计5 000颗微粒随机碰撞驱赶电极后的运动情况，得到微粒的碰撞电极后的初始落点位置分布，这里的初始落点位置是指微粒从启举到落点位置趋于稳定，即0.4 s内落在壳体上的轴向位置，仿真过程中未考虑微放电对粒子带电量的影响。
驱赶电极下微粒在壳体上的运动分布如图2所示，图中散点代表微粒在壳体上的分布位置，微粒碰撞驱赶电极后在电极与导体正下方A区内分布较为集中。将驱赶电极左侧轴向坐标设置为0 mm，通过计算可得微粒初始落点位置分布如图3所示，图3中每点包含了相邻5 mm范围内数据，得结论如下：在不加设驱赶电极时，微粒的初始落点位置较为分散，呈正态分布，在轴向位置25～35 mm处微粒出现的概率最大，为8.63 %；加设驱赶电极后，微粒的初始落点位置较为集中，且落点位置朝着远离绝缘子方向移动，在壳体轴向位置55～65 mm处微粒出现概率最大，为13.72 %。
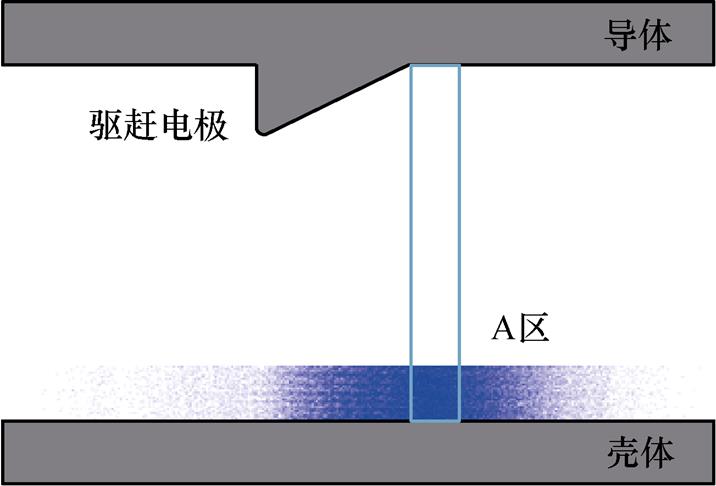
图2 驱赶电极下微粒运动分布
Fig.2 Distribution of particle motion under driving electrode
图3 微粒初始落点位置概率分布
Fig.3 Probability distribution of particle initial location
改变微粒大小，不同半径微粒初始落点位置概率分布如图4所示。由图4可知，微粒尺寸越小其碰撞电极后的轴向位置分布越远，即电极驱赶效果越明显，尺寸较大的微粒相较于小尺寸微粒的初始落点位置分布更集中；调整所施加的电压，由38 kV升压至48 kV，发现电压等级对微粒落点位置影响并不明显；不同半径、不同电压等级下的微粒碰撞驱赶电极后其初始落点位置仍具有集中性，均是在轴向50～60 mm处存在最大出现概率。
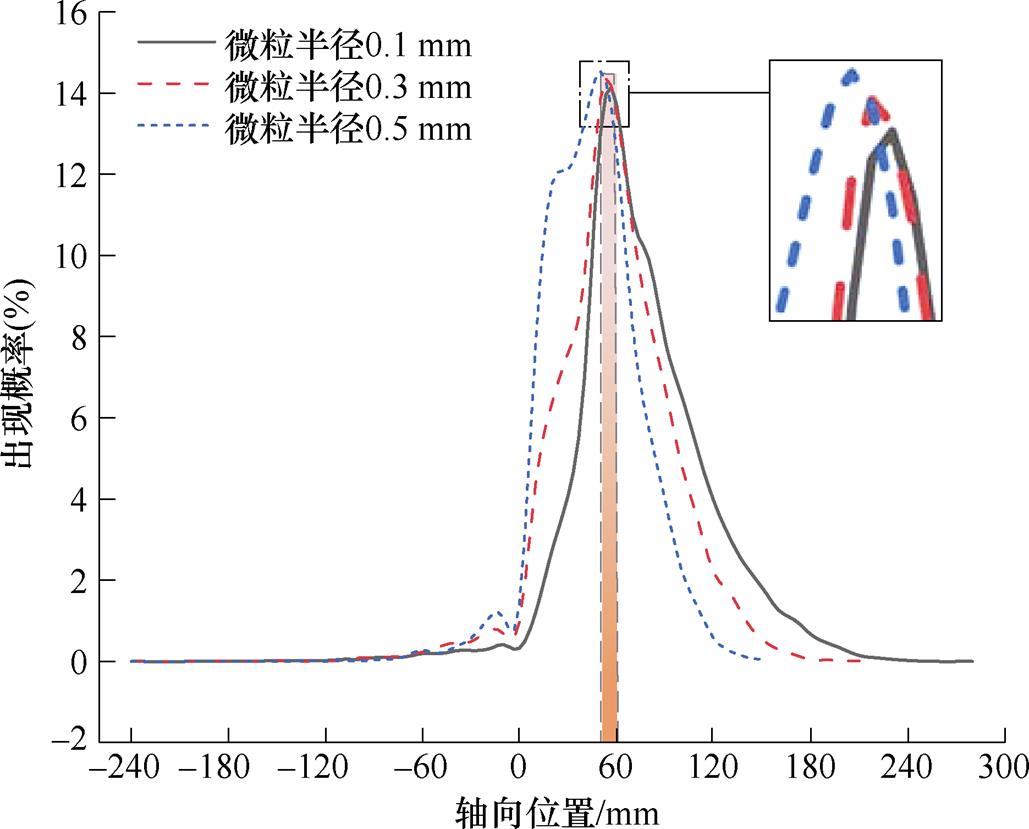
图4 不同半径微粒初始落点位置概率分布
Fig.4 Probability distribution of the initial location of particles with different radius
由以上分析可得出结论：驱赶电极能使得碰撞后的微粒朝着远离绝缘子方向运动，微粒初始落点位置具有强集中性，分布在导体与电极结合处附近A区范围内。
通过前述分析得到了驱赶电极的作用机制，驱赶电极示意图如图5所示。接下来对其进行设计，驱赶电极的关键参数包括电极凸起处长度、电极长度以及倾角等。
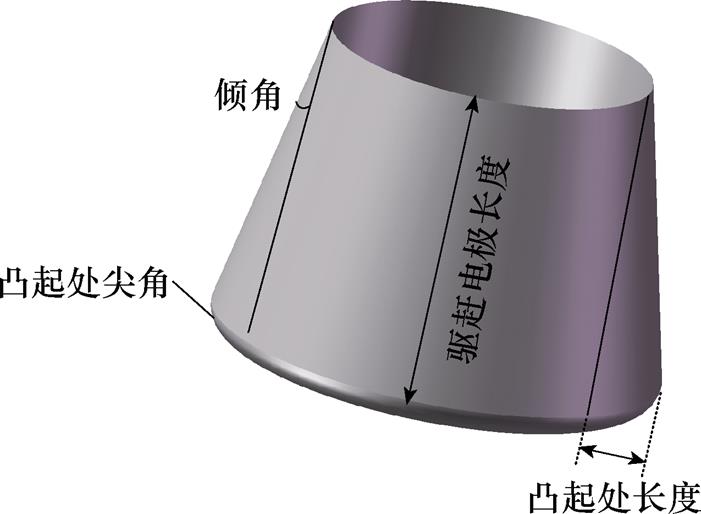
图5 驱赶电极示意图
Fig.5 Schematic diagram of driving electrode
电极凸起处长度会对电极的驱赶效果产生影响，该值越大，电极对微粒的驱赶效果越明显。但是随着电极凸起处长度值的增大，GIS/GIL内电场强度畸变越严重，由文献[23]可知，和设计导体外径的方法一致，当壳体内半径与驱赶电极外半径的比在2.1～3.9范围变化时，击穿电场强度的变化仅有5 %，是较为理想的状态。
类似地，随驱赶电极长度的增加，电极的驱赶效果减弱，电场畸变的范围增大，而驱赶电极太短会加剧附近电场的畸变程度，因此需要对驱赶电极长度进行限制。
与此同时，驱赶电极凸起处尖角也会造成电场发生较大畸变，需考虑对驱赶电极进行圆角处理。根据文献[24]中所指出的工频运行电压下内部及嵌件的设计电场强度值，安装驱赶电极后直流GIS/ GIL内部电场强度最大值应不超过4 kV/mm，以满足长期运行的要求。
综合以上因素，对于导体半径为20 mm、壳体内径为60 mm的模型，加设驱赶电极后导体的外径应该控制在20～28 mm，此时半径比在2.1～3.0之间，即设计驱赶电极凸起处长度为8 mm。本文固定驱赶电极凸起处长度，考虑电场畸变与微粒落点位置分布对驱赶电极的结构参数进行优化设计。
设驱赶电极左侧位置轴向坐标为0 mm，取驱赶电极倾角由5 °变化至14 °，仿真步骤与1.2节相同，得到不同倾角下驱赶效果及微粒集中落点分布结果如图6所示，下折线与左y轴对应，上折线与右y轴对应。当驱赶电极倾角大于5 °，微粒初始落点位置小于0 mm概率低，小于0.04 %，驱赶电极的驱赶效果好。计算不同倾角下电极周围电场发现，当倾角大于10 °，电场畸变较为严重，大于7 kV/mm，因此驱赶电极倾角设置在6 °～10 °是较为理想的状态。为减小内部电场的畸变，对驱赶电极进行圆角处理，当圆角半径为3 mm时，电场最大值减小到4 kV/mm以内，满足直流GIS/GIL长期运行要求。
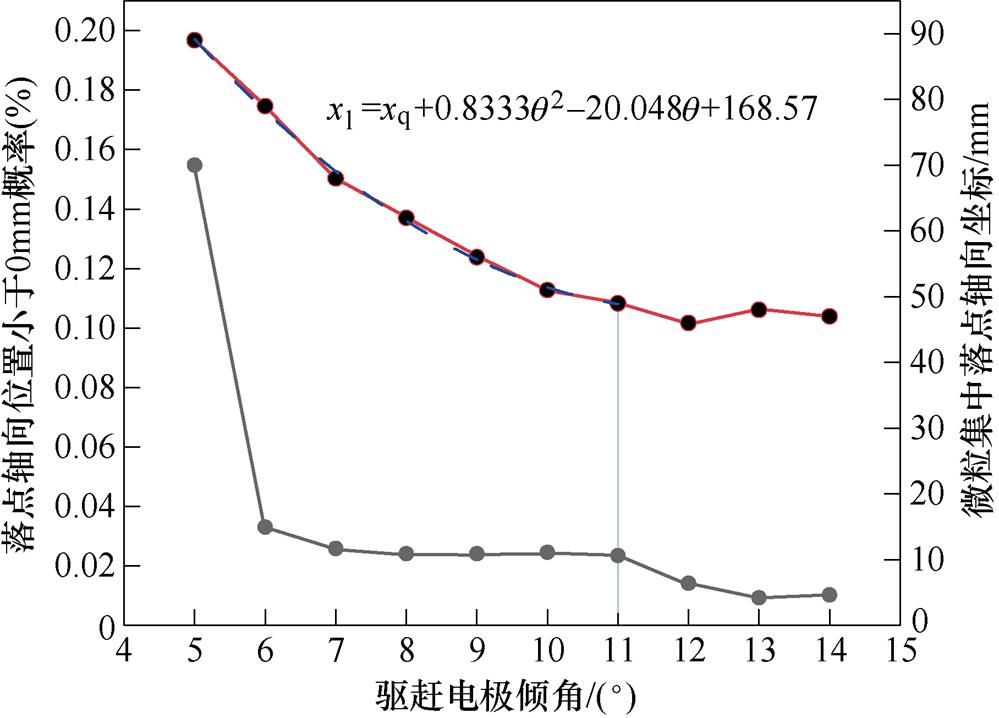
图6 不同倾角下驱赶效果及微粒集中落点分布
Fig.6 Driving effect and particle concentration point distribution at different inclinations
随着驱赶电极倾角增大，驱赶电极长度减小，微粒集中落点位置轴向坐标逐渐减小，根据计算结果，可拟合出不同驱赶电极倾角下微粒集中落点位置公式。当倾角在5 °～11 °时，微粒集中落点位置表示为
（10）
式中，xl为驱赶电极下微粒集中落点位置（mm）；xq为驱赶电极轴向初始位置，本文xq=0 mm；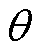
为驱赶电极几何倾角。
当倾角继续增大时，此时驱赶电极长度短，微粒难多次碰撞电极，微粒初始集中落点位置基本保持在相对驱赶电极50 mm处。
综上所述，对于导体半径为20 mm，壳体内径为60 mm的模型，驱赶电极凸起处长度应为8 mm，电极倾角设置为6 °～10 °，圆角半径为3 mm，驱赶电极下微粒碰撞电极后的集中落点位置分布具有规律性，可由公式统一表示。
根据微粒撞击驱赶电极后在壳体上初始落点位置具强集中性，本节进一步以微粒陷阱的捕获概率提升为目标，提出驱赶电极与微粒陷阱协同布置的优化设计方法，这里的捕获概率定义为陷阱捕获的微粒数量与运动的金属微粒数量比值的百分数。楔形陷阱易拆卸，其侧壁与底部呈一定倾角，有较高的捕获概率，可以和驱赶电极很好地配合，实现驱赶电极和楔形陷阱的协同优化。
基础的布置方案如图7所示：驱赶电极套接在高压电极上，布置在绝缘子附近，使绝缘子周围的金属微粒碰撞驱赶电极后朝着远离绝缘子方向运动；陷阱布置在驱赶电极与导体结合处下方，捕获被驱赶的微粒。
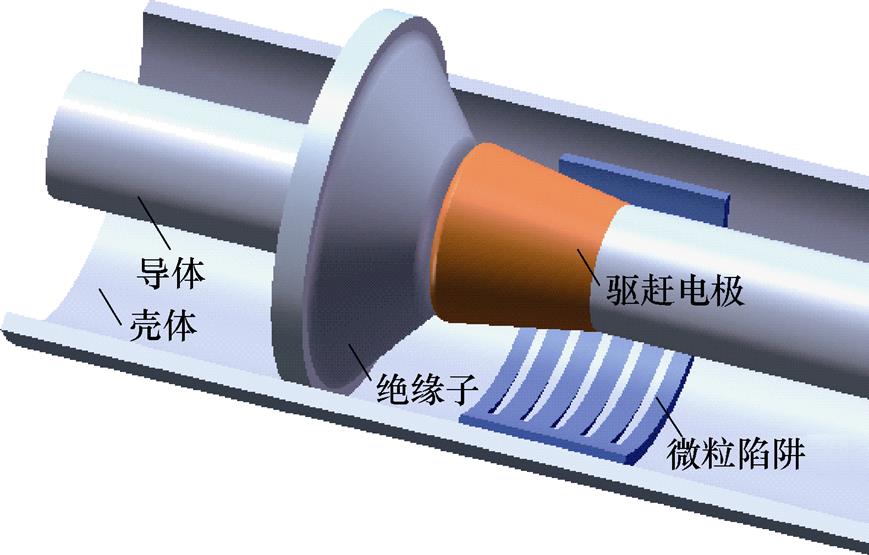
图7 驱赶电极和微粒陷阱布置方案
Fig.7 Drive electrode and particle trap layout scheme
设置模型的几何参数如下：模型外壳内径为60 mm，导体外径为20 mm，驱赶电极凸起处长度为8 mm，圆角半径为3 mm，选取电极长度50 mm，即电极倾角为9 °；楔形陷阱的捕获率随槽数增加而增大，为了简化分析，设置模型陷阱为单槽，几何参数如图8所示。绝缘子为盆式绝缘子，在电场力作用下，微粒易吸附于绝缘子凸面并引发绝缘子沿面闪络，为避免微粒向绝缘子运动，本文将驱赶电极设置在绝缘子凸面一侧进行分析。
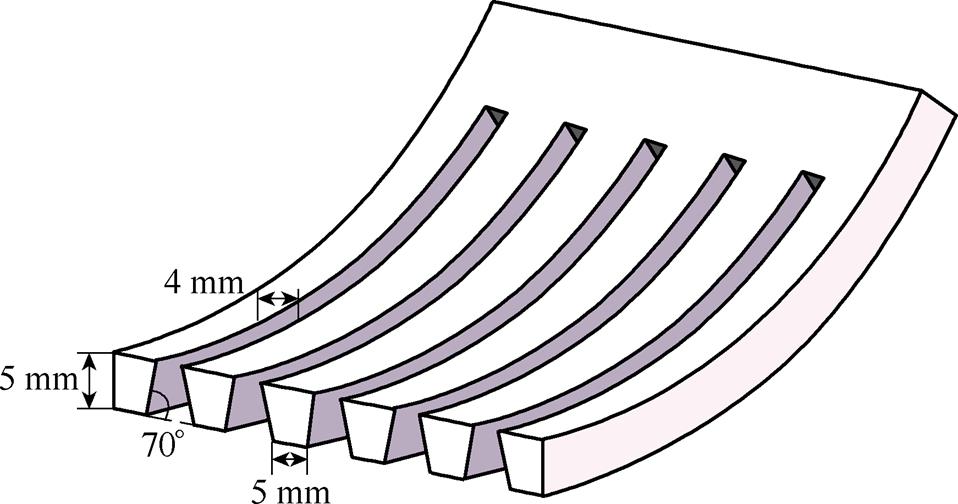
图8 微粒陷阱几何参数
Fig.8 Particle trap geometry parameters
微粒仍放置在驱赶电极正下方某一随机位置，陷阱放置在壳体上，通过仿真计算得到微粒从启举到陷阱捕获率达饱和，即6 s内的运动情况，微粒运动路径计算流程如图9所示。设置给定仿真参数，判断微粒是否发生碰撞，由式（8）和式（9）计算微粒未发生碰撞时的运动参数，由式（1）～式（7）计算微粒发生碰撞后的运动情况；当微粒进入陷阱时，若微粒径向坐标大于陷阱坐标，则认为微粒发生逃离，逃逸次数Nesc+1，若微粒反弹的径向速度小于0.3 m/s，则此时微粒不具有运动至陷阱上槽口的能力，可认为被陷阱捕获，捕获次数Ncap+1，仿真统计了6万颗微粒碰撞驱赶电极后陷阱的捕获概率。仿真过程中考虑了盆式绝缘子对微粒周围电场的影响，并认为当微粒运动到绝缘子侧时，驱赶电极驱赶作用失效，该微粒的运动过程不计入结果，不同布置方案下计算结果见表2。
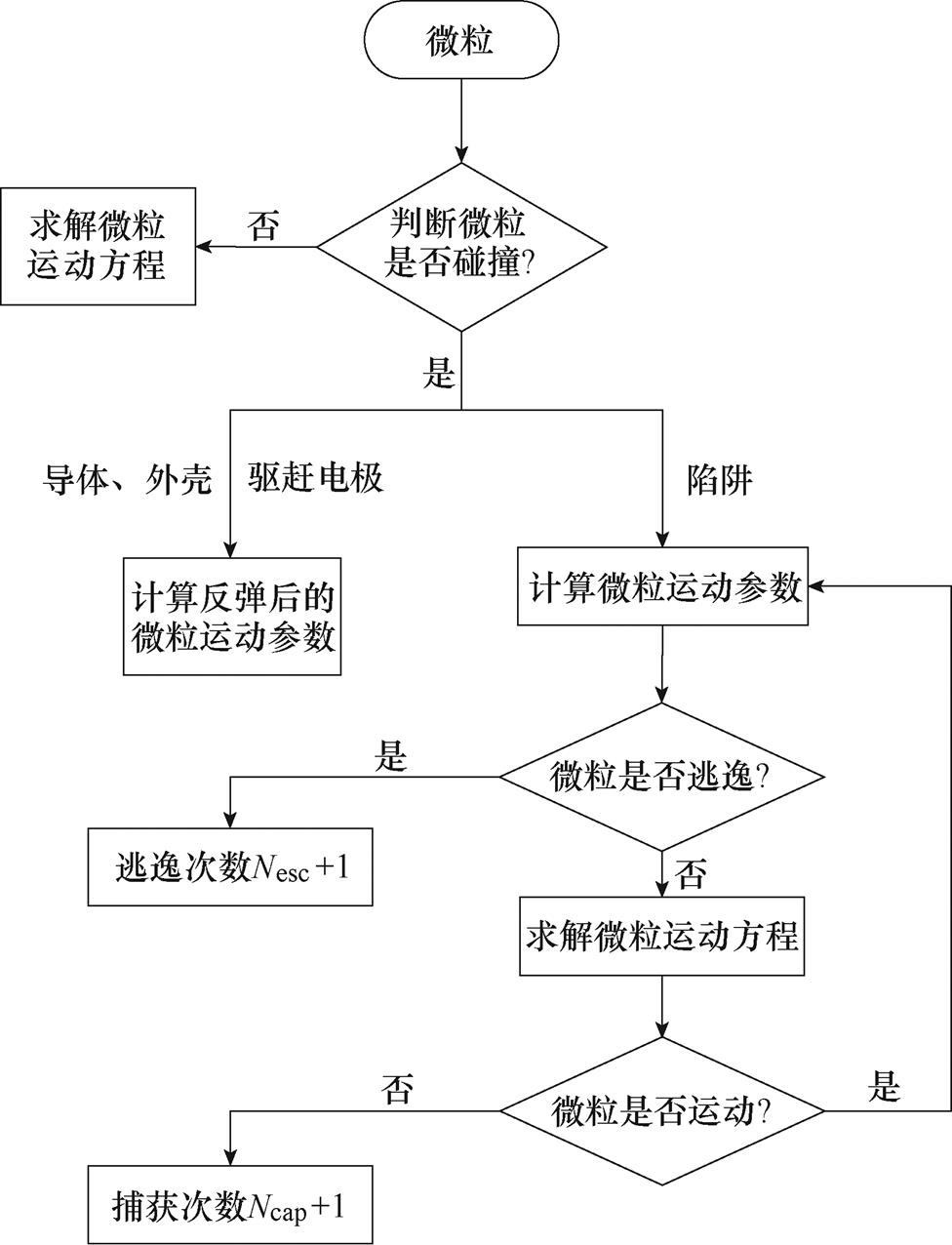
图9 微粒运动路径计算流程
Fig.9 Flow chart of particle path calculation
表2 不同布置方案结果比对
Tab.2 Comparison of results of different layout schemes
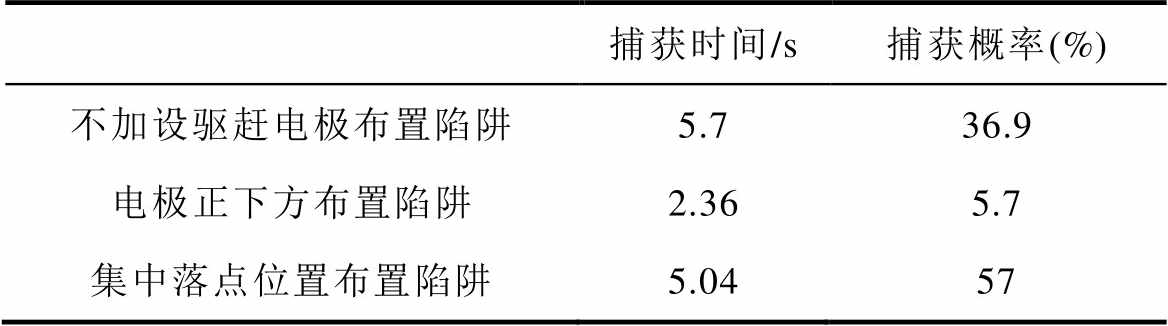
捕获时间/s捕获概率(%) 不加设驱赶电极布置陷阱5.736.9 电极正下方布置陷阱2.365.7 集中落点位置布置陷阱5.0457
直流GIS/GIL内不加设驱赶电极，由图3知此时微粒落点概率较大位置在轴向30 mm，将陷阱中心轴线轴向布置在该处，如图10所示，计算得到，此时捕获概率为36.9 %，对于被捕获的微粒，陷阱的平均捕获时间为5.7 s。
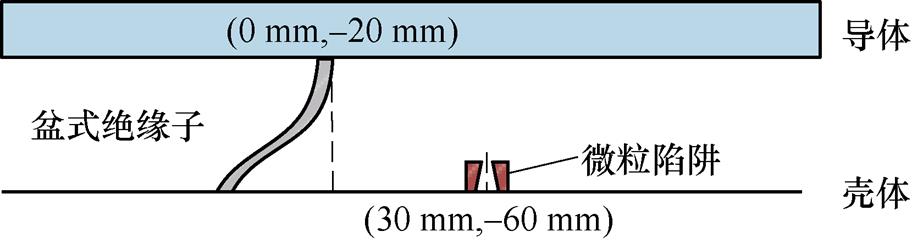
图10 不加设驱赶电极仿真布置
Fig.10 No driving electrode simulation layout is added
在导体上加设驱赶电极，布置如图11所示，当设置陷阱中心轴线轴向位置放置在10 mm处时，计算得到陷阱捕获微粒时间缩短，为2.36 s，但是陷阱捕获概率低，仅为5.7 %；当设置单个微粒陷阱槽中心轴线轴向位置放置在微粒集中落点位置60 mm处时，通过仿真得到陷阱平均捕获微粒时间为5.04 s，陷阱捕获概率增加，达到57 %。
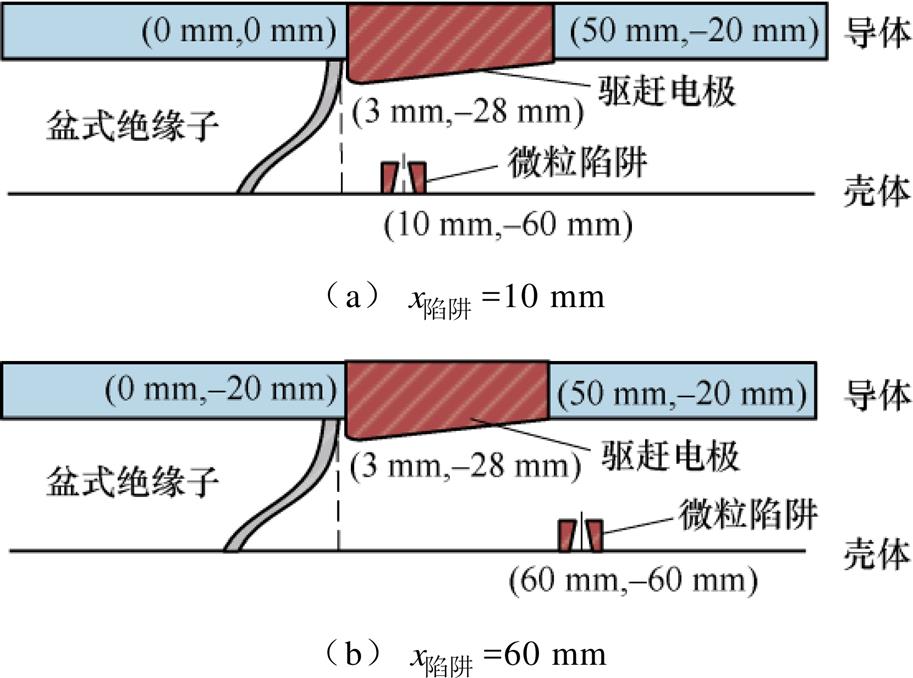
图11 加设驱赶电极仿真布置
Fig.11 Add driving electrode simulation layout
对比以上结果发现，加设驱赶电极后，微粒运动速度增加，陷阱捕获微粒的时间缩短，当陷阱布置在微粒集中落点位置时，陷阱捕获概率相较于无驱赶电极时提高了20 %。
分析陷阱捕获概率增加的原因，一方面是陷阱布置在了微粒集中落点位置；另一方面是驱赶电极使得陷阱中微粒的入射角减小。不加设驱赶电极时，由仿真可知，陷阱中微粒的入射角分布在85 °～90 °，此时初速度大的微粒进入陷阱后易发生逃逸；加设驱赶电极后，将陷阱布置在微粒集中落点处，此时微粒的入射角分布在50 °～90 °，其中55 %的微粒入陷的入射角小于85 °，从图12可以看出，入射角的减小会让微粒与陷阱壁面发生更多次碰撞，有利于陷阱对微粒的捕获。由以上分析可知，当微粒陷阱布置于微粒集中落点位置时，驱赶电极使入射角减小，增加了微粒在陷阱内碰撞次数，从而提高微粒陷阱捕捉能力。
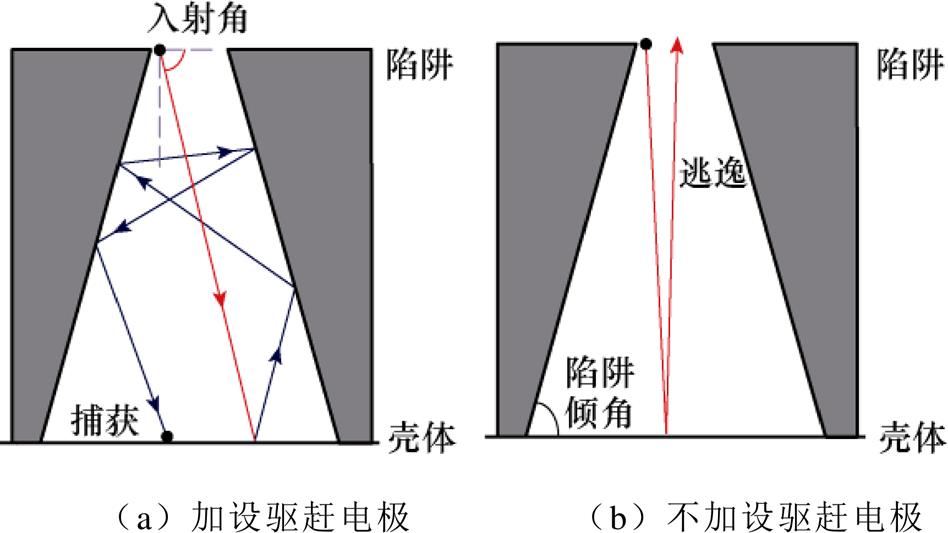
图12 微粒入陷示意图
Fig.12 Schematic diagram of particle entrapment
驱赶电极下微粒进入陷阱的入射角减小，可提高陷阱捕获微粒能力；而陷阱倾角大小也会影响入陷微粒的碰撞次数，陷阱倾角越小，其捕获入陷微粒的能力越强。因此，须对微粒陷阱与驱赶电极的结构参数进行协同优化。
改变驱赶电极倾角与微粒陷阱倾角，可得微粒捕获概率的变化情况，如图13所示。在不同驱赶电极倾角下，随着陷阱倾角增加，捕获概率均出现极大值，这是由微粒入射角、陷阱倾角和陷阱有效区域大小共同决定的。微粒入射角与陷阱倾角减小，会增加微粒在陷阱内的碰撞次数，但陷阱倾角过小会降低微粒进入陷阱的概率，因此会出现极值。随着驱赶电极倾角增大，微粒捕获概率最大情况下相应的微粒陷阱倾角逐渐增大，其中当驱赶电极倾角为8 °，陷阱倾角为50 °时，微粒的捕获概率达到最大，为69.8 %，是最优的几何设计方案，此时微粒入陷的入射角范围在48 °～90 °，有56 %的微粒入陷的入射角小于85 °。
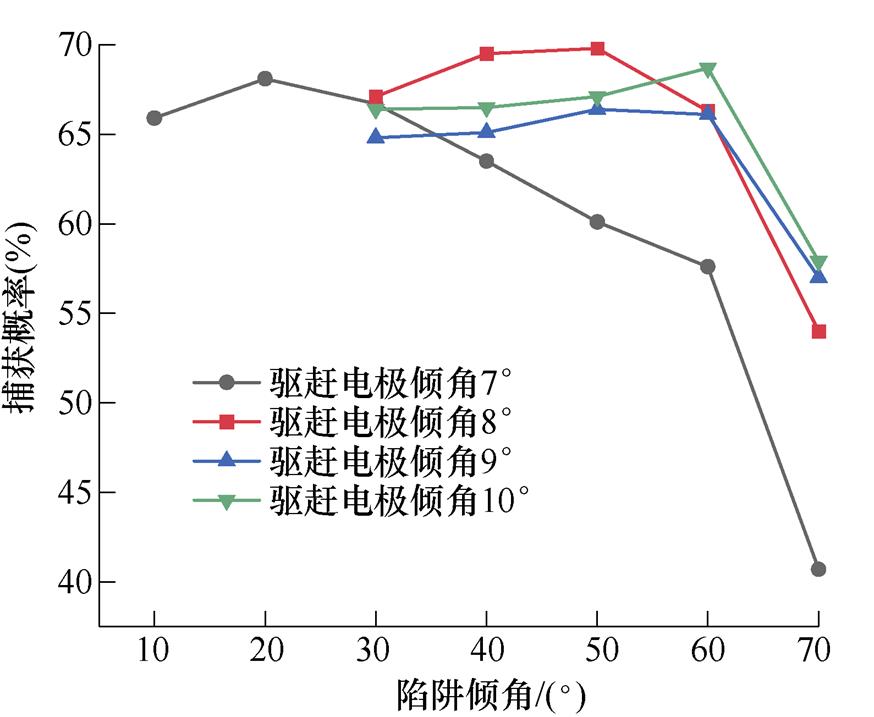
图13 捕获概率变化关系
Fig.13 Capture the relationship of probability variation
针对不同尺寸、不同电压等级的直流GIS/GIL，在驱赶电极下微粒初始落点位置均具有强集中性，将陷阱布置于微粒集中落点位置，能缩短陷阱捕获时间，减小微粒在陷阱中的入射角，提高陷阱捕获微粒能力，本文提出的驱赶电极与微粒陷阱协同优化方法具有普适性。利用直流气体绝缘设备的同轴缩比模型定量分析得到，相较于无驱赶电极时，陷阱布置在驱赶电极下微粒集中落点位置时捕获概率提升了20 %，当驱赶电极倾角为8 °、陷阱倾角为50 °时，微粒陷阱捕获概率最高，为69.8 %。
为验证仿真模型的正确性，搭建了如图14所示的真型实验平台。将电极置于有机玻璃内，放置在含有观察窗的方形密闭腔体中，通过套管对腔体采用逐步加压法施加直流电压；平台中驱赶电极凸起处长度为8 mm，电极长度为50 mm，驱赶电极套接在导体上，紧挨着盆式绝缘子凸面一侧放置；楔形陷阱布置在壳体上，导体外径、外壳内径和仿真模型参数相同。实验过程中通过高速相机拍摄微粒的运动行为，并用LED对相机进行补光。
首先观察驱赶电极驱赶效果：将直径为0.6 mm的铝球5个一组，随机放置在驱赶电极正下方，在电极上施加直流电压，通过高速相机拍摄微粒撞击驱赶电极的运动过程，重复20组实验，得到微粒运动路径如图15所示。驱赶电极下方的微粒撞击电极后朝着驱赶电极法向方向运动，微粒撞击电极后会集中出现在驱赶电极与导体结合处正下方壳体上，如图15所示的方框中，和前述微粒集中落点位置计算结果吻合。
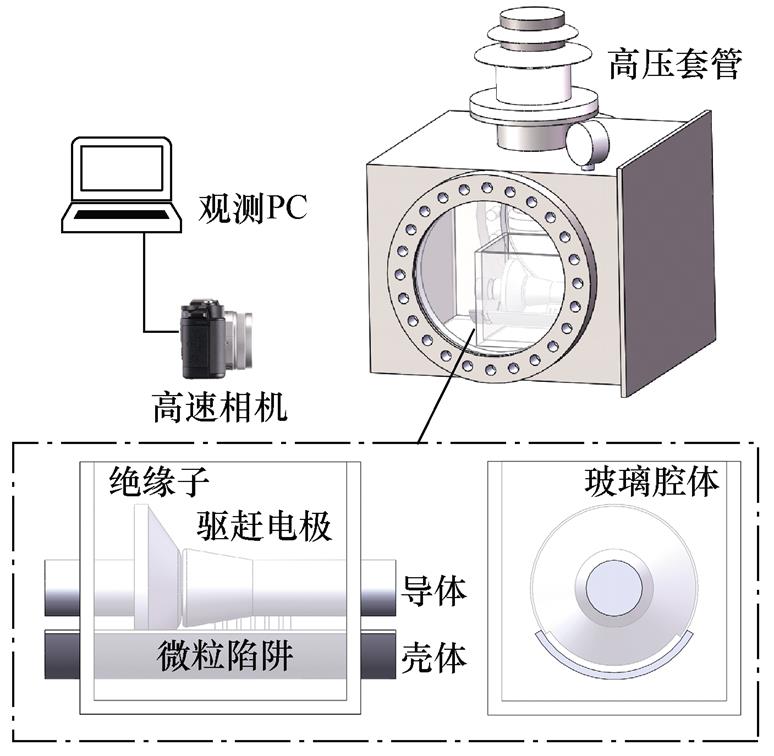
图14 实验平台
Fig.14 Experimental platform diagram
图15 微粒运动行为
Fig.15 Motion behavior of particles
接下来将楔形陷阱放置于半封闭式腔体底部，布置在微粒集中落点处，观察微粒入陷行为，同时统计陷阱的捕获概率，实验布置情况如图16所示。将半径为0.3、0.4、0.5 mm的微粒单一尺寸10个分成一组分别随机放置在驱赶电极正下方，电极上施加直流电压，重复50次实验，获得陷阱捕获概率。实验过程中将不加设驱赶电极和微粒陷阱直接放置在驱赶电极正下方的情况作为对照，得到微粒捕获概率如图17所示。
图16 实验布置
Fig.16 Experimental layout
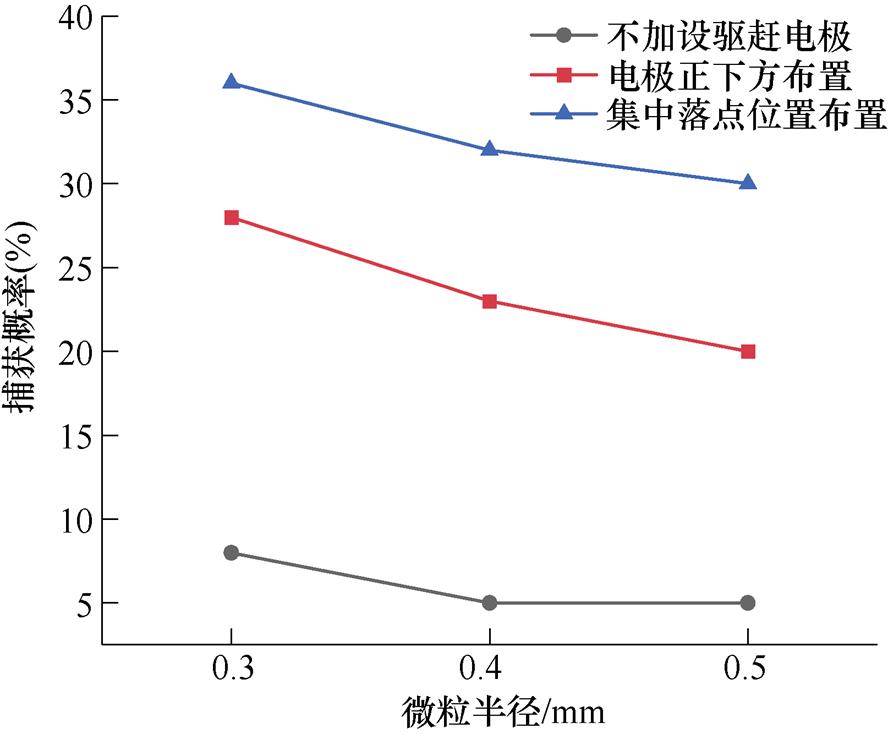
图17 微粒捕获概率
Fig.17 Particle capture probability
观察微粒运动路径发现，不加设驱赶电极时，直流电场下，微粒在电极与壳体间多做“谐振运动”，微粒陷阱难以捕获微粒，结合图17可知，该情况下微粒陷阱捕获概率较低。加设电极后，若直接在驱赶电极正下方布置微粒陷阱，微粒陷阱的捕获概率提高了15 %，在微粒集中落点处布置微粒陷阱，捕获概率最高，相较于无驱赶电极时提升了25 %，相较于正下方时提升了10 %，和仿真计算得到的陷阱捕获概率变化趋势基本一致，证实了仿真结果。
结合某实际交流特高压GIL，进一步讨论本文提出的协同布置方案与优化设计方法对不同电压等级设备的通用性、工程应用的可行性，以及有待探究的相关问题。
针对不同的GIS/GIL设备，驱赶电极结构参数的取值存在差异性，在实际应用中，可根据本文提出的驱赶电极设计方法，参考已有的屏蔽环大小以及相应电压等级下的电场强度阈值，设定驱赶电极的结构参数。在不同电压等级下，设备内的微粒启举后的运动情况也会不同，但微粒碰撞驱赶电极后的运动规律保持不变，本文基于特高压GIL真型结构，讨论提出的驱赶电极与微粒陷阱的协同优化方法的通用性。
该实际特高压GIL外壳内径为422 mm，导体外径为90 mm，通常在绝缘子两侧加设屏蔽环，加设屏蔽环处导体外径为150 mm。基于文中提出的驱赶电极设计方法，将已有的屏蔽环设计成驱赶电极。依据已有的屏蔽环处导体外径为150 mm，设置驱赶电极凸起处长度为60 mm，基于本文驱赶电极的设计方法，设置电极倾角在6 °～10 °，相较于同轴缩比模型，特高压等级下GIL内部电场强度更大，驱赶电极圆角半径应设置得更大。由特高压绝缘设计方法可知，对于工作气压为0.4～0.5 MPa的纯SF6绝缘GIS/GIL，雷电耐压下导体表面设计电场强度在19.9～24.5 kV/mm[25]，可设置驱赶电极圆角半径为50 mm，满足特高压GIL运行要求，设计结构如图18所示。
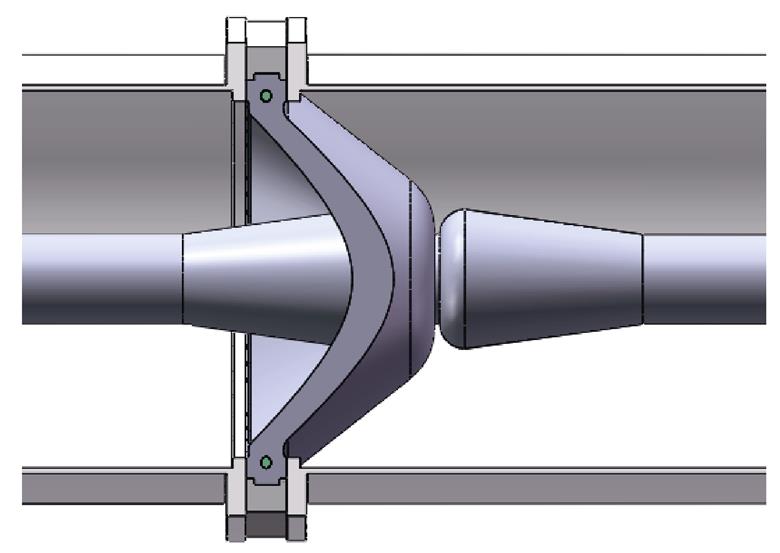
图18 1 000 kV交流特高压GIL真型设计结构
Fig.18 1 000 kV AC UHV GIL true design structure
利用本文提出的微粒与驱赶电极的碰撞动力学模型，搭建特高压GIL仿真模型，设置驱赶电极倾角为9 °，分析驱赶电极设置在绝缘子凸面一侧时微粒的运动情况，研究发现，相较于同轴缩比模型，电压等级升高后，微粒的运动速度会变快，微粒的分布范围会变大，但微粒碰撞驱赶电极后的初始落点仍集中分布在电极与导体连接处的正下方壳体上。利用图9所示的计算方法，得到模型中将陷阱布置在驱赶电极下微粒集中落点位置时的捕获概率，结果表明，相较于无驱赶电极时，陷阱的捕获概率提升了21 %，和同轴缩比模型中陷阱的捕获概率的变化趋势一致。改变驱赶电极倾角与微粒陷阱倾角，同样地，利用同图9所示的计算方法，得到微粒陷阱捕获概率的变化情况。具体结果表明，当驱赶电极倾角为8 °、陷阱倾角为50 °时，微粒陷阱的捕获概率出现极大值，达68.5 %，这与本文同轴缩比模型中获得的结果相符。由此，本文提出的驱赶电极与微粒陷阱协同优化方法具有普适性。
研究发现，交流GIL屏蔽罩下方大部分启举微粒的会聚集在远离绝缘子的位置，存在一个特征聚合区，因此利用已有的屏蔽罩将其设计为驱赶电极，具有工程可实施性。然而现阶段国内外专家学者仅从电场角度分析了同时布置驱赶电极与微粒陷阱时对运动微粒的抑制效果，研究过程中并未考虑微粒的碰撞随机特性，对于驱赶电极的作用机制也未给出定量表征。本文建立了微粒与驱赶电极的碰撞动力学模型，提出驱赶电极设计方法以及驱赶电极与微粒陷阱的协同优化方法，得到了更理想的微粒抑制效果。
在实际GIS/GIL设备中，其内部环境会比文中搭建的模型要复杂许多，本文仅通过同轴缩比的原型样机在实验室条件下进行实验验证，无法直接面向工程实际，相关问题还有待探究。在接下来的研究中，可进一步分析驱赶电极与盆式绝缘子的相对位置对电极周围电场的影响，探究不同相对位置下微粒运动路径的变化，需进一步考虑驱赶电极的表面粗糙度、驱赶电极的加工工艺、电晕放电离子风等对微粒运动的影响，从而调整驱赶电极的结构参数以及驱赶电极与微粒陷阱的协同布置方法。
由以上分析可知，本文提出的驱赶电极与微粒陷阱的协同设计方法适用于不同尺寸、不同电压等级的直流管道输电装备，对交流输电管道设计也具有参考价值。
1）本文考虑碰撞反射角的随机分布特性，建立了微粒与驱赶电极的碰撞动力学模型，发现驱赶电极下微粒初始落点位置具有强集中特征。研究表明，对于导体半径为20 mm、壳体内径为60 mm的气体绝缘设备缩比模型，将驱赶电极凸起处长度设置为8 mm、电极倾角在6 °～10 °、圆角半径为3 mm时，微粒初始落点位置分布于远离绝缘子侧，能有效抑制微粒向绝缘子运动。
2）以微粒陷阱捕获概率为优化目标，提出驱赶电极和微粒陷阱的协同布置策略与结构参数优化方法。将陷阱布置于驱赶电极下的微粒集中落点位置，能缩短陷阱捕获时间，减小微粒在陷阱中的入射角，提高陷阱捕获微粒能力。相较于无驱赶电极时，陷阱布置于微粒集中落点位置时捕获概率提升了20 %，当驱赶电极倾角为8 °、陷阱倾角为50 °时，微粒陷阱的捕获概率最高，可达69.8 %。本文提出的协同布置方案与优化设计方法可为当前工程中的微粒抑制技术提供量化依据。
3）搭建了包含驱赶电极与微粒陷阱的真型实验平台，实验结果表明，微粒陷阱布置于驱赶电极下的微粒集中落点处时，陷阱捕获概率最高。实验结果与仿真计算得到的微粒陷阱捕获概率变化趋势基本一致，验证了协同布置策略与参数优化方法的有效性。
4）本文提出的驱赶电极与微粒陷阱的协同设计方法适用于不同尺寸、不同电压等级的直流管道输电装备。未来将进一步探究驱赶电极与微粒陷阱协同方案对微粒飞萤运动的抑制效果，提高协同抑制方案的应用价值。
参考文献
[1] 张连根, 路士杰, 李成榕, 等. GIS中线形和球形金属微粒的运动行为和危害性[J]. 电工技术学报, 2019, 34(20): 4217-4225.
Zhang Liangen, Lu Shijie, Li Chengrong, et al. Motor behavior and hazard of spherical and linear particle in gas insulated switchgear[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4217-4225.
[2] Volpov E. Electric field modeling and field formation mechanism in HVDC SF6 gas insulated systems[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2003, 10(2): 204-215.
[3] Magier T, Tenzer M, Koch H. Direct current gas- insulated transmission lines[J]. IEEE Transactions on Power Delivery, 2018, 33(1): 440-446.
[4] 程涵, 魏威, Bilallqbal Ayubi, 等. 直流GIL中线形金属微粒电动力学行为研究[J]. 电工技术学报, 2021, 36(24): 5283-5293.
Cheng Han, Wei Wei, Ayubi B, et al. Study on the electrodynamic behavior of linear metal particles in DC gas insulated transmission line[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5283- 5293.
[5] 胡琦, 李庆民, 刘智鹏, 等. 基于表层梯度电导调控的直流三支柱绝缘子界面电场优化方法[J]. 电工技术学报, 2022, 37(7): 1856-1865.
Hu Qi, Li Qingmin, Liu Zhipeng, et al. Interfacial electric field optimization of DC tri-post insulator based on gradient surface conductance regulation[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1856-1865.
[6] 黄旭炜, 倪潇茹, 王健, 等. 苯硫醚聚酰亚胺电极覆膜材料合成及直流应力下对金属微粒运动特性的抑制作用[J]. 电工技术学报, 2018, 33(20): 4712- 4721.
Huang Xuwei, Ni Xiaoru, Wang Jian, et al. Synthesis of phenyl-thioether polyimide as the electrode coating film and its suppression effect on motion behavior of the metal particles under DC stresses[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4712-4721.
[7] 李杰, 李晓昂, 吕玉芳, 等. 正弦振动激励下GIS内自由金属微粒运动特性[J]. 电工技术学报, 2021, 36(21): 4580-4589, 4597.
Li Jie, Li Xiaoang, Lü Yufang, et al. Motion chara- cteristics of free metal particles in GIS under sinusoidal vibration[J]. Transactions of China Elec- trotechnical Society, 2021, 36(21): 4580-4589, 4597.
[8] Techaumnat B, Huynh V Q, Hidaka K. Numerical analysis and experiments on the electromechanical behavior of wired-shape conducting particles[J]. IEEE Transactions on Magnetics, 2018, 54(3): 1-5.
[9] 范建斌, 李鹏, 李金忠, 等. ±800kV特高压直流GIL关键技术研究[J]. 中国电机工程学报, 2008, 28(13): 1-7.
Fan Jianbin, Li Peng, Li Jinzhong, et al. Study on key technology of ±800kV UHVDC GIL[J]. Proceedings of the CSEE, 2008, 28(13): 1-7.
[10] Wang Jian, Hu Qi, Chang Yanan, et al. Metal particle contamination in gas-insulated switchgears/gas- insulated transmission lines[J]. CSEE Journal of Power and Energy Systems, 2019, 7(5): 1011-1025.
[11] Morcos M M, Ward S A, Anis H, et al. Insulation integrity of GIS/GITL systems and management of particle contamination[J]. IEEE Electrical Insulation Magazine, 2000, 16(5): 25-37.
[12] 詹振宇, 宋曼青, 律方成, 等. 交流环保GIL中微粒运动规律及陷阱抑制措施研究[J]. 中国电机工程学报, 2019, 39(增刊1): 278-286.
Zhan Zhenyu, Song Manqing, Lü Fangcheng, et al. Study on particle movement and trap suppression in AC environmentally friendly GIL[J]. Proceedings of the CSEE, 2019, 39(S1): 278-286.
[13] 李伯涛, 王健, 张圣富, 等. 直流GIL中附着导电微粒对绝缘子表面电荷积聚特性的影响分析[J]. 高压电器, 2017, 53(7): 80-86.
Li Botao, Wang Jian, Zhang Shengfu, et al. Influence of the DC-GIL conductive adherent particles on the charge accumulation of insulator surface[J]. High Voltage Apparatus, 2017, 53(7): 80-86.
[14] Berg T, Juhre K, Fedtke T, et al. Specific chara- cteristics of particle traps for application in DC gas-insulated transmission lines (DC GIL)[C]//VDE High Voltage Technology 2020, ETG-Symposium, Online, 2020: 1-8.
[15] 常亚楠, 王健, 李庆民, 等. 交直流气体绝缘管道输电装备微粒污染治理措施研究进展[J]. 高压电器, 2021, 57(10): 91-100, 110.
Chang Yanan, Wang Jian, Li Qingmin, et al. Research progress of particle contamination suppression measures in AC and DC gas-insulated transmission equipment[J]. High Voltage Apparatus, 2021, 57(10): 91-100, 110.
[16] Zhan Zhenyu, Wang Dong, Xie Jun, et al. Motion characteristics of metal powder particles in AC GIL and its trap design[J]. IEEE Access, 2021, 9: 68619- 68628.
[17] 刘鹏, 李智凯, 田汇冬, 等. 直流电压下气体绝缘输电线路中微粒运动特性研究及微粒陷阱效能分析[J]. 中国电机工程学报, 2022, 42(15): 5740-5751.
Liu Peng, Li Zhikai, Tian Huidong, et al. Research on motion characteristics of metal particles and capture efficiency of particle traps in gas insulated trans- mission lines under DC voltage[J]. Proceedings of the CSEE, 2022, 42(15): 5740-5751.
[18] 王健, 常亚楠, 王靖瑞, 等. 基于捕捉效用分析的直流GIL微粒陷阱设计与参数优化[J]. 中国电机工程学报, 2020, 40(15): 5050-5061.
Wang Jian, Chang Yanan, Wang Jingrui, et al. Design and optimization of particle traps in DC GIL based on the capture effect analysis[J]. Proceedings of the CSEE, 2020, 40(15): 5050-5061.
[19] Khan Y, Okabe S, Suehiro J, et al. Proposal for new particle deactivation methods in GIS[J]. IEEE Transa- ctions on Dielectrics and Electrical Insulation, 2005, 12(1): 147-157.
[20] 陈有兴. 天然沙颗粒—床碰撞起跃特性的实验测量研究[D]. 兰州: 兰州大学, 2016.
[21] 孙继星, 陈维江, 李志兵, 等. 直流电场下运动金属微粒的带电估算与碰撞分析[J]. 高电压技术, 2018, 44(3): 779-786.
Sun Jixing, Chen Weijiang, Li Zhibing, et al. Charge estimation and impact analysis of moving metal particle under DC electric field[J]. High Voltage Engineering, 2018, 44(3): 779-786.
[22] 葛藤, 贾智宏, 周克栋. 钢球和刚性平面弹塑性正碰撞恢复系数研究[J]. 工程力学, 2008, 25(6): 209- 213.
Ge Teng, Jia Zhihong, Zhou Kedong. Research on elastoplastic normal impact of steel spheres against a rigid plane[J]. Engineering Mechanics, 2008, 25(6): 209-213.
[23] 鲁加明, 曹伟伟, 周振华. 550kV GIL母线的结构设计[J]. 电气技术, 2015, 16(9): 59-63.
Lu Jiaming, Cao Weiwei, Zhou Zhenhua. The structural design of 550kV GIL bus[J]. Electrical Engineering, 2015, 16(9): 59-63.
[24] 黎斌. SF6高压电器设计[M]. 4版. 北京: 机械工业出版社, 2015.
[25] 李鹏, 李志兵, 孙倩, 等. 特高压气体绝缘金属封闭输电线路绝缘设计[J]. 电网技术, 2015, 39(11): 3305-3312.
Li Peng, Li Zhibing, Sun Qian, et al. Research on insulation design of UHV gas-insulated metal- enclosed transmission line[J]. Power System Tech- nology, 2015, 39(11): 3305-3312.
Abstract Moving metal particles in DC gas-insulated composite appliances and closed transmission lines is the main cause of insulation failure. The driving electrode can make particles move away from the insulator, and the capture probability of particle traps can be significantly improved when used together with driving electrodes.
This paper established the dynamic collision model between the particle and the driving electrode. It was found that the particles affected by the driving electrode have strong concentrations. Then, the structural parameters of the driving electrode were optimized by considering the electric field distortion characteristics and the distribution of the particles, as shown in Fig.A1. For the scaled model of gas-insulated equipment with a conductor radius of 20 mm and an internal shell radius of 60 mm, when the length of the convex part is set to 8 mm, the electrode dip angle is 6 °～10 °, and the fillet radius is 3 mm. The initial placement position of the particles is distributed away from the insulator side, which can effectively suppress the movement of the particles to the insulator.
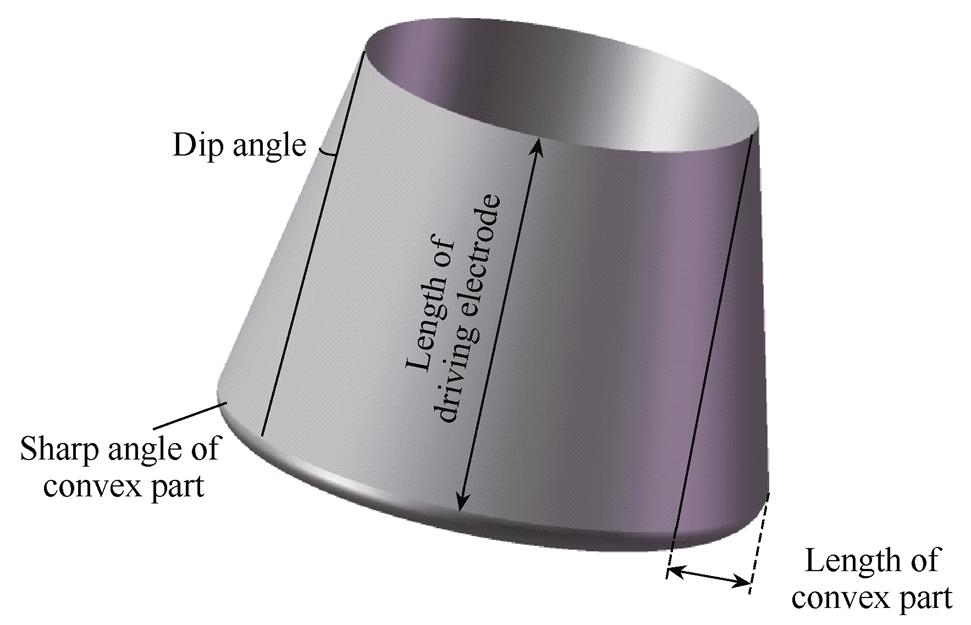
Fig.A1 Schematic diagram of driving electrode
Furthermore, aiming at optimizing particle trap capture probability, a synergistic arrangement strategy of the driving electrode and the particle trap was proposed, as shown in Fig.A2. The driving electrode is sleeved on the high-voltage electrode and arranged near the insulator. The particle trap is arranged at the concentrated drop point of the particles under the driving electrode. Compared with the case without the driving electrode, the capture probability of the trap at the location of particle concentration under the driving electrode is increased by 20 %.
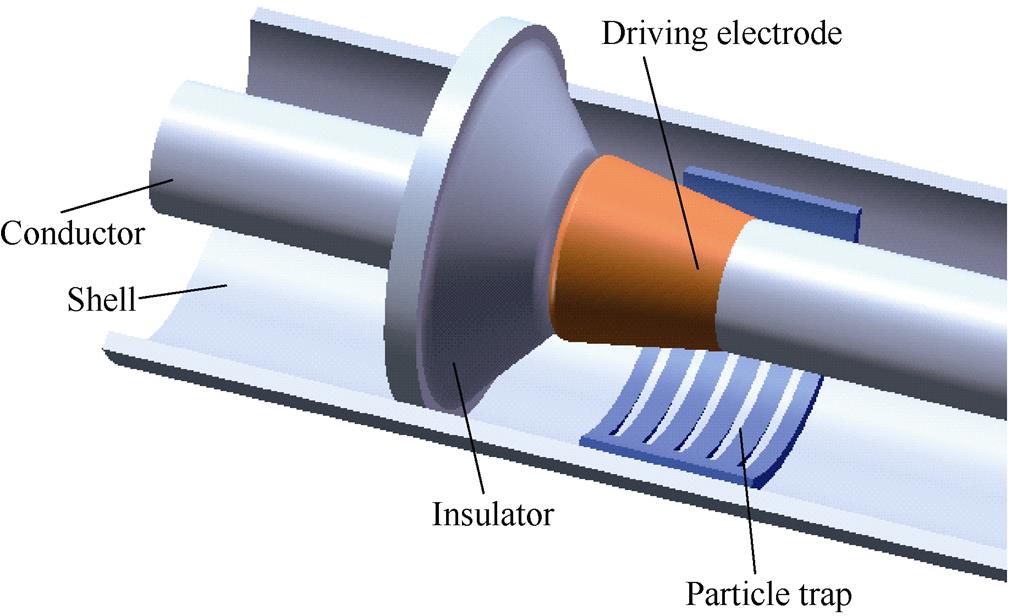
Fig.A2 Drive electrode and particle trap layout scheme
At the same time, considering the effect of the driving electrode on the incident angle of the particles in the trap, a synergistic optimization method of the driving electrode and the structural parameters of the particle trap was presented, which increased the collision times of particles in the trap and improved the capture probability of the particle trap. The results show that when the angle of the drive electrode is 8 ° and the angle of the trap is 50 °, and the capture probability of the particle trap is optimum, reaching 69.8 %. An experimental platform containing driving electrodes and particle traps was built to verify the effectiveness of the cooperative arrangement strategy and parameter optimization method.
Based on an actual UHV AC GIL, the versatility of the proposed method for different voltage-level equipment was discussed. Even though the particle motion characteristics at different voltages are numerically different, the motion law of the particles after collision with the driving electrode is the same for different voltages. Therefore, the proposed synergistic optimization method of driving electrode and particle trap is suitable for different sizes of DC gas-insulated equipment and can guide effective particle suppression in practical engineering.
keywords：Driving electrode, particle trap, synergistic inhibition, optimal design method
DOI: 10.19595/j.cnki.1000-6753.tces.220658
中图分类号：TM851
收稿日期2022-04-22
改稿日期 2022-05-09
胡智莹 女，1999年生，硕士研究生，研究方向为GIL金属微粒运动与抑制。E-mail: huzhiyingnuli@163.com
李庆民 男，1968年生，教授，博士生导师，研究方向为高电压与绝缘技术、放电物理。E-mail: lqmeee@ncepu.edu.cn（通信作者）
（编辑 郭丽军）