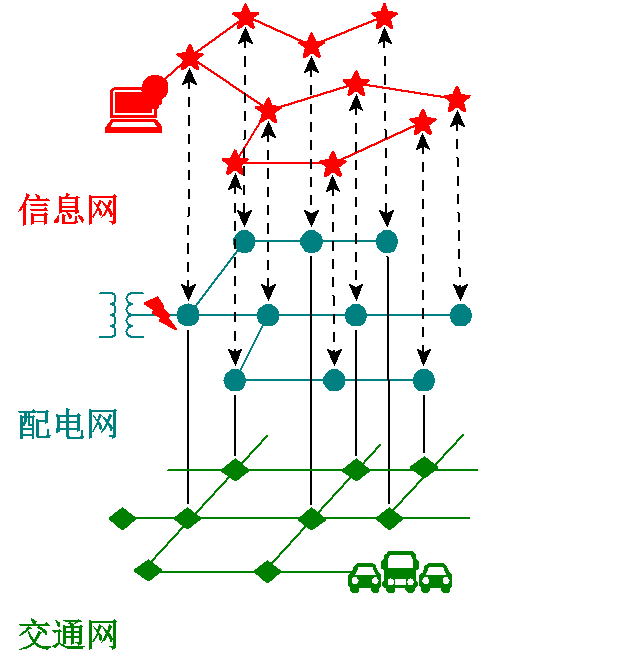
图1 物理-信息-交通网耦合关系
Fig.1 Physical- cyber- traffic network coupling relationship
摘要 信息通信技术的发展实现了配电网的可观可控,但当配电网受到严重灾害影响而导致大停电时,配电终端设备的有效性亦会对供电恢复产生影响。为此,提出一种考虑物理-信息-交通网耦合的配电网多时段动态供电恢复策略。首先,为保证负荷的可靠恢复,该策略深入探讨信息网与配电网的耦合关系对负荷恢复的影响;其次,为最大限度地恢复负荷,考虑移动储能系统(MESS)的功率支撑作用,动态优化MESS配置节点;接着,在MESS调度过程中计及交通道路和车流量的影响,选择Floyd算法获得最短路径,实现MESS与分布式能源的时空协同供电;最后,算例研究验证了所提策略的有效性和优越性。
关键词:配电网 供电恢复 物理-信息网络 移动储能系统
近年来,自然灾害、恶意破坏等极端情况给配电网带来了巨大冲击,造成长时间、大范围的停电事故。为应对大停电情况,各国政府不断推进建立“韧性电网”的发展战略[1],而提升配电网的恢复能力是提升韧性的重要手段之一。随着风电、光伏等分布式电源(Distributed Generation, DG)的接入,以及储能系统(Energy Storage System, ESS)、移动储能系统(Mobile Energy Storage System, MESS)的发展,配电网的应急规划、应急响应及应急恢复能力须要不断提高。如何充分发挥新型资源的灵活性,尤其是对MESS功率支撑能力的发掘和应用,已成为配电网供电恢复的研究热点[2]。与此同时,通信技术的进步为配电网的快速恢复提供了条件,加强了信息系统与电力系统的联系,使现代电力系统逐渐演变为深度融合的电力物理-信息系统。这种联系增强了配电网的状态感知能力和自动控制能力,同时也使电网变得更加复杂,进一步增加了配电网的薄弱环节和风险挑战[3]。在配电网故障恢复过程中,电力节点对应的终端通信设备能否正常工作起到关键作用[4]。例如,2015年乌克兰电网大停电,原因之一就是信息网络存在他人非法接入、窃取信息的风险,导致信息网络设备失效,进而影响物理供电系统[5]。因此,在上述背景下,研究利用MESS、DG等多种灵活性资源恢复供电,同时计及信息相关因素对恢复策略的影响具有重要意义。
配电网的供电恢复,可以通过划分多个孤岛的恢复方式[6-8],也可以采用协同多种电源的恢复策略[9-10],即利用本地电源互连形成一个尽量大的孤岛,在恢复供电过程中使系统更加稳定,这种恢复思路值得借鉴,但上述文献均未考虑MESS的供电支撑作用。文献[11]重点研究MESS在恢复配电网负荷时起到的有功时空支撑作用,但没有考虑交通网的影响,得出的结果过于理想。文献[12]应用Dijkstra算法求解MESS的调度方案,但其建立的交通路网模型未计及道路实时流量,且未充分发挥MESS的可移动作用。文献[13]采用预先分配MESS的位置,再对MESS进行实时调度的恢复方案,提高了系统韧性,但该恢复策略划分了多个孤岛,各DG间不连通,忽略了MESS和DG在空间上的互补协同能力,在一定程度上削弱了系统的负荷恢复能力。可见,协调多种电源恢复供电同时充分发挥MESS的时空移动性、考虑交通网对MESS调度的影响,都有待进一步研究。
在电力物理-信息系统相关研究方面,文献[14-16]立足于现实信息物理系统的功能结构和传输模式,研究信息系统对电力系统安全运行的影响。文献[3]提出了一种基于信息约束的智能电网应急响应最优潮流模型,为配电-信息耦合的供电恢复建模提供参考。文献[4]研究了台风灾害下电力系统的能量流与信息系统的信息流之间的交互作用,提出了计及信息网络约束的电力系统弹性评估方法,但对供电恢复策略未进行深入探索。文献[17]考虑信息耦合约束,构造的模型在满足配电网重构约束的同时还尽可能多地恢复信息节点,但该模型中信息系统与配电网的连通状态一致,而实际情况下,当电力线路断开时,线路两端电力节点所对应的信息节点未必处于断开状态[18]。因此,进一步深入研究信息网络对于恢复供电的影响,保证供电恢复可靠性,是有待解决的问题。
综上所述,在极端情况导致配电网长时间大停电的场景下,本文重点研究应急响应阶段[19-21],利用本地电源互连形成尽量大的孤岛,在恢复供电过程中使系统更加稳定。文中考虑负荷功率的波动性,建立多时段供电拓扑重构模型,实现配电网拓扑结构的动态优化。与此同时,建立MESS动态传输配置模型,时间上发挥其多时段功率支撑能力,空间上发挥其可移动作用,实现与其余DG的时空协调运行,且在进行MESS调度过程中计及交通流量对传输速度的影响,并利用Floyd算法优化传输路线。此外,本文从物理-信息系统的角度,建立信息网络与配电网的耦合模型,深入研究不同耦合程度对负荷恢复的影响,进而保证负荷恢复的有效性,最后应用IEEE 33节点配电-信息网与29节点交通网算例证明所建模型的优越性。
本文的物理网络特指配电网,信息网指对配电网起监测、控制作用的终端设备组成的网络,各配电节点所处的地理位置组成交通网。物理-信息-交通网耦合的关系如图1所示。

图1 物理-信息-交通网耦合关系
Fig.1 Physical- cyber- traffic network coupling relationship
考虑到在严重灾害中,给信息节点供电的不间断电源(Uninterruptible Power Supply, UPS)供电时长有限,电力网故障可能引发大规模连锁故障,会对信息网络造成供电影响,因此本文研究最严重情况,假设大停电情况下信息网络中仅有控制中心配置UPS,其余节点与电力网络节点具有直接耦合关系,即“一对一”相依关系[22]。配电网与其所对应的交通网之间有地理环境上的耦合关系,不同配电网节点在地理位置上对应不同的交通网节点,两网之间存在相互耦合的节点。在恢复供电过程中,考虑交通道路的影响,可以更可靠地发挥MESS的应急和移动作用。
2.1.1 恢复目标
配电网供电恢复的目标之一为最大化负荷恢复量,其次为优化故障恢复后的网络运行损耗。本文将恢复供电时段均分为T个时段,目标函数为各个时段的加权负荷功率恢复量和网络损耗的累加值,分别进行归一化处理,具体形式为
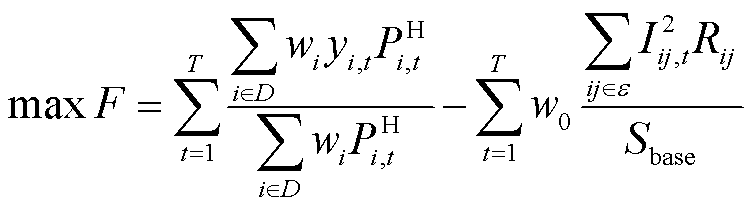 (1)
(1)
式中,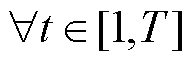 ;
;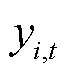 为0-1整数变量,表示t时段节点i处负荷是否被恢复;
为0-1整数变量,表示t时段节点i处负荷是否被恢复;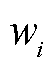 为节点i的负荷重要度,对于一、二、三级负荷,
为节点i的负荷重要度,对于一、二、三级负荷,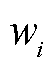 取值分别为10、5、1[23];
取值分别为10、5、1[23];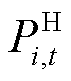 为t时段节点i的恢复功率;
为t时段节点i的恢复功率;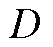 为负荷节点集合;
为负荷节点集合;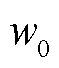 为网络损耗系数,保证主要目标的求解不受次要目标的影响,本文取0.5;
为网络损耗系数,保证主要目标的求解不受次要目标的影响,本文取0.5;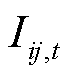 为t时段流经线路
为t时段流经线路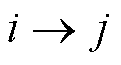 的电流;
的电流;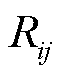 为线路
为线路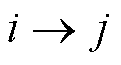 的电阻;
的电阻;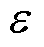 为目标孤岛内所有可用线路;
为目标孤岛内所有可用线路;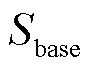 为基准功率。目标函数中计及网络损耗,也可以满足后续支路潮流约束中的凸松弛条件。
为基准功率。目标函数中计及网络损耗,也可以满足后续支路潮流约束中的凸松弛条件。
2.1.2 配电网故障恢复约束
1)负荷模型
主动配电网中的负荷可分为可控负荷和不可控负荷,充分发挥可控负荷的调节潜力,可以在不影响用户用电需求的情况下有效提高供电可靠性[24]。负荷恢复功率与负荷是否可控有直接关系,建立负荷恢复功率模型为
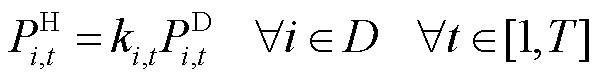 (2)
(2)
式中,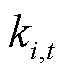 为t时段节点i处负荷恢复系数,负荷为可控负荷时,
为t时段节点i处负荷恢复系数,负荷为可控负荷时,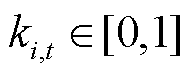 ,而当
,而当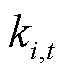 为1时,负荷等效为不可控负荷;
为1时,负荷等效为不可控负荷;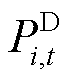 为t时段负荷i的负荷量。
为t时段负荷i的负荷量。
2)储能充放电约束
假设本地电源包括由光伏、风机和储能构成的风光储系统[12],其中储能可以抵御风光出力的波动性和不确定性,实现供需平衡。建立ESS的充放电模型为
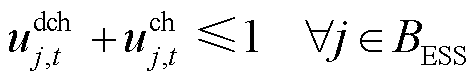 (3)
(3)
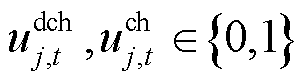 (4)
(4)
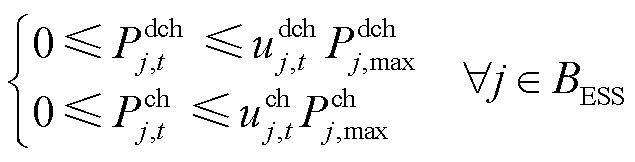 (5)
(5)
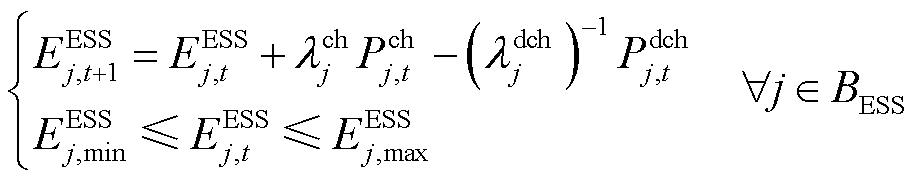 (6)
(6)
式中,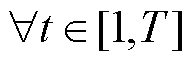 ;
;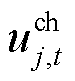 、
、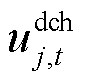 分别为第j个ESS在t时段的充、放电状态变量;
分别为第j个ESS在t时段的充、放电状态变量;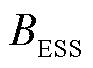 为ESS集合;
为ESS集合;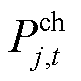 、
、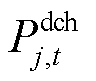 分别为第j个ESS在t时段的充、放电功率;
分别为第j个ESS在t时段的充、放电功率; 、
、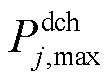 分别为第j个ESS的最大充、放电功率;
分别为第j个ESS的最大充、放电功率;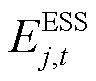 、
、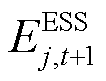 分别为第j个ESS在t时段、t+1时段的荷电状态;
分别为第j个ESS在t时段、t+1时段的荷电状态;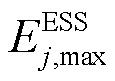 、
、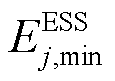 分别为第j个ESS的最大、最小荷电状态;
分别为第j个ESS的最大、最小荷电状态; 、
、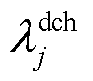 分别为第j个ESS的充、放电效率,均取0.9。
分别为第j个ESS的充、放电效率,均取0.9。
式(3)为充放电状态限制;式(5)为功率限制,本文假设ESS的无功补偿容量充足;式(6)为荷电状态约束。
3)辐射状拓扑约束
在配电网优化问题中,多数学者广泛采用生成树约束保证配电网的辐射状结构,但有学者证明该约束为辐射状拓扑的必要不充分条件,仅在某些条件下能够确保生成理想的辐射状拓扑[25]。相比于生成树约束,单商品流约束形式简单,引入的辅助变量数目和约束个数更少,而且是满足辐射状约束的充分必要条件,可以确保配电网的辐射状运行[26],因此本文基于虚拟潮流理论,建立单商品流约束模型[27],模型如下
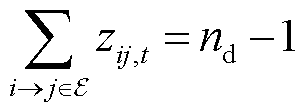 (7)
(7)
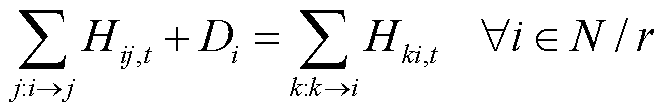 (8)
(8)
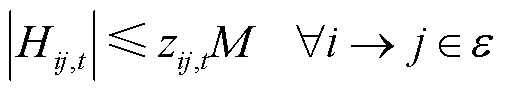 (9)
(9)
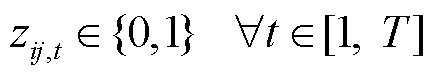 (10)
(10)
式中,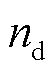 为配电网节点数;
为配电网节点数;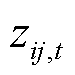 为0-1整数变量,表示t时段线路
为0-1整数变量,表示t时段线路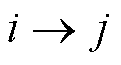 是否被恢复;
是否被恢复;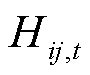 为连续变量,代表线路
为连续变量,代表线路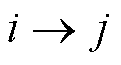 的虚拟潮流大小;
的虚拟潮流大小;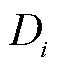 为非根节点虚拟需求,本文设为1;r为根节点编号;M为数值很大的正实数,本文设为配电网节点数目;
为非根节点虚拟需求,本文设为1;r为根节点编号;M为数值很大的正实数,本文设为配电网节点数目;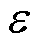 为配电网线路集合。
为配电网线路集合。
式(7)表示所有闭合线路的个数等于所有节点数减去1,该约束是保证生成的拓扑没有环路的必要条件;式(8)为虚拟潮流平衡约束,表示除根节点外,任意节点的虚拟潮流的流入流出量相等;式(9)表示当线路断开时,该线路不存在虚拟潮流,而当线路闭合时,对该线路的虚拟潮流不作约束,任一条线路i→j均属于配电网线路集合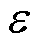 ;式(10)为变量取值范围约束。
;式(10)为变量取值范围约束。
4)支路潮流约束
本文考虑三相对称的辐射状配电网,采用二阶锥松弛线性化方法,列写单相模型为
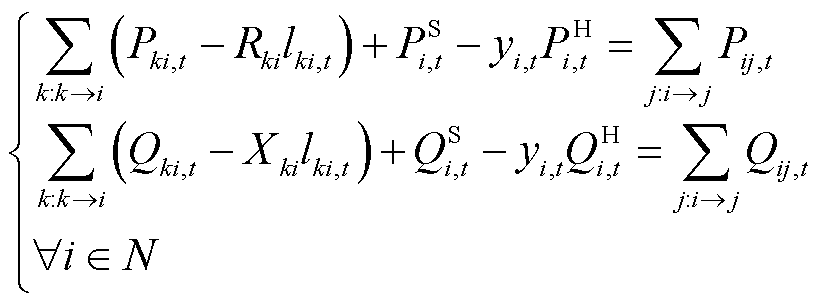 (11)
(11)
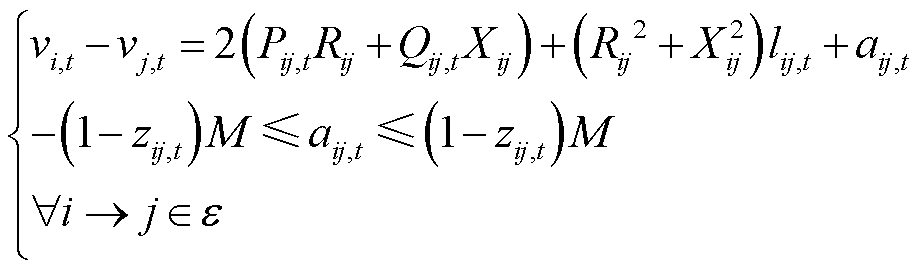 (12)
(12)
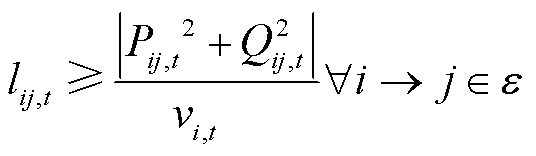 (13)
(13)
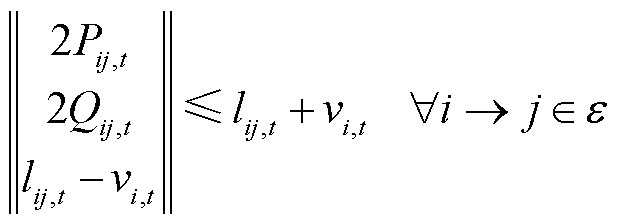 (14)
(14)
式中,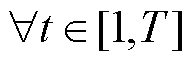 ;
;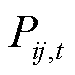 、
、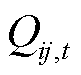 分别为t时段线路
分别为t时段线路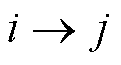 上单相流过的有功、无功功率;
上单相流过的有功、无功功率;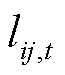 为t时段线路
为t时段线路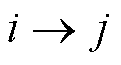 上单相流过的电流幅值的二次方;
上单相流过的电流幅值的二次方;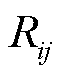 、
、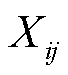 为常量,代表线路
为常量,代表线路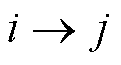 的电阻和电抗;
的电阻和电抗;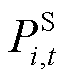 、
、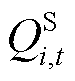 分别为t时段接入节点i的电源的有功、无功功率;
分别为t时段接入节点i的电源的有功、无功功率;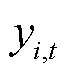 取值为0-1整数变量,表示t时段节点i处负荷是否被恢复;
取值为0-1整数变量,表示t时段节点i处负荷是否被恢复;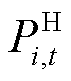 为t时段节点i恢复的有功功率;
为t时段节点i恢复的有功功率;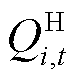 为t时段节点i恢复的无功功率;
为t时段节点i恢复的无功功率;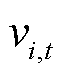 为t时段节点i上单相电压幅值的二次方,即
为t时段节点i上单相电压幅值的二次方,即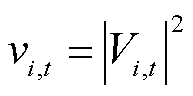 ;
;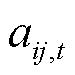 为辅助变量。
为辅助变量。
式(11)为节点有功和无功平衡方程,对于线路压降平衡方程,即式(12)是利用“大M法”,引进的辅助变量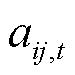 将电压降落大小和线路恢复状态
将电压降落大小和线路恢复状态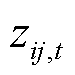 联系起来,若线路
联系起来,若线路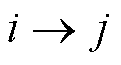 断开,则对于
断开,则对于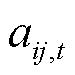 不做约束,反之则
不做约束,反之则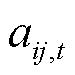 为0。式(14)是式(13)的标准二阶锥形式。
为0。式(14)是式(13)的标准二阶锥形式。
此外,还包括电源出力、节点电压,线路电流热极限安全约束。
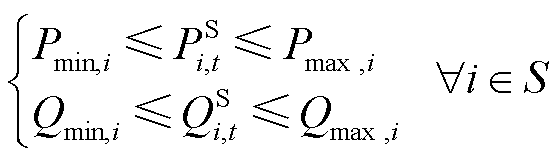 (15)
(15)
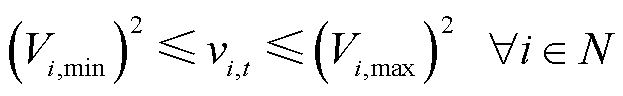 (16)
(16)
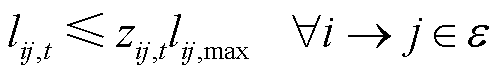 (17)
(17)
式中,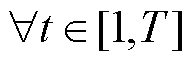 ;S为电源节点集合;
;S为电源节点集合;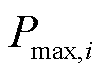 、
、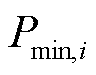 、
、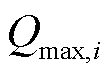 、
、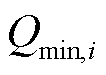 分别为节点i处电源的有功功率上限、下限,无功功率上限、下限;
分别为节点i处电源的有功功率上限、下限,无功功率上限、下限;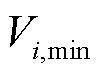 、
、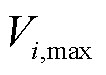 分别为节点i电压幅值的最小、最大值;
分别为节点i电压幅值的最小、最大值;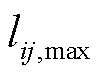 为电流幅值二次方允许最大值。
为电流幅值二次方允许最大值。
式(15)、式(16)分别是对电源出力、节点电压的安全限制;式(17)表示电流大小与支路是否恢复有关。
2.1.3 MESS运行约束
MESS运行约束包括储能电池的充放电约束和传输约束,充放电模型与上文中储能建模相同,建立传输配置模型如下。
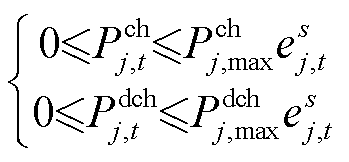 (18)
(18)
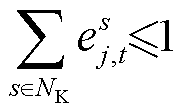 (19)
(19)
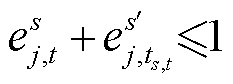 (20)
(20)
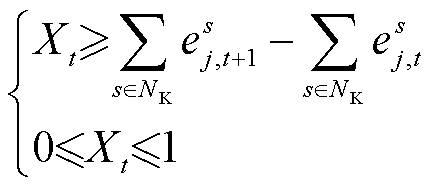 (21)
(21)
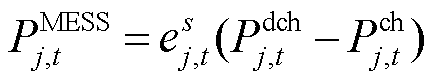 (22)
(22)
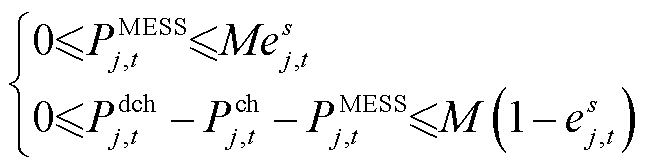 (23)
(23)
式中,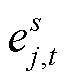 为t时段第j个MESS在配电网接入节点s处的标志位,
为t时段第j个MESS在配电网接入节点s处的标志位,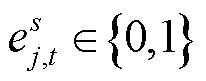 ;
;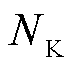 为可接入节点的集合;
为可接入节点的集合;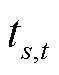 为t时段接入节点
为t时段接入节点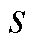 和
和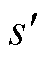 间的传输时间参数;
间的传输时间参数;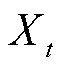 为t时段MESS传输指示变量,为1则表示传输;
为t时段MESS传输指示变量,为1则表示传输; 为t时段第j个MESS有功功率;M为值很大的正数。
为t时段第j个MESS有功功率;M为值很大的正数。
式(18)表示若MESS不停靠在配电网节点处,则不能进行充放电动作;式(19)规定第j个MESS 在各时段只能位于一个配电网节点处(值等于1)或处于传输状态(值为0);式(20)描述了若第j个MESS 在节点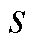 和
和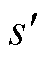 的传输途中,则接入标志位
的传输途中,则接入标志位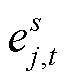 均为0;式(21)表示相邻时段的接入标志位差值为正时则进行传输,否则不传输;式(22)描述了第j个MESS 接入电网的输出功率关系式,该式中出现0-1变量与连续变量相乘的情况,采用大M法线性化处理如式(23)所示。
均为0;式(21)表示相邻时段的接入标志位差值为正时则进行传输,否则不传输;式(22)描述了第j个MESS 接入电网的输出功率关系式,该式中出现0-1变量与连续变量相乘的情况,采用大M法线性化处理如式(23)所示。
2.1.4 信息网络约束
信息网络的约束包括两方面:一方面,当信息网络节点有充足的能量供给,且能与控制中心存在通信流量时,则可认为该信息节点能够正常工作;另一方面,电力节点的正常运行和控制依赖所耦合的信息节点[3]。因此,基于信息网络与电力网络的相互作用关系,建立信息节点供能、信息网络流量及信息节点的控制作用约束模型。基于图论的相关概念,定义信息网络拓扑结构为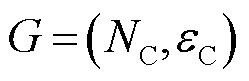 ,其中
,其中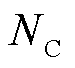 表示所有信息节点的集合,
表示所有信息节点的集合,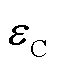 表示所有信息节点之间连接的集合。
表示所有信息节点之间连接的集合。
1)信息节点供能约束
在进行负荷供电恢复时,电力节点的负荷恢复量不小于信息节点的供能需求才可以使该信息节点工作。
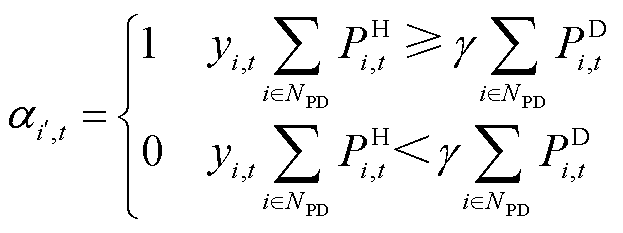 (24)
(24)
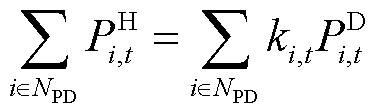 (25)
(25)
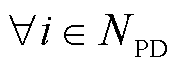
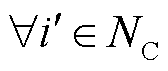
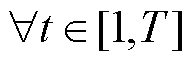 (26)
(26)
式中,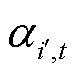 为t时段信息节点
为t时段信息节点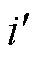 的供能有效性标志位;
的供能有效性标志位;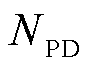 为与信息节点
为与信息节点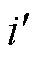 相连的电力节点的合集;
相连的电力节点的合集;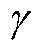 为信息网络与电力网络耦合强度的参数,
为信息网络与电力网络耦合强度的参数,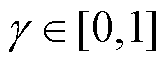 ,
,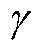 越大,关联性越强[3-4]。
越大,关联性越强[3-4]。
式(24)定义了信息节点供能状态与对应电力节点负荷恢复量的关系,当该电力节点的负荷恢复量大于等于对应信息节点的电量需求时,说明该电力节点有能力为信息节点供能,信息节点的供能有效标志位为有效状态;反之则失效。式(25)是对相应电力节点的负荷恢复量的定义。约束式(24)无法直接进行求解,因此引入辅助变量进行约束线性化。
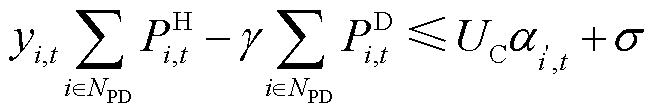 (27)
(27)
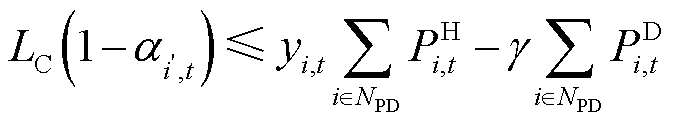 (28)
(28)
式中,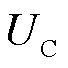 、
、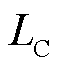 分别为
分别为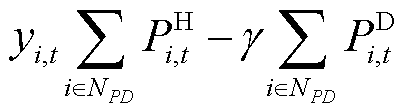 的上、下限;
的上、下限;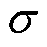 为一个极小正数。此处令
为一个极小正数。此处令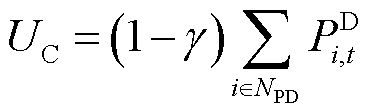 ,
,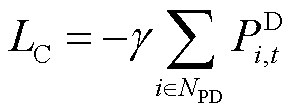 ,从而将约束式(24)完成线性化。
,从而将约束式(24)完成线性化。
2)信息网络流量约束
将通信网络流量建模为包含源节点、中继节点和目的节点的单向网络[22]。源节点为信息流的发出端,控制中心即为源节点;中继节点起到传输信息的作用,目的节点是负责配置同步相量测量单元(Phasor Measurement Unit, PMU)和发电控制设备的信息节点,也可以起到传输信息的作用。信息节点的工作状态受制于它的供能状态,还与该节点同控制中心间是否有通信流量有关,建立信息网络流量模型如下。
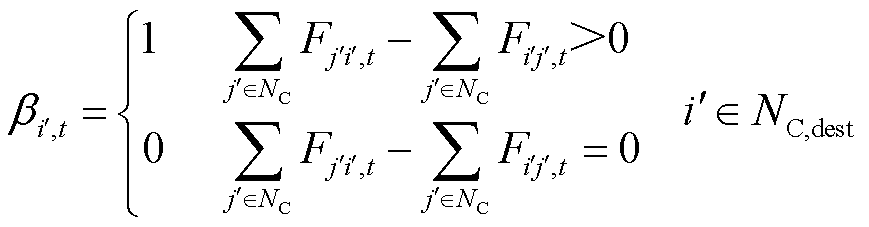 (29)
(29)
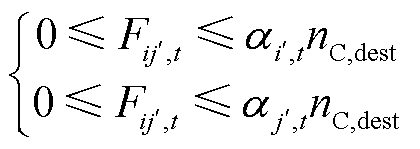 (30)
(30)
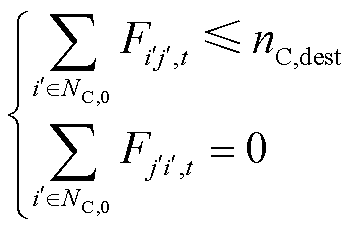 (31)
(31)
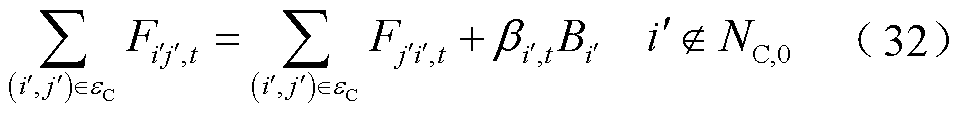
式中,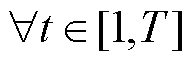 ;βi',t为t时段信息节点
;βi',t为t时段信息节点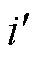 工作状态; Fj'i',t为流入信息节点i'的通信流量;Fi'j',t为流出信息节点i'的通信流量;NC,dest为信息流目的节点集;NC,0为信息流源节点集,即控制中心节点;nC,dest为信息终端个数;
工作状态; Fj'i',t为流入信息节点i'的通信流量;Fi'j',t为流出信息节点i'的通信流量;NC,dest为信息流目的节点集;NC,0为信息流源节点集,即控制中心节点;nC,dest为信息终端个数;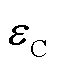 为信息网络链路集合;
为信息网络链路集合;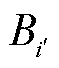 为节点
为节点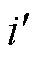 所需带宽,本文设每个目的节点所需带宽为1,即Bi'=1。
所需带宽,本文设每个目的节点所需带宽为1,即Bi'=1。
式(29)定义了信息节点的工作状态;式(30)表示信息链路上的通信流量受总业务量nC,dest和流经节点的供能状态αi',t、αj',t约束;式(31)表示源节点只有传出流量,且不能大于信息流目的节点数量;式(32)表示除源节点外,其余节点的入流量包括出流量和终端设备所需流量,当节点只起到业务传输的作用时,即βi',k =0,其对应的信息流的入流量和出流量应相等。
3)信息节点的控制作用约束
信息节点的失效将导致所对应的电力节点不可观且不可控。而在配电网中,主要考虑电力负荷、储能、分布式能源等电力设备的正常运行和控制。
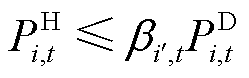 (33)
(33)
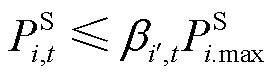 (34)
(34)
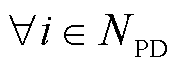
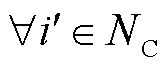 (35)
(35)
式中,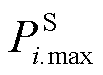 为接入i节点的电源的最大输出功率;式(33)表示在进行负荷恢复时,若该负荷节点对应的信息节点失效,由于不可控性,则该节点不能进行相应的恢复负荷操作。同理,式(34)表示供能类设备只有当其对应的信息节点正常工作时才能投入运行。
为接入i节点的电源的最大输出功率;式(33)表示在进行负荷恢复时,若该负荷节点对应的信息节点失效,由于不可控性,则该节点不能进行相应的恢复负荷操作。同理,式(34)表示供能类设备只有当其对应的信息节点正常工作时才能投入运行。
2.2.1 交通道路模型
利用图论方法来描述和说明交通路网的拓扑结构。用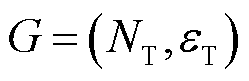 表示交通路网的图,其中:
表示交通路网的图,其中: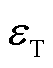 为路网中路段的集合;
为路网中路段的集合;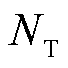 为顶点集,即路网中路段的端点或多个路段交叉点的集合。矩阵Droad为道路权值的邻接矩阵,用于描述各路段长度及节点连接关系,其元素
为顶点集,即路网中路段的端点或多个路段交叉点的集合。矩阵Droad为道路权值的邻接矩阵,用于描述各路段长度及节点连接关系,其元素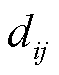 的赋值规则为
的赋值规则为
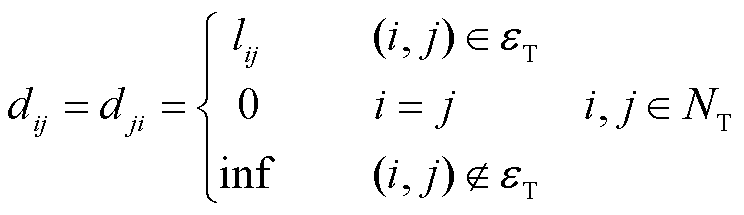 (36)
(36)
式中,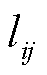 为节点i和节点j之间的路段长度;inf 表示两节点不相邻。
为节点i和节点j之间的路段长度;inf 表示两节点不相邻。
2.2.2 流量-速度模型
道路容量和车流量会对车辆行驶速度产生直接影响[28],因此在计算车辆行驶速度时,要计及这种影响,模型如下。
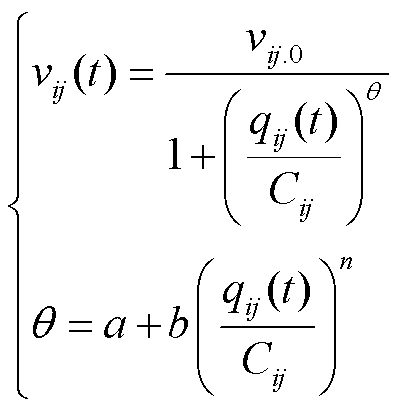 (37)
(37)
式中,vij(t)为t时段相邻交通节点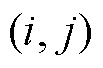 间车辆行驶速度;vij,0为相邻交通节点
间车辆行驶速度;vij,0为相邻交通节点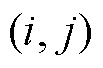 间的零流速度,即交通流量为0时的速度;qij(t)为t时段道路
间的零流速度,即交通流量为0时的速度;qij(t)为t时段道路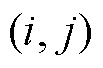 的道路流量;Cij为路段
的道路流量;Cij为路段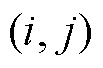 的通行能力,主要受道路等级的影响;qij(t)与Cij的比值为t时段道路
的通行能力,主要受道路等级的影响;qij(t)与Cij的比值为t时段道路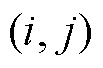 的饱和度;a、b、n为不同道路等级下的道路系数,道路等级不同,对应的系数也不同[28]。
的饱和度;a、b、n为不同道路等级下的道路系数,道路等级不同,对应的系数也不同[28]。
2.2.3 路径-时间模型
考虑到出发节点与目的节点间往往存在多条可行道路,本文假设所有应急车辆均选择最短路径行驶。常见的求解最短路径的方法有Floyd算法和Dijkstra算法。Floyd算法具有容易理解、编程简单、适应性强等优点,而Dijkstra 算法效率较低且应用范围有限[29-31],因此本文选用Floyd 算法求取不同出发-目的节点对间MESS的最短行驶路径。Floyd算法基于动态规划的思想,利用交通道路模型中的邻接矩阵Droad获得最短路径。算法可以描述为任意交通节点i、j之间的最短路径有两种情况:一种是节点i、j相邻,两点间存在直连路段;另一种是节点i、j不相邻,节点i到达节点j需经过若干中间节点k,当且仅当后者的距离小于前者时,更新Droad中对应的元素实现状态转移,该过程表示为
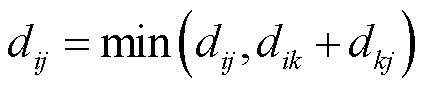 (38)
(38)
式中,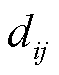 为节点i,j间的最短路径。算法通过外层循环控制迭代所有的交通节点,内层双重嵌套循环确定邻接矩阵中的对应节点的行列[32-34]。假设出发点i和目的点j之间有H段直连路段,行驶时间模型为
为节点i,j间的最短路径。算法通过外层循环控制迭代所有的交通节点,内层双重嵌套循环确定邻接矩阵中的对应节点的行列[32-34]。假设出发点i和目的点j之间有H段直连路段,行驶时间模型为
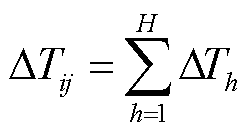 (39)
(39)
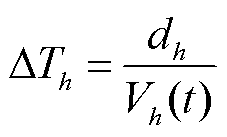 (40)
(40)
式中,DTij为节点i和j间的行驶总时间;DTh为第h段路段所需时间;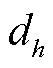 为第h段路段里程,由式(36)获得;
为第h段路段里程,由式(36)获得;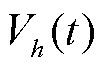 为由流量—速度模型得到的第h个直连路段行驶速度。
为由流量—速度模型得到的第h个直连路段行驶速度。
式(39)表示行驶总时间是各路段时间之和;式(40)定义了各路段行驶时间的计算方法。
事故发生后,应急指挥中心需迅速进行应急响应,采用本文的多时段动态供电恢复策略,恢复流程中所需参数及各阶段对应优化变量、对应的方程式如图2所示,图中t代表时段,T为预计停电时间总时段数。
首先,收集模型所需数据,包括停电期间各时段的负荷数据、分布式电源出力情况、线路破坏情况、信息网与配电网的耦合度、MESS参数及实时交通流量等数据。
对于第t个时段的具体恢复流程,可划分为两个阶段进行:第一阶段基于建立的物理-信息耦合的供电恢复模型,以式(1)作为目标函数,优化变量包括负荷恢复状态、信息节点有效状态、各电源输出功率、线路投运状态及MESS的接入节点,涉及配电网故障恢复、MESS运行和信息网络三方面约束,采用CPLEX求解器求解该二阶锥优化模型,可以得到t时段最优的网络拓扑结构、网络损耗以及信息节点、电力负荷的恢复情况,同时获得各时段MESS的最佳接入位置;第二阶段对交通路网建模,依据第一阶段得到的起始节点和目的节点,利用Floyd算法求解MESS最短调度路径,再结合t时段的交通流量数据,依据流量-速度模型计算MESS在各路段的行驶速度,最后利用路径-时间模型得到该最短路径的调度时间。
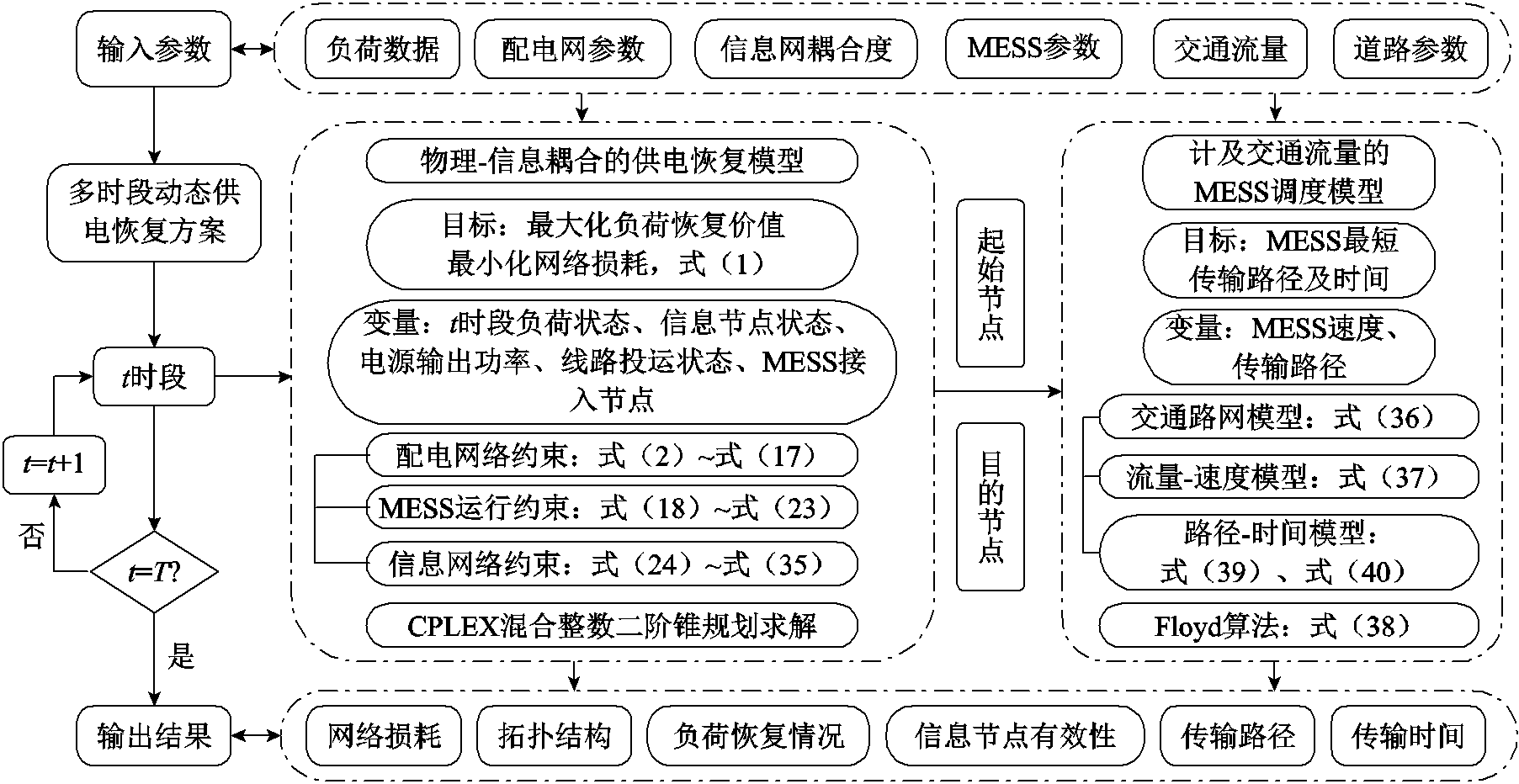
图2 多时段动态供电恢复流程
Fig.2 Multi-period dynamic power supply restoration process
按照上述流程对各时段进行迭代求解,最终可以获得整个停电期间的多时段动态供电恢复策略,输出动态变化的拓扑结构、负荷恢复情况、信息节点有效情况以及网络损耗、MESS动态调度策略等信息。
本文以改进的IEEE33节点配电网系统及其对应的信息网络作为算例,参考文献[28]的29节点交通网系统,其与配电网节点的耦合关系见附表1,测试系统如图3所示。
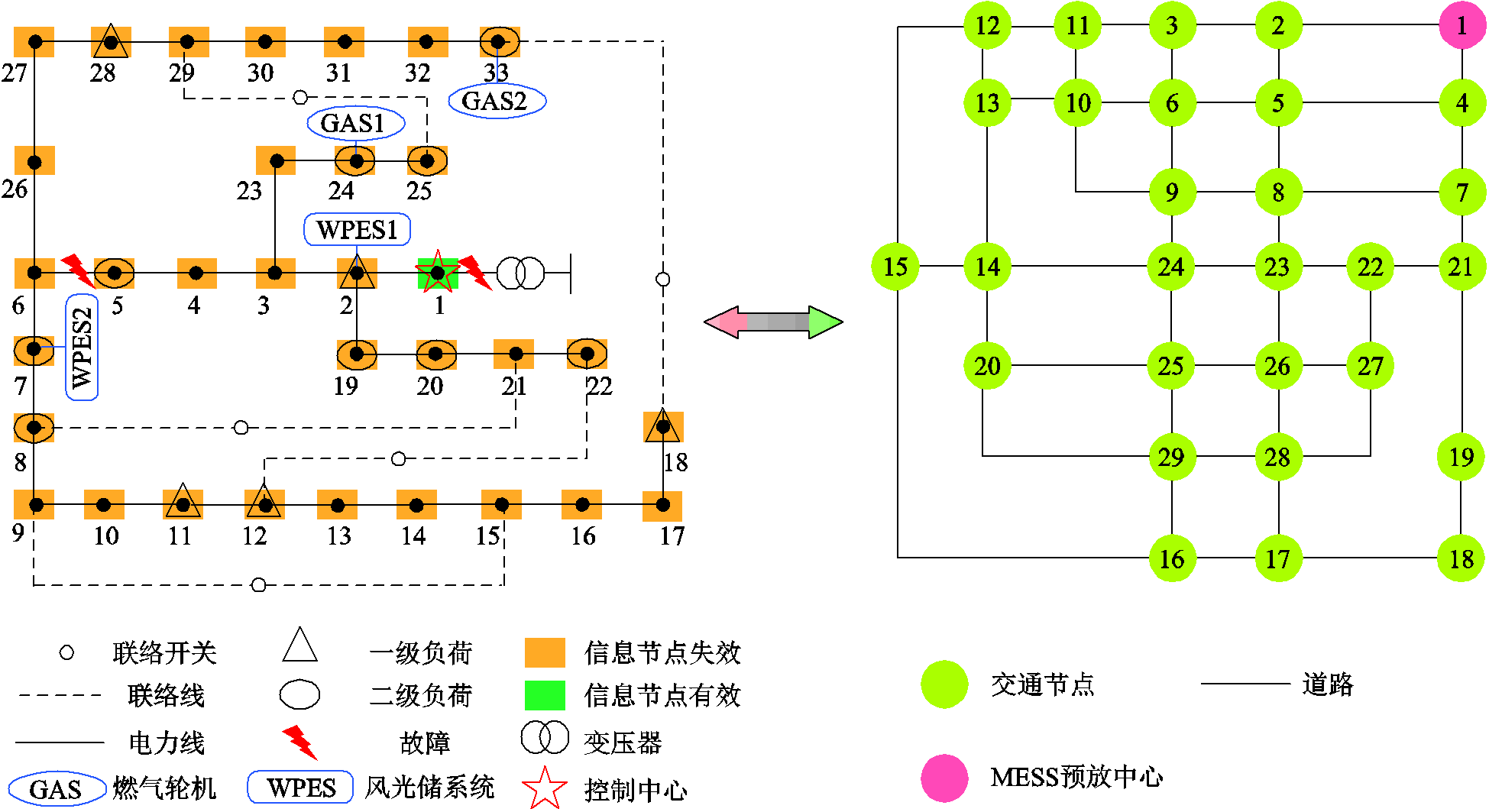
图3 本文的测试系统
Fig.3 The test system of this paper
图3中变电站失电,配电网支路5故障,整个配电网处于大停电状态,信息网中仅有位于配网1节点的控制中心正常工作,交通网1节点为MESS预放中心,即MESS初始停放位置;假设电力母线电压限值设为[0.94,1.06],配电网基准容量为1MV·A,本地可接入电源[35]包括2个风光储系统和2个燃气轮机,以及2个MESS,电源参数见表1、表2;负荷节点类型和可控性分别见表3、表4,各节点负荷功率见附表2,各节点负荷功率按百分比变化,如图4所示;设置道路等级主干道(I)和次干道(II),主干道的道路参数a、b、n分别取值1.726、3.15 和3,次干道的a、b、n分别取值 2.076、2.870 和 3,MESS零流速度为70 km/h,交通道路及流量数据与文献[28]一致。
表1 DG最大出力电路参数
Tab.1 Maximum output parameters of DG

编号电源类别节点位置最大发电功率/kW 1风光储系统12300 2风光储系统27250 3燃气轮机124180 4燃气轮机233150 5MESS1—250 6MESS2—200
表2 MESS参数
Tab.2 Parameters of MESS

编号有功出力最大值/kW容量/(kW·h) MESS12501 600 MESS22001 800
表3 负荷节点类型
Tab.3 Load node type

负荷等级等级系数节点 一级负荷102、11、12、18、28 二级负荷54、7、8、19、20、22、24、27、33 三级负荷1其余节点
表4 负荷可控性
Tab.4 Load controllability

负荷可控性节点 可控3、4、6、9、10、13-17、21、23、25、26、29-32 不可控其余节点
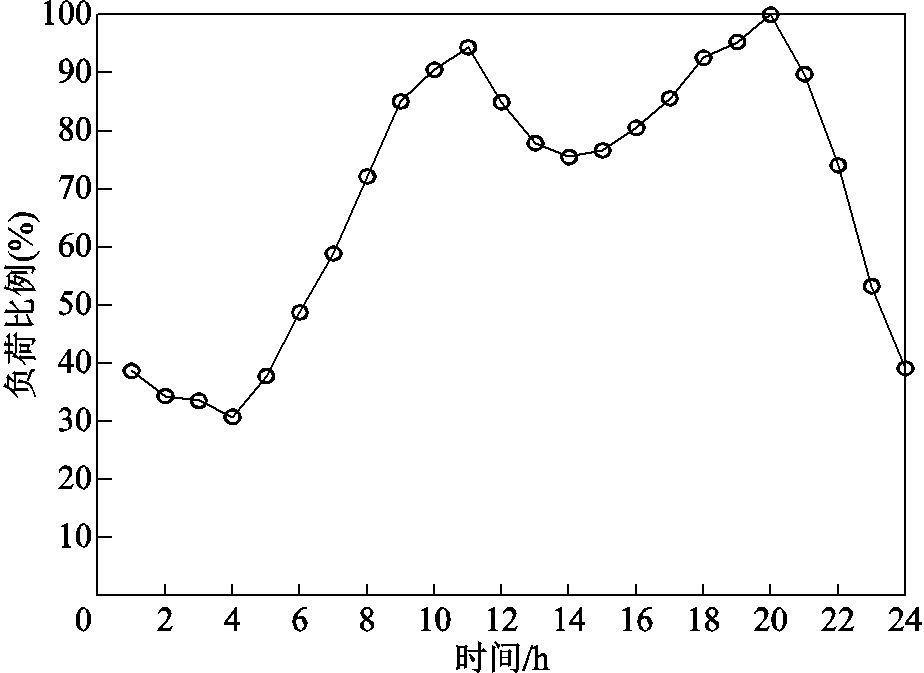
图4 负荷比例曲线
Fig.4 Load proportion curve
信息-物理耦合参数越大,代表信息网络对于配电网的供能需求越高。为研究耦合参数对于配电网N-k故障下负荷恢复的影响,本文设置四种故障情况,即k取1~4的四种断线情况,线路5、11、16、20分别为节点5、6,节点11、12,节点16、17以及节点20、21之间的线路;耦合系数γ分别取0、0.2、0.4、0.6、0.8、1来反映信息网络对配电网的供能需求程度,此处γ取0和1时为两种极端情况,为0即信息网络与配电网络完全解耦。应用本文恢复策略,选取18:00—19:00这一时间段进行恢复,以目标函数中加权负荷功率恢复比例来分析负荷恢复情况,同时分析对应的信息节点有效情况,结果分别如图5、图6所示。

图5 加权负荷功率恢复比例与耦合度的关系
Fig.5 Relationship between power recovery ratio of weighted load and coupling degree
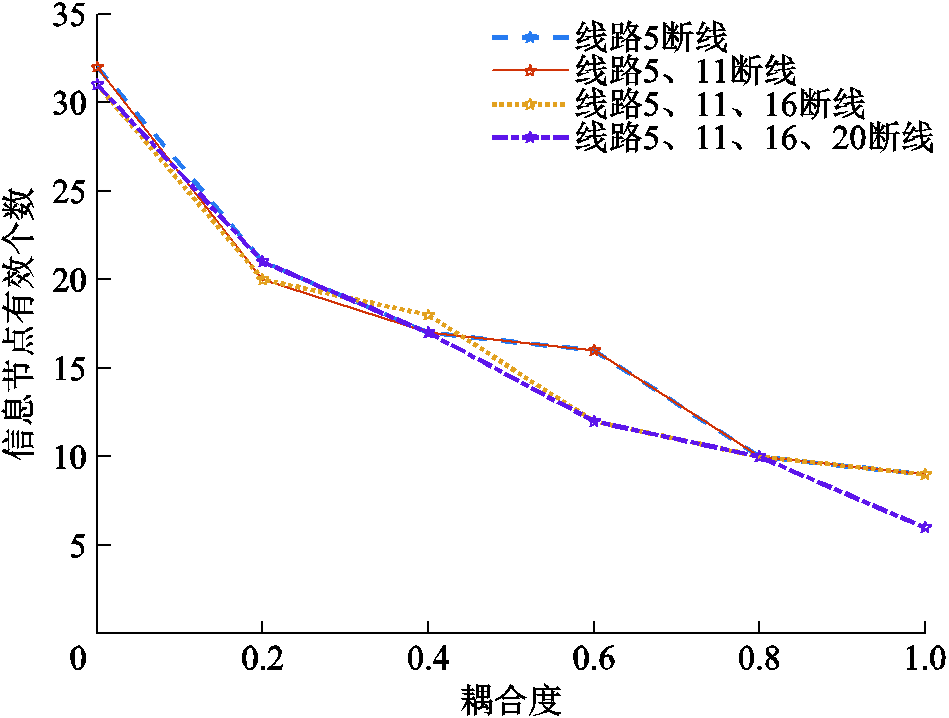
图6 信息节点有效个数与耦合度关系
Fig.6 Relationship between effective number of cyber nodes and coupling degree
从图5可以看出,耦合度较低(γ取0、0.2、0.4)时,不同k值对应的负荷恢复比例差别不明显,耦合度较高(γ取0.6、0.8、1)时;k越大,负荷恢复比例越小,可能的原因是受断开线路较多的影响,为满足配电网重构拓扑约束,配电网拓扑可选择性减少,导致可恢复负荷减少,而当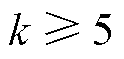 时,会出现不满足文中辐射状拓扑约束的情况。k相同时,随着信息网与配电网的耦合度增大,负荷恢复比例明显下降,说明当γ增加时,配电网各节点对应的终端设备更易因供电不足而失效,因此对负荷恢复的影响更加明显,此结论与文献[22]中相一致。
时,会出现不满足文中辐射状拓扑约束的情况。k相同时,随着信息网与配电网的耦合度增大,负荷恢复比例明显下降,说明当γ增加时,配电网各节点对应的终端设备更易因供电不足而失效,因此对负荷恢复的影响更加明显,此结论与文献[22]中相一致。
图6中,信息节点有效个数包含控制中心所对应的信息节点。可以发现,由于模型中负荷的恢复要求所对应的信息节点必须恢复,因此,信息节点的有效个数与负荷恢复量呈正相关,即耦合度越大,监测节点、通信中继节点和发电控制节点有效个数越少,信息网络越脆弱,耦合度为0时说明信息节点不需要配电网络电力支持,因此可能出现信息节点全部有效的情况;而γ相同,k越大信息节点有效个数亦有减少的趋势。
为了证明本文所提方案的可行性和优越性,设立三种不同的恢复方案进行负荷恢复,并对结果进行对比分析,耦合度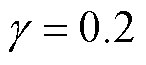 ,配电网停电时间为11:00—17:00共6 h,划分为6个时段,每个时段对应1h,如第一个时段对应11:00—12:00,依此类推,其余参数与算例信息一致。
,配电网停电时间为11:00—17:00共6 h,划分为6个时段,每个时段对应1h,如第一个时段对应11:00—12:00,依此类推,其余参数与算例信息一致。
方案一:考虑MESS时空移动性,优化MESS的动态配置,同时计及位置传输的时间损耗,即本文方法。
方案二:参考文献[12],考虑MESS参与,但仅在初始时间段进行位置优化,恢复过程中不再进行移动。该方案初始时段采用本文模型进行位置优化,其余时段不再移动。
方案三:未考虑MESS参与的配电网故障恢复。
分别采用上述三种方案进行负荷恢复,对比恢复结果见表5。
表5 6个时段累计恢复情况
Tab.5 Cumulative recovery in 6 periods

方案类别恢复加权功率/ kW恢复负荷数量网络损耗/ kW 一36 001.6692.27395.86 二34 026.9289.45458.33 三27 241.9865.29416.15
表5所示为6 h累计恢复情况,由此可知,方案一即本文方案恢复加权负荷功率和负荷数目最多,且6h内累计网络损耗也最小,证明了本文恢复方案的优越性。方案二考虑了MESS的作用,但没有考虑MESS的动态移动,因此其负荷恢复量高于方案三,但低于本文方案。方案三中未加入MESS,仅依靠分布式电源无法实现更多负荷的恢复,因此负荷恢复量与其他方案相差较多。其中恢复负荷含有小数是由于负荷的可控性,部分负荷未完全恢复。
各时段具体恢复情况如图7和图8所示,方案一和方案二中MESS调度情况如图9所示。在初始时段,方案二采用文中模型进行MESS位置优化,因此恢复结果和调度方案与方案一一致,即两方案的MESS均由配电网节点1出发,MESS1和MESS2分别接入节点8、27,但之后方案二不再进行MESS位置调度,而方案一中MESS按照优化结果进行移动。
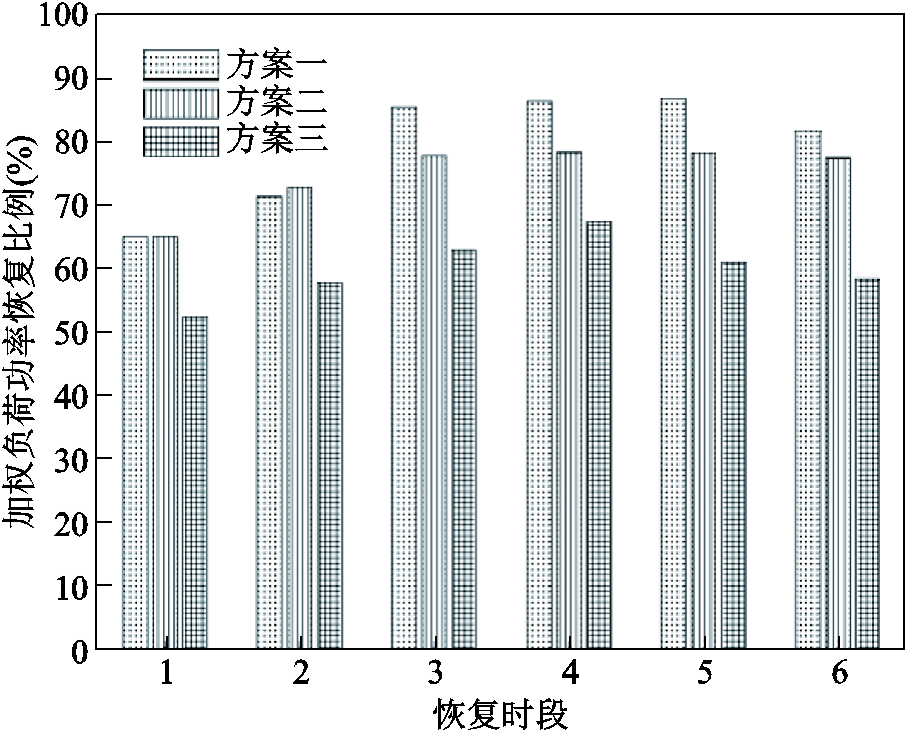
图7 加权负荷功率恢复比例对比
Fig.7 Comparison of weighted load power recovery ratio

图8 负荷恢复数量对比(各时段由左到右依此对应方案一、二、三)
Fig.8 Comparison of load recovery number (each period from left to right corresponds to scheme Ⅰ, Ⅱ and Ⅲ)
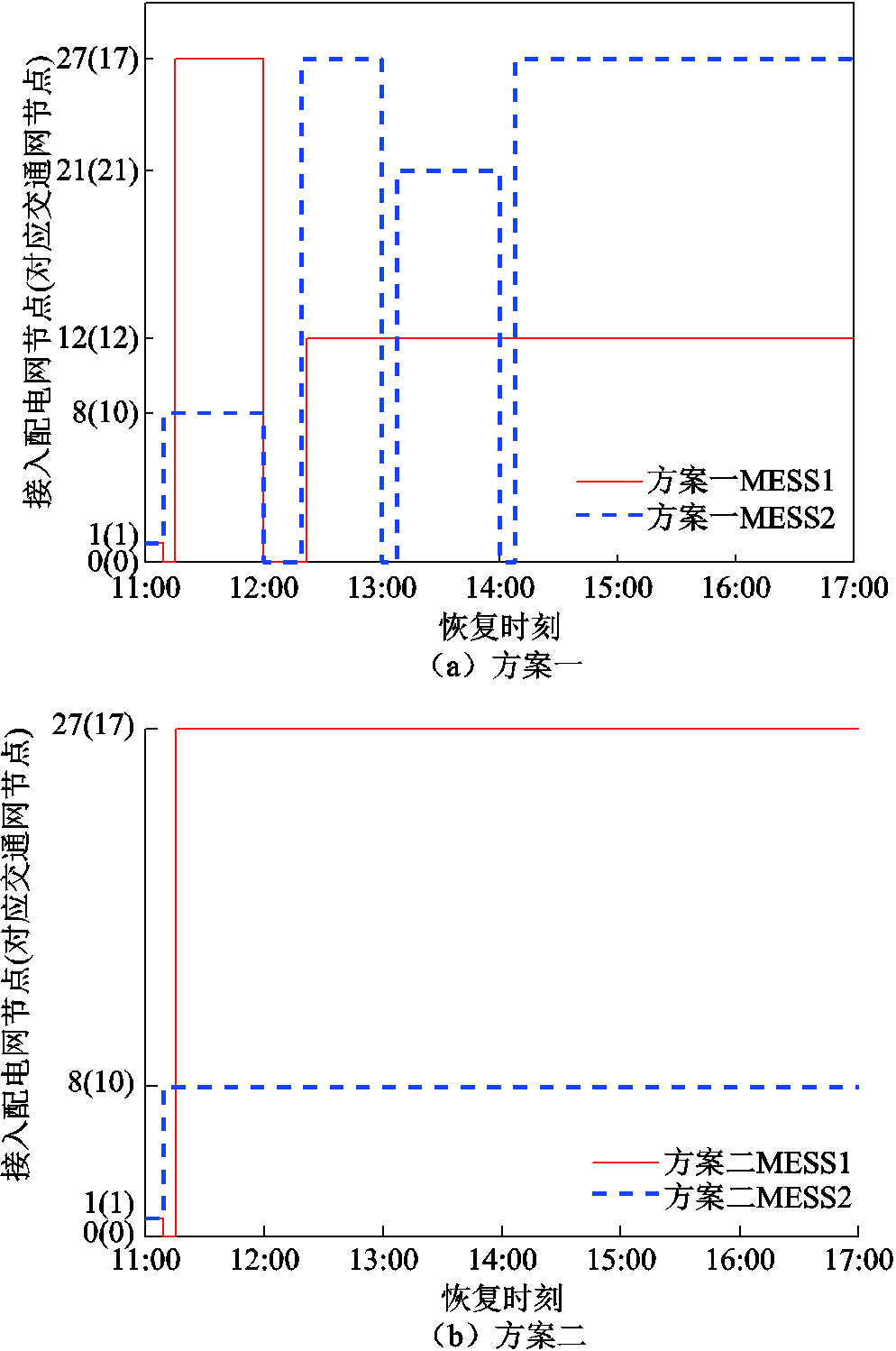
图9 MESS传输路径
Fig.9 MESS transmission path
第二个时段中,由于方案一中两个MESS均进行移动,如图9所示,MESS1由交通节点17移动到交通节点12,MESS2由交通节点10移动到交通节点17,调度时间较长,因此2时段方案二的恢复负荷比例稍高于方案一。在后续恢复过程中,方案二中MESS未进行实时的位置优化,而方案一中MESS2的位置进行了动态的优化,所以方案一的负荷恢复量较方案二多。图8中负荷恢复数目为累计数目,包含可控负荷恢复数目,因此会存在小数。由图8可知,方案一恢复了更多的一级、二级重要负荷,可见,尽管MESS的传输调度会减少供电时长,但对于长时间的停电场景,对MESS的位置进行多时段动态优化具有一定的优势,有利于实现更多重要负荷的恢复,提高配电网的韧性。
方案一部分时段的具体恢复结果和MESS调度方案如图10所示,其余时段参见附表3~附表5。由图10可以看出,本文的动态恢复策略体现在两个方面,其一,各节点负荷功率随时间波动,因此不同时段配电网拓扑也不同,通过断路器和联络开关的开断实现了配电网拓扑动态变化;其二,依据配电网与交通网节点对应关系,对MESS进行多时段动态调度,实现了MESS与DG的功率空间互补。图10所示路径均为交通网中起始—目的节点间最短路径,结合不同时段的交通流量信息,可以获得实时行驶速度,得到调度时间如图中标注所示。

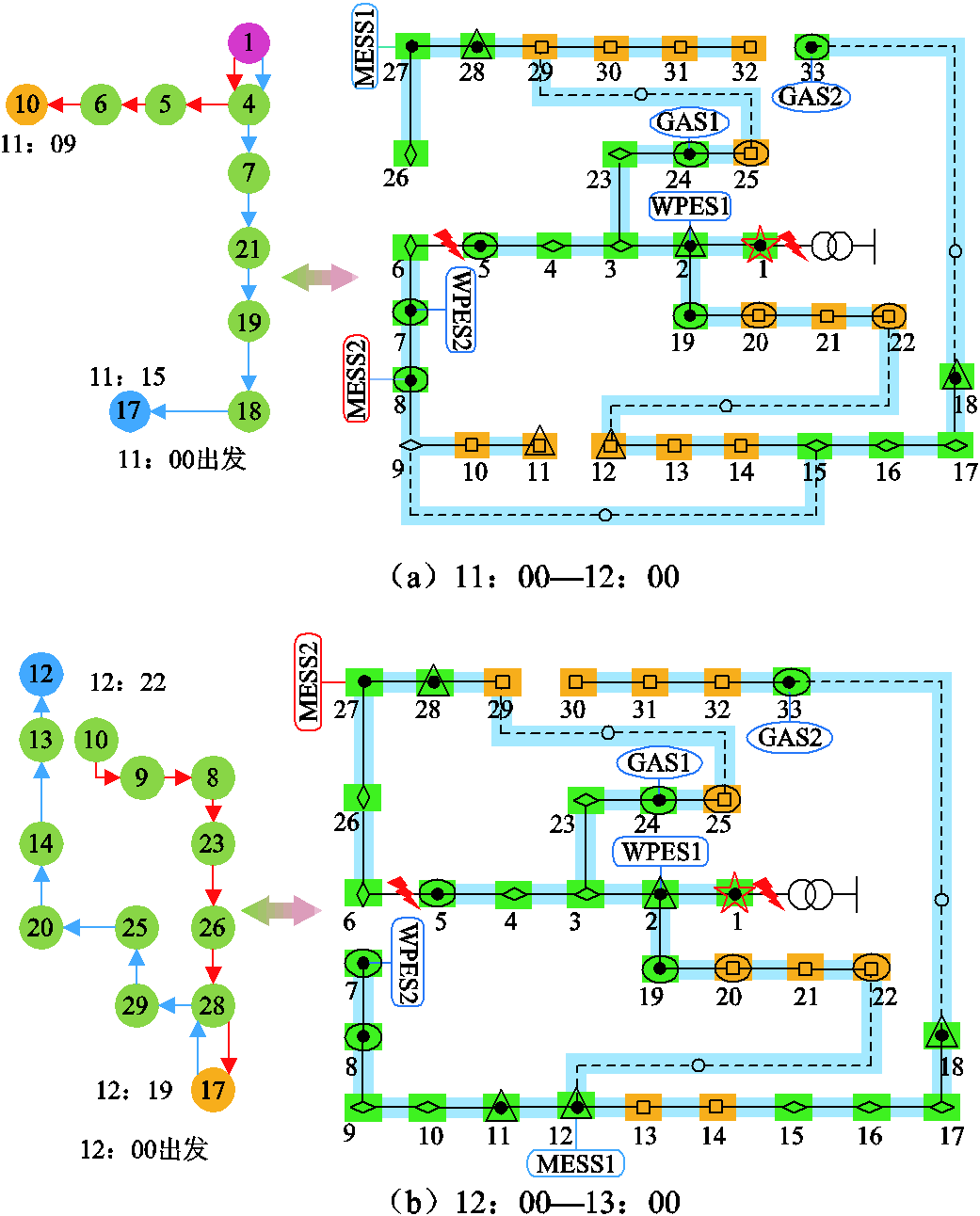
图10 方案一MESS调度及恢复结果
Fig.10 Scheme I MESS scheduling and recovery results
此外,恢复策略中计及相应信息节点的有效性,由图10可知只有信息节点有效时,对应的电力节点才可进行负荷恢复,且为了恢复尽可能多的负荷,电源接入节点所对应的信息节点均有效;失效的信息节点起到中继节点作用,用于传输信息,不消耗信息流量,有效的信息节点对应的终端设备发挥监测、控制作用;完全恢复的负荷节点中,均为一级、二级重要负荷,且实现了可控负荷的部分恢复。
MESS各时段的工作状态如图11所示。由图可知,MESS初始SOC均为0.9,恢复过程中始终处于放电状态。可见,后续若无能量补充,则无法再支持恢复。

图11 MESS工作状态
Fig.11 Operation states of MESS
针对长时间、大面积配电网停电情况,本文提出了一套综合物理-信息-交通网的配电网多时段动态供电恢复策略。该策略在已有的负荷恢复研究的基础上,考虑信息网络与配电网间的交互作用,以供能依赖和控制依赖作为建模依据,深入研究了耦合程度对负荷恢复量的影响。研究结果表明耦合程度越深,信息网络越脆弱,相应的配电网负荷恢复量越少。因此,在实际恢复过程中,有必要考虑信息网络的影响,以保证负荷恢复的可靠性和恢复策略的有效性。
此外,文中考虑MESS的移动供能能力,计及不同时段交通流量对MESS调度的影响,案例结果表明在长时间停电场景下,动态优化MESS位置的恢复方案具有一定的优越性,提升了配电网的恢复能力。但文中未计及交通阻塞、道路破坏等问题,假设该影响在MESS车辆的正常使用能力范围内,该问题将在今后的研究中进一步探讨。
附 录
附表1 配电网节点与交通网节点对应关系
App.Tab.1 Correspondence between distribution network node and traffic network node
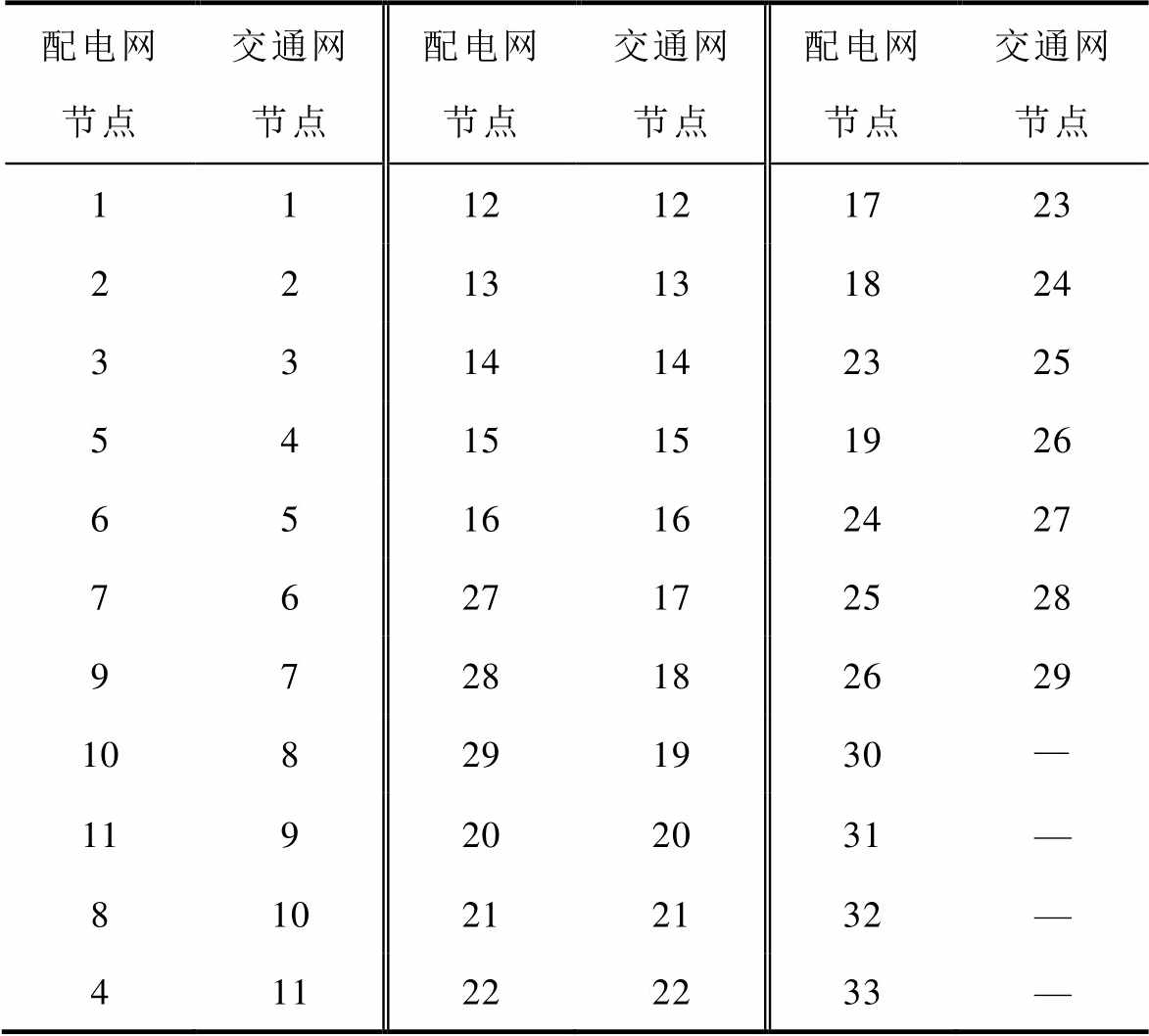
配电网节点交通网节点配电网节点交通网节点配电网节点交通网节点 1112121723 2213131824 3314142325 5415151926 6516162427 7627172528 9728182629 108291930— 119202031— 810212132— 411222233—
注:配电网节点30~33在交通网并无对应节点,故在路径规划中将其统一归为交通网节点29处。
附表2 配电网各负荷节点数据
App.Tab.2 Data of each load node in distribution network
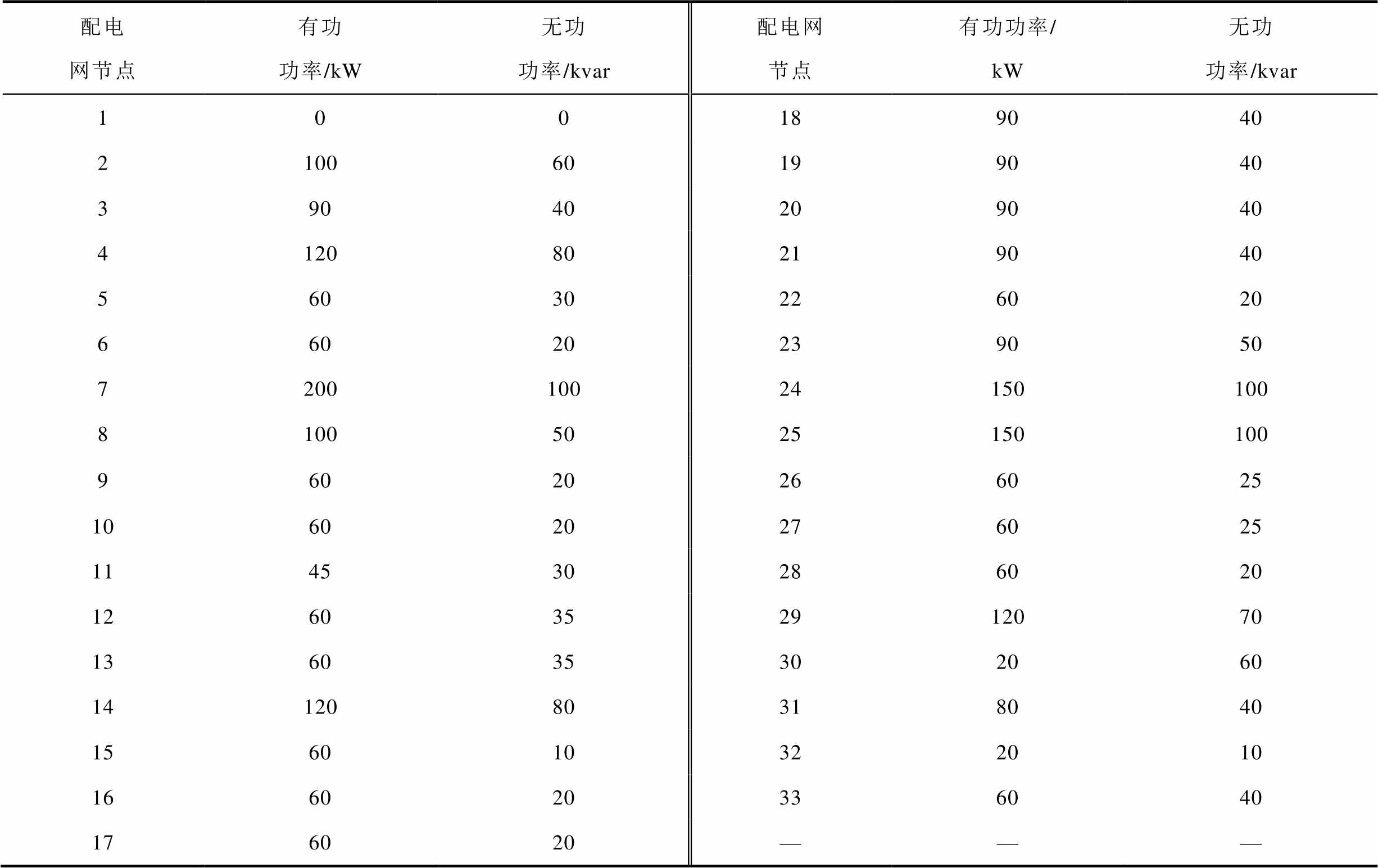
配电网节点有功功率/kW无功功率/kvar配电网节点有功功率/ kW无功功率/kvar 100189040 210060199040 39040209040 412080219040 56030226020 66020239050 720010024150100 81005025150100 96020266025 106020276025 114530286020 1260352912070 136035302060 1412080318040 156010322010 166020336040 176020———
附表3 配电网拓扑重构情况
App.Tab.3 Topology reconstruction of distribution network
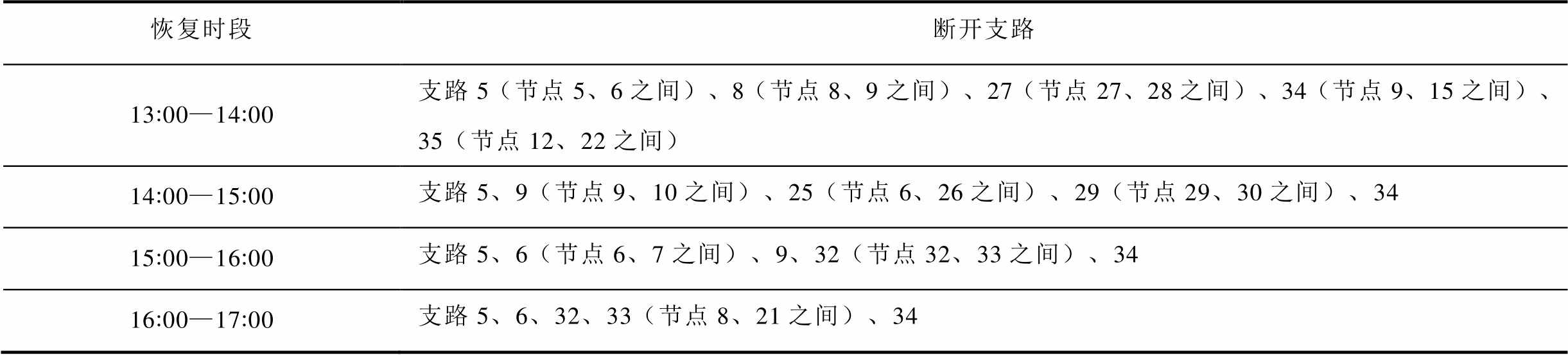
恢复时段断开支路 13:00—14:00支路5(节点5、6之间)、8(节点8、9之间)、27(节点27、28之间)、34(节点9、15之间)、35(节点12、22之间) 14:00—15:00支路5、9(节点9、10之间)、25(节点6、26之间)、29(节点29、30之间)、34 15:00—16:00支路5、6(节点6、7之间)、9、32(节点32、33之间)、34 16:00—17:00支路5、6、32、33(节点8、21之间)、34
附表4 信息节点有效情况
App.Tab.4 Cyber node valid results

恢复时段失效信息节点 13:00—14:00节点13、14、21、25、29-32 14:00—15:00同上 15:00—16:00同上 16:00—17:00节点13、14、20、21、25、29-32
附表5 负荷恢复结果
App.Tab.5 Load recovery results

恢复时段负荷完全恢复负荷未恢复 13:00—14:00节点1、2、5、7、8、11、12、18-20、22、24、27、28、33节点13、14、21、25、29-32 14:00—15:00同上同上 15:00—16:00同上同上 16:00—17:00节点1、2、5、7、8、11、12、18、19、22、24、27、28、33节点13、14、20、21、25、29-32
注:配电网其余负荷节点均为恢复部分负荷。
参考文献
[1] 王守相, 刘琪, 赵倩宇, 等. 配电网弹性内涵分析与研究展望[J]. 电力系统自动化, 2021, 45(9): 1-9. Wang Shouxiang, Liu Qi, Zhao Qianyu, et al. Connotation analysis and prospect of distribution network elasticity[J]. Automation of Electric Power Systems, 2021, 45(9): 1-9.
[2] 许寅, 和敬涵, 王颖, 等. 韧性背景下的配网故障恢复研究综述及展望[J]. 电工技术学报, 2019, 34(16): 3416-3429.Xu Yin, He Jinghan, Wang Ying, et al. A review on distribution system restoration for resilience enhancement[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3416-3429.
[3] Huang Gang, Wang Jianhui, Chen Chen, et al. Cyber-constrained optimal power flow model for smart grid resilience enhancement[J]. IEEE Transactions on Smart Grid, 2019, 10(5): 5547-5555.
[4] Ti Baozhong, Li Gengyin, Zhou Ming, et al. Resilience assessment and improvement for cyber-physical power systems under typhoon disasters[J]. IEEE Transactions on Smart Grid, 2022, 13(1): 783-794.
[5] 郭庆来, 辛蜀骏, 王剑辉, 等. 由乌克兰停电事件看信息能源系统综合安全评估[J]. 电力系统自动化, 2016, 40(5): 145-147. Guo Qinglai, Xin Shujun, Wang Jianhui, et al. Comprehensive security assessment for a cyber physical energy system: a lesson from Ukraine's blackout[J]. Automation of Electric Power Systems, 2016, 40(5): 145-147.
[6] 文娟, 谭阳红, 何怡刚, 等. 含分布式电源的复杂配电网多阶段故障恢复方法[J]. 电工技术学报, 2018, 33(14): 3332-3341. Wen Juan, Tan Yanghong, He Yigang, et al. A multi-stage service restoration method for complex distribution networks with distributed generators[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3332-3341.
[7] 陈厚合, 丛前, 姜涛, 等. 多能协同的配电网供电恢复策略[J]. 电工技术学报, 2022, 37(3): 610-622, 685. Chen Houhe, Cong Qian, Jiang Tao, et al. Distribution systems restoration with multi-energy synergy[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 610-622, 685.
[8] Demetriou P, Asprou M, Kyriakides E. A real-time controlled islanding and restoration scheme based on estimated states[J]. IEEE Transactions on Power Systems, 2019, 34(1): 606-615.
[9] Wang Ying, Xu Yin, He Jinghan, et al. Coordinating multiple sources for service restoration to enhance resilience of distribution systems[J]. IEEE Transactions on Smart Grid, 2019, 10(5): 5781-5793.
[10] Li Jiaxu, Xu Yin, Wang Ying, et al. Erratum to resilience-motivated distribution system restoration considering electricity-water-gas interdependency[J]. IEEE Transactions on Smart Grid, 2022, 13(3): 2495.
[11] 翁晓勇, 谭阳红. 考虑移动储能有功时空支撑的不对称配电网负荷恢复策略[J]. 电网技术, 2021, 45(4): 1463-1470. Weng Xiaoyong, Tan Yanghong. Load restoration strategy for unbalanced distribution network considering active power temporal-spatial supporting of mobile energy storage[J]. Power System Technology, 2021, 45(4): 1463-1470.
[12] 杨丽君, 赵宇, 赵优, 等. 考虑交通路网应急电源车调度的有源配电网故障均衡恢复[J]. 电力系统自动化, 2021, 45(21): 170-180. Yang Lijun, Zhao Yu, Zhao You, et al. Balanced fault recovery of active distribution network considering emergency power supply vehicle scheduling in traffic network[J]. Automation of Electric Power Systems, 2021, 45(21): 170-180.
[13] Lei Shunbo, Wang Jianhui, Chen Chen, et al. Mobile emergency generator pre-positioning and real-time allocation for resilient response to natural disasters[J]. IEEE Transactions on Smart Grid, 2018, 9(3): 2030-2041.
[14] Oyewole P A, Jayaweera D. Power system security with cyber-physical power system operation[J]. IEEE Access, 2020, 8: 179970-179982.
[15] Che Liang, Liu Xuan, Li Zuyi, et al. False data injection attacks induced sequential outages in power systems[J]. IEEE Transactions on Power Systems, 2019, 34(2): 1513-1523.
[16] Abianeh A J, Mardani M M, Ferdowsi F, et al. Cyber-resilient sliding-mode consensus secondary control scheme for islanded AC microgrids[J]. IEEE Transactions on Power Electronics, 2022, 37(5): 6074-6089.
[17] 陈健, 林咨良, 赵浩然, 等. 考虑信息耦合的电–气综合能源系统韧性优化方法[J]. 中国电机工程学报, 2020, 40(21): 6854-6864. Chen Jian, Lin Ziliang, Zhao Haoran, et al. Optimization method for resilience of integrated electric-gas system with consideration of cyber coupling[J]. Proceedings of the CSEE, 2020, 40(21): 6854-6864.
[18] 陈彬, 于继来, 周霞, 等. 基于网格化的极端灾后配电网电力–通信协调恢复策略[J]. 电网技术, 2021, 45(5): 2009-2017. Chen Bin, Yu Jilai, Zhou Xia, et al. Power-communication coordination recovery strategy based on gridding method after disasters[J]. Power System Technology, 2021, 45(5): 2009-2017.
[19] 秦清, 韩蓓, 李国杰, 等. 含智能软开关的配电网多阶段弹性力学映射与评估[J]. 电工技术学报, 2021, 36(21): 4444-4458. Qin Qing, Han Bei, Li Guojie, et al. Multi-stage elastic mechanical modelling and evaluation of distribution networks with soft open point[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4444-4458.
[20] 刘炜, 谢文君, 孙名刚, 等. 基于分层优化的分散式城轨供电系统网络化支援供电[J]. 电工技术学报, 2021, 36(11): 2306-2314. Liu Wei, Xie Wenjun, Sun Minggang, et al. Research on networked support power supply of urban rail power supply system based on hierarchical optimization[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2306-2314.
[21] 唐晓健, 林济铿, 郭其一. 基于网损估计的系统恢复新方法[J]. 电气技术, 2020, 21(10): 15-20. Tang Xiaojian, Lin Jikeng, Guo Qiyi. A new system recovery algorithm based on network loss estimation[J]. Electrical Engineering, 2020, 21(10): 15-20.
[22] 遆宝中, 李庚银, 王剑晓, 等. 计及监测与控制功能的电力信息物理系统关键输电线路辨识方法[J]. 中国电机工程学报, 2022, 42(7): 2556-2566. Ti Baozhong, Li Gengyin, Wang Jianxiao, et al. Identification of critical transmission lines in cyber-physical power system considering monitoring function and control function[J]. Proceedings of the CSEE, 2022, 42(7): 2556-2566.
[23] 周湶, 解慧力, 郑柏林, 等. 基于混合算法的配电网故障重构与孤岛运行配合[J]. 电网技术, 2015, 39(1): 136-142. Zhou Quan, Xie Huili, Zheng Bolin, et al. Hybrid algorithm based coordination between distribution network fault reconfiguration and islanding operation[J]. Power System Technology, 2015, 39(1): 136-142.
[24] 李丝雨, 张彼德, 彭丽维, 等. 考虑柔性负荷调节能力的主动配电网动态孤岛划分策略[J]. 高电压技术, 2019, 45(6): 1835-1842. Li Siyu, Zhang Bide, Peng Liwei, et al. Dynamic Island partitioning strategy for active distribution network considering adjustment ability of flexible load[J]. High Voltage Engineering, 2019, 45(6): 1835-1842.
[25] 王颖, 许寅, 和敬涵, 等. 基于断线解环思想的配电网辐射状拓扑约束建模方法[J]. 中国电机工程学报, 2021, 41(7): 2395-2404. Wang Ying, Xu Yin, He Jinghan, et al. Radiality constraint modelling method in distribution network based on cutting-line and opening-loop idea[J]. Proceedings of the CSEE, 2021, 41(7): 2395-2404.
[26] 王颖. 大面积停电场景下配电网多源协同故障恢复方法研究[D]. 北京: 北京交通大学, 2020.
[27] Lavorato M, Franco J F, Rider M J, et al. Imposing radiality constraints in distribution system optimization problems[J]. IEEE Transactions on Power Systems, 2012, 27(1): 172-180.
[28] 邵尹池, 穆云飞, 余晓丹, 等. “车–路–网”模式下电动汽车充电负荷时空预测及其对配电网潮流的影响[J]. 中国电机工程学报, 2017, 37(18): 5207-5219, 5519. Shao Yinchi, Mu Yunfei, Yu Xiaodan, et al. A spatial-temporal charging load forecast and impact analysis method for distribution network using EVs-traffic-distribution model[J]. Proceedings of the CSEE, 2017, 37(18): 5207-5219, 5519.
[29] 张英敏, 蒋容, 刘凯, 等. 含柔性直流电网的交直流系统潮流转移搜索与量化分析[J]. 高电压技术, 2019, 45(8): 2553-2561. Zhang Yingmin, Jiang Rong, Liu Kai, et al. Path search and analysis on power flow transferring of power system with VSC-HVDC grid[J]. High Voltage Engineering, 2019, 45(8): 2553-2561.
[30] 宋雨浓, 林舜江, 唐智强, 等. 基于动态车流的电动汽车充电负荷时空分布概率建模[J]. 电力系统自动化, 2020, 44(23): 47-56. Song Yunong, Lin Shunjiang, Tang Zhiqiang, et al. Spatial-temporal distribution probabilistic modeling of electric vehicle charging load based on dynamic traffic flow[J]. Automation of Electric Power Systems, 2020, 44(23): 47-56.
[31] 马钰, 韦钢, 李扬, 等. 考虑孤岛源-荷不确定性的直流配电网可靠性评估[J]. 电工技术学报, 2021, 36(22): 4726-4738. Ma Yu, Wei Gang, Li Yang, et al. Reliability evaluation of DC distribution network considering islanding source-load uncertainty[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4726-4738.
[32] 黄登一, 刘灏, 毕天姝, 等. 基于扰动传播时空相关性的电网扰动事件快速定位方法[J]. 中国电机工程学报, 2022, 42(6): 2045-2060. Huang Dengyi, Liu Hao, Bi Tianshu, et al. A novel method for fast event location based on the temporal and spatial relevance of disturbance propagation[J]. Proceedings of the CSEE, 2022, 42(6): 2045-2060.
[33] 孔顺飞, 胡志坚, 谢仕炜, 等. 含电动汽车充电站的主动配电网二阶段鲁棒规划模型及其求解方法[J]. 电工技术学报, 2020, 35(5): 1093-1105. Kong Shunfei, Hu Zhijian, Xie Shiwei, et al. Two-stage robust planning model and its solution algorithm of active distribution network containing electric vehicle charging stations[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1093-1105.
[34] 李婧祺, 王丹, 樊华, 等. 含移动式储能的主动配电网分层优化控制方法[J]. 电力系统自动化, 2022, 46(10): 189-198. Li Jingqi, Wang Dan, Fan Hua, et al. Hierarchical optimal control method for active distribution network with mobile energy storage[J]. Automation of Electric Power Systems, 2022, 46(10): 189-198.
[35] Zhang Zhu, Liu Yunfan, Wang Jingyuan. Optimal design of multi-channel water cooled radiator for motor controller of new energy vehicle[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(1): 87-94.
Abstract The frequency and intensity of natural disasters have greatly increased over the past decades, and they are expected to further increase in the coming future. As a consequence, it becomes a critical issue worldwide to deal with the disasters and their impacts. More and more scholars carry out research on "grid resilience". And improving the fault recovery capability of distribution network(DN) is an important means to improve the resilience. At the same time, with the continuous deepening of the application of modern information communication technology in the power system, the power information physical system has been formed. Many blackouts indicate that the failure or attack of the information system will affect the information system and the safe and stable operation of the physical system. In this context, a multi-period dynamic power supply restoration strategy of DN considering the coupling of physical- cyber- traffic network is proposed. The impact of information network on power supply restoration is discussed in depth, and the flexible resources such as mobile energy storage systems (MESSs) are fully used for power supply restoration.
Firstly, consider the fluctuation of load power and the regulation ability of controllable load. Taking load recovery as the main recovery objective. A multi-period power supply topology reconfiguration model is established to realize dynamic optimization of DN topology. Secondly, A dynamic scheduling model of MESS is established, Give play to its multi-period power support capability in time, and play its mobile role in space to achieve spatio-temporal coordinated operation with other Distributed generations. The impact of traffic flow on travelling speed of MESS is taken into account and Floyd algorithm is used for the transmission route optimization. In addition, the coupling model of information-distribution network is established based on the information-physical network. The influence of different coupling degrees on load recovery is deeply studied.
In the recovery process, the first stage is the emergency response for load power supply restoration. By increasing the output power of power sources, optimizing the DN topological structure and the location of MESSs, most critical loads can be restored. The purpose of the second stage is to find the optimal path of MESS, so that MESS can reach the destination node in the shortest time. According to the start node and destination node obtained in the first stage, Floyd algorithm is used to solve the shortest scheduling path of MESSs. Combined with the traffic flow data in t period, the MESS running speed of each section is calculated according to the flow-velocity model. Finally, the scheduling time of the shortest path is obtained by using the path-time model.
The following conclusions can be drawn through case analysis.
(1) With the deepening of information-distribution network coupling, the more fragile the information network is, the less the load recovery of DN will be. Therefore, in order to ensure the reliability of load recovery and the effectiveness of recovery strategies, it is necessary to consider the impact of information networks in the actual recovery process.
(2) This paper considers the mobile energy supply capacity of MESS and the impact of traffic flow in different periods on MESS dispatching. The case results show that the restoration scheme of dynamically optimizing the location of MESS has certain advantages in the case of long-term power outage, and improves the restoration capability of DN.
keywords:Distribution network, service restoration, physical-cyber network, mobile energy storage system
DOI:10.19595/j.cnki.1000-6753.tces.220497
中图分类号:TM732
国家重点研发计划资助项目(2020YFF0305800)。
收稿日期2022-04-04
改稿日期 2022-05-14
朱晓荣 女,1972 年生,博士,副教授,研究方向为新能源发电及并网技术、电力系统分析等。 E-mail:xiaorongzhu@ncepu.edu.cn
司 羽 女,1998 年生,硕士研究生,研究方向为配电网故障恢复等。 E-mail:772634962@qq.com(通信作者)
(编辑 赫 蕾)