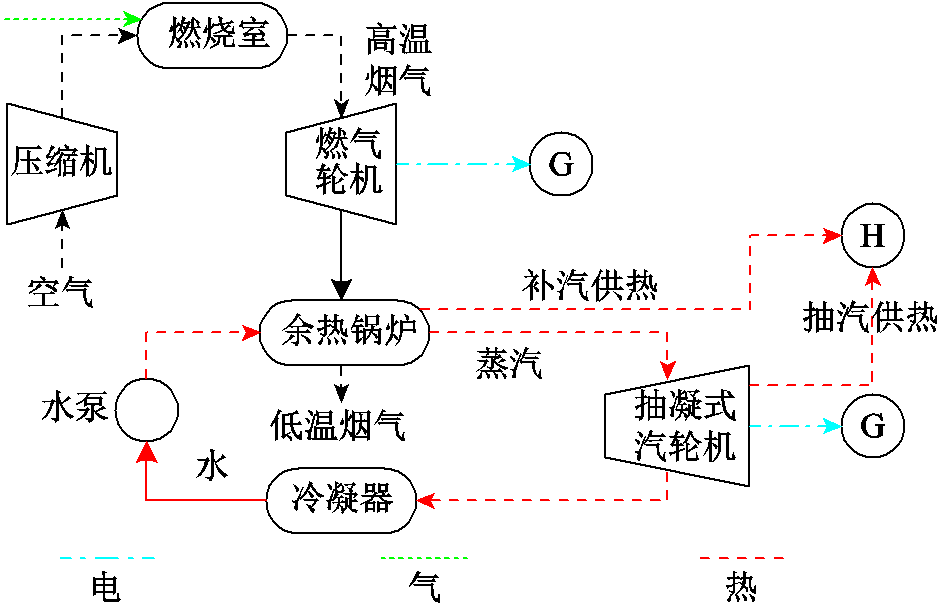
图1 热电联产系统典型结构
Fig.1 Typical structure of CHP unit
摘要 为提高区域综合能源系统可靠性评估的精度与效率,并从可靠性角度分析多能互补机理并量化对可靠性影响,该文提出一种考虑多能互补与多重热惯性的区域综合能源系统序贯模拟可靠性评估方法。首先,构建热电联产机组典型结构,分析热电联产机组正常运行、降电供热、降额供电及系统停运等运行状态,基于马尔科夫链建立热电联产机组的四状态可靠性模型;然后,分析热源起动惯性、热网传输惯性及建筑热惯性对系统可靠性的影响,基于差异化能流建模思想提出稳态的运行优化模型与考虑多重热惯性的动态最优切负荷模型,分别以运行经济性和等效失负荷量为目标建立优化模型;最后,计及用户舒适度特性对热网失负荷指标进行修正,采用序贯蒙特卡洛模拟实现对区域综合能源系统的可靠性评估。仿真验证了该方法的有效性,并深入分析了热电联产机组四状态可靠性模型、多能互补及热惯性对系统可靠性的影响,通过对比其他算法,以及采用更大系统验证所提方法的有效性,为系统规划设计提供参考。
关键词:区域综合能源系统 可靠性评估 热惯性 可靠性建模 序贯蒙特卡洛模拟
随着全球能源危机和环境污染的加剧,传统化石能源已经无法满足人类社会快速增长的能源需求,为提高能源利用效率并促进可再生能源消纳,低碳、绿色、持续发展的区域综合能源系统(Regional Integrated Energy System, RIES)应运而生[1]。现有研究中,RIES通常由电、气、热三种能源子系统耦合而成,相较于传统电力系统,RIES通过多能互补和能量的梯级利用提高了系统的可靠性,可靠性指标可为系统的规划和运行提供有价值的参考,因此准确地评价RIES的可靠性至关重要[2]。
目前,国内外学者已针对综合能源系统可靠性评估进行了深入的研究,并取得丰富的研究成果[3]。本文从元件停运模型、系统建模与评估方法和故障状态分析三个方面分别进行综述[4]。
元件停运模型是系统可靠性评估的基础。区域综合能源系统中元件按承载能质类型划分为独立型元件和耦合型元件[5]。独立型元件维持电、气、热各子系统自身独有的能质属性,如线路、管网、压缩机等;耦合型元件是实现电、气、热相互转换的核心设备,如电热锅炉(Electric Boiler, EB)、燃气轮机(Gas Turbine, GT)、热电联产机组(Combined Heat and Power, CHP)等。目前元件停运模型多采用“运行-故障”两状态概率模型[6],如文献[7]针对电热综合能源系统中热电联产机组、燃气轮机、余热锅炉等能源耦合设备分别建立为两状态停运模型。文献[8]将热电联产机组划分为天然气燃烧、供电和供热三个子系统,基于马尔科夫法建立三状态停运模型,但忽略了热电耦合对机组运行状态的影响。以热电联供为核心的耦合设备种类繁多,故障状态具有较大差异性,通过耦合带来的可靠性效益与其故障特征密切相关。因此,精细刻画热电联产机组等耦合设备可靠性模型,对提高系统可靠性评估的准确性具有重要意义。
系统可靠性建模是根据元件故障特性分析系统故障规律,建立与评估方法相适应的系统可靠性评估模型[9]。简单系统通常采用可靠性框图、故障树、马尔科夫状态空间等方法建模[10],并利用解析法进行评估。文献[11-12]忽略了RIES网络结构和能量传输特性,将系统抽象为能源枢纽,用矩阵方式表征系统内能量输入、转换、存储和输出的关系,并采用马尔科夫方程实现对电气冷热综合能源系统的可靠性评估,研究表明多能源耦合能够提高系统可靠性,而且热电联产机组的故障停运对系统可靠性影响最大。由于RIES具有源荷随机性、多能耦合性及储能状态时变性等特点,大多采用序贯蒙特卡洛方法[13]进行可靠性评估。而且为准确模拟系统故障前后状态变化,系统建模逐步精细化。文献[14]针对电气热耦合的RIES,在考虑网络结构基础上,计及天然气管道流量与节点压力的关系建立电气热系统运行模型,能够体现气体管道稳态传输过程,算例结果验证了线路故障增加负荷节点的削减量。为了进一步刻画天然气系统动态传输特性对可靠性的影响,文献[15]考虑天然气密度、温度以及流速等物理特性,建立了表征天然气网络短时流动过程的电气综合能源系统动态模型,表明故障时利用天然气“管存”特性能够减少系统电负荷削减量。文献[16]考虑热网热媒流速、热损及延时等动态特性,通过有限差分法将刻画系统时变过程的偏微分方程转换为代数方程,建立电热区域综合能源系统模型,能够精细模拟系统分钟级能量变化,将其用于可靠性评估能够准确获取故障时刻系统状态和故障后变化过程,提高计算精度,但对于非故障时刻的运行模拟大大增加了可靠性评估的运算规模且难以收敛,尤其对序贯模拟法的效率来说更是雪上加霜。
故障状态分析是在获取系统故障元件和系统状态前提下,模拟系统故障处理过程,评估故障后果。RIES在故障时可以通过协同调度配电网开关、能源转换设备运行状态、分布式电源出力、储能充放、需求侧资源等手段,尽可能减少多种负荷的削减。分析方法通常是建立以负荷削减量最小为目标的最优切负荷模型,并考虑如功率平衡、管道连续性方程等等式约束和线路容量、管道容量、设备出力区间等不等式约束,求解方法包括内点法、遗传算法等[17]。文献[18]针对电热区域综合能源系统,系统故障时通过配电网联络线实现负荷转供并建立了考虑配电网安全约束的热负荷削减模型,通过热泵实现对电热单向耦合,降低热网络故障对热负荷的影响。文献[19]针对电热冷区域综合能源系统,忽略气热传输时间延时和管道动态过程,以光伏、热电联产机组和电锅炉出力为控制变量建立了以等效负荷削减量经济性为目标的优化削减模型。充分利用短时间气热动态物理特性进一步提高可靠性[20],文献[21]针对大型综合能源系统建立两阶段优化调度模型,第一阶段为在故障发生后5 min内,以等效负荷削减量最小为目标,建立短时间尺度应急调度模型,实现对故障的快速响应;第二阶段以等效负荷削减量与系统运行成本之和最小为目标,建立常规调度模型,仿真表明充分利用天然气流速、管存等动态特性及热传递延迟能够减少17%的负荷削减量。但当管道长度较短、直径较小时,管存、延时与损耗等气热动态特性对系统故障后果分析的精确性具有较大的差异,为保障可靠性评估的实用性与准确性,亟须有针对性地开展建模研究。
综上所述,本文计及多重热惯性提出一种基于序贯蒙特卡洛模拟的区域综合能源系统可靠性评估方法。为平衡气、热能流特性对可靠性评估精度与效率的影响,提出正常和故障两阶段差异化能流建模思路。首先,正常情况下采用基于稳态的优化运行模型提高非故障时段运行模拟效率,为故障后果分析提供系统初始状态信息;其次,鉴于区域级综合能源系统管道长度较短、直径较细,忽略天然气动态特性对可靠性的影响,以电、气、热负荷等效经济削减量为目标,建立最优切负荷模型,考虑热源惯性与热网惯性对热源设备与热网设备故障恢复时间进行修正,并考虑热网传输延时建立管道动态约束,建筑储热效应与用户舒适度特性修正热负荷故障标准,形成了源、网、荷多重热惯性模型;最后,通过热电联产机组多状态元件模型、系统模型的精细化和差异化建模与改进,提出一种实用化评估方法,改善计算精度与计算效率,明确多能互补对系统可靠性影响,为实际系统设计和运行提供参考。
热电联产机组作为RIES主要能源耦合设备,由供电系统和供热系统构成,核心设备包括燃烧室、燃气轮机、余热锅炉、汽轮机等,针对水泵、冷凝器等辅助设备的故障概率叠加到机组核心设备故障状态,针对核心设备分别建立“运行-故障”两状态模型。因此,考虑机组结构与运行状态建立精确的元件可靠性模型是RIES可靠性评估的基础,热电联产系统典型结构如图1所示。

图1 热电联产系统典型结构
Fig.1 Typical structure of CHP unit
根据图1中CHP机组结构,若CHP机组无故障运行时为机组“正常运行”状态,针对内部关键设备故障时机组运行状态分析:当汽轮机发生故障时,其与余热锅炉、冷凝器、水泵构成的蒸汽循环发生故障,通过配合开高旁阀维持燃气轮机至预定出力,及时切换为补汽供热来保障热负荷供应,此时CHP机组处于“降电供热”状态;当余热锅炉故障时,燃气轮机应立减至预定出力,此时CHP机组处于“降额供电”状态;当燃气轮机或燃烧室发生故障时,均使CHP机组停运,处于“系统停运”状态。CHP机组状态模型见表1。
表1 CHP机组状态模型
Tab.1 State model of CHP system
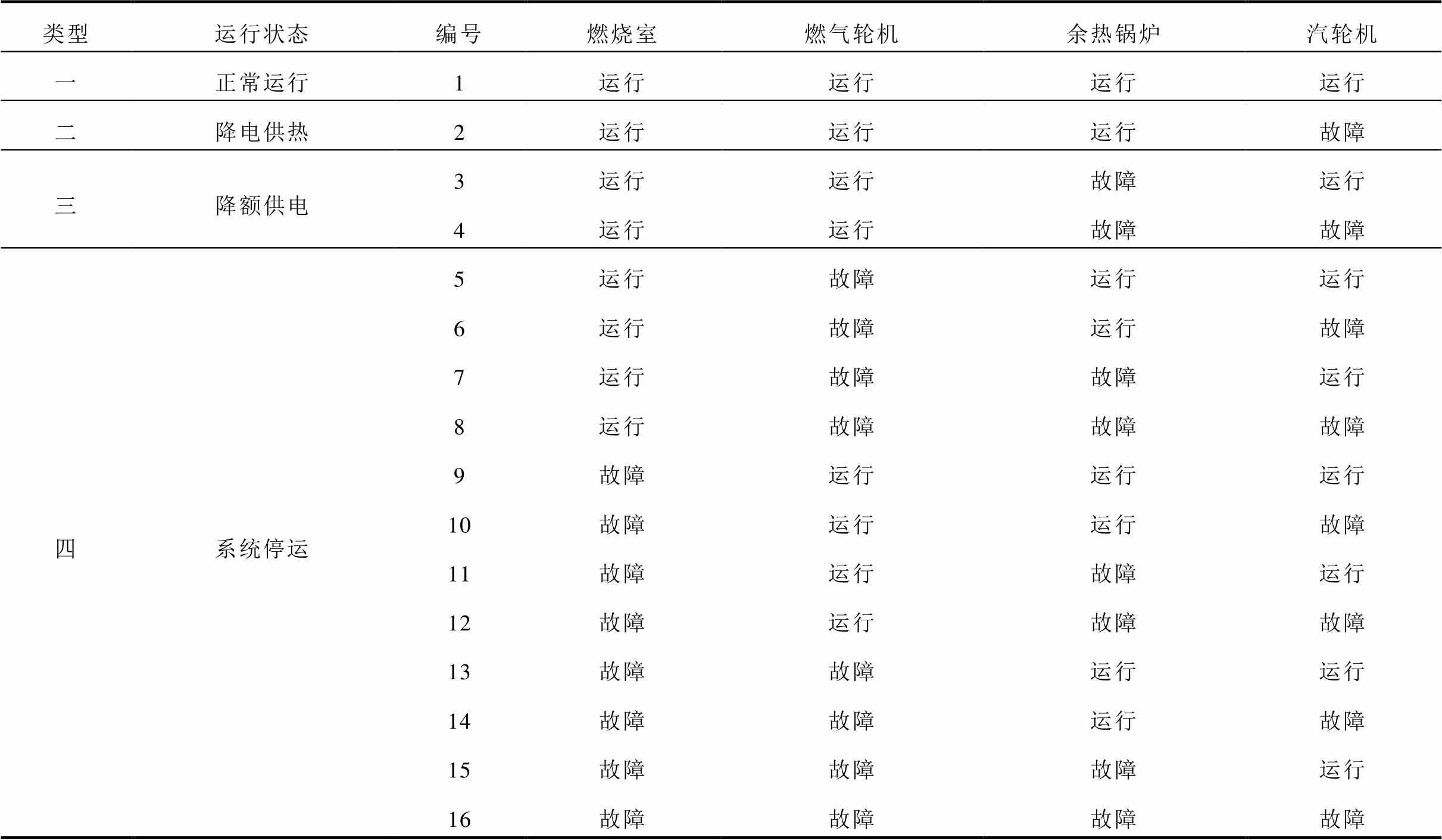
类型运行状态编号燃烧室燃气轮机余热锅炉汽轮机 一正常运行1运行运行运行运行 二降电供热2运行运行运行故障 三降额供电3运行运行故障运行 4运行运行故障故障 四系统停运5运行故障运行运行 6运行故障运行故障 7运行故障故障运行 8运行故障故障故障 9故障运行运行运行 10故障运行运行故障 11故障运行故障运行 12故障运行故障故障 13故障故障运行运行 14故障故障运行故障 15故障故障故障运行 16故障故障故障故障
通过对状态的合并,建立四状态系统空间。基于表1建立CHP机组四状态可靠性模型,如图2所示,图中,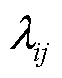 表示状态i到状态j的转移概率。
表示状态i到状态j的转移概率。
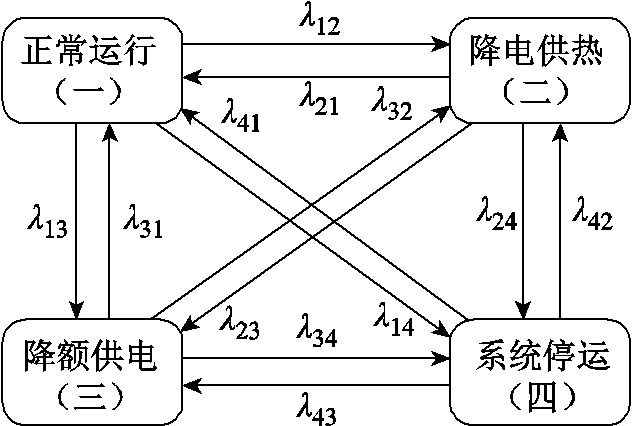
图2 CHP机组四状态可靠性模型
Fig.2 CHP unit four-state reliability model
对含有热电联产机组的RIES可靠性评估时,在利用序贯蒙特卡洛模拟法进行仿真过程中,根据热电联产机组四状态模型的状态概率抽取其随机状态,还需要根据其状态平均持续时间抽取该状态的实际持续时间。因此,针对图2中CHP机组四状态可靠性模型,基于马尔科夫链解析法计算出每个状态出现的概率和平均持续时间。
根据CHP机组状态表建立状态转移矩阵T,其维数为状态数,即每一状态对应于转移矩阵中的一列和一行。如果从状态i向状态j有转移,则转移率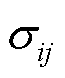 作为矩阵中第i行和第j列的元素,否则该元素为零。状态转移矩阵中对角线元素等于1减该行其余元素之和,其中矩阵中元素
作为矩阵中第i行和第j列的元素,否则该元素为零。状态转移矩阵中对角线元素等于1减该行其余元素之和,其中矩阵中元素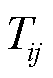 为
为
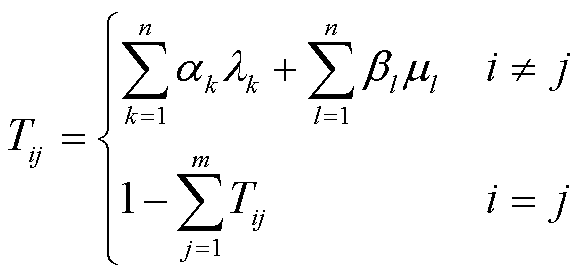 (1)
(1)
式中,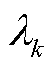 和
和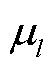 分别为元件的故障率和修复率;
分别为元件的故障率和修复率;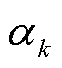 和
和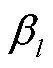 分别为的运行状态变化变量(0/1);
分别为的运行状态变化变量(0/1);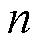 为元件个数;m为系统状态个数,
为元件个数;m为系统状态个数,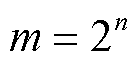 。
。
根据马尔科夫过程逼近原理得
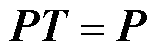 (2)
(2)
针对式(2)进行变换可得
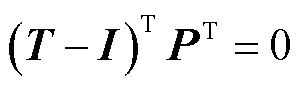 (3)
(3)
式中,I为单位矩阵;P为状态的概率矢量。
式(3)为具有N个未知数的线性方程组,但由于矩阵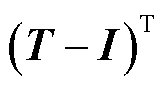 秩为N-1,因此需增加与式(3)中N个方程线性无关的方程,根据概率范数性与可列可加性,添加全概率条件方程,有
秩为N-1,因此需增加与式(3)中N个方程线性无关的方程,根据概率范数性与可列可加性,添加全概率条件方程,有
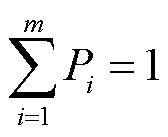 (4)
(4)
因此,替换到式(3)中任意一个方程,即可求解线性方程组,得机组各编号状态概率Pi。
根据CHP机组状态表中四种运行状态与16种设备状态编号对应关系,计算四种状态概率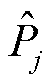 ,得到
,得到
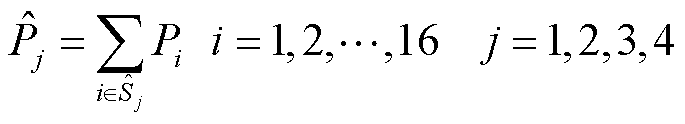 (5)
(5)
式中,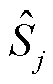 为CHP机组四种状态。
为CHP机组四种状态。
基于频率平衡原则,即遍历一个系统中,离开任一状态的频率等于进入该状态的频率。因此,每种状态频率为
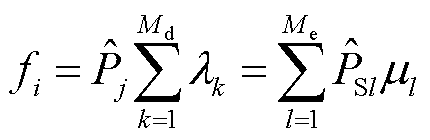 (6)
(6)
式中,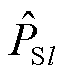 为与状态i直接连接状态的概率;Md为离开状态i的转移数;Me为进入状态i的转移数。
为与状态i直接连接状态的概率;Md为离开状态i的转移数;Me为进入状态i的转移数。
停留状态i的平均持续时间为
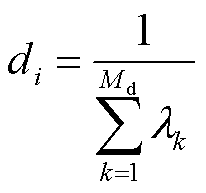 (7)
(7)
典型RIES通过变压器接入上级电网、压缩机接入上级气网,并通过CHP机组实现电、气、热子系统间相互耦合。系统可靠性建模不仅涉及系统拓扑结构和耦合关系,而且与子系统能流特性与运行方式密切相关。鉴于RIES运行的时序性,采用序贯蒙特卡洛方法进行可靠性评估。系统状态变化序列如图3所示。当t1时刻发生故障时,系统状态对切负荷大小具有一定影响,如分布式电源出力、热网管道出口温度、建筑室内温度等系统状态。由文献[22]可知,针对管道较短的区域级综合能源系统,天然气动态特性对其计算精度影响不大。因此,为保障模拟效率建立基于稳态模型的RIES运行优化模型。
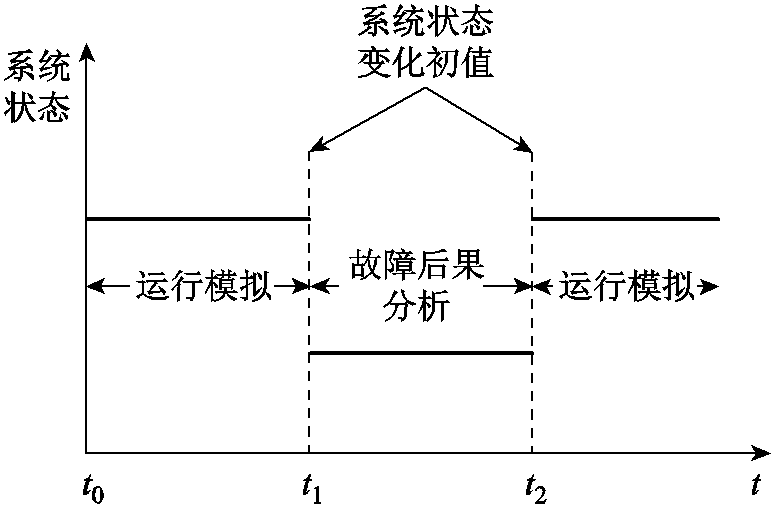
图3 系统状态变化序列
Fig.3 System state change sequence
在运行模拟时以分布式电源和变电站有功功率与无功功率、热电联产机组电、热功率,以及电热锅炉热功率为控制变量,目标是系统总运行费用最小。由于系统不具有外部热源,其运行费用主要包括:向上级电网、气网购电费用、购气费用以系统机组运行维护成本,模拟时间尺度为小时,优化运行目标函数为
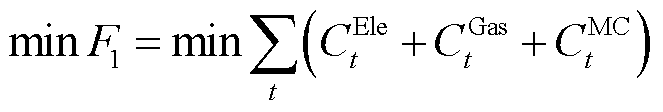 (8)
(8)
式中,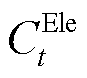 、
、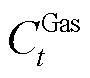 分别为t时刻向上级电网、天然气网购电、气费用;
分别为t时刻向上级电网、天然气网购电、气费用;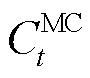 为t时刻各设备运行维护成本[23]。
为t时刻各设备运行维护成本[23]。
2.2.1 电网运行约束
Distflow潮流模型在辐射状配电网潮流分析中得到了广泛的应用,是一种从支路功率出发建立的潮流方程,相比于传统的基于节点功率的潮流计算法,更适用于辐射状配电系统的潮流计算。本文采用Distflow模型建立电网潮流约束,式(9)和式(10)分别表示节点有功功率和无功功率平衡约束,式(11)表示Distflow方程,式(12)~式(17)分别表示电压幅值、线路电流二次方、线路有功功率、线路无功功率、变电站有功功率、变电站无功功率上下限约束,式(18)和式(19)分别表示支路和DG的二阶锥约束。
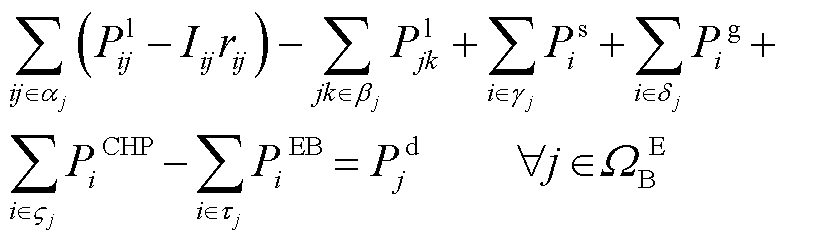 (9)
(9)
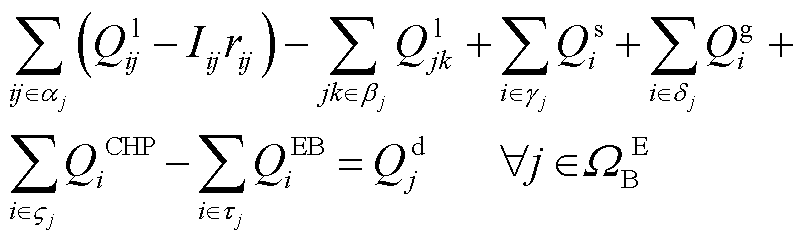 (10)
(10)
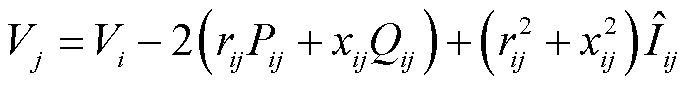 (11)
(11)
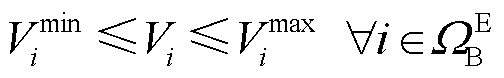 (12)
(12)
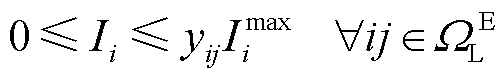 (13)
(13)
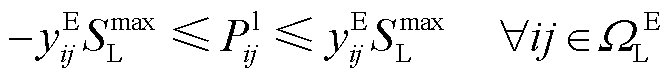 (14)
(14)
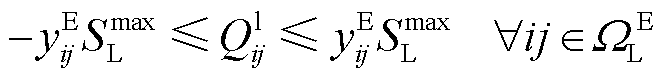 (15)
(15)
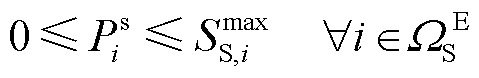 (16)
(16)
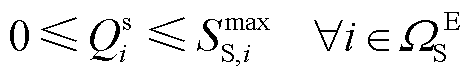 (17)
(17)
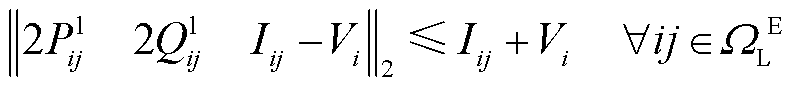 (18)
(18)
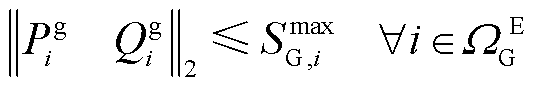 (19)
(19)
式中,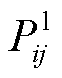 、
、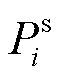 、
、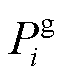 、
、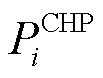 和
和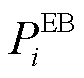 分别为线路ij有功功率、与节点i相连的变电站、DG、热电联产和电热锅炉的有功注入;
分别为线路ij有功功率、与节点i相连的变电站、DG、热电联产和电热锅炉的有功注入;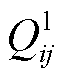 、
、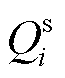 、
、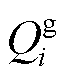 、
、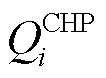 和
和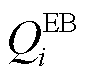 为对应设备无功功率;
为对应设备无功功率;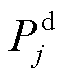 和
和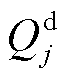 分别为节点
分别为节点 的有功负荷和无功负荷;
的有功负荷和无功负荷;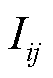 为线路ij电流的二次方;
为线路ij电流的二次方; 为节点i电压二次方;
为节点i电压二次方;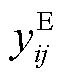 为电网线路ij状态的0-1变量;
为电网线路ij状态的0-1变量;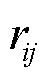 和
和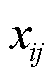 为线路ij阻抗;
为线路ij阻抗;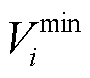 和
和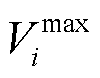 分别为节点i电压下、上限;
分别为节点i电压下、上限;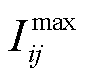 为线路ij电流上限;
为线路ij电流上限;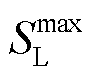 为线路容量;
为线路容量;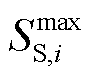 为变电站出力上限;
为变电站出力上限;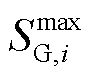 为DG出力上限;
为DG出力上限; 和
和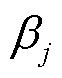 分别为由节点j首端或尾部线路构成的集合;
分别为由节点j首端或尾部线路构成的集合;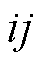 为支路索引;
为支路索引;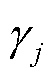 、
、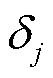 、
、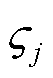 和
和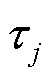 分别为与节点j相连的变电站、DGs、CHP机组和EB机组构成的集合;
分别为与节点j相连的变电站、DGs、CHP机组和EB机组构成的集合;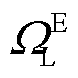 、
、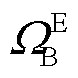 、
、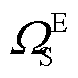 和
和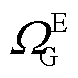 分别为电网中支路、节点、变电站和DG集合。
分别为电网中支路、节点、变电站和DG集合。
2.2.2 气网约束
天然气网满足流体力学质量守恒定律与伯努利方程,建立天然气稳态运行约束。其中,式(20)为天然气网络流量平衡方程,式(21)~式(24)表示管道流量与节点压力关系,式(25)~式(27)分别为管道流量、气源流量和节点压力上下限约束。由于式(21)表示的Weymouth流量方程具有强非线性特点,采用分段线性化处理[24]。
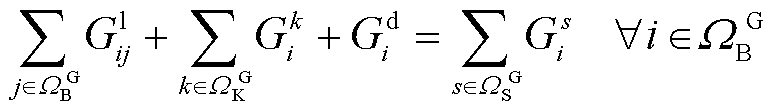 (20)
(20)
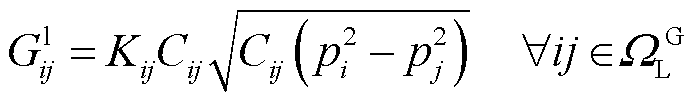 (21)
(21)
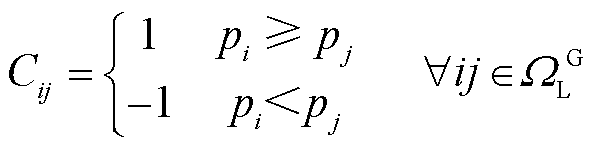 (22)
(22)
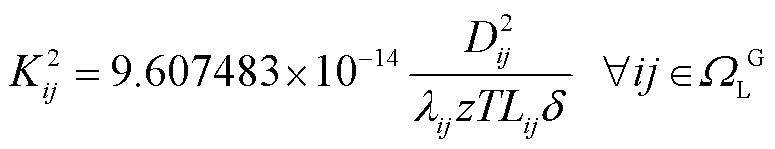 (23)
(23)
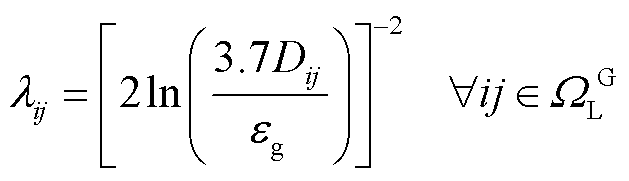 (24)
(24)
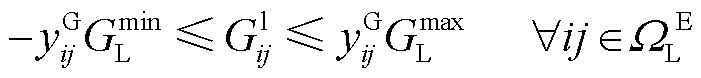 (25)
(25)
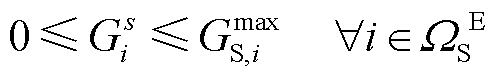 (26)
(26)
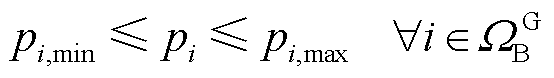 (27)
(27)
式中,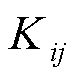 为管道常数;
为管道常数;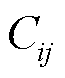 表示管道ij的气体流动方向;
表示管道ij的气体流动方向;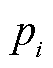 和
和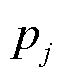 分别为i节点和j节点的气压;
分别为i节点和j节点的气压;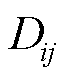 为管道内径;
为管道内径;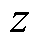 为气体压缩系数;
为气体压缩系数;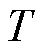 为气体温度;
为气体温度;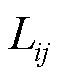 为管道长度;
为管道长度; 为天然气密度;
为天然气密度; 为管道绝对表面粗糙度;
为管道绝对表面粗糙度;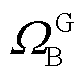 为所有天然气网络节点;
为所有天然气网络节点;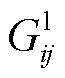 为节点i到节点j的天然气流量;
为节点i到节点j的天然气流量;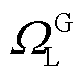 为气网管道集合;
为气网管道集合;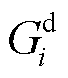 为节点i的气负荷;
为节点i的气负荷;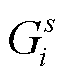 为与节点i相连气源s的天然气供应流量;
为与节点i相连气源s的天然气供应流量;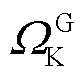 为CHP机组等能源转换设备;
为CHP机组等能源转换设备;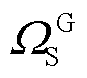 为气源节点;
为气源节点;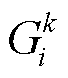 为与节点i相连的能源转换设备k消耗的天然气负荷;
为与节点i相连的能源转换设备k消耗的天然气负荷;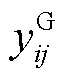 为气网管道状态的0-1变量;
为气网管道状态的0-1变量;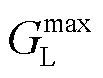 和
和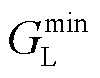 分别为管道流量上、下限;
分别为管道流量上、下限;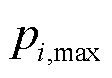 和
和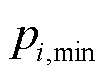 分别为节点i压力上、下限;
分别为节点i压力上、下限;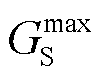 为气源出力最大值。
为气源出力最大值。
2.2.3 热网约束
典型的热力系统通常由热源、热网、热负荷组成。考虑热网供热媒介为热水,忽略供、回水管道因水温差异导致的微小流量变化,采用质调节模式对热网进行调控,预先通过水力模型计算管道质量流量。式(28)~式(37)分别为计及一次换热器的节点热源功率平衡方程、计及二次换热器的热负荷平衡方程、一次管网的供水网络管道稳态模型、回水网络管道稳态模型、供回水管网温度混合方程以及节点温度上下限约束。
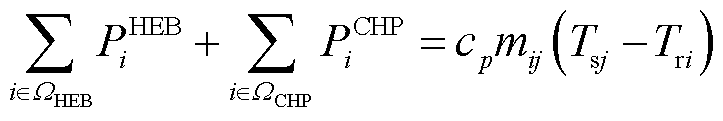 (28)
(28)
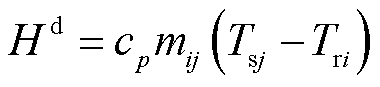 (29)
(29)
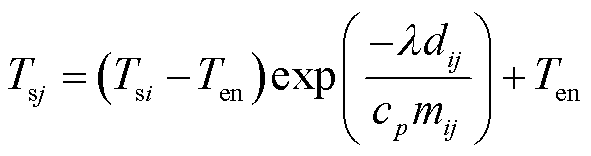 (30)
(30)
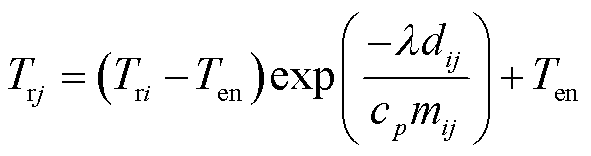 (31)
(31)
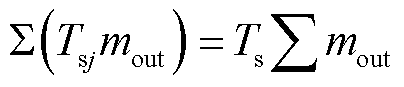 (32)
(32)
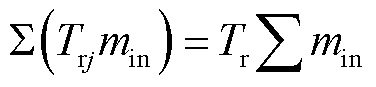 (33)
(33)
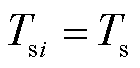 (34)
(34)
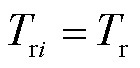 (35)
(35)
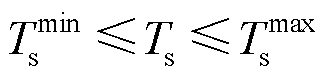 (36)
(36)
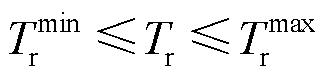 (37)
(37)
式中,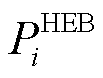 为电热锅炉制热功率;
为电热锅炉制热功率;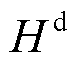 为热负荷;
为热负荷;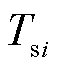 、
、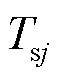 、
、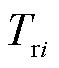 、
、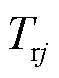 、
、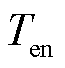 分别为供水管道始端i、末端j温度、回水管道始端i、末端j温度和室外环境温度;
分别为供水管道始端i、末端j温度、回水管道始端i、末端j温度和室外环境温度;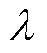 为单位长度管道的导热系数;
为单位长度管道的导热系数;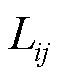 为管道ij的长度;
为管道ij的长度;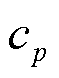 为水的比热容;
为水的比热容;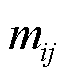 为管道ij的流量;
为管道ij的流量;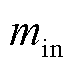 和
和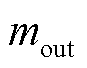 分别为节点流入质量流量和流出质量流量;
分别为节点流入质量流量和流出质量流量;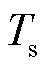 和
和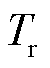 分别为供水网和回水网各节点温度;
分别为供水网和回水网各节点温度;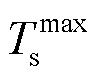 、
、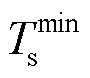 、
、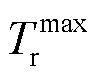 和
和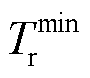 分别为供水网回水网各节点温度上、下限。通过水力模型和热力模型共同实现对热网的潮流建模。为保障系统水力工况稳定的关系,本文采用质调节模式,预先通过水力模型计算管道流量,在热源处只改变网路的供水温度。与此同时,管道流量为已知量,因而不存在非线性问题。
分别为供水网回水网各节点温度上、下限。通过水力模型和热力模型共同实现对热网的潮流建模。为保障系统水力工况稳定的关系,本文采用质调节模式,预先通过水力模型计算管道流量,在热源处只改变网路的供水温度。与此同时,管道流量为已知量,因而不存在非线性问题。
2.2.4 能量转换单位约束
本文在RIES中,通过CHP机组、电热锅炉实现天然气、电力及热力之间的相互转换,起到了耦合电、气、热三个系统的作用。
抽凝式热电联产机组的运行点位于其出力可行域范围,有
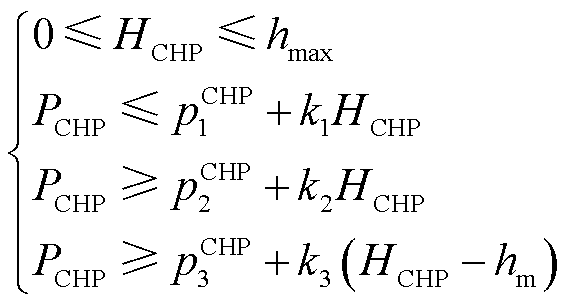 (38)
(38)
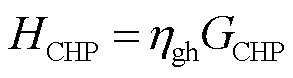 (39)
(39)
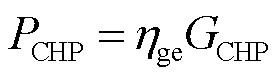 (40)
(40)
式中, 、
、 、
、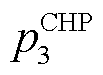 为对应可行域边界处;
为对应可行域边界处;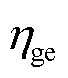 和
和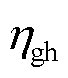 分别为CHP机组天然气发电效率和制热效率;
分别为CHP机组天然气发电效率和制热效率;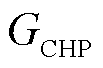 、
、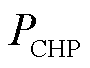 、
、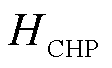 分别为CHP机组消耗天然气功率、发电功率和制热功率;
分别为CHP机组消耗天然气功率、发电功率和制热功率;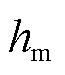 和
和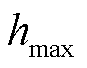 分别为机组发电功率最小时对应供热功率以及机组供热上限;k1、k2、k3为可行域边界斜率[8]。
分别为机组发电功率最小时对应供热功率以及机组供热上限;k1、k2、k3为可行域边界斜率[8]。
电热锅炉典型物理模型可表示为
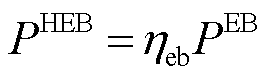 (41)
(41)
式中,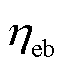 为电热锅炉制热效率。
为电热锅炉制热效率。
从源、网、荷角度依次分析热惯性对系统可靠性的影响。当热源如热电联产机组故障时,设备经修复后重新投入运行,存在设备起动时间。由机组启停操作规程可知,停机3 h以内,再次起动视为热起动;停机3~8 h内,再次起动视为温起动;停机8 h以上,再次起动视为冷起动。因此,当热源设备故障时,根据其故障持续时间与设备起动状态,延长相应故障持续时间,在系统状态抽样时对故障持续时间进行修正。
当热网管道发生故障时,经元件修复时间tf后故障修复,考虑热媒流速,即热能流延时tc小时后传输至用户,此时用户重新恢复供热。因此,考虑热网传输惯性,对管道故障持续时间修正,修正后的管道恢复时间为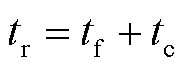 。
。
用户的建筑热惯性主要体现在对建筑内部进行加热或停暖时,建筑温度变化过程受建筑物结构、室外温度等因素对传热过程的影响,表现出一定的储热特性[25],即当热网故障时,室内温度不会瞬间降低到室外温度,结合用户舒适度特性将热负荷转换为柔性负荷,实现对用户故障后果的精确分析。通过采用建筑物热阻热容网络模型[20]建立建筑室内温度与室外温度时序变化过程,模型中建筑物通过热传导、热对流和热辐射三种方式进行热量交换,忽略窗户与相邻房间传热影响,考虑墙体热阻实现热交换,建立建筑区域热平衡微分方程,有
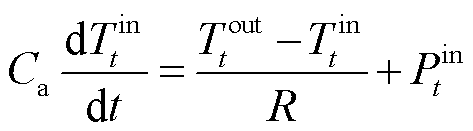 (42)
(42)
式中,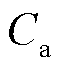 为建筑热容;
为建筑热容;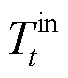 和
和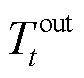 分别为t时刻室内温度和室外温度;R为建筑热阻;
分别为t时刻室内温度和室外温度;R为建筑热阻;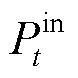 为t时段热源功率。
为t时段热源功率。
综上所述,为充分考虑RIES中热惯性对系统可靠性的影响,针对可靠性评估过程中多重热惯性影响分别进行建模。在可靠性评估多个环节中依次实现对多重热惯性的建模,即在元件抽样时考虑热源起动惯性与热网传输惯性对元件故障持续时间进行修正,在故障后果分析时建立最优切负荷模型中建筑热惯性约束。
在RIES故障恢复期间,可通过网络重构、调度分布式电源和耦合设备出力尽可能减少负荷削减。为实现对系统故障状态精细化分析,在稳态模型基础上进一步引入联络开关状态、切负荷控制变量,考虑热传输延迟与热负荷动态约束建立RIES最优切负荷模型,优化目标为系统电、气、热负荷最少削减量,其中包括各能源削减成本、电负荷各节点的重要程度,模型目标函数为
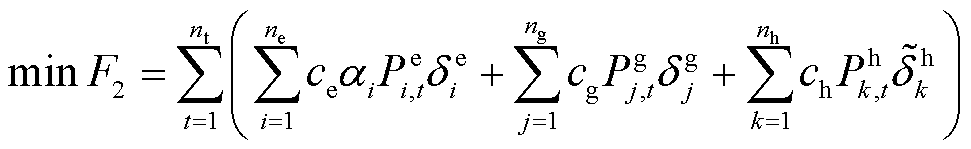 (43)
(43)
式中,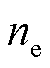 、
、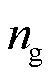 、
、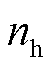 分别为电、气、热负荷节点数;
分别为电、气、热负荷节点数;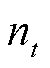 为故障恢复小时数;
为故障恢复小时数;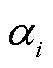 为配电网节点i负荷等级;
为配电网节点i负荷等级;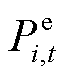 、
、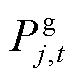 、
、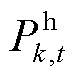 分别为t时刻节点i电负荷、节点j气负荷、节点k热负荷;
分别为t时刻节点i电负荷、节点j气负荷、节点k热负荷;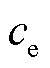 、
、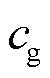 、
、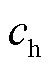 分别为电、气、热负荷削减成本;
分别为电、气、热负荷削减成本;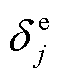 、
、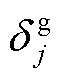 分别为电、气切负荷判别0/1变量;
分别为电、气切负荷判别0/1变量;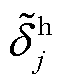 为考虑用户舒适度特性后修正的切热负荷变量。
为考虑用户舒适度特性后修正的切热负荷变量。
3.2.1 功率平衡约束
针对引入的电、气、热切负荷变量,与稳态的优化运行模型相比,对电、气、热网功率平衡约束进行修正。电网功率平衡约束修正为式(44)和式(45),分别表示有功功率和无功功率平衡约束;气网和热网功率平衡约束修正为式(46)和式(47)。
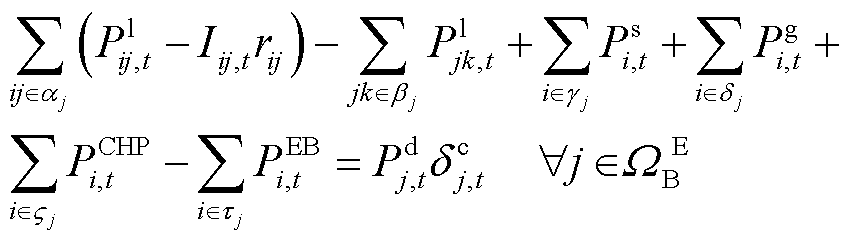 (44)
(44)
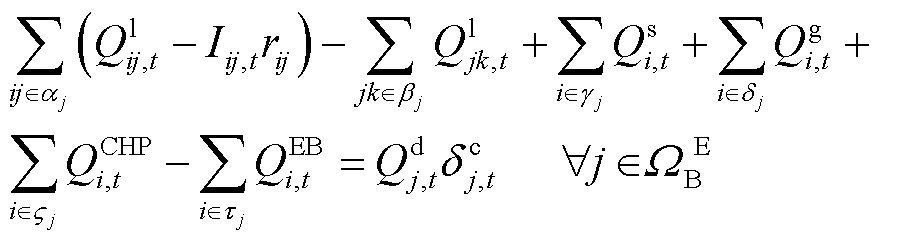 (45)
(45)
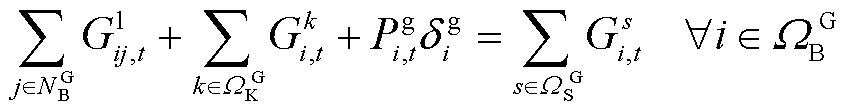 (46)
(46)
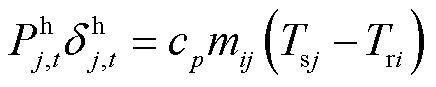 (47)
(47)
电网和气网其余约束与2.2节相同。
3.2.2 热网管道动态约束
由于2.2节中热网稳态模型未考虑管道动态特性,建立考虑动态特性的热网潮流约束。针对热网传输惯性采用简化的节点法建立供热管道传输动态方程,建立管道首末端口温度映射关系,将出口温度表示为过去某两个相邻时刻管道入口温度的线性组合。在质调节模式下,热水经供热管道ij的延迟时段数为
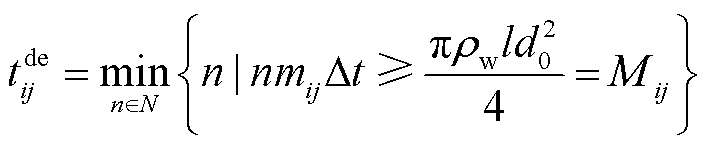 (48)
(48)
式中,n为正整数;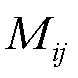 为管道ij内热水的总质量;
为管道ij内热水的总质量;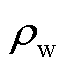 为水的密度;
为水的密度;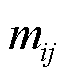 为管道ij内质量流量;
为管道ij内质量流量;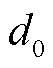 为管道内径;
为管道内径;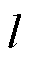 为管道长度;
为管道长度;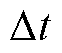 为调度时间间隔。
为调度时间间隔。
结合管道延迟时段数,建立供回水网管道模型为
 (49)
(49)
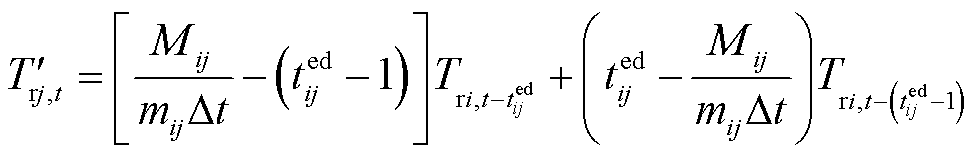 (50)
(50)
式中,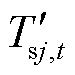 、
、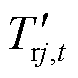 分别为忽略温度损耗时,t时刻供水网和回水网管道ij出口质块温度;
分别为忽略温度损耗时,t时刻供水网和回水网管道ij出口质块温度;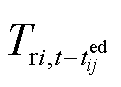 、
、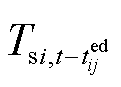 与
与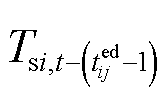 、
、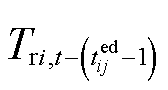 分别为供水网与回水网
分别为供水网与回水网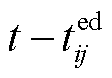 和
和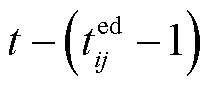 时刻注入管道的温度。
时刻注入管道的温度。
由于管道动态模型中忽略温度损耗,对稳态热网约束条件中式(30)和式(31)进行修正,计及传输热损时管道出口实际温度为
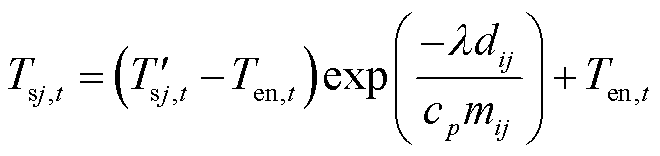 (51)
(51)
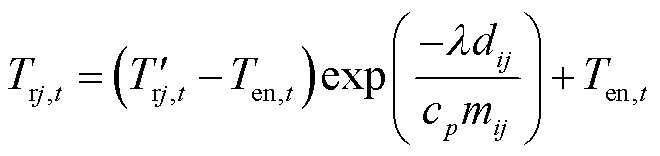 (52)
(52)
3.2.3 建筑热惯性约束
针对建筑热惯性,利用区域集总参数模型分析室内平均温度随时间变化规律,对式(42)进行差分变化计算可得建筑热平衡约束的代数方程,考虑用户舒适度区间对切负荷变量进行修正,建立热网热惯性约束为
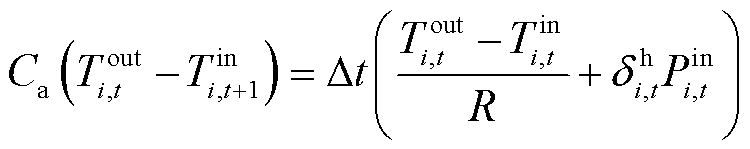 (53)
(53)
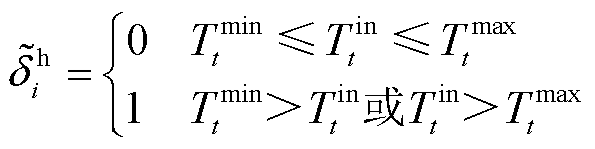 (54)
(54)
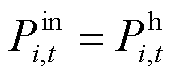 (55)
(55)
式中,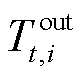 为t时刻节点i室外温度;
为t时刻节点i室外温度;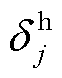 为热切负荷判别0/1变量;
为热切负荷判别0/1变量;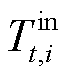 为t时刻节点i室内温度;
为t时刻节点i室内温度;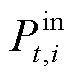 为节点i在t时段热源功率;
为节点i在t时段热源功率;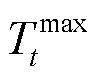 和
和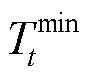 分别为t时刻室内温度上、下限。
分别为t时刻室内温度上、下限。
3.2.4 配电网辐射状约束
考虑配电网联络线进行负荷转供,建立相应辐射状结构约束为
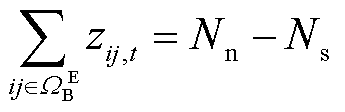 (56)
(56)
式中,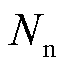 和
和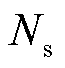 分别为系统节点总数与变电站总数;
分别为系统节点总数与变电站总数;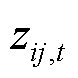 为表征支路和联络开关ij在时刻t开闭状态的0/1变量,闭合为1,断开为0。
为表征支路和联络开关ij在时刻t开闭状态的0/1变量,闭合为1,断开为0。
为衡量RIES可靠性水平,本文从能量损失和负荷损失概率角度分别建立可靠性评估指标。主要包括负荷损失概率(Loss of Load Probability, LOLP)、能量不足期望(Expected Energy Not Supplied, EENS)、系统平均中断频率指数(System Average Interruption Frequency Index, SAIFI)和系统平均中断持续时间指数(System Average Interruption Duration Index, SAIDI)。现有文献已经对可靠性指标进行了详细的描述[19],本文从用户舒适度角度出发,当建筑内室温低于适当温度范围时,热网才发生热负荷削减,因此对热网可靠性指标进行修正。
在t时刻提供给用户的热功率是指将温度从现有温度调节到合适温度所需的最小热功率[26]。
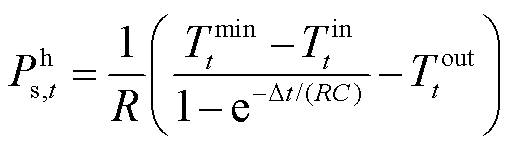 (57)
(57)
切负荷量为
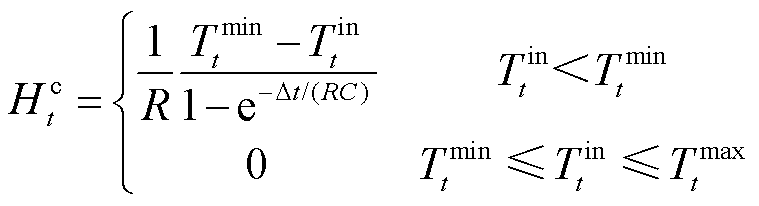 (58)
(58)
因此,热网期望失负荷概率LOLPh和失负荷量EENSh为
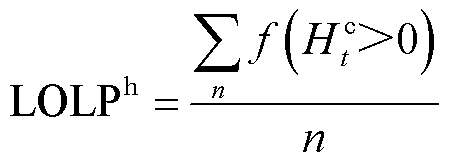 (59)
(59)
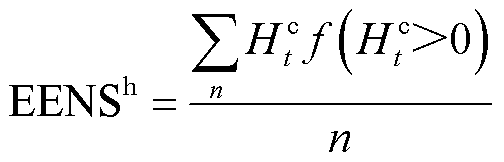 (60)
(60)
式中,n为蒙特卡洛采样个数;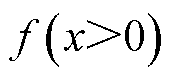 为采样过程中失负荷事件的发生次数。
为采样过程中失负荷事件的发生次数。
区域综合能源系统可靠性指标为
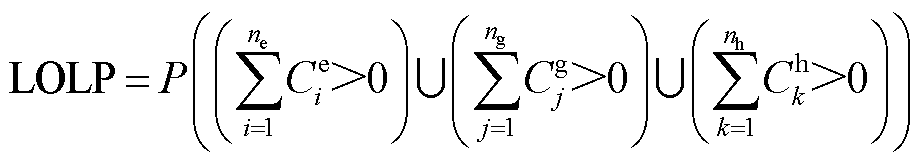 (61)
(61)
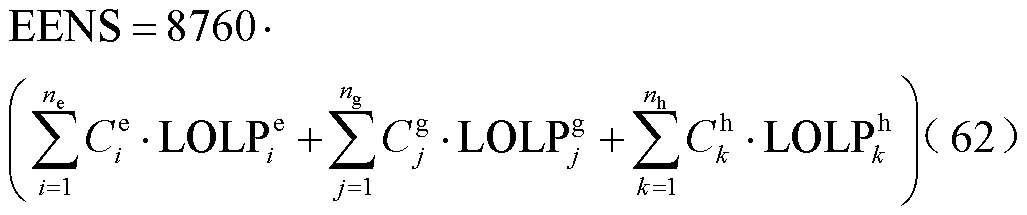
式中,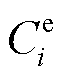 、
、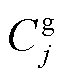 、
、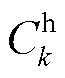 分别为电、气、热三个子系统分别在节点i、j、k的负荷削减;LOLPe、LOLPg和LOLPh分别为电、气、热子系统失负荷概率指标。
分别为电、气、热三个子系统分别在节点i、j、k的负荷削减;LOLPe、LOLPg和LOLPh分别为电、气、热子系统失负荷概率指标。
影响序贯蒙特卡洛模拟仿真精度的因素为仿真时间和收敛阈值,本文利用EENS的方差系数作为收敛阈值,定义为
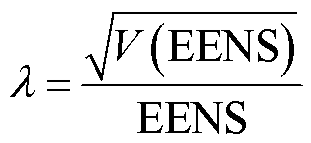 (63)
(63)
由于区域综合能源系统的耦合性与时序性,在元件多状态模型、运行优化模型、最优切负荷模型与可靠性评估指标基础上,提出一种基于多能流稳态模型与动态模型相结合的可靠性评估方法。在保证精度条件下进行以下假设:①所有元件都是可修复的;②仅考虑元件永久故障,不考虑瞬时故障,元件经修复后才可重新投入使用;③不考虑断路器等开关设备误动、拒动情况。具体评估流程如图4所示。
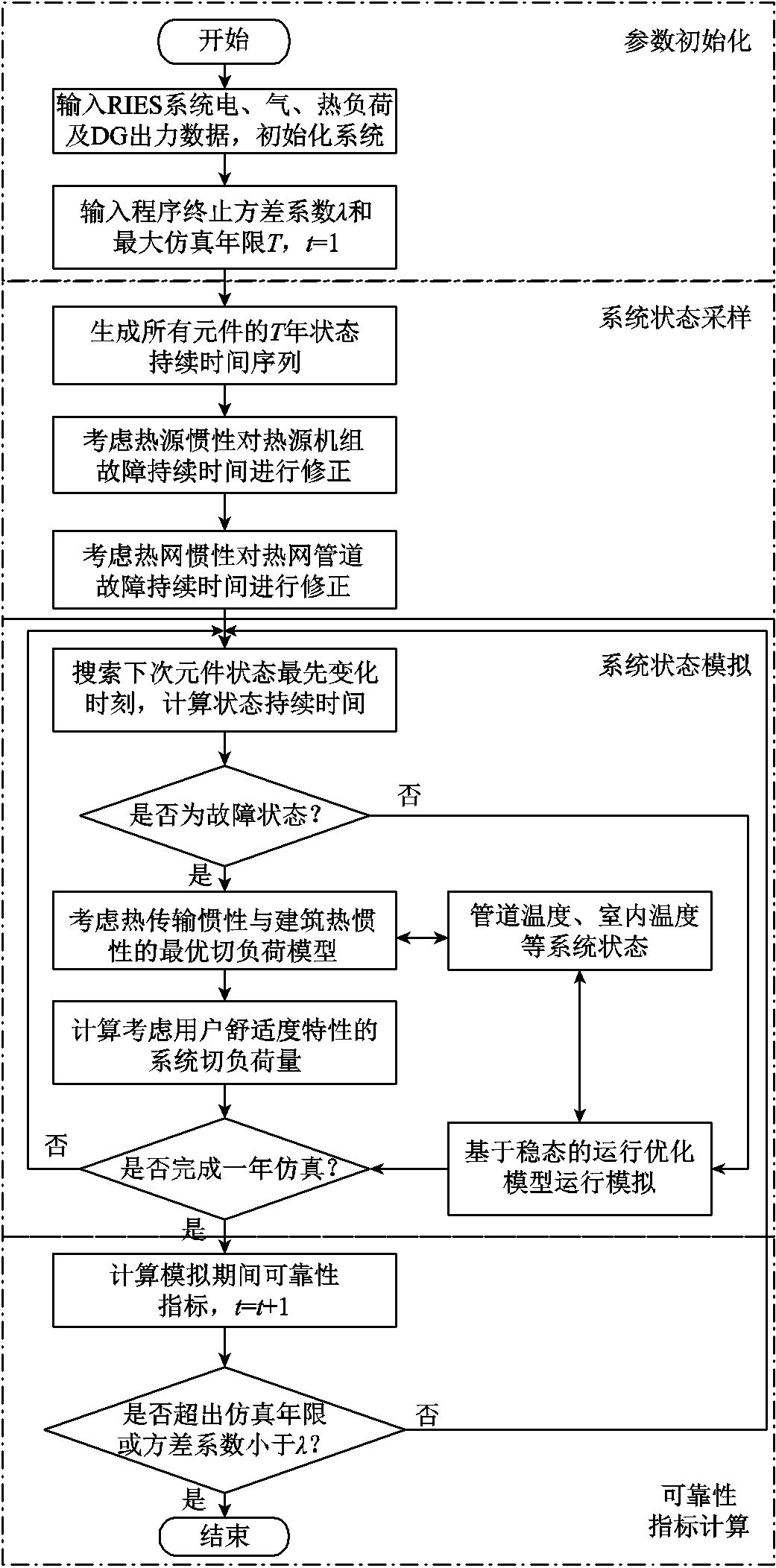
图4 RIES可靠性评估流程
Fig.4 Reliability assessment process of RIES
(1)参数初始化。输入RIES的原始数据,包括负荷数据、CHP机组参数、管道物理参数等。设定模拟时间为1 000年。
(2)系统状态采样。对系统中两状态元件与CHP机组四状态元件进行状态持续时间模拟,假定元件在每一状态的持续时间服从指数分布,通过建立多状态随机数抽取元件状态,再次结合反变换法与随机数抽取,通过双重抽样生成元件多状态时序序列,从而生成RIES状态序列。
(3)系统状态修正。根据热源惯性与热网惯性对元件故障持续时间的影响,结合热源起动时间与热能流传输时间分别进行修正。
(4)系统状态模拟。搜索元件状态变化时刻,当系统中元件无故障时,采用RIES运行优化模型逐时模拟;当系统中元件故障时,基于稳态运行优化模型获取当前系统状态初始值,并采用RIES最优切负荷模型计算故障恢复持续时间系统负荷削减量和削减时间。
(5)可靠性指标计算。根据式(57)~式(62)计算RIES系统级和用户级可靠性指标。
(6)收敛性检验。采用式(63)的方差系统作为收敛依据,若方差系数小于0.1[19]则终止系统状态模拟;否则执行步骤(3)。
本文算例在单台Intel(R) Core(TM) i5-960 0KF CPU(3.70 GHz)及内存为32 GB的个人计算机完成。本文基于Matlab和GUROBI平台,以33节点配电网、11节点配气网和32节点配热网构成的电-气-热耦合区域综合能源系统[14]为例,仿真验证所提的RIES可靠性评估方法,算例选取的综合能源系统如图5所示,热源设备起动时间见表2,配电网各负荷节点重要权重系数见表3,11、20、32节点接入额定总容量为0.1 MW的光伏发电机,系统可靠性参数见表4。其中,根据《室内空气质量标准》设定供暖室内温度为16~24℃,外部环境设定为-10℃,并假定当前供热室内温度为24℃[19]。
表2 热源设备起动时间
Tab.2 Heat source equipment start-up time

类型起动时间/h CHP机组电热锅炉 热态10 温态50 冷态80
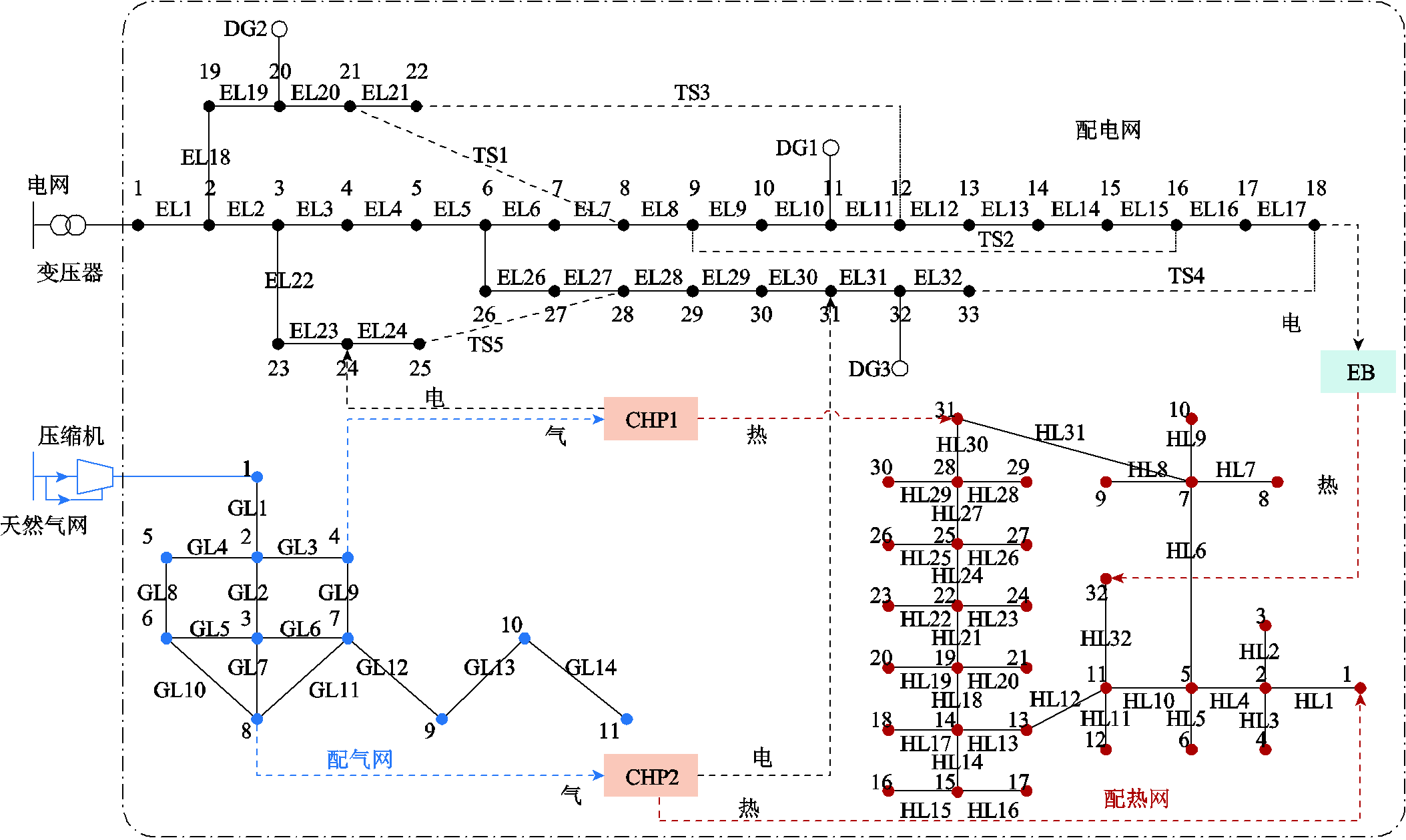
图5 区域综合能源系统拓扑结构
Fig.5 Topology structure of regional integrated energy system
表3 配电网节点负荷等级
Tab.3 Importance classification of node load in distribution network

负荷重要程度负荷节点权重系数 一级负荷11,12,20,21,31,321 二级负荷1,2,3,4,6,7,8,9,10,13,14,15,17,19,23,24,25,26,27,29,300.5 三级负荷5,16,18,22,28,330.1
表4 区域综合能源系统可靠性参数
Tab.4 reliability parameters for regional integrated energy system
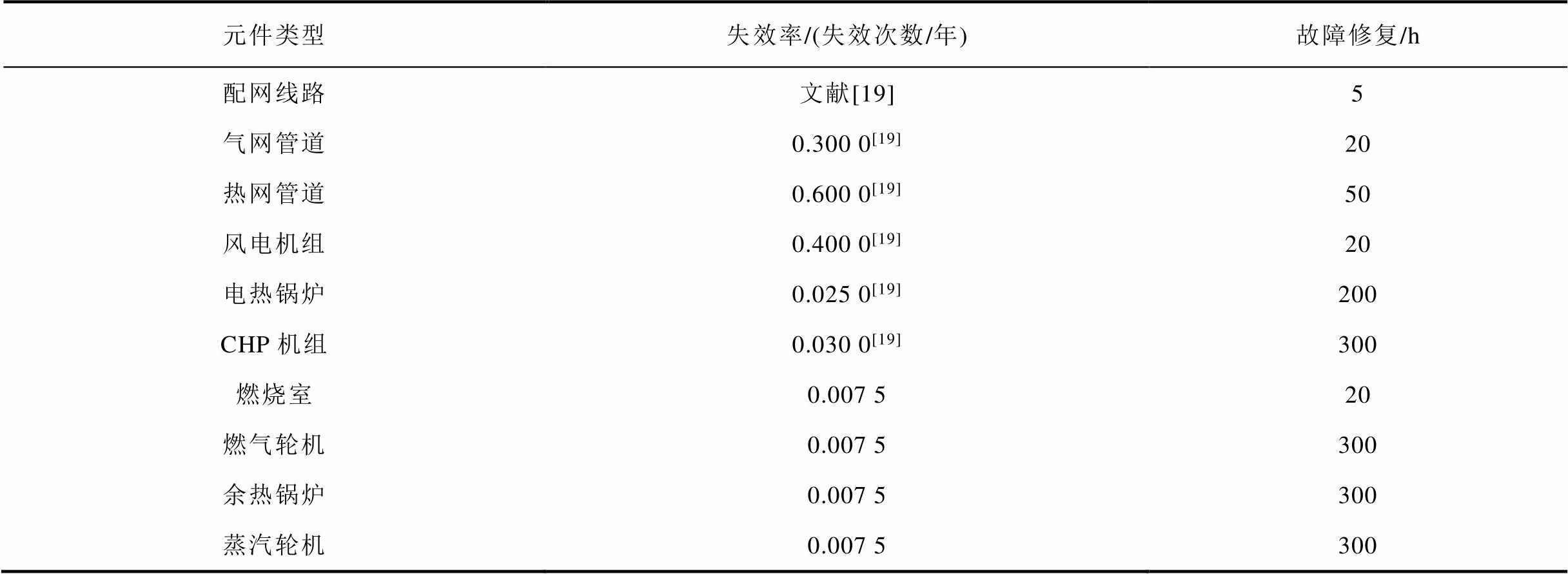
元件类型失效率/(失效次数/年)故障修复/h 配网线路文献[19]5 气网管道0.300 0[19]20 热网管道0.600 0[19]50 风电机组0.400 0[19]20 电热锅炉0.025 0[19]200 CHP机组0.030 0[19]300 燃烧室0.007 520 燃气轮机0.007 5300 余热锅炉0.007 5300 蒸汽轮机0.007 5300
5.2.1 耦合型元件可靠性建模分析
根据图1中CHP机组结构与表1中CHP机组状态,生成马尔科夫状态转移矩阵,见附表1。统计CHP机组各状态之间的转移概率,CHP机组四状态可靠性模型如图6所示。
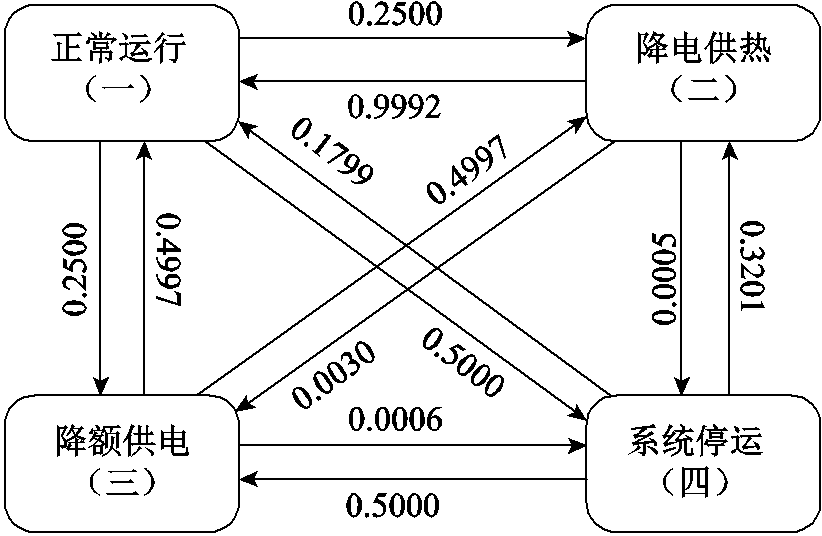
图6 CHP机组四状态可靠性模型
Fig.6 CHP unit four-state reliability model
基于马尔科夫链解析法计算各运行状态概率和平均持续时间,CHP机组可靠性指标见表5。
由表5可知,相比于传统两状态模型,四状态模型CHP机组停运概率降低了50%,供热和供电平均停电时间分别为221 h和261 h,分别降低了26.22%和12.89%,有效地提高了耦合设备可靠性建模的精度。
表5 CHP机组可靠性指标
Tab.5 Reliability indices of CHP system
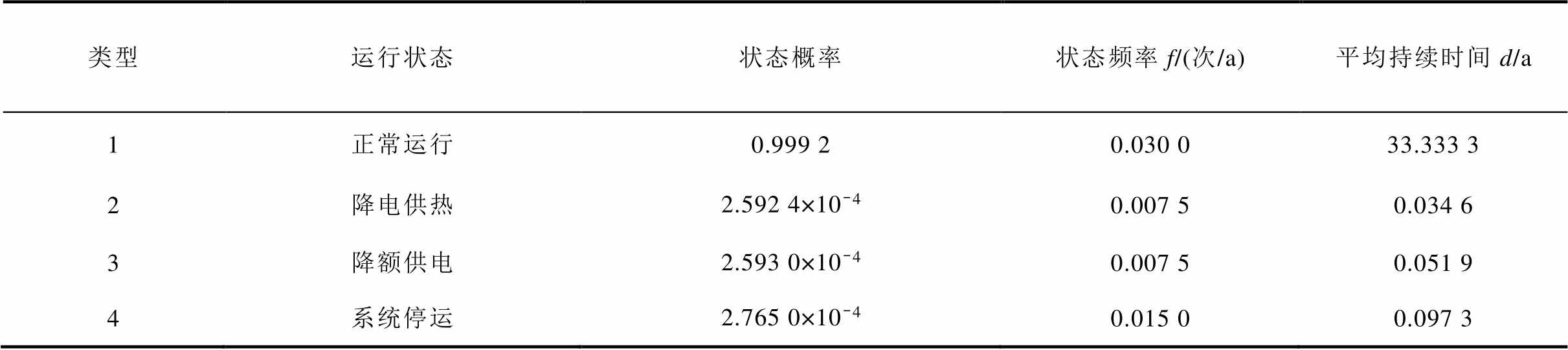
类型运行状态状态概率状态频率f/(次/a)平均持续时间d/a 1正常运行0.999 20.030 033.333 3 2降电供热2.592 4×10-40.007 50.034 6 3降额供电2.593 0×10-40.007 50.051 9 4系统停运2.765 0×10-40.015 00.097 3
5.2.2 区域综合能源系统可靠性评估分析
根据图4评估流程,基于序贯蒙特卡洛进行可靠性评估,仿真至300 a时方差系数小于0.1,仿真收敛。抽样获得故障场景48 944个,占比0.33%,其中一阶故障48 689个,二阶255个,电、气、热网故障次数分别为750、11 615、36 834。无故障运行模拟单个断面仿真时间为4.2 s,单次故障后果分析故障仿真时间为42.6 s。因此,针对中长期[27]的RIES可靠性评估,本文侧重于分析多能互补与能流差异对系统可靠性的影响,后续研究可通过重采样等方差减少技术进一步加快评估速度。
经仿真计算,可靠性指标见表6。
表6 RIES系统可靠性指标
Tab.6 Reliability indices for RIES

指标电气热RIES LOLP1.902 6×10-61.475 0×10-22.245 6×10-23.460 2×10-2 EENS1.402 0×10-15.016 2×1022.136 1×1027.153 7×102 SAIFI5.945 6×10-81.638 9×10-37.017 5×10-44.675 9×10-4 SAIDI4.381 3×10-35.573 56.675 39.667 2
在RIES中各类能源子系统中,气网总负荷为15.325 0 MW,相比电、热网具有更大的负荷需求。因此,表6中在气网LOLP指标远小于电网时,EENS指标反而最大。同时,由于热网相比气网具有更多的用户数,热网SAIFI与SAIDI指标比气网小得多。
在已知系统可靠性的基础上分析元件多状态建模的影响,仿真对比CHP机组四状态模型与两状态模型下RIES系统可靠性。两种CHP可靠性模型下可靠性指标对比见表7,其中,P1和P2分别表示两状态和多状态模型下失负荷概率,E1和E2分别表示失负荷期望。
表7 两种CHP可靠性模型下可靠性指标对比
Tab.7 RIES reliability evaluation indics with CHP unit reliability model

系统P1(pu)P2(pu)E1/(MW·h/a)E2/(MW·h/a) 电3.026 8×10-61.902 6×10-62.230 4×10-11.402 0×10-1 气1.475 0×10-21.475 0×10-25.016 2×1025.016 2×102 热3.321 6×10-22.245 6×10-22.895 2×1022.136 1×102 RIES4.796 6×10-23.460 2×10-27.911 5×1037.153 7×102
由表7可知,采用热电联产机组四状态模型下RIES失负荷概率与期望损失负荷更低,主要因为考虑了机组“降电供热”和“降额供电”状态,计及如汽轮机、余热锅炉等部分元件故障时通过调整机组运行方式继续保障电负荷与热负荷的供应,因此可靠性评估更接近实际场景,结果也更为准确。
进一步分析造成各子系统可靠性差异的影响因素,对网络中管道/线路平均故障率(S1)、平均故障修复时间(S2)、管道/线路数量(S3)、网络结构(S4)、故障恢复措施种类(S5)进行对比,结果见表8。
表8 RIES中电、气、热系统对比分析
Tab.8 Comparative analysis of electric, gas and heat systems in RIES

系统S1S2/hS3S4S5 电0.011 9537条冗余多重 气0.141 62014条部分冗余单一 热0.080 75032条单一单一
由表8可知,热网管道故障率相对较低,但由于其放射状、无冗余特点,故障恢复措施单一且故障恢复时间较长,导致热网失负荷概率最高,为0.022 46;与热网相比,气网管道设备故障率最高,是热网的1.75倍,但管道故障修复时间是热网的40%,管道数量相对较少且管网部分呈环型结构,具有一定冗余度,所以其失负荷概率相对较低,为热网的65.68%;电网失负荷概率最低,主要是因为线路故障率最低且故障恢复时间最短,同时由于联络线负荷转供使得电网结构具有很强的冗余特性,故障恢复措施涉及分布式电源、系统间多能互补、热惯性等手段多样,能够在故障时有效保障配网负荷的电力供应,提高供电可靠性。因此,降低气网和热网管道故障率,减少故障修复时间,增加备用管道能够有效提高系统可靠性。
5.2.3 多能互补机制对系统可靠性的影响
多能互补机制是RIES最关键的运行特征,为分析多能互补对系统可靠性影响,给出系统内各类负荷供应来源均值占比。RIES能源供应如图7所示,图中数值表示系统内电、气、热各类负荷供应均值占比。
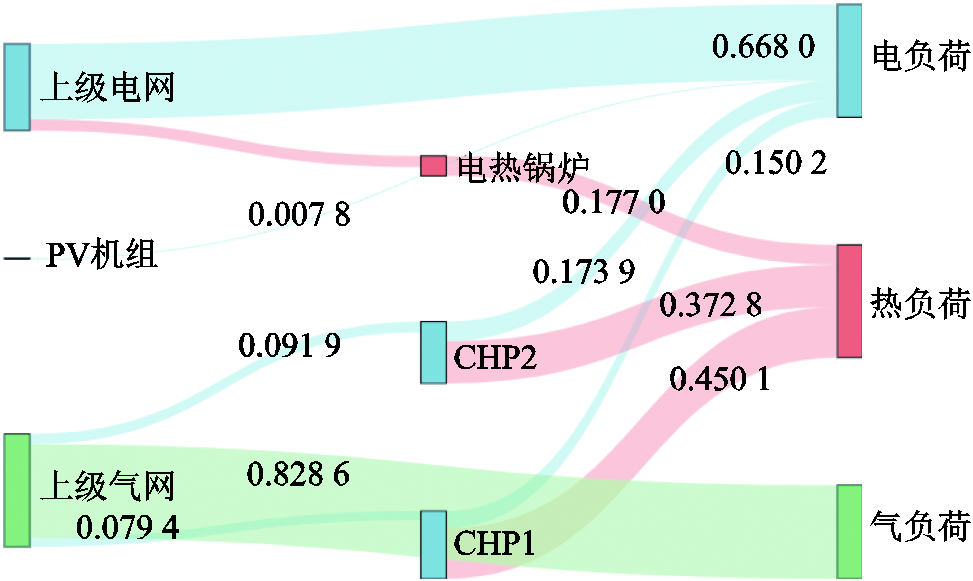
图7 RIES能源供应
Fig.7 RIES energy supply
在此基础上,分别计算各子系统耦合前后系统可靠性,结果如图8所示。图中圆形阴影区域分别表示电网、气网和热网耦合后的负荷供应概率,箭头表示此系统对另一系统可靠性的贡献程度,如箭头①表示电网与气网耦合后,气网提高电网0.51%可靠性,由于热网没有独立热源,箭头②和⑥表示图7中电网和气网供热占比。
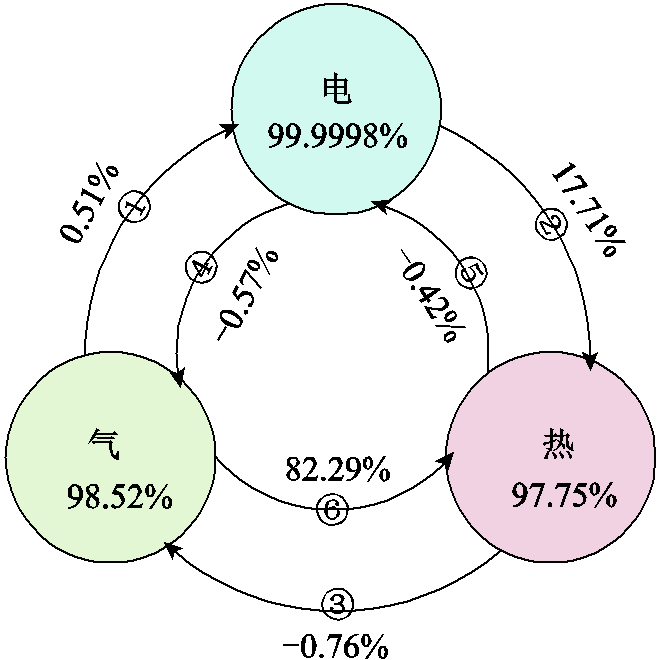
图8 RIES多能互补可靠性分析
Fig.8 RIES multi-energy complementary reliability analysis
由图7可知,电网正常情况下上级电网、热电联产机组、光伏机组供电占比分别为66.80%、32.42%、0.78%;由图8可知电网故障情况下,气网耦合贡献提高电网0.51%可靠性,热网耦合降低电网0.42%可靠性。在现有电网高可靠性基础上,多能互补进一步减少电网失负荷概率。
气网正常情况下负荷均由上级气网供应。故障情况下,与电网耦合降低气网0.57%可靠性,与热网耦合降低气网0.76%可靠性。由于图5系统结构中没有电转气的能源耦合设备,气网降低了1.33%的可靠性来保障电网和热网的可靠运行,因此,可增加气转电设备,在光伏弃光时以增加气源数量,能够在提高气网可靠性同时提高新能源消纳率。
由于热网缺少独立热源,正常情况下,热负荷由一台电热锅炉和两台热电联产机组供应,占比分别为17.70%、37.28%和45.01%;故障情况下,气网耦合贡献可靠性为82.3%,电网可靠性贡献为17.70%。由于电热锅炉容量限制,电网对热网可靠性贡献较低,因此,增大电转热设备容量,能够具有明显的可靠性增益。
5.2.4 热惯性对系统可靠性的影响
为分析热网惯性对可靠性的影响,针对是否计及热惯性的两种场景进行对比,可靠性指标见表9。P3和P4分别表示未考虑热惯性与考虑热惯性下失负荷概率,E3和E4分别表示失负荷期望。
表9 热惯性对系统可靠性的影响
Tab.9 Impact of thermal inertia on system reliability
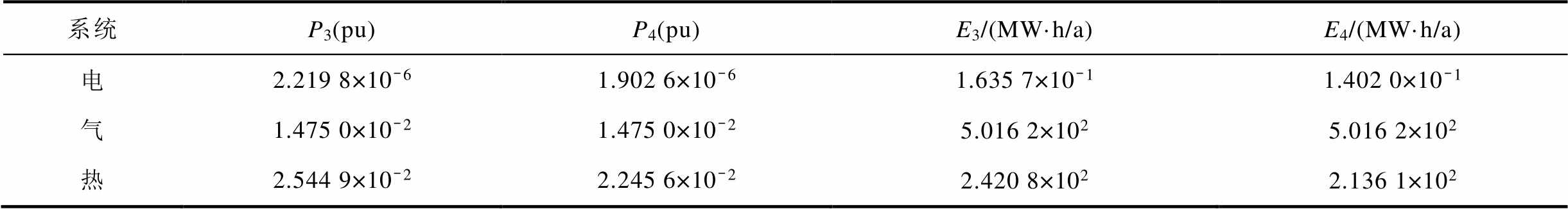
系统P3(pu)P4(pu)E3/(MW·h/a)E4/(MW·h/a) 电2.219 8×10-61.902 6×10-61.635 7×10-11.402 0×10-1 气1.475 0×10-21.475 0×10-25.016 2×1025.016 2×102 热2.544 9×10-22.245 6×10-22.420 8×1022.136 1×102
由表9可知,考虑热惯性后热网失负荷概率降低了11.76%,电网失负荷概率降低了14.29%,主要是因为考虑用户建筑热惯性以供热温度规定供热可靠性指标,牺牲了部分用户舒适度,在热网不影响自身可靠性基础上减供或停供,支撑故障时的电网或热网;热源惯性与热网惯性分别增加了2.33%和0.17%故障持续时间,同时当热网管道越长、管道直接越大对系统可靠性影响越大。
5.2.5 可行性分析
为表明本文所提方法的优越性,与现有研究进行对比分析,详情见附表3。由附表3可知,本文所提可靠性评估方法具有以下有优势:
(1)针对RIES可靠性评估,能够考虑源-网-荷多重热惯性,考虑元件多状态、多能耦合及用户舒适度特性,从而提高了可靠性评估的精确性。
(2)针对RIES中对可靠性影响较大的热惯性进行深入挖掘,并提出差异化建模思路,平衡精度与效率,所提方法更具有实用性。
(3)通过正常运行与故障后果分析,能够定量化设备重要性,有利于对设备重要程度进行评估,加快系统薄弱环节的识别。
同时,为了进一步验证所提方法的可扩展性,将其应用于由IEEE 123节点配电网、11节点配气网和32节点的配热网构成的区域电-气-热综合能源系统中,在节点14、49和104分别接入容量为 0.1 MW的光伏发电机,与图5采用相同的热电联产机组与电热锅炉,系统拓扑结构与耦合节点如图9所示。其中,配电网线路长度、线路故障率及节点用户数量等参数见文献[28]。
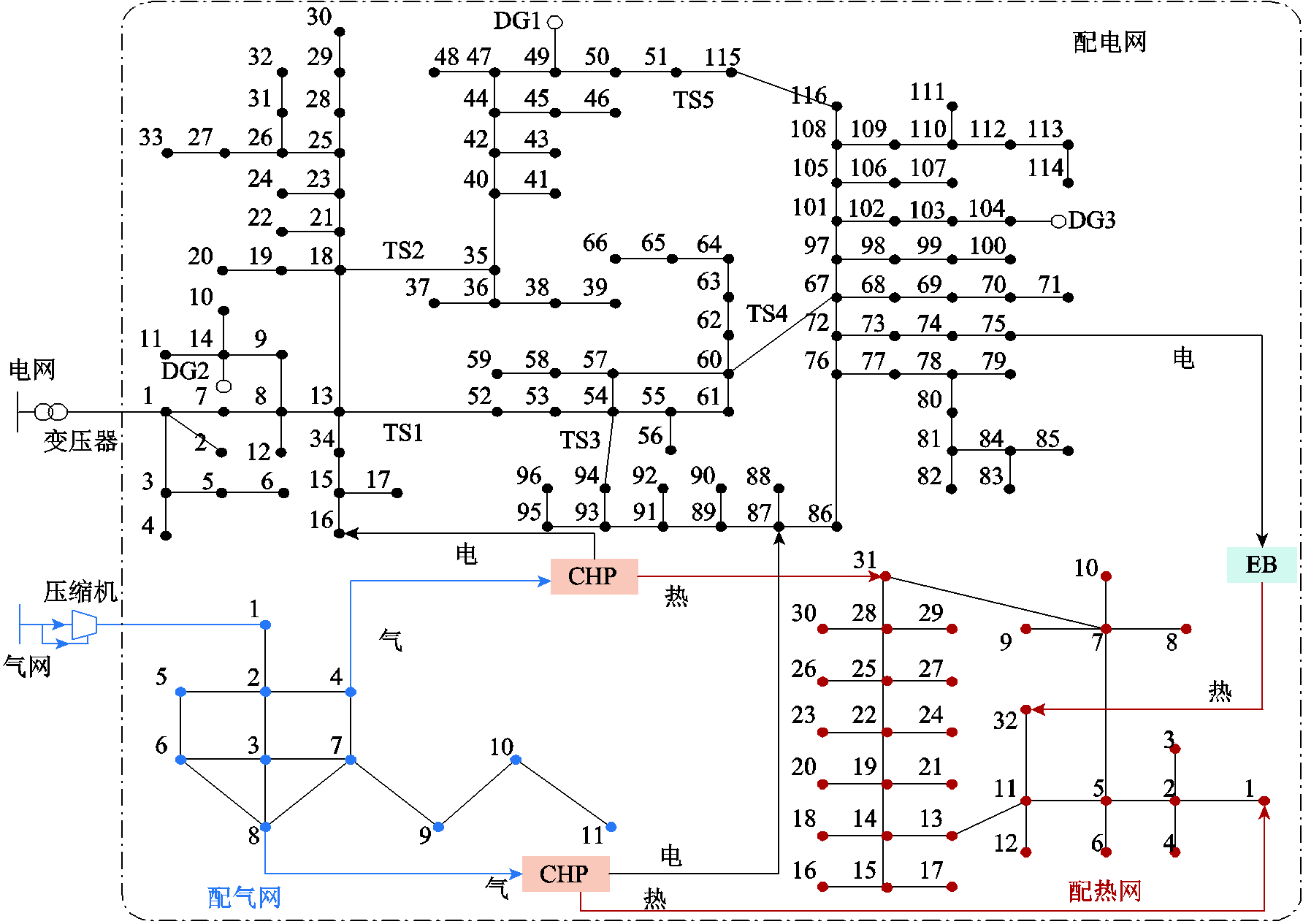
图9 E123G11H32 测试系统
Fig.9 E123G11H32 test system
采用本文所提可靠性评估方法进行仿真验证,仿真结果见表10。
表10 E123G11H32系统可靠性指标
Tab.10 Reliability indices for E123G11H32 system

指标电气热RIES LOLP3.734 2×10-31.475 0×10-26.516 8×10-27.946 9×10-2 EENS2.838 2×10-15.016 2×1026.199 0×1021.065 7×103 SAIFI2.926 1×10-11.638 9×10-32.036 5×10-32.962 9×10-1 SAIDI2.659 65.573 57.126 31.002 3×102
由表10可知,随着RIES中配电网规模的增大,系统故障情况增多。以SAIDI指标为例,可知配电网相比33节点测试算例系统平均停电时间增加,受电网故障影响,热网平均停电时间增加,表明多能耦合在提高系统可靠性的同时可能引起故障跨系统传播。同时,仿真结果表明本文所提方法具有实用性和可行性。
本文基于马尔科夫方法,建立了热电联产机组四状态可靠性模型,分别建立稳态的运行模拟模型与动态的最优切负荷模型,实现评估效率与精度的有机结合,基于序贯蒙特卡洛模拟实现了考虑多能互补与多重惯性的区域综合能源系统可靠性评估。经算例分析表明:
1)考虑热电联产机组运行状态,基于马尔科夫链解析法建立元件多状态可靠性模型,相比传统两状态模型针对供电和供热建模精度分别提高了26.22%和12.89%,降低了系统失负荷概率指标,可靠性评估更准确。
2)多能互补机制下气网与电网耦合对电网可靠性提升最大,提高了电网0.51%的可靠性。热电联产机组承担了电网32.41%与热网82.29%的能量供应,提高了耦合设备容量,令各子系统具有一定的源侧冗余度,能够带来较为明显的可靠性增益。
3)基于供热温度的供热可靠性指标,利用建筑热惯性能够提高热网11.76%的可靠性,热源惯性与热网惯性由于延长了热能传输到用户的时间,降低了系统可靠性,但利用光伏出力与用户需求时间差异性,以及在热源处配置热储,能够在运行时将热负荷转换为可平移负荷,提高系统运行经济性。
附 录
附表1 CHP机组状态转移矩阵
App.Tab.1 The state transfer matrix of CHP unit
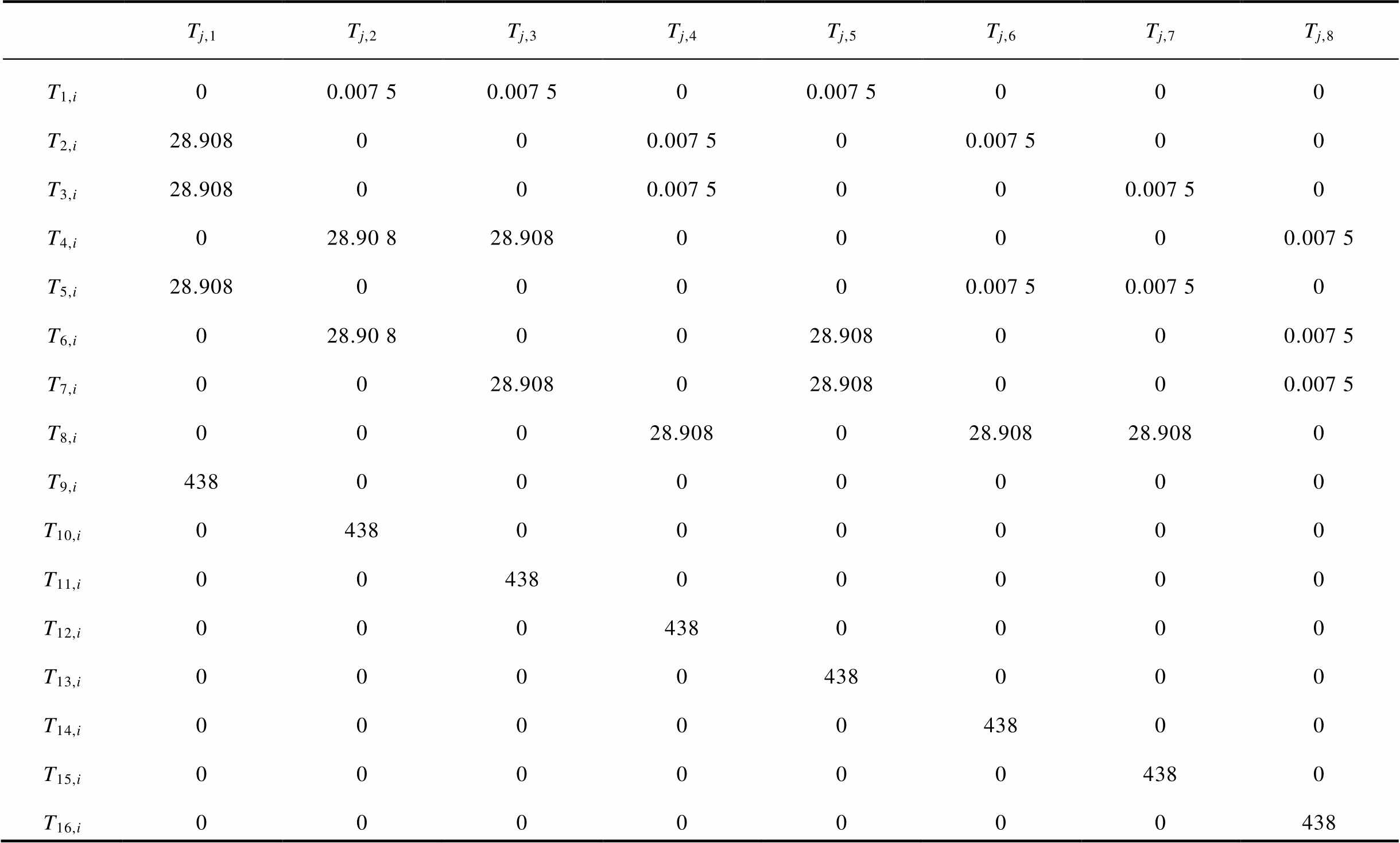
Tj,1Tj,2Tj,3Tj,4Tj,5Tj,6Tj,7Tj,8 T1,i00.007 50.007 500.007 5000 T2,i28.908000.007 500.007 500 T3,i28.908000.007 5000.007 50 T4,i028.90 828.90800000.007 5 T5,i28.90800000.007 50.007 50 T6,i028.90 80028.908000.007 5 T7,i0028.908028.908000.007 5 T8,i00028.908028.90828.9080 T9,i4380000000 T10,i0438000000 T11,i0043800000 T12,i0004380000 T13,i0000438000 T14,i0000043800 T15,i0000004380 T16,i0000000438
(续)
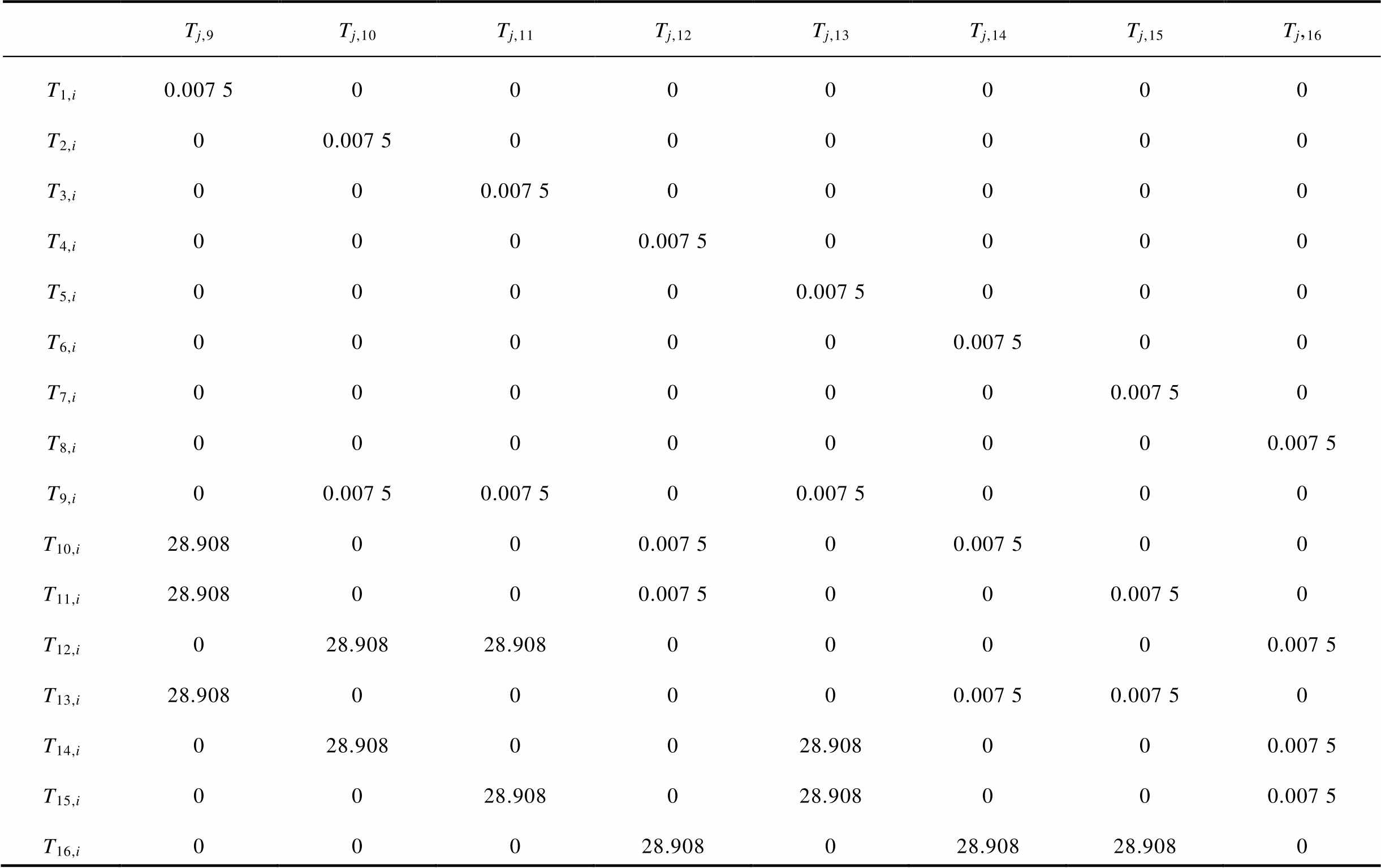
Tj,9Tj,10Tj,11Tj,12Tj,13Tj,14Tj,15Tj,16 T1,i0.007 50000000 T2,i00.007 5000000 T3,i000.007 500000 T4,i0000.007 50000 T5,i00000.007 5000 T6,i000000.007 500 T7,i0000000.007 50 T8,i00000000.007 5 T9,i00.007 50.007 500.007 5000 T10,i28.908000.007 500.007 500 T11,i28.908000.007 5000.007 50 T12,i028.90828.90800000.007 5 T13,i28.90800000.007 50.007 50 T14,i028.9080028.908000.007 5 T15,i0028.908028.908000.007 5 T16,i00028.908028.90828.9080
附表2 热网流速及管道传输时间
App.Tab.2 The mass flow and pipeline transmission time of heat network
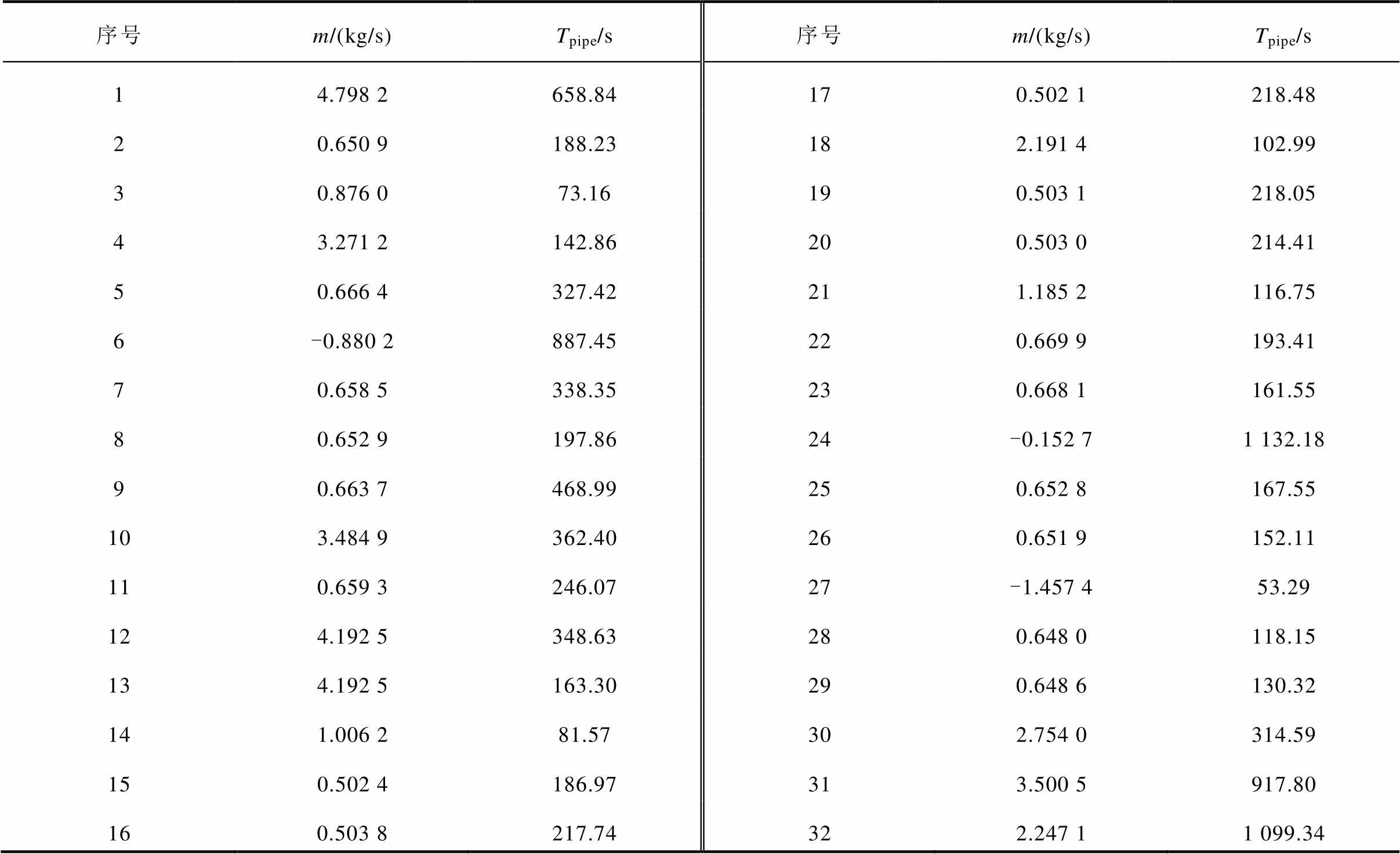
序号m/(kg/s)Tpipe/s序号m/(kg/s)Tpipe/s 14.798 2658.84170.502 1 218.48 20.650 9188.23182.191 4 102.99 30.876 073.16190.503 1 218.05 43.271 2142.86200.503 0 214.41 50.666 4327.42211.185 2 116.75 6-0.880 2887.45220.669 9 193.41 70.658 5338.35230.668 1 161.55 80.652 9197.8624-0.152 7 1 132.18 90.663 7468.99250.652 8 167.55 103.484 9362.40260.651 9 152.11 110.659 3246.0727-1.457 4 53.29 124.192 5348.63280.648 0 118.15 134.192 5163.30290.648 6 130.32 141.006 281.57302.754 0 314.59 150.502 4186.97313.500 5 917.80 160.503 8 217.74322.247 1 1 099.34
附表3 对比分析
App.Tab.3 Comparative analysis

时间精度网架元件状态动态特性用户舒适度 本文中高有多状态源网荷热惯性有 文献[29]短低有两状态无无 文献[7]短低无多状态无无 文献[14]中中有两状态无无 文献[19]中中有两状态热网惯性无 文献[21]长高有两状态气、热惯性有
参考文献
[1] 朱继忠, 骆腾燕, 吴皖莉, 等. 综合能源系统运行可靠性评估评述Ⅰ:模型驱动法[J]. 电工技术学报, 2022, 37(11): 2761-2776. Zhu Jizhong, Luo Tengyan, Wu Wanli, et al. A review of operational reliability assessment of integrated energy systems Ⅰ:model-driven method[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2761-2776.
[2] Bramerdorfer G. Multiobjective electric machine optimization for highest reliability demands[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(2): 71-78.
[3] 边晓燕, 史越奇, 裴传逊, 等. 计及经济性和可靠性因素的区域综合能源系统双层协同优化配置[J]. 电工技术学报, 2021, 36(21): 4529-4543. Bian Xiaoyan, Shi Yueqi, Pei Chuanxun, et al. Bi-level collaborative configuration optimization of integrated community energy system considering economy and reliability[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4529-4543.
[4] 马钰, 韦钢, 李扬, 等. 考虑孤岛源-荷不确定性的直流配电网可靠性评估[J]. 电工技术学报, 2021, 36(22): 4726-4738. Ma Yu, Wei Gang, Li Yang, et al. Reliability evaluation of DC distribution network considering islanding source-load uncertainty[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4726-4738.
[5] 臧海祥, 耿明昊, 黄蔓云, 等. 电-热-气混联综合能源系统状态估计研究综述与展望[J]. 电力系统自动化, 2022, 46(7): 187-199. Zang Haixiang, Geng Minghao, Huang Manyun, et al. Review and prospect of state estimation for electricity-heat-gas integrated energy system[J]. Automation of Electric Power Systems, 2022, 46(7): 187-199.
[6] 程林, 万宇翔, 齐宁, 等. 含多种分布式资源的配用电系统运行可靠性研究评述及展望[J]. 电力系统自动化, 2021, 45(22): 191-207. Cheng Lin, Wan Yuxiang, Qi Ning, et al. Review and prospect of research on operation reliability of power distribution and consumption system considering various distributed energy resources[J]. Automation of Electric Power Systems, 2021, 45(22): 191-207.
[7] 倪伟, 吕林, 向月, 等. 基于马尔科夫过程蒙特卡洛法的综合能源系统可靠性评估[J]. 电网技术, 2020, 44(1): 150-158. Ni Wei, Lü Lin, Xiang Yue, et al. Reliability evaluation of integrated energy system based on Markov process Monte Carlo method[J]. Power System Technology, 2020, 44(1): 150-158.
[8] 徐波, 孙宏斌, 鲁刚, 等. 基于机会维修的热电联产机组检修计划[J]. 电力建设, 2018, 39(12): 88-94. Xu Bo, Sun Hongbin, Lu Gang, et al. Maintenance optimization based on opportunistic maintenance for combined heat and power unit[J]. Electric Power Construction, 2018, 39(12): 88-94.
[9] 姚婷婷, 管乐诗, 石恩达, 等. 一种低母线电压尖峰的改进型Y源逆变器及其可靠性分析[J]. 电工技术学报, 2021, 36(增刊1): 209-217. Yao Tingting, Guan Yueshi, Shi Enda, et al. A low DC-link voltage spike modified Y-source inverter and its reliability evaluation[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 209-217.
[10] 廉永乐. 空管供配电系统可靠性分析[J]. 电气技术, 2021, 22(5): 89-96. Lian Yongle. Reliability analysis of power supply and distribution system of air transportation management[J]. Electrical Engineering, 2021, 22(5): 89-96.
[11] Geidl M, Koeppel G, Favre-Perrod P, et al. Energy hubs for the future[J]. IEEE Power and Energy Magazine, 2007, 5(1): 24-30.
[12] Koeppel G. Reliability modeling of multi-carrier energy systems[J]. Energy, 2009, 34(3): 235-244.
[13] 齐先军, 程桥, 吴红斌, 等. 激励型需求响应对配电网运行可靠性的影响[J]. 电工技术学报, 2018, 33(22): 5319-5326. Qi Xianjun, Cheng Qiao, Wu Hongbin, et al. Impact of incentive-based demand response on opreational reliability of distribution network[J]. Transactions of China Electrotechnical Society, 2018, 33(22): 5319-5326.
[14] Kou Yu. Reliability evaluation of multi-agent integrated energy systems with fully distributed communication[J]. Energy, 2021, 224: 120123.
[15] Fang Jiakun, Zeng Qing, Ai Xiaomeng, et al. Dynamic optimal energy flow in the integrated natural gas and electrical power systems[J]. IEEE Transactions on Sustainable Energy, 2018, 9(1): 188-198.
[16] Yao Shuai, Gu Wei, Lu Shuai, et al. Dynamic optimal energy flow in the heat and electricity integrated energy system[J]. IEEE Transactions on Sustainable Energy, 2021, 12(1): 179-190.
[17] 刘文霞, 富梦迪, 李涵深, 等. 计及信息失效的柔性配电系统集中-分散协调控制策略优化[J]. 电工技术学报, 2021, 36(22): 4749-4759. Liu Wenxia, Fu Mengdi, Li Hanshen, et al. Centralized-decentralized control strategies optimization for flexible distribution network considering cyber failures[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4749-4759.
[18] Zhang Shenxi, Wen Min, Cheng Haozhong, et al. Reliability evaluation of electricity-heat integrated energy system with heat pump[J]. CSEE Journal of Power and Energy Systems, 2018, 4(4): 425-433.
[19] 刘文霞, 杨粤, 李征洲, 等. 考虑多能流传输与热惰性的综合能源系统序贯模拟可靠性评估[J]. 电力自动化设备, 2020, 40(7): 10-16. Liu Wenxia, Yang Yue, Li Zhengzhou, et al. Reliability evaluation of integrated energy system considering multi-energy flow transmission and thermal inertia based on sequential simulation[J]. Electric Power Automation Equipment, 2020, 40(7): 10-16.
[20] Wang S, Shao C, Ding Y, et al. Operational reliability of multi-energy customers considering service-based self-scheduling[J]. Applied Energy, 2019, 254: 113531.
[21] Cao Maosen, Shao Changzheng, Hu Bo, et al. Reliability assessment of integrated energy systems considering emergency dispatch based on dynamic optimal energy flow[J]. IEEE Transactions on Sustainable Energy, 2022, 13(1): 290-301.
[22] Li Gengfeng, Huang Yuxiong, Bie Zhaohong. Reliability evaluation of smart distribution systems considering load rebound characteristics[J]. IEEE Transactions on Sustainable Energy, 2018, 9(4): 1713-1721.
[23] 崔艳妍, 刘伟, 苏剑, 等. 考虑最优负荷削减与热负荷惯性的综合能源系统可靠性评估[J]. 电力建设, 2021, 42(4): 40-48.Cui Yanyan, Liu Wei, Su Jian, et al. Reliability evaluation of integrated energy system considering optimal load reduction and thermal load inertia[J]. Electric Power Construction, 2021, 42(4): 40-48.
[24] Li Guoqing, Zhang Rufeng, Jiang Tao, et al. Optimal dispatch strategy for integrated energy systems with CCHP and wind power[J]. Applied Energy, 2017, 192: 408-419.
[25] 黄易君成, 王志强, 刘文霞, 等. 基于个体时空行为模拟的区域电供暖负荷特性建模[J]. 电力系统自动化, 2022, 46(11): 85-93. Huang Yijuncheng, Wang Zhiqiang, Liu Wenxia, et al. Characteristic modeling of regional electric heating load based on individual spatial-temporal behavior simulation[J]. Automation of Electric Power Systems, 2022, 46(11): 85-93.
[26] Gu Wei, Wang Jun, Lu Shuai, et al. Optimal operation for integrated energy system considering thermal inertia of district heating network and buildings[J]. Applied Energy, 2017, 199: 234-246.
[27] Yang Hejun, Zhang Yeyu, Ma Yinghao, et al. Reliability assessment of integrated energy system considering the uncertainty of natural gas pipeline network system[J]. IET Generation, Transmission & Distribution, 2019, 13(22): 5033-5041.
[28] Chen Houhe, Zhang Yutong, Zhang Rufeng, et al. Privacy-preserving distributed optimal scheduling of regional integrated energy system considering different heating modes of buildings[J]. Energy Conversion and Management, 2021, 237: 114096.
[29] 张雪寒, 余涛. 计及风速与负荷相关性的电-气互联系统概率可靠性评估方法[J]. 高电压技术, 2019, 45(10): 3263-3272. Zhang Xuehan, Yu Tao. Probabilistic reliability evaluation method of electricity-gas integrated energy system considering correlation of wind speeds and loads[J]. High Voltage Engineering, 2019, 45(10): 3263-3272.
Abstract In the real world, the energy crisis and environmental pollution problems are prominent. Traditional fossil energy has been unable to meet the rapidly growing energy demand of human society. The regionally integrated energy system came into being to meet the distribution network's green and low-carbon development needs. However, the development form of multi-energy complementation of regionally integrated energy systems brings incredible difficulties to its reliability assessment. In recent years, some reliability assessment methods for regional integrated energy systems have been proposed, but they lack practicality, and the calculation accuracy and efficiency are out of balance. A reliability assessment method for a regionally integrated energy system based on sequential Monte Carlo simulation considering multiple thermal inertias was proposed to solve this problem. A practical evaluation method is suggested by improving the calculation accuracy and efficiency from three aspects of the component outage model, system modeling, evaluation method, and fault state analysis.
Firstly, the typical structure of the CHP unit was constructed. The operating states of the CHP unit, such as normal operation, power-heat reduction, power supply reduction, and system shutdown, are analyzed. A four-state reliability model for the CHP unit was developed based on Markov chains. Secondly, the effects of heat source start-up inertia, heat network transmission inertia, and building thermal inertia on system reliability were analyzed. Based on differentiated energy flow modeling, an operation optimization model for steady-state and a dynamic optimal load-cutting model considering multiple thermal inertias were proposed. The optimization models were established with the objectives of operation economy and equivalent load loss amount, respectively. Finally, the heat network loss of load indices was corrected by counting user comfort characteristics. A sequential Monte Carlo simulation is used to evaluate the reliability of the regionally integrated energy system. The simulation results show that compared with the traditional two-state model, the four-state reliability model of components based on the Markov chain analytic method improves the modeling accuracy of power supply and heating by 26.22% and 12.89% respectively, and reduces the probability index of system load loss. It has higher evaluation accuracy. Under the multi-energy complementary mechanism, coupling the gas grid and power grid improves the power grid's reliability by 0.51%. The cogeneration unit undertakes 53.44% of the energy supply of the power grid and heat supply network. Therefore, increasing the capacity of coupling equipment and making each subsystem have certain source side redundancy can bring noticeable reliability gain. The reliability index of heating based on heating temperature is proposed. The reliability of the heating network can be improved by 11.76% by using building thermal inertia. Although the heat source inertia and heat network inertia reduce the system reliability due to the extension of the time for heat energy transmission to users, using the difference between photovoltaic output and user demand time and the configuration of heat storage at the heat source can convert the heat load into translatable load during operation, which can improve the system operating economy.
The following conclusions can be drawn from the simulation analysis: (1) The detailed description of the reliability model of CHP units can effectively improve the reliability evaluation of regionally integrated energy systems. (2) Analyzing the difference in energy flow in different subsystems and the idea of differential energy flow modeling in normal and fault phases can effectively improve the calculation accuracy and efficiency. (3) Full use of the multiple thermal inertias of the source, grid, and load in the thermal system can effectively reduce the frequency and duration of the system load loss event under fault conditions.
keywords:Regional integrated energy system, reliability evaluation, thermal inertia, reliability model, sequential Monte Carlo simulation
DOI:10.19595/j.cnki.1000-6753.tces.220367
中图分类号:TM73
国家重大科技专项资助项目(2020YFC0827001)。
收稿日期2022-03-14
改稿日期 2022-05-19
张 帅 男,1994年生,博士研究生,研究方向为综合能源系统可靠性评估。E-mail:zsrfkl@ncepu.edu.cn
刘文霞 女,1967年生,教授,博士生导师,研究方向为电力系统风险及可靠性评估、经济调度。E-mail:liuwenxia001@163.com(通信作者)
(编辑 赫 蕾)