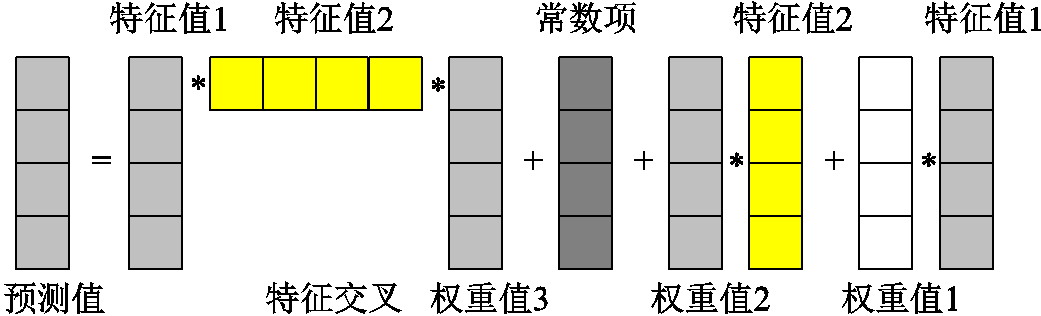
图1 特征交叉原理
Fig.1 Feature crossover principle
摘要 为提高短期风电功率预测精度，首先在卷积神经网络（CNN）-长短期记忆（LSTM）网络模型的基础上，引入特征交叉（FC）机制，对风电场数据集进行相关性分析并交叉组合，增加特征维度，加强非线性特征学习，挖掘隐藏关联，提高训练精度，构建形成FC-CNN-LSTM预测模型；然后，将该预测模型在风电预测中产生的误差值作为训练数据，训练生成误差补偿模型，利用该模型计算结果对风电预测数据进行补偿，进一步提高预测精度；最后，通过仿真验证该方法具有较高的预测精度，且相比传统预测模型，在分钟级超短期尺度上的预测性能具有显著优势。
关键词：卷积神经网络 长短期记忆网络 风功率预测 特征交叉 误差补偿
随着双碳目标和经济高质量发展要求的持续推进，以可再生能源为主体的新型电力系统逐渐成为我国未来电力系统发展的首要方向[1]，截至2021年底，我国风力发电装机容量突破3亿kW[2]。但风力发电具有随机性、间歇性、不确定性等特点，且受限于成本、空间等因素，储能系统难以大量存储电能，导致弃风率常年居高不下。因此，精确的风力发电功率预测是提高可再生能源消纳、保障电网安全稳定运行的首要条件[3]。
目前风电功率预测方法主要有物理建模、统计建模、人工智能算法建模三类[4-5]。传统的物理、统计建模方法由于物理数据收集、参数选择难度较大，处理大量数据的能力较弱，难以建立精确的预测模型[5]，所以在实际应用中通常采用人工智能算法对风功率预测进行建模。早期采用的人工智能算法主要包括人工神经网络（Artificial Neural Network, ANN）、支持向量机（Support Vector Machine, SVM）[6-7]。ANN虽然对非线性问题具有较强的处理能力，但其计算量与未知量数量成正比，容易陷入局部最优[8]；SVM不易陷入局部最优，但其算法参数选择没有规律，需要使用者凭经验选择[9]。
随着神经网络算法的不断发展，陆续有循环神经网络（Recurrent Neural Network, RNN）[10]、长短期记忆（Long Short Term Memory, LSTM）神经网络[11]、门控循环（Gated Recurrent Unit, GRU）神经网络[12]等序列数据预测的神经网络算法应用于风电功率预测。文献[13]基于长短期记忆网络提出了多变量超短期风电场发电功率预测方法，预测精度较ANN及SVM更高。文献[14-15]分别使用遗传、蜻蜓优化算法对LSTM进行改进，优化了LSTM中窗口大小和神经元数量等参数的选取。文献[16]首先利用小波变换对输入数据进行分解，然后使用卷积神经网络（Convolution Neural Network, CNN）对分解后每个频率中的非线性特征进行学习，实验证明该方法对于风电预测中的不确定性数据具有更精确的预测结果。文献[17]在对输入数据进行聚类的基础上，使用深度信念网络建立了风功率预测模型，预测精度较传统神经网络大幅提高。
上述对风功率预测的研究集中在对人工智能算法的使用和改进上，没有考虑数据中的不同特征与风电功率的相关性，以及特征表达关联性的能力差异，训练得到的模型只能建立单一、表面的关联，不能挖掘出更深层的关系，不利于风功率的短期预测。因此，本文引入特征交叉机制对特征数据进行预处理，特征交叉也称为特征组合，是在计算机推荐算法领域广泛应用的特征处理方法，本质是利用原有特征之间的相互运算产生新特征[18]。新特征除了可以增加特征维度，还因为包含了与待预测值之间的非线性关联，可以使模型学习到更为深层次的隐藏关系，增强模型拟合精度，得到更好的训练效果[19-20]。
综上所述，本文首先引入特征交叉机制，对数据特征进行相关性分析并交叉组合，增加特征维度，加强非线性特征和深层隐藏关联的学习能力，基于CNN-LSTM网络改进形成FC-CNN-LSTM预测模型；然后将该预测模型在预测中产生的误差值作为训练数据，训练生成误差补偿模型，利用计算产生的数据对风电预测数据进行补偿，进一步提高预测精度；最后通过某风电场实测数据验证了FC-CNN-LSTM模型具有较高的预测精度，且增加误差补偿流程后，相比传统预测方法，该模型可以进一步减小误差，具有显著的优势。
1.1.1 特征交叉基本原理
通常在实际预测中，风电功率往往与风速特征呈现出较强的线性关联，而并未与气压、空气密度、温度等特征表现出明显的线性关联。将这些表面上关联性不大的特征投入算法进行训练后，发现并不能提高预测的精确度，反而使训练时间加长，且模型更不稳定。原因在于这些特征除了与风电功率存在表面上的弱线性关联之外，还存在通过其他特征间接表现出的深层非线性关联。因此如果模型只利用原始的线性数据进行训练，就不能学习到这些深层的非线性关联，也就不能建立起风电功率与影响特征之间的准确联系。所以在实际操作中往往会将气压、空气密度、温度等弱关联特征的数据忽略，造成了数据的浪费和预测精度的降低。
因此本文引入特征交叉机制对风电预测中的弱关联特征进行处理，特征交叉是数据特征的一种处理方式，即将不同类型或不同维度的特征，以相乘或笛卡尔积的形式（连续特征相乘，离散特征做笛卡尔积）进行交叉组合，特征交叉原理如图1所示。以增加特征维度，表现出特征与待预测值之间的非线性关联，从而加强模型的非线性学习能力，提高训练精度。
采用乘积或笛卡尔积运算的目的是为了确保产生的新特征为非线性特征。任意两个线性或非线性特征在经过相乘之后均为非线性特征，而加减运算不能应对特征均为线性的情况，除法运算虽然也可以得到非线性特征，但会降低特征的数量级，不利于模型的学习。此外若再涉及其他的数学运算会使该过程更为复杂，因此不考虑。特征交叉的公式为
图1 特征交叉原理
Fig.1 Feature crossover principle
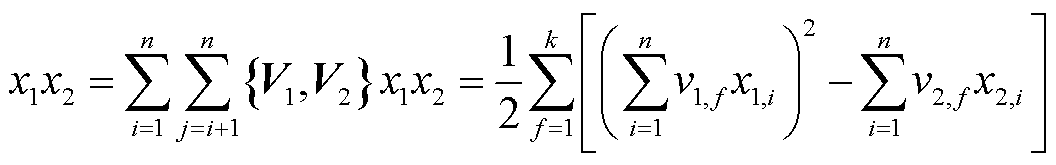（1）
式中，
、
为两个不同的特征；n为特征数据长度；
、
为特征辅助向量集（当特征数据为一维时可不取或均取1）；
为特征辅助向量宽度；
、
分别为辅助向量的第f个元素和特征的第i个元素。
假设在实际预测中存在式（2）所示的预测关系。
（2）
式中，
为预测值；
、
分别为特征值、对应的权重值；
为固定常数项。
在式（2）中，若预测值与特征值呈现出较强的关联特性，而未与特征值表现出明显的关联，但发现在多个相同时刻特征值、经常同时出现，说明特征值、之间具有一定的关联，因此可以认为特征值与预测值之间具有某种通过来表达的深层关系。但如果直接将特征值、在未进行组合的情况下投入模型进行训练，模型则难以发现并学习到此类深层次的关系，因此将其进行特征交叉处理，有
（3）
（4）
式中，
为特征交叉后的预测值；
为、经过特征交叉后形成的新特征值；
、
、
为特征交叉后各特征对应的新权重值；
为交叉后的固定常数项。
可以发现，预测值通过特征交叉得到了修正，修正后的表达式引入了新特征值。新特征值由于是通过、交叉得到，因此在包含了特征值、独立特征的同时，还会对特征值与之间的联系进行加强（特征交叉的特性），表现出与之间的联系。而由于预测值与特征值呈现出较强的关联特性，同时又包含了与之间的联系，所以可以通过特征值与预测值之间的关系，间接表现出特征值与预测值之间的深层联系，如图2所示。因此经过特征交叉修正之后的模型，在增加特征维度的同时，也提高了特征的表达能力，使模型可以通过新特征学习到更为深层次的非线性特征，增强拟合精度，得到更好的训练效果。
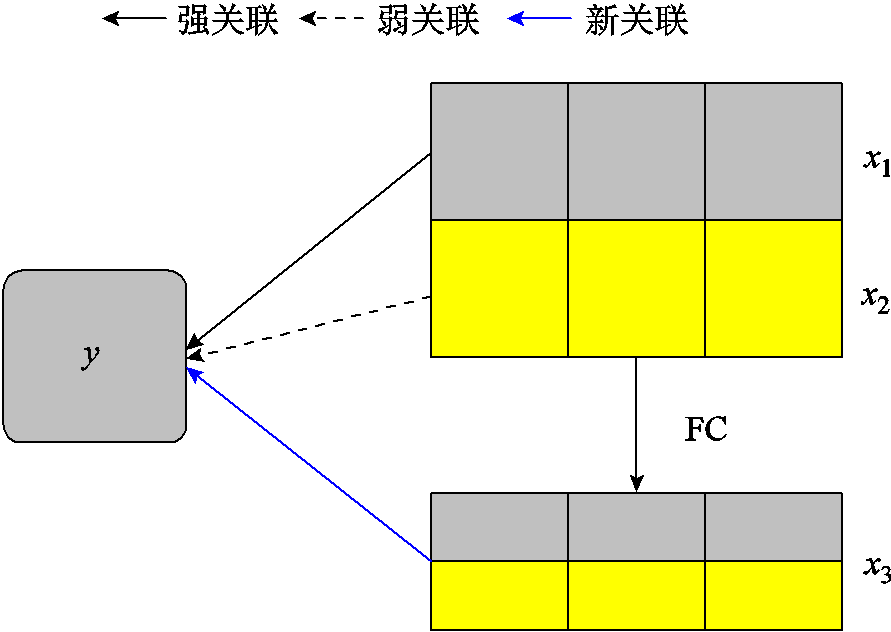
图2 特征交叉后新关联示意图
Fig.2 Schematic diagram of new association after feature intersection crossover
1.1.2 特征相关性分析
如1.1.1节所述，特征交叉的主要目的是加强对非线性特征的学习，建立新的关联，增强模型的深层学习能力，因此进行特征交叉的首要步骤就是对预测值与各特征值和特征值与特征值之间的相关性进行分析，常用皮尔逊相关系数公式进行分析，即
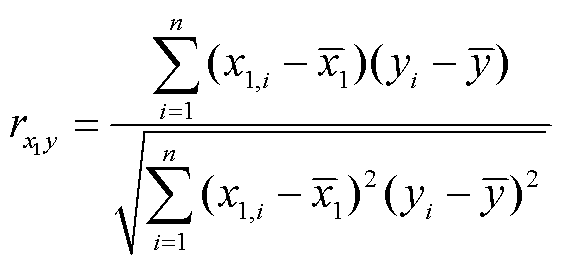（5）
式中，
为特征与之间的相关系数；
为第i个预测值；
为特征值第i个值；
、
分别为特征值、预测值的均值。
使用皮尔逊相关系数公式计算得到结果为正时，表示两者之间呈正相关关系；反之则为负相关。该结果的绝对值大小则表示两者之间的线性相关程度，绝对值越大则线性相关程度越高，相关系数绝对值与线性相关程度见表1。
表1 相关系数绝对值与相关程度关系
Tab.1 Relationship between absolute value of correlation coefficient and correlation degree
相关系数绝对值相关程度 0.8～1.0极强相关 0.6～0.8强相关 0.4～0.6中等相关 0.2～0.4弱相关 0.0～0.2极弱相关
本文对某小型风电场2012年1—2月监测数据进行分析，数据除风电场平均发电功率数值外，还包括100 m高度风向、100 m高度风速、温度、气压、轮毂高度空气密度（数据集中风电功率是该风电场所有风机的总体功率，风速、风向等数据来自风电场某一固定点的测量值），五个影响因素各自与风电功率的相关性和各影响因素之间的相关性见表2。
表2 各参数之间的相关系数
Tab.2 Correlation coefficient between parameters
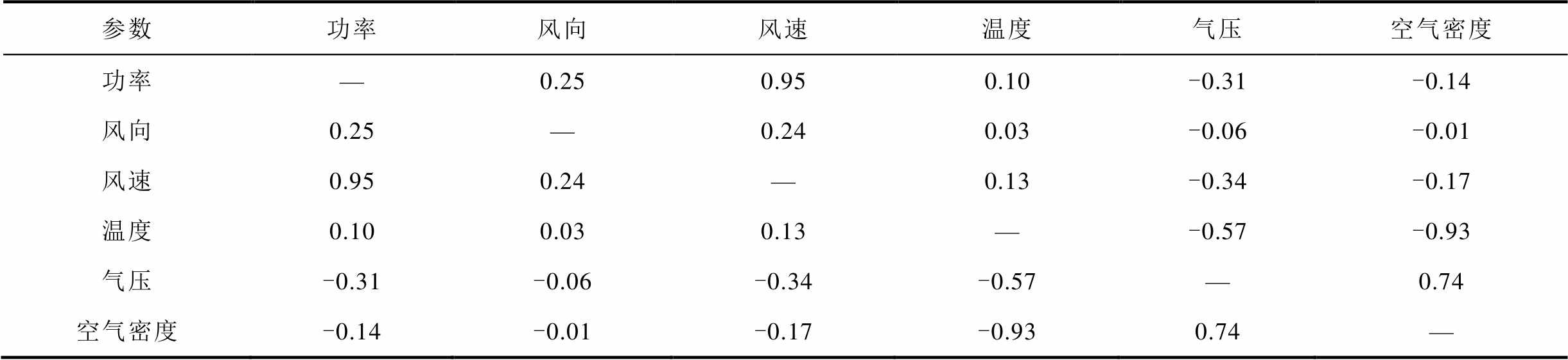
参数功率风向风速温度气压空气密度 功率—0.250.950.10-0.31-0.14 风向0.25—0.240.03-0.06-0.01 风速0.950.24—0.13-0.34-0.17 温度0.100.030.13—-0.57-0.93 气压-0.31-0.06-0.34-0.57—0.74 空气密度-0.14-0.01-0.17-0.930.74—
由表2可知，对风电功率影响最大的因素是风速，两者相关系数高达0.95，其后依次为气压-0.31、风向0.25、空气密度-0.14、温度0.1。可以发现，除风速与功率的相关程度达到了极强相关之外，其余因素与功率之间均为弱相关或极弱相关，但相关系数绝对值差距不大，因此不宜忽略其中的某个因素，所以在下文的模型训练中上述五个因素均设置为变量投入模型进行训练。
1.1.3 皮尔逊相关系数法的改进与特征选择
通过1.1.2节的分析可以非常清晰地看到风电功率与各因素之间的相关程度，但如前文所述，预测值与不同特征之间不仅存在直接、线性的表面关系，还存在诸多间接、非线性的内部深层联系，仅通过皮尔逊相关系数难以清楚地发现这些联系。因此本文提出隐藏相关系数和复合相关系数对皮尔逊相关系数法进行改进，用以表明特征与预测值之间的深层关联，以便筛选出需要进行交叉的特征。
直接相关系数指某特征与预测值通过皮尔逊相关系数法计算得到的相关系数。
隐藏相关系数用于判断特征与预测值之间是否存在深层关联，其定义是：若特征与预测值之间直接相关，且特征值、之间通过计算发现也具有相关性，则特征值与预测值之间存在通过特征值表达的隐藏相关性（与y是否存在隐藏相关与与y是否直接相关没有关系），计算得到的相关系数称为隐藏相关系数。
复合相关系数相较于使用皮尔逊相关系数公式计算得到的直接相关系数，可以更加综合和全面地评判各个特征对预测值的贡献程度，其定义是：若特征同时存在与预测值的直接相关和通过其他特征表现与预测值的隐藏相关，则其与预测值的复合相关系数等于直接相关系数与其他所有隐藏相关系数之和。其公式原理如下。
（6）
（7）
（8）
式中，
为特征与预测值通过特征间接计算得到的隐藏相关系数；
为特征与预测值通过除外的所有特征得到的总隐藏相关系数；
为特征与预测值之间复合相关系数；m为特征数量。
通过上述公式计算得到隐藏与复合相关系数见表3。表3中隐藏相关系数表示由列的特征通过行中某一特征向风电功率表达出来的相关性大小，复合相关系数表示横坐标中某一特征自身与风电功率的相关系数加上纵坐标中所有特征的隐藏相关系数之和。可以发现各特征的复合相关系数绝对值明显较表2中的皮尔逊相关系数数值更大，特别是风向、温度、气压、空气密度四个特征对风电功率的相关性从弱相关或极弱相关，提高到了中等相关或强相关。说明这几个特征与风电功率之间还存在更深层的非线性关联，而这种关联仅通过皮尔逊相关系数是不能够体现出来的。
表3 各参数与功率的隐藏和复合相关系数
Tab.3 Hidden and composite correlation coefficients between parameters and power
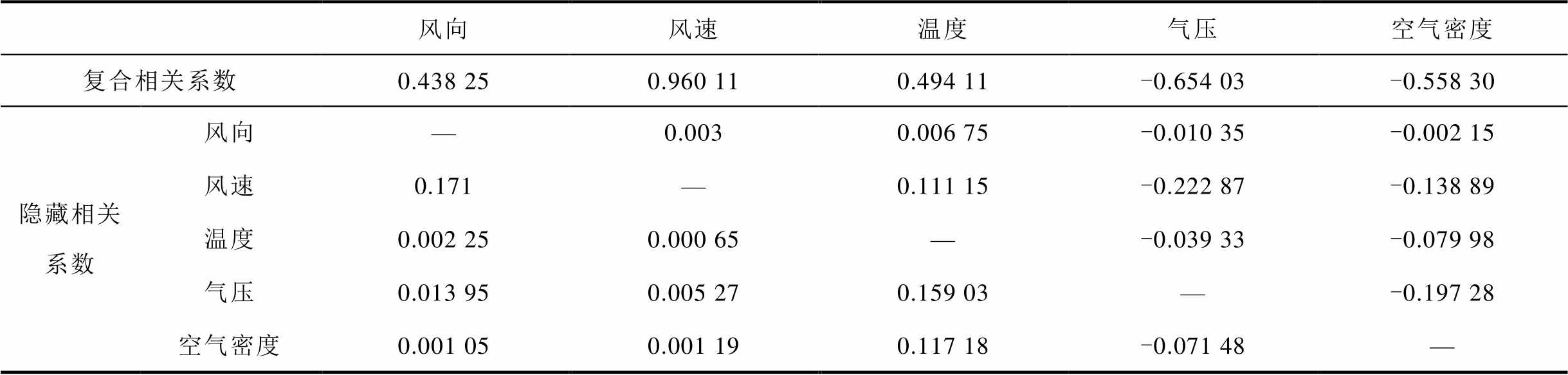
风向风速温度气压空气密度 复合相关系数0.438 250.960 110.494 11-0.654 03-0.558 30 隐藏相关系数风向—0.0030.006 75-0.010 35-0.002 15 风速0.171—0.111 15-0.222 87-0.138 89 温度0.002 250.000 65—-0.039 33-0.079 98 气压0.013 950.005 270.159 03—-0.197 28 空气密度0.001 050.001 190.117 18-0.071 48—
因此，如果根据皮尔逊公式的计算结果来选择参与模型训练的特征，就容易将风向、温度等特征忽略；但如果直接将这些弱关联特征投入模型进行训练，由于这些弱关联特征的非线性关联在原始数据中基本没有表现出来，模型训练时也就难以进行学习，因此需要对其进行交叉，得到可以表达出非线性关联的新特征，将其投入模型进行训练，才可以提高训练精度。
由表3可知，在第一列数据中，风速通过风向特征向风电功率表现出的隐藏相关系数达到了0.171，该值相对于该列中其他特征通过风速得到的隐藏相关系数更大（超过一个数量级），具有较强关联性，因此保留风速特征与风向特征进行交叉，其余特征忽略。同理，第二列数据中，纵坐标所有特征通过风速向风电功率表达出的隐藏相关系数远小于风速自身与风电功率的相关系数，所以均可忽略；第三列数据中，保留纵坐标中的风速、气压、空气密度三个特征与温度进行交叉；第四列数据中，保留纵坐标中的风速特征与气压进行交叉；第五列数据中，保留纵坐标中的风速、温度、气压特征三个与密度进行交叉。
由此，排除相同选项后，选择对（风向、风速）、（温度、风速、气压、空气密度）、（气压、风速）三个组合分别进行特征交叉。
1.2.1 CNN原理
CNN是一种利用卷积计算来降低特征维度，从而减少模型训练参数，简化模型复杂度的前馈神经网络。可以解决传统全连接神经网络中空间信息丢失、效率低下、训练困难和网络过拟合的问题，实现数据特征的高效快速提取，降低特征提取和分类过程中数据重建的复杂度。CNN网络主要结构卷积层的原理如图3所示。
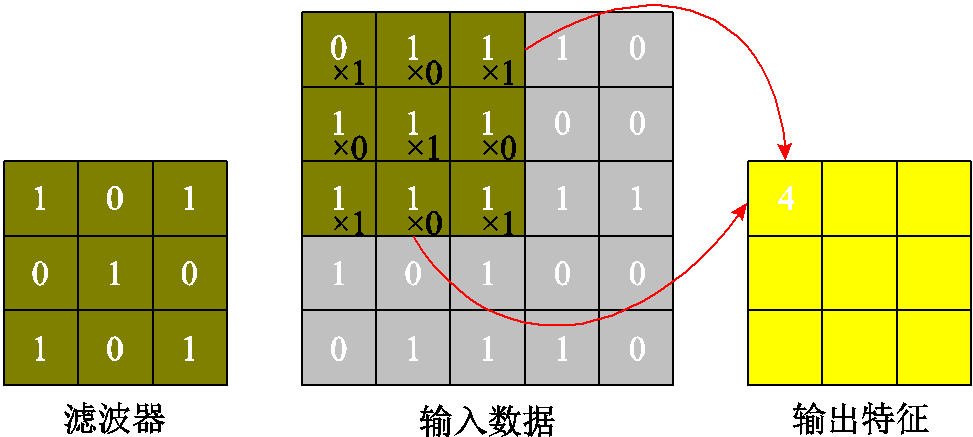
图3 卷积层原理图
Fig.3 Convolution layer principle
卷积层的作用是通过一个维度小于输入数据的滤波器，沿一个固定步长在输入数据内不断移动，对每次移动所取得的数据进行卷积运算，并将运算结果输出作为特征数据，从而达到降维的目的，其减少维度的多少取决于滤波器、步长的大小。
1.2.2 LSTM网络原理
LSTM网络是一种具有记忆长短期信息的能力的神经网络，通过引入门控机制来控制特征的存储和遗忘，从而获得增加和去除网络中所传输信息的能力。解决了传统循环神经网络长期依赖、梯度爆炸、消失的问题，可以很好地刻画具有时空关联的序列数据，实现基于事件序列的预测，且结构更为简单，其结构如图4所示。
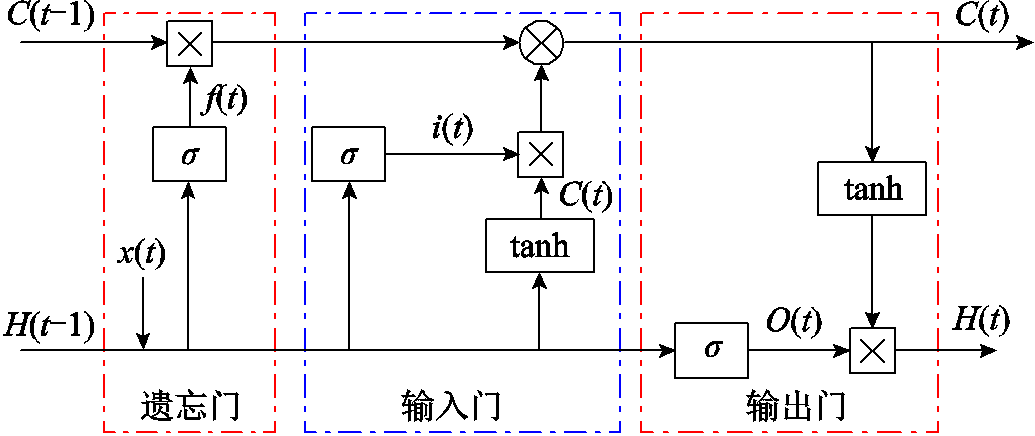
图4 LSTM网络结构
Fig.4 Network structure of LSTM
三个门的作用分别为：遗忘门，控制需要遗忘和保留的信息，避免梯度随时间反向传播时导致的梯度消失和梯度爆炸问题；输入门，确定哪些新的信息需要被保留在细胞状态中；输出门，基于细胞状态在过滤后进行输出。
FC-CNN-LSTM模型结构如图5所示，主要的改进是在传统CNN-LSTM模型基础上，将FC特征交叉模块添加到CNN模块的前端，对数据进行特征交叉预处理，增加特征维度和数据关联，增强特征的表达能力，使后续的CNN-LSTM模型可以学习到更深层次的非线性隐藏关联，增强拟合精度，得到更好的预测效果。
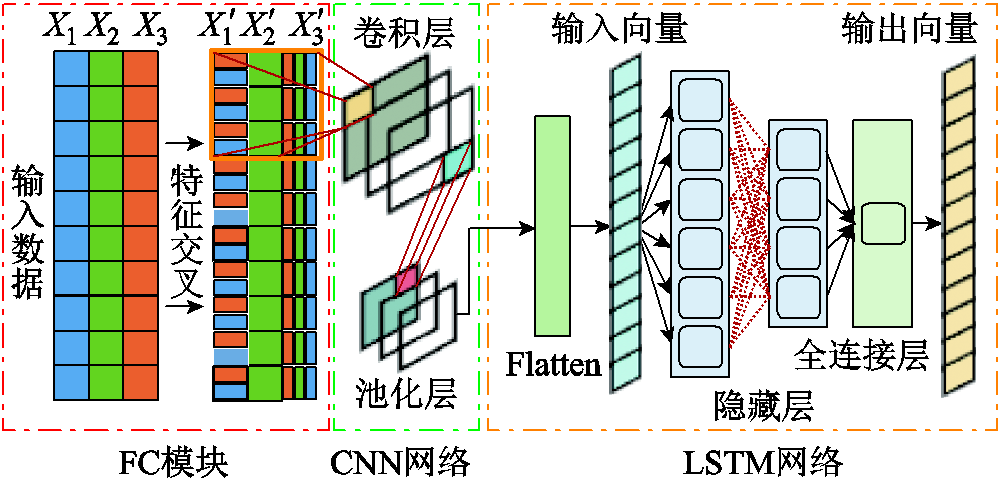
图5 FC-CNN-LSTM网络结构
Fig.5 Network structure of FC-CNN-LSTM
FC-CNN-LSTM模型预测流程如图6所示。首先将风电场初始数据输入FC模块，分析特征与风电功率之间的相关性，选择隐藏相关系数较大的特征进行交叉，增强特征强度和表达能力；其次，利用CNN算法对交叉后的特征数据在减少空间信息损失的情况下，进行降维和特征提取；最后，设定LSTM网络参数，利用LSTM网络训练并建立特征数据和风电功率之间的关联模型，实现基于特征数据的预测。
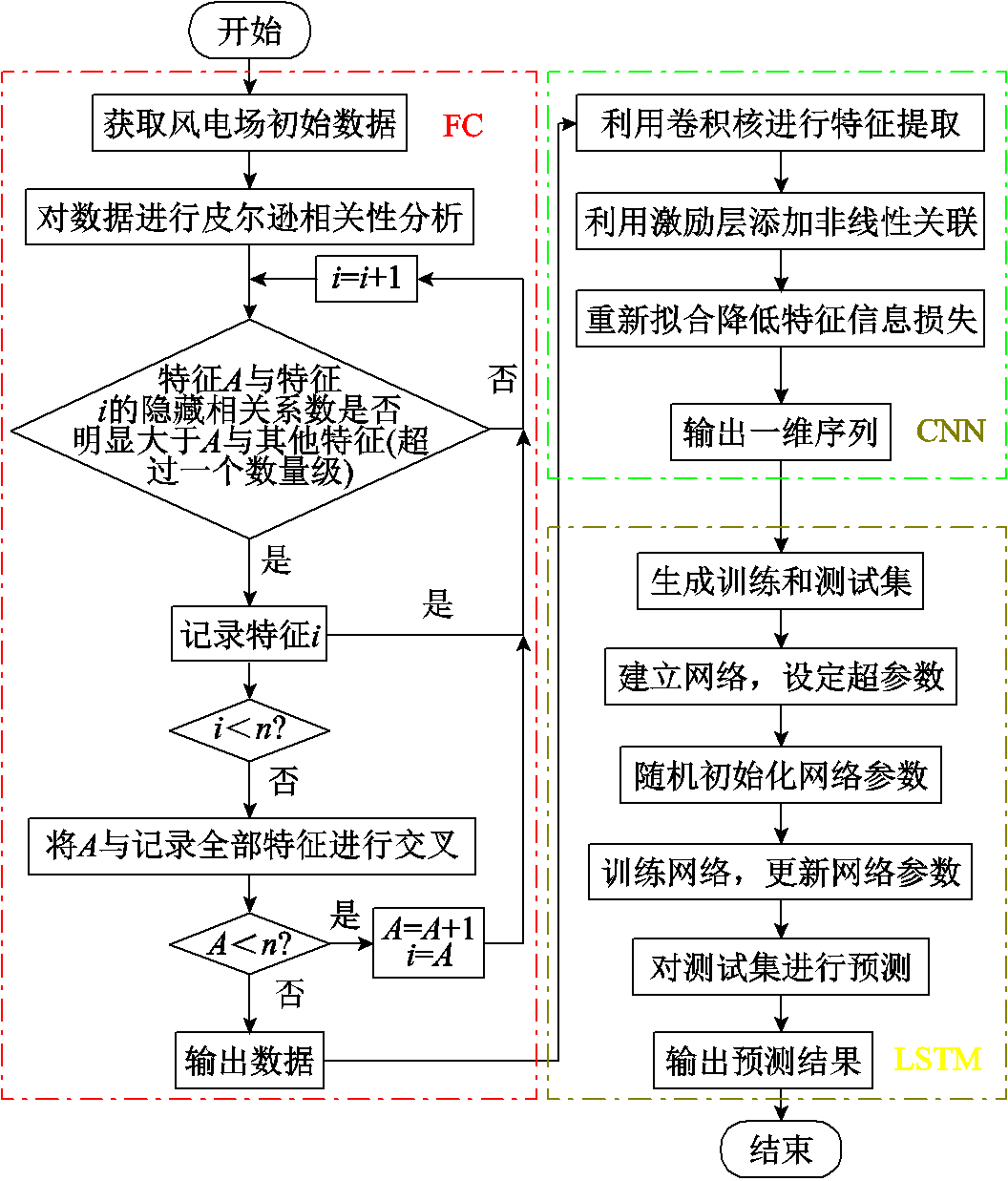
图6 FC-CNN-LSTM模型风电功率预测流程
Fig.6 FC-CNN-LSTM model wind power prediction process
风电预测误差补偿的原理是根据原有的影响因素和预测结果，生成一系列补偿数据，抵消预测结果中的误差，从而达到提高预测精度的目的。目前常用深度学习算法预测产生补偿数据[21-23]。
对于一个已经训练好的预测模型，其内部的网络、各单元结构、数据权重等所有参数均为定值。因此数据特征与预测数据之间的关系也是确定的，即使重复多次输入相同的数据特征得到的预测结果也是始终相同的。说明其模型内部具有一套固定的逻辑关系，而预测产生的误差既然是由该模型的计算结果通过对比实际数据得到的，因此也必然遵循该模型的逻辑关系，与用于功率预测的特征数据有所关联。所以可以将预测误差作为训练数据投入模型中进行训练，使模型建立起误差与用于功率预测的特征数据之间的关联网络，从而实现对误差的预测。
由于1.3节建立的FC-CNN-LSTM模型具有较高精度的预测能力，因此可对风电预测模型产生的误差进行预测，从而对风功率预测数据进行补偿和修正，误差补偿流程如图7所示。
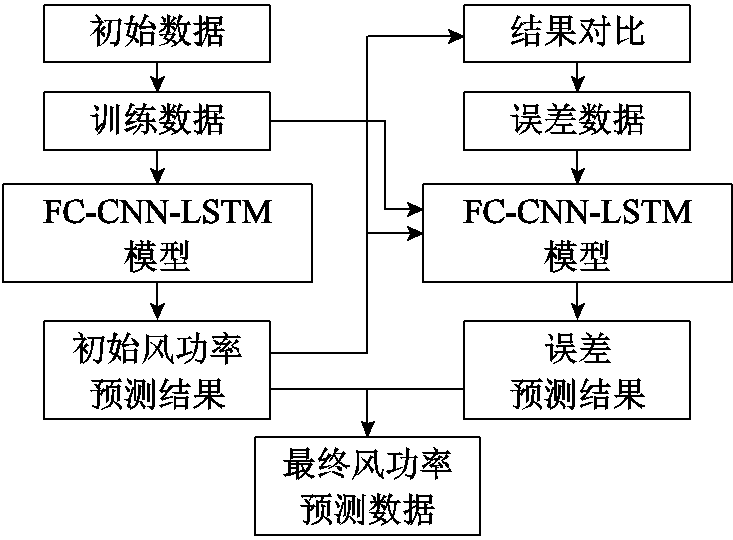
图7 误差补偿流程
Fig.7 Process of error compensation
如图7所示，初始数据首先经过划分产生训练数据，训练数据进入FC-CNN-LSTM模型训练，并计算得出初始风功率预测结果，与实际数据进行对比，产生误差数据。该误差数据与训练数据、初始风功率预测结果共同组成新的数据集，进入FC-CNN-LSTM模型，训练计算得到误差预测结果。最终将该误差预测数据与初始风功率预测结果相加补偿，得到最终的风功率预测数据。
本文以某小型风电场2012年监测数据集进行仿真验证，该数据集采集间隔时间为5 min，1月—2月共产生数据17 519条，取前80%（13 996条）作为训练数据，后20%（3 499条）作为预测验证数据。数据中的特征包括风电场风向、风速、实时气温、气压、轮毂高度空气密度、月份、日期、时间，共8个特征。分别使用CNN-LSTM、FC-CNN-LSTM模型、FC-CNN-LSTM+误差补偿模型进行对比，仿真环境为MatlabR2019a，CPU Ryzen R5 4600U，RAM 16GB，所使用的CNN-LSTM模型结构如图8所示。
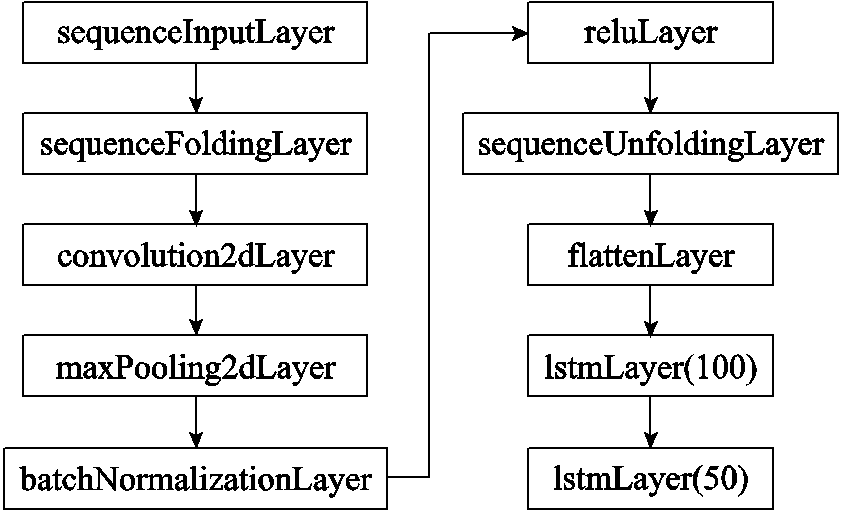
图8 神经网络结构
Fig.8 Neural network structure
模型参数分别为：最大训练周期40、梯度阈值1、初始学习率0.01、学习率降低周期2、学习率降低因子0.9。CNN-LSTM模型输入的训练集为：风向、风速、温度、气压、空气密度、月份、日期、时间8维矩阵与功率1维矩阵；FC-CNN-LSTM模型与FC-CNN-LSTM+误差补偿模型输入的训练集为：风向、风速、温度、气压、空气密度、月份、日期、时间及1.1.3节中经过特征交叉后产生的三个新特征共11维矩阵与功率1维矩阵（FC-CNN-LSTM+误差补偿为误差1维矩阵）。
图9所示为各模型对验证数据的预测结果，可以发现FC-CNN-LSTM模型与FC-CNN-LSTM模型+误差补偿在大部分区域较CNN-LSTM模型更贴近于实际功率曲线，且FC-CNN-LSTM模型+误差补偿的偏离程度更小，更趋近于实际功率曲线。
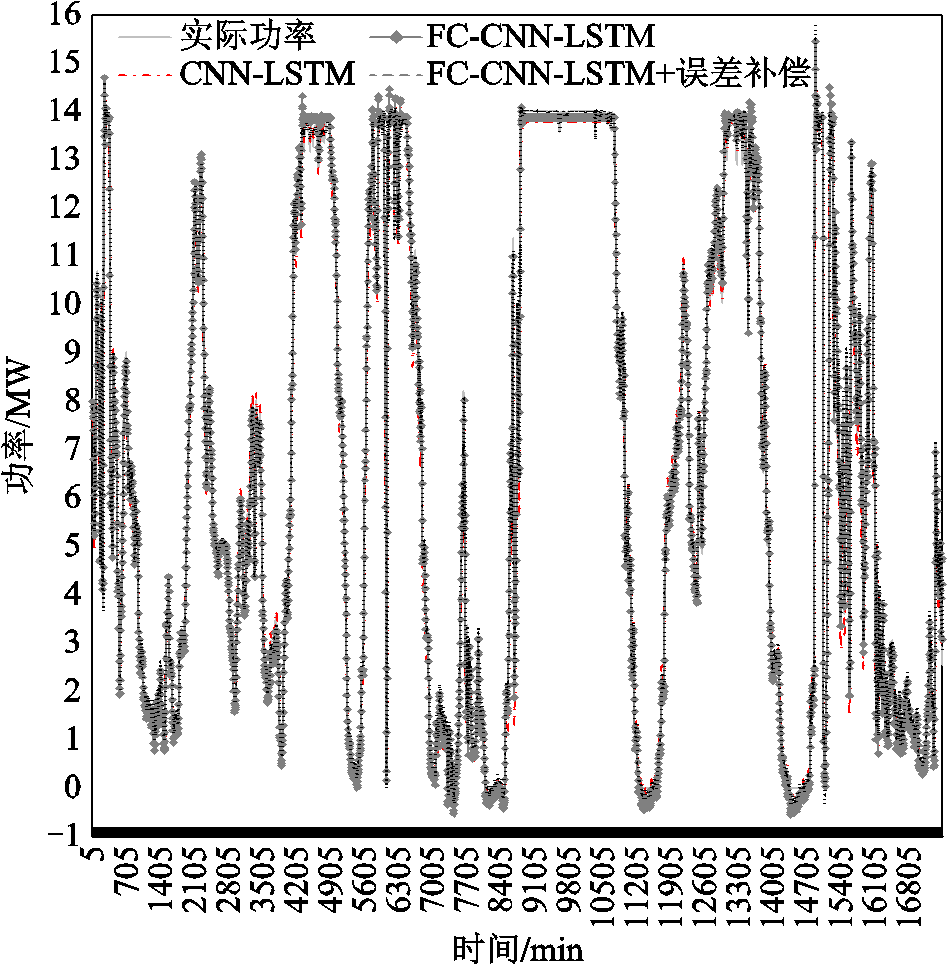
图9 各模型预测结果
Fig.9 Prediction results of each model
这一点通过表4的预测结果评价中也可以证明，FC-CNN-LSTM模型RMSE与MAE较CNN-LSTM分别下降了14.3%、12.55%；FC-CNN-LSTM模型+误差补偿RMSE与MAE较CNN-LSTM分别下降了54.16%、57.04%，较FC-CNN-LSTM分别下降了46.5%、50.88%，预测精度提升显著，充分说明了FC-CNN-LSTM模型与误差补偿的优越性。
表4 各模型预测结果评价
Tab.4 Evaluation of prediction results of each model
模型RMSEMAE CNN-LSTM0.413 990.257 02 FC-CNN-LSTM0.354 770.224 77 FC-CNN-LSTM+误差补偿0.189 790.110 41
当风电场周边气象因素剧烈变化时往往会造成风电功率的大幅变化，如何对此时的风电功率进行精确预测是目前研究中的难点。因此本文选取图9中7 495—7 995 min与15 300—15 995 min两个功率剧烈波动时段进行分析。功率剧烈波动时段各模型预测结果如图10所示。
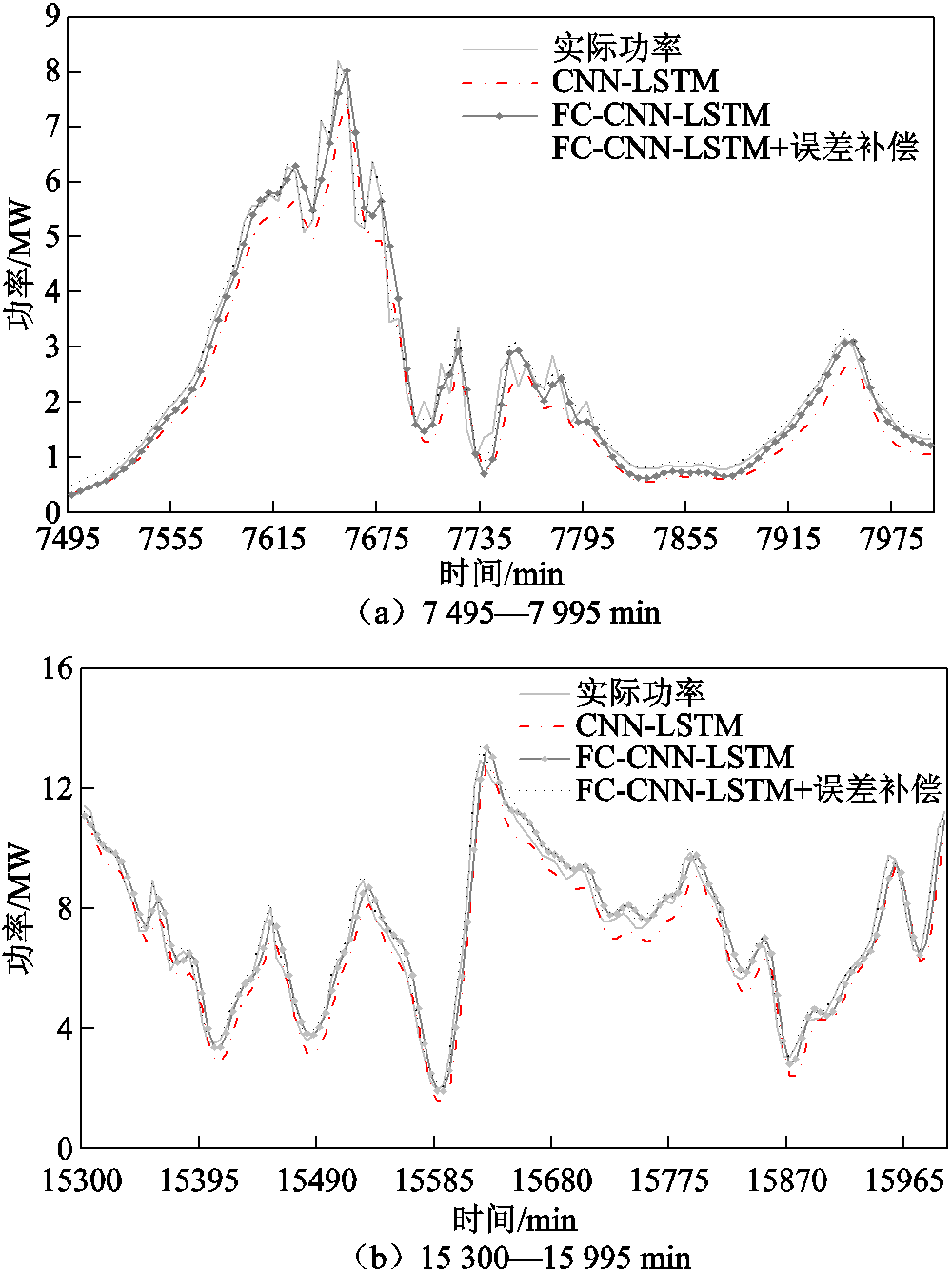
图10 功率剧烈波动时段各模型预测结果
Fig.10 Prediction results of each model in the period of severe power fluctuation
由图10可以发现，CNN-LSTM模型在功率剧烈波动情况下变化幅度较缓，不能很好地适应影响因素的快速变化，使其预测功率值往往小于实际功率，最终导致预测功率曲线较实际功率曲线偏差较大。而FC-CNN-LSTM模型则较CNN-LSTM模型在预测功率的变化幅度上有所提高，与实际功率的变化幅度更为接近，而当FC-CNN-LSTM模型经过误差补偿后，不仅变化幅度进一步提高，变化趋势也与实际功率曲线十分吻合，适应了环境影响因素的变化，预测准确度提升明显。
通过表5功率剧烈波动时段预测结果评价可以发现，在功率剧烈波动时段，CNN-LSTM模型的预测精度较表4中的总体预测结果精度更低，两个时段的RMSE较总体预测结果分别上升了20.29%、68.9%，而FC-CNN-LSTM模型与误差补偿带来的精度提升则更为显著。FC-CNN-LSTM模型与FC-CNN-LSTM模型+误差补偿的RMSE较CNN-LSTM模型在7 495—7 995 min时段分别下降了27.51%、60.3%；在15 300—15 995 min时段分别下降了20.46%、68.25%。对比表4总体预测结果中14.3%、54.16%的RMSE提高，FC-CNN-LSTM+误差补偿在功率剧烈波动时段预测精度的提升更为显著，充分说明FC-CNN-LSTM+误差补偿能够更好地适应气象因素的快速变化，做出准确的风电功率预测。
表5 功率剧烈波动时预测结果评价
Tab.5 Evaluation of prediction results when power fluctuates violently
模型评价指标7 495—7 995 min15 300—15 995 min CNN-LSTMRMSE0.497 970.699 22 MAE0.395 220.556 14 FC-CNN-LSTMRMSE0.360 960.529 40 MAE0.234 790.419 14 FC-CNN-LSTM+误差补偿RMSE0.197 700.221 99 MAE0.135 470.198 18
分析其原因在于，当风电场气象因素剧烈变化时，除强相关特征风速的变化外，风向、气温、气压、空气密度等弱相关特征也会出现波动不大但较为显著的变化，如图11所示。如果不能建立起这些弱相关特征与风电功率之间的良好联系，则当其发生细微变化时，模型就不能准确地将变化反映到预测功率上，从而导致预测值的偏差。而本文提出的FC-CNN-LSTM模型通过特征交叉加强了弱相关特征与风电功率的联系，增强了特征的表达能力，使其能够学习到更深层的隐藏关联，因此能够更好地应对风向、温度、气压等弱相关特征的细微变化，从而更加准确地对风电功率进行预测。
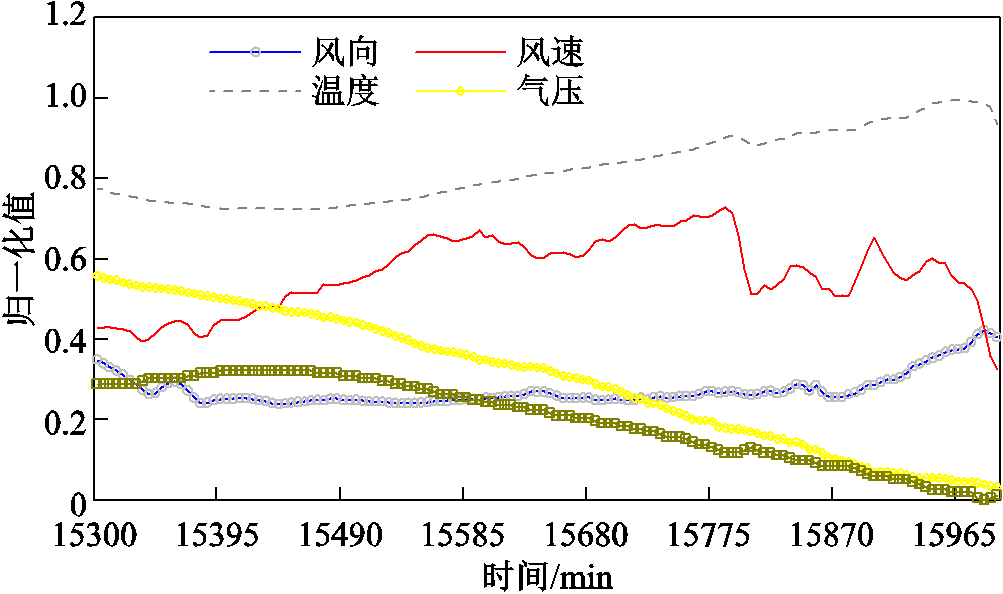
图11 15 300—15 995 min时段风电场气象条件变化
Fig.11 Variation curve of wind farm meteorological conditions during 15 300—15 995 min
从图9中可以发现，当风电实际功率接近0时，各个模型都出现了不同程度的预测功率为负值的情况，针对该问题选取图9中8 045—8 505 min与 14 245—14 770 min两个预测功率出现负值的时段进行分析。各模型预测结果为负值时段功率曲线如图12所示。
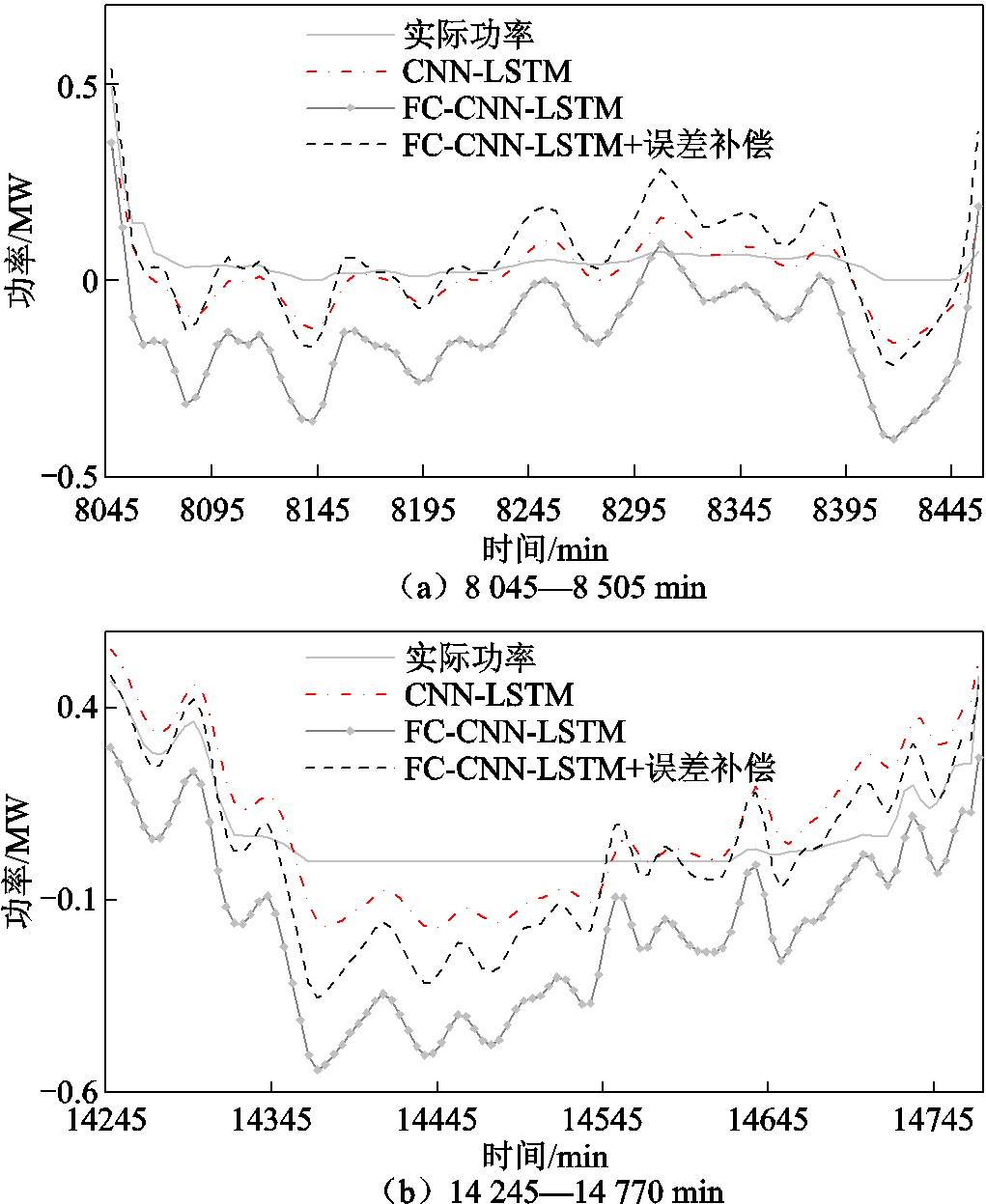
图12 各模型预测结果为负值时段功率曲线
Fig.12 The prediction results of each model are negative power curves
从图12中可以发现，当风电实际功率接近0时，各个模型的预测结果都出现了较大幅度的波动，甚至出现了预测功率为负值的情况。而其中CNN-LSTM模型的波动程度最小，更接近实际功率曲线，其次是FC-CNN-LSTM模型+误差补偿，FC-CNN-LSTM模型的波动幅度与偏离程度最大。预测功率为负值时结果评价见表6。通过表6也可以发现，在这两个时段中CNN-LSTM模型的预测结果RMSE与MAE均为最优，其次是FC-CNN-LSTM模型+误差补偿，FC-CNN-LSTM模型则最差。
表6 预测功率为负值时结果评价
Tab.6 Result evaluation when the predicted power is negative
模型评价指标8 045—8 505 min14 245—14 770 min CNN-LSTMRMSE0.068 380.112 50 MAE0.053 640.099 65 FC-CNN-LSTMRMSE0.209 970.288 24 MAE0.186 370.256 08 FC-CNN-LSTM+误差补偿RMSE0.102 900.148 33 MAE0.081 280.110 60
分析其原因在于，当风电实际功率接近0时，影响风电功率的强相关特征风速已经非常小，接近于0，而其他弱相关特征如风向、温度、气压等仍然在随时间发生变化，如图13所示。
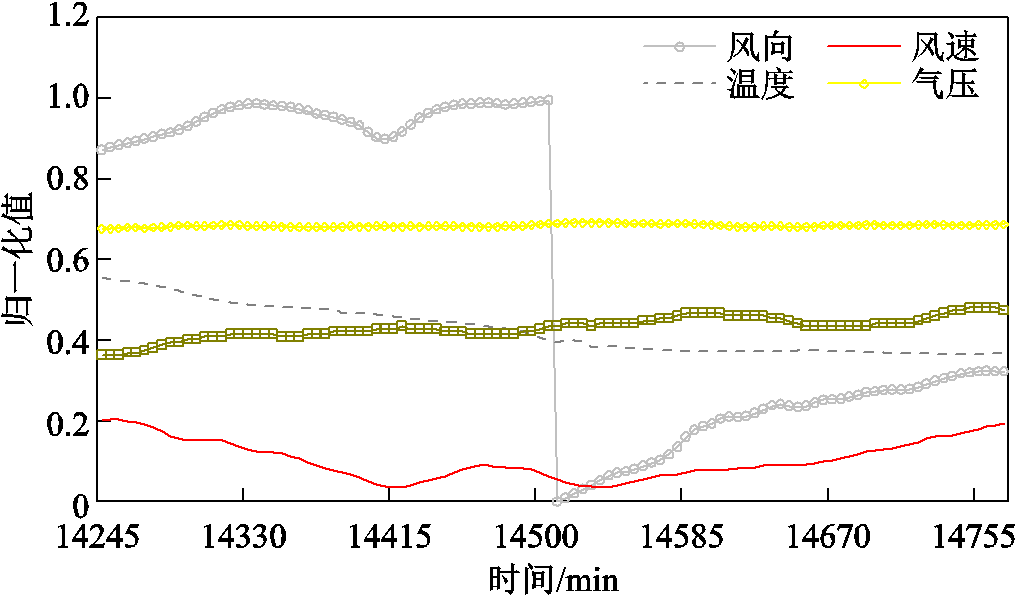
图13 14 245—14 770 min时段风电场气象条件变化
Fig.13 Variation curve of wind farm meteorological conditions during 14 245—14 770 min
当风速小于风机的最小风速时，在物理上风机就已经不能发出电力，但模型是根据各个特征的值进行预测，所以仍然可以取得一个非0的预测结果。而当风速的值减小时，其他弱相关特征的值就会相对变大，对于预测功率的贡献就会相对提高，导致弱相关特征的变化会比之前更明显地体现在预测功率中，具体表现就是预测功率的波动幅度增大。
而本文提出的FC-CNN-LSTM模型通过特征交叉加强了弱相关特征与风电功率的联系，挖掘出了弱相关特征与风电功率之间的深层联系，提高了应对弱相关特征细微变化的能力。因此在风速降低的情况下，FC-CNN-LSTM模型对于弱相关特征变化的放大会较CNN-LSTM模型明显，因此图11中FC-CNN-LSTM模型的波动幅度与偏离程度最高，即使经过误差补偿也不如CNN-LSTM模型。
这是其主要缺点，但该问题可通过设定风速下限值解决，同时考虑到其他情况下FC-CNN-LSTM模型更高的预测精度，总体上来看FC-CNN-LSTM模型仍要大幅优于CNN-LSTM模型。
本文充分考虑了风力发电功率预测中气压、气温等弱相关因素的影响，提出基于特征交叉机制和误差补偿的风力发电功率短期预测方法，通过案例验证得出以下结论：
1）将特征交叉之后得到的新特征与原始特征共同输入模型进行训练，可以有效提高模型对于非线性特征和深层隐藏关联的学习能力，从而提高模型预测精度，使FC-CNN-LSTM模型的预测精度较CNN-LSTM模型提高了14.3%。
2）误差补偿得益于FC-CNN-LSTM模型的高预测精度，可以较为准确地对功率预测模型的误差进行预测，极大地减小了预测误差，使补偿之后的预测精度相较于补偿前的FC-CNN-LSTM模型提高了46.5%。
3）在风电功率波动较为剧烈的时段，其影响风电功率的风速、风向等特征变化也较为剧烈。由于FC-CNN-LSTM具有对非线性特征和深层隐藏关联更强的学习能力，因此能够更加敏锐地捕捉到相关特征的细微变化，可以适应气象因素的快速变化，对风电功率进行更为准确的预测。
4）在风电功率较小，接近于零的时段，影响风电功率的主要特征风速大幅减小，在模型中其他弱相关特征的贡献就会相对提高，而这些弱相关特征虽然与风电功率具有一定关联，但并不像风速一样占据主要地位，所以在风速大幅降低的情况下，FC-CNN-LSTM模型由于提高了对弱相关特征的学习，因此导致其预测精度较CNN-LSTM模型更差。
本文建立了特征交叉与CNN-LSTM的组合模型用于风电功率预测，但未与目前较新提出的深度学习算法和误差补偿方法进行对比。同时可针对特征交叉是否适用于其他类型的深度学习算法，是否适用于其他类型的预测进行更深入的研究。
参考文献
[1] 马伟明. 关于电工学科前沿技术发展的若干思考[J]. 电工技术学报, 2021, 36(22): 4627-4636. Ma Weiming. Thoughts on the development of frontier technology in electrical engineering[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4627-4636.
[2] 宋琪, 吴可仲. 中国风电迎来“黄金时代”[N]. 中国经营报, 2022-01-03(D07).
[3] 李军徽, 张嘉辉, 李翠萍, 等. 参与调峰的储能系统配置方案及经济性分析[J]. 电工技术学报, 2021, 36(19): 4148-4160. Li Junhui, Zhang Jiahui, Li Cuiping, et al. Configuration scheme and economic analysis of energy storage system participating in grid peak shaving[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4148-4160.
[4] 潘超, 李润宇, 蔡国伟, 等. 基于时空关联分解重构的风速超短期预测[J]. 电工技术学报, 2021, 36(22): 4739-4748. Pan Chao, Li Runyu, Cai Guowei, et al. Multi-step ultra-short-term wind speed prediction based on decomposition and reconstruction of time-spatial correlation[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4739-4748.
[5] 沈小军, 周冲成, 付雪娇. 基于机联网-空间相关性权重的风电机组风速预测研究[J]. 电工技术学报, 2021, 36(9): 1782-1790, 1817. Shen Xiaojun, Zhou Chongcheng, Fu Xuejiao. Wind speed prediction of wind turbine based on the internet of machines and spatial correlation weight[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1782-1790, 1817.
[6] Lian Lian, He Kan. Wind power prediction based on wavelet denoising and improved slime mold algorithm optimized support vector machine[J]. Wind Engineering, 2022, 46(3): 866-885.
[7] 李智, 韩学山, 韩力, 等. 地区电网风电场功率超短期预测方法[J]. 电力系统自动化, 2010, 34(7): 90-94. Li Zhi, Han Xueshan, Han Li, et al. An ultra-short-term wind power forecasting method in regional grids[J]. Automation of Electric Power Systems, 2010, 34(7): 90-94.
[8] 韩自奋, 景乾明, 张彦凯, 等. 风电预测方法与新趋势综述[J]. 电力系统保护与控制, 2019, 47(24): 178-187. Han Zifen, Jing Qianming, Zhang Yankai, et al. Review of wind power forecasting methods and new trends[J]. Power System Protection and Control, 2019, 47(24): 178-187.
[9] 王渝红, 史云翔, 周旭, 等. 基于时间模式注意力机制的BiLSTM多风电机组超短期功率预测[J]. 高电压技术, 2022, 48(5): 1884-1892. Wang Yuhong, Shi Yunxiang, Zhou Xu, et al. Ultra-short-term power prediction for BiLSTM multi wind turbines based on temporal pattern attention[J]. High Voltage Engineering, 2022, 48(5): 1884-1892.
[10] Saeed A, Li Chaoshun, Gan Zhenhao, et al. A simple approach for short-term wind speed interval prediction based on independently recurrent neural networks and error probability distribution[J]. Energy, 2022, 238: 122012.
[11] Gu Bo, Zhang Tianren, Meng Hang, et al. Short-term forecasting and uncertainty analysis of wind power based on long short-term memory, cloud model and non-parametric kernel density estimation[J]. Renewable Energy, 2021, 164: 687-708.
[12] Wang Ruoheng, Li Chaoshun, Fu Wenlong, et al. Deep learning method based on gated recurrent unit and variational mode decomposition for short-term wind power interval prediction[J]. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(10): 3814-3827.
[13] 朱乔木, 李弘毅, 王子琪, 等. 基于长短期记忆网络的风电场发电功率超短期预测[J]. 电网技术, 2017, 41(12): 3797-3802. Zhu Qiaomu, Li Hongyi, Wang Ziqi, et al. Short-term wind power forecasting based on LSTM[J]. Power System Technology, 2017, 41(12): 3797-3802.
[14] Shahid F, Zameer A, Muneeb M. A novel genetic LSTM model for wind power forecast[J]. Energy, 2021, 223: 120069.
[15] Liu Hui, Chen Dihuang, Lin Fang, et al. Wind power short-term forecasting based on LSTM neural network with dragonfly algorithm[J]. Journal of Physics: Conference Series, 2021, 1748(3): 032015.
[16] Wang Huaizhi, Li Gangqiang, Wang Guibin, et al. Deep learning based ensemble approach for probabilistic wind power forecasting[J]. Applied Energy, 2017, 188: 56-70.
[17] Wang Kejun, Qi Xiaoxia, Liu Hongda, et al. Deep belief network based k-means cluster approach for short-term wind power forecasting[J]. Energy, 2018, 165: 840-852.
[18] 陆悦聪, 王瑞琴, 金楠. 基于多维特征交叉的深度协同过滤算法[J]. 计算机工程与应用, 2022, 58(22): 72-78. Lu Yuecong, Wang Ruiqin, Jin Nan. Deep collaborative filtering algorithm based on multi-dimensional feature crossover[J]. Computer Engineering and Applications: 2022, 58(22): 72-78.
[19] 王越, 于莲芝. 一个以注意力机制结合隐式和显式的特征交叉的CTR预估模型[J]. 小型微型计算机系统, 2021, 42(9): 1884-1890. Wang Yue, Yu Lianzhi. CTR prediction model combining implicit and explicit features with attention mechanism[J]. Journal of Chinese Computer Systems, 2021, 42(9): 1884-1890.
[20] 张思凡, 牛振东, 陆浩, 等. 基于图卷积嵌入与特征交叉的文献被引量预测方法：以交通运输领域为例[J]. 数据分析与知识发现, 2020, 4(9): 56-67. Zhang Sifan, Niu Zhendong, Lu Hao, et al. Predicting citations based on graph convolution embedding and feature cross: case study of transportation research[J]. Data Analysis and Knowledge Discovery, 2020, 4(9): 56-67.
[21] 边春元, 邢海洋, 李晓霞, 等. 基于速度变化率的无位置传感器无刷直流电机风力发电系统换相误差补偿策略[J]. 电工技术学报, 2021, 36(11): 2374-2382. Bian Chunyuan, Xing Haiyang, Li Xiaoxia, et al. Compensation strategy for commutation error of sensorless brushless DC motor wind power generation system based on speed change rate[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2374-2382.
[22] 周勇良, 余光正, 刘建锋, 等. 基于改进长期循环卷积神经网络的海上风电功率预测[J]. 电力系统自动化, 2021, 45(3): 183-191. Zhou Yongliang, Yu Guangzheng, Liu Jianfeng, et al. Offshore wind power prediction based on improved long-term recurrent convolutional neural network[J]. Automation of Electric Power Systems, 2021, 45(3): 183-191.
[23] Tao Cai, Lu Junjie, Lang Jianxun, et al. Short-term forecasting of photovoltaic power generation based on feature selection and bias compensation-LSTM network[J]. Energies, 2021, 14(11): 3086.
Abstract At present, wind power forecasting methods mainly include physical modeling, statistical modeling and artificial intelligence algorithm modeling. The traditional physical modeling and statistical modeling methods are difficult to collect data and select parameters, and have weak processing ability for a large number of data, so it is difficult to establish an accurate prediction model. Therefore, in practical applications, artificial intelligence algorithms are usually used to predict wind power. However, the current research on wind power prediction focuses on the use and improvement of artificial intelligence algorithms, and does not take into account the correlation between different features in the data and wind power, as well as the difference in the size of correlation. The model trained on this basis can only establish a single, superficial correlation, and cannotmine deeper relationships, which is not conducive to short-term prediction of wind power.
Therefore, this paper first introduces the feature crossover mechanism, analyzes the correlation of data features and cross combines them, increases feature dimensions, strengthens the learning ability of the algorithm for nonlinear features and deep hidden associations, and forms the FC-CNN-LSTM prediction model based on CNN-LSTM network improvement. Then, use the error value generated by the prediction model in the prediction as the training data, train and generate the error compensation model, and use the data generated by the error compensation model to compensate the wind power prediction data, so as to further improve the prediction accuracy. Finally, through the measured data of a wind farm, it is verified that the FC-CNN-LSTM model has a higher prediction accuracy, and after the error compensation process is added, it can further reduce the error compared with the traditional prediction methods, which has significant advantages.
The simulation results of the actual data in a region show that: (1) the feature crossing mechanism can effectively improve the learning ability of the model for nonlinear features and deep hidden associations, thus improving the prediction accuracy of the model. The prediction accuracy of the FC-CNN-LSTM model is 14.3% higher than that of the CNN-LSTM model; (2) The error compensation model based on FC-CNN-LSTM model can accurately predict the error of power prediction model, greatly reducing the prediction error, and greatly improving the prediction accuracy after compensation by 46.5% compared with the FC-CNN-LSTM model before compensation;
Finally, the following conclusions are drawn through analysis: (1) Compared with the CNN-LSTM model, the FC-CNN-LSTM model proposed in this paper has obvious advantages in the accuracy of the prediction of the ultra short termminute level wind power. It can more keenly capture the subtle changes of the characteristics related to the wind power, adapt to the rapid changes of meteorological factors, and more accurately predict the wind power, which is more suitable for practical engineering projects; (2) The error compensation mechanism based on FC-CNN-LSTM model proposed in this paper can further improve the accuracy of wind power prediction, and can be used in different application scenarios and with different algorithms, with high adaptability; (3) In addition, the disadvantage of the FC-CNN-LSTM model is that when the wind power is small and close to zero, the wind speed decreases significantly, and the contribution of other weak correlation features in the model will be relatively improved. Although these weak correlation features are related to the wind power to some extent, they do not occupy the same dominant position as the wind speed. Therefore, when the wind speed decreases significantly, the FC-CNN-LSTM model improves the learning of weak correlation features, The prediction accuracy will be worse than that of the CNN-LSTM model, which can be solved by setting a limit on the prediction results according to the wind speed.
keywords：Convolution neural network, short and long term memory network, wind power prediction, feature crossover, error compensation
DOI:10.19595/j.cnki.1000-6753.tces.220477
中图分类号：TM614; TM732
国家自然科学基金（51767023）和新疆维吾尔自治区研究生科研创新计划（XJ2022G041）资助项目。
收稿日期2022-04-01
改稿日期 2022-06-03
刘雨佳 男，1998年生，硕士研究生，研究方向电力系统控制与优化调度。E-mail：1104680459@qq.com
樊艳芳 女，1971年生，教授，博士生导师，研究方向为新能源并网技术及电力系统保护与控制。E-mail：fyf3985@xju.edu.cn（通信作者）
（编辑 赫 蕾）