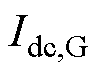 、
、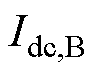 、
、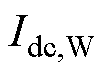 、
、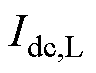 分别为换流器
分别为换流器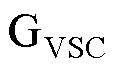 、
、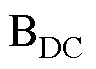 、
、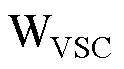 、
、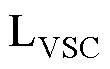 母线侧的电流。
母线侧的电流。摘要 为了提高直流电压的稳定性、动态特性以及安全性,提出一种基于预测模型控制的直流微电网虚拟惯性滚动优化方法。首先,建立含虚拟惯性控制单元的直流微电网线性离散模型,用以预测系统输出量的未来趋势。其次,设计模型预测控制器:以直流电压跟踪误差、虚拟惯性系数两者的加权二次方和最小为目标,希望直流电压维持稳定并且惯性响应的强度不要太大;以直流电压及其变化率限制为约束,防止因动态电压超过安全阈值而导致切机、切负荷甚至系统崩溃问题;在每个采样时刻,求解各控制单元的虚拟惯性系数并将其输出,从而实现虚拟惯性的优化控制。同时,通过控制性能分析,给出控制器主要参数的选取原则。最后,通过负荷突变、风速随机波动等典型工况下的硬件在环测试,验证了所提方法的可行性和有效性。
关键词:直流微电网 虚拟惯性优化控制 线性离散模型 模型预测控制
与交流电网相比,直流电网凭借转换环节少、线路损耗低、可控性高等优点受到工业界和学术界的广泛关注[1-3]。然而,由于换流器的隔离作用,直流电网无类似交流电网中同步发电机的旋转惯性作为支撑,采用传统的下垂控制或比例积分(Pro- portional Integral, PI)控制时,新能源功率波动和负荷突增、突减都会在一定程度上引起直流电压的快速波动[4-6]。
虚拟惯性控制是解决上述问题经济且有效的途径。直流系统的惯性反映了其阻止电压突变的能力,可用惯性时间常数度量,其值为直流侧电容在额定电压下存储的电能与直流端额定功率之比[7]。理论上,可通过增大母线电容提高系统的惯性,从而抑制直流电压的波动,但加装硬件设施会导致投资成本显著增加,不宜大规模推广。鉴于此,文献[8-9]提出一种虚拟电容的方法,通过控制模拟电容的充放电特性,提高了母线电压的抗扰动能力。另外,文献[10-11]根据交直流变量的对应关系,在类比交流系统中虚拟同步发电机(Virtual Synchronous Generator, VSG)的基础上提出了一种虚拟直流电机(Virtual DC Motor, VDCM)的方法,通过改变直流系统的惯性时间常数提高微电网的供电质量。上述方法通过惯性进行调压,在阻止电压突变的同时,不会对换流器稳态下的功率分配造成影响,并且能与一、二次调压相互配合从而形成多层次、多时间尺度的调压体系,但虚拟惯性是固定的,未充分利用换流器虚拟惯性灵活可调的特性,难以同时满足系统稳定性和快速性的要求。
因此,很多学者提出了自适应的虚拟惯性控制方法。文献[7, 12]鉴于下垂控制应用的广泛性,提出了一种基于下垂曲线调整的自适应虚拟惯性控制方法,该方法根据电压、电压变化率的动态变化实时计算下垂系数或下垂曲线截距,通过下垂曲线的快速摆动或平移为系统提供惯性支撑。文献[13-16]基于虚拟直流电机或虚拟电容的原理,建立虚拟惯性与电压、电压变化率的函数关系,提出了一种自适应的虚拟惯性控制方法。文献[17]在文献[16]的基础上,考虑稳定性、动态特性、实际运行需求及可实现性,实时计算换流器的稳定运行边界,提高了该方法的工程应用价值。此类方法虽然虚拟惯性有明确的解析式,但难以给出“最优”参数的计算方法,并且由于虚拟惯性根据当前状态确定,控制器的作用滞后于系统的变化,无法实现考虑动态电压约束的紧急预防控制,动态电压超过安全阈值会导致切机、切负荷,甚至系统崩溃等问题。
目前,考虑动态电压约束的虚拟惯性优化控制方法鲜见报道。近年来,因充分利用系统未来信息,对模型精度要求不高,求解的优化问题中很容易包含各种约束条件等优点,模型预测控制(Model Predictive Control, MPC)在微电网中得到广泛应 用[18-20]。文献[21]建立船舰直流微电网的动态模型,在此基础上,通过集中控制DC-DC换流器的占空比平抑冲击性负荷引起的电压波动。文献[22]以三端口DC-DC换流器为对象,采用MPC计算最优移相占空比,从而提高换流器的动态性能。文献[23-24]在VSG控制的基础上,通过附加MPC调节换流器的功率增量,改善了微电网的频率响应特性。上述文献未涉及虚拟惯性控制,或虽然涉及虚拟惯性控制,但是控制的并非虚拟惯性,且未对安全约束问题作进一步分析。以虚拟惯性系数为控制量的直流微电网动态模型虽然是非线性的,但可以通过雅克比矩阵在稳态点附近线性化。因此,可比较容易地将MPC应用于虚拟惯性的优化控制,若同时设置含动态电压的安全约束,则可兼顾直流电压的安 全性。
基于此,本文提出一种基于MPC的直流微电网虚拟惯性优化方法。首先建立含虚拟惯性控制的直流微电网线性离散模型,以预测直流电压等输出量的未来趋势;然后在每个采样时刻,以预测时域内直流电压跟踪误差、虚拟惯性系数(并网换流器下垂曲线纵截距调整系数、储能系统虚拟电容系数)最小为目标,在动态电压等约束下求解控制时域内虚拟惯性系数的最优值,并将优化解的第一组元素作用于系统。该方法能处理“多变量、多约束”的优化问题,将其应用于考虑动态电压约束的直流微电网虚拟惯性优化控制具有一定优势。
本文所研究的直流微电网拓扑如图1所示,主要由储能系统、交流电网、风电机组和交流负荷构成。图中,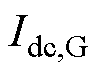 、
、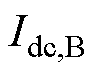 、
、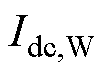 、
、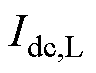 分别为换流器
分别为换流器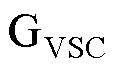 、
、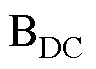 、
、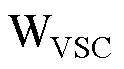 、
、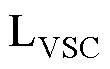 母线侧的电流。
母线侧的电流。
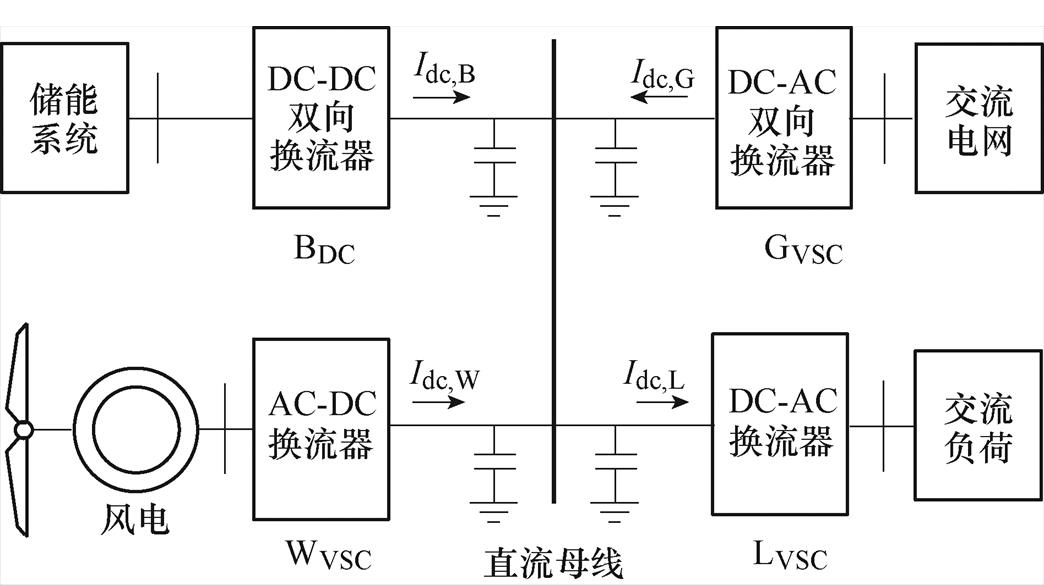
图1 直流微电网的拓扑
Fig.1 Topology of DC microgrid
该直流微电网中,各部分通过换流器并入直流母线,母线电压成为衡量供电质量的关键指标。为了尽可能地利用风能以提升发电效益,通常不考虑风电机组的调压能力。同时,负荷作为直流微电网的供电对象,一般不能轻易调整,对电压调节的贡献很小。交流电网、储能系统因功率双向流动等优点而成为电压调节的主力。
为了平抑直流电压的波动并体现控制方法的多样性,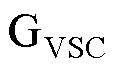 、
、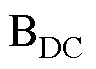 在传统控制的基础上采用不同的虚拟惯性控制方法。
在传统控制的基础上采用不同的虚拟惯性控制方法。
(1)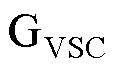 在电压下垂控制的基础上,采用下垂曲线截距调整的方式实现虚拟惯性控制[12],控制框图如图2所示。
在电压下垂控制的基础上,采用下垂曲线截距调整的方式实现虚拟惯性控制[12],控制框图如图2所示。
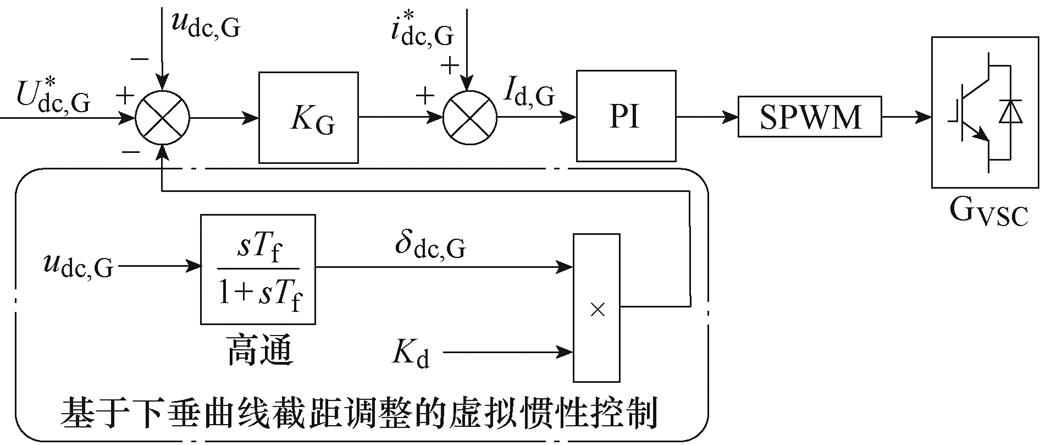
图2 基于下垂曲线截距调整的虚拟惯性控制
Fig.2 Virtual inertial control based on droop curve intercept adjustment
图2中,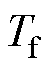 为高通滤波器的时间常数,
为高通滤波器的时间常数,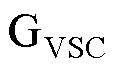 的d轴电流为
的d轴电流为
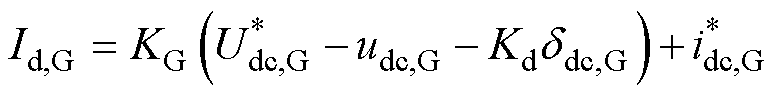 (1)
(1)
式中,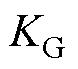 为下垂系数的倒数;
为下垂系数的倒数;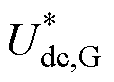 为
为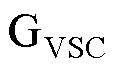 电压参考值;
电压参考值;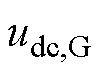 为
为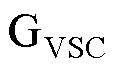 直流侧电压;
直流侧电压;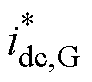 为上级下达至
为上级下达至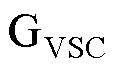 的调度指令;
的调度指令;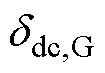 为
为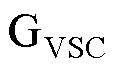 高通滤波器的输出,代替
高通滤波器的输出,代替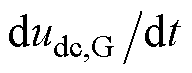 ;
;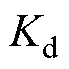 为下垂曲线纵截距调整系数,且
为下垂曲线纵截距调整系数,且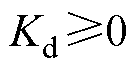 ,其值为常数时,虚拟电容近似恒定。
,其值为常数时,虚拟电容近似恒定。
与下垂控制相比,该方法中下垂曲线的纵截距由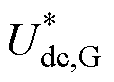 变为
变为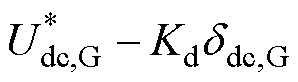 。电压下降,其变化率为负值,此时纵截距增加,换流器快速释放功率以减缓电压的下降速度;电压上升,则反之。换流器以此为直流微电网提供惯性支撑。
。电压下降,其变化率为负值,此时纵截距增加,换流器快速释放功率以减缓电压的下降速度;电压上升,则反之。换流器以此为直流微电网提供惯性支撑。
(2)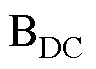 在定直流电压的基础上,采用虚拟电容控制提高系统的惯性[16],控制框图如图3所示。
在定直流电压的基础上,采用虚拟电容控制提高系统的惯性[16],控制框图如图3所示。
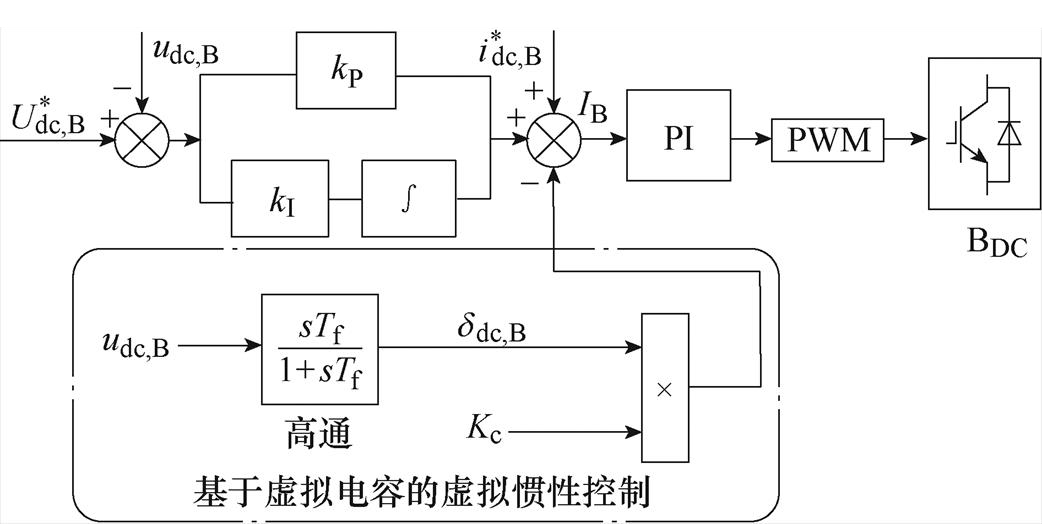
图3 基于虚拟电容的虚拟惯性控制
Fig.3 Virtual inertia control based on virtual capacitor
图3中,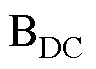 蓄电池侧的电流为
蓄电池侧的电流为
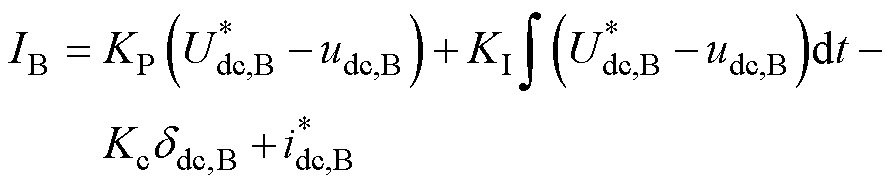 (2)
(2)
式中,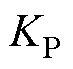 、
、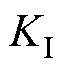 分别为
分别为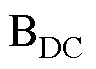 电压外环PI控制器的比例系数和积分系数;
电压外环PI控制器的比例系数和积分系数;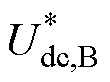 为
为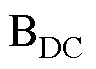 电压参考值;
电压参考值;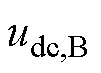 为
为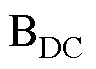 直流侧电压;
直流侧电压;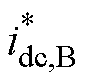 为上级下达至
为上级下达至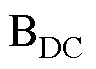 的调度指令;
的调度指令;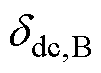 为
为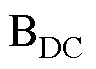 高通滤波器的输出,代替
高通滤波器的输出,代替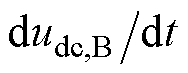 ;
;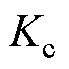 为虚拟电容调节系数,有
为虚拟电容调节系数,有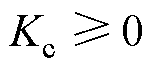 。
。
与定直流电压相比,该方法中电流内环的参考值附加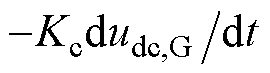 。虚拟电容充放电方向与电压变化方向相反,直流电压的波动得以平抑。
。虚拟电容充放电方向与电压变化方向相反,直流电压的波动得以平抑。
式(1)、式(2)中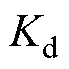 、
、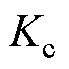 是固定的。选值过小,系统虚拟惯性响应强度不够;选值过大,系统动态响应变慢甚至出现稳定性问题。采用基于预测模型的滚动优化方法,则可以根据系统状态实时计算
是固定的。选值过小,系统虚拟惯性响应强度不够;选值过大,系统动态响应变慢甚至出现稳定性问题。采用基于预测模型的滚动优化方法,则可以根据系统状态实时计算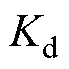 、
、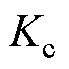 的优化值。
的优化值。
本文采用应用广泛的状态空间模型描述直流微电网的动态行为。图4为含虚拟惯性控制的直流微电网控制框图。图中,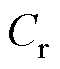 为直流母线等效电容;为了便于建模,对高通滤波器进行了等效变换,并引入了中间变量
为直流母线等效电容;为了便于建模,对高通滤波器进行了等效变换,并引入了中间变量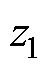 、
、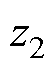 、
、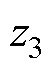 。以下假设系统全部状态量都是可以观测的,按照部分至整体的顺序进行建模。
。以下假设系统全部状态量都是可以观测的,按照部分至整体的顺序进行建模。
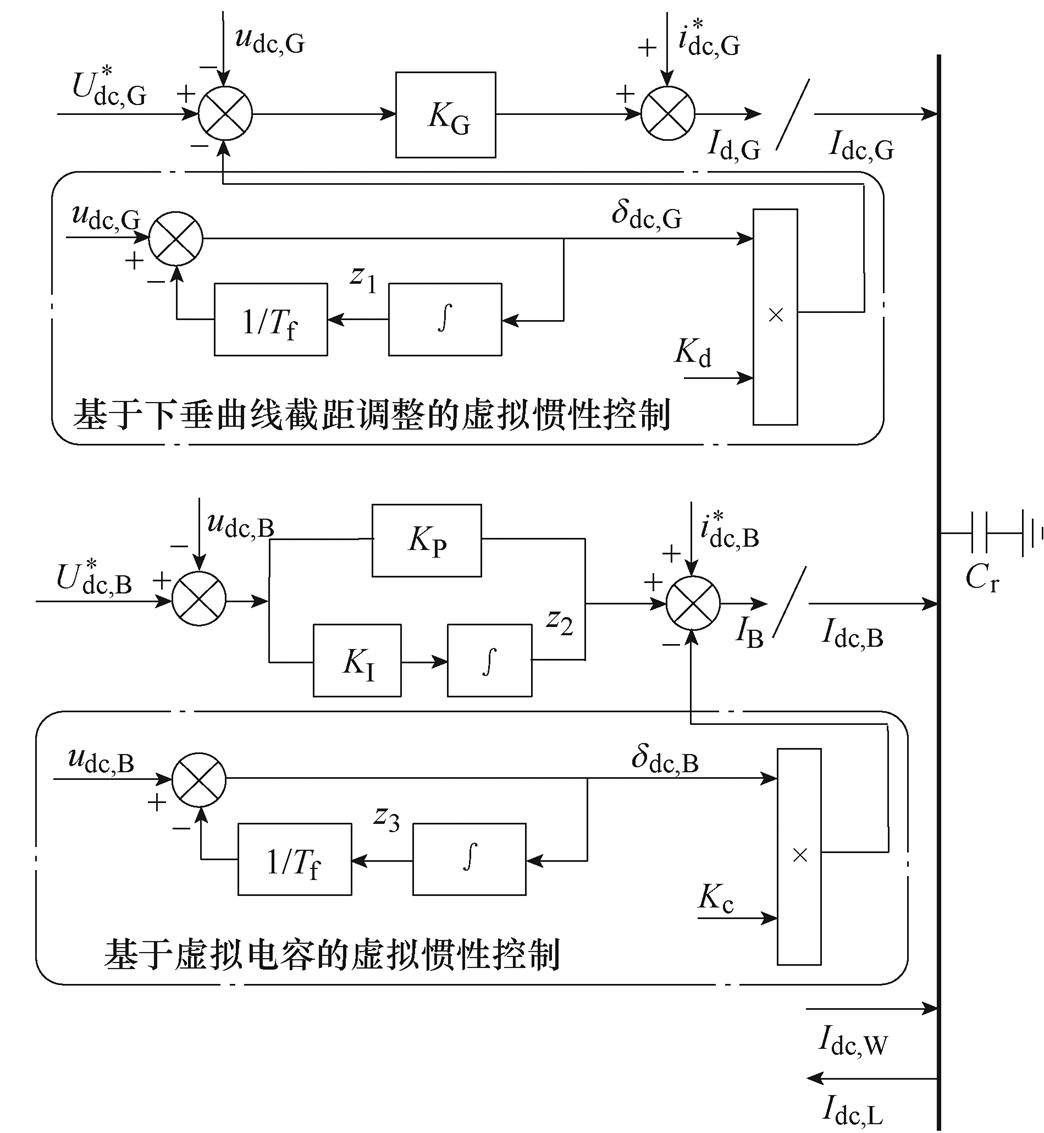
图4 含虚拟惯性控制的直流微电网控制框图
Fig.4 DC microgrid control block diagram with virtual inertial control
2.1.1 并网换流器微分方程
并网换流器电流内环的响应速度很快,可等效为一阶惯性环节甚至忽略不计。另外,采用电网电压定向矢量控制,电网电压恒定时其d轴分量为0,q轴电流几乎不影响直流侧的功率。因此,仅考虑并网换流器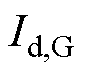 之前的部分。
之前的部分。
由图4可知,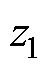 的微分方程为
的微分方程为
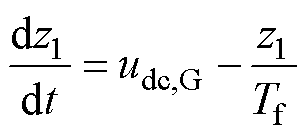 (3)
(3)
2.1.2 储能系统微分方程
与并网换流器类似,储能系统也仅考虑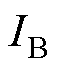 之前的部分。
之前的部分。
由图4可知,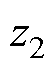 、
、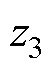 的微分方程为
的微分方程为
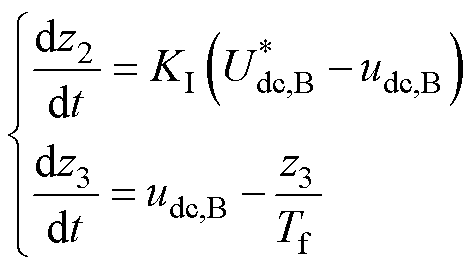 (4)
(4)
另外,储能本体的荷电状态(State of Charge, SOC)等参数,对设备安全运行起着非常重要的作用,因此可将其考虑在内。以SOC为例,其微分方程为
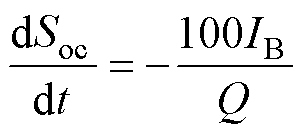 (5)
(5)
式中,Soc为蓄电池的SOC;IB为蓄电池电流;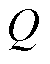 为蓄电池的容量。
为蓄电池的容量。
2.1.3 系统状态空间模型
为简化系统模型,假设各换流器直接连接至直流母线。根据基尔霍夫电流定律,得母线电压的微分方程为
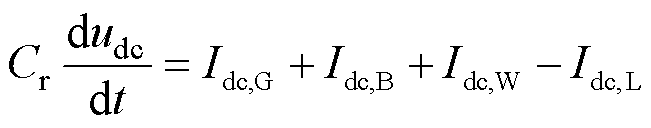 (6)
(6)
式中,Cr为直流母线的等效电容;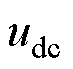 为母线电压。
为母线电压。
考虑换流器输入、输出功率平衡,上述电流可进一步表示为
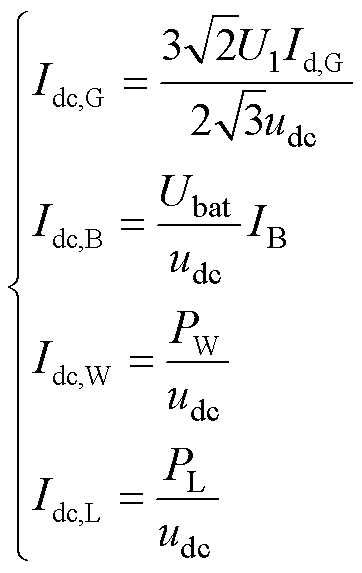 (7)
(7)
式中, 为
为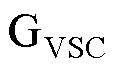 交流侧线电压的有效值;
交流侧线电压的有效值;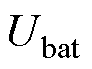 为蓄电池电压,文中假设其值恒定;
为蓄电池电压,文中假设其值恒定;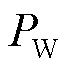 为风电机组的功率;
为风电机组的功率;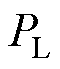 为负荷的功率。
为负荷的功率。
需要说明的是,在不考虑线路模型的情况下有
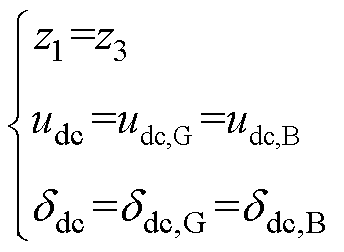 (8)
(8)
式中,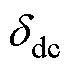 为
为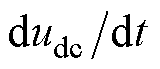 的替代量。
的替代量。
综上所述,直流微电网的微分方程组为
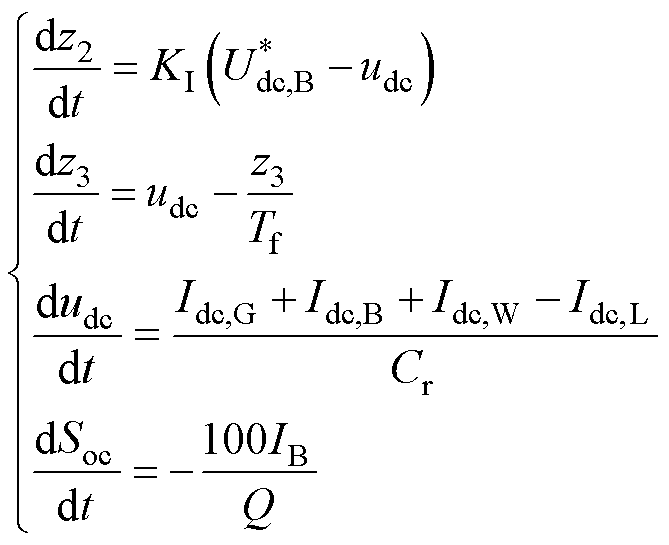 (9)
(9)
另外,以衡量虚拟惯性控制效果的直流电压及其变化率等指标为输出量,直流微电网的输出方程可表示为
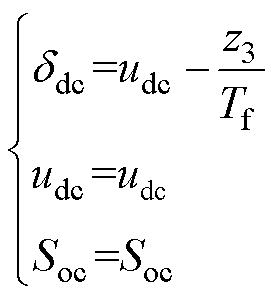 (10)
(10)
式中,等号左端为输出量,右端为状态量的线性组合,两端相等则表示该状态量直接作为输出量。
上述模型是连续的,且由于式(7)的作用,呈非线性特征。为了沿用相对成熟的线性递推方法预测系统的未来趋势,对模型进行线性化和离散化处理[21]。
本文建立的线性模型如式(11)所示。由于该模型用于虚拟惯性的优化控制,因此将虚拟惯性系数作为控制量。同时,由于风电和负荷具有一定的不确定性,将其功率增量视为扰动。
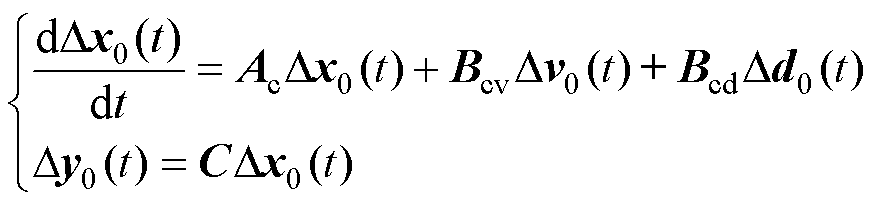 (11)
(11)
式中,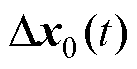 为状态量相对稳态点的增量,
为状态量相对稳态点的增量,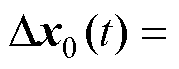
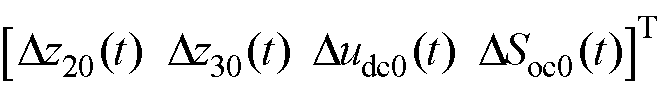 ;
;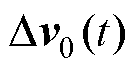 为控制量相对稳态点的增量,
为控制量相对稳态点的增量,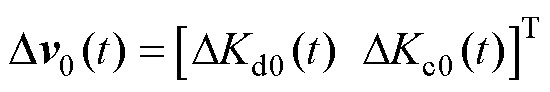 ;
;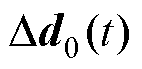
为扰动量相对稳态点的增量,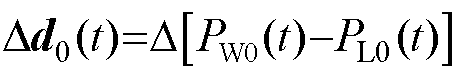 ;
;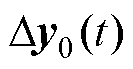 为输出量相对稳态点的增量,
为输出量相对稳态点的增量,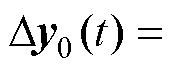
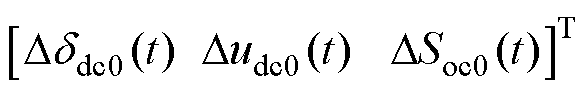 ;
;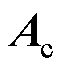 、
、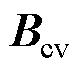 、
、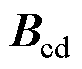 、
、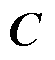 系数矩阵分别表示为
系数矩阵分别表示为
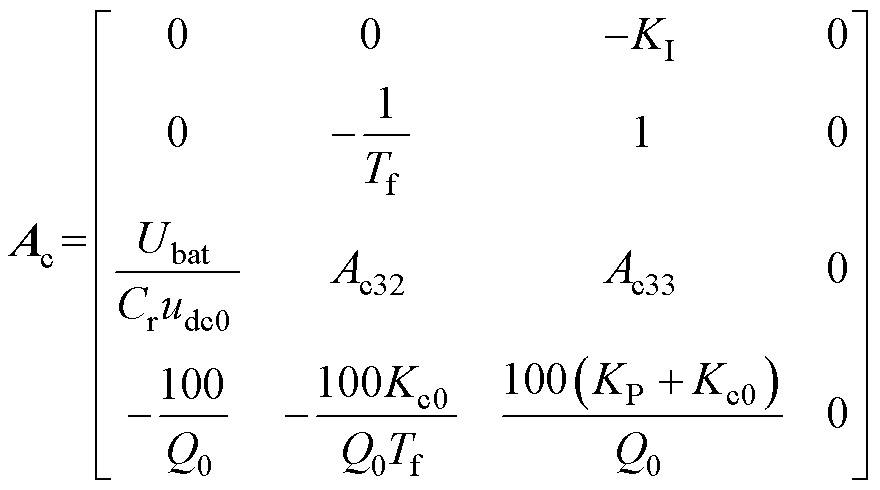
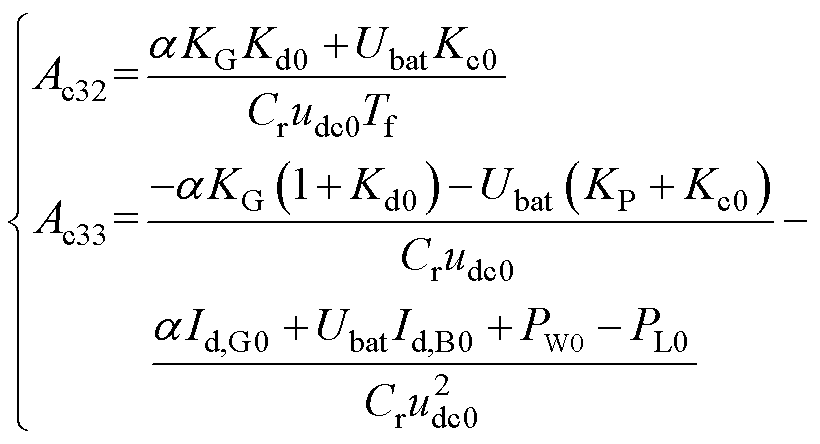
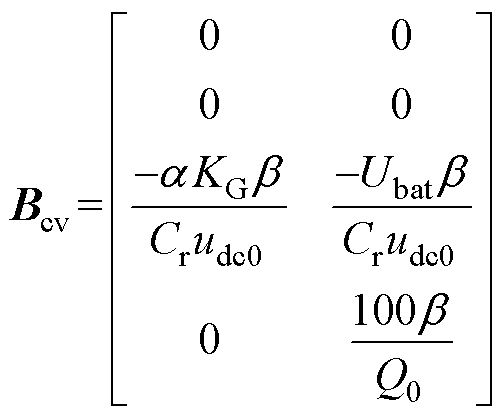
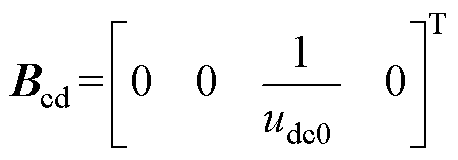
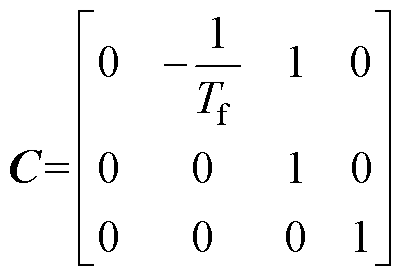
其中
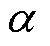 =
=
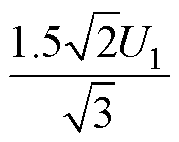
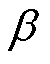 =
=
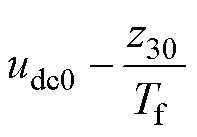
式中,下标“0”表示对应变量的稳态值,以下相同;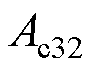 、
、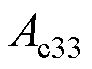 为矩阵元素。
为矩阵元素。
为了便于预测系统的未来动态,采用前向欧拉法将模型离散化,得线性离散预测模型为
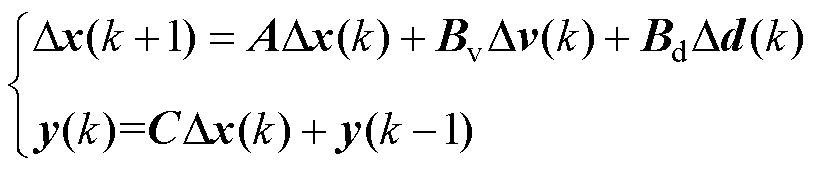 (12)
(12)
式中,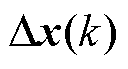 为当前时刻的状态增量,
为当前时刻的状态增量,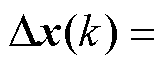
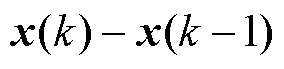 ;
;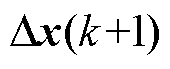 为下一个时刻的状态增量,以此类推,以下相同;
为下一个时刻的状态增量,以此类推,以下相同;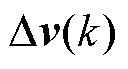 为当前时刻的控制增量;
为当前时刻的控制增量;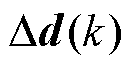 为当前时刻的扰动增量;
为当前时刻的扰动增量;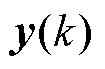 为当前时刻的输出量;
为当前时刻的输出量;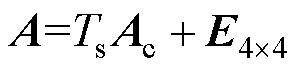 ,
,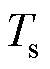 为采样周期,
为采样周期,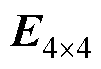 为4阶单位矩阵;
为4阶单位矩阵;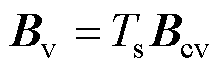 ;
;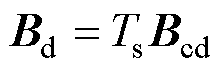 。
。
MPC是一种基于预测模型的控制方法,采用滚动优化的工作机制。MPC器在每个采样时刻预测系统的未来趋势,然后求解一个有限时域(预测时域p)的优化问题,最后将控制序列的第一组元素作用于系统。
MPC汲取了优化控制的思想,利用滚动的有限时域优化取代全局优化。这种建立在最新测量基础上的反复优化,能不断顾及模型失配、外部扰动等不确定性因素的影响并加以校正,要比只依靠模型的一次优化更适应实际控制过程。
然而,这种滚动机制也带来了计算量增大的问题。为了降低优化问题的规模,一个简单的方法是引入控制时域m(m≤p)的概念,并假设控制时域外控制增量为0。优化问题的独立变量数随之减少。
优化问题是MPC的核心内容,可采用式(13)描述[25-26],该式包括目标函数、预测模型和时域约束三部分。目标函数反映MPC对系统性能的要求。预测模型是根据质量守恒、能量守恒等定理建立的动力学方程,主要用于预测系统的未来动态。时域约束是为防止执行机构饱和、控制代价过大、输出量越限而设置的约束条件。
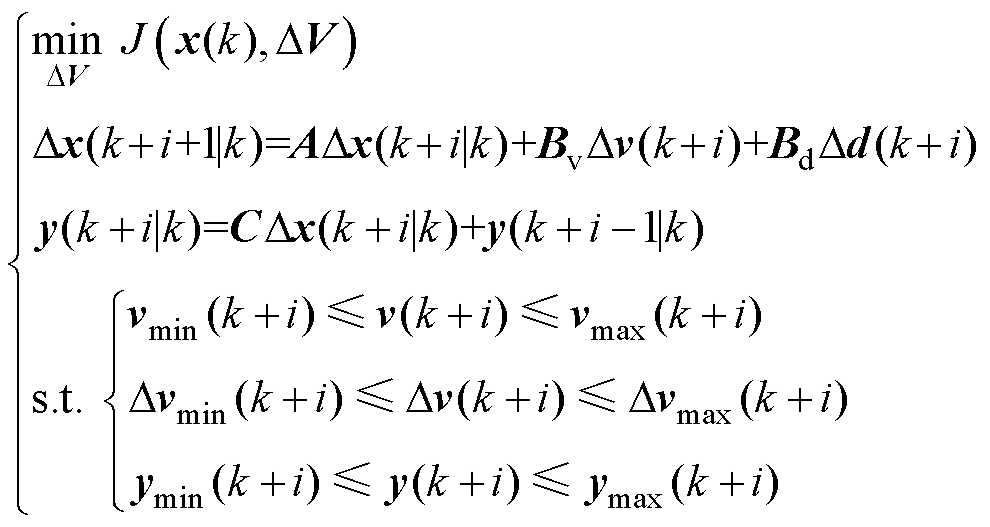 (13)
(13)
式中,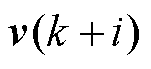 、
、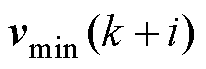 、
、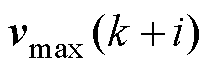 分别为
分别为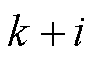 时刻的控制量及其最小值、最大值;
时刻的控制量及其最小值、最大值;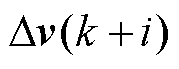 、
、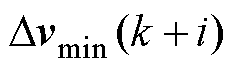 、
、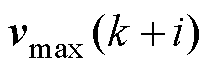 分别为
分别为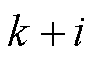 时刻的控制增量及其最小值、最大值;
时刻的控制增量及其最小值、最大值;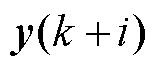 、
、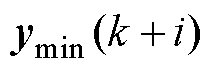 、
、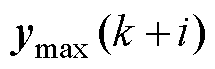 分别为
分别为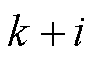 时刻的输出量及其最小值、最大值;
时刻的输出量及其最小值、最大值;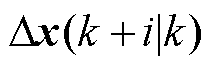 、
、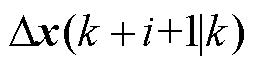 分别为
分别为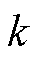 时刻预测的
时刻预测的 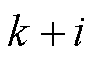 、
、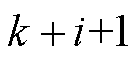 时刻的状态增量,以此类推,以下相同;
时刻的状态增量,以此类推,以下相同;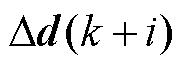 为
为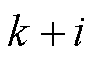 时刻的扰动增量,通常假设该值在
时刻的扰动增量,通常假设该值在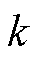 时刻之后为0;
时刻之后为0;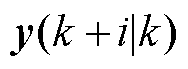 为
为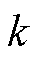 时刻预测的
时刻预测的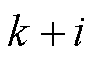 时刻的输出量;
时刻的输出量;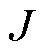 (x(k,
(x(k, 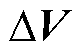 ))为目标函数,是
))为目标函数,是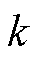 时刻状态量
时刻状态量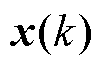 和控制序列
和控制序列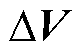 的函数,其中
的函数,其中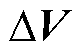 =
= 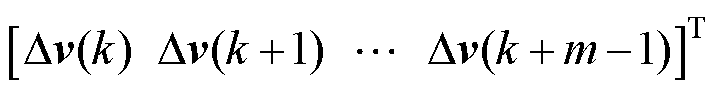 。
。
3.2.1 预测模型的作用
由式(13)可知,预测模型在优化问题中以约束的形式存在,通过预测时域内前后时刻状态变量、输出变量的线性关系,递推预测时域内的系统输出。定义系统输出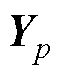 =
=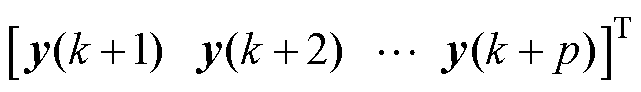 ,则预测方程为
,则预测方程为
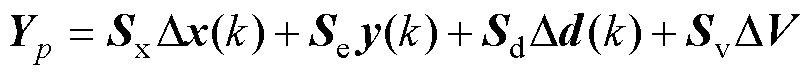 (14)
(14)
其中
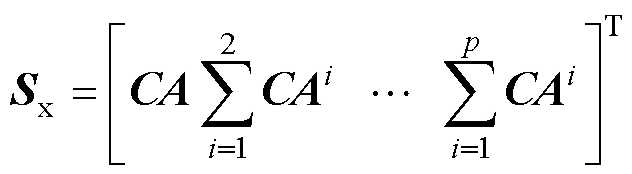
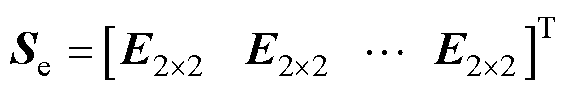
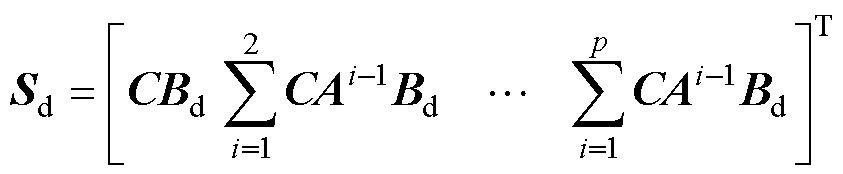
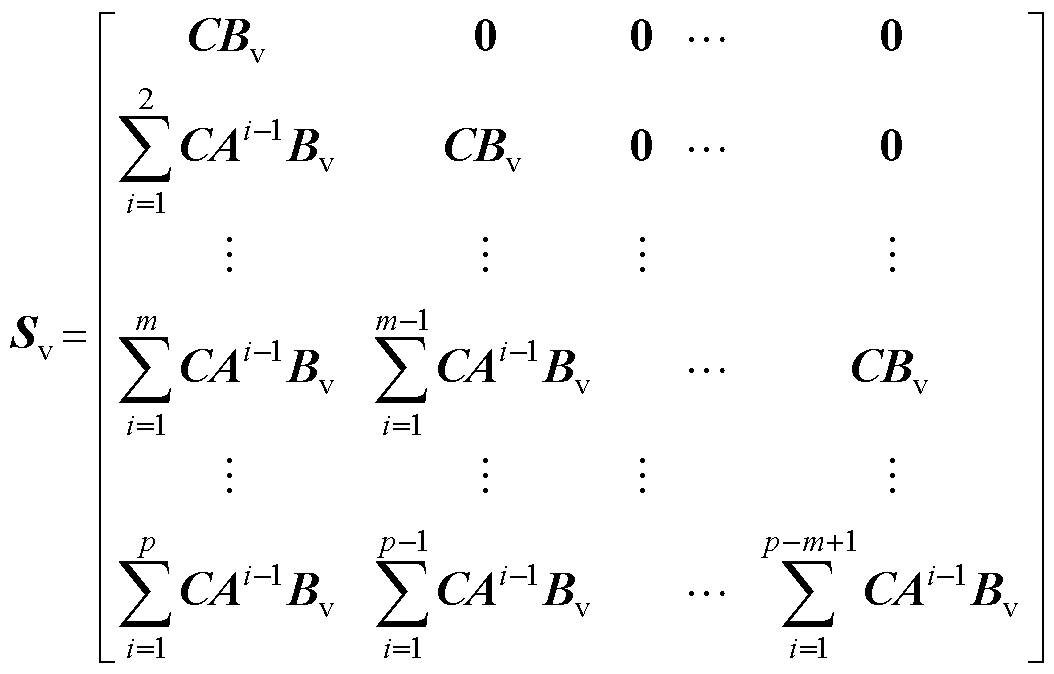
由式(14)可知,预测模型能根据当前状态和未来输入预测系统的未来输出。此时,与电力系统在线、离线仿真类似,可以任意给出未来的控制序列,然后观察系统在不同控制策略下的输出变化,从而为比较这些控制序列的优劣提供基础。
3.2.2 目标函数的设计
目标函数用于判断控制序列的优劣,一般而言,目标函数值越小,控制序列越优。本文希望直流电压保持稳定并且虚拟惯性响应强度不能太大,因此设计目标函数为
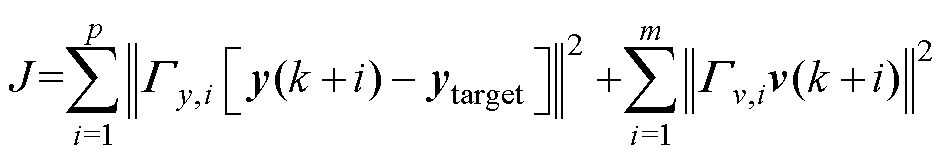 (15)
(15)
式中,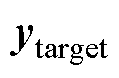 为输出量的跟踪目标,
为输出量的跟踪目标,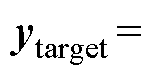
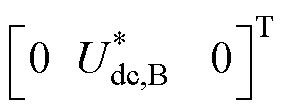 ;
;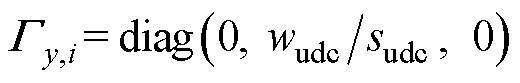 、
、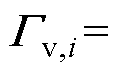
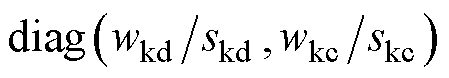 分别为输出量、控制量对应的权重矩阵,
分别为输出量、控制量对应的权重矩阵,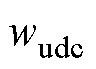 、
、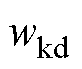 、
、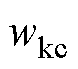 分别为
分别为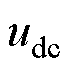 、
、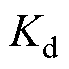 、
、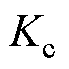 对应的权重系数,
对应的权重系数,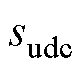 、
、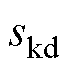 、
、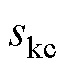 分别为
分别为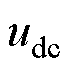 、
、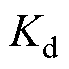 、
、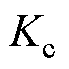 对应的尺度因子。
对应的尺度因子。
该目标函数分为两部分:第一部分对应直流电压保持稳定,由于未考虑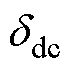 、
、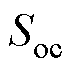 的跟踪,其对应的权重系数、跟踪目标均为0;第二部分对应虚拟惯性响应强度不能太大。通过最小化虚拟惯性系数减少辅助功率的调节量。
的跟踪,其对应的权重系数、跟踪目标均为0;第二部分对应虚拟惯性响应强度不能太大。通过最小化虚拟惯性系数减少辅助功率的调节量。
优化问题参数选取是一个难点,缺少统一且有效的理论指导。但就本文而言,由于目标函数仅包括一个输出量、两个控制量,参数选取的难度有所下降。选取原则如下:
(1)尺度因子:根据变量的最大值和最小值之差进行选取。各变量量纲不统一,且取值范围不同,为了消除其造成的影响,需对原始数据进行标准化处理。选取尺度因子为该变量最大值和最小值之差,相当于对变量进行了最大、最小标准化处理。
(2)权重系数:对于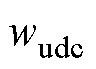 ,根据电压跟踪的重要性进行选取。
,根据电压跟踪的重要性进行选取。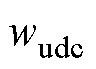 越大,跟踪目标越重要,此时
越大,跟踪目标越重要,此时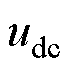 偏离目标的值越小,即电压偏差越小。对于
偏离目标的值越小,即电压偏差越小。对于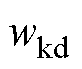 、
、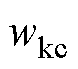 ,根据虚拟惯性支撑主次进行选取。权重系数越小,控制量越容易增大,换流器提供的惯性支撑力度更大。
,根据虚拟惯性支撑主次进行选取。权重系数越小,控制量越容易增大,换流器提供的惯性支撑力度更大。
需要说明的是,通过权重系数的调整可以实现并网换流器和储能系统的协调控制。增大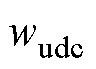 能提高并网换流器和储能系统的总惯量。增大
能提高并网换流器和储能系统的总惯量。增大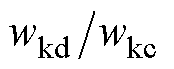 能提高储能系统虚拟惯量的分配比例;反之,则增强并网换流器的惯性响应强度。另外,在
能提高储能系统虚拟惯量的分配比例;反之,则增强并网换流器的惯性响应强度。另外,在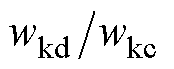 已知的情况下,根据式(7)可以估算两者注入母线的附加电流。
已知的情况下,根据式(7)可以估算两者注入母线的附加电流。
3.2.3 约束条件的设置
实际控制中,系统的电压、电压变化率等输出量越限,会引起安全性问题;MPC输出的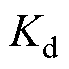 、
、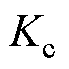 或
或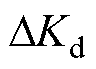 、
、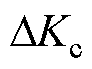 过大,会出现稳定性问题。因此,需要对这些变量在时域上的取值进行约束。
过大,会出现稳定性问题。因此,需要对这些变量在时域上的取值进行约束。
约束条件见式(13)时域约束部分,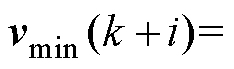
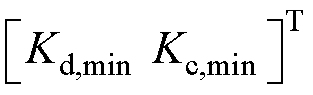 ,
,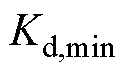 、
、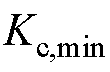 为虚拟惯性系数的最小值;
为虚拟惯性系数的最小值;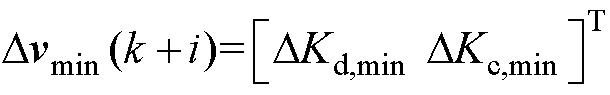 ,
,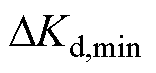 、
、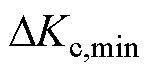 为虚拟惯性系数增量的最小值;
为虚拟惯性系数增量的最小值;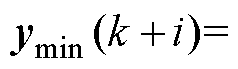
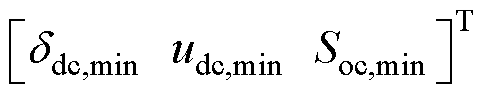 ,
,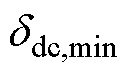 、
、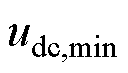 、
、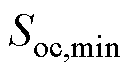 分别为电压变化率、电压、SOC的最小值;上述变量最大值的表达式与之类似,仅需将下标替换成“max”。
分别为电压变化率、电压、SOC的最小值;上述变量最大值的表达式与之类似,仅需将下标替换成“max”。
约束条件相关限值的选取原则如下:
(1)控制量:借鉴鲁汶大学的选取思想[27],并考虑下垂曲线纵截距调整与附加功率的关系,以及功率的双向流动,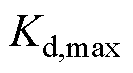 、
、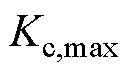 应满足
应满足
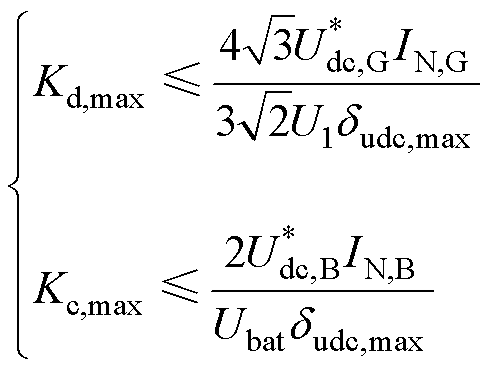 (16)
(16)
式中,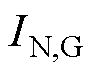 、
、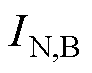 分别为
分别为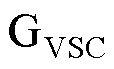 、
、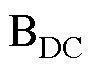 的额定电流。当
的额定电流。当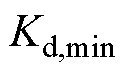 、
、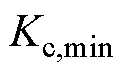 为0或比较小的正数时,可以提高系统恢复速度并抑制直流电压超调。
为0或比较小的正数时,可以提高系统恢复速度并抑制直流电压超调。
(2)输出量:根据直流微电网运行导则,选取电压、电压变化率的限值,以确保微电网的安全运行;根据蓄电池的充放电要求,选取荷电状态的限值,通常设置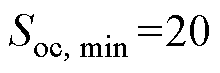 、
、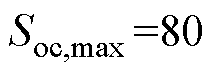 。
。
上述优化模型中,约束条件是必须满足的硬约束。实际运行中,由于存在不可测扰动、预测偏差等问题,电压、电压变化率等输出量违反边界约束的情况几乎是不可避免的。因此,首先应对约束进行软化,然后再求解优化模型。
软化约束不会对预测模型造成影响,只会改变目标函数和约束条件。目标函数更新为
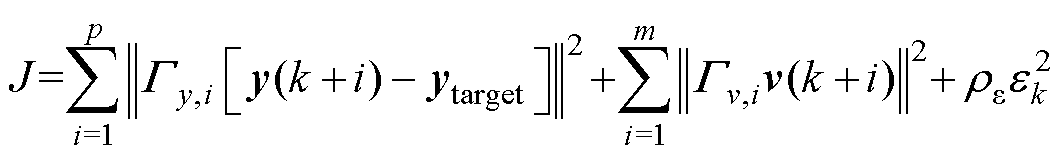 (17)
(17)
式中,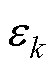 为因约束软化而引入的松弛变量,有
为因约束软化而引入的松弛变量,有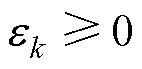 ,其本质上属于控制量;
,其本质上属于控制量;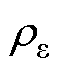 为违反约束的惩罚系数,其值越大,惩罚力度越大,
为违反约束的惩罚系数,其值越大,惩罚力度越大,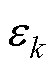 =0的可能性也越大。
=0的可能性也越大。
约束条件更新为
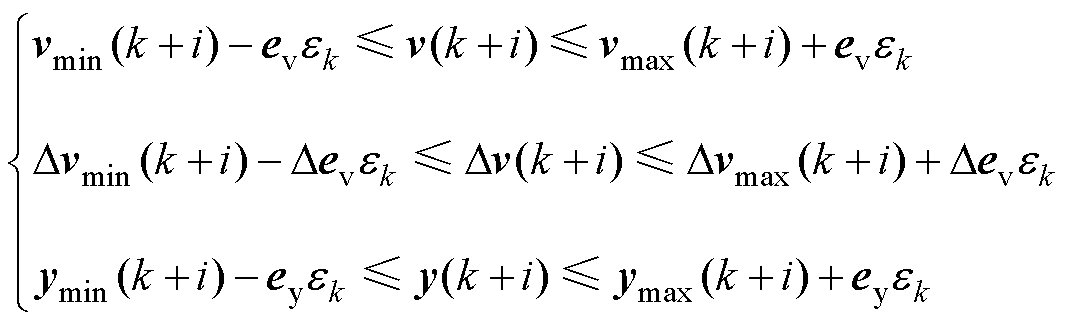 (18)
(18)
式中,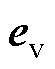 、
、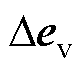 、
、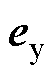 分别为
分别为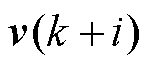 、
、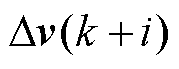 、
、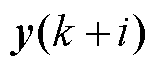 的松弛系数,其值越大,约束条件越宽松。
的松弛系数,其值越大,约束条件越宽松。
由新的目标函数和约束条件可知,该优化问题虽然引入了一个新的控制量,但依然是一个带线性约束的二次规划(Quadratic Programming, QP)问题,可采用积极集法和内点法进行求解[25]。实际运行中可能出现无解的问题。对于发生概率低且不连续的无解问题,MPC一般设置控制量与上一时刻相同,即保持不变;对于多次连续发生的无解问题,MPC可以退出运行,因为控制结构并未破坏,原系统在定直流电压和下垂控制下依然能稳定运行。
数值求解优化问题的快速性是困扰MPC应用的一个关键问题,但需要说明的是,随着求解算法的不断改进以及软硬件性能的持续提升,数值求解优化问题的速度将会大幅提升。
综上所述,基于MPC的虚拟惯性优化控制如图5所示。图5a中,增设的MPC器,通过光纤通信实现数据采集和控制量输出。图5b中,MPC器循环往复地执行三大步骤:①用运行数据刷新优化模型;②以预测模型为基础,求解刷新后的优化问题;③将所需优化解作用于控制单元,从而实现虚拟惯性的优化控制。
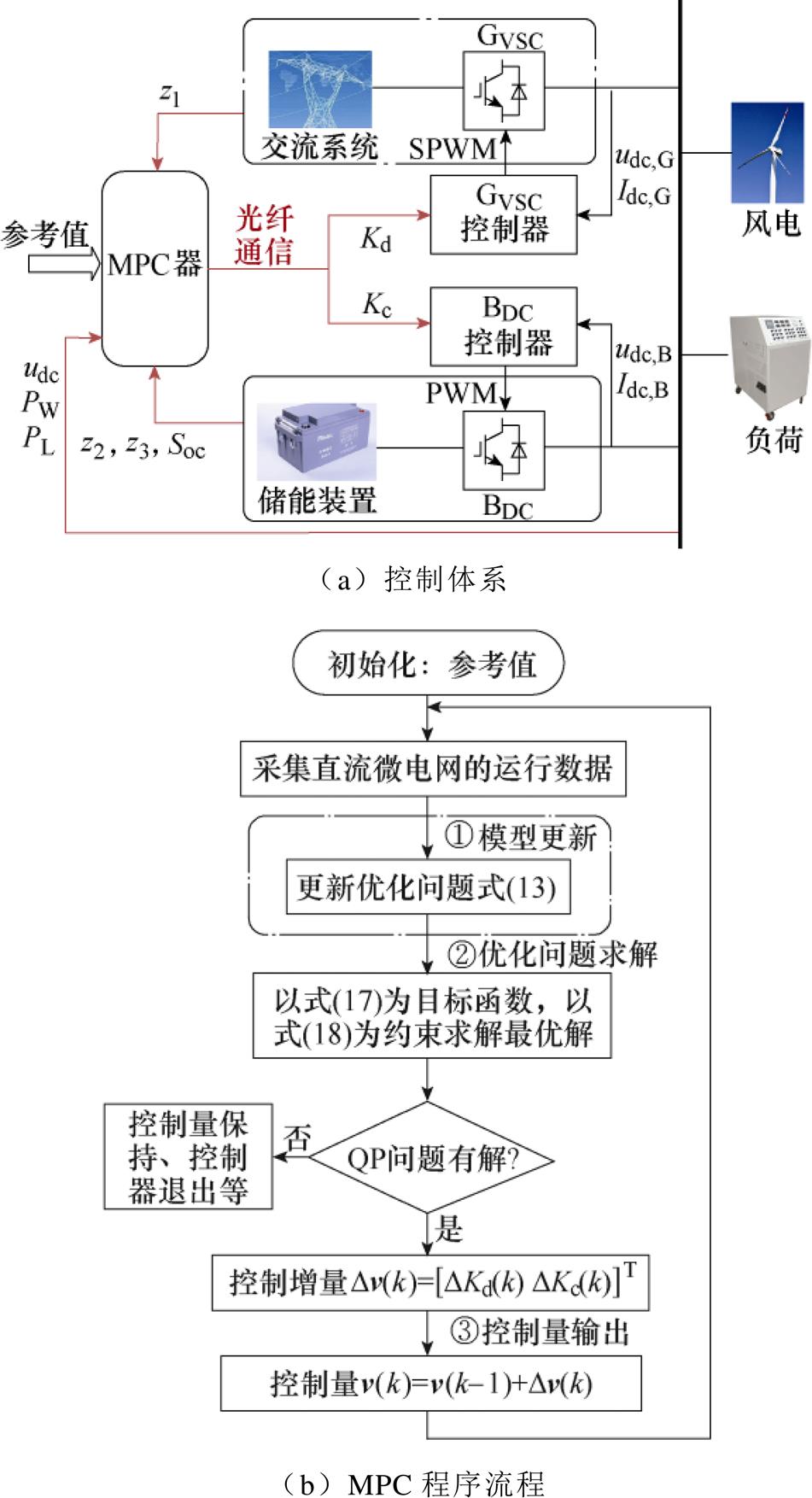
图5 基于MPC的虚拟惯性优化控制
Fig.5 Optimal control of virtual inertia based on MPC
为验证所提方法的有效性,本文搭建了如图6所示的硬件在环仿真系统[28]。该系统由RT-Lab实时仿真机、数字信号处理器(Digital Signal Processor, DSP)以及上位机(PC)等构成。MPC算法部署在DSP中,图1所示的直流微电网实时仿真模型通过上位机下载到RT-Lab中。由于光纤通信延迟为ms级[29],因此实验系统中未予以考虑,DSP与RT-Lab之间通过模拟端口实现数据交互。实验波形则通过RT-Lab前面板的min-BNC接口进行测量。
直流微电网中,直流母线额定电压为500 V,并网换流器、储能系统、风电和负荷额定功率分别为30 kW、15 kW、20 kW、30 kW,直流线路电阻、电感分别为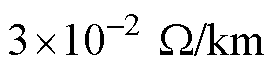 、
、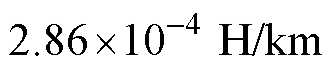 ,最小虚拟惯性系数为0,其他主要参数见表1。
,最小虚拟惯性系数为0,其他主要参数见表1。
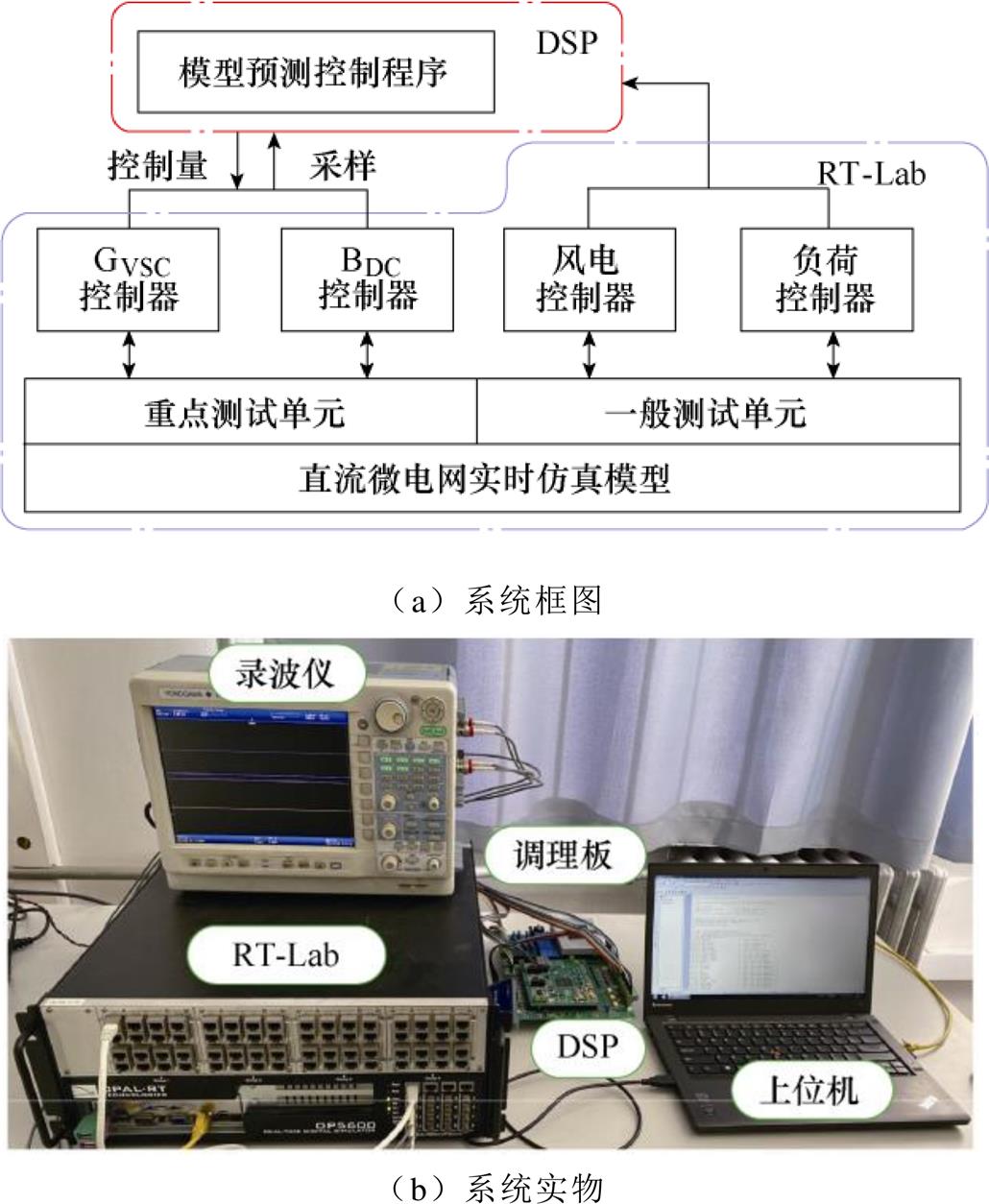
图6 硬件在环仿真系统
Fig.6 Hardware in the loop simulation system
表1 直流微电网其他主要参数
Tab.1 Other main parameters of the DC microgrid
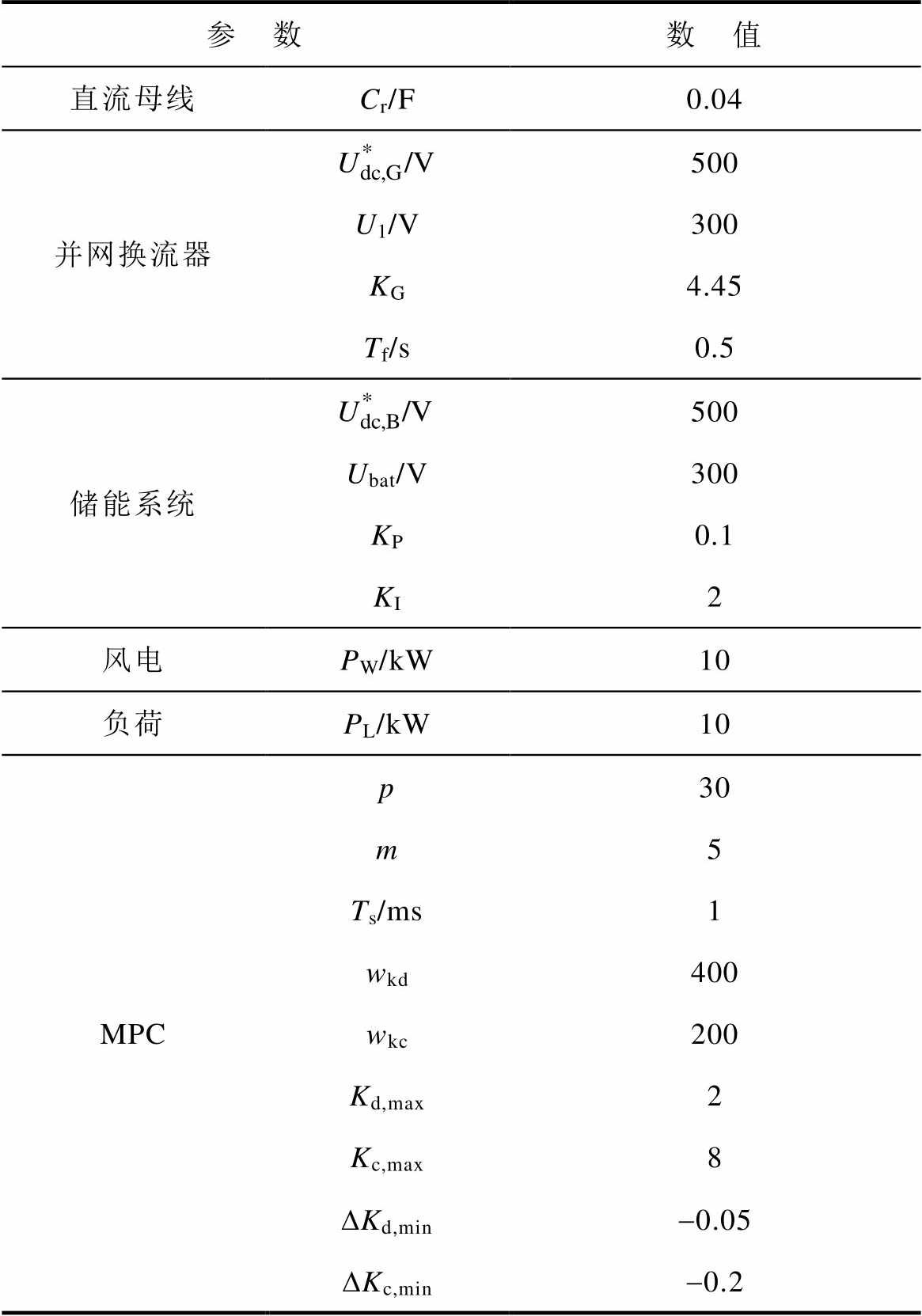
参 数数 值 直流母线Cr/F0.04 并网换流器500 U1/V300 KG4.45 Tf/s0.5 储能系统500 Ubat/V300 KP0.1 KI2 风电PW/kW10 负荷PL/kW10 MPCp30 m5 Ts/ms1 wkd400 wkc200 Kd,max2 Kc,max8 DKd,min-0.05 DKc,min-0.2
测试工况:负荷2 s时突增9.5 kW;自适应虚拟惯性控制,有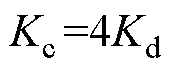 且
且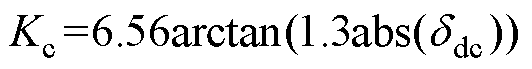 ;所提控制方法,有
;所提控制方法,有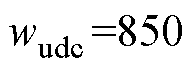 。同时,为了便于对比,假设两种控制下负荷突增瞬间惯性响应强度完全相同。
。同时,为了便于对比,假设两种控制下负荷突增瞬间惯性响应强度完全相同。
图7给出了两种控制方法下的对比结果。自适应虚拟惯性控制下:负荷突增,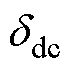 以及与之相关的
以及与之相关的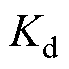 、
、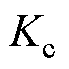 迅速增加以阻止电压正向偏离,3.8 s直流电压达到最低点495.7 V;之后,电压开始反向恢复,
迅速增加以阻止电压正向偏离,3.8 s直流电压达到最低点495.7 V;之后,电压开始反向恢复,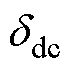 过0点,
过0点,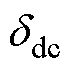 以及与之相关的
以及与之相关的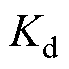 、
、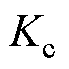 又开始增加,由于惯性较大,直流电压在参考值附近略微超调。所提控制方法下:负荷突增初期虚拟惯性系数迅速增大,为系统提供更有力的惯性支撑,直流电压的跌幅有所减小,4 s达到最低点496.1 V;然后,电压开始反向恢复,虚拟惯性系数减小至0,直流电压在前半段(8 s前)加速恢复减少了电压偏差,在后半段则降低速度消除了超调量。可见,与自适应虚拟惯性控制相比,所提方法在维持电压稳定、加快恢复速度和减少超调量方面具有优势。
又开始增加,由于惯性较大,直流电压在参考值附近略微超调。所提控制方法下:负荷突增初期虚拟惯性系数迅速增大,为系统提供更有力的惯性支撑,直流电压的跌幅有所减小,4 s达到最低点496.1 V;然后,电压开始反向恢复,虚拟惯性系数减小至0,直流电压在前半段(8 s前)加速恢复减少了电压偏差,在后半段则降低速度消除了超调量。可见,与自适应虚拟惯性控制相比,所提方法在维持电压稳定、加快恢复速度和减少超调量方面具有优势。
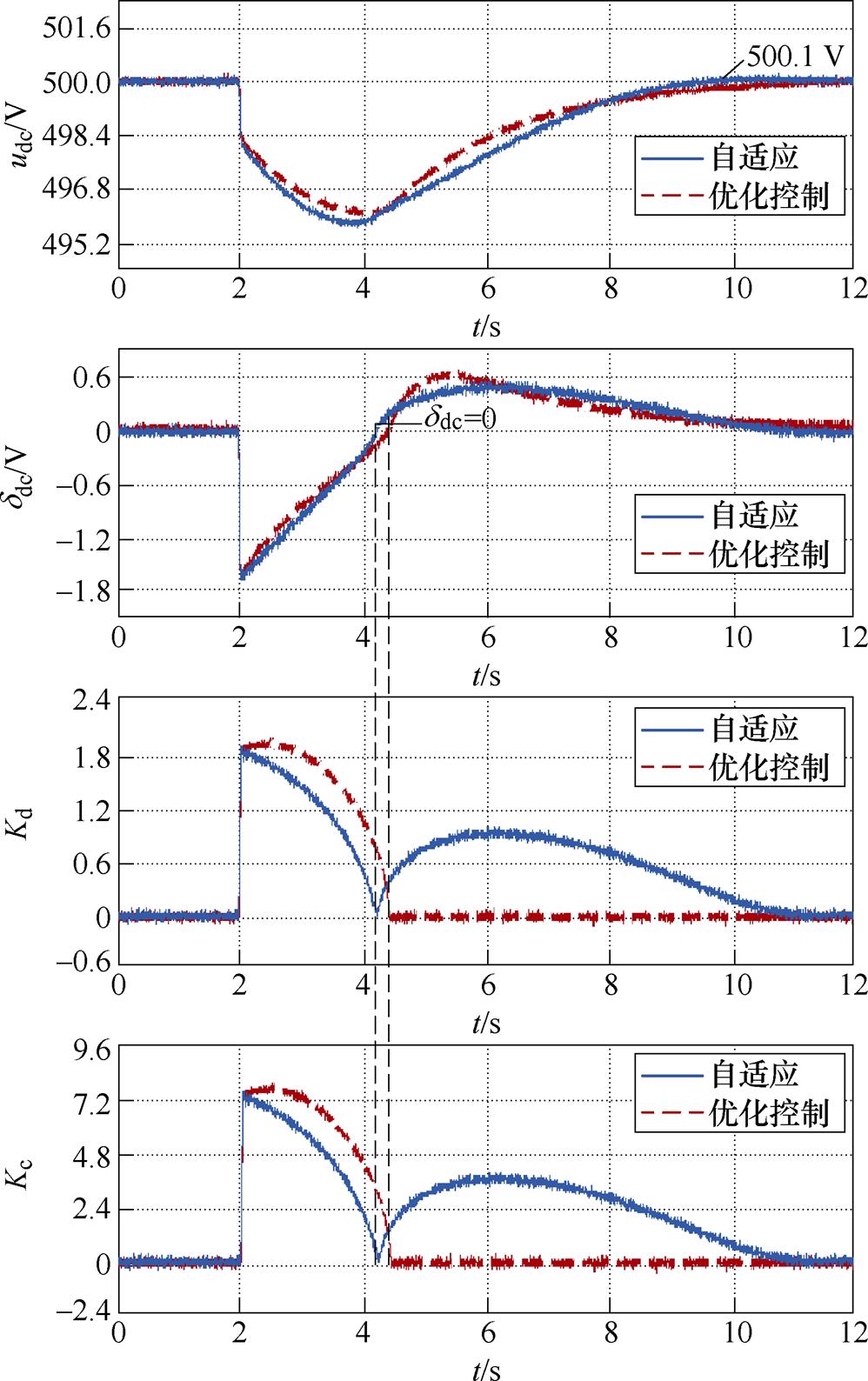
图7 稳定性与动态特性测试结果
Fig.7 Test results of stability and dynamic characteristics
测试工况:设置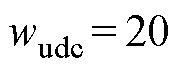 、
、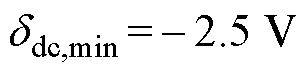 、
、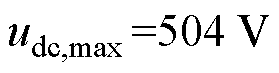 ;负荷于3 s、8 s分别发生9.5 kW的突增、突减。
;负荷于3 s、8 s分别发生9.5 kW的突增、突减。
图8给出了有无约束下的对比结果。无约束下,由于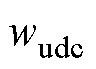 很小,并网换流器、储能系统的虚拟惯性响应很弱,负荷突增时
很小,并网换流器、储能系统的虚拟惯性响应很弱,负荷突增时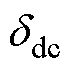 约为-5 V,负荷突减时
约为-5 V,负荷突减时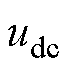 达到506.5 V,两者均超过限值。有约束下,负荷突增时虚拟惯性系数迅速增大以防
达到506.5 V,两者均超过限值。有约束下,负荷突增时虚拟惯性系数迅速增大以防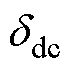 越限,但由于
越限,但由于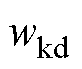 、
、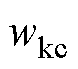 很大,并网换流器、储能系统仅提供满足约束的最小惯性支撑,
很大,并网换流器、储能系统仅提供满足约束的最小惯性支撑,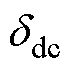 恰好控制在-2.5 V;与之类似,负荷突减时
恰好控制在-2.5 V;与之类似,负荷突减时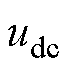 恰好控制在504 V。可见,采用所提方法能实现动态电压约束控制,从而提高系统的安全性。
恰好控制在504 V。可见,采用所提方法能实现动态电压约束控制,从而提高系统的安全性。
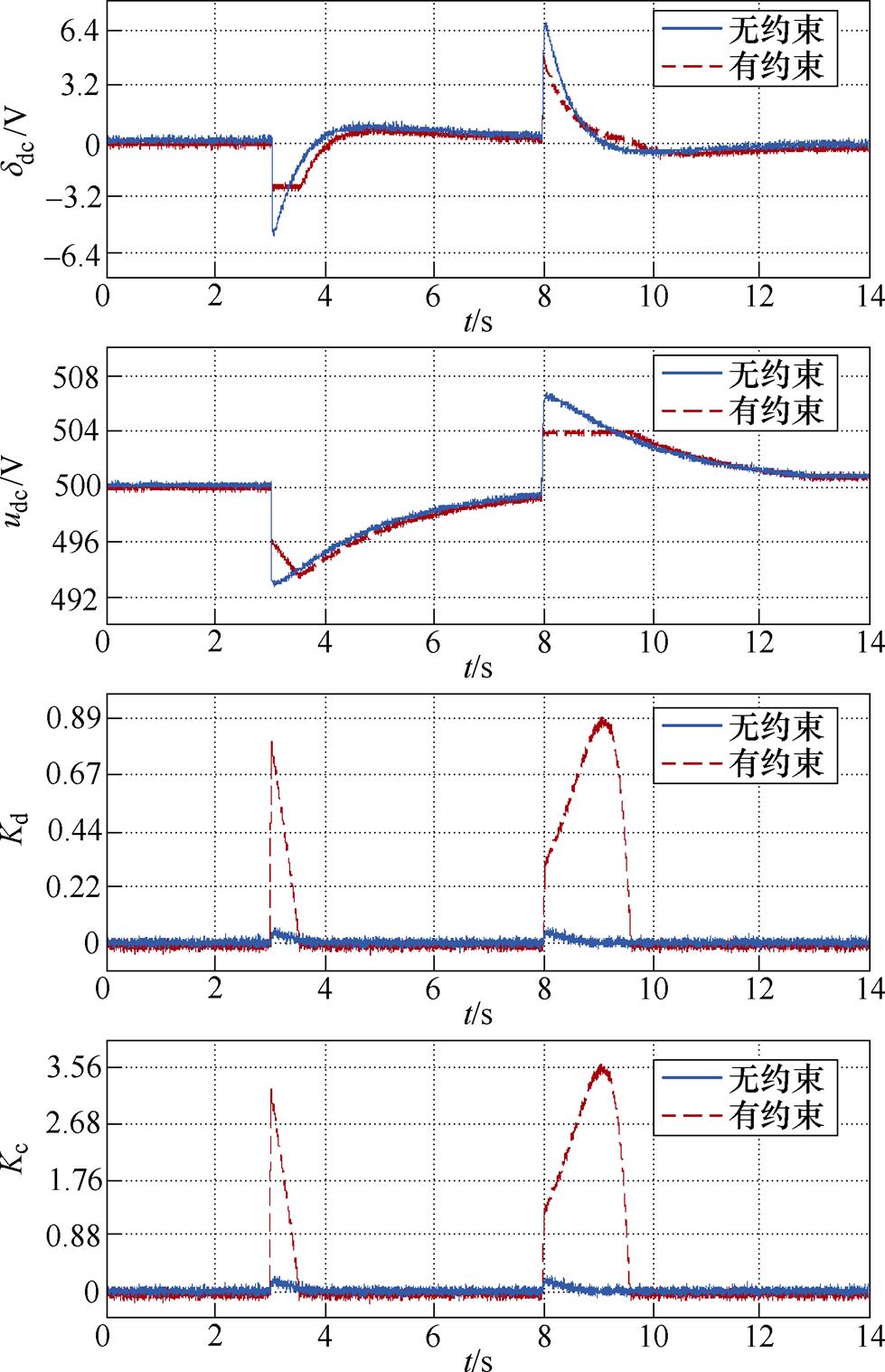
图8 约束控制测试结果
Fig.8 Test results of constraint control
在预测模型不变的情况下改变实时模型中的线路长度,以测试模型失配时控制器的性能。测试工况如下:设置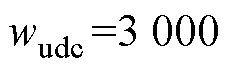 ,1 s时风速发生-0.5~0.5 m/s的随机波动;设置
,1 s时风速发生-0.5~0.5 m/s的随机波动;设置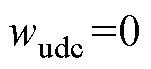 ,
,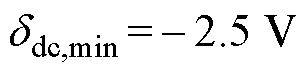 ,4 s时负荷发生9.5 kW的突增。
,4 s时负荷发生9.5 kW的突增。
图9给出了两种线路长度下的测试结果。1~4 s时,两者的运行曲线几乎重合;4 s时,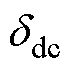 均能控制在限值以内,仅后者的
均能控制在限值以内,仅后者的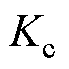 、
、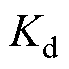 值略大。线路损耗的存在,使换流器功率与注入母线功率不再相等,
值略大。线路损耗的存在,使换流器功率与注入母线功率不再相等,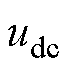 、
、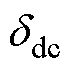 、
、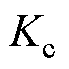 、
、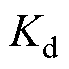 之间的关系发生改变,但优化的滚动实施对其进行了弥补,控制器的性能因此未受到大的影响。由此可知,本文所提方法对模型失配具有一定的耐受能力。
之间的关系发生改变,但优化的滚动实施对其进行了弥补,控制器的性能因此未受到大的影响。由此可知,本文所提方法对模型失配具有一定的耐受能力。

图9 模型失配测试结果
Fig.9 Test results of model mismatch
本文充分利用未来状态信息,提出一种基于MPC的直流微电网虚拟惯性优化方法,并给出主要参数的选取原则。通过理论分析和仿真证明,得到如下结论:
1)所提方法能提高直流电压的稳定性、动态特性以及安全性。以直流电压跟踪误差、虚拟惯性系数最小为目标,在维持电压稳定、加快恢复速度和减少超调量方面具有优势;以动态电压限制为约束,能防止因电压及其变化率超过阈值而导致切机切负荷甚至系统崩溃问题。
2)所提方法降低了优化问题的规模,有利于减轻MPC器的计算负担。对直流微电网的线路模型、换流器的内环控制进行简化处理,预测模型的阶数得以有效控制,优化问题的规模因此减小,控制器计算速度将会提升。
3)所提方法对线路模型失配具有一定的耐受能力。MPC采用滚动优化机制,用新的测量值刷新优化问题并重新求解,能顾及线路模型失配引起的不确定性。
本文采用的方法在虚拟惯性优化方面取得较好效果。但对考虑系统动态稳定、功率限制等因素的虚拟惯量边界以及多换流器协同控制问题,尚需进一步研究。
参考文献
[1] 熊雄, 季宇, 李蕊, 等. 直流配用电系统关键技术及应用示范综述[J]. 中国电机工程学报, 2018, 38(23): 6802-6813, 7115.
Xiong Xiong, Ji Yu, Li Rui, et al. An overview of key technology and demonstration application of DC distribution and consumption system[J]. Proceedings of the CSEE, 2018, 38(23): 6802-6813, 7115.
[2] 朱晓荣, 李铮, 孟凡奇. 基于不同网架结构的直流微电网稳定性分析[J]. 电工技术学报, 2021, 36(1): 166-178.
Zhu Xiaorong, Li Zheng, Meng Fanqi. Stability analysis of DC microgrid based on different grid structures[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 166-178.
[3] Alshareef M, Lin Zhengyu, Li Fulong, et al. A grid interface current control strategy for DC microgrids[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(3): 249-256.
[4] Li Yong, He Li, Liu Fang, et al. Flexible voltage control strategy considering distributed energy storages for DC distribution network[J]. IEEE Transa- ctions on Smart Grid, 2019, 10(1): 163-172.
[5] 曹建博, 王林, 黄辉, 等. 直流微电网多端口变换器虚拟惯性控制策略[J]. 电网技术, 2021, 45(7): 2604-2615.
Cao Jianbo, Wang Lin, Huang Hui, et al. Virtual inertia control strategy of multi-port converter used in DC micro-grid[J]. Power System Technology, 2021, 45(7): 2604-2615.
[6] 王勉, 唐芬, 赵宇明, 等. 虚拟直流电机的参数自适应控制策略[J]. 电力系统自动化, 2020, 44(14): 148-155.
Wang Mian, Tang Fen, Zhao Yuming, et al. Parameter adaptive control strategy of virtual DC machine[J]. Automation of Electric Power Systems, 2020, 44(14): 148-155.
[7] Wang Yi, Wang Chen, Xu Lie, et al. Adjustable inertial response from the converter with adaptive droop control in DC grids[J]. IEEE Transactions on Smart Grid, 2019, 10(3): 3198-3209.
[8] Zhu Xiaorong, Xie Zhiyun, Jing Shuzhi, et al. Distributed virtual inertia control and stability analysis of DC microgrid[J]. IET Generation Trans- mission & Distribution, 2018, 12(14): 3477-3486.
[9] Zhu Xiaorong, Meng Fanqi, Xie Zhiyun, et al. An inertia and damping control method of DC-DC converter in DC microgrids[J]. IEEE Transactions on Energy Conversion, 2020, 35(2): 799-807.
[10] 伍文华, 陈燕东, 罗安, 等. 一种直流微网双向并网变换器虚拟惯性控制策略[J]. 中国电机工程学报, 2017, 37(2): 360-372.
Wu Wenhua, Chen Yandong, Luo An, et al. A virtual inertia control strategy for bidirectional grid- connected converters in DC micro-grids[J]. Pro- ceedings of the CSEE, 2017, 37(2): 360-372.
[11] 张辉, 张凯涛, 肖曦, 等. 模拟直流发电机特性的储能变换器控制策略[J]. 电力系统自动化, 2017, 41(20): 126-132.
Zhang Hui, Zhang Kaitao, Xiao Xi, et al. Control strategy of energy storage converter for simulating DC generator characteristics[J]. Automation of Elec- tric Power Systems, 2017, 41(20): 126-132.
[12] 王慧, 赵书强, 孟建辉, 等. 基于下垂曲线截距调整的直流微电网自适应虚拟惯性控制[J]. 电力系统自动化, 2021, 45(24): 97-105.
Wang Hui, Zhao Shuqiang, Meng Jianhui, et al. Adaptive virtual inertia control for DC microgrid based on droop curve intercept adjustment[J]. Auto- mation of Electric Power Systems, 2021, 45(24): 97-105.
[13] 曹新慧, 刘昱良, 苗世洪, 等. 考虑参数自适应的直流微电网DC/DC变换器虚拟惯性控制策略研究[J]. 高电压技术, 2020, 46(4): 1281-1290.
Cao Xinhui, Liu Yuliang, Miao Shihong, et al. Research on virtual inertial control strategy of DC/DC converter in DC microgrid considering self-adaptive parameters[J]. High Voltage Engineering, 2020, 46(4): 1281-1290.
[14] 张祥宇, 李浩, 付媛. 含新型虚拟电机的直流微网动态稳定性分析与自适应电压惯性控制[J]. 高电压技术, 2021, 47(8): 2865-2874.
Zhang Xiangyu, Li Hao, Fu Yuan. Dynamic stability analysis and self-adaptive voltage inertia control of DC microgrids with novel virtual machine[J]. High Voltage Engineering, 2021, 47(8): 2865-2874.
[15] 张辉, 梁誉馨, 孙凯, 等. 直流微电网中多端口隔离型DC-DC变换器的改进虚拟电容控制策略[J]. 电工技术学报, 2021, 36(2): 292-304.
Zhang Hui, Liang Yuxin, Sun Kai, et al. Improved virtual capacitor control strategy of multi-port iso- lated DC-DC converter in DC microgrid[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(2): 292-304.
[16] 孟建辉, 邹培根, 王毅, 等. 基于灵活虚拟惯性控制的直流微网小信号建模及参数分析[J]. 电工技术学报, 2019, 34(12): 2615-2626.
Meng Jianhui, Zou Peigen, Wang Yi, et al. Small- signal modeling and parameter analysis of the DC microgrid based on flexible virtual inertia control[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2615-2626.
[17] 孟建辉, 宋美琪, 王毅, 等. 虚拟电容控制下并网型直流微网VSC多约束稳定运行边界[J]. 电力系统自动化, 2019, 43(15): 172-179, 199.
Meng Jianhui, Song Meiqi, Wang Yi, et al. Multi- constraint stable operation boundary of grid- connected voltage source converter of DC microgrid with virtual capacitance control[J]. Automation of Electric Power Systems, 2019, 43(15): 172-179, 199.
[18] 魏新迟, 许利通, 骆仁松, 等. 考虑饱和效应的无刷双馈发电机功率模型预测控制[J]. 电工技术学报, 2021, 36(17): 3721-3729.
Wei Xinchi, Xu Litong, Luo Rensong, et al. Model predictive power control of brushless doubly-fed induction generator considering saturation effect[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3721-3729.
[19] 周左, 汪洋, 李正明. 基于占空比控制的Vienna整流器模型预测控制策略[J]. 电力系统保护与控制, 2021, 49(10): 162-169.
Zhou Zuo, Wang Yang, Li Zhengming. Model predi- ctive control strategy of a Vienna rectifier based on duty cycle control[J]. Power System Protection and Control, 2021, 49(10): 162-169.
[20] 郭磊磊, 金楠, 李琰琰, 等. 并网逆变器无电网电压传感器模型预测控制[J]. 电工技术学报, 2020, 35(12): 2612-2622.
Guo Leilei, Jin Nan, Li Yanyan, et al. Grid voltage sensorless model predictive control for grid- connected inverters[J]. Transactions of China Elec- trotechnical Society, 2020, 35(12): 2612-2622.
[21] Mardani M M, Khooban M H, Masoudian A, et al. Model predictive control of DC-DC converters to mitigate the effects of pulsed power loads in naval DC microgrids[J]. IEEE Transactions on Industrial Electronics, 2019, 66(7): 5676-5685.
[22] 年珩, 叶余桦. 三端口隔离双向DC-DC变换器模型预测控制技术[J]. 电工技术学报, 2020, 35(16): 3478-3488.
Nian Heng, Ye Yuhua. Model predictive control of three-port isolated bidirectional DC-DC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3478-3488.
[23] 李帅虎, 向丽珍, 向振宇, 等. 用于改善VSG频率响应的模型预测控制方法[J]. 高电压技术, 2021, 47(8): 2856-2864.
Li Shuaihu, Xiang Lizhen, Xiang Zhenyu, et al. MPC control method for improving VSG frequency response[J]. High Voltage Engineering, 2021, 47(8): 2856-2864.
[24] 陈来军, 王任, 郑天文, 等. 改善独立微网频率动态特性的虚拟同步发电机模型预测控制[J]. 电力系统自动化, 2018, 42(3): 40-47.
Chen Laijun, Wang Ren, Zheng Tianwen, et al. Model predictive control of virtual synchronous generator to improve dynamic characteristic of frequency for isolated microgrid[J]. Automation of Electric Power Systems, 2018, 42(3): 40-47.
[25] 陈虹. 模型预测控制[M]. 北京: 科学出版社, 2013.
[26] 吴岩, 王玮, 吴学智, 等. 微电网跟踪调度计划双层双时间尺度实时控制策略[J]. 电力自动化设备, 2021, 41(1): 120-134.
Wu Yan, Wang Wei, Wu Xuezhi, et al. Two-layer double-time scale real-time control strategy of micro- grid for tracking scheduling plan[J]. Electric Power Automation Equipment, 2021, 41(1): 120-134.
[27] 宋琼, 张辉, 孙凯, 等. 多微源独立微网中虚拟同步发电机的改进型转动惯量自适应控制[J]. 中国电机工程学报, 2017, 37(2): 412-424.
Song Qiong, Zhang Hui, Sun Kai, et al. Improved adaptive control of inertia for virtual synchronous generators in islanding micro-grid with multiple distributed generation units[J]. Proceedings of the CSEE, 2017, 37(2): 412-424.
[28] Meng Jianhui, Wang Yi, Wang Chen, et al. Design and implementation of hardware-in-the-loop simu- lation system for testing control and operation of DC microgrid with multiple distributed generation units[J]. IET Generations Transmission & Distribution, 2017, 11(12): 3065-3072.
[29] Zhi Na, Ding Ke, Du Liang, et al. An SOC-based virtual DC machine control for distributed storage systems in DC microgrids[J]. IEEE Transactions on Energy Conversion, 2020, 35(3): 1411-1420.
Abstract To improve the stability and dynamic characteristics of microgrid DC bus voltage, researchers have proposed adaptive virtual inertial control methods. These methods have clear analytical formulas for virtual inertia, but providing the design details for the “optimal” parameters is challenging. Moreover, the operation state determines the virtual inertia, and the controller acts in a delayed manner with the system variations. As a result, emergency preventive control cannot be realized due to dynamic voltage constraints. Therefore, a model predictive controller has been proposed to realize the virtual inertia optimization of the DC microgrid by dynamically adjusting the units’ virtual inertia coefficients.
Firstly, the linear discrete model of a DC microgrid with virtual inertial control units was established to predict the future trend of system output. Secondly, the model predictive controller was designed to minimize the weighted sum of DC voltage tracking and virtual inertia, maintain the DC voltage stability, and make the intensity of the inertial response acceptable. Taking the DC voltage and its climbing rate as the constraints, preventing the excess safety threshold for the dynamic voltage is also crucial in case of machine cut-off, load cut-off, or even system collapse. At each sampling period, the individual virtual inertia coefficient is solved and updated to realize the optimization of virtual inertia. Finally, the selection principles of the main parameters are given through theoretical analysis.
Hardware-in-the-loop simulation experiments have been built to verify the proposed method. Compared with the adaptive virtual inertial control, the proposed method provides a stronger inertial support for the system, increases rapidly in the initial stage of the sudden load increase, and reduces the drop of DC bus voltage. In reverse recovery, the virtual inertia coefficients were reduced, so the DC voltage recovery is accelerated in the beginning, and the recovery speed is reduced in the following time to eliminate the overshoot. In addition, the test result shows that the proposed method can maintain a steady state and its climbing rate within the desired range. Finally, the model mismatch scenarios have also been tested. The result shows that, under the line model mismatch, the performance of DC bus voltage and virtual inertia coefficients do not degrade substantially by compensating for the optimized rolling, thus guaranteeing the controller’s adaptive performance.
Conclusions can be drawn: (1) The proposed method can improve the stability, dynamic characteristics, and safe operation of microgrid DC bus voltage. Aiming at minimizing DC voltage tracking error and virtual inertia coefficients, the proposed control has advantages in improving DC bus voltage stability, accelerating recovery speed, and reducing overshoot. It can also prevent the voltage and its climbing rate out of the thresholds. (2) The proposed method can reduce the optimization size problem, which is beneficial for optimizing the computational burden of the MPC controller. The prediction model can be effectively simplified and well controlled by simplifying the DC microgrid line model and converter control loops, thus reducing the optimization scale and contributing to accelerated calculation speed. (3) The proposed method provides certain tolerance to line model mismatch. MPC uses a rolling optimization mechanism to update the optimization problem with updated measured values, which mitigates the model uncertainty caused by the mismatch.
keywords:DC microgrid, virtual inertia optimal control, linear discrete model, model prediction control
DOI: 10.19595/j.cnki.1000-6753.tces.220691
中图分类号:TM712
国家自然科学基金资助项目(51807064)。
收稿日期 2022-04-27
改稿日期 2022-08-03
赵书强 男,1964年生,教授,博士生导师,研究方向为电力系统分析与控制。E-mail: zsqdl@163.com
王 慧 男,1982年生,博士研究生,高级工程师,研究方向为新能源电力系统稳定控制与经济调度。E-mail: wanghui@ncepu.edu.cn(通信作者)
(编辑 陈 诚)