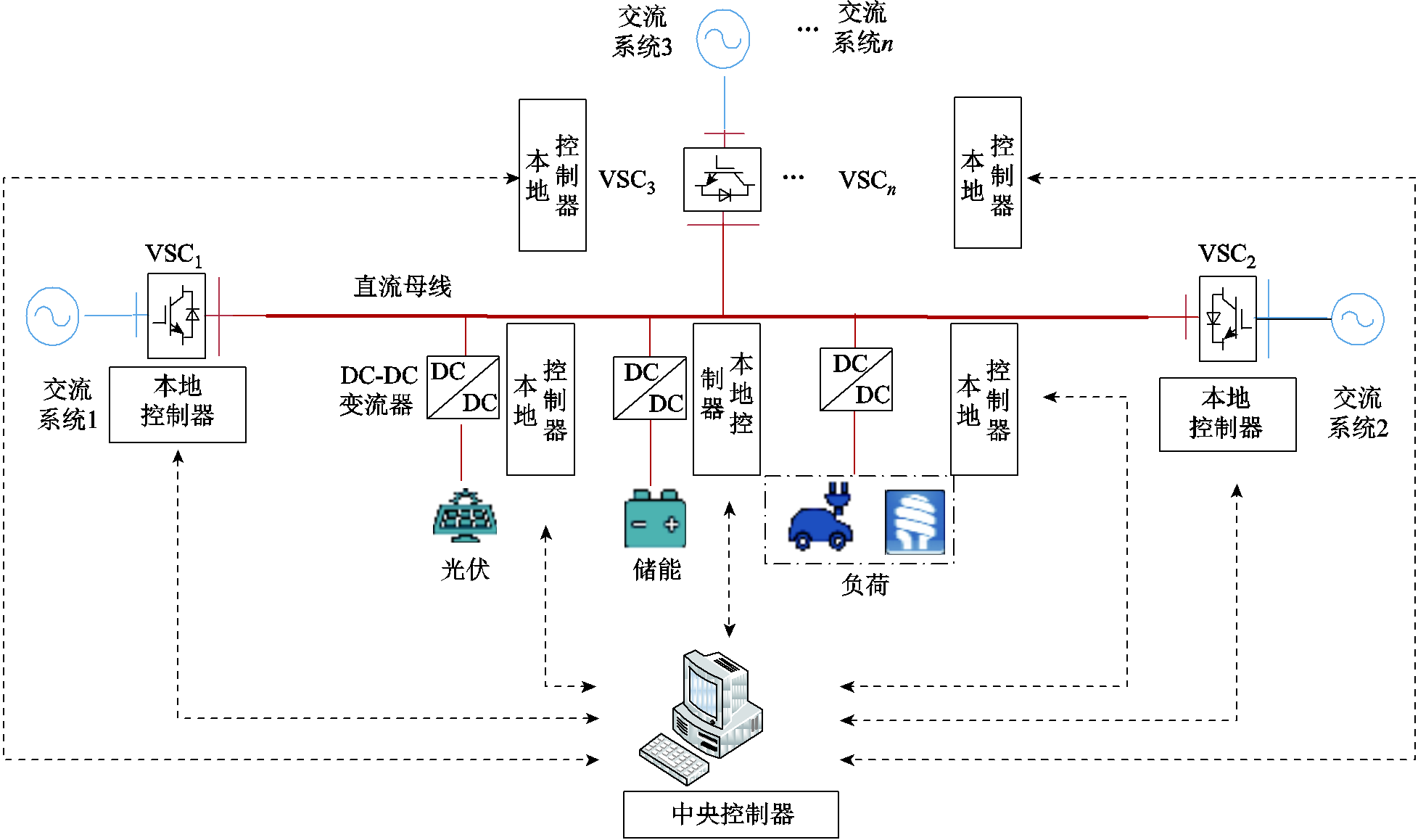
图1 多端直流系统示意图
Fig.1 Schematic diagram of multi-terminal low-voltage DC system
摘要 针对由低压多端直流系统中接入的可再生能源和直流负荷不确定性波动引起的系统直流电压波动、越限甚至跌落、振荡发散等电压稳定问题,提出一种主从控制下提高直流配电系统稳定性的时滞模型预测附加控制策略。首先,针对系统通信网络存在延时的情况,搭建了相应的系统时滞预测模型;然后,在此预测模型基础上,附加控制策略以系统直流电压波动最小和最小附加调节指令为目标,实现以最小出力平抑不确定扰动下系统直流电压的波动,进一步分析了通信延时对系统稳定性及附加控制策略性能的影响;最后,通过三端低压直流系统进行仿真和算例分析,结果表明,所提出的时滞模型预测附加控制策略能很好地平抑多端直流系统受不确定扰动带来的电压波动问题,提高系统稳定性,具有较好的鲁棒性。
关键词:低压多端直流系统 模型预测控制 分布式能源 附加控制 通信延时
分布式可再生能源的快速发展以及用户对直流负荷如电动汽车、LED(light-emitting diode)等需求的与日俱增,给传统交流配电网带来了如负荷多样化及网络架构庞杂等诸多挑战[1-3]。相较于传统交流配电网,低压多端直流系统具有减少直流负荷和可再生能源接入时的能量转换环节、结构多样及潮流灵活可控等优势,因此受到了广泛的关注与应用[4-6]。
多端直流系统具有高度电力电子化、弱阻尼、低惯性等特点,因此系统稳定性问题较为突出。一方面当系统中接入的可再生能源及负荷的功率发生波动或恒功率换流站交换功率发生波动时,会引起系统直流电压的波动;另一方面由恒功率负荷输入侧等效电容和线路阻抗形成的弱阻尼LC滤波,与并联在直流母线的换流器间相互作用,进一步降低系统稳定裕度[7],使系统面对不确定扰动更加敏感,加剧其直流电压波动变化趋势,易引发波动、闪变,甚至电压跌落、振荡发散等电压稳定问题,降低系统电能质量,严重影响系统安全运行[8-9]。
针对如何提高低压多端直流系统在多重不确定扰动下的电压稳定问题,国内外专家学者进行了大量研究。其中,附加控制因其结构简单易行,无需改变控制系统现有控制策略与环路结构,得到了比较广泛的研究[10]。文献[11-12]利用李雅普诺夫理论设计系统反馈控制率,并对多端直流系统各换流站施加附加电流控制,以达到平抑电压波动,提高系统稳定性的目的。文献[13]利用状态反馈的线性化方法(Linearization via State Feedback, LSF)构建控制函数,提高舰船多变换器直流供电系统的直流电压质量。此外,文献[14]利用非线性控制技术,针对多端直流系统,提出基于非线性鲁棒优化的双层控制策略,根据直流母线电压实际值与参考值偏差生成附加功率指令,解决电压越限、振荡等问题。
附加控制策略在改善多端直流系统在多重扰动下的电压稳定问题方面已取得一定的研究成果。然而文献[11-12]在设计反馈控制率时,对研究对象本身有一定要求,需要满足可状态反馈化的条件,适用场景有一定局限性,不易推广。且上述附加控制器在参数设计方面,大多依赖设计者经验,存在控制成本较高,无法保证达到最优控制效果的问题。此外,附加控制大多依赖上层中央控制器的调度,由于换流站本地控制器与上层中央控制器之间往往存在一定物理距离,因此通信延时的问题无法避免,会对附加控制效果造成一定影响。
对此,本文结合主从控制下多端直流系统的运行特征,提出一种时滞模型预测附加控制策略。该方法利用模型预测控制(Model Predictive Control, MPC)算法构建附加控制器。MPC也被称为滚动时域优化控制,基于一定系统预测模型,通过相应的约束条件可实现对控制成本的约束,进一步求解优化目标函数,可对多个参数变量进行在线优化控制,控制出力成本的同时达到最优控制效果。此外,针对系统通信网络存在的通信延时情况,本文搭建了系统时滞预测模型,可以更精确地描述时滞系统动态特性,提高控制策略鲁棒性。附加控制策略以系统电压波动最小和出力最小为优化目标,通过滚动优化和反馈校正,动态生成功率附加控制指令,从而起到平抑系统电压波动,系统安全运行的作用。最后通过Matlab/Simulink平台,完成了算例分析和仿真验证,证明了控制策略的有效性和准确性。
典型的低压多端直流系统结构图如图1所示。通常系统包含多个换流站、新能源发电单元、储能单元、直流母线以及直流负荷单元。上层中央控制器嵌入时滞模型预测附加控制策略,并负责采集各个设备端本地控制器的状态变量信息,下发附加控制指令到各个设备的本地控制器。起到实时监测直流母线电压,维持系统功率平衡的作用。需要指出的是,在实际工况中,本地控制器与中央控制器存在一定物理距离,因此附加控制指令在下发过程中会存在一定的通信延时。对于不同的多端直流系统,考虑工况与物理距离的不同,一般考虑通信延时在几个毫秒至几百毫秒不等[15-17]。各交流系统分别通过其对应的并网电压源换流器(Voltage Source Converter, VSC)实现柔性互联。VSC直流侧通过直流线路接入直流母线;光伏等新能源发电单元则由对应的DC-DC变流器接入直流母线;电动汽车及LED灯等作为主要直流负荷接入母线。

图1 多端直流系统示意图
Fig.1 Schematic diagram of multi-terminal low-voltage DC system
本文研究的低压多端直流系统,VSC换流站交流侧电网为强电网,因此下述建模分析中均忽略了锁相环的影响[18]。以多端直流系统中第n个VSC为例,拓扑结构为双闭环矢量控制的两电平换流站,其经典等效电路如图2所示。图2中,usan、usbn、uscn和isan、isbn、iscn分别代表VSCn交流并网侧ABC三相电压及电流,Lsn、Rsn分别代表VSCn交流侧滤波电感及等效电阻,uoan、uobn、uocn分别代表VSCn桥臂侧ABC三相电压,udcn表示VSCn直流侧电压。
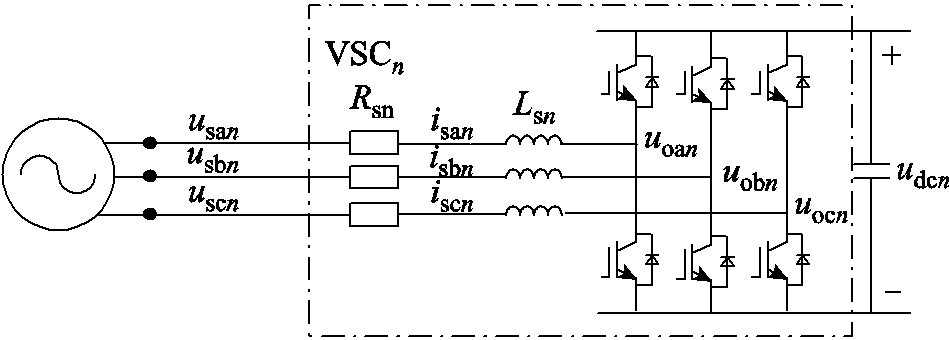
图2 VSC等效电路
Fig.2 VSC equivalent circuit
本文直流网络建模采用π型线路模型,由VSC直流侧直流线路、直流母线和直流母线负荷组成,直流网络示意图如图3所示。图3中udc为直流母线电压,Rn、Ln、Cn、Pdcn分别表示VSCn对应的直流网络电阻、电感、直流侧电容和直流有功功率,in、iload分别表示VSCn直流侧线路电流和流向直流母线处的负荷电流,C0表示直流母线电容。系统中储能与光伏发电单元一般经DC-DC变流器接入直流母线,而DC-DC变流器在闭环控制时会呈现恒功率负载特性[19]。因此,本文中将其等效为恒功率负载。并进一步与母线处的直流负荷等效并联,得到等效聚合负荷功率Peq。
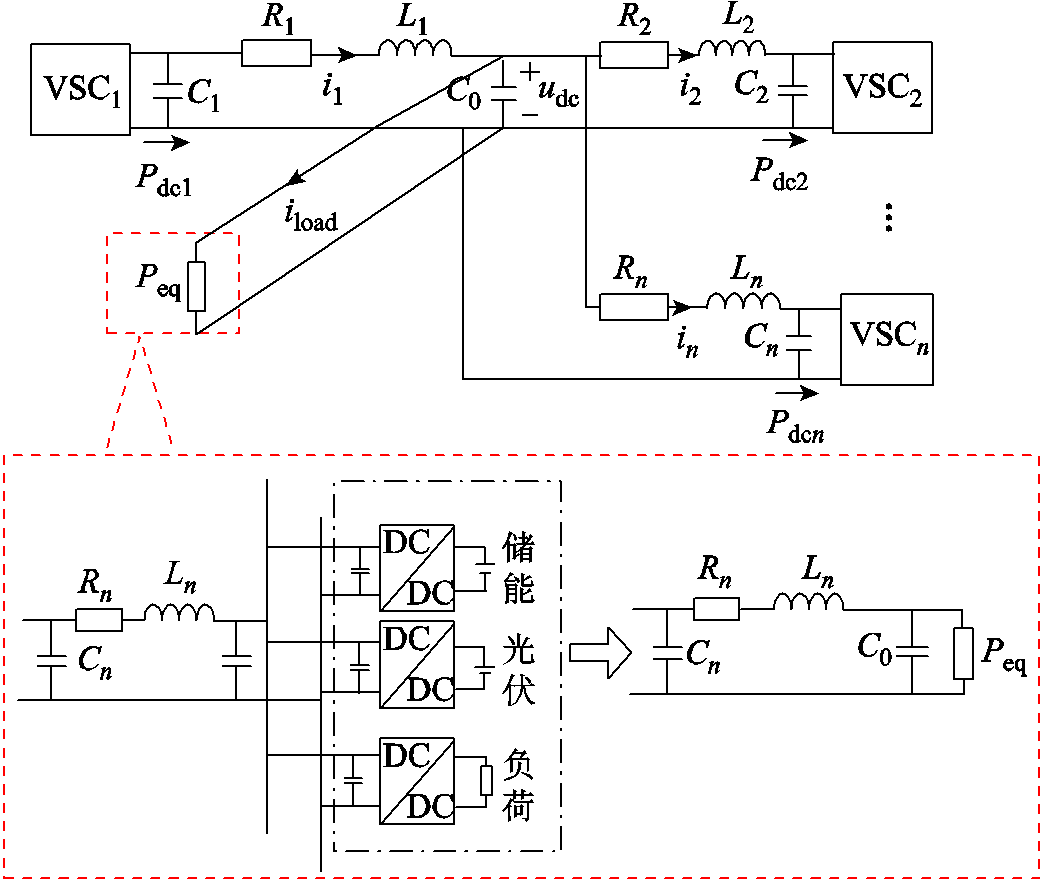
图3 直流网络示意图
Fig.3 Schematic diagram of DC network
本文研究的低压多端直流系统采用主从控制方式。系统内有且只有一个主站VSC,采用定直流电压控制策略,主要负责维持系统的电压稳定和功率平衡。其余VSC作为系统的从站,采用定功率控制策略。主站VSC采用的定电压控制原理和从站VSC采用的定功率控制原理分别如图4a和图4b所示,两者均采用双闭环控制原理,分为电压或功率控制外环和电流控制内环。图4中,Kpv、Kiv为定电压控制外环的PI控制参数,KpP、KiP和KpQ、KiQ分别为定功率控制外环的PI控制参数,Kpd、Kid和Kpq、Kiq分别为dq轴电流内环的PI控制参数,usdn、usqn分别为电压usan、usbn、uscn的dq轴分量,isdn、isqn分别为电流isan、isbn、iscn的dq轴分量,uodn、uoqn是电压uoan、uobn、uocn的dq轴参考值,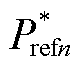 、
、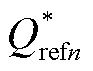 分别为有功功率、无功功率的控制指令,Pn、Qn分别为有功功率、无功功率的实际值,
分别为有功功率、无功功率的控制指令,Pn、Qn分别为有功功率、无功功率的实际值,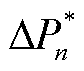 、
、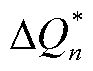 分别为时滞模型预测附加控制器实时求解得到的有功功率、无功功率附加控制指令。
分别为时滞模型预测附加控制器实时求解得到的有功功率、无功功率附加控制指令。
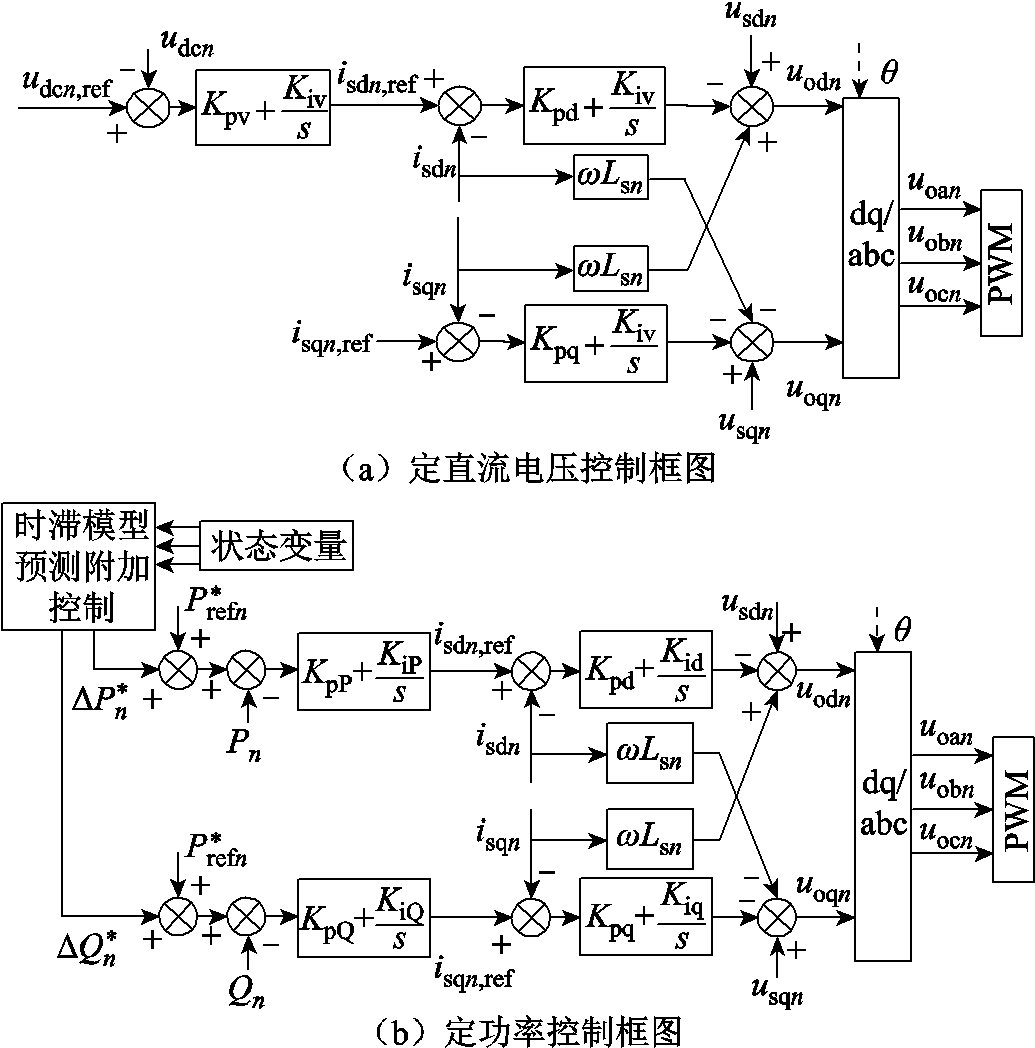
图4 主从控制策略
Fig.4 Master-slave control
时滞预测模型的附加控制策略主要是通过在线调节系统各从站功率附加控制指令以达到调整各站出力,平抑电压波动,解决电压波动、闪变、振荡发散等稳定性问题的目的。具体控制策略框图如图5所示。当系统测量到扰动后,嵌入中央控制器的附加控制策略开始工作,将采集的多端直流系统各换流站关键参数信息,如电压、电流、负载功率等,作为状态变量输入到系统时滞预测模型中,在线求解得到包含未来一定时间内最优附加功率序列的合集并下发至VSC本地控制器的从站功率外环。值得注意的是,为了减小控制误差,本地控制器只取优化附加控制序列的第一个值叠加到上一时刻的功率参考值,经PI控制器生成优化后的PWM 信号,完成一次附加功率优化控制。接着系统不断测量并更新状态变量输入到附加控制器中,完成滚动优化和反馈校正,提高了附加控制策略鲁棒性和控制性能。
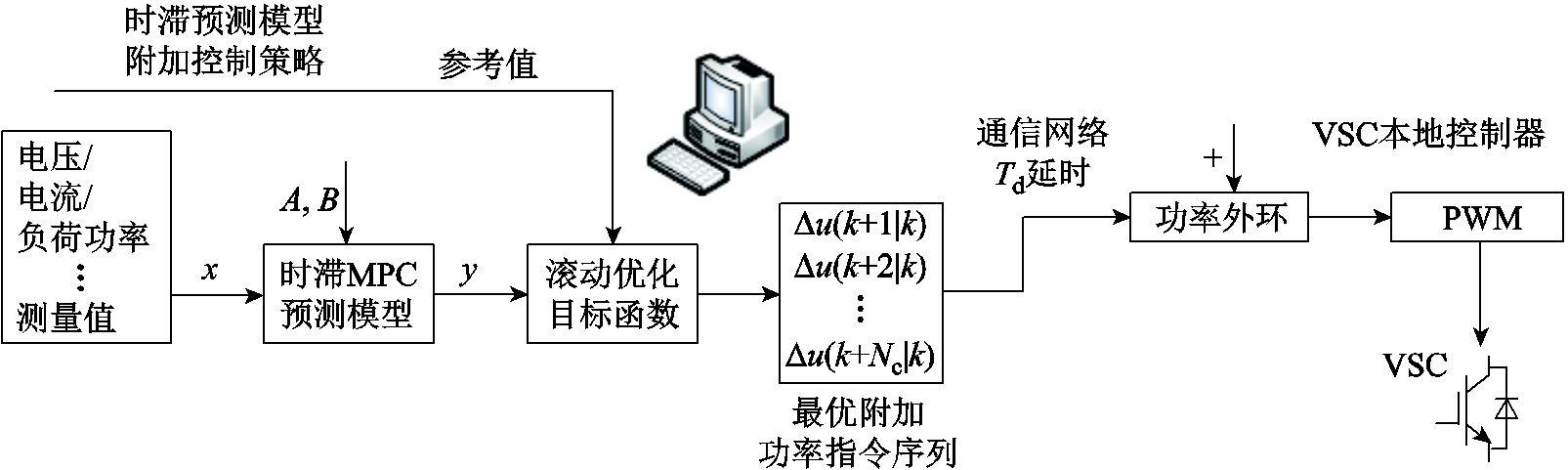
图5 基于MPC的附加控制策略
Fig.5 Control strategy of MPC based additional control
MPC是基于离散预测模型的有限时域闭环最优控制算法。主要分为模型预测、滚动优化和反馈校正三个部分[20-21]。MPC优化算法控制原理如图6所示。
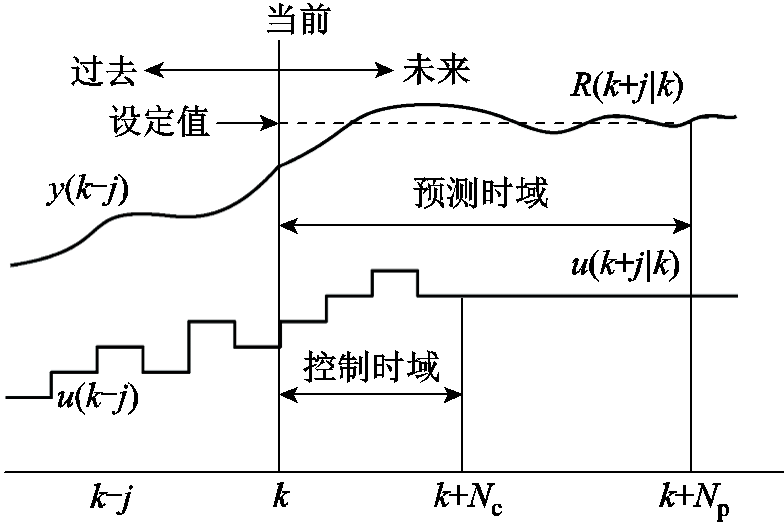
图6 MPC优化算法控制原理
Fig.6 Control principle of MPC optimization algorithm
图6中,Np为MPC优化算法的预测时域,Nc为控制时域,一般地,Nc≤Np。预测模型是MPC优化算法求解的基础。本文研究的低压多端直流系统时滞预测模型,在时滞系统的连续状态空间方程的基础上进行离散化处理,得到形式满足式(1)的状态空间方程。在k时刻,根据测量的系统状态变量x(k)和预测模型式(1),预测包含未来Np个时刻的系统状态变量序列[x(k+1|k) 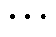 x(k+Np|k)]。
x(k+Np|k)]。
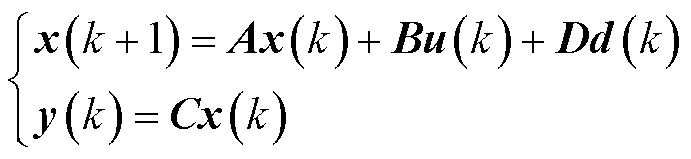 (1)
(1)
式中,A、B、C、D、d(k)和u(k)分别为预测模型的状态矩阵、输入矩阵、输出矩阵、扰动矩阵和扰动变量。
接着通过求解包含系统电压、功率和附加功率相关约束条件的最优化问题,得到包含Nc个时刻的最优附加功率控制指令,即[u(k|k) 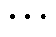 u(k+Nc-1|k)]并下发,完成一次优化控制过程。在下一控制时刻,即k+1时刻,测量并更新系统状态变量,重复上述步骤,完成滚动优化和对误差的反馈修正,不断更新最优控制指令,达到减小控制误差,提升系统性能的目的。
u(k+Nc-1|k)]并下发,完成一次优化控制过程。在下一控制时刻,即k+1时刻,测量并更新系统状态变量,重复上述步骤,完成滚动优化和对误差的反馈修正,不断更新最优控制指令,达到减小控制误差,提升系统性能的目的。
本文采用小信号分析方法搭建系统的预测模型。首先,搭建如图1所示的n端低压直流系统的完整小信号模型如式(2)所示。
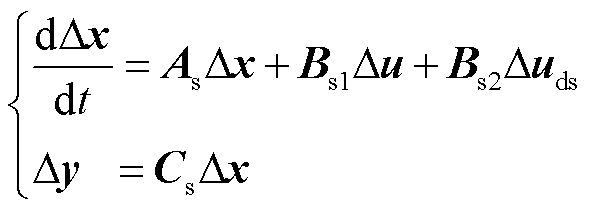 (2)
(2)
式中,Dx为系统的状态变量,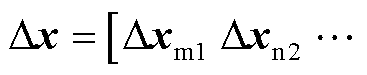
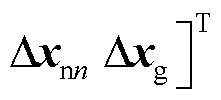 ;
;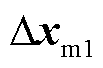 为主站VSC1对应的状态变量,
为主站VSC1对应的状态变量,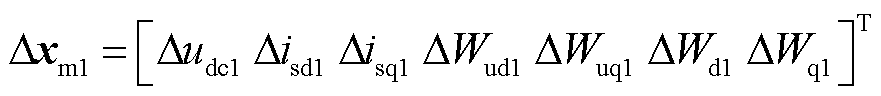 ,
,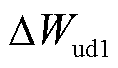 、
、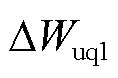 、
、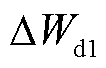 和
和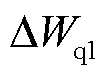 分别为dq轴电压外环调节器和电流内环调节器中的积分环节;
分别为dq轴电压外环调节器和电流内环调节器中的积分环节;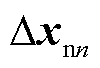 为从站VSCn对应的状态变量,其中
为从站VSCn对应的状态变量,其中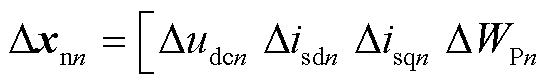
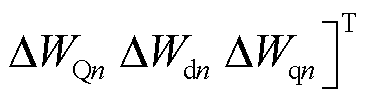 ;
;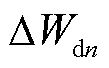 、
、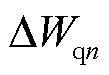 分别为dq轴功率外环调节器中的积分环节;
分别为dq轴功率外环调节器中的积分环节; 为直流网络状态变量,
为直流网络状态变量,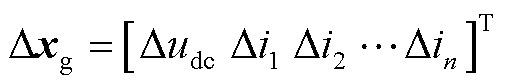 ;Du为输入控制变量,
;Du为输入控制变量,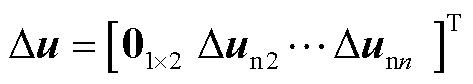 ;∆unn为从站VSCn对应的输入控制变量,
;∆unn为从站VSCn对应的输入控制变量,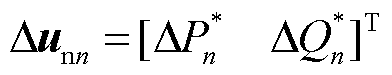 ;Duds为扰动变量,
;Duds为扰动变量,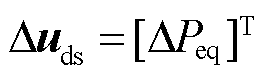 ;Dy为输出变量,
;Dy为输出变量,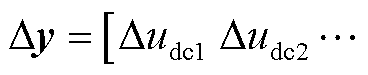
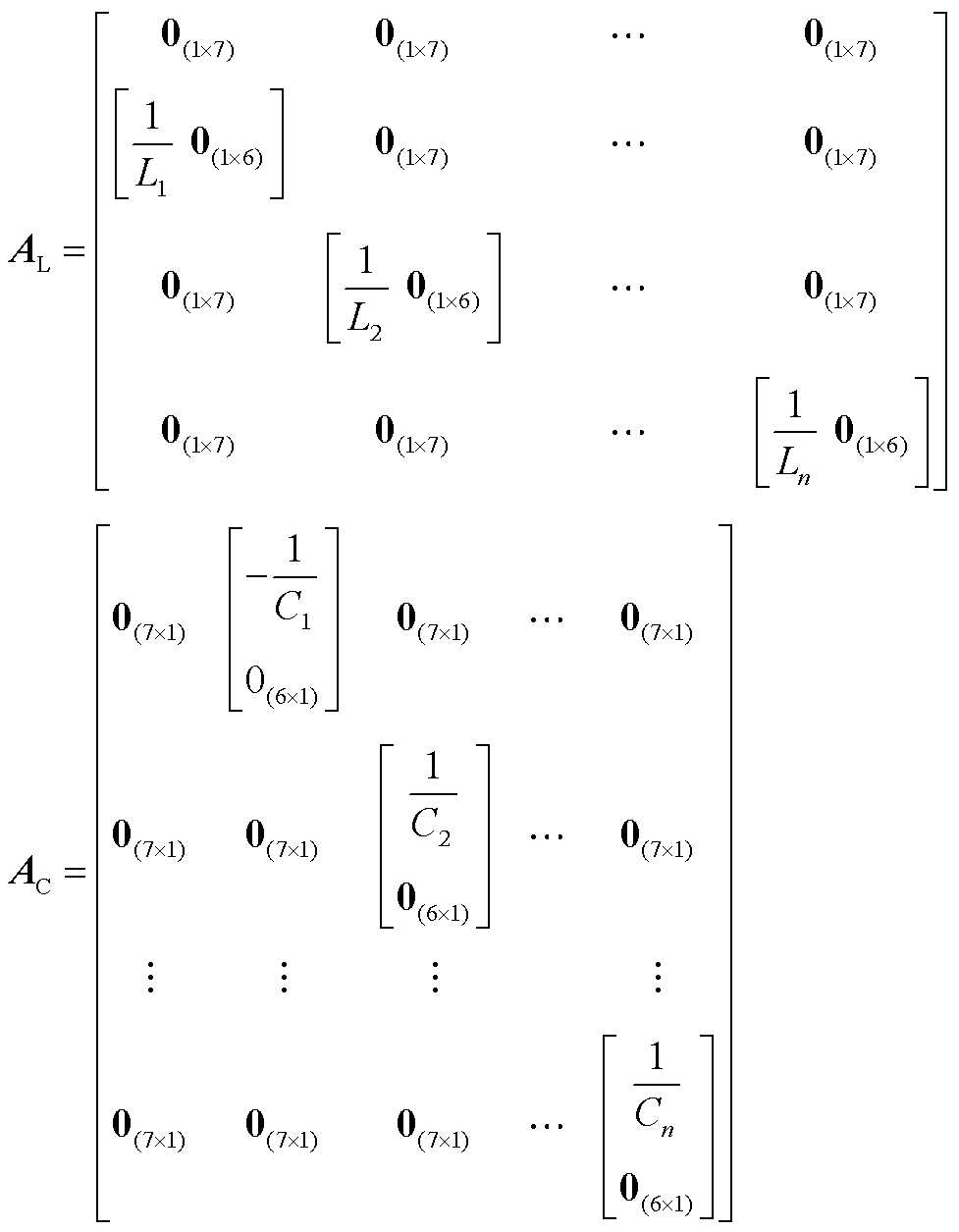
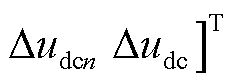 ;As、Bs1、Bs2和Cs分别为系统状态矩阵、输入矩阵、扰动矩阵和输出矩阵,详细推导过程和完整表达式见附录。
;As、Bs1、Bs2和Cs分别为系统状态矩阵、输入矩阵、扰动矩阵和输出矩阵,详细推导过程和完整表达式见附录。
上述小信号模型经离散化处理后可作为MPC优化算法的预测模型。然而在实际工况中,由于本地控制器与中央控制器存在一定的物理距离,所以从站功率外环实际接收到的附加控制指令,会存在Td的通信延时。这使得系统完整小信号模型式(2)无法准确地描述时滞系统的动态特性,影响附加控制效果。为了准确地描述时滞系统的动态特性,在式(2)的基础上,本文基于Pade近似方法搭建了系统时滞预测模型。
一般情况下,时滞系统系统通信延时由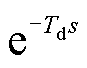 表示,其中Td表示通信延时时间,s为拉普拉斯算子,无法直接用状态空间方程表示。可以利用Pade近似的方法逼近系统真实时滞环节[22-23]。利用Pade近似的方法可以得到微分表达式为
表示,其中Td表示通信延时时间,s为拉普拉斯算子,无法直接用状态空间方程表示。可以利用Pade近似的方法逼近系统真实时滞环节[22-23]。利用Pade近似的方法可以得到微分表达式为
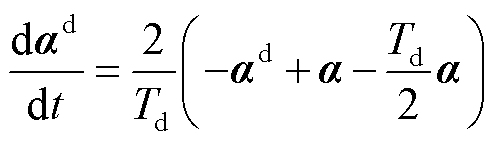 (3)
(3)
式中,α和αd分别为原始和延时后的变量序列。结合式(2)和式(3),进一步得到考虑通信延时的n端低压多端直流系统的完整小信号模型为
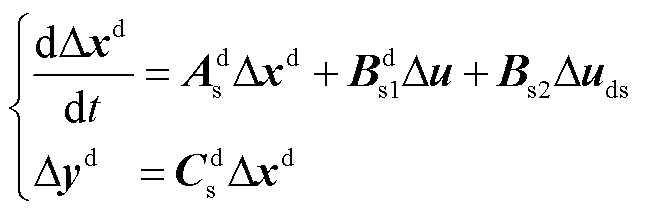 (4)
(4)
式中,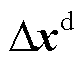 为系统的状态变量,
为系统的状态变量,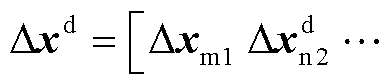
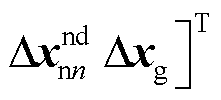 ;
;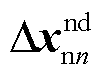 为从站VSCn对应的状态变量,
为从站VSCn对应的状态变量,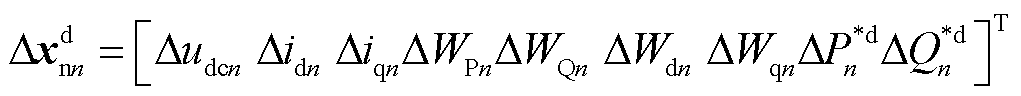 。主站和直流网络相关状态变量不涉及通信延时,因此小信号模型与之前一致。状态矩阵
。主站和直流网络相关状态变量不涉及通信延时,因此小信号模型与之前一致。状态矩阵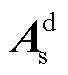 、输入矩阵
、输入矩阵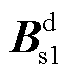 和输出矩阵
和输出矩阵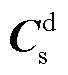 的完整表达式见附录。
的完整表达式见附录。
在连续状态空间方程式(4)基础上,利用欧拉法对系统完整的小信号模型进行离散化处理,设控制系统采样步长为Ts,进一步得到离散的系统预测模型。值得注意的是,为了减小计算稳态误差,本文利用增量式模型表示系统时滞预测模型,D表示离散变量相邻时刻内的增量,即
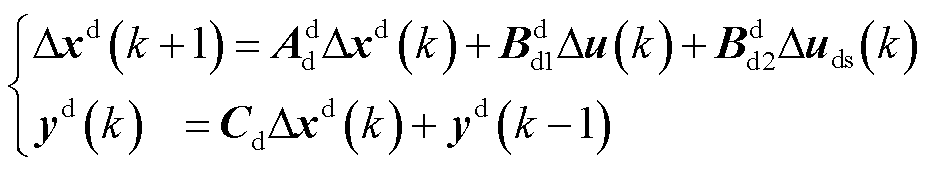 (5)
(5)
其中
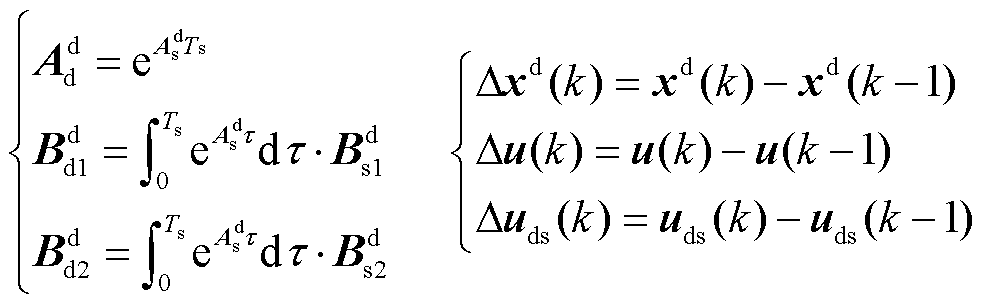
在k时刻,将系统实测值作为输入量的初始值,代入上述离散预测模型式(5)中,可得预测到未来Np时刻内状态变量及输出变量分别为
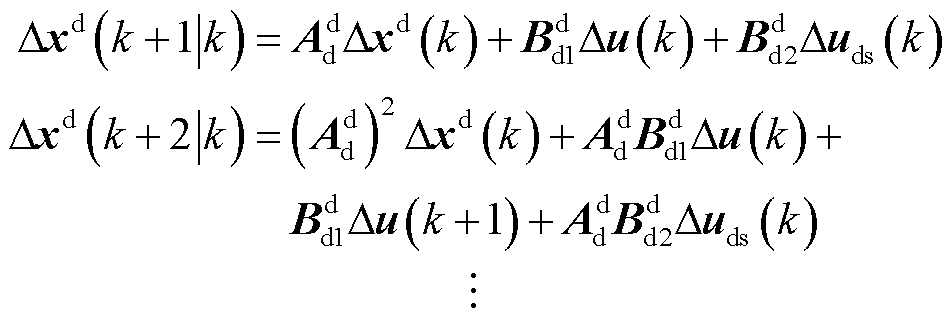
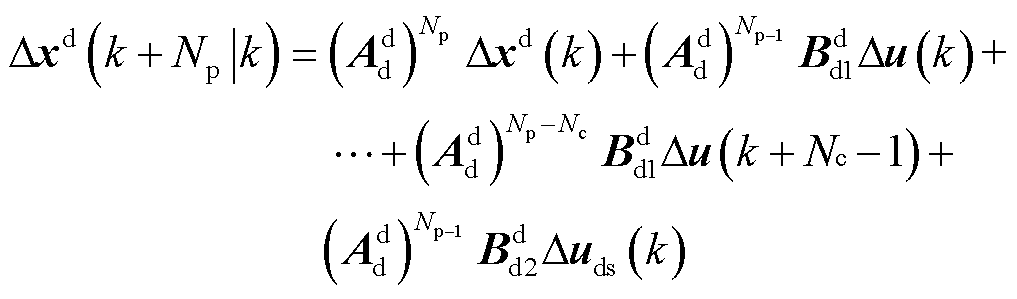 (6)
(6)
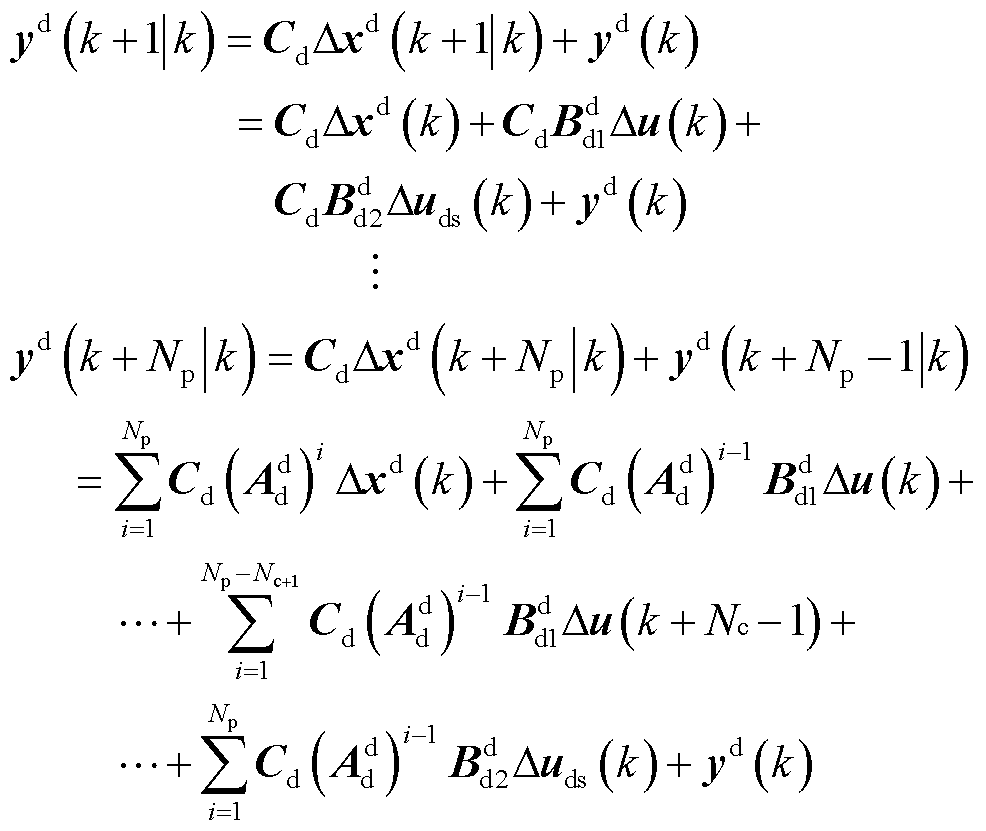 (7)
(7)
进一步将式(7)写成矩阵形式为
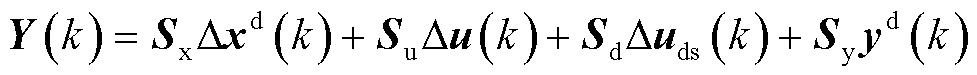 (8)
(8)
其中
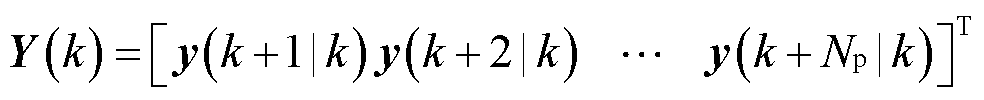
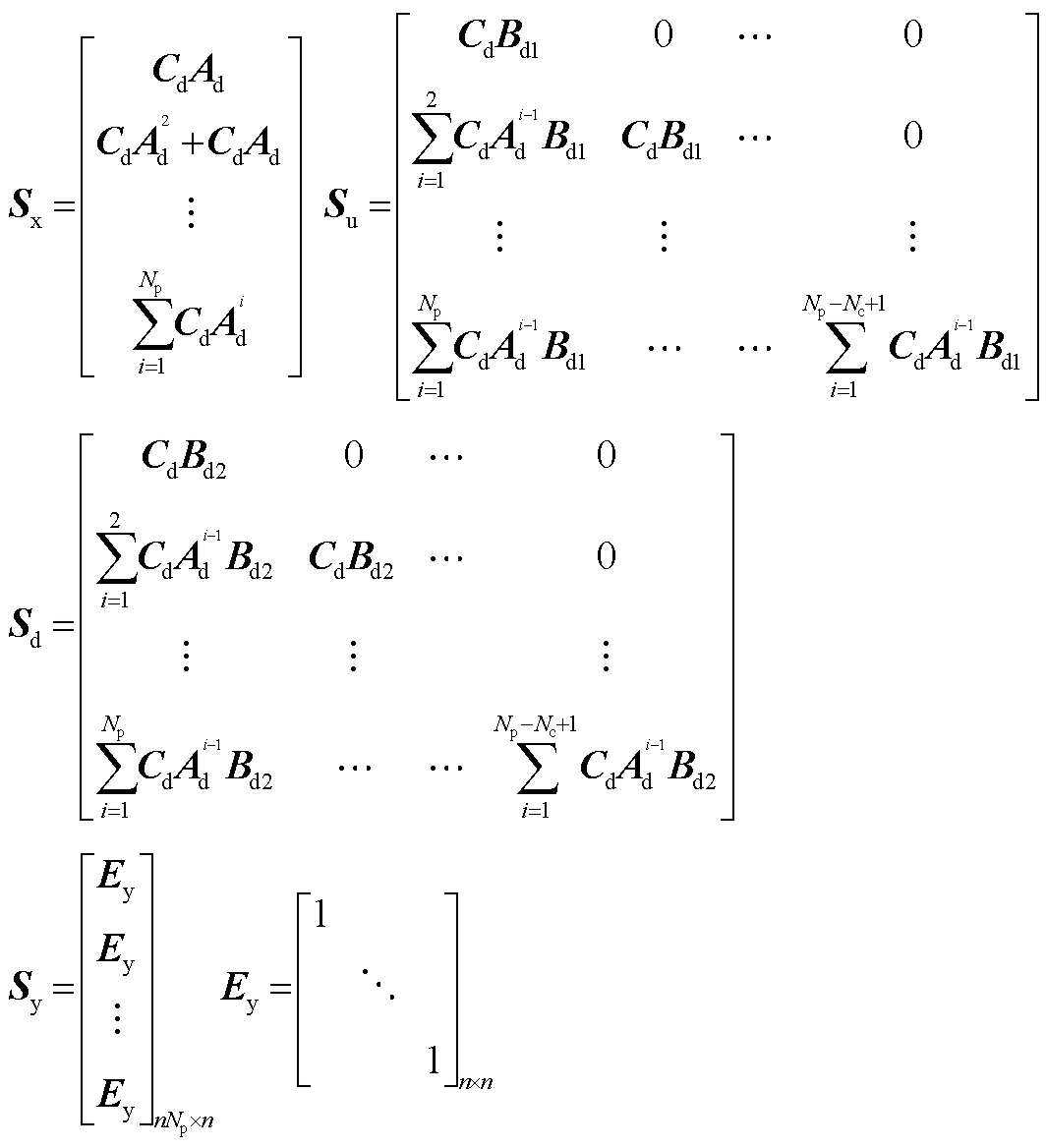
式中,Y(k)为k时刻MPC优化算法求得的未来时刻Np内预测输出序列;Su、Sx、Sy和Sd分别为输入变量、状态变量、输出变量和扰动变量在未来Np时刻内的系数矩阵,其完整表达式见附录。
设定附加控制变量在控制时域之外始终保持恒定,系统扰动变量在k时刻后保持恒定,即满足
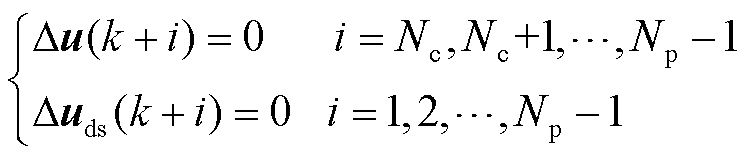
2.3.1 目标函数及约束条件
MPC优化算法目标函数的建立主要考虑以下几个方面:首先要保证直流电压的稳定,在扰动情况下避免直流电压振荡发散,即保证未来时刻Np内电压输出矩阵和参考矩阵绝对差值的最小化;其次在保证电压稳定情况下,确保每一时刻内附加功率调节指令绝对值之和的最小化,即保证最小出力下稳定系统直流电压,提高控制策略经济性,平抑电压波动。综合以上两点目标,建立系统优化目标函数为
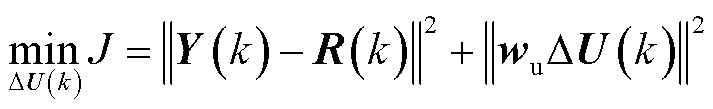 (9)
(9)
式中,R(k)为由系统额定电压urate组成的参考值矩阵,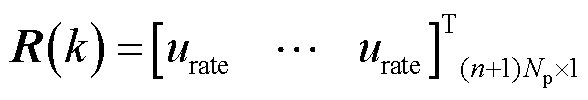 ; DU(k)为k时刻求得包含Nc时刻最优附加功率调节指令序列,
; DU(k)为k时刻求得包含Nc时刻最优附加功率调节指令序列,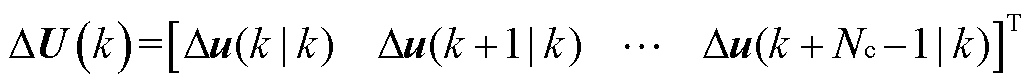 ;wu为功率附加控制指令的权重矩阵,用于评价MPC优化算法的性能和控制效果。
;wu为功率附加控制指令的权重矩阵,用于评价MPC优化算法的性能和控制效果。
此外,为了满足电压波动范围要求、保障附加控制效果,需要建立合理的约束条件。本文分别对k时刻系统输出电压矩阵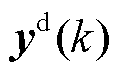 、控制矩阵
、控制矩阵 及附加控制矩阵
及附加控制矩阵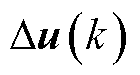 建立了相应的约束条件。对于输出电压矩阵,控制输出电压波动范围在额定电压的93%~107%之间,从站功率和附加功率控制指令变化范围应在额定功率的±50%和±10%之间。相应的表达式为
建立了相应的约束条件。对于输出电压矩阵,控制输出电压波动范围在额定电压的93%~107%之间,从站功率和附加功率控制指令变化范围应在额定功率的±50%和±10%之间。相应的表达式为
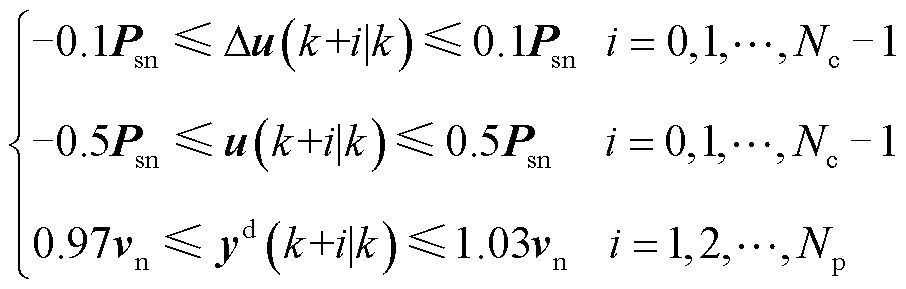 (10)
(10)
式中,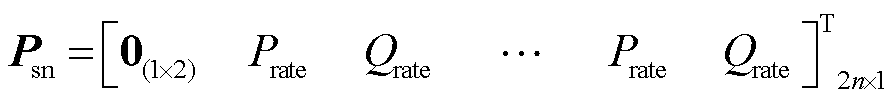 ;Prate、Qrate分别为系统有功功率和无功功率额定值;
;Prate、Qrate分别为系统有功功率和无功功率额定值;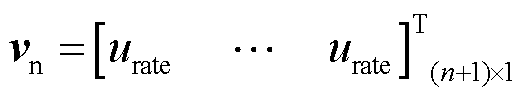 。
。
2.3.2 MPC优化算法求解
2.3.1节提到的优化算法是一类带有线性不等式约束的最小二乘问题,其本质是二次规划(Quadratic Programming, QP)问题的特殊形式,可以利用Matlab优化工具库quadprog函数进行快速求解。
将式(8)代入式(9),可将目标优化函数改写为
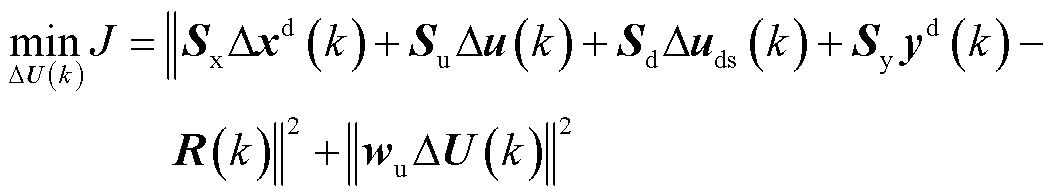 (11)
(11)
进一步将目标函数整理成标准QP问题形式,结果为
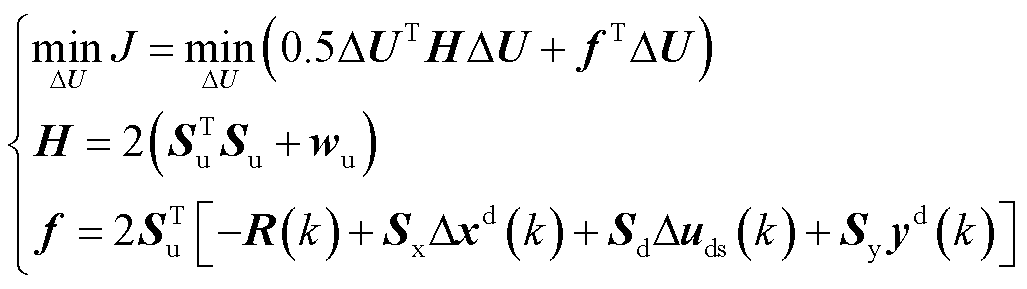 (12)
(12)
一般地,标准QP问题的约束条件为Ax≤b,改写式(10)中的不等式约束,可得到式(13)中三组符合标准QP问题的约束条件。
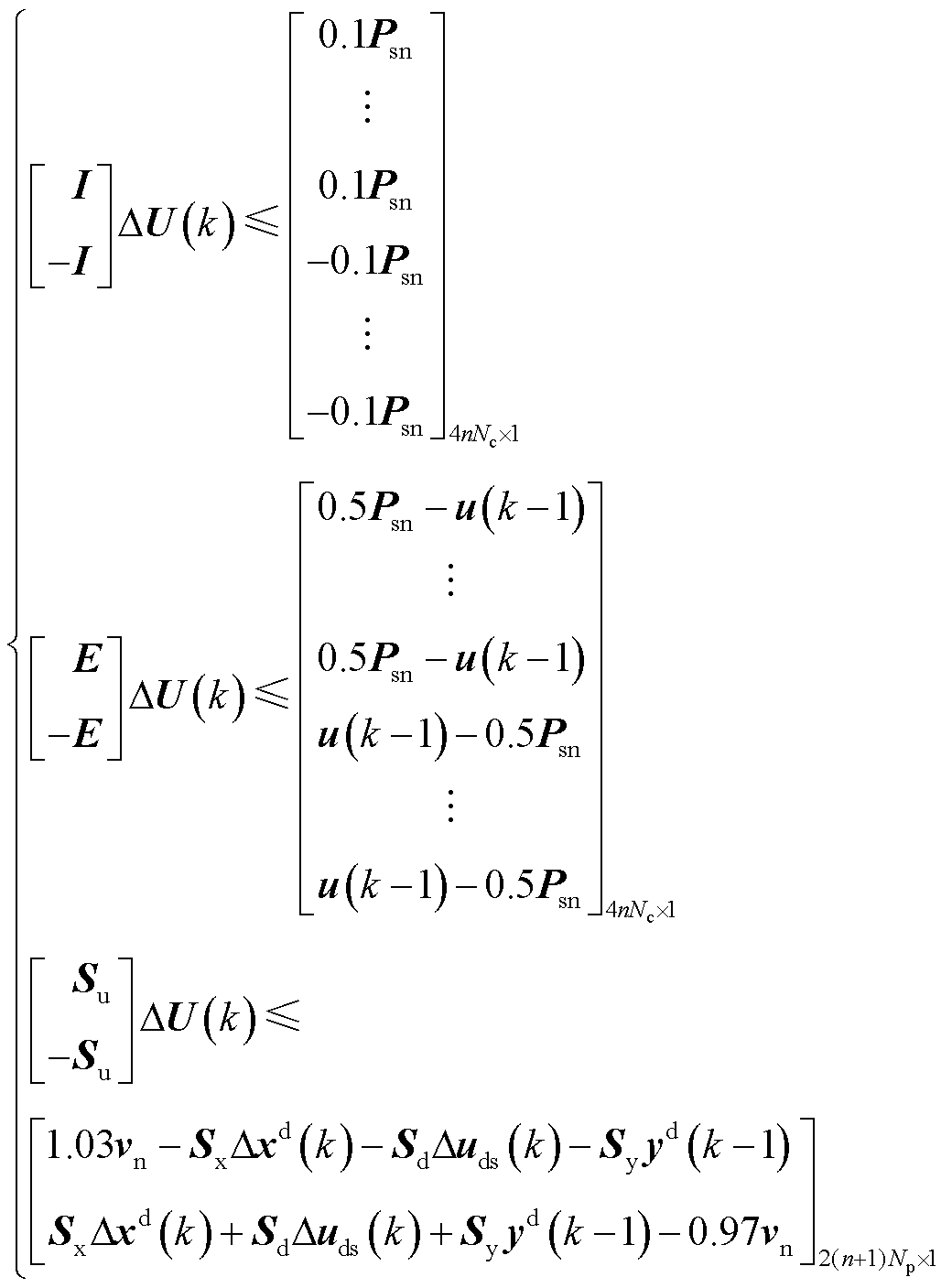 (13)
(13)
其中
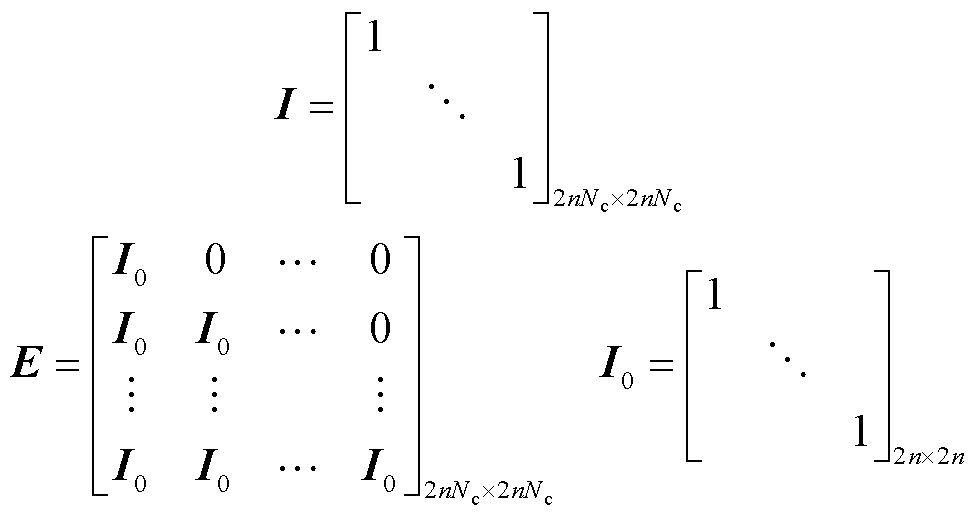
通过求解系统状态矩阵的特征根值,可对其稳定性进行分析。本文以三端低压直流配电系统为例,其系统结构如图1所示。其中VSC1为主站,电压参考值为800 V;VSC2、VSC3为从站,初始有功功率参考值为50 kW、30 kW,无功功率参考值均为0var。母线处接入由分布式能源、储能和直流负荷等效聚合成恒功率负载,额定功率为30 kW。其中时滞模型预测附加控制的额定电压设置为800 V,额定功率设置为100 kW,其余详细参数见表1。
对于采用传统主从控制的低压多端直流系统而言,其系统状态矩阵为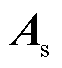 。当母线处负荷吸收功率Peq由30 kW增加至80 kW时,系统状态矩阵的
。当母线处负荷吸收功率Peq由30 kW增加至80 kW时,系统状态矩阵的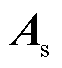 特征根变化轨迹如图7所示。
特征根变化轨迹如图7所示。
表1 三端低压直流配电系统参数
Tab.1 The parameters of three-terminal low-voltage DC distribution system

参数数值参数数值参数数值 Rs/mΩ1.5Kpv0.6isd2,0/A107 Ls/mH2Kiv100isd3,0/A64 C/μF600Kpq1Pdc3,0/kW30 Ldc1/mH0.5Kiq20Pdc1,0/kW110 Rdc1/Ω0.1Kpd1Pdc2,0/kW50 C1/μF1000Kid20udc1,0/V800 Ldc2/mH1KpQ0.6udc2,0/V773 Rdc2/Ω0.2KiQ100udc3,0/V786 C2/μF500KpP0.6uod1,0/V310.92 Ldc3/mH0.75KiP100uod2,0/V310.96 Rdc3/Ω0.15Np4uod3,0/V310.98 C3/μF500Nc4w/(rad/s)314 Ts/s0.01isd1,0/A235
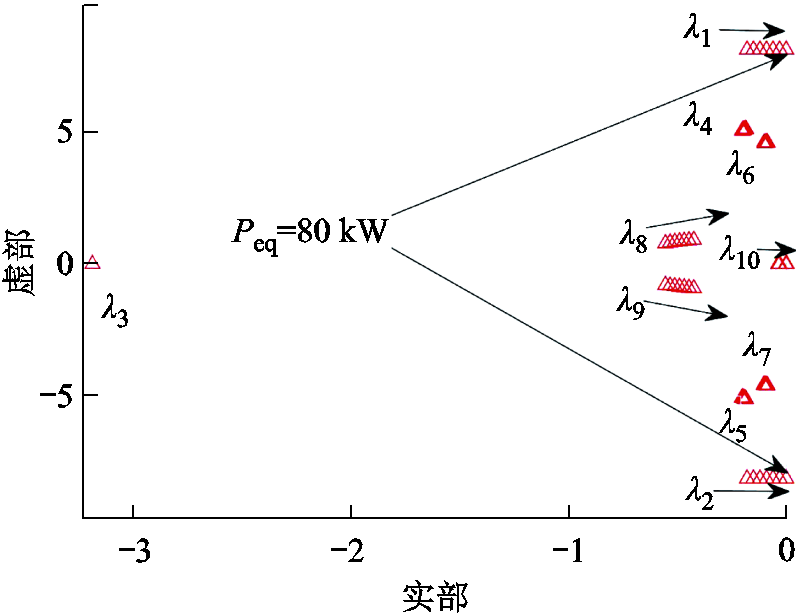
图7 负荷吸收功率Peq增加时系统根轨迹
Fig.7 The system eigenvalues under load power Peq increase
从图7可以看出,系统有三组特征根(λ1, λ2)、(λ8, λ9)和λ10对母线处负荷变化高度灵敏,并随着母线处负荷吸收功率的增加慢慢向右半平面移动,系统稳定性不断降低。当Peq吸收功率增加到80 kW时,特征根实值接近0,此时系统处于临界稳定的状态,即将失稳。对于未采用时滞模型预测附加控制的系统而言,当直流母线处负荷吸收功率超过80 kW时,各端换流站将无法再维持电压稳定和功率平衡,系统失稳。
当系统采用时滞模型预测附加控制后,由于通信系统存在延时,系统状态矩阵也因此发生了变化。当系统通信延时由0.1 s逐渐增加至0.4 s时,系统状态矩阵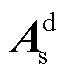 特征根变化轨迹如图8所示,此时母线处吸收功率为80 kW。
特征根变化轨迹如图8所示,此时母线处吸收功率为80 kW。
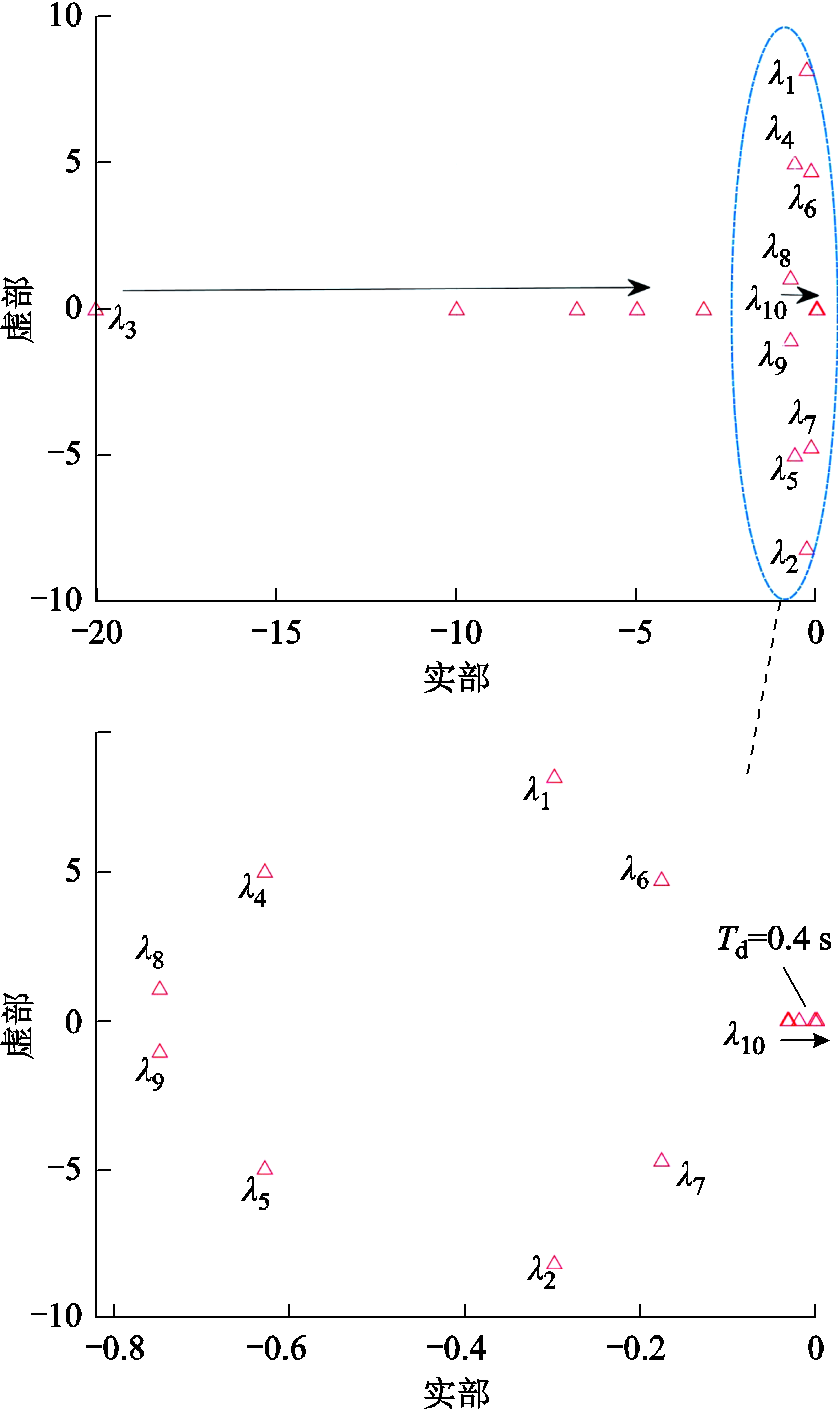
图8 通信延时增加时系统根轨迹
Fig8 The system eigenvalues under communication delay increase
从图8可以看出,状态矩阵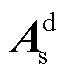 有两组特征根值,分别为λ3、λ10,对通信延时高度灵敏,且随着通信延时的增加慢慢向右半平面移动,系统稳定性不断降低。当系统通信延时Td小于0.1 s时,系统稳定性几乎不受影响,而当Td增加到0.4 s时,特征根实部逐渐逼近0,系统处于临界稳定的状态。对于采用时滞模型预测附加控制的系统而言,当直流母线处负荷吸收功率增加至80 kW时,系统通信网络延时同样会对稳定性产生影响。当Td超过0.4 s后,由于附加指令下发存在较大滞后,同样会导致系统失稳。
有两组特征根值,分别为λ3、λ10,对通信延时高度灵敏,且随着通信延时的增加慢慢向右半平面移动,系统稳定性不断降低。当系统通信延时Td小于0.1 s时,系统稳定性几乎不受影响,而当Td增加到0.4 s时,特征根实部逐渐逼近0,系统处于临界稳定的状态。对于采用时滞模型预测附加控制的系统而言,当直流母线处负荷吸收功率增加至80 kW时,系统通信网络延时同样会对稳定性产生影响。当Td超过0.4 s后,由于附加指令下发存在较大滞后,同样会导致系统失稳。
利用Matlab/Simulink搭建如图1所示低压三端直流配电系统仿真模型,详细参数见表1。设置当前系统工作在额定工况下(Pdc1=50 kW,Pdc2=30 kW,Peq=30 kW),t=2 s时,Peq发生跳变,功率增加至83 kW(Pdc1=50 kW,Pdc2=30 kW,Peq=83 kW),系统采用时滞模型预测附加控制策略,此时考虑通信延时为0.5 s。母线电压变化情况如图9所示。
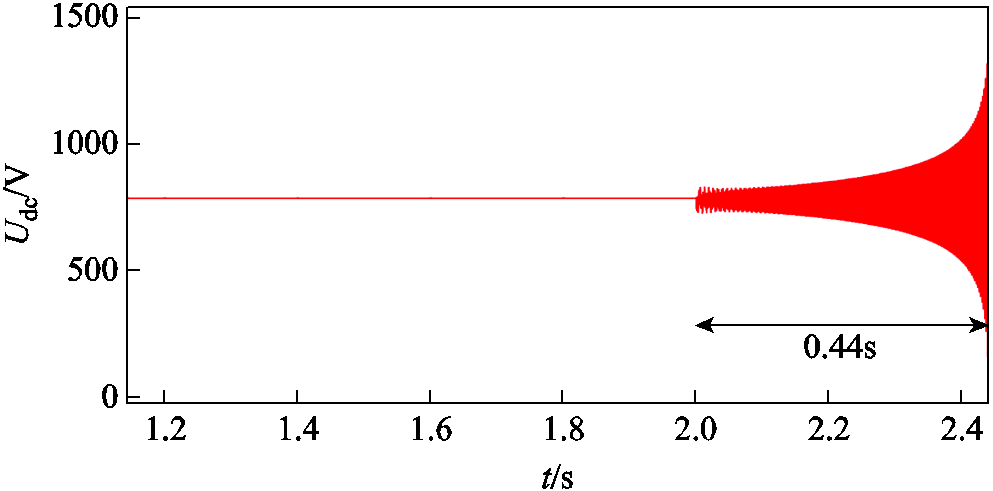
图9 通信延时为0.5 s时直流母线电压变化情况
Fig.9 DC bus voltage variation at Td=0.5 s
由图9可知,在外界扰动和通信网络延时的共同作用下,从站无法及时接收功率附加控制指令并调整出力,导致母线电压振荡失稳,上述仿真结果与图7和图8的理论分析一致。
利用Matlab/Simulink对本文提出的时滞模型预测附加控制策略进行仿真验证,对图1所示低压三端直流配电系统进行算例分析。对于本文研究的系统而言,通信延时一般在0.001~0.1 s。
4.1.1 短时随机功率波动
直流母线处负荷发生短时随机功率波动,功率变化情况如图10所示,持续时间28 s。此时系统通信延时较小,仅为0.001 s。
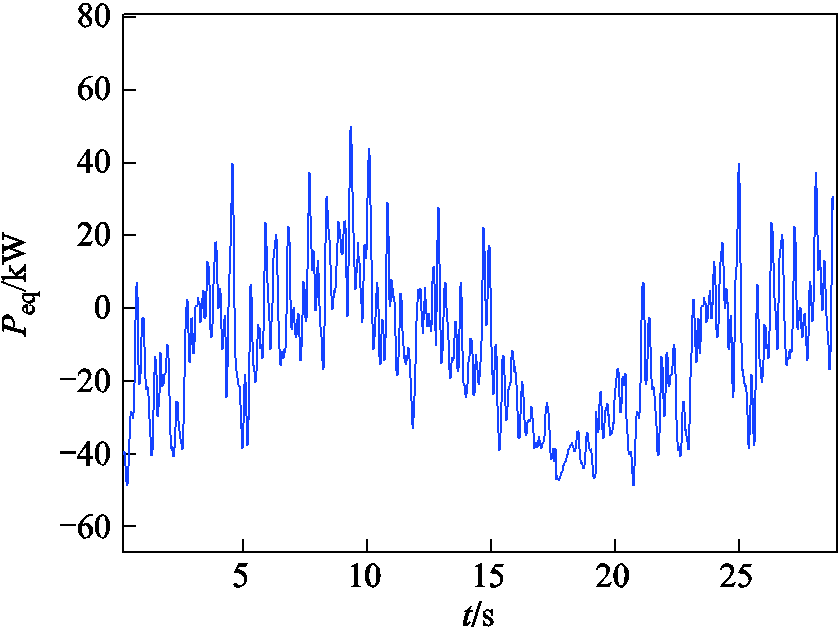
图10 直流母线处负荷功率
Fig.10 Load power at DC bus
同样工况下,系统采用传统主从控制策略和时滞模型预测附加控制策略两种不同方法,VSC直流出口侧电压变化情况如图11a和图11b所示。
对比图11a和图11b可知,采用传统主从控制策略的系统在母线负荷发生短时功率波动时,各端直流侧电压均有较大波动,出现了电压越限的问题,系统电能质量恶化。而采用本文提出的优化控制策略的系统,在同样工况下,各端直流电压波动明显减小,电压越限问题得到有效改善,且电压波动范围始终维持在额定电压的93%~107%区间内,满足电能质量要求。运行过程中,各个从站接收的功率附加控制指令变化情况如图12所示。
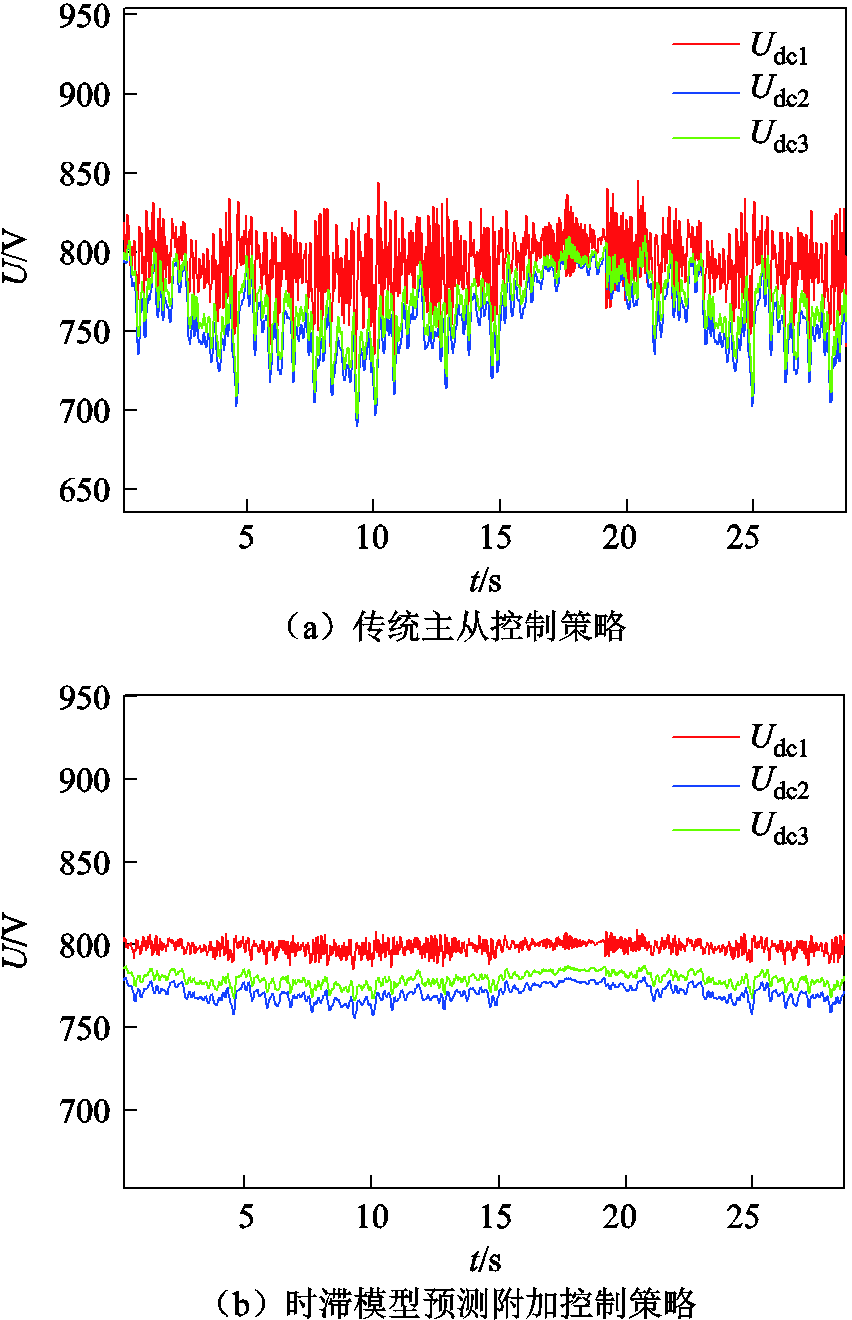
图11 VSC直流出口侧电压
Fig.11 Output voltage at VSC DC-side
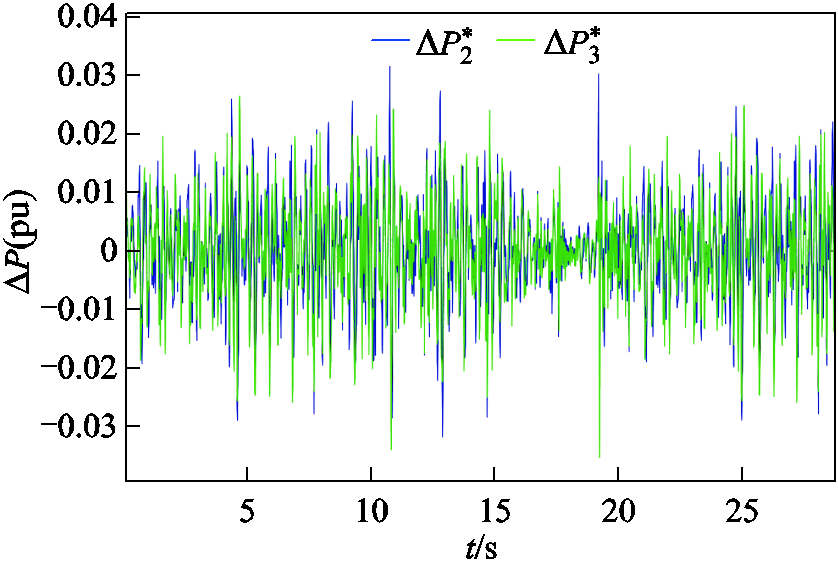
图12 短时随机功率波动下从站附加功率指令
Fig.12 Additional power instructions for slave stations under short-term random power fluctuation
由图12可知,当系统直流母线负荷发生短时随机扰动时,采用本文所提的附加控制策略,系统各从站功率附加控制指令均满足相应的约束要求,保障了以最小出力平抑由随机扰动下的直流电压波动,改善了系统电能质量,具有较好的经济性。
4.1.2 负荷功率跳变
设置当前系统工作在额定工况下(Pdc1=50 kW,Pdc2=30 kW,Peq=30 kW),t=2 s时,Peq发生跳变,吸收功率增加至90 kW(此时Pdc1=50 kW,Pdc2=30 kW,Peq=90 kW),采用传统主从控制和时滞模型预测附加控制策略两种不同控制方式的系统(通信延时为0.001 s),对应的直流母线电压变化情况,如图13所示。
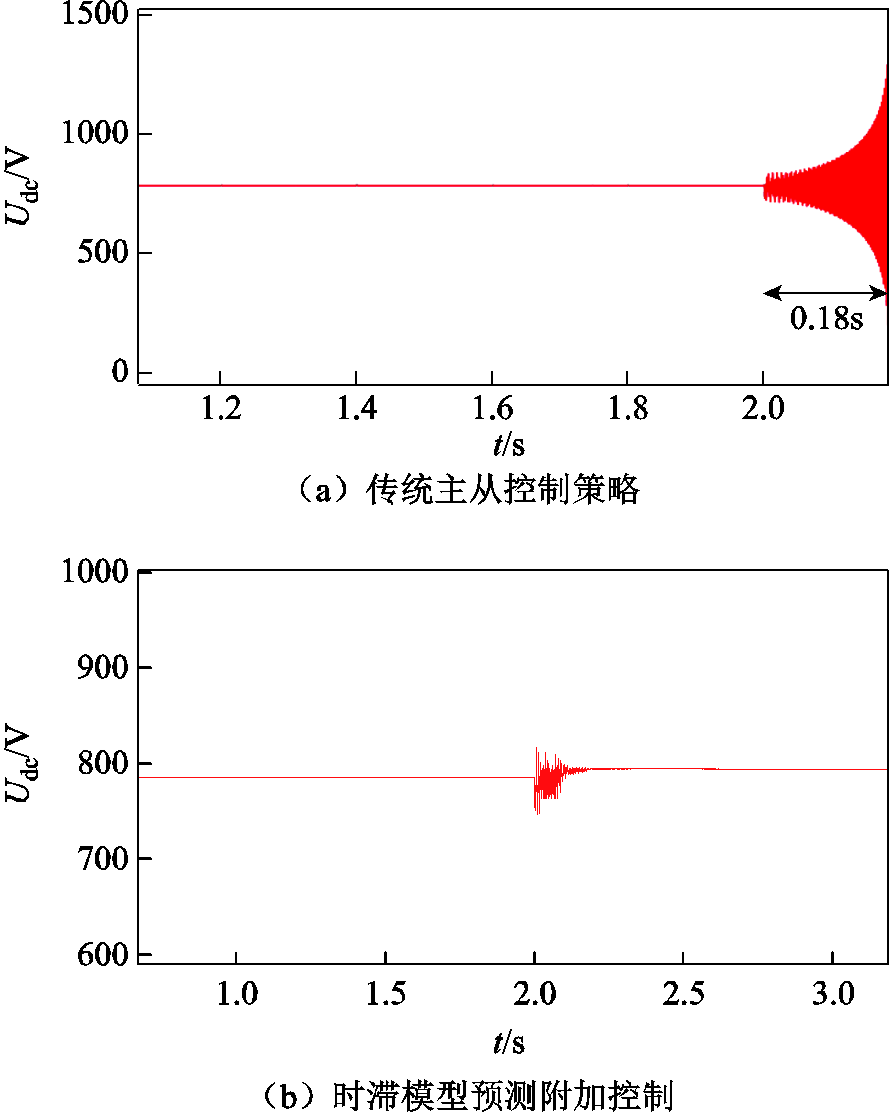
图13 通信延时为0.001 s时直流母线电压变化情况
Fig.13 DC bus voltage variation at Td=0.001 s
由图13可知,当直流母线负荷功率增加至 90 kW时,采用传统主从控制的系统直流母线电压会产生较大波动,并在约0.18 s后振荡失稳。此时系统各VSC功率调节裕度达到上限,无法保证系统内功率平衡,电压振荡失稳。如果采用本文提出的附加控制策略,直流母线电压在2 s时由于功率跳变发生了短暂波动,上层附加控制器开始工作,实时求解并下发最优功率附加控制指令至各从站,调节各站出力。经过约0.2 s后,直流母线电压重新达到稳态值,系统内功率恢复平衡。相应的功率附加指令变化情况如图14所示。
由图14可知,采用时滞模型预测附加控制策略的系统在运行过程中各从站附加功率指令均满足附加控制策略的约束条件。当负荷吸收功率瞬间增加,超过功率调节上限时,本文提出的附加控制策略可以快速调节系统各站出力,使电压迅速恢复稳态,提高了系统的稳定性,保障了系统的安全运行。
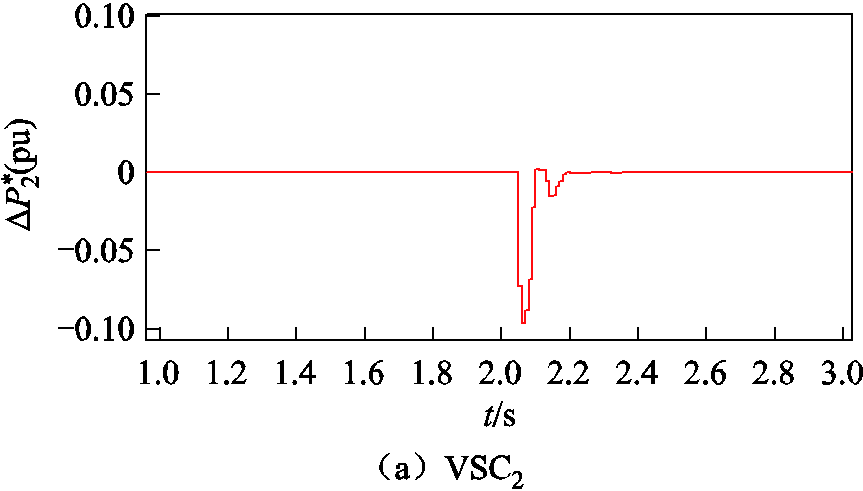
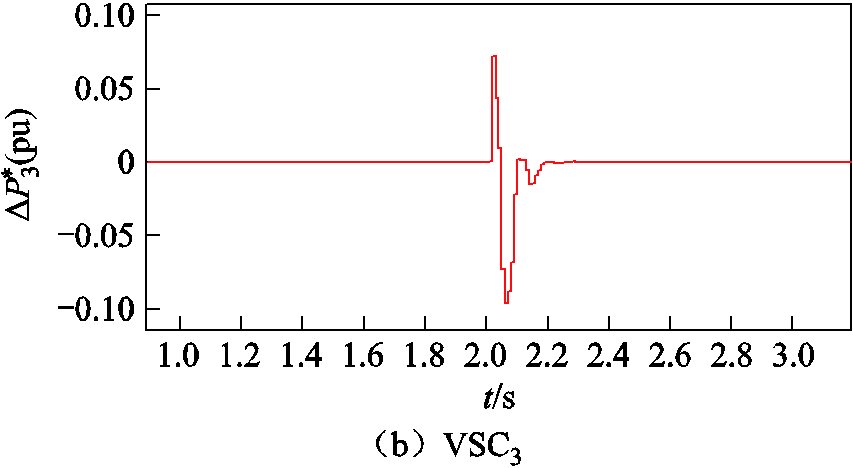
图14 负荷功率跳变时从站附加功率指令
Fig.14 Additional power instructions for slave stations at load power jump
系统在额定工况下(Pdc1=50 kW,Pdc2=30 kW,Peq=30 kW)运行,2 s时,Peq吸收功率增加至90 kW。此时通信系统延时为0.1 s,系统采用传统的MPC附加控制策略和本文提出的时滞模型预测附加控制两种不同控制方法,直流电压对应的变化情况如图15所示。
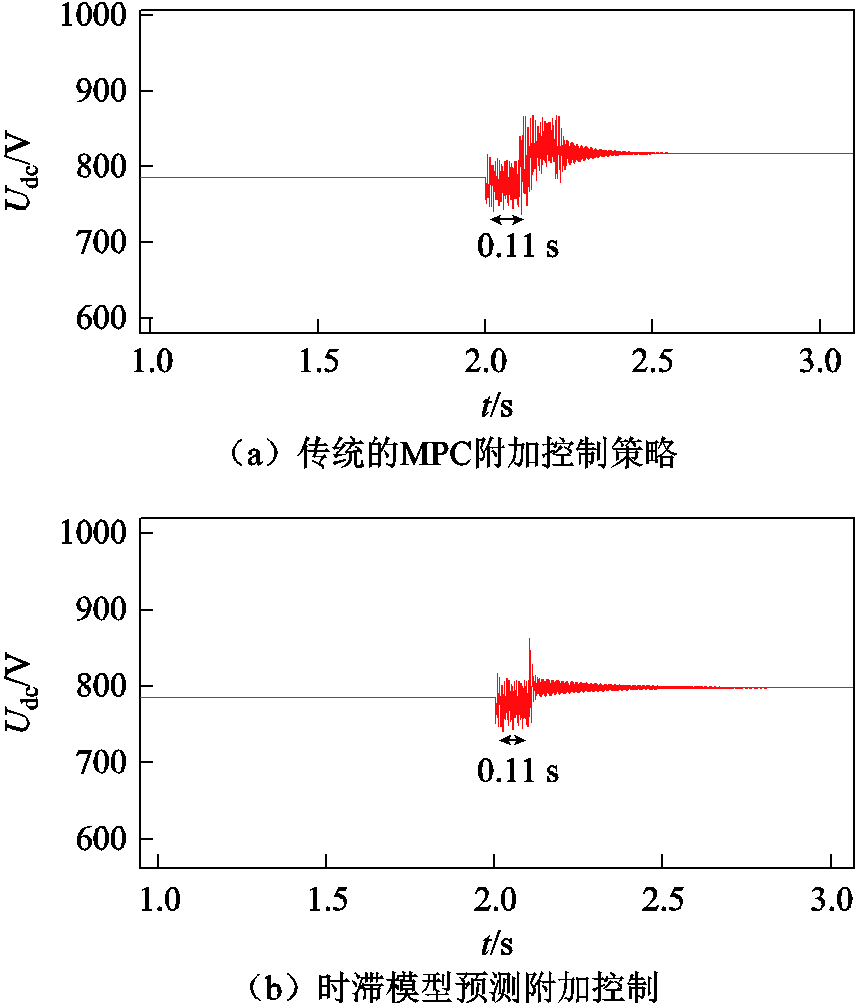
图15 通信延时为0.1 s时直流母线电压变化情况
Fig.15 DC bus voltage variation at Td=0.1 s
由图15a和图15b对比可知,采用两种不同控制方法的系统在母线处负荷功率增加时,电压均产生了短时振荡,且在约0.4 s后再次达到稳态,但图15b的直流母线电压波动在2.15 s后就得到了比较好的平抑。进一步地,对比图15a与图13b可知,采用传统MPC附加控制策略的系统,在系统通信延时增加后,母线电压恢复稳态的时间有了明显增加,且电压恢复稳态过程中波动幅度较大,最终达到的稳态值也有了比较明显的偏差。说明随着通信系统延时的增加,传统MPC附加控制策略的模型已无法准确描述时滞系统的动态特性,其控制效果和性能受到了较大影响。由图15b与图13b对比可知,尽管电压恢复稳态的时间有所增加,但电压最终达到的稳态值与图13b结果相比并无明显偏差。说明在一定范围内,随着系统通信延时的增加,采用时滞模型预测附加控制,仍可以有效平抑负荷变化引起的系统直流电压波动,保障系统的安全运行,该控制策略具有较好鲁棒性。
如果此时由于外界原因或突发的故障,导致通信延时进一步增加,超过0.17 s。由于本地控制器接收的上层功率附加控制指令存在较长的滞后,本地VSC将无法在0.18 s内接收到最优附加功率控制指令并及时调整出力。由图13a结果可知,系统母线电压将因为功率跳变而直接失稳。说明此时通信延时已对控制策略性能产生较大的影响,将无法平抑不确定扰动下的系统电压波动问题。
针对如何提高低压多端直流系统在可再生能源、直流负荷等不确定扰动下的运行稳定性问题,本文针对主从控制的低压多端直流系统提出一种时滞模型预测附加控制策略。分析了系统通信延时对稳定性和控制策略性能的影响,并通过算例分析验证了本文所提方法可以以最小出力平抑多端直流系统受到不确定扰动时的电压波动问题,提高系统电压稳定性和电能质量,具有较好的经济性。且当系统通信网络延时小于一定范围时,本文所提优化控制策略,可以很好地描述时滞系统动态特性,较好地平抑不确定扰动下的系统电压波动,保障系统的安全运行,具有较好的鲁棒性。未来可进一步研究在长通信延时甚至数据丢包等极端情况下,采用自适应变时间参数的方法进一步增加附加控制策略对通信延时的鲁棒性。
附 录
1. 本文研究的仿真算例的仿真步长为50 μs,仿真系统采样步长为0.001 s,VSC调制频率为6 kHz,滞模型预测附加控制的控制周期为0.01 s。
2. 以从站VSCn为研究对象,根据图2得到dq坐标系下交流侧小信号模型,D表示变量在稳态工作点P0附近的微小变化量。
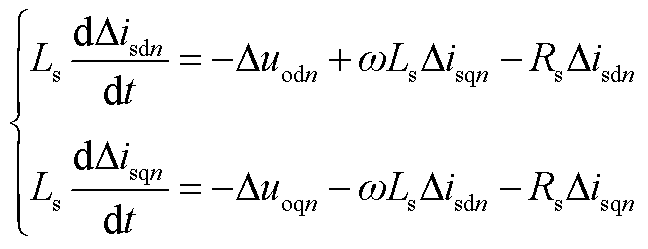 (A1)
(A1)
VSCn直流侧电容节点小信号模型为
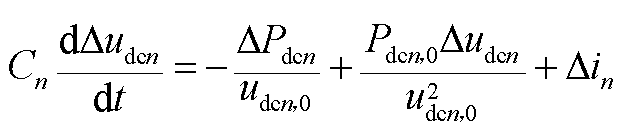 (A2)
(A2)
dq坐标下,VSCn交流侧有功功率、无功功率以及传递到直流侧功率分别为
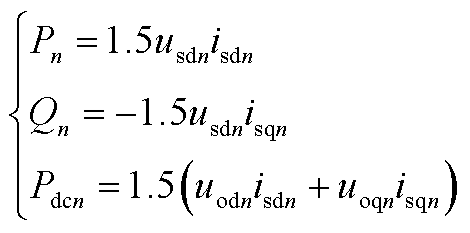 (A3)
(A3)
根据图3的控制框图,可以得到从站外环控制式小信号模型,下标“0”表示变量的稳态值。
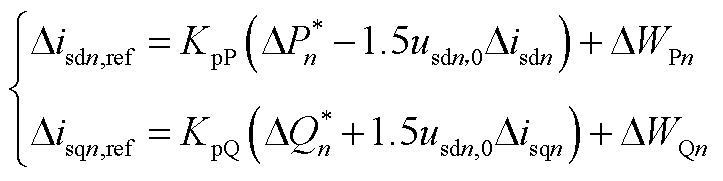 (A4)
(A4)
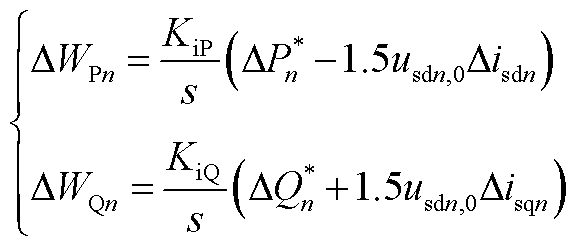 (A5)
(A5)
同样地,对于电流控制内环进行小信号处理,得到从站电流内环小信号模型,其中
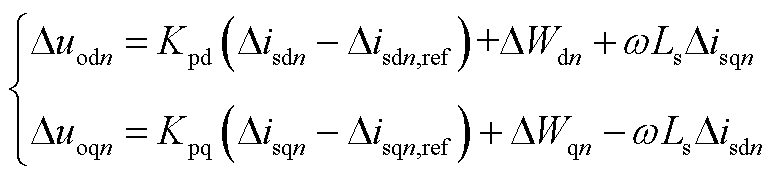 (A6)
(A6)
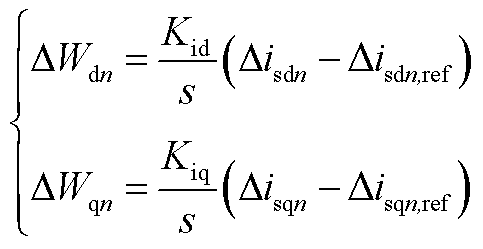 (A7)
(A7)
整合式(A1)~式(A7),可得主从控制下单个从站VSCn完整的小信号模型为
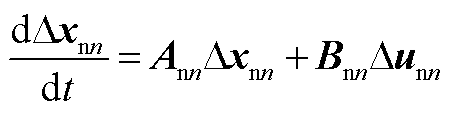 (A8)
(A8)
式中,Dxnn为从站VSCn完整小信号模型的状态变量,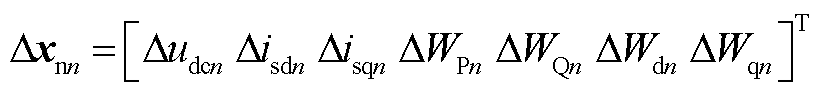 ;Dunn为从站输入控制变量,
;Dunn为从站输入控制变量,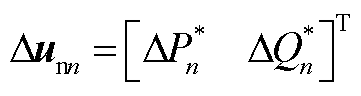 ;Ann为状态矩阵;Bnn为输入矩阵。
;Ann为状态矩阵;Bnn为输入矩阵。

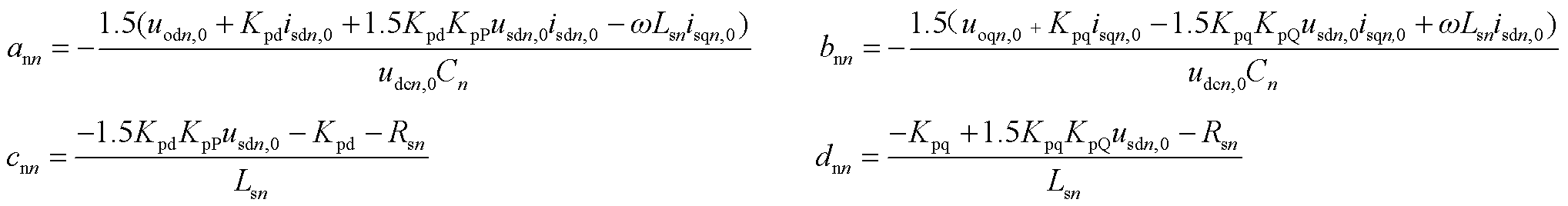
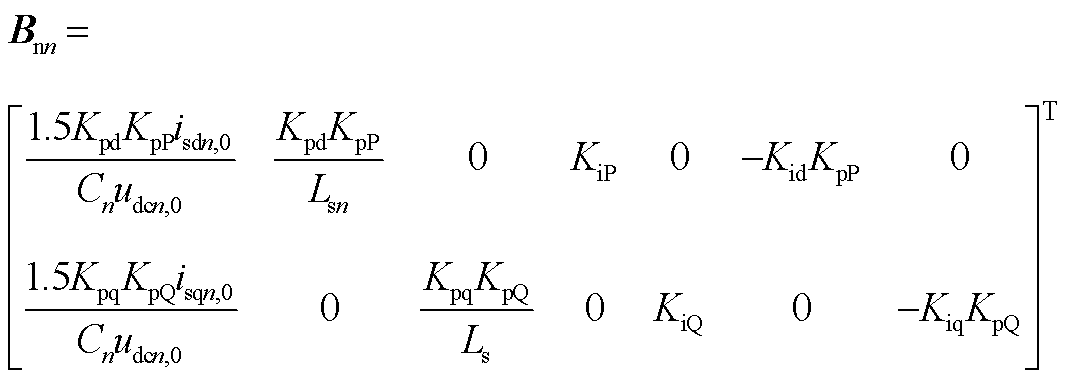
主站小信号建模方法与从站类似,具体过程不再赘述,其完整小信号模型为
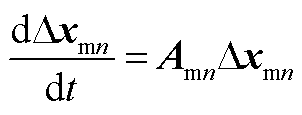 (A9)
(A9)
式中,Dxmn为主站VSCn完整小信号模型的状态变量,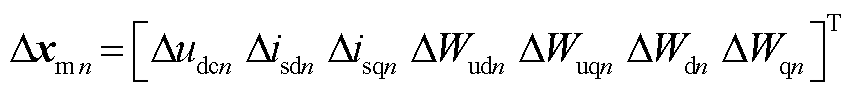 ;主站需要维持系统母线电压稳定,因此电压参考值恒定,无输入控制变量,Amn为状态矩阵,有
;主站需要维持系统母线电压稳定,因此电压参考值恒定,无输入控制变量,Amn为状态矩阵,有
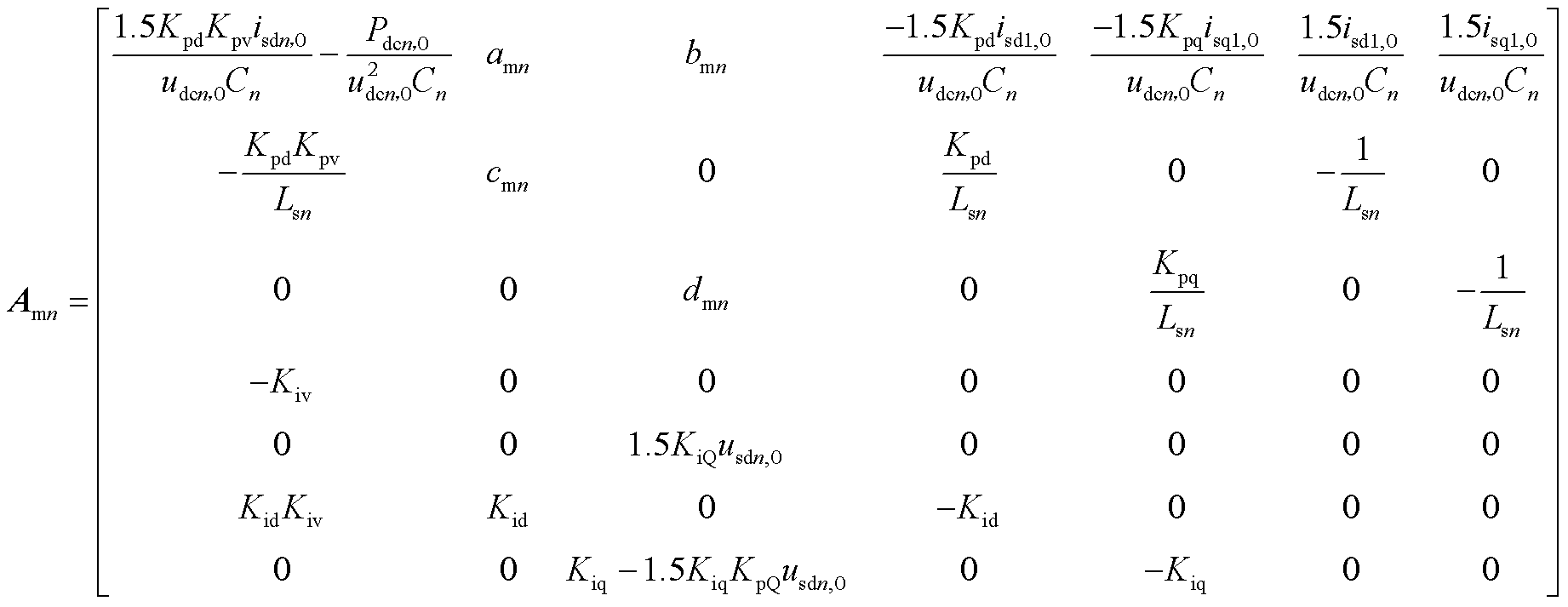
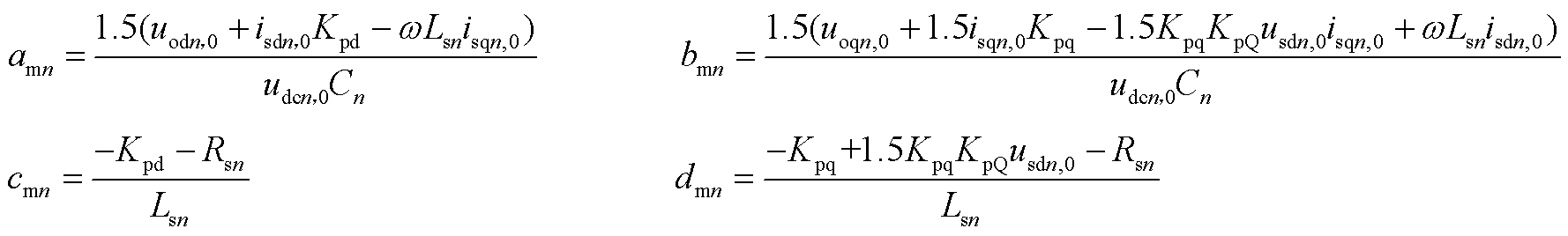
根据图3所示的系统直流网络结构图,可以得到直流网络数学模型为
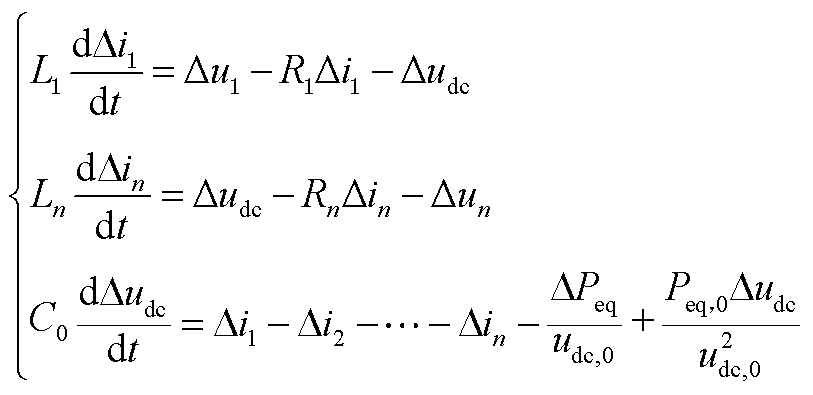 (A10)
(A10)
进一步整理得到系统直流网络小信号模型为
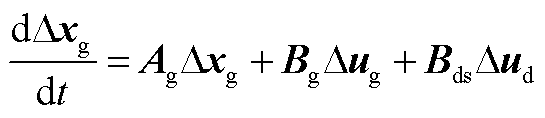 (A11)
(A11)
式中,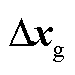 为直流网络状态变量,
为直流网络状态变量,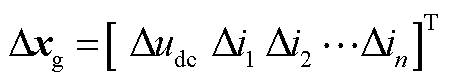 ;
;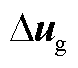 为输入变量,
为输入变量,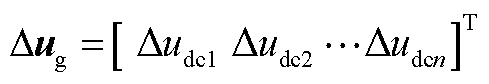 ;
;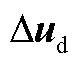 为由可再生发电单元和直流负载组成的等效聚合负载功率,
为由可再生发电单元和直流负载组成的等效聚合负载功率,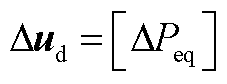 ;Ag和Bds分别为状态矩阵和扰动矩阵,表达式为
;Ag和Bds分别为状态矩阵和扰动矩阵,表达式为

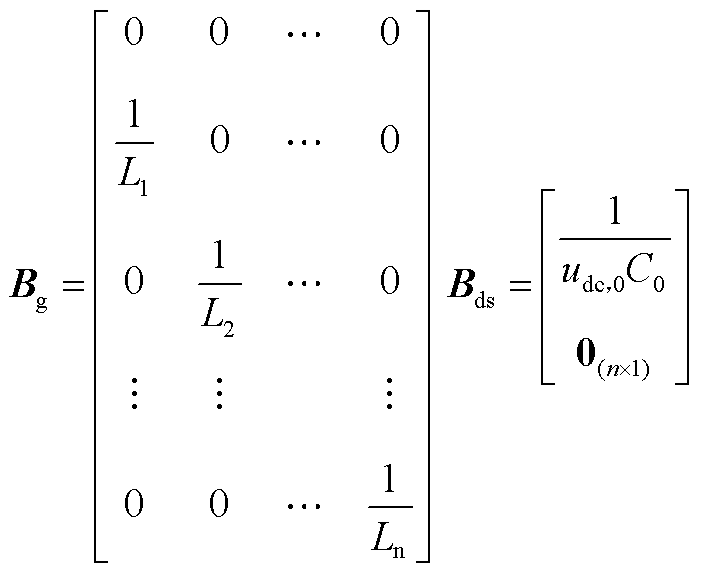 (A12)
(A12)
结合上述VSC和直流网络小信号模型,可以进一步整合得到n端主从直流系统的完整预测模型。
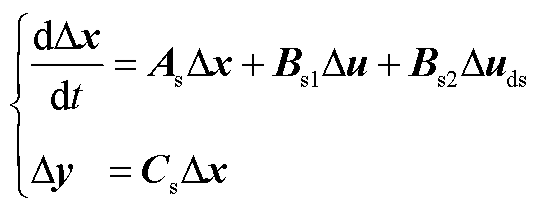 (A13)
(A13)
式中,Dx为系统状态变量,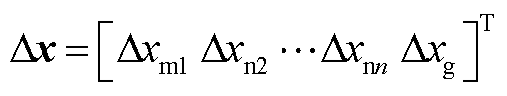 ;Du为输入控制变量,
;Du为输入控制变量,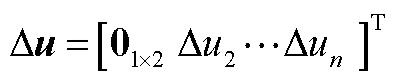 ;
;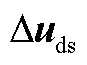 为扰动变量,
为扰动变量,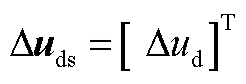 ;Dy为输出变量,
;Dy为输出变量,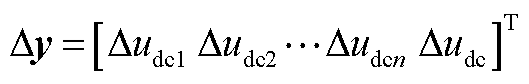 ;状态矩阵As、输入矩阵Bs1、扰动矩阵Bs2和输出矩阵Cs分别为
;状态矩阵As、输入矩阵Bs1、扰动矩阵Bs2和输出矩阵Cs分别为
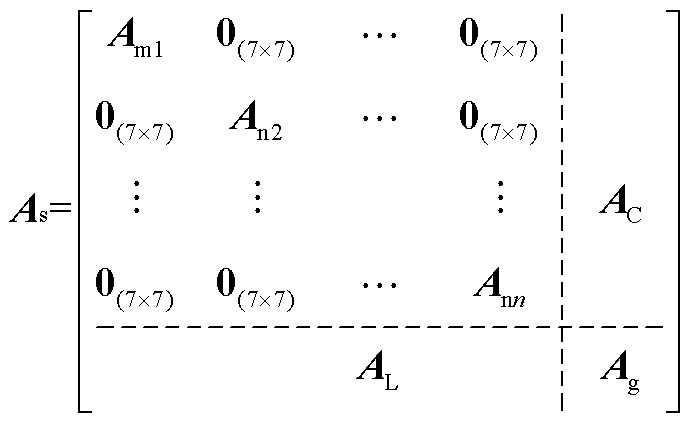
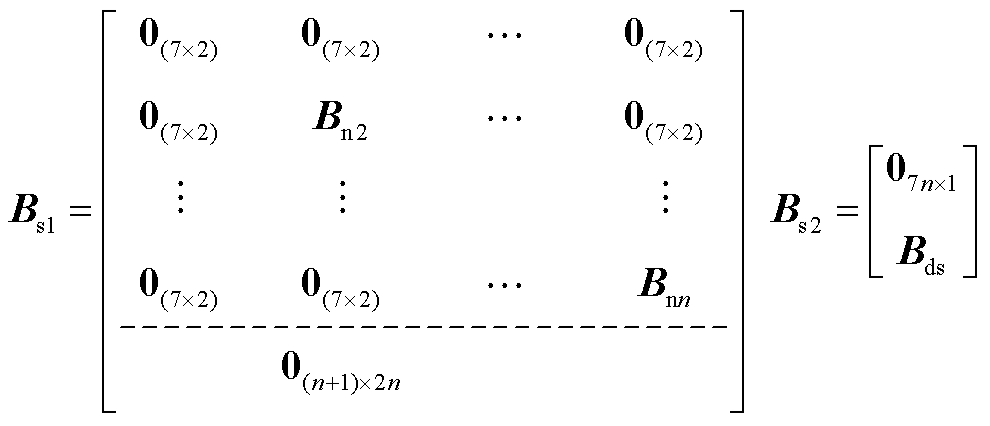
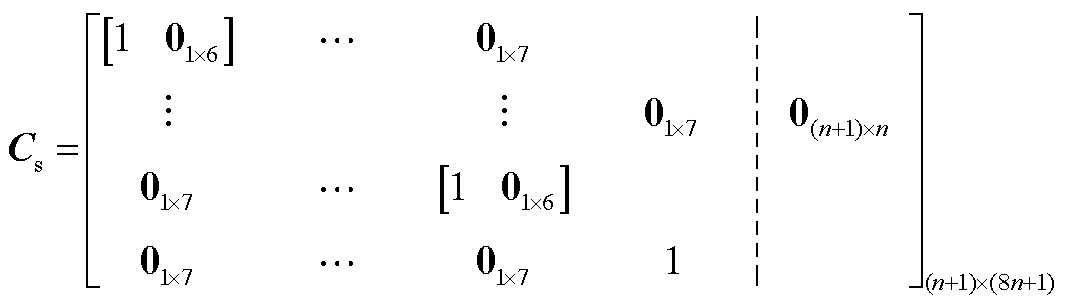
其中
3. 式(4)中,状态矩阵 、输入矩阵
、输入矩阵 和输出矩阵
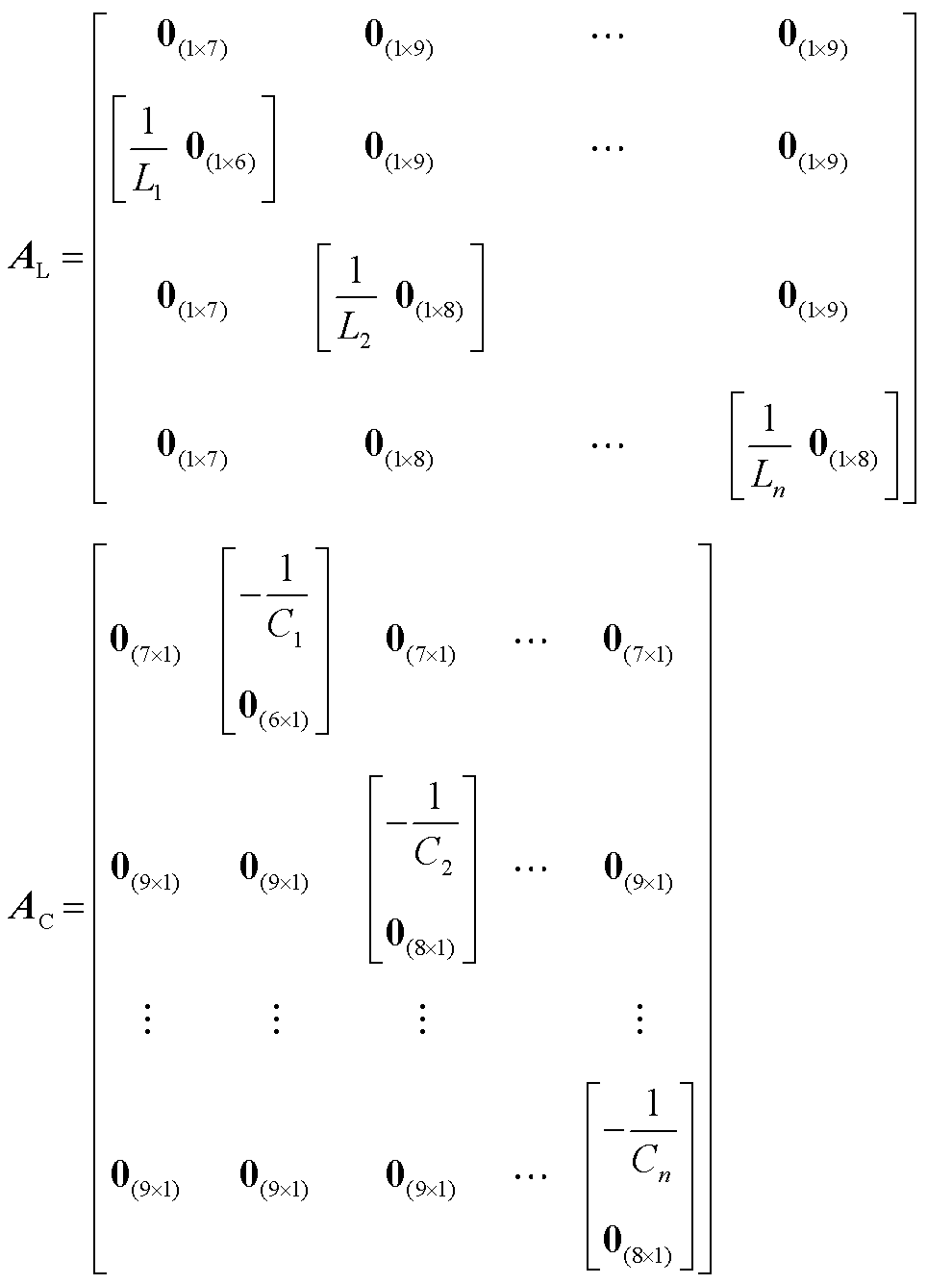
和输出矩阵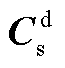 分别为
分别为


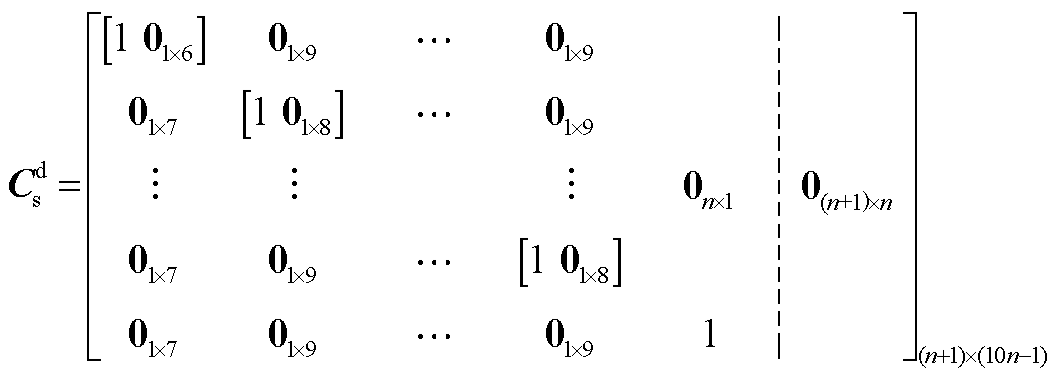
其中

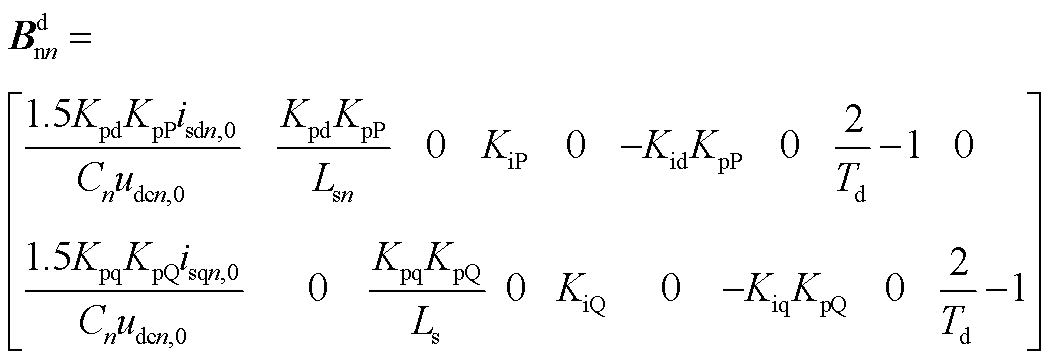
4. 式(8)中,输入矩阵Su、状态矩阵Sx、输出矩阵Sy和扰动矩阵Sd分别为
参考文献
[1] 李霞林, 郭力, 黄迪, 等. 直流配电网运行控制关键技术研究综述[J]. 高电压技术, 2019, 45(10): 3039-3049. Li Xialin, Guo Li, Huang Di, et al. Research review on operation and control of DC distribution networks[J]. High Voltage Engineering, 2019, 45(10): 3039-3049.
[2] 梁永亮, 吴跃斌, 马钊, 等. 新一代低压直流供用电系统在“新基建”中的应用技术分析及发展展望[J]. 中国电机工程学报, 2021, 41(1): 13-24. Liang Yongliang, Wu Yuebin, Ma Zhao, et al. Application and development prospect of new generation of LVDC supply and utilization system in “new infrastructure”[J]. Proceedings of the CSEE, 2021, 41(1): 13-24.
[3] 邓卫, 裴玮, 张释中, 等. 面向三端直流系统运行边界提升的集成参数优化配置研究[J]. 电工技术学报, 2020, 35(8): 1705-1715. Deng Wei, Pei Wei, Zhang Shizhong, et al. Research on integrated parameter optimization configuration for operational boundary improvement of three-multi-terminal DC system[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1705-1715.
[4] 李海波, 赵宇明, 刘国伟, 等. 基于时序仿真的商业楼宇交流与直流配电系统能效对比[J]. 电工技术学报, 2020, 35(19): 4194-4206.Li Haibo, Zhao Yuming, Liu Guowei, et al. The time sequential simulation based energy efficiency comparison of AC and DC distribution power system in commercial buildings[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4194-4206.
[5] 陈红坤, 夏方舟, 袁栋, 等. 直流配电网中含光伏的电动汽车快速充电站优化配置方案[J]. 电力系统自动化, 2020, 44(16): 53-60. Chen Hongkun, Xia Fangzhou, Yuan Dong, et al. Optimal configuration scheme of fast electric vehicle charging station with photovoltaic in DC distribution network[J]. Automation of Electric Power Systems, 2020, 44(16): 53-60.
[6] 金国彬, 潘狄, 陈庆, 等. 考虑源荷不确定性的直流配电网模糊随机日前优化调度[J]. 电工技术学报, 2021, 36(21): 4517-4528. Jin Guobin, Pan Di, Chen Qing, et al. Fuzzy random day-ahead optimal dispatch of DC distribution network considering the uncertainty of source-load[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4517-4528.
[7] 王成山, 李微, 王议锋, 等. 直流微电网母线电压波动分类及抑制方法综述[J]. 中国电机工程学报, 2017, 37(1): 84-97. Wang Chengshan, Li Wei, Wang Yifeng, et al. DC bus voltage fluctuation classification and restraint methods review for DC microgrid[J]. Proceedings of the CSEE, 2017, 37(1): 84-97.
[8] 彭克, 王琳, 李喜东, 等. 采用下垂控制的直流配电系统高频振荡分析及控制[J]. 电力系统自动化, 2021, 45(17): 43-50. Peng Ke, Wang Lin, Li Xidong, et al. Analysis and control of high-frequency oscillation for DC distribution system with droop control[J]. Automation of Electric Power Systems, 2021, 45(17): 43-50.
[9] 朱晓荣, 李铮, 孟凡奇. 基于不同网架结构的直流微电网稳定性分析[J]. 电工技术学报, 2021, 36(1): 166-178. Zhu Xiaorong, Li Zheng, Meng Fanqi. Stability analysis of DC microgrid based on different grid structures[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 166-178.
[10] 邓卫, 吴争, 孔力, 等. 交直流混联系统协调控制技术[J]. 高电压技术, 2019, 45(10): 3025-3038. Deng Wei, Wu Zheng, Kong Li, et al. Coordinated control technology for AC/DC hybrid system[J]. High Voltage Engineering, 2019, 45(10): 3025-3038.
[11] Deng Wei, Pei Wei, Li Luyang. Active stabilization control of multi-terminal AC/DC hybrid system based on flexible low-voltage DC power distribution[J]. Energies, 2018, 11(3): 502.
[12] Magne P, Nahid-Mobarakeh B, Pierfederici S. General active global stabilization of multiloads DC-power networks[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 1788-1798.
[13] Sulligoi G, Bosich D, Giadrossi G, et al. Multiconverter medium voltage DC power systems on ships: constant-power loads instability solution using linearization via state feedback control[J]. IEEE Transactions on Smart Grid, 2014, 5(5): 2543-2552.
[14] Hosseinzadeh M, Salmasi F R. Robust optimal power management system for a hybrid AC/DC micro-grid[J]. IEEE Transactions on Sustainable Energy, 2015, 6(3): 675-687.
[15] Chen Gang, Zhao Zhongyuan. Delay effects on consensus-based distributed economic dispatch algorithm in microgrid[J]. IEEE Transactions on Power Systems, 2018, 33(1): 602-612.
[16] 邓思成, 陈来军, 郑天文, 等. 考虑系统延时的微电网有功功率分布式控制策略[J]. 电网技术, 2019, 43(5): 1536-1542. Deng Sicheng, Chen Laijun, Zheng Tianwen, et al. Active power distributed control of microgrids considering system time delays[J]. Power System Technology, 2019, 43(5): 1536-1542.
[17] 吕振宇, 吴在军, 窦晓波, 等. 自治直流微电网分布式经济下垂控制策略[J]. 中国电机工程学报, 2016, 36(4): 900-910. Lü Zhenyu, Wu Zaijun, Dou Xiaobo, et al. A distributed droop control scheme for islanded DC microgrid considering operation costs[J]. Proceedings of the CSEE, 2016, 36(4): 900-910.
[18] Deng Wei, Pei Wei, Wu Qi, et al. Analysis of interactive behavior and stability of low-voltage multiterminal DC system under droop control modes[J]. IEEE Transactions on Industrial Electronics, 2022, 69(7): 6948-6959.
[19] 李鲁阳, 裴玮, 邓卫, 等. 改善直流配电网中VSC与线路交互失稳的有源阻尼策略[J]. 高电压技术, 2019, 45(9): 2884-2894. Li Luyang, Pei Wei, Deng Wei, et al. Active damping strategy for improving VSC and line interaction instability in DC distribution network[J]. High Voltage Engineering, 2019, 45(9): 2884-2894.
[20] 刘小龙, 李欣然, 刘志谱, 等. 基于风险量化与需求侧响应的综合能源系统储能事故备用优化利用[J]. 电工技术学报, 2021, 36(9): 1901-1913. Liu Xiaolong, Li Xinran, Liu Zhipu, et al. Study on the optimal utilization of integrated energy system emergency reserve based on risk quantification and demand side response[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1901-1913.
[21] Huang Wentao, Hua Wei, Fan Qigao. Performance analysis and comparison of two fault-tolerant model predictive control methods for five-phase PMSM drives[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(4): 311-320.
[22] 厉文秀. 随机时滞电力系统稳定性分析[J]. 电力与能源, 2015, 36(1): 10-15. Li Wenxiu. Stability analysis for stochastic time delay power system[J]. Power & Energy, 2015, 36(1): 10-15.
[23] 陈锦洲, 陈磊, 陈亦平, 等. 基于Pade近似的电力系统频率振荡模式延时轨迹分析[J]. 电力系统自动化, 2019, 43(14): 120-125. Chen Jinzhou, Chen Lei, Chen Yiping, et al. Trajectory analysis of time delay for frequency oscillation mode of power system based on Pade approximation[J]. Automation of Electric Power Systems, 2019, 43(14): 120-125.
Abstract Aiming at the voltage stability problems such as DC voltage fluctuation, voltage over-limit or even voltage drop, oscillation instability caused by uncertain fluctuation of distributed generation and DC loads connected to the low-voltage multi-terminal DC (MTDC) system, additional control strategy has been widely studied because of its simple structure and no need to change the system existing control loop structure. However, most of the current additional control strategy relies on the experience of designers in terms of parameter design, which leads to the problem that the control cost is high and the optimal control effect cannot be guaranteed. In addition, current method does not take into account of the communication time-delay. Since for centralized additional control mostly depends on the scheduling of the upper central controller and certain physical distance exists between the local controller of the converter station and the upper central controller, the problem of communication delay cannot be avoided, which will have a certain impact on the additional control effect that needs to be studied.
In order to solve the above problems, considering the characteristics of MTDC system under master-slave control, a time-delay model predictive additional control strategy is proposed which uses the model predictive control (MPC) algorithm to build the additional controller. Different from the traditional MPC method, the proposed method establishes a time-delay prediction model, which can more accurately describe the dynamic characteristics of system under communication time-delay, and improve the robustness of the control strategy. Firstly, the structure of a centralized MTDC system under master-slave control is studied. Secondly, a time-delay prediction model based on Pade approximation is constructed. Based on the time-delay prediction model, an additional controller which takes the minimum voltage fluctuation and the minimum output of system as the optimization goal is constructed, and through rolling optimization and feedback correction, the additional power control commands are generated in real-time, which are sent to the outer power loop of the local controller of slave VSC thus can stabilize the system voltage fluctuation and ensure the safe operation of the system under uncertain disturbance. Then, the influence of power disturbance and the communication time-delay on the stability and the additional control strategy performance is analyzed by studying the root locus diagram of the system. Finally, the simulation and case analysis of a three-terminal low-voltage DC system are carried out using Matlab/Simulink plate-form, which proves the effectiveness and robustness of the proposed method.
The following conclusions can be drawn from the theoretical and simulation analysis: (1) The proposed time-delay model predictive additional control strategy can solve the voltage instability problem when the MTDC system is subject to uncertain disturbance with minimum output, improve the system voltage stability and power quality, and has good economy. (2) When the system communication network delay is less than a certain range, the optimal control strategy proposed in this paper can well describe the dynamic characteristics of the time-delay system compared to the traditional additional control strategy, better suppress the system voltage fluctuation under the uncertain disturbance, ensure the safe operation of the system, and has good robustness.
Keywords:Low-voltage multi-terminal PC system, model predictive control, distributed generation, additional control, communication delay
DOI: 10.19595/j.cnki.1000-6753.tces.220459
中图分类号:TM76
中国科学院洁净能源先导科技专项(XDA21050000)和国家自然科学基金项目(52177122)资助。
收稿日期2022-03-29
改稿日期2022-06-22
庄 莹 女,1995年生,硕士,助理研究员,研究方向为多端直流系统稳定性分析与控制技术。E-mail: zhuangying@mail.iee.ac.cn
裴 玮 男,1982 年生,研究员,博士生导师,研究方向为交直流微网、主动配电网运行控制与分析。 E-mail:peiwei@mail.iee.ac.cn (通信作者)
(编辑 赫 蕾)