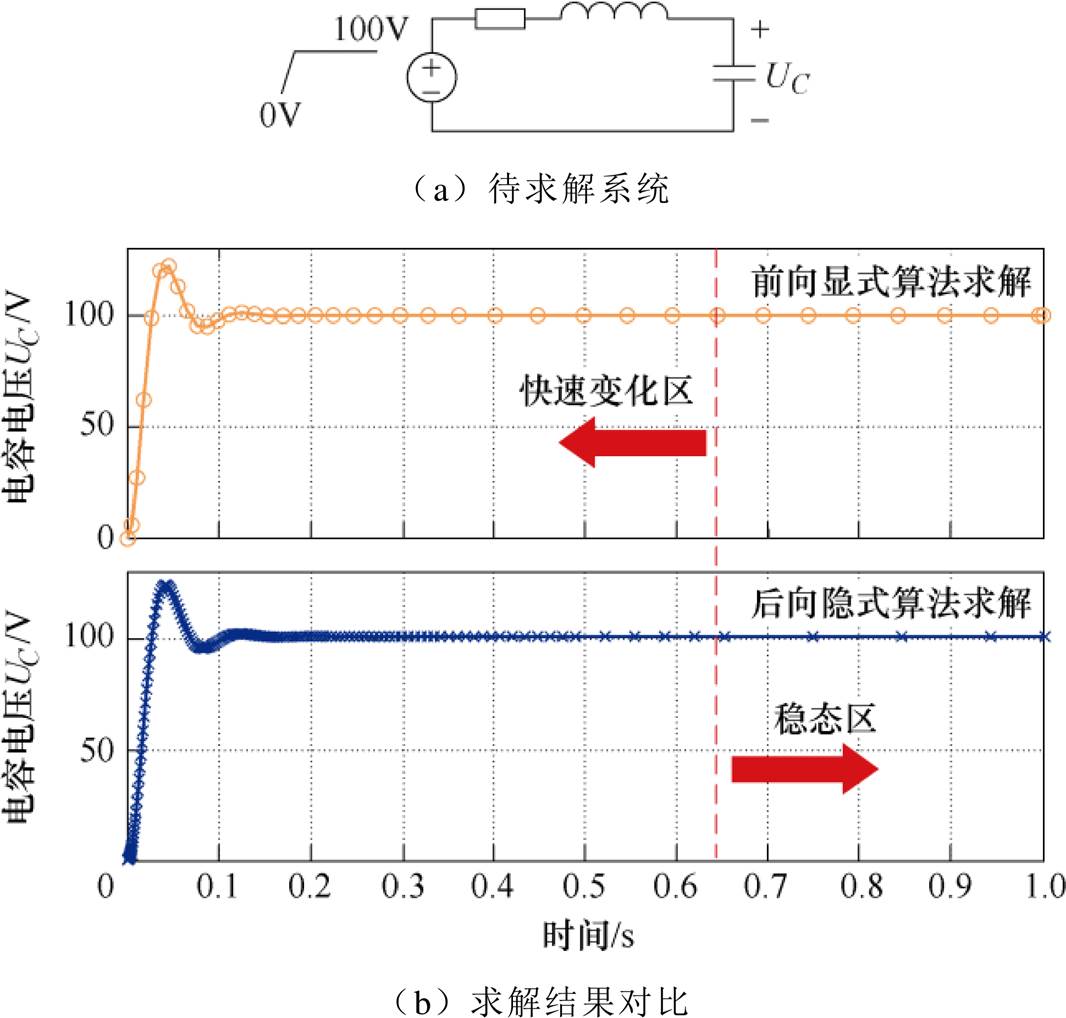
图1 使用显式算法和隐式算法求解某衰减振荡系统对比
Fig.1 Comparisons between explicit formula and implicit formula when solving an oscillation damping system
摘要 高性能仿真工具对电力电子系统的设计分析具有重要的支撑作用,而考虑杂散参数对装置可靠性的影响、实施参数扫描来辅助优化设计是目前仿真应用的重要趋势。但是,考虑杂散参数后,系统的数学性质更加复杂多变,可能在刚性和非刚性之间发生转变,此时仅使用单一的前向或者后向算法都不能达到最优仿真效率,给仿真解算带来挑战。离散状态事件驱动(DSED)仿真框架可以实现对电力电子系统的准确高效解算,相较于商业仿真软件具有明显优势。但现有的DSED框架无法对系统的数学性质进行自动识别,应对上述复杂场景时仿真效率仍然有较大提升空间。为此,该文深入分析不同数值算法的效率最优场景,提出一种自适应的数值算法切换策略。该方法构造一种额外计算成本较小的判据,实现对系统刚性程度的自动检测以及不同数值积分算法的平滑切换,在仿真全过程中始终选择更优的积分方法,从而提升整体求解效率。所提策略应用于一台10 kV-2 MW四端口电力电子变压器的高频振荡现象分析中,在同等精度的前提下,仿真总体速度相较于原有DSED仿真框架提升了约4倍,进而验证了所提方法的准确性和有效性。
关键词:电力电子系统仿真 刚性检测 离散状态事件驱动
电力电子装置在输配电网、电力传动、国防军工等领域得到了广泛的应用[1–3],而高性能仿真软件则是电力电子装置设计与分析的底层支撑工具[4]。近年来,随着装置设计精细化程度的不断提升,在仿真应用领域也出现了一些新的需求和趋势。首先,在大容量、高频装置中,杂散参数的作用愈加明显,它们可能导致过电压、过电流[5]、高频振荡[6-8]、电磁干扰[9-10]等诸多问题,严重影响系统的安全可靠运行,因此将其纳入仿真分析中具有重要意义。其次,对于复杂装置,电力电子系统的设计自动化成为新的研究热点[11–13],参数的批量扫描成为常见需求。上述需求对仿真工具提出了更高的要求——希望能在包含杂散参数的系统中、不同参数取值下、多次仿真时始终具有较高的解算效率。
然而,杂散参数的引入或者参数取值的变化可能使得系统中出现时间尺度极小的动态过程,数学模型呈现出“刚性”性质,大大增加了系统解算的难度。一般而言,刚性问题产生的原因是系统中包含至少一个负实部绝对值很大的特征值[14],该特征值对应于一个幅值衰减很快的解分量。常见的线性显式前向数值积分算法受到稳定域较小的限制,即使解分量已经迅速衰减到接近稳定,也不能采用大的步长,从而导致解算效率低下[14–16]。此时一般需要采用单步计算量高但稳定域更大的后向隐式数值积分公式进行解算[14],常见的算法包括后向差分公式、隐式龙格库塔方法等[16],它们在连续系统的刚性问题求解中取得了较好的效果。
对于电力电子系统而言,它既包含连续状态,也包含离散的开关事件,二者相互作用、相互影响,是一个典型的混杂系统[17]。这使得它区别于一般的连续系统,在求解时不仅需要考虑连续状态的数值积分,还需要同时考虑离散事件的定位。最近,相关研究提出了一种离散状态事件驱动(Discrete- State Event-Driven, DSED)建模仿真框架[18-21],它采用事件驱动而非时间驱动的方法推进仿真进程,避免离散点附近反复迭代,实现了对电力电子混杂系统的高效解算[19]。DSED框架充分考虑了电力电子系统连续和离散混杂的特性进行数值积分和事件定位优化,仿真速度相较商业软件有明显提升,展现出很大的应用潜力。
但是,如前文所述,目前电力电子装置的实际仿真需求多样,参数取值范围广,尤其是考虑了杂散参数之后,系统的数学性质更加难以判断,在仿真实践中经常会出现如下问题:
(1)开关动作会导致拓扑频繁变化,同样的杂散参数在不同拓扑下可能位于完全不同的回路,从而使系统的性质在非刚性和刚性之间发生转换。
(2)即使系统呈现出刚性性质,但是在解分量的快速变化区,本身为了精确刻画它的变化就需要采用较小的步长。此时步长主要受到精度制约而非稳定性约束,高阶的前向显式算法相较于后向隐式算法反而具有更高的效率[16]。图1为使用可变步长的前向显式算法和后向隐式算法求解同一衰减振荡系统的结果对比,可非常直观地展现出两种算法在不同时间段内的步长选择区别。在电力电子系统中,考虑到大量开关事件对时间轴的分隔,快变化阶段的总占比往往会上升。此时,简单地根据系统矩阵的数学性质直接选择后向方法,而不考虑变量所处的实际变化阶段以及离散事件的发生时刻,并不是一个最佳的选择。

图1 使用显式算法和隐式算法求解某衰减振荡系统对比
Fig.1 Comparisons between explicit formula and implicit formula when solving an oscillation damping system
(3)对于参数变化、多次仿真的情况,系统刚性和非刚性的界限可能变得模糊,用户在仿真之前也很难对系统性质做出全面评判,选择较优积分方法的难度大大提升。
现有的DSED框架只能提供单一的前向或后向数值积分方法,因此在仿真这类包含杂散参数的复杂系统时,仿真效率仍然有很大的提升空间。根据前文的分析,一种很自然的解决思路是结合不同类型数值求解器的优势,在仿真进行的过程中对系统的数学性质进行自动判断,始终选择当前情况下效率更优的数值积分公式进行求解。
上述思路在实现过程中的主要难点包括两点:一是如何保证求解器切换策略的可靠性和及时性;二是如何减少对系统性质进行检测所引入的额外成本。目前针对连续系统的刚性检测已经有一些相关的研究工作。恒定步长法基于当系统遇到刚性问题时前向显式方法的步长几乎不变的实践经验来进行判断,几乎无额外计算成本,但可靠性较差[22]。另外一类方法是将两种精度和稳定域各有优劣的数值积分公式进行配对比较[22],这类方法的切换判据形式与数值积分公式的形式紧密相关,需要根据具体采用的积分公式的特点进行设计,以减少刚性检测本身所产生的额外计算量。已有的工作大部分针对常用的显式龙格库塔方法或者显式Adams方法来构造对比公式和切换判据[23-29],但是这些文献中所采用的积分方法本身没有考虑混杂系统中离散事件的影响,作为单一求解器时仿真电力电子系统的效率仍然有较大的提升空间。另外还有一些方法直接对系统的特征值或者谱半径进行估计以辅助进行刚性程度的判断[22],但估计特征值的额外开销很大,对于电力电子系统这样方程频繁变化的场景来说并不实用。而仅估计谱半径无法区分绝对值最大的特征值是更接近于实轴还是更接近于虚轴;后者对应于高频振荡且几乎不衰减的分量,并不能认为导致了“刚性”问题,因此很容易产生误判。
针对以上问题,本文基于已有的DSED框架提出了一种针对电力电子混杂系统求解的自适应仿真算法。本文的创新点主要包括:
(1)深入分析了电力电子系统的数学性质以及不同类型算法在电力电子系统解算中效率最优的场景,提出了基于刚性检测的算法自适应切换思路。
(2)基于电力电子系统的混杂特性,具体地构造了电力电子系统的刚性检测判据以及不同求解器之间平滑切换的方法。该方法的额外计算量较低,可以以较小的代价实现对电力电子系统数学性质的实时检测及数值积分方法的自动切换。
因此,该方法可以保证始终能够选择更优的积分算法来进行解算,从而大大提升了电力电子系统的整体求解效率和仿真设置的自适应性。该策略应用于10 kV-2 MW四端口电力电子变压器中杂散参数引发的高频振荡分析,验证了所提方法的准确性和有效性。
本节主要对电力电子系统的建模方法进行介绍,对不同数值积分算法的最佳适用场景进行深入分析,从而为后续的自适应仿真算法提供理论基础。
电力电子系统可以采用一组分段线性的状态方程来进行建模,即
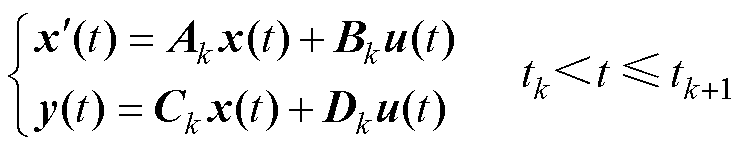 (1)
(1)
式中,x为一个n×1维的列向量,表示系统中的状态变量,一般为电容电压和电感电流;y为一个p×1维的列向量,表示系统中的输出变量,包含所有需要观测的变量;u为一个l×1维的列向量,表示系统的输入变量,一般由独立电源构成;Ak、Bk、Ck、Dk为第k个时间段内的系数矩阵,与系统当前的拓扑结构(由开关状态决定)和元件参数有关。由于后文主要讨论积分方法,不可能跨越离散点进行积分,因此相关场景下系数矩阵都保持恒定。为简便起见,在附录中提及系数矩阵Ak等时可省略下标k。
如引言部分所述,电力电子混杂系统与一般的连续系统不同,既包含连续动态,也包含离散事件,因此任何数值积分方法都应当综合考虑离散点的影响。由式(1)可得,在两次离散事件之间,系统建模为线性时不变常微分方程组,系统的解析解为
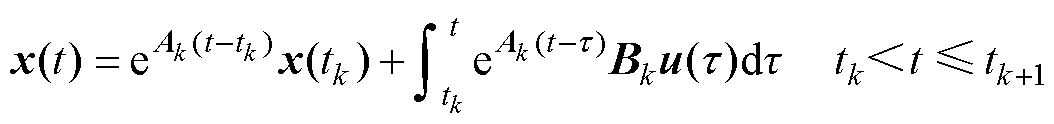 (2)
(2)
式中,解的第一部分即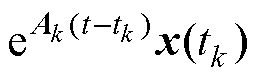 为系统的自由响应,只与系统的特征根有关;另一部分为系统的强迫响应,与系统的激励有关。由于电力电子系统的状态方程对应的是实际物理系统,满足能量守恒定律,因此Ak的全部特征根必然是非正的,自由响应部分会先经历一段暂态变化过程,最终衰减至稳态(0或者无衰减的三角函数振荡)。刚性问题的来源正是振荡衰减的自由响应部分已经接近稳态之后前向显式算法仍然需要采用小步长进行计算。
为系统的自由响应,只与系统的特征根有关;另一部分为系统的强迫响应,与系统的激励有关。由于电力电子系统的状态方程对应的是实际物理系统,满足能量守恒定律,因此Ak的全部特征根必然是非正的,自由响应部分会先经历一段暂态变化过程,最终衰减至稳态(0或者无衰减的三角函数振荡)。刚性问题的来源正是振荡衰减的自由响应部分已经接近稳态之后前向显式算法仍然需要采用小步长进行计算。
根据以上分析,本文希望提出一种自适应算法,充分发挥不同求解器在不同场景下的优势,提升解算效率。为了使得该方法既能准确检测系统的数学性质、及时选择最佳求解器,又不引入过多的额外计算量,算法设计时应当考虑如下因素:
1)不同求解器的效率最优场景以及启动刚性检测的时机
在电力电子混杂系统中,发生离散事件后的状态变量初值一般都偏离新阶段的稳态解,需要经过一段暂态过程才能到达新的稳态附近。因此,每当离散事件导致系统拓扑乃至方程发生变化的时候,应当首先选择单步计算量小、阶数高、精度高的前向显式方法(非刚性算法)作为初始算法,来匹配自由响应部分仍在快速变化的动态阶段;在自由响应部分进入稳态之后,再采用稳定域大的后向隐式算法(刚性算法)以能够使用大步长。
由于电力电子系统的方程在两个离散点之间线性时不变且解析解不发散,不会出现随着时间的推移,状态变量的变化反而越来越快的情况,因此对于求解器切换的检测仅需要在采用非刚性算法的时候进行,一旦确定了当前情况下采用刚性算法更优,后续就无需再进行反向切换。
在进行算法对比及刚性检测时,由于非刚性算法的单步计算量更小,因此在步长相似的情况下,必然优先选择非刚性算法。此外,刚性算法由于是隐式算法,需要求解线性方程组,往往需要在启动的时候进行一次LU分解,该分解的计算复杂度比后续的方程求解都大,因此刚性算法的启动步耗时最长,应尽量避免启动之后仅进行了极少计算就已经到达下一个离散点的情况。所以如果非刚性算法计算出的步长和两个离散点之间的距离相比差距并不悬殊,盲目切换至刚性算法反而得不偿失。
2)非刚性和刚性场景下积分算法的具体形式
自适应仿真算法中需要两种数值积分算法分别针对不同的动态过程进行求解。为了实现在各种场景下的仿真效率最优,所采用的数值积分方法应当契合电力电子混杂系统的本质,发挥DSED框架的已有优势。另外,用于检测刚性程度的数学判据在保证可靠性的前提下,额外计算量应当尽可能小。多步的数值积分算法可以使用历史值的组合来估计截断误差和最佳步长,无需真正完成一步数值积分。因此相比于单步法,多步的后向数值积分算法更适合与前向算法进行组合对比来构造切换判据。
本节根据第1节的分析结果具体介绍所提的自适应仿真算法,包括该方法中采用的数值求解器、刚性问题的实时检测判据以及求解器的切换策略。
现有的DSED框架针对非刚性电路提供了灵活自适应离散状态(Flexible Adaptive Discrete-State, FA-DS)积分方法[19]。该方法基于高阶的泰勒展开公式,是一种变步长、变阶数的前向显式算法。它针对电力电子系统的混杂特性进行专门设计,同时降低了计算点数和单步计算量,从而获得比一般的显式方法更高的计算效率[19]。由于FA-DS方法的良好性质,在本文所提的自适应仿真算法中,继续沿用FA-DS方法作为非刚性场景下的求解器。
针对刚性电路,已有的DSED框架提供了后向离散状态事件驱动积分(Backward Discrete-State Event Driven, BDSED)方法,它主要基于后向差分公式(Backward Difference Formula, BDF)。这是一种多步后向数值积分方法,具有变步长和变阶数的能力[15]。文献[20]中结合电力电子系统的混杂特性对BDF方法的步长和阶数变化策略进行了优化,从而进一步提升其在电力电子系统中的解算效率。
根据1.3节的分析,多步的后向积分算法更适宜与前向算法进行组合,以减少刚性检测和数值积分算法切换的额外成本。已有的BDSED方法能够在性质单一的场景下与DSED框架较好地契合,发挥事件驱动机制的优势,且其采用的数值积分公式本身为多步法,满足构造自适应算法的需求,因此本文所提的自适应仿真算法沿用BDSED方法以及BDF公式作为刚性场景下的求解器。
本小节主要介绍本文所提的自适应仿真算法的详细流程,包括刚性检测算法的启动策略、刚性问题的实时检测判据和不同求解器的切换及过渡 方法。
2.2.1 刚性检测算法的启动策略
根据第1节的分析,电力电子混杂系统的数值积分算法应当考虑两个离散点之间的时间段。假设两次离散事件的发生时刻分别为tdis,k和tdis,k+1,若tdis,k时刻的系统拓扑发生了变化,则需要重新进行算法初始化,初始算法选择为FA-DS方法。
假设(tdis,k, tdis,k+1)之间的某个积分点tm时刻选择的算法仍然为FA-DS方法,xm为tm时刻已经求解出的状态变量数值解,xm+1为tm+1时刻的待求值。以步长hFA积分至tm+1时刻,积分阶数为rFA。根据1.3节的分析,应当充分考虑后向数值积分算法启动的成本,尽量避免切换之后并未计算较多点就已经达到下一个离散点的状况。综上所述,当且仅当满足式(3)条件的时候才会进行刚性检测。
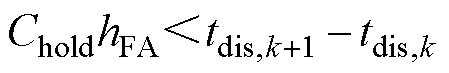 (3)
(3)
式中,Chold为自适应策略中可以调节的参数,Chold≥1,可以由FA-DS方法的单步计算量和BDSED方法启动的时候的单步计算量估算得到。
FA-DS方法主要基于高阶泰勒展开式进行计算,是一个变步长变阶数的算法,详细公式可参见附录。该算法以下一次离散事件的间隔作为步长选择的主要依据,由最低阶往上递增,直至达到最高阶数仍然不能满足误差要求才缩小步长。因此,如果解算遇到了刚性问题,那么必然代表阶数已经达到了最大设定值rFAmax。此时,FA-DS方法的单步计算量为rFAmaxn(n+l)+O(n)[19],其中 为状态变量维数,
为状态变量维数,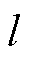 为输入变量维数。FA-DS方法中rFAmax=8。
为输入变量维数。FA-DS方法中rFAmax=8。
对于BDSED方法而言,它主要基于BDF公式,该方法为变步长、变阶数的多步法,求解过程中需要使用多个历史值,详细的公式可参见附录。由于BDSED方法为后向算法,需要求解方程组,因此无论计算步长如何,启动时都需要进行一次LU分解,该步的时间复杂度为2n3/3+O(n2)[30]。因此,对比FA-DS和BDSED方法的单步计算量,可取Chold为
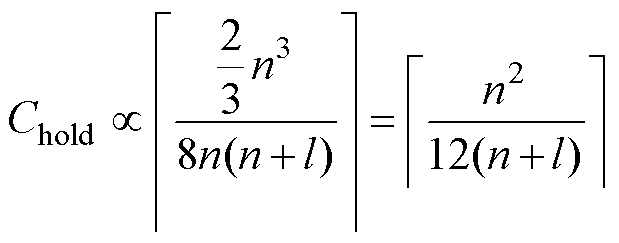 (4)
(4)
式中, 表示向上取整。
表示向上取整。
考虑到在每个离散的计算点除了进行数值积分以外,还需要进行输出变量等的计算,减少点数总能获得这一部分收益,因此Chold也不宜取太大。实践中可以取Chold为3~8。
2.2.2 刚性问题的实时检测判据
在满足式(3)的条件之后,需要进行检测,判断解算过程中是否遇到刚性问题。检测的基本思路是在每步FA-DS方法完成数值积分之后,对比同等精度下BDSED方法是否可能具有更优性能。为此,需要利用算法的截断误差估计公式来预测BDSED方法求解相同问题时能够达到的最大步长。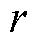 阶BDF积分公式的误差估计[15, 31]为
阶BDF积分公式的误差估计[15, 31]为
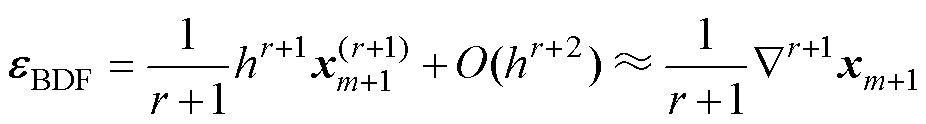 (5)
(5)
式中,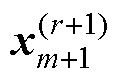 为状态变量在tm+1时刻的r+1阶导数;
为状态变量在tm+1时刻的r+1阶导数;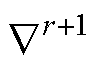 xm+1为tm+1时刻状态变量的r+1阶后向差分,
xm+1为tm+1时刻状态变量的r+1阶后向差分,
差分步长为积分步长h。但FA-DS方法是变步长方法,历史值不等于间距,无法直接计算出差分,因此需根据牛顿插值公式对后向差分进行估计。
由等距的牛顿插值多项式可知,当差分步长为h时,r+1阶的牛顿插值多项式N(t)为
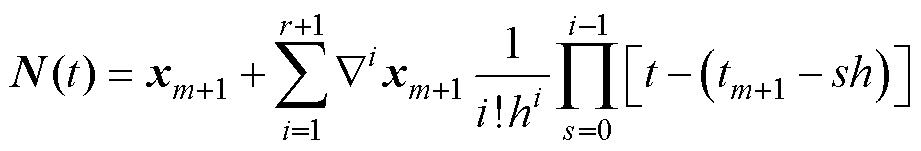 (6)
(6)
根据插值公式计算得到的结果应当与FA-DS方法已经计算得出的历史值相同,即应当满足
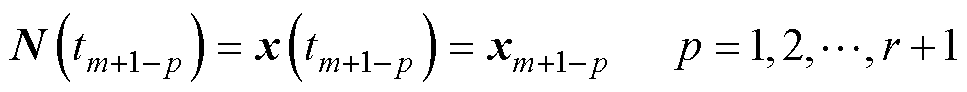 (7)
(7)
式中,tm+1−p为FA-DS方法选择得到的r+1个历史计算时刻。
为避免外插,在式(6)中可以取后向差分的步长h为历史积分步长的平均值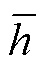 ,即
,即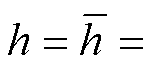
 ,联立式(6)和式(7)写成矩阵形式有
,联立式(6)和式(7)写成矩阵形式有
 (8)
(8)
式中,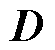 为状态变量的各阶差分排成的矩阵,有
为状态变量的各阶差分排成的矩阵,有
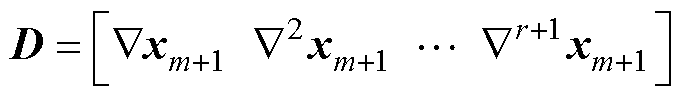 (9)
(9)
系数矩阵 为
为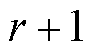 阶的方阵,第
阶的方阵,第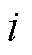 行第
行第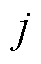 列的元素值为
列的元素值为
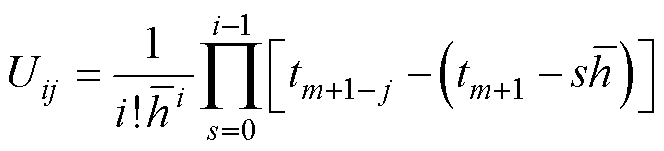 (10)
(10)
右端项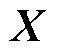 为
为
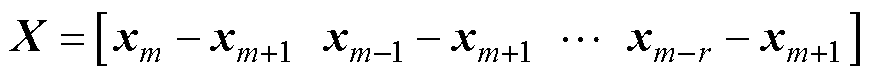 (11)
(11)
求解上述方程得到D,就可以得到xm+1处以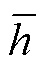 为步长的
为步长的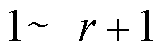 阶后向差分。代入式(5)中就可以估计得到在当前情况下以
阶后向差分。代入式(5)中就可以估计得到在当前情况下以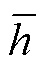 为步长用
为步长用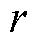 阶BDF公式计算得到的截断误差,而截断误差
阶BDF公式计算得到的截断误差,而截断误差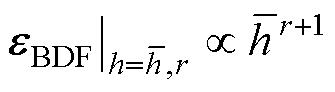 ,因此,在当前阶段,使用
,因此,在当前阶段,使用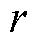 阶BDF公式进行数值积分,在下一个积分点所能采用的最大步长可估计为
阶BDF公式进行数值积分,在下一个积分点所能采用的最大步长可估计为
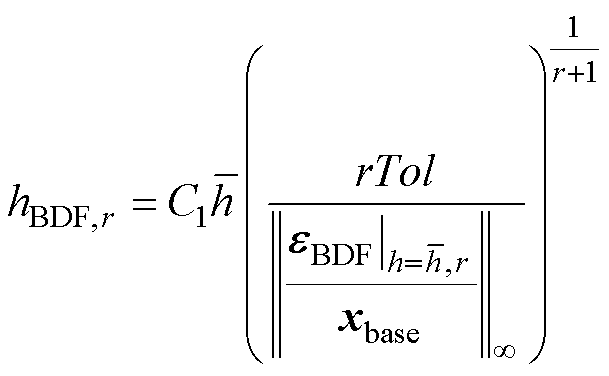 (12)
(12)
式中,rTol为算法的相对误差容限;xbase为状态变量的基值;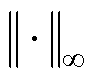 为无穷范数;C1为放缩系数,C1≤1,避免估计的步长过于乐观。参考Matlab中ODE求解器的源码以及一些经典变步长数值算法中的放缩系数[31-32],取C1≈1/1.4~1/1.2。
为无穷范数;C1为放缩系数,C1≤1,避免估计的步长过于乐观。参考Matlab中ODE求解器的源码以及一些经典变步长数值算法中的放缩系数[31-32],取C1≈1/1.4~1/1.2。
2.2.3 求解器的切换过渡方法
式(8)可以一次性计算出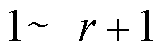 阶差分的全部值,可以从中选择步长最大的阶数作为切换到BDSED方法之后的启动阶数,即
阶差分的全部值,可以从中选择步长最大的阶数作为切换到BDSED方法之后的启动阶数,即
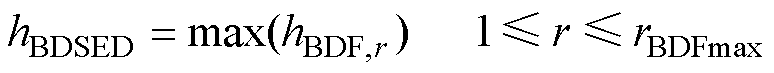 (13)
(13)
如果满足
 (14)
(14)
即采用BDSED方法所能够使用的潜在最大步长大于当前FA-DS方法使用的步长,就说明此时采用刚性算法是更优选择,应当切换至刚性算法,刚刚计算出的各阶差分可以保留,从而使得BDF公式可以直接以高阶启动后续的数值积分计算。
在切换到BDSED方法之后,就无需再进行反向检测,直接按照BDSED方法的策略进行正常的步长和阶数选择,直至达到下一个离散时刻计算点即可。上述算法的完整流程如图2所示。
本节以一台10 kV-2 MW四端口电力电子变压器高频振荡的仿真分析为例,验证所提自适应仿真算法在包含杂散参数的大规模电力电子系统仿真中的准确性和有效性。
近年来,多端口电力电子变压器(Power Elec- tronics Transformer, PET)在配电网领域得到了快速发展。多端口PET可以实现能量双向流动、电能灵活转换,被认为是交直流混合配电系统中的关键枢纽设备[33]。由于多端口PET的拓扑结构多样、参数设计复杂,对其进行准确快速的仿真分析成为重大需求。
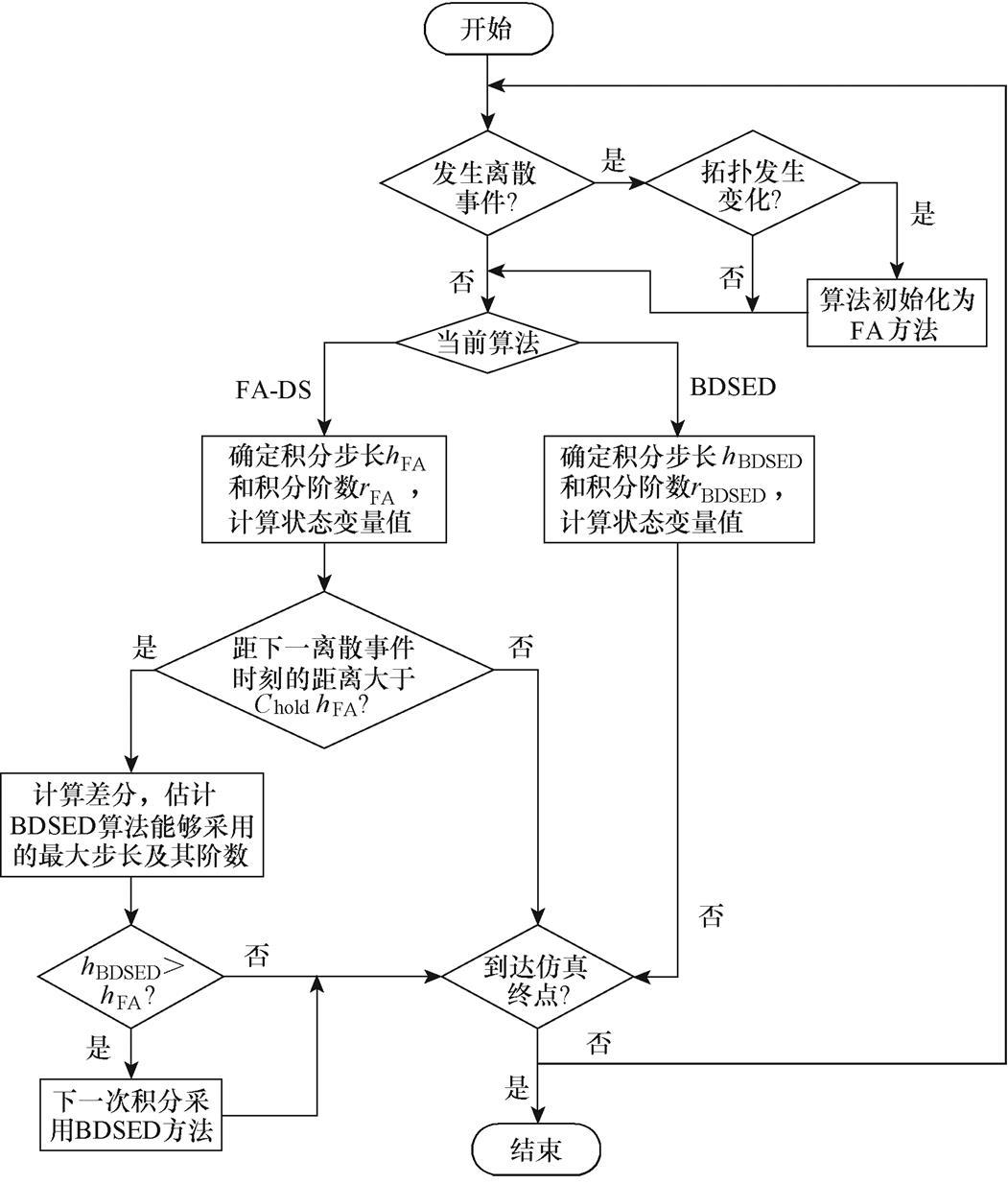
图2 所提自适应仿真算法的流程
Fig.2 The flowchart of the proposed method
本文所分析的案例是一台10 kV-2 MW四端口PET。四端口分别为10 kV高压交流(High-Voltage AC, HVAC)端口,380 V三相低压交流(Low-Voltage AC, LVAC)端口,10 kV高压直流(High-Voltage DC, HVDC)端口和±375 V低压直流(Low-Voltage DC, LVDC)端口。四个端口间创新性地使用了共高频母线的拓扑相连,以模块化多有源桥(Modular Multi-Active-Bridge, MMAB)为核心结构,一共包含87个子模块、72个高频变压器和578个开关器件,最高开关频率达到20 kHz[34-35]。目前该PET已经投入实际运行,图3和图4分别为该PET的拓扑示意图以及核心结构MMAB的连接示意图。
该PET采用的共高频母线结构可以减少电能变换环节,节省大量器件,降低损耗,在成本上具有显著优势[34]。但是相比于传统的共交流母线结构,高频母线运行在方波模式下,电压变化率高,因此很容易受到杂散参数的影响,控制策略较为复杂。
在实际装置中,在高频母线和MMAB的H桥出口电压波形上观察到MHz级别的高频振荡,实验中的高频交流母线的电压振荡现象如图5所示。这种电压高频振荡现象很容易导致电磁干扰现象,引起弱电设备的误动作,影响装置可靠运行,因此有必要对高频振荡的成因进行深入仿真分析,并探究相应的抑制办法。

图3 10 kV-2 MW电力电子变压器总体拓扑结构示意图
Fig.3 The overall topology of the 10 kV-2 MW PET

图4 模块化多有源桥的拓扑示意图
Fig.4 The schematic of the MMAB
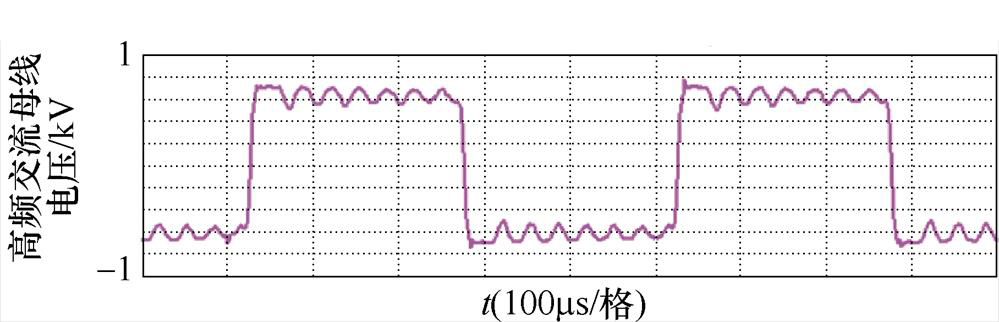
图5 实验中的高频交流母线的电压振荡现象
Fig.5 The voltage oscillation phenomenon of the high-frequency AC bus observed in experiments
文献[5, 7-8, 36]对高频振荡的原因进行了探究,针对MMAB的基本单元—双有源桥(Dual Active Bridge, DAB)进行了阻抗网络和振荡回路的分析。分析结果表明,当DAB模块工作在不同模式下的时候,会产生性质和频率不同的振荡。其中,当DAB的二次侧H桥闭锁时,二次侧H桥器件结电容与高频变压器的漏感会构成振荡回路[5, 36]。等效电路如图6所示。本文主要以该类振荡为例进行仿真分析。
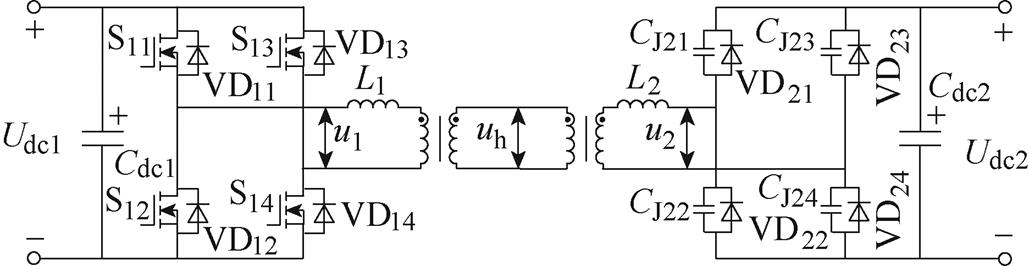
图6 双有源桥二次侧H桥闭锁时的等效拓扑
Fig.6 The equivalent circuit of the DAB when the H-bridge in the secondary side is blocked
在该PET中,开关器件采用了高压SiC MOSFET,由于电压和功率等级高,因此开关器件的输出结电容值也较大,结电容已经达到nF级,远大于高频变压器的杂散电容,因此文献[5, 36]中在进行机理分析时忽略了高频变压器杂散电容作用。
此时,一次侧的开关出口电压可以近似为一个方波,忽略漏阻、励磁电感和励磁电阻[5, 36],从一次侧的输出端口到二次侧H桥的通路的简化电路为如图7所示。
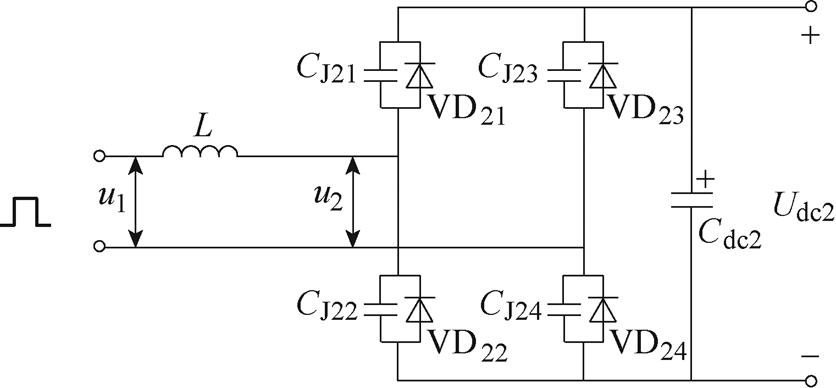
图7 简化等效电路
Fig.7 The simplified equivalent circuit
在后续的动态过程中,由于杂散电容的存在,电容电压不能突变,整流桥的状态会在截止、导通、截止之间循环。文献[5, 36]对该过程中的物理机理有详细的理论分析,此处不再赘述。结合实验可以看到,在该PET中开关寄生电容的存在以及双有源桥的方波运行机制会导致二次侧直流母线电压不断升高,进而还会导致高频母线电压产生高频振荡。前者会引发闭锁端口直流电容过电压击穿,后者会影响母线波形,从而影响其他端口的正常运行,导致电磁干扰、影响弱电装置。因此在这种场景中将杂散参数纳入考虑很有必要。
以上分析对高频振荡的原因进行了理论解释,但仅限于两个模块的情况。实际装置中采用了多模块串并联的设计,且包含四个端口,工况也更加复杂,因此对于这种大规模装置,只能采用仿真来进行时域分析才能获得更为准确直观的结果。
尽管大规模电路中几乎不可能通过理论分析得到解析结果,但是3.2节的结论仍然可以提供一些关于系统性质的定性信息。从仿真求解的角度来看,当整流桥完全截止的时候,变压器漏感和开关的寄生电容形成谐振回路,电路中的阻尼很小,状态方程的主导特征值应当为一对共轭虚根,状态变量中存在高频振荡且衰减较慢的分量,此时应当采用FA-DS方法刻画其快速变化;当整流桥导通的时候,SiC MOSFET的寄生电容和二极管的导通电阻并联,形成RC回路,使得方程中出现一个实部绝对值很大的特征值,容易引发刚性问题,此时应当使用BDSED方法来对刚性系统进行求解。
可以看到,在这样一个典型算例里,同样的杂散参数在不同的阶段参与了不同回路的动态过程,系统方程也呈现出不同性质。因此,采用自适应仿真算法对动态变化阶段进行时间上的划分、进行针对性求解对于提升总体仿真速度很有必要。
3.3.1 仿真准确性验证
本文选择的仿真场景为该PET单端口闭锁运行工况,用以模拟发生故障时需要闭锁端口的情况。在t=0 s前,所有端口都已经运行至稳态,t=0 s时,假设HVDC端口发生了某种故障,此时应当闭锁模块中所有端口,切除直流负载,其他端口保持正常运行。仿真观察该过程中高频母线的电压波形及HVDC子模块中直流母线的电压变化情况。系统中的主要参数范围见表1。
表1 电力电子变压器的系统规模及参数
Tab.1 System scales and parameters of the PET

参 数数 值 开关器件数578 子电路数87 高频变压器数72 最高开关频率/kHz20 非杂散电容数105 杂散电容数60 电感数166 电阻数356 非杂散电容取值范围250mF~15mF 杂散电容取值范围/nF10~30 电感取值范围1mH~5.6mH 电阻取值范围1mW~400W
1)与商业仿真软件对比
将本文所提策略的仿真结果与商业仿真软件A的仿真结果进行对比如图8、图9所示,二者采用了完全相同的电路模型。商业仿真软件A为电力电子领域的常用仿真工具,采用节点法框架,使用定步长求解器。节点法框架下一般采用梯形离散公式,数值稳定性较好,求解刚性系统不容易出现收敛性问题,所以将其选为对标软件。由于定步长求解器中最大步长的设置会对准确度有较大的影响,因此分别使用了1×10-6、1×10-7、1×10-8 s的步长进行仿真以确定合适的步长。从图8中可以看到,商业仿真软件A采用1×10-6、1×10-7 s步长的时候与采用更小步长时的仿真结果相比差异较大,因此选用1×10-8 s的步长才能在该软件中得到较为准确的结果。而从图9中可以看到,本文所提策略的仿真结果与商业仿真软件A采用1×10-8 s的仿真结果几乎完全相同,可以验证本文所提方法的准确性。
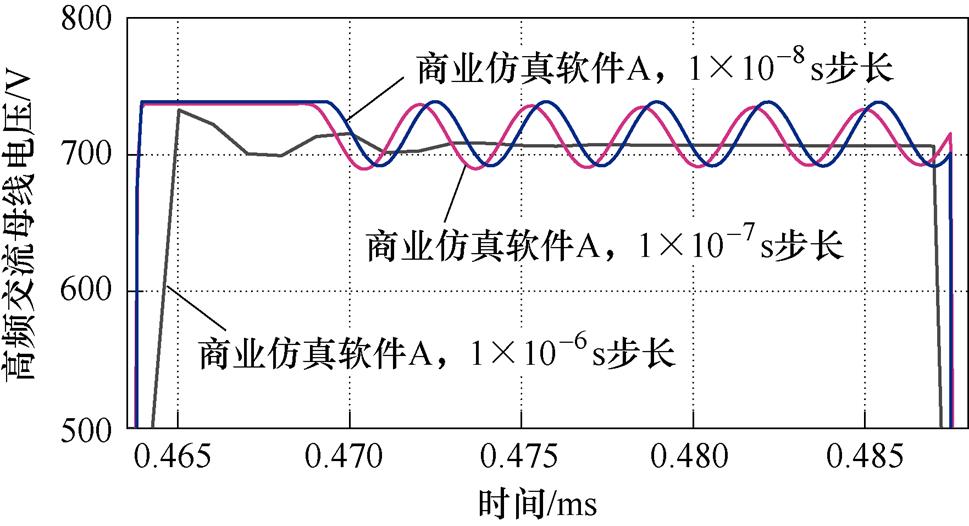
图8 商业仿真软件A使用不同仿真步长的波形对比
Fig.8 Comparisons of the simulated results by commercial software A with different step size
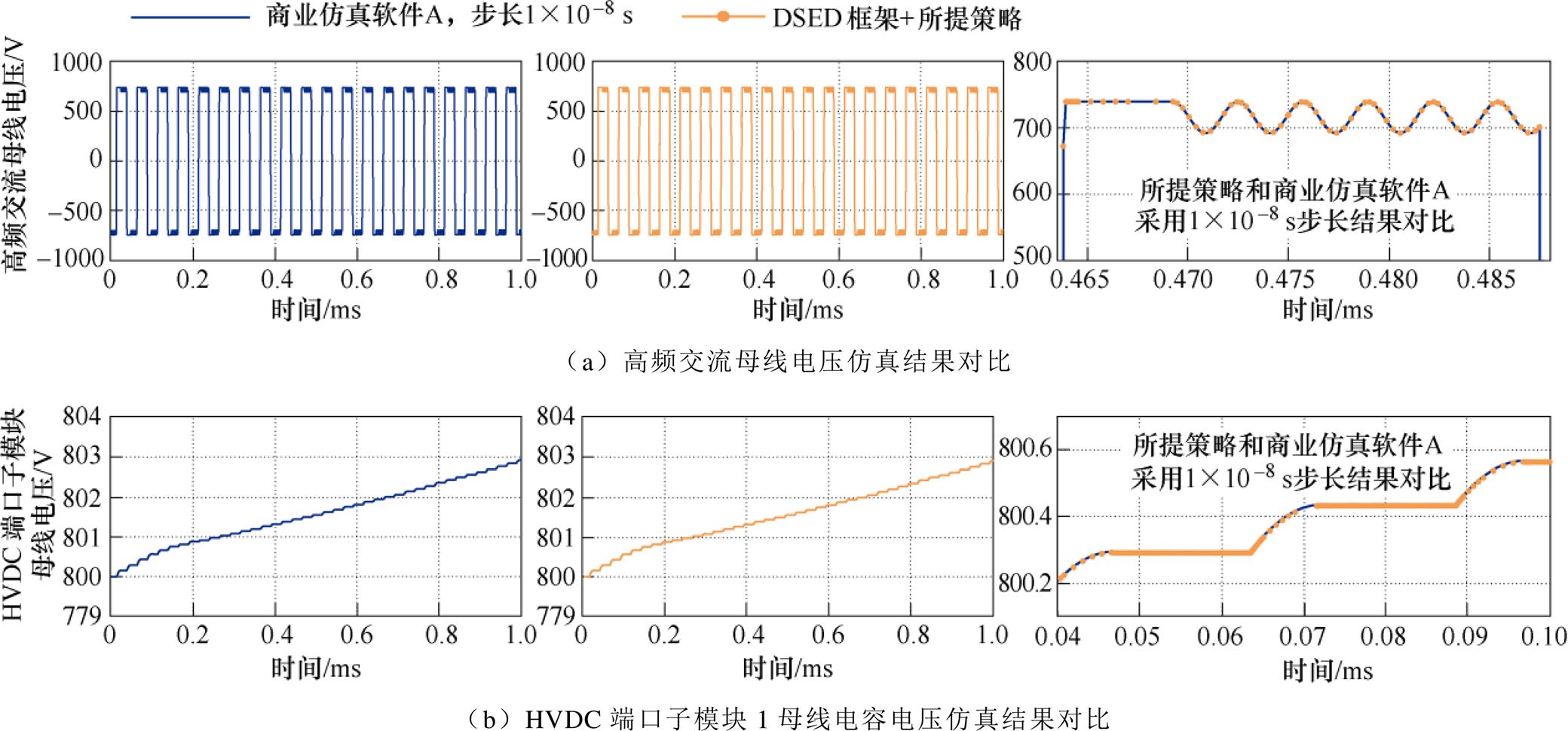
图9 所提策略和商业仿真软件仿真结果对比
Fig.9 Comparisons of the simulated results by the proposed method and commercial software
仿真结果相对误差和绝对误差的定量分析统计结果见表2,其中选取商业仿真软件A使用1×10-8 s步长的仿真结果作为参考波形。对比时,选取了高频交流母线电压、HVDC端口电压等5个有代表性的波形进行误差计算。定量分析的结果表明,所提策略和商业仿真软件的仿真结果对比,5个代表波形中相对误差平均值最大的也仅为千分之一左右,这进一步从定量的角度说明了所提策略仿真结果的准确性。
表2 所提策略相较于商业仿真软件的仿真误差
Tab.2 Simulation errors of the proposed method compared with commercial software

波形名称相对误差绝对误差 中位数90%分位数平均值中位数90%分位数平均值 高频交流母线电压1.94×10-48.43×10-44.78×10-40.13 V0.59 V0.28 V HVDC端口电压9.38×10-61.79×10-51.00×10-50.11 V0.22 V0.12 V HVDC子模块1,直流母线电容电压1.12×10-51.12×10-51.02×10-50.007 7 V0.014 8 V0.008 2 V HVDC子模块1,H桥出口电压1.67×10-31.68×10-31.03×10-30.38 V1.92 V0.76 V HVDC子模块1高频变压器电流1.20×10-31.94×10-31.20×10-30.015 A0.033 A0.018 A
2)与实验结果对比
用所提策略对实际装置进行仿真,HVDC子模块电压参考值为700 V,其余端口中子模块的电压参考值为600 V。仿真和实验的对比结果如图10所示。可以看到,实验中高频母线电压的变化模式,即先接近于直线,后以正弦模式进行振荡的现象与仿真分析得到的结果是一致的。在振荡周期上,仿真结果与实验结果也基本吻合,这进一步验证了所提方法求解结果的合理性和正确性。
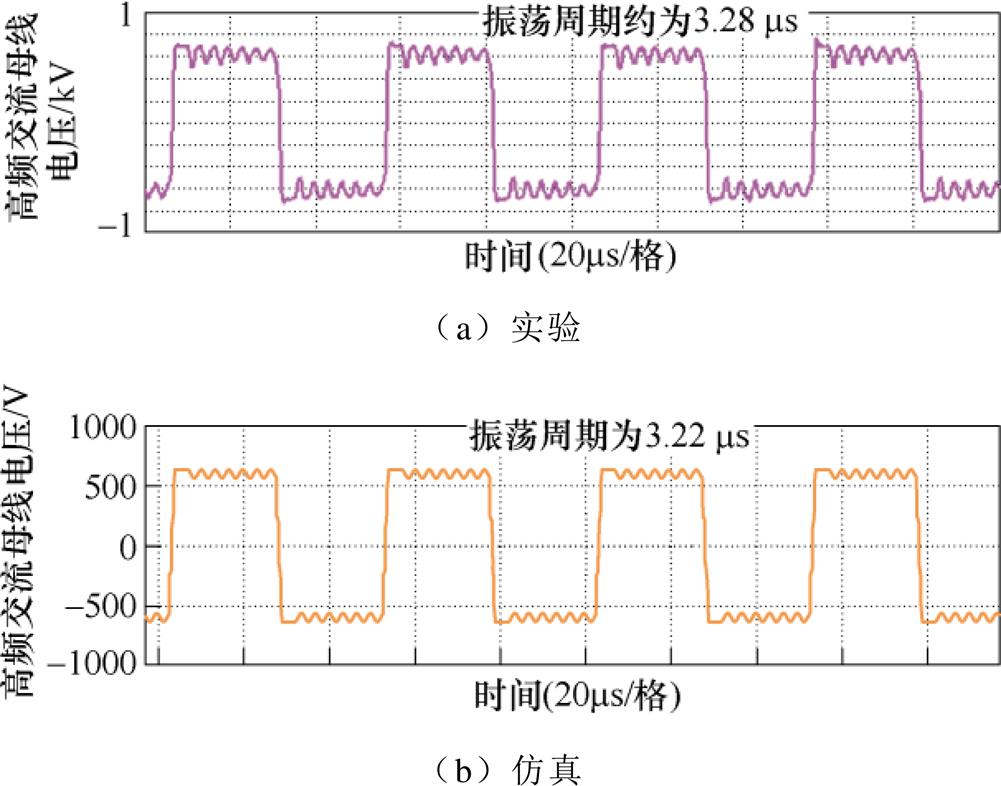
图10 仿真结果与实验结果对比
Fig.10 Comparisons between simulation and experiments
3.3.2 仿真速度比较
本文所提自适应仿真算法的主要思路是对动态变化过程的阶段进行时间上的划分,在每个阶段都采用最佳求解器。因此,本节将本文所提策略的仿真速度与DSED框架下全程采用FA-DS方法和DSED框架下全程采用BDSED方法进行了详细对比分析。三种方法都在DSED框架下实现,使用C++进行编程,除了数值积分策略以外的部分都保持一致,以此控制变量保证对比结果的合理性。
图11为高频母线电压波形的放大对比,图中列出了所提方法在不同阶段所自动选取的算法以及步长变化的情况。从图中可以看到,所提策略很好地识别了系统的刚性性质以及当前状态变量所处的变化阶段,算法切换点和状态变量的实际变化快慢情况相匹配。该策略能够始终选择步长更优的算法进行计算,总体的仿真计算点数远远少于采用单一的前向或者后向算法。这些现象说明了切换判据和切换策略的准确性和有效性。
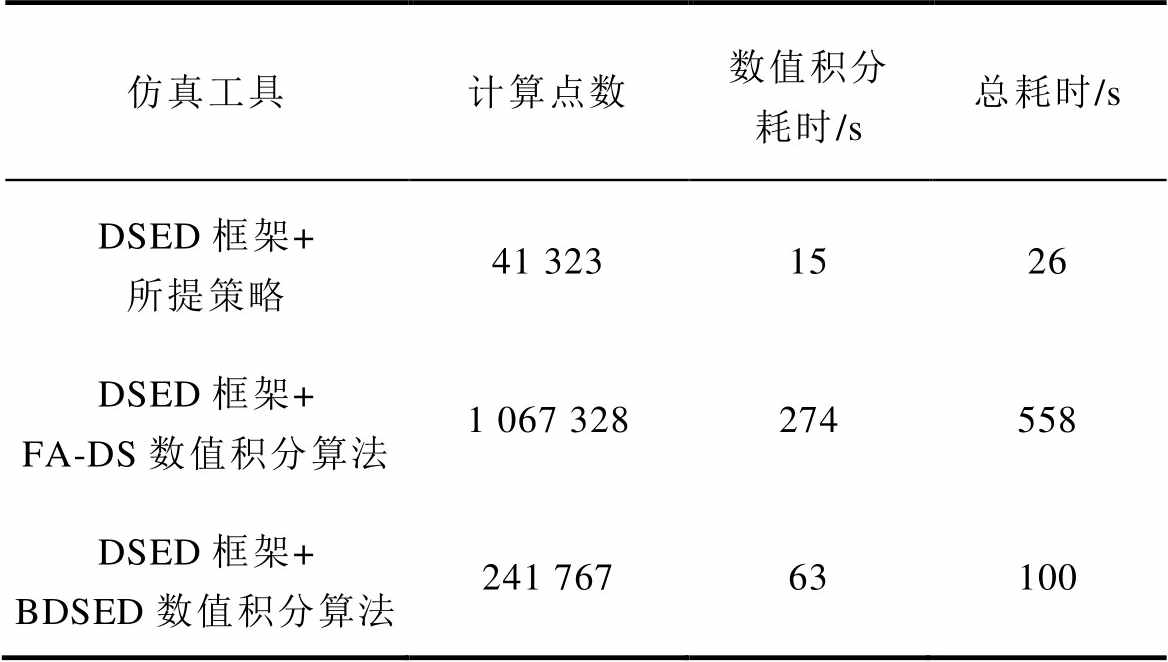
表3是DSED框架下不同方法的计算点数、数值积分的耗时以及总耗时的定量比较,总共仿真了0.01 s的动态过程进行数据统计。从表3中可以看到,所提策略的计算点数仅为纯FA-DS数值算法的3.8%,是BDSED数值算法的17%。由于计算的点数大大减少,因此无论是数值积分部分的计算,还是其他部分乃至整体的耗时,所提策略相较于已有算法都有明显提升。数值积分部分,所提策略相较于纯FA-DS方法速度提升到约18倍,较BDSED方法提升到4.35倍;总耗时方面,所提策略相较于纯FA-DS方法速度提升至约21.5倍,较BDSED方法提升至约3.85倍。这些结果充分说明了所提策略在提升仿真计算速度方面的效果。

图11 不同数值积分算法下步长选择对比
Fig.11 Comparisons of the step-size of different numerical integration methods
表3 DSED框架下不同数值积分算法的效率对比
Tab.3 Simulation efficiency comparisons of different numerical integration methods under the DSED framework
仿真工具计算点数数值积分耗时/s总耗时/s DSED框架+所提策略41 3231526 DSED框架+ FA-DS数值积分算法1 067 328274558 DSED框架+ BDSED数值积分算法241 76763100
表4给出了所提策略与商业仿真软件的速度比较,仿真了0.001 s的动态过程。可以看到,DSED框架结合所提策略,相较于商业仿真软件速度提升了几个数量级。由于DSED框架本身已经就针对电力电子系统的求解进行了大量优化,且商业仿真软件不开放仿真内核,无法进行精确的控制变量比较,因此这里列出相关数据仅是给出一个综合提速效果的参考。
表4 所提策略与商业仿真软件的速度对比
Tab.4 Simulation efficiency comparisons between the proposed method and commercial software

仿真工具总耗时 DSED框架+所提策略3 s 商业仿真软件A,步长1×10-8 s59 min 商业仿真软件A,步长1×10-7 s (不准确)53 min 商业仿真软件A,步长1×10-6 s(不准确)9 min24 s
仿真结果证明了本文所提出的自适应仿真算法可以很好地识别系统当前所处的性质,从而始终能够以更优的积分策略进行解算。这里进一步从理论角度对本文方法的有效性和额外计算量进行讨论。
在判据有效性上,本文采用的策略直接对比FA-DS方法和BDSED方法的潜在步长,符合刚性问题的本质特征。和采用恒定步长的策略相比,可靠性大大提升;和采用特征值或谱半径的策略相比,不仅避免了繁琐且不必要的计算,而且能够自适应地处理快变化区和稳态区两种情况,不会出现仅考虑特征值大小而不考虑变量所处实际变化阶段的误判情况。
在额外计算量方面,本文提出的自适应仿真算法考虑了电力电子混杂系统的特性,在每次离散事件发生之后,以和混杂系统高度契合的变阶数、变步长FA-DS方法为起始算法,满足特定条件之后再进行刚性检测。由于FA-DS方法的最高阶数较高,因此对于大部分的非刚性系统,特别是两次离散事件间隔不长的情况,FA-DS方法通常只采用低阶公式就能达到误差要求,或者是计算较少次数就能到达下一个离散点时刻。对于这种情况,本文所提出策略不会进行刚性检测,因此完全没有额外计算量。对于两次离散事件之间系统刚性较强的情况,状态变量一般会快速到达稳态附近,变量值在小范围内波动,此时切换判据会很快为真。在切换到刚性算法之后,该策略依据线性时不变系统的性质不会再进行反向检测,因此几乎也没有额外计算量。在最坏情况下,也就是一直采用FA-DS方法进行积分且点数较多(一般出现在高频振荡且衰减速度很慢的情况下),那么每一步都要进行刚性检测。由于BDF公式是多步法,使用差分来估算误差和步长,而不像其他单步隐式算法一样需要进行一步积分才能得到截断误差,因此额外计算量主要就是差分估计的计算量。在用于估计的式(8)中,系数矩阵U仅为(r+1)×(r+1)维,BDF公式的最高阶数为5,U最多不会超过6×6阶。因此切换判据的计算量其实并不大,远远小于FA-DS方法本身的单步计算量。
综上所述,所提出的切换判据及策略较为可靠,契合电力电子系统的本质特点和仿真的实际需求,且额外计算量很小,兼具了准确性和高效性。
电力电子系统的拓扑结构多变,换流回路复杂,参数选择范围广,这使得系统的数学性质可能不断发生变化。单一的前向或者后向数值积分算法无法自适应地匹配电力电子系统中模型数学性质的改变以及状态变量所处的变化阶段,因此在复杂场景中的仿真效率不尽人意。本文提出的自适应仿真算法构造了一种额外计算成本较小的判据,在已有的DSED仿真框架的基础上实现了对系统刚性程度的自动检测以及数值求解器的平滑切换,可以始终选择更优的数值积分算法来进行仿真求解,从而大大减少了仿真点数,提升了计算效率。文中将所提策略应用于一台10 kV-2 MW四端口电力电子变压器的高频振荡分析中,将仿真结果与商业软件和原始DSED框架进行比较。在同等精度条件下,所提策略相比于原始算法提速达到4倍左右,相较于商业仿真软件速度提升几个数量级,验证了所提策略的准确性和有效性。这种自适应、自动化的算法选择机制为用户提供了极大的便利,无需再手动调整仿真设置的就能始终保持仿真效率的最优,尤其适用于杂散参数作用机理较为复杂、工况切换、参数自动扫描等对系统性质难以提前判断的情况,具有很大的应用潜力。
附 录
1. 前向求解器:FA-DS方法
FA-DS方法基于高阶泰勒展开,状态变量在t=tm+1时刻的数值解[19]可表示为
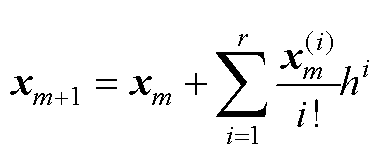 (A1)
(A1)
式中,xm为tm时刻已经求解出的状态变量数值解;xm+1为tm+1时刻的待求值;h为当前的积分步长,即h=tm+1−tm;r为积分阶数;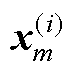 为状态变量在tm时刻的i阶导数,由于状态方程系数矩阵在两次离散事件之间为恒定矩阵,因此可以递推地计算出状态变量的各阶导数为
为状态变量在tm时刻的i阶导数,由于状态方程系数矩阵在两次离散事件之间为恒定矩阵,因此可以递推地计算出状态变量的各阶导数为
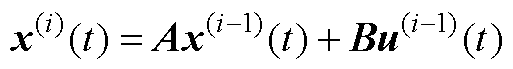 (A2)
(A2)
代入式(A1)即可得到下一个积分点处的数值解。
2. 后向求解器:BDSED方法
BDSED方法采用BDF公式,对于常微分方程组的一般形式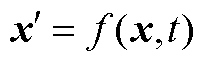 ,
,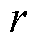 阶BDF公式[15, 31]为
阶BDF公式[15, 31]为
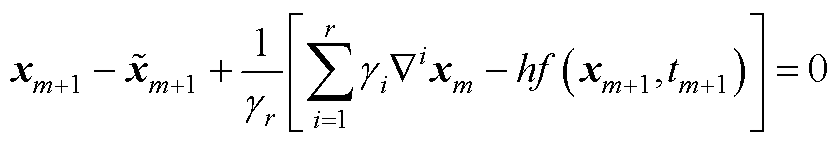 (A3)
(A3)
式中,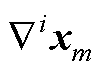 为
为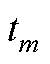 时刻状态变量的
时刻状态变量的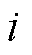 阶后向差分,差分间距为
阶后向差分,差分间距为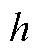 ;BDF为多步法,因此该差分项可以由历史信息得到;
;BDF为多步法,因此该差分项可以由历史信息得到; 为算法中用到的常数,由
为算法中用到的常数,由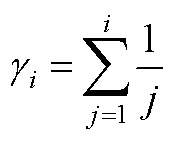 计算得到;
计算得到;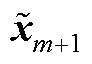 为
为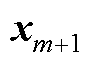 的迭代初值,由
的迭代初值,由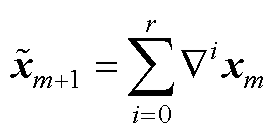 计算得到。
计算得到。
对于线性系统,式(A3)可以进行简化,求解如式(A4)所示的线性方程组,即可以得到下一个积分点处的数值解。
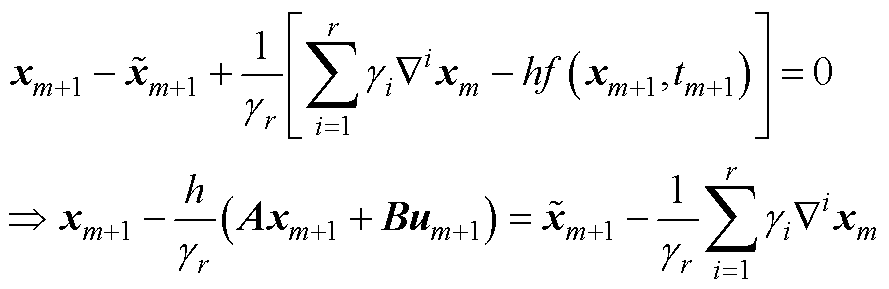
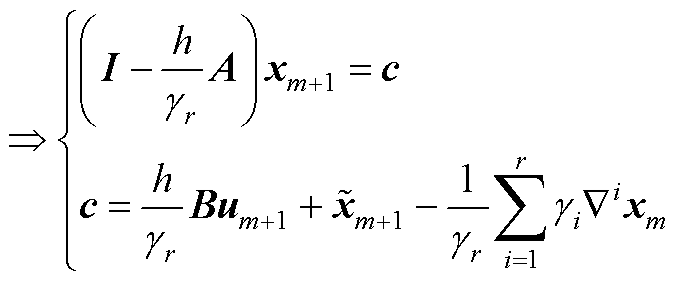 (A4)
(A4)
参考文献
[1] 张雪垠, 徐永海, 肖湘宁. 适用于中高压配电网的高功率密度谐振型级联H桥固态变压器[J]. 电工技术学报, 2018, 33(2): 310-321.
Zhang Xueyin, Xu Yonghai, Xiao Xiangning. A high power density resonance cascaded H-bridge solid- state transformer for medium and high voltage dis- tribution network[J]. Transactions of China Electro- technical Society, 2018, 33(2): 310-321.
[2] 刘计龙, 朱志超, 肖飞, 等. 一种面向舰船综合电力系统的模块化三端口直流变换器[J]. 电工技术学报, 2020, 35(19): 4085-4096.
Liu Jilong, Zhu Zhichao, Xiao Fei, et al. A modular three-port DC-DC converter for vessel integrated power system[J]. Transactions of China Electro- technical Society, 2020, 35(19): 4085-4096.
[3] Lee W, Li Silong, Han Di, et al. A review of integrated motor drive and wide-bandgap power electronics for high-performance electro-hydrostatic actuators[J]. IEEE Transactions on Transportation Electrification, 2018, 4(3): 684-693.
[4] 陈垣, 张波, 谢帆, 等. 电力电子化电力系统多时间尺度建模与算法相关性研究进展[J]. 电力系统自动化, 2021, 45(15): 172-183.
Chen Yuan, Zhang Bo, Xie Fan, et al. Research progress of interrelationship between multi-time-scale modeling and algorithm of power-electronized power system[J]. Automation of Electric Power Systems, 2021, 45(15): 172-183.
[5] Zhang Chunpeng, Li Huaru, Wen Wusong, et al. Study on DC-voltage rising of blocked port in high- frequency-link converters[C]//2020 IEEE Energy Con- version Congress and Exposition (ECCE), Detroit, MI, 2020: 1630-1635.
[6] 肖湘宁, 廖坤玉, 唐松浩, 等. 配电网电力电子化的发展和超高次谐波新问题[J]. 电工技术学报, 2018, 33(4): 707-720.
Xiao Xiangning, Liao Kunyu, Tang Songhao, et al. Development of power-electronized distribution grids and the new supraharmonics issues[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 707- 720.
[7] Wei Shusheng, Zhao Zhengming, Yuan Liqiang, et al. Voltage oscillation suppression for the high- frequency bus in modular-multiactive-bridge conver- ter[J]. IEEE Transactions on Power Electronics, 2021, 36(9): 9737-9742.
[8] Cui Bin, Shi Hongliang, Sun Qianhao, et al. A novel analysis, design, and optimal methodology of high-frequency oscillation for dual active bridge converters with WBG switching devices and nano- crystalline transformer cores[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 7665-7678.
[9] Dai Ning, Lee F C. Characterization and analysis of parasitic parameters and their effects in power electronics circuit[C]//PESC Record. 27th Annual IEEE Power Electronics Specialists Conference, Baveno, Italy, 2002: 1370-1375.
[10] Wang Shuo, Lee F C, van Wyk J D, et al. A study of integration of parasitic cancellation techniques for EMI filter design with discrete components[J]. IEEE Transactions on Power Electronics, 2008, 23(6): 3094-3102.
[11] De León-Aldaco S E, Calleja H, Aguayo Alquicira J. Metaheuristic optimization methods applied to power converters: a review[J]. IEEE Transactions on Power Electronics, 2015, 30(12): 6791-6803.
[12] Burkart R M, Kolar J W. Comparative h–r–s pareto optimization of Si and SiC multilevel dual-active- bridge topologies with wide input voltage range[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5258-5270.
[13] 袁立强, 陆子贤, 孙建宁, 等. 电能路由器设计自动化综述—设计流程架构和遗传算法[J]. 电工技术学报, 2020, 35(18): 3878-3893.
Yuan Liqiang, Lu Zixian, Sun Jianning, et al. Design automation for electrical energy router-design work- flow framework and genetic algorithm: a review[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3878-3893.
[14] Shampine L F, Gear C W. A user’s view of solving stiff ordinary differential equations[J]. SIAM Review, 1979, 21(1): 1-17.
[15] Hairer E, Wanner G. Solving ordinary differential equations II. stiff and differential-algebraic pro- blems[M]. Springer Verlag Series in Comput. Math.
[16] 李寿佛. 刚性微分方程算法理论[M]. 长沙: 湖南科学技术出版社, 1997.
[17] 赵争鸣, 施博辰, 朱义诚. 对电力电子学的再认识——历史、现状及发展[J]. 电工技术学报, 2017, 32(12): 5-15.
Zhao Zhengming, Shi Bochen, Zhu Yicheng. Recon- sideration on power electronics: the past, present and future[J]. Transaction of China Electrotechnical Society, 2017, 32(12): 5-15.
[18] Shi Bochen, Zhao Zhengming, Zhu Yicheng. Piece- wise analytical transient model for power switching device commutation unit[J]. IEEE Transactions on Power Electronics, 2019, 34(6): 5720-5736.
[19] Zhu Yicheng, Zhao Zhengming, Shi Bochen, et al. Discrete state event- driven framework with a flexible adaptive algorithm for simulation of power electronic systems[J]. IEEE Transactions on Power Electronics, 2019, 34(12): 11692-11705.
[20] Ju Jiahe, Shi Bochen, Yu Zhujun, et al. Backward discrete state event-driven approach for simulation of stiff power electronic systems[J]. IEEE Access, 2021, 9: 28573-28581.
[21] Yu Zhujun, Zhao Zhengming, Shi Bochen, et al. An automated semi-symbolic state equation generation method for simulation of power electronic systems[J]. IEEE Transactions on Power Electronics, 2021, 36(4): 3946-3956.
[22] Ekeland K, Owren B, Øines E. Stiffness detection and estimation of dominant spectrum with explicit runge- kutta methods[J]. ACM Transactions on Mathematical Software, 1998, 24(4): 368-382.
[23] Shampine L F. Stiffness and nonstiff differential equation solvers, II: detecting stiffness with Runge- Kutta methods[J]. ACM Transactions on Mathe- matical Software (TOMS), 1977, 3(1): 44-53.
[24] Shampine L F, Hiebert K L. Detecting stiffness with the Fehlberg (4, 5) formulas[J]. Computers & Mathe- matics with Applications, 1977, 3(1): 41-46.
[25] Shampine L F. Diagnosing stiffness for runge–Kutta methods[J]. SIAM Journal on Scientific and Statisti- cal Computing, 1991, 12(2): 260-272.
[26] Butcher J C. Order, stepsize and stiffness switching[J]. Computing, 1990, 44(3): 209-220.
[27] Sofroniou M, Spaletta G. Construction of explicit runge-Kutta pairs with stiffness detection[J]. Mathe- matical and Computer Modelling, 2004, 40(11/12): 1157-1169.
[28] Mazzia F, Nagy A M. Stiffness detection strategy for explicit runge Kutta methods[J]. AIP Conference Proceedings, 2010, 1281(1): 239-242 .
[29] Petzold L. Automatic Selection of methods for solving stiff and nonstiff systems of ordinary differ- ential equations[J]. SIAM Journal on Scientific and Statistical Computing, 1983, 4(1): 136-148.
[30] Golub G H. Matrix computations[M]. 4th ed Balti- more: Johns Hopkins University Press, 2013.
[31] Shampine L F, Reichelt M W. The MATLAB ODE suite[J]. SIAM Journal on Scientific Computing, 1997, 18(1): 1-22.
[32] Dormand J R, Prince P J. A family of embedded Runge-Kutta formulae[J]. Journal of Computational and Applied Mathematics, 1980, 6(1): 19-26.
[33] 赵争鸣, 冯高辉, 袁立强, 等. 电能路由器的发展及其关键技术[J]. 中国电机工程学报, 2017, 37(13): 3823-3834.
Zhao Zhengming, Feng Gaohui, Yuan Liqiang, et al. The development and key technologies of electric energy router[J]. Proceedings of the CSEE, 2017, 37(13): 3823-3834.
[34] Li Kai, Wen Wusong, Zhao Zhengming, et al. Design and implementation of four-port megawatt-level high-frequency-bus based power electronic transfor- mer[J]. IEEE Transactions on Power Electronics, 2021, 36(6): 6429-6442.
[35] Wen Wusong, Li Kai, Zhao Zhengming, et al. Analysis and control of a four-port Megawatt-level high-frequency-bus-based power electronic trans- former[J]. IEEE Transactions on Power Electronics, 2021, 36(11): 13080-13095.
[36] 魏树生. 共交流母线多端口电力电子变压器隔离级高频振荡研究[D]. 北京: 清华大学, 2021.
Abstract The high-efficiency simulation tool plays an important role in designing and analyzing power electronics systems. Meanwhile, modeling the parasitic elements to analyze their influences on system reliability and performing parameter sweep for optimal design have become trends in practical applications. However, the mathematical properties of the system can become complicated and may alternate between being stiff or non-stiff. In this situation, using a single forward or backward integration method cannot achieve the highest efficiency, which brings great challenges for simulation tools. A recently developed discrete-state event-driven (DSED) framework can achieve accurate and efficient simulation of power electronics systems and has shown great advantages over commercial software. However, it cannot automatically identify the mathematical properties of the system, so much space remains for improvement when dealing with complex simulation scenarios. This paper proposes an adaptive simulation method for power electronics systems based on stiffness detection. It can always select the better numerical solver during the simulation process with low extra cost, greatly improving the simulation efficiency.
Firstly, the optimal scenarios of different numerical algorithms in power electronics system simulation are analyzed. This paper points out that only when the step size is limited by the stability rather than the accuracy of the numerical method, the stiffness of the system will bring extra difficulty for simulation. Therefore, whenever the switching event happens in power electronics systems, the high-order explicit numerical method with high accuracy should be chosen as the initial solver. After the free responses have decayed to the steady state, the low-order implicit numerical method with a large stability region should be selected.
Secondly, the criterion to detect stiffness and automatically switch between different methods is constructed. The flexible-adaptive discrete-state (FA-DS) method under the DSED framework is chosen as the solver for non-stiff situations. It is a single-step variable-order variable-step method. The backward discrete-state event-driven (BDSED) method is chosen as the solver for stiff situations. It is based on the backward difference formula (BDF), a multi-step variable-order variable-step method. The adaptive solver uses the FA-DS solver as the initial solver after each switching event. Only when the order of the FA-DS solver has reached the highest order and the following calculation point is far away from the next discrete switching event, the detection will be started. Then, the adaptive solver estimates the maximum possible step size of the BDSED using the historical values and the Newton interpolation formula. If it is larger than the current step size, the BDSED solver will be used in the remaining interval until the next switching event. The computational cost of the detection is very low compared with the numerical integration process. Thus, the proposed method can always find the optimal solver to improve the overall simulation efficiency without much extra cost.
The proposed method analyzes the high-frequency voltage oscillations in a 10 kV-2 MW four-port power electronics transformer. The adaptive solver is implemented under the DSED framework. The simulation results are compared with those by commercial software, the DSED framework with a single FA-DS solver and the DSED framework with a single BDSED solver. With the same level of accuracy, it achieves about 4-fold speed-up, which confirms its accuracy and efficiency.
keywords:Power electronic system simulation, stiffness detection, discrete state event-driven
DOI: 10.19595/j.cnki.1000-6753.tces.230014
中图分类号:TM614
国家自然科学基金(U2034201)和中国博士后科学基金面上(2022M721776)资助项目。
收稿日期 2023-01-06
改稿日期 2023-02-16
虞竹珺 女,1996年生,博士研究生,研究方向为电力电子系统建模与仿真理论。E-mail: yuzhujun14@hotmail.com
施博辰 男,1995年生,博士,博士后,研究方向为电力电子系统建模仿真与开关电磁瞬变过程。E-mail: shbch03@126.com(通信作者)
(编辑 陈 诚)