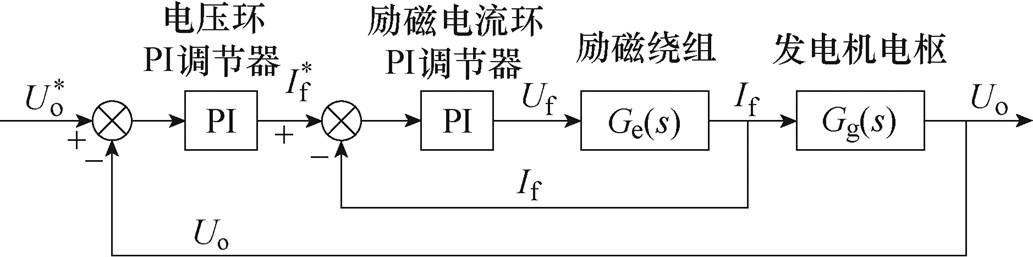
图1 直流发电系统双PI环控制框图
Fig.1 Dual PI control block diagram of DC power generation system
摘要 车载/机载电源系统对直流发电机的电压动态特性提出了要求。该文提出一种基于负载励磁映射关系的广义预测电压控制方法，替代传统的电压环PI调节器，以提高系统在负载扰动下的电压回复动态性能。采用增量式预测输出结合负载电流反馈的控制结构，经过负载励磁拟合函数得到励磁电流指令值。构建控制系统离散域下的传递函数，进行稳定性与系统抗负载扰动能力分析，考察控制参数与系统参数对控制性能的影响。实验证明，所提控制方案在系统负载突加和突卸情况下能够有效地抑制低电压与过电压，使系统平滑地过渡到稳态，拥有较快的动态响应 速度。
关键词：独立励磁直流发电系统 广义预测控制 负载扰动 动态性能
车载/机载发电机系统由发动机拖动的发电机及控制器和保护设备构成。交流发电机输出直流的方式包括可控整流和不控整流两种。其中，采用不控的二极管桥式整流（Diode Bridge Rectifier, DBR）结构的直流电源系统由于具有结构可靠、控制简单、安全性较高等特点而被广泛应用[1-3]。
独立励磁直流发电系统作为现如今种类众多的汽车、飞机中电能的主要来源之一，其电压控制性能在一定程度上决定了系统的输出电能质量[4]。采用DBR结构的直流发电系统中，发电机转速与负载的变化均会影响到输出电压，系统通过独立调节励磁电流使得输出端电压快速地回复至稳态以保证负载用电端正常工作。
PI控制具有算法简单、鲁棒性强、可靠性高等优点，位于外环的PI调节器可以保证电压的稳态控制精度，但其难以兼顾不同动态过程的电压调节性能[5]。国军标GJB 298-1987《军用车辆28伏直流电气系统特性》与GJB 181B-2012《飞机供电特性》对直流发电系统的瞬态特性均提出了瞬变上下峰值与动态恢复时间等要求。图1为一般的双PI环控制结构框图，采用电压外环、励磁电流内环的控制结构。当系统在不同工况下负载突变时，输出电压可能出现较大的过电压或低电压，影响直流发电系统的稳定性和可靠性。
图1 直流发电系统双PI环控制框图
Fig.1 Dual PI control block diagram of DC power generation system
预测控制方法具有动态响应快速和抗扰动能力强的特点，适合取代PI调节器以提升系统在负载突变情况下的动态性能[6]。其中，基于多步预测的广义预测控制（Generalized Predictive Control, GPC）具有参数设计灵活度高、预测长度足够的情况下鲁棒性强的特点，在电力电子与电力传动领域研究较广泛[6-8]。直流电源系统的多步预测控制方法研究多见于全控整流器的动态性能提升方面[9-13]，励磁直流发电系统的多步预测控制相关研究仍然空缺。文献[13]将GPC应用于并网三相可控整流的母线电压控制中，采用级联电压电流双环GPC，提高了系统的动态响应速度和抗扰动能力。对于全控整流的GPC方法，电压环预测输出量与旋转坐标系下的q轴电流存在功率约束，便于进行控制量给定值之间的转换。然而，对基于DBR的独立励磁直流发电机系统，电压环GPC输出与励磁电流没有类似的约束关系，针对这一点，本文提出利用负载电流与励磁电流的映射关系来处理电压环的预测输出结果。
针对独立励磁直流发电系统电压环采用PI调节器动态性能不足的问题，引入负载电流前馈是较为常见的解决思路。文献[14]根据误差大小在线自适应改变电压环PI参数，结合负载电流前馈补偿，减小了动态过程中输出电压波动的幅度，但动态响应时间仍然较长。文献[15]提出基于电容能量平衡的PI控制算法，用功率PI环替代电压PI环，PI调节器输出为瞬时功率给定增量，经过运算处理后得到励磁电流给定值，但是其外环PI调节器的存在使得动态过程仍存在明显超调。文献[16-18]均引入负载电流前馈以加快发电机中励磁系统的响应。上述文献提出的方案在一定程度上改善了基于DBR的直流发电系统在面对负载突变时的动态性能，但是仍然基于PI控制结构，且并未对控制系统进行分析，进而设计PI调节器参数，控制系统难以在不同负载突变时均具有较好的动态响应效果。
本文以独立励磁直流发电系统为研究对象，针对传统电压环PI调节器控制下系统动态性能不足的缺点，提出了一种基于负载励磁映射关系的GPC方法。外环GPC输出量结合负载电流反馈，经过负载电流、励磁电流、发电机转速三者对应的函数关系得到励磁电流指令值。励磁电流内环仍然采用PI调节器。对控制系统在离散域下的传递函数进行分析，证明了控制方案能够使系统稳定收敛，并讨论了控制器和系统参数对系统稳定性以及系统抗负载扰动能力的影响。最终，将所提控制方案与传统PI控制进行对比实验，验证了本文所提控制方案的有效性与优越性。
采用DBR结构的发电系统相较于全控整流的发电机系统省去了转子位置传感器，在车载/机载工况下更加安全可靠[3]，独立励磁直流发电系统拓扑如图2所示。励磁控制采用全桥能够提供反向弱磁电流，对于混合励磁发电机，其负载端出现短路故障时，适当的弱磁电流可以抵消永磁磁场实现完全灭磁，保障系统安全[5]。
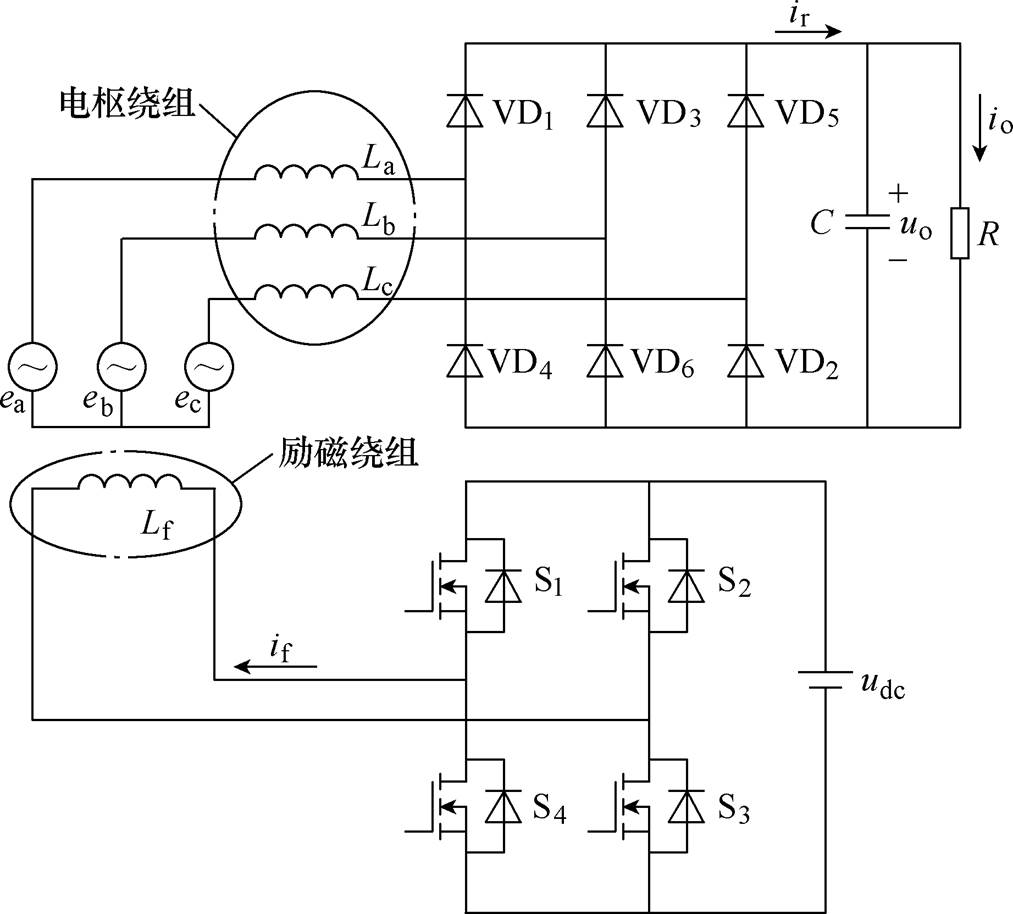
图2 独立励磁直流发电系统拓扑
Fig.2 Topology of independent excitation DC power generation system
图2中，ea、eb、ec为发电机三相反电动势，VD1～VD6为不控整流二极管，S1～S4为全控开关管，udc为励磁全桥端的电压源电压。
负载端电压的动态方程为
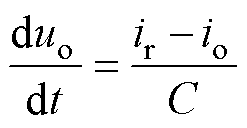（1）
式中，uo、io分别为负载端电压、负载电流；ir为整流电流；C为电容。
将式（1）中的微分写成前向差分形式，有
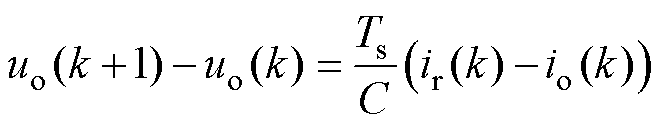（2）
式中，Ts为采样与控制周期；k为当前周期。
式（2）两端同乘前向差分算子
后得到
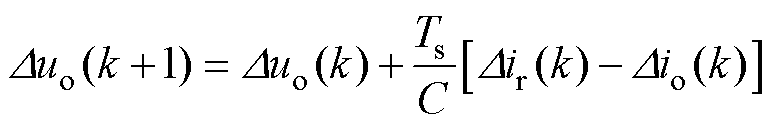（3）
由图1可知，励磁电流if直接控制整流电流ir，在控制器设计环节忽略负载扰动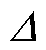
io(k)。
广义预测控制是随着自适应控制的研究发展起来的一种预测控制算法，其引入了控制时域长度的概念，适合用于多输入多输出系统。为了便于控制器的设计，将式（3）扩展为离散状态空间表达式，有
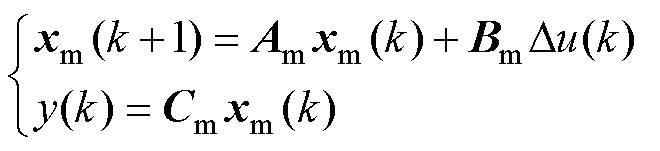（4）
其中
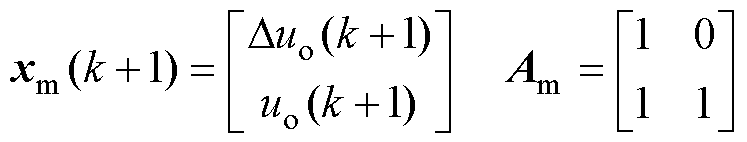
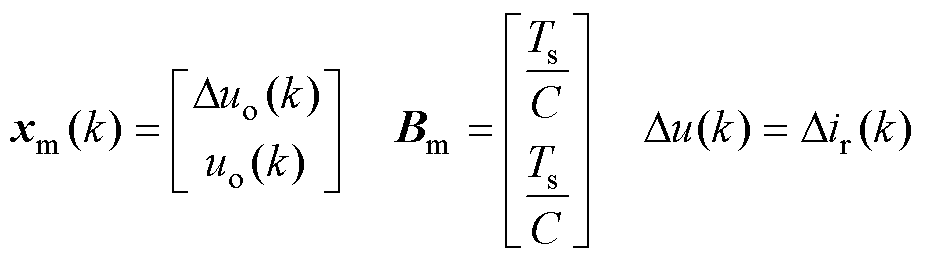
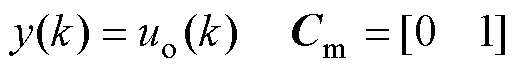
式中，xm(k)为扩展的状态变量；y(k)和Du(k)分别为输出变量和控制量增量；Am、Bm、Cm为系数矩阵。
式（4）递推N步后的对象预测模型的一般形式为
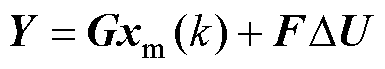（5）
其中
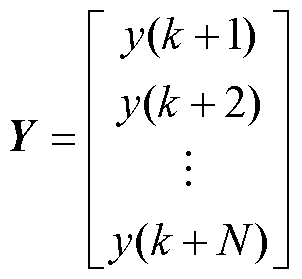
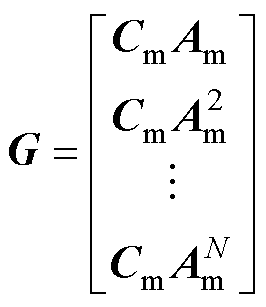
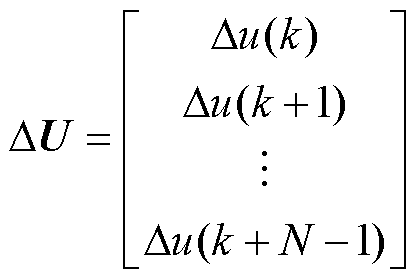
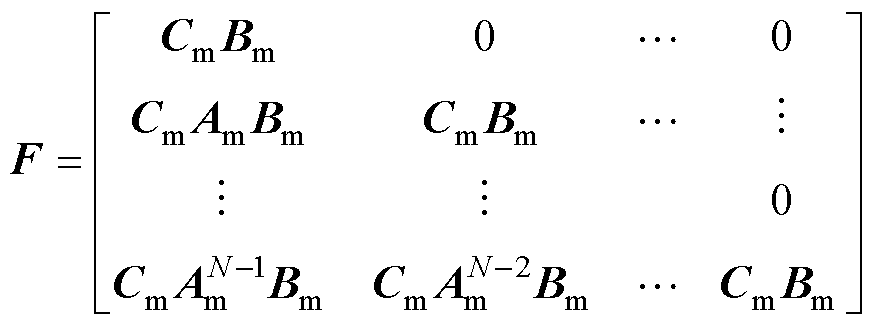
式中，Y为未来的预测输出；DU为当前和未来的控制增量向量；G和F为递推得到的系数矩阵；N为预测长度。
将性能指标函数表示为矩阵的形式，有
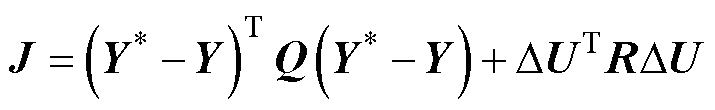（6）
式中，Q和R为半正定的权重系数对角矩阵；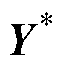
为输出电压给定，所有预测周期内使得预测输出Y趋向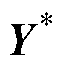的权重系数应相等，因此令Q为单位对角矩阵。
，
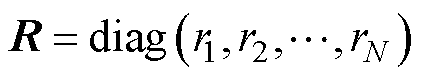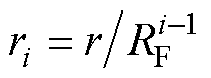，其中RF为系数因子。由于未来的控制序列DU是通过对式（6）极小化得到的，一般取RF＜1能够使得系统的预测输出轨迹在N个控制周期后更快地逼近期望输出。
性能指标函数式（6）对控制量增量取偏微分，令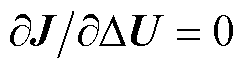
，得到滚动时域下最优N步控制量增量为
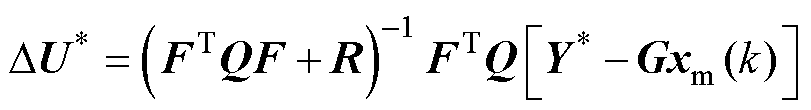（7）
取最优控制轨迹中的第一拍作为系统的实际控制量增量，即GPC控制器输出为
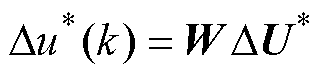（8）
其中
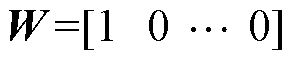
由式（5）～式（7）的推导可知，GPC控制器需要设计的参数包括预测长度N、控制量增量权重系数r及系数因子RF。此外，影响GPC输出的系统本身参数包括控制周期Ts、电容C，由式（4）中的Bm矩阵可知，二者讨论其一即可。
根据1.2节中对预测控制器的设计，GPC输出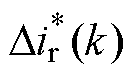
为电容前级整流电流的给定增量。而系统实际的控制量为励磁电流，GPC输出需要转化为励磁电流给定。发电机系统运行在稳态的情况下，即负载端电压一定时，负载电流io、转速n和励磁电流if三者存在一个相对固定的关系。图3中的三维曲面即为对本文的实验用混合励磁样机的稳态工作点拟合曲面，系统输出电压为28 V。三维曲面对应的励磁电流、负载电流、转速三者的函数关系为
（9）
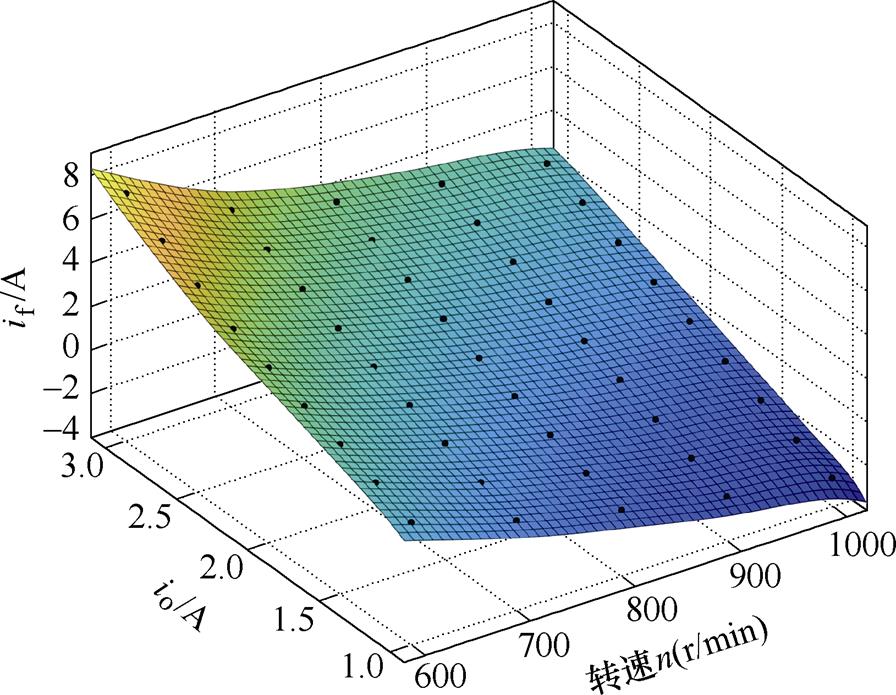
图3 负载励磁映射关系拟合曲面
Fig.3 Load excitation mapping fitting surface
图4为最终得到的系统整体控制框图。控制系统内环为对直流励磁电流的跟踪，且励磁电流环的等效时间常数较小，因此内环仍然使用PI调节器。系统在稳态情况下整流电流均值与负载电流相等，因此这里将图3拟合曲面所对应的函数关系式（9）等效为负载与励磁之间的映射系数K，得到励磁电流给定为
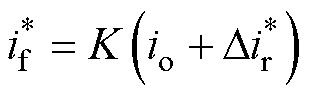（10）
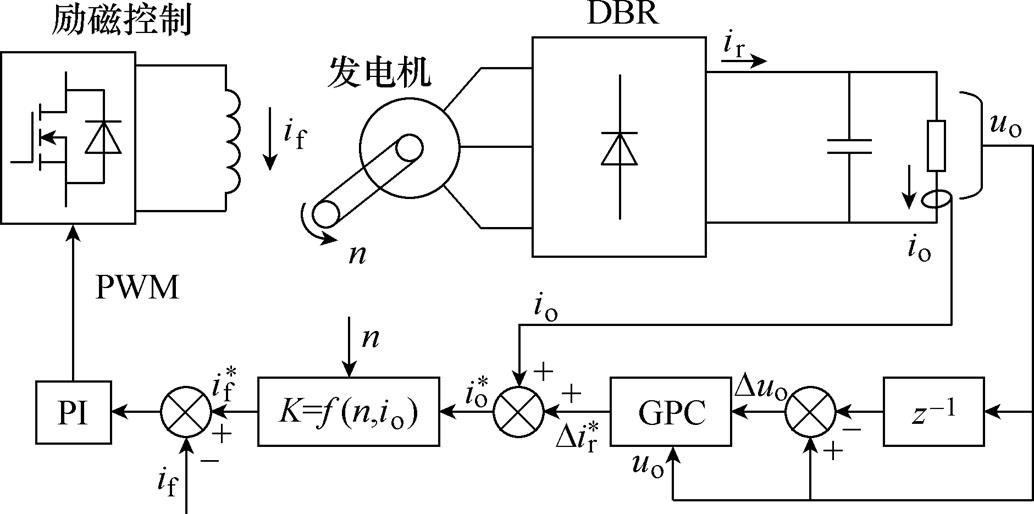
图4 基于负载励磁映射的GPC-PI级联系统控制框图
Fig.4 Control block diagram of GPC-PI cascade system based on load excitation mapping
式中，系数K由实时反馈的io和转速n决定，转速信号n采用测频测速法[19]得到，测量DBR交流侧两线电压同滞环比较得到含转速信息的方波信号。
本节根据图4的控制框图构建控制系统离散域下的传递函数，对GPC性能进行分析，考察不同控制系统对系统稳定性与抗负载扰动能力的影响。考虑到励磁电流内环的等效时间常数较小，将电流内环等效为单位比例函数。同时，忽略电机电磁时间常数的影响，假设系统实际增量等于控制增量，考虑一拍的延时，即
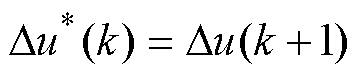（11）
根据式（4）和式（7），图5为等效后的系统离散控制结构。其中，以负载电流扰动为分界，式（4）表示系统的负载端，对应图中右半部分，式（7）表示反馈以及GPC的计算过程，对应图中左半部分。
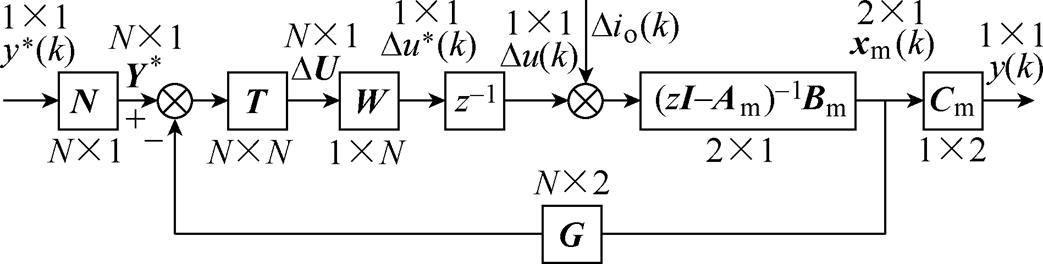
图5 离散域下的控制结构
Fig.5 Control structure diagram in discrete domain
图5中，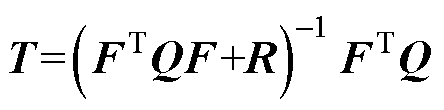
。得到系统输入到输出的z域传递函数为
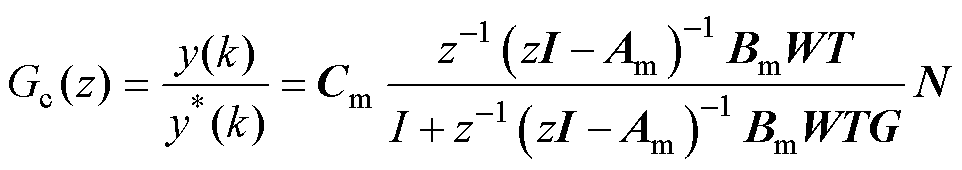（12）
负载电流扰动到输出的z域传递函数为
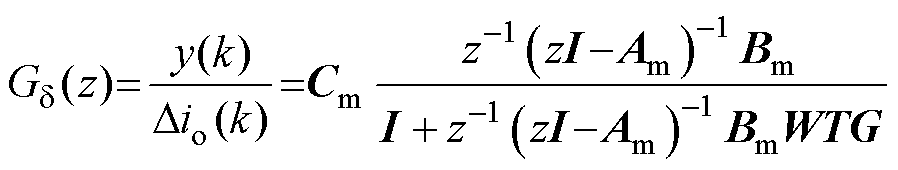（13）
传递函数分式均表示分子左乘分母矩阵的逆矩阵。
考察控制系统参数对系统稳定性的影响。对于离散域下矩阵形式的系统传递函数，当式（12）分母矩阵的特征根位于单位圆内时，认为控制系统稳定[20]。
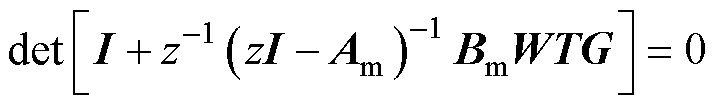（14）
求解式（14），所得即为离散控制系统闭环极点。需要讨论的控制参数与系统参数主要包括预测长度N、指标函数J中的权重系数r、系数因子RF及电容C，控制频率设定为10 kHz，即Ts=0.000 1 s。对式（14）求解得到3个特征根，随控制系统参数变化的特征根轨迹如图6所示，图中曲线箭头表示特征根随参数变化的趋势。由图6b可知，当权重系数r取值过小时，控制系统极点位于单位圆外，系统不稳定。在其他参数变化下，所求离散域下的闭环极点均在单位圆内部，使控制系统稳定的参数选取范围较宽。预测长度N决定了控制算法的计算量大小，受限于DSP的算力与控制频率，预测长度不宜取过大的值。
图6 离散域下系统闭环极点轨迹
Fig.6 Closed-loop pole locus of the system in discrete domain
稳定性分析能够总体上判断控制参数能否使系统稳定，但是无法明确具体参数取值的方向。本节从抗负载扰动能力的角度出发，考察不同的控制系统参数对系统负载扰动抑制能力的影响。
图7为式（12）负载电流至输出的传递函数对应的伯德图。对于本文讨论的独立励磁直流发电系统，如果对应的幅频曲线随参数的变化而变低，说明负载扰动导致的输出电压变化在该参数变化趋势上衰减更大。图7a中预测长度N取值较小时抗扰动能力不足，而当N取值从10到100，控制系统抗扰动能力提升有限。权重系数r取较小值时对系统抗扰动能力提升较大，系数因子RF的变化对抗扰能力作用有限。由图7d可知，输入GPC控制器的电容容值越大，系统对高频扰动抑制能力越强，然而负载扰动阶跃函数在频域下的幅值随频率升高呈指数衰减，因此，GPC下的系统对电容值这一参数敏感度一般，即使出现了较严重的参数失配，对控制性能影响也有限。电容值作为系统输出端时间常数，取值较小能够得到更快的动态响应速度，但稳定性不足，面对极端负载突变，可能会出现较大的过电压或低电压，危害系统后级设备。经以上讨论，实验采用的控制系统参数将在第3节给出。
图7 负载扰动环路伯德图
Fig.7 Bode diagram of load disturbance loop
为了验证基于独立励磁系统的GPC方法在提升负载突变下系统动态性能方面的有效性，实验以DSP28335为主控，对一台并列式混合励磁发电机进行控制。控制系统相关参数见表1。
表1 控制系统相关参数
Tab.1 Control system parameters
参 数数 值 负载端电容C/mF4 700 输出电压Uo/V28 控制频率f/kHz10 预测长度N20 权重系数r0.1 系数因子RF0.8
首先验证图4中根据拟合曲面函数得到的映射系数K的精确程度，这关系到GPC方法下系统输出电压的稳态控制精度。图8为GPC下转速变化时的系统输出波形，其中输出电压uo与励磁电流if在示波器中设置了20 V与2.5 A的偏置。实验证明了系数K能够将转速变化实时地反馈到控制回路中，GPC方法能够使系统的实际输出稳定跟踪给定值28 V。
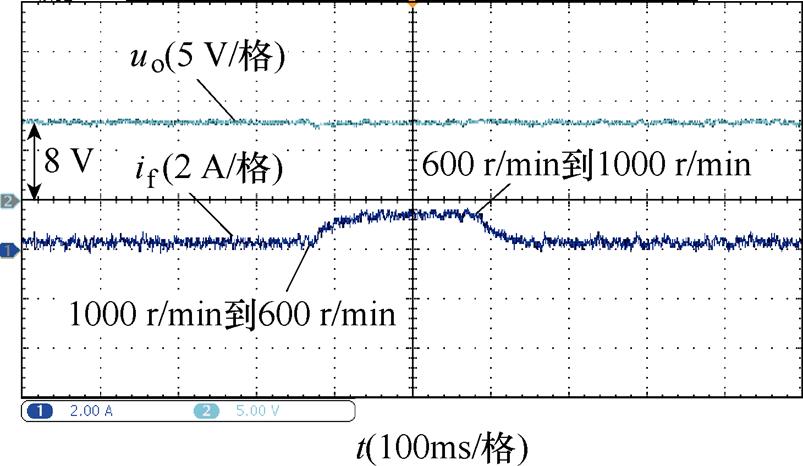
图8 转速变化下GPC稳态波形
Fig.8 GPC waveforms under rotational speed change
系统的机械时间常数远大于电气时间常数，即转速无法突变，因此无论是PI还是GPC，转速的变化对系统稳定输出的影响都较小。后文实验结果均在转速恒定的条件下得到。
考察相同的负载突变下不同PI参数与GPC的控制效果对比，二者励磁电流内环的PI调节器参数设置相同，电机转速为1 000 r/min，图9为负载电流由0.5 A突变到2.8 A的实验波形。图9a～图9c三组为PI控制下的动态波形，Kp和Ti分别为PI调节器的比例增益和积分时间常数。可以看出，在PI参数较差情况下，如图9b和图9c两组，动态调节时间较长，且图9c存在电压回复超调。即使是三组中效果最好的图9a组，仍然存在一定的超调量。图9d组在GPC下，动态过程平滑且快速，仅60 ms即恢复至稳态，在负载突加情况下，GPC方法对低电压的抑制作用更加明显。
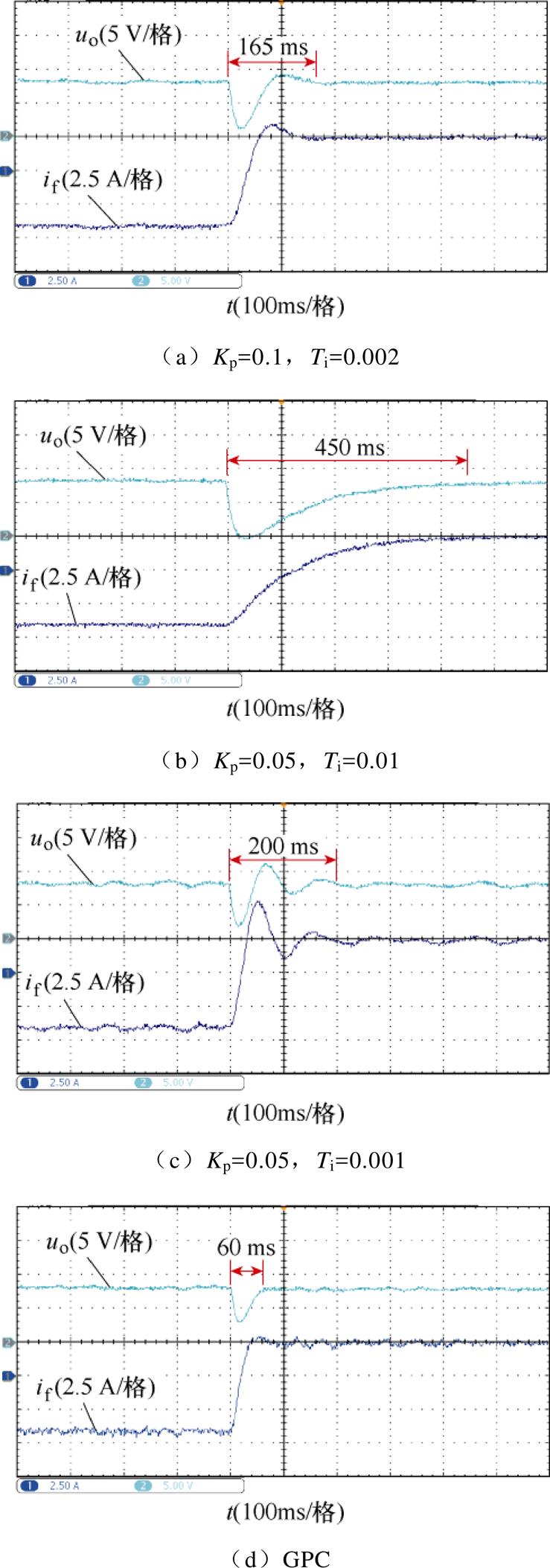
图9 相同负载突变下GPC与PI控制动态性能比较
Fig.9 Comparison of dynamic performance between GPC and PI control under the same load mutation
选择图9a组中的PI参数，在不同负载突变下同GPC进行比较，转速条件更换为800 r/min。实验结果如图10所示。不同负载突变下，GPC下的动态调节时间小于PI控制。
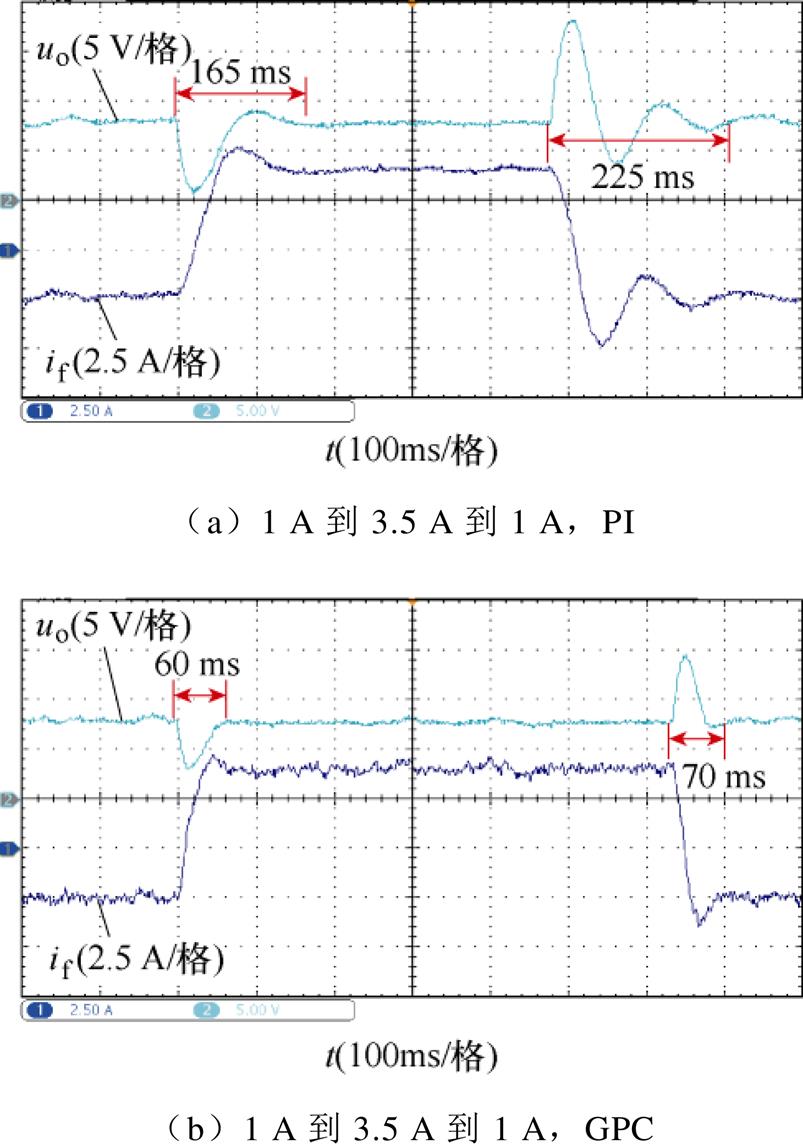
图10 不同负载突变下GPC与PI控制动态性能比较
Fig.10 Comparison of dynamic performance between GPC and PI control under different load mutations
对于实际的车辆28 V直流电气系统而言，负载突增造成的低电压，负载突减带来的过电压，如果幅值过大，可能会触发系统后级的低电压保护或过电压保护，在负载突减功率较大情况下损坏甚至会烧毁后级用电设备。对比图10a和图10b，PI控制下负载突减带来的过电压达到了10 V，而GPC下为7 V。面对负载突增突减两种情况，GPC相较于PI控制，均能有效地抑制负载扰动带来的输出电压变化。
观察GPC的励磁电流波形，相较于简单的PI控制，励磁电流的纹波更加明显。经分析，这是由于GPC方法基于负载励磁映射，引入了负载电流反馈与转速测量反馈，通过映射系数K得到励磁电流给定值。多个反馈通道，叠加了复杂的闭环控制机制导致了励磁电流纹波更加明显。
控制算法的复杂度可以用数字控制程序的执行时间来判断。GPC作为一种显示的多步预测控制算法，在每个控制周期需要进行矩阵运算，预测长度N的大小决定了相关参数矩阵初始化所占的空间大小，以及在中断中矩阵运算消耗的时间长短。
实验使用Matlab直接计算图5中的矩阵T和G，然后以二维数组的形式在主程序文件开头对矩阵进行初始化。在中断控制程序中，根据式（7），求解控制量的过程调用了两次矩阵乘法和一次矩阵减法。实验中断频率为10 kHz，对应周期100 ms，GPC不同预测步长下，在中断中的运算耗时见表2。当预测长度N达到20时，计算时间达到了68 ms，远大于PI控制中外环PI控制的计算耗时，叠加上采样、励磁电流内环计算耗时，整个中断程序耗时已经接近100 ms，因此，在实际应用中，预测长度N应综合考虑后折中选取。
表2 控制算法耗时
Tab.2 Control algorithm time consuming
算 法计算时间/ms GPC N=57 N=1015 N=1532 N=2068 外环PI4
独立励磁直流发电系统在负载变化较多的工况下，电压环采用PI调节器的控制方式难以取得较好的动态性能。本文提出一种基于负载励磁映射的广义预测控制方法应用于基于DBR的独立励磁直流发电系统中。对控制环路在离散域下的传递函数进行分析，为广义预测控制的控制参数设计提供了参考，对一般的基于不控整流的电励磁或混合励磁直流发电系统多步预测控制具有指导意义。经实验验证，相较于电压环PI控制方法，GPC下的直流发电系统，在面对不同负载突变时的动态性能提升效果明显。而当GPC的预测长度取值较大时，相较于简单的PI控制，GPC算法所需的空间与运算时间均较大。
参考文献
[1] Patin N, Vido L, Monmasson E, et al. Control of a hybrid excitation synchronous generator for aircraft applications[J]. IEEE Transactions on Industrial Elec- tronics, 2008, 55(10): 3772-3783.
[2] 甘志伟, 缪冬敏, 王云冲, 等. 宽转速范围永磁同步发电机系统稳压控制及参数优化[J]. 电工技术学报, 2020, 35(8): 1624-1633.
Gan Zhiwei, Miao Dongmin, Wang Yunchong, et al. Voltage stabilization control and parameters opti- mization for wide-speed-range permanent magnet synchronous generator systems[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1624-1633.
[3] 付兴贺, 江政龙, 吕鸿飞, 等. 电励磁同步电机无刷励磁与转矩密度提升技术发展综述[J]. 电工技术学报, 2022, 37(7): 1689-1702.
Fu Xinghe, Jiang Zhenglong, Lü Hongfei, et al. Review of the blushless excitation and torque density improvement in wound field synchronous motors[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1689-1702.
[4] Gao Fei, Bozhko S, Costabeber A, et al. Control design and voltage stability analysis of a droop- controlled electrical power system for more electric aircraft[J]. IEEE Transactions on Industrial Elec- tronics, 2017, 64(12): 9271-9281.
[5] Wang Yu, Deng Zhiquan. Hybrid excitation topo- logies and control strategies of stator permanent magnet machines for DC power system[J]. IEEE Transactions on Industrial Electronics, 2012, 59(12): 4601-4616.
[6] Vazquez S, Rodriguez J, Rivera M, et al. Model predictive control for power converters and drives: advances and trends[J]. IEEE Transactions on Indu- strial Electronics, 2017, 64(2): 935-947.
[7] 齐昕, 苏涛, 周珂, 等. 交流电机模型预测控制策略发展概述[J]. 中国电机工程学报, 2021, 41(18): 6408-6419.
Qi Xin, Su Tao, Zhou Ke, et al. Development of AC motor model predictive control strategy: an over- view[J]. Proceedings of the CSEE, 2021, 41(18): 6408-6419.
[8] Zhang Xiuyun, Shi Tingna, Wang Zhiqiang, et al. Generalized predictive contour control of the biaxial motion system[J]. IEEE Transactions on Industrial Electronics, 2018, 65(11): 8488-8497.
[9] Choi D K, Lee K B. Dynamic performance improve- ment of AC/DC converter using model predictive direct power control with finite control set[J]. IEEE Transactions on Industrial Electronics, 2015, 62(2): 757-767.
[10] 卜飞飞, 罗捷, 刘皓喆, 等. 双绕组感应发电机系统无差拍电流预测控制策略[J]. 电工技术学报, 2021, 36(24): 5213-5224.
Bu Feifei, Luo Jie, Liu Haozhe, et al. Deadbeat predictive current control strategy of dual winding induction generator system[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5213-5224.
[11] 徐伟, 陈俊杰, 刘毅, 等. 无刷双馈独立发电系统的改进无参数预测电流控制[J]. 电工技术学报, 2021, 36(19): 4002-4015.
Xu Wei, Chen Junjie, Liu Yi, et al. Improved nonparametric predictive current control for standalone brushless doubly-fed induction generators[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(19): 4002-4015.
[12] 肖蕙蕙, 魏苏东, 郭强, 等. 优化开关序列的PWM整流器模型预测控制策略[J]. 电工技术学报, 2022, 37(14): 3665-3675, 3700.
Xiao Huihui, Wei Sudong, Guo Qiang, et al. Model predictive control strategy for PWM rectifier with optimized switching sequence[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3665- 3675, 3700.
[13] Wang Tao, Zhu Z Q, Freire N M A, et al. Generalized predictive DC-link voltage control for grid-connected converter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(2): 1489-1506.
[14] 王莉, 曹小庆, 张卓然, 等. 电励磁双凸极无刷直流发电机非线性PI调压技术的研究[J]. 中国电机工程学报, 2006, 26(5): 153-158.
Wang Li, Cao Xiaoqing, Zhang Zhuoran, et al. Research of nonlinear PI voltage regulation for doubly salient brushless DC generator[J]. Proceedings of the CSEE, 2006, 26(5): 153-158.
[15] Xu Yanwu, Zhang Zhuoran, Bian Zhangming, et al. Capacitor-energy-based control of doubly salient brushless DC generator for dynamic performance optimization[J]. IEEE Transactions on Energy Con- version, 2020, 35(4): 1886-1896.
[16] 翟小飞, 马伟明, 欧阳斌, 等. 前馈控制在脉冲整流发电机数字励磁控制系统中的应用[J]. 电工技术学报, 2013, 28(7): 151-156.
Zhai Xiaofei, Ma Weiming, Ouyang Bin, et al. Application of feed forward control in the excitation system of pulse rectified generator[J]. Transactions of China Electrotechnical Society, 2013, 28(7): 151-156.
[17] 赵耀, 王慧贞, 张海波, 等. 基于励磁电流前馈调节的航空直流发电系统建模分析[J]. 航空学报, 2015, 36(4): 1230-1239.
Zhao Yao, Wang Huizhen, Zhang Haibo, et al. Modeling and analysis of aero DC generation system based on excitation current feedforward regulation[J]. Acta Aeronauticaet Astronautica Sinica, 2015, 36(4): 1230-1239.
[18] 刘金利, 马伟明, 翟小飞, 等. 带脉冲负载多相储能发电机励磁控制系统设计[J]. 海军工程大学学报, 2019, 31(3): 32-38.
Liu Jinli, Ma Weiming, Zhai Xiaofei, et al. Design of excitation control system for multi-phase energy storage generator with pulse load[J]. Journal of Naval University of Engineering, 2019, 31(3): 32-38.
[19] 阳习党, 翟小飞, 马伟明, 等. 整流充电发电机组励磁系统[J]. 电工技术学报, 2014, 29(5): 54-61.
Yang Xidang, Zhai Xiaofei, Ma Weiming, et al. Excitation system of rectified charging generators[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 54-61.
[20] Jury E, Gutman S. On the stability of the Amatrix inside the unit circle[J]. IEEE Transactions on Auto- matic Control, 1975, 20(4): 533-535.
Abstract The voltage closed-loop control based on the PI regulator is generally adopted in the inde- pendent excitation DC power generation system. PI control can ensure the steady-state control accuracy of the system output voltage. However, limited by the fixed PI regulator parameters and the system’s nonlinearity, the dynamic regulation characteristics of the output voltage may have problems such as slow response speed and extensive voltage recovery overshooting when the system faces load mutation under different working conditions. In recent years, predictive control has been widely used in power electronics with its characteristics of fast dynamic response and strong resistance to disturbance. Among them, the generalized predictive control (GPC) based on multi-step prediction has the characteristics of high flexibility in parameter design and strong robustness when the prediction length is sufficient. As an alternative to PI control, it can improve the dynamic voltage performance of the system under load disturbance.
Introducing load current feedforward is a standard method to solve the problem of the poor dynamic performance of PI control. Considering that the relation curve between excitation and load of the power generation system is coupled with the parameter of generator speed, the fitting function relation surface of excitation, load, and speed is constructed. After adding the feedback value of load current to the total generalized predicted output, the excitation current command value is obtained through the fitting function.
The control loop of the system is approximately linearized by the fitting function, and the transfer function in the discrete domain of the control system is constructed to analyze the system's stability and ability to resist load disturbance. The system’s stability is judged by the closed-loop pole position in the discrete domain. When the weight coefficient r of the performance index function is small, the system is unstable. When the predicted length N, the weight factor RF, and the estimated capacitance value C of the load end change within a specific range, the closed-loop pole trajectory of the control system always lies in the unit circle, and the system is stable. The control parameters used in the final experiment are determined by analyzing anti-load disturbance ability. The smaller r value and more considerable N value can give the system more excellent anti-disturbance ability. However, Considering the limited computing power of the MCU in the interrupt cycle, the N value must be manageable in the experiment.
Comparing the proposed GPC method with the PI method, the steady-state experiment, load disturbance dynamic experiment, and control algorithm complexity experiment are carried out, respectively. Finally, according to the experimental results, the following conclusions are drawn: (1) The GPC method based on the fitting function relationship can realize the closed-loop voltage control of the system with enough control accuracy when the speed changes. (2) Compared with the PI control method, the DC power generation system under the control of GPC has a significantly improved dynamic performance in the face of different load mutations. (3) When the prediction length of GPC is considerable, the MCU space and computing time required by the GPC algorithm are larger than the simple PI control.
keywords：Independent excitation DC generator system, generalized predictive control, load disturbance, dynamic performance
DOI: 10.19595/j.cnki.1000-6753.tces.220673
中图分类号：TM301
国家自然科学基金（51977107, U2141227）、江苏省六大人才高峰（XNYQC-005）和航空科学基金（2020HKZ0001）资助项目。
收稿日期2022-04-27
改稿日期 2022-09-08
夏宇航 男，1998年生，硕士研究生，研究方向为混合励磁发电及其控制。E-mail: surferx@nuaa.edu.cn
王 宇 男，1982年生，博士，副教授，研究方向为磁通切换电机及其控制。E-mail: Wanghaohao@163.com（通信作者）
（编辑 崔文静）