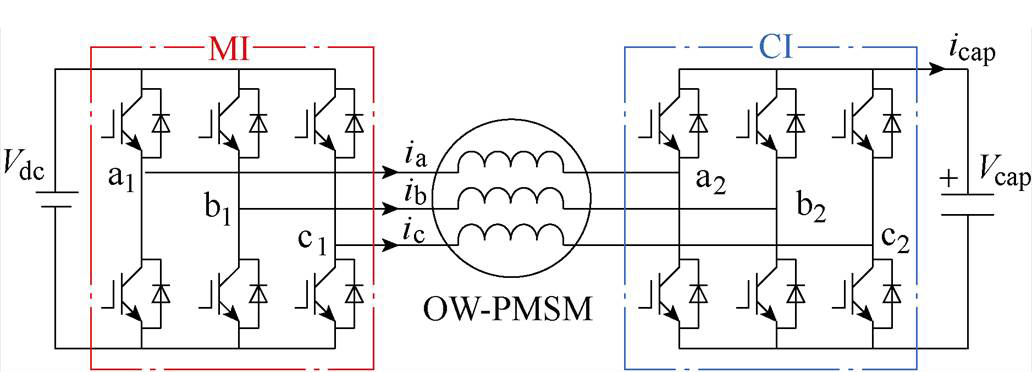
图1 混合供电型OW-PMSM系统拓扑结构
Fig.1 Topology of HI-OW-PMSM system
摘要 针对混合供电型开绕组永磁同步电机系统因功率分配约束难以执行过调制的问题,提出一种考虑功率分配的新型过调制方法。首先分析了传统过调制方法对系统功率平衡的影响,定义了有功电压调制度,使过调制区在考虑功率分配的情况下得到更清晰的界定。为了平衡过调制区的功率分配以及保障不同调制区的平滑切换,基于重新界定的过调制区分别提出定子电压矢量和有功电压的过调制方法。实验结果验证了所提新型过调制方法的有效性和优越性。
关键词:开绕组永磁同步电机 浮地电容 功率分配 过调制
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)因具有高效率、高功率密度等优点,被广泛用于交通、军事及航空航天等领域[1-4]。然而,由于其永磁体磁链固定,电机的反电动势随转速上升而增大,在有限直流母线电压的情况下限制了电机的速度运行范围。
目前,常见的提高PMSM运行范围的方法有弱磁控制、提高电压及提升电压利用率。其中,开绕组(Open Winding, OW)电机拓扑采用双逆变器供电,以增大机端供电电压的方式拓宽了电机的运行范围,获得了广泛关注[5-7]。
OW-PMSM拓扑具有三种常见供电类型[8-10]。其中,电容-电压混合供电型(Hybrid Inverter, HI)OW-PMSM借鉴电力系统中静止同步补偿器的思想[11-13],以一侧逆变器接电容的方式来增大电压并实现拓速,相比于双电源隔离母线型拓扑少用一个电源,具有成本低、体积小的优点,且无零序回路,避免了单电源共母线型拓扑中零序电流的抑制问题,具有一定优势[14-17]。
针对混合供电型开绕组拓扑,有学者研究采用弱磁控制方法[18-19]以提高电机的运行范围,但弱磁方法本质上是通过牺牲转矩输出能力来提高转速的方法,降低了系统效率。此外,弱磁控制后的参考电压仍被限制在线性调制区内,系统直流电压未被充分利用。为提高直流母线电压的利用率,有学者在该拓扑中引入了六步调制方法[20],但六步调制存在从线性调制区到六步调制区电压矢量的非线性切换问题,易引起电流和转矩脉动。
为解决线性调制区到六步调制区的非线性切换问题,需对中间的过调制区进行研究。目前,国内外对过调制算法已有一些研究。文献[21-22]分别提出了单模式和双模式的过调制方法,有效减小了过调制区中输出电压的谐波。文献[23-24]则在此基础上分别进行改进,使以上两种过调制方法更契合数字化的工程应用。此外,也有特殊拓扑结构过调制方法的研究,文献[25]提出适用于单电流传感器的过调制方法,文献[26]则解决了常规过调制方法对无电解电容PMSM系统的影响。
上述过调制方法都能有效提高系统的电压利用率,但均只适用于单逆变器供电的系统。针对双逆变器供电的OW系统,因双逆变器供电方式的不同,相应的过调制方法也存在较大的区别。双电源隔离型供电的OW-PMSM系统具有与单逆变器系统相似的电压矢量分布特性,因此该系统的过调制方法与传统单逆变器系统没有太多区别。但对于共直流母线型及混合供电型的OW-PMSM系统,其零序约束和电容电压约束与空间电压矢量存在高度耦合关系,导致这两种系统的线性调制区边界与传统拓扑不同,过调制方法也需要进行修正。针对共直流母线型及混合供电型的OW-PMSM系统,文献[27]提出一种三维空间矢量场景专用的过调制方案,将过调制边界校正为空间几何体内部的曲面。过调制的目标也不再是将参考电压压缩至六边形边界,而是压缩至空间几何体的外围面。
而对于混合供电型OW-PMSM系统,当考虑到电容电压和电压矢量的耦合关系时,难以对过调制区进行界定。因此,针对该拓扑的过调制方案目前只能在双逆变器上分别独立进行。然而,考虑到电容的充放电问题以及其仅能提供无功功率的限制,在控制时需对两个逆变器之间的功率进行分配,导致主逆变器(Main Inverter, MI)和辅逆变器(Com- pensatory Inverter, CI)的参考电压配比受到严格限制。而传统过调制方法通常需对参考电压进行修正,修正后的参考电压将不再能满足原来的功率分配需求,这将破坏系统的功率平衡,导致电机系统运行失稳。目前,针对混合供电型的OW-PMSM系统,还未见有能很好地兼顾电容电压稳定和输出低谐波的过调制方案的文献报导。
为使混合供电型OW-PMSM系统能稳定地运行在过调制区,进一步拓宽系统的运行范围,本文提出一种考虑功率分配的新型过调制方法。首先分析混合供电型OW-PMSM的功率分配机理,得到传统过调制方法无法移植到该拓扑的本质原因。为了在考虑功率分配的情况下更准确地界定系统的过调制区,定义有功电压调制度。根据重新界定的过调制区,分别提出定子电压矢量和有功电压的过调制方式,实现过调制区系统功率的平衡以及从线性调制区到过调制区再到六步调制区的平滑切换。最后通过实验验证所提方法的有效性和优越性。
混合供电型OW-PMSM系统的拓扑结构如图1所示。将常规PMSM定子绕组的中性点打开,定子绕组两侧分别与两个逆变器相连。其中,主逆变器(MI)由直流电压源供电,辅逆变器(CI)由电容器供电。图1中,Vdc为直流电压源的电压,Vcap为电容器的电压。
根据图1,电机的定子电压由主逆变器MI和辅逆变器CI共同提供,表示为

图1 混合供电型OW-PMSM系统拓扑结构
Fig.1 Topology of HI-OW-PMSM system
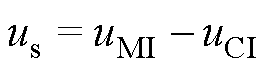 (1)
(1)
式中,u为电压;下标s为电机定子分量;下标MI和CI分别为由主逆变器MI和辅逆变器CI提供的分量。
混合供电型OW-PMSM在dq旋转坐标系下的电压方程可表示为
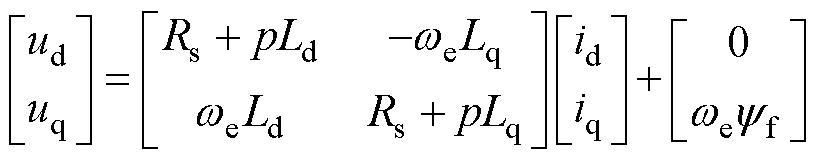 (2)
(2)
式中,下标d和q分别为旋转坐标系下的d轴和q轴分量;i为定子电流;Rs、L和yf分别为定子电阻、定子电感和转子磁链;p为电机的极对数;we为电机的电角速度。
辅逆变器直流侧的电容电压取决于流经辅逆变器的瞬时功率,其关系可表示为
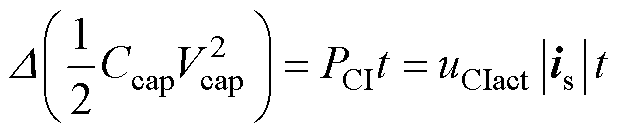 (3)
(3)
式中,Ccap为电容容值;PCI为流经辅逆变器的有功功率;|is|为定子电流幅值;uCIact为辅逆变器输出电压的有功分量; 为t时间内的增量。
为t时间内的增量。
由于电容是无源器件,因此辅逆变器只能向电机侧提供无功功率。此外,为了维持电容电压的稳定,辅逆变器需吸收一部分有功功率。满足以上约束关系后,系统所有的有功功率以及辅逆变器无法补偿的剩余无功功率均由主逆变器提供。恒定负载工况下,上述功率分配可等效为对电压矢量进行分配。基于电压矢量模型的功率分配原理如图2所示。图2中,qi为is与a 轴的夹角;上标ref为参考值;下标act为有功分量,所有有功分量均平行于is;下标react为无功分量,所有无功分量均垂直于is。
电机定子电压的有功和无功分量计算式为
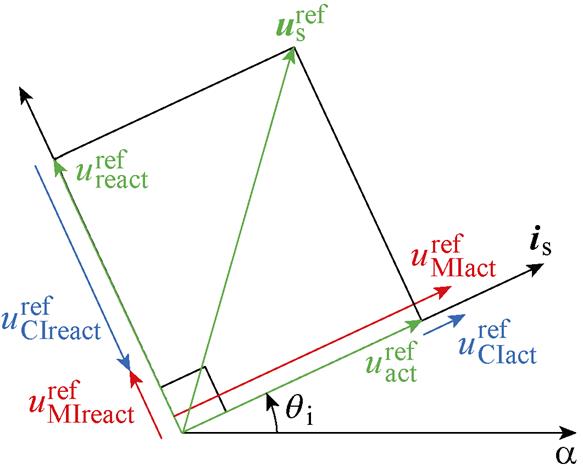
图2 功率分配原理
Fig.2 Principle of power distribution
 (4)
(4)
式中,qe为电机转子电角度。
辅逆变器所能提供的无功电压uCIreact受电容电压大小的限制,表示为
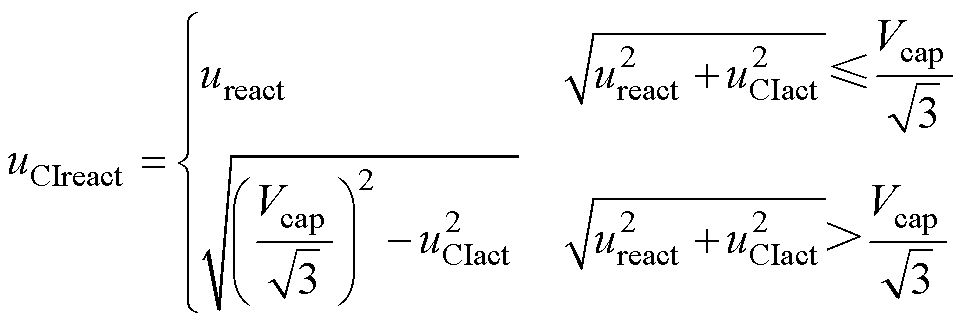 (5)
(5)
基于上述功率分配方法,可得混合供电型OW-PMSM系统传统矢量控制策略框图,如图3 所示。
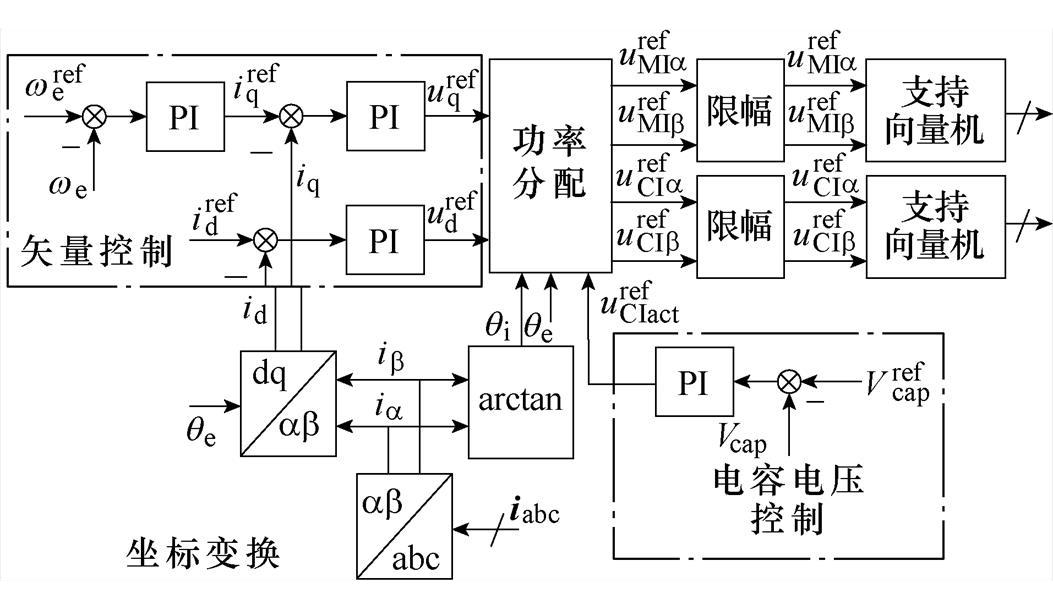
图3 混合供电型OW-PMSM系统传统矢量控制框图
Fig.3 Control block diagram of conventional field oriented control scheme for HI-OW-PMSM system
图3中,转速、电流及电容电压均采用PI调节器进行控制。将得到的电机定子电压参考值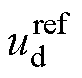 、
、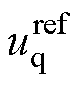 和辅逆变器的有功电压参考值
和辅逆变器的有功电压参考值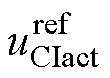 进行功率分配后再解耦,即可得到双逆变器的参考电压,如图4所示。
进行功率分配后再解耦,即可得到双逆变器的参考电压,如图4所示。
为了使输出电压不失真,传统调制方法将参考电压的幅值限制在线性调制区内,如图5所示。
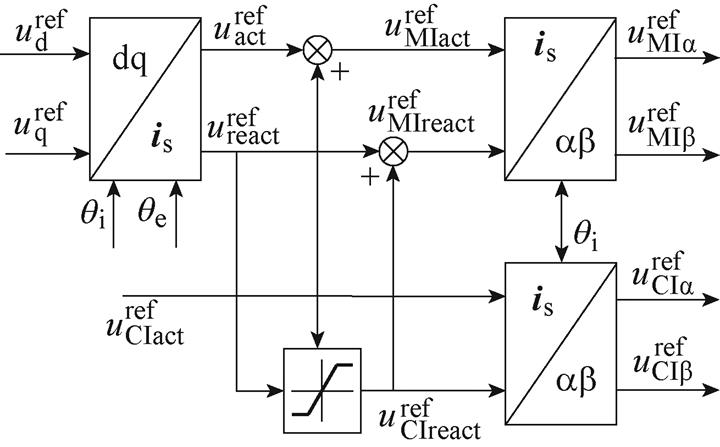
图4 功率分配控制框图
Fig.4 Control block diagram of power distribution
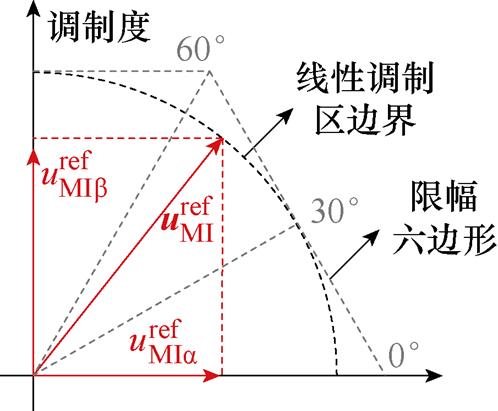
图5 线性调制区限制
Fig.5 Limitation of linear modulation region
 对应的调制度MMI定义为
对应的调制度MMI定义为
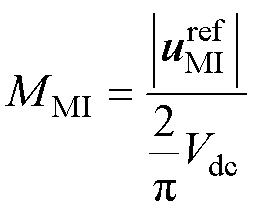 (6)
(6)
式中,(2/p)Vdc为逆变器六步调制时输出方波的基波幅值。
根据式(6)计算可知,当参考电压位于线性调制区内时,参考电压矢量的幅值最大为Vdc/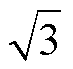 ,对应调制度为0.906 9,电压利用率较低。
,对应调制度为0.906 9,电压利用率较低。
为提高系统电压利用率,可采用过调制方法。然而,过调制方法通常需对参考电压矢量进行幅值或相位上的修正。而根据前面的分析可知,功率分配环节严格限制了双逆变器的参考电压配比。当任一个逆变器采用过调制方法时,修正后的参考电压将不再满足系统功率分配的需求,这将使电容电压以及电机的运行状态失稳。图6展示了主逆变器采用过调制算法对功率平衡的影响。图6中,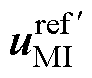 和
和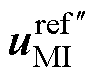 分别为主逆变器采用等幅值[21]和等相位过调制[22]修正后的参考电压,如图6a所示。可以发现,参考电压进行修正后,难以再次对其进行合理的功率分配,破坏了系统在该状态下的功率平衡,如图6b所示。
分别为主逆变器采用等幅值[21]和等相位过调制[22]修正后的参考电压,如图6a所示。可以发现,参考电压进行修正后,难以再次对其进行合理的功率分配,破坏了系统在该状态下的功率平衡,如图6b所示。
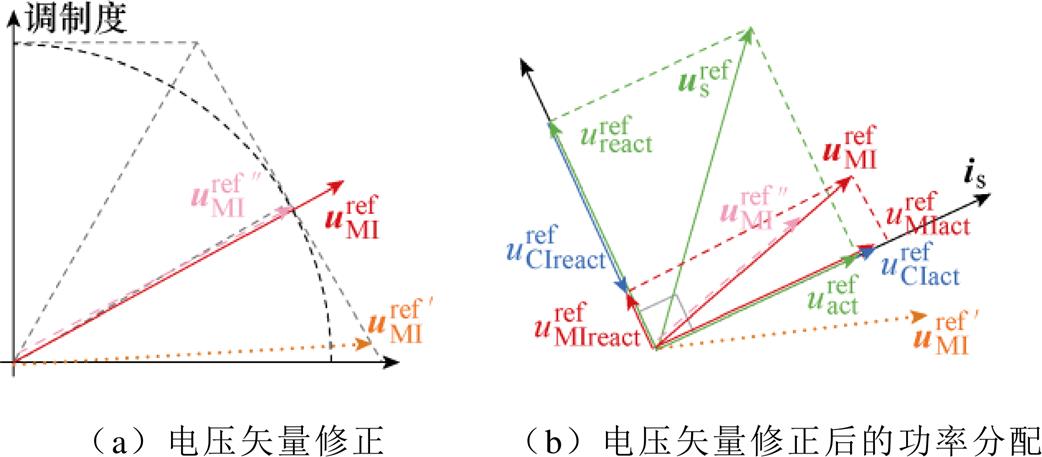
图6 传统过调制方法对功率平衡的影响
Fig.6 Influence of conventional overmodulation scheme on power balance
综合上述分析,常规的过调制方法无法直接移植到混合供电型的OW-PMSM系统中。为了在该系统中有效地实现过调制,本文提出一种考虑功率分配的新型过调制方法。考虑功率分配时,过调制区不能再简单地通过某一个逆变器的调制度进行判断,因此首先需对考虑功率分配的过调制区进行重新界定。根据重新界定的过调制边界,再分别提出当定子电压矢量和有功电压超过线性调制区时的过调制算法和六步调制算法,有效地提高了直流母线电压利用率。最后给出整个系统的控制框图。
传统方法都是以式(6)定义的某一个逆变器的电压矢量调制度作为线性调制区和过调制区的边界,导致电压矢量经由过调制修正后,难以重新对功率分配进行分析。考虑功率分配的情况下,需定义新的调制度对过调制区进行更清晰的界定。
结合混合供电型OW-PMSM功率分配的特点,本文以电机定子电压矢量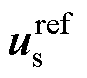 以及主逆变器的有功电压分量
以及主逆变器的有功电压分量 作为过调制区的判断依据。结合调制度的定义[23],
作为过调制区的判断依据。结合调制度的定义[23],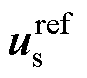 和
和 的调制度分别为其幅值与逆变器六步调制时输出方波的基波幅值
的调制度分别为其幅值与逆变器六步调制时输出方波的基波幅值 的比值,分别表示为M和MMIact,有
的比值,分别表示为M和MMIact,有
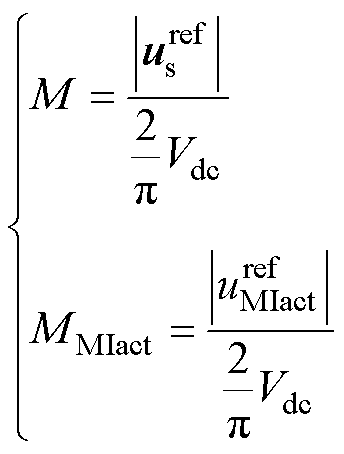 (7)
(7)
根据式(7)定义的调制度对过调制区进行重新界定,考虑功率分配时的过调制区界定见表1。当M≤0.906 9且MMIact≤0.906 9时,定子电压矢量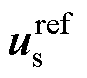 和有功电压
和有功电压 均位于线性调制区内,无需进行过调制;当M>0.906 9且MMIact≤0.906 9时,
均位于线性调制区内,无需进行过调制;当M>0.906 9且MMIact≤0.906 9时,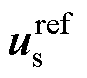 位于线性调制区外,
位于线性调制区外, 位于线性调制区内,进入定子电压矢量过调制区;当MMIact>0.906 9时,
位于线性调制区内,进入定子电压矢量过调制区;当MMIact>0.906 9时,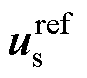 和
和 均位于线性调制区外,进入有功电压过调制区。
均位于线性调制区外,进入有功电压过调制区。
表1 考虑功率分配时的过调制区界定
Tab.1 Overmodulation region division considering power distribution

MMIactM调制区标志位nOM ≤0.906 9≤0.906 9线性调制区1 >0.906 9定子电压矢量过调制区2 >0.906 9—有功电压过调制区3
当M>0.906 9且MMIact≤0.906 9时,进入定子电压矢量过调制区,以0~p/3扇区为例,此时的过调制策略如图7所示。图7中,jMI为 和电流矢量is的夹角,即主逆变器的功率因数角。
和电流矢量is的夹角,即主逆变器的功率因数角。
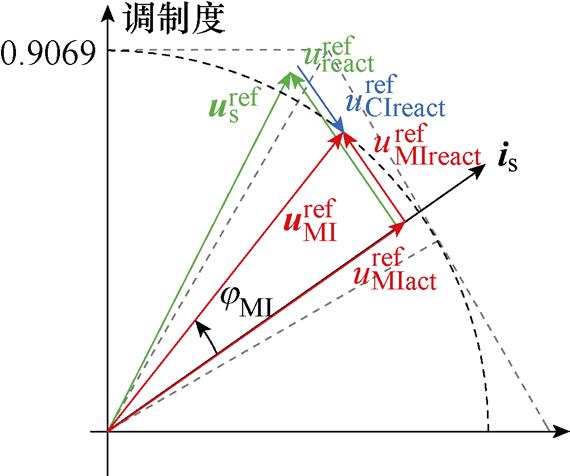
图7 定子电压矢量过调制分析
Fig.7 Overmodulation analysis for stator voltage
该情况下有功电压 仍处于线性调制区内,主逆变器仍有能力提供系统所需的有功功率。为了保证逆变器输出电压的正弦度并尽可能提高直流电压利用率,令主逆变器电压
仍处于线性调制区内,主逆变器仍有能力提供系统所需的有功功率。为了保证逆变器输出电压的正弦度并尽可能提高直流电压利用率,令主逆变器电压 沿着线性调制区边界运动。此时主逆变器无功电压由式(8)进行修正。
沿着线性调制区边界运动。此时主逆变器无功电压由式(8)进行修正。
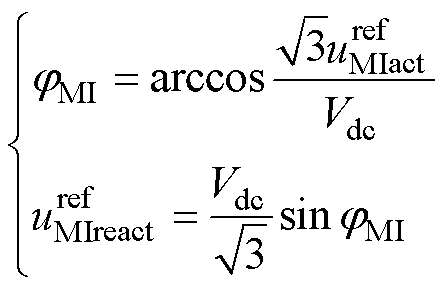 (8)
(8)
为了保证不同调制模式之间的平滑切换,需对该过调制区的边界情况进行分析,如图8所示。
定子电压矢量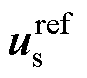 位于线性调制区边界上的情况(M=0.906 9)如图8a所示,此时jMI达到最大,即
位于线性调制区边界上的情况(M=0.906 9)如图8a所示,此时jMI达到最大,即 与
与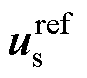 重合。并且,由图8a可以发现,当M≤0.906 9,即电机系统运行在线性调制区内时,定子电压矢量
重合。并且,由图8a可以发现,当M≤0.906 9,即电机系统运行在线性调制区内时,定子电压矢量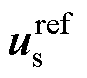 可以由主逆变器单独进行合成。图9给出了传统方法和本文所提方法在线性调制区内功率分配方案的区别。为了保证电机系统在不进行过调制矫正的情况下具有最大的运行范围,传统方案通常采用图9a所示方案进行功率分配(同图2),然而这样的方法在保证运行范围的同时给合成电压矢量引入了由辅逆变器直流侧的电容电压波动引起的谐波。而本文在线性调制区内采用图9b所示的方案,避免电容电压谐波引入的同时,与图8a所示过调制边界情况保持一致的功率分配关系,确保了线性调制区到过调制区的平滑切换。
可以由主逆变器单独进行合成。图9给出了传统方法和本文所提方法在线性调制区内功率分配方案的区别。为了保证电机系统在不进行过调制矫正的情况下具有最大的运行范围,传统方案通常采用图9a所示方案进行功率分配(同图2),然而这样的方法在保证运行范围的同时给合成电压矢量引入了由辅逆变器直流侧的电容电压波动引起的谐波。而本文在线性调制区内采用图9b所示的方案,避免电容电压谐波引入的同时,与图8a所示过调制边界情况保持一致的功率分配关系,确保了线性调制区到过调制区的平滑切换。
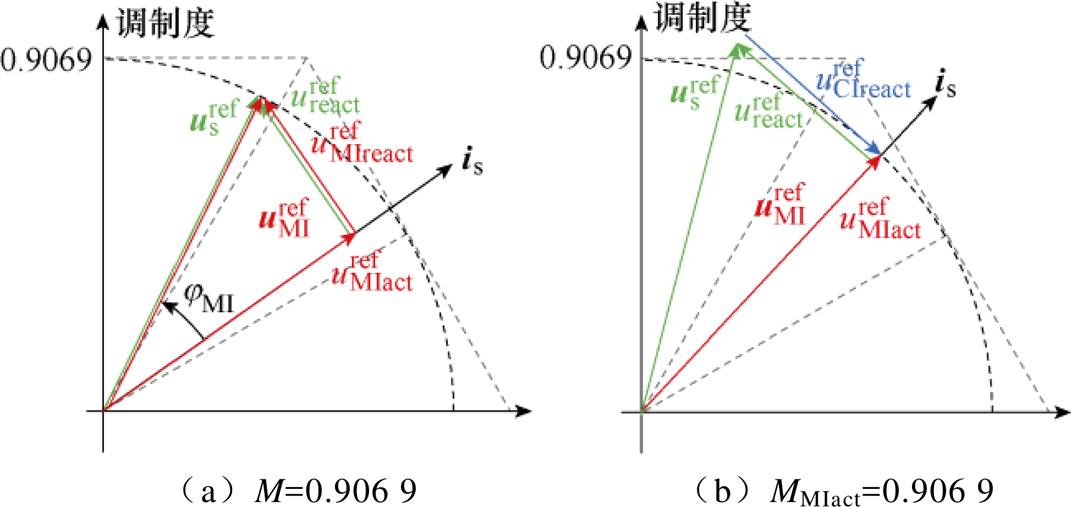
图8 定子电压矢量过调制边界情况
Fig.8 Boundary condition of stator voltage vector overmodulation
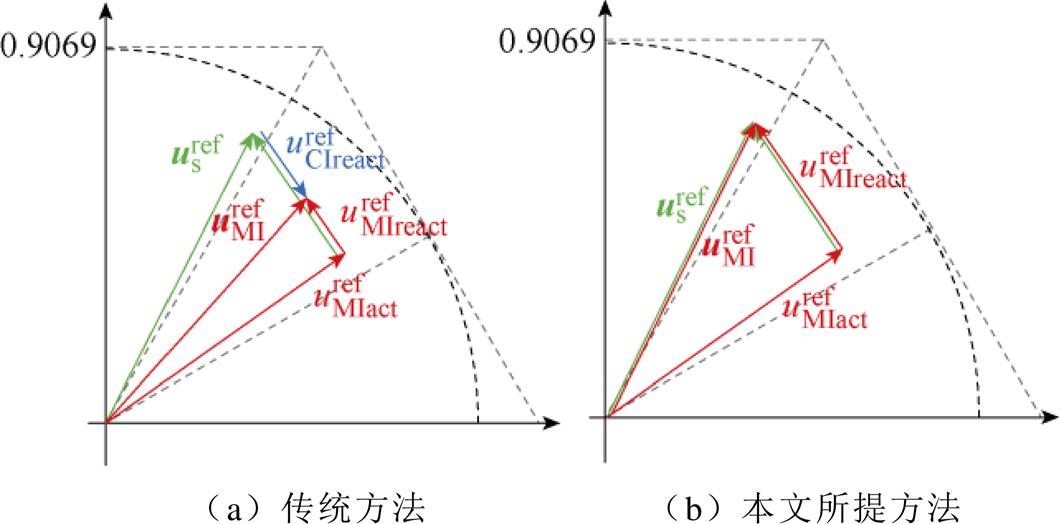
图9 线性调制分析
Fig.9 Analysis of linear modulation
根据图9b,线性调制区的功率分配关系为
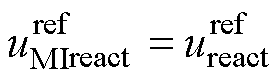 (9)
(9)
有功电压 达到线性调制区边界时的情况(MMIact=0.906 9)如图8b所示,此时jMI=0,
达到线性调制区边界时的情况(MMIact=0.906 9)如图8b所示,此时jMI=0,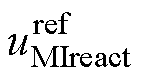 = 0,主逆变器输出电压将全被分解为有功分量,即
= 0,主逆变器输出电压将全被分解为有功分量,即 和
和 重合,主逆变器以单位功率因数运行。
重合,主逆变器以单位功率因数运行。
不难发现,当有功电压 达到主逆变器的线性调制区边界时,定子电压矢量
达到主逆变器的线性调制区边界时,定子电压矢量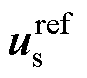 可以达到最大的不失真幅值。但当定子电压矢量进一步增大时,受线性调制区的限制主逆变器将不能再提供系统所需的有功功率。因此,需进一步对有功电压
可以达到最大的不失真幅值。但当定子电压矢量进一步增大时,受线性调制区的限制主逆变器将不能再提供系统所需的有功功率。因此,需进一步对有功电压 的过调制情况进行分析。
的过调制情况进行分析。
当MMIact>0.906 9时,进入有功电压的过调制区,以0~p/3扇区为例,此时的过调制策略如图10所示。图中,qMI为 与a 轴的夹角;红色实线圆弧为
与a 轴的夹角;红色实线圆弧为 的轨迹;红色虚线圆弧为
的轨迹;红色虚线圆弧为 的轨迹;qg为红色实线圆弧对应的临界角,其大小由
的轨迹;qg为红色实线圆弧对应的临界角,其大小由 的幅值决定,有
的幅值决定,有
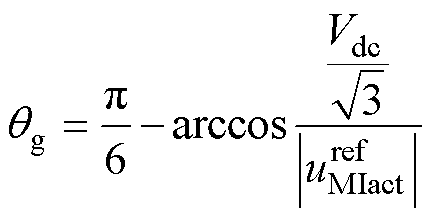 (10)
(10)
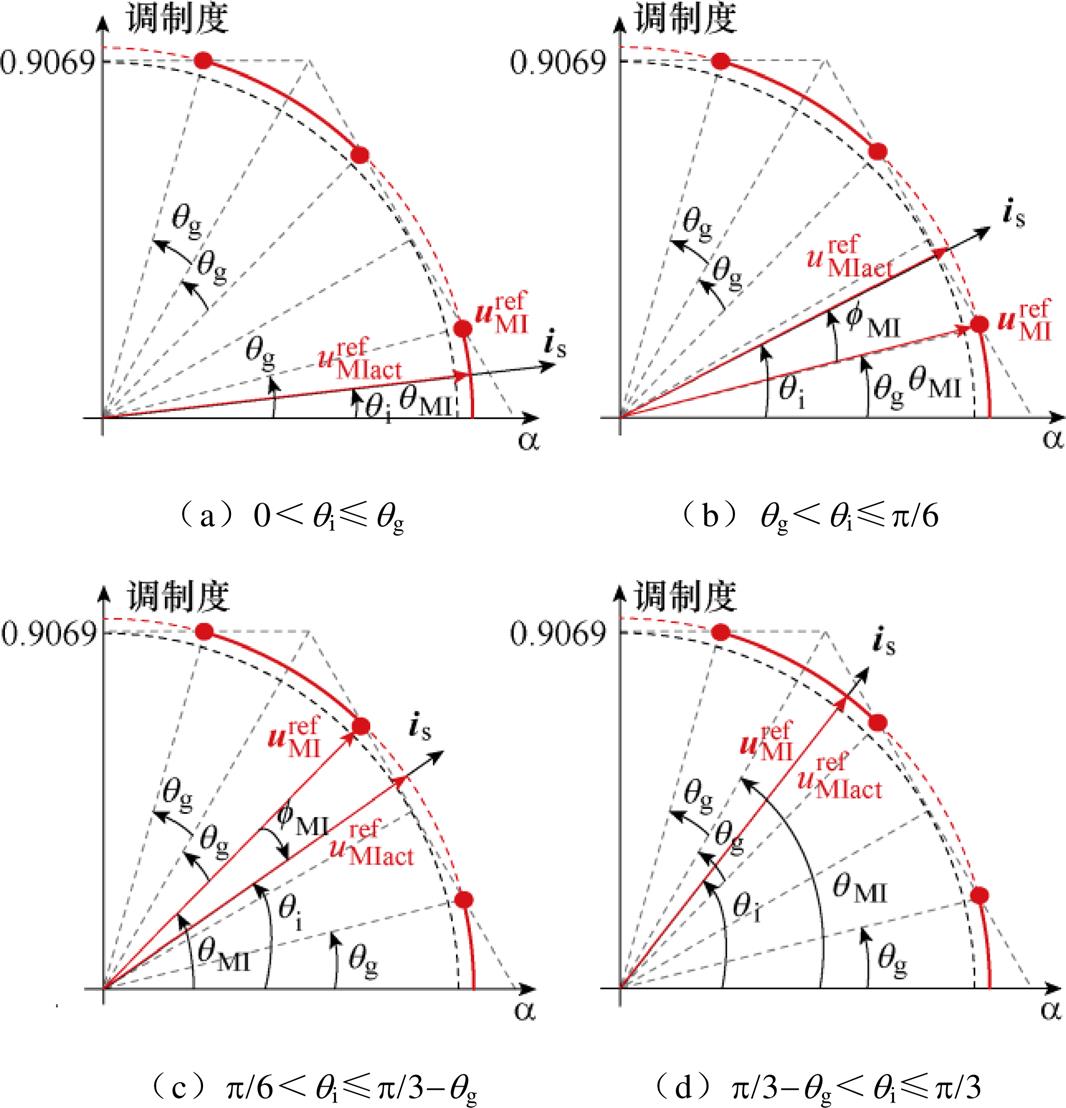
图10 有功电压过调制分析
Fig.10 Overmodulation analysis for active voltage
当MMIact=0.906 9时,qg=p/6,红色实线圆弧与线性调制区边界重合,即 在线性调制区边界上运行,与3.2节分析的定子电压矢量过调制时
在线性调制区边界上运行,与3.2节分析的定子电压矢量过调制时 的运行方式一致。说明从定子电压过调制区到有功电压过调制区的切换是平滑的。
的运行方式一致。说明从定子电压过调制区到有功电压过调制区的切换是平滑的。
根据图10, 和
和 具体运动方式可以总结如下:
具体运动方式可以总结如下:
(1)图10a展示了当电流角度qi小于临界角qg时的情况,此时 全被分解为有功分量,
全被分解为有功分量, 与
与 重合一起沿着红色实线运动。
重合一起沿着红色实线运动。
(2)图10b展示了当qi超过qg时的情况。由于 为主逆变器实际合成的电压,其轨迹必须全部位于限幅六边形内,此时
为主逆变器实际合成的电压,其轨迹必须全部位于限幅六边形内,此时 滞留在临界角处,
滞留在临界角处, 则随着电流矢量沿着红色虚线超过限幅六边形继续运动。
则随着电流矢量沿着红色虚线超过限幅六边形继续运动。
(3)图10c展示了当qi超过扇区中线时的情况,此时qi>p/6。为了防止主逆变器功率因数过低, 跃变到扇区上方的临界角处。
跃变到扇区上方的临界角处。
(4)图10d展示了当qi超过扇区上方临界角后的情况,此时 重新回到限幅六边形内,再次与
重新回到限幅六边形内,再次与 重合沿着红色实线运动。
重合沿着红色实线运动。
综合上述分析, 的相位qMI在0~p/3扇区内的表达式应修正为
的相位qMI在0~p/3扇区内的表达式应修正为
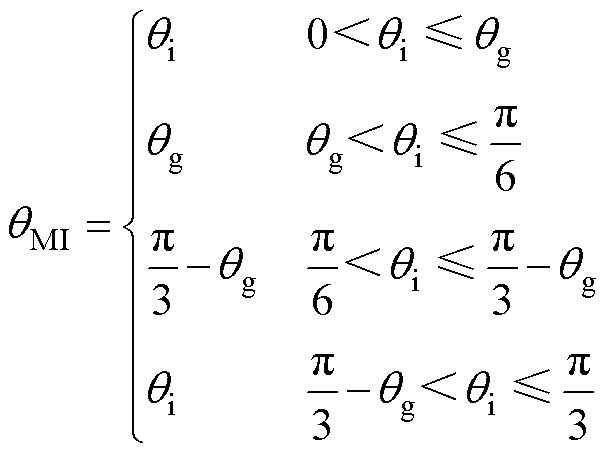 (11)
(11)
由图10b和图10c可以发现,所提的有功过调制方法中, 离开了限幅六边形后仍和
离开了限幅六边形后仍和 保持一致的幅值,而
保持一致的幅值,而 由于逆变器可调制范围的限制不能超出限幅六边形,将导致
由于逆变器可调制范围的限制不能超出限幅六边形,将导致 无法由
无法由 完整提供。有功电压修正如图11所示,
完整提供。有功电压修正如图11所示,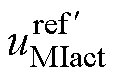 为此时
为此时 在is方向上的投影,即
在is方向上的投影,即 所能提供的最大有功分量,大于
所能提供的最大有功分量,大于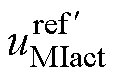 的部分将无法由
的部分将无法由 分解得到。
分解得到。
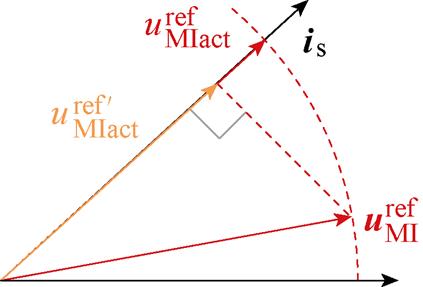
图11 有功电压修正
Fig.11 Active voltage correction
为了保证过调制情况下电压矢量可合成并维持功率分配的平衡,需将图10b和图10c的 根据图11分别修正为
根据图11分别修正为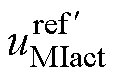 。修正后的电压矢量轨迹分别如图12a和图12b中的黄色弧线所示。图12中,落在黄色弧线上的任一矢量均为
。修正后的电压矢量轨迹分别如图12a和图12b中的黄色弧线所示。图12中,落在黄色弧线上的任一矢量均为 在该矢量方向上的投影,确保了修正后的
在该矢量方向上的投影,确保了修正后的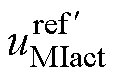 可完全由
可完全由 分解得到。
分解得到。
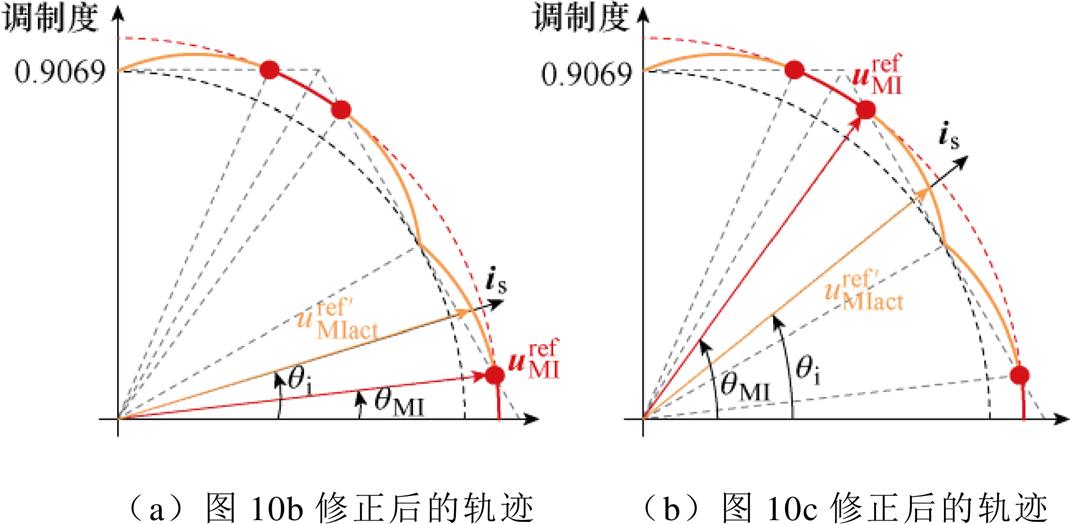
图12 有功电压修正后过调制分析
Fig.12 Overmodulation analysis after active correction
修正后的有功电压幅值表示为
 (12)
(12)
无功电压应该随着有功电压的修正进行相应的调整,表示为
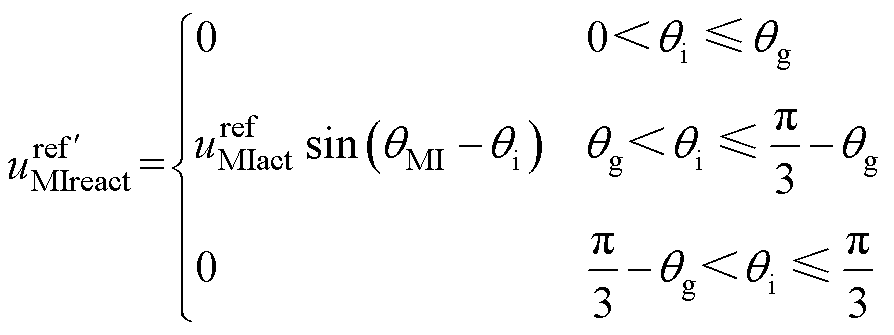 (13)
(13)
随着MMIact逐渐增大,边界角qg将逐渐减小。直到MMIact=1时,qg=0。此时 将滞留在限幅六边形的顶角处,以六步调制运行,如图13所示。
将滞留在限幅六边形的顶角处,以六步调制运行,如图13所示。 以六步调制运行时,
以六步调制运行时, 仍以修正后的轨迹运动,保证
仍以修正后的轨迹运动,保证 可合成的情况下提供最大的有功功率。
可合成的情况下提供最大的有功功率。

图13 六步调制分析
Fig.13 Analysis of six-step modulation
可以发现,该六步调制为上述有功电压过调制的边界情况,即从有功电压过调制区到六步调制区不存在电压矢量的非线性切换,过渡过程是平滑的。
综合上述分析,本文所提的考虑分配的新型过调制方法控制框图如图14所示。首先根据式(7)计算定子电压矢量调制度和有功电压调制度,并根据表1对调制区进行判断。当参考电压处于线性调制区,根据式(9)计算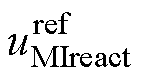 ;当参考电压处于定子电压过调制区,根据式(8)对
;当参考电压处于定子电压过调制区,根据式(8)对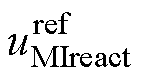 进行修正;当参考电压处于有功电压过调制区,则根据式(10)~式(13)对
进行修正;当参考电压处于有功电压过调制区,则根据式(10)~式(13)对 和
和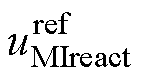 分别进行修正。
分别进行修正。
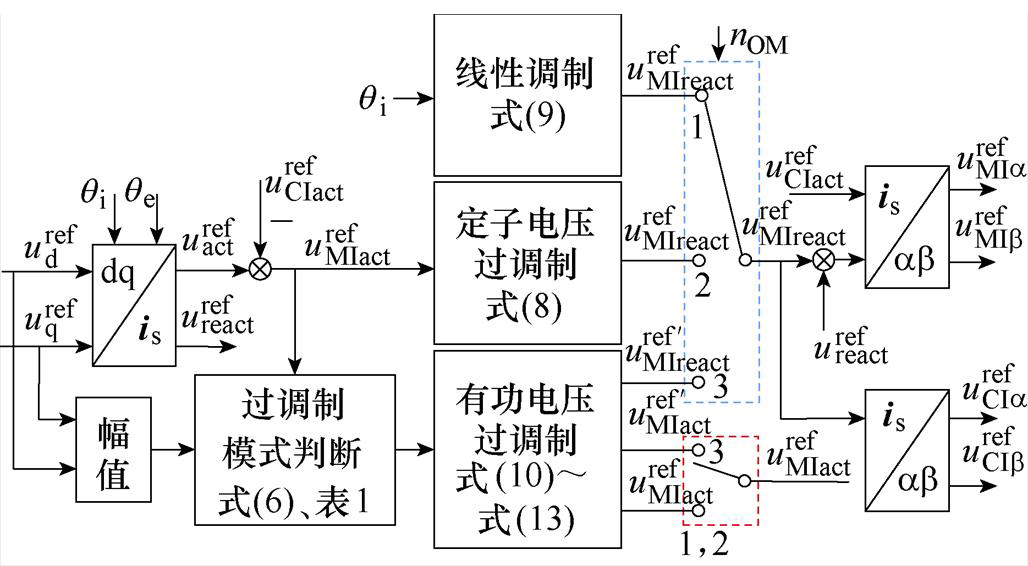
图14 考虑功率分配的新型过调制方法控制框图
Fig.14 Control block diagram of novel over-modulation scheme considering power distribution
基于所提过调制方法的控制框图如图15所示。所提方法将过调制与混合供电型OW-PMSM拓扑的功率分配环节进行了有效结合,解决了该拓扑因功率分配限制而导致的传统过调制难以执行的问题。
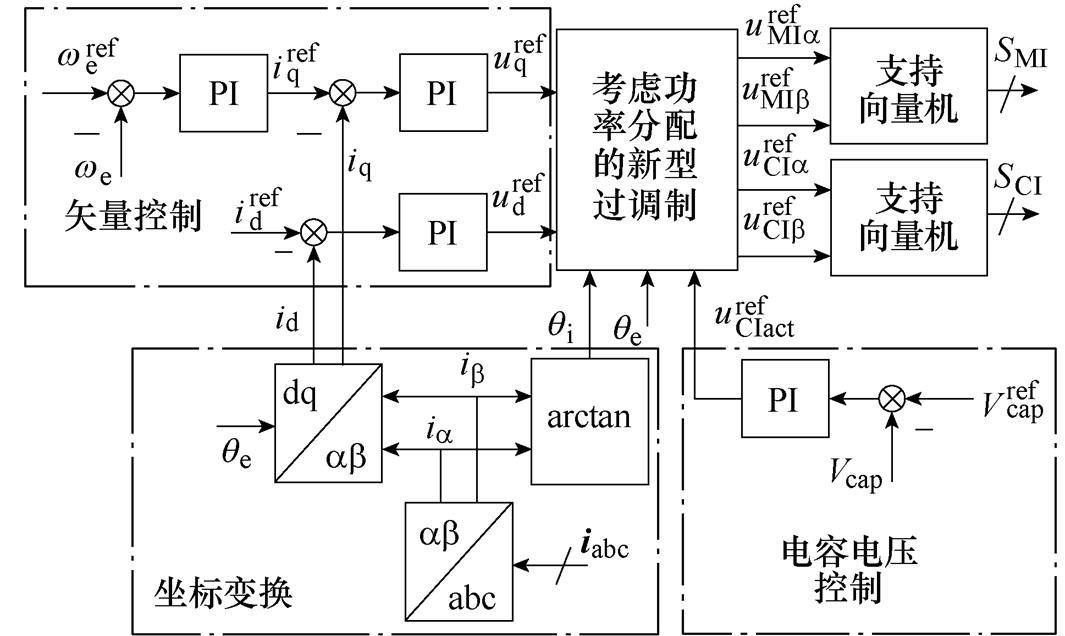
图15 基于所提过调制混合供电型OW-PMSM控制框图
Fig.15 Control block diagram for HI-OW-PMSM system based on proposed overmodulation method
为了验证所提考虑功率分配的新型过调制方法的正确性,本节对所提方法在多个工况下进行了实验研究。为了验证所提方法的优越性,进一步将仅含传统功率分配的矢量控制方法(策略Ⅰ)、在传统功率分配的基础上分别对两个逆变器进行等相位过调制修正[22]的矢量控制方法(策略Ⅱ)以及基于本文所提考虑功率分配过调制的矢量控制方法(策略Ⅲ)进行对比实验。
实验装置如图16所示。其中,主控芯片采用TI公司的DSP处理器,型号为TMS320F28335;双逆变器中的功率器件采用SEMIKRON公司生产的IGBT,型号为SKM75GB12T4;OW-PMSM定子绕组两端分别接主逆变器MI和辅逆变器CI,主逆变器直流侧接直流电压源,辅逆变器直流侧接浮地电容器;转子与迟滞测功机相连,并由迟滞测功机提供负载转矩;实验中参数设置为:直流母线电压Vdc=126 V,电容电压参考值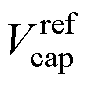 =Vdc=126 V,控制周期Ts=0.000 1 s;永磁电机极对数np=4,定子电阻Rs=1.35 W,定子电感Ld=5.86 mH、Lq=11.05 mH,永磁体磁链yf=0.154 7 Wb。
=Vdc=126 V,控制周期Ts=0.000 1 s;永磁电机极对数np=4,定子电阻Rs=1.35 W,定子电感Ld=5.86 mH、Lq=11.05 mH,永磁体磁链yf=0.154 7 Wb。

图16 实验装置
Fig.16 Picture of experimental platform
图17为所提方法带3 N·m额定负载在750、1 000、1 225、1 250 r/min四种转速下的电压电流稳态响应,分别对应电机运行在线性调制区、定子电压矢量过调制区、有功电压过调制区以及六步调制区的工况。图17中,从上到下分别为电机a相定子电流ia、主逆变器a相输出电压uMIa、辅逆变器a相输出电压uCIa及电机a相定子电压ua。
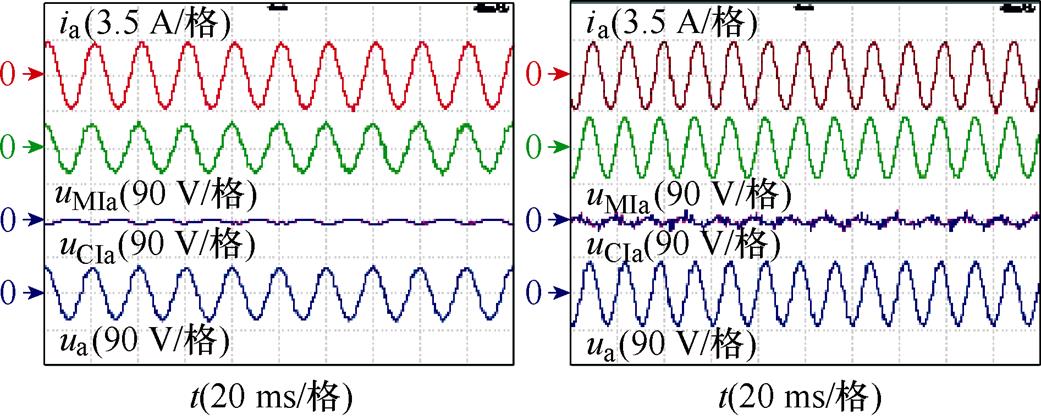
(a)750 r/min (b)1 000 r/min
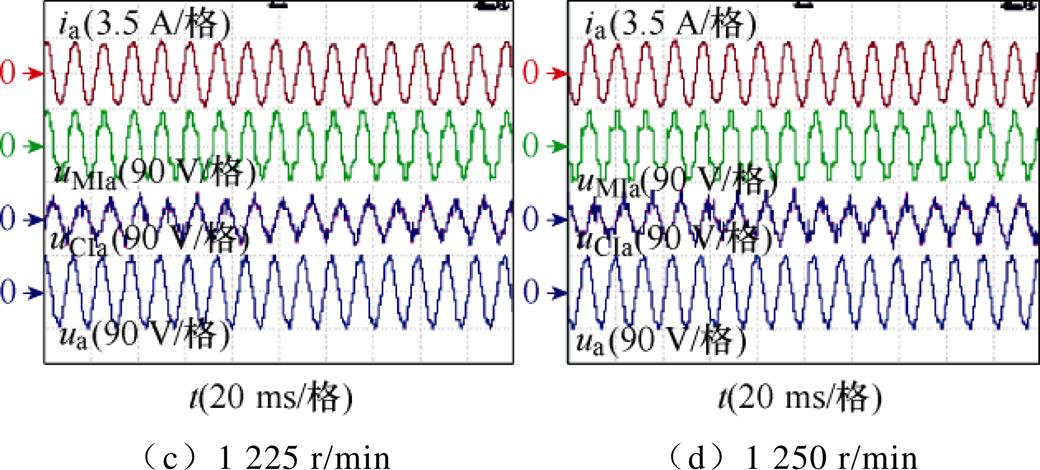
图17 所提过调制方法电流电压响应
Fig.17 Current and voltage response of proposed method
图17a中,uMIa、uCIa以及ua均具有较好的正弦度,uCIa幅值几乎为0,说明此时系统无功由主逆变器完全承担,这与图9b所示的电压矢量分配关系一致,说明此时线性调制区内算法的正确性。
图17b中,ua幅值约为81.3 V,此时电机超过线性调制区边界(72.75 V),运行在定子电压矢量过调制区。可以发现,uMIa以及ua均保持较好的正弦波形,与图7分析的电压矢量轨迹一致,证明了所提定子电压矢量过调制方法的正确性。
图17c中,电机运行在有功电压过调制区。其中uMIa因过调制出现明显失真,uCIa补偿因uMIa失真产生的谐波,保证了机端电压ua的正弦性。uMIa的波形与图12分析的电压矢量轨迹相对应,证明了所提有功电压过调制方法的正确性。
图17d中,电机运行在六步调制区域。uMIa每个周期仅有6个状态,同样因uCIa的补偿使ua不出现明显失真。图18进一步给出该状态下的有功电压uMIact和A相开关信号SMIa,此时SMIa的占空比约为50 %,uMIact以电压周期的六倍频脉动。uMIa和uMIact的波形与图13分析的电压矢量轨迹相对应,证明了所提有功电压过调制方法在六步调制情况下的正确性。
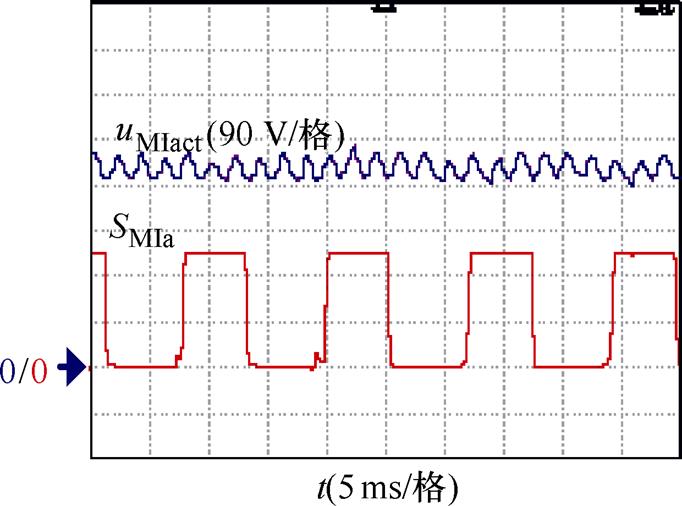
图18 六步调制时的有功电压和开关信号
Fig.18 Active voltage and switching signal of six-step modulation
图19~图21分别为策略Ⅰ至策略Ⅲ的稳态响应,从上到下分别是电机转速N、a相定子电流ia、电机输出转矩Te及电容电压Vcap。图19a、图19b中策略Ⅰ带3 N·m额定负载,分别以1 075 r/min及1 100 r/min参考转速运行。可以发现,当转速达到1 075 r/min时,已有明显转矩脉动;当转速再略微提高到1 100 r/min时,出现明显的转矩失稳现象,即电机在该转速下不足以支撑额定转矩。说明策略Ⅰ的临界转速位于1 075~1 100 r/min之间。图20a、图20b中,策略Ⅱ带3 N·m额定负载,分别以1 150 r/min及1 175 r/min参考转速运行。当参考转速达到1 175 r/min时,电机运行失稳,并且因电容电压的跌落(跌落至约109 V),导致实际电机转速不升反降。根据前文分析可知,在进行功率分配之后再分别对两个逆变器采用过调制方法进行矫正时,会使修正后的参考电压不再满足原本的功率分配需求,从而导致系统失去功率平衡,使电容电压和电机的运行状态失稳。图21a、图21b中策略Ⅲ带3 N·m额定负载,分别以1 225 r/min及1 250 r/min参考转速运行,此时电机转速达到1 250 r/min才开始失稳,说明采用所提过调制方法时,电机的临界转速位于 1225~1 250 r/min之间。相比于策略Ⅰ和策略Ⅱ,所提方法的临界转速分别提高约14 %和9 %,验证了本文所提方法的优越性。
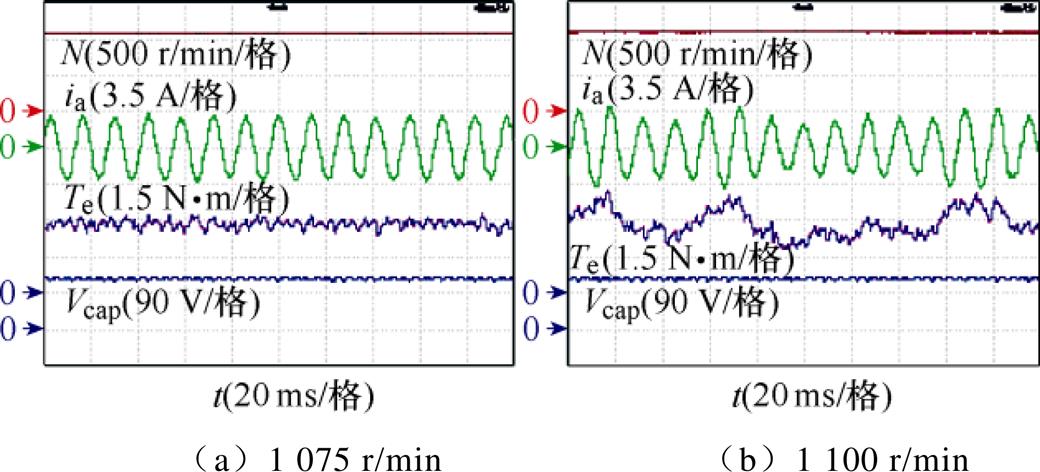
图19 策略Ⅰ的稳态响应
Fig.19 Static response of method Ⅰ
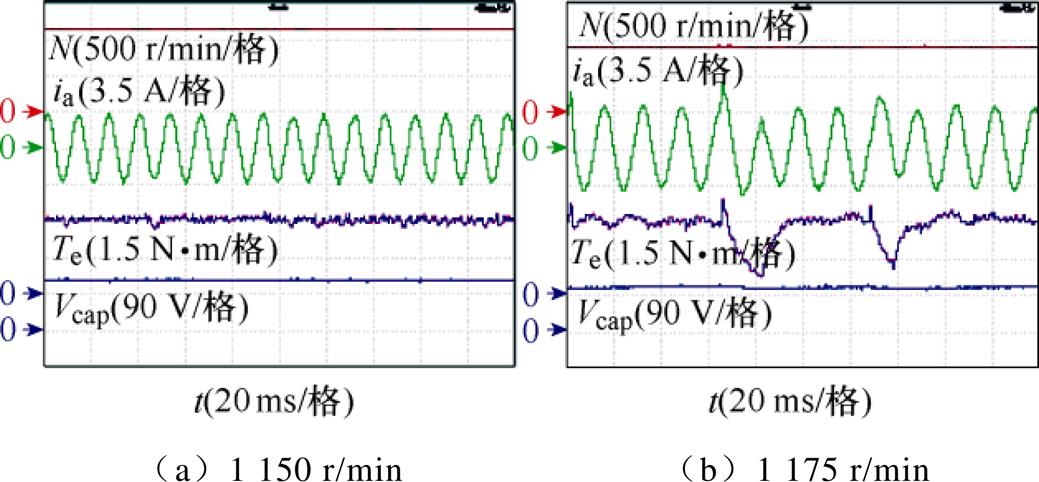
图20 策略Ⅱ的稳态响应
Fig.20 Static response of method Ⅱ
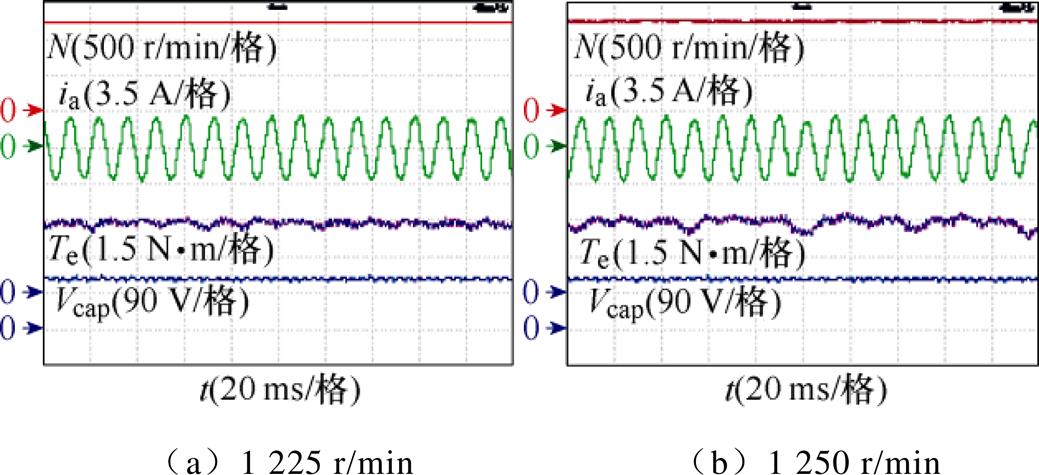
图21 策略Ⅲ的稳态响应
Fig.21 Static response of method Ⅲ
图22和图23分别给出了策略Ⅰ和策略Ⅱ在其临界转速(1 100 r/min和1 150 r/min)下与策略Ⅲ的电流总谐波畸变率(Total Harmonic Distortion, THD)频谱分析比较结果。图22中,运行于策略Ⅰ的临界转速(1 100 r/min)时,策略Ⅲ的电流THD为9.62 %,明显低于此时策略Ⅰ的电流THD值17.49 %;图23中,运行于策略Ⅱ的临界转速(1 150 r/min)时,策略Ⅲ的电流THD为10.45 %,同样小于此时策略Ⅱ的电流THD值12.83 %。由此证明了所提过调制方法在相同转速下具有比传统方法畸变率更小的电流响应波形。
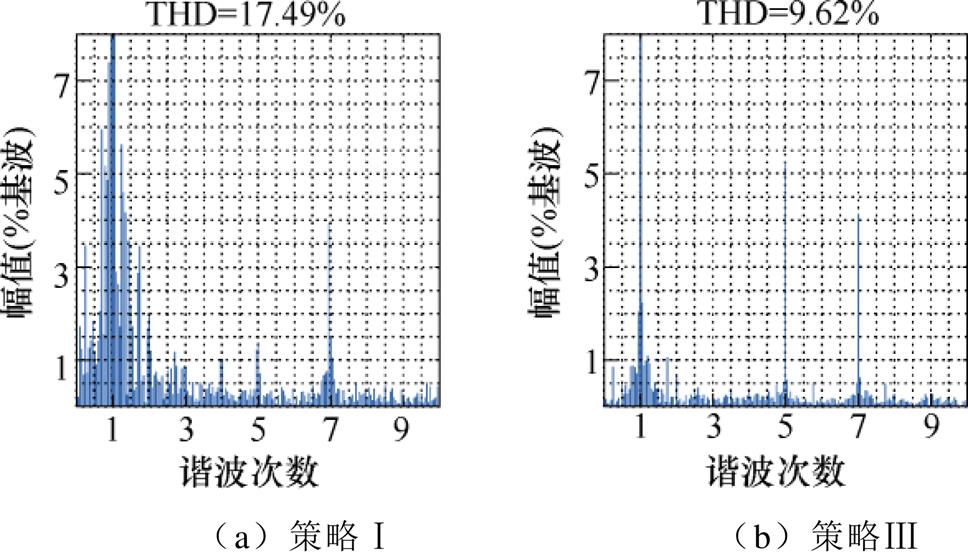
图22 策略Ⅰ临界转速下的电流THD比较
Fig.22 Comparision of current THD under the critical speed of method Ⅰ
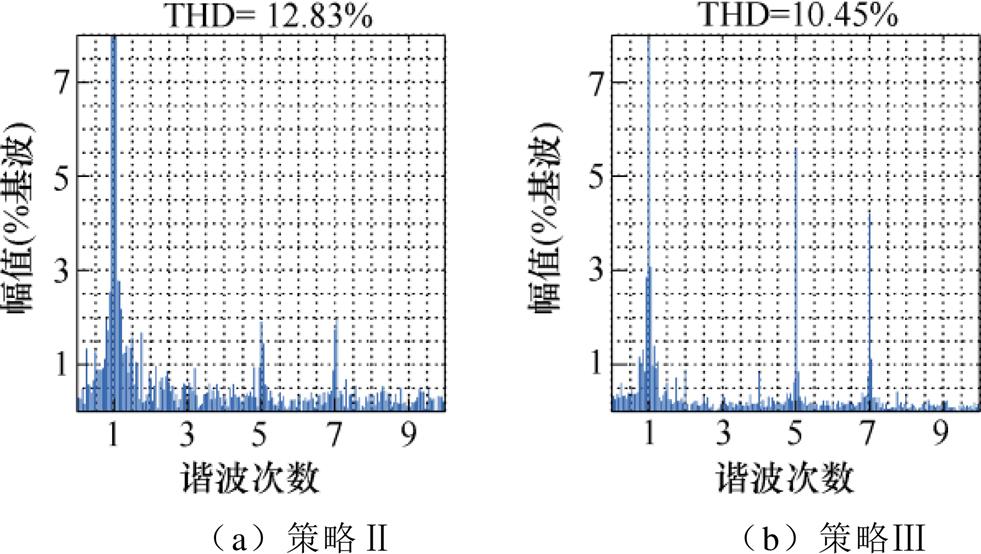
图23 策略Ⅱ临界转速下的电流THD比较
Fig.23 Comparision of current THD under the critical speed of method Ⅱ
图24进一步给出三种方法带额定负载3 N·m在不同转速工况下的电流THD对比。策略Ⅰ在参考电压超出线性调制区后电流THD显著增大。策略Ⅱ因采用了传统过调制方法,超出线性调制区后仍可短暂维持较好的电流响应,但随着转速进一步升高,过调制对参考电压的大程度矫正将严重破坏双逆变器功率分配的平衡,导致系统失稳。相比于策略Ⅰ和策略Ⅱ,策略Ⅲ在任一转速区域下均具有不高于传统方法的电流THD值。说明所提方法在拓宽电机运行范围的同时具有较低的电流谐波。
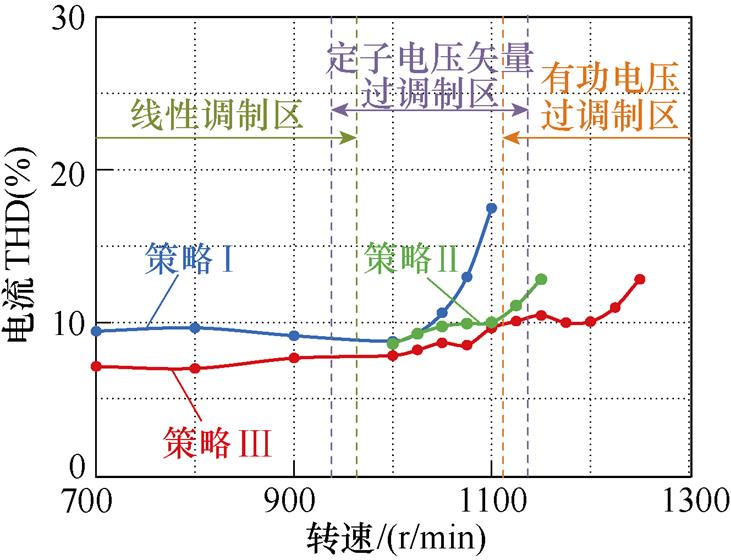
图24 不同转速下的电流THD比较
Fig.24 Comparision of current THD under different speed
图25~图27分别为三种策略带额定负载3 N·m时的变速实验暂态响应波形。图26为1 000 r/min阶跃至1 225 r/min。图27中的nOM为表1中定义的过调制区的标志位。
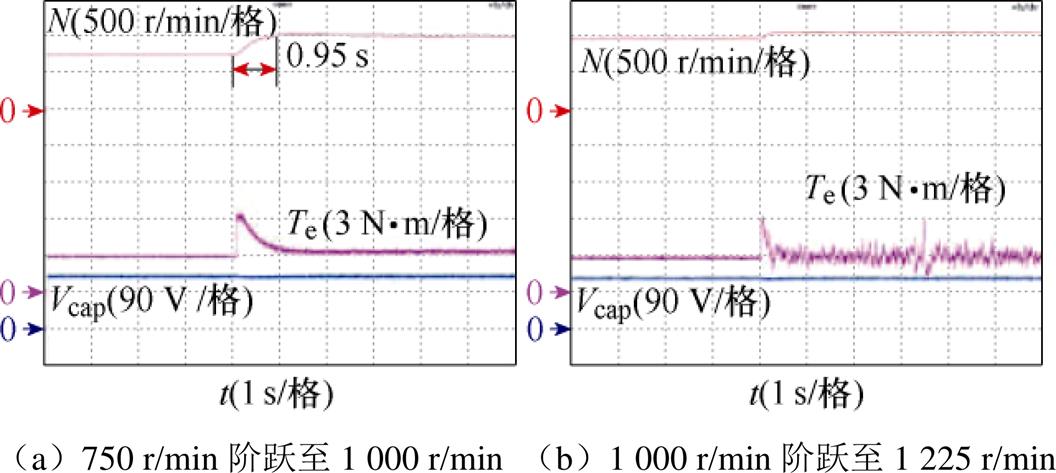
图25 策略Ⅰ的变速响应
Fig.25 Dynamic response of method Ⅰ
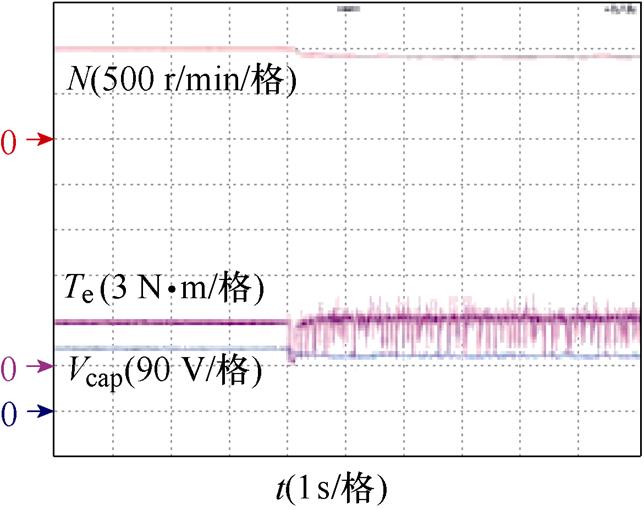
图26 策略Ⅱ的变速响应
Fig.26 Dynamic response of method Ⅱ
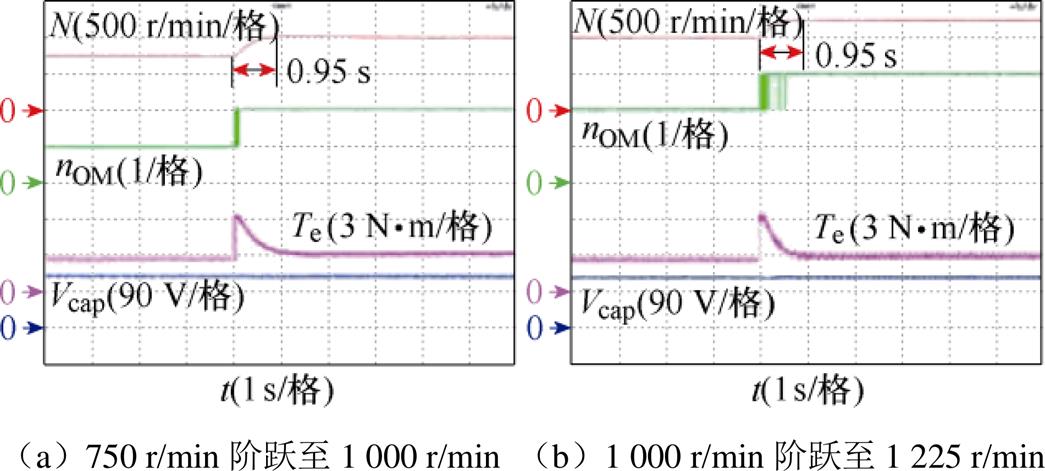
图27 策略Ⅲ的变速响应
Fig.27 Dynamic response of method Ⅲ
对比图25a和图27a,策略Ⅰ和策略Ⅲ的参考转速分别从750 r/min突变到1 000 r/min,实验结果表明,所提新型过调制方法与传统方法相比,具有同样快速的转矩和转速响应速度。对比图25b、图26和图27b,三种方法的参考转速分别从1 000 r/min突变到1 225 r/min。其中,策略Ⅰ中转速只能上升至约1 100 r/min处,并且伴随着较大的转矩脉动;策略Ⅱ更是由于采用传统过调制破坏了系统功率平衡,导致实际转速不升反降,电容电压出现明显跌落,电机运行失稳;而采用策略Ⅲ时,转速可以达到1 225 r/min稳定运行。以上实验结果表明,本文所提过调制方法在拓宽电机运行范围的同时,不会降低电机的暂态响应速度。
图27a、图27b中,策略Ⅲ从线性调制区(nOM=1)升速到定子电压矢量过调制区(nOM=2),再由定子电压矢量过调制区(nOM=2)升速到有功电压过调制区(nOM=3),升速过程中不存在因电压矢量非线性切换而引起的转矩脉动,说明本文所提过调制方法可以在不同调制区之间实现平滑切换。
本文针对混合供电型OW-PMSM系统,提出了一种考虑功率分配的新型过调制方法,解决了该混合供电型OW-PMSM系统因功率分配约束而导致的过调制难以执行的问题。定义了有功电压调制度,得到了功率平衡约束下更准确的过调制区边界。根据重新界定的过调制区,分别提出了定子电压矢量的过调制方法和有功电压的过调制方法,实现了过调制区功率分配的平衡以及过调制边界处的平滑切换。实验验证了所提过调制方法在保证高性能动稳态响应的情况下使混合供电型的OW-PMSM系统具有更宽的运行范围。
参考文献
[1] 张伟伟, 肖飞, 刘计龙, 等. 轨道交通车辆永磁同步牵引系统断电区穿越控制策略[J]. 电工技术学报, 2021, 36(16): 3483-3492.
Zhang Weiwei, Xiao Fei, Liu Jilong, et al. Power-off area traversing control strategy of permanent magnet synchronous motor traction system in rail transit vehicle[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3483-3492.
[2] Li Longfei, Xiao Jie, Zhao Yun, et al. Robust position anti-interference control for PMSM servo system with uncertain disturbance[J]. CES Transactions on Elec- trical Machines and Systems, 2020, 4(2): 151-160.
[3] 姜哲, 卜飞飞, 潘子昊, 等. 永磁同步电机伺服系统改进型无差拍电流控制算法[J]. 电力工程技术, 2020, 39(6): 177-183.
Jiang Zhe, Bu Feifei, Pan Zihao, et al. Improved deadbeat current control algorithm for permanent magnet synchronous motor servo system[J]. Electric Power Engineering Technology, 2020, 39(6): 177-183.
[4] Wang Tao, Guo L L, Wang K, et al. Generalized predictive current control for dual-three-phase PMSM to achieve torque enhancement through harmonic injection[J]. IEEE Transactions on Power Electronics, 2023, 39(5): 6422-6433.
[5] Takahashi I, Ohmori Y. High-performance direct torque control of an induction motor[J]. IEEE Transa- ctions on Industry Applications, 1989, 25(2): 257-264.
[6] 陈文汉, 孙丹, 王铭泽. 断相故障下开绕组永磁同步电机模型预测控制容错控制策略研究[J]. 电工技术学报, 2021, 36(1): 77-86.
Chen Wenhan, Sun Dan, Wang Mingze. Research on fault-tolerance strategy based on model predictive control for open-winding PMSM system under open- phase fault[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 77-86.
[7] Wei Yongqing, Qiao Mingzhong, Zhu Peng. Fault- tolerant operation of five-phase permanent magnet synchronous motor with independent phase driving control[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(1): 105-110.
[8] 孙丹, 林斌, 周文志. 开绕组电机系统拓扑及控制技术研究综述[J]. 电工技术学报, 2017, 32(4): 76-84.
Sun Dan, Lin Bin, Zhou Wenzhi. An overview of open winding electric machine system topology and control technology[J]. Transactions of China Electro- technical Society, 2017, 32(4): 76-84.
[9] 张晓光, 闫康, 张文涵. 开绕组永磁同步电机混合双矢量模型预测控制[J]. 电工技术学报, 2021, 36(1): 96-106.
Zhang Xiaoguang, Yan Kang, Zhang Wenhan. Hybrid double vector model predictive control for open- winding permanent magnet synchronous motor with common DC bus[J]. Transactions of China Electro- technical Society, 2021, 36(1): 96-106.
[10] Rovere L, Valente G, Formentini A, et al. Parameters and volt–ampere ratings of a floating capacitor open-end winding synchronous motor drive for extended CPSR[J]. IEEE Transactions on Industrial Electronics, 2022, 69(5): 4576-4586.
[11] 冯子木, 孙国强, 滕德红, 等. 永磁直驱风电机组低电压穿越研究综述[J]. 电力工程技术, 2021, 40(2): 75-85.
Feng Zimu, Sun Guoqiang, Teng Dehong, et al. Reviews of LVRT technology for D-PMSG[J]. Electric Power Engineering Technology, 2021, 40(2): 75-85.
[12] 陆道荣, 魏缪宇, 于宇, 等. 一种基于方波注入的星形级联静止同步补偿器的负序电流补偿策略[J]. 电工技术学报, 2022, 37(6): 1482-1494.
Lu Daorong, Wei Miaoyu, Yu Yu, et al. Zero- sequence-voltage injection based on square-wave to balance cluster voltages for star-connected cascaded STATCOM[J]. Transactions of China Electrotech- nical Society, 2022, 37(6): 1482-1494.
[13] 丘冠新, 朱鹏宇, 王灿, 等. 负载不平衡条件下MMC-STATCOM补偿策略研究[J]. 电力工程技术, 2020, 39(2): 35-42.
Qiu Guanxin, Zhu Pengyu, Wang Can, et al. The compensation method of MMC-STATCOM under unbalanced load condition[J]. Electric Power Engin- eering Technology, 2020, 39(2): 35-42.
[14] Kim J, Jung J, Nam K. Dual-inverter control strategy for high-speed operation of EV induction motors[J]. IEEE Transactions on Industrial Electronics, 2004, 51(2): 312-320.
[15] Amerise A, Rovere L, Formentini A, et al. Electric drive based on an open-end winding surface PM synchronous machine with a floating capacitor bridge[J]. IEEE Transactions on Industry Appli- cations, 2020, 56(3): 2709-2718.
[16] Lin Bin, Sun Dan, Chen Yin. Research on high-speed operation of hybrid-inverter fed open winding per- manent magnet synchronous motor[C]//International Conference on Electrical Machines and Systems (ICEMS), Busan, 2014: 1179-1183.
[17] Ewanchuk J, Salmon J, Chapelsky C. A method for supply voltage boosting in an open-ended induction machine using a dual inverter system with a floating capacitor bridge[J]. IEEE Transactions on Power Electronics, 2013, 28(3): 1348-1357.
[18] Sun Dan, Zheng Zhihao, Lin Bin, et al. A hybrid PWM-based field weakening strategy for a hybrid- inverter-driven open-winding PMSM system[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 857-865.
[19] Pan Di, Liang Feng, Wang Yang, et al. Extension of the operating region of an IPM motor utilizing series compensation[J]. IEEE Transactions on Industry Applications, 2014, 50(1): 539-548.
[20] Lee Y, Ha J I. Hybrid modulation of dual inverter for open-end permanent magnet synchronous motor[J]. IEEE Transactions on Power Electronics, 2015, 30(6): 3286-3299.
[21] Bolognani S, Zigliotto M. Novel digital continuous control of SVM inverters in the overmodulation range[J]. IEEE Transactions on Industry Applications, 1997, 33(2): 525-530.
[22] Holtz J, Lotzkat W, Khambadkone A. On continuous control of PWM inverters in the overmodulation range including the six-step mode[J]. IEEE Transa- ctions on Power Electronics, 1993, 8(4): 546-553.
[23] 张立伟, 刘钧, 温旭辉, 等. 基于基波电压幅值线性输出控制的SVPWM过调制新算法[J]. 中国电机工程学报, 2005, 25(19): 12-18.
Zhang Liwei, Liu Jun, Wen Xuhui, et al. A novel algorithm of SVPWM inverter in the overmodulation region based on fundamental voltage amplitude linear output control[J]. Proceedings of the CSEE, 2005, 25(19): 12-18.
[24] Lee D C, Lee G M. A novel overmodulation technique for space-vector PWM inverters[J]. IEEE Transa- ctions on Power Electronics, 1998, 13(6): 1144-1151.
[25] Sun Kai, Wei Qing, Huang Lipei, et al. An over- modulation method for PWM-inverter-fed IPMSM drive with single current sensor[J]. IEEE Transactions on Industrial Electronics, 2010, 57(10): 3395-3404.
[26] Wang Gaolin, Hu Haiming, Ding Dawei, et al. Over- modulation strategy for electrolytic capacitorless PMSM drives: voltage distortion analysis and boundary optimization[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 9574-9585.
[27] 王顺, 杨淑英, 李一, 等. 共中线开绕组拓扑三维空间矢量脉宽调制策略研究[J]. 中国电机工程学报, 2023, 43(3): 1163-1176.
Wang Shun, Yang Shuying, Li Yi, et al. Study on three-dimensional space-vector pulse-width modu- lation strategy used for open-end winding topology with common mode connected DC buses[J]. Pro- ceedings of the CSEE, 2023, 43(3): 1163-1176.
Abstract Hybrid-inverter driven open winding permanent magnet synchronous motor (HI-OW-PMSM) system has the advantages of high power factor, high voltage utilization, and high control accuracy. However, when the field-oriented control strategy is implemented in the HI-OW-PMSM system, an extra power distribution module is essential for the capacitor voltage constraint. The power distribution module limits the voltage ratio between two inverters, making a conventional overmodulation scheme challenging to be executed in the HI-OW-PMSM system. Therefore a novel overmodulation scheme considering power distribution is proposed.
The influence of the conventional overmodulation scheme on the power balance of the HI-OW-PMSM system is analyzed. The modulation index of the stator voltage and the active voltage are redefined, and the overmodulation region is divided more accurately when considering the power distribution. Accordingly, a novel overmodulation scheme considering power balance is proposed. To balance the power of the HI-OW-PMSM system in the stator voltage overmodulation region and smooth the switching process from the linear modulation region to the overmodulation region, a stator voltage overmodulation scheme is proposed, and the reactive voltage is indirectly corrected. Furthermore, an active voltage overmodulation scheme is proposed, and the active voltage is corrected. Then, the proposed active voltage overmodulation scheme is derived from the case of six-step modulation, and the operation range of the HI-OW-PMSM system is further extended.
In order to verify the superiority of the proposed method, comparative experimental studies among the conventional field-oriented control strategy (strategy Ⅰ), the conventional overmodulation strategy (strategy Ⅱ), and the proposed overmodulation strategy (strategy Ⅲ) are carried out in the experimental platform of the HI-OW-PMSM system. The static experimental results show that the critical speed of the proposed method is increased by about 14 % and 9 %, respectively. Besides, the current THD of the proposed method is smaller than strategy Ⅰ and strategy Ⅱ over the whole operation range. The dynamic experimental results show that the switching process among linear modulation, overmodulation, and six-step modulation regions is smooth.
The following conclusions can be drawn from theoretical derivation and experimental analysis: (1) The power distribution cannot keep balance when the conventional overmodulation method is directly applied to the HI-OW-PMSM system. (2) The active voltage modulation index has been defined, and a more accurate boundary of the over-modulation region has been obtained when considering the power distribution constraint. (3) The stator voltage overmodulation method and the active voltage overmodulation method have been proposed, respectively. Thus, the balance of the power distribution in the overmodulation region and the smooth switching at the overmodulation boundary are realized. (4) Comparative experiments have been carried out, which verified that the proposed method has a broader operating range and smaller current THD than the conventional overmodulation method.
keywords:Open winding permanent magnet synchronous motor, floating capacitor, power distribution, overmodulation
DOI: 10.19595/j.cnki.1000-6753.tces.220629
中图分类号:TM351
国家自然科学基金资助项目(51877197)。
收稿日期2022-04-20
改稿日期 2022-11-09
柯伟煌 男,1998年生,硕士研究生,研究方向为永磁电机控制技术。E-mail: kwh@zju.edu.cn
孙 丹 女,1975年生,教授,博士生导师,研究方向为交流电机高性能控制策略和新能源发电运行与控制技术。E-mail: sundan@zju.edu.cn(通信作者)
(编辑 崔文静)