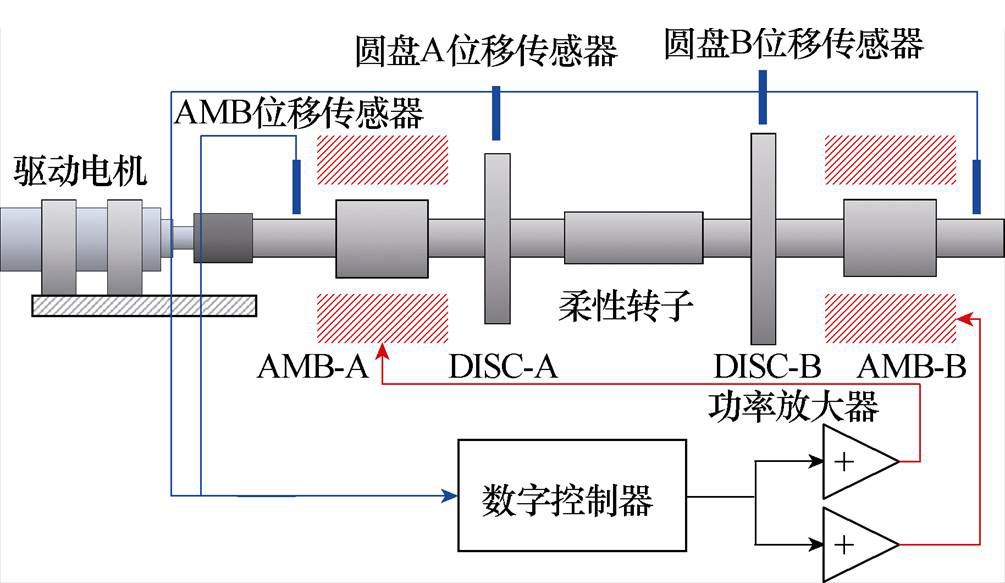
图1 AMBs-柔性转子系统
Fig.1 AMBs-flexible rotor system
摘要 工作在弯曲临界转速区的主动电磁轴承（AMBs）-柔性转子系统不能通过简单的几何关系从传感器位置的转子振动得到转子上目标位置的振动。为了实现转子系统的振动位移跟踪和估计，针对Luenberger状态观测器的观测滞后和观测器匹配条件难以满足等问题，基于二阶导数构建辅助输出，提出一种未知输入观测器（UIO）的柔性转子振动位移的高精度跟踪和估计方法。首先建立AMBs-柔性转子系统的动力学模型，阐述了Luenberger状态观测器获取转子系统振动位移的方法和滞后的不足；然后推导了基于二阶导数构建辅助输出的UIO，通过跟踪特性对比分析了UIO的优点，研究了模态可观性问题；最后在AMB-多盘柔性转子系统上进行了仿真和试验验证。结果表明，所提出的UIO能在0～6 000 r/min包括刚体和一阶弯曲临界转速的全转速范围内准确地跟踪系统输出信号，并可高精度地估计转子在目标位置的振动位移。
关键词：主动电磁轴承 柔性转子 状态观测器
主动电磁轴承（Active Magnetic Bearings, AMBs）可通过实时控制电磁力实现转子的稳定悬浮[1]，具有无接触、无磨损、无需润滑等优点，在各类高速旋转机械中得到了越来越广泛的应用[2-4]。随着旋转机械功率的进一步提高，转子的工作转速变得更高，转子的结构变得更为细长，这将导致支承在AMBs上的转子系统在一阶弯曲临界转速之上的转速区工作，这类转子称为柔性转子。
在AMBs-转子系统中，由于结构等原因传感器一般难以直接安装在AMBs的中心位置，出现所谓的不同位问题。此外，在转子系统中需要对一些特殊位置，如叶轮处的转子振动进行控制，而实际中在这些位置也难以安装传感器，这就需要从现有的传感器信息中获得这些目标位置的振动信息。
对于AMBs-刚性转子系统，转子上任意位置的振动位移都可用通过两端位移传感器的测量结果进行简单几何运算得到。但对于AMBs-柔性转子系统，转子发生弯曲变形且振型具有强烈的时变性，难以通过简单的运算从位移传感器的测量结果得到目标位置转子的振动位移。因此，利用有限个传感器位置处转子的振动信息来分析和估计目标位置处转子的振动位移具有重要的意义。
采用状态观测器的初衷是为了跟踪系统输出变量，估计出系统未知的状态变量[5]。D. G. Luenberger[6]于1964年提出了经典状态观测器的基本理论。随后他和L. Meier等[7]建立了线性常系数系统的观测器结构。对于一个无限自由度的柔性系统，当采用观测器对其进行观测时，只可能观测有限个状态变量。在研究早期，学者针对大维度系统进行了研究，这种大维度系统与柔性系统是类似的。T. S. Tang等[8]研究了大维度系统的观测器溢出效应。M. J. Balas[9]研究了大维度系统主动控制的特征，提出使用卡尔曼滤波器或Luenberger观测器获得缩减后系统的状态。近来，学者们对具体的被控模型进行了研究。曲志强等[10]研究了大型柔性空间结构的状态估计方法，指出若要精确观测n个模态需要n个位移和速度传感器，因此通过模态变换降低观测维数使得观测系统的状态方程可观测。在AMBs-转子系统中，利用有限个传感器位置处转子的振动信息分析和估计目标位置处转子的振动位移一般采用基于动力学模型的状态观测器及卡尔曼滤波器的方法来实现。王霈霈[11]提出使用卡尔曼滤波器进行转子位移信号获取的方法，在滤波器中使用了完整的转子系统模型。耿晓晓[12]提出不同位系统的位置重构方法，利用一个全阶状态观测器来估计出AMB节点处的实际位移。Z. Gosiewski等[13]针对柔性转子提出了状态观测器计算执行器位置状态量的虚拟重合方法。
以上观测系统均需要被控系统完整精确的动力学模型，受到的扰动均可视为相对缓慢且导数趋向于0，因此状态观测器可获得较好的观测效果。但是，观测结果对数学模型敏感，实际中很难获取精确的模型，同时，观测器的设计过程没有考虑扰动。在20世纪末，很多学者进行了观测器拓宽和改进方面的研究。从分析系统扰动的角度出发，一些学者提出了扰动观测器。Chen Wenhua等[14]系统地建立了基于扰动观测器的控制（Disturbance Observer Based Controller, DOBC）的概念，指出观测得到的扰动包括实际扰动和模型误差。基于这一概念，Peng Cong等[15]对电压控制的AMBs系统提出了基于扰动观测器的扰动抑制方法。Gong Lei[16]等提出使用扰动观测器来补偿AMBs-刚性转子系统中的陷波器在刚体临界转速前后进行极性切换时引起的突发振动。扩张状态观测器（Extended State Observer, ESO）由韩京清[17]于1995年提出，可同时解决扰动估计和补偿控制的问题。郭凯旋[18]将AMBs-刚性转子分离成4个单自由度SISO系统，以此为基础设计ESO。然而，ESO是基于无模型单输入单输出（Single Input Single Output, SISO）系统的状态方程设计的[19-20]，扩展到具有完整模型信息的多输入多输出（Multi Inputs Multi Output, MIMO）系统还有待研究。这些观测器的运行原理为将原系统模型和标称系统模型的输出作差，得到扰动量后补偿到控制输出中，本质上是一种补偿控制方法，而不是保证观测器能精确跟踪原系统的方法。
同属抗扰问题研究范畴内的未知输入观测器（Unknown Input Observer, UIO）于1978年由S. Bhattacharyya等[21]正式提出。P. Kudva等[22]建立了UIO的结构，并指出UIO设计的前提条件为观测器匹配条件。M. Darouach等[23]总结了线性系统中全阶UIO的设计方法，使用观测器匹配条件辅助推导过程，后续又对降阶UIO进行了研究[24]。与扰动观测器基于传递函数设计不同，未知输入观测器基于状态空间方法设计，可直接使用于MIMO系统。G. I. Bara等[25]的研究表明，未知输入观测器不仅可用于估计未知输入，也可用于估计输出干扰。以上研究的估计方法均在满足观测器匹配条件下才可成立。观测器匹配条件用于未知输入的解耦，但同时是一个限制性很强的条件，很多常见的物理系统并不满足，严重阻碍了UIO的应用。为了突破该限制，K. Kalsi等[26]提出相对阶的概念来构造辅助输出。张建成等[27]提出用正交矩阵乘以辅助输出的高阶分量，用于解决某些系统中相对阶构造方法仍然失败的问题。UIO在设计时就已经考虑了存在的扰动，关注的是未知输入、测量扰动解耦的问题。
从本质上讲，各类观测器均是使用系统输出变量来修正观测器运行，虽然各种观测器方法的研究深入而丰富，但大多基于已知系统和仿真模型，缺少对工程对象的试验研究。其中有几个重要原因：首先，建立工程对象准确的动力学模型是很困难的，特别是随时间或转速变化的旋转系统，当模型不准确时，观测器仅利用少量的输出来跟踪系统就会出现误差；其次，实际扰动经常在数学模型上难以预见、不可测量，并不是所有的扰动都是缓慢的且导数趋向于0，因而往往会造成离散观测器严重滞后；最后，噪声问题会使得高阶观测器的理论仿真与试验结果不相符，如求逆容易放大噪声，直接求导几乎不可能获得高阶导数信号。
针对AMBs-柔性转子系统中振动位移的跟踪和估计问题，本文提出了一种基于构造二阶导数辅助输出的UIO设计方法，将AMBs-柔性转子系统受到的不平衡力视为系统的未知输入，通过合理设计UIO，可以将系统状态和未知输入同时估计出来。首先，建立了AMBs-柔性转子系统的动力学模型；其次，分析了经典Luenberger状态观测器和滞后问题；然后，阐述了经典UIO的局限性和构造二阶导辅助输出的UIO设计方法，研究了跟踪特性和模态可观性问题；最后，针对AMBs-多盘柔性转子试验系统进行了仿真和试验。
AMBs-柔性转子系统的动力学模型是针对实验室建设的AMBs-柔性转子系统试验台来建立的，如图1所示。
用梁有限元法对转子建模，设节点数为N，转子系统动力学方程为
图1 AMBs-柔性转子系统
Fig.1 AMBs-flexible rotor system
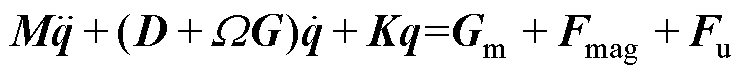（1）
式中，M、D、G、K分别为4N×4N维质量矩阵、阻尼矩阵、陀螺矩阵和刚度矩阵；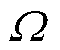
为转速；Fmag为4N×1维电磁力向量；Fu为4N×1维不平衡力向量；Gm为4N×1重力向量；q为位移向量。
AMBs的电磁力是线圈电流i和位移q的非线性函数。在工作点（q0, i0）附近进行线性展开，可表示为
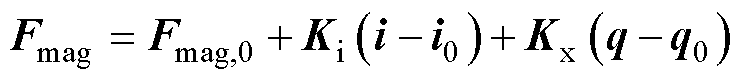（2）
式中，Ki及Kx分别为AMBs的电流刚度系数矩阵和位移刚度系数矩阵；Fmag,0为AMBs在工作点位置的电磁力。
由于两个AMB分别具有水平、垂直两个方向上的位移，AMBs-柔性转子系统是一个MIMO系统。MIMO系统的分析是建立在状态空间方程基础上的，其状态空间方程的表达式为
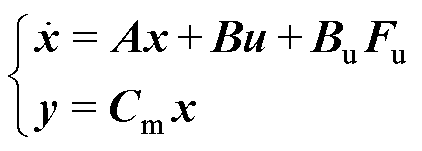（3）
其中
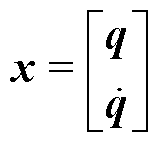
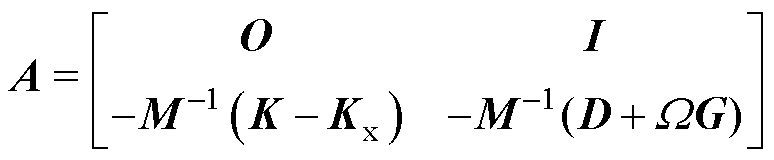
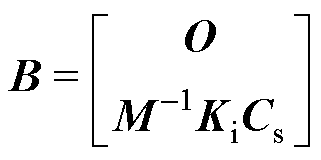
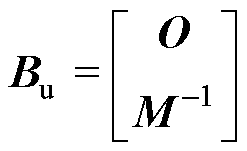
式中，Cs为AMB位置矩阵；Cm为传感器位置矩阵；y为实际转子系统输出；u为AMBs的输入向量；O为零矩阵；I为单位矩阵。
为了对转子有限元模型的准确性进行验证，对该柔性转子进行了自由悬挂状态下的模态试验。图2为转子模态试验的悬挂状态。
图2 模态试验示意图
Fig.2 Picture of modal test
从模态试验数据可以得到转子在自由悬挂状态下的前三阶弯曲模态的固有频率。其结果见表1。
表1 转子模态试验和建模结果对比
Tab.1 Results of modal test and modeling
阶次频率/Hz误差(%) 测试结果建模结果 173.274.92.3 2147.3139.35.4 3337.5345.82.5
经过对比可知，用所建立的有限元模型计算得到的转子在自由状态下的前三阶弯曲模态频率与试验测量结果之间的误差较小，可用作状态观测器的数学模型。
为了重构柔性转子目标位置的振动，可用观测器的方式从数学模型中提取振动信息。状态观测器与原系统并行，其原理是构建与实际转子系统形式相同的数学模型系统。所构建的数学模型系统具有所有的状态变量。经典Luenberger状态观测器的结构如图3所示。图3中，Cd、CdR分别为圆盘节点的输出矩阵，yd为圆盘处的位移。
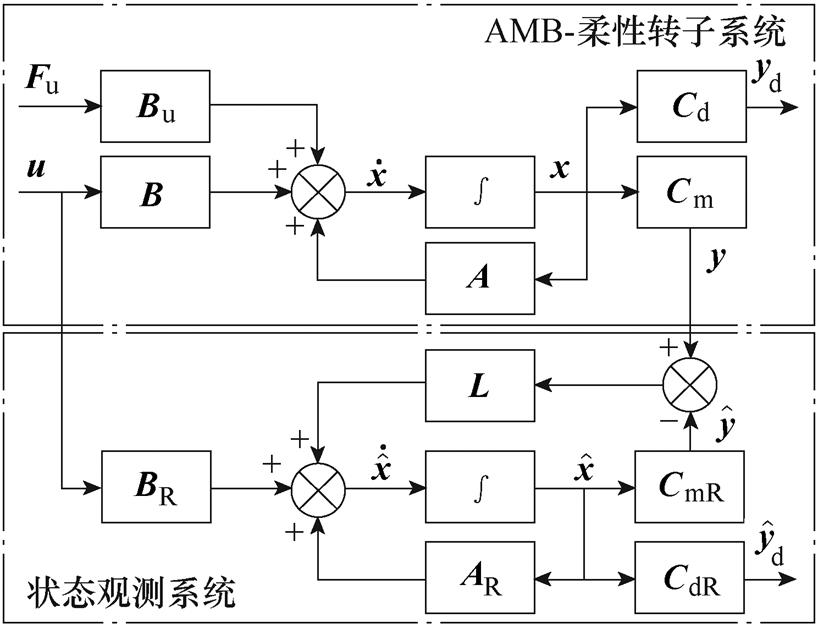
图3 Luenberger观测器结构
Fig.3 The structure of Luenberger observer
状态观测器的方程与转子系统的状态空间方程式（3）类似，为了使状态观测器的运行能正确地反映实际转子系统，用观测器输出与实际转子系统输出的误差乘以观测器增益L来修正状态观测值。其表达式为
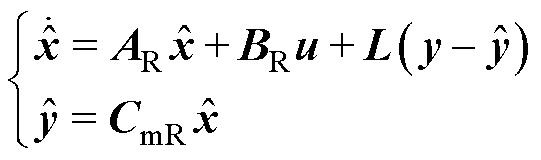（4）
式中，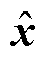
为估计的状态量；
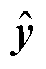为估计的输出量；L为增益矩阵；AR、BR、CmR为状态观测器的数学模型矩阵。
令跟踪误差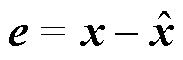
。此时的误差方程为
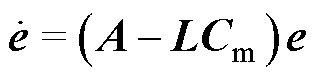（5）
在Luenberger观测器的设计中，选择适当的增益矩阵L，使得A-LCm为Hurwitz，误差状态方程就趋向于0，说明状态观测器渐近收敛到实际系统。增益矩阵L可以通过极点配置法和线性二次型法来配置。
分析状态观测器的过程中必须考虑模型不准确和与转速同频的不平衡力的干扰问题，假设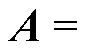
，
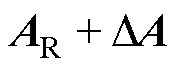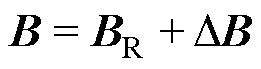，将转子状态方程与状态观测器的方程相减，得到误差状态方程为
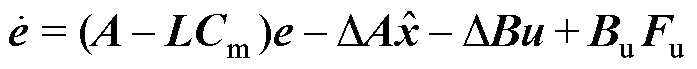（6）
AMBs系统是一个MIMO系统，其误差传递函数是一个矩阵。以其中一个通道的误差传递为例进行分析，其模型的形式为
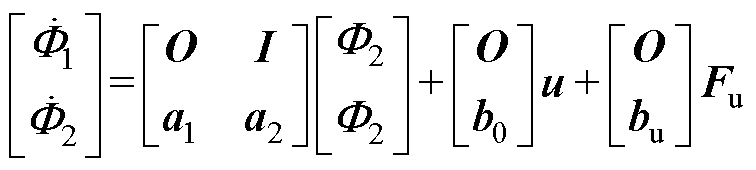（7）
可以推导出观测误差的表达式为
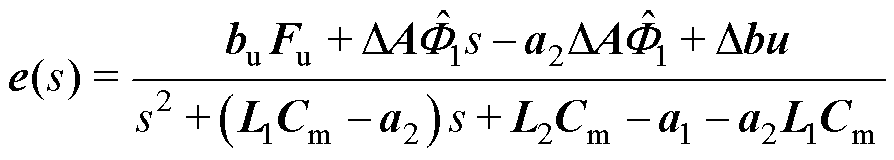（8）
式中，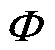
为转子的状态量；a1、a2、b0、bu分别对应单个通道的矩阵量；
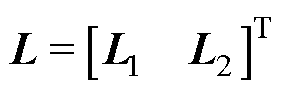。式（8）中考虑了模型不准确因素。
首先，稳态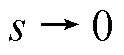
时，除了系统稳定时各个状态量均为0，输入亦为0的特殊情况，
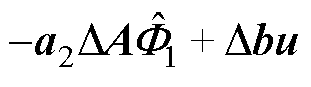不为0，误差方程有静差；其次，转子旋转时
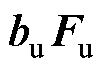项为正弦扰动。对一个通道的二阶物理系统，考察误差比例函数
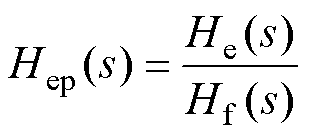（9）
式中，误差传递函数为
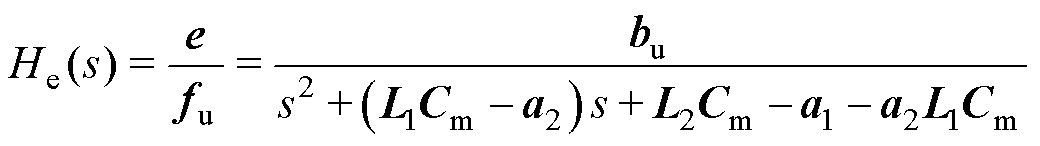（10）
式中，fu为等效为单个通道的不平衡力。
AMBs系统通过PID控制器进行稳定控制，PID控制器的闭环系统可看作为转子提供了等效刚度Ke和等效阻尼De，即AMBs的电磁力fmag为
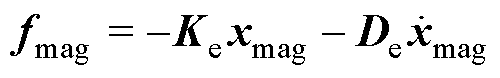（11）
式中，xmag为AMBs处的位移。对于一个具有等效质量me、等效刚度Ke和等效阻尼De的系统，向其中加入不平衡力F，其方程为
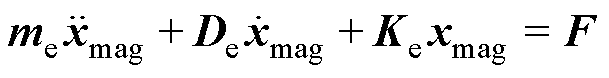（12）
经过拉氏变换，得到F产生的响应为
（13）
误差比例函数反映了观测器误差占总振动幅值的比例。以一个通道为例，将观测器特征方程的极点配置到不同位置时，幅频响应如图4所示。
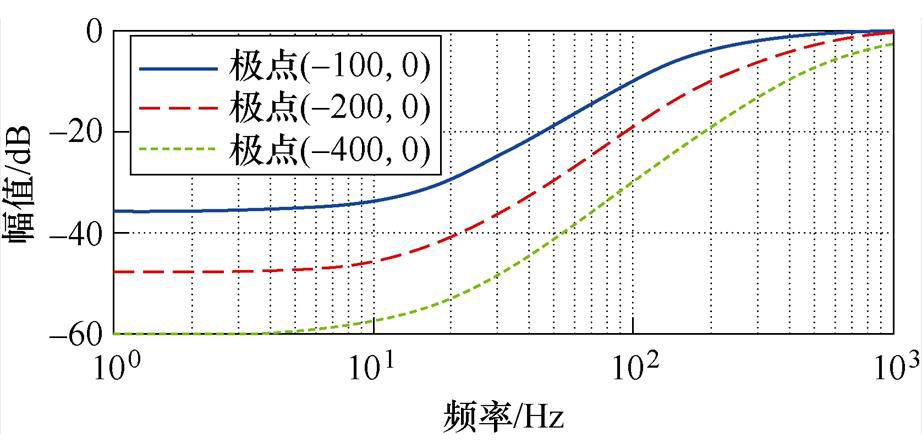
图4 误差比例函数的幅频特性
Fig.4 Amplitude-frequency characteristic of error ratio functions
然后，用误差传递函数考察滞后特性，其相频响应如图5所示。
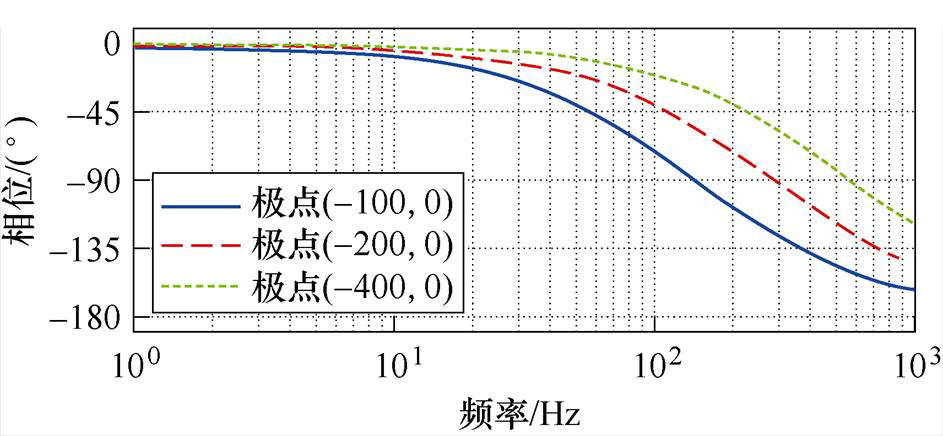
图5 误差传递函数的相频特性
Fig.5 Phase-frequency characteristic of error transfer functions
从图4和图5可知，扰动为正弦时，随着频率升高，状态观测器的误差表现出幅值增大、相位滞后的特征。虽然，调节状态观测器的特征极点（即增大观测器增益）可以减小误差和滞后，但是，一方面，观测器增益增大将大幅度降低抗噪声能力；另一方面，给MIMO系统配置足够大的观测器增益会变得困难。
AMBs-柔性转子系统在运行中持续受到与转速同频不平衡激励力的扰动，这个扰动是转子系统振动的来源。因此，经典Luenberger状态观测器不能准确观测运行的转子系统的状态。
在经典的UIO设计中，考虑具有不平衡力扰动的AMBs-柔性转子系统为
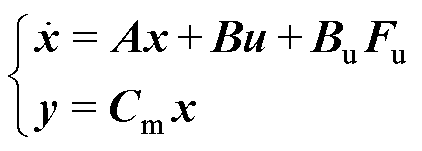（14）
若系统的系数矩阵A、B、Cm、Bu满足以下条件，则可设计对应的UIO：
（1）最小相位条件[22]。即系统（A, Cm, Bu）的不变复零点均位于左半平面。
定义
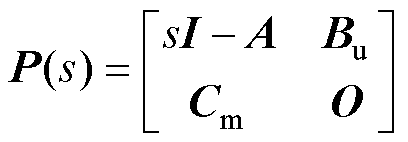（15）
将满足
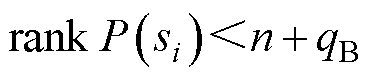（16）
的si定义为系统（A, Cm, Bu）的不变复零点。其中，n为A矩阵的维数，qB为Bu矩阵的列数。当不变复零点si的实部为负时，系统（A, Cm, Bu）为稳定。
该条件实际上与P(s)是列满秩矩阵且所有的特征值都具有负实部等价。一方面，P(s)是列满秩矩阵要求Bu是列满秩矩阵，即保证扰动都对状态量产生作用；另一方面，所有的特征值具有负实部要求原系统矩阵A稳定，即保证观测器系统是稳定的。在开环AMBs-转子系统中，不稳定的因素来源于AMBs自身具有的负位移刚度Kx，接入PID控制器形成稳定闭环系统后，AMBs产生了类似机械轴承的正刚度和正阻尼，因此可满足条件。
（2）观测器匹配条件[22]。即要求
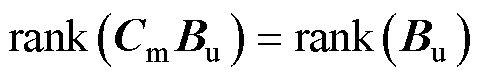（17）
满足以上条件时，可以设计对应的UIO。在设计UIO之前，首先对AMBs-转子系统的方程进行变换。对状态方程的输出矩阵求导可得
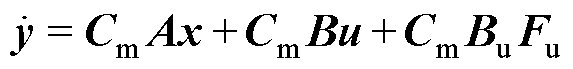（18）
令扩张的输出量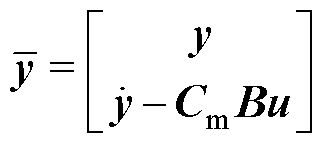
，则式（18）写为
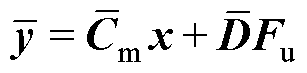（19）
其中
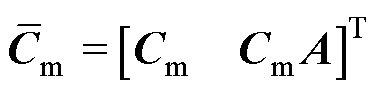
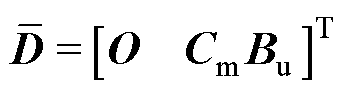
将AMBs-转子系统的扰动扩张为新的状态变量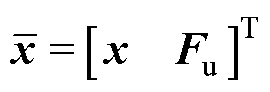
，记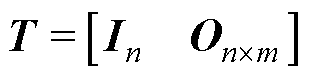
，
，m为Fu的列数。系统的状态方程变为
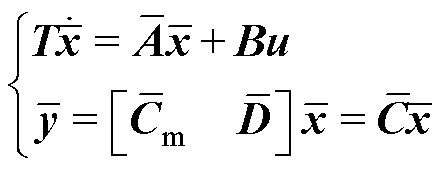（20）
对于矩阵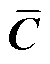
和T，当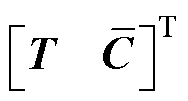
是列满秩矩阵时，存在矩阵G和H，使得
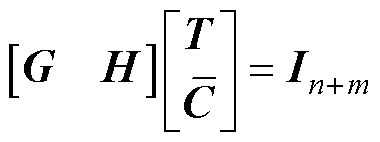（21）
记
，
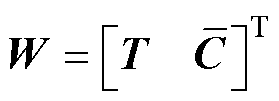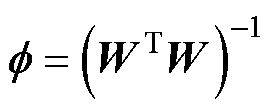，则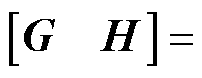
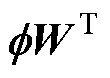，G和H分别为
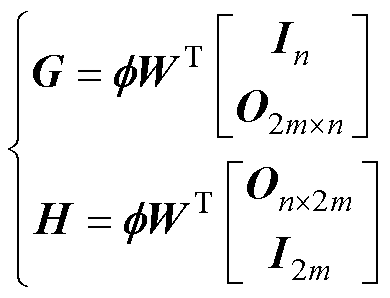（22）
此时
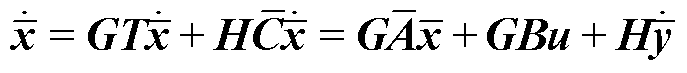（23）
被控的AMBs-转子系统方程变换为式（23）的形式以后，就可以对其设计观测器。经典UIO设计方法中假设rank(CmBu)=rank(Bu)，则
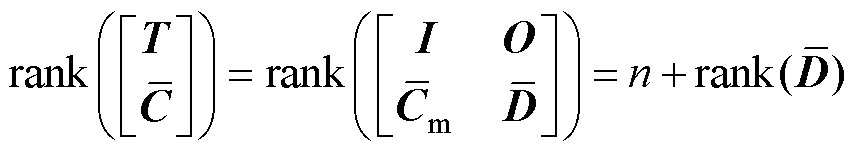（24）
该假设实际上是为了保证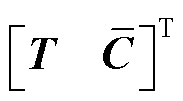
是列满秩矩阵，使得方程式（21）可解出G和H。并且可以看到，rank(CmBu)是状态变量
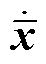中扰动Fu项与输出矩阵直接相关的维数。
设计观测器时，观测器矩阵与原系统相同，再加上修正增益与修正项的乘积。由式（23）可设计UIO状态方程为
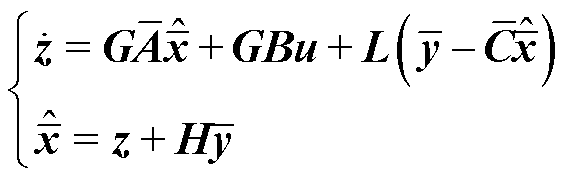（25）
其中
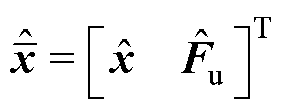
式中，z为观测器的中间状态量；L为增益矩阵。式（25）为系统式（23）的渐近收敛观测器。原系统的状态变量和扰动均可用单位输出矩阵得到。
证明：令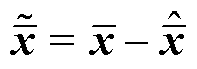
，用式（23）减式（25），得
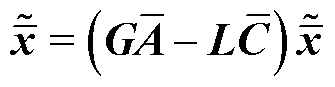（26）
选定增益矩阵L，使得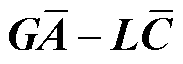
为Hurwitz，那么当t→∞时有
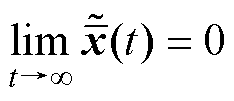，即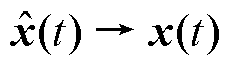
、
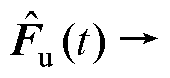
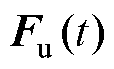，因此方程式（25）为原系统的渐近收敛观测器。
然而，观测器匹配条件在很多系统中并不满足。AMBs-柔性转子系统中，输出矩阵Cm为位移传感器信号，而不平衡力对系统的加速度产生作用，因此二者不匹配，rank(CmBu)实际上为0。观测器匹配条件不满足时，方程式（21）无解。为了实现观测器的匹配，本文基于高阶微分构造辅助输出的思想，提出一种构造辅助输出的实现方法。
在式（18）中，由于CmBu为O，y的一阶导数中不包含扰动信息。对式（18）再求一次导数得
（27）
新构建的扩张输出量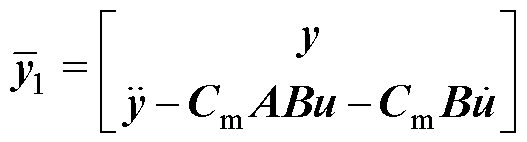
。对应地，有
，
，
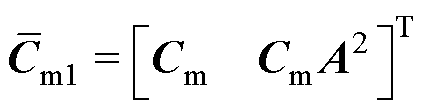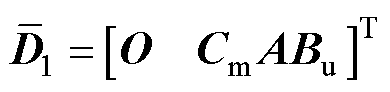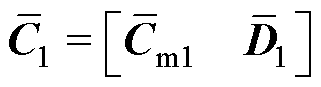。CmABu经计算得知为列满秩矩阵，故构造的扩张输出量满足了式（21）有解的条件。构成的UIO结构如图6所示。
通过计算观测器频率响应的方式来分析UIO观测器的精度，并与其他观测器进行比较。同样以一个AMBs-二阶转子系统为例，重写本文设计UIO的方程为
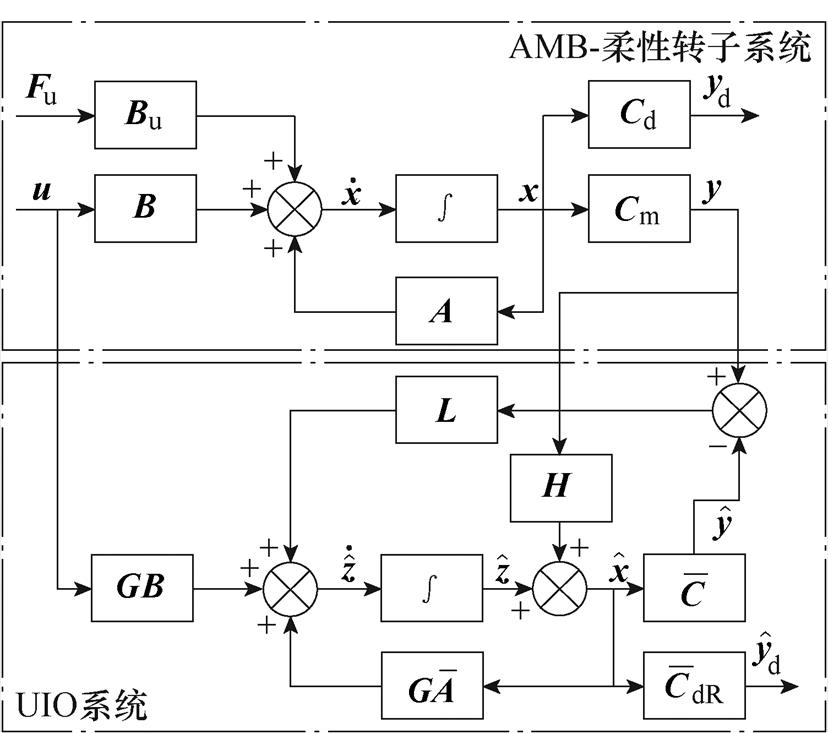
图6 UIO结构
Fig.6 The structure of UIO
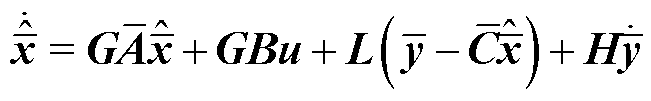（28）
暂时忽略控制量u，式（28）可用Laplace变换为
（29）
令Q矩阵为适当的行变换矩阵，使得左侧的矩阵变换为特征值对角矩阵，有
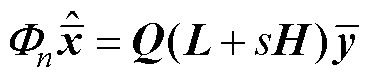（30）
其中
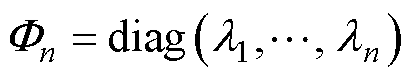
式中，li为特征值。由式（30）的第一行展开可以求得传感器输出y到估计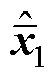
的传递函数表达式。
由式（25）可知，UIO采用了扩张状态项的方法使观测器矩阵快速收敛到物理系统，其特征是对扰动造成的误差具有高增益。Gao Zhiqiang等[28]基于自抗扰理论提出的线性扩张状态观测器（Linear ESO, LESO）也采用了扩张状态项的方法来提高跟踪精度。单通道LESO的方程为
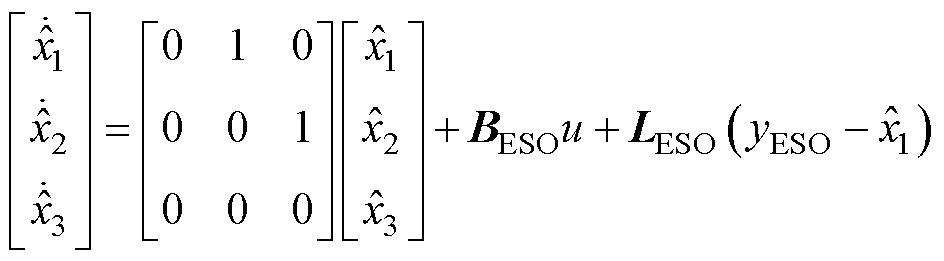（31）
式中，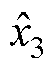
为扩张的扰动估计项；BESO为被观测系统的输入矩阵；LESO为增益矩阵；yESO为LESO的输入。通过将观测器的极点均配置到相同位置处，可得到LESO矩阵的值。与式（29）、式（30）类似，亦可求得Luenberger状态观测器和LESO的传递函数表达式。
采用计算频率响应的方法来验证观测器对输入信号的跟踪能力。此时把所有观测器的状态方程极点均配置到同一个位置（-400, 0），400 rad/s称为观测器带宽。以单个自由度为例，从观测器输入y到估计x1的频率响应如图7所示。
图7 各观测器从输入y到估计x1的频率响应
Fig.7 The frequency response of observers from input y to estimation x1
当输入信号的频率超过观测器带宽（63.7 Hz）后，Luenberger观测器、LESO和不带辅助输出（辅助输出项增益置零）的UIO的幅值不再能保持0 dB，相位开始滞后，说明跟踪精度均出现下降。其中Luenberger观测器的幅值下降最快、相位滞后最严重，在100 Hz附近的相位滞后约为-30 °。从图7的绿线可以看出，本文设计的带辅助输出UIO在0～1 000 Hz的范围内均能保持与原输入相等（0 dB附近），体现了跟踪幅值的优越性。带y二阶导的UIO在0～1 000 Hz的滞后能控制在-10 °以内，具有良好的跟踪特性。
综上所述，可得到如下结论：
（1）将不具有扩张状态项的Luenberger观测器与其他具有扩张状态项的观测器对比可知，扩张状态项在一定程度上提高了跟踪精度，但对于频率超过观测器带宽的输入信号仍然存在明显的精度下降。
（2）将不具有辅助输出的UIO、LESO与具有辅助输出项的UIO对比可知，加入辅助输出后大幅度改善了观测器的性能，在相当大的频率范围内均能保持良好的精度，证明了辅助输出的有效性。
状态可观性问题有两个方面，一为扰动系统能观问题，二为原物理系统的模态可观性问题。
首先，为了保证扰动系统的能观性，要求系统（A,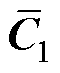 
, 
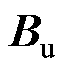）满足最小相位条件。若原系统中（A, Cm, Bu）满足最小相位条件，则
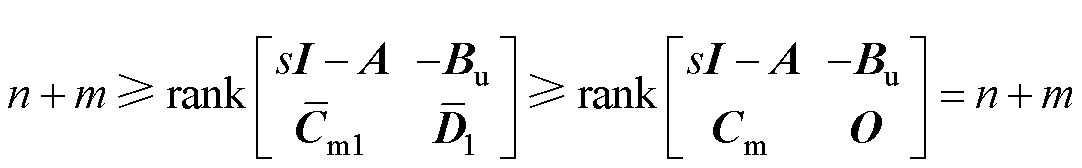（32）
因此，（A, 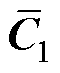, 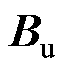）满足最小相位条件。此时原系统的能观性矩阵为
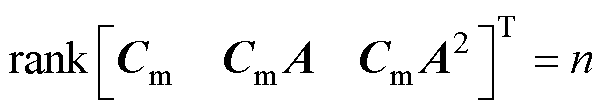（33）
扰动系统的能观性矩阵为
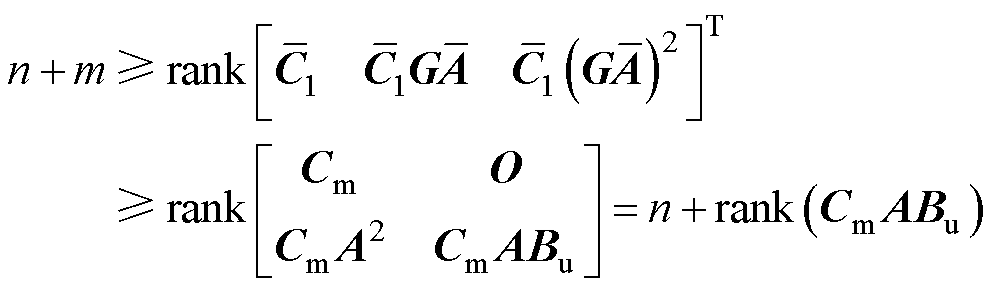（34）
通过计算扰动观测项CmABu列秩来判别扰动系统的能观性。当Cm中的有效行数（行秩）大于或等于Bu中的有效列数（列秩）时，rank(CmABu)=m。因此，扰动系统的可观性要求扰动数量不得超过传感器数量。
其次，原物理系统的模态可观性具有两个条件：
（1）传感器数量条件。使用下列可观性矩阵的秩来定性衡量是否可观
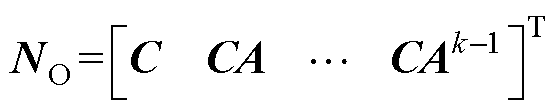（35）
式中，k为系统矩阵阶数。当rank(NO)=k时，系统可观。可观性计算矩阵结果指出，标准的AMBs-转子系统具有4个传感器，只能对刚性转子系统可观。每增加一阶弯曲模态，至少需要增加2个位移传感器。
（2）传感器位置条件。可用Gramian因子衡量系统可观性[29]。可观Gramian因子为
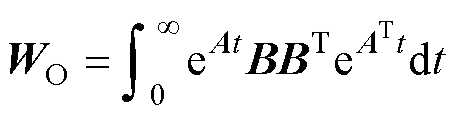（36）
可观Gramian因子可定量地计算出系统的可观性指标。当状态量之间的耦合较小时，Gramian矩阵是对角占优的，故可取Gramian的对角元素作为特征值的近似。
可观Gramian因子对角元素的大小反映了在任意输出中获得特定水平的能量所需的最小能量。当可观Gramian因子较大时，意味着同样的观测效果所需的传感器的放大倍数越小，即该模态可观性强；反之，较弱。刚体平动、锥动、一阶弯曲和二阶弯曲模态（模态序号1, 2, 3, 4）的归一化Gramian因子沿轴向距离变化的分布如图8所示。
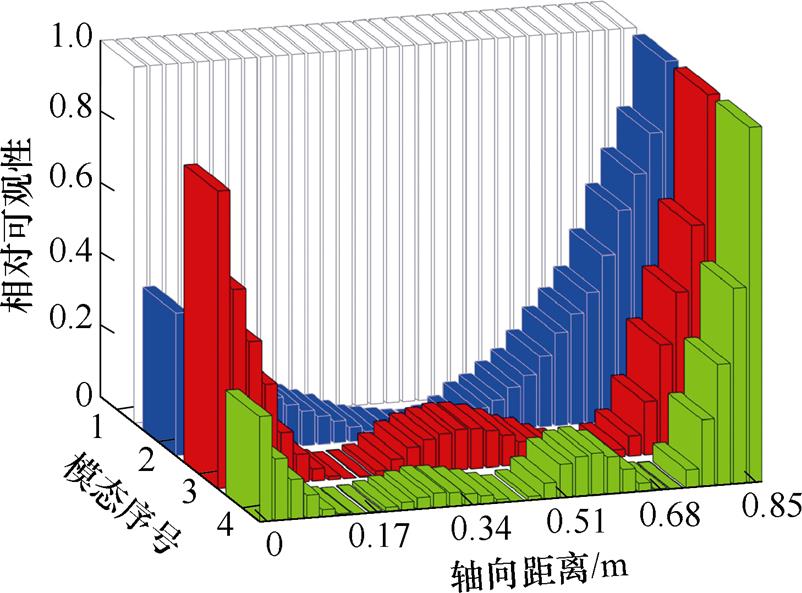
图8 AMBs-柔性转子系统低阶模态的Gramian因子
Fig.8 Gramian factors of lower order modes in AMBs-flexible rotor system
该柔性转子的前四阶振型如图9所示。
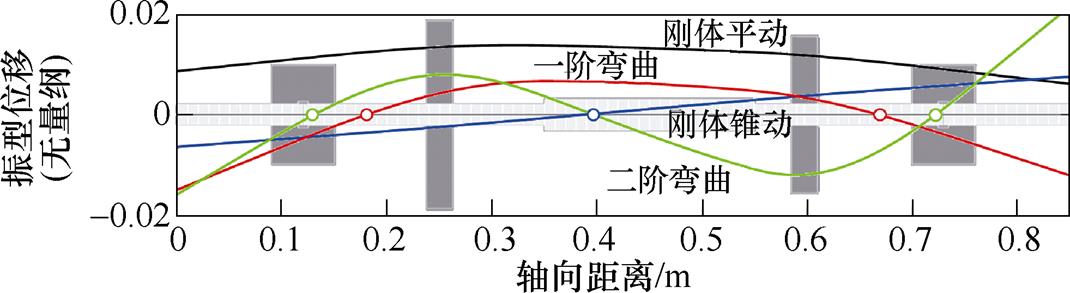
图9 柔性转子低阶模态振型
Fig.9 Mode shapes of flexible rotor
结合图8和图9可以看出，可观性与模态振型节点相关联。在模态节点附近，Gramian因子小、可观性弱。为了保证各受控低阶模态的可观性，要求位移传感器的节点不与某一阶模态节点重合。本文在两个AMBs轴颈之外的轴端和两个圆盘上安装位移传感器，对照图9可知，这些位置附近均没有节点，因此满足模态可观性条件。
为了验证本文提出的未知输入观测器对转子系统振动位移的跟踪和估计能力，搭建了如图10所示的AMBs-多盘柔性转子系统试验台。试验台采用了基于dSPACE 1006的磁悬浮控制器，用高速电机驱动柔性转子旋转。试验台上共安装了8个传感器，除了两对供AMB使用外，在两个刚性圆盘上各安装了一对传感器。柔性转子系统的相关参数见表2。
状态观测器的精度使用两个指标进行衡量，即跟踪精度和估计精度。在本文所研究的AMBs-柔性转子系统中，跟踪精度为观测器系统对已知位置的输出精度，估计精度为观测器系统对待估计位置的输出精度，试验中假设已知位置为AMBs和盘A，待估计位置为盘B。
图10 AMBs-柔性转子试验台
Fig.10 AMBs-flexible rotor test rig
表2 AMBs-柔性转子系统基本参数
Tab.2 Basic parameters of AMBs-flexible rotor system
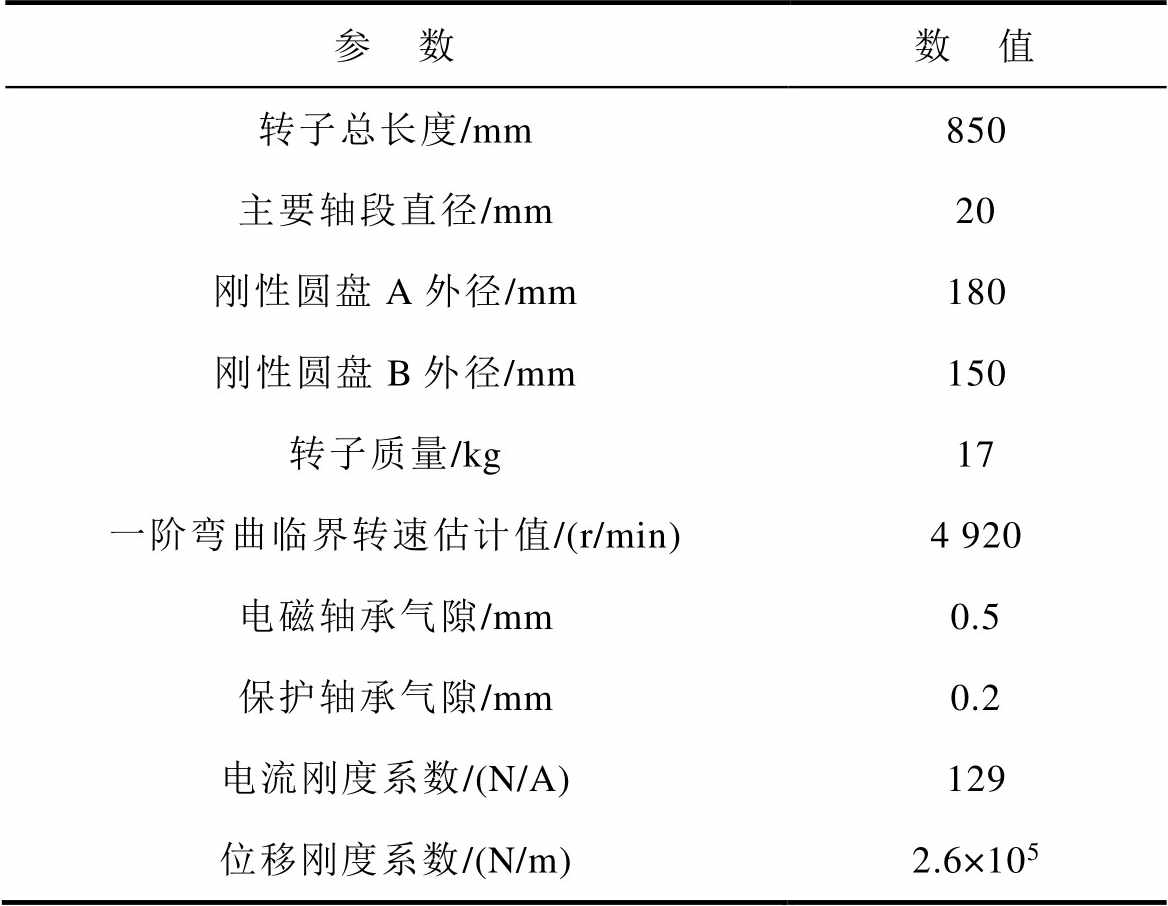
参 数数 值 转子总长度/mm850 主要轴段直径/mm20 刚性圆盘A外径/mm180 刚性圆盘B外径/mm150 转子质量/kg17 一阶弯曲临界转速估计值/(r/min)4 920 电磁轴承气隙/mm0.5 保护轴承气隙/mm0.2 电流刚度系数/(N/A)129 位移刚度系数/(N/m)2.6×105
Luenberger状态观测器和未知输入观测器的跟踪和估计性能仿真系统如图11所示。为了最大程度地模拟实际情况，观测器模型的节点数比主回路柔性转子模型的少，观测器输入不包括AMBs的位移刚度部分。
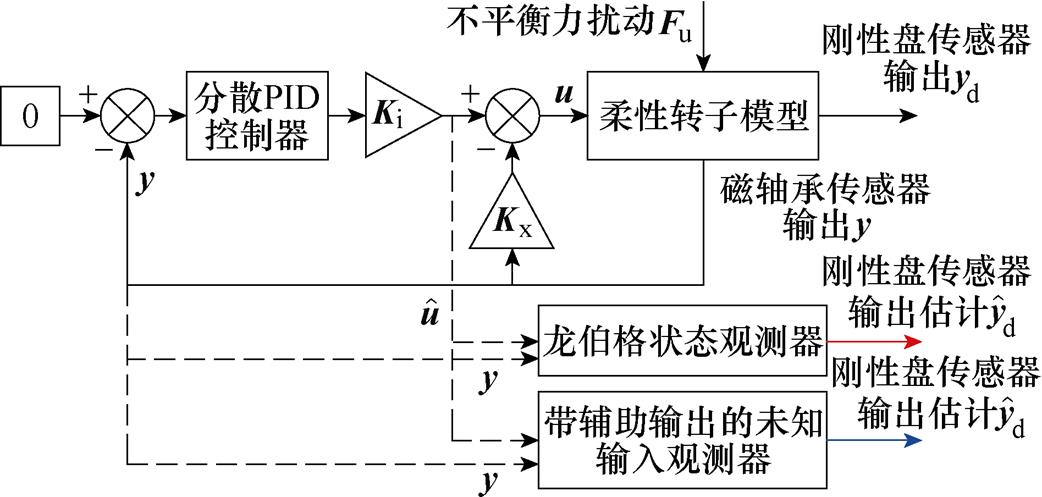
图11 仿真模型示意图
Fig.11 Schematic diagram of simulation model
设定柔性转子受到的恒定幅值电流激励从0 Hz扫描至100 Hz。4个传感器的Luenberger状态观测器（EO-4）、4个传感器的UIO（UIO-4）和6个传感器的UIO（UIO-6，在UIO-4的基础上增加两个盘A的传感器）的跟踪精度对比如图12所示。图12中，XA代表AMB-A的x方向振动位移。对刚性盘位移的估计精度如图13所示。图13中，DXB代表刚性圆盘B（待估计位置）的x方向振动位移。特别地，在转子的弯曲临界运行区间内的70 Hz附近，上述观测器的跟踪精度如图14所示。对刚性盘的估计精度如图15所示。
首先考察跟踪精度。由图12和图14可知，Luenberger状态观测器在低频段跟踪良好，在高频段出现明显的幅值误差和相位滞后；UIO-4和UIO-6在全转速范围都能保持准确跟踪。
图12 观测器跟踪精度的仿真结果
Fig.12 Simulation results of tracking performance
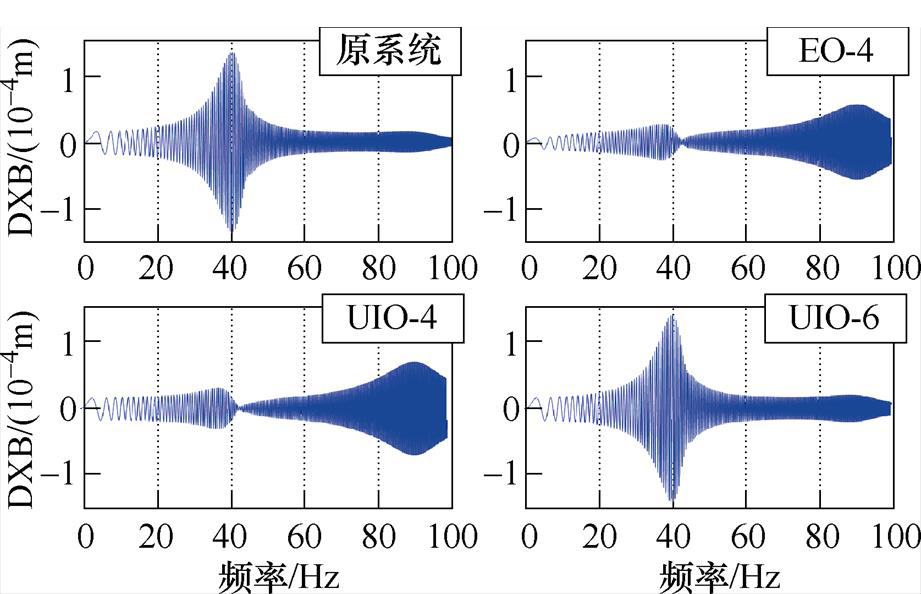
图13 观测器估计精度的仿真结果
Fig.13 Simulation results of estimation performance
图14 70 Hz时观测器的跟踪精度
Fig.14 Tracking performance of 70 Hz
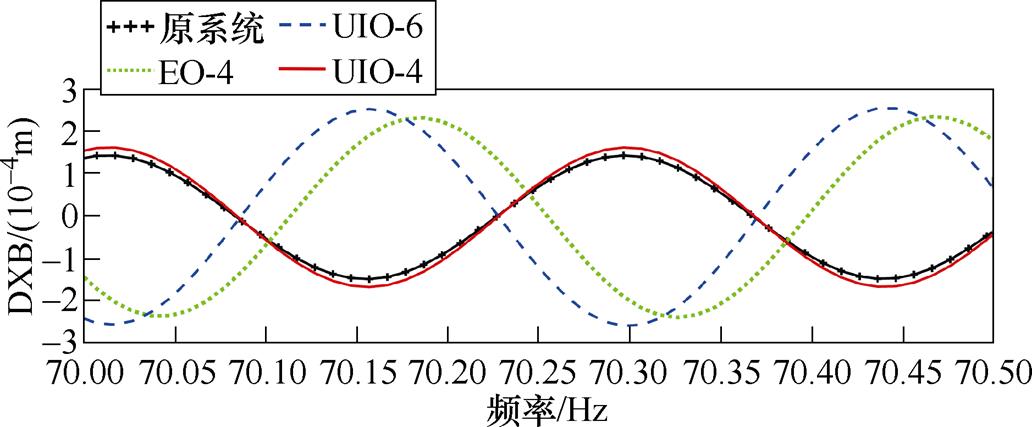
图15 70 Hz时观测器的估计精度
Fig.15 Estimation performance of 70 Hz
然后考察估计精度。由图13和图15可知，由于没有柔性模态信息，在高于刚体模态频率（30 Hz）后EO-4和UIO-4出现了估计错误。UIO-6在全转速范围实现了准确估计，其中，跟踪幅值误差不大于5 %，跟踪相位误差不大于5 °，估计幅值误差不大于10 %，估计相位误差不大于5 °。验证了本文提出的未知输入观测器的有效性。
在如图10所示的试验台上对观测器精度进行了试验验证。因求导会放大噪声，在实际系统中y的二阶导数几乎不能直接通过求导获得，考虑到转子的不平衡力扰动是一个与转速同频率的正弦扰动，其二阶导数恰好是其反相信号，因此将反相的位移信号乘以求导增益倍数作为y的二阶导数信号。
除此之外，为了抑制噪声，在观测器输入前串联二阶谐振器如下
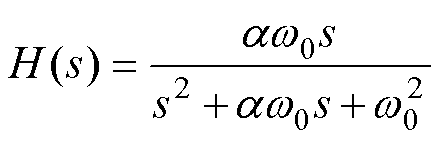（37）
式中，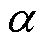
为参数，用于控制阻尼，即控制谐振峰的陡峭程度；w0为谐振器中心频率。
二阶谐振器只提取当前转速频率的分量，不仅能有效抑制高频噪声，还能抑制因传感器支架振动导致的电压零点漂移。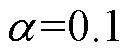
时二阶谐振器的伯德图如图16所示。
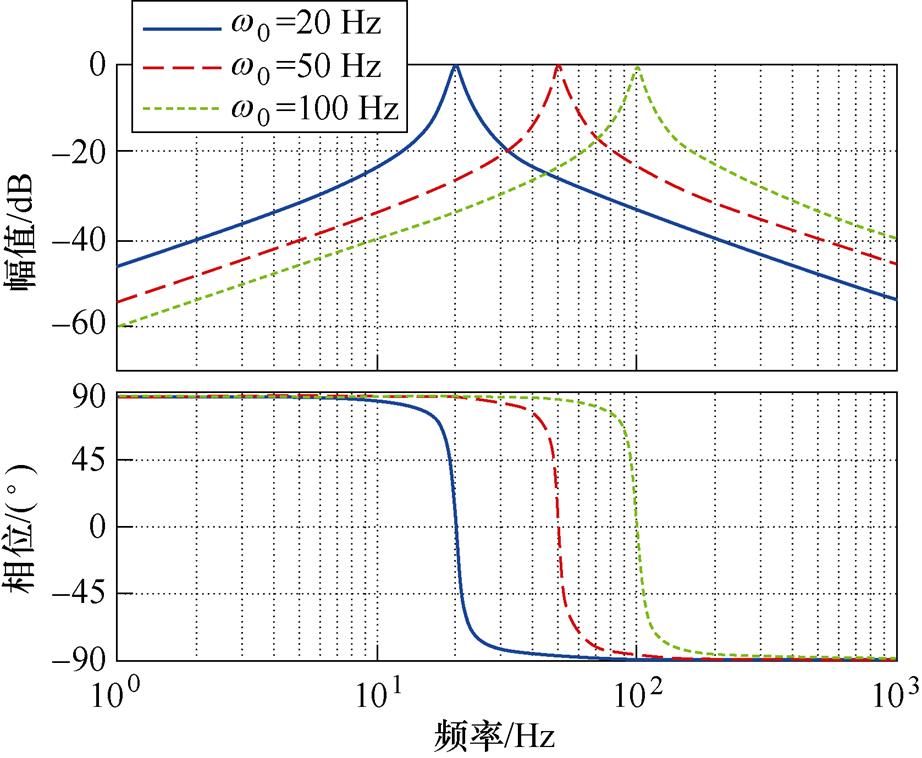
图16 二阶谐振器的伯德图
Fig.16 Bode plot of second order resonance
从仿真的结果得知，刚性盘在40～50 Hz之间出现位移峰值，该峰值处于转子的锥动临界和一阶弯曲临界转速之间；在刚体模态临界和一阶弯曲临界的位移都很小，因此，应重点考察50 Hz附近的跟踪精度和估计精度。
4.2.1 模拟电流激励试验
转子稳定悬浮时，向AMBs中施加旋转的电流激励来模拟旋转时受到的不平衡力。首先验证本文所述Luenberger观测器滞后问题和模态可观性，设定激励频率30 Hz。试验结果如图17所示。
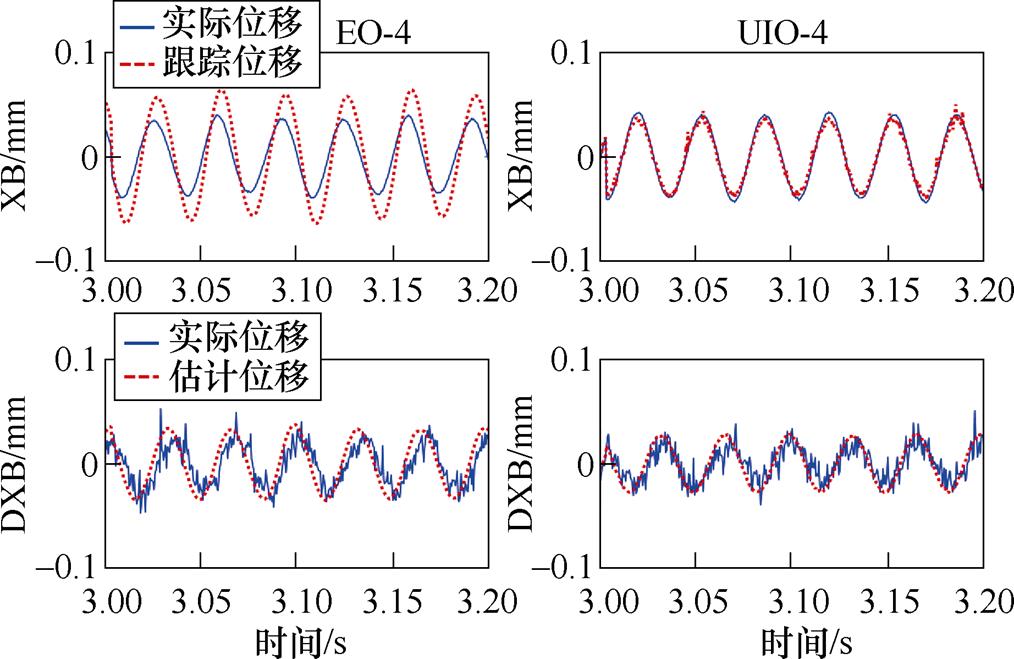
图17 模拟旋转电流激励试验结果
Fig.17 Experimental results of rotational current exciting
然后，设定激励频率为50 Hz。得到观测器的跟踪精度和估计精度的试验结果如图18所示。
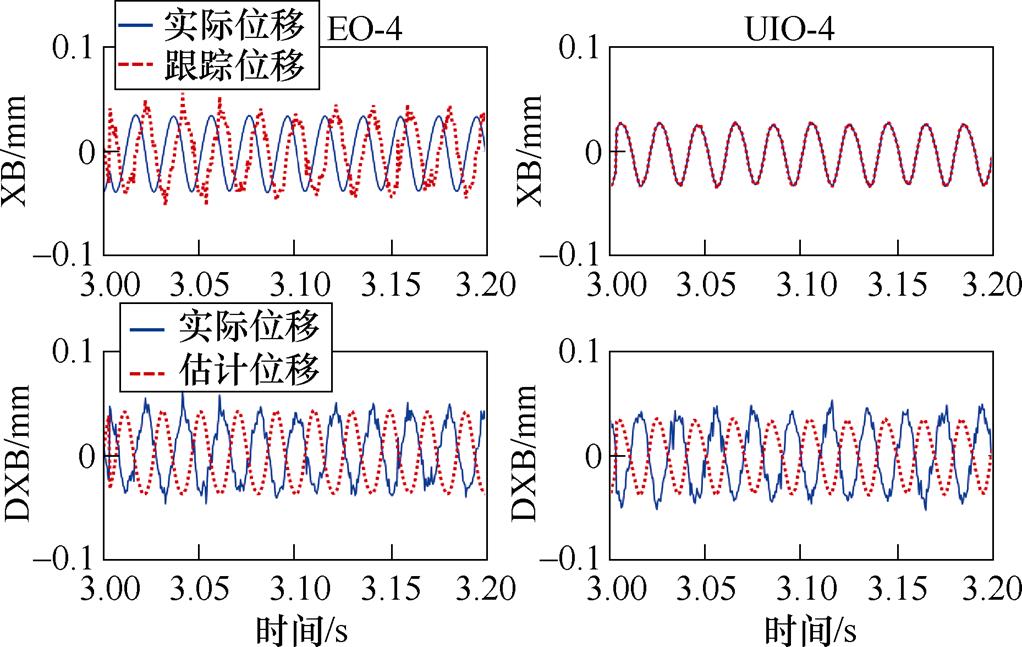
图18 模拟旋转电流激励的跟踪精度和估计精度
Fig.18 Tracking and estimation performance of rotational current exciting
用图17和图18上方的两个图考察跟踪精度，可知Luenberger状态观测器在低频和中频均有明显的相位滞后，而UIO-4具有很高的跟踪精度。用图17和图18下方的两个图考察估计精度，可知在30 Hz时两个观测器均能有效估计，而在50 Hz时两个观测器均出现观测错误。由此可得到以下结论：UIO-4相比Luenberger观测器具有更高的跟踪性能，但跨越过刚体临界后，估计得到的振动位移与实际位移反向。这是因为转子已经激发出一阶弯曲模态信号，只有4个传感器不满足模态可观条件，出现了估计错误。
分析得知，若需观测一阶弯曲模态，需要在原来4个传感器的基础上再增加2个传感器。以下进行UIO-6的试验。试验中AMBs附近的传感器为10 V/mm灵敏度，而安装在盘上的传感器为5 V/mm灵敏度，其输出信号中有更大的噪声，对UIO-6的跟踪提出了更高要求。
首先，考察UIO-6的跟踪精度。电流激励70 Hz的试验结果如图19所示。纵坐标的XA代表AMB-A的x方向位移，DXA代表盘A的x方向位移，其他类似。
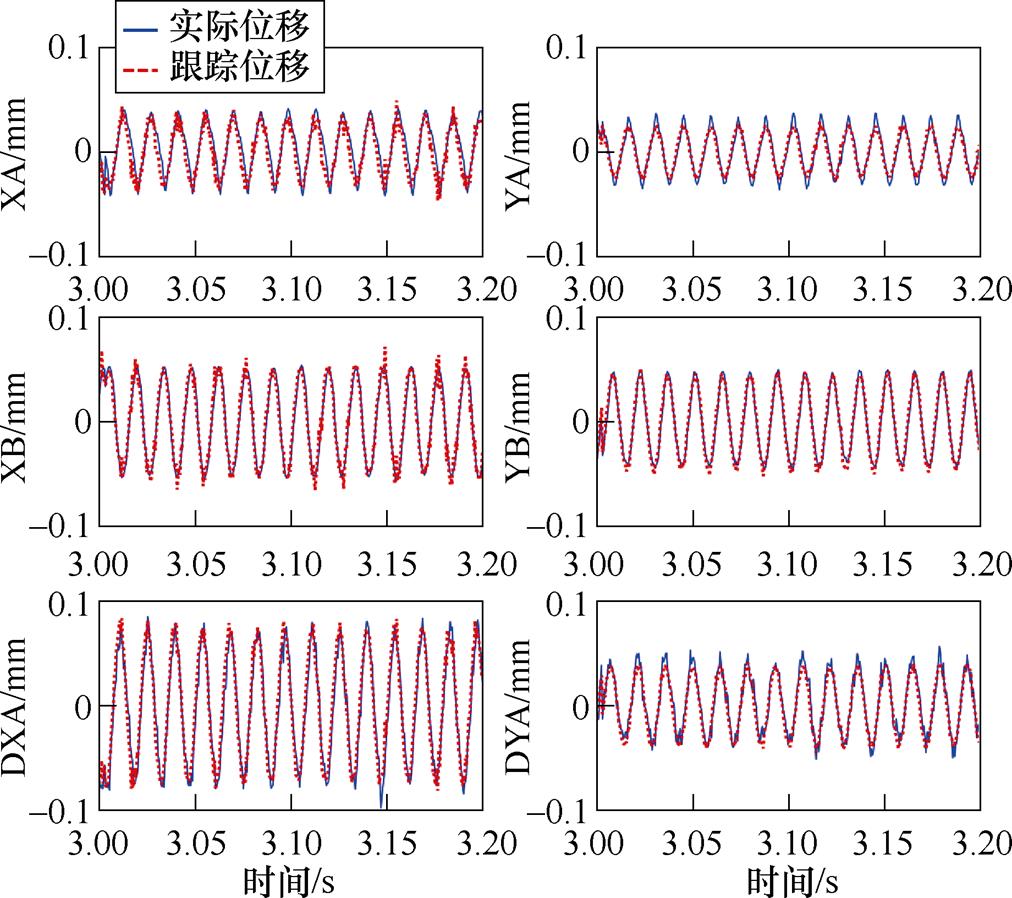
图19 70 Hz下6个输入通道的UIO-6的跟踪精度
Fig.19 Tracking performance of UIO-6 on 6 input channels in 70 Hz
从70 Hz激励的结果可以看出，UIO-6对4个轴承、2个盘A共6个传感器的振动都进行了高精度跟踪。因此，通过合理设计UIO，能在所有输入通道内全部达到高精度跟踪效果。
然后，考察UIO-6对盘B的估计精度。分别注入30、50和70 Hz激励电流的试验结果如图20所示。30 Hz恰好位于刚体临界处，因此振幅较大。UIO-6在低频段的估计位移接近正弦波，幅值与相位与实际位移相同。在一阶弯曲临界的70 Hz附近振动复杂，圆盘位移传感器的信号噪声强烈，但UIO-6仍能以小噪声准确估计，没有观测滞后。
4.2.2 旋转试验
转子旋转时，转子振动信号中加入了倍频分量，噪声比电流激励试验更大。首先，在转子旋转的1 800、3 000和4 200 r/min分别进行恒速试验。对盘B的估计结果如图21所示。
UIO-6的估计位移幅值准确，相位无滞后。其中，估计幅值误差不大于10 %，估计相位误差不大于20 °，在50 Hz附近振幅的尖峰位置对噪声具有较强的抑制能力。
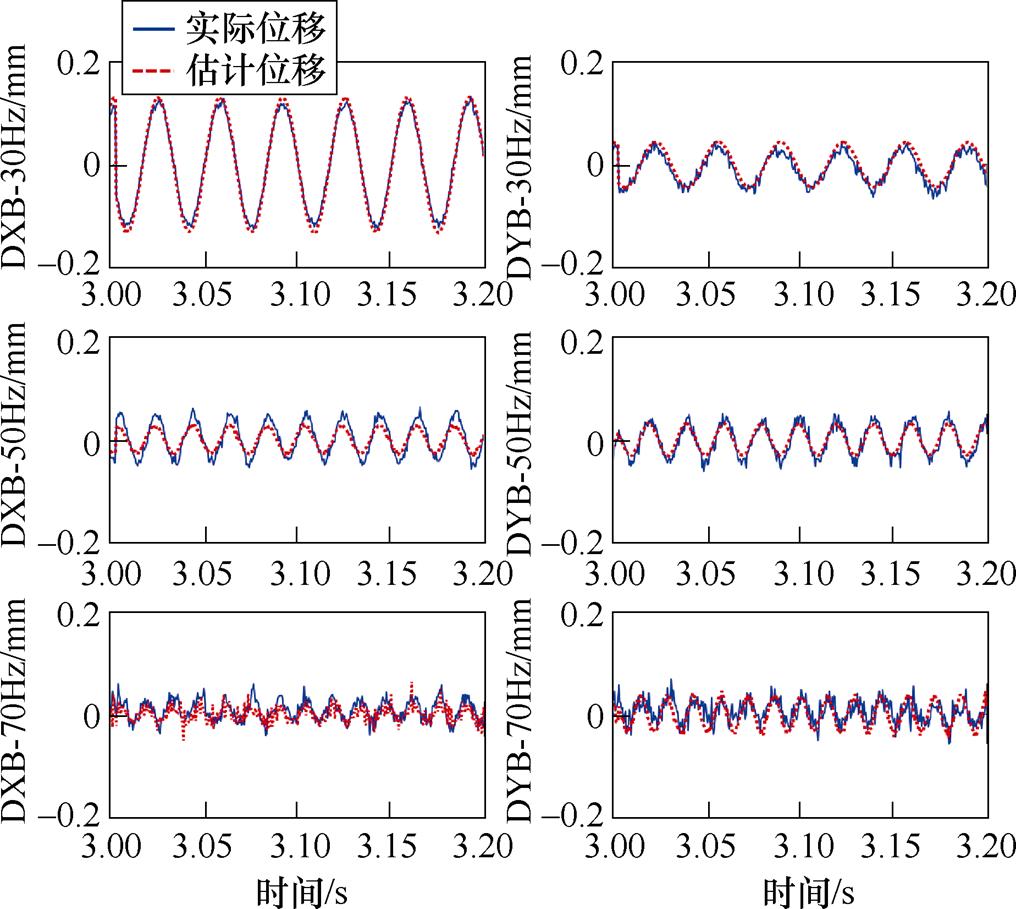
图20 不同转速频率下UIO-6的估计精度
Fig.20 Estimation performance of UIO-6 in different exciting frequencies
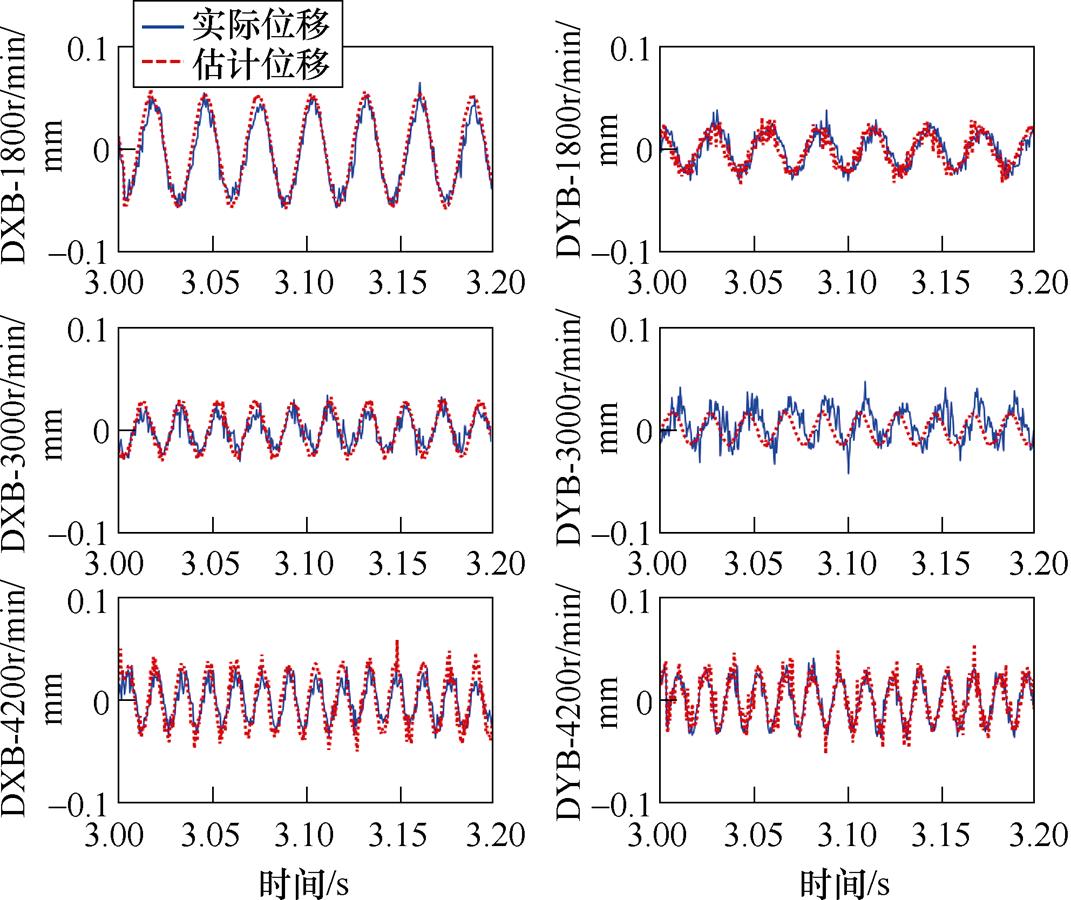
图21 不同转速试验中，UIO-6对盘B的估计精度结果
Fig.21 Estimation performance of disk-B of UIO-6 in different rotational speed
然后，进行转子加速试验。在电机轴上安装了键相传感器，用脉冲信号计算实时转速，计算结果用于谐振器的中心频率更新。转子从静止加速旋转至6 000 r/min（100 Hz），对6个传感器通道的跟踪精度和对盘B的估计精度分别如图22和图23所示。
考察UIO-6的跟踪精度。由图22可知，UIO在6个通道内都能准确跟踪加速旋转的转子系统，对复杂且不同通道不同时刻的振峰位移均能逐一贴合跟踪。圆盘传感器跟踪结果的噪声比实际少，说明观测器的跟踪信号降低了噪声灵敏度。
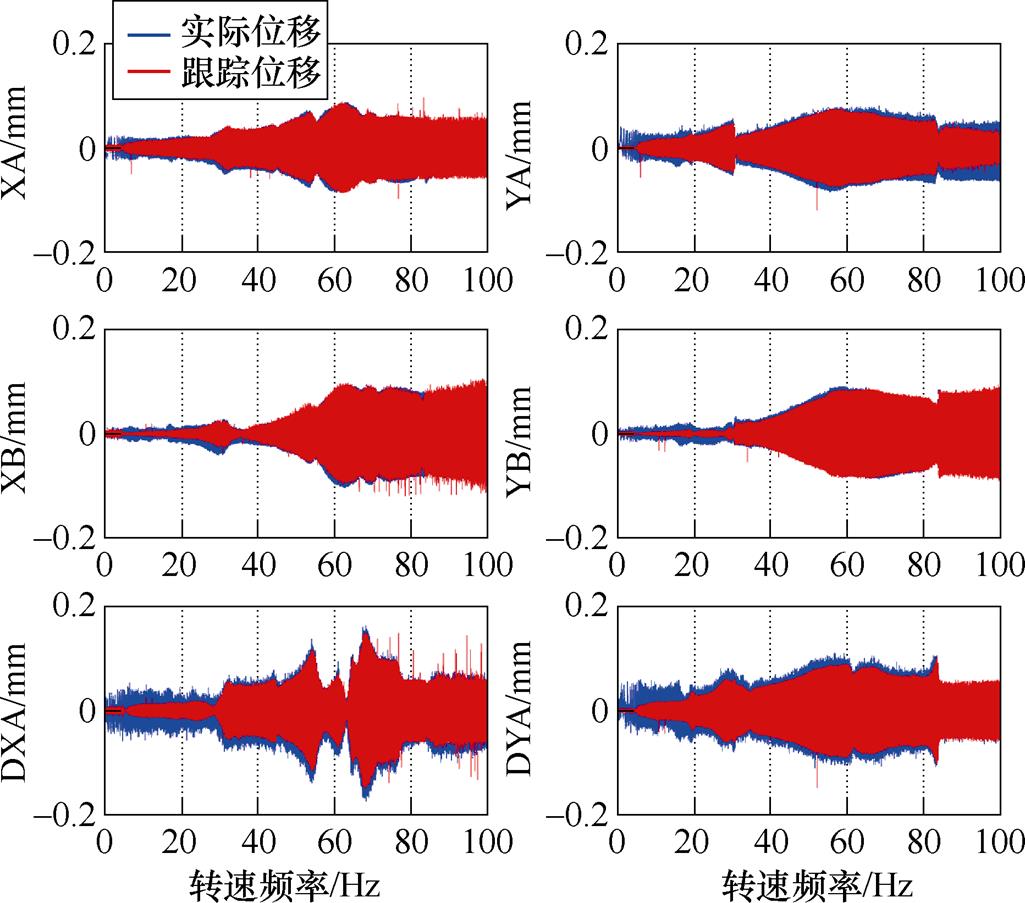
图22 加速过程中，UIO-6的跟踪精度结果
Fig.22 Tracking performance of UIO-6 in whole acceleration process
考察UIO的估计精度。由图23可知，水平方向上圆盘的位移具有两个明显的共振峰，分别是30 Hz左右的刚体临界峰和60～70 Hz的一阶弯曲临界峰。通过振幅对比可知，UIO在两个临界峰处均可有效估计；UIO的估计信号的噪声更少。
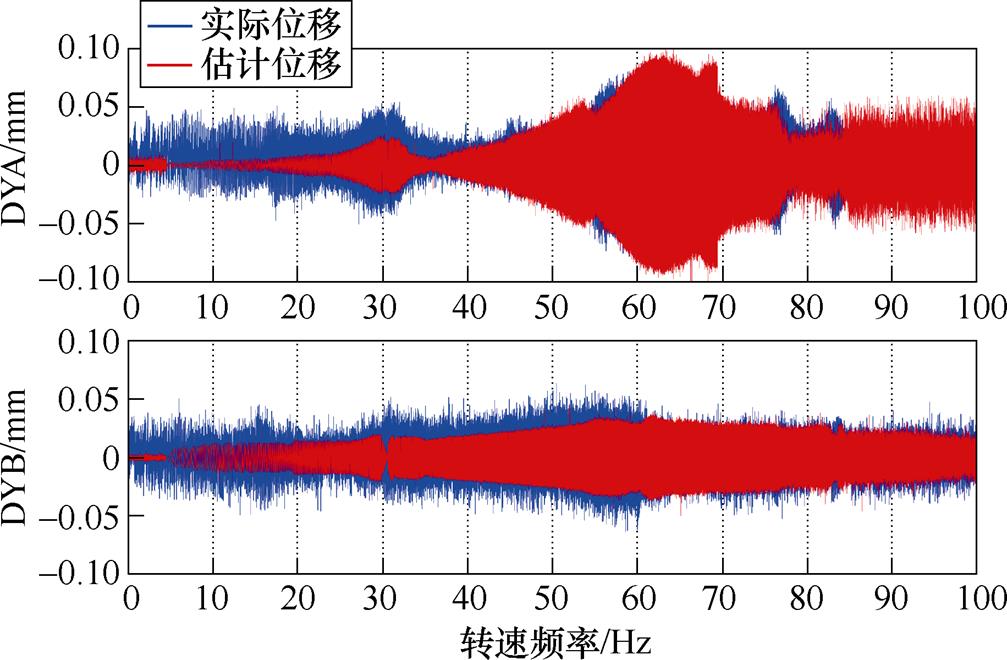
图23 加速过程中，UIO-6的估计精度结果
Fig.23 Estimation performance of UIO-6 in whole acceleration process
对比转子AMBs处振动与圆盘位置振动可知，转子在刚体区域内运行时，AMBs处振峰和圆盘振峰出现的频率相同，均为30 Hz；而转子在柔性区域内运行时，二者出现的频率不同，其中，AMBs处约为90 Hz且不明显，圆盘处为65 Hz附近。以上试验结果验证了本文提出的UIO-6能对AMBs-柔性转子系统的振动位移进行高精度的跟踪和估计。
由于圆盘直径较大便于安装电涡流传感器，本文以刚性圆盘的振动为跟踪和估计目标。实际上传感器也可安装在满足模态可观性条件的其他位置。
本文对AMBs-柔性转子系统轴段上目标位置的振动位移跟踪和估计进行了研究。针对经典Luenberger状态观测器存在的滞后，本文设计了未知输入观测器来观测转子系统，并提出基于二阶导数构造辅助输出的方法解决了观测器匹配条件不满足的问题，研究了跟踪特性和可观性。对AMBs-多盘柔性转子试验系统进行了仿真和试验，可得到如下结论：
1）本文利用传感器输出的二阶导数作为辅助输出构建UIO，在0～6 000 r/min的刚体和柔性运行区域均能实现高精度跟踪系统输出，并能准确估计目标位置的振动位移。
2）构造辅助输出保证了高精度跟踪，满足模态可观性，可完成状态的准确估计。
3）试验中利用可变中心频率的谐振器和以–y乘以导数增益作为y的二阶导数，可在不损失精度的前提下抑制噪声。
参考文献
[1] Maslen E H, Schweitzer G. Magnetic bearings: theory, design, and application to rotating machinery[M]. Berlin, Heidelberg: Springer, 2009.
[2] Siva Srinivas R, Tiwari R, Kannababu C. Application of active magnetic bearings in flexible rotordynamic systems-a state-of-the-art review[J]. Mechanical Systems and Signal Processing, 2018, 106: 537-572.
[3] 巩磊, 杨智, 祝长生. 主动电磁轴承-刚性转子系统加速响应的鲁棒性[J]. 电工技术学报, 2021, 36(2): 268-281.
Gong Lei, Yang Zhi, Zhu Changsheng. Acceleration responses robustness of active magnetic bearings- rigid rotor system[J]. Transactions of China Elec- trotechnical Society, 2021, 36(2): 268-281.
[4] 禹春敏, 邓智泉, 梅磊, 等. 基于精确磁路的新型混合型轴向-径向磁悬浮轴承研究[J]. 电工技术学报, 2021, 36(6): 1219-1228.
Yu Chunmin, Deng Zhiquan, Mei Lei, et al. Research of new hybrid axial-radial magnetic bearing based on accurate magnetic circuit[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1219-1228.
[5] 张静, 宋宝林, 谢松霖, 等. 基于状态估计的高速受电弓鲁棒预测控制[J]. 电工技术学报, 2021, 36(5): 1075-1083.
Zhang Jing, Song Baolin, Xie Songlin, et al. Robust predictive control of high-speed pantograph based on state estimation[J]. Transactions of China Electro- technical Society, 2021, 36(5): 1075-1083.
[6] Luenberger D G. Observing the state of a linear system[J]. IEEE Transactions on Military Electronics, 1964, 8(2): 74-80.
[7] Meier L, Luenberger D. Approximation of linear constant systems[J]. IEEE Transactions on Automatic Control, 1967, 12(5): 585-588.
[8] Tang T S, Huang G M. On control of large space structure[C]//1990 American Control Conference, San Diego, CA, USA, 2009: 2965-2970.
[9] Balas M J. Active control of flexible systems[J]. Journal of Optimization Theory and Applications, 1978, 25(3): 415-436.
[10] 曲志强, 高为炳. 大型柔性空间结构的状态估计及变结构控制[J]. 北京航空航天大学学报, 1989, 15(3): 17-25.
Qu Zhiqiang, Gao Weibing. State estimation and variable structure control of flexible spacecrafts[J]. Journal of Beijing University of Aeronautics and Astronautics, 1989, 15(3): 17-25.
[11] 王霈霈. 主动电磁轴承-柔性转子系统的振动分析与控制[D]. 杭州: 浙江大学, 2020.
[12] 耿晓晓. 电磁轴承-柔性转子系统过一阶弯曲临界转速区的滑膜振动控制[D]. 杭州: 浙江大学, 2020.
[13] Gosiewski Z, Kulesza Z. Virtual collocation of sensors and actuators for a flexible rotor supported by active magnetic bearings[C]//Proceedings of the 14th International Carpathian Control Conference (ICCC), Rytro, Poland, 2013: 94-99.
[14] Chen Wenhua, Yang Jun, Guo Lei, et al. Disturbance- observer-based control and related methods—an overview[J]. IEEE Transactions on Industrial Elec- tronics, 2015, 63(2): 1083-1095.
[15] Peng Cong, Fang Jiancheng, Xu Xiangbo. Mismatched disturbance rejection control for voltage-controlled active magnetic bearing via state-space disturbance observer[J]. IEEE Transactions on Power Electronics, 2015, 30(5): 2753-2762.
[16] Gong Lei, Zhu Changsheng. Vibration suppression for magnetically levitated high-speed motors based on polarity switching tracking filter and disturbance observer[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(6): 4667-4678.
[17] 韩京清. 一类不确定对象的扩张状态观测器[J]. 控制与决策, 1995, 10(1): 85-88.
Han Jingqing. The “extended state observer” of a class of uncertain systems[J]. Control and Decision, 1995, 10(1): 85-88.
[18] 郭凯旋. 基于自抗扰理论的磁悬浮轴承控制系统设计与研究[D]. 南京: 南京航空航天大学, 2017.
[19] 朱良红, 张国强, 李宇欣, 等. 基于级联扩张观测器的永磁电机无传感器自抗扰控制策略[J]. 电工技术学报, 2022, 37(18): 4614-4624.
Zhu Lianghong, Zhang Guoqiang, Li Yuxin, et al. Active disturbance rejection control for position sensorless permanent magnet synchronous motor drives based on cascade extended state observer[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4614-4624.
[20] 李思毅, 苏健勇, 杨贵杰. 基于自抗扰控制的永磁同步电机弱磁控制策略[J]. 电工技术学报, 2022, 37(23): 6135-6144.
Li Siyi, Su Jianyong, Yang Guijie. Flux weakening control strategy of permanent magnet synchronous motor based on active disturbance rejection control[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6135-6144.
[21] Bhattacharyya S. Observer design for linear systems with unknown inputs[J]. IEEE Transactions on Auto- matic Control, 1978, 23(3): 483-484.
[22] Kudva P, Viswanadham N, Ramakrishna A. Observersfor linear systems with unknown inputs[J]. IEEE Transa- ctions on Automatic Control, 1980, 25(1): 113-115.
[23] Darouach M, Zasadzinski M, Xu S J. Full-order observers for linear systems with unknown inputs[J]. IEEE Transactions on Automatic Control, 1994, 39(3): 606-609.
[24] Darouach M, Zasadzinski M, Hayar M. Reduced- order observer design for descriptor systems with unknown inputs[J]. IEEE Transactions on Automatic Control, 1996, 41(7): 1068-1072.
[25] Bara G I, Rafaralahy H, Zasadzinski M, et al. State observers for a class of bilinear descriptor systems subjected to unmeasurable disturbances[C]//Proceedings of the 38th IEEE Conference on Decision and Control, Phoenix, AZ, USA, 2002: 85-87.
[26] Kalsi K, Lian Jianming, Hui S, et al. Sliding-mode observers for systems with unknown inputs: a high- gain approach[J]. Automatica, 2010, 46(2): 347-353.
[27] 张建成, 朱芳来. 匹配条件不满足时线性系统未知输入观测器设计[J]. 控制理论与应用, 2017, 34(4): 441-448.
Zhang Jiancheng, Zhu Fanglai. Linear system unknown input observer design when the observer matching condition is not satisfied[J]. Control Theory & Applications, 2017, 34(4): 441-448.
[28] Gao Zhiqiang, Hu Shaohua, Jiang Fangjun. A novel motion control design approach based on active disturbance rejection[C]//Proceedings of the 40th IEEE Conference on Decision and Control, Orlando, FL, USA, 2002: 4877- 4882.
[29] 孟占峰, 韩潮. 模态密集柔性空间结构二阶内平衡降阶[J]. 航空学报, 2008, 29(2): 364-372.
Meng Zhanfeng, Han Chao. Second-order balanced reduction for flexible space structures with close modes[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(2): 364-372.
Abstract Supporting by active magnetic bearings (AMBs), the AMBs-flexible rotor system works near and above the first-order bending critical speed. Because of the deformation of the shaft, the displacement of other positions on the shaft cannot be inferred from the displacement of the two AMBs through simple mathematical calculations. Therefore, when controlling other positions is needed, an estimator construct by the observer is the key to tracking and obtaining the real-time displacement.
As the classical observer in control theory, the Luenberger observer can obtain the state of system by output. However, the design of the Luenberger observer needs to consider mathematical model error and continuous disturbance, which leads to less application in industry and lagging tracking. The Unknown Input Observer (UIO) is designed to keep track of unknown inputs in the system. Since the unbalance force in AMBs-flexible rotor system can be regarded as unknown input. It can be estimated by UIO to realize fast tracking and estimation.
There are two preconditions in the design of UIO. The first one is that the invariant zeros of the system (A, Cm, Bu) are all in the left half plane. This condition is equivalent to the disturbance input matrix Bu being full of rank and the system matrix A being stable. Since the AMB under the PID controller can provide positive stiffness and damping similar to mechanical bearings, the system matrix A is considered stable. The second condition is the observer matching condition, requiring rank(CmBu)=rank(Bu). While meeting these two conditions, the form of UIO can be designed as follows.
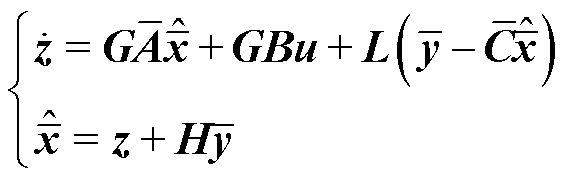
However, the observer matching condition is only satisfied in some systems. In the AMBs-flexible rotor system, the output matrix Cm is the position of the displacement sensors, and the unbalanced force acts on the acceleration of the system, resulting in rank (CmBu)=0. In order to achieve the matching of observers, this paper proposes an implementation method for constructing auxiliary outputs. By taking the second derivative of the output equation, the new output includes the original output y and auxiliary output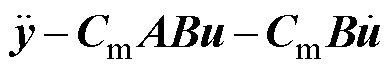 
. The new input matrix CmABu is full of rank, satisfying the matching condition.
The state observability needs to be solved before observing the AMBs-flexible rotor system. The first is the observable condition of the disturbance system, which requires that the number of disturbances cannot exceed the number of sensors. The second is the observable condition of the flexible rotor system, which requires at least n displacement sensors to estimate n nodes, including rigid modes. When observing the first-order bending mode, six displacement sensors are required. In addition, the observability of the system is calculated using the Gramian factor, and the positioning node of the sensor cannot be located near the mode shape node.
The tracking performance of the observers is studied by calculating the frequency response in the SISIO case. Compared with the Luenberger observer, the LESO with an extended disturbance state performs better but still suffers from phase lag when the input frequency exceeds the observer bandwidth. The UIO with auxiliary output can track the physics system accurately over a large frequency area.
Simulations and experiments are carried out to verify the proposed method. Tracking performance refers to the ability of the observer to track the existing output. Estimation performance refers to the ability to obtain the target position. In this paper, the existing outputs are 6 sensors of AMBs and disk A. The position to be estimated is the node of disk B. Simulations verify the estimating and tracking performance of UIO and the observability conditions. In the experiment, the second derivative in the auxiliary output is replaced by the square of the frequency multiplied by -1. A synchronous resonator is used to suppress the noise effect. The experimental result proves that the proposed method can track all system outputs with high precision in the region of 0～6 000 r/min and accurately estimate the displacement of the target position.
keywords：Active magnetic bearing, flexible rotor, state observer
DOI: 10.19595/j.cnki.1000-6753.tces.220519
中图分类号：TM133.3
国家科技重大专项（J2019-IV-0005-0073）和基础科研计划（2019110C026, 2020-ZD-232）资助项目。
收稿日期2022-04-06
改稿日期 2022-12-10
李翁衡 男，1998年生，博士研究生，研究方向为电磁轴承-柔性转子振动控制。E-mail: whengli@zju.edu.cn
祝长生 男，1963年生，教授，博士生导师，研究方向为转子系统动力学、高速电机及飞轮储能等。E-mail: zhu_zhang@zju.edu.cn（通信作者）
（编辑 崔文静）