图1 三相电压源型逆变器PMSM驱动系统拓扑结构
Fig.1 Topology structure of PMSM fed by three phase VSI
摘要 永磁同步电机(PMSM)模型预测转矩控制的代价函数中转矩与磁链具有不同的量纲,需要合理整定各自的权重系数,实现控制性能的优化。为此,该文在构建PMSM离散数学模型的基础上,首先将转矩误差与磁链误差表达式映射至两相静止坐标系下,分别等价为电压矢量终点到直线和到圆的距离表达式,两者因具有相同的量纲,可直接叠加构成该文所提代价函数,省去了权重系数的选取流程。然后将备选电压矢量依次代入代价函数,选取使代价函数最小的最优电压矢量作为下一控制周期的电压输入。最后建立仿真模型与实验平台,对该文所提无权重代价函数设计方法与其他PMSM预测转矩控制方法的稳态与动态性能进行比较,结果表明,所提方法具有良好的控制性能。
关键词:永磁同步电机(PMSM) 预测转矩控制 代价函数 权重系数
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)具有结构简单、高效高功率密度等优势[1],且随着碳化硅等宽禁带半导体技术的发展,PMSM驱动系统在电动汽车等工业伺服领域具有广泛的应用[2-3]。我国第十四个五年规划中指出,要突破新能源汽车高效驱动电机高性能动力系统等关键技术[4],而对PMSM的控制技术展开研究是提高电驱系统动力性能的必要途径。目前,常用的电机控制方法主要包括矢量控制(Field Oriented Control, FOC)、直接转矩控制(Direct Torque Control, DTC)及模型预测控制(Model Predictive Control, MPC)[5]。FOC的控制环路过多,需要对多个控制器参数进行配置,DTC动态响应快,但是电流纹波与转矩脉动较大。相比以上两种控制方法,MPC具有动态响应快、目标函数配置灵活、易于处理非线性约束等优势[6],近几年在功率变换器和电机驱动系统等领域得到了广泛的研究与应用。
MPC可分为模型预测电流控制(Model Predictive Current Control, MPCC)[7]和模型预测转矩控制(Model Predictive Torque Control, MPTC)[8]。与MPCC相比,MPTC通过将转矩和磁链引入目标函数,能够实现对转矩和磁链的直接控制。由于转矩与磁链量纲不同,MPTC在代价函数中磁链项加入一个权重系数,以调节磁链项对代价函数值的影响程度,而不同的权重系数对电机的控制性能存在很大的影响[9]。为此,文献[10-11]分别提出用模糊控制算法和粒子群算法实时整定权重系数,但是额外增加了控制算法的复杂度和运算量。文献[12]以最小转矩误差为原则配置权重系数,但是未考虑电流的谐波畸变问题。
为降低配置权重系数所带来的问题,一些无权重系数的MPTC被相继提出。文献[13]计算不同基本电压矢量作用下的转矩和磁链误差,分别对转矩和磁链误差排序,将选择排序后序号之和最小值对应的基本矢量作为最优矢量。文献[14]提出一种级联MPC方法,计算基本矢量作用下转矩误差并排序,选择使转矩误差最小的矢量集合,再从这些矢量集合中选择使磁链误差最小的矢量。文献[15]在文献[14]的基础上比较了磁链误差与转矩误差不同排序效果的优劣。文献[16]分别选择使转矩和磁链误差最小的两组矢量集合,每组包括3个基本矢量,再从两组矢量集合中选择共有的基本矢量作为最佳矢量。以上几种方法均需要完成两次排序,计算量较大。文献[17]通过相邻有效矢量的转矩和磁链预测误差的符号来选择有效矢量,然而其所建立的有效矢量选择表中,判定因素个数较多,不同组合的个数较多,运算量大。为了避免级联排序过程中进行多次比较而增加算法的执行时间,文献[18-20]将转矩和磁链预测误差转换为基本电压矢量和最优电压矢量距离之差。文献[21-22]将转矩误差转换为定子磁链误差,以上两种方法均是通过数学变换统一转矩与磁链的量纲,从而消除权重系数的设计过程。
本文在现有转矩预测控制相关文献的基础上,根据PMSM的离散数学模型,依次将转矩误差与磁链误差转换为电压矢量终点到直线和到圆的距离,统一了两者的量纲,构建以电压矢量为变量的代价函数。最后通过仿真与实验对本文方法的有效性和可行性进行验证。
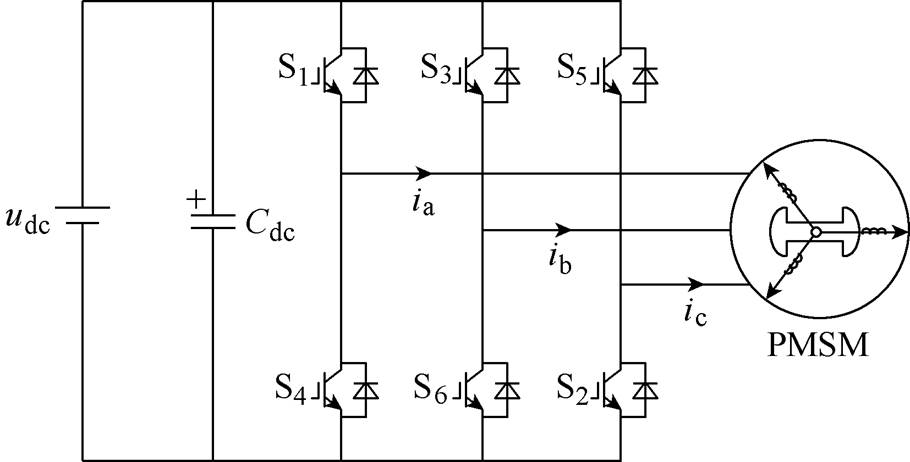
两电平电压源逆变器(two Level-Voltage Source Inverter, 2L-VSI)驱动永磁同步电机系统拓扑如图1所示。图中,udc为直流电压,Cdc为直流侧纹波吸收电容,S1~S6构成了三相电压型逆变桥,ia、ib、ic为三相PMSM定子电流。

图1 三相电压源型逆变器PMSM驱动系统拓扑结构
Fig.1 Topology structure of PMSM fed by three phase VSI
两相旋转dq坐标系下,PMSM电压方程可表示为
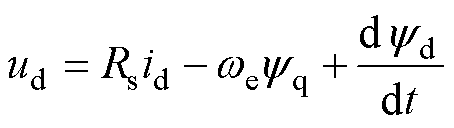 (1)
(1)
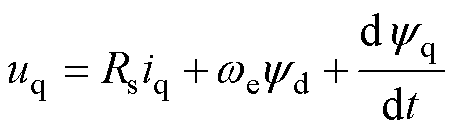 (2)
(2)
式中,Rs、we分别为定子电阻和电角频率;ud、uq分别为dq坐标系下d轴、q轴定子电压;id、iq分别为dq坐标系下d轴、q轴定子电流;yd、yq分别为dq坐标系下d轴、q轴定子绕组磁链,其表达式分别为
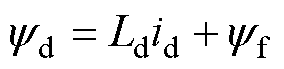 (3)
(3)
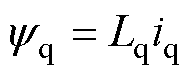 (4)
(4)
式中,Ld、Lq分别为d、q坐标系下的等效电感,对于表贴式PMSM,有Ld=Lq;yf为永磁体磁链。
dq坐标系下的转矩Te和磁链ys方程分别为
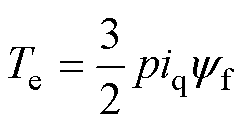 (5)
(5)
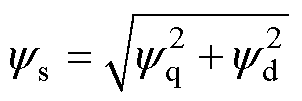 (6)
(6)
式中,p为极对数。
采用一阶欧拉式得到id、iq预测式为
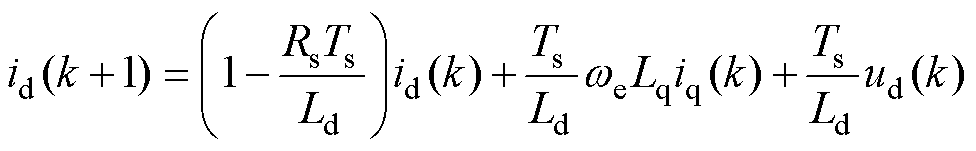 (7)
(7)
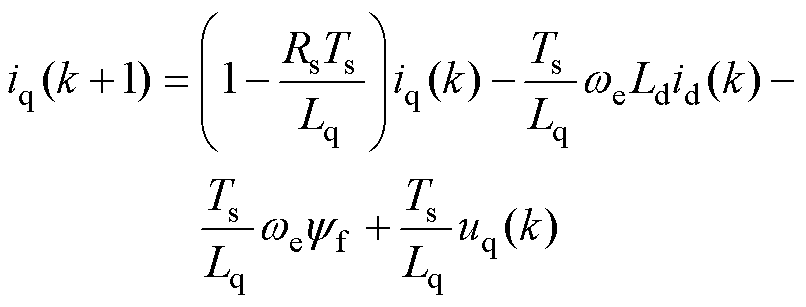 (8)
(8)
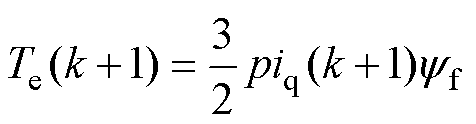 (9)
(9)
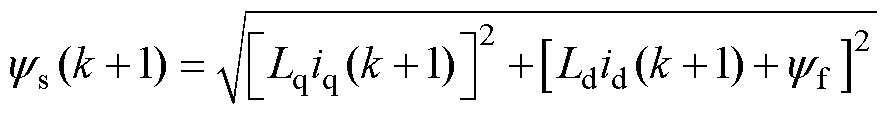 (10)
(10)
式中,id(k)、iq(k)分别为kTs时刻d、q轴电流采样值;ud(k)、uq(k)分别为kTs时刻d、q轴电压;id(k+1)、iq(k+1)分别为(k+1)Ts时刻d、q轴电流预测值;Te(k+1)、ys(k+1)分别为(k+1)Ts时刻转矩和磁链预测值;Ts为采样周期。
传统预测转矩控制代价函数如式(11)所示。将8个基本电压矢量代入式(7)~式(11),选择使代价函数g最小的基本电压矢量,输出给逆变器。
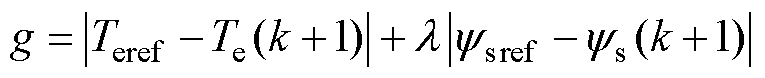 (11)
(11)
其中
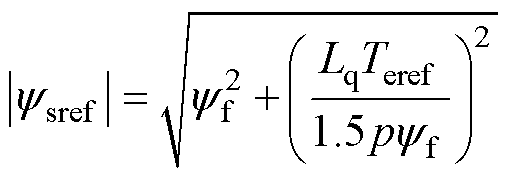 (12)
(12)
式中,Teref与ysref分别为转矩与磁链的给定值;l 为磁链项的权重系数,其取值方法为:记录多次不同l 的实验数据,选取综合性能最优情况下的取值。
对转矩和磁链单独定义代价函数,表示为
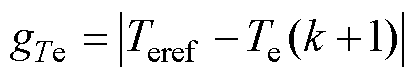 (13)
(13)
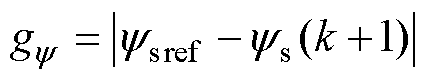 (14)
(14)
令式(5)中Te(k+1)=Teref,得到
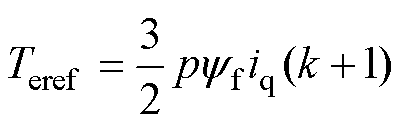 (15)
(15)
为了便于表述,将式(7)与式(8)分别表示为
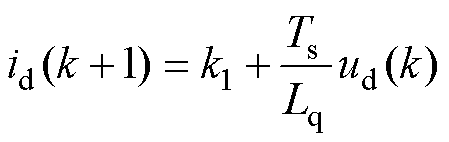 (16)
(16)
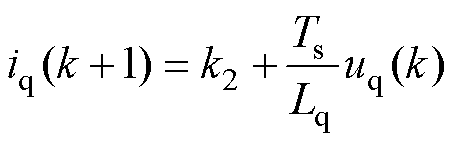 (17)
(17)
其中
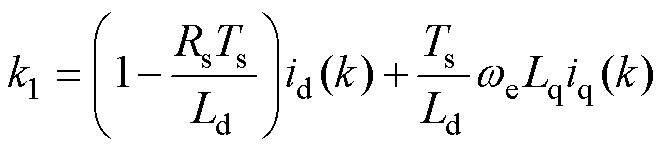 (18)
(18)
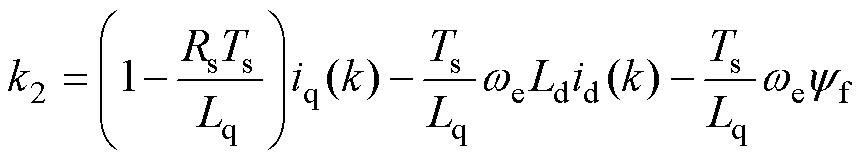 (19)
(19)
将式(16)~式(19)代入式(15)并转换到两相静止ab 坐标系,有
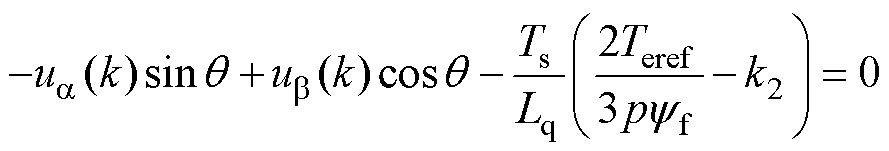 (20)
(20)
式中,ua(k)、ub(k)分别为ab 坐标系下a轴、b 轴的定子电压;q 为电压矢量的相位。令
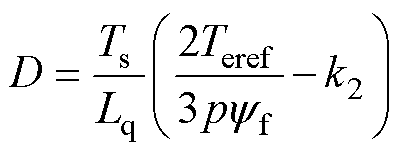 (21)
(21)
在ab 坐标系下,式(20)的几何意义为一条直线l,因此式(13)所示的转矩代价函数可以表示为电压矢量终点 (ua(k), ub(k)) 到l的距离dT,dT表达式为
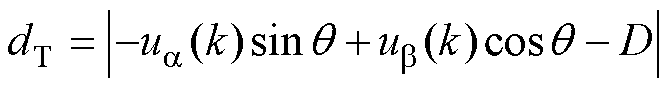 (22)
(22)
将式(15)~式(19)代入式(10),令ys(k+1)=ysref,进行Park逆变换至ab 坐标系,有
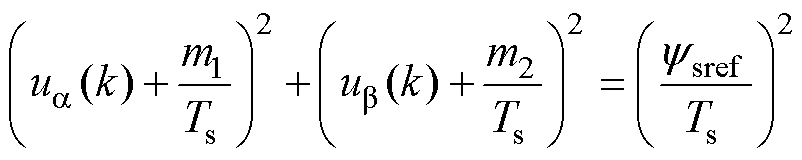 (23)
(23)
其中
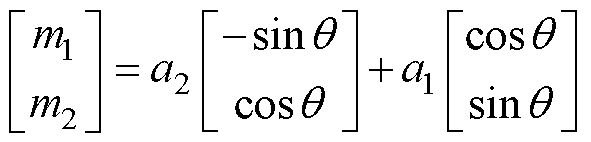 (24)
(24)
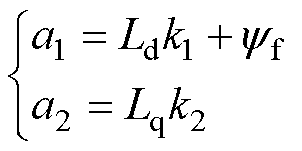 (25)
(25)
式中,m1与m2分别为磁链代价函数变换后的a、b 坐标系等效磁链。
式(24)在ab 坐标系下的几何意义为一个圆c,圆上任意点均满足磁链无差拍,可以将式(14)所示的磁链代价函数等效转换为电压矢量终点 (ua(k), ub(k)) 到c的距离dF,表达式为
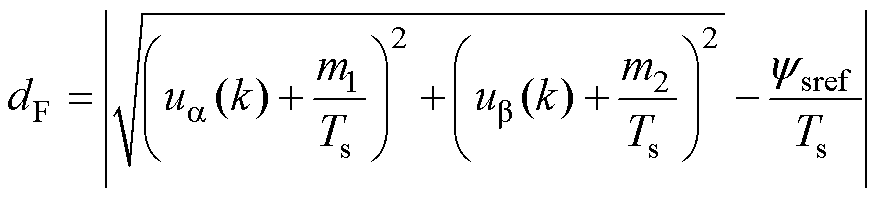 (26)
(26)
由式(22)和式(26)可知,dT和dF均为同一坐标系下的距离式,且具有相同的量纲,故构建新的无权重代价函数为
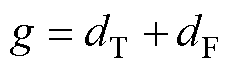 (27)
(27)
记所提方法为无权重代价函数的预测转矩控制(No Weighting Factor-Predictive Torque Control, NWF-PTC)方法,矢量选择示意图如图2所示。2L- VSI共有8种开关状态,对应8种基本电压矢量,包括6个有效矢量和2个零矢量。各电压矢量终点在ab 坐标系的坐标见表1。
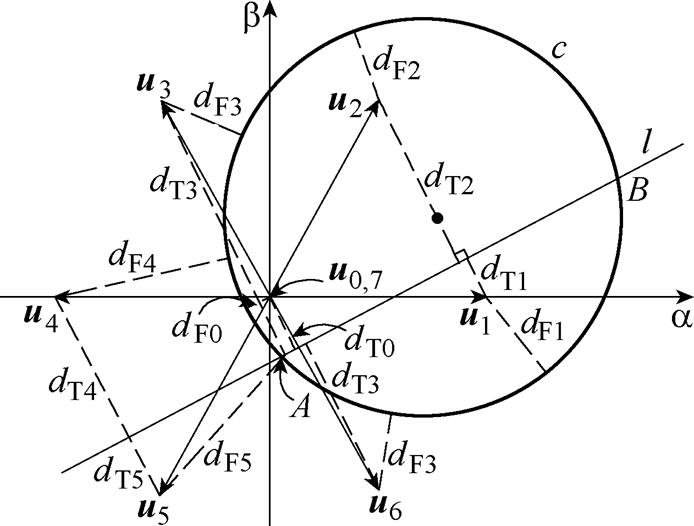
图2 矢量选择示意图
Fig.2 Vector selection schematic
图3为本文所提方法NWF-PTC的控制框图,对转速进行PI调节后得到转矩的指令值Teref,再代入式(12)的磁链指令值ysref,用Teref、ysref、当前第k次的采样电流id(k)、iq(k)以及转子位置角q 构造式(27)所示的基于距离的无权重代价函数g,将表1所示的各矢量坐标分别代入函数g,得到使代价函数取值最小的电压矢量,并产生下一周期的开关信号。
表1 备选电压矢量的坐标
Tab.1 Coordinates of voltage vectors

电压矢量a 轴b 轴 0 0 00 00
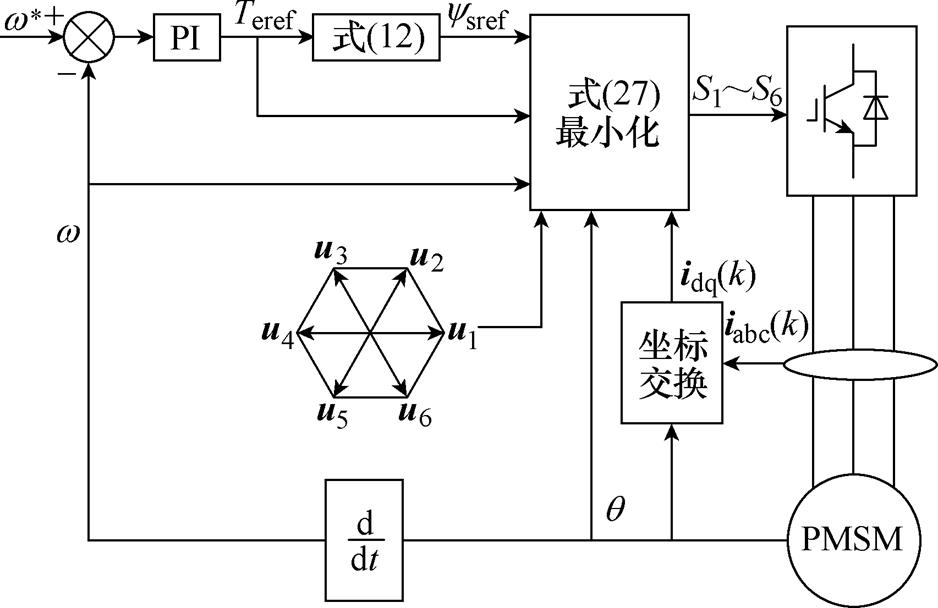
图3 本文所提方法的控制框图
Fig.3 Control diagram of NWF-PTC
转矩预测控制是一种根据离散模型获得电压输入矢量的控制方法,转矩环路没有具体形式的传递函数。根据转矩的单位阶跃响应特性,本文将转矩环路等效为带宽2 kHz的一阶惯性环节GTe(s),其表达式为
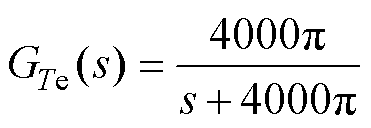 (28)
(28)
构建转速控制环路的等效模型,如图4所示。图中,kp与ki分别为转速PI控制器的比例系数与积分系数,J为电机转动惯量,J=0.01 kg·m2,TL为负载转矩。
利用Matlab的Sisotool工具整定转速PI控制器,当kp=21、ki=14.5时,转速闭环传递函数的幅频特性曲线如图5所示。转速环路的带宽为200 Hz,既具有良好的直流跟随特性,同时能够兼顾动态响应速度。
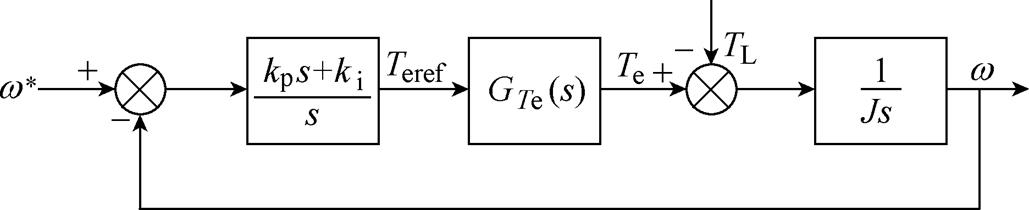
图4 转速控制环路
Fig.4 Closed-loop of speed control
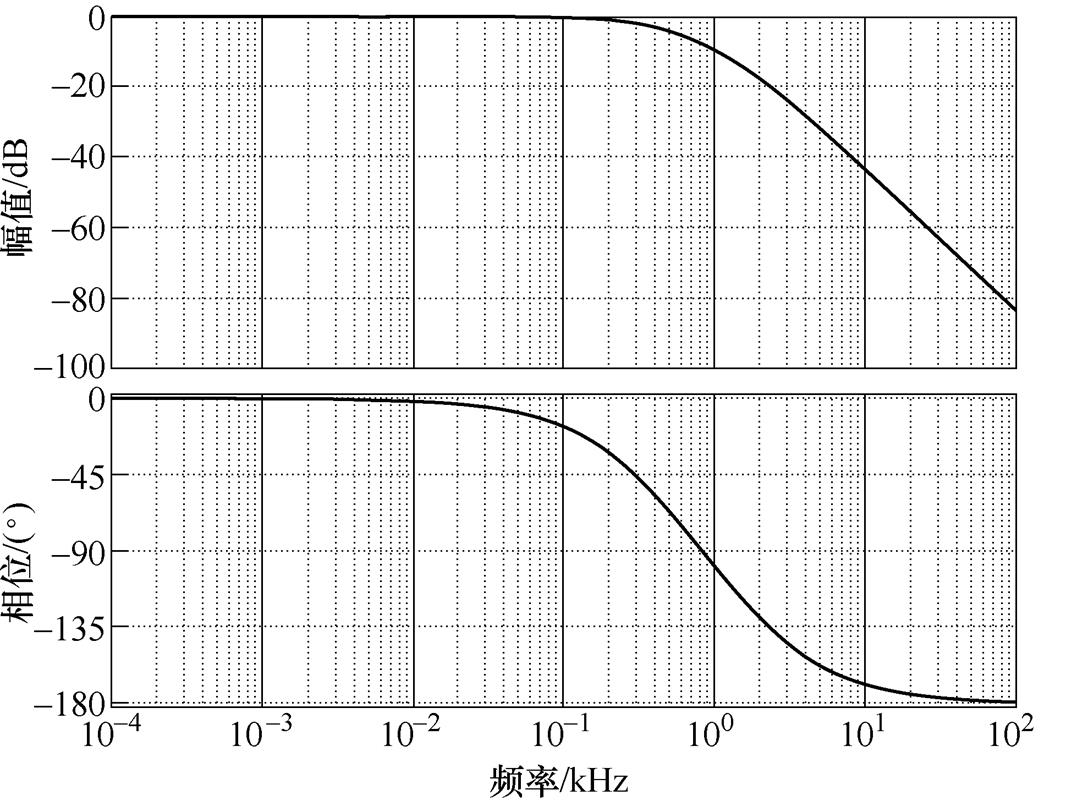
图5 转速闭环传递函数的幅频特性曲线
Fig.5 Bode plot of speed closed-loop transfer function
首先对本文所提方法NWF-PTC、传统预测转矩控制(Traditional Predictive Torque Control, TPTC)、文献[17]所提出的模型预测磁链控制(Model Predictive Flux Control, MPFC)三种方法的稳态性能进行比较,仿真中PMSM参数见表2,采样频率设置为20 kHz。
表2 永磁同步电机参数
Tab.2 Parameters of PMSM

参 数数 值 额定转速(r/min)3 000 极对数4 转动惯量/(kg·m2)0.004 78 定子电阻/W0.15 定子电感/mH1.625 额定转矩/(N·m)15 额定电流/A18
图6a与图6b分别给出了额定负载转矩、不同转速稳态运行及额定转速、不同负载转矩这两种工况下磁链脉动与转矩脉动的仿真比较结果,由于TPTC代价函数中选取使转矩脉动最小的权重系数,因此TPTC的转矩脉动是三种方法最小的,而本文所提方法NWF-PTC兼顾了磁链的控制,因此具有最小的磁链脉动效果,转矩脉动略高于TPTC,小于MPFC。
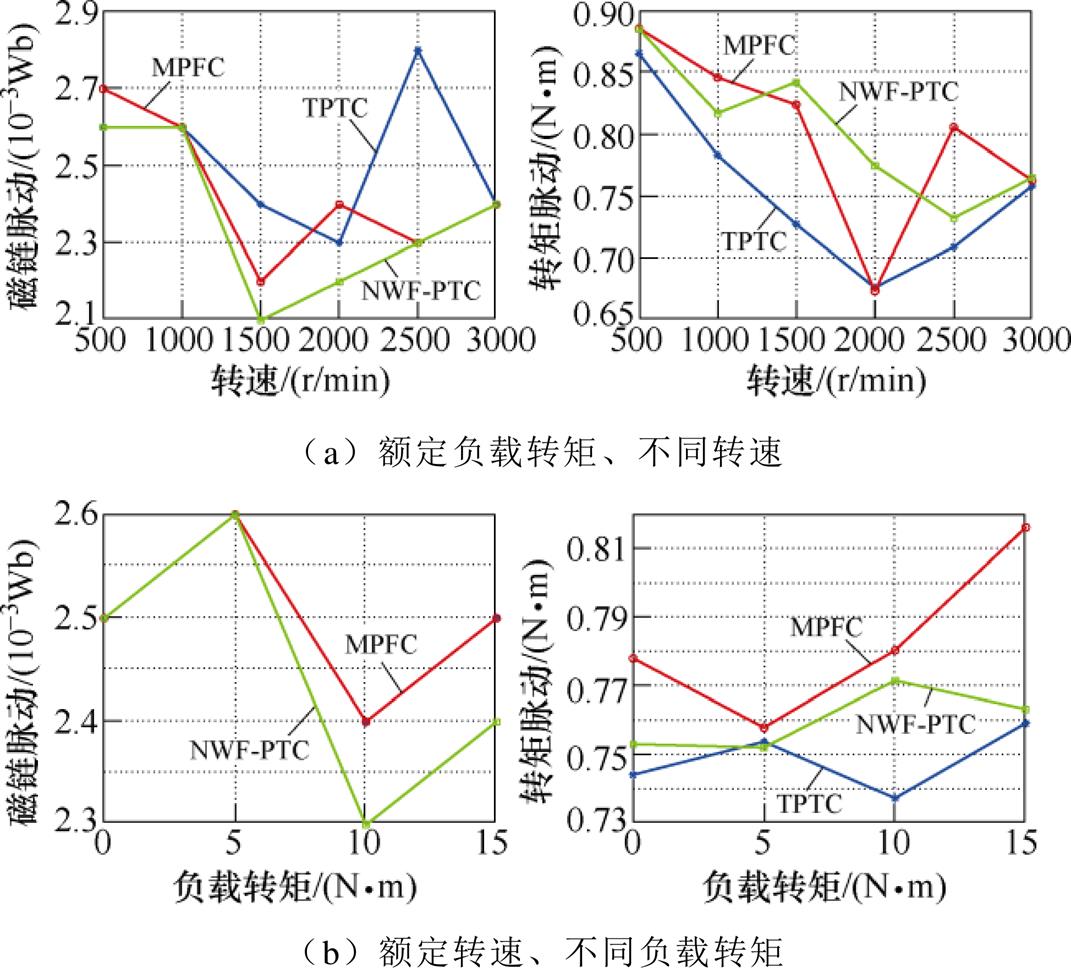
图6 不同控制方法下的转矩与磁链脉动的仿真比较
Fig.6 Simulation comparison of torque ripple and flux ripple under different control methods
对本文所提无权重代价函数进行等效变换,根据式(13)、式(22)可得转矩误差函数gTe与等效距离误差函数dT存在以下关系
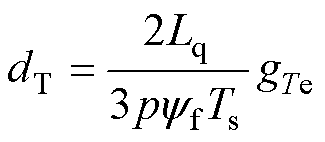 (29)
(29)
根据式(14)、式(26)可得磁链误差函数gy与其等效距离误差函数dF存在以下关系
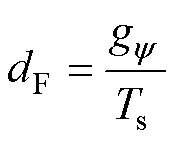 (30)
(30)
则式(27)可以改写为
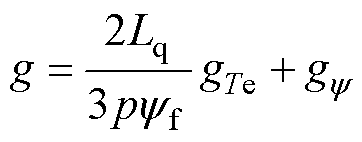 (31)
(31)
将式(31)转化等效为式(11)所示的代价函数表达形式,此时权重系数l 等效为
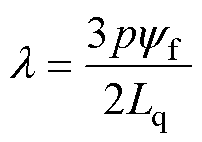 (32)
(32)
将表2中PMSM参数代入式(32),得到l= 369.23。为验证该取值下的稳态性能,表3给出了PMSM额定条件运行下不同l 取值的转矩脉动、磁链脉动以及定子电流总谐波畸变率(Total Harmonic Distortion, THD)的仿真比较结果,随着l 增大,磁链项在代价函数的重要性也随之增大,因此转矩脉动逐渐增加,而磁链脉动逐渐减小,但是当l>369后,磁链脉动对l 不再敏感。同时可以看出,当l= 369.23,电流THD小于其他l 取值,说明本文所提NWF-PTC能够兼顾转矩与磁链稳态性能,并使定子电流THD达到最小。
表3 额定条件下不同权重系数的转矩和磁链脉动及A相定子电流THD
Tab.3 Ripple of torque and flux, THD of stator current under rate condition and different l

权重系数l转矩脉动/(N·m)磁链脉动/Wb定子电流THD(%) 2000.650 10.003 18.14 3000.750 60.002 77.50 3200.752 40.002 67.42 3400.7540.002 57.38 3600.758 60.002 57.33 3690.761 20.002 47.31 3800.769 10.002 47.65 4000.778 70.002 47.82
图7给出了TPTC、MPFC及所提NWF-PTC方法的加减转速工况下的仿真波形。PMSM空载起动,0 s时给定转速2 000 r/min;0.2 s时突加10 N·m负载,并保持不变。0.3 s时给定转速由2 000 r/min下降至500 r/min;0.4 s时再给定转速增加到1 000 r/min。三种方法动态控制性能比较接近,起动时经过50 ms达到给定转速,且无超调,在加速与减速过程转矩与磁链均能够快速做出响应。

图7 三种控制方法的加减速仿真波形
Fig.7 Acceleration and deceleration simulation waveforms under different control method
图8给出了TPTC、MPFC及所提NWF-PTC方法的负载突变情况下的仿真波形。转速保持2 000 r/min,0.2 s时突加10 N·m负载,0.3 s时负载突变为15 N·m负载;0.4 s时将负载突减至5 N·m。三种控制方法均具有很好的转矩跟随性能,且磁链配合转矩做出相应的调整。
综合以上仿真结果,所提NWF-PTC方法与TPTC、MPFC相比,在无需对权重系数进行整定的情况下,能够兼顾转矩与磁链的稳态性能,实现最小电流谐波畸变,且不会影响动态性能。
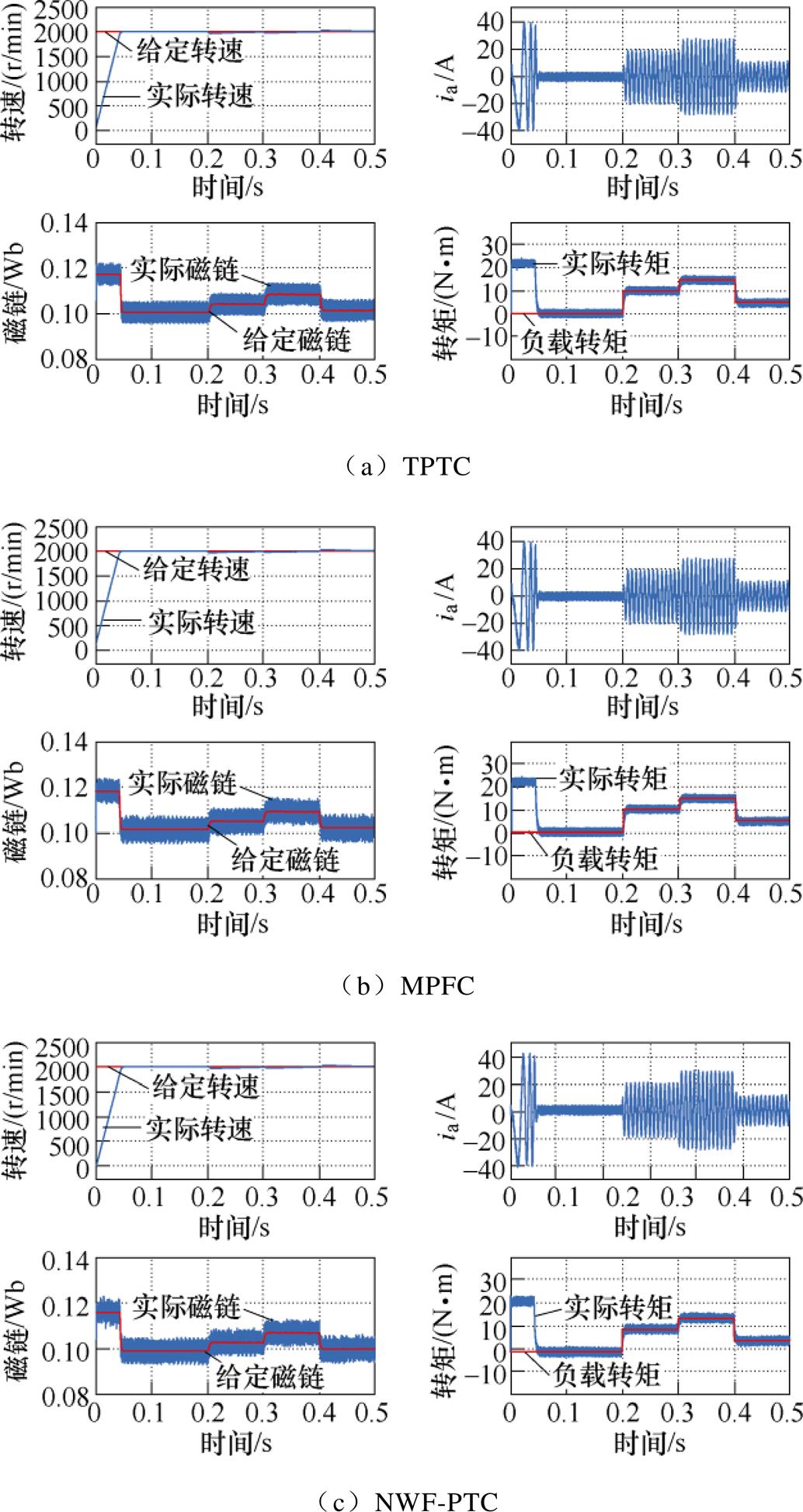
图8 加减负载仿真波形
Fig.8 Simulation waveforms under torque changing
在如图9所示的PMSM实验平台验证本文所提NWF-PTC方法的控制效果,其中采用瑞途优特信息公司研制的RTU-BOX作为数字信号处理器,将Matlab仿真模型转换为程序代码,电机参数与表2一致。

图9 实验平台
Fig.9 Experimental platform
图10为2 000 r/min、负载为10 N·m时TPTC、MPFC和所提方法NWF-PTC的稳态实验波形,定子电流的THD分别为8.14 %、8.05 %和7.82 %。说明NWF-PTC在兼顾转矩与磁链稳态性能的条件下,可降低定子电流的谐波畸变。
图11给出了转速给定值从2 000 r/min阶跃增加至2 500 r/min情况下三种控制方法的实验波形。三种方法的转速动态调整时间与振荡过程基本一致,经过100 ms转速重新跟踪给定,其中TPTC的转速超调为4.12 %,MPFC的转速超调为4.16 %,NWF-PTC的转速超调为2.47 %。
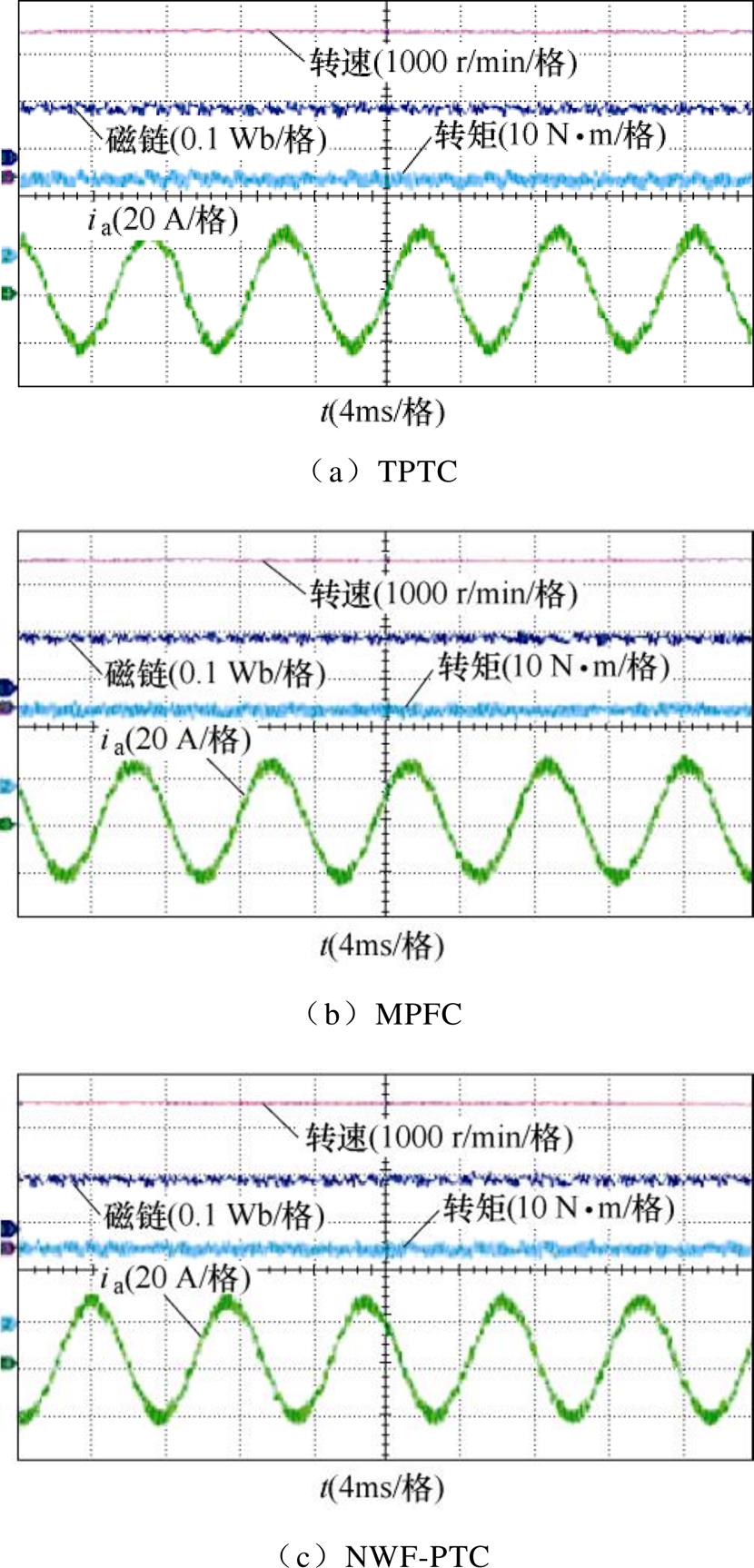
图10 三种控制方法的稳态实验波形
Fig.10 Experimental waveforms under three control methods
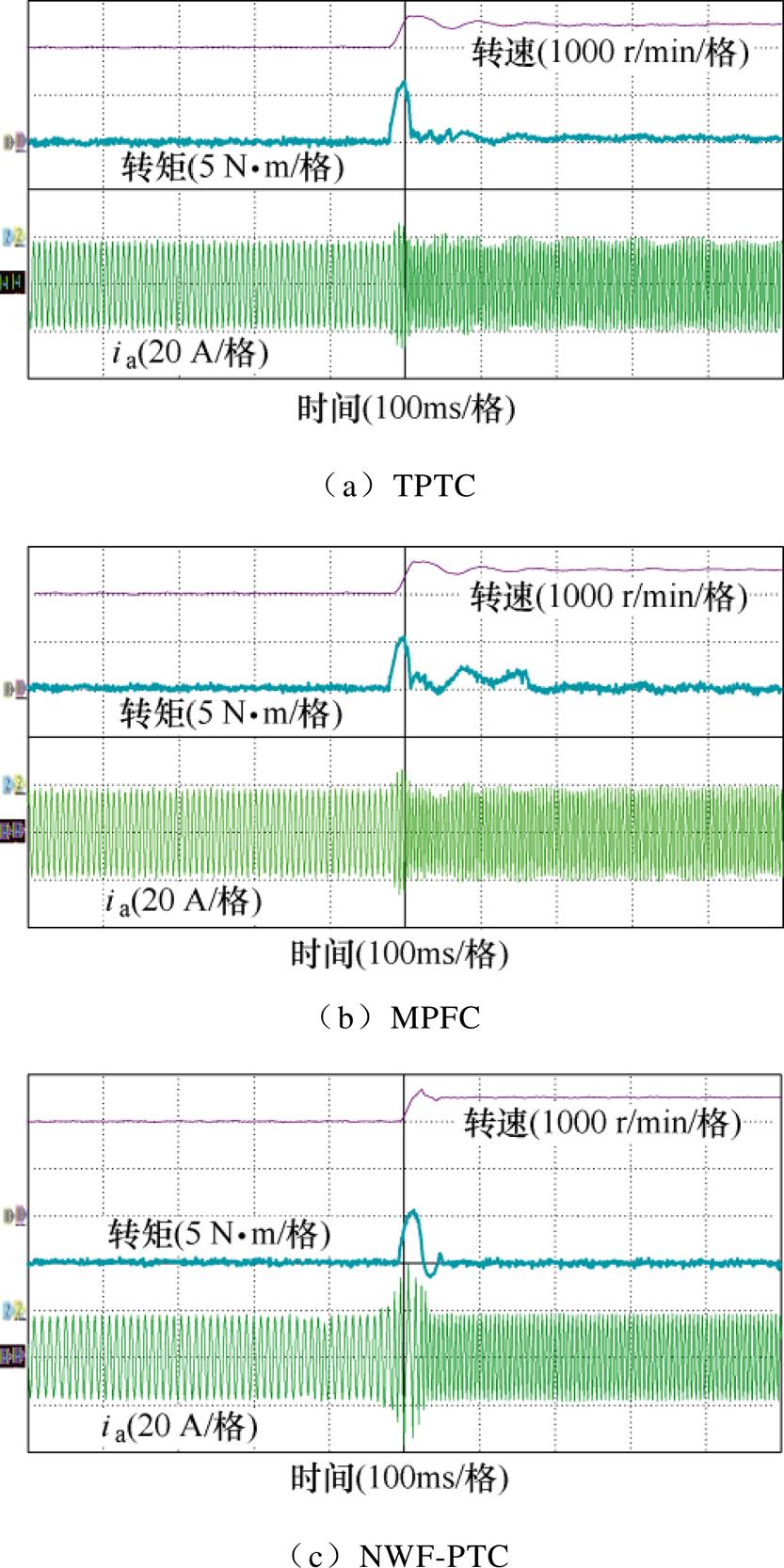
图11 加速工况下三种控制方法的实验波形
Fig.11 Experimental waveforms of three control methods under acceleration
图12为负载突变情况下三种控制方法的实验波形,PMSM以负载转矩5 N·m起动,参考转速设定为2 000 r/min。PMSM进入稳态后,负载突然增加10 N·m。三种控制方法的动态调整过程大致相同,当负载增加后,转速会立即下降,转速控制器会立即增加给定转矩,通过增加定子电流幅值,实现转矩的快速调整,仅经过100 ms,转速与转矩重新达到稳态。其中,本文所提NWF-PTC的转速脉动最小,转速超调量也最小。
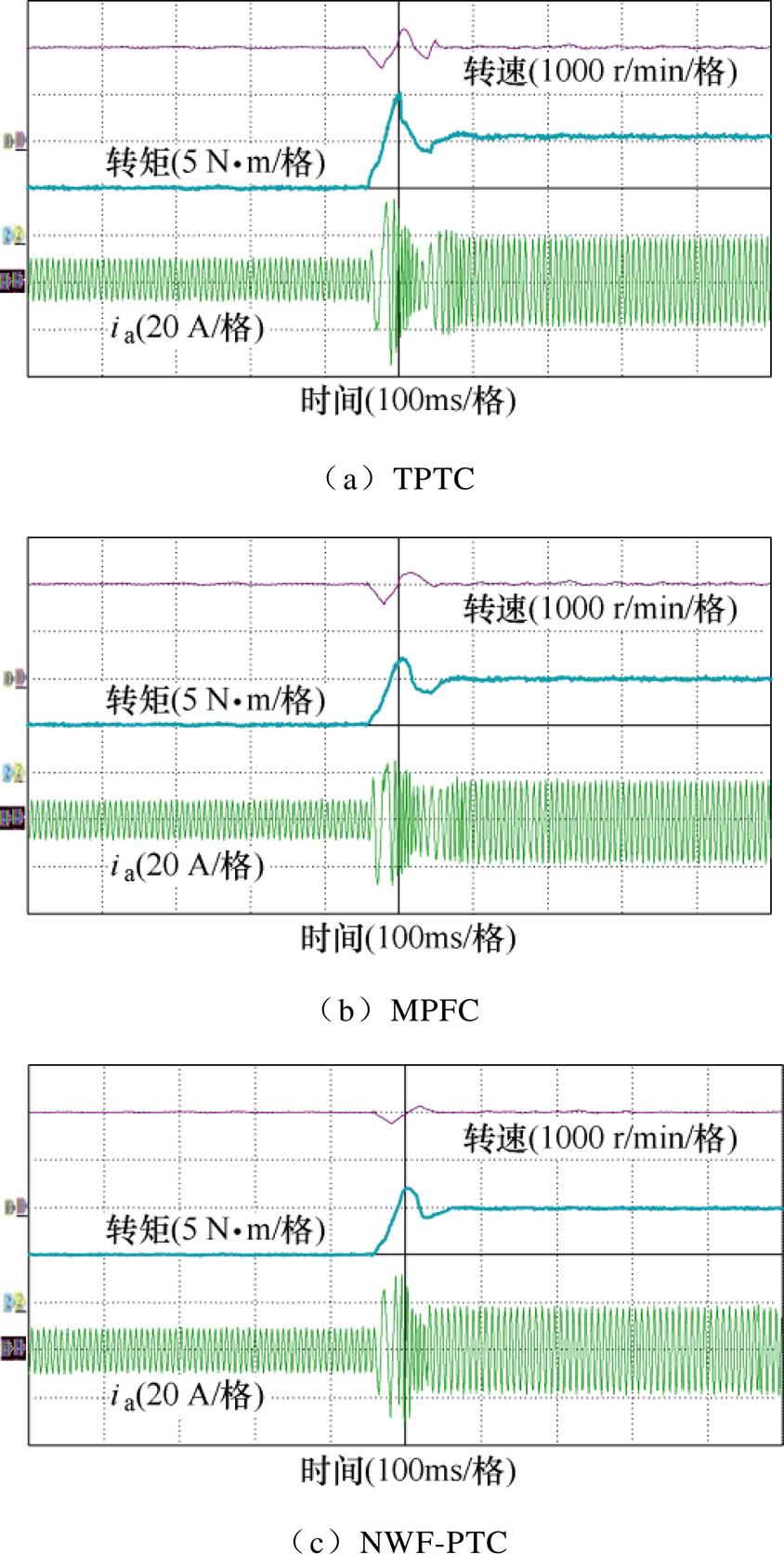
图12 负载突变情况下三种控制方法实验波形
Fig.12 Experimental waveforms of three control methods under torque suddenly changing
针对永磁同步电机预测转矩控制代价函数中权重系数的整定问题,本文通过数学变换,得到一种无权重系数的新型代价函数,并通过仿真与实验对所提方法的可行性与有效性进行验证,取得了良好的控制效果,并得到以下结论:
1)转矩误差函数可等效为电压矢量终点到直线的距离表达式,磁链误差函数可等效为电压矢量终点到圆的距离表达式,实现了量纲的统一。
2)在不影响动态性能的前提下,所提方法能够兼顾转矩与磁链的稳态性能,提高定子电流的波形质量。
参考文献
[1] Dong Zhiping, Liu Chunhua, Song Zaixin, et al. Suppression of dual-harmonic components for five- phase series-winding PMSM[J]. IEEE Transactions on Transportation Electrification, 2022, 8(1): 121- 134.
[2] 刘平, 陈梓健, 苗轶如, 等. 基于开关瞬态反馈的SiC MOSFET有源驱动电路[J]. 电工技术学报, 2022, 37(17): 4446-4457.
Liu Ping, Chen Zijian, Miao Yiru, et al. Active gate driver for SiC MOSFET based on switching transient feedback[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4446-4457.
[3] 刘平, 李海鹏, 苗轶如, 等. 基于内置温度传感器的碳化硅功率模块结温在线提取方法[J]. 电工技术学报, 2021, 36(12): 2522-2534.
Liu Ping, Li Haipeng, Miao Yiru, et al. Online junction temperature extraction for SiC module based on built-in temperature sensor[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2522- 2534.
[4] 王彦哲, 周胜, 王宇, 等. 中国核电和其他电力技术环境影响综合评价[J]. 清华大学学报(自然科学版), 2021, 61(4): 377-384.
Wang Yanzhe, Zhou Sheng, Wang Yu, et al. Com- prehensive assessment of the environmental impact of China’s nuclear and other power generation tech- nologies[J]. Journal of Tsinghua University (Science and Technology), 2021, 61(4): 377-384.
[5] Xiao Meng, Shi Tingna, Yan Yan, et al. Predictive torque control of permanent magnet synchronous motors using flux vector[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 4437-4446.
[6] 秦艳忠, 阎彦, 陈炜, 等. 永磁同步电机参数误差补偿-三矢量模型预测电流控制[J]. 电工技术学报, 2020, 35(2): 255-265.
Qin Yanzhong, Yan Yan, Chen Wei, et al. Three- vector model predictive current control strategy for permanent magnet synchronous motor drives with parameter error compensation[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 255- 265.
[7] Petkar S G, Eshwar K, Thippiripati V K. A modified model predictive current control of permanent magnet synchronous motor drive[J]. IEEE Transactions on Industrial Electronics, 2021, 68(2): 1025-1034.
[8] Niu Feng, Chen Xi, Huang Shaopo, et al. Model predictive current control with adaptive-adjusting timescales for PMSMs[J]. CES Transactions on Elec- trical Machines and Systems, 2021, 5(2): 108-117.
[9] Zhang Xiaoguang, Hou Benshuai. Double vectors model predictive torque control without weighting factor based on voltage tracking error[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2368-2380.
[10] 李家祥, 汪凤翔, 柯栋梁, 等. 基于粒子群算法的永磁同步电机模型预测控制权重系数设计[J]. 电工技术学报, 2021, 36(1): 50-59, 76.
Li Jiaxiang, Wang Fengxiang, Ke Dongliang, et al. Weighting factors design of model predictive control for permanent magnet synchronous machine using particle swarm optimization[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 50-59, 76.
[11] 梅杨, 易高. 间接矩阵变换器-异步电机调速系统模型预测控制权重系数自整定方法[J]. 电工技术学报, 2020, 35(18): 3938-3948.
Mei Yang, Yi Gao. A weighting factor self-tuning method in model prediction control for indirect matrix converter with induction motor system[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(18): 3938-3948.
[12] Alireza Davari S, Khaburi D A, Kennel R. An improved FCS-MPC algorithm for an induction motor with an imposed optimized weighting factor[J]. IEEE Transactions on Power Electronics, 2012, 27(3): 1540-1551.
[13] Kodumur Meesala R E, Kunisetti V P K, Kumar Thippiripati V. Enhanced predictive torque control for open end winding induction motor drive without weighting factor assignment[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 503-513.
[14] Norambuena M, Rodriguez J, Zhang Zhenbin, et al. A very simple strategy for high-quality performance of AC machines using model predictive control[J]. IEEE Transactions on Power Electronics, 2018, 34(1): 794- 800.
[15] Zhang Yongchang, Zhang Boyue, Yang Haitao, et al. Generalized sequential model predictive control of IM drives with field-weakening ability[J]. IEEE Transa- ctions on Power Electronics, 2019, 34(9): 8944- 8955.
[16] Kusuma E, Eswar K M R, Vinay Kumar T. An effective predictive torque control scheme for PMSM drive without involvement of weighting factors[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(3): 2685-2697.
[17] 陈炜, 曾思坷, 张国政, 等. 永磁同步电机改进型三矢量模型预测转矩控制[J]. 电工技术学报, 2018, 33(增刊2): 420-426.
Chen Wei, Zeng Sike, Zhang Guozheng, et al. Improved three-vector model predictive torque con- trol of permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 420-426.
[18] 张晓光, 张亮, 侯本帅. 永磁同步电机优化模型预测转矩控制[J]. 中国电机工程学报, 2017, 37(16): 4800-4809, 4905.
Zhang Xiaoguang, Zhang Liang, Hou Benshuai. Improved model predictive torque control of per- manent magnet synchronous motor[J]. Proceedings of the CSEE, 2017, 37(16): 4800-4809, 4905.
[19] 赵勇, 黄文新, 林晓刚, 等. 基于权重系数消除和有限控制集优化的双三相永磁容错电机快速预测直接转矩控制[J]. 电工技术学报, 2021, 36(1): 3-14.
Zhao Yong, Huang Wenxin, Lin Xiaogang, et al. Fast predictive direct torque control of dual three-phase permanent magnet fault tolerant machine based on weighting factor elimination and finite control set optimization[J]. Transactions of China Electrotech- nical Society, 2021, 36(1): 3-14.
[20] 夏长亮, 张天一, 周湛清, 等. 结合开关表的三电平逆变器永磁同步电机模型预测转矩控制[J]. 电工技术学报, 2016, 31(20): 83-92, 110.
Xia Changliang, Zhang Tianyi, Zhou Zhanqing, et al. Model predictive torque control with switching table for neutral point clamped three-level inverter-fed permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(20): 83-92, 110.
[21] Zhang Yongchang, Yang Haitao. Model-predictive flux control of induction motor drives with switching instant optimization[J]. IEEE Transactions on Energy Conversion, 2015, 30(3): 1113-1122.
[22] 於锋, 朱晨光, 吴晓新, 等. 基于矢量分区的永磁同步电机三电平双矢量模型预测磁链控制[J]. 电工技术学报, 2020, 35(10): 2130-2140.
Yu Feng, Zhu Chenguang, Wu Xiaoxin, et al. Two- vector-based model predictive flux control of three- level based permanent magnet synchronous motor with sector subregion[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2130-2140.
Abstract With high efficiency, high power density, and reliable operation, permanent magnet synchronous motors are widely used in electric vehicles, wind power generation, and high-performance servos. The research of PMSM high-performance control technology is the necessary way to improve the performance of PMSM systems. Compared with the two traditional control strategies of field-oriented control (FOC) and direct torque control (DTC), model predictive control (MPC) has the advantages of fast dynamic response, flexible objective function configuration, and easy-to-handle nonlinear constraints. MPC can be divided into model predictive current control (MPCC) and model predictive torque control (MPTC), which can directly control torque and magnetic chain by introducing torque and magnetic chain into the objective function. However, MPTC adds a weighting factor to the magnetic chain term in the cost function to regulate the degree of influence of the flux linkage term on the value of the cost function. Different weighting factors significantly impact the control performance of the motor. The currently proposed methods based on fuzzy, particle swarm, and cascade sorting all need to be revised to handle the problems of high computational power and complex implementation process. Therefore, a conversion method based on the cost function of the torque chain is proposed, which unifies the magnitudes of the two.
Firstly, the discrete current, torque, and flux linkage equations of PMSM are derived. After the torque equation is substituted into the current equation and the inverse Park transformation is performed on it, the torque cost function is converted into a distance expression from the endpoint of the voltage vector to a moving line. Similarly, the cost function of the flux linkage is converted into the expression of the distance from the endpoint of the voltage vector to a moving circle. Thus, the cost function composed of torque and flux linkage is replaced by the distance cost function, avoiding the weighting coefficient design due to the non-uniformity of dimensions. Finally, the design method of the outer speed loop PI controller is presented.
Simulation and experiment are carried out to compare the steady and dynamic performances of the three methods, namely NWF-PTC proposed in this paper, traditional predictive torque control (TPTC), and model predictive flux control (MPFC) proposed in Ref.[17]. NWF-PTC can consider the steady state performance of the torque and flux linkage and achieve the minimum current harmonic distortion without setting the weight coefficient. Under the two dynamic conditions of a sudden change of torque or the command value of the speed, the time of overshoot and adjustment of NWF-PTC is also slightly lower than those of the other two methods.
Simulation and experimental results verify the feasibility and correctness of the proposed method. The following two conclusions are as follows:
(1) The cost function of the torque and flux can be equivalent to the expression of the distance from the endpoint of the voltage vector to a moving line and a moving circle, respectively. Thus the unification of the dimensions is realized.
(2) On the premise of not deteriorating the dynamic performance, the proposed method can consider the steady-state performance of torque and flux, and improve the waveform quality of the stator current.
keywords:Permanent magnet synchronous motor (PMSM), predictive torque control, cost function, weighting factor
DOI: 10.19595/j.cnki.1000-6753.tces.220952
中图分类号:TM341
国家自然科学基金资助项目(52207051)。
收稿日期2022-05-30
改稿日期 2022-08-08
苗轶如 男,1988年生,博士,研究方向为电力电子变换器拓扑结构与控制技术。E-mail: miaoyiru@cqu.edu.cn
吕铭晟 男,1990年生,助理研究员,研究方向为高性能电机控制。E-mail: 289763620@qq.com(通信作者)
(编辑 崔文静)