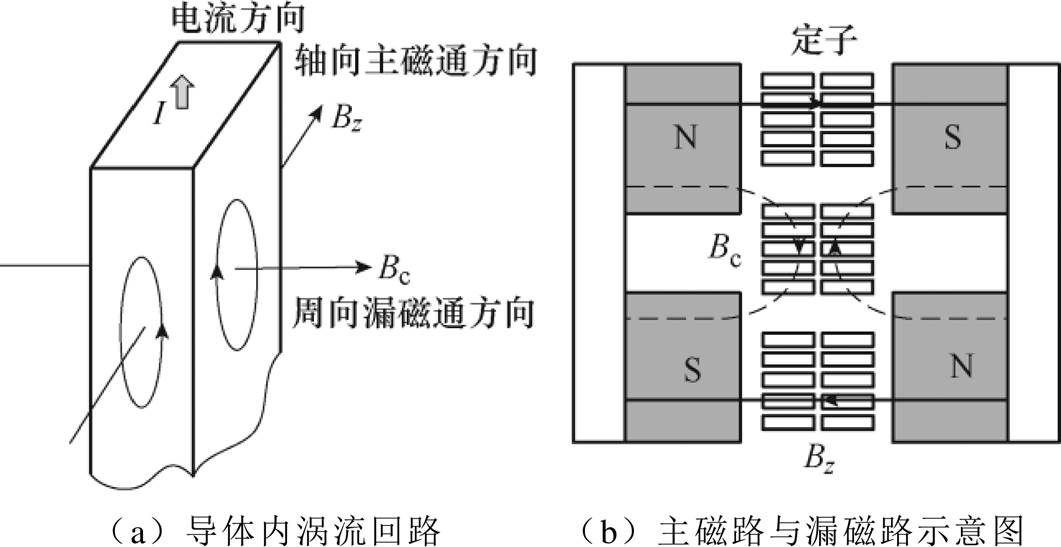
图1 主磁通与漏磁通产生涡流损耗
Fig.1 Eddy current loss caused by main flux and leakage flux
摘要 轴向磁通无铁心永磁电机的定子为无铁心结构，采用扁线绕制的定子绕组盘，具有槽满率高、平整度好、加工简单等特点。但是相对于圆形导线，矩形扁线具有截面积较大、涡流损耗大的缺点，导致电机损耗偏高、效率偏低。该文根据轴向无铁心电机磁场的三维分布特性，针对矩形扁线涡流损耗分布不均匀的特点，推导了定子无铁心扁线绕组特有的涡流损耗快速计算方法。在此基础上，基于涡流损耗的产生机理并以绕组铜耗最小为优化目标，建立了扁线绕组最优参数的求解公式。采用三维有限元软件仿真及样机测试的方法，验证了涡流损耗解析计算方法的有效性和准确性。结果表明，该文提出的涡流损耗计算公式以及导线参数优化方法可以实现扁线绕组的低损耗及电机的高效率，所得结论可为轴向无铁心电机定子绕组的设计及优化提供理论 依据。
关键词：无铁心永磁电机 扁线绕组 涡流损耗 绕组优化
无铁心轴向永磁同步电机（Coreless Axial Flux Permanent Magnet Synchronous Machine, CAFPMSM）以其结构紧凑、维护成本低、功率密度高、转矩大、效率高等优点[1-6]，越来越多地应用于各种工业和交通场合中。由于定子没有铁心，电机绕组直接暴露在气隙磁场中，导致其产生大量涡流损耗，当电机转速较高时这种现象会更加严重[7]。由于电机没有铁耗，涡流损耗成为电机的主要损耗，不合理的绕组设计将导致绕组的铜耗过大，降低电机的效率与功率密度，同时过高的温升降低了电机运行的可靠性[8-10]。所以，为了进一步提升电机的性能，精确计算无铁心电机定子绕组涡流损耗并通过合理的设计和优化以降低绕组铜损变得尤为重要。
利兹线或多股细圆线具有低交流铜损的优 势[11-13]，所以通常被用于制作无铁心电机定子绕组。但是由于利兹线或多股细圆线由多根独立绝缘的导体绞合或编制而成，有效导体的槽满率相对较低。且当电枢电流增大时，利兹线的直流铜损问题更加显著[14]。矩形扁线作为一种形状相对规则的导线，由于其可以充分利用定子空间，且传热性能好，有利于提高电机的功率密度，在有铁心电机中得到了广泛的应用，同时也非常适用于制作轴向无铁心电机绕组[15]。随着扁线绕组加工工艺越来越成熟，矩形扁线在电机绕组中的应用越来越广泛[16-18]。
由于定子没有铁心，电机的漏磁场与绕组产生交链，且矩形扁线对应于漏磁场的截面积较大，所以会产生更大的涡流损耗[14]，主磁通与漏磁通产生涡流损耗如图1所示。为了兼顾电机的高槽满率及高效率，精确计算并且降低扁线绕组的涡流损耗成为无铁心电机的研究重点。
文献[19]推导了轴向无铁心电机三维磁场的解析模型，得出气隙磁场在不同位置分布不均匀的结论。文献[20]在推导出无铁心电机的空载磁场三维解析模型的基础上，根据磁场特性推导出了各项损耗计算公式。但由于数学解析法求解得到气隙磁场的过程非常繁琐，且工作量太大，所以运用场路结合的思想，通过有限元软件求解磁场，结合电机实际模型可以更直观地得到轴向磁场和周向磁场的各次谐波幅值。文献[21]通过有限元软件得到气隙磁场各方向分量，并且根据轴向无铁心电机磁场特点，提出了圆形导线的涡流损耗计算公式，把绕组在轴向进行分层计算再求和，提高了涡流损耗计算精度。文献[22]同样利用分层的方法提出了利兹线的涡流损耗计算公式，由结论可以看出，利兹线可有效减小无铁心绕组的涡流损耗。利兹线采用多根导线并绕的形式，绕线形状相对不规则，会降低定子空间利用率，不利于电机功率密度的提升和散热。文献[23]基于等效磁网络模型的磁场计算结果进行绕组涡流损耗的解析计算，并对效率和温升进行了综合优化。文献[24]将盘式电机沿径向方向分为若干个环，用直线电机模型来等效每环，绕组总涡流损耗为所有直线电机损耗之和，该方法为求解多匝多层线圈的涡流损耗提供了思路。文献[25]提出矩形扁线的涡流损耗计算方法，计算出单根导线产生的涡流损耗。文献[26]对双凸极直流发电机扁线绕组的涡流损耗进行了计算和仿真，分析了槽漏磁对扁线绕组涡流损耗的影响。但是轴向磁通定子无铁心电机的磁场分布具有典型的三维分布特点，导体内涡流回路如图1所示，电机轴向主磁场与周向漏磁场均会在绕组上产生涡流。需要结合电机的磁场分布特性对扁线绕组的涡流损耗进行分析。
图1 主磁通与漏磁通产生涡流损耗
Fig.1 Eddy current loss caused by main flux and leakage flux
本文通过研究轴向无铁心电机气隙磁场分布特性，提出了一种适用于轴向无铁心电机扁线绕组的涡流损耗计算方法，对多层结构线圈的涡流损耗进行解析，着重分析漏磁场对涡流损耗的影响规律。根据绕组涡流损耗模型，以定子绕组铜损最低为目标，进一步对轴向无铁心电机扁线绕组的参数进行了优化。
本文以一台20极18槽电机为例，采用3D有限元的方法研究轴向无铁心电机气隙磁场分布特性，从而进一步推导轴向无铁心电机扁线绕组的交流铜耗。电机拓扑结构如图2所示，具体结构参数见表1。
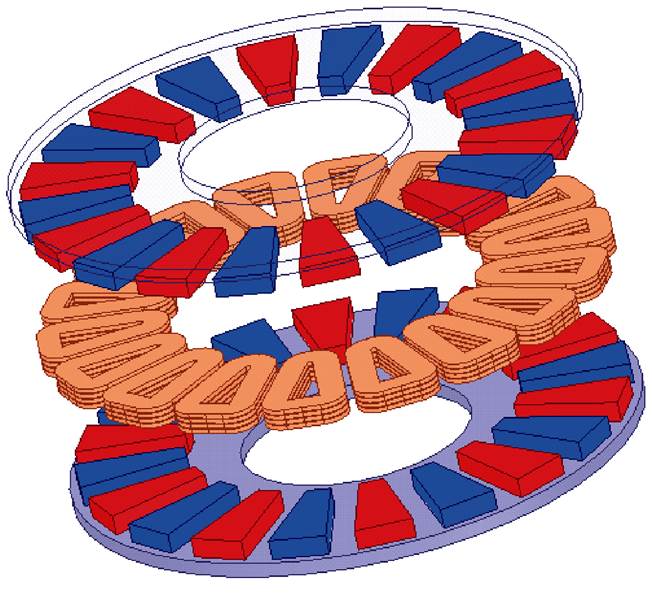
图2 电机拓扑结构
Fig.2 The topology of CAFPMSM
表1 无铁心轴向永磁同步电机模型参数
Tab.1 The model parameters of CAFPMSM
参 数数值 (型号) 转子轭外表面半径R1/mm100 永磁体外表面半径R2/mm96 定子槽数18 永磁体极对数p10 永磁体厚度/mm6.5 永磁体牌号N38UH 背铁厚度/mm6.5 气隙长度/mm1 额定转速n1/(r/min)3 600
以4层线圈为例，电机单个定子槽内绕组连接方式如图3所示。不同层线圈之间采用串联连接方式，以避免不同层绕组之间有环流，4层绕组在轴向方向叠加在一起。
在气隙中相邻永磁体中间位置建立观测面S1和气隙中心面S2，S1和S2两个平面互相垂直。采用有限元仿真可以得到气隙中周向漏磁场分布云图，如图4a所示。由图可知，观测面S1上靠近永磁体位置漏磁场强度较大而靠近气隙中心平面S2位置漏磁场强度基本为0，所以周向漏磁场在气隙中分布并不均匀，需要对其分布特性进行着重分析。如图4b所示为电机绕组简化模型，Bc1～Bcn代表漏磁场强度由高到低分布。由于矩形扁线对应于周向漏磁场的截面积S3相对较大，所以由周向漏磁场产生的涡流损耗，在导线上分布同样不均匀。从图中可以看出，由于同一根导线处于不同强度的周向漏磁场中，所以同一根导线内在不同轴向位置处的涡流回路产生的损耗也不相同。
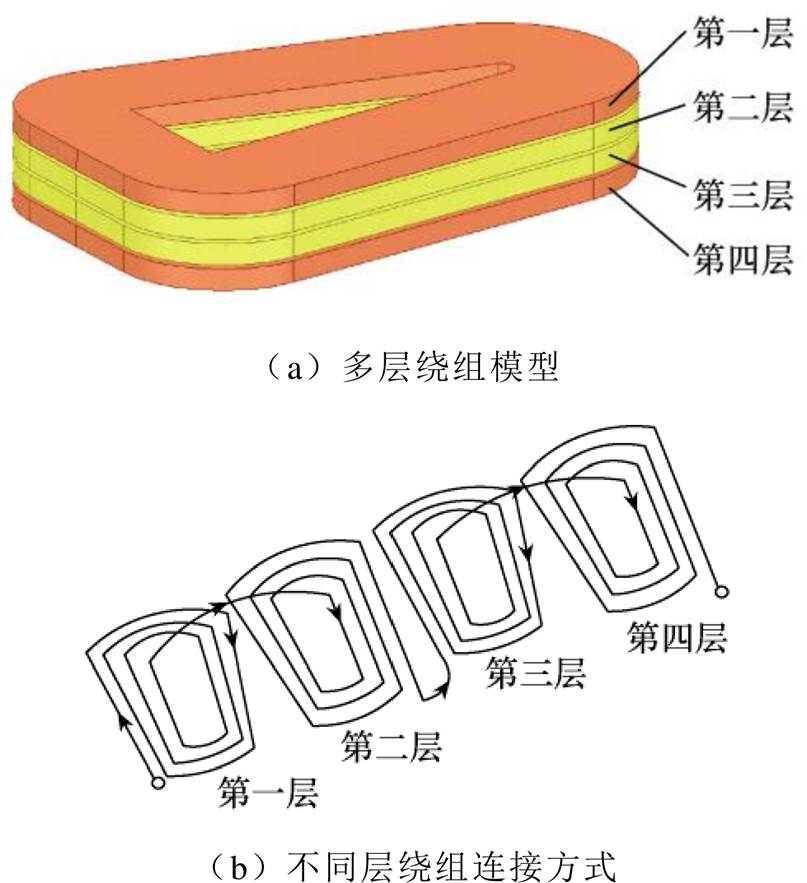
图3 电机单个定子槽内绕组连接方式
Fig.3 Schematic diagram of the coil connection in one slot
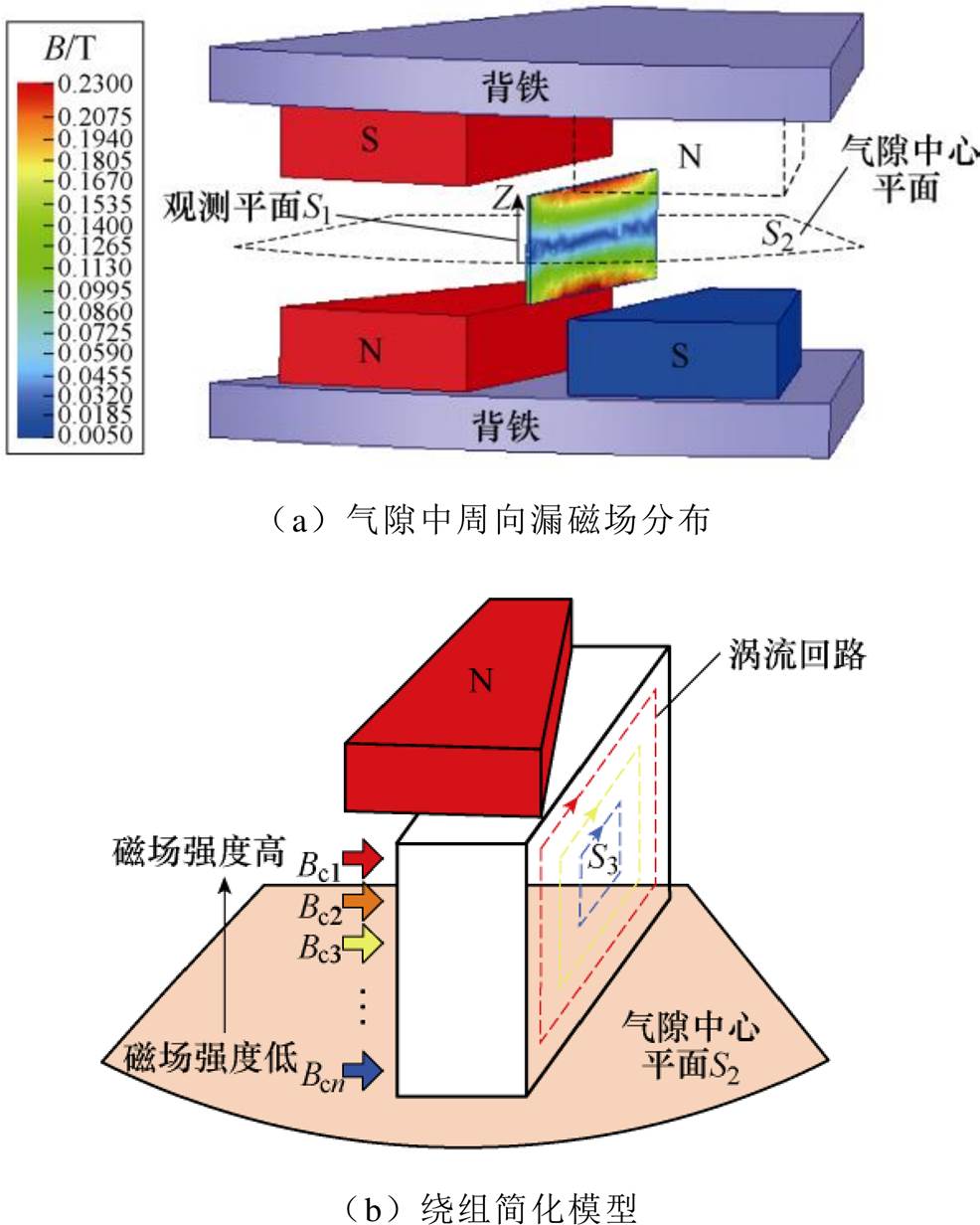
图4 周向漏磁场产生涡流损耗
Fig.4 Eddy current loss caused by leakage flux in circumferential direction
由图4a可得，周向漏磁场分布沿气隙中心平面S2上下对称，所以只需分析气隙中心平面S2以上部分磁场区域即可得到气隙内漏磁场整体分布特性。根据有限元仿真结果可知，气隙中周向漏磁场幅值最大处，为永磁体边缘正下方。在永磁体边缘正下方不同径向位置处设置如图5所示的观测线1～5，不同位置气隙磁场周向漏磁通密度幅值如图6所示。观测线1～5上漏磁通密度幅值基本相同，且气隙漏磁通密度幅值与其轴向位置呈近似线性关系，所以电机周向漏磁通密度幅值可以用轴向位置来表示，有
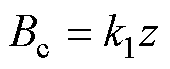（1）
式中，Bc为周向漏磁通密度幅值；z为气隙中心平面到绕组顶端的轴向距离；k1为1次谐波比例系数。当电机转子参数确定时，气隙中周向漏磁场分布也随之确定，所以比例系数k1可以通过式（1）得到。通过用轴向位置z表示Bc可以精确计算单根导体不同轴向位置周向漏磁通密度幅值。
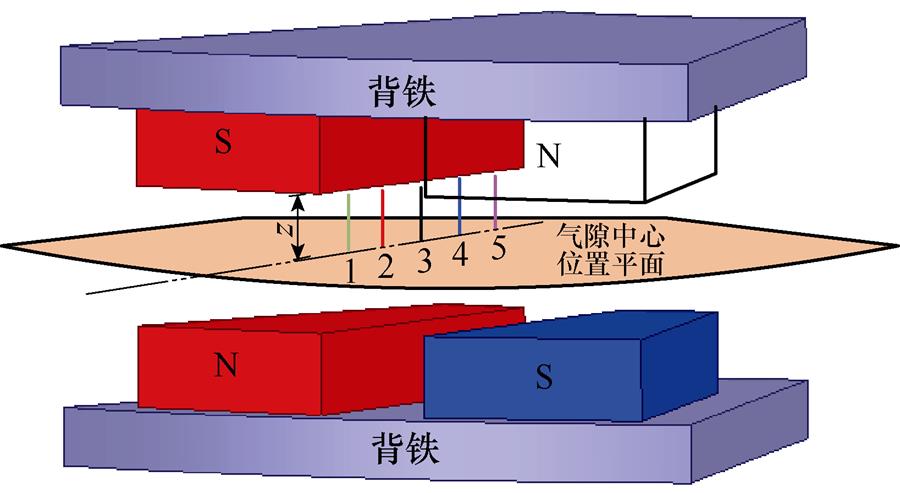
图5 周向漏磁场观测线示意图（一）
Fig.5 Observation lines for leakage flux in circumferential direction
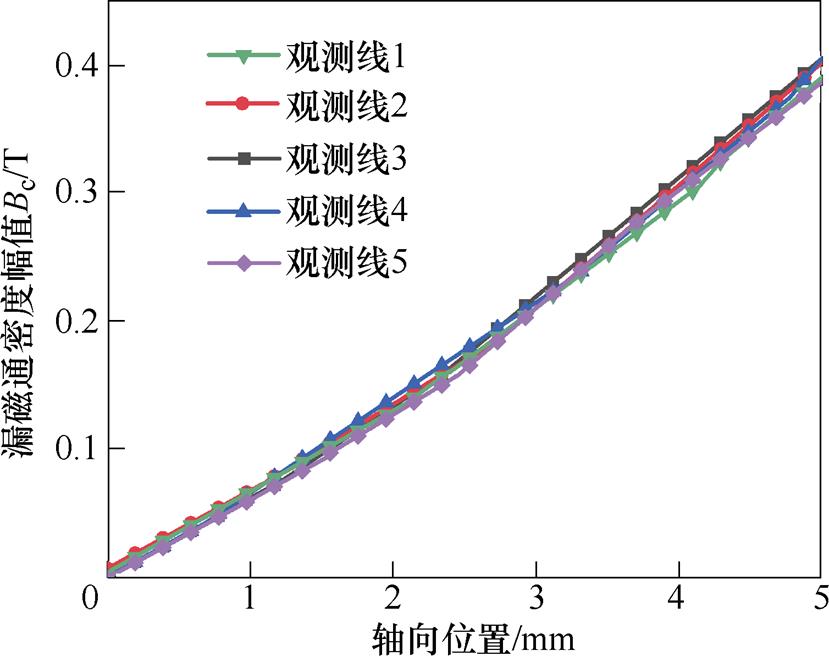
图6 漏磁通密度幅值Bc与轴向位置关系
Fig.6 Relationship between the amplitude of leakage flux density Bcand axial position
在永磁体正下方气隙轴向不同位置设置如图7所示的观测弧线。通过有限元仿真可以得到弧线上每一点切向方向的磁通密度幅值，得到周向漏磁通密度波形如图8所示。可以看出，靠近永磁体表面位置电机周向漏磁通密度波形幅值较大且谐波含量较多，畸变率较大。靠近气隙中心平面位置周向漏磁通密度波形幅值较小，且谐波含量较少，畸变率较小。由于空间谐波的频率较高，所以会产生更严重的涡流损耗。因此，必须要考虑由周向漏磁场内谐波产生的涡流损耗。
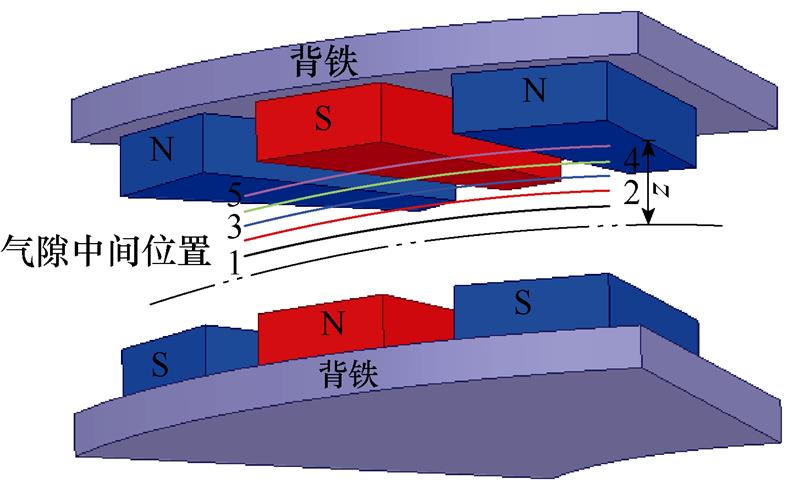
图7 周向漏磁场观测线示意图（二）
Fig.7 Observation lines for leakage flux in circumferential direction
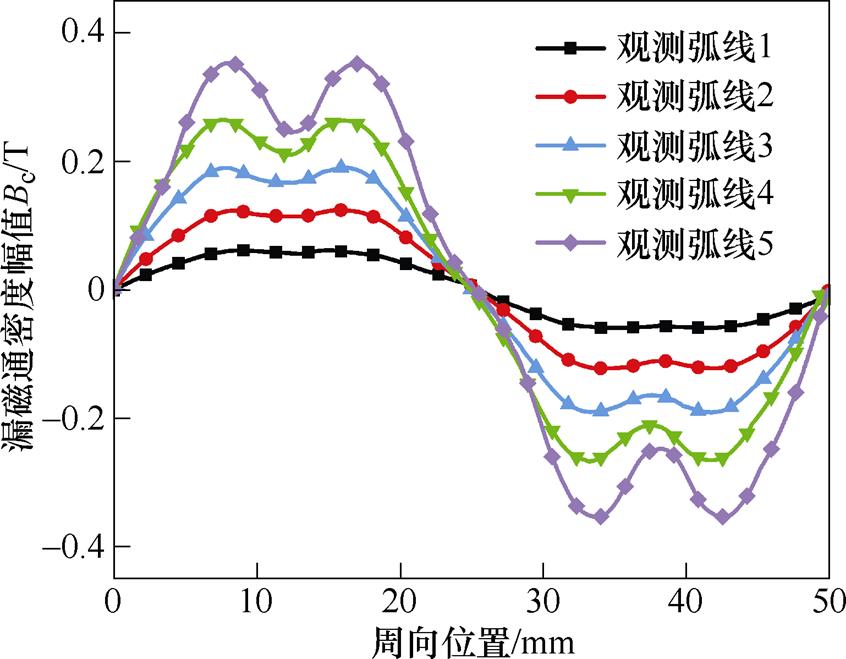
图8 周向漏磁通密度波形
Fig.8 Leakage flux density waveforms in circumferential direction
对观测弧线1～5所得漏磁通密度波形进行傅里叶分析，可以得到气隙中不同轴向位置处周向漏磁通密度谐波含量如图9所示。由图9可得，不同次谐波的周向漏磁通密度幅值Bcn与其轴向位置z也是基本呈线形关系，所以周向漏磁场中各次谐波幅值也可以由轴向位置z表示。考虑谐波时电机不同位置的周向漏磁通密度幅值为
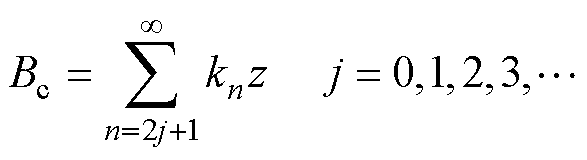（2）
式中，下角n为谐波次数；j为整数；kn为不同次数谐波比例系数。
通过测量观测弧线1～5上主磁场轴向分量，可以得到一个电周期内磁通密度轴向分量的波形如图10所示。为方便计算，取半径处的主磁通密度表示不同半径处磁通密度的平均值。对波形进行傅里叶分解，可以得到轴向主磁通密度波形各次谐波含量，轴向主磁通密度幅值Bz可表示为
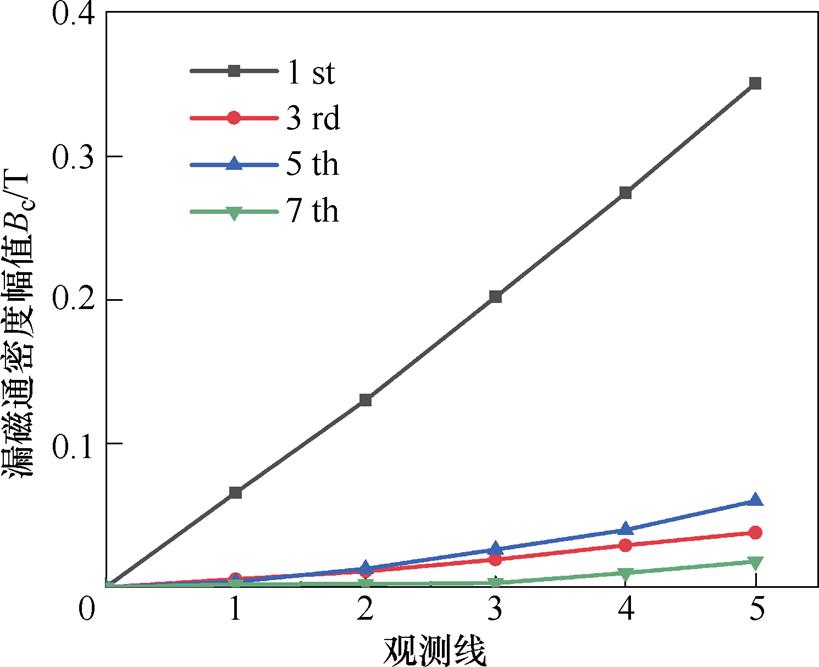
图9 周向漏磁场谐波含量
Fig.9 Harmonic content of leakage flux field in circumferential direction
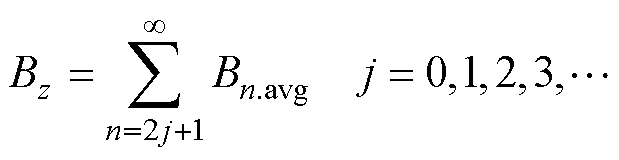（3）
式中，Bn.avg为各次谐波轴向主磁通密度幅值的平均值。
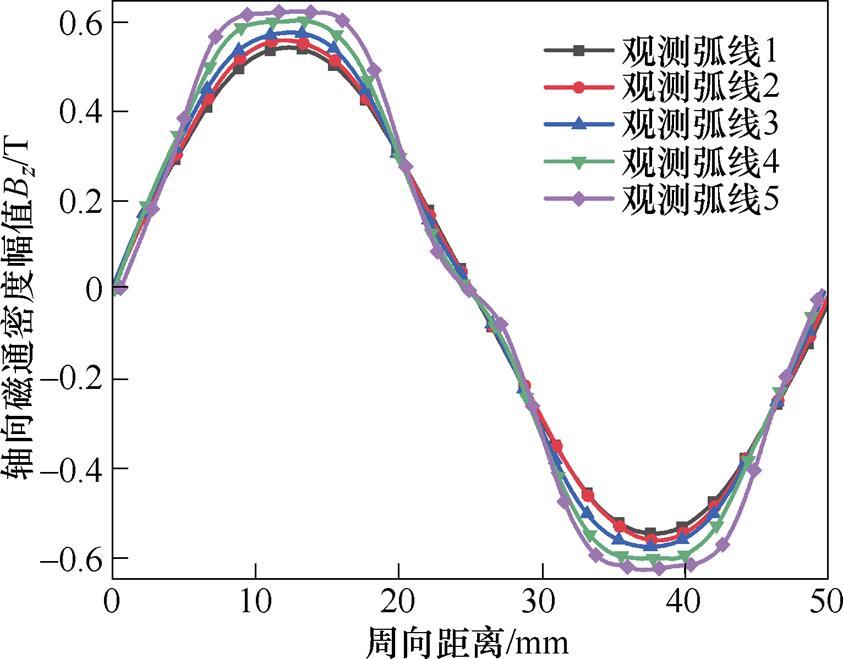
图10 轴向主磁通密度波形
Fig.10 Main flux density waveforms in axial direction
由于绕组所在不同位置的磁场可以分解为轴向分量和周向分量，不同分量都包含丰富的高次谐波。所以，定子绕组的涡流损耗，可以通过求出不同方向磁场以及各次谐波产生的涡流损耗，再进行求和得到。
气隙磁场周向分量产生涡流损耗如图11所示，L为矩形扁线径向长度，Wa为矩形扁线截面宽，Lb为矩形扁线截面长。为了求得矩形扁线的涡流损耗，假设电机气隙磁场轴向分量在Z轴方向以频率f交替变化，气隙磁场周向分量在X轴方向同样以频率f交替变化，两个方向磁场分量均以频率f切割定子绕组。
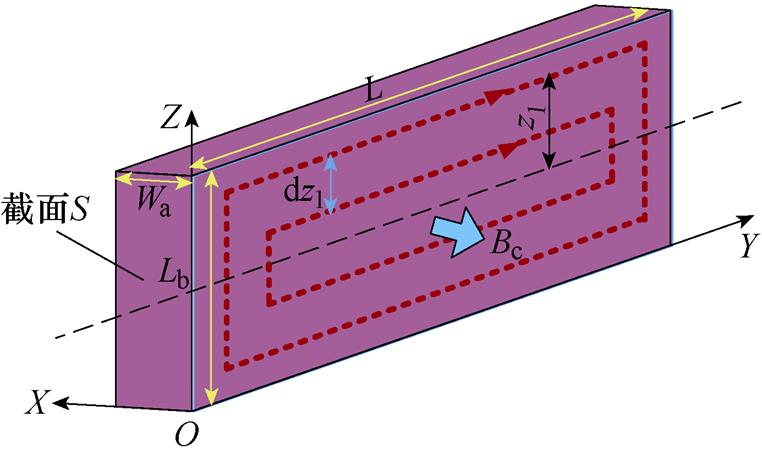
图11 气隙磁场周向分量产生涡流损耗
Fig.11 Eddy current loss caused by air gap flux field in circumferential direction
2.1.1 气隙磁场周向分量产生的涡流损耗
根据电磁感应定律可以得出由气隙磁场周向分量产生的涡流回路感应电动势E为
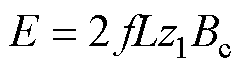（4）
式中，z1为涡流回路与绕组沿X方向截面中心对称线间的距离。忽略线圈端部，涡流回路的等效电阻R为
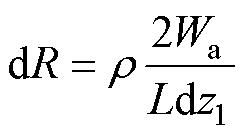（5）
式中，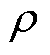
为导线电阻率。结合式（4）可以得到单根导体由气隙磁场周向分量产生的涡流损耗Pc为
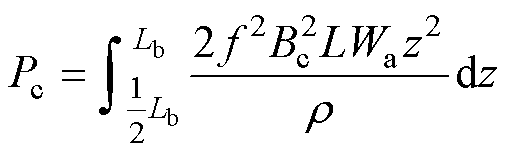（6）
根据式（1）所示的电机周向漏磁通密度幅值Bc与气隙轴向位置z的关系，并将其代入式（6）可得单根导体由气隙磁场周向分量产生的涡流损耗为
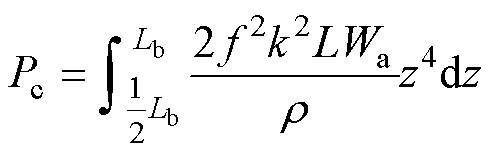（7）
式中，k为比例系数。
由式（7）可以得到导体中涡流损耗与轴向距离z之间的关系，从而可以准确计算由气隙磁场周向分量在单根导线上产生的涡流损耗。
2.1.2 气隙磁场轴向分量产生的涡流损耗
气隙磁场轴向分量穿过导线并以频率f切割导体，并且在导体的轴向截面上产生涡流。如图12所示为电机轴向主磁场产生的涡流回路。
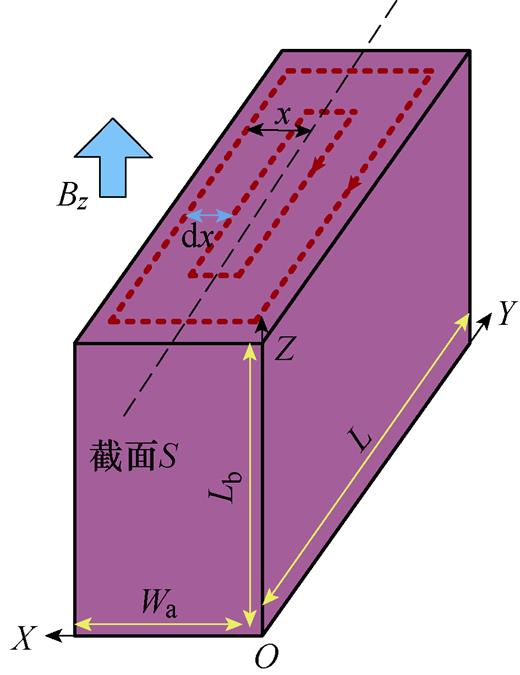
图12 气隙磁场轴向分量产生涡流损耗
Fig.12 Eddy current loss caused by air gap flux field in axial direction
假设气隙磁场的轴向分量在气隙中轴向不同位置处的幅值近似相等，取轴向中心线位置磁通密度幅值为通过导体的气隙磁场轴向分量幅值。则由气隙磁场轴向分量产生的涡流损耗Pz为
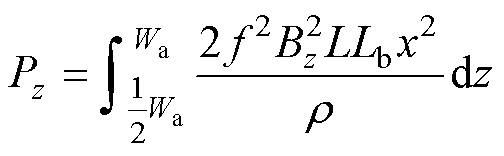（8）
式中，x为涡流回路与绕组沿Z方向截面中心对称线间距离。
2.1.3 单根导体产生的总涡流损耗
考虑气隙磁场内谐波含量，根据式（7）和式（8），周向磁场分量及轴向磁场分量产生的涡流损耗分别为
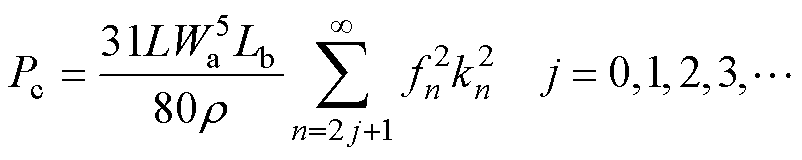（9）
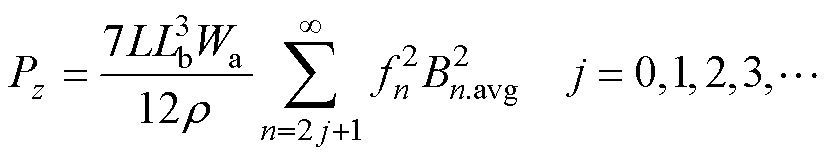（10）
式中，fn为不同次数谐波频率。
假设单根导体涡流损耗主要由气隙磁场内轴向分量与周向分量产生，忽略其他方向磁场分量对导体涡流损耗的影响。所以，单根导体产生的总涡流损耗Pall为气隙磁场轴向分量与气隙磁场周向分量产生的涡流损耗之和，有
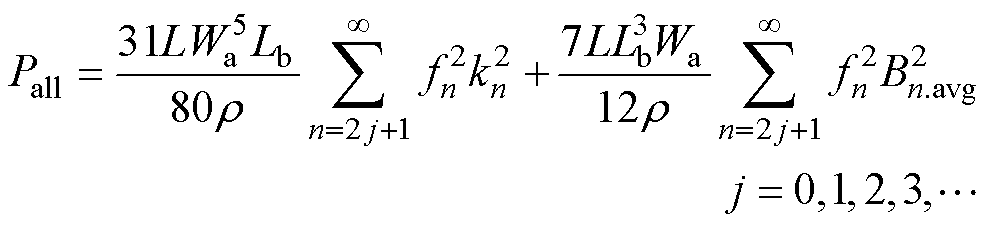（11）
轴向无铁心电机通常采用多层绕组线圈来抑制涡流损耗。由于气隙磁场的不均匀分布，不同层绕组产生的涡流损耗也不相同。以四层线圈的定子绕组为例，建立如图13所示的坐标系。由于气隙磁场的周向分量在轴向位置处的磁通密度幅值不相等，所以需要建立每一层绕组的涡流损耗模型。
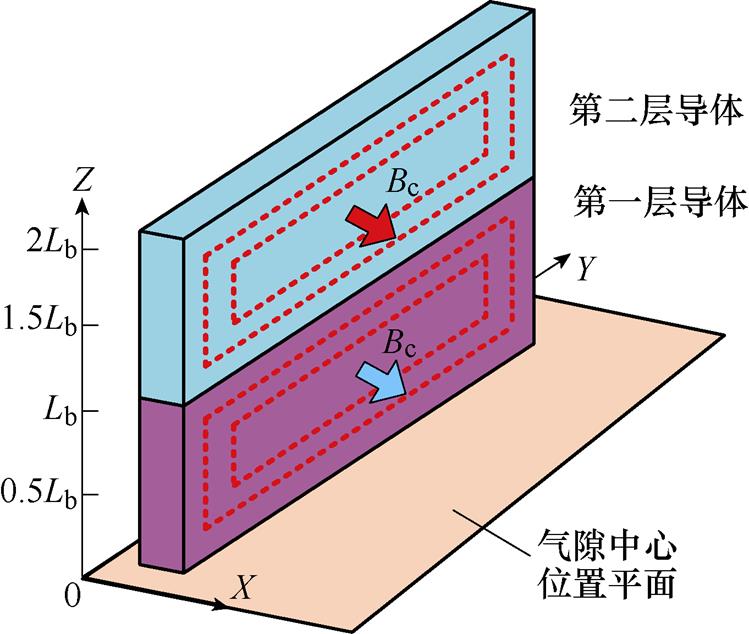
图13 气隙磁场周向分量在多层导体上产生的涡流损耗
Fig.13 Eddy current loss caused by air gap flux field in circumferential direction with multilayer conductors
2.2.1 气隙磁场周向分量产生的涡流损耗
由于第一层导体与第二层导体所处位置的气隙磁场轴向分量与周向分量均不相同，所以第二层导体的涡流损耗计算公式与第一层导体也不相同。通过式（7）计算第一层导体与第二层导体由周向漏磁场产生的涡流损耗，可以得到第一层导体与第二层导体由磁场周向分量产生的涡流损耗之和Pc-all为
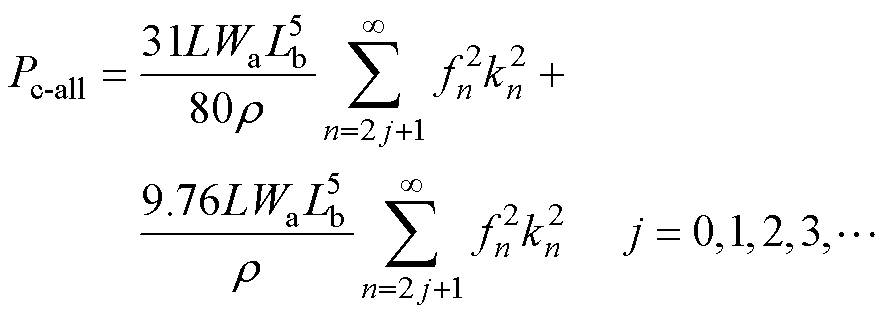（12）
2.2.2 气隙磁场轴向分量产生的涡流损耗
设第一层导体中心对称线位置轴向磁通密度幅值为Bz1，第二层导体中心对称线位置轴向磁通密度幅值为Bz2。由气隙磁场轴向分量在第一层与第二层导体上产生的总涡流损耗Pz-all为
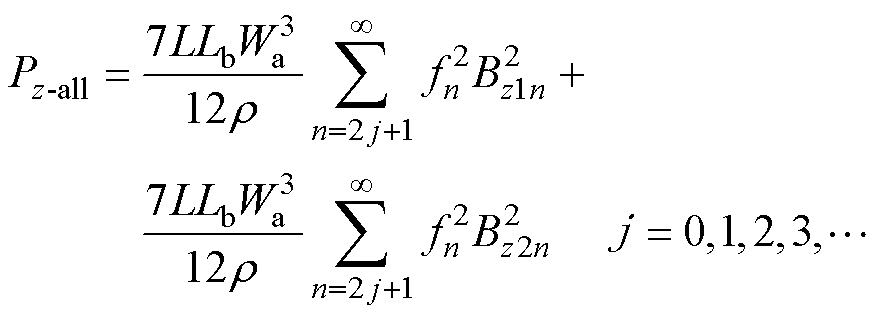（13）
2.2.3 多层导体产生的总涡流损耗
同单层导体产生的总涡流损耗求解公式，双层导体产生总的涡流损耗可表示为
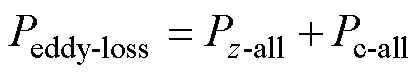（14）
将式（12）与式（13）代入式（14）可以得到双层导体产生的总涡流损耗Peddy-loss。
根据以上对双层导体产生涡流损耗的计算方法，同样也可以得到多层导体的涡流损耗。分别计算每一层导体的涡流损耗，再将每一层导体产生的涡流损耗相加即可得到整个线圈产生的涡流损耗。
根据涡流损耗的解析计算可知，涡流损耗大小与矩形导线的截面长Lb、截面宽Wa参数密切相关。由此可以看出，通过优化扁线参数可以降低绕组产生的涡流损耗。但是，当改变绕组参数降低涡流损耗的同时，绕组的直流损耗也会改变。由于导体趋肤效应的存在，改变扁线参数取值同样会对电机直流损耗产生影响。深入分析矩形导线的结构参数对直流损耗以及涡流损耗的影响，从而实现对矩形导线结构参数的优化，以减小电机绕组的铜耗。
当导体截面过大时趋肤效应的存在会使得电流在导体内部分布不均匀，增大直流损耗。以减少趋肤效应对直流损耗的影响为目标，首先计算导体趋肤深度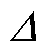
，以确定扁线绕组截面长与宽的最大取值范围。当绕组截面尺寸Wa、Lb均小于趋肤深度Δ时，趋肤效应对直流损耗产生的影响可忽略不计。趋肤深度 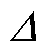计算公式[21]为
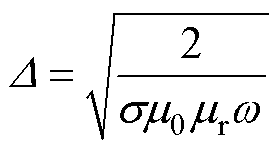（15）
式中，
为导线电导率；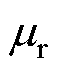
为相对磁导率；
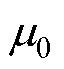为真空磁导率；
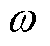为基波角频率。
绕组截面尺寸Wa、Lb均小于趋肤深度时，忽略趋肤效应对电机直流损耗产生的影响，直流损耗计算公式为
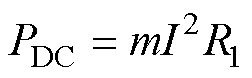（16）
式中，m为电机相数；I为电枢电流；R1为电机定子绕组电阻；PDC为电机绕组直流损耗。
以绕组矩形导线的电流密度为约束条件，即矩形导线的截面积不变，对导线截面的长度和宽度进行优化。如图14所示为扁线截面积S相同时，截面长Lb与宽Wa的不同设计方案。由于不同参数尺寸扁线的截面积S相同，所以当Lb、Wa均小于趋肤深度时，电机直流损耗与扁线截面长Lb和宽Wa无关。
图14 不同截面尺寸扁线绕组
Fig.14 Flat wire with different cross-sectional
根据约束条件，矩形导体的截面积S保持不变，多层绕组的涡流损耗与矩形导线结构参数之间的关系可表示为
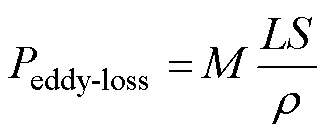（17）
式中，M为涡流损耗系数，有
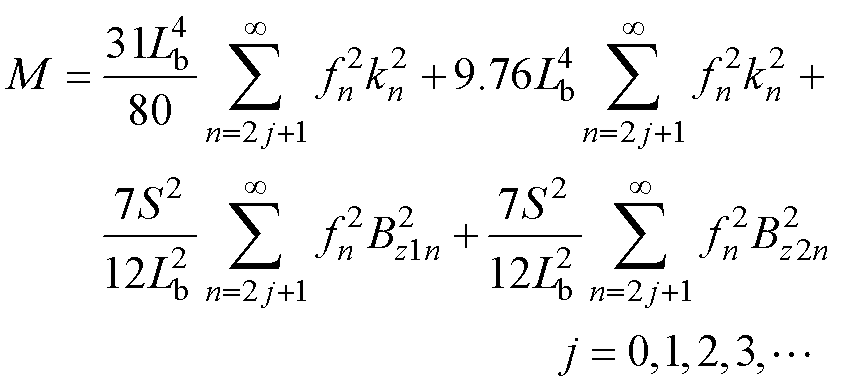（18）
由式（17）可以看出，导体涡流损耗与其系数M呈线性关系。绘制M与Lb的函数曲线，可得导体截面长Lb与绕组涡流损耗Peddy-loss的关系曲线，从而可以得到矩形导体结构参数与导体涡流损耗的关系如图15所示。由图中可以看出，矩形导体截面长度Lb取1.2 mm时电机涡流损耗最小，而当Lb的取值过大或过小时电机绕组涡流损耗都会增加。由此进一步可以得到涡流损耗最小时矩形导线的结构参数。
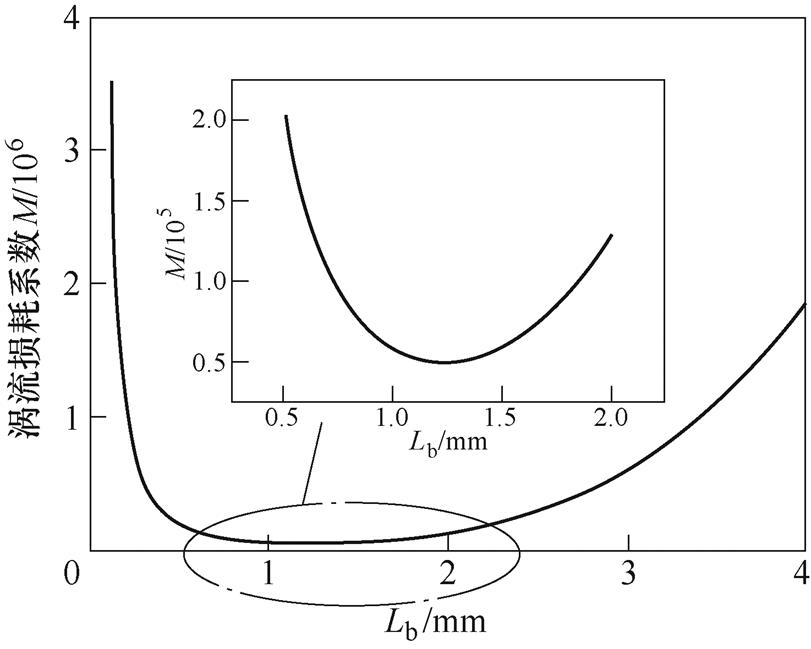
图15 涡流损耗系数M与截面长Lb关系
Fig.15 Relationship between the factor of eddy current loss M and the length of section Lb
利用有限元方法建立绕组等效模型。当改变导体截面参数时，由于在轴向同一层内，绕组从外到内各线圈，同一层绕组内圈与外圈线圈如图16所示，产生涡流损耗的变化趋势均相同，所以为了减少计算量，仿真计算时每一层绕组只取最外圈线圈，即可反映整个绕组线圈涡流损耗的变化趋势。
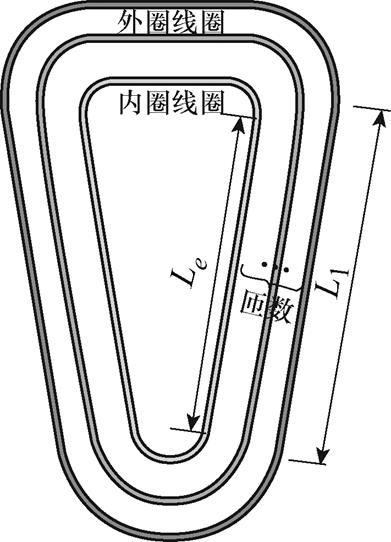
图16 同一层绕组内圈与外圈线圈
Fig.16 Inner and outer coils of the same winding layer
多匝线圈的示意模型如图16所示，忽略端部效应时，内外不同线圈之间只有径向长度L发生了变化。而根据式（6），涡流损耗与径向长度L呈线性关系，所以内圈绕组涡流损耗可以通过其径向长度与外圈绕组径向长度的比值进行折算，有
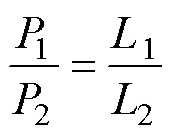（19）
式中，P1为第一匝线圈产生的涡流损耗；L1为第一匝线圈有效边长度；P2为第二匝线圈产生的涡流损耗；L2为第二匝线圈有效边长度。
通过将每一匝线圈都进行折算可以得出整个绕组线圈的涡流损耗，进而得到电机定子绕组总的涡流损耗为
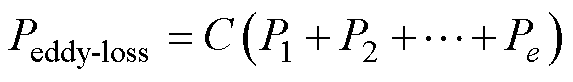（20）
式中，e为单个绕组线圈匝数；P1～Pe为从外到内不同匝线圈产生的涡流损耗；C为定子总线圈数。
对不同截面参数的绕组线圈进行建模仿真，得到不同截面参数线圈的涡流损耗仿真结果，如图17所示。仿真所得涡流损耗与截面长Lb关系曲线与计算所得曲线变化趋势一致，且当绕组的截面长度Lb取1.2 mm时电机最外圈线圈涡流损耗为最小值。仿真结果验证了理论推导的准确性。
为了验证理论推导以及有限元仿真的准确性，制造的实验样机参数见表2（实验样机结构参数与有限元仿真模型相同），同时搭建了无铁心永磁电机涡流损耗实验平台如图18所示。原动机为伺服电机，实验样机由原动机拖动至不同转速。通过高精度转矩测试仪测量输入转矩T，从而计算样机的输入功率P1，如式（21）所示。空载运行时，样机的输入功率P1即为电机的涡流损耗Peddy-loss与机械损耗Pmec之和。在电机无定子绕组时，可以测得样机在不同转速下的机械损耗Pmec。将相同转速条件下有定子与无定子输入功率测量结果相减，可以得到电机绕组在不同转速条件下的实际涡流损耗值Peddy-loss，如式（22）所示。
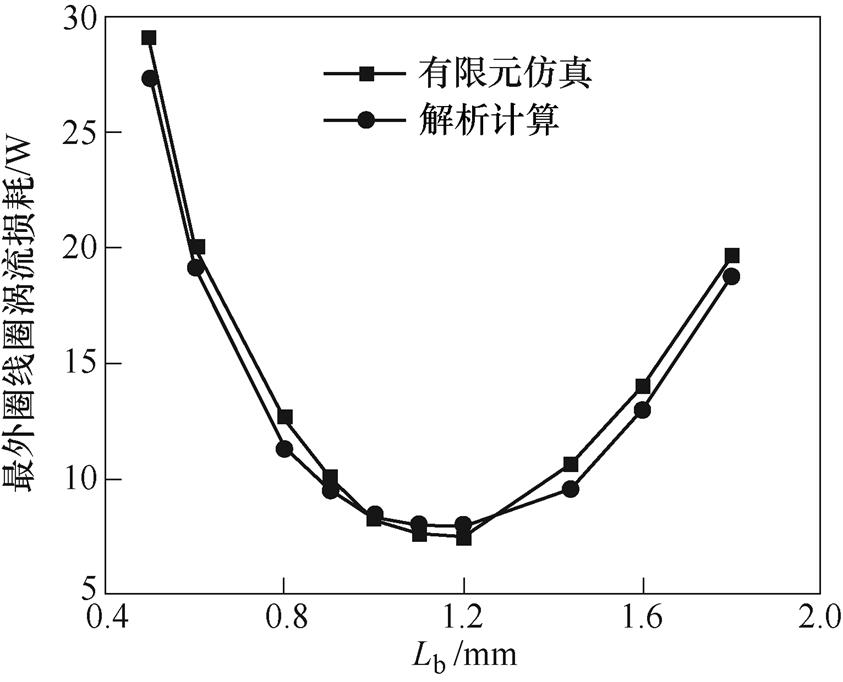
图17 最外圈线圈涡流损耗仿真结果
Fig.17 Analytical and simulation results of eddy current loss in the outermost coil
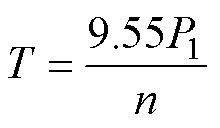（21）
式中，n为电机转速。
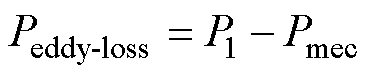（22）
表2 无铁心轴向永磁同步电机实验样机参数
Tab.2 The prototype parameters of CAFPMSM
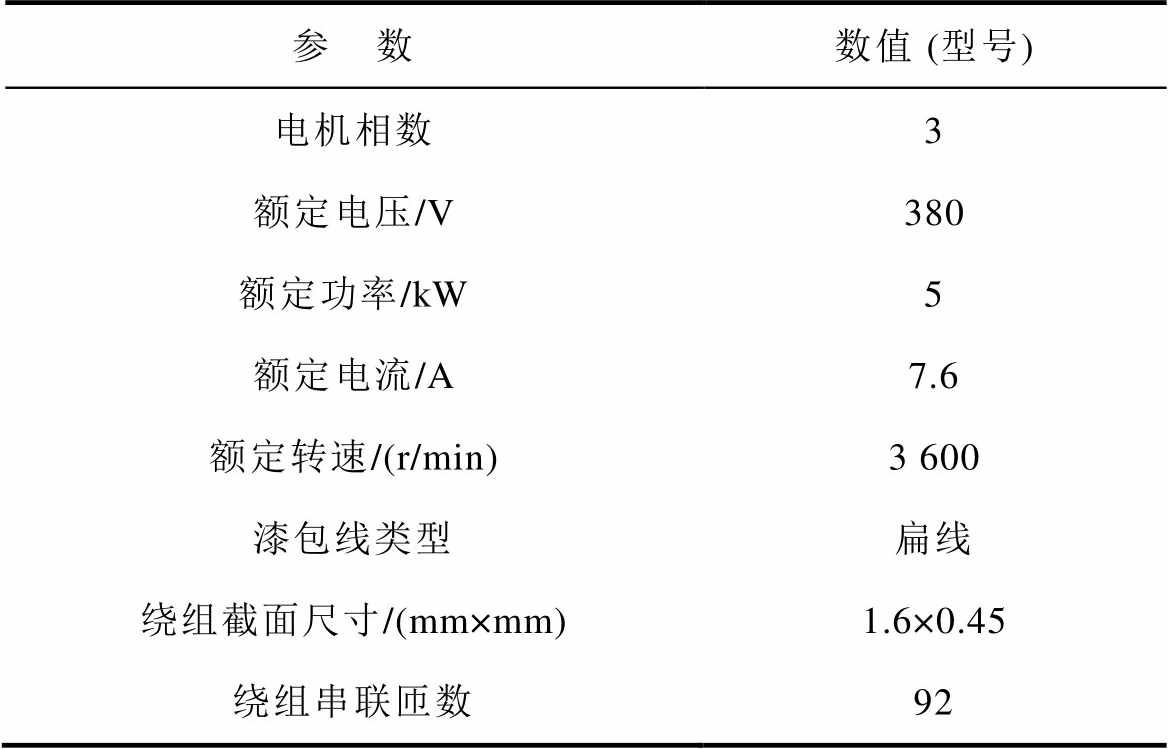
参 数数值 (型号) 电机相数3 额定电压/V380 额定功率/kW5 额定电流/A7.6 额定转速/(r/min)3 600 漆包线类型扁线 绕组截面尺寸/(mm×mm)1.6×0.45 绕组串联匝数92
对无铁心永磁电机进行测试，得到定子绕组的涡流损耗与转速之间的关系如图19所示。由图中涡流损耗测试结果与有限元仿真及解析计算结果可以看出，在达到额定转速3 600 r/min时电机涡流损耗测量值为232 W，解析计算值为218 W，误差为6%，主要是因为解析计算时没有考虑绕组的端部。实验结果与有限元仿真及解析计算结果吻合度较高，验证了解析计算方法的准确性。
图18 实验平台
Fig.18 Experimental platform
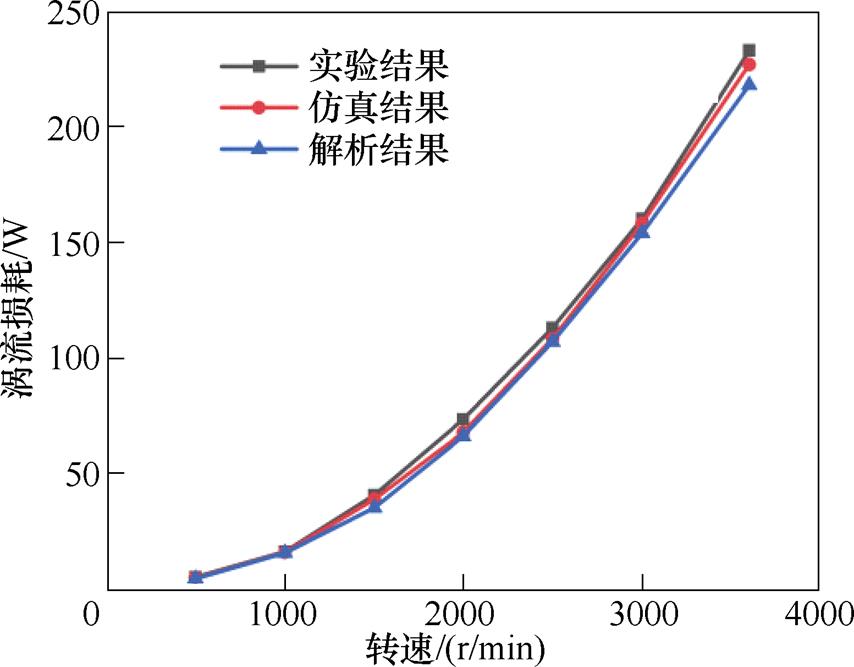
图19 涡流损耗解析、仿真与实验对比
Fig.19 Analytical, simulation and measurement of eddy current loss
本文针对矩形导线绕组的轴向无铁心电机无法精确计算绕组涡流损耗这一问题，基于轴向无铁心电机气隙磁场的分布特性，提出了扁线无铁心电机绕组涡流损耗的计算和优化方法，推导了绕组涡流损耗的快速计算公式。总结得到了以下结论：
1）针对定子无铁心电机，气隙磁场的轴向分量和周向分量均会在矩形导线中产生涡流损耗，即由转子漏磁场产生的涡流损耗不能忽略。
2）电机涡流损耗主要与扁线截面的长和宽比值以及气隙磁场强度有关系。通过改变截面长与宽的比值，可以保证电机绕组在直流损耗相同的条件下，涡流损耗最小。
3）样机不同转速情况下定子涡流损耗测试结果与理论解析、有限元分析结果基本一致，验证了解析计算与有限元结果的正确性，为扁线绕组在无铁心电机领域的应用提供了一定的参考价值。
参考文献
[1] Peng Bing, Zhuang Xiaoyu. Design and performance analysis of axial flux permanent magnet machines with double-stator dislocation using a combined wye- delta connection[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(1): 53-59.
[2] 张文晶, 徐衍亮, 李树才. 新型盘式横向磁通永磁无刷电机的结构原理及设计优化[J]. 电工技术学报, 2021, 36(14): 2979-2988.
Zhang Wenjing, Xu Yanliang, Li Shucai. Structure principle and optimization of a novel disk transverse flux permanent magnet brushless motor[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(14): 2979-2988.
[3] Wang Xiaoguang, Zhao Meng, Tang Lei, et al. Fault-tolerant analysis and design of AFPMSM with multi-disc type coreless open-end winding[J]. IEEE Access, 2020, 8: 171744-171753.
[4] Wang Xiaoguang, Wan Ziwei, Tang Lei, et al. Electromagnetic performance analysis of an axial flux hybrid excitation motor for HEV drives[J]. IEEE Transa- ctions on Applied Superconductivity, 2021, 31(8): 1-5.
[5] 唐任远, 赵清, 周挺. 稀土永磁电机正进入大发展的新时期[J]. 沈阳工业大学学报, 2011, 33(1): 1-8, 30.
Tang Renyuan, Zhao Qing, Zhou Ting. Rare earth permanent magnet electrical machines stepping a new period of rapid development[J]. Journal of Shenyang University of Technology, 2011, 33(1): 1-8, 30.
[6] He Mingjie, Li Weiye, Peng Jun, et al. Multi-layer quasi three-dimensional equivalent model of axial- flux permanent magnet synchronous machine[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(1): 3-12.
[7] 李修东, 郑晓钦, 王海峰, 等. 最大转矩范围内九相永磁同步电机缺相容错运行铜耗优化策略[J]. 电工技术学报, 2022, 37(17): 4355-4363.
Li Xiudong, Zheng Xiaoqin, Wang Haifeng, et al. Copper loss optimization strategy for nine-phase permanent magnet synchronous motors fault-tolerant operation in maximum torque range[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4355-4363.
[8] 骆凯传, 师蔚, 张舟云. 基于温度实验的永磁同步电机损耗分离方法[J]. 电工技术学报, 2022, 37(16): 4060-4073.
Luo Kaichuan, Shi Wei, Zhang Zhouyun. Method of loss separation of permanent magnet synchronous motor based on temperature experiment[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(16): 4060-4073.
[9] 佟文明, 侯明君, 孙鲁, 等. 基于精确子域模型的带护套转子高速永磁电机转子涡流损耗解析方法[J]. 电工技术学报, 2022, 37(16): 4047-4059.
Tong Wenming, Hou Mingjun, Sun Lu, et al. Analytical method of rotor eddy current loss for high-speed surface-mounted permanent magnet motor with rotor retaining sleeve[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4047-4059.
[10] 陈浈斐, 邢宁, 马宏忠, 等. 分数槽永磁电机永磁体谐波涡流损耗建模与分析[J]. 电工技术学报, 2022, 37(14): 3514-3527.
Chen Zhenfei, Xing Ning, Ma Hongzhong, et al. Analytical modeling and analysis of magnet harmonic loss in fractional slot permanent-magnet machines[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3514-3527.
[11] 徐衍亮, 赵建辉, 房建成. 高速储能飞轮用无铁心永磁无刷直流电动机的分析与设计[J]. 电工技术学报, 2004, 19(12): 24-28.
Xu Yanliang, Zhao Jianhui, Fang Jiancheng. Analysis and design of coreless permanent magnet brushless DC machine in high-speed energy storage flywheel application[J]. Transactions of China Electrotechnical Society, 2004, 19(12): 24-28.
[12] 刘向东, 马同凯, 赵静. 定子无铁心轴向磁通永磁同步电机研究进展综述[J]. 中国电机工程学报, 2020, 40(1): 257-273, 392.
Liu Xiangdong, Ma Tongkai, Zhao Jing. An overview on research progress of coreless stator axial flux permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2020, 40(1): 257-273, 392.
[13] Wang Shen, de Rooij M A, Odendaal W G, et al. Reduction of high-frequency conduction losses using a planar litz structure[J]. IEEE Transactions on Power Electronics, 2005, 20(2): 261-267.
[14] 高华敏, 张卓然, 王晨, 等. 定子无铁心轴向磁场永磁轮毂电机损耗分析及效率优化[J]. 中国电机工程学报, 2021, 41(6): 2002-2012.
Gao Huamin, Zhang Zhuoran, Wang Chen, et al. Loss analysis and efficiency optimization of ironless stator axial flux permanent magnet in-wheel machine[J]. Proceedings of the CSEE, 2021, 41(6): 2002-2012.
[15] Islam M S, Husain I, Ahmed A, et al. Asymmetric bar winding for high-speed traction electric machines[J]. IEEE Transactions on Transportation Electrification, 2020, 6(1): 3-15.
[16] Gonzalez D A, Saban D M. Study of the copper losses in a high-speed permanent-magnet machine with form-wound windings[J]. IEEE Transactions on Indu- strial Electronics, 2014, 61(6): 3038-3045.
[17] Soltani M, Nuzzo S, Barater D, et al. Considerations on the preliminary sizing of electrical machines with hairpin windings[C]//2021 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Modena, Italy, 2021: 46-51.
[18] Zhang Fengyu, Gerada D, Xu Zeyuan, et al. A thermal modeling approach and experimental validation for an oil spray-cooled hairpin winding machine[J]. IEEE Transactions on Transportation Electrification, 2021, 7(4): 2914-2926.
[19] 曹永娟, 陶少卿, 余莉. 轴向磁场无铁芯永磁电机绕组涡流损耗分析与计算[J]. 东南大学学报(自然科学版), 2016, 46(6): 1214-1220.
Cao Yongjuan, Tao Shaoqing, Yu Li. Analysis and calculation of winding eddy current loss in stator- coreless axial-flux permanent magnet machine[J]. Journal of Southeast University (Natural Science Edition), 2016, 46(6): 1214-1220.
[20] 董剑宁, 黄允凯, 金龙, 等. 定子无铁心轴向磁场永磁电机的解析设计[J]. 电工技术学报, 2013, 28(3): 43-49.
Dong Jianning, Huang Yunkai, Jin Long, et al. Analytical design method of stator-coreless axial flux permanent magnet machines[J]. Transactions of China Electrotechnical Society, 2013, 28(3): 43-49.
[21] 汤平华, 漆亚梅, 黄国辉, 等. 定子无铁心飞轮电机绕组涡流损耗分析[J]. 电工技术学报, 2010, 25(3): 27-32.
Tang Pinghua, Qi Yamei, Huang Guohui, et al. Eddy current loss analysis of ironless flywheel electric machine’s winding[J]. Transactions of China Elec- trotechnical Society, 2010, 25(3): 27-32.
[22] 王小雷. 一种功率型无铁芯AFPM电机绕组涡流损耗抑制方法[J]. 鱼雷技术, 2012, 20(4): 295-300.
Wang Xiaolei. A winding eddy current loss suppression method for power-type axial flux permanent magnet machine with coreless-stator[J]. Torpedo Technology, 2012, 20(4): 295-300.
[23] 陈晨, 王又珑. 基于效率及温升的轴向磁通永磁电机优化设计[J]. 中国电机工程学报, 2016, 36(6): 1686-1694.
Chen Chen, Wang Youlong. Optimal design of axial- flux permanent magnet motors based on the efficiency and temperature rise[J]. Proceedings of the CSEE, 2016, 36(6): 1686-1694.
[24] 邵非非, 陈钢. 无刷直流盘式电机涡流计算[J]. 微电机, 2011, 44(10): 13-16.
Shao Feifei, Chen Gang. Calculation of eddy current loss in the BLDC permanent magnet disc machine with coreless stator[J]. Micromotors, 2011, 44(10): 13-16.
[25] Wang Rongjie, Kamper M J. Calculation of eddy current loss in axial field permanent-magnet machine with coreless stator[J]. IEEE Transactions on Energy Conversion, 2004, 19(3): 532-538.
[26] Zhang Jian, Zhang Zhuoran, Xia Yiwen, et al. Thermal analysis and management for doubly salient brushless DC generator with flat wire winding[J]. IEEE Transactions on Energy Conversion, 2020, 35(2): 1110-1119.
Abstract Coreless axial flux permanent magnet synchronous machine (CAFPMSM) is increasingly used in industrial applications due to its advantages such as compact structure, low maintenance cost, high power density, high torque ratio, and power efficiency. Preformed flat wire has a relatively regular shape, which is adopted in CAFPMSM winding manufacturing because it can make full use of stator space and increase the power density of the machine. Since the coreless winding is directly exposed to the air gap flux field, the large across section of the flat wire will result in significant eddy current losses and will be more serious when the speed goes higher. Therefore, it is important to calculate the eddy current losses of the winding accurately. Some valuable methods have been presented to calculate the eddy current loss of the traditional round winding, but they are unsuitable for CAFPMSM with flat wire. This paper derives the formula specific to flat wire for the uneven distribution of eddy current losses generated by the air gap flux field. According to the theoretical analysis of eddy current loss and taking the minimum copper loss as the optimization objective, the solution of the optimal parameters of flat wire is established. The calculation formula and parameter optimization method can reduce the eddy current loss and improve efficiency.
Firstly, the distribution characteristics of both the flux field in the axial direction and circumferential direction have been analyzed. Secondly, the amplitude of leakage flux density between the two adjacent permanent magnets is approximately linear with the position in the axial direction. The amplitude of the leakage flux density in different positions can be expressed in terms of the distance in the axial direction. The eddy current loss produced by the leakage flux can be calculated. Thirdly, the amplitude of the main flux density waveform can be expressed by the average value, simplifying the calculation of the eddy current loss produced by the main flux. Finally, the theoretical analysis method has been proposed, and the eddy current loss of the winding can be obtained by the sum of the eddy current loss produced by the main flux and leakage flux. According to the proposed theoretical analysis, the length and width of the cross-section of flat wire are optimized with the constraint of the current density. Furthermore, the method for selecting the length and width of the cross-section is proposed to obtain the lowest eddy current loss of the winding. An equivalent model of the winding by finite element method is established, and the simulation results of the eddy current loss verify the correctness of the theoretical analysis. According to the established model, the prototype is manufactured. The measured results of the eddy current loss prove the accuracy of theoretical analysis, and the error is 6 %.
The following conclusions can be drawn from the analysis: (1) Both axial and circumferential components of the air gap flux field will produce eddy current loss in the rectangular conductor. The eddy current loss caused by the leakage flux field should be considered. (2) The eddy current loss of the machine is related to the length ratio, flat wire section width, and density of the air gap flux field. By changing the ratio of section length to width, the eddy current loss of the winding can be minimized with the same direct current loss. (3) The measured results of the prototype at different speeds are consistent with the theoretical and finite element analysis results, which verifies the correctness of the analytical calculation and finite element results. This paper provides a reference for designing machine windings with different structures.
keywords：Coreless axial flux permanent magnet synchronous machine, flat wire, calculation of eddy current loss, optimization of winding
DOI: 10.19595/j.cnki.1000-6753.tces.220911
中图分类号：TM351
湖北省教育厅科学技术研究计划重点资助项目（D20201407）。
收稿日期 2022-05-26
改稿日期 2022-06-29
王晓光 男，1984年生，副教授，研究方向为永磁电机及其控制。E-mail: xgwang84@foxmail.com（通信作者）
尹 浩 男，1997年生，硕士研究生，研究方向为永磁电机及其控制。E-mail: haoyinhbut@163.com
（编辑 崔文静）