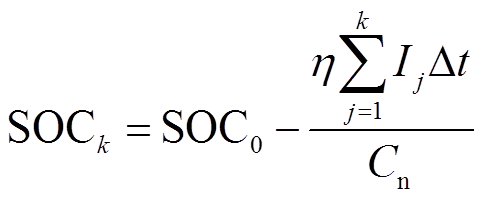 (1)
(1)
摘要 针对全寿命内复杂温度环境下锂离子电池内部状态难以快速精确估计难题,基于迁移模型提出一种宽温度全寿命荷电状态(SOC)与可用容量联合估计方法。选择传统二阶RC等效电路搭建迁移模型,并基于权值选择粒子滤波算法完成迁移因子的在线迁移,实现了宽温度全寿命内锂离子电池SOC快速准确的估算,基于得到的SOC估计值采用容量逆推实现了可用容量估计。结果表明,所提出方法在全寿命宽温度环境下估算SOC与可用容量具有计算量小、精度高的明显优势,SOC估计最大误差小于3%,容量估计最大误差小于2%。
关键词:锂离子电池 荷电状态 容量 迁移模型 温度 寿命
随着能源危机与全球变暖问题的日益严峻,发展电动汽车已成为缓解能源与气候危机、实现经济绿色可持续发展的迫切需求[1]。电动汽车相较于传统汽车主要依靠动力电池输出动力驱动汽车,具有节能环保的明显优势。目前车用动力电池以锂离子电池为主,包括磷酸铁锂电池和三元锂离子电池等[2]。为提高锂离子电池的使用性能和安全性,对其内部状态进行快速准确的实时监控是电池管理系统(Battery Management System, BMS)需要完成的重要工作之一[3],包括荷电状态(State of Charge, SOC)、健康状态(State of Health, SOH)、功率状态(State of Power, SOP)等。SOC反映了当前状态下电池内部剩余电量,精确地估算电池SOC可以更准确地控制充放电电流及截止时间,避免过充、过放和过负荷工作,提高电池使用安全性和延长使用寿命,同时SOC也是BMS进行电池均衡和故障诊断的重要依据[4]。然而受到电池老化后可用容量衰减及工作环境温度变化等多重因素耦合影响,如何实现全生命周期内复杂温度环境下的SOC精确估计一直是电池管理系统的难点[5]。同时,及时获取和了解电池使用过程中的可用容量状态,对于电池的可靠使用和及时更换也具有重要的作用和意义。
目前常用的SOC估算方法有安时积分法、黑箱SOC估计模型及基于状态空间模型的方法三类。安时积分法的优点是原理简单、计算速度快[6];缺点是高度依赖初始SOC精确度,且由于误差累计造成误差相对较大,因此通常在使用过程中与其他算法结合使用。常用的黑箱SOC估计模型有神经网络模型、模糊逻辑模型和支持向量回归模型等,这几种模型对实验数据质量的依赖性较高,且运算量很大,因此实用性不高[7]。基于状态空间模型是目前使用最多的方法,也被称为基于模型的方法。常见的模型有组合模型[8]、电化学模型[9]、等效电路模型等。其中以等效电路模型应用最多[10],其核心思想是利用数学模型来描述电池状态参数与电池外特性之间的变化关系,根据模型的电学方程建立电池SOC与开路电压(Open Circuit Voltage, OCV)之间的关系,并基于安时积分法获取电池SOC。常用的等效电路模型包括内阻模型、戴维南等效电路模型、PNGV模型和二阶RC等效电路模型等[11]。为了降低使用过程中数据采集噪声对估算精度的影响,该方法常结合各种滤波算法使用,包括扩展卡尔曼滤波(Extended Kalman Filter, EKF)[12]、粒子滤波[13]、H无穷滤波[14]及三种算法的衍生滤波算法等。由于基于状态空间模型的方法具有较好的在线应用能力、较高精度和初始误差纠正能力,被广泛地研究和应用于SOC估计。文献[15]将扩展卡尔曼滤波与考虑环境温度影响的锂离子电池改进双极化模型相结合,实现了不同温度下SOC的精确估计,其结果最大误差小于5%。文献[16]基于二阶RC等效电路模型通过模糊自适应扩展卡尔曼滤波器的方法完成了对SOC的估计,所提方法具有计算精度高、收敛速度快的优点。
然而基于状态空间模型的方法严重依赖于模型精度,且受到温度变化和电池老化的影响,进而造成全生命周期内和复杂温度环境下SOC估计精度的下降。文献[17]建立了温度补偿模型,并结合扩展卡尔曼滤波算法实现了锂离子电池SOC的动态估计,该方法虽然在建模过程中考虑了温度对模型的影响,有效提高了SOC的估计精度,但所需数据量较大,实际应用较为困难。文献[18]针对电池老化对SOC估计精度的影响,在参数辨识过程中融入了容量更新技术,通过容积卡尔曼滤波算法实现了不同老化范围的SOC估计,但该方法并未考虑温度对电池模型造成的影响,无法实现锂离子电池在宽温度范围的SOC有效估计。
针对上述问题,文献[19]中提出迁移模型的概念,该模型建立在传统等效模型的基础上,将外部温度和老化对模型精度影响程度定义为不确定量,仅需少量的数据即可建立起迁移模型,通过粒子滤波算法在线确定迁移因子,即可实现对温度和老化影响下的模型参数确定,大大减少了电池在复杂环境下建模所需要的数据量;文献[20]基于迁移模型实现了在温度和老化不确定的状态下对电池电量的估计。但文献[19-20]在迁移因子确定的过程中均采用传统的粒子滤波算法,而传统粒子滤波容易出现粒子退化现象,从而陷入粒子单一性,造成SOC估算精度下降。针对粒子单一问题,文献[21]提出了权值选择粒子滤波算法,该算法通过择优选择权重较大的粒子,可有效地解决粒子滤波的粒子退化问题,提高了粒子的多样性。
综上所述,本文在迁移模型理论的基础上融入权值选择粒子滤波算法,针对锂离子电池宽温度及全寿命范围内的SOC和可用容量估计进行研究,所提方法大幅度缩减了建模所需的数据量,并且估算得到的SOC值具有精度高、对初始值误差校正能力强等优点。此外,本文还通过将估计得到的精确SOC值通过容量逆推的方式实现可用容量的估计,所用方法计算简单,容易实现,具有实际工程应用的优势。
SOC用来反映电池的剩余容量,其定义表示为剩余容量与总容量的比值,用百分比表示。本文为了更好地表征迁移模型在电池温度及老化程度不确定情况下进行SOC估算的优势,采用两种不同的SOC定义来分析,即参考SOC和不精确SOC。
1)参考SOC
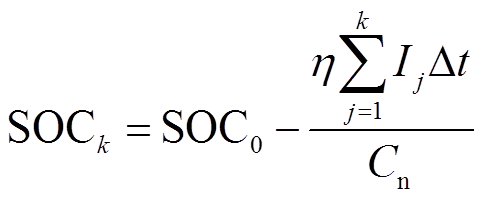 (1)
(1)
式中,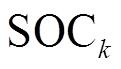 为
为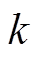 时刻的SOC值;
时刻的SOC值;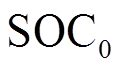 为初始时刻的SOC值;
为初始时刻的SOC值;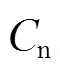 为电池的实际可用容量;
为电池的实际可用容量;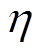 为库伦效应,本文中设为100%;
为库伦效应,本文中设为100%;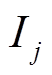 为
为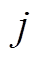 时刻的电流值;
时刻的电流值;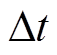 为采样时间,本文设置为1s。
为采样时间,本文设置为1s。
参考SOC是指在默认电池的实际可用容量和初始SOC值为已知的情况下,通过安时积分法得到的SOC值,该SOC定义将被运用在第1.3.2节中的参数辨识中来获取准确的模型参数信息搭建迁移模型,以及第4节中的SOC估算验证中与通过迁移模型得到的SOC值做对比。但是,电池的实际可用容量和初始时刻的SOC值一般是未知的,因此,提出不精确SOC定义。
2)不精确SOC
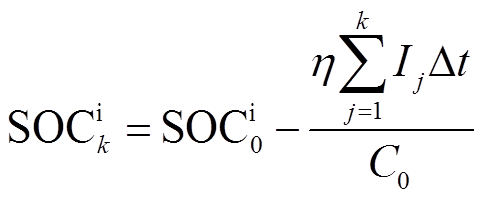 (2)
(2)
式中,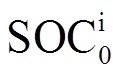 为初始时刻通过开路电压法得到的SOC值;
为初始时刻通过开路电压法得到的SOC值;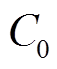 为电池的额定容量。
为电池的额定容量。
不精确SOC指的是电池在实际运用过程中通过安时积分法得到的SOC值,该SOC定义将会运用到第1.3节迁移模型建立中,通过线性迁移不精确的SOC值可以转换为精确的SOC值。
由于二阶RC等效电路模型能够较好地反映电池的极化现象,并且计算强度适中[22],因此本文选取二阶RC等效电路模型作为初始模型,其结构如图1所示。
图1中,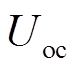 为开路电压(OCV),
为开路电压(OCV),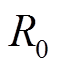 为欧姆电阻,
为欧姆电阻,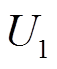 为电阻
为电阻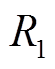 和电容
和电容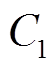 两端的电压,
两端的电压,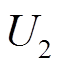 为电阻
为电阻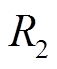 和电容
和电容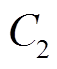 两端的电压,
两端的电压,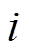 为电池的电流,
为电池的电流,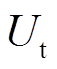 为电池的端电压。由于温度变化对模型参数影响较大,因此,模型参数应能随温度T而变化,所选取的二阶RC等效电路模型参数为
为电池的端电压。由于温度变化对模型参数影响较大,因此,模型参数应能随温度T而变化,所选取的二阶RC等效电路模型参数为
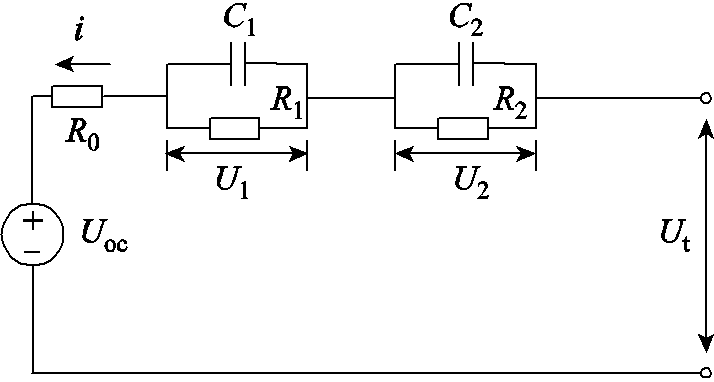
图1 二阶RC等效电路模型图
Fig.1 Second-order RC equivalent circuit model diagram
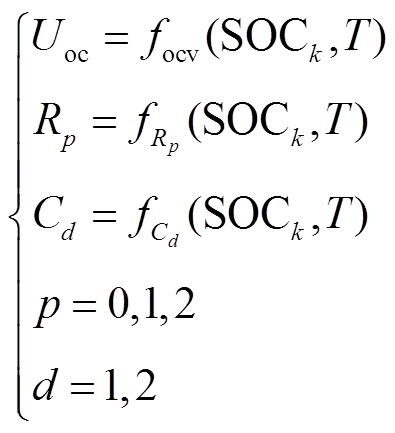 (3)
(3)
根据基尔霍夫定理,该二阶RC等效电路模型电路方程可表示为
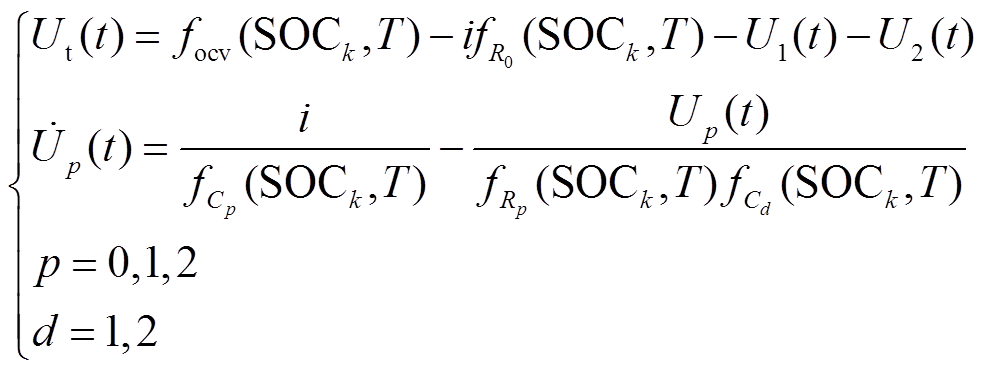 (4)
(4)
文本选取额定容量为4A·h的三元锂离子电池作为实验对象,该电池详细参数信息见表1。为研究不同温度及不同老化状态下的电池特征,首先在-10~50℃之间以10℃为间隔开展单体电池性能实验,实验内容包括定容实验、混合功率脉冲特性(Hybrid Pulse Power Characteristic, HPPC)工况测试实验及城市道路循环(Urban Dynamometer Driving Schedule, UDDS)工况测试实验。之后在常温状态下(25℃)进行电池老化实验测试。老化实验过程中,以0.5C电流恒流恒压(CCCV)方式对电池充电,然后以0.5C恒流放电,使电池不断老化,同时每50个循环进行一次不同温度下的HPPC及UDDS实验测试,当电池老化至SOH=80%,达到电池退役要求,实验结束。全部实验流程如图2所示。
表1 电池参数信息
Tab.1 Battery parameter information

参数数值 额定容量/(A·h)4 允许电压范围/V2.75~4.2 允许充电温度/℃0~45 允许放电温度/℃-20~60
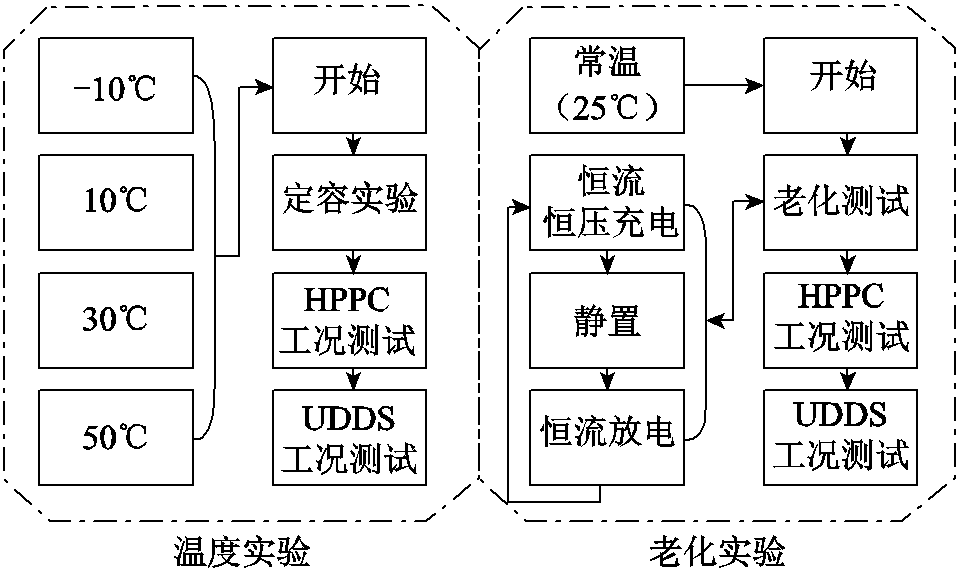
图2 实验设计流程
Fig.2 Experimental design flowchart
1.4.1 模型参数辨识
本文选取实验电池在常温全新状态下的HPPC放电实验数据作为辨识模型的数据集,基于所选择的二阶RC等效电路模型,待辨识的参数为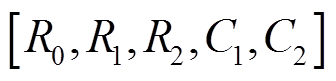 ,使用带遗忘因子的递推最小二乘法对待辨识的参数进行辨识,获得电池模型在常温全新状态下的精确参数值。
,使用带遗忘因子的递推最小二乘法对待辨识的参数进行辨识,获得电池模型在常温全新状态下的精确参数值。
为了使带遗忘因子的最小二乘法在辨识过程中更好地获得精确的模型参数,本文将遗忘因子设为0.95,使其算法能够更好地跟随电池放电时电流变化。带遗忘因子的最小二乘法递推关系为
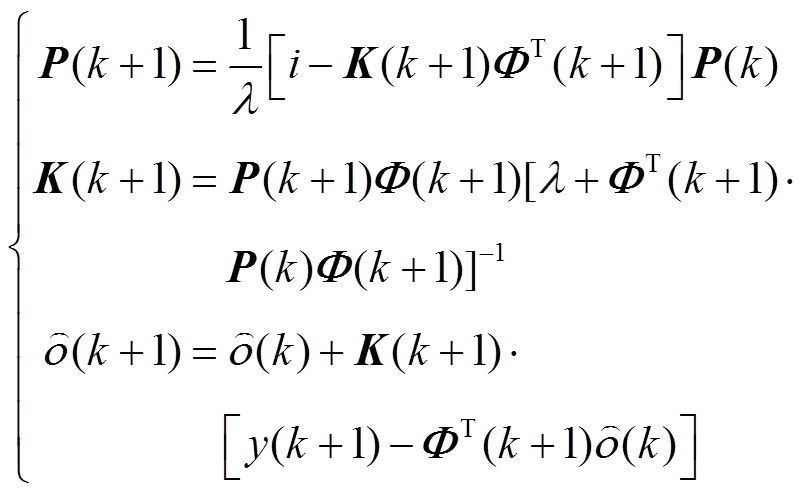 (5)
(5)
式中,P为协方差;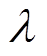 为遗忘因子;K为增益矩阵;
为遗忘因子;K为增益矩阵;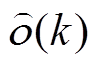 为系统估计参考值;
为系统估计参考值;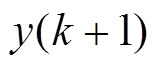 为系统实际观测值;
为系统实际观测值;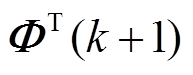 为观测值矩阵。
为观测值矩阵。
根据式(5)求出参考值向量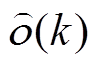 与模型参数之间的关系,即可得到待辨识参数值,其辨识均值结果见表2。
与模型参数之间的关系,即可得到待辨识参数值,其辨识均值结果见表2。
表2 参数辨识均值结果
Tab.2 Parameter identification mean results

参数数值 0.050 7 R1/W0.021 0 R2/W0.034 2 C1/F605 C2/F722
1.4.2 模型参数与SOC关系曲线拟合
由于SOC与模型参数之间存在非线性关系,因此本文将模型参数建立为SOC的函数,采用多项式拟合法将通过第1.4.1节辨识得到的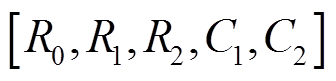 与SOC之间进行关系曲线拟合,具体拟合公式为
与SOC之间进行关系曲线拟合,具体拟合公式为
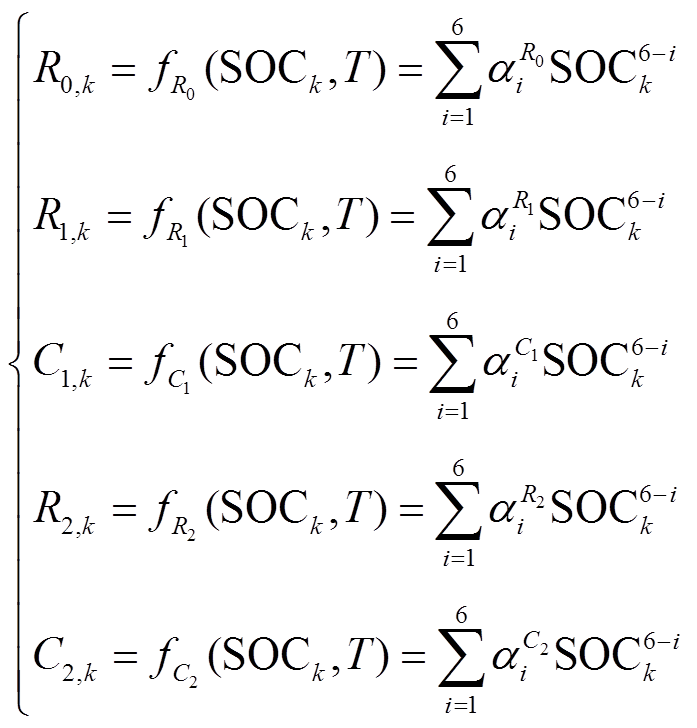 (6)
(6)
式中,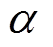 为模型拟合系数。
为模型拟合系数。
电池在实际的工作过程中,温度变化及电池老化会对电池模型参数造成较大影响,且影响程度很难精确掌握。因此在传统建模过程中往往需要大量的数据不断辨识和修正模型参数,以弥补温度及老化对模型精确度的影响。迁移模型通过对模型参数的在线迁移,即可实现对温度和老化影响下的模型参数确定,并且由于迁移之后得到的新模型是建立在基础模型的基础上,可以有效减少在建模时所需的数据量,提高计算速度。因此本文应用迁移模型来实现宽温度及全寿命范围SOC及容量的联合估计。
在迁移模型建模过程中,假设已经使用了足够多的数据建立起一个精确的电池模型,整个建模过程称之为“基础过程”,那么在描述一个类似的“新过程”时,可以将基础过程融入到一个新的过程中,即仅使用较少的数据,来获得一个新的模型。基于迁移模型构建原理,本文将外部温度和老化对模型精度的影响程度定义为不确定量,通过斜率与偏差校正现有模型参数,进而得到真实的模型参数,对基础模型进行线性变化,完成对迁移模型建立。通过在线确定迁移因子,实现模型真实参数信息的在线确定,进一步地,通过将不精确的SOC值迁移可以得到温度和老化影响下的真实SOC值。迁移模型的结构框架可以描述为
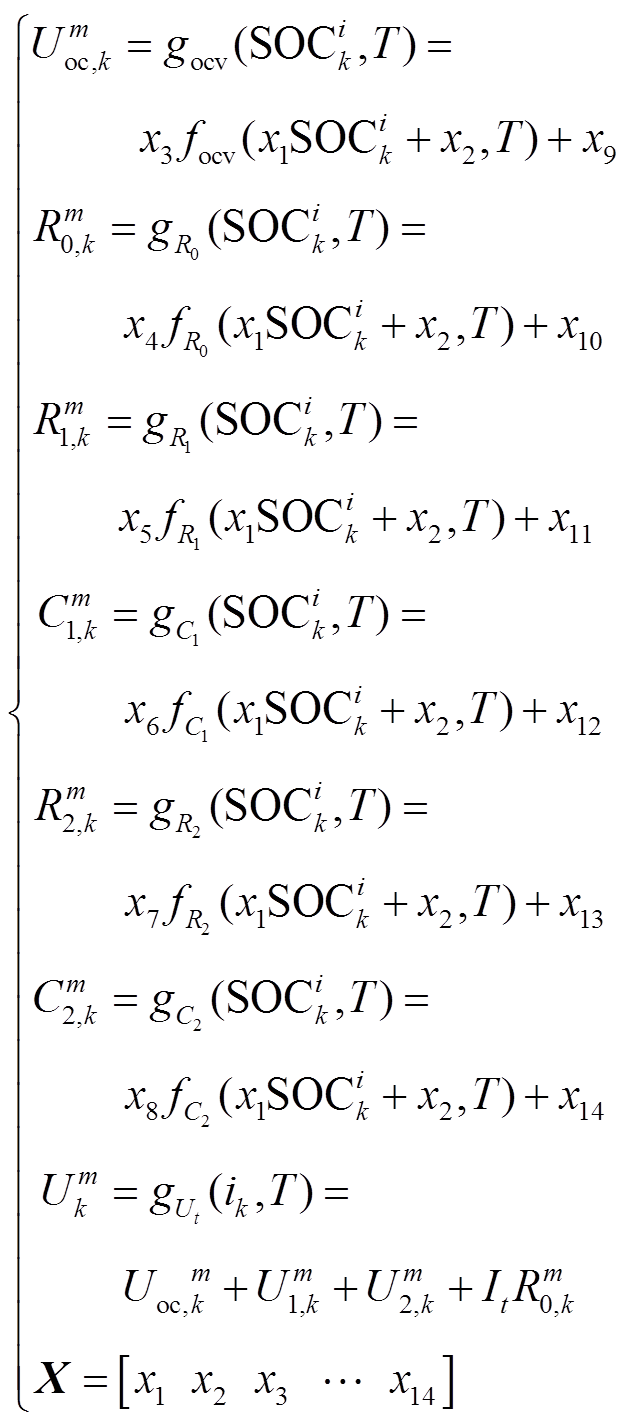 (7)
(7)
式中,X为待确定的迁移因子;上标m为迁移后得到的电池模型参数;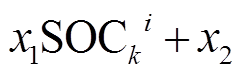 为修正后的真正SOC值。
为修正后的真正SOC值。
迁移因子作为迁移模型在线迁移过程中校正电池初始模型与SOC的重要参数,其确定的过程不仅与迁移模型对电池特性的描述能力有关,还与电池SOC估计精度相关。迁移因子的确定是一个非线性和非高斯的过程,需要选用非线性非高斯的滤波算法对其进行在线确定。粒子滤波算法适用于非线性非高斯的状态估计,但是传统的粒子滤波算法容易出现粒子退化现象,从而导致粒子单一性,影响SOC估算精度。因此,为了解决这一问题,本文采用权值选择粒子滤波算法进行迁移因子的在线确定。权值选择粒子滤波算法中全部粒子都将参与粒子滤波过程,但只选择粒子权重较大的粒子进行电池状态估计,从而解决传统的粒子滤波算法的粒子退化问题,提高粒子的多样性。
随着时间迁移,迁移矩阵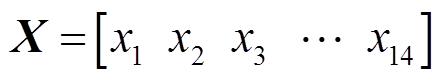 服从高斯分布,因此将迁移矩阵作为系统状态变量,电池端电压作为系统的观测量,建立系统离散状态方程,有
服从高斯分布,因此将迁移矩阵作为系统状态变量,电池端电压作为系统的观测量,建立系统离散状态方程,有
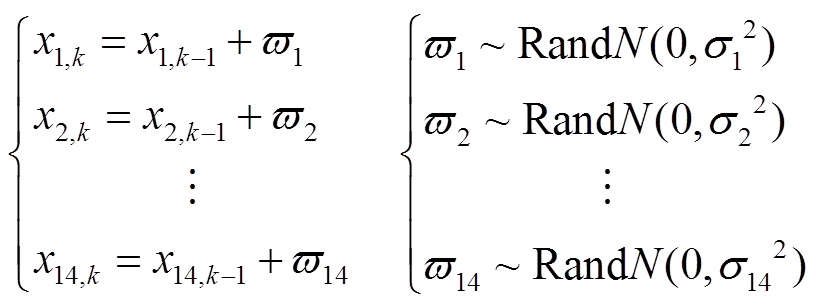 (8)
(8)
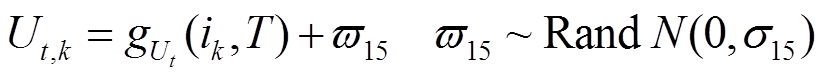 (9)
(9)
式中,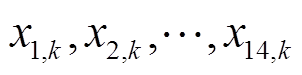 为系统的状态方程;
为系统的状态方程;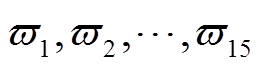 为系统噪声;
为系统噪声;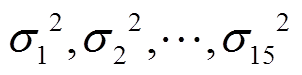 为系统测量噪声的方差;
为系统测量噪声的方差;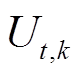 为系统的观测方程;电流
为系统的观测方程;电流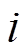 为输入变量。
为输入变量。
通过权值选择粒子滤波算法进行迁移因子确定的具体步骤为:
1)粒子初始化。采用先验概率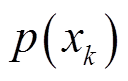 产生
产生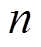 个初始粒子:
个初始粒子: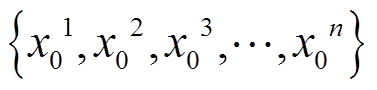 ,每个粒子权重为
,每个粒子权重为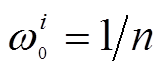 。
。
2)预测。已知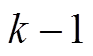 时刻状态
时刻状态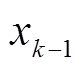 ,预测
,预测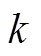 时刻
时刻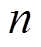 个粒子的状态
个粒子的状态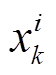 ,并计算每个
,并计算每个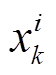 所对应预测端电压值。
所对应预测端电压值。
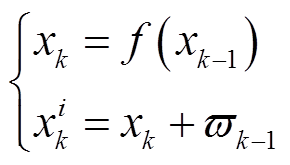 (10)
(10)
3)更新粒子权重。
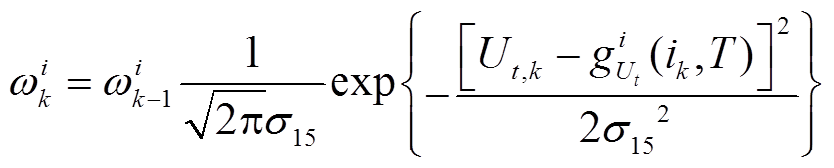 (11)
(11)
式中,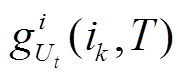 为k时刻第i个粒子
为k时刻第i个粒子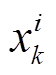 的系统输出值;
的系统输出值;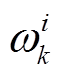 为更新后的粒子权重。
为更新后的粒子权重。
4)择优选择。选择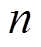 个粒子中权重最大的
个粒子中权重最大的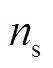 个。
个。
5)粒子权重归一化。
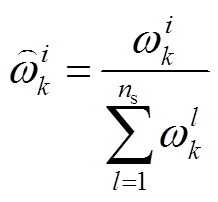 (12)
(12)
式中,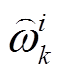 为归一化后的粒子权重。
为归一化后的粒子权重。
6)滤波估计。将选中的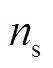 个粒子,计算后验概率密度,即
个粒子,计算后验概率密度,即
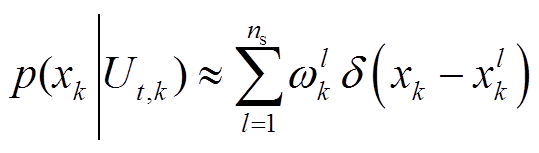 (13)
(13)
式中,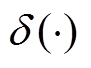 为狄利克雷函数。
为狄利克雷函数。
7)权值恢复及均一化。
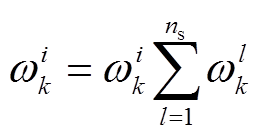 (14)
(14)
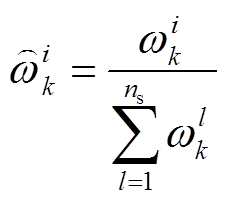 (15)
(15)
8)端电压计算。
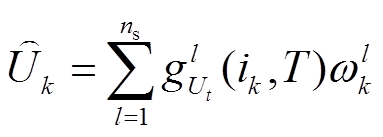 (16)
(16)
9)SOC估计。
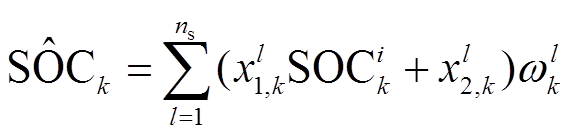 (17)
(17)
在迁移因子确定的过程中,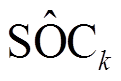 将随着迁移因子
将随着迁移因子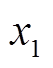 、
、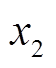 的估计值变化而上下波动,而迁移因子
的估计值变化而上下波动,而迁移因子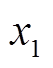 、
、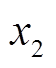 的估计会受到系统测量噪声的方差
的估计会受到系统测量噪声的方差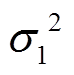 和
和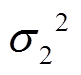 的影响,过大或者过小的系统噪声方差将会影响迁移因子
的影响,过大或者过小的系统噪声方差将会影响迁移因子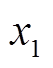 、
、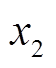 的估值波动范围,从而影响
的估值波动范围,从而影响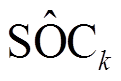 的估计精度。针对这一问题,本文采用塞维茨基-戈莱滤波器对迁移模型中
的估计精度。针对这一问题,本文采用塞维茨基-戈莱滤波器对迁移模型中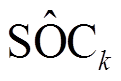 估计值进行降噪处理,降低过大的
估计值进行降噪处理,降低过大的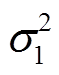 、
、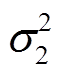 值给
值给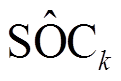 估计值带来的影响。塞维茨基-戈莱滤波器是一种利用局部多项式最小二乘法对噪声数据进行平滑滤波的时域滤波器,对噪声数据进行滤波时能够保持数据形状和宽度不变,广泛地应用于数据平滑去噪领域[23-24]。本文将迁移模型计算得到的
估计值带来的影响。塞维茨基-戈莱滤波器是一种利用局部多项式最小二乘法对噪声数据进行平滑滤波的时域滤波器,对噪声数据进行滤波时能够保持数据形状和宽度不变,广泛地应用于数据平滑去噪领域[23-24]。本文将迁移模型计算得到的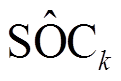 作为塞维茨基-戈莱滤波器的输入,对式(17)初步得到的SOC值进行降噪处理。
作为塞维茨基-戈莱滤波器的输入,对式(17)初步得到的SOC值进行降噪处理。
电池容量是电池内部状态的重要参数,会随电池老化程度的增加而出现非线性的衰退,对电池SOC值具有较大的影响。本文所提的SOC估计方法在进行锂离子电池SOC估计时不需要当前电池可用容量就可以实现精确的SOC估计,但当前电池可用容量可以影响SOC估计的精确程度。因此,在获取不同老化状态下电池准确SOC基础上,本文提出一种基于SOC的容量逆推的方式来获取电池的可用容量,当电池的第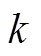 个循环满足电池为满充状态且静置时间超过1h的条件,可在其随后的放电过程中对电池第
个循环满足电池为满充状态且静置时间超过1h的条件,可在其随后的放电过程中对电池第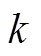 个循环的可用容量
个循环的可用容量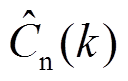 进行估计,其计算公式为
进行估计,其计算公式为
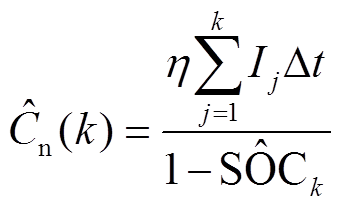 (18)
(18)
式中,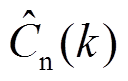 为逆推得到的可用容量值;采样时间
为逆推得到的可用容量值;采样时间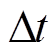 在本文中设置为1s。
在本文中设置为1s。
为了验证本文基于迁移模型所搭建的电池模型在宽温度及全寿命范围内的准确性,利用30℃、50℃环境温度下和老化前期(SOH=96.7%)、老化中期(SOH=93.1%)两种不同老化状态下的电池UDDS循环工况实验数据对模型的准确性进行验证,对比迁移模型在不同环境温度和老化状态下计算输出端电压和实际测量端电压之间的差异。通过迁移模型得到的电池端电压信息如图3、图4所示,误差结果见表3、表4。
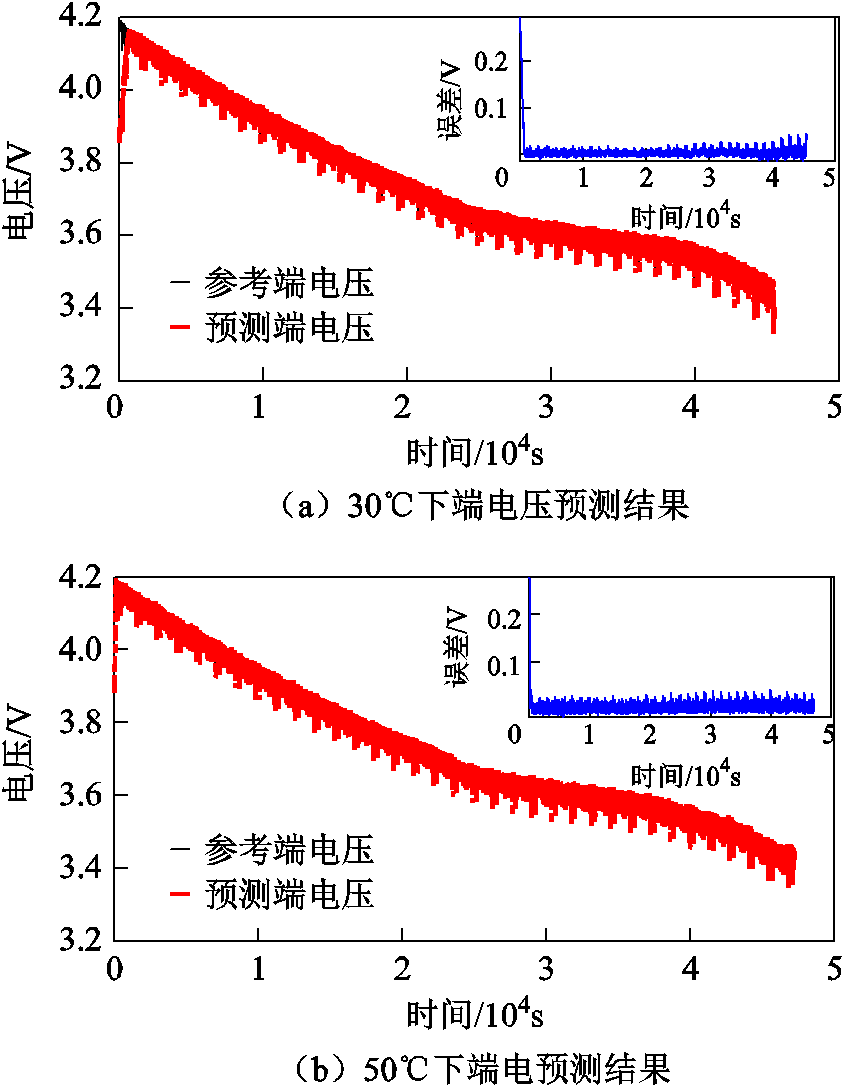
图3 不同温度状态下端电压预测
Fig.3 Prediction of terminal voltage under different temperature conditions
表3 不同温度状态下端电压预测误差
Tab.3 Prediction error of terminal voltage under different temperature conditions

温度/℃RMSE/VMAE/VMAX/V 300.0190.0020.047 500.0090.0010.041
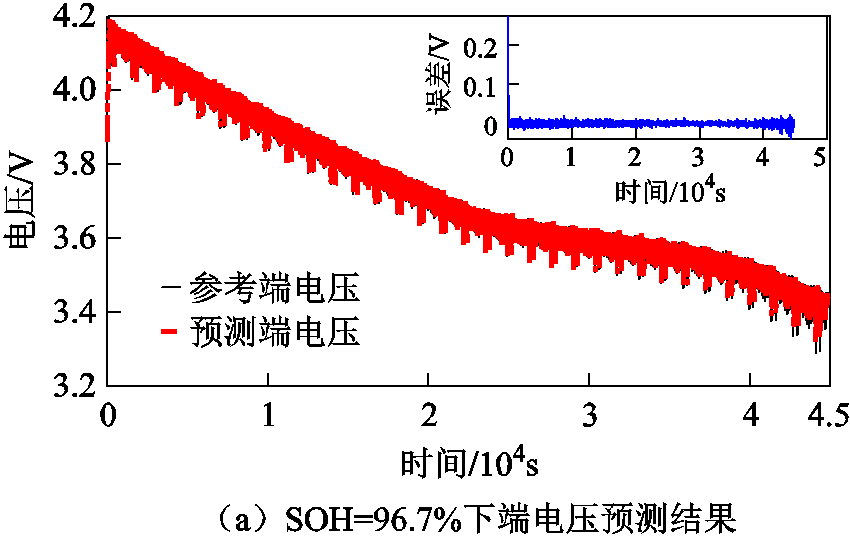
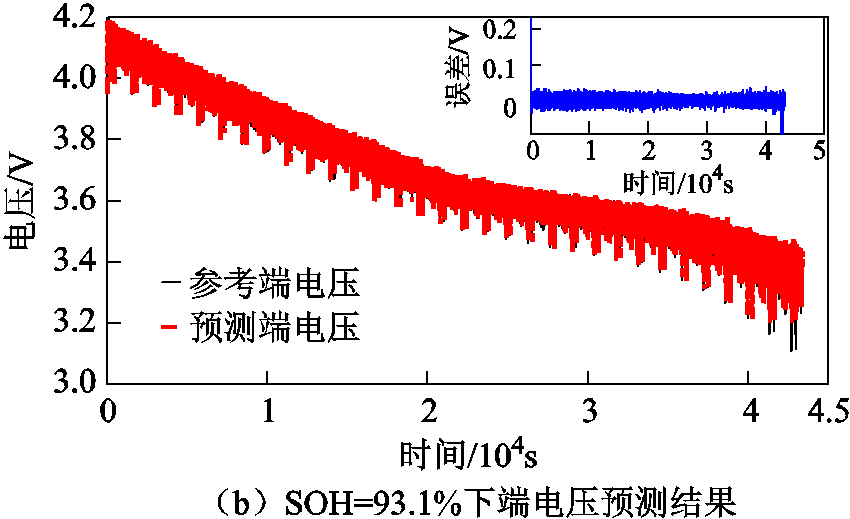
图4 不同老化状态下端电压预测
Fig.4 Prediction diagram of terminal voltage under different aging states
表4 不同老化状态下端电压预测误差
Tab.4 Prediction error of terminal voltage under different aging states

SOH(%)RMSE/VMAE/VMAX/V 96.70.0080.0010.039 93.10.0320.0050.095
在本文结果分析中,使用方均根误差(Root Mean Square Error, RMSE)、平均绝对误差(Mean Absolute Error, MAE)和最大误差(Maximum absolute error, MAX)来评估性能,计算公式为
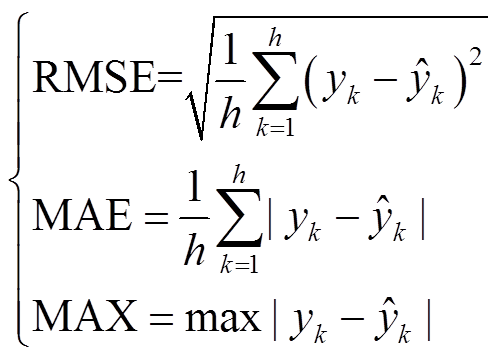 (19)
(19)
式中,h为测试数据的长度;k为测试数据的序号;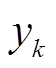 为测试集的参考值;
为测试集的参考值;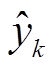 为经过迁移模型得到的估算值。
为经过迁移模型得到的估算值。
由上述端电压误差统计结果可以得出,不同温度状态下迁移模型端电压预测值的RMSE范围在0.009~0.019V,MAE范围在0.001~0.002V,MAX范围在0.041~0.047V。不同老化状态下迁移模型端电压预测值的RMSE均在0.008~0.026V,MAE均在0.001~0.004V,MAX均在0.039~0.095V,表明所构建的迁移模型框架在不同温度和老化状态下均具有很高的精度,可以较好地描述电池充放电特性。
锂离子电池在实际工作过程中所处的环境温度复杂多变,从而导致在不同环境温度下锂离子电池内部参数发生改变。为了验证迁移模型在宽温度环境下对电池SOC的估计精度,分别在-10℃、10℃、30℃及50℃环境下进行UDDS循环工况实验验证。同时为了验证算法对初始误差的校正能力,将算法中SOC初始值设置为75%,而电池实际初始SOC值为100%。同时与传统扩展卡尔曼滤波以及自适应扩展卡尔曼滤波(Adaptive Extended Kalman Filter, AEKF)算法进行SOC估计结果对比,以验证迁移模型相较于传统模型进行SOC估算的优势。上述两种算法均基于传统二阶RC等效电路模型,并采用最小二乘法算法对模型参数进行在线辨识。不同算法宽温度环境下SOC估计结果如图5所示,使用式(19)进行性能分析,此时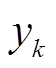 为参考SOC的值,
为参考SOC的值,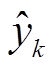 为通过迁移模型、EKF及AEKF算法得到的SOC值,误差统计见表5。
为通过迁移模型、EKF及AEKF算法得到的SOC值,误差统计见表5。
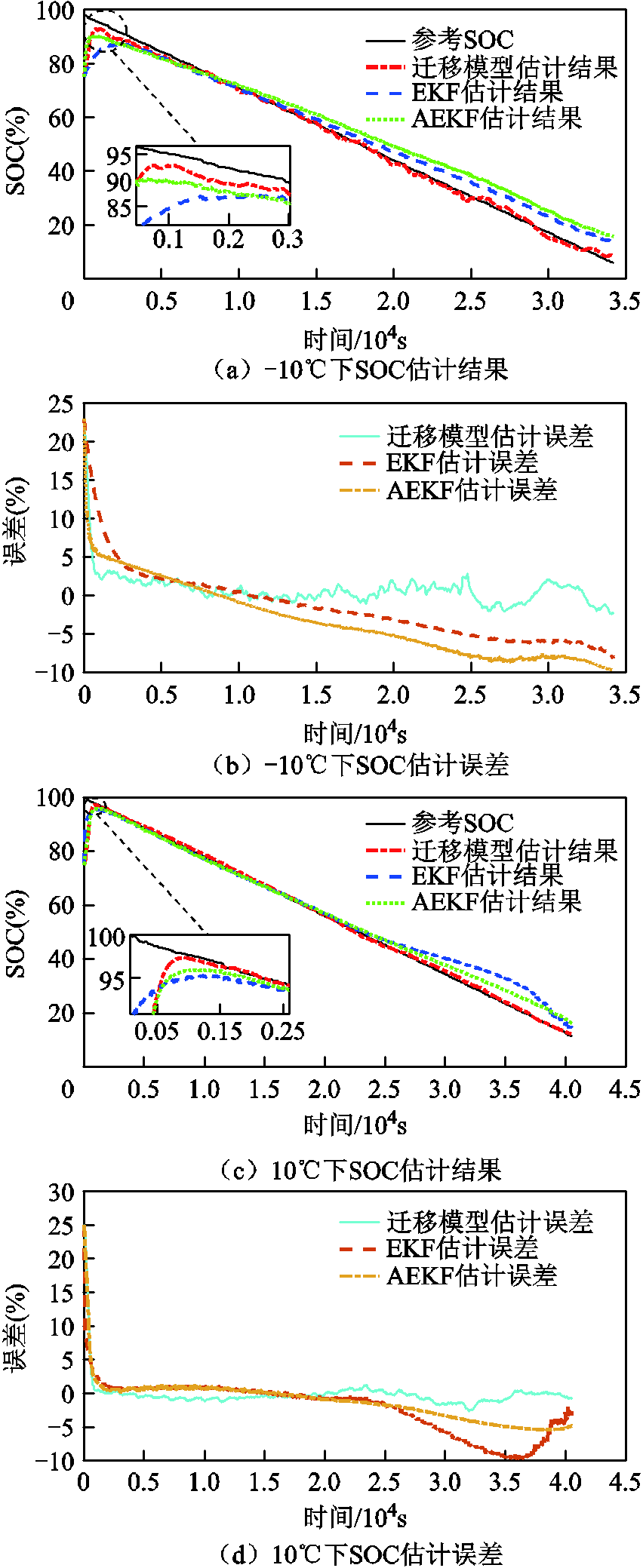
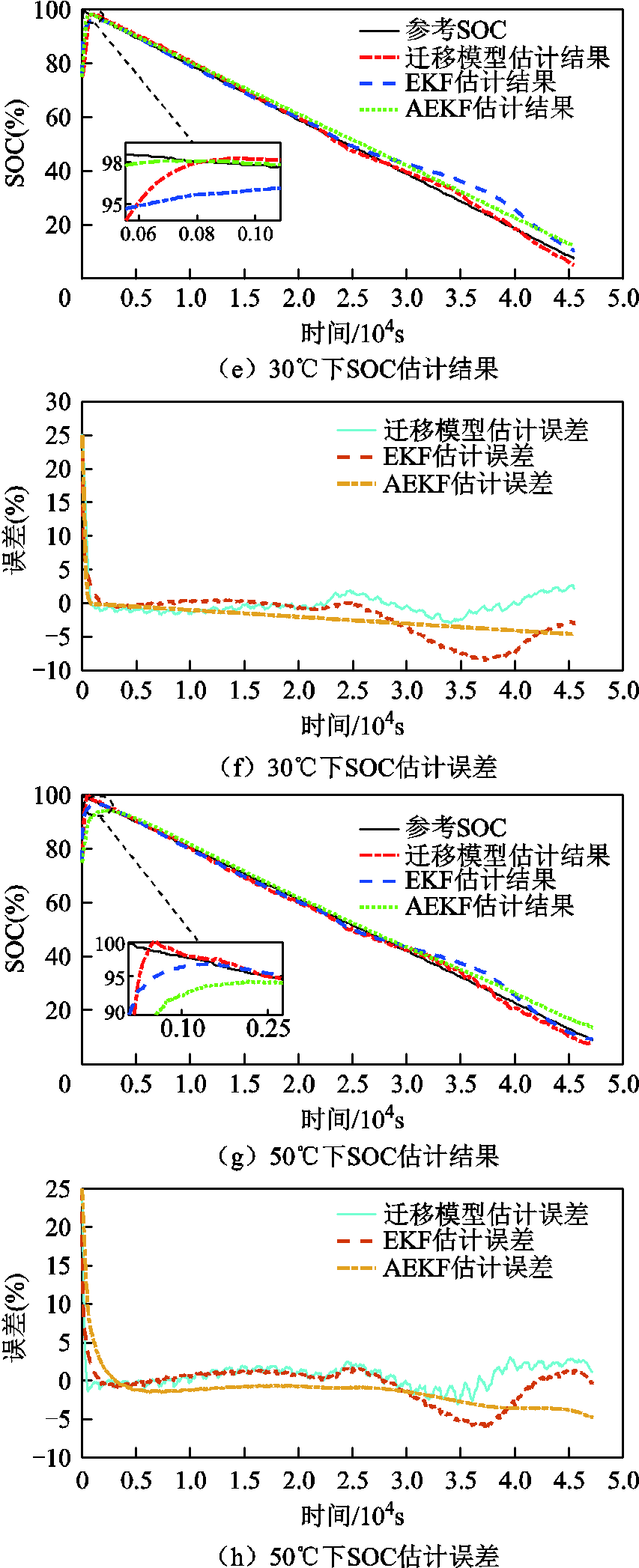
图5 不同温度状态下SOC估计结果
Fig.5 SOC estimation results under different temperature conditions
表5 不同温度状态下SOC估计误差
Tab.5 SOC estimation error under different temperature conditions
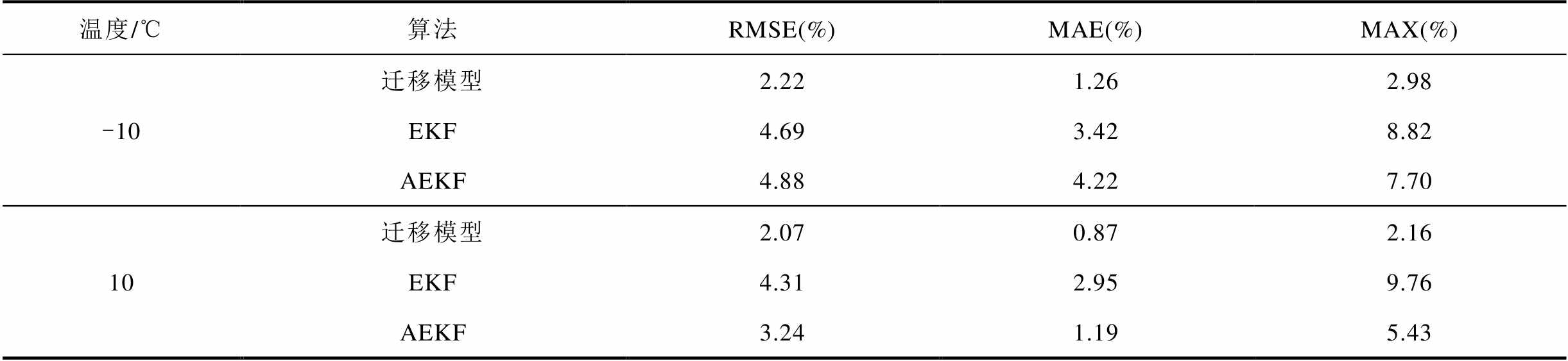
温度/℃算法RMSE(%)MAE(%)MAX(%) -10迁移模型2.221.262.98 EKF4.693.428.82 AEKF4.884.227.70 10迁移模型EKFAEKF2.070.872.16 4.312.959.76 3.241.195.43
(续)
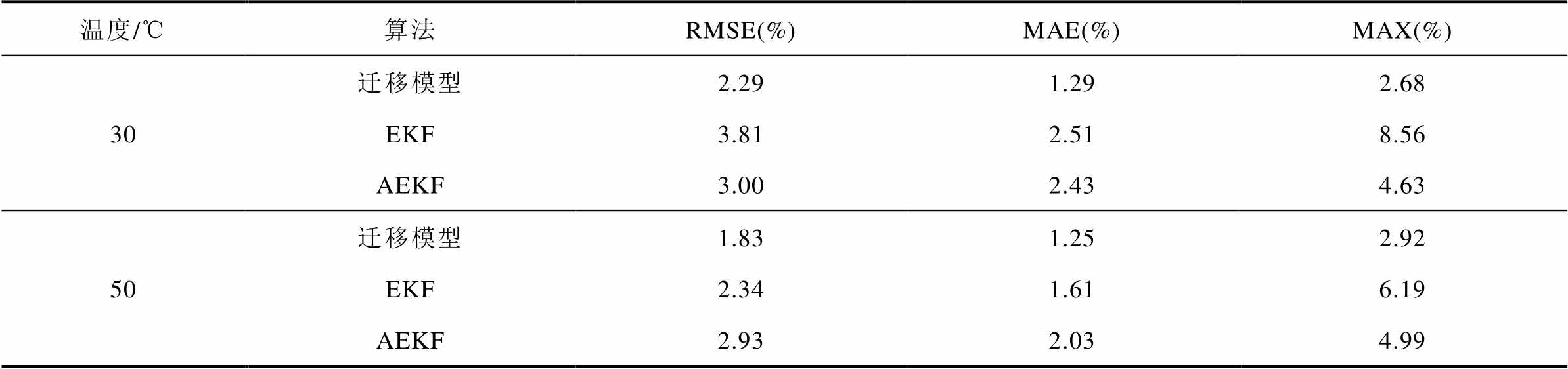
温度/℃算法RMSE(%)MAE(%)MAX(%) 30迁移模型EKFAEKF2.291.292.68 3.812.518.56 3.002.434.63 50迁移模型1.831.252.92 EKF2.341.616.19 AEKF2.932.034.99
1)由图5a、图5c、图5e、图5g可以看出,三种算法均可以实现电池SOC初始误差的有效修正,其中迁移模型在-10℃、10℃、30℃及50℃环境下收敛至真实值2%误差带范围内用时分别为550s、700s、750s、600s,EKF分别为3 000s、2 000s、2 000s、900s,AEKF分别为2 500s、800s、600s、2 000s。虽然AEKF算法在常温状态下也可以较快收敛至真实值附近,但在低温和高温状态下,基于迁移模型的方法收敛速度远远快于EKF和AEKF。
2)由图5b、图5d、图5f、图5h及表5可知,在四种不同温度下,迁移模型所得到的SOC估算结果最大误差均小于3%,在宽温度范围始终能够保持良好的估算精度。而EKF算法在四种温度下的最大误差为8.82%、9.76%、8.56%及6.19%,精确度远落后于迁移模型。虽然AEKF方法在10℃、30℃及50℃环境下的最大误差为5.43%、4.63%和4.99%,但在低温-10℃环境下精度明显降低,最大误差达到7.70%,表明迁移模型相较传统EKF和AEKF方法在宽温度范围内具有明显的优势。
3)在-10℃、10℃、30℃及50℃宽温度环境下,迁移模型得到的SOC估算结果最大误差分别为2.98%、2.16%、2.68%和2.92%。造成迁移模型在不同温度下估计精度有所差别的原因是锂离子电池在低温和高温时内部参数变化相对较大,迁移因子在校正过程中的波动较大,但误差也在可接受范围之内。
以上分析表明,使用迁移模型对宽温度范围内SOC进行估算具有较高的估算精度,同时对初始值误差有较好的修正能力。此外,由于基于迁移模型的SOC估算方法只需建立起一个温度的基准迁移模型,通过在线迁移即可获得其他温度下的模型信息,而传统模型在进行不同温度SOC估算过程中,则需要分别搭建不同温度下的模型或实时辨识和更新模型参数,然后进行SOC估算。因此使用迁移模型进行SOC估算可以大大缩减建模所需的数据量,减少计算时间。
随着电池的不断老化,电池的充放电特性也会随之产生非线性变化,进而造成模型参数发生变化和影响SOC估计精度。为了验证迁移模型在全寿命周期内不同老化状态下的电池SOC估计精度,分别在锂离子电池老化初始阶段(SOH=96.7%)、中度老化(SOH=93.1%)及老化后期(SOH=85.1%)三种状态下基于UDDS工况数据进行验证。在算法中设置电池初始SOC值为75%,而电池实际初始SOC值为100%。同时与EKF、AEKF算法估算结果进行对比。不同老化状态下SOC估计结果如图6所示。不同老化状态下SOC预测误差见表6。
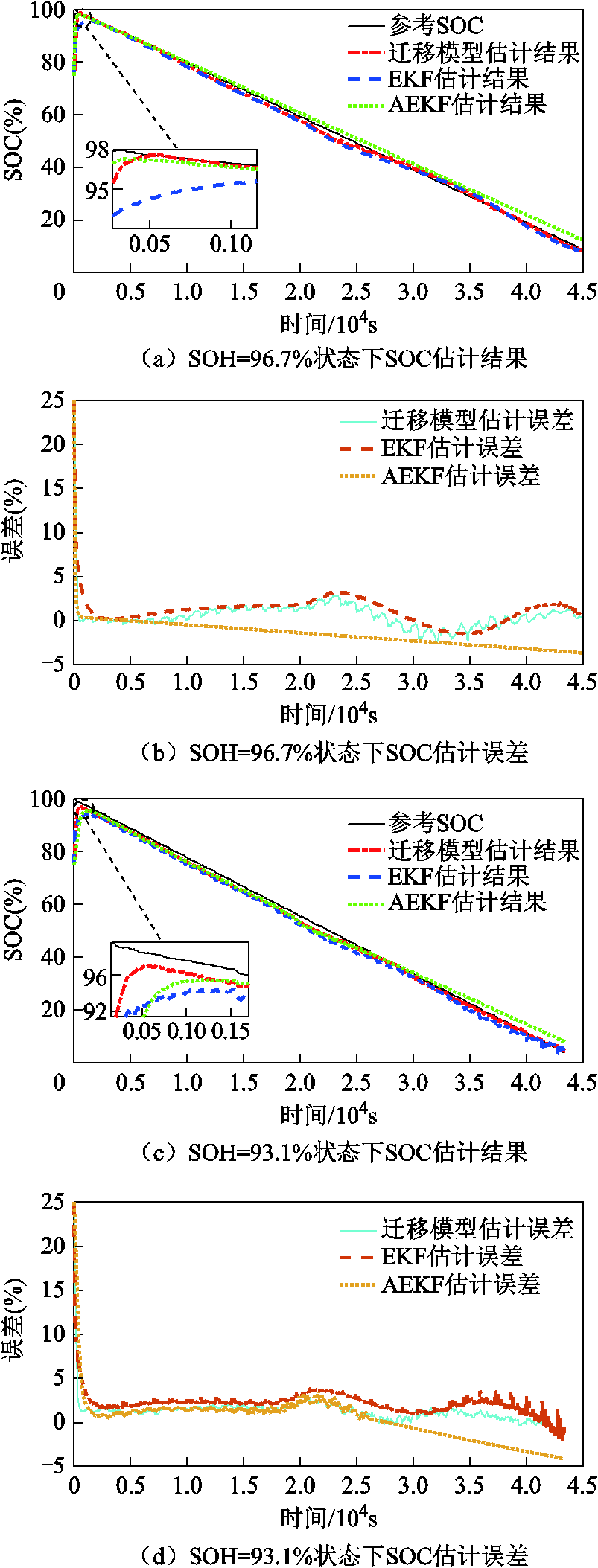
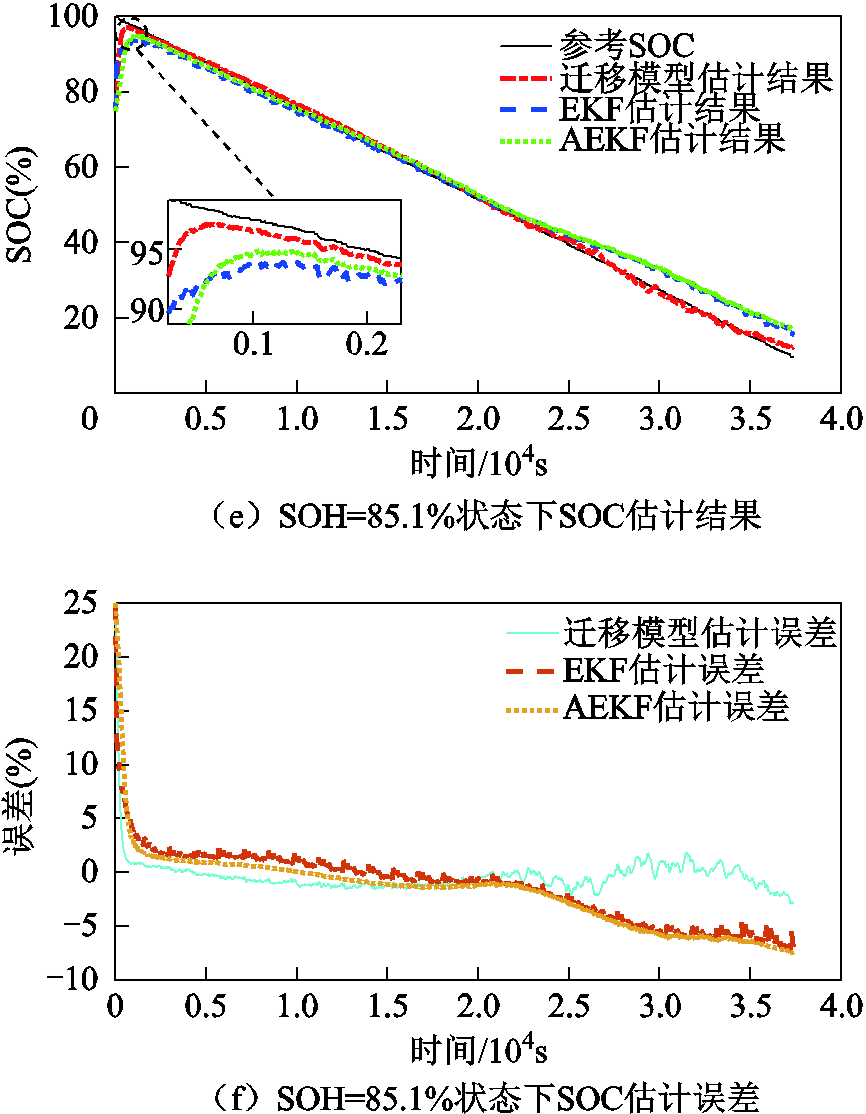
图6 不同老化状态下SOC估计结果
Fig.6 SOC estimation results under different aging conditions
表6 不同老化状态下SOC预测误差
Tab.6 SOC prediction error under different aging conditions
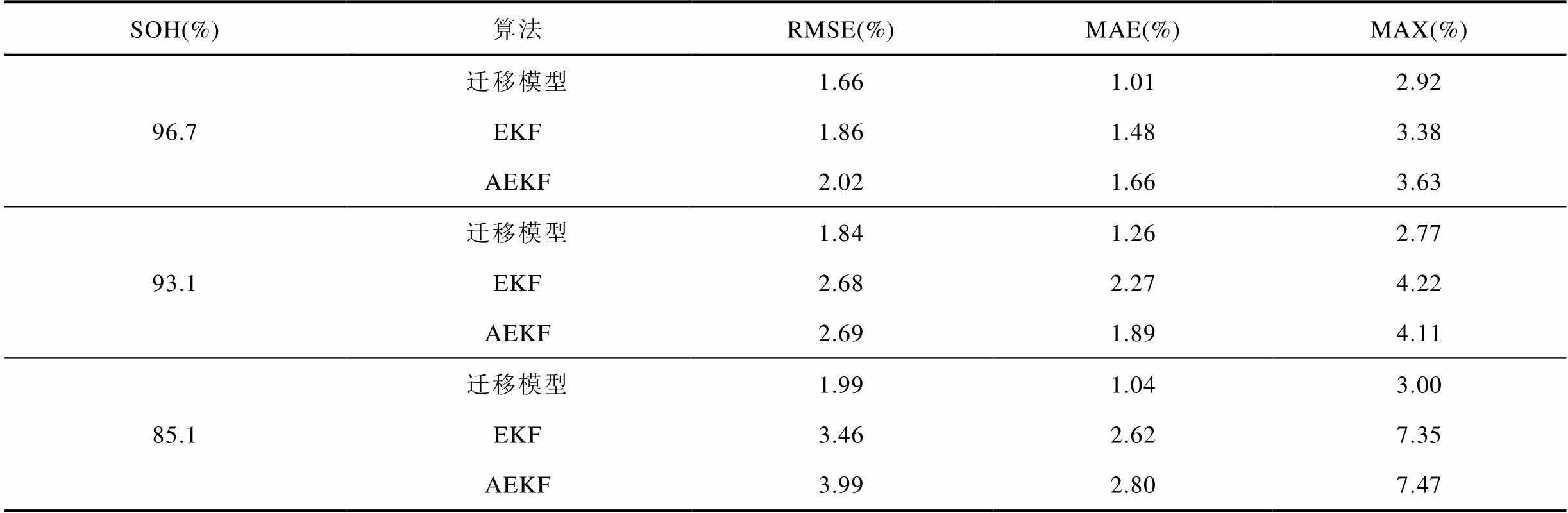
SOH(%)算法RMSE(%)MAE(%)MAX(%) 96.7迁移模型1.661.012.92 EKF1.861.483.38 AEKF2.021.663.63 93.1迁移模型1.841.262.77 EKF2.682.274.22 AEKF2.691.894.11 85.1迁移模型1.991.043.00 EKF3.462.627.35 AEKF3.992.807.47
1)由图6a、图6c、图6e可知,当电池老化状态SOH=96.7%、SOH=93.1%和SOH=85.1%时,基于迁移模型的SOC估计结果曲线最多只需500s即可收敛至SOC真实值2%误差范围内,而基于传统二阶RC等效电路模型的EKF和AEKF两种方法,随着电池老化程度的加深,特别是在电池老化后期则需要1 200s左右才能收敛至SOC真实值2%误差范围内。
2)由图6b、图6d、图6f及表6可知,在三种不同老化状态下,基于迁移模型的SOC估算结果最大误差分别为2.92%、2.77%及3%,而EKF与AEKF的两种方法得到的SOC估计结果最大误差均大于3%。其主要原因在于随着电池的不断老化,电池内部参数信息发生变化,而EKF与AEKF两种SOC算法过度依赖于所搭建模型精度,当模型精度降低时,会导致SOC估算精度显著下降。
上述分析表明,本文提出的基于迁移模型的SOC估计方法在全寿命范围同样具有较高的精度和较好的初始值误差修正能力。
为了验证本文提出的迁移模型进行容量估计的准确性,使用所选电池的老化实验数据,每间隔50个循环对不同老化阶段电池容量估算结果进行验证。不同老化状态下容量预测结果如图7所示。
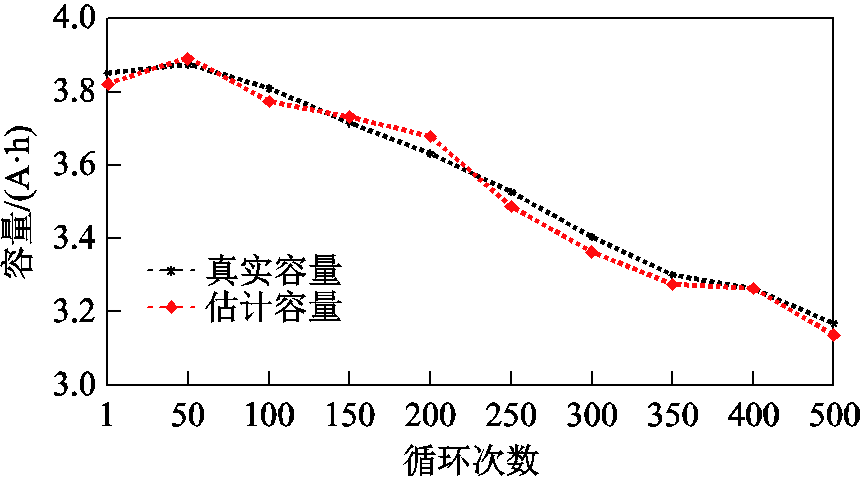
图7 容量估计结果
Fig.7 Capacity estimation results
由容量估算结果可知,在电池全生命周期内不同老化阶段下真实容量与模型估计容量之间最大误差为0.047A·h,小于2%。表明本文提出的容量估计方法具有较高的估算精度,在SOC估计完成的同时,只要达到满充且静置超过1h的条件,即可实现可用容量的联合估计,大幅降低了计算量,缩短了计算时间,具有明显的工程应用的优势。
为了解决宽温度全寿命范围内锂离子电池SOC与可用容量快速精确难题,本文选取二阶RC等效电路模型作为基础模型,利用带遗忘因子的递推最小二乘法对模型参数进行辨识,并进一步使用多项式拟合了模型参数与SOC之间的关联关系,进而完成迁移模型搭建;利用权值选择粒子滤波算法实现迁移因子的在线迁移;在不同温度和不同老化状态下验证了所建立迁移模型的精确性。不同温度和不同老化状态下电池SOC与可用容量仿真结果表明,所提方法在宽温度全寿命范围内电池SOC估计最大误差小于3%,可用容量估计最大误差小于2%,具有估算精度高和计算速度快的显著优点。
参考文献
[1] 索鎏敏, 李泓. 锂离子电池过往与未来[J]. 物理, 2020, 49(1): 17-23. Suo Liumin, Li Hong. The past, present and future of lithium ion batteries[J]. Physics, 2020, 49(1): 17-23.
[2] Zhang Xu, Wang Yujie, Yang Duo, et al. An on-line estimation of battery pack parameters and state-of-charge using dual filters based on pack model[J]. Energy, 2016, 115: 219-229.
[3] Liu Kailong, Li Kang, Peng Qiao, et al. A brief review on key technologies in the battery management system of electric vehicles[J]. Frontiers of Mechanical Engineering, 2019, 14(1): 47-64.
[4] Weng Caihao, Cui Yujia, Sun Jing, et al. On-board state of health monitoring of lithium-ion batteries using incremental capacity analysis with support vector regression[J]. Journal of Power Sources, 2013, 235: 36-44.
[5] 程泽, 吕继考, 刘继光, 等. 等效滞回模型在锂离子电池SOC估计中的应用[J]. 湖南大学学报(自然科学版), 2015, 42(4): 63-70. Cheng Ze, Lv Jikao, Liu Jiguang, et al. Application of equivalent hysteresis model in estimaion of state of charge of lithium-ion battery[J]. Journal of Hunan University (Natural Sciences), 2015, 42(4): 63-70.
[6] Sun Li, Li Guanru, You Fengqi. Combined internal resistance and state-of-charge estimation of lithium-ion battery based on extended state observer[J]. Renewable and Sustainable Energy Reviews, 2020, 131: 109994.
[7] 胡晓松. 电动车辆锂离子电池模型辨识、优化与状态估计[D]. 北京: 北京理工大学, 2012.
[8] Shi Meihua, Yuan Jingchao, Dong Li, et al. Combining physicochemical model with the equivalent circuit model for performance prediction and optimization of lead-acid batteries[J]. Electrochimica Acta, 2020, 353: 136567.
[9] 武龙星, 庞辉, 晋佳敏, 等. 基于电化学模型的锂离子电池荷电状态估计方法综述[J]. 电工技术学报, 2022, 37(7): 1703-1725. Wu Longxing, Pang Hui, Jin Jiamin, et al. A review of SOC estimation methods for lithium-ion batteries based on electrochemical model[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1703-1725.
[10] Xiong Rui, He Hongwen, Sun Fengchun, et al. Evaluation on state of charge estimation of batteries with adaptive extended Kalman filter by experiment approach[J]. IEEE Transactions on Vehicular Technology, 2013, 62(1): 108-117.
[11] 来鑫, 李云飞, 郑岳久, 等. 基于SOC-OCV优化曲线与EKF的锂离子电池荷电状态全局估计[J]. 汽车工程, 2021, 43(1): 19-26. Lai Xin, Li Yunfei, Zheng Yuejiu, et al. An overall estimation of state-of-charge based on SOC-OCV optimization curve and EKF for lithium-ion battery[J]. Automotive Engineering, 2021, 43(1): 19-26.
[12] Vasebi A, Partovibakhsh M, Bathaee S M T. A novel combined battery model for state-of-charge estimation in lead-acid batteries based on extended Kalman filter for hybrid electric vehicle applications[J]. Journal of Power Sources, 2007, 174(1): 30-40.
[13] 谢长君, 费亚龙, 曾春年, 等. 基于无迹粒子滤波的车载锂离子电池状态估计[J]. 电工技术学报, 2018, 33(17): 3958-3964. Xie Changjun, Fei Yalong, Zeng Chunnian, et al. State-of-charge estimation of lithium-ion battery using unscented particle filter in vehicle[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 3958-3964.
[14] 熊巍, 梅华平, 徐刚, 等. 基于改进H无穷滤波的锂离子电池SOC估计[J]. 电源技术, 2020, 44(10): 1488-1491, 1528. Xiong Wei, Mei Huaping, Xu Gang, et al. Lithium-ion battery SOC estimation based on improved H-infinity filter[J]. Chinese Journal of Power Sources, 2020, 44(10): 1488-1491, 1528.
[15] 庞辉, 郭龙, 武龙星, 等. 考虑环境温度影响的锂离子电池改进双极化模型及其荷电状态估算[J]. 电工技术学报, 2021, 36(10): 2178-2189. Pang Hui, Guo Long, Wu Longxing, et al. An improved dual polarization model of Li-ion battery and its state of charge estimation considering ambient temperature[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2178-2189.
[16] 宫明辉, 乌江, 焦朝勇. 基于模糊自适应扩展卡尔曼滤波器的锂电池SOC估算方法[J]. 电工技术学报, 2020, 35(18): 3972-3978. Gong Minghui, Wu Jiang, Jiao Chaoyong. SOC estimation method of lithium battery based on fuzzy adaptive extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3972-3978.
[17] 刘新天, 彭泳, 何耀, 等. 基于温度补偿的动力锂电池SOC估算方法[J]. 计算机仿真, 2021, 38(5): 66-69, 328. Liu Xintian, Peng Yong, He Yao, et al. State of charge estimation of lithiumion power battery considering temperature influence[J]. Computer Simulation, 2021, 38(5): 66-69, 328.
[18] 郑涛, 张里, 侯杨成, 等. 基于自适应CKF的老化锂电池SOC估计[J]. 储能科学与技术, 2020, 9(4): 1193-1199. Zheng Tao, Zhang Li, Hou Yangcheng, et al. SOC estimation of aging lithium battery based on adaptive CKF[J]. Energy Storage Science and Technology, 2020, 9(4): 1193-1199.
[19] Tang Xiaopeng, Wang Yujie, Zou Changfu, et al. A novel framework for lithium-ion battery modeling considering uncertainties of temperature and aging[J]. Energy Conversion and Management, 2019, 180: 162-170.
[20] Tang Xiaopeng, Wang Yujie, Yao Ke, et al. Model migration based battery power capability evaluation considering uncertainties of temperature and aging[J]. Journal of Power Sources, 2019, 440: 227141.
[21] 李亚滨, 袁学庆, 汤琦, 等. 基于权值选择粒子滤波的锂电池RUL预测研究[J]. 计算机仿真, 2020, 37(11): 75-80. Li Yabin, Yuan Xueqing, Tang Qi, et al. Research on RUL prediction of lithium-ion batteries based on weight select particle filter[J]. Computer Simulation, 2020, 37(11): 75-80.
[22] Farmann A, Sauer D U. Comparative study of reduced order equivalent circuit models for on-board state-of-available-power prediction of lithium-ion batteries in electric vehicles[J]. Applied Energy, 2018, 225: 1102-1122.
[23] Krishnan S R, Seelamantula C S. On the selection of optimum savitzky-golay filters[J]. IEEE Transactions on Signal Processing, 2013, 61(2): 380-391.
[24] Press W H, Teukolsky S A. Savitzky-golay smoothing filters[J]. Computers in Physics, 1990, 4(6): 669-672.
Abstract At present, the traditional equivalent circuit model is widely used in the research of joint estimation of state of charge (SOC) and available capacity. However, this method seriously depends on the model accuracy, and is affected by temperature changes and battery aging, which leads to the decline of estimation accuracy of SOC and available capacity in the whole life cycle and under complex temperature environment. To solve the above problems, this paper integrates the weight selection particle filter algorithm on the basis of the migration model theory, and studies the estimation of SOC and usable capacity in the wide temperature and full life range of lithium-ion batteries. The proposed method can greatly reduce the amount of data required for modeling, and the estimated SOC value has the advantages of high accuracy and strong ability to correct the initial value error.
First of all, this paper selects the traditional second-order RC equivalent circuit model as the basic model for building the migration model, the recursive least square method with forgetting factor is employed to identify the model parameters, and further uses polynomials to fit the correlation between the model parameters and SOC to complete the construction of the migration model. Secondly, the weight selection particle filter algorithm is used to realize the online migration of migration factors and complete the online determination of the real parameter information of the model. Further, the inaccurate SOC value can be migrated to obtain the real SOC value under the influence of temperature and aging. Finally, the available capacity estimation is realized by capacity inversion based on the obtained SOC estimation value.
In order to verify the estimation accuracy of the migration model for the battery SOC in a wide temperature environment, UDDS cycle condition experiments were conducted at -10℃, 10℃, 30℃ and 50℃ respectively. In addition, the initial value of SOC in the algorithm was set to 75%, while the actual initial value of the battery SOC was 100%, to verify the ability to correct the initial error. The results show that under the wide temperature environment of -10℃, 10℃, 30℃ and 50℃, the root mean square error (RMSE) of SOC estimation obtained by the migration model is 2.22%, 2.07, 2.29% and 1.83% respectively, and the time taken to converge to the true value within the 2% error band is 550s, 700s, 750s and 600s respectively, which shows that the migration model has a high estimation accuracy and a good correction ability for the initial value error in estimating SOC in a wide temperature range. At the same time, in order to verify the estimation accuracy of the battery SOC of the migration model under different aging conditions during the whole life cycle, it was verified based on the data of UDDS operating conditions in the initial aging stage (SOH=96.7%), moderate aging (SOH=93.1%) and late aging stage (SOH=85.1%) of the lithium-ion battery. The results show that under three different aging conditions, the RMSE of SOC estimation results based on migration model is 1.66%, 1.84% and 1.99%, respectively, indicating that the proposed migration model based SOC estimation method has high accuracy in the whole life range. Finally, this paper uses the aging experimental data of the selected battery to verify the battery capacity estimation results at different aging stages every 50 cycles. The capacity estimation results show that the maximum error between the real capacity and the model estimated capacity at different aging stages in the battery life cycle is 0.047A·h, less than 2%. It shows that the capacity estimation method proposed in this paper has high estimation accuracy.
keywords:Lithium-ion battery, state of charge, capacity, migration model, temperature, life
DOI:10.19595/j.cnki.1000-6753.tces.220216
中图分类号:TM912
国家自然科学基金资助项目(52162051)。
收稿日期 2022-02-17
改稿日期 2022-04-10
申江卫 男,1984年生,高级实验师,硕士生导师,研究方向为新能源汽车动力电池管理。E-mail:shenjiangwei6@kust.edu.cn
陈 峥 男,1982年生,教授,博士生导师,研究方向为新能源汽车节能控制与动力电池管理、智能网联汽车优化控制。E-mail:chen@kust.edu.cn(通信作者)
(编辑 赫蕾)