
图1 雪峰山野外科学观测研究站
Fig.1 Xuefeng Mountain Field Science Observation and Research Station
摘要 高海拔地区风能资源丰富,然而建设于此的风力发电机面临严重覆冰问题。覆冰会破坏叶片气动结构,造成输出功率损失,影响供电质量。了解不同工况下的风力发电机输出功率情况,有助于电力部门进行合理的电力调度。该文提出了一种适用于洁净和覆冰条件下的风力发电机输出功率计算方法。该方法以叶素动量理论为基础,同时引入二维计算流体动力学(CFD)仿真方法来计算叶素的升力与阻力系数。将计算结果与现场试验运行结果对比发现,该计算方法可以在工程应用允许的误差范围内获得风力发电机的输出功率。此外,通过比较基于该方法获得的关键气动参数在不同风速下沿叶片翼展方向的分布发现,冰层的存在会降低叶片对风能的利用率,减小叶片旋转扭矩,从而导致输出功率降低;并且随着风速的增加,覆冰所带来的负面影响更加明显。
关键词:风力发电机 输出功率 叶素动量理论 覆冰
近年来,新能源受到世界各国高度重视并得到迅速发展[1-2],其中,开发利用新能源已经成为世界各国建设低碳社会的普遍共识[3-4]。截至2020年,风力发电产业和技术都取得了巨大发展,全球范围的海上风电单年新增装机容量创历史新高[5]。我国风电累计装机容量达到28.153 GW,占全国电源总装机容量的12.8%。英国、美国等发达国家均设立了2023年风电扩充建设的总目标。
位于高海拔山地的风力发电机能捕获更多风能,但它们在冬季也更容易结冰[6-7]。风力发电机覆冰的危害主要包括:影响测量设备工作,产生运行参数测量误差;改变叶片气动结构,导致风力发电机出力损失;叶片的不均匀覆冰会导致风力发电机叶片异常振动,对风机结构稳定产生威胁;在离心作用下脱落的冰块对周围人群和建筑产生潜在威胁[8-9]。
自21世纪初以来,相关研究人员开始对覆冰风力发电机的运行状态进行监测和报告,他们发现风力发电机每年因覆冰而导致的电能损失可达总发电量的10%~20%[10-12]。研究不同覆冰情况对风力发电机输出功率的影响,对于电力部门进行合理的电力调度、保证电网安全稳定运行十分重要。通常,对风力发电机叶片三维模型进行仿真,可以准确地计算出复杂流场对气动参数的影响,从而获得精度较高的输出功率信息。文献[13]利用仿真软件对风力发电机雨凇覆冰三维模型进行仿真计算,并通过人工试验进行验证,发现仿真结果与试验结果具有一致性。文献[14]通过对二维与三维风力发电机叶片翼型进行覆冰仿真发现,三维仿真冰型与实际覆冰情况更相符,这主要是由于三维仿真考虑了更多复杂的流场信息。然而,采用三维模型仿真覆冰叶片的功率特性也存在一些问题,例如,不规则覆冰模型会使划分的网格变形,降低仿真的稳定性;三维模型模拟功率特性时需要耗费大量计算时间。研究发现,将一个三维的覆冰叶片模型划分为400万个网格并在Fluent软件中进行仿真,获得功率特性结果需要花费大约2天的时间[15]。而在工程应用中,电力工作人员更多关注的是覆冰对输出功率的影响从而做出合理的调度操作,对流场信息的要求并不放在第一位,因此,提出一种更高效、精度稳定的覆冰风力发电机输出功率计算方法更符合工程应用的需要。
叶素动量(Blade Element Momentum, BEM)理论以二维叶片截面(叶素)为研究对象,忽略了叶片展向流场变化,计算耗时短,可以在较短时间内获得风力发电机叶片的功率特性。因此,本文提出了一种基于BEM理论的风力发电机输出功率快速计算方法,通过Matlab软件编程实现。在采用BEM理论计算输出功率时,需要获得不同叶素的升力与阻力系数,而冰层的存在改变了叶片原有的升力和阻力系数。因此,本文还利用了Fluent软件对叶素进行二维计算流体动力学(Computational Fluid Dynamics, CFD)仿真来获得不同覆冰叶素的升力和阻力系数。同时,利用经验公式并基于风力发电机的结构建立不同坐标系来对不同的气动参数进行修正。为了验证计算方法的准确性,在雪峰山野外科学观测研究站进行了现场试验。试验结果发现,该方法在工程应用允许的误差范围内可以较为准确地计算洁净和覆冰条件下风力发电机的输出功率。同时,通过该方法计算获得了不同风速下的关键气动参数沿叶片翼展的分布情况,经过分析可知,冰层的存在会降低叶片对风能的利用率,减小叶片旋转扭矩,从而导致输出功率降低;并且随着风速的增加,覆冰带来的负面影响更明显。
风力发电机现场试验于雪峰山野外科学观测研究站开展,如图1所示。据统计,该研究站年平均覆冰时长可达60天,雨凇最大厚度可达500 mm,最大风速可达25 m/s,为开展户外覆冰研究提供了良好的试验条件。

图1 雪峰山野外科学观测研究站
Fig.1 Xuefeng Mountain Field Science Observation and Research Station
现场试验对象为一台安装NREL S819型号叶片的300 kW风力发电机,其采用变速恒频发电系统,从而可以获取风力发电的最大转换效率,保证输出电压和频率的稳定。风力发电机的主要技术参数见表1。风力发电机叶片被条标定块分割成均匀的七份(忽略叶根处的部分),每一份的长度为2 m。标定块的作用是为用图像处理法[16]测量标记处的叶素覆冰厚度时提供参考尺寸。为区分不同标定块的叶素,采用叶素到叶根的距离r与叶片长度R的比值进行表示,如图2所示。
表1 风力发电机主要技术参数
Tab.1 The primary technical parameters of wind turbine

参数数值参数数值 额定功率/kW300切出风速/(m/s)25 额定转速/(r/min)400旋转直径/m31 额定风速/(m/s)13叶片长度/m14.6 切入风速/(m/s)3轮毂高度/m31

图2 叶素在叶片的位置
Fig.2 The position of blade elements on blade
风速的测量由安装在机舱上的BLF1-S型风速传感器进行采集,测量精度为0.1 m/s,如图3a所示;相对湿度和环境温度由WPH2-WX520型数字气象传感器进行采集,如图3b所示。风力发电机的运行参数(转子转速、桨距角、输出功率等)由德国Beckhoff PLC控制器以1 Hz的采样频率进行记录,该控制器广泛应用于风电行业,其软件运行界面如图4所示。在风力发电机塔架高度为18 m、23 m和28 m的三个位置各安装了一台高清摄像机,如图5所示,用于对叶片不同区域的覆冰情况进行监测。通过图像处理法对高清摄像机拍摄的照片进行处理,获得叶片覆冰厚度信息。
图3 环境参数测量设备
Fig.3 The environmental parameters measurement devices

图4 控制器软件运行界面
Fig.4 The interface of controller running software

图5 高清摄像机安装位置
Fig.5 The position of high definition cameras.
本文选取的覆冰工况如图6所示,覆冰冰型为均匀流线型,且选择风力发电机在覆冰条件下依然旋转运行的工况来进行计算方法的验证。由于覆冰为均匀流线型,故本文忽略了冰层表面不规则变化带来的影响,近似地认为相邻叶素间的冰层为线性均匀分布。
图像处理法获得覆冰厚度示意图如图7所示。首先,利用图像处理来获得冰层、叶片及标定块边缘的清晰轮廓。由于叶片的背面覆冰量少,因此可以近似地将冰层边缘与叶片边缘的距离作为覆冰厚度。然后,以标定块的水平边与垂直边为基准建立像素点直角坐标系,确定标定块、叶片和冰层边缘的像素点坐标,则叶片前缘的实际覆冰厚度d为

图6 选取的覆冰工况
Fig.6 The selected icing case
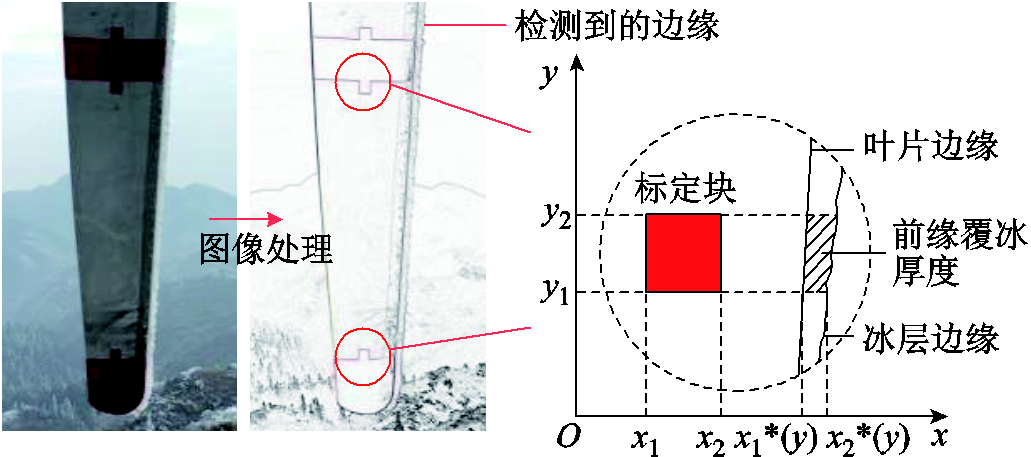
图7 图像处理法获得覆冰厚度示意图
Fig.7 The ice thickness obtained by image processing
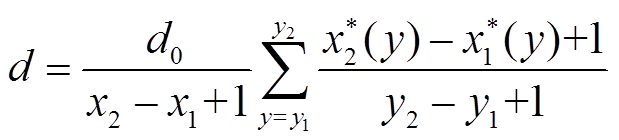 (1)
(1)
式中,d0为标定块实际长度;x1、x2、y1、y2为标定块边缘像素点的坐标;x1*(y)、x2*(y)分别为叶片边缘及冰层边缘像素点的坐标;x2-x1+1为标定块左右边缘之间的像素点个数;y2-y1+1为标定块上下边缘之间的像素点个数;x2*(y)-x1*(y)+1为y坐标下冰层边缘与叶片边缘之间的像素点个数。
根据上述方法,获得不同叶素的覆冰厚度见表2,洁净与覆冰条件下风速与输出功率随时间变化的监测数据如图8所示。
表2 不同叶素的覆冰厚度
Tab.2 The ice thickness of different blade elements

r/R覆冰厚度/mmr/R覆冰厚度/mm 0.0400.5917.9 0.17800.72631.2 0.3151.20.86342.6 0.4526.1152.1
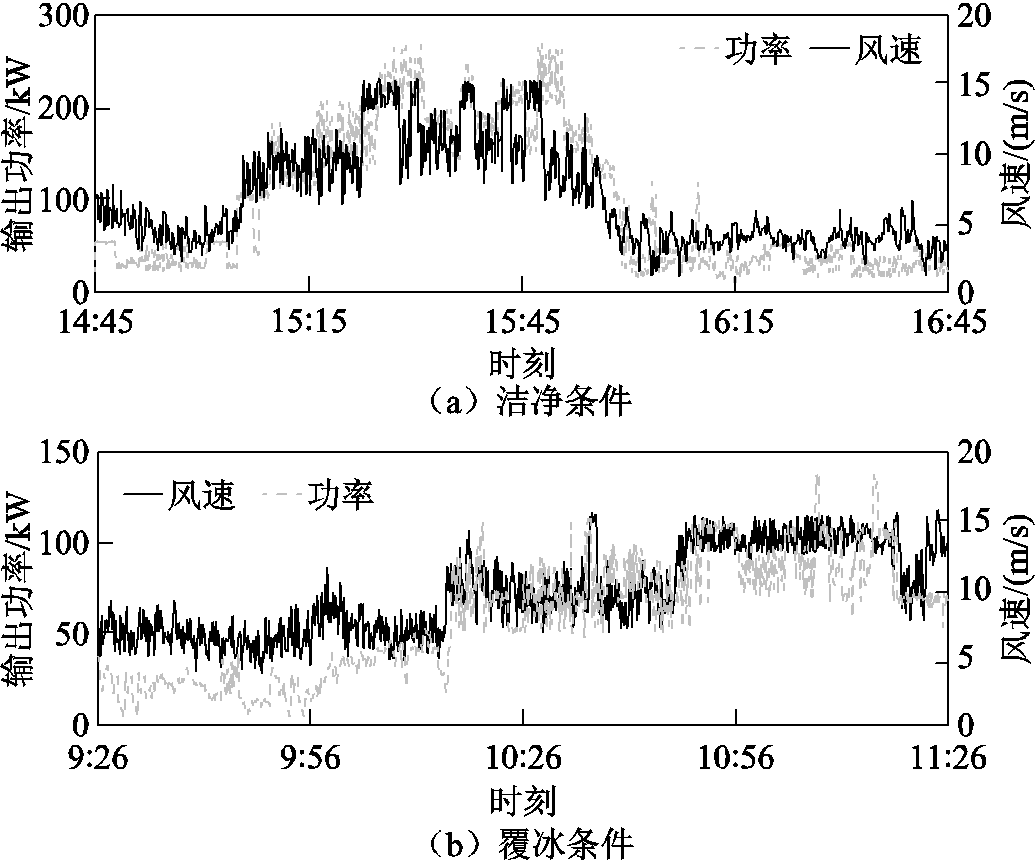
图8 风速和输出功率随时间变化数据
Fig.8 Time varying data of wind speed and output power
2.1.1 叶素绘制
由于临近叶尖三分之一长度的叶片对风力发电机输出功率的贡献达到了90%[17],并且叶根处翼型变化不规则,其对输出功率的贡献可以忽略[18]。因此,本文计算输出功率只考虑了从r/R=0.315~1处的叶片部分。基于图像处理法和无人机拍摄的照片,绘制标定块处叶素的覆冰轮廓如图9所示,叶片从里到外对应的叶素分别为r/R=1, 0.863, 0.726, 0.59, 0.452, 0.315。

图9 不同叶素覆冰轮廓
Fig.9 The ice outlines of different blade elements
2.1.2 仿真设置
仿真设置示意图如图10所示,仿真计算域尺寸为20c×20c(c为叶素弦长)。对轮廓线前缘表面进行网格加密,确保网格总数控制在1.0×105,满足网格独立性的要求。叶素轮廓设置为无滑移边界条件,仿真域上、下轮廓设置为无穷远压力边界条件。入流风速的湍流参数和粘度系数分别设定为5%和10%。压力出口参数设置为0 Pa,湍流参数为5%。

图10 仿真设置示意图
Fig.10 Diagram of simulation settings
2.2.1 BEM理论
根据BEM理论,将风轮平面分成无数个微小的流管单元,如图11所示。图中,p0为气流静压;p为风轮迎风面压力;Δp为风轮损耗压力;u1为尾流风速。轴向推力作用在气流方向,使来流风速从v0减小到u,作用在厚度为dr的单元流管上的轴向推力dT和力矩dM[19-20]分别为
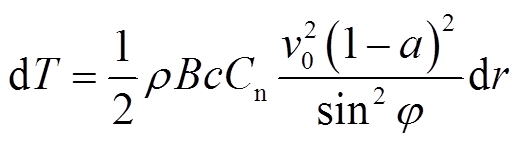 (2)
(2)
 (3)
(3)
式中,ρ为空气密度;B为叶片数量;Cn为法向力系数;Ct为切向力系数;ω为风机旋转角速度;a为轴向诱导因子;b为切向诱导因子;φ为相对风速与风轮平面的夹角;r为单元流管所在半径位置(也指单元流管对应叶素到叶根的距离)。
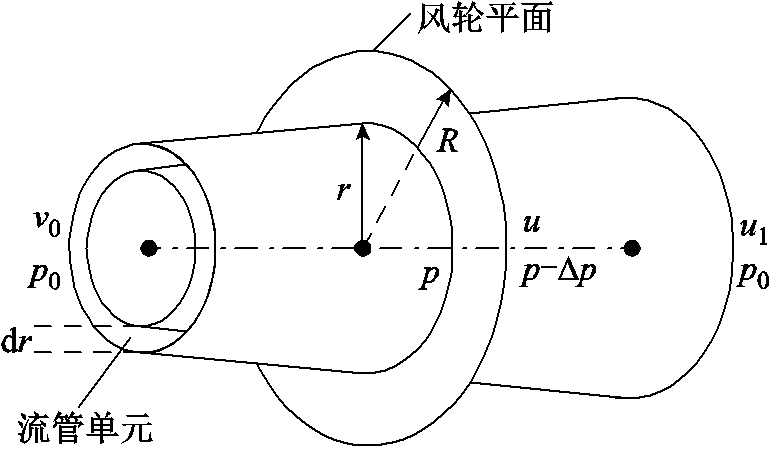
图11 风轮平面流管单元模型
Fig.11 Model of flow tube unit on wind rotor swept plane
叶素上的风速关系如图12所示,其中va为轴向诱导速度,vb为切向诱导速度,α为相对风速vrel与叶素之间的攻角。va和vb的数值[19-20]分别为
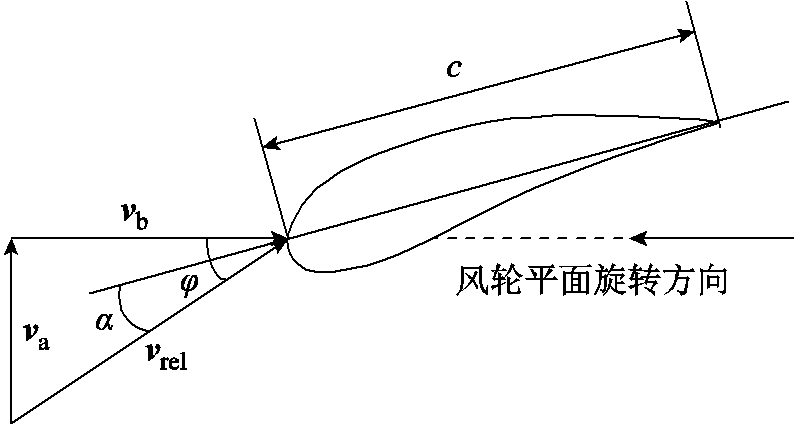
图12 叶素上的不同风速
Fig.12 The velocities on blade element
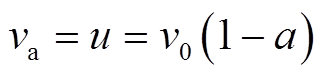 (4)
(4)
 (5)
(5)
叶素上的受力如图13所示。通过矢量分解,由升力L与阻力D的合力Fr得到切向力PT和法向力PN,升力、阻力、切向力和法向力的大小[19-20]分别为
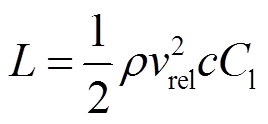 (6)
(6)
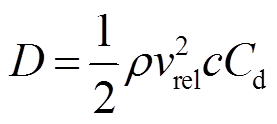 (7)
(7)
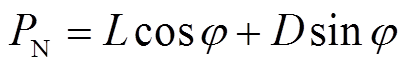 (8)
(8)
 (9)
(9)
式中,Cl为升力系数;Cd为阻力系数。联立表达式(6)~式(9)可得
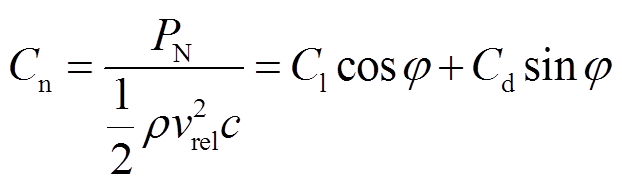 (10)
(10)
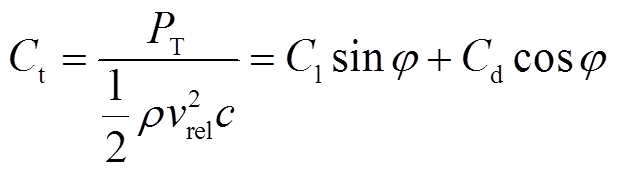 (11)
(11)
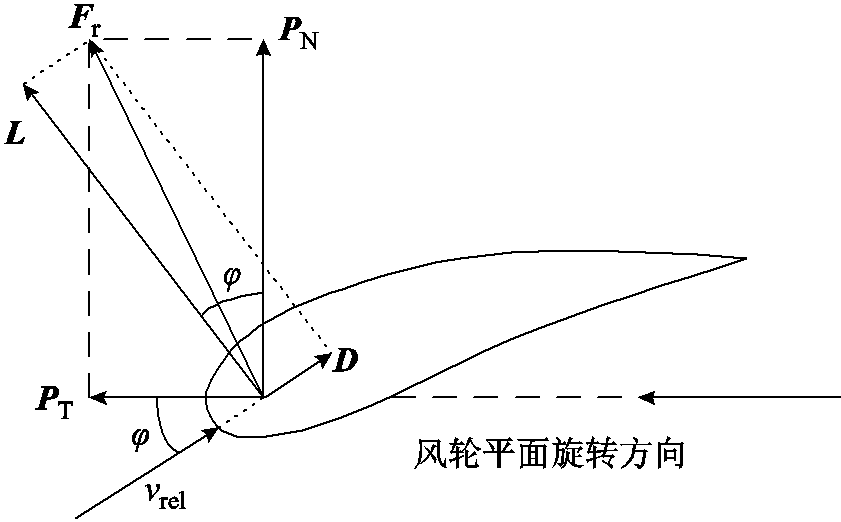
图13 叶素上的受力
Fig.13 The forces on blade element
2.2.2 诱导因子修正
根据BEM理论可知轴向诱导因子a和切向诱导因子b的表达式[21]分别为
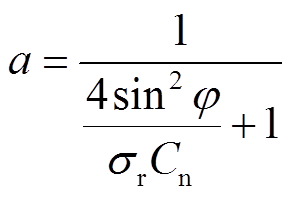 (12)
(12)
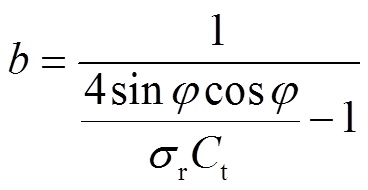 (13)
(13)
其中,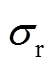 =Bc/(2πr)。
=Bc/(2πr)。
由于靠近叶尖与轮毂处的气流会在上下表面压力差的作用下产生二次流动,而叶素理论忽略了此处的影响,因此需要进行叶尖损失和轮毂损失修正,修正公式[21]分别为
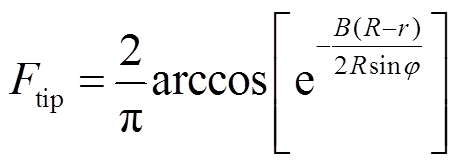 (14)
(14)
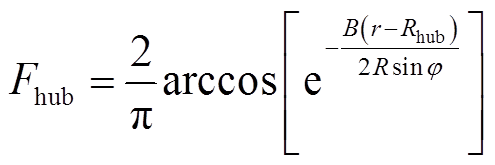 (15)
(15)
式中,Ftip为叶尖损失因子;Fhub为轮毂损失因子;Rhub为轮毂半径。因此,式(12)和式(13)修正为
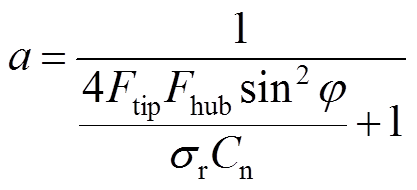 (16)
(16)
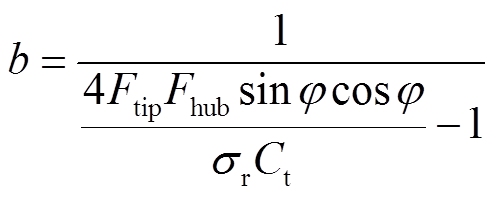 (17)
(17)
2.2.3 攻角修正
考虑到叶片厚度和宽度对气流的影响,引入Cascade理论,对流入叶素气流的攻角进行修正,修正公式[18]为
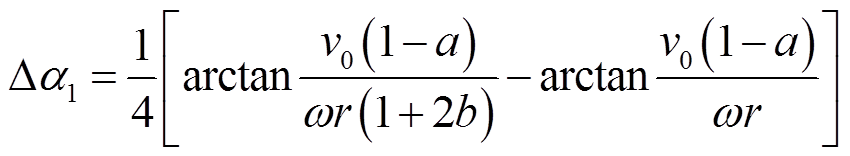 (18)
(18)
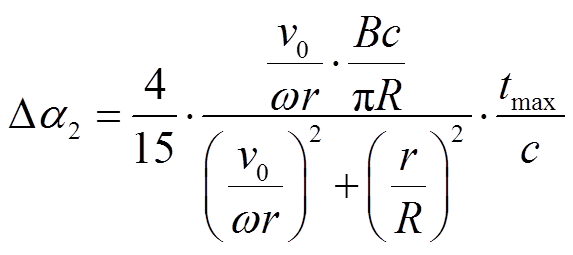 (19)
(19)
式中,tmax为叶素最大厚度;Δα1为叶素宽度引起的攻角变化;Δα2为叶素厚度引起的攻角变化。攻角总变化量Δα=Δα1+Δα2。
2.2.4 相对风速修正
考虑到风力发电机的结构参数对相对风速的影响,建立一个系统的坐标系对相对风速进行修正,坐标系系统如图14所示。其中,惯性坐标系S以塔架中心O为原点,z轴垂直指向水平地面,y轴与风轮转轴处于同一平面并与x轴形成平行于地面的水平面;塔架坐标系Sn则是由惯性坐标系S沿x轴旋转角度 得到,其中角度
得到,其中角度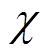 为风轮转轴的倾角;轮毂坐标系Sh则以轮毂中心Oh为原点,由塔架坐标系Sn沿yn轴平移距离Lh所得到,其中距离Lh为塔架中心与轮毂中心的距离;风轮坐标系Sr是随风机叶片旋转而不断改变的坐标系,由轮毂坐标系Sh绕yh轴按顺时针方向旋转角度θ0所得,其中定义叶尖垂直朝上时,风轮方位角θ=0°,则图14c在坐标系Sr下的风轮方位角为θ=180°+θ0;叶片坐标系Sp由风轮坐标系Sr绕xr轴旋转角度β0得到,其中β0为风机叶片与叶片扫掠平面形成的锥角。
为风轮转轴的倾角;轮毂坐标系Sh则以轮毂中心Oh为原点,由塔架坐标系Sn沿yn轴平移距离Lh所得到,其中距离Lh为塔架中心与轮毂中心的距离;风轮坐标系Sr是随风机叶片旋转而不断改变的坐标系,由轮毂坐标系Sh绕yh轴按顺时针方向旋转角度θ0所得,其中定义叶尖垂直朝上时,风轮方位角θ=0°,则图14c在坐标系Sr下的风轮方位角为θ=180°+θ0;叶片坐标系Sp由风轮坐标系Sr绕xr轴旋转角度β0得到,其中β0为风机叶片与叶片扫掠平面形成的锥角。
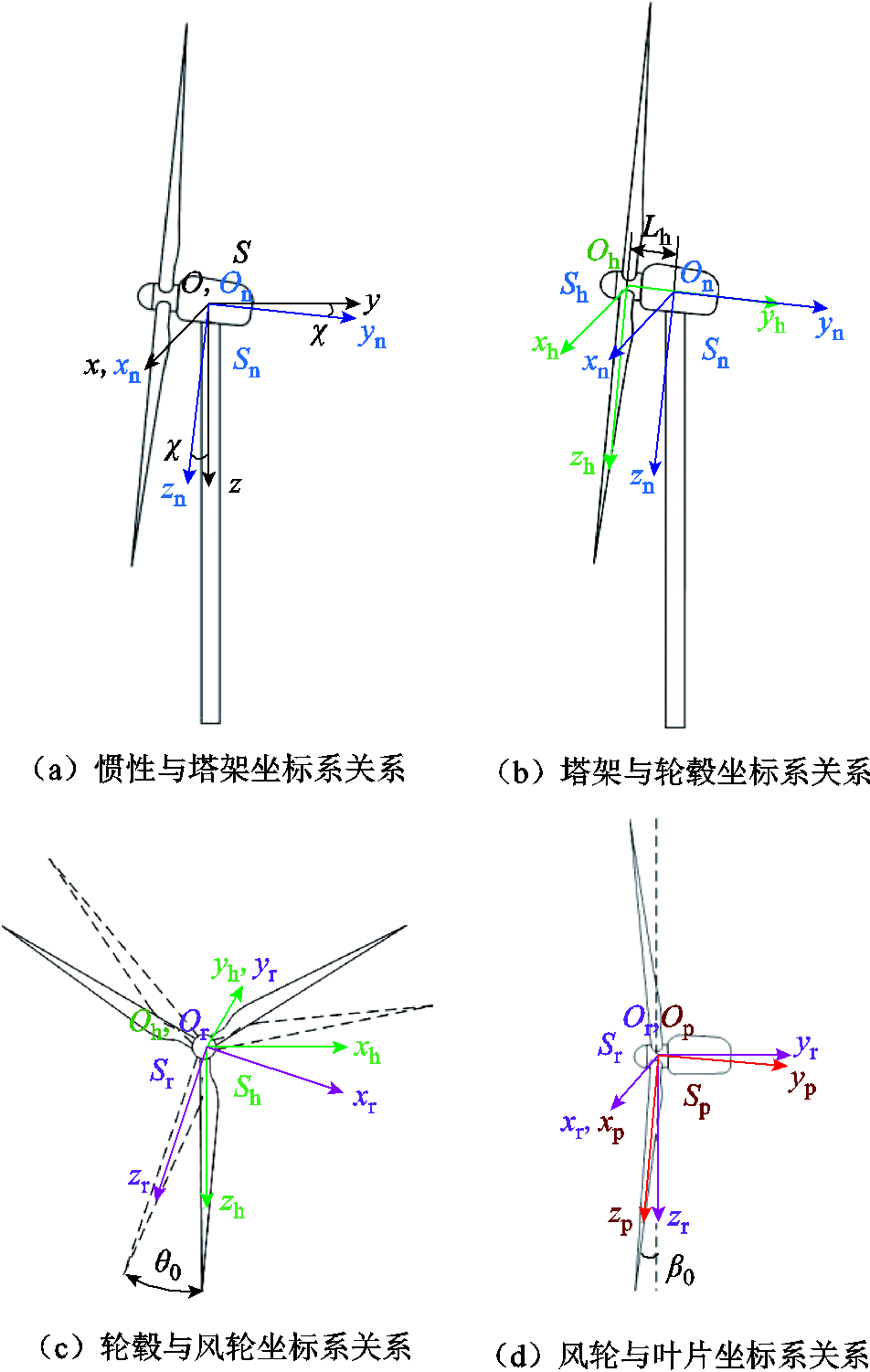
图14 坐标系的转换
Fig.14 Transformation of coordinate systems
根据上述描述的坐标系关系,设惯性坐标系S中的位置矢量s表示为
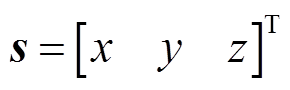 (20)
(20)
则其他坐标中的位置矢量可分别表示为
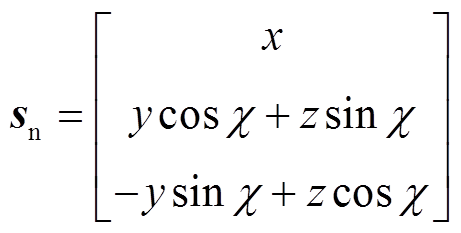 (21)
(21)
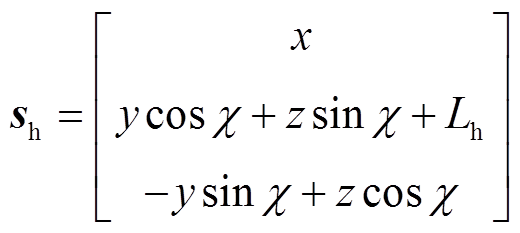 (22)
(22)
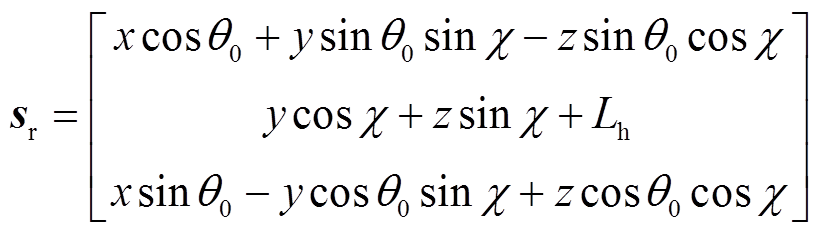 (23)
(23)
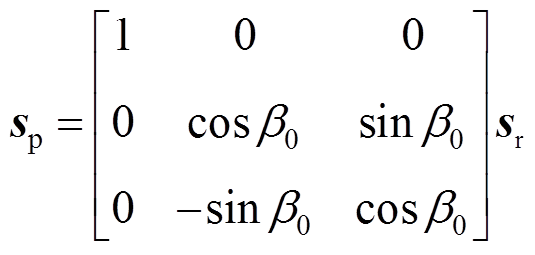 (24)
(24)
由于来流的风速并不是垂直吹向风轮平面,它们之间存在一定的偏航角γ。因此,当来流风速为v0时,以叶片坐标系Sp为基本坐标系可得各坐标轴的风速分量为
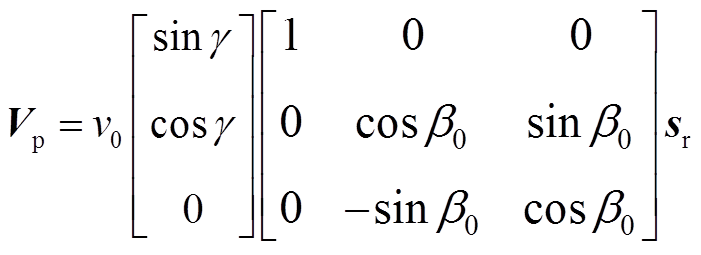 (25)
(25)
2.2.5 输出功率计算
当风力发电机叶片数目为K、叶素数目为N时,通过式(9)可以计算出叶素上的切向力大小。在计算整个风力发电机的输出功率时,假定每两个相邻叶素ri和ri+1之间的切向力PT,i为线性分布,其可以表示[22]为
 (26)
(26)
其中
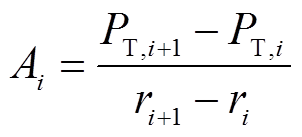 (27)
(27)
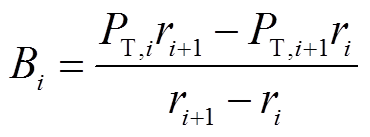 (28)
(28)
所以,第i片叶素在单位长度dr上受到的力矩dMi可表示为
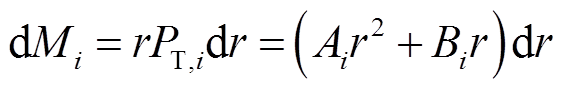 (29)
(29)
从叶素位置为ri到ri+1之间的风力发电机局部叶片所受转矩Mi,i+1为
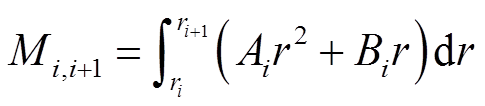 (30)
(30)
从而整个风力发电机的输出功率P可表示为
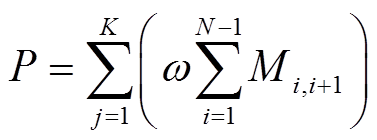 (31)
(31)
洁净和覆冰条件下的风力发电机输出功率计算流程如图15所示,通过Matlab软件编程实现。各叶素的升力与阻力系数由Fluent软件仿真获得。

图15 输出功率计算流程
Fig.15 Flow chart of output power calculation
3.1.1 洁净条件
洁净条件下风力发电机运行参数见表3,风力发电机额定功率、场地试验测量功率和计算功率的对比结果如图16所示。由图16可知,当风速小于11 m/s时,计算结果与测量结果十分吻合;而当风速超过11 m/s时,两者间出现显著差异。试验测量结果较小的原因是实际运行中高风速持续时间较短,在风力发电机达到相应的工作状态之前,风速已经降低,导致对应风速下的平均输出功率较低。当风速为13 m/s时,计算结果大于额定功率。这是由于在实际运行中,当风速超过额定值时,风力发电机会改变桨距角以保持额定输出功率,然而计算方法中并未考虑此处的非线性变化。整体而言,计算结果与测量结果的最大相对误差小于10%,说明该模型能够较为准确地计算出洁净条件下风力发电机的输出功率。
表3 洁净条件下风力发电机运行参数
Tab.3 The operation parameters of wind turbine under clean condition

风速/(m/s)5678910111213 转速/(r/min)30323436384041.54344 偏航角/(°)000000025
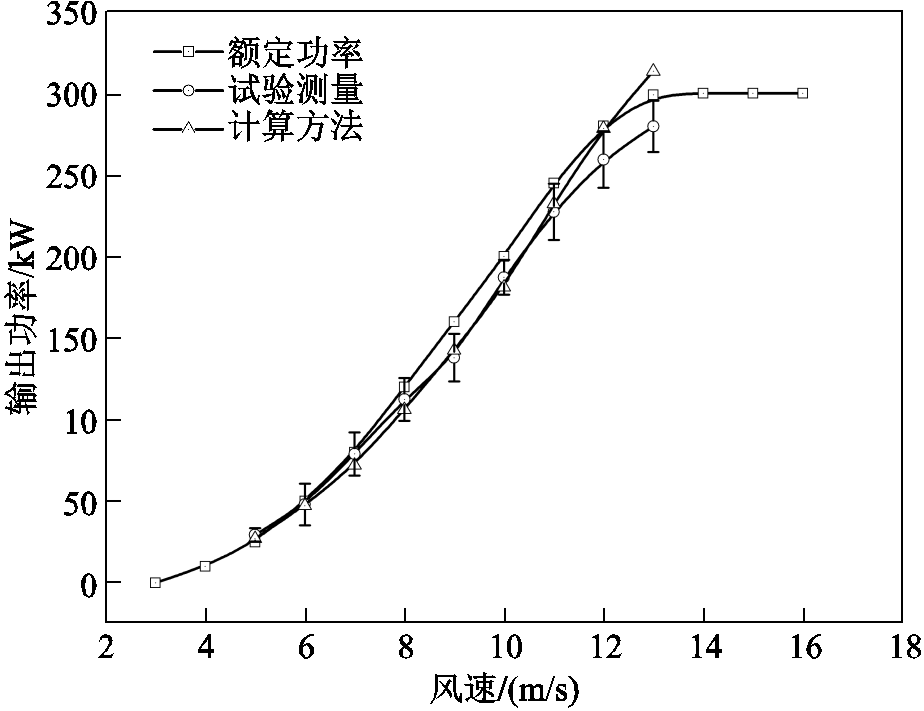
图16 洁净条件下的功率对比
Fig.16 Power comparison under clean condition
3.1.2 覆冰条件
覆冰条件下风力发电机运行参数见表4,风力发电机额定功率、场地试验测量功率和计算功率的对比结果如图17所示。由图17可知,计算结果与测量结果的趋势基本一致。随着风速的增加,平均测量功率与计算功率的差值越来越大,原因有二:①BEM理论和二维CFD仿真忽略了展向流场变化的影响,只考虑了流场二维平面的变化;②冰面的粗糙程度会使背风面上的气流分离点提前,导致涡流增加,能量损失增大。整体而言,两者间的最大相对误差小于14.1%,说明该模型能够较准确地计算出覆冰条件下风力发电机的输出功率。
表4 覆冰条件下风力发电机运行参数
Tab.4 The operation parameters of wind turbine under icing condition

风速/(m/s)5678910111213 转速/(r/min)2929292929.530303232 偏航角/(°)000000023
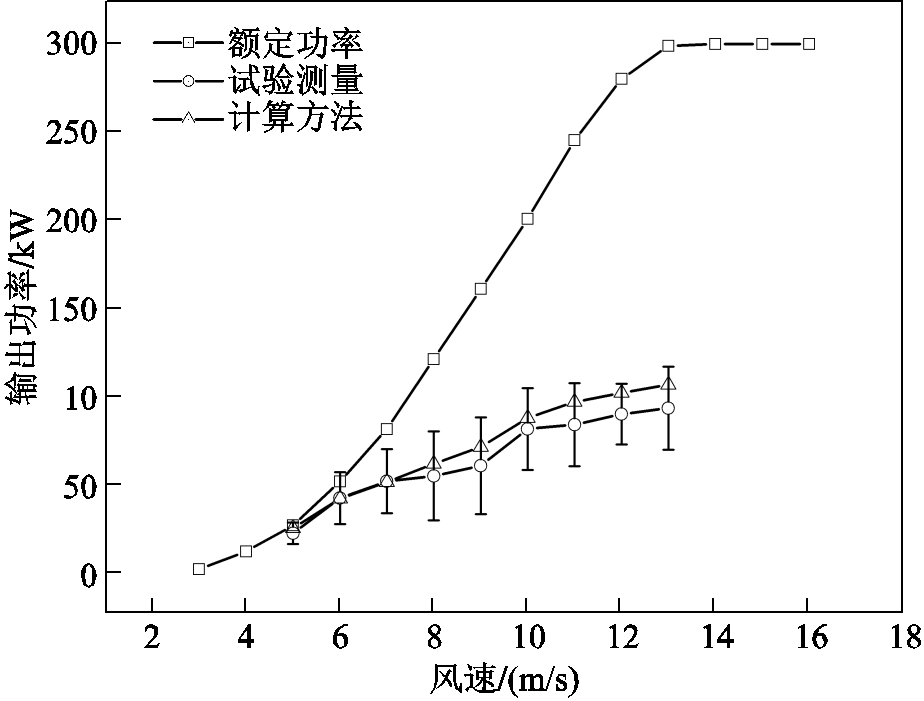
图17 覆冰条件下的功率对比
Fig.17 Power comparison under icing condition
3.2.1 轴向诱导因子a和切向诱导因子b
不同风速下,轴向和切向诱导因子沿洁净和覆冰风力发电机叶片翼展方向的分布规律如图18所示。
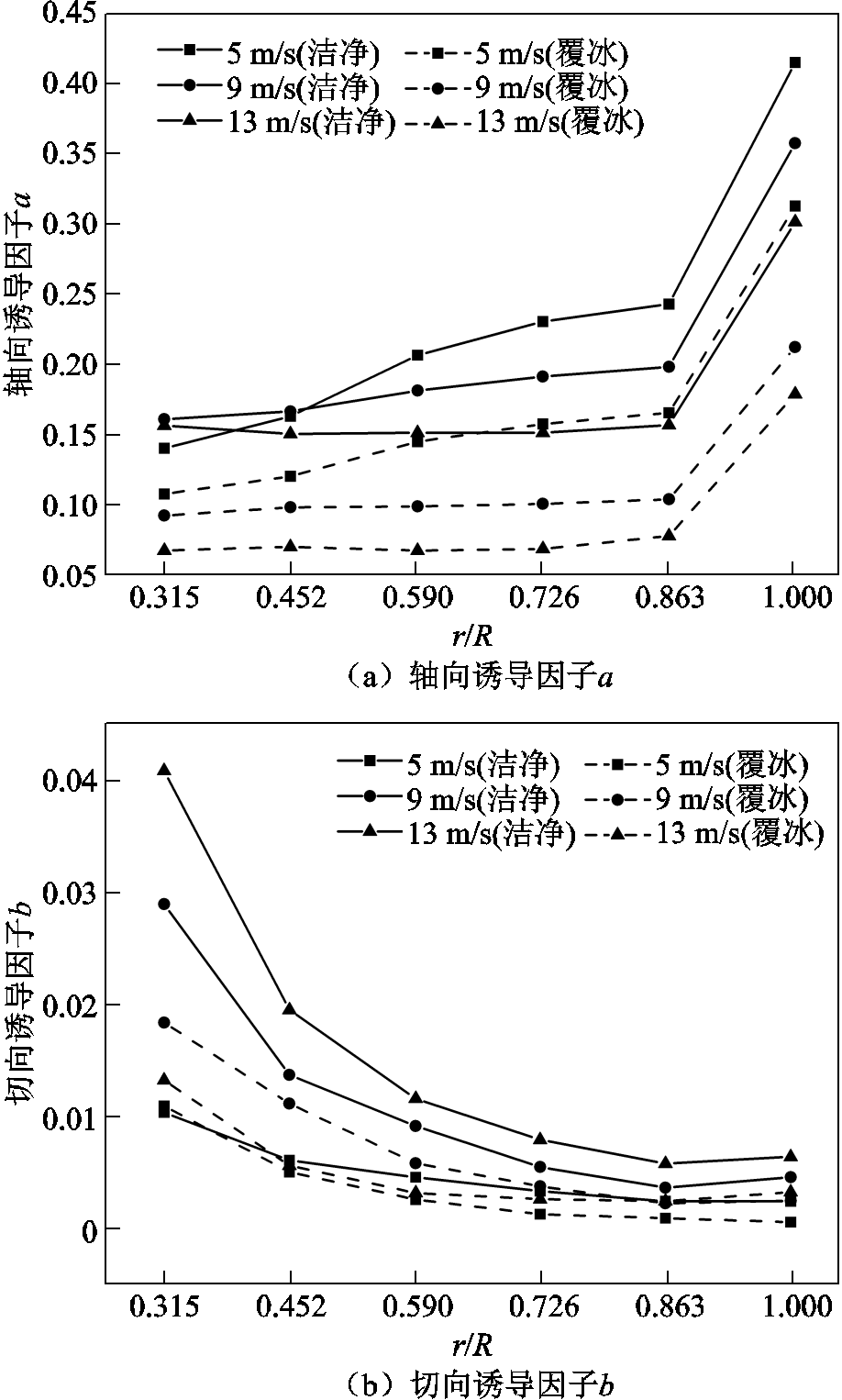
图18 诱导因子对比
Fig.18 Comparison of inducing factors
1)从图18可以看出,轴向诱导因子a沿翼展方向逐渐增大,切向诱导因子b沿翼展方向逐渐减小。在叶尖附近,因子a的增长速率明显增加,而因子b的下降趋势趋于稳定,这表明风能在叶尖处的利用最为充分。
2)在覆冰工况下,随着风速增加,切向诱导因子b呈现先增大后减小的趋势。说明在高风速下,覆冰严重地破坏了风机叶片前缘气动结构,对切向诱导因子b产生的影响更明显。
3)与洁净条件下的结果相比,在相同风速下,覆冰条件下轴向、切向诱导因子a、b均有不同程度的下降。这表明覆冰会降低叶片对风能的利用率并减小叶片旋转扭矩,从而导致输出功率降低。
3.2.2 切向力和法向力
不同风速下,切向力和法向力沿洁净和覆冰风力发电机叶片翼展方向的分布规律如图19所示。
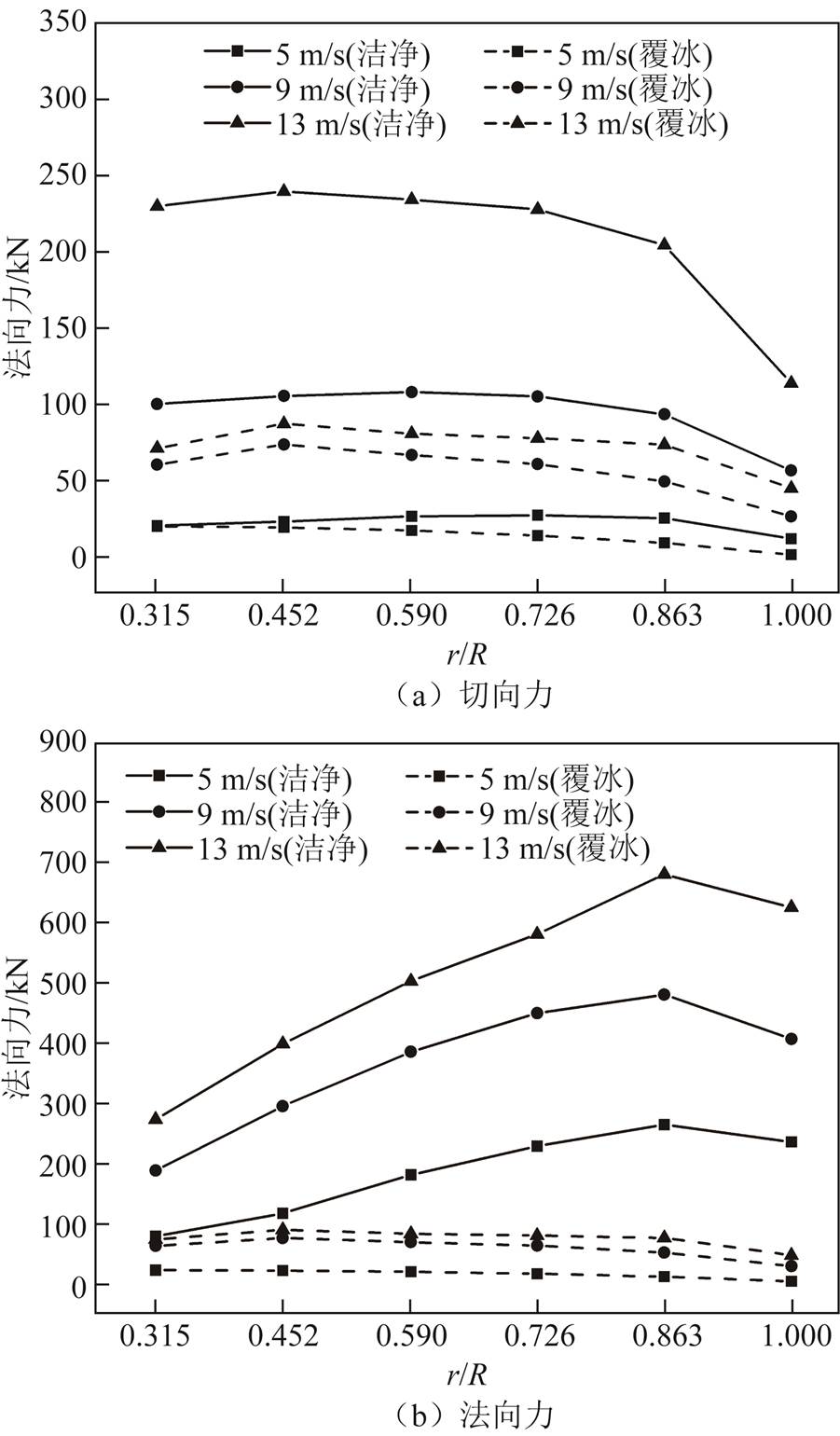
图19 叶素受力分析对比
Fig.19 Comparison of forces on blade elements
1)从图19可以看出,洁净和覆冰条件下,随着风速的增加,法向力和切向力均增大,说明风速的提高可以增加风力发电机的输出功率。
2)覆冰条件下的法向力小于洁净条件下的法向力,这是因为冰层的存在减少了风力发电机对风能的利用率,背风区压力相应增加所导致。
3)覆冰条件下,切向力也明显减小,这是由于冰层破坏了叶片原有气动结构,导致阻力增大,升力减小。当风速增加时,这种差异更加显著。
本文提出了一种基于BEM理论的洁净和覆冰条件下风力发电机输出功率计算方法,并且通过现场试验验证了该方法的准确性,主要结论如下:
1)在低风速洁净条件下时,该计算模型能够准确地计算出风力发电机的输出功率,与场地试验结果高度吻合;但当风速大于11 m/s时,二者偏差开始增加,这主要是因为场地试验过程中风速波动速度快、波动幅度大所导致,但在本文工况下二者最大相对误差不超过10%。
2)在覆冰条件下,该计算模型所获得的风力发电机输出功率随风速变化的趋势与场地试验结果有较好的吻合度。随着风速的增加,二者之间的偏差略微增加。计算数值较大的原因除了风速波动影响外,还可能是由于本计算方法忽略了展向流场的变化,以及忽略了冰层表面粗糙度对风力发电机输出功率带来的影响,但在本文工况下二者最大相对误差不超过14.1%。
3)覆冰会导致轴向和切向诱导因子均有不同程度的降低,说明覆冰会降低叶片对风能的利用率并减小叶片旋转扭矩。随着风速的增加,覆冰所带来的影响越严重。
4)覆冰会导致叶素所受切向力和法向力均出现不同程度的降低。随着风速的增加,覆冰所带来的影响也更加明显,这也进一步证实覆冰会通过改变叶片空气动力结构来减少风能的利用率,从而导致出力损失。
参考文献
[1] 颜湘武, 王德胜, 杨琳琳, 等. 直驱风机惯量支撑与一次调频协调控制策略[J]. 电工技术学报, 2021, 36(15): 3282-3292. Yan Xiangwu, Wang Desheng, Yang Linlin, et al. Coordinated control strategy of inertia support and primary frequency regulation of PMSG[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3282-3292.
[2] 陆秋瑜, 马千里, 魏韡, 等. 基于置信容量的风场配套储能容量优化配置[J]. 电工技术学报, 2022, 37(23): 5901-5910. Lu Qiuyu, Ma Qianli, Wei Wei, et al. Optimal configuration of energy storage parameters based on confidence capacity of wind farms[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 5901-5910.
[3] 徐海亮, 吴瀚, 李志, 等. 低短路比电网下含负序控制双馈风机稳定性研究的几个关键问题[J]. 电工技术学报, 2021, 36(22): 4688-4702. Xu Hailiang, Wu Han, Li Zhi, et al. Several key issues on stability study of DFIG-based wind turbines with negative sequence control during low short-circuit ratio power grids[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4688-4702.
[4] 朱东海, 邹旭东, 胡家兵, 等. 双馈风电机组无撬棒故障穿越技术研究综述[J]. 电工技术学报, 2022, 37(19): 4895-4910. Zhu Donghai, Zou Xudong, Hu Jiabing, et al. Review of crowbarless fault ride through technology for doubly-fed induction generator-based wind turbines[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4895-4910.
[5] 符杨, 张耀楠, 刘璐洁, 等. 海上风电场维护任务动态调度策略[J]. 电力系统自动化, 2021, 45(21): 48-56. Fu Yang, Zhang Yaonan, Liu Lujie, et al. Dynamic dispatching strategy for maintenance tasks of offshore wind farm[J]. Automation of Electric Power Systems, 2021, 45(21): 48-56.
[6] 胡琴, 王欢, 邱刚, 等. 风力发电机叶片覆冰量化分析及其应用[J]. 电工技术学报, 2022, 37(21): 5607-5616. Hu Qin, Wang Huan, Qiu Gang, et al. Quantitative analysis of wind turbine blade icing and its application[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5607-5616.
[7] 龚妙, 李录平, 刘瑞, 等. 风力机叶片覆冰状态监测基准值与分级诊断标准研究[J]. 太阳能学报, 2021, 42(2): 172-178. Gong Miao, Li Luping, Liu Rui, et al. Research on ice accretion conditon monitoring reference value and grading diagnosis standard of wind turbine blades[J]. Acta Energiae Solaris Sinica, 2021, 42(2): 172-178.
[8] Parent O, Ilinca A. Anti-icing and de-icing techniques for wind turbines: critical review[J]. Cold Regions Science and Technology, 2011, 65(1): 88-96.
[9] Drapalik M, Zajicek L, Purker S. Ice aggregation and ice throw from small wind turbines[J]. Cold Regions Science and Technology, 2021, 192: 103399.
[10] Dierer S, Oechslin R, Cattin R. Wind turbines in icing conditions: performance and prediction[J]. Advances in Science and Research, 2011, 6(1): 245-250.
[11] Pérez J M P, Márquez F P G, Hernández D R. Economic viability analysis for icing blades detection in wind turbines[J]. Journal of Cleaner Production, 2016, 135: 1150-1160.
[12] Gao Linyue, Hu Hui. Wind turbine icing characteristics and icing-induced power losses to utility-scale wind turbines[J]. Proceedings of the National Academy of Sciences of the United States of America, 2021, 118(42): e2111461118.
[13] 梁健, 舒立春, 胡琴, 等. 风力机叶片雨淞覆冰的三维数值模拟及试验研究[J]. 中国电机工程学报, 2017, 37(15): 4430-4436, 4584. Liang Jian, Shu Lichun, Hu Qin, et al. 3-D numerical simulations and experiments on glaze ice accretion of wind turbine blades[J]. Proceedings of the CSEE, 2017, 37(15): 4430-4436, 4584.
[14] Jin J Y, Virk M S, Hu Qin, et al. Study of ice accretion on horizontal axis wind turbine blade using 2D and 3D numerical approach[J]. IEEE Access, 2020, 8: 166236-166245.
[15] Shu Lichun, Li Hantao, Hu Qin, et al. 3D numerical simulation of aerodynamic performance of iced contaminated wind turbine rotors[J]. Cold Regions Science and Technology, 2018, 148: 50-62.
[16] Akhloufi M, Benmesbah N. Outdoor ice accretion estimation of wind turbine blades using computer vision[C]//2014 Canadian Conference on Computer and Robot Vision, Montreal, QC, Canada, 2014: 246-253.
[17] Hochart C, Fortin G, Perron J, et al. Wind turbine performance under icing conditions[J]. Wind Energy, 2008, 11(4): 319-333.
[18] Wilson R E, Lissaman P B S, Walker S N. Aerodynamic performance of wind turbines[R]. Energy Research and Development Administration, 1976.
[19] Hansen M O L. 风力发电机空气动力学[M]. 肖劲松,译. 2版. 北京:中国电力出版社, 2009.
[20] 韩巧丽, 马广兴. 风力发电原理与技术[M]. 北京: 中国轻工业出版社, 2018.
[21] 李岩, 王绍龙, 冯放. 风力机结冰与防除冰技术[M]. 北京: 中国水利水电出版社, 2017.
[22] 蔡新, 潘盼, 朱杰. 风力发电机叶片[M]. 北京: 中国水利水电出版社, 2014.
Abstract Wind energy resources are abundant in high-altitude areas, but wind turbines built here suffer serious icing problems. The accumulated ice will destroy the original aerodynamic structure of wind turbine blades, resulting in output power loss, which has bad influences on the power supply quality. Understanding the influences of different icing cases on the output power is helpful for the power department to carry out reasonable power dispatching during icing season. Therefore, a method for calculating the output power of wind turbine under clean and icing conditions was proposed.
The proposed method is based on the Blade Element Momentum (BEM) theory and this theory ignores the variation of flow field along the wind turbine blades, which could increase efficiency by reducing computation time. To improve the calculation accuracy and make the calculation results more fit the actual condition, empirical formulas were introduced to correct the axial inducing factor, the tangential inducing factor, and attack angle. Because the accumulated ice changes the original aerodynamic structure of the wind turbine blades, the 2D CFD simulation based on commercial software Fluent was introduced to obtain the lift and drag coefficients of iced blade elements. Considering the influences of wind turbine structural parameters, different coordinate systems were established to correct the relative wind velocity working on the blade rotation plan. Because the contribution of one-third length blade near tip to output power reaches 90%, the proposed calculation method ignores the contribution of blade root on output power to save the computation time.
To verify the accuracy and feasibility of the calculation method, field tests of the NREL S819 type wind turbine under clean and icing conditions were carried out in Xuefeng Mountain Energy Equipment Safety National Observation and Research Station. Under the icing condition, the uniform and streamline ice was chosen as the research object.
Comparing the calculated results and test measured results, it is found that: (1) When the wind velocity is less than 11 m/s under clean or icing condition, the calculation method can accurately calculate the output power of wind turbine, which is in good agreement with the test measured results. (2) When the wind velocity exceeds 11 m/s, the differences between calculated results and test measured results increase gradually, and this is because the wind speed fluctuates fast and the fluctuation range is large during the field test. The maximum relative errors between two of them under clean and icing conditions are 10% and 14.1% respectively, which meet the engineering application error requirements.
Based on this method, the key aerodynamic parameters along wingspan direction under different wind velocity were calculated. Results showed that: (1) The ice on wind turbine blades will decrease the axial and tangential inducing factor, which indicates that it could reduce the rotational torque of blades. (2) Icing could reduce the tangential and normal force, and the effects of icing become more pronounced as wind velocity increases. (3) The attenuation of tangential and normal force is obvious near the blade tip, which indicates that the ice will reduce the utilization of wind energy near blade tip more easily.
keywords:Wind turbine, output power, blade element momentum, icing
DOI: 10.19595/j.cnki.1000-6753.tces.220234
国家自然科学基金资助项目(52077020, 51977016)。
中图分类号:TM315
收稿日期 2022-02-22
改稿日期 2022-04-26
舒立春 男,1964年生,博士,教授,博士生导师,研究方向为高电压与绝缘技术、输电线路和风力发电机覆冰及防护等。E-mail:lcshu@cqu.edu.cn(通信作者)
于 周 男,1994年生,博士研究生,研究方向为风力发电机覆冰及防护。E-mail:yuzhoucqu@163.com
(编辑 李冰)