图1 SFSZ7-31 500/110变压器实物图
Fig.1 Photo of SFSZ7-31 500/110 transformer
摘要 为了研究变压器绕组在多次短路冲击的累积效应影响下逐步机械形变问题，开展了多次110 kV真型变压器短路试验，采集了振动暂态信号和轴向压力稳态值，分析了历次短路过程中振动偏离和加权时频谱熵的变化趋势。结果表明，累积效应导致的绕组机械劣化会使振动加速度偏离未形变状态基准值，且加权时频谱熵增大；结合材料力学及绕组轴向振动动力学模型，推导出当振动加速度呈正偏离时，短路侧绕组形变形式为轴向外凸膨胀，反之为轴向内凹压缩的关联规律。最后提出并验证了一种基于振动偏差模值及加权时频谱熵联合分析的绕组形变辨识方法，该方法较传统阻抗法能够在绕组早期微小形变时更早发现机械稳定性下降。研究结果对变压器绕组形变预警具有一定指导意义。
关键词：变压器绕组 累积效应 短路冲击试验 时频特征分析 形变辨识
电力变压器是电能输送的关键设备，其安全稳定运行对整个电网系统而言至关重要。据统计，由短路引起的绕组形变是造成变压器故障的主要原因之一。正常绕组一般能承受单次短路冲击，严重失稳形变往往是多次短路冲击后在累积效应作用下突然发生[1]。因此，研究绕组在多次短路冲击下的机械形变具有重要的工程意义[2-3]。
传统绕组形变诊断方法具有一定的局限性，如频率响应法、低压脉冲法需变压器退出运行后才能进行[4-7]，短路阻抗法在检测电抗变化率小于2%的绕组形变时灵敏度不高[8-9]。而变压器的振动信号往往能够灵敏反映绕组的状态信息，且可实现带电采集，与系统无电气连接，因此振动法目前广泛用于变压器绕组的状态诊断[10-12]。文献[13]通过建立绕组两体振动模型，推导了模型的振动数学方程，获得了绕组的多倍频振动特性。文献[14]分析了换流变压器在起动、停运以及降功率运行等状态下的振动特性及铁心、绕组振动贡献，通过分离振动来源为变压器机械状态监测提供了有效的振动频率适用区段与数据支持。
上述文献明确了振动法对变压器绕组机械状态诊断的指导意义，但未对绕组的形变识别提出明确方法。为此，文献[15]提取了绕组振动信号的时域、频域以及信息域的特征量，基于线性判别式分析（Linear Discriminant Analysis, LDA）投影算法实现了不同负载电流下绕组的正常、松动状态的准确识别。文献[16]建立了多种故障状态的绕组振动及电抗信息数据集，提出了能够检测到绕组松动、轻微变形状态的绕组状态综合监测方法，灵敏度和实用性更高，为绕组形变诊断提供了理论参考依据。
但前人在研究过程中形变故障类型往往是人为设计，不具有状态连续性，对绕组在经历多次短路冲击时产生的累积效应聚焦不足，而累积效应导致绕组结构松动、导线屈服强度下降等故障致使变压器抗短路能力下降是其损坏事故的重要原因[17-19]，因此为准确监测绕组机械状态，必须关注累积效应自绕组早期微小形变至严重失稳形变期间的影响。同时，现有研究往往分析的是50 Hz激励下的振动信号，当绕组应变程度较低时，稳态激励对振动信号特征影响不明显，而短路过程中暂态短路电流能够有效地放大振动响应，因此对暂态振动信号进行特征分析能够更灵敏地反映累积效应的影响。
针对上述问题，本文首先开展了110 kV真型变压器多种工况下连续多次短路冲击试验，采集短路过程中振动加速度暂态信号和短路前后绕组轴向压力稳态值，有针对性地分析冲击过程中振动信号的时频特征，获得了历次试验过程中振动加速度测量值与基准值的偏离趋势；然后结合绕组轴向振动动力学模型，验证了振动加速度偏移趋势与轴向压力、绕组形变趋势的关联关系；最后提出了振动加速度偏移模值与加权时频谱熵双特征量联合分析方法，实现了考虑累积效应的绕组形变状态及机械性能监测，为变压器绕组形变预警及状态评估提供了参考。
为探究变压器绕组在多次短路冲击下的机械形变问题，以图1所示SFSZ7-31 500/110型变压器为研究对象，于沈阳变压器研究院国家变压器质量监督检验中心开展连续多次短路试验，变压器具体参数见表1。
图1 SFSZ7-31 500/110变压器实物图
Fig.1 Photo of SFSZ7-31 500/110 transformer
表1 变压器产品参数
Tab.1 Transformer product parameters
参数数值（型号） 额定容量/(kV×A)31 500 额定电压/kV(110±3×2.5%):(38.5±2×2.5%):10.5 联结组别YN yn0 d11 冷却方式ONAN/ONAF
绕组失稳前的微小形变难以在变压器投运过程中仅通过外置传感器直接监测，但机械状态变化会使压板的轴向压力发生改变，进而影响绕组的振动特性，因此可以通过布置内置轴向压力传感器和外置振动加速度传感器进行绕组机械状态监测。
轴向压力传感器布置于每相钢压板和压钉之间。振动加速度传感器布置于靠近短路相的油箱外壁。两种传感器通过屏蔽光纤接入实时录波采集系统，具体布置如图2所示。
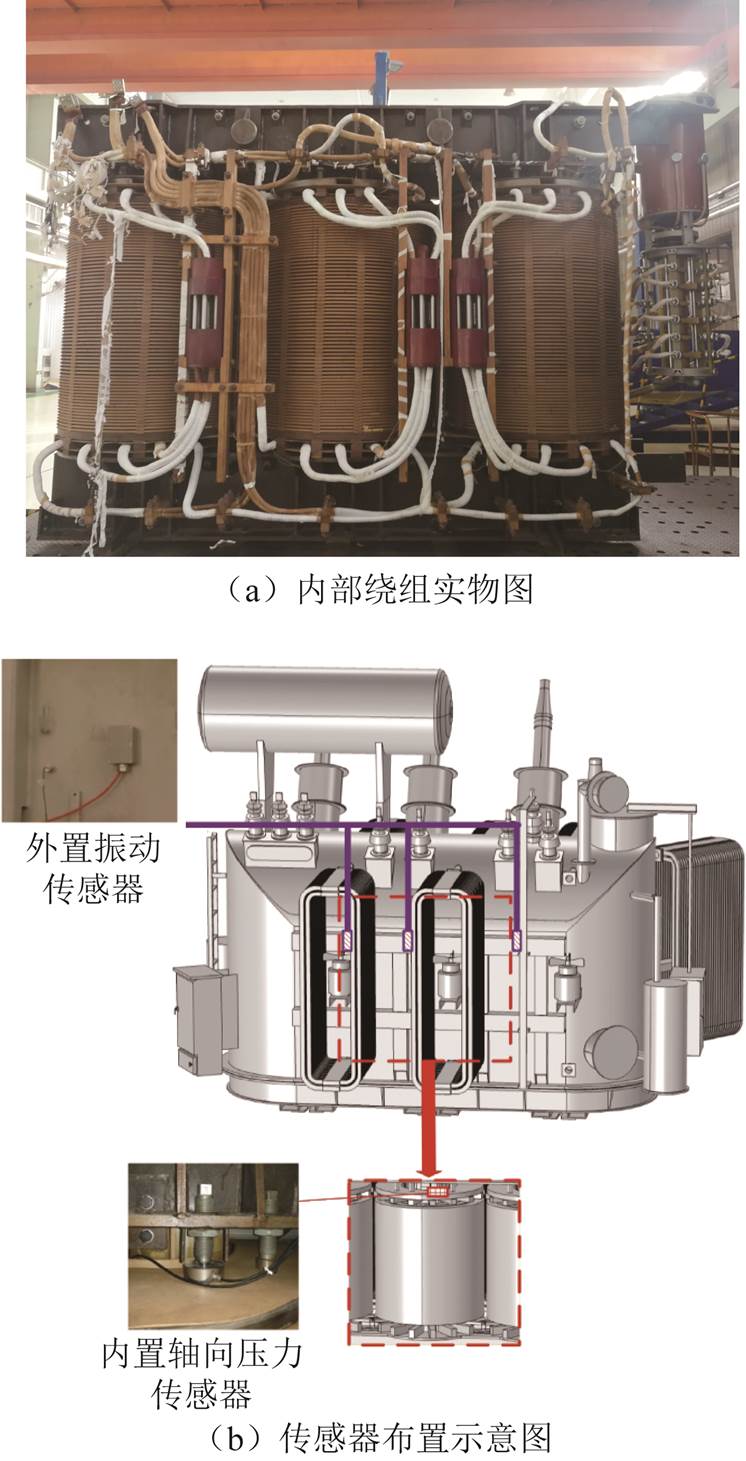
图2 试验变压器及传感器布置
Fig.2 Test transformer and arrangement of sensors
压力传感器量程为20 t；振动传感器量程为±20 g，分辨率为0.001 g，频率测量范围可至5 000 Hz。传感器参数能够有效满足测量需求。
传感器安装完成后通过全部出厂试验，确保传感器不会对变压器运行造成影响。
依据GB/T 1094.5—2016[20]要求，开展了三相变压器连续多次短路冲击试验。每次短路试验激励持续时间为（250±25）ms，由于短路试验为破坏性试验，每次试验后需测量绕组电抗值，当电抗较初始值变化超过2%或单次短路后电抗变化率大于0.8%，即认为绕组发生严重形变，此时停止该工况短路试验。为防止过热危险并给予电抗足够的变化保持时间，每两次短路试验时间间隔为5 min。
为尽可能获得多种工况下的绕组振动信号，且避免绕组严重形变影响其他工况的短路试验，先后开展了高压对中压B相短路（H-M B）、中压对低压A相短路（M-L A）和中压对低压C相短路（M-L C）三种工况的短路试验。试验具体工况及施加的短路电流见表2。
表2 试验电流设置
Tab.2 Test current settings
工况序号短路电流（%）额定峰值/A电抗变化率(%) 高压对中压B相短（H-M B）1601 4880.11 2800.18 3850.25 4900.25 51000.39 61050.50 71050.57 81052.28 中压对低压 A相短路（M-L A）1535 2470.30 2680.30 3720.30 4761.49 中压对低压C相短路(M-L C)1805 2470.30 2857.81
以H-M B相试验为例，高压侧采用1.5相单电源激励接线，中压侧三相短接，并使低压侧开路。通过调节高压侧的电压使高压侧流过一定比例（53%～105%）的额定电流，此时流过中压绕组的电流为短路电流，其值为表2中短路电流百分比与额定峰值的乘积。接线原理图如图3所示，高压与中压绕组均处于额定分接。
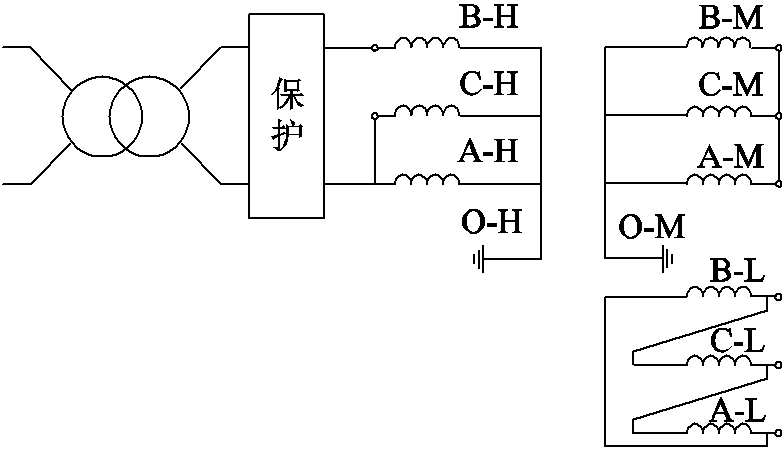
图3 H-M B相短路试验接线原理图
Fig.3 Test wiring diagram of H-M B-phase short-circuit
试验过程中实时采集振动加速度波形，并记录短路冲击前后压板轴向压力的稳态值。
变压器绕组在遭受短路故障时，即使能够抵御单次冲击，其支撑刚度、阻抗等电气、机械参数均发生不可逆转的微小变化，进而影响下次短路冲击时绕组的振动响应，造成如振动幅值、激振频率的改变。因此提取振动信号的关键特征量，分析其在多次短路冲击过程中的变化规律，建立特征量与绕组状态的关联关系对研究多次短路冲击造成的累积效应影响有重要意义。
变压器振动一般分为磁致伸缩引起的铁心振动和电磁力引起的绕组振动两部分。在变压器正常投运时，变压器振动主要来源于铁心，但当变压器遭受短路冲击，绕组电流迅速增大数十至数百倍，此时铁心振动可忽略不计，振动贡献主要来源于绕组。
为确定振动加速度与轴向压力之间的关联关系，本节仅考虑绕组轴向振动特性。
变压器绕组振动结构是一个多自由度机械结构系统，满足质量-弹簧-阻尼动力学模型。在求解绕组振动的动态过程中，每饼绕组均可建立一个振动方程，但绕组尺寸大、线饼多，为简化计算，认为各线圈之间的振动形式相似，即可建立绕组的单自由度轴向振动系统如图4所示。
图4 单自由度轴向振动系统
Fig.4 Single-degree of freedom axial vibration system
绕组轴向振动动力学微分方程[21]为
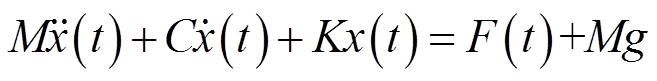（1）
式中，M为绕组质量；C为阻尼；K为刚度；x(t)为绕组轴向位移；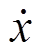
(t)为绕组轴向速度；
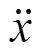(t)为绕组轴向加速度。
根据式（1），绕组振动特性与其质量、阻尼以及刚度有关，当绕组存在形变、位移等缺陷时，绕组轴向压力将发生变化，使绕组之间出现高度差，进而影响安匝平衡及漏磁场分布，最终导致振动时频特征即振动幅值、振动频率发生相应变化。
离散时域信号的特征主要有幅值、峰-峰值、有效值、平均值等。其中，幅值、峰-峰值为局部特征，在一定程度上能够反映信号的剧烈程度，有效值、平均值为整体特征，能够反映激励的能量大小。较其他特征量，有效值能够更好地反映非平稳信号的时域特征。通过方均根计算有效值为
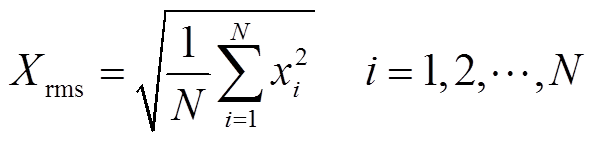（2）
根据GB 1094.5—2016，每次短路激励施加时长为(250±25)ms。为保证分析的信号段为外激励状态响应，本节选取短路过程冲击起始至200 ms的暂态振动时域信号。
由2.1节分析，当绕组的质量、阻尼、刚度矩阵不发生变化即绕组机械性能不变时，绕组振动加速度有效值与电流呈二次方关系[22]，则在不同电流I1、I2激励下，振动加速度a1、a2满足
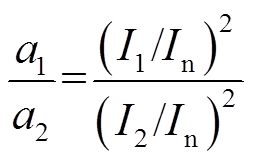（3）
式中，In为额定电流。
由于试验场地使用时间有限，各短路工况未进行空载试验，因此定义每种工况第一次短路电流试验后绕组机械状态为正常基准状态，并以该组振动加速度测量有效值作为振动加速度基准值，由式（3）拟合出不同工况不同短路电流下的振动加速度基准值并与实际测量值进行对比，提出振动偏离的时域特征。三种工况下历次短路冲击过程中振动加速度基准值和测量值的对比结果如图5所示。
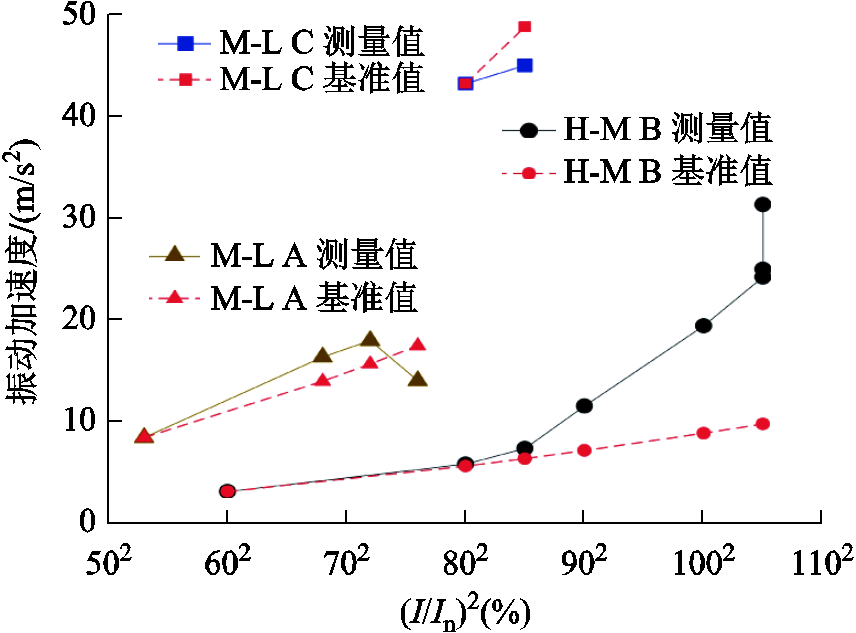
图5 振动加速度基准值和测量值对比
Fig.5 Comparison between reference value and measured value of vibration acceleration
由图5所示，在连续多次短路冲击的过程中，振动加速度的变化规律呈现以下三个特点：①振动加速度测量值与短路电流的二次方出现明显的非线性，且逐渐偏离基准值；②在H-M B相105%短路电流的三次短路冲击试验，测量值偏离程度也发生了变化，且随重复次数增加而增大；③测量值偏离趋势有所不同，H-M B相试验中，测量值呈正偏离，即大于基准值，M-L C相试验中，测量值呈负偏离，即小于基准值，而M-L A相试验中，测量值前三次小幅正偏离，在最后一次冲击时出现负偏离。
特点①、②说明绕组在承受多次短路冲击后机械性能逐渐变化，即产生了累积效应；特点③反映短路冲击会导致绕组产生不同类型的形变。为研究振动偏离方向与形变的联系，对每次短路冲击后短路相的轴向压力稳态值进行分析，轴向压力稳态值见表3。
表3 连续短路冲击轴向压力、电抗变化率及振动偏离变化
Tab.3 Change of axial pressure, impedance change and vibration deviation during multiple short-circuit
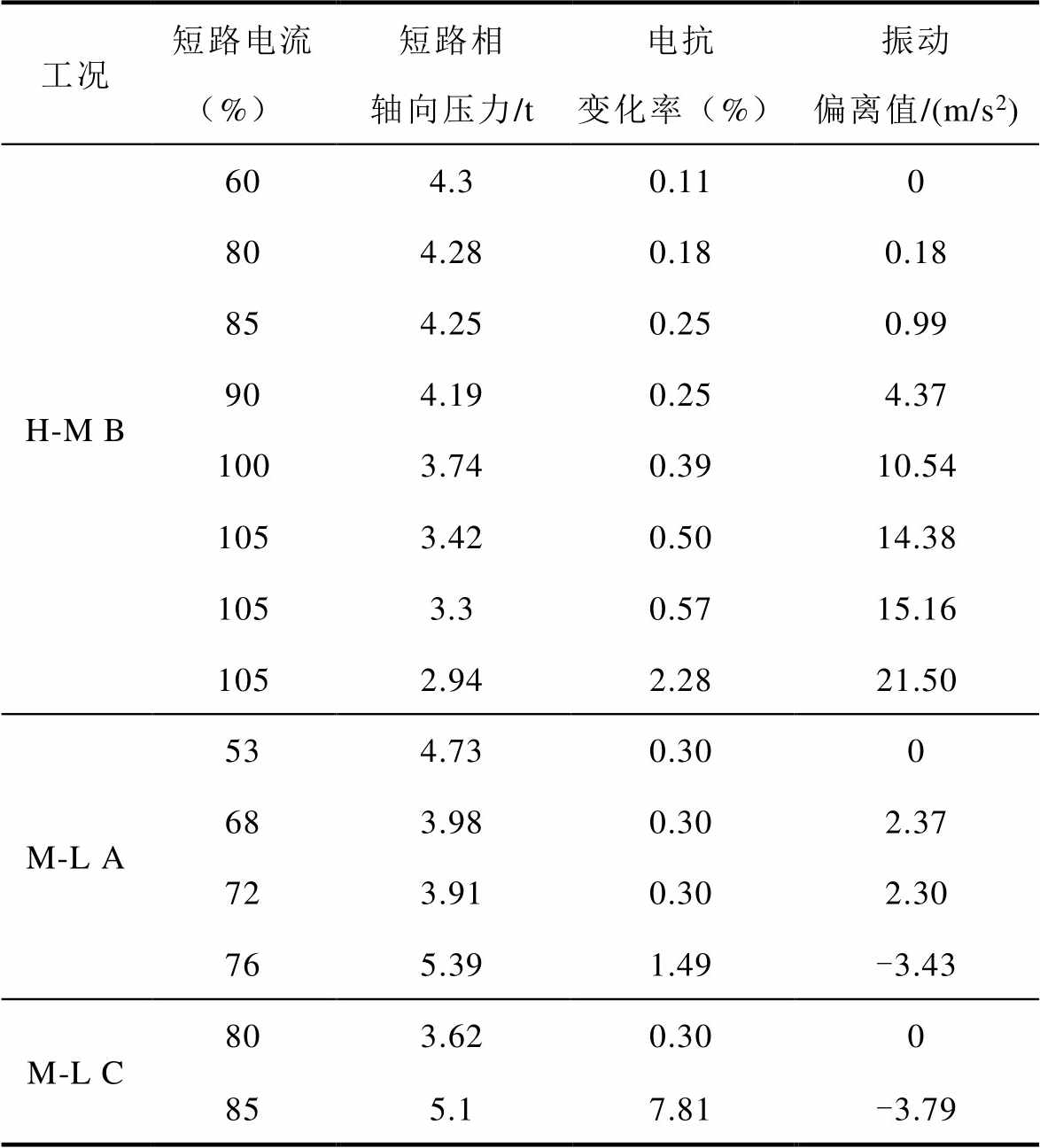
工况短路电流（%）短路相轴向压力/t电抗变化率（%）振动偏离值/(m/s2) H-M B604.30.110 804.280.180.18 854.250.250.99 904.190.254.37 1003.740.3910.54 1053.420.5014.38 1053.30.5715.16 1052.942.2821.50 M-L A534.730.300 683.980.302.37 723.910.302.30 765.391.49-3.43 M-L C803.620.300 855.17.81-3.79
由表3所示，对于H-M B工况和M-L C工况，短路相的稳态轴向压力值较试验前分别逐渐减小和增大；而对于M-L A工况，压力值先减小后增大。三种工况在致使失稳形变的最后一次短路冲击后压力值均发生明显突变。
结合振动加速度和稳态轴向压力的变化趋势可以发现，在连续短路冲击作用下，当绕组的轴向压力逐渐减小，振动加速度将呈正偏离；反之，当短路相的轴向压力逐渐增大时，振动加速度将呈负偏离。为验证上述定性规律，需建立振动加速度与轴向压力之间的数值关系，但由于两者没有直接的物理关系，因此考虑以刚度K为中间参量进行数理分析。首先根据材料的力学方程确定刚度K与轴向压力之间的定量关系。
绕组轴向压力对绝缘垫块产生的应力σ与应变ε关系满足[22]
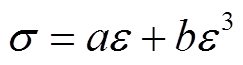（4）
式中，a、b分别为垫块的线弹性常数和硬化系数。
当绕组承受轴向压力T时，绕组与垫块的接触面积为S，应力可表示为
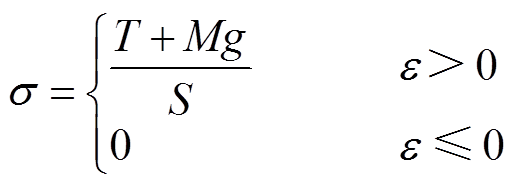（5）
对于厚度为l的垫块，其弹性模量E及等效刚度K定义为
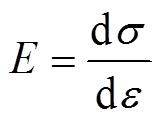（6）
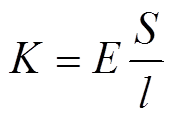（7）
将式（5）、式（6）代入式（7），可得
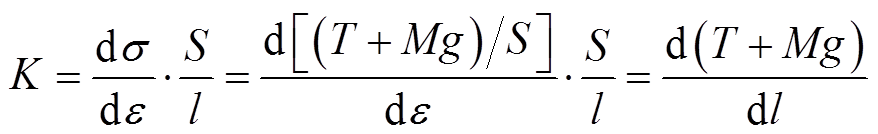（8）
由式（8）可知，轴向压力的变化与刚度呈正相关关系。
同时，将式（4）代入式（7）可得
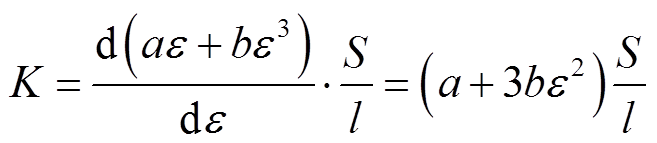（9）
由式（9）可知，刚度与应变呈正相关关系。综上所述，当轴向压力T减小时，垫块刚度K和应变ε相应减小，则其宏观表征为短路侧绕组出现轴向外凸膨胀形变；反之轴向压力T增大，垫块刚度K和应变ε也随之增大，此时宏观表征为短路侧绕组轴向内凹压缩形变。
基于上述轴向压力T与刚度K的数值关系，随后搭建变压器轴向振动模型以计算振动加速度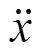随刚度K的变化趋势。
短路过程中的绕组轴向振动模型的输入激励为电磁力和重力，对于短路侧绕组，式（1）可展开为
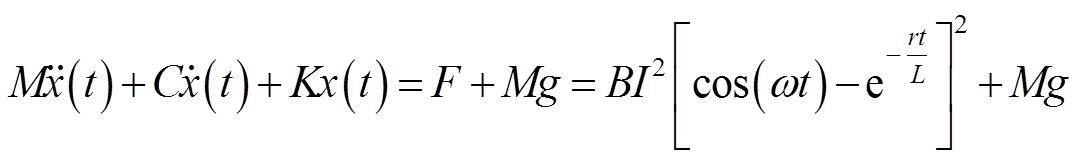
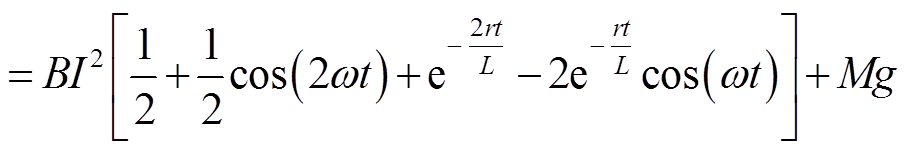（10）
式中，B为常参数；ω为激励频率，取50 Hz；r、L为绕组阻抗参数。
其特征方程及特征根为
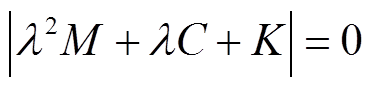（11）
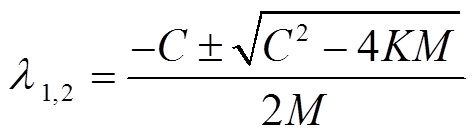（12）
由式（12）可知，质量、刚度和阻尼系数之间的数值关系影响了特征根性质，宏观上表现为振动加速度的衰减形式会有所不同。为不失一般性，做出以下合理假设[22-23]：
（1）多次短路冲击不会使绕组的质量和变压器油的阻尼发生变化。
（2）绕组振动系统始终满足欠阻尼条件，即C2-4KM＜0。
求解式（10）获得振动加速度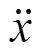随刚度K变化的变化趋势规律如图6所示。轴向压力、振动偏离及绕组形变类型关联关系见表4。
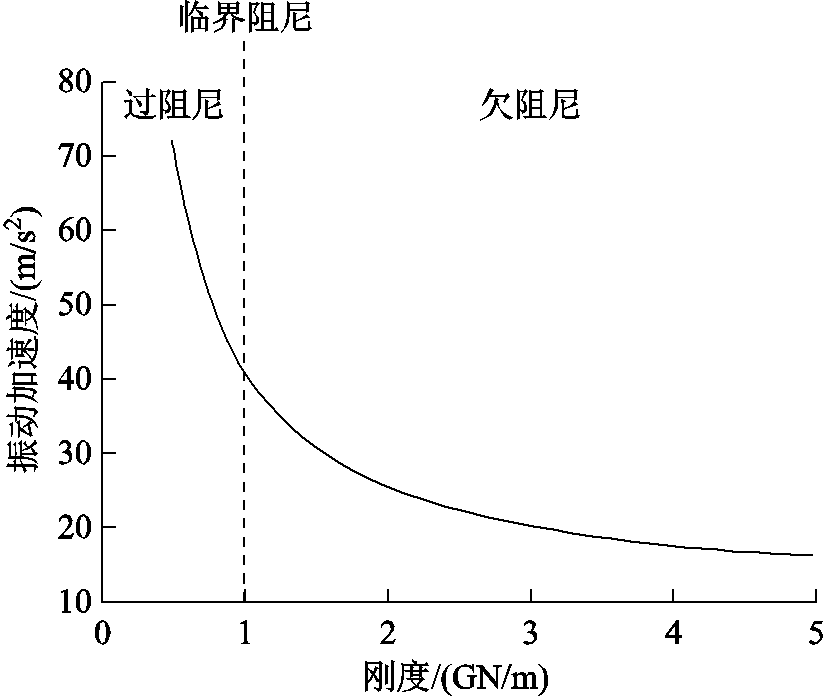
图6 不同刚度下的振动加速度曲线
Fig.6 Curve of vibration acceleration under different stiffness
表4 轴向压力、振动偏离及绕组形变类型关联关系
Tab.4 The relation between axial pressure, vibration deviation and deformation type
工况轴向压力支撑刚度振动偏离形变类型 H-M B减小减小正偏离外凸 M-L A先减后增先减后增先正后负先凸后凹 M-L C增大增大负偏离内凹
如图6及表4所示，刚度增大，振动加速度减小，而刚度减小，振动加速度增大，与前文所述试验规律相符。同时，根据轴向振动模型，刚度值的瞬时变化会实时改变振动加速度，因此在三种工况最后一次冲击时，轴向压力的突变也会导致刚度及对应振动加速度的突变，这与图5所示趋势亦相符。
综上所述，多次短路冲击会导致绕组的机械性能发生变化，导致振动信号的时域特征也即振动加速度测量有效值与基准值出现偏差，同时根据轴向振动方程及应力计算式，推导了振动偏离可以辨识短路侧绕组形变类型。但如表3、表4所示中压对低压A相短路工况，当绕组形变类型连续改变时，振动偏离模值仅由第二次试验的2.37 m/s2增至第四次的3.43 m/s2，变化较小，在这种情况下单一关注振动偏离会忽视绕组机械性能变化，具有一定局限性。考虑到引起振动加速度偏离的非线性成分反映在高次谐波上，因此对振动加速度频域信号进行分析。
不同短路电流激励的相位差异会导致漏磁、振动的时域响应波形有所区别，但其频域特征却不易受到影响。因此除时域信息外，同时掌握信号的频率信息对全面、真实地分析信号特征非常重要。
对于频域信号，频率分布是最直观的特征。传统的傅里叶变换具有很好的全局统计特性，但无法处理频率信息时变局部特征问题。对于本文所讨论的非平稳信号，通过傅里叶变换获得其频谱会丢失重要的时间分布特性。因此本节采用短时傅里叶变换（Short-Time Fourier Transform, STFT）对振动信号进行频域分析。
短时傅里叶变换的原理是将原始时域信号x(n)划分为多个有限长度的短信号也即加窗，随后进行傅里叶变换，从而获得同时具有时间信息和频率信息的时频谱。汉明窗（Hamming window）具有主瓣集中、旁瓣能量较低的特点，能够较好地改善加窗带来的频谱泄漏问题。汉明窗函数w(n)及离散傅里叶变换X(k)计算式为[24]
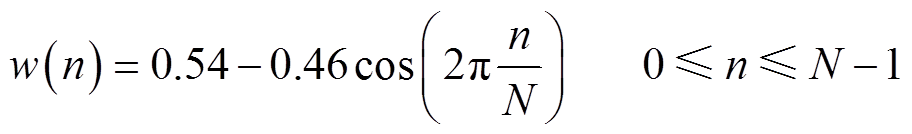（13）
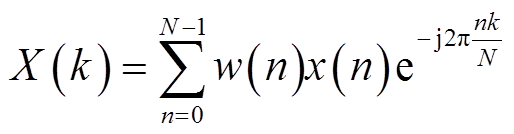（14）
式中，N为汉明窗的窗宽；k为频率点序号。
考虑到振动信号主频为100 Hz，其理论周期应为10 ms，但为了避免短信号在延拓过程中畸变导致信号失真，帧长即截取信号长度，取20 ms，重叠为帧长的一半。
在连续多次短路冲击试验过程中，试验电流不同等因素会导致各次试验中采集到的振动信号幅值存在差异，为消除这种影响，在后续绕组的机械响应分析中引入新的变量，对经短时傅里叶变换后的时频谱进行归一化处理，获得占比时频谱Pi(k)，计算式为
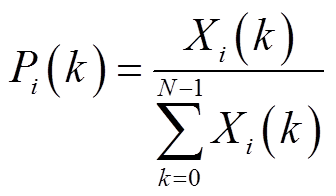（15）
式中，i为帧数。
图7为三种工况中首次和末次短路冲击试验占比时频谱图。
图7 不同工况短路试验的首次和末次时频谱
Fig.7 Time-frequency spectrums of the first and last short circuit tests under different condition
对比各工况的两组时频谱图，频谱的主要成分为主频100 Hz和倍频200 Hz，但在多次短路冲击后，三种工况均呈现频谱成分更复杂，主频能量占比明显降低。
为量化上述特征，本节通过计算频谱熵进行整体特征分析。谱熵能够从整体上体现频谱的复杂程度，谱熵越高则频率分量越分散，分布越复杂。
一般地，谱熵Hf可定义为[25]
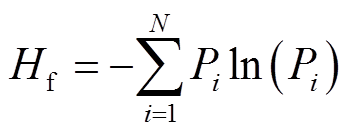（16）
式（16）适用于分析一整段信号的频率分布情况，而本文讨论的是短路冲击暂态过程中每帧的频率分布，需要对式（16）进行修正，因此提出并构建加权时频谱熵，较谱熵更能够准确、全面地反映暂态过程的频率成分复杂程度。计算方法如图8所示。
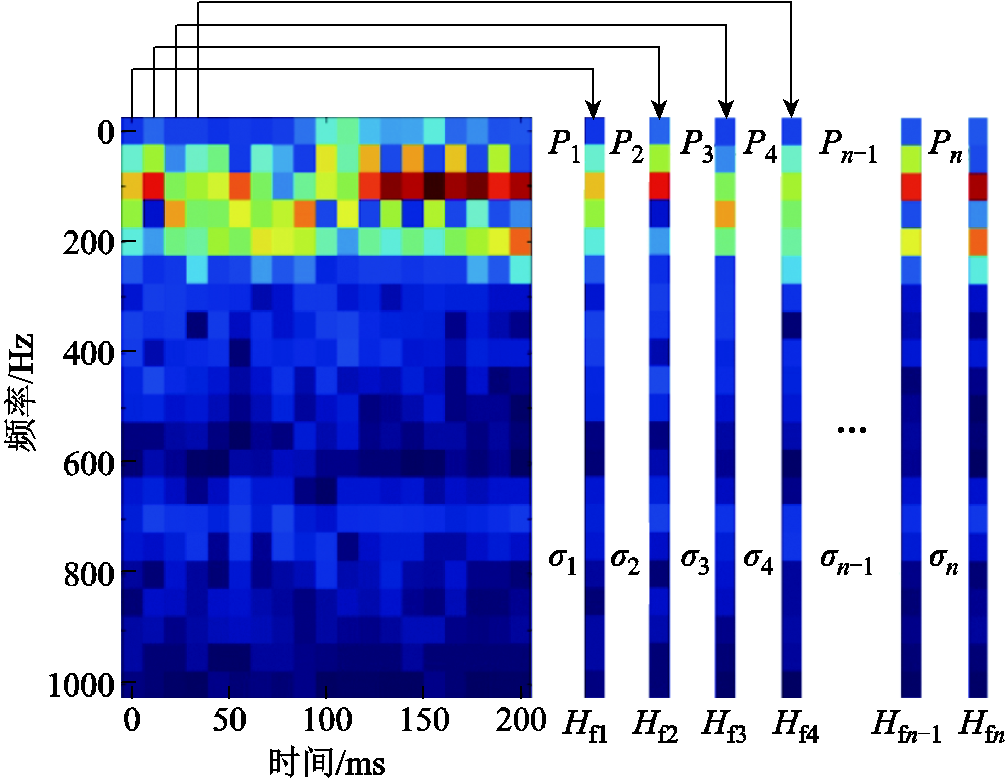
图8 加权时频谱熵计算示意图
Fig.8 Schematic diagram of weighted time-frequency entropy calculation
首先计算每帧的振动能量在整个信号段中的能量占比权重σi，即
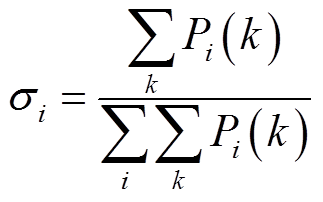（17）
随后计算每帧的谱熵Hfi以及加权时频谱熵H，即
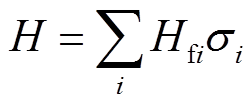（18）
根据上述方法计算获得三种工况下多次短路冲击试验下的谱熵见表5。
表5 多次短路冲击试验加权时频谱熵
Tab.5 Weighted time-spectrum entropy of multiple short-circuit tests
工况序号短路电流（%）加权时频谱熵 H-M B1603.803 2803.712 3853.773 4903.917 51003.848 61053.775 71053.901 81054.100 M-L A1534.261 2684.332 3724.383 4764.990 M-L C1803.386 2855.295
由表5可知，在连续多次短路冲击的过程中，振动加速度加权时频谱熵整体呈增大的趋势；其中，H-M B相组在前六次试验中谱熵在3.712～3.917之间振荡，随后在第七、第八次逐渐增至4.100；M-L A相组在历次试验中，加权时频谱熵逐步由4.261增至4.990；M-L C组由于第二次试验后就出现严重形变，由3.386跃升至5.295，缺少谱熵中间变化过程。三种工况在最后一次试验中加权时频谱熵值均明显增大。
综上所述，振动信号的频域特征表明多次短路冲击会导致变压器绕组机械性能变化，频率成分趋于复杂，从而出现时域有效值与电流呈非线性关系的现象。因此，振动加速度加权时频谱熵的变化能够反映绕组的机械状态变化。但谱熵也存在一定的缺陷，在多次短路前期不够敏感，因此需要采用多特征联合分析来确定多次短路冲击对振动信号的影响。
如上文所述，单一的特征量难以较好准确描述累积效应这一复杂问题，本节将振动加速度的时域偏移特征和频域谱熵特性进行联合分析如图9所示，以全面观察连续多次短路冲击对振动信号的影响。
由图9所示，对于H-M B相短路工况，加权时频谱熵在前六次试验中于3.712～3.917之间振动，随后增至4.100。而振动偏离模值在多次试验过程中逐渐增大至15.16 m/s2，弥补了加权时频谱熵的不敏感问题。在八次试验后，两种特征量均呈现增大的趋势，说明绕组机械性能不断劣化，这与最终电抗变化率达2.28%相符。
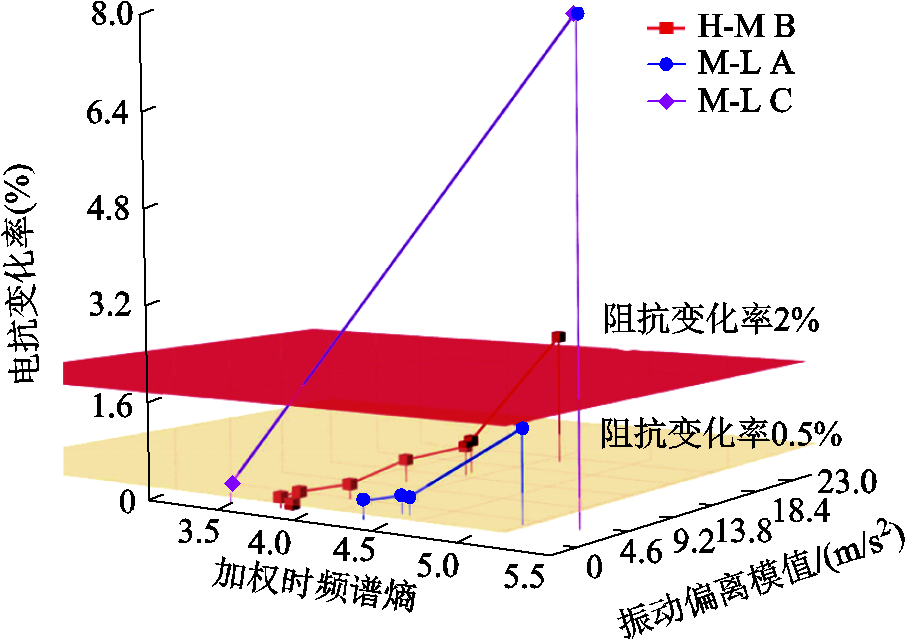
图9 振动偏离模值及加权熵联合分析
Fig.9 Combined analysis of acceleration deviation and weighted entropy
类似地，对于M-L A相短路工况，振动偏离模值在第二次试验后增至2.37 m/s2后，试验偏离模值变化范围仅为±1.1 m/s2，而振动谱熵在多次试验过程中由4.261逐渐增至4.990，弥补了振动偏离反向带来的偏离模值变化不明显的问题。在八次试验后，两种特征量均呈现增大的趋势，说明绕组机械性能不断劣化，这与第三与第四次试验之间电抗单次变化率逾0.8%相符。
对于M-L C短路工况，由于连续两次短路冲击后绕组就发生明显形变，振动加速度偏移和加权时频谱熵不能反映累积效应的逐步影响过程，但第二次试验时，两种特征量均明显增大，说明绕组机械性能不断劣化，这与最终电抗变化率达7.81%相符。
综上所述，振动加速度偏离模值和加权时频谱熵的变化能够反映绕组机械性能的变化，而对两种特征量进行联合监测能够更准确地确定绕组劣化形变的发生，即当短路冲击过程中的振动加速度偏离幅值和加权时频谱熵明显增大时，可判断为绕组已经开始受到累积效应的影响，机械性能稳定、抗短路能力下降，此时应提出运行检修建议。
本文通过开展连续多次短路冲击试验，记录试验过程中暂态振动信号以及试验前后每相压板的稳态轴向压力值，分析了振动信号的时频特征以及两种信号的变化规律，得到以下结论：
1）对于本文所示欠阻尼振动系统，H-M B相短路多次短路冲击试验下，振动加速度时域信号有效值逐渐产生正偏离，在最后一次试验中偏离值高达21.50 m/s2，对应历次轴向压力由3.15 t减小至2.77 t；类似地，M-LA相短路试验下，振动加速度先在第二次试验时产生2.37 m/s2正偏离，随后逐渐降低，在最后一次实验中呈-3.43 m/s2负偏离，对应历次轴向压力先由4.29 t降至4.17 t随后增至4.43 t。因此根据变压器振动加速度的正、负偏离可实现绕组的轴向形变类型辨识，即当振动加速度呈正偏离时，轴向压力降低，短路侧绕组形变形式为端部轴向外凸膨胀形变，当振动加速度呈负偏离时，轴向压力增大，此时短路侧绕组形变形式为端部轴向内凹压缩形变。
2）对于本文所示欠阻尼振动系统，开展连续多次短路冲击试验过程中，高对中B相短路工况、中对低A相短路工况及中对低C相短路工况的加权时频谱熵分别由3.803增至4.100、4.261增至4.990、3.386增至5.295。即加权时频谱能作为辨识绕组形变是否产生的有效频域特征。
3）联合分析振动加速度偏离模值和加权时频谱熵两种特征量可避免单一特征量在轴向形变类型发生变化或微小形变早期等情况下变化不明显的问题，实现对绕组机械稳定性能的有效可靠监测。当振动加速度时域有效值偏离模值和加权时频谱熵明显增大时，绕组机械稳定性将降低。该方法能够在绕组电抗变化率达到2%或连续两次变化率超过0.8%前显示出绕组机械劣化，具有更加灵敏的优势，更有效地反映累积效应的影响，且振动信号易于采集，不影响变压器的正常运行，这对变压器绕组的运行维修和形变预警具有一定的指导意义。
参考文献
[1] Zhang Bo, Li Yan. Research on radial stability of large transformers windings under multiple short-circuit conditions[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(7): 1-4.
[2] 刘云鹏, 王博闻, 李欢, 等. 结合载纤绕组形变测量法的大型变压器绕组多次短路冲击暂态声纹特征[J]. 中国电机工程学报, 2022, 42(1): 434-447. Liu Yunpeng, Wang Bowen, Li Huan, et al. Transient acoustics characteristics of large transformer windings under multiple short-circuit impulse combined with fiber-carrying winding deformation measurement[J]. Proceedings of the CSEE, 2022, 42(1): 434-447.
[3] 吴振宇, 周利军, 周祥宇, 等. 基于振荡波的变压器绕组故障诊断方法研究[J]. 中国电机工程学报, 2020, 40(1): 348-357, 401. Wu Zhenyu, Zhou Lijun, Zhou Xiangyu, et al. Research on fault diagnosis method of transformer winding based on oscillatory wave[J]. Proceedings of the CSEE, 2020, 40(1): 348-357, 401.
[4] 刘云鹏, 李欢, 田源, 等. 基于分布式光纤传感的绕组变形程度检测[J]. 电工技术学报, 2021, 36(7): 1347-1355. Liu Yunpeng, Li Huan, Tian Yuan, et al. Winding deformation detection based on distributed optical fiber sensing[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1347-1355.
[5] 李典阳, 张育杰, 冯健, 等. 变压器故障样本多维诊断及结果可信度分析[J]. 电工技术学报, 2022, 37(3): 667-675. Li Dianyang, Zhang Yujie, Feng Jian, et al. Multi-dimensional diagnosis of transformer fault sample and credibility analysis[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 667-675.
[6] Secue J R, Mombello E. Sweep frequency response analysis (SFRA) for the assessment of winding displacements and deformation in power transformers[J]. Electric Power Systems Research, 2008, 78(6): 1119-1128.
[7] Prema Kumar N, Amarnath J, Shrivastava K D, et al. Identification of winding faults in power transformers by low voltage impulse test and neutral current method using wavelet transform approach[C]//CEIDP '05. 2005 Annual Report Conference on Electrical Insulation and Dielectric Phenomena, Nashville, TN, USA, 2005: 140-143.
[8] 王琦, 付超, 王欣盛, 等. 变压器绕组短路电抗在线测量工程应用研究[J]. 高电压技术, 2020, 46(11): 3943-3950. Wang Qi, Fu Chao, Wang Xinsheng, et al. Research on online measurement engineering application of transformer winding short circuit reactance[J]. High Voltage Engineering, 2020, 46(11): 3943-3950.
[9] 中华人民共和国国家发展和改革委员会. DL/T 1093—2008 电力变压器绕组变形的电抗法检测判断导则[S]. 北京: 中国电力出版社, 2008.
[10] 赵书涛, 许文杰, 刘会兰, 等. 基于振动信号谱形状熵特征的高压断路器操动状态辨识方法[J]. 电工技术学报, 2022, 37(9): 2170-2178. Zhao Shutao, Xu Wenjie, Liu Huilan, et al. Identification method for operation state of high voltage circuit breakers based on spectral shape entropy characteristics of vibration signals[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2170-2178.
[11] 高树国, 汲胜昌, 孟令明, 等. 基于在线监测系统与声振特征预测模型的高压并联电抗器运行状态评估方法[J]. 电工技术学报, 2022, 37(9): 2179-2189. Gao Shuguo, Ji Shengchang, Meng Lingming, et al. Operation state evaluation method of high-voltage shunt reactor based on on-line monitoring system and vibro-acoustic characteristic prediction model[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2179-2189.
[12] 赵莉华, 徐立, 刘艳, 等. 基于点对称变换与图像匹配的变压器机械故障诊断方法[J]. 电工技术学报, 2021, 36(17): 3614-3626. Zhao Lihua, Xu Li, Liu Yan, et al. Transformer mechanical fault diagnosis method based on symmetrized dot patter and image matching[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3614-3626.
[13] 师愉航, 汲胜昌, 张凡, 等. 变压器绕组多倍频振动机理及特性[J]. 高电压技术, 2021, 47(7): 2536-2544. Shi Yuhang, Ji Shengchang, Zhang Fan, et al. Multi-frequency vibration mechanism and characteristics of transformer windings[J]. High Voltage Engineering, 2021, 47(7): 2536-2544.
[14] 吴书煜, 汲胜昌, 孙建涛, 等. 在运换流变压器振动监测及其变化规律[J]. 高电压技术, 2022, 48(4): 1561-1570. Wu Shuyu, Ji Shengchang, Sun Jiantao, et al. Vibration monitoring and variation law of converter transformer in operation[J]. High Voltage Engineering, 2022, 48(4): 1561-1570.
[15] 赵莉华, 张振东, 张建功, 等. 运行工况波动下基于振动信号的变压器故障诊断方法[J]. 高电压技术, 2020, 46(11): 3925-3933. Zhao Lihua, Zhang Zhendong, Zhang Jiangong, et al. Diagnosis methods for transformer faults based on vibration signal under fluctuating operating conditions[J]. High Voltage Engineering, 2020, 46(11): 3925-3933.
[16] 曹辰, 徐博文, 李辉. 基于振动与电抗信息的变压器绕组形变状态综合监测方法[J]. 高电压技术, 2022, 48(4): 1518-1530. Cao Chen, Xu Bowen, Li Hui. Composite monitoring method for the state of transformer winding deformation based on vibration and reactance information[J]. High Voltage Engineering, 2022, 48(4): 1518-1530.
[17] 李冰阳. 电力变压器短路冲击累积效应的机理研究[D]. 武汉: 华中科技大学, 2016.
[18] 闫荣格, 焦佩林, 董正予. 基于多测点振动信号的变压器绕组形变故障诊断研究[J]. 变压器, 2020, 57(12): 27-31. Yan Rongge, Jiao Peilin, Dong Zhengyu. Research on fault diagnosis of transformer winding deformation based on vibration signals at multiple measuring points[J]. Transformer, 2020, 57(12): 27-31.
[19] 陈世彪, 邓祥力, 杨欢红. 基于变压器最优漏磁信息的绕组变形分类方法[J]. 水电能源科学, 2018, 36(11): 173-177. Chen Shibiao, Deng Xiangli, Yang Huanhong. Classification method of winding deformation based on transformer leakage field information[J]. Water Resources and Power, 2018, 36(11): 173-177.
[20] 国家质量监督检验检疫总局. GB 1094.5—2003 电力变压器第5部分: 承受短路的能力[S]. 北京: 中国标准出版社, 2004.
[21] 胡异炜. 基于空间振动分布和工况模态分析的变压器绕组故障诊断方法研究[D]. 杭州: 浙江大学, 2020.
[22] 徐樊浩. 基于振动信号分析方法的电力变压器状态评估研究[D]. 北京: 华北电力大学, 2017.
[23] 刘晓丽, 刘文里, 王铭, 等. 电缆变压器短路时绕组轴向振动特性的探讨[J]. 变压器, 2011, 48(3): 18-21. Liu Xiaoli, Liu Wenli, Wang Ming, et al. Discussion on characteristics of winding axial vibration in short circuit of cable transformer[J]. Transformer, 2011, 48(3): 18-21.
[24] 权文杰, 童晓阳, 张广骁. 基于S变换行波能谱矩阵相似度的柔性直流单端保护方案[J]. 电力系统自动化, 2022, 46(7): 178-186. Quan Wenjie, Tong Xiaoyang, Zhang Guangxiao. Single-end flexible DC protection scheme based on similarity of S-transform energy spectrum matrix of traveling wave[J]. Automation of Electric Power Systems, 2022, 46(7): 178-186.
[25] 杨挺, 张璐, 张亚健, 等. 基于信息熵计算模型的电力信息物理系统融合控制方法[J]. 电力系统自动化, 2021, 45(12): 65-74. Yang Ting, Zhang Lu, Zhang Yajian, et al. Fusion control method for cyber-physical power system based on information entropy calculation model[J]. Automation of Electric Power Systems, 2021, 45(12): 65-74.
Abstract The accumulative effect of transformer windings under multiple short-circuit impulse will eventually lead to sudden instability failure, so it is essential to study the mechanical deformation of windings under multiple short-circuit.
Firstly, the multiple short-circuit tests under various working conditions on an 110 kV full-scale transformer were carried out, and the transient vibration acceleration signals during the short-circuit process and the steady-state values of the axial pressure of the windings before and after the multiple short-circuit were collected, the time-frequency characteristics of which were analyzed. According to the linear relationship between the vibration acceleration and the square of the current, the deviation trend between the measured value and the reference value is obtained, and the time domain characteristic of the vibration deviation is proposed. Then, combined with the winding axial vibration dynamics model, the relation between axial pressure, vibration deviation and deformation type is determined. Under HV-MV B-phase multiple short-circuit tests, the effective value of the vibration acceleration gradually produced a positive deviation. In the last test, the deviation value was 21.5 m/s2, and the corresponding axial pressure was reduced from 3.15 t to 2.77 t. Similarly, under MV-LV A-phase multiple short-circuit tests, the vibration acceleration first produced a positive deviation of 2.37 m/s2 in the second test, and then gradually decreased. In the last test, it showed a negative deviation of -3.43 m/s2, and the corresponding axial pressure decreased from 4.29 t to 4.17 t and then increased to 4.43 t. According to the positive or negative deviation of the vibration acceleration under multiple-short circuit, the axial deformation type identification of the winding can be realized. When the vibration acceleration presents a positive deviation, the axial pressure decreases. The deformation form of the winding on the short circuit side is the outwards expansion of the end shaft. When the vibration acceleration presents a negative deviation, the axial pressure increases. At this time, the deformation form of the winding on the short circuit side is the inward concave compression of the end shaft. And the frequency domain characteristics of vibration weighted spectral entropy are proposed. For the HV-MV B-phase short-circuit condition, and M-L C-phase short circuit condition, the weighted entropy increases from 3.803 to 4.1, and 3.386 to 5.295 respectively. The weighted time-frequency spectrum entropy can be used as an effective frequency domain feature to identify whether the winding deformation occurs. The above result shows that when the mechanical degradation of winding caused by accumulative effect is occurred, the vibration acceleration will deviate the reference value of the undeformed state of winding, and the weighted time-frequency spectrum entropy will increase. Finally, a winding deformation identification method based on the joint analysis of vibration deviation and weighted time-frequency spectrum entropy is proposed and verified. This combined analysis method can avoid the problem that when the axial deformation type changes or the extend of deformation is small the characteristic quantity does not change significantly. Compared with the traditional impedance method, it is able to detect the mechanical degradation of winding earlier, which is more effectively to reflect the impact of the accumulative effect. The vibration signal is easy to collect, and the normal operation of the transformer will not be disturbed during collecting the signal, so as to realize the effective and reliable monitoring of the mechanical stability of the winding.
Keywords：Transformer winding, accumulative effect, short circuit impact test, time-frequency analysis, mechanical deformation identification
DOI: 10.19595/j.cnki.1000-6753.tces.221028
中图分类号：TM407
河北省自然科学基金资助项目（E2021521004）。
收稿日期 2022-06-02
改稿日期 2022-07-22
律方成 男，1963年生，教授，博士生导师，研究方向为电气设备绝缘机理和状态检修、电气设备在线监测与故障诊断等。E-mail：lfc@ncepu.edu.cn
汪鑫宇 男，1996年生，博士研究生，研究方向为电气设备在线监测与故障诊断。E-mail：wangxy1996@ncepu.edu.cn（通信作者）
（编辑 郭丽军）