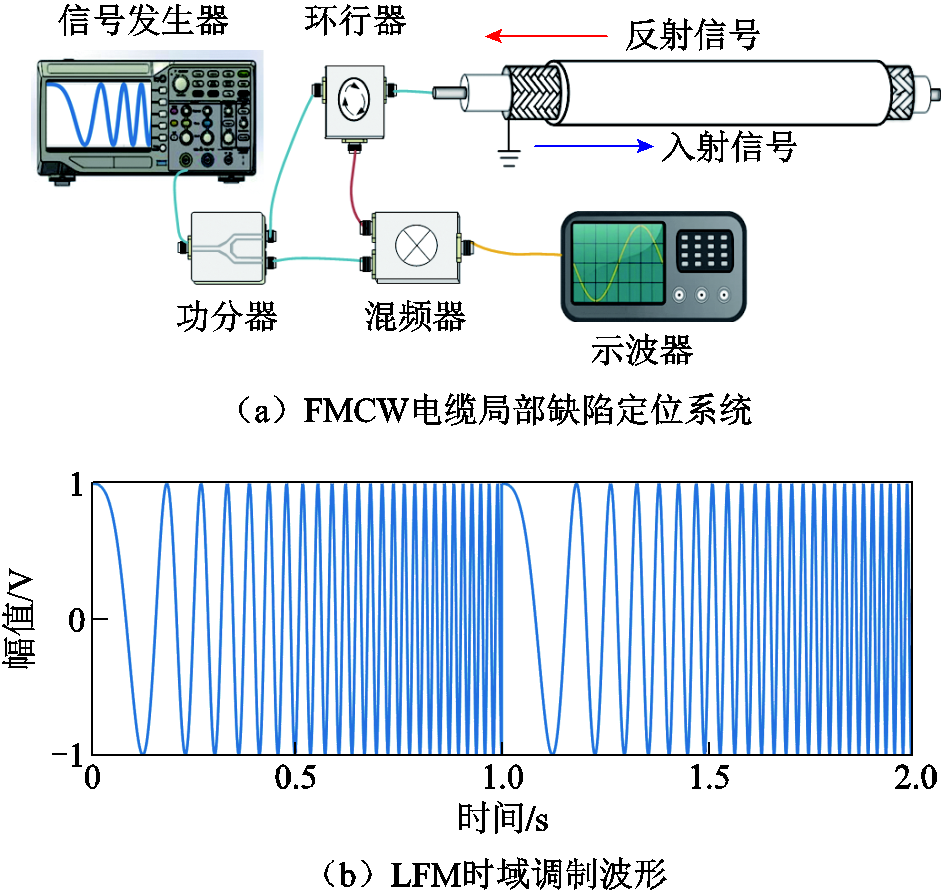
图1 FMCW电缆局部缺陷定位方法原理示意图
Fig.1 Schematic diagram of local defect location of cables based on FMCW technology
摘要 灵敏地检测和定位电缆缺陷对于电缆安全运行具有重要的作用。调频连续波（FMCW）法是一种基于频域反射法的电缆缺陷检测方法，该方法相对于宽频阻抗谱法具有更高的缺陷检测灵敏度及抗干扰能力。该文在现有FMCW方法的基础上，提出利用FMCW的相位敏感特性对电缆缺陷进行检测的方法，提高了现有FMCW方法缺陷检测的灵敏度。首先，结合FMCW相位敏感特性与电缆分布参数模型进行了电缆缺陷检测仿真；然后，在实验室的射频同轴电缆、10 kV交联聚乙烯（XLPE）电缆上模拟不同程度的缺陷并测试，观察缺陷处相位的变化情况，验证了所提方法的有效性。结果表明：相敏-FMCW方法对于射频及10 kV XLPE电缆上模拟的缺陷敏感，不同严重程度的缺陷相位变化量不同，缺陷处对应相位变化的取值区间可为180°。定义缺陷引起的相位、幅值变化量占取值区间的比例为灵敏度，相敏-FMCW方法可以提高现有FMCW方法对该文中所设缺陷检测的灵敏度：对于电缆局部异常温升造成的容性缺陷，当局部温差为37℃时，可将灵敏度由36%提升至71%；对于电阻性、电导性及铜屏蔽破损缺陷，相敏-FMCW方法的灵敏度均优于传统FMCW方法，检测灵敏度提升了7%～62%。
关键词：相位敏感 调频连续波（FMCW） 同轴电缆 缺陷检测
在现代社会的各种电气设备或机器中，电能、信息和控制信号大多通过聚合物绝缘同轴电缆传输。电缆在社会运转中起着十分重要的作用，与工业生产、人民生活息息相关[1-5]。电缆上产生的轻微缺陷会逐渐发展为严重缺陷，最终导致电缆发生故障。因此，检出并定位电缆上的缺陷非常重要[6]。
频域反射法（Frequency Domain Reflectometry, FDR）因在电缆缺陷、故障定位方面比时域反射法（Time Domain Reflectometry, TDR）具有更高的灵敏度，得到了快速发展[7-8]。近年来，基于FDR的宽频阻抗谱（Broadband Impedance Spectroscopy, BIS）方法成为了电缆缺陷定位领域的研究热点[9]。2006年，挪威Halden核电站的P. F. Fantoni等基于电缆的宽频阻抗谱提出了线性共振分析技术（Line Resonance Analysis, LIRA）[10]，但并未公开具体算法。2011年日本学者Y. Ohki等提出了基于快速傅里叶逆变换（Inverse Fast Fourier Transform, IFFT）的电缆BIS缺陷定位分析算法[7,11]，但不能评估局部老化的严重程度[12]。2015年华中科技大学周志强使用积分变换分析法实现了电缆局部缺陷的定位与缺陷状态评估[12]，但并未将该方法应用到中间接头的缺陷定位诊断上[13]。电缆中间接头本身就是一个阻抗不连续点，因此很难通过阻抗突变来判定中间接头是否存在缺陷，2019年，四川大学李蓉等采用加Blackman窗的离散傅里叶变换提高了BIS方法对中间接头受潮定位诊断的灵敏度[13-14]。BIS方法目前已实现电缆的局部老化、局部破损及10 kV电缆中间接头的受潮等缺陷定位，并可评估缺陷的严重程度。
BIS方法通过测量电缆在不同频率下的电压和电流幅值得到阻抗谱，电压、电流信号的测量结果可以用其虚部和实部的幅值表示，也可以用其幅值和相位的形式表示，是一种基于信号幅值测量的方法。随着缺陷距离的增加，反射信号越来越小，而测量端的入射信号幅值基本不变。由于测量端的反射信号远小于入射信号，准确地测量反射信号极为困难。在现场测试时，背景噪声将干扰小信号的准确测量。针对BIS方法存在的问题，文献[15]提出了一种基于调频连续波（Frequency Modulated Continuous Wave, FMCW）的电缆局部缺陷定位方法。FMCW方法测量的是入射信号和反射信号之间由于时间延迟而产生的频率差，相对于BIS方法测量幅值，具有更好的抗噪性。在相同的条件下，FMCW方法对缺陷检测具有更高的灵敏度，可在更远的位置检出缺陷，并对其进行定位[15]。
虽然FMCW方法通过测量频率差的方式获取了高于BIS方法的灵敏度，但依然无法满足现场测量的需求。受FMCW方法在液位测量时利用相位提高了距离准确度[16]的启发，本文基于FMCW中相位对电缆缺陷敏感的特性提出了一种电缆缺陷检测方法，该方法可以提高FMCW方法检测缺陷的灵敏度。
FMCW信号调制方法在雷达领域具有广泛的应用，如汽车防撞系统、液面高度测量等领域[16-17]。FMCW电缆局部缺陷定位系统如图1a所示，主要由信号发生器、功分器、环行器、混频器、示波器、计算机等构成。信号发生器产生如图1b所示的连续调频信号，经过功分器和环行器后注入电缆中。入射信号遇到线缆中的局部缺陷将发生反射；反射信号被环行器接收后，与发射耦合信号混频后经傅里叶变换解调，对电缆缺陷进行测距和定位。
图1 FMCW电缆局部缺陷定位方法原理示意图
Fig.1 Schematic diagram of local defect location of cables based on FMCW technology
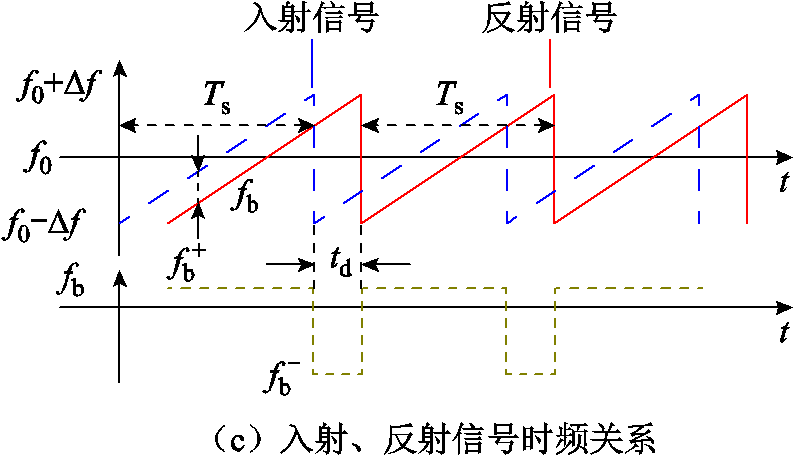
FMCW所用的调制信号为线性调频信号（Linear Frequency Modulation, LFM），典型的LFM波形如图1b所示，在时域中可表达[15,18]为
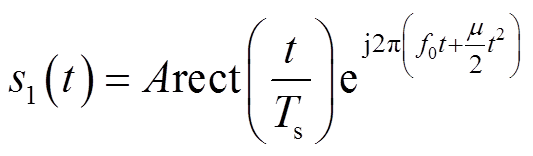（1）
式中，A为信号幅值；Ts为调制周期；rect(t/Ts)为宽度为Ts的矩形脉冲；f0为中心频率；t、m分别控制信号的持续时间与频带宽度。为便于分析，信号s1可写为
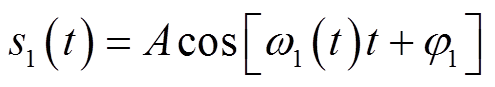（2）
式中，ω1(t)为s1信号的角频率；φ1为信号s1的初相位。在一个调制周期内，线性调频信号s1的频率f随时间线性变化，如图1c所示，f可表示为
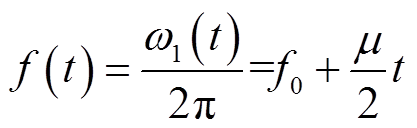（3）
假设信号s1传输到阻抗不匹配点时的距离为D，则接收到的信号sr为
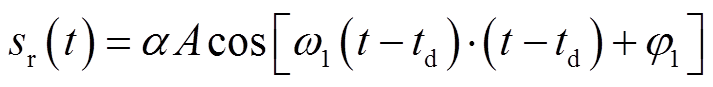（4）
式中，α为信号传输衰减因子；td为到达目标的双向时延，td=2D/v，v为电磁波在电缆中的传输速度。则接收信号的频率fr为
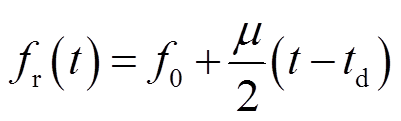（5）
将接收信号sr与参考信号s1进行混频，输出的信号可表示为
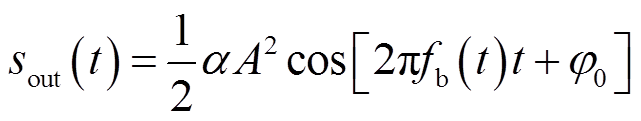（6）
式中，fb(t)为频差，可表示为
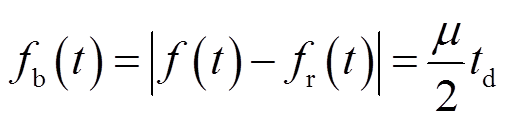（7）
设φ(t)为sout的相位，随时间变化，表达式见式（8），则φ0为信号sout的初相位，φ0 = φ(t = 0)。
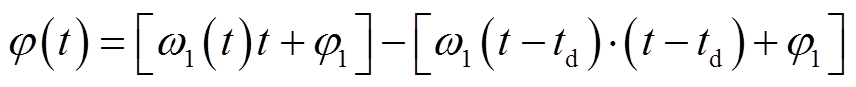（8）
fb(t)的波形如图1c所示，其中信号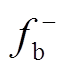
持续时间非常短，可忽略。因此，fb主要由信号fb+构成对混频信号进行低通滤波处理，即可获取图1c中的信号fb+，信号fb可由式（7）改写为
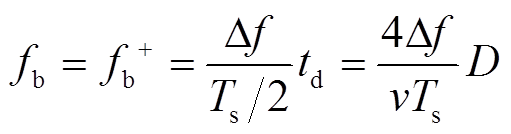（9）
式中，∆f为图1c中频率调制带宽的一半。由图1c可知，时间差td与目标距离D正相关，与频率差fb成正比，则目标距离D为
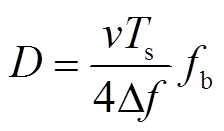（10）
在实际中，从混频器输出端测得信号sout后经过快速傅里叶变换（Fast Fourier Transform, FFT）即能算出信号sout的频谱，以幅频谱作为定位谱、相频谱作为相位谱，则现有的FMCW电缆缺陷定位都采用定位谱。定位谱中的谱线对应的频率根据式（10）换算即可确定电缆中各处的位置。由于电缆中各频率信号的波速不同，在处理时可按中心频率f0的传输速度确定波速，或者直接根据电缆末端所对应的谱线频率及电缆长度计算波速用于缺陷定位。
根据1.1节中的推导，假设电缆中缺陷位置为D，混频输出信号为sout，该信号由频率和相位两个量确定，式（6）中φ0为信号sout的初相位。为说明FMCW的相位敏感原理，将信号sout改写为
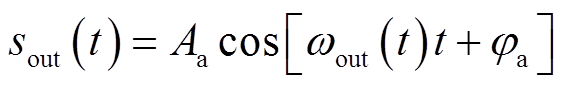（11）
式中，Aa和φa分别为信号sout的幅值和相位；ωout(t)为信号sout的角频率。
图2展示了调频周期为1 s，起止频率分别为 50 Hz和100 Hz的LFM信号频谱。如图2所示，由于LFM信号的特性，在调制频带外也会产生不同频率的信号，其中包含了与信号sout同频的信号分量s2，可表示为
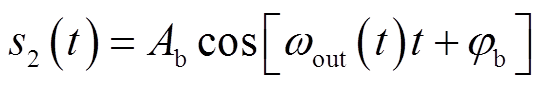（12）
式中，Ab和φb分别为信号s2的幅值和相位。
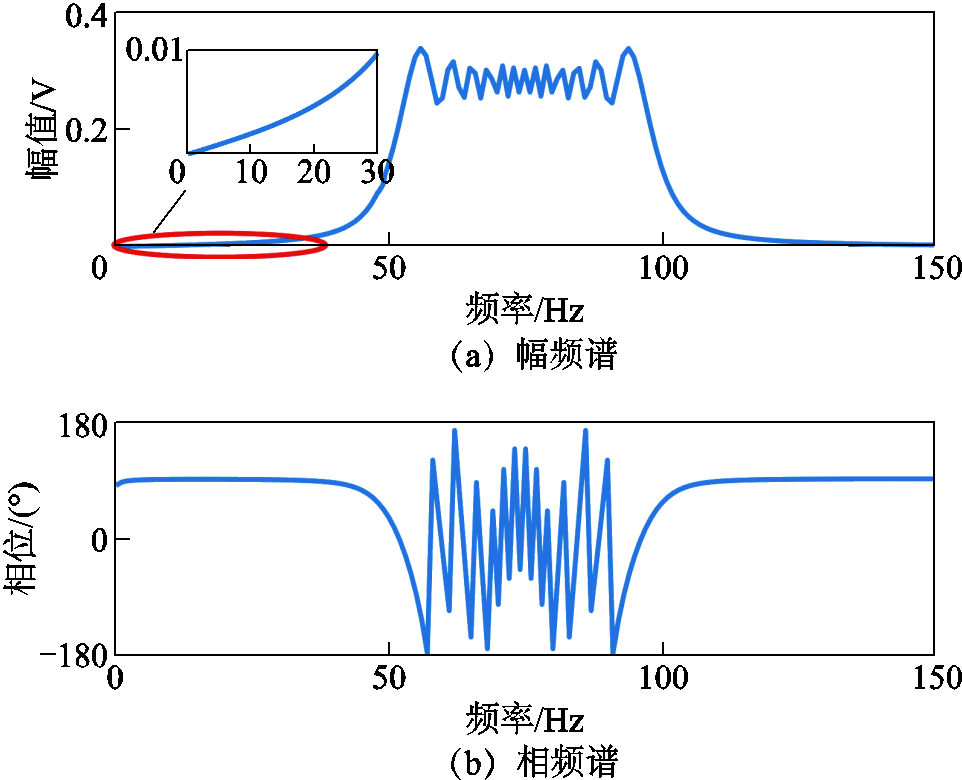
图2 LFM信号的频谱
Fig.2 Spectrum of LFM signal
在理想情况下，信号sout仅由入射、反射信号混频生成，但由于混频器的信号泄漏等原因形成了基准谱线，信号sout还应考虑LFM入射信号的信号分量s2的影响。由于s2的影响，sout叠加s2后的信号表示为
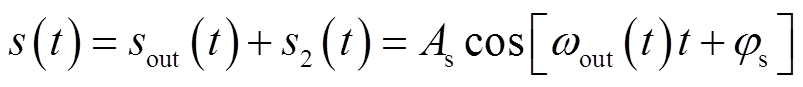（13）
式中，As和φs分别为信号s的幅值和相位。则信号s对应的相位φs可以表示为
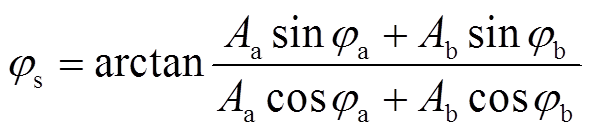（14）
因此，最终测得的信号s为sout与s2的合信号，其相位φs会受到LFM信号的影响，即相位信号同时受到幅值与相位的双重调制。当反射信号发生变化时，相位φs也会随之改变。电缆中缺陷的位置不变，缺陷严重程度引起的反射信号强弱变化会导致输出信号的相位改变，这是FMCW方法对缺陷相位敏感的基本原理。
根据G. C. Stone和S. A. Boggs在1982年提出的塑料电缆等效分布参数电路模型[19]，建立电缆分布参数模型，如图3所示。图3中，R0、L0、G0、C0分别为正常电缆单位长度的电阻、电感、电导和电容；电缆中局部缺陷处分布参数与正常电缆不同，记为R0d、L0d、G0d、C0d。
局部缺陷的存在会导致该处电缆特征阻抗Z0改变，信号源发出的信号遇到电缆中的阻抗不匹配点则发生反射。电缆分布参数模型是基于FMCW进行电缆缺陷定位仿真的基础。
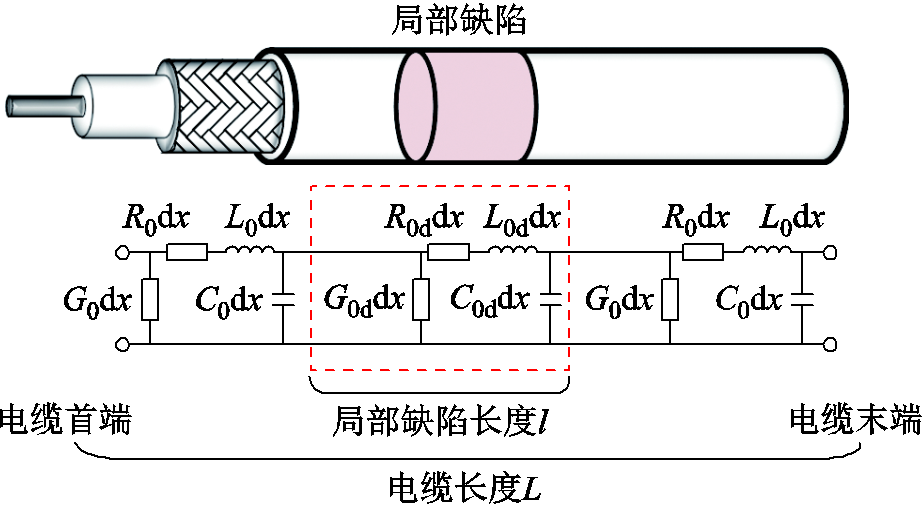
图3 电缆分布参数模型
Fig.3 Cable distribution parameter model
电缆的特征阻抗Z0为
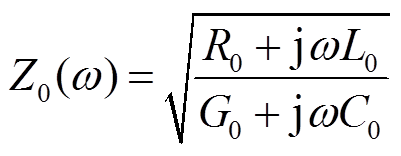（15）
在高频下，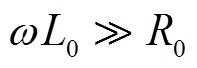
、
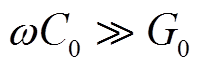，特征阻抗Z0可近似为
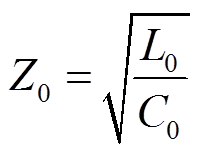（16）
2.1.1 电缆缺陷参数
常见的电缆本体典型缺陷（受潮、老化、铜屏蔽层缺损）均将改变电缆局部单位电容C，形成阻抗不连续缺陷[12-14]。根据电缆的分布参数模型，在总长度为300 m的电缆上进行FMCW仿真实验，电缆150 m处设置缺陷。正常电缆单位电容为C0，缺陷处的单位电容改变，电缆仿真参数见表1。表中4号电缆无缺陷，R0、L0、G0、C0计算涉及的参数取自文献[12]。
表1 电缆仿真参数
Tab.1 Simulation parameters for cable samples
编号缺陷位置/m缺陷参数 1150.0～150.1C1=90%C0 2150.0～150.1C2=95%C0 3150.0～150.1C3=98%C0 4无缺陷C4=100%C0
2.1.2 LFM信号调制参数
LFM信号调制主要由频带和调制周期两个参数决定。仿真时，从电缆首端注入LFM调制信号，信号频带为1～50 MHz，调制周期为1 ms。
基于FMCW与相敏-FMCW方法的电缆缺陷仿真结果如图4所示，图4a为电缆的混频信号，对混频信号做FFT运算即可获得图4b和图4c中的电缆定位谱及相位谱。图4b中上图为混频信号进行FFT之后的幅频谱，依据式（10）可计算出谱线对应的电缆位置，如图4b中下图所示。相位谱与定位谱相对应，缺陷处的相位发生改变，而其余位置几乎不变。
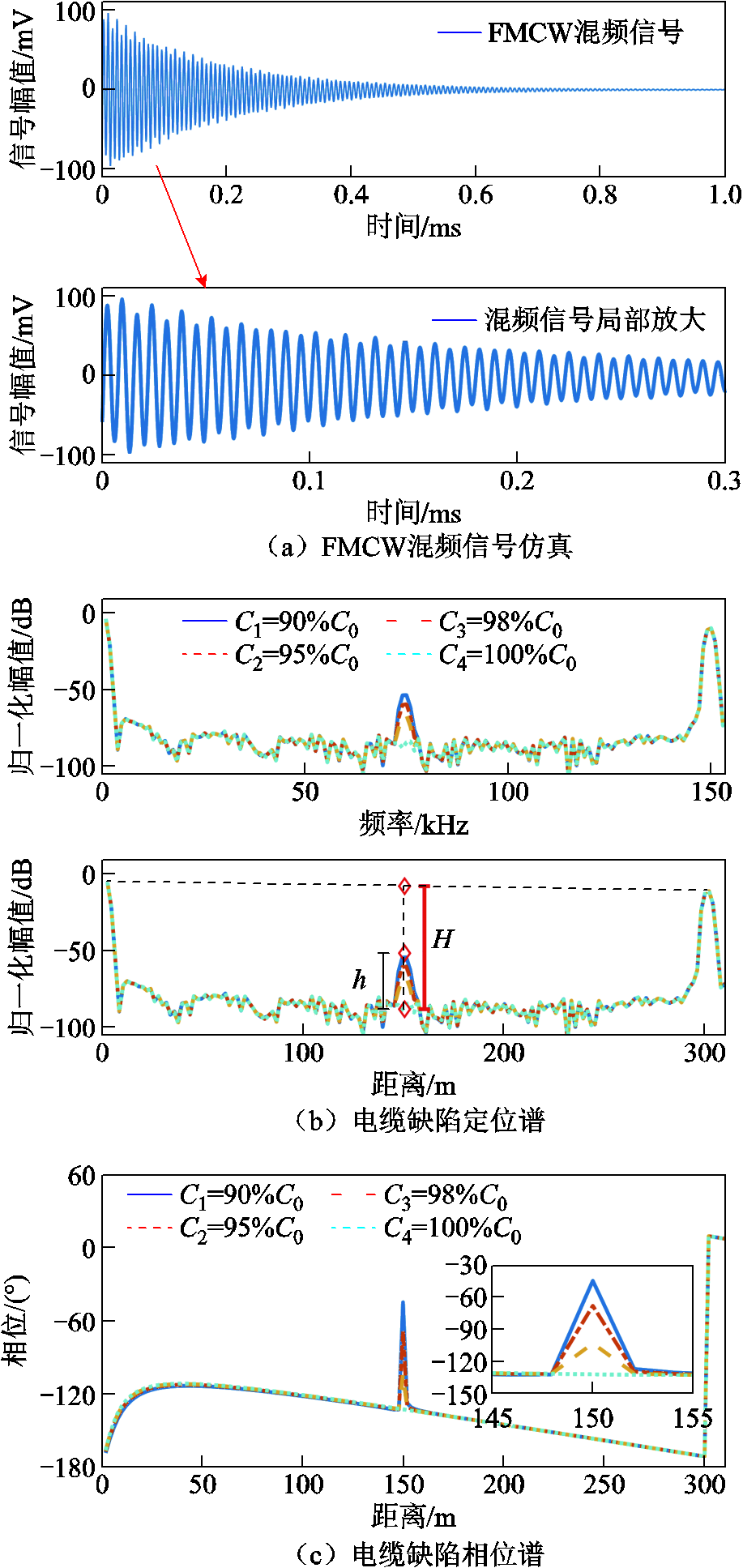
图4 电缆FMCW与相敏-FMCW仿真结果
Fig.4 FMCW and phase-sensitive FMCW simulation results
图4b中，4号电缆的定位谱在300 m处形成一定位峰，该处为电缆末端。相比于4号电缆，缺陷电缆的定位谱均在150 m处形成了定位峰，表明该处存在阻抗不连续点，准确地定位了预设的缺陷。因为缺陷严重程度不同，1号～3号电缆的缺陷定位峰大小不同，缺陷越轻微，定位峰峰值越小。
电缆的FMCW相位谱与定位谱具有对应关系，可共同描述电缆中各处的“状态”。如图4c中150m处，因缺陷严重程度不同，对应的相位变化亦不同，这与式（14）的推导结果相符。
将缺陷处对应的峰值和相位列于表2中，可知电缆缺陷处的峰值与相位随着缺陷处分布电容差的增大而逐渐增加。为进一步对比峰值与相位对缺陷检测的灵敏度，需对表2中的峰值、相位数据进行处理。首先，本文将缺陷处峰值、相位相对于各自取值范围的比例定义为灵敏度，由此说明峰值与相位对于缺陷检测灵敏度的关系。计算方法如下：在图4b的电缆定位谱中绘制一条黑色虚线连接电缆的首末端定位峰，据此估计缺陷处断路时电缆定位峰的最大值。本文在试验中测试了不同长度电缆的末端峰值，结果表明峰值取值符合这一规律。则图4b中150 m位置处电缆定位峰的最大峰值即为该处黑色虚线的数值，为-7 dB，无缺陷的4号电缆在该处的基准值为-84 dB，因此缺陷处的最大峰峰值为77 dB，记为H，如图4b中红色线段所示；1号～3号电缆缺陷处定位峰的峰值记为h，如图4b中黑色线段所示；则h占最大峰峰值H的比例即为峰值灵敏度。相位谱的灵敏度计算也采用此方法，根据仿真结果，缺陷处相位的变化范围约为180°，电缆缺陷处的相位与基准相位的差值占180°的比例即为相位灵敏度。
表2 电缆仿真试验结果统计
Tab.2 Defective cable simulation test results
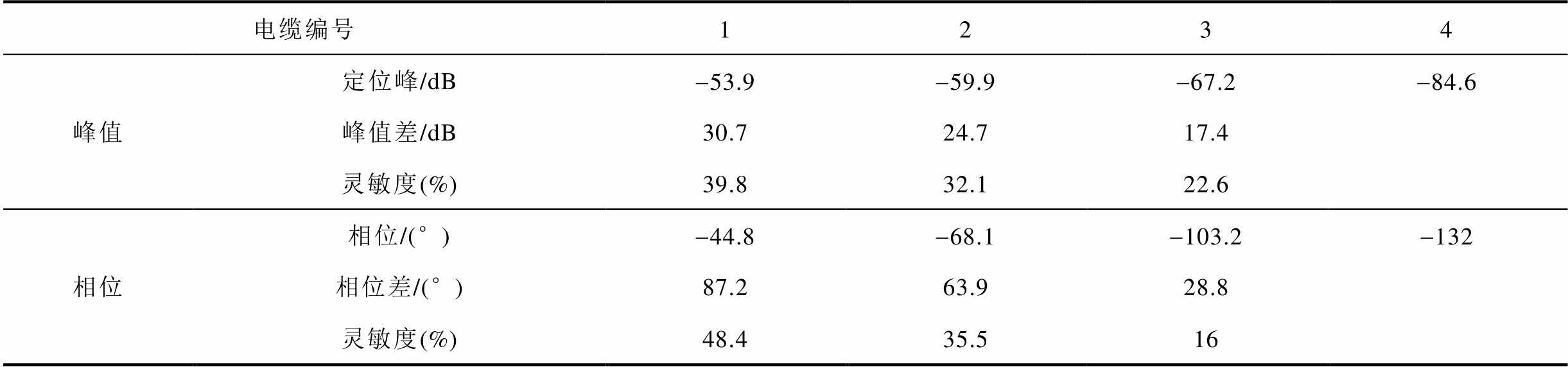
电缆编号1234 峰值定位峰/dB-53.9-59.9-67.2-84.6 峰值差/dB30.724.717.4 灵敏度(%)39.832.122.6 相位相位/(°)-44.8-68.1-103.2-132 相位差/(°)87.263.928.8 灵敏度(%)48.435.516
峰值、相位灵敏度的对比如图5所示，取50%灵敏度范围进行展示。当电容差（缺陷与正常电缆缺陷处分布电容之间的差值）小于4%时，相位灵敏度小于峰值灵敏度；当电容差达到4%后，相位灵敏度优于峰值灵敏度。图5中灵敏度轴（绿色坐标轴）右侧区域为相位更灵敏区间，当缺陷发展至该区间后，相位灵敏度高于峰值灵敏度。当电容差为10%时，峰值的灵敏度为39.8%，相位的灵敏度为48.4%，可见相敏-FMCW方法提高了FMCW方法的灵敏度。
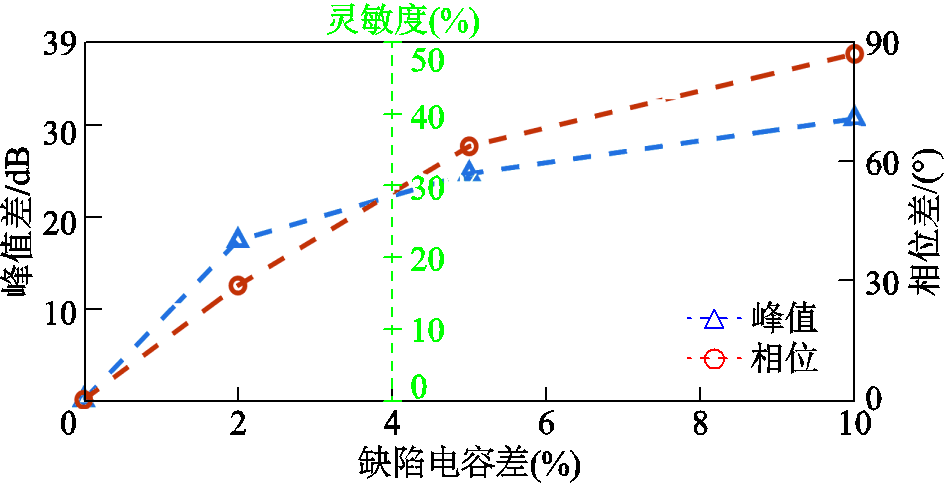
图5 相敏-FMCW与FMCW方法灵敏度对比
Fig.5 Phase-sensitive FMCW and FMCW method sensitivity simulation comparison
本节仿真结果表明，基于FMCW的电缆定位谱可以有效地定位电缆缺陷位置；利用FMCW的相敏特性可以检测电缆局部缺陷；电缆本体缺陷刚产生时FMCW方法更灵敏，缺陷更为严重后，相敏-FMCW方法更灵敏。
由第2节可知，常见的电缆本体典型缺陷（受潮、老化、铜屏蔽层缺损）均将改变电缆局部单位电容C[12-14]，由于低密度聚乙烯（Low Density Polyethylene, LDPE）、交联聚乙烯（Cross Linked Polyethylene, XLPE）等聚合物绝缘材料的相对介电常数在温升后下降[20-22]，导致局部单位电容C下降，本文以此方式模拟电缆中常见的局部缺陷。因射频同轴电缆（LDPE绝缘）的信号传输特性与电力电缆（XLPE绝缘）具有相似性，本文选用SYV50-3-1同轴电缆（Z0=50W）作为测试对象，射频电缆缺陷参数见表3。
表3 试验电缆参数
Tab.3 Parameters for cable samples
编号电缆长度/m加热位置/m加热温度/℃ T0311无缺陷23 T131110230 T231110240 T331110250 T431110254 T531110260
表3中T0号电缆无缺陷；如图6所示，对T1号～T5号电缆在102 m处进行水浴加热以模拟电缆缺陷，加热长度为0.2 m，加热温度见表3。从电缆首端注入LFM调制信号，信号带宽为1～50 MHz，调制周期为1 ms。
容性缺陷测试结果如图7所示，图7a为电缆的混频信号，对混频信号做FFT运算即可获得图7b和图7c中的电缆定位谱及相位谱。与仿真结果相似，图7b在102 m位置，仅室温电缆T0未形成定位峰，其余电缆定位峰均指向该处（103 m，误差小于0.5%）。该结果说明，对电缆进行局部加热可以模拟电缆中的局部缺陷，并且FMCW的定位谱可对这些缺陷进行定位。
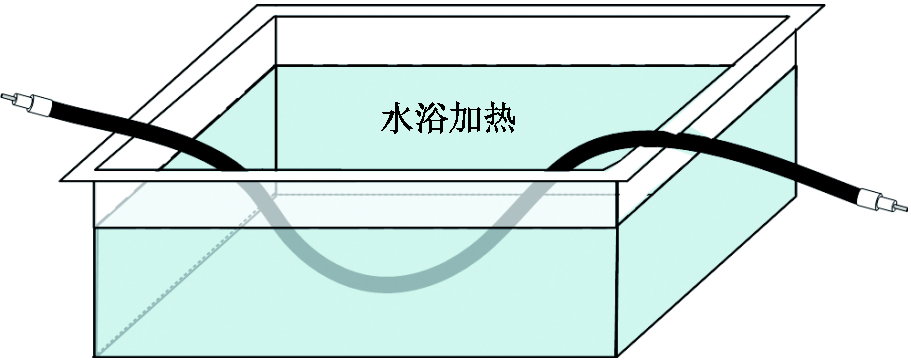
图6 模拟电缆缺陷示意图
Fig.6 Schematic diagram of simulated cable defects
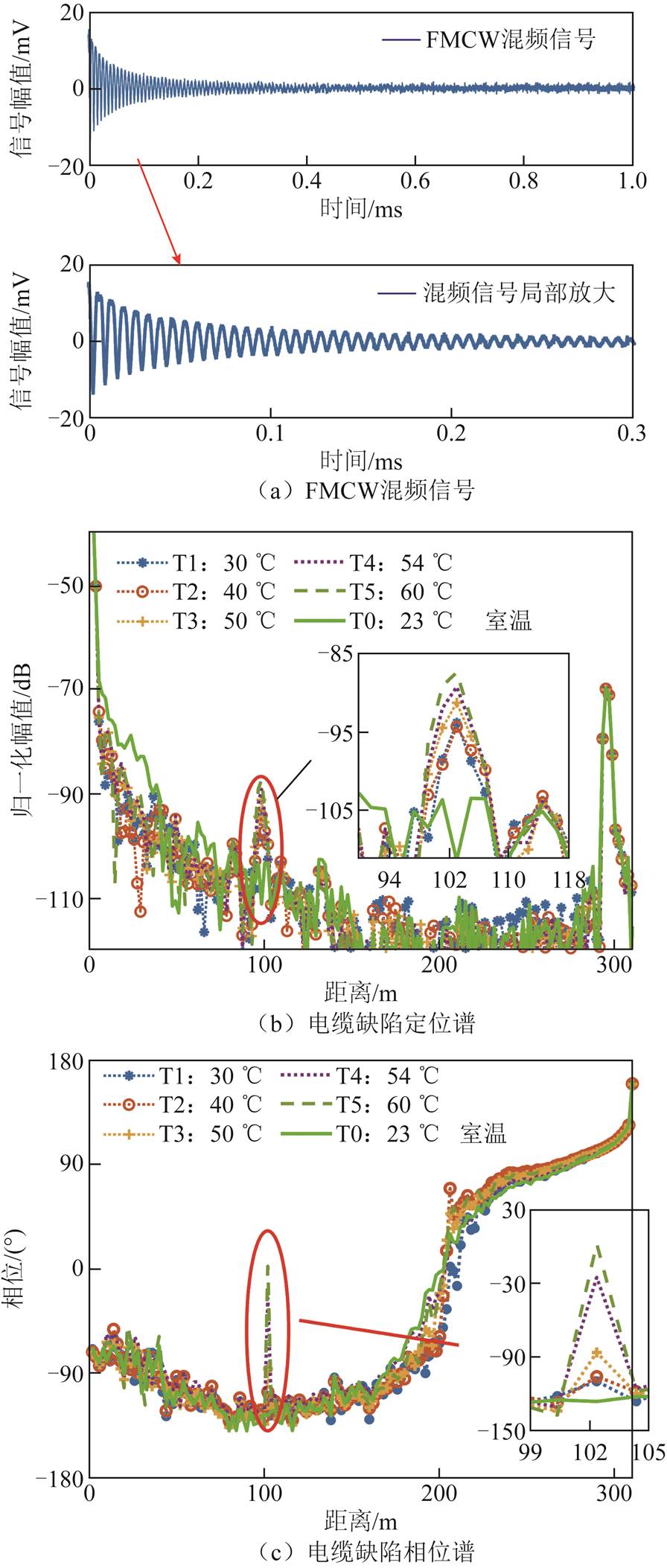
图7 容性缺陷测试结果
Fig.7 Capacitive defect test results
图7c是电缆局部温升缺陷的FMCW相位谱测试结果，相位谱与定位谱对应，缺陷处相位发生改变，而其余位置几乎不变。这表明，相敏-FMCW方法对于不同严重程度的缺陷相位变化量不同，可以作为检测电缆局部缺陷的一种手段。
统计电缆局部温升试验的结果见表4。为对相敏-FMCW与FMCW方法检测电容性缺陷的灵敏度进行对比，按2.2节中仿真数据的处理方法，对表4中的结果进行处理绘成图8。由图7可知，实测102 m处电缆定位峰的最大峰值为-44 dB，T0号电缆102 m处定位谱基准值为-111.4 dB，因此该处缺陷峰峰值的取值范围最大约为67 dB；根据仿真结果，相位差的取值范围限定为180°；将峰值、相位相对于各自取值范围的比例定义为灵敏度；以室温23℃为基准，计算各组数据的温差。
表4 电缆局部温升试验结果统计
Tab.4 Statistics of local temperature rise test results of cables
编号T0T1T2T3T4T5 缺陷温度/℃233040505460 峰值定位峰/dB-111.4-93.9-94.4-91.4-89.4-87.5 峰值差/dB17.517202223 灵敏度(%)26.1025.4029.9032.8035.70 相位相位/(°)-126.4-109.9-106.2-86.4-25.32.1 相位差/(°)16.520.240101.1128.5 灵敏度(%)9.2011.2022.2056.2071.40
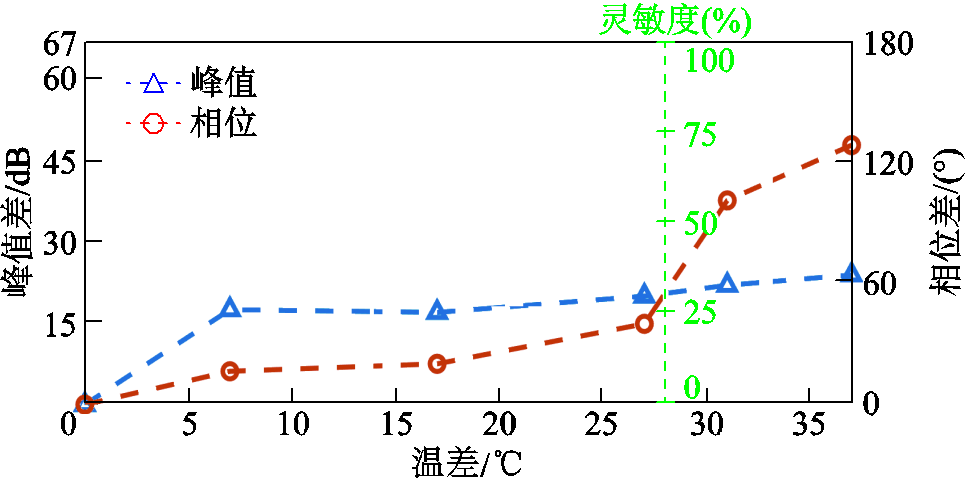
图8 容性缺陷灵敏度对比
Fig.8 Capacitive defect sensitivity comparison
从图8中可知，相位的灵敏度一开始小于峰值灵敏度，当温差大于28℃后，相位灵敏度优于峰值灵敏度。图8中灵敏度轴（绿色坐标轴）右侧区域是相位更灵敏的区间。当温差为37℃时，峰值灵敏度为36%，相位灵敏度为71%，因此，相敏-FMCW方法提高了FMCW方法检测电缆容性缺陷的灵敏度。
限于试验条件，本文选择在180 m长的10 kV XLPE电缆上设置铜屏蔽破损缺陷来模拟电缆受间接外力破坏的情况。电缆受损后还能继续运行一段时间，但最终仍会引发故障[23]。试验所用电缆由远东电缆公司生产，导体截面积为150 mm2。电缆铜屏蔽破损缺陷的设置过程如图9所示：首先在电缆150 m处剥除0.3 m的橡胶外护套，使铜屏蔽暴露于空气中；之后在该处中心位置环绕切除宽度小于5 mm的铜屏蔽，避免损伤外半导电层及主绝缘；最后使用四块边长为3 cm的薄铜片环绕裹覆破损处，电缆铜屏蔽层周长为8 cm，裹覆后该处铜屏蔽层导通。试验时，初始状态四块铜片均裹覆在破损处，测量后抽走一片，再次测量后从对侧抽走一片并测量，直至剩下最后一片，共测量四次。
图9 铜屏蔽破损缺陷示意图
Fig.9 Broken copper shielding defect
10 kV XLPE电缆的测试结果如图10所示。以四块铜片裹覆破损时的结果作为基准值，可见各电缆定位谱均在150 m处有一定位峰，因此对于铜屏蔽层破损缺陷，即使用铜皮覆盖修复仍能清晰地定位。图10b中相位谱对应的150 m位置，其相位变化量随着裹覆铜片的减少而逐步增加。对试验数据进行如下处理：实测XLPE电缆150 m处铜屏蔽完全断开时该处的定位谱峰值为-51 dB，四块铜片裹覆时该处的峰值约为-86 dB，因此该处缺陷峰的取值范围最大为35 dB；根据仿真结果，相位差的取值范围限定为180°；将峰值、相位相对于各自取值范围的比例定义为灵敏度，则两种方法的灵敏度对比如图11所示。
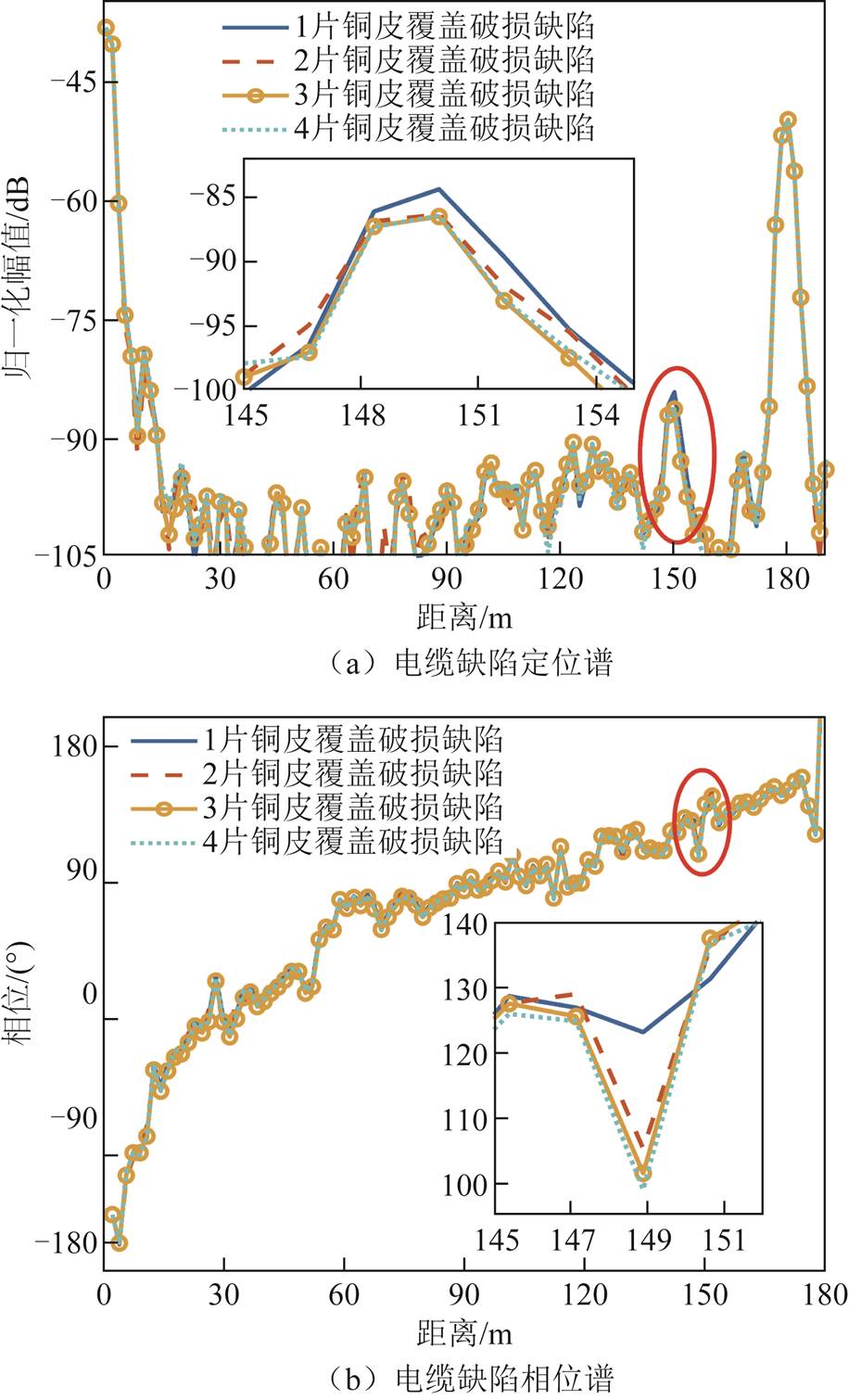
图10 铜屏蔽破损缺陷测试结果
Fig.10 Copper shield broken defect test results
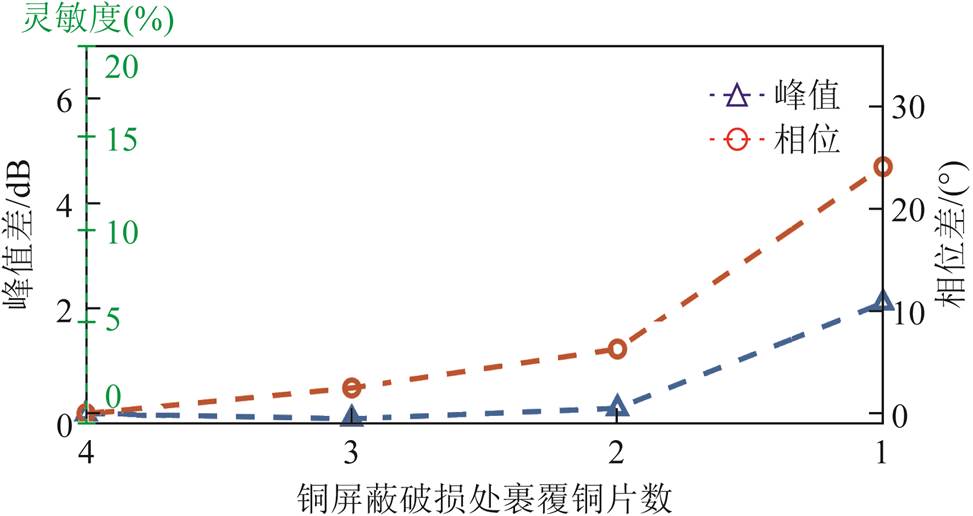
图11 铜屏蔽破损缺陷灵敏度对比
Fig.11 Sensitivity comparison of copper shield damage defects
由图11可知，对于本文中设置的铜屏蔽破损缺陷，相敏-FMCW方法的灵敏度始终优于FMCW方法。当缺陷处裹覆的铜片数量为1时，使用相敏-FMCW方法可将灵敏度由FMCW方法的6%提升至13%，灵敏度提高了7%。数据统计结果及灵敏度对比见表5。
该试验说明，相敏-FMCW方法不仅对于射频电缆上的缺陷有效，对于10 kV XLPE电缆也有效。
表5 铜屏蔽破损缺陷试验结果统计
Tab.5 Statistics of test results of copper shield damage defects
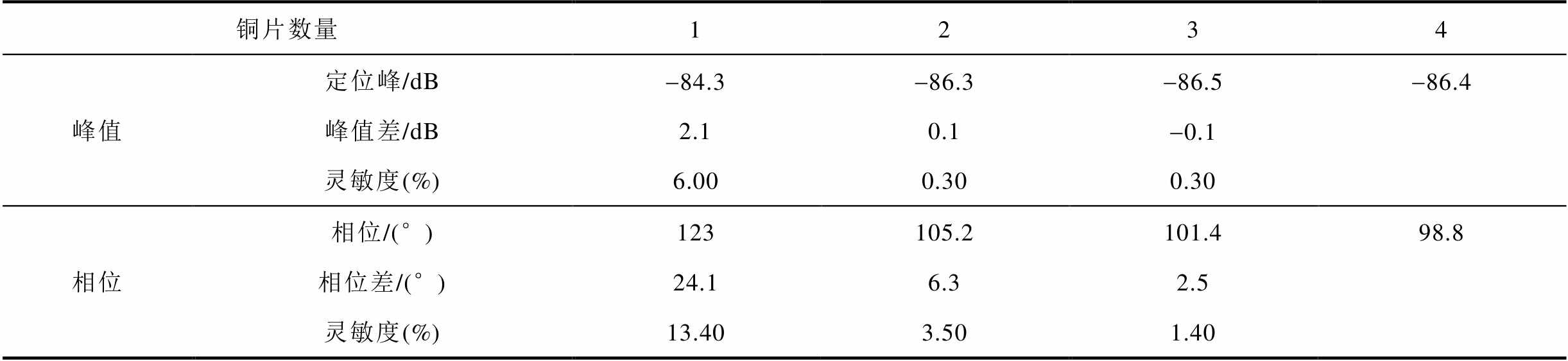
铜片数量1234 峰值定位峰/dB-84.3-86.3-86.5-86.4 峰值差/dB2.10.1-0.1 灵敏度(%)6.000.300.30 相位相位/(°)123105.2101.498.8 相位差/(°)24.16.32.5 灵敏度(%)13.403.501.40
为了检验本文所提方法对其他类型缺陷检测的有效性，还进行了对电阻性缺陷与电导性缺陷的试验。
3.3.1 电缆电阻性缺陷试验
连接长度分别为200 m与410 m的射频电缆（SYV 50-3-1）的线芯，在电缆铜屏蔽线的连接处串联电阻进行测试。串联电阻的阻值为0.1～100 W，这将改变该处的分布电阻数值。两段电缆的铜屏蔽线经电阻连接，整个连接处的尺寸小于55 mm。电缆局部电阻性缺陷的试验结果如图12所示。
图12 电缆电阻性缺陷测试结果
Fig.12 Cable resistive defect test results
为便于展示，在图12a和图12b中展示了串联电阻阻值为0.1、0.2、0.5、1.0、2.0、3.0 W的测试结果，在图12c中则展示了所有的数据点。图12a为阻性缺陷的定位谱，定位谱缺陷处的定位峰峰值随着串联电阻值的增大而增大。图12b中，串联电阻从0.1 W增至3 W时，相位谱200 m位置处的相位变化量随着串联电阻值的增加而逐步增加。计算灵敏度时，相位范围取180°，峰值范围取24 dB，灵敏度对比结果如图12c所示。由图12c可知，对于阻性缺陷，相敏-FMCW方法比传统FMCW方法更具有优势。当串联电阻为5 W时，FMCW方法的灵敏度为8%，使用相敏-FMCW方法可将灵敏度提升至70%，灵敏度提高了62%；当串联电阻为100 W时，相敏-FMCW方法可将灵敏度由70%提升至86%，灵敏度提高了16%。
3.3.2 电缆电导性缺陷试验
将两段SYV50-3-1电缆经T型接头（射频同轴连接器-BNC三通转接头）连接，接头位于200 m处。经FLUKE-17B+万用表测量，线芯与地线间的绝缘电阻大于40 MW。在电缆的T型接头线芯与地线上连接电阻，电阻与电缆的分布电导G呈并联状态，该并联电阻将改变该处的绝缘电阻。电导性缺陷（线芯与地线间的绝缘电阻缺陷）可归类为高阻故障，高阻故障的绝缘电阻一般大于10Z0[24]。由于绝缘电阻远大于并联电阻，该处绝缘电阻主要由并联电阻决定。取并联电阻阻值为1 kΩ～2 MΩ[25]，电缆局部电导性缺陷的试验结果如图13所示，可见定位谱、相位谱均能准确地定位缺陷所在位置。
在图13a和图13b中，FMCW方法的定位峰几乎重合，难以分辨各种阻值的缺陷；而相敏-FMCW的相位峰峰值随着该处并联电阻阻值逐步下降而发生改变，可见相敏-FMCW方法的测试结果更直观、更显著。计算灵敏度时，相位范围取180°，峰值范围取29 dB，灵敏度对比结果如图13c所示。随着并联电阻值的下降，FMCW方法的峰值差出现了波动，甚至在1.0 kΩ附近时为负值，因此FMCW方法难以检测出电导性缺陷；而相敏-FMCW方法的相位差随着缺陷加重而增大，说明相敏-FMCW方法对于电缆绝缘电阻的变化敏感。因此，对于电导性缺陷（高阻故障），相敏-FMCW方法的灵敏度始终优于FMCW方法。当并联电阻为1.0 kW时，相敏-FMCW方法可将灵敏度提升至18%。
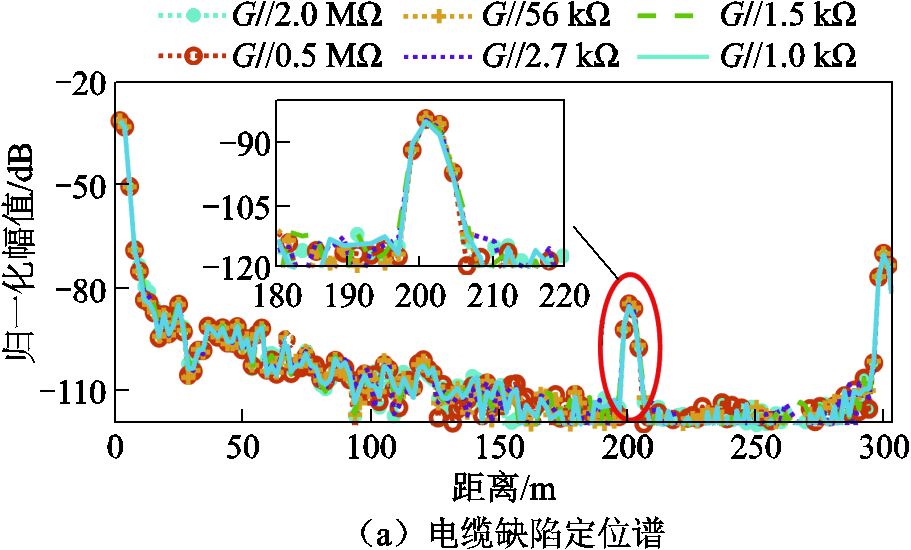
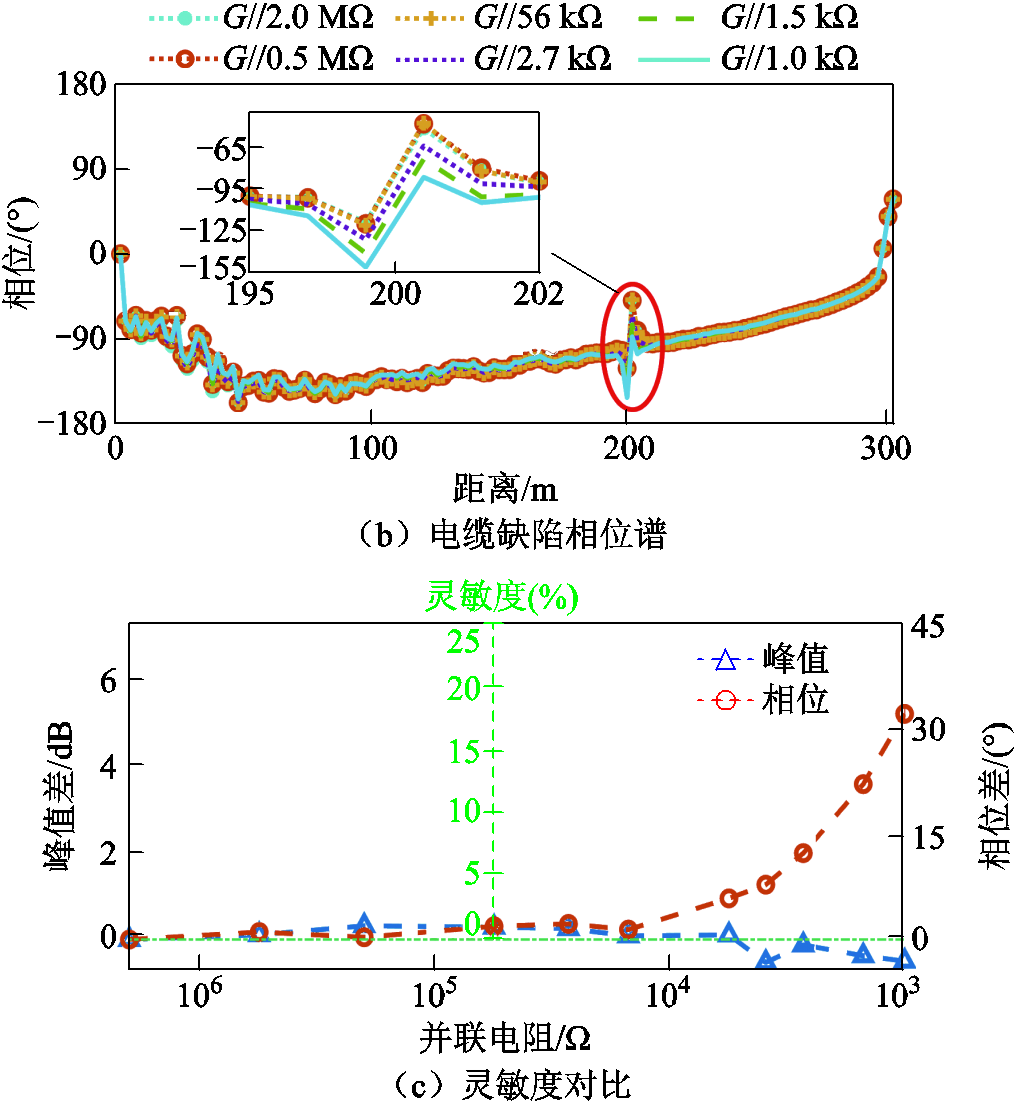
图13 电缆电导性缺陷测试结果
Fig.13 Cable conductivity defect test results
目前的试验结果表明，相敏-FMCW方法对于高阻故障有一定的检测能力，但能否满足现场的需求还有待实际测量的考验。在现场应用时，三相电缆可以互为参照进行对比，通过峰值或相位变化来检测缺陷及故障。
本节对射频电缆、XLPE电缆及不同类型的缺陷进行了试验，结果表明，相敏-FMCW方法对于电缆的多种缺陷敏感，对于不同严重程度的缺陷其相位变化量不同，相敏-FMCW方法是一种有效的检测电缆局部缺陷的方法。对于本文列举的几种缺陷，除温升缺陷（容性缺陷）以外，相敏-FMCW的灵敏度均优于传统FMCW方法。对于温升缺陷，只在温升试验开始时相敏-FMCW方法的灵敏度低于传统方法，随着温差增加至28℃后，相敏-FMCW方法则更为灵敏。
本文中计算相位灵敏度时，将相位的取值区间设为180°，本节将结合试验数据与算例进行验证。
图14a展示了铜屏蔽串联电阻与相位的对应关系，随着串联电阻值越来越大，对应的相位值从0°趋近于155°，相位变化范围约为155°。图14a中的拟合曲线显示了相位取值范围，且此范围有进一步扩大并最终趋于稳定的趋势。据此推测，由于缺陷变化引起的FMCW相位变化范围应不大于180°，与仿真结果吻合。
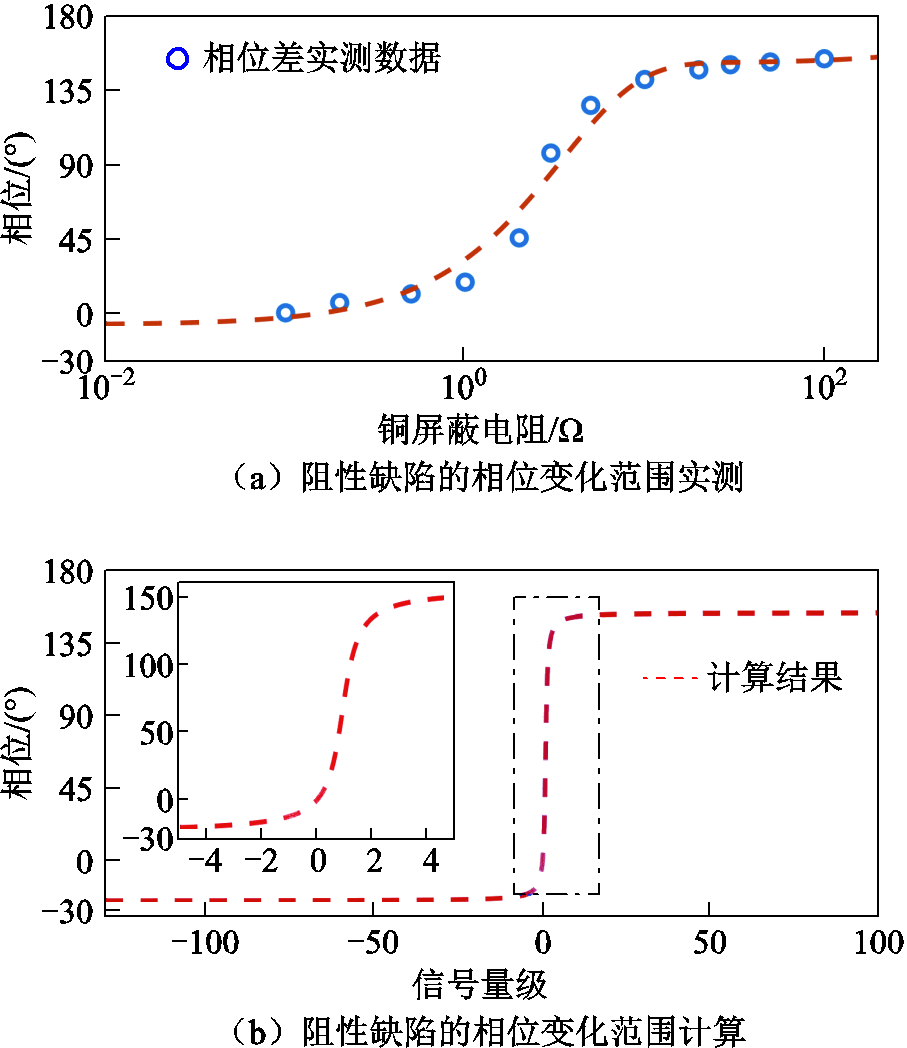
图14 缺陷的相位变化范围计算
Fig.14 Phase variation range simulation of defects
下面进行相位取值范围理论值的计算。根据式（11）～式（14）的推导，假设电缆中缺陷位置为D，LFM信号经缺陷反射回到测量端后与参考信号混频，会产生频率对应位置D的余弦信号sout，该信号的相位同时受到反射信号强度、LFM入射信号在该频率产生的信号s2的初相位与幅值的共同影响。在算例中，信号s2的幅值相对固定，设为1，初相位设为0°；信号sout初相位设为155°，由于不确定反射系数，故幅值可在实数域任意取值。如果不存在信号s2，则相位谱中该处的相位应为155°。按式（13）和式（14）计算，由于信号s2的影响，最终输出信号的相位分布如图14b所示。
可见，算例相位分布范围为180°，该结果与电缆电阻性缺陷试验的结果相符。根据仿真、试验及算例的验证，可以确定相敏-FMCW方法中缺陷处相位的取值范围最大为180°。
缺陷所在的位置及电缆总长度都可能影响缺陷检测，为了说明这些因素对试验的影响，选择全长为300 m与610 m的电缆进行试验，缺陷类型为电阻性缺陷。缺陷位于300 m电缆的100 m处及610 m电缆的200 m处。从电缆的两端分别测量，得到不同电缆长度、不同缺陷位置的峰值及相位数据，绘制成灵敏度对比图，如图15所示。
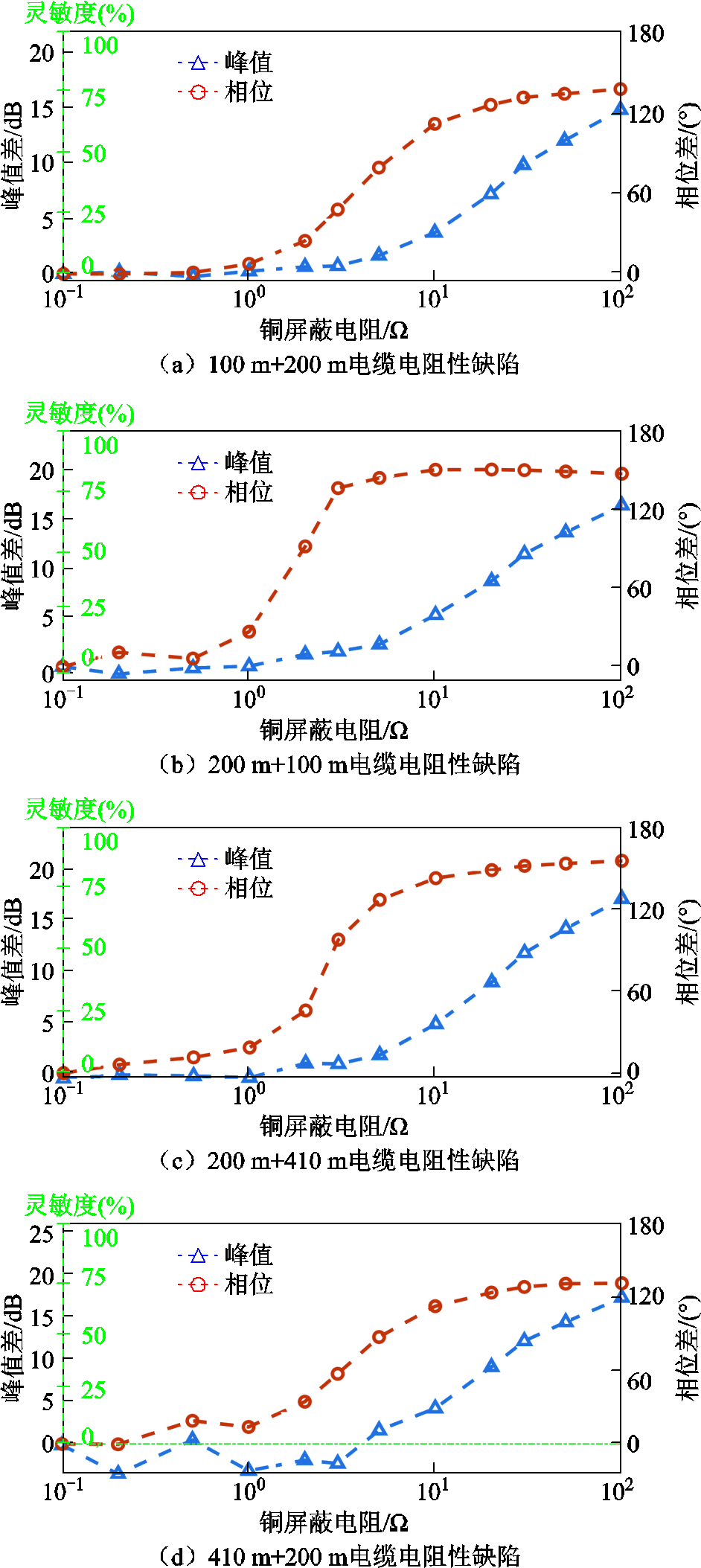
图15 电缆长度变化对测量的影响
Fig.15 Influence of cable length change on measurement
图15a与图15b为总长度为300 m的电缆测试结果，图15c与图15d为总长度为610 m的电缆测试结果，可见相敏-FMCW方法的灵敏度均优于传统FMCW方法，电缆的总长度不影响相敏-FMCW方法的测量。对比图15c与图15d中的数据，缺陷位于410 m处时的相位值略有下降，说明随着缺陷距离的增加，相敏-FMCW方法对于轻微缺陷的灵敏度略有下降，但仍优于FMCW方法。图15d中，当串联电阻值小于3 Ω时，FMCW方法测得的峰值差没有规律性变化，说明传统FMCW方法感知微小缺陷的能力随缺陷距离的增加而下降。综上所述，不同长度电缆试验的结果显示相敏-FMCW方法的测量具有良好的可重复性。
BIS方法与FMCW方法同属于FDR方法，且BIS方法是目前电缆缺陷检测的常用方法。本节通过对比BIS方法与FMCW方法，进一步说明相敏-FMCW方法相对于现有BIS方法的提升。以本文所提的容性温升缺陷和电导性缺陷为例，运用宽频阻抗谱仪分别进行测量，测试结果如图16所示。宽频阻抗谱仪测试频率设置为100 kHz～50 MHz，测试点数为4 990个。
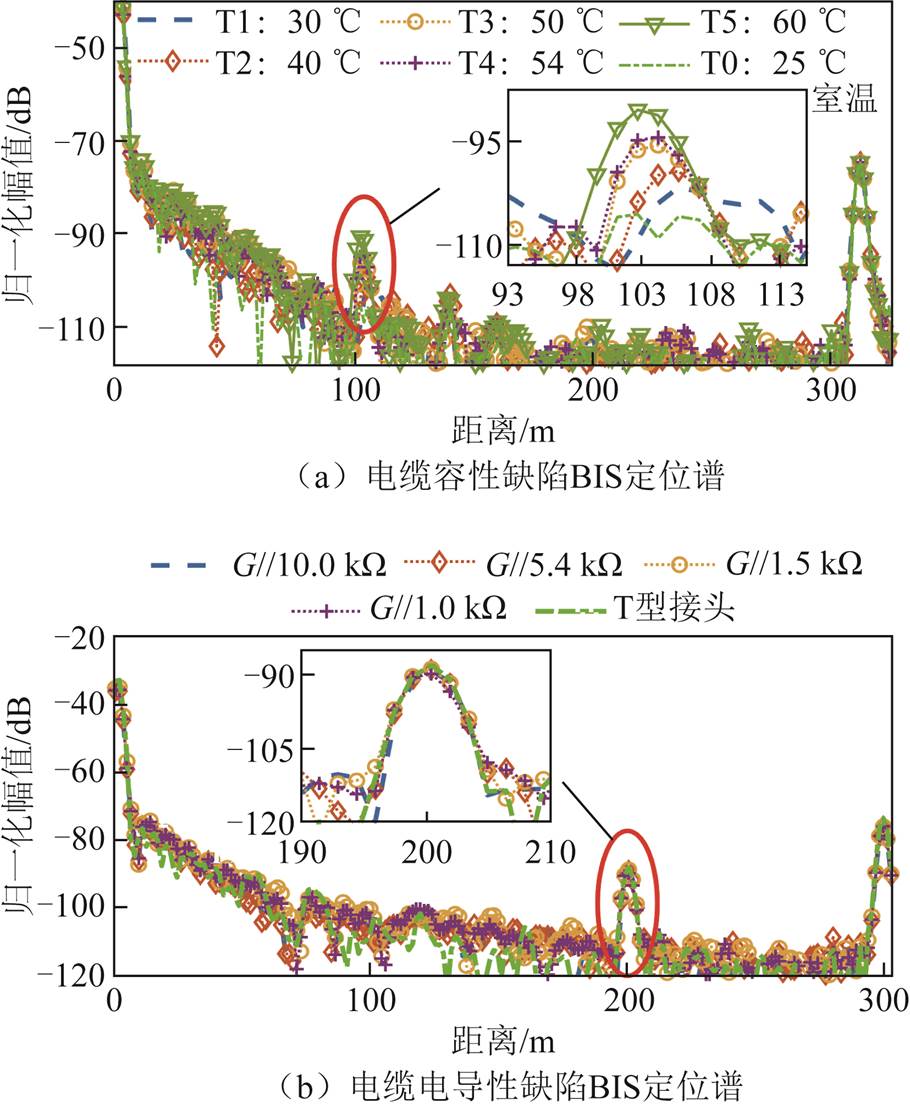
图16 基于BIS的电缆缺陷定位谱
Fig.16 Cable defect location spectrum based on BIS
对于加热温度不同而导致的容性缺陷，BIS方法在25℃、30℃、40℃时的缺陷定位峰产生一定偏移，按偏移规律取缺陷位置附近最大峰为定位峰，各温度相对于室温电缆的峰值差分别为：4 dB（30℃）、7 dB（40℃）、10 dB（50℃）、11 dB（54℃）、15 dB（60℃）。此时，FMCW方法定位谱中各温度相对于室温电缆的峰值差分别为：18 dB（30℃）、17 dB（40℃）、20 dB（50℃）、22 dB（54℃）、23 dB（60℃）。对于电导性缺陷（高阻故障），BIS与FMCW方法的定位谱可以观察到定位峰，但难以观察到缺陷电导变化导致的峰值变化。其中BIS方法产生的定位峰高度为22.7 dB，FMCW方法产生的定位峰高度为27.8 dB。
通过对比，FMCW方法与BIS方法均具有定位缺陷的能力，且FMCW方法测得的缺陷峰值相对于BIS方法更显著。综上所述，相敏-FMCW方法的灵敏度也优于BIS方法。
1）本文提出了一种基于调频连续波相位敏感特性的电缆局部缺陷检测方法，该方法可以提高FMCW方法对电缆缺陷检测的灵敏度。
2）通过仿真、试验及计算阐明了相位变化与缺陷严重程度之间的关系，解释了相位敏感-FMCW方法的原理，确定了缺陷处相位变化的范围最大为180°。
3）相敏-FMCW方法对于射频电缆及10 kV XLPE电缆上设置的缺陷均有效。以缺陷引起的相位、峰值变化量占取值区间的比例为灵敏度，可得对电缆局部异常温升造成的容性缺陷，当局部温差为37℃时，相敏-FMCW方法较传统基于峰值的FMCW方法可将灵敏度由36%提升至71%；对于电阻性、电导性（高阻故障）及铜屏蔽破损缺陷，相敏-FMCW方法的灵敏度均优于FMCW方法，本文所提方法可提升7%～62%的检测灵敏度。
相敏-FMCW方法对于高阻故障有一定的检测能力，但能否满足现场的需求还有待实际测量的考验。如果能定期对同一根电缆进行检测，可以根据其相位谱的变化趋势来判断缺陷的发展情况。本文所提的根据相位变化来跟踪电缆缺陷的检测方法有望为目前电缆缺陷检测提供新的工具。
参考文献
[1] 周远翔, 赵健康, 刘睿, 等. 高压/超高压电力电缆关键技术分析及展望[J]. 高电压技术, 2014, 40(9): 2593-2612. Zhou Yuanxiang, Zhao Jiankang, Liu Rui, et al. Key technical analysis and prospect of high voltage and extra-high voltage power cable[J]. High Voltage Engineering, 2014, 40(9): 2593-2612.
[2] 赵健康, 赵鹏, 陈铮铮, 等. 高压直流电缆绝缘材料研究进展评述[J]. 高电压技术, 2017, 43(11): 3490-3503. Zhao Jiankang, Zhao Peng, Chen Zhengzheng, et al. Review on progress of HVDC cables insulation materials[J]. High Voltage Engineering, 2017, 43(11): 3490-3503.
[3] 田野, 郭金明, 傅明利, 等. 超高压交流XLPE电缆输电工程应用现状综述[J]. 南方电网技术, 2016, 10(9): 30-36, 48. Tian Ye, Guo Jinming, Fu Mingli, et al. Review on power transmission projects with UHVAC XLPE cables[J]. Southern Power System Technology, 2016, 10(9): 30-36, 48.
[4] 单秉亮, 李舒宁, 杨霄, 等. XLPE配电电缆缺陷诊断与定位技术面临的关键问题[J]. 电工技术学报, 2021, 36(22): 4809-4819. Shan Bingliang, Li Shuning, Yang Xiao, et al. Key problems faced by defect diagnosis and location technologies for XLPE distribution cables[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4809-4819.
[5] 王昊月, 王晓威, 孙茂伦, 等. XLPE电缆绝缘热老化的高压频域介电谱诊断方法[J]. 电工技术学报, 2022, 37(17): 4497-4507. Wang Haoyue, Wang Xiaowei, Sun Maolun, et al. High voltage frequency domain dielectric spectroscopy diagnosis method for thermal aging of XPLE cables[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4497-4507.
[6] 牛海清, 徐涛, 黄嘉盛, 等. 单芯电缆外护层绝缘缺陷及其差异化检修策略[J]. 绝缘材料, 2015, 48(11): 64-68. Niu Haiqing, Xu Tao, Huang Jiasheng, et al. Insulation defects in outer sheath of single-core cable and its differential maintenance strategy[J]. Insulating Materials, 2015, 48(11): 64-68.
[7] Hirai N, Yamada T, Ohki Y. Comparison of broadband impedance spectroscopy and time domain reflectometry for locating cable degradation[C]// 2012 IEEE International Conference on Condition Monitoring and Diagnosis, Bali, Indonesia, 2012: 229-232.
[8] Ohki Y, Hirai N. Location attempt of a degraded portion in a long polymer-insulated cable[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2018, 25(6): 2461-2466.
[9] 潘文霞, 赵坤, 朱正鼎. 一种基于阻抗相位变化比率的长电缆局部缺陷定位新方法[J]. 中国电机工程学报, 2020, 40(12): 4043-4051. Pan Wenxia, Zhao Kun, Zhu Zhengding. A new method for local defect location of long cable based on impedance phase change ratio[J]. Proceedings of the CSEE, 2020, 40(12): 4043-4051.
[10] Fantoni P F, Nordlund A. Wire system aging assessment and condition monitoring (WASCO)[R]. Copenhagen: Nordic Nuclear Safety Research (NKS- 130), 2006.
[11] Ohki Y, Yamada T, Hirai N. Diagnosis of cable aging by broadband impedance spectroscopy[C]//2011 Annual Report Conference on Electrical Insulation and Dielectric Phenomena, Cancun, Mexico, 2011: 24-27.
[12] 周志强. 基于宽频阻抗谱的电缆局部缺陷诊断方法研究[D]. 武汉: 华中科技大学, 2015.
[13] 李蓉, 周凯, 万航, 等. 基于频域反射法的10 kV配电电缆中间接头受潮定位[J]. 电网技术, 2021, 45(2): 825-832. Li Rong, Zhou Kai, Wan Hang, et al. Moisture location of 10 kV cable joints in medium voltage distribution grid based on frequency domain reflection[J]. Power System Technology, 2021, 45(2): 825-832.
[14] 李蓉, 周凯, 万航, 等. 基于输入阻抗谱的电力电缆本体局部缺陷类型识别及定位[J]. 电工技术学报, 2021, 36(8): 1743-1751. Li Rong, Zhou Kai, Wan Hang, et al. Identification and location of local defects in power cable body based on input impedance spectroscopy[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1743-1751.
[15] Zhao Shujing, Gong Liangtao, Yan Ruijian, et al. Defect location for cables based on frequency modulated continuous wave[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2022, 29(3): 1095-1102.
[16] 齐国清. FMCW液位测量雷达系统设计及高精度测距原理研究[D]. 大连: 大连海事大学, 2001.
[17] Stove A G. Linear FMCW radar techniques[J]. IEE Proceedings F Radar and Signal Processing, 1992, 139(5): 343.
[18] Jankiraman M. FMCW radar design[M]. Norwood: Artech House, 2018.
[19] Stone G C, Boggs S A. Propagation of partial discharge pulses in shielded power cable[C]//Conference on Electrical Insulation & Dielectric Phenomena - Annual Report, Amherst, MA, USA, 1982: 275-280.
[20] Gouda O E, Matter Z. Effect of the temperature rise on the XLPE dielectric properties[C]//Proceedings of the 35th Midwest Symposium on Circuits and Systems, Washington, DC, USA, 1992: 95-98.
[21] Hasegawa Y, Ohki Y, Fukunaga K, et al. Complex permittivity spectra of various insulating polymers at ultrawide-band frequencies[J]. Electrical Engineering in Japan, 2017, 198(3): 11-18.
[22] Hasegawa Y, Takihana J, Ohki Y. Estimation of thermal expansion coefficients of polymeric insulating films from temperature dependence of dielectric permittivity[J]. Japanese Journal of Applied Physics, 2014, 53(7): 071501.
[23] 罗俊华, 邱毓昌, 杨黎明. 10kV及以上电力电缆运行故障统计分析[J]. 高电压技术, 2003, 29(6): 14-16. Luo Junhua, Qiu Yuchang, Yang Liming. Operation fault analysis of CLPE power cable above 10 kV[J]. High Voltage Engineering, 2003, 29(6): 14-16.
[24] 李蓉, 周凯, 饶显杰, 等. 基于输入阻抗谱的电缆故障类型识别及定位[J]. 高电压技术, 2021, 47(9): 3236-3245. Li Rong, Zhou Kai, Rao Xianjie, et al. Identification and location of cable faults based on input impedance spectrum[J]. High Voltage Engineering, 2021, 47(9): 3236-3245.
[25] 陶宇航, 张熹, 宫祥龙. 10kV电缆故障测距及定位典型案例分析[J]. 电气技术, 2022, 23(2): 88-93. Tao Yuhang, Zhang Xi, Gong Xianglong. Typical cases analysis of 10kV cable fault location[J]. Electrical Engineering, 2022, 23(2): 88-93.
Abstract Cables play a very important role in the operation of society and are closely related to industrial production and people's lives. Minor defects develop into serious defects that eventually lead to cable failure. In this regard, it is important to be able to detect and locate defects in cables before they occur. Frequency domain reflectometry (FDR) is developing rapidly because it has higher sensitivity than time domain reflectometry (TDR) in terms of cable defects and fault location. In recent years, the broadband impedance spectroscopy (BIS) method based on FDR has made great progress in the field of cable defect location. The BIS method measures the impedance spectrum of the cable through instruments, and analyzes the impedance spectrum to obtain the location spectrum of the cable. However, the BIS method is easily interfered by noise. In order to improve the anti-noise ability of the FDR method, a frequency modulated continuous wave (FMCW) method based on FDR was developed. With the same background noise, FMCW measurements are better and can locate defects further away.
FMCW has obtained higher sensitivity than BIS method by measuring the frequency difference, but it is still not sensitive enough for the detection of minor defects in cables that are further developed into serious defects due to the influence of operating environment and other factors. In response to this difficulty, inspired by the use of phase characteristics to improve the distance resolution of the FMCW method in the process of high-precision liquid level measurement, we propose a phase-sensitive-FMCW method to improve the sensitivity of the FMCW method to the measurement of cable defect state changes.
First, based on the principle of FMCW cable defect location, the basis for using FMCW phase characteristics to detect defects is proposed: the phase of the mixing signal is affected by the chirp signal, and the phase signal is double modulated by both amplitude and phase. When the reflected signal changes, the phase also changes. Even if the defect position remains unchanged, the strength of the reflected signal will cause the final output signal phase to be different, which is the basic principle that the FMCW signal is sensitive to the defect phase.
Then, the cable defect detection simulation experiment is carried out in combination with the cable distribution parameter model. The simulation test results show that the cable location spectrum based on FMCW can effectively locate the location of cable defects; the cable phase spectrum based on FMCW can effectively reflect the changes of cable defects, and the phase-sensitive characteristics of the phase spectrum can be used to detect the changes of local cable defects. After that, the RF coaxial cable in the laboratory is simulated and tested with different degrees of defects, and the phase change at the defect is observed. There are four types of defects, namely capacitive defects caused by heating, defects caused by copper screen breakage, and resistive defects on the copper shield and conductive defects caused by parallel resistance.
The simulation and experimental results show that: (1) This paper proposes a local defect detection method for cables based on the phase-sensitive characteristic of FMCW, which can improve the sensitivity of the FMCW method to the detection of cable defects. (2) Through simulation, experiment and calculation, the relationship between phase change and defect severity is clarified, the principle of phase sensitive-FMCW method is explained, and the maximum range of phase change at defect is 180°. (3) Taking the ratio of the phase and amplitude changes caused by the defect to the value interval as the sensitivity, the sensitivity of the capacitive defect caused by the local abnormal temperature rise of the cable can be increased from 36% to 71% when the local temperature difference is 37℃. The sensitivity of phase sensitive FMCW method is better than that of FMCW method for resistance, conductivity and copper shield damage defects, which can increase the detection sensitivity by 7%～62%.
keywords：Phase-sensitive, frequency modulated continuous wave (FMCW), coaxial cable, defect detection
DOI:10.19595/j.cnki.1000-6753.tces.221790
中图分类号：TM247
国网山西省电力公司科技项目资助（52053020000V）。
收稿日期 2022-09-21
改稿日期 2022-11-08
赵书静 男，1993年生，博士研究生，研究方向为电力设备状态的监测与故障诊断。E-mail：zhaoshujing2015@163.com
王 伟 男，1979年生，副教授，硕士生导师，研究方向为电力设备状态的监测与故障诊断等。E-mail：ww790324@163.com（通信作者）
（编辑 李冰）