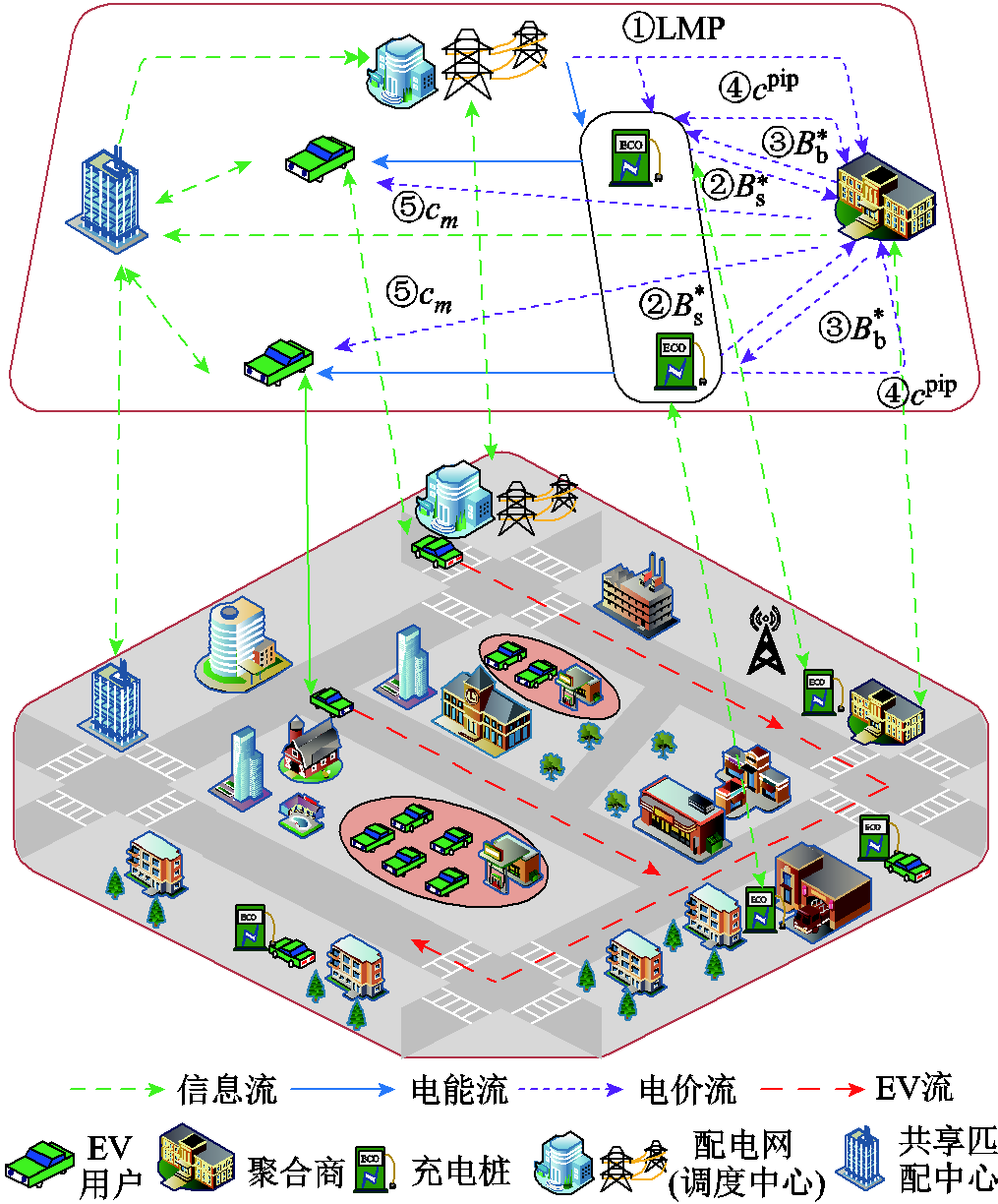
图1 车桩匹配示意图
Fig.1 Schematic diagram of vehicle and pile matching
摘要 充电桩共享是缓解车桩配置不平衡的一种可行方案。该文综合考虑配电网、电动汽车(EV)用户、充电桩、聚合商四方主体利益,提出一种基于主从博弈的充电桩共享方法。给出了基于车桩匹配中心的充电桩共享多主体博弈框架,并分别建立四个主体的成本和效益函数;提出考虑节点边际电价的车-桩-网三阶段主从博弈经济调度模型,并给出基于静态不完全信息博弈的充电桩及其聚合商最优报价策略和基于最小费用最大流的车桩匹配策略;结合图论最短路最大流理论,提出基于Ford-Fulkerson最大流算法的主从博弈双层迭代求解方法。算例分析表明,该文所提方法能有效提升四方主体经济效益、车桩匹配成功数和充电桩使用率。
关键词:节点边际电价 主从博弈 最小费用最大流 贝叶斯均衡 充电桩共享
我国“双碳”战略下,电动汽车(Electric Vehicle, EV)保有量将快速增长[1],促进节能减排[2]的同时,也将给充电设施配置带来一系列问题:①充电桩数量不足,充电设施配备速度严重滞后于车辆发展速度[3];②存在大量充电桩闲置的情况,充电桩分布不合理[4];③庞大的充电需求对电网运行带来冲击[5-6]。自2014年国家电网开放电动汽车充电桩市场以来,私人充电桩共享服务在我国出现,有效地缓解了公共充电设施紧张问题。星星充电、华商三优等为EV用户搭建了充电桩共享平台,平台仅提供充电桩信息查询与预约服务,EV用户受出行习惯与城市交通影响集中于部分桩充电,造成排队以及部分桩闲置两种现象发生,打击了部分桩主参与共享的积极性,因此研究合理有效的EV-充电桩匹配(简称车桩匹配)方法十分有必要。
当前,在EV和充电站匹配方面,充电价格是重要的控制信号。文献[7-8]以充电站收益最大为目标,建立充电站间的非合作博弈模型,制定充电站最优充电电价,以引导EV选择充电站。文献[9]采用事件驱动建立充电站的动态充电队列模型,提出了一种基于队列拥堵程度来调整电价的定价策略,调度EV有序充电,使充电站间设备利用率分布均衡,并减少EV排队时间。文献[10]利用EV用户的价格敏感性,提出充电站最优定价策略,来指导和协调EV充电过程,以减少放弃充电的EV数量。上述文献中充电电价均以充电站收益为制定目标,来控制EV充电行为,忽略了EV负荷并网对配电网的影响,导致匹配方案有可能冲击电网安全,增加其运营成本负担。进一步,文献[11]考虑了EV充电需求对电价的影响,提出一种基于聚合博弈模型的现货市场定价策略。但未能考虑电价变化导致EV充电选择发生改变,忽略了EV用户、配电网之间的主从博弈竞争关系[12]。此外,在车桩匹配方面,一般利用充电桩聚合商实现EV用户和电网的协调,充电桩聚合商获取某一区域内多个充电桩的代理权,代表充电桩参与共享,为EV用户提供充放电服务的同时获取相应利润。
现有充电策略的研究局限于单一主体最优,对实现EV用户、聚合商、充电桩、配电网多主体共赢的充电策略研究较少。文献[13]侧重于EV充电成本最优,提出将EV充电调度问题转换为约束马尔可夫决策过程,采用安全深度强化学习生成最优充电计划,使EV充电成本最小化,同时确保充满电。文献[14]侧重于充电桩的收益,考虑信息不对称条件下,基于轮流讨价还价博弈,构建了以充电桩桩主、配电网和EV用户为主体的双边议价博弈模型,确定充电桩最优共享服务电价,增加了桩主共享收益、降低了EV用户充电成本。文献[15]侧重于配电网安稳运行,提出利用柔性EV充电负荷帮助电网实现填谷,使电力负荷分布平缓。
针对上述研究不足,本文从配电网、EV用户、充电桩、聚合商四方共赢出发,建立了充电桩共享匹配主从博弈模型。论文亮点工作主要包括:①提出利用节点边际电价[16-17](Location Marginal Price, LMP)优化博弈主体模型,引导车桩匹配;②提出利用最小费用最大流模型,构建以车桩匹配对数最大为首目标、EV总充电成本最优为次目标的车桩匹配双目标从体博弈模型;③利用静态不完全信息博弈理论和最小费用最大流双目标从体博弈模型,实现车桩最优匹配,前者确定充电桩共享价格定价策略,后者实现车桩最优匹配;④利用双层迭代法求解博弈模型,并提出基于Bellman-Ford增广路算法的Ford-Fulkerson最大流算法,高效求解车桩匹配从体博弈模型。
充电桩共享涉及EV用户、聚合商、充电桩、配电网(调度中心)、共享匹配中心五个主体。其中,聚合商指区域内共享充电桩的代理商,充电站、充电桩属于特殊的聚合商,仅代理自身的充电机,一个聚合商可代理多个充电桩,而充电桩仅能由一个聚合商代理共享。共享匹配中心为设计车桩匹配策略且独立于其他主体的充电桩共享服务平台。各主体之间的关系如图1所示。
EV预计电量不足时,向共享匹配中心发出充电请求,上传其实时数据。充电桩、聚合商以不计入EV负荷时节点边际电价为配电网初始电价,通过静态非完全信息博弈,确定充电桩共享电价cpip,以及聚合商m售电电价cm、共享充电桩数Num,并实时发送给共享匹配中心。共享匹配中心结合实时充电设施和交通数据,快速匹配EV与充电桩。配电网调度中心计算拟接入配电网各节点的EV充电负荷大小,通过潮流计算修正各配电网节点LMP,并将电价数据传送给聚合商、充电桩。聚合商与充电桩重新博弈来更新cpip、cm、Num。共享匹配中心接收到更新后的cm、Num,重新匹配车桩并再次将EV充电负荷反馈至配电网调度中心,配电网调度中心和共享匹配中心反复进行此过程,直至博弈趋于稳定,各方决策不再变化。此时,配电网调度中心下发LMP至聚合商和充电桩,共享匹配中心向EV推送充电位置以及推荐路径。相关变量含义见表1。

图1 车桩匹配示意图
Fig.1 Schematic diagram of vehicle and pile matching
表1 EV用户数据及图1中价格变量
Tab.1 EV user data and price variables in figure 1
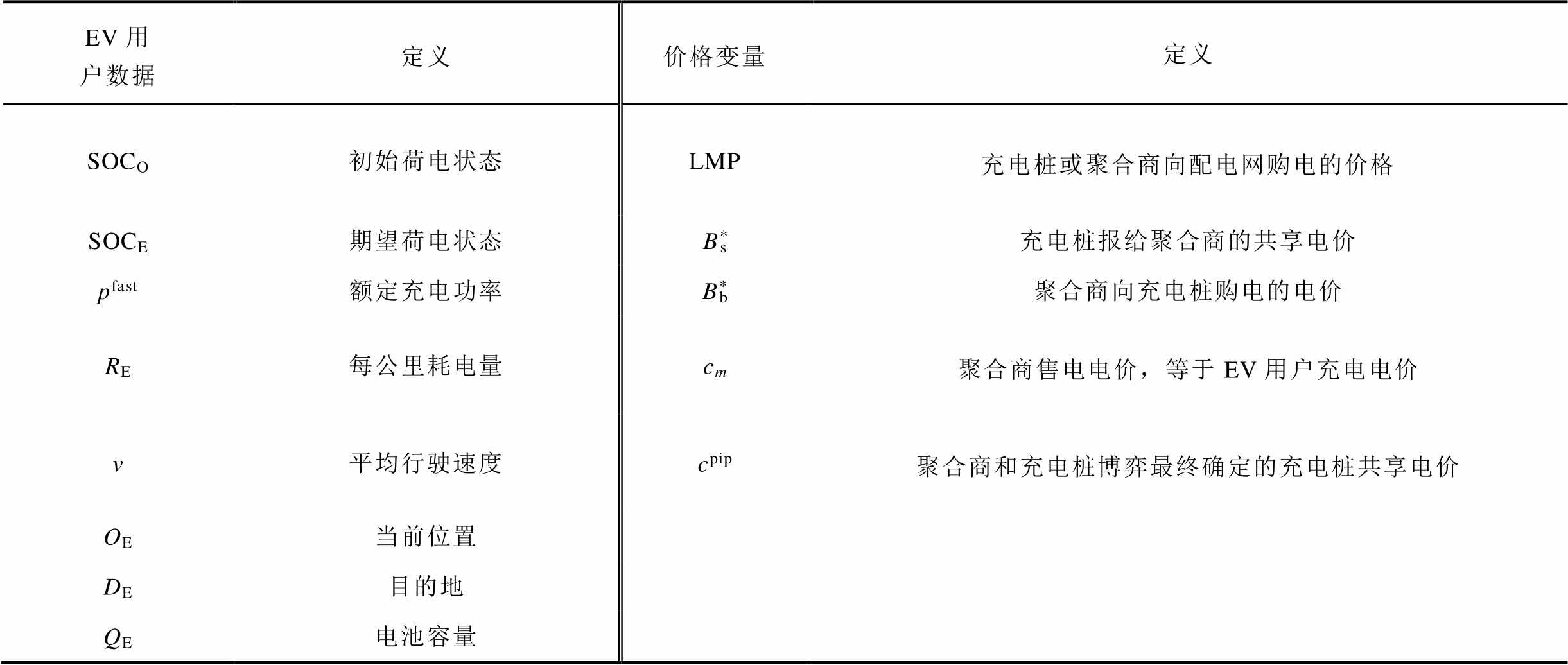
EV用户数据定义价格变量定义 SOCO初始荷电状态LMP充电桩或聚合商向配电网购电的价格 SOCE期望荷电状态B*s充电桩报给聚合商的共享电价 pfast额定充电功率B*b聚合商向充电桩购电的电价 RE每公里耗电量cm聚合商售电电价,等于EV用户充电电价 v平均行驶速度cpip聚合商和充电桩博弈最终确定的充电桩共享电价 OE当前位置 DE目的地 QE电池容量
注:表格中电价均为单位功率电价。
基于上述背景,本文提出以配电网为主体,以聚合商、充电桩、EV用户为从体的主从博弈模型,定义为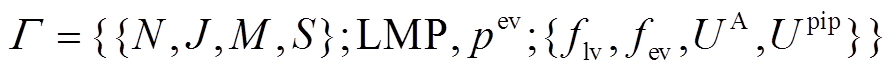 ,各组成部分定义如下:
,各组成部分定义如下:
(1)参与者集合:N个EV用户、J个充电桩、M个聚合商、配电网S构成参与者集合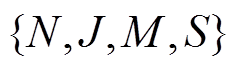 。
。
(2)决策变量:主体配电网S的决策变量节点边际电价LMP,是各节点下充电桩、聚合商每单位电能的购电成本的集合;博弈从体的决策变量为EV充电负荷的分布pev。
(3)效用函数:配电网、EV用户、聚合商、充电桩的效用函数分别为flv、fev、UA、Upip。
配电网购电成本主要由内部分布式燃汽轮机组出力成本、向外部电网购电成本两部分构成。本文将一天划为T个调度时刻,对任意时刻t,配电网优化运行目标为配电网购电成本flv最小[18],即
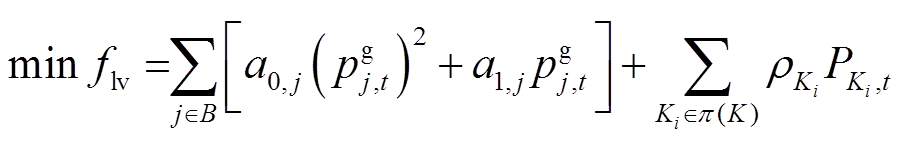 (1)
(1)
式中,B为节点集合;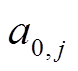 与
与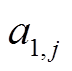 分别为节点j处分布式燃汽轮机组二次、一次成本系数;
分别为节点j处分布式燃汽轮机组二次、一次成本系数;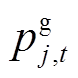 为t时段节点j处分布式燃汽轮机组有功出力;p(K)为与外网联络线集合;ρi为与外网的协议电价;
为t时段节点j处分布式燃汽轮机组有功出力;p(K)为与外网联络线集合;ρi为与外网的协议电价;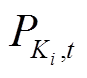 为t时段从外网Ki购买的电量。等号右边第一项为分布式燃气轮机组发电成本,第二项为向外网购电成本。
为t时段从外网Ki购买的电量。等号右边第一项为分布式燃气轮机组发电成本,第二项为向外网购电成本。
本文以单辐射状配电网为例进行研究,采用支路潮流模型描述交流配电网潮流,对"tÎ[1,T]均满足如下潮流约束[18]。
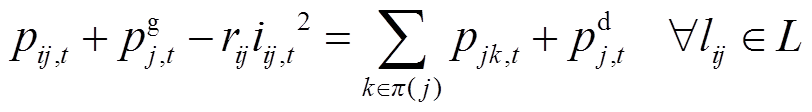 (2)
(2)
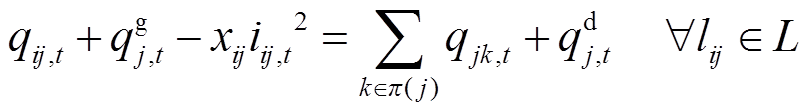 (3)
(3)
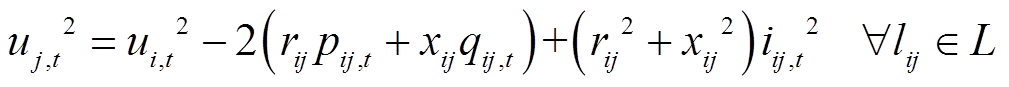 (4)
(4)
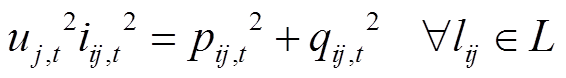 (5)
(5)
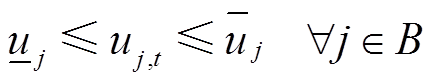 (6)
(6)
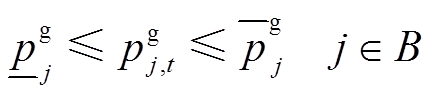 (7)
(7)
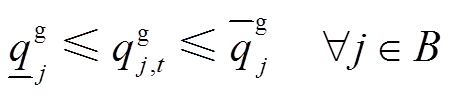 (8)
(8)
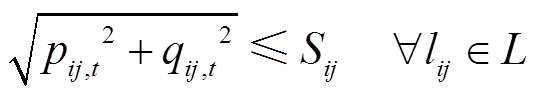 (9)
(9)
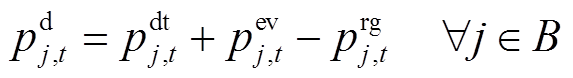 (10)
(10)
根据支路潮流模型,式(2)、式(3)为节点i到节点j的支路lij的有功功率、无功功率平衡方程,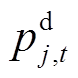 、
、 分别为t时段节点j处有功、无功负荷;
分别为t时段节点j处有功、无功负荷;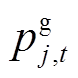 、
、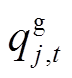 分别为t时段节点j处分布式燃汽轮机组有功、无功出力;
分别为t时段节点j处分布式燃汽轮机组有功、无功出力;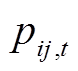 、
、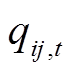 分别为t时段支路lij的有功、无功潮流;rij、xij分别为支路lij的电阻、电抗;iij,t为t时段支路lij的流过电流;p(j)为所有首端为j的支路的末端节点集合;L为支路集合。式(4)为电压平衡方程,ui,t、uj,t分别为t时段节点i、j处的电压。式(5)为支路首端功率方程。式(6)~式(8)分别为各节点的电压幅值、分布式燃汽轮机组有功出力、无功出力所受约束,
分别为t时段支路lij的有功、无功潮流;rij、xij分别为支路lij的电阻、电抗;iij,t为t时段支路lij的流过电流;p(j)为所有首端为j的支路的末端节点集合;L为支路集合。式(4)为电压平衡方程,ui,t、uj,t分别为t时段节点i、j处的电压。式(5)为支路首端功率方程。式(6)~式(8)分别为各节点的电压幅值、分布式燃汽轮机组有功出力、无功出力所受约束,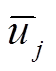 、
、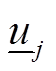 、
、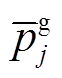 、
、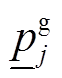 、
、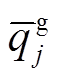 、
、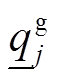 分别为节点j的电压幅值上下限、分布式燃汽轮机组有功出力上下限、无功出力上下限。式(9)为支路复功率Sij幅值约束。式(10)表示接入负荷的组成,
分别为节点j的电压幅值上下限、分布式燃汽轮机组有功出力上下限、无功出力上下限。式(9)为支路复功率Sij幅值约束。式(10)表示接入负荷的组成,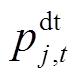 为t时段节点j的基础负荷;
为t时段节点j的基础负荷;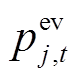 为t时段接入节点j的EV充电负荷;
为t时段接入节点j的EV充电负荷;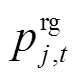 为t时段分布式能源出力。
为t时段分布式能源出力。
对潮流模型进行二阶锥松弛,将配电网最优潮流问题转换为二阶锥规划(Second-Order Cone Programming, SOCP)问题[19],过程见附录。
配电网LMP指考虑配电网潮流约束下,节点增加单位负荷时配电网新增边际运营成本,通常可衡量当前时刻配电网稳定运行条件下,节点处变化的单位电能价值。聚合商向电网购电的电价即为LMP。LMP计算步骤如下:首先,构造拉格朗日函数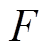 ,公式见附录;然后,对各节点负荷求偏导得到LMP并发布给聚合商和充电桩[20-21],有
,公式见附录;然后,对各节点负荷求偏导得到LMP并发布给聚合商和充电桩[20-21],有
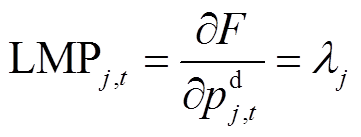 (11)
(11)
式中,LMPj,t为t时段节点j的节点边际电价;λj为附录中式(A1)对应的对偶乘子。考虑网损等因素影响,传统辐射状配电网中LMP会随潮流流向递增,然而分布式燃气轮机组的接入改变了传统配电网潮流单向流动的特点,进而影响各节点间LMP大小关系。
EV行驶过程中发现剩余电量不足以支撑达到目的地,或无法克服用户的里程焦虑时,会向共享匹配中心申请充电。
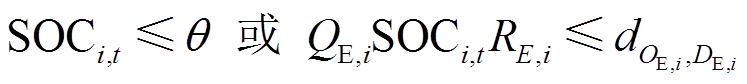 (12)
(12)
式中,SOCi,t为EV用户i在t时刻的EV电池荷电状态;θ为能源焦虑系数;QE,i、RE,i、OE,i、DE,i分别为EVi的电池容量、每公里耗电量、当前位置和目的地;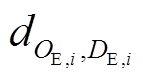 为从OE,i到目的地DE,i的最短距离。
为从OE,i到目的地DE,i的最短距离。
1)充电距离成本
EV申请充电的位置OE,i到目的地DE,i之间通常存在多条路径可选,共享匹配中心从用户心理考虑,假设用户选择最短的路径,根据Floyd路径搜索算法规划充电路径。最短路径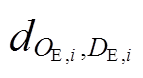 距离公式为
距离公式为
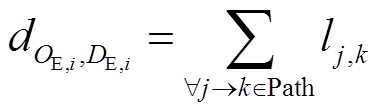 (13)
(13)
式中,Path:Oi→j→k→…→Di表示算法搜索的一条可行最短路径;j→k表示从交通节点j直接到达节点k,路段长度为lj,k。
当共享匹配中心为EV成功匹配到充电桩,EV先到达桩所在位置x,完成充电后前往原目的地。若充电设施不在原规划路径上,EV必须行驶的最短距离会增加,增加的行驶距离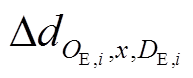 为
为
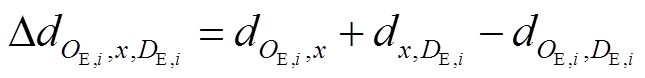 (14)
(14)
行驶的距离增加,将导致EV用户产生额外的耗电、行驶时间,即EV用户充电的距离成本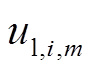 由额外耗电成本与行驶时间成本组成,即
由额外耗电成本与行驶时间成本组成,即
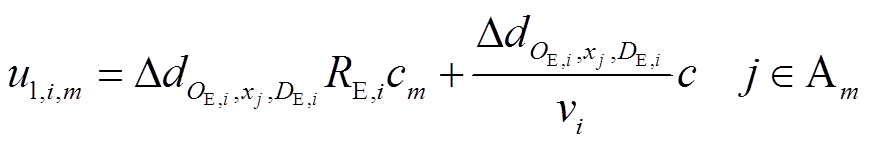 (15)
(15)
式中,xj为充电桩j的位置;vi为EVi的出行速度;c为时间成本系数,其值取中国城市标准人均小时收入13.5元/h;jÎAm表示EVi选择的充电桩j由聚合商Am代理。
2)充电时间成本
大多数共享充电桩的功率小于充电站快充功率。相较于充电站快充模式,EV用户选择共享充电桩充电花费的时间要长,导致EV用户产生充电时间成本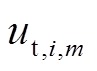 ,具体为
,具体为
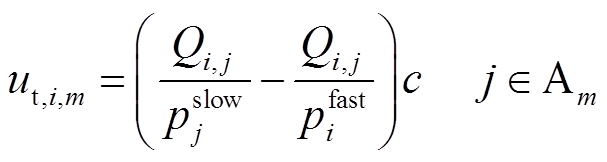 (16)
(16)
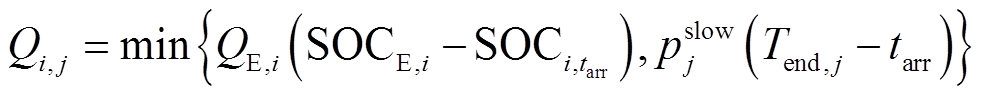 (17)
(17)
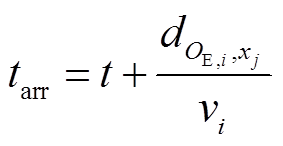 (18)
(18)
式中,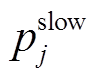 为充电桩j的充电功率;
为充电桩j的充电功率;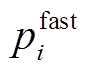 为EVi的额定充电功率;tarr为EVi到达充电桩j所在位置的时间;SOCE,i、
为EVi的额定充电功率;tarr为EVi到达充电桩j所在位置的时间;SOCE,i、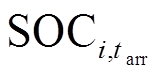 分别为EVi的期望荷电状态、tarr时刻荷电状态;Qi,j为EVi在充电桩j处的充电电量,当充电桩j的共享时间不足以使EVi电池充电达到期望SOCE,i时,EVi选择在充电桩j结束共享时间Tend,j时刻离开,否则充满电再离开。
分别为EVi的期望荷电状态、tarr时刻荷电状态;Qi,j为EVi在充电桩j处的充电电量,当充电桩j的共享时间不足以使EVi电池充电达到期望SOCE,i时,EVi选择在充电桩j结束共享时间Tend,j时刻离开,否则充满电再离开。
3)充电经济成本
充电经济成本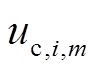 是EV选择聚合商Am充电服务需支付的电费,有
是EV选择聚合商Am充电服务需支付的电费,有
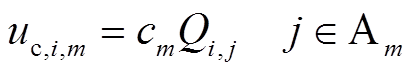 (19)
(19)
EV的剩余电量必须保证能够支撑到达聚合商Am代理的充电桩j的位置,否则EV不会选择聚合商Am充电,即
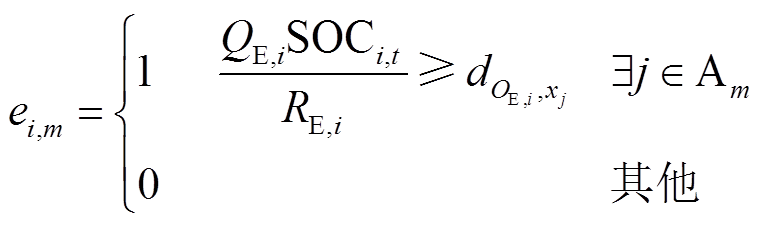 (20)
(20)
式中,ei,m为0-1变量,当值为1时,表示EV剩余电量可支撑到达充电桩j的位置充电,共享匹配中心允许双方匹配;否则为0。
综上所述,EV用户充电成本函数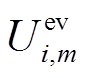 为
为
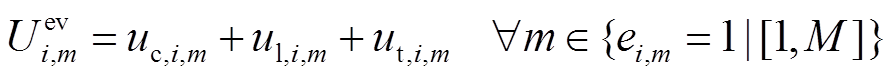 (21)
(21)
式中,M为聚合商数量。
充电桩参与共享服务时,需向聚合商上报共享时段开始时间Tinit和停止时间Tend。充电桩成本收益分为三部分:充电桩共享收入、充电桩购电成本、抵触效用,其中抵触效用指共享带来的电池损耗、维护成本等,效益函数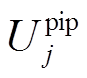 [22-23]为
[22-23]为
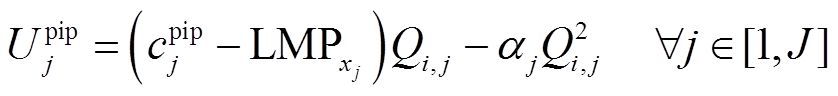 (22)
(22)
式中,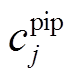 为充电桩j与聚合商博弈确定的充电桩共享电价,详细计算可见3.1节;
为充电桩j与聚合商博弈确定的充电桩共享电价,详细计算可见3.1节;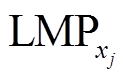 为交通节点xj处节点边际电价;αj为充电桩j抵触系数。
为交通节点xj处节点边际电价;αj为充电桩j抵触系数。
聚合商效益是提供EV用户充电获取的售电利润,其效益函数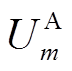 为
为
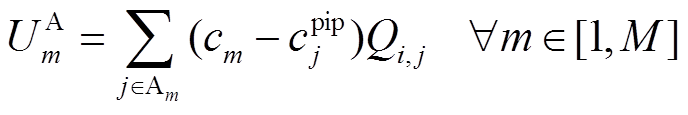 (23)
(23)
基于Stackelberg博弈的车桩匹配过程如图2所示,分为三个阶段。
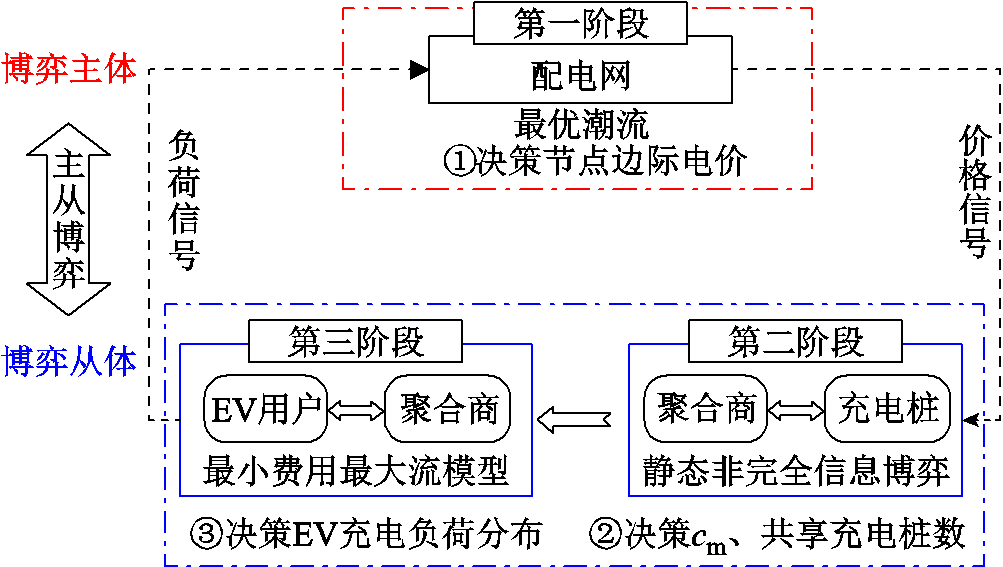
图2 车-桩-网主从博弈流程
Fig.2 Flow chart of master-slave game of vehicle-pile-net
(1)博弈主体决策阶段。配电网调度中心更新各配电网节点接入负荷大小,以配电网运行成本最小为优化目标,得到各节点边际电价LMP,下发给聚合商和充电桩。
(2)博弈从体-聚合商和充电桩基于节点边际电价进行一对一定价博弈,构建静态非完全信息博弈模型,将博弈的贝叶斯纳什均衡解作为最终成交价格。基于聚合商与充电桩完全理性的假设,充电桩确定其是否参与共享,聚合商统计该时刻其代理的、可参与共享的充电桩数量Num,详细见3.1.1节分析。
(3)共享匹配中心根据EV上报的信息,以及第二阶段聚合商、充电桩决策确定的cm、Num,基于2.2节EV的成本收益计算公式,以车桩成功匹配对数最多、EV用户总充电成本最优为目标,构建基于最小费用最大流模型的一对多车桩匹配模型,求解模型生成车桩匹配列表,计算各配电网节点EV负荷接入向量pev,返回第一阶段,详见3.1.2节分析。
3.1.1 基于静态不完全信息博弈的充电桩共享价格定价策略
1)充电桩报价策略
充电桩j 在时刻t参与共享充电任务时,首先,需要提前对式(22)成本函数求导来估算自身参与共享充电的单位成本cs,j,cs,j见式(24),结合充电桩共享报价上限cs,max(由市场规律与历史交易数据预测推出),得到定价范围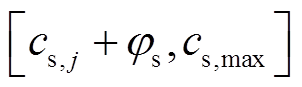 ,其中φs为必须保证的充电桩最低利润价差;然后,考虑自身偏好等因素确定可接受的最低共享电价bs,见式(25);最后,充电桩向聚合商提交的桩共享报价Bs(bs)采用线性策略,见式(26)。考虑到当前市场环境下用户真实报价策略难以预测,因此本文重点探讨不失一般性的线性报价策略研究方法。
,其中φs为必须保证的充电桩最低利润价差;然后,考虑自身偏好等因素确定可接受的最低共享电价bs,见式(25);最后,充电桩向聚合商提交的桩共享报价Bs(bs)采用线性策略,见式(26)。考虑到当前市场环境下用户真实报价策略难以预测,因此本文重点探讨不失一般性的线性报价策略研究方法。
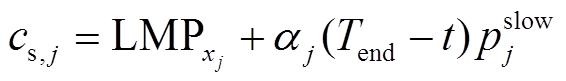 (24)
(24)
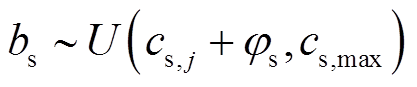 (25)
(25)
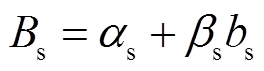 (26)
(26)
其中,假定式(25)充电桩接受的最低共享电价bs服从均衡分布,U(·)代表均匀分布。式(26)表示充电桩采用线性价格策略提供EV充电电价报价,αs、βs分别为报价策略的常数项和一次项系数。
2)聚合商报价策略
聚合商Am首先根据LMP制定聚合商售电电价cm,见式(27);然后得到购买充电桩服务电价的出价范围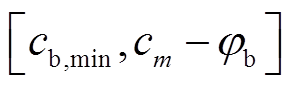 ,其中cb,min为聚合商的出价下限,由市场规律与历史交易数据预测得到,φb为必须保证的聚合商最低利润价差,同理假定聚合商对此时共享任务的最高接受出价bb,服从均衡分布,如式(28);最后,聚合商按照类似充电桩的线性价格策略设置购买充电桩服务的电价Bb(bb),如式(29)。
,其中cb,min为聚合商的出价下限,由市场规律与历史交易数据预测得到,φb为必须保证的聚合商最低利润价差,同理假定聚合商对此时共享任务的最高接受出价bb,服从均衡分布,如式(28);最后,聚合商按照类似充电桩的线性价格策略设置购买充电桩服务的电价Bb(bb),如式(29)。
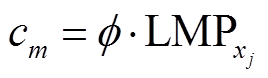 (27)
(27)
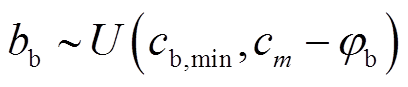 (28)
(28)
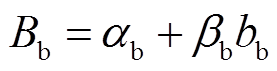 (29)
(29)
式中,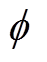 为价格系数,反映聚合商售电电价cm与配电网节点边际电价成线性关系;αb、βb分别为聚合商策略函数的常数项、一次项系数。
为价格系数,反映聚合商售电电价cm与配电网节点边际电价成线性关系;αb、βb分别为聚合商策略函数的常数项、一次项系数。
由式(25)、式(26)、式(28)、式(29),Bs、Bb分别与bs、bb存在线性关系,bs、bb服从均匀分布,聚合商、充电桩可推导对方的报价Bs、Bb也服从均匀分布,即
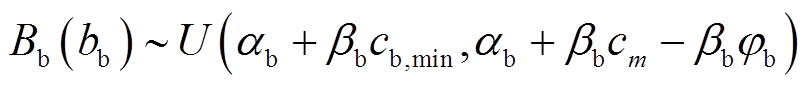 (30)
(30)
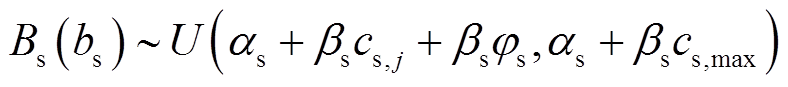 (31)
(31)
3)双边议价交易流程
充电桩、聚合商同时公布报价Bs、Bb,当满足Bb≥Bs时,即聚合商出价不低于充电桩报价,符合双方意愿可交易,取报价平均值(Bb+Bs)/2作为充电桩共享电价;否则,交易失败。
4)基于静态不完全信息博弈的定价策略
报价双方信息部分公开,例如:充电桩接受共享的最低电价bs、聚合商的最高接受出价bb取值范围以及服从的概率分布信息完全公开;但聚合商不知道充电桩bs的具体值,同样充电桩也不知道聚合商bb的具体值。因此,该问题属于静态不完全信息博弈问题。
聚合商面对充电桩任何可能的报价Bs(bs),以自身期望效益最大为目标来选取报价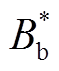 ;同理,充电桩对聚合商任何可能发生的报价Bb(bb),选取最优报价
;同理,充电桩对聚合商任何可能发生的报价Bb(bb),选取最优报价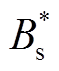 使自身期望效益最大。当交易成功时,对于聚合商来说,通过报价策略节省的效益为bb-(Bb+Bs)/2,而对于充电桩,通过报价策略增加的效益为超出价格bs的部分,即(Bb+Bs)/2-bs;交易失败,充电桩不参与此时段共享,则双方效益为0。由贝叶斯定理和期望效应理论,聚合商、充电桩的期望效益函数分别为
使自身期望效益最大。当交易成功时,对于聚合商来说,通过报价策略节省的效益为bb-(Bb+Bs)/2,而对于充电桩,通过报价策略增加的效益为超出价格bs的部分,即(Bb+Bs)/2-bs;交易失败,充电桩不参与此时段共享,则双方效益为0。由贝叶斯定理和期望效应理论,聚合商、充电桩的期望效益函数分别为
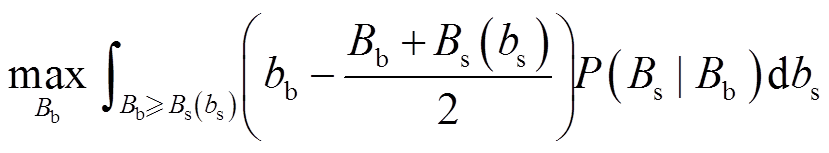 (32)
(32)
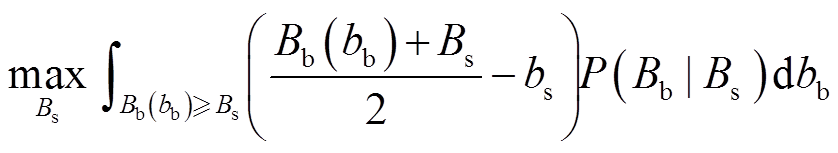 (33)
(33)
式中,P(Bs|Bb)为在Bb发生的条件下Bs发生的概率。若存在一组解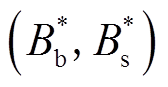 同时满足式(32)、式(33),则博弈存在贝叶斯纳什均衡解。
同时满足式(32)、式(33),则博弈存在贝叶斯纳什均衡解。
已知双方报价的概率分布,如式(30)、式(31),对式(32)、式(33)求二阶导数为负数,即存在最大值;令一阶导数取0,推导得
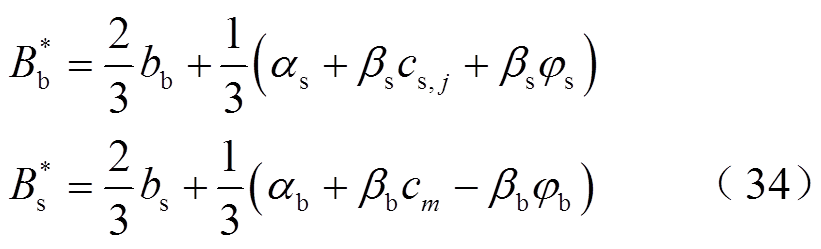
与式(26)、式(29)对照,可求得βs、βb均为2/3,αs、αb分别为(cs,j+φs)/4+(cm-φb)/12、(cs,j+φs)/ 12+(cm-φb)/4。综上所述,静态非完全信息博弈的贝叶斯纳什均衡解,即双方最优报价策略为
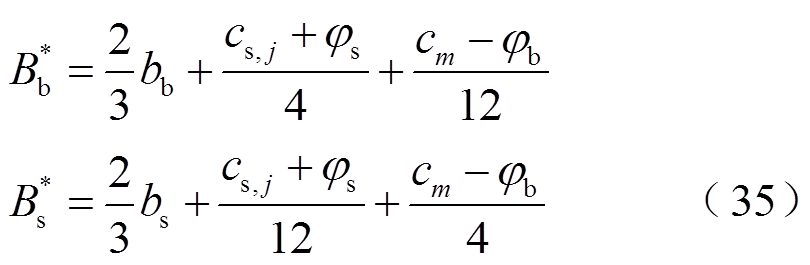
若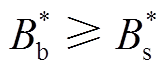 ,聚合商与充电桩成功交易,充电桩共享电价为式(36);否则,交易失败,充电桩此时段不参与共享。统计成功交易的充电桩数量Numm,即为t时刻聚合商Am的代理充电桩数量,见式(37)。其中,
,聚合商与充电桩成功交易,充电桩共享电价为式(36);否则,交易失败,充电桩此时段不参与共享。统计成功交易的充电桩数量Numm,即为t时刻聚合商Am的代理充电桩数量,见式(37)。其中,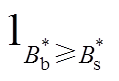 表示当
表示当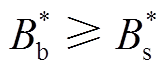 成立,值为1,否则为0。
成立,值为1,否则为0。
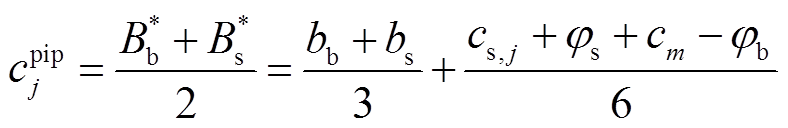 (36)
(36)
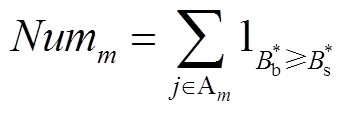 (37)
(37)
3.1.2 基于最小费用最大流模型的车桩匹配策略
聚合商与充电桩在时刻t完成定价博弈后,立刻向共享匹配中心上传代理充电桩数Numm、EV充电电价cm。若所提出的匹配列表无法令EV用户满意,EV用户有可能不接受共享匹配中心给出的匹配方案,导致方案失效。为激励EV用户接受方案,共享匹配中心优先考虑EV的需求,以车桩成功匹配对数最多为首要目标、EV用户总充电成本最优为次要目标,对车桩进行匹配,引导EV用户充电。
本文将车桩匹配问题抽象为有向网络流图G=(V,E,Cap,Cost),如图3所示,其中V、E、Cap、Cost分别为图的点、边、边容量、边费用。
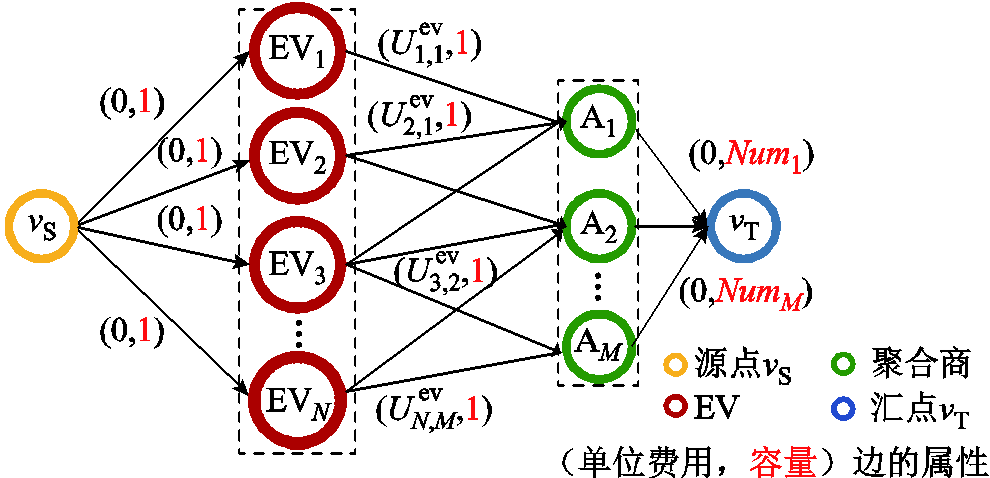
图3 EV与聚合商充电匹配电网络流图
Fig.3 Network flow chart of EVs charging matching with aggregators
点集V分为三类:①源点vS、汇点vT;②N个EV用户节点EVi;③M个充电桩聚合商节点Am。
边集E分为三类:①N条由源点流向EV用户节点的边E(vS,EVi),容量均为1,限制了每个EV用户最多匹配一个聚合商,单位费用均为0;②仅当ei,m=1,EV用户节点EVi与聚合商节点Am连边,即边E(EVi,Am),容量均为1,保证EVi最多匹配聚合商Am所代理的一台充电桩,单位费用为充电费用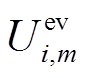 ;③M条由聚合商节点流向汇点的边E(Am, vT),容量为Numm,约束聚合商Am最多匹配Numm个EV用户,单位费用均为0。
;③M条由聚合商节点流向汇点的边E(Am, vT),容量为Numm,约束聚合商Am最多匹配Numm个EV用户,单位费用均为0。
通过图论中最小费用最大流模型将车桩匹配问题建模成双目标整数线性规划问题:车桩匹配对数最多,等价为网络流图G中从源点vS输送到汇点vT的最大可行流Maxflow,作为优化的主要目标FirstObj;在保证FirstObj最优的条件下,优化次要目标SecondObj,即EV用户总成本最小,等价为输送流量Maxflow最大时的最小费用fev,数学优化模型为
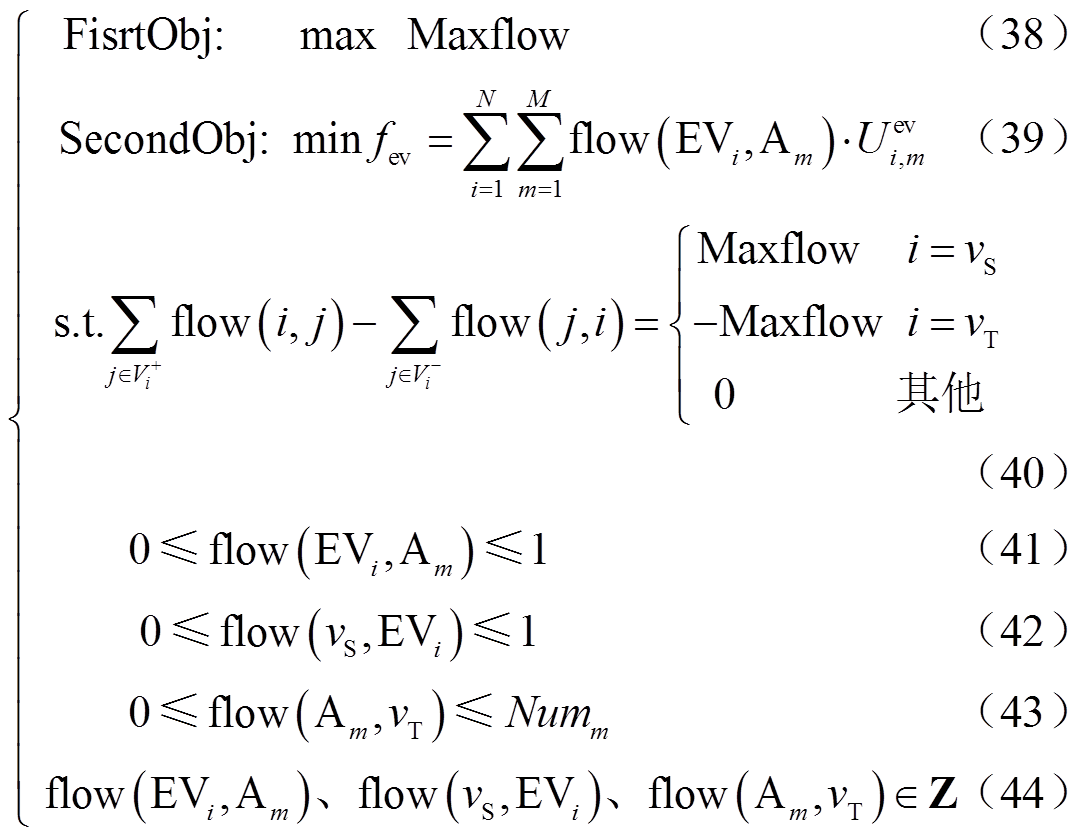
式中,flow(i,j)为从节点i流向节点j的实际流量;式(40)为节点流量平衡,源点vS流出流量、汇点vT流入流量均等于Maxflow,其余节点流入流量等于流出流量,其中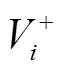 为以节点i为起点的边集、
为以节点i为起点的边集、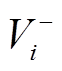 为以节点i为终点的边集;式(41)~式(43)是网络流的容量约束,边上流量不得超过容量;式(44)表示流量为整数变量,Z为整数集。
为以节点i为终点的边集;式(41)~式(43)是网络流的容量约束,边上流量不得超过容量;式(44)表示流量为整数变量,Z为整数集。
主从博弈求解常用方法如KKT(Karush-Kuhn-Tucker)条件将从体模型转换为主体模型的约束条件,将主从博弈模型转换为一类含非线性互补条件的均衡约束数学规划问题,从双层规划问题转变为求解单层规划问题。但由于本文从体模型中最小费用最大流模型存在大量整数变量,导致不满足转KKT的前提条件——regularity条件,即无法保证单层的最优解与原问题的最优解的等价性。因此本文采用双层迭代方法。依次求解主体、从体模型,博弈主从双方针对对方实施的策略,重新计算自身策略来回应,双方的策略耦合并不断迭代,直到形成一个不动点,此时达到Stackelberg均衡点,停止求解,基于此时的稳定策略来完成车桩网调度。博弈均衡解存在性证明[24]见附录。
本文博弈主体配电网调度中心优化模型为二阶锥模型,可调用Gurobi等商业求解器[25]来求解配电网各节点分布式燃汽轮机组最优出力,并获取约束相对应的对偶因子,以此制定各节点LMP。
博弈从体中,由式(38)~式(44)可知车桩匹配模型是一个整数规划问题,一般做法可直接调用Gurobi求解。但由本文3.1.2节可知,该车桩匹配问题可以用图论最短路最大流方法求解。因此,本文提出基于Bellman-Ford增广路算法的Ford-Fulkerson最大流算法求解车桩匹配问题,通过Bellman-Ford算法在图中寻找一条最小费用路径,对路径所有边的容量减去路径流量(新图简称“容量残余图”),基于Ford-Fulkerson最大流算法不断搜寻最小费用路径,修正边的容量,更新容量残余图,直至无法找到一条增广路径,完成全部EV充电匹配。具体博弈求解算法流程如图4所示。
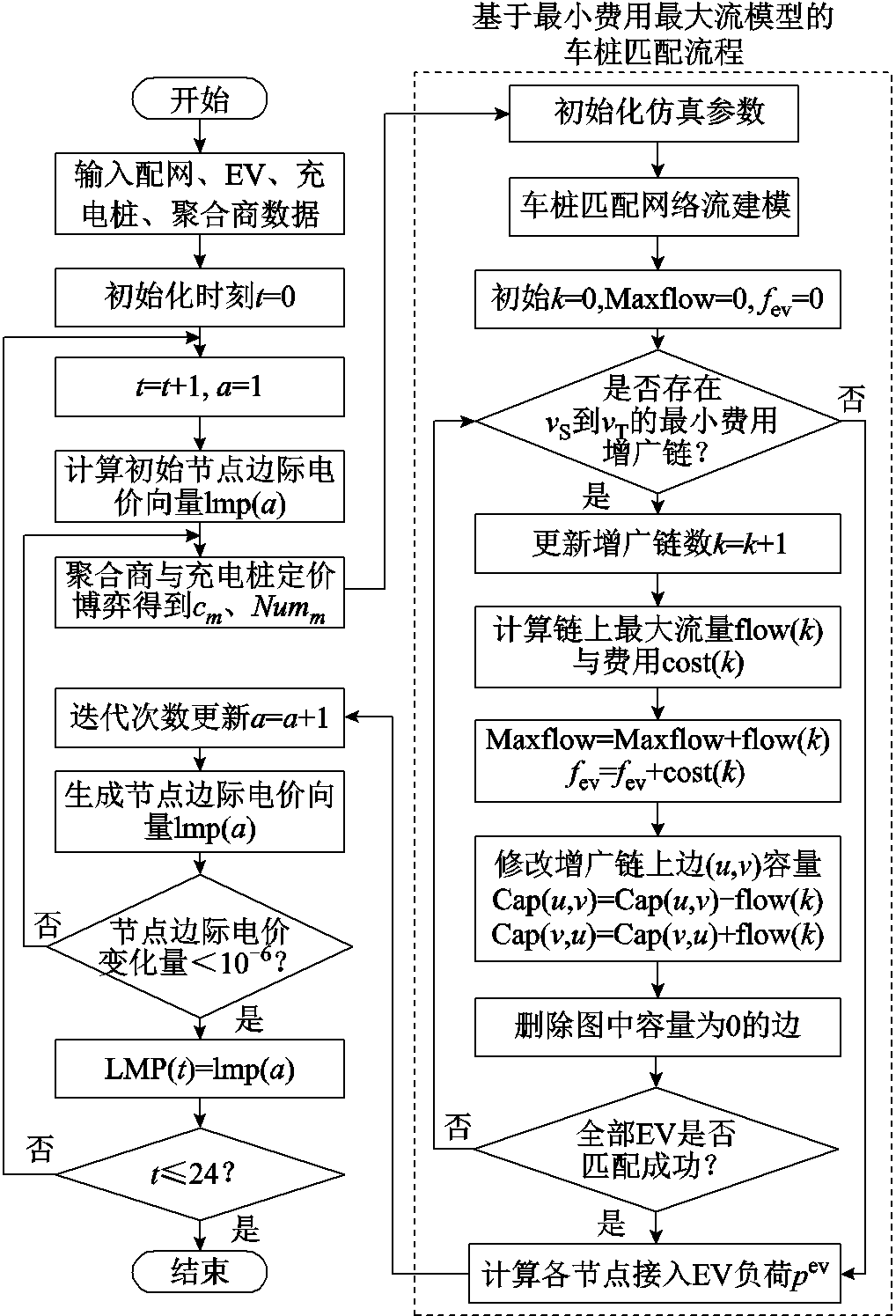
图4 Stackelberg博弈双层迭代求解流程
Fig.4 Flow chart of Stackelberg game bilevel iterative solution
本文选用改进的34节点-55路段的城市交通网[9]与IEEE 33节点配电网构造电力-交通耦合网络,网络拓扑结构如图5所示。
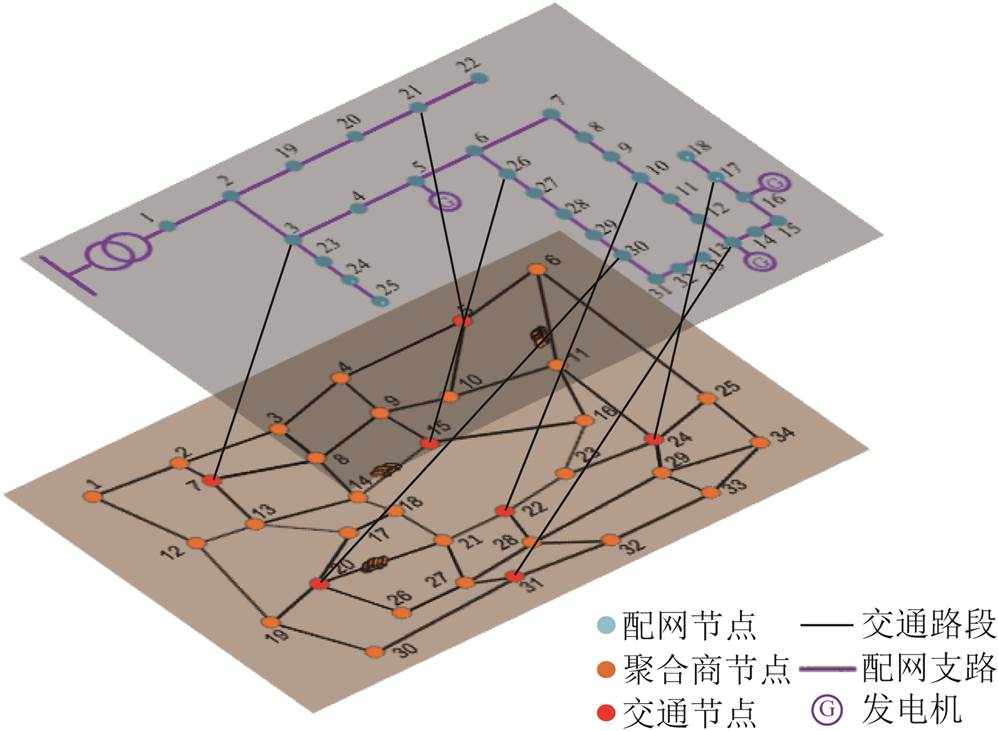
图5 电力-交通耦合网络
Fig.5 Coupled power-transportation network
交通节点与配电网节点的连接关系见附表1。采用的实验系统配置为Intel Core i5-8250U CPU 1.8 GHz,8 GB内存。各主体参数设置如下:
1)交通网:交通节点坐标见附表2。
2)配电网:仅配电网节点5、13、16存在分布式燃汽轮机组,其有功出力的价格系数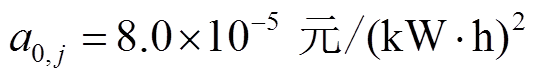 、
、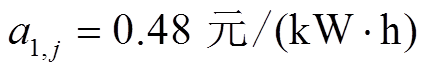 ,节点1与外网相连,协议电价ρi=0.896元/(kW·h);基准电压选取12.66 kV,基准功率为10 MW,以下潮流参数均为标幺值,电压幅值边界为
,节点1与外网相连,协议电价ρi=0.896元/(kW·h);基准电压选取12.66 kV,基准功率为10 MW,以下潮流参数均为标幺值,电压幅值边界为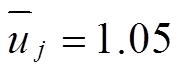 、
、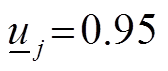 ,分布式燃汽轮机组功率边界为
,分布式燃汽轮机组功率边界为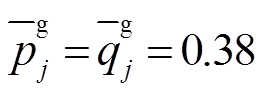 、
、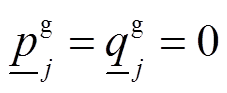 ,支路复功率幅值边界
,支路复功率幅值边界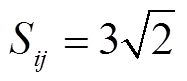 ;节点基础负荷
;节点基础负荷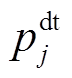 以IEEE 33节点负荷乘以随机数来模拟全天24 h各节点接入负荷大小,数据参考文献[26-28]并做修改。
以IEEE 33节点负荷乘以随机数来模拟全天24 h各节点接入负荷大小,数据参考文献[26-28]并做修改。
3)EV:参与匹配仿真的EV共6 000辆,按电池容量、额定功率、每百公里耗电量分为四种类型,详细数据见附表3;蒙特卡洛模拟每辆EV发起请求充电的时间、当前位置OE、目的地DE、电池荷电状态SOCo、期望荷电状态SOCE、EV平均行驶速度均为30 km/h。
4)充电桩:充电桩总计765个,分布在7个交通节点下。值得注意的是,实际中聚合商完全可以代理不同交通或配电网节点的充电桩,由于本文不考虑聚合商之间的竞争,充电桩产生的收益只和充电桩相关,即无论由哪个聚合商代理桩收益都相同。为使算例更直观,设定一个交通节点处的充电桩由同一个聚合商代理,对仿真分析无影响。具体分布数据见表2。假设向共享匹配中心上报共享时段均为全天0:00—24:00,电池抵触系数均为αj=0.000 3元/ (kW·h)2,预测允许的最低报价、最高报价cmin=1元/ (kW·h)、cmax=2元/(kW·h)。
表2 充电桩参数与位置分布
Tab.2 The parameters and distribution of charging piles
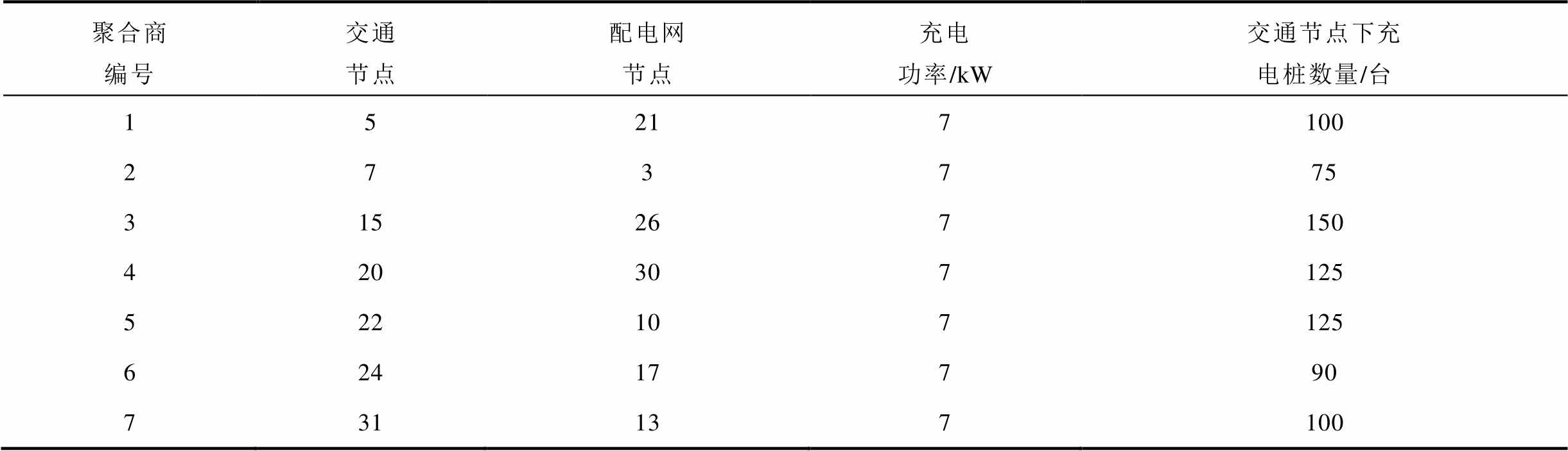
聚合商编号交通节点配电网节点充电功率/kW交通节点下充电桩数量/台 15217100 273775 315267150 420307125 522107125 62417790 731137100
为验证所提匹配策略的可行性,本文设置四组场景对比分析:
场景1:EV无序充电,配电网按照分时电价确定充电价格,EV不接受共享匹配中心引导,直接前往充电成本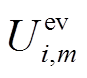 最小的聚合商处充电,分时电价参数见表3[29]。
最小的聚合商处充电,分时电价参数见表3[29]。
表3 分时电价
Tab.3 Time of use electricity price (单位:元/(kW·h))

类别时段从电网购电电价 峰平谷10:00—14:00;20:00—23:001.090 2 8:00—10:00;14:00—20:000.715 2 0:00—8:000.356 4
场景2:仅考虑上层配电网制定的节点边际电价引导,EV不接受共享匹配中心引导,直接前往EV充电成本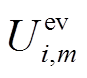 最优的聚合商处充电。
最优的聚合商处充电。
场景3:仅考虑下层车桩匹配,EV基于分时电价而非节点边际电价接受共享匹配中心引导充电。
场景4:基于本文提出的节点边际电价和Stackelberg主从博弈策略进行车桩匹配,引导EV充电。
24h内聚合商成功匹配EV数量如图6所示,统计得到四种场景下的车桩匹配总数分别为:4 648、5 004、5 195、5 195。基于本文所提策略,EV成功充电数量比前两种场景分别多了547辆、191辆。其中,805辆EV的剩余SOC足够支撑到目的地,无充电需求。
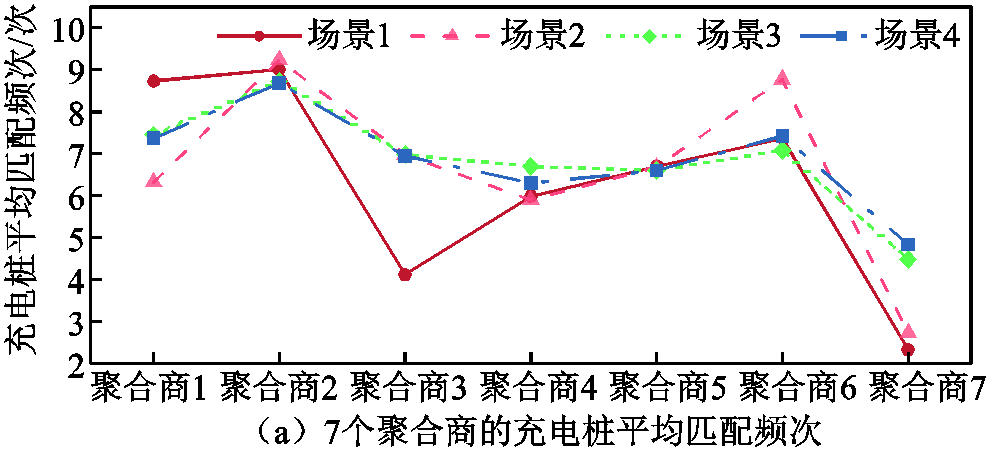
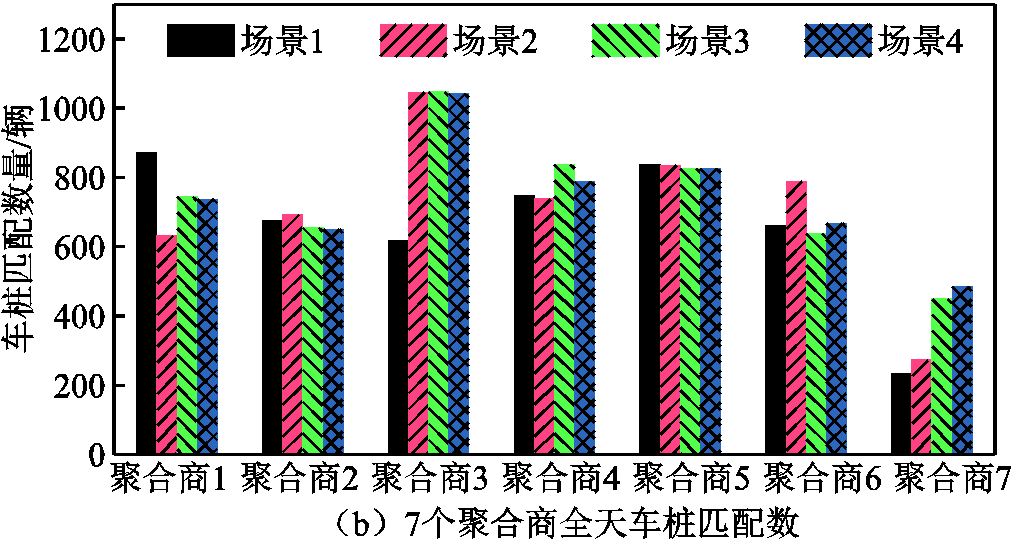
图6 车桩匹配数与充电桩平均匹配频次
Fig.6 Matching number of vehicles and average matching frequency of charging piles
1)LMP对充电桩共享的影响
结合图5、图6,以聚合商4、7作分析。聚合商4、7所处位置靠近,但聚合商7处于城市边缘,聚合商4靠近城市中心地带,EV用户多选择聚合商4充电,导致聚合商7的充电桩平均匹配频次非常低。图6b中,对比场景3,场景4在LMP引导下,令部分EV增加绕路距离,放弃了充电价格高的聚合商4,前往聚合商7充电。可见,LMP提高了聚合商7处充电桩利用率。另一方面,根据图6a,各场景下聚合商代理充电桩平均匹配频次的标准差分别为2.24、1.97、1.17、1.09。对比场景1、2或场景3、4,可见考虑LMP的场景标准差都小于不考虑LMP的场景,反映了LMP使不同充电桩的利用率更加均衡,提高了聚合商、充电桩参与共享的积极性。
2)最小费用最大流对车桩匹配的影响
场景1、2的匹配成功总数低于场景3、4,归因于EV用户不接受匹配,造成部分充电桩忙碌、部分充电桩空闲。以场景1、4中聚合商1、聚合商3的匹配为例,具体情况如图7所示。场景1中,EV用户不接受匹配中心调度,选择充电成本最小的聚合商充电,造成大量EV前往聚合商1处充电,而聚合商1处有共享充电桩100个,所有充电桩在6:00—24:00均处于忙碌状态,请求充电的EV数量大于空闲桩数,大量EV匹配失败,只能在聚合商处等待充电;而聚合商3拥有150个共享充电桩,几乎全天存在充电桩空闲。相反,场景4通过最小费用最大流模型的匹配策略,引导场景1中前往聚合商1充电的部分EV用户前往聚合商3处充电,提高了聚合商3下闲置充电桩的利用率和车桩总匹配数量。
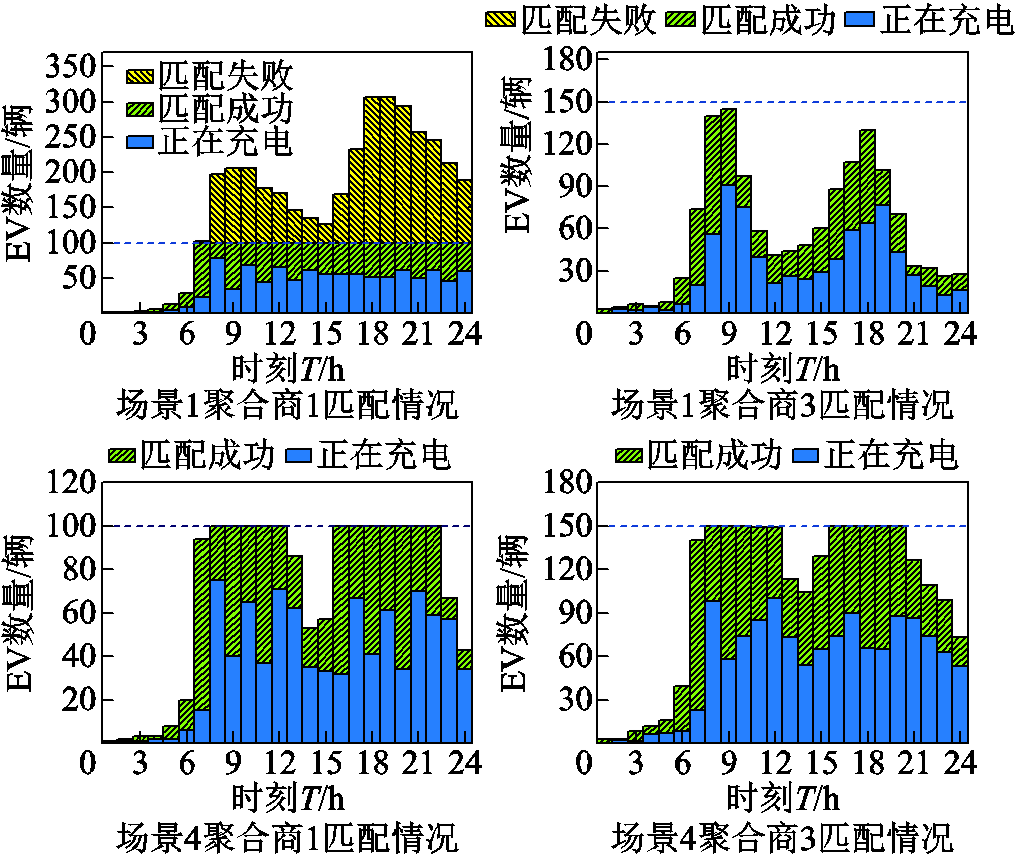
图7 场景1、4中聚合商1、3匹配情况对比
Fig.7 Comparison of the matching of aggregate quotients 1 and 3 in scenarios 1 and 4
为进一步比较不同场景策略的优劣,采用TOPSIS(Technique for Order Preference by Similarity to Ideal Solution)[30-32]法对各场景车桩匹配状况进行综合评价,各场景优化的目标主要为各主体的成本收益与车桩匹配对数。考虑博弈主体地位平等,设置各优化目标的权重相等,引入接近度刻画各场景方案与理想方案的接近程度,值越大越接近理想方案,则方案越优,接近度计算结果见表4。
表4 各场景的车-桩-网各主体成本收益
Tab.4 The cost and benefit of each subject of vehicle-pile-net in each scenario
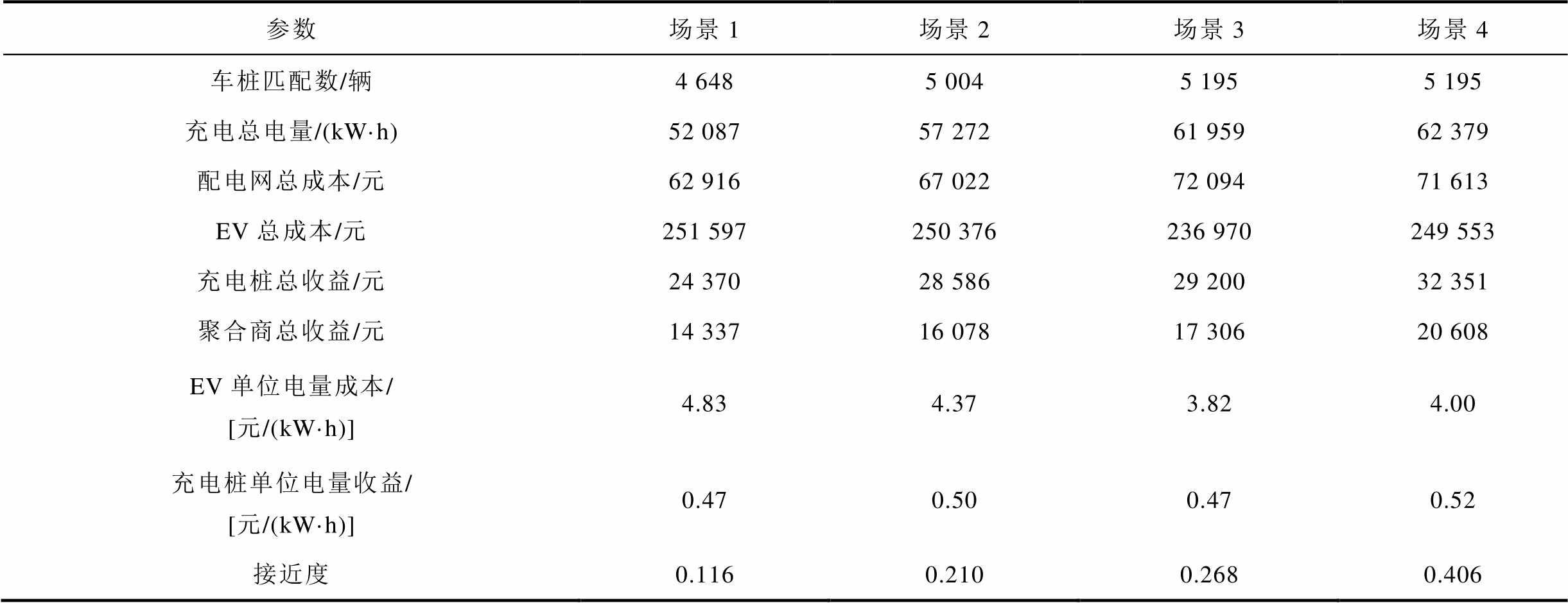
参数场景1场景2场景3场景4 车桩匹配数/辆4 6485 0045 1955 195 充电总电量/(kW·h)52 08757 27261 95962 379 配电网总成本/元62 91667 02272 09471 613 EV总成本/元251 597250 376236 970249 553 充电桩总收益/元24 37028 58629 20032 351 聚合商总收益/元14 33716 07817 30620 608 EV单位电量成本/ [元/(kW·h)]4.834.373.824.00 充电桩单位电量收益/[元/(kW·h)]0.470.500.470.52 接近度0.1160.2100.2680.406
注:EV单位电量成本=EV总成本/充电总电量;充电桩单位电量收益=充电桩总收益/充电总电量。
3)主体博弈对成本收益的影响
四种场景下配电网、车、桩、聚合商各主体的成本或收益数值见表4。场景3、4,两者均接受共享匹配中心引导。
由表4可知,场景4考虑节点边际电价,使EV充电负荷分布更加均衡,降低了配电网成本。结合表5可知,由于充电电量增加,造成EV充电经济成本增加,同时,充电桩、聚合商的总收益增加。虽然场景4中EV总成本高于场景3,但两种场景的EV单位电量成本相差不大,能被EV用户接受。且通过TOPSIS法分析对比各场景,场景4的接近度高于场景3,证明了场景4的方案优于场景3。由此可得,考虑配电网节点边际电价策略的主体模型有助于降低配电网成本,提高充电桩和聚合商收益。
表5 各场景的EV总成本的组成
Tab.5 Composition of EV total cost for each scenario

成本场景1场景2场景3场景4 充电距离成本/元13 52521 59920 96321 397 充电时间成本/元160 283139 198122 510122 750 充电经济成本/元77 78989 57993 497105 406
4)从体博弈对成本收益的影响
对比场景2和场景4,配电网均以节点边际电价定价,区别在于是否接受共享匹配中心引导充电,由表4、表5对比得到对四个主体不同的影响:①对于充电桩、聚合商来说,场景2中EV用户增加了行驶距离,前往电价低的聚合商处充电,使充电经济成本得到下降,从而引起充电桩、聚合商总收益下降;②EV用户虽然充电经济成本下降了16 000元左右,但由于发生了严重的充电拥挤现象,场景2的充电时间成本比场景4高出了16 500元左右,EV总成本高了823元;③对于配电网,总成本下降了4 591元,归因于其车桩匹配数辆少于场景4,EV充电总量减少。采用TOPSIS法综合比较各目标,场景4的接近度大大高于场景2。综上所述,引入从体模型分析充电桩共享匹配问题是有必要的。
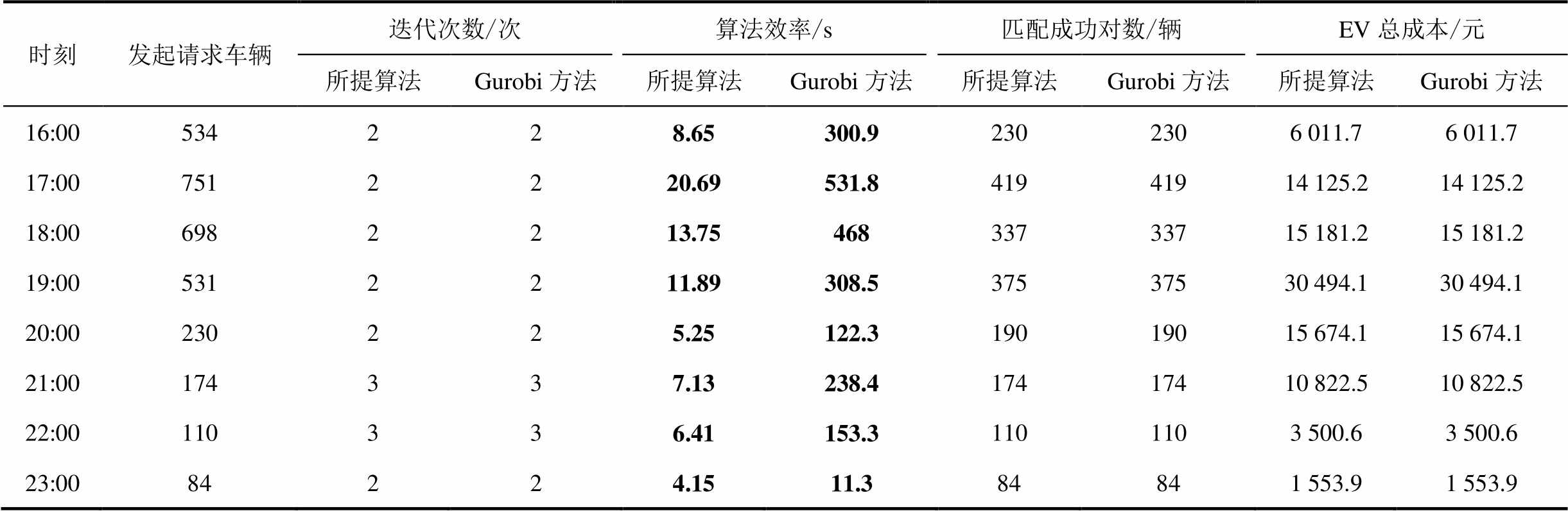
由3.2节可知,本文主体博弈二阶锥模型直接调用Gurobi求解,而从体博弈模型采用基于Bellman-Ford增广路算法的Ford-Fulkerson最大流算法求解。为了验证本文所提算法的性能,引入双层均采用Gurobi求解的迭代方法(以下简称“Gurobi方法”)进行对比分析,仿真结果见附表4。由附表4可知,两种算法在任一时刻的优化结果均相同,求解迭代次数也相同且不超过4次,两者都有较好的收敛性,这表明了本文所提求解方法的有效性。此外,相比Gurobi方法,本文求解方法用时更短,更能满足车桩实时匹配对计算速率的要求。
12:00时刻配电网调度中心与共享匹配中心进行博弈的具体收敛过程如图8所示,设置迭代次数15次,图8a、图8b分别为配电网购电成本、EV总成本收敛曲线,可见,前后两次误差逐渐减小,当迭代3次之后,迭代误差、配电网运营成本、EV总成本均收敛到固定值,迭代15次后结束迭代。此时,配电网得到最优成本下的发电计划与各节点边际电价,共享匹配中心得到车桩最优匹配方案,配电网中心最优运营成本收敛到3 449.6元,EV最优总成本收敛到7 702.04元,也进一步证实了本文提出的匹配策略存在均衡点、所提算法存在快速收敛的特性。
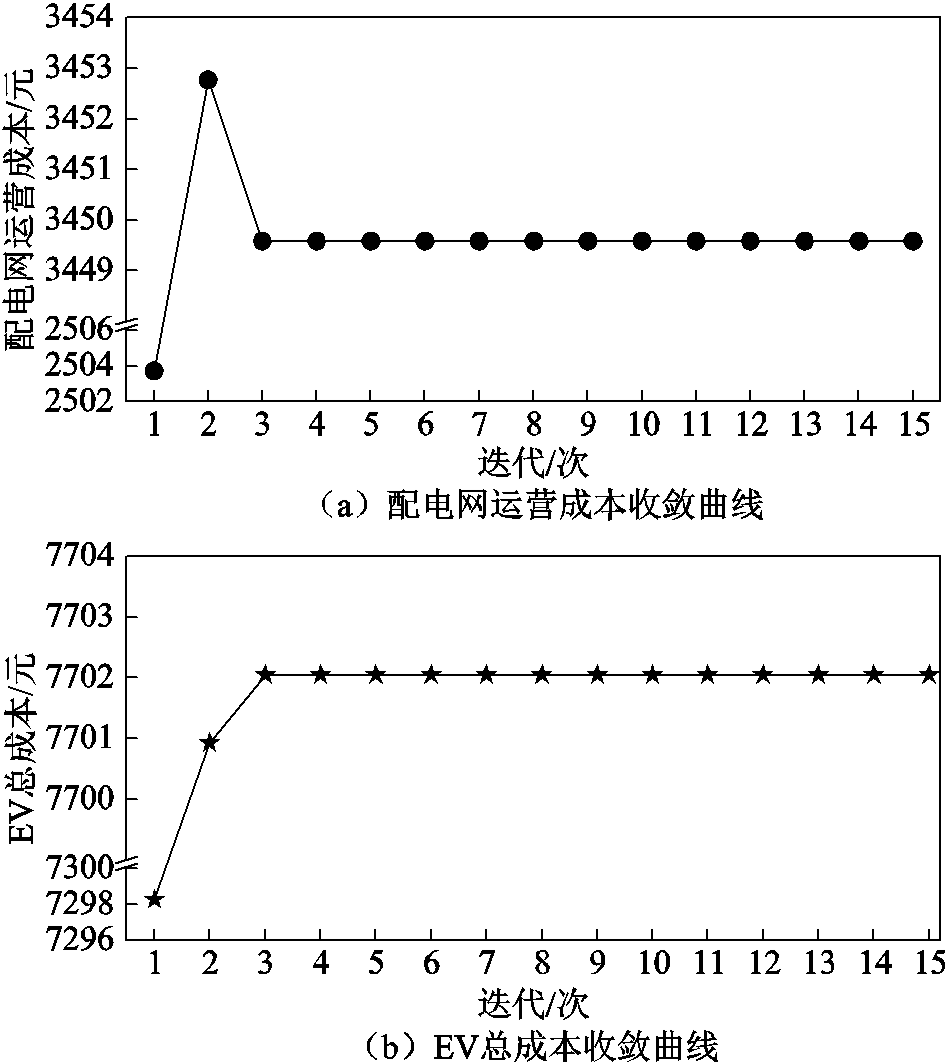
图8 12:00pm时,配电网与EV博弈过程中成本收敛曲线
Fig.8 At 12:00pm, the cost convergence curve in the process of distribution network and EVs game
为验证本文所提算法的普适性,即同时发出充电申请的EV规模大小不影响算法的有效性,对比EV规模为100、1 000、5 000、10 000辆时算法运行效率,结果见表6。
表6 不同EV规模下算法求解时间
Tab.6 Computational time of algorithms in different scale EVs

EV规模/辆求解时间 本文所提算法/sGurobi方法 100513.1 s 1 00040.3737 s 5 000252.8>4 h 10 000907.3>4 h
由表6可见,在求解大规模EV匹配问题时,随着EV规模进一步扩大(不少于5 000辆),Gurobi方法出现长时间无法收敛的情况,当求解时间超4 h时内存溢出。但是,即使EV规模为10 000辆时,本文所提求解算法仍能正常求解,且求解时间在900 s左右,这进一步说明了本文所提算法在处理大规模EV匹配场景中的有效性。
本节比较了场景3、场景4下各时段的配电网网损,结果见附图1。场景4中配电网各时段网损都较低,特别在负荷高峰期(9:00—11:00),网损明显少于场景3。归因于场景4考虑LMP来引导EV负荷空间转移,如图9所示,场景4中11:00时聚合商4处节点边际电价远高于聚合商6、7处电价,使得部分EV负荷(场景3中选择聚合商4)改变不考虑LMP时的充电选择,前往聚合商6、7处充电。在一定程度上调整有功分布平衡,有效降低负荷高峰期配电网网损。
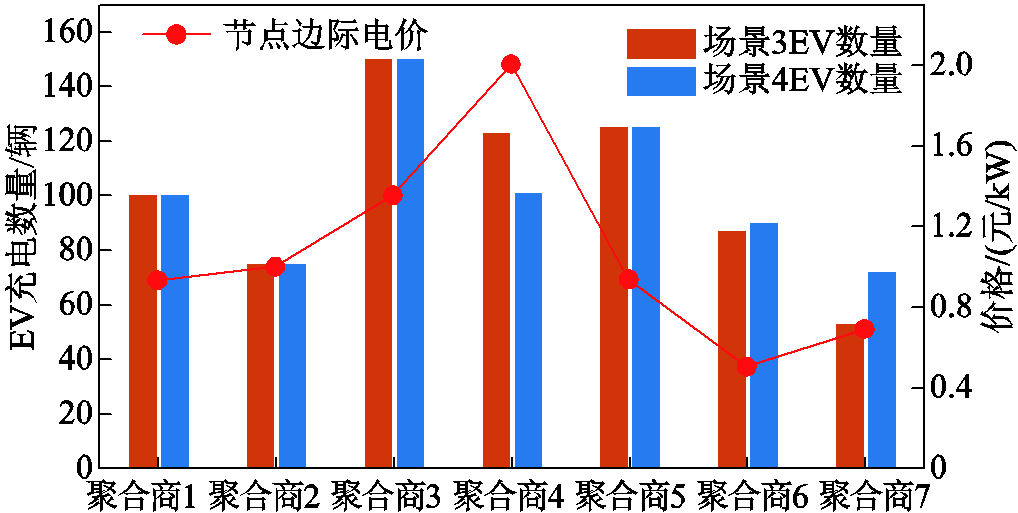
图9 11:00时,EV负荷与节点边际电价的空间分布
Fig.9 At 11:00, the spatial distribution of EV loads and LMP
附图2给出了场景3、场景4下配电网节点电压分布情况。两种场景的电压质量均在安全运行范围内。两种场景9:00时节点33的电压标幺值最低,电压标幺值分别为0.95、0.954,场景4的电压跌落略少于场景3。两种场景下配电网潮流优化结果见表7。结合表7可知,场景4的日电压偏移量累计值较场景3减少了0.39(pu),全天网损比场景4减少了1 MW·h左右。显然,在LMP作用下,配电网潮流得到了优化,这在一定程度上提高配电网电能质量并降低购电成本。因此,LMP有助于配电网安全经济运行。
表7 两种场景下配电网潮流优化结果
Tab.7 Optimization results of distribution power flow in two scenarios

场景总有功网损/ (kW·h)日电压偏移量累计值(pu)日电压偏移量累计值= 场景36 035.114.55 场景45 064.5414.16
本文针对网、车、桩、聚合商多主体共赢的充电桩共享问题展开研究,提出了多主体博弈共赢的电动汽车充电桩共享方法。得到以下主要结论:
1)基于Stackeleberg主从博弈的车桩匹配策略能大大提高共享充电桩的匹配成功数量,使各充电桩、同一充电桩不同时段利用率更加均衡,避免了部分充电桩使用过于频繁而部分充电桩闲置的情况,对于解决当前阻碍电动汽车和充电基础设施发展的瓶颈问题具有一定工程价值。
2)本文提出的充电桩共享策略能增加充电桩、聚合商的收益,降低EV用户成本,且有助于配电网降低网损、减小电压偏差,对各方均有益。
3)基于图论理论将车桩匹配问题转换为最小费用最大流模型,提出基于Bellman-Ford增广路算法的Ford-Fulkerson最大流算法求解该模型。相比于传统方法,所提双层迭代算法提高了求解效率。通过仿真,进一步验证了所提算法在大规模EV匹配问题中仍具有较高求解效率。
需要指出的是,本文研究节点边际电价引导负荷空间转移时重点分析其对经济调度问题的影响,尚未考虑配电网重构的影响;此外,本文忽略了聚合商之间的竞争,未来研究中将基于非合作博弈理论解决聚合商合作竞争问题。
1. 潮流约束二阶锥松弛
潮流模型中含有大量二次项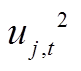 、
、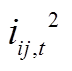 ,对目标函数的求解带来困难,使用一次项变量Uj,t、Iij,t替换
,对目标函数的求解带来困难,使用一次项变量Uj,t、Iij,t替换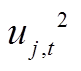 、
、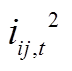 ,则式(2)~式(6)修正为
,则式(2)~式(6)修正为
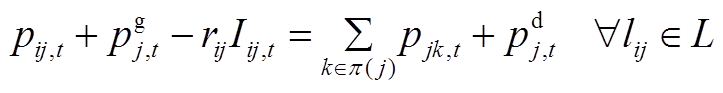 (A1)
(A1)
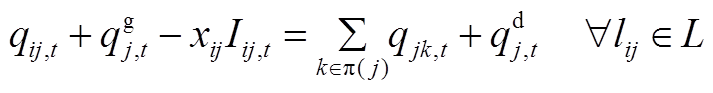 (A2)
(A2)
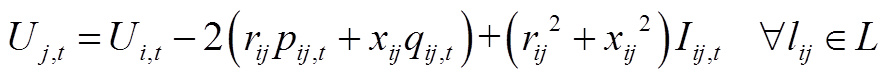 (A3)
(A3)
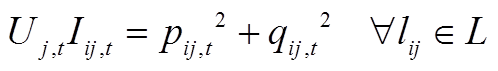 (A4)
(A4)
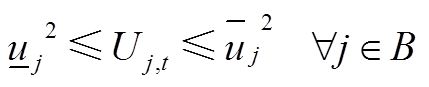 (A5)
(A5)
式(A4)为二阶非凸等式,通过将其松弛为二阶锥不等式,以便于商业求解器求解,具体过程为
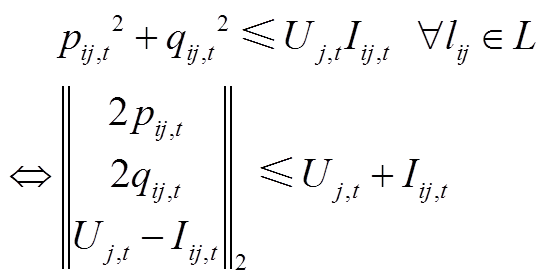 (A6)
(A6)
2. 配电网购电成本函数的拉格朗日函数公式
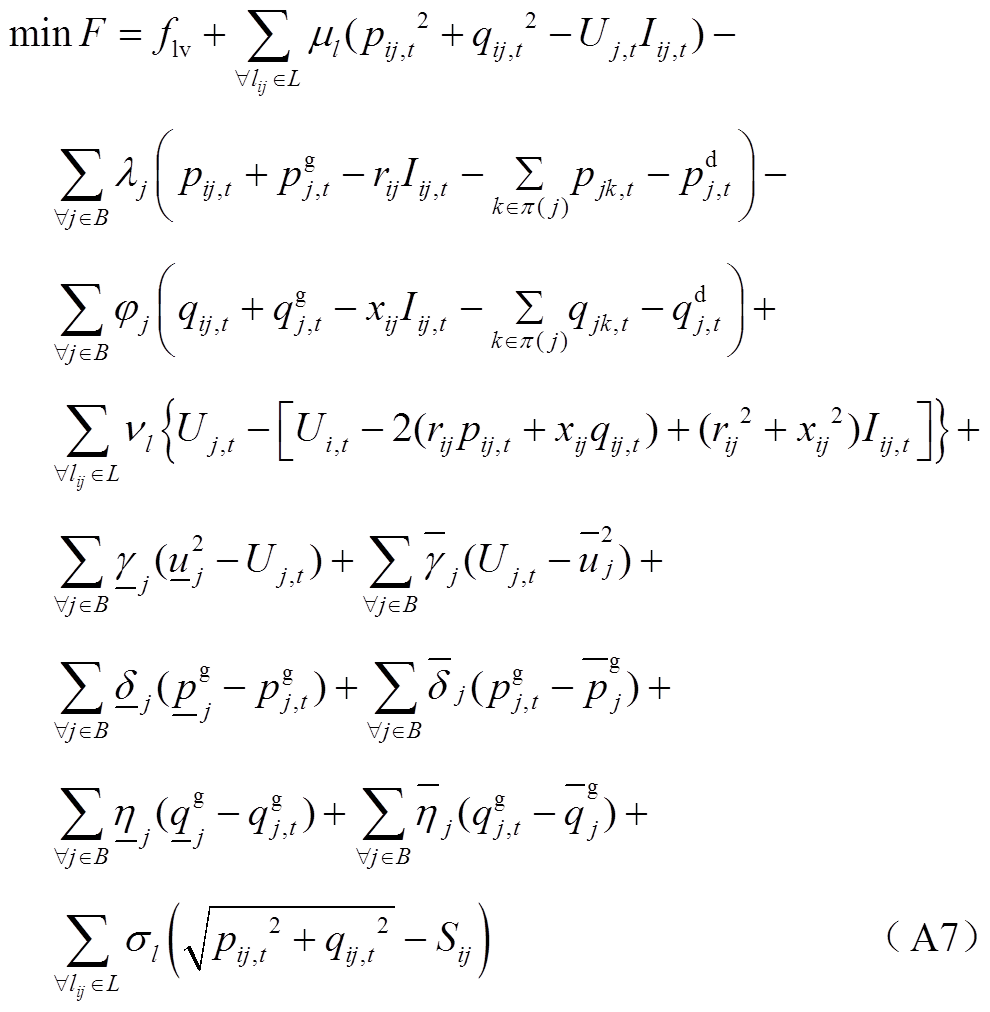
式中,μl、λ、φ、νl、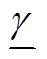 、
、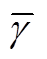 、δ、
、δ、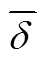 、
、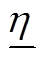 、
、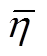 、σl分别为对应潮流约束的拉格朗日乘子。
、σl分别为对应潮流约束的拉格朗日乘子。
3. 博弈均衡解存在性证明
当Stackelberg博弈Г满足以下条件时,其博弈均衡解存在。
条件1:策略集LMP、pev均为关于其欧式空间的非空、凸的、有界的子集。
条件2:flv是关于LMP、pev的连续函数。
条件3:fev、Upip、UA是关于LMP、pev的连续函数。
条件4:fev是关于LMP、pev的拟凹函数,Upip、UA是关于LMP、pev的拟凸函数。
配电网成本flv由式(A7)计算得到,显然LMP、pev满足条件1,flv关于LMP、pev连续,条件2易证。
式(38)、式(22)、式(23)中,fev、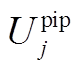 、UA均为关于LMP、cm、Qij的一次函数,因pev为各节点下EV充电量Qij的线性和,cm与LMP呈线性关系,所以fev、UA均为LMP、pev的线性连续函数,线性函数既是凸函数,又是凹函数,可证fev是关于LMP、pev的拟凹函数,UA是关于LMP、pev的拟凸函数。同理, Upip为LMP的一次函数,关于pev的二次凸函数,可证Upip是关于LMP、pev的拟凸函数,条件3、4成立。综上所述,证明了本文博弈Г的均衡解存在。
、UA均为关于LMP、cm、Qij的一次函数,因pev为各节点下EV充电量Qij的线性和,cm与LMP呈线性关系,所以fev、UA均为LMP、pev的线性连续函数,线性函数既是凸函数,又是凹函数,可证fev是关于LMP、pev的拟凹函数,UA是关于LMP、pev的拟凸函数。同理, Upip为LMP的一次函数,关于pev的二次凸函数,可证Upip是关于LMP、pev的拟凸函数,条件3、4成立。综上所述,证明了本文博弈Г的均衡解存在。
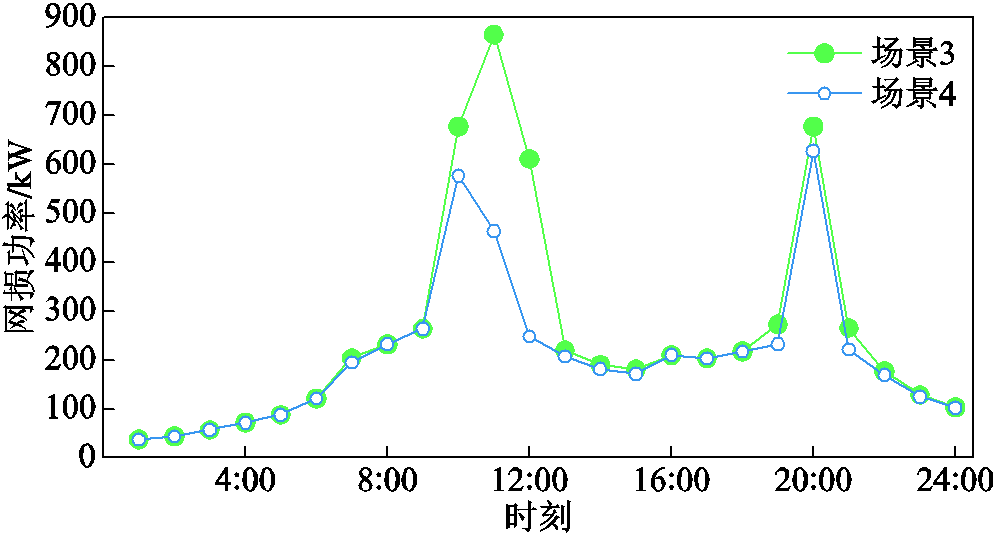
附图1 两种场景的有功网损功率对比
App.Fig. 1 Comparison of active power loss in two scenarios
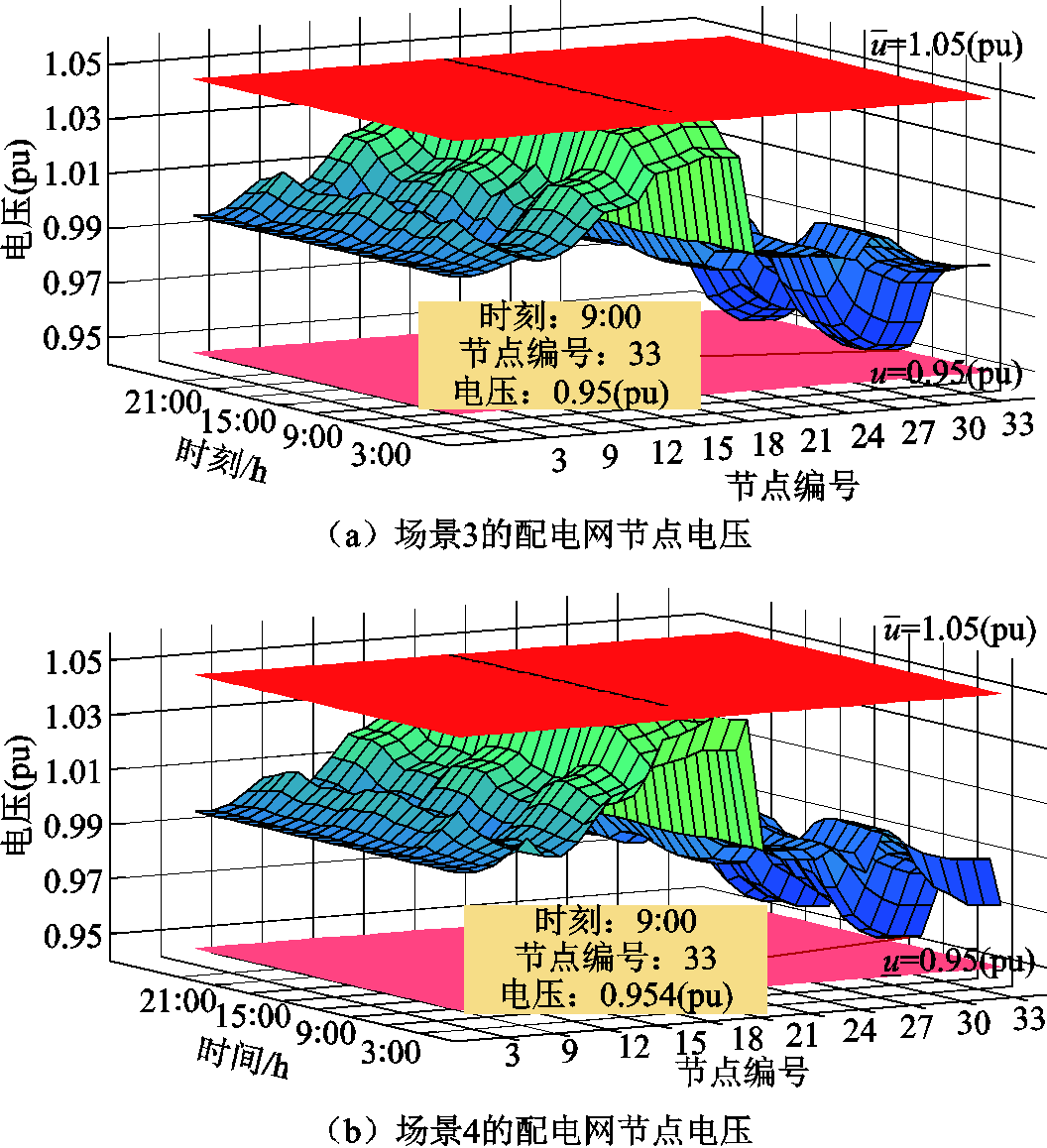
附图2 两种场景的配电网节点电压
App.Fig.2 Voltage of distribution network node in two scenarios
附表1 交通节点与配电网节点连接关系
App.Tab. 1 Connection relationship between traffic nodes and distribution network nodes

配电网节点交通网节点配电网节点交通网节点配电网节点交通网节点 1113312519 2214322615 3715332714 4816292818
(续)
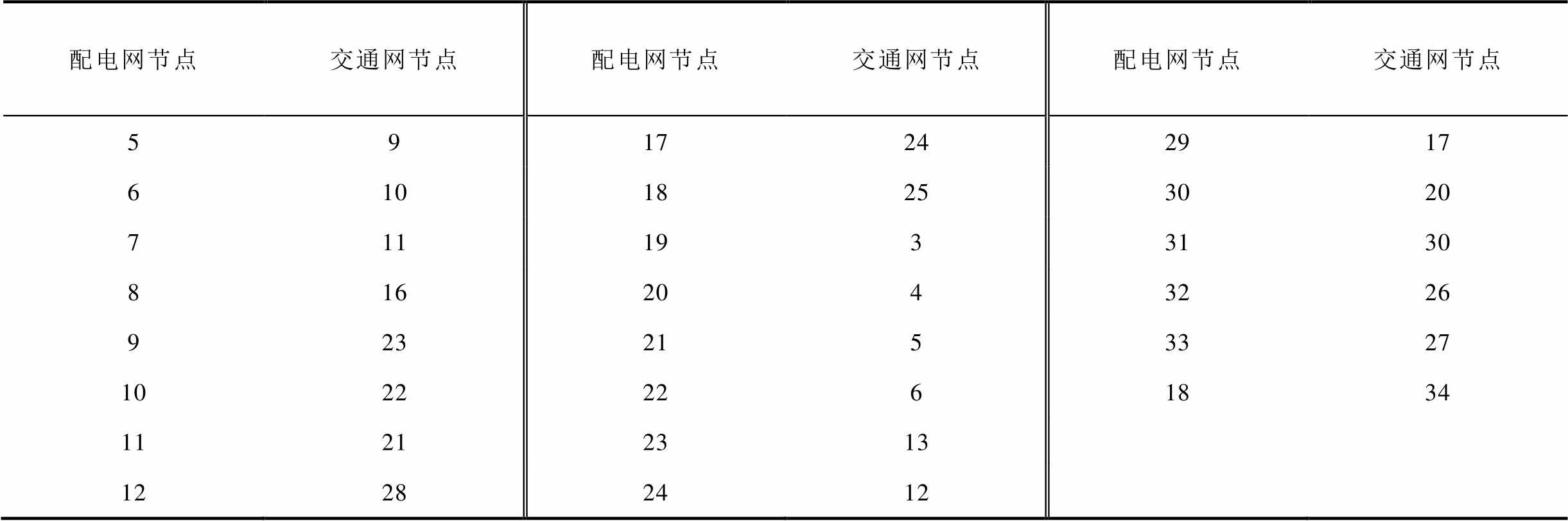
配电网节点交通网节点配电网节点交通网节点配电网节点交通网节点 5917242917 61018253020 7111933130 8162043226 9232153327 10222261834 11212313 12282412
附表2 改进的交通网节点坐标
App.Tab.2 Improved traffic network node coordinates
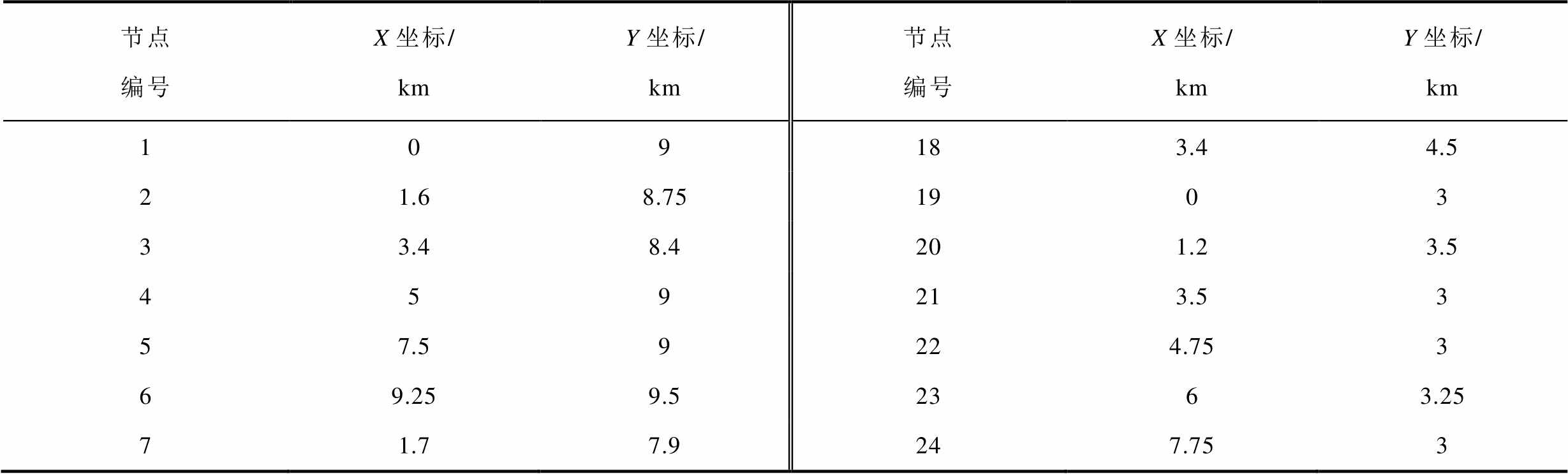
节点编号X坐标/ kmY坐标/ km节点编号X坐标/ kmY坐标/ km 109183.44.5 21.68.751903 33.48.4201.23.5 459213.53 57.59224.753 69.259.52363.25 71.77.9247.753
(续)
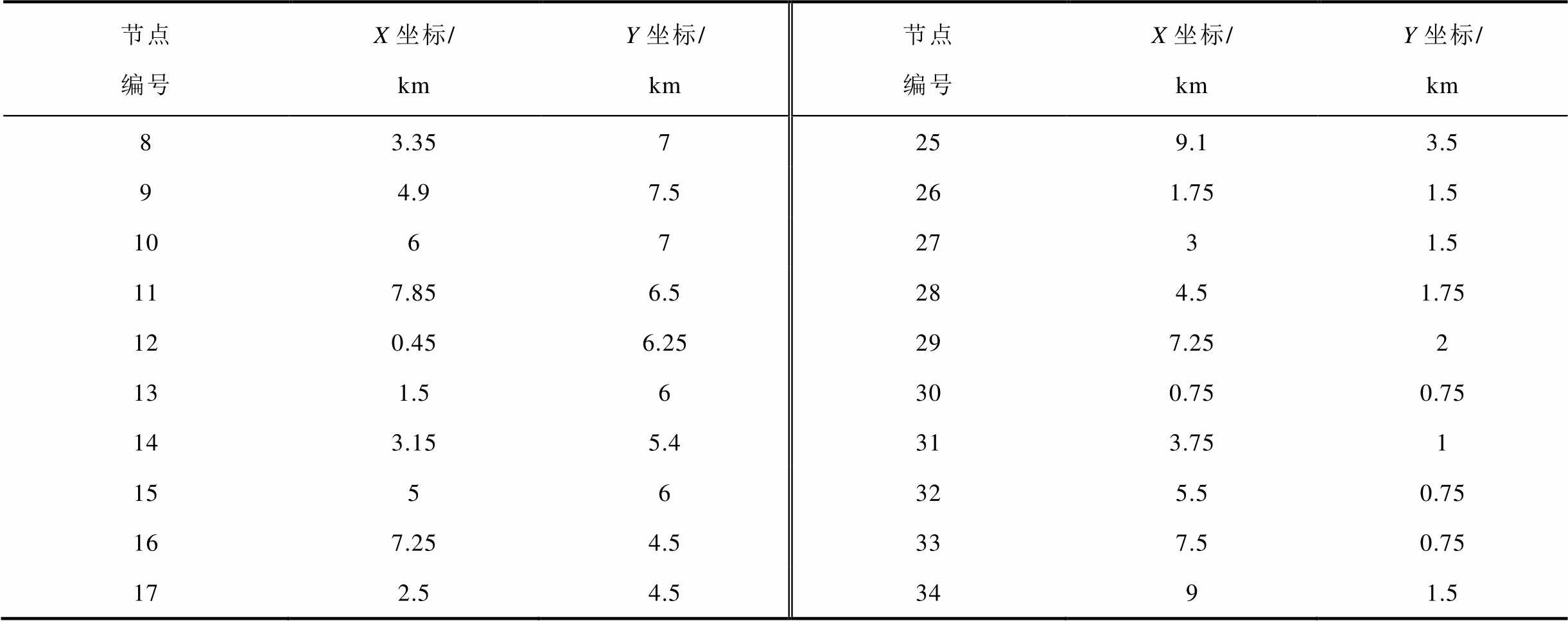
节点编号X坐标/ kmY坐标/ km节点编号X坐标/ kmY坐标/ km 83.357259.13.5 94.97.5261.751.5 10672731.5 117.856.5284.51.75 120.456.25297.252 131.56300.750.75 143.155.4313.751 1556325.50.75 167.254.5337.50.75 172.54.53491.5
附表3 4种EV的性能数据以及数量占比
App.Tab.3 Performance data and quantity proportion of four EVs
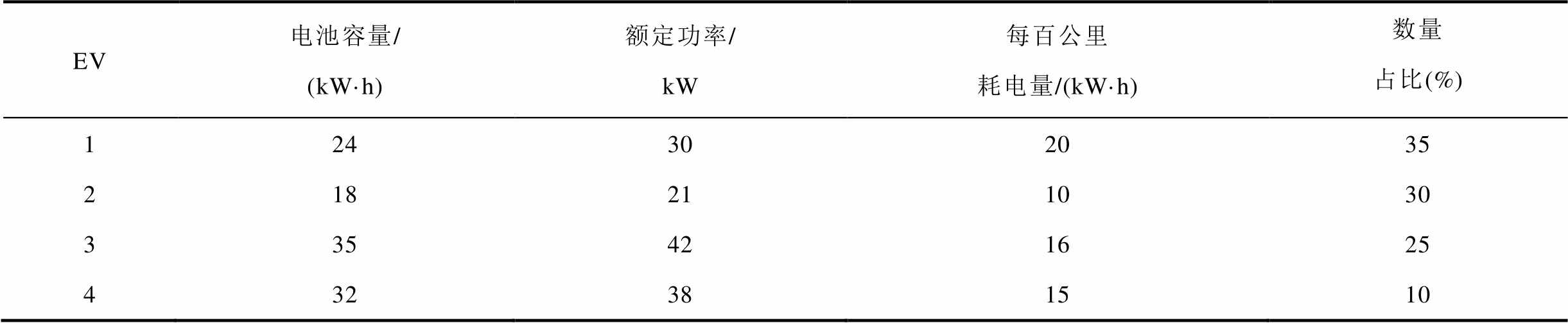
EV电池容量/ (kW·h)额定功率/ kW每百公里耗电量/(kW·h)数量占比(%) 124302035 218211030 335421625 432381510
附表4 不同算法求解时间和优化结果对比
App.Tab.4 Comparison of solution time and optimization results of different algorithm
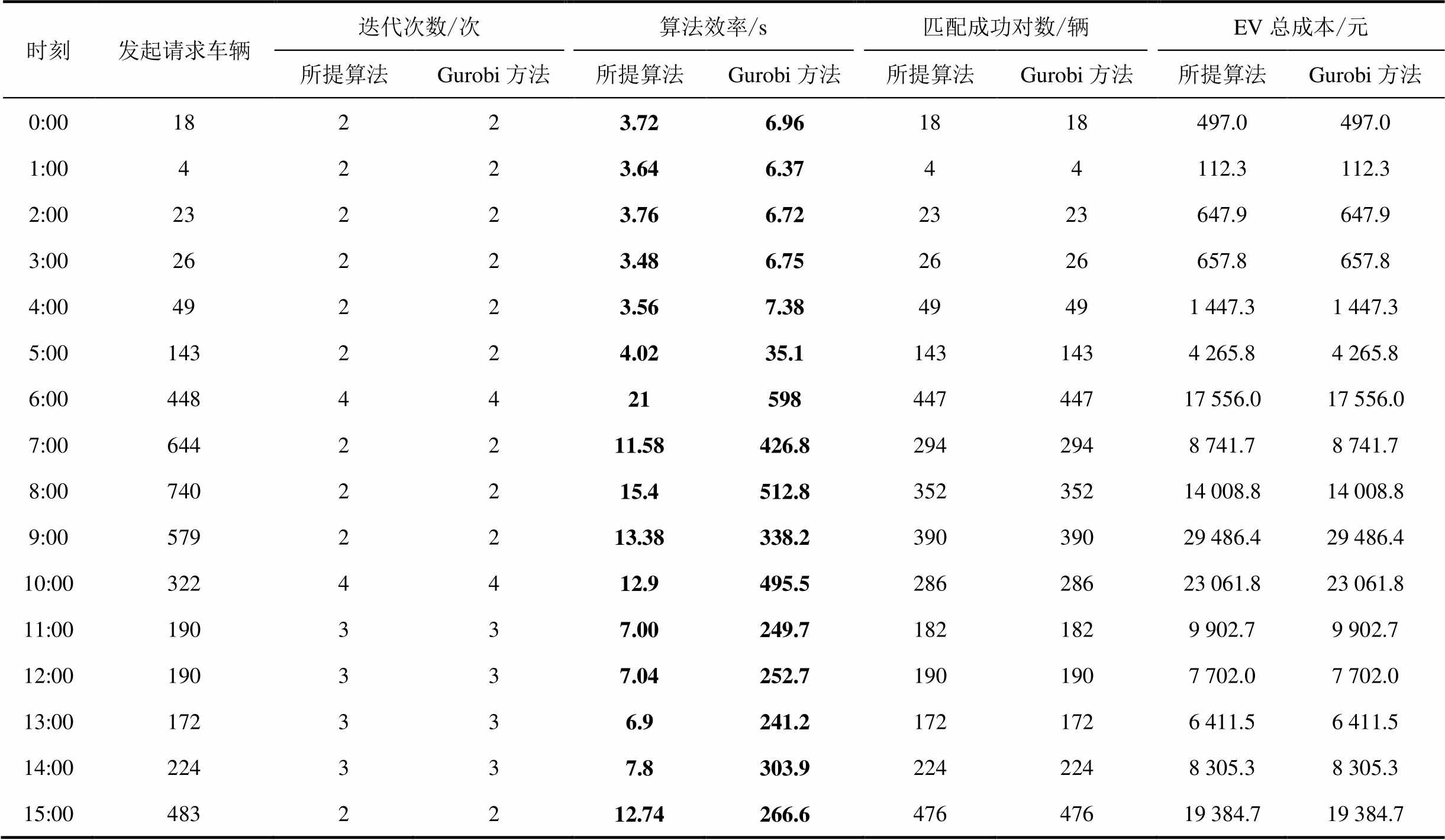
时刻发起请求车辆迭代次数/次算法效率/s匹配成功对数/辆EV总成本/元 所提算法Gurobi方法所提算法Gurobi方法所提算法Gurobi方法所提算法Gurobi方法 0:0018223.726.961818497.0 497.0 1:004223.646.3744112.3 112.3 2:0023223.766.722323647.9 647.9 3:0026223.486.752626657.8 657.8 4:0049223.567.3849491 447.3 1 447.3 5:00143224.0235.11431434 265.8 4 265.8 6:00448442159844744717 556.0 17 556.0 7:006442211.58426.82942948 741.7 8 741.7 8:007402215.4512.835235214 008.8 14 008.8 9:005792213.38338.239039029 486.4 29 486.4 10:003224412.9495.528628623 061.8 23 061.8 11:00190337.00 249.71821829 902.7 9 902.7 12:00190337.04252.71901907 702.0 7 702.0 13:00172336.9241.21721726 411.5 6 411.5 14:00224337.8303.92242248 305.3 8 305.3 15:004832212.74266.647647619 384.7 19 384.7
(续)
时刻发起请求车辆迭代次数/次算法效率/s匹配成功对数/辆EV总成本/元 所提算法Gurobi方法所提算法Gurobi方法所提算法Gurobi方法所提算法Gurobi方法 16:00534228.65300.92302306 011.7 6 011.7 17:007512220.69531.841941914 125.2 14 125.2 18:006982213.7546833733715 181.2 15 181.2 19:005312211.89308.537537530 494.1 30 494.1 20:00230225.25122.319019015 674.1 15 674.1 21:00174337.13238.417417410 822.5 10 822.5 22:00110336.41153.31101103 500.6 3 500.6 23:0084224.1511.384841 553.9 1 553.9
参考文献
[1] 杨镜司, 秦文萍, 史文龙, 等. 基于电动汽车参与调峰定价策略的区域电网两阶段优化调度[J]. 电工技术学报, 2022, 37(1): 58-71. Yang Jingsi, Qin Wenping, Shi Wenlong, et al. Two-stage optimal dispatching of regional power grid based on electric vehicles' participation in peak-shaving pricing strategy[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 58-71.
[2] Aiso K, Akatsu K. High speed SRM using vector control for electric vehicle[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(1): 61-68.
[3] Mobarak M H, Bauman J. Vehicle-directed smart charging strategies to mitigate the effect of long-range EV charging on distribution transformer aging[J]. IEEE Transactions on Transportation Electrification, 2019, 5(4): 1097-1111.
[4] Chen Jie, Huang Xiaoqing, Cao Yijia, et al. Electric vehicle charging schedule considering shared charging pile based on Generalized Nash Game[J]. International Journal of Electrical Power & Energy Systems, 2022, 136: 107579.
[5] 许刚, 张丙旭, 张广超. 电动汽车集群并网的分布式鲁棒优化调度模型[J]. 电工技术学报, 2021, 36(3): 565-578. Xu Gang, Zhang Bingxu, Zhang Guangchao. Distributed and robust optimal scheduling model for large-scale electric vehicles connected to grid[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 565-578.
[6] Li Ruoyang, Wu Qiuwei, Oren S S. Distribution locational marginal pricing for optimal electric vehicle charging management[J]. IEEE Transactions on Power Systems, 2014, 29(1): 203-211.
[7] Tan Jun, Wang Lingfeng. Real-time charging navigation of electric vehicles to fast charging stations: a hierarchical game approach[J]. IEEE Transactions on Smart Grid, 2017, 8(2): 846-856.
[8] Lu Zhigang, Shi Lina, Geng Lijun, et al. Non-cooperative game pricing strategy for maximizing social welfare in electrified transportation networks[J]. International Journal of Electrical Power & Energy Systems, 2021, 130: 106980.
[9] Li Xuecheng, Xiang Yue, Lü Lin, et al. Price incentive-based charging navigation strategy for electric vehicles[J]. IEEE Transactions on Industry Applications, 2020, 56(5): 5762-5774.
[10] Zhang Yongmin, You Pengcheng, Cai Lin. Optimal charging scheduling by pricing for EV charging station with dual charging modes[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(9): 3386-3396.
[11] Liu Zhaoxi, Wu Qiuwei, Huang Shaojun, et al. Optimal day-ahead charging scheduling of electric vehicles through an aggregative game model[J]. IEEE Transactions on Smart Grid, 2018, 9(5): 5173-5184.
[12] 史一炜, 冯冬涵, Zhou E, 等. 基于主从博弈的充电服务商充电引导方法及其定价策略[J]. 电工技术学报, 2019, 34(增刊2): 742-751. Shi Yiwei, Feng Donghan, Zhou E, et al. Stackelberg game based on supervised charging method and pricing strategy of charging service providers[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 742-751.
[13] Li Hepeng, Wan Zhiqiang, He Haibo. Constrained EV charging scheduling based on safe deep reinforcement learning[J]. IEEE Transactions on Smart Grid, 2020, 11(3): 2427-2439.
[14] Zhao Zhenli, Zhang Lihui, Zhu Jinrong, et al. Pricing of private charge sharing service based on bilateral bargaining game[J]. Sustainable Cities and Society, 2020, 59: 102179.
[15] Hu Zechun, Zhan Kaiqiao, Zhang Hongcai, et al. Pricing mechanisms design for guiding electric vehicle charging to fill load valley[J]. Applied Energy, 2016, 178: 155-163.
[16] Bai Linquan, Wang Jianhui, Wang Chengshan, et al. Distribution locational marginal pricing (DLMP) for congestion management and voltage support[J]. IEEE Transactions on Power Systems, 2018, 33(4): 4061-4073.
[17] 郑重, 苗世洪, 李超, 等. 面向微型能源互联网接入的交直流配电网协同优化调度策略[J]. 电工技术学报, 2022, 37(1): 192-207. Zheng Zhong, Miao Shihong, Li Chao, et al. Coordinated optimal dispatching strategy of AC/DC distribution network for the integration of micro energy Internet[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 192-207.
[18] Wei Wei, Wu Lei, Wang Jianhui, et al. Network equilibrium of coupled transportation and power distribution systems[J]. IEEE Transactions on Smart Grid, 2018, 9(6): 6764-6779.
[19] Farivar M, Low S H. Branch flow model: relaxations and convexification—part I[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2554-2564.
[20] 谢仕炜, 林伟伟, 张亚超. 基于变分不等式理论的电力-交通耦合网络均衡状态研究[J]. 中国电机工程学报, 2022, 42(17): 6220-6239. Xie Shiwei, Lin Weiwei, Zhang Yachao. Research on coupled power-transportation network equilibrium state based on variational inequality theory[J]. Proceedings of the CSEE, 2022, 42(17): 6220-6239.
[21] Shi Xiaoying, Xu Yinliang, Guo Qinglai, et al. A distributed EV navigation strategy considering the interaction between power system and traffic network[J]. IEEE Transactions on Smart Grid, 2020, 11(4): 3545-3557.
[22] Tushar W, Chai Bo, Yuen C, et al. Energy storage sharing in smart grid: a modified auction-based approach[J]. IEEE Transactions on Smart Grid, 2016, 7(3): 1462-1475.
[23] He Li, Zhang Jie. A community sharing market with PV and energy storage: an adaptive bidding-based double-side auction mechanism[J]. IEEE Transactions on Smart Grid, 2021, 12(3): 2450-2461.
[24] 熊宇峰, 司杨, 郑天文, 等. 基于主从博弈的工业园区综合能源系统氢储能优化配置[J]. 电工技术学报, 2021, 36(3): 507-516. Xiong Yufeng, Si Yang, Zheng Tianwen, et al. Optimal configuration of hydrogen storage in industrial park integrated energy system based on stackelberg game[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 507-516.
[25] 王昀, 谢海鹏, 孙啸天, 等. 计及激励型综合需求响应的电-热综合能源系统日前经济调度[J]. 电工技术学报, 2021, 36(9): 1926-1934. Wang Yun, Xie Haipeng, Sun Xiaotian, et al. Day-ahead economic dispatch for electricity-heating integrated energy system considering incentive integrated demand response[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1926-1934.
[26] 詹祥澎, 杨军, 吴赋章, 等. 基于去中心化交易模式的充电站日前购电策略[J]. 电力系统自动化, 2019, 43(24): 23-31, 49. Zhan Xiangpeng, Yang Jun, Wu Fuzhang, et al. Day-ahead electricity purchasing strategy of charging station based on decentralized trading mode[J]. Automation of Electric Power Systems, 2019, 43(24): 23-31, 49.
[27] 谢仕炜, 胡志坚, 王珏莹. 考虑时–空耦合的城市电力–交通网络动态流量均衡[J]. 中国电机工程学报, 2021, 41(24): 8408-8424. Xie Shiwei, Hu Zhijian, Wang Jueying. Dynamic flow equilibrium of urban power and transportation networks considering the coupling in time and space[J]. Proceedings of the CSEE, 2021, 41(24): 8408-8424.
[28] 文云峰, 林晓煌. 孤岛与并网模式下微电网最低惯量需求评估[J]. 中国电机工程学报, 2021, 41(6): 2040-2053. Wen Yunfeng, Lin Xiaohuang. Minimum inertia requirement assessment of microgrids in islanded and grid-connected modes[J]. Proceedings of the CSEE, 2021, 41(6): 2040-2053.
[29] 李咸善, 方子健, 李飞, 等. 含多微电网租赁共享储能的配电网博弈优化调度[J]. 中国电机工程学报, 2022, 42(18): 6611-6625. Li Xianshan, Fang Zijian, Li Fei, et al. Game-based optimal dispatching strategy for distribution network with multiple microgrids leasing shared energy storage[J]. Proceedings of the CSEE, 2022, 42(18): 6611-6625.
[30] 祁兵, 刘思放, 李彬, 等. 共享风险链路组与风险均衡的电力通信网路由优化策略[J]. 电力系统自动化, 2020, 44(8): 168-175. Qi Bing, Liu Sifang, Li Bin, et al. Routing optimization strategy for power communication network with shared risk link group and risk balance[J]. Automation of Electric Power Systems, 2020, 44(8): 168-175.
[31] 曾博, 徐富强, 刘一贤, 等. 综合考虑经济-环境-社会因素的多能耦合系统高维多目标规划[J]. 电工技术学报, 2021, 36(7): 1434-1445. Zeng Bo, Xu Fuqiang, Liu Yixian, et al. High-dimensional multiobjective optimization for multi-energy coupled system planning with consideration of economic, environmental and social factors[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1434-1445.
[32] 罗志刚, 韦钢, 朱兰, 等. 含分布式电源的城市配电网交直流改造方案综合决策[J]. 电力系统自动化, 2020, 44(11): 87-94. Luo Zhigang, Wei Gang, Zhu Lan, et al. Comprehensive decision on AC/DC transformation scheme of urban distribution network with distributed generator[J]. Automation of Electric Power Systems, 2020, 44(11): 87-94.
Abstract With the rapid growth of electric vehicles (EVs), it brings a series of problems to the configuration of charging facilities: (1) the configuration of charging piles is lagging behind the development speed of vehicles seriously; (2) unreasonable distribution of charging piles leads to a large number of idle piles; (3) the huge charging demand has impact on the operation of the power grid. For these problems, charging pile sharing is a feasible solution to alleviate the imbalance of vehicle-pile configuration. The four subjects of EV users, aggregators, charging piles and distribution network participate in shared charging activities. However, researches on this are limited to the single subject optimization, ignoring the master-slave game competition between EV users and distribution network. Towards the win-win goal of distribution network, EV users, charging piles and aggregators, a master-slave game model of charging pile sharing and matching is established.
The model can be divided into three stages: in the first stage, the distribution network updates the access load of each distribution network node, takes the minimum operation cost of distribution network as the optimization objective, calculates the locational marginal price (LMP), and sends it to the aggregators and charging piles. In the second stage, the aggregators and the charging piles play a one-to-one pricing game based on the LMP, and the Bayesian Nash equilibrium solution of the game is taken as the final transaction price. In the third stage, the shared matching center aims at maximizing the number of successful matching pairs of vehicle-piles and optimizing the total charging cost of EV users, builds a one-to-many vehicle pile matching model based on the minimum cost and maximum flow model, solves the model to generate a vehicle-pile matching list, calculates the power vector of each distribution network node accessing EV load, and returns to the first stage.
Simulation results the charge sharing data show that, the number of EV charges successfully matched by the experimental group using the proposed method is 5 195, which is 547, 191 and 0 more than other control groups respectively. In the control group, the standard deviation of the average frequency of charging piles used by aggregators is 2.24, 1.97, 1.17, respectively, compared with 1.09 in the experimental group. The result shows that the strategy can greatly increase the number of successful matching of shared charging piles, make the utilization ratio of each charging pile more balanced at different times, and avoid the situation that some charging piles are frequently used while some charging piles are idle.
The study shows that the proposed charging pile sharing strategy can increase the revenue of charging piles and aggregators, reduce the cost of EV users. It is also helpful to reduce network loss and voltage deviation of distribution network, which is beneficial to all parties. Compared with the traditional method, the proposed bilevel iterative algorithm improves the solution efficiency. In large-scale EV matching problems, this method still has high efficiency.
keywords:Locational marginal price, master-slave game, minimum cost maximum flow, Bayesian equilibrium, charging pile sharing
DOI: 10.19595/j.cnki.1000-6753.tces.220142
中图分类号:TM73
国网江苏省电力有限公司科技项目资助(J2020119)。
收稿日期 2022-01-28
改稿日期 2022-05-31
黄小庆 女,1981年生,博士,副教授,研究方向为电动汽车接入电网研究、微电网分析。E-mail:huangxiaoqing@hnu.edu.cn(通信作者)
李隆意 男,1998年生,硕士研究生,研究方向为电动汽车并网研究、博弈论。E-mail:lilongyi@hnu.edu.cn
(编辑 赫蕾)