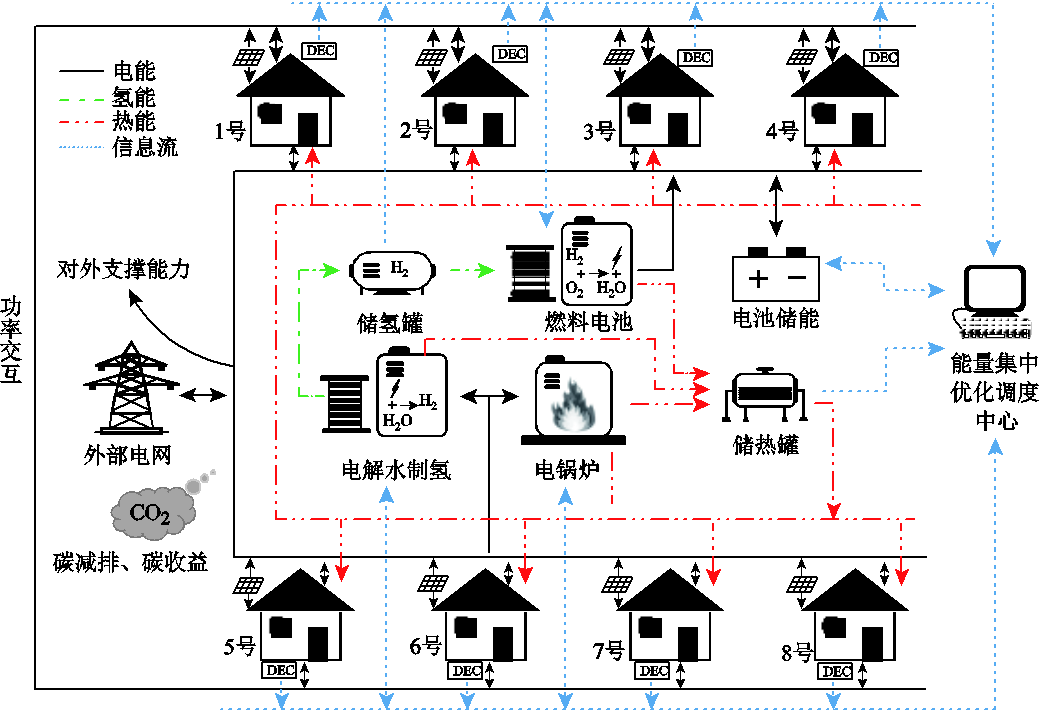
图1 电氢园区能源系统结构
Fig.1 Energy system structure of electric hydrogen park
摘要 针对园区电-氢-热低碳能源系统分布与集中交互优化调度问题,提出一种基于交替方向乘子法(ADMM)的园区电-氢-热能源双层能量低碳优化调度方法。通过将分布式(屋顶光伏、园区建筑电、热负荷)与集中式(电池储能、氢储能、电蓄热)能源相结合,上层基于ADMM求解园区内各建筑可用于共享的交互能量值,下层以园区能源系统运行总成本最小为目标,利用上层求取的建筑交互能量及各建筑剩余功率,基于混合整数规划求解各建筑间交互能量及园区内各集中式能源设备最优出力,实现多主体能源点对点能量精准最优交互。最后,通过吉林市某低碳产业园能源架构进行算例分析,验证了所提低碳优化调度方法的有效性。
关键词:园区电-氢-热系统 分布式与集中式交互 交替方向乘子法 双层优化调度
随着能源低碳化转型和“双碳”目标的推进,减少煤炭资源利用,充分利用太阳能、风能等清洁能源已成为社会能源发展的共识。氢能具有无碳排放且可实现热电联供等的特点,可与电能、热能等多种能源形式互补,是实现“双碳”目标的重要途径[1-5]。为提高用户用能的灵活性与协调性,以可再生能源为基础的电氢多能互补的园区能源系统是我国能源低碳化转型的重要支点[6],因此园区电-氢-热低碳化能源系统如何实现经济优化运行将成为专家学者关注的焦点。
目前,对于多主体分布式优化问题,国内外已展开很多研究。文献[7]提出了一种用于配电网与搭载光伏-风机的微电网之间的双层优化协调能量管理模型,采用改进层次结构的遗传算法进行求解,利用交互式博弈矩阵协调功率交互,有效改善系统的电能质量,提高供电可靠性。文献[8-11]在充分利用清洁能源的同时,各微电网之间相互配合,在满足有限资源的条件下,求解最优潮流问题,准确排序并给出最优互联规划方案,减少系统电力损失,适用于微电网集群最优功率分配问题。文献[12]结合本地电力市场、零售市场的电网交易,在考虑居民侧装有光伏发电及小型储能系统的情况下,实现居民间能量的点对点交易。文献[13]提出了一种将消费者和分布式控制功能相结合的智能综合能源系统,利用多代理相互交互信息的方法查找和优化解决方案,在达到系统中设定目标的同时实现系统的优化运行。文献[14]开发了一种结合太阳能的新型分布式能源系统,在考虑设备配置和运行策略的条件下,通过对比不同场景,验证了其节能效果的客观性。文献[15]从储能元件运行寿命的角度出发,考虑到微电网自身运行成本,各微电网的风机、光伏在满足自身负荷的条件下,其富余功率优先由自身储能元件吸收,其次传递给其他微电网,实现各微电网储能元件有序充放电。文献[16]提出一种分散式优化调度方法,其无需全局协调,各设备交换信息少,目标函数为凸保证收敛,对计算和通信资源要求低,为智能电网发展提供了新的模式。文献[17]提出一种微电网群分布式双层优化策略,通过对比不同拓扑下的运行结果,验证其有较好的收敛性。文献[18]借鉴北欧电力市场模型,建立了综合能源楼宇群能源系统,通过楼宇群代理商监管各建筑,并与电力市场及配电网通信,通过交替方向乘子法(Alternating Direction Method of Multipliers, ADMM)实现日前分布式调度,保证线路容量的同时实现楼宇间能量共享。文献[19]将模型预测控制与ADMM相结合,各子微电网求解本地子问题,在优化的同时对系统状态进行校正,消除误差影响,有效降低系统运行成本,并保证良好的收敛性。文献[20]构建了分层分布式双层优化调度模型,在解决多主体利益冲突问题的同时实现多园区能源系统最优运行。文献[21]在考虑微电网的运行效率受风电、光伏不确定性的条件下,建立可有效降低系统运行成本、保证多主体之间多能共享的多微网能量管理模型。文献[22]利用ADMM算法有效求解输-配-天然气系统优化问题,通过二阶锥松弛将天然气网优化问题转为凸优化问题,实现了在满足系统热负荷的条件下可调节耗电量和耗气量,并且其储能元件配合风力发电对系统起到削峰填谷的作用。文献[23]通过利用氢能可灵活参与微电网系统能量交换的特点,构建了含氢储能的微电网主从博弈框架,有效改善微电网系统能量平衡的同时提高微电网运营商收益。
以上文献存在各主体为交替求解自身优化问题,无法实现真正并行求解,从而影响整个系统运行的经济性和稳定性。当多个主体参与系统分布式优化时,系统无法做出点对点交互功率的精准调控。并且负荷类型较少,无法满足用户需求的多样性,由于天然气的使用且未设置碳回收装置,系统不满足低碳要求,同时均未考虑园区对外的支撑能力和碳减排收益等。
本文将分布式与集中式相结合,提出园区电-氢-热系统双层优化调度方法。上层优化基于交替方向乘子法,园区各建筑以自身运行成本最小为目标,独立求解自身可用于能量共享的功率值以及自身剩余功率,能量集中优化调度中心负责协调各建筑期望的交互功率,兼顾用户隐私的同时降低运算时间;下层优化基于混合整数规划数学模型,以整个园区运行成本最小为目标,在各能源设备运行约束下,求取各建筑间交互功率精确值以及各能源设备最优出力,实现了园区电-氢-热能源系统交互优化运行。最后,通过吉林市某低碳产业园的能源结构,验证本文所提方法的有效性。
本文以吉林市某低碳产业园能源结构为基础,电氢园区能源系统结构如图1所示。园区能源系统由建筑屋顶光伏发电、氢储能(电解水制氢、储氢罐、燃料电池发电)、电池储能、电蓄热储能组成。园区内各建筑均装有分布式能量控制器(DistributedEnergy Controller, DEC),监控楼内负荷及资源情况,计算出各建筑的期望交互功率,并与能量集中优化调度中心进行通信。能量集中优化调度中心负责协调各建筑交互功率并检测园区各能源设备运行状态,各建筑负荷与各能源之间可实现灵活功率交换。园区建筑屋顶光伏发电可直接用于园区负荷,各建筑作为独立的个体,在自身光伏发电充足的情况下,可对其他光伏发电不足的建筑提供一定电力支撑,也可由电解水制氢吸收转换为氢能或由电池储能存储。当园区能源系统出现功率缺额时,燃料电池和电池储能作为电能提供者,和电网相配合为园区提供一定电能支撑,并且在电解水制氢和燃料电池发电余热配合电锅炉满足园区热负荷的同时,剩余热量由储热罐存储,充分提高清洁能源利用率。园区对外具有一定支撑能力,在外部负荷高峰时,园区能源系统调用其内部可控资源为电网分担一定负荷。由于清洁能源的使用,园区从电网购电量减少以降低CO2排放,根据各设备出力计算碳减排量,并与碳交易市场进行交易,获取相应碳收益。

图1 电氢园区能源系统结构
Fig.1 Energy system structure of electric hydrogen park
光伏发电模型在文献[24]已有论述,在此不再赘述。电解水制氢、燃料电池发电、储氢具体模型已在文献[25]论述。
任意时刻电池储能SOC为
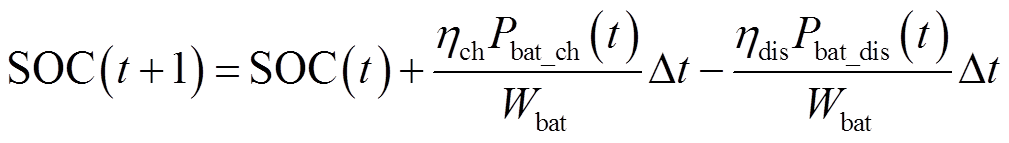 (1)
(1)
式中,Pbat_dis为电池储能的放电功率;Pbat_ch为电池储能的充电功率;SOC(t)为电池储能t时刻荷电状态;Δt为时间步长;Wbat为电池储能额定容量;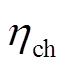 为电池储能充电效率;
为电池储能充电效率;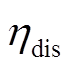 为电池储能放电效率。
为电池储能放电效率。
本文采用碱性电解水制氢模型[25],碱性电解水制氢产氢速率为
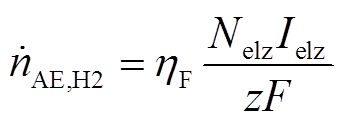 (2)
(2)
式中,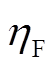 为法拉第效率;Ielz为直流电流;Nelz为电解水制氢串联模块个数;z为每次反应电子转移数;F为法拉第常数。
为法拉第效率;Ielz为直流电流;Nelz为电解水制氢串联模块个数;z为每次反应电子转移数;F为法拉第常数。
PEMFC模块输出电压[25]为
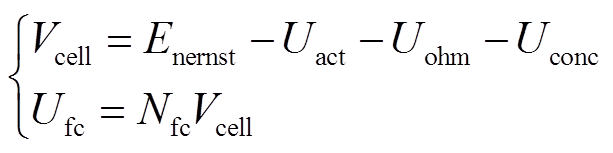 (3)
(3)
式中,Vcell为单模块输出电压;Ufc为燃料电池模块输出电压;Enernst为热力学电动势;Uact为活化过电压;Uohm为欧姆过电压;Uconc为浓差过电压;Nfc为串联电池的数量。
任意Δt时间储氢罐储氢量[25]为
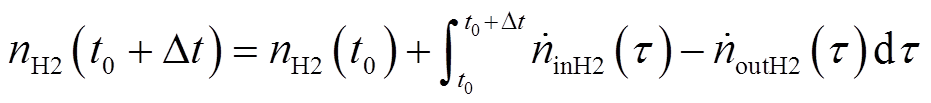 (4)
(4)
式中,nH2(t0)为t0时刻储氢罐储氢量;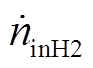 为储氢罐进氢率;
为储氢罐进氢率;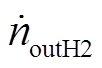 为储氢罐出氢率。
为储氢罐出氢率。
氢水平为当前储氢量与最大储氢量的比值,即
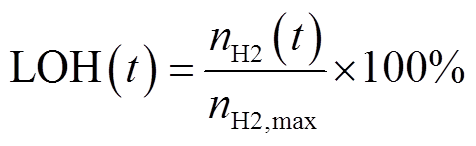 (5)
(5)
式中,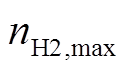 为储氢罐最大储氢量。
为储氢罐最大储氢量。
电蓄热锅炉输出热功率为
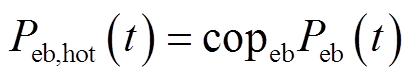 (6)
(6)
式中,Peb,hot(t)为t时刻电锅炉输出热功率;Peb(t)为t时刻电锅炉输入电功率;copeb为电锅炉能量转换系数。
园区电-氢-热能源双层能量优化调度模型流程如图2所示。
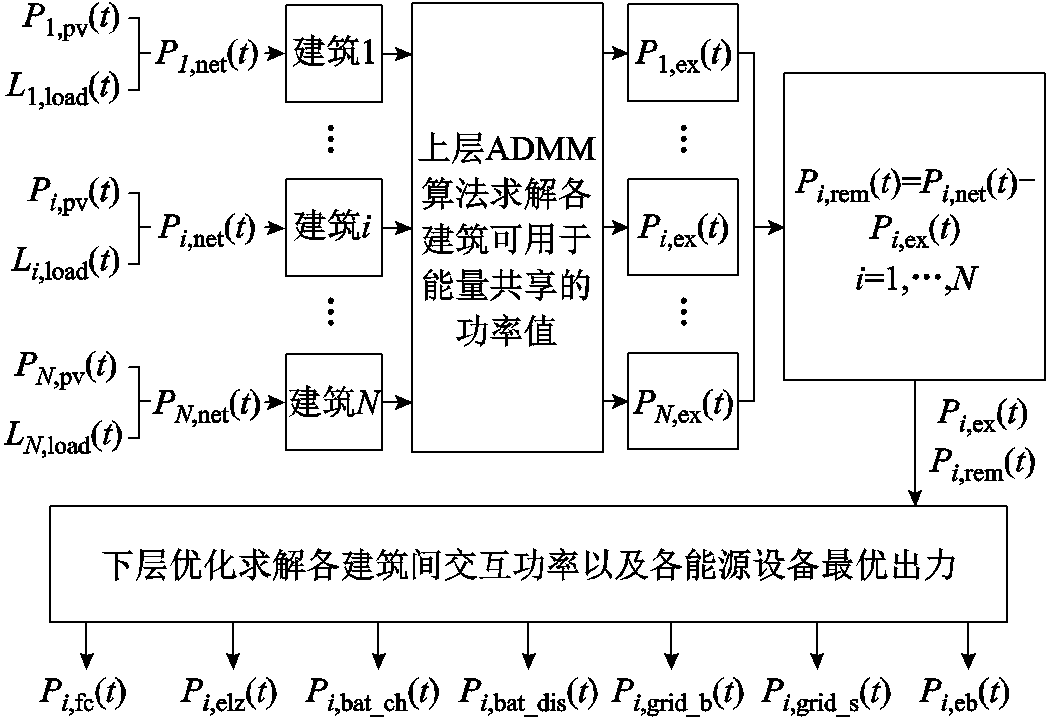
图2 双层优化调度模型流程
Fig.2 Schematic diagram of the two-tier optimal scheduling model
对于单个建筑,在光伏和负荷功率已知的前提下,制定每个调度周期内各建筑间交互功率和各可控电源出力值,使园区运行成本最小。建筑净功率值为
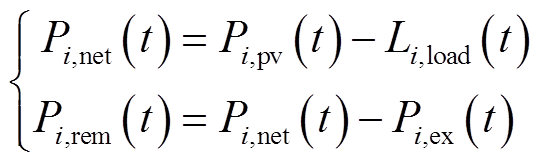 (7)
(7)
式中,Pi,net(t)为建筑i在t时段的净功率;Pi,pv(t)为建筑i在t时段的光伏出力;Li,load(t)为建筑i在t时段的电负荷;Pi,rem(t)为建筑i在t时段在功率交互后的剩余功率;Pi,ex(t)为建筑i在t时段与其他建筑的互济功率,正值为发出功率,负值为接受功率;i为建筑编号,i=1,…, N;t为时段编号。
上层优化调度模型以园区建筑i与电网之间功率交互成本、设备运行维护成本、各建筑间功率交互成本及碳收益为综合成本最小为目标,其数学表达为
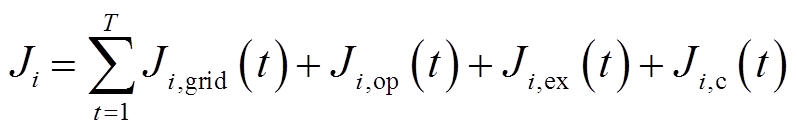 (8)
(8)
式中,Ji为建筑i总成本;Ji,grid(t)为建筑i与电网之间功率交互成本;Ji,op(t)为建筑i对应各能源设备运行维护成本;Ji,ex(t)为各建筑之间交互功率传输成本;Ji,c(t)为建筑i碳收益;T为时段集合。
与电网间功率交互成本为
 (9)
(9)
式中,Ri,grid_b(t)为t时段的电网购电电价;Pi,grid_b(t)为建筑i在t时段的电网购电功率;Ri,grid_s(t)为t时段的电网售电电价;Pi,grid_s(t)为建筑i在t时段的向电网售电功率。
各设备运行维护成本为
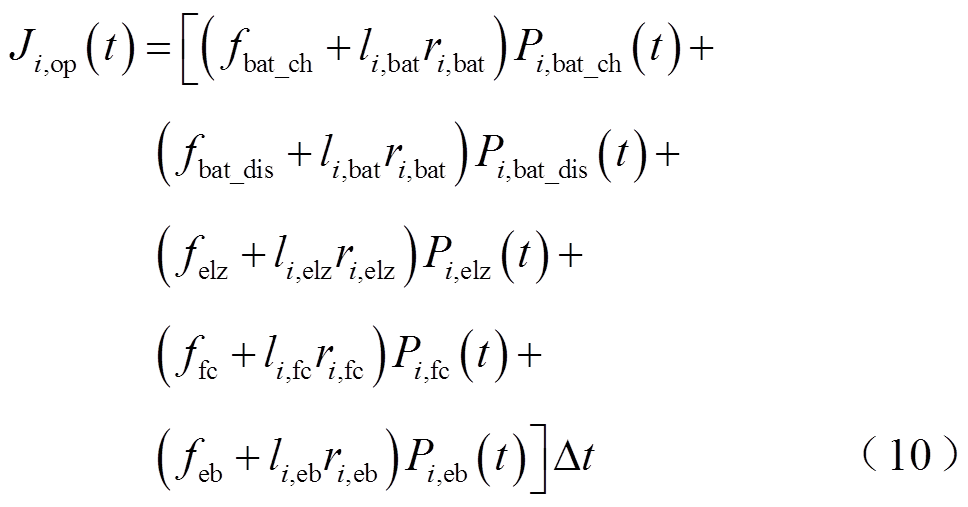
式中,Pi,bat_ch(t)为建筑i在时段t对电池储能的充电功率;Pi,bat_dis(t)为建筑i在时段t电池储能的放电功率;Pi,elz(t)为建筑i在时段t电解水制氢功率;Pi,fc(t)为时段t燃料电池对建筑i的发电功率;Pi,eb(t)为建筑i在时段t的电锅炉功率;fbat_ch为电池储能充电成本系数;fbat_dis为电池储能放电成本系数;felz为电解水制氢成本系数;ffc为燃料电池发电成本系数;feb为电锅炉运行成本系数;li,a为建筑i与能源设备a之间的导线距离;ri,a建筑i与能源设备a之间传输单位功率损耗系数,a=bat、elz、fc、eb。
各建筑交互功率成本为
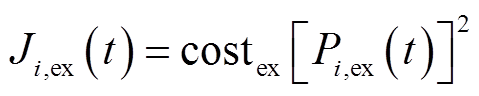 (11)
(11)
式中,costex为各建筑间交换功率的二次项系数。
碳收益为
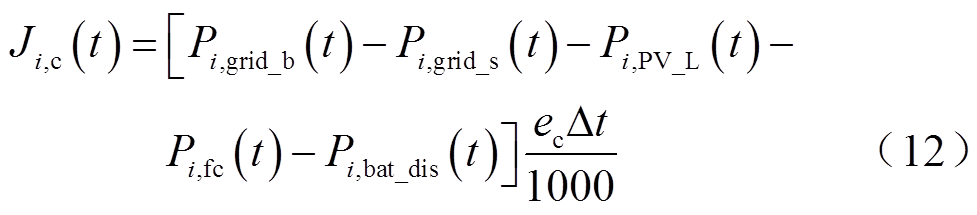
式中,ec为碳收益系数;Pi,PV_L(t)为建筑i的屋顶光伏在t时段为负荷提供的功率。
下层优化调度模型以园区与电网之间功率交互成本,设备运行维护成本、各建筑间功率交互成本及碳收益为综合成本最小为目标,其数学表达为
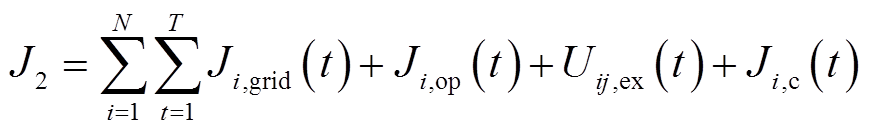 (13)
(13)
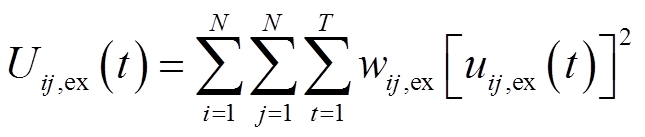 (14)
(14)
式中,J2为园区总成本;Uij,ex(t)为各建筑之间交互功率总成本;uij,ex(t)为t时段建筑i向建筑j传输的功率,正值为发出,负值为接受;wij,ex为建筑i与建筑j之间传输功率的二次项系数,与两者之间导线距离有关。
园区能源系统的约束可以分为各建筑内部约束和园区全局约束。单个建筑内部约束包括内部电功率和热功率平衡约束,包括电池储能、电解水制氢、燃料电池发电、电蓄热锅炉的出力上下限约束,建筑间互济功率的上、下限约束。园区全局约束指各建筑间的交换功率平衡约束,即全部建筑的输入和输出功率之和为零。各建筑间交换功率平衡约束为
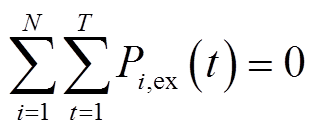 (15)
(15)
1)上层单个建筑运行约束
电功率平衡约束为

当Pi,net(t)<0时,热平衡约束为
 (17)
(17)
式中,Hi,load(t)为建筑i在t时段的热负荷;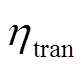 为换热器传热效率;ΔH为氢气焓变。
为换热器传热效率;ΔH为氢气焓变。
当Pi,net(t)>0时,储热约束为
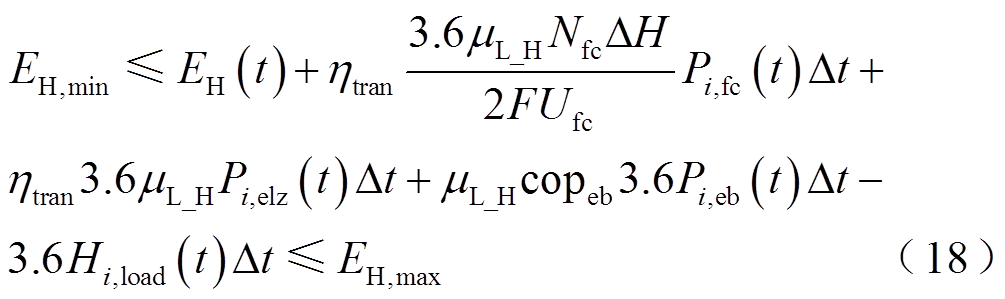
式中,EH(t)为t时段储热罐的储热量;EH,min为储热量下限;EH,max为储热量上限;µL_H为传热效率。
2)下层园区运行约束
电功率平衡约束为
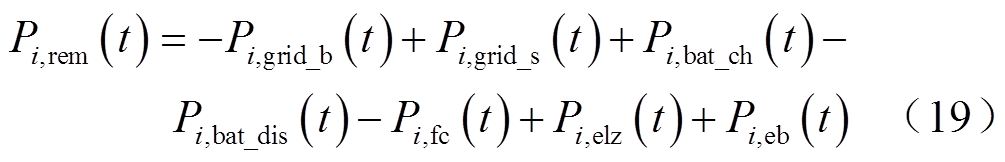
交互功率约束为
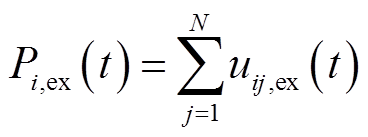 (20)
(20)
热约束为
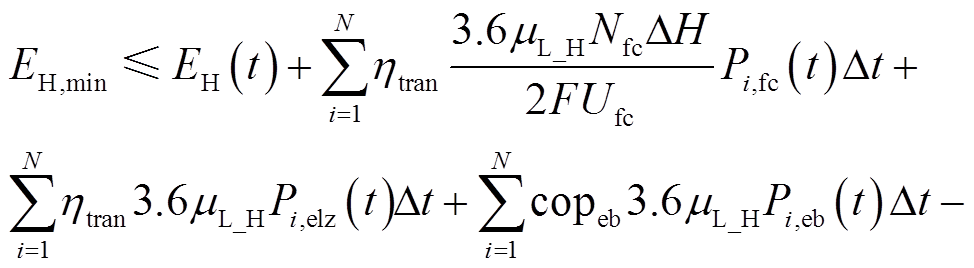
 (21)
(21)
储电约束为
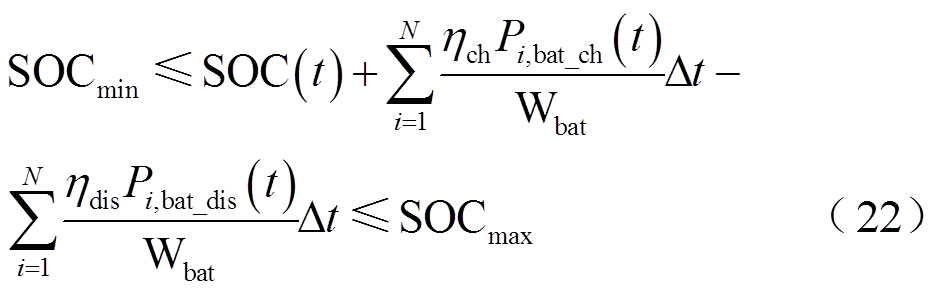
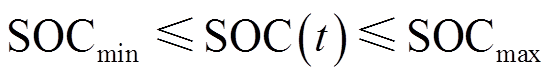 (23)
(23)
式中,SOCmin和SOCmax分别为电池储能荷电状态的下限和上限。
储氢约束为
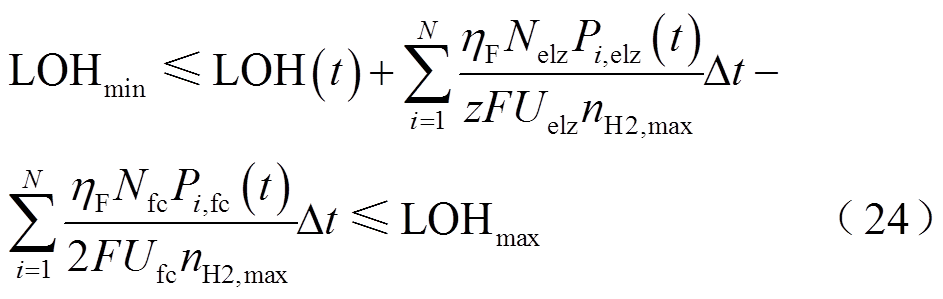
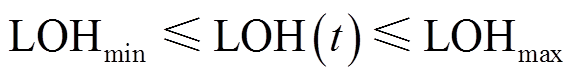 (25)
(25)
式中,LOHmin和LOHmax分别为储氢罐氢水平的下限和上限。
电网交互功率约束为
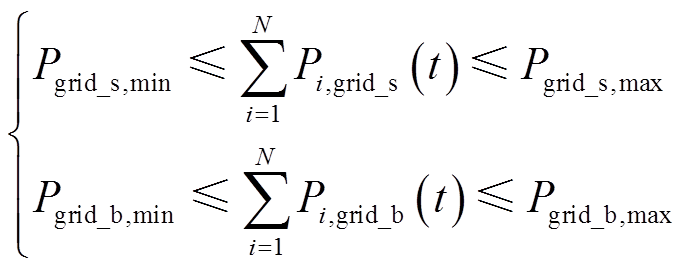 (26)
(26)
式中,Pgrid_s,min和Pgrid_s,max分别为园区向电网售电功率的最小值和最大值;Pgrid_b,min和Pgrid_b,max分别为电网购电功率的最小值和最大值。
各能源设备运行约束
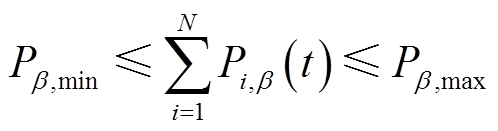 (27)
(27)
式中,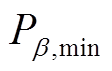 和
和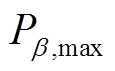 分别为设备β出力下限和上限;β=bat_dis、bat_ch、elz、fc、eb。
分别为设备β出力下限和上限;β=bat_dis、bat_ch、elz、fc、eb。
在优化模型中,用向量xi(t)表示优化变量,f(xi(t))为优化目标函数,有
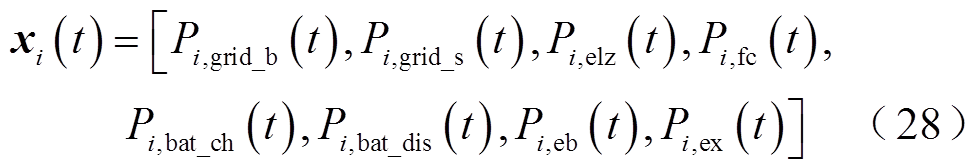
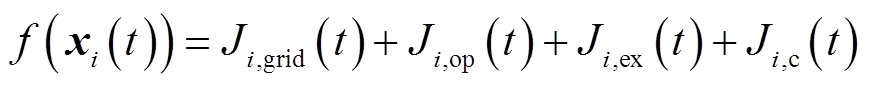 (29)
(29)
为了解耦各建筑间互联功率,定义辅助变量m和函数 [26]。
[26]。
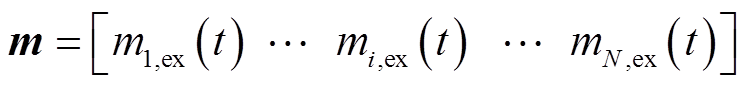 (30)
(30)
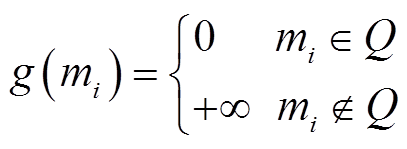 (31)
(31)
其中
 (32)
(32)
因此,上述目标函数可以写为
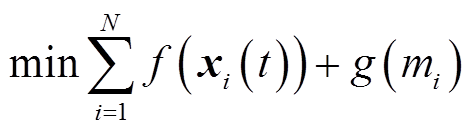 (33)
(33)
约束为
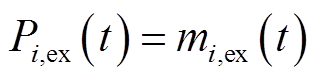 (34)
(34)
对目标函数(33)及约束(34)进行松弛处理,得到增广拉格朗日函数
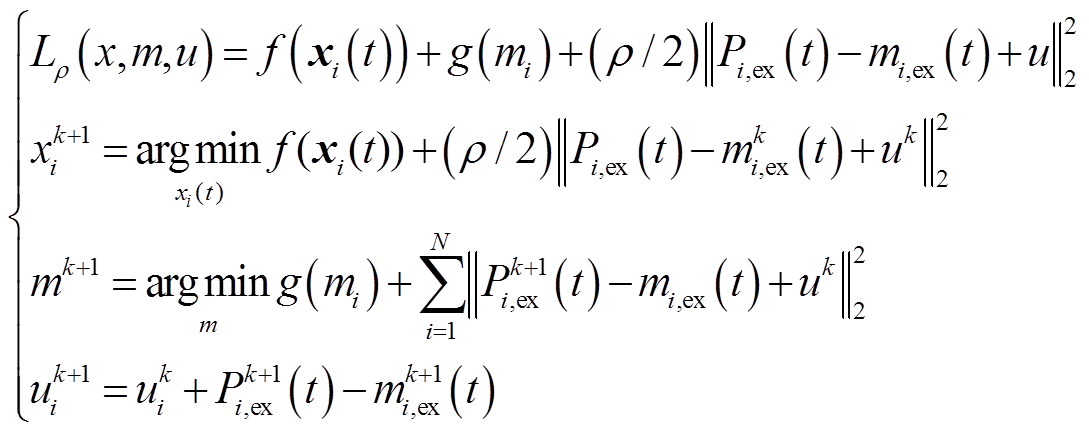 (35)
(35)
式中,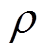 为惩罚因子,
为惩罚因子,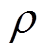 >0;k为迭代次数;‖·‖2为矩阵的2范数;u为拉格朗日乘子。
>0;k为迭代次数;‖·‖2为矩阵的2范数;u为拉格朗日乘子。
为简化迭代过程,本文采用同步式算法,最终迭代形式为
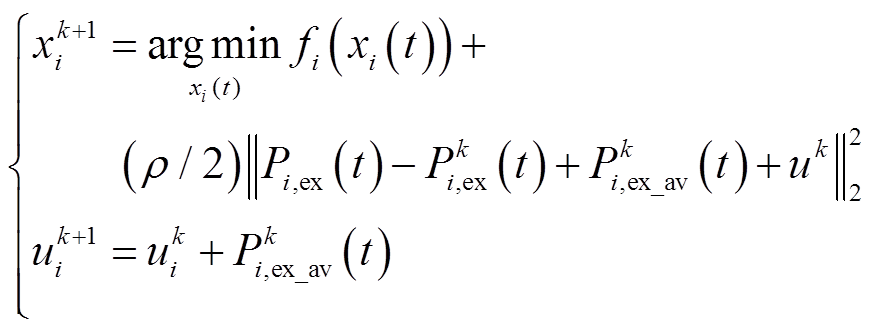 (36)
(36)
式中,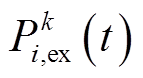 为第k次迭代中交换功率的优化结果;
为第k次迭代中交换功率的优化结果;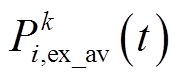 为第k次迭代中全部建筑交换功率优化结果的平均值。每个建筑进行第k次迭代优化前,选取第k-1次计算的期望交换功率的修正值作为本次迭代的参考值,其修正值为第k-1次计算的期望交换功率减去全部建筑期望交换功率的平均值。
为第k次迭代中全部建筑交换功率优化结果的平均值。每个建筑进行第k次迭代优化前,选取第k-1次计算的期望交换功率的修正值作为本次迭代的参考值,其修正值为第k-1次计算的期望交换功率减去全部建筑期望交换功率的平均值。
基于ADMM原理,采用残差作为收敛标准,即
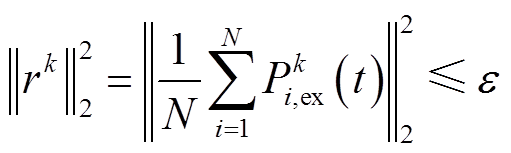 (37)
(37)
园区电氢系统双层优化求解流程如图3所示。园区上层优化采取分布式算法根据系统输入的原始数据,各建筑自治求解优化问题得出Pi,ex(t),并将Pi,rem(t)和Pi,ex(t)作为输入传递给园区下层集中式优化,求取各设备最优出力以及各建筑交互功率精确值。
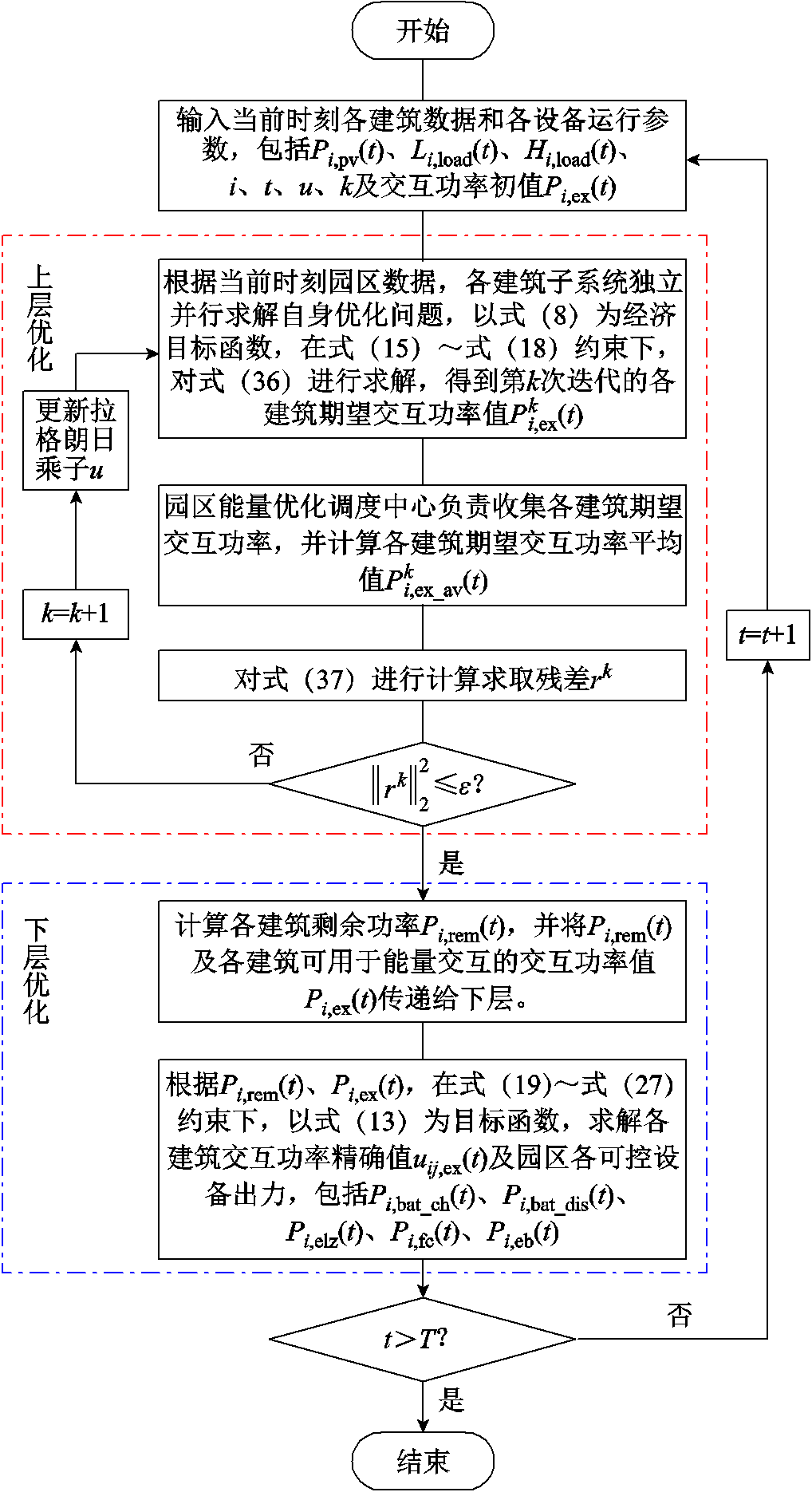
图3 算法流程
Fig.3 Algorithm flow chart
本文以吉林市某低碳产业园能源结构为例(如图1所示)。园区各建筑均装设有屋顶光伏,建筑1~4为工业建筑,铺设光伏容量400 kWp,建筑5~8为办公/公寓建筑,铺设光伏容量50 kWp,调度周期T为24 h,以15 min为一个时段,共96个。园区电-氢-热系统参数设置见附表1。各建筑间交换功率的二次项系数costex为0.001,辅助变量m初值均为1,拉格朗日乘子u初值为1,残差ε为0.01。
建筑1~8屋顶光伏出力、电负荷、热负荷数据如图4所示。光伏资源在8:00—16:00较为充足,最大为370.88 kW,工业负荷在0:00—4:00、10:00—15:00及21:00—24:00较大,最大为177.66 kW,由图4d可知,工业建筑1~4无热负荷,不计冷负荷。
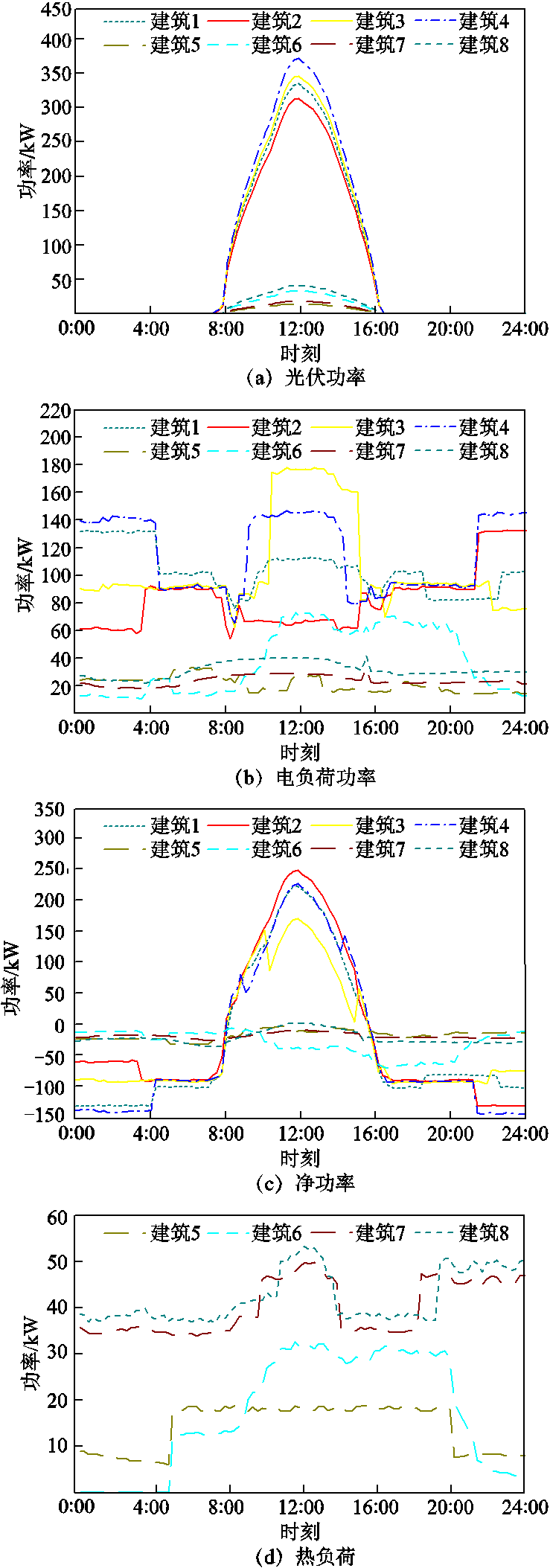
图4 光伏发电及负荷功率
Fig.4 Photovoltaic power generation and load power
24 h园区建筑1~8的能源优化结果如附图1所示,电池储能及其荷电状态变化如图5所示,电解水制氢-燃料电池及氢水平变化如图6所示,产热量、耗热量及储热量变化如图7所示。
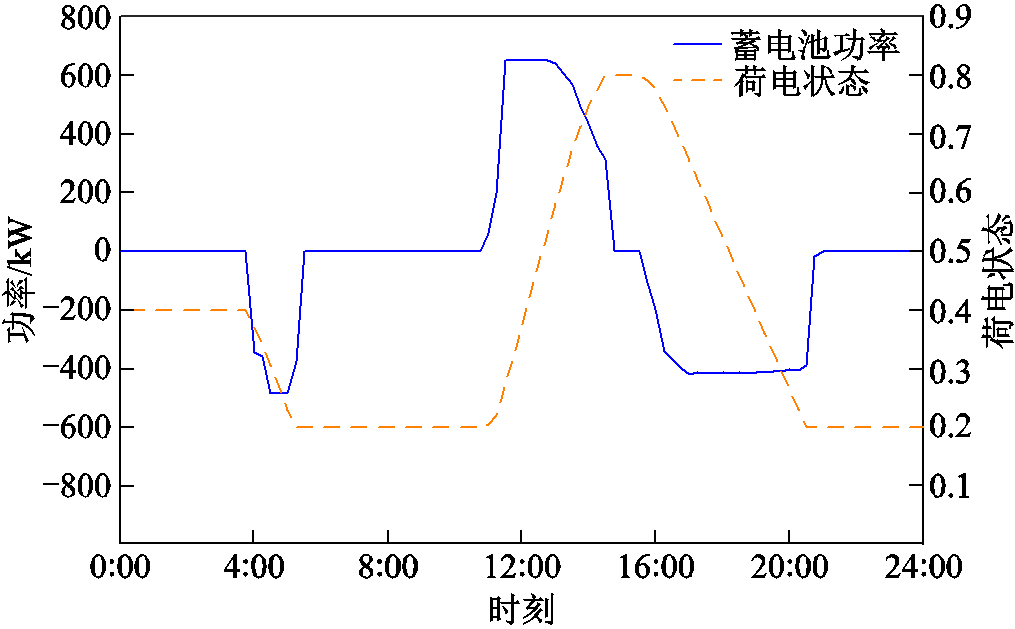
图5 电池储能及其荷电状态优化调度曲线
Fig.5 Battery and state-of-charge optimization scheduling curve
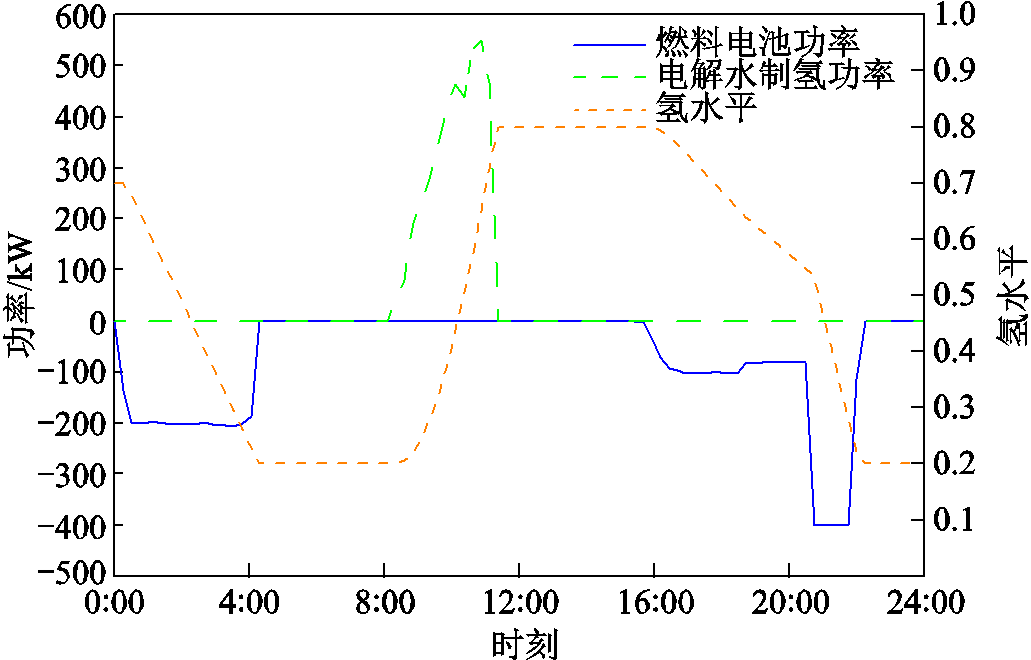
图6 电解水制氢-燃料电池及氢水平优化调度曲线
Fig.6 Electrolyzer-fuel cell and hydrogen level optimization scheduling curve
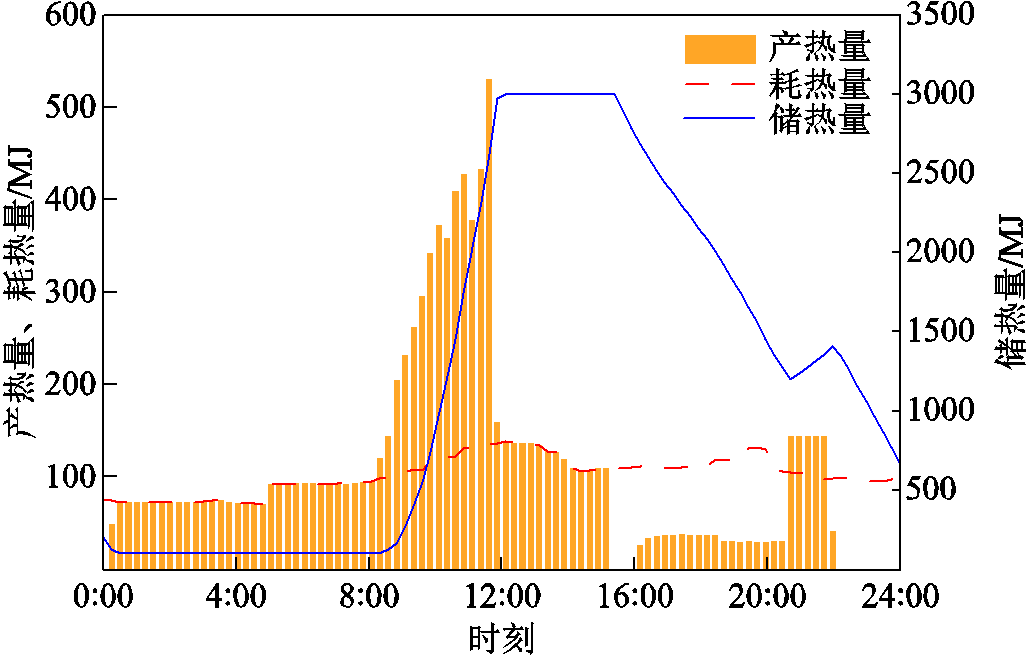
图7 产热量、耗热量及储热量优化调度曲线
Fig.7 Optimal scheduling curve of heat production, heat consumption and heat storage
由附图1a~附图1h分析可知,在各建筑无富余电能时,其负荷由电池储能、燃料电池及电网满足,在光伏资源充足时,其富余电能用于功率交互的同时,剩余功率由园区各能源设备和电网消纳。结合图5、图6和图7知,在4:15,储氢罐氢水平为0.2,达到运行下限,此时燃料电池停机,并且储热罐达到储热下限。在4:15—8:00,园区热负荷由电锅炉满足,维持在储热下限。在4:00—5:30,根据分时电价,电池储能放电满足园区电负荷,最大运行功率为485 kW。在5:30,电池储能荷电状态为0.2,达到运行下限,电池储能停机,负荷由电网满足。在8:30—15:00,由于建筑1~4光伏资源较为充足,在满足自身负荷的同时,将富余电能输送给其余建筑,光伏在满足园区负荷的同时,富余电能由电解水制氢和燃料电池吸收,制氢余热由储热罐存储,电解水制氢最大制氢功率为532.4 kW。由于制氢功率较大,园区产热量大于耗热量,在12:00,储热量为3 000 MJ,达到储热上限。在11:00,储氢罐氢水平为0.8,达到储氢上限,电解水制氢装置停机,其余电能由电池储能吸收,最大充电功率为650 kW,在15:00,荷电状态达到上限0.8。在16:00—20:30,光伏无法满足园区负荷,由于园区储热量较大,电锅炉未启动,各建筑热负荷由储热装置满足,电池储能作为电能提供者满足大部分负荷,最大发电功率为415 kW,其余少量负荷由燃料电池补充,产热量小于耗热量,储热量下降。在20:30,荷电状态达到下限,电池储能停机,其余负荷由燃料电池满足。在22:00,氢水平达到下限,燃料电池停机,其余负荷由电网满足。
各调度周期收敛后各建筑交互功率最终如图8所示。
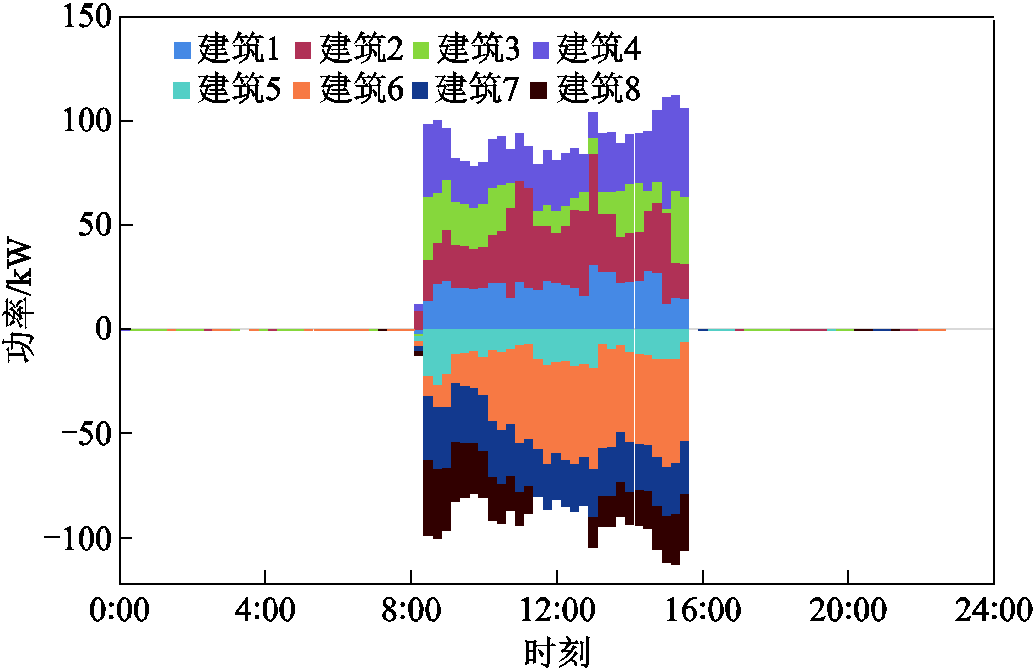
图8 交互功率优化调度结果
Fig.8 Interactive power optimization scheduling results
由图8可知,各建筑通过交互功率充分利用光伏资源,在建筑净功率为正时可对外输出电能,实现分布式优化。在0:00—8:00,15:45—24:00,各建筑净功率均为负,无交互功率。
各优化调度周期残差收敛结果如图9所示。
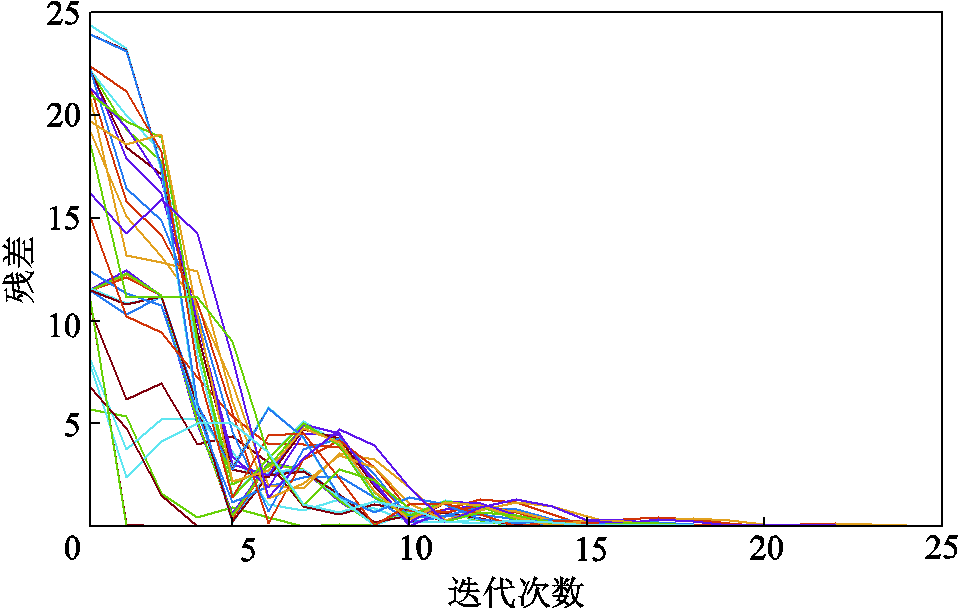
图9 所有调度周期残差收敛结果
Fig.9 Residual convergence results for all scheduling periods
从图9中可以看出,大部分周期能够在15~20次迭代内收敛,说明ADMM算法对求解上层各建筑共享功率值有较好的性能。
园区内各集中能源设备除满足自身负荷外,在留有相应裕度的前提下应具有对外输出电能的能力。本文设置电池储能荷电状态和储氢罐氢水平在留有40%裕度的前提下,园区对外电力、电量支撑能力如图10所示。
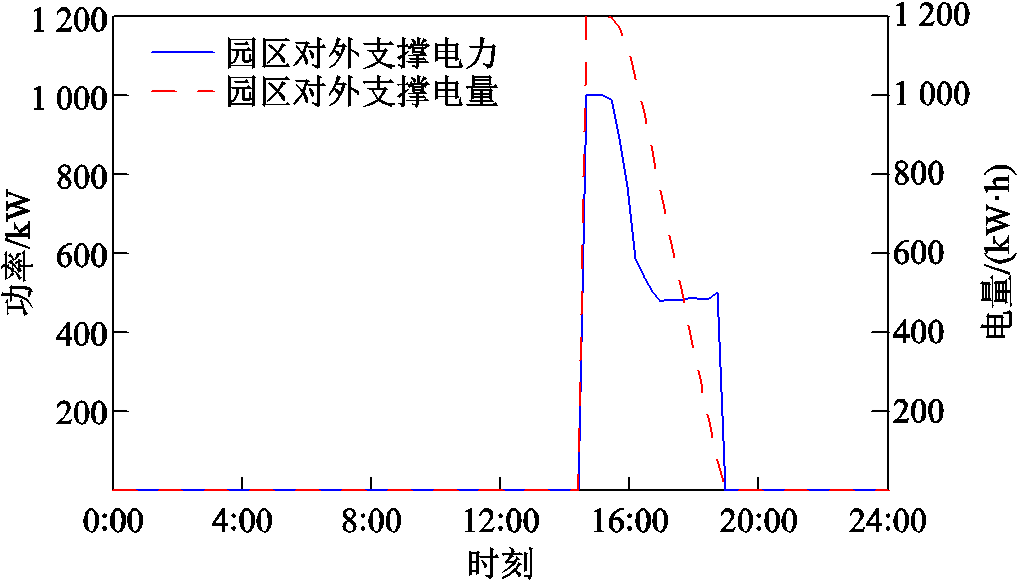
图10 园区对外支撑能力
Fig.10 The external support capacity of the park
由图10可知,在14:30—19:00园区可对外提供电能,最大功率支撑为1 000 kW,最大电量支撑为1 200 kW·h。
园区电-氢-热低碳优化调度各时段可实现碳减排如图11所示。
由图11可知,在0:00—3:45、5:15—7:45、21:45—24:00,园区能源系统碳减排为负值,大部分园区负荷由电网满足;在3:45—5:15,7:45—21:45,大部分负荷由光伏、电池储能、燃料电池及电网满足,可再生能源出力大于从电网购电量,碳减排为正值。经计算得到园区能源系统24 h碳减排总量为4.56 t,可获得的碳收益为547.2元。
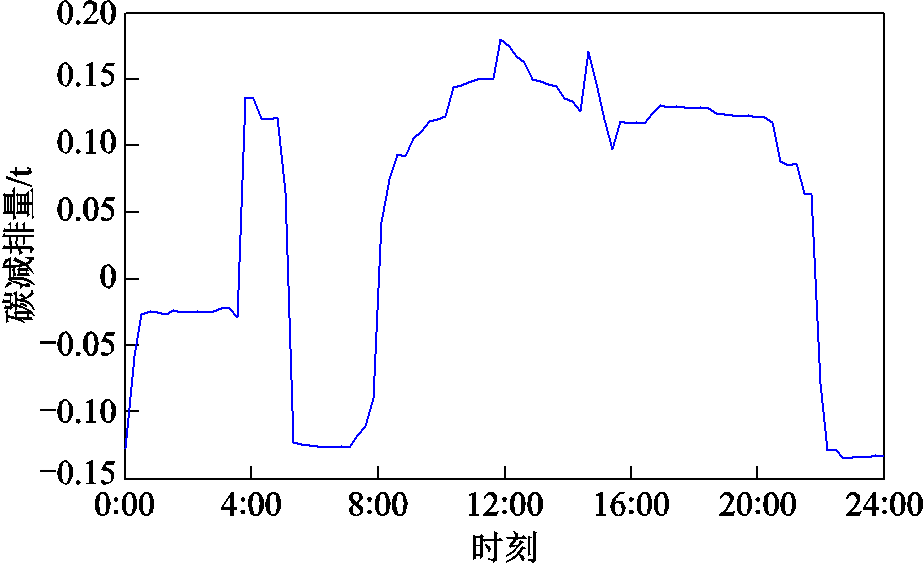
图11 各时段园区能源系统碳减排量
Fig.11 The external support capacity of the park
本文针对园区电-氢-热能源系统分布与集中联合优化调度,实现多主体能源系统点对点功率精准交互以及集中能源最优调控,提出了一种基于交替方向乘子法的电氢系统双层优化调度方法,通过算例分析得出以下结论:
1)园区内各建筑均可并行求解自身优化问题,求解期望交互功率并上传至能量集中优化调度中心,同时兼顾用户数据隐私。
2)实现园区多建筑、多能源(电、氢、热)能量精准交互,在上层交替方向乘子法的支持下,求解各建筑可用于能量共享的交互功率值,下层基于混合整数规划模型根据系统运行经济性精准求解各建筑间交互功率以及园区内各可控能源出力。
3)园区能源系统在满足自身负荷的前提下,其内部可调控设备在保留相应裕度的同时具有对外灵活支撑能力。本文方法可根据各能源设备出力精确地计算园区碳减排量和碳收益,实现园区电-氢-热系统低碳优化调度。
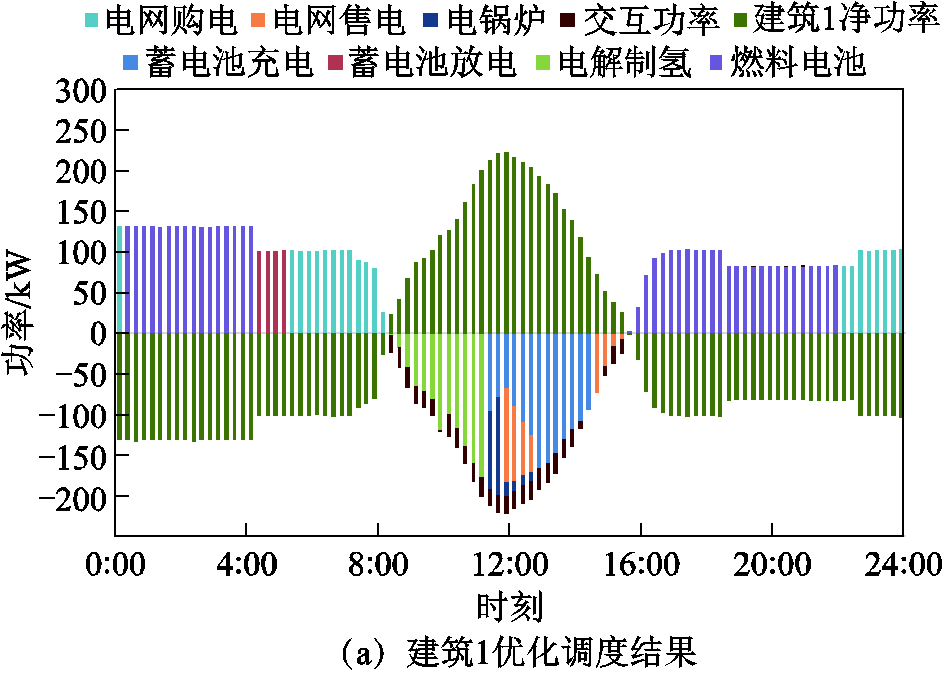
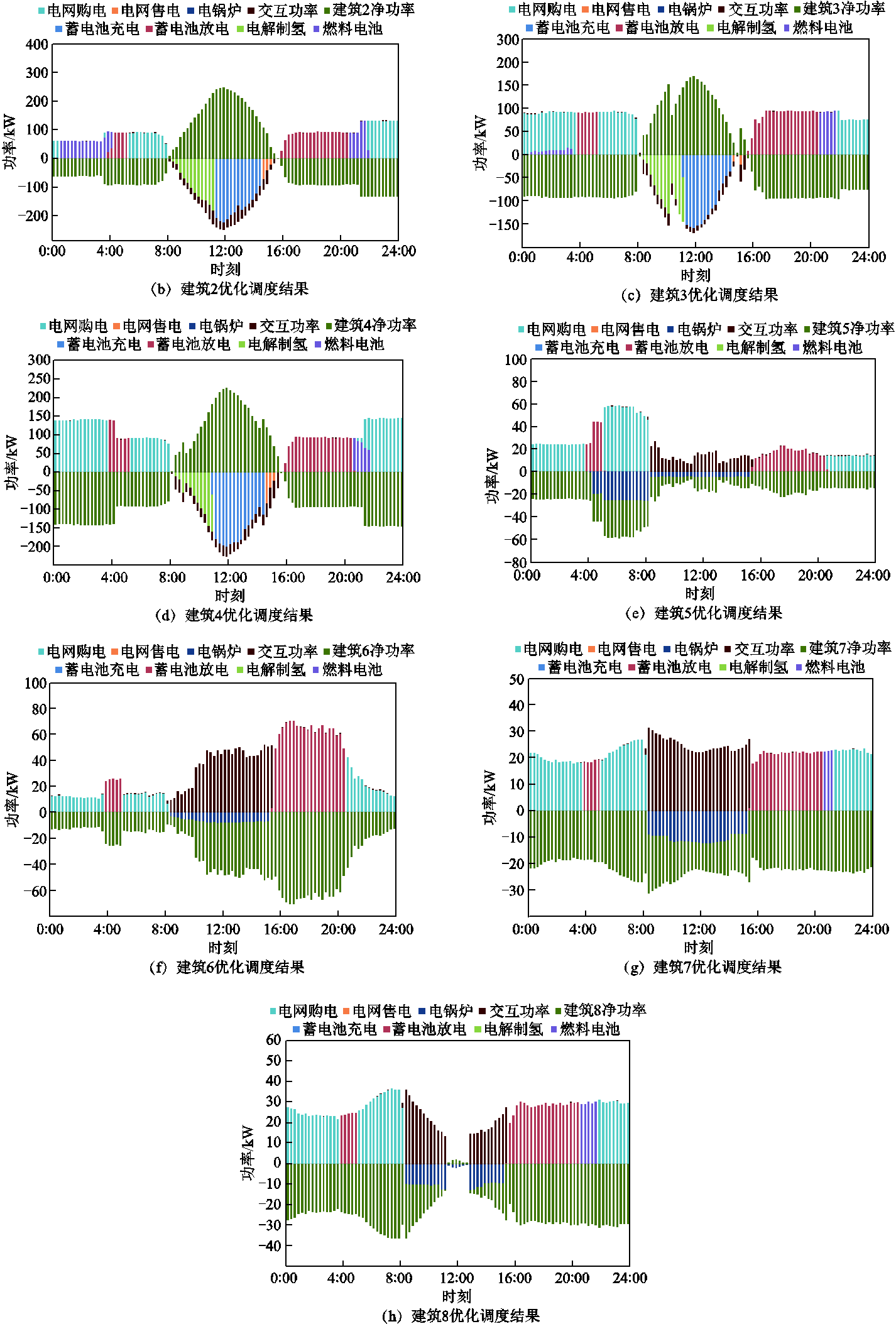
附图1 园区内建筑1~8优化调度结果
App.Fig.1 Optimized dispatching results of buildings 1~8 in the park
附表1 园区内各能源设备变量参数
App.Tab.1 Variable parameters of energy equipment in the park

参数数值电池储能电池储能充电功率下限Pbat_ch,min/kW0电池储能充电功率上限Pbat_ch,max/kW650电池储能放电功率下限Pbat_dis,min/kW0电池储能放电功率上限Pbat,dis,max/kW600荷电状态下限SOCmin0.2荷电状态上限SOCmax0.8电池储能容量Wbat/(kW·h)3 000电池储能充电成本fbat_ch/[元/(kW·h)]0.035电池储能放电成本fbat_dis/[元/(kW·h)]0.035电池储能充电效率ηch0.95电池储能放电效率ηdis0.95电蓄热电锅炉功率下限Peb,min/kW0电锅炉功率上限Peb,max/kW300为电锅炉能量转换系数copeb4电锅炉运行维护成本feb/[元/(kW·h)]0.025 5储热罐储热量上限EH,max/MJ3 000储热罐储热量上限EH,min/MJ100传热效率µL_H0.98氢储能燃料电池功率下限Pfc,min/kW0燃料电池功率上限Pfc,max/kW400燃料电池运行维护成本ffc/[元/(kW·h)]0.045电解水制氢功率下限Pelz,min/kW0电解水制氢功率上限Pelz,max/kW550电解水制氢运行维护成本felz/[元/(kW·h)]0.036法拉第常数F/(C/mol)96 485氢罐体积nH2,max/(Nm3)400氢水平下限LOHmin0.2氢水平上限LOHmax0.8碳收益碳收益系数ec/(元/t)120购电电价/ [元/(kW·h)]22:00—4:000.254:00—8:000.758:00—14:000.9514:00—18:000.7518:00—22:000.95售电电价/ [元/(kW·h)]22:00—4:000.24:00—8:000.658:00—14:000.814:00—18:000.6518:00—22:000.8
参考文献
[1] Zhu Dafeng, Yang Bo, Liu Qi, et al. Energy trading in microgrids for synergies among electricity, hydrogen and heat networks[J]. Applied Energy, 2020, 272: 115225.
[2] 袁铁江, 孙传帅, 谭捷, 等. 考虑氢负荷的新型电力系统电源规划[J]. 中国电机工程学报, 2022, 42(17): 6316-6325. Yuan Tiejiang, Sun Chuanshuai, Tan Jie, et al. Generation planning of new power system considering hydrogen load[J]. Proceedings of the CSEE, 2022, 42(17): 6316-6325.
[3] 沈小军, 聂聪颖, 吕洪. 计及电热特性的离网型风电制氢碱性电解槽阵列优化控制策略[J]. 电工技术学报, 2021, 36(3): 463-472. Shen Xiaojun, Nie Congying, Lü Hong. Coordination control strategy of wind power-hydrogen alkaline electrolyzer bank considering electrothermal charact-eristics[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 463-472.
[4] 李奇, 赵淑丹, 蒲雨辰, 等. 考虑电氢耦合的混合储能微电网容量配置优化[J]. 电工技术学报, 2021, 36(3): 486-495. Li Qi, Zhao Shudan, Pu Yuchen, et al. Capacity optimization of hybrid energy storage microgrid considering electricity-hydrogen coupling[J]. Trans-actions of China Electrotechnical Society, 2021, 36(3): 486-495.
[5] 孔令国, 蔡国伟, 李龙飞, 等. 风光氢综合能源系统在线能量调控策略与实验平台搭建[J]. 电工技术学报, 2018, 33(14): 3371-3384. Kong Lingguo, Cai Guowei, Li Longfei, et al. Online energy control strategy and experimental platform of integrated energy system of wind, photovoltaic and hydrogen[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3371-3384.
[6] 范宏, 于伟南, 柳璐, 等. 双碳目标下考虑电氢互补的智慧园区多楼宇协调调度[J]. 电力系统自动化, 2022, 46(21): 42-51. Fan Hong, Yu Weinan, Liu Lu, et al. Method of Multi-building coordinated dispatch in smart park considering electricity and hydrogen complementary with dual carbon targets[J]. Automation of Electric Power Systems, 2022, 46(21): 42-51.
[7] Lu Tianguang, Wang Zhaoyu, Ai Qian, et al. Interactive model for energy management of clustered microgrids[J]. IEEE Transactions on Industry Applications, 2017, 53(3): 1739-1750.
[8] Meng Lexuan, Shafiee Q, Trecate G F, et al. Review on control of DC microgrids and multiple microgrid clusters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(3): 928-948.
[9] Han Yang, Zhang Ke, Li Hong, et al. MAS-based distributed coordinated control and optimization in microgrid and microgrid clusters: a comprehensive overview[J]. IEEE Transactions on Power Electronics, 2018, 33(8): 6488-6508.
[10] Boroojeni K, Amini M H, Nejadpak A, et al. A novel cloud-based platform for implementation of oblivious power routing for clusters of microgrids[J]. IEEE Access, 2016, 5: 607-619.
[11] Che Liang, Zhang Xiaping, Shahidehpour M, et al. Optimal interconnection planning of community microgrids with renewable energy sources[J]. IEEE Transactions on Smart Grid, 2017, 8(3): 1054-1063.
[12] Faia R, Soares J, Pinto T, et al. Optimal model for local energy community scheduling considering peer to peer electricity transactions[J]. IEEE Access, 2021, 9: 12420-12430.
[13] Stennikov V, Barakhtenko E, Mayorov G, et al. Coordinated management of centralized and distributed generation in an integrated energy system using a multi-agent approach[J]. Applied Energy, 2022, 309: 118487.
[14] Liu Zhijian, Li Ying, Fan Guangyao, et al. Co-optimization of a novel distributed energy system integrated with hybrid energy storage in different nearly zero energy community scenarios[J]. Energy, 2022, 247: 123553.
[15] 王程, 刘念. 基于交替方向乘子法的互联微电网系统分布式优化调度[J]. 电网技术, 2016, 40(9): 2675-2681. Wang Cheng, Liu Nian. Distributed optimal dispatching of interconnected microgrid system based on alternating direction method of multipliers[J]. Power System Technology, 2016, 40(9): 2675-2681.
[16] 李佩杰, 陆镛, 白晓清, 等. 基于交替方向乘子法的动态经济调度分散式优化[J]. 中国电机工程学报, 2015, 35(10): 2428-2435. Li Peijie, Lu Yong, Bai Xiaoqing, et al. Decentralized optimization for dynamic economic dispatch based on alternating direction method of multipliers[J]. Proceedings of the CSEE, 2015, 35(10): 2428-2435.
[17] 王皓, 艾芊, 吴俊宏, 等. 基于交替方向乘子法的微电网群双层分布式调度方法[J]. 电网技术, 2018, 42(6): 1718-1727. Wang Hao, Ai Qian, Wu Junhong, et al. Bi-level distributed optimization for microgrid clusters based on alternating direction method of multipliers[J]. Power System Technology, 2018, 42(6): 1718-1727.
[18] 杨昭, 艾欣. 考虑电能共享的综合能源建筑群分布式优化调度[J]. 电网技术, 2020, 44(10): 3770-3776. Yang Zhao, Ai Xin. Distributed optimal scheduling for integrated energy building clusters considering energy sharing[J]. Power System Technology, 2020, 44(10): 3770-3776.
[19] 吴成辉, 林声宏, 夏成军, 等. 基于模型预测控制的微电网群分布式优化调度[J]. 电网技术, 2020, 44(2): 530-538. Wu Chenghui, Lin Shenghong, Xia Chengjun, et al. Distributed optimal dispatch of microgrid cluster based on model predictive control[J]. Power System Technology, 2020, 44(2): 530-538.
[20] 牟晨璐, 丁涛, 李立, 等. 基于分层分布式调度的多园区服务商与综合能源供应商两级协调优化运行模型[J]. 电网技术, 2021, 45(11): 4336-4348. Mu Chenlu, Ding Tao, Li Li, et al. Coordinated optimization operation model of multiple load-serving entities and energy supply companies based on two-level distributed scheduling[J]. Power System Technology, 2021, 45(11): 4336-4348.
[21] 冯昌森, 任冬冬, 沈佳静, 等. 计及多能共享的互联微能源网的分布式协同优化调度[J]. 电力系统自动化, 2022, 46(11): 47-57. Feng Changsen, Ren Dongdong, Shen Jiajing, et al. Distributed coordinated optimal scheduling of interconnected micro-energy grids considering multi-energy sharing[J]. Automation of Electric Power Systems, 2022, 46(11): 47-57.
[22] 兰鹏, 沈晓东, 吴刚, 等. 基于交替方向乘子法的输-配-天然气系统分布式优化调度[J]. 电力系统自动化, 2021, 45(23): 21-30. Lan Peng, Shen Xiaodong, Wu Gang, et al. Distributed optimal scheduling for transmission-distribution-natural-gas system based on alternating direction method of multipliers[J]. Automation of Electric Power Systems, 2021, 45(23): 21-30.
[23] 熊宇峰, 司杨, 郑天文, 等. 基于主从博弈的工业园区综合能源系统氢储能优化配置[J]. 电工技术学报, 2021, 36(3): 507-516.
Xiong Yufeng, Si Yang, Zheng Tianwen, et al. Optimal configuration of hydrogen storage in industrial park integrated energy system based on stackelberg game[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 507-516.
[24] 孔令国, 于家敏, 蔡国伟, 等. 基于模型预测控制的离网电氢耦合系统功率调控[J]. 中国电机工程学报, 2021, 41(9): 3139-3149. Kong Lingguo, Yu Jiamin, Cai Guowei, et al. Power regulation of off-grid electro-hydrogen coupled system based on model predictive control[J]. Proceedings of the CSEE, 2021, 41(9): 3139-3149.
[25] 孔令国. 风光氢综合能源系统优化配置与协调控制策略研究[D]. 北京: 华北电力大学(北京), 2017.
[26] Boyd S, Parikh N, Chu E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends® in Machine Learning, 2011, 3(1): 1-122.
Abstract With the transition to low-carbon energy and the promotion of the "double carbon" goal, the full use of clean energy has become the consensus of social development. Hydrogen energy, which has no carbon emissions and can realize combined heat and power supply, is an important way to achieve the goal of "double carbon". In order to improve the flexibility and coordination of users' energy use, the renewable energy-based electric-hydrogen multi-energy complementary park energy system has become the focus of attention of experts and scholars, so how to achieve economic and optimal operation of the park electric-hydrogen-thermal decarbonized energy system. To solve this problem, this paper proposes a double-layer energy optimal scheduling method of electric-hydrogen-thermal energy in park based on the alternating direction method of multipliers (ADMM). By combining distributed (rooftop photovoltaic, park building electricity, thermal load) and centralized (battery storage, hydrogen storage, electric heat storage) energy, it realizes precise and optimal interaction of point-to-point energy of multiple subjects.
First, the mathematical model of each building is established based on the power interaction cost between buildings and grid, equipment operation and maintenance cost, power interaction cost between buildings and carbon benefit, and the final economic function of the upper level optimization is obtained by decoupling the interaction power between buildings through ADMM. Second, as each building solves its own optimization problem synchronously, its interactive power values need to be coordinated by a centralized energy optimization scheduling center to achieve a balance between supply and demand. Third, the lower layer optimization uses the building interaction energy and the residual power of each building obtained from the upper layer to solve the exact interaction power among buildings and the optimal output of each centralized energy equipment in the park based on mixed integer programming with the objective of minimizing the park operation cost.
Simulation results for the electric-hydrogen-thermal system of the park show that each building, as an independent entity, can provide certain electric power support to other buildings with insufficient PV power generation when its own PV power generation is sufficient, or it can be absorbed by the electrolyzer and converted into hydrogen energy or stored by battery storage. When there is a power shortage in the park's energy system, fuel cells and battery storage act as power providers to meet the park's load in conjunction with the grid. In addition, while hydrogen production by electrolysis of water and waste heat of fuel cell power generation are matched with electric boilers to meet the heat load of the park, the remaining heat is stored by the heat storage tank, which fully improves the utilization rate of clean energy. The park has a certain support capacity externally, and the energy system of the park can share a certain load for the grid when the external load peaks. The park calculates carbon emission reductions and carbon benefits based on the output of each equipment.
The following conclusions can be drawn from the simulation analysis: (1) Each building in the park can solve its own optimization problem in parallel, solve the desired interactive power and upload it to the centralized energy optimization scheduling center, while taking into account the privacy of user data. (2) Realize the precise interaction of energy from multiple buildings and multiple energy sources (electricity, hydrogen, heat) in the park. solving for the interactive power values available for energy sharing in each building with the support of the ADMM algorithm. The lower layer is based on a mixed integer planning model to accurately solve for the interactive power between buildings and the output of each controllable energy source in the park according to the system operation economy. (3) The adjustable equipment of the park energy system has the ability to support external flexibility while retaining the corresponding margin, and the system can calculate the carbon emission reduction and carbon revenue of the park according to the output of each equipment, so as to realize the low-carbon optimal scheduling of the park electricity-hydrogen-heat system.
keywords:Park electricity-hydrogen-heat system, distributed and centralized interaction, alternating direction method of multipliers (ADMM), double-layer optimized scheduling
DOI:10.19595/j.cnki.1000-6753.tces.220773
中图分类号:TM73
国家重点研发计划(2018YFB1503100)和国家自然科学基金(51907021)资助项目。
收稿日期 2022-05-10
改稿日期 2022-08-13
孔令国 男,1984年生,博士,副教授,研究方向为可再生能源耦合氢能关键技术。E-mail:klgwin@neepu.edu.cn
石振宇 男,1993年生,硕士,助理实验师,研究方向为低碳配电系统关键技术。E-mail:601547794@qq.com(通信作者)
(编辑 赫蕾)