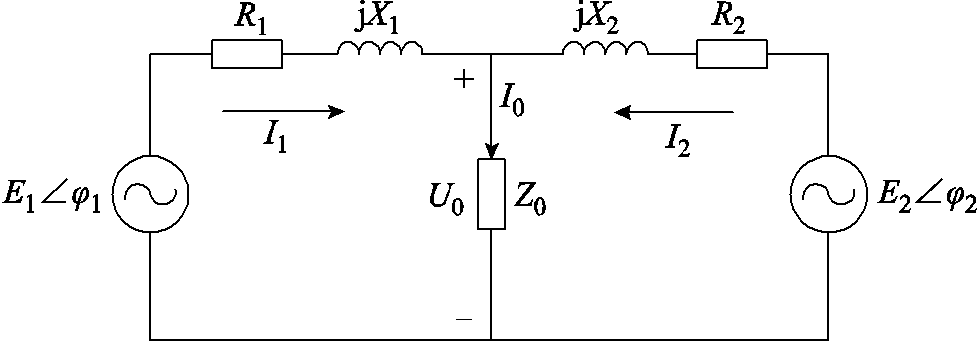
图1 逆变器并联运行等效电路
Fig.1 Equivalent model diagram of parallel operation of inverters
摘要 针对大型光伏电站各发电单元位置差异导致的并网接线阻抗不同，以及光伏电站内各单元最大输出光伏功率运行状况不一致的问题，建立以时变追踪并网光伏电站最大输出功率为目标的无功优化数学模型，并给出相应的快速求解方法。该模型建立和求解是在量测、通信技术完备的前提下，借助逆变器可快速调制有功功率和无功功率输出的电力电子化技术，依据秒级优化周期内光伏系统状态量变化微小的特点，对非线性优化模型实施泰勒展开、线性拟合等线性化近似处理，通过灵敏度计算对逆变器无功功率运行基点进行快速求解，必要时将自动弃光，达到时变追踪光伏电站最大并网输出功率并满足并网点电压水平要求的目的。最后，以某地区大型光伏电站并网系统为例进行仿真，结果验证了所提方法的有效性和合理性。
关键词：大型光伏电站 光伏逆变器 并联运行 时变追踪 无功优化
我国光伏发电呈现“分散开发，低压接入，就地消纳”和“集中开发，高压并网，远距离送出”两种发展方式并举的格局[1]。就后者而言，由于受光照等自然因素限制，光伏发电功率具有很强的时变性、波动性和间歇性[2-3]，若运行控制措施不当，大型光伏电站并网会带来冲击，影响电网经济稳定的运行[4-5]。可见，跟踪与控制发电功率并网点的电压支撑问题就成为关注的焦点。
同时，对于大型光伏电站的并网运行，站内的电压支撑问题同样值得关注。①大型光伏电站由诸多光伏单元有机构成，每个光伏单元都要通过集电线并联到主变压器低压侧母线公共连接点（Point of Common Coupling, PCC），集电线长短不同，阻抗就不同[6]，即各个光伏单元汇集到并网母线的电气距离存在差异；②各个光伏单元所在位置光照强度不同，发电功率存在差异，以及光照的波动性与间歇性导致光伏发电功率具有极强的波动性[7-8]，由此造成各个光伏单元运行状况的不一致。上述两点给满足并网条件的光伏电站调度与控制带来困难，若偏离并网条件严重，将在各个光伏单元间产生电磁环流，不仅损耗大而且影响运行效率，同时对设备造成危害，轻者影响寿命，重者损坏元件，发生运行事故。可见，就并网光伏发电全消纳而言，关注并网点及其内部各点的电压支撑是关键，对其进行深入研究具有重要的理论和现实意义。
目前针对光伏电站并网电压问题的研究主要集中在两个方面：①PCC母线附近配置储能及无功补偿设备来提供电压支撑[9-11]；②挖掘光伏逆变器的无功调节能力来支撑并网点电压[12-14]。额外配置储能及无功补偿设备需要增加一定的成本，且难以实现对内部多个逆变器满足并行协调运行条件的控制，且多为长时间尺度协调配合决策，并不能时变追踪不确定性的光伏功率，逆变器快速的无功功率调节能力也难以得到有效发挥。因此，依靠光伏逆变器剩余容量的无功电压控制，不仅有利于并网点电压支撑水平的控制，也会间接考虑光伏电站内部运行状况不一致与接线阻抗不相等带来的协调配合问题。
现有的研究大多聚焦于大型光伏电站站内无功补偿设备与逆变器对于并网点电压的协调控制。如文献[15-16]以并网点电压恒定为目标，通过PI控制器内部灵敏度计算环节获取所需无功功率参考量；文献[17]在协调无功补偿装置和逆变器的无功容量提供电压支撑的基础上，根据线路流动无功产生的有功损耗对逆变器无功功率进行优化分配；文献[18]建立光伏电站双层无功优化模型，上层跟踪并网点电压控制目标，下层将上层优化结果在各组无功补偿单元之间进行分配，实现光伏电站参与电网主动调压的精细化控制；文献[19]基于光伏单元不同无功裕度的计算，采用可变下垂系数实现无功功率的协调分配；文献[20]综合无功可变下垂控制、有功自动削减控制和无功补偿三种方式，对并网电压进行控制。这些方法在一定程度上提高了光伏并网运行的稳定性，但研究关注的焦点在于维持并网点电压水平，对于如何消除站内各个发电单元之间接线阻抗和运行参量的差异以便于更好地满足并网点及其他节点电压水平的实现研究不够。
对此，在假设光伏电站没有其他调压措施的前提下，本文研究时变追踪最大光伏功率发电并网的无功优化问题[22-23]，仅依靠光伏逆变器的快速无功调节能力来提供电压支撑，必要时自动弃光，保证并网电压满足要求。首先针对光伏单元并联运行的特性，分析接线阻抗与输出功率对于并网电压的影响[21]。在此基础上，假设量测、通信技术完备，建立考虑接线阻抗不相等与运行状况不一致的时变追踪大型光伏电站最大输出功率并网的无功优化数学模型，并给出相应的快速求解方法。该方法依据极短决策时段内光伏系统状态量变化极小的特点，基于泰勒展开与线性拟合将优化周期内的目标函数与约束条件进行线性化处理，构造罚函数，通过灵敏度计算对逆变器的运行基点进行快速求解，达到时变追踪光伏电站最大输出功率并网，并满足并网点电压水平要求的目的。
逆变器是光伏发电将直流电转变为交流电输送到电网的关键设备，因此在光伏电站内部，光伏发电单元的并行问题可以等效为逆变器的并联问题来思考。以两台逆变器并联运行为例，对并联系统的环流问题进行分析。
逆变器并联运行的等效电路如图1所示。其中，R1、R2和X1、X2分别为逆变器和输出线路的等效电阻和电抗，I1和I2为逆变器输出电流，I0为并联电路输出电流，U0为并联电路输出电压，Z0为外电路等效阻抗，E1、E2和φ1、φ2分别为逆变器输出电压的幅值和相位。
图1 逆变器并联运行等效电路
Fig.1 Equivalent model diagram of parallel operation of inverters
若使系统正常运行，就必须保证各逆变器输出电压的幅值、相位及频率严格一致。但在系统实际运行中，由于各逆变器的参数存在一定差异，以及输出线路阻抗也不能保证完全一致，因此，实际运行的并联系统中都会存在环流以及功率均分的问题。如果不加以抑制，就会影响系统的正常运行。
逆变器并联系统中各逆变单元输出的电压不一致是导致环流产生的主要原因，其中电压的不一致又包括电压幅值和相位的不一致，环流可以表示为
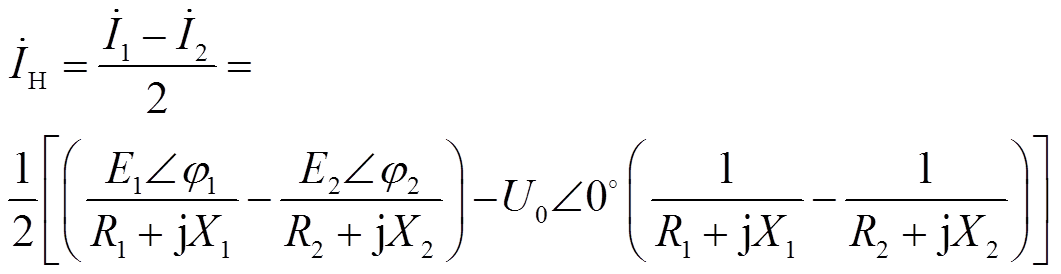（1）
式中，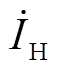
为两逆变器并联运行产生的环流相量；
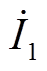和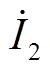
为逆变器输出的电流相量。
可以看出，环流的大小随两台逆变器等效阻抗差值与输出电压差值的增大而增大。阻抗值无法改变，所以调节电压是消除并联环流的有效措施。若E1≠E2，环流大小与幅值差成正比，可通过调节有功功率来减少环流；若φ1≠φ2，环流随相位差的增大而增大，可通过调节其无功功率来减少环流。
两个光伏发电单元并行接入无穷大系统的简化示意图如图2所示。其中，P1+jQ1和P2+jQ2分别表示光伏发电单元1和2中并网逆变器输出的功率，R1+jX1和R2+jX2分别表示光伏发电单元1和2连接到PCC母线的集电线路的等效阻抗，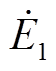
和
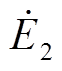分别表示光伏发电单元1和2中并网逆变器的网侧输出电压，
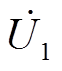和
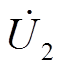分别表示光伏发电单元1和2连接到PCC母线处的电压。
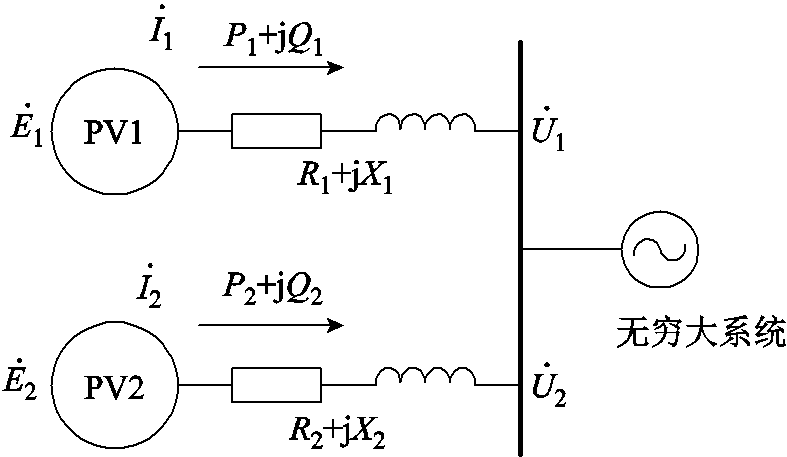
图2 光伏发电单元并行接入无穷大系统简化示意图
Fig.2 Simplified diagram of photovoltaic cell parallel access infinite system
下面分析光伏发电单元并联运行时阻抗和逆变器网侧输出电压对于并网母线电压的影响。由于同一个光伏电站的变压器、逆变器等一般采用相同厂家生产的设备，其参数都相同，不会对光伏单元并行产生影响，故分析过程中忽略其阻抗。
光伏单元的并联运行要保证其电压相同，有
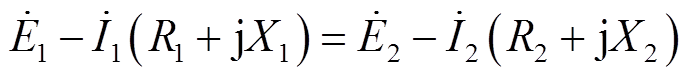（2）
同时，对于并网逆变器并网侧输出功率与电流的关系，有
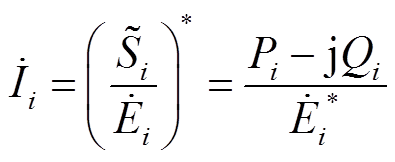（3）
式中，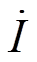
、
、
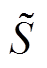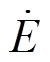、P、Q分别为逆变器并网侧输出电流、视在功率、电压、有功功率、无功功率；*表示共轭；下标i为光伏发电单元的标号，i = 1,2。
一般情况下，为保证光伏功率被有效利用，光伏发电都要遵循最大功率点跟踪（Maximum Power Point Tracking, MPPT）控制方式，尽可能保证输出最大有功功率[24]。由式（2）和式（3）可以看出，在追求最大有功功率的前提下，要想保证并网电压一致，只能调节光伏输出的无功功率。如果光伏单元集电线路阻抗较大，那么逆变器输出的无功功率就要相对增大，来降低流经的电流大小，以此减小阻抗上的电压降，保证并网母线处电压是一致的，才能使光伏单元顺利并网运行。
综上所述，如果要使并联运行的光伏发电单元顺利并网，就要保证到达PCC母线的电压的幅值、相位及频率相等。相应地，如果对光伏逆变器输出无功功率进行控制，来消除集电线路阻抗不同与光伏输出功率不同带来的光伏电站内部的运行不一致问题，就能在一定程度上保证各单元并网电压一致。
以光伏逆变器的输出有功功率、无功功率为决策变量，建立其在满足潮流约束、电压水平约束、光伏发电输出功率约束条件下，追求整个光伏电站并网功率最大为目标的数学优化模型。
1）目标函数
（4）
式中，N为光伏电站系统所有节点的集合；NG为所有光伏发电单元及其对应节点的集合；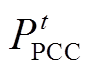
为t时刻光伏电站PCC处输出的有功功率；
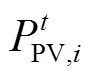为t时刻光伏发电单元i输出的有功功率；
为t时刻光伏电站系统的有功功率损耗；Rij为线路ij的电阻；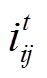
为t时刻线路ij流过的电流。
2）约束条件
（1）光伏电站内部潮流约束
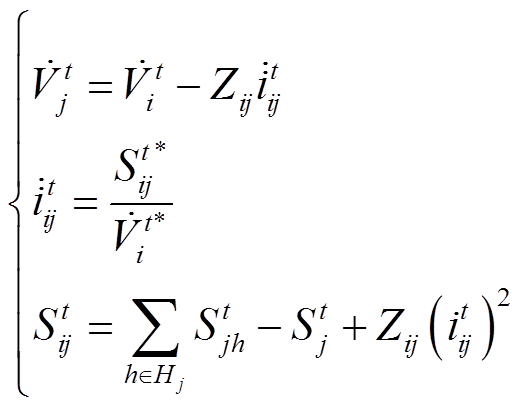（5）
式中，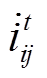
为t时刻线路ij流过的电流相量；
、
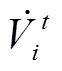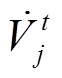分别为t时刻光伏电站节点i和j的电压相量；
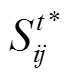为t时刻光伏电站线路ij的视在功率的共轭值；
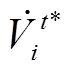为t时刻光伏电站节点i的电压相量的共轭值；
、
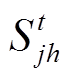分别为t时刻光伏电站线路ij和jh的视在功率；
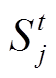为t时刻光伏电站节点j注入的复功率；Zij为光伏电站线路ij的阻抗。
（2）节点电压、线路电流约束
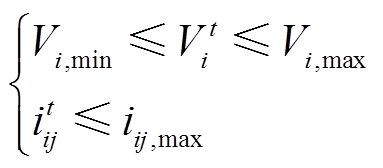（6）
式中，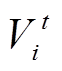
为t时刻光伏电站节点i的电压幅值；Vi,max、Vi,min分别为节点i的允许电压幅值上、下限；iij,max为线路ij的允许电流上限。
（3）光伏逆变器输出功率约束
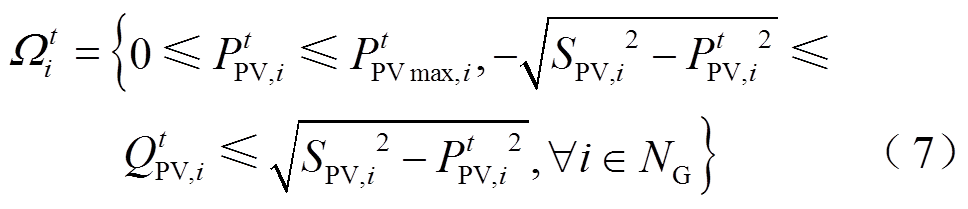
式中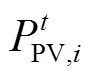，为t时刻节点i光伏逆变器有功功率输出；
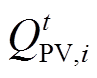为t时刻节点i光伏逆变器无功功率输出；
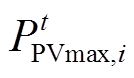为t时刻节点i光伏逆变器有功输出的上限，根据光伏逆变器MPPT控制系统获得；
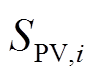为节点i光伏逆变器的额定容量。
2.1节建立了t时刻时变追踪光伏发电最大并网功率的无功优化模型。该模型是非线性规划问题，直接求解时速度难以满足对逆变器控制基点的快速决策要求。在量测、通信技术完备的前提下，假设光伏电站系统状态可观、可控，即t时刻可观，依此可优化t-1时刻决策量，当这两个时刻相差时间极短时，该模型可转变为线性优化模型，从而达到时变追踪光伏逆变器有功功率和无功功率控制基点的效果。
令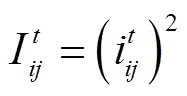
，
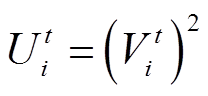，在目标函数式（4）中引入电压、电流不等式约束的罚函数，构造增广目标函数式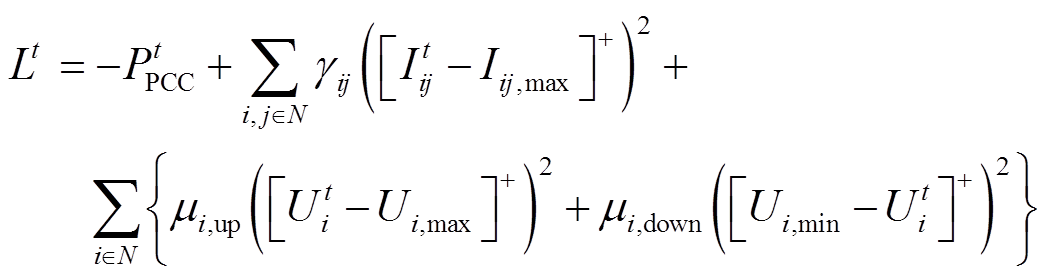（8）。
（8）
式中，[•]+的数学含义是max{•,0}；γij为t时刻光伏电站线路ij的电流约束的惩罚系数；μi,up和μi,down分别为光伏电站节点i的电压约束上限和下限的惩罚系数。
基于以下迭代过程求解：
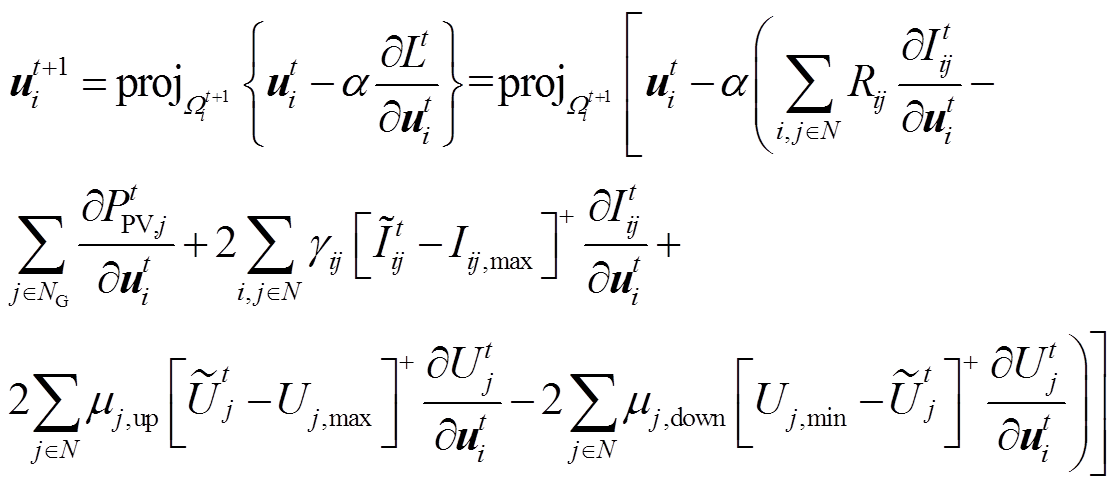（9）
式中，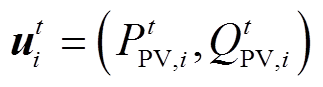
为决策变量；
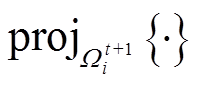为限定范围函数，将
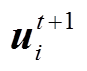限定在逆变器运行约束
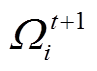内；α为迭代步长；
、
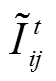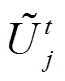分别为光伏电站内各线路电流量测值的二次方和各节点电压量测值的二次方。
由上述分析，问题的关键就转换为灵敏度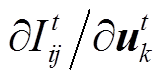
和
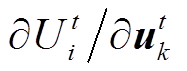的计算。
假设通过量测可得决策时段t初始时刻任一支路的送端功率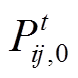
、
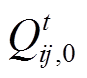及相应节点的电压幅值
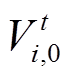。令
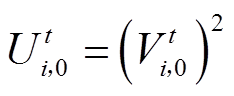，在(,,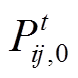
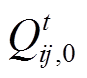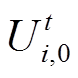)处对潮流约束中的非线性项
进行泰勒展开，并忽略其二阶及高阶项，得
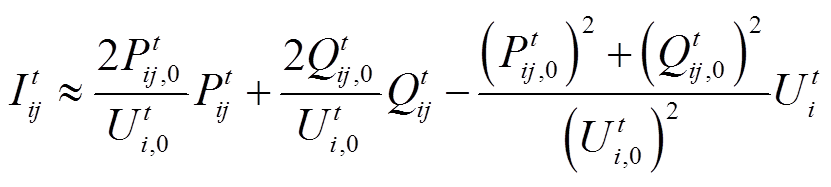（10）
式中，
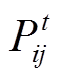和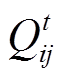
分别为线路ij的送端有功功率和无功功率；
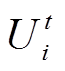为节点i的电压幅值的二次方。
式（10）将非线性项转换为随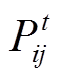、、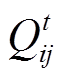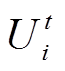变化的线性项，代入式（5），可将模型中的潮流约束转换为以、、、
、
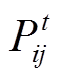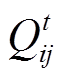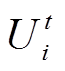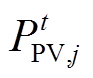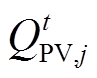为变量的线性表示形式，由此潮流方程得以线性化表示。
可将灵敏度分别展开为
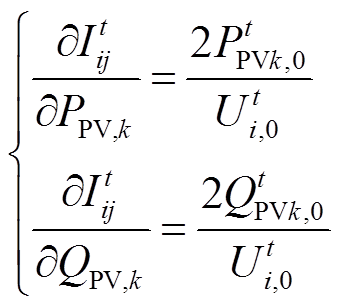（11）
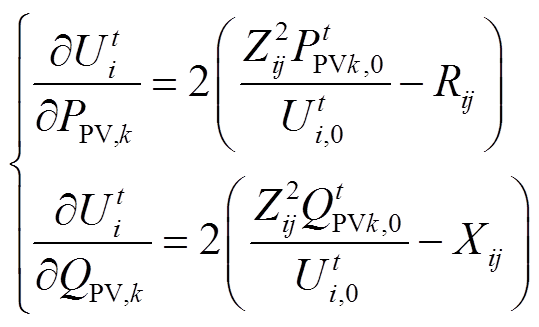（12）
式中，PtPVk,0、QtPVk,0分别为通过量测获得的决策时段t初始时刻的光伏有功、无功输出，即光伏单元对应支路的送端功率；Uti,0为通过量测获得的决策时段t初始时刻的节点电压幅值的二次方值；Xij为线路ij的电抗。
由此，将2.1节模型的目标函数和潮流约束中的非线性量进行线性化处理，下一步对于逆变器的输出功率约束利用线性拟合的方法处理，就可以使该模型变成线性的追踪优化模型。
对于光伏逆变器输出约束式（7），其有功功率和无功功率关系的二维图形如图3a所示，对其通过多条直线进行拟合，如图3b所示。当拟合直线足够多时，可以将拟合误差缩小到任意范围。由此将非线性约束式以多个线性不等式约束进行代替。
本文按照圆心角相等原则将光伏逆变器圆方程进行等分，设第一象限圆弧被九等分，得(0,1)、(0.17,0.98)、(0.34,0.94)、(0.5,0.87)、(0.64,0.77)、(0.77,0.64)、(0.87,0.5)、(0.94,0.34)、(0.98,0.17)、(1,0)10个分段点，相邻两点可确定一条直线，综合第一和第四象限共有18条直线对式（7）进行拟合，将非线性约束式（7）转换为线性约束。
直线集合表示为
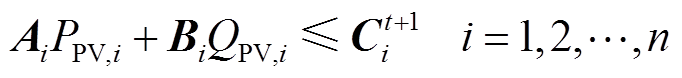（13）
式中，Ai、Bi分别为第i个逆变器功率拟合表达式中的常系数矩阵；Cit+1为与PtPVmax,i有关的矩阵。
图3 光伏逆变器输出约束线性化
Fig.3 Output constraint linearization of photovoltaic inverter
基于以上模型与方法，可以实现对时变光伏发电最大功率并网追踪的无功优化计算。进一步，各逆变器不断将计算结果予以实现，达到对大型光伏电站时变光伏功率的快速追踪，以及对逆变器控制基点的快速求解决策。具体步骤如下：
（1）基于量测获取光伏并网系统的实时运行状态，包括各节点电压幅值Vti,0和各支路功率Ptij,0、Qtij,0，根据MPPT原理得到光伏发电单元在时段t的最大有功功率限值PtPVmax,i。根据2.1节和2.2节公式构建时变追踪光伏发电最大功率的无功优化模型。
（2）求解得到时段t内各逆变器的有功、无功功率设定点uit=(PtPV,i,QtPV,i)。
（3）将uit传送给各台逆变器控制系统，通过PQ控制执行有功功率、无功功率控制指令。
（4）返回步骤（1），进行下一时段迭代运算。
随着步骤（1）～步骤（4）的不断循环，得到如图4所示的两光伏单元并联运行拓扑结构示意图，最终实现对时变光伏发电最大功率的快速追踪。
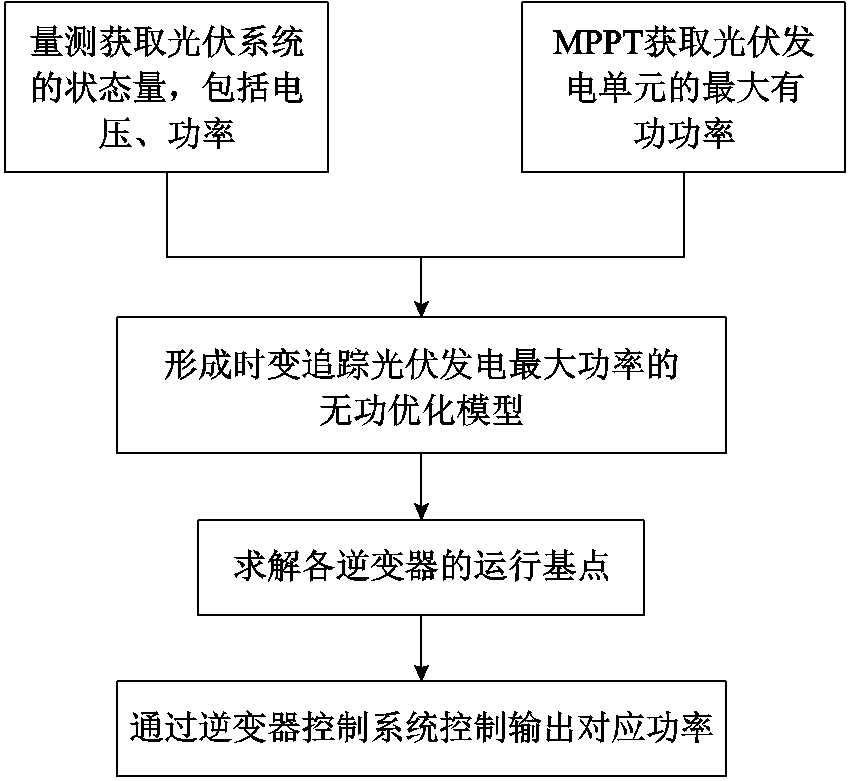
图4 时变追踪光伏电站最大功率的无功优化算法求解框图
Fig.4 Block diagram of reactive power optimization algorithm for time-varying tracking maximum power of photovoltaic power station
本节采用两单元并联模型为例，对光伏电站并行机理进行分析，其拓扑结构示意图如图5所示。其中，U1、U2表示光伏电站中并网逆变器的并网侧电压，也表示各个光伏单元的节点电压，U3和UPCC分别表示主变压器低压侧和高压侧并网公共点电压，U0表示电网电压，T1、T2表示光伏发电单元出口处的箱式升压变压器，T3表示连接光伏电站与电网的主变压器。
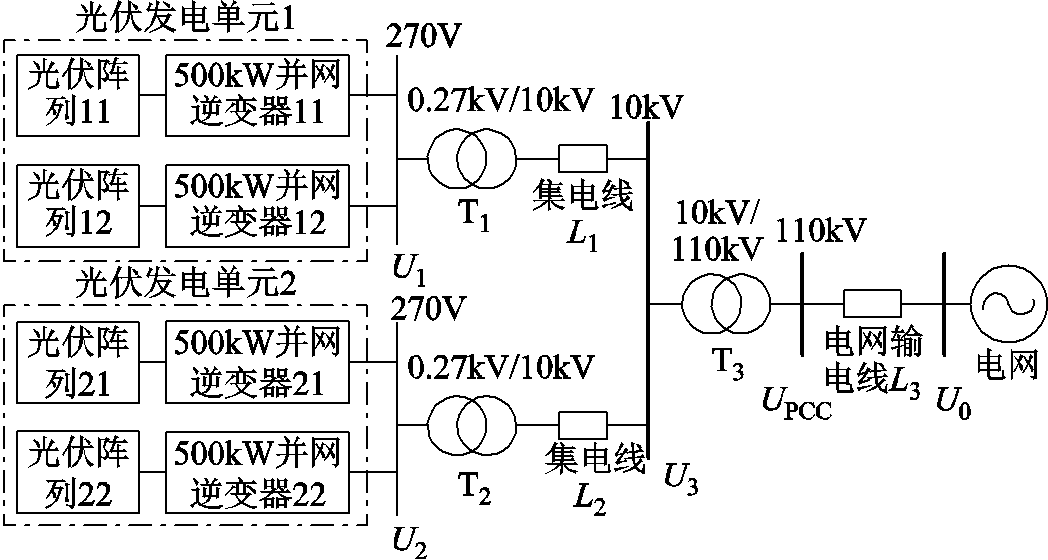
图5 两光伏单元并联运行拓扑结构示意图
Fig.5 Schematic diagram of topology structure of parallel operation of two PV units
该模型具体参数数据见附表1～附表3。两个光伏发电单元经箱式升压变压器和电缆集电线路并联接入主变压器低压侧10 kV母线，经主变压器升压之后通过输电线接入电网。并网逆变器出口直接连接箱式升压变压器，目的是减少不必要的损耗。集电线路L1、L2长度不同，所以各光伏单元连接到PCC母线的阻抗不同；光伏发电单元地理位置差异，接受光照不同，所以最大有功功率输出能力不同。
选取1 min内光伏单元历史光照数据进行计算，参考文献[25]中光伏电池模型公式可得光伏有功功率输出，使用Matlab软件YALMIP工具箱调用FMINCON函数求解2.1节无功优化模型，计算结果如图6所示。
图6a展示了两个光伏发电单元输出的最大有功功率情况。可以看出，由于位置差异，同一时刻两个光伏单元的输出功率有一定差异，随光照强度的改变而改变，造成光伏电站内部运行参量的不一致。同时，两个光伏发电单元的变压器采用相同配置，集电线采用相同材质，但由于位置差异，集电线路长度不同造成阻抗不同。图6b为光伏发电单元输出无功功率情况，可以看出，在两个单元有功功率差别不大但是L1＞L2的情况下，1号单元比2号单元要输出更多的无功功率才能消除结构上的差异，保证光伏电站PCC母线处并联运行电压一致。根据1.2节公式推导，两个光伏单元输出有功功率不同，且线路阻抗不相等的情况下，要想保持每个单元到达PCC母线的电压一致，就要调控各个光伏逆变器输出不同的无功功率。也就是说，由于1号光伏发电单元的集电线路较长，其阻抗值大，意味着逆变器需要输出更多的无功功率，来降低其线路阻抗上产生的电压降，保证1号与2号光伏单元到达PCC母线的电压是一致的，这与1.2节的理论分析非常吻合。
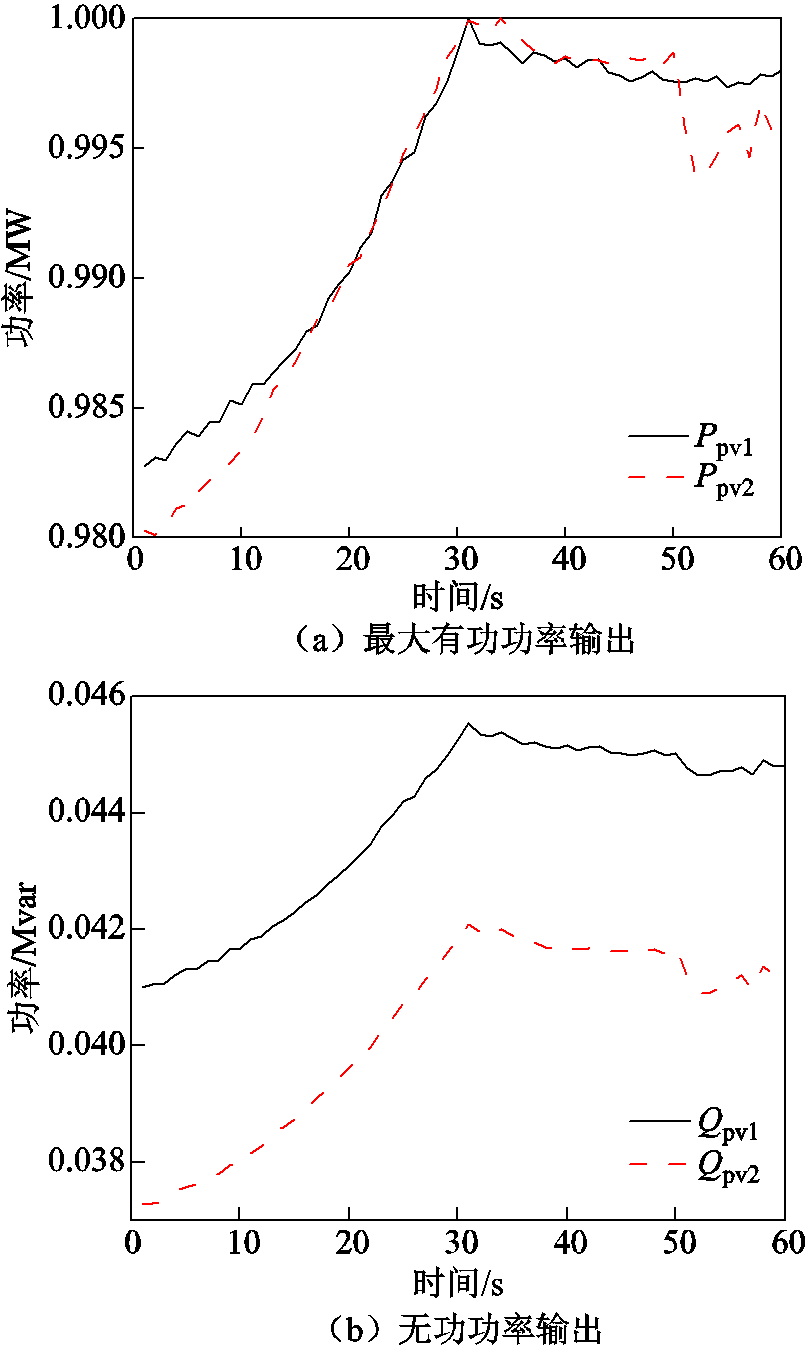
图6 光伏发电单元输出功率对比
Fig.6 Comparison of power output of photovoltaic cells
以山东东营某光伏发电项目为例进行算例分析。光伏电站共有40组发电单元，每组发电单元的额定功率为1 MW。各发电单元均通过400 V/10 kV变压器接到5条10 kV的集电线路上，各集电线路长短不一，最终汇集到10 kV/110 kV主变压器的低压母线，经变压器升压后通过5 km输电线路接入110 kV变电站实现并网。其拓扑结构见附图1，光伏电站内部线路参数信息见附表4，其中U0为电网电压，集电线采用LGJ-95型号线，高压输电线采用LGJ-300型号线。
利用某天00:00～24:00的24 h历史光照数据进行计算分析，各单元的光照、功率输出情况各不相同，同时，假设光伏电站内各个节点、支路和逆变器等关键设备处均配有量测和通信设备。
本文所提算法是以2.1节无功优化模型为基础，构造罚函数，引入在线量测信息线性化，进而实现对光伏电站时变最大功率的追踪优化。计算所用计算机硬件配置为：2.70GHz Intel(R) Core(TM) i5-6400 CPU，8GB RAM；运行软件为：Matlab R2018a。将2.1节优化模型直接利用非线性优化方法求解与本文所提罚函数线性化方法求解进行对比，速度对比结果见表1，本文方法的模型平均计算时间为0.012 s，可以实现光伏逆变器运行基点的快速决策，相比较非线性方法求最优解时用时36.091 s，具有显著的速度优势。
表1 求解速度对比
Tab.1 Solution speed comparison
求解方法单次求解所用时间/s 非线性优化方法t136.091 本文方法t20.012
分析时变追踪并网光伏电站最大输出功率情况，结果如图7所示。可以看出，相比于MPPT输出功率，在10:00～15:00光照很强这段时间内，本文方法计算结果自动弃光，降低光伏发电单元输出的有功功率，通过有功功率让位于无功功率来保证电压满足约束。
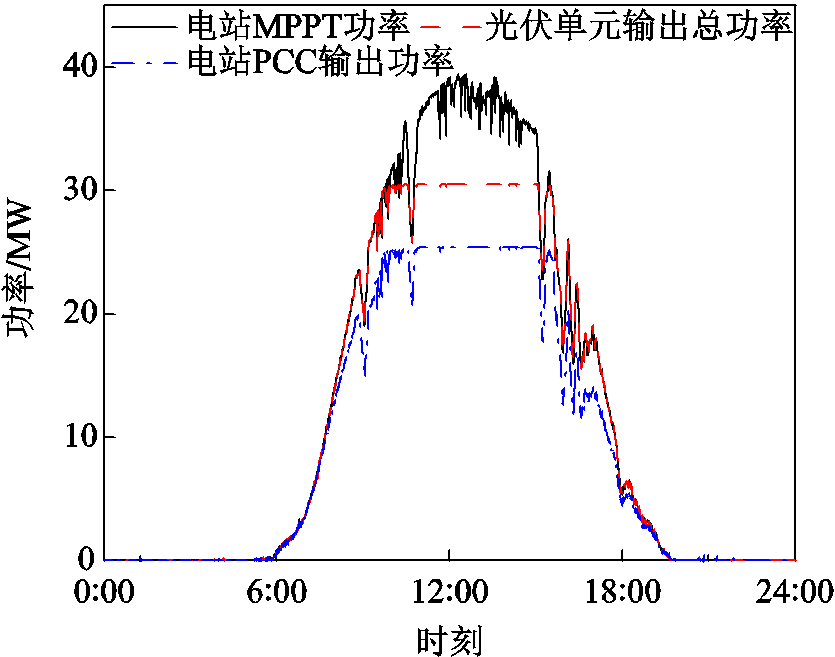
图7 光伏电站输出功率对比
Fig.7 Comparison of output power of photovoltaic power station
分析采用本文算法前后无功电压控制效果，其中节点电压幅值变化情况如图8a所示，光伏发电单元无功功率输出情况如图8b所示。可以看出，采用本文算法前，在11:00～17:00时段内光伏电源高发，使得节点电压超过上限，而在其余时间段，光伏电源少发或不发，容易使电压低于下限。采用本文算法后，可以将节点电压控制在允许范围之内。同时，当光伏电源高发导致节点电压超过上限时，逆变器吸收无功功率增多，从而抵消一部分光伏高发对电压的提升作用，当光伏电源零发或少发导致电压越下限时，逆变器会增加无功功率的输出，保证电压不低于下限。
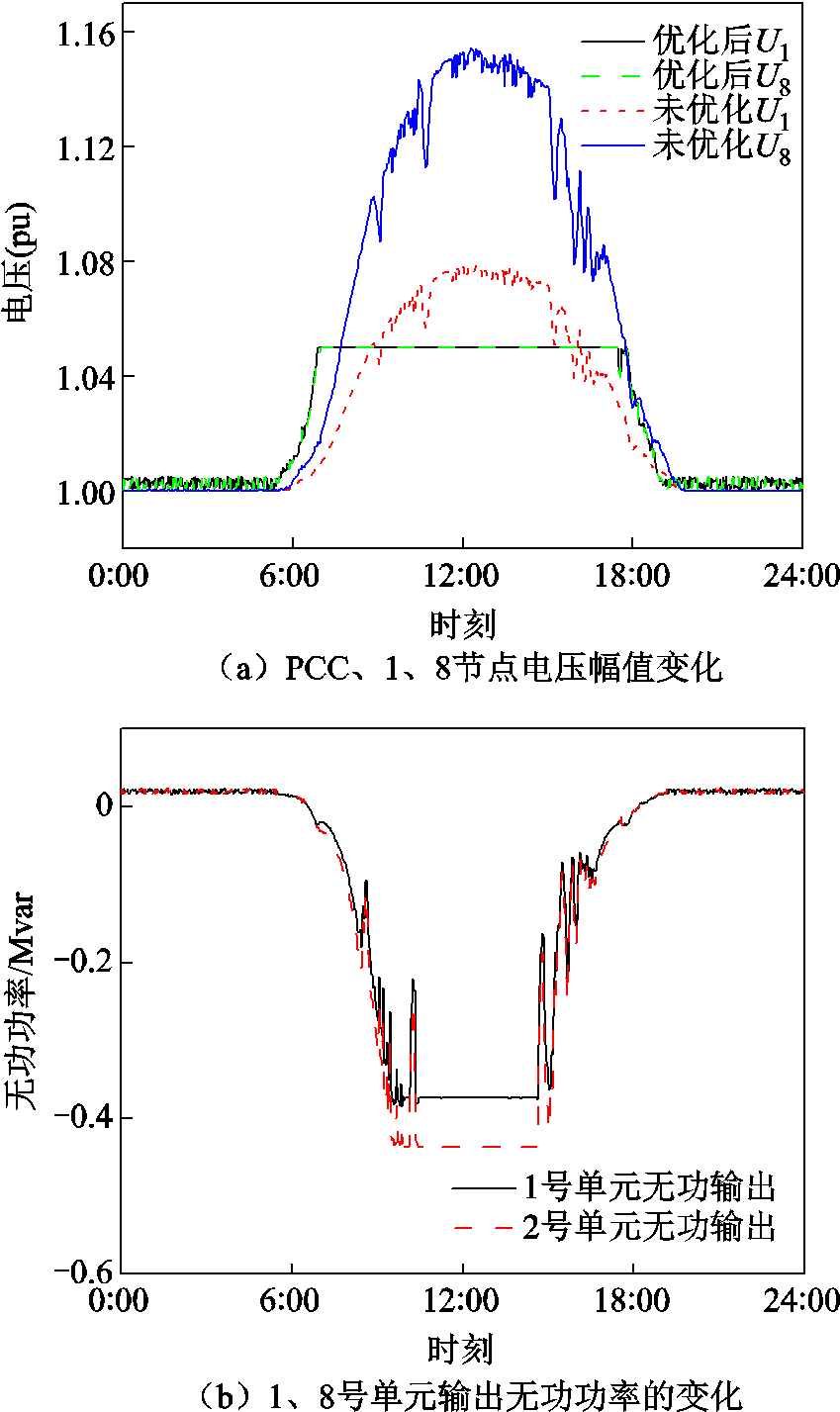
图8 采用本文算法的光伏电站无功电压控制效果
Fig.8 The reactive voltage control effect of photovoltaic power station using the algorithm in this paper
为进一步分析本文所提算法的有效性，对比采用本算法前后光伏电站并网系统损耗情况，结果如图9所示。可以看出，采用本算法前光伏电站按单位功率因数并网，一天中最大损耗为7.856 4 MW，采用本算法后，以光伏并网功率最大为目标，间接追求系统损耗最小，逆变器实时调控输出功率，一天中最大损耗为5.769 8 MW。图9中两条曲线之间差值即为采用本文算法能够降低的损耗，对其积分可得一天节省电量为61.8 kW·h。
图9 采用本文算法的光伏电站损耗降低情况
Fig.9 Loss reduction of photovoltaic power station using the algorithm in this paper
本文聚焦于光伏电站没有其他调压措施的前提下，考虑连同内部结构的统一时变追踪最大光伏功率发电的优化问题，依靠光伏逆变器的无功调节能力来提供电压支撑，保证并网电压稳定。通过快速决策逆变器有功功率、无功功率的控制基点，挖掘光伏电站自身的无功电压调控潜力。得出结论如下：
1）类比同步发电机的并联运行，光伏电站内部光伏单元的并联运行也需要满足到达PCC母线的电压与电流幅值、相位及频率完全一致。频率的一致由逆变器控制系统依照电网频率来进行控制，在此不做考虑。由于各个光伏发电单元到PCC母线的集电线路阻抗不同，各个单元发出的有功功率也不同，要保持并网电压一致的前提下，需要对并网逆变器输出无功功率进行分别调控，来保证并网条件的满足。
2）利用分布在光伏电站内部各个单元光伏逆变器自身的有功、无功调节能力，解决集中式补偿无法有效解决的光伏电站内部电压问题。基于实时量测与通信设备，结合电力电子化设备的快速控制，可以实现对各发电单元的功率输出的快速决策与控制，充分挖掘光伏电站自身的无功电压调节潜力。结果表明，该方法具有较高的计算精度，能够快速决策逆变器的功率设定点，通过快速调节逆变器无功功率的输出来解决光伏电站内部的电压问题，利用算法的实时性有效应对光伏发电的不确定性。
目前的研究是对光伏电站自身调控能力的深度挖掘，而且是基于电网完全接纳光伏功率的前提下。当电网要求光伏电站参与调度时，光伏逆变器自身的调节能力可能无法满足，需要储能、无功补偿等辅助设备的合作配合，这些问题将在后续研究中进一步深入。
附表1 线路参数
App.Tab.1 Line parameters
编号线路长度/kmUN/kVR/(Ω/km)X/(Ω/km)B/(S/km) L130100.008 20.001 2— L220100.008 20.001 2— L31001100.2700.7852.78×10-6
附表2 变压器参数
App.Tab.2 Transformer parameter
编号SN/MWk1/k2P0/kWPk/kWUk(%)I0(%) T110.4/10.51.15510.34.50.5 T210.4/10.51.15510.34.50.5 T3210.5/12129.44148.210.50.3
附表3 光伏电池板参数
App.Tab.3 Photovoltaic panel parameter
Um/VIm/AUOC/VISC/A 24.68.7430.79.15
附表4 光伏电站内部线路参数
App.Tab.4 Internal circuit parameters of photovoltaic power station
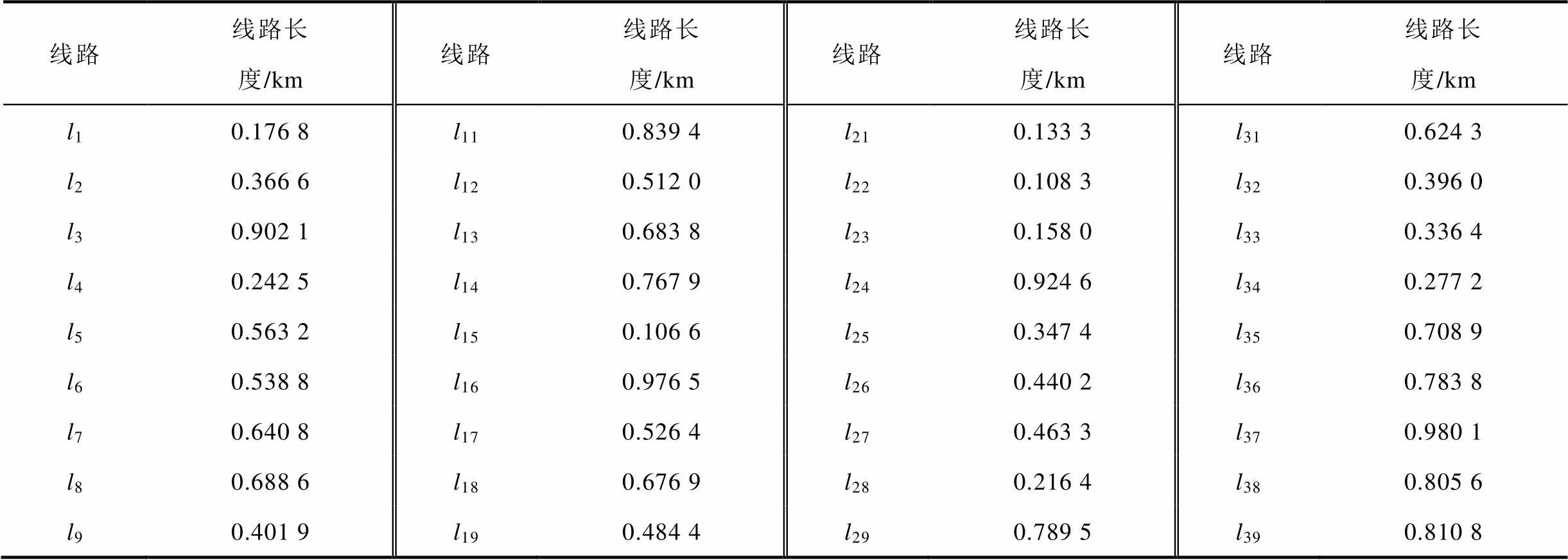
线路线路长度/km线路线路长度/km线路线路长度/km线路线路长度/km l10.176 8l110.839 4l210.133 3l310.624 3 l20.366 6l120.512 0l220.108 3l320.396 0 l30.902 1l130.683 8l230.158 0l330.336 4 l40.242 5l140.767 9l240.924 6l340.277 2 l50.563 2l150.106 6l250.347 4l350.708 9 l60.538 8l160.976 5l260.440 2l360.783 8 l70.640 8l170.526 4l270.463 3l370.980 1 l80.688 6l180.676 9l280.216 4l380.805 6 l90.401 9l190.484 4l290.789 5l390.810 8
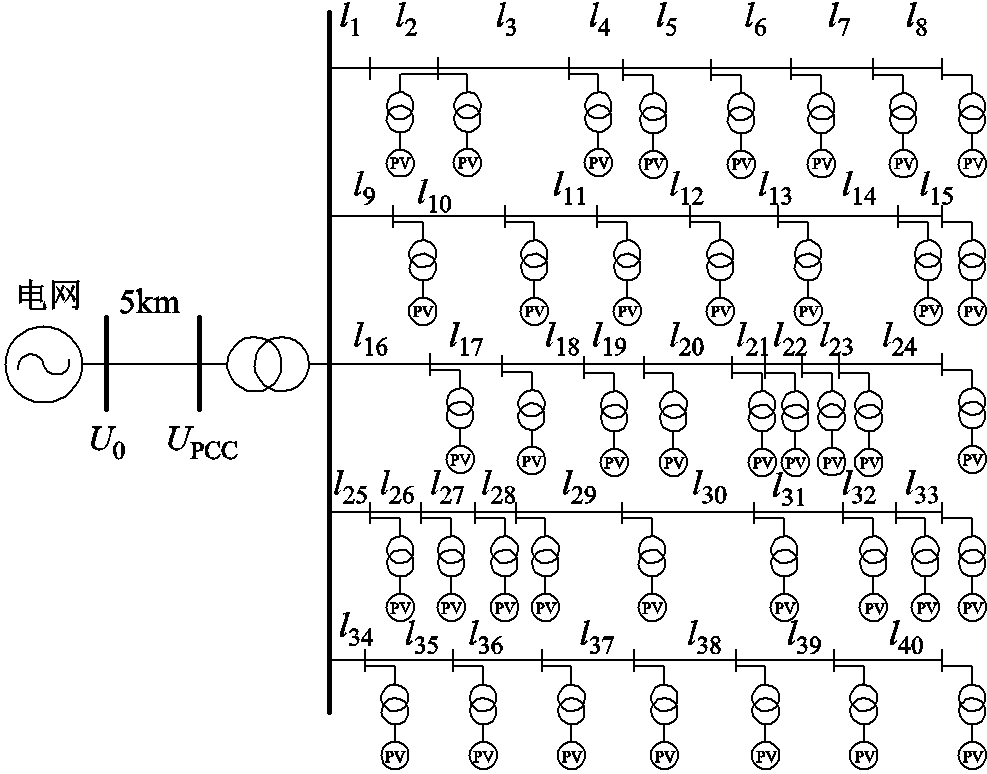
附图1 光伏电站内部拓扑结构示意图
App.Fig.1 Diagram of internal topological structure of photovoltaic power station
参考文献
[1] 郭立东, 雷鸣宇, 杨子龙, 等. 光储微网系统多目标协调控制策略[J]. 电工技术学报, 2021, 36(19): 4121-4131. Guo Lidong, Lei Mingyu, Yang Zilong, et al. Multi-objective coordinated control strategy for photovoltaic and energy-storage microgrid system[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4121-4131.
[2] Zhu Xiaonan, Wang Hongliang, Zhang Wenyuan, et al. A novel single-phase five-level transformer-less photovoltaic (PV) inverter[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(4): 329-338.
[3] 谢丽蓉, 郑浩, 魏成伟, 等. 兼顾补偿预测误差和平抑波动的光伏混合储能协调控制策略[J]. 电力系统自动化, 2021, 45(3): 130-138. Xie Lirong, Zheng Hao, Wei Chengwei, et al. Coordinated control strategy of photovoltaic hybrid energy storage considering prediction error compensation and fluctuation suppression[J]. Automation of Electric Power Systems, 2021, 45(3): 130-138.
[4] 丁明, 王伟胜, 王秀丽, 等. 大规模光伏发电对电力系统影响综述[J]. 中国电机工程学报, 2014, 34(1): 1-14. Ding Ming, Wang Weisheng, Wang Xiuli, et al. A review on the effect of large-scale PV generation on power systems[J]. Proceedings of the CSEE, 2014, 34(1): 1-14.
[5] 陈炜, 艾欣, 吴涛, 等. 光伏并网发电系统对电网的影响研究综述[J]. 电力自动化设备, 2013, 33(2): 26-32, 39. Chen Wei, Ai Xin, Wu Tao, et al. Influence of grid-connected photovoltaic system on power network[J]. Electric Power Automation Equipment, 2013, 33(2): 26-32, 39.
[6] 李璐璐, 韩学山, 朱星旭, 等. 双馈风电机群并网系统时变最优潮流的优化追踪方法[J]. 电力自动化设备, 2021, 41(2): 56-62, 96. Li Lulu, Han Xueshan, Zhu Xingxu, et al. Method for time-varying optimal power flow tracking of doubly-fed wind turbine grid-connected system[J]. Electric Power Automation Equipment, 2021, 41(2): 56-62, 96.
[7] Zhao Liang, Qu Linan, Ge Luming, et al. An active power control strategy for large-scale clusters of photovoltaic power stations[C]//PES General Meeting | Conference & Exposition, Nanjing China, 2014.
[8] 徐潇源, 王晗, 严正, 等. 能源转型背景下电力系统不确定性及应对方法综述[J]. 电力系统自动化, 2021, 45(16): 2-13. Xu Xiaoyuan, Wang Han, Yan Zheng, et al. Overview of power system uncertainty and its solutions under energy transition[J]. Automation of Electric Power Systems, 2021, 45(16): 2-13.
[9] 郑浩, 谢丽蓉, 叶林, 等. 考虑光伏双评价指标的混合储能平滑出力波动策略[J]. 电工技术学报, 2021, 36(9): 1805-1817. Zheng Hao, Xie Lirong, Ye Lin, et al. Hybrid energy storage smoothing output fluctuation strategy considering photovoltaic dual evaluation indicators[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1805-1817.
[10] Long Chao, Ochoa L F. Voltage control of PV-rich LV networks: OLTC-fitted transformer and capacitor banks[J]. IEEE Transactions on Power Systems, 2016, 31(5): 4016-4025.
[11] 朱星旭, 韩学山, 杨明, 等. 含分布式光伏与储能配电网时变最优潮流追踪的分布式算法[J]. 中国电机工程学报, 2019, 39(9): 2644-2658. Zhu Xingxu, Han Xueshan, Yang Ming, et al. A distributed algorithm for time-varying optimal power flow tracking in distribution networks with photovoltaics and energy storage[J]. Proceedings of the CSEE, 2019, 39(9): 2644-2658.
[12] 李克强, 韩学山, 李华东, 等. 配网中光伏逆变器最优潮流追踪的分布式算法[J]. 中国电机工程学报, 2019, 39(3): 711-720, 950. Li Keqiang, Han Xueshan, Li Huadong, et al. Distributed algorithm for optimal power flow pursuit by photovoltaic inverters in distribution systems[J]. Proceedings of the CSEE, 2019, 39(3): 711-720, 950.
[13] Alam M J E, Muttaqi K M, Sutanto D. A multi-mode control strategy for VAr support by solar PV inverters in distribution networks[J]. IEEE Transactions on Power Systems, 2015, 30(3): 1316-1326.
[14] 朱泓晖, 屈艾文, 周扬忠. 基于储能型准Z源光伏并网逆变器的改进型自适应粒子群最大功率点跟踪算法研究[J]. 电气技术, 2021, 22(3): 6-13. Zhu Honghui, Qu Aiwen, Zhou Yangzhong. Research on improved adaptive particle swarm optimization maximum power point tracking algorithm based on energy-stored quasi-Z-source photovoltaic grid-connected inverter[J]. Electrical Engineering, 2021, 22(3): 6-13.
[15] 周林, 任伟, 廖波, 等. 并网型光伏电站无功电压控制[J]. 电工技术学报, 2015, 30(20): 168-175. Zhou Lin, Ren Wei, Liao Bo, et al. Reactive power and voltage control for grid-connected PV power plants[J]. Transactions of China Electrotechnical Society, 2015, 30(20): 168-175.
[16] 周林, 邵念彬. 大型光伏电站无功电压控制策略[J]. 电力自动化设备, 2016, 36(4): 116-122, 128. Zhou Lin, Shao Nianbin. Reactive-power and voltage control for large-scale grid-connected photovoltaic plants[J]. Electric Power Automation Equipment, 2016, 36(4): 116-122, 128.
[17] Dai Jianfeng, Tang Yi, Xu Yan, et al. Reactive power optimization coordinated control strategy of the large-scale PV power station[C]//2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 2019: 1632-1637.
[18] 王贤, 刘文颖, 夏鹏, 等. 光伏电站参与电网主动调压的无功优化控制方法[J]. 电力自动化设备, 2020, 40(7): 76-83. Wang Xian, Liu Wenying, Xia Peng, et al. Reactive power optimization control method for PV station participating in active voltage regulation of power grid[J]. Electric Power Automation Equipment, 2020, 40(7): 76-83.
[19] 朱慧敏, 苑舜, 李春来. 基于可变下垂系数的光伏电站无功电压控制策略[J]. 可再生能源, 2020, 38(8): 1103-1108. Zhu Huimin, Yuan Shun, Li Chunlai. Reactive voltage control strategy of photovoltaic power station based on variable droop coefficient[J]. Renewable Energy Resources, 2020, 38(8): 1103-1108.
[20] 俞智鹏, 汤奕, 戴剑丰, 等. 基于有功自适应调整的光伏电站无功电压控制策略[J]. 电网技术, 2020, 44(5): 1900-1907. Yu Zhipeng, Tang Yi, Dai Jianfeng, et al. Voltage/var control strategy of PV plant based on adaptive adjustment of active power[J]. Power System Technology, 2020, 44(5): 1900-1907.
[21] 谢志为, 陈燕东, 伍文华, 等. 弱电网下多逆变器并网系统的全局高频振荡抑制方法[J]. 电工技术学报, 2020, 35(4): 885-895. Xie Zhiwei, Chen Yandong, Wu Wenhua, et al. A global high-frequency oscillation suppression method for multi-inverter grid-connected system in weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 885-895.
[22] 赵冬梅, 陶然, 马泰屹, 等. 基于多智能体深度确定策略梯度算法的有功-无功协调调度模型[J]. 电工技术学报, 2021, 36(9): 1914-1925. Zhao Dongmei, Tao Ran, Ma Taiyi, et al. Active and reactive power coordinated dispatching based on multi-agent deep deterministic policy gradient algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1914-1925.
[23] Dall'Anese E, Dhople S V, Giannakis G B. Photovoltaic inverter controllers seeking AC optimal power flow solutions[J]. IEEE Transactions on Power Systems, 2016, 31(4): 2809-2823.
[24] 李畸勇, 张伟斌, 赵新哲, 等. 改进鲸鱼算法优化支持向量回归的光伏最大功率点跟踪[J]. 电工技术学报, 2021, 36(9): 1771-1781. Li Jiyong, Zhang Weibin, Zhao Xinzhe, et al. Global maximum power point tracking for PV array based on support vector regression optimized by improved whale algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1771-1781.
[25] 谢宁, 罗安, 陈燕东, 等. 大型光伏电站动态建模及谐波特性分析[J]. 中国电机工程学报, 2013, 33(36): 10-17, 4. Xie Ning, Luo An, Chen Yandong, et al. Dynamic modeling and characteristic analysis on harmonics of photovoltaic power stations[J]. Proceedings of the CSEE, 2013, 33(36): 10-17, 4.
Abstract For parallel operation of large photovoltaic power station, connection impedance is different because of different location of each power generation unit, and operation status of the maximum output photovoltaic power of generation units are inconsistent. They generate difficulty on the interconnection conditions of photovoltaic power plant scheduling and control. If deviating from the parallel conditions, the electromagnetic circulation will be generated between each photovoltaic unit, which will cause great loss and harm to the operation of the equipment, and affect the operation efficiency. Recently, some methods were presented to control the grid connection of photovoltaic power generation, which focus on maintaining the voltage level of the grid connection point, but most of them suffered from eliminating the differences of wiring impedance and operation parameters among the power generation units in the station. To address these issues, this paper establishes a mathematical model of reactive power optimization for time-varying tracking of maximum output power of grid-connected photovoltaic power station, and gives a fast solution method. By quickly solving the control base point of inverter, the purpose of tracking the maximum grid-connected output of photovoltaic power station with time is achieved.
Firstly, taking the output active power and reactive power of photovoltaic inverter as decision variables, a mathematical optimization model is established to maximize the grid-connected power of the whole photovoltaic power plant under the constraints of power flow, voltage level and photovoltaic power output. The state change of photovoltaic grid-connected system is small in very short time interval, so the nonlinear optimization model is linearized by Taylor expansion and linear fitting. Through sensitivity calculation, the operating basis point of the reactive power of the inverter is quickly solved, and the light will be automatically discarded when necessary. This model uses the concept of sensitivity to solve the control point based on the online optimization iterative process, thus leading to a computationally fast model.
Simulation results show that, if two photovoltaic power generation units operate in parallel, and the photovoltaic output active power has little difference, the inverter output reactive power is approximately proportional to the line impedance distribution to maintain grid voltage consistency. Using illumination data from 00:00 to 24:00 and compared with the maximum power point tracking (MPPT) output, the results show that, during the period of strong illumination (10:00-15:00), this method automatically abandon light, reduce the active power output of photovoltaic power generation unit, and ensure the voltage meets the constraint by giving way of active power to reactive power. At the same time, the voltage control effect analysis also verifies this point. Before the algorithm in this paper is adopted, the photovoltaic power supply is high during 11:00-17:00, making the node voltage exceed the upper limit. While the node voltage can be controlled within the allowable range by using this algorithm. When the node voltage exceeds the upper or lower limit due to the high or less photovoltaic power generation, the inverter will absorb or emit reactive power to ensure the voltage within limit.
The following conclusions can be drawn from the simulation analysis: ①Compared with the traditional nonlinear optimization, the proposed method significantly reduces the solution time and improves the computational speed. ②The model uses the fast regulation of the inverter to quickly solve the active and reactive power operating base points through online optimization, and discards light to ensure the grid-connected voltage when necessary. So the maximum output power of the photovoltaic power station can be tracked time-varying. ③The model aims at maximizing the grid-connected power of PV and indirectly seeks to minimize the system loss. By regulating the output power in real time through the inverter, the active power loss is significantly reduced compared with the operation of the power station before this method is adopted.
Keywords：Large photovoltaic power station, photovoltaic inverter, parallel operation, time-varying track, reactive power optimization
DOI:10.19595/j.cnki.1000-6753.tces.220161
中图分类号：TM615；TM732
国家自然科学基金资助项目（51477091）。
收稿日期 2022-01-29
改稿日期 2022-03-21
李 桐 女，1998年生，硕士研究生，研究方向为电力系统运行与控制。E-mail：litongsduer@163.com
韩学山 男，1959年生，教授，博士生导师，研究方向为电力系统运行与控制、优化调度等。E-mail：xshan@sdu.edu.cn（通信作者）
（编辑 赫蕾）