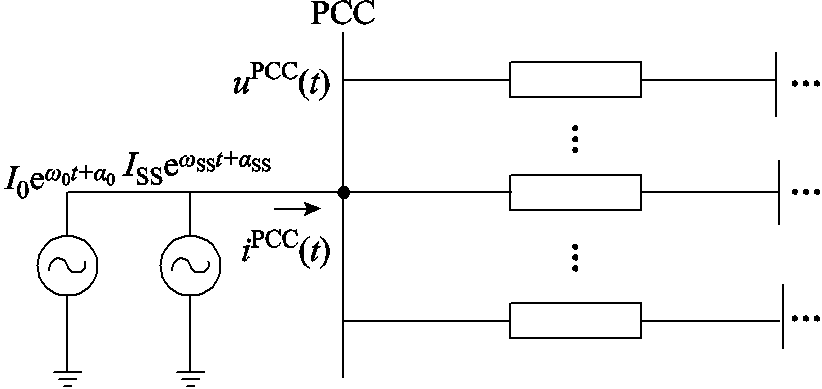
图1 并网点等效电路
Fig.1 Parallel network equivalent circuit diagram
摘要 大规模新能源并网引发的次同步振荡严重威胁电力系统的安全稳定运行。为满足次同步振荡在线告警需求，需要分析宽频测量数据并快速提取振荡分量，快速检测到次同步振荡并精准切除振荡源已是迫切需要解决的关键技术。该文推导了对称和不对称三相电路中含有次同步频率电源时的瞬时功率表达式，揭示了瞬时功率主要为恒定功率分量和次同步频率的交变功率量；在此基础上，提出基于整周期瞬时功率差的次同步振荡频率提取方法，相比于快速傅里叶变换的计算速度大幅提升，避免了栅栏效应和频谱泄露问题；并提出了利用半周期瞬时功率差的次同步振荡源识别方法，可以对多风电场集中并网系统进行次同步振荡源定位，进而为精准切机提供支撑。时域仿真结果表明，该文提出的次同步振荡频率提取方法的计算速度相比快速傅里叶变换有显著提升，振荡源机组辨识方法具有较高的精度。
关键词：风电场 次同步振荡 瞬时功率 振荡频率提取 振荡源识别
为保证“碳达峰、碳中和”能源发展目标的持续推进，构建以新能源为主体的电力系统刻不容缓，随着高比例新能源大量接入电力系统，引发的新能源机组并网次同步振荡问题亟待解决[1]。次同步振荡问题一直是威胁电力系统安全稳定运行的动态稳定问题，近年来国内外多次发生风电并网引发的严重次同步振荡事件。从2009年美国得克萨斯州双馈风场发生次同步振荡到2011年我国冀北沽源地区的双馈风场低风速下频繁发生的次同步振荡事件，都对电力系统安全稳定造成了严重的影响[2-4]。双馈风机出现的次同步振荡现象一般认为是双馈风机变流器控制处于低风速时在次同步频率下会等效为负电阻，同时其阻值大于等效电网的正电阻阻值，从而导致谐振发散[5-6]。此外，还有文献定义风机转子所产生的次同步频率下功率为次同步功率（Subsynchronous Power, SSP），认为风机产生的次同步功率驱动和支持了次同步振荡[7]，并对潮流、线路阻抗特性在次同步功率传播中的影响效果进行分析，但未涉及多模态次同步频率耦合对次同步功率的影响，也未进一步探究其在频率提取及振荡源识别中的应用。本文将基于瞬时功率，研究次同步振荡频率提取及振荡源识别方法。
次同步振荡分量的常用提取方法有Prony算法、希尔伯特-黄变换（Hilbert-Huang Transform, HHT）分析、快速傅里叶分解算法等。Prony分析通过将波形分解为不同形式指数函数的组合，计算得到各指数函数的振幅、相位、衰减因子及频率[8]，但其计算效率较低，拟合次同步振荡功率所需阶数较高且计算精度不高。快速傅里叶分解将时域信号转换到频域进行计算，能够检测出信号中的频率和幅值信息[9]，但会受到信号选择时间窗的影响，同时存在栅栏效应和频谱泄露等问题。为解决算法引起的误差，现有文献通常采用加窗函数的插值方法以获得频谱补偿[10-11]。HHT方法首先利用经验模态分解法将原信号划分为有限个数的固有模态信号，进一步计算得到Hilbert边际谱[12]，但由于经验模态分解是单通道分解方法，不能很好地适应多机系统的参数辨识。此外，文献[13-14]将参数辨识转换为模态参数提取，通过重构信号有效辨识了次同步振荡参数。
在振荡源定位方面，国内外学者进行了大量研究，主要可以分为基于模型和基于量测数据两类。文献[15-16]利用小信号分析状态空间矩阵，计算风机振荡下的参与因子。文献[17-18]利用阻抗分析等效电路，利用奈奎斯特判据对稳定性进行分析。这些方法都需要获知电力系统各元件相应的数据，但风机控制器参数、风机内部结构等模型参数难以获取，且构建系统模型所需阶数很高，计算耗时长，多用于离线分析，很难对次同步振荡进行在线定位。因此，有学者基于量测数据进行振荡源的识别定位。能量函数法在振荡源定位中应用广泛[19-21]，通过分析振荡下能量流的组成，推导出振荡暂态能量流和阻尼的关系，进而进行振荡源的定位。但研究以汽轮发电机为主，主要研究低频振荡强迫振荡源的定位，在次同步振荡源定位方面的普适性仍有待考证。此外，能量函数在实际工程应用中需要进行积分运算，计算复杂而难以在线应用。以机器学习、迁移学习为主的人工智能方法可以对海量数据进行处理学习，降低对系统模型的依赖，故在振荡源定位方面也有了较多研究[22-25]。人工智能方法通过学习振荡特征和振荡源位置之间的关系，实现振荡源定位。但目前机器学习的数据多来自仿真模型，其在实际电力系统中的适应性、准确性仍有待研究。
宽频测量系统正在开发、部署和实施，在高精度数据采集的基础上可以实现次/超同步间谐波分量的提取、传输[25]。基于瞬时功率的频率提取和振荡源识别方法可以直接使用宽频测量系统得到的电压和电流量，数据易于获取，同时计算方法简便。一般振荡分量提取技术需要考虑非整周期截断引起的栅栏效应和频谱泄露，如快速傅里叶变换（Fast Fourier Transform, FFT）分析要求加窗并插值补偿。本文提出的振荡频率提取方法对截断时间点没有要求，可以任意选择时间序列段，避免了截断点引起的测量精度问题。此外，大多数参数辨识手段需要将大量时序数据进行时域向频域的转换，基于瞬时功率的频率提取可以规避时频转换的计算量，提高计算速度，更适用于配置宽频测量系统的电力系统在线监测。
基于上述分析，本文提出一种利用宽频测量系统的电压电流计算瞬时功率，进而实现次同步振荡频率提取及振荡源识别的方法。该方法从量测数据出发，基于瞬时功率推导双馈风机经串补接入交流电网在三相对称和三相不对称情况下多模态次同步功率的解析表达式，从而得到次同步功率在两种情况下的主导分量；利用主导分量中交变量特性进行次同步振荡频率提取，进而以此为基础研究多机系统下次同步振荡源识别方法。该方法相较于传统参数辨识方法计算速度快、计算量更小、精度更高。同时瞬时功率相比于传统能量方法将更适应于实际电力系统振荡源识别，为实际工程中双馈风电场次同步振荡源在线识别提供了一种解决思路。
当风电场并网系统发生次同步振荡时，风机侧会同时出现工频和次同步频率的电压和电流。本文将风电场等效为电流源，包括工频电流源和次同步频率电流源，如图1所示。
图1 并网点等效电路
Fig.1 Parallel network equivalent circuit diagram
假定次同步振荡发生时，三相电路完全对称，利用叠加定理可知三相瞬时功率表达式为[6]
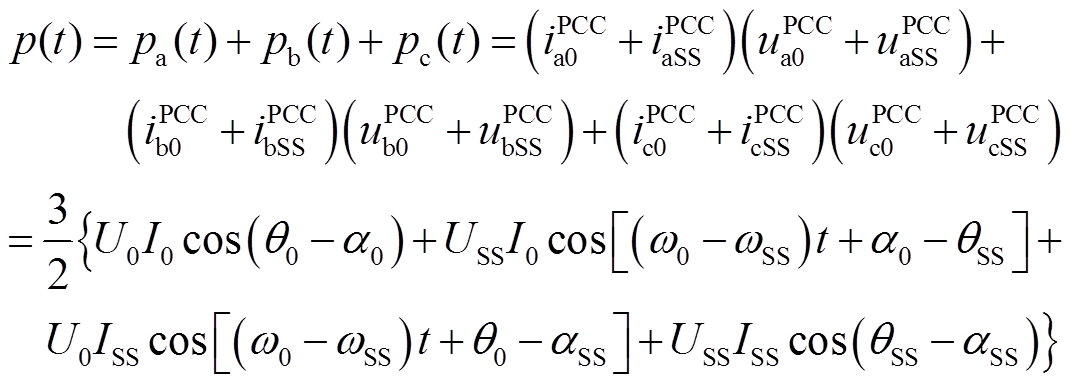（1）
式中，I0和U0分别为基频电流和电压幅值；ISS和USS分别为次同步频率电流和电压幅值；ω0为基频角频率；ωSS为次同步频率角频率；α0、θ0分别为基频电流和电压的初相位；αSS、θSS分别为次同步频率电压和电流的初相位。
瞬时功率包含恒定功率分量和交变频率分量两部分。其中交变的频率成分包括次同步频率、超同步频率、两倍基频和两倍次同步频率。恒定功率分量由工频电源和次同步频率电源产生；次同步频率分量和超同步频率分量是由工频电源和次同步频率电源共同作用产生的；两倍工频分量由工频电源作用产生；两倍次同步频率分量由次同步频率电源作用产生。
对称的三相电路中超同步分量、两倍基频和两倍次同步频率分量功率相互抵消，故而三相对称时瞬时功率由恒定功率量和次同步频率交变量两部分构成。
此处需要说明，瞬时功率中含有的恒定量和交变量都是由次同步频率电源与工频电源产生的，故而本文将其统称为次同步功率分量。次同步功率分量包括次同步分量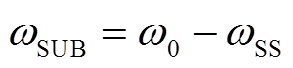
和与次同步频率互补的超同步分量
。
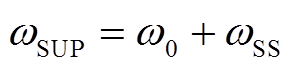当多个双馈风电场汇集至电网出现多模态次同步振荡现象时，等效电流源应包含多种模态的次同步频率谐波源。假设有n个模态，则三相瞬时功率的交变分量表达式见式（2），具体推导见附录。
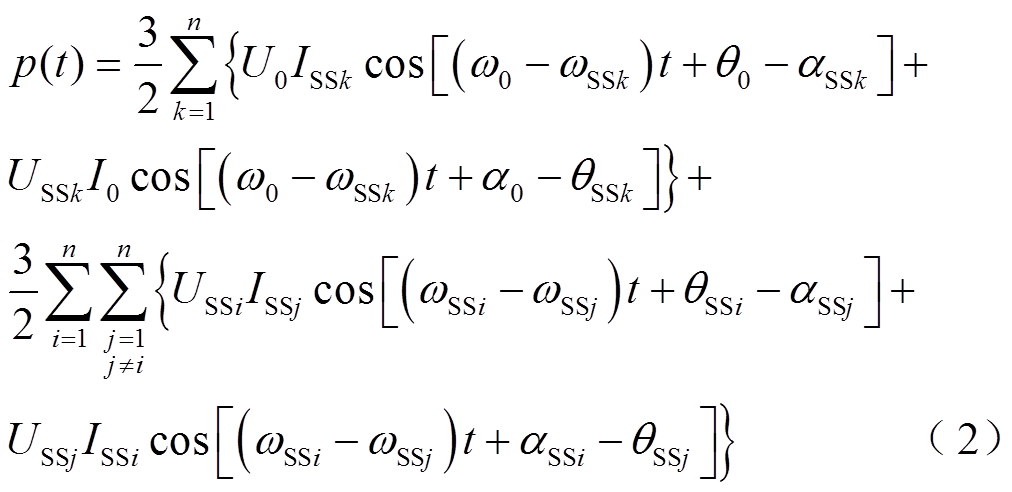
式（2）由两部分组成，一部分为各模态次同步分量和工频分量之间的耦合项，另一部分为各模态次同步分量之间的耦合项。与单模态相比，多模态下瞬时功率的交变分量出现了各模态次同步分量之间的耦合项，其幅值远小于各模态次同步分量和工频分量之间耦合项的幅值。因此，瞬时功率交变量的主导分量仍为次同步频率分量。
故而，本文将基于瞬时功率中次同步分量的交变量特性进行次同步频率提取和振荡源识别。
单模态谐波源在不对称的三相电路中三相瞬时功率中的超同步分量、二倍基频分量、二倍次同步频率分量不能互相抵消，故在不对称三相电路中需要对各个交变量分别分析。
1）次同步分量
首先分析不对称三相电路瞬时功率的次同步分量。a相中瞬时功率次同步分量为
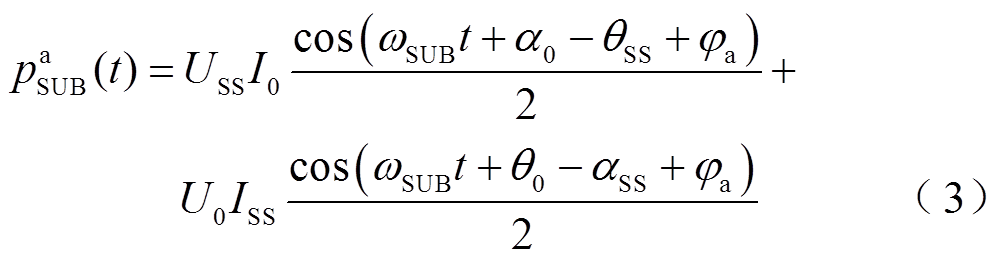
由式（3）可知，不对称电路中单相瞬时功率次同步分量包含两项。负荷不平衡等情况会引起三相电路电压电流发生不平衡。由于次同步频率的电压相较于工频电压的幅值较小，故为了推导简便，在不对称三相瞬时功率推导时主要考虑各相瞬时功率次同步分量的第二项。
将三相不对称时各相瞬时功率次同步分量第二项进行叠加可以得到
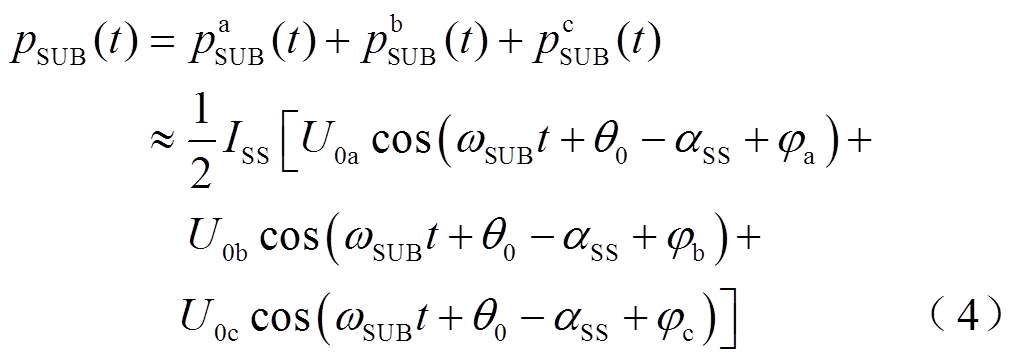
式中，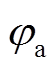
、
、
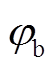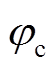为三相工频电压电流不平衡时导致的相位差偏移。
2）超同步分量
其次分析不对称三相电路瞬时功率的超同步分量。a相中瞬时功率超同步分量为
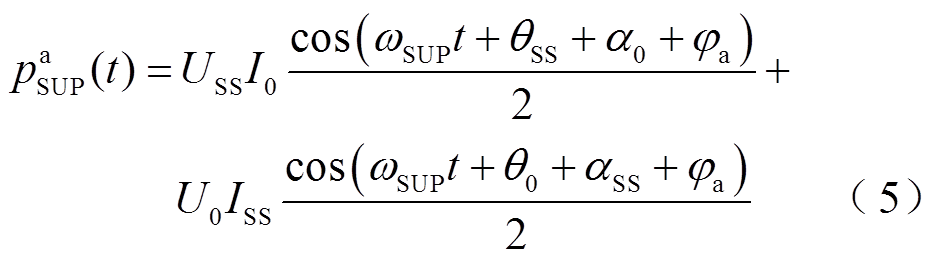
超同步分量与单相瞬时功率的次同步分量具有相似的结果，同理主要考虑各相瞬时功率超同步分量的第二项。将三相不对称时各相瞬时功率超同步分量第二项进行三相叠加可以得到
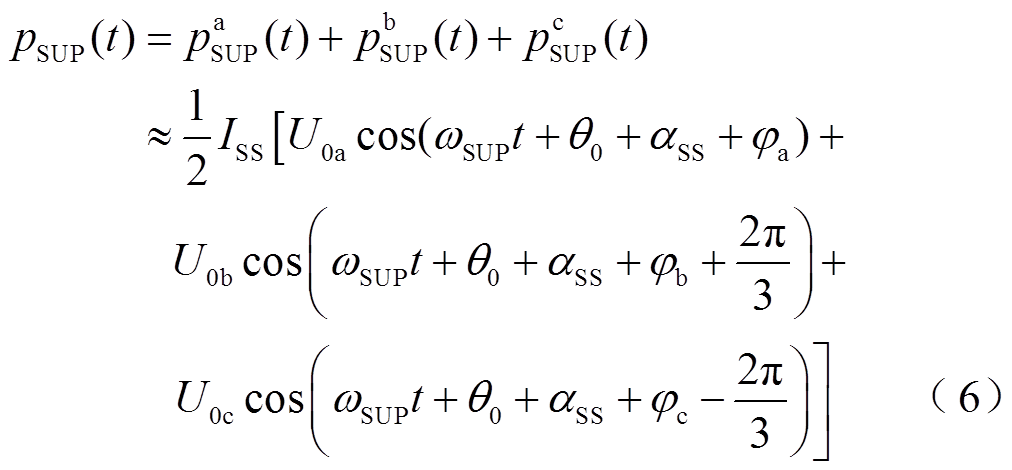
3）二倍次同步频率分量
a相中二倍次同步频率分量为
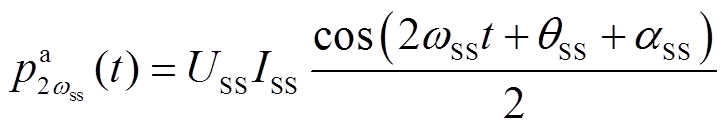（7）
对于两倍次同步频率分量而言，由于三相不对称时主要是三相工频电压电流不平衡，而二倍次同步频率在单相瞬时功率中不存在工频相关量，故可以在公式推导中忽略三相不对称对两倍次同步频率分量的影响，认为其在三相不对称情况下大多数被抵消。
4）两倍基频分量
a相中瞬时功率二倍基频分量为
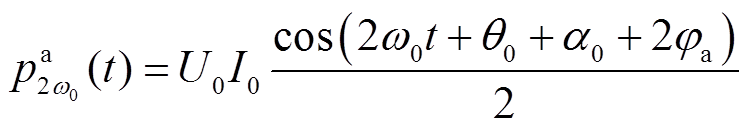（8）
结合次同步振荡和输电线路特性可知，在实际电力系统中线路两端的压降很小，故而可以假设压降幅值接近于0。此外，次同步功率发散的主要原因就在于在次同步频率下线路阻抗值接近0，故而可得
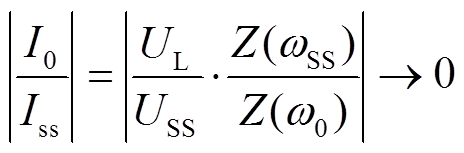（9）
式中，UL为交流线路两端的电压降落幅值。两倍基频分量与次同步分量比值为
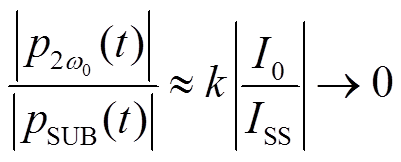（10）
式中，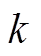
为两倍基频分量与次同步分量比值的其他项。
同时由文献[6]可知，超同步分量不超过次同步分量的4%，故而在单模态不对称三相电路中交变量的主导项仍为次同步分量。
在不对称三相电路中，多模态次同步振荡的瞬时功率交变量出现了新的振荡分量，其频率为各模态次同步频率之和。由于新振荡分量的幅值为各次同步频率电压电流的乘积，远小于次同步分量。因此，多模态谐波源在不对称三相电路中瞬时功率的主导项仍为次同步分量。
此外，工程实际中可以在瞬时功率计算结果后加入带通滤波环节，滤除次同步分量以外的其他频率分量，从而可以提高三相不对称情况下频率提取及振荡源识别的准确性。
综合上述分析可以得到，在对称和不对称的三相电路中，次同步功率的主要分量都为恒定量和次同步频率交变量，故可以基于次同步功率中唯一的次同步频率交变量进行次同步振荡的频率提取和振荡源识别。
基于第1节对次同步功率在对称及不对称三相电路情况的分别讨论，可得在两种情况下三相次同步功率的主导分量都为恒定量及次同步频率交变量，故以三相对称情况为例进行讨论。
从式（1）可知在瞬时功率交变量中唯一的正弦量是次同步分量，利用正弦函数的周期性可以对时序数据进行分析，从而提取次同步频率。
以不同周期对瞬时功率进行采样并计算对应的整周期瞬时功率差，不同频率对应的整周期瞬时功率差定义为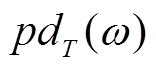
，即
式中，T为角频率ω对应的采样周期，T=2π/(ω0-ω)。由正弦函数周期性可知，当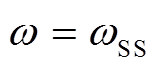
时整周期瞬时功率差等于零，记为
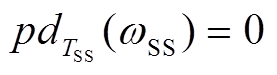。在实际工程中可以使用上述结论来检测次同步振荡瞬时功率中对应的次同步频率。
由于整周期瞬时功率差为时变量，为便于提取次同步振荡频率，定义整周期瞬时功率差绝对均值F1(ω)为
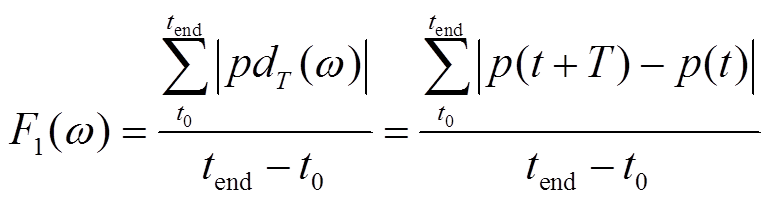（12）
对比不同频率对应的F1(ω)，其最小值所对应的频率即为次同步振荡频率。双馈风机在经串补并网时有时会出现频率漂移问题，直接进行频率提取会导致F1(ω)在某段频率区间内不能得到明显的最值。这种情况下可以缩短采样周期，以确定各个小区间内所属频率，进而得到频率变化范围。但该方法在剧烈频率漂移问题中需要极小的步长才能进行频率提取，后续将对剧烈频率漂移问题中的频率提取方法展开研究。
特别地，多模态谐波源在联络线处会出现多模态次同步振荡，根据第1节对多模态次同步功率的推导可知，振荡发生时联络线处频率提取结果为各个等值双馈风电场次同步频率的加权和，其提取频率接近电压电流幅值最大谐波源。对比各双馈风电场以及联络线的频率提取结果，可以提取多模态次同步振荡中的主导次同步频率，并确定主导频率对应的双馈风电场，从而为振荡源识别奠定基础。
该频率提取方法处理时间序列时可以灵活选取截断点，从而对任意采样时间下的功率时序数据进行计算，避免了采样端点不连续导致的频谱泄露风险；同时由于次同步功率可以直接使用宽频量测系统得到的瞬时功率，获取方便。目前对于频率分量的检测多使用FFT，但功率时序数据需进行时域到频域的转换。此外FFT与时间窗选取有关，在不同时间窗下其检测结果可能存在误差。在实际工程中也常用Prony方法对功率序列进行分析，提取振荡频率等信息，但Prony方法要完全拟合振荡功率所需阶数较高，同时计算量较大，提取所得的频率精度不高。
本文基于瞬时功率理论对功率时序序列中的次同步频率进行检测，避免了对庞大时序数据进行时频转换，同时其检测频率与截断点选取无关，计算量小，且所提取的次同步频率精度高，在工程应用中具有较大价值。
风电场大多按照集群分布，在发生次同步振荡后切掉风电场的全部风机将产生巨大损失，故需要精确识别风电场内产生次同步振荡的振荡源风机。此外，风场发生次同步振荡时可能存在多台机组共同起振，故需要对风电场内振荡源风机的重要程度进行排序。
双馈风机在发生次同步振荡时仅有振荡源风机存在次同步频率电源，其产生的电流流经其他风机和并网连接的交流电网，等效电路如图2所示。图中，Z(ωSS)为振荡源风机等效阻抗，Zi(ωSS)(i=1,2,×××,k)为非振荡源风机等效阻抗，Zsys(ωSS)为交流线路等效阻抗。
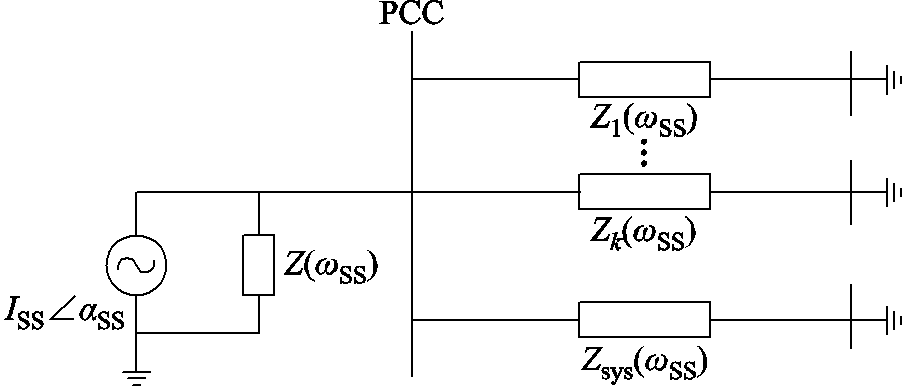
图2 并网点次同步频率等效电路
Fig.2 Parallel subsynchronous frequency equivalent circuit
图2等效电路可以说明，振荡源处量测到的次同步频率电压为最大值，同时由于风电机组间的并联关系，振荡源所处位置次同步频率电流也为最大值，由此可利用振荡源特性即可对振荡源进行识别。
本文基于次同步功率中次同步频率交变量进行振荡源的识别，以次同步频率对应半周期对瞬时功率时序序列进行采样，计算次同步频率对应的半周期瞬时功率差，定义为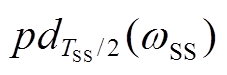
。即
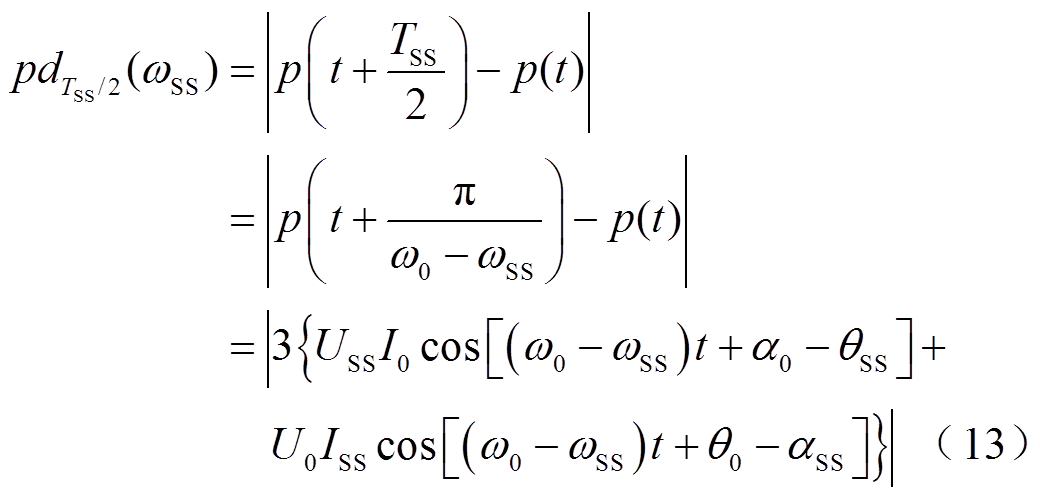
式中，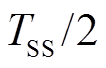
为角频率ωSS对应的采样周期，TSS/2= π/(ω0-
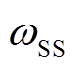)。基于次同步功率提取得到的次同步频率ωSS计算不同机组以次同步频率对应周期采样得到的
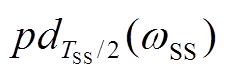。振荡源处存在次同步频率下的最大电压电流，而各风电场的工频电压电流相近，故而次同步振荡源处
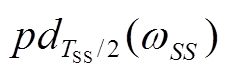的幅值最大。
基于次同步频率检测的结果，比较各风机处的半周期瞬时功率差幅值即可识别振荡源。同时基于此特性可以对振荡源风机影响程度进行排序，风机的半周期瞬时功率差幅值越大，次同步振荡源幅值越大，造成的影响程度就越大，可以此为依据在切机时对风电机组进行评估。
定义半周期瞬时功率差绝对平均值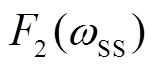
，通过对比不同机组对应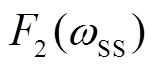，即可量化振荡源风机对次同步振荡的影响程度。
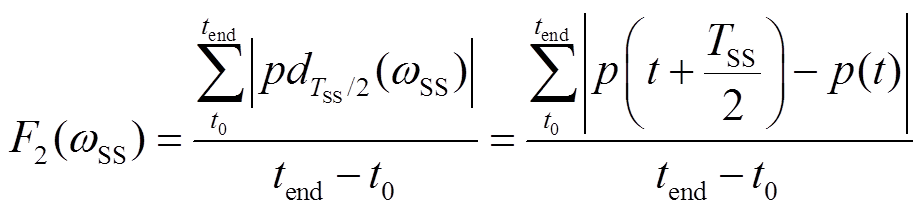（14）
本文提出的次同步振荡源识别方法基于瞬时功率，仅需对时序序列进行四则计算。与暂态能量流等能量方法相比，避免了能量的积分运算，极大地提高了振荡源识别的计算速度。且瞬时功率仅需要宽频量测系统得到的电压电流的瞬时值，数据易于获取，相较于模型方法更符合实际系统，识别准确性高，更适用于工程中快速对振荡源进行识别的要求。
为验证本文基于瞬时功率提出的次同步振荡频率提取及振荡源识别方法的正确性，在电磁暂态仿真平台PSCAD/EMTDC中搭建双馈风电场经串补并入无穷大电网模型进行时域仿真。通过对时序数据进行处理，验证不同情况下所提方法的理论分析是否正确。
在PSCAD/EMTDC中搭建如图3所示的双馈风机并入含串联补偿系统，以此为代表验证双馈风机在三相对称及三相不对称情况下所提频率提取方法的正确性。等值双馈风机由30台相同的额定功率为1.5 MW的双馈风机组成，假设风电场所有风电机组的运行状态相同，可以使用单台双馈风机代表所有风电机组，其等值参数可以由单台风电机组参数获得，单台风机参数见附表1。
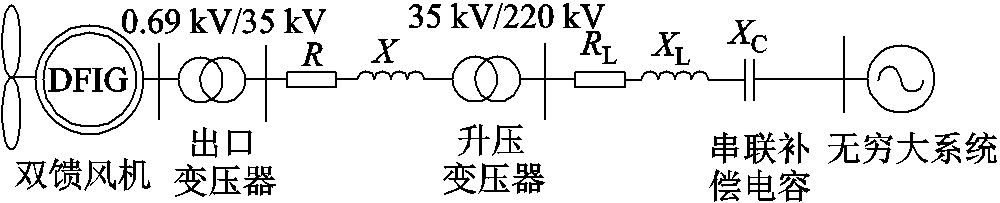
图3 双馈风电场并入含串联补偿系统等值模型
Fig.3 Equivalent model of a double-fed wind farm integrated into a system with series compensation
双馈风机分别由0.69 kV/35 kV、35 kV/220 kV两个升压变压器经串补线路接入交流电网。
3.1.1 三相对称情况下频率提取
设置300μF的串补电容（线路串补度为48.2%）在10 s投入输电线路，引发双馈风机出现次同步振荡。在投入串补后，并网点功率逐渐振荡发散产生次同步振荡，计算不同频率对应采样周期下的整周期瞬时功率差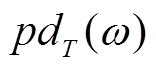，三相对称情况频率提取如图4a所示。对比不同频率对应的F1(ω)，7.3 Hz所对应整周期瞬时功率差绝对平均值最小，由此得出次同步振荡频率为7.3 Hz。
图4b中选取双馈风机起动后的时域波形，并计算不同采样周期下的整周期瞬时功率差，可以看出14 s后各采样周期下的整周期瞬时功率差都发生了等幅振荡，这是由于在14 s左右限幅环节发挥了作用。本文基于叠加定理对瞬时功率进行推导，故而在非线性环节加入后整周期瞬时功率差不能保持在零附近，但从图4a中可以看出，
在限幅环节起作用后仍然相对更小，说明即使在非线性电力系统中，本文所提次同步频率提取方法同样有效。
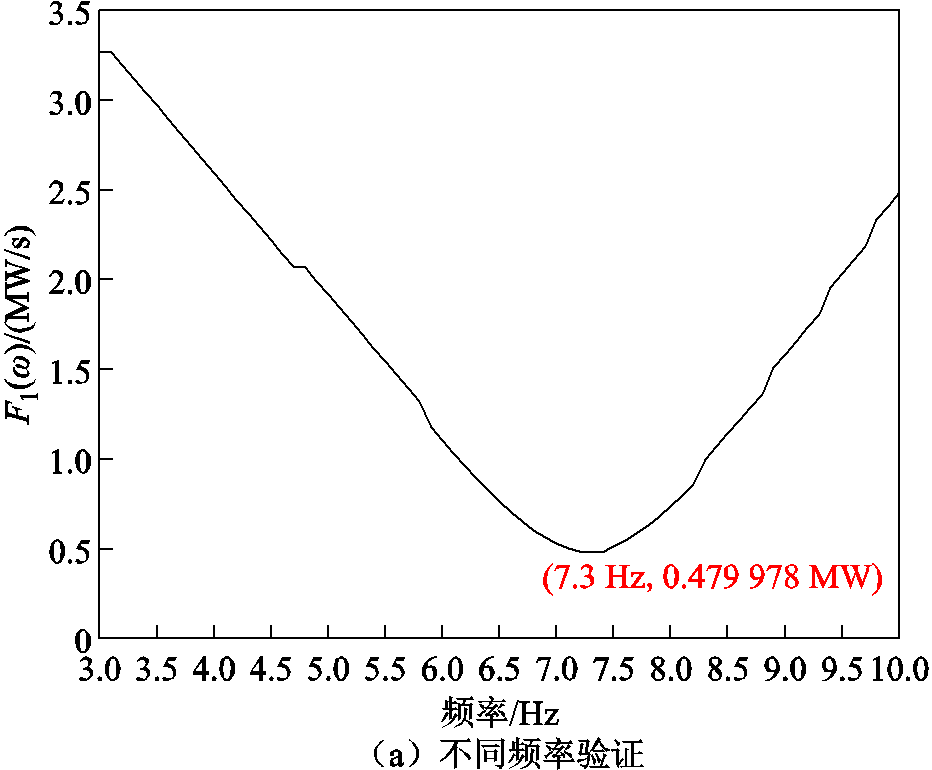
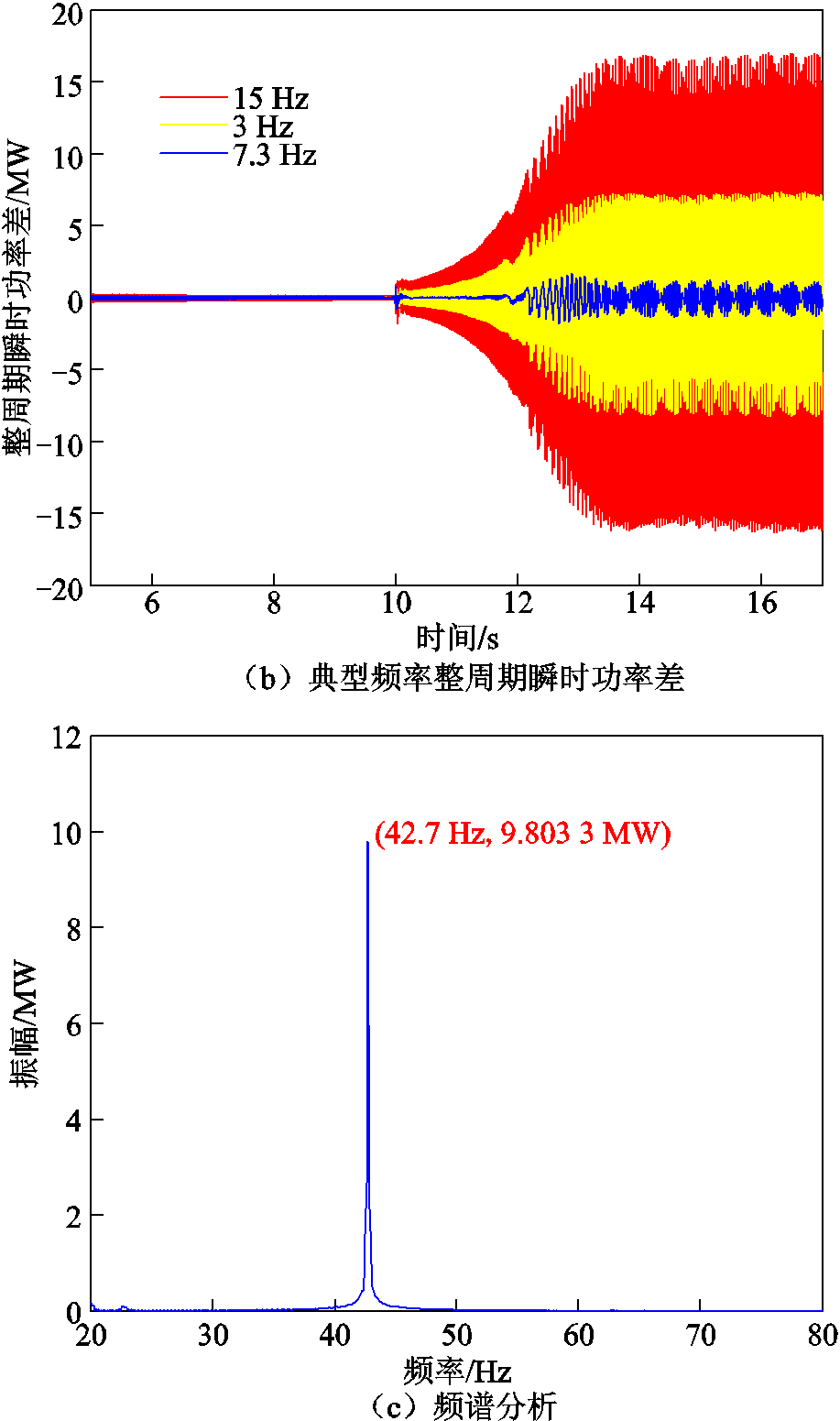
图4 三相对称情况频率提取
Fig.4 Three-phase symmetric case frequency extraction
图4c对发生振荡后的功率进行FFT分析，可以得出功率中含有的分量为42.7 Hz（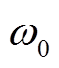
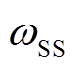-），次同步频率为7.3 Hz，证明了所提频率提取方法的正确性。
此外，测试不同时序数据下不同算法的程序运行时间，计算机处理器为12 th Gen Intel(R) Core(TM) i9-12900K 3.20 GHz，三相对称时计算不同时序数据计算时间对比结果见表1。由表1可知，时序数据每增加5s，本文所提频率提取方法的计算时间约增加0.3 ms，FFT方法的计算时间约增加2 ms，二者相差一个数量级。因此，本文所提频率提取方法在计算速度上具有明显优势。这是由于FFT分析需要对数据进行时域到频域的转换，时序数据越长时频转换工作量越大，导致FFT频率提取需要更长的时间。
表1 三相对称时计算不同时序数据计算时间对比
Tab.1 Comparison of calculation time for different time series data in three-phase symmetric case
时序数据计算时间/s 瞬时功率的频率提取FFT方法 10 s时序数据0.002 6300.003 515 15 s时序数据0.002 9110.005 529 20 s时序数据0.003 4230.007 650
本文用Prony分析对同一段振荡功率进行分析，在拟合阶数为200时得到Prony分析结果如图5所示。
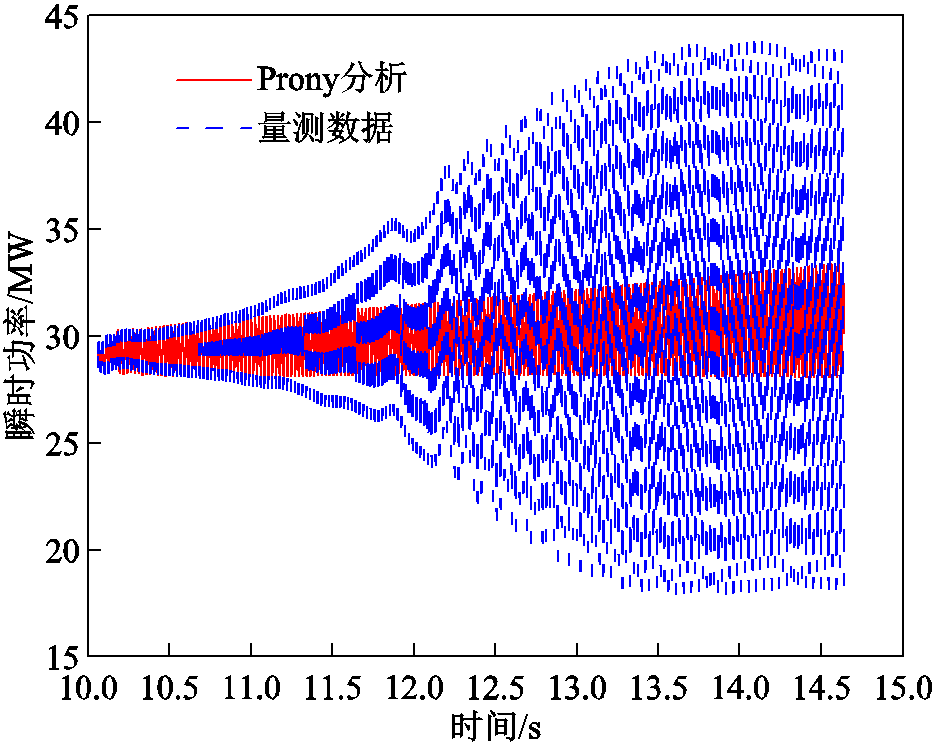
图5 Prony分析结果
Fig.5 Prony analysis results
选取Prony分析结果中幅值前三的频率分量，见表2。
表2 Prony分析结果
Tab.2 Prony analysis results
幅值排列频率/Hz幅值/MW阻尼比 10580.009 4 2430.630.22 3180.2-24
由于功率时域波形十分复杂，Prony方法要完全拟合次同步振荡功率所需计算阶数很高。从表2中可以发现，在拟合阶数高达200阶时仍未达到较好的拟合效果，同时其频率提取误差已达到0.3 Hz，计算误差相比于其他方法更大，不适用于次同步振荡频率的精准提取。
基于瞬时功率进行频率提取具有较高的准确性，同时其计算速度更快，不受时序数据截断点的影响，更适应电力系统在线监测的要求。
为验证多模态次同步振荡频率提取方法的正确性，设置两台经不同串补度接入电网的双馈风场。双馈风电场1投入350 μF串补电容（线路串补度为41.4%），双馈风电场2投入250 μF串补电容（线路串补度为57.3%）。各个双馈风电场出口以及联络线处的频率提取结果如图6所示。
对比不同频率对应的整周期瞬时功率差绝对平均值F1(ω)可知，双馈风电场1振荡频率为6.8 Hz，双馈风电场2振荡频率为8.1 Hz。联络线处功率频谱分析中频率分量为41.9 Hz和43.2 Hz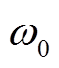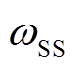（-），对应次同步频率为8.1 Hz和6.8 Hz，证明了多模态频率提取方法的正确性。根据算例验证结果可以看出，由于8.1 Hz谐波源的电压电流幅值相对较大，联络线处频率提取结果更接近8.1 Hz。通过对比F1(ω)，可以确定多模态次同步振荡中主导模态对应的双馈风电场，从而为风电场内振荡源的识别奠定基础。
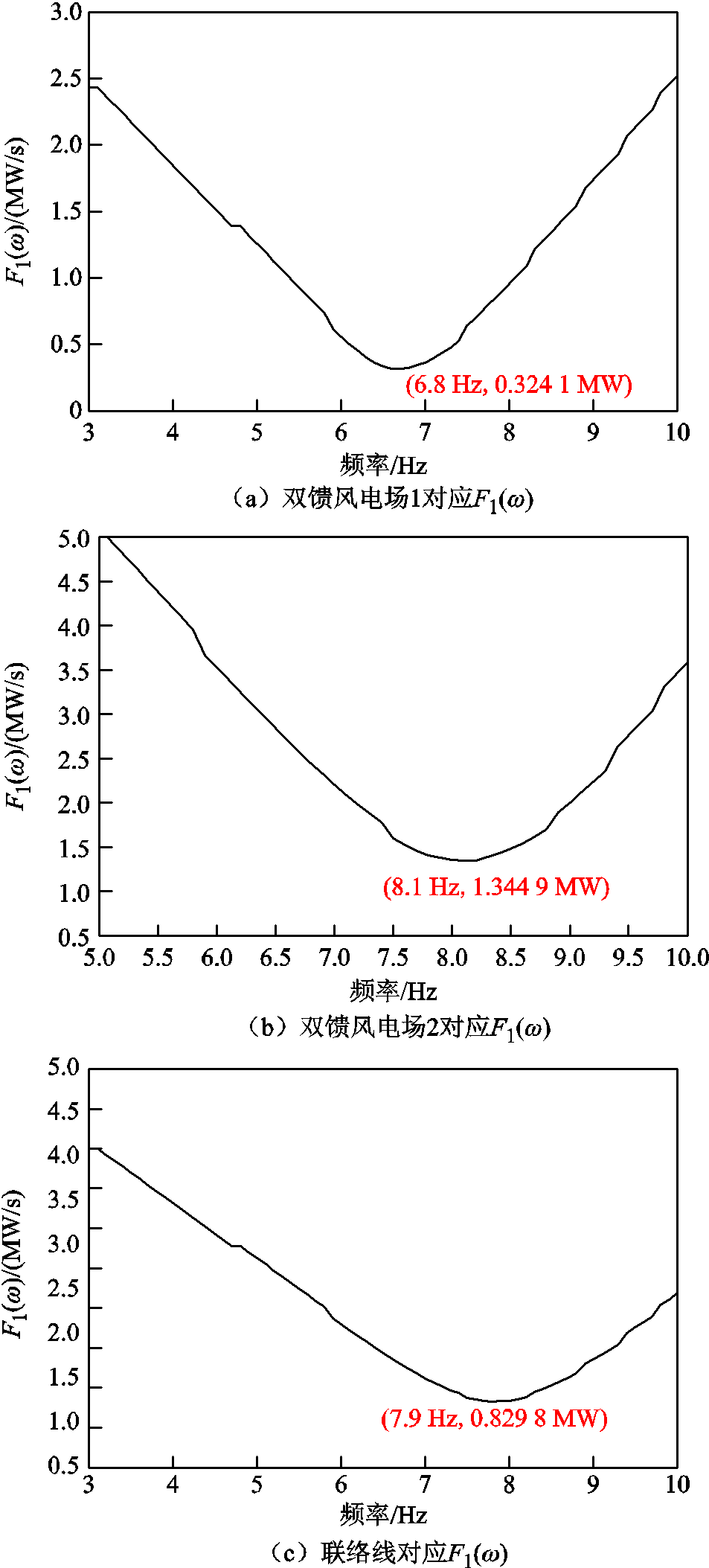
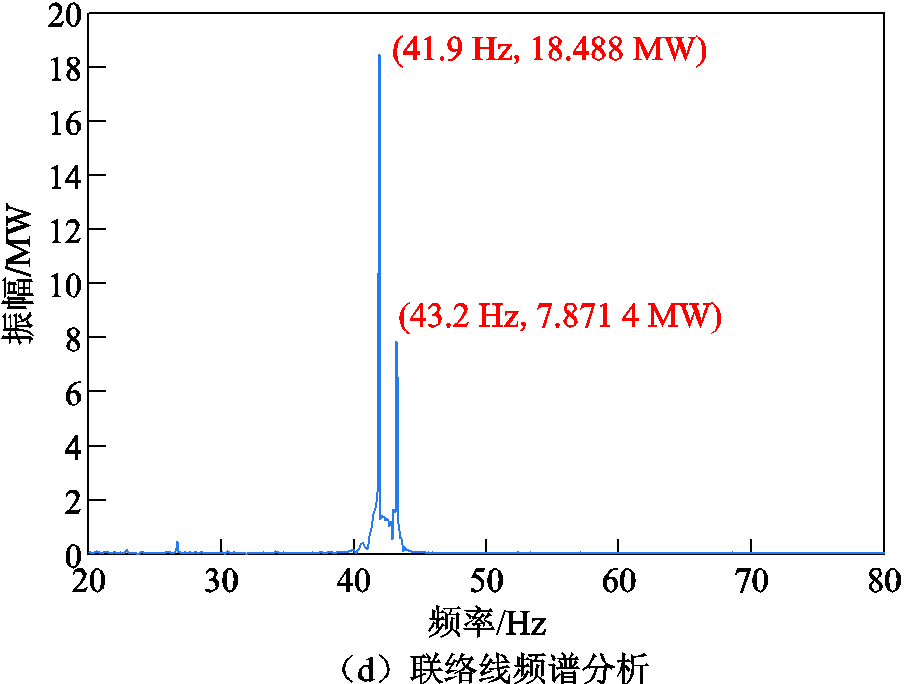
图6 多模态下频率提取
Fig.6 Frequency extraction under multimodality
3.1.2 三相不对称情况下频率提取
设置300 μF的串补电容在10 s投入输电线路，引发双馈风机出现次同步振荡，同时调整线路负荷使得三相不平衡。计算不同频率对应采样周期下的整周期瞬时功率差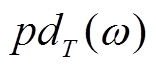
，如图7所示。在投入串补后，并网点功率逐渐振荡发散，对比不同频率下整周期瞬时功率差，6.7 Hz对应整周期瞬时功率差相较于其他频率下更小。此时由于改变了线路参数，在串补电容值未发生改变的情况下次同步频率发生了改变。
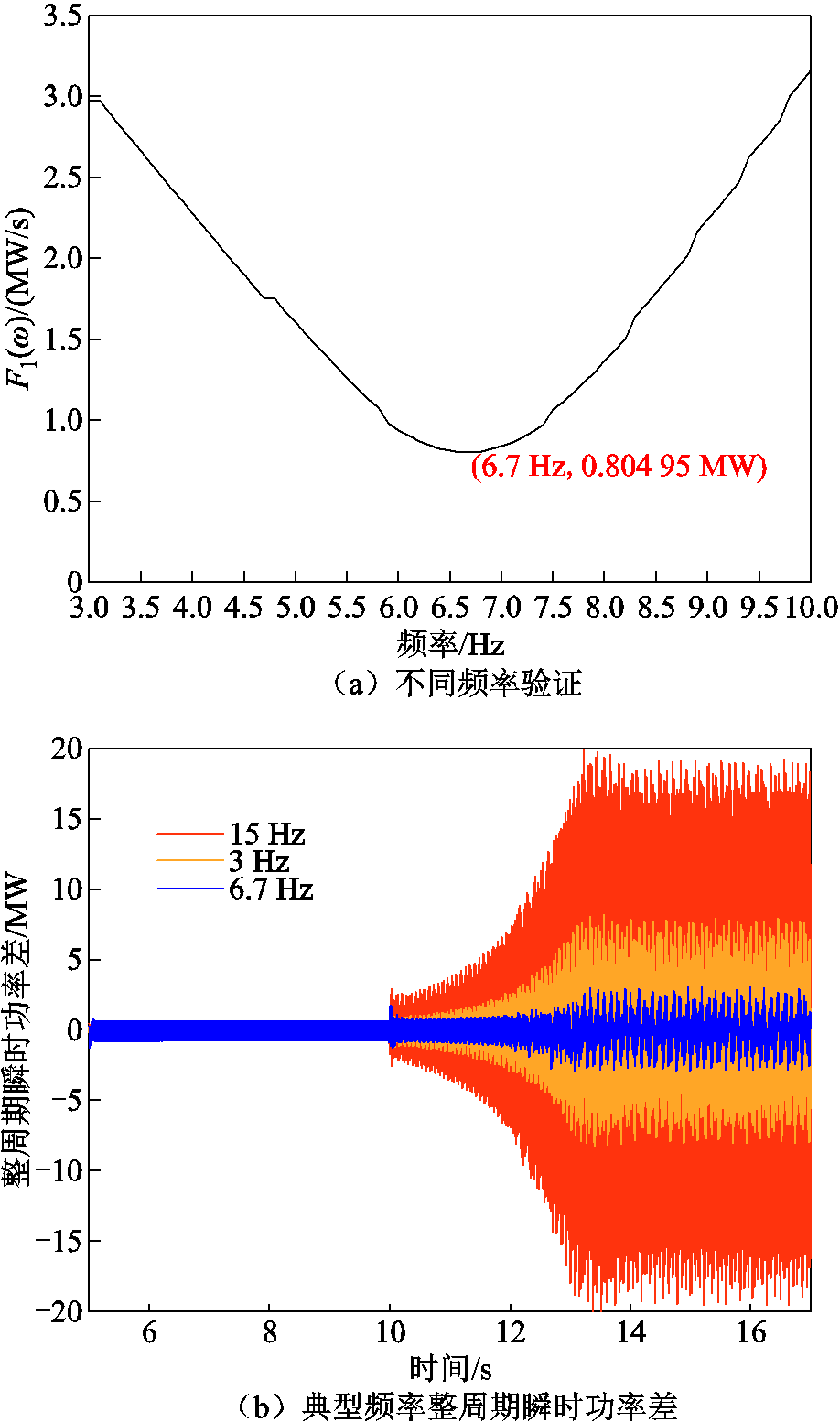
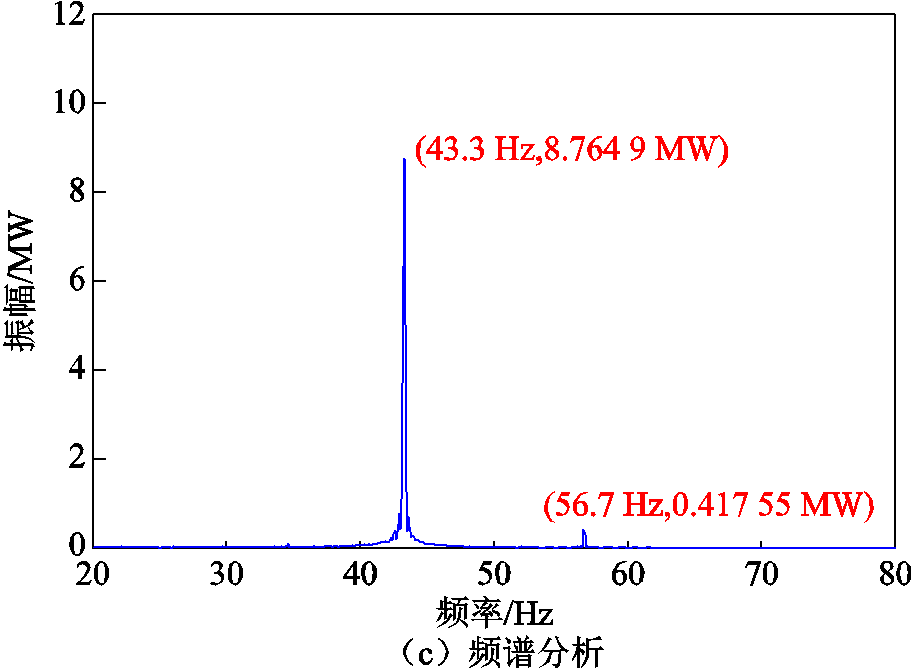
图7 三相不对称情况频率提取
Fig.7 Three-phase asymmetry case frequency extraction
同样对振荡发生后的功率进行频谱分析，结果如图7c所示。图7c表明，在三相不对称情况下次同步功率存在次同步分量43.3 Hz和超同步分量56.7 Hz，且超同步分量相比于次同步分量很小，在证明频率提取方法有效性的同时，也证明了在三相不对称情况下超同步分量与次同步分量的比值确实较小，次同步功率交变量的主导分量是次同步分量。
此外，测试不同算法在三相不对称时的不同时序数据计算时间，计算机处理器为12 th Gen Intel(R) Core(TM) i9-12900 K 3.20 GHz，三相不对称时计算不同时序数据计算时间对比结果见表3。由表3同样可以得出本文所提频率提取方法速度远快于FFT方法。
表3 三相不对称时计算不同时序数据计算时间对比
Tab.3 Comparison of calculation time for different time series data in three-phase asymmetry case
时序数据计算时间/s 瞬时功率的频率提取FFT方法 10 s时序数据0.002 9270.003 730 15 s时序数据0.003 1970.005 833 20 s时序数据0.003 8140.008 206
在三相不对称情况下，由于忽略了超同步分量、两倍基频和两倍次同步分量的影响，各频率的整周期瞬时功率差相较于三相对称下较大。通过在瞬时功率提取后增加带通滤波器，限制提取功率分量的频率范围，可以降低整周期瞬时功率差的误差，从而保证频率提取的准确性。这里使用无限冲击响应（Infinite Impulse Reponse, IIR）带通滤波器，陡度值设置为0.5，滤波后频率验证可以看到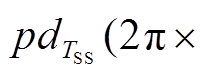
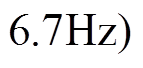相较于滤波前更接近零，计算准确性经过滤波得到了提升。
图8 滤波后频率验证
Fig.8 Frequency verification after filtering
风机大多集群分布，在发生次同步振荡时很难准确识别出风场内发生次同步振荡的机组，同时也很难快速对振荡源风机的重要程度进行排序。本算例以集群分布的风机向电网输送功率，单台或多台风机受到串补线路影响发生次同步振荡为例，研究其次同步振荡源识别方法，并对其重要程度进行排序。多台双馈风电场并入含串联补偿系统等值模型如图9所示。
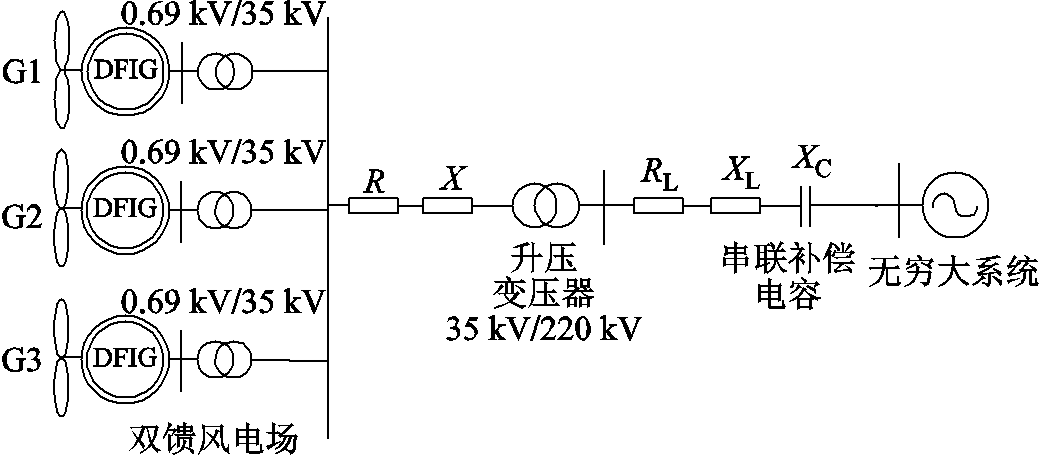
图9 多台双馈风电场并入含串联补偿系统等值模型
Fig.9 Equivalent model of multiple doubly-fed wind farms integrated into a system with series compensation
3.2.1 单振荡源
首先对单独双馈机组引发次同步振荡进行分析，增加G1的RSC电流内环比例系数至1.5，使G1发出次同步功率，单振荡源识别结果如图10所示。
从图10a中可以直观地看出，在次同步频率对应采样周期下，G1双馈风机的半周期瞬时功率差最大，而G2、G3和并网点处的半周期瞬时功率差相比于G1较小。同时计算不同机组对应半周期瞬时功率差绝对平均值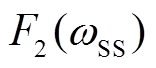
，G1为7.821 MW/s，G2为2.286 MW/s，G3为2.459 MW/s。可以得到G1对应的瞬时功率差平均值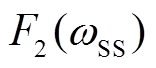最大。这是由于G1作为振荡源，其次同步频率的电压和电流相比其他位置更大，从而使得其在次同步频率下对应的半周期瞬时功率差绝对平均值的幅值更大。
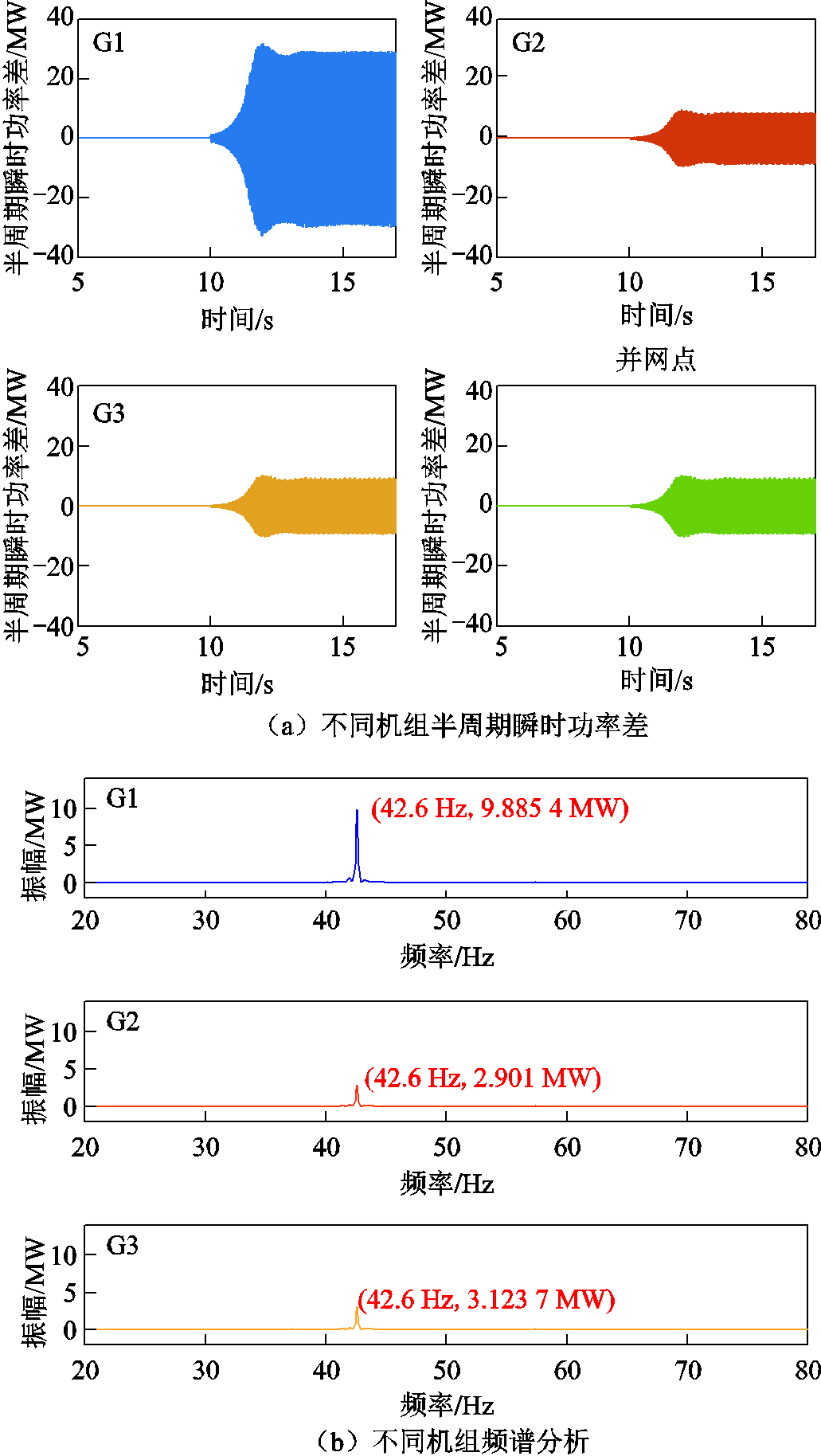
图10 单振荡源识别结果
Fig.10 Difference of power in different positions
3.2.2 多振荡源
算例以三台30 MW双馈风电机场经串补引发次同步振荡为例进行研究。分别增加G1、G2的转子侧变流器（Rotor Side Converter, RSC）电流内环比例系数至2.0和1.5，使得G1和G2发出次同步功率。对比各机组在次同步频率下半周期瞬时功率差，结果如图11所示。
计算不同机组对应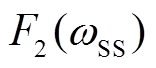，G1为9.920 MW/s，G2为8.804 MW/s，G3为0.592 MW/s，可以得出G1机组半周期瞬时功率差绝对平均值最大，G2机组其次。图11b中的FFT分析可以表明，在G1机组处含有最大含量的次同步功率分量，G2机组其次，验证了上述理论分析和时域仿真结果的正确性。
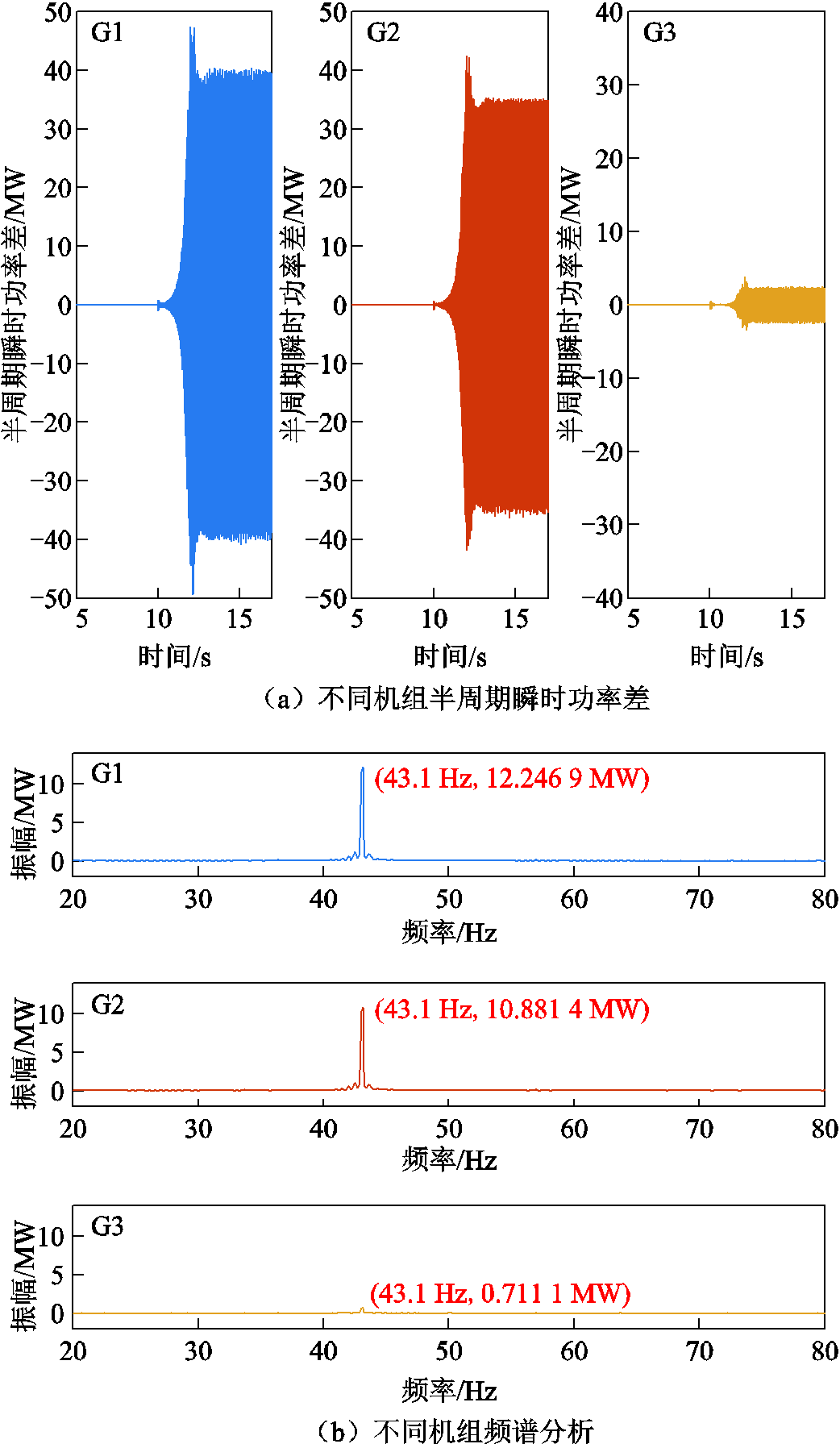
图11 多振荡源识别
Fig.11 Multi-oscillation source positioning
基于半周期瞬时功率差的结果，可以对三台机组进行振荡源重要程度排序，为切机策略提供参考，即必要时先切掉G1机组，如次同步振荡仍未消失，则继续切除G2机组。不同机组功率差值如图12所示。通过对振荡机组进行重要性排序，可以合理规划次同步振荡时的紧急应对措施，避免全部切除风机造成的经济损失。
通过图12对比不难看出，机组瞬时功率差值最大的为两个振荡源机组，而非振荡源机组与振荡源机组之间的功率差值相对较小。对比振荡源机组G1和G2相对于G3之间的瞬时功率差值，可得G1和G3之间的瞬时功率差值相对较大。由此可以得出在双馈机组之中G1机组发出的瞬时功率是最大的，即G1机组造成的次同步振荡影响最大。但此方法仅适用于风电机组数量较少时进行判断，当振荡机组数量增加后所需对比的机组数量将大大增加，因此该方法辨别多机组振荡源相对困难。而利用半周期瞬时功率差绝对平均值可以直接量化不同机组对次同步振荡的重要程度，从而快速地对振荡源的重要性进行排序。
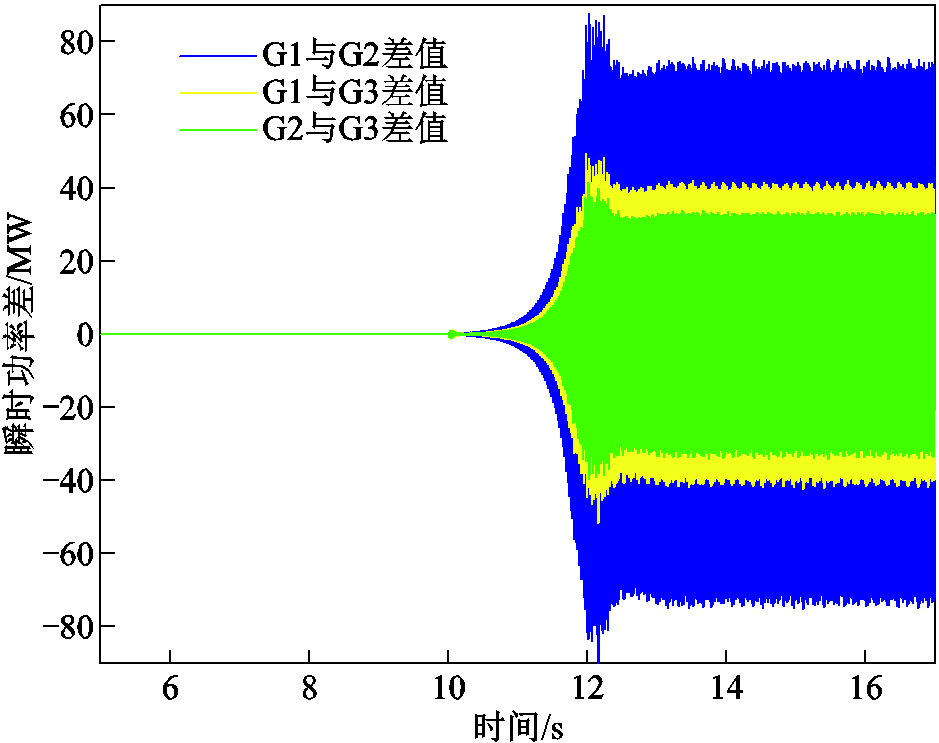
图12 不同机组功率差值
Fig.12 Power difference of different units
本文从瞬时功率概念出发，推导出次同步振荡时瞬时功率的主要分量，进而基于瞬时功率的交变量特性，提出次同步振荡频率提取方法和振荡源识别方法，并在PSCAD/EMTDC上进行了时域仿真验证，主要结论如下：
1）风电并网系统发生次同步振荡时，在对称和不对称的三相电路中瞬时功率的主要分量都为恒定量和次同步频率交变量。
2）提出了基于整周期瞬时功率差的次同步振荡频率提取方法。该方法通过设置不同频率下对应的采样周期，整周期瞬时功率差绝对平均值最小时对应的频率即为次同步振荡频率。
3）提出了基于半周期瞬时功率差的多机次同步振荡源识别方法，即振荡源引发次同步振荡时，其在次同步频率对应采样周期下的半周期瞬时功率差最大，由此识别出振荡源机组。
1. 多模态公式推导
假设存在双模态谐波源，则公共连接点PCC处的电流如下所示。
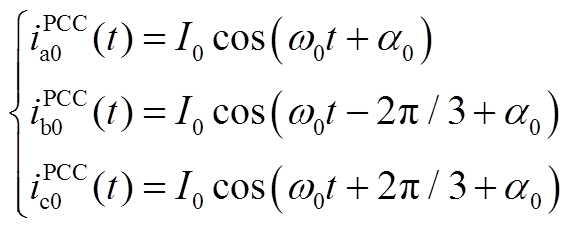（A1）
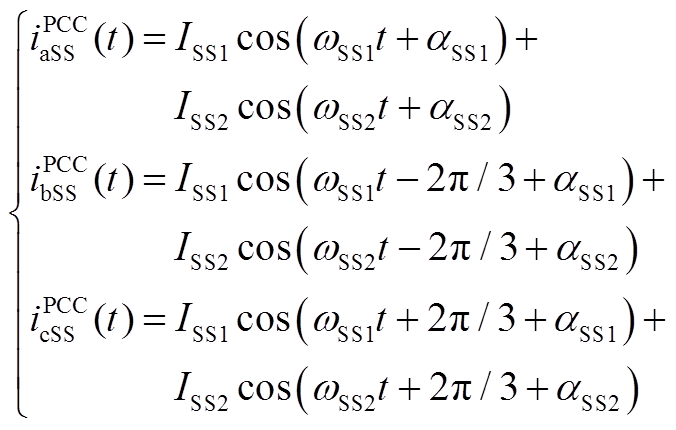（A2）
同理PCC点处电压可以表示为
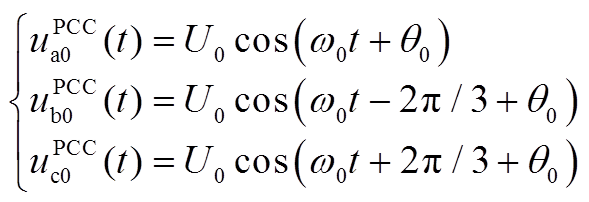（A3）
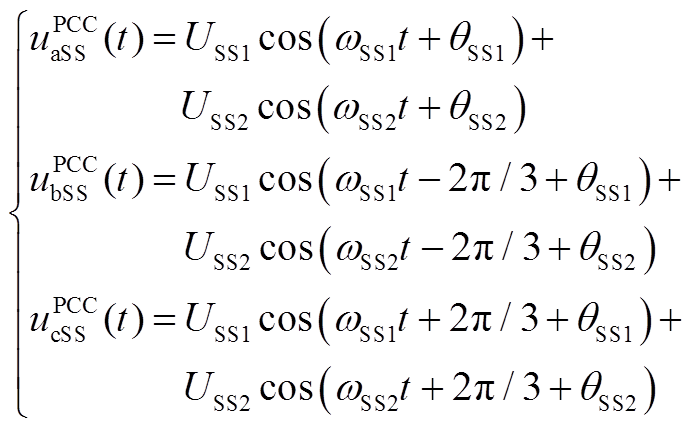（A4）
式中，I0和U0分别为基频电流和电压幅值；ISS和USS为次同步频率电流和电压幅值；ω0为基频角频率；ωSS1和ωSS2为多模态次同步频率角频率；α0、θ0分别为基频电流和电压的初相位；αSS1、αSS2、θSS1、θSS2分别为两种模态下次同步频率电压和电流的初相位。
假设次同步振荡发生时三相电路对称，则两模态三相瞬时功率表达式为
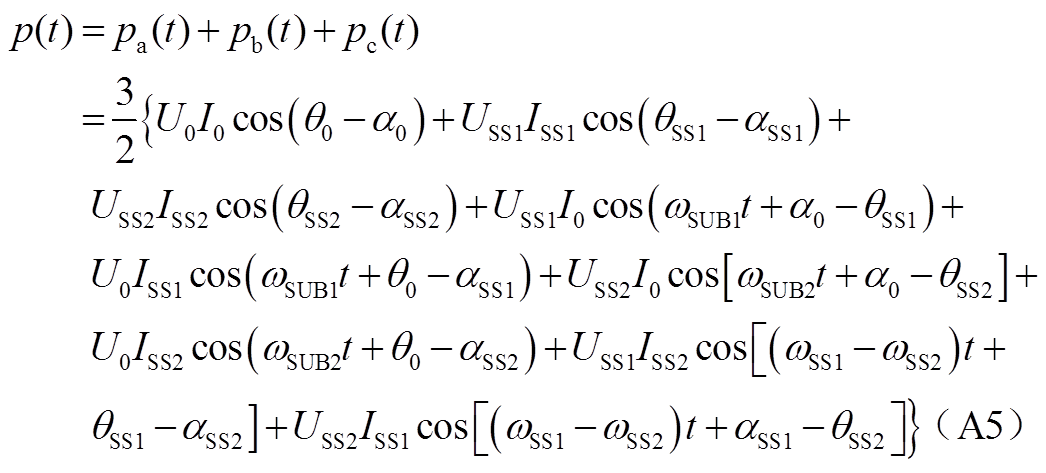
式中，次同步分量为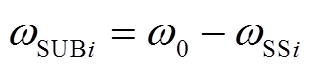
；超同步分量为
。
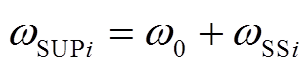拓展至n维，则三相瞬时功率中交变量的表达式为
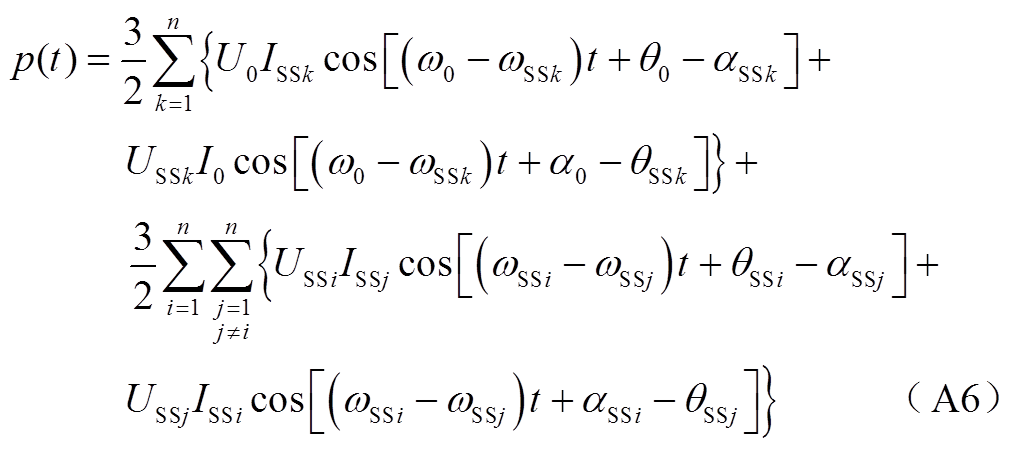
2. 仿真系统参数设置
双馈风机转子侧采用定子磁链矢量控制技术，实现有功功率和无功功率的解耦控制。网侧变流器采取定子电压定向的策略，实现交流侧单位功率因数控制和直流环节电压稳定控制。单台双馈风机具体参数见附表1。
附表1 单台双馈风机具体参数
App.Tab.1 Specific parameters of single DFIG
参数数值 额定功率/MW1.5 额定电压/kV0.69 风速/(m/s)8 RSC有功功率环， RSCq轴电流环， RSC无功功率环， RSCd轴电流环， GSC直流电压环， GSCd轴电流环， GSC无功功率环， GSCq轴电流环， 锁相环，
参考文献
[1] 肖湘宁,罗超, 廖坤玉. 新能源电力系统次同步振荡问题研究综述[J]. 电工技术学报, 2017, 32(6): 85-97. Xiao Xiangning, Luo Chao, Liao Kunyu. Review of the research on subsynchronous oscillation issues in electric power system with renewable energy sources[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 85-97.
[2] 王伟胜, 张冲, 何国庆, 等. 大规模风电场并网系统次同步振荡研究综述[J]. 电网技术, 2017, 41(4): 1050-1060. Wang Weisheng, Zhang Chong, He Guoqing, et al. Overview of research on subsynchronous oscillations in large-scale wind farm integrated system[J]. Power System Technology, 2017, 41(4): 1050-1060.
[3] 李明节, 于钊, 许涛, 等. 新能源并网系统引发的复杂振荡问题及其对策研究[J]. 电网技术, 2017, 41(4): 1035-1042. Li Mingjie, Yu Zhao, Xu Tao, et al. Study of complex oscillation caused by renewable energy integration and its solution[J]. Power System Technology, 2017, 41(4): 1035-1042.
[4] Wang Liang, Xie Xiaorong, Jiang Qirong, et al. Investigation of SSR in practical DFIG-based wind farms connected to a series-compensated power system[J]. IEEE Transactions on Power Systems, 2015, 30(5): 2772-2779.
[5] 张剑, 肖湘宁, 高本锋, 等. 双馈风力发电机的次同步控制相互作用机理与特性研究[J]. 电工技术学报, 2013, 28(12): 142-149, 159. Zhang Jian, Xiao Xiangning, Gao Benfeng, et al. Mechanism and characteristic study on sub-synchronous control interaction of a DFIG-based wind-power generator[J]. Transactions of China Electrotechnical Society, 2013, 28(12): 142-149, 159.
[6] Xu Yanhui, Gao Tianchu. Sub-synchronous frequency domain-equivalent modeling for wind farms based on rotor equivalent resistance characteristics[J].Global Energy Interconnection, 5(3): 293-300.
[7] 马闻达, 王西田, 解大. 大规模风电场并网系统次同步振荡功率传播特性研究[J]. 中国电机工程学报, 2020, 40(16): 5217-5229. Ma Wenda, Wang Xitian, Xie Da. Characteristics of subsynchronous oscillation power propagation in the large-scale wind farm integrated system[J]. Proceedings of the CSEE, 2020, 40(16): 5217-5229.
[8] 丁屹峰, 程浩忠, 吕干云, 等. 基于Prony算法的谐波和间谐波频谱估计[J]. 电工技术学报, 2005, 20(10): 94-97. Ding Yifeng, Cheng Haozhong, Lü Ganyun, et al. Spectrum estimation of harmonics and interharmonics based on Prony algorithm[J]. Transactions of China Electrotechnical Society, 2005, 20(10): 94-97.
[9] Yang Xiaomei, Zhang Jianing, Xie Xiaorong, et al. Interpolated DFT-based identification of sub-synchronous oscillation parameters using synch-rophasor data[J]. IEEE Transactions on Smart Grid, 2020, 11(3): 2662-2675.
[10] Romano P, Paolone M. Enhanced interpolated-DFT for synchrophasor estimation in FPGAs: theory, implementation, and validation of a PMU prototype[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(12): 2824-2836.
[11] 马钺, 蔡东升, 黄琦. 基于Rife-Vincent窗和同步相量测量数据的风电次同步振荡参数辨识[J]. 中国电机工程学报, 2021, 41(3): 790-803. Ma Yue, Cai Dongsheng, Huang Qi. Parameter identification of wind power sub-synchronous oscillation based on Rife-Vincent window and synchrophasor data[J]. Proceedings of the CSEE, 2021, 41(3): 790-803.
[12] 李天云, 赵妍, 季小慧, 等. HHT方法在电力系统故障信号分析中的应用[J]. 电工技术学报, 2005, 20(6): 87-91. Li Tianyun, Zhao Yan, Ji Xiaohui, et al. Application of HHT method for analysis of fault signal in electric power system[J]. Transactions of China Electrotechnical Society, 2005, 20(6): 87-91.
[13] 王杨, 晁苗苗, 谢小荣, 等. 基于同步相量数据的次同步振荡参数辨识与实测验证[J]. 中国电机工程学报, 2022, 43(3): 899-908. Wang Yang, Chao Miaomiao, Xie Xiaorong, et al. Identification of subsynchronous oscillation parameters and field tests based on PMU data[J]. Proceedings of the CSEE, 2022, 43(3): 899-908.
[14] Ma Yue, Huang Qi. Application of multisynchros-queezing transform for subsynchronous oscillation detection using PMU data[C]//2020 IEEE Industry Applications Society Annual Meeting, Detroit, MI, USA, 2021: 1-7.
[15] Varma R K, Moharana A. SSR in double-cage induction generator-based wind farm connected to series-compensated transmission line[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2573-2583.
[16] Ali Mohammadpour H, Santi E. Modeling and control of gate-controlled series capacitor interfaced with a DFIG-based wind farm[J]. IEEE Transactions on Industrial Electronics, 2015, 62(2): 1022-1033.
[17] Liu Huakun, Xie Xiaorong, Zhang Chuanyu, et al. Quantitative SSR analysis of series-compensated DFIG-based wind farms using aggregated RLC circuit model[J]. IEEE Transactions on Power Systems, 2017, 32(1): 474-483.
[18] Karaagac U, Mahseredjian J, Jensen S, et al. Safe operation of DFIG-based wind parks in series-compensated systems[J]. IEEE Transactions on Power Delivery, 2018, 33(2): 709-718.
[19] 余一平, 闵勇, 陈磊, 等. 基于能量函数的强迫功率振荡扰动源定位[J]. 电力系统自动化, 2010, 34(5): 1-6. Yu Yiping, Min Yong, Chen Lei, et al. Disturbance source location of forced power oscillation using energy functions[J]. Automation of Electric Power Systems, 2010, 34(5): 1-6.
[20] 任怡娜, 陈磊, 闵勇, 等. 次同步振荡中暂态能量流与电功率和阻尼转矩的关系[J]. 电力系统自动化, 2018, 42(22): 52-58. Ren Yina, Chen Lei, Min Yong, et al. Relationship between transient energy flow, electric power and damping torque in subsynchronous oscillation[J]. Automation of Electric Power Systems, 2018, 42(22): 52-58.
[21] Chen Lei, Min Yong, Chen Yiping, et al. Evaluation of generator damping using oscillation energy dissipation and the connection with modal analysis[J]. IEEE Transactions on Power Systems, 2014, 29(3): 1393-1402.
[22] 陈剑, 杜文娟, 王海风. 基于对抗式迁移学习的含柔性高压直流输电的风电系统次同步振荡源定位[J]. 电工技术学报, 2021, 36(22): 4703-4715. Chen Jian, Du Wenjuan, Wang Haifeng. Location method of subsynchronous oscillation source in wind power system with VSC-HVDC based on adversarial transfer learning[J]. Transactions of China Electrotech-nical Society, 2021, 36(22): 4703-4715.
[23] 陈剑, 杜文娟, 王海风. 采用深度迁移学习定位含直驱风机次同步振荡源机组的方法[J]. 电工技术学报, 2021, 36(1): 179-190. Chen Jian, Du Wenjuan, Wang Haifeng. A method of locating the power system subsynchronous oscillation source unit with grid-connected PMSG using deep transfer learning[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 179-190.
[24] Huang Tong, Freris N M, Kumar P R, et al. A synchrophasor data-driven method for forced oscillation localization under resonance conditions[J]. IEEE Transactions on Power Systems, 2020, 35(5): 3927-3939.
[25] Liu Hao, Qi Yuan, Zhao Junbo, et al. Data-driven subsynchronous oscillation identification using field synchrophasor measurements[J]. IEEE Transactions on Power Delivery, 2022, 37(1): 165-175.
[26] Li Jinsong, Liu Hao, Li Wenzhuo, et al. Data network traffic analysis and optimization strategy of real-time power grid dynamic monitoring system for wide-frequency measurements[J]. Global Energy Intercon-nection, 2022, 5(5): 131-142.
Abstract The subsynchronous oscillation has been a dynamic stability problem that threatens the safe and stable operation of power systems, and serious subsynchronous oscillation events have occurred frequently in recent years around the world. Therefore, it is important to promptly extracting the oscillation components and precisely remove the oscillation source by monitoring the wide-frequency measurement data online. Most of conventional subsynchronous component extraction methods, however, have sluggish calculation times and low calculation accuracy, making it challenging to meet the oscillation monitoring demands of a wide-frequency measurement system. To address these issues, this paper suggests a method of calculating instantaneous power using the voltage and current from the wide-frequency measurement system, realizing the extraction of the frequency of the subsynchronous oscillation and the identification of the oscillation source.
Based on the instantaneous power from the measured data, the analytical formulas for the multimodal subsynchronous power of a doubly-fed induction generator grid-connected system were derived in this article. The major components of the subsynchronous power were extracted in the three-phase symmetric and asymmetric situations. Afterwards, using the features of the alternating power component in the main component of subsynchronous power, it was suggested to develop a frequency extraction method based on the whole-cycle instantaneous power difference. This method is faster and more accurate than the traditional method, avoiding the picket fence effect and spectrum leakage issues. Additionally, a method of the identification for subsynchronous oscillation source utilizing half-cycle instantaneous power difference was proposed based on the subsynchronous frequency extraction. This method can locate the subsynchronous oscillation source for the centralized grid-connected system of multiple wind farms and support for cutting machines.
To validate the suggested method, a doubly-fed induction generator was simulated in PSCAD by incorporating it into an infinite grid model using series complementation. The frequency extraction was carried out for the of three-phase symmetric and asymmetric situations in the subsynchronous frequency extraction example. When comparing the FFT analysis results, it shows that the instantaneous power-based frequency extraction results have good accuracy. For every 5 s increase in the studied time series, the computing time of the approach in this study grows by roughly 0.3 ms while the FFT method increases by about 2 ms, the difference between which is an order of magnitude. The result demonstrates how the suggested approach has clear advantages in the processing performance. Meantime, the approach reduces the possibility of spectrum leakage caused by discontinuous sampling endpoints in FFT analysis, and permits variable selection of truncation points for measurement data. The oscillation source identification was done for two scenarios in the multi-machine synchronous oscillation source identification examples: single oscillation source and multi-oscillation source. The simulations demonstrate that the voltage and current at the subsynchronous frequency of the generator where the oscillation source is located are larger than those at other generators. As a result, the corresponding half-cycle instantaneous power difference at the subsynchronous frequency has a larger amplitude. The findings can be used to accurately identify the oscillation source generators in the centralized grid-connected system of multiple wind farms. Furthermore, the magnitude of the absolute mean value of the half-cycle instantaneous power difference can be used to rank the significance of the oscillation sources and to rationally plan emergency response actions in the event of subsynchronous oscillations.
The simulated analysis leads to the following conclusions: (1) The primary elements of the instantaneous power in the symmetric and asymmetric three-phase circuits are a constant power component and an alternating power component of subsynchronous frequency when the subsynchronous oscillation occurs in the wind power grid-connected system. (2) The frequency corresponding to the smallest absolute mean value of the whole-cycle instantaneous power difference is the subsynchronous oscillation frequency, based on which this paper suggests a method for extracting the subsynchronous oscillation frequency. The approach can avoid the picket fence effect problem and offers improved calculation accuracy and speed compared to FFT. (3) The oscillation source, the wind generator, in the centralized grid-connected system of multiple wind farms can be detected because the half-cycle instantaneous power difference of the oscillation source generator at the subsynchronous sampling period is the biggest.
keywords：Wind farms, subsynchronous oscillation, instantaneous power, oscillation frequency extraction, oscillation source identification
DOI:10.19595/j.cnki.1000-6753.tces.220279
中图分类号：TM712
国家重点研发计划资助项目（2021YFB2400800）。
收稿日期 2022-02-28
改稿日期 2022-04-12
徐衍会 男，1978年生，教授，博士生导师，研究方向为动态电力系统分析与负荷建模。E-mail：xuyanhui23@sohu.com（通信作者）
成蕴丹 女，1999年生，硕士研究生，研究方向为风电并网系统次同步振荡。E-mail：yundan@ncepu.edu.cn
（编辑 郭丽军）