（1）
摘要 在高比例可再生能源和高比例电力电子设备接入背景下，配电网中的谐波污染和耦合谐振特性逐渐向高频段扩展。高频谐振特性分析时，现有基于开关周期平均的电压源型变换器（VSC）单频阻抗模型难以满足奈奎斯特频率以上的阻抗建模精度需求。为此，该文分析了VSC控制器采样和脉冲宽度调制（PWM）环节产生的边带分量与扰动量之间的频率耦合机理；同时考虑两类边带分量的频率耦合，建立了适用于奈奎斯特频率以上的VSC多频耦合输入导纳模型；分析了PWM采样方式、抗混叠滤波器截止频率对VSC输入导纳的影响规律。基于硬件在环仿真平台的频率扫描和稳定性分析结果，验证了计及边带分量频率耦合的VSC输入导纳模型和相关理论分析的准确性。
关键词：电压源型变换器 采样 脉冲宽度调制 边带分量 输入导纳
近年来，电压源型变换器（Voltage Source Converter, VSC）作为交直流配电网互联[1]、新能源并网运行[2-3]、储能接入等场景中的关键端口设备，在配电网中得到广泛应用[4]。然而，基于高带宽闭环控制器的VSC端口阻抗特性与电缆化配电线路、无功补偿设备、各类设备端口滤波器等设备交互作用[5-6]，导致系统谐振点分布宽频化，配电网高频谐振风险越发严重。相关案例在新能源并网、铁路牵引供电等领域均有发生，例如，某市30 MWp光伏并网项目出现谐波谐振问题，导致其110 kV线路中52次谐波电流达到基波的3倍，造成全站58台逆变器停止工作、逆变器模组的变频风扇和隔离变压器烧毁等严重损失；在铁路方面，我国某段高速铁路的供电系统、牵引网与动车组牵引变换器之间曾发生开关频率以上的高频耦合谐振，严重的谐波畸变导致避雷器爆炸、牵引供电线路过电压跳闸等问题，严重威胁列车安全稳定运行[7]。作为配电网谐振特性分析的基础，VSC高频段输入导纳的精确建模研究已成为近几年国内外学者的关注重点。
VSC的控制器采样过程和脉冲宽度调制（Pulse Width Modulation, PWM）过程均存在边带效应[8]。当扰动信号频率超过奈奎斯特频率，受频谱混叠和控制器低通滤波特性影响，采样和PWM边带分量的幅值将高于原扰动量，导致边带分量与扰动量间的频率耦合效应明显，进而影响VSC输入导纳特性[9]。多年来，国内外学者在VSC阻抗建模方面已开展了大量研究。基于移动平均算子的小信号平均阻抗模型将系统变量在开关周期内平均化处理，建模过程相对简单，在变换器控制参数设计、稳定性分析等领域应用广泛[9-11]。然而该类方法采用的移动平均处理会滤除开关周期内采样和PWM边带分量等高频信息，导致1/2开关频率以上的高频段输入导纳分析缺乏，精度不足[12-13]。
动态相量法、谐波状态空间模型等基于广义平均的多频建模方法为精确分析边带量频率耦合对VSC输入导纳的影响提供了理论工具。文献[14]建立了VSC序分量动态相量谐波分析模型，用于含多VSC配电网高频谐振特性分析，但模型仅考虑了开关次特征谐波影响。文献[15]考虑采样边带分量影响，提出了单相VSC多频阻抗模型，提高了1/2开关频率以上的VSC阻抗模型精度。文献[16]进一步提出三相VSC多频阻抗模型，并分析了采样边带量对VSC谐波稳定性的影响。文献[17]则考虑PWM边带量频率耦合影响，建立了VSC多频耦合阻抗模型。文献[18]将考虑PWM边带分量频率耦合的多输入多输出模型简化为单输入单输出形式，在保留PWM边带频率耦合效应的同时便于直观地进行VSC稳定性分析。现有文献多针对采样或PWM边带量单独作用时的VSC输入导纳特性开展研究，且通常忽略采样器前端抗混叠滤波环节对边带分量的影响。然而，VSC实际运行时两类边带分量同时影响VSC输入导纳特性，现有研究对采样和PWM边带量共同作用时各分量间的频率耦合机理以及对VSC输入导纳特性的影响规律仍缺少全面分析。
本文首先分析了VSC采样边带分量和PWM边带分量的产生机理，以及与扰动量之间的频率耦合机理；然后，同时考虑两类边带分量耦合效应影响，提出了满足奈奎斯特频率以上精确分析需求的VSC多频耦合输入导纳模型；基于所提模型，进一步研究PWM采样方式、抗混叠滤波器参数等因素对VSC输入导纳特性的影响规律；最后，搭建硬件在环仿真算例，频率扫描和稳定性分析结果验证了本文所提模型和理论分析的正确性。
数字控制系统中，A-D转换包括采样和量化两个过程，忽略量化误差影响并假设为理想采样，原始信号f(t)采样后得到采样信号fs(t)，其时域表达式为
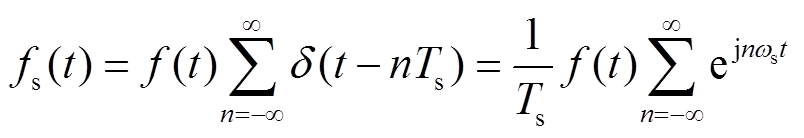（1）
式中，δ为冲击函数；Ts为采样周期；ωs为采样角频率；n为采样边带系数。
对于角频率为ωp的扰动信号，采样器输出的采样信号频域表达式为
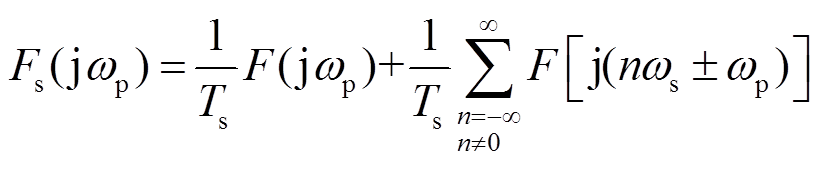（2）
式中，Fs(jω)为采样信号频域形式；F(jω)为扰动信号频域形式。
采样信号频谱如图1所示，包含扰动分量和以采样频率为周期的无穷多采样边带分量（nωs±ωp，n=1,2,3,…）。
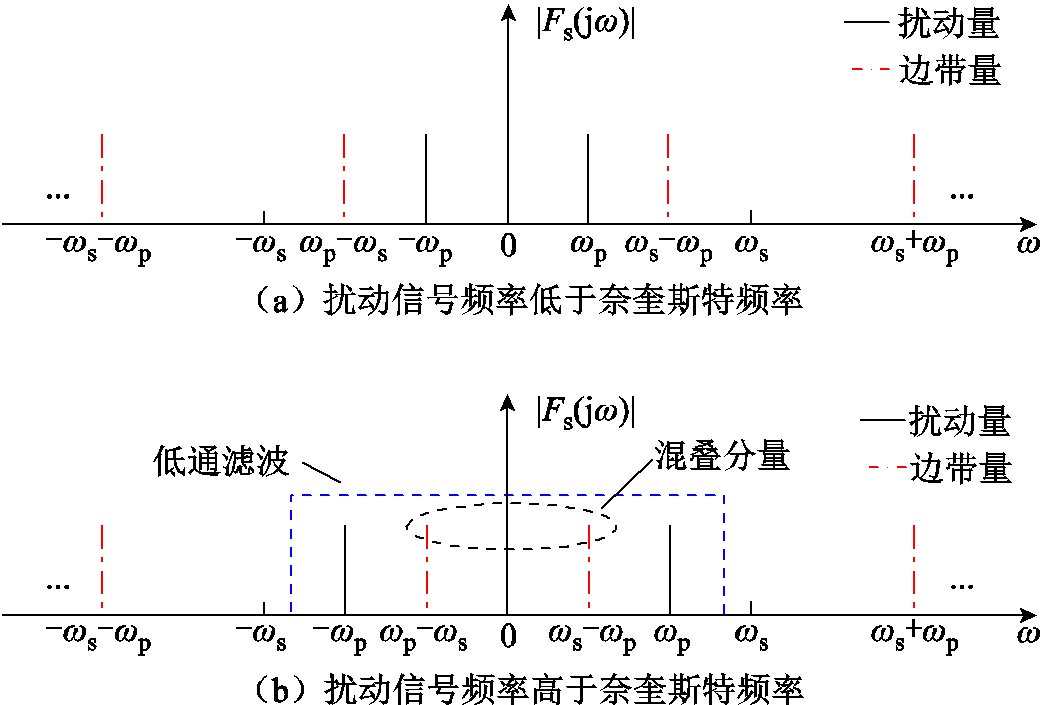
图1 扰动信号采样频谱
Fig.1 Sampling spectrum of disturbance signal
将扰动量ωp的边带量kωs±ωp(k=1,2,3,…)表示为ωp1。对于闭环控制VSC，ωp1分量经控制-物理环路再次反馈至采样器，由式（3）可知，ωp1分量的采样边带中包含与扰动量ωp同频率的额外分量。
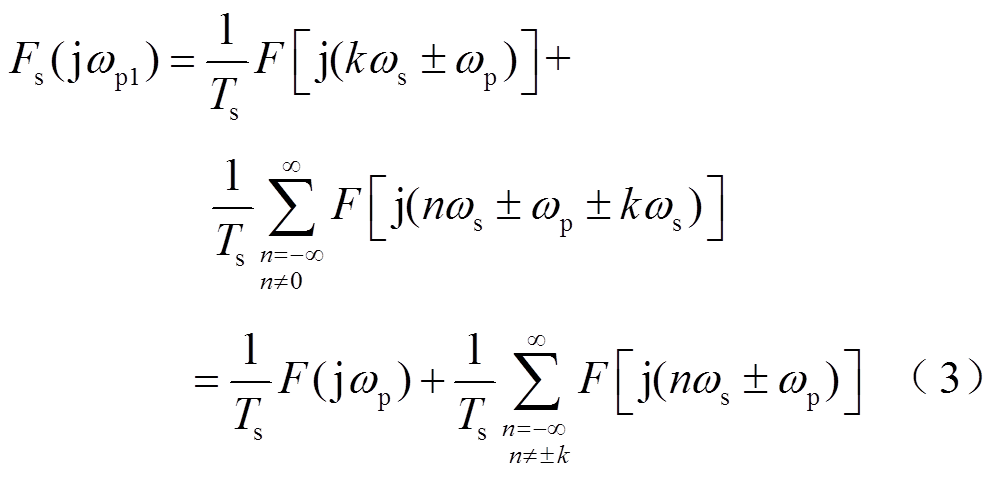
采样边带分量与扰动量信号在边带效应作用下，通过VSC控制系统和物理电路间的反馈环路实现频率耦合，从而影响VSC端口阻抗特性，频率耦合机理如图2所示。
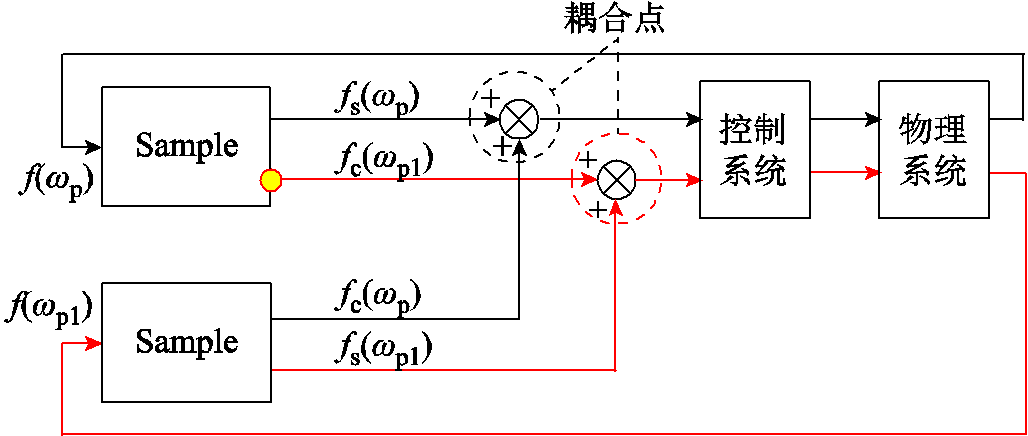
图2 扰动信号与采样边带分量耦合作用机理
Fig.2 Coupling mechanism of disturbance signal and sampling sideband component
在VSC控制系统中，通常利用零阶保持器（Zero-Order-Hold, ZOH）的低通特性实现采样信号频谱恢复。ZOH传递函数形式如式（4）所示，对应幅频特性如图3所示。
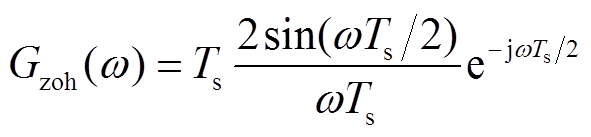（4）
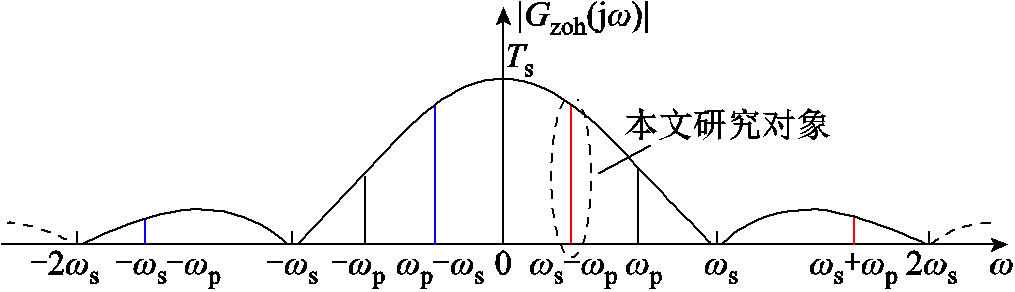
图3 ZOH幅频特性曲线
Fig.3 Frequency characteristic curve for amplitude of ZOH
当ωp＞0.5ωs时，根据奈奎斯特采样定理，会产生图1b所示的频谱混叠现象，即ωs－ωp边带量的频率低于扰动量ωp。由图3可知，ZOH环节对混叠边带分量的抑制效果明显小于扰动频率分量，因此，高频段扰动量的采样边带分量更易经图2所示耦合路径影响VSC阻抗特性。而当扰动量频率较低时，ωs－ωp接近采样频率，采样边带量几乎被ZOH环节滤除，所以中低频段VSC阻抗建模时忽略采样边带量影响，几乎不影响模型精度。
受ZOH环节、端口滤波器和采样器前端的抗混叠滤波器影响，采样频率以上边带量与扰动量之间的频率耦合效应被显著削弱。因此，本文后续分析仅考虑图3所示的ωp1=ωs－ωp采样边带分量[15]。
PWM输出信号频谱特征与其采样方式直接相关[19]。当PWM调制过程为对称规则采样，即调制信号每个开关周期更新一次（ωs=ωc,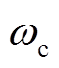 
为开关角频率）时，包含基波和扰动分量的调制信号可以表示为
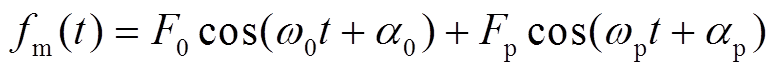（5）
式中，F0、ω0和α0分别为基波分量的幅值、角频率和相角；Fp、ωp和αp分别为扰动分量的幅值、角频率和相角。则PWM输出信号的傅里叶变换可以表示为
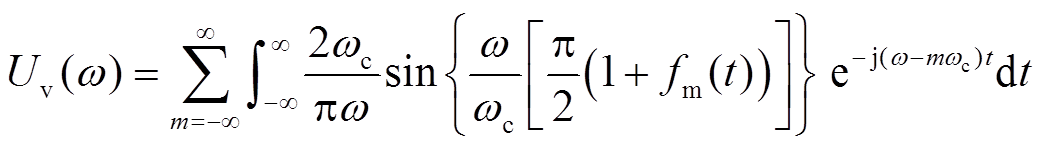（6）
对式（6）进行积分运算，最终计算得到式（7）所示的PWM边带分量表达式。
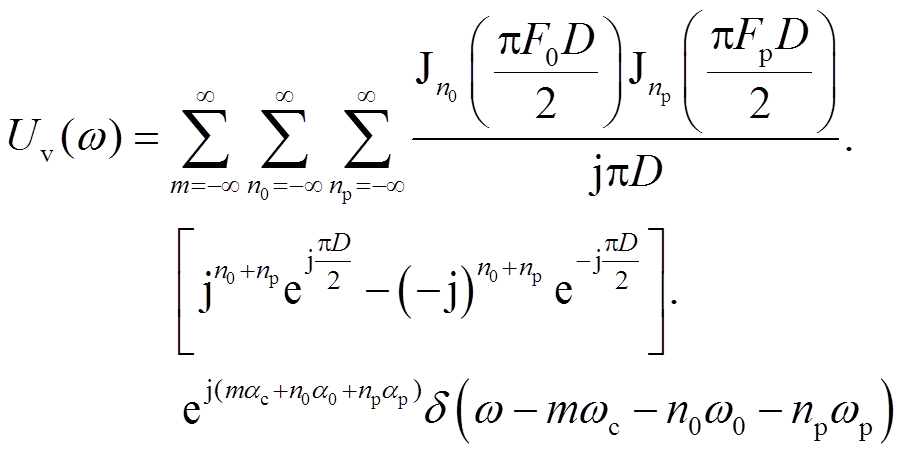（7）
式中，Ji为第一类贝塞尔函数；αc为载波初相位；n0、np和m为边带系数；中间变量D的具体形式为
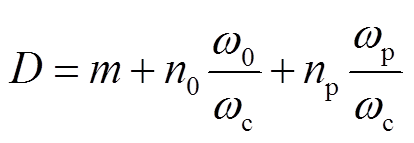（8）
当PWM调制采用非对称规则采样，即调制信号每个开关周期更新两次（ωs=2ωc）时，同理可计算得到PWM边带分量为
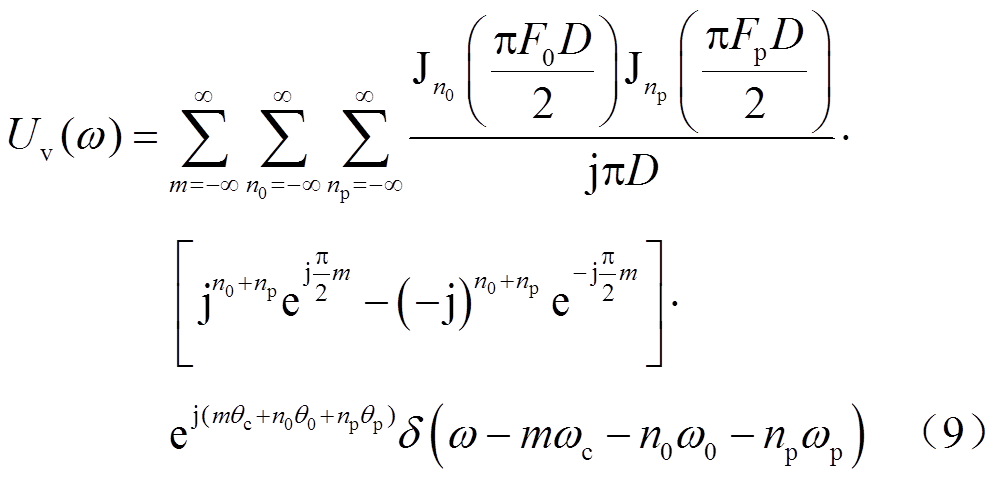
与采样边带频率耦合相似，扰动量ωp经PWM调制后产生的边带分量ωp2（ωp2=mωc+n0ω0+npωp）经物理-控制环路再次反馈至PWM调制模块，调制后将产生与扰动分量ωp同频率的额外边带分量，进而实现与扰动信号间的频率耦合。由式（7）和式（9）推导可知，ωp1分量与ωp2分量之间同样存在上述频率耦合路径。上述频率耦合机理如图4所示。图4中，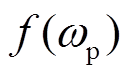
、
、
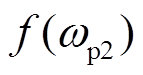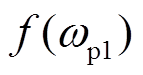为PWM调制模块输入量，
、
、
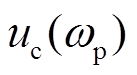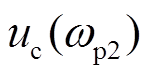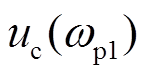为PWM调制模块输出量。
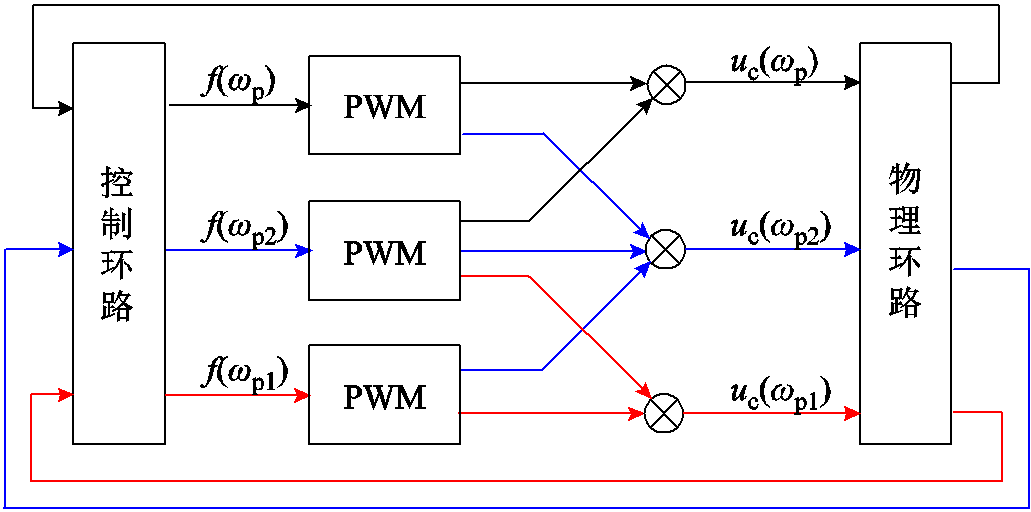
图4 扰动信号与PWM边带分量频率耦合机理
Fig.4 Coupling mechanism of disturbance signal and PWM modulation sideband harmonic component
同理，在ZOH和滤波器等环节对PWM边带中高频分量的抑制作用下，可仅考虑低于开关频率的ωc－ωp－ω0和ωc－ωp+ω0频率边带分量影响。若扰动信号f(ωp)三相对称，根据式（7）和式（9）计算可知，ωc－ωp+ω0频率的边带量为零序分量，VSC端口电流中将不包含该频率分量，因此，后续分析中仅分析ωp2=ωc－ωp－ω0的PWM边带分量频率耦合[17]。
本节针对VSC高频段阻抗特性开展研究，目标频段在1/2开关频率附近至采样频率之间。因此，可忽略带宽较低的锁相环和电压外环部分[14-18]，模型考虑电流内环、系统电压前馈、控制器计算延迟、采样环节和PWM调制等环节的影响。
计及采样与PWM边带量频率耦合的VSC控制框图如图5所示，控制框图同时考虑了采样边带分量与扰动量、PWM边带分量与扰动量，以及两种边带分量之间的频率耦合效应。
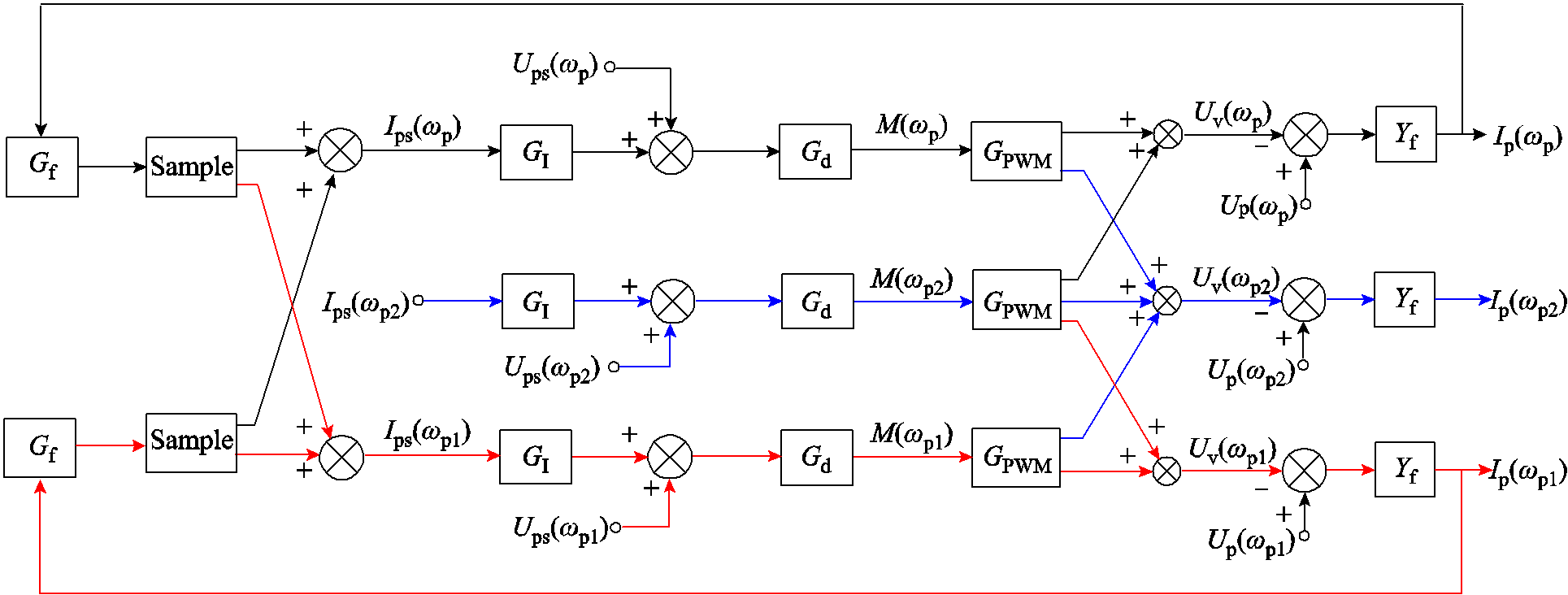
图5 同时考虑采样和PWM边带分量耦合效应的VSC控制框图
Fig.5 VSC control block diagram considering coupling effect of sampling and PWM sideband components
图5中，Yf为端口滤波器传递函数，Gf为抗混叠滤波器传递函数，Gs为采样环节传递函数，GI为内环传递函数，Gd为控制器等效延迟传递函数，GPWM为PWM环节传递函数。为简化书写，将扰动频率分量用角标p表示，采样边带分量用角标p1表示，PWM边带分量用角标p2表示。
假设系统中存在小扰动电压为
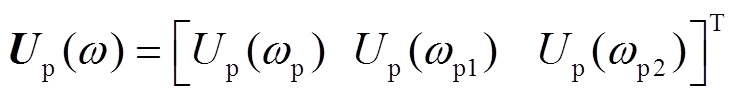（10）
由扰动电压引起的VSC端口电压、电流为
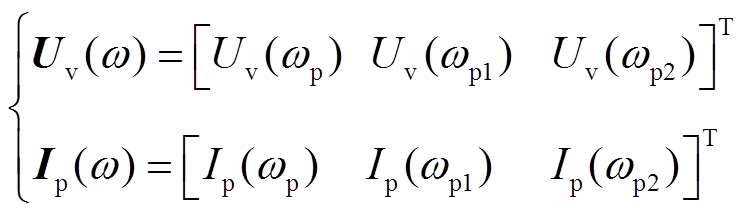（11）
VSC端口电压、电流与系统扰动电压间的关系为
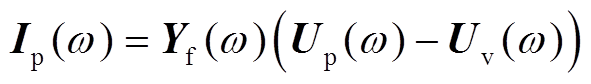（12）
其中，滤波器传递函数矩阵为
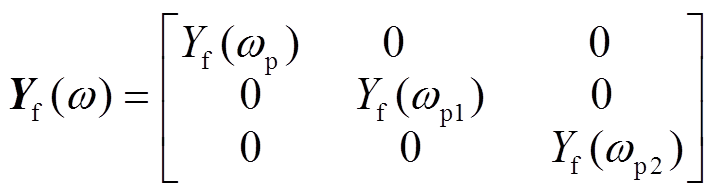（13）
在A-D采样器前端设置抗混叠滤波器是工程中抑制采样混叠的重要方式，一般可采用巴特沃斯低通滤波器或低通+陷波滤波器[13,20]。本文采用四阶巴特沃斯低通滤波器进行抗混叠滤波，其传递函数表示为Gf(ω)。
考虑采样边带效应引起的频率耦合以及抗混叠滤波，控制器中采样电压、电流可表示为
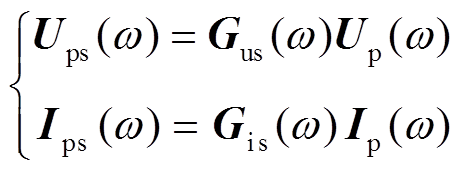（14）
其中，电压采样和电流采样传递函数矩阵分别为
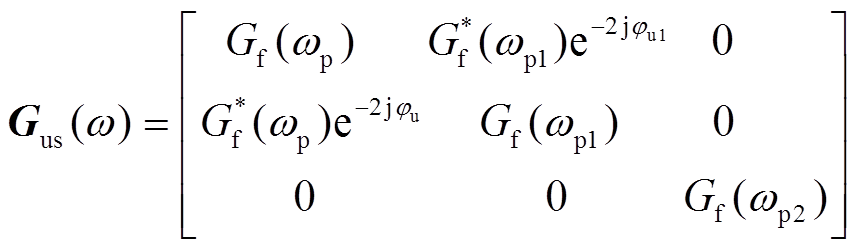（15）
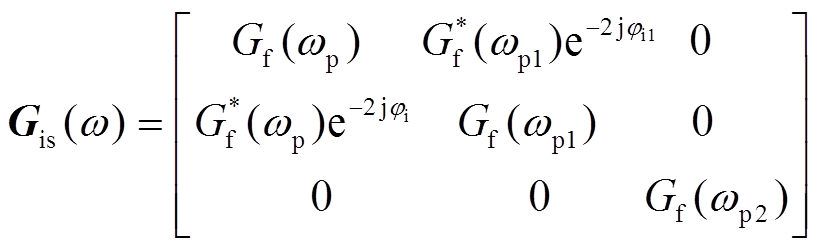（16）
式中，φu、φi、φu1、φi1分别为扰动频率电压、电流及采样边带电压、电流的初相位；*表示对应分量的共轭形式。
根据图5所示控制框图，控制器输出调制信号分量可表示为
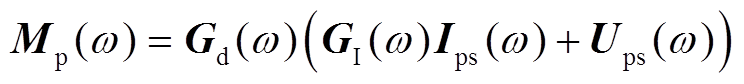（17）
式中，等效延迟传递函数矩阵如式（18）所示，等效延迟时间设为Ts；电流内环采用PI控制，传递函数矩阵如式（19）所示。
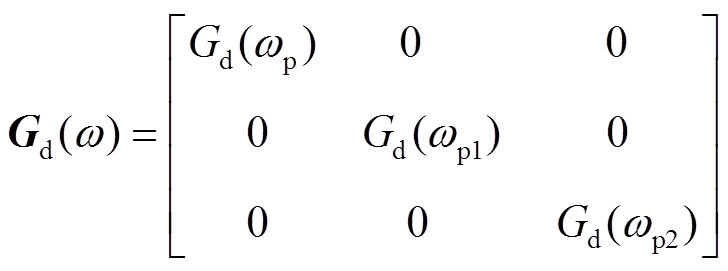（18）
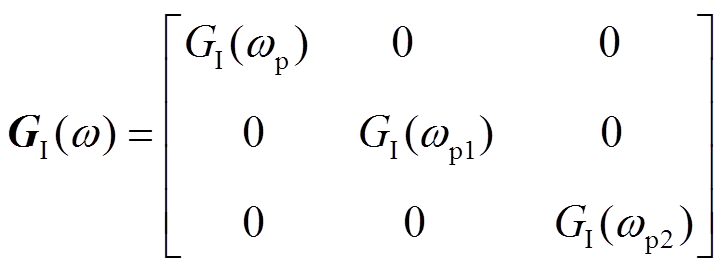（19）
考虑PWM边带效应造成的各分量之间频率耦合，VSC端口电压与调制信号之间的对应关系可以表示为
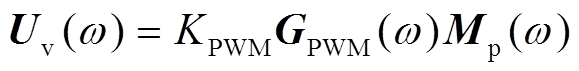（20）
式中，KPWM为PWM等效增益；PWM边带传递函数形式为
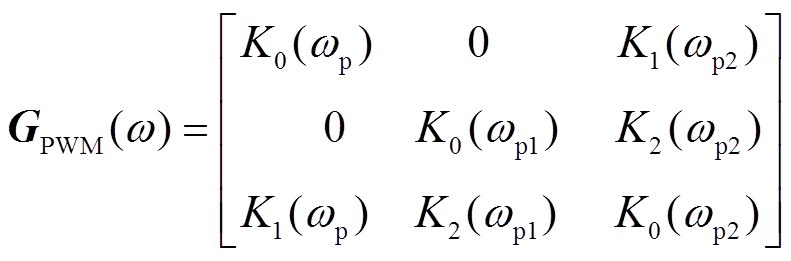（21）
采用对称规则采样时，式（21）矩阵中各元素对应传递函数可根据式（7）推导得到，具体表达式见附录式（A1）。当采用不对称规则采样时，可根据式（9）计算得到PWM边带传递函数矩阵，参数计算可见附录式（A2）。
扰动电压、电流与VSC输入导纳之间的关系为
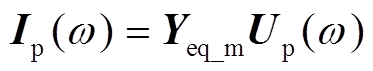（22）
综合式（10）～式（21），可计算得到VSC计及采样和PWM边带量频率耦合的多输入多输出（Multiple-Input Multiple-Output, MIMO）导纳模型为
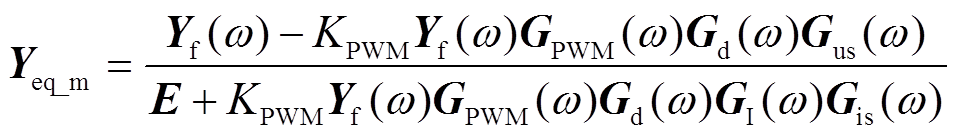（23）
式中，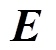
为3×3单位矩阵。
式（23）所示MIMO导纳模型为3×3多维矩阵形式，可利用广义奈奎斯特判据进行稳定性分析。然而，将VSC导纳模型应用于多VSC并网的系统稳定性和谐振特性研究时，MIMO模型导致系统导纳矩阵维数大幅增加，且不易直观地反映单台VSC对系统谐振特性的影响规律[18,21]。为此，可在保留采样和PWM边带分量频率耦合效应的前提下，将式（21）转换为单输入单输出（Single-Input Single-Output, SISO）形式，即考虑系统中仅存在单一扰动频率电压时，计及该电压在VSC端口引起的边带电压、电流分量频率耦合对扰动频率电流的影响，重建扰动电压、扰动电流与输入导纳间的关系式。对式（21）矩阵进行降维数学变换[21]，计算得到VSC考虑采样和PWM边带分量频率耦合效应的SISO输入导纳模型为
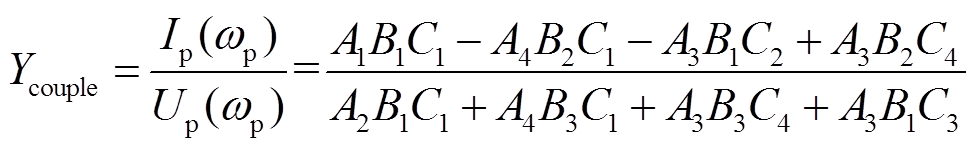（24）
其中，中间参数Ai、Bi、Ci具体定义为
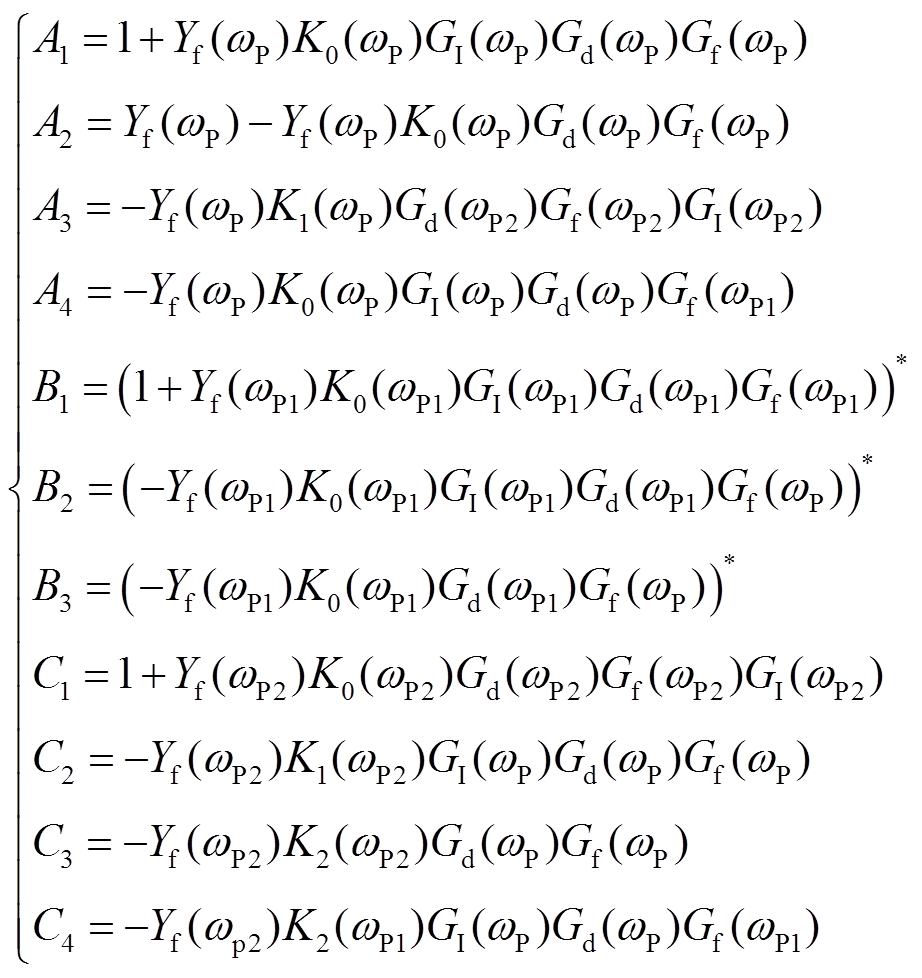（25）
当忽略采样边带分量和PWM边带分量频率耦合效应时，式（24）可简化为式（26）所示纯单频导纳模型[13]，即现有研究中常采用的输入导纳模型。
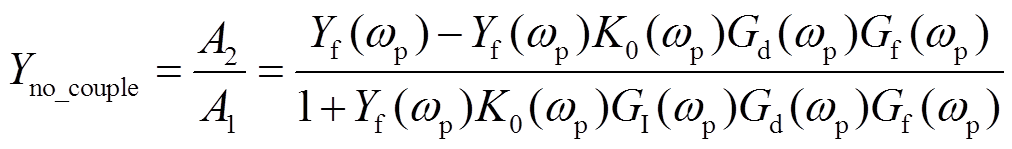（26）
为衡量输出电流中采样和PWM边带谐波分量大小，可将采样边带分量Ip(ωp1)及PWM边带分量Ip(ωp2)与扰动电压分量Up(ωp)的比值定义为衍生导纳。基于式（10）～式（24）推导，可得到式（27）所示两种边带分量衍生导纳表达形式。
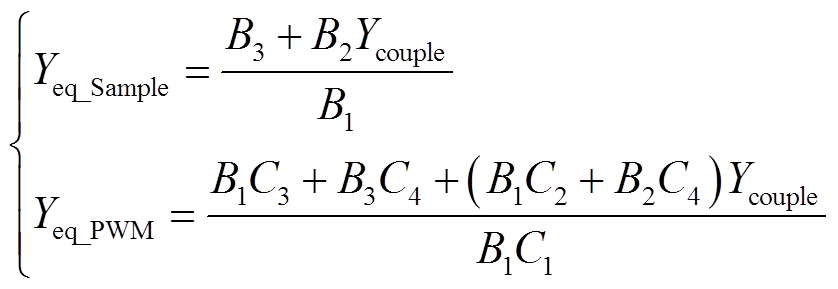（27）
为验证本文提出的计及边带量频率耦合效应的VSC输入导纳模型准确性，参照表1所示参数搭建图6所示并网VSC硬件在环仿真电路。验证平台包含DSP控制器（TMS320F28069）、RT-BOX硬件模拟器以及连接二者的接口板电路三部分，使用示波器通过接口板上AO接口测量VSC输出电流，通过频率扫频对理论分析进行验证。由于采样和 PWM 边带分量由控制环节的非线性特征引起，采用硬件在环仿真能够满足采样和PWM边带分量频率耦合效应分析的验证需求。
表1 VSC电路和控制主要参数
Tab.1 Main parameters of VSC circuit and controller
参数数值 电网线电压Ug/kV10 直流侧电压Udc/kV20 基波频率f0/Hz50 开关频率fc/kHz2 控制器采样频率fs/kHz2 滤波器电感Lf/mH7 抗混叠滤波器截止频率fcut/kHz2 电流内环PI参数kip, kii5, 50 PWM采样方式对称规则采样
图6 实验验证平台
Fig.6 Experimental verification platform
在分析频段以25 Hz为步长进行逐点频率扫描测试，基于扰动电压和扰动电流波形的快速傅里叶变换（Fast Fourier Transform, FFT）分析计算不同扰动频率下的输入导纳的幅值和相角大小。（注：表1中采样频率是指VSC控制器的采样频率，与扰动电流波形FFT分析时的采样频率无关，对1/2控制器采样频率以上的电压、电流波形FFT分析不违背奈奎斯特采样定理）
图7为VSC输入导纳理论分析与实验对比。如图7a所示，本文提出的计及边带量频率耦合的输入导纳模型与频率扫描结果基本吻合，而忽略采样和PWM边带量频率耦合效应时，输入导纳模型的幅值和相角特性在奈奎斯特频率（1 kHz）附近及以上频段均存在一定误差，证明了本文理论分析的正确性和必要性。图7b为采样边带分量和PWM边带分量衍生导纳理论分析与实验结果对比。可以看出，采样和PWM边带分量同时存在，但采样边带分量衍生导纳随频率的升高显著增大，在奈奎斯特频率以上的高频段，采样边带分量衍生导纳明显高于PWM边带分量衍生导纳。
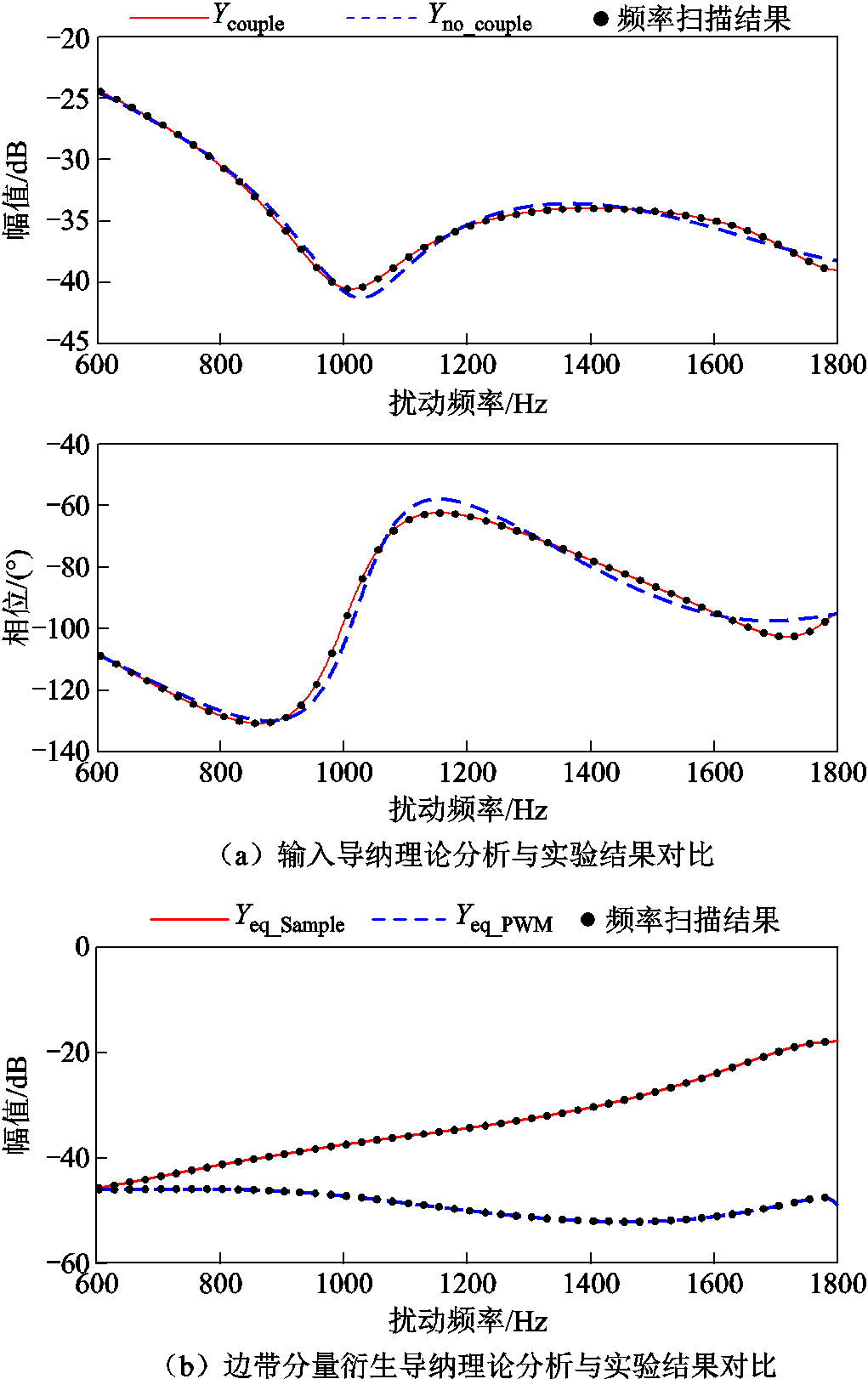
图7 VSC输入导纳理论分析与实验结果
Fig.7 Theoretical analysis and experimental results of VSC input admittance
图8为注入频率为1 600 Hz、幅值为3.5%Ug的小扰动电压时VSC输出电流波形测量结果，基于波形图FFT分析计算得到的边带量谐波含有率如图8b所示。结果与图7理论分析一致，即在奈奎斯特频率以上的高频段PWM边带谐波电流含量较低，而采样边带谐波电流含量甚至高于扰动频率电流，其与扰动频率电流分量之间的耦合效应更强，采样边带分量对VSC输入导纳特性的影响占主导作用。
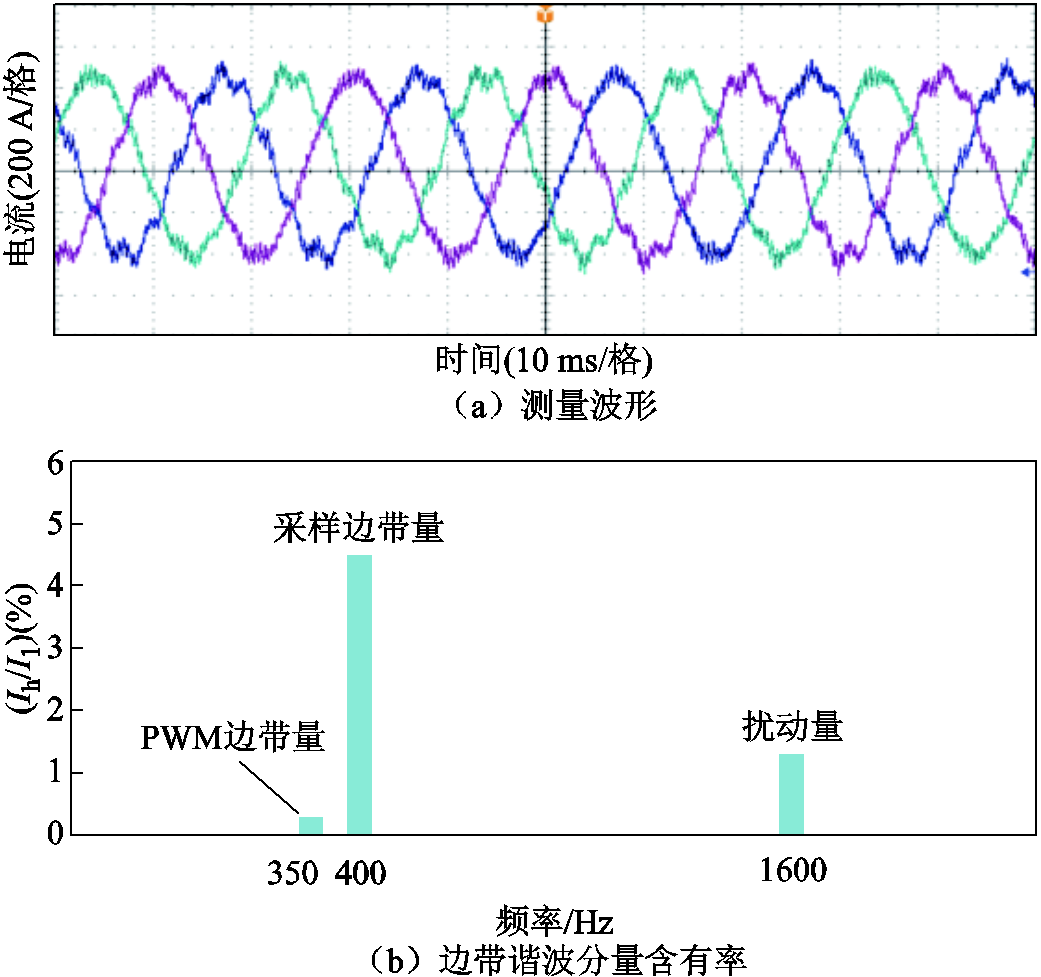
图8 小扰动注入时VSC输出电流波形
Fig.8 VSC output current waveform during small disturbance injection
图9为抗混叠滤波器截止频率设置为800 Hz时输入导纳理论分析与实验结果。结合图7a对比可知，抗混叠滤波器截止频率由2 kHz降低为800 Hz时，计及边带量频率耦合的输入导纳模型与忽略频率耦合的单频导纳模型更为接近，原因在于较低截止频率的抗混叠滤波器对采样和PWM边带分量具有显著抑制作用，从而削弱边带分量与扰动量之间的频率耦合效应。
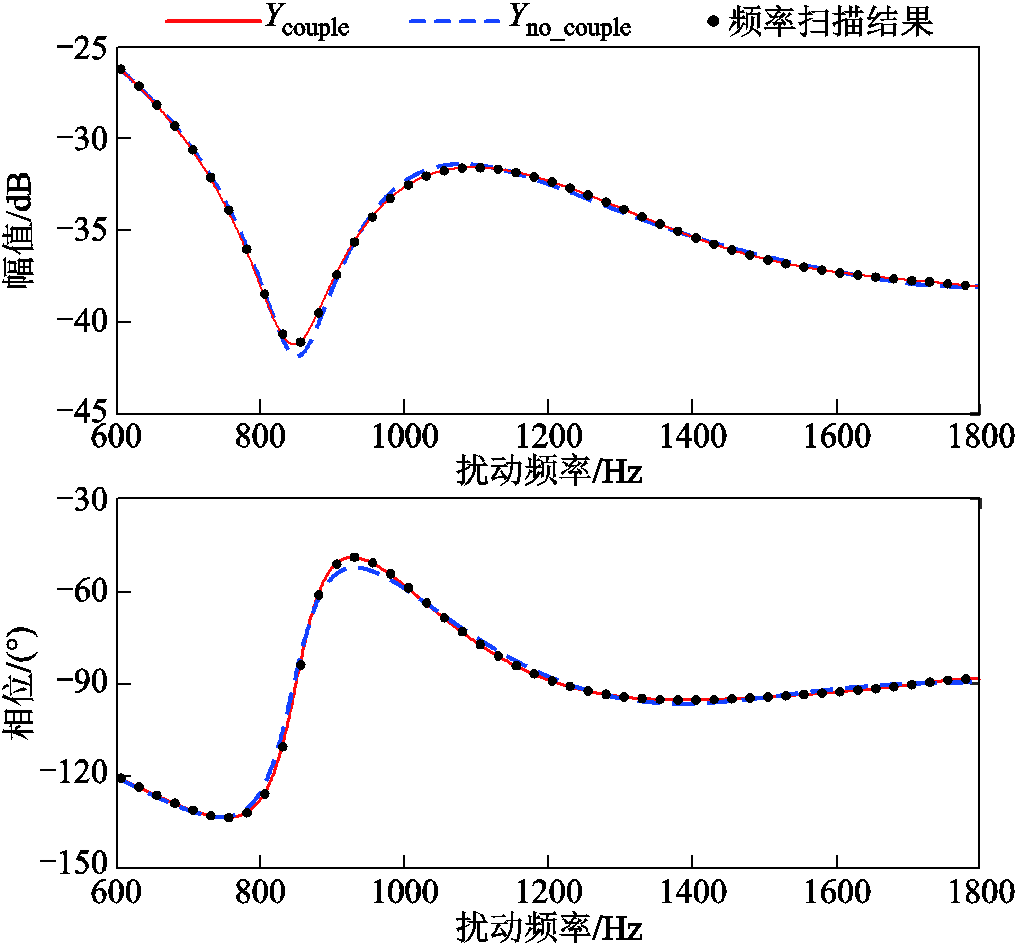
图9 fcut=800 Hz时VSC输入导纳理论分析与实验结果
Fig.9 Theoretical analysis and experimental results of VSC input admittance when fcut=800 Hz
图10对比了对称规则采样和不对称规则采样时VSC输入导纳特性。
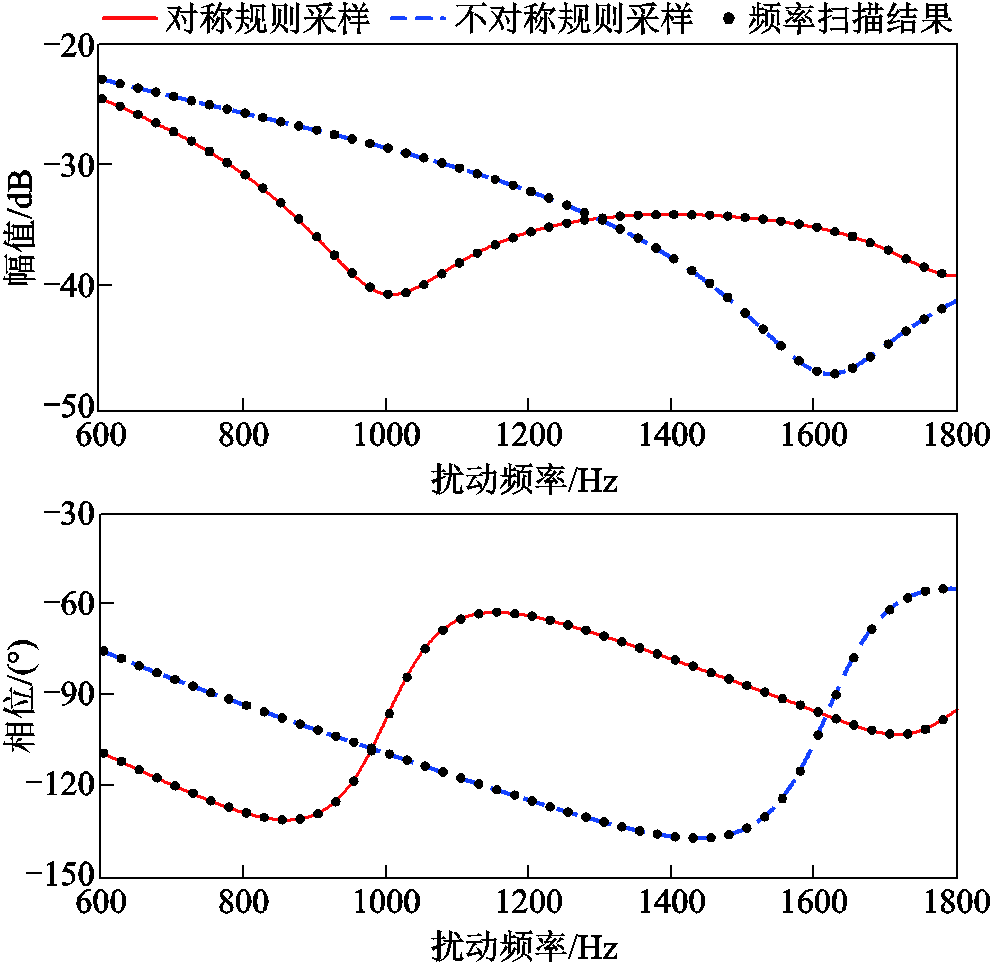
图10 对称规则采样模型与不对称规则采样模型对比
Fig.10 Comparison between symmetric regular sampling model and asymmetric regular sampling model
可以看出PWM采样方式对VSC导纳特性具有显著影响，原因在于：
1）由式（7）和式（9）对比可知，不同采样方式下PWM调制的非线性特性不一致，导致PWM边带量与扰动量之间频率耦合效应不同。
2）开关频率相同时，不对称规则采样频率是对称规则采样频率的2倍，不同采样频率下控制器计算延迟和ZOH环节等效延迟时间常数不一致。
为进一步验证本文提出的计及边带分量频率耦合VSC输入导纳模型有效性，进行VSC接入电网稳定性分析。考虑线路等效电感、对地电容及支路等效电阻影响，系统等效导纳表示为
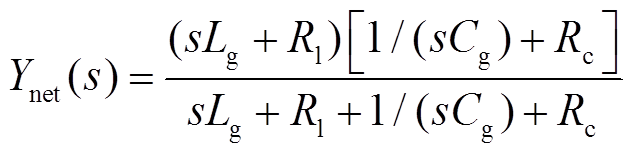（28）
当VSC参数如表1所示，且Lg=1 mH、Rl=0.1 Ω、Cg=10 μF、Rc=0.1 Ω时，VSC输入导纳与系统等效导纳伯德图如图11所示。在1 702 Hz处，两种VSC输入导纳模型对应幅频特性曲线均与系统导纳幅频特性曲线相交，不考虑边带分量频率耦合效应时，对应相位裕度为5°；考虑边带分量频率耦合效应时，系统相位裕度为-2°，即系统处于谐振不稳定状态。
图12为基于上述电网参数的VSC输出电流波形测量结果，VSC并网后在1 700 Hz附近发生谐振不稳定现象，振荡电流分量的谐波含有率接近20%。
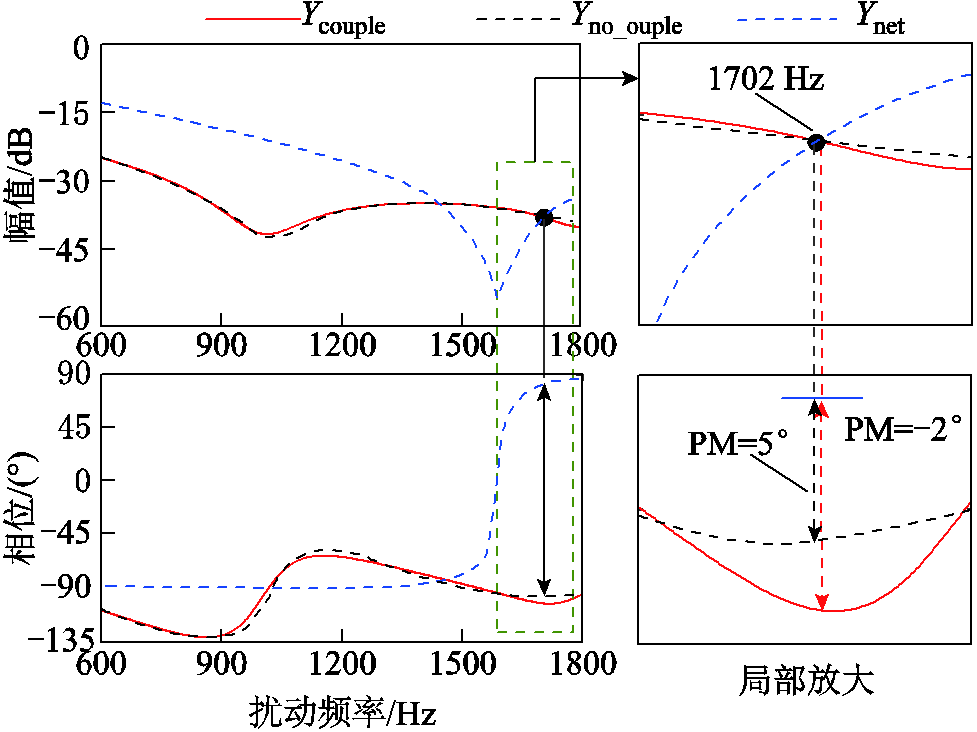
图11 VSC输入导纳与系统导纳伯德图
Fig.11 Bode diagram of VSC input admittance and system admittance
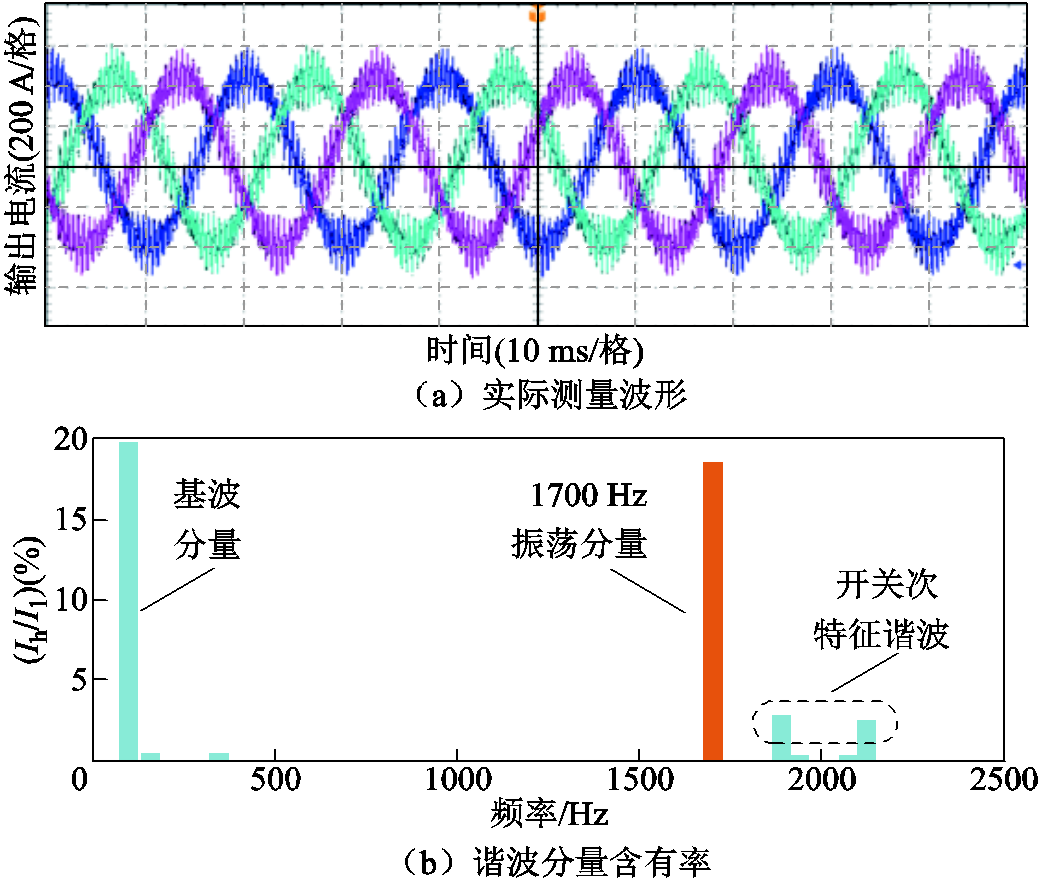
图12 VSC并网电流波形
Fig.12 VSC grid connected current waveform
由图12分析可知，系统实际谐振频率（1 700 Hz）与图11理论分析结果（1 702 Hz）比较吻合，证明了论文所提考虑边带分量频率耦合的VSC输入导纳建模方法在系统稳定性分析时的有效性。也说明了奈奎斯特频率以上VSC导纳特性分析时考虑边带分量频率耦合的必要性。
本文同时考虑VSC采样边带分量和PWM边带分量的频率耦合效应，提出了满足奈奎斯特频率以上分析需求的VSC多频耦合输入导纳模型，利用硬件在环仿真平台对算例进行了验证，得到如下结论：
1）本文所提模型在奈奎斯特频率以上的高频段相对于现有单频模型具有更高精度，能够满足含VSC配电网的高频谐振特性精确分析需求。
2）采样边带分量和PWM边带分量均会影响VSC高频段输入导纳特性，但采样边带分量含量更高，其与扰动量之间的耦合效应更强。
3）抗混叠滤波器可影响采样和PWM边带分量的频率耦合效应，在控制器A-D采样环节的前端添加截止频率较低的抗混叠滤波器，可有效削弱边带分量频率耦合对VSC输入导纳的影响。
4）PWM调制的采样方式对VSC输入导纳特性具有显著影响，该影响一方面来自于不同采样方式导致PWM调制的非线性特征不相同，另一方面来自于不同采样方式带来的延迟效应不相同。
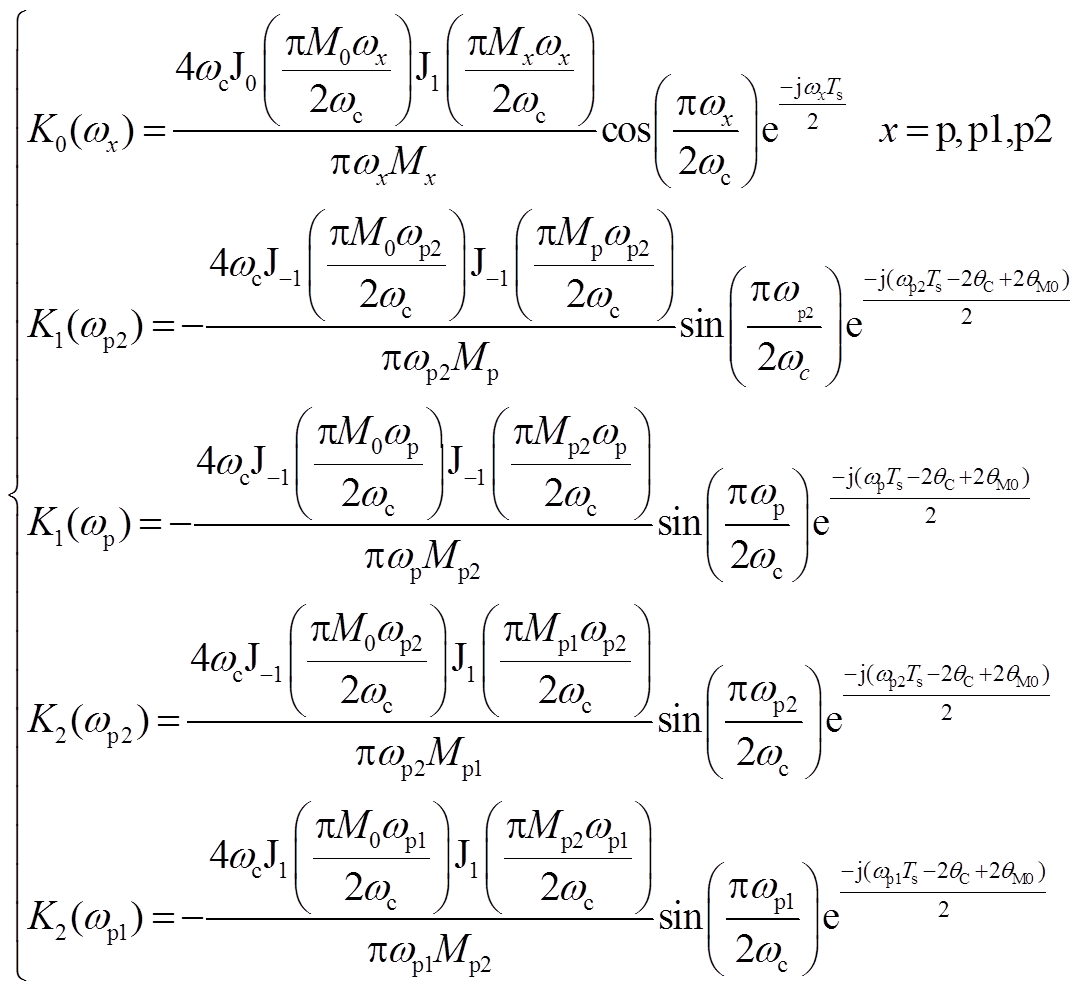（A1）
式中，M0为基波调制信号幅值；Mp1、Mp2、Mp3为对应频率的边带谐波调制信号幅值。
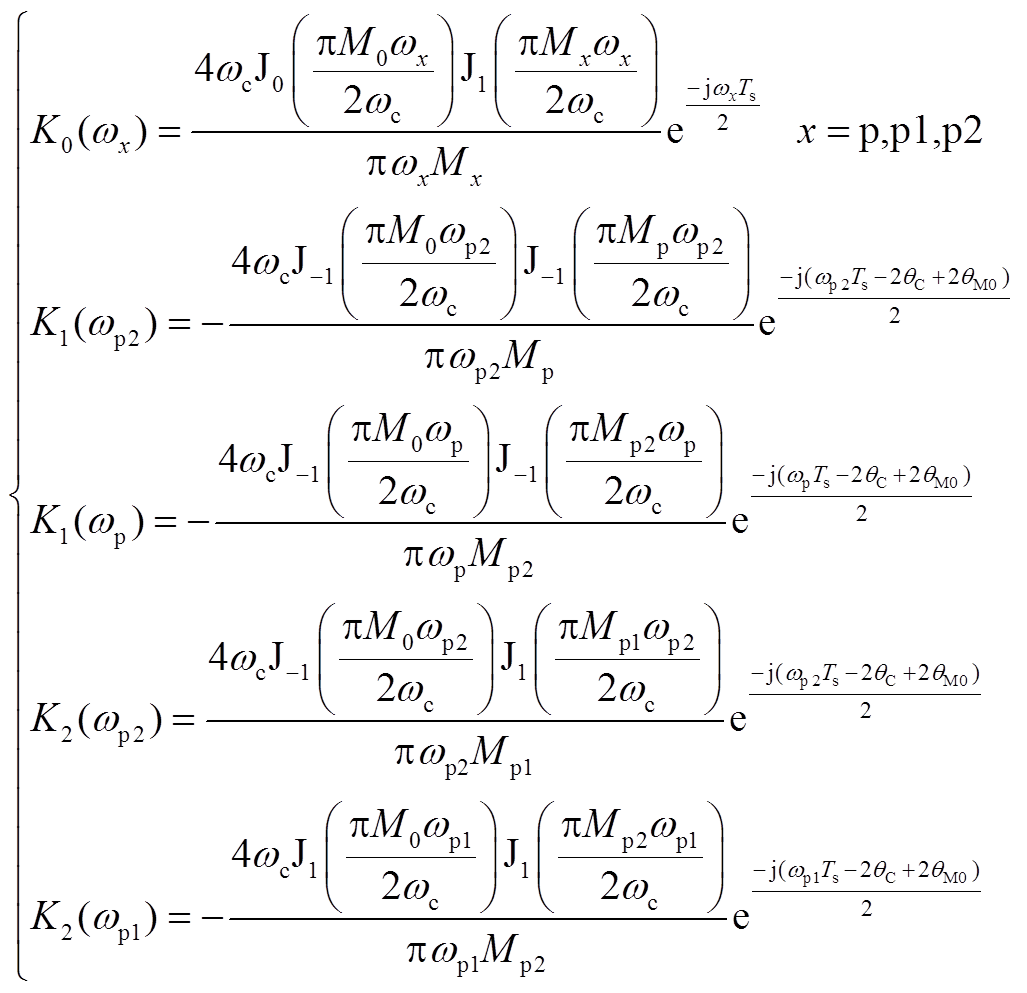（A2）
参考文献
[1] 姜涛, 李雪, 李国庆, 等. 含多端柔性直流的交直流电力系统静态电压稳定域构建方法[J]. 电工技术学报, 2022, 37(7): 1746-1759. Jiang Tao, Li Xue, Li Guoqing, et al. A predictor-corrector algorithm for forming voltage stability region of hybrid AC/DC power grid with inclusion of VSC-MTDC[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1746-1759.
[2] 李军徽, 侯涛, 穆钢, 等. 电力市场环境下考虑风电调度和调频极限的储能优化控制[J]. 电工技术学报, 2021, 36(9): 1791-1804. Li Junhui, Hou Tao, Mu Gang, et al. Optimal control strategy for energy storage considering wind farm scheduling plan and modulation frequency limitation under electricity market environment[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1791-1804.
[3] 秦本双, 徐永海. 多虚拟同步机并网系统功频振荡模态分析[J]. 中国电机工程学报, 2021, 41(19): 6570-6581. Qin Benshuang, Xu Yonghai. Modal analysis of multi-virtual synchronous machine grid-connected power-frequency oscillation[J]. Proceedings of the CSEE, 2021, 41(19): 6570-6581.
[4] 于彦雪, 马慧敏, 陈晓光, 等. 弱电网下基于准静态模型的混合控制微电网逆变器同步稳定性研究[J]. 电工技术学报, 2022, 37(1): 152-164. Yu Yanxue, Ma Huimin, Chen Xiaoguang, et al. Synchronous stability research of inverters in hybrid microgrid based on the quasi-static models under weak grid[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 152-164.
[5] 马宁宁, 谢小荣, 贺静波, 等. 高比例新能源和电力电子设备电力系统的宽频振荡研究综述[J]. 中国电机工程学报, 2020, 40(15): 4720-4732. Ma Ningning, Xie Xiaorong, He Jingbo, et al. Review of wide-band oscillation in renewable and power electronics highly integrated power systems[J]. Proceedings of the CSEE, 2020, 40(15): 4720-4732.
[6] 朱晓娟, 胡海涛, 陶海东, 等. 光伏并网系统的谐波不稳定产生机理及影响规律[J]. 电工技术学报, 2017, 32(10): 33-41. Zhu Xiaojuan, Hu Haitao, Tao Haidong, et al. The mechanism and influence of harmonic instability for photovoltaic grid-connected system[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 33-41.
[7] Tao Haidong, Hu Haitao, Zhu Xiaojuan, et al. High-frequency instability evaluation in railway system considering frequency-coupling dynamics[C]//2019 IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 2020: 1796-1800.
[8] Qiu Yang, Xu Ming, Yao Kaiwei, et al. The multi-frequency small-signal model for buck and multiphase interleaving Buck converters[C]//Twentieth Annual IEEE Applied Power Electronics Conference and Exposition, Austin, TX, USA, 2005: 392-398.
[9] Wang Xiongfei, Blaabjerg F. Harmonic stability in power electronic-based power systems: concept, modeling, and analysis[J]. IEEE Transactions on Smart Grid, 2018, 10(3): 2858-2870.
[10] Fu Qiang, Du Wenjuan, Wang Haifeng. Analysis of harmonic oscillations caused by grid-connected VSCs[J]. IEEE Transactions on Power Delivery, 2021, 36(2): 1202-1210.
[11] 刘一锋, 周小平, 洪乐荣, 等. 虚拟惯性控制的负荷变换器接入弱电网的序阻抗建模与稳定性分析[J]. 电工技术学报, 2021, 36(4): 843-856. Liu Yifeng, Zhou Xiaoping, Hong Lerong, et al. Sequence impedance modeling and stability analysis of load converter with virtual inertia control connected to weak grid[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 843-856.
[12] Yue Xiaolong, Wang Xiongfei, Blaabjerg F. Review of small-signal modeling methods including frequency-coupling dynamics of power converters[J]. IEEE Transactions on Power Electronics, 2018, 34(4): 3313-3328.
[13] Tao Haidong, Hu Haitao, Zhu Xiaojuan, et al. A multifrequency model of electric locomotive for high-frequency instability assessment[J]. IEEE Transactions on Transportation Electrification, 2020, 6(1): 241-256.
[14] 钟庆, 冯俊杰, 王钢, 等. 含多电压源型换流器配电网高频谐振特性分析[J]. 电力系统自动化, 2017, 41(5): 99-105. Zhong Qing, Feng Junjie, Wang Gang, et al. Analysis on high frequency resonance characteristics of distribution network with multiple voltage source converters[J]. Automation of Electric Power Systems, 2017, 41(5): 99-105.
[15] Harnefors L, Finger R, Wang Xiongfei, et al. VSC input-admittance modeling and analysis above the nyquist frequency for passivity-based stability assessment[J]. IEEE Transactions on Industrial Electronics, 2017, 64(8): 6362-6370.
[16] Freijedo F D, Ferrer M, Dujic D. Multivariable high-frequency input-admittance of grid-connected converters: modeling, validation, and implications on stability[J]. IEEE Transactions on Industrial Electronics, 2019, 66(8): 6505-6515.
[17] Yang Dongsheng, Wang Xiongfei, Blaabjerg F. Sideband harmonic instability of paralleled inverters with asynchronous carriers[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 4571-4577.
[18] Meng Xiangyu, Liu Zhigang, Li Guorong, et al. A multi-frequency input-admittance model of locomotive rectifier considering PWM sideband harmonic coupling in electrical railways[J]. IEEE Transactions on Transportation Electrification, 2022, 8(3): 3848-3858.
[19] du Toit Mouton H, McGrath B, Holmes D G, et al. One-dimensional spectral analysis of complex PWM waveforms using superposition[J]. IEEE Transactions on Power Electronics, 2014, 29(12): 6762-6778.
[20] 马春艳, 段青, 张博, 等. 并网逆变器高频纹波抗混叠滤波器设计研究[J]. 电力电子技术, 2021, 55(11): 33-37. Ma Chunyan, Duan Qing, Zhang Bo, et al. Study of the design of grid-connected inverter high-frequency ripple anti-aliasing filter[J]. Power Electronics, 2021, 55(11): 33-37.
[21] 刘洋铭, 吴思奇, 孟祥宇, 等. 考虑谐波耦合的车网系统谐波域SISO阻抗建模[J]. 电网技术, 2022, 46(4): 1594-1604. Liu Yangming, Wu Siqi, Meng Xiangyu, et al. SISO equivalent impedance modeling of vehicle network system in harmonic domain considering harmonic coupling[J]. Power System Technology, 2022, 46(4): 1594-1604.
Abstract Under the background of high proportion of renewable energy and high proportion of power electronic equipment access, the harmonic pollution and coupling resonance characteristics in the distribution grid gradually expand to the high frequency band. The controller sampling process and pulse width modulation (PWM) process of voltage source converter (VSC) have sideband effect. When the frequency of the disturbance signal exceeds the Nyquist frequency, the amplitude of the sampling and PWM sideband components will be higher than the original disturbance due to the influence of spectrum aliasing and the low-pass filtering characteristics of the controller, resulting in an obvious frequency coupling effect between the sideband components and the disturbance, thus affecting the VSC input admittance characteristics. In the analysis of high-frequency resonant characteristics, the existing single frequency impedance model of VSC based on switching cycle averaging is difficult to meet the impedance modeling accuracy requirements above Nyquist frequency. Therefore, this paper analyzes the frequency coupling mechanism between the sideband component and disturbance generated by VSC controller sampling and PWM link; Considering the frequency coupling of two kinds of sideband components, the VSC multi-frequency coupling input admittance model above Nyquist frequency is established.
Firstly, the generation mechanism of VSC sampling sideband component and PWM sideband component and the frequency coupling mechanism with disturbance are analyzed. Under the action of sideband effect, sampling sideband component, PWM sideband component and disturbance signal realize frequency coupling through feedback loop between VSC control system and physical circuit, thus affecting VSC port impedance characteristics. Considering the suppression effect of ZOH and filter on high frequency components in the sideband, the model can only retain ωs－ωp and ωc－ωp－ω0 sideband component. Considering the influence of current inner loop control, system voltage feedforward control, controller calculation delay effect, the sampling procedure and PWM modulation, the multi-frequency input admittance model of VSC is established. A grid connected VSC hardware in the loop simulation platform is built to verify the theoretical analysis result. The input admittance model which takes into account the frequency coupling of sidebands is basically consistent with the frequency scanning results of hardware in the loop simulation. When the frequency coupling effect of sampling and PWM sidebands is ignored, the amplitude and phase angle characteristics of the input admittance model have certain errors in the frequency bands near and above the Nyquist frequency, which proves the necessity of this study.
The following conclusions can be drawn from the simulation analysis: (1) The VSC multi-frequency coupling input admittance model considering the coupling effect of sampling and PWM sideband components has higher accuracy in the high frequency band above Nyquist frequency. (2) Both the sampling sideband component and PWM sideband component will affect the admittance characteristics of VSC in the high frequency band, but the influence of sampling sideband component on the admittance characteristics of VSC in the high frequency band is more significant. (3) The anti-aliasing filter can significantly suppress the frequency coupling effect of sampling and PWM sideband components. When the cut-off frequency of the anti-aliasing filter is low, the influence of sideband frequency coupling effect on VSC input admittance can be ignored. (4) The sampling mode of PWM modulation has a significant impact on the impedance characteristics of VSC. On the one hand, the delay effect caused by different sampling modes is different, and on the other hand, the nonlinear characteristics of PWM modulation are different due to different sampling modes.
keywords：Voltage source converter (VSC), sampling, pulse width modulation (PWM), sideband component, input admittance
DOI:10.19595/j.cnki.1000-6753.tces.222053
中图分类号：TM464
南方电网公司科技资助项目（090000KK52220014/ SZKJXM20220021）。
收稿日期 2022-10-31
改稿日期 2022-12-12
徐少博 男，1994年生，博士研究生，研究方向配电网电能质量。E-mail：13021085107@163.com
陶 顺 女，1972年生，副教授，硕士生导师，研究方向为智能配电网与电能质量。E-mail：tao_shun@sina.com（通信作者）
（编辑 赫蕾）