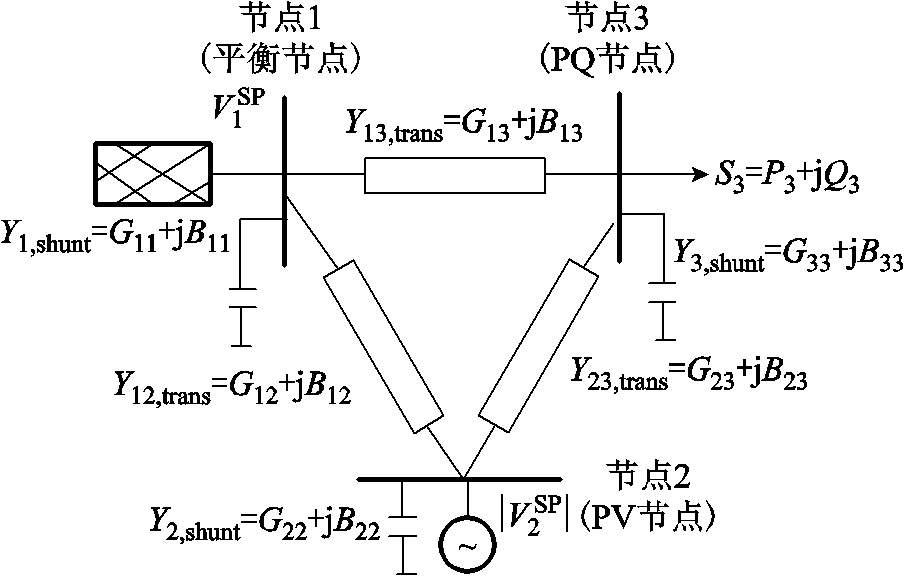
图1 1个PQ节点、1个PV节点和1个平衡节点构成的3节点系统
Fig.1 A system composed of a PQ bus, a PV bus and a swing bus
摘要 通过求解电力系统最优潮流获得各发电机的有功出力对于电力系统经济运行具有重要意义。全纯嵌入法是一种用于潮流计算的非迭代算法。该文将全纯嵌入法应用于最优潮流的求解，首先推导出约束条件和KKT条件的全纯嵌入形式；然后通过上述两组方程交叉得到求解通式，递归地计算出节点电压和发电机有功出力的表达式；最后根据解析表达式直接得到各发电机的有功出力，进而计算系统的最低发电成本。在IEEE 3节点、4节点、30节点、118节点和新英格兰39节点电力系统上的仿真结果验证了所提方法的可行性和准确性。
关键词：最优潮流 全纯嵌入法 非迭代 KKT条件 发电成本
我国电力行业的快速发展，对电力系统资源的优化配置提出了更高的要求[1]。在确保系统安全稳定的运行条件下，优化电力系统的调度运行，降低系统的能量损耗，得到发电成本最低的潮流分布，正是最优潮流（Optimal Power Flow, OPF）所要解决的问题之一。因此，最优潮流自诞生之日起便是电力系统中研究的热点问题，对于电力系统的节能环保低碳和经济性运行有着重要的理论和实践意义[2]。
最优潮流的概念在1962年由J. Carpentier首次提出[3]，为了适应电力系统的飞速发展，最优潮流的优化模型与求解方法也在不断更新。根据潮流的类型不同分为直流最优潮流[4]和交流最优潮流；根据网络的拓扑结构可以分为辐射型网络最优潮流[5]和环型网络最优潮流[6]。当前求解最优潮流的方法主要可以分为三类：①线性近似处理[7-8]；②非线性优化方法[9-15]；③智能算法[16-19]。第①类方法将交流潮流约束近似为直流潮流约束，求解直流最优潮流，同时也避免了OPF模型中的非凸问题，但将交流潮流近似为线性问题得到的结果可能不是交流潮流中的可行解。第②类方法主要采用传统的内点法[9]、梯度法[10]、牛顿法[11]等数学上常用的求解算法对非线性优化问题的进行求解，由于这些方法容易陷入局部最优，近年来针对约束条件进行松弛的凸松弛算法（如半正定规划松弛[12]，二阶锥规划松弛[13-15]等）一直是研究的热点，对非凸问题进行松弛，将优化问题松弛为凸问题，从而能够应用内点法等求解算法得到问题的最优解，在精确松弛的前提下，可以保证得到的解为全局最优解，但不同的优化问题对于松弛有不同的精确要求，在松弛不精确时所得到的解可能为系统的不可运行点[2]。第③类方法为近几年发展迅速的智能算法，如粒子群算法[16]、进化算法[17-18]、遗传算法[19]等，这些启发式算法不采用传统的内点法作为求解器，而是通过经验选择行之有效的方法。
全纯嵌入法是由西班牙学者A. Trias于2012年提出的。该方法最初被应用在潮流计算中，它避免了许多传统方法（如牛顿-拉夫逊法[20]、快速分解法[21]等）过于依赖初始点选取而导致不收敛的缺陷，该方法通过适当的全纯嵌入形式以保证收敛性，同时能够将计算结果解析化。全纯嵌入法已在电力系统在线电压稳定评估、薄弱节点辨识和动态仿真方面有了较多的应用[22-26]，但在系统有功最优潮流的研究方面，目前相关的文献研究较少。由于全纯嵌入法存在非迭代、递归性、解析性、不依赖初始点的选取、所得到的解为可运行点等优点，因此该方法在有功最优潮流的计算中有较大的应用潜力。
本文将全纯嵌入的方法用于有功最优潮流的求解，提出了基于全纯嵌入法的电力系统有功最优潮流的计算方法。首先构造出电力系统最优潮流约束条件和KKT条件的全纯嵌入形式；然后推导出节点电压和发电机有功出力解析表达式幂级数系数的递推方程组；最后通过上述两组方程组交叉递归求得解析表达式中的系数，得到优化后系统发电机的出力以及发电成本。本文通过IEEE 3节点、4节点、30节点、118节点和新英格兰39节点系统有功最优潮流的算例仿真，验证了该方法的可行性及准确性。
为了验证本文所提的基于全纯嵌入的最优潮流算法的可行性，本文以有功最优潮流为例，优化电力系统发电机的有功出力，目标函数为最小发电成本。
在传统的最优潮流问题中在针对经济调度问题时一般不考虑PV节点，但发电机还是有自身的电压控制功能，所以为方便推导及理解，本文将发电机节点考虑为PV节点。
同时为了便于理解且不失一般性，本节以3节点系统模型为例，包含1个平衡节点（节点1）、一个PV节点（节点2）和一个PQ节点（节点3），如图1所示。其中方程中所有的大写字母表示常数，小写字母表示变量。同时，附录给出了由m个PQ节点、p个PV节点和1个平衡节点构成的电力系统的推导方程。
图1 1个PQ节点、1个PV节点和1个平衡节点构成的3节点系统
Fig.1 A system composed of a PQ bus, a PV bus and a swing bus
该最优模型是一个发电成本最小化模型，目标函数为最小化发电成本，即
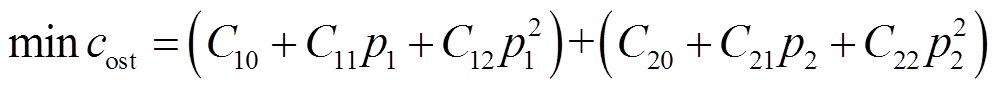（1）
式中，p1和p2分别为节点1和节点2处的发电机有功出力，发电成本表示为发电机有功出力的二次函数；Cij为成本系数，视为常数项。平衡节点和PV节点的有功出力p1和p2为控制变量，而PQ节点的有功输出P3和无功输出Q3为已知量。
以直角坐标系下的潮流方程组以及全网的有功平衡方程作为约束条件。
约束1：平衡节点1的潮流方程
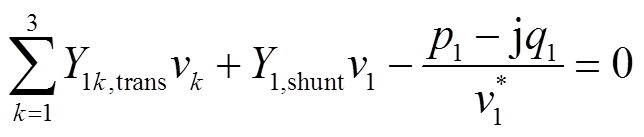（2）
同时平衡节点1的电压固定，即
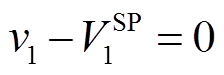（3）
约束2：PV节点2的潮流方程
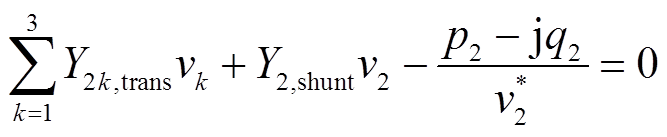（4）
同时PV节点2的电压幅值固定，即
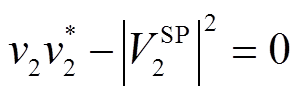（5）
约束3：PQ节点3的潮流方程
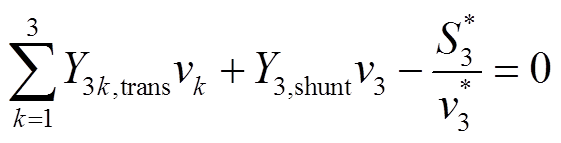（6）
约束4：全网有功平衡方程
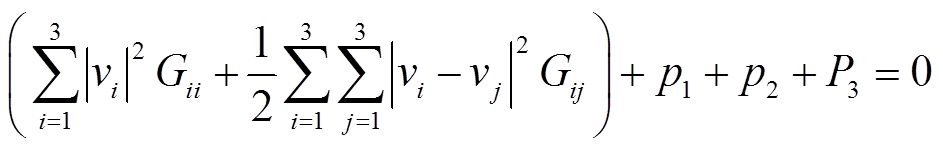（7）
式中，vi为节点i的电压；ViSP为固定值，表示平衡节点或PV节点的电压值；q1和q2分别为节点1和节点2处的发电机无功出力；Gij为节点i到节点j之间的互电导；Gii为节点i的对地电导；Bij为节点i到节点j之间的互电纳；Bii为节点i的对地电纳；Yi,shunt为节点i对地的导纳；Yij,trans为节点i和节点j之间的互导纳；Si为节点i处的视在功率，如图1所示；上标*表示共轭算子。式（7）中左端第一项为网络损耗，分为节点对地的导纳产生的损耗和节点之间互导纳产生的损耗。同时目标函数里的p1和p2应是发电机的有功出力，而约束里的P是指对应节点的有功注入，即发电机和负荷的共同效果。图1中所示的3节点系统中节点1、2只有发电机，节点3只有负荷，故不需要考虑此类问题。
目前为止本文只考虑了等式约束，没有涉及不等式约束，在数学上求取考虑不等式约束条件目标函数最小值的方法已有很多[27]，同时文献[28]解决了全纯嵌入法在潮流计算中考虑控制上下限的问题，上述解决不等式约束的方法均可以和本文所提方法相结合。本文侧重于首度探索全纯嵌入法在有功优化方面的可行性，因此考虑不等式约束的有功优化将可以作为后续研究内容。
根据目标函数式（1）和约束条件式（2）～式（7），构造拉格朗日方程为
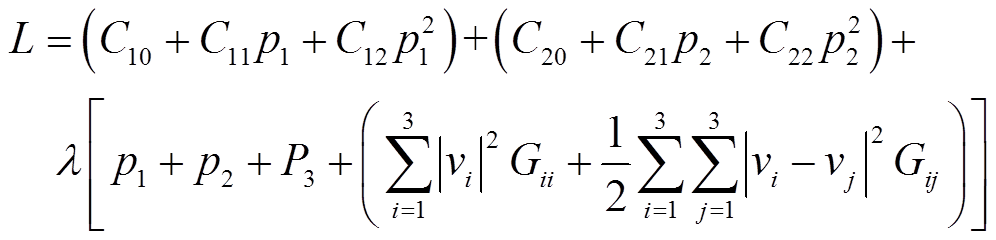（8）
式中，λ为拉格朗日乘子。
根据拉格朗日数乘法计算极值的规则，得到KKT条件为
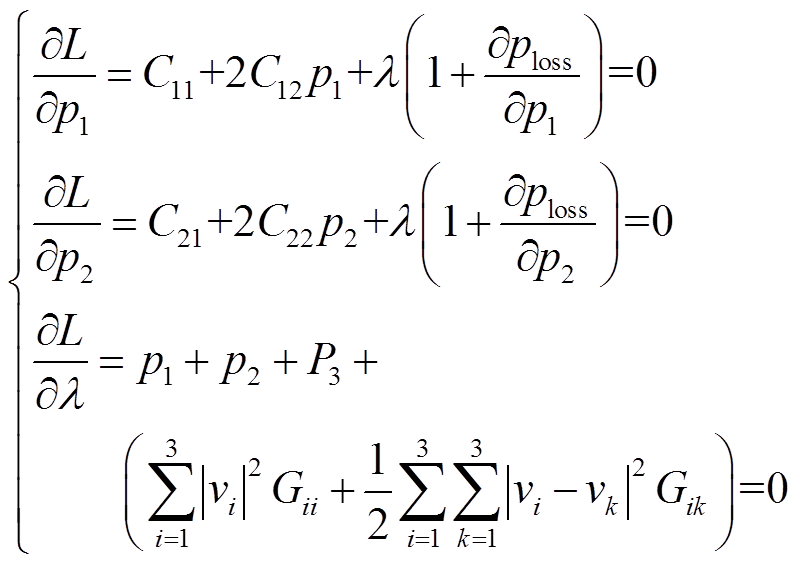（9）
虽然式（7）中左端第一项括号中的线路损耗没有表示出与发电机有功出力的相关性，但由于约束条件式（2）～式（5）的存在使得发电机有功出力的改变会改变节点处的电压，所以网络的有功损耗既是所有节点电压的函数，也是所有节点有功输入的函数[29]，在计算拉格朗日函数对发电机有功出力的偏导时，线路损耗对有功出力的偏导数不能忽略，用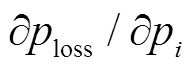
来表示，也称作网损微增率。
全纯嵌入法及其构造规则在文献[25]中已有介绍，若单复变函数x(s)在复数s0的邻域U内复可微，则称函数x(s)是复数域U上的全纯函数。
全纯函数能够在该复数域内展开成幂级数的形式，有
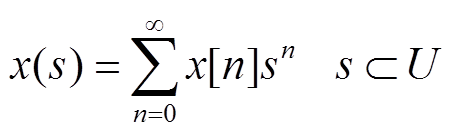（10）
应用全纯嵌入法的求解潮流方程等非线性方程组的重点是在待求解的变量中嵌入复变量s，令求解过程变为从初始状态延伸到所求解，将所要求解的潮流平衡方程g(x)=0按照一定的规则将其变量x（如节点电压v和发电机的有功出力p）构建成全纯函数x(s)，可以得到复合函数g(x(s))=0，其中只要计算出式（10）中各个变量的幂级数系数x[n]，则能得到变量的解析表达式。本文所有幂级数系数均使用方括号表示，函数使用小括号表示。
全纯嵌入函数的构造可按照如下规则：
1）当s=0时表示系统的初始条件，且能够满足g(x(0))=0，如在潮流计算中可以表示为发电机在没有有功输入、系统没有负荷时的状态。
2）当s=1时表示所要计算的目标解，同时也能够满足g(x(1))=0，即为原始的常规潮流平衡方程。
3）s在取其他值时不代表系统的任何运行状态。
4）在s从0到1变化的过程中，复合函数g(x(s))需是解析连续的。
对于幂级数系数x[n]的计算，可以通过方程g(x(s))=0左右两侧s同阶系数相同构造的递推关系求得[7]。
将s=0代入式（10）中，由上述构造规则1）可知，得到每个变量的第0阶幂级数x[0]即为系统初始条件的值。同时将s=1代入式（10）中，根据构造规则2）可知，所有幂级数系数之和即为变量的目标解，当求得的幂级数阶数越高，目标解就越精确，越接近变量的实际值。
根据约束条件式（2）～式（7）与全纯嵌入的基本构造规则，节点电压的初始值设为v(0)=1，将复变量s嵌入到方程组中，构造全纯嵌入方程，有
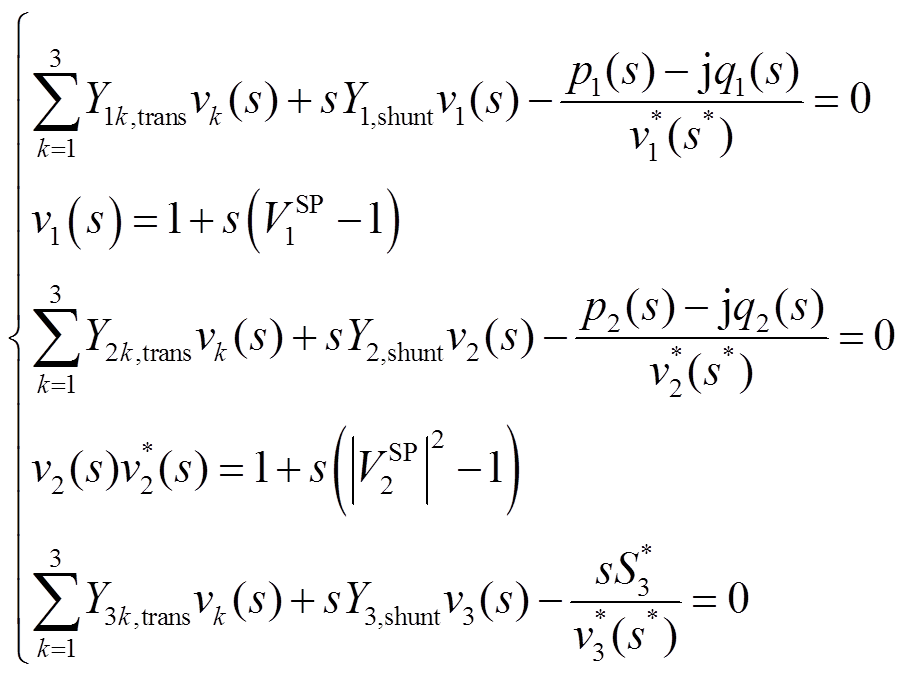（11）
由式（11）可推出当s=0时，系统在初始运行状态下节点电压的值v(0)=1，理论上该初始值也可以取其他值，只需要构造的全纯嵌入形式满足构造规则即可。同时在s=1时，上述方程则变为前文中的约束条件。所以本文提出的方法不依赖于系统实际初始点的选取，与系统实际的初始点无关。
将式（10）代入约束方程的全纯嵌入方程中，采用附录中的方式，将电压的实部e和虚部f分开，可以得到s在不同阶数时的电压的实部与虚部表达式（12）。
式中，Re(·)表示取实部；Im(·)表示取虚部；Gij和Bij分别为节点i与节点j之间互电导和互电纳；Gii和Bii分别为节点i的对地电导和对地电纳；当n=i时，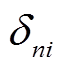
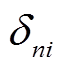=1，否则=0；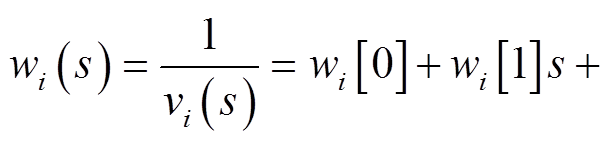
；
-
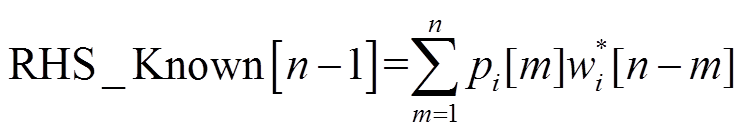。所有的幂级数系数均为低阶系数或已经通过其他步骤计算得到。
同时节点2的电压实部e2[n]可以通过附录中PV节点的电压幅值恒定公式推导得到。
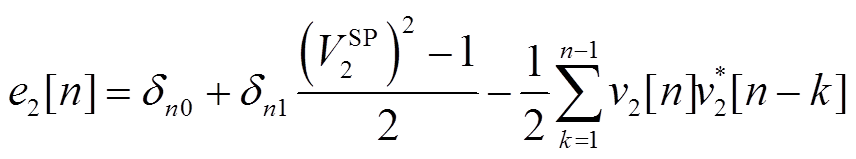（13）
将表达式右端项对应PV节点的节点2的无功变量q2[n]移到等式左侧，将左侧节点2的电压实部e2[n]移到等式的右侧，可以得到节点电压幂级数系数的递推公式为
由式（14）可以看出，等式右侧均为低阶幂级数系数或能够通过式（13）计算得到的系数，所以能够通过式（14）逐渐递推出节点电压高阶的幂级数系数。
由2.1节可知，将s=0代入式（11）可以得到节点电压的初始值（ei[0]，fi[0]），后续的系数（ei[n]，fi[n]）可以通过式（13）、式（14）进行递推求解，直至达到所设定的计算精度，节点电压的解析表达式可以由式（15）表示。
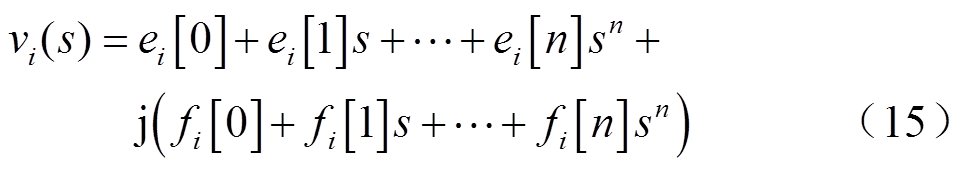
将s=1代入式（15），根据构造规则2）可知，所有幂级数的和即为节点电压的目标解，计算的阶数越高，得到的节点电压值越精确，相应的计算量也会增加。所以递推的过程就是在逐步更新节点电压值，使结果逐渐接近电压实际值的过程。
根据拉格朗日方程式（8）、式（9）与全纯嵌入的基本数学规定，设置系统初始运行条件下发电机没有有功出力，将复变量s嵌入到KKT条件中，得到全纯嵌入形式为
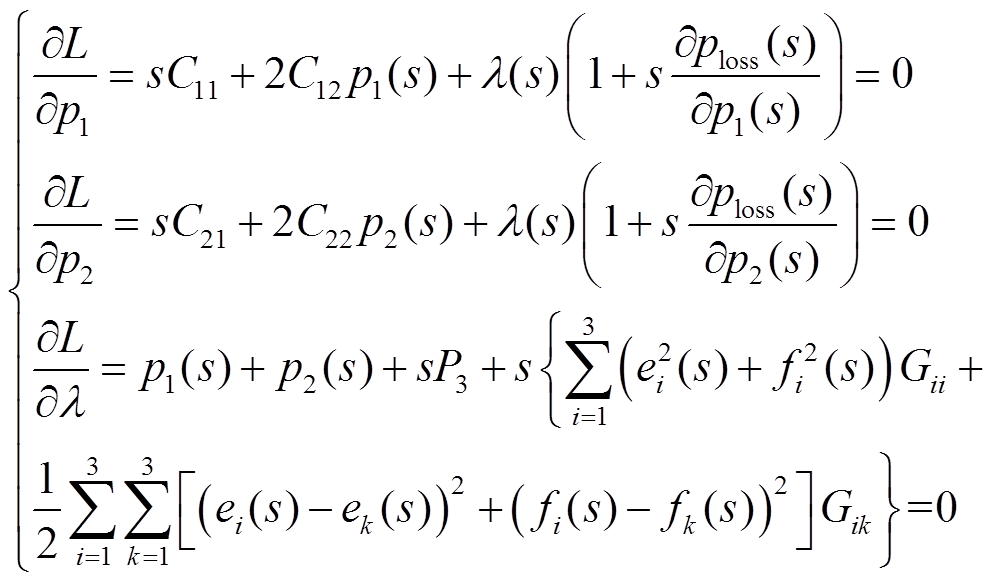（16）
同理在s=0时，由式（16）可以推出系统在初始运行状态下发电机有功出力与拉格朗日乘子pi(0)=0、λ(0)=0；同时在s=1时，上述方程则变为KKT条件的原始方程。若发电机的有功出力初始值不同，只需要改变全纯嵌入的形式，再次体现了本文所提方法不依赖于系统实际初始点的选取。
将式（10）代入式（16）中，根据附录中介绍的方法，可以得到发电机的输出功率pi[n]和拉格朗日乘子λ[n]的递推公式为
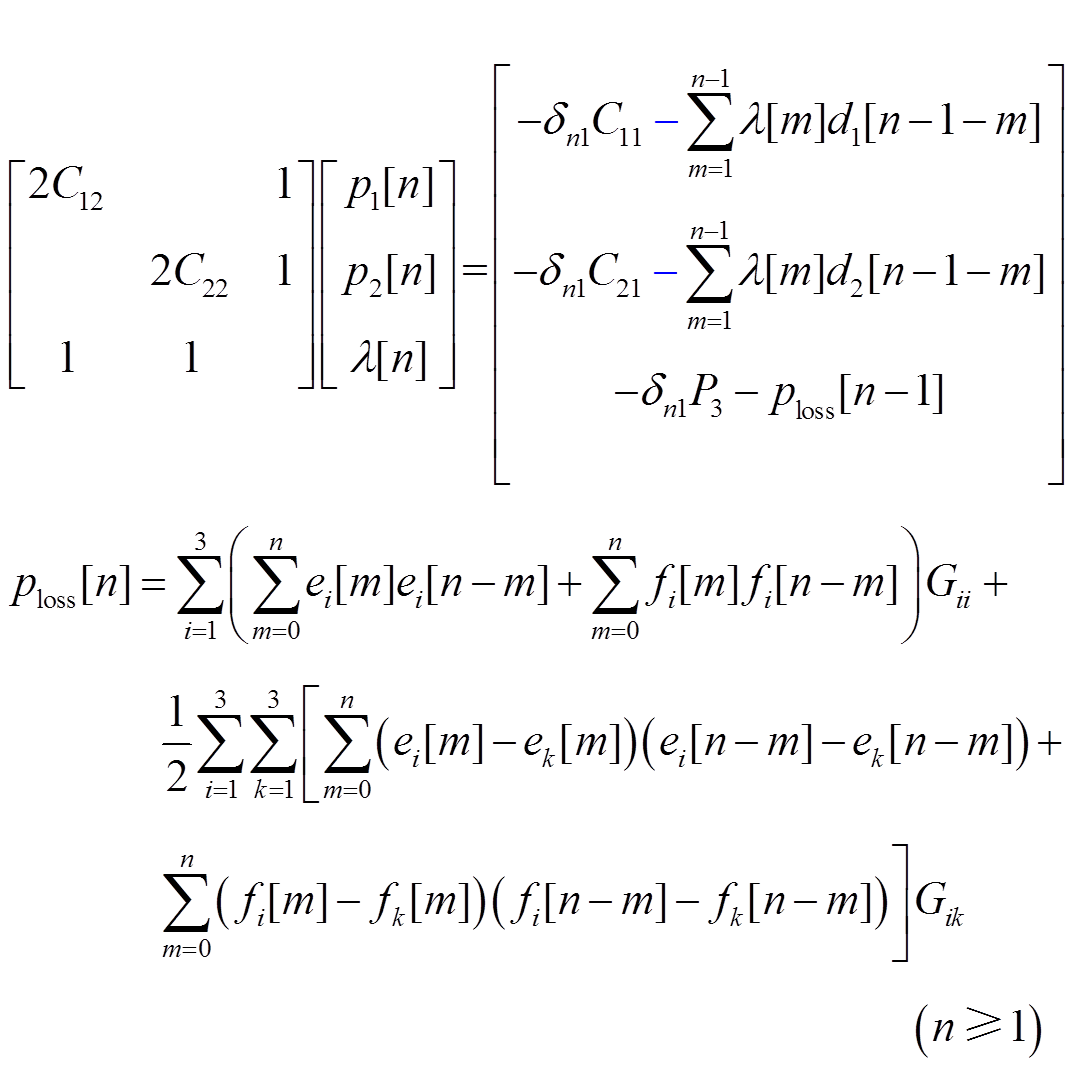（17）
其中用di(s)表示系统网损对第i台发电机输出功率的偏导，即网损微增率，有
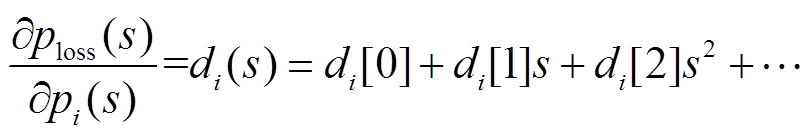
将s=0代入式（16）可以得到未知量的初始解（pi[0]，λ[0]），后续系数（pi[n]，λ[n]）根据式（17）递推得到，直至达到所设定的计算精度。发电机的有功出力解析表达式为
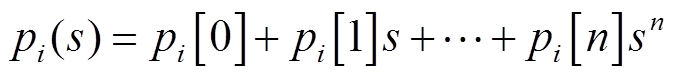（18）
同理，递推的过程就是在逐步更新发电机有功出力值，使结果逐渐接近有功出力实际值的过程。
然而，由于式（7）中网损部分没有发电机的有功出力项，所以不能直接通过网损公式求得di(s)。由于前文提到网损是所有节点电压和功率的函数，可得
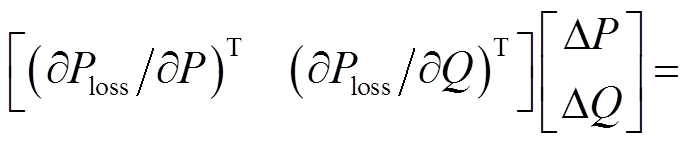
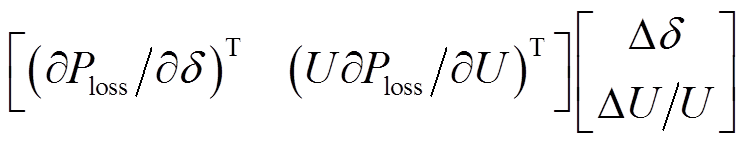（19）
式中，U和δ分别为电压的幅值和相位。
将潮流计算的修正方程式代入式（19）中，能够得到采用转置雅克比矩阵法求解网损微增率的计算公式为
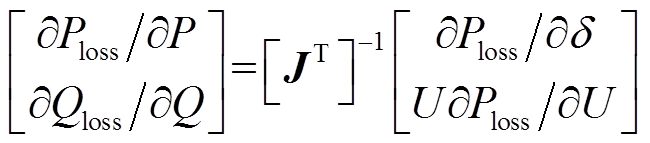（20）
式中，J为潮流计算中的雅克比矩阵。在计算电压幂级数系数的过程中，逐步更新节点电压信息，同时更新雅克比矩阵，从而可以得到每一步的网损微增率。
本文所提的基于全纯嵌入的最优潮流求解流程如图2所示，其中KKT条件与约束条件的递推计算交替进行。首先根据网络的数据构建约束条件递推方程（14）与KKT条件递推方程（17）左侧矩阵，为计算节点电压和发电机有功出力的幂级数展开系数做准备。给定系统的初始状态，根据前文的推导过程，令所有节点电压实部ei[0]=1，虚部fi[0]=0，发电机有功输入pi[0]=0，此时由于系统中没有潮流流过，所以初始状态下系统也没有有功损耗。
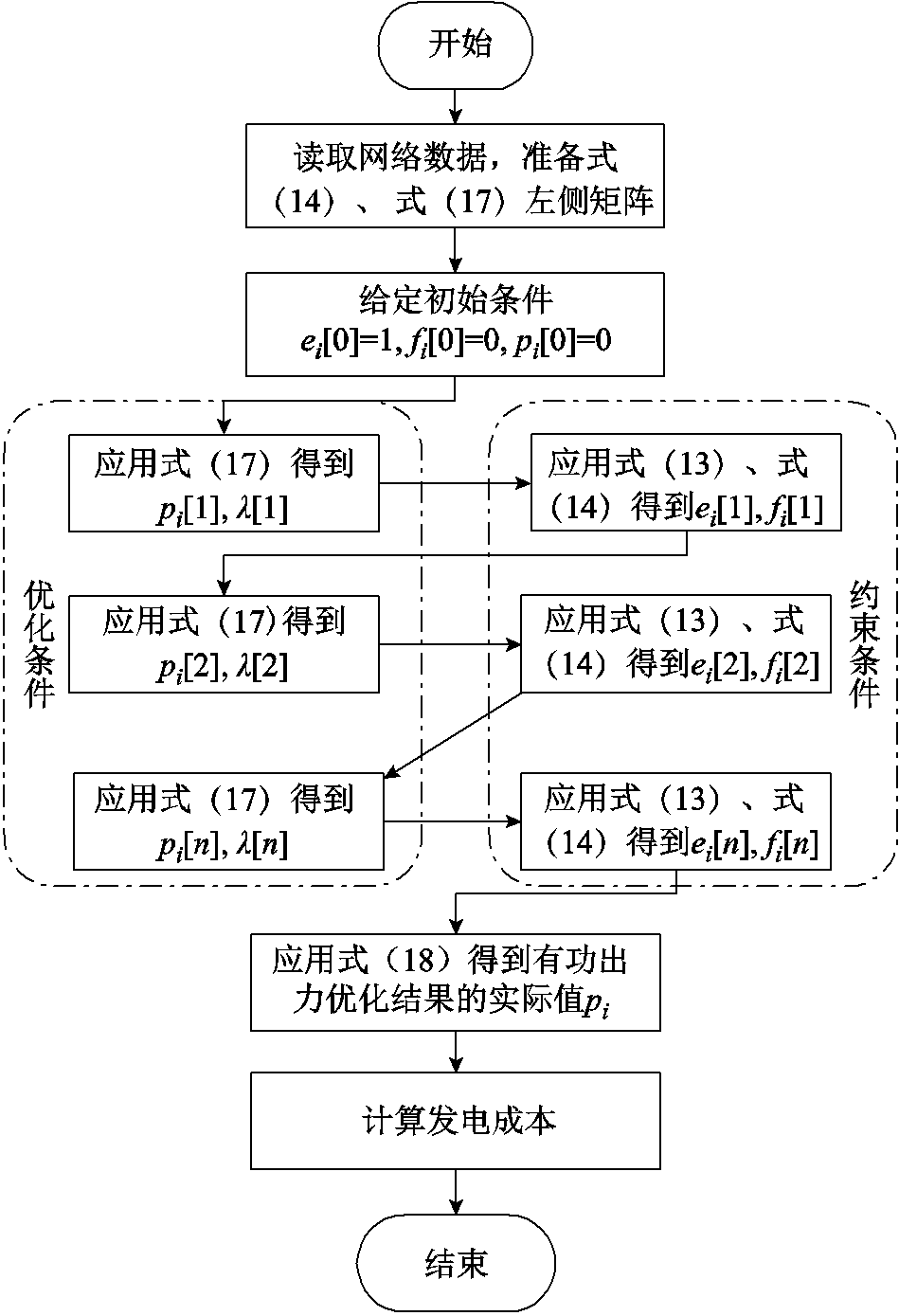
图2 应用全纯嵌入法交叉求解有功最优潮流流程
Fig.2 Framework of holomorphic embedding method for solving optimal power flow
根据初始的条件应用式（17）计算发电机有功出力p第一次递推的值，再应用约束条件的递推式（13）、式（14）得到节点电压v的第一阶幂级数系数；再由得到的所有变量的第一阶系数应用式（17）计算发电机出力的第二阶系数，然后再应用式（13）、式（14）得到节点电压的第二阶幂级数系数，循环递推。递推的过程就是不断更新发电机出力和节点电压的过程，当计算的递推阶数越高，由式（15）、式（18）计算得到的变量实际值越接近目标解。当变量实际值变化达到所设置的计算精度要求时，停止递推，并计算实际的发电成本。
由于在进行递推求解的过程中，每一步都包含KKT条件和约束条件的计算，所以得到的解满足约束条件，即为系统的可运行点，同时由全纯嵌入的规则可知，该方法不依赖于初始点的选取。
应用全纯嵌入法求解有功最优潮流伪代码见表1。
表1 基于全纯嵌入法的最优潮流求解的伪代码
Tab.1 Pseudocode of holomorphic embedding method for solving optimal power flow
算法：基于全纯嵌入法的优化潮流算法输入：系统参数输出：发电成本cost 开始 初始化，准备式（14）、式（17）中左侧矩阵 给定初始条件ei[0], fi[0], pi[0] While(网损变化值＜设置精度)应用式（17）计算得到pi[n], λ[n]应用式（13）、式（14）计算得到ei[n], fi[n]应用式（15）、式（18）更新节点电压与有功出力的实际值更新雅克比矩阵J应用式（19）网损微增率应用式（7）计算网络损耗n = n+1end 应用式（1）计算发电成本 结束
为了验证2.2节和2.3节中推导的全纯嵌入方法在有功最优潮流中的可行性与准确性，本文采用IEEE 3节点、4节点、30节点、新英格兰39节点电力系统和IEEE 118电力系统算例进行仿真计算，同时与内点法的计算结果做比较，仿真软件采用Matlab 2020a，在配置为Intel Core i5-9400 CPU @ 2.90 GHz、8 GB内存的计算机上运行，内点法的优化潮流结果应用Matpower4.1工具箱计算得到。
为了验证本文所提的基于全纯嵌入的潮流计算方法计算有功最优潮流的可行性，全纯嵌入法在IEEE 3节点和4节点电力系统中的发电机有功出力和节点电压的仿真结果与参考值见表2和表3。图3和图4分别表示全纯嵌入法在IEEE 30节点和新英格兰39节点电力系统的仿真结果与参考值对比，图5表示全纯嵌入法在四个系统的仿真过程收敛情况。有功网络损耗变化的精度设置为1×10-6(pu)。由仿真结果可知，全纯嵌入法在求解电力系统的有功优化潮流递推过程中收敛，发电机有功出力的收敛结果和节点电压值与参考值接近，前两个系统的误差小于1%，四个系统分别递推至第6、8、10、12阶系数时达到所设置的收敛精度。
表2 发电机有功出力
Tab.2 Active output of generator （单位：MW）
发电机全纯嵌入法内点法 IEEE 3节点系统1164.33164.54 2163.78163.56 IEEE 4节点系统1190.28189.97 2187.98188.30
表3 节点电压
Tab.3 The bus voltage （pu）
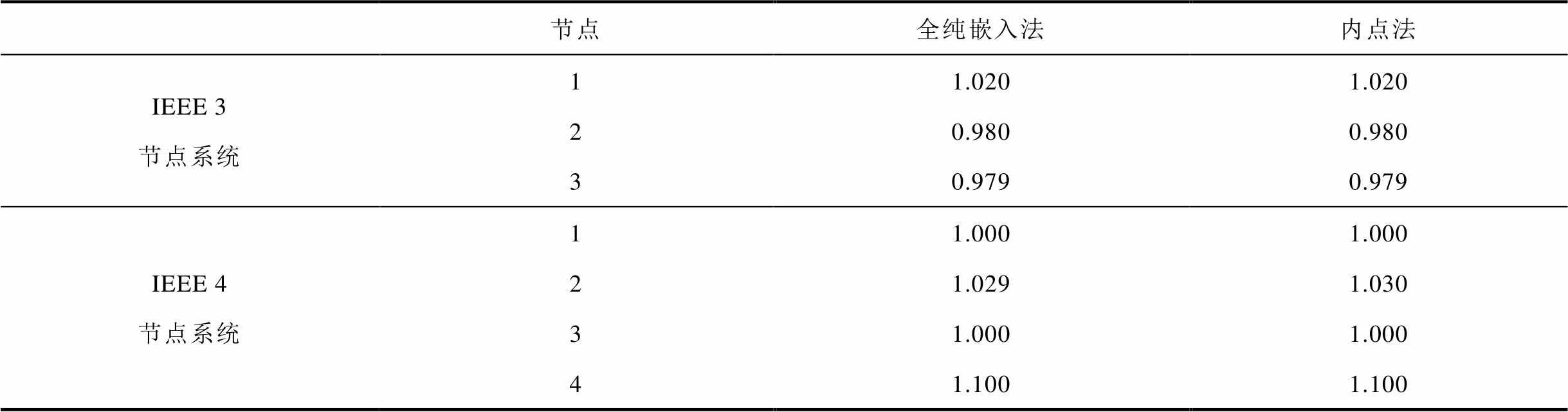
节点全纯嵌入法内点法 IEEE 3节点系统11.0201.020 20.9800.980 30.9790.979 IEEE 4节点系统11.0001.000 21.0291.030 31.0001.000 41.1001.100
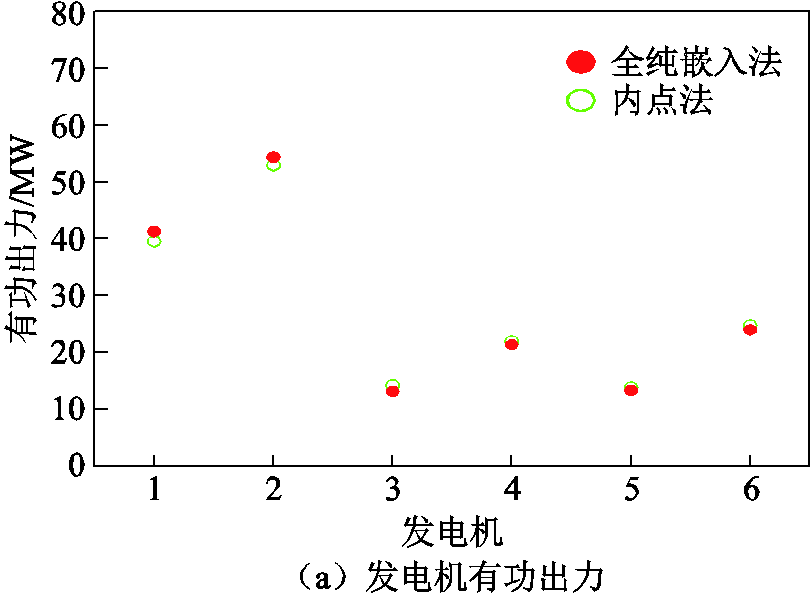
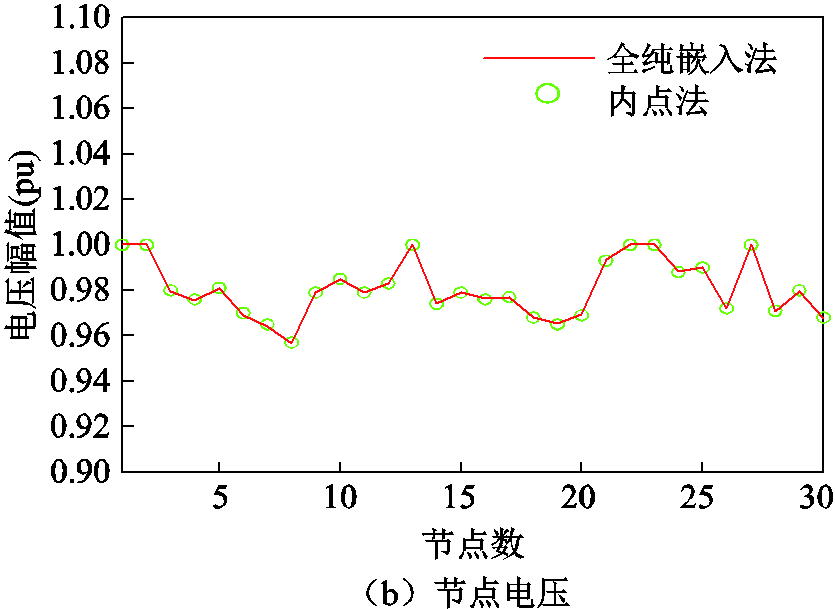
图3 IEEE 30节点系统仿真结果
Fig.3 Simulation results of IEEE 30-bus power system
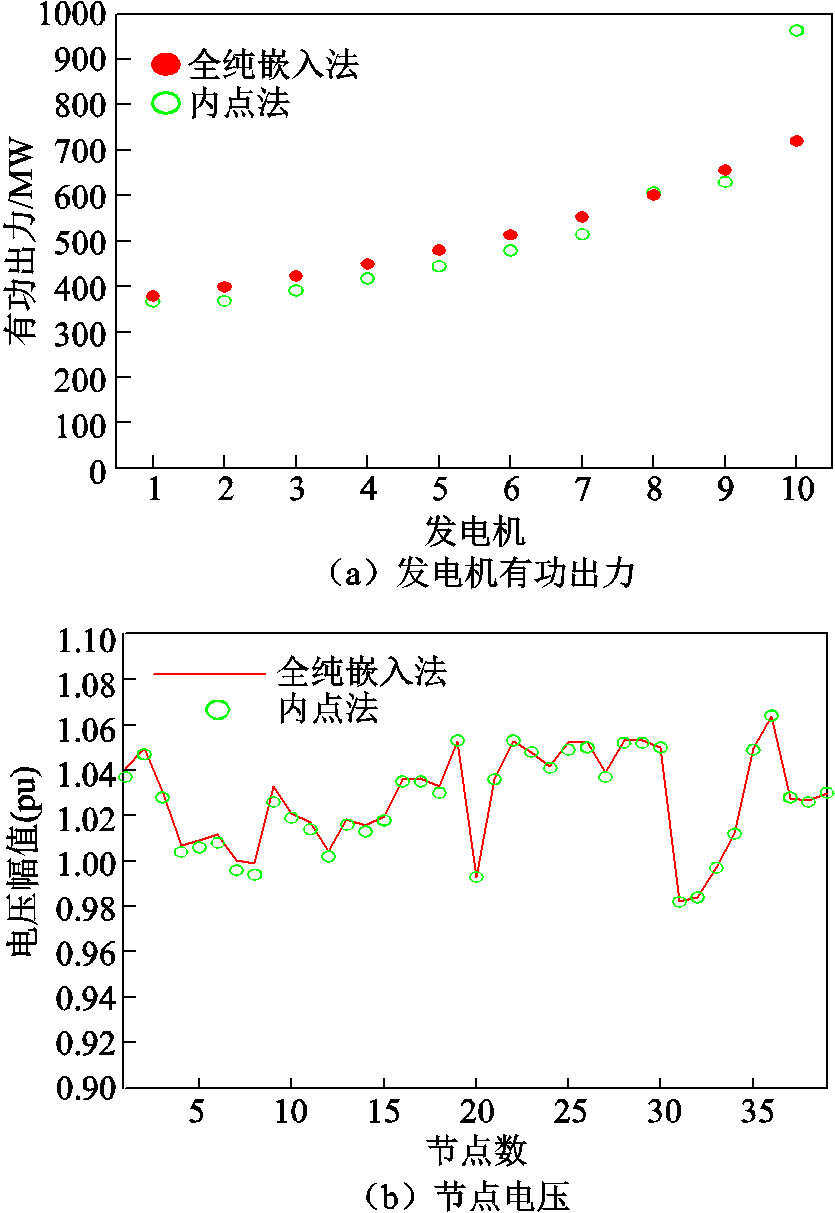
图4 新英格兰39节点电力系统仿真结果
Fig.4 Simulation results of 39-bus power system in New England
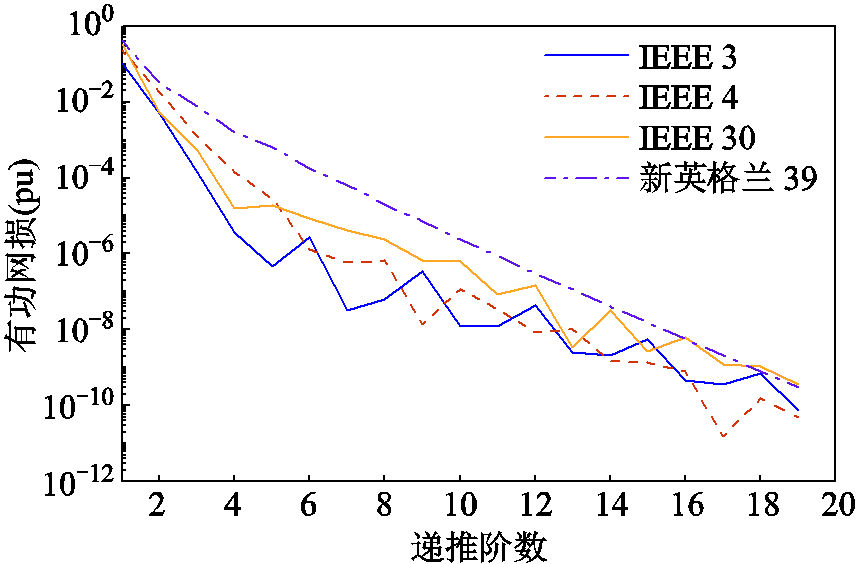
图5 有功网络损耗的变化
Fig.5 Variation of active power loss
接下来对本文所提的全纯嵌入方法的准确性进行验证，比较全纯嵌入法与内点法计算得到的系统发电成本（目标函数）和全网有功网络损耗。优化后的系统发电成本和有功网络损耗见表4和表5，发电机的发电成本系数C0～C2见表6。相对误差采用|(x-x*)/x*|计算，其中x为全纯嵌入法的计算结果，x*表示内点法的计算结果。由表4和表5可知，全纯嵌入法计算前两个系统的相对误差均为10-6数量级，计算结果满足精度要求，误差来源为递推的阶数，每次递推的过程都是使结果逐渐逼近精确解的过程。误差随着系统规模的增大而增大，在新英格兰39节点系统中误差较大，是因为在该系统中没有考虑不等式约束条件，使得有功出力较为理想化，从而使发电成本和有功网络损耗都偏小。所以接下来要对考虑不等式约束的全纯嵌入法进行深一步的研究。但本文通过仿真实例证实了该方法的可行性，为电力系统有功优化潮流计算提供了新思路。
表4 发电成本
Tab.4 Power generating cost
IEEE节点系统全纯嵌入法/（$/h）内点法/（$/h）相对误差 IEEE 37 861.407 861.391.27×10-6 IEEE 49 936.139 936.103.02×10-6 IEEE 303.1193.3025.54×10-2 IEEE 3939.12245.7291.44×10-1
表5 有功网络损耗
Tab.5 Active power loss
IEEE节点系统全纯嵌入法/MW内点法/MW相对误差 IEEE 36.1046.1031.64×10-4 IEEE 48.2678.2643.63×10-4 IEEE 303.1193.3025.542×10-2 IEEE 3939.12245.7291.44×10-1
表6 发电机成本系数
Tab.6 Generator cost coefficients
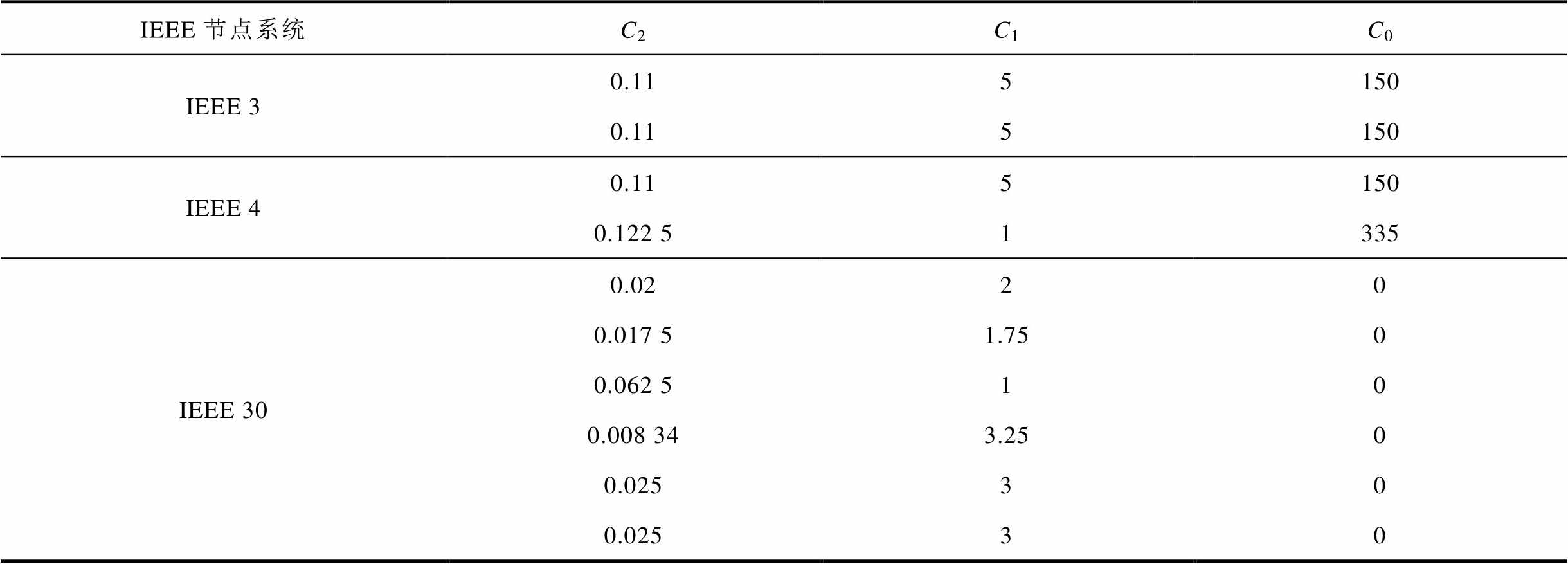
IEEE节点系统C2C1C0 IEEE 30.115150 0.115150 IEEE 40.115150 0.122 51335 IEEE 300.0220 0.017 51.750 0.062 510 0.008 343.250 0.02530 0.02530
（续）
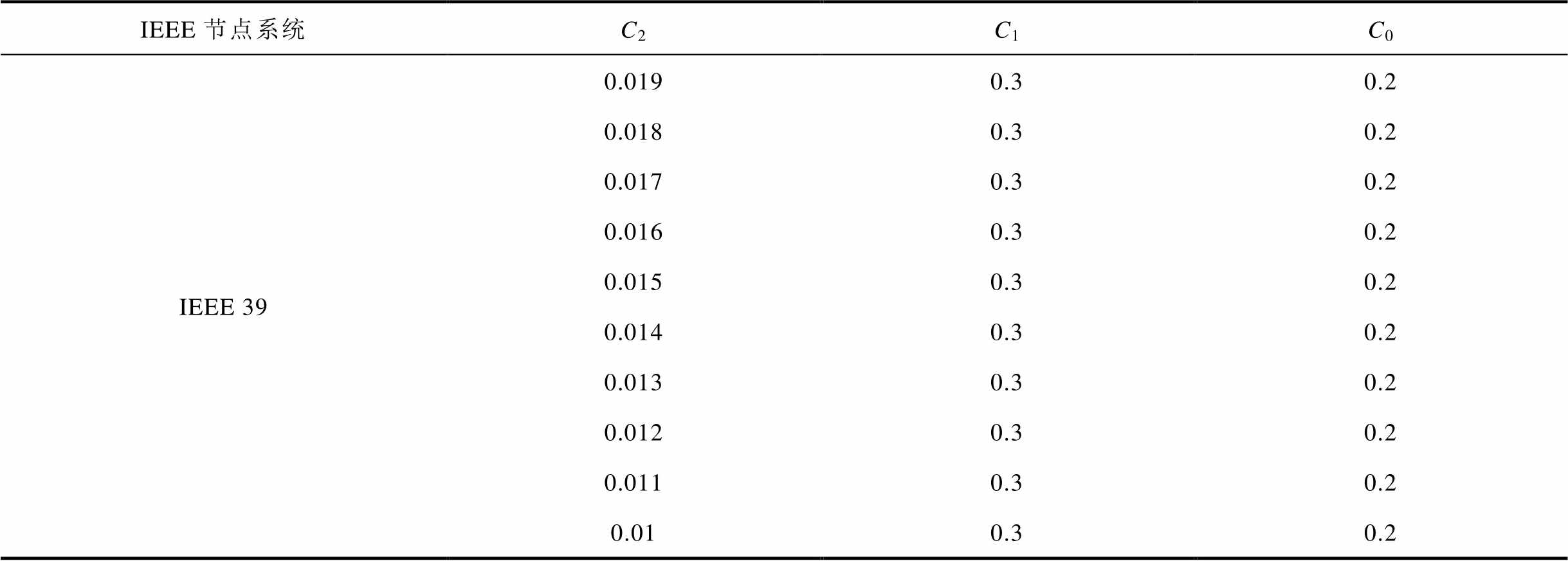
IEEE节点系统C2C1C0 IEEE 390.0190.30.2 0.0180.30.2 0.0170.30.2 0.0160.30.2 0.0150.30.2 0.0140.30.2 0.0130.30.2 0.0120.30.2 0.0110.30.2 0.010.30.2
由2.4节可知，全纯嵌入法计算有功最优潮流的时间与递推的阶数相关。图6展示了全纯嵌入法在对四个系统进行仿真时递推阶数与计算时长的关系，过多的递推次数在增加计算精度的同时必定会耗费更多的时间，因此在满足精度的情况下选择合适的递推次数即可，在合适的递推精度下全纯嵌入法有着较好的计算效率。在本文所设置精度下全纯嵌入法与内点法的计算时长见表7。
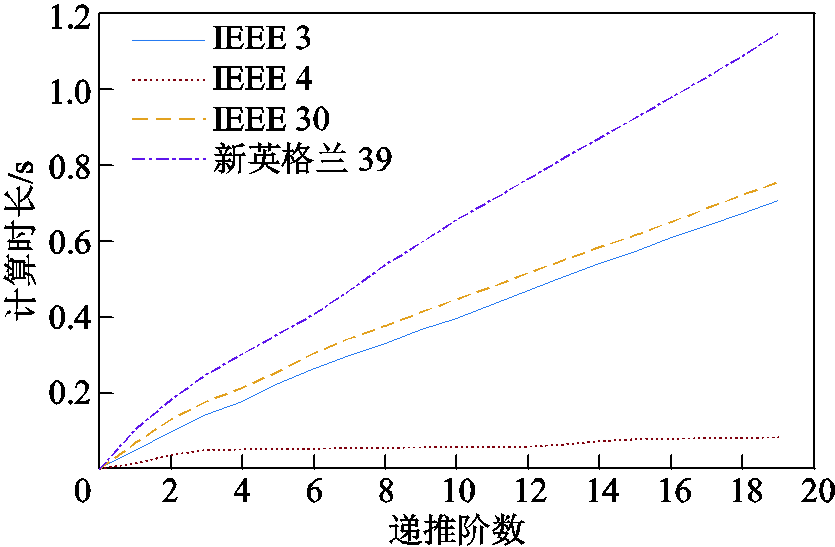
图6 不同递推阶数下的计算时长
Fig.6 Calculation time under different recursion orders
表7 计算时长
Tab.7 Calculation time （单位：s）
系统全纯嵌入法内点法 IEEE 30.0590.42 IEEE 40.0720.26 IEEE 300.4160.30 新英格兰390.8190.39
可以看出，在系统规模较小的情况下，本文所提出的全纯嵌入法在满足精度的前提下计算时长要短于内点法的计算时长。但在IEEE 30节点和新英格兰39节点系统中的计算时长要高于内点法。考虑到内点法的应用较为成熟且商业化程度较高，本文所提的全纯嵌入法的计算程序还可以进一步优化。
本文所提方法的优越性在于构造全纯嵌入函数时所选取的初始点与系统的当前运行状态无关，且能够在递推计算时考虑以潮流计算为约束条件，进而确保计算结果为可运行解，同时约束条件和KKT条件的全纯嵌入方程左侧矩阵固定，可以离线推导得到，所以能够减少在线应用的计算时长。
为了验证本文全纯嵌入方法在大规模系统中的有效性，以IEEE 118节点系统为仿真算例，发电机的发电成本系数C0～C2均为0、40、0.01，发电机出力和节点电压的仿真结果如图7所示，目标函数（发电机的发点成本）为59 122.7 $/h，计算时长为4.83 s。应用内点法计算得到的目标函数为58 140.5 $/h，本文所提方法的相对误差为1.6%，同时内点法计算时长为1.0 s。
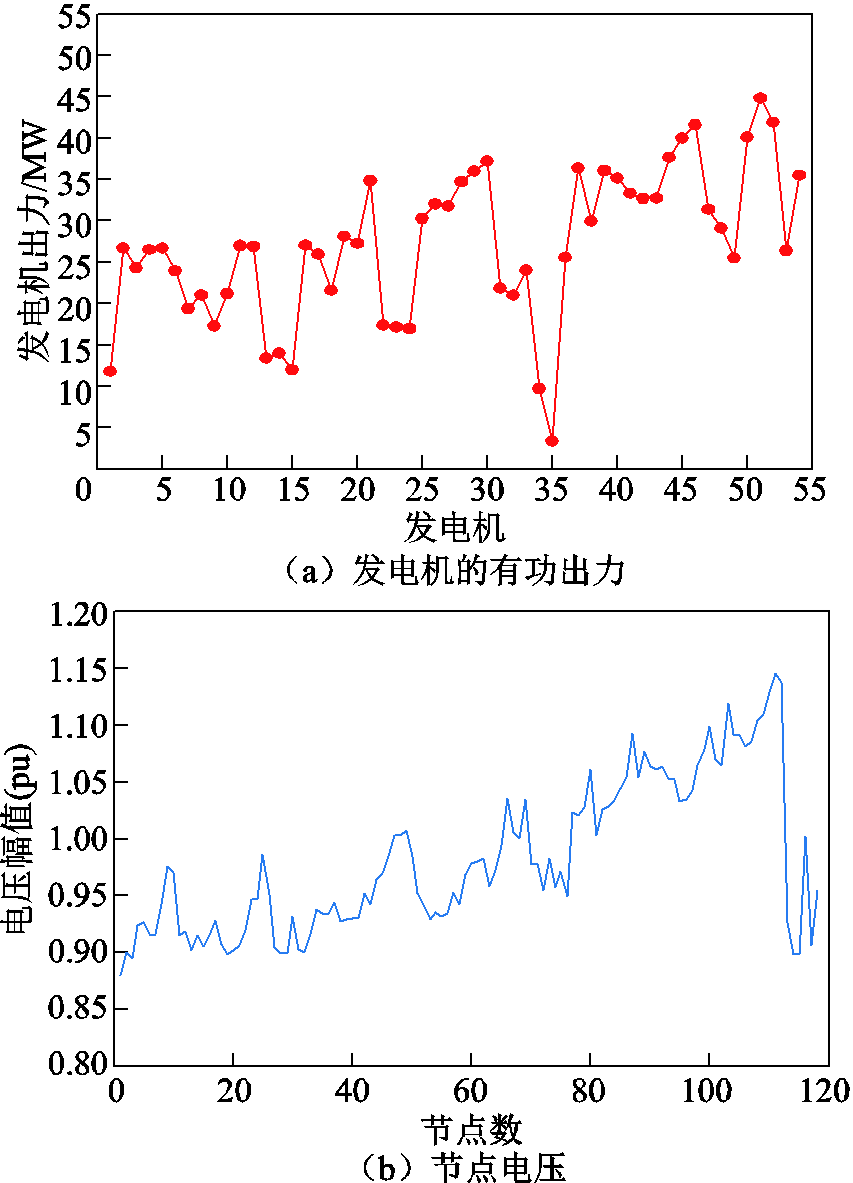
图7 IEEE 118节点系统仿真结果
Fig.7 Simulation results no IEEE 118-bus power system
上述结果表明，所提的基于全纯嵌入的最优潮流计算方法在大规模系统中具有可行性，展现了良好的准确性和计算效率。
本文建立了以全纯嵌入法为基础的有功最优潮流的计算方法，从有功最优潮流的基本数学模型入手，在约束条件和KKT条件中嵌入复变量，构造约束条件和KKT条件的全纯嵌入方程组，再通过递推求解的方式得到节点电压与发电机有功出力的幂级数系数，从而得到二者的解析解，最终得到优化后的发电成本。在IEEE 3节点、4节点、30节点、118节点和新英格兰39节点系统中的仿真结果验证了所提方法的可行性与准确性。主要结论如下：
1）应用全纯嵌入法能够得出节点电压和发电机有功出力的解析表达式，通过KKT条件和约束条件两部分交叉进行非迭代的递推计算，求得解析表达式幂级数的系数。
2）由于计算过程中包含了潮流计算的约束条件，所以得到的最优结果为稳态的可运行点，同时有着不依赖于系统实际初始点选取的优点。
3）采用全纯嵌入法可以将有功最优潮流的求解变为递推求解系统节点电压和发电机有功出力的过程，逐步更新节点电压和有功出力，计算结果满足精度要求，同时证明了本文所提方法的可行性。
本文所提出的基于全纯嵌入的方法为大型电力系统最优潮流求解提供了新的思路，具有一定的参考价值。但本文在构建全纯嵌入函数时，发电机节点不含有负荷，如果考虑在发电机节点侧的恒定负荷，只需要根据全纯嵌入的规则将潮流约束的全纯嵌入方程组稍加修改。同时本文没有考虑不等式约束条件，在文献[25]中提供了全纯嵌入法考虑不等式约束的潮流计算应用，所以考虑不等式约束的基于全纯嵌入法的有功最优潮流计算值得进一步深入研究。
1. 约束条件的递推公式推导
3节点系统潮流方程的全纯嵌入表达式在2.2节中已得到，现推广至m个PQ节点、p个PV节点和1个平衡节点构成的电力系统，有
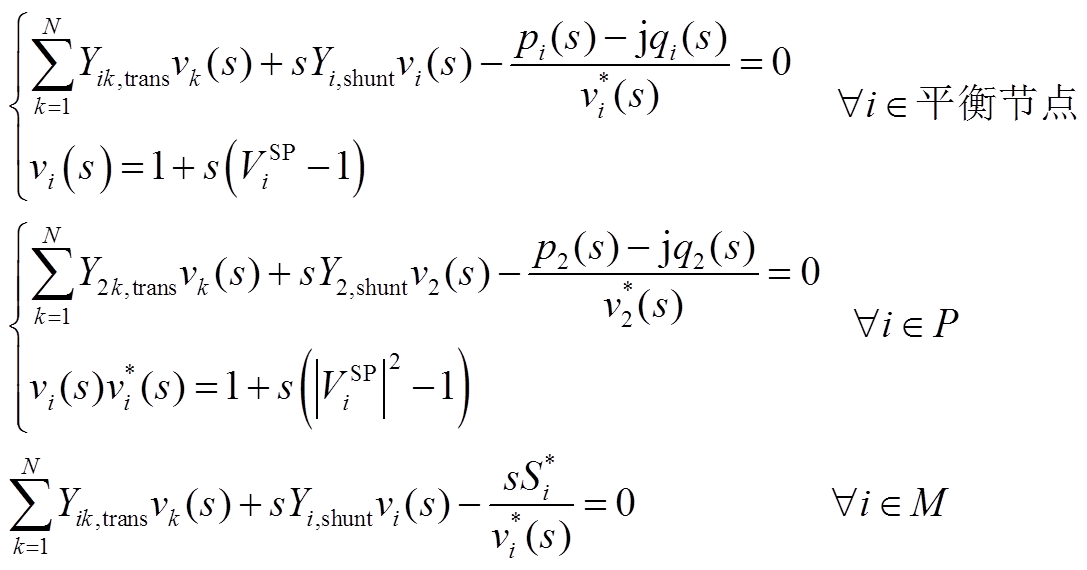（A1）
式中，N为系统节点总数；P和M分别为PV节点和PQ节点的集合。
1）平衡节点
对于平衡节点，由于其电压固定，根据式（A1）中平衡节点公式可得其节点电压全纯嵌入的表达式为
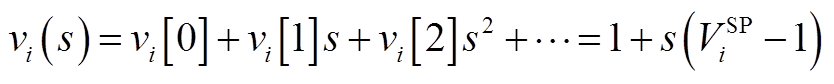（A2）
根据式（A2），令等式两侧s同阶系数相同可得
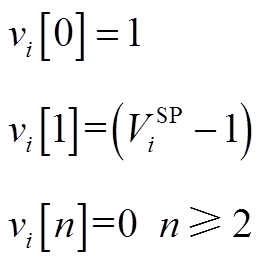
为了计算简便，一般取ViSP为实数，所以容易得到平衡节点电压的实部和虚部幂级数系数的递推公式为
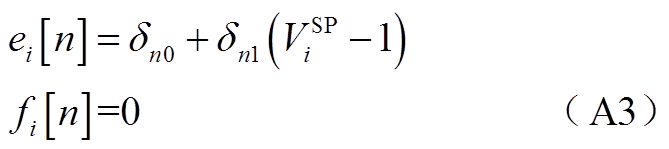
2）PV节点
对于PV节点，将式（A1）中PV节点部分拆写为实部和虚部两部分，能够得到
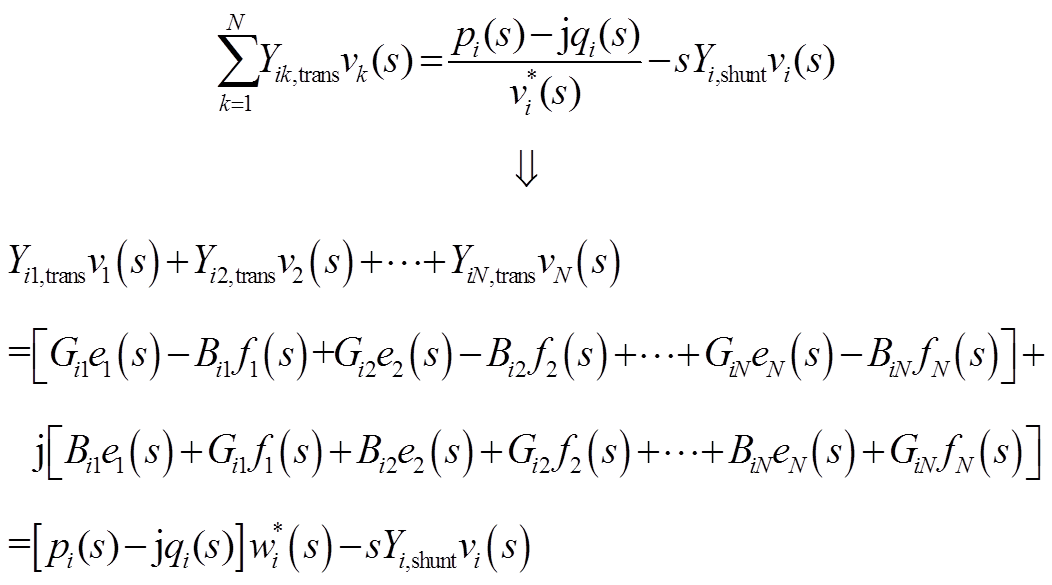
将等式左右两侧所有变量写成式（10）表示的幂级数形式，再令等式两侧s相同阶数的系数相同，由初始条件p2[0]=0、q2[0]=0、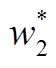
[0]=1，所以上式第n阶幂级数系数实部和虚部可以分别表示为
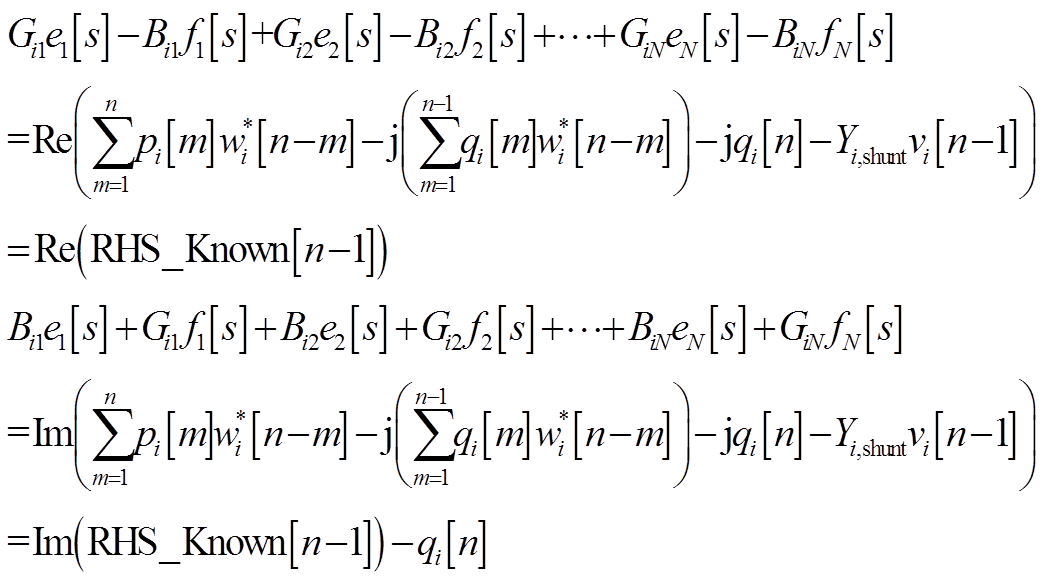
所以PV节点的电压实部和虚部幂级数系数的递推表达式为
根据式（A1）中PV节点电压方程式可以得到
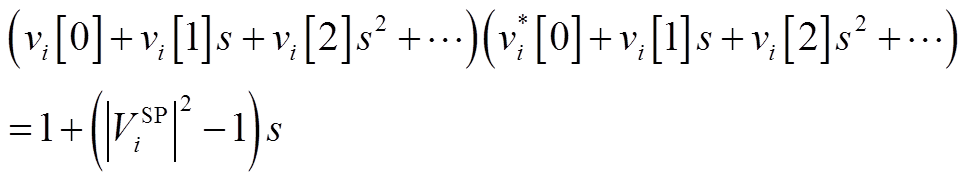
令等式两侧s相同阶数的系数相同，写出不同阶数下的系数，其中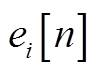
表示PV节点的电压实部第n阶幂级数的系数，可以得出PV节点电压实部幂级数系数的递推表达式为
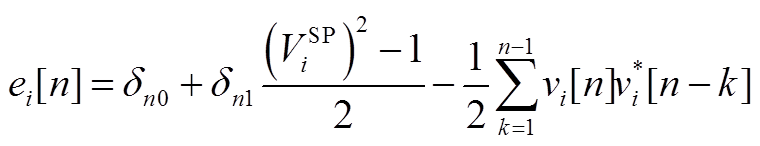（A5）
3）PQ节点
对于PQ节点，将式（A1）中PQ节点潮流方程按同样的方式拆写为实部和虚部两部分，能够得到
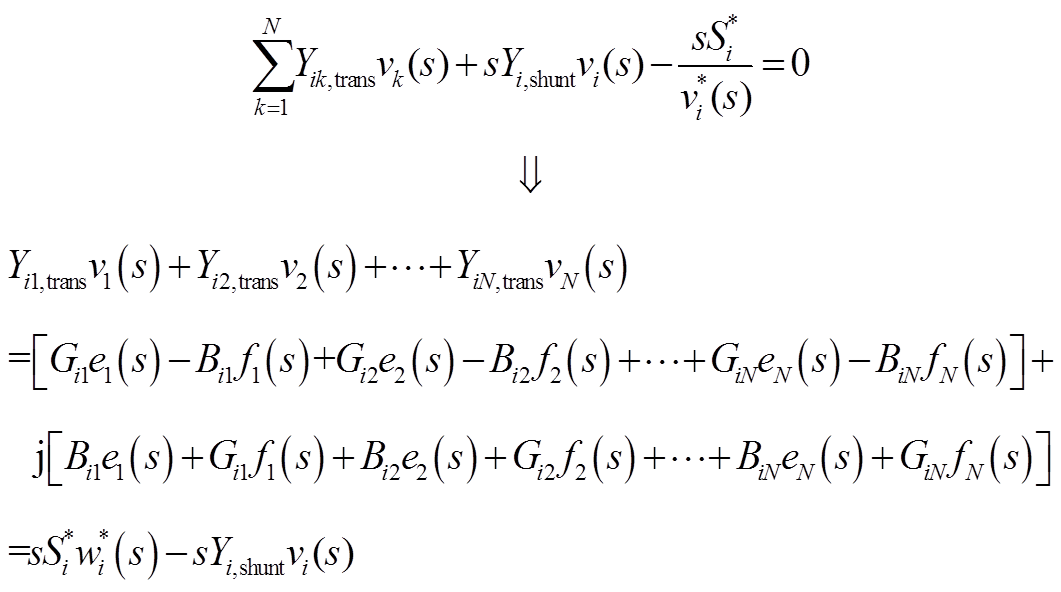
将上式左右两侧所有变量写成幂级数的形式，再令等式两侧s相同阶数的系数相同，能够得到PV节点的电压实部和虚部幂级数系数的递推表达式为
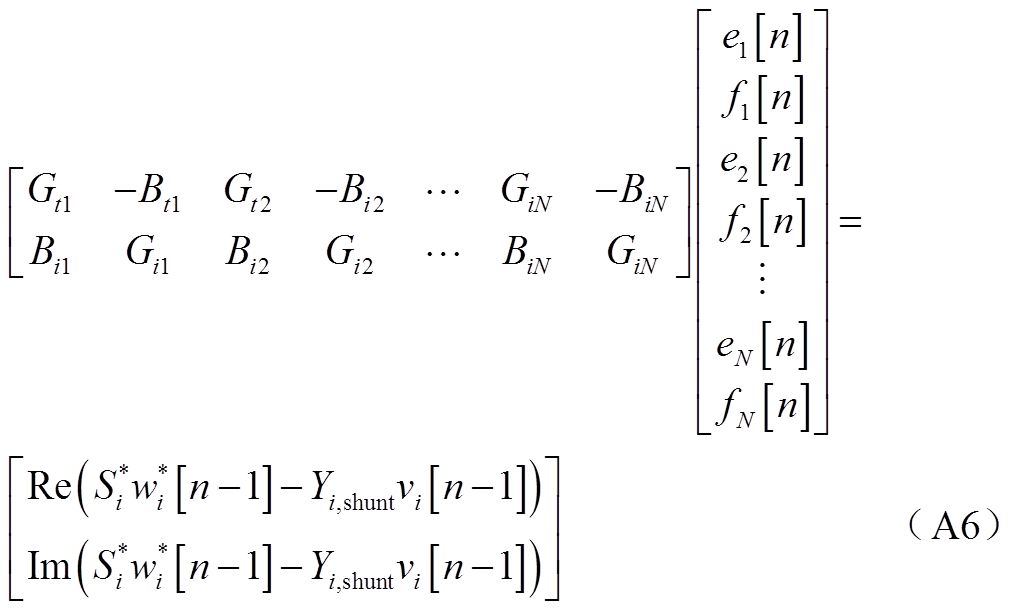
2. KKT条件的递推公式推导
如正文所述，拉格朗日方程要取得最值的条件为满足等微增率准则，KKT条件的全纯嵌入表达式在2.2节中以得到，现重写为
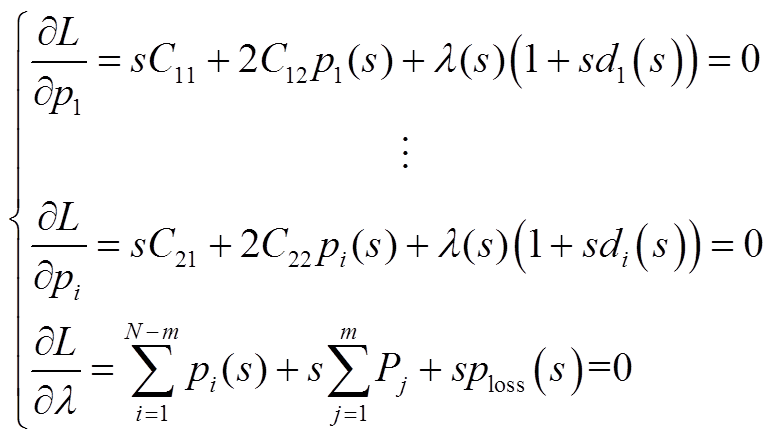（A7）
其中，
。
与约束条件的推导方法类似，将式（A7）写为幂级数展开的形式，再令等式左右两侧s相同阶数的系数相同，所以能够得到PV节点和平衡节点的发电机有功出力pi、拉格朗日乘子λ的递推公式，有
（A8）
参考文献
[1] 国家发展改革委, 国家能源局. 电力发展“十三五”规划[R]. 2016．
[2] 林哲, 胡泽春, 宋永华. 最优潮流问题的凸松弛技术综述[J]. 中国电机工程学报, 2019, 39(13): 3717-3728. Lin Zhe, Hu Zechun, Song Yonghua. Convex relaxation for optimal power flow problem: a recent review[J]. Proceedings of the CSEE, 2019, 39(13): 3717-3728.
[3] Carpentier J. Contribution to the economic dispatch problem[J]. Bulletin de la Societe Francoise des Electriciens, 1962, 3(8): 431-447.
[4] 刘科研, 盛万兴, 李运华. 互联电网的直流最优潮流分解算法研究[J]. 中国电机工程学报, 2006, 26(12): 21-25. Liu Keyan, Sheng Wanxing, Li Yunhua. Research on decomposition algorithm of DC optimal power flow in large scale interconnection power grids[J]. Proceedings of the CSEE, 2006, 26(12): 21-25.
[5] 王峥, 丛培杰. 基于改进前推回代法的辐射状配电网潮流计算[J]. 东北电力技术, 2008, 29(2): 7-10. Wang Zheng, Cong Peijie. Power flow calculation for radial distribution network based on forward and backward substitution method[J]. Northeast Electric Power Technology, 2008, 29(2): 7-10.
[6] 麻秀范. 含分布式电源的配电网规划与优化运行研究[D]. 北京: 华北电力大学, 2013.
[7] Zhang Ning, Cheng Jiangnan, Wang Yi. Probabilistic optimal energy flow of district multienergy systems: an MPLP-based online dictionary-learning approach[J]. IEEE Transactions on Industrial Informatics, 2019, 15(9): 4867-4877.
[8] Pan Shixian, Li Zhigang, Zheng J H, et al. A non-iterative solution method for DC optimal power flow based on holomorphic embedding[C]//2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, 2022: 1865-1870.
[9] 朱泽安, 王承民, 马明, 等. 基于拉格朗日函数鞍距分配的广义内点法[J]. 电力系统自动化, 2018, 42(5): 18-24. Zhu Zean, Wang Chengmin, Ma Ming, et al. Generalized interior-point method based on Lagrange function saddle space distribution[J]. Automation of Electric Power Systems, 2018, 42(5): 18-24.
[10] Gan Lingwen, Low S H. An online gradient algorithm for optimal power flow on radial networks[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(3): 625-638.
[11] 唐坤杰, 董树锋, 朱炳铨, 等. 大规模输配一体化系统牛顿法潮流计算性能分析及改进方法[J]. 电力系统自动化, 2019, 43(6): 92-99. Tang Kunjie, Dong Shufeng, Zhu Bingquan, et al. Performance analysis and improvement of Newton method for power flow calculation of large-scale integrated transmission and distribution network[J]. Automation of Electric Power Systems, 2019, 43(6): 92-99.
[12] Luo Zhiquan, Ma W K, So A M C, et al. Semidefinite relaxation of quadratic optimization problems[J]. IEEE Signal Processing Magazine, 2010, 27(3): 20-34.
[13] 巨云涛, 黄炎, 张若思. 基于二阶锥规划凸松弛的三相交直流混合主动配电网最优潮流[J]. 电工技术学报, 2021, 36(9): 1866-1875. Ju Yuntao, Huang Yan, Zhang Ruosi. Optimal power flow of three-phase hybrid AC-DC in active distribution network based on second order cone programming[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1866-1875.
[14] 李洪美, 崔翰韬, 万秋兰. 考虑电动汽车充电策略的配网重构二阶锥规划模型[J]. 中国电机工程学报, 2015, 35(18): 4674-4681.Li Hongmei, Cui Hantao, Wan Qiulan. Distribution network reconfiguration based on second-order conic programming considering EV charging strategy[J]. Proceedings of the CSEE, 2015, 35(18): 4674-4681.
[15] 郭清元, 吴杰康, 莫超, 等. 基于混合整数二阶锥规划的新能源配电网电压无功协同优化模型[J]. 中国电机工程学报, 2018, 38(5): 1385-1396. Guo Qingyuan, Wu Jiekang, Mo Chao, et al. A model for multi-objective coordination optimization of voltage and reactive power in distribution networks based on mixed integer second-order cone programming[J]. Proceedings of the CSEE, 2018, 38(5): 1385-1396.
[16] Sennewald T, Linke F, Reck J, et al. Parameter optimization of differential evolution and particle swarm optimization in the context of optimal power flow[C]//2020 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), Hague, Netherlands, 2020: 1045-1049.
[17] 刘明凯, 王占山, 邢彦丽. 基于强化多目标差分进化算法的电-气互联系统最优潮流计算[J]. 电工技术学报, 2021, 36(11): 2220-2232. Liu Mingkai, Wang Zhanshan, Xing Yanli. Enhanced multi-objective differential evolutionary algorithm based optimal power flow calculation for integrated electricity and gas systems[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2220-2232.
[18] 王浩翔, 赵冬梅, 陶然, 等. 基于分解的多目标进化算法的含MMC-HVDC交直流混合系统最优潮流研究[J]. 电工技术学报, 2020, 35(17): 3691-3702. Wang Haoxiang, Zhao Dongmei, Tao Ran, et al. Study on optimal power flow for AC/DC hybrid system incorporating MMC-HVDC based on MOEA/D[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3691-3702.
[19] Moeini-Aghtaie M, Abbaspour A, Fotuhi-Firuzabad M, et al. A decomposed solution to multiple-energy carriers optimal power flow[J]. IEEE Transactions on Power Systems, 2014, 29(2): 707-716.
[20] Koh C S, Ryu J S, Fujiwara K. Convergence acceleration of the Newton-Raphson method using successive quadratic function approximation of residual[J]. IEEE Transactions on Magnetics, 2006, 42(4): 611-614.
[21] Li Mingyang, Zhao Qianchuan, Luh P B. Decoupled load flow and its feasibility in systems with dynamic topology[C]//2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 2009: 1-8.
[22] 姜涛, 张勇, 李雪, 等. 电力系统交直流潮流的全纯嵌入计算[J]. 电工技术学报, 2021, 36(21): 4429-4443, 4481. Jiang Tao, Zhang Yong, Li Xue, et al. A holomorphic embedded method for solving power flow in hybrid AC-DC power system[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4429-4443, 4481.
[23] Liu Chengxi, Wang Bin, Hu Fengkai, et al. Online voltage stability assessment for load areas based on the holomorphic embedding method[C]//2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, 2018: 1.
[24] Liu Chengxi, Sun Kai, Wang Bin, et al. Probabilistic power flow analysis using multi-dimensional holomorphic embedding and generalized cumulants[C]// 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 2019: 1.
[25] 刘承锡, 赖秋频, 姚良忠, 等. 基于全纯嵌入法的电力系统解耦模型：薄弱节点辨识[J]. 中国电机工程学报, 2022, 42(5): 1736-1748. Liu Chengxi, Lai Qiupin, Yao Liangzhong, et al. Power system decoupling model based on holomorphic embedding method: weak bus identification[J]. Proceedings of the CSEE, 2022, 42(5): 1736-1748.
[26] Yao Rui, Liu Yang, Sun Kai, et al. Efficient and robust dynamic simulation of power systems with holomorphic embedding[J]. IEEE Transactions on Power Systems, 2020, 35(2): 938-949.
[27] Kundur P, Balu N J, Lauby M G. Power system stability and control[M]. New York: McGraw-Hill, 1994
[28] Trias A, Marín J L. A Padé-Weierstrass technique for the rigorous enforcement of control limits in power flow studies[J]. International Journal of Electrical Power & Energy Systems, 2018, 99: 404-418.
[29] 陈珩. 电力系统稳态分析[M]. 3版. 北京: 中国电力出版社, 2007.
Abstract It is very important to obtain the active power output of each generator by solving the optimal power flow (OPF) for the economic operation of power system. The traditional methods mainly include simplified model, convex relaxation and intelligent algorithm, but these methods also have some shortcomings such as imprecision and dependence on the initial value. Holomorphic embedding method (HEM) is a new method used in power flow calculation and it ensures convergence through proper holomorphic embedding forms. HEM has the advantages of non-iteration, recursion, analyzability, no dependence on the initial value, and the obtained solution is a runnable point. Based on these above advantages, HEM is used to solve the OPF flow, and a non-iterative OPF calculation method based on HEM is proposed.
Firstly, taking a 3-bus power system as an example, the objective function is the lowest generating cost, and the active power output of the generator is optimized. Secondly, constraints and KKT conditions of the optimization model are listed. Based on the basic construction rules of HEM, the holomorphic embedding forms of constraints and KKT conditions are constructed. Thirdly, according to the basic properties of holomorphic functions, the recursive equations of power series coefficients of analytic expressions of bus voltage and generator active power output are derived. Finally, coefficients can be obtained by the cross recursion of the above two sets of equations, and the generating cost is obtained.
Simulation results on IEEE 3-bus, 4-bus, 30-bus and 39-bus New England power systems show that the HEM is convergent when solving the OPF. The calculation result of the active power output of generators and the bus voltage are close to the reference value, and the error is less than 1% in the first two power systems. In the four systems, the convergence accuracy is achieved at the 6th, 8th, 10th and 12th order respectively. For the result of the objective function, the error of the results calculated by HEM reaches to 10-6 in the first two systems. The source of error is the order of recursion, and the process of each recursion is to make the result gradually approximate to the exact solution. However, the error increases with the increase of the scale of the system. In New England 39-bus system, the error is larger because inequality constraints are not considered in the system, which makes the active power output more ideal, so that the generating cost and active power loss are smaller. In the case of a small system scale, the holomorphic embedding method proposed in this paper has a shorter computing time than the interior point method (IPM). However, the computing time in IEEE 30-bus and New England 39-bus systems is longer than the IPM. Finally, the feasibility of the HEM in IEEE 118 bus power system is verified.
The following conclusions can be drawn through the simulation analysis: (1) HEM can be used to obtain the analytical expressions of the bus voltage and the active power output of the generator. The coefficients of the power series are obtained through the cross recursion of the KKT condition and constraints in holomorphic embedding form. (2) Due to the constraint of power flow included in the model, the optimal result obtained is operable in the real system, which has the advantage of being independent of the initial value. (3) The calculation results of HEM meet the accuracy requirements, and it is proved that HEM is feasible in the calculation of OPF.
Keywords：Optimal power flow, holomorphic embedding method, non-iterative, KKT conditions, generating cost
DOI:10.19595/j.cnki.1000-6753.tces.220334
中图分类号：TM744
国家自然科学基金资助项目(52007133)。
收稿日期 2022-03-10
改稿日期 2022-06-12
刘承锡 男，1975年生，教授，博士生导师，研究方向为电力系统仿真计算，电力系统稳定与控制。E-mail：liuchengxi@whu.edu.cn（通信作者）
徐慎凯 男，1997年生，硕士研究生，研究方向为电力系统最优潮流计算。E-mail：xushenkai@whu.edu.cn
（编辑 赫蕾）