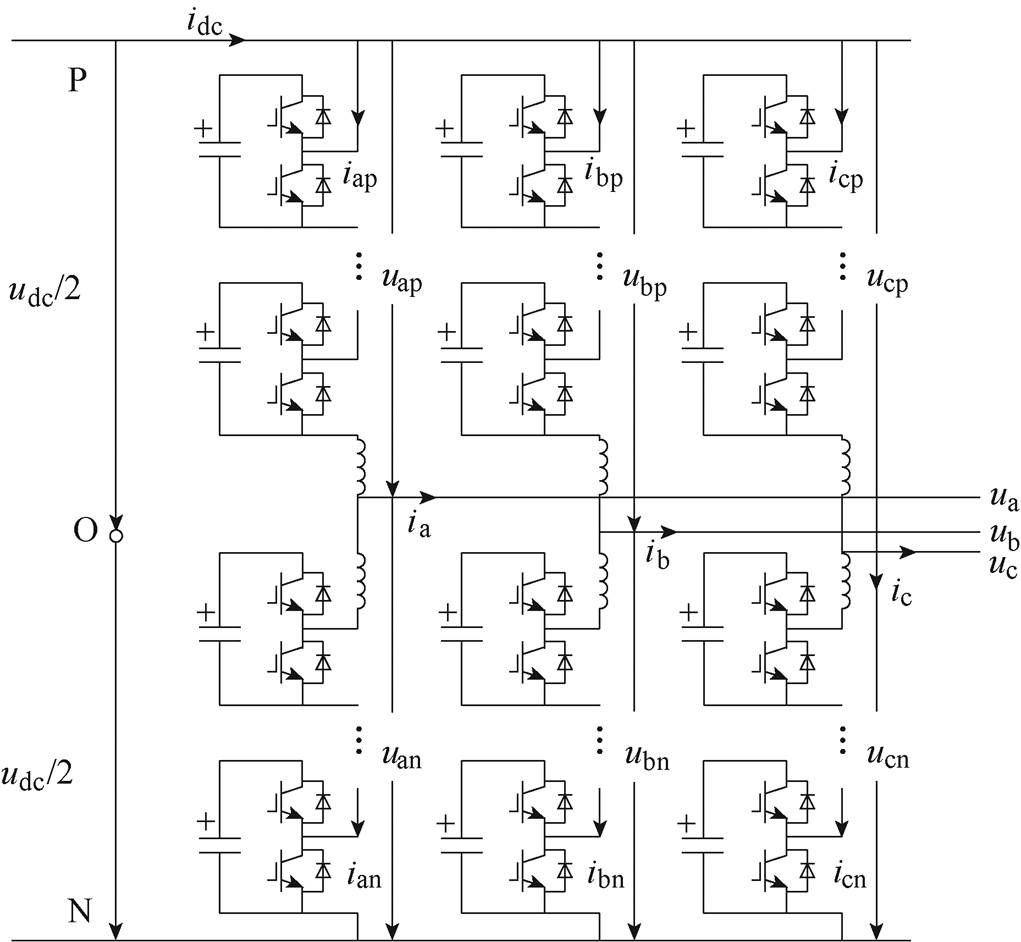
图1 三相模块化多电平换流器拓扑结构
Fig.1 3-phase modular multilevel converter topology
摘要 模块化多电平换流器（MMC）的子模块开路故障隐蔽性强，可以及时有效地识别故障位置，防止故障蔓延影响其他组件，提高换流系统的可靠性。为了诊断子模块开路故障，该文提出一种基于多元高斯分布异常检测模型的故障检测方法。首先，分析子模块开路故障特性，选择子模块电容电压作为故障检测的关键指标，并提取子模块电容电压的12个特征量组成特征向量用于故障诊断。然后，根据多元高斯分布特性，提出基于多元高斯分布的异常检测模型构建方法，并基于此模型提出子模块开路故障诊断策略，可在故障样本偏少致使样本不均衡时，实现高准确率、高效率的故障诊断。最后，通过仿真和实验验证了所提出的MMC子模块开路故障诊断方法的有效性。
关键词：模块化多电平换流器 开路故障检测 多元高斯分布
随着模块化多电平换流器（Modular Multilevel Converter, MMC）的广泛应用，柔性直流输电系统向高电压化、大容量化、多端口化的趋势发展[1-4]。2020年昆柳龙直流工程投产，输送容量达到8 000 MW，直流母线电压高达±800 kV[5]。为满足更高的指标要求，MMC的结构也越发复杂化[6-7]。与此同时，可再生能源富集地大多都是极寒或酷热的环境恶劣地区，如张北工程建造时正值北方极寒天气，工程师及技师维护响应速度较慢，单次维护成本较高[8-9]。综合以上两方面，复杂的换流结构和严苛的系统工况大大增加了柔性直流输电工程中发生子模块故障的概率，对MMC的运行可靠性造成了严重威胁[10-11]。换流器中子模块故障会在直流系统中快速传播并可能引起整个系统的连锁反应[12-13]。为降低故障发生的概率，需要可靠的运维手段来确保整个系统的稳定性。
经统计研究，功率器件是电力电子换流器中最易失效的组件之一[14]。功率器件故障可以分为短路故障和开路故障。功率器件短路故障通常由硬件保护电路进行检测，方案常规且成熟[15-17]。然而，功率器件开路故障隐蔽性强，不易识别，且任其发展会导致系统出现联锁故障，造成其他设备的损坏[18-19]。由于MMC结构高度模块化的特点，在工程应用中若出现子模块开路故障，只需将相应的故障子模块更换以保证整个系统继续正常运行。因此，子模块开关管开路故障诊断的目标是定位到发生开路故障的具体子模块，从而能够进行故障子模块切除并启用健康子模块进行替代。现有子模块开路故障诊断方法根据故障诊断是否改变硬件传感器装置，可分成传感器法与模型法。
传感器法的诊断速度快、准确率高，但传感器法提高了子模块搭建成本，并引入新的潜在故障点，且无法应用于已投运的MMC工程，故该方法适配能力严重受限[20-23]。模型法无需添加额外传感器，可根据是否基于数据驱动，进一步分为机理模型法和机器学习法。机理模型法主要是通过滑模观测器、卡尔曼滤波器等数学手段，结合电路的实际参数建立换流器的数学机理模型，通过比较特征参数的理论值与实测值从而判断子模块是否发生故障[24-25]。机理模型法对系统参数和环境噪声较为敏感，鲁棒性弱。同时，随着子模块数量的增加，数学模型越发复杂，计算量大。机器学习法是数据驱动模型训练，无需精确的机理模型和人为设定阈值，具有高经济性、强鲁棒性的优势，可以直接适配于已有的MMC工程，是具有广阔前景的开路故障诊断方法[26-27]。文献[28-29]基于卷积神经网络算法构建有监督多分类器模型，选用子模块端电压及电流作为样本特征，将每个位置的子模块开路故障作为一个分类类别。文献[30-32]中是基于聚类（Clustering）算法构建的无监督模型，均选用桥臂电流及子模块电容电压作为样本特征。文献[33-34]基于支持向量机或支持张量机算法构建多分类器模型，能够通过故障及正常运行的数据，将开路故障诊断转化为分类问题，从而实现开路故障的诊断。然而，在实际工程中时常出现一些情况未知的故障或者故障样本难以获得以及故障工况不足的情形，分类器无法根据已有数据情况进行学习，导致方法诊断准确率受限，诊断错误率较高。
针对故障子模块样本量不均衡这一情况，本文提出了基于多元高斯分布异常检测模型的开路故障诊断方法。异常检测模型可用于判断样本是“正常”或“故障”，通常适用于系统故障情况部分未知的场景，从而实现在故障样本较少致使样本失均情况下的高准确率诊断。
三相半桥型MMC由6桥臂组成，其拓扑结构如图1所示。交流侧电压、电流分别为uj和ij（j=a, b, c），直流侧电压、电流可表示为Udc和Idc。
半桥子模块由上、下两个IGBT开关管VTu和VTl，及其反并二极管VDu和VDl，以及一个储能电容C组成，半桥子模块拓扑结构如图2所示。图2中，uC为储能电容电压，uSM为子模块端电压，iSM为流经子模块的电流。
根据开路故障发生的位置不同，半桥子模块开路故障可分为上管开路故障和下管开路故障两种类型。当器件发生开路故障时，半桥子模块电容电压会与正常电容电压产生差异，可将uSM作为开路故障的表征量。
图1 三相模块化多电平换流器拓扑结构
Fig.1 3-phase modular multilevel converter topology
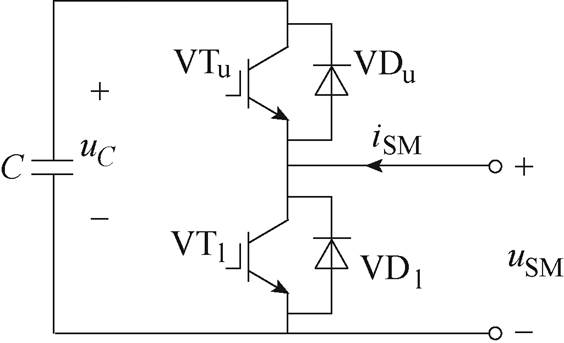
图2 半桥子模块拓扑结构
Fig.2 Half-bridge sub-module topology
为获取故障诊断所需的数据样本，本文采用滑动窗口法对离线数据进行分割处理，动态更新传感器所获得的数据。为了减小样本的特征维度以加快训练模型的速度，本文通过统计学对电压数据集合进行描述，表1为从不同角度给出的描述子模块电压特征的12种特征量。
表1 子模块电压特征表达式
Tab.1 Expression of sub-module voltage features
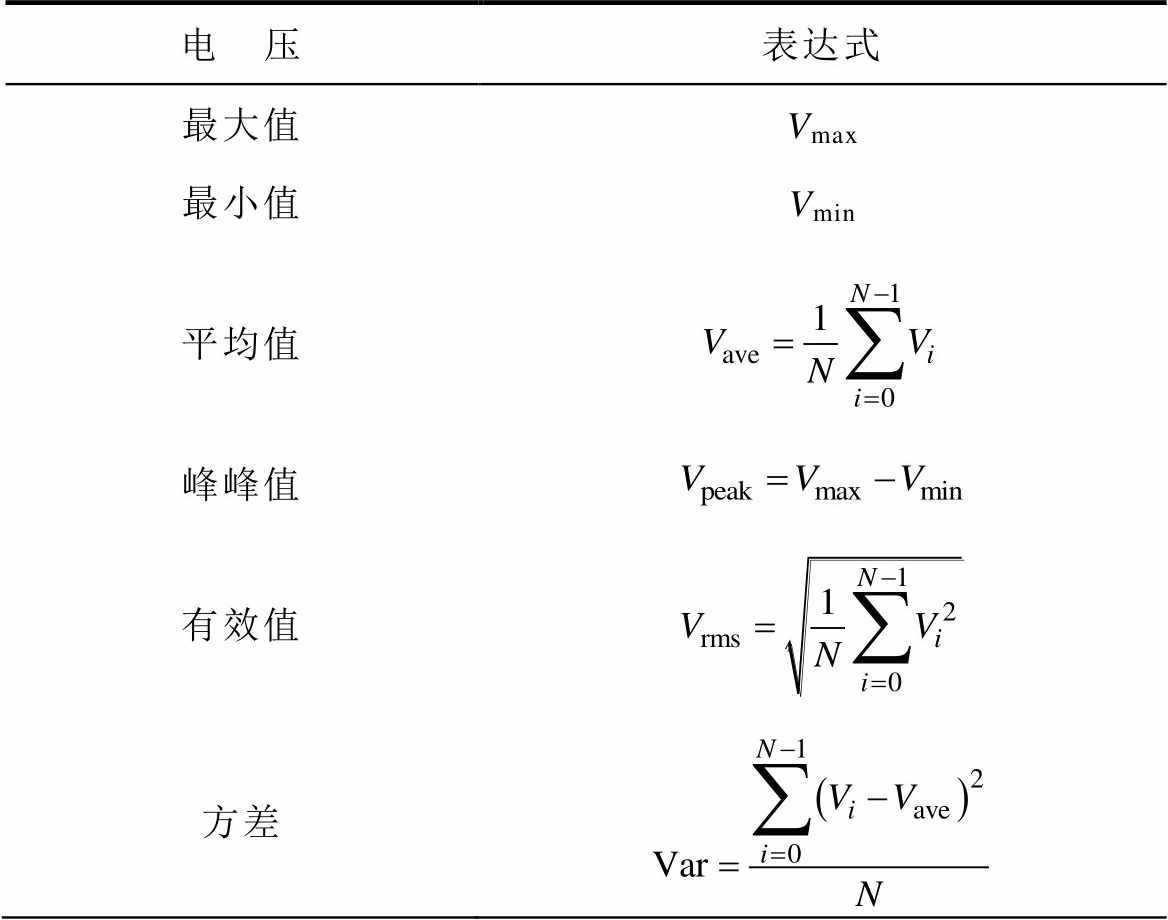
电 压表达式 最大值Vmax 最小值Vmin 平均值 峰峰值 有效值 方差
（续）
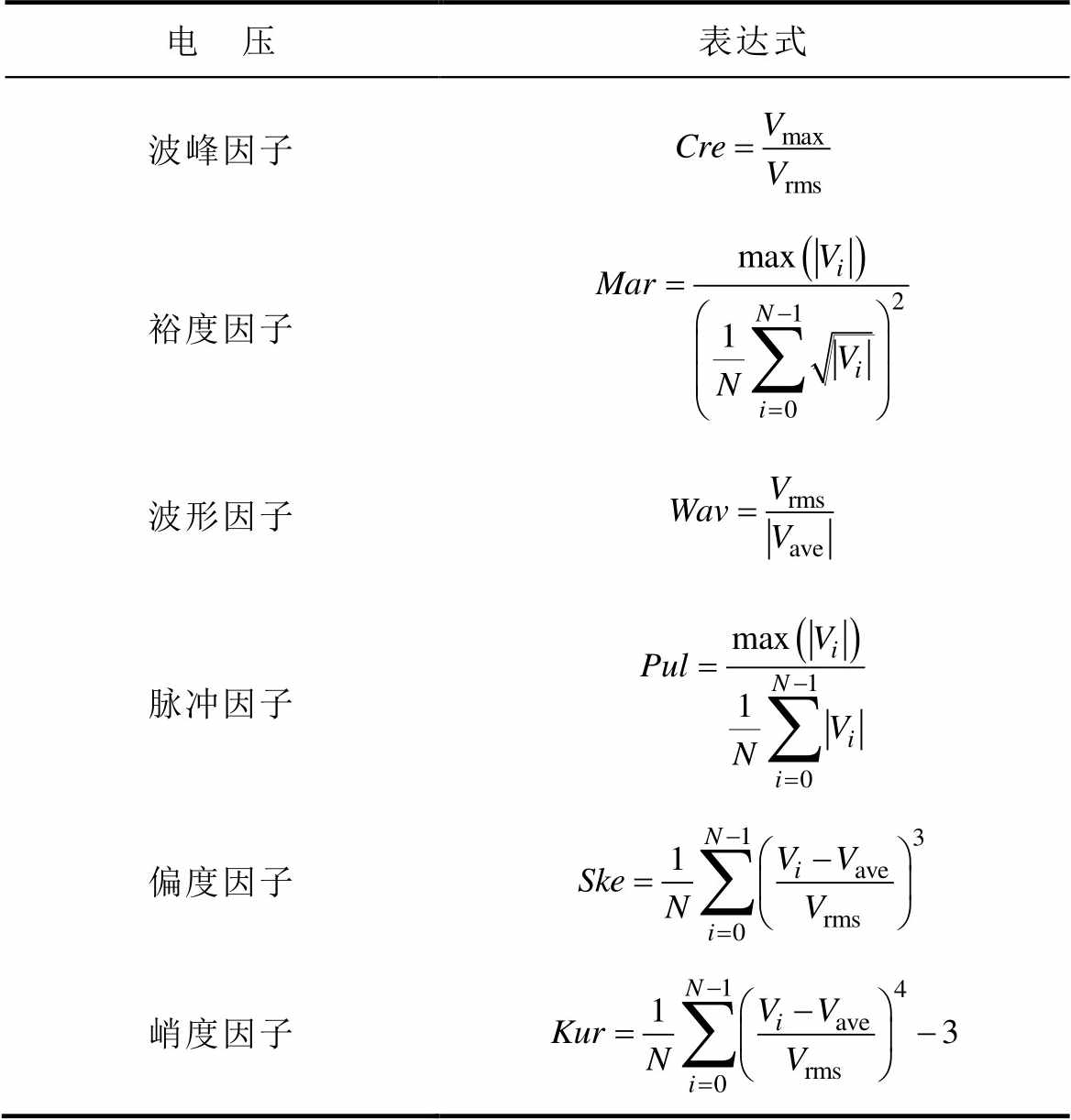
电 压表达式 波峰因子 裕度因子 波形因子 脉冲因子 偏度因子 峭度因子
表1中，平均值表示电压的平均状态；峰峰值表示取样点中电压最大值与最小值的差值，即电压信号的波动范围；方均根（Root Mean Square, RMS）值在电学中也可以表示为有效值，电学含义是电压信号片段的能量；方差用于描述数值的离散程度；波峰因子为波峰值与有效值的比值，在电路出现故障而导致波形产生畸变时，波峰因数会发生异常变化；裕度因子为电压峰值与方均根幅值的比值，通常用于诊断设备老化状况；波形因子为有效值与平均值的比值，在交直流侧功率相等的情况下，其波形因子表示为直流电压与交流电压的比值；脉冲因子为电压波峰值与整流平均值的比值，通常用于诊断设备是否受到冲击，如果电力系统出现瞬时过电压的情况，则脉冲因子很大；偏度因子为三阶中心矩与标准差三次方的比值，统计学含义是样本偏离中心的程度，偏度因子为负时，整个分布呈现左偏，偏度为正时，整个分布呈现右偏；峭度因子为四阶中心矩与标准差四次方的比值与正态分布峰度的差，统计学含义是变量分布的陡峭程度，超峰度为正数时，整个分布相比于正态分布更陡峭，超峰度为负数时，整个分布相比于正态分布更加平缓。由12个子模块电容电压特征量组成的特征向量x如式（1）所示，x中的物理量含义详见表1。
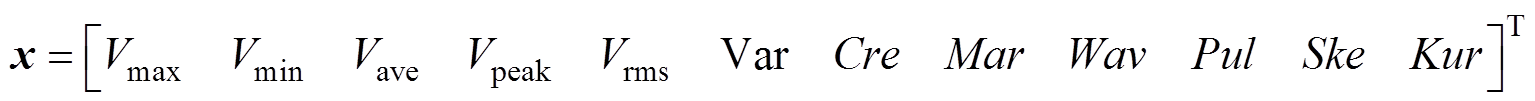（1）
高斯分布由于自身的拟合特性常用于特征工程及实际应用。多元高斯分布是能够适用于一组非独立的分别服从高斯分布的变量，是多元标准高斯分布的通用情况。多元标准高斯分布的理论基础是一元高斯分布。若随机变量X服从一元高斯分布，则概率密度函数p(x)满足
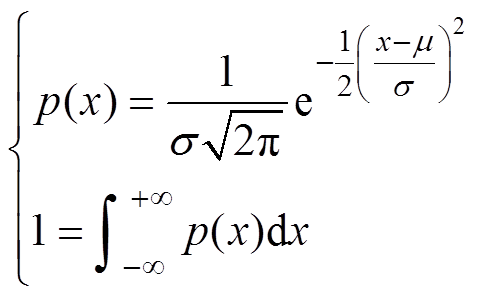（2）
式中，s 为随机变量的方差；m 为随机变量的期望；e为自然对数的底数。
为消去量纲以及分布差异，将全体数据进行标准化。Z-score标准化方法在机器学习中是一种常用的数据预处理方法，可以将不同数量单位的数据去量纲化。Z-score标准化通过数据与平均值的差值除以标准差的方式，实现随机变量X的标准化，通过使用G进行换元，即
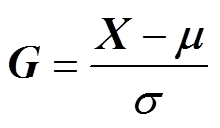（3）
基于式（3）的标准化，可以推导出服从一元标准高斯分布G的密度函数为
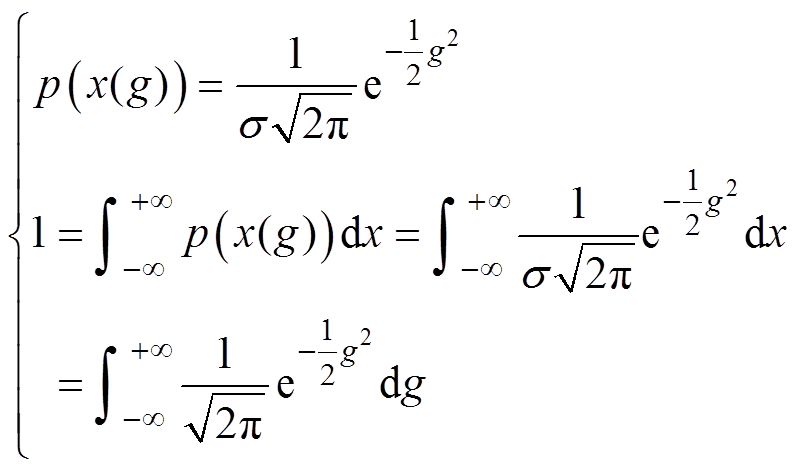（4）
从而可以得到均值为0、方差为1的一元标准高斯分布，且换元后的随机变量概率密度函数为
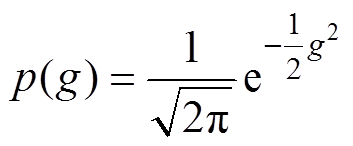（5）
随后，通过一元标准高斯分布推广到多元高斯标准分布。假设随机向量G由一组随机变量G1～Gn组成，其中每个随机变量都服从一元标准高斯分布，且各个变量之间彼此独立。可以根据一元标准高斯分布的概率密度函数及变量间的独立性，得到这组随机向量的概率密度函数为
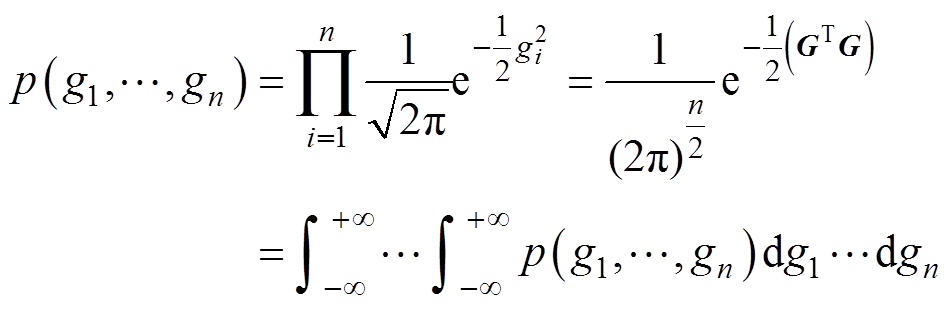（6）
继而可以得到服从均值为零向量，协方差矩阵为单位矩阵的多元标准高斯分布，协方差矩阵为
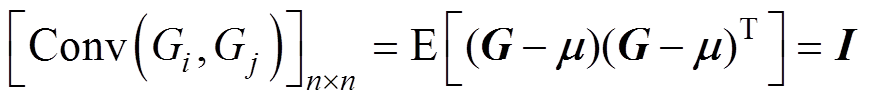（7）
各个随机变量不独立的多元高斯分布可将随机变量进行相关变换，从而构造出独立的随机变量，即可服从多元标准高斯分布，并通过式（6）求出联合概率密度函数。假设随机向量X由一组随机变量X1～Xn组成，其中各随机变量均服从一般性的高斯分布，而各个变量之间彼此不独立。若均值向量为实向量，且协方差矩阵为半正定实对称矩阵，则存在一个满秩矩阵B满足
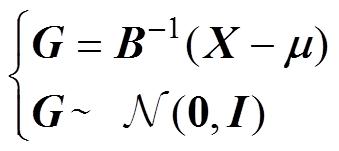（8）
式中，随机向量G服从均值向量为零向量，协方差矩阵为单位矩阵的高斯分布。基于式（8），可以对非独立的随机向量进行变换，将其代入式（6）中可以得到联合概率密度函数为
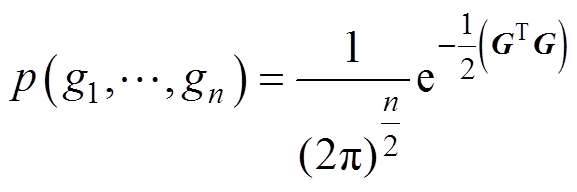（9）
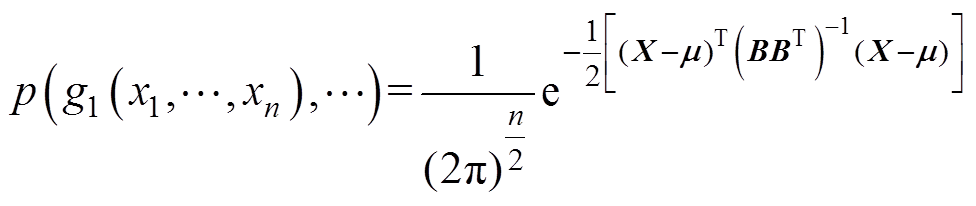（10）
其概率密度函数满足
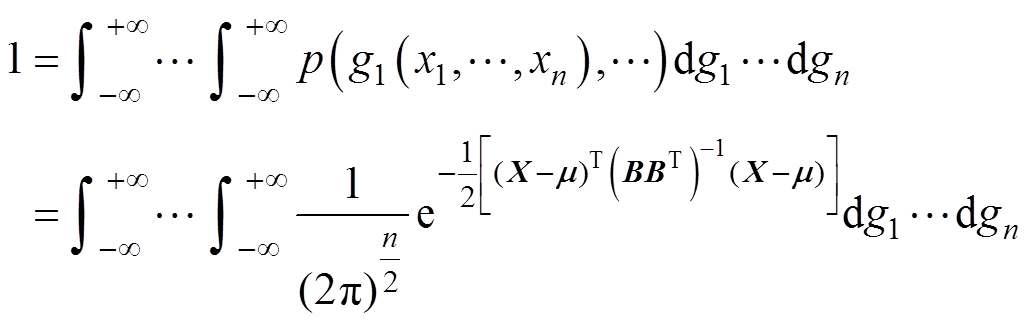（11）
为实现多元函数换元，由式（8）可得随机向量G变换为X的雅可比行列式为
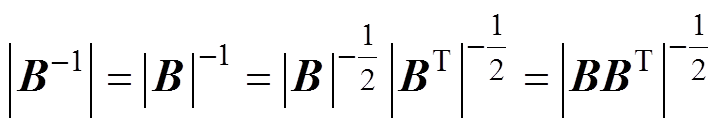（12）
将式（11）及式（12）合并化简，可得概率密度函数满足
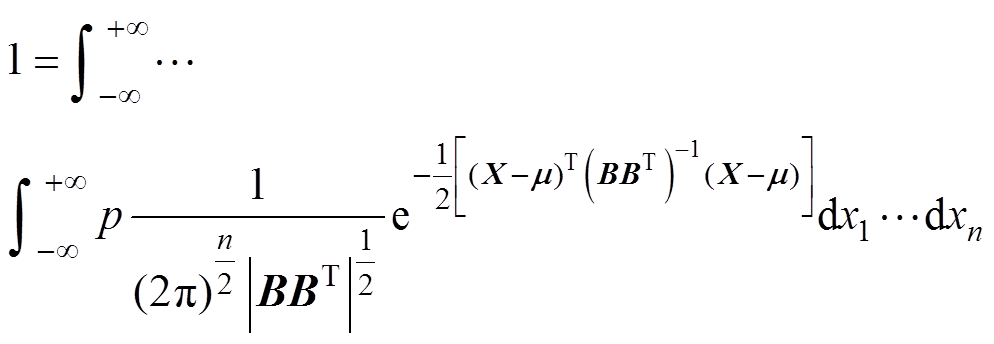（13）
从而可以得到普适性的多元高斯分布的联合概率密度函数为
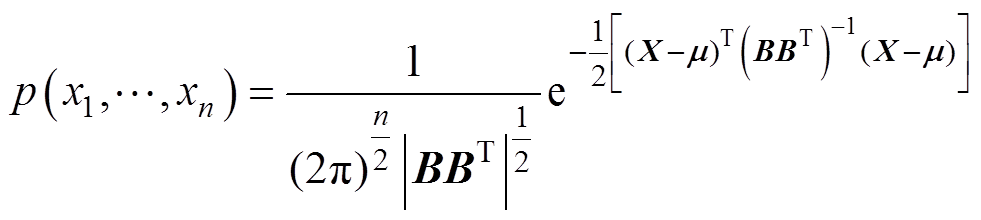（14）
其协方差矩阵可以表示为
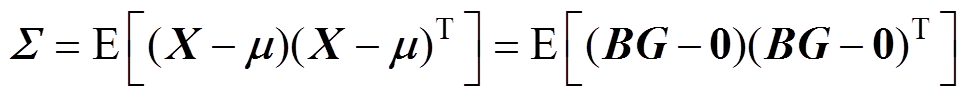
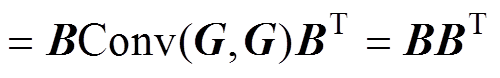（15）
式中，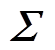
为协方差矩阵。
将协方差矩阵代入式（14）化简，即可得到一般情况下多元高斯分布的联合概率密度函数为
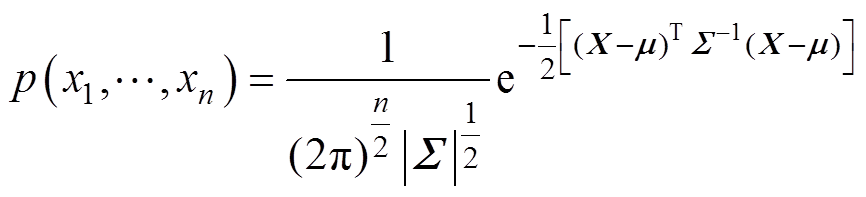（16）
MMC子模块在均压策略的作用下，电容电压在参考电压附近小范围波动，表1中给出的子模块电容电压特征量近似符合高斯分布。高斯分布可以用于描述误差，观测值与真值差距越大，观测实例越少；观测值与真值差距越小，观测实例越多。因此，可以根据大量正常子模块电容电压的周期性特征估算真值，并认为偏离此真值较远即概率过低的样本为异常点，从而实现开路故障子模块异常检测。但是由于特征提取所得到的各个特征均来源于电压这个原始表征量，多个特征并非相互独立。针对多个相关联的非独立变量，多元高斯分布模型可契合地描述特征变量。因此，根据子模块电容电压的特征提取，可以将子模块开路故障诊断问题转化为多元高斯异常检测问题，开路故障诊断模型构造流程如图3所示，主要分为五个步骤：
1）基于子模块电容电压构建特征数据集
在进行数据集建立时，子模块数据的类型可分为工作状态已知与工作状态未知。对两种类型的数据处理与特征提取的方法相同，均使用子模块的电压传感器对电容电压分别进行离线存储。随后对多组电压数据进行周期性分割及特征量提取，从而构建一个多维特征向量的数据特征集。对于工作状态未知的子模块数据样本，由于将其作为验证集会使阈值设定不准确，将其作为测试集会导致测试准确率与模型的实际情况不符，故这部分样本只能作为训练集，并设为正常标签。对于工作状态已知的正常工作子模块数据，设置样本标签“0”代表“未发生故障”，并按照一定比例分为机器学习的训练集、验证集和测试集三部分。对于工作状态已知的开路故障子模块数据样本，设置样本标签“1”代表“发生故障”，并按照一定比例分为机器学习验证集与测试集两部分。
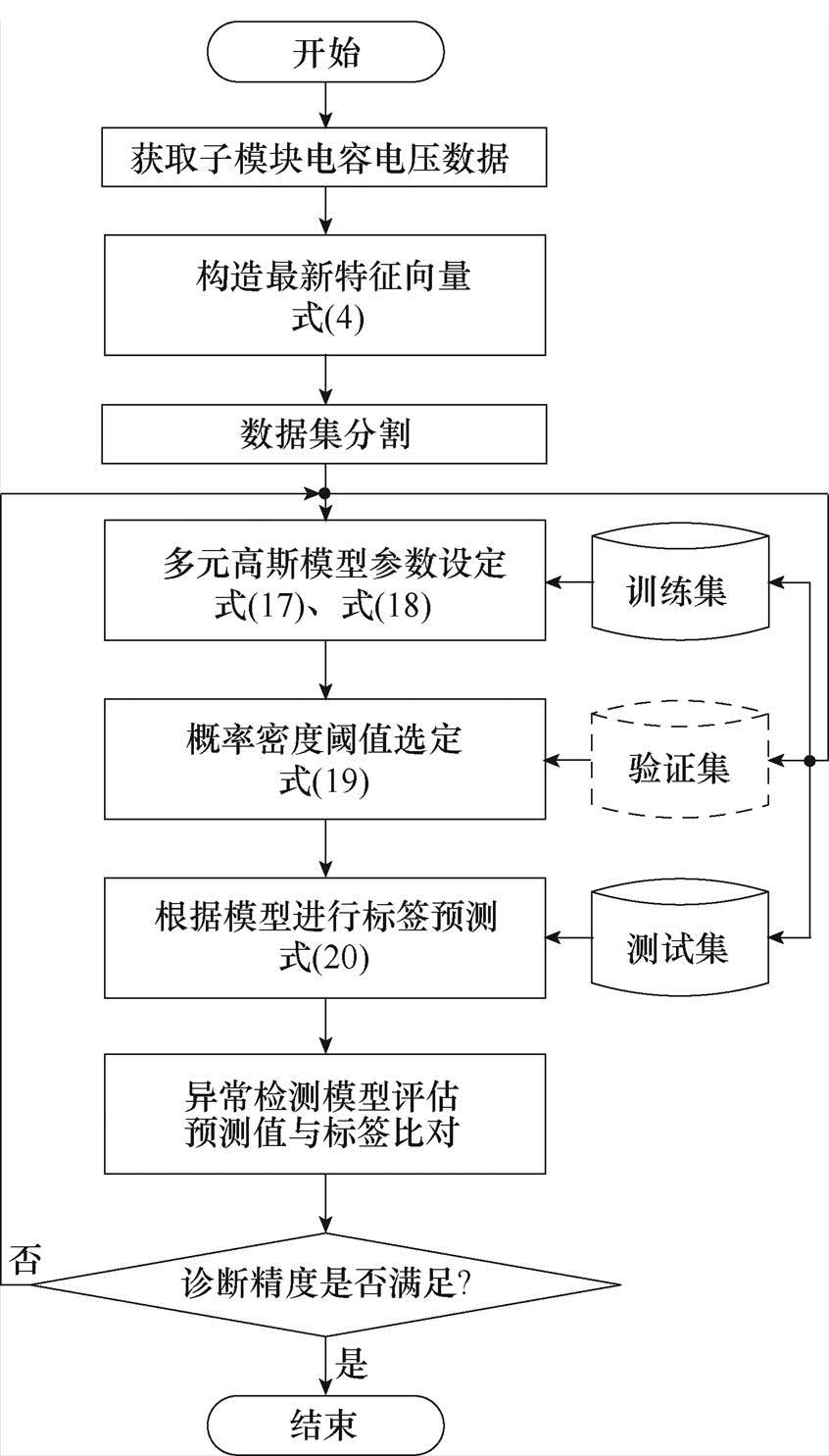
图3 基于多元高斯分布异常检测的诊断模型
Fig.3 Anomaly detection model based on multivariate Gaussian distribution
2）基于电压特征构建模型参数
首先，为构建多元高斯模型，使用步骤1）中得到的电压特征数据训练集，计算模型参数。首先计算特征均值向量m 为
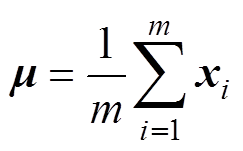（17）
式中，xi为从电压数据提取出的特征向量；m为特征向量的样本数量。基于所得到的均值向量，计算训练集特征向量的协方差矩阵∑为
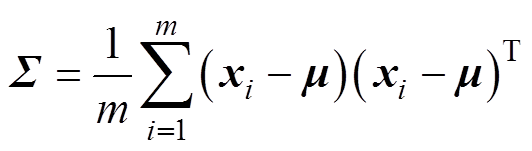（18）
3）选定模型概率密度阈值
在步骤2）构建的模型参数基础上，进一步进行阈值选用。基于步骤1）中构成的验证集，分别代入式（19）中计算相应的概率密度值。
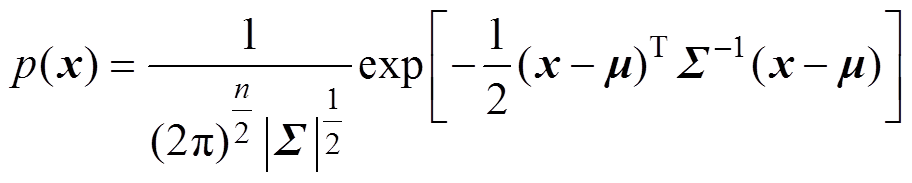（19）
阈值可设定为正常工作子模块数据样本的概率密度最小值、开路故障子模块数据样本的概率密度最大值，或者根据样本量将二者结合进行加权平均。
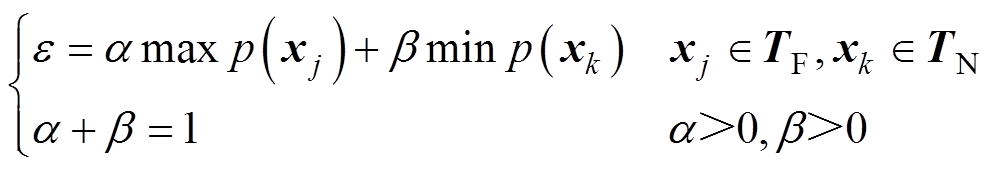（20）
式中，e 为所选取的阈值；TF、TN分别为开路故障特征向量矩阵、正常子模块的特征向量矩阵；a、b为权重值。
4）使用训练好的模型进行预测
为了独立训练和评估所提出的模型，需要用步骤1）中分割好的测试集进行相关指标的测试。基于步骤2）、步骤3）所计算的参数与阈值，进行测试集的标签预测：若计算所得的概率密度小于等于阈值，则标签输出为“1”，代表发生开路故障；若计算所得的概率密度大于阈值，则标签输出为“0”，代表正常运行。
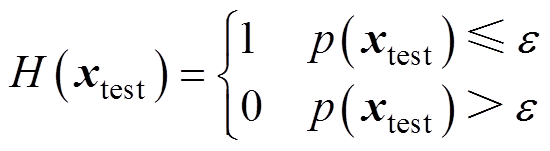（21）
通过计算样本标签预测正确的情况，可以评估模型的准确度。还可以通过召回率、F1分数等参数指标综合评估训练得到的诊断模型，其中召回率指预测为某类且实际也为该类的样本与全部实际为该类别的样本比例；F1分数指召回率与准确度的加权调和平均值，可用于衡量故障预测的正确程度。
5）迭代提高模型性能
在所得模型准确度不能达到理想情况的时候，可以通过交叉验证的方式来比对参数组合对模型的影响，如式（20）中a、b 权重值的设定。交叉验证能够充分利用数据，选定最契合的参数组合，从而达到最优的故障诊断效果。
在子模块传感器获取各电容电压后，更新滑动窗口数据并计算出窗口内各特征，从而组成当前状态的待诊断向量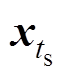
。将待诊断向量输入到训练好的多元高斯分布异常检测模型中，根据式（19）进行概率密度的计算。
若待诊断向量的概率密度值大于阈值，则可以判定该子模块为正常运行状态；若待诊断向量的概率密度值小于等于阈值，则判定该子模块为故障状态，表示为
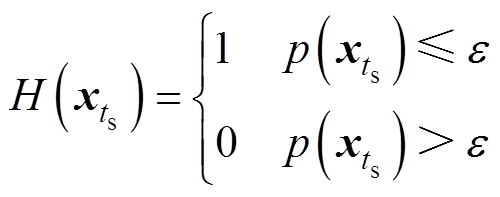（22）
由于单次诊断存在误诊的可能性，所以通过叠加多个周期进行判断。若连续N个周期均诊断到同一子模块开路故障，则进行故障判定。随后根据各子模块上传数据的属性直接定位到指定故障子模块，从而进行后续的切除并使用健康子模块进行替换。
为证明所提出的子模块开路故障诊断方法的有效性，在Matlab/Simulink中搭建可设置开路故障信号的三相21电平MMC仿真模型，主要参数见表2。
表2 三相21电平MMC仿真模型主要参数
Tab.2 Simulation parameters of 21-level MMC
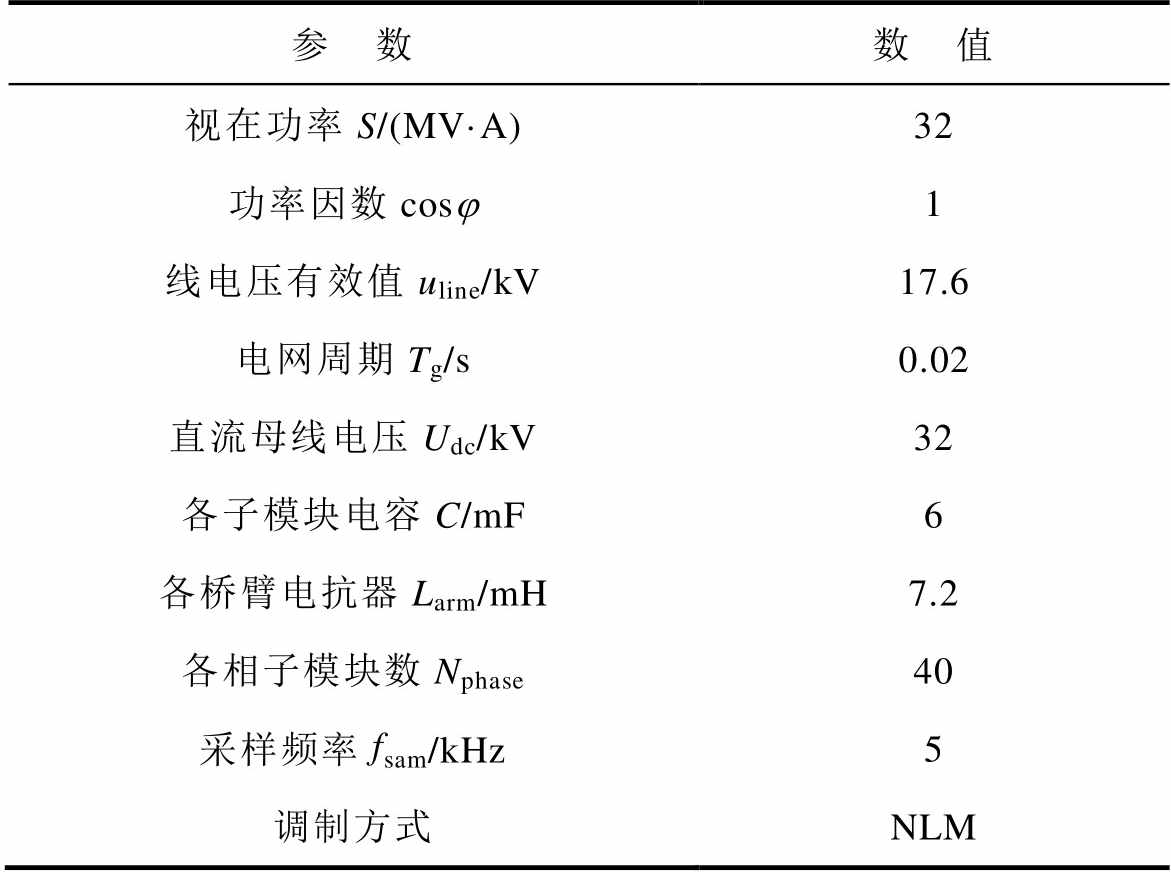
参 数数 值 视在功率S/(MV·A)32 功率因数cosj1 线电压有效值uline/kV17.6 电网周期Tg/s0.02 直流母线电压Udc/kV32 各子模块电容C/mF6 各桥臂电抗器Larm/mH7.2 各相子模块数Nphase40 采样频率fsam/kHz5 调制方式NLM
首先验证故障特征提取方法的有效性。根据各样本的预测值与实际值可以计算模型准确率，见表3。由表3可知，在提取最大值与方差2个特征（方差、标准差）时虽然平均准确率为99 %，然而故障样本的诊断准确率仅有92 %，存在大量误诊的情况，在提取4个特征（最大值、方差、标准差、偏态）时，故障样本的诊断准确率小于99 %。在提取12个特征时，由于没有预测错误的样本，平均准确率为100 %，证明本方法能实现高准确率的故障诊断。分别提取2个特征、4个特征、12个特征，在同一机器学习模型下进行多组不同故障点的故障诊断效率测试。多组开路故障实验的平均诊断时间见表3。由表3可知，在提取方差及标准差2个特征时，诊断时间平均为22.64 ms。在提取12个特征时诊断效率较为理想，诊断时间在19.38 ms左右，相比减少了25 %，证明本方法所提取的特征能在确保诊断准确率的基础上，有效提高模诊断效率。
表3 不同特征提取方法下的诊断准确率
Tab.3 Model accuracy with different feature extraction methods
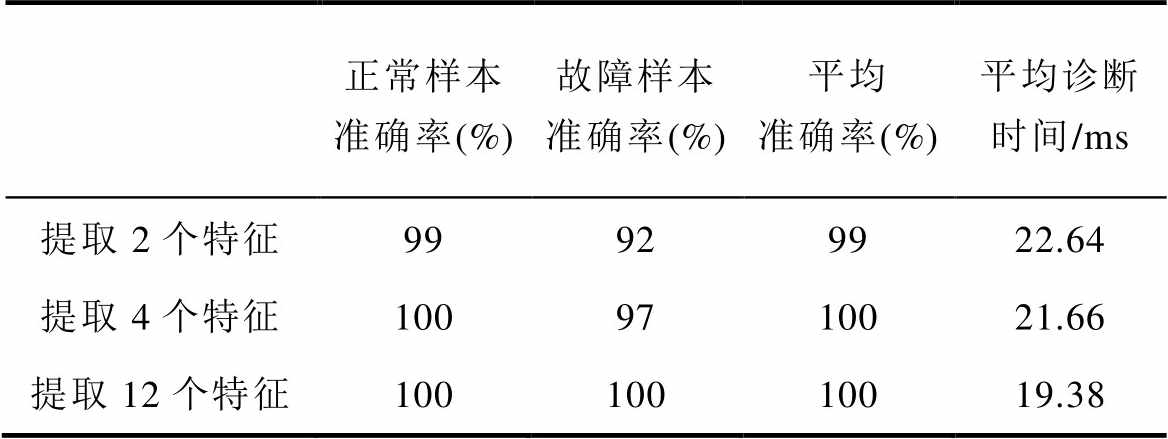
正常样本准确率(%)故障样本准确率(%)平均准确率(%)平均诊断时间/ms 提取2个特征99929922.64 提取4个特征1009710021.66 提取12个特征10010010019.38
仿真条件下，模型的混淆矩阵热力如图4所示，混淆矩阵热力图表示各个区域数值密度情况，即由深红到深蓝表示密度百分比的由高到低。在混淆矩阵中，横轴和纵轴分别代表预测标签与实际标签。由图可知，模型的准确率较高，平均准确率为99.97 %，证明了模型具有较好的诊断准确率性能。异常检测模型的两类样本数量差异较大，仅用准确率不能全面评价模型性能。
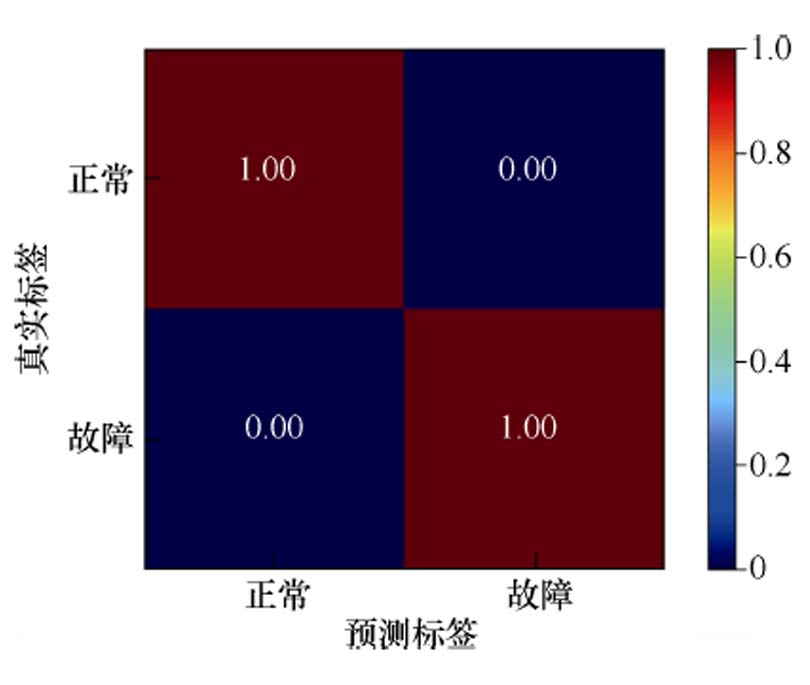
图4 混淆矩阵热力图形式
Fig.4 Confusion matrix presenting the strategy accuracy
为了更确切地对模型的性能进行评估，使用由准确度、召回率、F1分数指标构成的评价矩阵，见表4，对于正常运行的样本，三种指标都接近100 %；对于发生开路故障的样本，准确度为100 %，召回率为99.61 %，F1分数为99.80 %，说明所提方法能够高准确率地实现开路故障诊断。对于其中极少量被误诊的正常样本，可以通过连续叠加诊断窗口的方式在端到端的故障诊断中消除误诊，在3.2节将给出验证。
表4 异常检测模型评价指标矩阵
Tab.4 Evaluation index matrix of anomaly detection model（单位: %）
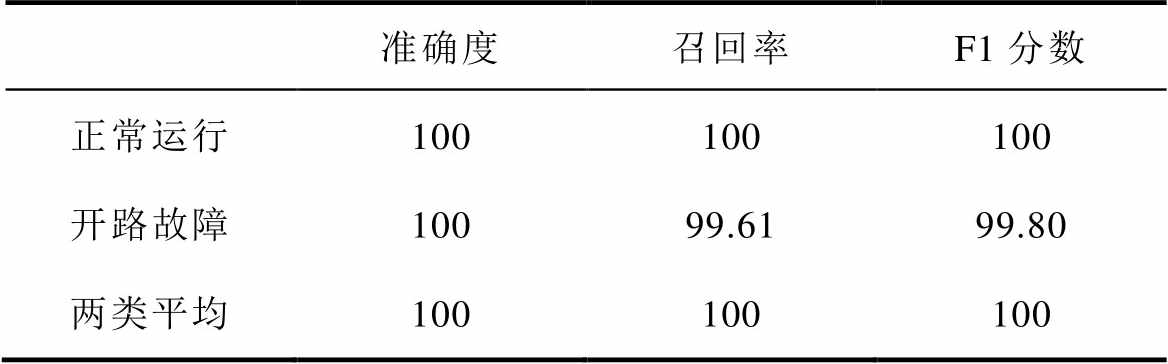
准确度召回率F1分数 正常运行100100100 开路故障10099.6199.80 两类平均100100100
通过滑动窗口与特征提取，获取各个子模块最新特征向量，将训练好的模型加载并对各个向量进行标签预测即可实现故障诊断。分别在逆变模式下设置了上桥臂第1个子模块开路故障，在整流模式下设置了上桥臂第10个子模块故障，使用多元高斯异常检测模型进行故障诊断。逆变模式下，诊断过程中各子模块电容电压波形如图5所示，开路故障在1.5 s时发生并在1.516 8 s处诊断完成，故障定位在第1个子模块，诊断过程用时16.8 ms。整流模式下，诊断过程中各子模块电容电压波形如图6所示，开路故障在1.5 s时发生并在1.524 8 s处诊断完成，故障定位在第10个子模块，诊断过程用时24.8 ms。
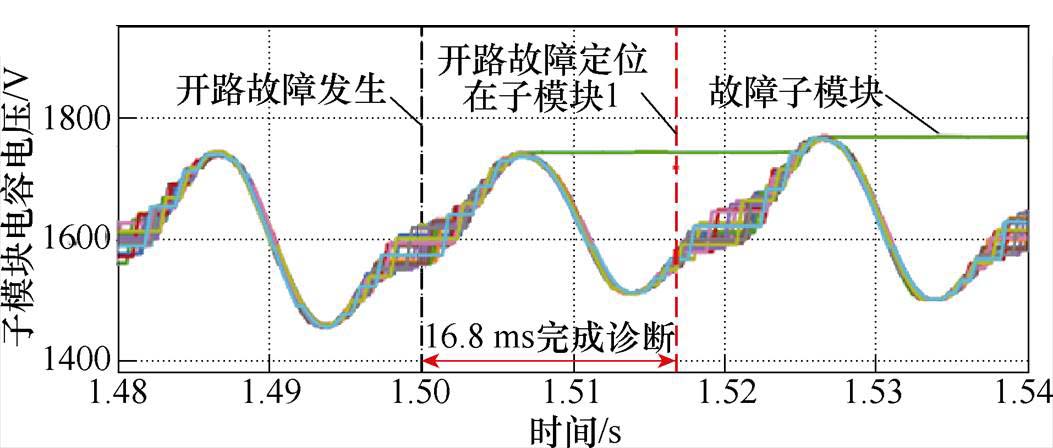
图5 逆变模式下子模块开路故障诊断结果
Fig.5 SM fault diagnosis results in inverter mode
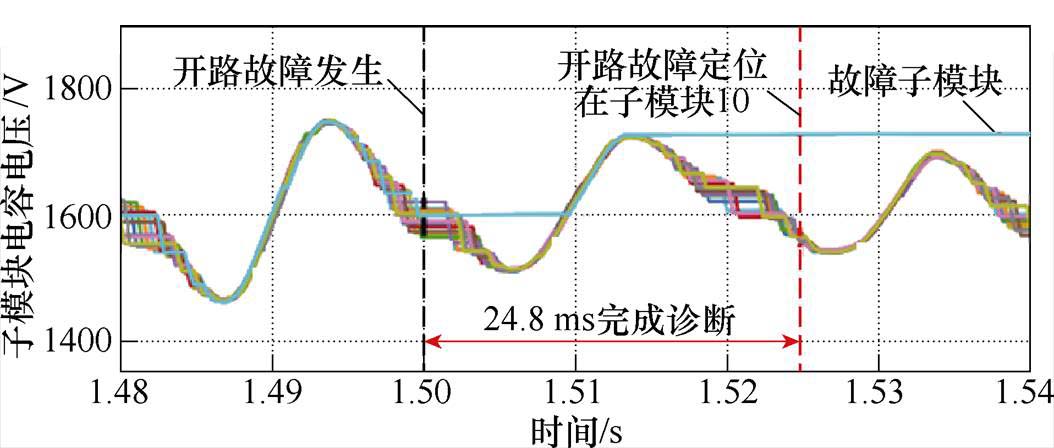
图6 整流模式下子模块开路故障诊断结果
Fig.6 SM fault diagnosis results in rectifier mode
逆变及整流模式下诊断过程中各子模块决策标签变化如图7所示。逆变及整流模式下的故障子模块决策标签分别如图7a与图7b所示。在逆变模式下，第1个子模块的决策标签由0跳变至1且连续保持5个周期后，将开路故障定位在第1个子模块。在整流模式下，第10个子模块的决策标签由0跳变至1且连续保持5个周期后，将开路故障定位在第10个子模块。逆变及整流模式下存在误诊情况的正常子模块决策标签分别如图7c与图7d所示。由于噪声干扰等因素存在一定误诊的概率，正常子模块的决策标签断续由0跳变至1，但是持续周期均较短，故可以通过连续5个周期叠加可以消除误诊的情况。逆变及整流模式下无误诊情况的正常子模块决策标签分别如图7e与图7f所示，在无误诊情况下正常子模块的决策标签保持为0。
为了更准确地评估方法的诊断效率，分别设置了不同工作状态下（整流/逆变）、不同位置的子模块开路故障，进行20组子模块开路故障测试。故障诊断时间的直方图如图8所示，20组测试的诊断时间均小于40 ms，平均诊断时间为32.6 ms，且其中6组诊断时间在30 ms内，可以证明本方法具有高诊断效率。
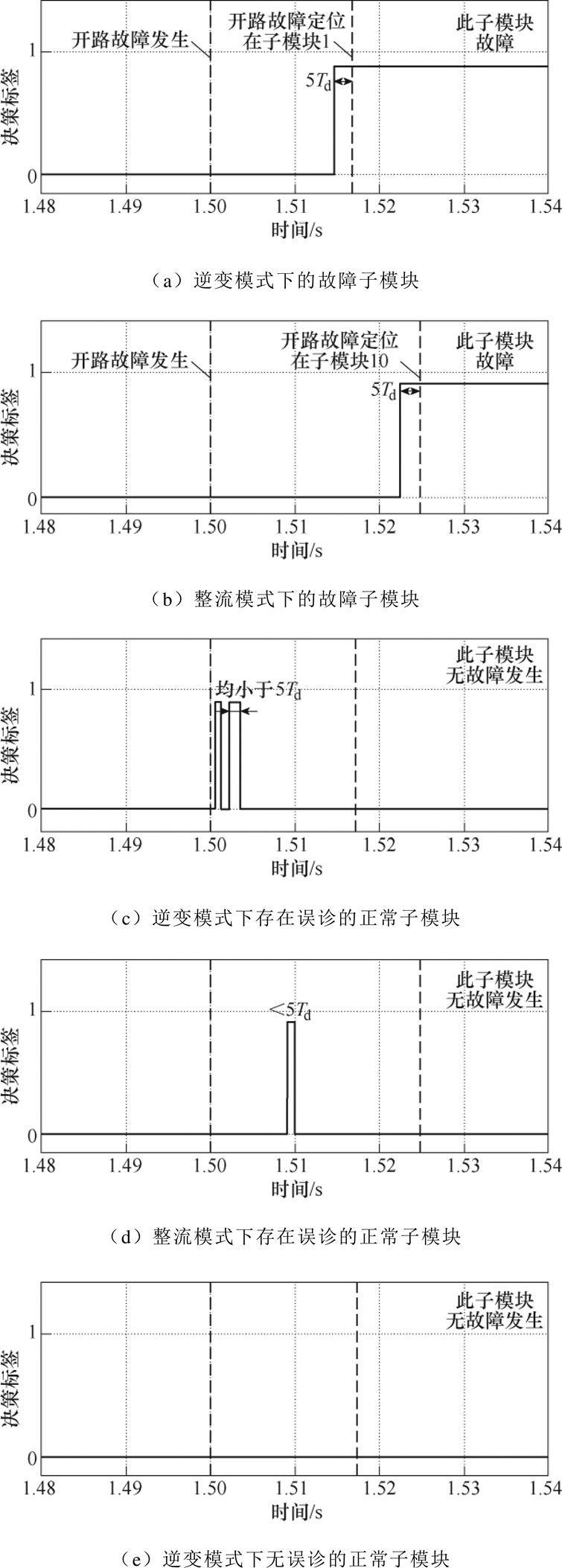
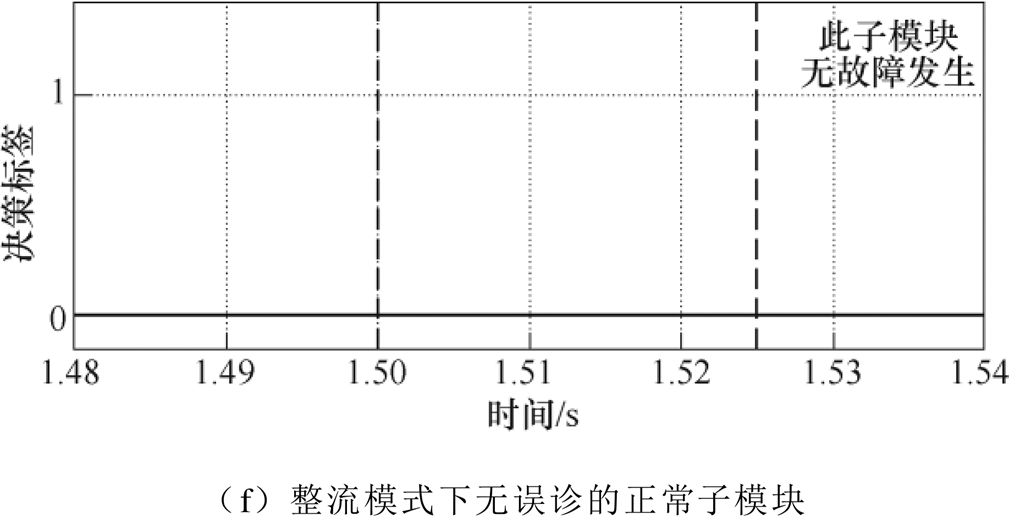
图7 逆变及整流模式下诊断过程中子模块决策标签变化
Fig.7 Sub-module diagnosis label process in inverter and rectification mode
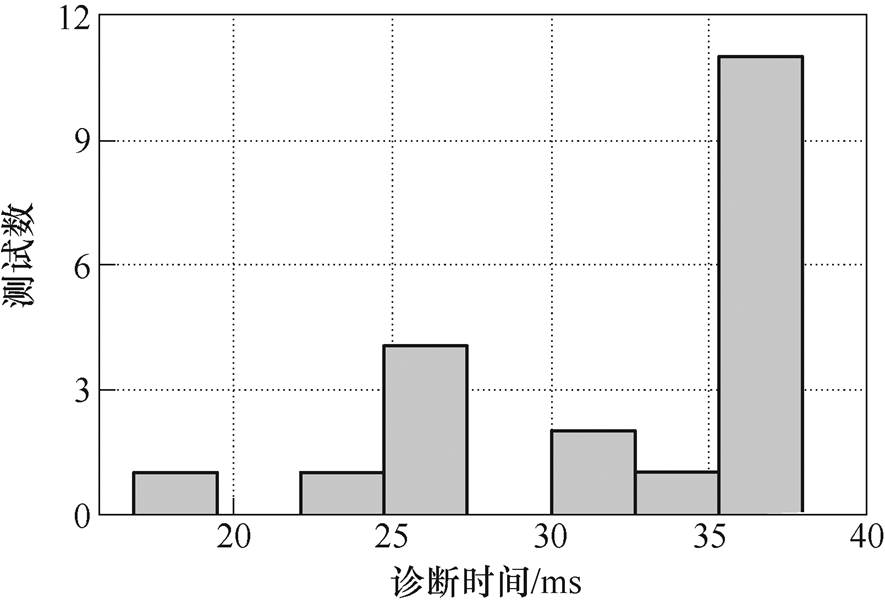
图8 开路故障诊断时间直方图
Fig.8 Histogram of time for open-circuit fault detection
为验证所提出的基于多元高斯分布的开路故障诊断方法，搭建了三相MMC实验平台，主要参数见表5。
表5 三相MMC实验平台主要参数
Tab.5 Experimental parameters of MMC test bench
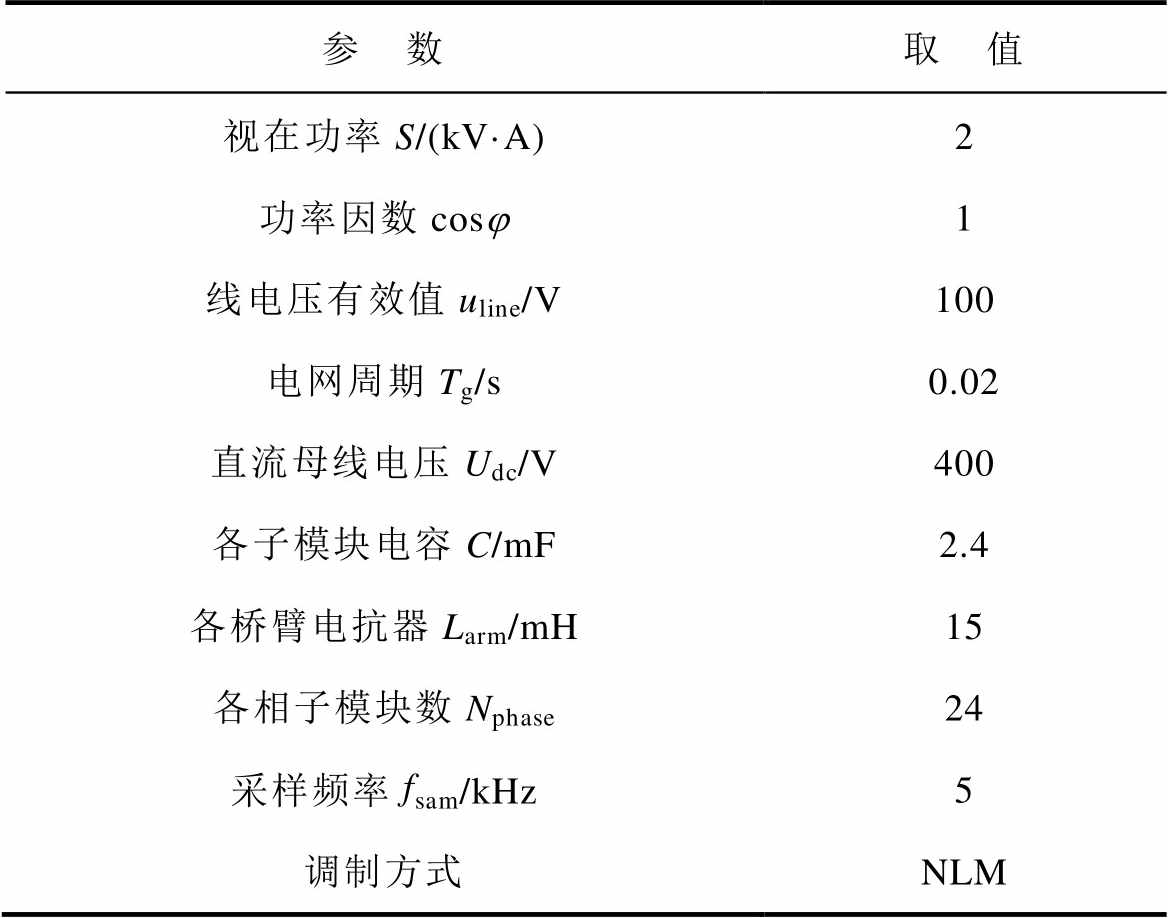
参 数取 值 视在功率S/(kV·A)2 功率因数cosj1 线电压有效值uline/V100 电网周期Tg/s0.02 直流母线电压Udc/V400 各子模块电容C/mF2.4 各桥臂电抗器Larm/mH15 各相子模块数Nphase24 采样频率fsam/kHz5 调制方式NLM
在如图9所示的实验平台上设置不同子模块发生开路故障，共进行5次实验，收集到417组子模块电容电压序列。滑动窗口长度设置为250个采样点，即为50 ms，滑动步长设置为1个样本点，即0.2 ms，总样本量为60 300，并根据子模块实际运行状态分别设置故障标签或正常标签。将所得数据集分为训练集、验证集及测试集，分别用于训练模型参数与阈值，并完成模型测试。
图9 三相MMC实验平台
Fig.9 MMC test platform of three phase
开路故障模型的混淆矩阵热力形式如图10所示，各指标评价矩阵见表6。
由图10可知，模型的整体准确率较高，平均准确率为99.96 %，证明了模型具有较好的诊断性能。由表6可知，正常样本的准确度等指标均接近99.99 %，而存在约1 %的预测故障样本实际为正常样本。对于少量被误诊的正常样本，可以通过连续叠加诊断窗口的方式在端到端的故障诊断中消除，在4.2节将给出验证。
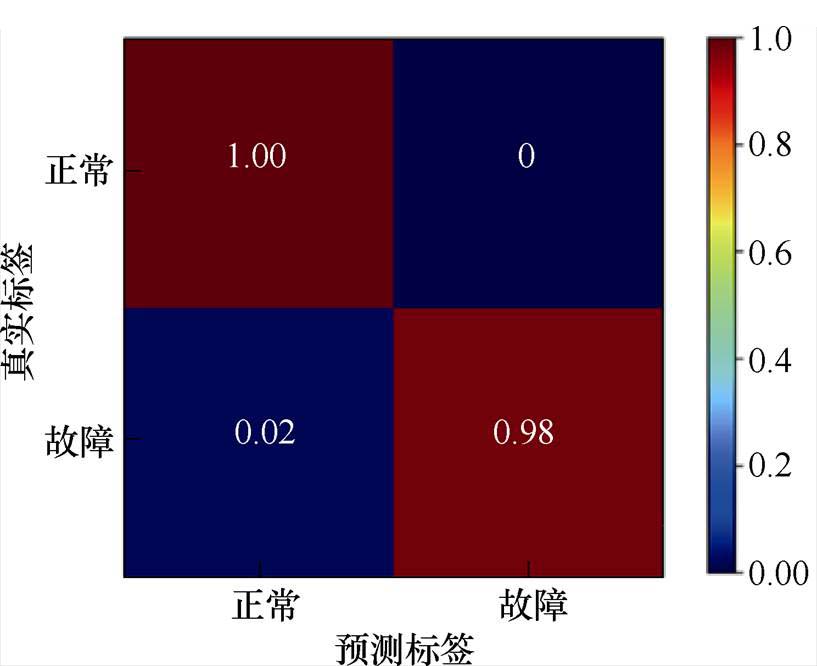
图10 混淆矩阵热力图形式
Fig.10 Confusion matrix presenting the strategy accuracy
表6 异常检测模型评价指标矩阵
Tab.6 Evaluation index matrix of anomaly detection model（单位: %）
准确度召回率F1分数 正常运行99.9899.9899.99 开路故障98.5098.5098.50 两类平均99.9699.9699.96
通过滑动窗口与特征提取，获取各个子模块最新特征向量，将训练好的模型加载并对各个向量进行标签预测即可实现故障诊断。在1.05 s时，设置了上桥臂第4个子模块开路故障，根据故障诊断流程进行故障定位。
开路故障诊断过程中各子模块电容电压波形如图11a所示。开路故障在1.05 s时发生，在1.107 s处诊断完成，诊断用时50.7 ms。第4个子模块的决策标签随时间变化如图11b所示，在第4个子模块的决策标签由0跳变至1且连续保持5个周期后，实现故障诊断并定位在此子模块。无误诊的正常子模块决策标签如图11c所示。在无误诊情况下，正常子模块的决策标签保持为0，没有出现断续跳变。存在误诊的正常子模块决策标签如图11d所示，由于噪声干扰等因素存在一定误诊的概率，所以正常子模块的决策标签断续由0跳变至1，但是持续周期均较短，故通过连续5个周期叠加可以消除误诊的情况。
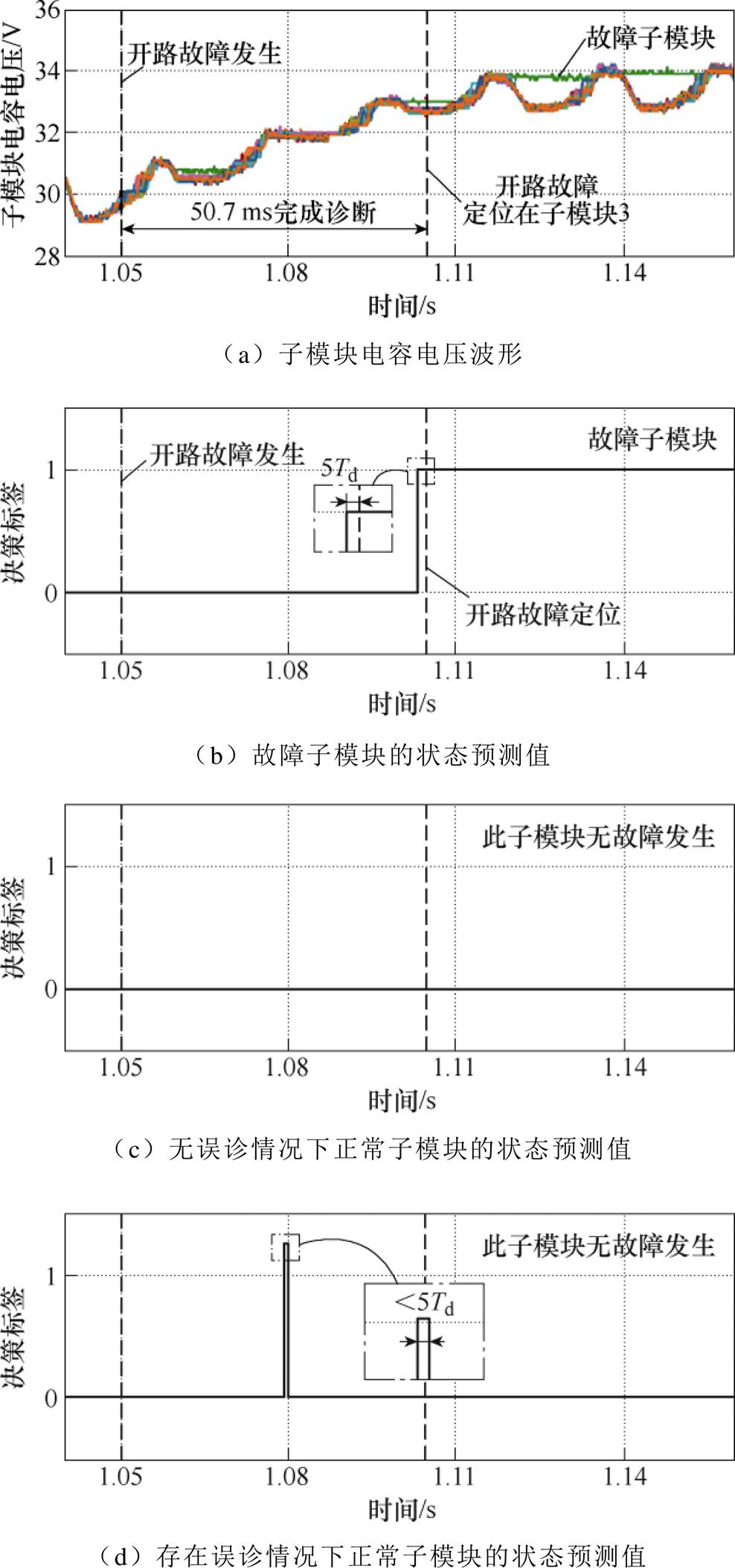
图11 子模块开路故障诊断过程
Fig.11 Diagnosis process for sub-module open-circuit fault detection and location
为了更准确地评估所提方法的诊断效率，分别设置了不同位置的子模块开路故障，进行12组子模块开路故障实验测试。12组实验的故障诊断时间直方图如图12所示。由图12可知，12组测试的诊断时间均小于65 ms，平均诊断时间为52.73 ms，且至少6组的诊断时间小于55 ms。各组均可以在开路故障造成实质性危害前进行诊断与故障子模块切除，证明了该方法的高诊断效率。
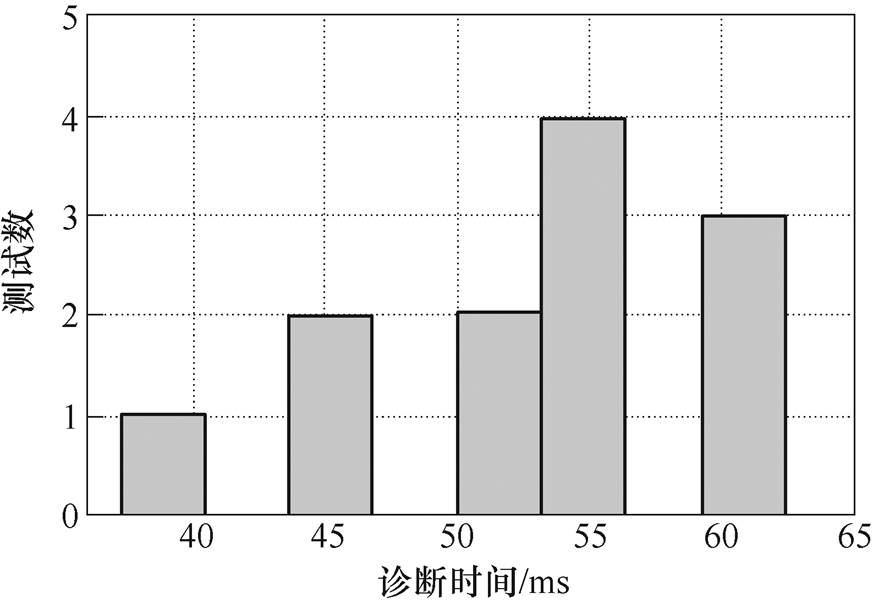
图12 开路故障诊断时间直方图
Fig.12 Histogram of time for open-circuit fault detection
本文首先针对模块化多电平换流器子模块开路故障数据样本不足的情况，将开路故障诊断问题转化为异常检测问题。随后，提出了基于多元高斯分布的异常检测模型构建方法，并基于此模型提出了子模块开路故障诊断策略，可在故障样本偏少致使样本不均衡时，实现高准确率、高效率的故障诊断。最后，通过仿真及实验从诊断准确率、召回率、诊断效率等多方面对子模块开路故障诊断方法的有效性进行了验证。
参考文献
[1] 徐殿国, 李彬彬, 周少泽. 模块化多电平高压变频技术研究综述[J]. 电工技术学报, 2017, 32(20): 104-116.
Xu Dianguo, Li Binbin, Zhou Shaoze. Overview of the modular multilevel converter based high voltage motor drive[J]. Transactions of China Electro- technical Society, 2017, 32(20): 104-116.
[2] 贺永杰, 向往, 周家培, 等. LCC-MMC串联型混合直流输电系统小信号建模[J]. 电工技术学报, 2021, 36(7): 1492-1506.
He Yongjie, Xiang Wang, Zhou Jiapei, et al. Small- signal modelling of LCC-MMC series hybrid HVDC transmission system[J]. Transactions of China Elec- trotechnical Society, 2021, 36(7): 1492-1506.
[3] 彭浩, 邓焰, 王莹, 等. 模块化多电平变换器模型及稳态特性研究[J]. 电工技术学报, 2015, 30(12): 120-127.
Peng Hao, Deng Yan, Wang Ying, et al. Research about the model and steady-state performance for modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 120- 127.
[4] 常浩, 厉璇, 马玉龙, 等. 舟山多端柔性直流输电工程直流系统放电特性[J]. 高电压技术, 2017, 43(1): 9-15.
Chang Hao, Li Xuan, Ma Yulong, et al. Discharge characteristics of DC system in Zhoushan multi-terminal VSC-HVDC transmission project[J]. High Voltage Engineering, 2017, 43(1): 9-15.
[5] 谢惠藩, 付超, 李诗旸, 等. 昆柳龙多端直流线路故障恢复及换流站在线退站的系统稳定特性分析[J]. 南方电网技术, 2021, 15(6): 7-14.
Xie Huifan, Fu Chao, Li Shiyang, et al. Analysis on system stability characteristic of DC line fault reco- very and converter station online disconnection of KLL MTDC[J]. Southern Power System Technology, 2021, 15(6): 7-14.
[6] 张建坡, 崔涤穹, 田新成, 等. 自阻自均压模块化多电平换流器子模块拓扑及控制[J]. 电工技术学报, 2020, 35(18): 3917-3926.
Zhang Jianpo, Cui Diqiong, Tian Xincheng, et al. Self-block and voltage balance modular multilevel converter sub module topology and control[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3917-3926.
[7] 杨晓峰, 李泽杰, 薛尧, 等. 增强型柔性逆阻模块化多电平换流器的故障阻断特性分析[J]. 电工技术学报, 2019, 34(12): 2549-2557.
Yang Xiaofeng, Li Zejie, Xue Yao, et al. Fault blocking performance analysis of enhanced flexible reverse blocking multilevel modular converter[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2549-2557.
[8] 杜晓磊, 郭庆雷, 吴延坤, 等. 张北柔性直流电网示范工程控制系统架构及协调控制策略研究[J]. 电力系统保护与控制, 2020, 48(9): 164-173.
Du Xiaolei, Guo Qinglei, Wu Yankun, et al. Research on control system structure and coordination control strategy for Zhangbei demonstration project of MMC- HVDC grid[J]. Power System Protection and Control, 2020, 48(9): 164-173.
[9] 汤广福, 王高勇, 贺之渊, 等. 张北500kV直流电网关键技术与设备研究[J]. 高电压技术, 2018, 44(7): 2097-2106.
Tang Guangfu, Wang Gaoyong, He Zhiyuan, et al. Research on key technology and equipment for Zhangbei 500kV DC grid[J]. High Voltage Engin- eering, 2018, 44(7): 2097-2106.
[10] 汤广福, 罗湘, 魏晓光. 多端直流输电与直流电网技术[J]. 中国电机工程学报, 2013, 33(10): 8-17, 24.
Tang Guangfu, Luo Xiang, Wei Xiaoguang. Multi- terminal HVDC and DC-grid technology[J]. Pro- ceedings of the CSEE, 2013, 33(10): 8-17, 24.
[11] 邹毅军, 魏明洋. 模块化多电平换流器子模块故障模拟方法[J]. 电气技术, 2022, 23(4): 96-101.
Zou Yijun, Wei Mingyang. Fault simulation method for sub-module in modular multilevel converter[J]. Electrical Engineering, 2022, 23(4): 96-101.
[12] Deng Fujin, Lü Yongqing, Liu Chengkai, et al. Over- view on submodule topologies, modeling, modulation, control schemes, fault diagnosis and tolerant control strategies of modular multilevel converters[J]. Chinese Journal of Electrical Engineering, 2020, 6(1): 1-21.
[13] Nami A, Liang Jiaqi, Dijkhuizen F, et al. Modular multilevel converters for HVDC applications: review on converter cells and functionalities[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 18-36.
[14] Choi U M, Blaabjerg F, Lee K B. Study and handling methods of power IGBT module failures in power electronic converter systems[J]. IEEE Transactions on Power Electronics, 2015, 30(5): 2517-2533.
[15] Wang Zhiqiang, Shi Xiaojie, Tolbert L M, et al. A di/dt feedback-based active gate driver for smart switching and fast overcurrent protection of IGBT modules[J]. IEEE Transactions on Power Electronics, 2014, 29(7): 3720-3732.
[16] Krone T, Xu Chengzhi, Mertens A. Fast and easily implementable detection circuits for short circuits of power semiconductors[J]. IEEE Transactions on Industry Applications, 2016, 53(3): 2871-2879.
[17] Lamb J, Mirafzal B. Open-circuit IGBT fault detection and location isolation for cascaded multi- level converters[J]. IEEE Transactions on Industrial Electronics, 2017, 64(6): 4846-4856.
[18] 于泳, 蒋生成, 杨荣峰, 等. 变频器IGBT开路故障诊断方法[J]. 中国电机工程学报, 2011, 31(9): 30-35.
Yu Yong, Jiang Shengcheng, Yang Rongfeng, et al. IGBT open circuit fault diagnosis method for inver- ter[J]. Proceedings of the CSEE, 2011, 31(9): 30-35.
[19] Lu Bin, Sharma S. A literature review of IGBT fault diagnostic and protection methods for power inverters[J]. IEEE Transactions on industry appli- cations, 2009, 45(5): 1770-1777.
[20] Liu Chengkai, Deng Fujin, Cai Xu, et al. Submodule open-circuit fault detection for modular multilevel converters under light load condition with rearranged bleeding resistor circuit[J]. IEEE Transactions on Power Electronics, 2022, 37(4): 4600-4613.
[21] Bi Kaitao, An Quntao, Duan Jiandong, et al. Fast diagnostic method of open circuit fault for modular multilevel DC/DC converter applied in energy storage system[J]. IEEE Transactions on Power Electronics, 2017, 32(5): 3292-3296.
[22] Zhang Jianzhong, Hu Xing, Xu Shuai, et al. Fault diagnosis and monitoring of modular multilevel converter with fast response of voltage sensors[J]. IEEE Transactions on Industrial Electronics, 2020, 67(6): 5071-5080.
[23] Wang Jun, Ma Hao, Bai Zhihong. A submodule fault ride-through strategy for modular multilevel con- verters with nearest level modulation[J]. IEEE Transactions on Power Electronics, 2018, 33(2): 1597-1608.
[24] Liu Zehao, Xiao Lan, Wang Qin, et al. Open-circuit fault diagnosis for MMC based on event-triggered and capacitor current state observation[J]. IEEE Transa- ctions on Circuits and Systems II: Express Briefs, 2022, 69(2): 534-538.
[25] Deng Fujin, Chen Zhe, Khan M R, et al. Fault detection and localization method for modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2015, 30(5): 2721-2732.
[26] Pang Yuqi, Ma Gang, Xu Xiaotian, et al. RNN-based fault detection method for MMC photovoltaic grid- connected system[J]. Recent Advances in Electrical & Electronic Engineering, 2021, 14(7): 755-766.
[27] Kiranyaz S, Gastli A, Ben-Brahim L, et al. Real-time fault detection and identification for MMC using 1-D convolutional neural networks[J]. IEEE Transactions on Industrial Electronics, 2019, 66(11): 8760-8771.
[28] Deng Fujin, Jin Ming, Liu Chengkai, et al. Switch open-circuit fault localization strategy for MMCs using sliding-time window based features extraction algorithm[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(10): 10193-10206.
[29] An Yang, Sun Xiangdong, Yuan Qing. IGBT open circuit fault diagnosis method for a modular multi- level converter based on PNN-MD[C]//2020 4th International Conference on HVDC (HVDC), Xi'an, China, 2020: 911-916.
[30] Jiang Siyu, Wang Bin, Xu Wanwan. Fault diagnosis of modular multilevel converter based on principal component analysis and support vector machine[J]. Journal of Physics: Conference Series 2021, 2030(1): 012086.
[31] Qu Xiaoyu, Dong Kun, Zhao Jianfeng, et al. An identification and location method for power quality disturbance sources in MMC converter based on KNN algorithm[C]//2021 4th International Conference on Energy, Electrical and Power Engineering (CEEPE), Chongqing, China, 2021: 170-177.
[32] Yang Qichen, Qin Jiangchao, Saeedifard M. Analysis, detection, and location of open-switch submodule failures in a modular multilevel converter[J]. IEEE Transactions on Power Delivery, 2016, 31(1): 155- 164.
[33] Li Cui, Liu Zhenxing, Zhang Yong, et al. Diagnosis and location of the open-circuit fault in modular multilevel converters: an improved machine learning method[J]. Neurocomputing, 2019, 331: 58-66.
[34] 李翠, 刘振兴, 柴利, 等. 模块化多电平换流器的子模块开路故障检测方法[J]. 中国电机工程学报, 2017, 37(23): 6995-7003, 7091.
Li Cui, Liu Zhenxing, Chai Li, et al. An open circuit fault detection method for sub-modules in modular multi-level converters[J]. Proceedings of the CSEE, 2017, 37(23): 6995-7003, 7091.
Abstract Modular multilevel converter (MMC) is drawing increasing attention in high-voltage direct- current (HVDC) transmission. Due to the numerous cascaded sub-modules (SMs), safety is one of the most important challenges for MMC. The open-circuit faults for SMs may distort the output voltage and current of MMC and even destroy the system if the faults are not handled in time. Therefore, this paper will concentrate on SM open-circuit faults. In general, the research for fault detection and location (FDL) of SM open-circuit is mainly divided into three basic approaches: (1) sensor-based, (2) model-based, and (3) machine learning (ML)-based. Sensor-based methods can realize FDL quickly but need extra hardware costs, which may also add potential points of fault. Model-based methods are relatively sensitive to uncertain system parameters and environmental noise because of the requirement for an accurate mechanism model of the circuit. This paper proposes a diagnostic strategy based on machine learning (ML) to detect and locate the sub-module open-circuit fault.
Firstly, the operation principle of MMC and SMs are analyzed to find that the capacitor voltages of faulty SMs will be different from the normal capacitance voltage. SM capacitor voltages can be regarded as the indicator for fault detection and location. The sliding window divides the long original data into multiple short data fragments, and 12 features of SM capacitor voltages are extracted as the feature vectors for the anomaly detection model. Secondly, the open circuit fault diagnosis problem can be transformed into a multivariate Gaussian anomaly detection problem according to the feature extraction of the capacitor voltage of SMs. The model based on multivariate Gaussian distribution is demonstrated to make predictions for anomaly detection and trace back the predicted faulty SM. Then, the fault detection and location method based on multivariate Gaussian distribution is presented to locate the faulty SM. If the probability density of the vector to be diagnosed is greater than the threshold value, it can be determined that the SM is normal. If the probability density is less than the threshold value, the SM is in a fault state. When the open circuit fault is diagnosed for N consecutive cycles, the SM is judged as faulty. Finally, simulation and experiment verify the effectiveness of the proposed FDL method.
In summary, an SM open-circuit FDL method based on multivariate Gaussian distribution is proposed in this paper. After the analysis of the fault characteristics, the voltages of SM are chosen as the indicators of FDL. Sliding window and feature extraction are used to construct the dataset for the ML model. The model based on multivariate Gaussian distribution is trained for anomaly detection. After the fault is detected, it can be located by tracing the corresponding SM number. This method can get high generalization accuracy without extra sensors or an accurate mathematical model of MMC. According to the simulation and experiment results, the effectiveness of the proposed method can be proven by the different evaluation indexes.
keywords：Modular multilevel converter, open-circuit fault detection, multivariate Gaussian distribution
DOI: 10.19595/j.cnki.1000-6753.tces.220777
中图分类号：TM46
国家自然科学基金资助项目（52007166, 52107214）。
收稿日期 2022-05-10
改稿日期 2022-08-30
杨贺雅 女，1991年生，博士，特聘副研究员，研究方向为大功率变流与控制技术。E-mail: yangheya@zju.edu.cn
向 鑫 男，1990年生，博士，研究员，研究方向为新能源发电并网和柔性直流输配电技术。E-mail: xiangxin@zju.edu.cn（通信作者）
（编辑 陈 诚）