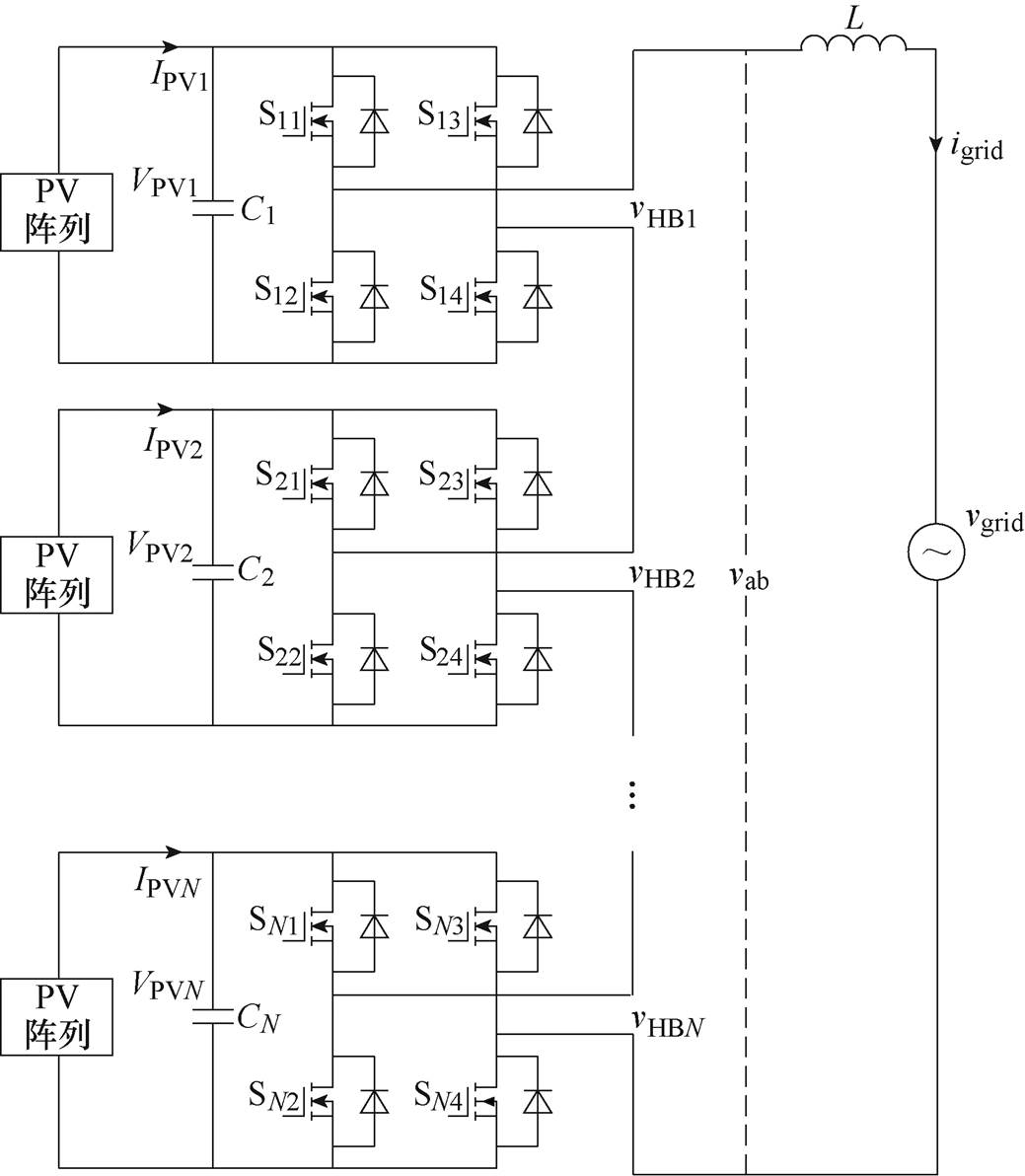
图1 级联H桥光伏并网逆变器主电路
Fig.1 Digram of cascaded H-bridge PV grid-tied inverter
摘要 在光伏逆变等以传递有功功率为主的应用场合，由于部分光伏模块光照被遮挡、老化等原因造成模块间功率不平衡较严重时，传统调制波注入策略控制的级联H桥并网逆变器会出现并网电流畸变的问题。传统调制波注入策略中不平衡模块的调制信号微调量为部分调制波，而该文提出由方波（与电流同相位）和共同调制波的部分差值量作为微调量，从而实现功率不平衡下的控制。该文所提方法除了具有谐波补偿法的优点（最高调制比达1.27），同时还具有以下两个特点：①能够进一步提高功率较高模块的工作能力（所提方法不仅使高功率模块的调制波基波峰值可达到1.27，而且使此模块的基波电压和电流同相位，从而传输最大有功功率）；②能够克服谐波补偿法中的低功率模块因叠加过多反向谐波而部分区域过调制导致的并网电流畸变问题。仿真和实验验证了所提方法的有效性。
关键词：级联H桥 电流畸变 功率不平衡 改进策略
开发新能源、减少化石能源的消耗进而降低二氧化碳的排放，是人类的共识。在新能源中，光能具有丰富且转化方便的优点，因而得到广泛的应用。多电平变换器能够提高光伏逆变器的输出电流质量，还具有减小滤波器体积、减小电磁噪声等特点。在多电平变换器中，级联H桥和其他多电平逆变器相比，具有模块化、布局简单、高可靠性等优点，从而获得了广泛的应用[1-7]。
级联H桥变换器直流侧可以接光伏电池板，实现每个模块直流侧光伏电池板的独立最大功率点跟踪（Maximum Power Point Tracking, MPPT），具有提高光伏逆变器效率的优势[8-9]。另外，级联H桥光伏逆变器具有模块级监控功能，能够使每个模块工作在较低开关频率且输出较高质量的并网电流。
然而，实际运行时由于直流侧光伏电池板被遮挡、老化等原因导致级联H桥各个模块直流侧功率不一致（不匹配），部分H桥功率变低，调制比降低；相对地，另一部分H桥调制比升高，会出现超出工作范围、过调制现象。过调制导致电感电流畸变，不符合并网要求，严重时则可能导致振荡、过电流以及逆变器停机。因此，对于级联H桥功率不平衡问题，国内外学者进行了较多研究。文献[10-11]中，调制波注入策略（Modulation Waveform Injection Strategy, MWIS）把共同调制波的一部分被叠加到不平衡模块的调制波中，进而改变每个模块的调制波幅值，实现电容电压跟踪参考值（最大功率点电压）。文献[12-13]中，通过注入有功分量（所注入量与交流电流同相位）实现电容电压跟踪参考值。文献[10-13]所示方法在模块调制比大于1的情况下，系统进入非线性调制区[14-15]。针对此问题，文献[16]提出提高过调制模块的给定电压的控制策略，这种方法能够使得过调制模块重新进入线性调制区，达到降低电感电流（并网电流）总谐波畸变率（Total Harmonic Distortion, THD）的目的，但提高直流侧电压使得高功率模块偏离了最大功率点，导致光伏利用效率降低。文献[17-18]采用无功功率补偿策略（Reactive Power Compensation Strategy, RPCS）扩大不平衡工作范围，同样能够使过调制模块重回线性调制区，但RPCS降低了系统的功率因数。
文献[19-21]使用3次谐波补偿策略（Third Harmonic Compensation Strategy, THCS），把系统的线性调制范围从1扩展到1.155。THCS在单相中的工作原理为在高功率模块中注入正向3次谐波，同时在低功率模块中注入反向3次谐波，从而使得逆变器交流侧总输出电压中3次谐波相互抵消。THCS提高了高功率H桥的电压利用率，间接地提高了高功率模块的调制比及线性调制范围。混合调制 法[22-24]根据模块功率的相对大小及基于排序算法，选择1、0、-1或PWM模式控制相应的模块，实现电容电压平衡，但会导致光伏电压出现较大的脉 动[25-27]。基于3次谐波补偿策略，文献[25-27]提出了谐波补偿策略（Harmonic Compensation Strategy, HCS），通过在过调制模块中注入多重谐波，在非过调制模块中补偿相应量的反向谐波，从而使所注入的谐波在总输出电压中相互抵消。相比于3次谐波注入的THCS，HCS把系统的线性调制范围从1.155扩展到1.27；但高功率模块的调制波基波在工作范围上限并非和交流电流同相位，所以高功率H桥有功功率并没有被扩展到其所能输出的最大值。另外，文献[25-27]所示方法在功率不平衡严重时，若多个过调制模块的反向谐波注入到个别非过调制模块，非过调制模块可能会发生过调制（反向过调制），导致电感电流畸变。
针对文献[25-27]所存在的上述两个问题，本文提出改进的调制波注入策略（Modified Modulation Waveform Injection Strategy, MMWIS）：以与电流同相位的幅值为±1的方波和共同调制波的差值量的一部分作为微调量代替传统调制波注入策略中的微调量，从而把高功率模块的最高调制比扩展到1.27，且极限状态下高功率模块输出电压基波分量和电流同相位，使其输出有功功率达到其所能输出的最大值，从而把工作范围扩展到极限状态。本方法除了拥有谐波补偿法的优点外，同时还具有以下两个特点：①能够进一步提高功率最高模块的工作能力（本文所提方法不仅使功率最高模块的调制波基波峰值达到1.27，而且使此模块的基波电压和电流同相位，从而传输最大有功功率）；②能够克服谐波补偿法中的低功率模块部分区域过调制导致的并网电流畸变问题。
图1所示为N个H桥级联构成的光伏并网逆变器主电路，每个H桥的直流侧接滤波电容和光伏模块，每个H桥交流侧串联后形成含2N+1个电平的多电平电压vab，经过滤波电感L后并入电网vgrid。VPVi、IPVi、Ci分别为第i个模块的直流侧光伏模块输出电压、电流和滤波电容。Si1～Si4为第i个模块的开关管。
图1 级联H桥光伏并网逆变器主电路
Fig.1 Digram of cascaded H-bridge PV grid-tied inverter
级联H桥光伏并网逆变器要实现两个功能:直流端口要能具有MPPT功能，控制光伏板的电压VPVi工作于MPPT输出的最大功率点参考电压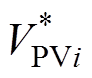
；级联H桥系统输出端口要能向电网输出高质量的交流电流，进行单位功率因数并网。根据上面两个基本要求，常使用如图2和图3所示的含总电压环和电流环、最大功率跟踪环的基本环路控制框图。
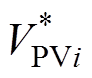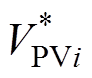图2中，变换器工作时，MPPT模块产生每个光伏模块的最大功率点参考电压。总与实际反馈的总VPVi经过PI调节后产生并网电流的有功幅值指令
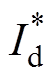。系统没有无功补偿要求情况下，无功指令
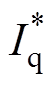为零。锁相环（Phase Locked Loop, PLL）输出电网电压的实时角度wt和峰值Vm。并网电流信号igrid及其延迟90 °的信号igD经过Park变换后产生dq坐标系下的有功反馈量Id和无功反馈量Iq。参考值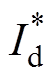、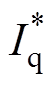以及反馈量Id、Iq经过内环的PI调节后产生有功和无功控制量vsd、vsq，从而得到内环输出的共同调制比M和共同调制信号角度a 分别为
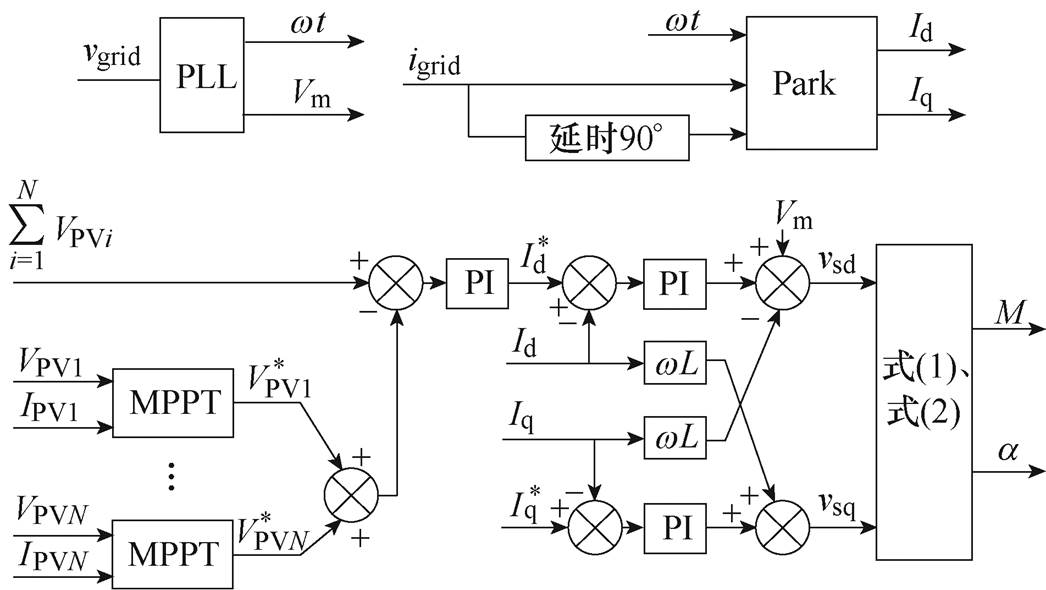
图2 系统总直流电压和并网电流控制框图
Fig.2 Block diagram of total DC voltage and current control
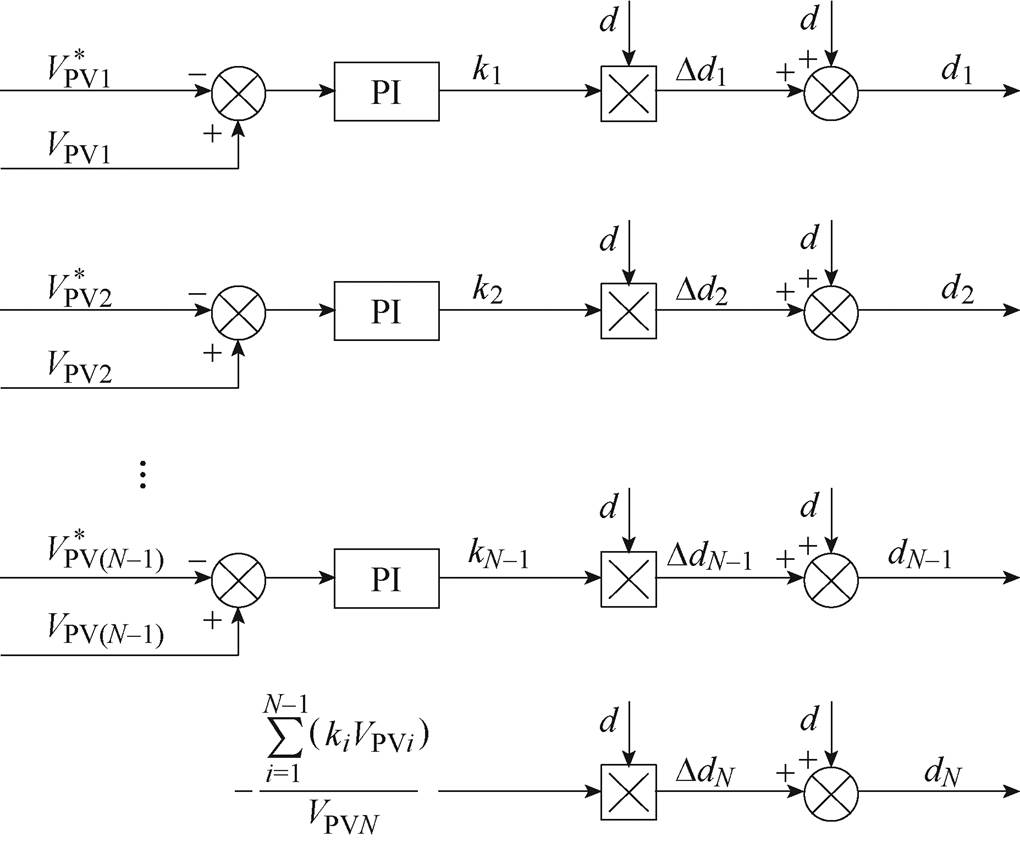
图3 传统调制波注入法直流电压跟踪指令电压控制框图
Fig.3 Control block diagram of individual DC voltage tracking its reference in conventional MWIS
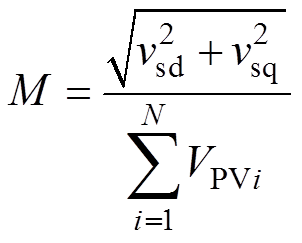（1）
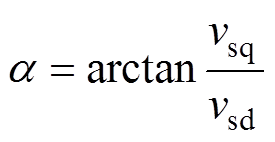（2）
由式（1）、式（2）得到共同调制信号为
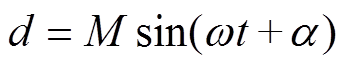（3）
当第i个光伏模块的输出电压高于参考值时，其对应的H桥需要提高其有功功率以降低其直流侧电容电压，通过注入和共同调制信号d同相位的微调量Ddi，从而提高该模块的调制波幅值，让光伏输出电压向参考值靠拢。调制信号微调量Ddi由电容电压平衡PI调节器输出值ki和共同调制信号d相乘得到，即
（4）
式中，最后一个模块的微调量系数kN为
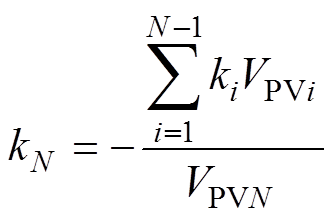（5）
式（5）可以保证每个H桥微调量Ddi所调制出的微调电压总和为零，即
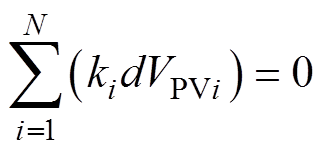（6）
每个模块的调制信号由共同调制信号及其微调量构成，即
（7）
由于调制比最大值为1，Ddi的最大值为(1-M)sin(wt+a)。调制信号可扩展区域如图4所示。图4a中的A区域为注入量可调节区域。当ki=0时，Ddi=0，di对应图4a中的Msin(wt+a)曲线；当ki= (1-M)/M时，di对应图4a中的单位调制波sin(wt+a)曲线，Ddi对应A区域；当0＜ki＜(1-M)/M时，Ddi对应A区域的一部分，即相当于A区域的一部分被注入到每个H桥的调制信号中。
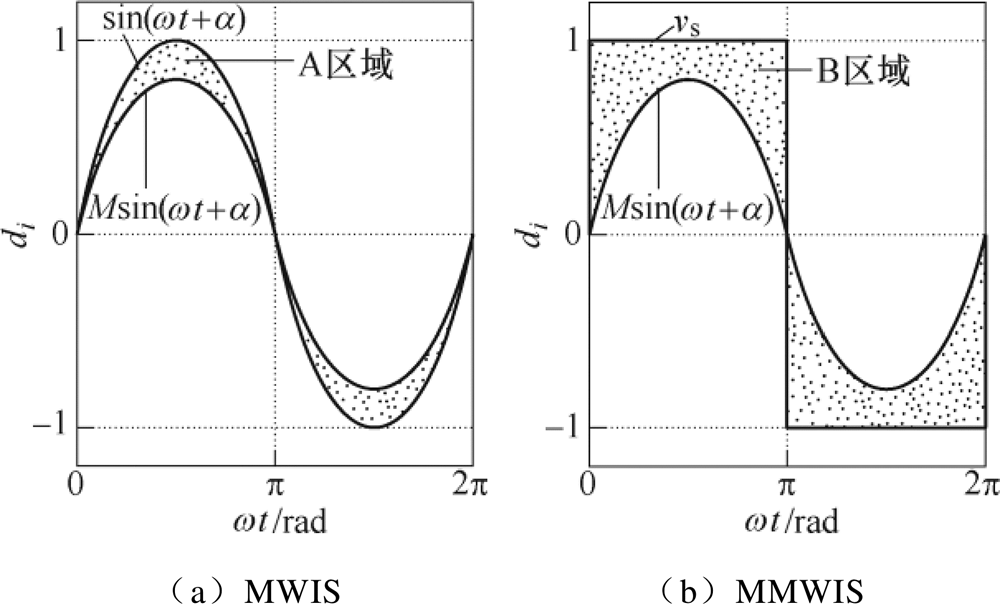
图4 调制信号可扩展区域
Fig.4 Modulation signal expandable region
当功率不平衡时，把图4b中B区域部分乘以系数ki叠加到原有调制波中，则功率较高的模块将能够传输更多的有功功率，不平衡功率处理能力将得到加强。若图4b中的方波vs的相位和电感电流同相位，当把B区域全部注入到此模块原调制信号中时，此模块的调制波为方波，并且和电流igrid同相位，意味着在流经此模块的交流侧电流Ig（igrid的有效值）的情况下，将输出有功功率的最大值，从而把不平衡运行能力扩展到最大。
当高功率模块被注入正向B区域微调分量时，低功率模块将被注入反向B区域调节分量。反向调节分量有可能会造成低功率模块调制波幅值超出载波幅值，即反向过调制问题，这个问题也将在本文得到解决。
图4b中，和电感电流同相位的方波vs定义为
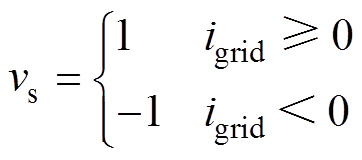（8）
图4b中的B区域表示方波和共同调制波差值部分，可描述为
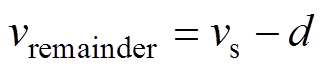（9）
MMWIS待注入的波形如图5所示。
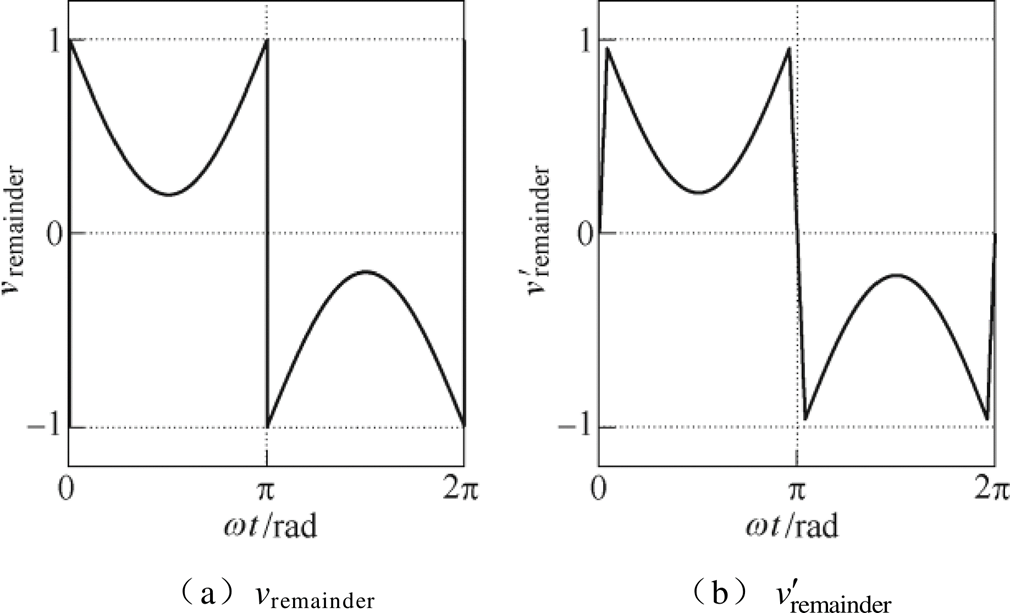
图5 MMWIS待注入的波形
Fig.5 Waveforms to be injected by MMWIS
当功率不平衡时，把vremainder的一部分即kivremainder注入到此模块的调制波中实现电容电压跟踪控制。但是，图5a所示的vremainder含有阶跃变化，DSP数字控制的载波移相单极性PWM载波互相延迟p/N，调制信号一般不立即更新，而是在三角载波的顶点或零点更新。因为延迟更新，调制波的阶跃变化在载波移相调制下会导致并网电流畸变。为消除阶跃变化，把vremainder中的阶跃变化部分替换为斜坡，得到如图5b所示的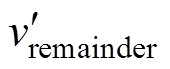
，其可描述为
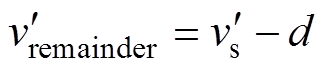（10）
其中
（11）
在实际应用中，斜坡的斜率小于一定值以后，调制信号阶跃变化不对并网电流THD产生影响。对THD无影响的斜率可以通过仿真和实验获取。
根据每个模块的电容电压调节器输出值（即注入系数）ki，每个H桥的调制信号di被注入了微调量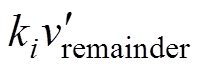
，即
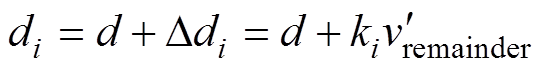（12）
式中，第N个模块的微调系数kN仍按式（5）进行求解，从而能够保证每个H桥微调信号Ddi所调制出的电压总和为0，即
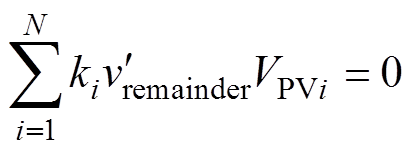（13）
调制信号di构成示意图如图6所示。当ki取不同值时，di的波形如图6c和图6f所示。以M=0.8为例，共同调制信号d如图6a所示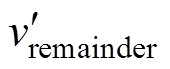，如图6b中ki=1所示曲线。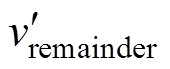乘以不同系数ki得到图6b中各条曲线；图6b中各微调信号曲线和共同调制信号d相加得到图6c所示的调制信号波形；当ki=1时，di的曲线和
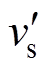的曲线重合。
当ki=1时，表示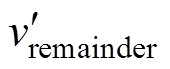全部注入到此模块的原调制波中，达到最大值状态，所以输出ki的比例积分（PI）调节器的最大饱和值应设置为1，如此将不会造成高功率模块调制信号幅值大于1或小于-1的问题（过调制问题）。注入反向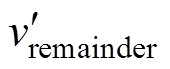导致过调制及其解决方法如图7所示。
但对于一个ki＜0的低功率模块，由于被注入反向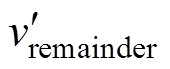，则可能会导致调制信号幅值超出载波幅值±1的过调制问题，如图7a所示。造成此问题的原因为系统中多个H桥的微调量为正向微调量，少数模块为反向微调量，因为所有H桥微调量产生的微调电压总和应该为0，所以造成少数低功率模块出现反向微调量幅值相对较大，继而导致过调制问题。反向过调制问题在HCS中也存在，会导致并网电流畸变，影响并网电能质量，需要加以解决。
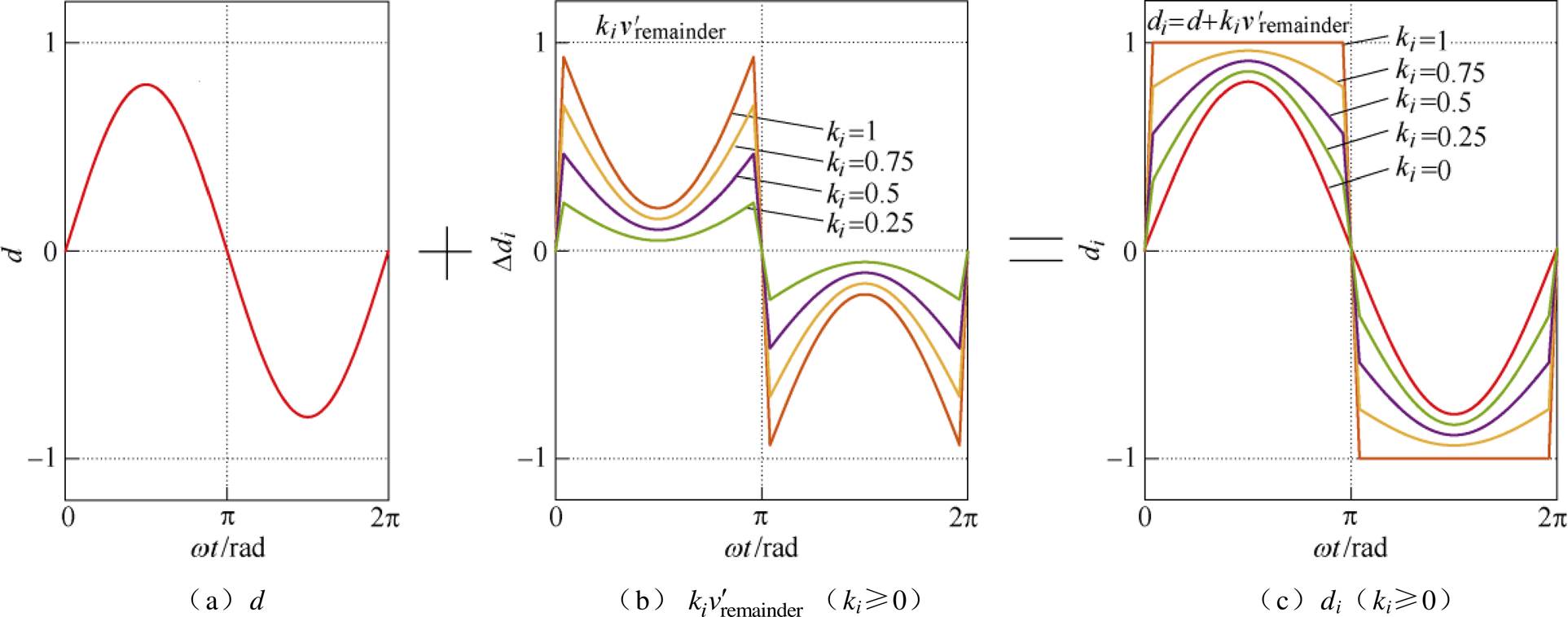
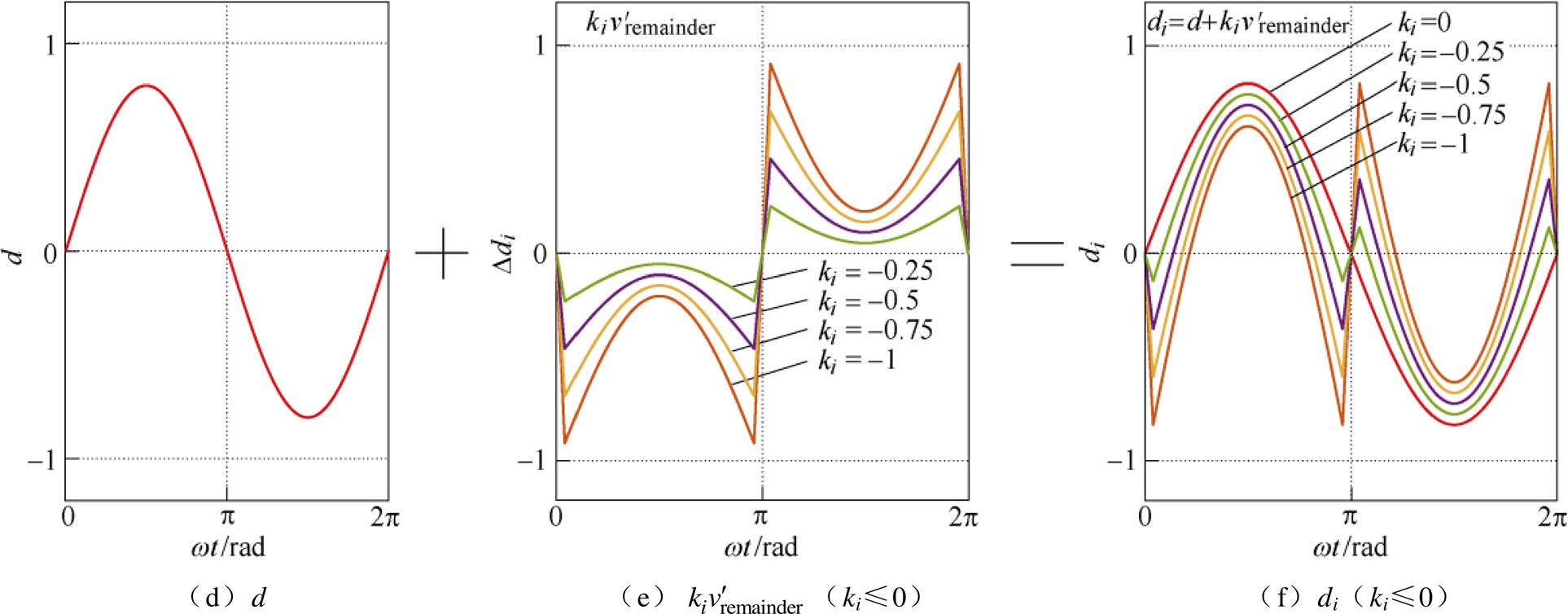
图6 调制信号di构成示意图
Fig.6 Components of the modulation signals
反向过调制解决方法如图7所示。图7a j 处的调制信号di中的共同调制信号d的瞬时值为正，其所能叠加的最大反向调节量Ddi的幅值为|d+1|；但此时式（12）中的微调量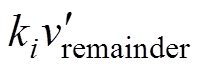的幅值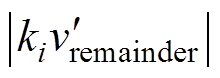
＞|d+1|，所以造成了di此刻低于-1。从式（13）可以看出，微调量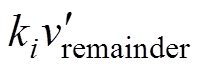乘以一个系数以后，式（13）仍然成立；即每个H桥由微调信号Ddi所调制出的微调电压总和为零。每个模块调制信号di中的微调量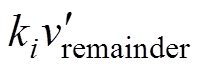可以同乘以一个共同的系数以解决j 处的过调制问题，反而不引起并网电流畸变。把j 处的微调量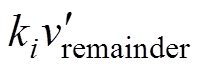乘以系数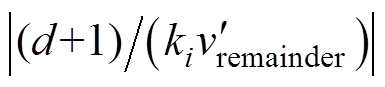
后，可以正好让此时的di变为-1，从而解决了di＜-1的过调制问题。
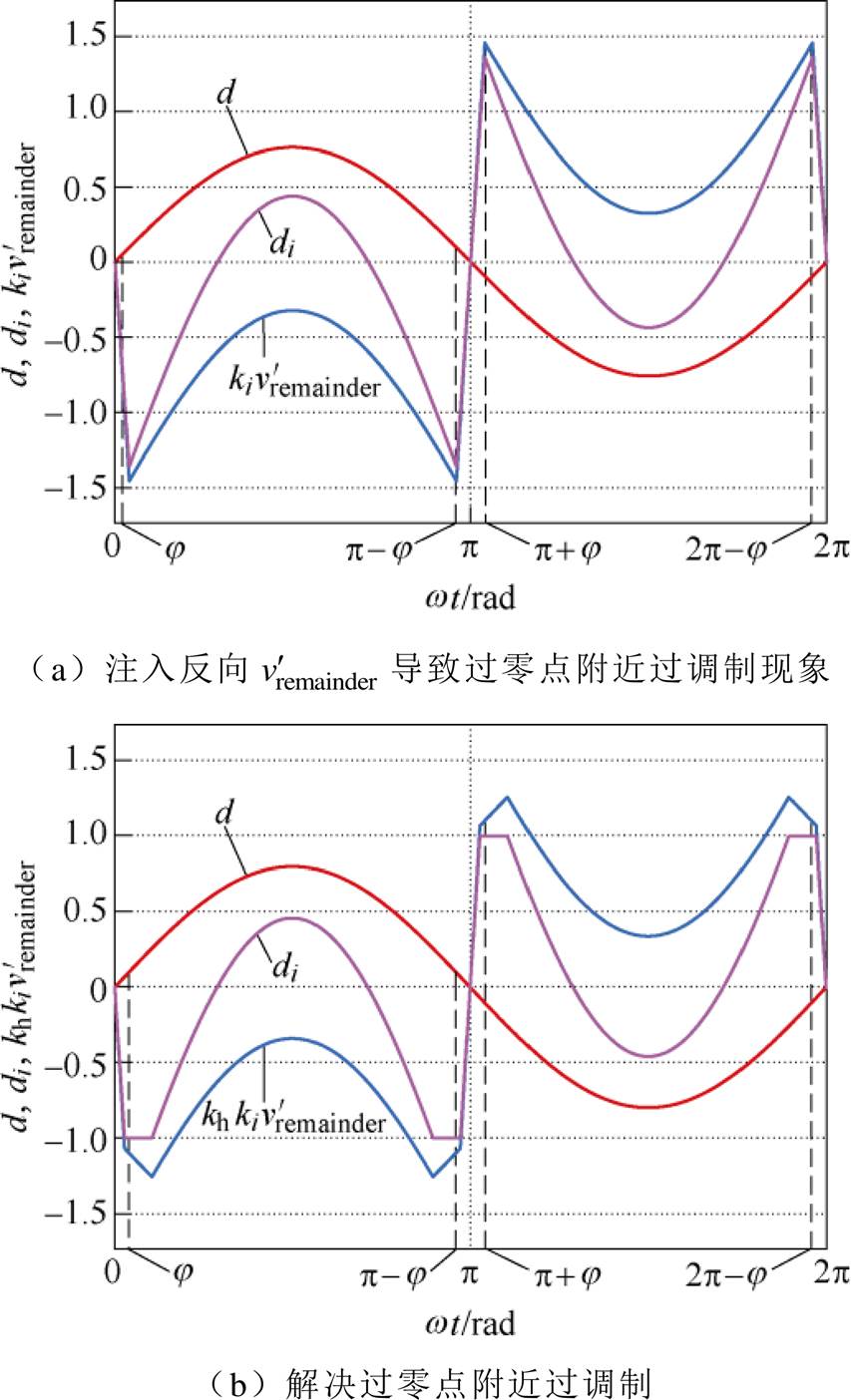
图7 注入反向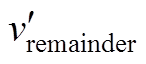
导致过调制及其解决方法
Fig.7 Injection of reverse 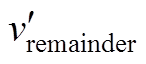leads to overmodulation and its solution
每个模块微调量Ddi应该被乘以的系数为
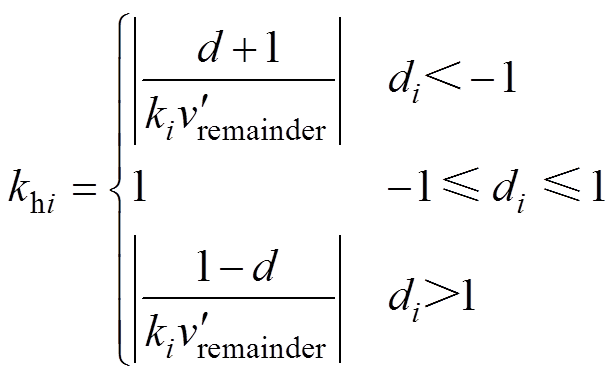（14）
为保证式（13）成立，每个H桥的同一运算执行周期中微调量Ddi应该被乘以该时刻共同的系数。应取khi（i=1, 2,…, N）中最小值作为该共同系数，即
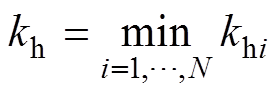（15）
把每个模块调制波中的微调量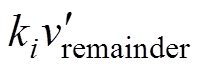乘以系数kh，然后和共同调制信号d组合成新的调制信号
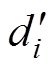为
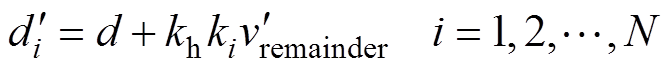（16）
式中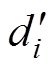，为最终和三角载波比较的调制信号。
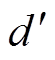乘以系数kh后，虽然过零点附近j 处的注入量减少了，但均压环会通过PI调节器自动使电容电压维持在给定值；最终的结果是，其他区域的注入量增加，从而使总注入量保持不变。
MMWIS调制波产生过程小结如下：首先求出H桥的共同调制信号d。功率不平衡时需要注入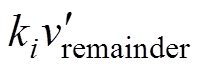（高功率模块ki为正，低功率模块ki为负）。对于功率不平衡严重时，会出现反向过调制的情况，本文利用基本平衡公式，解决了反向注入
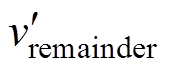而导致的过调制问题。经过以上三步，得出了MMWIS调制波完整实现式（16），其在不平衡下的效果和现有控制方法的性能比较，将在仿真和实验中得到 展现。
本节对MMWIS控制策略进行仿真证明，并且和MWIS、RPCS、THCS、HCS等控制策略进行了对比，比较了这五种控制方法在功率不平衡状态下的调制信号、并网电流质量、直流侧的电压波动量。仿真参数见表1。
级联H桥变换器在平均调制比较高，即直流电压总和较低的时候，处理不平衡功率的能力变弱，此时出现模块间功率不平衡，对系统的危害更大。光伏电池板夏天在强烈的光照下温度较高，最大功率点电压较低，直流电压总和较低，所以仿真时光伏模块的温度设置为45°。
表1 仿真参数
Tab.1 Simulation parameters
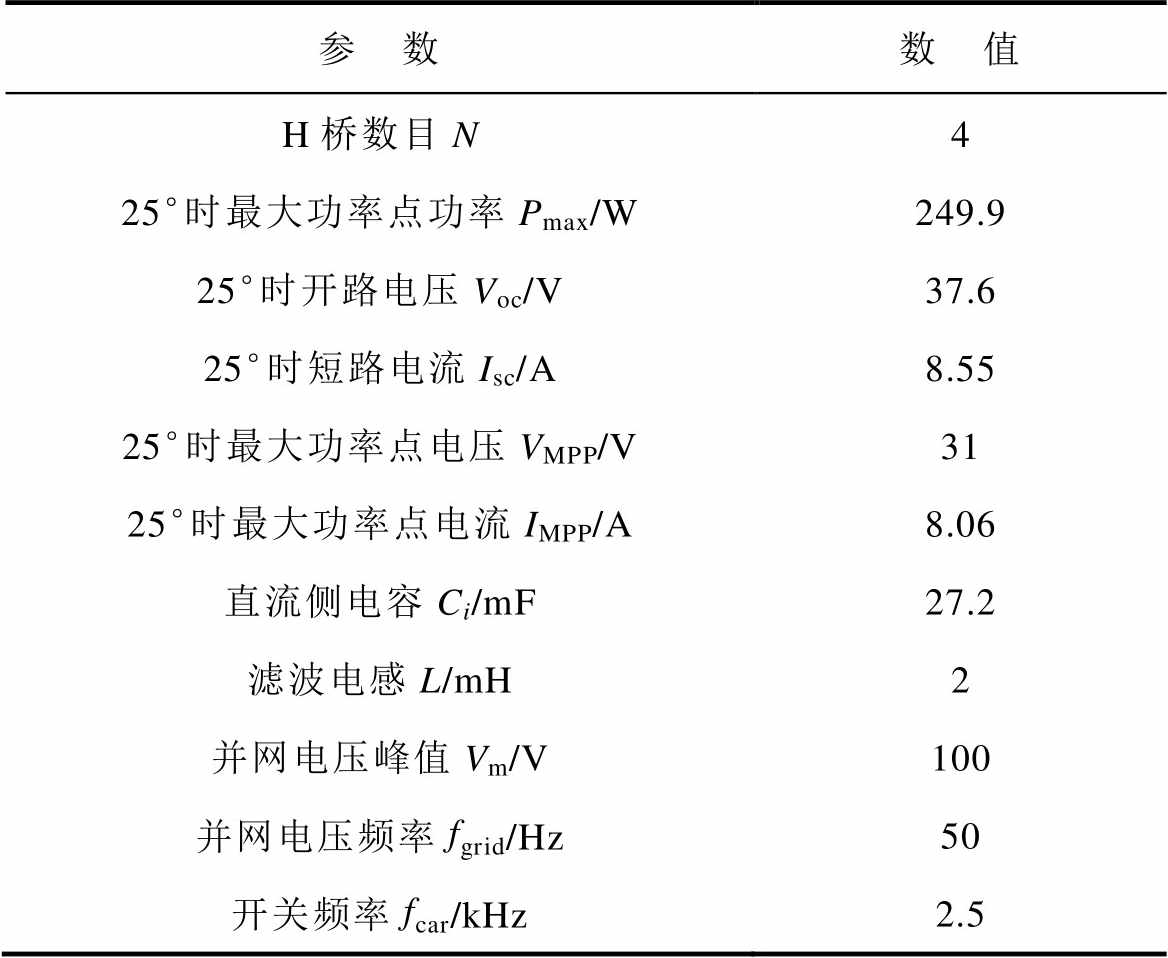
参 数数 值 H桥数目N4 25°时最大功率点功率Pmax/W249.9 25°时开路电压Voc/V37.6 25°时短路电流Isc/A8.55 25°时最大功率点电压VMPP/V31 25°时最大功率点电流IMPP/A8.06 直流侧电容Ci/mF27.2 滤波电感L/mH2 并网电压峰值Vm/V100 并网电压频率fgrid/Hz50 开关频率fcar/kHz2.5
图8展示了MMWIS控制策略下几种不平衡状态时的仿真波形。在0.52 s前，4个模块功率平衡，光照强度E1=E2=E3=E4=900 W/m2，P1=P2=P3=P4=206 W，调制比M=0.88，并网电流THD=1.0 %，光伏模块1输出电压的波动量Du=0.87 V。t=0.52 s时模块3光照强度变为E3=600 W/m2，输出功率变为P3=137 W，其他模块的光照强度和功率保持不变；该状态下并网电流THD=1.5 %，Du=0.77 V，模块1和模块2的调制比最高，为0.97。t =0.77 s时，模块4的光照强度E4变为300 W/m2，输出功率变为67 W，其他模块光照强度和功率维持不变。该工况下THD= 2.2 %，Du=0.62 V，模块1和模块2的调制比为1.20。从图8可以看出，MMWIS不仅动态过程无畸变，而且稳态下并网电流畸变小。
图9比较了MWIS、MMWIS、RPCS、THCS、HCS方法的控制效果，采用同样的仿真参数：E1= 1 000 W/m2，E2=E3=900 W/m2，E4=100 W/m2，P1= 229 W，P2=P3=206 W，P4=20 W，温度为45 °。此工况下光伏模块输出功率不平衡差异较大，系统的最高调制比达到了1.24。图9a为MWIS的仿真波形，THD=45.3 %，并网电流畸变严重，谐波含量非常大；而本文所改进的MMWIS仿真波形如图9b所示，THD=2.1 %。
对于RPCS，从图9c中可以看到，变换器不再是单位功率因数（Power Factor, PF）运行，PF=0.41。为了消除过调制现象，功率因数被降低；使用MMWIS时，电感电流峰值只有14 A，而采用RPCS时，电感电流为29 A，大大增加了变换器的电流应力，易出现过电流的危险。
图8 MMWIS仿真波形
Fig.8 Simulation waveforms of MMWIS
图9d为3次谐波注入法THCS仿真波形，由于THCS最高等效调制比只能达到1.155，第1个模块出现了过调制，如图9d中的d1所示，并网电流出现畸变，THD=12.2 %。
对于HCS（见图9e），前3个模块调制波中基波含量以外的谐波被分配在模块4的调制波d4中，由于模块4的调制波d4被补偿了过量的谐波，导致其在部分区域调制信号的幅值大于载波的最大值1或小于载波的最小值-1，导致并网电流畸变，THD= 7.6 %。本文所提的式（16）使得本文所提方法克服了这一问题；在相同的工况下，本文所提方法仍然能够输出高质量的并网电流，并使得每个模块都工作在MPPT状态。
直流电压二倍频纹波与瞬时功率波动有关。当调制比等于1时，MWIS、RPCS、THCS、HCS的调制波峰值达到1，而本文所提方法只有在调制比达到1.27时，调制波峰值才达到1。所以，在图9中，MMWIS控制下，第一个H桥的瞬时功率峰值较小、瞬时功率波动较小，使得直流电压波动较小。
通过对比可以看出，本文所提的MMWIS比RPCS有更高的功率因数。在严重不平衡下比MWIS、HCS和THCS有更低的THD。本文所提的MMWIS在功率不平衡较大时性能优越。
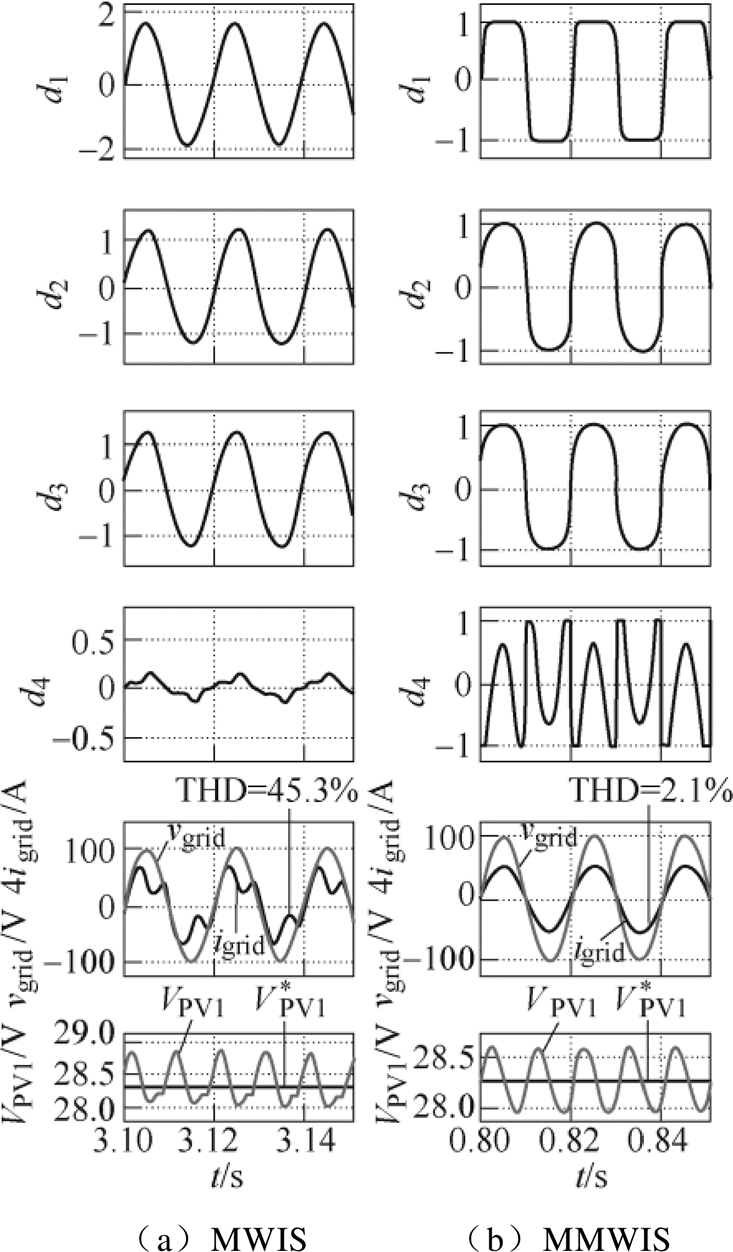
图9 严重不平衡时MWIS、MMWIS、RPCS、THCS、HCS控制策略下仿真波形对比
Fig.9 Comparison of simulation waveforms of MWIS, MMWIS, RPCS, THCS, and HCS under severe unbalanced strategies
为了通过实验验证MMWIS方法的可行性和优越性，搭建了如图10所示基于数字控制芯片TMS320F28377D的4模块级联H桥光伏并网逆变器实验平台，将4个光伏模拟器（Chroma62150H- 1000S）发出的能量回馈至电网模拟器（Chroma 61830）。实验参数和仿真参数相同。
图10 实验平台
Fig.10 Experimental platform
图11为MMWIS的动态和稳态实验波形。图11a为4个模块从工况1（4个模块功率平衡，光照强度E1=E2=E3=E4=900 W/m2，P1=P2=P3=P4=206 W）突变到工况2（模块3光照强度变为E3=600 W/m2，输出功率变为P3=137 W，其他模块不变）的过程。图11b为从工况2突变到工况3（模块4光照强度E4变为300 W/m2，输出功率变为67 W）过程中的主要波形。图11c～图11e分别为工况1、2、3时的稳态波形。由图11实验波形可见，不管是暂态过程还是稳态过程，MMWIS能够输出较好的电能质量，3个工况下的THD分别为1.0 %，1.6 %，2.3 %。
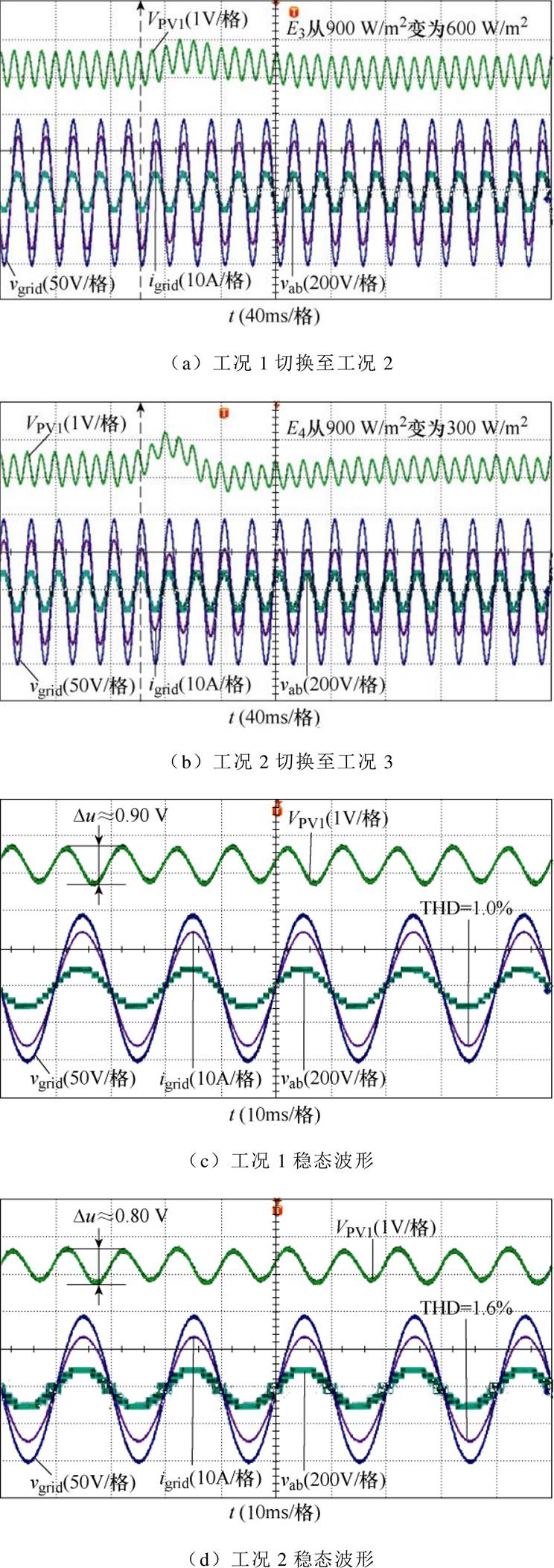
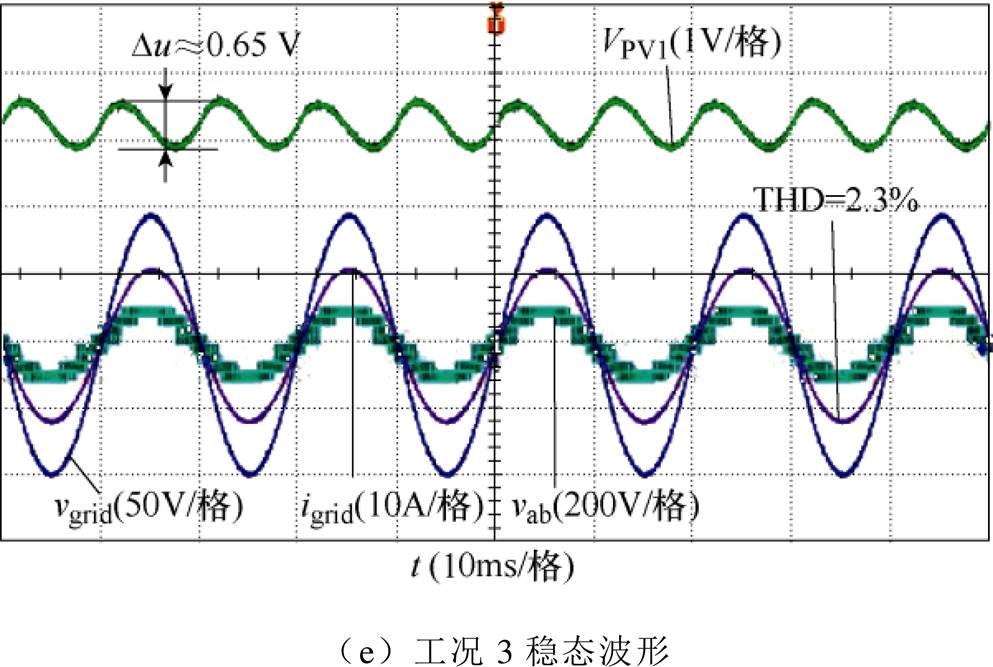
图11 MMWIS的动态和稳态实验波形
Fig.11 Dynamic and steady state experimental waveforms of MMWIS
图12～图16分别为功率不平衡工况下MWIS、RPCS、THCS、HCS、MMWIS控制策略下的实验波形。实验采用和仿真相同的参数：E1=1 000 W/m2，E2=E3=900 W/m2，E4=100 W/m2，P1=229 W，P2=P3= 206 W，P4=20 W，温度为45 °。图12为MWIS实验波形，THD=45.6 %，光伏模块1输出电压波动Du= 0.85 V，并网电流畸变严重，谐波含量非常大。
而对于RPCS，从图13中可以看到，变换器不再是单位功率因数运行，PF=0.41。为了取消过调制现象，降低功率因数。所注入的无功导致并网电流的幅值（29 A）变为实际所需电流（14 A）的2.07倍，使变换器出现过电流的风险。
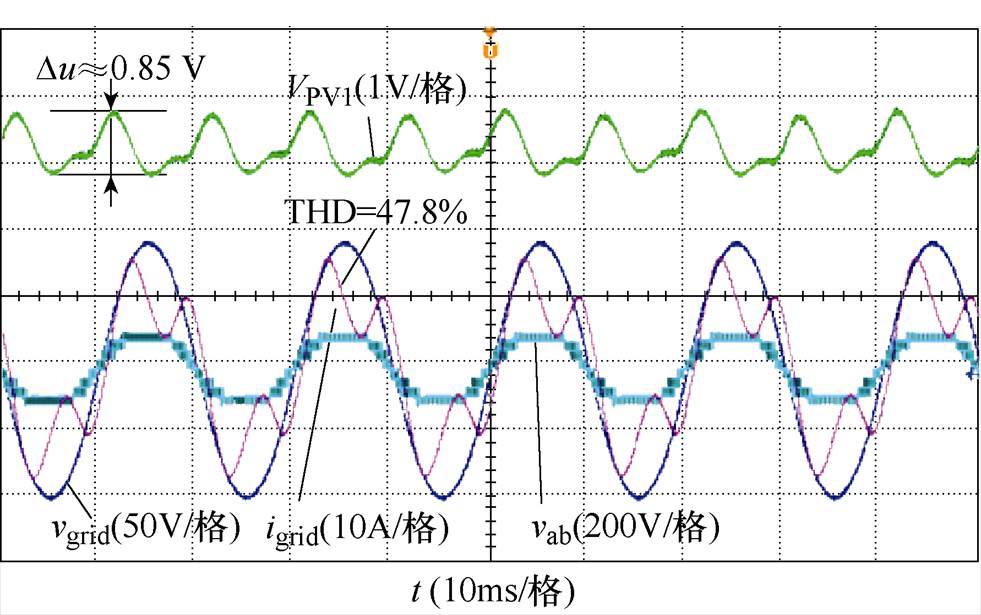
图12 MWIS实验波形
Fig.12 Experimental waveforms of MWIS
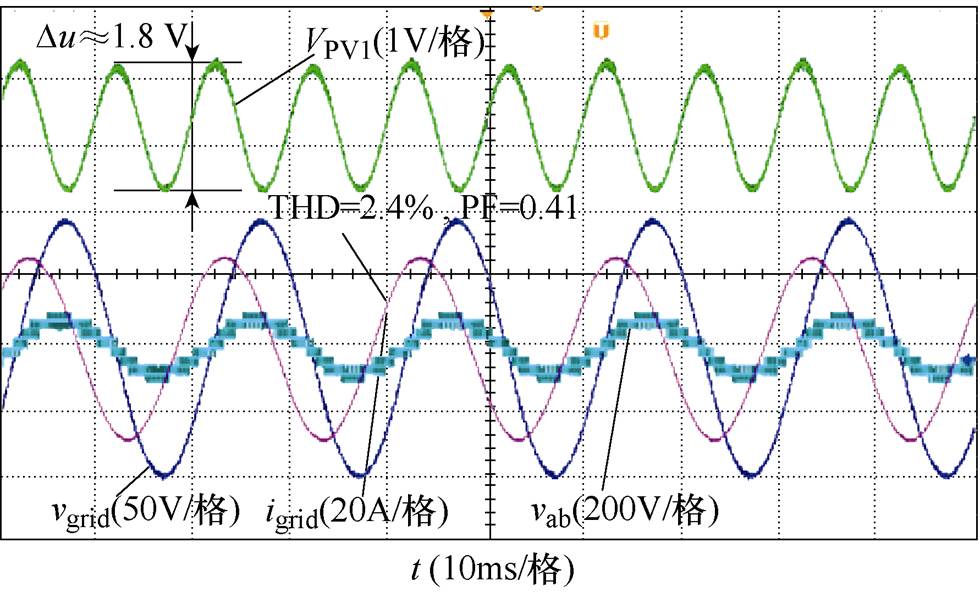
图13 RPCS实验波形
Fig.13 Experimental waveforms of RPCS
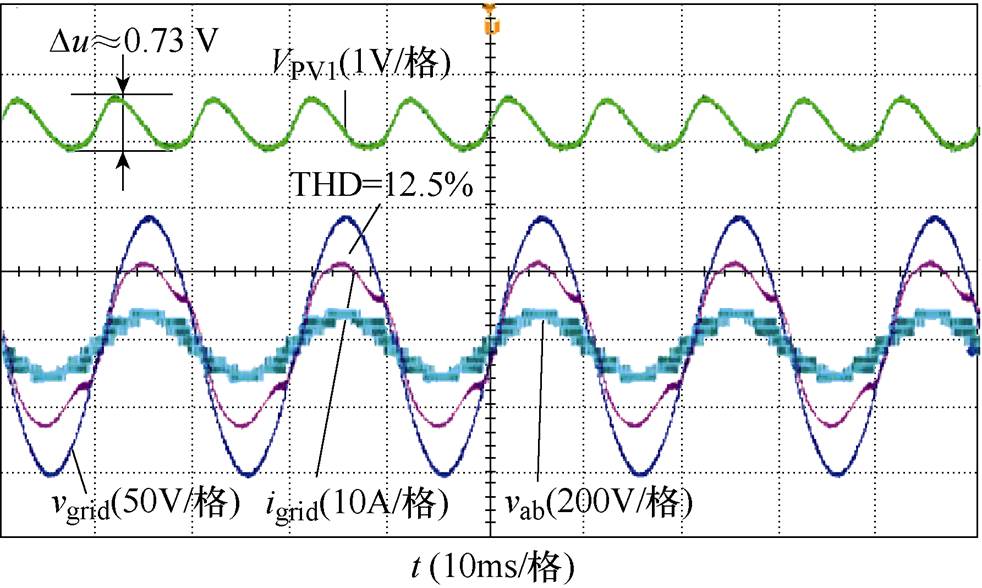
图14 THCS实验波形
Fig.14 Experimental waveforms of THCS
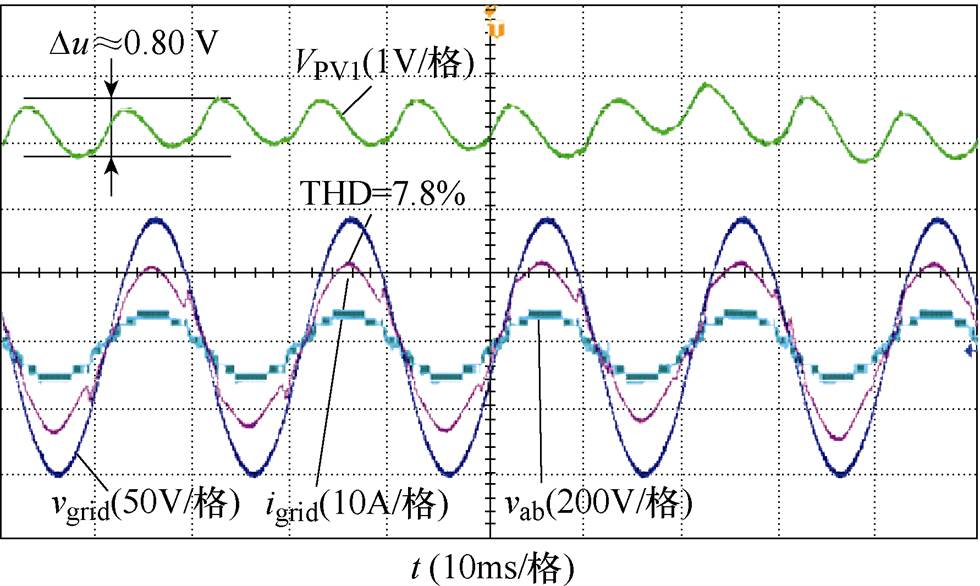
图15 同工况下HCS实验波形
Fig.15 Experimental waveforms of HCS under the same condition
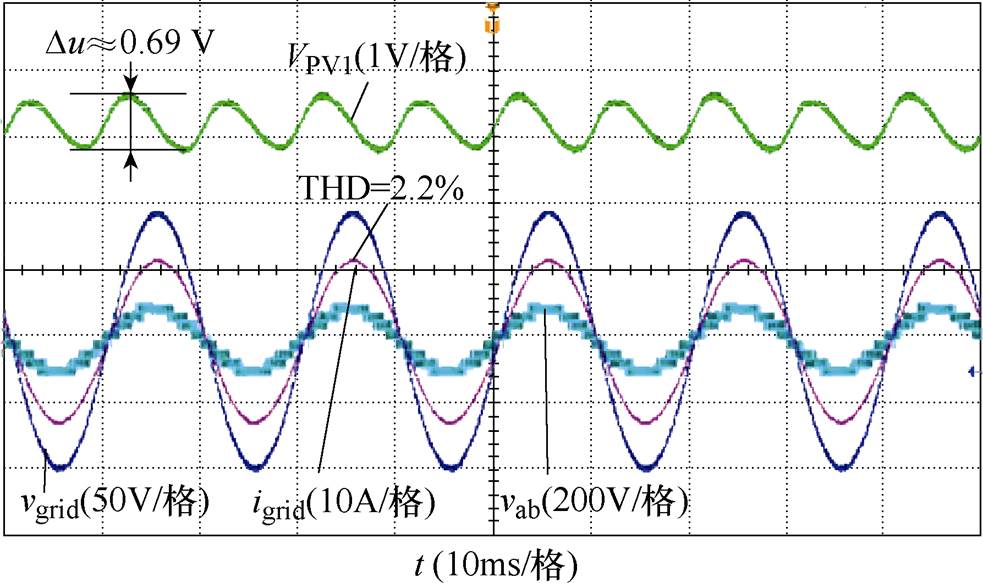
图16 MMWIS实验波形
Fig.16 Experimental waveforms of MMWIS
图14为3次谐波补偿法THCS实验波形，由于THCS最高等效调制比只能达到1.155，这种比较大的不平衡工况超出了THCS的工作范围，导致了其输出较大的谐波含量，并网电流出现畸变，THD= 12.5 %。而图15所示的HCS实验波形中，并网电流THD=7.8 %，直流电压波动为Du=0.80 V。
与MWIS、RPCS、THCS、HCS相比，图16所示的MMWIS波形不仅使系统维持了单位功率因数运行和较小电容电压波动量Du=0.69 V，而且具有较小的电流畸变（THD=2.2 %）。对比之下，本文所提的MMWIS在功率不平衡较大时性能优越。
针对级联H桥光伏并网逆变器中光伏模块输出功率不平衡工况下，系统出现过调制、并网电流畸变问题，本文提出一种新的控制方法。主要结论如下：
1）本文所提方法用与电感电流同相位的方波和共同调制波的差值量的一部分作为每个模块调制信号的微调量，实现功率不平衡下的控制。与原方法相比，本文所提控制方法进一步提高了高功率模块的工作能力，不仅使高功率模块的调制波的基波峰值达到1.27，而且使此模块的基波电压和电流同相位，从而使此模块可传输最大有功功率。
2）本文所提方法解决了低功率模块部分区域过调制（反向过调制）导致的并网电流畸变问题，提出的反向过调制解决方法很好地保证了功率严重不平衡时的电流质量，从而克服了谐波补偿策略中低功率模块存在的反向过调制问题。
参考文献
[1] 叶满园, 任威, 李宋, 等. 基于控制载波自由度的级联H桥逆变器改进型PWM技术[J]. 电工技术学报, 2021, 36(14): 3010-3021.
Ye Manyuan, Ren Wei, Li Song, et al. Improved PWM technology of cascaded H-bridge inverter based on control of carrier degree of freedom[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(14): 3010-3021.
[2] Babaei E, Laali S, Alilu S. Cascaded multilevel inver- ter with series connection of novel H-bridge basic units[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12): 6664-6671.
[3] 王琛琛, 李永东. 多电平变换器拓扑关系及新型拓扑[J]. 电工技术学报, 2011, 26(1): 92-99.
Wang Chenchen, Li Yongdong. Multilevel converter topologies and two novel topologies[J]. Transactions of China Electrotechnical Society, 2011, 26(1): 92-99.
[4] Zhang Zhiyu, Zhao Hengyang, Fu Shihang, et al. Voltage and power balance control strategy for three- phase modular cascaded solid stated transfor- mer[C]//2016 IEEE Applied Power Electronics Con- ference and Exposition (APEC), Long Beach, CA, 2016: 1475-1480.
[5] 陈轶涵, 郭鸿浩, 陈家伟. 基于载波移相控制的模块化串并联逆变器非理想条件谐波特性分析[J]. 电工技术学报, 2020, 35(8): 1690-1704.
Chen Yihan, Guo Honghao, Chen Jiawei. Analysis of harmonic characteristics in non-ideal conditions of modular series/parallel inverter based on carrier phase shift control[J]. Transactions of China Electrotech- nical Society, 2020, 35(8): 1690-1704.
[6] Zhang Yang, Chen Xin, Sun Jian. Sequence impe- dance modeling and analysis of MMC in single-star configuration[J]. IEEE Transactions on Power Elec- tronics, 2020, 35(1): 334-346.
[7] 李响, 郭希铮, 游小杰, 等. 一种改进的级联H桥整流器直流电压平衡策略[J]. 电工技术学报, 2017, 32(4): 66-75.
Li Xiang, Guo Xizheng, You Xiaojie, et al. An advanced DC voltage balance strategy for cascaded H-bridge rectifier[J]. Transactions of China Electro- technical Society, 2017, 32(4): 66-75.
[8] Yu Yifan, Konstantinou G, Hredzak B, et al. Oper- ation of cascaded H-bridge multilevel converters for large-scale photovoltaic power plants under bridge failures[J]. IEEE Transactions on Industrial Elec- tronics, 2015, 62(11): 7228-7236.
[9] Chavarria J, Biel D, Guinjoan F, et al. Energy-balance control of PV cascaded multilevel grid-connected inverter under level-shifted and phase-shifted PWMs[J]. IEEE Transactions on Industrial Electro- nics, 2013, 60(1): 98-111.
[10] Wang Liang, Zhang Donglai, Wang Yi, et al. Power and voltage balance control of a novel three-phase solid-state transformer using multilevel cascaded H-bridge inverters for microgrid applications[J]. IEEE Transactions on Power Electronics, 2016, 31(4): 3289-3301.
[11] Blahnik V, Kosan T, Peroutka Z, et al. Control of a single-phase cascaded H-bridge active rectifier under unbalanced load[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 5519-5527.
[12] 王书征, 赵剑锋, 姚晓君, 等. 级联型光伏并网逆变器在光照不均匀条件下的功率平衡控制[J]. 电工技术学报, 2013, 28(12): 251-261.
Wang Shuzheng, Zhao Jianfeng, Yao Xiaojun, et al. Power balanced controlling of cascaded inverter for grid-connected photovoltaic systems under unequal irradiance conditions[J]. Transactions of China Elec- trotechnical Society, 2013, 28(12): 251-261.
[13] She Xu, Huang A Q, Zhao Tiefu, et al. Coupling effect reduction of a voltage-balancing controller in single-phase cascaded multilevel converters[J]. IEEE Transactions on Power Electronics, 2012, 27(8): 3530- 3543.
[14] 王昕, 王琛琛, 顾长彬. 级联H桥整流器稳定运行区域和直流侧电压平衡策略的调节能力分析[J]. 电工技术学报, 2019, 34(14): 2970-2979.
Wang Xin, Wang Chenchen, Gu Changbin. Analysis about steady-state operating region and regulation capacity of voltage balance strategy for cascaded H-bridge rectifier[J]. Transactions of China Electro- technical Society, 2019, 34(14): 2970-2979.
[15] Eskandari A, Javadian V, Iman-Eini H, et al. Stable operation of grid connected cascaded H-bridge inverter under unbalanced in solation conditions[C]// Proceeding of the Third International Conference on Electrical Power Energy Conversion System, Istanbul, Turkey, 2014: 1-6.
[16] Iman-Eini H, Bacha S, Frey D. Improved control algorithm for grid-connected cascaded H-bridge photovoltaic inverters under asymmetric operating conditions[J]. IET Power Electronics, 2018, 11(3): 407-415.
[17] Liu Liming, Li Hui, Xue Yaosuo, et al. Reactive power compensation and optimization strategy for grid-interactive cascaded photovoltaic systems[J]. IEEE Transactions on Power Electronics, 2014, 30(1): 188-202.
[18] Liu Liming, Li Hui, Xue Yaosuo, et al. Decoupled active and reactive power control for large-scale grid- connected photovoltaic systems using cascaded modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 176-187.
[19] Xiao Bailu, Hang Lijun, Mei Jun, et al. Modular cascaded H-bridge multilevel PV inverter with istri- buted MPPT for grid-connected applications[J]. IEEE Transactions on Industry Applications, 2015, 51(2): 1722-1731.
[20] Ko Y, Andresen M, Buticchi G, et al. Power routing for cascaded H-bridge converters[J]. IEEE Transa- ctions on Power Electronics, 2017, 32(12): 9435- 9446.
[21] Zhao Tao, Zhang Xing, Mao Wang, et al. An opti- mized third harmonic compensation strategy for single-phase cascaded H-bridge photovoltaic inver- ter[J]. IEEE Transactions on Industrial Electronics, 2018, 65(11): 8635-8645.
[22] Zhao Tao, Zhang Xing, Mao Wang, et al. A modified hybrid modulation strategy for suppressing DC voltage fluctuation of cascaded H-bridge photovoltaic inverter[J]. IEEE Transactions on Industrial Electro- nics, 2018, 65(5): 3932-3941.
[23] Miranbeigi M, Iman-Eini H. Hybrid modulation technique for grid-connected cascaded photovoltaic systems[J]. IEEE Transactions on Industrial Elec- tronics, 2016, 63(12): 7843-7853.
[24] Moosavi M, Farivar G, Iman-Eini H, et al. A voltage balancing strategy with extended operating region for cascaded H-bridge converters[J]. IEEE Transactions on Power Electronics, 2014, 29(9): 5044-5053.
[25] Wang Mingda, Zhang Xing, Zhao Tao, et al. Harmonic compensation strategy for single-phase cascaded H-bridge PV inverter under unbalanced power conditions[J]. IEEE Transactions on Industrial Electronics, 2020, 67(12): 10474-10484.
[26] Zhao Tao, Zhang Xing, Mao Wang, et al. Harmonic compensation strategy for extending the operating range of cascaded H-bridge PV inverter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 1341-1350.
[27] Zhao Tao, Chen Daolian. A power adaptive control strategy for further extending the operation range of single-phase cascaded H-bridge multilevel PV inver- ter[J]. IEEE Transactions on Industrial Electronics, 2022, 69(2): 1509-1520.
Abstract The maximum modulation index of the cascaded H-bridge photovoltaic grid-connected inverter controlled by the conventional sinusoidal modulation wave injection strategy (MWIS) is 1, so the working range is small. When the power imbalance is severe, the MWIS will have the problem of over-modulation, leading to the distortion of the grid-connected current. As a result, the output current cannot meet the grid-connected standard, thereby reducing the harvesting ability of photovoltaic energy. In the MWIS, the fine-tuning signal of the modulation signal of each H-bridge module is a part of the modulation wave signal. This paper proposes a modified modulation wave injection strategy (MMWIS). The sinusoidal modulation wave fine-tuning signal in the MWIS can be replaced with a part of the difference between the square wave signal in the same phase as the inductor current and the common modulation wave signal, thereby improving the active power transmission range of the system.
The implementation procedures of the MMWIS are as follows. First, the PI controller in the total voltage outer loop calculates the amplitude signal of the grid-connected current. The current inner loop calculates the common modulation signal of each H-bridge unit, and the voltage produced by this modulation signal represents the multi-level voltage on the AC side of the cascaded H-bridge inverter. Second, the remainder of the common modulation wave signal subtracted from the square wave signal (in the same phase as the ac current) is multiplied by the injection coefficient output by the voltage balancing PI controller of each H-bridge unit. The modification signal of each H-bridge unit can be obtained to replace the sine wave modification signal in the MWIS. Third, the low-power cells may be over-modulated around the zero-crossing point due to the large opposite injected modification signals. During the over-modulation period of the low-power modules, the fine-tuning amounts of all modules must be multiplied by the same coefficient to solve the over-modulation problem. At the same time, this common coefficient ensures that the sum of the AC voltages produced by the modulation wave of each H-bridge unit is equal to that produced by the common modulation signal.
The simulation and experimental results are as follows. First, the MMWIS can achieve a smooth transition between various working conditions, and the inductor current distortion is small. Second, when the power imbalance is large, compared with conventional methods such as the sinusoidal modulation wave injection strategy and third harmonic compensation strategy, the MMWIS can still maintain high grid-connected current quality. Third, the DC voltage fluctuation of the high-power module is small under the control of MMWIS. Because the peak value of the modulation wave reaches 1 only when the modulation ratio is equal to 1.27 in this method, the instantaneous power fluctuation of the high-power H-bridge unit is small.
The conclusions are as follows. The MMWIS can further improve the ability of high-power modules to transmit active power. The AC side fundamental voltage and current of the high-power module are in the same phase when the peak value of the modulation wave reaches 1.27, thereby transmitting the maximum active power. In addition, the MMWIS can overcome the problem of grid-connected current distortion caused by over-modulation in some areas due to the superposition of too many reverse adjustment quantities for low-power modules.
keywords：Cascaded H-bridge, current distortion, power imbalance, modified strategy
DOI: 10.19595/j.cnki.1000-6753.tces.220762
中图分类号：TM46
江苏省研究生科研与实践创新计划资助项目（KYCX18_0286）。
收稿日期 2022-05-07
改稿日期 2022-08-15
李金玉 男，1989年生，博士研究生，研究方向为多电平变换器控制。E-mail: lijinyu@nuaa.edu.cn
陈 杰 男，1982年生，副教授，研究方向为航空航天供电系统、新能源发电与电能变换技术、电力电子变换器建模与控制技术等。E-mail: chen_jie@nuaa.edu.cn（通信作者）
（编辑 陈 诚）