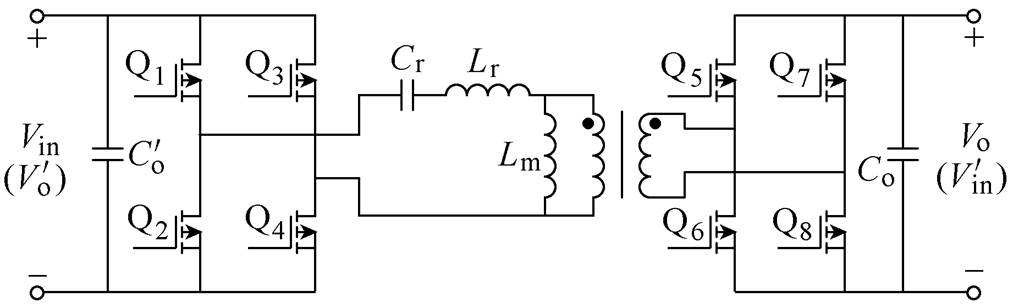
图1 双向LLC谐振变换器拓扑结构
Fig.1 Topology of bidirectional LLC resonant converter
摘要 近年来，双向LLC-DCX在电源系统中得到了越来越广泛的应用。为应对系统功率等级的提升，多模块并联成为实现系统扩容的重要方法。然而，均流性能是LLC谐振变换器并联系统的设计难点，各模块微小的谐振参数差异即可引起较大的电流不均衡。该文根据双向LLC谐振变换器的增益特性，定量分析双向LLC-DCX的并联特性，提出一种通过优化谐振网络参数提升并联均流性能的方法。最后，搭建一套三模块双向LLC-DCX并联系统样机，实验结果验证了所提方法的可行性和有效性。
关键词：双向LLC-DCX 多模块并联系统 谐振网络优化 并联均流
近年来，LLC谐振变换器因高效率、高功率密度的优势，在相关领域得到了广泛的应用。然而宽增益范围的设计会严重影响LLC变换器的效率[1]，在宽电压范围场合，通常采用LLC+非隔离变换器的两级式拓扑[2]。其中LLC变换器作为直流变压器（DC Transformer, DCX）使用，称为LLC-DCX，在谐振点附近开环定频工作，具有极高的效率、极低的控制复杂度和成本，在系统中起到直流母线变压器的作用，并逐渐成为LLC变换器的应用趋势[3]。此外，随着可再生能源和新能源汽车等的发展，双向功率变换的需求日益增加，同样对系统中的LLC-DCX提出了双向工作的要求[4-5]。
除了效率和功率密度的要求，模块化也是如今电力电子变换器的发展趋势，有利于系统扩容和变换器的标准化生产[6-7]。在低压大电流场合，多模块并联是实现系统扩容的重要方法，可降低主电路元器件的电流应力和热应力，提高系统可靠性。然而LLC变换器本身并不具备良好的并联性能，受工艺水平限制，LLC的谐振参数存在偏差，并联系统的均流性能对谐振参数偏差非常敏感，研究表明，谐振参数5 %的偏差即可引起高达50 %以上的电流不均衡度[8]。因此，为充分发挥LLC变换器的性能优势，LLC变换器并联技术具有重要的研究意义。
目前，LLC变换器的并联均流方法可分为两类。第一类是调整拓扑结构的均流方法：如文献[9-10]提出了共用谐振电感和谐振电容的方法，避免谐振参数偏差对均流的影响；文献[11]提出了谐振电感耦合的均流方法，通过谐振电感的耦合作用抑制各路谐振电流的不均衡。上述方法调整了并联系统的拓扑结构，模块间存在大电流交流连接点，并限制了系统的进一步扩容。第二类是通过数字控制实现的均流方法：如文献[12]提出了一种调频均流控制方法，采用双环控制调节各模块开关频率使电压增益相等，进而实现均流；文献[13]提出了基于虚拟阻抗的均流方法，在电压环中加入虚拟阻抗补偿单元，调节各模块的等效阻抗实现均流。上述均流控制方法无需调整电路结构，可在一定程度上实现模块化并联，但各模块间仍存在控制和通信上的耦合，对于LLC-DCX，均流控制增加了控制复杂度，重新加入了已省去的控制成本。因此，如何在无需均流控制、完全模块化的基础上提升均流性能成为了LLC-DCX并联系统的设计难点。
由于LLC-DCX逐渐成为LLC变换器的主要应用方向，而面对不断增加的并联扩容需求，开环不控均流是LLC-DCX最理想的并联均流方式，因此开展LLC-DCX开环并联均流研究具有重要的意义。本文提出了一种针对双向LLC-DCX多模块并联系统的均流方法。通过优化设计谐振网络参数，优化谐振网络的阻抗分配，提升双向LLC-DCX的自然并联均流性能。从而无需闭环控制，实现各模块完全解耦、完全模块化的开环并联均流，最大限度简化控制、降低成本。首先分析了双向LLC变换器的拓扑和增益特性；然后在此基础上对双向LLC- DCX的并联特性进行了定量分析，提出了一种通过优化谐振网络参数提升并联均流性能的方法；最后基于一套三模块并联系统原理样机，验证了所提方法的可行性和有效性。
图1给出了双向LLC谐振变换器的拓扑结构。图中，谐振电容Cr、谐振电感Lr和励磁电感Lm共同构成双向LLC变换器的谐振网络。变换器正向工作时，Q1～Q4为主控管，Q5～Q8为同步整流管；反向工作时，Q5～Q8为主控管，Q1～Q4为同步整流管。
图1 双向LLC谐振变换器拓扑结构
Fig.1 Topology of bidirectional LLC resonant converter
Cr、Lr和Lm为双向LLC谐振变换器的3个谐振参数。变换器的谐振频率fr表达式为
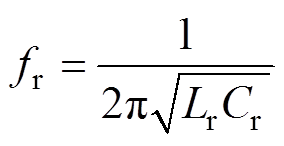（1）
双向LLC谐振变换器正向工作时，电路为全桥LLC谐振变换器，根据基波分析法，可得到正向基波等效电路如图2所示[14]。
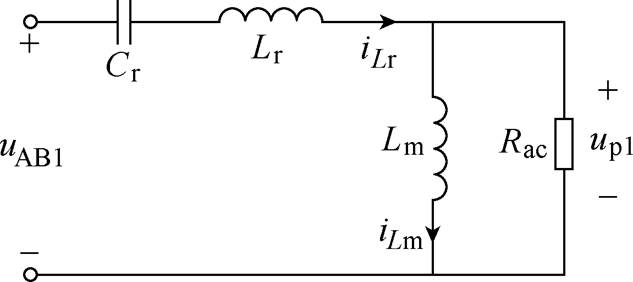
图2 正向基波等效电路
Fig.2 Forward fundamental wave equivalent circuit
图2中，Rac为正向交流等效负载电阻，表示为
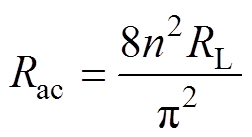（2）
式中，RL为正向负载电阻。根据图2，可得到变换器正向工作的直流电压增益表达式为
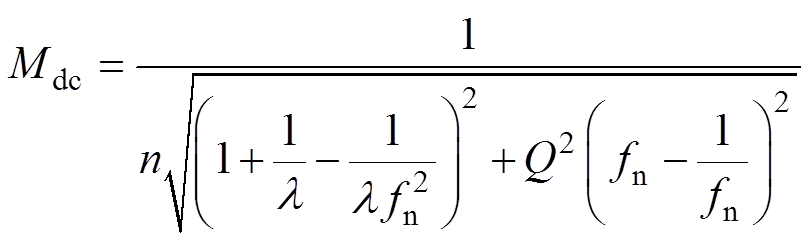（3）
式中，fn为归一化频率，定义为开关频率fs和谐振频率fr之比；l 为电感比，定义为Lm和Lr之比；Q为品质因数，其表达式为
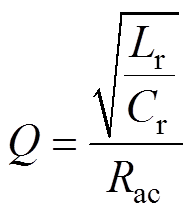（4）
根据式（3），图3给出了变换器正向工作时l固定、不同Q下的增益曲线。
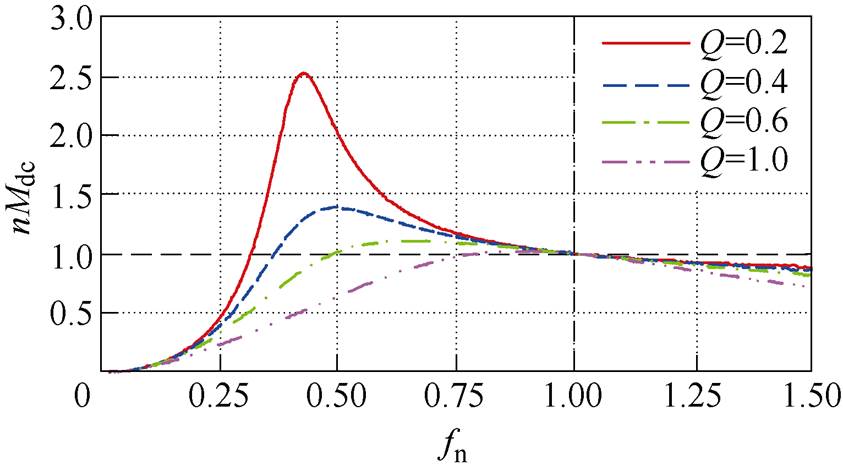
图3 正向增益曲线（l=5）
Fig.3 Forward gain curves (l=5)
根据式（3），当fs=fr时正向电压增益仅取决于变压器匝比，不受负载变化影响，变换器具有良好的理想直流变压器特性。因此，双向LLC-DCX正向工作时，一般开关频率设置在谐振频率附近。
双向LLC谐振变换器反向工作时，Lm始终被输入电压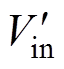
钳位，Lm不参与谐振，电路等效为全桥串联谐振变换器。同样根据基波分析法，可得到其基波等效电路如图4所示[15]。
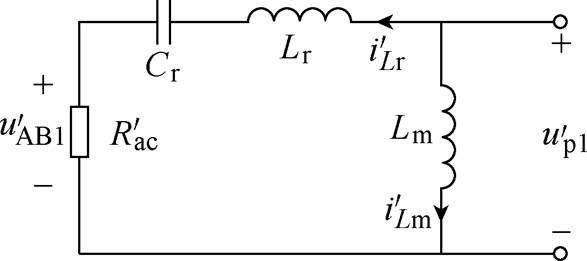
图4 反向基波等效电路
Fig.4 Reverse fundamental wave equivalent circuit
图4中，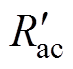
为反向交流等效负载电阻，其值为
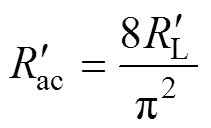（5）
式中，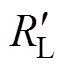
为反向负载电阻。根据图4，可得到变换器反向工作的直流电压增益表达式为
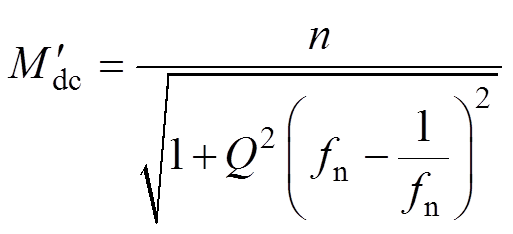（6）
根据式（6），图5给出了变换器反向工作时不同Q下的增益曲线。
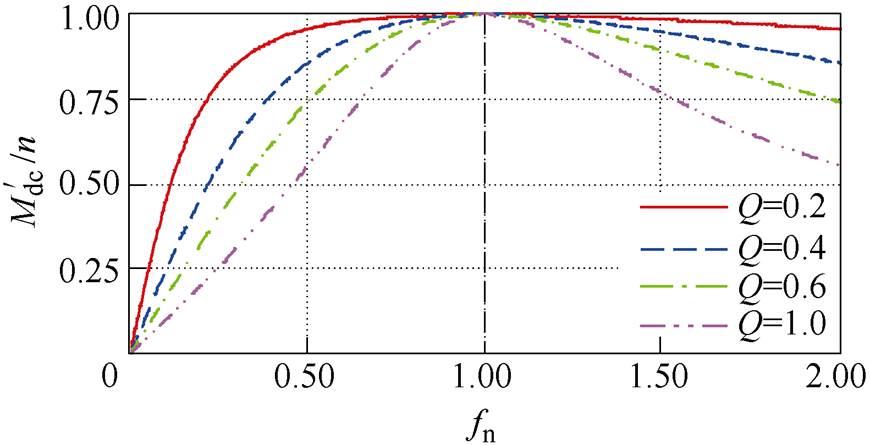
图5 反向增益曲线
Fig.5 Reverse gain curves
根据式（6），当fs=fr时，与正向工作情况类似，反向电压增益同样仅取决于变压器匝比，不受负载变化影响，变换器具有良好的理想直流变压器特性。因此，双向LLC-DCX反向工作时，一般开关频率也设置于谐振频率附近。
双向LLC-DCX正向多模块并联工作时，各模块谐振参数偏差使得相同负载下的电压增益不同，由于输入输出电压强制相等，各模块会自动调节各自分配的负载使电压增益相等，导致负载电流不均衡。对于LLC谐振变换器，并联均流性能对谐振参数偏差十分敏感，微小的谐振参数偏差将导致严重的电流不均衡。本节将分析双向LLC-DCX的正向并联特性，提出一种针对LLC-DCX的开环并联均流方法，通过优化谐振网络参数，降低均流性能对谐振参数偏差的敏感度，无需闭环调节，各模块凭借其外特性可实现良好的自然并联均流。
首先对变换器的正向外特性（Vo-Io特性）进行分析。输出电压随着负载电流的增大而减小，形成负载调整率，输出电压的负载调整率由增益的负载调整率和内阻压降两个因素共同决定。考虑谐振参数偏差，为保证同步整流管的零电流软开关（Zero Current Switching, ZCS），一般使开关频率略小于所设计的谐振频率，根据式（3），当fn＜1时，随着负载电流增大，Q值增大，增益降低，根据式（3）可推导正向增益的负载调整率的表达式为
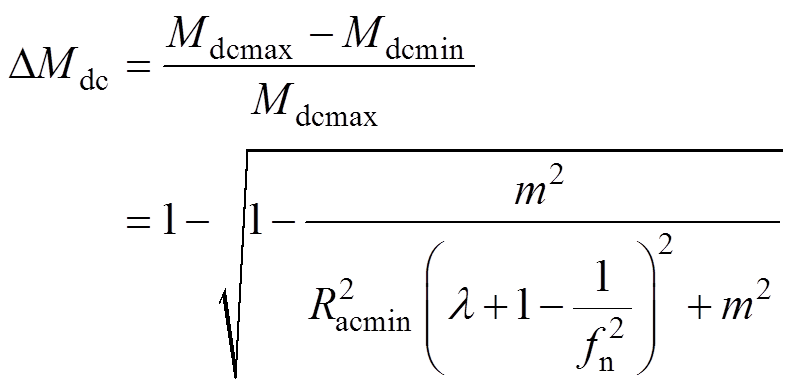（7）
其中
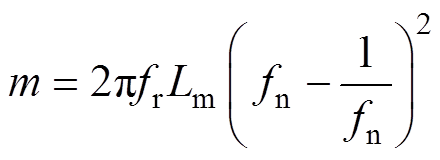（8）
式中，Mdcmax为正向空载增益；Mdcmin为正向满载增益；Racmin为满载时的交流等效负载电阻。
对于双向LLC-DCX，Lm的值由双向零电压软开关（Zero Voltage Switching, ZVS）条件确定，在满足ZVS条件的前提下Lm尽可能取大，从而获得最优的效率。Lm确定后，m为常数，根据式（7），正向增益的负载调整率DMdc仅和电感比l 有关，随l 的增大而减小。图6给出了变换器DMdc随l 的变化曲线，足够大的l 可基本消除正向增益的负载调整率，输出电压的负载调整率基本只与内阻压降有关。
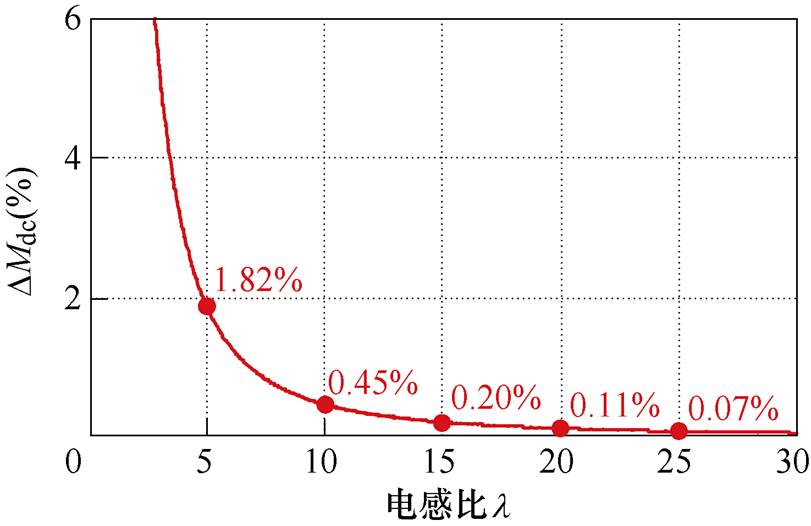
图6 正向增益的负载调整率随电感比变化曲线
Fig.6 Load regulation curve of forward gain with l
理想直流变压器特性是衡量LLC-DCX性能的主要指标，要求其输出电压负载调整率尽可能小，又由于LLC-DCX中电感比l 的取值不受调压能力限制，因此须尽可能增大l 的取值使得增益的负载调整率DMdc可忽略。
忽略正向增益的负载调整率DMdc，考虑内阻压降，变换器输出电压表达式为
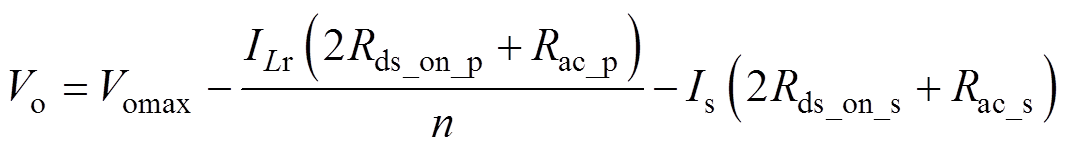（9）
式中，Vomax为正向空载输出电压；ILr、Is分别为正向工作时谐振电流和变压器二次电流的有效值；Rds_on_p、Rds_on_s分别为一次侧开关管（Q1～Q4）和二次侧开关管（Q5～Q8）的导通电阻；Rac_p、Rac_s分别为变压器一次、二次绕组的交流电阻。由于Lm足够大，有iLr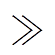
iLm，则Is≈n2ILr，式（9）可简化为
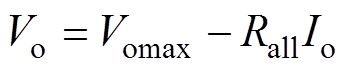（10）
式中，Io为正向负载电流。
定义Rall为变换器总等效内阻，表示为
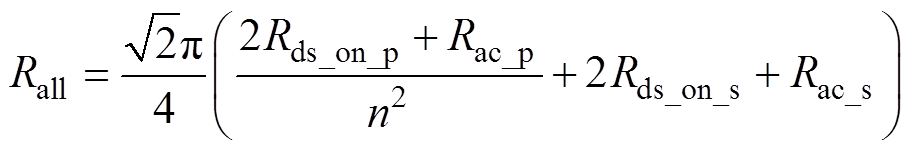（11）
式（10）即为双向LLC-DCX的正向外特性曲线方程，其图像为一条以Vomax为纵截距、以-Rall为斜率的直线。
根据双向LLC-DCX的正向外特性分析其多模块并联特性。考虑谐振参数偏差和内阻偏差，多模块正向并联的外特性曲线如图7所示。
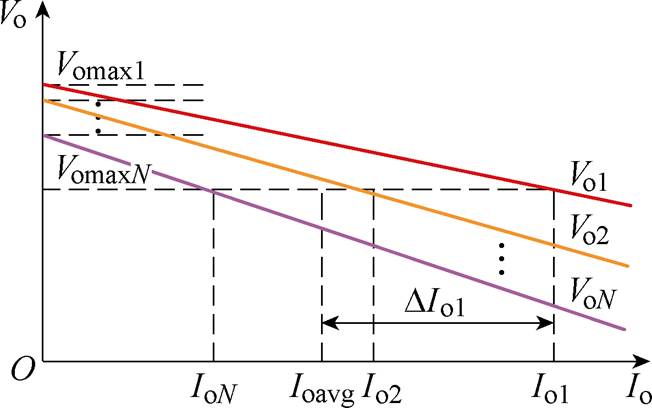
图7 多模块正向并联的外特性曲线
Fig.7 External characteristic curves of forward paralleled multiple modules
N个模块的外特性曲线方程为
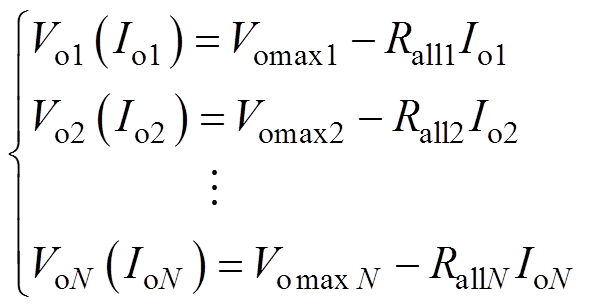（12）
并联工作时，N个模块的输出电压均相等，总负载电流为平均负载电流Ioavg的N倍，则可得到方程组
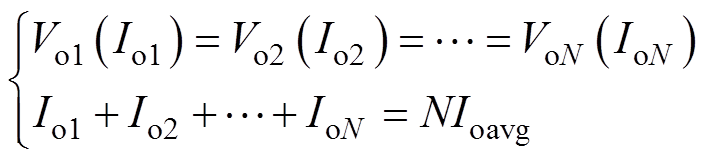（13）
将式（12）代入式（13），根据方程组可解出并联系统中N个模块各自分配的负载电流。解得并联系统中第i个模块的负载电流表达式为
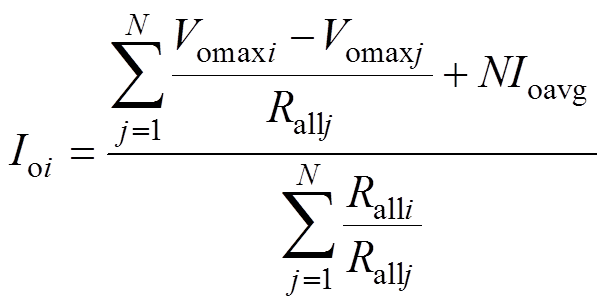（14）
定义第i个模块的电流不均衡度DIoi计算式为
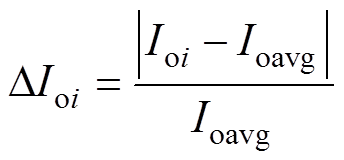（15）
将式（14）代入式（15），可得到第i个模块的电流不均衡度DIoi的定量表达式为
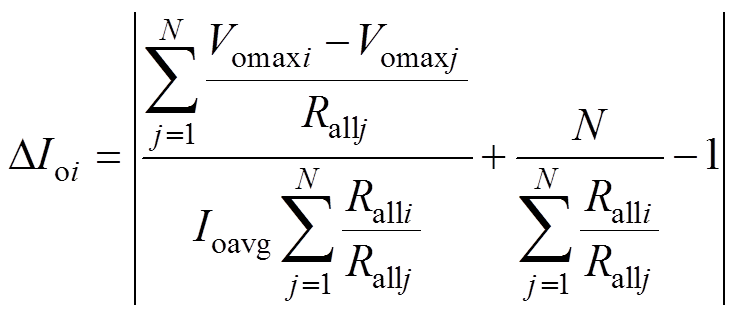（16）
根据式（16），电流不均衡度DIoi由两项相加组成；第一项与各模块的空载输出电压偏差有关，该偏差由谐振参数偏差产生；第二项由内阻偏差产生，是仅与各模块内阻有关的定值。
由于内阻偏差产生的不均衡度为定值，不便于调节，因此为了提升均流性能，需要尽可能减小谐振参数偏差产生的不均衡度。根据式（16），需要在谐振参数偏差一定时，尽可能减小各模块的空载输出电压偏差。根据图2，变换器空载下的正向基波等效电路如图8所示。
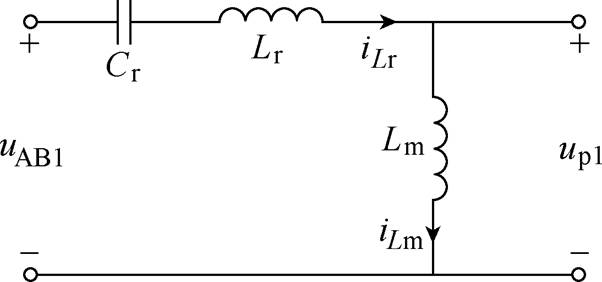
图8 空载下的正向基波等效电路
Fig.8 Forward fundamental equivalent circuit at no load
根据图8，谐振网络的正向空载增益即为励磁电感阻抗在3个谐振元件总阻抗中的占比，即
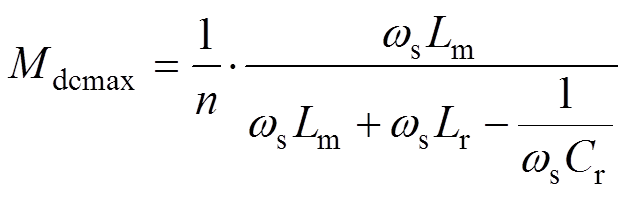（17）
式中，
为开关角频率。
根据图8及式（17），将Lr和Cr的串联谐振阻抗设计得尽可能小，从而尽可能增大Lm阻抗的占比，那么当谐振参数存在偏差时，各模块谐振网络的正向空载增益均近似为1，空载增益对谐振参数偏差不敏感，从而可减小各模块的空载输出电压偏差，改善均流性能。
根据式（17），由于Lm取值已确定，设计时可尽可能增大电感比l，从而尽可能减小Lr和Cr的串联谐振阻抗，尽可能增大励磁电感阻抗的占比。该方法通过优化分配谐振网络阻抗，降低空载增益对谐振参数偏差的敏感度，提升并联系统的均流性能。
接下来定量推导空载输出电压偏差与电感比l之间的关系。考虑谐振参数偏差，设i、j两模块的实际谐振参数分别为Lri=aiLr、Cri=biCr、Lmi=ciLm，Lrj=ajLr、Crj=bjCr、Lmj=cjLm（i≥1, j＜N）。根据式（3），可得i、j两模块的正向空载增益分别为
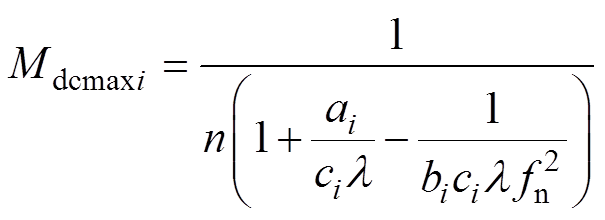（18）
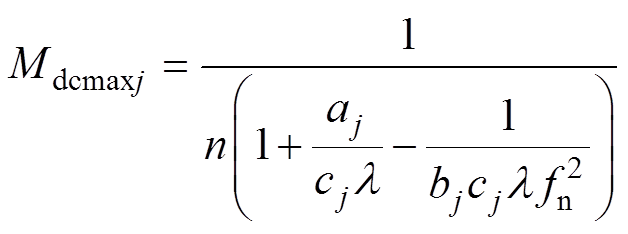（19）
式中，ai、bi、ci、aj、bj、cj为谐振参数实际值与设计值的比值。
根据式（18）和式（19），可推导出i、j两模块之间的空载输出电压偏差Vomaxi-Vomaxj的表达式为
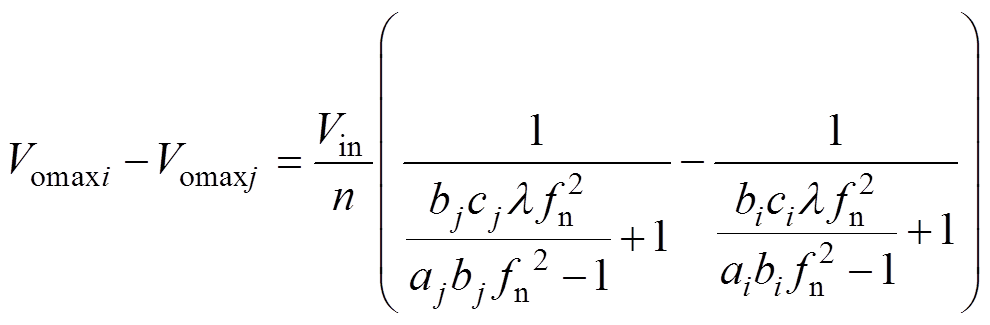（20）
根据式（20），谐振参数偏差一定时，空载输出电压偏差仅与电感比l 的值有关，分析其单调性可得空载输出电压偏差的绝对值|Vomaxi-Vomaxj|随l 增大而单调递减。因此，在谐振参数偏差一定时，增大l 可减小模块间的空载输出电压偏差，使各模块外特性曲线的纵截距更接近，从而降低并联电流不均衡度对谐振参数偏差的敏感度，改善正向并联系统的均流性能。
以三模块正向并联系统为例，设谐振参数偏差情况为a1=b1=c1=0.95、a2=b2=c2=1、a3=b3=c3=1.05，图9给出了各模块的空载输出电压Vomax随l 的变化曲线，随着l 的增大，各模块间的空载输出电压偏差明显减小。
进一步考虑内阻偏差，设Rall1=0.95Rall、Rall2= Rall、Rall3=1.05Rall，图10给出了满载下各模块分配的负载电流随l 的变化曲线。各模块负载电流随l的增大而趋向均衡，当l=20时，最大电流不均衡度达65.7 %；而当l=200时，最大电流不均衡度仅有11.1 %，并联系统的均流性能得到明显改善。
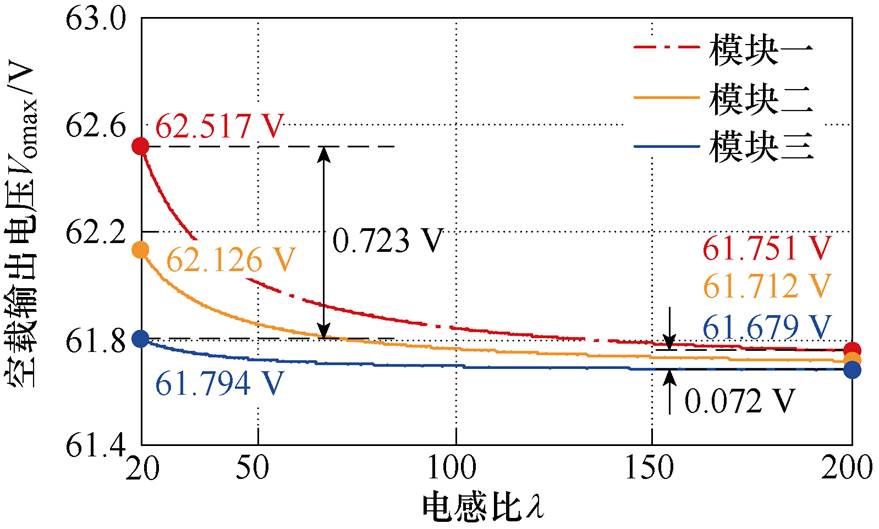
图9 各模块空载输出电压随电感比变化曲线
Fig.9 Curves of each module’s Vomax withl
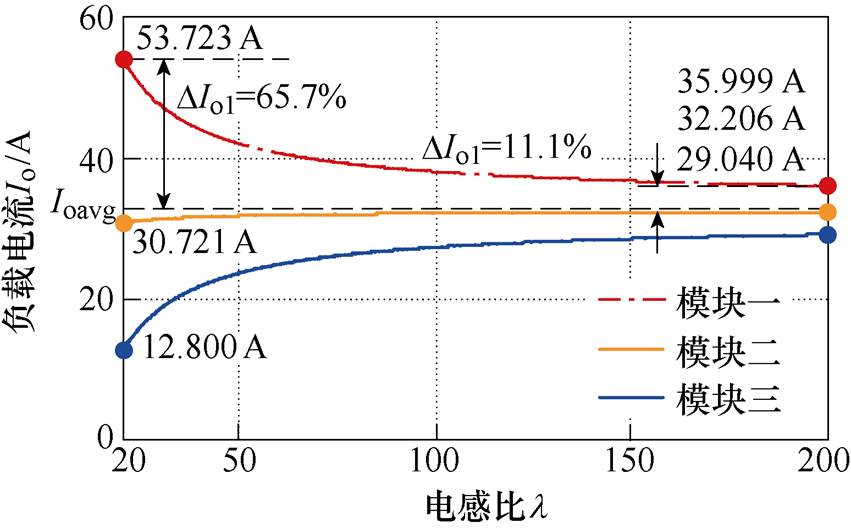
图10 各模块负载电流随电感比变化曲线
Fig.10 Curves of each module's load current withl
根据以上分析，对于双向LLC-DCX正向并联系统，增大电感比l 的值可有效减小谐振参数偏差产生的电流不均衡度，从而减小总的电流不均衡度，改善正向并联系统的均流性能。由此，可根据并联系统的均流指标要求，定量求解l 的取值范围，优化设计谐振参数。求解时须考虑参数偏差范围内的最不均衡情况，对于N模块正向并联系统，电流不均衡度最大的情况出现在仅有一个模块的谐振参数和内阻均为最小值，其余N-1个模块的谐振参数和内阻均为最大值时，多模块正向并联最不均衡情况的外特性曲线如图11所示。
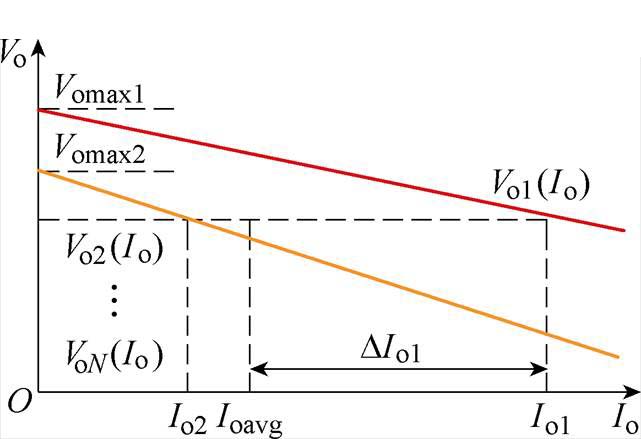
图11 多模块正向并联最不均衡情况的外特性曲线
Fig.11 External characteristic curves of forward paralleled multiple modules under most unbalanced case
根据图11，此时模块一具有理论上最大的电流不均衡度，根据式（16），此时模块一的电流不均衡度的表达式为
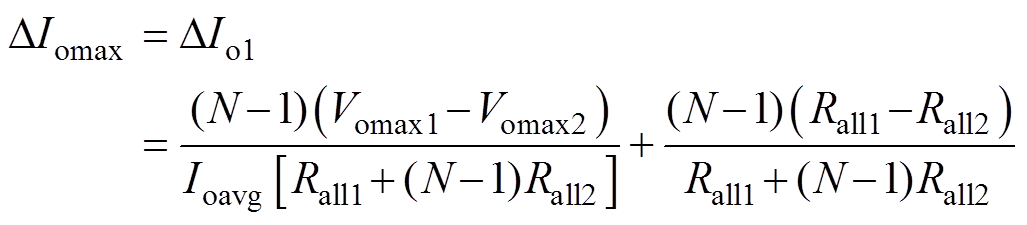（21）
式中，Vomax1和Vomax2分别取谐振参数偏差范围内空载输出电压的最大值和最小值；Rall1和Rall2分别取内阻偏差范围内的最大值和最小值。根据式（21），令DIomax小于指标要求的电流不均衡度DIoreq，解出l 的取值范围，即
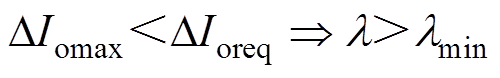（22）
在Lm的值由双向ZVS条件确定的前提下，通过减小Lr的值来获得较大的l 值。因此，可将变压器漏感作为Lr，在获得较大l 值的同时可很方便地实现谐振电感和变压器的磁集成。
该谐振网络优化方法通过优化分配谐振网络阻抗，可实现双向LLC-DCX正向并联系统开环下的自然均流，各模块仍各自保持开环工作，无需加入均流控制或其他措施，实现了各模块完全解耦的开环模块并联。并联系统中，变换器完全模块化，易于进行系统的功率扩展，并可最大限度地简化系统的控制、降低成本。
此外，由于所提方法优化了变换器本身的自然均流性能，因此在负载突变的动态过程中，各模块在每一时刻都能均衡地分配负载，均流不受动态过程影响。而在常规的闭环调频均流方法中，变换器本身不具备良好的自然均流性能，受限于环路带宽等因素，动态过程中可能存在不均流。因此，所提方法具有理论上最好的动态均流特性。
值得一提的是，闭环调频控制的LLC变换器为了满足调压范围要求，l 不能过大，否则升压特性会受到限制。而LLC-DCX开环定频工作在谐振点附近，故设计时无需根据增益调节范围限制l 的取值，可通过增加l 提升均流特性。因此，该方法对LLC-DCX并联系统普遍适用。
双向LLC-DCX反向多模块并联工作时，与正向类似，根据其反向外特性分析其多模块并联特性。首先对其反向外特性进行分析，输出电压的负载调整率同样由增益的负载调整率和内阻压降两个因素共同决定。然后根据式（6），可推导反向增益的负载调整率的表达式为
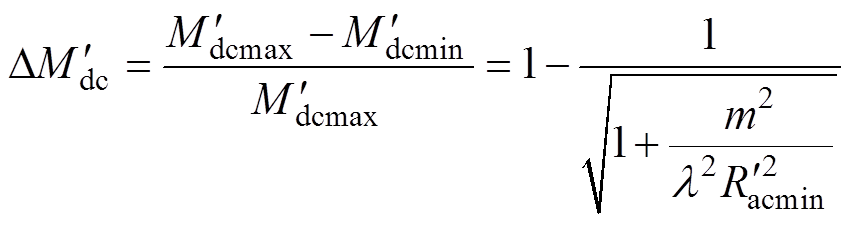（23）
式中，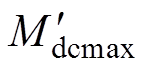
为反向空载增益；
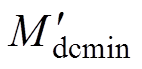为反向满载增益。
根据式（23），反向增益的负载调整率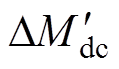
同样仅和电感比l 有关，并随l 的增大而减小。图12给出了变换器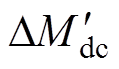随l 的变化曲线，与正向相同，足够大的l 值可基本消除反向增益的负载调整率，输出电压负载调整率基本只与内阻压降有关。
图12 反向增益负载调整率随电感比变化曲线
Fig.12 Load regulation curve of reverse gain with l
与正向类似，忽略反向增益的负载调整率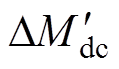，考虑内阻压降，变换器输出电压表达式为
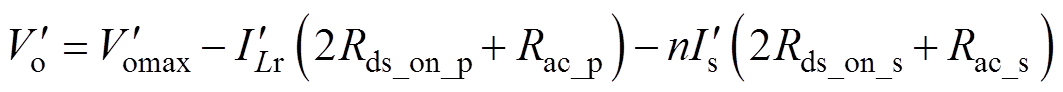（24）
式中，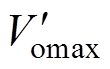
为反向空载输出电压；
、
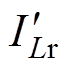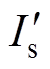分别为反向工作时的谐振腔电流和变压器二次电流的有效值。由于Lm足够大，有
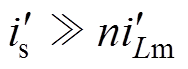，则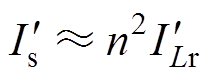
I，式（24）可简化为
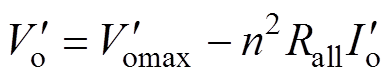（25）
式中，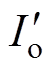
为反向负载电流。
式（24）即为双向LLC-DCX的反向外特性曲线方程，其图像为一条以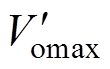为纵截距、以-n2Rall为斜率的直线。
根据图4，变换器空载下的反向基波等效电路如图13所示。
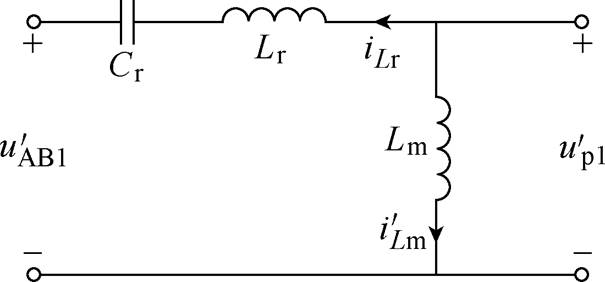
图13 空载下的反向基波等效电路
Fig.13 Reverse fundamental equivalent circuit at no load
根据图13，与正向所不同的是，变换器谐振网络的反向空载增益为定值1，与谐振参数无关。因此各模块谐振参数偏差不会导致空载输出电压偏差，各模块外特性曲线的纵截距保持相等。由此，考虑内阻偏差，多模块反向并联的外特性曲线如图14所示。
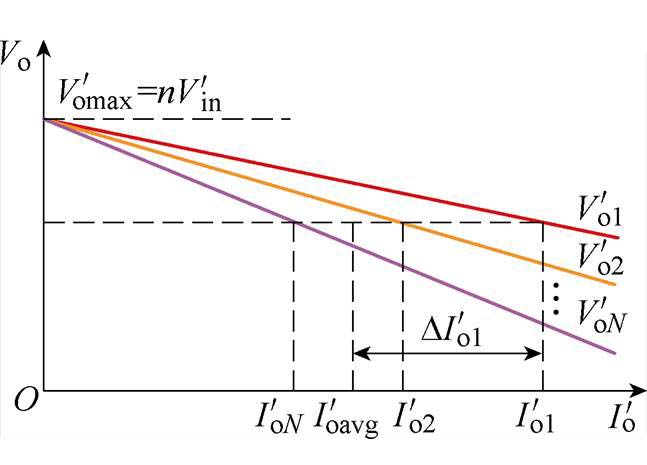
图14 多模块反向并联的外特性曲线
Fig.14 External characteristic curves of reverse paralleled multiple modules
对于N模块反向并联系统，与正向类似，根据N个模块的反向外特性曲线方程，可得方程组
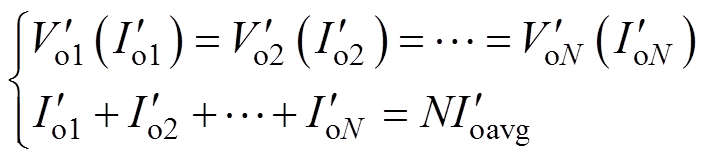（26）
根据方程组式（26）可解得并联系统中第i个模块的负载电流表达式为
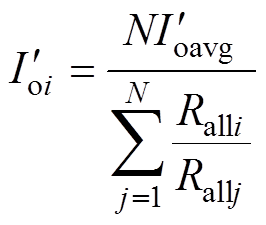（27）
相应地，可得到第i个模块的电流不均衡度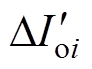
的表达式为
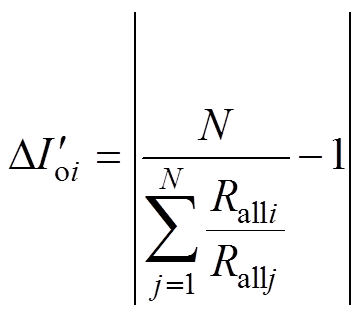（28）
变换器反向工作时，并联系统的均流性能不受谐振参数偏差影响，仅与内阻偏差有关。因此对于双向LLC-DCX反向并联系统，无需针对均流性能优化设计谐振参数，谐振参数只需使增益的负载调整率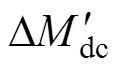
较小，变换器就会自然具有良好的开环并联均流能力。
根据上述分析，若设计单向工作且有并联需求的DCX，可将谐振腔放在变压器二次侧，使其工作在反向LLC-DCX状态，从而能够自然实现良好的开环并联均流，可进一步简化变换器的设计。
综合双向工作下的分析，对所提均流方法与常用的数字控制均流方法作一个对比。所提方法的主要优点是无需均流控制、可实现完全模块化的并联扩容和良好的动态均流，具有高可靠性以及较低的系统复杂度和成本，非常适用于无需闭环控制的LLC-DCX并联系统；主要缺点有：①不均衡度无法完全消除，由式（16）和式（28），所提方法可尽可能减小谐振参数偏差产生的不均衡度，而内阻偏差产生的不均衡度为定值，无法被消除；②所提方法只适用于开环的LLC-DCX，而不适用于闭环控制的LLC变换器，因为增大l 会限制调压范围，不利于闭环调节。
为验证所提谐振参数优化方法的有效性，搭建了三台双向LLC-DCX模块样机如图15所示，构成三模块并联系统，样机的指标参数和主要元器件选型见表1。样机高压侧采用SiC MOSFET，谐振电感用变压器漏感实现，经谐振参数优化，模块一的电感比l 由136.8增大至290.5。设置谐振参数偏差，谐振参数优化前后，令模块二的3个谐振参数均比模块一偏大约5 %，令模块三的3个谐振参数均比模块一偏小约5 %。
图15 双向LLC-DCX样机
Fig.15 Bidirectional LLC-DCX prototype
表1 双向LLC-DCX指标参数和元器件选型
Tab.1 Bidirectional LLC-DCX specifications and device selection
参 数数值 (型号) 正向输入电压（反向输出电压）/V370 正向输出电压（反向输入电压）/V61.7 最大输出功率/W2 000 开关频率/kHz140 谐振电感/mH模块一2.91 (优化前) 1.37 (优化后) 模块二3.08 (优化前) 1.43 (优化后) 模块三2.78 (优化前) 1.30 (优化后) 谐振电容/nF模块一375 (优化前) 817 (优化后) 模块二389 (优化前) 850 (优化后) 模块三355 (优化前) 779 (优化后) 励磁电感/mH模块一398 模块二418 模块三380 高压侧开关管Q1～Q4IMW65R027M1H (SiC) 低压侧开关管Q5～Q8IAUT150N10S5N035 (Si)
图16和图17分别给出了双向LLC-DCX三模块正向并联系统半载和满载下的实验波形（输入电压Vin=370 V，输出电压Vo=61.7 V），图中iLr1、iLr2、iLr3分别为三模块谐振腔电流，io1、io2、io3分别为三模块负载电流。谐振参数优化前，半载和满载下的最大电流不均衡度DIomax分别为16.9 %和8.7 %，谐振参数优化后，DIomax分别减小至4.2 %和1.0 %。经过谐振参数优化，正向并联系统的均流特性得到了有效改善。
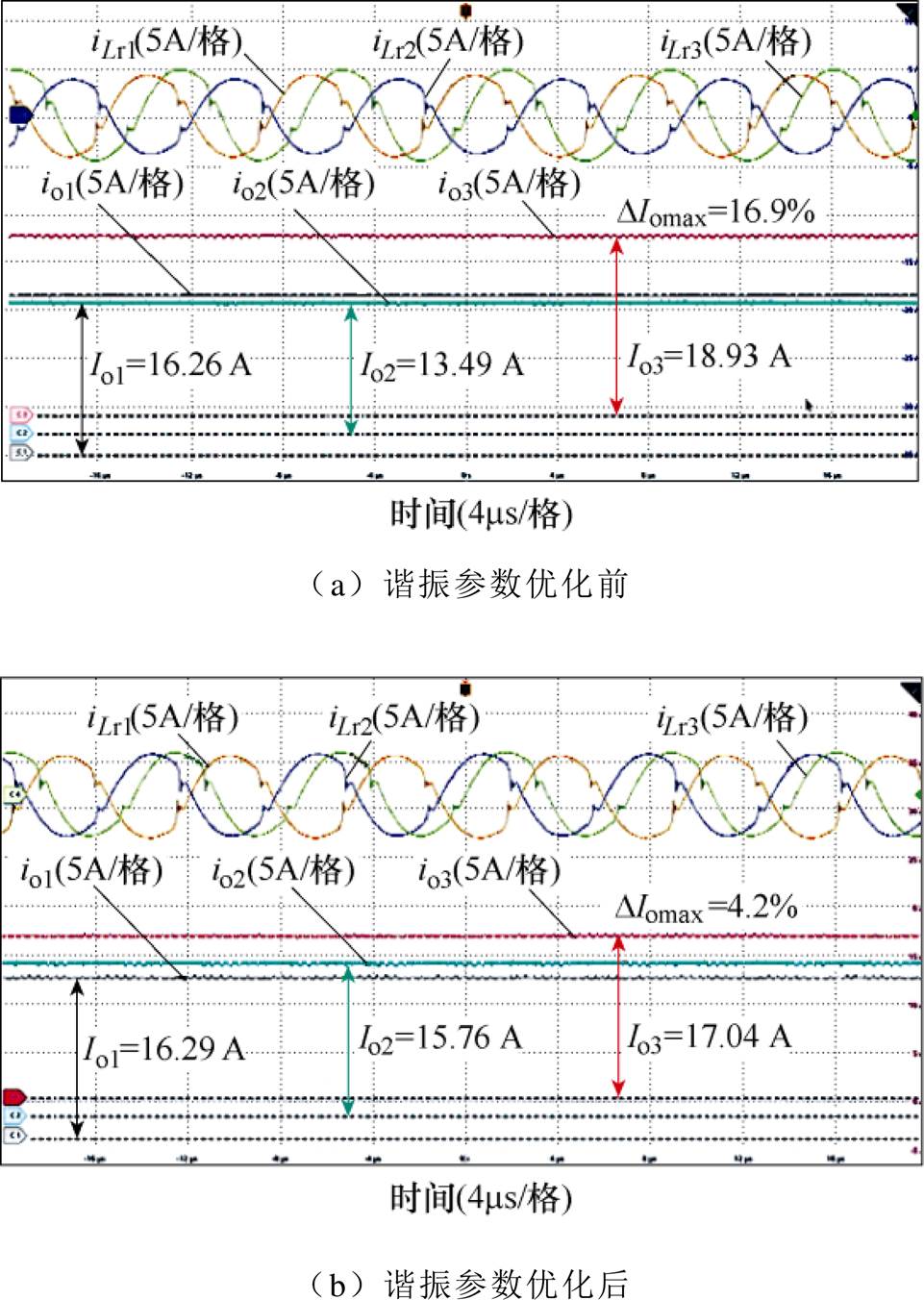
图16 半载（3 000W）下三模块正向并联实验波形
Fig.16 Experimental waveforms of forward paralleled three modules at half load (3 000W)
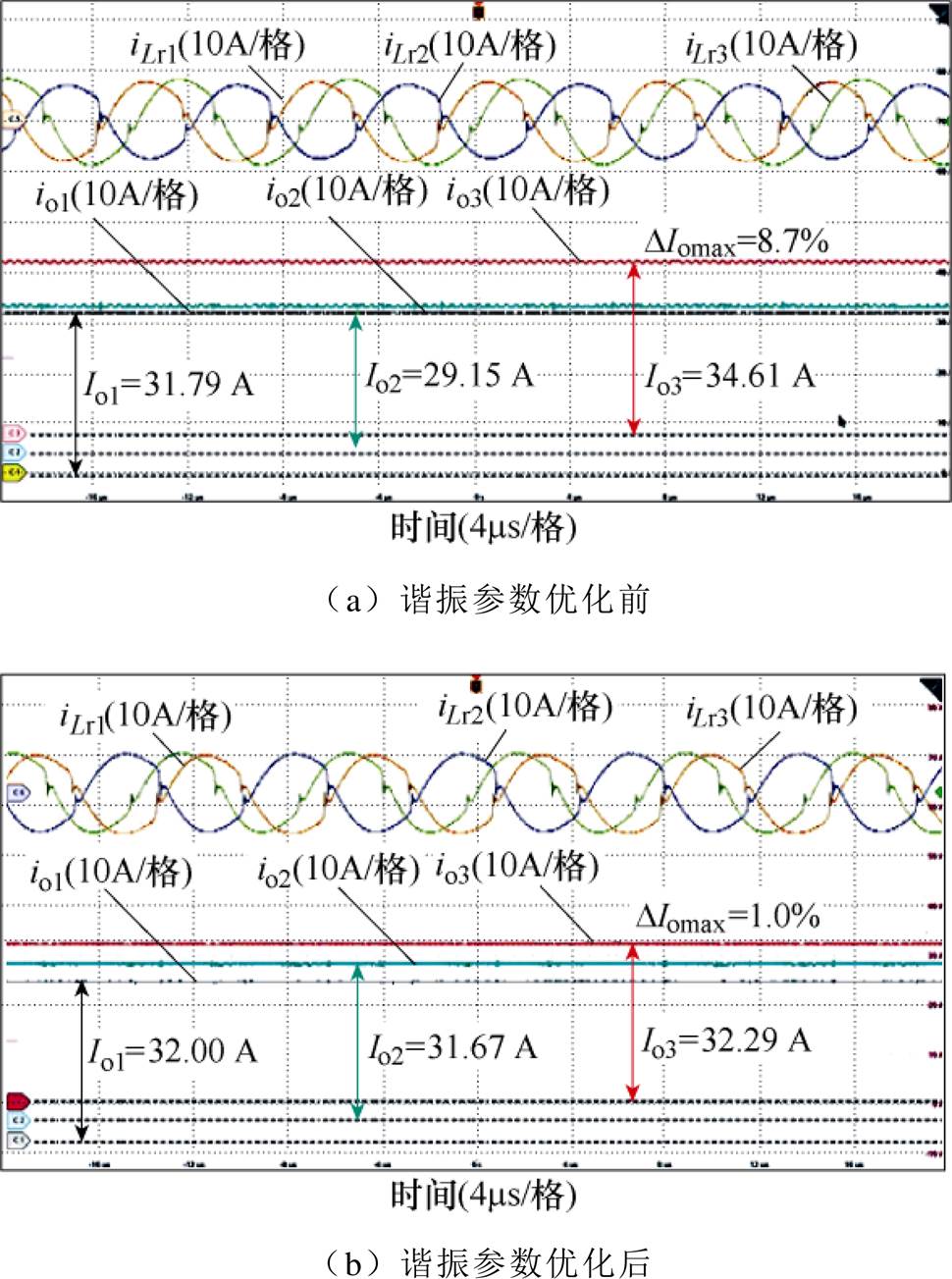
图17 满载（6 000W）下三模块正向并联实验波形
Fig.17 Experimental waveforms of forward paralleled three modules at full load (6 000W)
图18给出了谐振参数优化后，三模块正向并联系统从轻载到满载范围内，负载电流和对应的最大电流不均衡度的变化曲线（输入电压Vin=370 V，输出电压Vo=61.7 V）。可以看出，电流不均衡度随负载增大逐渐减小，根据式（16），随着负载增大，谐振参数偏差对均流的影响减小，内阻偏差对均流的影响不变，当谐振参数偏差影响占主导时，电流不均衡度随负载增大而减小，实验结果与理论相符。在半载以上，最大电流不均衡度均不超过5 %，正向并联系统具有良好的均流性能。
图18 正向并联电流不均衡度随功率变化曲线
Fig.18 Curves of forward parallel current unbalance with power
图19和图20分别给出了双向LLC-DCX三模块反向并联系统半载和满载下的实验波形（输入电压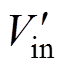
=61.7 V，输出电压
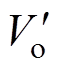=370 V），图中
、
、
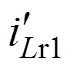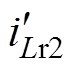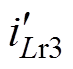分别为三模块谐振腔电流，
、
、
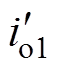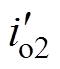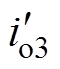分别为三模块负载电流。谐振参数优化前后，电流不均衡度均很小且无明显差异，反向并联系统无需额外的谐振参数设计则可自然实现良好的开环并联均流，与理论分析相符。
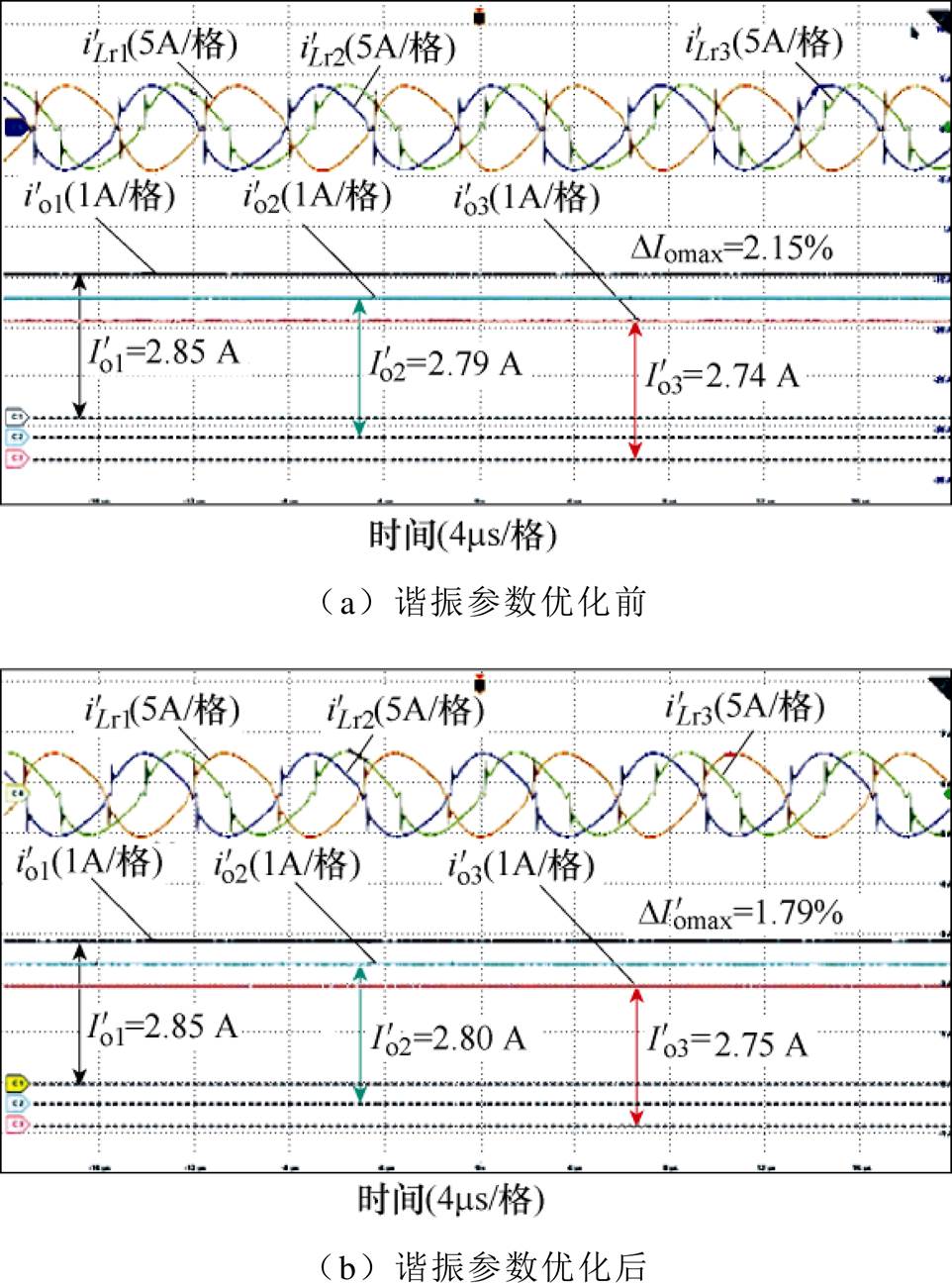
图19 半载（3 000W）下三模块反向并联实验波形
Fig.19 Experimental waveforms of reverse paralleled three modules at half load (3 000W)
图21给出了谐振参数优化后，三模块反向并联系统从轻载到满载范围内，负载电流和对应的最大电流不均衡度的变化曲线（输入电压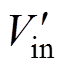=61.7 V，输出电压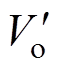=370 V）。全负载范围内电流不均衡度均很小，并几乎不随负载变化，根据式（28），电流不均衡度仅取决于内阻偏差，与负载电流无关，实验结果与理论相符。在全负载范围内，最大电流不均衡度基本均在2 %以内，反向并联系统具有十分良好的并联均流效果。
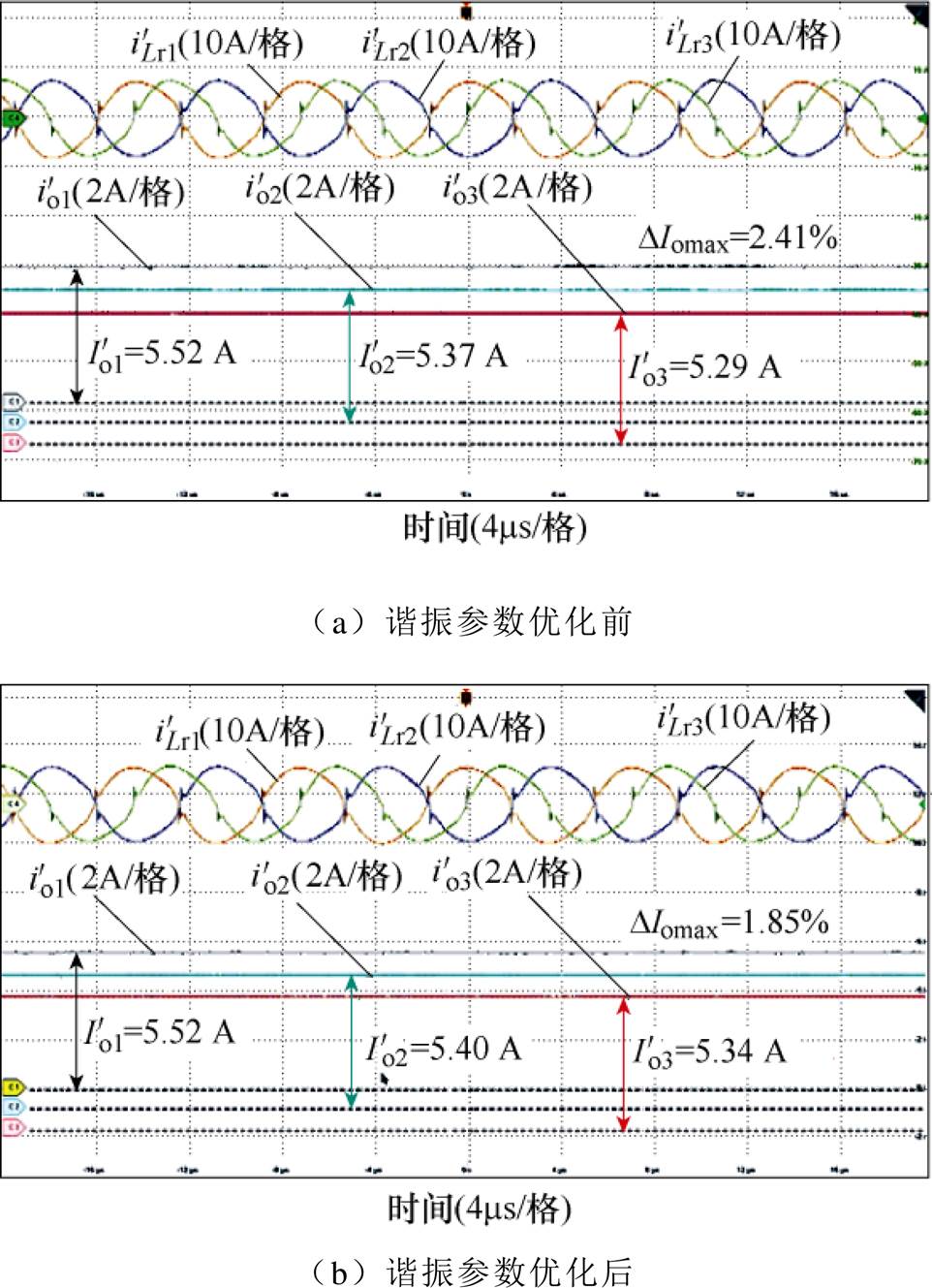
图20 满载（6 000W）下三模块反向并联实验波形
Fig.20 Experimental waveforms of reverse paralleled three modules at full load (6 000W)
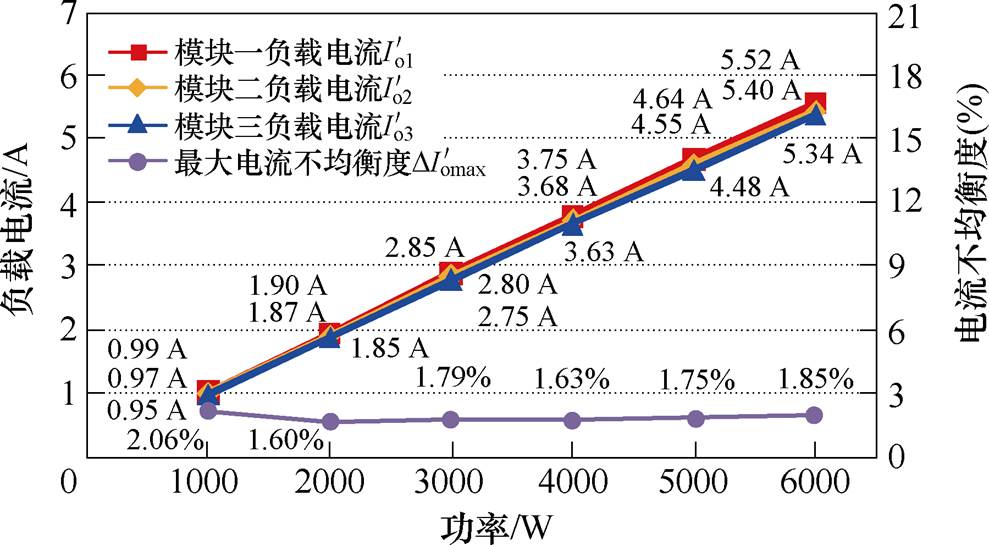
图21 反向并联电流不均衡度随功率变化曲线
Fig.21 Curves of reverse parallel current unbalance with power
图22和图23分别给出了谐振参数优化后，三模块正向和反向并联系统中，当负载以200 A/ms的速率从10 %到100 %满载跳变的过程中，各模块负载电流的动态波形（低压侧电压Vin=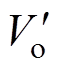=370 V，高压侧电压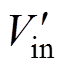=Vo=61.7 V）。动态过程中，各模块负载电流均匀上升，双向并联系统均具有良好的动态均流性能。
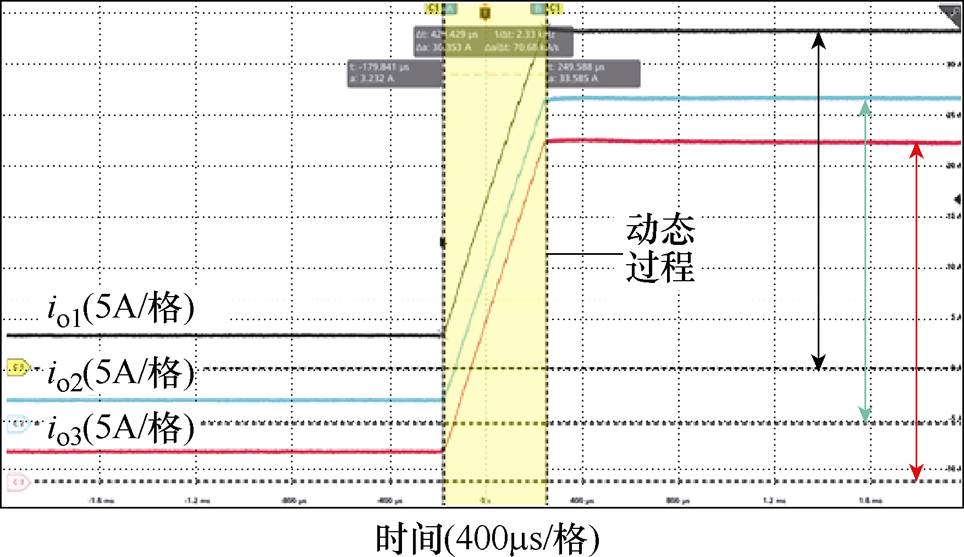
图22 三模块正向并联动态实验波形
Fig.22 Experimental waveforms of forward paralleled three modules in dynamic experiment
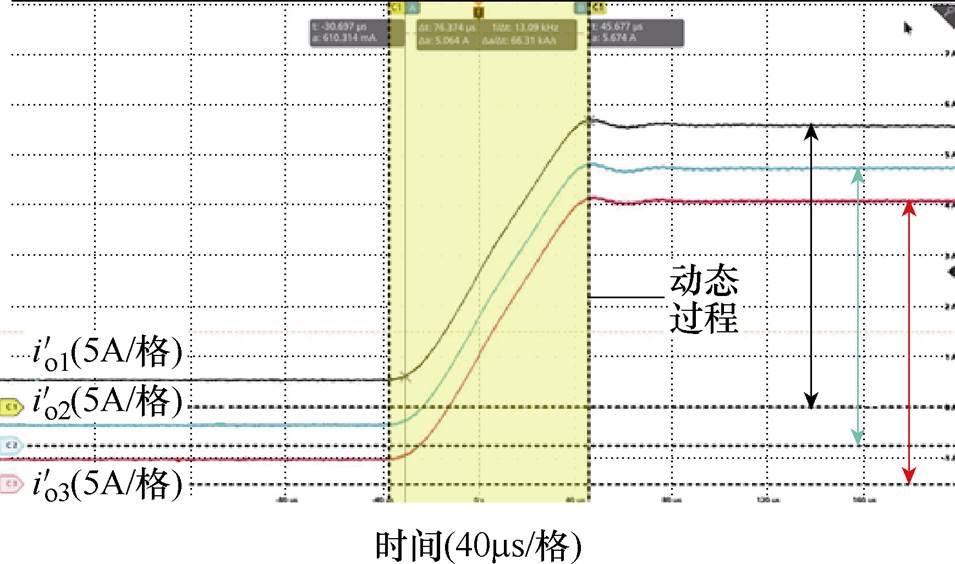
图23 三模块反向并联动态实验波形
Fig.23 Experimental waveforms of reverse paralleled three modules in dynamic experiment
本文推导分析了双向LLC-DCX多模块并联系统的均流特性与谐振网络参数之间的定量关系，得出增大电感比l 的值可优化谐振网络的阻抗分配，有助于提高正向并联均流性能，而反向并联本身即具备良好的均流性能，故无需额外设计。以此为据，提出了一种基于谐振网络优化的并联均流设计方法，实现了双向LLC-DCX完全模块化的开环并联，实验结果验证了该方法的有效性。
参考文献
[1] 杨东江, 段彬, 丁文龙, 等. 一种带辅助双向开关单元的宽输入电压范围LLC谐振变换器[J]. 电工技术学报, 2020, 35(4): 775-785.
Yang Dongjiang, Duan Bin, Ding Wenlong, et al. An improved LLC resonant converter with auxiliary bi-directional switch for wide-input-voltage range applications[J]. Transactions of China Electro- technical Society, 2020, 35(4): 775-785.
[2] Tan D F D. A review of immediate bus architecture: a system perspective[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(3): 363-373.
[3] Ren Ren, Liu Shuo, Wang Jinlong, et al. High frequency LLC DC-transformer based on GaN devices and the dead time optimization[C]//International Power Electronics and Application Conference and Exposition, Shanghai, China, 2015: 462-467.
[4] Jean-Pierre G, El Shafei A, Altin N, et al. A multiport bidirectional LLC resonant converter for grid-tied photovoltaic-battery hybrid system[C]//International Conference on Renewable Energy Research and Applications (ICRERA), Brasov, 2020: 755-760.
[5] Li Haoran, Zhang Zhiliang, Wang Shengdong, et al. A 300-kHz 6.6-kW SiC bidirectional LLC onboard charger[J]. IEEE Transactions on Industrial Electro- nics, 2020, 67(2): 1435-1445.
[6] 林霖, 裴忠晨, 蔡国伟, 等. 混合式隔离型模块化多电平变换器[J]. 电工技术学报, 2021, 36(16): 3319-3330.
Lin Lin, Pei Zhongchen, Cai Guowei, et al. Hybrid isolated modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3319-3330.
[7] 任小永, 张强, 庞振进, 等. 输入串联输出准并联的多路输出变换器[J]. 中国电机工程学报, 2016, 36(13): 3582-3589, 3377.
Ren Xiaoyong, Zhang Qiang, Pang Zhenjin, et al. Input-series output-quasi-parallel multiple output converter[J]. Proceedings of the CSEE, 2016, 36(13): 3582-3589, 3377.
[8] Jang J, Choi S, Choi B, et al. Average current mode control to improve current distributions in multi- module esonant DC-to-DC converters[C]//International Conference on Power Electronics-ECCE Asia, Jeju, 2011: 2312-2319.
[9] Wang Hongliang, Chen Yang, Qiu Yajie, et al. Common capacitor mutiphase LLC converter with passive current sharing ability[J]. IEEE Transactions on Power Electronics, 2018, 33(1): 370-387.
[10] Wang Hongliang, Chen Yang, Liu Yanfei, et al. A passive current sharing method with common inductor multiphase LLC resonant converter[J]. IEEE Transa- ctions on Power Electronics, 2017, 32(9): 6994- 7010.
[11] 杨玉岗, 吴晗, 关婷婷. 交错并联LLC谐振变换器的磁集成均流特性[J]. 电工技术学报, 2019, 34(12): 2529-2538.
Yang Yugang, Wu Han, Guan Tingting. Magnetic integrated current sharing characteristics of inter- leaved LLC resonant converter[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2529- 2538.
[12] Yang Gang, Dubus P, Sadarnac D. Double-phase high-efficiency, wide load range high-voltage/low- voltage LLC DC/DC converter for electric/hybrid vehicles[J]. IEEE Transactions on Power Electronics, 2015, 30(4): 1876-1886.
[13] 任小永, 王亚坤, 陈宇, 等. 基于虚拟阻抗的LLC谐振变换器并联均流控制[J]. 电工技术学报, 2019, 34(21): 4540-4550.
Ren Xiaoyong, Wang Yakun, Chen Yu, et al. Parallel current sharing control of LLC resonant converter based on virtual impedance[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4540-4550.
[14] 刘硕, 苏建徽, 赖纪东, 等. LLC谐振变换器PO模式增益公式与模式边界条件分析[J]. 电力系统自动化, 2020, 44(6): 164-170.
Liu Shuo, Su Jianhui, Lai Jidong, et al. Analysis on gain formula and mode boundary condition for LLC resonant converter in PO mode[J]. Automation of Electric Power Systems, 2020, 44(6): 164-170.
[15] Pledl G, Tauer M, Buecherl D. Theory of operation, design procedure and simulation of a bidirectional LLC resonant converter for vehicular applications[C]// IEEE Vehicle Power and Propulsion Conference, Lille, France, 2011: 1-5.
Abstract In recent years, bidirectional LLC DC transformers (DCX) have been widely applied in power supply systems. Multi-module parallel has become an important way to increase the power level of the system. However, the current sharing performance is the design difficulty of an LLC resonant converter parallel system. For LLC-DCX, if conventional current sharing methods are adopted, the fully decoupled modular parallel cannot be realized, and the current sharing control will reintroduce the control cost that has been saved. A current sharing method for a bidirectional LLC-DCX parallel system is proposed. By optimizing the resonant parameters, the natural current sharing performance of the converter can be improved, and the fully decoupled and modularized open-loop current sharing can be realized, which can simplify the control and reduce the cost to the maximum extent.
Firstly, according to the equivalent circuit of the bidirectional LLC converter, the gain characteristics of the bidirectional operation are derived. Next, the forward parallel characteristics of bidirectional LLC-DCX are quantitatively analyzed. According to the forward equivalent circuit, the external characteristic curve equation is derived, and the expression of the current imbalance of each module in the forward parallel system is further derived. The current imbalance is composed of two parts. The first part is related to the no-load output voltage deviation of each module, and the second part is related to the internal resistance deviation of each module. According to the forward gain characteristics, the analysis shows that increasing the inductance ratio can optimize the impedance distribution of the resonant network, then reduce the first part of the current imbalance. Therefore, we can calculate the value range of the inductance ratio according to the requirement, then optimize the design of resonant parameters, to improve the current sharing performance of the forward parallel system.
Next, the reverse parallel characteristics of bidirectional LLC-DCX are quantitatively analyzed. Similarly, the expression of the current imbalance of each module in the reverse parallel system is derived. Because the reverse no-load output voltage is constant, the current-sharing performance is only related to the internal resistance deviation. Therefore, the reverse parallel system naturally has a good current sharing performance without requiring to design of resonant parameters.
Finally, a prototype of a three-module bidirectional LLC-DCX parallel system is built for the experiment. After optimizing resonant parameters, the current sharing performance of the forward parallel system is improved. Before and after the resonant parameter optimization, the reverse parallel system has good current sharing performance, and there is no noticeable difference. The forward parallel system and reverse parallel system have good dynamic current-sharing performance. The experimental results verify the feasibility and effectiveness of the proposed method. By optimizing the resonant parameters, the fully decoupled and modularized open-loop current sharing can be realized in a bidirectional LLC-DCX parallel system.
keywords：Bidirectional LLC-DCX, multi-module parallel system, resonant parameters optimization, parallel current sharing
DOI: 10.19595/j.cnki.1000-6753.tces.220713
中图分类号：TM46
国家自然科学基金资助项目（52177181）。
收稿日期 2022-05-04
改稿日期 2022-06-22
李加明 男，1997年生，硕士，研究方向为宽禁带器件电力电子变换技术。E-mail: 306550028@qq.com
任小永 男，1979年生，博士，博士生导师，研究方向为高功率密度集成技术、高电压调节模块、分布式电源系统和GaN晶体管应用技术。E-mail: renxy@nuaa.edu.cn（通信作者）
（编辑 陈 诚）