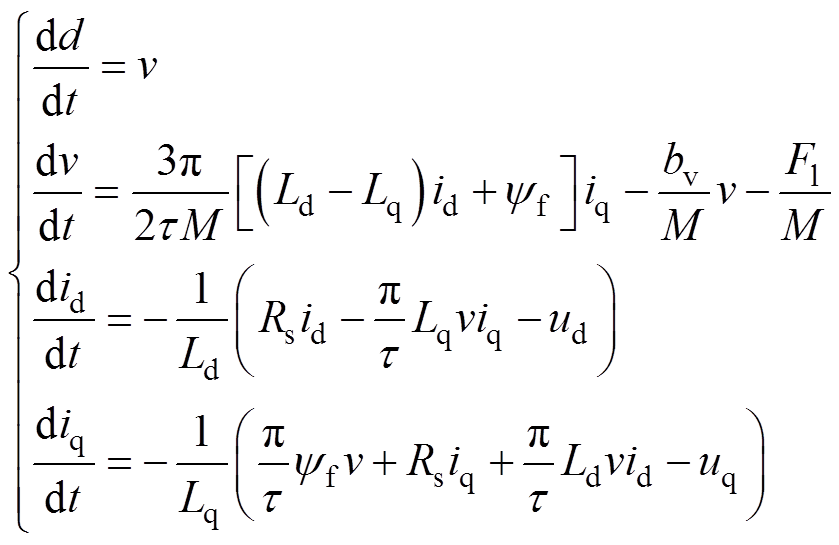 (1)
(1)
摘要 针对永磁直线同步电机易受参数摄动、负载扰动等不确定因素的影响,该文提出一种分数阶微分型边界层非奇异快速终端滑模控制(FO-NFTSMC)策略。首先,采用NFTSMC方法来抑制不确定因素对系统的影响,保证了跟踪误差在有限时间快速收敛,避免了奇异性;其次,在系统不确定上界未知的情况下,将Riemann-Liouville分数阶微分定义和边界层技术结合,实现一种新的分数阶微分型边界层控制,不仅具有整数阶边界层的输出特性,还具备“大误差大增益,小误差小增益”的功能,化解了整数阶边界层控制中的“弱抖振”与“快收敛”之间的矛盾,使得系统全局快速收敛;最后,实验结果表明,该策略提高了系统的跟踪精度与响应速度,对负载扰动和参数变化具有很强的抑制能力,同时有效地削弱了抖振现象。
关键词:永磁直线同步电机 非奇异快速终端滑模控制 分数阶微分型边界层 抖振
永磁直线同步电机(Permanent Magnet Linear Synchronous Motor, PMLSM)具有高响应、高刚度、高精度等优点,满足高精密直线伺服驱动的需求,在光刻机、精密切割机和高精密数控机床等各类高精度工业伺服场合具有重要应用价值[1-2]。PMLSM结构上省去中间机械传动环节,有效地解决了机械损耗、齿侧间隙等问题,但易受参数摄动和负载扰动等不确定因素的影响[3-5]。为此,如何克服不确定性对系统的不利影响是亟待解决的关键问题。
近年来,非线性滑模控制作为一种非线性系统控制方法逐渐发展起来[6]。因其强大的鲁棒性以及可以实现系统状态有限时间收敛,非常适合于PMLSM伺服系统。其中,非奇异终端滑模是非线性滑模中的一个重要分支,为当前应用的主流。但在机械系统中,由文献[7]相轨迹曲线分析可知,非奇异终端滑模控制的“滑动阶段”收敛速度低于经典终端滑模控制。因此,有学者对滑动阶段的“提速”问题进行深入研究,在文献[8-9]中分别提出混合终端滑模控制、非奇异快速终端滑模控制。但针对存在不确定扰动的PMLSM系统,仅加快“滑动阶段”的收敛速率并不能保证系统的全局收敛时间。因此,在保证“滑动阶段”快速收敛的同时兼顾着趋近阶段的收敛速度是实现全局快速收敛的关键。
然而,滑模趋近阶段的“提速”常常伴随着抖振现象,抖振的强弱会影响系统的稳定性,在实际的工业应用中有着较大的局限性。通常通过调整切换增益来削弱抖振现象。文献[10]提出自适应鲁棒滑模控制,对系统不确定性进行实时估计,改善了系统鲁棒性,削弱了抖振。但却为了选取合适的切换增益来平衡鲁棒性能和跟踪性能,而忽略了收敛速率。文献[11]采用死区迟滞函数代替切换控制律中的符号函数,降低了抖振幅度,但文中没有实验验证,缺少鲁棒性能的详细说明。文献[12]通过引入边界层的方式设计滑模控制方案,利用饱和函数代替符号函数,有效地减弱抖振,但控制方案中切换控制律过度依赖系统集总不确定上界,无法平衡“快收敛”与“弱抖振”之间的关系。如果切换增益过小或边界层厚度值过大,则会导致系统状态收敛速度变慢,稳态误差变大。如果切换增益过大或边界层的厚度值过小,则系统会出现明显抖振现象。
分数阶微积分学是整数阶微积分学的延伸,先后有日本学者S. Manabe教授、法国学者A. Oustaloup教授等分别提出分数阶控制观点[13]和分数阶鲁棒控制技术[14]。近些年,由于计算机技术高速发展,分数阶微积分算子的近似方法不断改进,分数阶滑模控制技术成为当前研究热点。在电机控制领域中,文献[15]将传统整数阶滑模面扩展为分数维空间,即滑模面增加了一个额外的控制参数,设计了一种分数阶滑模等效控制律,并采用模糊算法对切换增益进行实时估计,实验结果表明,分数阶系统性能优于整数阶系统。文献[16]设计了分数阶积分滑模等效控制律,并采用模糊算法和概率模糊神经网络观测器对扰动进行估计和观测,提高了系统跟踪性能。但以上分数阶系统设计过于复杂,不能很好地体现分数阶系统的优越性。尽管分数阶微积分理论在电机控制领域得到了广泛应用,但在PMLSM控制领域报道较少。此外,由于分数阶系统模型的建立存在局限性,大部分学者对分数阶滑模控制的研究主要集中在等效控制律[17],而切换控制律是实现非线性系统状态轨迹快速收敛到滑模面的关键。
因此,本文为了解决PMLSM动子运动过程中易受系统参数摄动、负载扰动等不确定因素影响的问题,并考虑到分数阶微积分算子具有较好的灵活性,以滑模切换律为切入点,将滑模控制算法分数阶化,提出了一种分数阶微分型边界层(fractional order differential boundary layer)非奇异快速终端滑模控制(Non-singular Fast Terminal Sliding Mode Control, NFTSMC)策略。该控制策略在抑制不确定因素影响的同时避免“奇异”问题,提高了系统状态的收敛速率。为了进一步减小有限稳定时间,实现全局快速收敛,并消弱“抖振”现象,将分数阶微分型饱和函数替代整数阶饱和函数,实现分数阶微分型边界层控制。最后,通过实验验证了本文所提控制策略的可行性。
忽略电机初级绕组和永磁体阻尼作用,不考虑磁路饱和、铁心损耗等次要因素的影响,并假设反电动势为理想正弦波,由Park变换得旋转坐标系dq下的PMLSM方程[18]为
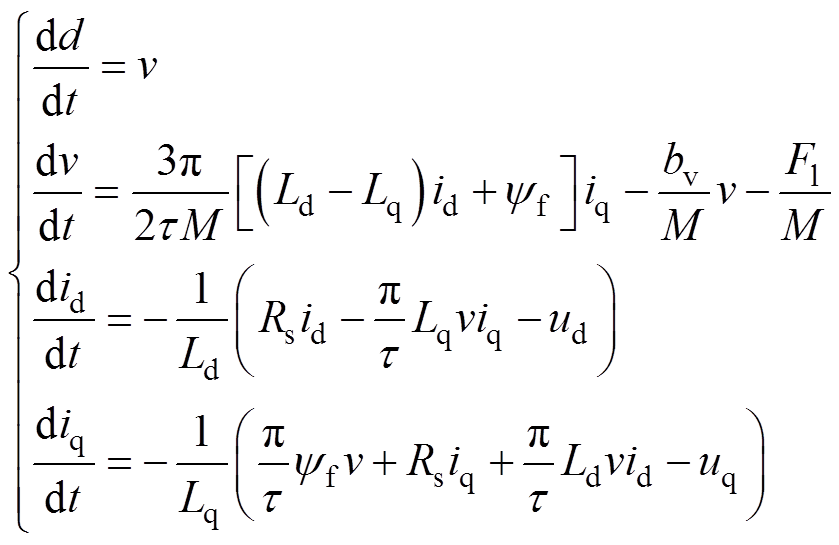 (1)
(1)
式中,ud、uq、id、iq、Ld、Lq分别为dq轴动子电压、电流和电感;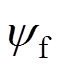 为定子永磁体磁链;d为动子所在位置;v为运动速度;F1为系统外部扰动、非线性摩擦力等;M为PMLSM的动子总质量(包括动子及加在动子上的负载);
为定子永磁体磁链;d为动子所在位置;v为运动速度;F1为系统外部扰动、非线性摩擦力等;M为PMLSM的动子总质量(包括动子及加在动子上的负载);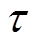 为极距;bv为粘滞摩擦因数;Rs为电阻。
为极距;bv为粘滞摩擦因数;Rs为电阻。
为了保证稳态时id不影响iq或uq,采用磁场定向控制(id=0),由式(1)可得
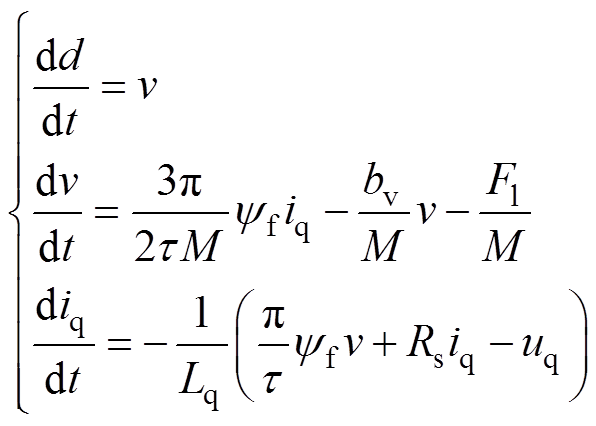 (2)
(2)
当考虑系统参数摄动,式(2)中动态方程改写为
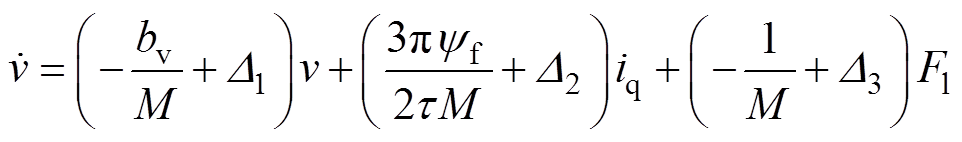
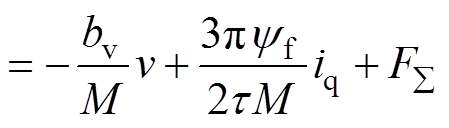 (3)
(3)
式中,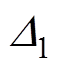 、
、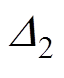 和
和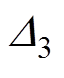 为系统参数的不确定性;
为系统参数的不确定性;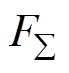 为系统总不确定项,表示为
为系统总不确定项,表示为
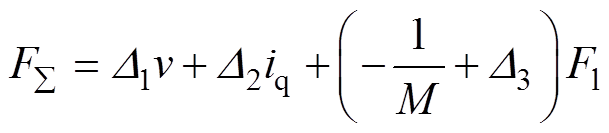 (4)
(4)
假设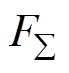 有界,即
有界,即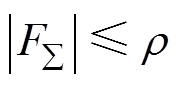 ,
,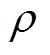 为正常数,是系统总不确定项上界,同时作为NFTSMC的切换增益。该数学模型用于第3节和第4节中控制器的设计。
为正常数,是系统总不确定项上界,同时作为NFTSMC的切换增益。该数学模型用于第3节和第4节中控制器的设计。
本文采用Riemann-Liouville(RL)型分数阶微分初始化[19]定义为
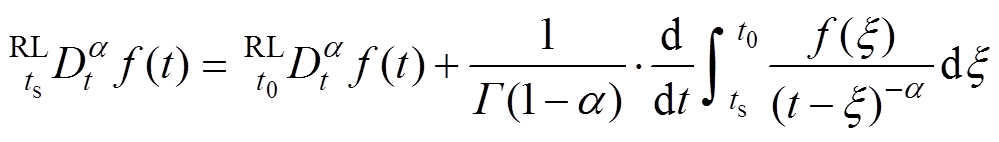 (5)
(5)
式中,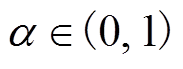 为其阶次;
为其阶次;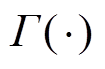 为Gamma函数;ts和t分别为分数阶微分算子的上、下限;
为Gamma函数;ts和t分别为分数阶微分算子的上、下限;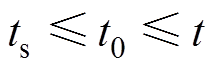 ,
,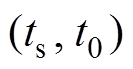 区间为初始化阶段。则分数阶微分型饱和函数设计为
区间为初始化阶段。则分数阶微分型饱和函数设计为
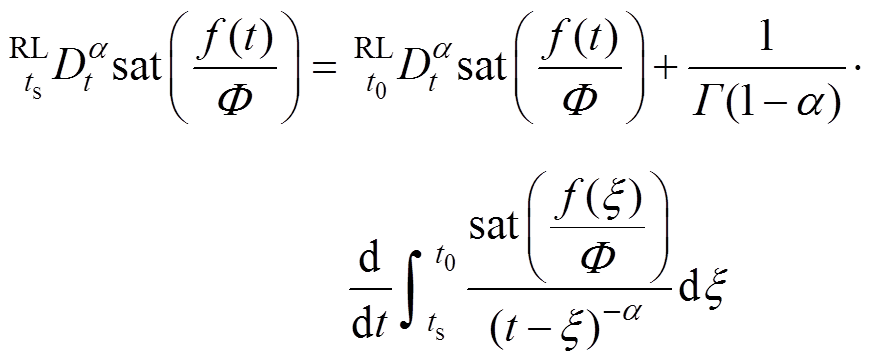 (6)
(6)
其中,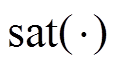 为饱和函数,表示为
为饱和函数,表示为
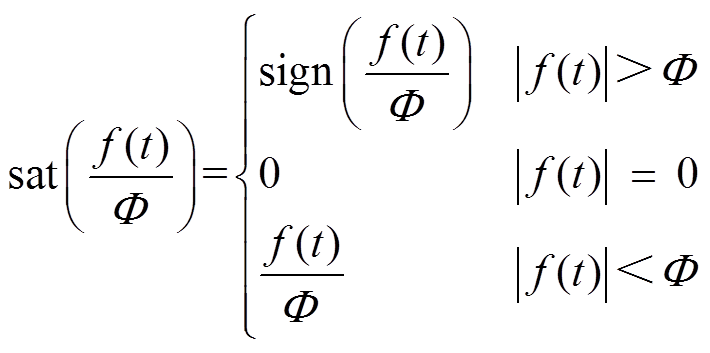 (7)
(7)
式中,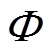 为边界层厚度值。为了直观表现式(6)性质,将分数阶微分型饱和函数和饱和函数进行对比分析。图1为0.2、0.5、0.7阶次分数阶微分型饱和函数与整数阶饱和函数(0阶次分数阶饱和函数)的数值变化对比。输入为一个周期变化的信号,输出为饱和函数和分数阶微分型饱和函数的函数值。根据图1数值对比,总结出分数阶微分型饱和函数的两点性质。
为边界层厚度值。为了直观表现式(6)性质,将分数阶微分型饱和函数和饱和函数进行对比分析。图1为0.2、0.5、0.7阶次分数阶微分型饱和函数与整数阶饱和函数(0阶次分数阶饱和函数)的数值变化对比。输入为一个周期变化的信号,输出为饱和函数和分数阶微分型饱和函数的函数值。根据图1数值对比,总结出分数阶微分型饱和函数的两点性质。
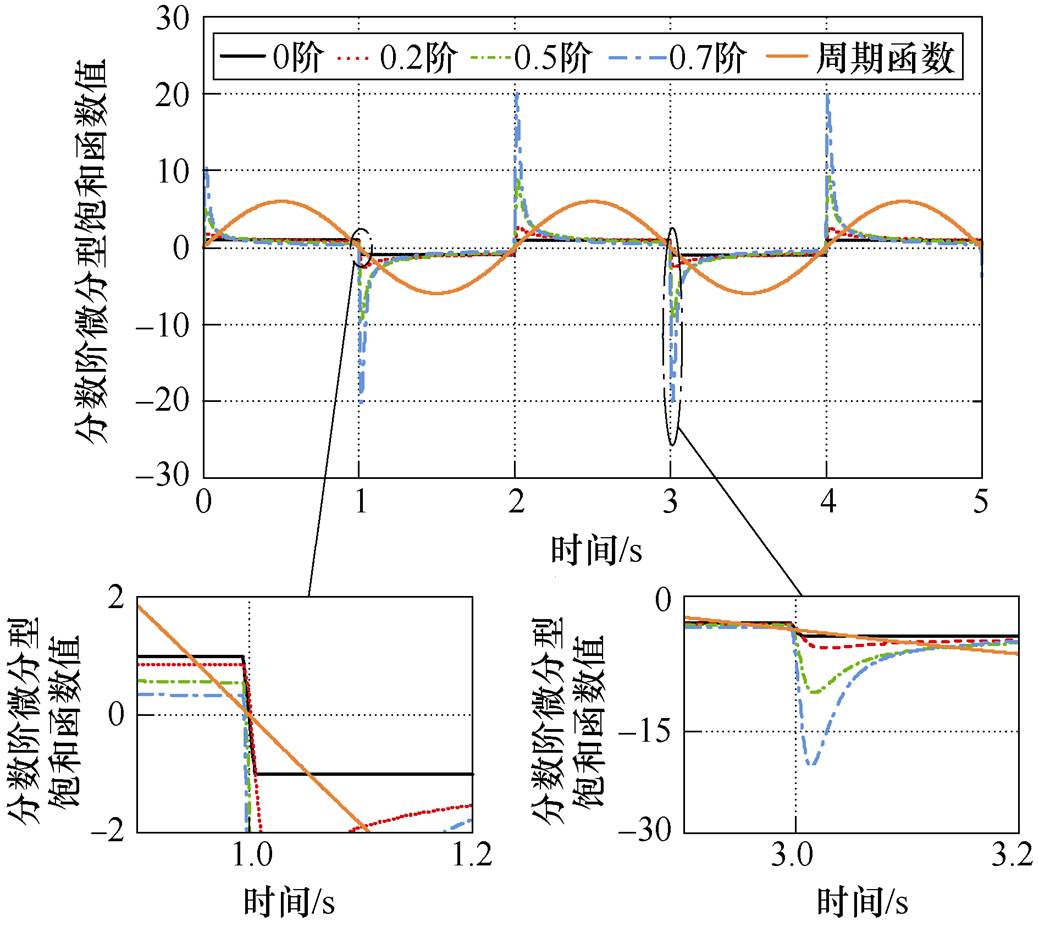
图1 不同阶次分数阶微分型饱和函数值
Fig.1 Fractional order differential saturation function values with different order
(1)性质1。在初始时刻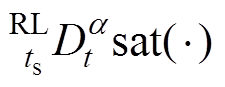
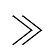
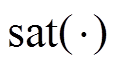 ,且函数值会随着时间增长而衰减到一个小于1的数,
,且函数值会随着时间增长而衰减到一个小于1的数,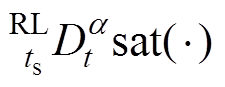 值沿着偏差的变化“方向”而变化,即“大偏差大增益、小偏差小增益”的特性。
值沿着偏差的变化“方向”而变化,即“大偏差大增益、小偏差小增益”的特性。
(2)性质2。在一定条件下,分数阶微分型饱和函数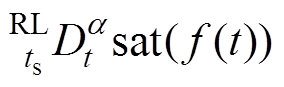 可以提取f(t)的符号,其中f(t)为连续函数,即
可以提取f(t)的符号,其中f(t)为连续函数,即
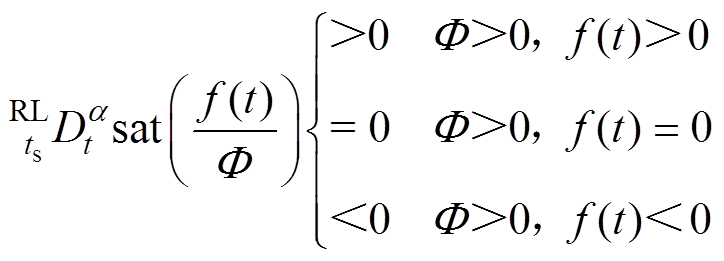 (8)
(8)
为了平衡切换控制“快收敛”与“弱抖振”的关系,将2.1节中的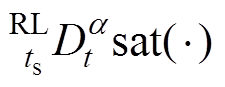 代替传统指数切换控制律中的
代替传统指数切换控制律中的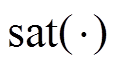 ,则分数阶边界层滑模切换控制律为
,则分数阶边界层滑模切换控制律为
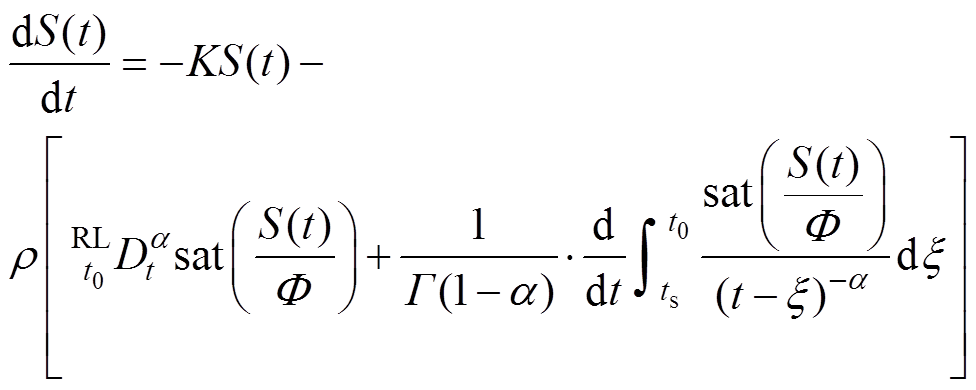 (9)
(9)
式中,K为正常数;S(t)为滑模面;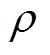 为切换控制增益。
为切换控制增益。
系统受到不确定影响时,致使系统状态轨迹偏离S(t)。当系统状态变量运行轨迹距S(t)较远时,按照分数阶速率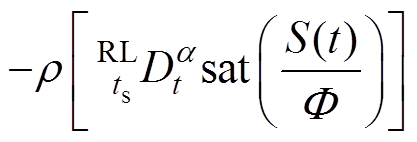 和指数项-KS(t)趋向S(t)。当接近S(t)时,指数项趋近于0,分数阶项起主要作用。此时为滑模控制的关键时期,分数阶项利用“大偏差大增益,小偏差小增益”的功能,将系统状态快速地“拉回”到S(t),且能够减缓在S(t)附近时的收敛速度。因此,不需要较大的切换增益值也能够实现快速收敛,削弱抖振现象。当系统状态轨迹到达边界层内,其线性结构又滤除了系统剩余“抖振”。
和指数项-KS(t)趋向S(t)。当接近S(t)时,指数项趋近于0,分数阶项起主要作用。此时为滑模控制的关键时期,分数阶项利用“大偏差大增益,小偏差小增益”的功能,将系统状态快速地“拉回”到S(t),且能够减缓在S(t)附近时的收敛速度。因此,不需要较大的切换增益值也能够实现快速收敛,削弱抖振现象。当系统状态轨迹到达边界层内,其线性结构又滤除了系统剩余“抖振”。
为验证其优越性,以式(10)所示的典型系统为例对分数阶微分型边界层切换控制律进行分析研究。
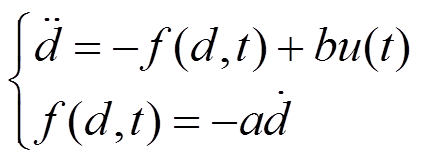 (10)
(10)
取系统的滑模面为
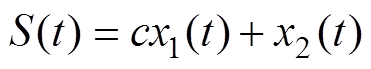 (11)
(11)
式中,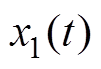 、
、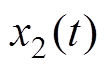 为状态变量;c>0,a>0;
为状态变量;c>0,a>0;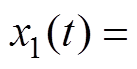
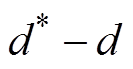 ,
,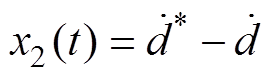 ,
,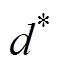 为参考信号,d为实际信号。
为参考信号,d为实际信号。
根据式(9)~式(11)可得控制函数为
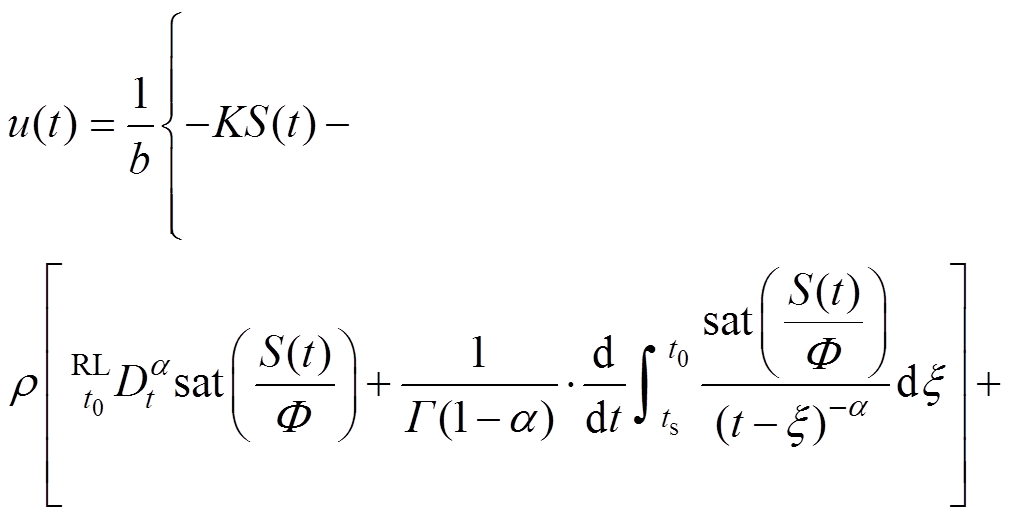
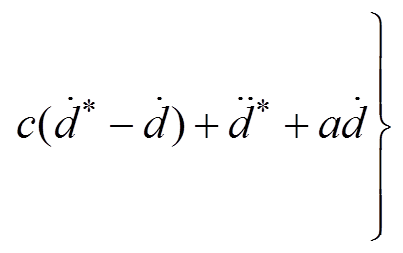 (12)
(12)
式中,a=25;b=133;c=15;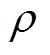 =10;K=10;a=0.2、0.5、0.7;
=10;K=10;a=0.2、0.5、0.7;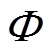 =0.01;x1(0)=10。
=0.01;x1(0)=10。
为了方便比较,整数阶系统的条件与分数阶系统相同。分数阶系统与整数阶系统的性能对比如图2所示,仿真结果表明,无论是收敛速度还是抑制抖振效果,分数阶系统均优于整数阶系统,具体分析如下。
由图2a、图2b、图2d、图2e可见,当系统状态轨迹远离滑模面时,分数阶系统收敛时间小于整数阶系统。由图2e中局部放大图可知,不同阶次分数阶系统均可在0.1 s附近收敛到滑模动态面,其中0.7阶次收敛时间<0.5阶次收敛时间<0.2阶次收敛时间。图2c和图2f为控制输入曲线,从图2c和图2f可以看出,分数阶系统在保证快速收敛的前提下,“抖振”强度明显低于整数阶系统。
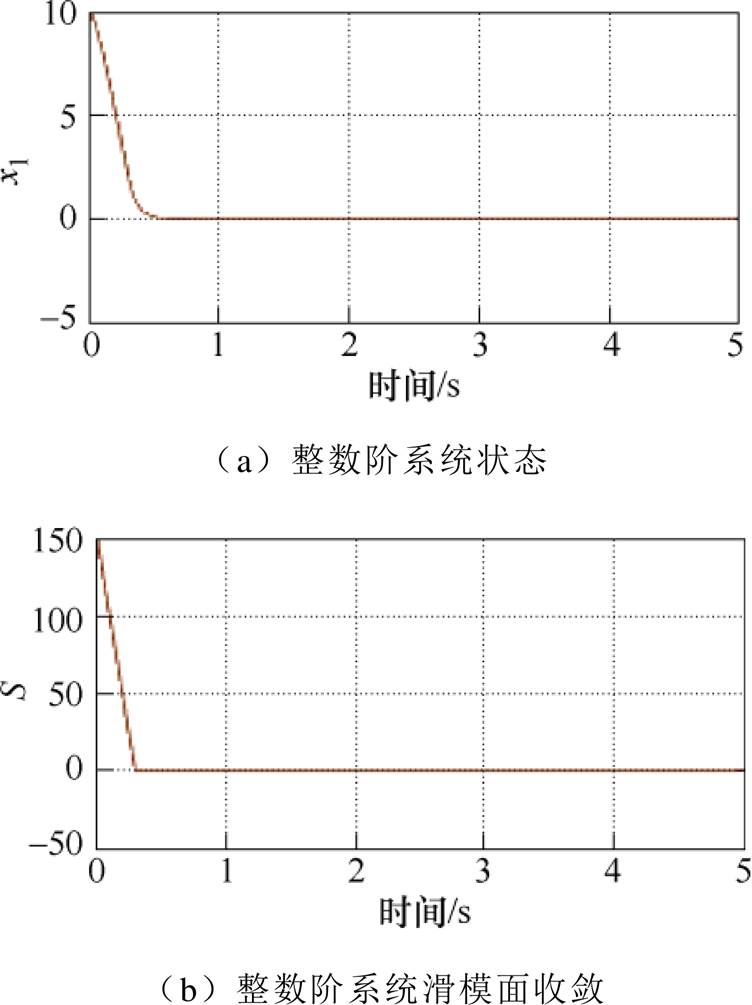
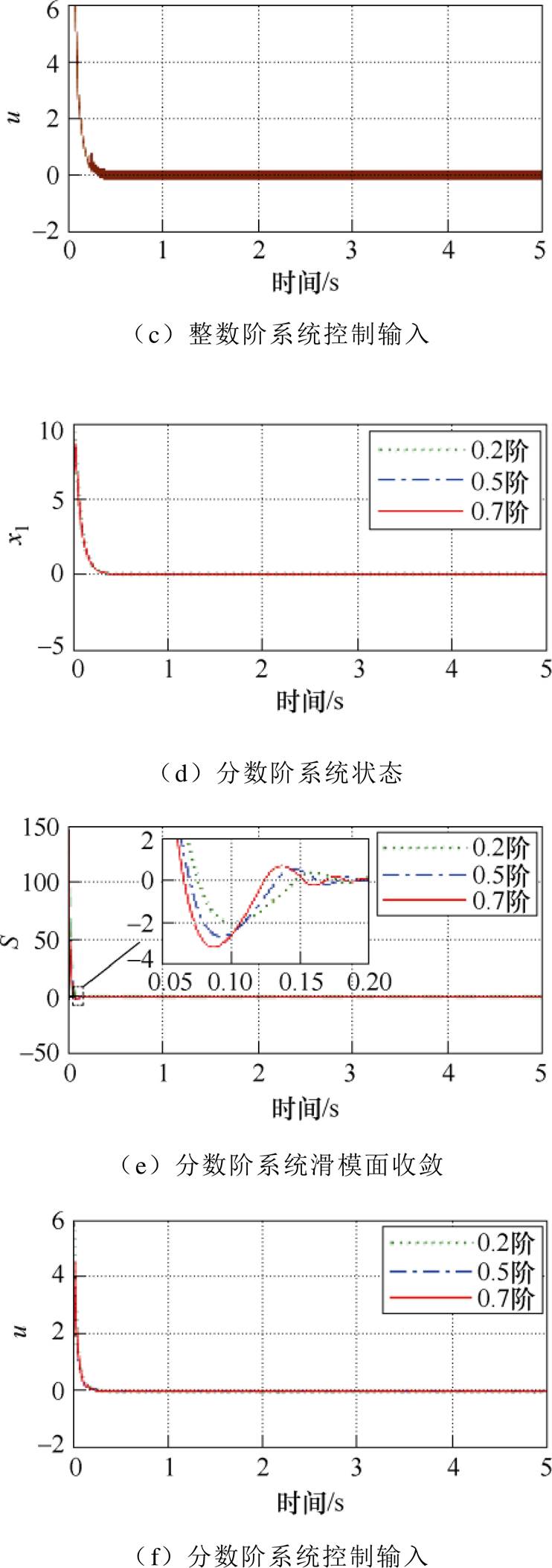
图2 分数阶系统与整数阶系统的性能对比
Fig.2 Performance comparison of fractional and integer order systems
综上所述,本文所设计分数阶边界层相对于整数阶边界层而言,抖振抑制效果较好,减少了收敛时间。
高精度位置控制要求PMLSM系统在不确定性存在时,电机动子仍能够准确快速地跟踪不同的位置参考轨迹,则位置跟踪误差e为
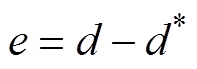 (13)
(13)
定义滑模面
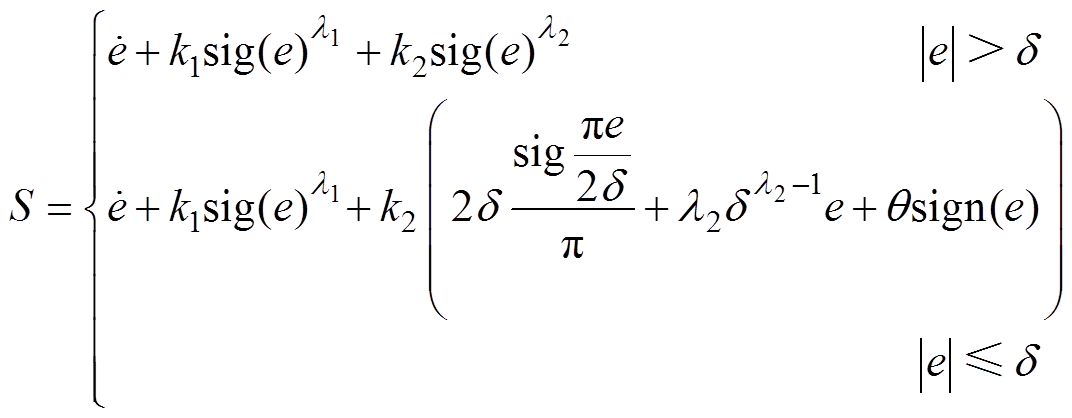 (14)
(14)
其中
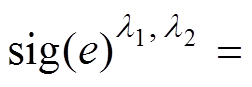
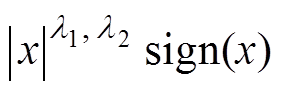
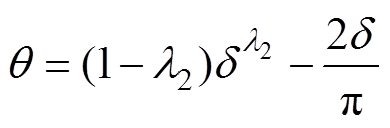
式中,k1、k2为正常数;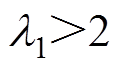 ;
;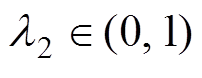 ;
;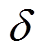 为设定值,
为设定值,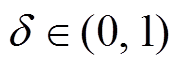 。
。
系统状态远离平衡点: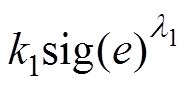 项解决了由于系统状态导数比相同参数的线性滑模面小而影响收敛速度的问题,减少了收敛时间。
项解决了由于系统状态导数比相同参数的线性滑模面小而影响收敛速度的问题,减少了收敛时间。
系统状态接近平衡点:当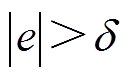 时,
时,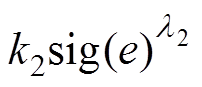 项与经典终端滑模非线性部分相同;当
项与经典终端滑模非线性部分相同;当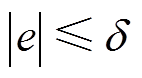 时,
时,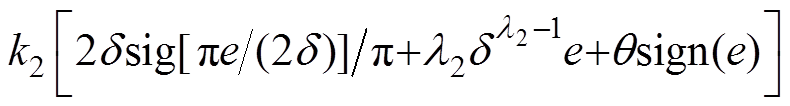 保证有限时间快速收敛,且避免了控制律中的负指数项趋近无穷。
保证有限时间快速收敛,且避免了控制律中的负指数项趋近无穷。
此外,在原点S的导数定义为
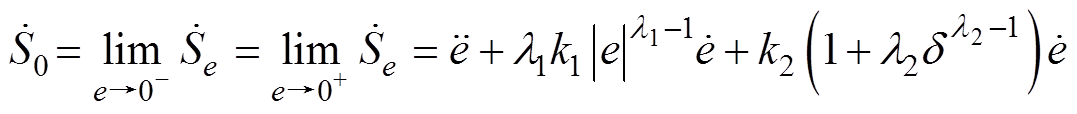 (15)
(15)
将式(3)、式(13)代入式(14),并对其求导,有
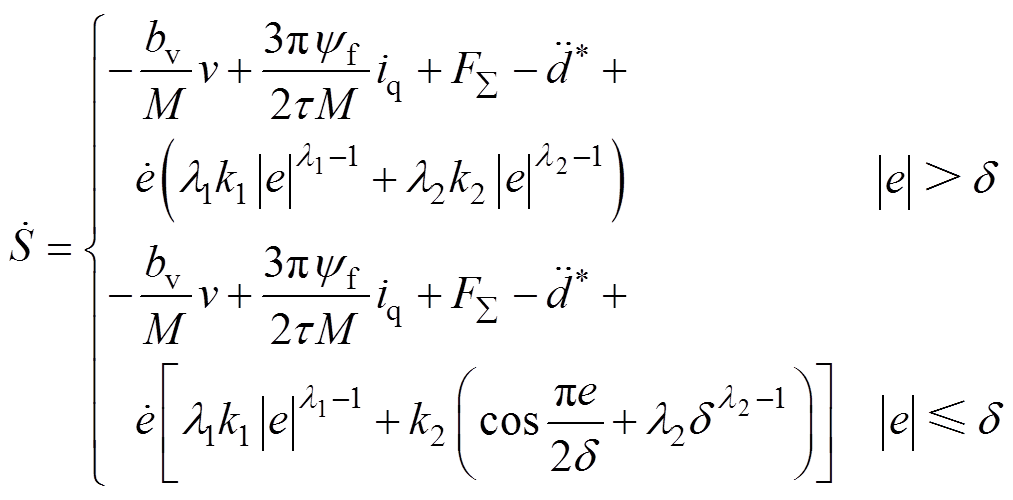 (16)
(16)
为保证系统稳定性,设计分数阶边界层非奇异快速终端滑模控制(Fractional Order boundary layer Nonsingular Fast Terminal Sliding Mode Control, FO-NFTSMC)的控制律,其由等效控制律和切换控制律组成,表示为
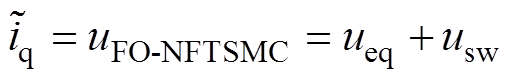 (17)
(17)
其中
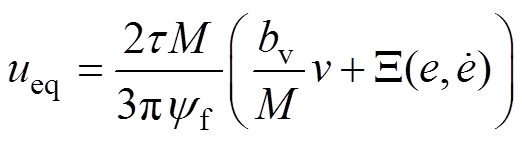
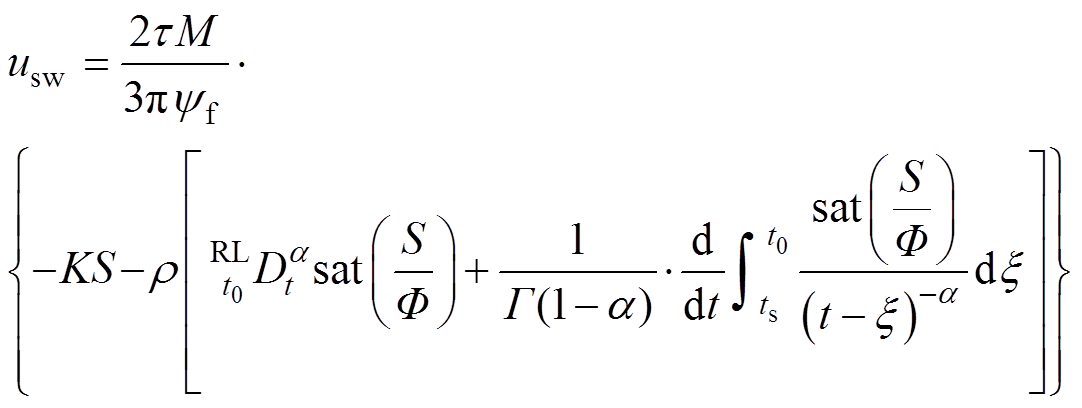
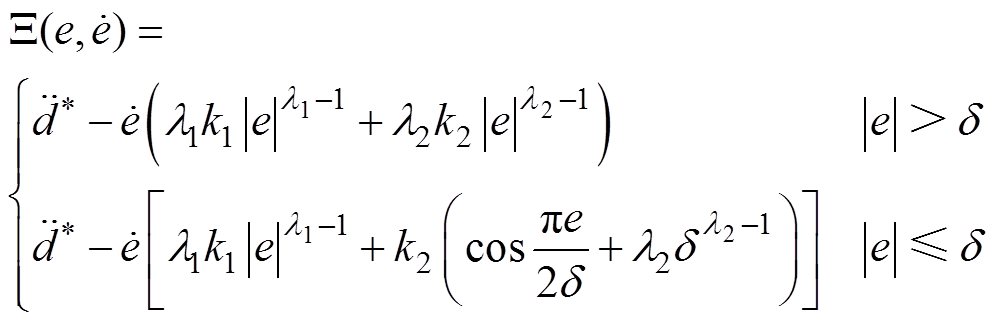 (18)
(18)
式中,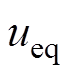 为等效控制律;
为等效控制律;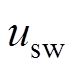 为切换控制律;
为切换控制律;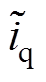 、
、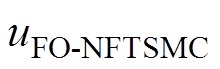 为FO-NFTSMC的控制律。
为FO-NFTSMC的控制律。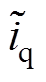 可使系统状态轨迹在有限时间内快速收敛到滑模面上,并保持在滑模面附近运动,从而达到削弱抖振、减小跟踪误差的效果,实现PMLSM伺服系统高精度控制要求。基于FO-NFTSMC的PMLSM系统控制原理框图如图3所示。
可使系统状态轨迹在有限时间内快速收敛到滑模面上,并保持在滑模面附近运动,从而达到削弱抖振、减小跟踪误差的效果,实现PMLSM伺服系统高精度控制要求。基于FO-NFTSMC的PMLSM系统控制原理框图如图3所示。
为了证明系统的稳定性,选取Lyapunov函数V=S2/2,并对其进行两种情况讨论:
(1)当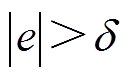 时,对V求导,并将式(16)、式(17)代入可得
时,对V求导,并将式(16)、式(17)代入可得
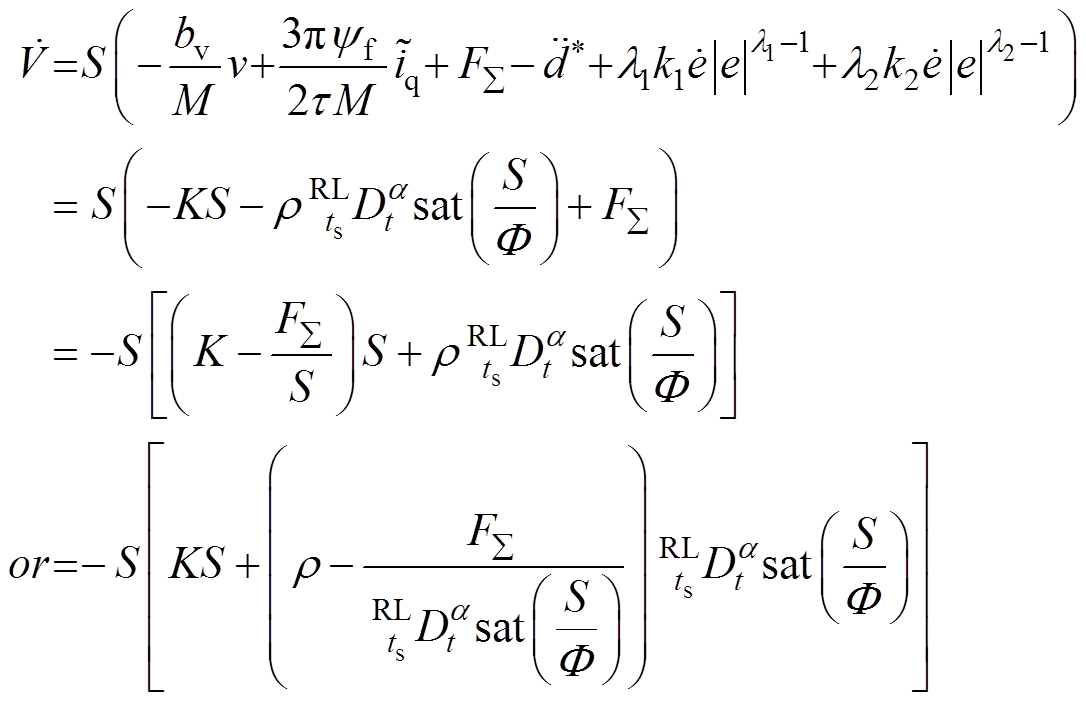 (19)
(19)
显然,根据式(19)可得,欲使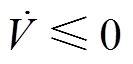 ,需满足
,需满足
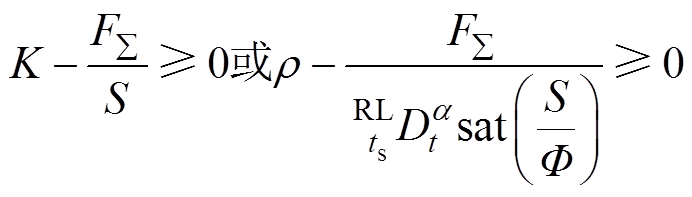 (20)
(20)
因此,系统滑模有限时间收敛集合为
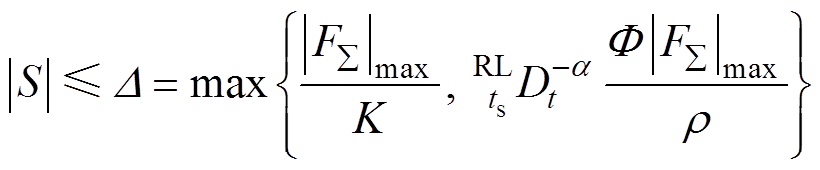 (21)
(21)
式中,D 为收敛集合。
(2)当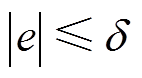 时,对V求导,并将式(16)、式(17)代入可得
时,对V求导,并将式(16)、式(17)代入可得

图3 系统控制原理框图
Fig.3 Block diagram of the system control principle
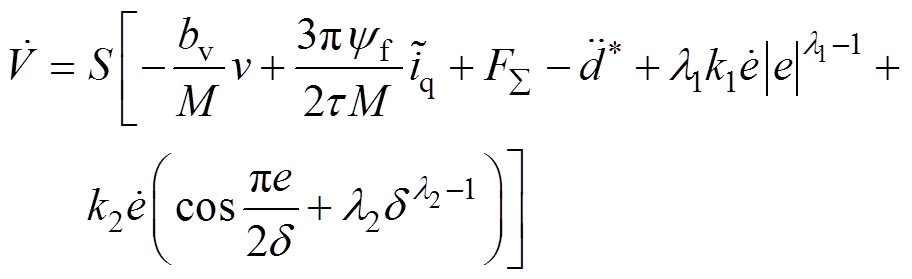
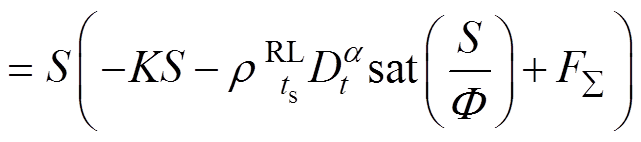 (22)
(22)
同理,情况(2)滑模面收敛集合与情况(1)相同。因此,由Lyapunov稳定判据可以证明在参数变化、外部扰动等不确定性存在的情况下,FO- NFTSMC的系统仍是稳定的。
为了验证本文采用方法的可行性,搭建了基于cSPACE的半实物仿真平台,如图4所示。系统主要由PMLSM、驱动器、光栅位移传感器、cSPACE控制箱、计算机(Matlab/Simulink)、DSP控制卡等组成。在Simulink中搭建算法模型,用cSPACE模块替换输入输出接口,然后编译整个模块生成DSP代码,在控制卡上运行后生成相应的控制信号。运行过程中可以在线修改控制参数,并在操作界面上实时显示多个变量,非常适合于PMLSM的多变量动态模型。最后,将显示的变量数据下载保存到硬盘中,并利用Origin软件处理数据,完成图像化显示。PMLSM中主要电机参数为: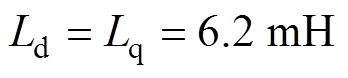 ,
,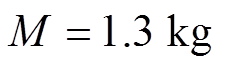 ,
,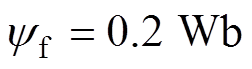 ,
,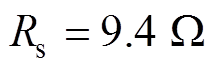 ,
,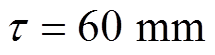 。
。

图4 PMLSM实验平台
Fig.4 Experimental platform of PMLSM
本实验采用整数阶非奇异快速终端滑模控制(Integer Order boundary layer Nonsingular Fast Terminal Sliding Mode Control, IO-NFTSMC)与本文所设计的分数阶边界层非奇异快速终端滑模控制(FO-NFTSMC)进行对比分析。则基于式(3)数学模型,IO-NFTSMC设计为
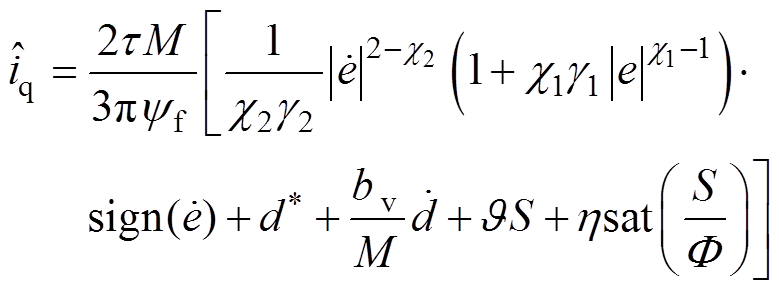 (23)
(23)
式中,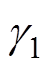 、
、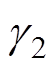 、
、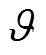 、
、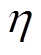 为正常数;
为正常数;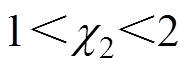 ,
, 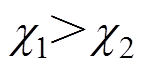 。
。
在实验中,为验证所提出FO-NFTSMC策略的有效性,需要进行四组对比实验。
首先,向系统输入两类不同的时变信号。然后在直线电机运动平台上依次进行三组位置跟踪对比实验(Case 1,Case 2,Case 3),来测试提出的算法的快速性、准确度以及鲁棒性。此外,为了确定分数阶参数a 对控制系统的影响,额外进行1组实验(Case 4)。
(1)Case 1。在标称参数条件下的幅值为50 mm的阶跃信号。
(2)Case 2。在标称参数条件和参数变化条件下的幅值为10 mm的正弦信号。
(3)Case 3。在负载扰动条件下的幅值为10 mm的正弦信号。
(4)Case 4。在标称参数条件下的幅值为10 mm的正弦信号(不同a 对应边界层值相同)。
考虑到系统稳定性和操作环境,本文经过多次重复实验与测试,最终确定了每种控制策略的一组参数,如下:IO-NFTSMC: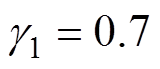 ,
,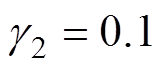 ,
,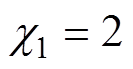 ,
,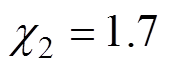 ,
,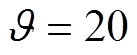 ,
,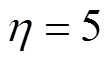 ,
,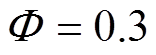 ;FO-NFTSMC:
;FO-NFTSMC: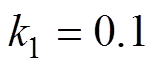 ,
,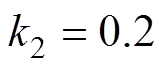 ,
,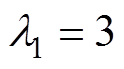 ,
,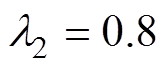 ,
,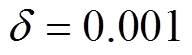 ,
,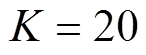 ,
,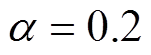 ,
,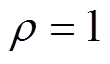 ,
,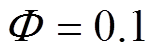 。
。
为了将分数阶微积分应用到实际的运动控制系统中,本实验选择分数阶系统的频率段为[0.01, 100] Hz。此外,综合考虑系统的动态性能和稳态性能,本文实验部分选择a=0.2来验证控制器的控制性能。
以上参数可以保证系统获得较好的控制性能。
(1)Case 1。在标称状态条件下采用IO-NFTSMC和FO-NFTSMC两种策略下的位置响应如图5所示。在保证高精度的情况下,虽然FO-NFTSMC策略在初始响应有一定超调,但超调在工业要求指标的合理范围之内,且达到平衡点的时间明显比IO- NFTSMC策略短。为方便对比,图5b给出放大100倍的细节。从位置响应曲线细节可以看出,FO- NFTSMC策略的偏离给定跟踪曲线的值较小,具有更好的跟踪性能。而IO-NFTSMC策略的偏离给定跟踪曲线的值较大,偏离值高达12.8 mm。图6为两种控制策略下的系统跟踪误差,从图6b可以直观地发现,FO-NFTSMC策略下的位置误差幅值大约保持在5 mm左右,而IO-NFTSMC策略下的位置误差幅值大约保持在10 mm左右,可见FO- NFTSMC策略下的系统抖振现象更弱。
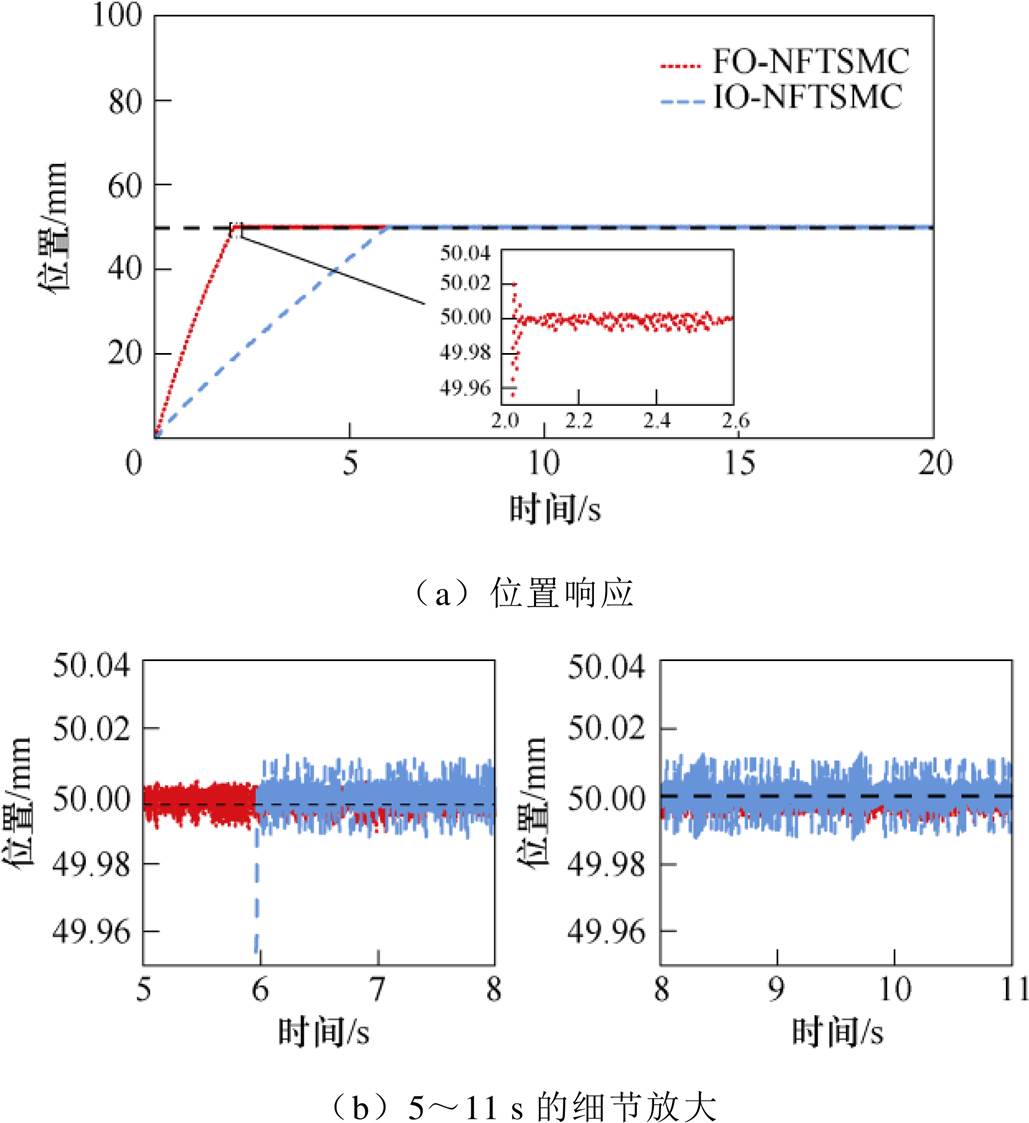
图5 两种控制策略下的位置响应
Fig.5 Position response under two control strategies
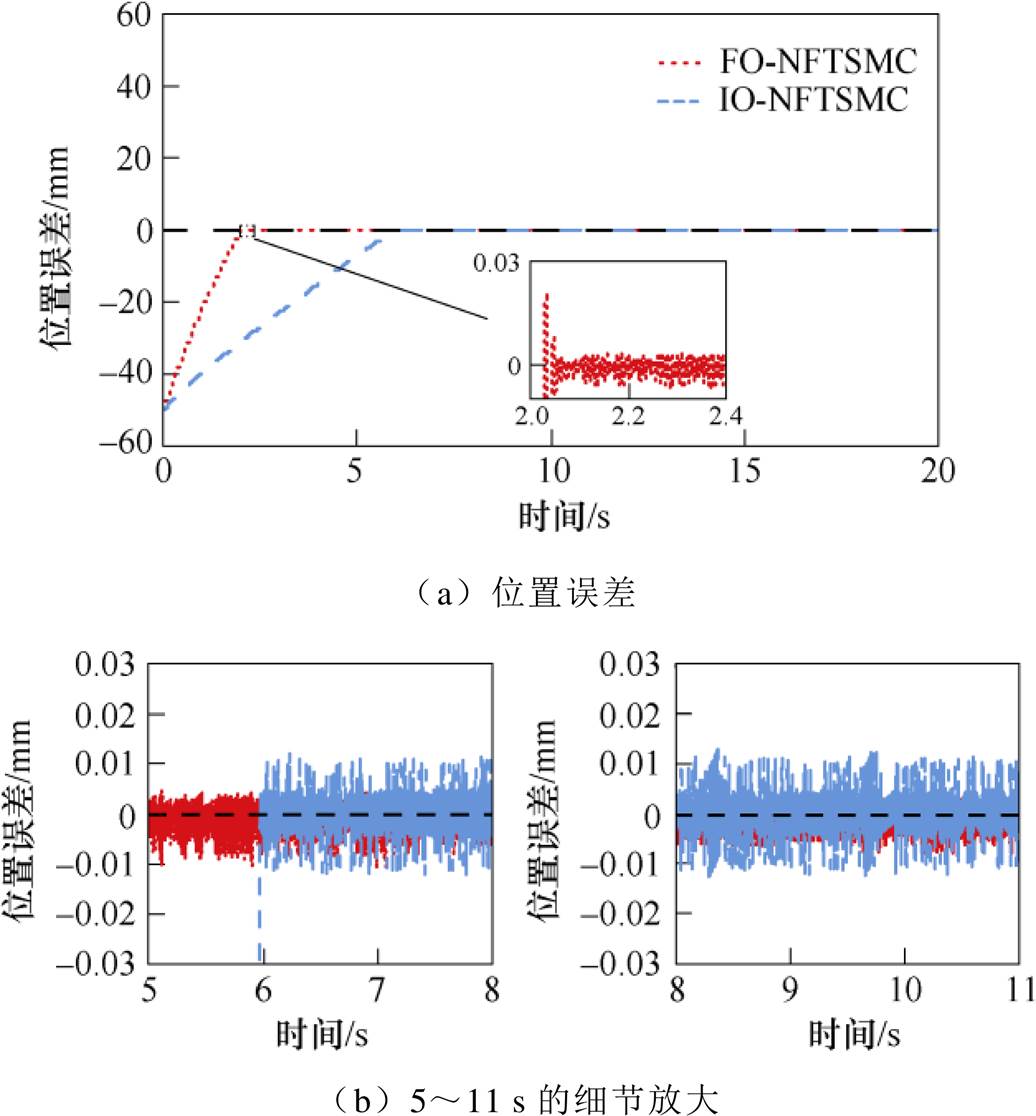
图6 两种控制策略下的位置误差
Fig.6 Position error under two control strategies
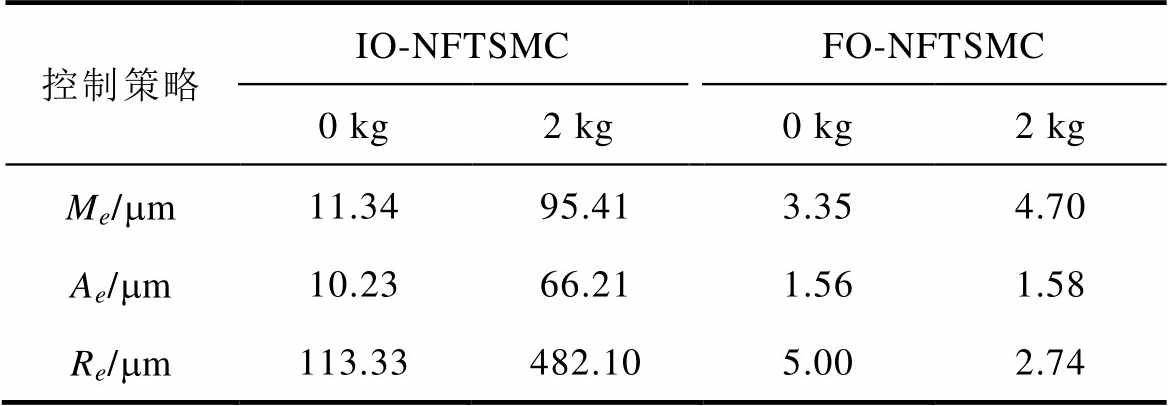
(2)Case 2。在标称参数条件下采用IO-NFTSMC和FO-NFTSMC两种策略下的位置响应如图7所示。虽然这两种控制策略均可以使电机动子跟踪给定参考轨迹,但FO-NFTSMC明显地削弱了抖振现象,并且FO-NFTSMC跟踪曲线的偏差较小,而IO- NFTSMC跟踪曲线与给定位置曲线的偏差较大,两种控制策略具体的位置误差如图8所示。该结果表明,FO-NFTSMC策略无论是在抖振现象还是位置跟踪性能方面均有更好的控制效果。进一步研究永磁直线同步电机控制系统中电机质量和摩擦力变化时的影响。考虑两种情况,分别是没有有效负载、具有2 kg的附加有效负载。其中,图9与图10分别为参数变化条件下的FO-NFTSMC和IO-NFTSMC位置跟踪误差。对比图9a与图9b,参数变化下的FO-NFTSMC策略稳态误差曲线波动频率大于标称状态的稳态误差曲线波动频率,但跟踪误差的波动幅值变化不大,这证明了该控制策略对于参数变化不确定的影响具有较好的抑制效果。对比图9、图10参数变化误差曲线看出,当附加2 kg有效负载时,FO-NFTSMC与IO-NFTSMC相比,具有更小的跟踪误差,跟踪误差减小了60 %左右,且值约为-5~5 mm。此外,从图10细节可以看出,当系统施加2 kg有效负载,系统响应初期IO-NFTSMC策略响应速度稍慢,在0.1 s左右才能达到稳态。而FO-NFTSMC设计中所采用的分数阶边界层不仅具有边界层的输出特性,还具备“大误差大增益”的功能,利用分数阶系统快收敛特性,保证了系统的收敛时间。因此,在参数变化存在时,FO-NFTSMC策略能够更好地克服不确定性对系统的影响。
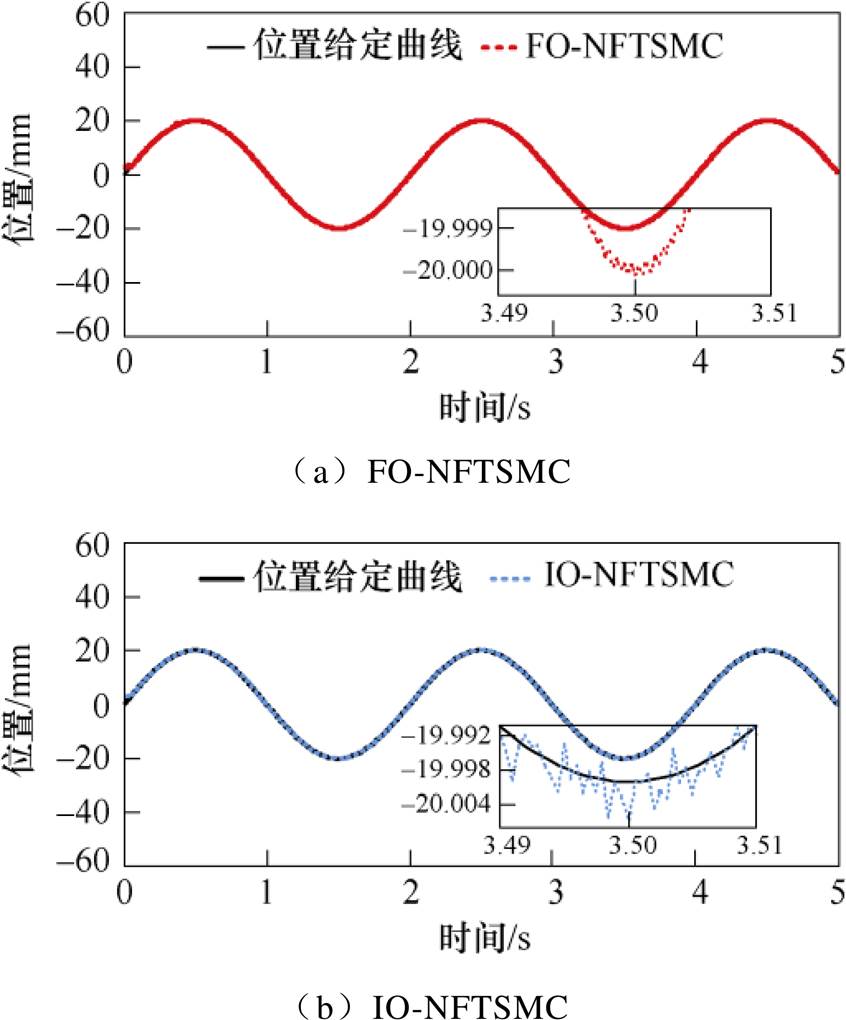
图7 位置响应(标称状态)
Fig.7 Position response(nominal condition)
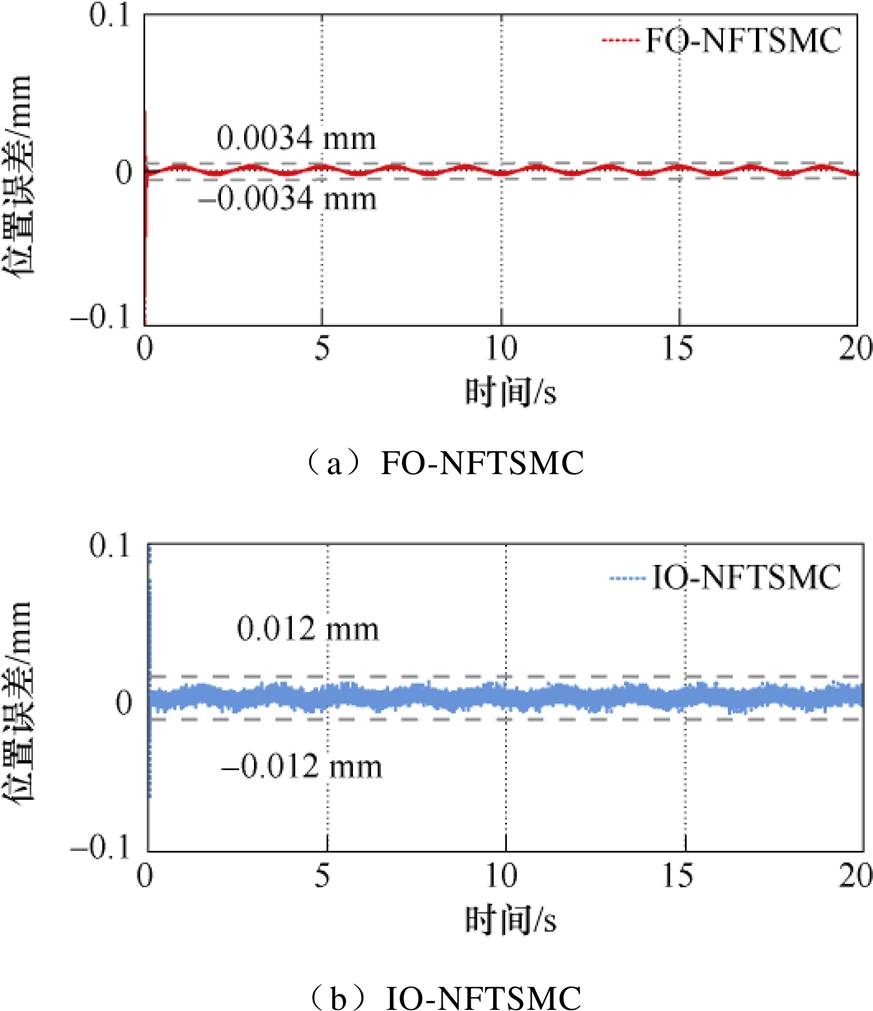
图8 跟踪误差(标称状态)
Fig.8 Tracking error (nominal condition)
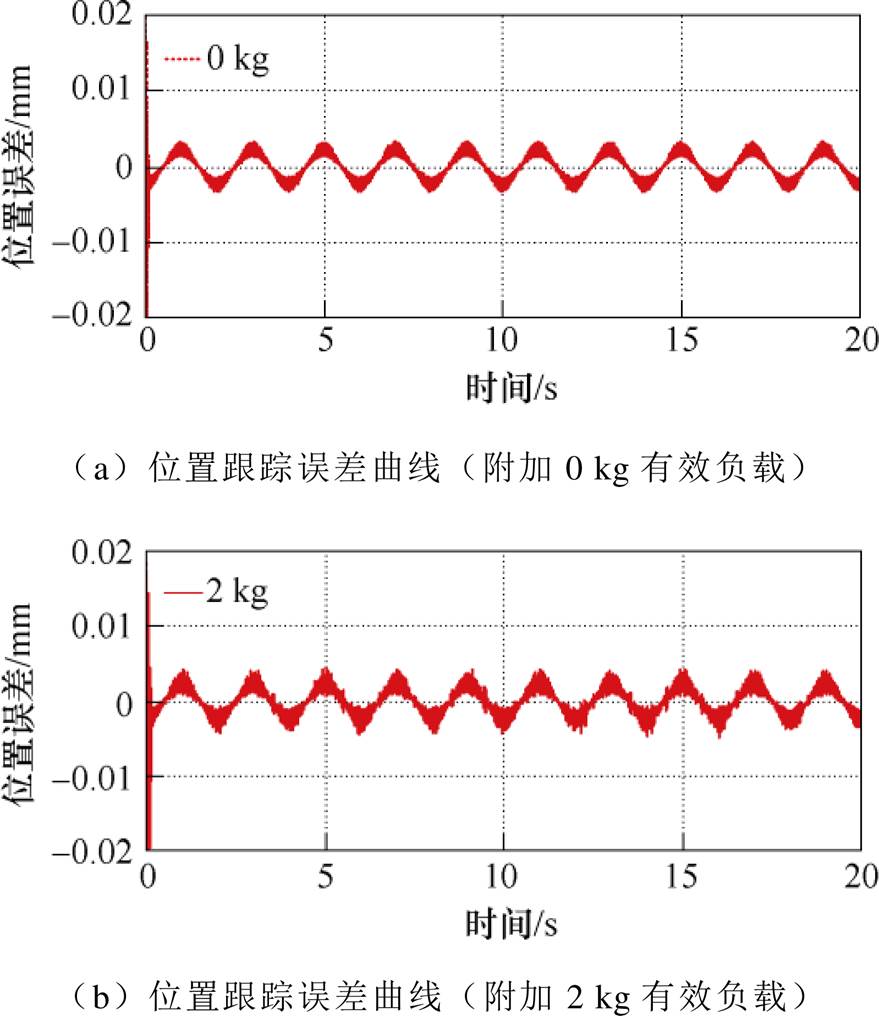
图9 FO-NFTSMC跟踪误差(参数变化)
Fig.9 FO-NFTSMC tracking error (parameter variations)
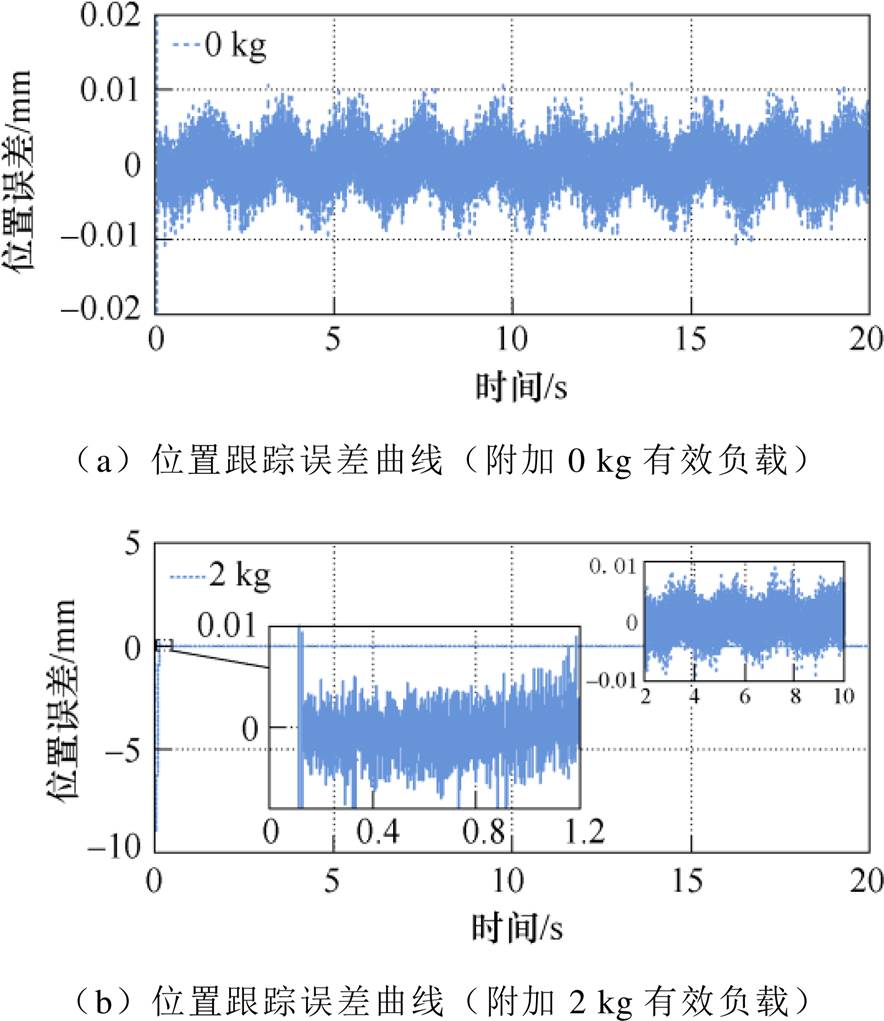
图10 IO-NFTSMC跟踪误差(参数变化)
Fig.10 IO-NFTSMC tracking error (parameter variations)
此外,为了更加方便清晰地比较两种方法的跟踪性能,针对位置跟踪误差,分别定义最大绝对值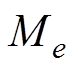 、平均值
、平均值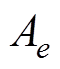 和方均根
和方均根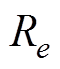 ,有
,有
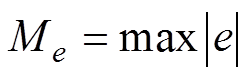 (24)
(24)
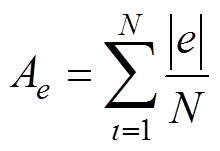 (25)
(25)
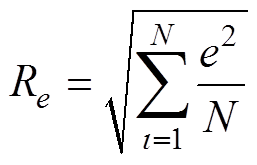 (26)
(26)
式中,N为位置误差信号序列长度。位置误差的详细数据见表1。
表1 质量变化下稳态性能的比较
Tab.1 The comparison of steady-state performance in the presence of the variation of mass
控制策略IO-NFTSMCFO-NFTSMC 0 kg2 kg0 kg2 kg Me/mm11.3495.413.354.70 Ae/mm10.2366.211.561.58 Re/mm113.33482.105.002.74
(3)Case 3。在6 s时向永磁直线同步电机系统突然添加5 N的干扰负载,以验证系统的抗干扰能力。两种控制策略下的位置误差如图11所示。在突加负载的条件下,两种控制策略均出现了明显波动,但FO-NFTSMC策略的跟踪误差曲线的波动幅值较小,仍保持在10 mm以内。而IO-NFTSMC策略的跟踪误差曲线的波动幅值较大,最大幅值达到30 mm左右,两种控制策略详细的性能指标见表2。本组实验证明了FO-NFTSMC系统具有较好的抗干扰能力。这是由于FO-NFTSMC方法中分数阶边界层部分起到关键性作用,由于分数阶微分算子增加了新的自由度,导致参数选择范围更大,以至于系统稳定区域变窄,这就使系统在切换平面上的鲁棒性加强。因此,在保证跟踪精度前提下,分数阶系统的鲁棒性能也优于整数阶系统。
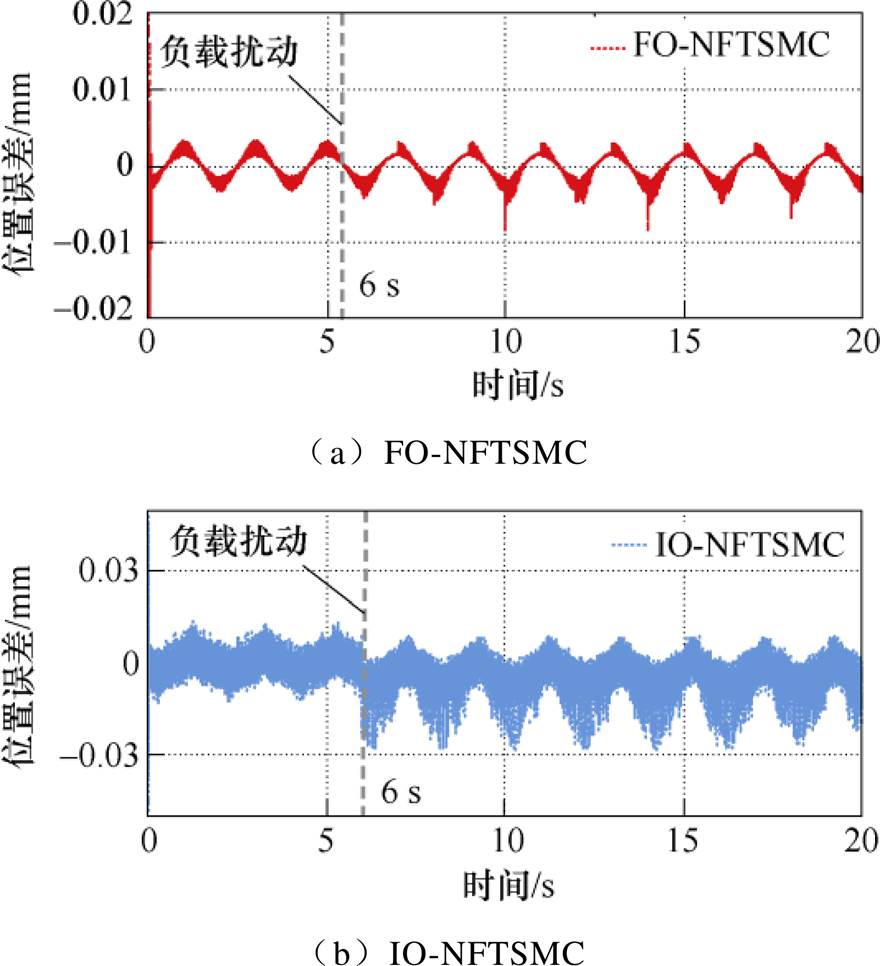
图11 跟踪误差(存在扰动)
Fig.11 Tracking error (presence of disturbance)
表2 突加负载下稳态性能的比较
Tab.2 Comparison of steady-state performance under sudden loading
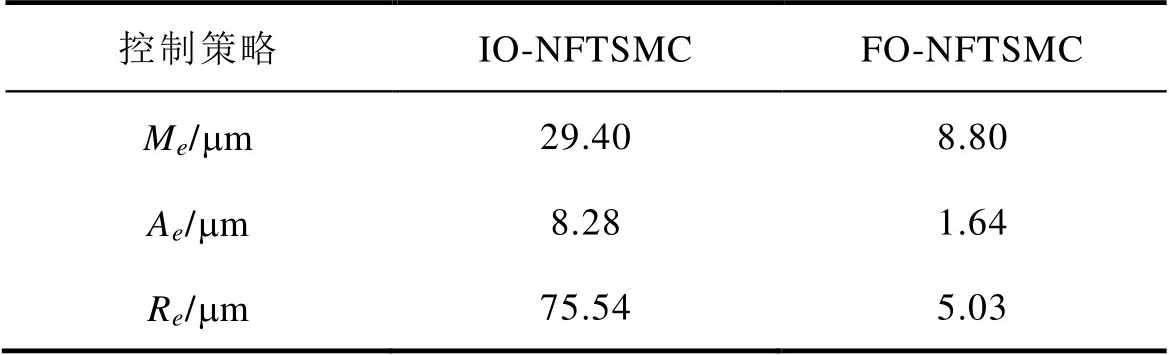
控制策略IO-NFTSMCFO-NFTSMC Me/mm29.408.80 Ae/mm8.281.64 Re/mm75.545.03
(4)Case 4。在其他条件不变的情况下,只改变控制器中阶次a 值,则a=0.1, 0.5, 0.7时的位置跟踪误差如图12所示。当a=0.1时,跟踪误差曲线相较于另外两组参数更为平坦,但是在系统响应初期,其响应时间太慢,这是由于a 越小,分数阶系统发挥的作用越弱,降低了收敛速度。当a=0时,分数阶滑模控制系统也就退化为整数阶滑模控制系统,分数阶系统完全失去了功能;当a=0.5时,跟踪误差的波动频率有所增大,且前期明显有较强的抖振现象;当a=0.7时,跟踪误差的波动幅值、频率大幅度增加,抖振现象较大。这是由于随着阶次的增加,分数阶系统发挥的作用增强,导致分数阶边界层的绝对值过大,使得切换控制过饱和,产生较大的抖振现象,甚至实验结果已经无法保证高精度跟踪性能,此实验现象与理论分析结果基本一致。
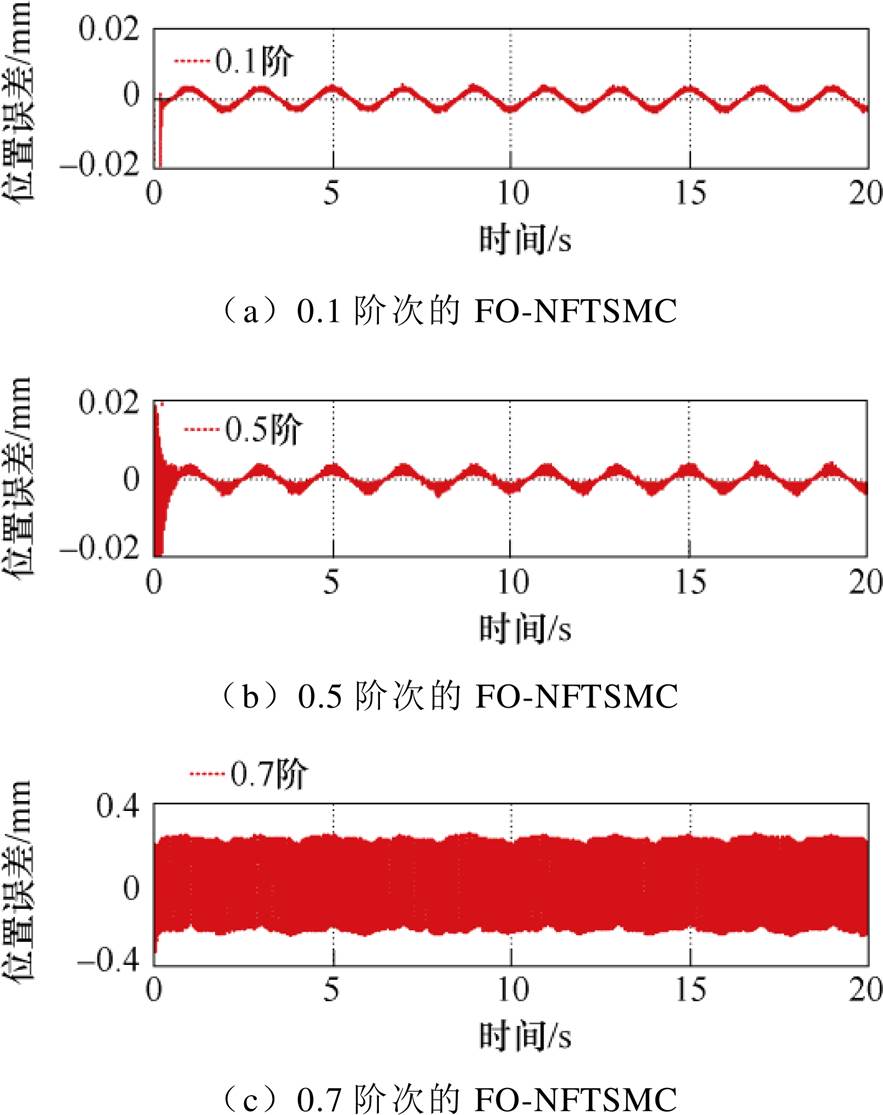
图12 跟踪误差(不同阶次)
Fig.12 Position error (different order)
相较于Case 2中实验结果,以上实验结果均不理想。因此,为了保证整个直线电机伺服系统的跟踪精度,并且误差曲线尽量平滑以及响应速度快,本实验分数阶参数适宜在a=0.2附近进行选择。
为了提高PMLSM伺服系统的跟踪精度,抑制不确定性影响,提出了一种分数阶边界层非奇异快速终端滑模控制方法,使系统状态有限时间收敛到一个集合。并基于Lyapunov稳定性理论,分析证明了闭环系统的稳定性。最后通过对比实验进行验证,得到以下结论:
1)与IO-NFTSMC方法相比,FO-NFTSMC方法响应速度快、抖振现象不明显,提高了PMLSM伺服系统位置跟踪精度和鲁棒性能。
2)分数阶边界层不仅具有整数阶边界层的输出特性,还具备“大误差大增益,小误差小增益”的功能,改善了PMLSM伺服系统的动态品质以及稳态性能。
3)分数阶控制系统相较于整数阶控制系统,具有更广的参数选择范围。
参考文献
[1] 张春雷, 张辉, 叶佩青, 等. 两相圆筒型永磁同步直线电机无传感算法[J]. 电工技术学报, 2019, 34(23): 4901-4908.
Zhang Chunlei, Zhang Hui, Ye Peiqing, et al. Rese- arch on sensorless algorithm of two-phase tubular permanent magnet synchronous linear motor[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4901-4908.
[2] 李雄松, 崔鹤松, 胡纯福, 等. 平板型永磁直线同步电机推力特性的优化设计[J]. 电工技术学报, 2021, 36(5): 916-923.
Li Xiongsong, Cui Hesong, Hu Chunfu, et al. Optimal design of thrust characteristics of flat-type permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 916-923.
[3] 张康, 王丽梅. 基于反馈线性化的永磁直线同步电机自适应动态滑模控制[J]. 电工技术学报, 2021, 36(19): 4016-4024.
Zhang Kang, Wang Limei. Adaptive dynamic sliding mode control of permanent magnet linear syn- chronous motor based on feedback linearization[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4016-4024.
[4] 孙宜标, 仲原, 刘春芳. 基于LMI的直线伺服滑模位移跟踪控制[J]. 电工技术学报, 2019, 34(1): 33-40.
Sun Yibiao, Zhong Yuan, Liu Chunfang. LMI-based sliding mode displacement tracking control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 33-40.
[5] Li Longfei, Xiao Jie, Zhao Yun, et al. Robust position anti-interference control for PMSM servo system with uncertain disturbance[J]. CES Transactions on Elec- trical Machines and Systems, 2020, 4(2): 151-160.
[6] Kao Yonggui, Wang Changhong. H∞ sliding mode control for uncertain neutral-type stochastic systems with Markovian jumping parameters[J]. Information Sciences, 2015, 314(3): 200-211.
[7] 穆朝絮, 余星火, 孙长银. 非奇异终端滑模控制系统相轨迹和暂态分析[J]. 自动化学报, 2013, 39(6): 902-908.
Mu Chaoxu, Yu Xinghuo, Sun Changyin. Phase traje- ctory and transient analysis for nonsingular terminal sliding mode control systems[J]. Acta Automatica Sinica, 2013, 39(6): 902-908.
[8] Wang Yaonan, Zhang Xizheng, Yuan Xiaofang, et al. Position-sensorless hybrid sliding-mode control of electric vehicles with brushless DC motor[J]. IEEE Transactions on Vehicular Technology, 2011, 60(2): 421-432.
[9] 张贝贝, 赵东亚, 高守礼, 等. 自适应边界层非奇异快速终端滑模控制[J]. 控制工程, 2019, 26(4): 717-723.
Zhang Beibei, Zhao Dongya, Gao Shouli, et al. A novel nonsingular fast terminal sliding mode control with adaptive boundary layer[J]. Control Engineering of China, 2019, 26(4): 717-723.
[10] Ghaebi P P, Ataei M, Mirzaeian B, et al. A robust adaptive sliding mode control for PMLSM with variable velocity profile over wide range[J]. Research Journal of Applied Sciences, Engineering and Technology, 2015, 10(9): 997-1006.
[11] 张月玲, 党选举. 基于死区迟滞函数的永磁同步直线电机滑模控制[J]. 中国电机工程学报, 2011, 31(3): 67-74.
Zhang Yueling, Dang Xuanju. Sliding mode control based on dead-zone hysteresis function for PMLSM[J]. Proceedings of the CSEE, 2011, 31(3): 67-74.
[12] 赵希梅, 赵久威. 永磁直线同步电机的互补滑模变结构控制[J]. 中国电机工程学报, 2015, 35(10): 2552-2557.
Zhao Ximei, Zhao Jiuwei. Complementary sliding mode variable structure control for permanent magnet linear synchronous motor[J]. Proceedings of the CSEE, 2015, 35(10): 2552-2557.
[13] Manabe S. The non-integer integral and its appli- cation to control systems[J]. Electrotechnical Journal of Japan, 1961, 6(3-4): 83-87.
[14] Oustaloup A, Moreau X, Nouillant M. From fractal robustness to non-integer approach in vibration insulation: the CRONE suspension[C]//Proceedings of the 36th IEEE Conference on Decision and Control, San Diego, CA, USA, 2002: 4979-4984.
[15] 张碧陶, 皮佑国. 基于分数阶滑模控制技术的永磁同步电机控制[J]. 控制理论与应用, 2012, 29(9): 1193-1197.
Zhang Bitao, Pi Youguo. Fractional order sliding- mode control for permanent magnet synchronous motor[J]. Control Theory & Applications, 2012, 29(9): 1193-1197.
[16] Chen S Y, Chiang H H, Liu T S, et al. Precision motion control of permanent magnet linear syn- chronous motors using adaptive fuzzy fractional-order sliding-mode control[J]. IEEE/ASME Transactions on Mechatronics, 2019, 24(2): 741-752.
[17] Yin Chun, Huang Xuegang, Chen Yangquan, et al. Fractional-order exponential switching technique to enhance sliding mode control[J]. Applied Mathe- matical Modelling, 2017, 44: 705-726.
[18] 孙宜标, 杨雪, 夏加宽. 采用鲁棒微分器的永磁直线同步电机二阶滑模控制[J]. 中国电机工程学报, 2007, 27(33): 6-10.
Sun Yibiao, Yang Xue, Xia Jiakuan. Second order sliding mode control for PMLSM using robust differ- entiator[J]. Proceedings of the CSEE, 2007, 27(33): 6-10.
[19] Zhang Fengrong, Li Changpin. Remarks on the initialization of Caputo derivative[C]//Proceedings of 2012 IEEE/ASME 8th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications, Suzhou, China, 2012: 325-329.
Abstract Due to its high reliability, low cost, and simple structure, the permanent magnet linear synchronous motor (PMLSM) has been increasingly used in high-precision industrial servo applications. However, the lack of mechanical transmission in the structure makes it more susceptible to uncertainties such as parameter variations and load disturbance. Therefore, a fractional order boundary layer nonsingular fast terminal sliding mode control (FO-NFTSMC) strategy is proposed.
Firstly, the dynamic model of PMLSM containing uncertainties is established. Then, the nonsingular fast terminal sliding mode control (NFTSMC) method is used to suppress the influence of uncertainties on the system, ensuring that the tracking error converges to zero in a finite time and avoiding the singularity problem. In addition, the Riemann-Liouville fractional order differential definition and the boundary layer technique are combined to realize a new fractional order differential boundary layer control. The fractional order boundary layer has the output characteristics of the integer boundary layer. It can also change the output value with the direction of change of the state trajectory, solving the contradiction between “Weak chattering” and “fast convergence” in the traditional integer order boundary layer control.
The contrast experiments based on the FO-NFTSMC method and IO-NFTSMC method are carried out on a linear motor system. When tracking a given step command, the actual trajectory based on the FO-NFTSMC deviates less from the given tracking trajectory, and the steady-state error remains around 5 mm. In addition, the deviation value of the IO-NFTSMC strategy is larger, and the steady-state error remains around 10 mm. Therefore, the system based on the FO-NFTSMC has better tracking performance and weaker chattering. A linear motor mounted with a 2 kg payload can track a given sine signal to further study the effects of motor mass and friction on the PMLSM control system. The position tracking error of FO-NFTSMC has a smaller value than IO-NFTSMC, with a reduction of about 60 %. In addition, the IO-NFTSMC strategy responds slower at the beginning of the system response, reaching a steady state in about 0.1 s, while the FO-NFTSMC ensures the convergence time of the system. Also, the load disturbance of 5 N is suddenly added to the PMLSM system at the nominal condition to verify the anti-interference ability of the system. The experimental results show that the error curves of both control strategies fluctuate significantly, with the fluctuation amplitude of FO-NFTSMC being smaller and remaining within 10 mm. In contrast, the tracking error curve of IO-NFTSMC strategy has a larger fluctuation amplitude, with the maximum magnitude reaching about 30 mm. Finally, to verify the effect of the fractional-order boundary layer control on the system performance, an additional set of experiments were carried out to change only the fractional order. The experimental results show that the 0.2 order-based control system has good dynamic performance.
The following conclusions can be drawn from the experimental analysis: (1) Compared with the IO-NFTSMC method, the FO-NFTSMC method improves the position tracking accuracy and robustness performance of the PMLSM system. (2) Using the fractional order boundary layer control, the sliding mode chattering is reduced, and the dynamic performance of PMLSM servo system is improved. (3) Fractional-order control systems have a wider range of parameter selection than integer-order control systems.
keywords:Permanent magnet linear synchronous motor, non-singular fast terminal sliding mode control, fractional order differential boundary layer, chattering
DOI: 10.19595/j.cnki.1000-6753.tces.220287
中图分类号:TM359.4
国家自然科学基金资助项目(51875366)。
收稿日期 2022-03-02
改稿日期 2022-03-29
赵鑫宇 男,1996年生,博士研究生,研究方向为永磁直驱伺服系统及其控制。E-mail: zhaoxy_sut@163.com
王丽梅 女,1969年生,教授,博士生导师,研究方向为交流伺服驱动技术。E-mail: wanglm@sut.edu.cn(通信作者)
(编辑 崔文静)