图1 单自由度电磁悬浮体差动结构
Fig.1 The single degree of freedom electromagnetic bearing differential structure
摘要 自传感电磁悬浮系统利用线圈电感电流与定、动子间气隙的函数关系估计动子位移信息，减少位移传感器的使用，具有成本低、可靠性好和集成度高的优点。该文针对传统单线圈电流纹波变化率检测法估计误差大、易受干扰的问题，基于两相三桥臂开关功率放大器的差动电流控制，建立了两相线圈电流纹波变化率检测的差动位移估计方法，提高了自传感控制精度。首先，阐述了两相三桥臂拓扑的工作原理和电流纹波的特性，明确了差动控制下电流纹波变化率与动子位移的函数关系，给出自传感差动位移估计的实现方法。然后，结合实验分析了线路电阻、偏置电流和母线电压等参数对电流纹波变化率的影响。最后，在单自由度电磁悬浮平衡梁实验平台上开展了自传感动态悬浮控制实验，验证了所提方法的有效性。
关键词：电磁悬浮 共桥臂拓扑 自传感 电流纹波
电磁悬浮技术因其无摩擦、少维护和动力学特性可调等优异特性，近年来受到广泛的关注和研 究[1-2]，并在轨道交通、高速电机、飞轮储能、航空航天等领域获得了应用[3-4]。
电磁悬浮系统因其开环不稳定特性，通常需要使用位移传感器实时检测动子位移并进行闭环反馈控制。位移信号的实时性与准确性直接决定了悬浮系统的稳定性和动态性能。目前，采用电涡流、电容等类型传感器检测动子位移的系统，存在系统成本高、装配繁琐、轴向尺寸大等缺点。此外，在柔性系统中，还存在传感器和执行器不同位的问 题[5-6]。而自传感技术（也称无传感器技术）利用执行器自身实现动子的位移估计，能有效解决上述问题，对降低系统的成本、提高系统集成度和可靠性具有重要意义。
自传感技术的实现方法主要有三类：第一类是基于电磁悬浮系统的数学模型，通过构建状态观测器实现对悬浮体位移的估计[7]，这种方法易受模型参数变化的影响，鲁棒性较差[8]。第二类是根据动子位移与定子线圈电感之间的近似线性关系，通过对线圈电感值的在线检测来获得，称之为参数估计法。具体实现方法有高频小信号注入法[9]、差动变压器检测法、开关谐波解调法[10-13]和电流变化率检测法等[14-16]。其中，高频小信号注入法会引起额外的振动和损耗。差动变压器检测法需要改造定子本体并增加线圈数量，相当于内置了互感型传感器。开关纹波解调法直接利用开关功率放大器（简称“功放”）驱动下的高频电流谐波作为检测线圈电感变化的信号源，通过信号解调提取动子位置信息。电流变化率检测法利用了电流纹波变化率与线圈电感的函数关系以获取动子位移。第三类是具有非线性映射能力的智能算法，如群优化支持向量机、神经网络等方法来预测动子位移[17-18]。
在上述方法中，电流变化率测量法的硬件电路简单、滤波器数量少，且可在一个开关周期内完成对动子位移的检测，动态性能良好[19-20]，但单个开关周期内有限的电流采样点数，以及开关暂态和涡流等因素的干扰，影响了位移估计的精度[21]，若能在不降低开关频率或不增加采样率的前提下增加电流采样点数，就可以有效改善上述问题。近年来，有学者提出了使用共用桥臂的开关功放[22-23]，将多个线圈的电流驱动集成到一个拓扑结构内，以减少开关功率放大器的元器件数量，提高系统可靠性。这种结构虽然使得线圈电流在控制上存在耦合，但有利于通过差动控制实现两相控制桥臂的同步动作和电流纹波的互补，提高单个开关周期中电流纹波上升沿和下降沿的有效采样点数，从而改善电流变化率测量法的位移检测精度。目前，基于共用桥臂开关功放实现自传感电磁悬浮系统的研究尚未被报道。
针对上述问题，本文提出了一种基于两相三桥臂开关功放驱动的电磁悬浮系统的动子位移自传感检测方法，通过检测两相差动电流的纹波变化率来估计悬浮体位移，相比仅检测单相电流，能够有效减小开关暂态和噪声对位移估计准确性的影响。并在一个单自由度的刚性电磁悬浮实验平台上，实现了动子的自传感电磁悬浮，验证了所提方法的有效性。
开关功率放大器是电磁悬浮系统的重要组成部分，将控制信号的线性转换为电磁线圈的驱动电流，进而产生电磁力以实现动子的悬浮控制。
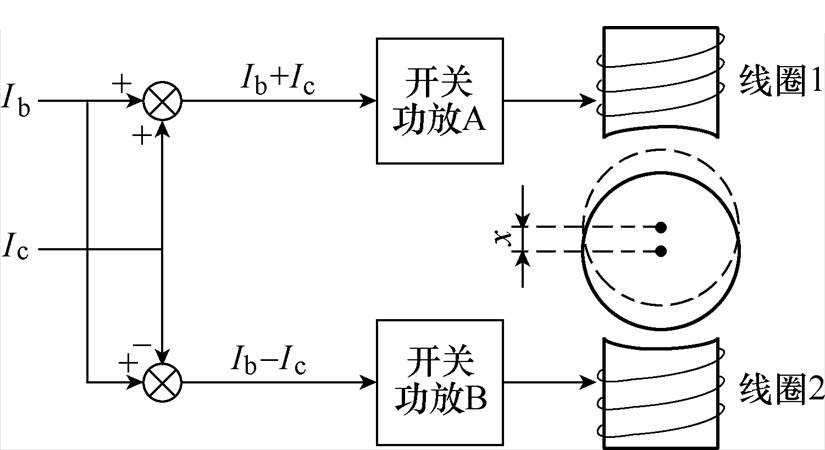
电磁悬浮系统通常使用电磁线圈的差动布置方案来进行各自由度上的转子位移控制。图1所示为垂直方向上差动结构的电磁悬浮控制方案。图1中，Ib为偏置电流，Ic为差分控制电流，x为动子距离中心位置的偏移量。当Ic变化时，上、下线圈电流的大小向相反方向变化，产生的电磁力合力是单个线圈的两倍，进而有效地提高了悬浮系统的刚度。
图1 单自由度电磁悬浮体差动结构
Fig.1 The single degree of freedom electromagnetic bearing differential structure
两相三桥臂开关功放的拓扑结构如图2a所示，能够同时驱动两个电磁线圈。其中，每个线圈的电流由一个控制桥臂和公共桥臂共同控制。相比之下，传统全桥开关功放的拓扑如图2b所示，仅能驱动一个电磁线圈。两相三桥臂拓扑可视为两个全桥型拓扑共用一个桥臂后形成的电路结构，其相比传统的单相全桥功放，可以在基本功能和电流纹波特性不变的条件下，减少1/4开关器件的使用，不仅使得电路的集成度得到提高，而且减少了控制器输出脉冲宽度调制（Pulse Width Modulation, PWM）信号以及驱动电路的数量，有利于系统整体集成度的提高。
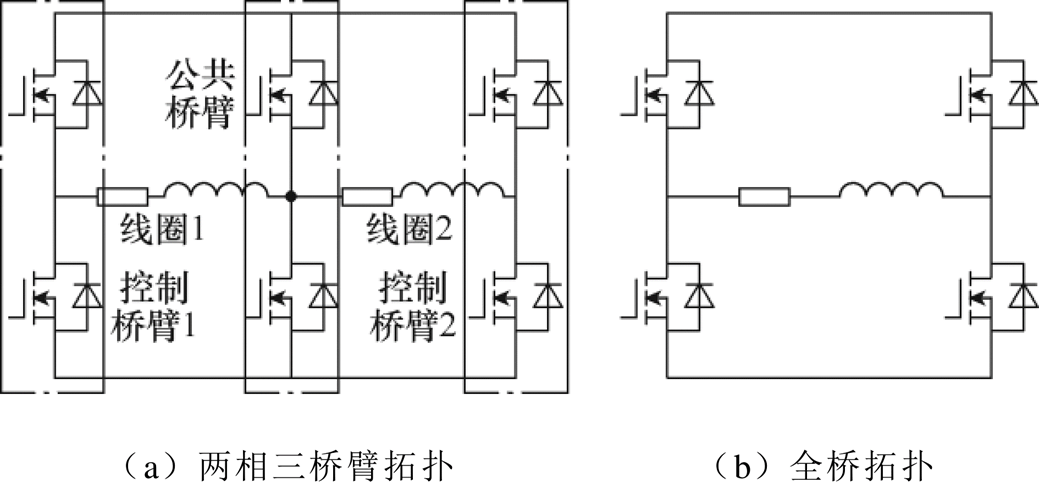
图2 开关功放拓扑
Fig.2 The topology of switching power amplifier
两相三桥臂开关功放的公共桥臂采用50%固定占空比的调制方式，控制桥臂采用可变占空比的调制方式。当控制桥臂的开关管和与其相对应的公共桥臂的开关管都导通时，回路处于正向导通状态；当控制桥臂的开关管和与其相对应的公共桥臂的开关管都关断时，回路处于负向导通状态；当控制桥臂的开关管和与其相对应的公共桥臂的开关管仅有一个导通时，回路处于续流状态。其调制方式及线圈电流如图3所示。
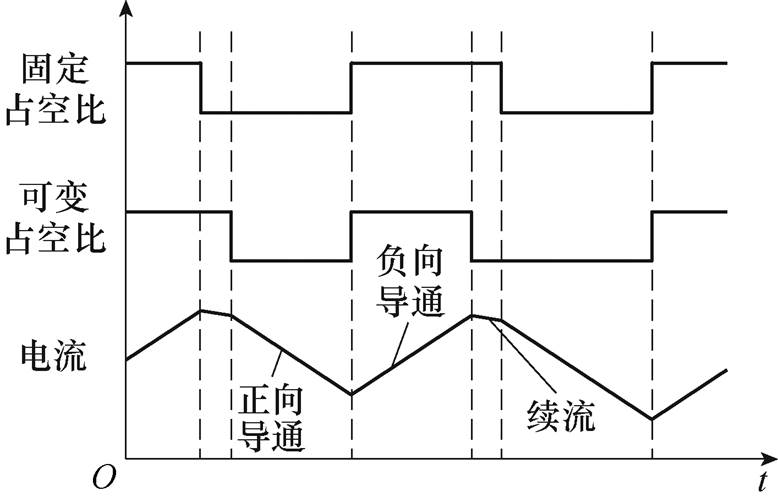
图3 调制方式及线圈电流
Fig.3 Modulation mode and coil current
以单个线圈为例，图4给出了线圈1电压的开关组合。图中，VL为线圈的端电压。图4a为电感充电状态，此时功放控制桥臂的上开关管和公共桥臂的下开关管导通，电磁线圈电流在输入电压Vin条件下快速上升（11模式）；图4b和图4c为电感续流状态，图4b中功放控制桥臂的上开关管开通，其余开关管均关断，电感电流处于续流状态（10模式），图4c中功放公共桥臂的下开关管开通，其余开关管均关断，电感电流处于续流状态（01模式）；图4d为电感放电状态，此时功放控制桥臂的下开关管和公共桥臂的上开关管导通，电磁线圈电流在输入电压-Vin条件下快速减小（00模式）。
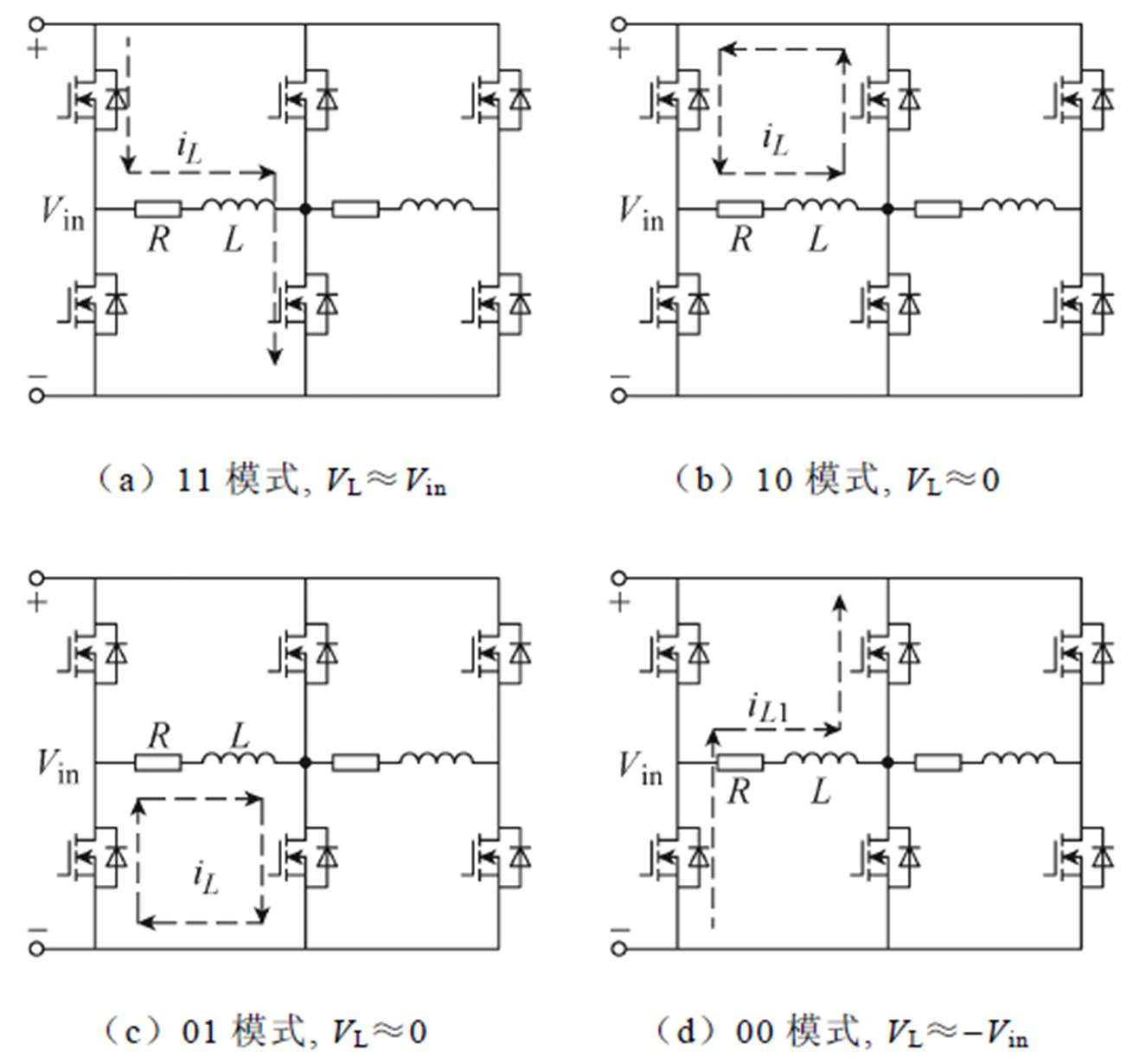
图4 两相三桥臂开关功放的工作状态
Fig.4 The working state of two phase three bridge legs switching power amplifier
在本文中的两相三桥臂开关功放由碳化硅（SiC）MOSFET和肖特基续流二极管构成，相比于普通的硅器件，新型SiC宽禁带器件具有更小的导通内阻、寄生参数和更高的耐压等级，使得两相三桥臂开关功放可以工作在更高的母线电压和开关频率下，同时降低了系统的损耗。图5a和图5b分别给出了当采用SiC器件和Si器件在四种工作模式下的功率损耗分布。由图5对比可知，采用SiC器件降低了开关功放的损耗。
图5 功率损耗分布
Fig.5 Power loss distribution
多自由度电磁悬浮系统的执行器经解耦或忽略磁耦合的条件下，可简化为如图6所示的单自由度差动电磁悬浮系统。
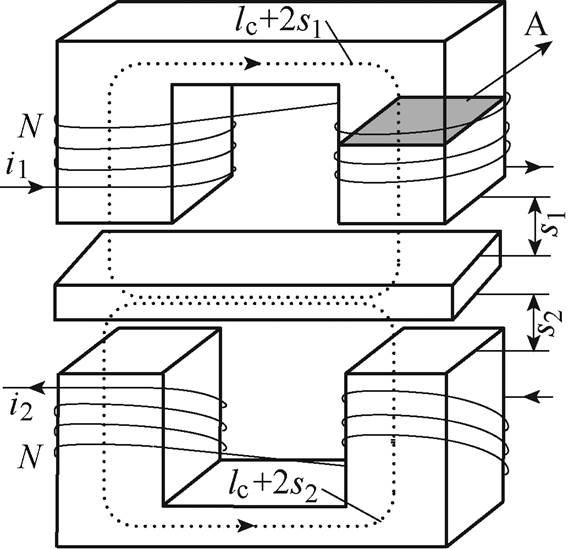
图6 单自由度电磁悬浮体模型
Fig.6 Single degree of freedom electromagnetic bearing model
为简化分析，进一步忽略涡流、漏磁以及边缘效应，并假设穿过铁心和气隙的磁通密度是均匀分布的，则根据磁路理论和安培环路定律，主磁通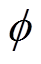
和线圈电流i的关系可表示为
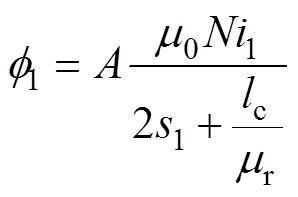（1）
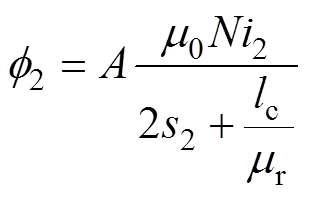（2）
线圈的电感可表示为
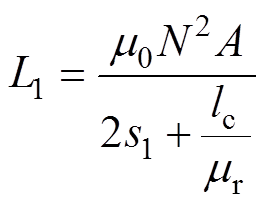（3）
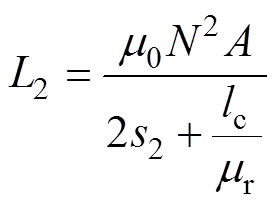（4）
式中，A为磁极面积；N为线圈匝数；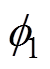
、
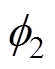分别为图6中上、下两个磁路的主磁通；
、
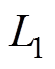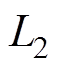分别为图6中上、下两个线圈的电感；
、
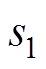为气隙长度，且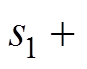
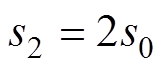，s0为动子位于平衡位置时定子与动子的气隙大小；lc为铁磁材料内部磁路的平均长度；m0为空气磁导率；mr为铁磁材料的相对磁导率。
根据基尔霍夫电压定律以及法拉第电磁感应定律得到绕组线圈的激励电压为
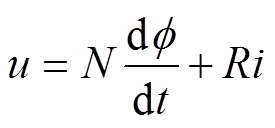（5）
式中，u为线圈母线电压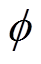；为磁通；R为线圈电阻。将式（1）～式（4）代入式（5），整理可得
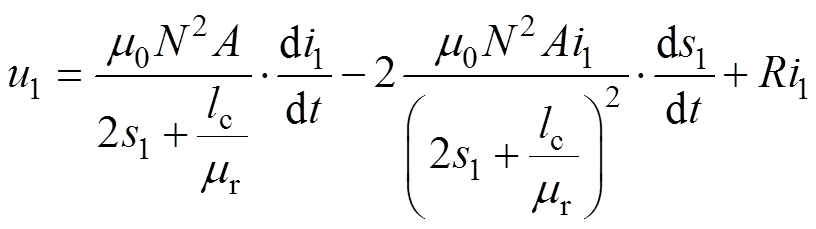（6）
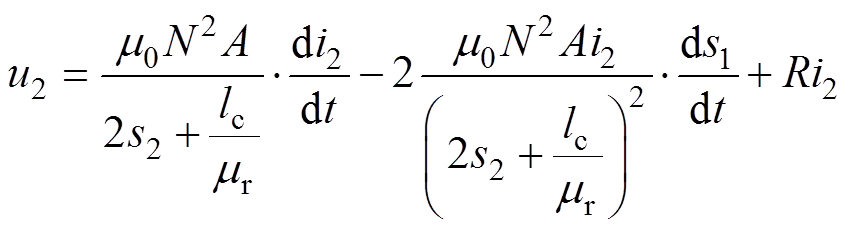（7）
由于电磁悬浮系统的机械时间常数通常远大于电气时间常数，即电流变化率远远大于位移变化率，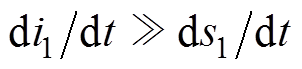
、
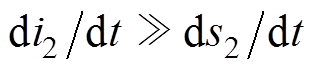，又由于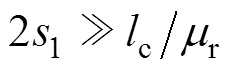
、
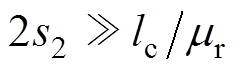，故式（6）、式（7）可以简化为
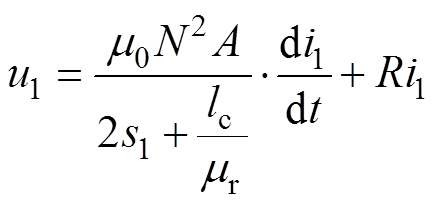（8）
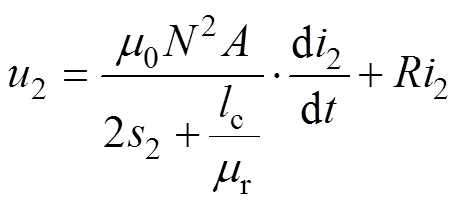（9）
通过简单的数学变换，由式（8）、式（9）可得到
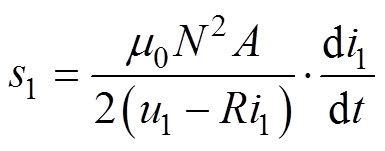（10）
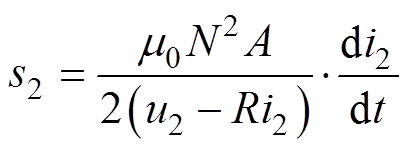（11）
由式（10）和式（11）可知，通过测量电流纹波的变化率，可以获取动子位移信息。此时，执行器兼具位移传感器的功能，即实现了自传感电磁悬浮系统。相比于其他方法，通过电流纹波变化率来实现磁悬浮位移自传感，不需要改动原有的系统定子结构，也不需要其他额外的信号注入和解调电路，同时，采集电流纹波的电流传感器与开关功放电流控制所需的电流传感器可以共用，因此电路结构简单、易于实施。
由2.1节的分析可知，两相三桥臂开关功放根据功率器件通断状态的不同有四种工作模式。在实际电磁悬浮系统中，功放控制桥臂的PWM占空比会在围绕稍大于0.5的常数值动态变化，电感续流状态（10和01模式）相比于电感充电状态（11模式）和电感放电状态（00模式）的时间比较短暂，可近似认为两相三桥臂开关功放工作在两电平模式。
假设开关功率放大器的给定电流在单个开关周期内可视为常数，则可以得到如图7所示的输出电流波形。图7中，T为载波的周期，t1为电流上升时间，imin为一个周期内电流的最小值，imax为一个周期电流最大值，Ia为输出电流平均值。
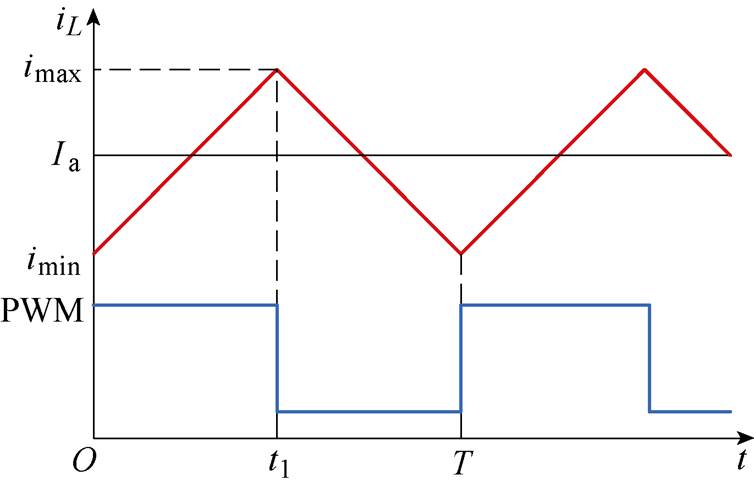
图7 开关功放输出理想电流波形
Fig.7 Output idea current waveforms of switching power amplifier
结合图7可以得到在电感电流上升和下降阶段的电压方程为
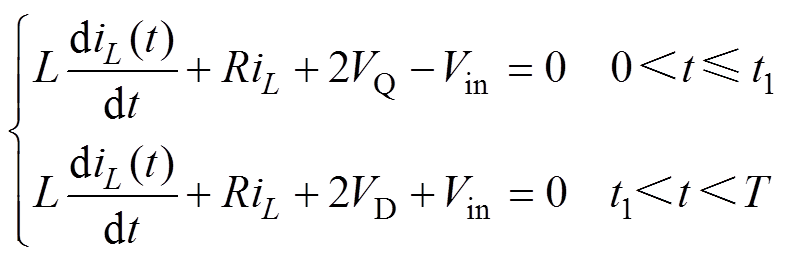（12）
可以解得在两种状况下的电流表达式为
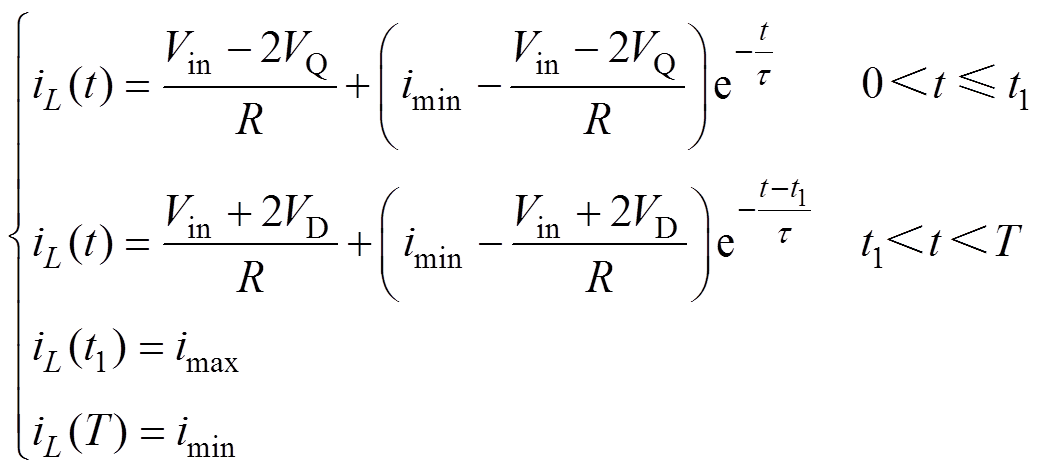（13）
式中，VD、VQ分别为SiC MOSFET和续流二极管的导通压降；t 为电感线圈的时间常数，t =L/R。由式（13）求解可得
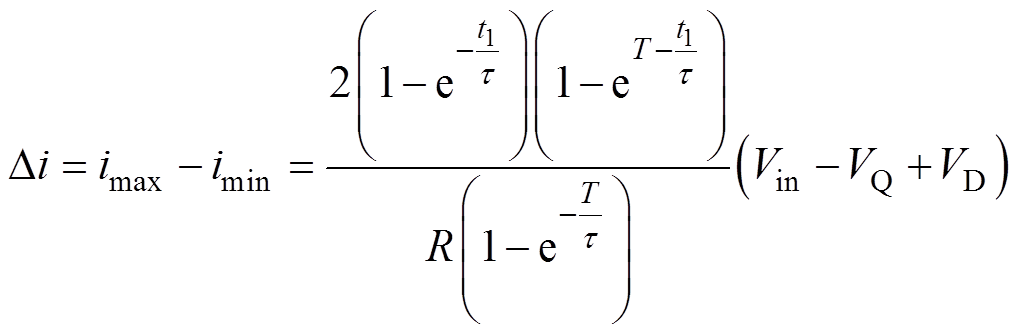（14）
由于开关功放的开关频率较高，因此t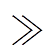 
T，根据等价无穷小可知，当变量x很小时，有1- e-x=x，则式（14）可简化，整理得到电流纹波与状态切换时刻t1的表达式为
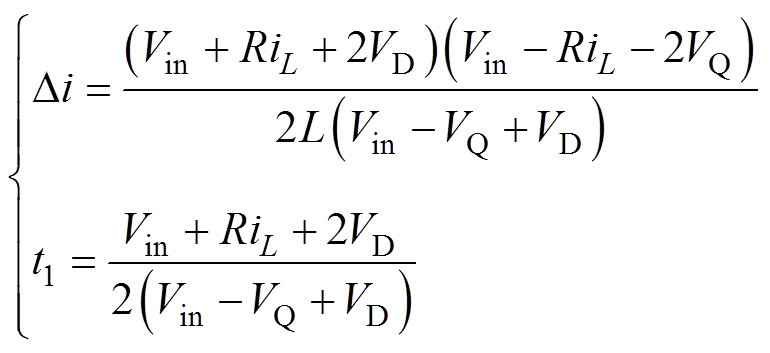（15）
考虑到线圈电阻R，SiC MOSFET和续流二极管的压降VD和VQ均比较小，可以忽略不计，式（15）可进一步简化为
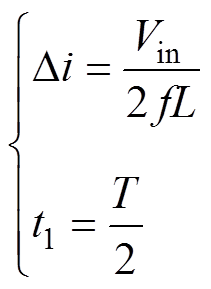（16）
由式（16）可知，在理想情况下，开关功率放大器输出电流的纹波幅值与输入电压大小成正比，与开关频率和电感大小成反比。在母线电压以及开关频率确定的条件下，电流纹波的幅值仅与线圈电感的大小有关，第2.1节推导已证明线圈电感的大小与动子位移近似为线性关系，因此，通过测量电流纹波的变化率来实现动子位移自传感的方法是可行的。
受器件开关瞬态、传感器噪声干扰以及铁心磁滞、涡流等因素的干扰，实际的线圈电流纹波如图8所示，相对理想三角波在电流上升阶段、下降阶段以及开关时刻附近存在噪声干扰。为保证电流采样数据的准确性，在采样时需要进行滤波，以消除尖峰噪声。
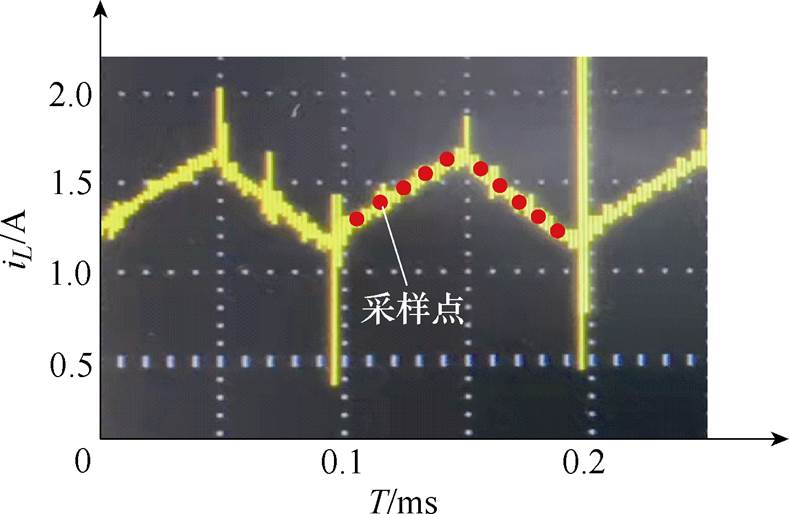
图8 开关功放输出实际电流波形
Fig.8 Output the actual current waveform of switching power amplifier
差动位移估计方法同时利用两相线圈电流纹波变化率的信息，采样点数翻倍，从而有效提高了电流纹波变化率的测量精度，具体实现算法结合图8进行说明。对于纹波电流的第n个周期，在上升沿上采样X个点，在下降沿上采样Y个点，X和Y不是固定的，并随PWM占空比的动态变化而变化，但X和Y的总和是固定的。以线圈1为例，采样后的电流和时间可以表示为一个数组，有
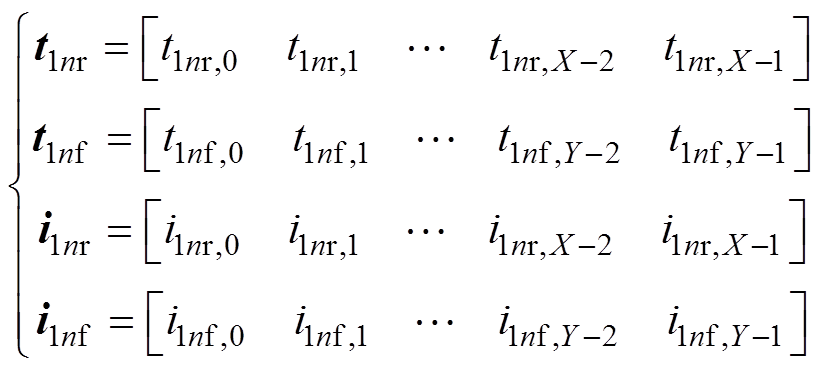（17）
式中，t1nr、t1nf分别为电流纹波上升和下降阶段的采样时间值向量；i1nr、i1nf分别为电流纹波上升和下降阶段的电流采样值向量。
采样时间和电流的平均值为
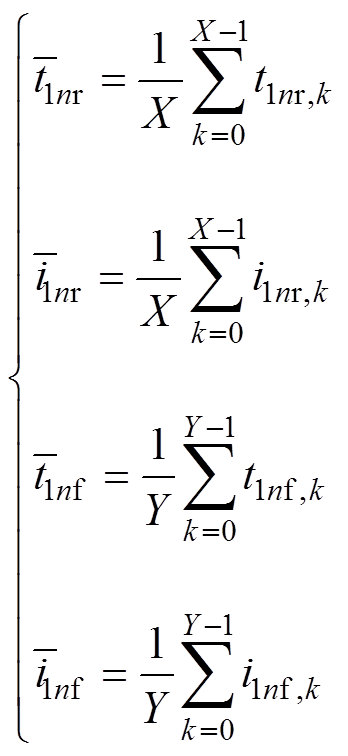（18）
利用采样电流上升沿上的X个点和下降沿上的Y个点，可以使用最小二乘法计算第n个周期中的电流纹波变化率为
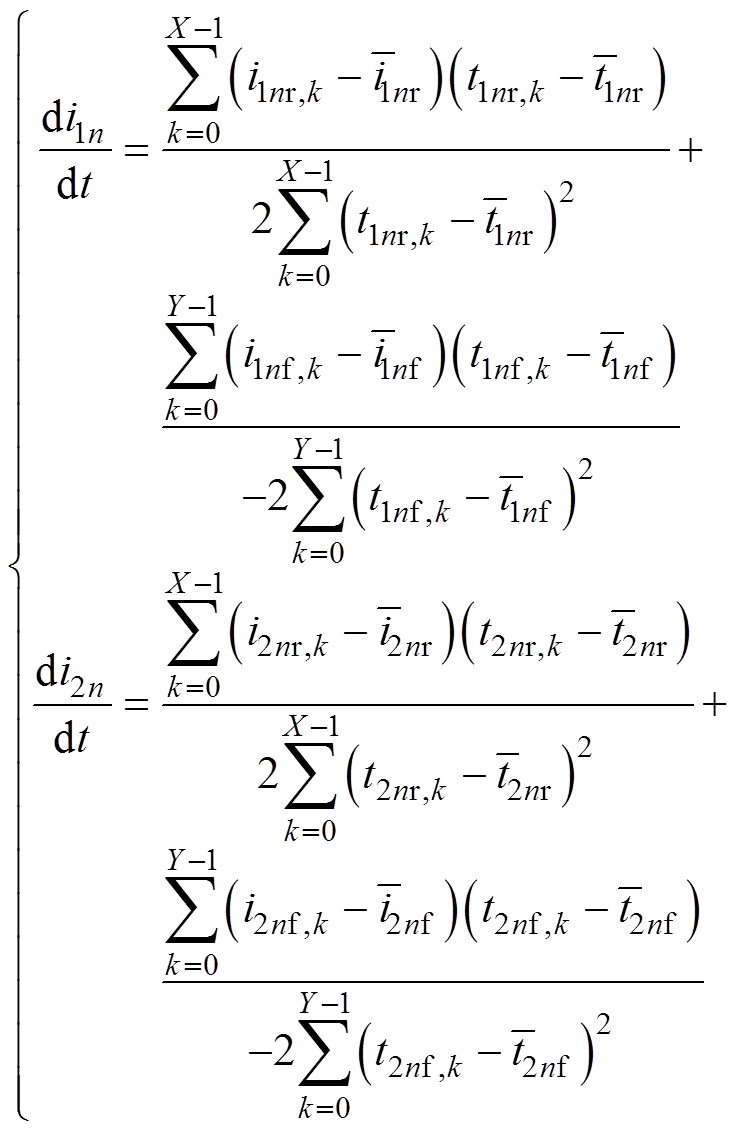（19）
式中，tn,k=tn,0+kTs，Ts定值。将式（18）、式（19）和母线电压代入（10）和式（11），可求得差动位移s1、s2。
此外，由于差动控制下两侧电磁铁的尺寸和材料是完全相同的，磁滞、涡流等因素对两侧电流纹波变化率的影响近似等效，因此进一步对差动位移s1、s2进行加权可以减小涡流、磁滞等非线性因素引起的位移估计值误差，有
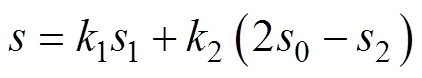（20）
式中，k1、k2为加权系数，k1=k2=0.5。通过差动位移估计法能够得到位移估计误差，从而提高位移估计精度。
利用电流传感器同时采集两相差动线圈的电流信号，经滤波后送入控制板的AD采样模块，采样程序由PWM信号上升沿触发，保证了每个开关周期内采样点与电流纹波的同步性，同时避免了开关时刻附近的噪声影响，提高了采样的准确性。单侧线圈的电流采样点如图8所示，均匀布置在电流纹波的上升和下降阶段，同步采样差动线圈电流可获得相对于单侧线圈两倍的采样点，有效改善电流纹波斜率的计算精度。数字信号处理器（Digital Signal Processing, DSP）基于两路电流信号的采样值，计算出各自的电流纹波平均值和电流纹波变化率，其中纹波电流平均值作为开关功放的反馈信号以实现线圈电流的闭环控制；电流纹波变化率用于计算动子位移，即通过对电流纹波变化率与悬浮体位移的关系，计算出当前周期位移量s1、s2，两路位移估计值通过加权平均后反馈给电磁悬浮系统的控制器。上述算法的流程如图9所示。
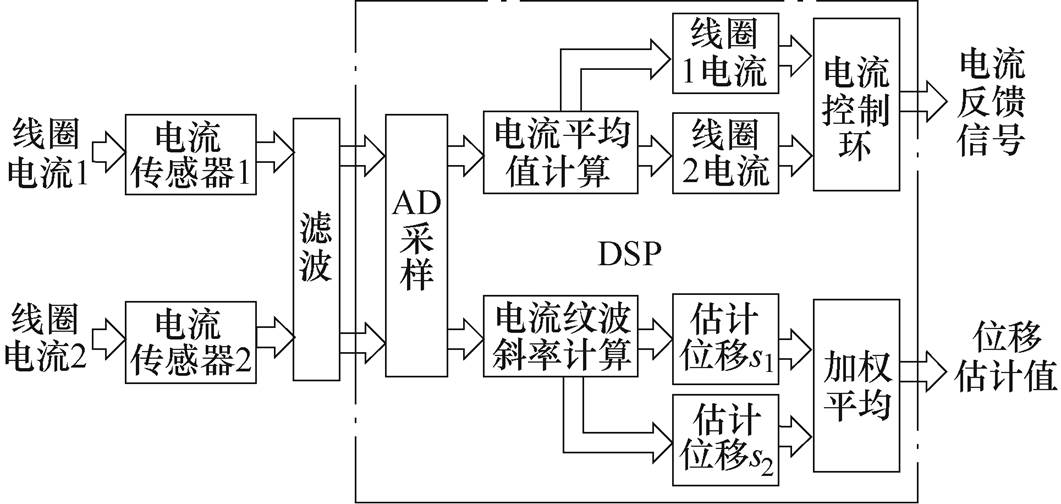
图9 算法流程
Fig.9 Algorithm flow chart
结合式（15）、式（16）可知，在式（15）简化的过程中，忽略了器件以及线路内阻的影响。实际功率器件及线路内阻受温度等因素的影响，会对电流纹波变化率的检测结果产生影响。为此，分析了不同母线电压、电流平均值下回路内阻对电流纹波变化率的影响，以及气隙大小与电流纹波变化率的线性度关系。
由式（10）、式（11）可知，在估计位移时忽略了器件导通电阻以及回路电阻，导致了电流纹波斜率的计算误差。在不同的电流平均值下，受温度等因素的影响，电流纹波变化率的实际值会小于理论值，且偏差值随着电流平均值的增大，呈非线性增大。为此，在实验中通过调整偏置电流大小改变电流平均值，保持开关频率为10 kHz，定动子气隙为0.5 mm，在母线电压分别为50 V、80 V、100 V、120 V时，分析电流纹波变化率与偏置电流的变化关系，实验结果如图10所示。
由图10可知，随着偏置电流的增大，电流纹波的变化率非线性下降，这是因为在偏置电流增大时，线圈电阻以及功率器件的导通压降随之增大，致使电流纹波变化率的下降并不是线性增加的。
当母线电压增大时，功率器件的开关损耗增大，热效应增强，从而导致电流纹波变化率进一步下降。例如，在偏置电流由0 A增大到1 A的过程中，母线电压为50 V和120 V时，电流纹波变化率的下降值分别为0.05 A/ms和0.06 A/ms。
图11给出了在母线电压为100 V、开关频率为10 kHz、偏置电流为1.5 A时，电流纹波变化率与气隙的关系曲线。
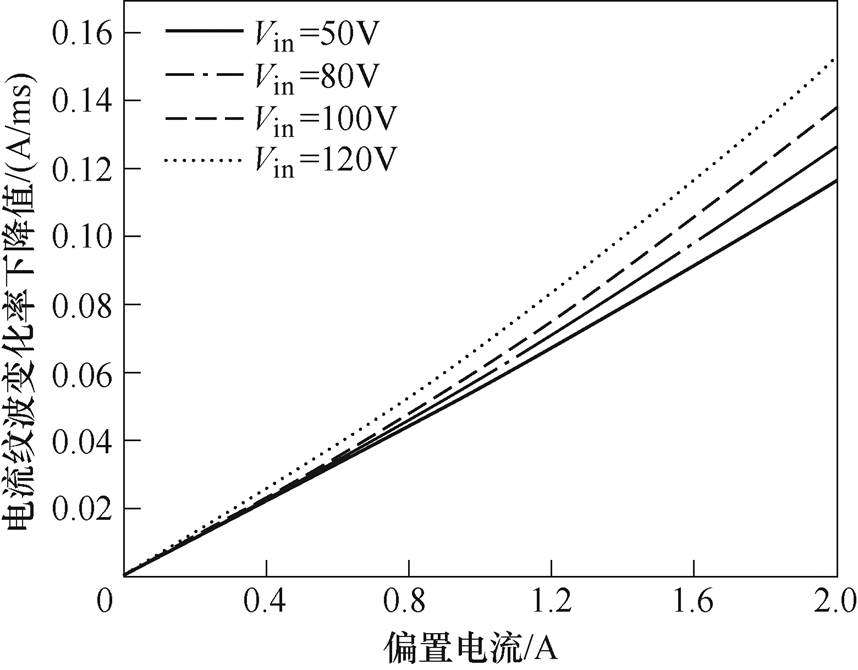
图10 母线电压、偏置电流与电流纹波变化率的关系
Fig.10 The relationship between bus voltage, bias current and current ripple rate of decline
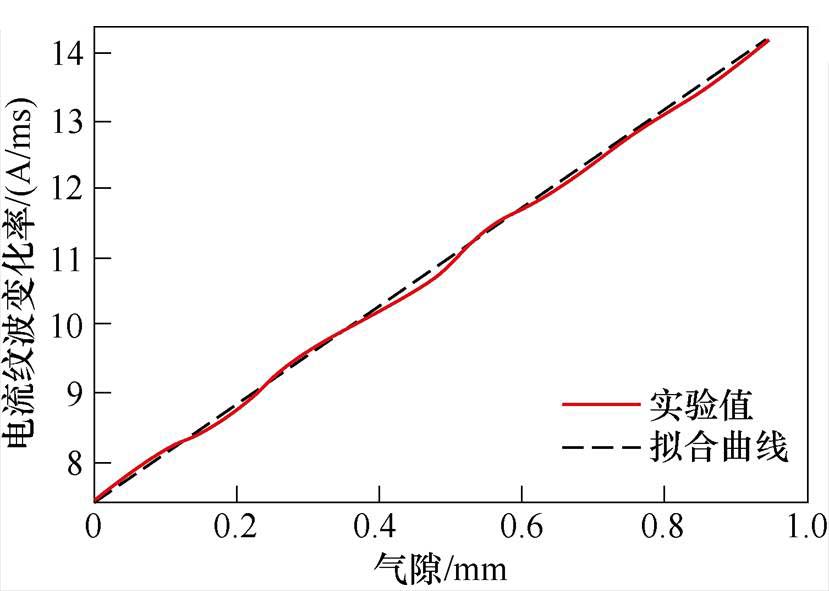
图11 气隙与电流纹波变化率线性度
Fig.11 Linearity of air gap and current ripple rate
由图11可以看出，气隙与电流纹波变化率近似为线性关系，误差产生的原因主要是高频噪声对采样数据的干扰。结合图10和图11可知，当母线电压为100 V时，气隙每增大0.1 mm，电流纹波变化率增大约0.7 A/ms，而电流平均值每增大1 A，电流纹波变化率下降约0.06 A/ms。因此，在实际电磁悬浮系统中，线圈电流动态变化会影响电流纹波变化率的测量结果，进而引起动子位移的观测误差。基于本文提出的自传感差动计算方法，可以有效利用差动控制的特性减小控制电流变化引起的误差。
为验证所提方法的有效性，在一个单自由度的刚性电磁悬浮平衡梁实验平台上开展了自传感动态悬浮实验，实验平台的硬件结构和实物分别如图12和图13所示。
该系统主要包括单自由度电磁悬浮平衡梁，梁体中心位置与底座活动支撑，两侧可上下运动。两组电磁铁分别位于梁体两端的下方，利用刚性梁体的对称性，实现梁体的差动电磁力控制。在梁体一端的上方，对应电磁铁的中心位置，安装了一个电涡流位移传感器以检测动子位移，不参与电磁悬浮控制，仅与自传感动子位移的估计值进行对比。两相三桥臂开关功放采用了SiC的MOSFET与续流二极管。使用了带宽HNC025A霍尔电流传感器以检测线圈电流，其带宽能够满足电流纹波斜率测量的精度和实时性要求；控制器采用TI公司的TMS320F28335 DSP。
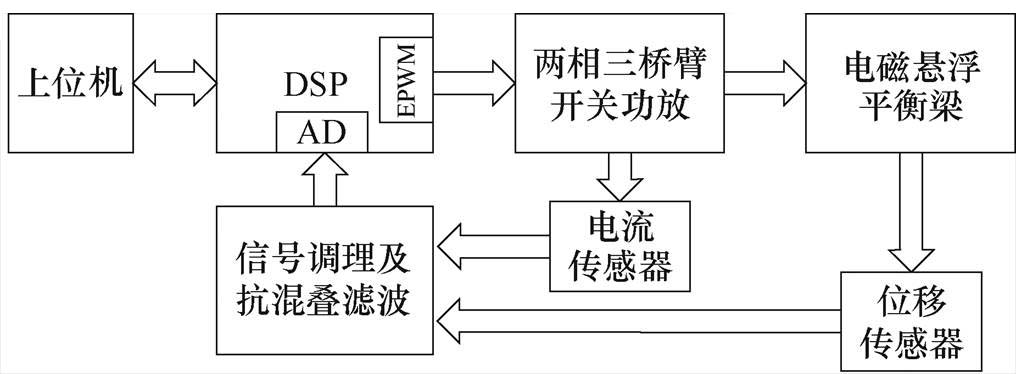
图12 实验平台硬件结构
Fig.12 Hardware structure diagram of the test rig
图13 单自由度刚性电磁悬浮平衡梁实验平台
Fig.13 Single degree of freedom rigid electromaglev balance beam experimental platform
单自由度刚性磁悬浮平衡梁实验平台主要参数见表1。
表1 实验平台主要参数
Tab.1 Main parameters of the experimental platform
参 数数 值 功放直流母线电压Vs/V100 功放开关频率fs/kHz10 磁极线圈匝数N100 额定气隙g0/mm0.5 线圈电阻R/W0.8 偏置电流I0/A1.5 额定线圈电感L0/mH8.2 梁体长度l/mm400 梁体质量M/kg0.6
实验分为两部分：
（1）通过单线圈电流纹波变化率对梁体的位移进行估计，并与电涡流位移传感器输出的实际动子位移对比，实验结果如图14a所示。由图14a可以看出，位移估计值相对实际值在位移变化的峰值位置存在明显误差。
（2）基于所提出的差动位移估计方法，通过检测两相差动线圈电流纹波变化率对梁体位移进行估计，实验中两路电流传感器测量两个线圈中的电流纹波变化率，其中一路电磁线圈中电流纹波变化率增大的同时，另一路电磁线圈电流纹波变化率对应减小，构成差动关系。差动位移估计值与电涡流位移传感器测量值的对比如图14b所示，可以看出，动子位移的估计值和实际值基本吻合，滤波器和信号处理引起的延迟是引起估计误差的主要原因。
对比图14a和图14b可知，采用单线圈的电流变化率来估计悬浮体位移，估计值与实际值的最大误差为13 mm，而采用两相差动线圈的电流变化率估计悬浮体位移，估计误差减小至6 mm，进而有效提高了控制的准确度和可靠性。
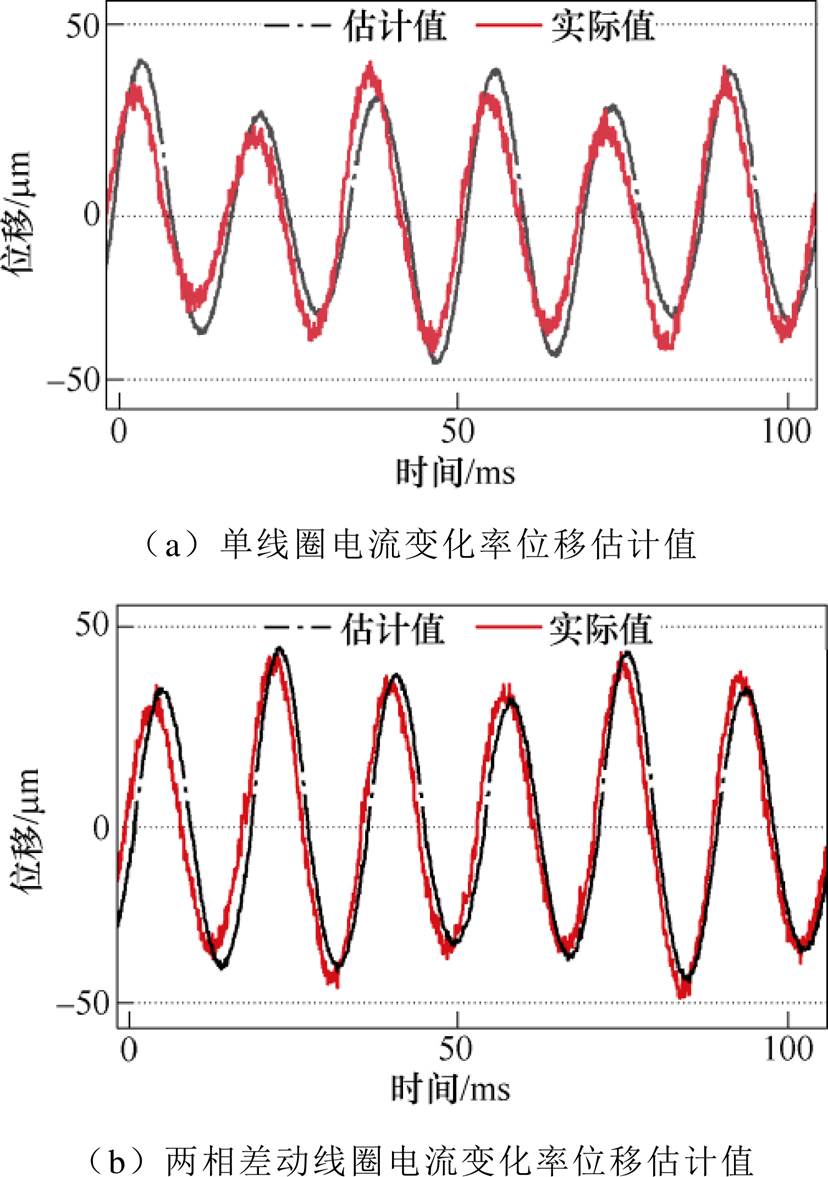
图14 自传感动态电磁悬浮的实验结果
Fig.14 The experimental results of self-sensing dynamic electromagnetic levitation
悬浮体稳定悬浮时，以一相电磁线圈为例，图15a和图15b分别给出了电磁线圈的电压和电流波形。由图15可知，两相三桥臂输出的电压电流波形与全桥拓扑开关功放输出的电流波形基本相同。
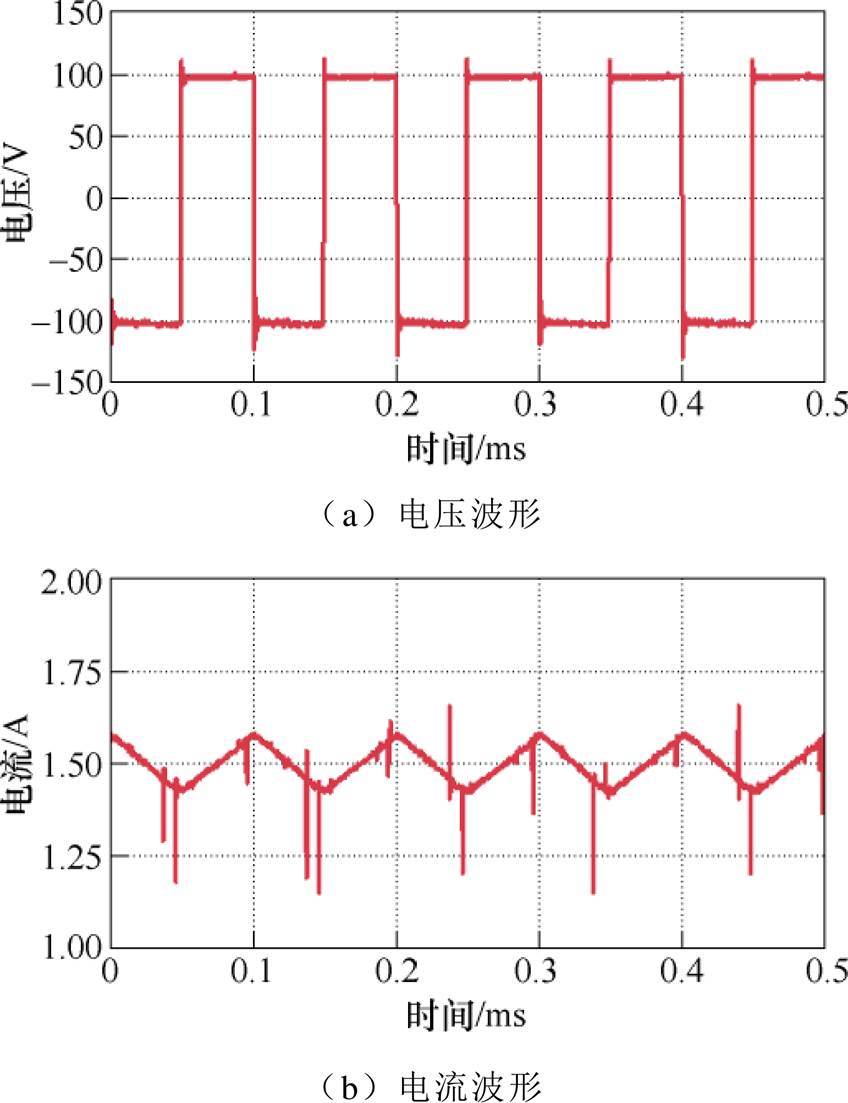
图15 悬浮体稳定悬浮时电磁线圈电压和电流波形
Fig.15 Voltage and current waveforms of electromagnetic coil when the suspension is stably suspended
在悬浮体稳定悬浮时，根据实际线圈电压、电流波形的测量结果，计算得出两相三桥臂拓扑开关功放的功率损耗，如图16所示。由图16可知，两相三桥臂拓扑开关功放的SiC MOSFET的损耗为3.78 W，SiC二极管的损耗为0.65 W，母线电容的损耗为0.16 W。
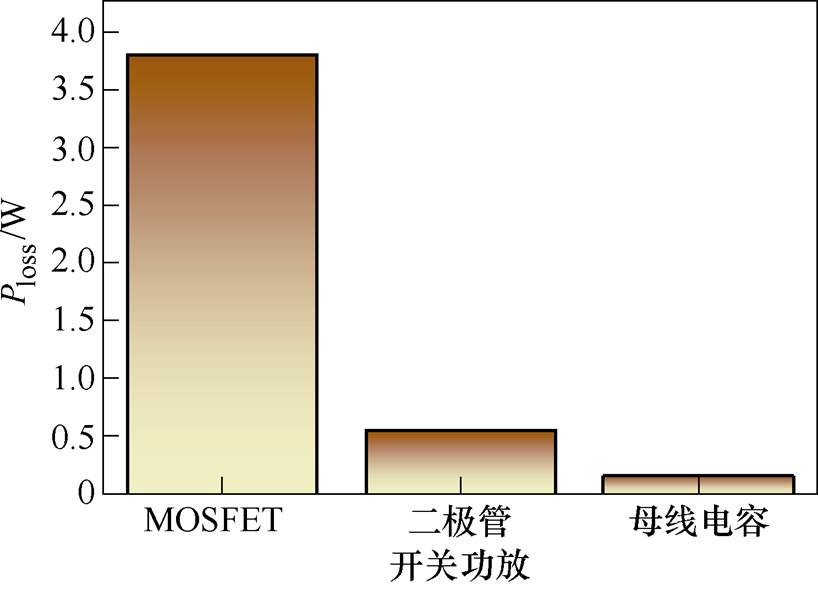
图16 两相三桥臂开关功放的功率损耗
Fig.16 Power loss of two phase three bridge arm switching power amplifier
本文针对两相三桥臂开关功放拓扑结构，基于开关电流纹波的变化率计算获得动子位移信息，实现了单自由度电磁悬浮平衡梁的自传感控制；提出通过差动位移估计方法来提高精度，并进行了实验验证，得出相关结论如下：
1）在电流平均值增大的情况下，电流纹波的变化率会因为功率器件导通电阻和线路电阻等因素的影响而略有下降，进而引起位移估计误差。
2）与检测单线圈的电流变化率估计悬浮体位移相比，采用两相线圈电流变化率同步检测的差动位移估计方法，能够有效减小电流采样不准确等偶然因素造成的位移估计误差，提高估计精度。
3）该方法可拓展用于多相共桥臂拓扑开关功放驱动的多自由度电磁悬浮系统的自传感控制。
参考文献
[1] 张维煜, 朱熀秋, 袁野. 磁悬浮轴承应用发展及关键技术综述[J]. 电工技术学报, 2015, 30(12): 12-20.
Zhang Weiyu, Zhu Huangqiu, Yuan Ye. Study on key technologies and applications of magnetic bearings[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 12-20.
[2] 胡烽, 孙宏博, 蒋栋, 等. 基于四相全桥的磁悬浮轴承开关器件开路故障容错控制策略[J]. 电工技术学报, 2022, 37(9): 2295-2305, 2340.
Hu Feng, Sun Hongbo, Jiang Dong, et al. Fault- tolerant strategy of four-phase full-leg for active magnetic bearing in case of open circuit fault of switching device[J]. Transactions of China Electro- technical Society, 2022, 37(9): 2295-2305, 2340.
[3] 张涛, 刘欣凤, 莫丽红, 等. 磁悬浮高速电机系统建模与控制[J]. 电机与控制学报, 2018, 22(4): 98-104.
Zhang Tao, Liu Xinfeng, Mo Lihong, et al. Modeling and control of magnetic suspension high-speed motor[J]. Electric Machines and Control, 2018, 22(4): 98-104.
[4] 余志强, 孙晓云, 邱清泉, 等. 电机外置式径向型高温超导飞轮储能系统样机悬浮测试及旋转实验[J]. 电工技术学报, 2019, 34(10): 2166-2175.
Yu Zhiqiang, Sun Xiaoyun, Qiu Qingquan, et al. Levitation test and rotation experiment of radial-type superconducting flywheel energy storage system prototype with external motor[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2166- 2175.
[5] 刘程子, 湛江, 杨艳, 等. 主动磁悬浮轴承-柔性转子的研究和发展综述[J]. 中国电机工程学报, 2020, 40(14): 4602-4614, 4739.
Liu Chengzi, Zhan Jiang, Yang Yan, et al. Review of research status and development of flexible rotor- magnetic bearing[J]. Proceedings of the CSEE, 2020, 40(14): 4602-4614, 4739.
[6] Tang Enqiong, Han Bangcheng, Zhang Yin. Optimum compensator design for the flexible rotor in mag- netically suspended motor to pass the first bending critical speed[J]. IEEE Transactions on Industrial Electronics, 2016, 63(1): 343-354.
[7] Song Xinda, Fang Jiancheng, Han Bangcheng, et al. Adaptive compensation method for high-speed surface PMSM sensorless drives of EMF-based position estimation error[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1438-1449.
[8] Noshadi A, Shi Juan, Lee W S, et al. System identi- fication and robust control of multi-input multi-output active magnetic bearing systems[J]. IEEE Transa- ctions on Control Systems Technology, 2016, 24(4): 1227-1239.
[9] Park Y H, Han D C, Park I H, et al. A self-sensing technology of active magnetic bearings using a phase modulation algorithm based on a high frequency voltage injection method[J]. Journal of Mechanical Science and Technology, 2008, 22(9): 1757-1764.
[10] Yu Jie, Wu Xinzhen, Zhang Yuhao, et al. A novel differential estimation method of rotor displacement for active magnetic bearings[C]//2019 22nd Inter- national Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 2019: 1-5.
[11] 于洁, 祝长生, 吴新振. 解调型自传感电磁轴承的位移估计误差分析[J]. 中国电机工程学报, 2019, 39(19): 5876-5884, 5916.
Yu Jie, Zhu Changsheng, Wu Xinzhen. The analysis of displacement estimation errors of demodulation type self-sensing active magnetic bearings[J]. Pro- ceedings of the CSEE, 2019, 39(19): 5876-5884, 5916.
[12] Jiang Yinxiao, Ma Xin, Fan Yahong. Rotor displace- ment self-sensing approach for permanent magnet biased magnetic bearings using double-axis PWM demodulation[J]. IEEE Sensors Journal, 2018, 18(19): 7932-7940.
[13] Jiang Yinxiao, Wang Kun, Sun Maolin, et al. Displacement self-sensing method for AMB-rotor systems using current ripple demodulations combined with PWM command signals[J]. IEEE Sensors Journal, 2019, 19(14): 5460-5469.
[14] Xiong Haojie, Xiao Jun, Yang Dongsheng, et al. Displacement estimation of self-sensing magnetic bearings based on biorthogonal spline wavelet[J]. IEEE Access, 2021, 9: 76213-76223.
[15] Tian Zhongliang, Wei Zhengyuan, Guo Bin, et al. A rotor displacement estimation method for magnetic bearings with direct measurement of the ripple current slope[C]//2019 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 2019: 1848-1853.
[16] Wang Jinou, Binder A. Self-sensing magnetic bearings using multiple sampling of currents alone[C]//2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2013: 1-10.
[17] Tang Ming, Zhu Changsheng. New method of position estimation for self-sensing active magnetic bearings based on artificial neural network[C]//2010 International Conference on Electrical and Control Engineering, Wuhan, China, 2010: 1355-1358.
[18] Sadighi A, Kim W J. Adaptive-neuro-fuzzy-based sensorless control of a smart-material actuator[J]. IEEE/ASME Transactions on Mechatronics, 2011, 16(2): 371-379.
[19] 周亮, 李黎川. 电流驱动和电压驱动下实心磁路磁轴承的系统辨识[J]. 中国电机工程学报, 2016, 36(1): 268-273.
Zhou Liang, Li Lichuan. System identification of solid-core active magnetic bearings under current drive and voltage drive[J]. Proceedings of the CSEE, 2016, 36(1): 268-273.
[20] 钟建朋, 李黎川. 实心磁路磁轴承的分数阶系统辨识[J]. 中国电机工程学报, 2013, 33(18): 170-177, 25.
Zhong Jianpeng, Li Lichuan. Fractional-order system identification of a solid-core active magnetic bearing[J]. Proceedings of the CSEE, 2013, 33(18): 170-177, 25.
[21] 叶品州, 李红伟, 于文涛, 等. 考虑材料非线性及涡流影响的径向电磁轴承等效磁路建模[J]. 电工技术学报, 2020, 35(9): 1858-1867.
Ye Pinzhou, Li Hongwei, Yu Wentao, et al. Equi- valent magnetic circuit modeling of radial active magnetic bearing considering material nonlinearity and eddy current effects[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1858-1867.
[22] 胡载东, 蒋栋, 孙宏博. 一种应用于磁悬浮轴承的四相四桥臂电力电子变换器[J]. 电工技术学报, 2020, 35(20): 4325-4335.
Hu Zaidong, Jiang Dong, Sun Hongbo. A four-phase four-leg power electronics converter for active magnetic bearing drive[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4325-4335.
[23] Jiang Dong, Li Tian, Hu Zaidong, et al. Novel topologies of power electronics converter as active magnetic bearing drive[J]. IEEE Transactions on Industrial Electronics, 2020, 67(2): 950-959.
Abstract Electromagnetic levitation technology has been widely concerned and studied in recent years because of its excellent characteristics such as no friction, less maintenance, and adjustable dynamic characteristics. However, the integration, reliability, and cost of its system restrict the application and development of electromagnetic levitation technology. The appearance of displacement self-sensing has effectively solved the above problems. Because the traditional displacement self-sensing estimation method uses a single coil to estimate the displacement of the suspension according to the change rate of the current ripple, there are many problems, such as large displacement estimation error and easy to be disturbed by the external environment. Therefore, this paper proposes a displacement self-sensing detection method of an electromagnetic suspension system driven by a two-phase, three-leg switching power amplifier. The displacement of the suspension body is estimated by detecting the ripple change rate of the two-phase differential current. Compared with detecting single-phase current, it can effectively reduce the impacts of switching transients and noise on the accuracy of displacement estimation. The self-induced electromagnetic levitation of the mover is realized on a single degree of freedom rigid electromagnetic levitation experimental platform, which verifies the effectiveness of the proposed method.
Firstly, the structure of the differential control system of a single degree for freedom electromagnetic suspension is introduced. Then, the topology of the two-phase, three-leg switching power amplifier is analyzed. Compared with the traditional full bridge switching power amplifier, the two-phase, three-leg switching power amplifier can reduce 1/4 switching devices while its basic functions and current ripple characteristics remain unchanged. It not only improves the integration of the circuit, but also reduces the number of PWM signals output by the controller and the number of driving circuits, which is conducive to the improvement of the overall integration of the system. Accordingly, the working principle and the modulation mode of the two-phase, three-leg switching power amplifier are introduced.
This paper analyzes the self-sensing principle of the differential electromagnetic levitation system by modeling the single degree of freedom suspension. Through theoretical analysis and derivation, it is proved that the magnitude of the coil inductance is approximately linear with the mover displacement, and the relationship between the differential displacement and the current ripple change rate is obtained. Then, the current ripple characteristics of the two-phase, three-leg switching power amplifier are analyzed theoretically. It is verified that the amplitude of the current ripple is only related to the inductance of the coil under the condition that the bus voltage and the switching frequency are determined. Moreover, the method for measuring the change rate of the current ripple is feasible to realize the self-sensing of the mover displacement. The change rate of the two-phase current ripple is obtained by sampling the rising edge and the falling edge of the current ripple and using the least square method.
In the derivation of differential displacement self-sensing theory, the influence of device and line internal resistance is neglected. The actual power device and the internal resistance of the line are affected by temperature and other factors, which will affect the detection results of the current ripple change rate. Therefore, the influence of loop internal resistance on the current ripple change rate under different bus voltage and current average values is analyzed. The linear relationship between the air gap size and the current ripple change rate is also analyzed. It can be seen from the analysis that the influence of the loop internal resistance change on the displacement estimation accuracy can be ignored in the actual application of the electromagnetic suspension system.
The self-sensing dynamic suspension experiment was carried out on a single degree of freedom rigid electromagnetic suspension balance beam experimental platform. Experimental results show that the differential displacement estimation method based on detecting the current ripple changing rate of two-phase coils can significantly improve the accuracy of displacement estimation compared with the traditional displacement estimation method based on detecting the current ripple changing rate of a single coil.
keywords：Electromagnetic levitation, common bridge arm topology, self-sensing, current ripple
DOI: 10.19595/j.cnki.1000-6753.tces.220286
中图分类号：TM315
山东省自然科学基金项目（ZR2021QE118）、基础加强计划重点基础研究项目（2019-JCJQ-ZD-015-00）、山东省高等学校“青年创新团队计划”项目（2022KJ150）资助。
收稿日期 2022-03-02
改稿日期 2022-07-26
张友军 男，1996年生，硕士研究生，研究方向为开关功率放大器设计及控制。E-mail: 2020025741@qdu.edu.cn
于洁 男，1988年生，讲师，硕士生导师，研究方向为主动电磁轴承控制、多相电机控制等。E-mail: yujie_ee@qdu.edu.cn（通信作者）
（编辑 崔文静）