
图1 永磁同步电机模型
Fig.1 Permanent magnet synchronous motor model
摘要 将集总参数热网络(LPTN)模型应用于永磁电机温度在线估计能够预防电机因过温而造成的电机损坏,特别是降低永磁体的不可逆退磁风险,提高永磁电机使用的安全性。该文首先针对LPTN模型应用于温度估计过程中存在灰度模型的不确定性,对永磁电机LPTN模型进行比较,建立不同节点的低阶灰箱永磁电机LPTN模型。搭建永磁电机变工况温度实验平台,基于实验数据进行模型对比分析,得到用于永磁电机在线温度估计的最优节点数LPTN模型。同时为克服扩展卡尔曼滤波算法出现的滤波发散及热阻参数在变工况下非线性导致温度估计累积误差问题,利用加权多新息强跟踪扩展卡尔曼滤波(WMI-STEKF)算法对永磁电机LPTN模型进行在线参数辨识及温度估计,将温度估计误差降低至3 ℃,提高非线性系统在变工况条件下参数辨识过程的鲁棒性。最后,通过仿真和温度实验结果对比分析,证明该方法的正确性和准确性。
关键词:集总参数热网络 永磁电机 温度估计 加权多新息强跟踪扩展卡尔曼滤波(WMI- STEKF)
在不同的永磁电机拓扑结构中,内置式永磁电机由于固有的高功率密度、高效率以及高转矩利用率等优势,成为汽车等牵引领域应用最广泛的电机之一[1]。然而,与其他一些应用领域不同的是,车辆在很宽的温度范围内运行,在温度变化下,内置式永磁电机的性能将会受到很大的影响,甚至在极端情况下会造成永磁体的不可逆退磁,直接影响到电机安全运行[2-3]。因此,需要对运行中的永磁电机进行温度在线监测,特别是转子永磁体的温度监测,防止电机由于过温而造成损坏,同时可为高性能的电机控制策略提供温度参数,提高控制精度。
针对永磁电机的在线温度监测技术,在线直接测量技术由于安装空间、成本等因素未能被广泛接受,目前仅适合应用在实验室验证阶段[4];永磁电机温度间接估计方法成为解决这一问题的主要途径。其中,基于电机电参数模型的间接方法,如电机参数估计法[5]、高频信号注入法[6]、直流电压信号注入法[7],因可靠性、对电机电参变化引起的误差不敏感等因素受到一定制约。基于电机热参数模型的集总参数热网络(Lumped Parameter Thermal Network, LPTN)法将电机的主要部件按照结构及散热情况划分成温度单元,通过求解得到单元温度,是温度在线估计的另一种可行性解决方案。然而,创建集总热网络模型需要考虑到电机几何外形、传热及冷却系统,建立适用于温度在线估计的热网络模型,从而提高温度估计的准确性和可靠性成为这一方法应用在永磁电机在线估计的关键。
文献[8]提出了一种新的观测器拓扑结构,它利用与速度相关的Gopinath式通量观测器,结合了以低速运行的四节点LPTN模型和以中速和高速运行的基于电压模型的观测器,以提升温度估计方面的抗干扰能力。文献[9]将流动网络模型和集总热网络模型耦合在一起来解决油冷分段定子电机的热计算,该方法提供了一种快速但精确的模拟工具,可以识别哪些分段极片将处于最高温度。文献[10]利用LPTN和二维分析热模型协同作用的混合热模型来解决这个问题并预测准确的临界温度,特别是有源绕组和末端绕组的平均和最高温度。以上研究通过LPTN与其他温度估计方法融合来提高温度估计的准确性和可靠性。然而,LPTN模型的误差主要来源于模型热参数的不确定性,如热阻值受到电机工况等诸多因素影响从而变动。文献[11]结合永磁电机实验温升数据,利用扩展卡尔曼滤波算法对热网络模型进行关键参数的辨识,建立任意工况下的参数模型。文献[12]通过改进直流热测试,估计了热网络中的一些重要热参数,如外壳与环境之间的等效热阻、绕组与叠片之间的等效热导率,再借助热网络可以预测每个电机组件的温度。文献[13]通过建立四节点热网络模型,基于综合实验训练数据的方法和粒子群优化算法识别热参数进行电机临界温度的监测。针对以上利用LPTN法进行电机温度特别是永磁体温度的在线估计中,不同规模的网络拓扑对在线估计的速度、精度方面的影响未有深入研究。同时热阻单元在变工况下的非线性以及损耗计算造成的误差累积都会造成估算温度与实际值的偏差,因此如何提高参数识别在变工况条件下的鲁棒性,以及温度估计精度成为亟待解决的关键问题。
本文首先对集总热网络模型进行分析,选择低阶灰箱热网络模型为永磁电机温度估计的首选模型,并对不同节点的灰箱热网络模型进行建模,通过实验对不同节点模型的温度估计结果进行分析对比,得到最优温度估计模型,然后利用多新息理论和强跟踪扩展卡尔曼算法对卡尔曼滤波的非线性系统适用性和过程参数变化的鲁棒性进行改进;最后通过对变工况下的电机温度实验数据与仿真数据进行对比,验证了模型及温度估计算法的正确性和准确性。
以一台内置“V”型转子磁极结构的高密度永磁电机为原型,其额定功率为45 kW,电机三维模型如图1所示,基本参数见表1。

图1 永磁同步电机模型
Fig.1 Permanent magnet synchronous motor model
表1 电机的基本参数
Tab.1 Basic parameters of the motor

参 数数 值 额定功率/kW45 额定转速/(r/min)3 500 直流母线电压/V300 额定电流/A200 额定扭矩/(N·m)123 定、转子铁心外径/mm230, 163 定、转子铁心内径/mm165, 100 定转子铁心长度/mm140 气隙长度/mm1
永磁电机温度的辨识需要特定的数学模型及相关参数。将电机传热过程等效为电路网络进行在线温度估计可利用白箱及灰箱LPTN模型。白箱LPTN模型通常根据内置式电机的几何形状,建立复杂的热网络模型,同时考虑轴向和径向的热流,具有较高的计算精度,但也存在一定的难点。首先,节点数量多,如对绕组等关键部件要求非常高的局部离散水平建模,这必然增加了计算量,降低了计算速度。其次,过多的节点必然出现过多的热阻,白箱LPTN模型的热阻通常是通过计算给定值甚至有一些热阻值是经验值。而热阻值受温度、流速、面积、材料等诸多影响,如材料导热系数受到材料性能和部件制造等因素影响,材料之间的对流换热系数为一个变动系数,其在不同温度范围下计算公式不同,且受气流状态影响,因此换热系数只能在特定条件下测出,在实际工程应用中往往用经验值。最后,节点过多需要对电机损耗进行精准分布计算。综上所述,白箱LPTN模型可以进行精确电机温度计算,但计算复杂、电机热参数难计算、时间长,不适用于电机温度的在线快速估计。
灰箱LPTN模型则在白箱模型基础上进行了大量简化,能够采用参数估计的方法进行电机温度的求解,不仅缩短了计算时间,也解决了未知电机热参数问题。常见的灰箱模型有深灰箱LPTN及浅灰箱LPTN两种。深灰箱LPTN去掉无关紧要的热交换过程,通过2~5个节点模拟最主要的热路径。而浅灰箱LPTN则根据传热理论,对重要的电机组件进行建模,节点约为5~15个,然而节点数的增加对参数估计的算法要求逐渐升高。因此,灰箱模型是进行电机温度估计的最佳选择,但灰箱模型节点个数的具体取值需要进一步验证。
基于以上各灰箱LPTN模型分析结论,综合考虑温度估计需求及在线参数估计的可行性,以及兼顾永磁电机中最受关注的永磁体温度,采用灰箱LPTN模型,该类模型对电机结构进行强抽象化,建模时做出如下假设:①各部件的损耗分布均匀;②永磁电机是均匀对称的;③只考虑转轴和槽内绕组的轴向传热,其他部件仅考虑径向传热;④电机内部空气为理想气体,不考虑温度对其温度的影响;⑤环境温度的变化忽略。
通过分析电机内部传热过程对电机关键部位进行建模,建立四种不同低阶灰度网络模型。
(1)三节点模型。将电机关键结构分为定子铁心、绕组和转子三个节点,即将转子铁心、永磁体及轴承简化至转子节点。三节点等效热网络模型示意图如图2所示。在三节点模型中,定子铁心温度节点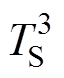 通过热阻
通过热阻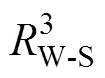 和绕组温度节点
和绕组温度节点 相连,通过气隙热阻
相连,通过气隙热阻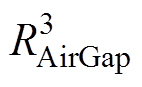 与转子温度节点
与转子温度节点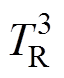 相连,通过热阻
相连,通过热阻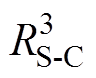 与电机冷却水道入水口温度TC连接。转子温度节点
与电机冷却水道入水口温度TC连接。转子温度节点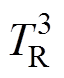 通过热阻
通过热阻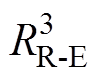 与环境温度TE连接。
与环境温度TE连接。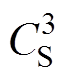 、
、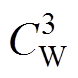 、
、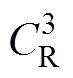 分别为简化定子铁心热容、绕组热容和转子热容。永磁电机内部的热源主要为各种损耗,其中PS、
分别为简化定子铁心热容、绕组热容和转子热容。永磁电机内部的热源主要为各种损耗,其中PS、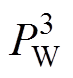 、
、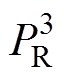 分别为定子铁心损耗、绕组损耗及转子损耗,转子损耗包括转子铁心损耗、永磁体涡流损耗和轴承损耗。
分别为定子铁心损耗、绕组损耗及转子损耗,转子损耗包括转子铁心损耗、永磁体涡流损耗和轴承损耗。
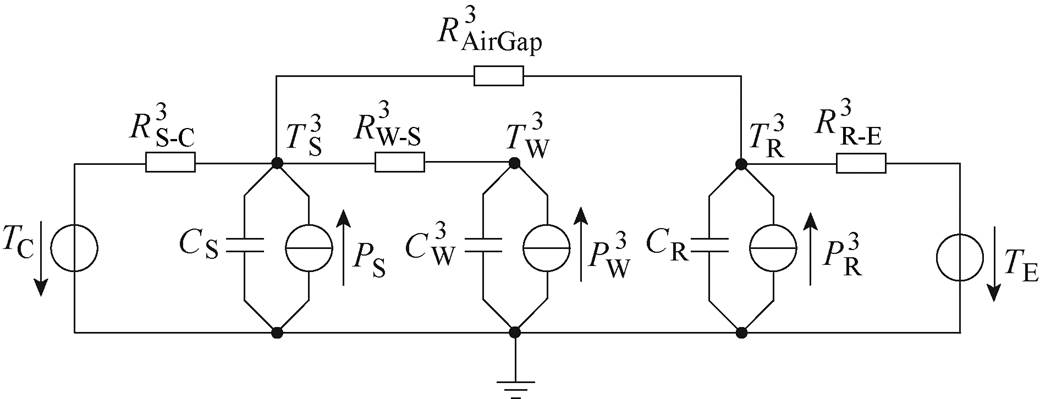
图2 三节点等效热网络模型示意图
Fig.2 Schematic diagram of three-node equivalent thermal network model
(2)四节点模型。在三节点模型基础上将轴承部分从转子节点中分离,同时考虑绕组槽内和端部因传热途径不同,从而导致端部绕组和槽内绕组温差较大,因此四节点模型去除定子铁心部分,将绕组部分细化为端部和槽内两部分,最后电机结构简化为槽内绕组、端部绕组、永磁体及轴承四个节点模型,如图3所示。四节点模型中,槽内绕组节点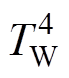 通过热电阻
通过热电阻 连接到电机冷却水道入水口温度TC,通过热阻
连接到电机冷却水道入水口温度TC,通过热阻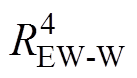 连接到端部绕组节点
连接到端部绕组节点 ,通过热电阻
,通过热电阻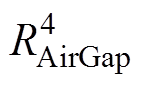 连接到永磁体节点
连接到永磁体节点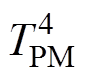 。转子与转轴节点
。转子与转轴节点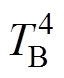 通过热阻
通过热阻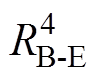 与环境温度节点TE相连,通过热电阻
与环境温度节点TE相连,通过热电阻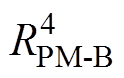 与永磁体节点
与永磁体节点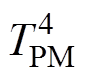 相连。CEW、CW、CB、CPM分别为简化端部绕组热容、槽内绕组叠加定子铁心热容、轴承热容及永磁体叠加转子铁心热容。永磁电机内部的热源主要为各种损耗,其中PW、PEW、PPM、PB分别为槽内绕组叠加定子铁心损耗、端部绕组损耗、永磁体涡流损耗和轴承损耗。
相连。CEW、CW、CB、CPM分别为简化端部绕组热容、槽内绕组叠加定子铁心热容、轴承热容及永磁体叠加转子铁心热容。永磁电机内部的热源主要为各种损耗,其中PW、PEW、PPM、PB分别为槽内绕组叠加定子铁心损耗、端部绕组损耗、永磁体涡流损耗和轴承损耗。

图3 四节点等效热网络模型示意图
Fig.3 Schematic diagram of four-node equivalent thermal network model
(3)五节点模型。五节点模型则在四节点模型基础上,将定子铁心节点考虑进去,分为定子铁心、槽内绕组、端部绕组、永磁体和轴承五个节点,如图4所示。由图4可知,定子铁心温度节点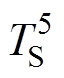 通过热阻
通过热阻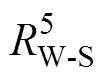 和槽内绕组温度节点
和槽内绕组温度节点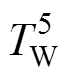 相连,通过气隙热阻
相连,通过气隙热阻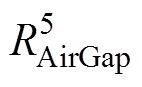 与永磁体温度节点
与永磁体温度节点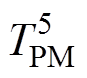 相连,通过热阻
相连,通过热阻 与电机冷却水道入水口温度TC连接。轴承温度节点
与电机冷却水道入水口温度TC连接。轴承温度节点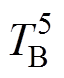 通过热阻
通过热阻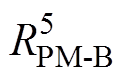 与永磁体温度节点
与永磁体温度节点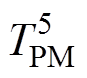 相连,通过热阻
相连,通过热阻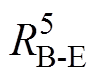 与环境温度TE连接。定子端部绕组温度节点
与环境温度TE连接。定子端部绕组温度节点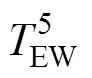 通过热阻
通过热阻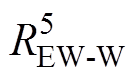 与定子槽内绕组温度节点
与定子槽内绕组温度节点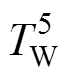 相连。
相连。
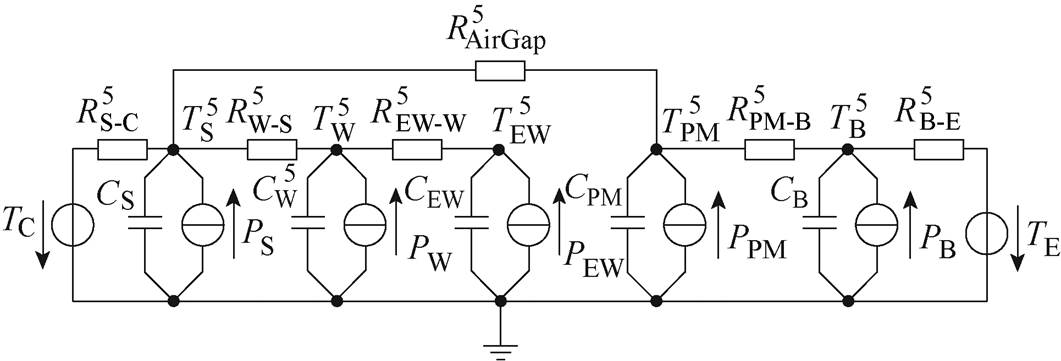
图4 五节点等效热网络模型示意图
Fig.4 Schematic diagram of five-node equivalent thermal network model
(4)六节点模型。六节点模型则是在五节点模型上细化,增加转子铁心部分,分为定子铁心、槽内绕组、端部绕组、永磁体、转子铁心和轴承六个节点,如图5所示。六节点模型中,定子铁心温度节点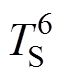 通过热阻
通过热阻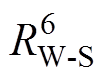 和槽内绕组温度节点
和槽内绕组温度节点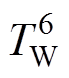 相连,通过气隙热阻
相连,通过气隙热阻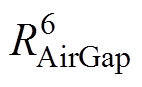 与转子节点
与转子节点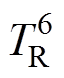 相连,通过热阻
相连,通过热阻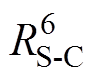 与电机冷却水道入水口温度TC连接。轴承温度节点
与电机冷却水道入水口温度TC连接。轴承温度节点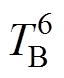 通过热阻
通过热阻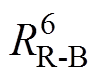 与转子温度节点
与转子温度节点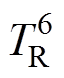 相连,通过热阻
相连,通过热阻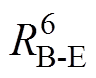 与环境温度TE连接。定子端部绕组温度节点
与环境温度TE连接。定子端部绕组温度节点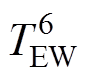 通过热阻
通过热阻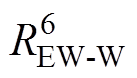 与定子槽内绕组温度节点
与定子槽内绕组温度节点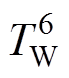 相连。转子温度节点
相连。转子温度节点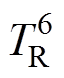 通过热阻
通过热阻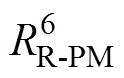 与永磁体温度节点
与永磁体温度节点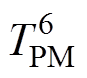 相连。图5中,PR为转子铁心损耗。
相连。图5中,PR为转子铁心损耗。
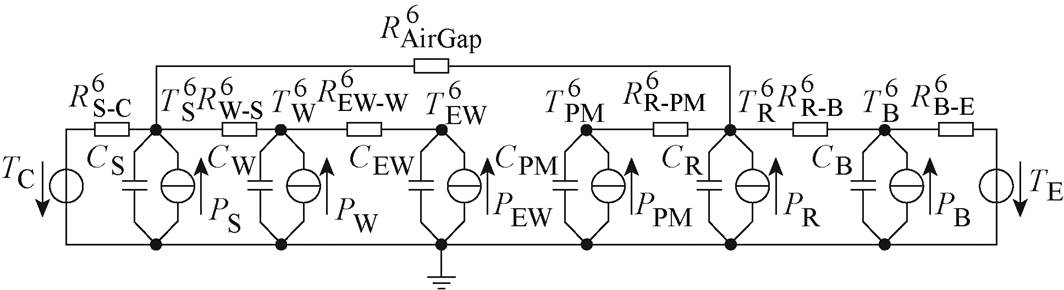
图5 六节点等效热网络模型示意图
Fig.5 Schematic diagram of six-node equivalent thermal network model
各节点模型中的热容C可根据基本传热学理论进行计算,计算公式为
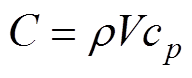 (1)
(1)
式中,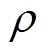 为物体密度;V为物体体积;cp为物体的比热容。
为物体密度;V为物体体积;cp为物体的比热容。
同时,通过分析电机内部热传递方式可将热网络中的热阻分为热传导电阻和热对流电阻。如定子铁心和定子槽内线圈之间热阻即属于热传导电阻,可利用式(2)进行计算,定子端部线圈与转子铁心之间的热阻属于热对流电阻,可利用式(3)进行计算。
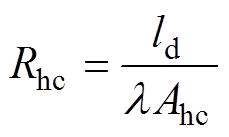 (2)
(2)
 (3)
(3)
式中,Rhc为热传导热阻;ld为两个节点之间的距离;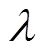 为材料导热系数;Ahc为传导区域的面积;Rtc为热对流热阻;h为对流换热系数;Atc为热对流区域的面积。
为材料导热系数;Ahc为传导区域的面积;Rtc为热对流热阻;h为对流换热系数;Atc为热对流区域的面积。
将以上四种不同节点的LTPN模型建立热平衡方程,其状态空间方程可表示为
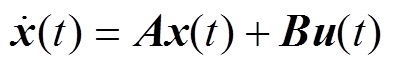 (4)
(4)
式中,u(t)为状态空间方程输入,包含各种损耗、环境及水道温度;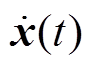 为各节点的温度状态变量;A和B分别为由热阻和热容共同组成的状态转移矩阵和输入矩阵。
为各节点的温度状态变量;A和B分别为由热阻和热容共同组成的状态转移矩阵和输入矩阵。
LPTN模型的输入主要依赖于永磁电机各部分损耗,这些损耗与运行参数,如转速、转矩及各部分的温度密切相关。
(1)铁心损耗。铁心损耗受高次谐波、磁路饱和、旋转磁化等因素的影响,目前常用的铁耗计算模型是由Bertotti提出的包含磁滞损耗、经典涡流损耗及异常损耗三项的铁心损耗模型。同时考虑电机的运行参数、电机转速n、电机输入的交直轴电流id、iq,以及永磁体随着温度tpm的上升导致铁心磁通密度的变化,可以建立以上因素的有限元仿真模型计算铁心损耗,并利用非线性回归方法得到模型电机在整个工作域上的铁心损耗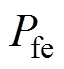 [14],定转子铁心损耗为
[14],定转子铁心损耗为
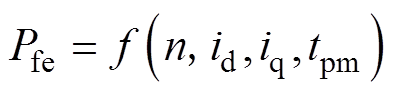 (5)
(5)
(2)永磁体涡流损耗。气隙磁场中产生空间和时间谐波分量会在转子永磁体产生涡流损耗。同样考虑电机转速、电机输入的交直轴电流及永磁体温度四个主要的影响损耗因素,建立以上因素的有限元仿真模型计算永磁体涡流损耗,并利用非线性回归方法可得到模型电机在整个工作域上的永磁体涡流损耗PPM[14]为
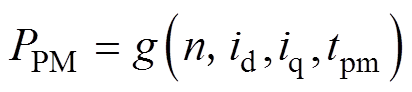 (6)
(6)
(3)绕组铜耗。绕组铜耗是电流流过绕组产生的电阻损耗,受本身温度影响较大,因电机线径原因,忽略绕组存在趋肤效应和邻近效应,槽内绕组及端部绕组铜耗PCu为
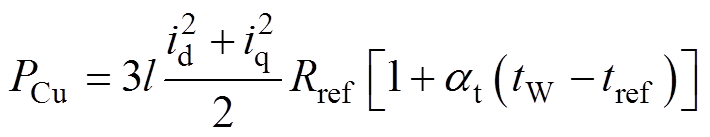 (7)
(7)
式中,l为绕组长度;Rref为参考绕组阻值;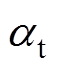 为绕组的温度系数;tW为绕组温度;tref为参考温度。
为绕组的温度系数;tW为绕组温度;tref为参考温度。
(4)轴承损耗。轴承损耗主要受电机转速以及各摩擦力矩的影响,当轴承温度达到90 ℃影响到润滑脂时,损耗才会急剧变大,可以忽略轴承温度的影响。由此,轴承损耗PB表达式为
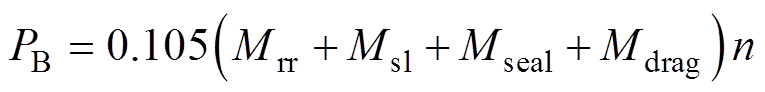 (8)
(8)
式中,Mrr为滚动摩擦力矩;Msl为滑动摩擦力矩;Mseal为密封件的摩擦力矩;Mdrag为润滑油润滑脂拖拽、涡流和飞溅等导致的摩擦力矩。
为验证温度估计模型及算法的准确性,设计一个用于永磁电机各部分温度测量的实验平台。如 图6所示,实验平台由被测电机、驱动模块、发电机三个主要部分组成。其中被测电机通过直接测量法对定子端部绕组、机壳、进出水道、环境及转子永磁体进行实时温度测量。转子永磁体部分测温通过在转子铁心与永磁体之间开槽安置温度传感器,温度传感器采用电阻温度系数大、稳定性好的PT100铂热电阻传感器,并通过转子同步旋转发射模块将实时的温度数据传输至监测终端。

图6 模型电机实验平台
Fig.6 Experiment platform of model motor
利用四种不同节点数的灰箱热网络模型,通过实时输入电机的转速及交直轴电流参数,即可进行电机各部分温度估计。但变工况运行中,各部分热阻参数会随着运行工况及温度的变化而变化,在温度估计中误差会不断累积,最终影响温度估计的精度。因此,可以利用扩展卡尔曼滤波(Extended Kalman Filter, EKF)算法对热阻参数及永磁电机温度进行同步辨识更新,从而提高模型在各工况下的辨识精度。
以五节点模型为例,首先增广状态空间变量 ,其中包含需要辨识温度变量及热阻值,如式(9)所示。同时,由于目前永磁电机为了保证电机安全使用,通常在永磁电机定子端部线圈设立温度传感器,因此利用这一固定测温值作为观测向量y,如式(10)所示。
,其中包含需要辨识温度变量及热阻值,如式(9)所示。同时,由于目前永磁电机为了保证电机安全使用,通常在永磁电机定子端部线圈设立温度传感器,因此利用这一固定测温值作为观测向量y,如式(10)所示。
 (9)
(9)
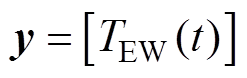 (10)
(10)
将五节点热网络数学模型离散化可简化表示为
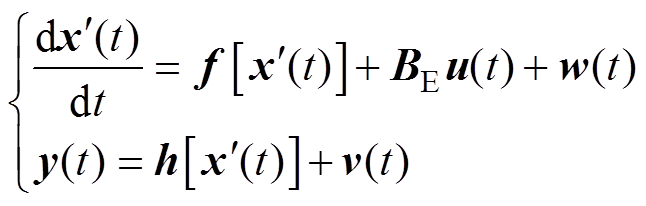 (11)
(11)
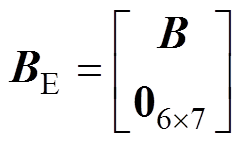 (12)
(12)
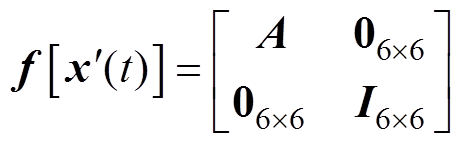 (13)
(13)
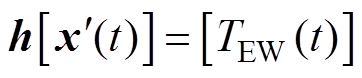 (14)
(14)
式中,BE为扩展输入矩阵;w(t)、v(t)为均值的高斯白噪声;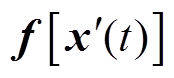 和
和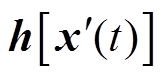 为非线性项;
为非线性项;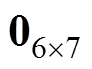 为6´7阶零矩阵;
为6´7阶零矩阵;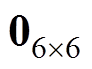 为6´6阶零矩阵;
为6´6阶零矩阵;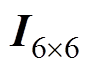 为6´6阶单位矩阵;TEW(t)为t时刻的端部绕组温度。非线性项
为6´6阶单位矩阵;TEW(t)为t时刻的端部绕组温度。非线性项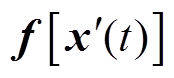 和
和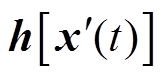 进行线性化,定义雅可比矩阵
进行线性化,定义雅可比矩阵
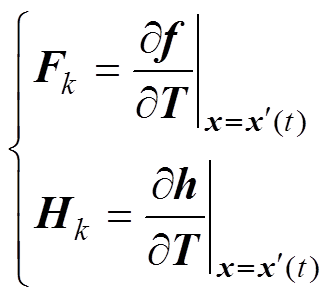 (15)
(15)
状态转移矩阵 为
为

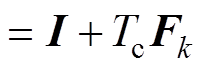 (16)
(16)
式中,I为单位矩阵;Tc为采样周期,Tc=1 s。
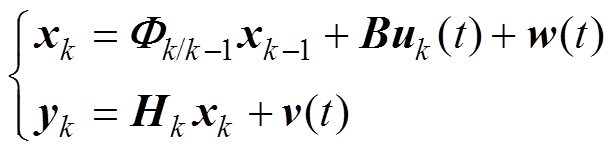 (17)
(17)
式中,xk为tk时刻的增广状态矩阵;uk(t)为tk时刻的输入矩阵;yk为tk的量测矩阵;Hk为观测矩阵。
离散型EKF方程包括每个运算周期状态预测和状态更新两个分部,状态预测为
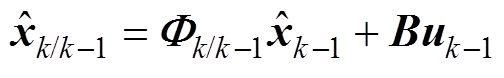 (18)
(18)
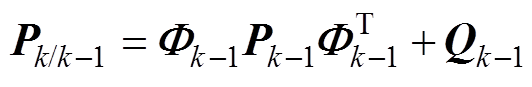 (19)
(19)
状态更新为
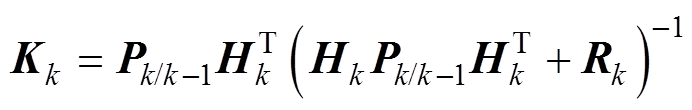 (20)
(20)
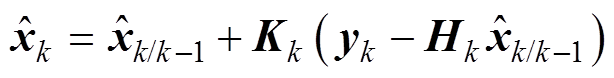 (21)
(21)
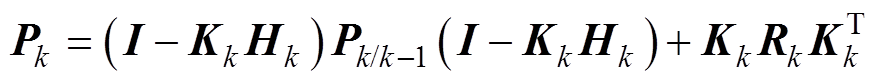 (22)
(22)
式中,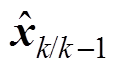 为本时刻的预测值;
为本时刻的预测值;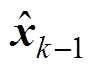 为上一时刻最优结果;uk-1为上一时刻的状态空间输入;Pk/k-1为本时刻预测的协方差矩阵;Qk-1为过程噪声协方差矩阵;Pk-1为上一时刻的协方差矩阵;Kk为卡尔曼增益;Rk为观测噪声协方差矩阵;
为上一时刻最优结果;uk-1为上一时刻的状态空间输入;Pk/k-1为本时刻预测的协方差矩阵;Qk-1为过程噪声协方差矩阵;Pk-1为上一时刻的协方差矩阵;Kk为卡尔曼增益;Rk为观测噪声协方差矩阵;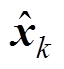 为本时刻更新的最优结果;Pk为本时刻的协方差矩阵。
为本时刻更新的最优结果;Pk为本时刻的协方差矩阵。
通过采用EKF算法并结合永磁电机热网络模型辨识电机的热阻及永磁体温度。同理可以进行三、四和六节点的热网络模型的热阻及电机温度估计。
为比较用于在线电机温度估计的热网络模型,利用永磁电机温度实验平台将实验采集的实测永磁体温度数据与利用四个不同节点模型进行温度估计的结果进行对比分析。
通过在不同工况下对四个不同节点模型进行仿真估计,得到永磁体实际温度与不同节点估计温度如图7所示。从图7可得,综合考虑收敛速度、精度、稳定性及对各个工况的适应性等诸多方面,在不同工况下进行比较,五节点模型相对其他节点模型适用性最好,五节点模型的精度、收敛速度及稳定性最好。五节点模型在采样时间150 s左右收敛且估计误差最小。而六节点模型的估计误差相对较小,但其模型细化程度较高、参数增多,开始时利用观测向量较好,收敛较快,但在参数变化过程中,过多的未知参数会导致收敛性和鲁棒性不如其他的模型,因为随着节点数的增加,模型中未知变量也增加,状态向量达到13维,导致辨识过程中模型收敛性和鲁棒性难以保障。


图7 不同工况下永磁体估计温度与实际温度对比
Fig.7 Comparison of estimated and actual permanent magnet temperatures under different operating conditions
对各节点模型在不同工况下进行仿真后,不同节点的平均误差和最大误差结果见表2。可见,不同工况下的永磁体温度估计,五节点模型温度估计结果无论是平均误差还是最大误差都小于其他节点数模型。因此,作为低阶灰度热网络的四种备选节点模型,五节点模型具有较好的温度估计收敛性及温度估计精度。
表2 各工况下不同热网络模型转子永磁体温度估计误差
Tab.2 The temperature estimation error of rotor permanent magnets in different thermal network models under various working conditions

节点数平均估计误差/℃最大估计误差/℃最大百分比估计误差(%) 310.5114.0015.50 46.618.639.55 53.535.876.50 64.287.808.63
利用EKF算法进行热阻更新,并进行永磁电机温度估计发现,EKF算法将非线性问题转化为线性问题,EKF法的辨识精度依赖模型数学建模的准确性及过程参数误差水平,若模型建模不准确、初始值设置不合适及过程参数误差过大,则辨识精度会明显下降甚至出现发散现象[15-17]。故需要对EKF算法进行改进,提高其对过程参数变化的鲁棒性和强非线性系统的适用性。
EKF计算中经常出现滤波异常甚至发散的现象,为了解决这一问题,提出了强跟踪EKF算法[18]。即在EKF算法中引入时变渐消因子进行实时增益矩阵调整,提高模型的鲁棒性,进而提升EKF辨识的精度。
对式(21)进行改进。令残差序列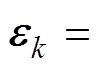

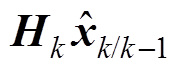 ,则
,则
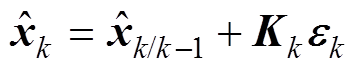 (23)
(23)
为了实现强跟踪性,确定增益矩阵Kk时,需要满足
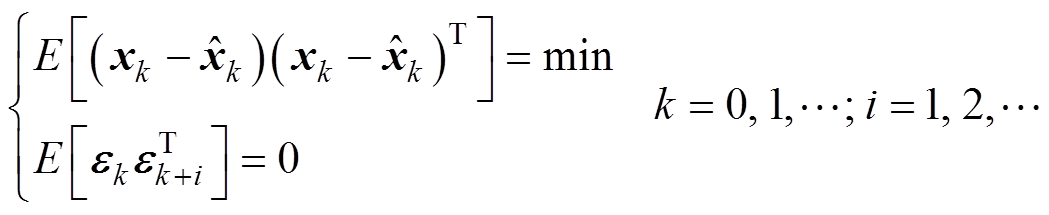 (24)
(24)
式中,当估计值与实际值差别较大,通过在线确定增益矩阵,若估计值准确,则强跟踪EKF退化为普通EKF。
因此,对EKF的误差协方差矩阵更新式(19)改进为式(25),引入渐消因子实现EKF的强跟踪特性。
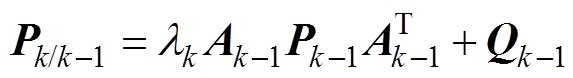 (25)
(25)
式中,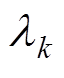 为时变渐消因子,且
为时变渐消因子,且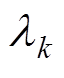 ≥1,其求解为
≥1,其求解为
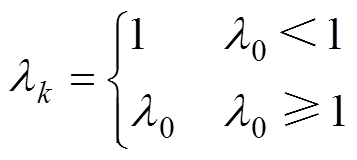 (26)
(26)
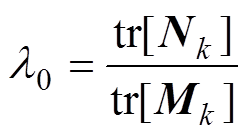 (27)
(27)
其中,Nk、Mk定义为
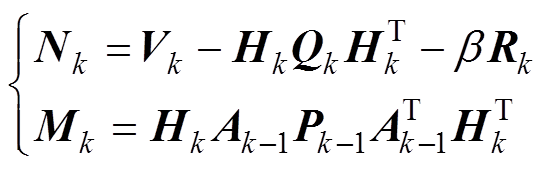 (28)
(28)
式中,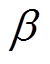 为弱化因子,且
为弱化因子,且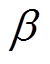 ≥1;Vk为残差序列的协方差矩阵,有
≥1;Vk为残差序列的协方差矩阵,有
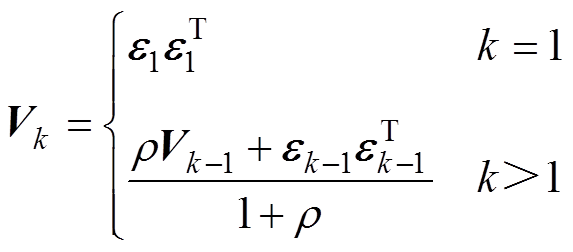 (29)
(29)
式中,0<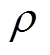 <1为遗忘因子,通常取为0.95。
<1为遗忘因子,通常取为0.95。
当系统具有较强非线性时,为了提高EKF算法在这类系统中的适应性,将标量的新息扩展为新息向量,进而将新息向量拓展为新息矩阵,建立一种基于新息矩阵的辨识理论与方法。通过利用多个时刻数据信息的方式将算法中的残差标量扩展为新息矩阵来替换原本算法中使用当前时刻的新息对估计值的修正,建立了基于新息的辨识理论和方法,从而达到精度提升的效果[19]。
基于多新息理论,将式(21)中新息额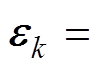
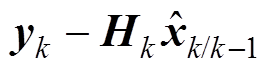 扩展为新息矩阵,有
扩展为新息矩阵,有
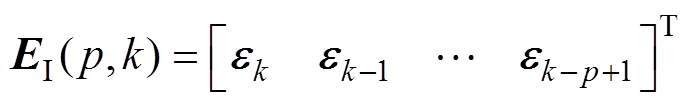 (30)
(30)
式中,p≥1为多新息向量的长度。
则卡尔曼增益扩展为
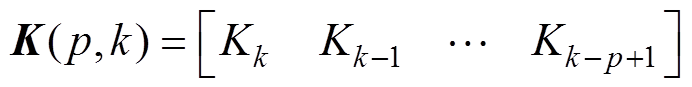 (31)
(31)
由于矩阵中不同时刻的新息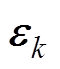 的所处时刻不同,其中包含的信息量也不同,因此不能简单地把所有新息都按照同等的计算方式引入算法中。因此,要为不同时刻的新息配置不同的权重因子。
的所处时刻不同,其中包含的信息量也不同,因此不能简单地把所有新息都按照同等的计算方式引入算法中。因此,要为不同时刻的新息配置不同的权重因子。
采用高斯分布函数进行加权,为不同时刻的新息配置不同的权重因子[20]。首先建立高斯分布函数为
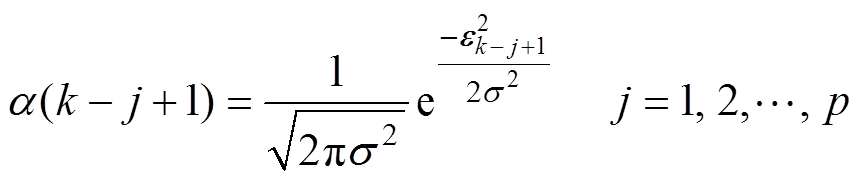 (32)
(32)
进行归一化
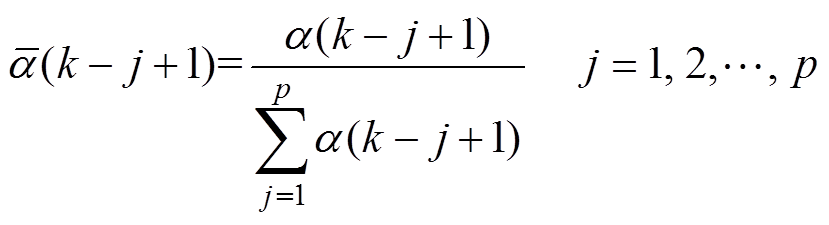 (33)
(33)
加权多新息扩展卡尔曼滤波算法中假定所有权重的和为p。
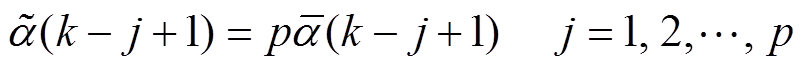 (34)
(34)
加权后新息矩阵为
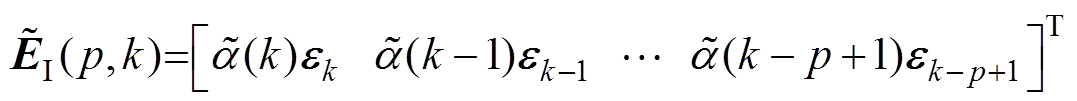 (35)
(35)
则状态更新方程为
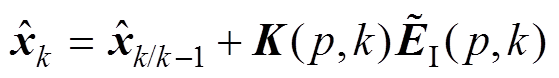 (36)
(36)
由此,结合强跟踪理论和加权多新息理论对EKF进行改进后,加权多新息强跟踪扩展卡尔曼滤波(Weighted Multi-Interest Strong Tracking Extended Kalman Filter, WMI-STEKF)算法流程如图8所示。
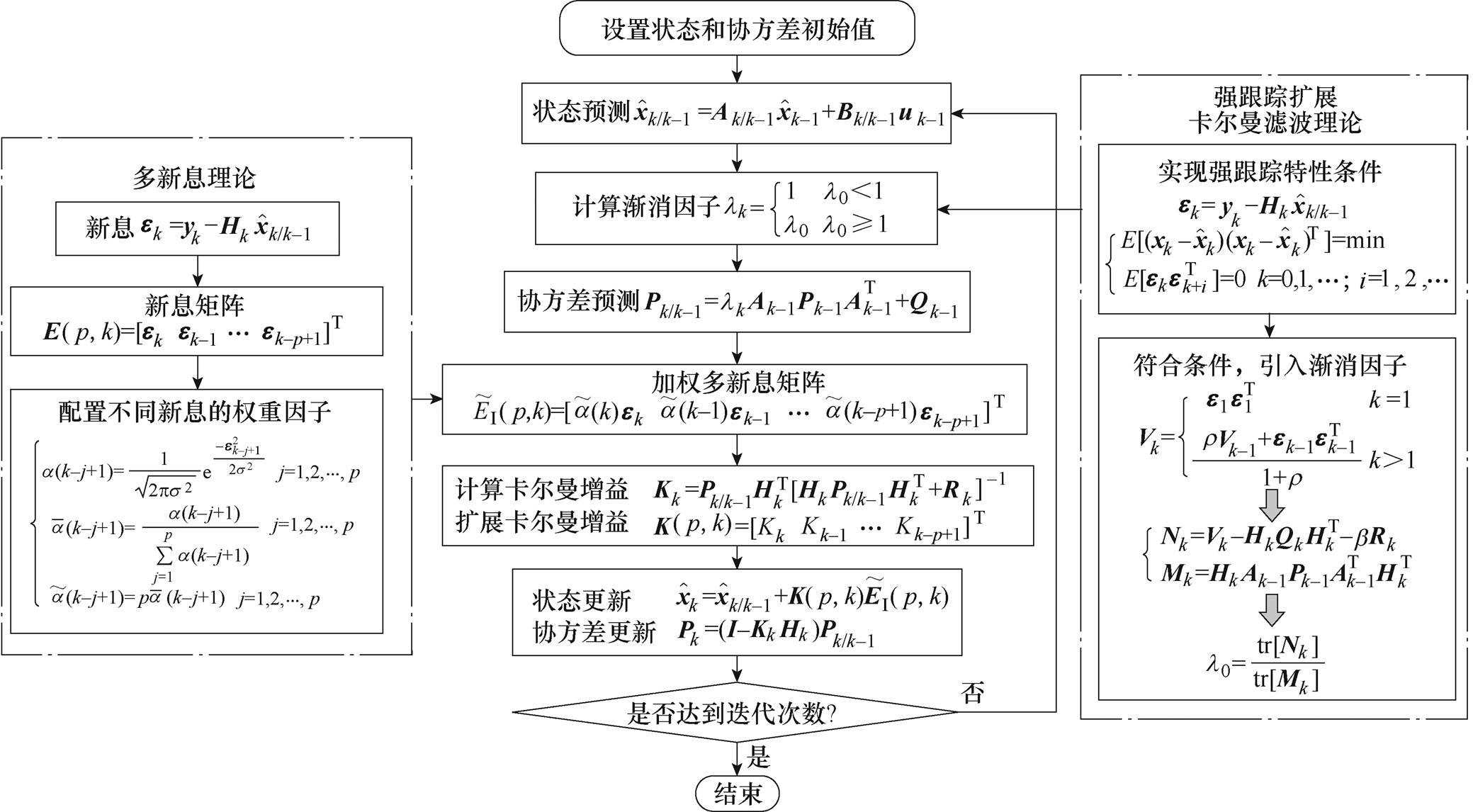
图8 WMI-STEKF算法流程
Fig.8 WMI-STEKF algorithm flow chart
基于WMI-STEKF算法进行永磁电机温度在线估计时,首先根据电机参数计算其热容参数和初始热阻值。当电机在某一工况下运行时,将永磁电机的实时转速、交直轴电流以及端部绕组温度实时采样,采样周期为1 s,同时输入全域空间损耗计算模型中进行损耗计算后,输入永磁体温度在线估计模块,即可利用WMI-STEKF算法估计电机五个节点的温度及辨识热阻参数。考虑电机温度惯性较大,设置输出周期ts=60 s,在输出周期内不断将辨识的热阻参数及估计的节点温度更新至温度估计模型,同时将估计的节点温度更新至全域空间损耗模型。当温度估计时间t>60 s后,输出电机五个节点温度,具体的永磁电机温度在线估计流程如图9所示。在线温度估计过程中,会采用上一个邻近工况下辨识出来的热阻值输入到下一工况作为初始值,这样可以在加快计算速度的同时保持工况转换时温度辨识的准确性。
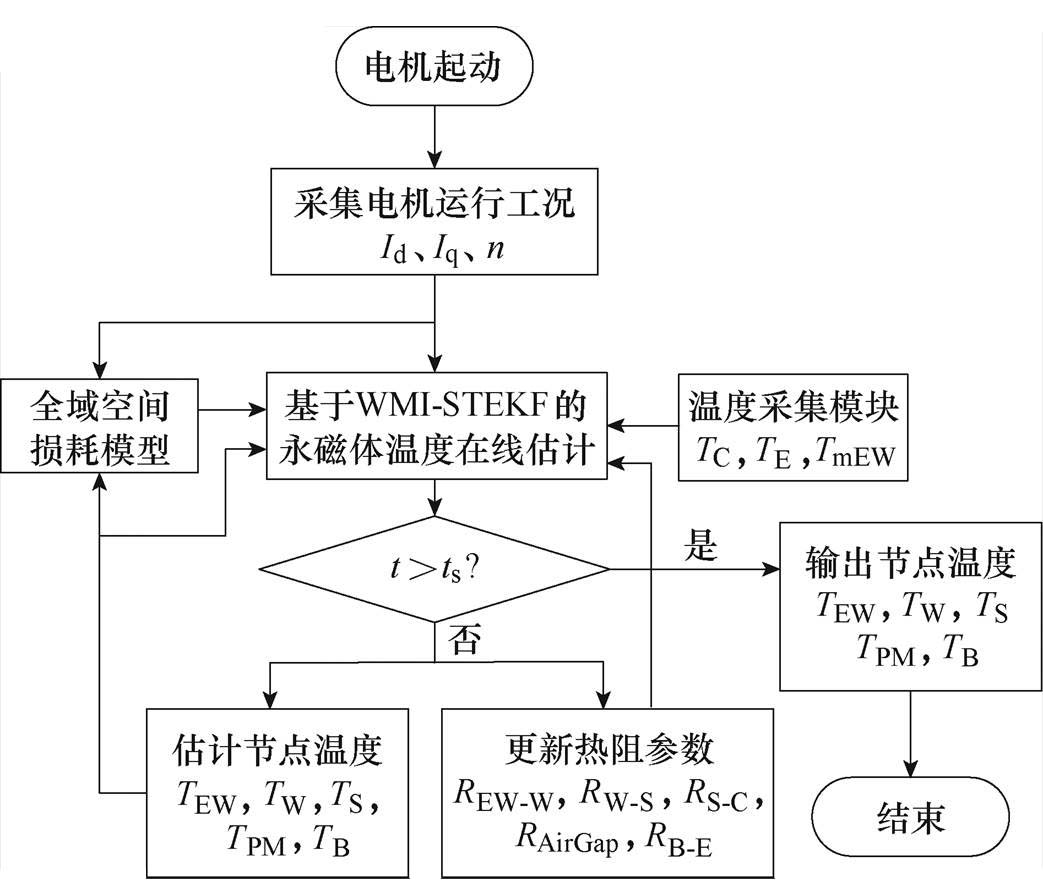
图9 永磁电机温度在线估计流程
Fig.9 Flow chart of on-line estimation of permanent magnet motors
为了验证永磁电机的温度估计方法的准确性,在永磁电机温度实验平台上,进行电机额定工况及多个连续变工况下的温升实验。利用温度估计模块进行实时永磁体温度估计及热阻参数辨识,此时热阻除了受到电机工况的影响,还受到电机本身温升的影响,电机初始运行在额定工况(45 kW, 3 500 r/min)下的热阻及永磁体温度辨识结果如图10所示。

图10 额定工况下热阻辨识结果
Fig.10 Thermal resistance identification results under rated conditions
五节点模型分别利用WMI-STEKF算法与常规EKF算法进行热阻辨识更新,并进行节点温度估计。在工况45 kW,3 750 r/min时作为初始估计点,得到两种估计算法与实际永磁体温度的对比如图11所示,从图中可以看出,WMI-STEKF算法较传统EKF算法温度估计精度更高。
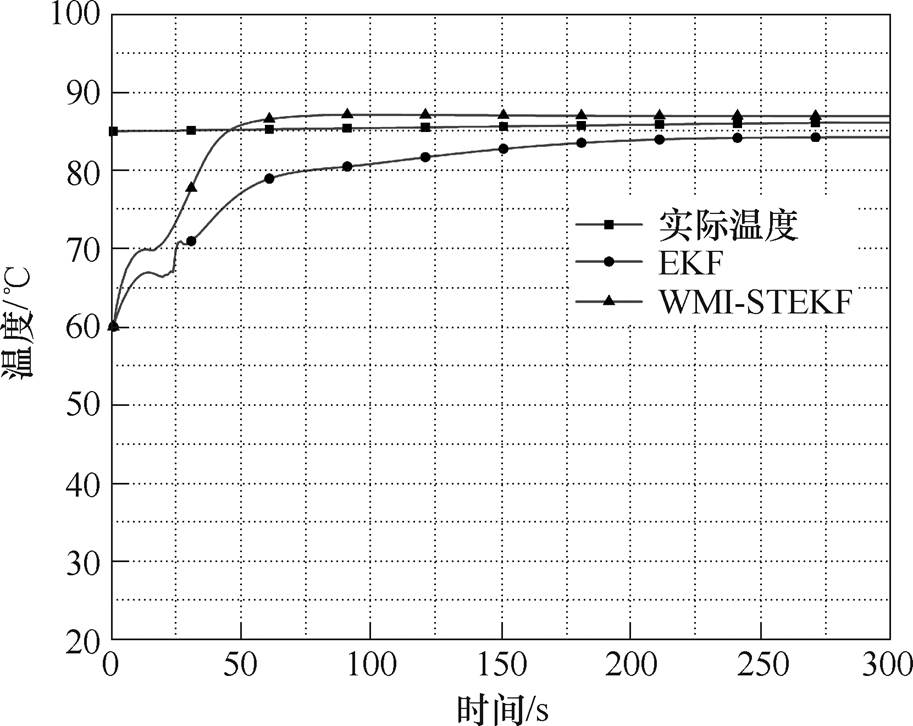
图11 45 kW, 3 750 r/min工况下不同算法永磁体估计温度与实际温度对比
Fig.11 Comparison of estimated and actual permanent magnet temperatures for different algorithms at 45 kW, 3 750 r/min
为验证连续工况下,该永磁电机温度估计算法的准确性,利用永磁电机温度实验平台进行变工况温度测试,温度估计模块在测试中间段进行永磁电机温度估计,60 s输出一组估计值,取变工况下永磁体估计温度与实测温度进行对比,如图12所示,永磁体估计误差分析见表3。
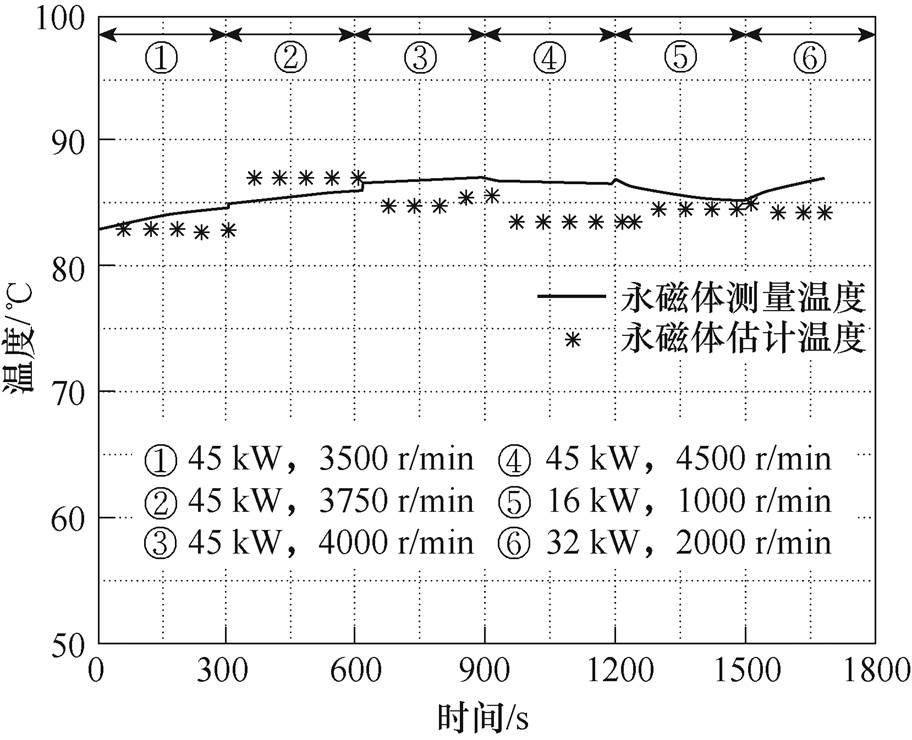
图12 变工况永磁体估计温度结果对比
Fig.12 Comparison of estimated temperature results of permanent magnet under continuous working conditions
表3 永磁体温度估计误差分析
Tab.3 Error analysis of permanent magnet temperature identification

平均估计误差(%)最大估计误差/℃最大百分比估计误差(%) 1.4333.1
由图12及表3可看出,该永磁电机温度估计方法估计的永磁体温度与实测永磁体温度误差较小,在3 ℃以内,具有较高的精度。
本文采用集总参数热网络模型法进行永磁体温度估计,相较于现有的温度估计方法,重点在不同节点模型选择和提高温度辨识精度方面,以满足永磁电机变工况运行下电机温度在线监测需求。
1)采用低阶灰度LPTN模型满足温度在线估计需求,便于实现在电机控制系统中的嵌入。针对低阶灰度模型节点的选择,通过系统辨识和实验数据进行不同工况下的模型对比并量化温度估计指标,得到五节点模型为最优在线估计模型。
2)利用多新息理论和强跟踪扩展卡尔曼滤波理论对扩展卡尔曼滤波算法进行改进。在电机变工况运行过程中,有效地弥补了模型简化和热阻变化带来的温度估计过程中的累计误差,提高了算法在电机热模型强非线性系统的适用性和参数辨识中过程参数变化的鲁棒性。
3)对永磁电机温度实验中变工况的电机温度进行估计。通过对变工况下采集的电机温度数据与仿真数据进行对比,证明了本文的LPTN模型及设计的WMI-STEKF辨识算法在永磁电机温度在线辨识方面具有较高的精度,估计误差达到3 ℃以内。
参考文献
[1] 李晓华, 赵容健, 田晓彤, 等. 逆变器供电对电动汽车内置式永磁同步电机振动噪声特性影响研究[J]. 电工技术学报, 2020, 35(21): 4455-4464.
Li Xiaohua, Zhao Rongjian, Tian Xiaotong, et al. Study on vibration and noise characteristics of interior permanent magnet synchronous machine for electric vehicles by inverter[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4455-4464.
[2] Shi Wei, Zhou Xuan. Online estimation method for permanent magnet temperature of high-density per- manent magnet synchronous motor[J]. IEEJ Transa- ctions on Electrical and Electronic Engineering, 2020, 15(5): 751-756.
[3] 张业成, 刘国海, 陈前. 基于电流波动特征的永磁同步电机匝间短路与局部退磁故障分类诊断研究[J]. 电工技术学报, 2022, 37(7): 1634-1643, 1653.
Zhang Yecheng, Liu Guohai, Chen Qian. Dis- crimination of interturn short-circuit and local demagnetization in permanent magnet synchronous motor based on current fluctuation characteristics[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1634-1643, 1653.
[4] 朱元, 肖明康, 陆科, 等. 电动汽车永磁同步电机转子温度估计[J]. 电机与控制学报, 2021, 25(6): 72-81.
Zhu Yuan, Xiao Mingkang, Lu Ke, et al. Rotor temperature estimation for permanent magnet syn- chronous motors in electric vehicles[J]. Electric Machines and Control, 2021, 25(6): 72-81.
[5] Reigosa D D, Fernandez D, Tanimoto T, et al. Permanent-magnet temperature distribution estimation in permanent-magnet synchronous machines using back electromotive force harmonics[J]. IEEE Transa- ctions on Industry Applications, 2016, 52(4): 3093- 3103.
[6] Reigosa D D, Fernandez D, Yoshida H, et al. Permanent-magnet temperature estimation in PMSMs using pulsating high-frequency current injection[J]. IEEE Transactions on Industry Applications, 2015, 51(4): 3159-3168.
[7] 刘平, 王鑫, 孙千志, 等. 永磁同步电机定子绕组温度估计的信号注入策略优化[J]. 电机与控制学报, 2019, 23(11): 18-26.
Liu Ping, Wang Xin, Sun Qianzhi, et al. Signal injection strategy optimization of stator winding temperature estimation for permanent magnet syn- chronous motor[J]. Electric Machines and Control, 2019, 23(11): 18-26.
[8] Gaona D, Wallscheid O, Böcker J. Fusion of a lumped-parameter thermal network and speed-dependent flux observer for PM temperature estimation in synchronous machines[C]//IEEE Southern Power Electronics Conference (SPEC), Puerto Varas, Chile, 2018: 1-6.
[9] Camilleri R, Howey D A, McCulloch M D. Predicting the temperature and flow distribution in a direct oil-cooled electrical machine with segmented stator[J]. IEEE Transactions on Industrial Electronics, 2016, 63(1): 82-91.
[10] Liang Dawei, Zhu Z Q, Zhang Yafeng, et al. A hybrid lumped-parameter and two-dimensional analytical thermal model for electrical machines[J]. IEEE Transactions on Industry Applications, 2021, 57(1): 246-258.
[11] 师蔚, 靳荣华. 基于扩展卡尔曼滤波的永磁电机热网络参数辨识[J]. 电机与控制学报, 2020, 24(12): 106-112.
Shi Wei, Jin Ronghua. Thermal network parameters identification of permanent magnet motor based on extended Kalman filter[J]. Electric Machines and Control, 2020, 24(12): 106-112.
[12] Wang Wenbo, Zhou Yubin, Chen Yangsheng. Investigation of lumped-parameter thermal model and thermal parameters test for IPMSM[C]//17th Inter- national Conference on Electrical Machines and Systems, Hangzhou, China, 2015: 3246-3252.
[13] Wallscheid O, Böcker J. Global identification of a low-order lumped-parameter thermal network for permanent magnet synchronous motors[J]. IEEE Transactions on Energy Conversion, 2016, 31(1): 354-365.
[14] 骆凯传, 师蔚, 张舟云. 基于温度实验的永磁同步电机损耗分离方法[J]. 电工技术学报, 2022, 37(16): 4060-4073.
Luo Kaichuan, Shi Wei, Zhang Zhouyun. Method of loss separation of permanent magnet synchronous motor based on temperature experiment[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(16): 4060-4073.
[15] 巫春玲, 胡雯博, 孟锦豪, 等. 基于最大相关熵扩展卡尔曼滤波算法的锂离子电池荷电状态估计[J]. 电工技术学报, 2021, 36(24): 5165-5175.
Wu Chunling, Hu Wenbo, Meng Jinhao, et al. State of charge estimation of lithium-ion batteries based on maximum correlation-entropy criterion extended Kalman filtering algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5165-5175.
[16] 刘芳, 马杰, 苏卫星, 等. 基于自适应回归扩展卡尔曼滤波的电动汽车动力电池全生命周期的荷电状态估算方法[J]. 电工技术学报, 2020, 35(4): 698- 707.
Liu Fang, Ma Jie, Su Weixing, et al. State of charge estimation method of electric vehicle power battery life cycle based on auto regression extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 698-707.
[17] Wu Pengfei, Shi Zhangsong, Yan Penghao. Improved EKF-SLAM algorithm of unmanned helicopter auto- nomous landing on ship[C]//37th Chinese Control Conference, Wuhan, China, 2018: 5287-5292.
[18] Cheng Yan, Chang Qing. A carrier tracking loop using adaptive strong tracking Kalman filter in GNSS receivers[J]. IEEE Communications Letters, 2020, 24(12): 2903-2907.
[19] 丁锋. 系统辨识(6): 多新息辨识理论与方法[J]. 南京信息工程大学学报(自然科学版), 2012, 4(1): 1-28.
Ding Feng. System identification. part F: multi- innovation identification theory and methods[J]. Journal of Nanjing University of Information Science & Technology (Natural Science Edition), 2012, 4(1): 1-28.
[20] Han Yiyang, Ding Jie, Chen Jiazhong, et al. SOC estimation method for lithium-ion batteries: extended Kalman filter with weighted innovation[C]//Chinese Control and Decision Conference, Nanchang, China, 2019: 5074-5078.
Abstract The online temperature estimation of permanent magnet motors (PMM) can prevent motor damage caused by over temperature, especially reduce the risk of irreversible demagnetization of permanent magnet and improve the safety of PMM. For traditional online temperature estimation of lumped parameter thermal network (LPTN), the influence of LPTN topology with different scales on the speed and accuracy of on-line estimation has yet to be deeply studied. At the same time, the thermal resistance unit nonlinearity and the error accumulation from loss calculation generate the deviation between the estimated temperature and the actual value. Therefore, after comparing the low-order gray box LPTN models of PMM with different nodes, this paper proposes the weighted multi-innovation strength tracking extended Kalman filter (WMI-STEKF) algorithm to carry out on-line parameter identification and temperature estimation with high accuracy under variable working conditions.
Firstly, the LPTN gray box models of PMM with different nodes are established. Next, the experimental temperature platform of variable condition temperature of PMM is built. Based on the experimental temperature data, the models are compared and analyzed. The optimal LPTN model for online temperature estimation of PMM is obtained. Third, the time-varying fading factor is introduced into the extended Kalman filtering algorithm to adjust the real-time gain matrix to improve the robustness of the model and the accuracy of the extended Kalman filtering algorithm identification. At the same time, the residual scalar in the extended Kalman filtering algorithm is extended to the innovation matrix to improve the adaptability of the system to nonlinear systems. WMI-STEKF algorithm is used in on-line parameter identification and temperature estimation.
The grey box thermal network models with four different node models are evaluated according to the experimental temperature data. The five-node model has the best accuracy, convergence speed, and stability. The average error and maximum error of the temperature estimation results are 3.53 ℃ and 5.87 ℃, respectively, lower than other node number models. In the online parameter identification and temperature estimation of the LPTN model using the WMI-STEKF algorithm, six consecutive working conditions of 45 kW, 3 500 r/min; 45 kW, 3 750 r/min; 45 kW, 4 000 r/min; 45 kW, 4 500 r/min; 16 kW, 1 000 r/min; 32 kW, 2 000 r/min are implemented. After temperature identification, the error between the estimated and measured permanent magnet temperatures is within 3 ℃.
The following conclusions are drawn: (1) The low-order gray five-node LPTN model can meet the needs of online temperature estimation. Through system identification and experimental data, the proposed model is the optimal online estimation model for experimental motors under different working conditions and quantitative temperature estimation index evaluation. (2) Based on multi-innovation theory and strong tracking extended Kalman filter algorithm, the accumulated error in the temperature estimation process caused by model simplification and thermal resistance change is effectively compensated under different working conditions. This algorithm improves the applicability in the strongly nonlinear system of motor thermal model and the robustness of process parameter changes in parameter identification. It has high accuracy in online temperature identification.
keywords:Lumped parameter thermal network, permanent magnet motor, temperature estimation, weighted multi-innovation strength tracking extended Kalman filter (WMI-STEKF)
DOI: 10.19595/j.cnki.1000-6753.tces.220385
中图分类号:TM351
国家“十三五”科技部重研发计划资助项目(2016YFB0100700)。
收稿日期 2022-03-17
改稿日期 2022-04-18
师 蔚 女,1981年生,博士,副教授,硕士生导师,研究方向为永磁电机及其控制技术。E-mail: cane914@126.com(通信作者)
骆凯传 男,1996年生,硕士研究生,研究方向永磁电机损耗计算及温度估计。E-mail: 531370502@qq.com
(编辑 崔文静)