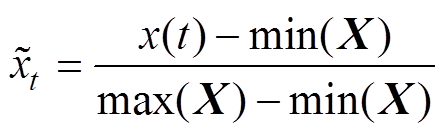（1）
摘要 针对一维机械振动信号在输入卷积神经网络时无法充分提取相对位置关系的问题，提出一种基于格拉姆角场（GAF）和小尺寸卷积的胶囊网络的轴承故障诊断分类方法。利用GAF对采集到的振动信号进行编码，可以很容易地进行角度透视，从而识别出不同时间间隔内的时间相关性并产生相应特征图。胶囊网络对小尺寸图像相对位置比较敏感，特征提取具有优势，同时考虑到VGG网络优秀的特征提取能力，在结合胶囊网络和VGG网络的基础上，加入深度小尺寸卷积层。将GAF编码的振动图像输入到改进的CapsNet网络进行训练，组成GAF-CapsNet模型对轴承故障进行诊断。该模型在凯斯西储大学轴承数据集上进行试验，结果表明，格拉姆角和场（GADF）编码方式相比格拉姆角差场（GASF）编码效果差，效果较好的GADF-CapsNet有99.27 %准确率，较差的GASF-CapsNet也有98.83 %准确率，相较其他编码方式和卷积神经网络，该模型性能表现普遍比其他模型具有更高准确率。
关键词：轴承 故障诊断 格拉姆角场 胶囊网络
随着现代机械的高速发展，滚动轴承的应用场合也趋向更高工作强度和更恶劣的工作环境，在所有电机机械故障中，高达30 %的损坏是由轴承故障造成[1]，这使得轴承的故障诊断和维护更加重要。当前在“工业4.0”的大环境下，机械设备也向着智能化的方向发展[2]，数据采集的速度大大加快[3]，数据驱动的背景下故障诊断可以利用大量的机械数据，使轴承的故障诊断方法向智能化方向发展。
传统的智能故障诊断方法在处理大数据时，因为其特征提取的泛化能力差，难以取得良好的效果。通过支持向量机[4]（Support Vector Machines, SVM）则需要足够的先验知识，对于不同的故障诊断任务需要重新设计不同的特征提取器[5]，使系统的设计成本增加。而近年来，由于训练资源的大幅增加和计算能力的快速发展，深度学习逐渐成为智能故障诊断领域中的新秀[6]。V. N. Ghate等[7]发现神经模糊和神经网络（Neural Network, NN）的故障检测方法在大型机器上表现良好，针对中小型三相异步电动机，开发了基于径向-基函数-多层感知器级联的故障检测方案；Chen Zhiqiang等[8]采用了三种深度神经网络模型深度波尔茨曼机（Deep Boltzmann Machines, DBM）、深度置信网络（Deep Belief Networks, DBN）和堆栈自编码器（Stacked Auto Encoders, SAE）来识别滚动轴承的故障状况并进行研究，发现深度波尔茨曼机、深度置信网络和堆栈式自编码器取得了良好的效果；余啸等[9]采用经验模态分解（Empirical Mode Decomposition, EMD）的方法分析振动信号，再通过极限学习机的特征选择方法，去除原始特征中的冗余和干扰，最后利用深度信念网络进行故障诊断。
作为神经网络最有代表性的网络之一，卷积神经网络（Convolutional Neural Network, CNN）因其强大的特征提取和分类能力[10-12]，在图像分类领域取得了巨大成功，但是对于机械故障中的一维振动信号却无法直接通过卷积神经网络进行学习。因此，先将一维振动信号通过编码使其转换为二维图像再输入卷积神经网络成为了行之有效的处理方式。张西宁等[13]将时域振动信号输入网络，以原信号与重构信号的差值最小为目标，对卷积核和反卷积核进行优化，迭代后输入全连接层（Full Connection layer, FC）和分类器，用标签样本调整，以获得一个深度卷积自编码网络；宫文峰等[14]提出了一种融合了卷积神经网络CNN和支持向量机SVM的方法用于电机轴承的故障诊断，该方法采用1×1的过渡卷积层与全局均值池化层的组合代替传统CNN的全连接网络层结构；刘炳集等[15]使用振动信号进行短时傅里叶变换得到时频图，把时频图作为卷积神经网络的输入进行训练，在凯斯西储大学轴承数据集上得到了97.63 %的准确率；袁建虎等[16]对振动信号进行连续小波变换得到时频图，并将图像输入CNN网络进行训练分类；另外，闫佳瑛[17]、仝钰[18]、陈德伦[19]等分别使用变分模态分解（Variational Mode Decomposition, VMD）、格拉姆角差场（Gramian Angular Difference Fields, GADF）、符号聚合近似（Symbolic Aggregate Approximation, SAX）等不同的数据处理方式对振动信号进行编码，然后输入深度卷积网络进行训练，均取得了良好的效果，这些研究都证明了卷积神经网络在轴承故障分类问题上的有效性。但是，由于卷积神经网络的平移不变性，2017年G. E. Hinton团队[20]提出了胶囊网络（capsule network）的概念，克服了卷积神经网络的固有缺陷——平移不变性。
胶囊网络用向量的胶囊单元代替了卷积神经网络的标量，图像上的元素用胶囊表示，用胶囊之间的关系建立起元素间的位置关系，使得网络的感受野变得更大。在提出胶囊网络的首次试验中，胶囊网络在经典数据集MNIST上获得了99.76 %准确率，展现了胶囊网络在小尺寸图像上超强的特征提取和识别能力。张振良等[21]把胶囊网络运用到轴承故障诊断问题上，用粒子群优化的稀疏盲源分离后的振动信号通过S域转换的时域图输入胶囊网络，取得了较好的效果，说明胶囊网络在一维振动信号转换的图像上能够提取到深层次特征并进行识别。但转换的时域图关键内容较少，一旦被网络忽略就完全遗失了这部分特征，使得胶囊网络的特征提取过程中更容易遗漏相关信息从而降低了网络的准确率。
本文提出一种新的GAF-CapsNet模型：采用格拉姆角场（Gramian Angular Field, GAF）编码方式将原始数据转换为特征明显的图像，分别运用格拉姆角和场（Gramian Angular Summation Fields, GASF）、GADF进行编码，并将产生的两组特征图分别输入小卷积核的卷积层进行信息读取和特征提取，再输入胶囊网络进行更深层次的特征提取与故障识别，最后通过数字胶囊层的十个胶囊来对应不同故障类型。最后使用美国凯斯西储大学（Case Western Reserve University, CWRU）轴承故障数据库中的滚动轴承数据测试GAF-CapsNet模型的性能。结果表明，使用GADF编码的模型表现更好，所提出的GAF-CapsNet相比其他图像编码方式或卷积神经网络在对滚动轴承故障进行诊断时具有更高的识别精度，并在噪声环境中兼具更好的性能。
GAF[22]是一种将一维时间序列转化为二维图像的编码方式。考虑到CapsNet在图像分类中对特征提取的优势，本文通过GAF基于极坐标的矩阵将时间序列编码成图像，保持一维信号与时间序列的相关性，在Gramian矩阵，每个元素实际上是角度的三角函数值。原始时间序列X首先被归一化为介于0和1之间，这在式（1）中被定义。
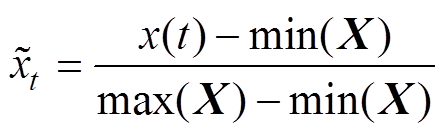（1）
式中，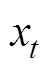
为原始t时刻的振动信号，
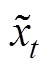为缩放后该时刻的信号；min(X)、max(X)分别为X中最小值和最大值。因此，可以用极坐标来表示重新缩放的时间序列
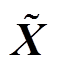。时间戳为半径，公式为
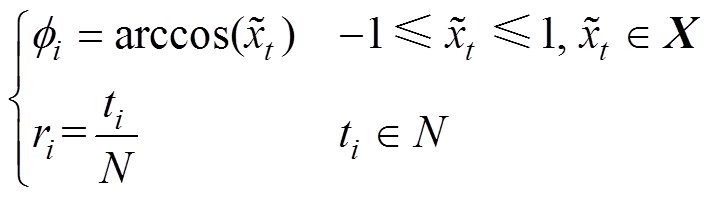（2）
式中，ti为该点时刻的时间戳码；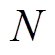
为常数因子，将区间[-1, 1]或[0, 1]分为N等份；ri为极轴，保留了时间上的关系；
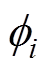为极角，保留了数值上的关系。在将重新标定的时间序列转换到极坐标系后，可以通过每一个点之间的三角和/差来利用角度的视角识别不同时间间隔内的时间相关性。使用GASF[22]和GADF分别编码，编码方式分别定义为
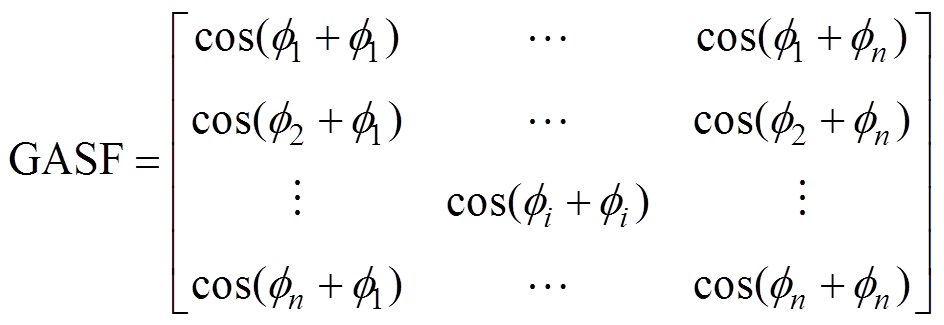（3）
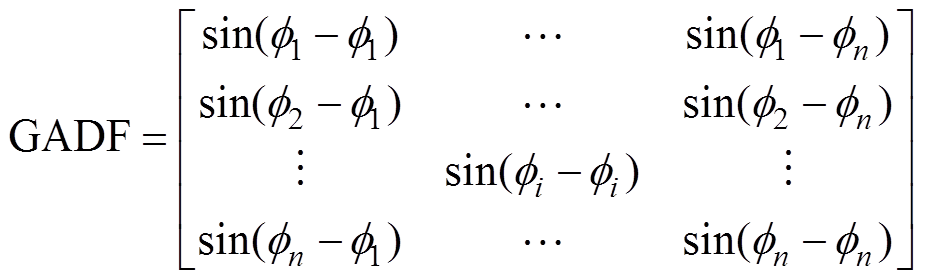（4）
式中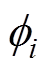，为第i序列的角度值。可以看出，通过该方式编码后，保留了二维图像上对于时间从左上到右下的顺序。在正对角线位置上保留了原始信息，其他区域表达了不同时序间的关系。对于一个原始时间序列长度为n的振动信号，通过GAF编码得到尺寸为n×n的数值矩阵。
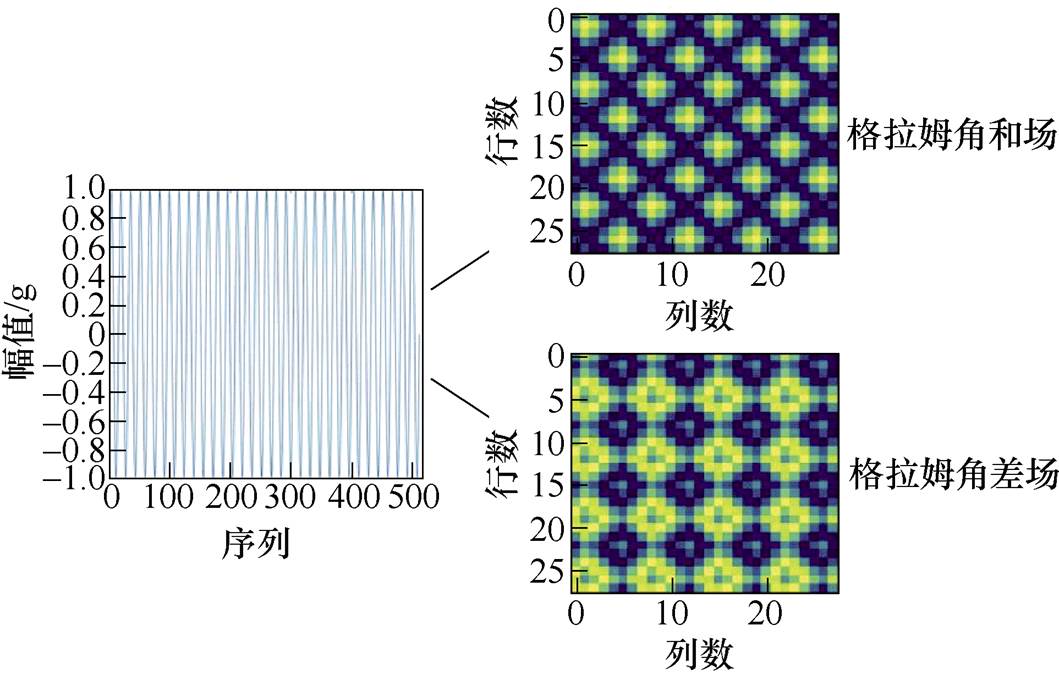
图1 GAF两种编码方式
Fig.1 Two types of GAF encoding
胶囊网络由Hinton在2017年提出，胶囊网络的单元被称为胶囊，每个胶囊包含多个神经元，与传统卷积神经网络的标量模型不同，胶囊用向量来标记图片中各个部分的位置关系。向量的方向和长度分别代表着指向该方向的概率，长度越大则表示概率越大。通常胶囊网络包含两层胶囊层，低层胶囊做出预测后向高层胶囊提供参数信息，多个预测结果一致时激活高层胶囊，激活函数squash[20]为
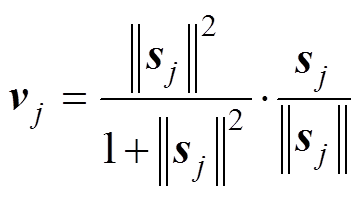（5）
式中，vj为胶囊j的输出；sj为胶囊j所有的输入。
由于胶囊是不同于神经元标量的向量单元，卷积神经网络的迭代更新算法将不再适用，对于向量的更新，胶囊网络使用的是动态路由（dynamic routing）算法，通过动态路由更新胶囊中权重参数bij，bij由预测向量和输出向量进行点乘，点积越大则说明预测与结果的相似度越高。具体的权重更新方式如下。
预测向量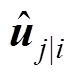
，迭代次数r，对于输入胶囊i和输出胶囊j，定义一个参数bij。
通过式（6）更新向量cij，使得cij非负且和为1。
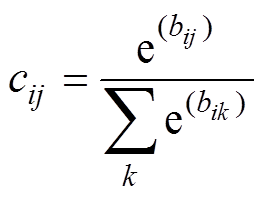（6）
通过式（7）得到输入胶囊sj，并用squash函数（见式（5））更新vj。
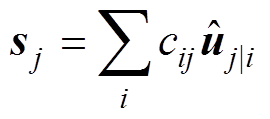（7）
通过式（8）更新bij并回到式（6）进行迭代计算。
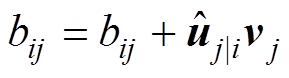（8）
迭代r次后返回最终输出向量vj。
尽管胶囊网络有着优异的特征提取能力，但是在大尺寸图像输入时会产生过多的参数，降低了网络的训练速度。为降低胶囊网络的参数量，提高网络训练速度，同时不造成过多信息丢失，在胶囊层之前构建小卷积层来压缩图像尺寸，并加大深度来保证输入图像信息的完整性。
以此构建了适合故障诊断的胶囊网络结构，包括输入层、卷积层、池化层和胶囊层。由于输入的GAF编码图像的尺寸较大，为了更好的提取特征，先通过两层3×3小卷积核卷积层和一层5×5卷积层，经过一层池化层压缩，再通过一层5×5卷积层，再输入胶囊层，该胶囊层有32个胶囊，每个胶囊有16个维度，再输入数字胶囊层，数字胶囊层有10个胶囊，分别对应10种故障类型。改进的胶囊网络结构见表1。胶囊网络的网络结构示意图如图2所示。
表1 改进的胶囊网络结构
Tab.1 Improved capsule network structure
层卷积核步长输出尺寸 输入128×128×1 卷积层13×3×1281128×128×128 卷积层23×3×641128×128×64 卷积层35×5×641128×128×64 池化层2×2×64264×64×64 卷积层45×5×128164×64×128 胶囊层32×32×16×32 数字胶囊层32×10 输出10
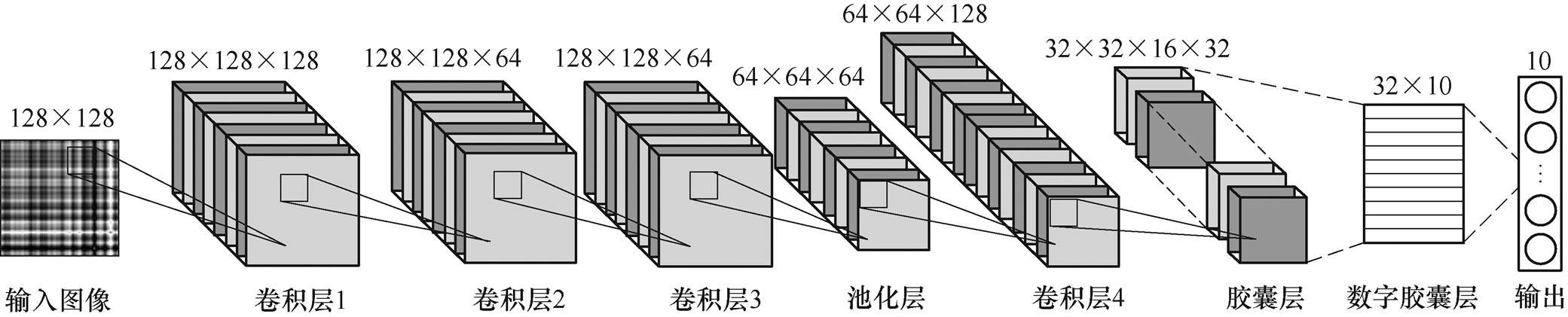
图2 胶囊网络结构示意图
Fig.2 Capsule network structure diagram
因为胶囊中的向量不同于标量，用向量的长度来表示正相关的概率，所以本文的模型边际函数（margin loss）为损失函数，每个胶囊k使用单独的边际损失Lk表示，有
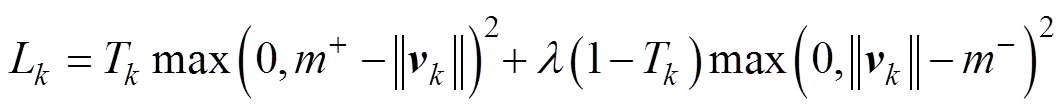（9）
式中，k为分类数；Tk为分类的指示函数；m+与m-分别为上、下边界；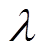
为比例系数；vk为第k个胶囊的输出。当m+=0.9、m-=0.1时，对k类存在的维度将取Tk=1，对缺失类别用系数
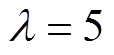降权，阻止训练过程对数字胶囊的压缩，总损失函数为每个数字胶囊边际损失Lk的和，有
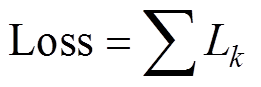（10）
GAF-CapsNet滚动轴承故障诊断流程如下：试验获取的振动信号，通过窗函数将振动信号采样截断，并采用GAF对信号进行编码处理，生成二维灰度图像。依据交叉验证的方式将图像数据集划分为训练集和测试集，将训练集输入胶囊层，通过胶囊层获取不同类型轴承故障GAF图像特征信息，再将其输入到数字胶囊层对故障进行预测。GAF-CapsNet故障诊断流程如图3所示。
试验使用凯斯西储大学的轴承数据集，数据集涵盖了采样频率为12 kHz、48 kHz的驱动端轴承试验数据和采样频率12 kHz的风扇端轴承数据[23]。试验设备包括一台1.5 kW三相异步电机、一个转矩传感器/译码器和一个功率测试计。试验平台如图4所示。
轴承的故障设置采用电火花加工的单点损伤。本试验使用采样频率12 kHz的驱动端轴承试验数据集，此数据集共设计了三种故障类型：外圈故障（Outer race Fault, OF）、滚动体故障（Roll Fault, RF）和内圈故障（Inter race Fault, IF）。每种类型的故障设置了三种受损程度：受损直径为0.177 8、0.355 6、0.533 4 mm。再加一组无故障的对照数据（Normal, NO），这些数据分别在四种负载0 HP、1 HP、2 HP、3 HP（1 HP=0.73 kW），电机转速分别为1 797、1 772、1 750、1 730 r/min条件下的试验数据。每组试验共采集120 000组数据，每组数据包括驱动端加速度数据（Drive End, DE）、风扇端加速度数据（Fan End, FE）、基座加速度数据（Base Accelerometer, BA）。每组故障信号数据集中都有120 000采样数据点，无故障数据集中有240 000采样数据点。
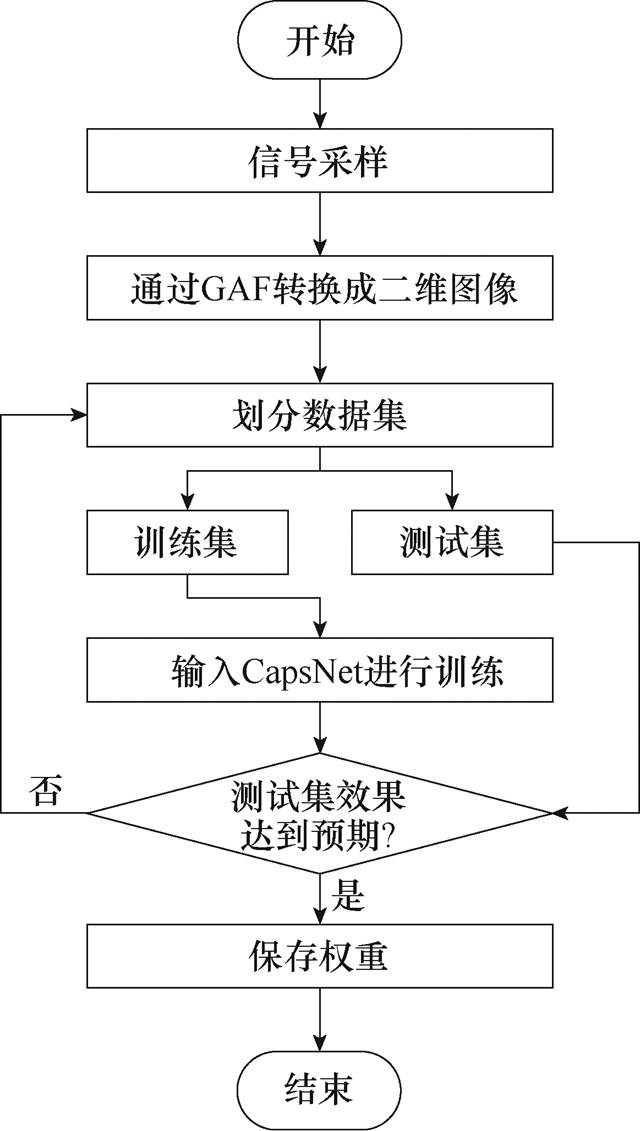
图3 GAF-CapsNet故障诊断流程
Fig.3 GAF-CapsNet bearing fault diagnosis flow chart
图4 凯斯西储大学轴承数据集试验平台
Fig.4 Experimental platform for CWRU bearing datasets
本文所有训练及试验都在个人电脑“OMEN by HP”上实现，处理器（CPU）为Intel(R) Core(TM) i7-10750H CPU@2.60 GHz；显示卡（GPU）为NVIDIA GeForce RTX2070super 8G；计算机系统为Windows 10；环境配置为Python 3.6.12、CUDA 10.1、tensorflow-gpu 2.3.0、numpy 1.19.2、Keras 2.4.3；使用软件工具为Spyder3、matlab2020a。
在选取的试验数据集中，每组故障数据有12万个数据采样点。通过采用矩形滑窗函数来截取指定信号片段，从而输入到GAF-CapsNet网络。为了保证网络中卷积层不丢失信息，在经过预试验后，确定四种可用的采样尺寸分别为64、128、256、512。
为了探究这四种尺寸对最终试验结果的影响，选取内圈0.177 8 mm故障在1 797 r/min的数据进行试验，四种尺寸通过GAF编码后得到图像如图5所示。
如图5所示，64尺寸未能包含足够的振动信息，而128、256、512三种尺寸均包含了足够的信号信息。明显看到，256和512尺寸因为像素的压缩，图像相似度提高，特征反而不明显。为了验证结论，设计了一个VGG三分类网络，分别用以上四种采样尺寸采集无故障对照组和外圈0.177 8 mm故障在1 797 r/min的数据，进行三分类试验，图6为四种尺寸在VGG分类网络的数据结果。
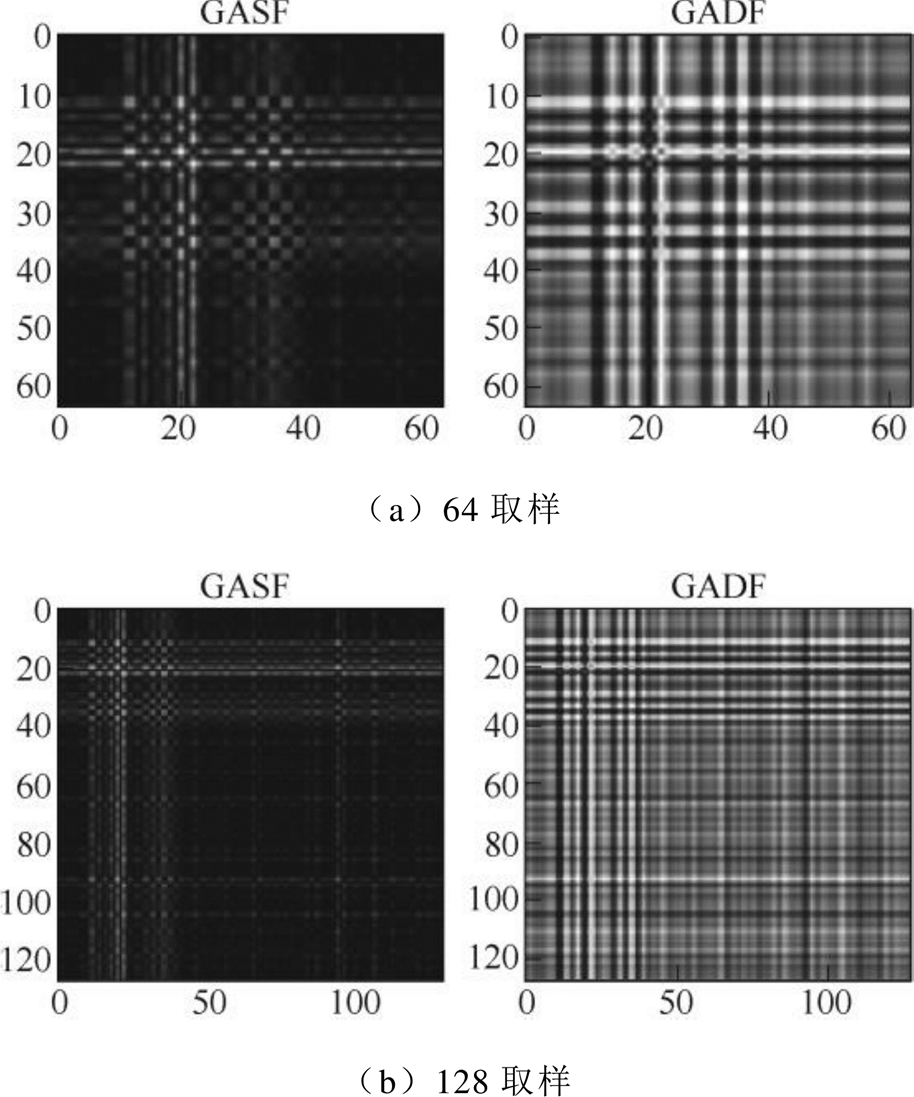
图5 GAF编码图像
Fig.5 GAF-encoded images
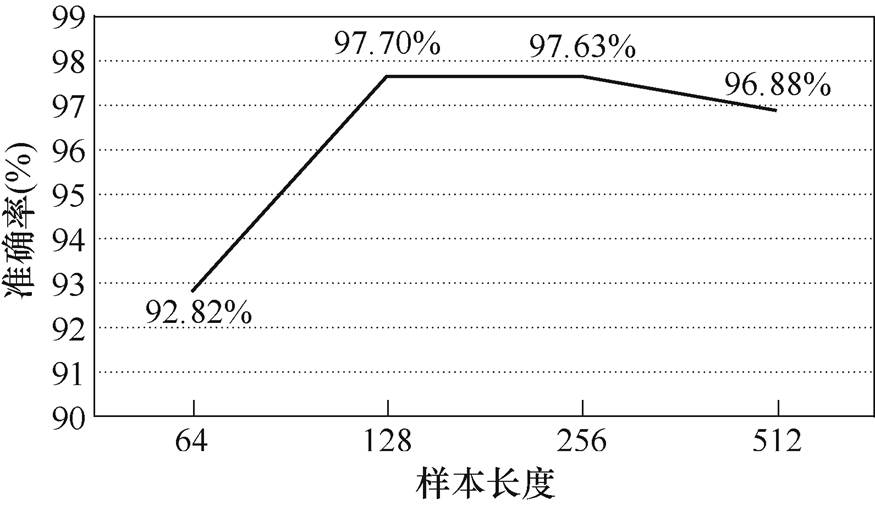
图6 四种样本长度预试验的准确率对比
Fig.6 Pre-experiment accuracy comparison of four sample length
试验表明，小于128尺寸的采样会丢失部分信息，使精度下降。而512尺寸的采样虽然包含足够的信息，但是在卷积神经网络的池化层中信息丢失导致精度下降。256尺寸与128尺寸准确率相差无几，然而在神经网络中，更大的尺寸意味着更多的训练参数，试验中发现，256尺寸的试验时间要长于128尺寸的试验时间。因此，本方法将采用128尺寸作为信号样本的时间点长度，本文试验数据集划分见表2。试验轴承数据集按照不同故障类型以及严重程度将其分为10类故障。数据集按照8
2的比例划分为训练集与测试集。表2中，数据集A代表在0HP下的10类故障数据集。本文将使用包含0～3HP负载的故障数据集E来验证提出模型的故障诊断效果。
表2 轴承故障数据集样本分布
Tab.2 Sample distribution of bearing fault dataset
故障直径/mm00.180.360.53载荷 正常内圈外圈滚动体内圈外圈滚动体内圈外圈滚动体 故障标签0123456789 A训练集7517517517517517517517517517510 HP (0 kW) 测试集187187187187187187187187187187 B训练集7517517517517517517517517517511 HP (0.745 7 kW) 测试集187187187187187187187187187187 C训练集7517517517517517517517517517512 HP (1.491 4 kW) 测试集187187187187187187187187187187 D训练集7517517517517517517517517517513 HP (2.237 1 kW) 测试集187187187187187187187187187187 E训练集3 0043 0043 0043 0043 0043 0043 0043 0043 0043 0040～3 HP 测试集748748748748748748748748748748
通过以上的信号采样后，将GAF编码后的10分类样本图像数据集输入CapsNet进行训练，对GAF的两种编码方式分别进行训练，数据集分割为训练集和测试集的分割比例为82，通过交叉验证的方式分为五组，两种编码方式准确率迭代图如图7所示。
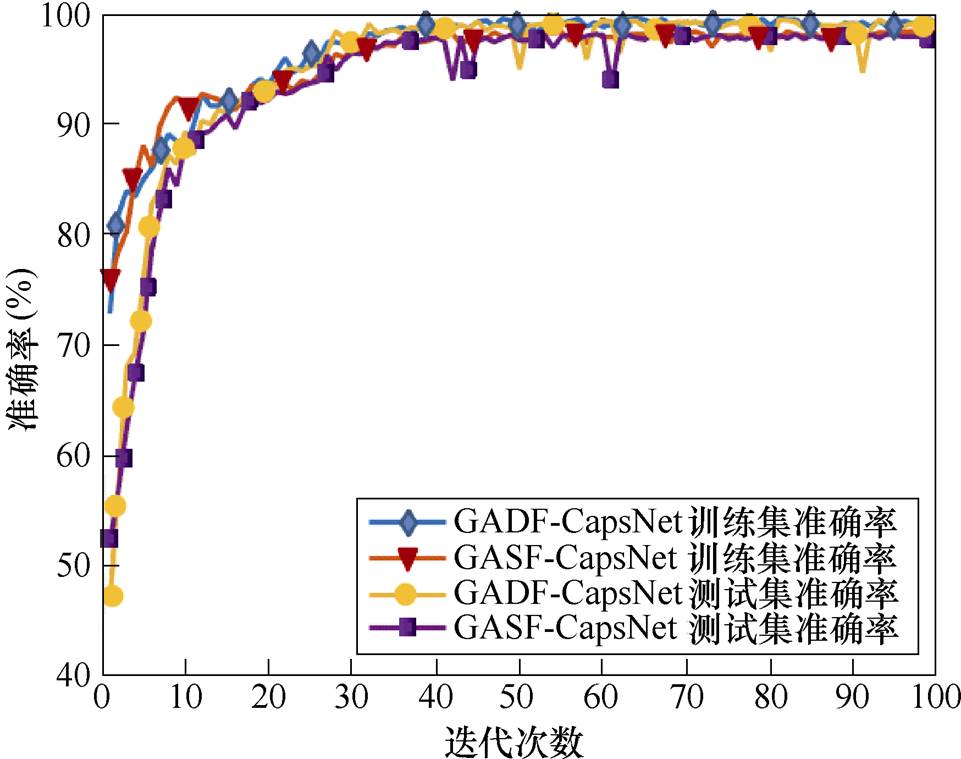
图7 两种编码方式准确率迭代图
Fig.7 Iterative graphs of the accuracy of the two coding methods
如图7所示，两种编码方式的网络模型分别达到了99.31 %和99.03 %的准确率，其中相比于GASF编码，GADF的编码方式具有更快的收敛速度和更高的准确率。通过交叉验证进行五组试验，最终求取试验中达到的最高准确率的平均值，详细的平均准确率见表3。
表3 两种编码方式准确率对比
Tab.3 Comparison of the accuracy of the two coding methods
编码方式测试准确率(%)训练准确率(%) GADF99.2799.82 GASF98.8399.03
由表3可以看出，GADF编码方式准确率高于GASF的编码方式，为了进一步研究模型的性能，绘制GADF-CapsNet的混淆矩阵，如图8所示。
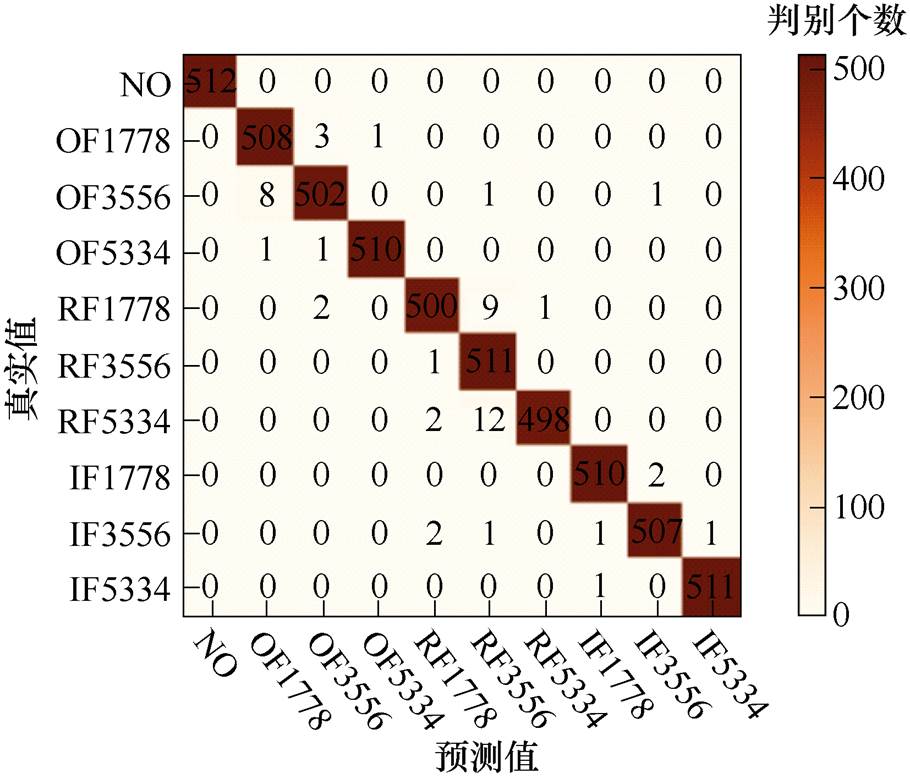
图8 GADF-CapsNet混淆矩阵
Fig.8 GADF-CapsNet confusion matrix
图8中，横轴是预测值，纵轴是真实值，标签中NO、OF、RF、IF分别表示正常、外圈故障、滚动体故障和内圈故障，1 778、3 556、5 334分别表示故障所在位置为0.177 8 mm、0.355 6 mm、0.533 4 mm。
将数据集按照82的比例进行划分，使得混淆矩阵每个类别有512张图片。矩阵中主对角线的数字代表正确分类的数量，其他地区代表预测错误的数量。从图8可以明显发现，样本是否存在故障可以完全被网络识别出来；其次，在故障类型方面，所有滚动体故障的样本全部被正确识别，其他两种故障也具有较高的识别度；此外，在预测每种故障的严重程度方面，滚动体故障表现略差，但也具有较高的准确率。说明GAF-CapsNet在轴承故障诊断试验中取得较好的效果。
为进一步研究GAF-CapsNet的性能，采用其他编码方式和网络进行试验并比较。其他常用的编码方式有时频图、短时傅里叶变换（Short Time Fourier Transform, STFT）、小波包分解（Wavelet Packet Decomposition, WPD）、谱峭度（Spectral Kurtosis, SK）图等；常用的网络结构有卷积神经网络，比如VGGNet[24]、ResNet[25]等。Wen Long等[26]直接将一维振动信号图片输入进CNN网络进行分类；李恒等[27]使用短时傅里叶变换把振动信号构造成时频图，再输入CNN网络进行训练；S. S. Udmale等[28]使用谱峭度对不同频段的振动信号编码，然后研究不同级别谱峭度在故障诊断中效果；陈里里等[29]通过小波包变换将信号转换成时频图，输入到VGG19网络进行训练。庞俊等[30]把振动的灰度纹理图输入带有残差单元的卷积神经网络。GAF-CapsNet与以上方法进行比较，准确率对比如图9所示。
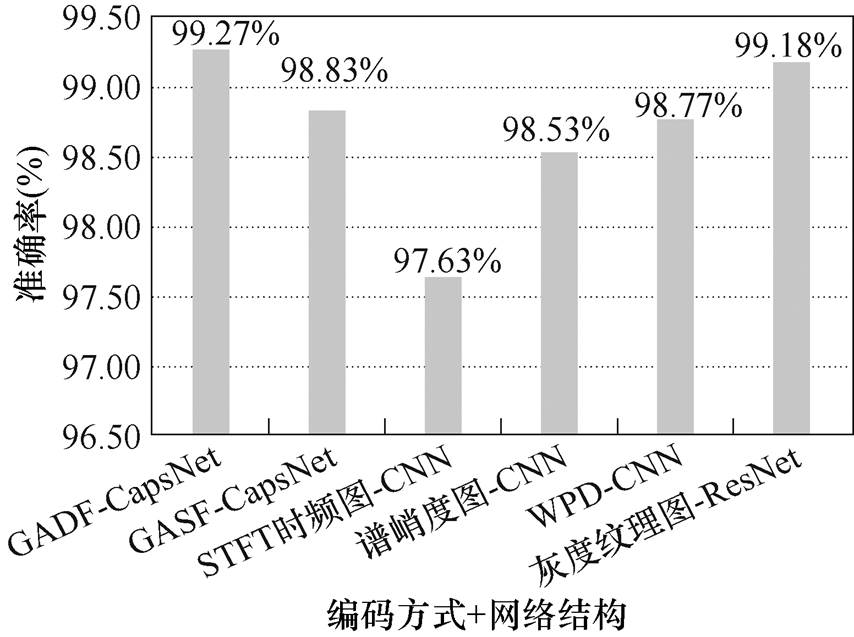
图9 不同模型准确率对比
Fig.9 Comparison of the accuracy of different models
通过图9可以看出，本文提出的GAF-CapsNet与其他编码方式以及网络结构相比准确率更高，其中GADF-CapsNet模型在这些模型中准确率最高，达到了99.27 %。
噪声在电机实际工况中不可避免，因此模型在噪声环境下的性能分析是必要的。在仿真试验中，通常使用高斯白噪声来模拟实际工作状态的噪声影响。本文中模型是用CWRU提供的原始数据训练，后用噪声数据进行测试，在原始信号中加入加性白高斯噪声，合成不同信噪比的信号。信噪比的定义为
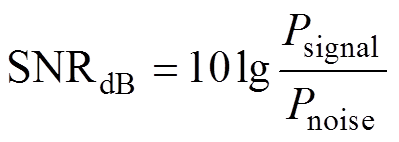（11）
式中，Psignal和Pnoise分别为信号和噪声的功率。信噪比SNR越大，噪声的影响越小，当信噪比SNR=0时，噪声功率与信号功率为11。使用GAF-CapsNet在信噪比为-4～10dB范围内进行噪声环境试验，与GAF-CNN、多层感知机（Multilayer Perceptron, MLP）、一维卷积网络（One Dimensional CNN, 1DCNN）进行比较，各种模型在不同噪声环境下的表现如图10所示。
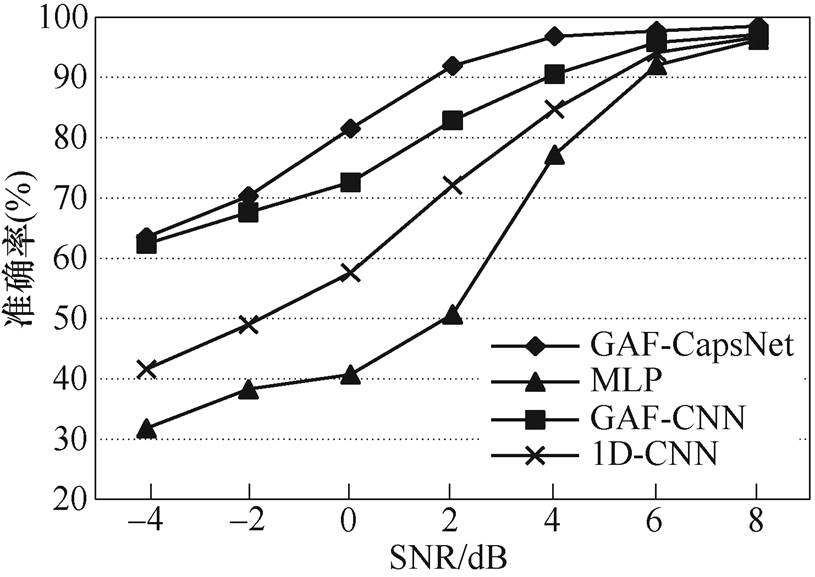
图10 不同噪音环境下的分类准确率比较
Fig.10 Comparison of classification accuracy under different noisy environment
由图10可见，通过GAF编码之后的二维图像在深度学习中性能更好，这是由于原始振动信号通过编码之后，自身的特征信号经过重复处理，使得包含故障特征的振动信息多次重复，增加了故障特征在噪声下的信号比重。对比CapsNet和CNN两种网络模型，在高噪声环境（-4～-2dB）下性能差距不大，随着信噪比的增大，CapsNet的网络性能略高于CNN，这说明改进后的胶囊网络有更好的深度特征的提取能力。通过试验对比发现，相比其他模型，本文提出的CapsNet模型在噪声环境下相比其他模型拥有更好的性能。
本文首次把胶囊网络作为故障诊断的模型，将原始振动信号通过GAF编码，输入改进的胶囊网络，进行了电机滚动轴承智能故障诊断的试验研究，得出以下结论：
1）在GAF编码的两个方式中，GADF编码的图像在胶囊网络中的表现优于GASF编码。整体来看，GAF的编码方式保留较完整的原始振动信号的故障特征。因不同采样尺寸对于准确率的影响，通过试验证明128采样尺寸为改进胶囊网络效果最好的输入尺寸。
2）本文提出的模型在电机轴承故障诊断中的准确率达到了99.27 %，高于其他常用网络模型，最大差值达到1.64 %。其次，在混淆矩阵试验中，提出的模型能够较为准确预测故障位置及其严重程度。最后，通过在抗噪性能试验中验证，相比于一维卷积及其他网络，提出的模型具有较强的抗噪性能，在信噪比为-4dB的情况下模型准确率仍能达到65 %以上。
参考文献
[1] 张神林. 基于卷积神经网络的滚动轴承及行星齿轮箱故障诊断方法[D]. 马鞍山: 安徽工业大学, 2018.
[2] 于寅虎. 控制智能化拉开工业4.0生产方式的序幕[J]. 电子技术应用, 2015, 41(2): 8, 10.
Yu Yinhu. Intelligent control kicked off the pro- duction mode of Industry 4.0[J]. Application of Electronic Technique, 2015, 41(2): 8, 10.
[3] Wang Dong, Tse P W. Prognostics of slurry pumps based on a moving-average wear degradation index and a general sequential Monte Carlo method[J]. Mechanical Systems and Signal Processing, 2015, 56/57: 213-229.
[4] 李泽, 王辉, 钱勇, 等. 基于加速鲁棒特征的含噪局部放电模式识别[J]. 电工技术学报, 2022, 37(3): 775-785.
Li Ze, Wang Hui, Qian Yong, et al. Pattern recog- nition of partial discharge in the presence of noise based on speeded up robust features[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 775- 785.
[5] 任世锦, 潘剑寒, 李新玉, 等. 基于ELMD与改进SMSVM的机械故障诊断方法[J]. 南京航空航天大学学报, 2019, 51(5): 693-703.
Ren Shijin, Pan Jianhan, Li Xinyu, et al. Novel machinery fault diagnosis approach via ELMD and improved SMSVM[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2019, 51(5): 693-703.
[6] 李世晓, 杜锦华, 龙云. 基于一维卷积神经网络的机电作动器故障诊断[J]. 电工技术学报, 2022, 37(增刊1): 62-73.
Li Shixiao, Du Jinhua, Long Yun. Fault diagnosis of electromechanical actuators based on one-dimensional convolutional neural network[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 62-73.
[7] Ghate V N, Dudul S V. Cascade neural-network-based fault classifier for three-phase induction motor[J]. IEEE Transactions on Industrial Electronics, 2011, 58(5): 1555-1563.
[8] Chen Zhiqiang, Deng Shengcai, Chen Xudong, et al. Deep neural networks-based rolling bearing fault diagnosis[J]. Microelectronics Reliability, 2017, 75: 327-333.
[9] 俞啸, 范春旸, 董飞, 等. 基于EMD与深度信念网络的滚动轴承故障特征分析与诊断方法[J]. 机械传动, 2018, 42(6): 157-163.
Yu Xiao, Fan Chunyang, Dong Fei, et al. Fault feature analysis and diagnosis method of rolling bearing based on empirical mode decomposition and deep belief network[J]. Journal of Mechanical Trans- mission, 2018, 42(6): 157-163.
[10] 王艳新, 闫静, 王建华, 等. 基于域对抗迁移卷积神经网络的小样本GIS绝缘缺陷智能诊断方法[J]. 电工技术学报, 2022, 37(9): 2150-2160.
Wang Yanxin, Yan Jing, Wang Jianhua, et al. Intelligent diagnosis for GIS with small samples using a novel adversarial transfer learning in convolutional neural network[J]. Transactions of China Electro- technical Society, 2022, 37(9): 2150-2160.
[11] 王卓, 王玉静, 王庆岩, 等. 基于协同深度学习的二阶段绝缘子故障检测方法[J]. 电工技术学报, 2021, 36(17): 3594-3604.
Wang Zhuo, Wang Yujing, Wang Qingyan, et al. Two stage insulator fault detection method based on collaborative deep learning[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3594-3604.
[12] 葛磊蛟, 廖文龙, 王煜森, 等. 数据不足条件下基于改进自动编码器的变压器故障数据增强方法[J]. 电工技术学报, 2021, 36(增刊1): 84-94.
Ge Leijiao, Liao Wenlong, Wang Yusen, et al. Data augmentation method for transformer fault based on improved auto-encoder under the condition of insufficient data[J]. Transactions of China Electro- technical Society, 2021, 36(S1): 84-94.
[13] 张西宁, 向宙, 唐春华. 一种深度卷积自编码网络及其在滚动轴承故障诊断中的应用[J]. 西安交通大学学报, 2018, 52(7): 1-8, 59.
Zhang Xining, Xiang Zhou, Tang Chunhua. A deep convolutional auto-encoding neural network and its application in bearing fault diagnosis[J]. Journal of Xi’an Jiaotong University, 2018, 52(7): 1-8, 59.
[14] 宫文峰, 陈辉, 张美玲, 等. 基于深度学习的电机轴承微小故障智能诊断方法[J]. 仪器仪表学报, 2020, 41(1): 195-205.
Gong Wenfeng, Chen Hui, Zhang Meiling, et al. Intelligent diagnosis method for incipient fault of motor bearing based on deep learning[J]. Chinese Journal of Scientific Instrument, 2020, 41(1): 195- 205.
[15] 刘炳集, 熊邦书, 欧巧凤, 等. 基于时频图和CNN的滚动轴承故障诊断[J]. 南昌航空大学学报(自然科学版), 2018, 32(2): 86-91.
Liu Bingji, Xiong Bangshu, Ou Qiaofeng, et al. Fault diagnosis of rolling bearing based on time-frequency representations and CNN[J]. Journal of Nanchang Hangkong University (Natural Sciences), 2018, 32(2): 86-91.
[16] 袁建虎, 韩涛, 唐建, 等. 基于小波时频图和CNN的滚动轴承智能故障诊断方法[J]. 机械设计与研究, 2017, 33(2): 93-97.
Yuan Jianhu, Han Tao, Tang Jian, et al. An approach to intelligent fault diagnosis of rolling bearing using wavelet time-frequency representations and CNN[J]. Machine Design & Research, 2017, 33(2): 93-97.
[17] 闫佳瑛, 朱希安. 基于VMD与CNN的滚动轴承故障诊断方法[J]. 北京信息科技大学学报(自然科学版), 2020, 35(6): 84-89.
Yan Jiaying, Zhu Xi’an. Fault diagnosis method of rolling bearing based on VMD and CNN[J]. Journal of Beijing Information Science & Technology University, 2020, 35(6): 84-89.
[18] 仝钰, 庞新宇, 魏子涵. 基于GADF-CNN的滚动轴承故障诊断方法[J]. 振动与冲击, 2021, 40(5): 247- 253, 260.
Tong Yu, Pang Xinyu, Wei Zihan. Fault diagnosis method of rolling bearing based on GADF-CNN[J]. Journal of Vibration and Shock, 2021, 40(5): 247-253, 260.
[19] 陈德伦, 梁晓瑜, 曾九孙. 基于SAX和CNN的滚动轴承故障诊断方法研究[J]. 计算机仿真, 2020, 37(12): 299-306.
Chen Delun, Liang Xiaoyu, Zeng Jiusun. Rolling element bearing fault diagnosis using a symbolic representation and convolutional neural networks[J]. Computer Simulation, 2020, 37(12): 299-306.
[20] Sabour S, Frosst N, Hinton G E. Dynamic routing between capsules[C]//Proceedings of the 31st Inter- national Conference on Neural Information Pro- cessing, 2017: 3859-3869.
[21] 张振良, 刘君强, 张曦, 等. 基于粒子群优化以及深度胶囊网络的轴承故障诊断[J]. 计算机与数字工程, 2021, 49(2): 333-339, 352.
Zhang Zhenliang, Liu Junqiang, Zhang Xi, et al. Bearing fault diagnosis based on PSO and CapsNet[J]. Computer & Digital Engineering, 2021, 49(2): 333- 339, 352.
[22] 侯东晓, 穆金涛, 方成, 等. 基于GADF与引入迁移学习的ResNet34对变速轴承的故障诊断[J]. 东北大学学报(自然科学版), 2022, 43(3): 383-389.
Hou Dongxiao, Mu Jintao, Fang Cheng, et al. Fault diagnosis of variable speed bearings based on GADF and ResNet34 introduced transfer learning[J]. Journal of Northeastern University (Natural Science), 2022, 43(3): 383-389.
[23] Smith W A, Randall R B. Rolling element bearing diagnostics using the case western reserve university data: a benchmark study[J]. Mechanical Systems and Signal Processing, 2015, 64/65: 100-131.
[24] Simonyan K, Zisserman A J A E-P. Very deep con- volutional networks for large-scale image recog- nition[J/OL]. 2014, https://ui.adsabs.harvard.edu/abs/ 2014arXiv1409.1556S.
[25] He Kaiming, Zhang Xiangyu, Ren Shaoqing, et al. Deepresidual learning for image recognition[EB/OL]. 2015, https://ui.adsabs.harvard.edu/abs/2015arXiv151203385H.
[26] Wen Long, Li Xinyu, Gao Liang, et al. A new convolutional neural network-based data-driven fault diagnosis method[J]. IEEE Transactions on Industrial Electronics, 2018, 65(12): 9953-10107
[27] 李恒, 张氢, 秦仙蓉, 等. 基于短时傅里叶变换和卷积神经网络的轴承故障诊断方法[J]. 振动与冲击, 2018, 37(19): 124-131.
Li Heng, Zhang Qing, Qin Xianrong, et al. Fault diagnosis method for rolling bearings based on short- time Fourier transform and convolution neural net- work[J]. Journal of Vibration and Shock, 2018, 37(19): 124-131.
[28] Udmale S S, Patil S S, Phalle V M, et al. A bearing vibration data analysis based on spectral kurtosis and ConvNet[J]. Soft Computing, 2019, 23(19): 9341- 9359.
[29] 陈里里, 付志超, 凌静, 等. 基于WPD-CNN二维时频图像的滚动轴承故障诊断[J]. 组合机床与自动化加工技术, 2021(3): 57-60, 65.
Chen Lili, Fu Zhichao, Ling Jing, et al. Rolling bearing fault diagnosis based on WPD-CNN two- dimensional time-frequency image[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2021(3): 57-60, 65.
[30] 庞俊, 刘鑫, 段敏霞, 等. 基于改进卷积神经网络轴承故障诊断[J]. 组合机床与自动化加工技术, 2021(3): 66-69.
Pang Jun, Liu Xin, Duan Minxia, et al. Fault diagnosis based on improved convolutional neural network[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2021(3): 66-69.
Abstract In mechanical motor faults, up to 30 % of the damage is caused by bearing faults, which makes bearing fault diagnosis and maintenance more critical. Traditional intelligent fault diagnosis methods are challenging to achieve good results when dealing with big data because of their poor generalization ability of feature extraction. In recent years, due to the substantial increase in training resources and the rapid development of computing power, deep learning has gradually become a new player in intelligent fault diagnosis.
This paper proposes a new GAF-CapsNet model to solve the problem that the relative position relationship cannot be fully extracted when one-dimensional mechanical vibration signals are input into the convolutional neural network. The Gramian Angular Field (GAF) encoding method converts the original data into images with conspicuous features. The Gramian Angular Summation Fields (GASF) and Gramian Angular Difference Fields (GADF) are used, respectively. Two groups of feature maps are input into the convolution layer of the small convolution kernel for information reading and feature extraction and then into the capsule network for deeper feature extraction and fault identification. Finally, ten capsules of the digital capsule layer correspond to different fault types.
The Gram-angle field encodes the collected vibration signals, which can be quickly perspective to identify the temporal correlations in different time intervals and generate corresponding feature maps. The Capsule network is sensitive to the relative position of small-size images and has advantages in feature extraction. At the same time, considering the excellent feature extraction ability of the VGG network, a deep small-size convolutional layer is added based on the combination of the capsule network and the VGG network. The vibration images encoded by the Gram Angle field were input to the improved CapsNet network for training, and the GAF-CapsNet model was formed to diagnose bearing faults. Among the two methods of GAF coding, GADF coding performs better than GASF coding in a capsule network. Overall, the GAF encoding method retains relatively complete fault characteristics of the original vibration signal. Due to the influence of different sampling sizes on the accuracy, the experiment proves that the 128 sampling size is the best input size for improving the capsule network.
The performance of the GAF-CapsNet model is tested on the rolling bearing data in the bearing fault database of Case Western Reserve University (CWRU). The results show that the GASF coding method has a poor effect compared with theGADF coding method. Gadfly-cabinet with a sound effect has 99.27 % accuracy, and GASF-CAPSNet with a poor effect has 98.83 %. Compared with other coding methods and convolutional neural networks, the performance of this model is generally higher than that of other models. The maximum difference was 1.64 %.
Finally, the proposed model can accurately predict the fault location and severity in the confusion matrix experiment. Compared with one-dimensional convolution and other networks, the proposed model performs strongly in the anti-noise experiment. The model's accuracy can reach more than 65 % when the SNR is -4dB.
keywords：Bearing, fault diagnosis, Gramian angular field, capsule network
DOI: 10.19595/j.cnki.1000-6753.tces.220312
中图分类号：TM307
国家自然科学基金（51777048）和黑龙江省普通高校基本科研业务专项资金（145209409）资助项目。
收稿日期 2022-03-07
改稿日期 2022-09-06
张 辉 男，1982年生，博士研究生，副教授，研究方向为电机智能化与故障诊断。E-mail: zhanghui_zdh@163.com
戈宝军 男，1960年生，教授，博士生导师，研究方向为电机基础理论与应用。E-mail: gebj@hrbust.edu.cn（通信作者）
（编辑 崔文静）