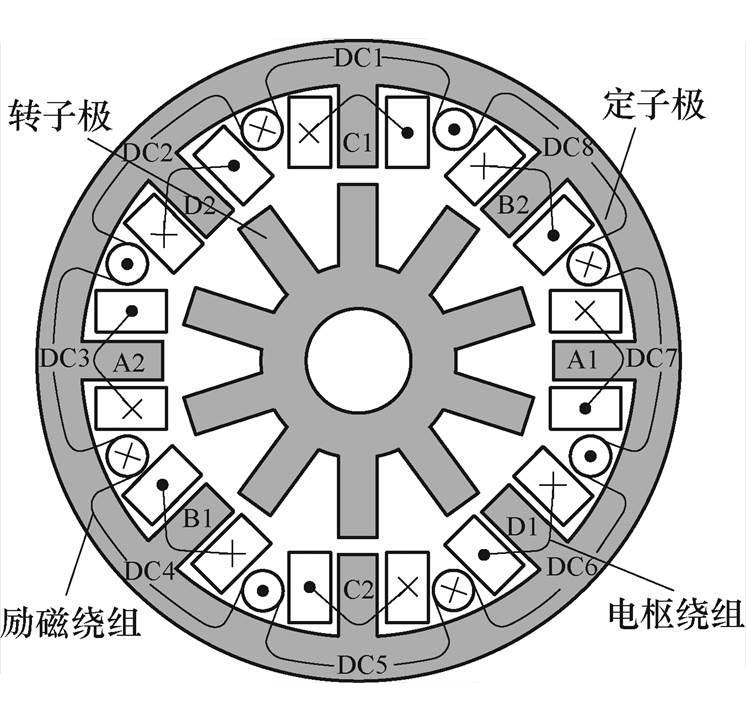
图1 四相8-10极WFDSM
Fig.1 Four-phase 8-10 pole WFDSM
摘要 电励磁双凸极电机(WFDSM)具有结构简单、可靠性高等优点,适用于航空航天等环境恶劣领域。当发生小匝数短路故障时,由于其电流、振动等信号不会产生明显的变化,难以用传统的检测手段区分。因此,该文提出一种基于特征层面多源信号融合和改进神经网络的WFDSM匝间短路故障诊断方法,用于诊断极端环境下WFDSM早期匝间短路故障。首先,对电流信号进行经验模态分解,获得本征模态函数,同时对振动信号进行小波包变换,并对分解后的各个频段提取峭度和裕度特征,同时计算能量占比;然后,将上述特征矩阵处理后输入改进卷积神经网络训练模型中;最后,通过实验表明,采取特征融合的计算方法诊断准确率可达98 %,较数据层面和结果层面的融合计算方法准确率有明显的提升,并且对极端运行环境下的噪声,该方法具有很强的抗干扰能力。
关键词:电励磁双凸极电机 经验模态分解 特征层融合 改进卷积神经网络 极端环境
电励磁双凸极电机(Wound-Field Doubly Salient Machine, WFDSM)结构简单、控制方便,由于其转子上没有任何绕组,它在发电运行环境下表现优异,适合于风力发电、航空航天等极端环境应用领域[1-3]。虽然,WFDSM励磁回路独立,且具有较高的可靠性,但极端场合下的故障诊断能够进一步提高电机的可靠性和环境适应能力。定子绕组匝间短路是WFDSM最常见的故障之一,由于匝间短路故障在早期阶段现象不明显,难以被察觉,因此容易导致电机局部发热严重。最终,随着电机的运行,导致设备产生损坏,严重时甚至可能引发安全事故[4]。同时,极端环境下信号容易受到干扰,传统电机故障检测方法更难判断电机运行状态,因此准确诊断极端环境下WFDSM的匝间短路故障对电机安全稳定运行具有十分重要的意义。
目前,针对磁阻电机的优化设计、容错分析等方面已经进行了大量研究[5-10],但对于其故障诊断方面研究较少。针对磁阻电机的故障,当前主流诊断方法主要有三类[11]:一是通过构建数学模型进行故障预测;二是通过信号处理方法如奇异值分解、小波包变换将部分信号的变化作为故障判断依据;三是通过智能算法,依靠大数据智能判断电机的运行状态。
构建数学模型是故障诊断中最为常见的方法,已在同步电机特别是磁阻电机诊断中得到了广泛的应用。文献[12]通过构建磁阻电机在正常、故障等不同工况下的模型,确定不同故障下的转矩特征,并由此判断故障类型。文献[13]对磁阻电机的功率变换器建立模型,分析了斩波信号和特定位置电流信息的关系,以相电流作为诊断量进行故障诊断,并在12/8开关磁阻电机上验证了该方法的有效性。文献[14]构建了双凸极电机功率变换器模型,分析了不同开路故障下相电流的变化趋势,通过检查反电动势电流的大小来判断开路故障类型,并在双凸极电机实验平台上验证了该方法的有效性。但由于实际电机运行存在不确定性,转速、负载等因素的变化均可能导致实际结果无法与模型预测的结果完全相符。
除了建立模型之外,也有文献通过信号处理进行故障诊断,文献[15]通过采集四相电机的相电流,采用派克变换确定故障特征,并用幅值大小判断故障类型。文献[16]对开关信号和电流信号进行空间复变换,并用变换后的信号作为故障指示信号,在8-6极开关磁阻电机(Switched Reluctance Motor, SRM)模型上得到了验证。文献[17]采取了改进对称分量法提取磁阻电机断相故障特征,分析电流信号的幅值和相位变化,并在五相电机中得到验证。文献[18]通过小波包变换处理电流信号,并以小波包节点能量的离散度作为特征诊断磁阻电机的变流器故障。文献[19]利用变分模态分解的方法对振动信号进行分解,解决了振动信号噪声过多的问题,将多尺度散布熵作为特征识别出多极发电机匝间短路故障。使用信号处理的方法进行特征提取往往存在提取过程复杂、算法通用性弱的问题。
得益于近年来智能算法的开发和推广,可以将难以识别的海量数据通过智能算法进行区分,辨识出其中隐含的故障特征信息。文献[20]采取生成对抗网络的增强数据方法得到高质且足量数据,用其建立性能良好的模型,并在电机轴承数据集中得到验证。文献[21]将采集到的转速信号直接输入深度置信网络中,通过网络自身的特征提取能力进行数据分类,并在风力发电机仿真数据中得到97.1 %的准确率。文献[22]通过采集永磁同步电机的负序电流和转矩信号,利用生成式对抗神经网络完成样本数据扩张,结合稀疏自编码网络实现故障分类诊断,并通过实验验证,该方法在同步电机上准确率可达99.4 %。但智能算法往往是基于单一检测量进行研究,而单一信号的采集易受传感器故障影响,同时复杂的工况还可能引起测量误差,导致诊断结果不准确。
此时,采用数据融合的方法检测故障即可减小单一检测量带来的测量误差问题。数据融合通过综合考虑多个变量,全面考虑各检测量内部的故障信息,从而提高故障诊断的精确性。文献[23-24]通过融合电流和振动信号,识别磁阻电机在变速条件下的故障类型。文献[25]通过电机附近的多个磁通传感器提取敏感谐波,并通过置信函数理论融合分析多个传感器位置的数据,使得其在同步电机故障诊断中具有较高的准确率。文献[26]通过融合电流和振动信号的频谱特征,进而更准确地描述故障特征,并在同步电机的匝间短路故障诊断中得到验证。文献[27]融合不同传感器采集的振动波形信号,并将其输入一维卷积神经网络中进行分类识别,最终在实际航空发电机数据集上得到验证。但传统的融合算法往往是基于结果的融合,虽然可以减小大量的运算,使得容错性更高,但是也损失了大量的数据特征。因此,本文采取了特征融合的方法,在减小了融合的数据量的同时,又保存了大部分的故障 特征。
WFDSM作为磁阻电机,电流、振动等物理量谐波含量多且复杂,同时运行环境复杂多变,特征检测容易受到各种环境因素影响。因此,本文采取多种信号特征融合的方法对极端环境下WFDSM发生匝间短路故障进行诊断。首先,分别通过小波包变换法对不同工况下的振动信号、经验模态分解法对不同工况下的电流信号进行分解和特征向量的提取;然后,对特征进行并行排列,对形成的特征矩阵进行区间缩放、归一化处理;最后,将融合完成后的特征矩阵作为特征向量输入改进的卷积神经网络中。实验证明,相较于单一检测量故障诊断、数据层面融合诊断和结果层面融合诊断,本文采取的特征层融合诊断准确度更高,同时收敛速度也更快,具有更好的故障分辨效果,且在极端情况下信号受到噪声干扰时具有较好的抗干扰能力。
8-10极WFDSM是一种特殊的四相分布励磁双凸极电机,其结构如图1所示。由于四相电机相较于三相电机具有更强的容错能力,与五相电机相比具有更高的功率密度,在容错能力和功率密度之间达到了较好的平衡,因此本文选择了四相8-10极WFDSM作为实验电机[28]。

图1 四相8-10极WFDSM
Fig.1 Four-phase 8-10 pole WFDSM
为了对8-10极WFDSM匝间短路故障进行研究,样机的抽头设置如图2所示。以A相为例,每相电枢绕组共有40匝,在绕组首端和第10匝分别引出抽头记为A1和A2,则A相绕组被A1和A2分为了10匝和30匝两个部分。本文通过改变抽头的连接方式研究不同类别的匝间短路故障。在实验时,将A相的A1抽头和A2抽头通过短路电阻经由导线连接称为Ⅰ类匝间短路故障,将A1、B2两抽头短接称为Ⅱ类匝间短路故障,实验采用全桥整流电路进行电能变换。
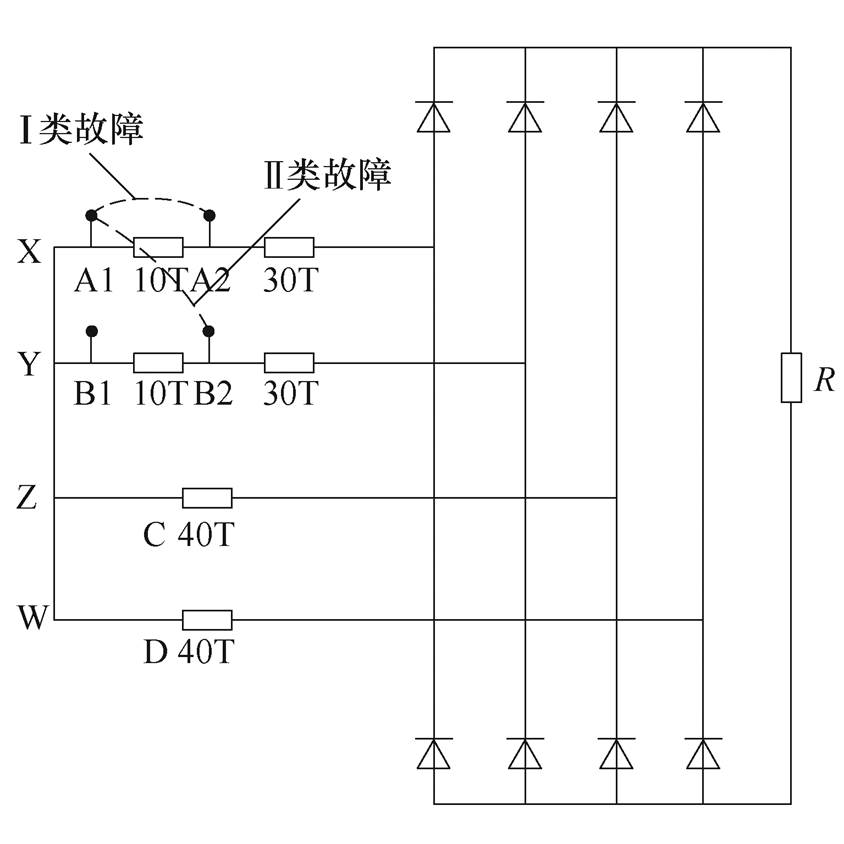
图2 电枢绕组故障拓扑结构
Fig.2 Armature winding fault topology structure
电枢绕组通入相差90 °的四相对称电流后,假设A相发生Ⅰ类短路故障,产生了短路故障电流,则此时四相电流表达式为
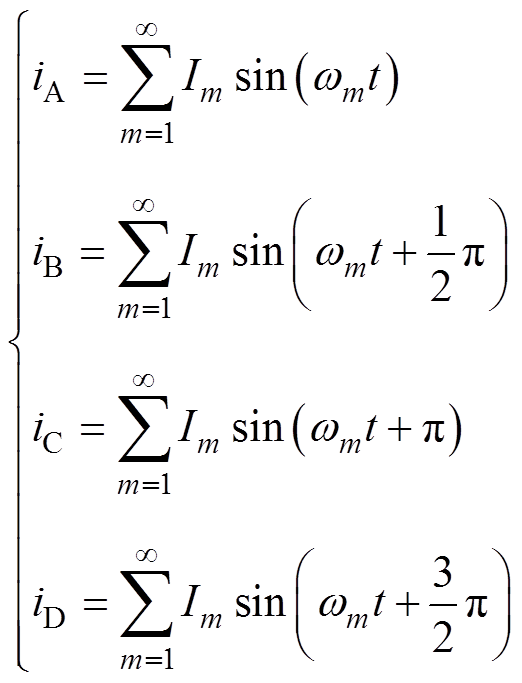 (1)
(1)
式中,iA、iB、iC、iD为四相电流表达式;Im为电流幅值;wm为电角速度;t为时间。则四相绕组的v对极的磁动势分别为
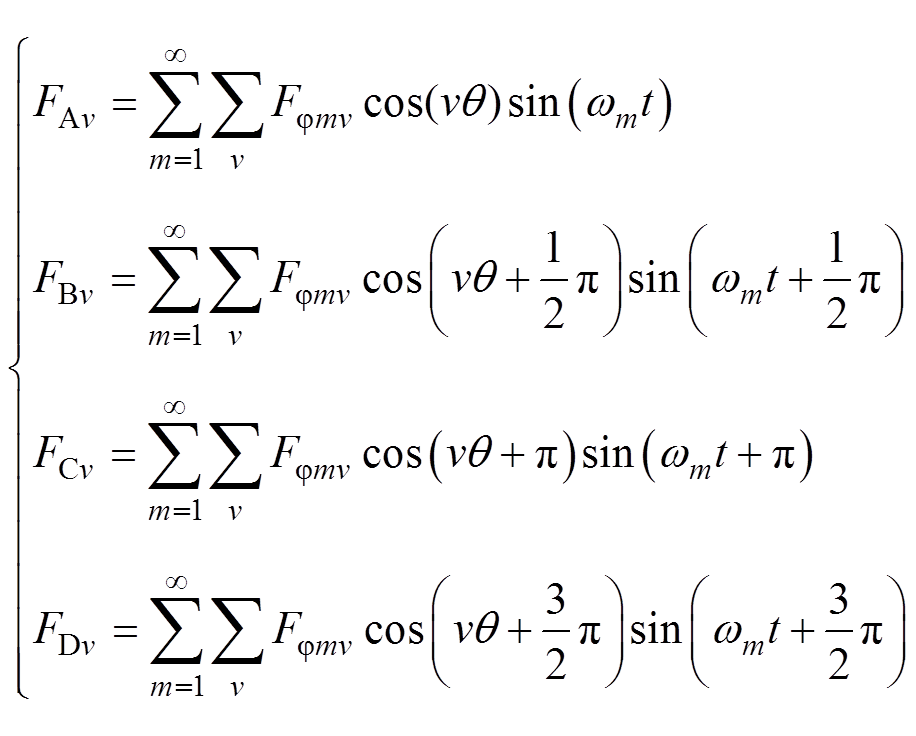 (2)
(2)
式中,FAv、FBv、FCv、FDv为四相绕组v对极的磁动势;Fjmv为磁动势幅值;q 为电角度。此时四相绕组产生的磁动势合成后为
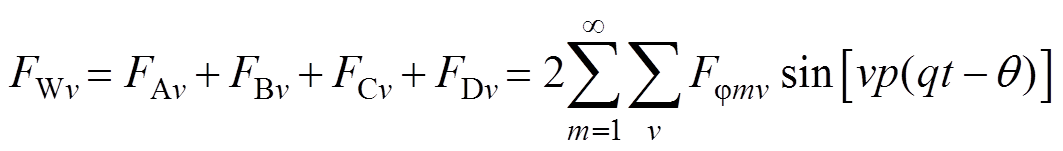 (3)
(3)
式中,FWv为四相合成磁动势;p为定子极对数;q为旋转机械角速度。
根据WFDSM定子结构,可以得到气隙磁导波形,如图3所示,相应的气隙磁导L(q )为
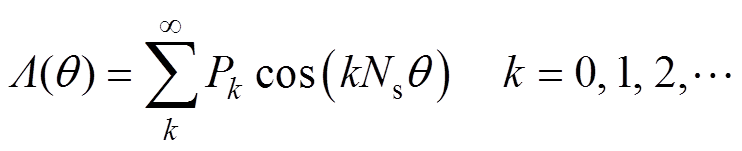 (4)
(4)
式中,Pk为电机各槽的磁导系数;Ns为定子槽数。则此时经过齿槽调制后的磁场为
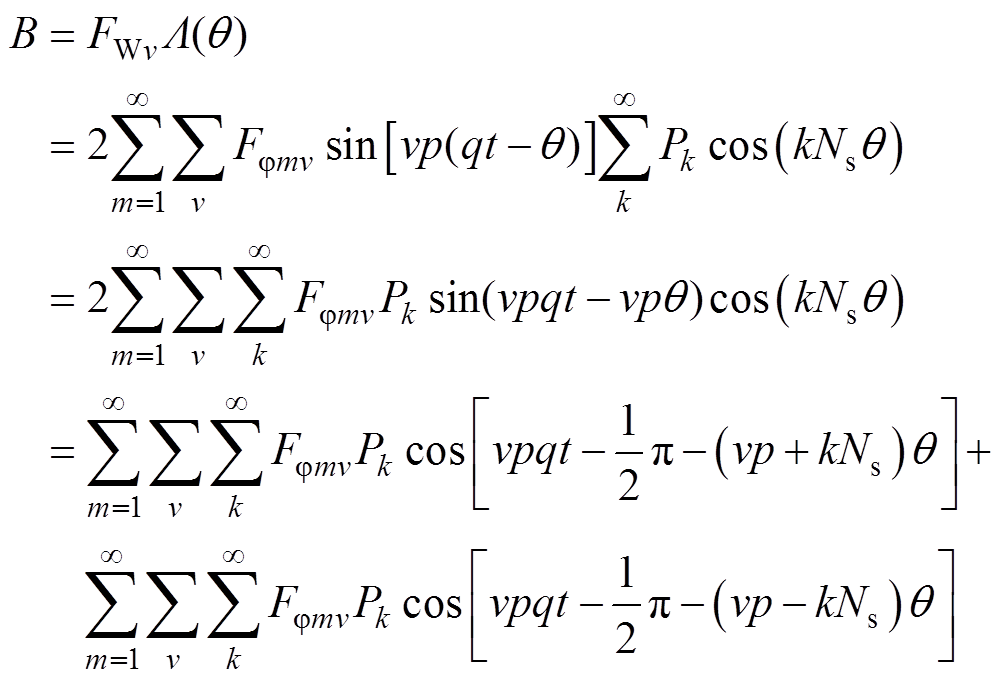 (5)
(5)
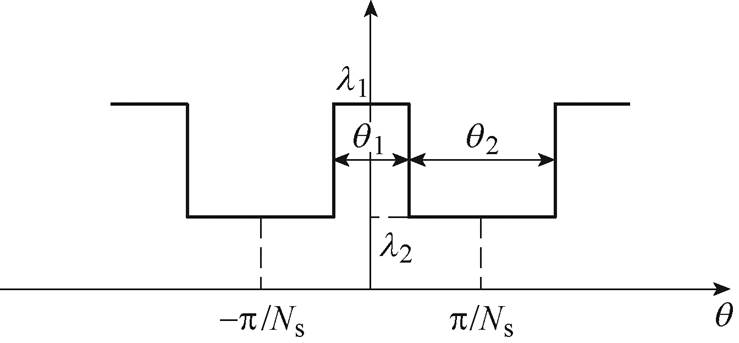
图3 WFDSM气隙磁导
Fig.3 WFDSM slot vector composition
故在发生匝间短路故障时气隙磁通密度会产生|vp±kNs|(v=1, 3, 5,…;k=0, 1, 2, 3)的谐波阶次,因此短路故障的发生会导致磁场的畸变。根据电磁感应定律,变化的磁场会导致电流的变化,因此电流可以作为故障的检测量。
在电机运行过程中,各次谐波磁场交变产生的电磁力会引发电磁振动。根据麦克斯韦定律,定子表面单位面积上的径向电磁力和磁通密度呈正相关关系,而在WFDSM实际运行中,径向磁通密度远大于切向磁通密度,故而电磁振动主要由径向磁拉力决定,即
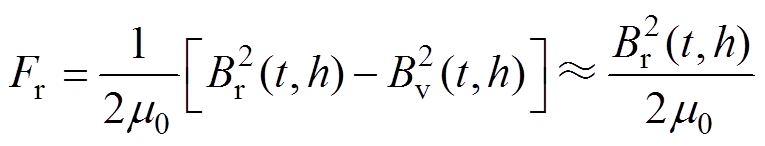 (6)
(6)
则由于磁拉力产生的转矩Te(t)为
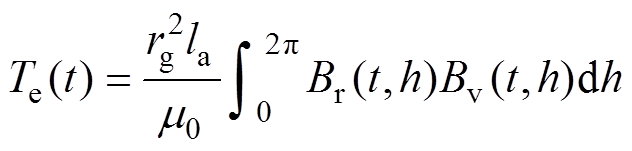 (7)
(7)
式中,rg为气隙半径长度;la为有效轴向长度;m0为真空磁导率;Br(t,h)和Bv(t,h)分别为气隙磁通密度的径向分量和切向分量,两分量可进一步展开为傅里叶形式,有
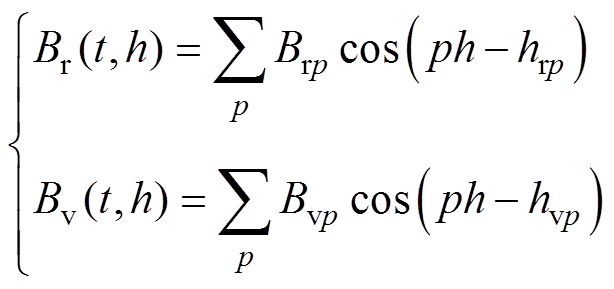 (8)
(8)
式中,Brp和Bvp分别为Br和Bv的p(p=0, 1, 2,…)次傅里叶分解系数;hrp和hvp分别为p次Br和Bv所对应的初始相位,则p次谐波产生的转矩Tp(t)可表示为
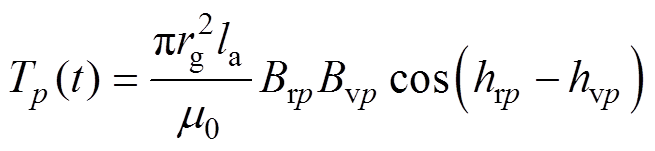 (9)
(9)
故而通过有限元法可求得各阶次谐波相应的Brp和Bvp,hrp和hvp,代入式(9)即可求得多余谐波贡献的转矩大小。
根据上述分析可得,变化的磁场会引发磁拉力的变化,进而导致发电机的振动特性、转矩大小发生变化,因此振动量可以作为特征量来进行故障诊断。
综上所述,可以通过电流和振动量实现对故障的诊断。
在对8-10极WFDSM进行故障诊断的过程中,需要采集大量的电流、振动信号用以判断电机的运行状态。对于这些信号,一般需要根据实际数据特征进行一定的数学处理以提取所需的特征量。
图4、图5所示分别是正常、Ⅰ类匝间短路、Ⅱ类匝间短路三种工况下四相电流波形对比以及A相电枢电流经过快速傅里叶变换(Fast Fourier Transform, FFT)得到的频谱图。由图中信息可以得知,故障前后的电流在时域上的变化较小,但在频域上变化较为明显,出现较多的低次谐波,可以较好地分辨出WFDSM的工况。同时由于WFDSM的电流信号是非平稳特征信号,因此选取更适合于非平稳信号的经验模态分解[29](Empirical Mode Decomposition, EMD)方法对电流信号进行处理。
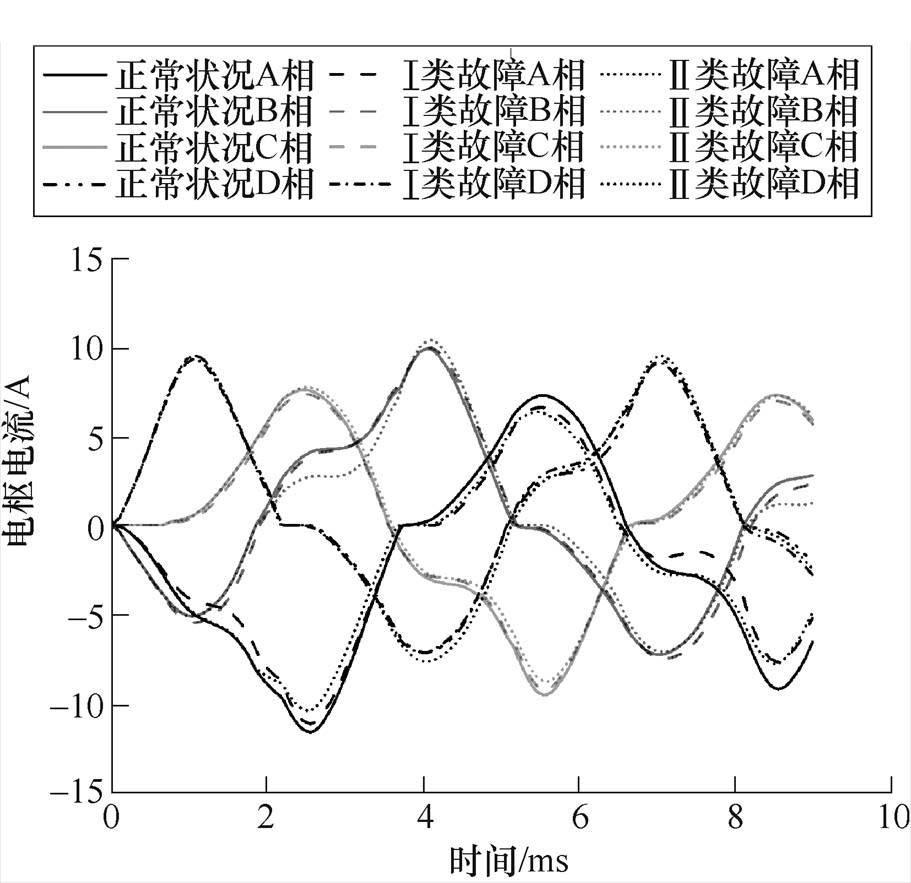
图4 不同工况下四相电流对比
Fig.4 Four-phase current comparison of different operating conditions
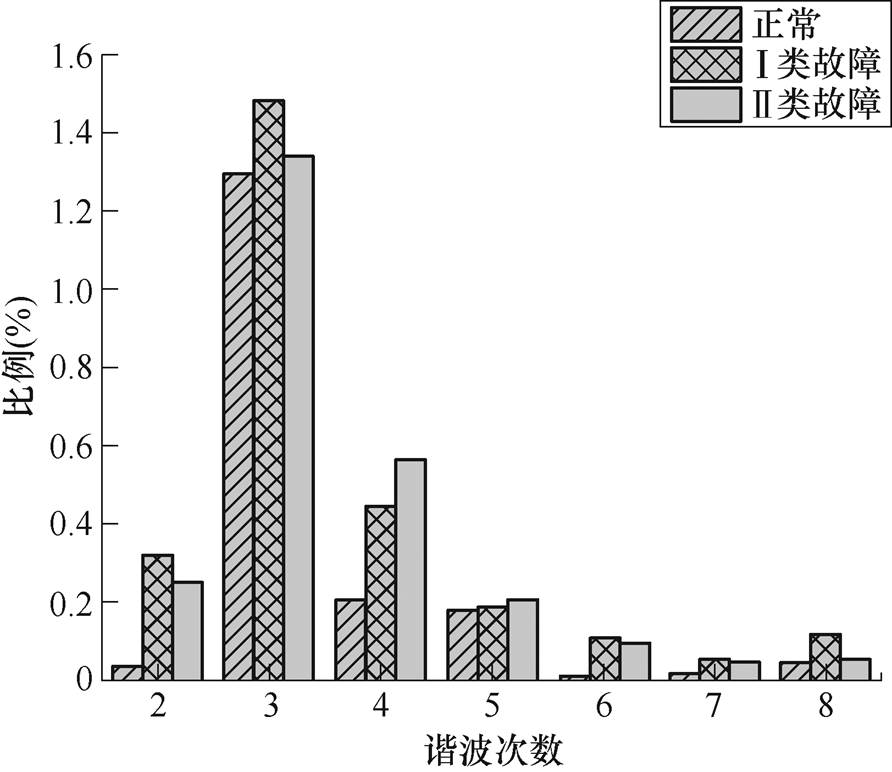
图5 不同工况下A相电流傅里叶频谱
Fig.5 A-phase current Fourier spectral decomposition of different operating conditions
EMD是时频变换方法的一种,主要适用于处理复杂的非平稳信号,其主要思想是将频率不规则的信号转化为多个单一频率的本征模态函数和残差的形式。对比其他窄波段滤波手段,EMD在保留信号非平稳频率的同时,克服了基函数无自适应性的问题,同时不需要预先分析和研究,就可以直接进行分解。本文中,由于故障导致磁场产生多余谐波进而影响电流的组成,通过EMD的方法可以很好地识别出不同工况下电流信号的分量。
EMD可以将在一段时间内时变的频率转化为数个IMF分量和相应的残存函数,其表达式为
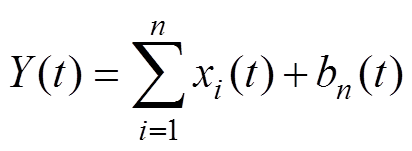 (10)
(10)
式中,Y(t)为初始信号;xi(t)为第i个IMF分量;bn(t)为相应的残存函数。
经由上述的介绍可以得知,EMD方法相较于传统的傅里叶分析等方法,其优势在于EMD并非采用常用的三角级数对信号进行分解,因此其得到的是大小、频率时变的IMF分量,故而可以应用在如WFDSM电流这种非平稳特征信号的分解中。本文采用了EMD方法对电流信号进行时频分析,并通过EMD观察信号在时频域的变化,最终采取经过EMD后得到的本征模态函数作为特征对象。
不同工况下振动对比如图6所示。由图6可知,故障前后的振动信号在时域上发生了较大的变化,包括波形由平缓变得更为尖锐,这和反映数据尖峰情况的峭度因子密切相关。峭度因子被定义为关于平均值的标准化四阶矩,是四阶累积量,因此被用作度量数据尖峰的一种统计指标,可以描述波形的平缓程度,衡量样本的峰度。因此,往往用来检测与旋转机械相关的信号中的故障冲击信息强弱。对应地,图像上波形的陡峭程度是由反映振动严重程度的裕度因子体现,其物理含义是信号峰值与方根幅值的比值。
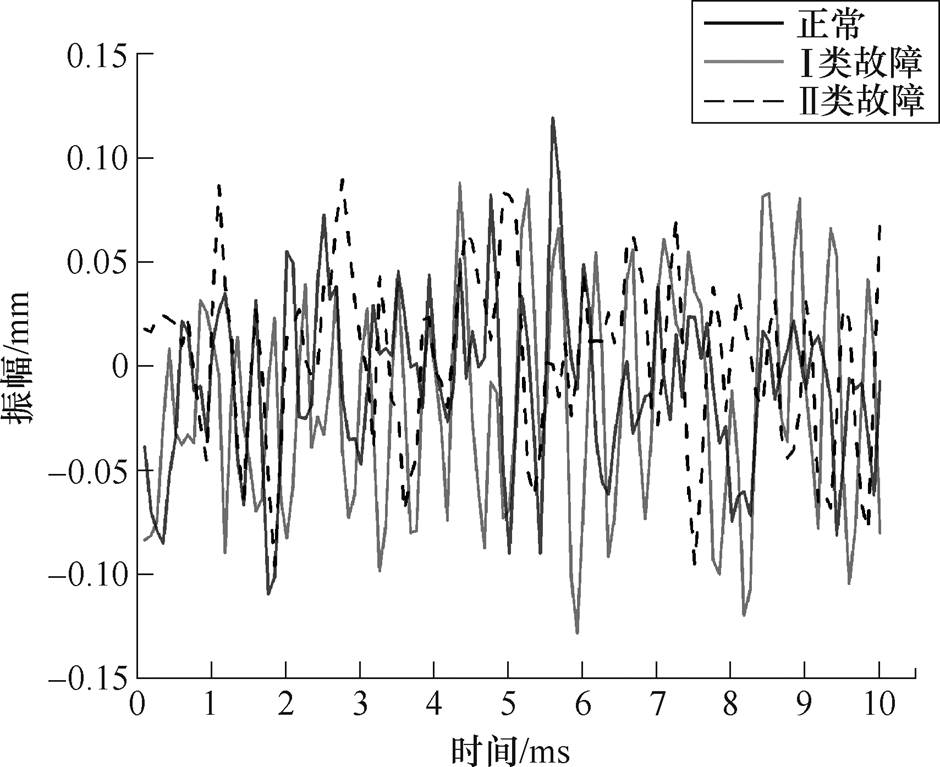
图6 不同工况下振动对比
Fig.6 Vibration comparison of different operating conditions
不同工况下A相振动信号的傅里叶频谱如图7所示,对故障前后振动从时域转化到频域采用傅里叶变换进行分析可以得知,WFDSM故障后转矩多了大量高次谐波,但由于变化情况相对复杂,本文选择多频段进行分析。由于小波包变换对低次和高次信号都有较好的识别能力,因此选取小波包变换方法处理振动信号。
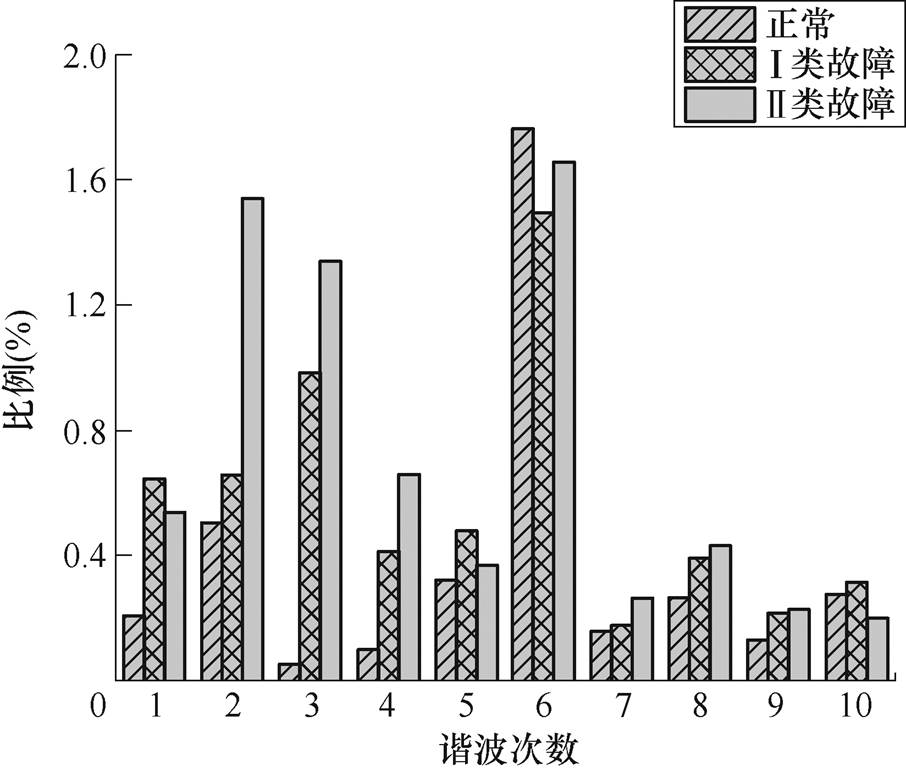
图7 不同工况下A相振动信号的傅里叶频谱
Fig.7 A-phase vibration Fourier spectral decomposition of different operating conditions
在WFDSM发生匝间短路故障时,电机本身会受到脉冲力的作用,在靠近脉冲力时,振动信号的能量较大,相反在远离脉冲力时,振动信号会包含平稳时的振动信号、噪声和低频干扰,相对来说,此时的信号能量较小,因此能量占比可以较好地反映故障情况。故而在对原信号进行8层小波包变换后,对每个频段求取能量值,并求其占据总的能量的比重即能量占比作为特征量之一。
小波包变换是在小波变换基础上衍生的信号处理方法,它在每一级信号分解时,对高低频子带都进行分解,最后通过最小化一个代价函数,计算出最优的信号分解路径,并以此分解路径对原始信号进行分解。
小波函数是一种时频函数,可以被描述为
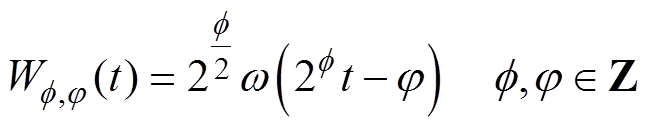 (11)
(11)
式中,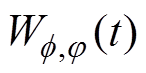 为小波包系数,整数f 和j 分别为尺度坐标和位置坐标。
为小波包系数,整数f 和j 分别为尺度坐标和位置坐标。
特征层融合指的是先由各个传感器分别采集信号,待采集完成后分别提取故障特征,而后将信号特征进行融合的融合方法。
当前对WFDSM的故障诊断的主流做法是使用单一信号量进行研究,从而判断其是否发生故障。然而单一信号量较易受到外界干扰的影响,如传感器故障,外界的噪声、抖动等,使得诊断的鲁棒性较差,同时诊断结果也会受到影响。而采用信息融合技术,综合考虑多个变量,可以最大程度地减轻上述问题带来的误差,提高故障诊断的准确性。本文采用的电流和振动信号是从机电融合角度来检测故障,在一定层面上形成互补,提高故障诊断的准确性。同时相较于数据层面融合和结果层面融合,本文特征层融合方法的优势在于,在减小融合的数据量的同时,又保存了大部分的故障特征,从而大大加快了运行速度。
由于存在着量纲不同、特征定性与定量的区别等问题,未经处理的特征不能直接进行故障诊断,需要进行特征预处理操作。首先,不同信号的特征不属于同一量纲,数据的规格大小存在明显的区别,无法进行同类比较,故而需要将其转化为同一区间,常用区间缩放、标准化等方法处理;其次,由于某些采样时间的差异,极少数点存在值缺失的现象,需采取补零办法或众数法来处理;同时,由于某些算法的原因,只能输入定量特征,此时需要为定性值制定定量值,往往采用哑编码的方式进行性量转换。本文采取了区间缩放、归一化、缺失值计算等特征层处理方法,因篇幅有限,故介绍较为重要的区间缩放和归一化两部分内容。
3.2.1 区间缩放
由于特征矩阵是由电流和振动两部分物理量构成,因此进行信息融合时需要进行去量纲、归一化等步骤。设某一传感器输出的特征向量为tl(l=1, 2, 3,…, e),综合得到的特征向量为At,则二者之间的关系为
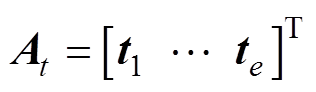 (12)
(12)
式中,e为样本数量。
At的元素组成为
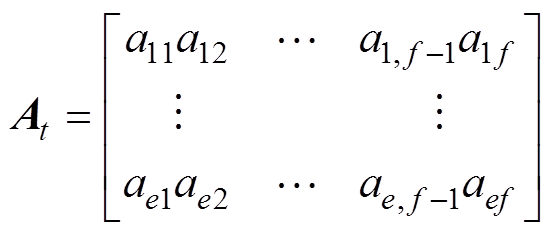 (13)
(13)
式中,f为特征值数量。
由式(13)可知,特征矩阵的每列元素都是来自同一传感器的同一特征,每行元素是来自不同传感器的不同特征,而相同位置的元素需要进行比较,故而不同量纲的数据需要进行一定的预处理,变为同一范围后才能进行对比。去量纲的过程如下,设特征矩阵每列向量为Wg(g=1, 2,…, f)。
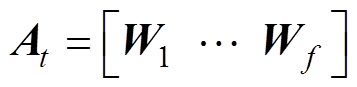 (14)
(14)
设去量纲后的特征矩阵为Bt,Bt内的元素为bef,为使处理后的数据的最小值为0,则
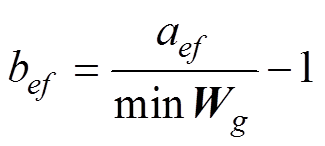 (15)
(15)
此时每列元素最大值为Mg,每列特征向量的取值范围为(0, Mg),有
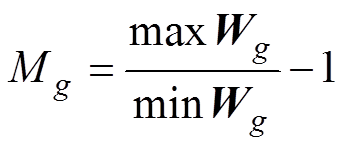 (16)
(16)
3.2.2 归一化处理
在去除量纲后,所有的特征值都转换为正值,但由于特征本身来自于不同传感器,同一列中不同数据的值可能会存在较大差异,因此要对其进行归一化处理才能输入神经网络中分类。传统的归一化方法是将整个矩阵的数据都转换到同一区间下,但由于本文特征矩阵的数据分属于不同领域,且振动信号中能量占比、峭度、裕度三者的差别较大,因此无法进行全局的转换,需要对每一列数据分别进行0均值归一化处理。0均值归一化方法如图8 所示。
由于本文采集的电流、振动两类信号在经过信号处理后具有特征多、维数大的特点,因此在处理上述信号时需要同时兼顾高维度和大数据。而卷积神经网络(Convolutional Neural Network, CNN)作为一种前馈式的深度学习方法,由于其共享卷积核的结构,适合处理高维度的大量数据,同时CNN相较于其他网络而言参数较少,故而诊断效率更高。
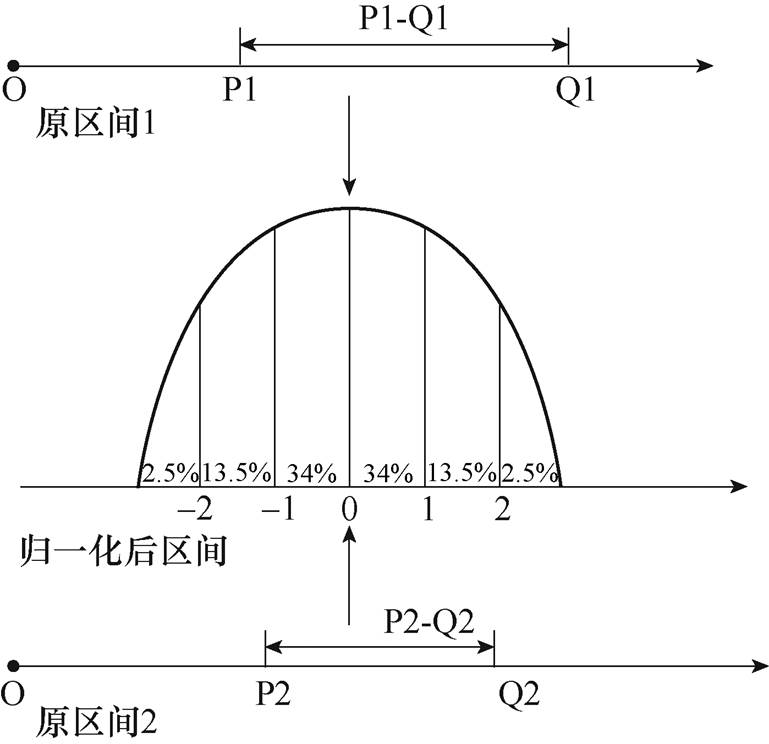
图8 0均值归一化方法
Fig.8 0-means normalization method
典型的CNN结构由输入层、卷积层、池化层、全连接层、输出层组成,通过卷积核间隔一定的步长对上一层信号进行卷积,同时经过池化层缩减模型大小、提高计算速度,最后经由全连接层连接到下一个层级并分类诊断。传统的CNN结构由于其卷积层池化层交替排布,使得模型具有良好的诊断特性。
传统CNN可以在计算过程中减少节点数,进而减少冗余参数,这对于高维数据输入有着十分重要的意义。但由于本文的特殊性在于输入神经网络的数据是提取好的特征,已经减少了大量的参数,经由池化层后可能会使得部分关键特征发生变化,甚至可能导致最终诊断输出结果错误。因此,本文提出的改进模型在每个池化后增加了批标准化层(Batch Normalization, BN),这样在减小数据损失的同时,还可以有效保留数据特征。但由于神经网络是递进式的,每一层面的变化都会显著影响到接下来的层面,BN层在保留数据特征的同时也严重减缓了网络的运行速率。因此,本文采取自适应力矩对梯度进行优化,该方法不仅运行效率高,同时对内存要求低,在数据较多时其优势更为明显。改进CNN基本结构如图9所示。
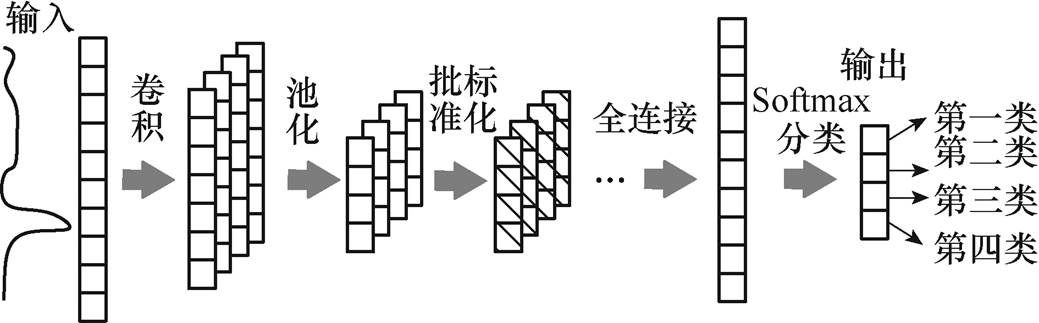
图9 改进CNN结构
Fig.9 Structure of improving CNN
4.1.1 批标准化层
批标准化层可以在卷积网络训练时,通过求取不同组别输入数据的均值和标准差,将前一层的输出向量进行标准化,进而提高模型的准确度。
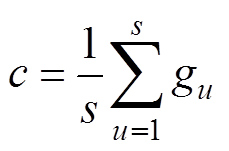 (17)
(17)
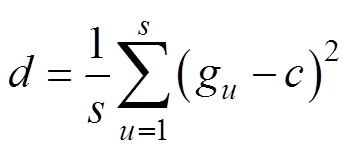 (18)
(18)
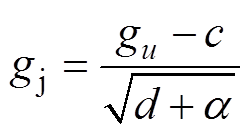 (19)
(19)
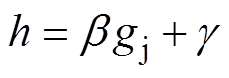 (20)
(20)
式中,c为均值;s为批处理大小;gu为激活后的数据;gj为标准化后的数据;d为方差;h为BN层输出;a、b、g 均为重构参数。
4.1.2 自适应力矩
自适应力矩将动量法和方均根传播算法结合,通过矩估计动态调整参数的学习率。该方法不仅可以减小随机梯度在局部最优解处的波动,同时也加快了计算速度。其中,mt和vt分别为在t时刻对梯度的一阶矩和二阶矩的估计。
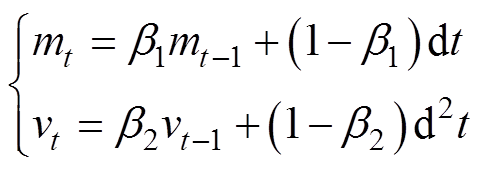 (21)
(21)
式中,b1和b2分别为一阶矩、二阶矩的指数衰减率;dt为导数。
通过计算偏差校正后的一阶矩和二阶矩估计为
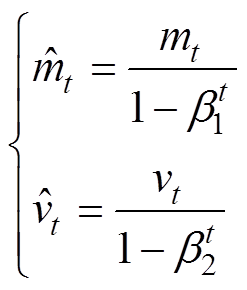 (22)
(22)
最后,利用上述矩估计更新参数
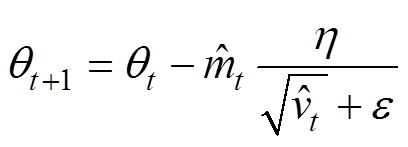 (23)
(23)
式中,h 为学习步长;e 为防止除零的保护量。
4.1.3 超参数优化
为避免CNN在训练时可能出现的过拟合现象,在加入dropout层的同时需要对超参数进行优化,其中最重要的参数为学习率。通过对学习率的优化,不仅可以避免损失值发生较大波动导致模型难以收敛,同时也加速了收敛的过程。本文将准确率作为优化指标,假设第t次学习率的值为l,模型优化过程中逐步减小l 的值,直到第t次模型的准确率较第t+1次、t+2次更小,则结束优化,输出第t次的模型。
基于深度学习和信息融合的WFDSM故障诊断流程见附图1,包括如下步骤:①采集原始信号,包括电流信号、振动信号;②对采集到的信号进行处理,本文采用的是经验模态分解和小波包变换;③对分解后的信号提取特征并对其进行归一化、区间缩放等处理;④对处理后的信号进行融合并作为输入改进卷积神经网络模型;⑤对测试集进行故障诊断;⑥判断故障情况,输出诊断结果。
为实现不同转速下WFDSM匝间短路故障的智能诊断,本文使用了实际的8-10极WFDSM的实验数据对所提出方法的性能进行验证。该电机具体结构参数见表1,实验平台如图10所示。
表1 四相8-10极WFDSM主要参数
Tab.1 Parameters of four-phase 8-10 pole wound-field doubly salient machine
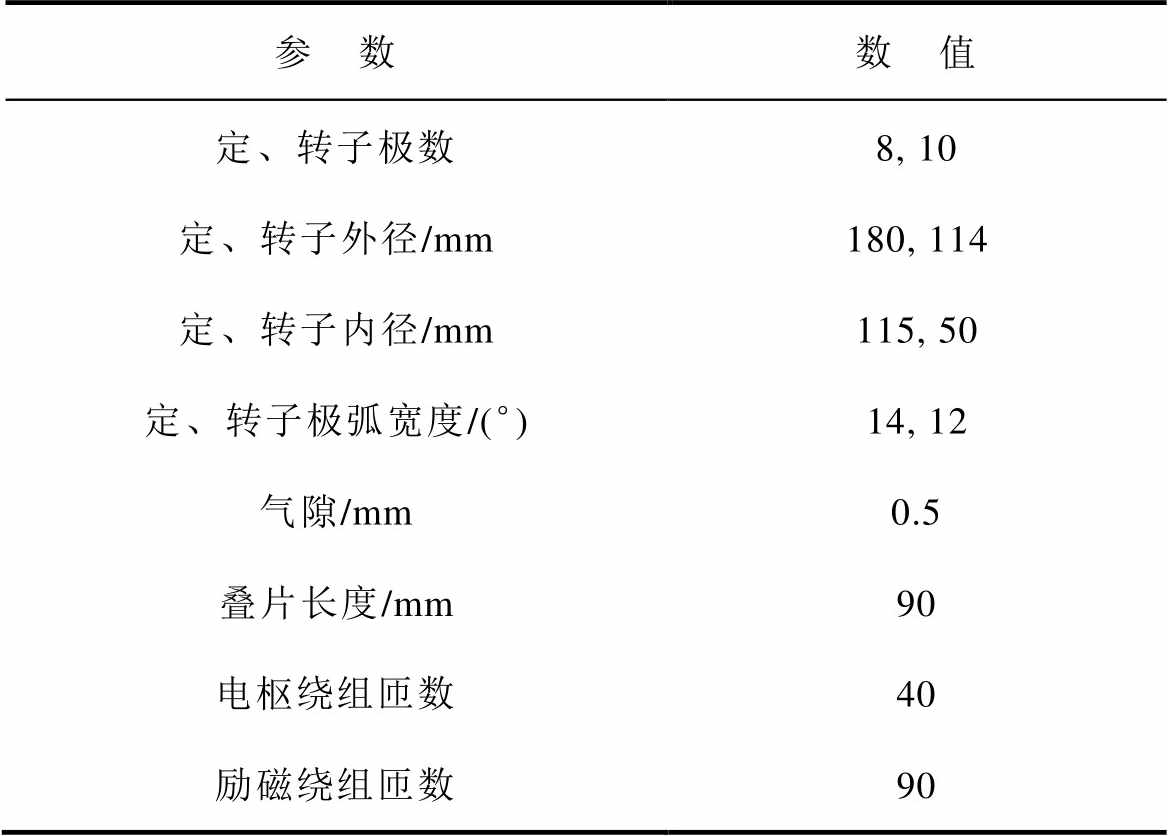
参 数数 值 定、转子极数8, 10 定、转子外径/mm180, 114 定、转子内径/mm115, 50 定、转子极弧宽度/(°)14, 12 气隙/mm0.5 叠片长度/mm90 电枢绕组匝数40 励磁绕组匝数90
本文所采集的数据为WFDSM在不同转速下的四相电流信号和振动加速度信号,其中电流信号由电子示波器采集四相电枢电流得到,而振动信号则通过安装在实验台不同位置和方向的加速度传感器采集得到。
由于实际电机的运行工况差异的主要因素为转速,转速对电流和振动信号的故障影响较大。因此,通过改变转速的快慢,来模拟实际电机运行工况的差异,用以验证在多种工况下本诊断方法的鲁棒性。本实验在10 A的电流励磁下,分别以800、1 000、1 200 r/min的转速运转,外加的负载由直流负载提供,有0.5、1、5 Ω三种情况,在每种工况下又有正常、Ⅰ类故障、Ⅱ类故障三种运行状态,因此实验共计27种运行状态,确保消除运行状态对于诊断方法的影响。

图10 实验平台
Fig.10 Experimental platform
实验的四相电流信号由电子示波器采集,其采样频率为20 kHz,而振动信号由4个加速度传感器采集,其采样频率为12 kHz。
通过EMD对75组四相电流信号进行处理,每相电流信号取维度为101维的本征模态函数,因此每种运行状态的电流特征矩阵为300组长度为101维的数据。同时,应用小波包变换对振动信号进行处理,每个传感器得到256维的能量占比、峭度和裕度,因此每种运行状态的振动特征矩阵为300组长度为768维的数据,将两者并行排布后按4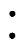 1的比例将每组数据随机划分为训练集和测试集。
1的比例将每组数据随机划分为训练集和测试集。
原始特征矩阵在经过区间缩放,归一化、缺失值处理等特征处理后,作为输入进入卷积神经网络进行分类。矩阵经过卷积和池化后,通过批归一化层有效保留数据特征,最后由Flatten层压平并传递到Softmax分类器中进行分类。在实际运行中还引入了dropout层,同时对学习率进行寻优来保证模型在较高分类效率,不会发生过拟合的情况。
本文对三种不同转速下的8-10极WFDSM数据进行检测,检测的故障类别分为短路发生在A相内部的Ⅰ类匝间短路故障和短路发生在A、B相之间的Ⅱ类匝间短路故障,并与正常状态进行对比实验,用以验证该方法应用于实际的价值,相同转速下各故障类别和相应的标签对应见表2。
不同转速下各检测量故障诊断准确率见表3,可以看出,在三种不同转速下,仅采用电流信号的时候,800 r/min和1 000 r/min的工况下的准确率仅为82.8 %和83.7 %,仅采用振动信号的准确率为85.7 %和84.3 %,同时其收敛速度相对较慢,且训练时也会出现一定的波动。而当采取本文提出的多特征融合的故障诊断方法时,准确率最高可达98.3 %,且模型收敛速度也明显加快,相较于单电流信号和单振动信号的准确率有着较大的提升,这表明综合利用电流和振动信号对于故障的区分有着明显的作用,因此可以满足实际工程需求,具有良好的应用前景。
表2 电机运行工况数据集标签
Tab.2 Labels of WFDSM data set

故障状态样本数量/组样本长度/维分类标签 训练集测试集电流振动 正常7201801017681 Ⅰ类故障7201801017682 Ⅱ类故障7201801017683
表3 不同转速下各检测量故障诊断准确率
Tab.3 Labels of fault diagnosis accuracy on different rotor speed
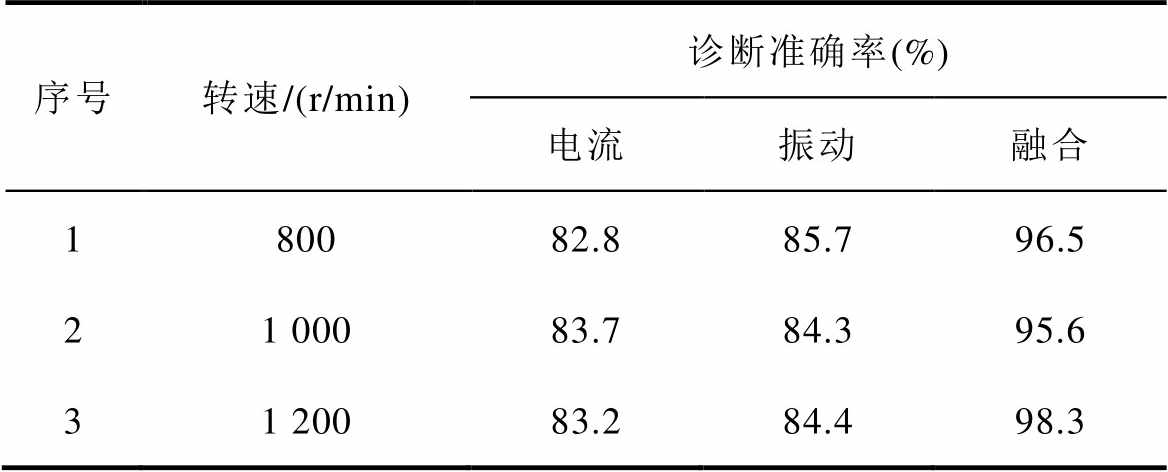
序号转速/(r/min)诊断准确率(%) 电流振动融合 180082.885.796.5 21 00083.784.395.6 31 20083.284.498.3
以800 r/min的融合诊断结果为例,模型准确率和损失值变化如图11所示,由图11可知,在模型迭代的过程中,损失值在快速下降并逐渐收敛于0,同时准确率快速上升并很快趋近于100 %,这表明该诊断模型对于WFDSM故障数据的输入特征能够进行有效识别,同时学习效果明显。
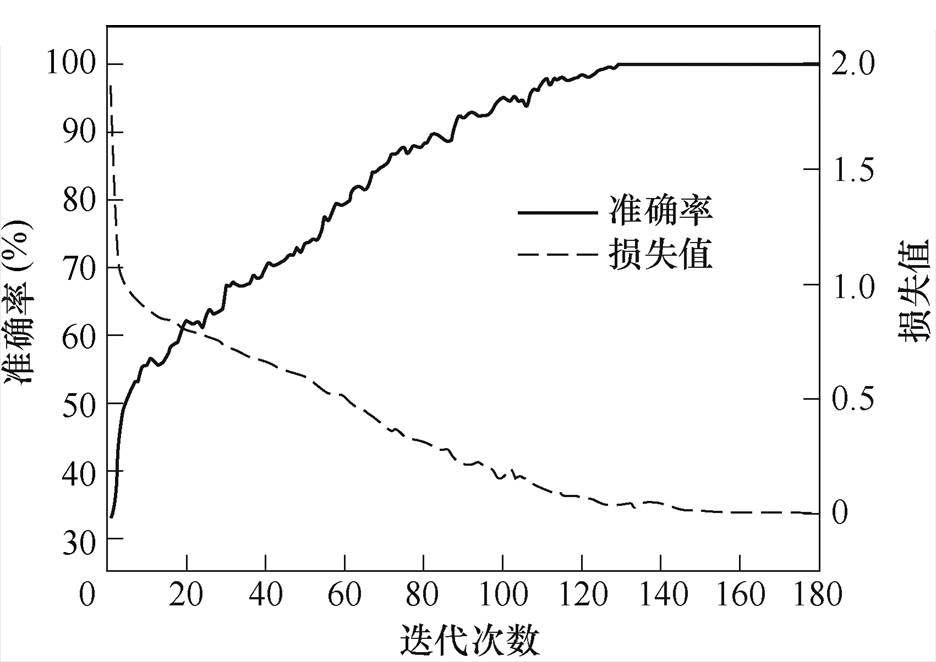
图11 准确率和损失值
Fig.11 Accuracy and loss value
为具体分析三种不同诊断方式对于不同故障的识别情况,以1 200 r/min数据诊断结果为例作出如图12所示的混淆矩阵。由图12中可以看出,单电流量的诊断方法对Ⅰ类故障电机识别效果最差,仅有67 %的诊断准确率,且极大可能将其判断为正常运转,同时对于正常运转的电机也难以做到完全识别,仍存在14 %的误诊断情况,但对于Ⅱ类故障能够较好地识别。而单一振动诊断方法虽然Ⅰ型故障能够做到99 %识别,但对于正常情况也还是存在着较大的识别误差,对于Ⅱ型故障也难以做到100 %诊断。而本文提出的信号融合方法结合了两种单一信号量诊断方法的优势,对正常电机和Ⅰ类故障电机都能够做到100 %识别,同时对Ⅱ类故障也有较高的识别率,相较于其余两种单一故障量诊断方法更为优越,效果更好。

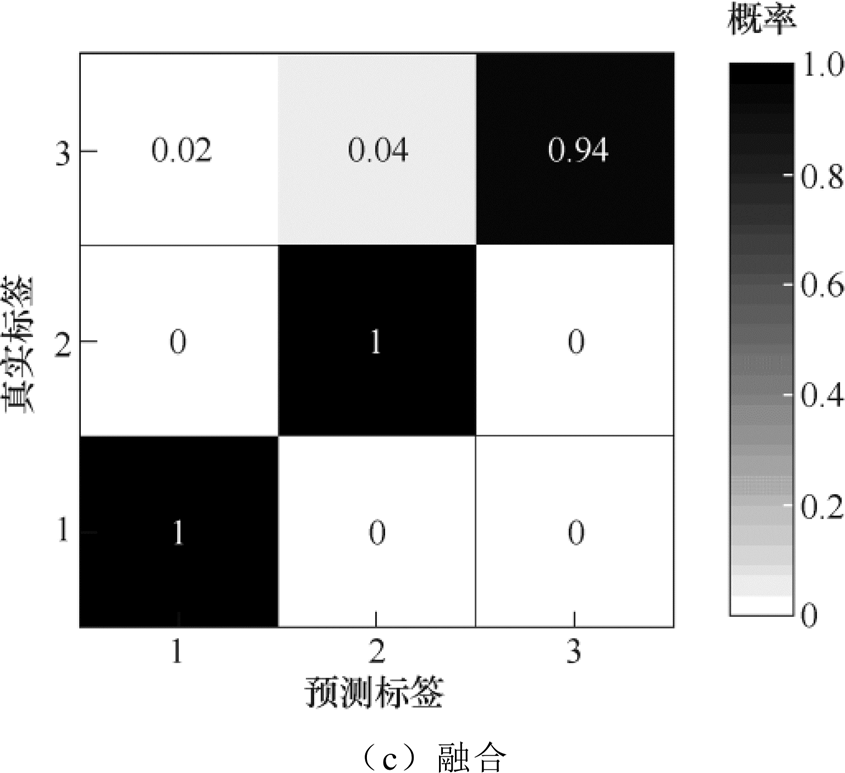
图12 1 200 r/min不同诊断方式混淆矩阵
Fig.12 Confusion matrix of different diagnostic methods on 1 200 r/min
以800 r/min为例比较特征融合方法和其余两种融合方法的差异,其中数据融合方法不对数据作任何处理,直接对原始数据融合后进行故障诊断;结果融合方法在分别对原始数据直接进行诊断后,采取D-S证据理论对两者诊断结果进行融合[30]。不同融合方法故障诊断准确率和时间见表4,本文采取特征融合方法的用时为228 s,其余两种融合方法所需时间分别为300 s和168 s。虽然,本文特征融合方法相较于结果融合的用时更长,但基于特征融合的故障诊断方法较其余两种诊断方法的准确率有显著的提升,且收敛速度更快,综合考虑下特征融合方法更具有优势。
表4 不同融合方法故障诊断准确率和时间
Tab.4 Fault diagnosis accuracy and time of different fushion methods
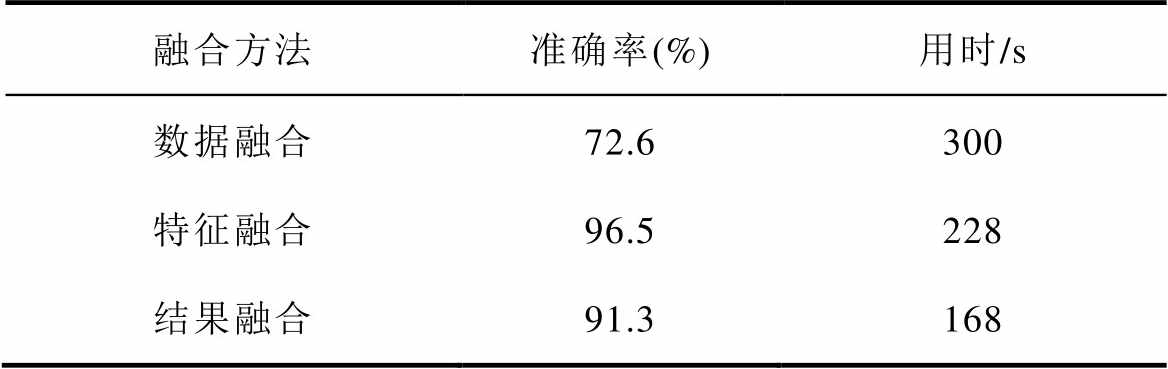
融合方法准确率(%)用时/s 数据融合72.6300 特征融合96.5228 结果融合91.3168
由于WFDSM实际往往运行于极端环境下,难以忽略外界噪声的干扰,致使振动信号失真。实际工程中的信噪比往往在0~30 dB间,为检验本文提出方法在极端环境下的准确性,选取800 r/min的数据样本,加入不同程度高斯白噪声来模拟实际环境,最终在噪声干扰下的实验结果见表5。
由表5可知,有噪声干扰时的三种融合方法相较于实验室条件下的故障诊断准确率都有了不同程度的下降,其下降幅度由低到高分别为特征融合方法、数据融合方法、结果融合方法。特征融合方法在信噪比大于20 dB时准确率几乎没有变化,仍在95 %以上,能够较好地识别故障,同时即使在噪声较大的极端情况下,该方法的准确率较其余两种方法更高,具有较好的抗干扰能力。综上所述,本文提出的特征层融合的故障诊断方法的抗干扰能力较好,其特征域特征几乎不会被噪声所掩盖,泛化能力更好。
表5 不同融合方法极端环境下故障诊断准确率
Tab.5 Labels of fault diagnosis accuracy of different fusion methods in extreme environments
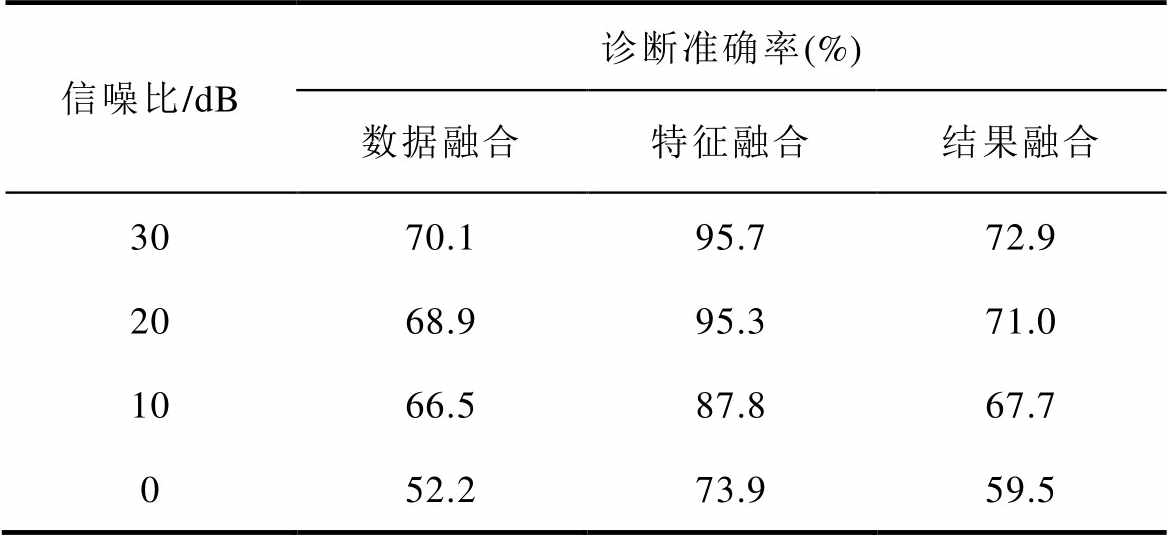
信噪比/dB诊断准确率(%) 数据融合特征融合结果融合 3070.195.772.9 2068.995.371.0 1066.587.867.7 052.273.959.5
针对不同转速下WFDSM故障诊断过程中的时频特征提取和智能诊断问题,本文提出了基于多信号特征融合提取和改进神经网络算法的智能诊断方法,挖掘出不同信号故障特征的同时也为WFDSM的故障检测提供了新思路。
通过对于故障状态的分析,不同工况数据的采集、特征提取和分类,并将采用不同信号量、不同融合方法的诊断结果进行对比,可以得到以下 结论:
1)WFDSM在发生短路故障时,其磁场会发生畸变,有额外高次谐波产生,并间接导致了电流量和振动量较正常时发生变化。
2)提出了多信号特征融合的故障诊断方法,该方法相较于单信号诊断方法、数据层面融合诊断方法、结果层面融合诊断方法的准确率和收敛速度均有较大的提升。
3)在模拟极端运行情况的有噪声干扰场景下的故障诊断实验结果表明,相较于其余两种融合方法,本文提出的特征层面融合的诊断方法在扰动较大时仍具有较高的准确率,抗干扰能力更强。
4)作为对比的单一电流和振动检测量方法也均有着较高准确率,证明了通过EMD和小波包变换提取的特征在故障识别方面有着良好的作用,同时改进卷积神经网络对于故障也具有较好的分类 效果。
故障诊断流程如附图1所示。
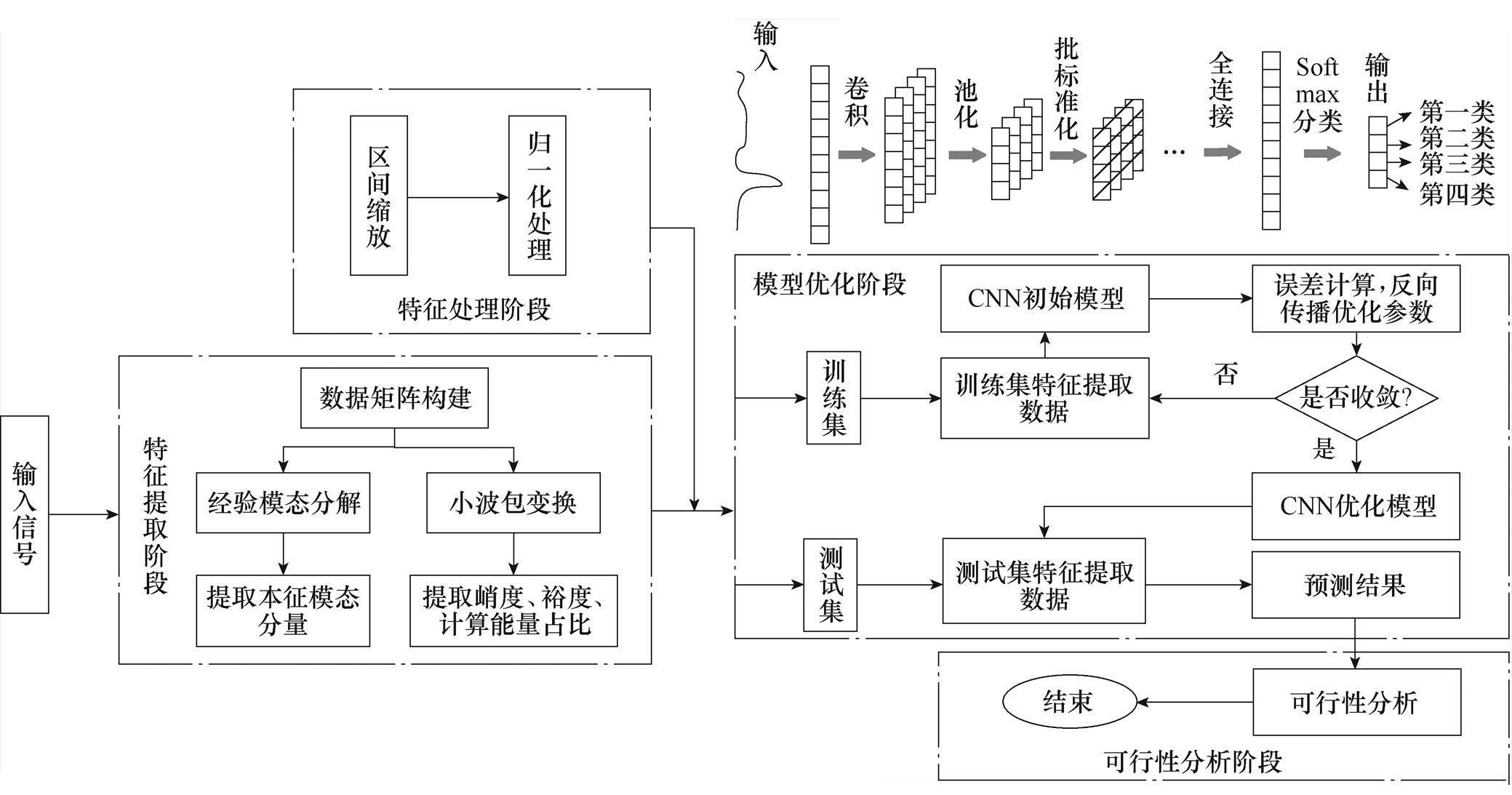
附图1 故障诊断流程
App.Fig.1 Fault diagnosis process
参考文献
[1] 于立, 张卓然, 张健, 等. 多电发动机内装式高速起动发电机研究与实践[J]. 中国电机工程学报, 2020, 40(14): 4615-4628, 4740.
Yu Li, Zhang Zhuoran, Zhang Jian, et al. Study and implementation on high-speed starter/generator for more electric engine application[J]. Proceedings of the CSEE, 2020, 40(14): 4615-4628, 4740.
[2] 王逸洲, 王慧贞, 刘伟峰, 等. 新型电励磁双凸极电机发电系统建模研究[J]. 中国电机工程学报, 2017, 37(17): 5162-5170, 5236.
Wang Yizhou, Wang Huizhen, Liu Weifeng, et al. A novel modeling method for power generator systems of wound-excited doubly salient machines[J]. Proceedings of the CSEE, 2017, 37(17): 5162-5170, 5236.
[3] 陈云云, 朱孝勇, 全力, 等. 基于参数敏感度的双凸极永磁型双定子电机的优化设计和性能分析[J]. 电工技术学报, 2017, 32(8): 160-168.
Chen Yunyun, Zhu Xiaoyong, Quan Li, et al. Parameter sensitivity optimization design and per- formance analysis of double-salient permanent- magnet double-stator machine[J]. Transactions of China Electrotechnical Society, 2017, 32(8): 160-168.
[4] 张健, 朱锡庆, 张卓然, 等. 电励磁双凸极无刷直流发电机热网络建模与热特性研究[J]. 中国电机工程学报, 2023, 43(1): 318-329.
Zhang Jian, Zhu Xiqing, Zhang Zhuoran, et al. Thermal network modeling and thermal characteri- stics analysis of doubly salient brushless DC generator with stator field winding[J]. Proceedings of the CSEE, 2023, 43(1): 318-329.
[5] 闫文举, 陈昊, 马小平, 等. 不同转子极数下磁场解耦型双定子开关磁阻电机的研究[J]. 电工技术学报, 2021, 36(14): 2945-2956.
Yan Wenju, Chen Hao, Ma Xiaoping, et al. Development and investigation on magnetic field decoupling double stator switched reluctance machine with different rotor pole numbers[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2945- 2956.
[6] 郭佳强, 刘旭, 李珊瑚. 计及电枢和零序回路电阻压降的可变磁通磁阻电机弱磁控制[J]. 电工技术学报, 2021, 36(18): 3911-3921.
Guo Jiaqiang, Liu Xu, Li Shanhu. Flux weakening control of variable flux reluctance machine con- sidering resistive voltage drops in armature and zero-sequence loop[J]. Transactions of China Electro- technical Society, 2021, 36(18): 3911-3921.
[7] 丁文, 李可, 付海刚. 一种12/10极模块化定子混合励磁开关磁阻电机分析[J]. 电工技术学报, 2022, 37(8): 1948-1958.
Ding Wen, Li Ke, Fu Haigang. Analysis of a 12/10-pole modular-stator hybrid-excited switched reluctance machine[J]. Transactions of China Electro- technical Society, 2022, 37(8): 1948-1958.
[8] 孙毅, 蔡顺, 林迎前, 等. 永磁辅助同步磁阻电机顶层优化设计[J]. 电工技术学报, 2022, 37(9): 2306-2318.
Sun Yi, Cai Shun, Lin Yingqian, et al. Top-level design pattern of PM-assisted synchronous reluctance machines[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2306-2318.
[9] 王瑾, 李岩, 于占洋, 等. 永磁同步磁阻电动机全负载区域功率因数特性分析[J]. 电工技术学报, 2021, 36(增刊2): 451-459.
Wang Jin, Li Yan, Yu Zhanyang, et al. Analysis of power factor characteristics of permanent magnet synchronous reluctance motor in whole load range[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 451-459.
[10] Zhang Minjie, Ali N, Gao Qiang. Winding inductance and performance prediction of a switched reluctance motor with an exterior-rotor considering the magnetic saturation[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(3): 212-223.
[11] Gan Chun, Chen Yu, Qu Ronghai, et al. An overview of fault-diagnosis and fault-tolerance techniques for switched reluctance machine systems[J]. IEEE Access, 2019, 7: 174822-174838.
[12] Park J K, Babetto C, Berardi G, et al. Comparison of fault characteristics according to winding confi- gurations for dual three-phase synchronous reluctance motor[J]. IEEE Transactions on Industry Applications, 2021, 57(3): 2398-2406.
[13] Chen Hao, Han Guoqiang, Shi Xianqiang, et al. Phase current digital analysis of power converter for freewheeling diode fault diagnosis on switched reluctance motor drive[J]. IEEE Transactions on Industrial Electronics, 2019, 66(8): 6613-6624.
[14] 夏一文, 张卓然, 张健, 等. 基于反电势电流的电励磁双凸极电机驱动电路单管开路故障诊断研究[J]. 电工技术学报, 2020, 35(23): 4888-4897.
Xia Yiwen, Zhang Zhuoran, Zhang Jian, et al. Research on single power switch open circuit fault diagnosis of doubly salient eletromagnetic motor drive circuit based on the back electromotive force current[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4888-4897.
[15] Alam M, Shah V, Payami S. Online fault diagnosis of static and dynamic eccentricity in switched reluctance motors using parks vector algorithm[C]//The 10th International Conference on Power Electronics, Machines and Drives (PEMD 2020), Online Con- ference, 2021: 885-889.
[16] Fonseca D S B, Marques Cardoso A J. On-line inter-turn short-circuit fault diagnosis in switched reluctance motors[C]//2019 IEEE International Elec- tric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 2019: 198-202.
[17] Arafat A, Choi S, Baek J. Open-phase fault detection of a five-phase permanent magnet assisted syn- chronous reluctance motor based on symmetrical components theory[J]. IEEE Transactions on Indu- strial Electronics, 2017, 64(8): 6465-6474.
[18] Gan Chun, Wu Jianhua, Yang Shiyou, et al. Wavelet packet decomposition-based fault diagnosis scheme for SRM drives with a single current sensor[J]. IEEE Transactions on Energy Conversion, 2016, 31(1): 303-313.
[19] 何玉灵, 孙凯, 王涛, 等. 基于变分模态分解与精细复合多尺度散布熵的发电机匝间短路故障诊断[J]. 电力自动化设备, 2021, 41(3): 164-172.
He Yuling, Sun Kai, Wang Tao, et al. Fault diagnosis of generator interturn short circuit fault based on variational mode decomposition and refined com- posite multiscale dispersion entropy[J]. Electric Power Automation Equipment, 2021, 41(3): 164- 172.
[20] 肖雄, 肖宇雄, 张勇军, 等. 基于二维灰度图的数据增强方法在电机轴承故障诊断的应用研究[J]. 中国电机工程学报, 2021, 41(2): 738-749.
Xiao Xiong, Xiao Yuxiong, Zhang Yongjun, et al. Research on the application of the data augmentation method based on 2D gray pixel images in the fault diagnosis of motor bearing[J]. Proceedings of the CSEE, 2021, 41(2): 738-749.
[21] 李梦诗, 余达, 陈子明, 等. 基于深度置信网络的风力发电机故障诊断方法[J]. 电机与控制学报, 2019, 23(2): 114-122.
Li Mengshi, Yu Da, Chen Ziming, et al. Fault diagnosis and isolation method for wind turbines based on deep belief network[J]. Electric Machines and Control, 2019, 23(2): 114-122.
[22] 李垣江, 张周磊, 李梦含, 等. 采用深度学习的永磁同步电机匝间短路故障诊断方法[J]. 电机与控制学报, 2020, 24(9): 173-180.
Li Yuanjiang, Zhang Zhoulei, Li Menghan, et al. Fault diagnosis of inter-turn short circuit of per- manent magnet synchronous motor based on deep learning[J]. Electric Machines and Control, 2020, 24(9): 173-180.
[23] Wang Xiaoxian, Lu Siliang, Chen Kang, et al. Bearing fault diagnosis of switched reluctance motor in electric vehicle powertrain via multisensor data fusion[J]. IEEE Transactions on Industrial Infor- matics, 2022, 18(4): 2452-2464.
[24] 施耀华, 冯延晖, 任铭, 等. 融合电流和振动信号的永磁同步风电系统变流器故障诊断方法研究[J]. 中国电机工程学报, 2020, 40(23): 7750-7760.
Shi Yaohua, Feng Yanhui, Ren Ming, et al. Study on fault diagnosis method of converter in permanent magnet synchronous wind power system by fusion of current and vibration signals[J]. Proceedings of the CSEE, 2020, 40(23): 7750-7760.
[25] Irhoumah M, Pusca R, Lefevre E, et al. Information fusion with belief functions for detection of interturn short-circuit faults in electrical machines using external flux sensors[J]. IEEE Transactions on Indu- strial Electronics, 2018, 65(3): 2642-2652.
[26] 陈勇, 梁洪, 王成栋, 等. 基于改进小波包变换和信号融合的永磁同步电机匝间短路故障检测[J]. 电工技术学报, 2020, 35(增刊1): 228-234.
Chen Yong, Liang Hong, Wang Chengdong, et al. Detection of stator inter-turn short-circuit fault in PMSM based on improved wavelet packet transform and signal fusion[J]. Transactions of China Elec- trotechnical Society, 2020, 35(S1): 228-234.
[27] 杨洁, 万安平, 王景霖, 等. 基于多传感器融合卷积神经网络的航空发动机轴承故障诊断[J]. 中国电机工程学报, 2022, 42(13): 4933-4941.
Yang Jie, Wan Anping, Wang Jinglin, et al. Aero- engine bearing fault diagnosis based on convolutional neural network for multi-sensor information fu- sion[J]. Proceedings of the CSEE, 2022, 42(13): 4933-4941.
[28] Zhao Yao, Teng Denghui, Li Dongdong, et al. Com- parative research on four-phase dual armature- winding wound-field doubly salient generator with distributed field magnetomotive forces for high- reliability application[J]. IEEE Access, 2021, 9: 12579-12591.
[29] 刘素贞, 魏建, 张闯, 等. 基于FPGA的超声信号自适应滤波与特征提取[J]. 电工技术学报, 2020, 35(13): 2870-2878.
Liu Suzhen, Wei Jian, Zhang Chuang, et al. Adaptive filtering and feature extraction of ultrasonic signal based on FPGA[J]. Transactions of China Electro- technical Society, 2020, 35(13): 2870-2878.
[30] 王栋悦, 谷怀广, 魏书荣, 等. 基于机电信号融合的DFIG定子绕组匝间短路故障诊断[J]. 电力系统自动化, 2020, 44(9): 171-178.
Wang Dongyue, Gu Huaiguang, Wei Shurong, et al. Diagnosis of inter-turn short-circuit fault in stator windings of DFIG based on mechanical and electrical signal fusion[J]. Automation of Electric Power Systems, 2020, 44(9): 171-178.
Abstract The Wound-Field Doubly Salient Machine (WFDSM) has a simple structure and high reliability, suitable for aerospace and other applications in harsh environments. However, traditional diagnosis methods are challenging to diagnose an inter-turn short-circuit fault due to slight changes in currents and vibration. Therefore, a novel WFDSM inter-turn short circuit diagnosis method is proposed in this paper based on multi-signal fusion at the feature level and improved convolutional neural network (CNN).
Firstly, current and vibration data are collected from the 8-10 WFDSM. The 75 sets of four-phase current signals are processed by Empirical Mode Decomposition (EMD), and Intrinsic Mode Function (IMF) of length 101 is taken from each phase current. Thus, each condition of the current feature matrix is 300 sets of length 101. At the same time, the wavelet packet transform is applied to the vibration signal, and each sensor gets kurtosis, margin and energy ratio of length 256. Thus, each condition of the vibration feature matrix is 300 sets of length 768. Interval scaling, normalization, missing value processing, and other feature processing are taken after two sets are arranged in parallel. Each group is randomly divided into the training set and test set of 4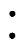 1. After the input matrix is convolved and pooled, the data features are effectively preserved by the batch normalization layer, next the flattened layer is laminated and finally passed to the SoftMax classifier for diagnosis. The dropout layer is also applied in the diagnosis, while the learning rate is optimized to ensure high classification efficiency without overfitting.
1. After the input matrix is convolved and pooled, the data features are effectively preserved by the batch normalization layer, next the flattened layer is laminated and finally passed to the SoftMax classifier for diagnosis. The dropout layer is also applied in the diagnosis, while the learning rate is optimized to ensure high classification efficiency without overfitting.
The diagnosis results of different detection quantities show that when only current signals are used, the accuracy can reach 82.8 % on 800r/min and 83.7 % on 1 000 r/min. when only vibration signals are used, the accuracy can reach 85.7 % and 84.3 %. In contrast, when the multi-signal fusion at feature level method is adopted, the accuracy can reach up to 98.3 %, while the model convergence speed accelerates significantly. In order to simulate extreme conditions, different degrees of white Gaussian noise are added to the experiment. The fusion accuracy at the feature level method barely changed when the SNR>20 dB, which is still above 95 %. Meanwhile, when SNR=10 dB, the accuracy remains at 87.8 %. Considering the accuracy and solving efficiency, the fusion at the feature level method is superior to the fusion method at the data or result levels.
The following conclusions can be drawn. (1) The magnetic field of WFDSM will be distorted with additional harmonics generated when a short-circuit fault occurs, which also indirectly leads to the change of the current and vibration. (2) Compared with the single signal diagnosis method, the accuracy and convergence speed of the proposed model are greatly improved. (3) The proposed model performs better and has a strong anti-interference ability under extreme conditions. (4) The features extracted by EMD and wavelet packet transformation play an essential role in fault identification, and the improved CNN also has a good classification effect.
keywords:Wound-field doubly salient machine, empirical mode decomposition, feature fusion, improved convolutional neural network, extreme conditions
DOI: 10.19595/j.cnki.1000-6753.tces.220516
中图分类号:TM352
国家自然科学基金(51977128)、上海市青年科技启明星计划(21QC1400200)和上海市自然科学基金(21ZR1425400)资助项目。
收稿日期 2022-04-06
改稿日期 2022-04-28
赵 耀 男,1987年生,博士,副教授,硕士生导师,研究方向为电力设备故障诊断、新能源发电。E-mail: nihaozhaoyao@163.com
李东东 男,1976年生,博士,教授,博士生导师,研究方向为电力设备故障诊断、风力发电与电力系统稳定控制、智能用电。E-mail: powerldd@163.com(通信作者)
(编辑 崔文静)