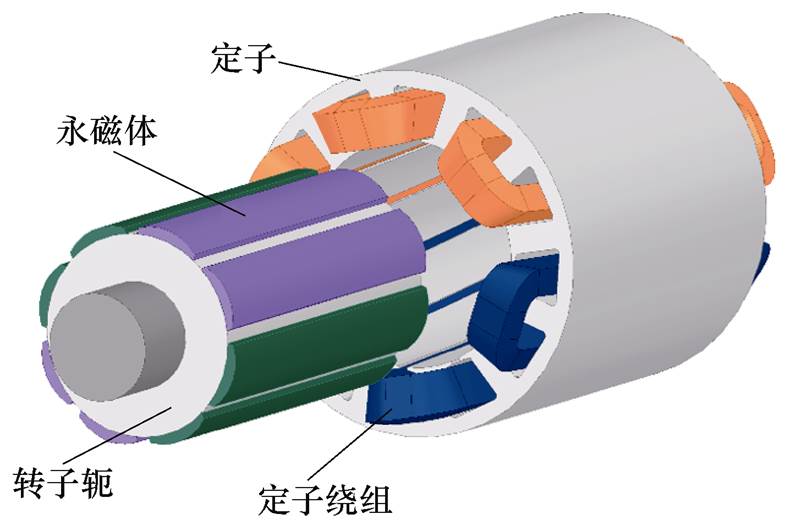
图1 DRPMSM结构模型
Fig.1 Structure model of DRPMSM
摘要 针对双余度永磁同步电机(DRPMSM)的多目标优化设计问题,该文采用Pearson相关系数分析法,在参数敏感度分析的基础上,提出一种改进迭代田口法的多目标优化设计方法。该方法利用单余度模式下的田口法优化设计结果作为双余度模式下优化因子水平取值的依据,对优化因子的水平取值进行了优化选择。既考虑了各工作模式下的优化设计,又解决了不同水平值之间无法寻优的问题。以800 W双余度永磁同步电机为例,利用有限元仿真,对比分析了优化前后的效率、转矩等关键性能参数,验证了所提优化方法的有效性。最后,制作了实验样机,实验测试结果与优化设计结果有较高的吻合度,证明该文所提出方法可有效解决多余度电机的多目标优化设计问题,拓宽了对于该类电机的优化设计思路。
关键词:双余度永磁同步电机 敏感度分析 迭代田口法 多目标优化 有限元分析
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)具有体积小、功率密度大、效率高等诸多优点,广泛应用于各种系统中。为了提高系统运行的可靠性和容错能力,增加一个机电单元,构成双余度永磁同步电机(Dual-Redundancy Permanent Magnet Synchronous Motor, DRPMSM)。DRPMSM具有串联和并联两种结构形式。相对于串联结构,并联结构的DRPMSM具有更高的功率体积比和功率质量比,深受相关研究者的关注[1-2]。
永磁同步电机的优化设计需要综合考虑多个参数对关键性能的影响,可采用多目标优化的设计方法[3-7]。为了增强优化的针对性并提高优化效率,首先需要对参数进行敏感度分析,筛选出敏感度大的待优化设计参数[8-10];进而采用全局或局部优化法对筛选出来的参数进行优化设计。其中,全局优化方法的函数构建较为复杂,多参数耦合搜寻能力较差,求解周期长[11-14]。田口法是应用广泛的局部优化方法,该方法能够综合考虑多个参数对优化目标的影响程度,效率高、计算量小,能够有效地实现多目标优化[15-18]。文献[19]使用田口法建立正交试验表对永磁球形电机进行优化,选取径向气隙磁场密度和最大输出转矩两个优化目标,未做参数敏感度分析。文献[20]首先通过参数敏感度分析将电机相关参数进行分层,然后分别应用分层响应面法和改进的带精英策略的非支配排序遗传算法(elitist Non- dominated Sorting Genetic Algorithm, NSGA-II)方法对不同层级的参数进行了优化。文献[21]通过转子应力和转子动力学分析,基于响应面法以及Pareto前沿,对电机的效率和热负荷做了多目标优化设计,优化函数的建立较为繁琐。相对于PMSM而言,DRPMSM的工作状态多,优化设计的参数也更多,并且大多要求余度单元的性能一致、余度单元间的耦合度低。目前,DRPMSM的优化设计借鉴PMSM的优化设计方法,难以满足DRPMSM多工作模式下的优化需求。
为解决DRPMSM多目标优化设计问题,文献[22]中提出了初步的迭代田口法多目标优化思想。但两种工作模式的田口法优化相对独立;未考虑传统田口法两个水平值之间是否存在非劣最优解;且优化因子依靠经验选择,并未对各优化因子的参数敏感度进行分析。
本文针对以上存在的问题,提出基于参数敏感度分析的改进迭代田口法多目标优化算法。采用Pearson相关系数分析法,在参数敏感度分析的基础上,针对正常运行的双余度工作模式和容错运行的单余度模式,展开双余度永磁同步电机的迭代优化设计研究。在考虑不同工作模式的同时,兼顾考虑两个水平值之间的寻优问题。为了提升双余度电机的容错运行能力,首先考虑容错运行时的单余度模式的优化,单余度模式的优化结果也进一步缩小了双余度模式的寻优范围。实验样机测试结果证明,本文提出的改进迭代田口法优化设计方法的有效性。
本文以8极12槽的DRPMSM为对象,其结构模型如图1所示。

图1 DRPMSM结构模型
Fig.1 Structure model of DRPMSM
DRPMSM具有两套独立的定子绕组,定子绕组常见分布方式有半球连续分布和全球隔槽分布,如图2所示。

图2 DRPMSM定子绕组分布示意图
Fig.2 Winding distribution diagram of DRPMSM
定子绕组采用半球连续分布时,同一余度的绕组邻近排列,连接绕组线圈与三相中性点的端部绕组导线用量较少,可节约电机的制造成本并降低电机运行过程中的铜损耗;其次,两个余度绕组在空间排列位置上不存在交叉,可以最大限度地降低两个余度端部绕组的交叉重叠,从而降低余度之间的电磁耦合,使得当某一余度发生故障时,另一余度所受的影响较小。但是,采用半球连续分布时,不同余度的三相绕组在空间排列上不对称,增加了电机输出转矩波动,因此,在设计时,应该重点考虑电机的输出转矩及其波动大小。
定子绕组采用全球隔槽分布时,两个余度的绕组交叉隔槽排列,同一余度下,连接绕组线圈与三相中性点的端部绕组长度增加,电机的铜损耗上升;其次,余度间的电磁耦合要大于半球连续分布结构。因此,在设计采用全球隔槽分布的双余度永磁同步电机时,应该重点考虑两个余度之间的电磁耦合关系以及铜损耗引起的电机温升问题。
本文选用半球连续分布的电枢绕组形式,兼顾容错运行的单余度模式和正常运行的双余度模式,基于改进迭代田口算法展开双余度永磁同步电机的性能优化研究。
依据应用需求,设计DRPMSM的约束参数见表1。
表1 DRPMSM的约束参数
Tab.1 Constraint parameters of DRPMSM

约束参数数 值 单余度额定功率/W400 双余度额定功率/W800 单余度额定转矩/(N·m)1.50 双余度额定转矩/(N·m)3.05 额定转速/(r/min)2 500 效率(%)≥85
本文所采用的迭代田口法的DRPMSM多目标优化设计方法流程如图3所示。
首先,选取电机关键性能指标作为优化目标,并选取6个典型结构尺寸参数,确定其初值和优化范围。建立单余度运行模式和双余度运行模式的有限元模型,分别在两种模式下对选择的结构尺寸参数做敏感度分析,筛选出对优化目标影响较大的4个参数作为优化因子。
其次,先在单余度模式下建立正交试验,并应用田口法进行初次优化分析,筛选出单余度运行模式下的四组准最优参数集。将选取出来的准最优参数组作为依据,建立双余度模式下的正交试验表,进行双余度模式下的二次优化分析,最终得到考虑DRPMSM不同运行模式的最优参数组。
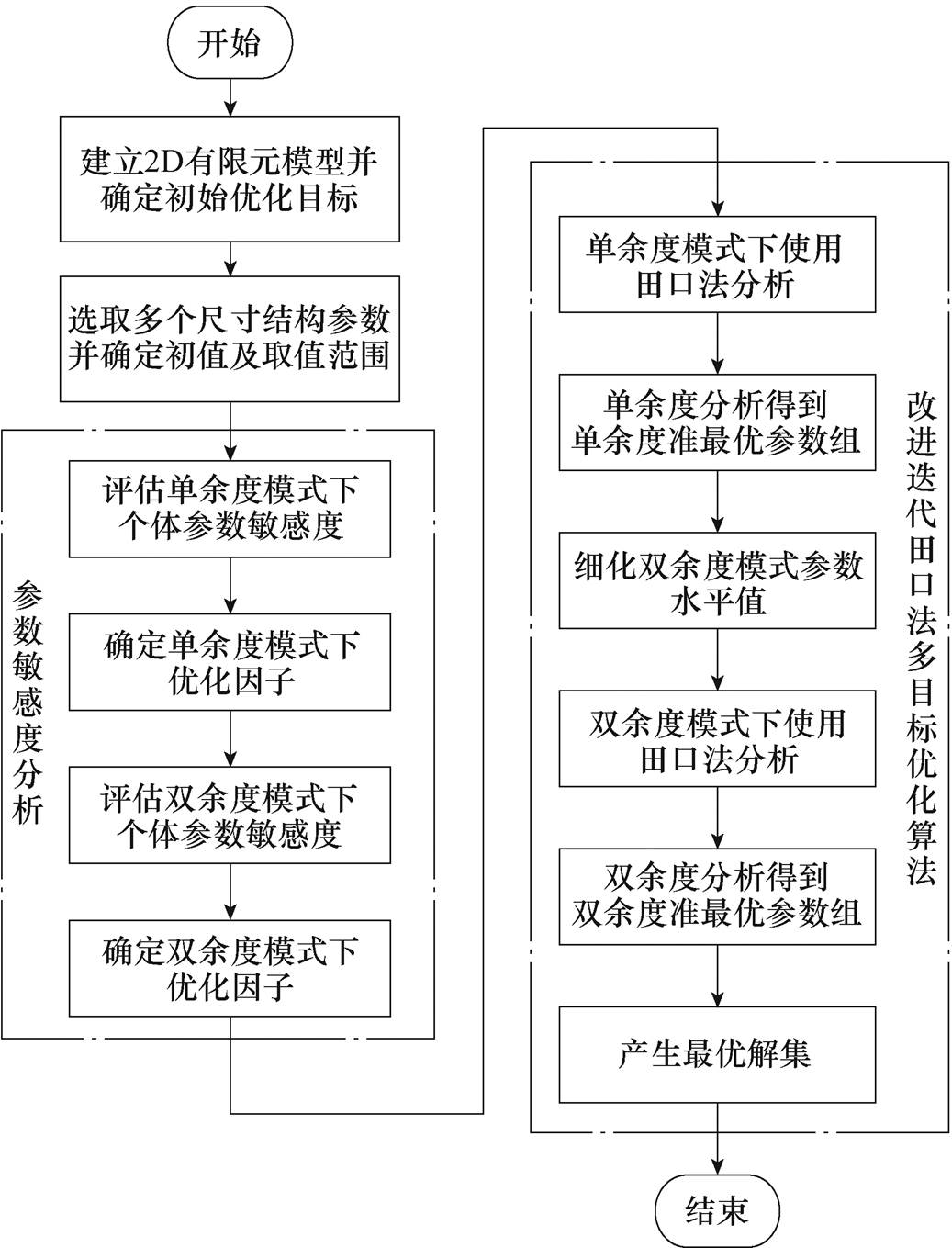
图3 迭代田口法优化设计方法流程
Fig.3 Flowchart optimization design method of iterative Taguchi method
最后,基于优化后的设计参数加工原理样机,并进行相关测试。
考虑到本文所设计的电机样机正常运行时为双余度模式,单余度模式为其容错工作模式,为提升容错运行性能,应用改进迭代田口法进行优化时,先针对单余度模式进行优化;再应用田口法对双余度模式进行优化,可得到兼顾正常运行模式和容错运行模式的准最优参数组。优先针对单余度模式进行优化的显著优点是:①可缩小双余度优化参数的取值范围,初步解决了传统田口法无法考虑两个水平值之间寻优的问题;②考虑了双余度中由于敏感度较低而未被考虑的优化因子的取值(磁极偏心距);③确保了单余度容错运行时的电机性能。而最终优化参数取值由双余度模式确定,可保证正常运行模式的优化性能。
DRPMSM是由两个PMSM单元复合而成,每个PMSM单元的视在电磁功率[23-24]为
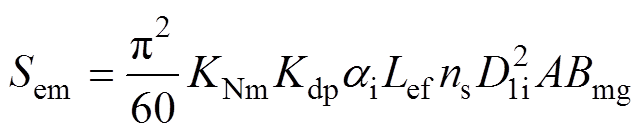 (1)
(1)
式中,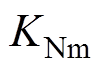 为气隙磁场的波形系数;
为气隙磁场的波形系数;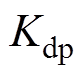 为电枢的绕组系数;
为电枢的绕组系数;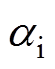 为极弧系数;Lef为电机的等效长度;
为极弧系数;Lef为电机的等效长度;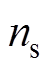 为电机转子的同步转速;
为电机转子的同步转速;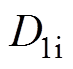 为定子内径;
为定子内径;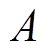 为线负荷,定义为沿电枢圆周单位长度上的安培导体数;
为线负荷,定义为沿电枢圆周单位长度上的安培导体数;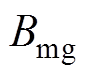 为气隙磁通密度,由于本文电机采用不等厚永磁体的平行充磁方式,因此气隙磁通密度是当前位置与磁极中心线夹角
为气隙磁通密度,由于本文电机采用不等厚永磁体的平行充磁方式,因此气隙磁通密度是当前位置与磁极中心线夹角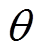 的函数,有
的函数,有
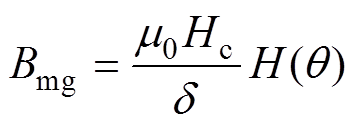 (2)
(2)
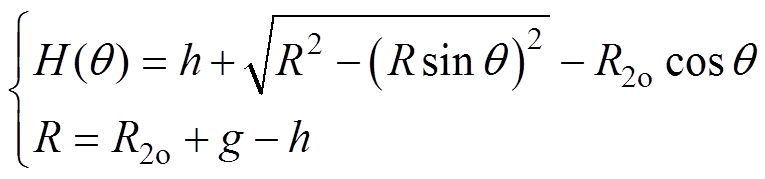 (3)
(3)
式中,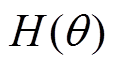 为当前位置处的磁场强度;
为当前位置处的磁场强度;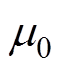 为真空磁导率;
为真空磁导率;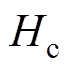 为永磁体的矫顽力;
为永磁体的矫顽力;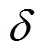 为气隙长度;
为气隙长度;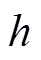 为磁极偏心距;
为磁极偏心距;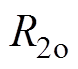 为转子外半径;
为转子外半径;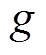 为不等厚磁极的最大厚度;
为不等厚磁极的最大厚度;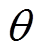 为永磁体上任意一点和该磁极中心线的偏移角度。
为永磁体上任意一点和该磁极中心线的偏移角度。
最大电磁功率表示为
 (4)
(4)
式中,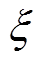 为永磁体的利用系数;
为永磁体的利用系数; 为转子励磁磁通的波形系数;
为转子励磁磁通的波形系数;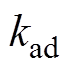 为d轴电枢反应系数;
为d轴电枢反应系数;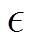 为在空载下转子励磁磁通形成的感应电动势与输入电压比,
为在空载下转子励磁磁通形成的感应电动势与输入电压比,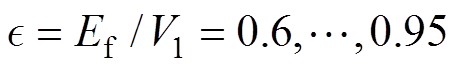 ;
;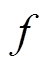 为输入电流的频率;
为输入电流的频率;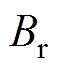 为永磁体的剩余磁通密度;
为永磁体的剩余磁通密度;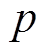 为PMSM的极对数;
为PMSM的极对数;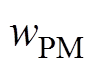 、
、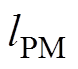 分别为永磁体的宽度以及永磁体的长度。
分别为永磁体的宽度以及永磁体的长度。
记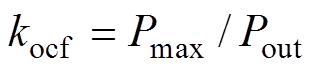 为PMSM的过载系数,
为PMSM的过载系数,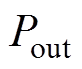 为PMSM的额定输出功率;
为PMSM的额定输出功率;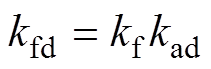 ,PMSM的额定输出功率表示为
,PMSM的额定输出功率表示为
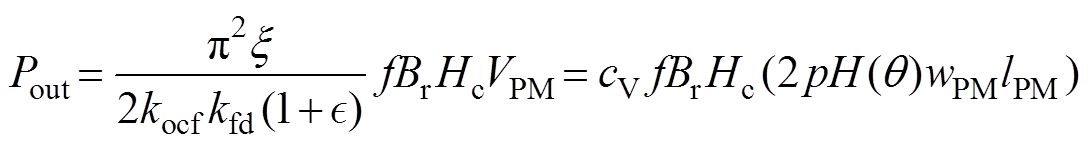 (5)
(5)
其中
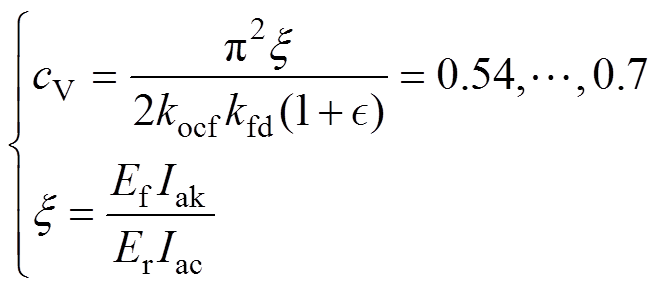
式中,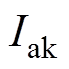 为永磁体的退磁曲线与负载线的交点K点(永磁体的工作点)的电枢电流;
为永磁体的退磁曲线与负载线的交点K点(永磁体的工作点)的电枢电流;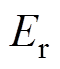 为当转子励磁磁感应强度为永磁体的剩磁密度
为当转子励磁磁感应强度为永磁体的剩磁密度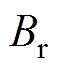 时的电枢感应电动势;
时的电枢感应电动势;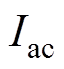 为永磁体矫顽力
为永磁体矫顽力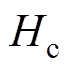 所对应的电枢电流。
所对应的电枢电流。
根据输出功率与输出转矩之间的关系,可得到PMSM的输出转矩为
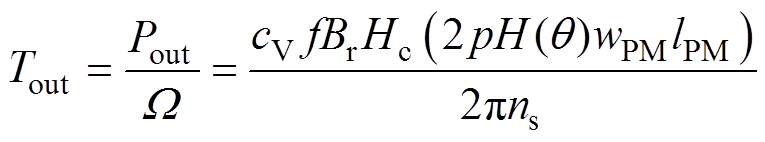 (6)
(6)
式中,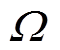 为电机转子的机械角速度。
为电机转子的机械角速度。
结合式(1)、式(4)、式(6),可以得到电机效率的公式为
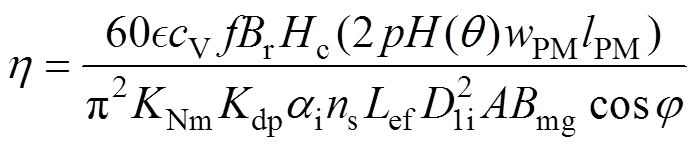 (7)
(7)
式中, 为电机的功率因数。
为电机的功率因数。
电机的转矩脉动系数为
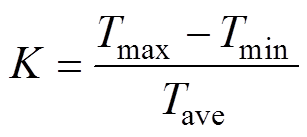 (8)
(8)
式中,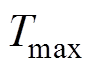 为电机的最大输出转矩;
为电机的最大输出转矩;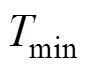 为最小输出转矩;
为最小输出转矩;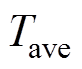 为平均输出转矩。
为平均输出转矩。
可知,电机的输出性能由永磁体、电机尺寸、绕组等多个参数决定。通过对定子铁心、磁极和气隙长度等参数的优化设计能够使得输出转矩、转矩脉动系数得到优化,并在一定程度上提升电机效率。
根据式(6)、式(7),综合考虑电机的应用需求、工作模式及基本电磁参数等因素,选取效率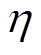 、转矩
、转矩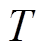 和转矩脉动系数
和转矩脉动系数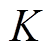 为优化设计目标。
为优化设计目标。
电机外形尺寸一般会受安装空间及安装方式的约束,本文所研究DRPMSM的外径及长度均为给定值。
根据选取的优化目标,选择气隙长度、磁极中心线的磁极厚度、极弧系数、磁极偏心距作为设计优化参数。
气隙长度较小时,可以减少永磁体的用量,降低定子绕组的励磁电流;但气隙过小,会导致装配难度急剧增加,且当转子发生不可避免的振动时,气隙的缓冲余量不足,转子与定子间会产生摩擦碰撞。受工艺精度影响,一般气隙长度应大于0.2 mm,考虑本文所设计电机的转速较低,且经过优化后转矩脉动较小,因此气隙长度的下限值定为0.3 mm;当气隙长度较大时,气隙磁场的基波幅值无法得到保证,不能在定子绕组中产生足够的反电动势。根据有限元仿真分析,当气隙长度大于0.6 mm,气隙磁场的基波幅值下降明显。因此,气隙长度的取值范围为0.3~0.6 mm。
永磁体的厚度较小时,无法提供足够的励磁磁场;当永磁体的磁极厚度较大时,易导致定子铁心发生磁饱和。根据有限元仿真分析,磁极厚度在2.4~3 mm时,可以基本保持足够的励磁磁场强度,同时不会导致定子铁心饱和。
根据实际工程经验,极弧系数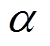 的取值一般在0.7~0.9之间。在本文的有限元模型中,经过仿真分析,确定极弧系数的取值范围为0.7~0.85。
的取值一般在0.7~0.9之间。在本文的有限元模型中,经过仿真分析,确定极弧系数的取值范围为0.7~0.85。
永磁体的磁极偏心距主要是使永磁体产生的气隙励磁磁场波形更正弦。当磁极偏心距取值较小时,对励磁磁场波形的修饰作用不明显,当磁极偏心距取值较大时,又会使得励磁磁场波形畸变严重。根据本文的有限元分析,磁极偏心距的取值范围在8~14 mm时,可以达到对永磁体励磁磁场波形的修饰作用,且不会使得磁场波形发生严重畸变。
根据以上的分析,优化参数及其约束范围见表2。
表2 DRPMSM优化因子及其约束范围
Tab.2 Optimization parameters and their constraint range of DRPMSM

参数数值合理约束范围 气隙长度d/mm0.30.3~0.6 磁极厚度g/mm2.42.4~3 极弧系数a0.80.7~0.85 磁极偏心距h/mm128~14
表2给出了优化因子的合理约束范围,在该范围内,根据田口法选取优化因子水平值的一般原则,在取值范围内等距地选取4个水平值,分别命名为水平值Ⅰ、Ⅱ、Ⅲ、Ⅳ,待优化参数水平数见表3。
表3 待优化参数水平数
Tab.3 Level value of parameters

参数水平Ⅰ水平Ⅱ水平Ⅲ水平Ⅳ 气隙长度d/mm0.30.40.50.6 磁极厚度g/mm2.42.62.83 极弧系数a0.70.750.80.85 磁极偏心距h/mm8101214
在对DRPMSM优化设计过程中,先借助有限元分析软件完成主要参数的敏感度分析,得出各参数对于某一优化目标的Pearson相关系数r,再根据优化目标在电机设计中的权重,得出某一参数xi对于优化目标的敏感度Q(xi)。
Pearson相关系数r以及敏感度Q(xi)的定义分别为
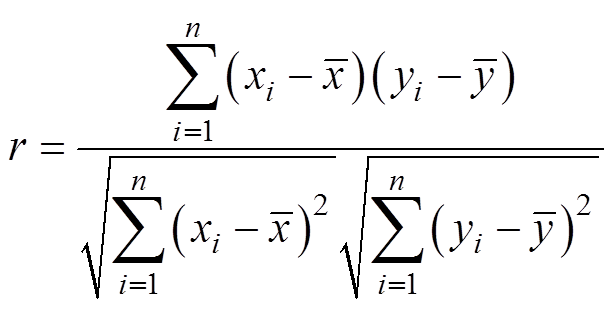 (9)
(9)
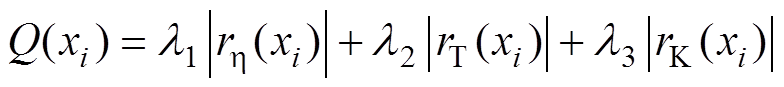 (10)
(10)
式中,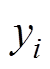 为结构参数xi所对应优化目标取值;
为结构参数xi所对应优化目标取值;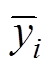 为参数xi取不同值时,优化目标
为参数xi取不同值时,优化目标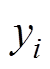 的平均值;
的平均值;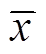 为结构参数xi的平均值;
为结构参数xi的平均值;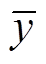 为参数xi取不同值时,优化目标
为参数xi取不同值时,优化目标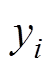 的平均值;
的平均值;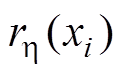 、
、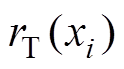 、
、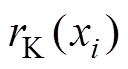 分别为效率、转矩、转矩脉动系数的Pearson相关系数;
分别为效率、转矩、转矩脉动系数的Pearson相关系数; 、
、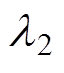 、
、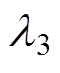 分别为效率、转矩、转矩系数的权重系数。
分别为效率、转矩、转矩系数的权重系数。
本文主要在保证输出转矩的情况下,考虑电机的效率和转矩脉动系数的优化。因此对于式(10)中加权参数的选择为: ,
,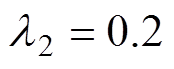 ,
,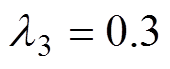 。
。
2.3.1 单余度运行模式参数敏感度分析
在单余度运行模式下,得出各结构尺寸参数在不同水平值下所对应的不同优化目标值,并计算其Pearson相关系数,结果如图4所示。
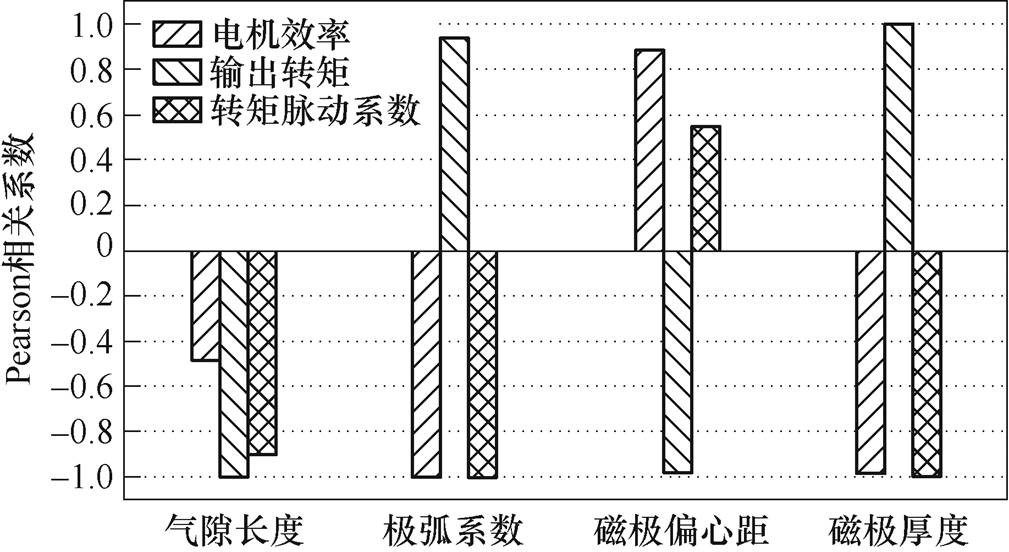
图4 单余度工作模式Pearson相关系数
Fig.4 The Pearson correlation coefficient of optimization objective in single mode
由式(10)可得到单余度模式下各优化目标的参数敏感度,如图5所示。
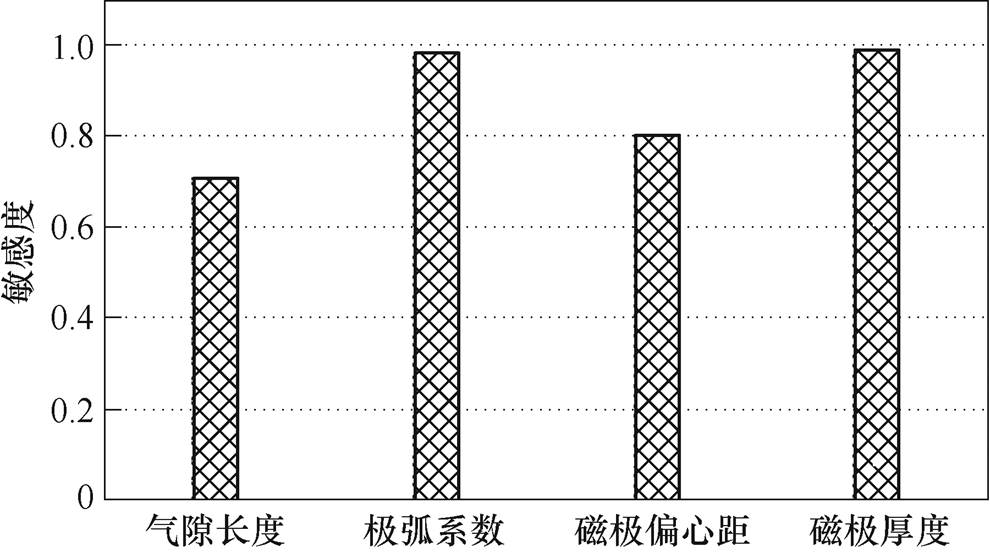
图5 单余度运行模式尺寸参数的敏感度
Fig.5 Sensitivity of parameters in single mode
由图5可知,不同的结构尺寸参数对于不同的优化目标,影响程度不尽相同。其中,磁极厚度、极弧系数和磁极偏心距对于电机关键性能的影响更为突出,因此在单余度模式下初选以上三种结构参数作为优化因子。
2.3.2 双余度运行模式参数敏感度分析
同理,可得出双余度工作模式下,各结构参数对应不同优化目标的Pearson相关系数,结果如图6所示。
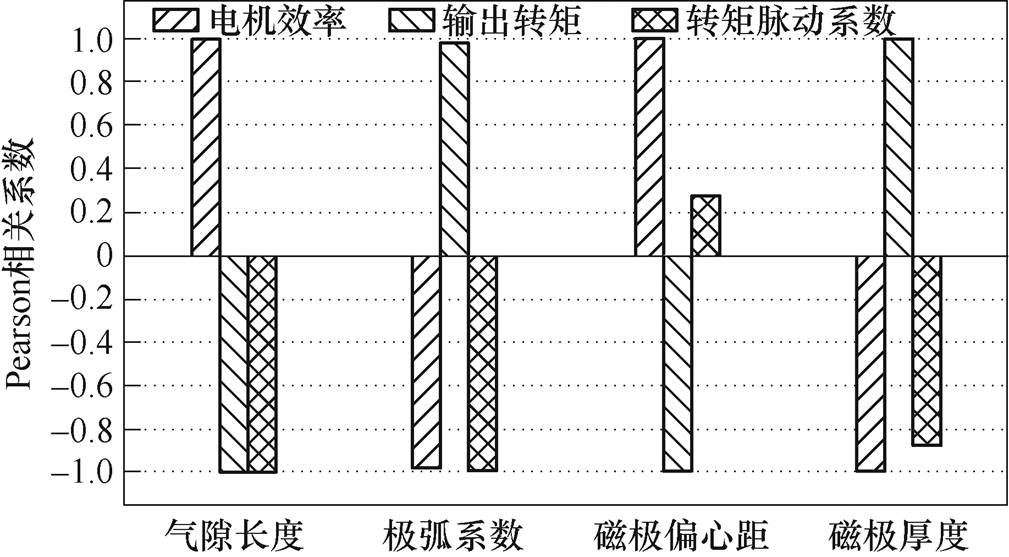
图6 双余度模式Pearson相关系数
Fig.6 The Pearson correlation coefficient of optimization objective in dual mode
由上述计算结果可得到双余度模式下,优化目标的参数敏感度,如图7所示。
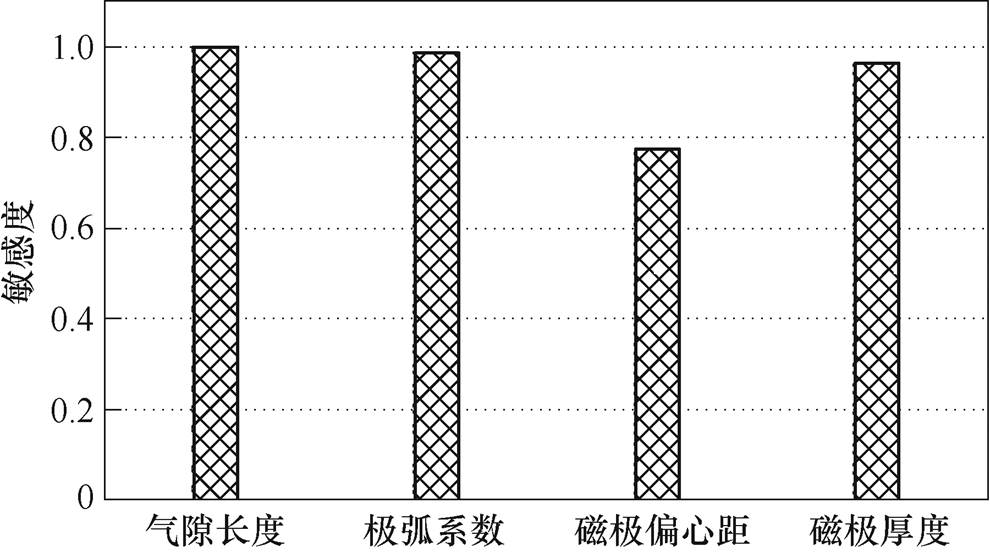
图7 双余度运行模式尺寸参数的敏感度
Fig.7 Sensitivity of parameters in dual mode
由图7可知,在双余度模式下应该选取气隙长度、磁极厚度、极弧系数作为优化因子。
2.4.1 单余度模式的多目标优化
通过参数敏感度分析,已经筛选出在不同工作模式下,对优化目标影响较大的参数作为优化因子。在单余度模式下,选择磁极厚度、极弧系数和磁极偏心距3个优化因子;在双余度模式下,选择气隙长度、磁极厚度和极弧系数3个优化因子。表3已经给出所选优化因子的水平值。
若使用传统排列组合的试验设计方法,则对于一个工作模式,需要进行34=81次计算,使用正交试验方法,建立L16(43)正交试验表,只需要进行16次计算,很大程度上缩短了电机多目标优化设计的计算次数。单余度模式正交试验有限元计算结果见表4。
表4 单余度模式正交试验结果
Tab.4 Orthogonal test results of single mode

计算序号优化因子优化目标 磁极厚度g/ mm极弧系数a磁极偏心距h/mm效率h(%)转矩T/ (N·m)转矩脉动系数K(%) 12.40.7884.611.536 44.678 5 22.40.751084.691.520 73.092 0 32.40.81284.881.503 02.202 6 42.40.851484.771.422 82.347 5 52.60.71084.701.521 64.322 2 62.60.75884.141.549 12.840 8 72.60.81484.891.449 62.559 1 82.60.851284.761.562 21.270 5 92.80.71284.861.513 94.305 5 102.80.751484.941.455 33.294 1 112.80.8883.541.646 62.701 7 122.80.851083.981.639 92.704 2 1330.71484.971.468 23.858 2 1430.751284.611.580 43.326 1 1530.81083.821.636 52.167 5 1630.85882.911.702 64.261 8
由表4可知,第16组参数的转矩最大,第8组参数的转矩脉动系数最小,第13组参数的效率最高。
为进一步分析,计算优化目标的平均值,单余度模式正交试验结果平均值见表5。
表5 单余度模式正交试验结果平均值
Tab.5 The average value of orthogonal test results in single mode

优化目标效率h(%)转矩T/(N·m)转矩脉动系数K(%) 平均值84.441.544 33.120 8
在不同水平值下,各优化因子对应优化目标的平均值结果如图8所示。
根据正交试验结果,计算优化目标的Pearson相关系数所占比重,探究不同优化因子对优化目标的影响程度。Pearson相关系数计算公式按照式(10)计算。
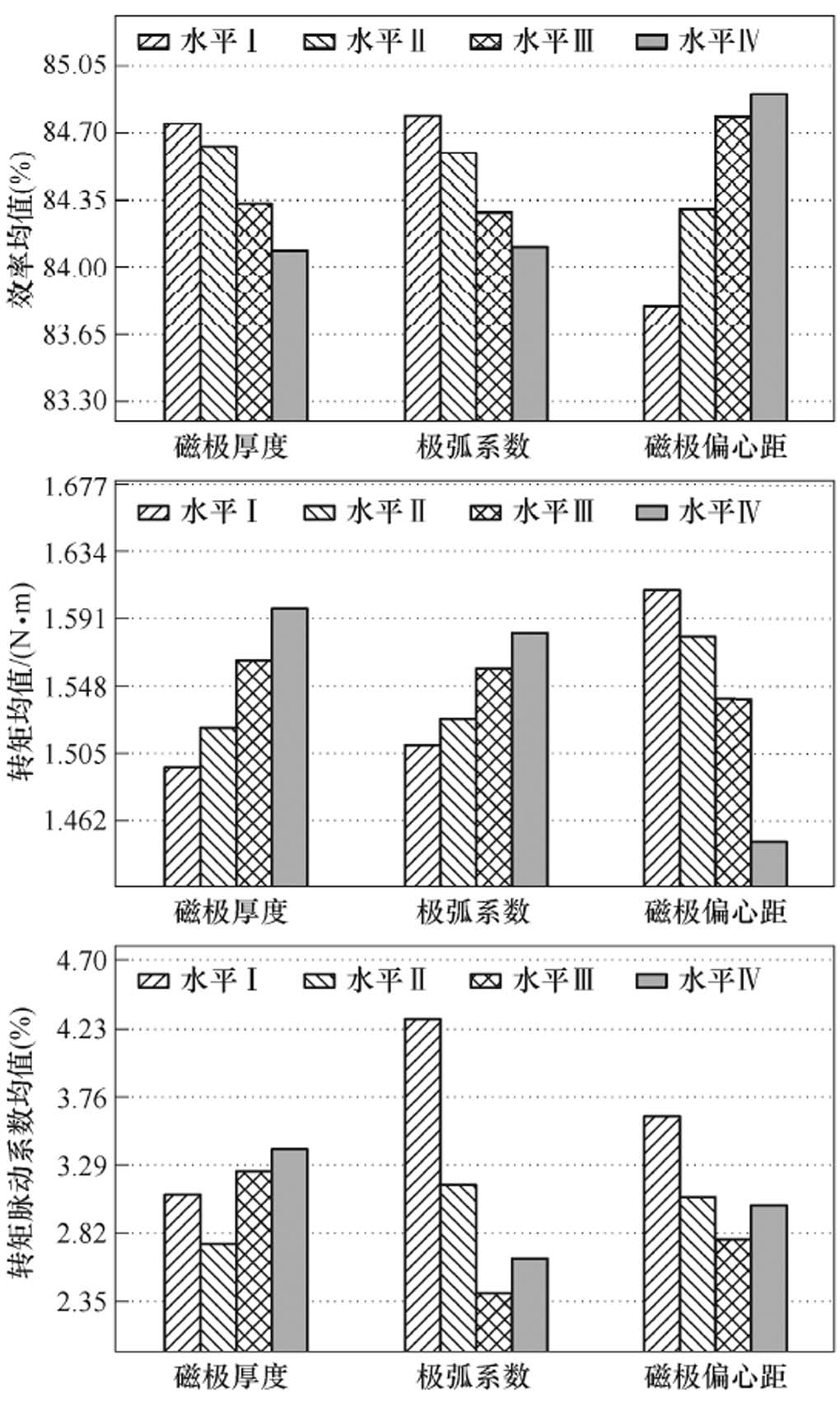
图8 单余度模式各水平值下的优化目标平均值
Fig.8 Average value of optimization objective under each level value of single mode
所求Pearson相关系数占比如图9所示。由图9可知,磁极厚度对于效率和转矩的影响较大,当优化转矩脉动系数时,应重点顾及极弧系数的值。
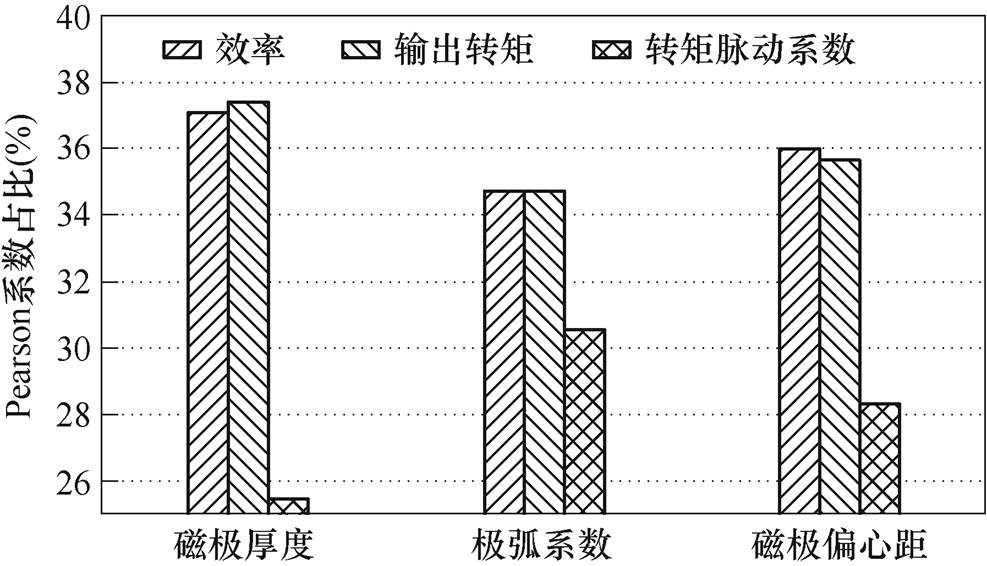
图9 单余度模式下Pearson系数占比
Fig.9 Pearson coefficients ratio of optimization objective in single mode
根据田口法,结合本设计对3个优化目标的侧重点,磁极厚度和磁极偏心距按照效率最大、输出转矩最大的原则选取;极弧系数的选取按照转矩脉动系数最小的原则。单余度模式下,田口法选取的参数组为g(3 mm)a(0.85)h(14 mm)。
由于田口法选取的参数组是各优化目标的折衷,单一优化目标无法达到最优,因此添加上述单一优化目标最优的三组参数,得到单余度模式下的四组准最优参数组,见表6。
表6 单余度运行模式下的准最优参数组
Tab.6 Quasi-optimal parameter groups in single mode

筛选依据准最优参数组 效率最大g(3 mm)a(0.7)h(14 mm) 转矩最大g(3 mm)a(0.85)h(8 mm) 转矩脉动系数最小g(2.6 mm)a(0.85)h(12 mm) 单余度田口法最优g(3 mm)a(0.85)h(14 mm)
2.4.2 双余度模式的多目标优化
由表6结合双余度模式参数敏感分析结果可确定,在四组准最优参数中,对各优化因子的参数水平值进行优化,优化后的水平值见表7。
表7 双余度模式参数水平表
Tab.7 Level value of parameters in dual mode

参数水平Ⅰ水平Ⅱ水平Ⅲ 气隙长度d/mm0.30.50.7 极弧系数a0.70.750.85 磁极厚度g/mm2.62.83
在单余度模式筛选出的准最优参数组基础上,对双余度模式进行优化。此时可建立三因素三水平的正交试验表L9(33),双余度模式下,设计参数水平值以及正交试验数据结果见表7和表8。
表8 双余度模式正交试验结果
Tab.8 Orthogonal test results of dual mode

计算序号优化因子优化目标 磁极厚度g/mm极弧系数a气隙长度δ/mm效率h(%)转矩T/ (N·m)转矩脉动系数K(%) 12.60.70.391.393.510 78.234 4 22.60.750.591.913.387 25.058 1 32.60.850.792.263.264 84.182 2 42.80.70.591.773.372 68.062 8 52.80.750.390.673.637 15.337 6 62.80.850.792.003.341 04.651 5 730.70.591.413.425 37.533 1 830.750.791.883.324 64.405 9 930.850.389.873.784 47.810 9
由表8可知,第3组参数下的效率最高,第3组参数下的转矩脉动系数最低,第9组参数下的转矩最大。
同样,计算优化目标的平均值,见表9。
表9 双余度模式仿真试验结果平均值
Tab.9 The average value of orthogonal test results in dual mode

优化目标效率h(%)转矩T/(N·m)转矩脉动系数K(%) 平均值91.463.449 86.14
分别计算3个优化因子在不同水平值下的优化目标平均值,结果如图10所示。
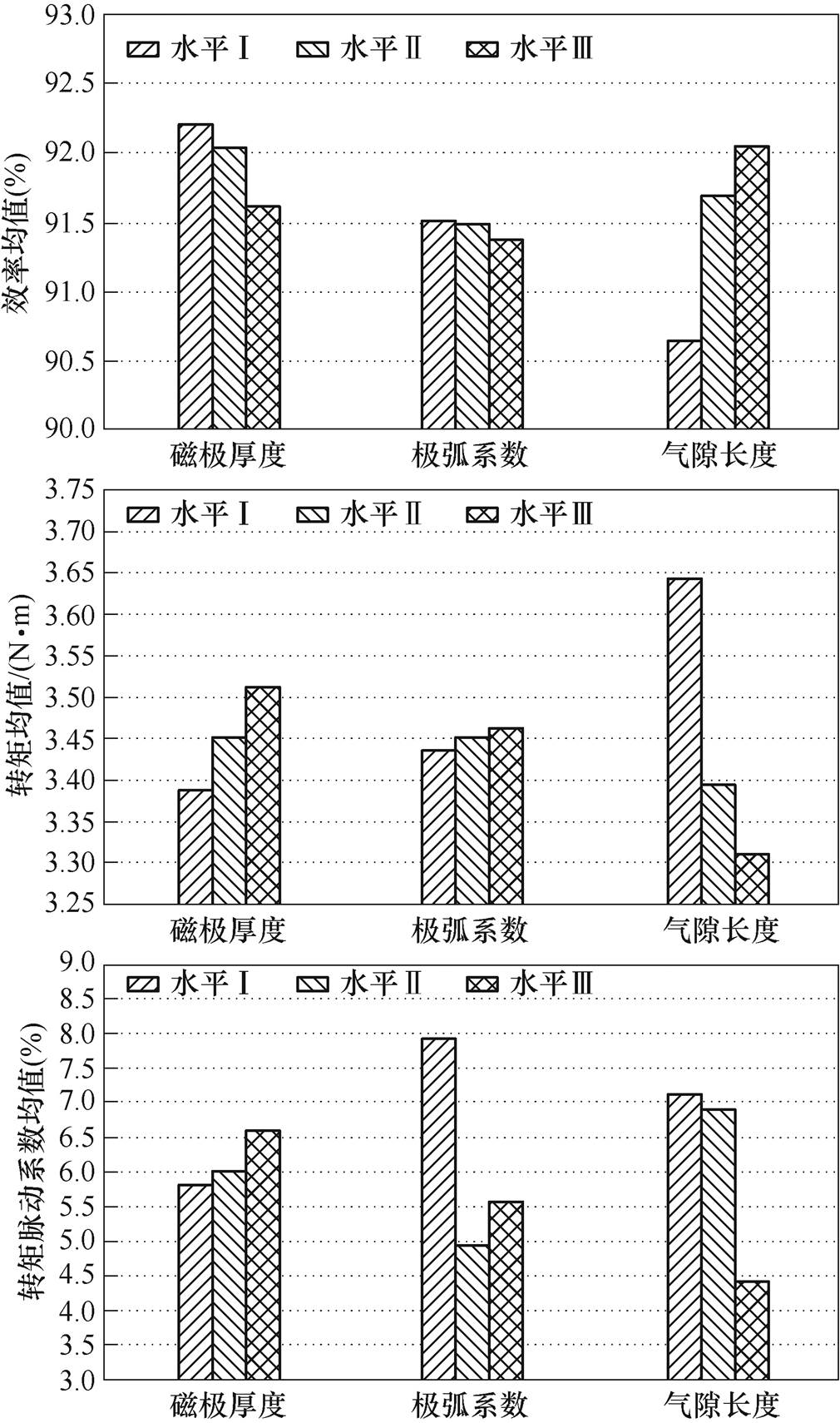
图10 双余度运行模式优化目标平均值
Fig.10 Average value of optimization objective under each level value of dual mode
根据式(10)计算各优化因子对于优化目标的方差,并统计其所占比重,探究优化因子对优化目标的影响程度,优化目标的方差所占比重结果如图11所示。
由图11可知,极弧系数对于效率和转矩脉动系数的影响大,气隙长度和磁极厚度对转矩的影响较大。
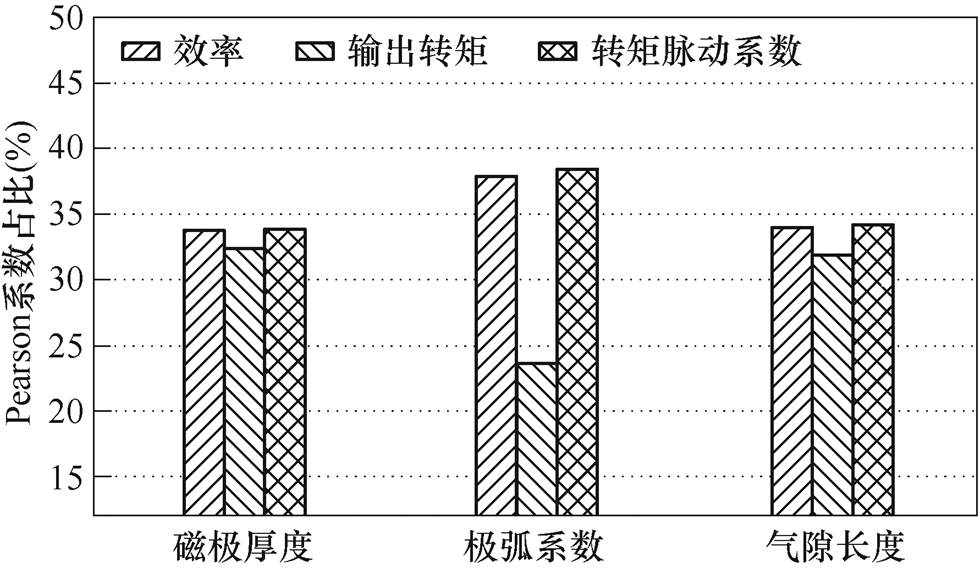
图11 双余度模式下Pearson系数占比
Fig.11 Pearson coefficients ratio of optimization objective in dual mode
根据田口法,磁极厚度的选取考虑效率、转矩和转矩脉动折中选择的原则;极弧系数按照转矩脉动系数最小、效率最高的原则选取;气隙长度按照输出转矩大的原则选取。在双余度模式下,田口法选取的最优参数组为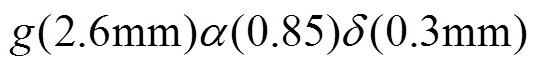 。
。
同理,由于田口法选取的最优参数是对各优化目标的折中,因此添加单一优化目标最优的三组参数组,得到双余度模式下的四组准最优参数组,见表10。
表10 双余度模式筛选的准最优参数组
Tab.10 Quasi-optimal parameter groups in dual mode

筛选依据准最优参数组 效率最大g(2.6 mm)α(0.85)δ(0.7 mm) 转矩最大g(3 mm)α(0.85)δ(0.3 mm) 转矩脉动系数最小g(2.6 mm)α(0.85)δ(0.7 mm) 双余度田口法最优g(2.6 mm)α(0.85)δ(0.3 mm)
由表10及图11,选取的最优参数组为g(2.6 mm)a(0.85)d(0.3 mm),即气隙长度为0.3 mm,磁极厚度为2.6 mm,极弧系数为0.85。
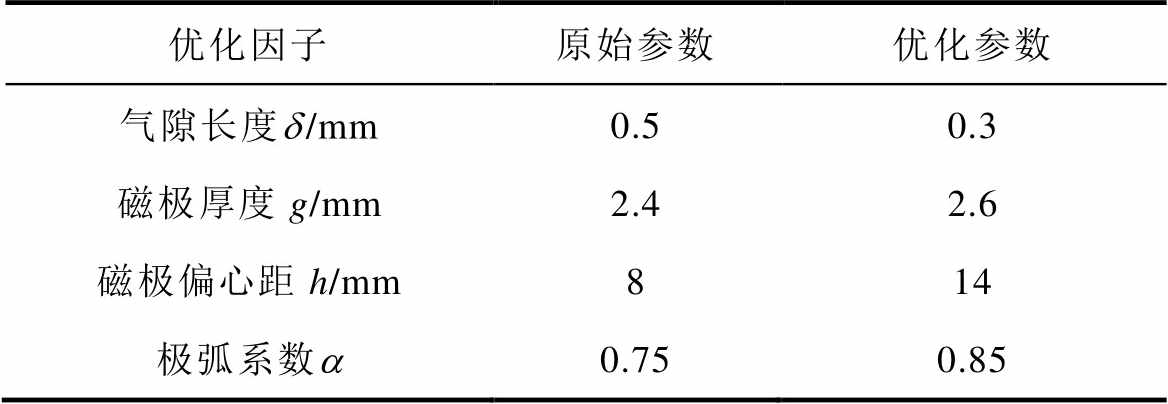
应用两次迭代田口法后,对优化因子的值调整,优化前后的优化因子数值对比见表11。
表11 优化前后的优化因子数值对比
Tab.11 Comparison of optimization factor before and after optimization
优化因子原始参数优化参数 气隙长度d/mm0.50.3 磁极厚度g/mm2.42.6 磁极偏心距h/mm814 极弧系数a0.750.85
单余度和双余度模式优化前后,电机的优化目标有限元计算结果对比见表12和表13。
表12 单余度模式优化前后目标参数值对比
Tab.12 Comparison of objective values before and after single mode

效率h(%)输出转矩T/(N·m)转矩脉动系数K(%) 优化前84.363 11.483 72.891 4 优化后84.993 31.500 92.098 7 优化率(%)0.751.1627.42
表13 双余度模式优化前后目标参数值对比
Tab.13 Comparison of objective values before and after dual mode

效率h(%)输出转矩T/(N·m)转矩脉动系数K(%) 优化前90.372 13.446 87.842 1 优化后92.048 83.468 15.954 3 优化率(%)1.860.6224.07
单余度模式的转矩脉动系数优化率为27.42 %,双余度模式转矩脉动系数的优化率为24.07 %。两种模式下均使得效率和转矩脉动系数得到明显提升,转矩的提升较小,但完全满足设计要求。
基于以上优化设计结果,制作原理样机,并搭建测试平台展开实验验证,其测试平台如图12所示。

图12 原理样机测试平台
Fig.12 Prototype and test platform
应用泰克示波器MDO3024测得样机的线反电动势波形及其谐波,如图13所示。
实测线反电动势峰峰值为324 V,有效值为114.6 V,而有限元计算的线反电动势为115.1 V,误差为0.5 V。分析线反电动势的谐波,其总谐波畸变率(Total Harmonic Distortion, THD)为1.38 %。
应用泰克MDO3024示波器测试余度之间相位差值如图14所示。两余度的同相线反电动势相位差仅为1.607 °电角度。
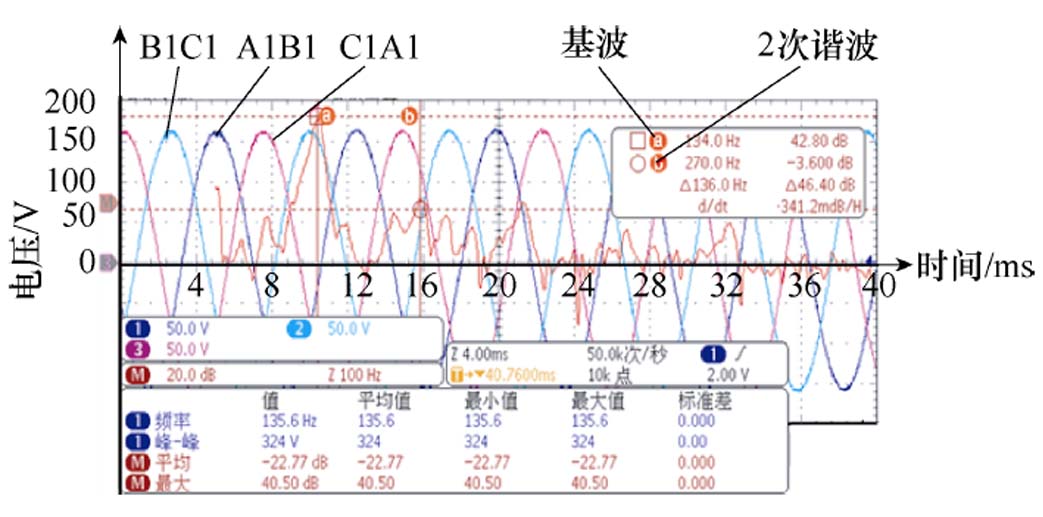
图13 样机线反电动势波形
Fig.13 Line back-electromotive force waveforms
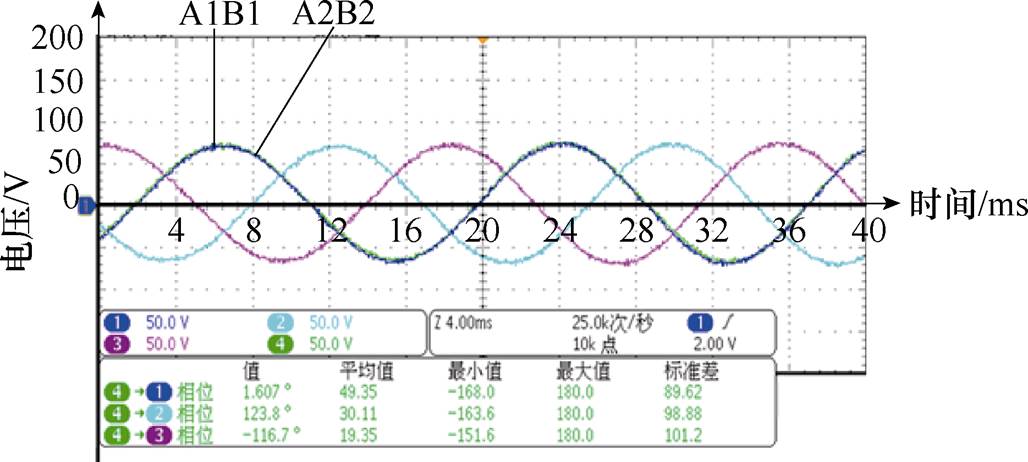
图14 余度间相位差测试
Fig.14 Phase difference between redundancies
在加载工况下,分别测试样机的额定转矩。单余度模式下,样机输出转矩平均值为1.494 3 N·m,输出转矩脉动系数为2.32 %。双余度模式下,样机输出转矩平均值为3.450 9 N·m,转矩脉动系数为6.52 %。
在不同的工作模式下,样机效率、转矩以及转矩脉动系数有限元分析结果与实测结果对比见表14。
表14 有限元分析结果和实测结果对比
Tab.14 Comparison of finite element analysis and experimental results

优化目标单余度模式双余度模式 设计值实测值误差(%)设计值实测值误差(%) 电机效率(%)84.9983.821.4092.0590.491.72 输出转矩T/(N·m)1.500 91.494 30.443.468 13.450 90.50 转矩脉动系数(%)2.102.329.485.956.528.74
由表14对比数据可知,效率和转矩的实测值与设计值吻合度较高,而转矩脉动系数的设计值和实测值的误差稍大,这是因为实测时存在轴心偏差、联轴器形变等因素,导致实测值与理想设计值有较大误差。单余度模式下的设计吻合度与双余度模式下的设计吻合度接近,表明样机在容错运行时能保持相应的性能。
本文针对DRPMSM电机迭代田口法多目标优化算法存在的不足,提出基于Pearson相关系数参数敏感度分析的改进迭代田口法多目标优化算法。该算法考虑了电机的双余度正常运行工作模式和单余度容错运行工作模式两种工况,可解决田口法两个水平值之间无法寻优的问题。通过优化前后的性能参数对比分析及样机的实验结果分析,验证了本文所提改进迭代田口法优化算法的有效性及实用性,总结研究过程及其结果,可得到以下结论:
1)引入Pearson相关系数,可以直观量化优化因子对电机性能的影响敏感度,有助于优化设计前期对优化因子的筛选。
2)采用先针对单余度运行模式,再针对双余度运行模式的顺序进行迭代优化,可确保电机容错运行模式下的性能,并缩小正常工作模式下优化因子的寻优范围,使得田口法优化结果能兼顾多模式运行工况。
3)针对不同工作模式进行迭代优化,能够兼顾不同运行模式下敏感度较高的优化因子,对优化因子的选取更加全面。既考虑了同一工作模式下优化因子对电机性能的敏感度,也考虑了不同工作模式下,同一优化因子的参数敏感度变化。
4)基于改进迭代田口法优化的样机实验,验证了本文所提优化方法的有效性。其中,转矩脉动系数的优化效果明显,单余度模式下降低了27.42 %,双余度模式下降低了24.07 %。
参考文献
[1] Marignetti F, Volpe G, Mirimani S M, et al. Electro- magnetic design and modeling of a two-phase axial- flux printed circuit board motor[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 67-76.
[2] Yang Yukai, Chen Yiguang, Hao Weijie, et al. Vibration analysis of dual redundant permanent magnet synchronous motor in two operating condi- tions[C]//2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 2019: 1-6.
[3] 戴睿, 张岳, 王惠军, 等. 基于多物理场近似模型的高速永磁电机多目标优化设计[J]. 电工技术学报, 2022, 37(21): 5414-5423.
Dai Rui, Zhang Yue, Wang Huijun, et al. Multi- objective optimization design of high-speed per- manent magnet machine based on multi-physics approximate model[J]. Transactions of China Elec- trotechnical Society, 2022, 37(21): 5414-5423.
[4] 李祥林, 李金阳, 杨光勇, 等. 电励磁双定子场调制电机的多目标优化设计分析[J]. 电工技术学报, 2020, 35(5): 972-982.
Li Xianglin, Li Jinyang, Yang Guangyong, et al. Multi-objective optimization analysis of electric- excitation double-stator field-modulated machine[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 972-982.
[5] 赵玫, 于帅, 邹海林, 等. 聚磁式横向磁通永磁直线电机的多目标优化[J]. 电工技术学报, 2021, 36(17): 3730-3740.
Zhao Mei, Yu Shuai, Zou Hailin, et al. Multi- objective optimization of transverse flux permanent magnet linear machine with the concentrated flux mover[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3730-3740.
[6] 谢冰川, 张岳, 徐振耀, 等. 基于代理模型的电机多学科优化关键技术综述[J]. 电工技术学报, 2022, 37(20): 5117-5143.
Xie Bingchuan, Zhang Yue, Xu Zhenyao, et al. Review on multidisciplinary optimization key tech- nology of electrical machine based on surrogate models[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5117-5143.
[7] 吉敬华, 沈人洁, 徐亮, 等. 考虑运行工况的模块化双永磁游标电机多工作点优化设计[J]. 电工技术学报, 2022, 37(22): 5649-5659.
Ji Jinghua, Shen Renjie, Xu Liang, et al. Multi- working point optimization of modular double permanent-magnet vernier motor considering oper- ation condition[J]. Transactions of China Electro- technical Society, 2022, 37(22): 5649-5659.
[8] Chen Hao, Lee C H T. Parametric sensitivity analysis and design optimization of an interior permanent magnet synchronous motor[J]. IEEE Access, 2019, 7: 159918-159929.
[9] 刘国海, 王艳阳, 陈前. 非对称V型内置式永磁同步电机的多目标优化设计[J]. 电工技术学报, 2018, 33(增刊2): 385-393.
Liu Guohai, Wang Yanyang, Chen Qian. Multi- objective optimization of an asymmetric V-shaped interior permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 385-393.
[10] 徐磊, 朱孝勇, 张超, 等. 磁极径向组合轴向磁场永磁电机转矩品质分析与优化设计[J]. 中国电机工程学报, 2021, 41(6): 1971-1983.
Xu Lei, Zhu Xiaoyong, Zhang Chao, et al. Torque quality analysis and optimization design of axial field machine with radial combined permanent magnet poles[J]. Proceedings of the CSEE, 2021, 41(6): 1971-1983.
[11] Gao Jian, Dai Litao, Zhang Wenjuan. Improved genetic optimization algorithm with subdomain model for multi-objective optimal design of SPMSM[J]. CES Transactions on Electrical Machines and Systems, 2018, 2(1): 160-165.
[12] Assaad B, El kadri Benkara K, Vivier S, et al. Thermal design optimization of electric machines using a global sensitivity analysis[J]. IEEE Transa- ctions on Industry Applications, 2017, 53(6): 5365- 5372.
[13] Chakkarapani K, Thangavelu T, Dharmalingam K, et al. Multiobjective design optimization and analysis of magnetic flux distribution for slotless permanent magnet brushless DC motor using evolutionary algorithms[J]. Journal of Magnetism and Magnetic Materials, 2019, 476: 524-537.
[14] Wu Shengnan, Sun Xiangde, Tong Wenming. Opti- mization design of high-speed interior permanent magnet motor with high torque performance based on multiple surrogate models[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(3): 235-241.
[15] Lei Gang, Liu Chengcheng, Li Yanbin, et al. Robust design optimization of a high-temperature super- conducting linear synchronous motor based on Taguchi method[J]. IEEE Transactions on Applied Superconductivity, 2019, 29(2): 1-6.
[16] Guo Youquan, Si Jikai, Gao Caixia, et al. Improved fuzzy-based Taguchi method for multi-objective optimization of direct-drive permanent magnet syn- chronous motors[J]. IEEE Transactions on Magnetics, 2019, 55(6): 1-4.
[17] 司纪凯, 严作光, 聂瑞, 等. 120°相带环形绕组圆筒型永磁直线发电机定位力降低的优化设计(英文)[J]. 电工技术学报, 2021, 36(6): 1138-1148.
Si Jikai, Yan Zuoguang, Nie Rui, et al. Optimal design of a tubular permanent magnet linear generator with 120°phase belt toroidal windings for detent force reduction[J]. Transactions of China Electro- technical Society, 2021, 36(6): 1138-1148.
[18] Arkadan A A, Al Aawar N. Taguchi-EM-AI design optimization environment for SynRM drives in traction applications[C]//2020 International Applied Computational Electromagnetics Society Symposium (ACES), Monterey, CA, USA, 2020: 1-2.
[19] He Jingxiong, Li Guoli, Zhou Rui, et al. Optimization of permanent-magnet spherical motor based on Taguchi method[J]. IEEE Transactions on Magnetics, 2020, 56(2): 1-7.
[20] 曹永娟, 冯亮亮, 毛瑞, 等. 轴向磁场永磁记忆电机多目标分层优化设计[J]. 中国电机工程学报, 2021, 41(6): 1983-1992.
Cao Yongjuan, Feng Liangliang, Mao Rui, et al. Multi-objective stratified optimization design of axial-flux permanent magnet memory motor[J]. Pro- ceedings of the CSEE, 2021, 41(6): 1983-1992.
[21] Du Guanghui, Zhou Qixun, Liu Shulin, et al. Multiphysics design and multiobjective optimization for high-speed permanent magnet machines[J]. IEEE Transactions on Transportation Electrification, 2020, 6(3): 1084-1092.
[22] 张玉峰, 孟庆品, 苏涛, 等. 基于田口法的双余度永磁同步电机优化设计[J]. 微电机, 2021, 54(9): 37-42.
Zhang Yufeng, Meng Qingpin, Su Tao, et al. Optimal design of dual-redundancy permanent magnet syn- chronous motor based on Taguchi method[J]. Micro- motors, 2021, 54(9): 37-42.
[23] Gieras J F. Permanent magnet motor technology: design and applications[M]. 3rd Edition. Boca Raton: CRC Press, 2009.
[24] 陈世坤. 电机设计[M]. 北京: 机械工业出版社, 2000.
Abstract Compared with the permanent magnet synchronous motor (PMSM), the dual redundancy permanent magnet synchronous motor (DRPMSM) has more working states and optimized design parameters. Most of the multi-objective optimization methods for DRPMSM are based on the optimization design methods of PMSM, which is difficult to meet the optimization requirements of DRPMSM in multiple working states. Moreover, the traditional Taguchi method cannot optimize the gap between the two-level values of the parameters. Therefore, this paper proposes an improved iteration Taguchi method for the DRPMSM, combining the Taguchi method with a sequential optimization strategy. The sensitivity of parameters based on the Pearson correlation coefficient is filtered. The effectiveness of the proposed method is verified by the finite element analysis (FEA) and experimental results.
Firstly, the sensitivity of parameters was calculated, and the parameters were screened for the single redundancy working state and dual redundancy working state, respectively. Secondly, the Taguchi method was used in the single redundancy working state. Four groups of parameters were obtained, namely, the optimal efficiency, the optimal torque, the optimal torque ripple coefficient, and the optimal Taguchi. Next, the gap of two-level values of the parameters was scaled down under the dual redundancy working state. In addition, the Taguchi method was used again to optimize the DRPMSM motor in the dual redundancy working state. Finally, the optimal values of the parameters were selected. In the improved iterative Taguchi method, the parameters set obtained from single redundancy working state limits the gap of two-level values of the dual redundancy working state parameters. The issue that the traditional Taguchi method cannot optimize the gap of two-level values was addressed.
Simulation results on the DRPMSM show that, for single redundancy working state, the efficiency of the motor is increased by 0.75 %, the output torque is increased by 1.16 %, and the torque ripple coefficient is decreased by 27.42 %. Furthermore, for dual redundancy working state, the efficiency of the motor is increased by 1.86 %, the output torque is increased by 0.62 %, and the torque ripple coefficient is decreased by 24.07 %. The error of the FEA results is less than 10 % compared with the experimental test of the prototype. The error of efficiency and the error output torque of the FEA and experimental are less than 2 %. The error of the FEA and experimental torque ripple coefficient is large due to the axial deviation and coupler deformation. The design motor performances in single and dual redundancy working states are close to that of the experimental test of the prototype, which indicates that the prototype can maintain the corresponding performance in single and dual redundancies.
The following conclusions can be drawn from the simulation analysis and the prototype experiment. (1) The introduction of the Pearson correlation coefficient is helpful to select parameters. (2) The combination of the Taguchi method and sequential optimization strategy can address the issue of optimizing the gap of two-level values of the parameter in the Taguchi method. Different working states of the motor can also be considered. (3) The parameters with high sensitivity under different states can be considered, and the selection among parameters is comprehensive.
keywords:Dual-redundancy permanent magnet synchronous motor (DRPMSM), sensitivity analysis, iterations Taguchi method, multi-objective optimization, finite element analysis (FEA)
DOI: 10.19595/j.cnki.1000-6753.tces.220768
中图分类号:TM351
国家自然科学基金面上资助项目(52177056)。
收稿日期 2022-05-09
改稿日期 2022-10-31
张玉峰 男,1977年生,副教授,硕士生导师,主要研究方向为高性能电机设计及控制、超导应用技术等。E-mail: xkdzhangyufeng@xust.edu.cn(通信作者)
高文韬 男,1996年生,硕士研究生,研究方向为永磁电机设计及多目标优化等。E-mail: gaowentao0704@163.com
(编辑 崔文静)