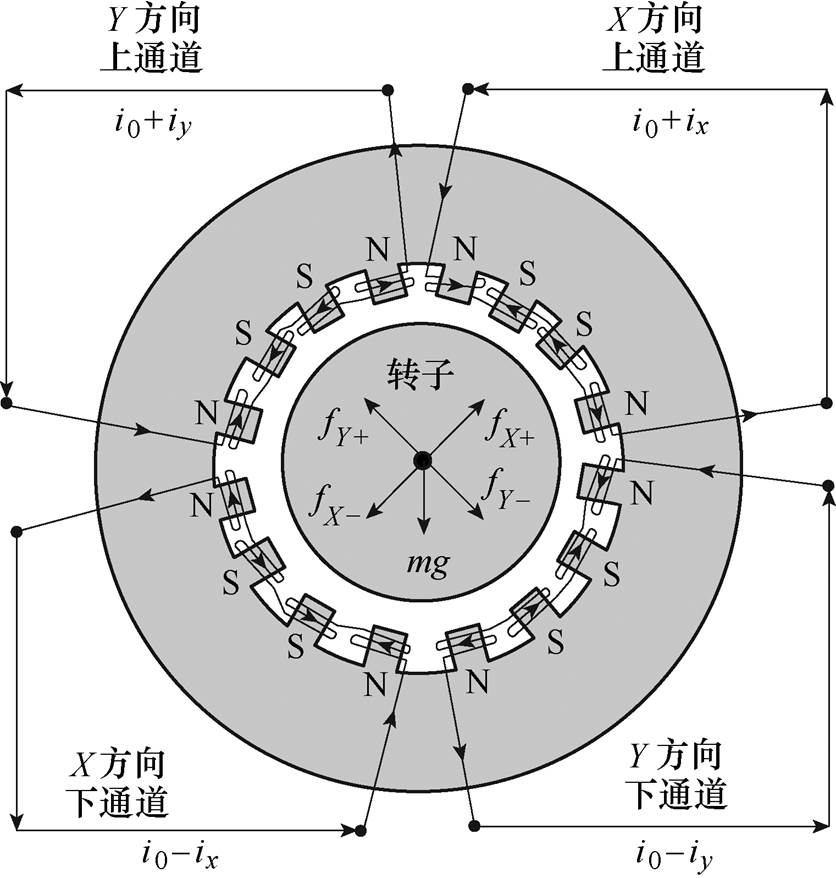
图1 16极径向磁轴承线圈分布
Fig.1 Distribution of coils in 16-pole radial AMB
摘要 通道故障后，磁轴承系统的动态承载力将发生变化，该文建立了考虑部分通道故障的磁轴承系统模型以分析该变化。首先以单自由度模型为例，分析由转子位移及通道电流计算系统动态承载力的方法。其次建立考虑动载荷、转子不平衡量以及故障通道电磁力变化的四自由度系统模型，并将单自由度系统承载力分析方法应用于该系统模型，从而得到四自由度系统动态承载力。然后分析通道故障后控制参数对系统动态承载力的影响。最后进行仿真与实验的对比。结果表明，故障前后转子最大位移幅值误差小于3.9 %，验证了所建模型用于计算系统动态承载力的有效性。
关键词：磁轴承 动态承载力 不平衡量 通道故障 控制参数
主动磁轴承（Active Magnetic Bearings, AMB）（以下称磁轴承）通过可控电磁力实现定转子的无机械接触，因此具有运行过程中无磨损、无需润滑等优点，在飞轮储能、高速电机等领域已得到了广泛应用[1-2]。为确保磁轴承系统的安全稳定运行，国内外学者针对磁轴承系统的故障诊断和容错控制开展了许多研究[3-4]，对产生电磁控制力的磁轴承电磁线圈通道（以下称通道）故障进行容错控制是其中一个重要的研究方向。但现有研究主要集中于通道故障诊断以及产生故障后系统稳定运行[5-6]，对故障前后系统动态承载力变化的相关研究较少。然而，对磁轴承系统尤其是通道故障后的系统而言，准确计算动态承载力是确定系统运行工况的前提，因此本文通过建立含故障通道的磁轴承系统模型对其动态承载力进行分析。
根据侧重点的区别可将已有研究分为重点考虑动载荷频率的影响以及重点考虑动载荷幅值的影响两类。
（1）根据转子动力学理论，转子在临界转速运行时振动幅值会大幅增大[7]，此时动载荷频率对系统稳定性影响远大于幅值影响，因此相关研究主要考虑变化的动载荷频率带来的影响，可分为搭建系统模型以计算临界转速与设计控制算法以实现跨临界转速运行两类。
在系统建模方面，文献[8]根据磁轴承系统的结构框图得到动载荷与转子位移的幅相关系，由此定义了复阻尼系数与复刚度系数，并分析了该系数与动载荷频率的关系，但模型为单自由度（Degrees of Freedom, DOF）磁轴承系统。文献[9-12]在上述方法的基础上，考虑径向四自由度模型的交叉刚度与交叉阻尼，通过集总质量法或有限元法建立转子的动力学方程，并通过实验证明该方程能准确计算系统临界转速。为验证理论分析得到的系统复刚度的准确性，文献[13]基于傅里叶分析的方法设计了复刚度的自动测量程序。
为实现磁轴承系统的跨临界转速运行，已有研究主要采用零传递力补偿与零电流补偿两种思路[14-15]。零传递力补偿的控制目标是使转子绕惯性主轴旋转，以此减小转子传递到定子的电磁力的反作用力，但此时转子位移振动幅值较大；零电流补偿的控制目标是使转子绕几何轴线转动，转子位置精度高，但电磁力的反作用力会带来定子的振动。
（2）当转子工作转速远离临界转速时，动载荷频率对系统稳定性的影响较小，相关研究主要分析动载荷幅值对系统动态性能的影响，文献[16]分析了转子所受动静载荷幅值比与转子位移气隙比的关系，并由此计算了动态承载力，但仅进行了公式推导，没有进行实验验证。文献[17]假设电磁力交流分量与动载荷反相，此时转子的位移幅值由电磁力与动载荷的幅值差决定，由此可计算系统动态承载力，但单纯采用PID控制无法实现交流电磁力与扰动力等大反相。因此，文献[18]基于变角度搜索算法计算转子位移幅值与相位，并由此计算产生与扰动力等大反相的电磁力所需控制电流，但为了提高搜索速度需要增大搜索步长，结束搜索后的电磁力仍不可能与扰动力完全反相，且难以分析转子位移幅值与动载荷的关系。发生通道故障后，差动磁轴承结构变为非差动结构，文献[19]证明在系统参数相同情况下，差动磁轴承的动态承载力是非差动磁轴承的两倍以上，但该结论同样基于电磁力与动载荷反相的理想条件。
由于本文研究的磁轴承系统的工作转速远离临界转速，因此主要考虑动载荷幅值对系统稳定性的影响。
对于本文研究的典型磁轴承结构，通道故障后无法通过广义偏置电流线性化的方法[20]维持系统的线性控制，已有研究针对非差动结构开展了非线性控制的研究，主要有反馈线性化、基于BP神经网络[21-22]等方法，但均没有对通道故障后的系统动态承载力进行分析，且已有研究在考虑动载荷幅值对系统稳定性的影响时大多停留在理论分析层面，忽略了转子不平衡量对实际系统的影响，所建模型与实际偏差较大。
针对上述不足，本文建立了考虑部分通道故障的磁轴承系统模型，并由此分析系统动态承载力。首先考虑动载荷、转子不平衡量以及故障通道电磁力变化的影响，建立了磁轴承系统模型。基于该模型得到各自由度转子位移、通道电流，并由此计算系统动态承载力。仿真与实验结果的对比证明了该模型用于计算故障前后系统动态承载力的准确性，能为磁轴承系统选择合适的运行工况提供理论依据。
本文以典型的16极径向磁轴承为对象开展研究，其拓扑结构和线圈绕制方式如图1所示。相邻4个磁极以NSSN的形式构成一组，4组线圈分别嵌放于4组磁极上，可分别产生fX+、fX-、fY+、fY- 4个方向的电磁力。每组线圈与对应的控制器、功率放大器一起构成一个通道。为便于区分，本文将产生电磁力（fX+、fY+）效果为克服转子重力的称为上通道，反之称为下通道。
图1 16极径向磁轴承线圈分布
Fig.1 Distribution of coils in 16-pole radial AMB
根据虚功原理，单个通道产生的电磁力F为
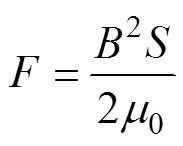（1）
式中，B为气隙磁通密度；S为通道磁极在转子上的投影面积；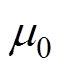
为真空磁导率。忽略铁磁材料饱和和漏磁，气隙磁通密度B为
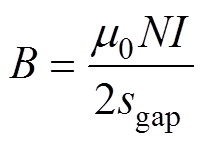（2）
式中，N为线圈匝数；I为线圈电流；sgap为电磁气隙长度。综合式（1）、式（2）可得
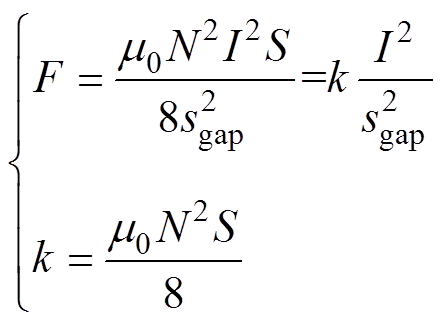（3）
式中，k为与磁轴承结构有关的常数。以X方向为例，当采用差动控制时，假设上、下通道偏置电流为i0，转子在X方向上偏离平衡位置位移x时控制电流为ix，则X方向上、下通道电流分别为i0±ix，设转子在平衡位置处时的电磁气隙长度为s0，则通过对电磁力求偏导可求出电流刚度ki、位移刚度ks分别为
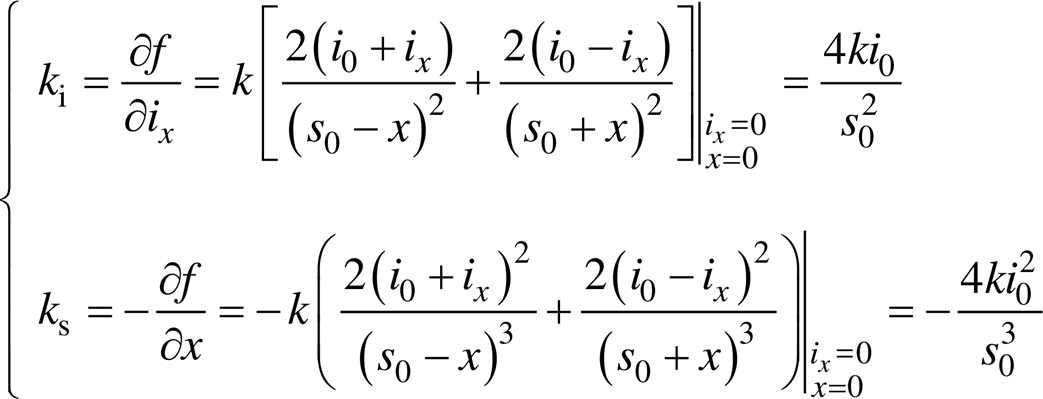（4）
磁轴承系统控制架构采用最典型的分散PID+双闭环系统，其中内环为电流环，外环为位移环。由于内环带宽通常远大于外环，故本文暂忽略电流内环的动态特性。这时控制电流可以计算为
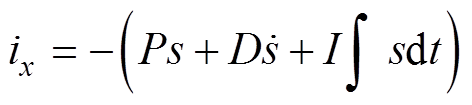（5）
式中，P、I、D分别为比例、积分、微分参数；s为位移传感器测得转子位移。将式（5）代入式（4）得差动通道产生电磁力Fnet为
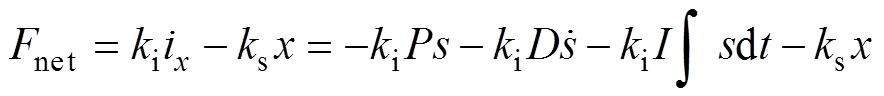（6）
式中，x为轴承处转子位移，与s值不同。
在单自由度电磁力表达式的基础上可以对实际的磁轴承系统进行动力学建模。对于本文研究的含有两个径向磁轴承和一个轴向磁轴承的磁轴承系统，由于轴径向解耦，在考虑径向动载荷对系统的影响时可以仅分析径向四自由度动力学模型。由于本文研究的磁轴承系统的工作转速小于一阶临界转速的50 %，故将转子视为刚体建立动力学模型。为区分转子两端，将与电机相连一端称为伸端，另一端称为非伸端，四自由度转子受力示意图如图2 所示。
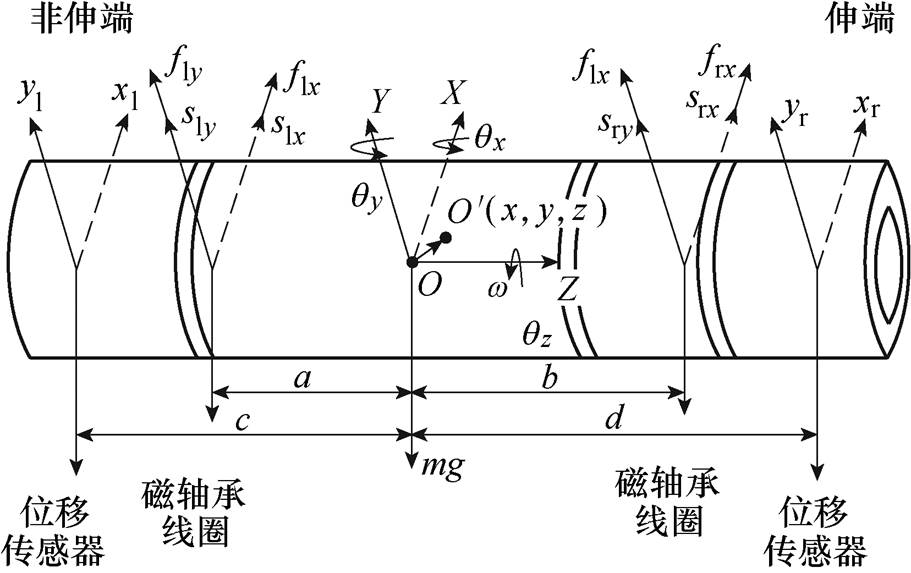
图2 四自由度转子受力示意图
Fig.2 Diagram of force on 4-DOF rotor
以转子处在平衡位置时的质心O点为原点建立OXYZ定子坐标系，在该坐标系下，转子运动后的质心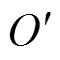
点的坐标为（x, y, z），非伸端、伸端位移传感器的Z轴方向位移为c、d，非伸端、伸端径向磁轴承的Z轴方向位移为a、b，非伸端、伸端磁轴承线圈处的转子X方向位移为slx、srx，Y方向为sly、sry，非伸端、伸端位移传感器测得转子X方向位移为xl、xr，Y方向为yl、yr，非伸端、伸端在X、Y方向电磁合力为flx、fly、frx、fry，mg为转子重力，m为转子质量，g为重力加速度，转子绕X、Y、Z轴旋转的弧度分别为qx、qy、qz，转动惯量分别为Jx、Jy、Jz，由于转子绕X、Y轴转动范围受定子限制，qx、qy值相对较小，而qz值随时间t与转子动角速度w 变化。
考虑陀螺效应，列写四自由度转子动力学方程为
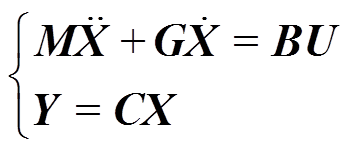（7）
其中
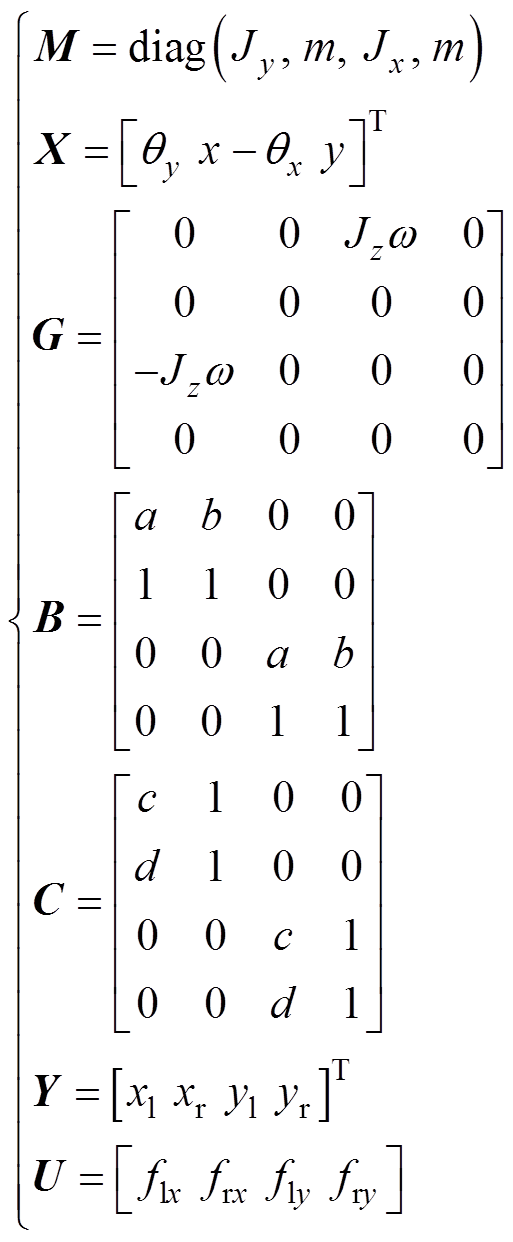（8）
系统稳定后，可忽略积分环节对控制电流的影响，当各自由度参考位移均为0时，式（7）变为
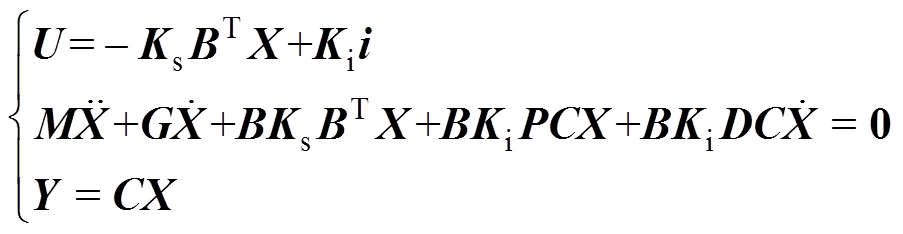（9）
当各自由度的控制参数、系统参数相同时有
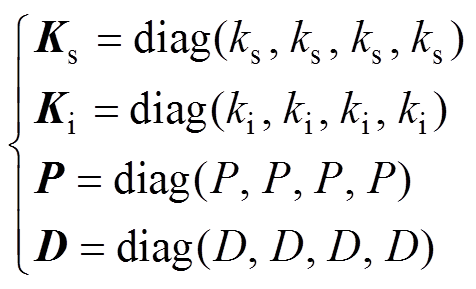（10）
首先以单自由度磁轴承为例分析系统的动态承载力。此时转子仅受一对差动的磁轴承控制，在频率为f的动载荷作用下达到稳定状态时转子位移、控制电流的交流分量角速度w=2pf，忽略积分环节对控制电流的影响，各变量的交流分量幅值及相互关系可用相量图表示，单自由度转子受力分析如图3所示。图3中，xm为转子位移幅值，im为控制电流交流分量幅值，fdynm为动载荷幅值，fcoilm为电磁力交流分量幅值，mw2xm为加速度力幅值，a 为动载荷与转子位移相位差。
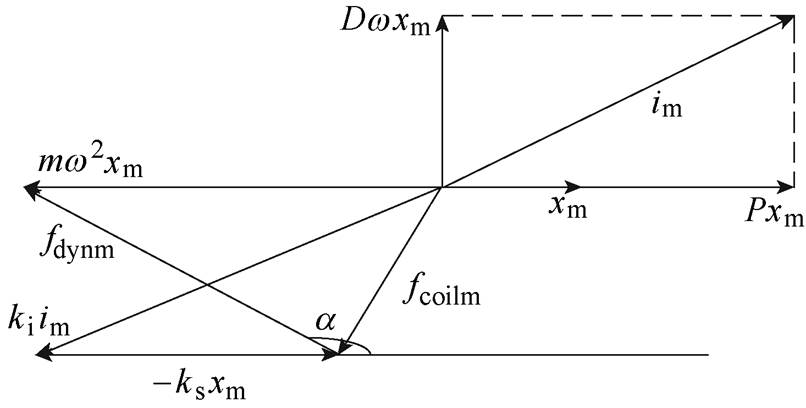
图3 单自由度转子受力分析
Fig.3 Analysis of force on single DOF rotor
当转子仅受重力作用在平衡位置静态悬浮时，静态控制电流is为
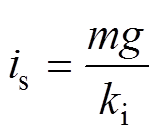（11）
fcoilm与xm之比用kfx表示为
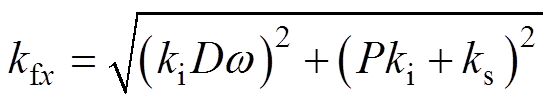（12）
对于这样一个线性系统，在动载荷幅值逐渐增大的过程中，转子位移幅值逐渐增大会与定子发生碰撞。由于磁轴承系统的定子上装有保护轴承以防止碰撞损害线圈等部件，转子从平衡位置运动到发生碰撞的位移幅值就是保护气隙值xtd。由于本文研究的纯电励磁磁轴承的通道电流方向固定，因此通道电流最小值为零。通道电流过大时气隙磁通密度饱和不可忽略，稳定运行边界不易确定，因此本文将磁轴承饱和电流作为临界状态下的最大电流imax，一般为两倍偏置电流。
正常情况下，差动的上下通道电流和为2i0，当其中一个通道达到最大（小）电流临界状态时，另一个通道同时达到最小（大）电流临界状态，因此仅需考虑上或下通道电流即可。本文以上通道为例，由于is恒为正，在fdynm增大过程中，上通道电流将先达到最大电流。因此，当磁轴承参数固定时，随着动载荷幅值的增大可根据转子质量定义两种临界状态。
（1）转子质量较小，is较小。在上通道电流达到最大值之前，转子位移幅值达到保护气隙值。
（2）转子质量较大，is较大。在转子位移幅值达到保护气隙值前，上通道电流达到最大值。
当xm=xtd时，系统达到位移临界状态，由图3可知，此时临界控制电流幅值ilj为
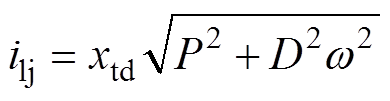（13）
在两类临界状态的分界点处，两个临界状态同时满足
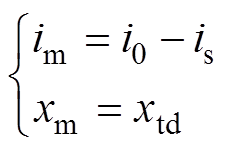（14）
对应的转子质量mfj为
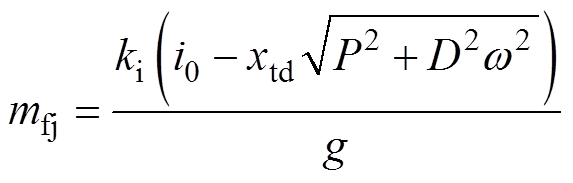（15）
由图3有
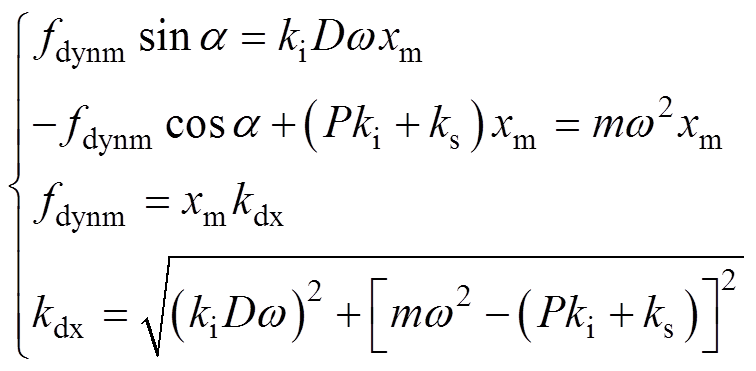（16）
式中，kdx为fdynm与xm的比值。由此可确定不同转子质量下的动态承载力幅值fdynmax为
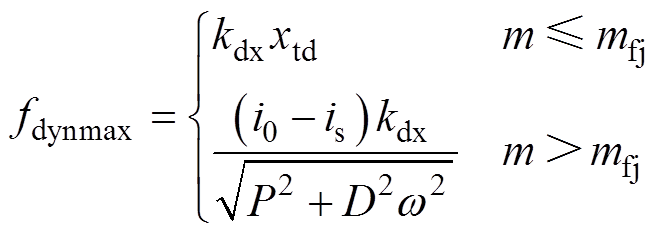（17）
对于四自由度磁轴承系统，已有研究往往忽略了动载荷作用点的轴向位移所带来的力矩影响，所建动力学模型难以准确计算转子实际位移幅值。为提高模型准确性，本节所建模型中动载荷幅值为fdyn作用点的轴向位移为ldyn。当转子以w 的角速度旋转t时间后，动载荷在X、Y方向的投影fdynx、fdyny为
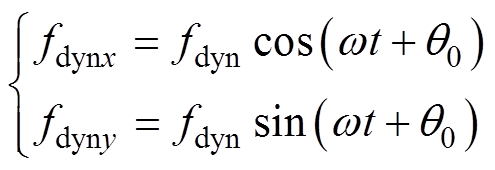（18）
式中，q0为动载荷初始相位。对于细长型转子，可以忽略陀螺效应的影响，此时四自由度转子动力学方程由式（9）变为
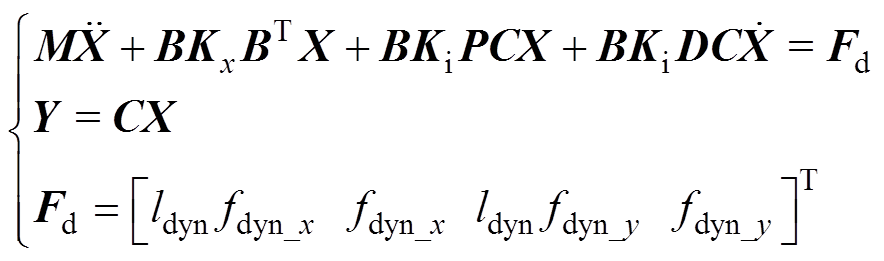（19）
式中，Fd为外力及其力矩组成的向量。
由于实验中得到的位移为传感器测量位移，因此将状态空间方程转化为对测量矩阵Y的表达式可直接分析外部载荷与位移测量值的关系。以外力fdyn_x对应的相平面相位为参考相位，即q0=0，根据外部力、力矩以及测量位移相量在相平面的幅值、相位，四自由度转子受动载荷作用响应分析如图4所示，可将其用虚数坐标表示，有
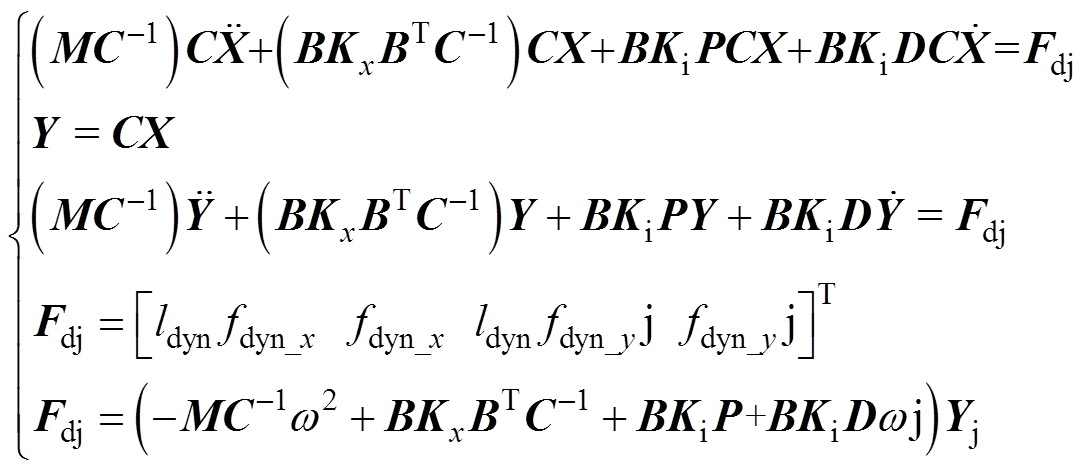（20）
式中，j为虚数单位；Fdj为Fd在复平面的向量；Yj为Y在复平面的向量。
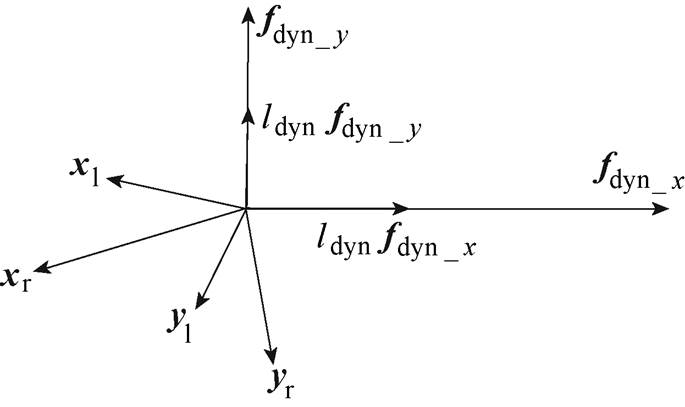
图4 四自由度转子受动载荷作用响应分析
Fig.4 Analysis of response in 4-DOF rotor with dynamic load
尽管经过了动平衡调校，磁轴承转子仍会存在一定的不平衡质量，该不平衡质量将与外部动载荷一起影响转子动态性能，故需要对磁轴承转子不平衡质量的相关参数进行测定。
转子不平衡质量的测量方法如图5所示，在转子上固连一个开有燕尾槽的圆盘，通过在燕尾槽内布置不同数量的质量块，并使转子在同一转速下旋转，可得到不同质量块对应的动载荷幅值fc1、fc2，以及附加动载荷力矩幅值Mc1（Mc2未标出）。设等效初始不平衡质量随转子旋转产生的离心力为fc0、力矩为Mc0，将实验得到的两端位移幅值以及相位差代入式（20）可得总的动载荷幅值以及动载荷力矩幅值，最后可由图5中的三角关系计算fc0及Mc0的幅值以及与质量块的夹角。
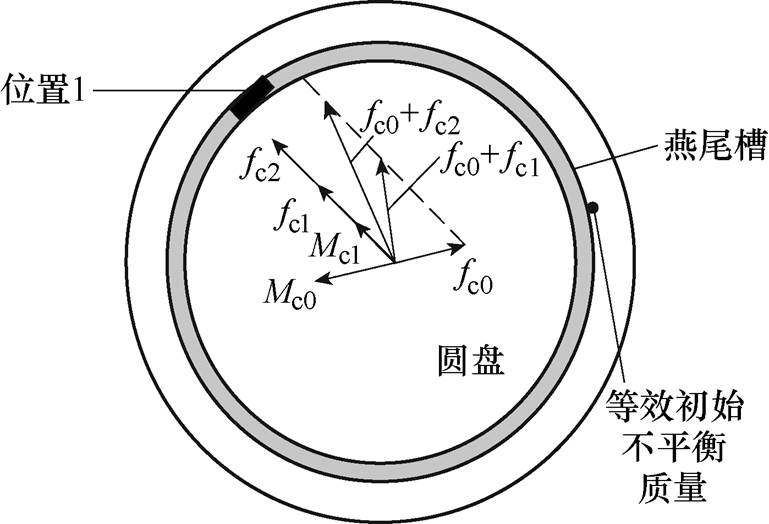
图5 转子不平衡质量测量方法
Fig.5 Unbalance mass measurement of rotor
将不平衡质量与附加不平衡量的和代入式（20）可得转子位移信息，由此可根据两种临界状态对系统的动态承载性能进行分析。
对于图1所示的典型径向磁轴承结构，由于每个自由度只有一对差动的线圈提供电磁吸力，而转子重力分量始终指向下通道方向，因此上通道故障后转子无法继续悬浮。下通道故障后，故障所在自由度上通道静态电流ies与上通道故障前的静态控制电流is的关系为
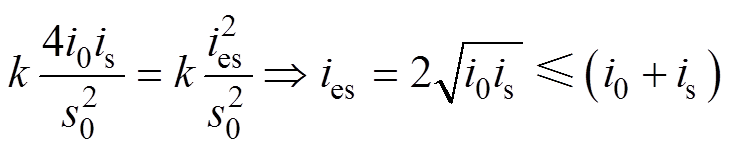（21）
可知，只要故障前转子能够静态悬浮，故障后仅靠上线圈仍可维持转子静态悬浮。若故障后仍保持PID控制，控制电流与位移的幅值相位关系与正常时相同。系统稳定后位移直流分量接近零，则仍可用两种临界状态作为判断系统动态承载力的依据，所不同的是，由于ies＜i0，上通道电流可能会达到零电流临界状态。
由于系统临界状态由位移幅值与通道电流幅值定义，且通道电流幅值与位移幅值之比与P、I、D控制参数有关，尤其是与P、D参数相关，因此P、D参数在变化时系统动态承载力也会随之变化。
正常状态下的P、D参数可根据文献[23]中的方法并结合实际经验确定，以|2ks/ki|作为正常状态下的P参数值；取阻尼比为0.3，得到正常状态下的D参数值；由于积分环节用于消除系统静态偏差，当磁轴承转速较高时，对系统动态性能影响较小，因此忽略其对系统动态性能的影响。
由于故障后系统的非线性增强，系统的动力学方程无法表示成式（21）的形式，下文主要通过搭建仿真模型的方法对动态承载力进行分析。
基于式（19）建立磁轴承的仿真模型，模型框图如图6所示。模型系统参数见表1。
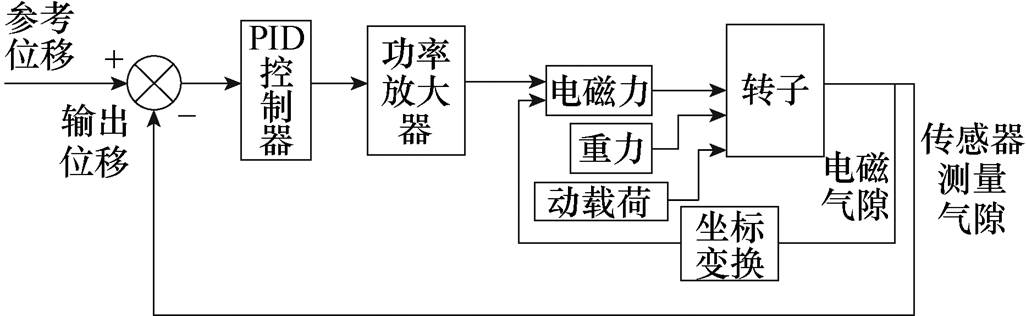
图6 磁轴承系统框图
Fig.6 Block diagram of AMB system
表1 磁轴承系统参数
Tab.1 Parameter of AMB system
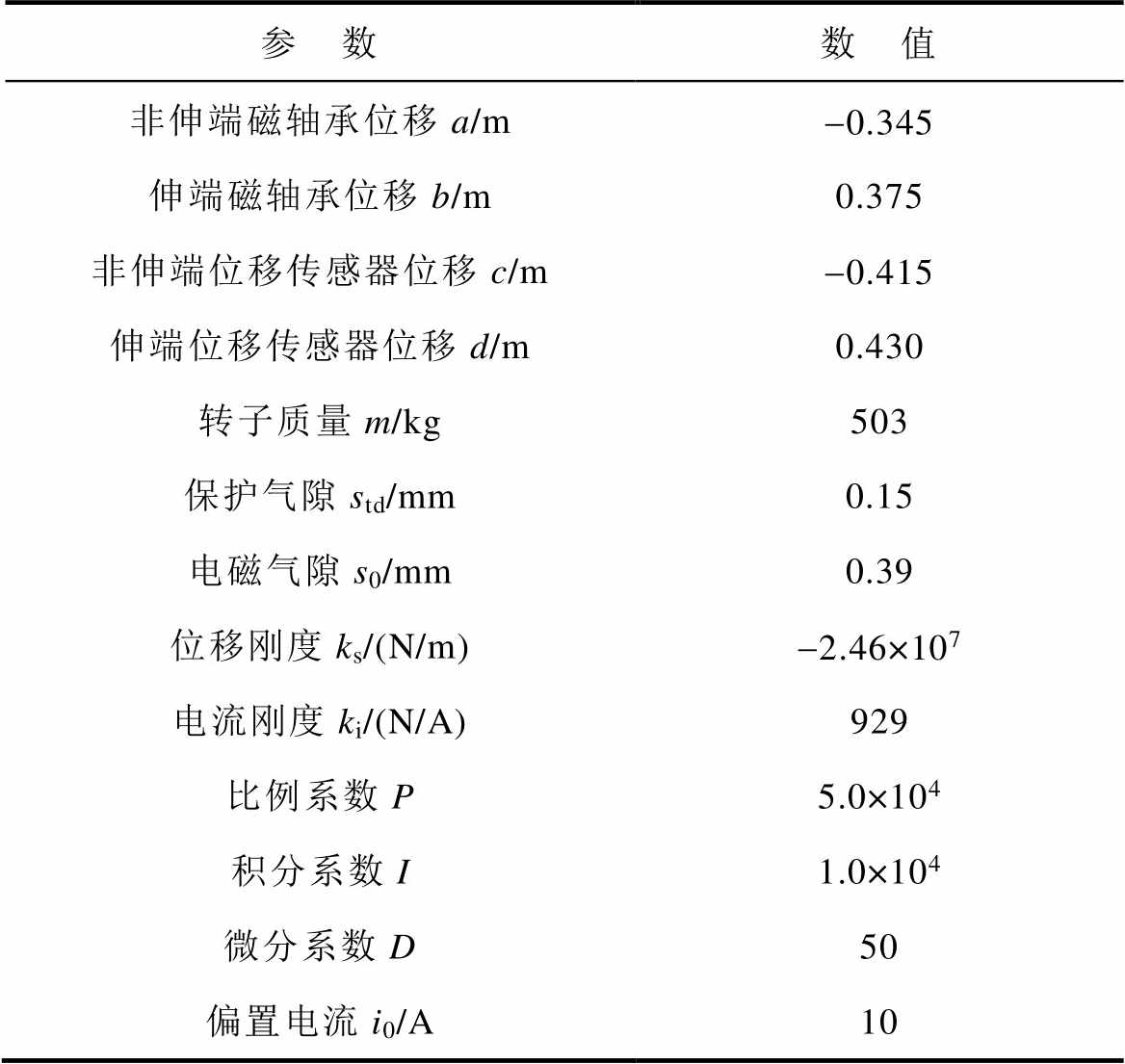
参 数数 值 非伸端磁轴承位移a/m-0.345 伸端磁轴承位移b/m0.375 非伸端位移传感器位移c/m-0.415 伸端位移传感器位移d/m0.430 转子质量m/kg503 保护气隙std/mm0.15 电磁气隙s0/mm0.39 位移刚度ks/(N/m)-2.46×107 电流刚度ki/(N/A)929 比例系数P5.0×104 积分系数I1.0×104 微分系数D50 偏置电流i0/A10
为验证单自由磁轴承系统的动态承载力，可将图6模型中各状态变量阶数改为一阶并代入表1参数。将式（17）计算的动态承载力幅值作为动载荷幅值代入模型，通道最大电流、转子位移幅值及理论动态承载力分别如图7所示。
图7a和图7b中虚线分别代表系统的通道电流、转子位移临界值。根据式（15）以及表1中的数据计算得到的两种临界状态对应的转子质量分界值为368 kg，仿真结果显示：在转子质量大于400 kg时，动载荷作用下系统先达到电流临界状态；在转子质量小于400 kg时，动载荷作用下系统先达到位移临界状态，与理论分析一致。系统动态承载力幅值随转子质量增大先增大后减小。
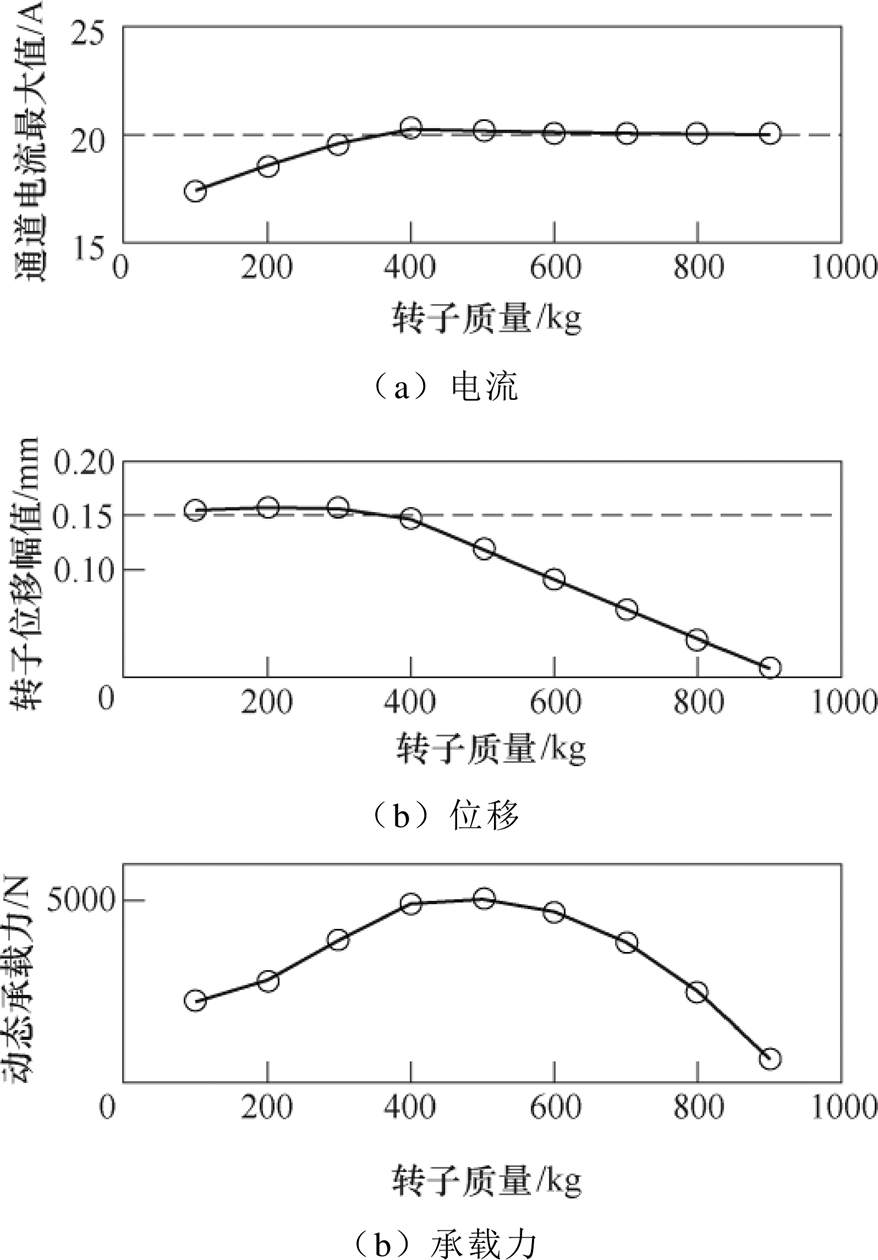
图7 单自由度磁轴承动态承载力与临界状态
Fig.7 Dynamic capacity and critical state of single DOF AMB system
对于四自由度模型，本节主要分析动荷载作用点轴向位移ldyn对转子两端位移幅值的影响。
在动载荷幅值为1 000、2 000、3 000 N，频率为50 Hz时，改变动载荷作用点的位置，得到伸端位移与非伸端位移的幅值比如图8所示。当ldyn=0时，比值为0.92，等于伸端与非伸端磁轴承轴向距离的反比。可以看出，不同幅值的动载荷作用对两端幅值比的影响很小；可根据幅值比确定动载荷作用点轴向位移符号。
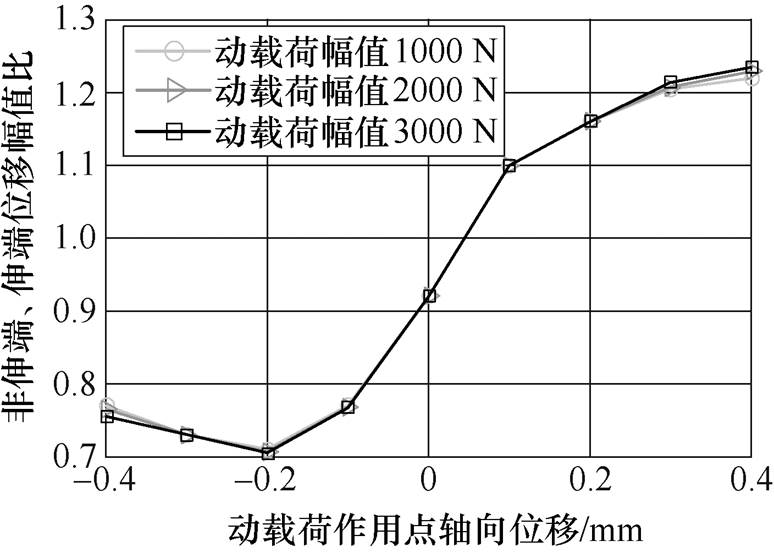
图8 动载荷作用点与转子两端位移幅值比关系
Fig.8 Relationship between ratio of displacement amplitude and load axial position
以m=500 kg为例，在仿真模型中增大动载荷幅值以寻找临界状态，4个自由度的转子位移幅值及4个通道电流中的最大值变化如图9所示。可以看出，当转子位移幅值达到保护气隙值时，四个通道的最大电流值距离imax还有一定的裕量，因此在后续仿真、实验分析中以最大转子位移幅值为依据计算系统动态承载力。
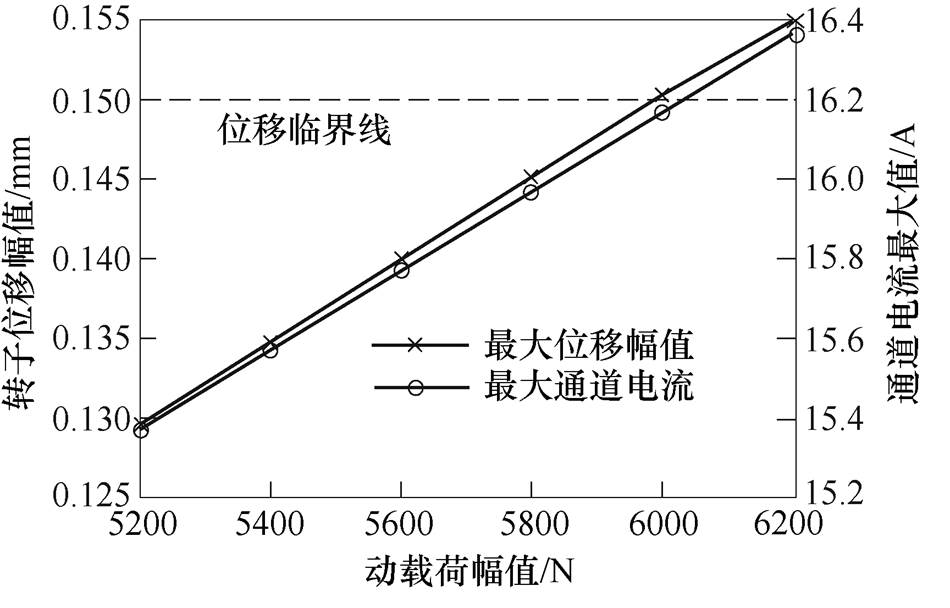
图9 四自由度磁轴承系统临界状态
Fig.9 Critical state of 4-DOF AMB system
进一步在四自由度模型上检验用转子两端位移计算动载荷以及动载荷力矩的有效性，见表2。
表2 动载荷、动载荷力矩幅值计算
Tab.2 Calculation of amplitude of dynamic load and dynamic torque
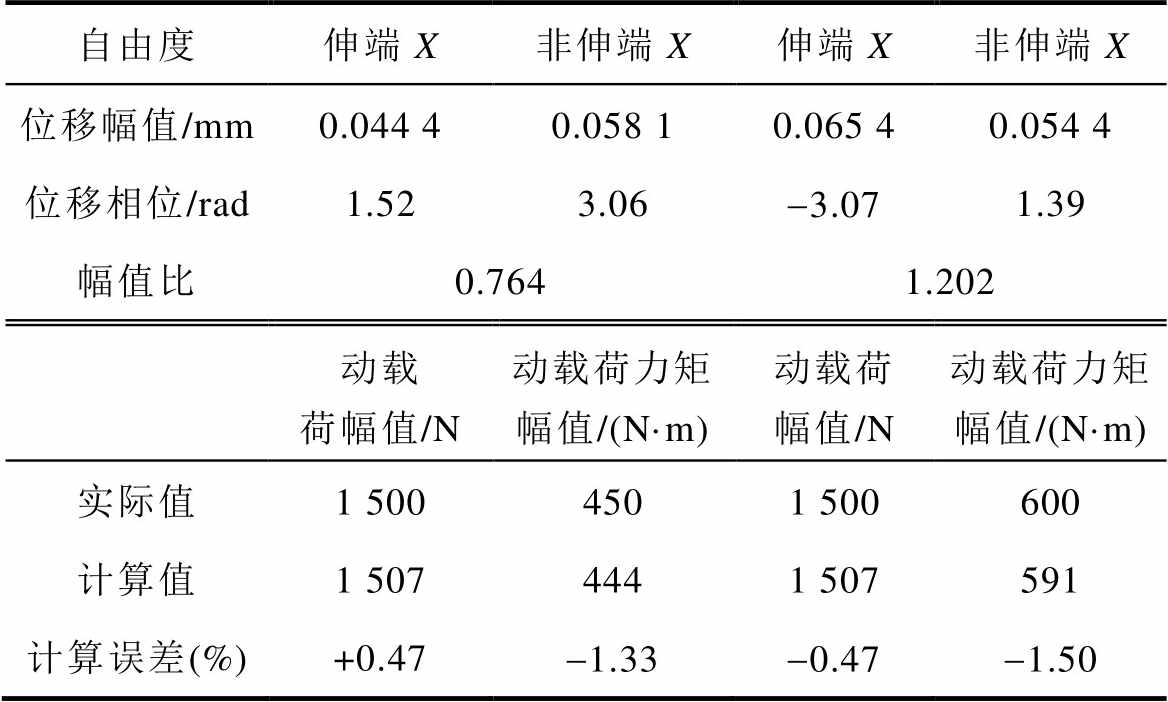
自由度伸端X非伸端X伸端X非伸端X 位移幅值/mm0.044 40.058 10.065 40.054 4 位移相位/rad1.523.06-3.071.39 幅值比0.7641.202 动载荷幅值/N动载荷力矩幅值/(N·m)动载荷幅值/N动载荷力矩幅值/(N·m) 实际值1 5004501 500600 计算值1 5074441 507591 计算误差(%)+0.47-1.33-0.47-1.50
表2中设定转子转速为3 000 r/min，动载荷幅值为1 500 N，动载荷作用点的轴向位移分别为-0.3 m及+0.4 m，代入仿真模型得到转子两端位移信息，并由式（20）得到动载荷与动载荷力矩幅值的计算值，可以看出，动载荷以及动载荷力矩幅值的计算值与实际给定值相比误差较小，这说明陀螺力矩与积分环节的影响的确可以忽略。
为在仿真中模拟下通道故障，可在t =te时刻，改变某一自由度电磁力表达式，将电磁力计算公式由式（6）变为式（3），通道故障仿真如图10所示。
由于下通道故障后ies＜i0，因此在考虑电流临界状态时，只需考虑电流最小值达到0的情况。仿真得到转子位移幅值、故障自由度上通道电流最小值与动载荷幅值如图11所示，可以看出，此时系统先达到转子位移临界状态。
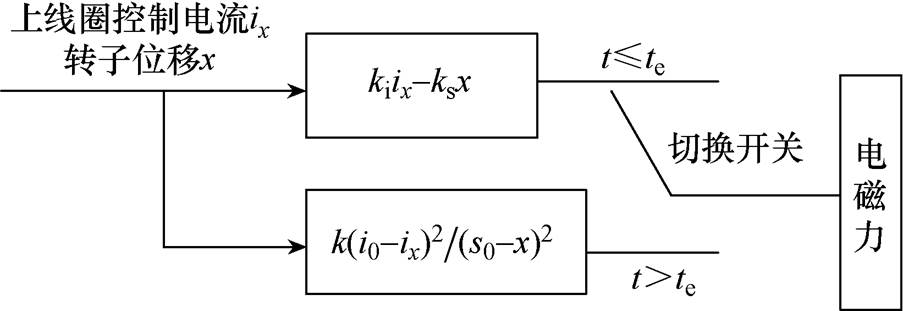
图10 通道故障仿真
Fig.10 Simulation of channel failure
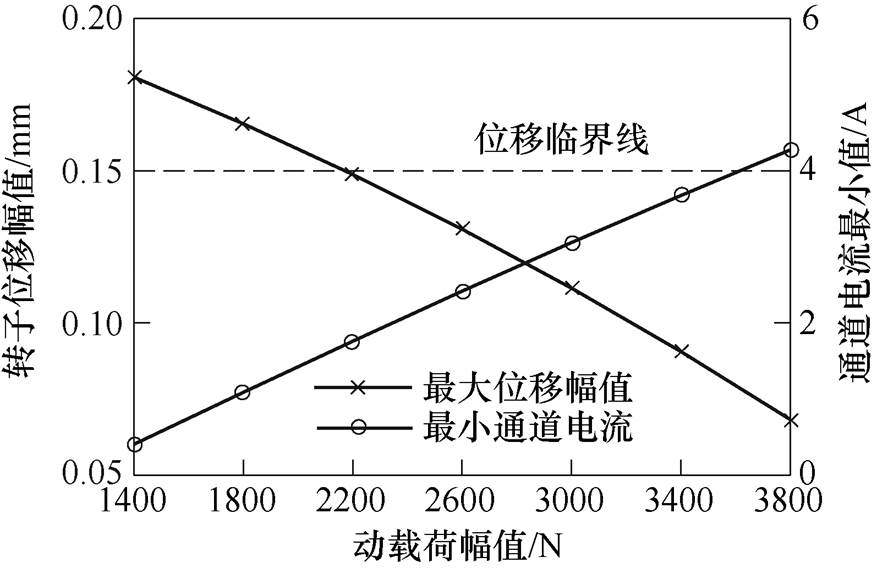
图11 通道故障后磁轴承系统临界状态
Fig.11 Critical state of AMB system after channel failure
本文所用的实验平台如图12所示，实验平台参数与表1中参数相同，平台工作转速为3 500 r/min。
图12 实验平台
Fig.12 Experimnet platform
首先通过实验确定转子的不平衡质量，在图5中的燕尾槽内分别固定17.2 g及34.4 g质量块在转速为3 000 r/min时进行实验，实验数据及不平衡质量的计算过程见表3。表3中除附加载荷848 N时根据X、Y方向数据计算的合力矩幅值相差较大，其余基于X、Y方向数据计算得到的力与力矩幅值相差较小，可互为验证。
计算得到初始动载荷幅值为207 N、附加动载荷幅值为105 N·m，由此可将转子的初始不平衡质量等效为一个质量8.3 g，到轴线垂直距离0.25 m的质量块，轴向位移为-0.5 m，初始不平衡力与附加动载荷夹角为1.14 rad。
表3 转子不平衡质量计算
Tab.3 Unbalance mass calculation of rotor
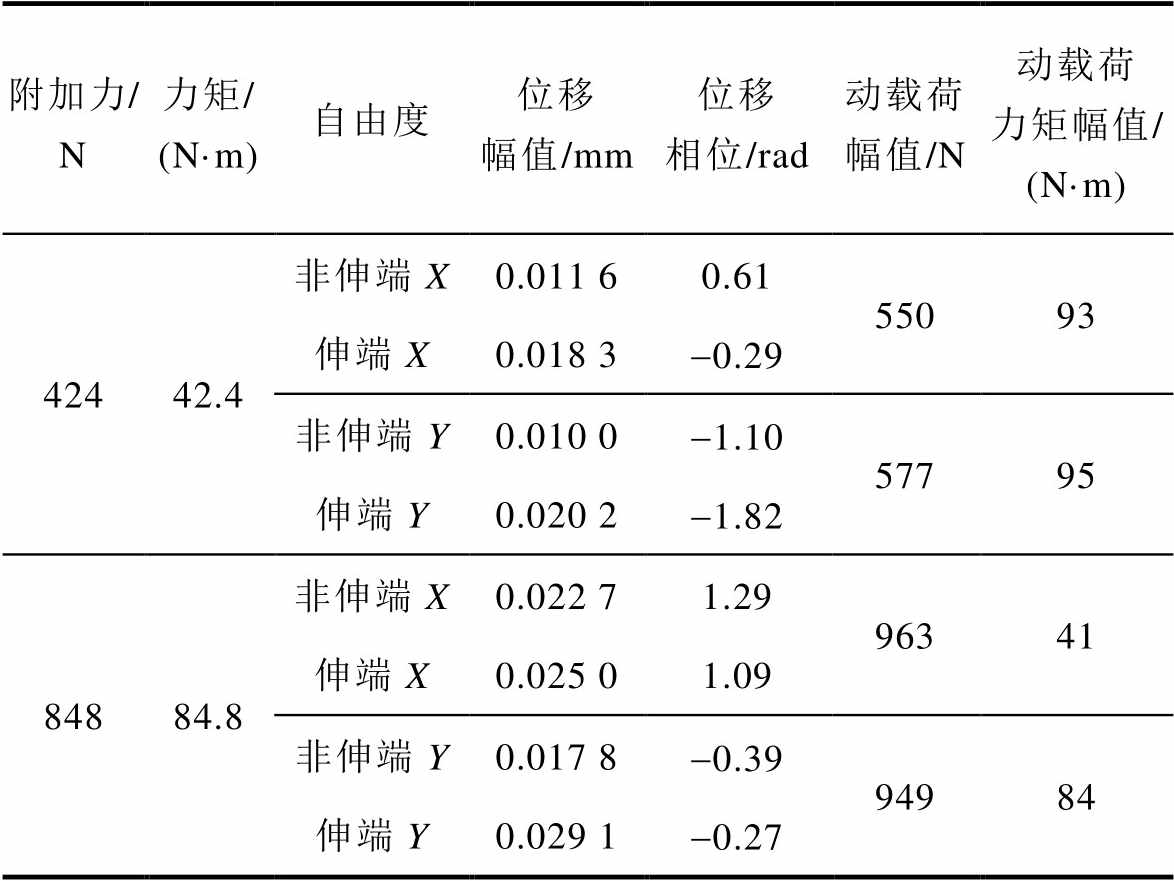
附加力/ N力矩/ (N·m)自由度位移幅值/mm位移相位/rad动载荷幅值/N动载荷力矩幅值/ (N·m) 42442.4非伸端X0.011 60.6155093 伸端X0.018 3-0.29 非伸端Y0.010 0-1.1057795 伸端Y0.020 2-1.82 84884.8非伸端X0.022 71.2996341 伸端X0.025 01.09 非伸端Y0.017 8-0.3994984 伸端Y0.029 1-0.27
为进一步验证四自由度转子动力学模型的准确性并考虑到实验的安全性，分别在位置1安装4、6块质量块（分别为34.4 g与51.6 g）得到3 000 r/min、3 500 r/min转速下伸端、非伸仿真值与实验值对比。转速为3 500 r/min转速时附加4块质量块下的仿真与实验端轨迹对比如图13所示。
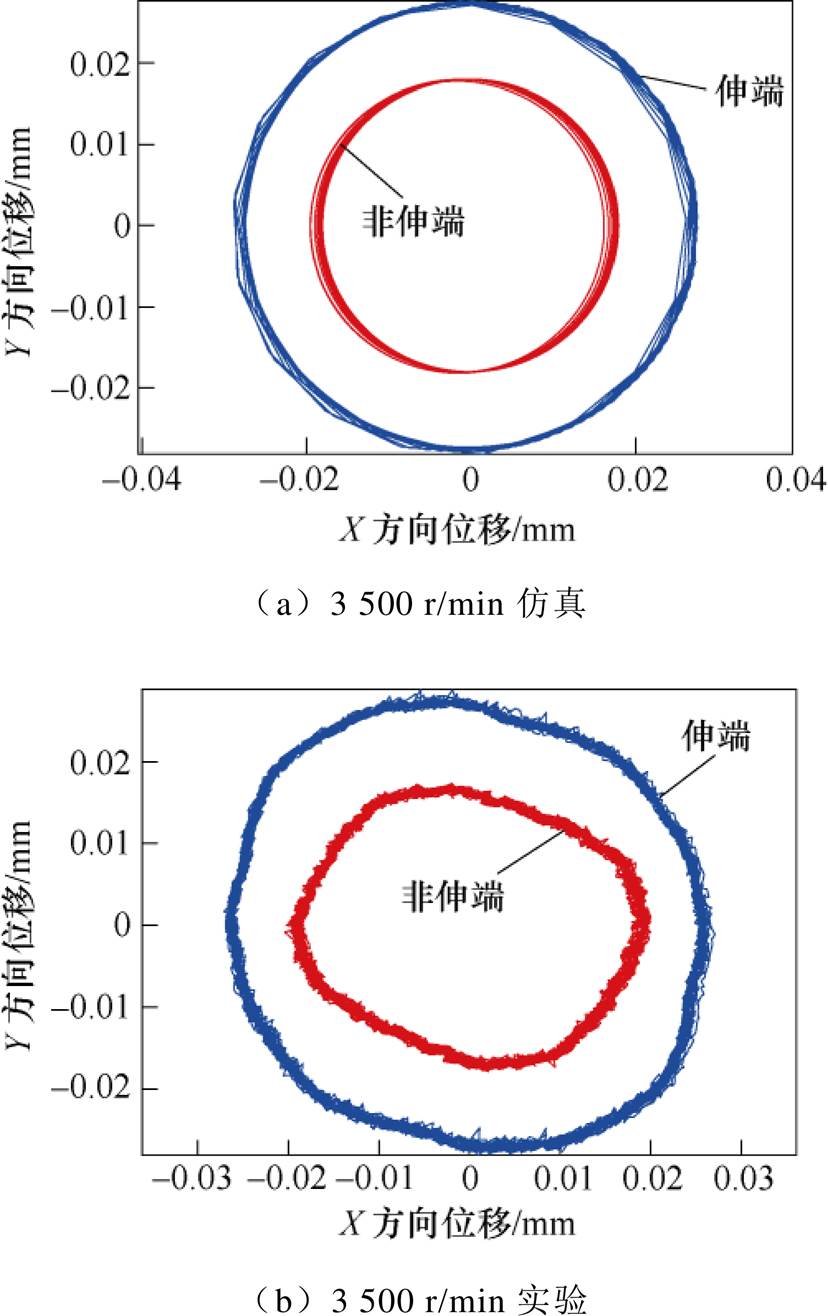
图13 正常情况下转子轨迹
Fig.13 Rotor trajectory under normal conditions
取转子两端轨迹上距离平衡点的最大值为最大位移幅值，仿真与实验值对比见表4。因为加工制造误差以及实验过程中定转子温升差异引起的气隙变化等原因，实际电流、位移刚度值与理论值存在一定的偏差，所以仿真值与实验值也存在一定的误差。但从表4可以看出，仿真模型计算最大位移幅值的误差不超过3.9 %，说明该模型能用于计算系统动态承载力。考虑不平衡质量，可由模型计算得到正常情况下的系统动态承载力为5 100 N。
表4 正常情况下最大位移幅值仿真值与实际值
Tab.4 Simulation and experiment value of maximum displacement amplitude under normal conditions
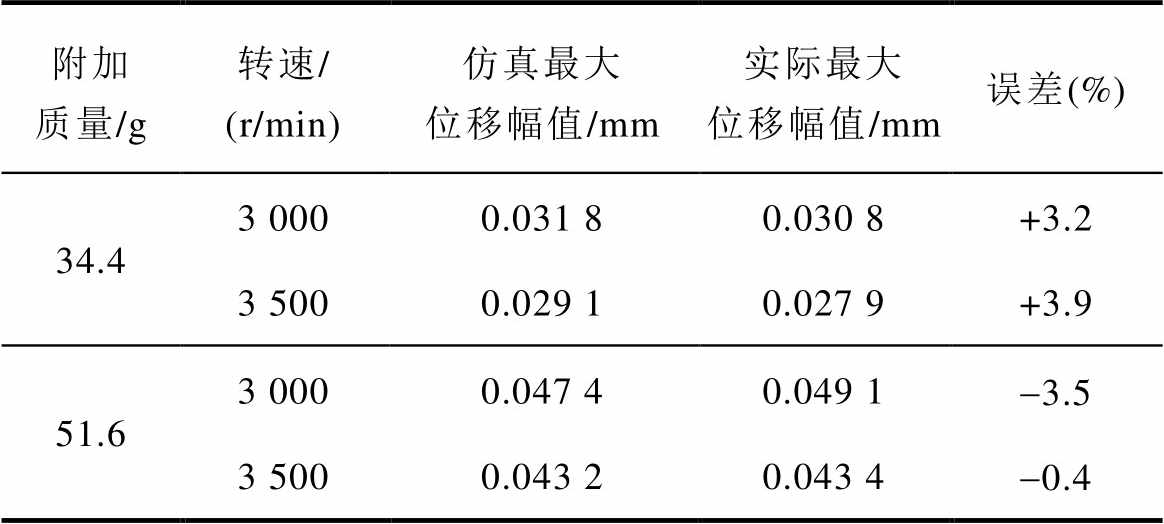
附加质量/g转速/ (r/min)仿真最大位移幅值/mm实际最大位移幅值/mm误差(%) 34.43 0000.031 80.030 8+3.2 3 5000.029 10.027 9+3.9 51.63 0000.047 40.049 1-3.5 3 5000.043 20.043 4-0.4
为在实验中模拟下通道故障，可将某自由度下通道开关管的使能信号置为低电平，使该通道电流降为零。由于附加34.4 g质量块时转子位移幅值较小，对通道故障后的系统动态性能变化体现不够明显，故在附加质量51.6 g，转子转速为3 000 r/min、3 500 r/min时进行非伸端磁轴承Y方向下通道故障的仿真及实验，3 500 r/min时转子两端轨迹对比如图14所示。由图14可知，非伸端磁轴承Y方向下通道故障后，由于通道故障后非伸端X、Y方向的位移相位不再正交，因此轨迹为近似斜椭圆形状。伸端Y方向位移受到非伸端Y方向位移影响而增大，也产生倾斜。下通道故障后，在转速为3 500 r/min时分别在一定范围内改变P、D参数值，得到转子最大位移幅值的仿真与实验结果如图15所示。可以看出，在一定范围内增大P、D参数，磁轴承系统的最大位移幅值减小，由图11可知，此时系统动态承载力增大，但由于过大的P参数会使该自由度电磁力增大，可能导致失稳；过大的D参数会放大噪声对系统稳定性的影响。因此，通过改变P、D参数增大系统动态承载力的能力有限。
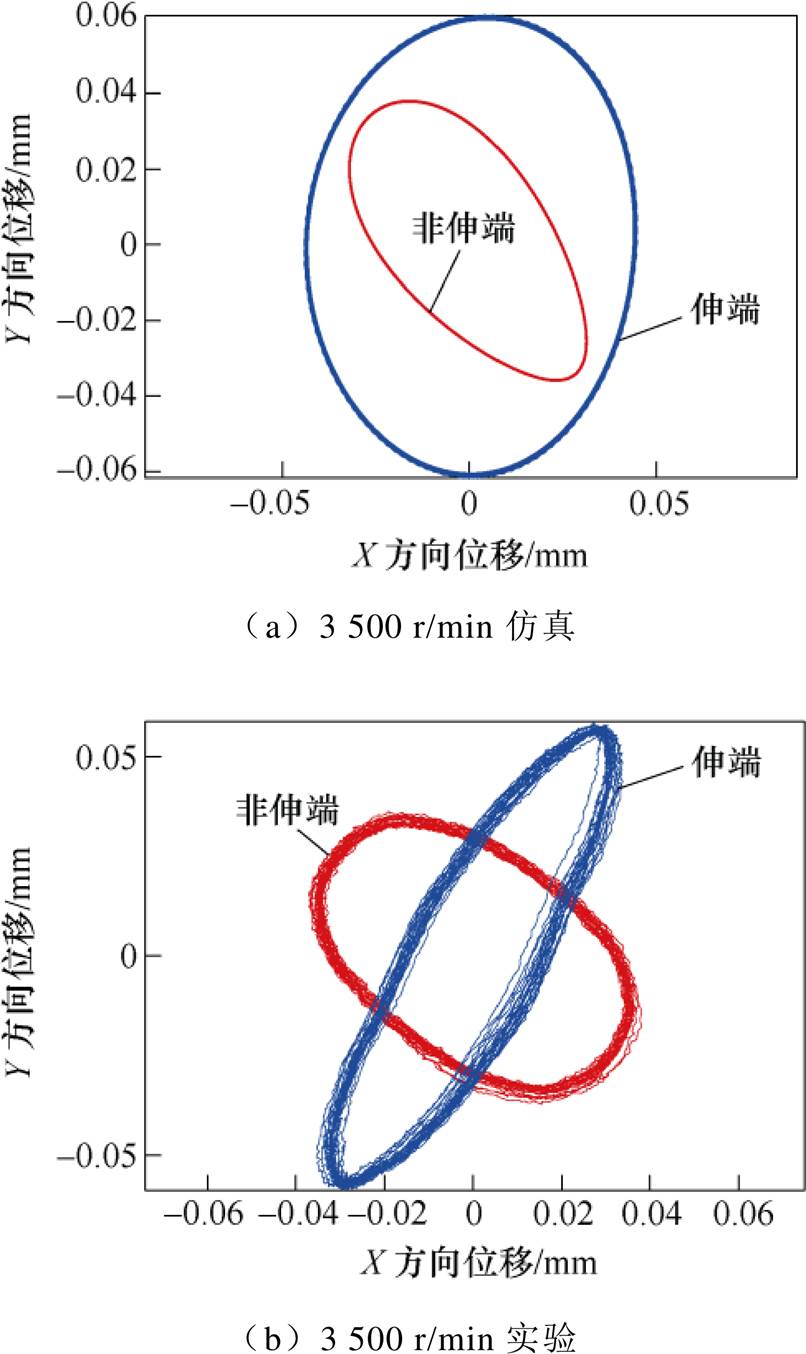
图14 部分通道故障后转子轨迹
Fig.14 Rotor trajectory with partial channel failure
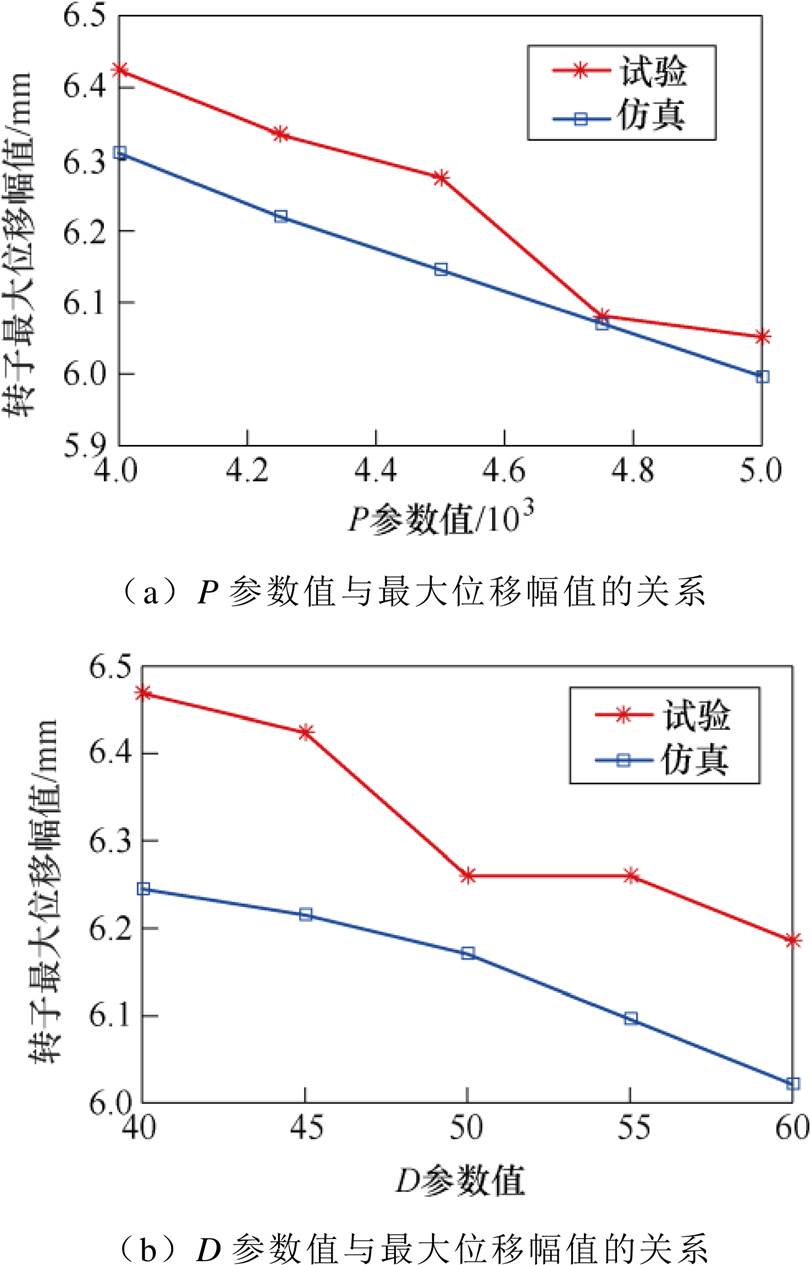
图15 P、D参数值与转子最大位移幅值的关系
Fig.15 Relationship between P、D parameters and maximum displacement amplitude of rotor
同样，受实际装置中各自由度位移、电流刚度值与理论值偏差的影响，仿真得到的最大位移幅值与实际值存在一定误差。但由图15a、图15b可知，仿真与实验误差分别小于2 %、3.5 %，证明仿真模型能对下通道故障后的系统动态承载力进行估算。基于改前的P、D参数计算得到通道故障后的系统动态承载力约为3 600 N，相较于正常情况减小了29 %。
本文建立了考虑部分通道故障的四自由度磁轴承系统模型，并由此对故障前后的系统动态承载力进行了分析，通过仿真与实验证明：
1）正常情况下，随着动载荷幅值增加，磁轴承系统存在两种临界状态：①转子位移幅值过大至定转子碰撞；②通道电流达到零或最大值。根据这两类临界状态可以确定磁轴承系统的动态承载力，由仿真可知，动态承载力幅值随转子质量增加的变化规律为先增大后减小。
2）所搭建的四自由度转子动力学模型计算动载荷作用下的转子最大位移幅值与实际值相比，误差小于3.9 %，可用于计算正常情况下转子动态承载力。
3）当发生部分通道故障后，仿真模型计算的动载荷作用下的最大位移幅值与实际值相比误差小于3.5 %。
4）通过改变P、D参数可以改变系统动态承载力，但改变范围有限。
参考文献
[1] 姜豪, 苏振中, 王东. 运动平台上磁轴承-转子系统的动力学建模[J]. 电工技术学报, 2019, 34(23): 4880-4889.
Jiang Hao, Su Zhenzhong, Wang Dong. Dynamic modeling of magnetic bearing-rotor system on moving platform[J]. Transactions of China Electro- technical Society, 2019, 34(23): 4880-4889.
[2] 黄威, 邓智泉, 李克翔, 等. 一种磁悬浮轴承支承刚性转子现场动平衡方法[J]. 电工技术学报, 2020, 35(22): 4636-4646.
Huang Wei, Deng Zhiquan, Li Kexiang, et al. A filed dynamic balancing method for rigid rotor supported by magnetic bearings[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4636-4646.
[3] 胡烽, 孙宏博, 蒋栋, 等. 基于四相全桥的磁悬浮轴承开关器件开路故障容错控制策略[J]. 电工技术学报, 2022, 37(9): 2295-2305.
Hu Feng, Sun Hongbo, Jiang Dong, et al. Fault- tolerant strategy of four-phase full-leg for active magnetic bearing in case of open circuit fault of switching device[J]. Transactions of China Electro- technical Society, 2022, 37(9): 2295-2305.
[4] 李志, 苏振中, 胡靖华, 等. 磁轴承复合位移传感设计与实验研究[J]. 电工技术学报, 2021, 36(7): 1425-1433.
Li Zhi, Su Zhenzhong, Hu Jinghua, et al. Design and experimental research of magnetic bearing compound displacement sensor[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1425-1433.
[5] Jiang Dong, Li Tian, Hu Zaidong, et al. Novel topologies of power electronics converter as active magnetic bearing drive[J]. IEEE Transactions on Industrial Electronics, 2020, 67(2): 950-959.
[6] Cheng Xin, Cheng Baixin, Lu Meiqian, et al. An online fault-diagnosis of electromagnetic actuator based on variation characteristics of load current[J]. Automatika, 2020, 61(1): 11-20.
[7] 钟一谔, 何衍宗. 转子动力学[M]. 北京: 清华大学出版社, 1987.
[8] Wang Xiping, Yu Liang, Wan Jingui, et al. Analysis on stiffness and damping performance of active magnetic bearing system[J]. Journal of Shanghai University (English Edition), 1998, 2(3): 221-225.
[9] 汪希平, 朱礼进, 于良, 等. 主动磁轴承转子系统动力学特性的研究[J]. 机械工程学报, 2001, 37(11): 7-12.
Wang Xiping, Zhu Lijin, Yu Liang, et al. Investi- gation on dynamic performance of active magnetic bearing rotor system[J]. Chinese Journal of Mecha- nical Engineering, 2001, 37(11): 7-12.
[10] 田拥胜, 孙岩桦, 虞烈. 高速永磁电机电磁轴承转子系统的动力学及实验研究[J]. 中国电机工程学报, 2012, 32(9): 116-123, 18.
Tian Yongsheng, Sun Yanhua, Yu Lie. Dynamical and experimental researches of active magnetic bearing rotor systems for high-speed PM machines[J]. Proceedings of the CSEE, 2012, 32(9): 116-123, 18.
[11] 张舒月, 李青, 伍继浩. 磁悬浮冷压缩机转子的动力学分析和试验研究[J]. 湖南大学学报(自然科学版), 2021, 48(10): 57-66.
Zhang Shuyue, Li Qing, Wu Jihao. Dynamic analysis and experiments on cold compressor research of magnetic suspension rotor[J]. Journal of Hunan University (Natural Sciences), 2021, 48(10): 57-66.
[12] 李胜远, 郑龙席. 磁轴承激励下转子系统动力学特性[J]. 中国机械工程, 2021, 32(8): 901-907.
Li Shengyuan, Zheng Longxi. Dynamics characteristics of rotor systems under magnetic bearing excitation[J]. China Mechanical Engineering, 2021, 32(8): 901- 907.
[13] 杨作兴, 赵雷, 赵鸿宾. 电磁轴承动刚度的自动测量[J]. 机械工程学报, 2001, 37(3): 25-29.
Yang Zuoxing, Zhao Lei, Zhao Hongbin. Automatic measurement of dynamic stiffness for active magnetic bearings[J]. Chinese Journal of Mechanical Engin- eering, 2001, 37(3): 25-29.
[14] 吴海同, 周瑾, 纪历. 基于单相坐标变换的磁悬浮转子不平衡补偿[J]. 浙江大学学报(工学版), 2020, 54(5): 963-971.
Wu Haitong, Zhou Jin, Ji Li. Unbalance compensation of magnetically suspended rotor based on single phase coordinate transformation[J]. Journal of Zhejiang University (Engineering Science), 2020, 54(5): 963- 971.
[15] 周天豪, 陈磊, 祝长生, 等. 基于自适应变步长最小均方算法的磁悬浮高速电机不平衡补偿[J]. 电工技术学报, 2020, 35(9): 1900-1911.
Zhou Tianhao, Chen Lei, Zhu Changsheng, et al. Unbalance compensation for magnetically levitated high-speed motors based on adaptive variable step size least mean square algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1900- 1911.
[16] Rao D K, Brown G V, Lewis P, et al. Stiffness of magnetic bearings subjected to combined static and dynamic loads[J]. Journal of Tribology, 1992, 114(4): 785-789.
[17] Maslen E, Hermann P, Scott M, et al. Practical limits to the performance of magnetic bearings: peak force, slew rate, and displacement sensitivity[J]. Journal of Tribology, 1989, 111(2): 331-336.
[18] 巩磊, 祝长生. 基于变角度搜索算法的磁悬浮高速电机刚性转子系统的不平衡补偿方法[J]. 中国电机工程学报, 2021, 41(19): 6769-6778.
Gong Lei, Zhu Changsheng. Unbalance compensation method of an active magnetic bearings-rigid rotor system for high-speed motors based on variable angle seeking algorithm[J]. Proceedings of the CSEE, 2021, 41(19): 6769-6778.
[19] Bornstein K R. Dynamic load capabilities of active electromagnetic bearings[J]. Journal of Tribology, 1991, 113(3): 598-603.
[20] Maslen E H, Meeker D C. Fault tolerance of magnetic bearings by generalized bias current linearization[J]. IEEE Transactions on Magnetics, 1995, 31(3): 2304- 2314.
[21] 何海婷, 柳亦兵, 巴黎明, 等. 基于BP神经网络的飞轮储能系统主动磁轴承非线性动力学模型[J]. 中国电机工程学报, 2022, 42(3): 1184-1198.
He Haiting, Liu Yibing, Ba Liming, et al. Nonlinear dynamic model of active magnetic bearing in flywheel system based on BP neural network[J]. Proceedings of the CSEE, 2022, 42(3): 1184-1198.
[22] 汤继强, 隗同坤, 宁梦月, 等. 基于反馈线性化的MSCMG转子稳定控制[J]. 北京航空航天大学学报, 2020, 46(6): 1063-1072.
Tang Jiqiang, Wei Tongkun, Ning Mengyue, et al. Stable control of MSCMG rotor based on feedback linearization[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(6): 1063- 1072.
[23] 王忠博, 毛川, 祝长生. 主动电磁轴承-刚性转子系统PID控制器设计方法[J]. 中国电机工程学报, 2018, 38(20): 6154-6163.
Wang Zhongbo, Mao Chuan, Zhu Changsheng. A design method of PID controller for active magnetic bearings-rigid rotor systems[J]. Proceedings of the CSEE, 2018, 38(20): 6154-6163.
Abstract The dynamic capacity of the active magnetic bearing (AMB) system changes due to its channel failure. The accurate calculation of dynamic capacity is required to determine AMB system operation conditions. However, the AMB system model with partial channel failure in existing studies greatly deviates from reality. In order to improve the model accuracy for calculating the dynamic capacity of the AMB system, considering the external load and initial unbalance mass from the rotor, this paper establishes the four degrees of freedom (DOF) AMB system models with or without channel failure. Based on the system model, dynamic capacity can be calculated with the relations between external load, rotor displacements, and channel current.
Firstly, based on the single DOFAMB system model, this paper elaborates on two critical states related to rotor mass: rotor displacement critical state and channel current critical state. Then, the 4-DOF model is established considering external load and initial unbalance mass from the rotor. Secondly, the initial unbalance mass from the rotor is calculated according to the rotor displacement amplitude, which changes by placing various external loads on the rotor. Finally, according to the two critical states, the dynamic capacity of the system with or without partial channel failure is calculated, and the influence of control parameters is analyzed for the AMB system with partial channel failure.
By changing the external load value or rotor mass on a single DOF AMB system, we find that the rotor displacement amplitude reaches the critical value (collision value) for the low-mass rotor, and the channel current reaches the critical value (saturation value) for the big-mass rotor. The ratio of rotor displacement amplitude at the stretch side and non-stretch side is related to the load axial position. Therefore, the axial position sign of the load can be determined according to the ratio value. The rotor displacement amplitude can be obtained by substituting the dynamic load into the model, and the error of dynamic load of calculated and set value is less than 1.5 %. The dynamic load calculated by rotor displacement amplitude at 4-DOF from experiment data can also be mutually verified, proving the method of calculating dynamic load from rotor displacement amplitude works. Experiments at different rotor speeds and additional extern loads are conducted. The result shows that the maximum amplitude error in rotor displacement from the experiment and simulation does not exceed 3.9 %. By changing the proportional and differential coefficient value in a limited range of the AMB system with lower channel failure, the maximum displacement amplitude error of the simulation and experiments does not exceed 3.5 %. Since the rotor mass of the experiment platform is relatively small, the dynamic capacity of the AMB system with or without failure can be calculated from the rotor displacement amplitude. The dynamic capacity of the AMB system with/without failure is 3 600 N/5 100 N.
The following conclusions can be drawn through simulation analysis and experiments: (1) As the dynamic load changes, the AMB system has two critical states. That is, rotor displacement amplitude and channel current reach a critical value. According to the critical states, the dynamic capacity of the AMB system can be calculated. The value of the dynamic capacity increases first and then decreases in the process of rotor mass increases. (2) The error of the maximum displacement amplitude of simulation and experiments does not exceed 3.9 % without channel failure, and the error does not exceed 3.9 % with channel failure. It indicates that the model can be used to calculate the dynamic capacity of AMB systems with or without channel failure. (3) The dynamic capacity of the AMB system is associated with the proportional and differential coefficient values, but the adjustment range is limited.
keywords：Active magnetic bearing, dynamic capacity, unbalance mass, channel failure, control parameters
DOI: 10.19595/j.cnki.1000-6753.tces.220356
中图分类号：TM359.9
国家自然科学基金资助项目（51707201, 51690181, 51825703）。
收稿日期 2022-03-11
改稿日期 2022-06-15
刘 奇 男，1995年生，博士，研究方向为磁轴承及其容错控制。E-mail: 1159591124@qq.com
苏振中 男，1989 年生，副研究员，硕士生导师, 研究方向为磁悬浮技术、电力集成技术。 E-mail: suayst@163.com（通信作者）
（编辑 崔文静）