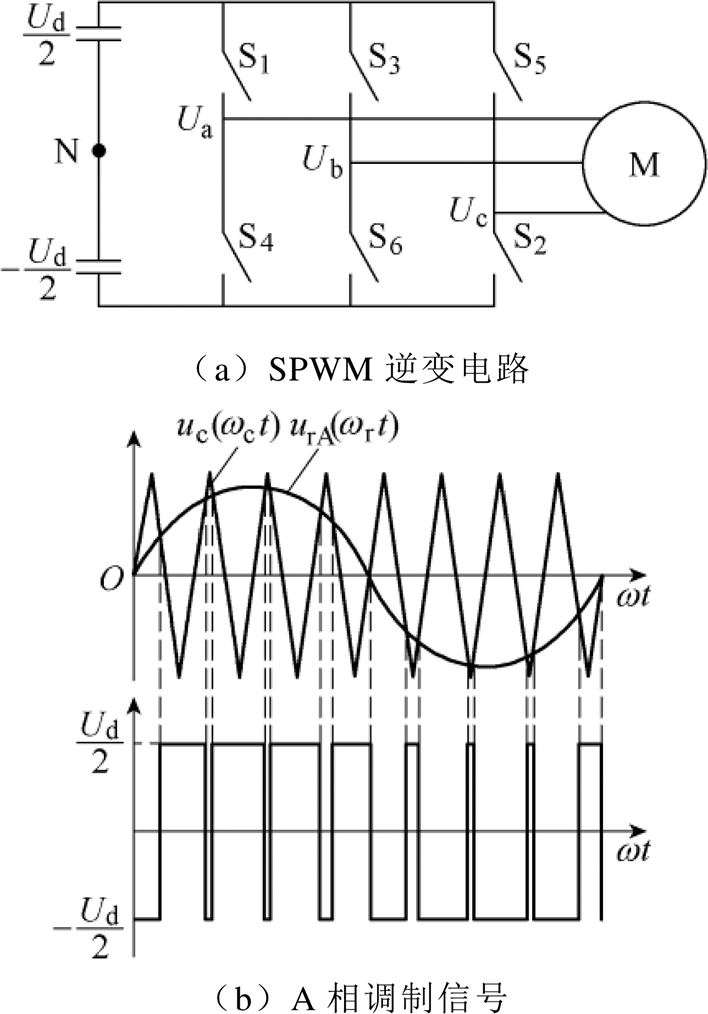
图1 SPWM逆变电路与调制信号
Fig.1 SPWM inverter circuit and modulation signal
摘要 针对变频驱动下双斜槽转子感应电机振动性能研究的不足，对变频驱动下双斜槽转子感应电机的径向电磁力展开研究。首先从变频器的输出谐波特性出发，采用解析法分析了气隙磁通密度成分，并通过分析各个磁通密度谐波的相互作用得到了径向电磁力的幅值、阶次、频率的表达式。然后采用分层有限元法结合二维快速傅里叶分解，得到了平均径向电磁力的时空分布频谱。通过不同供电方式与不同转子结构下气隙径向电磁力的对比，发现双斜槽转子结构能够有效地削弱由变频供电引入的部分高频附加径向电磁力。最后通过实验对比不同供电方式下电动叉车用双斜槽转子感应电机机壳表面的振动频谱，进而验证分析的正确性。
关键词：感应电机 双斜槽转子 径向电磁力 电磁振动
笼型感应电机具有结构简单、制造成本低、维护简单、运行可靠性高等优点，是新能源汽车电驱系统的重要电机类型[1]。随着我国国民生活质量的提高及新能源汽车技术和市场的日趋成熟，变频感应电机的低振动噪声性能已经成为衡量新能源电动汽车舒适性能的一项重要指标[2]。
感应电机通常采用转子单斜槽来降低振动噪声，但仍满足不了一些特殊场合的需求，且带来了轴向力的不利影响。因此有学者提出了双斜槽转子结构[3]。Wang Lang等[4]采用解析推导与实验验证相结合，指出该转子结构可以有效削弱同步附加转矩，解决了定转子等槽配合时的起动问题。Xu Wei等[5]提出了一种双斜槽转子斜槽角度和交错角度的优化设计方法，在不影响电机振动噪声性能的基础上，进一步提高了电机的电磁转矩。王春雨[6]分析了电动叉车用双斜槽转子感应电机的振动噪声特性，指出该结构可以进一步降低振动噪声，并削弱转子偏心带来的部分附加径向电磁力，但其在分析的过程中忽略了变频器的不利影响。
变频供电的电流谐波对电机的振动噪声有重要的影响，受到了国内外学者的广泛关注。浙江大学的祝长生等[7]分析了正弦脉冲宽度调制（Sinusoidal Pulse Width Modulation, SPWM）变频器的输出特性，研究了变频供电电机的输出响应并提出了降低该类电机振动噪声的方法。Du Jiamin等[8]分析了PWM逆变器产生的电流谐波对感应电机径向电磁力和振动响应的影响，指出PWM供电会加剧电机的振动响应，总的振动加速度水平会随着开关频率的增加而降低。A. C. Binojkumar等[9]采用实验的方法研究了不同调制波频率和不同开关频率下感应电机的振动噪声特性，并指出高频电磁噪声相对噪声的机械和空气动力成分占主导地位。J. Le Besnerais等[10]推导了感应电机由于PWM供电而产生的径向振动的分析特征，并通过可视化定子的一些运行偏转形状，验证了这些力波的节点数和速度。李文 等[11]通过变频驱动异步电机振动频率的特征分析，指出变频驱动下，一阶转频引起的强迫振动与自由振动波形会发生畸变，且电机的振动幅值增加。左曙光等[12]基于异步电机的磁动势和磁导的时空分布特性，理论推导了考虑变频器谐波电流的电磁力的时空特性，指出了变频谐波电流会在开关频率附近引入新的径向电磁力波，而加大电机噪声。肖阳等[13]通过有限元法建立了变频供电电机的电磁-固-声多场耦合仿真计算模型，指出变频输入的谐波会辐射大量频率的噪声，使得电机更加容易发生共振。I. P. Tsoumas等[14]分析了不同逆变调制策略下电机噪声的变化，突出强调了调制技术在变速驱动器噪声产生中所起的重要作用。A. Ruiz-Gonzalez等[15]提出了一种开关频率的控制策略，该策略产生高质量的电压，每个周期的换向次数很少，并且在减少换向损耗和辐射噪声方面非常有效。
上述研究主要分别关注双斜槽转子结构或变频器供电对感应电机振动性能的影响，未对二者同时存在的情况进行过分析。针对以上不足，本文对变频供电下双斜槽转子的气隙径向电磁力特性展开了细致的研究。首先，从变频器的输出谐波特性出发，考虑双斜槽转子结构，采用解析法推导了气隙径向电磁力的数学分析模型，分析了变频驱动下径向电磁力的空间阶次和时间谐波成分，并总结一般规律。然后，通过分层有限元法对变频驱动下双斜槽转子结构下的径向电磁力进行了仿真，结合二维快速傅里叶分解（2 Dimension-Fast Fourier Transform, 2D-FFT）法将得到的径向电磁力进行时空分解，对理论分析进行验证。最后，通过振动实验测得不同供电方式下双斜槽转子感应电机机壳的振动频谱，验证理论分析的正确性。
在以变频驱动的三相感应电机调速系统中，电机的输入电压与电流不再是具有恒定频率的正弦波，而是包含大量的高次时间谐波[16]。SPWM是电机变频调速领域使用最为广泛的方法，其基本原理是将正弦波等效成一系列等幅不等宽的矩形脉冲波，其脉冲宽度是由正弦波和三角波自然相交生成的。图1a所示为典型的三相桥式SPWM逆变电路，图中Ua、Ub、Uc为逆变电路的三相桥臂，S1～S6为逆变电路的六个开关器件，通过控制开关器件的通断可以得到输出幅值相等而宽度不等的方波脉冲序列。
开关管的控制信号是通过三角形载波与三相调制正弦波相互作用得到的，其中三相调制正弦波通常公用一个三角形载波。以A相调制信号为例，如图1b所示。当调制波urA大于三角载波uc时，开关管S1导通而S4关断，则A相的输出电压UAN=Ud/2。当调制波urA小于三角载波uc时，开关管S4导通而S1关断，则A相的输出电压UAN=-Ud/2。B、C两相的调制信号与A相依次相差120 °，其开关管控制规律与A相类似。
图1 SPWM逆变电路与调制信号
Fig.1 SPWM inverter circuit and modulation signal
SPWM逆变电路可以使输出电压、电流接近正弦波，但由于载波对正弦信号的调制作用，也产生了与载波有关的谐波分量[17]。为了便于分析三相SPWM输出电压的谐波特性，首先做出以下假设：①输入电压为理想的直流电压源，忽略纹波对逆变器输出电压的影响；②视功率开关器件为理想器件，即有理想的开关特性；③忽略开关管的死区时间。
在以上的假设条件下，通过对输出电压进行双重傅里叶分解结合Bessel理论，可以得到SPWM逆变电源输出相电压的傅里叶级数[18]表示为
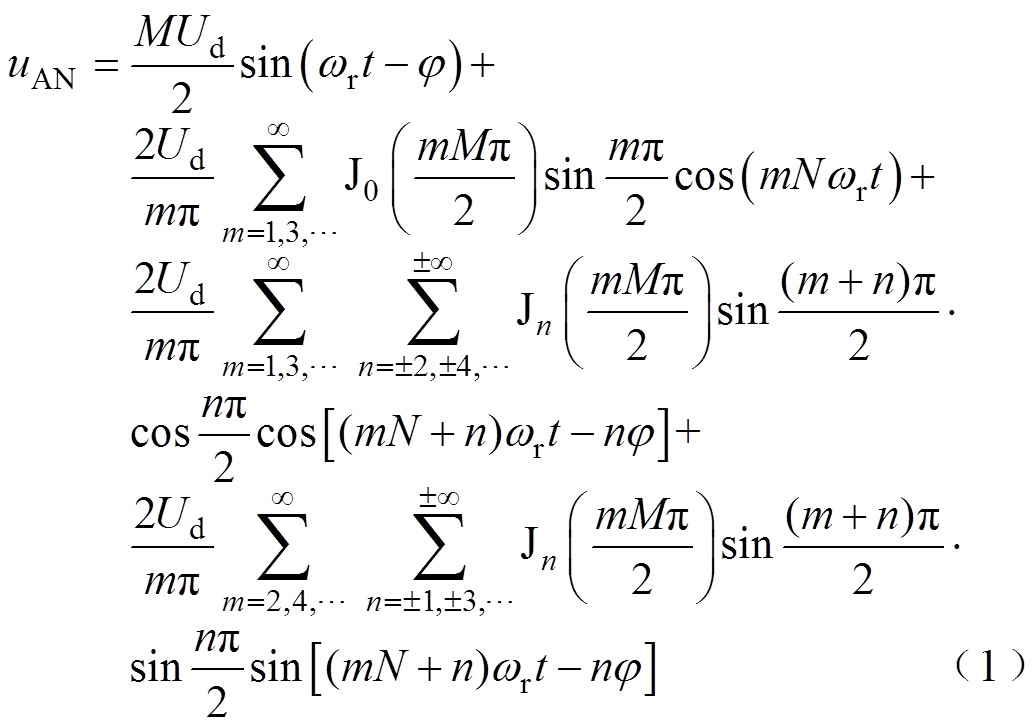
式中，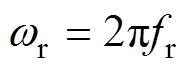
，fr为调制波频率；Ud为直流侧的电源电压；M=Ur/Uc为调制度，Ur为调制波幅值，Uc为载波幅值；N为载波比，N=fc/fr，fc为载波的频率；m为相对于载波的谐波次数；n为相对于调制波的谐波次数；
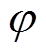为调制波的初相位；J0～Jn为第一类Bessel函数。
同理可以得到B、C两相电压uBN、uCN的表达式，在此不再赘述。根据相线电压之间的关系
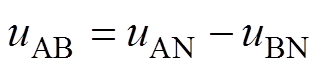（2）
可以得到输出线电压的级数展开式为
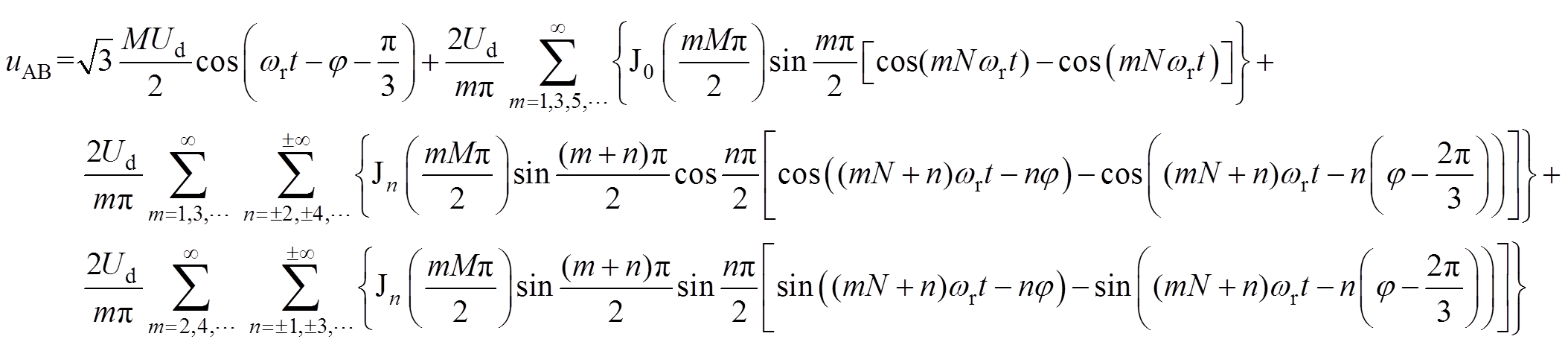（3）
对式（3）进行归纳可知，输出的电压主要包括基波分量和高次谐波分量[19]。基波分量表达式为
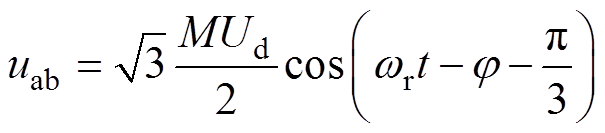
高次谐波分量，其频率为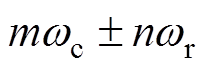
。当m=1, 3, 5,…时，有
，
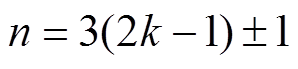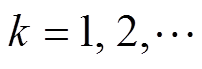；当m=2, 4, 6,…时，有
，
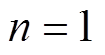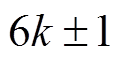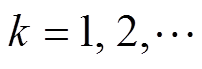，。可以看到，输出线电压幅值为相电压的
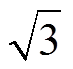倍，输出的高次谐波分量主要集中在载波频率
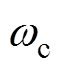附近，且不包含其整数倍的谐波分量。
双斜槽转子实物如图2所示。从图中可以看出，整个转子沿着轴向方向分为两半部分，每一半相当于普通的单斜槽转子，并通过中间环连接以保证良好的导电性能。上、下两半部分的转子导条反向扭斜以抵消轴向力作用，并且相互交错半个转子槽距。
图2 双斜槽转子实物
Fig.2 Physical drawing of double skewed rotor
双斜槽转子削弱谐波的原理如图3所示，其基本的原理是通过上半转子导条和下半转子导条的交错效应，使得两部分转子相对转子的齿谐波相位相反，这样一阶以及奇数阶转子齿谐波在两部分转子内产生的谐波负作用可以相互抵消。
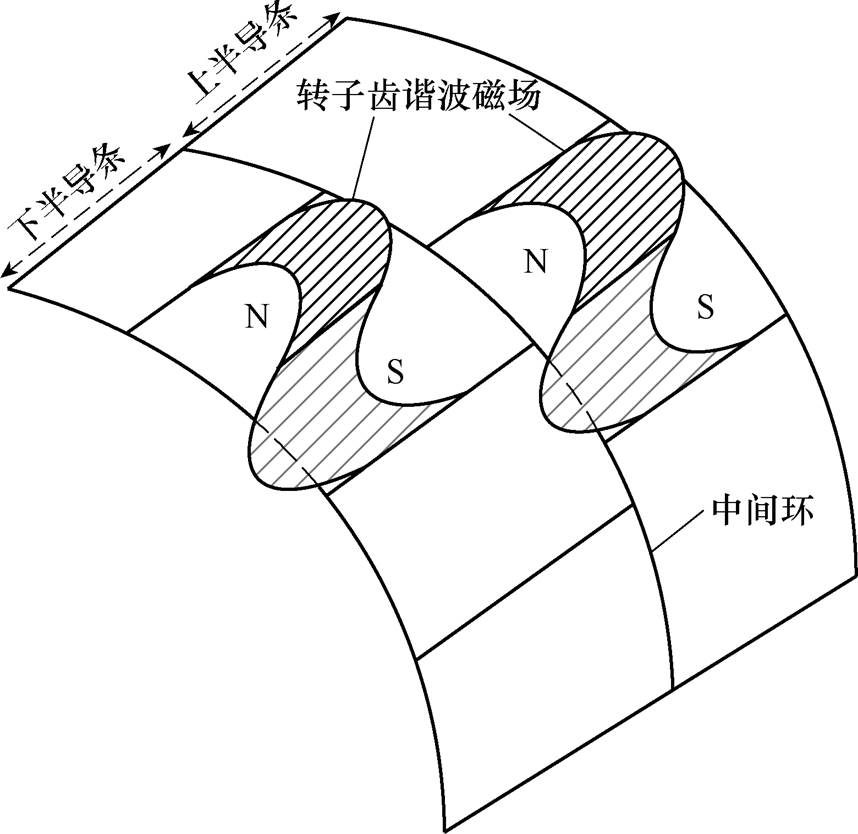
图3 双斜槽转子削弱谐波的原理
Fig.3 Schematic diagram of double skewed rotor attenuating harmonics
通过1.2节的分析可知，SPWM供电会引入开关频率及其整数倍附近的高次时间谐波电压。由时间谐波电压或电流产生的电机磁场具有相同的极距与极对数但频率却各不相同[20]。由于双斜槽转子结构的特殊性，变频驱动时，双斜槽感应电机的三相绕组气隙合成磁动势可以分为两部分，有
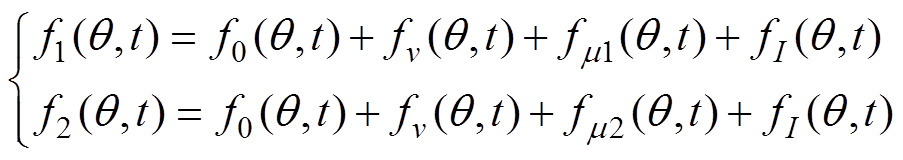（4）
式中，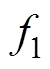
、
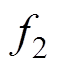分别为上、下两部分气隙合成磁动势；
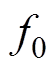为基波磁动势；
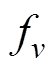为定子v次谐波磁动势；
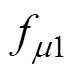和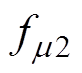
分别为两段转子绕组产生的m1次和m2次谐波磁动势；
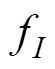为变频器引入的附加时间谐波磁动势；
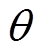为定子静止坐标系下的空间机械位置角；t为时间。
式（4）中的各部分表达式的具体展开如下
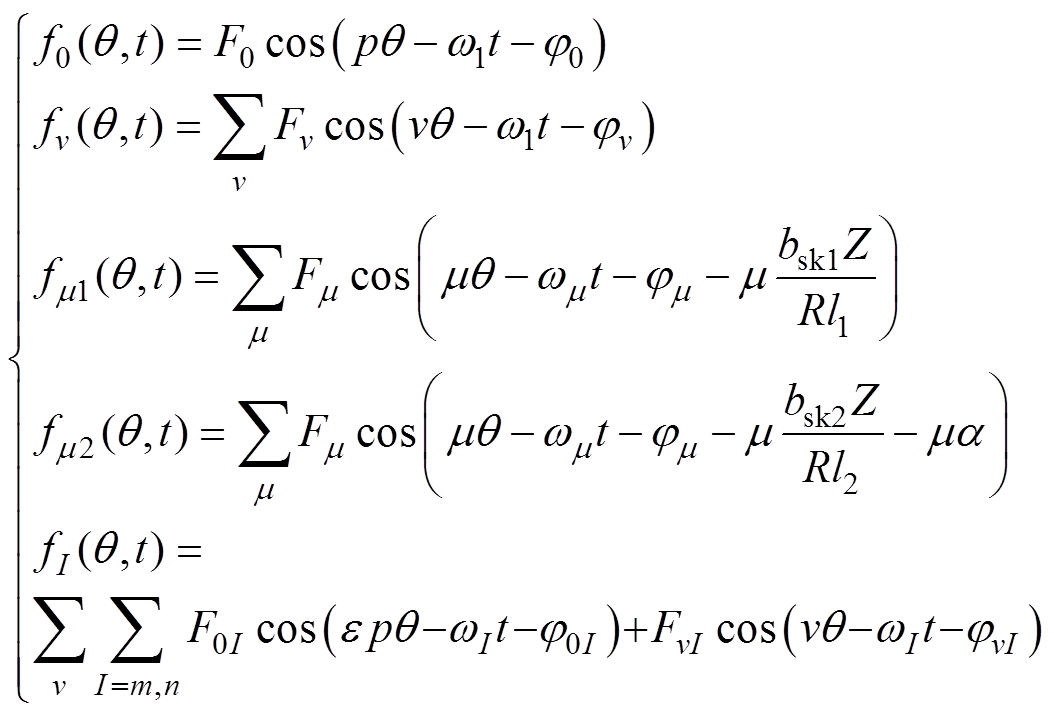（5）
式中，p为电机极对数；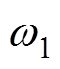
为定子基波的角频率； 
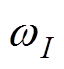为定子谐波电流的时间角频率，
；
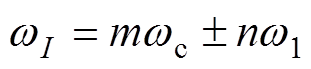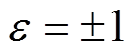为附加主波磁动势的旋转方向；v、
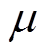为定、转子谐波的阶次；
、
、
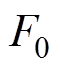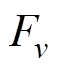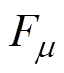分别为主波、定、转子绕组谐波磁动势的幅值；
、
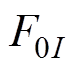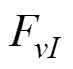分别为附加主波、附加定子谐波磁动势的幅值；
、
、
、
、
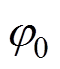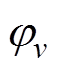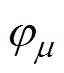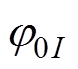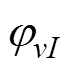分别对应各磁动势的初相位；bsk1、bsk2分别为上、下两部分转子的斜槽距离；
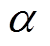为上半转子和下半转子相互错开的角度；Z为轴向位置；l1、l2分别为两部分转子轴向长度；R为电机转子半径；
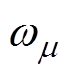为转子谐波时间角频率，其表达式为
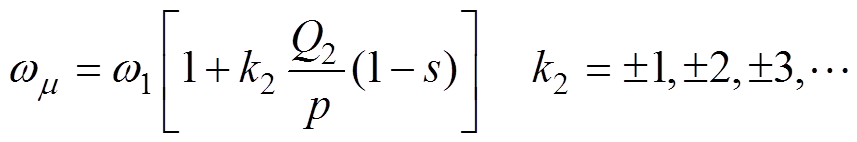（6）
式中，Q2为电机转子的槽数；s为转差率；k2为不为0的整数。
在分析气隙磁通密度之前，首先对磁导进行分析。类似于磁动势的分析，电机的磁导也分两部分分析，当考虑定、转子开槽以及转子斜槽的影响时，双斜槽转子的气隙磁导可表示为
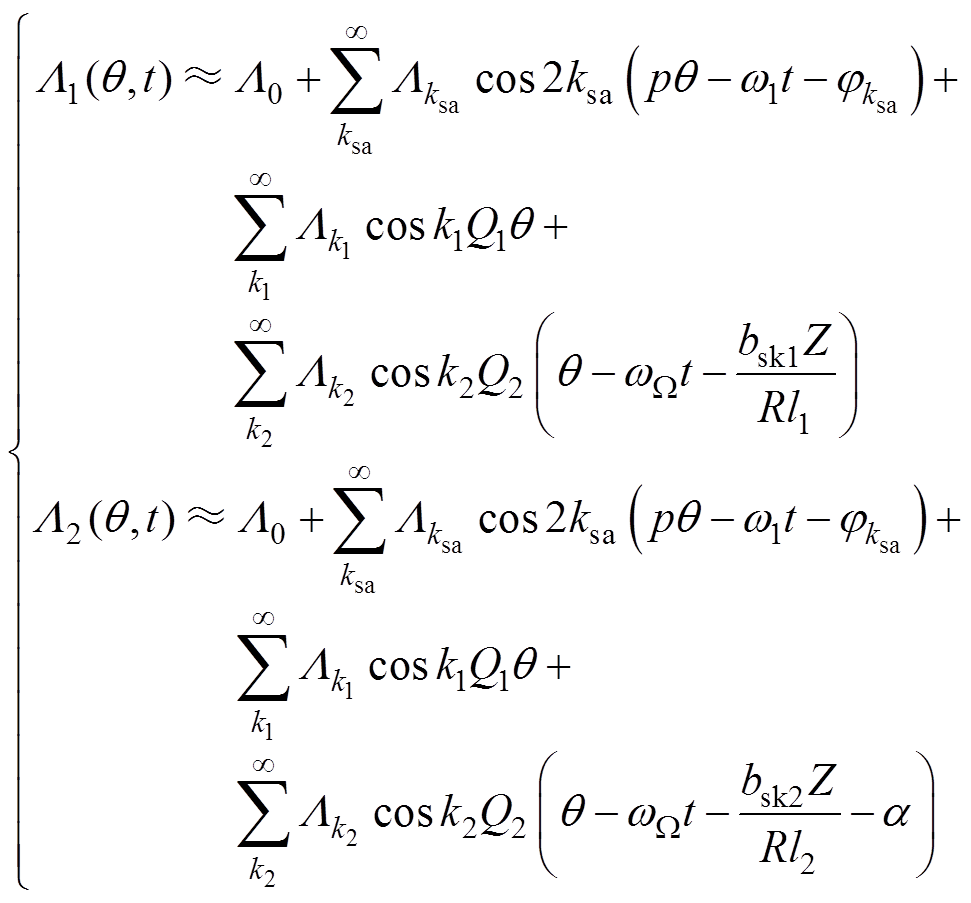（7）
式中，Q1为定子槽数；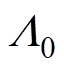
为气隙磁导的不变部分；
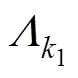为转子光滑时定子开槽引起的齿k1次谐波磁导幅值；
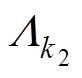为定子光滑时转子开槽引起的齿k2次谐波磁导幅值；
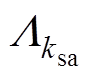为饱和谐波磁导的幅值；
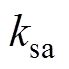为饱和谐波的次数；
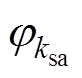为其初相位；
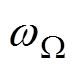为转子旋转的机械角速度，
。
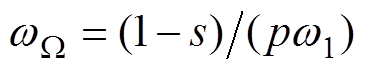由磁动势和磁导交叉相乘可以得到变频驱动下双斜槽感应电机气隙磁通密度的表达式为
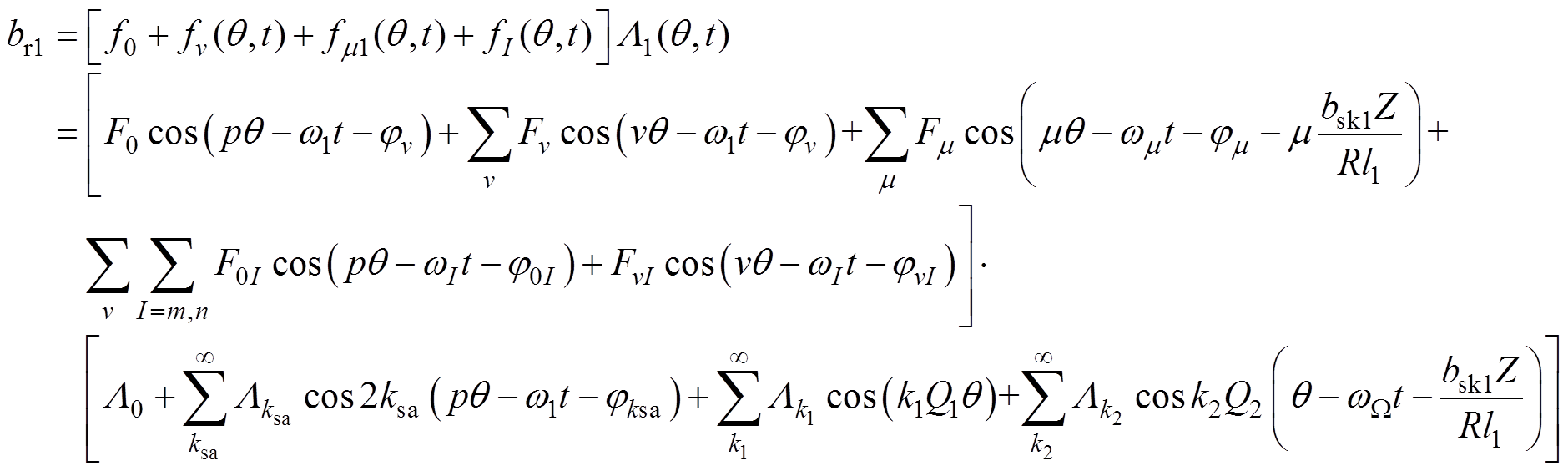（8）
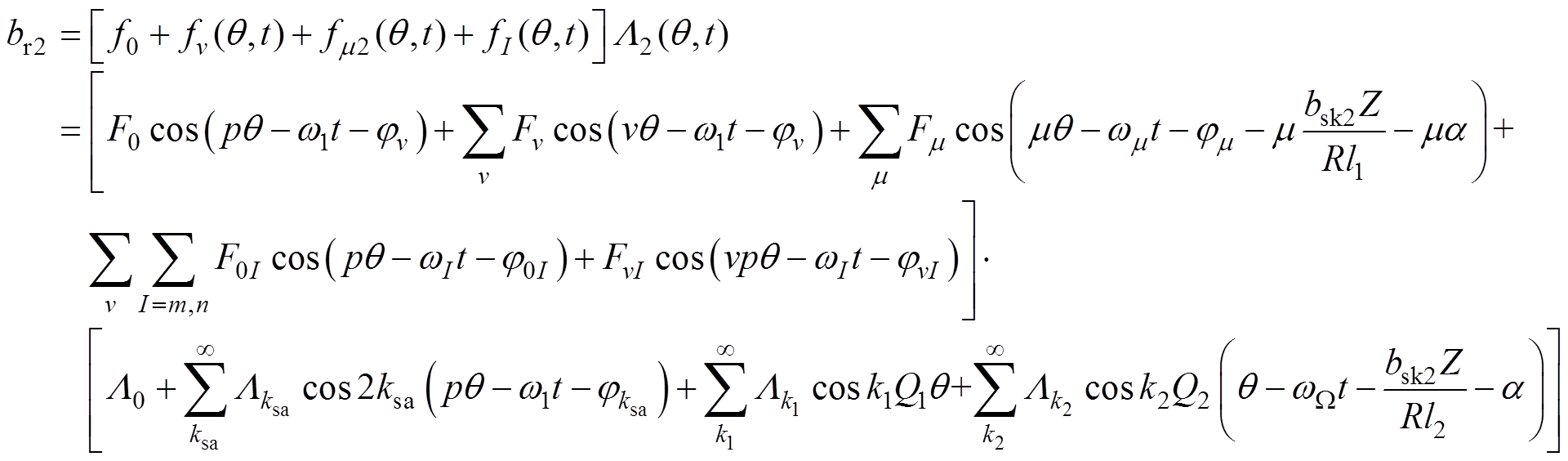（9）
式中，br1和br2分别为两半转子对应的气隙合成径向磁通密度，为了简化分析，忽略其中的次要成分，进而得到双斜槽转子感应电机正弦供电下气隙磁通密度表达式和变频器引入的重要的附加谐波磁通密度的表达式，即
（10）
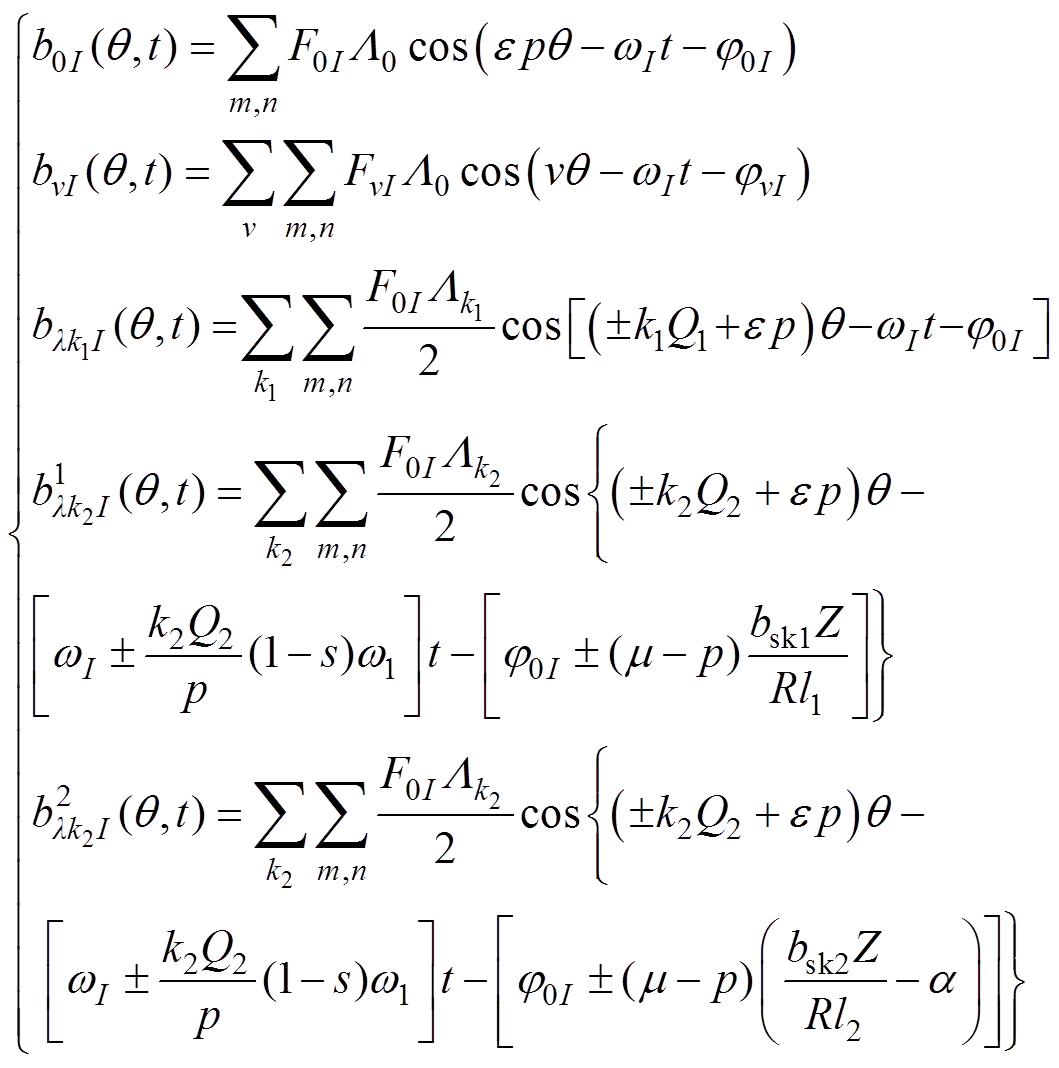（11）
式中，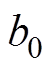
为主波磁通密度；
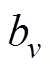为定子谐波磁通密度；
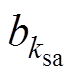为饱和谐波磁通密度；
、
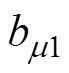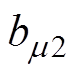分别为上、下两半转子绕组建立的转子谐波磁通密度；
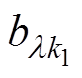为定子磁导齿谐波磁通密度；
、
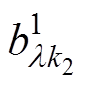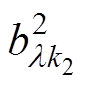分别为上、下两半转子磁导齿谐波磁通密度；
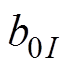为变频供电下附加主波磁通密度；
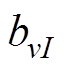为附加定子谐波磁通密度；
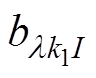为附加定子磁导齿谐波磁通密度；
、
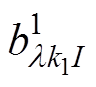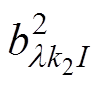分别为上、下两半转子附加转子磁导齿谐波磁通密度。
通过气隙磁通密度波的作用，在电机定子齿上产生的电磁力有径向和切向两个分量。其中径向分量使定子铁心产生的振动变形，是感应电机振动噪声的主要来源[21]。根据麦克斯韦尔应力张量理论电机气隙单位面积上的径向电磁力的瞬时表达式[22-23] 为
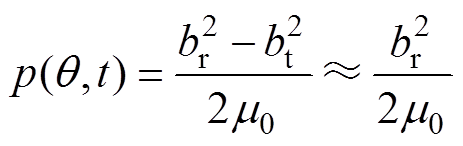（12）
式中，br为径向磁通密度；bt为周向磁通密度，气隙周向磁通密度幅值较小可忽略不计；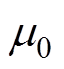
为真空磁导率。
双斜槽转子感应电机在全轴长上的平均径向电磁力可以表现两部分转子对应的平均径向电磁力在电机全轴长上的矢量合成，其表达式为
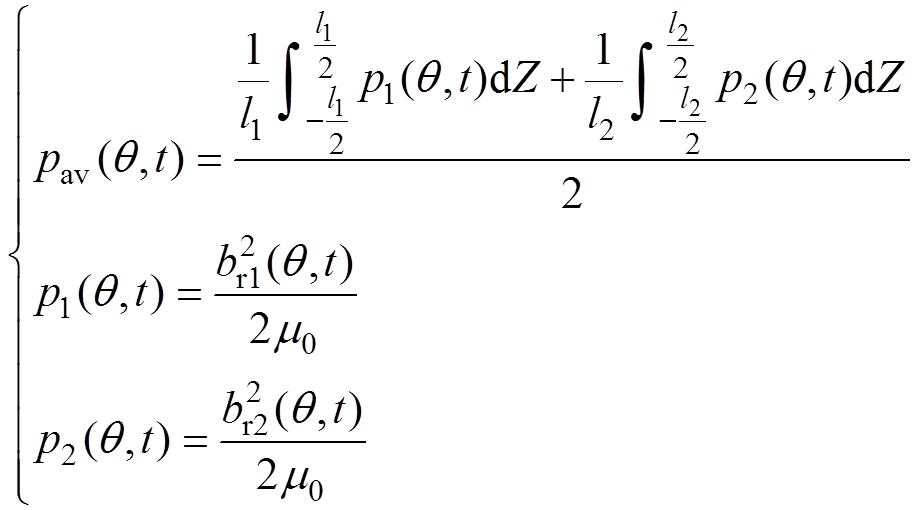（13）
式中，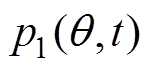
为上半转子对应的径向电磁力波；
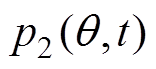为下半转子对应的径向电磁力波。
令bsk1=bsk2=bsk，l1=l2=l，将式（8）～式（11）代入式（13）可以得到一系列不同空间阶次与不同时间频率的径向电磁力波。忽略力波中对振动噪声影响较小的次要分量，提取主要径向电磁力波幅值、空间阶次、时间频率见表1。
表1中序号1～5为正弦供电下电机内磁场相互作用产生的径向电磁力，其中，4、5为饱和谐波磁通密度与主波磁通密度相互作用产生的径向电磁力；6、7为附加主波磁通密度与主波磁通密度相互作用产生的径向电磁力波；8、9为附加主波磁通密度与饱和谐波磁通密度相互作用产生的径向电磁力；10为附加转子磁导谐波磁通密度与定子磁导谐波磁通密度相互作用产生的径向电磁力；11、12为附加定子谐波磁通密度与转子谐波磁通密度相互作用产生的径向电磁力。表1中，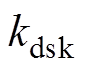
和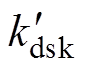
为对应电磁力波下的斜槽系数，具体表达式为
表1 变频供电下双斜槽感应电机的径向电磁力波
Tab.1 Radial electromagnetic force wave of double skewed rotor induction motor under variable frequency power supply
序号幅值空间阶次时间频率 100 22p 3 4 5 6 7 8 9 10 11 12
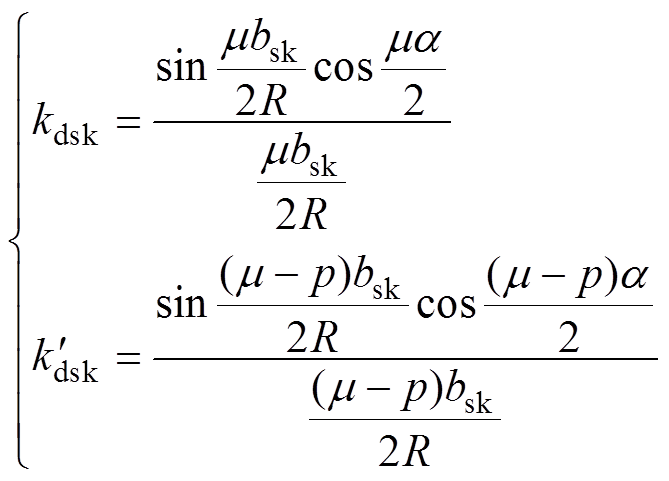（14）
式中，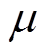
为转子齿谐波的次数，
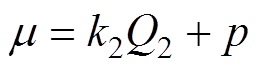。对于三相笼型感应电机有
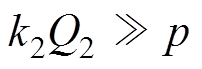，所以有
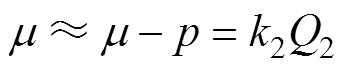（15）
当取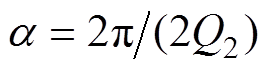
，即为1/2转子齿距时，将式（15）代入式（14）可得
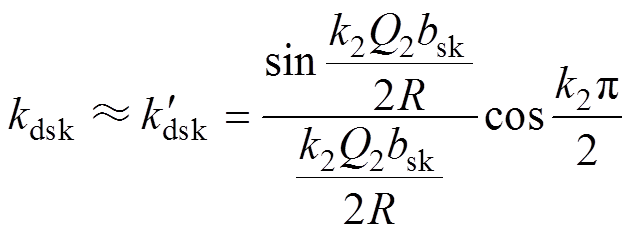（16）
归纳可知
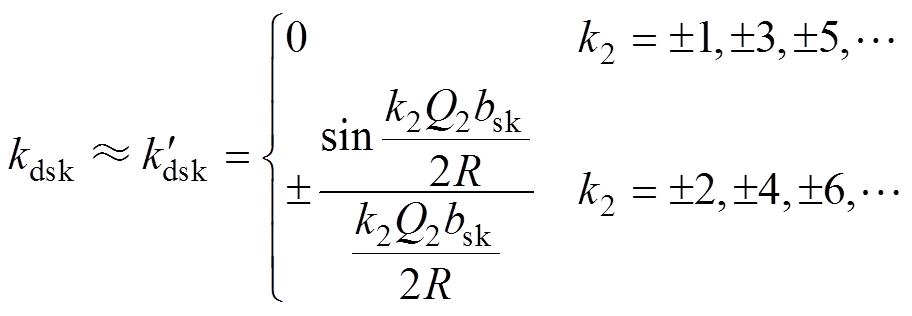（17）
由式（17）以及表1可以看出，当双斜槽转子的两段转子的长度与斜槽角度相同，且交错距离为半个转子齿距时，主波磁通密度与附加主波磁通密度以及附加主波磁通密度与饱和谐波磁通密度相互作用所产生的径向电磁力不会被削弱，但由变频器引入的奇数次附加转子磁导谐波所产生的附加径向电磁力以及转子谐波与附加定子谐波相互作用产生的附加径向电磁力可以被有效地削弱。
对于双斜槽转子感应电机，通常情况下，需采用三维有限元法进行仿真分析，但是三维模型的网格数量巨大，计算速度缓慢。因此有学者提出用改进的等效二维有限元法来对双斜槽转子感应电机的径向电磁力进行仿真计算，并通过对比验证了其良好的效果[24-25]。双斜槽转子的分层模型示意图如图4所示，具体的做法是将电机的转子沿着轴向分为K段，每一段转子沿轴向偏斜不同的机械角度，其中上半转子的各段与下半转子的各段需要进一步错开半个转子齿距。
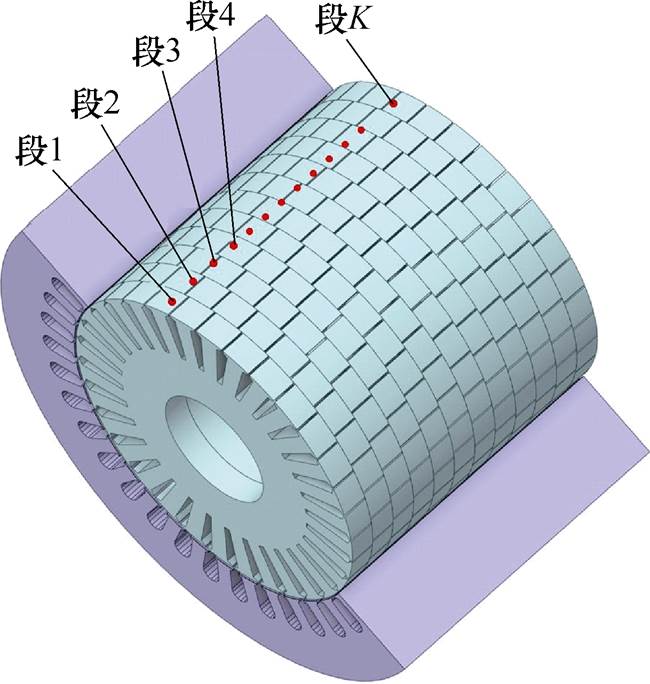
图4 双斜槽转子分层模型示意图
Fig.4 Schematic diagram of the multi-slice model of the double skewed rotor
双斜槽感应电机的仿真参数见表2，电机的转速为2 964 r/min（s=0.012）。为了考虑变频器的输出特性，采用Maxwell circuit插件搭建SPWM外电路对模型施加激励。取分段数K=12，双斜槽的等效二维有限元模型如图5所示。
表2 双斜槽转子感应电机的参数
Tab.2 Parameters of double skewed rotor induction motor
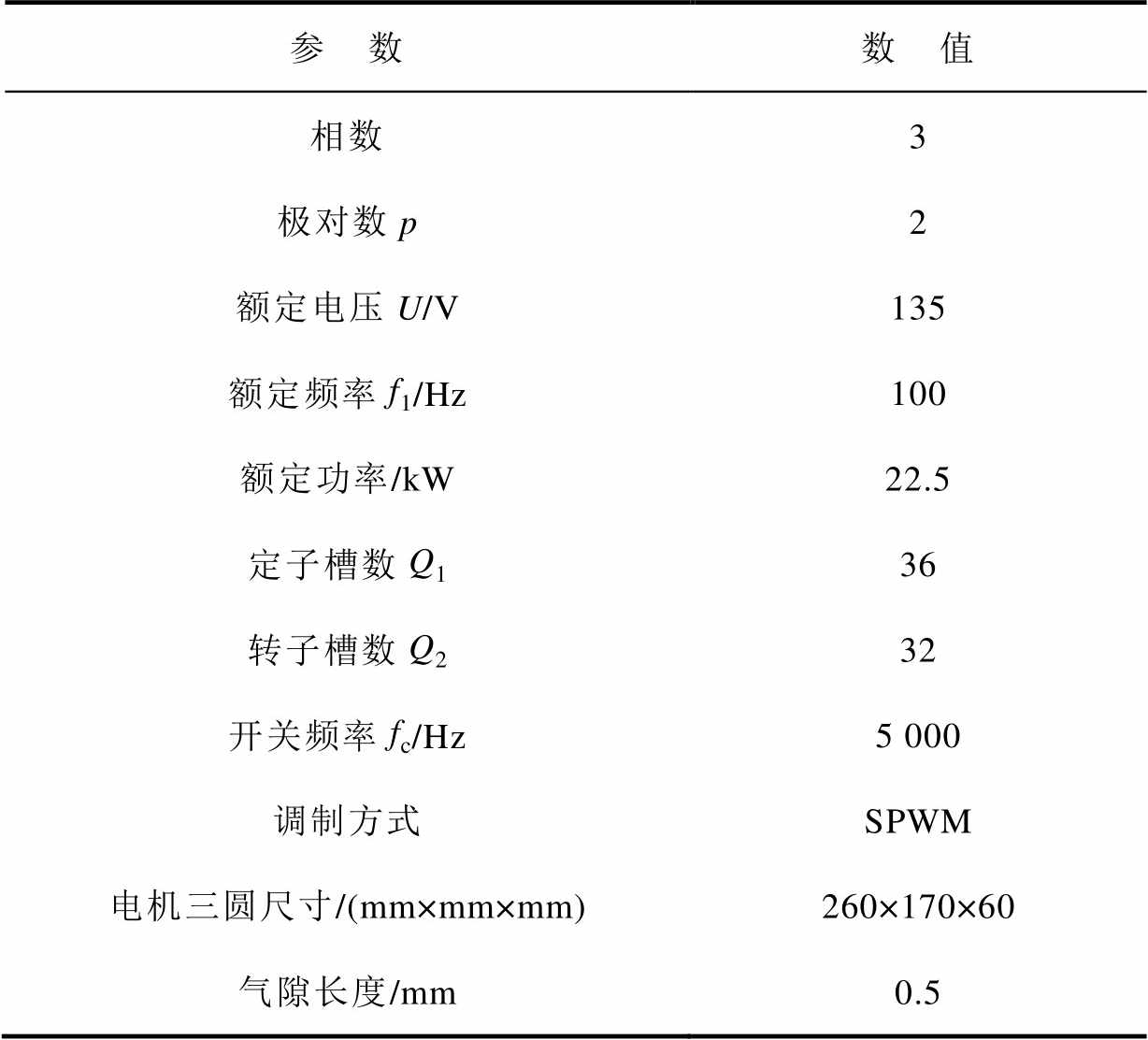
参 数数 值 相数3 极对数p2 额定电压U/V135 额定频率f1/Hz100 额定功率/kW22.5 定子槽数Q136 转子槽数Q232 开关频率fc/Hz5 000 调制方式SPWM 电机三圆尺寸/(mm×mm×mm)260×170×60 气隙长度/mm0.5
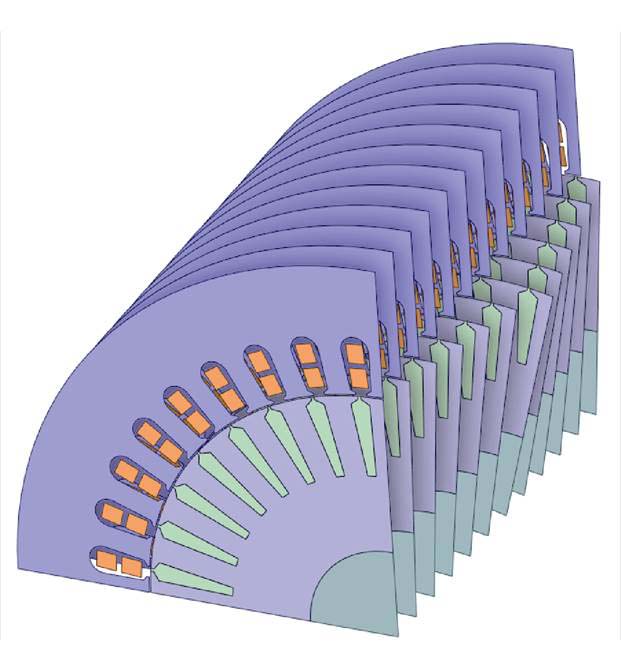
图5 等效二维有限元模型
Fig.5 Equivalent 2D finite element model
仿真得到的电机稳态时不同供电方式下的定子相电流波形如图6所示。对SPWM供电下定子相电流进行快速傅里叶分解，得到的结果如图7所示。
通过观察SPWM供电下定子相电流的快速傅里叶分解结果可以看出，在除基波以外，在频率4 800、5 200、9 900、10 100 Hz等高频处均出现了较高的幅值，分别对应的频率为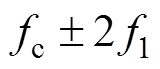
、
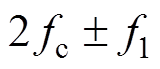，与上文的分析一致，为SPWM引入的高次时间谐波。
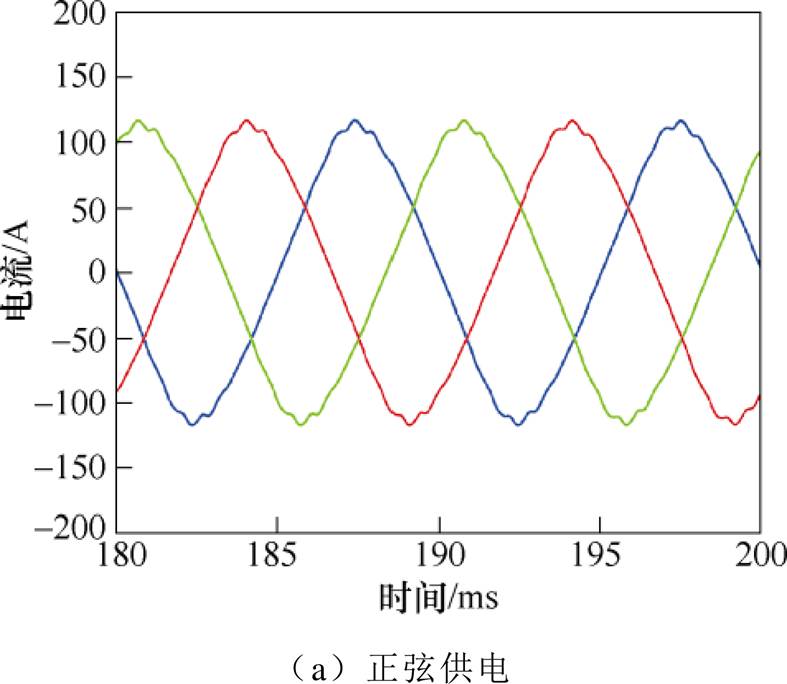
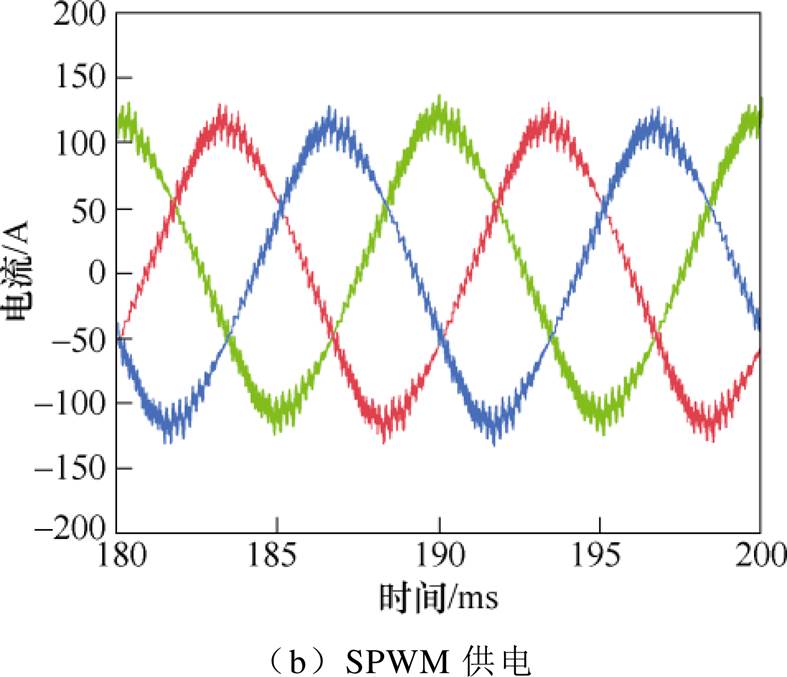
图6 不同供电方式下定子相电流波形
Fig.6 Stator phase current waveforms under different power supply modes
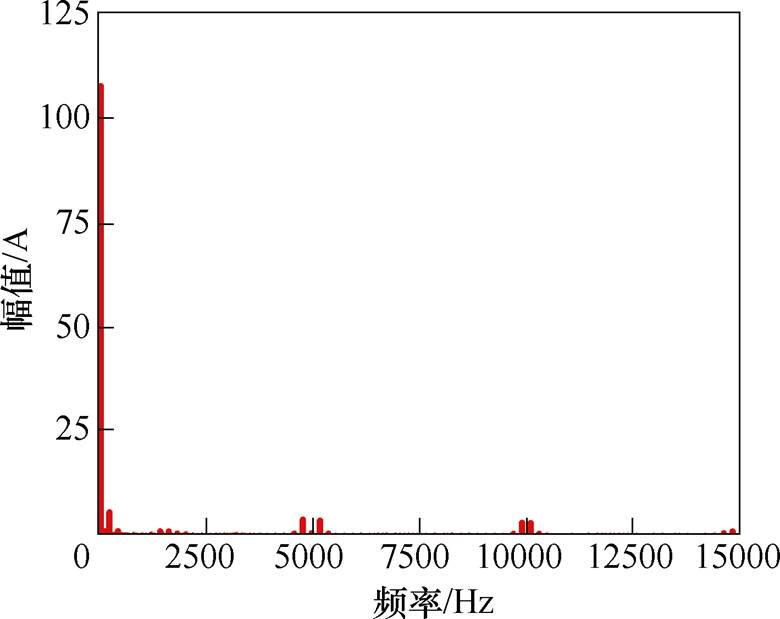
图7 SPWM供电下定子相电流的FFT
Fig.7 FFT of stator phase current under SPWM power supply
图8为仿真得到的双斜槽转子下气隙径向电磁的时空分布。取气隙的定子齿下的某一点，得到该点的径向电磁力随时间的变化波形如图9所示。可以看出，双斜槽的径向电磁力波形相较于直槽而言，“毛刺”更少，具有更好的正弦度。这也意味着双斜槽径向电磁力的时间谐波含量更少。为了进一步观察径向电磁力的时空谐波成分，对气隙径向电磁力进行时空上的（2D-FFT），得到的结果如图10 所示。
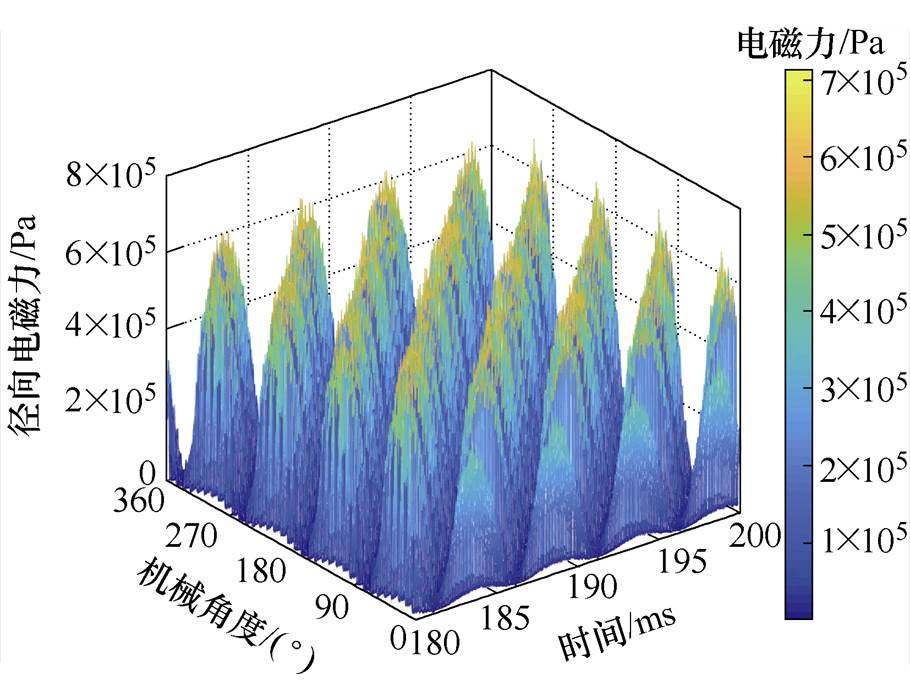
图8 双斜槽转子下径向电磁力的时空分布
Fig.8 Space-time distribution of radial electromagnetic force in double skewed rotor
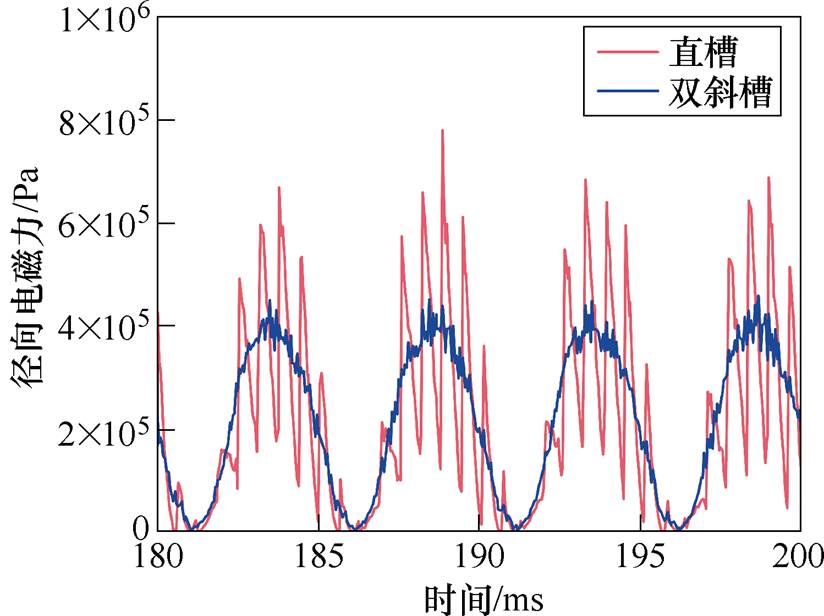
图9 双斜槽径向电磁力的时间分布
Fig.9 Time distribution of radial electromagnetic force of double skewed rotor
通过观察正弦供电直槽转子下的气隙径向电磁力2D-FFT结果可以看出，气隙的低阶次径向电磁力主要集中在0、4、8阶次，这是由于电机采用的槽配合为36～32，极对数为2造成的。对比变频供电与正弦供电下的径向电磁力分解结果看出，变频供电不会改变径向电磁力的空间阶次，但会引入新的频率的力波，而且新引入幅值较高的径向电磁力频率主要集中在3 000～7 000 Hz。
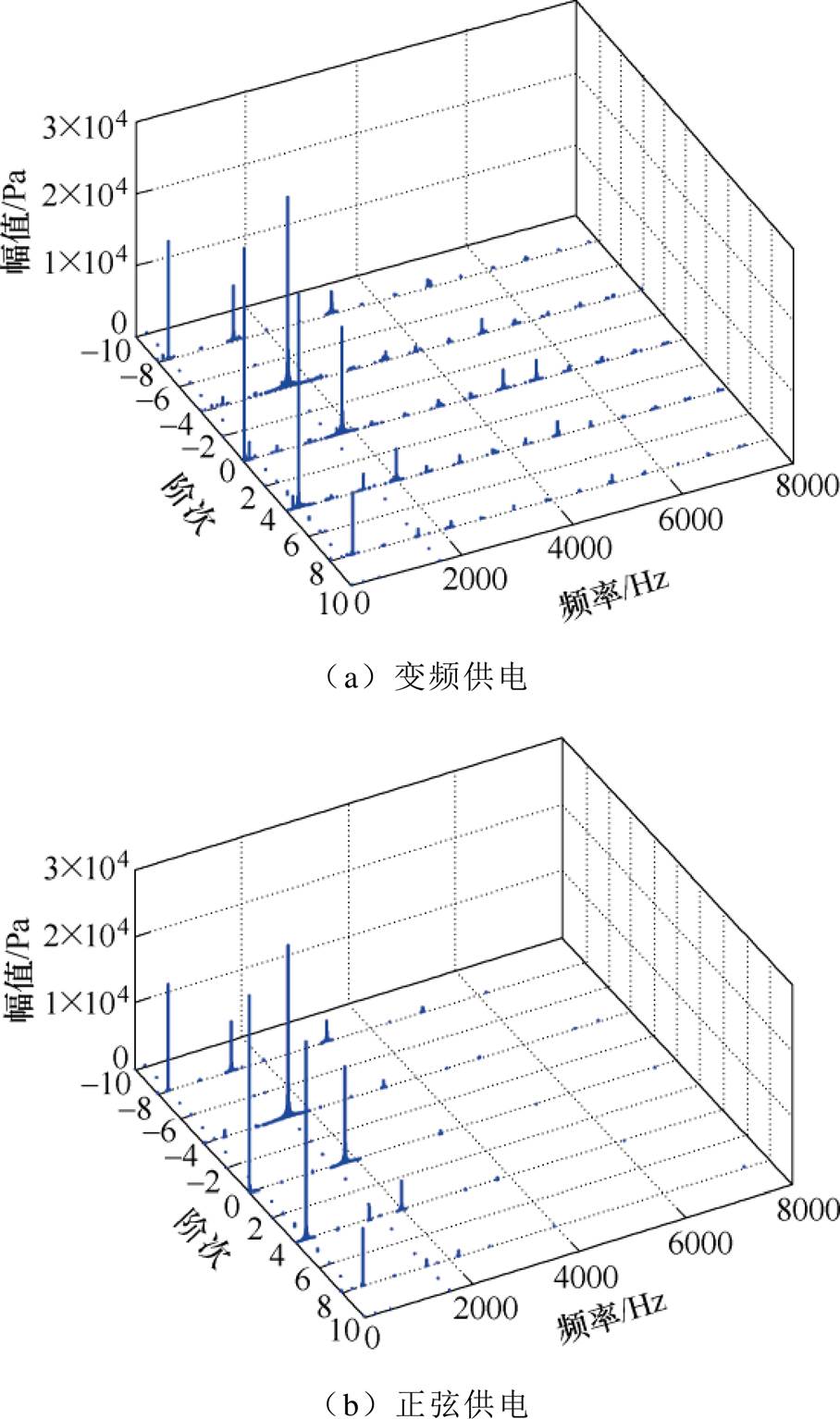
图10 直槽转子下径向电磁力的2D-FFT
Fig.10 2D-FFT of radial electromagnetic force under straight slot rotor
图11所示为变频供电下直槽和双斜槽的主要径向电磁力谐波的二维傅里叶对比，将二维傅里叶分解得到的结果进行整理，得到的变频供电引入的主要附加径向电磁力波见表3。
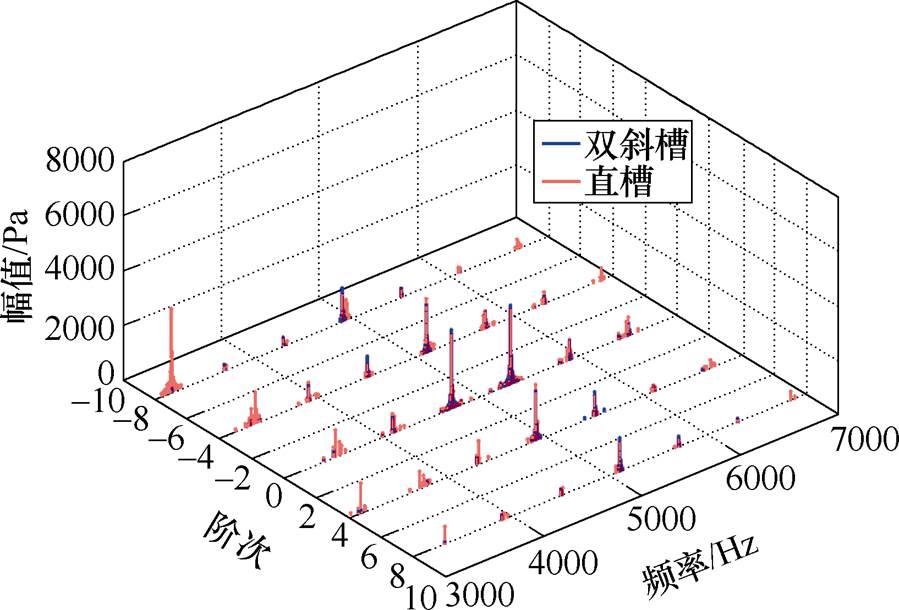
图11 变频供电下直槽和双斜槽的径向电磁力的2D-FFT
Fig.11 2D-FFT of radial electromagnetic force of straight rotor and double skewed rotor under inverter power supply
通过表3中的数据可以看出，主波与附加主波相互作用产生的附加径向电磁力及附加主波与饱和谐波相互作用产生的附加径向电磁力不能被双斜槽削弱，但与附加转子磁导谐波相互作用引入的附加径向电磁力波以及转子谐波与附加定子谐波相互作用产生的径向电磁力波可以被明显削弱。
径向电磁力是电机机壳表面振动的激励源，为了验证上述分析的正确性，对不同供电方式下的电机机壳表面的振动加速度频谱进行测试。双斜槽样机及实验平台如图12所示。
将加速度传感器黏着在电机的机壳表面，待电机稳态运行后，采用振动分析仪记录1 min的机壳测点的振动加速度，然后改变供电方式，重复记录数据，得到的不同供电方式下机壳表面的振动加速度频谱如图13所示。
表3 变频供电引入的重要附加径向电磁力
Tab.3 The main radial electromagnetic force wave under variable frequency power supply
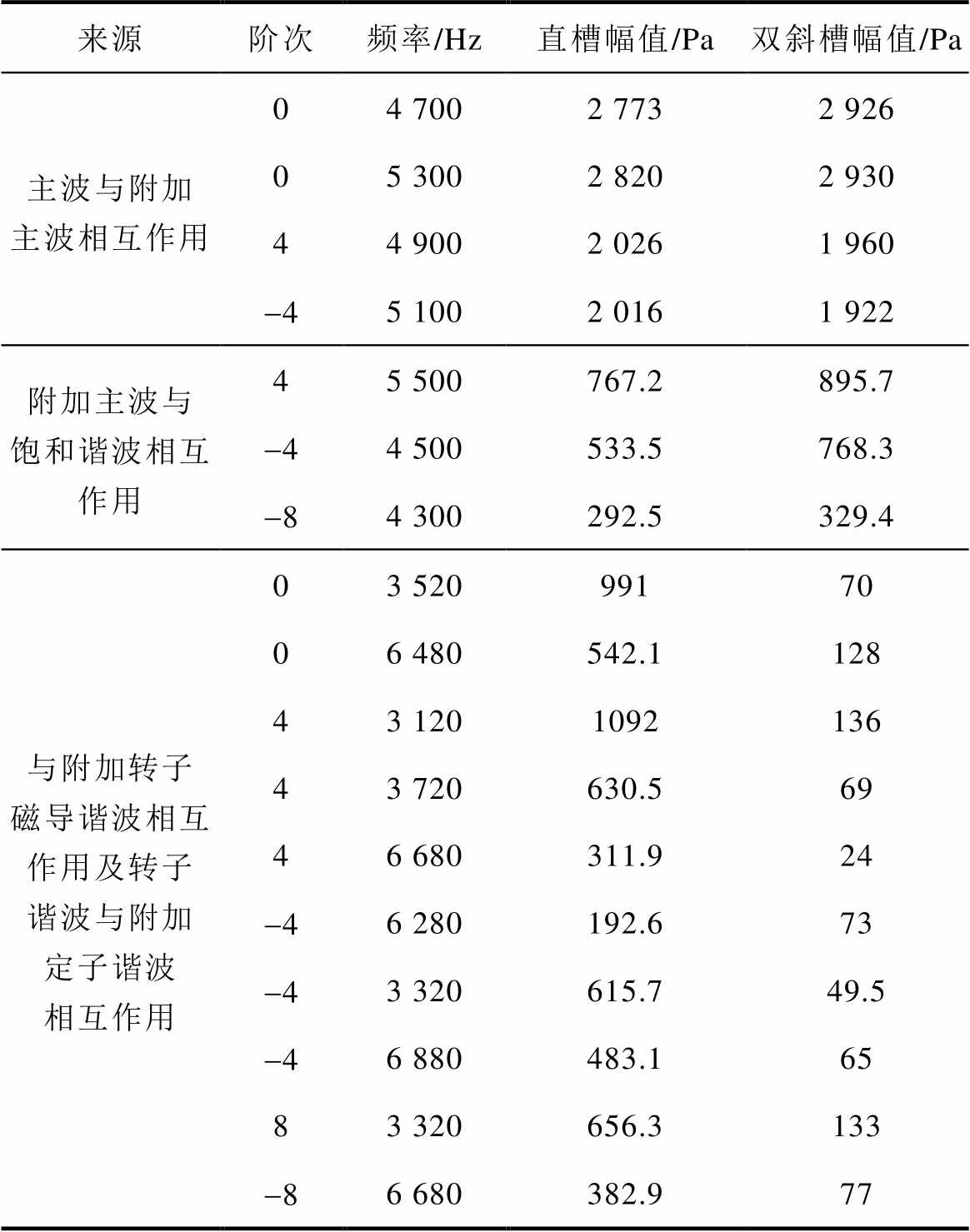
来源阶次频率/Hz直槽幅值/Pa双斜槽幅值/Pa 主波与附加主波相互作用04 7002 7732 926 05 3002 8202 930 44 9002 0261 960 -45 1002 0161 922 附加主波与饱和谐波相互作用45 500767.2895.7 -44 500533.5768.3 -84 300292.5329.4 与附加转子磁导谐波相互作用及转子谐波与附加定子谐波相互作用03 52099170 06 480542.1128 43 1201092136 43 720630.569 46 680311.924 -46 280192.673 -43 320615.749.5 -46 880483.165 83 320656.3133 -86 680382.977
图12 双斜槽样机及实验平台
Fig.12 Double skewed prototype and test platform
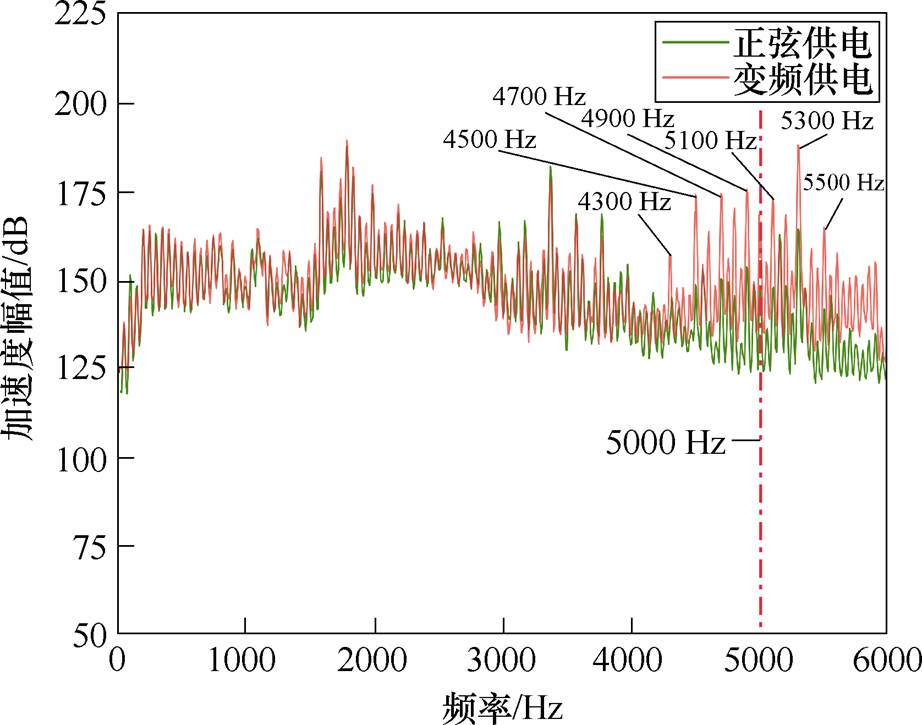
图13 振动频谱
Fig.13 Vibration spectrogram
通过观察不同供电方式下机壳表面的振动加速度可以发现，由于主波与附加主波以及附加主波与饱和谐波的相互作用，在频率为4 300、4 500、4 700、4 900、5 100、5 300、5 500 Hz处均出现了较大的振动加速度，其中5 300 Hz处的振动加速度幅值最大，为188 dB。当频率低于4 300 Hz时，由于双斜槽转子结构的谐波削弱作用，不同供电方式下双斜槽感应电机的振动加速度频谱基本相同。
本文对变频驱动下双斜槽感应电机的径向电磁力进行了研究。从变频器的输出谐波特性出发，采用解析法分析了变频供电下双斜槽感应电机径向电磁力的时空分布，并利用分层有限元法与二维傅里叶分解得到了附加电磁力波的阶次、频率与幅值，结合样机实验可以得出以下结论：
1）变频供电不会改变径向电磁力的空间阶次，但会引入新的高频径向电磁力。
2）主波磁场和附加主波磁场相互作用产生的径向电磁力及附加主波与饱和谐波相互作用产生的径向电磁力不会被双斜槽的结构削弱，因此在开关频率附近存在较大的径向电磁力，使得电机在该频率点处振动幅值增加。
3）与变频器引入的附加转子磁导谐波相互作用所产生的径向电磁力及转子谐波与附加定子谐波相互作用所产生的径向电磁力可以被双斜槽结构有效的削弱，其中幅值最大的径向电磁力波削弱也最明显，从1 092 Pa降低到136 Pa，降低了956 Pa。因此在远离开关频率处电机机壳的振动特性与正弦供电下的机壳振动特性基本相同。
以上的分析与理论分析相符，为进一步的变频驱动下双斜槽感应电机噪声的研究及其故障诊断技术奠定基础。
参考文献
[1] Yang Zhi, Shang Fei, Brown I P, et al. Comparative study of interior permanent magnet, induction, and switched reluctance motor drives for EV and HEV applications[J]. IEEE Transactions on Transportation Electrification, 2015, 1(3): 245-254.
[2] 黄闯, 代颖, 罗建. 新能源汽车异步电机驱动系统的电磁振动与噪声分析[J]. 工业控制计算机, 2019, 32(5): 160-161, 164.
Huang Chuang, Dai Ying, Luo Jian. Analysis of elec- tromagnetic vibration and noise in induction motor drive system of new energy vehicle[J]. Industrial Control Computer, 2019, 32(5): 160-161, 164.
[3] 陈永校. 电机噪声的分析和控制[M]. 杭州: 浙江大学出版社, 1987.
[4] Wang Lang, Bao Xiaohua, Di Chong, et al. Analysis of synchronous parasitic torque in dual skew cage rotor induction motors with equivalent slot number[J]. IET Electric Power Applications, 2017, 11(8): 1357- 1365.
[5] Xu Wei, Bao Xiaohua, Di Chong, et al. Optimal angle combination for improving electromagnetic torque in induction motor with double-skewed rotor[J]. IEEE Transactions on Magnetics, 2017, 53(11): 1-5.
[6] 王春雨. 电动叉车用双斜槽转子感应电机的振动噪声分析[D]. 合肥: 合肥工业大学, 2018.
[7] 祝长生, 陈永校. 变频器供电的三相异步电机的噪声特性[J]. 中小型电机, 1997, 24(5): 9-12.
Zhu Changsheng, Chen Yongxiao. Noise characteri- stics of three-phase asynchronous motor powered by frequency converter[J]. S & M Electric Machines, 1997, 24(5): 9-12.
[8] Du Jianmin, Li Yan, Yu Zhanyang, et al. Research on radial electromagnetic force and vibration response characteristics of squirrel-cage induction motor fed by PWM inverter[J]. IEEE Transactions on Applied Superconductivity, 2021, 31(8): 1-4.
[9] Binojkumar A C, Saritha B, Narayanan G. Acoustic noise characterization of space-vector modulated induction motor drives—an experimental approach[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3362-3371.
[10] Le Besnerais J, Lanfranchi V, Hecquet M, et al. Characterization and reduction of audible magnetic noise due to PWM supply in induction machines[J]. IEEE Transactions on Industrial Electronics, 2010, 57(4): 1288-1295.
[11] 李文, 赵慧敏, 邓武. 变频器驱动异步电机振动频谱特征分析[J]. 电机与控制学报, 2012, 16(8): 67-73.
Li Wen, Zhao Huimin, Deng Wu. Analysis of vibration spectrum characteristics for asynchronous motor driven by inverter[J]. Electric Machines and Control, 2012, 16(8): 67-73.
[12] 左曙光, 李凡, 胡潇睿. 考虑变频器供电影响的异步电机电磁噪声特性分析[J]. 机电一体化, 2021, 27(4): 12-21.
Zuo Shuguang, Li Fan, Hu Xiaorui. Characteristics analysis of electromagnetic noise in induction motor considering the influence of inverter[J]. Mechatronics, 2021, 27(4): 12-21.
[13] 肖阳, 宋金元, 屈仁浩, 等. 变频谐波对电机振动噪声特性的影响规律[J]. 电工技术学报, 2021, 36(12): 2607-2615.
Xiao Yang, Song Jinyuan, Qu Renhao, et al. The effect of harmonics on electromagnetic vibration and noise characteristic in inverter-duty motor[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(12): 2607-2615.
[14] Tsoumas I P, Tischmacher H. Influence of the inverter’s modulation technique on the audible noise of electric motors[J]. IEEE Transactions on Industry Applications, 2014, 50(1): 269-278.
[15] Ruiz-Gonzalez A, Vargas-Merino F, Perez-Hidalgo F, et al. Low switching PWM strategy to reduce acoustic noise radiated by inverter-fed induction motors[C]// 2010 IEEE International Symposium on Industrial Electronics, Bari, Italy, 2010: 1353-1358.
[16] 宁榕. SPWM型变频器供电下异步电机电磁噪声[J]. 电机与控制应用, 2014, 41(7): 39-42.
Ning Rong. Electromagnetic noise of induction motor under SPWM inverter power supply[J]. Electric Machines & Control Application, 2014, 41(7): 39-42.
[17] 翟国富, 李永虔, 刘玥怡, 等. 基于空间域谐波控制的电磁超声Lamb波模态抑制方法[J]. 电工技术学报, 2021, 36(16): 3467-3473.
Zhai Guofu, Li Yongqian, Liu Yueyi, et al. Mode suppression method of lamb wave excited by electromagnetic acoustic transducers based on spatial harmonic control[J]. Transactions of China Electro- technical Society, 2021, 36(16): 3467-3473.
[18] 李新君, 张敏. 三相SPWM逆变器的谐波分析及其抑制策略[J]. 防爆电机, 2008, 43(1): 18-20, 32.
Li Xinjun, Zhang Min. Harmonic analysis of three- phase SPWM inverter and its inhibition scheme[J]. Explosion-Proof Electric Machine, 2008, 43(1): 18-20, 32.
[19] 王兆安, 刘进军. 电力电子技术[M]. 5版. 北京: 机械工业出版社, 2009.
[20] 汤蕴璆, 张奕黄, 范瑜. 交流电机动态分析[M]. 北京: 机械工业出版社, 2005.
[21] 刘东浩, 张小平, 郭宇轩, 等. 基于内切圆弧的交流牵引电机齿肩削角降噪方法[J]. 电工技术学报, 2021, 36(6): 1259-1268.
Liu Donghao, Zhang Xiaoping, Guo Yuxuan, et al. Method for reducing shoulder noise of AC traction motor based on inscribed arc[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1259- 1268.
[22] 洪剑锋, 王善铭, 孙宇光, 等. 高模数电磁力对永磁电机电磁振动影响[J]. 电工技术学报, 2022, 37(10): 2446-2458.
Hong Jianfeng, Wang Shanming, Sun Yuguang, et al. The influence of high-order force on electromagnetic vibration of permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2446-2458.
[23] 罗玉涛, 卢若皓. 基于结构参数分级优化的电机电磁噪声抑制[J]. 电工技术学报, 2021, 36(14): 2957- 2970.
Luo Yutao, Lu Ruohao. Hierarchical optimization of structural parameters for motor electromagnetic noise suppression[J]. Transactions of China Electro- technical Society, 2021, 36(14): 2957-2970.
[24] Bao X, Di C, Zhou Y. Calculation of electromagnetic excitation forces in double skewed motors[J]. Journal of Electrical Engineering and Technology, 2018, 13(2): 812-821.
[25] Du Jianmin, Li Yan, Yu Zhanyang, et al. Research on electromagnetic vibration response of squirrel-cage induction motor based on multi-section method[C]// 2020 IEEE International Conference on Applied Super- conductivity and Electromagnetic Devices (ASEMD), Tianjin, China, 2020: 1-2.
Abstract Inverter power supply is a common method for new energy drive motors, greatly broadening the operating range of induction motors. However, the output voltage of the inverter contains a large number of harmonic components, which will deteriorate the vibration and noise performance of the motor. There have been many related types of research on the vibration and noise of permanent magnet motors and traditional induction motors under the inverter power supply. However, more research must be done on the vibration and noise of double-skewed rotor induction motors (DSRIM) under the inverter power supply. Therefore, this paper has carried out a detailed study on the radial electromagnetic force of the DSRIM driven by an inverter.
Firstly, based on the output harmonic characteristics of the inverter, the air-gap flux density component of the induction motor is analyzed by analytical method, and the expressions of the amplitude, order, and frequency of the radial electromagnetic force are obtained by analyzing the interaction of each flux density harmonic. Then the time-space distribution spectrum of the average radial electromagnetic force is obtained using the multi-slice finite element method and 2-D fast Fourier decomposition. Compared with air gap radial electromagnetic force under different power supply modes and rotor structures, the DSRIM can effectively weaken some of the additional high-frequency radial electromagnetic force introduced by the inverter power supply. Finally, the correctness of the analysis is verified by the vibration experiment of the prototype.
The simulation results of the radial electromagnetic force of the motor under the inverter power supply show that the inverter power supply will not change the spatial order of the radial electromagnetic force. However, it will introduce new frequency force waves mainly concentrated in 3 000～7 000 Hz. The additional radial electromagnetic force wave introduced by the interaction with the additional rotor permeance harmonic and the radial electromagnetic force wave generated by the interaction between the rotor harmonic and the additional stator harmonic can be significantly weakened. The weakening of the radial electromagnetic force wave with the largest amplitude is also the most obvious, decreasing from 1 156 Pa to 60 Pa, decreasing by 1 096 Pa. The experimental results of the prototype show that the motor has significant vibration acceleration at the frequencies of 4 300 Hz, 4 500 Hz, 4 700 Hz, 4 900 Hz, 5 100 Hz, 5 300 Hz, and 5 500 Hz under the inverter power supply, but when the frequency is lower than 4 300 Hz, due to the harmonic weakening effect of the DSRIM, the vibration acceleration spectrum of the DSRIM under different power supply modes is the same.
The following conclusions can be drawn: (1) Inverter power supply will not change the spatial order of radial electromagnetic force but will introduce new high-frequency radial electromagnetic force. (2) The structure of DSRIM does not weaken the radial electromagnetic force generated by the interaction of the main and additional main wave magnetic fields. Moreover, the radial electromagnetic force generated by the interaction of the additional main wave and the saturated harmonic magnetic field will not be weakened. Therefore, there is a large radial electromagnetic force near the switching frequency, which increases the vibration amplitude of the motor at this frequency point. (3) The DSRIM can effectively weaken the radial electromagnetic force generated by the interaction with the additional rotor permeance harmonics introduced by the inverter and the radial electromagnetic force generated by the interaction between the rotor slot harmonics and the additional stator harmonics. Therefore, the vibration characteristics of the motor casing at a place far away from the switching frequency are the same as those of the casing under a sinusoidal power supply.
This paper lays a foundation for further research on noise and fault diagnosis technology of DSRIM driven by an inverter.
keywords：Induction motor, double skewed rotor, radial electromagnetic force, electromagnetic vibration
DOI: 10.19595/j.cnki.1000-6753.tces.220663
中图分类号：TM346+.2
国家自然科学基金（51977055）、安徽省科技重大专项（201903a05020042）和合肥工业大学智能制造技术研究院2019年度智能网联及新能源汽车技术科技成果转化及产业化专项资金（IMIWL2019001）资助项目。
收稿日期 2022-04-25
改稿日期 2022-06-12
鲍晓华 男，1972年生，教授，博士生导师，研究方向为电机设计理论和技术、电机电磁场理论分析及计算、大型电机及高速电机的可靠性技术。E-mail: sukz@ustc.edu（通信作者）
明 帅 男，1998年生，硕士研究生，研究方向为电机振动噪声的分析和控制。E-mail: 2020110345@mail.hfut.edu.cn
（编辑 郭丽军）