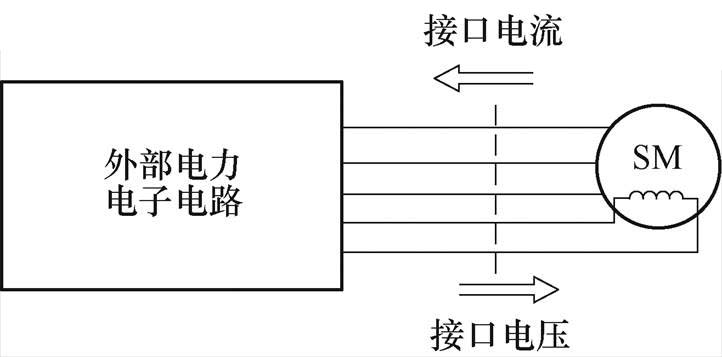
图1 包含电励磁同步电机的系统
Fig.1 System with electrically excited synchronous machine
摘要 微电网系统可以实现分布式电源、储能和负载的灵活接入,目前受到了广泛关注。建模仿真方法是微电网系统分析和设计的基础工具。但是,由于微电网系统往往含有多种直流、交流电源以及大量的电力电子装置,对系统进行准确解算耗时很长,仿真速度慢已成为系统分析设计的瓶颈问题之一。离散状态事件驱动(DSED)方法能够针对大规模电力电子变换器进行高效的解算,具备在微电网系统仿真中应用的潜力,但是由于建模解算均基于线性状态方程,该方法目前无法求解电励磁同步电机这一微电网系统中的非线性基本元件。该文提出了基于DSED方法的电励磁同步电机建模解算方法——状态变量接口解耦解算方法,使得DSED方法能够对包含电励磁同步电机的非线性微电网系统进行高效解算,从而提高仿真效率。在微电网系统算例研究中,与商业仿真软件相比,基于该文所提方法可以在相同精度下提高解算速度40余倍,从而可以为包含非线性旋转设备的大规模微电网系统准确高效的分析和设计提供仿真工具。
关键词:离散状态事件驱动 电励磁同步电机 电力电子系统仿真 微电网
由于微电网在提高分布式新能源利用率以及供电可靠性方面具有较大的发展潜力,其发展所需的相关技术得到了广泛研究[1-4]。针对微电网系统的建模仿真是相关研究的基础工具之一。相关研究借助建模仿真工具来验证各种与微电网系统相关的控制算法[5-8]。然而,微电网的电源类型多样,既包含旋转电机设备,也包含多种可再生能源和电力电子变换器,系统往往具有规模大、半导体开关器件数量多、连续状态与离散开关事件混杂的特点。这些特点导致对微电网系统开展建模仿真时,经常需要花费大量的时间进行准确解算[9-10]。
最近,相关工作提出的离散状态事件驱动(Discrete State Event-Driven, DSED)建模仿真方法,可以实现大规模电力电子系统的高效解算[11]。DSED方法充分利用了电力电子系统的混杂特性(连续状态和离散开关事件的混杂[12-14]),并利用分段解析瞬态(Piecewise Analytical Transient, PAT)模型[15]以及自适应积分方法[11]对系统进行解算。已有研究表明,DSED已经可以高效解算大规模的变换器系统[11],但是目前版本无法直接解算由非线性的状态方程所建模的系统,如含有电励磁同步电机的微电网,其中电励磁同步电机被广泛地应用于发电领域,同时也有被拓展到电气化轨道交通等领域的潜力[16]。之所以无法直接解算上述系统,是因为DSED方法将电力电子电路建模为分段线性状态方程组,而电励磁同步电机等非线性器件无法被建模成分段线性状态方程组的形式。
针对以上问题,一种可行的思路是将非线性部分与线性部分进行解耦。在已有研究中,系统解耦解算方法主要包括延迟插入法[17-18]、模型降阶 法[19-20]等。延迟插入法通过插入人工的时延以实现将一个大系统解耦为若干子系统。该方法的优势在于可以利用不同的数值解算法以及多速率来计算不同的子系统[17]。基于该优势,借助延迟插入法对线性部分采用DSED的自适应积分方法进行解算并用其他数值解算方法解算非线性的电机部分,但是该方法可能会引起数值解算不稳定的问题,这主要是由接口变量的数值交换存在时延引起的[18]。模型降阶方法则是将系统分为主导分量部分与非主导分量部分,并主要解算主导分量,从而实现解耦和提高解算效率。在已有研究中,该方法可以在线性系统中实现较高的解算速度提升[19]。但是该方法忽略了非主导特征值所对应的状态变量,降阶后的模型的计算结果与完整模型的结果可能会存在较大误差。
因此,为了在保证解算精度的前提下实现高效的解算,本文提出了一种适应于DSED方法的状态变量接口解耦方法。该方法的主要目的是将电机部分的非线性方程与外部的线性电力电子电路进行解耦,从而可以保证线性电路部分依然可以用DSED方法解算;同时通过接口电压和接口电流导数的及时传递,保证解算精度。
结合本文所提出的方法,DSED方法将能够准确高效地求解含有电励磁同步电机的系统,例如包含旋转设备的微电网系统;并且本文所提出的方法可以向其他非线性系统拓展,因此可以进一步拓展DSED方法的应用范围。
本文首先介绍本文所面向的系统结构以及利用DSED方法求解该系统的关键难点;其次介绍状态变量接口解耦方法的具体内容以及如何实现电机模型状态变量的各阶导数的计算;然后搭建一个微电网算例并对比基于DSED方法的仿真平台与商用软件的仿真解算结果以及解算效率;最后给出本文的结论。
本小节介绍所解算系统的一般结构以及现有的DSED方法的建模解算方法,进而解释本文在应用DSED方法解算包含电励磁同步电机系统时所要解决的问题。
本文所针对的建模解算系统是包含电励磁同步电机(Synchronous Machine, SM)的电力电子电路系统,其基本结构如图1所示。系统中包含电机部分以及电机以外的电力电子电路部分。对于电励磁同步电机以外的电力电子电路部分,DSED方法将其建模为分段线性状态方程的形式[11]。
电力电子系统是一个混杂系统,其中包含连续状态变量如电容电压和电感电流,以及离散的开关事件。基于这样的混杂特点,DSED方法将电力电子电路建模为分段线性状态方程组的形式,有

图1 包含电励磁同步电机的系统
Fig.1 System with electrically excited synchronous machine
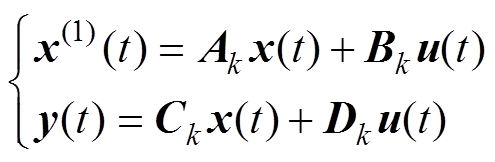 (1)
(1)
式中,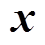 为
为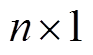 维的状态变量;
维的状态变量;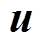 为
为 维的输入变量;
维的输入变量;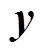 为
为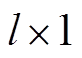 维的输出变量;
维的输出变量;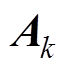 为
为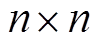 的矩阵;
的矩阵;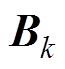 为
为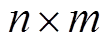 的矩阵;
的矩阵;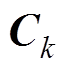 为
为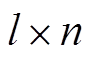 的矩阵;
的矩阵;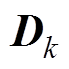 为
为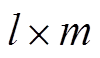 的矩阵。不同的开关状态会改变电路的拓扑进而引起上述矩阵的变化。这些矩阵的下标
的矩阵。不同的开关状态会改变电路的拓扑进而引起上述矩阵的变化。这些矩阵的下标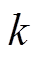 对应着第
对应着第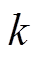 种开关状态所对应的矩阵。
种开关状态所对应的矩阵。
DSED方法利用自适应积分方法对式(1)进行数值解算[11],有
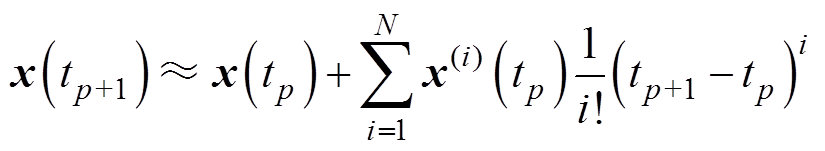 (2)
(2)
式中,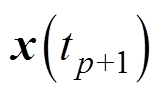 和
和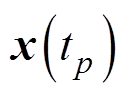 分别为状态方程式(1)中的状态变量在时刻
分别为状态方程式(1)中的状态变量在时刻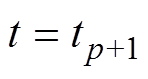 和
和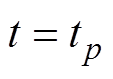 的数值解;
的数值解;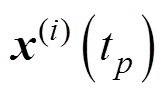 为状态变量在
为状态变量在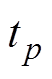 时刻的
时刻的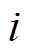 阶导数值;
阶导数值;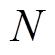 为算法设定的最高导数阶数,
为算法设定的最高导数阶数,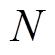 越大则数值求解方法具有更高的代数精度。
越大则数值求解方法具有更高的代数精度。
值得注意的是,如式(2)所示的基于泰勒展开的常微分方程求解方法并不是常用的常微分方程数值求解方法,因为对于一般的常微分方程组,计算各个状态变量的高阶导数往往是较为困难且计算量较大的。然而对于式(1)所示的系统,其状态变量的各阶导数可以通过式(3)所示的迭代公式得到。
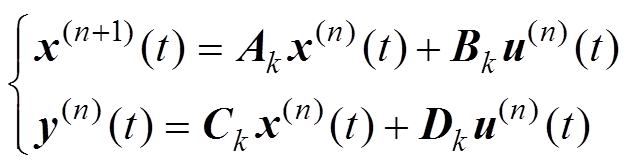 (3)
(3)
在知道状态变量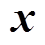 的初值以及输入变量
的初值以及输入变量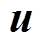 的初值和1~N阶的导数值时,便可以利用式(3)求出状态变量
的初值和1~N阶的导数值时,便可以利用式(3)求出状态变量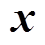 和输出变量
和输出变量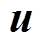 的1~N阶的导数,进而可以利用式(2)得到下一个时刻的状态变量数值解。
的1~N阶的导数,进而可以利用式(2)得到下一个时刻的状态变量数值解。
相比于常用的显式Runge-Kutta方法,自适应积分方法应用在线性系统时具有更高的计算效率,这主要得益于以下两个特点:
(1)对于相同的线性状态方程以及相同阶数的积分公式,自适应积分方法的单步计算量小于显式Runge-Kutta方法。表1展示了自适应积分的计算量与Runge-Kutta 45方法的对比。Runge-Kutta 45方法是一个变步长的4阶5阶方法,自适应积分方法想要达到相同的精度只需要计算最高的5阶导数,即表1中的r=5。乘法计算次数约为Runge-Kutta 45方法的 。除此之外,自适应积分方法可以用更高阶数(5、6、7阶)的算法进行计算以显著提高计算步长从而减少计算次数。
。除此之外,自适应积分方法可以用更高阶数(5、6、7阶)的算法进行计算以显著提高计算步长从而减少计算次数。
表1 自适应积分方法与Runge-Kutta 45算法的计算量对比
Tab.1 Computation comparison between the flexible adaptive algorithm and Runge-Kutta 45 algorithm

算法乘法次数加法次数 r阶自适应积分方法 Runge-Kutta 45方法
(2)自适应积分方法利用了当前点的导数信息从而可以实现灵活的变阶数与变步长,因此可以在当前点的时刻距离开关动作时刻较长时采用较高阶数的算法从而减少计算点数,反之在较短时采用较低阶数的算法。如式(2)所示,得到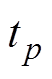 时刻状态变量的各阶导数值后,自适应积分方法在更改步长时只需要用新的步长代入式(2)进行计算,不需要重新计算导数值,而显式Runge-Kutta方法则需要重新计算所有中间点的值才能实现变步长。
时刻状态变量的各阶导数值后,自适应积分方法在更改步长时只需要用新的步长代入式(2)进行计算,不需要重新计算导数值,而显式Runge-Kutta方法则需要重新计算所有中间点的值才能实现变步长。
自适应积分方法可以灵活选取最为合适的解算阶数与步长求解离散状态之间的连续状态变量的变化,进而显著提高解算速度。
第一个难点来自于高阶导数的计算。如式(2)所示,DSED方法采用的自适应积分方法充分地利用了电路的线性特征,通过计算线性状态变量的高阶导数实现了灵活的变阶数与变步长。然而,电励磁同步电机的状态方程并不是线性状态方程,并且其状态变量的导数计算公式十分复杂。本文2.2节部分会介绍其导数计算公式的复杂性。这样的复杂性会导致:①推导公式繁琐;②计算高阶导数的计算量较大。因此,可能需要合理地简化高阶导数的计算。
第二个难点来自于包含电励磁同步电机的系统无法被统一建模为式(1)的形式。这是由于电励磁同步电机的状态方程具有非线性(见下文式(4)、式(5))。对这两个相互耦合但却具有不同方程形式的部分进行解算时,需要设计一种可以实现解耦的算法进行解算。
本小节首先介绍本文所采用的电励磁同步电机模型,然后推导电励磁同步电机状态变量的导数迭代计算公式以及状态变量接口解耦方法的算法流程。
本文所使用的电励磁同步电机的模型基于磁路线性以及互感随转子角度的变化呈现正弦变化的假设条件,并且考虑了凸极效应。基于上述假设,可以得到在转子dq0坐标系下的电励磁同步电机模 型[21],包括式(4)所示的电磁系统部分以及式(5)所示的机械系统部分。本文所采用的绕线式同步电机是无中线的,因此模型中的零轴电流分量为零。
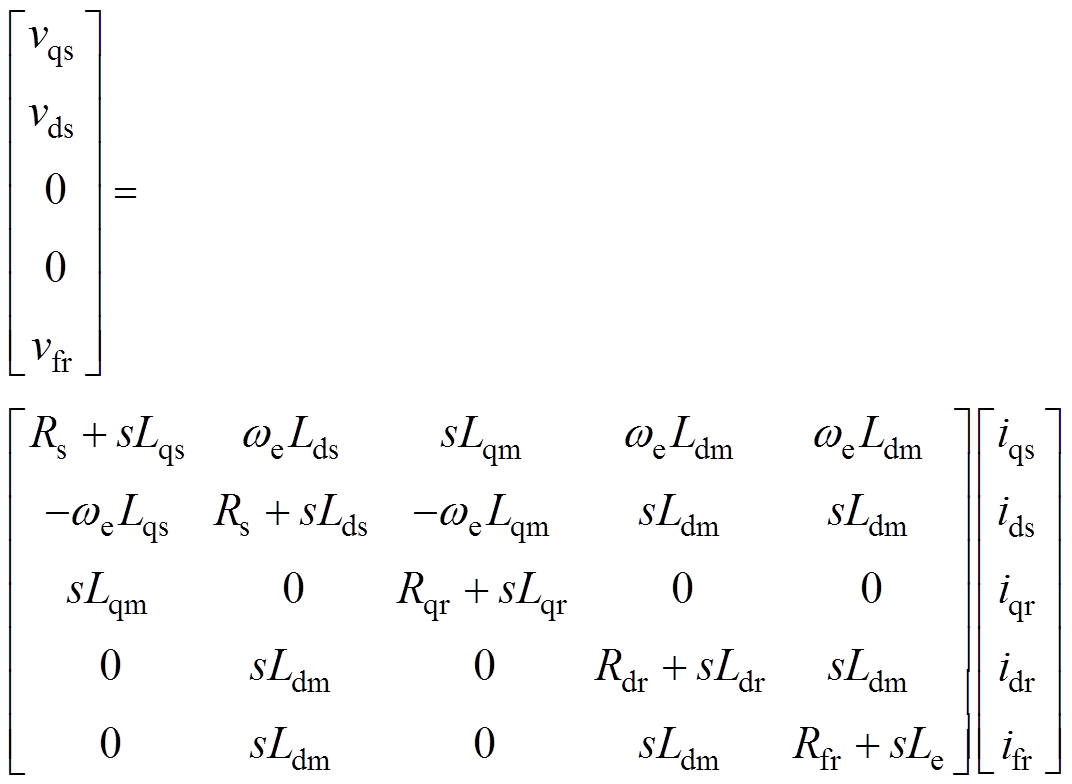 (4)
(4)
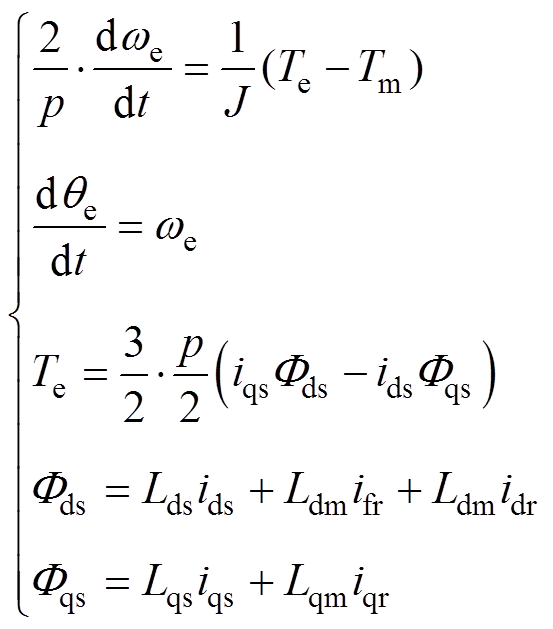 (5)
(5)
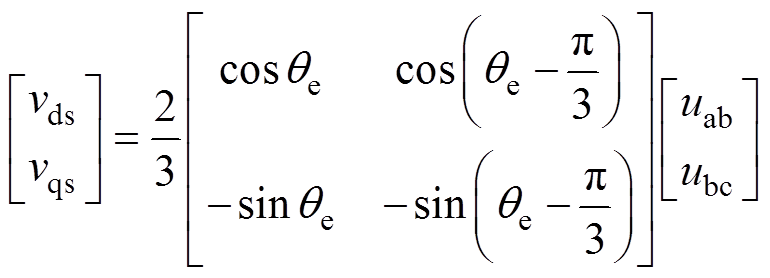 (6)
(6)
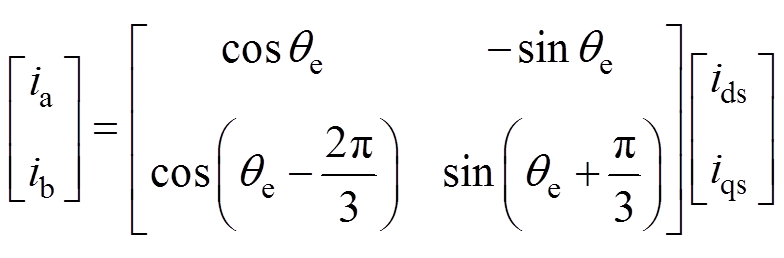 (7)
(7)
式中,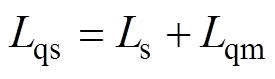 ;
;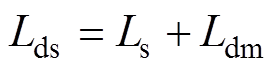 ;
;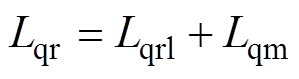 ;
;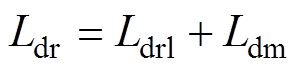 ;
;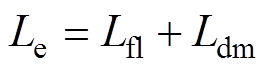 ;
;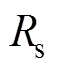 为定子电阻;
为定子电阻;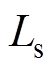 为定子漏感;
为定子漏感;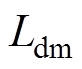 为d轴励磁电感;
为d轴励磁电感;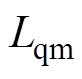 为q轴电感;
为q轴电感;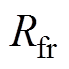 为折算到定子侧的磁绕组电阻;
为折算到定子侧的磁绕组电阻;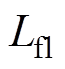 为折算到定子侧的励磁绕组漏感;
为折算到定子侧的励磁绕组漏感;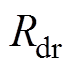 为折算到定子侧的转子阻尼绕组的d轴电阻;
为折算到定子侧的转子阻尼绕组的d轴电阻;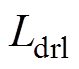 为折算到定子侧的阻尼绕组d轴漏感;
为折算到定子侧的阻尼绕组d轴漏感;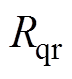 、
、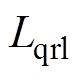 分别为折算到定子侧的转子绕组的q轴电阻与q轴漏感;p为电机极对数;
分别为折算到定子侧的转子绕组的q轴电阻与q轴漏感;p为电机极对数;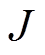 为电机的转动惯量;
为电机的转动惯量;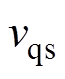 、
、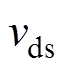 分别为通过式(3)所示的变换得到的q轴和d轴定子电压;uab、ubc分别为ab相和bc相的线电压;
分别为通过式(3)所示的变换得到的q轴和d轴定子电压;uab、ubc分别为ab相和bc相的线电压;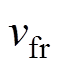 为励磁绕组的电压;
为励磁绕组的电压;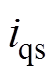 、
、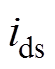 为通过所示的变换得到a相和b相电流;
为通过所示的变换得到a相和b相电流;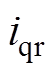 、
、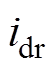 分别为q轴和d轴转子电流;
分别为q轴和d轴转子电流;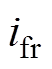 为励磁绕组电流;ia、ib分别为a、b相的相电流;
为励磁绕组电流;ia、ib分别为a、b相的相电流;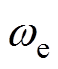 、
、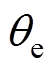 分别为电角速度和电角度;Te为电转矩;
分别为电角速度和电角度;Te为电转矩;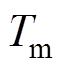 为外部机械转矩;
为外部机械转矩;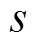 为微分算子。
为微分算子。
结合上述的电励磁同步电机模型可以得到完整的系统方程,有
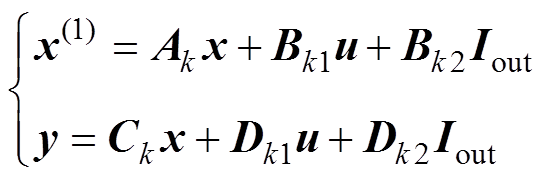 (8)
(8)
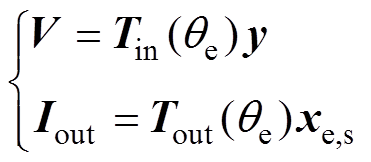 (9)
(9)
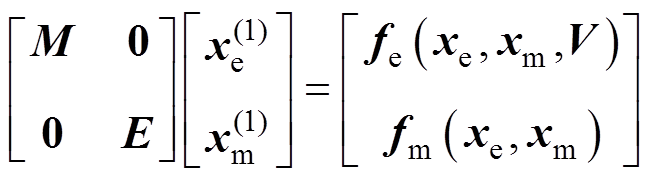 (10)
(10)
式中,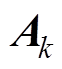 、
、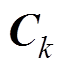 、
、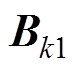 、
、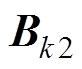 、
、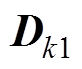 、
、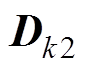 为线性系统的系统矩阵;
为线性系统的系统矩阵;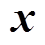 、
、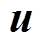 分别为线性系统中的状态变量以及独立源;
分别为线性系统中的状态变量以及独立源;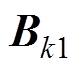 、
、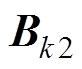 为线性系统的输入矩阵;
为线性系统的输入矩阵;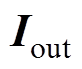 为电机的定子电流,是电机与线性电路进行耦合的接口电流;
为电机的定子电流,是电机与线性电路进行耦合的接口电流;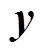 为线性电路的输出变量;
为线性电路的输出变量;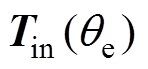 为输入时的变换矩阵,具体形式如式(6)所示;
为输入时的变换矩阵,具体形式如式(6)所示;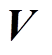 为由
为由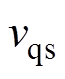 、
、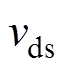 组成的向量,是线性电路与电机进行耦合的接口电压;
组成的向量,是线性电路与电机进行耦合的接口电压;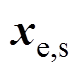 为由
为由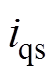 、
、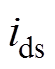 构成的向量,是电机输出给线性电路的状态变量;
构成的向量,是电机输出给线性电路的状态变量;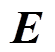 为单位矩阵;
为单位矩阵;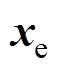 、
、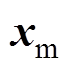 分别为电机中与电磁系统相关的状态变量以及与机械系统相关的状态变量;
分别为电机中与电磁系统相关的状态变量以及与机械系统相关的状态变量;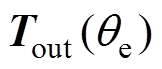 为输出时的变换矩阵,具体形式如式(7)所示;
为输出时的变换矩阵,具体形式如式(7)所示;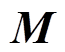 、
、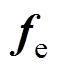 与
与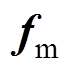 由式(4)、式(5)整理得到,其具体分量表示为
由式(4)、式(5)整理得到,其具体分量表示为
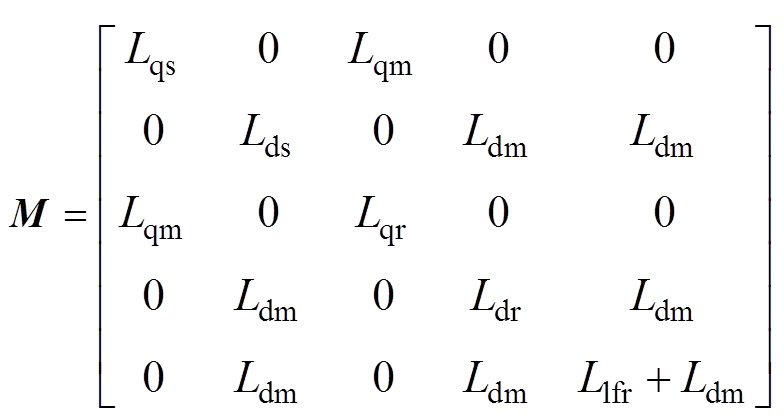 (11)
(11)
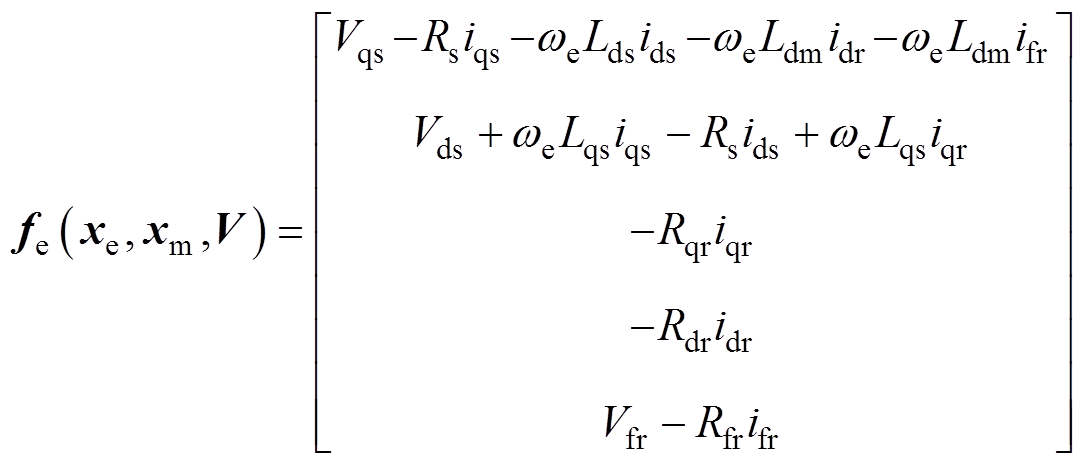 (12)
(12)
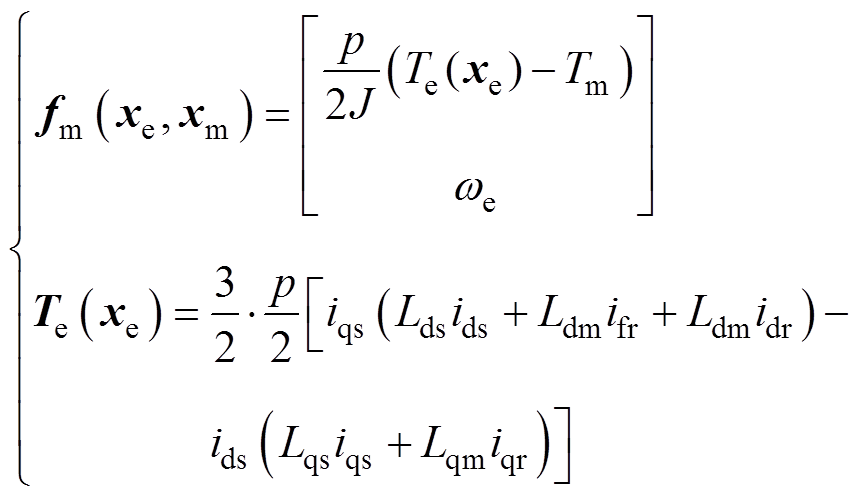 (13)
(13)
对于线性电路部分,其状态变量的各阶导数的计算可以利用式(6)迭代公式进行计算,而对于式(4)~式(7)所示的电机模型则显然无法应用线性系统所用的迭代公式进行计算。
为了计算电励磁同步电机的状态变量的各阶导数,首先需要计算式(9)中的接口电压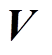 的导数值。对式(9)两侧求
的导数值。对式(9)两侧求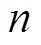 阶导数,可以得到
阶导数,可以得到
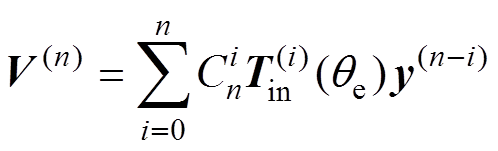 (14)
(14)
式中,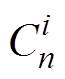 为组合数,变量的上标表示变量关于时间的导数阶数。
为组合数,变量的上标表示变量关于时间的导数阶数。
在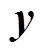 的n阶导数已知的情况下便可以按照式(14)进行导数计算,但是该公式的推导复杂且计算量较大。这是因为
的n阶导数已知的情况下便可以按照式(14)进行导数计算,但是该公式的推导复杂且计算量较大。这是因为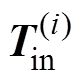 的计算较为复杂,注意到
的计算较为复杂,注意到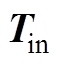 是关于
是关于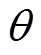 的函数,同时
的函数,同时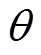 是关于时间的函数,表2展示了
是关于时间的函数,表2展示了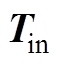 关于时间的1~5阶导数的计算公式。可以看到,随着导数阶数的增加,导数的计算公式变得更加复杂,并且计算量随着项数的增加而显著增加。
关于时间的1~5阶导数的计算公式。可以看到,随着导数阶数的增加,导数的计算公式变得更加复杂,并且计算量随着项数的增加而显著增加。
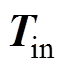 为旋转矩阵,乘以二维向量后,向量旋转
为旋转矩阵,乘以二维向量后,向量旋转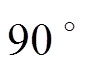 且幅值扩大
且幅值扩大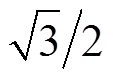 倍。
倍。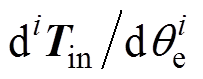 仍然是旋转矩阵,其乘以向量后,向量旋转
仍然是旋转矩阵,其乘以向量后,向量旋转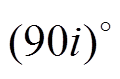 且幅值扩大
且幅值扩大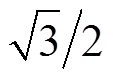 倍。见表2,
倍。见表2,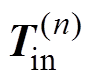 可以看作是
可以看作是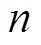 个旋转矩阵
个旋转矩阵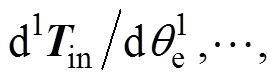
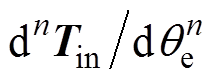 的线性组合,因此简化
的线性组合,因此简化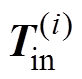 计算的原则是省去对应系数较小的旋转矩阵项。大部分情况下,转速
计算的原则是省去对应系数较小的旋转矩阵项。大部分情况下,转速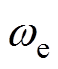 的2阶以及更高的导数值可以忽略,这是由于转速2阶导数值以及更高阶的导数值与转矩的导数值有关,而转矩的大小变化速度相对较小。按照以上原则,接口电压
的2阶以及更高的导数值可以忽略,这是由于转速2阶导数值以及更高阶的导数值与转矩的导数值有关,而转矩的大小变化速度相对较小。按照以上原则,接口电压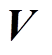 的导数值可以简化为
的导数值可以简化为
表2 变换矩阵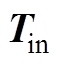 导数计算公式
导数计算公式
Tab.2 Formulas of transformation matrix 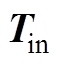 ’s derivatives
’s derivatives

导数阶数计算公式 1 2 3 4 5
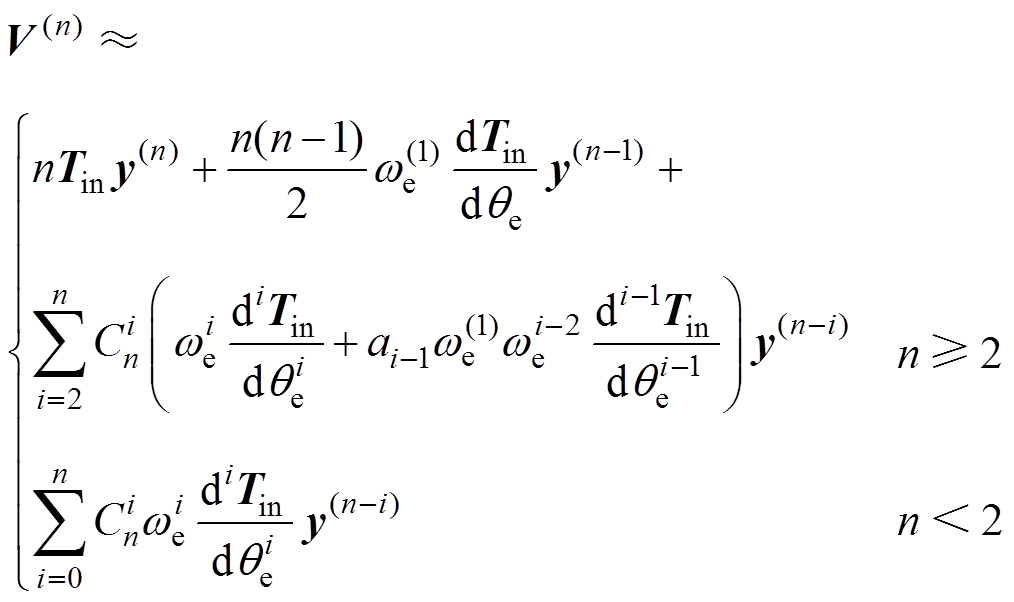 (15)
(15)
其中
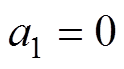
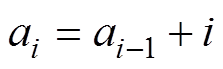 i≥2
i≥2
同理,接口电流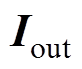 的导数值计算可以进行相似的简化,有
的导数值计算可以进行相似的简化,有
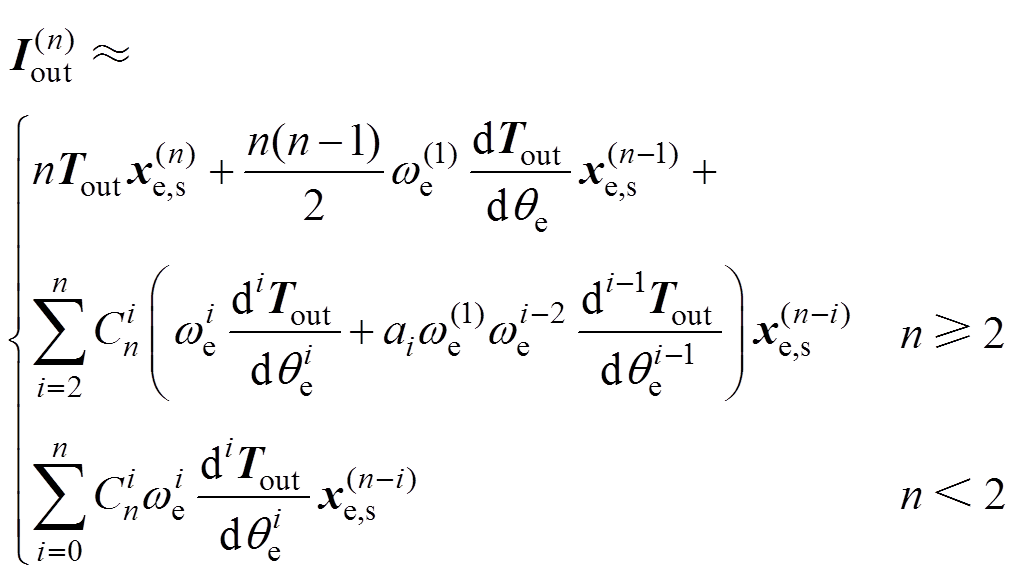 (16)
(16)
值得注意的是,应用上述公式进行计算时,不需要进行矩阵乘法,而是可以直接借助旋转矩阵的特点,计算旋转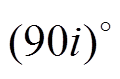 后的向量值。利用这一特点又进一步简化了导数计算。
后的向量值。利用这一特点又进一步简化了导数计算。
除此之外,还需要对上述简化公式进行误差分析,从而可以在进行数值解算时控制误差。
设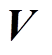 在
在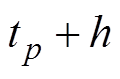 时刻的准确值为
时刻的准确值为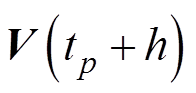 ,利用式(5)以及近似导数计算式(15)可以得到
,利用式(5)以及近似导数计算式(15)可以得到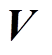 在
在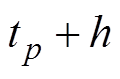 时刻的近似数值解
时刻的近似数值解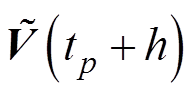 。
。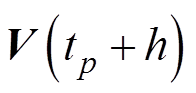 与
与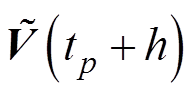 之间的差距是由导数简化以及泰勒展开截断引起的数值误差。误差主项为
之间的差距是由导数简化以及泰勒展开截断引起的数值误差。误差主项为
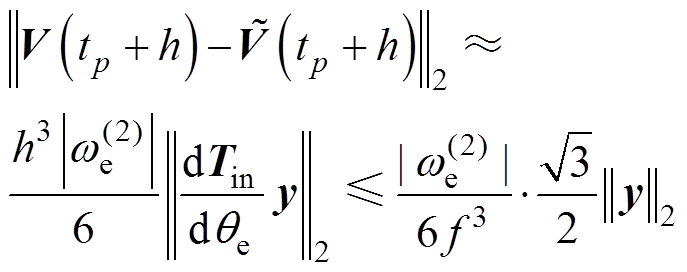 (17)
(17)
式中,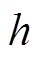 为解算步长;
为解算步长;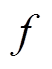 为系统中最高的开关频率。需要注意的是,系统中没有开关器件时,步长
为系统中最高的开关频率。需要注意的是,系统中没有开关器件时,步长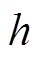 也会被数值精度的要求限制。
也会被数值精度的要求限制。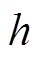 与系统最小的时间常数相关,一般来说,其典型值小于等于1×10-5 s。
与系统最小的时间常数相关,一般来说,其典型值小于等于1×10-5 s。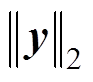 约为电机线电压的幅值。因此,根据式(17),误差主项的数量级一般会小于1×10-6。即使当该误差不满足数值解算误差要求时,也可以根据式(17)调整步长以满足误差要求。
约为电机线电压的幅值。因此,根据式(17),误差主项的数量级一般会小于1×10-6。即使当该误差不满足数值解算误差要求时,也可以根据式(17)调整步长以满足误差要求。
得到接口电压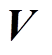 的各阶导数值后便可以计算电机状态变量的导数值。对式(10)左右两侧同时求
的各阶导数值后便可以计算电机状态变量的导数值。对式(10)左右两侧同时求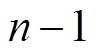 阶导数,可以得到
阶导数,可以得到
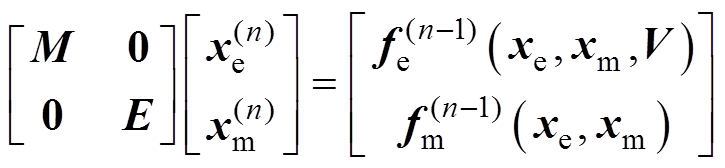 (18)
(18)
如式(12)、式(13)所示,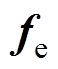 、
、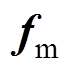 中存在状态变量的相乘项,如
中存在状态变量的相乘项,如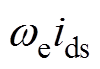 、
、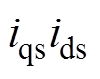 等项,根据牛顿莱布尼兹公式,计算类似两个状态变量相乘项的
等项,根据牛顿莱布尼兹公式,计算类似两个状态变量相乘项的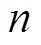 阶导数值为
阶导数值为
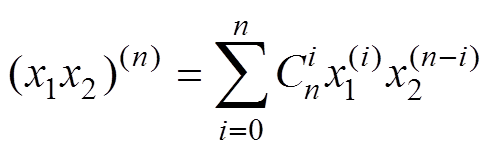 (19)
(19)
式中,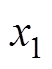 、
、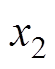 为任意两个状态变量。
为任意两个状态变量。
至此,已经得到了电机状态变量的导数计算公式并且在不影响计算精度的情形下实现了导数计算的简化。
电励磁同步电机以及外部电路所对应的数学模型以及各自的状态变量、输入变量以及输出变量见表3。
表3 各系统方程以及变量汇总
Tab.3 The summary of mathematical models and variables

系统数学模型状态变量输入变量输出变量 电励磁同步电机 外部电路
如表3所示,电励磁同步电机的输入变量为接口电压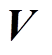 ,外部电路的输入变量包含接口电流
,外部电路的输入变量包含接口电流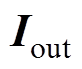 。接口变量由式(9)变换得到。两个系统的解算依靠接口电压以及接口电流进行导数值的交换以计算得到各自状态变量的各阶导数值,并最终利用式(5)完成数值解算。
。接口变量由式(9)变换得到。两个系统的解算依靠接口电压以及接口电流进行导数值的交换以计算得到各自状态变量的各阶导数值,并最终利用式(5)完成数值解算。
从物理意义上看,在求解外部的电力电子电路时,电机部分被视作等效电流源。此时,电机定子侧的电流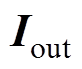 是电机部分输出给外部电路的输入变量。
是电机部分输出给外部电路的输入变量。
在求解电机部分时,外部电路被视作等效电压源。电机定子侧的电压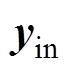 是外部电路输出给电机部分的输入变量。
是外部电路输出给电机部分的输入变量。
需要注意的是,电机部分与外部电力电子电路部分在解算时不仅可以得到接口电压和接口电流的当前值,还可以得到其各阶导数值,因此可以在解耦解算的同时保证解算精度。
图2为状态变量接口解耦方法的流程。借助接口电流以及接口电压,状态变量接口解耦方法的具体过程如下所示:
(1)在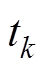 时刻,电机系统以及外部电路的状态变量的初值已知。设
时刻,电机系统以及外部电路的状态变量的初值已知。设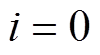 ,则电机以及外部电路的
,则电机以及外部电路的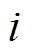 阶导数已知(初值也可以记作0阶导数)。
阶导数已知(初值也可以记作0阶导数)。
(2)首先利用电机状态变量的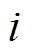 阶导数以及式(16)计算接口电流
阶导数以及式(16)计算接口电流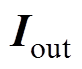 的
的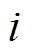 阶导数,再利用式(3)计算出外部电路状态变量的
阶导数,再利用式(3)计算出外部电路状态变量的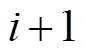 阶导数以及外部电路输出变量
阶导数以及外部电路输出变量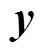 的
的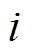 阶导数。
阶导数。
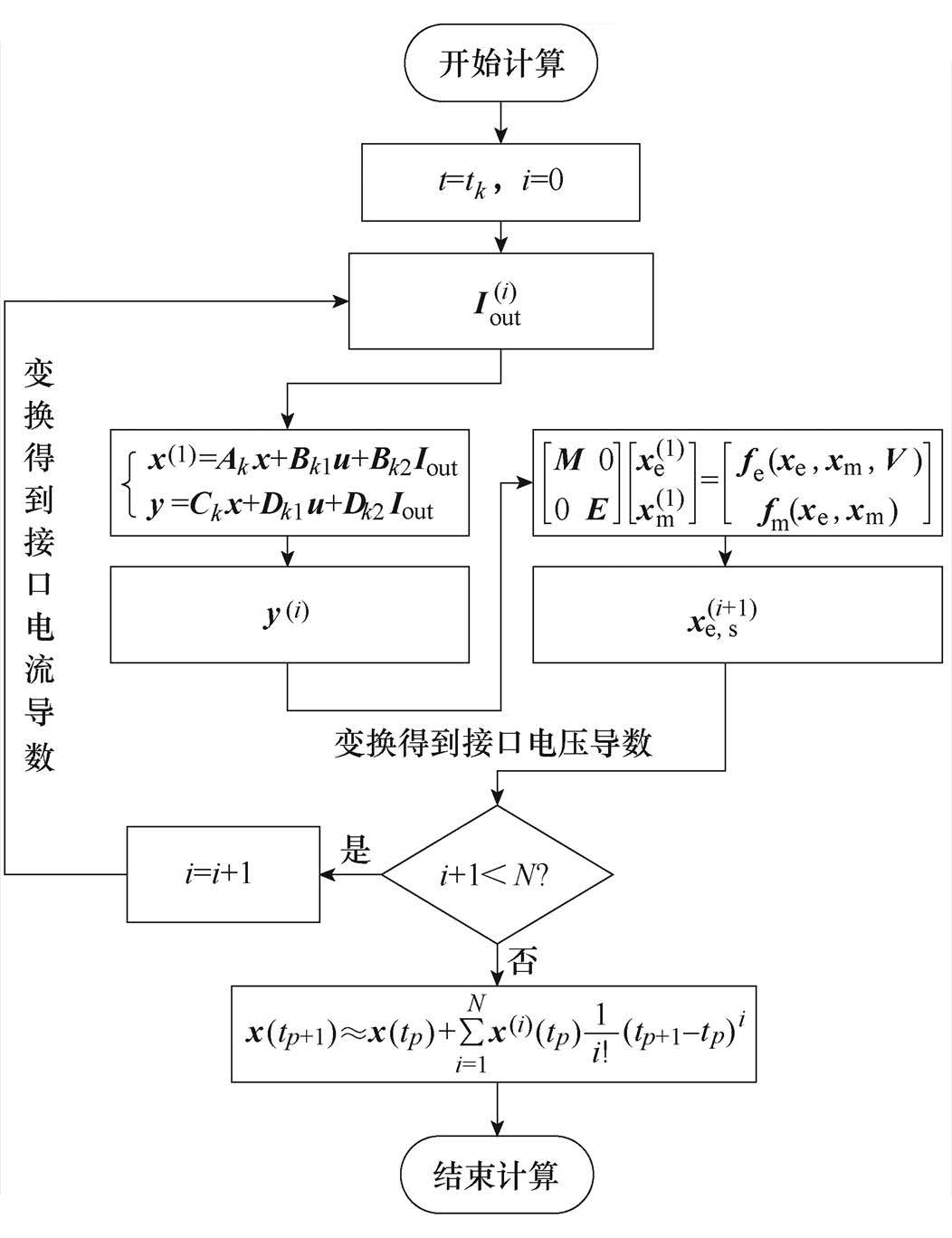
图2 状态变量接口解耦方法流程
Fig.2 The flowchart of state-variable-interfaced decoupling strategy
(3)首先利用步骤(2)中计算得到的外部电路输出变量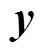 的
的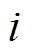 阶导数以及式(15)计算出接口电压
阶导数以及式(15)计算出接口电压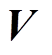 的
的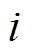 阶导数,再利用式(18)计算电励磁同步电机的状态变量
阶导数,再利用式(18)计算电励磁同步电机的状态变量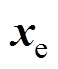 、
、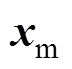 的
的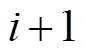 阶导数。
阶导数。
(4)设置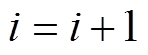 ,并重复步骤(2)、步骤(3),直到
,并重复步骤(2)、步骤(3),直到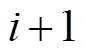 =N(N为设置的最高求导阶数)。
=N(N为设置的最高求导阶数)。
(5)根据计算得到的状态变量的各阶导数值并利用式(5)计算下一个时刻的状态变量的数值解。设置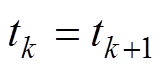 并回到步骤(1)继续解算下一个时刻的状态变量值。
并回到步骤(1)继续解算下一个时刻的状态变量值。
通过以上的算法,借助接口电压以及接口电流实现了电机部分以及外部电路部分的解耦解算。两个部分之间通过交换彼此的接口电压以及接口电流的导数值便实现了同一时刻的解算,因此解决了第1节中提到的难点二。这样的方法能保证线性部分的电路仍然可以采用自适应积分方法进行解算,从而实现灵活地变阶数与变步长。
利用本文提出的状态变量接口解耦解算方法,DSED方法可以解算包含电励磁同步电机以及大量电力电子器件的系统。本节搭建了一个微电网系统进行算例研究,通过对比商用软件PSIM的仿真结果来验证基于DSED方法的仿真平台的解算准确性和求解高效性。
交流微电网往往既包含逆变器型微电源又包含柴油发电机、微型燃气轮机等交流电源[1-2]。本算例包含了逆变器型微电源以及电励磁同步电机,并且仿真了一个微电网脱网运行的过程。
本节搭建的微电网系统的总体结构如图3a所示,其包含两个交流电源(电励磁同步电机)以及3个逆变器型电源。交流电源内部的具体结构如图3b所示。对于交流电源,其控制目标是稳定电压以及频率。逆变器型电源的内部结构如图3c所示。对于逆变器型电源,其控制目标是控制输出的有功功率以及无功功率。微电网系统主要的参数见表4。

图3 微电网拓扑结构
Fig.3 Topology of Micro-grid
表4 微电网系统参数
Tab.4 The parameters of micro-grid
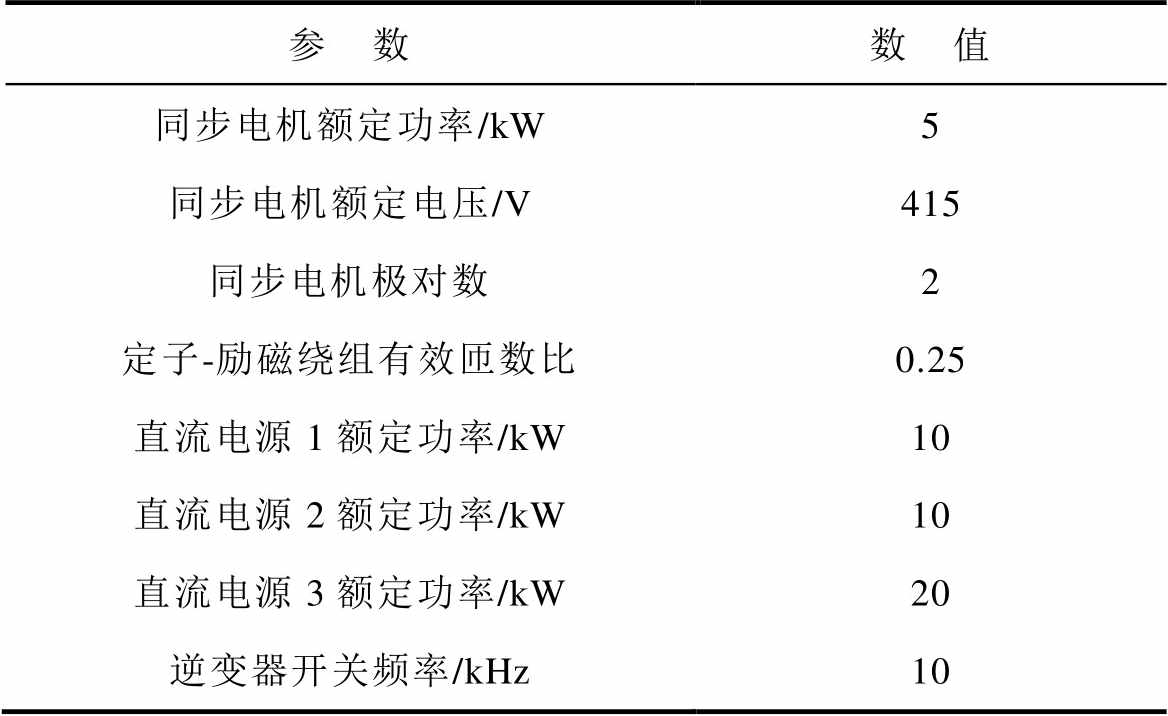
参 数数 值 同步电机额定功率/kW5 同步电机额定电压/V415 同步电机极对数2 定子-励磁绕组有效匝数比0.25 直流电源1额定功率/kW10 直流电源2额定功率/kW10 直流电源3额定功率/kW20 逆变器开关频率/kHz10
所仿真的工况为:初始时,仅有直流电源供电,且微电网与电网相连;在0.2 s时,投入交流电源,即电励磁同步电机;在0.4 s时,微电网与电网断开,由交流电源支撑线路电压以及频率。
分别利用PSIM以及基于DSED方法的解算平台对上述过程进行仿真。不同解算平台的计算结果的相对误差见表5。PSIM所选取的解算步长是1 ms,该步长是表5中逆变器开关周期的百分之一,以保证仿真得到的结果具有较高的可靠性。
表5 不同解算平台的计算结果的相对误差
Tab.5 The relative error between different simulation platforms’ results

波形物理量误差(%) 同步电机1励磁电流0.54 同步电机2励磁电流0.70 同步电机1 AC线电压0.32 同步电机2 AC线电压0.19
图4为上述工况下的关键变量的波形,包括两个电励磁同步电机定子侧线电压波形以及两个电励磁同步电机的励磁电流波形。通过波形对比,可以看到,基于DSED方法的仿真平台的仿真结果与商用仿真软件PSIM的仿真结果吻合较好。
进一步可以通过数据误差计算验证结果的吻合程度。两个仿真平台得到的结果之间的差距见表5。差距衡量所用的计算公式为
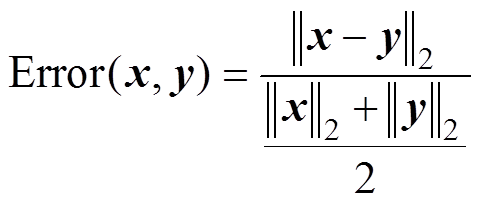 (20)
(20)
式中,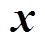 、
、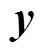 分别为进行对比的两组解算结果;
分别为进行对比的两组解算结果;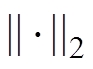 为二范数。
为二范数。
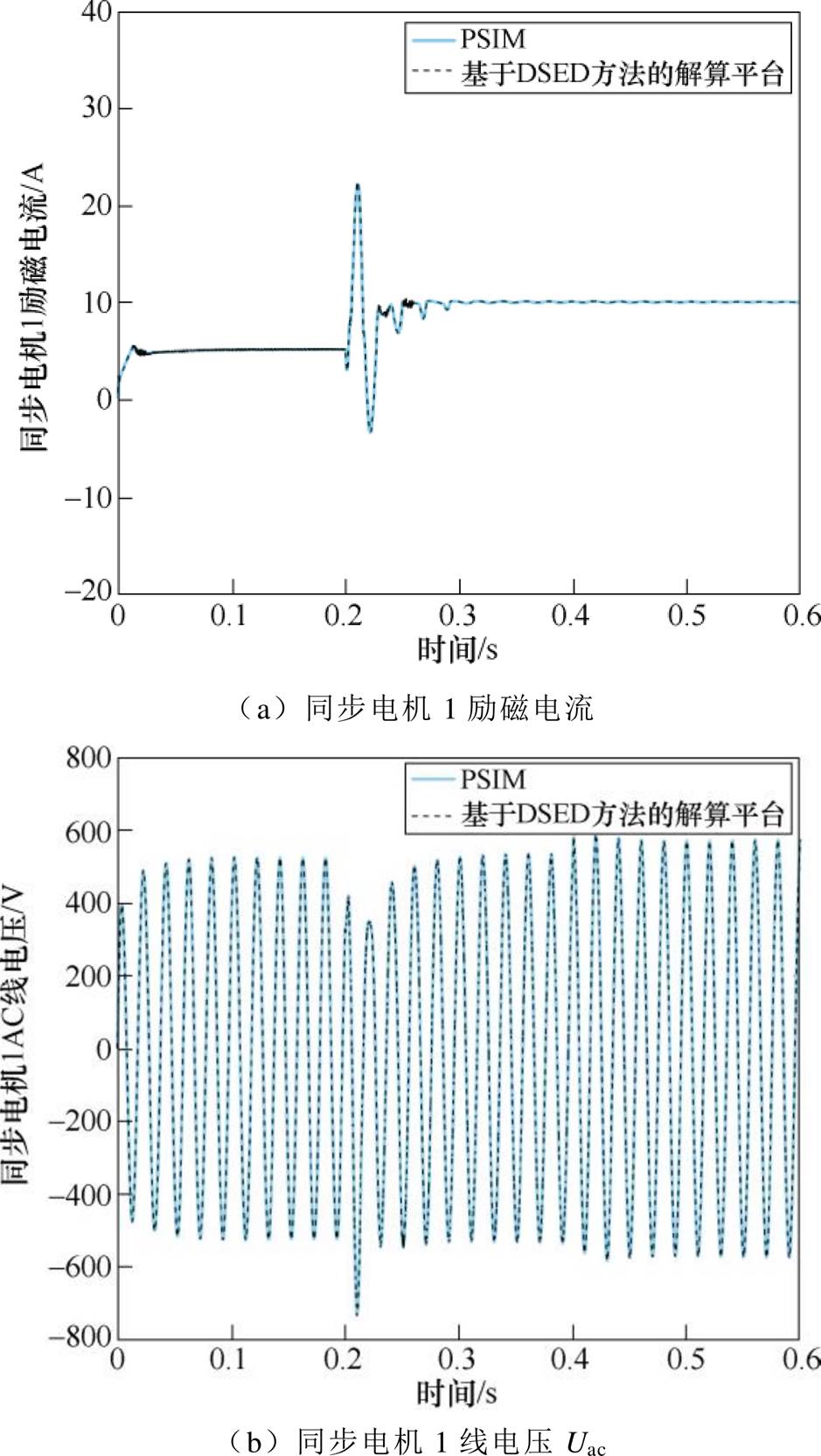
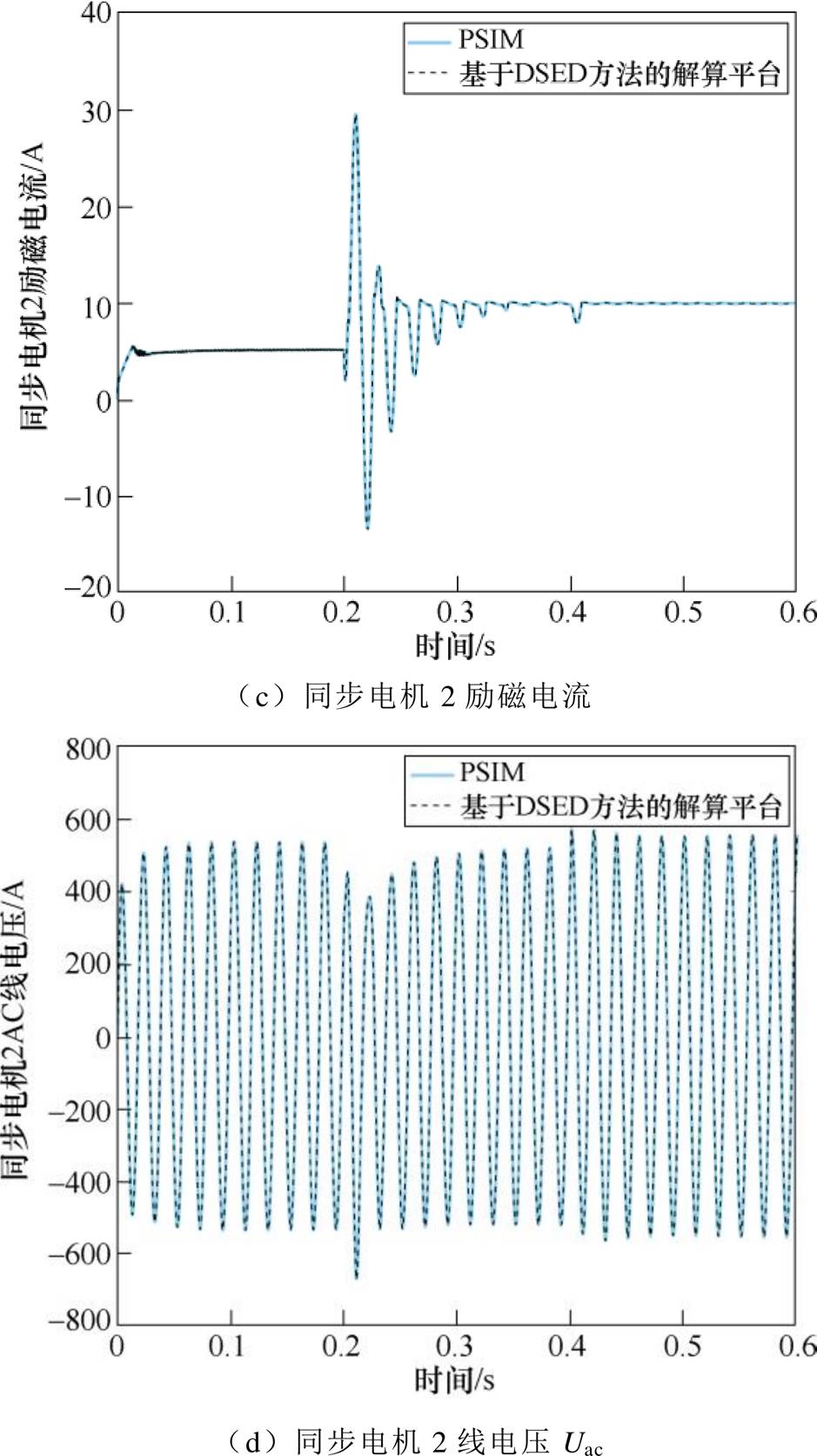
图4 PSIM与基于DSED方法的仿真平台的仿真结果对比
Fig.4 Numerical results simulated by PSIM and DSED
由于基于DSED方法的仿真平台在解算时采用的是自适应变步长变阶数的解算方法,因此需要首先利用插值得到与PSIM的定步长算法一致的采样点后再利用式(20)进行结果比较。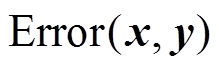 越小,意味着解算结果越接近。
越小,意味着解算结果越接近。
表5中所展示的结果说明两种仿真平台得到的仿真结果之间的相对误差在1 %之内,这意味着基于DSED方法的仿真平台的解算结果与PSIM仿真平台的解算结果十分接近。
在解算结果十分接近的条件下,进一步对两个平台的解算时间进行对比,从而比较两个平台的解算效率。
两个仿真平台均运行在同一台配备了Intel(R) Core(TM) i5-10500 CPU和16 GB内存的个人计算机上。两种仿真平台的解算时间见表6。可以看到,表6中PSIM的仿真计算时间是基于DSED方法的仿真计算时间的40余倍。
表6 仿真时间
Tab.6 Simulation time

仿真平台仿真计算时间 PSIM15 min 基于DSED方法的仿真平台22 s
计算效率的提高主要得益于两方面:其一是自适应积分方法的单步计算量低于常用的显式Runge-Kutta方法,见表1。PSIM采用的数值积分算法虽然不是显式Runge-Kutta算法,而是梯形积分算法,但是该算法每一步都涉及到线性方程组的求解,因此其单步计算量更大。其二是DSED方法考虑到了离散事件,利用事件驱动,在事件点之间对连续状态变量进行数值积分,减少了计算点数。PSIM与基于DSED方法的仿真平台单个开关周期内的仿真点数对比如图5所示,在单个开关周期中,基于DSED方法的解算平台计算了8个点;PSIM由于采取的是低阶算法且没有考虑到离散的开关事件,因此需要较多点数才能达到相同的精度。
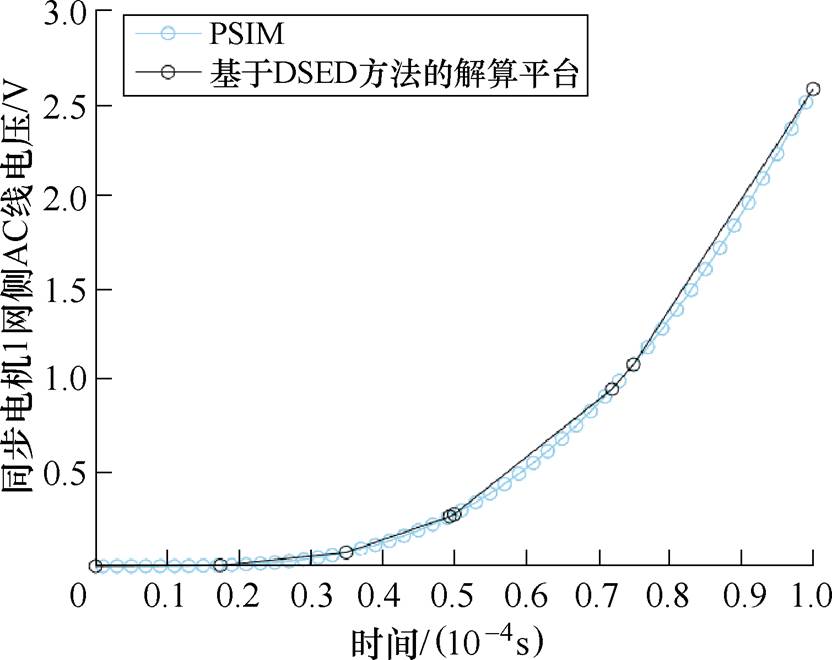
图5 PSIM与基于DSED方法的仿真平台单个开关周期内的仿真点数对比
Fig.5 Simulation points within one switching period comparison between PSIM and DSED
DSED方法能够针对大规模电力电子变换器进行高效的解算,但是无法求解以电励磁同步电机为代表的非线性系统。原因是DSED方法针对线性电路利用自适应积分方法进行解算,而电励磁同步电机无法被建模为线性状态方程。为此,本文提出了一种适应于DSED方法的状态变量接口解耦方法,实现了电机部分与线性电路部分的解耦解算。该方法使得DSED方法能够对包含电励磁同步电机的电力电子系统进行高效解算,并且具有拓展到解算其他类型电机以及其他非线性元件的潜力。最终,通过对比基于DSED方法的仿真平台以及商用软件对于同一个微电网算例的仿真结果以及仿真速度,验证了本文所提方法的有效性。
致谢:感谢富士电机株式会社(FUJI Electric Co. Ltd)对本文研究工作的支持。
参考文献
[1] 杨新法, 苏剑, 吕志鹏, 等. 微电网技术综述[J]. 中国电机工程学报, 2014, 34(1): 57-70.
Yang Xinfa, Su Jian, Lü Zhipeng, et al. Overview on micro-grid technology[J]. Proceedings of the CSEE, 2014, 34(1): 57-70.
[2] 鲁宗相, 王彩霞, 闵勇, 等. 微电网研究综述[J]. 电力系统自动化, 2007, 31(19): 100-107.
Lu Zongxiang, Wang Caixia, Min Yong, et al. Over- view on microgrid research[J]. Automation of Electric Power Systems, 2007, 31(19): 100-107.
[3] 王成山, 武震, 李鹏. 微电网关键技术研究[J]. 电工技术学报, 2014, 29(2): 1-12.
Wang Chengshan, Wu Zhen, Li Peng. Research on key technologies of microgrid[J]. Transactions of China Electrotechnical Society, 2014, 29(2): 1-12.
[4] 周林, 黄勇, 郭珂, 等. 微电网储能技术研究综述[J]. 电力系统保护与控制, 2011, 39(7): 147-152.
Zhou Lin, Huang Yong, Guo Ke, et al. A survey of energy storage technology for micro grid[J]. Power System Protection and Control, 2011, 39(7): 147-152.
[5] 杨美辉, 周念成, 王强钢, 等. 基于分布式协同的双极直流微电网不平衡电压控制策略[J]. 电工技术学报, 2021, 36(3): 634-645.
Yang Meihui, Zhou Niancheng, Wang Qianggang, et al. Unbalanced voltage control strategy of bipolar DC microgrid based on distributed cooperation[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 634-645.
[6] 张伟亮, 张辉, 支娜, 等. 基于节点源荷电流差分的直流微电网储能变换器控制策略[J]. 电工技术学报, 2022, 37(9): 2199-2210.
Zhang Weiliang, Zhang Hui, Zhi Na, et al. Control strategy of DC microgrid energy storage converter based on node differential current[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2199- 2210.
[7] 王宇彬, 杨晓东, 谢路耀, 等. 基于滑模控制的直流微电网一致性控制策略[J]. 电工技术学报, 2021, 36(增刊2): 530-540, 553.
Wang Yubin, Yang Xiaodong, Xie Luyao, et al. Consensus algorithm strategy of DC microgrid based on sliding mode control[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 530-540, 553.
[8] 胡长斌, 王慧圣, 罗珊娜, 等. 计及直流微电网扰动抑制的残差动态分散补偿控制策略[J]. 电工技术学报, 2021, 36(21): 4493-4507, 4543.
Hu Changbin, Wang Huisheng, Luo Shanna, et al. Residual dynamic decentralized compensation control strategy considering disturbance suppression in DC microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4493-4507, 4543.
[9] Zhu Yicheng, Zhao Zhengming, Shi Bochen, et al. Discrete state event-driven framework for simulation of switching transients in power electronic systems[C]// 2019 IEEE Energy Conversion Congress and Expo- sition (ECCE), Baltimore, MD, USA, 2019: 895-900.
[10] 施博辰, 赵争鸣, 朱义诚, 等. 离散状态事件驱动仿真方法在高压大容量电力电子变换系统中的应用[J]. 高电压技术, 2019, 45(7): 2053-2061.
Shi Bochen, Zhao Zhengming, Zhu Yicheng, et al. Discrete state event-driven simulation framework for high-voltage power electronic hybrid systems[J]. High Voltage Engineering, 2019, 45(7): 2053-2061.
[11] Zhu Yicheng, Zhao Zhengming, Shi Bochen, et al. Discrete state event-driven framework with a flexible adaptive algorithm for simulation of power electronic systems[J]. IEEE Transactions on Power Electronics, 2019, 34(12): 11692-11705.
[12] van der Schaft A J, Schumacher J M. An introduction to hybrid dynamical systems in lecture notes in control and information sciences[M]. London, New York: Springer, 2000.
[13] Gupta P, Patra A. Hybrid mode-switched control of DC-DC Boost converter circuits[J]. IEEE Transa- ctions on Circuits and Systems II: Express Briefs, 2005, 52(11): 734-738.
[14] Sreekumar C, Agarwal V. A hybrid control algorithm for voltage regulation in DC-DC Boost converter[J]. IEEE Transactions on Industrial Electronics, 2008, 55(6): 2530-2538.
[15] Shi Bochen, Zhao Zhengming, Zhu Yicheng. Piece- wise analytical transient model for power switching device commutation unit[J]. IEEE Transactions on Power Electronics, 2019, 34(6): 5720-5736.
[16] 付兴贺, 江政龙, 吕鸿飞, 等. 电励磁同步电机无刷励磁与转矩密度提升技术发展综述[J]. 电工技术学报, 2022, 37(7): 1689-1702.
Fu Xinghe, Jiang Zhenglong, Lü Hongfei, et al. Review of the blushless excitation and torque density improvement in wound field synchronous motors[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1689-1702.
[17] Benigni A, Monti A, Dougal R A. Latency-based approach to the simulation of large power electronics systems[J]. IEEE Transactions on Power Electronics, 2014, 29(6): 3201-3213.
[18] Grégoire L A, Blanchette H F, Bélanger J, et al. A stability and accuracy validation method for multirate digital simulation[J]. IEEE Transactions on Industrial Informatics, 2017, 13(2): 512-519.
[19] Khan H, Bazaz M A, Ahmad N S. Singular perturbation-based model reduction of power elec- tronic circuits[J]. IET Circuits, Devices & Systems, 2019, 13(4): 471-478.
[20] Davoudi A, Jatskevich J, Chapman P L, et al. Multi- resolution modeling of power electronics circuits using model-order reduction techniques[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2013, 60(3): 810-823.
[21] [美]博斯. 现代电力电子学与交流传动[M]. 北京: 机械工业出版社, 2005.
Abstract Microgrids can realize the flexible access of distributed generations, energy storages, and loads. A typical microgrid system often contains various DC and AC power supplies and many power electronic devices, challenging conventional simulation tools. Recently, the discrete state event-driven (DSED) approach has been proposed and can efficiently solve large-scale power electronic converters. This method models power electronic converters as piecewise linear (PWL) state equations and consists of a flexible, adaptive integration method based on the Taylor series. It can solve PWL systems but cannot solve the system containing electrically excited synchronous machines. Therefore, this paper proposes a state-variable-interfaced decoupling strategy based on the DSED approach.
The state-variable-interfaced decoupling strategy can decouple the electrically excited synchronous machine from the whole system. The electrically excited synchronous machine and the other part systems exchange high-order time derivatives of interface variables to assure the simulation accuracy. In addition, a method for simplifying the time derivative calculation of electrically excited synchronous machines’ state variables is proposed. The time derivatives can be obtained recursively, and the complicated and troublesome high-order derivative expressions can be avoided. The numerical errors introduced by the simplifying method are analyzed and can be well controlled using the proposed error equations.
In the case study of a microgrid system, compared with commercial simulation software, the proposed method can improve the calculation speed by more than 40 times with the same accuracy. The simulated microgrid system consists of two distributed synchronous machines as AC generations and three DC generations with inverters. The simulated working conditions are as follows: initially, only DC power supplies are available, and the microgrid is connected to the power grid; At 0.2 s, put AC power into operation, that is, electrically excited synchronous machines; At 0.4 s, the microgrid is disconnected from the power grid, and the AC power supply supports the line voltage and frequency. The simulated results show good agreement with the commercial simulation software. The improvement of computing efficiency mainly benefits from two aspects. The single-step computational cost of the adaptive integration method is lower than that of the commonly used explicit Runge-Kutta method under the same order. The DSED method considers events and uses an event-driven strategy to conduct numerical integration of continuous state variables between event points, reducing the number of calculation points.
The following conclusions can be drawn from the simulation analysis: (1) When adopting the ideal switched model, power electronic systems contain discrete switch events and continuous state events. The DSED method adopts a flexible, adaptive Taylor series-based integration method to adapt to this hybrid nature and achieve high simulation efficiency. (2) The proposed state-variable-interfaced decoupling strategy makes the DSED method efficiently solve the microgrid with electrically excited synchronous machines. (3) The proposed method has the potential to be transferred to solve systems containing other motors, such as induction motors.
keywords:Discrete state event-driven approach, electrically excited synchronous machine, power electronic system simulation, microgrid
DOI: 10.19595/j.cnki.1000-6753.tces.220308
中图分类号:TM743
“台达电力电子科教发展计划”资助项目。
收稿日期 2022-03-07
改稿日期 2022-04-14
许 涵 男,1999年生,硕士研究生,研究方向电力电子系统建模仿真。E-mail: xuhan21@mails.tsinghua.edu.cn(通信作者)
赵争鸣 男,1959年生,教授,博士生导师,研究方向为大容量电力电子变换器、太阳能光伏发电系统。E-mail: zhaozm@mail.tsinghua.edu.cn
(编辑 崔文静)