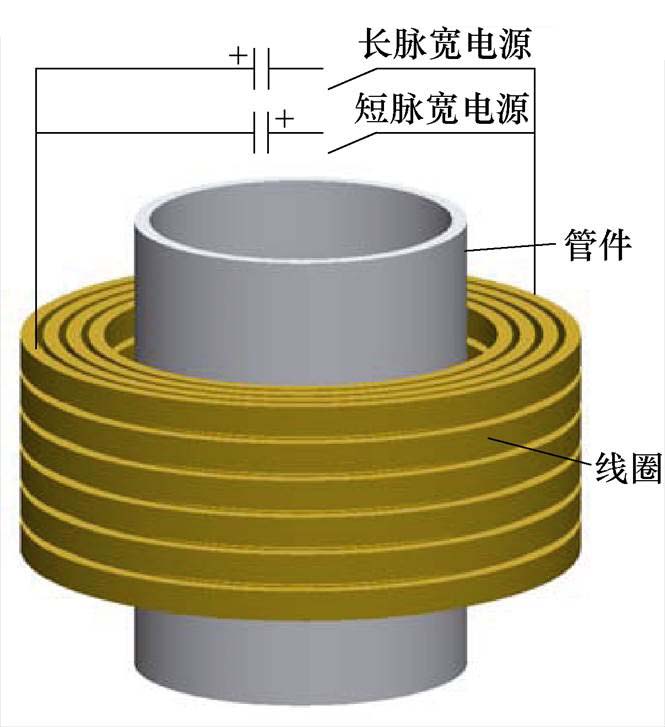
图1 吸引式电磁成形原理示意图
Fig.1 Schematic diagram of attractive electromagnetic forming
摘要 镁合金作为目前工程应用中最轻质的金属结构材料之一，因其多种优良特性而广泛应用于轻量化设备制造中。然而，镁合金在室温下的塑性形变能力较差，传统加工工艺难以满足镁合金工件成形制造的需求。利用电磁力驱动金属材料发生高速变形的电磁成形技术可有效解决上述问题，其极高的应变速率能显著改善镁合金材料的成形性能，提升室温下的成形极限。然而，目前关于镁合金电磁成形的研究，大多使用驱动片与加热装置辅助，其工装较为复杂，且工件变形质量难以保证；辅助装置的添加也难以用于微小管件的成形。因此该文提出室温下的镁合金管件电磁吸引式成形方法，通过建立有限元仿真模型，在理论上验证了其成形方案的可行性；进一步分析了放电参数、电磁参数对管件运动状态的调控规律，阐明管件变形过程中工件的动态特性。上述结论可为线圈结构设计和放电参数设计提供指导。
关键词：电磁成形 动态特性 管件 吸引力 AZ31镁合金
我国是世界上镁矿资源储备最丰富的国家，大力发展以镁合金为首的轻质合金材料可有效降低航空航天、汽车等领域的耗能[1]，是早日实现“双碳战略”的重要途径之一。
镁合金作为目前工程应用中最轻质的金属结构材料，其相较于铝合金，具有更高的比强和比刚度，延展性也更强[2]。但由于其结构呈密排六方晶体结构，室温下的镁合金独立滑移系少于铝合金，因此镁合金的塑性形变能力更差，在室温下成形性能弱于铝合金。采用传统冲压工艺进行准静态加工时，容易出现材料流动不均匀的现象，造成工件起皱。其他加工手段如液压、挤压成形，则均存在多向变形困难、二次塑性加工难度大等问题。因此目前的镁合金加工需要多次加热与退火，工序过于复杂，也带来了高昂的模具设计和炉具成本[3-4]。如何提升镁合金在室温下的成形性能，是目前镁合金加工的研究重点之一。
利用脉冲强磁场与感应涡流共同产生电磁力驱动工件发生形变的电磁成形（Electromagnetic Forming, EMF）技术，因其在室温下可显著提升材料成形极限，抑制工件回弹、减小起皱，已成为当今轻质合金加工制造技术的热点[5-7]。EMF技术中电磁力大小、方向灵活可控，现已广泛应用于铝合金管板类工件塑性加工[8-10]，且在管件翻边[11-13]、胀形[14-18]等工艺上的研究较为成熟，但针对镁合金管件的电磁成形工艺研究鲜有文献记载。
与铝合金材料相比，镁合金导电率更低，导致同等参数下镁合金工件上所受电磁力更小，再加上镁合金的屈服强度更高，导致常规EMF技术也难以实现镁合金工件在室温下的塑性加工，需要借助其他导电性更好的金属材料作为驱动片或者加热装置来辅助成形[19]。徐俊瑞在室温下采用铝合金作为驱动片，开展了镁合金板件磁脉冲成形实验，提高了室温下AZ31板材EMF成形性能[20]。国外学者E.Uhlmann等[21]采用加热配合EMF技术，使镁合金板件成形性能得到了显著提升，板件的胀形高度随温度提升而提升；I. Ulacia等[22]进行了AZ31B镁合金板件从室温到250℃下的EMF研究，结果表明：随着其成形温度的升高，材料的屈服点会降低，但导电系数却随之下降，因而电磁力降低。武汉理工大学的黄尚宇课题组[23]将温热成形与EMF技术相结合，指出提高放电电压较提升电容对增大镁合金板件胀形高度有更明显的效果；随后Xu Junrui等采用电磁力冲击介质产生压力，驱动温热的镁合金板件发生塑性形变，为镁合金成形提供了新的加工思路[24-25]。
以上研究需要驱动片或加热等辅助成形装置，实验平台搭建较为复杂，且加热条件下线圈温度更高使用寿命难以保证。另一方面，镁合金电导率随温度上升而显著下降，需使用更大的放电能量，才能补偿因电导率降低而造成的电磁力减弱。采用驱动片虽然免去了加热的麻烦，但驱动片在碰撞冲击工件后将在工件表面留下冲击痕迹，影响表面质量，最终影响使用性能；此外，采用驱动片受限于空间限制，不能满足微小管件成形的需求。
故本文提出了室温下的镁合金管件电磁吸引式成形方法，无需加热、驱动片等辅助成形装置，特别适用于微小镁合金管件的成形。本文选用工程上广泛使用的AZ31镁合金，建立了其成形过程中的有限元仿真模型，从理论上研究其成形方案的可行性。进一步地，通过模型分析放电参数、电磁参数对管件运动过程的调控规律，阐明管件变形过程中工件的动态特性，为后续线圈结构设计、放电参数选取提供理论指导。
本文选用AZ31B镁合金管件，其内径为10 mm，长度100 mm，属于微小管件。由于操作空间限制，难以将线圈置于管件内部实现胀形；且在实际工程中，线圈内径过小将降低其结构强度进而使线圈绝缘性能难以保证[26]。
为解决上述问题，可将线圈置于管件外侧，其成形原理示意图如图1所示，采用文献[16]所使用的单线圈-双电源成形系统，利用双频电流法产生吸引力驱动管件成形。
图1 吸引式电磁成形原理示意图
Fig.1 Schematic diagram of attractive electromagnetic forming
由文献[16]中可知，通过两组电源的时序配合，即可产生吸引力驱动管件高速变形，管件所受电磁力密度方向与环向感应涡流密度Jephi和轴向合成磁通密度Bz的方向相关。
由于电磁成形速度极快且十分复杂，实验不能得到详细数据随时间的变化趋势来反映吸引式成形的动态变化关系，因此必须借助仿真详细探究吸引式电磁成形过程中，放电参数、电磁参数、运动状态三者间的关系以及对成形效果的影响。因此本文采用文献[15-17]中的有限元法分析电磁成形的物理过程。
本文采用型号为AZ31B的镁合金管件作为研究对象，该管件壁厚2 mm，外直径24 mm，长度100 mm，建立了考虑管件位移与变形速率影响的全耦合仿真模型，其具体方案示意图及结构参数如图2所示。
线圈选用铜导线，横截面积为1 mm´4 mm，共6层，每层12匝。本文采用两组放电电流脉宽不同的电源系统，其等效电路拓扑如图3所示，放电参数见表1。
铜线圈材料与AZ31镁合金管件材料参数见表2。
考虑到镁合金材料在高应变率成形过程中与准静态下材料成形情况大不相同，因此本文采用文献[20]中使用的Cowper-Symonds本构模型对管件的变形过程进行分析，其应力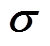
可表示为
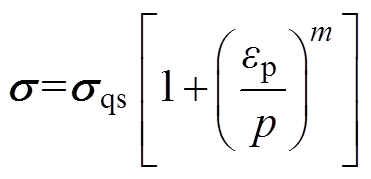（1）
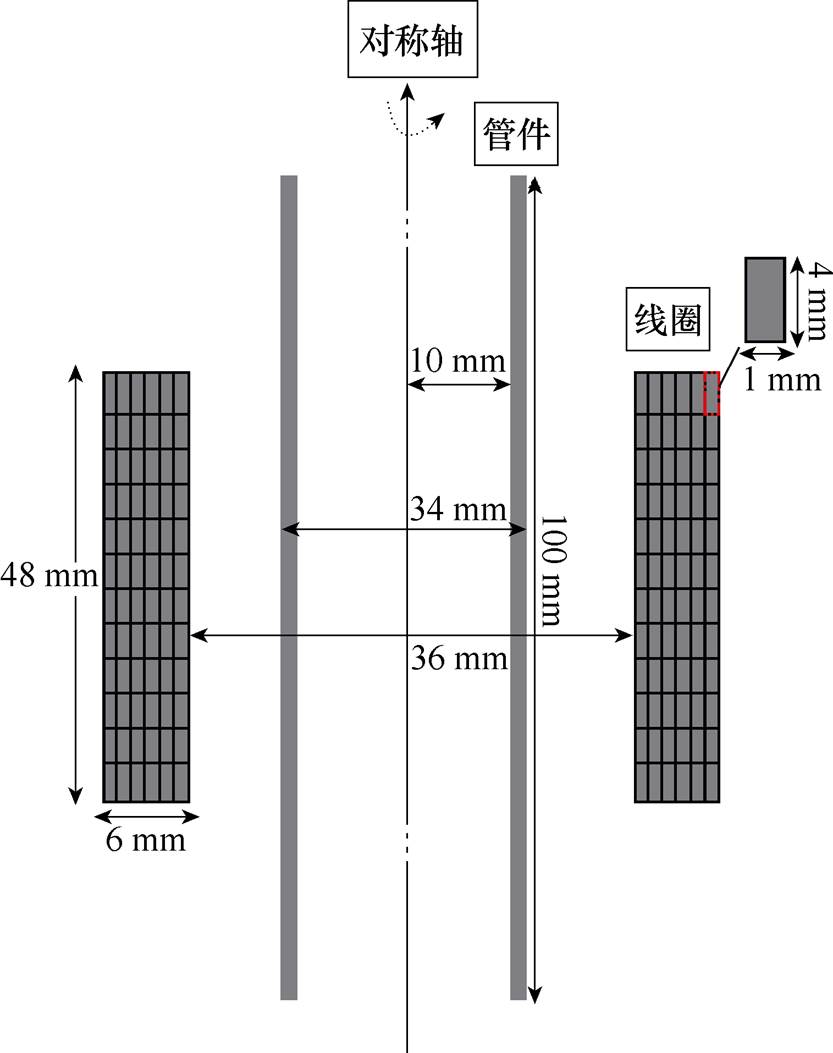
图2 管件吸引式成形仿真模型
Fig.2 Simulation model of tube attractive forming
表1 双电源系统电参数
Tab.1 Dual power supply system parameters
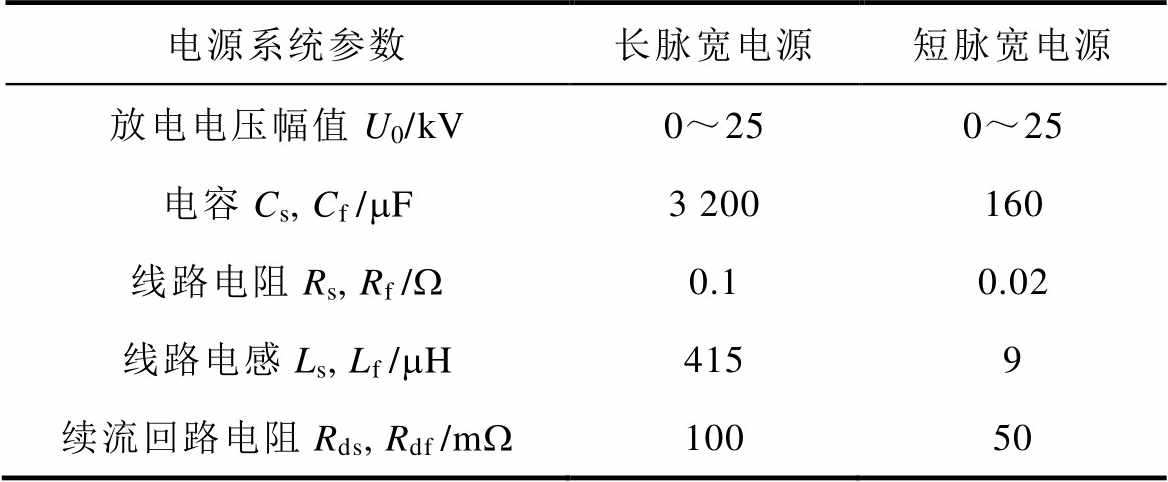
电源系统参数长脉宽电源短脉宽电源 放电电压幅值U0/kV0～250～25 电容Cs, Cf /mF3 200160 线路电阻Rs, Rf /W0.10.02 线路电感Ls, Lf /mH4159 续流回路电阻Rds, Rdf /mW10050
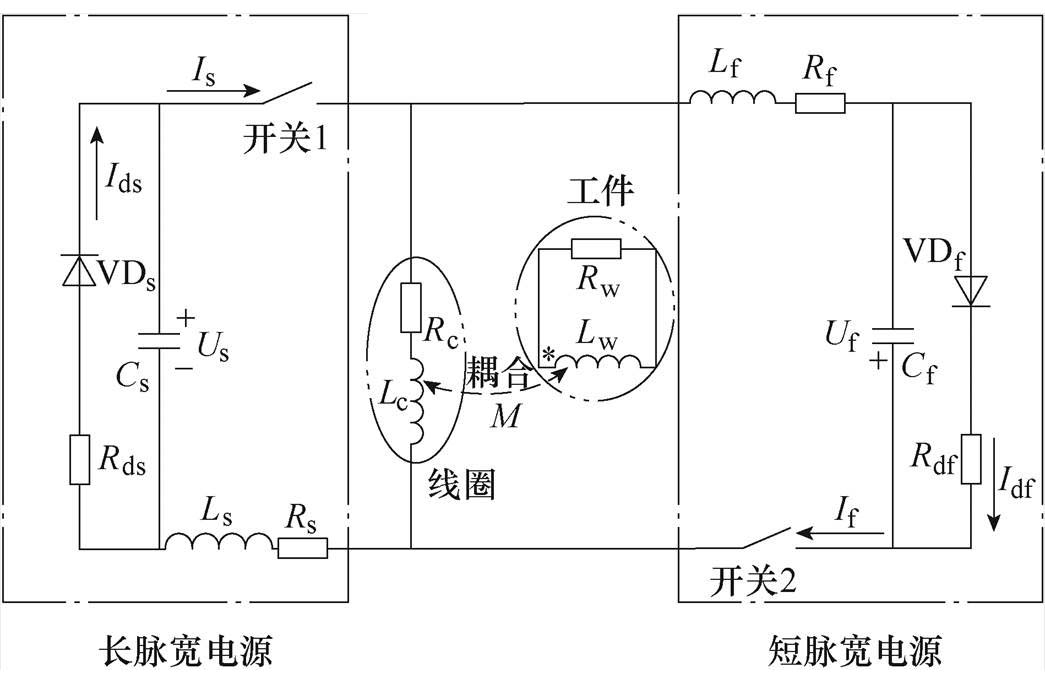
图3 双频电流法电路拓扑等效模型
Fig.3 Dual-frequency current method discharge system
式中，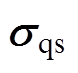
为准静态应力（MPa）；
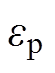为塑性应变率；而对于镁合金管件；p、m为应变率参数，p= 24 124.9 s-1；m=0.323。
由于EMF过程涉及电路-磁场-结构场之间的耦合，因此为了提升计算精度，本文采用文献[27]中使用的线圈、工件网格划分方法。该划分方式已通过实验验证，准确度较高。COMSOL Multiphysics有限元模型网格划分如图4所示，线圈与管网格划分处的最大网格单元尺寸设置为0.5 mm，空气域网格划分处最大网格单元尺寸为40 mm与80 mm。
表2 线圈和管件的材料参数
Tab.2 Material parameters of coils and tubes
材料参数铜线圈AZ31B镁合金管件 密度/(kg/m3)8 9301 780 电导率/(S/m)5.998×1071.1×107 相对介电常数11 相对磁导率11 杨氏模量/Pa1.1×10114.5×1010 泊松比0.330.29 初始屈服应力/MPa250160
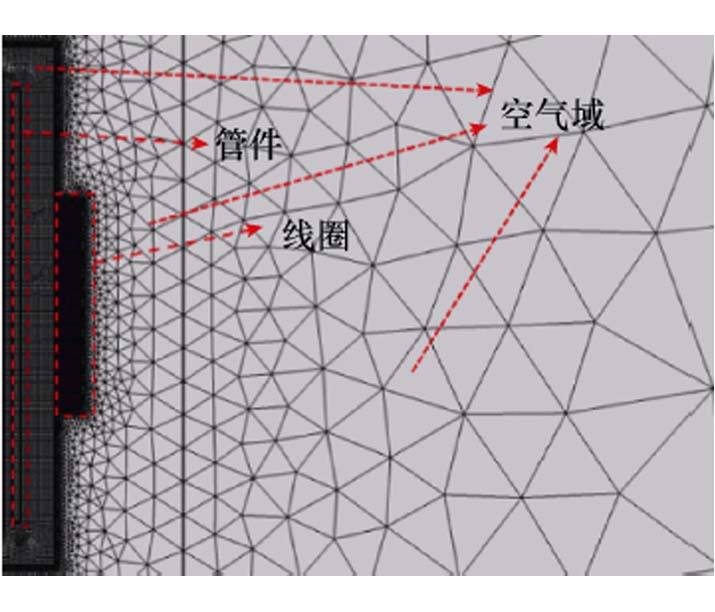
图4 COMSOL Multiphysics有限元模型网格划分
Fig.4 COMSOL Multiphysics finite element model meshing diagram
电磁成形的动态过程极其复杂，管件所受电磁力密度、径向速度的大小、方向（运动状态）与管件上的感应涡流密度、空间上产生的合成磁通密度（下称磁通密度）的大小、方向（电磁参数）高度相关。而电磁参数又与电源系统的放电参数（电压、电容、电感、电阻等）密切相关。故想要具体分析管件的运动状态，首先需要明确放电参数与电磁参数的动态变化过程。
双电源系统产生的线圈电流波形如图5所示，此时长脉宽电源电压Us=7 kV，短脉宽电源电压Uf = 13 kV。长脉宽电流Is先缓慢上升至峰值，t =1.9 ms时短脉宽电流If导通，此时线圈中合成急速下降的电流波形。合成电流谷值点应尽量靠近0点以确保管件具有较好的变形效果[28-29]。
在该放电参数下，管壁中点的电磁参数变化如图6所示，在0～1.9 ms即长脉宽电流上升沿阶段，磁通密度与感应涡流密度的符号相反（在此规定长脉宽电源电流方向为正，其产生的磁通密度为正，感应涡流密度方向为负）；1.9 ms时短脉宽电流导通后，感应涡流密度迅速反向，但轴向磁通密度方向不变，此时磁通密度与感应涡流密度符号相同。
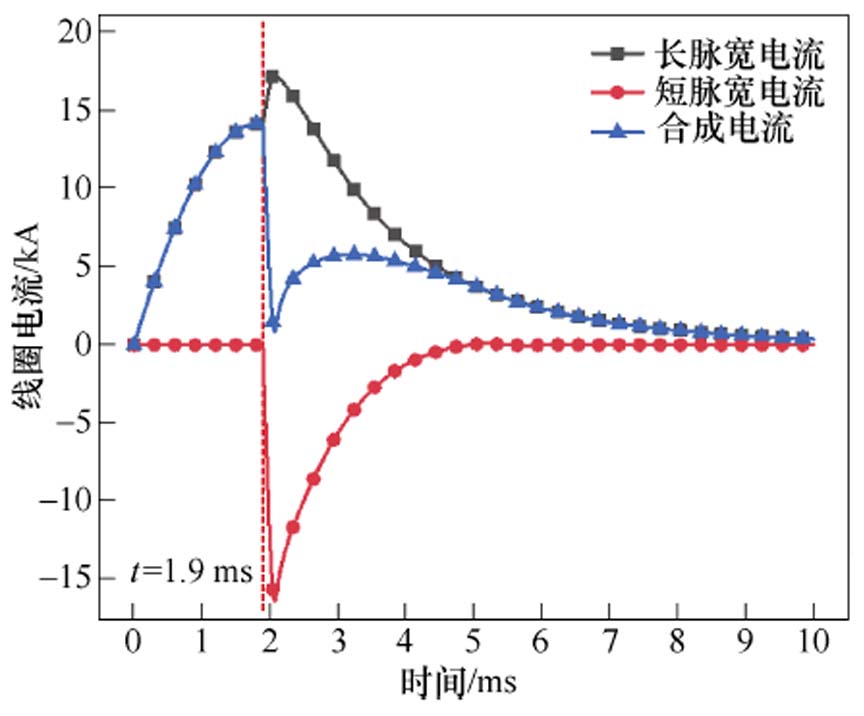
图5 Us=7.4 kV、Uf =13 kV时电流波形
Fig.5 Current waveforms of Us=7.4 kV, Uf =13 kV
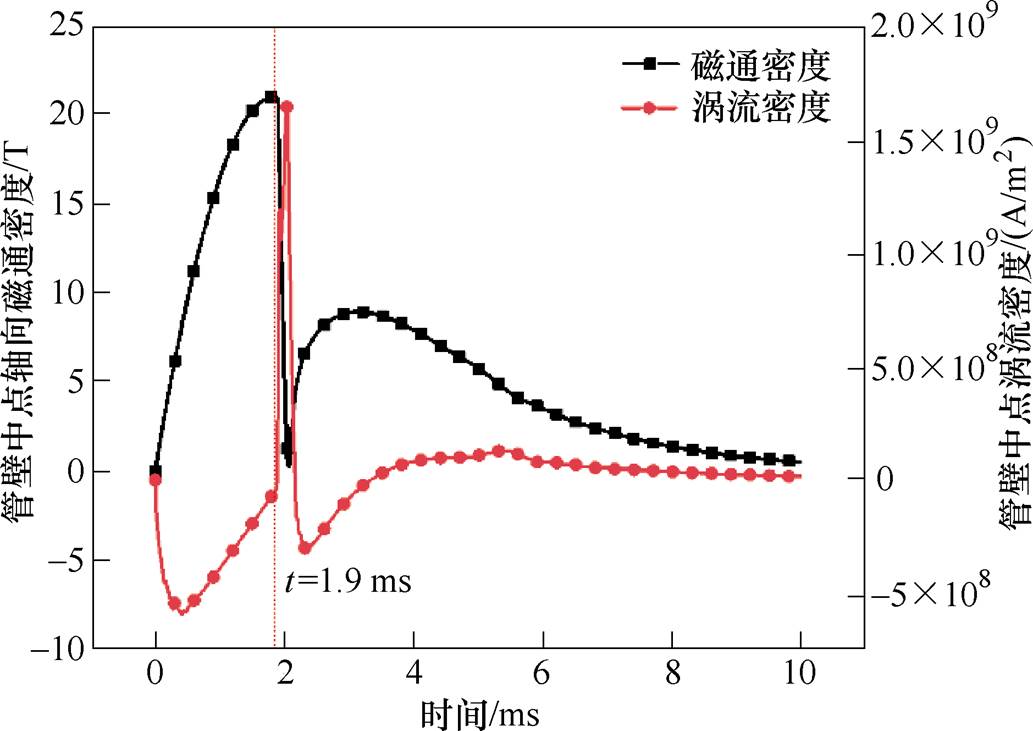
图6 电磁参数变化
Fig.6 Electromagnetic parameters change
管件的运动状态是电磁参数相互作用的直观表现形式，根据图6中管壁中点电磁参数的变化规律，可以得出管壁中点电磁力密度与径向位移随时间的变化如图7所示，管件所受电磁力密度的空间分布如图8所示。在0～1.9 ms内管件上的电磁参数符号相反，故在该阶段内管件受方向向内（收缩）的排斥力作用，但管壁中点的径向位移并没有发生明显变化；1.9 ms后，管件上的电磁参数方向相同，管件在极短的时间（10-4 s）内受吸引力驱动向外高速膨胀，其径向位移在0.2 ms内达到峰值。在电磁参数相互作用产生的电磁力驱动下，管件在0～2.3 ms内的径向位移变化决定了其最终的变形效果。
管件径向位移时空分布如图9所示，由于1.9 ms前，管件并未发生明显变形，故选择1.9～2.3 ms内管件的径向位移时空分布进行分析。
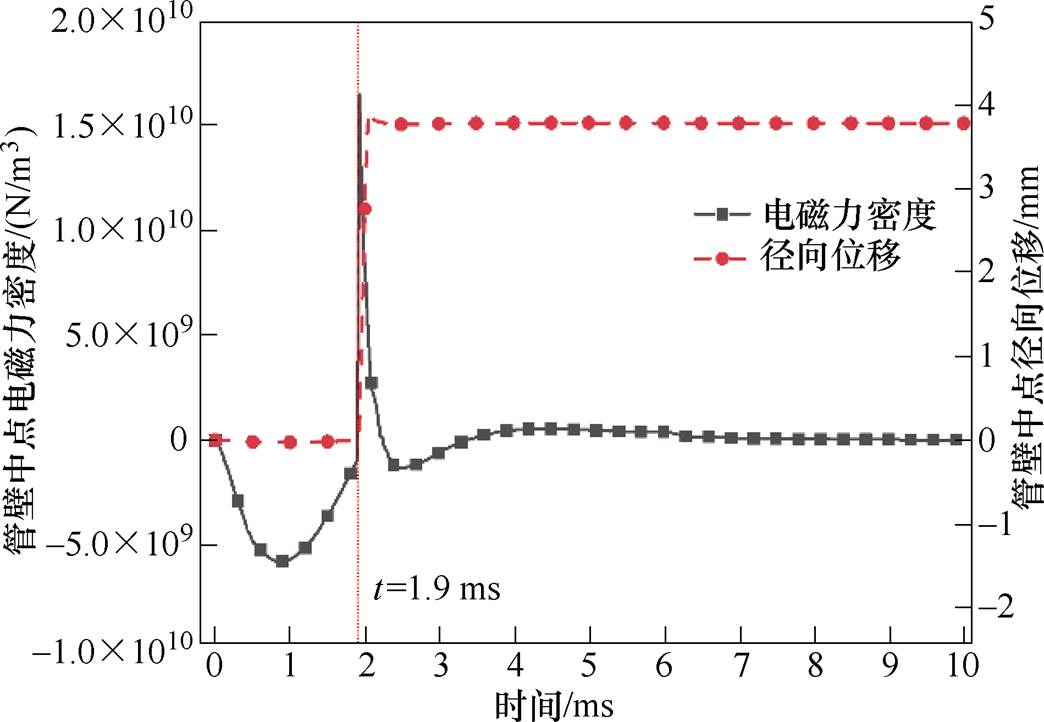
图7 电磁力密度与径向位移变化
Fig.7 Electromagnetic force density and radial displacement change
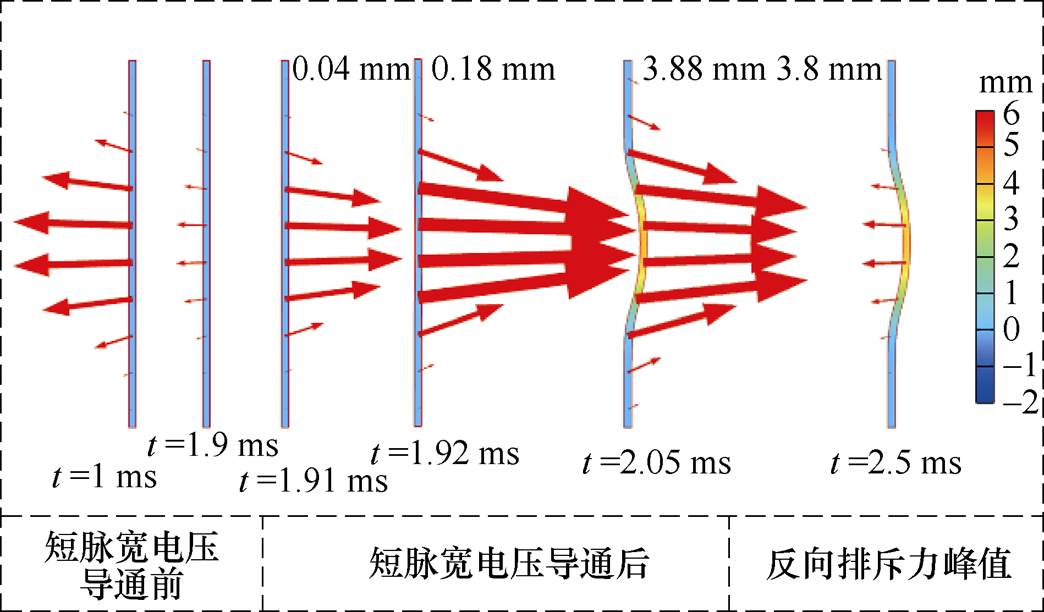
图8 电磁力密度空间分布
Fig.8 Electromagnetic force density spatial distribution
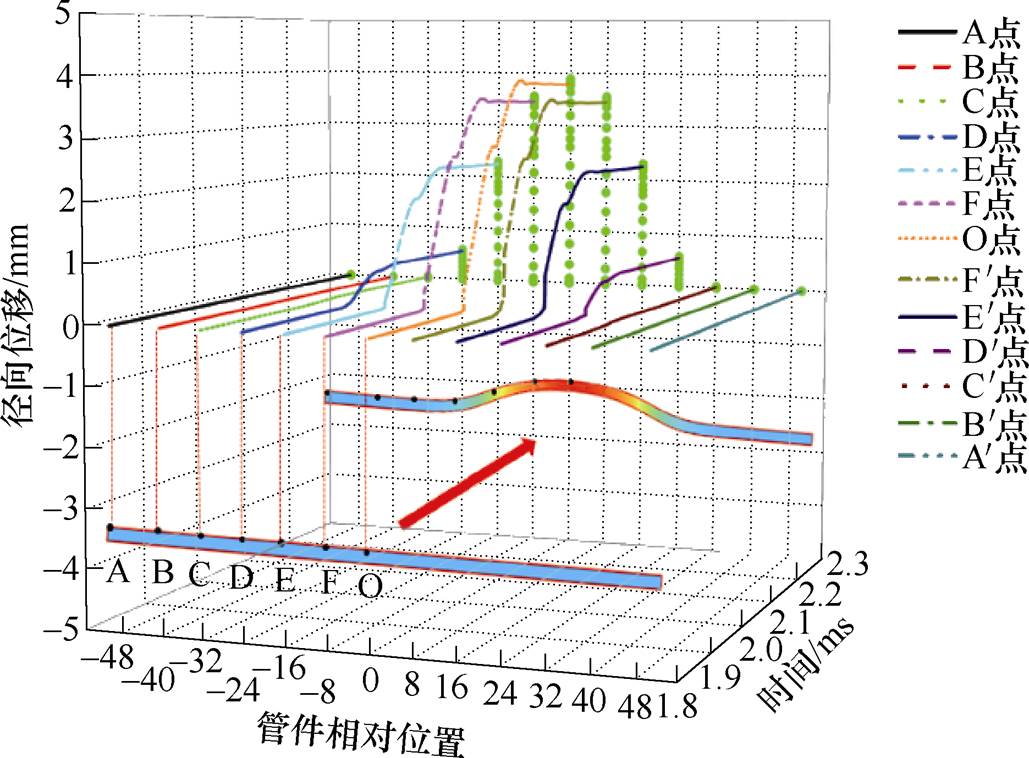
图9 管件径向位移时空分布
Fig.9 Time-space distribution of radial displacements of tube
以管壁中间点为O点，沿管件轴向向上每8 mm取一个点共取7个点A、B、C、D、E、F。以管件的相对位置为X轴，时间为Y轴，径向位移为Z轴，即可建立管件外壁径向位移的时空分布。如图9所示，对Y、Z轴的数据分析可知：在1.9～2.3 ms内，管件迅速发生形变并趋于稳定状态；对X、Z轴的数据分析可知：越靠近管壁中间点O，径向位移越大。
通过上述分析，可以得知管壁中点O的运动变化趋势最为显著，故分析该点电磁参数与运动状态随时间的变化趋势，即可反映管件电磁成形的动态特性。O点的电磁力密度、径向速度、径向位移随时间变化如图10所示。
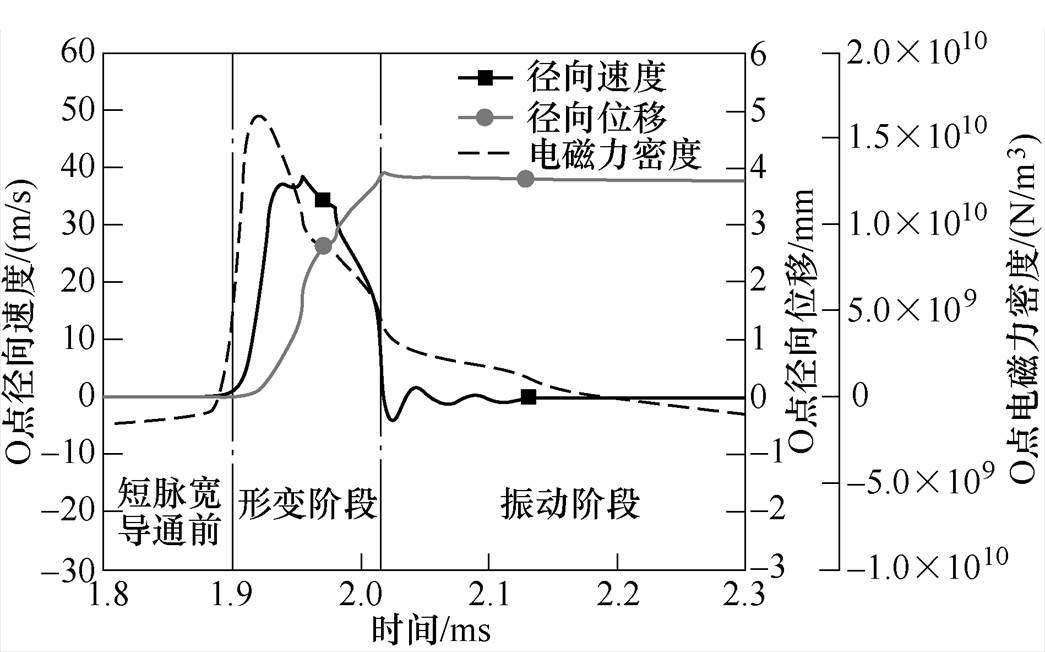
图10 O点的运动状态变化
Fig.10 Movement states change of O point
在0～1.9 ms内即短脉宽电流导通前，管件受排斥力驱动，O点的径向速度与位移并未发生明显变化；短脉宽电流在1.9 ms时导通，管件受吸引力驱动而发生高速形变，O点的径向膨胀速度迅速上升至38.5 m/s。当O点的径向膨胀速度首次为0时，其径向膨胀位移达到峰值3.89 mm，此后O点的径向速度在0点上下波动，径向位移回落并且具有上下振动的趋势。
管件运动状态由电磁参数相互作用决定，电磁参数的方向与大小由放电参数宏观调控，这也正是电磁力灵活可控的体现。本文中衡量管件变形效果的标准是其膨胀方向的径向位移，也是宏观放电参数控制工件运动状态的直接体现。因此熊奇等提出的吸引式成形过程的涡流竞争[9]与电磁力竞争[30]，均为工件运动状态改变的本质原因。故可根据上述的分析，将管件吸引式成形过程分为以下三个阶段：
（1）0～1.9 ms内为长脉宽电源电流上升阶段，管件受排斥力驱动，称该阶段为短脉宽电流导通前阶段。
（2）1.9 ms后至管件径向膨胀位移到达峰值时刻为形变阶段。在该阶段，短脉宽电源电流导通并达到峰值，合成磁场与合成涡流符号相同且相互作用，电磁力迅速由排斥力变为吸引力，管件径向膨胀高速变形，在该阶段管件的径向膨胀速度的峰值时间并不是电磁力为0的时间，这是由于管件自身的几何约束使其径向膨胀速度减小。
（3）当管件径向膨胀速度为0时，形变阶段结束，管件运动状态将由自身几何约束与电磁力共同决定，这一过程为振动阶段。
根据前文的分析可知，放电参数宏观调控管件吸引式成形的运动状态，因此本节将对长脉宽电源放电参数对管件成形三个阶段的影响进行分析。
通过增加长脉宽电源电压Us等级，即可调控长脉宽电源电流Is幅值。当放电电容容值以及线路电阻、电感不变时，短脉宽电源电压Uf为13 kV。将长脉宽电源电压Us由4.4 kV提升至7.4 kV，此时线圈电流波形如图11所示。
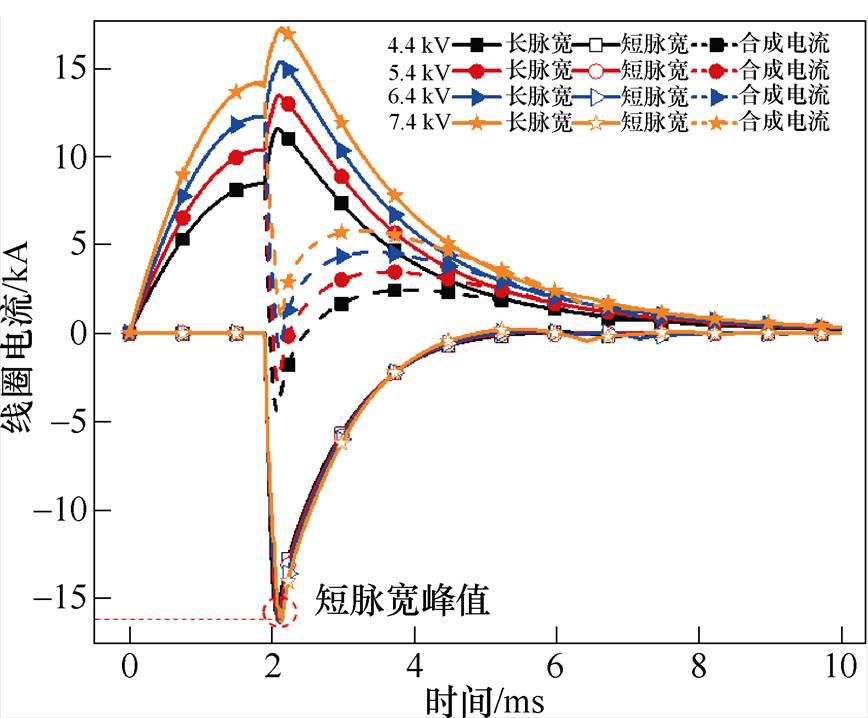
图11 不同Us下的电流波形
Fig.11 Current waveforms under different Us
Is幅值随Us增大而增大，因此在相同时间（导通时间1.9 ms）下，Us越大，合成电流谷值点也随Us等级提升而上移。因此在不同Us下，O点电磁参数在1.8～2.3 ms内变化如图12所示。
Is幅值决定了1.9 ms空间中O点轴向磁通密度的幅值，当Us=7.4 kV时磁通密度幅值为Us=4.4 kV时的1.7倍；在短脉宽电源电流If幅值不变的前提下，Is幅值越小，O点的轴向磁通密度达到反向峰值的时间就越早，感应涡流密度越大。当Us＜7.4 kV，O点的轴向磁通密度发生反向时，感应涡流密度方向并未立即改变，故此时管件的运动状态也将发生改变。
电磁力密度、径向速度随时间变化如图13所示，在形变阶段，由于Us＜7.4 kV时合成电流谷值点将越过0点进而使O点轴向磁通密度反向，但感应涡流密度方向不变。故在该阶段，O点的电磁力将由吸引力变为排斥力，与径向膨胀速度方向相反。进而使得O点的径向膨胀速度在反向电磁力与自身几何约束共同作用下迅速下降至0，Us越小，则径向膨胀速度为0时间越早。
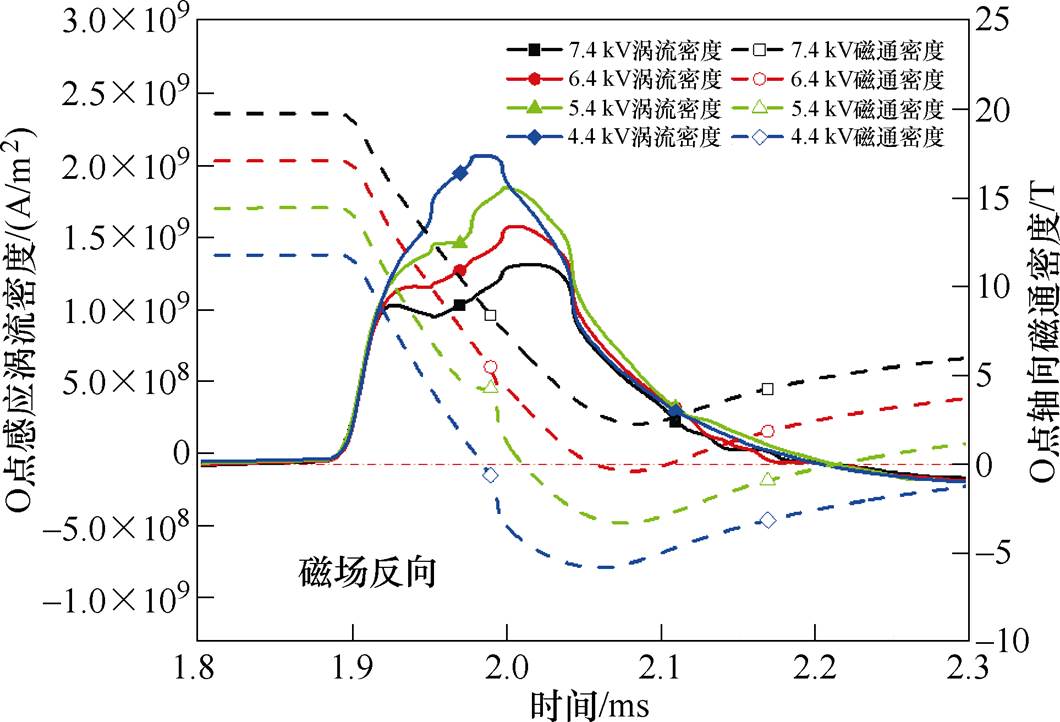
图12 不同Us电磁参数变化
Fig.12 Electromagnetic parameters change under different Us
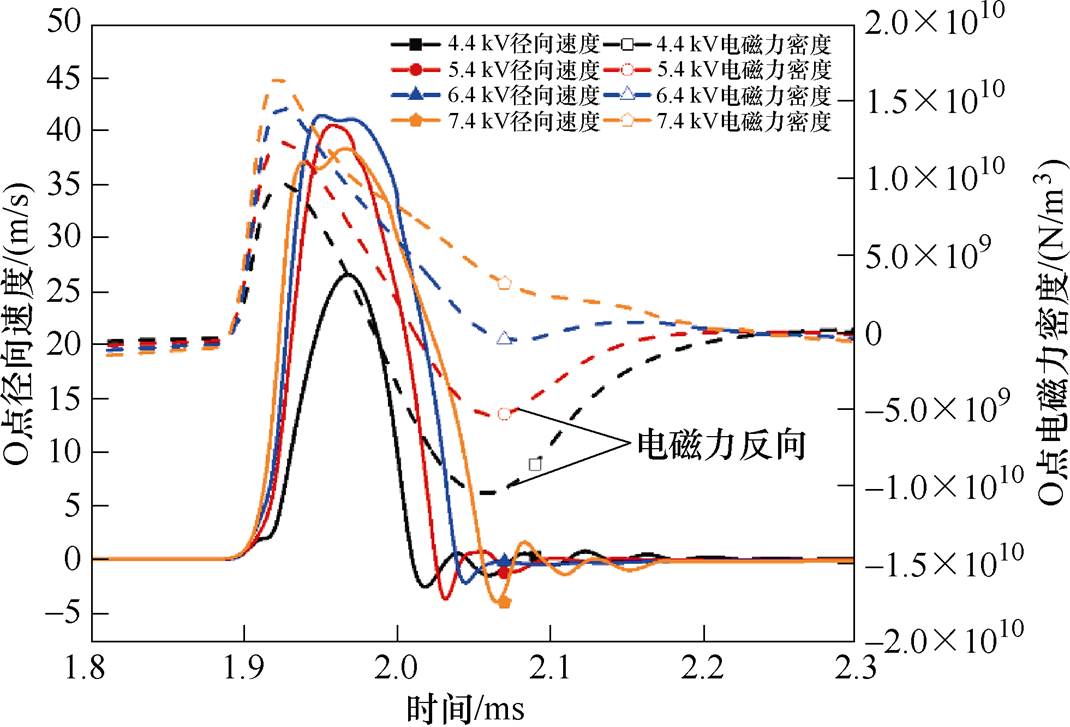
图13 不同Us下运动状态变化
Fig.13 Change of motion states under different Us
管件在不同Us下最终径向位移的空间分布如图14所示。Us越小将使管件在形变阶段内的电磁力由吸引力变为排斥力，因此吸引力的作用时间将变短。在振动阶段管件运动趋势相同的情况下，形变阶段吸引力作用时间越短，其径向膨胀位移越小。故Us为4.4 kV时，径向膨胀位移仅为1.57 mm，Us为7.4 kV时，径向膨胀位移为3.77 mm，后者约为前者的2.4倍。
因此提升长脉宽电源电压Us，可以使合成电流的谷值点上移，进而使O点轴向磁通密度反向峰值减小或者不发生反向。保证形变阶段的电磁力不会产生因吸引力与排斥力竞争而出现径向膨胀速度下降过快的现象。吸引力作用时间更长，则形变阶段径向位移越大，管件最终变形效果就更好。
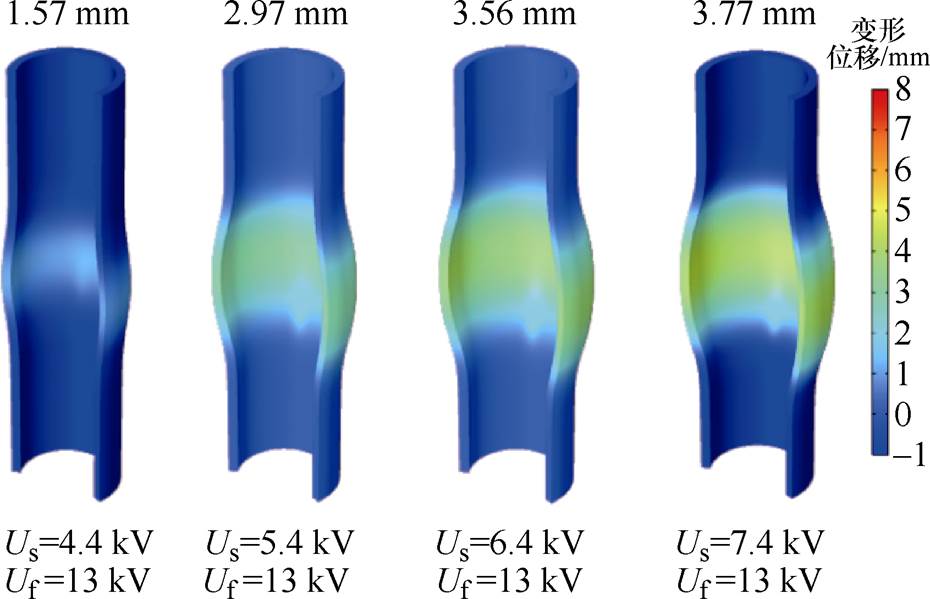
图14 不同Us下管件最终位移
Fig.14 Final displacement of tubes under different Us
当Us继续增大时，O点的电磁参数变化如图15所示。当Us＞7.4 kV值时，Is幅值也将增大，在短脉宽电源导通时间不变的前提下，将使Is上升沿阶段感应涡流密度显著提升，并且在空间中产生的轴向磁通密度也将增大。
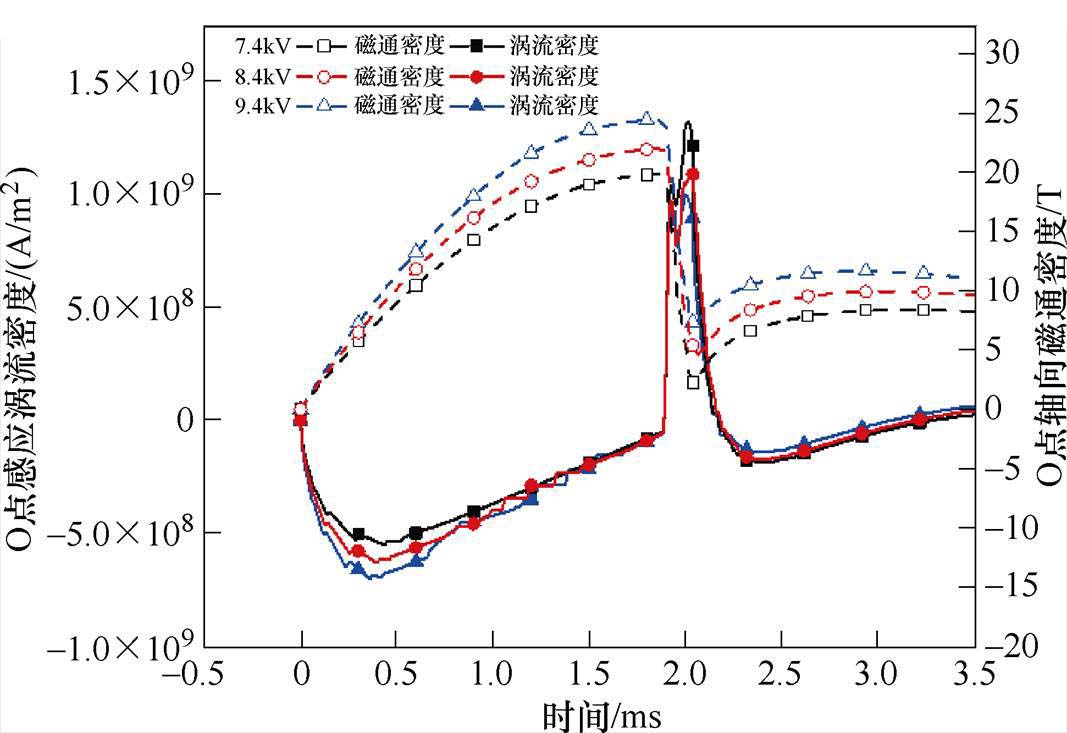
图15 不同Us电磁参数变化
Fig.15 Electromagnetic parameters change under different Us
O点电磁力密度、径向位移随时间变化与最终成形效果空间分布如图16所示。Us=9.4 kV时，短脉宽导通前阶段管件所受排斥力过大，导致管件在该阶段径向收缩，其收缩位移为0.27 mm，最终径向膨胀位移为3.2 mm，远低于8.4 kV时的3.9 mm，且管件中间区域出现凹痕，变形平整度较差。
综上所述，长脉宽电源电压Us主要影响吸引力成形动态过程的前两个阶段，即短脉宽导通前阶段与形变阶段。当Us＞8.4 kV时，管件上产生的感应涡流密度、空间上产生的轴向磁通密度过大。在此电磁参数的相互作用下，短脉宽电源导通前阶段管件受排斥力驱动发生径向收缩，收缩位移为0.27 mm，故最终径向膨胀位移低于8.4 kV的膨胀位移。当Us＜8.4 kV时，随着Us的增大，形变阶段吸引力作用时间更长，因此最终径向膨胀位移增大，管件变形效果更好。
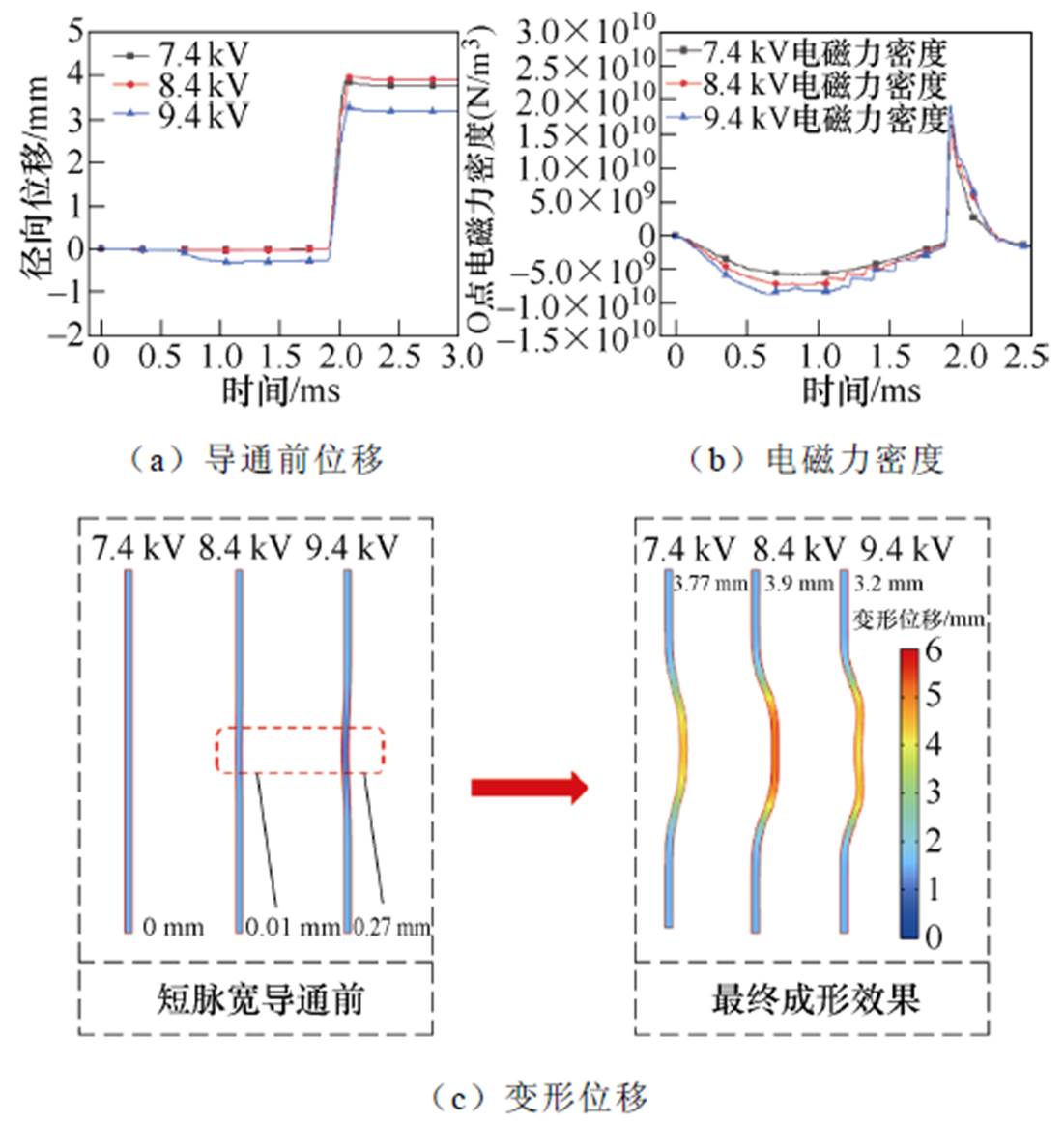
图16 不同Us下仿真结果示意图
Fig.16 Schematic diagrams of simulation results under different Us
急剧下降的合成电流波形是由短脉宽电源放电参数所决定的，因此短脉宽电源放电电压Uf越大，电流If的幅值越大（方向与Is相反，幅值与正负无关）。当长脉宽电源Us不变，为8.4 kV时，增加短脉宽电源放电电压Uf，线圈电流If波形如图17所示。
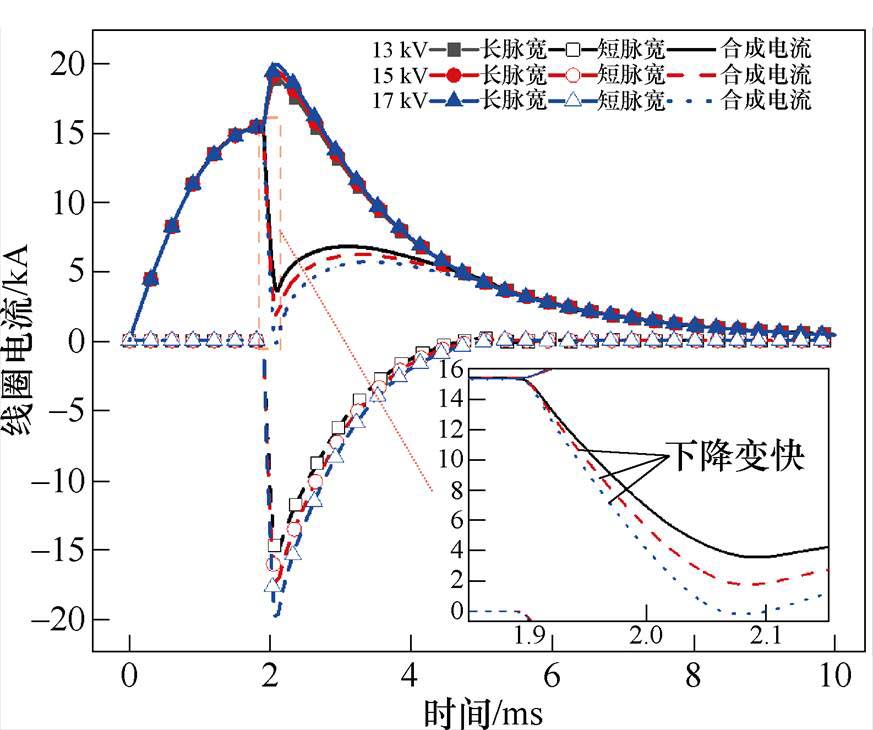
图17 不同Uf下的电流波形
Fig.17 Current waveforms under different Uf
当长脉宽电源放电参数不变时，在1.9 ms前合成电流峰值是相同的。因此短脉宽电源Uf越大，If峰值越大，且到达峰值时刻相同，故1.9 ms后，合成电流下降沿的变化率（斜率）将增大。
不同Uf下电磁参数的变化如图18所示。不同Uf等级下，O点的电磁参数在1.8～2.3 ms内随时间的变化关系可得知：随着Uf由13 kV提升至17 kV，O点轴向磁通密度在1.9 ms时下降的速度将变快，因此O点产生的感应涡流密度也随之增大。当Uf= 17 kV时，O点轴向磁通密度将在2.03 ms时反向，但感应涡流密度的方向并未发生改变。
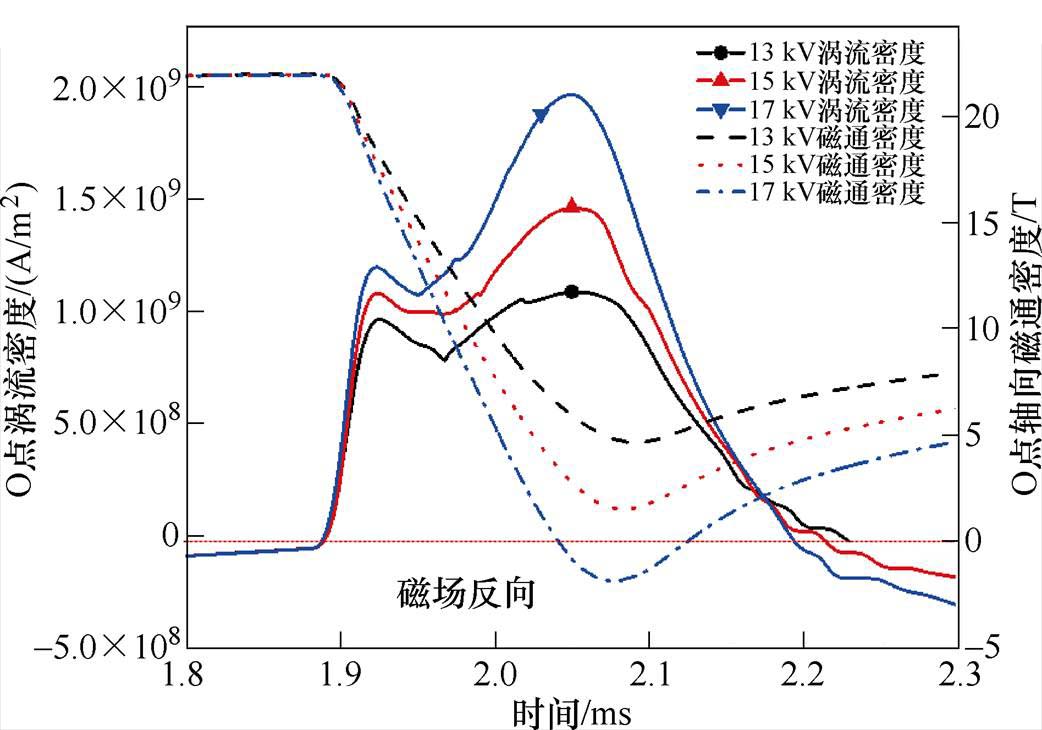
图18 不同Uf电磁参数变化
Fig.18 Electromagnetic parameters change under different Uf
故在上述电磁参数相互作用下，O点的电磁力密度与径向速度在1.8～2.3 ms内随时间的变化如图19所示。从图19中可知，在形变阶段，Uf为17 kV时O点的电磁力密度峰值相比Uf =13 kV时，提升113%，故O点的径向膨胀速度也随之变大。Uf = 17 kV时O点轴向磁通密度发生反向，电磁力方向也发生改变。此时形变阶段将出现吸引力与排斥力在时间上的竞争关系，但由于此时排斥力较小，因此并未使得管件的运动状态发生改变；在振动阶段时，管件的运动状态由自身几何约束与电磁力共同决定，因此Uf =17 kV时，虽然在振动阶段管件仍受排斥力作用，但并未主导其形变阶段的运动状态，故振动阶段O点的径向速度变化趋势几乎相同。
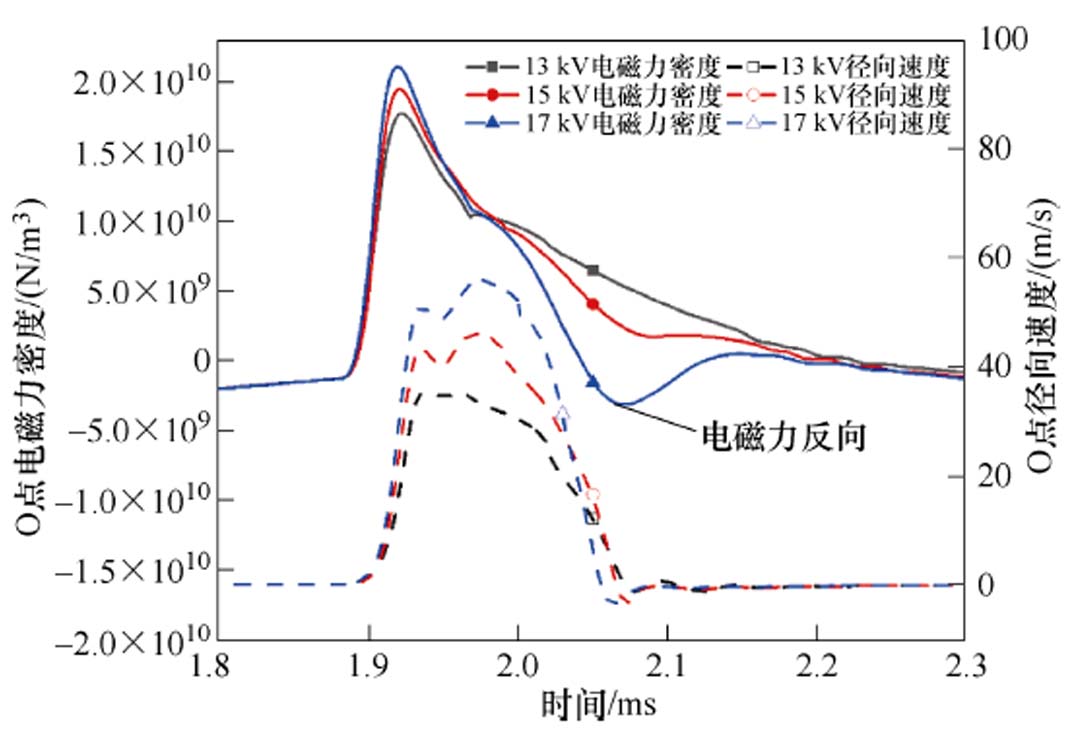
图19 不同Uf下运动状态变化
Fig.19 Change of motion states under different Uf
Uf由13 kV提升至17 kV，管件最终的变形效果如图20所示，其中右轴颜色范围表示管件位移大小，越靠近红色区域，管件膨胀径向位移越大。Uf = 17 kV时管件最大位移为6.02 mm，较Uf =13 kV时提升154%。因此增大Uf，可提升管件形变阶段吸引力与径向膨胀速度大小，使管件径向膨胀位移更大。
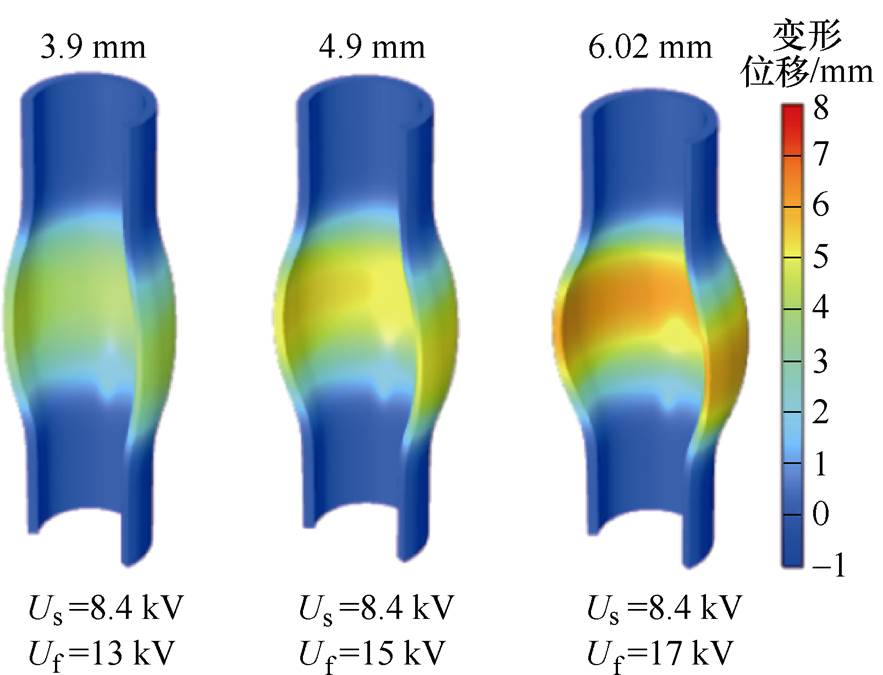
图20 不同Uf下管件最终成形位移
Fig.20 Final forming displacement of tubes under different Uf
但另一方面，当Uf为17 kV时，合成电流谷值越过0点，O点轴向磁通密度反向，故形变阶段将出现吸引力与排斥力相互竞争的现象。但这一现象并没有影响Uf为17 kV时管件的运动状态，针对这一问题，继续增大Uf，其电磁参数在1.8～2.3 ms内随时间变化关系如图21所示。
当Uf由19 kV增加至23 kV时，O点轴向磁通密度反向峰值将增大且下降速度更快，故感应涡流密度也将增大但方向不变。因此在该电磁参数的相互作用下，管件在1.8～2.3 ms内随时间变化如图22所示。
由图22中可知，随着Uf由19 kV提升至23 kV时，O点电磁力增大，故在形变阶段的径向膨胀速度与电压呈正相关。由于O点轴向磁通密度反向，管件在形变阶段均存在吸引力与排斥力在时间上的竞争关系；当Uf =23 kV时，排斥电磁力密度峰值约为吸引电磁力密度峰值的1.8倍。管件在Uf由19 kV增加至23 kV的过程中，管件径向位移与形变量1.8～2.3 ms内时空分布如图23所示。
形变阶段结束时，Uf为23 kV时的最大径向位移是大于Uf为21 kV、19 kV时刻的，但在振动阶段，由图22中Uf为21 kV与19 kV时O点的径向速度可以看出，虽然此时电磁力为排斥力，但并未明显增大19 kV时的径向收缩速度；但Uf为23 kV时O点的排斥力过大，使其径向收缩速度增大至46 m/s，是19 kV与21 kV时径向收缩速度的3.8倍。故Uf =23 kV时，在振动阶段除了管件自身几何约束将使管件出现振动，排斥力将主导振动阶段的运动状态，径向收缩速度显著提升，使得管件径向收缩位移增大，最终变形效果不如低电压等级。
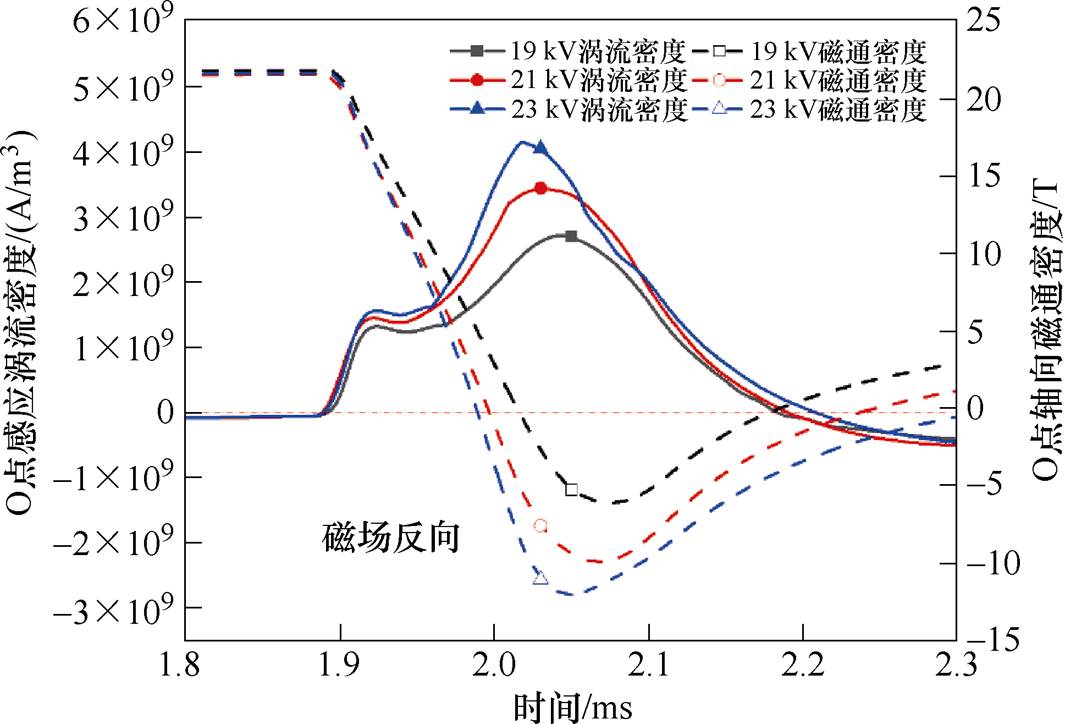
图21 Uf＞17 kV时电磁参数变化
Fig.21 Electromagnetic parameters change under Uf＞17 kV
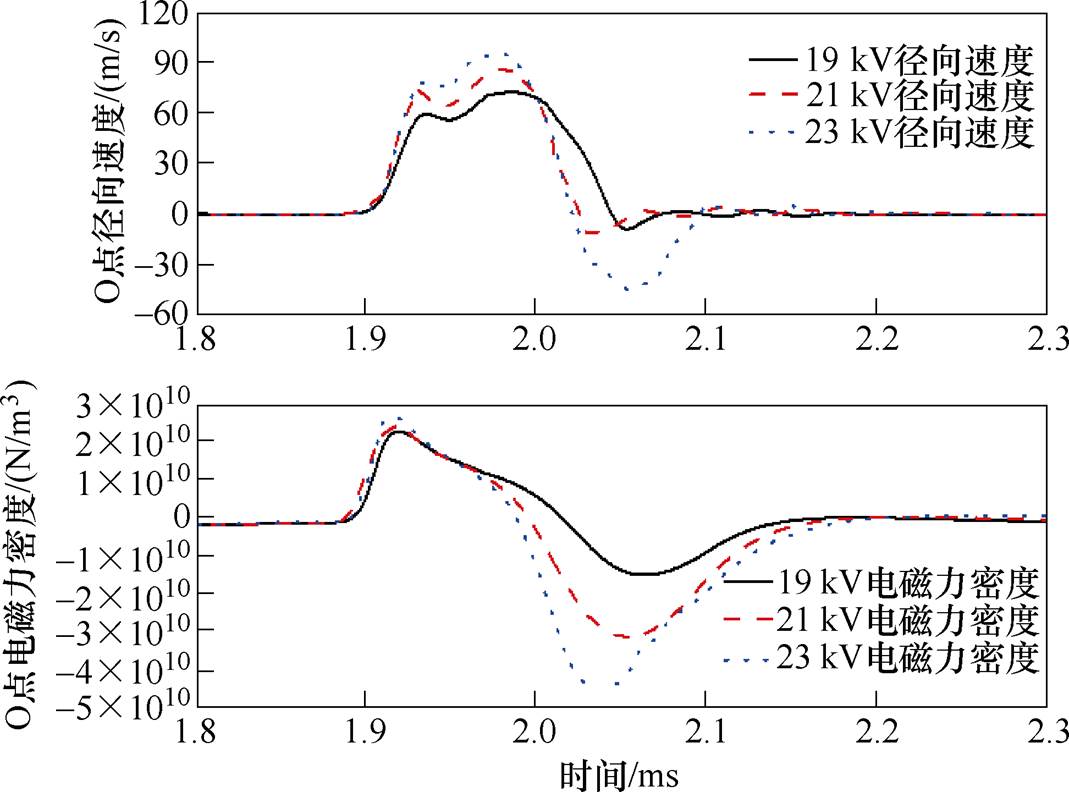
图22 不同Uf下运动状态变化
Fig.22 Change of motion states under different Uf
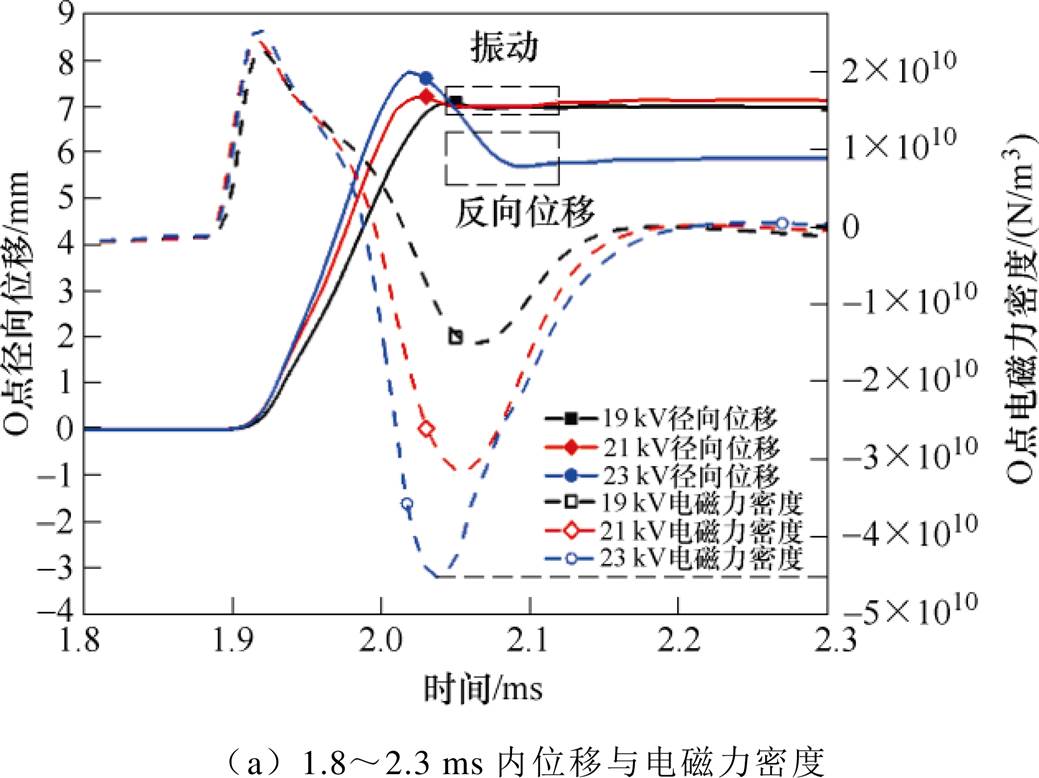
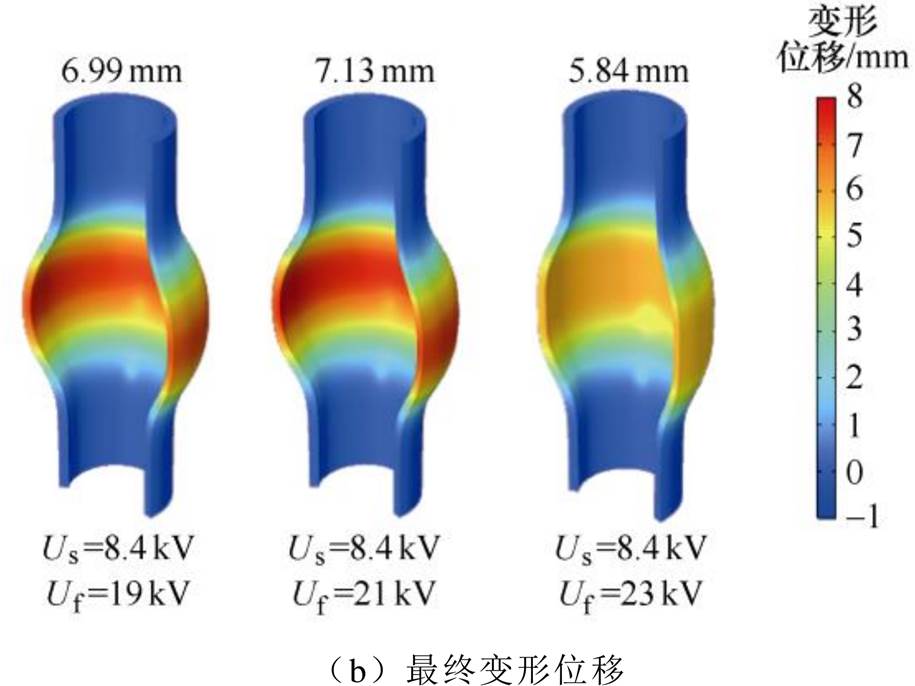
图23 Uf为19～23 kV下仿真结果示意图
Fig.23 Schematic diagrams of simulation results of Uf 19～23 kV
为了验证振动阶段发生的反向位移是否是由排斥力过大造成的。将Uf由21 kV增加至23 kV，每级增加0.5 kV，O点的径向速度与径向位移在1.8～2.3 ms内随时间变化如图24a所示，最终成形位移空间分布如图24b所示。
当Uf为21.5 kV与22 kV时，振动阶段O点的径向位移回落并振动主要由自身几何约束与排斥力共同决定，其径向收缩速度最大值为12.8 m/s与13.4 m/s，二者差别不大；当Uf为22.5 kV时，由于此时O点的排斥力过大，足以在振动阶段管件的运动状态中占据主导地位，使O点的径向收缩速度显著提升至32.9 m/s，因此排斥力将驱动管件径向收缩。Uf为22.5 kV时管件的最终变形位移为6.52 mm，较Uf为21.5 kV时的7.36 mm减小了11%，变形效果不佳。
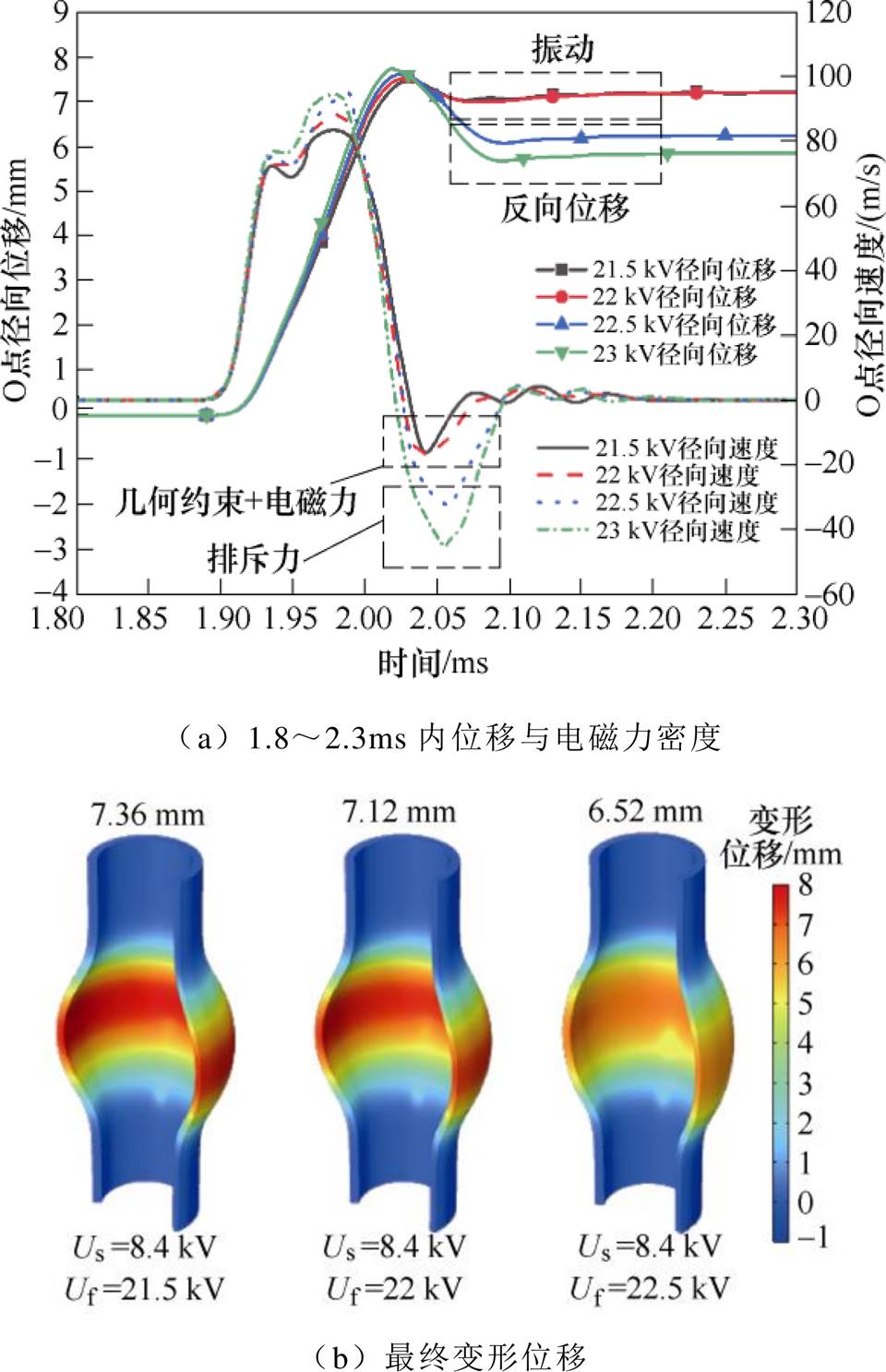
图24 21.5～23 kV下仿真结果示意图
Fig.24 Schematic diagrams of simulation results of 21.5～23 kV
综上所述，短脉宽电源电压Uf主要影响管件吸引式成形动态过程中形变阶段与振动阶段。随着Uf的增大，管件在形变阶段所受吸引力越大，径向膨胀速度越快，形变阶段结束时膨胀位移也越大；当Uf增加至22 kV以上时，虽然在形变阶段管件所受吸引力与管件的径向膨胀速度均大于Uf为22 kV以下时，但在振动阶段，管件运动状态将由排斥力主导，因此其径向收缩速度显著提升，管件径向位移由上下振动变为径向收缩，使得最终变形效果不佳。
本文建立了室温下AZ31镁合金管件吸引式成形的仿真模型，分析了吸引式成形过程中放电参数、电磁参数对管件运动状态的影响。得到如下结论：
1）当Us＞8.4 kV时，在短脉宽导通前阶段管件将受排斥力驱动径向收缩，故最终变形效果将变差。因此在实际工程设计中，应考虑Us是否会引起工件在该阶段产生颈缩现象。
2）当Us＜8.4 kV、Uf不变时，增大Us可提升形变阶段吸引力作用的时间；当Us为4.4、5.4、6.4 kV时，将使该阶段出现电磁力的竞争现象，吸引力的作用时间变短，故管件变形效果变差。
3）当Us不变，增大Uf可提升形变阶段管件所受吸引力及膨胀速度。因此在实际工程设计中，由于Us具有较低的上限，故增大Uf较增大Us更能提升管件的变形效果。
4）当Uf＞22 kV时，在振动阶段管件运动状态将由排斥力主导，进而使管件收缩，降低其变形效果。因此在实际工程设计中，Uf的上限将由管件在振动阶段的运动状态决定，即该阶段管件的速度运动趋势应大致相同。若出现收缩速度显著增大的现象，则不能继续增加Uf。
参考文献
[1] 潘复生, 蒋斌. 镁合金塑性加工技术发展及应用[J]. 金属学报, 2021, 57(11): 1362-1379.
Pan Fusheng, Jiang Bin. Development and application of plastic processing technologies of magnesium alloys[J]. Acta Metallurgica Sinica, 2021, 57(11): 1362-1379.
[2] Zhang Jianyue, Jian Yongxin, Zhao Xuzhe, et al. The tribological behavior of a surface-nanocrystallized magnesium alloy AZ31 sheet after ultrasonic shot peening treatment[J]. Journal of Magnesium and Alloys, 2021, 9(4): 1187-1200.
[3] Medina J, Garces G, Pérez P, et al. High temperature mechanical behaviour of Mg-6Zn-1Y alloy with 1 wt % calcium addition: reinforcing effect due to I-(Mg3Zn6Y1) and Mg6Zn3Ca2 phases[J]. Journal of Magnesium and Alloys, 2020, 8(4): 1047-1060.
[4] Cui Xuejun, Ning Chuangming, Zhang Guangan, et al. Properties of polydimethylsiloxane hydrophobic modified duplex microarc oxidation/diamond-like carbon coatings on AZ31B Mg alloy[J]. Journal of Magnesium and Alloys, 2021, 9(4): 1285-1296.
[5] Psyk V, Risch D, Kinsey B L, et al. Electromagnetic forming—a review[J]. Journal of Materials Pro- cessing Technology, 2011, 211(5): 787-829.
[6] Wu Zelin, Cao Quanliang, Fu Junyu, et al. An inner- field uniform pressure actuator with high performance and its application to titanium bipolar plate for- ming[J]. International Journal of Machine Tools and Manufacture, 2020, 155: 103570.
[7] 邱立, 李彦涛, 苏攀, 等. 电磁成形中电磁技术问题研究进展[J]. 电工技术学报, 2019, 34(11): 2247- 2259.
Qiu Li, Li Yantao, Su Pan, et al. Research on electromagnetic problems in electromagnetic forming process[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2247-2259.
[8] 熊奇, 唐红涛, 王沐雪, 等. 2011年以来电磁成形研究进展[J]. 高电压技术, 2019, 45(4): 1171-1181.
Xiong Qi, Tang Hongtao, Wang Muxue, et al. Research progress of electromagnetic forming tech- nique since 2011[J]. High Voltage Engineering, 2019, 45(4): 1171-1181.
[9] 熊奇, 杨猛, 周丽君, 等. 双线圈吸引式板件电磁成形过程中的涡流竞争问题[J]. 电工技术学报, 2021, 36(10): 2007-2017.
Xiong Qi, Yang Meng, Zhou Lijun, et al. Eddy currents competition in electromagnetic forming process of plates by double-coil attraction[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(10): 2007-2017.
[10] Cao Quanliang, Xia Liangyu, Li Xian, et al. The importance of coil conductivity and eddy current effects in the analysis of electromagnetic forming process[J]. High Voltage, 2022, 7(2): 390-404.
[11] Xiong Qi, Huang Hao, Xia Liangyu, et al. A research based on advance dual-coil electromagnetic forming method on flanging of small-size tubes[J].The Inter- national Journal of Advanced Manufacturing Tech- nology, 2019, 102(9/10/11/12): 4087-4094.
[12] 张望, 王于東, 李彦涛, 等. 基于双向电磁力加载的管件电磁翻边理论与实验[J]. 电工技术学报, 2021, 36(14): 2904-2911.
Zhang Wang, Wang Yudong, Li Yantao, et al. Theory and experiment of tube electromagnetic flanging based on bidirectional electromagnetic force loading[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2904-2911.
[13] Xiong Qi, Li Zhe, Tang Jianhua, et al. A flexible and economical method for electromagnetic flanging of tubes with field shapers[J]. The International Journal of Advanced Manufacturing Technology, 2021, 116(3/4): 1169-1177.
[14] Qiu Li, Yu Yijie, Yang Yuqi, et al. Analysis of electromagnetic force and experiments in electro- magnetic forming with local loading[J]. International Journal of Applied Electromagnetics and Mechanics, 2018, 57(1): 29-37.
[15] 邱立, 余一杰, 聂小鹏, 等. 管件电磁胀形过程中的材料变形性能问题与电磁力加载方案[J]. 电工技术学报, 2019, 34(2): 212-218.
Qiu Li, Yu Yijie, Nie Xiaopeng, et al. Study on material deformation performance and electromag- netic force loading in electromagnetic tube expansion process[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 212-218.
[16] Xiong Qi, Tang Hongtao, Wang Muxue, et al. Design and implementation of tube bulging by an attractive electromagnetic force[J]. Journal of Materials Pro- cessing Technology, 2019, 273: 116240.
[17] Ouyang Shaowei, Wang Chen, Li Changxing, et al. Improving the uniformity and controllability of tube deformation via a three-coil forming system[J]. The International Journal of Advanced Manufacturing Technology, 2021, 114(5/6): 1533-1544.
[18] 王紫叶, 杨猛, 熊奇. 电磁成形过程中线圈温升及结构优化[J]. 电工技术学报, 2021, 36(18): 3891- 3901.
Wang Ziye, Yang Meng, Xiong Qi. Coil temperature rise and structure optimization in electromagnetic forming[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3891-3901.
[19] 徐俊瑞, 王元丰, 王宇阳, 等. 镁合金板材磁脉冲成形研究进展[J]. 精密成形工程, 2021, 13(5): 10-21.
Xu Junrui, Wang Yuanfeng, Wang Yuyang, et al. Research progress of magnetic pulse forming of magnesium alloy sheet[J]. Journal of Netshape Forming Engineering, 2021, 13(5): 10-21.
[20] 徐俊瑞. AZ31镁合金板材磁脉冲成形性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2013.
[21] Uhlmann E, Jurgasch D. New impulses in the forming of magnesium sheet metals[C]//Proceeding 1st Inter- national Conference on High Speed Forming, Dortmund, 2004: 229-241.
[22] Ulacia I, Arroyo A, Eguiy I, et al. Warm electro- magnetic forming of AZ31B magnesium alloy sheet[C]// Proceeding 4th International Conference on High Speed Forming, Ohio, 2010:159-168.
[23] 孟正华, 黄尚宇, 胡建华, 等. 镁合金板材温热电磁复合成形试验研究[J]. 机械工程学报, 2011, 47(10): 38-42.
Meng Zhenghua, Huang Shangyu, Hu Jianhua, et al. Experimental research on warm and electromagnetic hybrid forming of magnesium alloy sheet[J]. Journal of Mechanical Engineering, 2011, 47(10): 38-42.
[24] Xu Junrui, Xie Xueyun, Wen Zhisheng, et al. Deformation behaviour of AZ31 magnesium alloy sheet hybrid actuating with Al driver sheet and temperature in magnetic pulse forming[J]. Journal of Manufacturing Processes, 2019, 37: 402-412.
[25] Xu Junrui, Wang Yuyang, Wen Zhisheng, et al. Electromagnetic impacting medium forming (EIMF): a new method forming process for magnesium alloy sheet[J]. The International Journal of Advanced Manufacturing Technology, 2020, 109(1/2): 553- 563.
[26] 唐红涛. 基于吸引式电磁力的金属管件电磁胀形设计与实现[D]. 宜昌: 三峡大学, 2019.
[27] 杜立蒙. 可调阻尼系数下的电磁成形工件变形及线圈焦耳热特性研究[D]. 武汉: 华中科技大学, 2020.
[28] Xiong Qi, Tang Hongtao, Deng Changzhen, et al. Electromagnetic attraction-based bulge forming in small tubes: fundamentals and simulations[J]. IEEE Transactions on Applied Superconductivity, 2018, 28(3): 1-5.
[29] Cao Quanliang, Lai Zhipeng, Xiong Qi, et al. Electromagnetic attractive forming of sheet metals by means of a dual-frequency discharge current: design and implementation[J]. The International Journal of Advanced Manufacturing Technology, 2017, 90(1/2/3/4): 309-316.
[30] 熊奇, 周丽君, 杨猛, 等. 单脉冲电磁成形中洛伦兹力在时间上的双向竞争关系及其对成形效果的影响[J]. 电工技术学报, 2022, 37(14): 3453-3463.
Xiong Qi, Zhou Lijun, Yang Meng, et al. The two- way competitive relationship of Lorentz force in time in single pulse electromagnetic forming and its influence on forming effect[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3453-3463.
Abstract Electromagnetic forming (EMF) technology can effectively improve the forming limit of light alloys at room temperature, suppress the spring-back of the workpiece, and reduce wrinkling. It has been widely used in the plastic processing of aluminum alloy workpieces. However, compared with aluminum alloys, magnesium alloys have lower electrical conductivity and higher yield strength, so conventional EMF technology can not satisfy the plastic processing of magnesium alloy workpieces at room temperature. Recently, some scholars used high-conductivity alloys as driving plates or heating devices to assist in forming. However, the tooling was complex, and the forming quality needed to be guaranteed. It is not even suitable for small tube forming. Therefore, this paper proposes an electromagnetic attraction forming method for magnesium alloy tubes at room temperature. By establishing a finite element simulation model, the feasibility of the forming scheme, the discharge and electromagnetic parameters, and the workpiece deformation were studied.
Firstly, AZ31B magnesium alloy tubes with an inner diameter of 10 mm, a length of 100 mm, and a thickness of 2 mm are selected. The dual-frequency discharge current method is used to generate attractive forces to drive the forming of the tube. Secondly, due to the extremely fast and complex electromagnetic forming, it is necessary to use simulation to explore the relationship between the parameters in the attractive electromagnetic forming process in detail. Finally, a finite element model has been developed considering the influence of tube displacement and deformation. The method realizes the full coupling between the electromagnetic fields and workpiece deformation.
Simulation results show that the electromagnetic forming process can be divided into three stages: the stage before the short pulse current is turned on, the deformation stage, and the vibration stage. Changing the long-pulse voltage Us or the short-pulse voltage Uf can change the time-space distribution of electromagnetic parameters at point O and ultimately regulate the motion state of the tube. During the short-pulse current conduction stage, the electromagnetic parameters at point O have opposite signs, and the tube is subjected to a repulsive force. When Us is 9.4 kV and Uf is 13 kV, the tube is radially contracted by 0.27 mm, the final deformation area dent marks appear, and the deformation flatness is poor. In the deformation stage, the electromagnetic parameters at point O have the same sign, and the attractive force deforms the tube. When Uf is 13 kV, Us increases from 4.4 kV to 8.4 kV, and the action time of the attractive force in the deformation stage will become longer. The final radial expansion displacement of the tube will become larger. When Us is 8.4 kV and Uf is raised from 13 kV to 23 kV, the electromagnetic force and radial expansion velocity of point O in the deformation stage increase. However, the final displacement at 23 kV is only 5.84 mm, much lower than 7.13 mm at 21 kV. Uf was raised from 21 kV to 23 kV (0.5 kV intervals) to study this phenomenon. In the vibration stage, the peak shrinkage radial velocity at 21 kV and 21.5 kV were 12.8 m/s and 13.4 m/s, respectively, and the peak shrinkage velocity increased to 32.9 m/s at 22.5 kV. At this time, the repulsive force will dominate the motion state of the tube in the vibration stage, so the final deformation effect is not good.
The following conclusions can be drawn: (1) In practical engineering, whether Us will cause necking in the workpiece before the short pulse is turned on should be considered. (2) Since Us has a lower upper limit, increasing Us is more effective than increasing Uf. It can improve the deformation effect of the tube fitting. (3) The upper limit of Uf will be determined by the motion state of the tube fitting in the vibration stage. That is, the velocity movement trend of the tube fitting in this stage should be roughly the same. If the shrinkage speed is significantly increased, Uf cannot be further increased.
keywords：Electromagnetic forming, dynamic characteristics, tube, attraction force, AZ31 magnesium alloy
DOI: 10.19595/j.cnki.1000-6753.tces.220495
中图分类号：TM154
国家自然科学基金（51707104）和武汉强磁场学科交叉基金（WHMFC202121）资助项目。
收稿日期 2022-04-01
改稿日期 2022-07-13
熊 奇 男，1990年生，博士，副教授，博士生导师，IEEE Senior Member，研究方向为电磁场工业应用。E-mail: pandaqi0218@gmail.com（通信作者）
朱鑫辉 男，1996年生，硕士研究生，研究方向为电磁场分析及应用。E-mail: 540022126@qq.com
（编辑 郭丽军）