图1 双层丝阵Z箍缩[5]
Fig.1 Nested wire array Z pinches[5]
摘要 能量法计算导体段电感的理论完备自洽，计算结果准确，但对全场域的积分复杂，计算效率低。磁链法只需对导体区域积分，计算简单，已广泛应用于导体段电感计算。但现有基于磁链法的电感计算方法因不满足电流连续性定律，计算结果存在误差，因此基于磁链法求得的电感用于计算并联导体段的电流分配也会导致误差，而现有文献尚未对其进行系统研究。该文首先针对工程中常见的电流单端注入单端流出的并联细导体段模型，推导磁链法计算并联支路电流的误差公式，揭示了误差电流正比于真实电流，且只与并联导体组的自感以及总电流注入、流出点的距离有关。该文的理论分析与计算修正了采用磁链法计算的并联细导体电流分配结果，在不降低计算速度的同时提高了计算的准确度，可为工程应用提供参考。
关键词：并联细导体段 电流分配 电感 磁链法 能量法
闭合回路中并联导体段的电流分配问题是工程中的常见问题，尤其对于多支路并联的导体，支路电流的准确测量受测量仪器尺寸、抗干扰能力、插入阻抗等因素的影响往往十分困难[1]。因此并联导体段电流分配的准确计算非常重要。
在工程实践中，当并联导体段所在的闭合回路过于复杂或连接情况尚不清楚时，有时也只考虑这一局部的多分支并联导体段的电流分配来开展计 算[2]，以近似看作实际闭合回路中的电流分布。并联细导体段的电流分配问题在工程应用中并不罕见，如双层金属丝阵负载Z箍缩中的内外层电流分配就是其中的代表性问题。
Z箍缩是一种将电磁能高效地转化为X射线辐射能的技术途径，在惯性约束聚变、高能量密度物理等诸多领域有广泛的应用前景[3]。如图1所示的双层金属丝阵负载的Z箍缩相比于单层可提高辐射功率高达40 %[4]，其中内外层丝阵的电流分配是影响内爆动力学过程的关键因素[5]。在最大值为几兆安培，持续时间为几十纳秒的电流脉冲过程中，丝阵电感决定了其初始电流分配，丝阵电阻的影响可忽略不计[6]。同心双层丝阵的电流经由阳极极板流入平行于丝阵的回流柱，通过回流柱再流入阴极极板[7]。在电流脉冲过程中，两个极板的电流分布并不清楚，其与丝阵及回流柱的电磁耦合作用难以量化表征，电感参数的提取比较困难，因此实际计算中往往只考虑双层金属丝阵与回流柱的电感效应，以确定丝阵中的电流分配。
图1 双层丝阵Z箍缩[5]
Fig.1 Nested wire array Z pinches[5]
美国海军研究实验室的J. Davis等[8]将Nw根金属丝和Nb根回流柱组成个Nw×Nb个回路，先将金属丝及回流柱视为无限长，在此磁场分布下求出金属丝实际长度对应的回路自感及其间互感，以获得金属丝阵的电流分布。密歇根大学的T. S. Strickler等[9]将Nw×Nb个回路简化为Nw+Nb-1个支路，仍在无限长的近似下求出支路的电感及其间互感，将金属丝阵电流分布的计算时间减小了5个数量级。俄罗斯学者E. V. Grabovskiĭ等[10]将Nw+Nb-1个回路进一步简化为内层丝阵与回流柱，外层丝阵与回流柱组成的两个回路，沿用了丝阵与回流柱无限长的近似，提出了两支路并联的电路模型，更方便计算内外层丝阵的电流分配。目前的研究都采用了沿丝阵轴线磁场分布不变的假设[11]，因此将金属丝和回流柱简化为无限长，然而考虑到目前外层丝阵的高度与半径之比一般在1～3之间[11]，无限长的近似在计算丝阵与回流柱电感时会导致较大误差，直接影响内外层丝阵电流分配的计算结果，因此必须采取针对有限长导体段的电感计算方法以获得准确的金属丝阵内外层电流分配。
从对Z箍缩中的内外层电流分配问题的讨论中可以看出，为了获得实际中并联细导体段的电流分配情况，保证细导体段的自感以及段间的互感的计算结果的准确性十分关键。美国学者A. E. Ruehli[12]和C. L. Holloway等[13]结合导体闭合回路的电感定义，基于采用矢量磁位表示的磁链法，将闭合回路导体的电感计算公式分段表示，从而得到了分段导体的部分电感及相应物理模型。这种方法称为磁链法，采用磁链法计算导体段电感时，只需对有存在电流的区域积分，而不用对全域进行积分，大大减小了计算量，提高了计算速度。
但是上述采用磁链法推导出的导体段自感和互感的计算公式，与采用能量法推导出来的结果并不相同[14]。导致它们不相同的根本原因在于所采用的导体段模型不满足电流连续性定理，因此不能完整地反映各分支导体段之间磁场的相互作用。为解决此问题，倪筹帷等[15]在细导体段模型的两端点添加积累的等值极性相反的点电荷，使得模型实现了电流连续。并在此基础上推导了端点处累积点电荷所产生矢量磁位的解析式，从而获得与能量法计算结果一致的导体段自感和互感的计算公式。
然而，倪筹帷等提出的细导体段两端积累电荷的模型并不适用直流情况，同时导体段部分自感和互感的计算公式中包含较多积分，计算复杂，而且未从理论上说明载流导体间互感的对称性。为解决此问题，华北电力大学崔翔课题组[16]提出了细导体段两端电流以球对称形式注入和流出的模型，满足电流连续性定理且适用于直流情况，同时推导了具有极简单形式的细导体段自感和互感的解析式，论证了载流导体间互感的对称性，且计算结果与能量法一致。
采用能量法计算并联导体段自感和互感虽然理论完备自洽、计算结果准确，但由于要对整个空间场域积分，导致计算复杂、计算效率低的缺陷。磁链法的积分场域仅局限于并联细导体所在区域，使得计算效率大大提高，已广泛应用于细导体段电感的计算[17-18]。但由于磁链法的导体模型并不满足电流连续性定理，因此计算细导体段电感时存在固有的计算误差，这直接导致采用磁链法计算并联细导体段电流分配时也存在误差[19-20]，现有文献尚未对其开展研究。
以文献[16]中能量法计算的电感为基准，本文通过理论分析和计算，对磁链法计算下并联细导体段电流分配误差开展了系统研究。获得了电流注入点空间位置，并联细导体段尺寸等关键参数对电流分配误差的影响规律。修正了磁链法计算的并联细导体电流分配结果，在不降低磁链法计算速度的同时提高了计算的准确度。
Z箍缩中通过电缆向金属丝阵负载注入电流可抽象为如图2所示的电流单端注入单端流出模型，可以描述工程中广泛存在的通过引线连接实现电流注入与流出的并联导体组。设A点是引线始端电流注入点，B点是电流注入端引线与并联细导体组的连接点，C点是电流流出端引线与并联细导体组的连接点，在BC两点间并联了n个细导体段，D点是引线末端电流流出点。
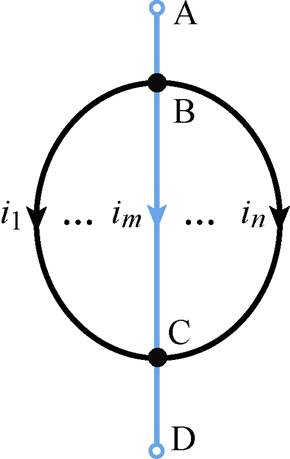
图2 电流单端注入单端流出并联细导体段模型
Fig.2 Parallel filament conductor segments model with single-ended injection and multi-ended outflow
假设细导体段中流过频率为f的交流电流，且细导体段的电阻与其电抗相比足够小可忽略不计，同时导体段足够细可不考虑其涡流效应。在图2所示的电流单端注入单端流出模型中，支路电流的分布完全由导体段的自感以及导体段间的互感决定。
图2中共包含n+2个细导体段（AB、CD，以及BC间n个细导体段），若考虑这n+2个细导体段的自感与互感列写KVL方程，不仅形式复杂且难以揭示磁链法与能量法计算并联支路电流分配之间的联系。因此本文引入了可以互相重叠的“部分回路”的概念，将沿AB经第m条并联支路到CD定义为并联细导体的第m条“部分回路”（在图2中用蓝色实线A—B—C—D表示），则图2中的n支路并联的导体组分为n条在AB和CD相互重合的“部分回路”，类似于电路分析中的网孔电流法。并联导体组两端电压与n条“部分回路”电流之间关系为
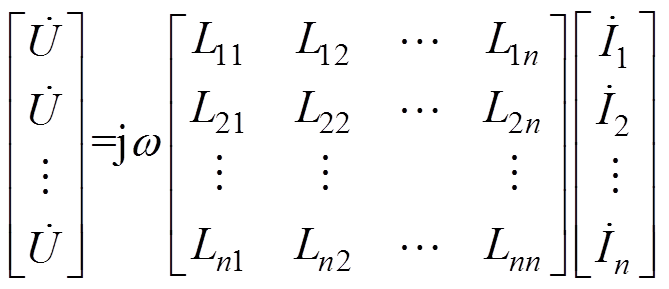（1）
式中，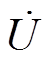
为n段细导体并联两端所加的电压相量；w 为交流电流对应的角频率；
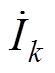为第k条部分回路的电流相量（亦即并联导体组中第k个细导体段的电流相量）；Lkk为第k条“部分回路”的自感；Lkm为第k条“部分回路”与第m条“部分回路”的互感。
磁链法计算细导体段的自感与互感的解析公式为
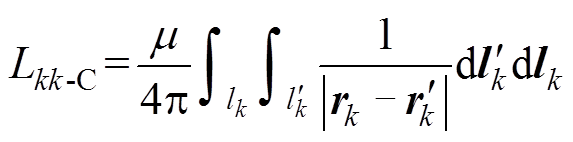（2）
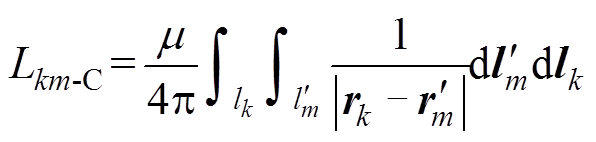（3）
式中，Lkk-C为磁链法计算的第k段细导体自感；Lkm-C为磁链法计算的第k段细导体与第m段细导体的互感；m 为磁导率。根据本文作者前期工作，可避免计算复杂的全场域积分求得能量法下细导体段的自感与互感，推导了形式简单的解析公式[16]为
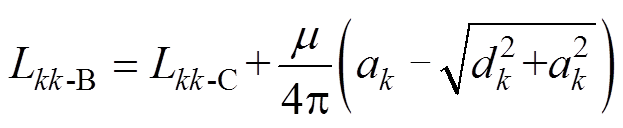（4）
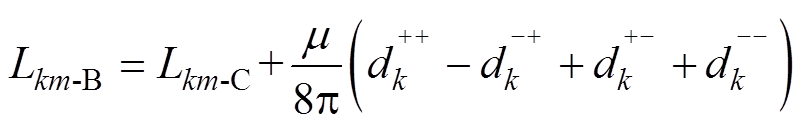（5）
式中，Lkk-B为能量法计算的第k段细导体自感，与磁链法计算结果相比多了与细导体半径与始末端位置有关的项；Lkm-B为能量法计算的第k段细导体与第m段细导体的互感，与磁链法计算结果相比多了与细导体始末端位置有关的项；ak为第k段细导体半径；dk为第k段细导体始末端的直线距离；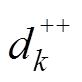
为第k段细导体末端与第m段细导体末端的直线距离；
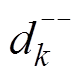为第k段细导体始端与第m段细导体始端的直线距离；
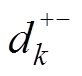为第k段细导体末端与第m段细导体始端的直线距离；
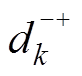为第k段细导体始端与第m段细导体末端的直线距离。两个细导体段模型如图3所示。
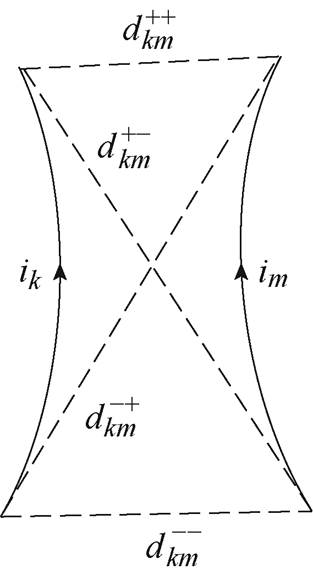
图3 两个细导体段模型
Fig.3 Two filament conductor segments
根据式（2）、式（3）中磁链法计算的导体电感，可以构建相应的电感矩阵LC，代入式（1）中，可得并联细导体段各支路电流
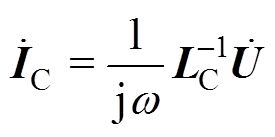（6）
其中
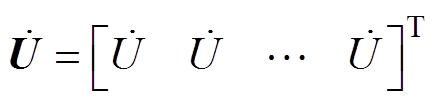
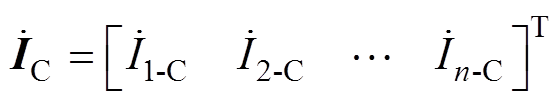
式中，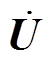
为施加在各细导体段上的电压列向量；
为导体电感用磁链法计算时并联细导体组的支路电流列向量。
同理，根据式（4）、式（5）中能量法计算的导体电感，可以构建相应的电感矩阵LB，代入式（1）中，导体电感用能量法计算时并联细导体组的支路电流列向量可表示为
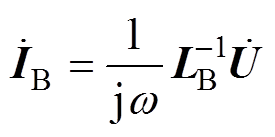（7）
由于磁链法和能量法计算所计算导体电感存在差异，其相应的电感矩阵LC和LB也因此不同，所以在并联细导体组两端所加电压给定的情况下求出的并联细导体段各支路电流向量和
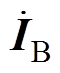并不一致。
以通过能量法计算得出的并联细导体段各支路电流向量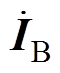为基准，分析依据磁链法计算得出的并联细导体段各支路电流向量相对于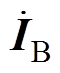的误差，此处只对图2a所示的电流单端注入单端流出模型展开讨论。
对于细导体段，导体半径远小于导体尺寸，即在式（4）中应满足ak
dk，而且电流单端注入单端流出模型中每个部分回路电流注入端（见图2中的点A）和流出端（见图2中的点D）的位置相同，即对于每个部分回路电流注入端和流出端之间的距离可用一个参数d表示，因此式（4）可化简为
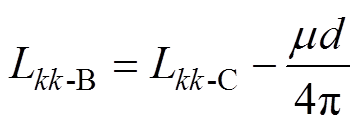（8）
对于电流单端注入单端流出模型，式（5）可化简为
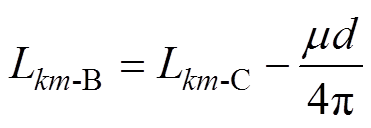（9）
式（8）、式（9）用矩阵统一表示为
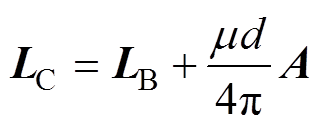（10）
式中，A为所有元素皆为1的n×n矩阵，将式（10）代入到式（6）中，得到
（11）
在式（11）两端同时左乘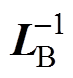
，整理得
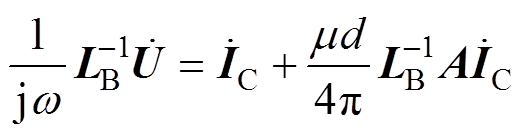（12）
由式（7），式（12）可化简为
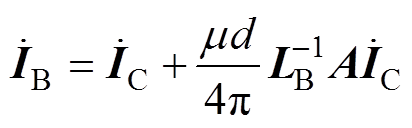（13）
将A表示为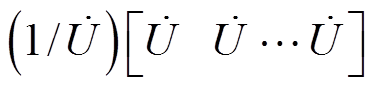
，并代入式（7）得
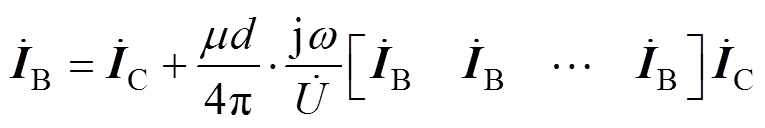（14）
进一步可表示为
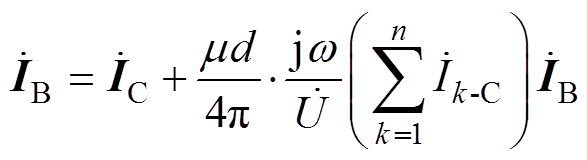（15）
注意到
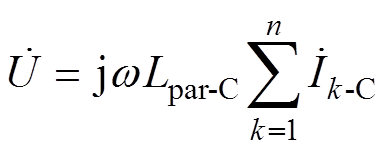（16）
式中，Lpar-C为磁链法计算得到的并联细导体组的等效自感，因此式（15）可化简为
（17）
由式（6）、式（16）可得
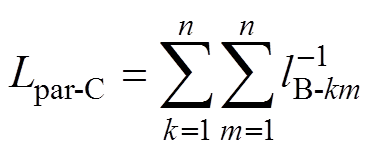（18）
式中，
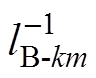为矩阵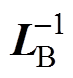的第k行、第m列元素。
式（17）表明，对图2a所示的电流单端注入单端流出模型，给定并联细导体组两端所加电压，导体电感用磁链法计算时支路电流列向量与导体电感用能量法计算时支路电流列向量成正比，比值大于0小于1。因此，磁链法计算的支路电流的分布规律与能量法计算结果相同，但是其支路电流幅值小于能量法计算结果。此外，磁链法计算的支路电流幅值误差仅与电流注入端与流出端的距离以及磁链法计算的并联细导体组的等效自感有关。对于闭合的并联细导体组回路（见图2中的点A与点D重合），即式（17）中d=0，磁链法与能量法计算的支路电流完全一致。
考虑图2所示的电流单端注入单端流出模型，引线AB、CD长度和形状（影响AD的距离）的变化不仅会直接影响电流注入和流出端距离d的大小，还会同时改变磁链法计算的并联细导体组的等效自感Lpar-C，因此有必要进一步研究引线对磁链法计算支路电流误差的影响规律。
仅关注并联细导体组一侧引线（AB）的影响，将引线CD的长度设为0。假设引线AB为长直导线，且为了研究引线长度所导致的误差，假设引线AB的长度dAB远大于BC间并联支路的长度dBC。因此电流注入端和流出端的距离近似等于引线AB的长度，即d≈dAB，磁链法计算的并联细导体组的等效自感近似等于引线AB的自感，即Lpar-C≈LAB-C。
引线AB足够长时，其自感可近似表示[16]为
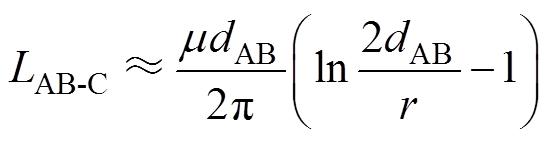（19）
式中，r为引线AB的半径。由式（17），磁链法计算支路电流的误差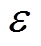
为
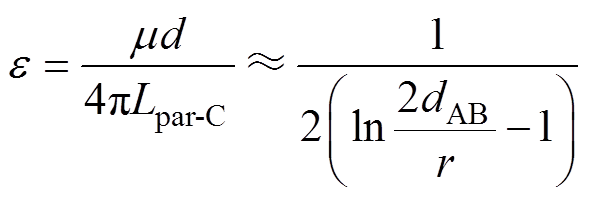（20）
式（20）表明，磁链法计算的支路电流误差仅与引线长度dAB和引线半径r的比值有关，且引线半径一定时，误差随着引线长度的增大而趋于0，但值得注意的是，此时误差的衰减是非常缓慢的，当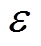=12 %时，dAB=100r；当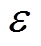=5 %时，dAB=29 937r，取r=1 mm，dAB≈30 m；当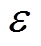=1 %时，dAB=7×1021r，此时引线的长度已经不可想象了。因此，在引线长度足够长时，误差对引线长度的变化非常不敏感。
以n个沿直线排列且各段相互平行的细导体段为例，验证磁链法计算误差公式的正确性。细导体段沿直线等间距排列的电流单端注入单端流出模型如图4所示。相邻细导体段间距都为h，引线AB与CD平行于各细导体段，引线AB的长度为dAB，引线CD的长度忽略不计。B点和C点分别位于并联导体组电流注入侧和流出侧的中点。
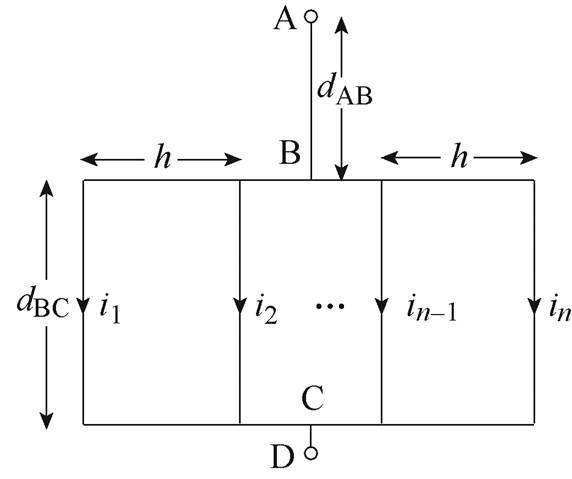
图4 细导体段沿直线等间距排列的电流单端注入单端流出模型
Fig.4 Single-ended injection and multi-ended outflow model with filament conductor segments arranged equidistantly along straight line
取并联细导体支路数n=5，并联细导体长度dBC=0.1 m，半径r=1 mm。设并联细导体组两端所加电压幅值为1 V，利用式（6）、式（7）计算对于并联细导体，引线长度dAB=0.1dBC，间距h分别为0.2dBC、0.5dBC、dBC时，采用磁链法和能量法得到的各并联支路电流如图5所示；间距h=0.2dBC，引线长度dAB分别为0.2dBC、dBC、10dBC时，采用磁链法和能量法得到的各并联支路电流如图6所示（本文中磁链法和能量法计算所得结果均按能量法计算的支路电流最大值归一化）。取并联细导体支路数n=10，引线长度dAB=0.1dBC，间距h分别为0.2dBC、0.5dBC、dBC时，采用磁链法和能量法得到的各并联支路电流如图7所示；间距h=0.2dBC，引线长度dAB分别为0.2dBC、dBC、10dBC时，采用磁链法和能量法得到的各并联支路电流如图8所示。
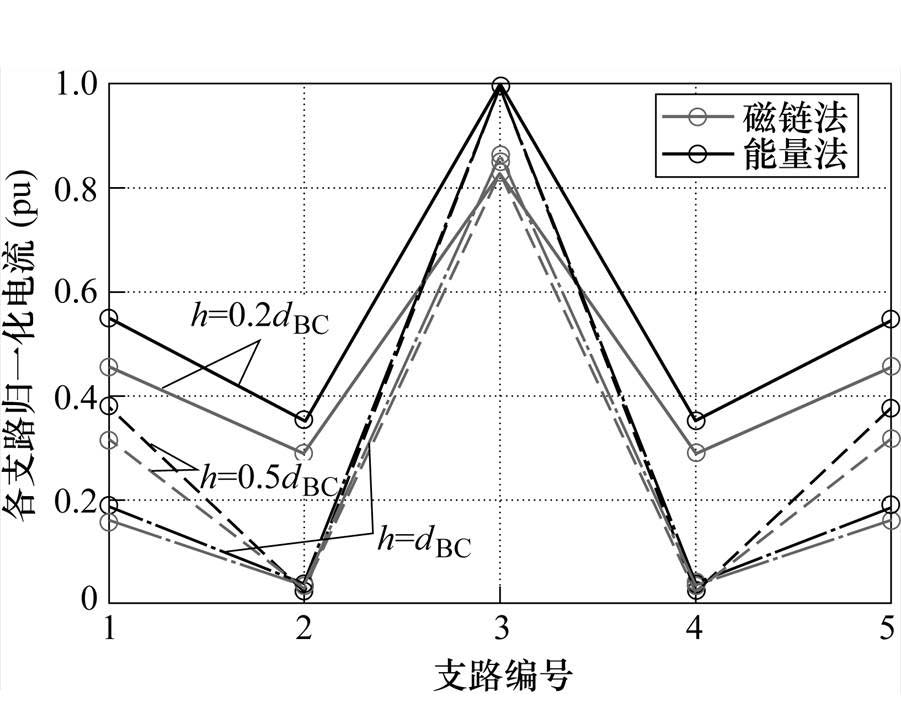
图5 dAB=0.1dBC，h=0.2dBC、0.5dBC、dBC时，电流单端注入单端流出模型中磁链法与能量法计算并联5支路电流对比
Fig.5 The comparison between five paralleled branch currents calculated by flux method and energy method under single-ended injection and single-ended outflow model with dAB=0.1dBC, h=0.2dBC, 0.5dBC, dBC
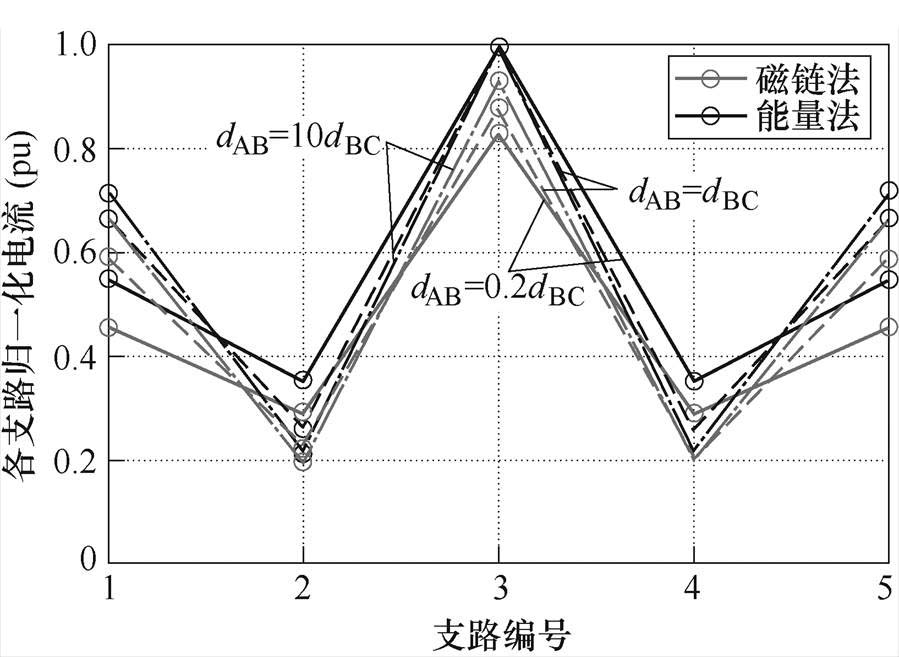
图6 h=0.2dBC，dAB=0.2dBC、dBC、10dBC时，电流单端注入单端流出模型中磁链法与能量法计算并联5支路电流对比
Fig.6 The comparison between five paralleled branch currents calculated by flux method and energy method under single-ended injection and single-ended outflow model with h=0.2dBC, dAB=0.2dBC, dBC, 10dBC
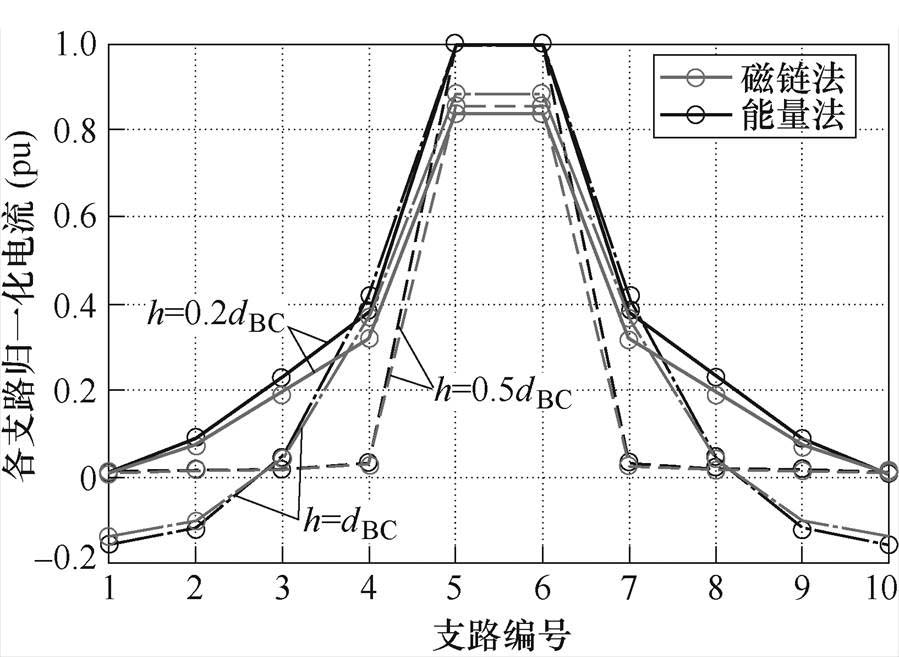
图7 dAB=0.1dBC，h=0.2dBC、0.5dBC、dBC时，电流单端注入单端流出模型中磁链法与能量法计算并联10支路电流对比
Fig.7 The comparison between ten paralleled branch currents calculated by flux method and energy method under single-ended injection and single-ended outflow model with dAB=0.1dBC , h=0.2dBC, 0.5dBC, dBC
图5～图8表明，在图4所示模型中，由于中间位置的导体长度更短，自感更小，因此支路电流的总体分布规律是从中间向两侧减小。同时，当引线长度和细导体段间距变化时，始终满足磁链法计算的支路电流绝对值小于能量法计算的支路电流绝对值，与式（17）的结论相符。
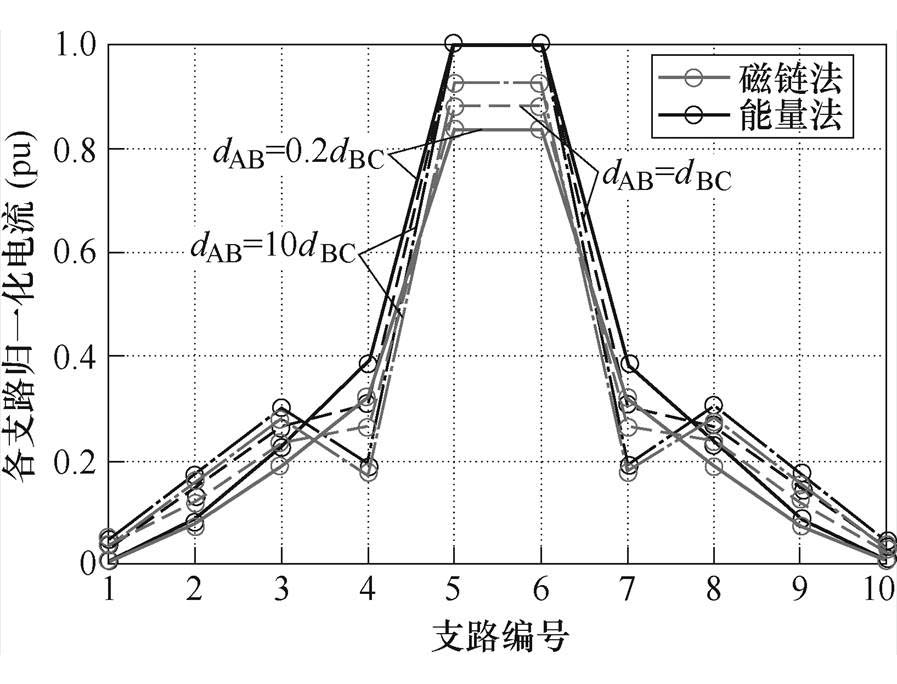
图8 h=0.2dBC，dAB=0.2dBC、dBC、10dBC时，电流单端注入单端流出模型中磁链法与能量法计算并联10支路电流对比
Fig.8 The comparison between five paralleled branch currents calculated by flux method and energy method under single-ended injection and single-ended outflow model with h=0.2dBC, dAB=0.2dBC, dBC, 10dBC
从图5、图7可以看出，当并联细导体段的间距增大时，磁链法计算支路电流的误差会略微减小，这是因为随着各支路距离的增大，各部分回路长度增大，自感也随之增大，导致并联细导体组的等效自感增大，而电流注入端和流出端之间的距离不变，由式（17）可知，磁链法误差会减小。进一步地，以支路数为5，引线长度dAB=0.2dBC，间距h分别为0.2dBC、0.5dBC、dBC为例，磁链法计算的误差见表1。
表1 单端注入单端流出模型中并联导体间距对磁链法下支路电流误差的影响
Tab.1 Influence of space between paralleled conductors to five paralleled branch currents calculated by flux method under single-ended injection and single-ended outflow model
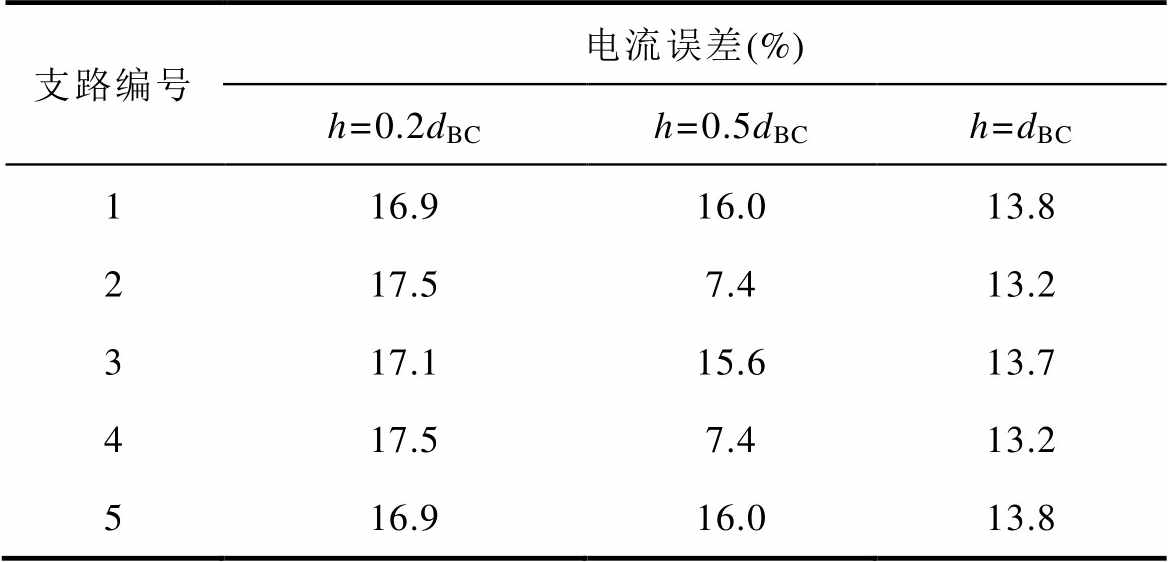
支路编号电流误差(%) h=0.2dBCh=0.5dBCh=dBC 116.916.013.8 217.57.413.2 317.115.613.7 417.57.413.2 516.916.013.8
表1中，h=0.2dBC时计算的支路电流误差与从式（17）推出误差17.5 %相比并不严格相等，这时因为前述推导中作了式（8）的近似，与17.5 %相差最大的支路电流误差16.9 %差值为0.6 %，仅为解析值的3 %，表明计算值与式（17）有较好的一致性。h=dBC时计算的支路电流误差与从式（17）推出误差14 %相比，与14 %相差最大的支路电流误差13.2 %差值为0.8 %，仅为解析值的6 %，表明计算值与式（17）有较好的一致性。h=0.5dBC时计算的支路电流误差与从式（17）推出误差15.9 %相比，与15.9 %相差最大的支路电流误差7.4 %差值为8.5 %，为式（17）解析值的53 %，解析值与数值计算值相差较大是因为支路2和支路4的电流本身非常小（磁链法和能量法计算结果分别为0.022(pu)和0.026(pu)），因此算出的支路电流的微小改变会导致计算磁链法相对能量法的相对误差发生很大变化，但是其绝对误差与解析值仍有较好的一致性。
从图6、图8可看出，当引线长度dAB增大时，磁链法计算支路电流的误差减小，与式（20）结论一致。进一步地，将支路数n=5，细导体段间距h= 0.2dBC、0.5dBC、dBC，计算引线长度dAB=0.2dBC、dBC、10dBC、100dBC、500dBC时中心位置导体电流磁链法的误差与近似解析式（20）进行对比，如图9所示，当引线长度dAB=0.2dBC时，并联细导体段的间距对磁链法计算结果误差的影响较大，且导体段间距越大，近似解析式越不准确。如导体段间距为dBC，近似解析式结果为18.5 %，数值计算结果为13.9 %，相差33 %。随着引线长度dAB增大，近似解析式的误差越来越小，如引线长度dAB=dBC时，与导体段间距为dBC的数值计算结果只相差4.5 %。引线长度更长时，用式（20）近似计算磁链法的误差非常 有效。
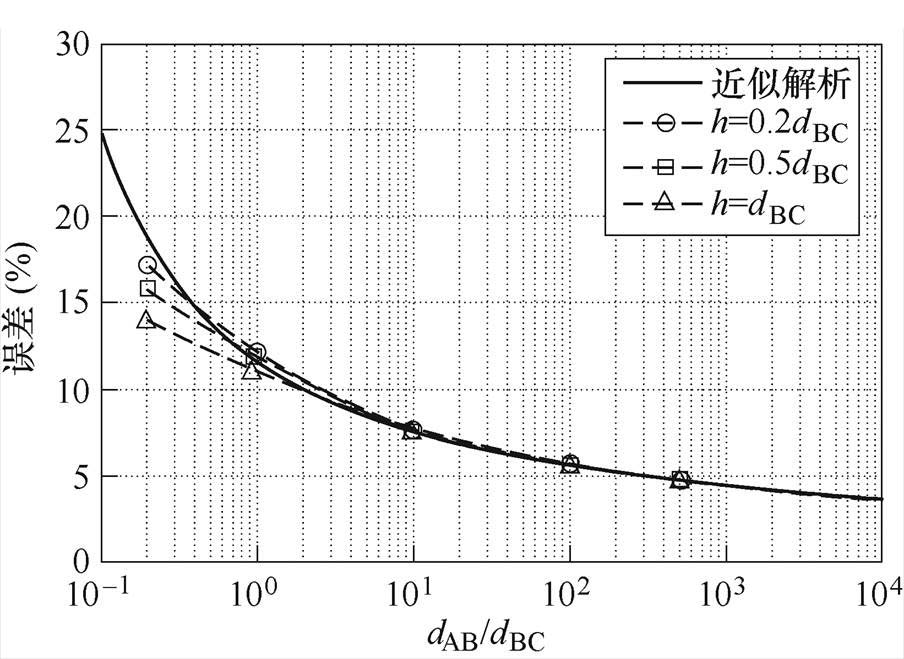
图9 单端注入单端流出模型中近似解析与数值计算的引线长度对磁链法误差影响对比
Fig.9 Comparison between influences of lead length to five paralleled branch currents calculated by approximate analysis and numerical method under single-ended injection and single-ended outflow model
当并联支路数增大时，磁链法计算支路电流的误差会略微减小，这是因为随着各支路距离的增大，并联导体组的回路面积增大，使其等效自感增大，而电流注入端和流出端之间的距离不变，由式（17）可知磁链法误差会减小。
Z箍缩中金属丝阵与回流柱所连接的极板一般被认为是等电位体，因此可以只考虑丝阵与回流柱的电感而忽略极板的影响，使得计算得到大大简化。在工程实际中，除了图2中的电流单端注入单端流出的细导体段并联方式，也存在大量与Z箍缩中金属丝阵与极板类似的连接方法，即图2中引线AB或CD并不直接与并联细导体段连接，而是连接至大体积的金属体（如极板、汇流母排等），同时并联细导体也与此大金属体相连。如果大金属体的电位变化远小于并联细导体两端的电位差，可认为金属体为等电位体。基于此，提出了具有工程实际意义的电流多端注入多端流出的并联细导体组，如图10a所示；以及电流单端注入多端流出的并联细导体组，如图10b所示，其中蓝色实线连接的并联细导体段端点电位相等。与图2相比，图10中模型并联细导体段的电流注入点或流出点分裂为n个不相互重合的端点。在磁链法和能量法下分别计算图10a的细导体段以及图10b中的“部分回路”的自感和互感，再利用式（1）即可求出各支路电流。
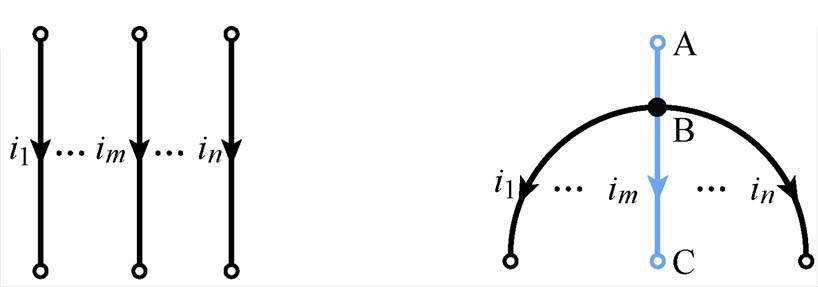
（a）电流多端注入多端流出 （b）电流单端注入多端流出
图10 电流多端流出的并联细导体段模型
Fig.10 Parallel filament conductor segments model with single-ended injection and multi-ended outflow
n个细导体段沿直线排列且各段相互平行，各细导体段长度为dBC，相邻导线间距都为h，如图11所示。
取并联细导体支路数n=5，并联细导体长度dBC=0.1 m，半径r=1 mm。设并联细导体组两端所加电压幅值为1 V，利用式（6）、式（7）计算对于并联细导体间距h分别为0.2dBC、0.5dBC、dBC时，采用磁链法和能量法得到的各并联支路电流，如图12所示。取并联细导体支路数n=5，间距h分别为0.2dBC、0.5dBC、dBC时，采用磁链法和能量法得到的各并联支路电流如图13所示。
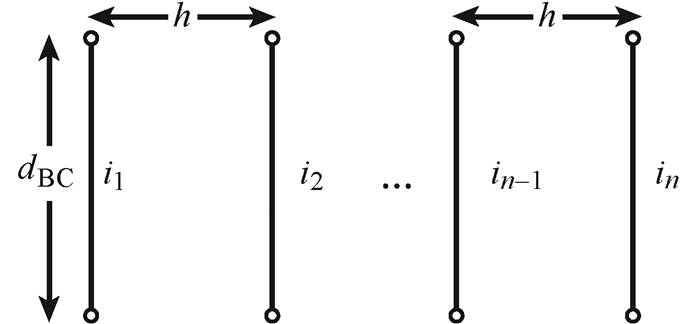
图11 细导体段沿直线等间距排列的电流多端注入多端流出模型
Fig.11 Multi-ended injection and multi-ended outflow model with filament conductor segments arranged equidistantly along straight line
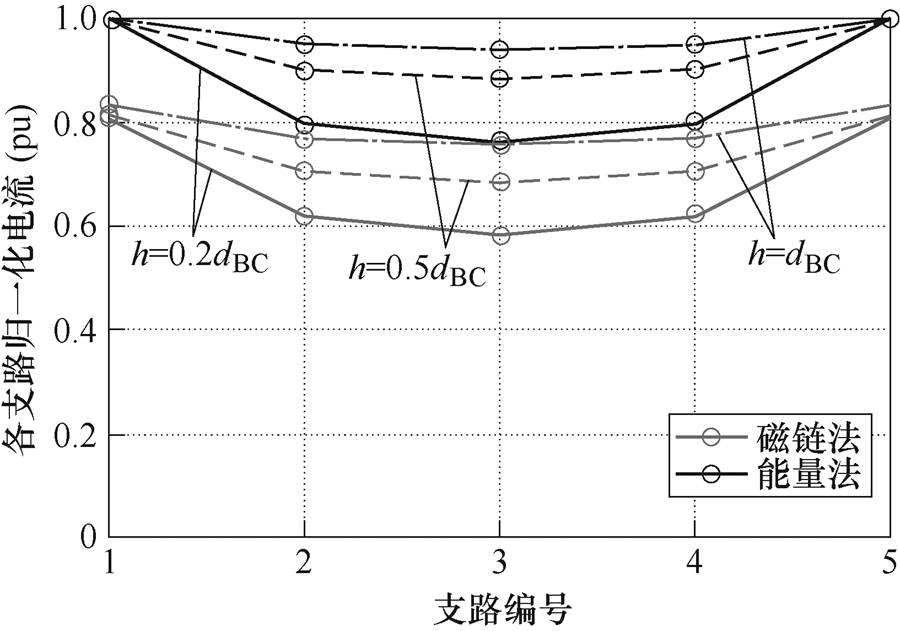
图12 n=5，h=0.2dBC、0.5dBC、dBC时，电流多端注入多端流出模型中磁链法与能量法计算并联5支路电流对比
Fig.12 The comparison between five paralleled branch currents calculated by flux method and energy method under multi-ended injection and multi-ended outflow model with h=0.2dBC, 0.5dBC, dBC
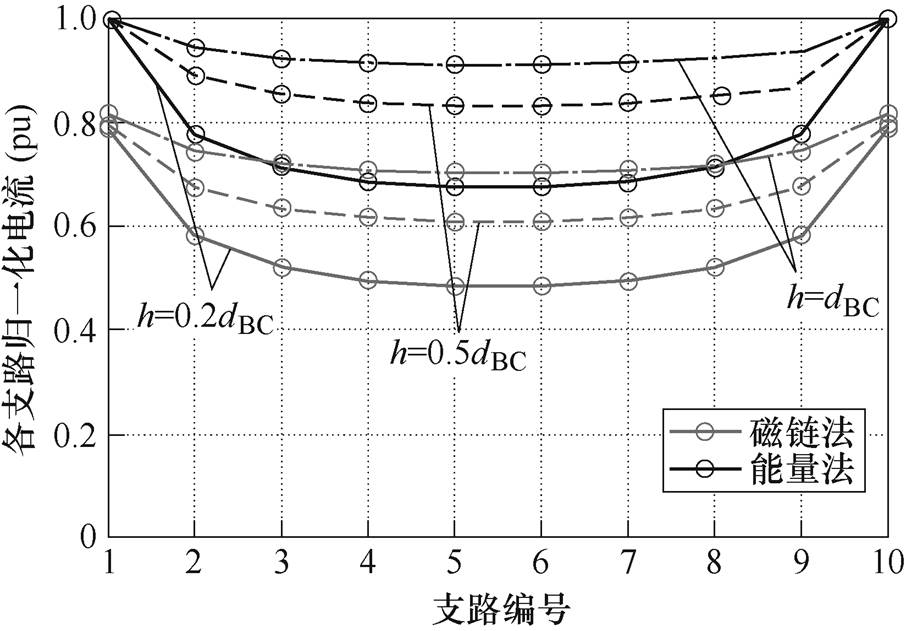
图13 n=10，h=0.2dBC、0.5dBC、dBC时，电流多端注入多端流出模型中磁链法与能量法计算并联10支路电流对比
Fig.13 The comparison between ten paralleled branch currents calculated by flux method and energy method under multi-ended injection and multi-ended outflow model with h=0.2dBC, 0.5dBC, dBC
与图5所示模型不同，图11模型中各并联细导体段的自感都相等，各细导体段间的互感决定了支路电流分布。由于位于中心位置的细导体段距离两侧较近，受其他支路电流起抑制作用的电磁耦合更强，因此其电流更小，这使得并联支路的电流分布呈“U”型。当并联细导体段的间距增大时，支路电流受其他支路电流的电磁耦合作用减弱，因此支路电流分布趋于均匀。
考虑并联细导体间距对磁链法计算误差的影响，以支路数为5，间距h分别是0.2dBC、0.5dBC、dBC为例，求得磁链法计算的误差见表2。
表2 多端注入多端流出模型中并联导体间距对磁链法下支路电流误差的影响
Tab.2 Influence of space between paralleled conductors to five paralleled branch currents calculated by flux method under multi-ended injection and multi-ended outflow model
支路编号电流误差(%) h=0.2dBCh=0.5dBCh=dBC 119.218.616.8 222.421.919.2 323.222.719.8 422.321.919.2 519.218.616.8
对于图11所示模型，由于磁链法计算的电感矩阵LC与能量法计算的电感矩阵LB不再满足式（10），因此磁链法计算的各支路电流误差不相等，由表1可知，支路电流误差从位于中间导体段向两侧减小。当并联细导体段的间距增大时，磁链法计算的各支路电流误差会一致减小。当导线间距足够大时，磁链法计算的并联导体间的互感与自感相比可以忽略不计，能量法计算结果中并联导体与导线始末位置有关的项趋于定值，因此磁链法计算误差会趋于某一定值。
随着并联支路数增大，位于中心位置细导体与边缘导体间电磁耦合随之增强，中心导体电流受到进一步抑制，并联导体组的电流不均衡度增大。边缘导体磁链法计算的各支路电流误差几乎不变，中心导体的电流计算误差略微增大。
n个细导体段沿直线排列且各段相互平行，相邻细导体段间距都为h，引线AB与CD平行于各细导体段，引线AB的长度为dAB。B点位于并联导体组电流注入侧的中点，细导体段沿直线等间距排列的电流单端注入多端流出模型如图14所示。
图14 细导体段沿直线等间距排列的电流单端注入多端流出模型
Fig.14 Single-ended injection and multi-ended outflow with filament conductor segments arranged equidistantly along straight line
取并联细导体支路数n=5，并联细导体长度dBC=0.1 m，半径r=1 mm。设并联细导体组两端所加电压幅值为1 V，利用式（6）、式（7）计算对于并联细导体，引线长度dAB=0.1dBC，间距h分别为0.2dBC、0.5dBC、dBC时，采用磁链法和能量法得到的各并联支路电流如图15所示；间距h=0.2dBC，引线长度dAB分别为0.2dBC、dBC、10dBC时，采用磁链法和能量法得到的各并联支路电流如图16所示（磁链法和能量法所得结果按能量法计算的支路电流最大值归一化，后同）。取并联细导体支路数n=10，引线长度dAB=0.1dBC，间距h分别为0.2dBC、0.5dBC、dBC时，采用磁链法和能量法得到的各并联支路电流如图17所示；间距h=0.2dBC，引线长度dAB分别为0.2dBC、dBC、10dBC时，采用磁链法和能量法得到的各并联支路电流如图18所示。
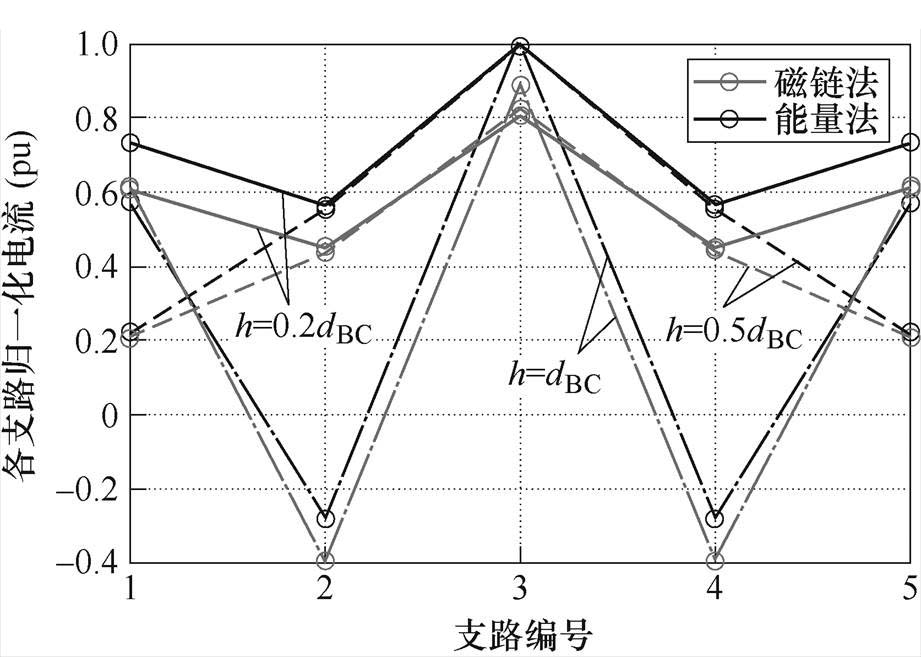
图15 dAB=0.1dBC，h=0.2dBC、0.5dBC、dBC时，电流单端注入多端流出模型中磁链法与能量法计算并联5支路电流对比
Fig.15 The comparison between five paralleled branch currents calculated by flux method and energy method under single-ended injection and multi-ended outflow model with dAB=0.1dBCand h=0.2dBC, 0.5dBC, dBC
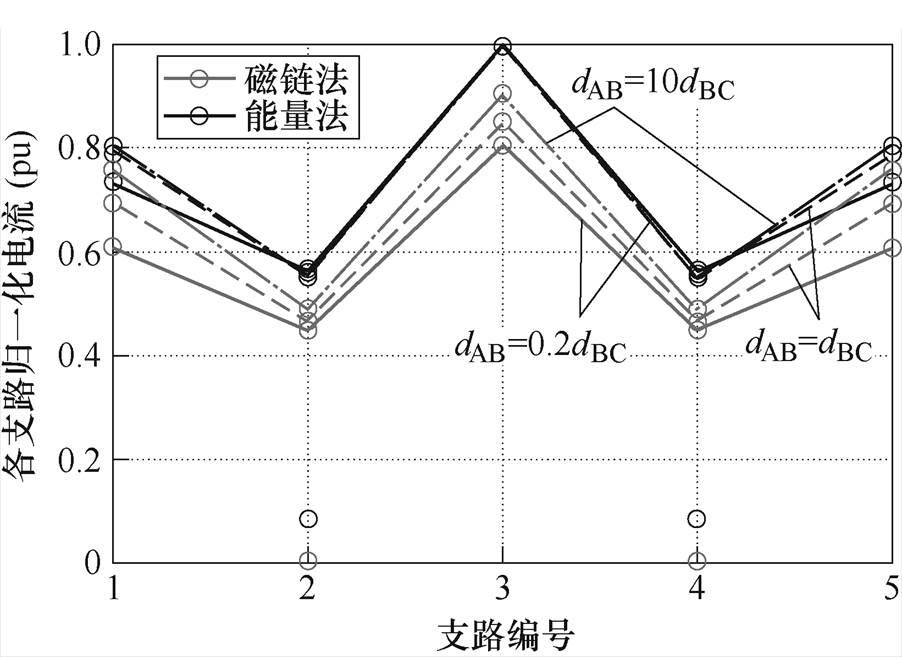
图16 h=0.2dBC，dAB=0.2dBC、dBC、10dBC时，电流单端注入多端流出模型中磁链法与能量法计算并联5支路电流对比
Fig.16 The comparison between five paralleled branch currents calculated by flux method and energy method under single-ended injection and multi-ended outflow model with h=0.2dBC, dAB=0.2dBC, dBC, 10dBC
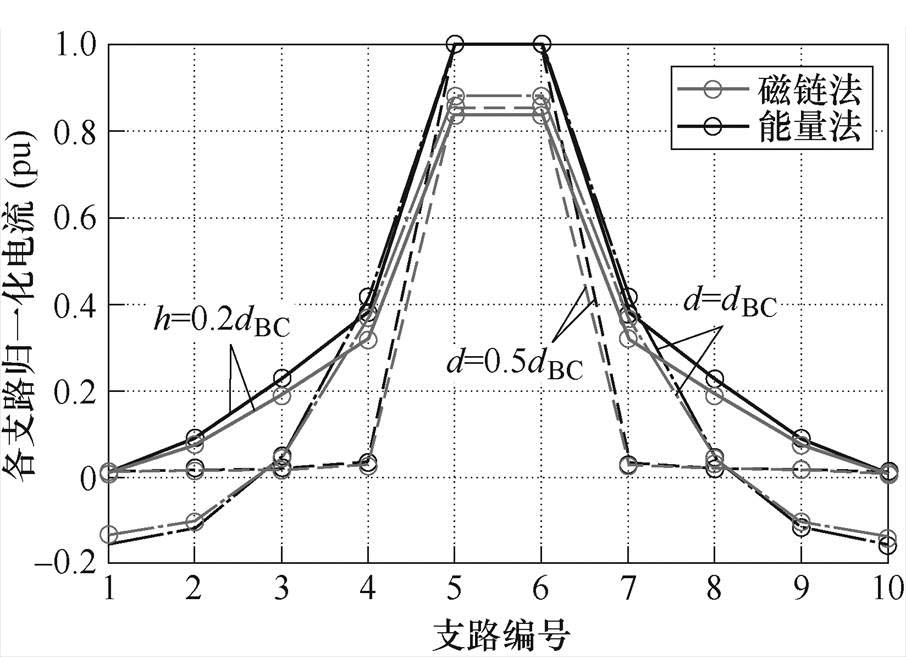
图17 dAB=0.1dBC，h=0.2dBC、0.5dBC、dBC时，电流单端注入多端流出模型中磁链法与能量法计算并联10支路电流对比
Fig.17 The comparison between ten paralleled branch currents calculated by flux method and energy method under single-ended injection and multi-ended outflow model with dAB=0.1dBC, h=0.2dBC, 0.5dBC, dBC
图14所示电流单端注入多端流出模型可视为图4所示电流单端注入单端流出模型与图11所示电流多端注入多端流出模型的结合，因此其支路电流分布规律和磁链法计算支路电流误差性质与这两种模型类似。如由于中间位置的导体长度更短，自感更小，因此支路电流的总体分布规律与电流单端注入单端流出模型一致，从中间向两侧减小。且当并联细导体段的间距增大时，磁链法计算位于中间细导体段电流的误差会略微减小，边缘导体电流误差增大，见表3。当并联导体间距h=dBC时，与前述电流单端注入多端流出模型及电流单端注入单端流出模型的磁链法计算支路电流误差不同，只有中心细导体段电流的误差为正，即磁链法计算支路电流小于能量法计算支路电流，而其余4条支路的细导体段电流的误差为负，这意味着磁链法计算支路电流大于能量法计算支路电流。
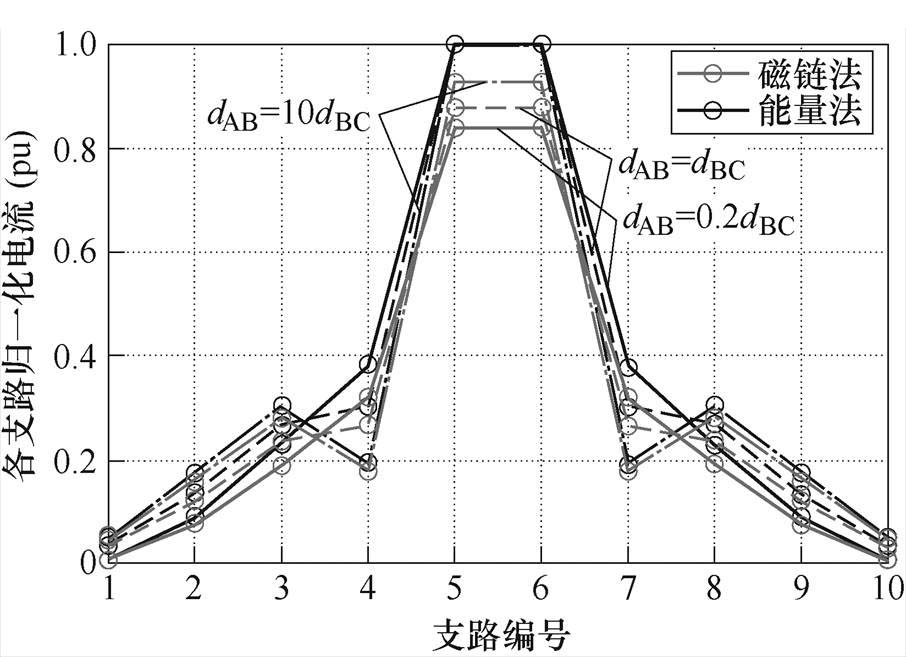
图18 h=0.2dBC，dAB=0.2dBC、dBC、10dBC时，电流单端注入多端流出模型中磁链法与能量法计算并联10支路电流对比
Fig.18 The comparison between five paralleled branch currents calculated by flux method and energy method under single-ended injection and multi-ended outflow model with h=0.2dBC, dAB=0.2dBC, dBC, 10dBC
表3 单端注入多端流出模型中并联导体间距对磁链法下支路电流误差的影响
Tab.3 Influence of space between paralleled conductors to five paralleled branch currents calculated by flux method under single-ended injection and multi-ended outflow model
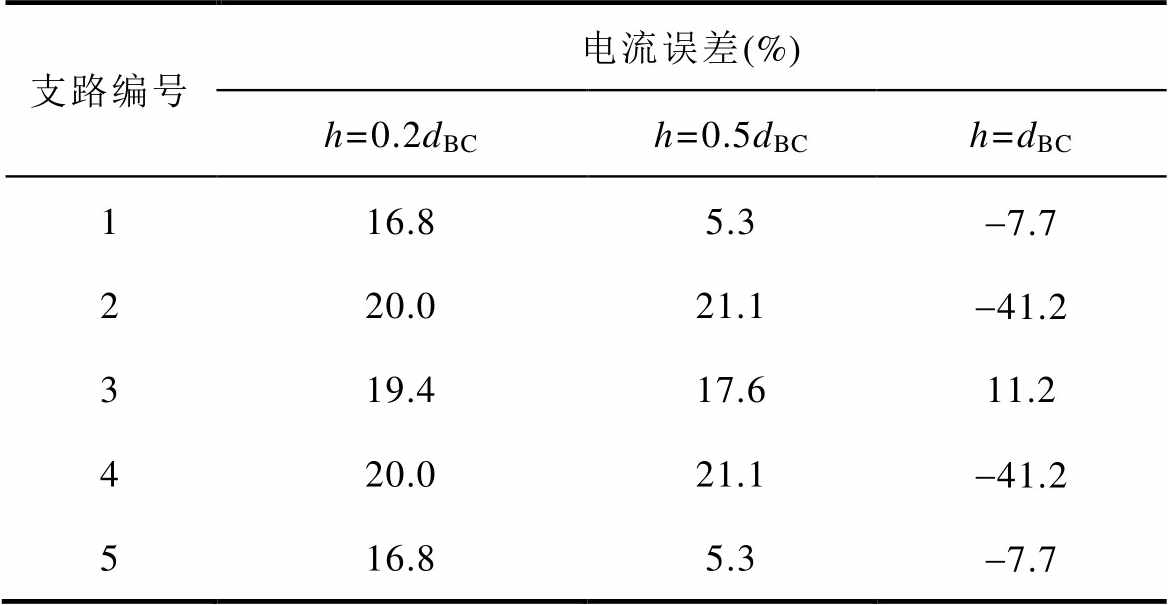
支路编号电流误差(%) h=0.2dBCh=0.5dBCh=dBC 116.85.3-7.7 220.021.1-41.2 319.417.611.2 420.021.1-41.2 516.85.3-7.7
随着并联支路数增加，电流仍然主要集中于中心导体，导致边缘导体电流占比快速衰减至接近为0。由于并联细导体组的等效自感增大，中心导体磁链法计算支路电流误差随之减小。对于边缘导体，由于能量法与磁链法计算的支路电流都接近于0，此时考虑其电流计算误差意义不大。
从图16、图18可看出，随着引线长度增大时，磁链法计算的支路电流与能量法计算结果越来越接近，图16中磁链法的计算误差见表4，其更清楚地表明了引线长度增大，磁链法计算支路电流的误差会一致减小，这与电流单端注入单端流出模型的规律相同。
表4 单端注入多端流出模型中引线长度对磁链法下支路电流误差的影响
Tab.4 Influence of lead length to five paralleled branch currents calculated by flux method under single-ended injection and multi-ended outflow model
支路编号电流误差(%) dAB=0.2dBCdAB=dBCdAB=10dBC 116.812.05.4 220.015.911.1 319.415.09.6 420.015.911.1 516.812.05.4
本文系统研究了采用磁链法计算细导体段电感导致的并联细导体电流分配误差。针对电流单端注入单端流出的并联细导体段模型进行了深入的理论研究，提出了磁链法计算支路电流分配的误差公式，揭示了磁链法计算的各支路电流幅值均小于真实电流，但各支路电流的相对比值与真实电流一致。其误差仅与并联细导体组的等效自感以及电流注入与流出两端点的距离有关。推导了电流注入引线长度影响计算误差的近似公式，当电流注入引线的长度为其半径100倍时，磁链法计算的支路电流误差约为12 %。特殊地，当引线与并联细导体段构成完整闭合回路时没有计算误差。
针对工程中常见的多端流出的并联细导体模型的计算结果表明，对于电流多端注入多端流出并联细导体段，并联细导体间距越大，磁场耦合越弱，互感越小，磁链法计算支路电流误差随之减小，趋于单个导体的电流计算误差。对电流单端注入多端流出并联细导体段，并联导体的磁场耦合程度介于单端注入单端流出和多端注入多端流出之间。引线长度越大，磁链法计算支路电流误差随之增大，但误差增长速度逐渐减小，近似满足对数规律；并联导体间距越大，中心导体电流误差减小，边缘导体电流误差增大，导体间距足够大时，甚至出现边缘导体电流磁链法计算结果远大于真实电流的现象。
参考文献
[1] 傅实, 邓二平, 赵志斌, 等. 压接型IGBT器件多物理量测试方法综述[J]. 中国电机工程学报, 2020, 40(5): 1587-1605.
Fu Shi, Deng Erping, Zhao Zhibin, et al. Overview of measurement methods of multiple physical parameters in press pack IGBTs[J]. Proceedings of the CSEE, 2020, 40(5): 1587-1605.
[2] Ni Chouwei, Zhao Zhibin, Cui Xiang. Notice of retraction: partial inductance of conductor segments with coulomb gauge in quasi-static field[J]. IEEE Transactions on Electromagnetic Compatibility, 2017, 59(4): 1125-1132.
[3] 周林, 薛飞彪, 司粉妮, 等. Z箍缩等离子体电流分布实验研究[J]. 物理学报, 2012, 61(19): 195207.
Zhou Lin, Xue Feibiao, Si Fenni, et al. Experimental sduty of current distribution in wirearray Z pinch plasma[J]. Acta Physica Sinica, 2012, 61(19): 195207.
[4] Deeney C, Douglas M R, Spielman R B, et al. Enhancement of X-ray power from a Z pinch using nested-wire arrays[J]. Physical Review Letters, 1998, 81(22): 4883-4886.
[5] 叶繁, 薛飞彪, 褚衍运, 等. 双层丝阵Z箍缩电流分配实验研究[J]. 物理学报, 2013, 62(17): 175203.
Ye Fan, Xue Feibiao, Chu Yanyun, et al. Experi- mental study on current division of nested wire array Z pinches[J]. Acta Physica Sinica, 2013, 62(17): 175203.
[6] 丁宁, 张扬, 刘全, 等. 电感分布对双层丝阵Z箍缩内爆动力学模式的影响[J]. 物理学报, 2009, 58(2): 1083-1090.
Ding Ning, Zhang Yang, Liu Quan, et al. Effects of various inductances on the dynamic models of the Z-pinch implosion of nested wire arrays[J]. Acta Physica Sinica, 2009, 58(2): 1083-1090.
[7] 赵屾, 朱鑫磊, 石桓通, 等. 用X-pinch对双丝Z箍缩进行轴向X射线背光照相[J]. 物理学报, 2015, 64(1): 015203.
Zhao Shen, Zhu Xinlei, Shi Huantong, et al. Axial backlighting of two-wire Z-pinch using an X-pinch as an X-ray source[J]. Acta Physica Sinica, 2015, 64(1): 015203.
[8] Davis J, Gondarenko N A, Velikovich A L. Fast commutation of high current in double wire array Z-pinch loads[J]. Applied Physics Letters, 1997, 70(2): 170-172.
[9] Strickler T S, Gilgenbach R M, Johnston M D, et al. Efficient computation of current in multiwire Z-pinch arrays[J]. IEEE Transactions on Plasma Science, 2003, 31(6): 1384-1387.
[10] Grabovskiĭ E V, Zukakishvili G G, Mitrofanov K N, et al. Study of the magnetic fields and soft X-ray emission generated in the implosion of double wire arrays[J]. Plasma Physics Reports, 2006, 32(1): 32-46.
[11] Giuliani J L, Commisso R J. A review of the gas-puff: pinch as an X-ray and neutron source[J]. IEEE Transa- ctions on Plasma Science, 2015, 43(8): 2385-2453.
[12] Ruehli A E. Inductance calculations in a complex integrated circuit environment[J]. IBM Journal of Research and Development, 1972, 16(5): 470-481.
[13] Holloway C L, Kuester E F, Ruehli A E, et al. Partial and internal inductance: two of clayton R. Paul’s many passions[J]. IEEE Transactions on Electro- magnetic Compatibility, 2013, 55(4): 600-613.
[14] 倪筹帷. 多导体段的电感参数计算方法[D]. 北京: 华北电力大学, 2018.
[15] 倪筹帷, 赵志斌, 崔翔. 考虑位移电流的部分电感计算方法[J]. 中国电机工程学报, 2017, 37(17): 5181-5187, 5238.
Ni Chouwei, Zhao Zhibin, Cui Xiang. Computing method partial inductance for conductor segments by considering displacement current[J]. Proceedings of the CSEE, 2017, 37(17): 5181-5187, 5238.
[16] 崔翔. 电流连续的细导体段模型的磁场及电感[J]. 物理学报, 2020, 69(3): 034101.
Cui Xiang. Magnetic field and inductance of filament conductor segment model with current continuity[J]. Acta Physica Sinica, 2020, 69(3): 034101.
[17] 金亮, 祝登锋, 杨庆新, 等. 超高压电抗器电感计算灰箱模型与优化[J]. 电工技术学报, 2022, 37(23): 6093-6103.
Jin Liang, Zhu Dengfeng, Yang Qingxin, et al. Grey box model and optimization for inductance calcu- lation of EHV reactors[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6093-6103.
[18] 刘博, 刘伟志, 董侃, 等. 基于全碳化硅功率组件的变流器母排杂散电感解析计算方法[J]. 电工技术学报, 2021, 36(10): 2105-2114.
Liu Bo, Liu Weizhi, Dong Kan, et al. Analytical calculation method for stray inductance of converter busbar based on full silicon carbide power module[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2105-2114.
[19] 张春雷, 张辉, 叶佩青, 等. 两相无槽圆筒型永磁同步直线电机电感计算与分析[J]. 电工技术学报, 2021, 36(6): 1159-1168.
Zhang Chunlei, Zhang hui, Ye Peiqing, et al. Inductance analysis of two-phase slotless tubular permanent magnet synchronous linear motor[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 1159-1168.
[20] 李巍, 王浩淞, 陈伟. 永磁同步电机交直轴增量电感计算与测量研究[J]. 电机与控制学报, 2022, 26(12): 19-27.
Li Wei, Wang Haosong, Chen Wei. Research on calculation and measurement of d-axis and q-axis incremental inductance of permanent magnet syn- chronous motor[J]. Transactions of China Electro- technical Society, 2022, 26(12): 19-27.
Abstract The energy method is complete and self-consistent in calculating the inductance of conductor segments with accurate calculation results. However, integrating the whole field is complicated, and the calculation efficiency could be higher. It is necessary to integrate the conductor area, and the calculation is simple using the magnetic flux method. Therefore it has been widely used in the inductance calculation of conductor segments. However, the method does not satisfy the current continuity law, which leads to calculation errors. Accordingly, the current distribution of parallel conductor segments based on the magnetic flux method also has errors that have yet to be studied in the existing literature.
This paper is specified to parallel filament conductors with single-end injection and single-end outflow, which are common in engineering. The inductance matrices of the parallel filament conductors are extracted by the flux method and the energy method, respectively. The parallel branch currents are derived by the flux method and the energy method. The error formula of parallel branch current by magnetic flux method is obtained. The error is proportional to the actual current and only related to the self-inductance of the parallel conductor and the distance between injection and outflow points. The correctness of the proposed error formula is verified by the current distribution calculation results of the filament conductors with 5 branches and 10 branches in parallel. When the length of the current injection lead is 100 times its radius, the error of the branch current calculated by the magnetic flux method is 12 %.
For parallel filament conductor segments with multi-ended outflow, the influence of distance and length of parallel conductors and the length of the connecting lead on calculation error are studied through systematic theoretical calculation. Regarding the parallel filament conductor segments with multi-ended injection and multi-ended current outflow, the larger the distance between the parallel fine conductors, the weaker the magnetic field coupling and the smaller the mutual inductance. Moreover, the current calculation error of the branch by the flux method decreases, which tends to the current calculation error of a single conductor. The magnetic field coupling of the parallel filament conductor segments with single-ended injection and multi-ended current outflow is between that with single-ended injection and multi-ended outflow model and that with multi-ended injection and multi-ended outflow model. With the increase of lead length, the error of the flux method increases, but its rate gradually decreases, approximately satisfying the logarithmic law. When the distance between parallel conductors is large enough, the current error of the center conductors decreases, and the current error of the edge conductors increases. When the distance between conductors is large enough, the edge conductor current of the flux method is even much larger than the real current.
This paper's theoretical analysis and calculation revise the current distribution results of parallel filament conductors calculated by the magnetic flux method, improve the calculation accuracy without reducing the calculation speed and provide references for engineering applications.
keywords：Parallel filament conductor segments, current distribution, inductance, magnetic flux method, energy method
DOI: 10.19595/j.cnki.1000-6753.tces.220689
中图分类号：TM12
国家自然科学基金委员会-国家电网公司智能电网联合基金（U1766219）资助项目。
收稿日期 2022-04-26
改稿日期 2022-07-24
傅 实 男，1995年生，博士研究生，研究方向为高压大功率半导体器件。E-mail: fu_shi@126.com
崔 翔 男，1960年生，教授，博士生导师，研究方向为电磁场理论及其应用、先进输电、高压大功率电力电子器件等。E-mail: x.cui@ncepu.edu.cn（通信作者）
（编辑 郭丽军）