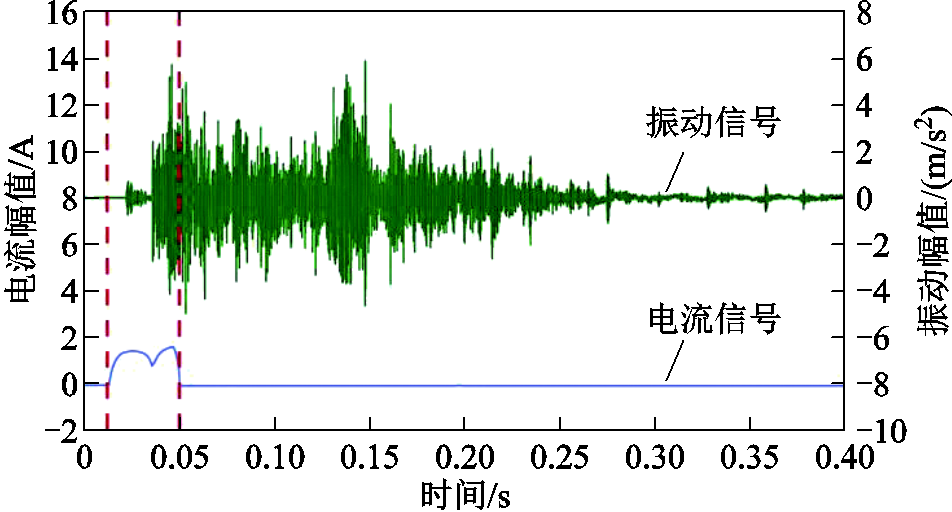
图1 ZN63-12断路器合闸过程监测信号
Fig.1 Monitoring signal of full cycle closing process of ZN63-12 circuit breaker
摘要 针对利用电流-振动信号联合进行高压断路器故障分类过程中原始特征集维数较高,因而造成识别率低、分类性能退化的问题,该文提出一种适用于高维小样本的类聚几何敏感特征优选方法。首先,利用广义维数谱和敏感维数定量刻画经魏格纳-威尔分布处理的振动信号时频图,结合线圈电流信号的突变信息,构建断路器完整动作过程的电-振联合多征兆域原始特征集;其次,通过定义“变异系数”细致描绘特征在样本类内和类间的波动性,由“赏函数”对类间发散性强的特征予以加权,根据特征敏感因子优选得到不同故障类型下的类聚几何最优特征集;最后,采用支持向量机和其他识别方法进行故障分类。试验结果表明采用最优特征集识别准确率明显提高,具有工程应用价值。
关键词:高压断路器 电流-振动信号联合 类聚几何 特征优选 敏感维数
高压断路器是电力系统的关键安全控制设备,其故障造成的损失远超自身价值[1-3]。断路器动作涉及二次电气回路控制和机械部件间能量传动过程,其复杂的结构和恶劣的运行环境容易导致发生电气故障或机械故障[4-5]。
控制线圈电流和传动过程振动信号是分析断路器操动状态异常的有效特征量。非平稳、非线性振动信号是能量变化的优良载体,衰减小且易捕捉,因此基于振动信号的断路器故障诊断方法受到了学者们的关注[6-9]。但振动分析法对于电气控制回路缺陷不敏感,控制线圈电流信号蕴藏完整的二次回路和电磁铁控制信息[10-11]。“电流-振动”联合分析(以下简称“‘电-振’联合分析”)实现断路器动作全过程的故障研判更具优势,可有效填补断路器部件开始动作前电气信息的空白。文献[12-13]将由振动、电流信号提取的原始特征全部纳入特征集进行识别。而断路器结构复杂,传动过程各部件之间相互关联、紧密耦合,导致建立的原始特征集维数过高,不仅增加了计算时间,也造成分类性能退化和识别率降低。
特征优选能够根据定量的评价准则来度量特征对目标分类的敏感程度,从高维的特征中筛选出能够有效识别目标的最小特征子集[14]。文献[15-18]在高压断路器的机械故障诊断中运用传统的Relief算法进行特征降维处理,但对于特定故障类型与低维特征向量的映射关系未进行进一步的研究。文献[19]提出了用于医学影像识别的基于核空间的距离测量,有效提高了线性不可分数据集的高维特征筛选能力,但先验知识直接关系到核参数的选择,影响了分类精度。文献[20]通过定义“紧密度”和“分离度”函数,更为细致地描述了弹道目标识别多特征的类内类间距离,但忽略了由于样本的波动而引起的变异性,并且“松紧度”权重对于类间发散性不敏感。
鉴于此,本文提出一种适用于高维小样本的类聚几何敏感特征优选方法。通过广义维数谱和敏感维数挖掘潜藏在振动信号时频图像中的二维信息,以时域突变点提取电流信号波形变异信息,构成断路器多征兆域原始特征集。在此基础上,定义“变异系数”、“赏函数”和“特征敏感因子”量化特征对于特定故障类型的分类敏感性,构造与支持向量机(Support Vector Machine, SVM)模型匹配的最优特征集,明确了故障类型与最优特征集之间的对应关系。最后通过试验验证了本文方法对于断路器不同故障类型最优特征集优选的有效性,提高了目标分类的识别准确率。
弹簧操动机构动作线圈通电后,电磁铁中电磁吸力大于阻力时铁心开始运动,到达预设位置时触发脱扣装置释放弹簧势能,驱动主轴、凸轮、拐臂和拉杆等机构部件联动,直至动触头到位切除线圈电源,完成一个完整操动过程。电流信号从出现到衰减为零呈现双峰分布,振动信号在能量传递和动静触头强烈冲击下呈现非平稳的振荡衰减过程。ZN63—12断路器合闸过程监测到的电流和振动信号如图1所示。
由静转动、再到动转静的断路器操动过程伴随的电流、振动信号特征与电气和机械状态息息相关。当出现操作电压过高或过低、控制回路电阻异常等电气故障,断路器分合闸线圈电流波形会发生明显变化;弹簧疲劳、轴销脱落等机械故障的振动信号也会有明显差异。引入电流信号延展了振动信号分析时间历程,包含部件运动发生前二次回路和电磁铁触发机构动作的全过程。电流和振动信号联合分析可涵盖断路器动作的电气故障和机械故障。建立故障类型与最优特征集映射关系至关重要,因此提出面向断路器故障分类的类聚几何敏感特征优选模型。甄选故障最优特征集流程如图2所示。

图1 ZN63-12断路器合闸过程监测信号
Fig.1 Monitoring signal of full cycle closing process of ZN63-12 circuit breaker
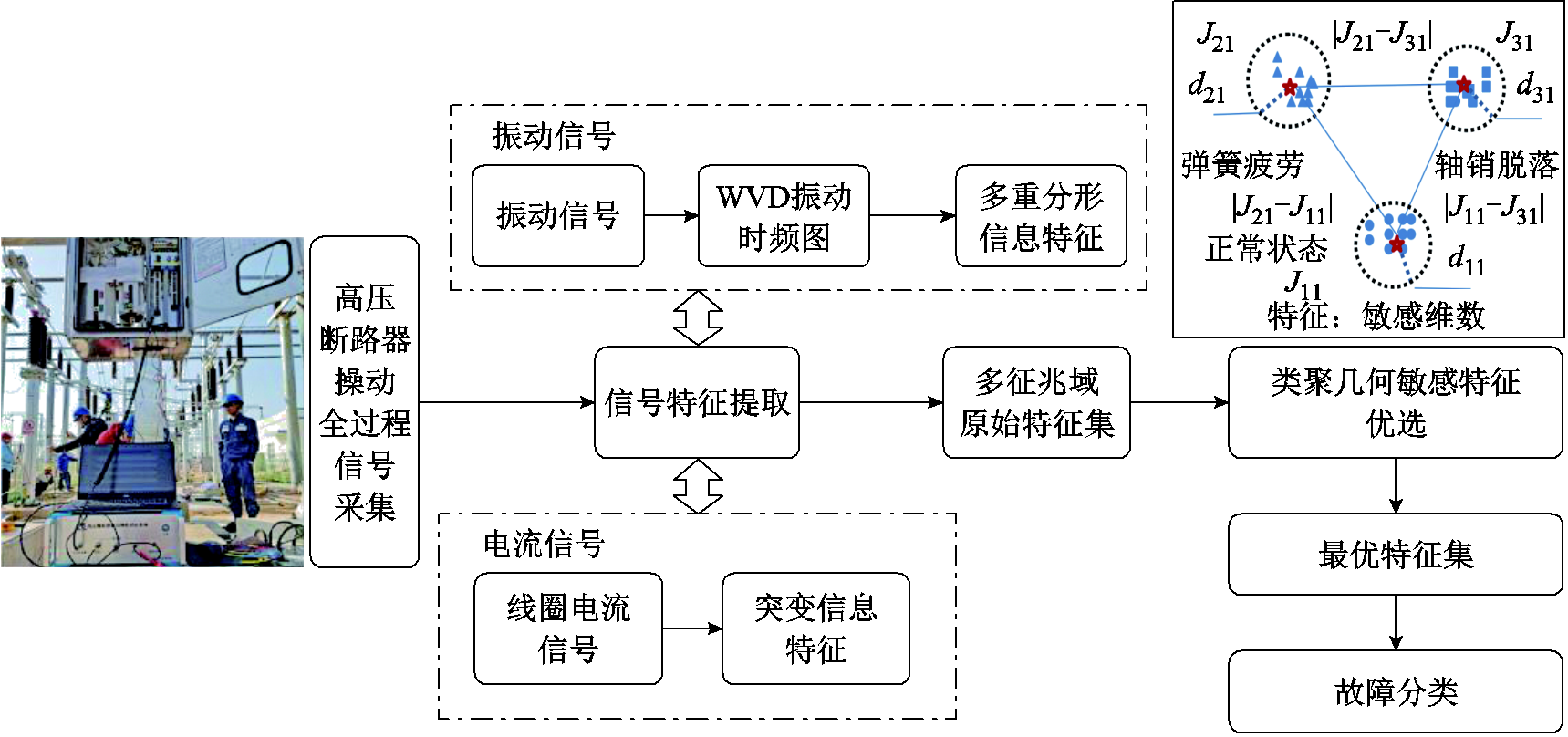
图2 基于特征优选的断路器故障分类流程
Fig.2 Fault classification flow of circuit breaker based on feature optimization
科学提取振动信号和电流信号有效特征及遴选最优特征子集是识别断路器故障类型的关键环节。
2.1.1振动信号时频图
振动信号时频图从时间、频率、能量三个维度呈现断路器分合闸的动作特性,魏格纳-威尔分布(Wigner-Ville Distribution, WVD)时频分析方法[21]适用于处理瞬时冲击、频率时变的非平稳信号。
对振动信号Z(t)进行WVD时频变换,可得
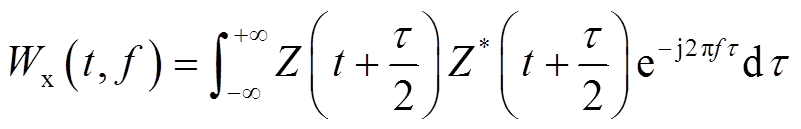 (1)
(1)
式中,f为频率;t为积分变量;Z*为Z的共轭。
对断路器铁心卡涩、轴销脱落、弹簧疲劳和正常状态的合闸振动信号进行WVD处理得到图3所示时频图。图3中振动信号在频率和时间方面的能量差异均以色阶形式体现出来,四种状态的时频图均有明显的差异性。基于WVD处理的时频图细致描述了振动信号的时频特征。
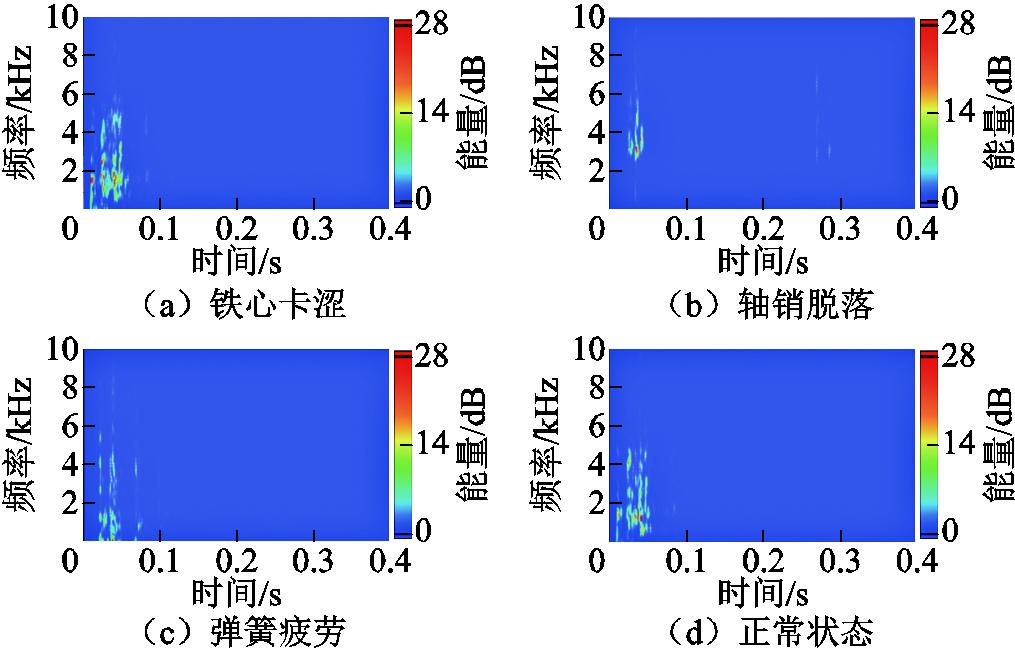
图3 正常及三种故障状态合闸振动信号时频图
Fig.3 Time frequency diagram of closing vibration signal in normal and three fault states
2.1.2 多重分形信息特征
分形理论是处理工程中不规则图形强有力的工具[22]。多重分形维数是在单一分形维数发展的基础上,由不同阶数的维数构成的高阶特征集合,在刻画非线性复杂机械系统时不易出现状态混叠现象。采用覆盖法[23]来描述多重分形的广义维数谱。
使用尺度为l的相同大小的盒子对整个分形集Y进行覆盖,设所需盒子的总数为N,设点落入第i个盒子的概率为pi(l),给定参数q,可以计算General信息熵Kq(l),即
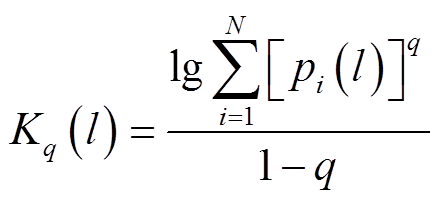 (2)
(2)
式中,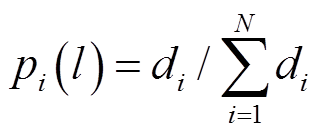 ,
,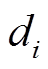 为第
为第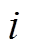 个盒子覆盖住的“点数”,
个盒子覆盖住的“点数”,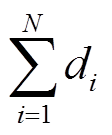 为所有盒子覆盖住的“点数”。
为所有盒子覆盖住的“点数”。
改变l的大小可计算出一系列Kq(l)值,从而在lgl-lgKq(l)图上得到标度律的存在范围,该范围的斜率的绝对值就是给定参数q的广义维数D(q),即
 (3)
(3)
式中,当![]() 时,
时,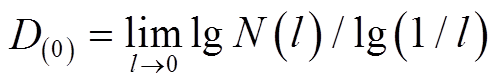 为盒维数;当
为盒维数;当![]() 时,
时,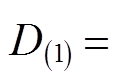
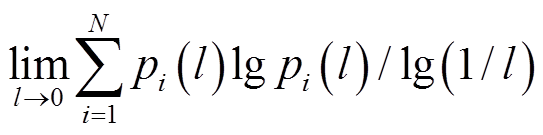 为信息维数;当
为信息维数;当![]() 时,
时,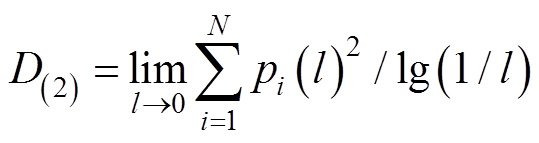 为关联维数。
为关联维数。
广义维数谱涵盖了分形理论中的盒维数、信息维数和关联维数等典型维数。当q的取值不同时,便可以得到不同标度的广义维数谱{D(0), D(1), D(2),  , D(q)},从而更全面地刻画不规则图形的细节信息。q取值选择为[-7, 7],图3中四种状态时频图的广义维数谱如图4所示。
, D(q)},从而更全面地刻画不规则图形的细节信息。q取值选择为[-7, 7],图3中四种状态时频图的广义维数谱如图4所示。
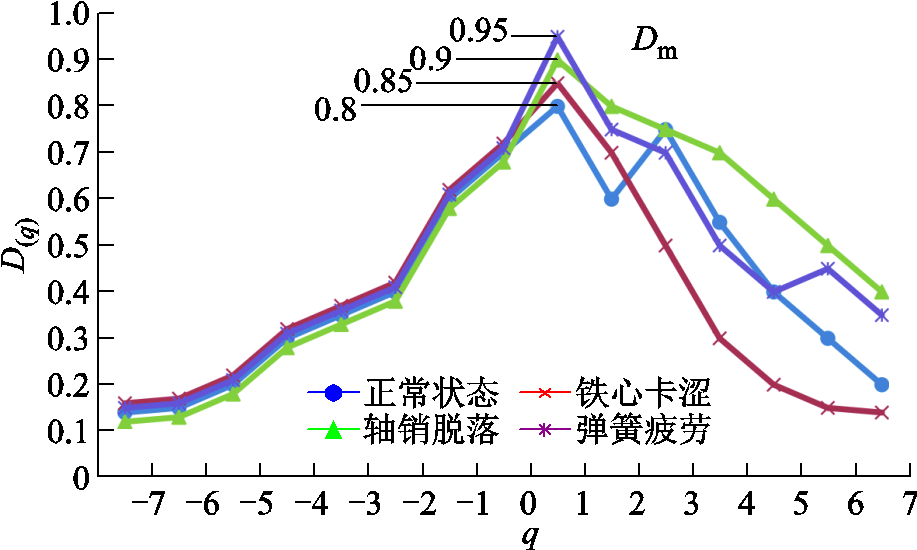
图4 四种状态的广义维数谱
Fig.4 Generalized dimension spectrum of four states
引入敏感维数描绘广义维数谱的突变性,将曲线上突变点所对应的维数定义为敏感维数,记为Dm。通过最小二乘法可计算得出广义维数谱曲线最大值的敏感维数,由图4可知断路器操动的四种状态的敏感维数分别为0.8、0.85、0.9和0.95,具有较大的差异性。
线圈电流信号是典型的双峰波形,操作时标准电压和电压偏低都会对线圈电流信号产生影响。以断路器合闸为例,正常和故障状态下的线圈电流信号如图5所示。
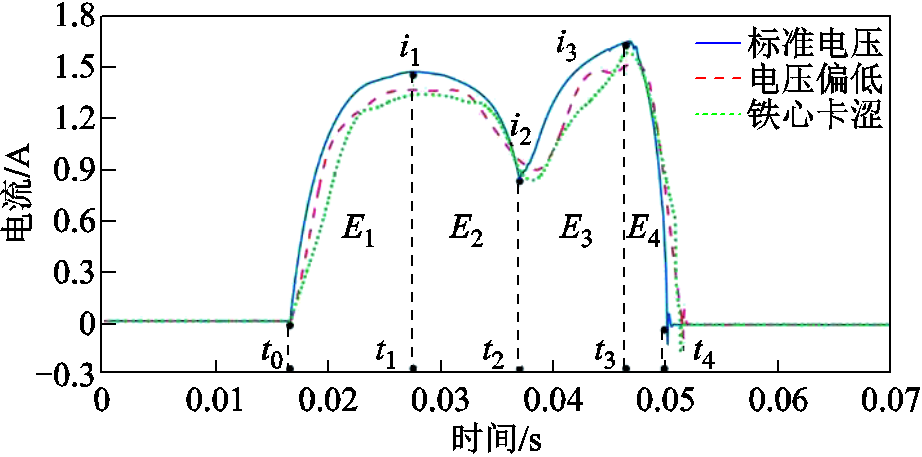
图5 合闸线圈电流信号
Fig.5 Closing coil current signal
操作电压的变化体现为相对于正常双峰波形的时延和幅值大小变异。铁心卡涩直接影响撞击脱扣装置时刻,其电流波形与正常操作状态存在差异。故通过提取线圈电流信号对断路器二次回路和操动过程进行辨识,以线圈电流波形突变点信息作为信号特征。
(1)突变电流特征和时间特征
根据图5所示的合闸线圈电流信号可将分合闸操作分为四个时间段,获取波峰和波谷的突变电流特征i1~i3以及起始、波峰、波谷及结束时间特征t0~t4。
(2)累积能量特征
为了全面地反映电流信号的波形形状,进一步提取各时间段累积能量E1~E4作为补充信号特征。累积能量可定量反映线圈电流波形在每个阶段的波形斜率、波形抖动等信息。
设某阶段的线圈电流信号为C(T),T=1, 2, , n,则该阶段的累积能量为
, n,则该阶段的累积能量为
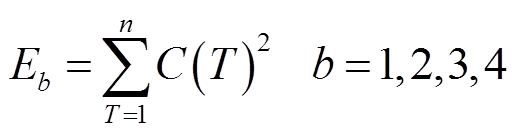 (4)
(4)
式中,T为线圈电流信号采样点;n为采样长度。
构建“电-振”联合原始特征集,取振动信号的多重分形信息特征,广义维数谱的q的取值范围选择为[-7, 7],包含15个特征,加上1个敏感维数特征Dm,共有16个特征量;对于电流信号的突变信息特征,包含3个电流特征(i1~i3)、5个时间特征(t0~t4)和4个累积能量特征(E1~E4),共有12个特征量。因此,“电-振”联合原始特征集共有28个特征量,如图6所示。
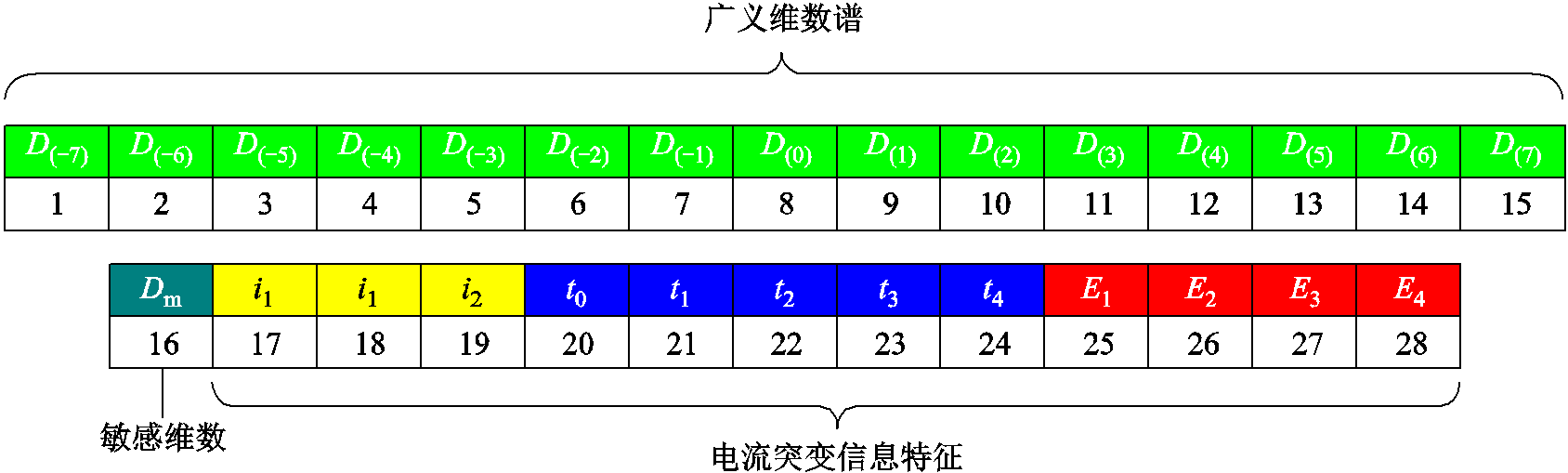
图6 “电-振”联合原始特征集
Fig.6 Original feature set of “current vibration combination”
“电-振”联合原始特征集涵盖了断路器操动过程的全部动作信息。但对于特定故障类型,一部分特征是与故障息息相关的,一部分特征则是冗余的。冗余的特征可能会干扰断路器的故障识别,并且高维原始特征集可能将带来较大计算时间开销,同时造成分类性能退化或识别率降低。
为提高分类模型的识别率和泛化能力,必须筛选出“好”的敏感特征,剔除“坏”的冗余特征。类聚几何敏感特征优选算法通过“变异系数”细致描绘特征类内的一致性和类间的区分度,并定义“赏函数”对类间发散性强的特征进行加权,以特征敏感因子定量刻画特征对于不同故障的敏感性。计算步骤如下。
假设有l类目标状态,m维特征,第c类的特征集样本数为k,则第c类的特征矩阵可表示为
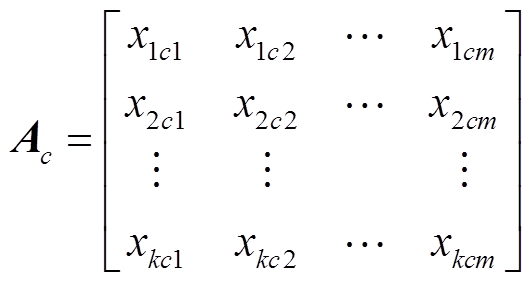 (5)
(5)
式中,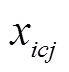 为第
为第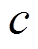 类的第
类的第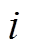 个样本的第
个样本的第![]() 维特征值。
维特征值。
(1)归一化,消除特征在不同量纲量级之间的影响。归一化后的特征值为
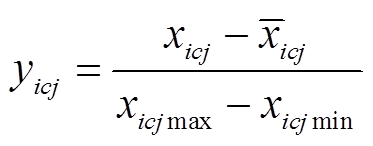 (6)
(6)
式中,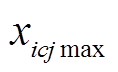 、
、 分别为第
分别为第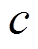 类第
类第![]() 维特征的最大值与最小值;
维特征的最大值与最小值;![]() 为相应均值;
为相应均值;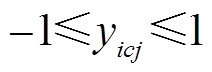 ,
,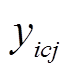 在不改变原数据固有特性的基础上,可反映
在不改变原数据固有特性的基础上,可反映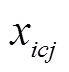 的大小波动情况。
的大小波动情况。
(2)计算第c类第![]() 维特征的类内平均距离,即
维特征的类内平均距离,即
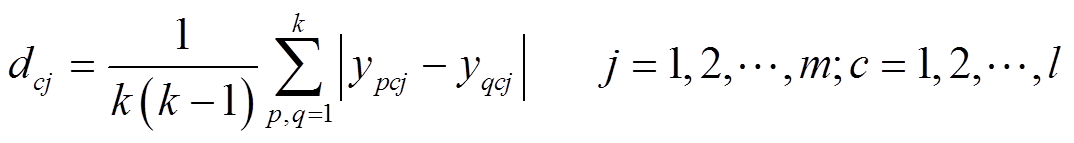 (7)
(7)
式中, 和
和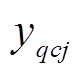 分别为第
分别为第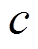 类中第
类中第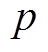 、
、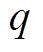 个样本中第
个样本中第![]() 维特征的归一化值。由此可以得到
维特征的归一化值。由此可以得到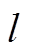 类第
类第![]() 维特征类内平均距离的平均值为
维特征类内平均距离的平均值为
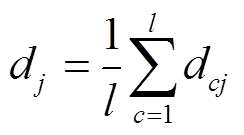 (8)
(8)
(3)计算第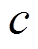 类第
类第![]() 维特征的平均值,即
维特征的平均值,即
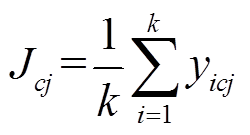 (9)
(9)
式中,![]() 为第
为第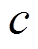 类第
类第![]() 维特征的类中心。然后计算第
维特征的类中心。然后计算第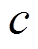 类每个样本到类中心的平均距离为
类每个样本到类中心的平均距离为
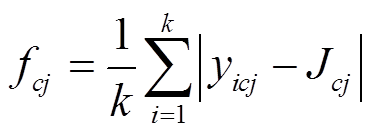 (10)
(10)
式(10)即为样本的标准差,表征了同类样本内特征的波动情况,其值越小,波动越小。从而得到l类第j维特征的每个样本到类中心的平均距离的平均值为
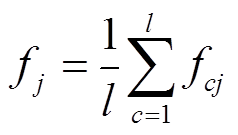 (11)
(11)
(4)定义第![]() 维特征“类内变异系数”,用于描述类内样本聚集性,即
维特征“类内变异系数”,用于描述类内样本聚集性,即
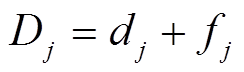 (12)
(12)
Dj是根据统计学中的相关知识定义的,可衡量同变量在不同样本间的变异程度,直观反映特征在类内样本的波动情况,其值越小,波动越小,类内样本的紧密程度越高。
(5)计算第![]() 维特征在
维特征在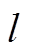 类样本类间平均距离,即
类样本类间平均距离,即
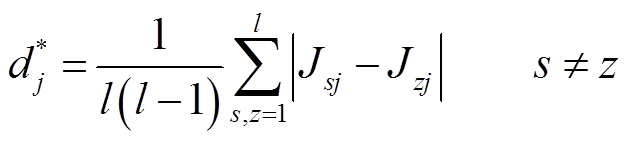 (13)
(13)
式中,Jsj和Jzj分别为第s个和第z个类的第![]() 维特征的平均值。
维特征的平均值。
(6)计算所有类的第![]() 维特征的中心,即
维特征的中心,即
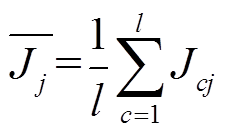 (14)
(14)
计算每个类中心到所有类的中心的平均距离,即
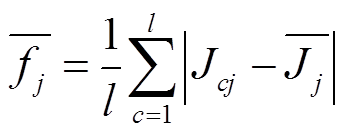 (15)
(15)
(7)将两个类近似看成几何图形的两个圆,则两个类区分性的优劣可以根据两个圆的相对位置来判断,若两个圆相交说明类间具有模糊性;若两个圆相离则说明在类间有很好的区分度。定义“赏函数”来“奖励”“相离”伴随的强区分性,减弱“相交”的模糊性。
令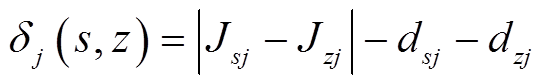 ,当
,当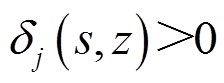 时,表明两个圆相离;
时,表明两个圆相离;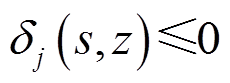 时,表明两个圆相交或相切。
时,表明两个圆相交或相切。
定义类间“赏函数”为
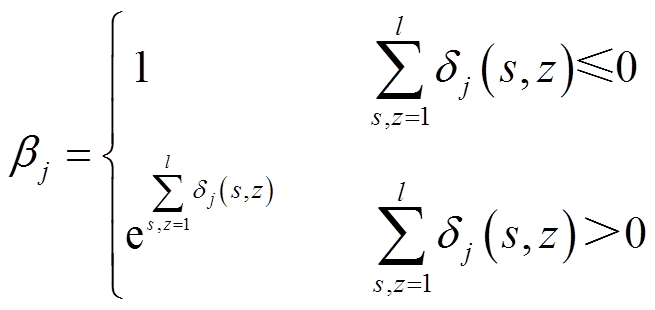 (16)
(16)
引入赏函数bj对类间强发散性的特征予以加权,能够有效地提高类间分类性好的特征敏感性,更好地体现有效特征对分类能力的影响。
(8)定义第![]() 维特征“类间变异系数”,用于描述类间样本区分性,表达式为
维特征“类间变异系数”,用于描述类间样本区分性,表达式为
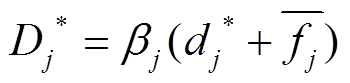 (17)
(17)
(9)定义第![]() 维特征敏感因子为
维特征敏感因子为
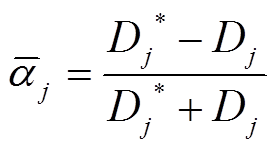 (18)
(18)
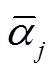 反映了第
反映了第![]() 维特征对
维特征对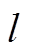 类目标分类的敏感性。显然,Dj越小(即类内特征差异度越小)且Dj*越大(即类间特征区分度越大)时,
类目标分类的敏感性。显然,Dj越小(即类内特征差异度越小)且Dj*越大(即类间特征区分度越大)时,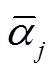 越大,越容易分类,说明该特征对目标分类的敏感性越高。若
越大,越容易分类,说明该特征对目标分类的敏感性越高。若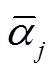 出现负值,表明该特征类内的差异度大于类间的区分度,可直接剔除该特征。根据特征敏感因子
出现负值,表明该特征类内的差异度大于类间的区分度,可直接剔除该特征。根据特征敏感因子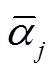 从大到小的顺序即可筛选出最优特征集。
从大到小的顺序即可筛选出最优特征集。
对本文所用的数据样本选取10组数据进行分析,由于篇幅所限,选取二维特征,即振动信号的敏感维数Dm和电流第一波峰特征i1;目标状态选取三种,分别为正常合闸、弹簧疲劳和轴销脱落。具体结果如图7所示。
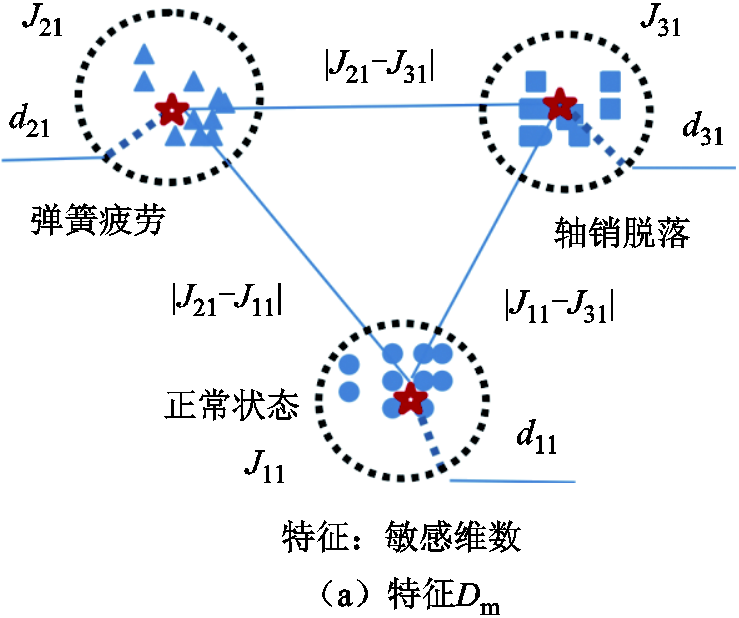
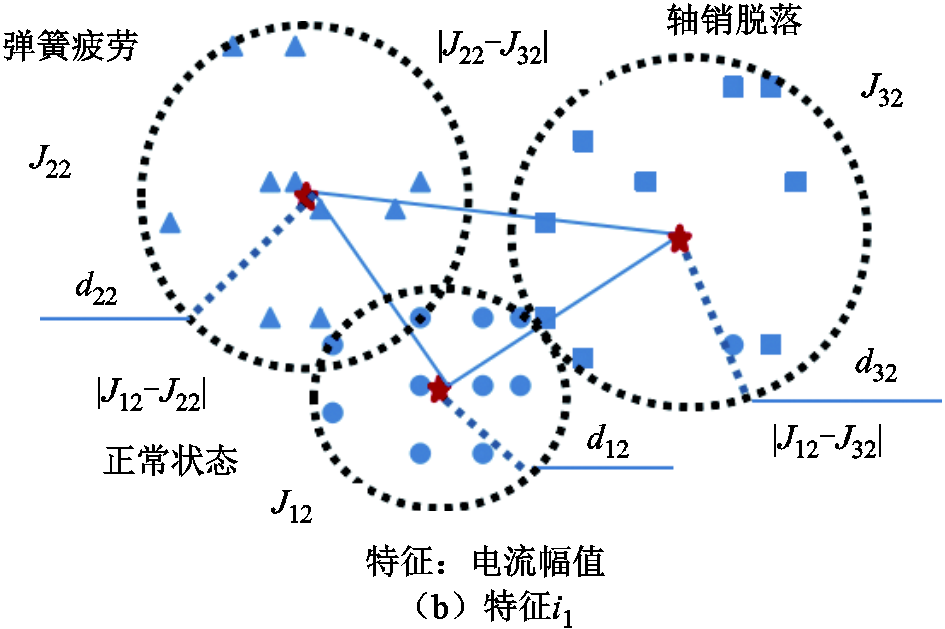
图7 特征敏感性比较示意图
Fig.7 Comparison of feature sensitivity
图7中特征Dm对于三种状态的类内平均距离dc1(虚线圆的半径d11、d21、d31)与每个类样本到类中心的平均距离fcj比特征i1的小,所以显得比较集中。因此特征Dm比特征i1的类内变异系数小(D1<D2)。同时,特征Dm的三种状态的几何圆是相离的,而特征i1的几何圆是相交的,说明特征Dm类间平均距离比特征i1的大,类间显得比较分散。因此特征Dm比特征i1的类间变异系数大(D1*>D2*)。
由式(18)可知,在三种状态分类问题上,特征Dm比特征i1更敏感。
类聚几何敏感特征优选方法具有明确的几何意义,并且计算量不大,直观清晰,符合断路器故障分类特征优选的原则。
以ZN63—12型高压断路器为研究对象搭建故障模拟实验平台,选取24位自带高速IEPE恒流源输出的信号采集设备,将AD50S振动传感器通过强磁座吸附在断路器操动机构顶壁,霍尔开口式电流钳夹在控制线圈上,由上位机记录断路器操动时的电流和振动信号。实验平台如图8所示。

图8 实验平台
Fig.8 Experimental platform
利用实验平台模拟断路器九种状态,采集数据样本集的每个子集对应一种运行状态,9个子集各包含50组样本。每种状态随机选择30组样本数据用于训练,余下的20组用于测试。断路器的九种状态及状态标记见表1,状态包括电气故障、机械故障1、机械故障2和复合故障四大类。
表1 断路器的九种运行状态
Tab.1 Nine operating states of circuit breaker

故障状态类型故障模拟方式状态标记 正常合闸状态正常合闸1 操作电压偏高调整二次回路输入电压至240V2 操作电压偏低调整二次回路输入电压至200V3 铁心卡涩铁心中混入异物模拟4 合闸掣子行程偏大调整合闸掣子螺栓5 弹簧疲劳减少合闸弹簧预压缩模拟6 轴销脱落摘除连接轴销模拟7 操作电压偏低且弹簧疲劳调整二次回路输入电压至200V且减少合闸弹簧预压缩模拟8 铁心卡涩且弹簧疲劳铁心中混入异物且减少合闸弹簧预压缩模拟9
对于表1中的九种运行状态,划分为四类目标状态组,见表2。
表2 四类目标状态组
Tab.2 Category four target status group

目标状态组状态标记 Ⅰ类电气故障1, 2, 3 Ⅱ类机械故障11, 4, 5 Ⅲ类机械故障21, 6, 7 Ⅳ类复合故障1, 8, 9
表1包含断路器运行中常见的故障类型,但断路器实际运行环境恶劣,故障复杂多样,如现场温度、湿度和沙尘等因素会引起电流波形变异和机构动作延缓,但这些缺陷都可以归类为表2的电气故障、机械故障或复合故障,其造成的影响可以体现为“电-振”联合原始特征集的变化。
由于篇幅有限,选择Ⅲ类目标状态,随机列举三种状态下样本构建原始特征集,见表3。对于断路器正常、弹簧疲劳和轴销脱落三种状态,振动信号16个特征区分度都较明显,而线圈电流信号12个特征中只有特征i2存在较大差异性。
针对每类目标状态组,分别计算特定状态组的特征敏感因子,具体结果如图9所示。由图9可知,在不同目标状态组,同一特征敏感因子不同。由振动信号提取的敏感维数特征Dm对于以机械故障有关的目标状态表现出较高的敏感性。
表3 Ⅲ类目标状态的原始特征集
Tab.3 Original feature set of class III target state
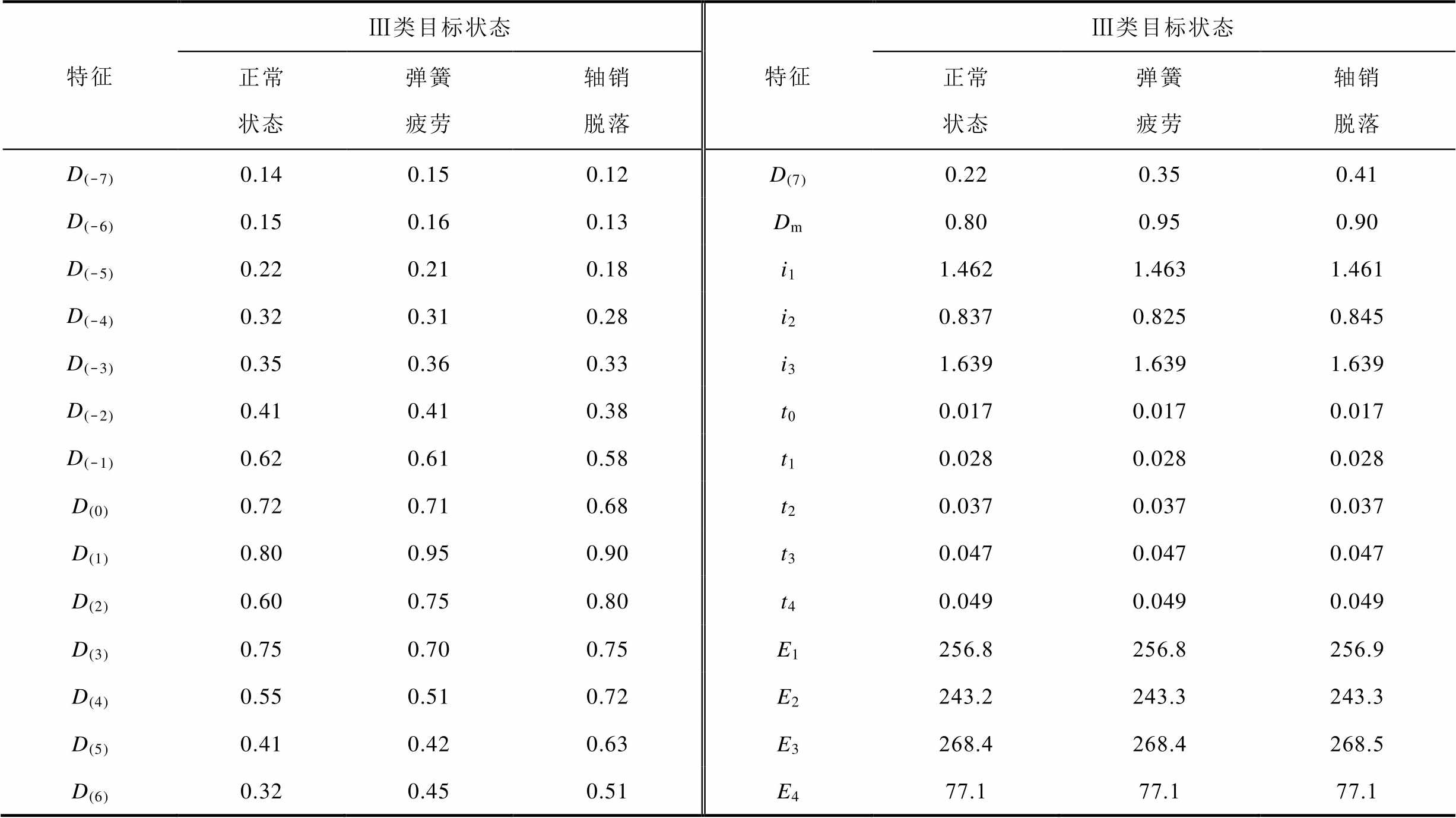
特征Ⅲ类目标状态特征Ⅲ类目标状态 正常状态弹簧疲劳轴销脱落正常状态弹簧疲劳轴销脱落 D(-7)0.140.150.12D(7)0.220.350.41 D(-6)0.150.160.13Dm0.800.950.90 D(-5)0.220.210.18i11.4621.4631.461 D(-4)0.320.310.28i20.8370.8250.845 D(-3)0.350.360.33i31.6391.6391.639 D(-2)0.410.410.38t00.0170.0170.017 D(-1)0.620.610.58t10.0280.0280.028 D(0)0.720.710.68t20.0370.0370.037 D(1)0.800.950.90t30.0470.0470.047 D(2)0.600.750.80t40.0490.0490.049 D(3)0.750.700.75E1256.8256.8256.9 D(4)0.550.510.72E2243.2243.3243.3 D(5)0.410.420.63E3268.4268.4268.5 D(6)0.320.450.51E477.177.177.1

图9 各特征在不同目标状态的敏感性
Fig.9 Sensitivity of each feature in different target state
特征优选的最终目的是为明确不同故障类型的最优特征集。针对断路器在运行中操作较少,导致用于故障分类的数据样本有限的问题,采用支持向量机方法[24]进行故障分类。
通过训练样本优选特征时,将全部特征按照敏感因子降序排列,先由前两个敏感因子构成特征集,然后特征集数依次加1来得到不同特征数的分类精度,四类目标状态组的识别准确率随特征组合数变化的结果如图10所示。
由图10可知,不同特征组合数下,四类目标状态的识别准确率均呈现为先上升后下降。在特征组合数由2不断增大的前期,各类的识别准确率迅速递增,直至稳定于识别准确率最大值附近,并以最大识别准确率对应的最小特征子集作为最优特征集。随着敏感因子低的特征的加入,各类的识别准确率明显下降,说明敏感因子较低的冗余特征对断路器故障分类起到干扰作用,在后续故障分类时将直接剔除。四类故障类型下的最优特征集与最大识别准确率见表4。
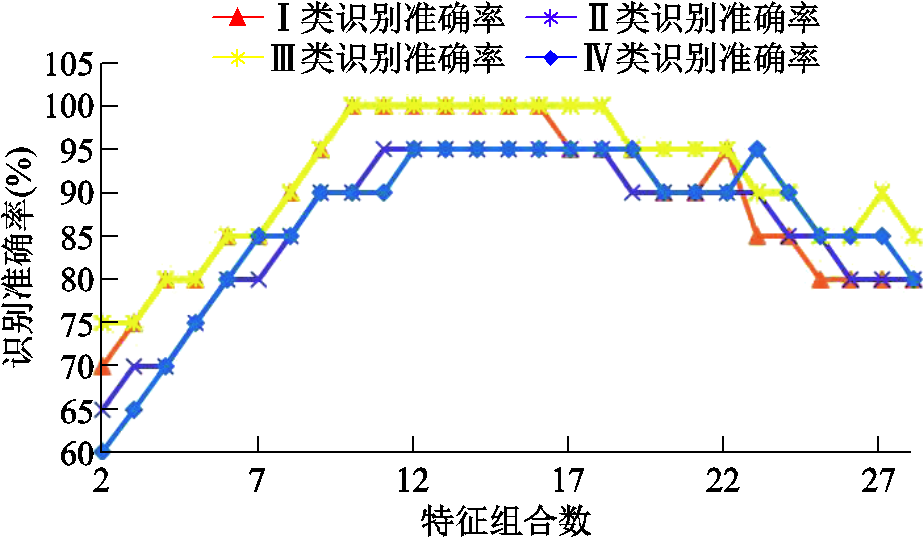
图10 不同特征组合数的识别精度对比
Fig.10 Comparison of recognition accuracy of different feature combinations
表4 四类故障类型下的最优特征集与最大识别准确率
Tab.4 Optimal feature set and maximum recognition accuracy under four fault types

目标状态组状态标记最优特征集最大识别准确率(%) Ⅰ类1, 2, 3E2, E3, i1, i3, t2, t3, i2, Dm, D(1)100 Ⅱ类1, 4, 5t2, i1, Dm, t4, E2, E3, i3, D(1), D(0), D(2)95 Ⅲ类1, 6, 7Dm, D(1), D(0), D(2), D(6), D(-1), D(-2), D(5), i2100 Ⅳ类1, 8, 9Dm, E3, E2, D(1), D(0), D(2), i1, i3, D(6), D(-1), D(-2)95
由表4可知,对于四类目标状态组,最优特征集均是由电流和振动信号的特征共同构造的,说明断路器操动过程“电-振”联合分析的必要性。值得注意的是,敏感维数Dm包含在每类故障的最优特征集中,充分展示其定量描绘振动信号时频图的能力。另外,表4给出了典型故障类型对应的最优敏感特征集,可为后续对典型故障的研究提供借鉴意义。
为了验证典型故障类型对应最优特征集的通用性,选用实验室LW34—40.5断路器操动机构继续进行故障模拟试验。通过减少合闸弹簧预压缩来模拟合闸弹簧疲劳故障,重复试验30次,正常状态与弹簧疲劳状态的“电-振”信号对比如图11所示。两种状态的电流信号基本一致,弹簧疲劳状态的振动信号幅值略小,并出现一定的时延。
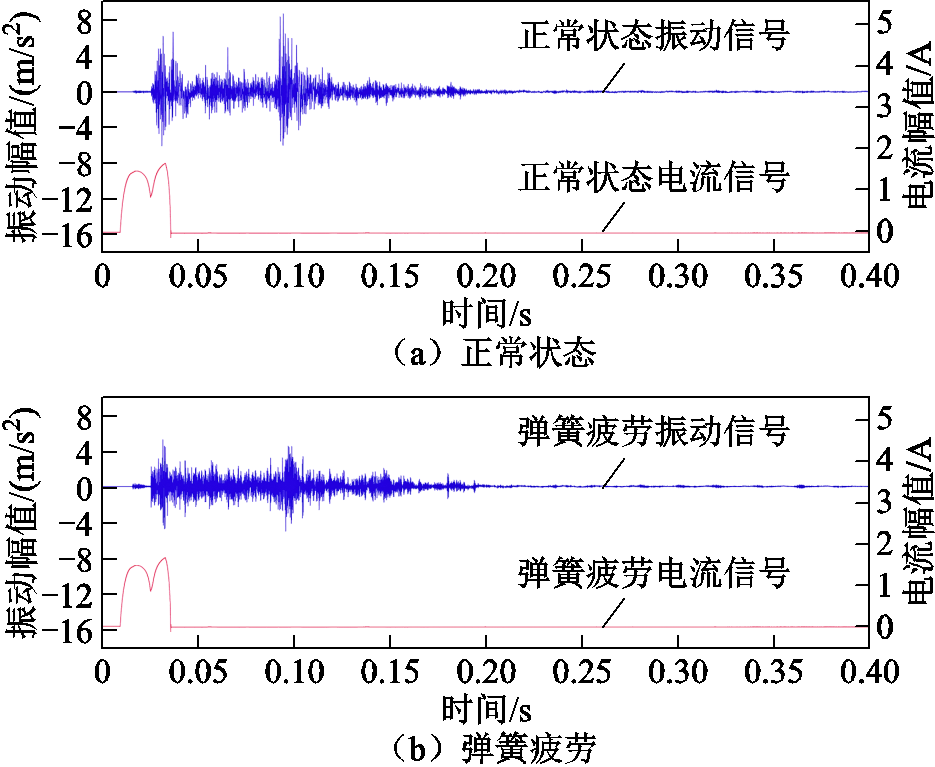
图11 正常与弹簧疲劳状态的“电-振”信号
Fig.11 “Current-vibration” signal of normal and spring fatigue state
采用类聚几何敏感特征优选方法确定最优特征集为Dm, D(1), D(0), D(2), D(6), D(-1), D(-2), D(5),与表4中Ⅲ类机械故障的最优特征集对比,缺少了i2,可见最优特征集虽稍有差别,但本文的优选方法仍具有通用性。表4中的最优特征集可在同类典型故障的后续研究中优先考虑。
断路器故障识别准确率能够直观反映特征优选方法的优劣。为了进一步验证本文方法的识别精度,分别采用SVM、反向传播神经网络(Back Propagation Neural Network, BPNN)、K近邻(k-Nearest Neighbor, KNN)和随机森林(Random Forest, RF)对比识别效果。随机选择30组样本数据进行训练,20组样本进行测试,计算各识别方法对于四类目标状态组的最大平均准确率,结果如图12所示。

图12 不同模式识别算法识别精度对比
Fig.12 Comparison of recognition accuracy of different pattern recognition algorithms
由图12可知,SVM方法的识别准确率平均值达到97.5%,BPNN、KNN和RF识别算法的识别准确率平均值比SVM方法略低,但也达到91.25%以上,验证了类聚几何特征优选方法在断路器故障识别中的有效性。
断路器操作过程伴随着控制线圈电流突变和机构振动冲击,故障分类准确性和快速性取决于电-振信号联合特征提取及优选。本文得到如下结论:
1)提出基于WVD振动时频图的多重分形信息特征提取方法。时频图以色阶形式体现断路器振动信号能量差异性;广义维数谱和敏感维数Dm定量刻画时频图的局部特性、细致捕捉时频变化,并将Dm纳入了所有故障类型的最优特征集。
2)结合电流信号的突变信息,延展振动信号的时间历程,构建断路器完整动作过程的电-振联合多征兆域原始特征集,能够全面反映断路器的电气故障、机械故障和复合故障。
3)提出类聚几何敏感特征优选方法来解决故障分类的高维小样本问题,通过更全面的“奖惩”科学地筛选了面向不同故障类型的最优特征集。试验表明基于类聚几何优选特征集的SVM方法兼顾了故障分类准确率和计算性能,四类状态组的识别准确率平均值达97.5%。
参考文献
[1] 杨秋玉, 王栋, 阮江军, 等. 基于振动信号的断路器机械零部件故障程度识别[J]. 电工技术学报, 2021, 36(13): 2880-2892.
Yang Qiuyu, Wang Dong, Ruan Jiangjun, et al. Fault severity estimation method for mechanical parts in circuit breakers based on vibration analysis[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2880-2892.
[2] 游颖敏, 王景芹, 舒亮, 等. 断路器保护特性测试电流的自适应控制策略[J]. 电工技术学报, 2020, 35(15): 3203-3213.
You Yingmin, Wang Jingqin, Shu Liang, et al. Research on adaptive current control method in circuit breaker protection characteristic test[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3203-3213.
[3] 王昱皓, 武建文, 马速良, 等. 基于核主成分分析-SoftMax的高压断路器机械故障诊断技术研究[J]. 电工技术学报, 2020, 35(增刊1): 267-276.
Wang Yuhao, Wu Jianwen, Ma Suliang, et al. Mechanical fault diagnosis research of high voltage circuit breaker based on kernel principal component analysis and SoftMax[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 267-276.
[4] Carvalho A, Cormenzana M L, Furuta H, et al. CIGRÉ technical brochure 510: final report of the 2004-2007 international enquiry on reliability of high voltage equipment, part 2 - reliability of high voltage SF6 circuit-breakers[M]. Paris: CIGRÉ, 2012.
[5] Yang Qiuyu, Ruan Jiangjun, Zhuang Zhijian, et al. Chaotic analysis and feature extraction of vibration signals from power circuit breakers[J]. IEEE Transactions on Power Delivery, 2020, 35(3): 1124-1135.
[6] 李建鹏, 赵书涛, 夏燕青. 基于双谱和希尔伯特-黄变换的断路器故障诊断方法[J]. 电力自动化设备, 2013, 33(2): 115-119, 125.
Li Jianpeng, Zhao Shutao, Xia Yanqing. Fault diagnosis based on bispectrum and Hilbert-Huang transform for circuit breaker[J]. Electric Power Automation Equipment, 2013, 33(2): 115-119, 125.
[7] 马强, 荣命哲, 贾申利. 基于振动信号小波包提取和短时能量分析的高压断路器合闸同期性的研究[J]. 中国电机工程学报, 2005, 25(13): 149-154.
Ma Qiang, Rong Mingzhe, Jia Shenli. Study of switching synchronization of high voltage breakers based on the wavelet packets extraction algorithm and short time analysis method[J]. Proceedings of the CSEE, 2005, 25(13): 149-154.
[8] 马速良, 武建文, 袁洋, 等. 多振动信息下的高压断路器机械故障随机森林融合诊断方法[J]. 电工技术学报, 2020, 35(增刊2): 421-431.
Ma Suliang, Wu Jianwen, Yuan Yang, et al. Mechanical fault fusion diagnosis of high voltage circuit breaker using multi-vibration information based on random forest[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 421-431.
[9] 杨秋玉, 阮江军, 张灿, 等. 基于定量递归分析的高压断路器机械缺陷辨识及应用[J]. 电工技术学报, 2020, 35(18): 3848-3859.
Yang Qiuyu, Ruan Jiangjun, Zhang Can, et al. Study and application of mechanical defect identification for high-voltage circuit breakers using recurrence quantification analysis[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3848-3859.
[10] 赵书涛, 朱继鹏, 王波, 等. 断路器控制线圈电流特征诊断故障的技术分析及展望[J]. 华北电力大学学报(自然科学版), 2018, 45(5): 70-77.
Zhao Shutao, Zhu Jipeng, Wang Bo, et al. Technical analysis and prospect of circuit breaker fault diagnosis based on control coil current characteristics[J]. Journal of North China Electric Power University (Natural Science Edition), 2018, 45(5): 70-77.
[11] 韩宇, 董波. 一种基于线圈电流的高压断路器机械故障诊断方法[J]. 高压电器, 2019, 55(9): 241-246.
Han Yu, Dong Bo. Mechanical fault diagnosis method for high voltage circuit breaker based on coil current[J]. High Voltage Apparatus, 2019, 55(9): 241-246.
[12] 赵科, 王飞, 杨元威, 等. 基于信号特征融合与优化的高压断路器机械状态评估[J]. 高压电器, 2018, 54(4): 14-19.
Zhao Ke, Wang Fei, Yang Yuanwei, et al. Mechanical condition evaluation of high voltage circuit breaker based on the features fusion and optimization of different signals[J]. High Voltage Apparatus, 2018, 54(4): 14-19.
[13] 万书亭, 李聪, 豆龙江, 等. 基于振电结合的高压断路器特征提取及分类方法研究[J]. 华北电力大学学报(自然科学版), 2019, 46(4): 31-38, 53.
Wan Shuting, Li Cong, Dou Longjiang, et al. Study on the signal feature extraction and classification of high voltage circuit breaker based on vibration signal and current signal[J]. Journal of North China Electric Power University (Natural Science Edition), 2019, 46(4): 31-38, 53.
[14] 姚旭, 王晓丹, 张玉玺, 等. 特征选择方法综述[J]. 控制与决策, 2012, 27(2): 161-166, 192.
Yao Xu, Wang Xiaodan, Zhang Yuxi, et al. Summary of feature selection algorithms[J]. Control and Decision, 2012, 27(2): 161-166, 192.
[15] 张浩, 赵莉华, 景伟, 等. 基于Relief特征量优化及SOM网络的断路器操作机构状态评估[J]. 高压电器, 2017, 53(9): 240-246.
Zhang Hao, Zhao Lihua, Jing Wei, et al. Condition assessment of the circuit breaker operating mechanism based on Relief feature vector optimization and SOM network[J]. High Voltage Apparatus, 2017, 53(9): 240-246.
[16] 杨秋玉, 阮江军, 黄道春, 等. 基于振动信号时频图像识别的高压断路器分闸缓冲器状态评估[J]. 电工技术学报, 2019, 34(19): 4048-4057.
Yang Qiuyu, Ruan Jiangjun, Huang Daochun, et al. Opening damper condition evaluation based on vibration time-frequency images for high-voltage circuit breakers[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4048-4057.
[17] 李邦彦, 齐伟强, 桂媛, 等. 基于Relief F和灰色关联分析的高压断路器机械故障诊断[J]. 高压电器, 2020, 56(6): 197-203, 210.
Li Bangyan, Qi Weiqiang, Gui Yuan, et al. Mechanical fault diagnosis of high voltage circuit breaker based on Relief F and grey relation analysis[J]. High Voltage Apparatus, 2020, 56(6): 197-203, 210.
[18] 邵阳, 武建文, 马速良, 等. 用于高压断路器机械故障诊断的AM-ReliefF特征选择下集成SVM方法[J]. 中国电机工程学报, 2021, 41(8): 2890-2901.
Shao Yang, Wu Jianwen, Ma Suliang, et al. Integrated SVM method with AM-ReliefF feature selection for mechanical fault diagnosis of high voltage circuit breakers[J]. Proceedings of the CSEE, 2021, 41(8): 2890-2901.
[19] 蔡哲元, 余建国, 李先鹏, 等. 基于核空间距离测度的特征选择[J]. 模式识别与人工智能, 2010, 23(2): 235-240.
Cai Zheyuan, Yu Jianguo, Li Xianpeng, et al. Feature selection algorithm based on kernel distance measure[J]. Pattern Recognition and Artificial Intelligence, 2010, 23(2): 235-240.
[20] 吴瑕, 周焰, 杨龙坡, 等. 基于聚类分析与几何的目标特征敏感性评估算法[J]. 控制与决策, 2012, 27(6): 914-918.
Wu Xia, Zhou Yan, Yang Longpo, et al. Target feature sensitivity evaluation method based on clustering analysis and geometry[J]. Control and Decision, 2012, 27(6): 914-918.
[21] 穆利智, 李泽文, 吕佳佳, 等. 结合EMD-WVD和布谷鸟搜索算法的输电线路故障暂态保护[J]. 电力系统自动化, 2020, 44(16): 137-144.
Mu Lizhi, Li Zewen, Lü Jiajia, et al. Transient protection for transmission line fault combining empirical mode decomposition-Wigner ville distribution and cuckoo search algorithm[J]. Automation of Electric Power Systems, 2020, 44(16): 137-144.
[22] Kantelhardt J W, Zschiegner S A, Koscielny-Bunde E, et al. Multifractal detrended fluctuation analysis of nonstationary time series[J]. Physica A: Statistical Mechanics and Its Applications, 2002, 316(1-4): 87-114.
[23] 徐玉秀, 张剑, 侯荣涛. 机械系统动力学分形特征及故障诊断方法[M]. 北京: 国防工业出版社, 2006.
[24] 谢桦, 亚夏尔·吐尔洪, 陈昊, 等. 基于支持向量机算法的配电线路时变状态预测方法[J]. 电力系统自动化, 2020, 44(18): 74-80.
Xie Hua, Yaxar Turgun, Chen Hao, et al. Prediction method for time-variant states of distribution line based on support vector machine algorithm[J]. Automation of Electric Power Systems, 2020, 44(18): 74-80.
Abstract High voltage circuit breaker is the key safety control equipment of power system, and the loss caused by its failure is far more than its own value. The action of the circuit breaker involves the secondary electrical circuit control and the energy transmission process between mechanical components. Its complex structure and harsh operating environment are easy to cause electrical or mechanical failures. The control coil current and the vibration signal in the transmission process are effective characteristics for analyzing the abnormal operating state of the circuit breaker. In the process of fault classification of high-voltage circuit breakers using current vibration signals, the dimension of the original feature set is high, resulting in low recognition rate and degradation of classification performance. This paper proposes a clustering geometric sensitive feature optimization method suitable for high-dimensional and small samples.
Firstly, the time-frequency diagram of vibration signal processed by Wigner-Ville Distribution (WVD) is quantitatively characterized by generalized dimension spectrum and sensitive dimension. The time-frequency diagram reflects the energy difference of the circuit breaker vibration signal in the form of color scale. The generalized dimension spectrum and sensitive dimension quantitatively depict the local characteristics of the time-frequency diagram, and carefully capture the time-frequency changes. Secondly, using the mutation information of the coil current signal decomposed by singular value decomposition to extend the time history of the vibration signal, the original feature set of the electrical vibration joint multi symptom domain for the complete action process of the circuit breaker is constructed. Finally, the "coefficient of variation" is defined to describe the volatility of the characteristics in the samples within and between classes, the "reward function" is used to weight the characteristics of strong divergence between classes, and the optimal collection of clustering geometry under different fault types is obtained according to the optimization of feature sensitivity factors. The corresponding relationship between the fault types and the optimal feature set is clarified.
Taking ZN63-12 high-voltage circuit breaker as the research object, a fault simulation experiment platform is built. The experimental platform is used to simulate nine states of the circuit breaker, including normal, electrical fault, mechanical fault and compound fault. For each type of target state group, the feature sensitivity factor of a specific state group is calculated respectively, and the support vector machine (SVM) method is used to classify faults, and finally the optimal feature set under a specific fault type is selected. The experiment shows that: ①The original feature set of electrical vibration combined multi symptom domain in the complete action process of the circuit breaker can fully reflect the electrical fault, mechanical fault and compound fault of the circuit breaker. ②The optimization method of clustered geometric sensitive features is proposed to solve the problem of high-dimensional small samples of fault classification, and the optimal feature set for different fault types is scientifically screened through more comprehensive "rewards and punishments". ③The SVM method based on clustering geometric optimization feature set gives consideration to the accuracy of fault classification and computational performance, and has engineering application value.
Keywords:High voltage circuit breaker, current-vibration combination, aggregation geometry, feature optimization, sensitive dimension
DOI: 10.19595/j.cnki.1000-6753.tces.220639
中图分类号:TM561
刘会兰 女,1986年生,博士研究生,工程师,研究方向为电力设备故障诊断、智能电器监测技术及分布式电源并网技术。E-mail:liuhuilan111@163.com(通信作者)
许文杰 男,1997年生,硕士研究生,研究方向为电力设备在线监测与故障诊断。E-mail: xuwenjie19784624@126.com
中央高校基本科研业务费专项资金资助项目(2021MS064)。
收稿日期 2022-04-23
改稿日期 2022-05-12
(编辑 李冰)