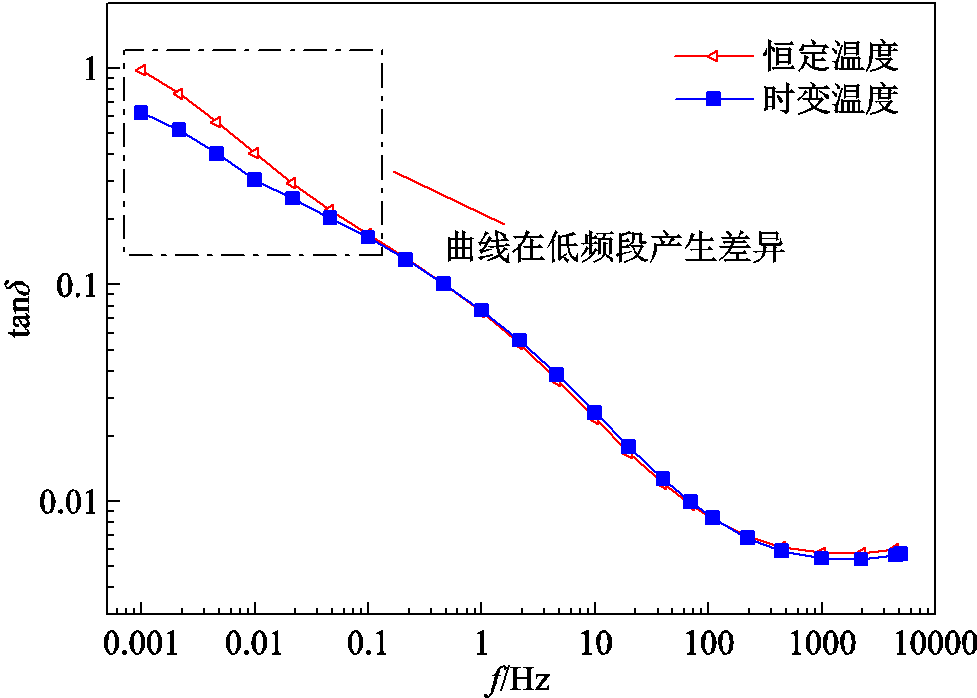
图1 恒温与变温条件下的tand-f曲线
Fig.1 The tand-f curves under constant temperature and time-varying temperature
摘要 频域介电谱(FDS)技术被广泛应用于油纸绝缘电力设备状态诊断中。但FDS在低频段测试时间较长,测试时设备往往处于动态降温过程,所获得的FDS曲线与评估数据库差别较大,使用时变温度FDS曲线进行绝缘状态评估的结果存在一定误差。为将时变温度条件下的FDS曲线校正到恒定温度,该文通过仿真获得套管温度场分布,采用粒子群优化(PSO)算法反演出不同温度下介电弛豫Havriliak-Negami(H-N)模型的特征参数。在此基础上,基于最小二乘法(LS)计算出时变温度条件下每个频点的等效温度,由此实现了曲线校正。结果表明:校正后的曲线与参考温度曲线具有较好的一致性,有助于电力设备绝缘状态的精确评估。
关键词:时变温度 频域介电谱(FDS) Havriliak-Negami模型 粒子群优化-最小二乘法(PSO-LS)算法 绝缘状态评估
随着碳达峰、碳中和战略目标的提出,跨省跨区域电网建设逐渐成为资源优化配置的必要手段,其中电力设备寿命周期精细化管理是构建安全高效智能电网的关键。电容型高压套管作为电力系统中最重要的设备之一,堪称电力系统的“咽喉”,其剩余寿命主要取决于内部油纸绝缘状态[1]。运行期间,套管在各种应力的作用下逐渐受潮并发生老化,威胁着电力系统的安全稳定运行。如何准确获取并有效表征套管绝缘状态成为油纸绝缘领域研究的热点问题[2]。
目前,基于介电响应原理的油纸绝缘设备无损检测方法主要有回复电压法(Recovery Voltage Method, RVM)、极化/去极化电流(Polarization and Depolarization Current, PDC)法和频域介电谱(Frequency Domain Spectroscopy, FDS)法[3]。相比于前两种方法,频域介电谱法抗干扰能力更强,携带信息更加丰富,在油纸设备绝缘状态现场评估方面具备更大潜力[4]。
K. Bandara等[5]使用频域介电谱法研究了四种绝缘油在不同恒定温度下的绝缘特性,并基于活化能表征了其介电响应的频率依存性。张大宁等[6]通过制备不同受潮程度与老化程度的样本,研究了温度对油纸绝缘低频段非线性电导损耗特性的影响。M. Gutten等[7]发现套管中水分与温度都会对FDS曲线产生影响,为此提出了基于补偿因子g的曲线校正方法,将其他稳态温度下的FDS曲线校准到基准温度条件下。
以上研究均为基于稳态温度下的FDS曲线评估方法,但实际工况下环境复杂,尤其由于地域、气候等外界因素的影响,设备在停运检修时往往处于动态降温过程[8]。此外,由于现场检修的“时间窗口”较短,进行介电响应测试的时间有限,无法在套管温度稳定后再进行介电响应评估,所获得的FDS曲线与恒定温度曲线差别较大[9-11]。因此,需要将时变温度曲线校正到恒定温度条件,可以大幅度提升绝缘状态的评估精度。
为此,西南交通大学王东阳等[11]提出了一种基于稳态直流电导率和离子迁移率的时变温度FDS曲线校正方法,采用优化方法计算得到了三种不同温度变化率下介电谱的校正值。广西大学刘捷丰等[12]将介质损耗因数分解为连续幂级数的表达形式,使用曲面拟合的方法构建了样品含水率、测试温度及介质损耗因数的非线性关系,通过求解相关参数得到了不同温度下的校准曲线。上述方法在考虑恒定散热速率条件的基础上,以套管或变压器油温为基础数据,为曲线校正提供了便捷的方法。实际现场中受套管绝缘的热传导、空气与套管的热对流及套管自身的热辐射的影响,其散热速率往往是随时间变化的。同时,套管或变压器内部温度较难获得,现有的测试方法在现场应用中仍存在一定困难,其油温与真实绝缘温度存在差异,不利于工况下时变温度曲线的准确校正。
本文在充分考虑套管真实结构及散热条件的基础上,基于有限元仿真研究了工况下套管停电后内部绝缘温度的变化特性,为时变温度下FDS曲线校正提供了基础。进一步地通过测试得到多组恒温条件下的FDS曲线。在此基础上,采用粒子群优化(Particle Swarm Optimization, PSO)算法反演出了Havriliak-Negami(H-N)介电弛豫模型特征参数与温度的非线性关系,将仿真温度作为初值基于最小二乘(Least Square, LS)法计算出时变温度条件下FDS曲线中每个频点的等效温度,并使用Arrhenius公式实现了暂态温度下逐个频点数据的精准校正。最后,通过实验模拟套管的散热过程获得时变温度下套管的FDS曲线,并依据上述方法将曲线校准到指定基准温度,验证了模型的准确性。
FDS测试的频率范围通常为1mHz~5kHz。低频段测试周期较长,导致工况下测试起始温度与结束温度差别较大,测试曲线与稳态温度下的FDS曲线也将产生较大偏差。恒温与变温条件下的介质损耗因数tanδ与频率f的关系曲线如图1所示[11]。

图1 恒温与变温条件下的tand-f曲线
Fig.1 The tand-f curves under constant temperature and time-varying temperature
从图1可以看出,FDS在高频段的测试时间较短,温度基本没有发生变化,时变温度曲线与恒温曲线差别较小。随着测试频率的降低,测试时间增长,时变温度曲线出现了向下偏移的趋势,与恒温曲线差异逐渐增大。而FDS低频段与油纸绝缘的受潮老化状态密切相关,曲线低频段的差异会降低绝缘状态评估结果的准确性。
此外,传统的FDS评估数据库往往是基于恒定温度材料数据构建的,工况下需要把时变温度曲线校正为恒定温度曲线,才能实现电力设备绝缘状态的准确评估。
首先,为获取电力设备内部的绝缘温度,研究温度随时间的变化特性,构建时变温度条件下FDS曲线校正方法,对油纸绝缘套管进行了温度场仿真。
套管仿真模型的结构及材料与实际套管相同,包括中心载流导体、绝缘纸、铝箔、变压器油、外护套和空气间隙[13],仿真模型如图2所示。

图2 套管仿真模型
Fig.2 The simulation model of bushing
套管的主绝缘可等效为多层铝箔电极所构成的同轴串联电容器,其中心载流导体采用具有高导热系数的铜导体,外壳为聚甲基丙烯酸甲酯材质的有机玻璃。套管模型参数见表1。
表1 套管模型参数
Tab.1 Bushing model parameters

极板层数厚度/mm上极差/mm下极差/mm极板长度/mm 0———260 11.6246220 21.6298180 31.6348140 41.6571665
套管中,电容芯子零屏半径R0为16.5mm,长度L0为260mm。同时,电容型油纸套管模型结构包括固、液、气三种物质形态,依据实际套管运行工况,设置模型内部绝缘初始温度为85℃,空气间隙和外护套初始温度与环境温度相同,采用二维轴对称结构对其温度分布进行计算,具体仿真流程如图3所示。
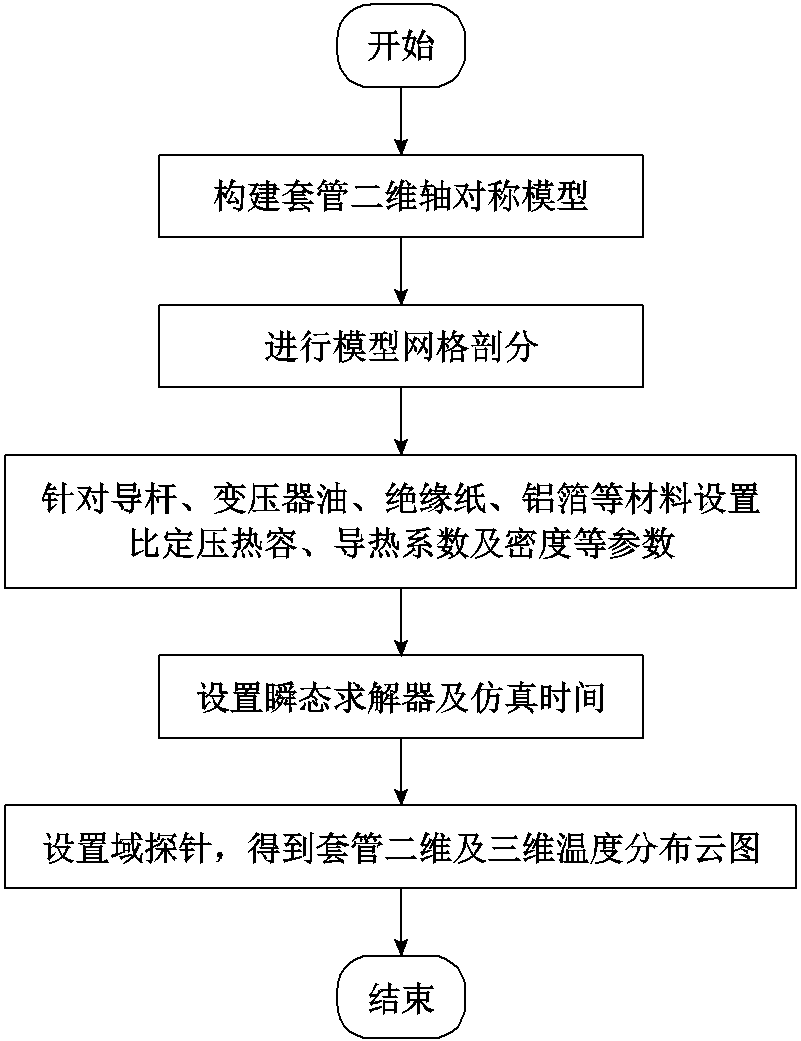
图3 套管内部温度仿真流程
Fig.3 The flow chart of bushing temperature simulation
套管在运行时始终承受工频交流电压,其整体温度保持恒定。当停电检修时,套管温度会由于介质间的热传导、空气与套管间的热对流及套管自身的热辐射而发生变化。但工况下所获得的温度往往为套管油温,无法真实地反映套管绝缘温度。研究表明[14],选取电力设备内部绝缘温度代替油温进行温度校正,可以得到更加准确的结果。
因此,本文运用COMSOL有限元仿真对套管内部散热过程进行分析。结合套管散热环境,本文主要考虑以下三种散热过程。
1)传导散热
热传导是固、液、气三种状态下介质内分子无宏观运动时的传热现象,其微分方程[13]为
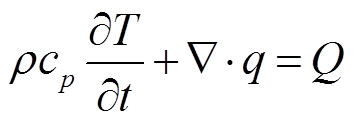 (1)
(1)
 (2)
(2)
式中,T为温度,K;x,y,z为坐标值,m;k为导热系数,W/(m×K);cp为比定压热容,J/(kg×K);r为密度,kg/m3;t为时间,s;Q为单位体积发热功率,W/m3。
2)对流换热
介质表面和流体之间会发生对流换热。对于电容式油纸套管,最外层与空气接触,由于垂直方向存在温差,在空气浮力作用下导致气体流动发生对流换热,属于自然对流换热。变压器油密封在套管中,与套管发生密封腔自然对流换热。热对流的基本方程[15]如下。
质量守恒方程:
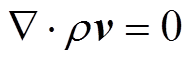 (3)
(3)
动量守恒方程:
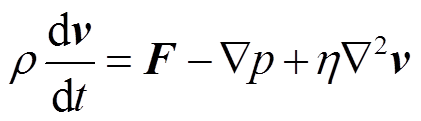 (4)
(4)
能量守恒方程:
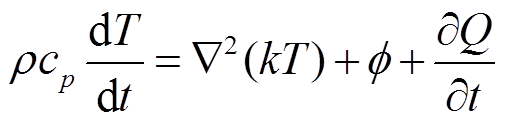 (5)
(5)
式中,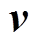 为速度,m/s;F为流体受到的重力,N;p为流体压强,Pa;h为动力粘度,kg/m;f为损耗方程。
为速度,m/s;F为流体受到的重力,N;p为流体压强,Pa;h为动力粘度,kg/m;f为损耗方程。
外表面通过自然对流耗散热量时的损耗特征通常采用表面传热系数h进行表征,其表达式为[16]
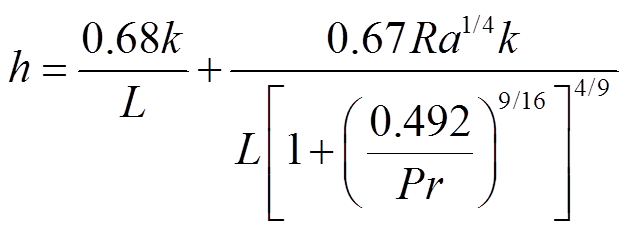 (6)
(6)
式中,L为物体尺寸,m; 和Pr分别为无量纲的瑞利数和普朗特数。
和Pr分别为无量纲的瑞利数和普朗特数。
3)辐射散热
套管表面也会通过向外辐射电磁能进行散热,热量以波的形式从发热体辐射到温度较低的周围介质中,热辐射能量大小与套管温度和其表面物性有关。热辐射过程中物体表面最大辐射流密度为[13]
 (7)
(7)
式中,Ts为物体表面温度,K;s为斯蒂芬-玻耳兹曼常数,s=5.67´10-8。
仿真过程中各材料散热参数见表2。
表2 材料散热参数
Tab.2 Heat dissipation parameters

材料比定压热容/[J/(kg×K)]导热系数/[W/(m×K)]密度/(kg/m3)表面辐射率 铝箔9002382 700— 导杆3854008 960—
(续)

材料比定压热容/[J/(kg×K)]导热系数/[W/(m×K)]密度/(kg/m3)表面辐射率 绝缘纸8000.15900— 变压器油2 1000.128895— 空气cp(T)k(T)r(p,T)— 有机玻璃7031.382 2030.85
仿真模型考虑了电容芯子内部的传导散热,垂直壁、水平壁的外部对流散热以及外护套表面对环境的辐射散热,仿真得到不同散热时间下套管的温度分布云图如图4所示。
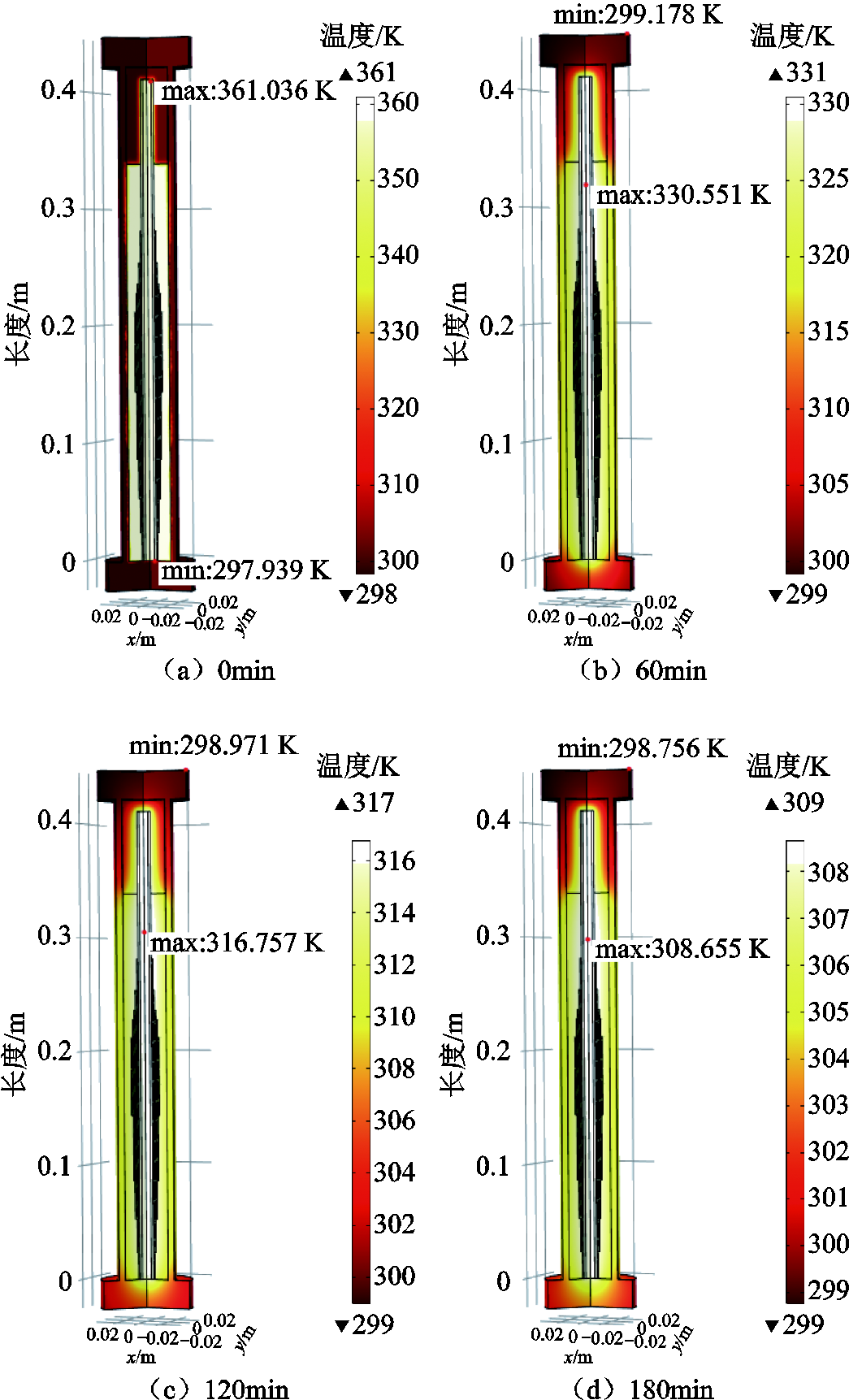
图4 套管温度分布云图
Fig.4 Temperature distribution of bushing
从图4a~图4d可以看出,套管的最高温度出现于电容芯子处,最低温度出现于套管外护套顶点处。随着散热时间的增加,套管内部温度逐渐降低,散热过程中电容芯子径向与轴向温度始终呈现均匀分布状态。
为了更加直观地了解套管内部绝缘温度随散热时间的变化关系,选取套管电容芯子为研究对象,得到其散热曲线如图5所示。
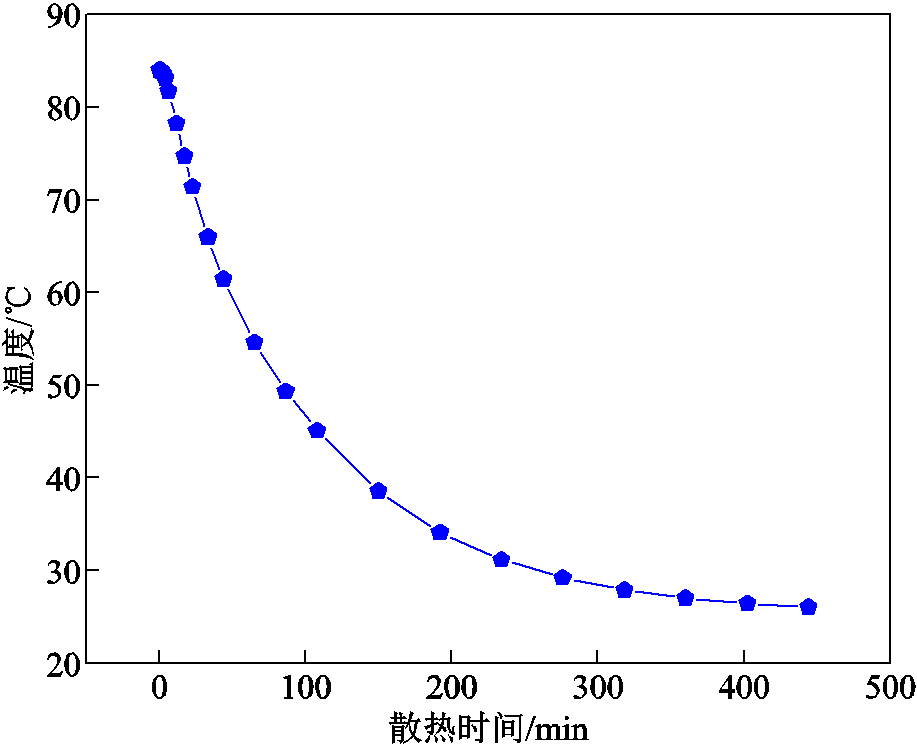
图5 套管电容芯子温度随时间变化关系曲线
Fig.5 Temperature curve of bushing capacitor core varying with time
从图5可以看出,随着散热时间的增加,套管内部绝缘的温度并非以恒定速率下降,而是呈现指数下降趋势,最高温度为起始温度,最低温度为环境温度,散热速率由快变慢。通过拟合可以得到套管的散热方程为
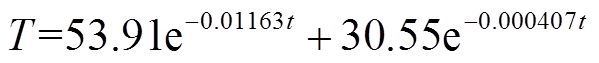 (8)
(8)
由此,可以获得套管散热过程中任意时刻的绝缘温度。相比于使用油温,基于此温度表达式进行时变温度FDS曲线校正会更加准确。
在电介质经典理论中,常用单一弛豫时间的Debye模型来描述介电响应过程。但大多数情况下,弛豫时间是服从最大概率分布的。研究表明,Cole-Cole函数和Davidson-Cole函数可以描述具有弛豫时间分布的介电响应过程,但在多种介电过程下绘制出的曲线与实际测量曲线仍有一定偏差[17]。为此,Havriliak和Negami提出一种普适的模型函数,可以更加精确地描述包含界面极化的弛豫过程[18-19],称为Havriliak-Negami(H-N)弛豫函数,其表达式为[20]
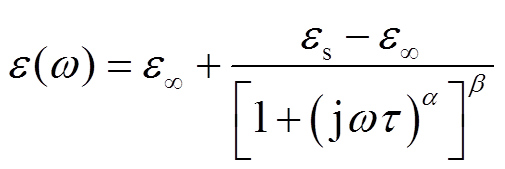 (9)
(9)
式中,t为弛豫时间;es和e¥分别为静态介电常数与光频介电常数;a、b为与弛豫时间分布相关的形状参数,0≤a≤1,0≤b≤1;ω为角频率。
根据复分析理论,可得到其复介电常数实部和虚部的表达式分别为[20]
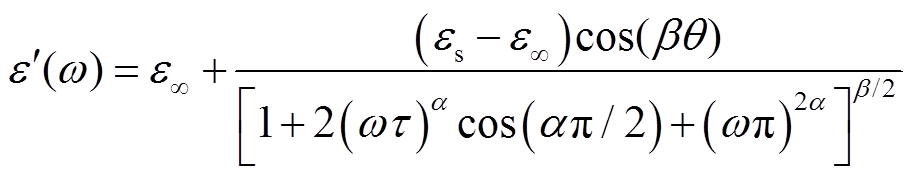 (10)
(10)
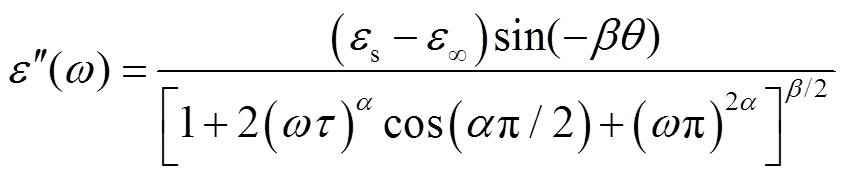 (11)
(11)
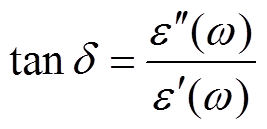 (12)
(12)
其中
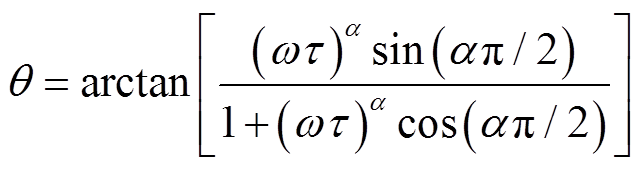 (13)
(13)
对于不同温度下的FDS曲线,es、t、a、b的值均有所不同。其中,es可以表示为电子极化的微观极化率ae和偶极极化的微观极化率a0的函数。因为原子中的电子结构与温度无关,故ae不受温度影响;而分子在不同温度下能量不同,其取向极化程度有所差异,故a0与温度相关[21]。另一方面,介质的弛豫是由系统内粒子间的能量传递所引起的,温度越高,能量传递越快,则弛豫时间t越小。而粒子的能量又是服从玻耳兹曼分布的,故弛豫时间t与温度存在指数关系[22]。a和b为形状参数,无物理意义。
由此可推导出介质损耗因数与温度T的函数关系[21]为
 (14)
(14)
其中
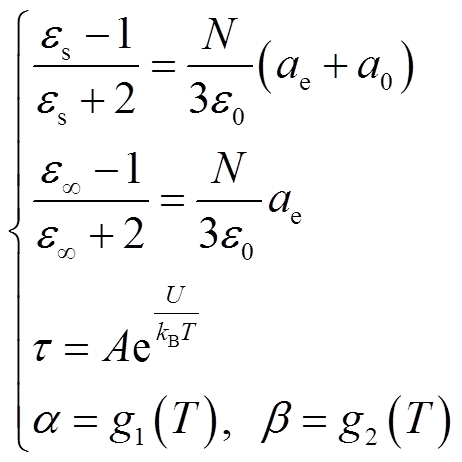 (15)
(15)
式中,N为独立永久偶极子个数;e0为真空介电常数;A为常系数;U为分子活化能;kB为Boltzmann常数,kB=1.38×10−23J/K。在时变温度条件下,由于低频段(1mHz~0.1Hz)FDS测试时间较长,所对应测试频点的温度不是定值,在进行曲线温度校正时需要获得其等效温度。
依据式(14)与式(15),在已知介电谱某点的频率及介质损耗因数时,可以获得相应的等效温度为
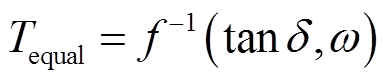 (16)
(16)
由于式(16)较为复杂,无法得出其显式表达式,故本文采用LS方法进行求解。
获得等效温度后,依据Arrhenius公式[23]可将时变温度下的频点平移到所需的恒定温度条件下,即
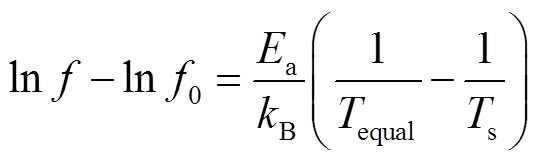 (17)
(17)
式中,Ts为校正的目标温度;f0为等效温度Tequal下FDS曲线某点平移前所对应的频率;f为平移后该点在温度Ts下所对应的频率;Ea为活化能。
为获取上述H-N介电弛豫等效温度模型在不同温度下的参数,在实验室内对干燥油纸绝缘套管进行了不同恒定温度下的FDS测试。实验平台如图6所示。
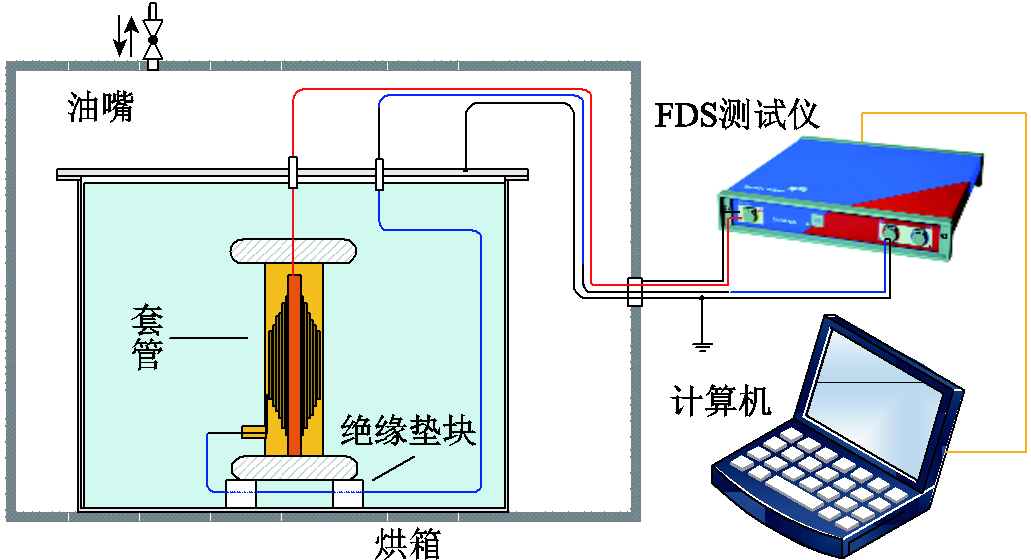
图6 实验平台
Fig.6 Schematic diagram of experimental platform
将套管竖直放置于恒温恒湿箱中,频域介电谱测试仪选用Omicron公司研制的DIRANA,通过烘箱内嵌的电极将高压端与测试端分别接于套管的导杆及末屏。
实验温度包含30℃、40℃、50℃、60℃、70℃、80℃和90℃。针对本文所使用的套管,采用梯度升温的方式,每个温度下保持5h即可实现温度分布稳定。介质损耗因数tand、复电容实部C¢和复电容虚部C²随频率变化的结果如图7~图9所示。
由图7可知,不同温度的tand-f曲线在中高频段存在明显的交点。在tand-f曲线中频率小于交点的低频部分,介质损耗因数随着温度的升高而变大;在tand-f曲线中频率大于交点的高频部分,介质损耗因数随着温度的增加而减小。tand-f曲线整体符合平移趋势。
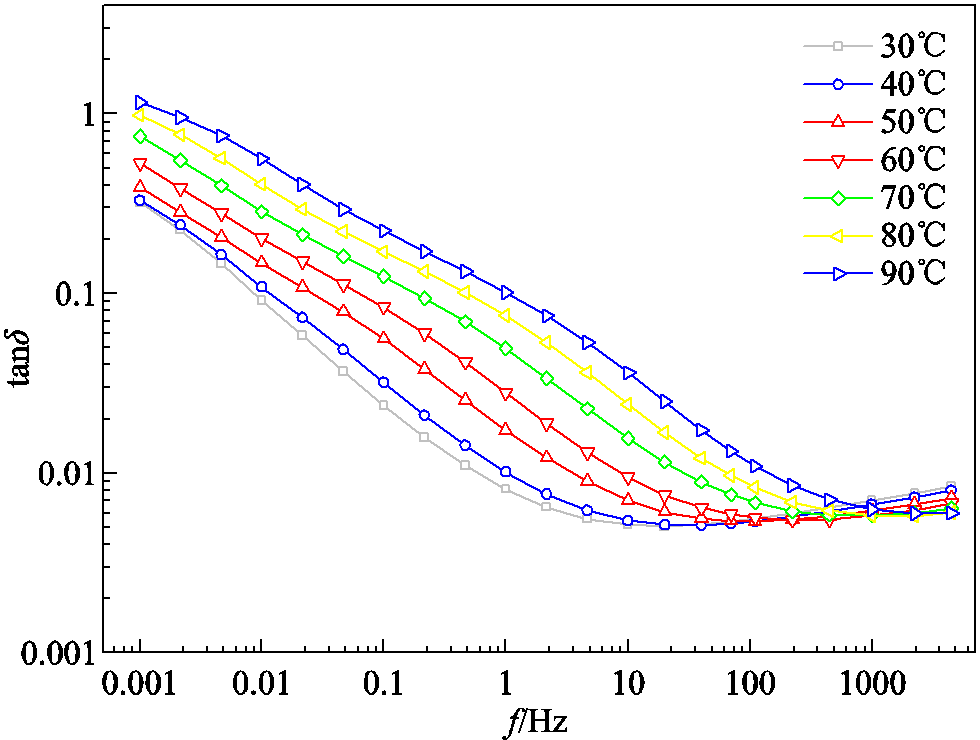
图7 不同恒定温度下的tanδ-f曲线
Fig.7 The tanδ-f curves at different constant temperatures
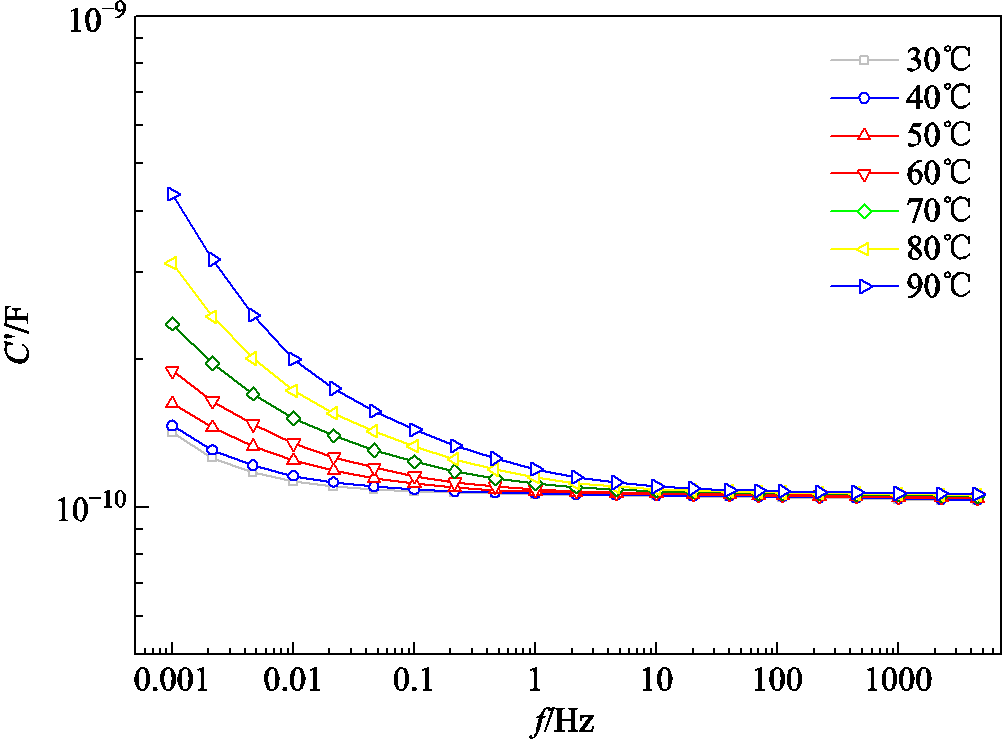
图8 不同恒定温度下的C′-f曲线
Fig.8 C′-f curves at different constant temperatures
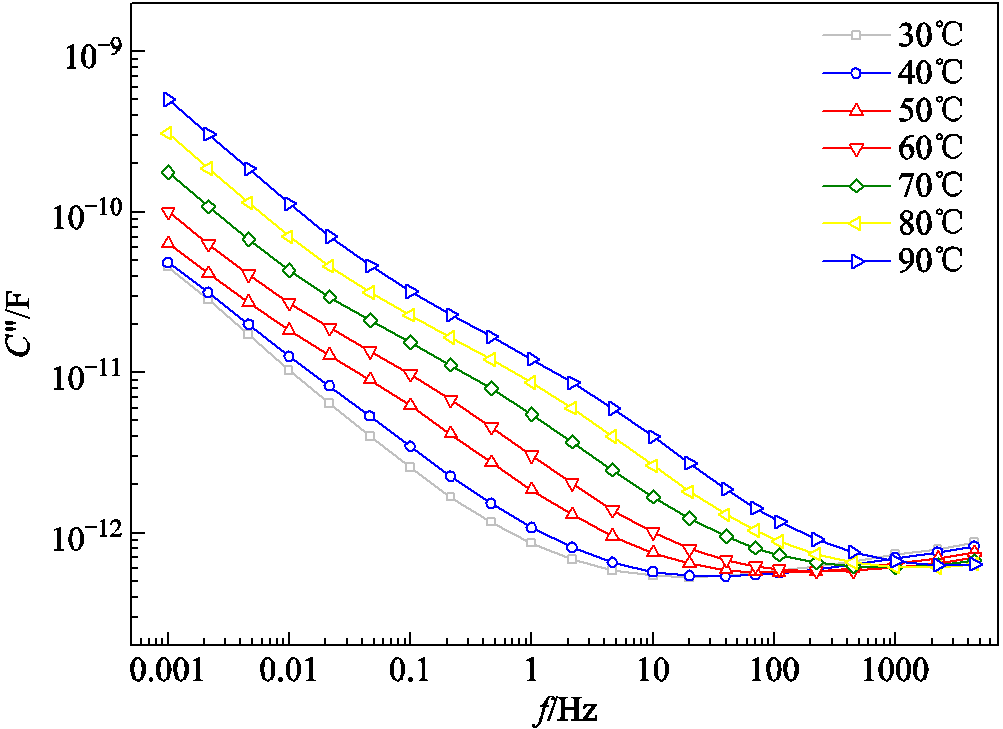
图9 不同恒定温度下的C″-f曲线
Fig.9 C″-f curves at different constant temperatures
如图8所示,对于C¢-f曲线,随着温度增加,曲线在低频部分出现明显的上翘。主要有两种原因:①温度增加使得油纸之间的界面极化时间常数减小,界面极化在更短的时间内完成;②依据低频弥散理论[24],高频段离子的振荡过程中复合和解离趋于平衡,随着频率的降低,一部分离子因行程增大而被阻挡束缚,进而导致复电容实部上升。而温度加剧了离子的复合和解离,使得低频弥散更加明显。
如图9所示,C²-f曲线低频部分主要反映电导损耗,由于温度的增加,油纸绝缘内载流子的迁移率大幅增加;C²-f曲线高频部分主要反映极化损耗,温度的增加使得分子热运动加剧,分子转向极化难度增大,极化损耗减小。
由式(10)~式(13)可知,H-N模型表达式较为复杂,使用传统方法求解其参数与温度的关系属于NP难问题,且求解过程具有离散化、多指标、非线性和不确定性等特点,同时求解多个参数的时间成本与空间成本巨大。另一方面,传统方法对参数拟合的初值要求较高,偏离最优解较远的初值会导致模型性能退化,求解结果误差变大。
为此,本文采用启发式算法PSO求解不同恒定温度下H-N模型的参数。PSO算法的优势在于其流程简单、容易实现且待调整参数较少。在粒子群寻优过程中,通过调整关系权重系数、自我学习因子及社会学习因子,可以在寻优前期更趋向于全局搜索,获得良好的开发能力,在后期更趋向于局部搜索,从而提高解的精度[25-26]。
为确保结果的准确性,以计算所得的复介电常数与实测复介电常数方均误差最小为目标函数,以H-N模型参数为解,将问题转换为最优化问题。算法过程如下:
在可行域内由n个粒子组成粒子群,每个粒子的位置表示一种可行解,则第i个粒子第k+1次迭代后的位置可表示为
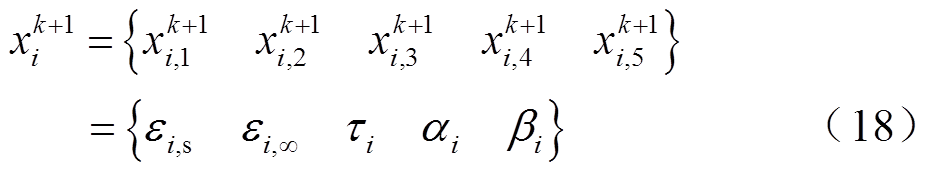
式中,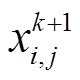 为第i个粒子第k+1次迭代后的H-N模型的第j维参数。
为第i个粒子第k+1次迭代后的H-N模型的第j维参数。
粒子自我学习因子c1、社会学习因子c2及最大迭代次数ngen等参数的选取会影响PSO算法的收敛速度和算法性能。考虑H-N模型特性,PSO算法的参数设置见表3。
表3 PSO算法参数
Tab.3 PSO algorithm parameters

参数数值 种群数量5 000 维数d5 c1min0
(续)

参数数值 c1max1.5 c2min0 c2max1.5 ngen500
可行解的更新通过粒子的移动来完成,则第i个粒子在维度d下第k+1次迭代后的位置为[27]
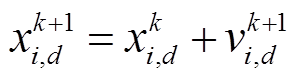 (19)
(19)
式中,v为粒子群的速度,可以表示为[27]
 (20)
(20)
式中,m为惯性权重;r1和r2为[0,1]范围内的随机数,以增加搜索的随机性;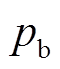 为粒子i的历史最佳位置;
为粒子i的历史最佳位置;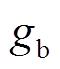 为整个粒子群的历史最佳位置。粒子的移动向量由三个部分组成:粒子个体原本移动方向、个体当前位置与历史最佳位置差值、个体当前位置与种群最佳位置差值。PSO算法粒子移动规则如图10所示。
为整个粒子群的历史最佳位置。粒子的移动向量由三个部分组成:粒子个体原本移动方向、个体当前位置与历史最佳位置差值、个体当前位置与种群最佳位置差值。PSO算法粒子移动规则如图10所示。
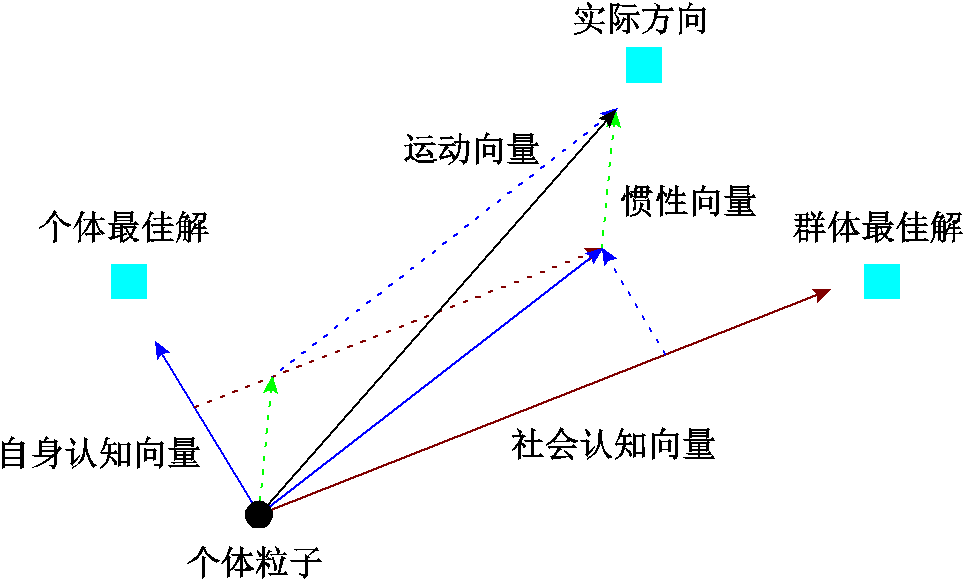
图10 PSO算法粒子移动规则
Fig.10 Particle moving rules of PSO
PSO算法中通过粒子适应度来衡量解的优劣,定义粒子适应度函数为
式中,下标pso代表将粒子群算法的最优结果代入式(10)与式(11)获得的计算值;下标test代表FDS实测值;s为FDS的测试频点数。
基于式(14)与式(15),使用不同恒定温度下的FDS数据可以反演出H-N模型中对应的5个参数值,见表4。
由于需要校正的时变温度在30~90℃,采用三次样条插值函数构造H-N模型各参数与温度的准确关系。
表4 不同温度下H-N模型参数
Tab.4 H-N model parameters at different temperatures

T/℃ese¥tab 301.1410.987382.810.5540.191 401.5711.037115.120.7880.386 502.7410.98137.470.7760.522 603.3651.00313.050.8320.499 705.5220.9874.830.9650.435 809.872 20.9711.890.7250.635 9012.9010.9730.780.9510.477
在此基础上,将以上参数替换为温度的函数代入式(10)和式(11)中求解等效温度。由于式(16)无法表示为显式的表达式,且已知数据多于待求解参数个数,故本文采用最小二乘法进行等效温度的求解。
最小二乘法是一种数学优化技术。它通过最小化误差的二次方和来寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得H-N模型的未知参数,并使得这些参数与实际数据之间的误差的二次方和最小。但最小二乘法严重依赖初始值,初始值的选取会对最终的结果造成很大的影响[28]。为此,通过式(8)将仿真得到的绝缘内部温度作为最小二乘法的初值可以保证计算结果的准确性。时变温度校正的流程如图11所示。
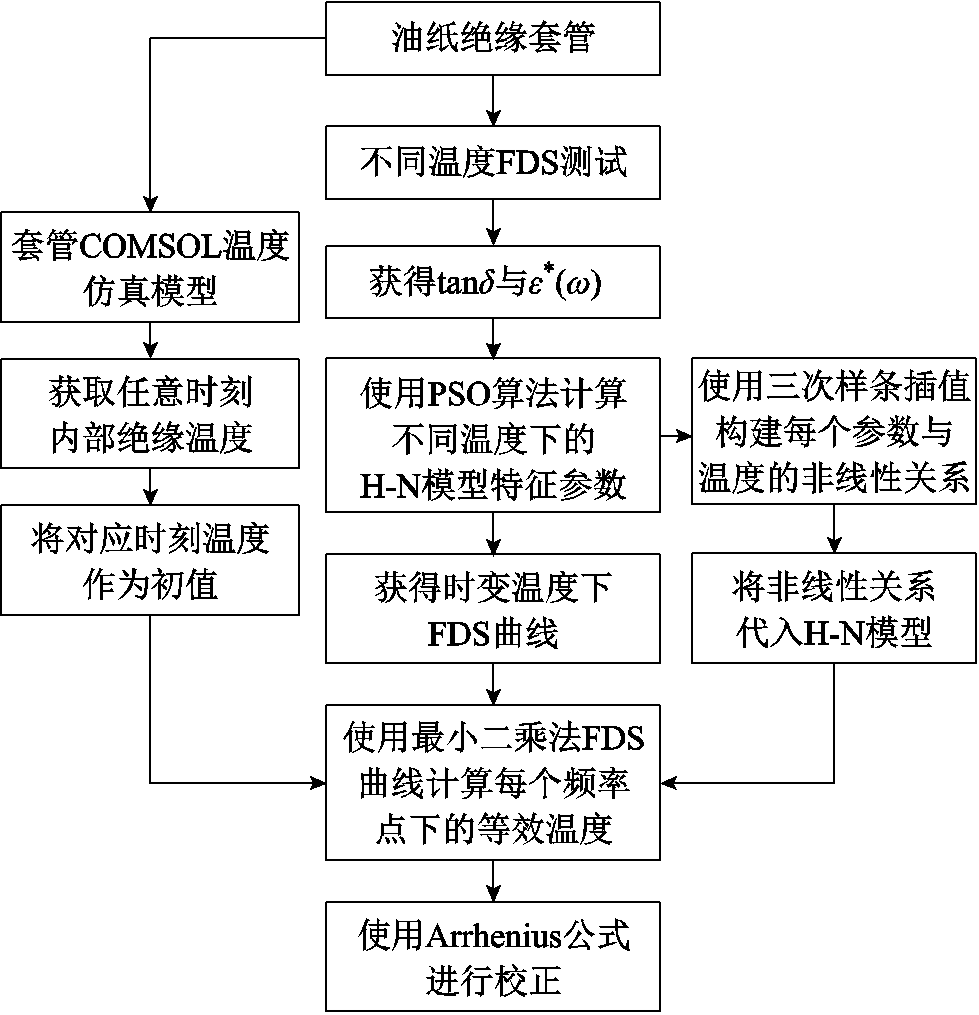
图11 时变温度FDS曲线校正流程
Fig.11 The flow chart of time-varying temperature FDS curves correction
为验证时变温度FDS曲线校正方法的准确性,在实验室内对油纸绝缘套管进行了时变温度下FDS曲线测量。
由于实验过程无法获取套管电容芯子内部温度,故选择更易测量的套管油温与仿真数据进行对比。实验中,首先将套管放置于恒温恒湿箱中升温至85℃并稳定5h;之后立刻取出套管进行FDS测试,并将T型热电偶布置于变压器油中,散热总时长为200min,监测散热过程中套管的温度变化。时变温度实验布置图如图12所示。

图12 时变温度实验布置图
Fig.12 Layout of time-varying temperature experiment
套管油温随时间变化的实验曲线与仿真曲线对比如图13所示。可以看出,仿真曲线和实验曲线的形状与对应数值基本相同,相对误差小于6%,由此验证了仿真模型及套管散热特性的准确性。此外,随着散热时间的增加,实验与仿真所得温度并非以恒定速率下降,而是呈现指数下降趋势,最高温度为起始温度,最低温度为环境温度,散热速率呈现由快变慢的趋势。

图13 油温的实验曲线与仿真曲线对比
Fig.13 Comparison between experimental curve and simulation curve of oil temperature
实验过程中,套管散热总时长为200min,分别测试套管在25~76min(Case1)、84~135min(Case2)与143~194min(Case3)的时变温度FDS曲线,如图14所示。
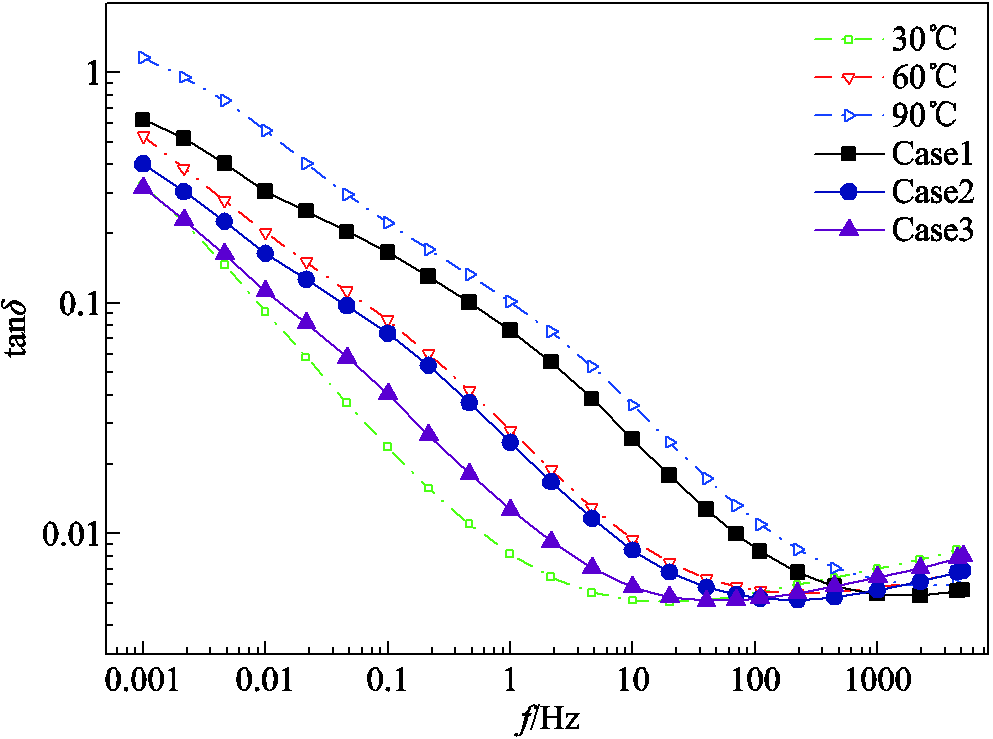
图14 时变温度条件下FDS曲线
Fig.14 FDS curves under time-varying temperature
由图14可以看出,中高频部分(0.1Hz~5kHz)的测试结果与恒定温度曲线基本一致。随着测试温度降低,三种情况下小于0.1Hz的FDS曲线出现了向下偏移的趋势,相较于恒定温度曲线数据差别较大。这是由于频率较高时所对应的频点FDS测试周期较短,温差变化小,tand值与恒温下的测量值接近。随着测试频率降低,对应频点下电场变化周期逐渐变长,在FDS低频段套管绝缘温度呈指数规律下降,tand值发生向下偏移。
为了将三种情况下的时变温度曲线校准到任意恒定基准温度,基于式(16)使用LS法可以计算得到低频段(1mHz~0.1Hz)下每个频点的等效温度,其中LS方法中使用的初始温度可以根据由式(8)获得。每个频点下的等效温度见表5。
表5 时变温度条件下每个频点的等效温度
Tab.5 The equivalent temperature of each frequency point under time-varying temperature conditions

f/Hz等效温度/℃ Case1Case2Case3 0.00166.2850.8537.61 0.00268.5253.5338.54 0.00570.5154.2140.61 0.01071.8355.6142.21 0.02275.7457.1543.89 0.04678.4858.3144.45 0.10080.2859.1444.59
本文以30℃、60℃、90℃为基准温度,基于式(17)对三种情况下的时变温度曲线进行校正,其中活化能采用经验值0.98eV[29]。校正结果与FDS测试结果对比如图15所示。由图15可以看出,相比于30℃、60℃、90℃参考温度条件下的测试结果,时变温度条件下的测试结果在低频部分发生畸变,曲线呈现向下偏移趋势;三种情况下校正的结果与参考温度30℃、60℃、90℃下测试的结果基本一致,曲线重合程度较好,验证了校正模型的准确性。

图15 时变温度条件下曲线校正结果
Fig.15 Curve correction results under time-varying temperature
因此,可以得出结论:根据所提出的校正方法能够有效地修正时变温度条件下的测试结果,由此实现时变温度下电力设备绝缘状态的准确评估。
本文以消除测试温度变化对套管绝缘状态评估的影响为目标,构建了时变温度条件下FDS曲线校正方法,研究分析了套管内部绝缘的温度分布规律,通过PSO算法对不同恒定温度下的H-N模型参数进行了反演,进而求解出时变温度条件下每个频点对应的等效温度,实现了FDS曲线的校正。本文主要得到以下结论:
1)随着散热时间的增加,套管内部绝缘温度并非以恒定速率下降,而是呈现指数下降趋势,散热速率由快变慢。
2)利用PSO-LS算法获得了H-N模型参数与温度的关系,并基于此构建了时变温度下不同频点的等效温度计算模型。
3)实验表明,套管油温随时间变化的温度曲线与仿真曲线的误差小于6%,验证了仿真的准确性。时变温度条件下,FDS中高频段(0.1Hz~5kHz)测试结果与参考温度曲线一致。随着测试温度的降低,FDS低频段(1mHz~0.1Hz)曲线出现了向下偏移的趋势,相较于恒定温度曲线差别增大。
本文提出的曲线校正方法能够有效地修正时变温度条件下的测试结果,具有较高的工程应用价值。
参考文献
[1] 杨峰, 唐超, 周渠, 等. 基于等效电路的油纸绝缘系统受潮状态分析[J]. 电工技术学报, 2020, 35(21): 4586-4596.
Yang Feng, Tang Chao, Zhou Qu, et al. Analyzing the moisture state of oil-paper insulation system using an equivalent circuital model[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4586-4596.
[2] 范贤浩, 刘捷丰, 张镱议, 等. 融合频域介电谱及支持向量机的变压器油浸纸绝缘老化状态评估[J]. 电工技术学报, 2021, 36(10): 2161-2168.
Fan Xianhao, Liu Jiefeng, Zhang Yiyi, et al. Aging evaluation of transformer oil-immersed insulation combining frequency domain spectroscopy and support vector machine[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2161-2168.
[3] 邓映鑫, 杨丽君, 燕飞东, 等. 受潮油纸绝缘的非线性介电响应特性及H-W模型在时-频转换中的应用[J]. 电工技术学报, 2020, 35(21): 4609-4619.
Deng Yingxin, Yang Lijun, Yan Feidong, et al. Nonlinear dielectric response characteristics of damp oil-impregnated pressboard insulation and application of H-W model in time-frequency conversion[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4609-4619.
[4] Yao Huanmin, Mu Haibao, Ding Ning, et al. Evaluation method for moisture content of oil-paper insulation based on segmented frequency domain spectroscopy: from curve fitting to machine learning[J]. IET Science, Measurement & Technology, 2021, 15(6): 517-526.
[5] Bandara K, Ekanayake C, Saha T K. Analysis of frequency domain dielectric response of pressboard insulation impregnated with different insulating liquids[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2016, 23(4): 2042-2050.
[6] Zhang Daning, Yun Hao, Zhan Jiangyang, et al. Insulation condition diagnosis of oil-immersed paper insulation based on non-linear frequency-domain dielectric response[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2018, 25(5): 1980-1988.
[7] Gutten M, Korenciak D, Brncal P, et al. Frequency diagnostics of insulating system of power transformers[J]. Electrical, Control and Communication Engineering, 2020, 16(1): 1-7.
[8] Chakravorti S, Dey D, Chatterjee B. recent trends in the condition monitoring of transformers[M]. London: Springer London, 2013.
[9] Fofana I, Hemmatjou H, Meghnefi F, et al. On the frequency domain dielectric response of oil-paper insulation at low temperatures[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2010, 17(3): 799-807.
[10] Zukowski P, Rogalski P, Koltunowicz T N, et al. Influence of temperature on phase shift angle and admittance of moistened composite of cellulose and insulating oil[J]. Measurement, 2021, 185: 110041.
[11] Wang Dongyang, Zhou Lijun, Wang Lujia, et al. Frequency domain dielectric response of oil gap in time-varying temperature conditions[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(2): 964-973.
[12] Liu Jiefeng, Fan Xianhao, Zhang Yiyi, et al. Frequency domain spectroscopy prediction of oil-immersed cellulose insulation under diverse temperature and moisture[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2020, 27(6): 1820-1828.
[13] 冀田. 油纸电容式套管电场及温度场分析[D]. 沈阳: 沈阳工业大学, 2015.
[14] Montsinger V M. Loading transformers by temperature[J]. Transactions of the American Institute of Electrical Engineers, 1930, 49(2): 776-790.
[15] 王青于, 杨熙, 彭宗仁, 等. 应用三维电磁–热–流耦合场分析法计算换流变压器干式套管的温度场分布[J]. 中国电机工程学报, 2016, 36(22): 6269-6275.
Wang Qingyu, Yang Xi, Peng Zongren, et al. 3D coupled electromagnetic-thermal-fluid method for computation of temperature field of converter transformer RIP bushings[J]. Proceedings of the CSEE, 2016, 36(22): 6269-6275.
[16] Bergman T L, Incropera F P, DeWitt D P, et al. Fundamentals of heat and mass transfer[M]. 7th ed. Hoboken, NJ: John Wiley, 2011
[17] 周利军, 李先浪, 王东阳, 等. 基于Havriliak–Negami介电弛豫模型的油纸绝缘状态评估[J]. 高电压技术, 2016, 42(1): 153-162.
Zhou Lijun, Li Xianlang, Wang Dongyang, et al. Status assessment of oil-paper insulation based on Havriliak Negami dielectric relaxation model[J]. High Voltage Engineering, 2016, 42(1): 153-162.
[18] Shan Zhiduo, Chen Qingguo, Fu Qiang. Analysis of dielectric response of epoxy-mica insulation with temperature normalization[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2020, 27(2): 574-580.
[19] Dong Ming, Ren Ming, Wen Fuxin, et al. Explanation and analysis of oil-paper insulation based on frequency-domain dielectric spectroscopy[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2015, 22(5): 2684-2693.
[20] Scaife B K P. Principles of dielectrics[M]. New York: Oxford University Press, 1989.
[21] 赵孔双. 介电谱方法及应用[M]. 北京: 化学工业出版社, 2008.
[22] 王力衡. 介质的热刺激理论及其应用[M]. 北京: 科学出版社, 1988.
[23] Shroff D H, Stannett A W. A review of paper aging in power transformers[J]. IEE Proceedings C (Generation,Transmission and Distribution), 1985, 132(6): 312-319.
[24] 胡一卓, 董明, 谢佳成, 等. 空间电荷引起的油纸绝缘低频弛豫现象研究[J]. 中国电机工程学报, 2020, 40(6): 2026-2038.
Hu Yizhuo, Dong Ming, Xie Jiacheng, et al. Study of low frequency domain relaxation of oil-paper insulation caused by space charge[J]. Proceedings of the CSEE, 2020, 40(6): 2026-2038.
[25] 赵小军, 徐华伟, 刘小娜, 等. 基于PSO-Powell混合算法的软磁复合材料二维矢量磁滞特性模拟[J]. 电工技术学报, 2021, 36(14): 2893-2903.
Zhao Xiaojun, Xu Huawei, Liu Xiaona, et al. Two-dimensional vector hysteresis simulation of soft magnetic composite materials based on the hybrid algorithm of PSO-Powell[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2893-2903.
[26] 任京攀, 马宏伟, 姚明清. 基于粒子群算法的飞轮阵列协调控制策略[J]. 电工技术学报, 2021, 36(增刊1): 381-388.
Ren Jingpan, Ma Hongwei, Yao Mingqing. A coordinated control strategy of flywheel array based on particle swarm optimization algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 381-388.
[27] Clerc M. Particle swarm optimization[M]. London: ISTE, 2006.
[28] de Campos Souza P V. Pruning method in the architecture of extreme learning machines based on partial least squares regression[J]. IEEE Latin America Transactions, 2018, 16(12): 2864-2871.
[29] Emsley A M, Stevens G C. Review of chemical indicators of degradation of cellulosic electrical paper insulation in oil-filled transformers[J]. IEE Proceedings - Science, Measurement and Technology, 1994, 141(5): 324-334.
Abstract In recent years, frequency domain spectroscopy (FDS) has been widely used in the insulation status diagnosis of oil-paper bushing. However, at present, FDS testing can only be realized at steady temperature. The environment under actual working conditions is complex. Especially affected by external factors such as region and climate, the equipment is often in a dynamic cooling process when it is out of service for maintenance. In addition, due to the short “time window” of on-site maintenance, the time for FDS testing is limited. Therefore, it is impossible to conduct dielectric response assessment after the bushing temperature is stabilized, and the obtained FDS curves are quite different from the constant temperature curves. In order to solve these problems, this paper obtains the equivalent temperature of each frequency point of the FDS curves under the condition of time-varying temperature based on Havriliak-Negami (H-N) model, so as to realize FDS curve correction and improve the accuracy of insulation state evaluation.
Firstly, the heat dissipation simulation model was constructed with full consideration of the real structure of the casing. On this basis, the conduction heat dissipation inside the bushing capacitor core, the external convection heat dissipation of the vertical wall and horizontal wall, and the radiation heat dissipation of the outer sheath surface to the environment were studied, and the temperature distribution characteristics of the bushing under different heat dissipation times were obtained. It is found that with the increase of heat dissipation time, the insulation temperature inside the bushing does not decrease at a constant rate, but shows an exponential downward trend, and the heat dissipation rate changes from fast to slow. In addition, the experiment shows that the error between the temperature curve of bushing oil temperature changing with time and the simulation curve is less than 6%, which verifies the accuracy of simulation. Furthermore, the FDS curves of several groups at constant temperature were obtained through testing. H-N relaxation function can accurately describe the relaxation process including interface polarization. Therefore, the nonlinear relationship between the characteristic parameters of the H-N dielectric relaxation model of the constant temperature FDS curves and temperature was inversed by using the particle swarm optimization (PSO) algorithm. Since the equivalent temperature cannot be expressed as an explicit expression, and the known data are more than the number of parameters to be solved, this paper uses the least square method (LS) to calculate the equivalent temperature of each frequency point in the FDS curves under the condition of time-varying temperature. Finally, the Arrhenius formula was used to achieve accurate correction of frequency point by point data under transient temperature.
With 30℃, 60℃ and 90℃ as the reference temperature, the time-varying temperature curves under three different conditions were corrected. The results show that compared with the test results under 30℃, 60℃ and 90℃, the test results under time-varying temperature conditions are distorted in the low frequency part, and the curve shows a downward shift trend. The calibration results under three conditions are basically consistent with the test results under 30℃, 60℃ and 90℃, and the curve overlap well, which verifies the accuracy of the calibration model.
Therefore, it can be concluded that the proposed correction method can effectively correct the test results under time-varying temperature conditions, which is helpful to the accurate evaluation of the insulation status of power equipment.
keywords:Time-varying temperature, frequency domain spectroscopy (PDS), Havriliak-Negami model, particle swarm optimization-least square (PSO-LS) method, insulation state evaluation
DOI:10.19595/j.cnki.1000-6753.tces.211475
中图分类号:TM85
姚欢民 男,1998年生,博士研究生,研究方向为电力设备运行状态监测及绝缘性能提升等。E-mail:yaohuanmin2010@163.com
穆海宝 男,1982年生,副教授,博士生导师,研究方向为电力设备状态检测与评估技术,电气设备绝缘耐电性能提升技术以及微放电等离子体基础与应用技术。E-mail:haibaomu@mail.xjtu.edu.cn(通信作者)
国家自然科学基金青年基金(52107165)、陕西省重点研发计划(2021GXLH-Z-061,2022GY-269)和西安市碑林区科技计划(GX2124)资助项目。
收稿日期 2021-09-15
改稿日期 2021-12-23
(编辑 李冰)