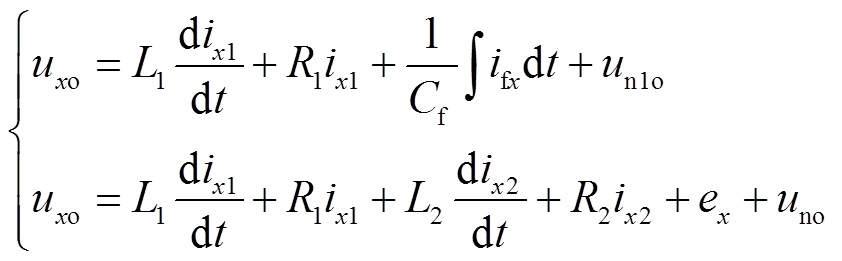（1）
式中，x = a、b、c；uxo为逆变器输出电压；ix1为桥臂电流；ix2为并网电流；ifx为交流电容电流；ex为电网电压；un1o、uno为n1点、n点相对于O点的电压；L1、L2为滤波电感；R1、R2为电路等效电阻。
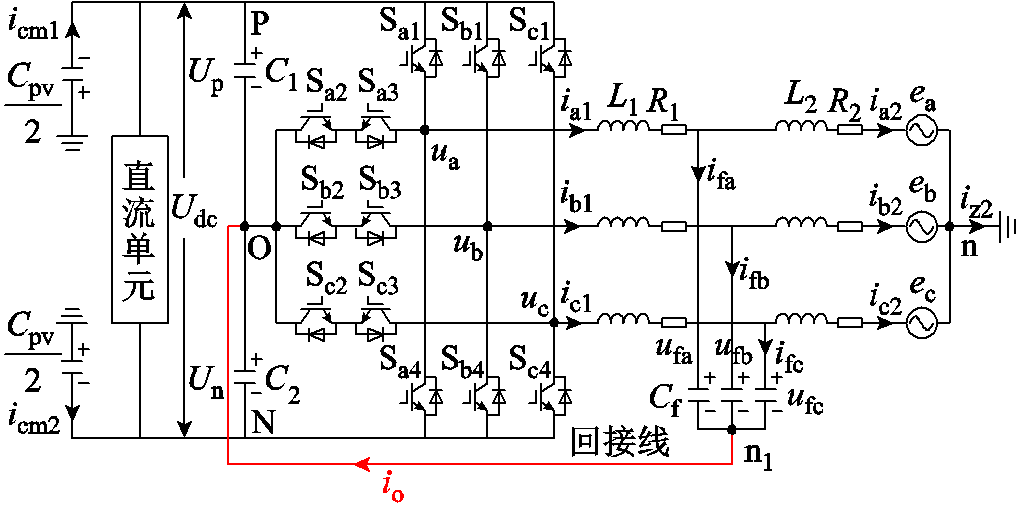
图1 非隔离T型三电平逆变器拓扑
Fig.1 Topology of non-isolated T-type three-level inverter
摘要 三电平逆变器具有损耗小、谐波低等优势，在非隔离型光伏系统中广泛应用。因其常采用中点回接型LCL滤波器抑制漏电流，易引发共模谐振电流，影响并网系统稳定性。为此，该文揭示了共模谐振电流的产生机理，研究了调制策略对共模谐振电流的影响。提出一种自适应3次谐波注入算法，有效降低了共模谐振电流。首先，为保证调制的正确性，推导了3次谐波注入系数的取值范围；然后，根据直流电压和调制度，提出了3次谐波注入系数的自适应律，以提升逆变器系统并网性能；最后，为便于工程应用，降低控制器的计算负担，推导了基于电流闭环控制的3次谐波注入实现方法，该方法计算量小、稳定性好、适用范围广。该方法为3次谐波注入调制算法的应用提供了理论支撑和实现途径，具有较强的工程应用价值。仿真和实验结果证明了不同工况下提出方法的正确性及有效性。
关键词：非隔离型光伏系统 共模谐振电流抑制 自适应3次谐波注入调制 闭环控制算法
随着光伏系统装机容量的不断增加，光伏发电将成为未来电力能源的重要组成部分[1-4]。逆变器作为光伏发电系统中的能量转换单元，将光伏电池板产生的直流电变换为交流电，作用十分关键[5-6]。其中T型三电平非隔离型逆变器因具有体积小、谐波低、效率高等优势，在光伏系统中得到广泛应用[7]。
由于光伏电池板与大地之间存在寄生电容，在非隔离型并网系统中易产生漏电流，危及设备寿命与人身安全[8-12]。为此，通常将LCL滤波器的电容公共点回接至直流母线中点（本文称作：中点回接型LCL滤波器）[13]。该漏电流抑制方法具有结构简单、成本低等优势，但却极易引发共模谐振电流，引起桥臂电流振荡，并网系统失稳。因此研究共模谐振电流抑制方法意义重大[14-15]。传统的增加阻尼电阻的谐振抑制方法，使系统损耗增加并降低了滤波器滤波性能[16]。文献[14-15]分别提出共模差模解耦的输出滤波器方案和零序电流闭环控制方案以抑制共模谐振电流，保证系统稳定。然而，上述方法或滤波器设计复杂，或需增加额外的控制器，系统设计与稳定性分析复杂。
另一方面，调制策略的选择直接影响LCL滤波器中共模电压的频谱特性，进而影响共模谐振电流。在光伏系统中，为提高直流电压利用率以保证高发电量，通常采用零序电压注入调制（Zero Sequence Voltage Injection Modulation, ZSVIM）方法[17-19]。通过在正弦调制波中注入特定的零序电压可以等效实现多种调制策略，工程应用中常见的有：空间矢量调制（Space Vector Pulse Width Modulation，SVPWM）策略、鞍形波调制（Saddle Pulse Width Modulation, SAPWM）策略以及三次谐波注入调制（Third Harmonic Injection Pulse Width Modulation, THIPWM）策略[20-24]。此外，为了满足其他性能要求，国内外学者还研究了其他形式的零序电压注入方法。例如，文献[25-26]研究了断续脉宽调制（Discontinuous Pulse Width Modulation, DPWM）策略，该策略通过在一定时间内保持开关管不动作以降低开关损耗，提高逆变器效率。文献[27-28]通过注入某种零序电压实现低共模调制以抑制漏电流，但该类方法舍弃了部分电压矢量。上述调制方法虽然可以实现某种特定的功能，但由于长时间保持开关管不动作或舍弃部分矢量，并网电流波形质量较低。因此，本文主要对比分析工程中常用的SVPWM、SAPWM和THIPWM策略。
在SVPWM策略与SAPWM策略中，注入零序电压是根据三相调制波的瞬时值计算获得，计算简单，但其共模电压谐波含量高，在基于中点回接型LCL滤波器的逆变器中影响桥臂输出电流波形质量，导致逆变器并网电流控制精度差。采用THIPWM策略时共模电压谐波含量低，有利于减小谐振电流，提高逆变器输出波形质量。但该策略需通过获取三相调制波的幅值与相位信息确定零序电压值，计算量大，且相位信息易受噪声干扰。因此，研究工程上简单易用且稳定性好的3次谐波注入实现算法十分重要。
此外，THIPWM策略的3次谐波注入系数没有确定的计算方法，而如何选定该参数至关重要，选取不当易引起脉宽调制失效，造成系统失稳。文献[29-32]中指出：3次谐波注入系数可选用1/4、1/6等，也可选用与系统控制器参数或电气参数相关的可变系数。不同的3次谐波注入系数对系统的直流电压利用率、效率等性能影响不同，但目前尚未见中点回接型LCL滤波器的逆变器中关于研究3次谐波注入系数选取的报道。
为此，本文基于中点回接型三电平逆变器数学模型，揭示了共模谐振电流产生机理，研究了三种调制策略对共模谐振电流的影响，进而提出一种自适应3次谐波注入算法。该方法不仅能有效抑制共模谐振电流，保证系统安全稳定运行；还能根据直流电压及调制度自适应调整3次谐波注入系数，进一步提高并网变换器性能。此外，本文推导了所提算法在电流闭环控制策略下的实现方法，以方便工程应用。最后，仿真和实验验证了所提方法的正确性及有效性。
T型三电平非隔离光伏并网逆变器的拓扑结构如图1所示，其采用了中点回接型LCL滤波器以抑制漏电流。以O点为参考点，每相桥臂可以输出正电平（P）、零电平（O）和负电平（N）三种状态。
根据基尔霍夫电压定律，建立逆变器数学模型
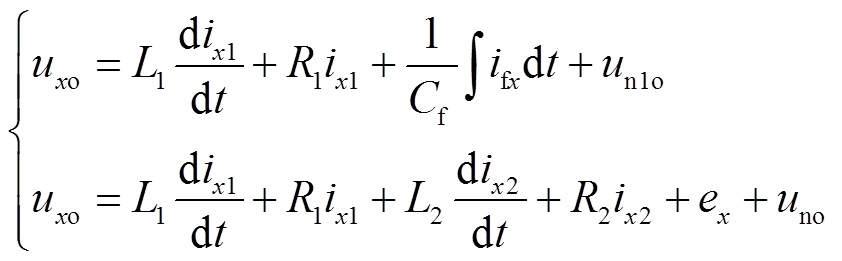（1）
式中，x = a、b、c；uxo为逆变器输出电压；ix1为桥臂电流；ix2为并网电流；ifx为交流电容电流；ex为电网电压；un1o、uno为n1点、n点相对于O点的电压；L1、L2为滤波电感；R1、R2为电路等效电阻。
图1 非隔离T型三电平逆变器拓扑
Fig.1 Topology of non-isolated T-type three-level inverter
将三相数学模型相加，可得到逆变器共模回路的数学模型为
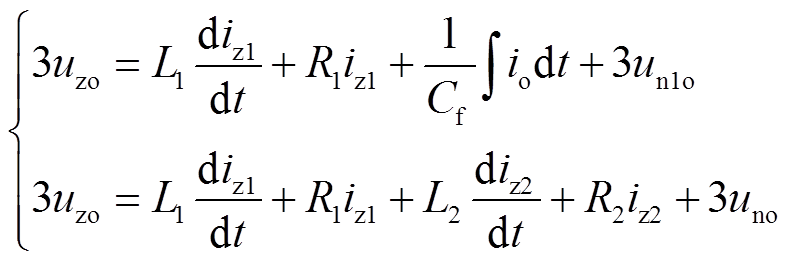（2）
式中，uzo为逆变器输出共模电压，uzo=(ua1+ub1+uc1)/3；iz1为桥臂共模电流，iz1=ia1+ib1+ic1；iz2为系统漏电流，iz2=ia2+ib2+ic2；io为回接线电流，io=ifa+ifb+ifc。
光伏电池板的正负极对大地存在寄生电容，逆变器运行时通过该寄生电容产生系统漏电流，根据基尔霍夫电压定律得
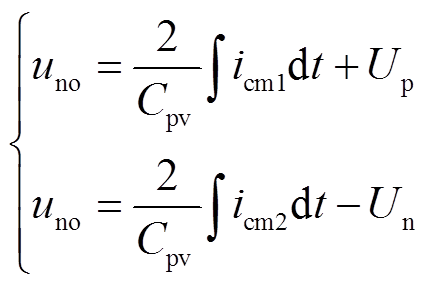（3）
将式（3）相加并考虑到iz2=icm1+icm2，得
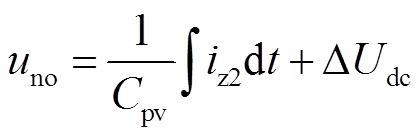（4）
式中，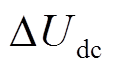
为直流中点电位偏移电压，ΔUdc=(Up−Un)/2。
综合上述分析得到图2所示的系统共模等效电路。当采用传统型LCL滤波器时，n1点与O点无导线连接，io = 0，iz1 = iz2，此时系统仅有一条共模电流路径，如图2a所示。当采用回接型LCL滤波器时，n1点与O点连接，un1o = 0，其共模等效电路如图2b所示。对比图2a、图2b可以看出，回接型LCL滤波器在共模回路中增加了一条低阻抗容性共模电流路径，因此可有效抑制高频漏电流。
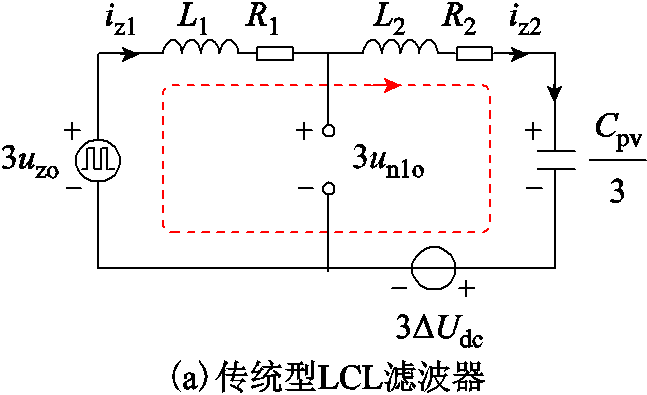
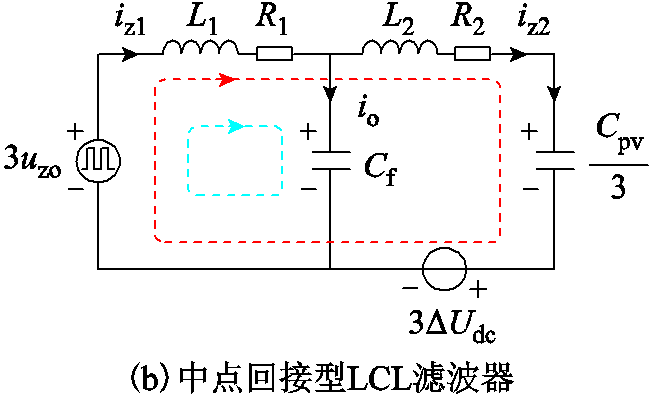
图2 两种滤波器连接方式下的共模等效电路
Fig.2 Common-mode equivalent circuit with two filter-connection types
然而，由于增加了并联支路Cf，回接型LCL滤波器共模回路的等效阻抗降低，在相同共模电压的激励下，其共模电流iz1必然要增大。同时，由于回路等效电阻R1通常很小，基于中点回接型LCL滤波器的共模回路存在共模电流谐振的风险，其共模谐振频率可近似表示为[15]
（5）
以额定功率为20kW的逆变器为例，逆变侧滤波电感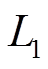
选为500μH，滤波电容
选为4.7μF，则其共模谐振频率
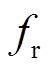在3.2kHz附近。
图2中，共模回路由共模电压uzo、中点偏移电压ΔUdc和RLC阻抗网络组成。其中，ΔUdc 可通过中点平衡控制算法予以有效抑制，而uzo为高频开关量，是产生共模谐振电流的主要激励源。共模电压uzo的特性由调制策略决定，故本文从调制的角度研究共模谐振电流抑制方法。
如前所述，改善激励源谐波特性是抑制共模电流谐振的有效手段。共模激励源特性由调制策略决定，为此，本节分析三种调制策略对共模激励源的影响。其中，三相正弦调制波可表示为
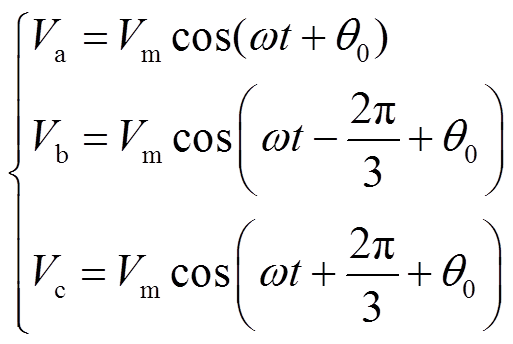（6）
式中，Vm为正弦调制波幅值；ω为正弦调制波角频率；θ0为正弦调制波初始相位。
正弦调制波幅值Vm与调制度m的关系为
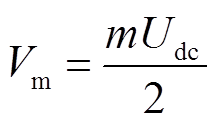（7）
通过向正弦调制波中注入特定零序电压可以实现多种性能指标，下面分析工程中三种常用调制策略的零序电压注入方法。
（1）SVPWM策略的原理是按照最近三矢量原则进行参考矢量合成，并保证冗余矢量的作用时间相同，其等效注入的零序电压可表示为[33]
（8）
式中，x=a、b、c；kx为中间变量。当Vx≥0时，kx=0；当Vx＜0时，kx=Udc/2。
（2）SAPWM策略的本质是保证三相正弦调制波最大值至Udc/2的距离等于其最小值至−Udc/2的距离，故注入的零序电压被唯一确定为[18]
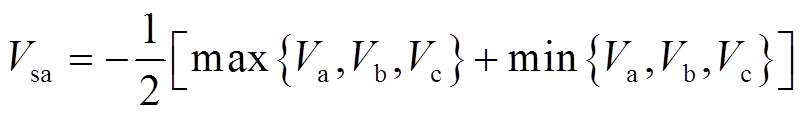（9）
（3）THIPWM策略是在正弦调制波中注入3次正弦电压，注入的零序电压可表示为
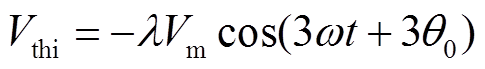（10）
式中，λ为3次谐波注入系数。
图3为上述三种调制策略调制波与零序电压波形，仿真参数Udc=600V，m=1，λ=1/6。可以看出，三种调制策略注入的零序电压形状不同，其对共模回路的影响也必然不同。
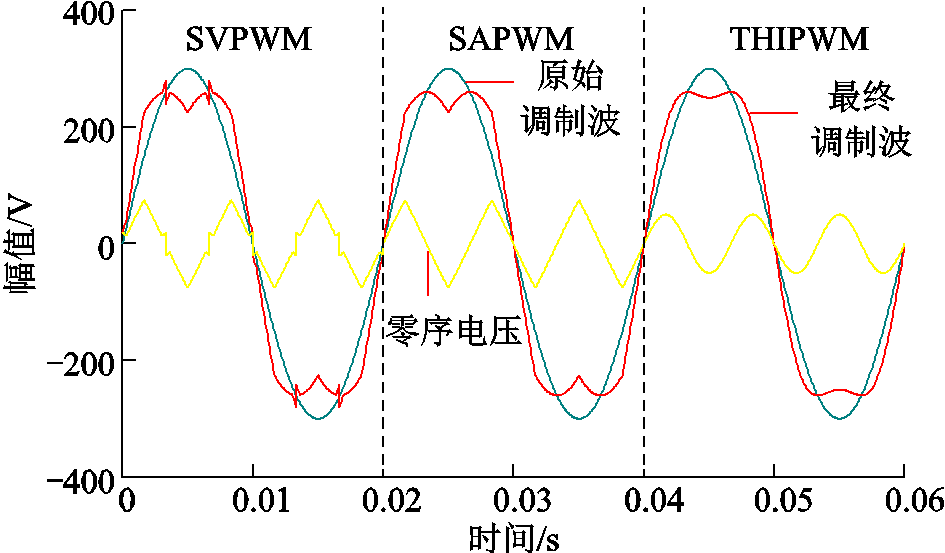
图3 三种调制策略调制波与零序电压波形
Fig.3 Modulation waveforms and zero-sequence voltages of three modulation strategies
图4给出了Udc=600V时三种调制策略共模电压频谱特性的仿真结果，Udc=600V和Udc=760V时的仿真数值结果见表1。其中，λ根据后文所提出的自适应律计算，其他仿真参数见表2。
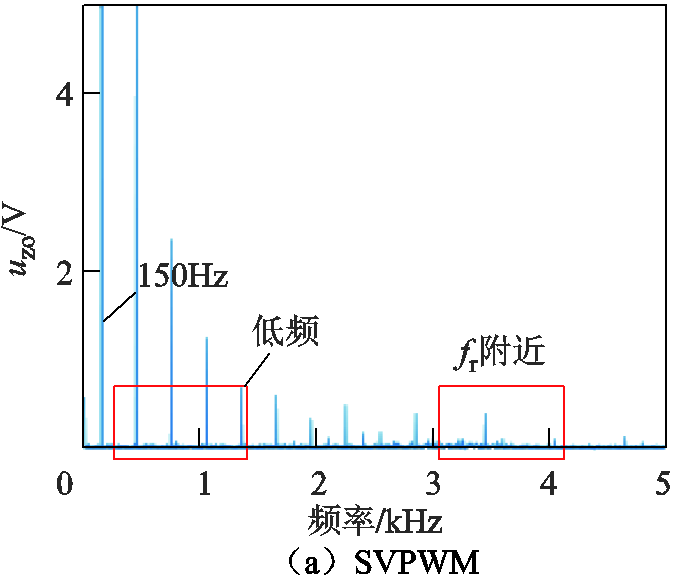
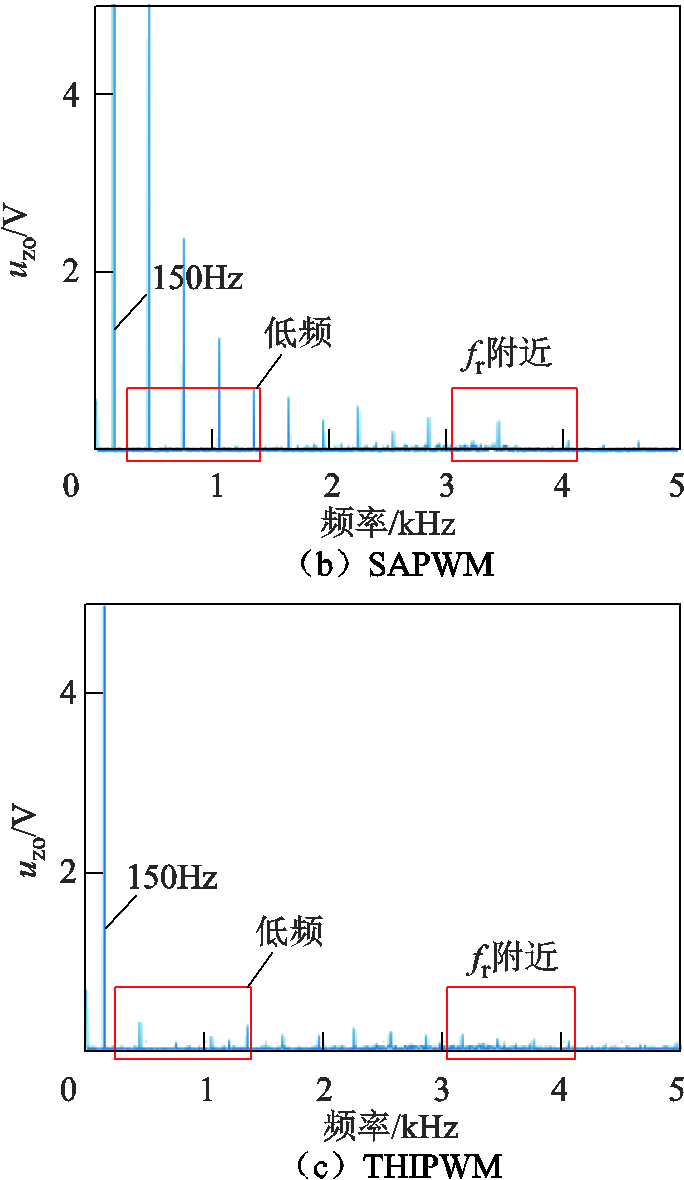
图4 Udc=600V时三种调制策略共模电压FFT分析
Fig.4 FFT analysis of common-mode voltages under three modulation strategies when Udc=600V
表1 三种调制策略共模电压频谱特性
Tab.1 Frequency spectrum characteristic of common-mode voltage
直流电压/V调制策略电压有效值/V 150Hz低频(f≤2kHz)fr附近(3.2kHz≤f≤3.8kHz) 600SVPWM4850.426 SAPWM4850.391 THIPWM380.460.276 760SVPWM49112.106 SAPWM4850.729 THIPWM290.480.439
根据图4和表1的仿真结果可知，基于SVPWM策略的共模电压谐波含量最高，SAPWM策略次之，THIPWM策略最低。在谐振频率fr附近，Udc=600V时三种策略共模电压有效值分别为0.426V、0.391V和0.276V，Udc=760V时则分别为2.106V、0.729V和0.439V。fr附近的共模电压易引发共模谐振电流，因此THIPWM策略的谐振抑制效果最好。
表2 仿真与实验参数
Tab.2 Simulation and experimental parameters
参数数值 额定输出功率P/kW20 电网电压有效值Erms/V230 电网电压频率fg/Hz50 直流母线电压Udc/V600/680/760 直流母线支撑电容C1,C2/μF1 630 开关频率fs/kHz16 控制频率fc/kHz16 逆变器侧初始电感L1/μH500 电网侧初始电感L2/μH50 交流滤波电容Cf/μF4.7
在低频附近，Udc=600V时三种策略共模电压有效值分别为5V、5V和0.46V，Udc=760V时则分别为11V、5V和0.48V。此外，还可以看出THIPWM策略在150Hz处的有效值也最低。低频共模电压在回路中将产生低频共模电流，增加系统损耗[14]。另一方面，由于逆变器实际控制系统中存在电流采样延时与误差，当较高的低频共模电流叠加到差模电流时，采样误差会降低差模电流的控制精度。显然，THIPWM策略的低频共模电压含量最低，其低频共模电流最小，有利于提高并网电流质量。
总之，基于上述分析可知，THIPWM策略不仅能有效抑制共模谐振电流，还能有效降低低频共模电流，进而提高并网电流性能。
3次谐波注入调制策略中，注入系数λ决定了该调制策略的调制性能，其合理选值十分关键。脉宽调制需保证调制波幅值不大于载波幅值，否则将引起调制失效。当注入系数选取较小、调制度较高时易出现上述调制失效问题；注入系数选取较大时则会使共模电流低频分量增加。
为得到合理的3次谐波注入系数，本节首先根据调制原理约束，通过数学推导确定注入系数λ的取值范围。在此基础上，提出3次谐波注入系数的自适应律，其兼顾了直流电压利用率与低频共模电流指标。
首先，为简化算法推导且不失一般性，假设初始相位θ0=0°，此时，注入3次谐波后的调制波为
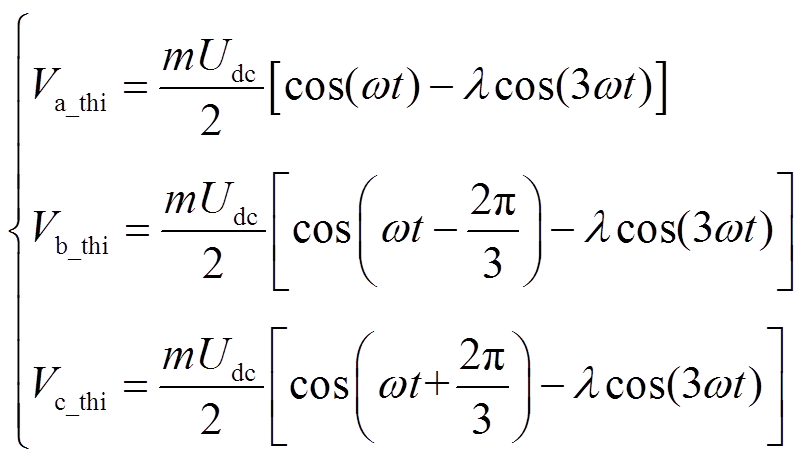（11）
式中，Va_thi、Vb_thi、Vc_thi为注入3次谐波后的三相调制波。
为保证调制策略有效，需要限制调制波Va_thi、Vb_thi、Vc_thi的幅值不大于Udc/2，即
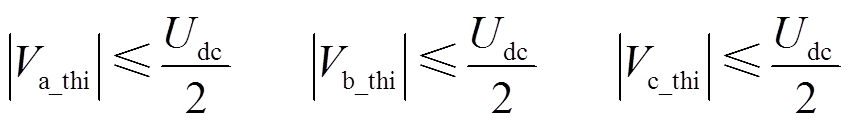（12）
根据三相对称性与正负对称性，仅需分析A相调制波的最大值情况。由函数极值点求解理论，当在某点t使调制波Va_thi的一阶导数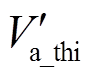
=0，二阶导数
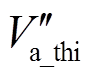＜0时，该点是极大值点。为此，分别求出Va_thi的一阶导数和二阶导数，即
（13）
（14）
由于正弦波的周期性特点，同时考虑到注入系数λ的取值不宜过大，限定−π/2≤ωt≤π/2，0≤λ＜1/3。令Va_thi的一阶导数等于零并利用三角函数公式进行化简可得
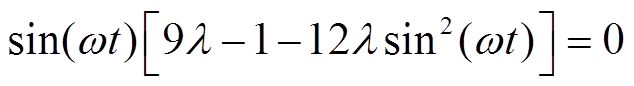（15）
欲使等式（15）成立，需满足条件sin(ωt)=0或9λ−1−12λsin2(ωt)=0，现分别讨论如下。
（1）sin(ωt)=0
由限定条件−π/2≤ωt≤π/2可知，此时cos(ωt)=1，将其代入式（14），可得
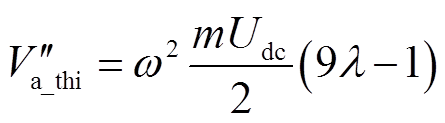（16）
令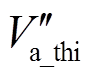＜0，可知当0≤λ＜1/9时，等式sin(ωt)=0对应的t点是Va_thi的极大值点，且其极大值为
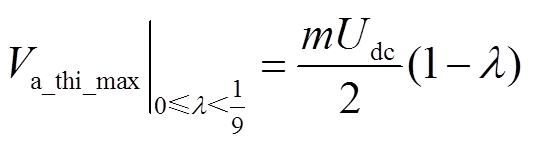（17）
为保证调制算法的有效性，根据式（12）对调制波的要求，得到满足条件的m和λ的约束条件为
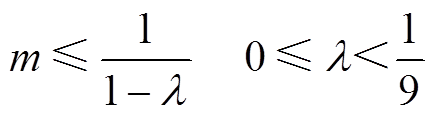（18）
（2）9λ−1−12λsin2(ωt) = 0
此时sin2(ωt)=(9λ−1)/(12λ)，由三角函数公式求得cos2(ωt)=(3λ+1)/(12λ)，再次由限定−π/2≤ωt≤π/2知cos(ωt)≥0，故式（14）可整理为
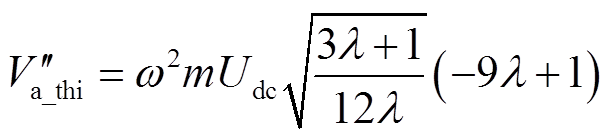（19）
同样地，令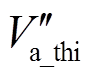＜0，可知当1/9＜λ＜1/3时，等式9λ−1−12λsin2(ωt)=0对应的点是Va_thi的极大值点，其极大值为
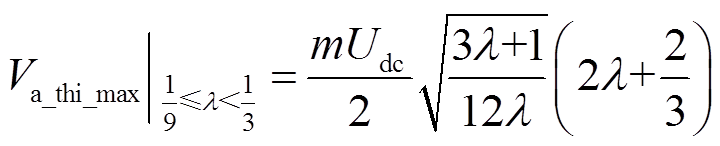（20）
根据式（12）对调制波的要求，同时将λ=1/9纳入讨论，得到此时m和λ应当满足的约束条件为
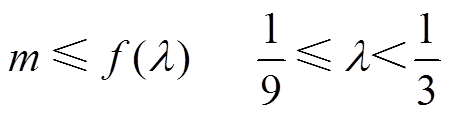（21）
其中，f(λ)的表达式为
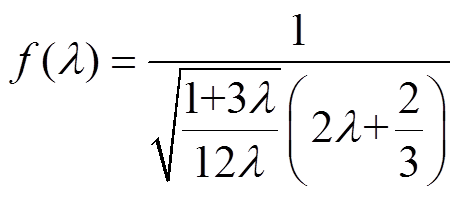（22）
为得到THIPWM策略可达到的最大调制度，在区间1/9≤λ＜1/3上，分别对f(λ)求一阶导数和二阶导数，可得λ=1/6是f(λ)的极大值点，且极大值为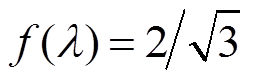
，因此采用3次谐波注入调制策略时，可达到的最大调制度是
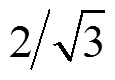，这与SVPWM和SAPWM可达到的最大调制度相同。
综上所述，注入系数λ的取值范围应当满足式（18）与式（21）的约束，由函数m=1/(1−λ)、m=f(λ)及λ预设的最大值确定，如图5所示。其中，当调制度m=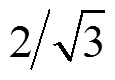时，λ选取为1/6才能保证调制策略在整个工频周期内有效；当调制度m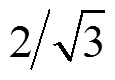＜时，可根据系统需要选取不同的λ值，这为系统控制提供了更多自由度。
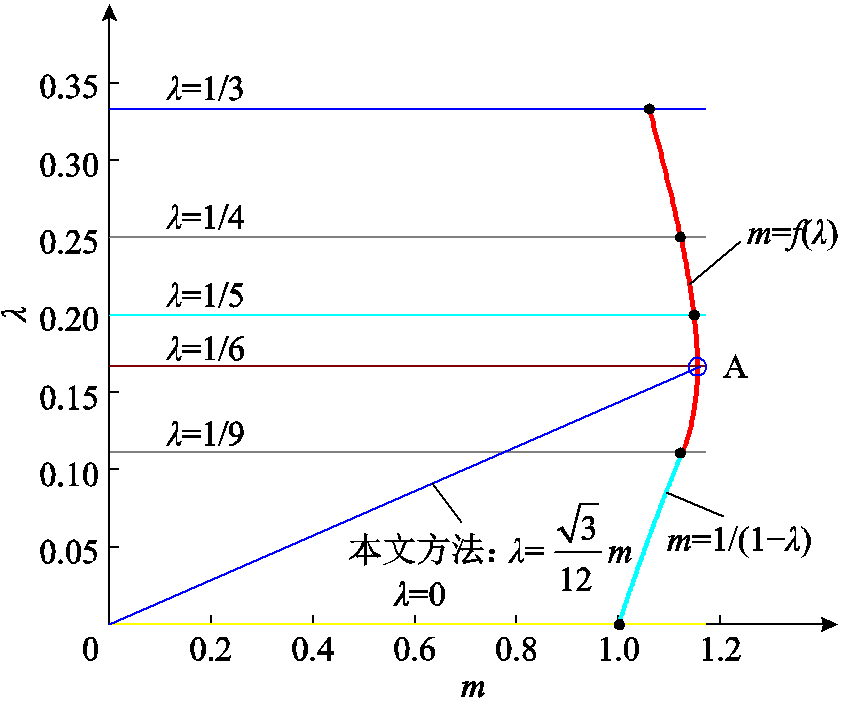
图5 注入系数λ取值范围示意图
Fig.5 Value range diagram of injection coefficient λ
为减小低频共模电流，并保证THIPWM策略注入零序分量的连续性，本文给出3次谐波注入系数的自适应律。注入系数的选取如图5所示。其中，极值点A对应的工况为λ=1/6,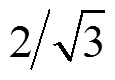。将该点与坐标原点相连，可得本方法注入系数与调制度对应关系，即
（23）
当直流母线电压较低时，为保证较高的电压利用率，提高光伏系统发电量，调制度设置得较高。此时，应将注入系数λ平滑地增大，直至1/6。当直流母线电压较高时，调制度设置得较低。此时，应将注入系数λ平滑地减小以降低低频回接电流。
经过上述分析与理论推导，得到本文所提THIPWM策略的3次谐波为
（24）
式（24）中，根据设定的调制度m、正弦调制波幅值Vm、正弦调制波频率ω以及正弦调制波初始相位θ0，可实时计算3次谐波的瞬时值。
基于自适应3次谐波注入调制策略的闭环控制系统如图6所示，包括直接电流闭环控制部分、自适应3次谐波注入闭环算法部分、中点平衡控制部分和PWM生成部分。这里需要指出的是，电流控制分为间接电流控制与直接电流控制，间接电流控制策略虽简单易实现，但动态响应慢且并网电流的波形质量难以保证。为了解决该问题，山东大学张承慧教授等提出直接电流闭环控制方法[34]，通过引入实际电流反馈，构建电流闭环控制系统，不仅提高了系统的动态性能和电流的波形质量，也提高了系统的鲁棒性。为此，本文电流环采用文献[34]提出的直接电流控制方法，即在同步旋转坐标系下实现桥臂电流闭环控制，控制器输出为Vd和Vq。进一步地，根据本文提出的自适应3次谐波注入调制算法，通过Vd、Vq、Udc和电网锁相环输出θ计算得到调制信号，并与载波进行比较进行PWM。有关自适应3次谐波闭环实现算法的详细阐述见下文。此外，三电平逆变器的中点平衡控制采用文献[15]中的方法。
图6 基于自适应3次谐波注入的并网控制框图
Fig.6 Close-loop control block diagram of the adaptive third harmonic injection
根据Vd、Vq和θ可得到三相原始正弦调制波，其中，A相调制波Va可表示为
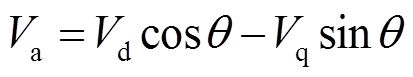（25）
由三角函数公式，可以进一步推得
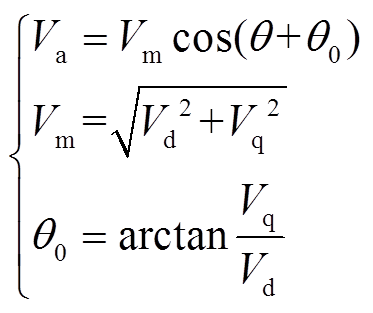（26）
式中，θ0为等效的初始相位，与开环调制波表达式（6）中的含义相同。
然后，为得到自适应3次谐波，根据图5计算注入系数λ，并将式（26）代入式（10），得到精确的3次谐波注入公式为
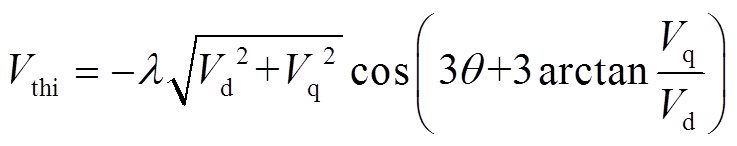（27）
由式（27）可知，实现THIPWM策略需要用到除法函数、三角函数、反三角函数和求根函数等复杂函数计算，占用较多的控制器资源。复杂计算增加了控制延时，难以保证控制实时性，易出现程序运行超时现象，导致系统失稳。此外，初始相位θ0通过对Vq、Vd的比值求反正切获得，Vq、Vd作为电流控制器的输出，其值存在一定波动，导致该方法的实际计算精度有限，易受噪声干扰。因此，需研究易于工程化应用的THIPWM实现方法。
逆变器并网运行时，由于滤波电感L1、L2上的电压较小，因此Vq2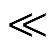
Vm2，进而sin2θ0可近似为零。根据三角函数公式，得到
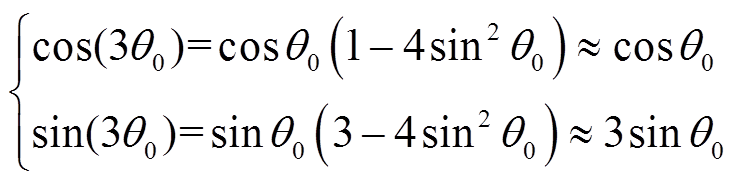（28）
结合式（26）～式（28），得到简化的自适应THIPWM策略的实现方法为
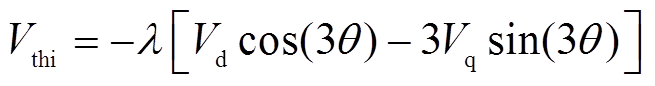（29）
为了进一步说明简化方法的合理性，对逆变器输出无功功率和有功功率的情况进行分析，三种功率因数工况下简化算法合理性分析如图7所示。当仅输出无功功率时，逆变器输出电压矢量Ui与电网电压矢量Ug方向相同，此时sin2θ0=0，简化方法（29）与精确方法（27）等价。当仅输出有功功率时，由于电感电压矢量UL的幅值远小于电网电压矢量Ug的幅值，因此sin2θ0可合理近似为零。
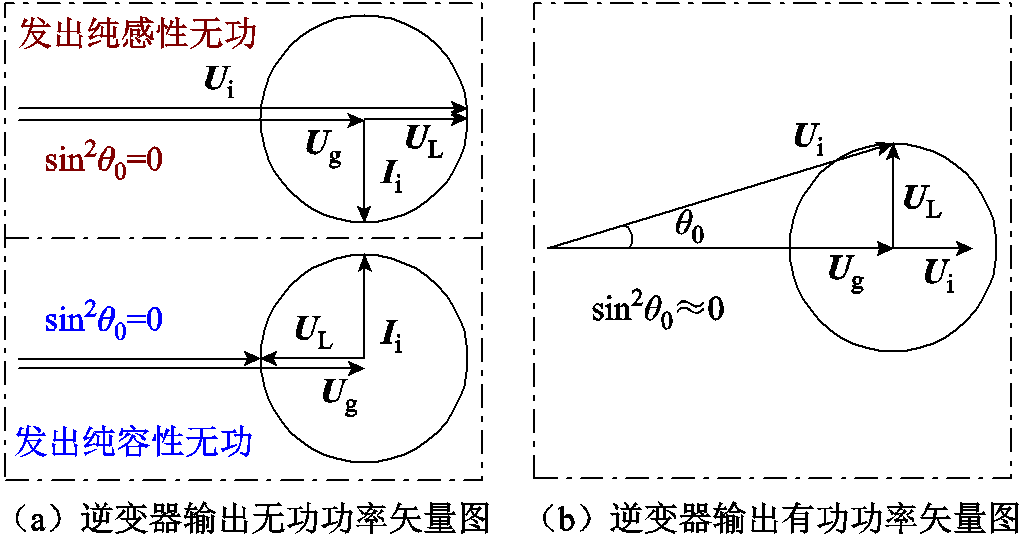
图7 三种功率因数工况下简化算法合理性分析
Fig.7 Rationality analysis of simplified algorithm under three power factor conditions
由式（28）知，三角函数cos(3θ)、sin(3θ)可由电网电压锁相环输出cosθ、sinθ经过乘法运算和加法运算精确求出。对比式（27）和式（29）可以看出，简化后的THIPWM策略避免了耗时的函数运算。由于DSP中乘法运算和加法运算耗时极少，因此该方法能有效降低其计算负担，保证控制算法的实时性。同时式（29）中的相位θ为电网锁相环的输出，其值更加稳定，因此更有利于控制系统稳定，且更加便于工程应用。
为了验证本文提出方法的有效性及分析的正确性，首先用Simulink软件进行仿真验证，然后搭建了一台额定功率20kW的逆变器样机并进行实验验证。仿真和实验参数见表2。
仿真时THIPWM策略的3次谐波计算方法由式（23）和式（29）给出。逆变器仿真运行工况为：功率因数cosφ=1，给定电流有效值iref=29A。
图8为Udc变化时，基于自适应THIPWM策略的仿真波形，包括直流电压、注入系数、零序电压、调制波和桥臂电流。其中，零序电压和调制波通过Udc/2进行了归一化处理。仿真时电网电压保持为230V，当直流电压上升时，调制度降低。
图8 基于自适应THIPWM算法的暂态波形
Fig.8 Transient waveforms of adaptive THIPWM method
由图8可以看出，当直流电压上升引起调制度降低时，注入系数根据调制度的变化自适应平滑降低。此时，归一化零序电压平滑下降，桥臂电流波形质量良好。
为验证不同调制度下提出算法的有效性，图9和图10分别给出了不同直流电压和不同调制策略下的仿真波形。波形包括共模电流iz1和桥臂电流ia1、ib1、ic1的波形以及其对应的FFT分析结果。
图9为Udc=600V时，三种调制策略的仿真波形。可以看出，与SVPWM策略和SAPWM策略的结果相比，基于自适应THIPWM策略的共模电流在低频和谐振频率处含量最低，与理论分析相符。与之相对应的是，基于自适应THIPWM策略的桥臂电流在低频和谐振频率处谐波含量也最低。
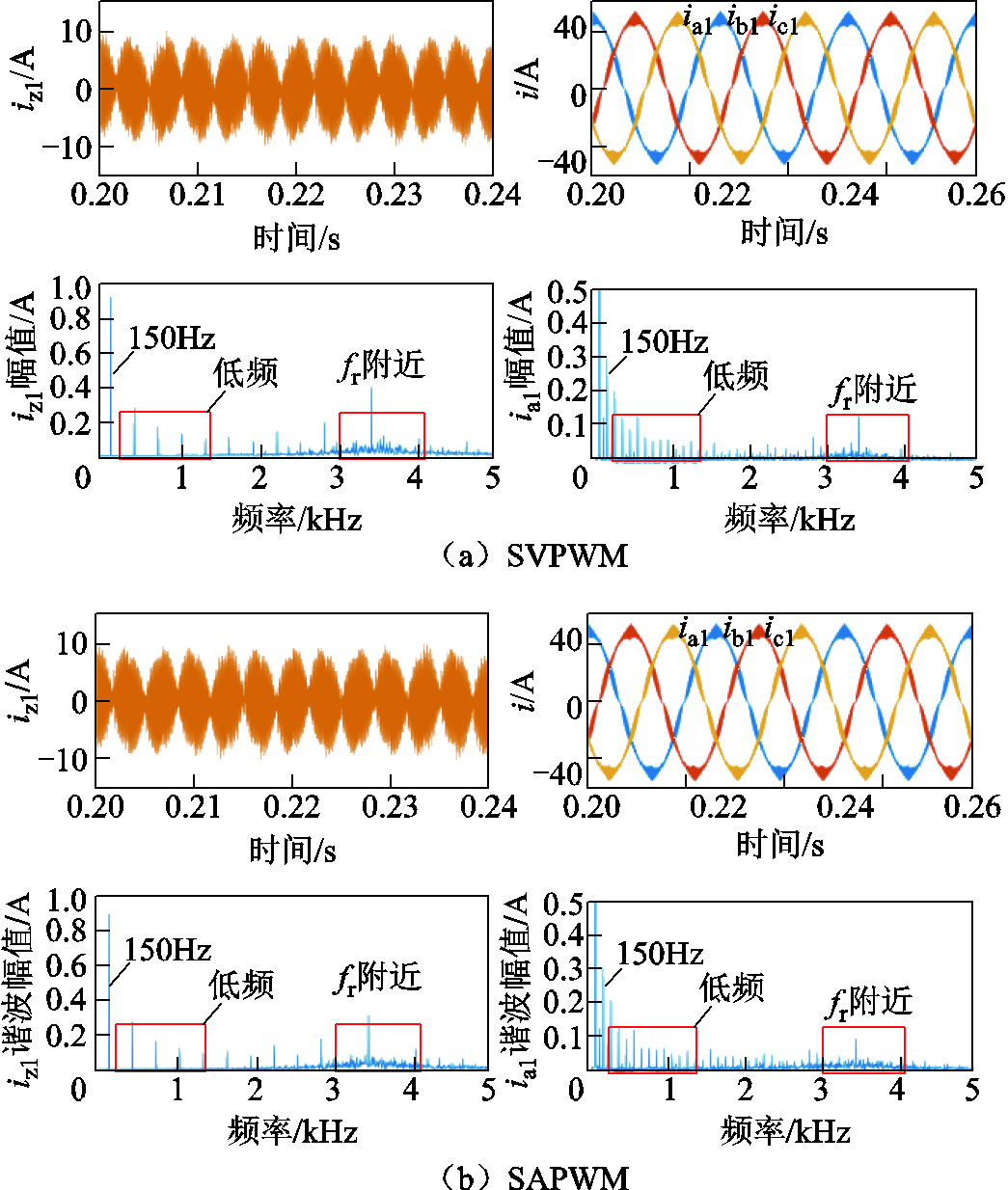
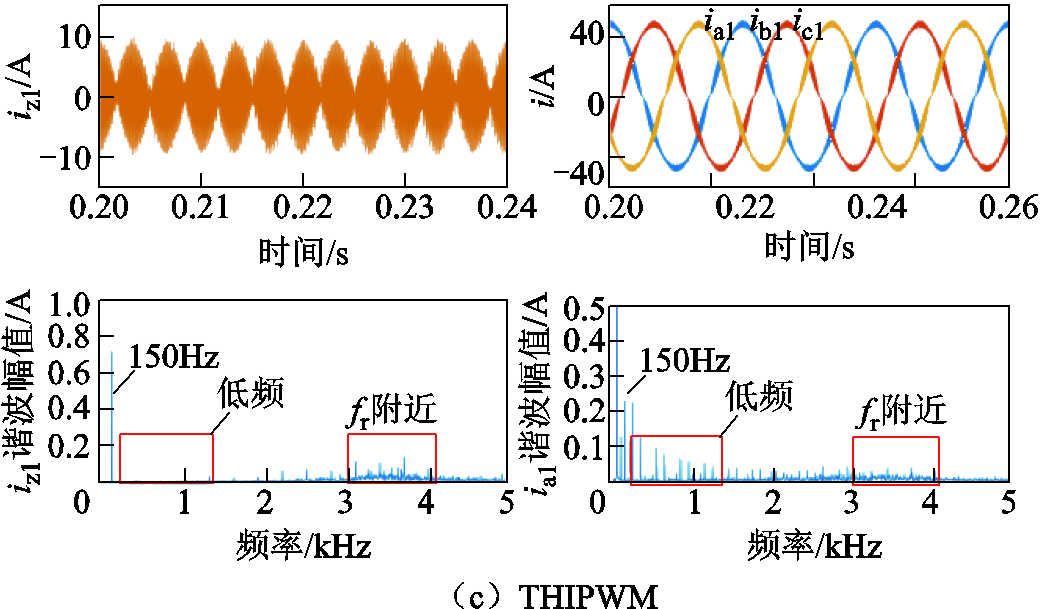
图9 Udc=600V时三种调制策略的波形及频谱分析
Fig.9 Waveforms and spectrum analysis under three modulation strategies when Udc=600V
图10为Udc=760V时，基于三种调制策略的输出波形。该直流电压等级下，基于SVPWM调制策略的共模电流和桥臂电流发生明显畸变，在谐振频率处谐波含量明显增多。虽然SAPWM策略电流波形质量得到改善，但FFT波形分析显示其电流仍有振荡。采用自适应THIPWM策略的波形质量最好。图10中的波形对比效果与图9相似，说明提出的自适应THIPWM策略在不同直流电压等级（不同调制度）下对共模谐振电流的抑制能力最优。
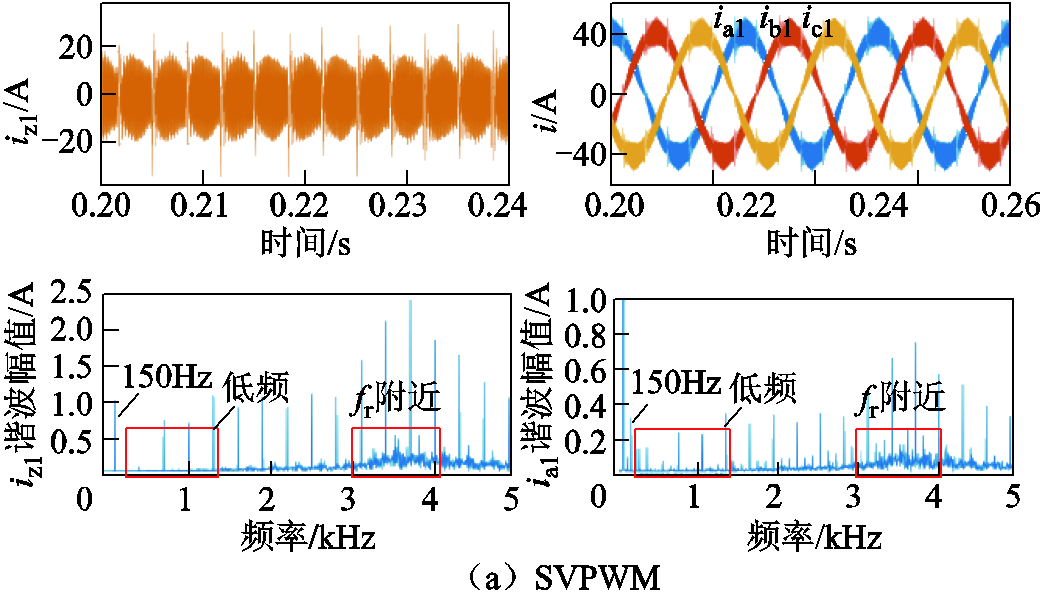
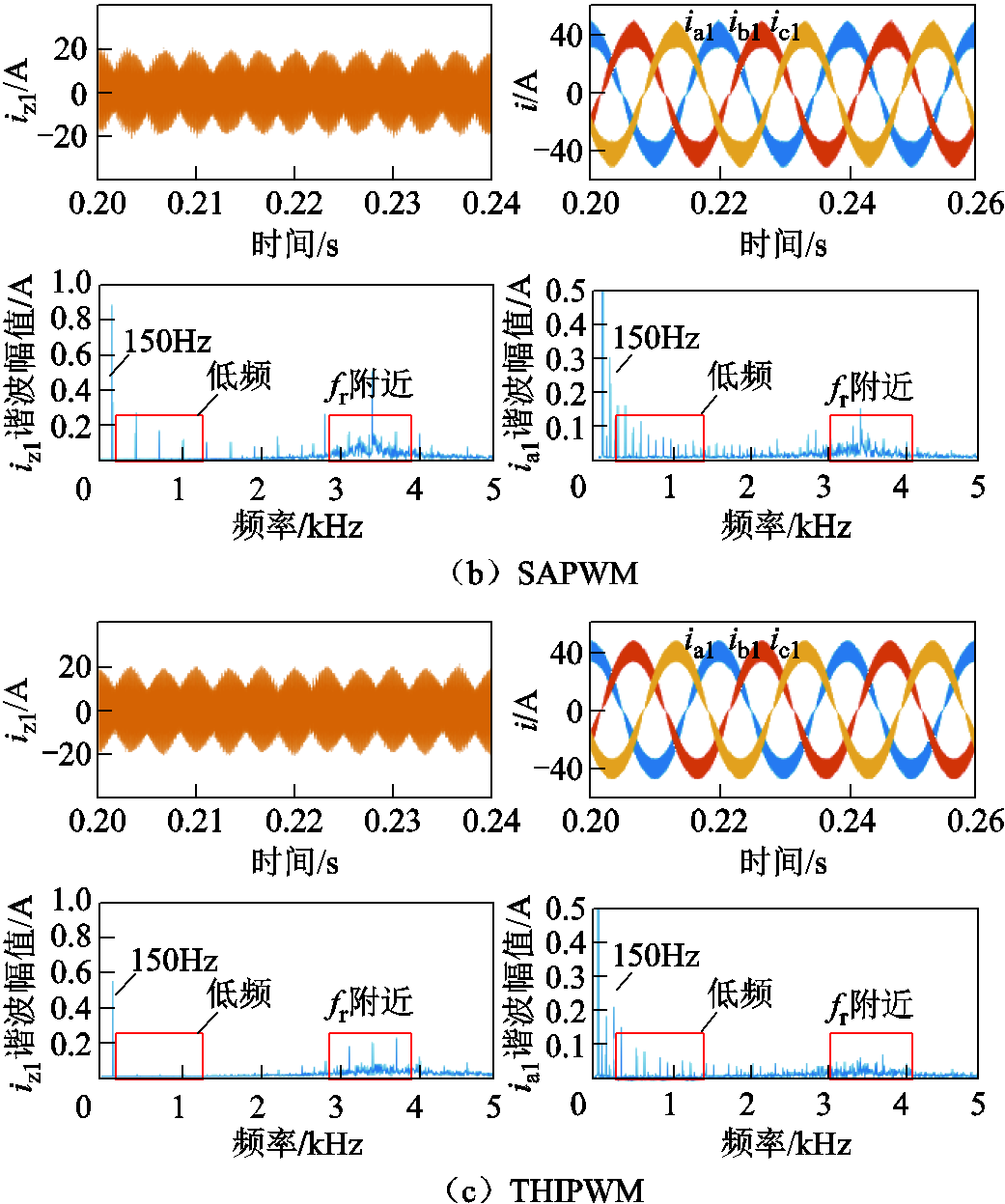
图10 Udc=760V时三种调制策略的波形及频谱分析
Fig.10 Waveforms and spectrum analysis under three modulation strategies when Udc=760V
表3总结了上述两种工况下，基于不同调制策略的共模电流在不同频率处的含量。其中，谐振频率附近谐波含量为3 200～3 800Hz各谐波分量占比的总和。可以看出，与SVPWM策略和SAPWM策略相比，本文所提出的自适应THIPWM策略在谐振频率附近的谐波含量明显降低，150Hz处的基波幅值也更小。
表3 共模电流频谱特性
Tab.3 Frequency spectrum characteristic of common-mode current
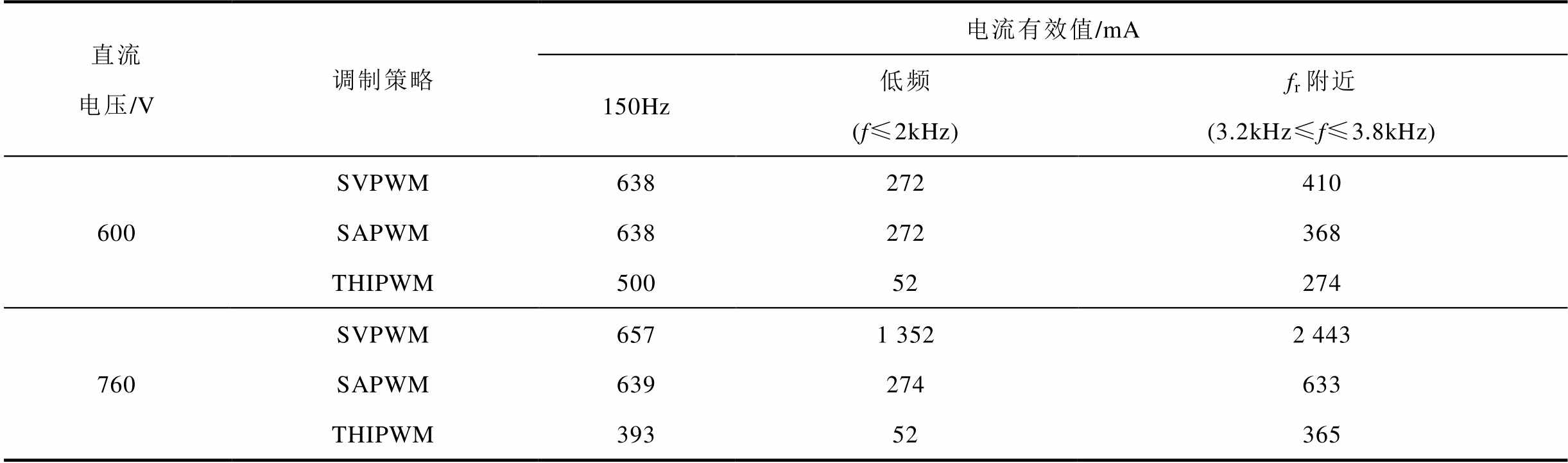
直流电压/V调制策略电流有效值/mA 150Hz低频(f≤2kHz)fr附近(3.2kHz≤f≤3.8kHz) 600SVPWM638272410 SAPWM638272368 THIPWM50052274 760SVPWM6571 3522 443 SAPWM639274633 THIPWM39352365
为了进一步验证本文方法的有效性，在20kW逆变器样机平台上进行了相关实验。图11所示为系统实验平台。其中，主控芯片型号为TI公司的定点型数字处理器TMS320F2812，工作频率最高为150MHz。
图11 实验平台
Fig.11 Experimental platform
实验给出了不同直流电压、不同功率因数下三种调制策略的输出波形。实验波形中依次给出了桥臂输出电压、共模电压FFT分析、共模电流、共模电流FFT分析、桥臂电流和A相桥臂电流的FFT分析。
图12为cosφ=1、Udc=600V、iref=27A时，三种调制策略的实验波形。该条件下，SVPWM策略与SAPWM策略共模电压及共模电流的谐波特性相近，在低频及谐振频率处谐波含量较高，导致桥臂侧电流含有一定的谐振电流，影响系统性能。而采用自适应THIPWM策略时，输出的共模电压、共模电流在低频及谐振频率处的谐波含量最低，桥臂电流频谱分析结果最好。
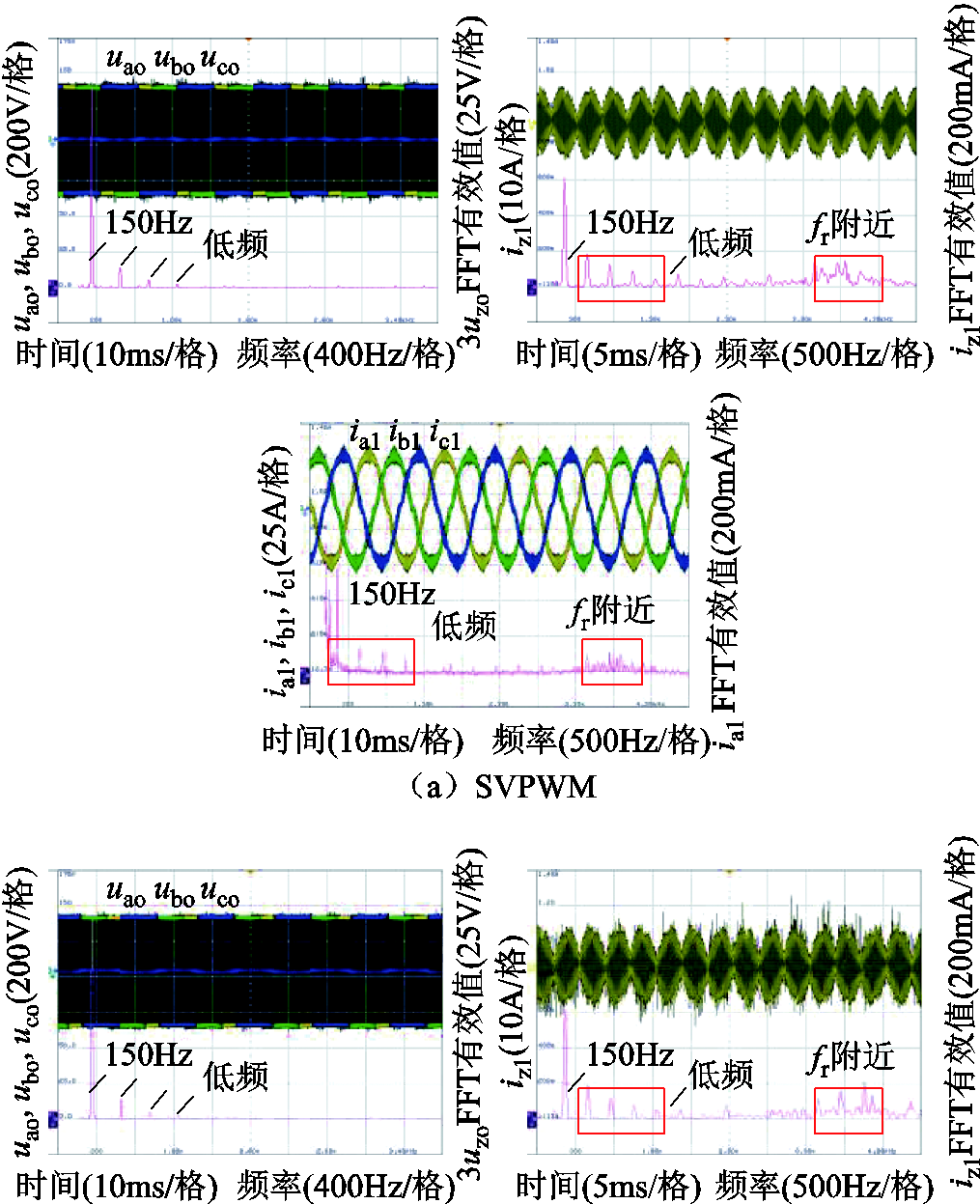
图12 cosφ=1、Udc=600V、iref=27A时三种调制策略波形及频谱分析
Fig.12 Waveforms and spectrum analysis under three modulation strategies when cosφ=1,Udc=600V,iref=27A
为验证不同调制度下提出方法的有效性，图13给出了cosφ=1、Udc=760V、iref=27A实验条件下的输出波形。图13a为采用SVPWM策略的实验结果，可以看出共模电流、三相桥臂电流波形质量差，振荡明显。运行时滤波电感发出啸叫声，易引起损坏设备。图13b为采用SAPWM策略的实验结果，波形质量有了大幅提升，但在共模电流在低频及谐振频率处的谐波含量仍然较高。图13c为采用自适应THIPWM策略的实验结果，可以看出共模谐振电流被有效抑制，且低频处的谐波含量较低，电流波形质量最佳。
图13 cosφ=1、Udc=760V、iref=27A时三种调制策略波形及频谱分析
Fig.13 Waveforms and spectrum analysis under three modulation strategies when cosφ=1,Udc=760V,iref=27A
为验证提出方法在不同功率因数下的有效性。图14给出了cosφ=0.92、Udc=600V、iref=27A实验条件下的输出波形。由图可以看出，提出的自适应THIPWM策略的共模电压、共模电流、桥臂电流在低频处及谐振频率处谐波含量最低，对共模谐振抑制效果最好。
图15为不同直流电压下基于自适应THIPWM策略的并网电流波形。可以看出，采用该方法的并网电流波形平滑、正弦度高。为进一步对比不同调制策略的并网电流质量，表4给出了不同直流电压下SVPWM策略、SAPWM策略和所提THIPWM策略A相并网电流的总谐波畸变率（Total Harmonic Distortion, THD）。可以看出，应用本文所提THIPWM策略时并网电流THD更小，证明了本文提出方法有利于并网电流控制。
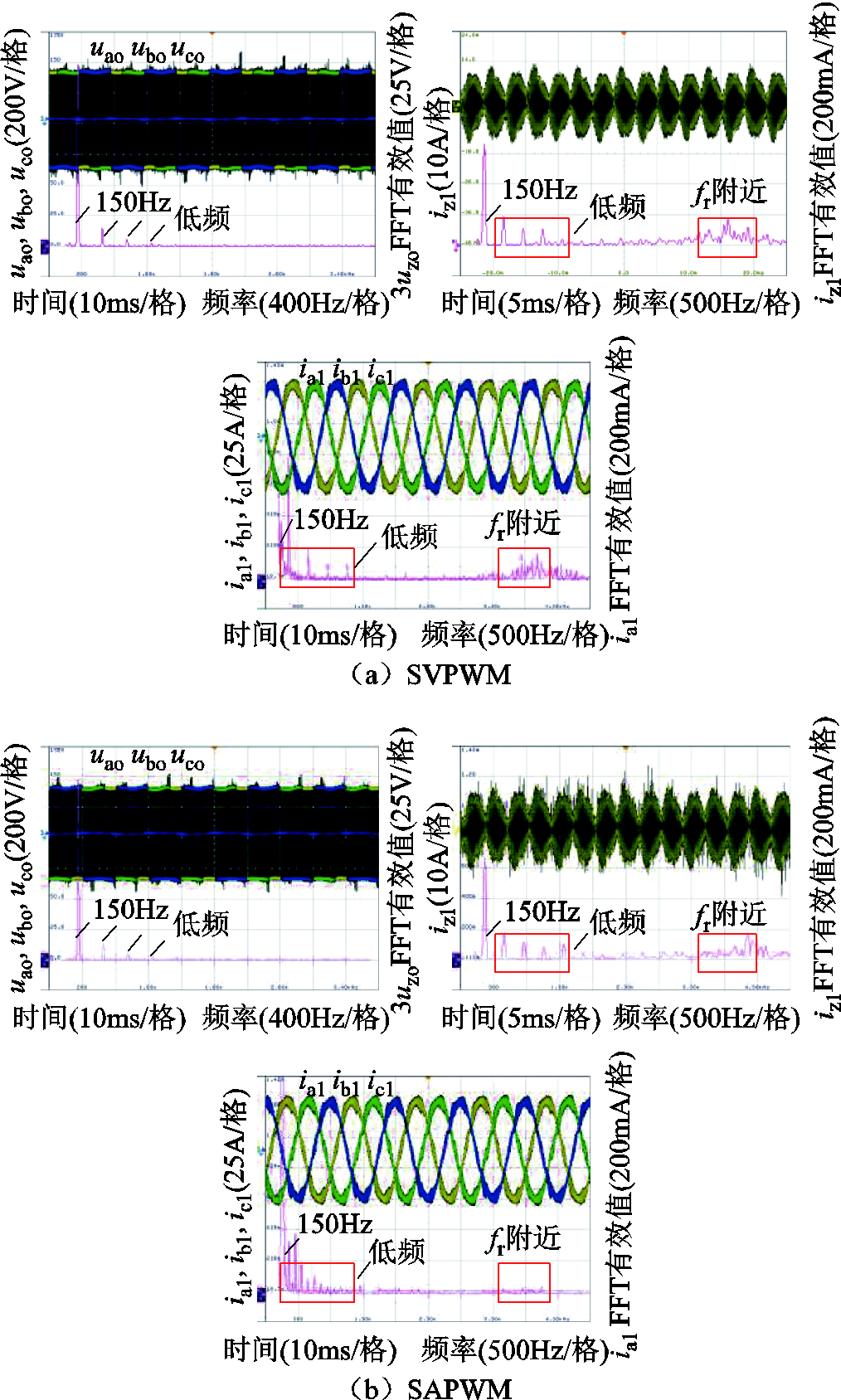
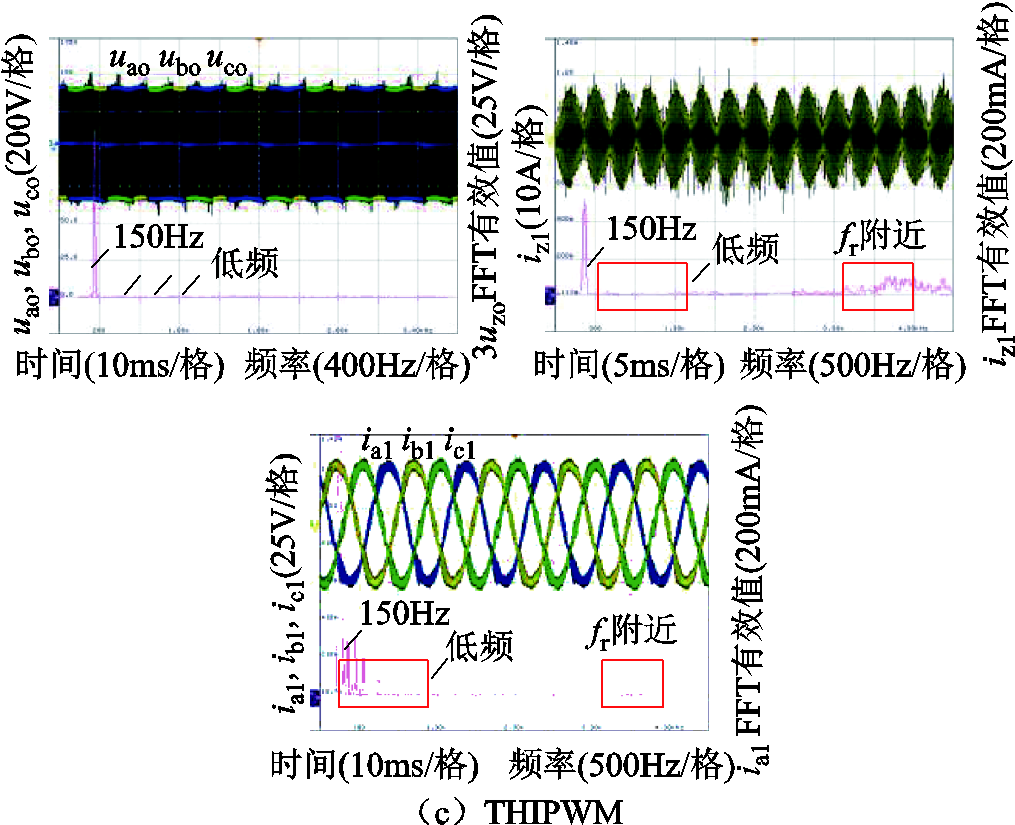
图14 cosφ=0.92、Udc=600V、iref=27A时三种调制策略波形及频谱分析
Fig.14 Waveforms and spectrum analysis under three modulation strategies when cosφ=0.92,Udc=600V,iref=27A
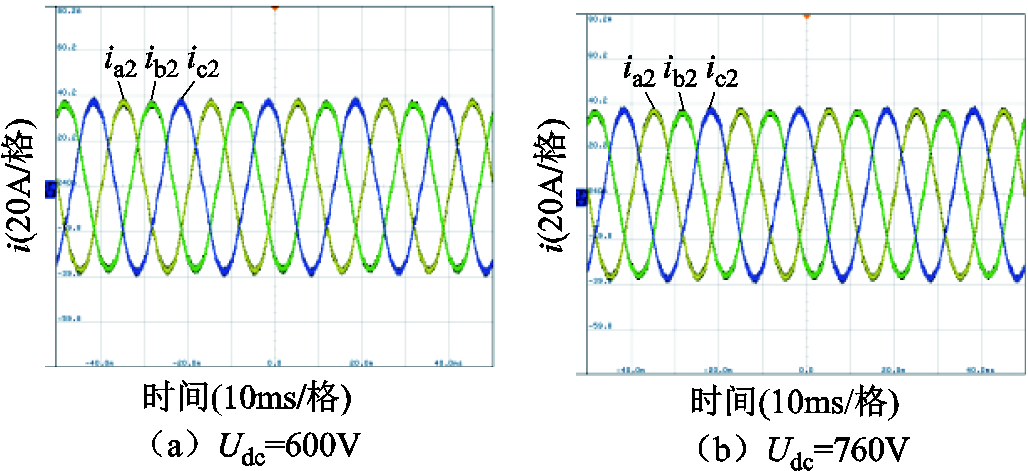
图15 不同直流电压下，基于自适应THIPWM调制的并网电流
Fig.15 Grid current waveforms of adaptive THIPWM method under different DC voltages
表4 A相并网电流总谐波畸变率（THDi）
Tab.4 THDi of grid current of phase A
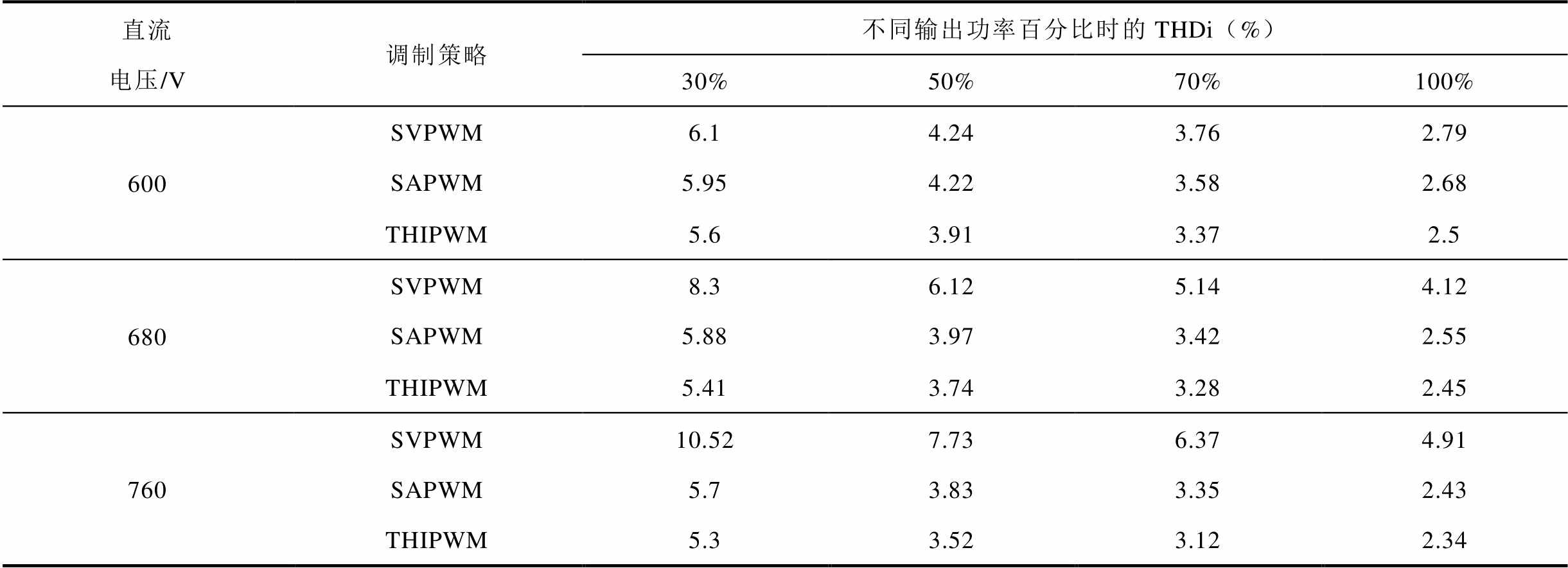
直流电压/V调制策略不同输出功率百分比时的THDi（%） 30%50%70%100% 600SVPWM6.14.243.762.79 SAPWM5.954.223.582.68 THIPWM5.63.913.372.5 680SVPWM8.36.125.144.12 SAPWM5.883.973.422.55 THIPWM5.413.743.282.45 760SVPWM10.527.736.374.91 SAPWM5.73.833.352.43 THIPWM5.33.523.122.34
三电平逆变器直流电容电压Up、Un和线电压Uab的波形如图16所示。由图可知，加入中点平衡控制算法后，可有效实现不同直流电压下的中点平衡控制，即将Up与Un控制至相同，这有利于维持系统稳定。此时，输出线电压为标准五电平，提高了并网电流波形质量。
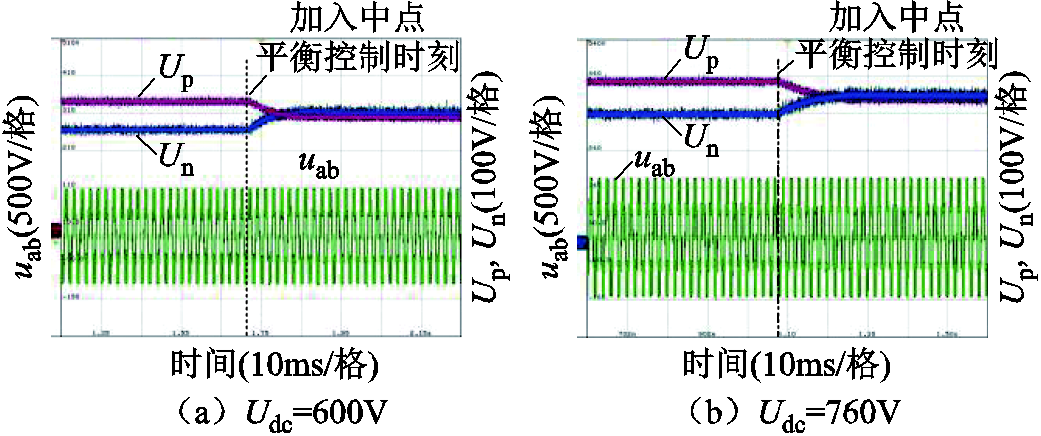
图16 不同直流电压下中点平衡控制效果与线电压波形
Fig.16 Performance of neutral-point balance control and line voltage waveform under different DC voltages
针对基于中点回接型LCL滤波器的三电平逆变器共模谐振电流抑制问题，本文分析了三种调制策略共模激励源的谐波特性及其对共模谐振电流的影响，提出了一种自适应3次谐波注入算法，该算法不仅可以有效抑制共模谐振电流，同时可以降低低频共模电流含量，进而提高并网电流性能。为方便工程应用，本文推导了基于电流闭环控制的3次谐波注入调制的实现方法。最后，通过仿真和实验验证了不同工况下提出算法的正确性和有效性。本文所提理论与方法已在山东奥太电气有限公司非隔离型光伏逆变器系列产品中推广应用，效果良好。
参考文献
[1] 王文静, 王斯成. 我国分布式光伏发电的现状与展望[J]. 中国科学院院刊, 2016, 31(2): 165-172.
Wang Wenjing, Wang Sicheng. Status and prospect of Chinese distributed photovoltaic power generation system[J]. Bulletin of Chinese Academy of Sciences, 2016, 31(2): 165-172.
[2] Kouro Samir, Leon Jose I, Vinnikov Dimitri, et al. Grid-connected photovoltaic systems: an overview of recent research and emerging PV converter technology[J]. IEEE Industrial Electronics Magazine, 2015, 9(1): 47-61.
[3] 薛世伟, 贾清泉, 李盼, 等. 提高组串光伏发电效率的直流动态重构控制策略[J]. 电工技术学报, 2021, 36(9): 1761-1770.
Xue Shiwei, Jia Qingquan, Li Pan, et al. Efficiency improvement control strategy for photovoltaic generation through DC dynamic reconfiguration[J]. Transaction of China Electrotechnical Society, 2021, 36(9): 1761-1770.
[4] Zhu Xiaonan, Wang Hongliang, Zhang Wenyuan, et al. A novel single-phase five-level transformer-less photovoltaic (PV) inverter[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(4):329-338.
[5] 秦昌伟. 三电平光伏逆变器系统高性能调控技术研究[D]. 济南: 山东大学, 2019.
[6] Liao Huanyue, Zhang Xin, Ma Zhijun. Robust dichotomy solution-based model predictive control for the grid-connected inverters with disturbance observer[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(2): 81-89.
[7] 王要强, 袁艺森, 陈天锦, 等. T型开关电容可扩展多电平逆变器[J]. 电工技术学报, 2020, 35(24): 5115-5124.
Wang Yaoqiang, Yuan Yisen, Chen Tianjin, et al. Extensible T-type switched capacitor multilevel inverter[J]. Transaction of China Electrotechnical Society, 2020, 35(24): 5115-5124.
[8] Guo Xiaoqiang, Zhou Jiale, He Ran, et al. Leakage current attenuation of a three-phase cascaded inverter for transformerless grid-connected PV systems[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 676-686.
[9] 邱继浪, 何英杰, 焦乾明, 等. 非隔离型三电平逆变器漏电流抑制与中点电位平衡控制[J]. 电力系统自动化, 2021, 45(17): 161-170.
Qiu Jilang, He Yingjie, Jiao Qianming, et al. Leakage current suppression and neutral point potential balance control of non-isolated three-level inverter[J]. Automation of Electric Power Systems, 2021, 45(17): 161-170.
[10] 王付胜, 李祯, 付航, 等. 一种抑制系统漏电流非隔离型三电平逆变器中点平衡载波调制算法[J]. 电工技术学报, 2017, 32(增刊2): 128-138.
Wang Fusheng, Li Zhen, Fu Hang, et al. A new pulse-width modulation algorithm for the comprehensive neutral-point balancing and leakage current reducing in the three-level transformerless inverter[J]. Transaction of China Electrotechnical Society, 2017, 32(S2): 128-138.
[11] Zhang Li, Sun Kai, Xing Yan, et al. H6 transformerless full-bridge PV grid-tied inverters[J]. IEEE Transactions on Power Electronics, 2014, 29(3): 1229-1238.
[12] Zhu Xiaonan, Wang Hongliang, Zhang Wenyuan, et al. A novel single-phase five-level transformer-less photovoltaic (PV) inverter[J]. CES Transactions on Electrical Machines and Systems, 2020,4(4): 329-338.
[13] Akagi Hirofumi, Tamura Shunsuke. A passive EMI filter for eliminating both bearing current and ground leakage current from an inverter-driven motor[J]. IEEE Transactions on Power Electronics, 2006, 21(5): 1459-1469.
[14] 任康乐, 张兴, 王付胜, 等. 非隔离型三电平并网逆变器的输出滤波器优化设计[J]. 电力系统自动化, 2015, 39(3): 117-123.
Ren Kangle, Zhang Xing, Wang Fusheng, et al. Optimized design of output filter for transformerless three-level grid-connected inverter[J]. Automation of Electric Power Systems, 2015, 39(3): 117-123.
[15] Li Xiaoyan, Xing Xiangyang, Zhang Chenghui, et al. Simultaneous common-mode resonance circulating current and leakage current suppression for transformerless three-level T-type PV inverter system[J]. IEEE Transactions on Industrial Electronics, 2019, 66(6): 4457-4467.
[16] Kouchaki Alireza, Nymand Morten. Analytical design of passive LCL filter for three-phase two-level power factor correction rectifiers[J]. IEEE Transactions on Power Electronics, 2018, 33(4): 3012-3022.
[17] 高瞻, 李耀华, 葛琼璇, 等. 低载波比下三电平中点钳位变流器改进型同步载波脉宽调制策略研究[J]. 电工技术学报, 2020, 35(18): 3894-3907.
Gao Zhan, Li Yaohua, Ge Qiongxuan, et al. Research on improved synchronized carrier based PWM for three-level neutral point clamped converter under low carrier ratio[J]. Transaction of China Electrotechnical Society, 2020, 35(18): 3894-3907.
[18] 王东毅. 三电平变流器调制策略研究[D]. 合肥: 合肥工业大学, 2016.
[19] Pou Josep, Zaragoza Jordi, Ceballos Salvador, et al. A carrier-based PWM strategy with zero-sequence voltage injection for a three-level neutral-point- clamped converter[J]. IEEE Transactions on Power Electronics, 2012, 27(2): 642-651.
[20] Holmes D G, Lipo T A. Pulse width modulation for power converters: principles and practice[M]. New York: John Wiley & Sons, 2003.
[21] 李杰, 陈国呈, 王得利, 等. 三相PWM整流器直接电流控制中进行SAPWM调制的新方法[J]. 电工电能新技术, 2007, 26(4): 36-40.
Li Jie, Chen Guocheng, Wang Deli, et al. A new method for SAPWM in direct current control of PWM rectifier[J]. Advanced Technology of Electrical Engineering and Energy, 2007, 26(4): 36-40.
[22] Younis M A A, Rahim N A, Mekhilef S. Simulation of grid connected THIPWM-three-phase inverter using SIMULINK[C]//IEEE Symposium on Industrial Electronics and Applications, Langkawi, Malaysia, 2011: 133-137.
[23] Kumbhare Jyoti M, Deshmukh Ankush C, Renge Mohan M, et al. THIPWM technique applied to three level ANPC converter for grid tied PV applications[C]// 21st Century Energy Needs-Materials, Systems and Applications, Kharagpur, India, 2016: 1-5.
[24] 陈杰, 沈禹廷, 沈佳茜, 等. 三相VIENNA整流器的混合空间矢量脉宽调制策略[J]. 电工技术学报, 2021, 36(增刊2): 665-675.
Chen Jie, Shen Yuting, Shen Jiaqian, et al. Hybrid space vector pulse width modulation strategy for three-phase VIENNA rectifier[J]. Transaction of China Electrotechnical Society, 2021, 36(S2): 665-675.
[25] 罗锐, 何英杰, 陈晖, 等. 三电平变流器中点电位平衡及低开关损耗SVPWM策略[J].电工技术学报, 2018, 33(14): 3245-3254.
Luo Rui, He Yingjie, Chen Hui, et al. SVPWM scheme for three-level converters with neutral-point potential balancing and switching loss reduction[J]. Transaction of China Electrotechnical Society, 2018, 33(14): 3245-3254.
[26] Mukherjee S, Giri S K, Banerjee S. A flexible discontinuous modulation scheme with hybrid capacitor voltage balancing strategy for three-level NPC traction inverter[J]. IEEE Transactions on Industrial Electronics, 2019, 66(5): 3333-3343.
[27] Guo Xiaoqiang, Wei Baoze, Zhu Tieying, et al. Leakage current suppression of three-phase flying capacitor PV inverter with new carrier modulation and logic function[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2127-2135.
[28] Qin Changwei, Zhang Chenghui, Chen Alian, et al. A space vector modulation scheme of the quasi-Z-source three-level T-type inverter for common-mode voltage reduction[J]. IEEE Transactions on Industrial Electronics, 2018, 65(10): 8340-8350.
[29] Albatran S, Allabadi A S, Khalaileh A R A, et al. Improving the performance of a two-level voltage source inverter in the overmodulation region using adaptive optimal third harmonic injection pulsewidth modulation schemes[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 1092-1103.
[30] Park Jin-Hyuk, Lee June-Seok, Lee Kyo-Beum. Sinusoidal harmonic voltage injection PWM method for vienna rectifier with an LCL filter[J]. IEEE Transactions on Power Electronics, 2019, 36(3): 2875-2888.
[31] Ojha S, Sharma C, Pandey A K. Comparative analysis of close loop three level voltage source inverter using sinusoidal pulse width modulation and third harmonic injection method for different loads[C]//Second International Conference on Electrical, Computer and Communication Technologies, Coimbatore, India, 2017: 1-6.
[32] Albatran S, Khalaileh A R A, Allabadi A S. Minimizing total harmonic distortion of a two-level voltage source inverter using optimal third harmonic injection[J]. IEEE Transactions on Power Electronics, 2020, 35(3): 3287-3297.
[33] 张子成. T型三电平逆变器并联系统控制策略研究[D]. 济南: 山东大学, 2017.
[34] 张承慧, 叶颖, 陈阿莲, 等. 基于输出电流控制的光伏并网逆变电源[J]. 电工技术学报, 2007, 22(8): 41-45.
Zhang Chenghui, Ye Ying, Chen Alian, et al. Research on grid-connected photovoltaic inverter based on output current control[J] Transactions of China Electrotechnical Society, 2007, 22(8): 41-45.
Abstract Due to the parasitic capacitance between the photovoltaic array and the ground, the leakage current is easily generated in non-isolated photovoltaic grid-connected system, which will reduce the equipment life and endanger personal safety. Therefore, the modified LCL filter with neutral-point back connection is often adopted for non-isolated system to provide a low-impedance bypass path and suppress the leakage current. However, the LCL filter modification brings potential risk of common-mode (CM) resonance in CM loop which will cause inverter-side current oscillation, leakage current increment, and system instability. Passive and active damping methods have been proposed to overcome the drawback of CM current but will bring extra power losses or complex controller design tasks. To address the CM resonance issue, this paper proposes an adaptive third harmonic injection algorithm based on the analysis of different modulation strategy influences on the CM resonant current.
Firstly, the mathematical model and generation mechanism of CM resonant current are introduced briefly and the CM voltage spectrums of space vector pulse width modulation (SVPWM) method, saddle pulse width modulation (SAPWM) method and third harmonic injection pulse width modulation (THIPWM) method are compared, which shows the advantage of THIPWM method on CM resonant current suppression. Secondly, the exact available range of the third-harmonic injection coefficient is derived to ensure the correctness of modulation and determine the adjustable range of the coefficient. Thirdly, according to DC voltage and modulation index, an adaptive law for the injection coefficient is proposed to improve the performance of the grid-connected inverter. Fourthly, the third-harmonic injection implementation method for current closed-loop control is derived in order to facilitate engineering application and reduce the calculation burden of the controller.
To verify the effectiveness of the proposed method, simulation and experiment are performed on Matlab/Simulink platform and on a 20kW inverter prototype. In simulation, transient waveforms of adaptive is firstly given to verify the adaptive law of injection coefficient. Then, waveforms of the CM current and the bridge currents as well as their FFT analysis results are given. These waveforms and analysis data validate that the adaptive THIPWM method can efficiently suppress the CM resonant current and reduce low-frequency CM currents. As for experiments, the waveforms of the bridge output voltage, the CM current, the bridge currents and relevant FFT analysis results under different DC voltages and different power factors are given in detail. These results further show that the proposed method is effective under different conditions. Then, grid current waveforms of the adaptive THIPWM method under different DC voltages are provided. The total harmonic distortions (THD) of grid current under three modulation methods are also given to validate the performance improvement of the proposed method. Finally, the performance of neutral-point balance control is verified.
The following conclusions can be drawn from the simulation and experimental analyses: ①The CM resonant current is effectively suppressed and the low-frequency CM currents are reduced by the proposed method. ②Smooth transient performance of the adaptive THIPWM method can be achieved. ③Compared with SVPWM and SAPWM, the grid current quality is improved when applying the adaptive THIPWM method. ④The performance improvement including CM resonant current suppression and grid current THD reducing can be achieved under different operating conditions.
Keywords：Non-isolated photovoltaic system, common-mode resonant current suppression, adaptive third harmonic injection modulation, algorithm for current closed-loop control
DOI: 10.19595/j.cnki.1000-6753.tces.220806
中图分类号：TM46
张洪亮 男，1981年生，博士研究生，高级工程师，研究方向为新能源与电力电子技术。E-mail：18660138145@163.com
张子成 男，1991年生，博士研究生，研究方向为新能源并网发电与电力电子技术。E-mail：15634103621@163.com（通信作者）
国家自然科学基金资助项目（61821004, 61733010）。
收稿日期 2022-05-11
改稿日期 2022-06-01
（编辑 郭丽军）