（1）
摘要 针对内置式永磁同步电机（IPMSM）速度环中存在的内部参数摄动与外部负载扰动等问题，为了提高速度控制系统的动态性和鲁棒性，该文提出一种基于改进型双幂次趋近律（IDPRL）与全局快速终端滑模观测器（GFTSMO）的滑模控制方法。所提趋近律在幂次项中引入系统状态变量，减少了稳态误差，解决了快速趋近滑模面和抖振抑制之间的矛盾。设计一种基于IDPRL的IPMSM滑模速度控制器。为了进一步减少系统状态的稳态误差，设计了一种GFTSMO，该观测器不仅能够减少趋近律的开关增益，还能实现系统扰动的准确补偿。仿真和实验结果验证了所提的滑模控制方法的可行性和有效性。
关键词：内置式永磁同步电机 滑模趋近律 全局快速终端滑模观测器
内置式永磁同步电机（Interior Permanent Magnet Synchronous Motor, IPMSM）因其具有高效、高功率密度、调速范围宽等优点，在航天、伺服系统、电动汽车、风力发电等领域中得到广泛应用[1-3]。目前，IPMSM调速系统的控制普遍采用传统的比例积分（Proportional Integral, PI）控制，该控制方法具有算法简单、易于实现和调节方便的优点，在一定范围内能满足控制要求。然而，实际的IPMSM的调速系统具有非线性、强耦合、变参数的特性，仅采用PI控制算法等线性控制方法很难使系统获得较快的响应速度和较强的鲁棒性[4-6]。
针对上述问题，国内外学者做了大量研究，包括鲁棒控制[7]、自适应控制[8]、滑模控制（Sliding Mode Control, SMC）[9]、预测控制[10]在内的许多先进控制理论被成功应用于IPMSM的调速系统中。滑模控制以其鲁棒性强、动态响应快等优点，在IPMSM调速系统中被广泛应用，具有良好的研究前景[11-14]。滑模控制在IPMSM调速系统中主要有两种方式：一种是将滑模控制和矢量控制或者直接转矩控制结合的位置、速度或者电流控制；另一种则是以滑模观测器的形式应用于IPMSM中，如电机参数识别、集总扰动补偿和电机无传感器控制。文献[15]将一种基于滑模控制的混合控制方法用于控制电机的转速和电流，提高了永磁同步电动机驱动系统的动态响应。文献[16]将SMC应用到无传感器的直接转矩控制系统中，构建了滑模状态观测器，解决了传统直接转矩控制中转矩和磁链脉动大以及电机运行于空载或突加负载时直轴电流分量较大等问题。然而，滑模控制也并非完美，由于开关的频繁切换所造成的控制不连续性，滑模控制系统中将不可避免地产生抖振现象。因此，抑制抖振现象是滑模控制方法的研究热点。
抖振现象是系统轨迹对滑模面的趋近过程不理想所导致的，而趋近过程的理想与否与趋近律的品质是直接相关的，因此，研究高品质趋近律是抑制系统抖振的关键。文献[17]基于新型控制律设计了永磁同步电机伺服系统的二阶滑模控制器。理论和仿真结果表明，在具有外界干扰的情况下，系统仍能满足精度要求。文献[18]将一种新型趋近律与小波模糊神经网络相结合，设计了一个智能二阶滑模控制系统，该系统具有良好的干扰抑制效果。文献[19]采用饱和函数来替代开关函数以消除系统抖振，在一定程度上抑制了抖振现象，但系统收敛速度比较慢，且鲁棒性也明显降低。文献[20]提出了一种基于反双曲正弦函数的新型趋近律，该趋近律有效抑制了调速系统的稳态抖振，提高了系统的响应速度。文献[21]将幂次项和系统状态变量相结合，幂次项受开关函数的绝对值的约束，该方法不仅能有效地抑制系统固有的抖振，而且能提高系统状态到达滑动模态表面的速度。上述方法在扰动的情况下会降低系统状态变量的稳态精度。此外，趋近律方法在干扰较小时能很好地抑制抖振，而在扰动较大或扰动上限未知时，为了保证系统具有较强的抗干扰性和鲁棒性，趋近律的开关函数增益必须设置得足够大，这样必然会加剧SMC的抖振。而开关函数增益太小，则系统的抗干扰性和鲁棒性便会受损。因此，将扰动观测器与滑模控制方法结合可以有效解决上述问题。
基于扰动观测器（Disturbance Observer, DO）控制的基本思想最早于1987年被K. Ohnishi提出。传统的DO采用线性控制，该控制方法由于结构简单，所以在不同的工业领域中得到了广泛的应用，但其动态性能和鲁棒性受到限制。为了解决这一问题，非线性DO被认为是一种很有前途的方法。文献[22]提出了一种非线性控制系统的模糊DO，明显提高了系统的稳定性和跟踪精度。在交流电机调速中，负载转矩估计是一个关键问题。在文献[23]中，提出了一种以负载转矩为扩展状态的扩展状态观测器（Extended State Observer, ESO），用于永磁同步电机的速度控制。然而，ESO本质上是一种线性DO，在电机和负载侧参数不匹配的情况下，其抗扰性能会下降。与基于DO的方法相比，基于滑模观测器（Sliding Mode Observer, SMO）的方法具有抗干扰性强、对参数变化不敏感、参数调整灵活等优点[24]。
为了提高IPMSM调速系统的动态性和鲁棒性，本文提出了一种基于改进的双幂次趋近律（Improved Double Power Reaching Law, IDPRL），相比于传统趋近律，所提的新型趋近律有效地解决了抖振抑制和快速响应的矛盾，并减少了稳态误差。为了进一步减小系统状态变量的稳态误差，本文设计了一种全局快速终端滑模观测器（Global Fast Terminal Sliding Mode Control, GFTSMO），该观测器能对速度控制器的扰动进行前馈补偿，提高调速系统的抗干扰性能，减小趋近律的开关增益，削弱滑模抖振。采用最大转矩电流比（Maximum Torque Per Ampere, MTPA）的控制策略，设计了基于IDPRL和GFTSMO调速系统，并通过仿真和实验对该系统性能进行了验证。
在滑模控制过程中，良好的趋近律保证了系统趋近运动的动态品质。高为炳院士设计了指数趋近律（Exponent Reaching Law, ERL）[17]，即
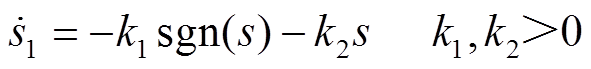（1）
式中，k1、k2为任意正实数；s为滑模面。
对式（1）两侧求积分且t1时刻s(t1) = 0时，可得系统状态到达滑模面的时间为
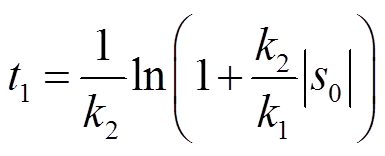（2）
式中，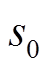
为滑模面初始位置。
由式（2）可知，增大等速项k1可以减少到达滑模面的时间和提高系统的抗干扰能力。但当系统初始状态与估计状态误差较大时，等速项仍以固定增益使趋近律运动到滑模面，不能随系统状态进行自适应调节，这将会使系统产生严重抖振和较大的偏差。
文献[25]基于传统指数趋近律，提出一种在指数项和等数项中引入系统状态变量的滑模趋近律（State Variables Exponential Researching Law, SVERL），即
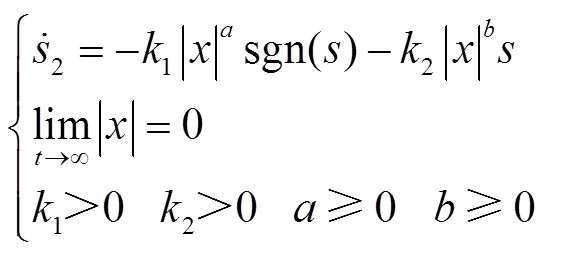（3）
式中，a、b、k1、k2为任意正实数；x为系统状态变量。
对式（3）两侧求积分且t2时刻s(t2) = 0时，可得系统状态到达滑模面的时间为
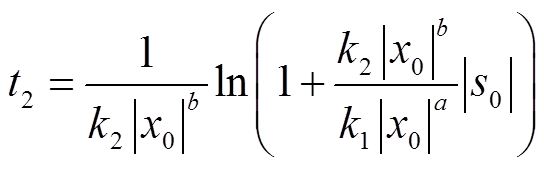（4）
式中，x0为初始状态，即x0＞0。
通过对比式（4）和式（2），可以得到
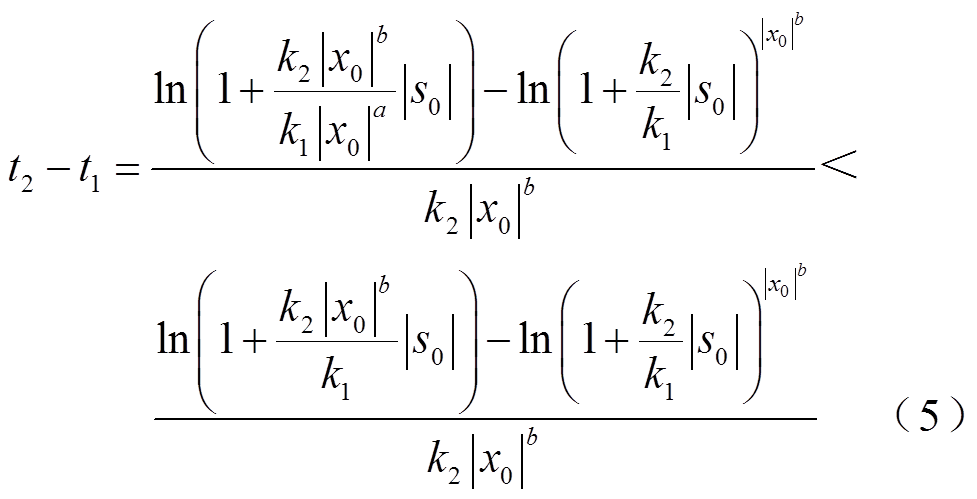
通过式（5）可以推导出，当x0＞1时，t2-t1＜0；当0＜x0＜1时，t2-t1＞0。引入系统状态变量，可以有效削弱抖振带来的影响，但收敛时间却受到了s0和x0的影响。此外，在指数项和等速项均引入状态变量，SVERL的抗干扰性能也会被削弱。
为了解决上述趋近律的问题，本文提出一种基于状态变量的改进型双幂次趋近律（IDPRL），即
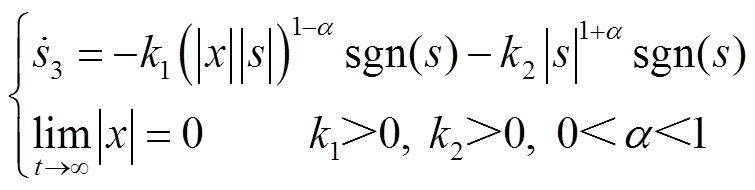（6）
式中，α、k1、k2为任意正实数；x为系统状态变量。
该趋近律由两部分组成：基于状态变量的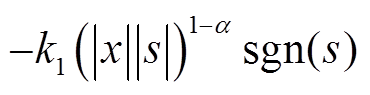幂次项
和幂次项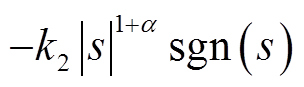
。当系统远离滑模面s=0时，即|s|＞1，幂次项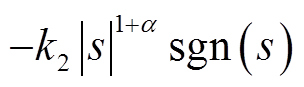起主要作用，此时
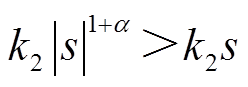且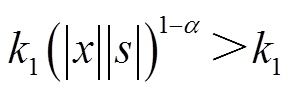
，说明本文所提的趋近律在该阶段比指数趋近律快，保证系统快速到达滑模面；当系统状态接近滑模面时，即|s|＜1，幂次趋近项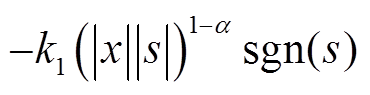起主要作用，此时存在
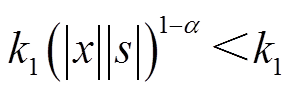和
，指数部分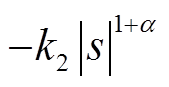
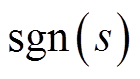趋近速度近似为零。等速项系数
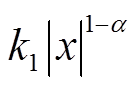会随着系统状态x的减小而减小，解决了固定的等速项系数带来较大抖振的问题。
本文所提的趋近律有如下优点：①系统可以在短时内收敛至滑模面，所提趋近律的收敛时间不受初始值s0的影响；②相比于SVERL，所提趋近律选取的参数更少；③与ERL和SVERL相比，所提趋近律同时具有快速响应能力、抖振抑制能力和更好的抗扰性能。
定理1 系统状态在IDPRL的作用下，当|x0|＞1时，可从任意初始位置s0在有限时间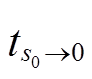
内达到滑模面s = 0，且收敛时间t3存在与状态初值s0无关的上限时间Tmax，其中
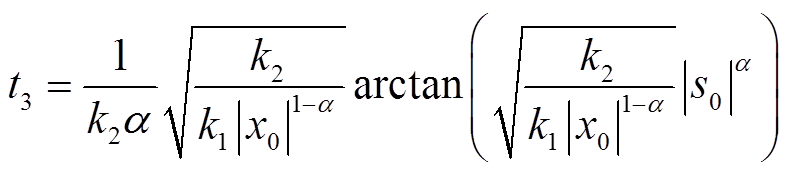（7）
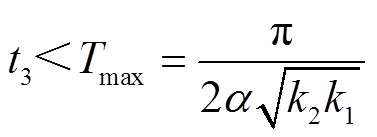（8）
证明 根据李雅普诺夫定理可得
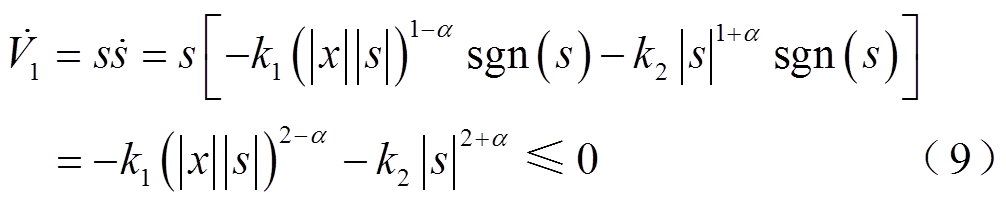
综上所述，当且仅当s=0时，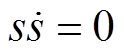
。下面推导过程证明了系统可以在有限时间内收敛至平衡点。
当s＞0时，式（6）可化简为
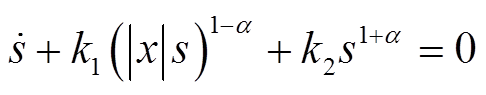（10）
对式（10）两边同时除以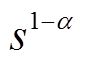
，可得到
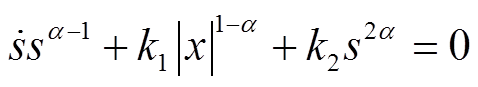（11）
令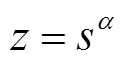
，并将z代入式（11）中，可简化为黎卡提微分方程
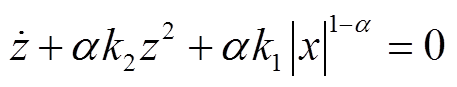（12）
式（12）的通解为
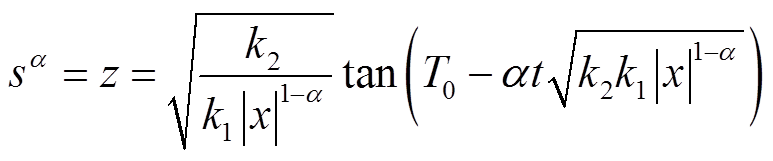（13）
由s(0) = s0可得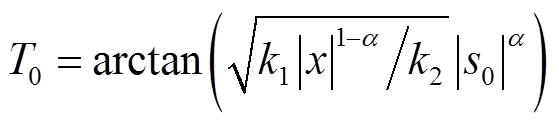
，当s(t) = 0时可求得t3为
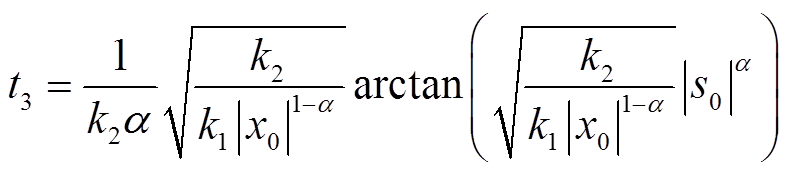（14）
在式（14）中，系统状态的初始值出现在arctan函数中，而arctan函数的取值范围是(-π/2, π/2)，因此，当|x0|＞1时，式（14）的最大值为
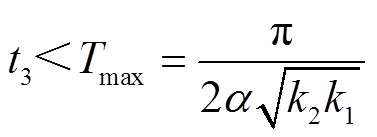（15）
因此，定理1得证。
通过比较式（2）、式（4）和式（15）可知，t3是有界的，而t1和t2会随着初始值的大小而改变。所以当初始值s0较大时，本文所提趋近律有更快的趋近速度。从式（5）可知，当|x0|＞1时，t2＜t1，下面具体比较在|x0|＞1时t2和t3的关系。
将式（4）减去式（14），并对s0求导后可得
（16）
由式（16）可知，当α=b且|s0|≥|x0|≥0时，t2-t3为单调递增函数，故s0=0时，t2-t3为极小值。因此，当|s0|≥|x0|＞1时，存在t3＜t2。
考虑如下带有扰动的被控系统
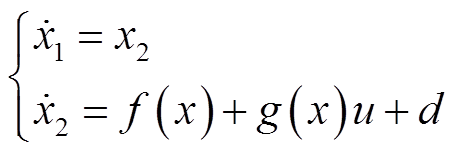（17）
式中，x(t)为系统状态；f(x)和g(x)已知，且b＞0；u为控制输入；d为集总扰动。
设计滑模函数为
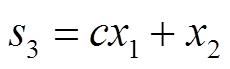（18）
其中c＞0。
对s求导可得
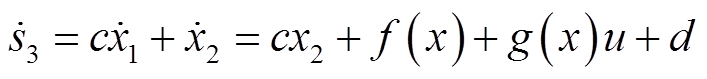（19）
假设g(x)为非奇异函数，集总扰动d未知且有界，即|d| ≤M。可得到基于IDPRL的等效控制律为
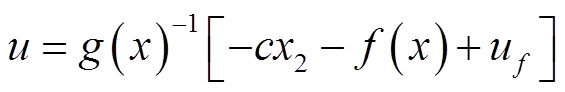（20）
其中
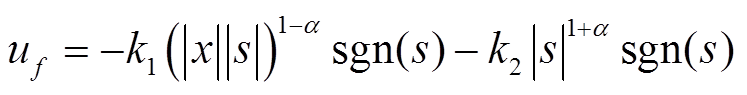
将式（20）代入式（19）可得
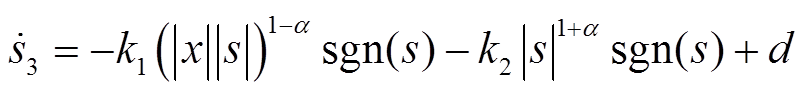（21）
引理1 令
，
，
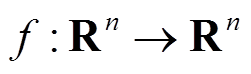为定义在平衡点领域D内的连续函数，假设存在连续函数V满足以下条件：①V是正定的；②
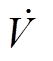除平衡点外是负定的；③存在实数α和β均大于零和邻域
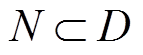，使得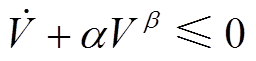
，则函数s在平衡点有限时间收敛[26]。
定理2 式（21）中的s3在有限时间内会收敛到以下区域
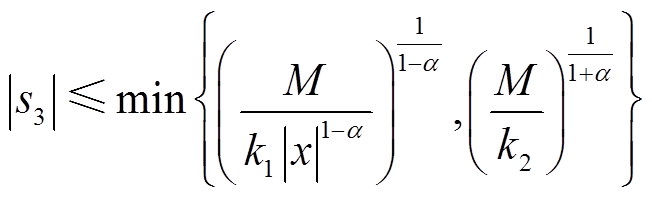（22）
证明 考虑李雅普诺夫定理函数V = 0.5s2，对V沿式（18）求导，可得
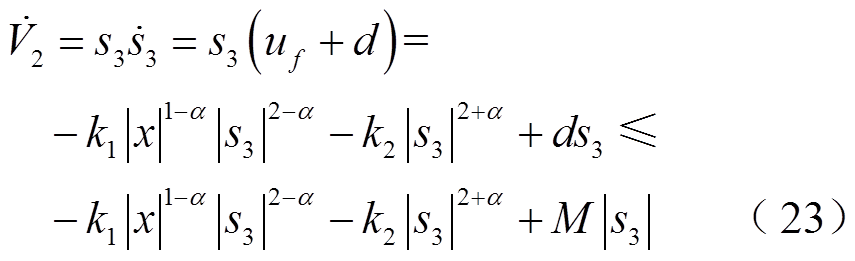
式（23）可以写成
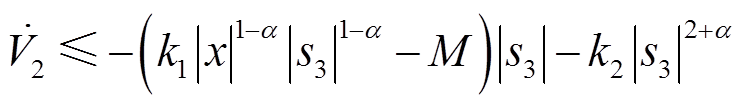（24）
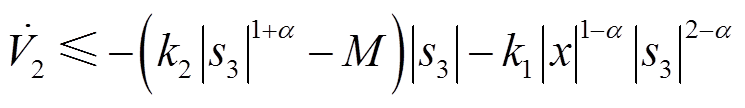（25）
式（23）成立的条件是
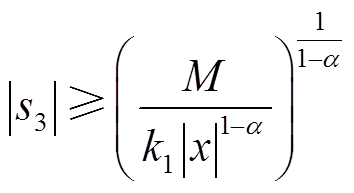
即
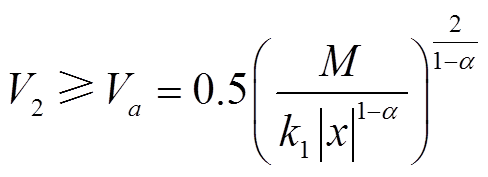
此时，由式（23）可知
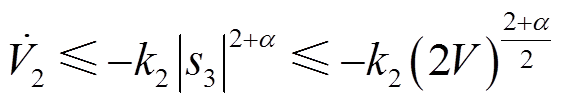（26）
因此，由引理1可知，s关于平衡点有限时间收敛，收敛区域为
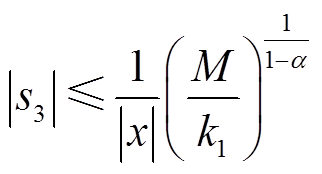（27）
同理，由式（24）可以求得滑模面s3的收敛域。综上所述，当存在扰动时，所提趋近律s3会在有限时间内收敛到如下区域
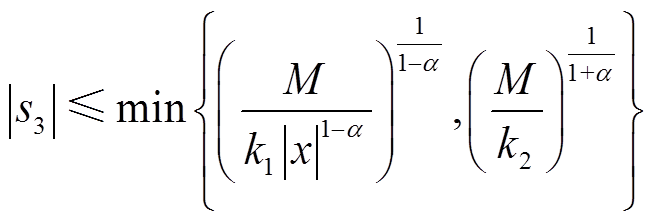（28）
因此，定理2得证。
由定理2可以求得趋近律ERL和SVERL的状态s会在有限时间内分别收敛到如下区域
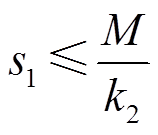（29）
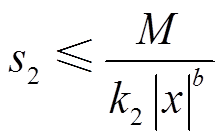（30）
对x1≠0，滑模函数s可以改写为
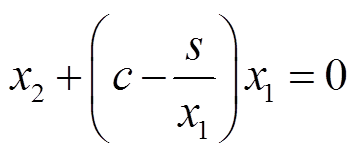（31）
式（31）保证状态x1收敛的条件是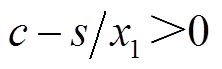
，通过引理1并结合式（28）可得收敛域
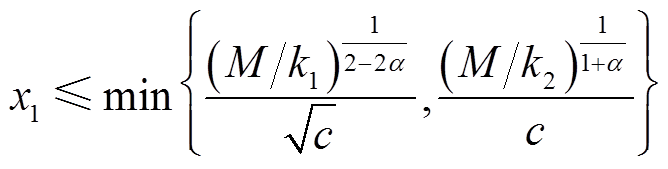（32）
同理可得式（29）和式（30）的状态x分别收敛到如下区域
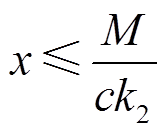（33）
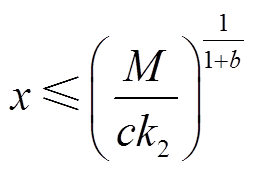（34）
假设α=b，当M/k2＞1时，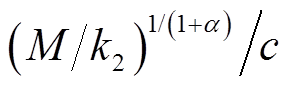
最小。当M/k2＜1时，且0.5＜α＜1，
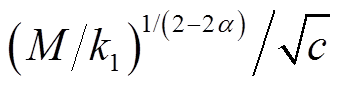最小，若0＜α＜0.5，
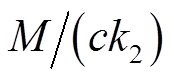最小。因此，当系统遇到扰动时，所提趋近律能够抑制扰动并减少稳态误差。
对于1.4节中带有扰动的二阶系统，取指令信号xd(t)=sin(t)，被控对象初始状态[x,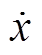 
]为[-2, -2]，f(x, t)=25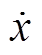，d(t)=10sin(πt)。分别采用ERL、SVERL和IDPRL进行仿真。趋近律参数为k1=15，k2=135，α=a=b=0.1。
图1～图3是ERL、SVERL和IDPRL的控制性能对比图。从图1～图3的a图和b图可以看出，所提趋近律IDPRL具有更快的跟踪速度。图1c中的抖振非常明显，图2c中的抖振次之，而本文所提的趋近律如图3c，抖振基本被抑制。图1d、图2d和3d的系统收敛精度分别为0.004 65，0.014 9和 0.004 8。由于取值范围为（0, 0.5），故指数趋近律具有更小的收敛精度，与1.4节中分析一致。
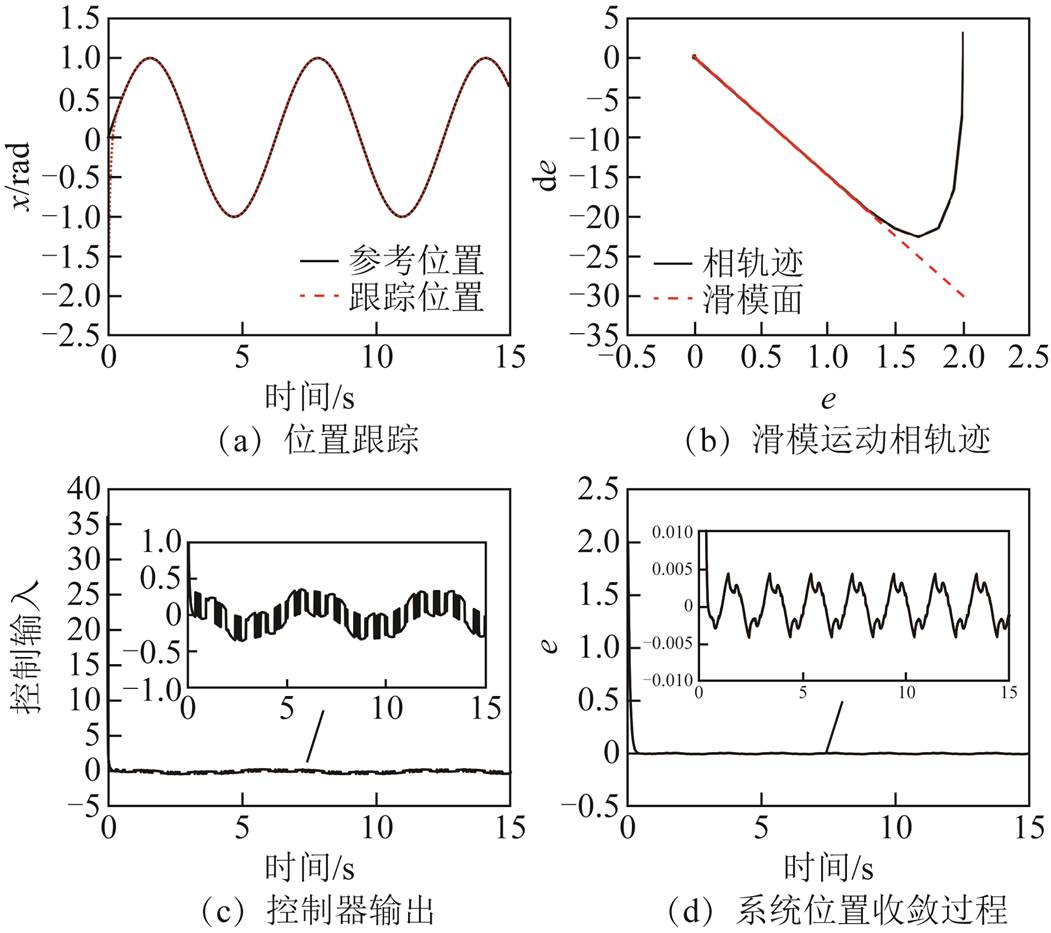
图1 ERL的控制性能图
Fig. 1 Control performance diagram of the ERL
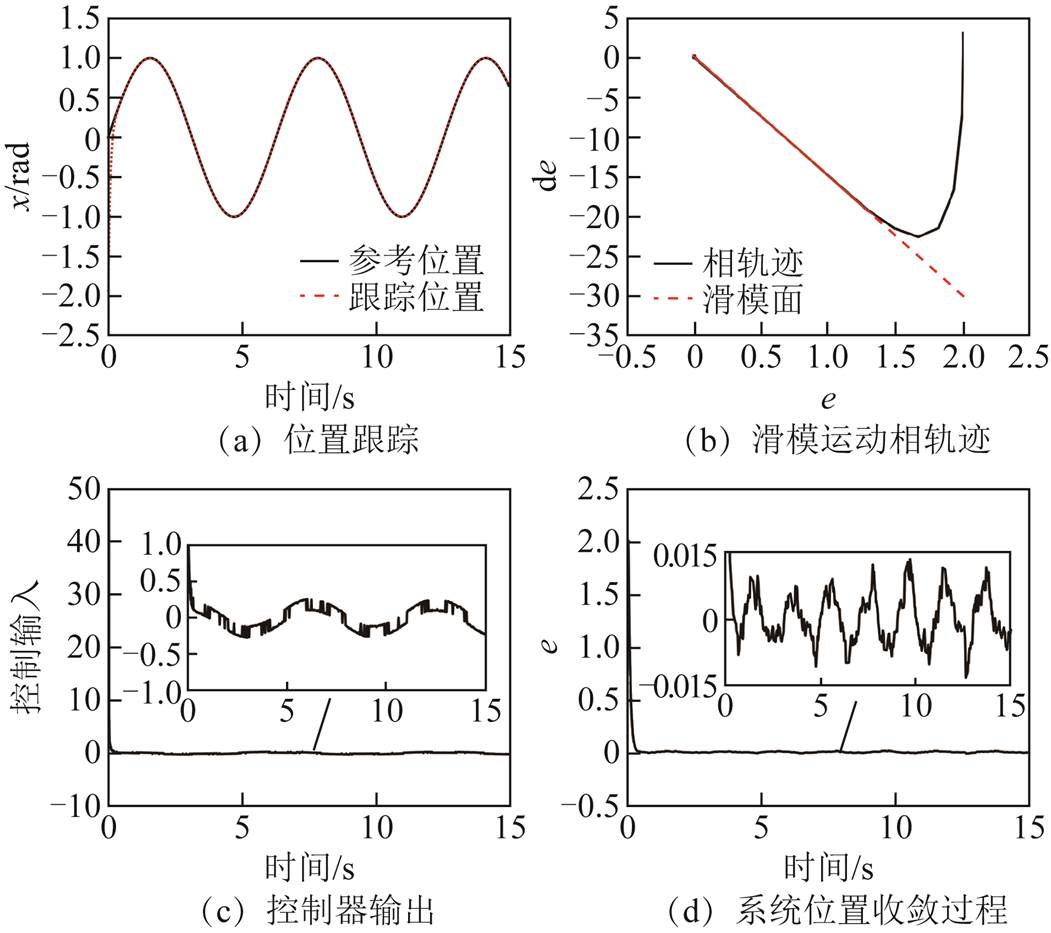
图2 SVERL的控制性能图
Fig.2 Control performance diagram of the SVERL
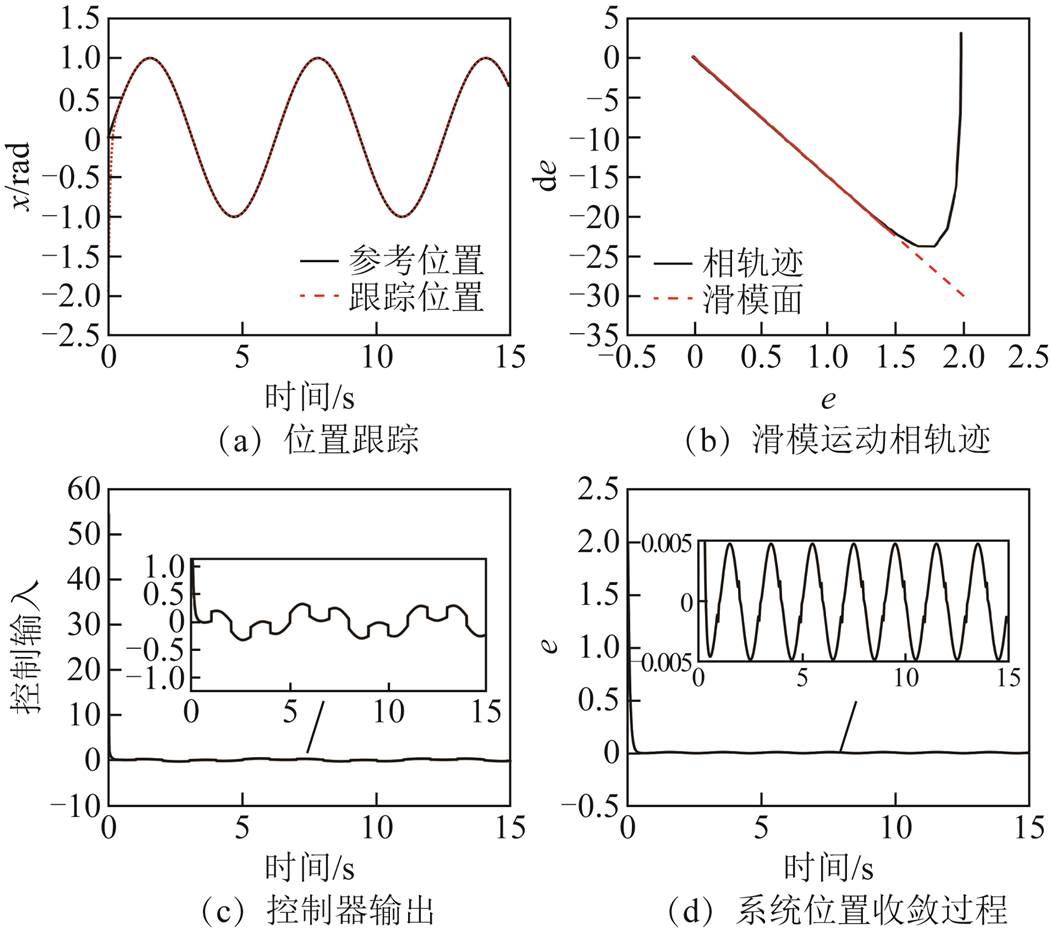
图3 IDPRL的控制性能图
Fig.3 Control performance diagram of the IDPRL
建立同步旋转坐标系即dq坐标系的IPMSM，其电机运动方程为
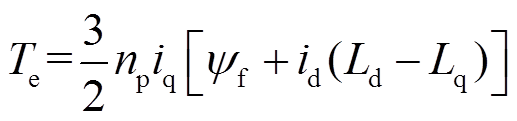（35）
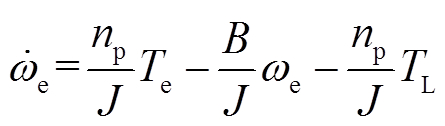（36）
式中，id、iq分别为d轴和q轴的电流；Ld、Lq分别为d轴和q轴电感；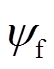
为电机永磁体磁链，ωe为电角速度；np为电机极对数；J为转动惯量；B为阻尼系数；TL为负载转矩。
考虑参数变化的情况下，永磁同步电动机的动态运动方程可以表示为
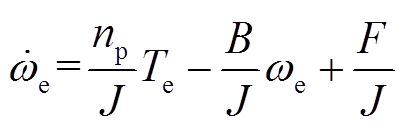（37）
其中
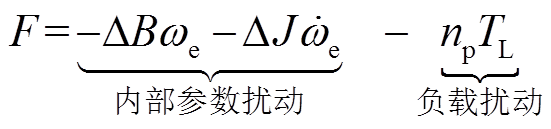
式中，ΔB和ΔJ分别为系统参数B和J所引起的不确定量；F为系统总扰动。
为了设计速度控制器，将一滑模变量s定义为调节误差的函数，即e = ω*-ω，其中，ω*为参考电角速度。假定x1 = e, x2 =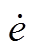
，所以，IPMSM速度误差的状态方程可表示为
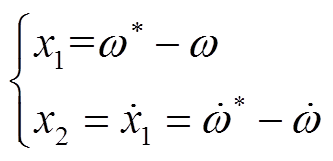（38）
将式（37）代入式（38），速度误差的导数可表示为
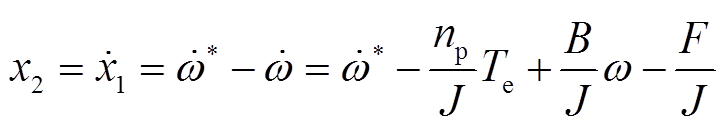（39）
为了消除稳态误差，提高控制精度，本文在传统滑模面的基础上增加了状态量的积分量，积分滑模面计算式为
（40）
结合式（6）、式（40），可得滑模控制器的方程为
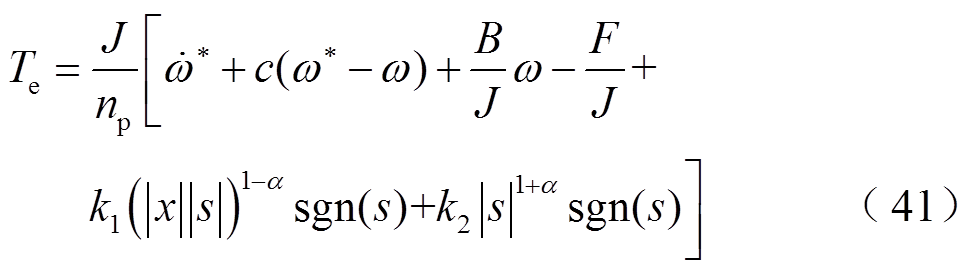
通过调节参数c、k1、k2、α，滑模变量s将在有限时间内趋近于0。
由于IPMSM交、直轴电感不对称，为充分发挥电机性能，本文采用最大转矩电流比的控制策略，由转速调节器得到Te参考信号，通过MTPA模块输出为d、q轴给定电流。系统控制结构框图如图4所示。
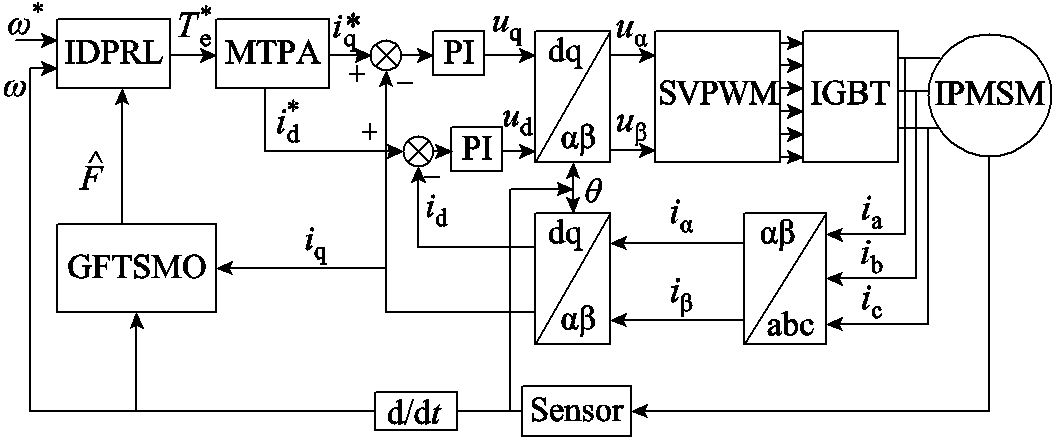
图4 IPMSM调速系统结构框图
Fig.4 Structure diagram of IPMSM speed control system
从式（41）可以看出，利用积分滑动面设计的控制律中包含了总扰动F，由定理2的分析可知，该总扰动会影响电机速度控制系统转速精度。为了提高系统的鲁棒性，针对永磁同步电机因参数变化、负载扰动等带来的非匹配扰动，本文设计了全局快速终端滑模观测器（GFTSMO）估计IPMSM系统中的扰动量，并用于前馈补偿控制。
以电角速度ω和系统总扰动F为状态变量，将q轴定子电流iq和电角速度ω分别定义为系统的输入和输出。IPMSM扩展状态空间方程为
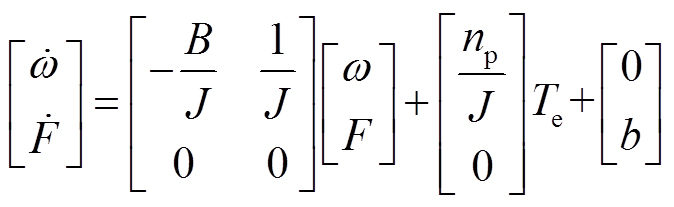（42）
式中，b为总扰动F的导数，且F和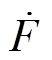
的导数有界。
通过式（42）可得负载转矩观测器的扩展状态空间方程可以表示为
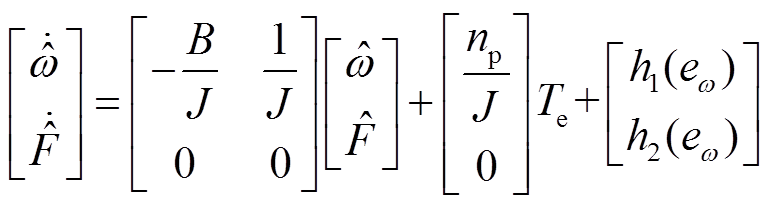（43）
式中，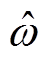
为转子电角速度的估计值；
为系统总扰动的估计值；h(eω)为观测误差eω对应的滑模控制律。电角速度eω和系统总扰动ef的观测误差率定义为
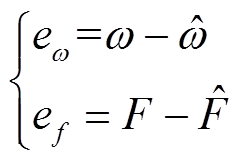（44）
由式（42）、式（43）和式（44）可得到观测器的误差方程为
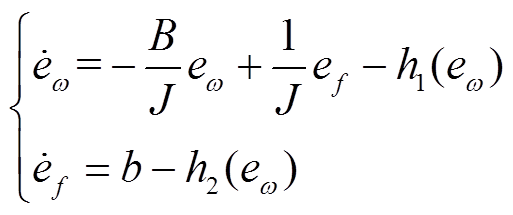（45）
滑模面的设计决定了滑模观测器的观测质量，为了获得更快的收敛时间和更好的跟踪精度，设计了一种全局快速终端滑模（GFTSM）曲面为
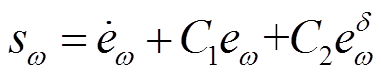（46）
式中，C1、C2和δ均为常数，且满足C1、C2＞0， 1＞δ＞0。
针对误差方程式（45），设计了一种高阶滑模控制律[27]，使eω和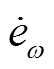
在有限时间内收敛到零。
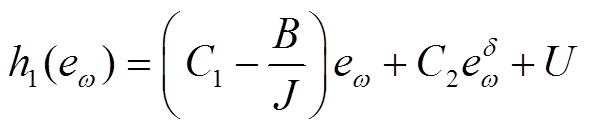（47）
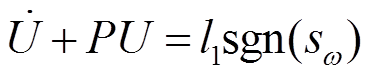（48）
式中，U、P、l1为式（48）控制律的设计参数。其中U的初始值U(0)=0。
此外，系统扰动导数的设计为
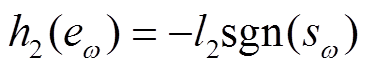（49）
式中，l2为设计参数。
图5是GFTSMO的结构图，通过适当地调整设计参数，GFTSMO可以获得令人满意的跟踪效果。
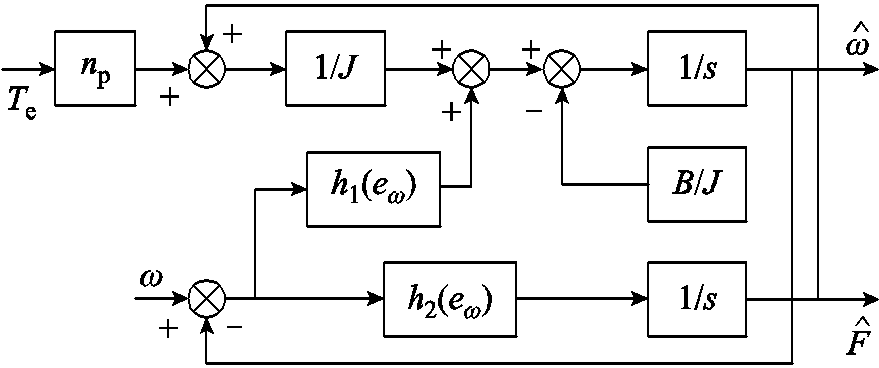
图5 全局快速终端滑模观测器结构
Fig.5 Structure of the GFTSMO
将式（45）的第一式与式（46）和式（47）相结合，滑模面函数s可重写为
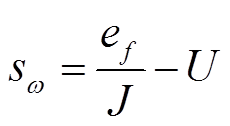（50）
s对时间t的导数可以表示为
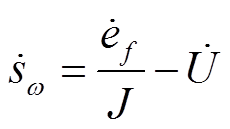（51）
将式（45）的第二项与式（48）代入式（51）可得
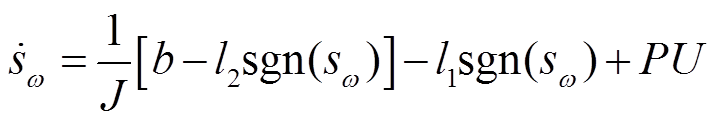（52）
结合李雅普诺夫函数和式（52）可得
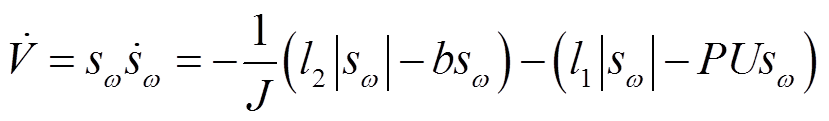（53）
根据有限时间李雅普诺夫稳定性理论，要使得
，则必须满足条件
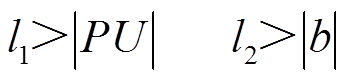（54）
由式（54）可取l1=2|PU|，减少了GFTSMO参数选取。
为验证所提方法的有效性和正确性，基于Matlab/Simulink平台建立仿真模型，仿真时的电机参数见表1。×
为了证明所提控制方法的有效性，下文对基于ERL、SVERL、IDPRL、基于GFTSMO的IDPRL控制方法进行了仿真对比，五种控制方法的参数分别如下。ERL参数：c=70，k1=10，k2=200；SVERL参数：c=70，k1=10，k2=200，a=0.55，b=0.55；IDPRL参数：c=70，k1=10，k2=200，α=0.55；GFTSMO参数：C1=100，C2=200，δ=0.9，P=200，l2=-500。
表1 永磁同步电机参数
Tab.1 Parameters of the IPMSM
参数数值 额定功率PN/kW1.5 额定电压UN/V380 额定电流IN/A2.7 额定转速nN/(r/min)1 500 极对数2 摩擦系数B/(N·m·s)0.000 1 定子电阻R/Ω3.678 d轴电感Ld/mH37.78 q轴电感Lq/mH119.62 转子磁链ψ/Wb0.803 转动惯量J/(kg·m2)0.003 01
图6比较了空载起动下四种控制方式的性能，速度始终保持在1 000r/min，表2给出了四种控制方式性能对比的具体数值。从图6a中可知所提的方法能够抑制超调，提高响应速度，降低转速和转矩波动。ERL和SVERL在空载起动时出现了较小的转速超调，而所提控制方法光滑地跟踪了参考速度。结合表2可以算出所IDPRL+GFTSMO方法在空载起动时转速的响应时间分别是ERL、SVERL、IDPRL的80.74%、85.51%和90.9%；转速稳态误差分别是ERL、SVERL和IDPRL的32.56%、38.89%和51.22%。同理，由图6b和表2可以算出所提控制方法在空载起动时的转矩脉动分别是ERL、SVERL、IDPRL的53.57%、56.6%和66.67%。
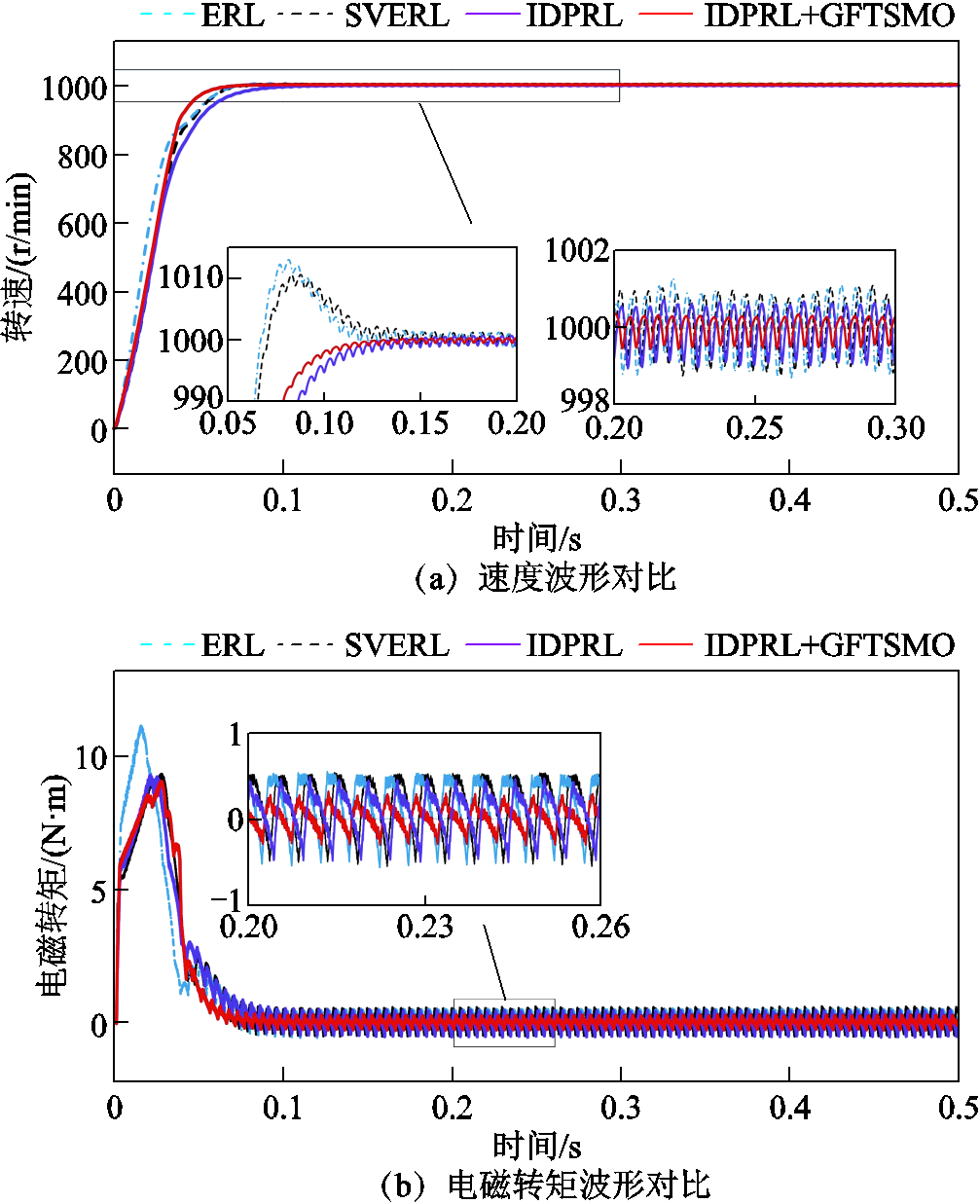
图6 空载起动时的四种控制方法性能对比
Fig.6 Performance comparison of four control methods under no-load condition
表2 空载起动时四种控制方式性能比较
Tab.2 Performance comparison of four control methods under no-load condition
性能指标ERLSVERLIDPRLIDPRL+GFTSMO 速度上升时间/ms161152143130 速度稳态误差/(r/min)1.291.080.820.42 速度超调/(r/min)10.5913.0200 转矩稳态误差/(N×m)0.560.530.450.3
为了验证设计的GFTSMO具有良好的动态性能，增加了基于SMO的仿真对比。图7中比较了阶跃负载下的五种控制方法，负载在0.3s时加载至6N×m，在0.6s卸载至0N·m，在0.6s时又加载至6N×m，速度始终保持在1 000r/min，表3给出了加载后四种控制方式性能对比的具体数值。从图7a中可知，所提的IDPRL+GFTSMO方法能具有较好的抗干扰性能，在加载和减载后能快速跟踪指定速度且抑制了转速波动。结合表3可以算出所提的控制方法在加载后的速度掉落分别是ERL的21.54%，是SVERL的24.1%，是IDPRL的68.9%和IDPRL+SMO的90.77%。6N×m负载转矩下ERL的转矩脉动最大，脉动范围为5.33～6.6N×m，转矩脉动为21.2%；SVERL的脉动范围为5.35～6.6N×m，转矩脉动为20.8%；IDPRL的脉动范围为5.38～6.46N·m，转矩脉动为18%；IDPRL+SMO的脉动范围为5.55～6.5N×m，转矩脉动为15.8%；IDPRL+ GFTSMO最小，脉动范围为5.6～6.36N×m，转矩脉动为12.7%。通过分析可知，所提控制方法能有效降低转矩脉动。
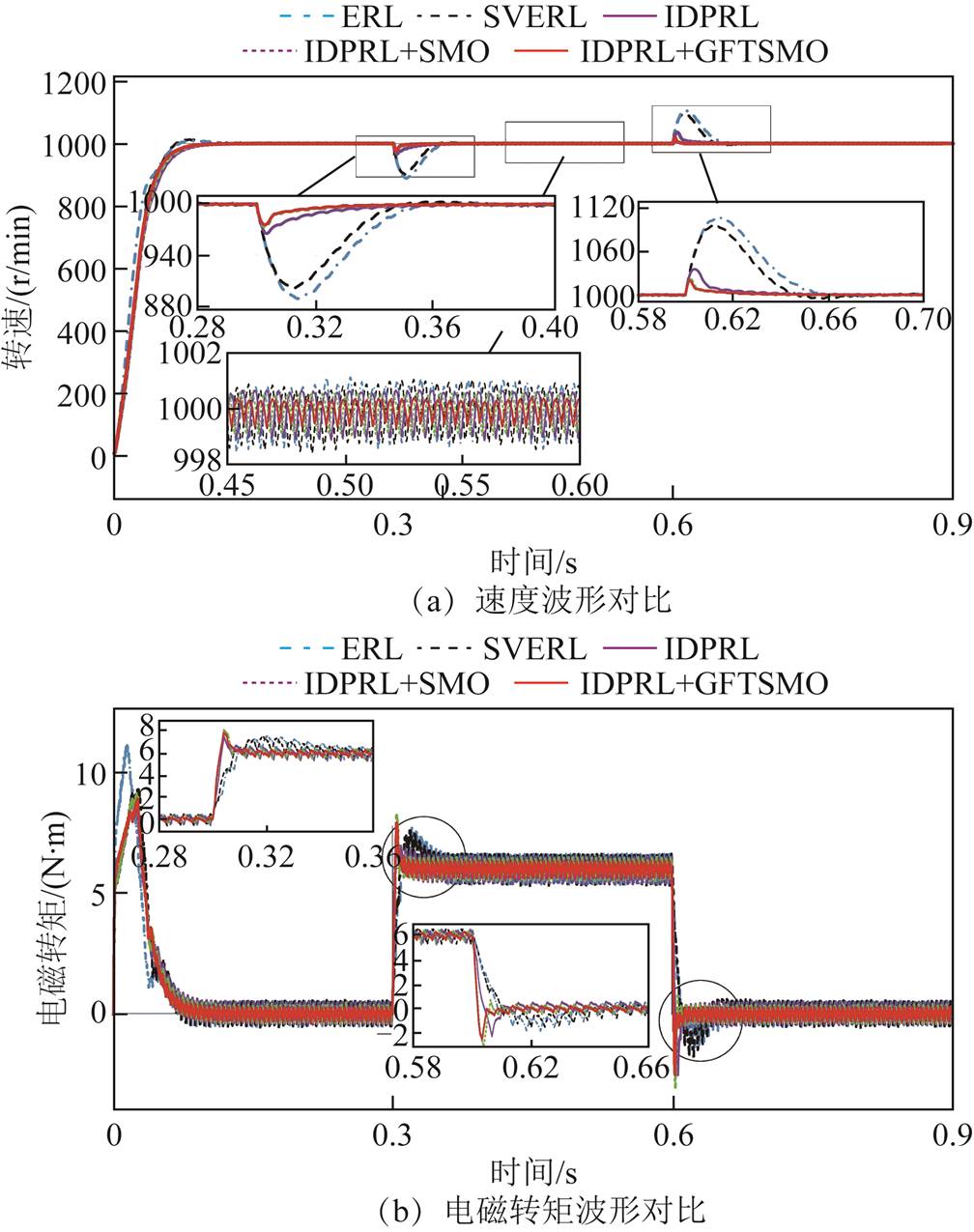
图7 阶跃负载的五种控制方法性能对比
Fig.7 Performance comparison of five control methods under step load condition
表3 阶跃负载的四种控制方式性能比较
Tab.3 Performance comparison of four control methods under step load condition
性能指标ERLSVERLIDPRLIDPRL+SMOIDPRL+ GFTSMO 速度上升时间/ms133115988568 速度稳态误差/(r/min)1.291.250.920.80.52 速度掉落/(r/min)110.599.134.526.323.8 转矩上升时间/ms5847251815 转矩稳态误差/(N×m)0.640.630.540.480.38
图8对比了两种观测器的控制性能，SMO在起动时有较大的脉动，而GFTSMO很好地抑制了起动后的脉动，实现了光滑的输出。从局部放大图可以看出SMO的观测曲线有较大的抖振，响应时间为0.11s，且观测误差大于0.005N×m，而GFTSMO较好地抑制了抖振，响应时间为0.012s，且观测误差为0.005N·m，表明了GFTSMO具有良好的跟踪性能。
图8 观测器性能对比
Fig.8 Performance comparison of observer
为进一步验证基于所提方法的速度控制器具有响应速度快、转矩脉动小、抗干扰强等优点，搭建了以dSPACE1104为控制核心的实验平台和硬件系统，如图9所示。控制器参数与仿真参数一致。
图9 实验平台
Fig.9 Experimental platform
图10为空载起动时四种控制方式的转速和电磁转矩的实验波形。相比基于ERL和SVERL控制方法，由图10a～图10c可知，所提的IDPRL方法的速度响应时间和速度在稳定状态的脉动均优于ERL和SVERL方法。其中，IDPRL的响应时间为2.79s，SVERL为3.11s，ERL为3.55s。ERL、SVERL和IDPRL方法的速度稳态脉动分别为56r/min，54r/min和51r/min。而所提的IDPRL+GFTSMO控制方法可以进一步提高系统的动态性和鲁棒性，其响应时间为2.25s，稳态时的转速和转矩脉动分别是48r/min和1N×m，这表明所提控制方法能够有效提高系统的快速性，并较好地抑制了转速和转矩脉动。
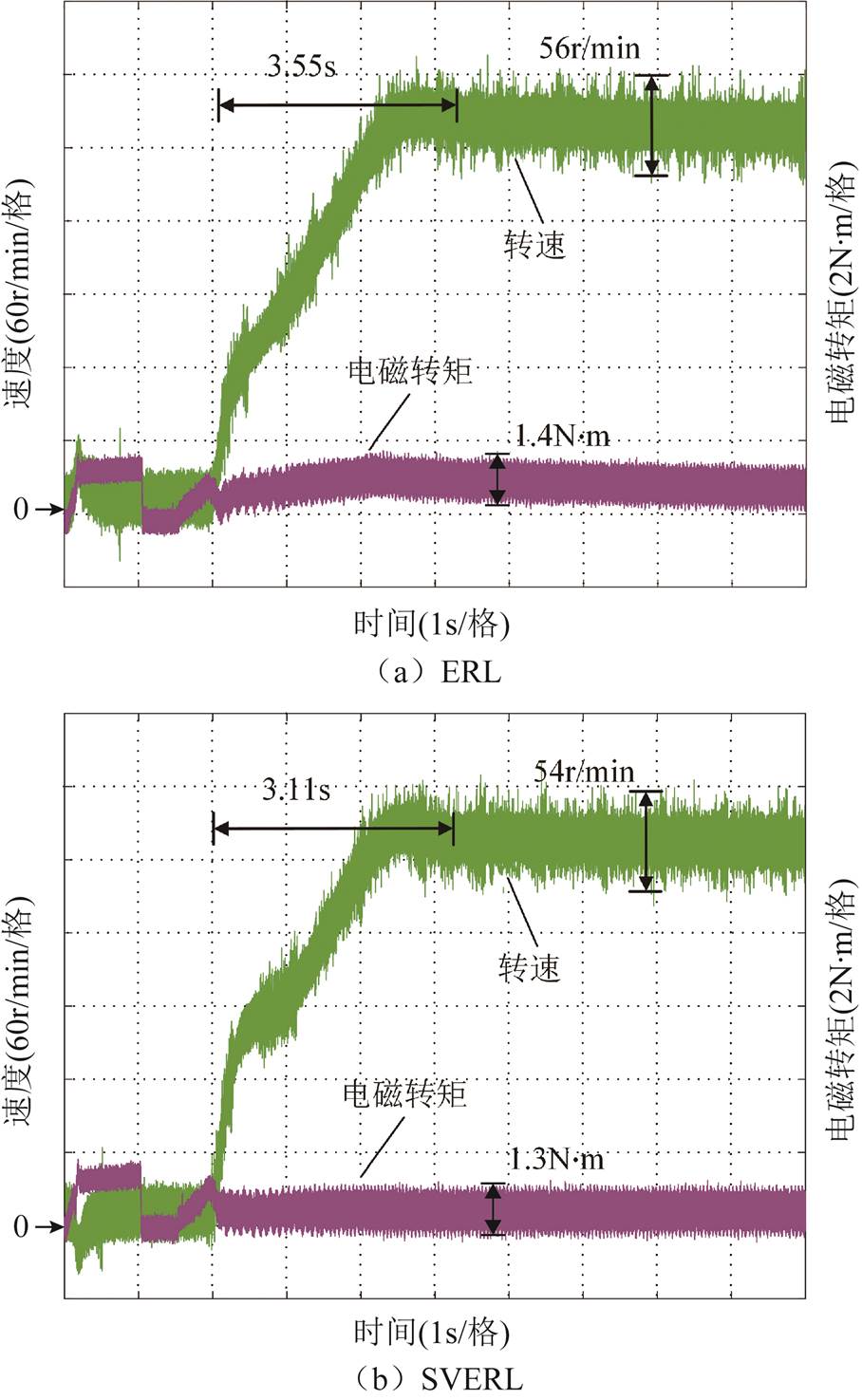
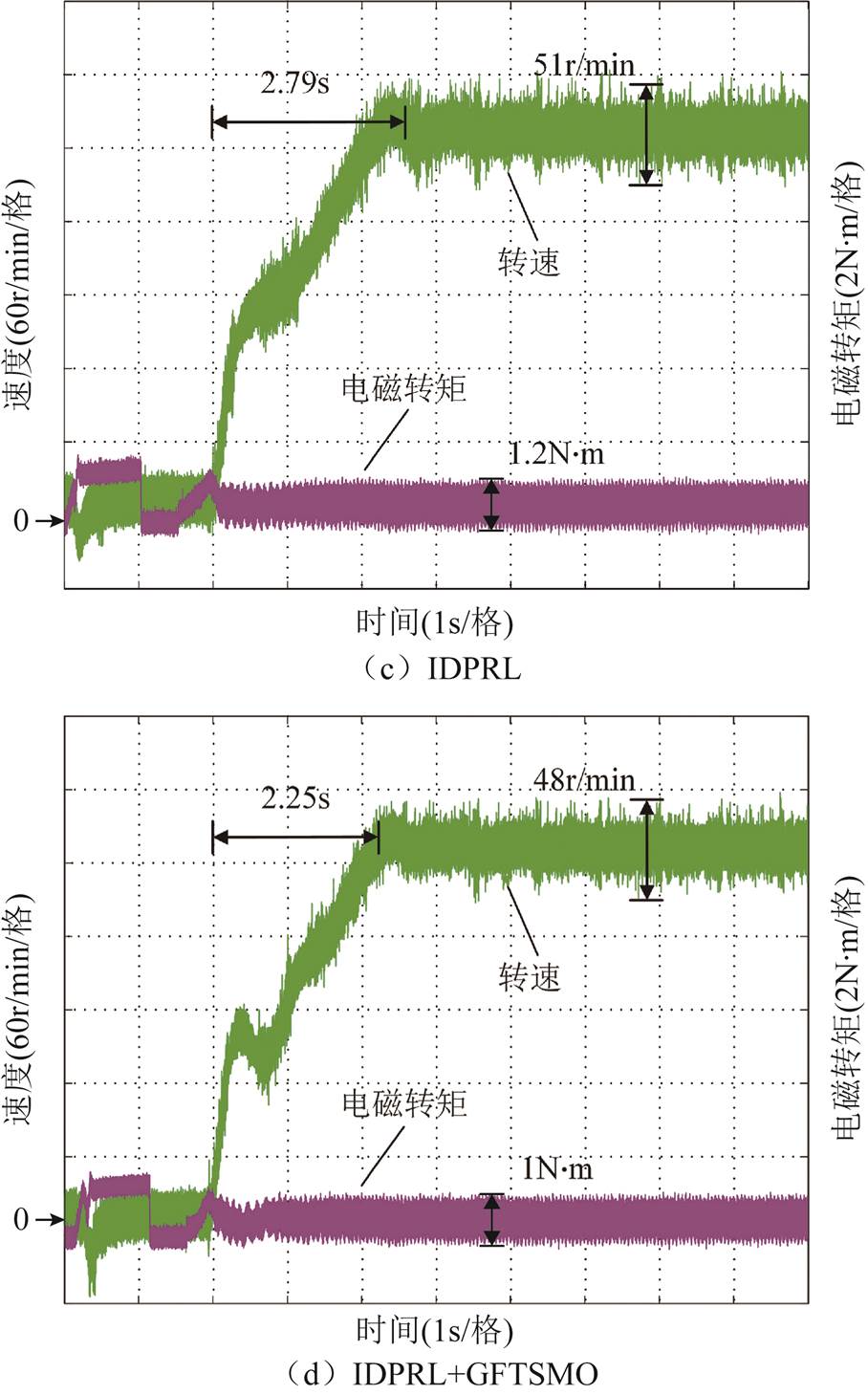
图10 IPMSM空载启动时下的转速和电流对比
Fig.10 Comparison of the speed and torque of IPMSM under no-load condition
图11为加减载时转速和电磁转矩在不同控制方法的实验波形。由图11可知，所提的IDPRL方法能够很好地抑制负载扰动，在加载时的速度掉落分别是ERL的83.33%，是SVERL的85.86%，在减载时的速度上升分别是ERL和SVERL的84.78%和88.63%。此外，IDPRL在加载时的转矩脉动和速度波动也均小于ERL和SVERL。而IDPRL+ GFTSMO方法进一步提升了上述指标，验证了本文所提控制方法具有较好的扰动抑制能力。
图12为转速从300r/min增加到600r/min的四种控制方法实验对比。由图12可知，所提的IDPRL+ GFTSMO和IDPRL方法在速度变换时的响应时间略小于SVERL方法，远小于ERL方法，证实了所提方法的快速性。相比于ERL和SVERL方法，IDPRL+GFTSMO和IDPRL方法的速度和转矩脉动大大减小，验证了所提方法能够大大减小稳态抖振的特性。
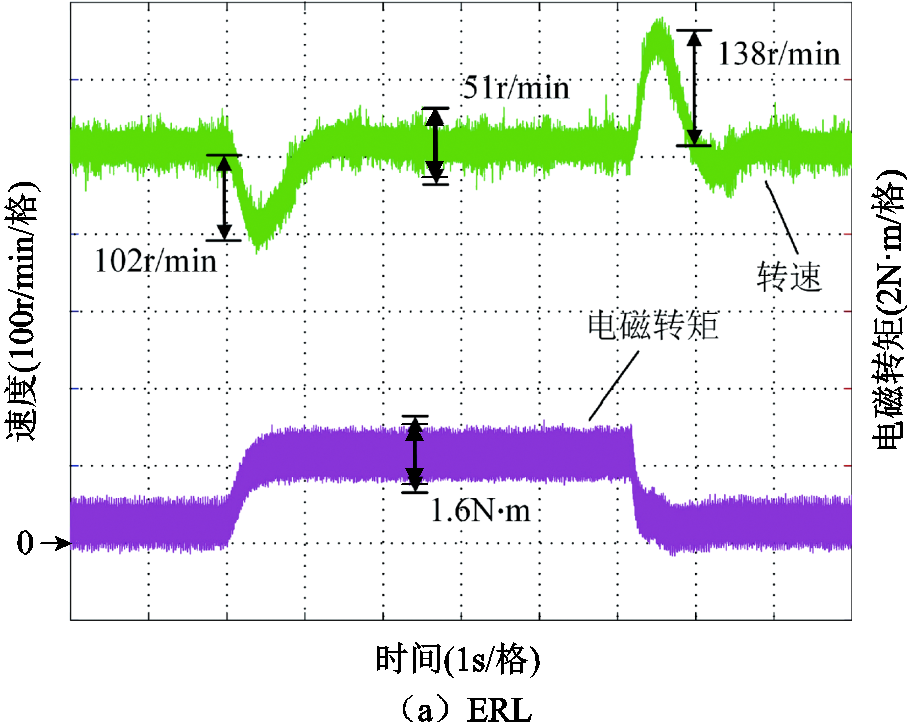
图11 加减载时的转速和电磁转矩对比
Fig.11 Comparison of speed andtorque under sudden loading and unloading conditions
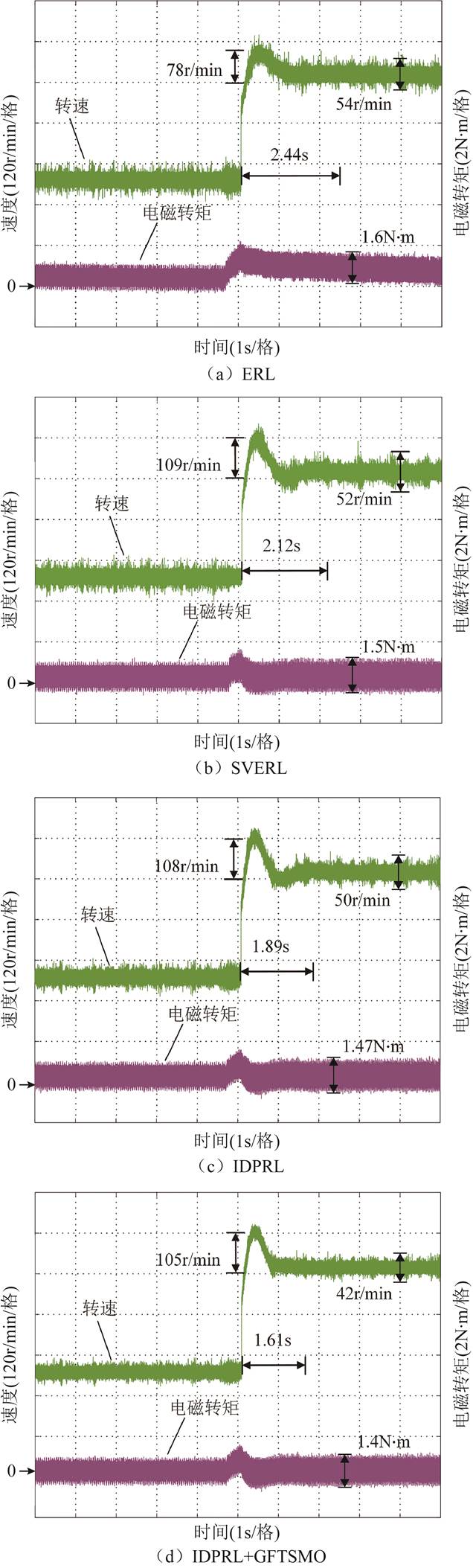
图12 不同方法的速度和电磁转矩响应
Fig.12 The speed and torque response of different methods
为了提高IPMSM调速系统的动态性，本文提出了一种基于状态变量的改进的双幂次趋近律，相比于现存的滑模趋近律，该趋近律具有参数少，在减少稳态误差、削弱抖振的同时快速到达滑模面的优点。为了进一步减少IPMSM调速系统的稳态误差，本文在采用所提趋近律设计的速度控制器的基础上，设计了一种全局快速终端滑模观测器，该观测器能对速度控制器的扰动进行前馈补偿，提高调速系统的快速性和抗干扰性。仿真和实验结果表明，所提方法能够有效地提高系统的响应速度，抑制转矩转速脉动，提高对外部负载的抗干扰性能。
参考文献
[1] 叶宇豪, 彭飞, 黄允凯. 多电机同步运动控制技术综述[J]. 电工技术学报, 2021, 36(14): 2922-2935.
Ye Yuhao, Peng Fei, Huang Yunkai. Overview of multi-motor synchronous motion control technology[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2922-2935.
[2] 刘春强, 骆光照, 涂文聪, 等. 基于自抗扰控制的双环伺服系统[J]. 中国电机工程学报, 2017, 37(23): 7032-7039, 7095.
Liu Chunqiang, Luo Guangzhao, Tu Wencong, et al. Servo systems with double closed-loops based on active disturbance rejection controllers[J]. Proceedings of the CSEE, 2017, 37(23): 7032-7039, 7095.
[3] Li Longfei, Xiao Jie, Zhao Yun, et al. Robust position anti-interference control for PMSM servo system with uncertain disturbance[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(2): 151-160.
[4] 付东学, 赵希梅. 永磁直线同步电机自适应非奇异快速终端滑模控制[J]. 电工技术学报, 2020, 35(4): 717-723.
Fu Dongxue, Zhao Ximei. Adaptive nonsingular fast terminal sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 717-723.
[5] 左月飞, 刘闯, 张捷, 等. 永磁同步电动机转速伺服系统PI控制器的一种新设计方法[J]. 电工技术学报, 2016, 31(13): 180-188.
Zuo Yuefei, Liu Chuang, Zhang Jie, et al. A novel design method of PI controller for permanent magnetic synchronous motor speed servo system[J]. Transactions of China Electrotechnical Society, 2016, 31(13): 180-188.
[6] 吕广强, 许文敏, 王谱宇. 基于变论域模糊PI自适应控制的电力弹簧控制策略[J]. 电力系统自动化, 2020, 44(18): 172-178.
Lü Guangqiang, Xu Wenmin, Wang Puyu. Control strategy for electric spring based on fuzzy proportional-integral self-adaptive control in variable universe[J]. Automation of Electric Power Systems, 2020, 44(18): 172-178.
[7] Shao Meng, Deng Yongting, Li Hongwen, et al. Robust speed control for permanent magnet synchronous motors using a generalized predictive controller with a high-order terminal sliding-mode observer[J]. IEEE Access, 2019, 7: 121540-121551.
[8] 魏惠芳, 王丽梅. 永磁直线同步电机自适应模糊神经网络时变滑模控制[J]. 电工技术学报, 2022, 37(4): 861-869.
Wei Huifang, Wang Limei. Adaptive fuzzy neural network time-varying sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 861-869.
[9] 李政, 胡广大, 崔家瑞, 等. 永磁同步电机调速系统的积分型滑模变结构控制[J]. 中国电机工程学报, 2014, 34(3): 431-437.
Li Zheng, Hu Guangda, Cui Jiarui, et al. Sliding-mode variable structure control with integral action for permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2014, 34(3): 431-437.
[10] 姚绪梁, 黄乘齐, 王景芳, 等. 两相静止坐标系下的永磁同步电动机模型预测功率控制[J]. 电工技术学报, 2021, 36(1): 60-67.
Yao Xuliang, Huang Shengqi, Wang Jingfang, et al. Model predictive power control of permanent magnet synchronous motor in two-phase static coordinate system[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 60-67.
[11] 陈闯, 王勃, 于泳, 等. 基于改进指数趋近律的感应电机滑模转速观测器研究[J]. 电工技术学报, 2020, 35(增刊1): 155-163.
Chen Chuang, Wang Bo, Yu Yong, et al. An improved exponential reaching law based-sliding mode observer for speed-sensorless induction motor drives[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 155-163.
[12] Yin Zhonggang, Gong Lei, Du Chao, et al. Integrated position and speed loops under sliding-mode control optimized by differential evolution algorithm for PMSM drives[J]. IEEE Transactions on Power Electronics, 2019, 34(9): 8994-9005.
[13] Zhang Xiaoguang, Sun Lizhi, Zhao Ke, et al. Nonlinear speed control for PMSM system using sliding-mode control and disturbance compensation techniques[J]. IEEE Transactions on Power Electronics, 2013, 28(3): 1358-1365.
[14] 张国荣, 侯立凯, 彭勃, 等. 柔性多状态开关反馈线性化滑模控制[J]. 电力系统自动化, 2020, 44(1): 126-133.
Zhang Guorong, Hou Likai, Peng Bo, et al. Feedback linearization sliding mode control strategy for soft open point[J]. Automation of Electric Power Systems, 2020, 44(1): 126-133.
[15] Jiang Yajie, Xu Wei, Mu Chaoxu, et al. Improved deadbeat predictive current control combined sliding mode strategy for PMSM drive system[J]. IEEE Transactions on Vehicular Technology, 2018, 67(1): 251-263.
[16] Fan Ying, Zhang Li, Cheng Ming, et al. Sensorless SVPWM-FADTC of a new flux-modulated permanent-magnet wheel motor based on a wide-speed sliding mode observer[J]. IEEE Transactions on Industrial Electronics, 2015, 62(5): 3143-3151.
[17] Gao Weibing, Hung J C. Variable structure control of nonlinear systems: a new approach[J]. IEEE Transactions on Industrial Electronics, 1993, 40(1): 45-55.
[18] Lin F J, Hung Y C, Ruan Kaichun. An intelligent second-order sliding-mode control for an electric power steering system using a wavelet fuzzy neural network[J]. IEEE Transactions on Fuzzy Systems, 2014, 22(6): 1598-1611.
[19] 陆婋泉, 林鹤云, 冯奕, 等. 永磁同步电机无传感器控制的软开关滑模观测器[J]. 电工技术学报, 2015, 30(2): 106-113.
Lu Xiaoquan, Lin Heyun, Feng Yi, et al. Soft switching sliding mode observer for PMSM sensorless control[J]. Transactions of China Electrotechnical Society, 2015, 30(2): 106-113.
[20] 樊英, 周晓飞, 张向阳, 等. 基于新型趋近律和混合速度控制器的IPMSM调速系统滑模变结构控制[J]. 电工技术学报, 2017, 32(5): 9-18.
Fan Ying, Zhou Xiaofei, Zhang Xiangyang, et al. Sliding mode control of IPMSM system based on a new reaching law and a hybrid speed controller[J]. Transactions of China Electrotechnical Society, 2017, 32(5): 9-18.
[21] Wang Yaoqiang, Feng Yutao, Zhang Xiaoguang, et al. A new reaching law for antidisturbance sliding-mode control of PMSM speed regulation system[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 4117-4126.
[22] Kim E. A fuzzy disturbance observer and its application to control[J]. IEEE Transactions on Fuzzy Systems, 2002, 10(1): 77-84.
[23] Liu Huixian, Li Shihua. Speed control for PMSM servo system using predictive functional control and extended state observer[J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 1171-1183.
[24] Lian Chuanqiang, Xiao Fei, Gao Shan, et al. Load torque and moment of inertia identification for permanent magnet synchronous motor drives based on sliding mode observer[J]. IEEE Transactions on Power Electronics, 2019, 34(6): 5675-5683.
[25] 张晓光, 赵克, 孙力, 等. 永磁同步电机滑模变结构调速系统动态品质控制[J]. 中国电机工程学报, 2011, 31(15): 47-52.
Zhang Xiaoguang, Zhao Ke, Sun Li, et al. Sliding mode control of permanent magnet synchronous motor based on a novel exponential reaching law[J]. Proceedings of the CSEE, 2011, 31(15): 47-52.
[26] Marks G, Shtessel Y, Gratt H, et al. Effects of high order sliding mode guidance and observers on hit-to-kill interceptions[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, California, Reston, Virginia, USA, 2005: 5967.
[27] Levant A. Higher-order sliding modes, differentiation and output-feedback control[J]. International Journal of Control, 2003, 76(9/10): 924-941.
Abstract Interior permanent magnet synchronous motors (IPMSM) are widely used in aerospace, servo systems, electric vehicles, wind power and other fields because of their high efficiency, high power density, and wide speed range. However, IPMSM has the characteristics of nonlinearity, strong coupling, and variable parameters. It is difficult to obtain fast response speed and strong robustness of the system only by using linear control methods such as PI control algorithm. Sliding mode control is widely used in IPMSM speed control system due to its advantages of strong robustness and fast dynamic response. The frequent switching of switches leads to the control discontinuity, which will bring inevitable chattering to the control system. In addition, a larger load disturbance requires a higher switching gain to ensure the robustness of the system, which will aggravate the chattering of the control system. To address these problems, a sliding mode control for IPMSM speed regulation system based on an improved double power reaching law (IDPRL) and a global fast terminal sliding mode observer (GFTSMO) is proposed.
The structure of this paper is as follows. Firstly, the existing problems of sliding mode reaching law, i.e., exponential reaching law (ERL) and exponential reaching law based on state variables (SVERL) are analyzed. Secondly, the IDPRL based on state variables is proposed. According to the theoretical derivation and analysis, it is shown that the proposed control method has the following characteristics: ①the system can converge to the sliding mode surface in a short time, and the convergence time of the proposed reaching law is not affected by the initial value; ② the proposed reaching law simultaneously has fast response ability, chattering suppression ability and better anti-interference performance. Thirdly, the IPMSM speed control system based on IDPRL and GFTSMO is designed, and its stability is proved theoretically. Fourthly, the simulation and experimental comparisons are conducted to verify the effectiveness of the proposed method. Finally, the conclusion is presented.
The simulation results show that, under the case of the system reference speed of 1 000r/min and no load, the speed response time of the proposed IDPRL+GFTSMO method is 80.74%, 85.51% and 90.9% of ERL, SVERL, IDPRL, respectively. The steady-state errors of IDPRL+GFTSMO are 32.56%, 38.89% and 51.22% of ERL, SVERL and IDPRL, respectively. Under the case of the system reference speed of 1000r/min and the load of 6N×m, the speed drop of the proposed IDPRL+GFTSMO method after loading is 21.54%, 24.1%, 68.9% and 90.77% of ERL, SVERL, IDPRL, IDPRL+SMO. Under the load torque of 6N·m, the torque ripple of ERL is the largest, the ripple range is 5.33～6.6N×m, and the torque ripple is 21.2%. The pulsation range of SVERL is 5.35～6.6N×m, the torque pulsation is 20.8%. The pulsation range of IDPRL is 5.38～6.46N×m, and the torque pulsation is 18%. The ripple range of IDPRL+SMO is 5.55～6.5N×m, and the torque ripple is 15.8%. For IDPRL+GFTSMO, the ripple range is the smallest (5.6～6.36N×m), and the torque ripple is 12.7%. The experimental results show that, under the case of the system reference speed of 300r/min and no-load startup, the speed response times of IDPRL+GFTSMO, IDPRL, SVERL and ERL are 2.25s, 2.79s, 3.11s and 3.55s, respectively. The steady-state speed fluctuations of ERL, SVERL, IDPRL and IDPRL+GFTSMO methods are 56r/min, 54r/min, 51r/min, and 48r/min, respectively. The speed drop scores of the proposed IDPRL+GFTSMO method during loading are 70.58%, 72.72% and 84.71% of ERL, SVERL and IDPRL. The speed increase at load shedding is 69.56%, 72.73% and 82.05% of ERL, SVERL and IDPRL, respectively. Under the case of the rotational speed from 300r/min to 600r/min, the transient response time of the proposed IDPRL+GFTSMO and IDPRL methods are both smaller than those of the SVERL and ERL methods.
Simulation and experimental results show that the proposed method can effectively improve the system response speed, reduce the torque and speed ripple, and improve the anti-interference performance of external loads.
Keywords：Interior permanent magnet synchronous motor, sliding mode reaching law, global fast terminal sliding-mode observer
DOI:10.19595/j.cnki.1000-6753.tces.211602
中图分类号：TM341
郭 昕 男，1994年生，博士研究生，研究方向为非线性控制及电机控制。E-mail：hnu_csgx@hnu.edu.cn
黄守道 男，1964年生，博士，教授，研究方向为主要研究方向为电力电子传动装置及控制、特种电机及控制、大型风力发电技术、磁耦合谐振式无线电能传输系统。E-mail：hsd1962@hnu.edu.cn（通信作者）
国家重点研发计划（2019YFB1503700）和国家自然科学基金（51737004）资助项目。
收稿日期 2021-10-11
改稿日期 2022-02-08
（编辑 郭丽军）