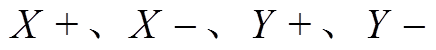 四个方向的电磁力。根据虚功原理,每组磁极产生的电磁力
四个方向的电磁力。根据虚功原理,每组磁极产生的电磁力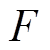 为
为摘要 对于传统磁轴承系统,发生单个下执行器失效故障后,悬浮的转子通常会与保护轴承发生碰撞,影响运行稳定性,甚至导致悬浮系统失稳,危害系统安全运行。在不改变磁轴承硬件架构的基础上,通过容错控制可以避免该碰撞,对于提高系统可靠性具有重要意义。为此,该文首先建立考虑部分执行器故障的两自由度转子动力学模型,提出针对上执行器的Bang-Bang控制算法,实现了故障磁轴承侧转子回到平衡位置的时间最优控制,并结合前馈控制使转子在Bang-Bang控制结束后直接达到稳定状态。仿真和实验结果表明,在全转速范围内故障侧最大位移幅值与转子正常轴振幅值相差不超过0.04mm,且转子在0.2s内恢复至稳定悬浮,故障侧轴承座振动加速度在0.03s内恢复到正常幅值,避免了定转子碰撞,证明了该算法的有效性。
关键词:磁轴承 执行器故障 容错控制 Bang-Bang控制 前馈控制
主动磁悬浮轴承(Active Magnetic Bearing, AMB,以下简称磁轴承)通过可控电磁力实现定转子的无机械接触,并由此带来运行过程中无摩擦、无磨损和无需润滑等优点,在飞轮储能、高速电机、涡轮机械等领域已得到了较广泛的应用[1-2]。然而,磁轴承系统较为复杂,控制通道和组成元件数量较多,由此带来的可靠性问题成为制约其发展的难题[3-5]。近年来随着磁轴承技术在航空航天、船舶、核能发电等领域的应用,对磁轴承的运行可靠性提出了更高的要求[6],因此可靠性问题亟须进一步深入研究和解决。作为提高系统可靠性的重要手段,容错控制是在磁轴承故障发生前后,根据检测的故障信息,针对不同故障源与故障特征,采取相应的控制措施,尽量保证磁轴承正常运行。通常,磁轴承系统主要由位移传感器、控制器、功率放大器、轴承本体(主要为电磁铁组件)等结构组成,其中功率放大器与轴承本体构成执行器。目前磁轴承容错控制研究主要集中在位移传感器故障的容错控制[7-8]和执行器故障的容错控制[9]两个方面。
本文针对执行器故障开展容错控制研究。根据故障对象进行划分,现有研究大致可以分为磁轴承本体故障和功放故障两类。针对磁轴承本体故障,文献[10]在径向布置6个磁极,并将相对的2个磁极作为一个独立的控制轴,3组磁极之间相互错开120°,任何一个磁极故障,剩余两个控制轴可继续保持系统的稳定运行。尽管该方法具有较强的容错能力,但需要布置冗余磁极,会额外增加磁轴承的设计成本。文献[11]提出一种广义偏置电流线性化方法,当检测到某一执行器通道开路后,通过重配置其他执行器电流实现水平、垂直方向电磁力的线性化控制,该方法适用各种分布形式线圈故障容错控制,但对应的电流重配置矩阵有无穷多解。文献[12]以故障后最大承载力为优化目标,对电流分配矩阵进行求解,但仍停留在理论分析层面。为证明该方法的有效性,文献[13]通过仿真分析了采用该容错控制算法的五种不同结构磁轴承故障后位移变化,证明该方法对于不同磁轴承结构均具有良好的容错控制性能,但同样未进行实验验证。文献[14]在一个磁路耦合的六极径向磁轴承上采用该方法进行了容错控制实验,结果表明,该方法能够在三个线圈失效的情况下维持转子静态悬浮,但全工况的运行性能未得到验证。除基于广义偏置电流线性化的电流重配置方法外,文献[15]针对弱耦合径向磁轴承结构,基于力补偿原理设计了电流重配置算法,并通过实验验证该算法的有效性,但该方法需要进行复杂的矩阵求解,会极大地增加控制算法的复杂度。对此,文献[16]提出了简化计算的参数解方法,但该方法只适用于线圈为偶数且等面积均匀间距分布的径向磁轴承。上述方法均没有对故障后转子动态性能进行分析,为此文献[17]通过实验说明提高电流重构速度能减小重构过程中转子最大幅值,证明了离线计算电流分配矩阵的重要性。文献[18-19]通过对功放调制过程中电流变化特征进行理论分析,根据正常负载电流的等效斜率定义故障诊断阈值,能快速诊断断路及部分短路故障,在与广义偏流线性化方法结合后能避免定转子碰撞。整体看来,上述容错控制算法能够在一个以上的执行器故障后维持转子稳定悬浮,但需将传统的差动控制方式改为独立控制,这将增加功放数量。针对故障后的单线圈控制,文献[20]介绍了将模糊Bang-Bang控制应用于单线圈控制的单自由度(Degree of Freedom, DOF)磁轴承上,在一定程度上解决了Bang-Bang控制稳态响应中存在的高频抖振问题。针对功放故障,文献[21]设计了一种新的开关管拓扑结构,将三相全桥等效为两套三相半桥的组合从而实现功放冗余,但采用三相半桥结构会降低直流母线电压利用率。从上述研究内容来看,现有的执行器容错控制方法普遍需要增加磁极数量、功放数量或改变功放开关管拓扑结构。增加硬件既增加了磁轴承的设计成本,又增大了整个系统的体积,而改变功放拓扑将降低直流母线电压利用率。
为克服上述缺陷,本文以卧式旋转设备用径向磁轴承作为研究对象,分析如何在不改变磁轴承硬件架构的基础上,针对单个执行器失效故障进行容错控制。为此,本文首先建立了两自由度转子动力学模型;然后在此基础上提出了执行器故障诊断方法以及基于Bang-Bang+前馈的容错控制策略,利用相平面分析法得到Bang-Bang控制切换曲线方程,并基于动力学模型得到前馈控制电流值;最后通过仿真与实验验证了该容错控制策略的有效性。
本文以典型的16极径向磁轴承为对象开展研究,其拓扑结构和线圈绕制方式如图1所示。相邻4个磁极构成一组,4个线圈分别嵌放于4组磁极上,可分别产生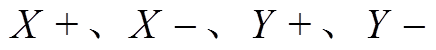 四个方向的电磁力。根据虚功原理,每组磁极产生的电磁力
四个方向的电磁力。根据虚功原理,每组磁极产生的电磁力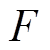 为
为
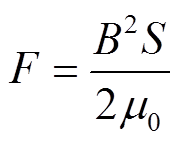 (1)
(1)
式中,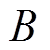 为气隙磁通密度;
为气隙磁通密度;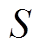 为每组磁极在转子上的投影面积;
为每组磁极在转子上的投影面积;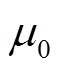 为真空磁导率。
为真空磁导率。
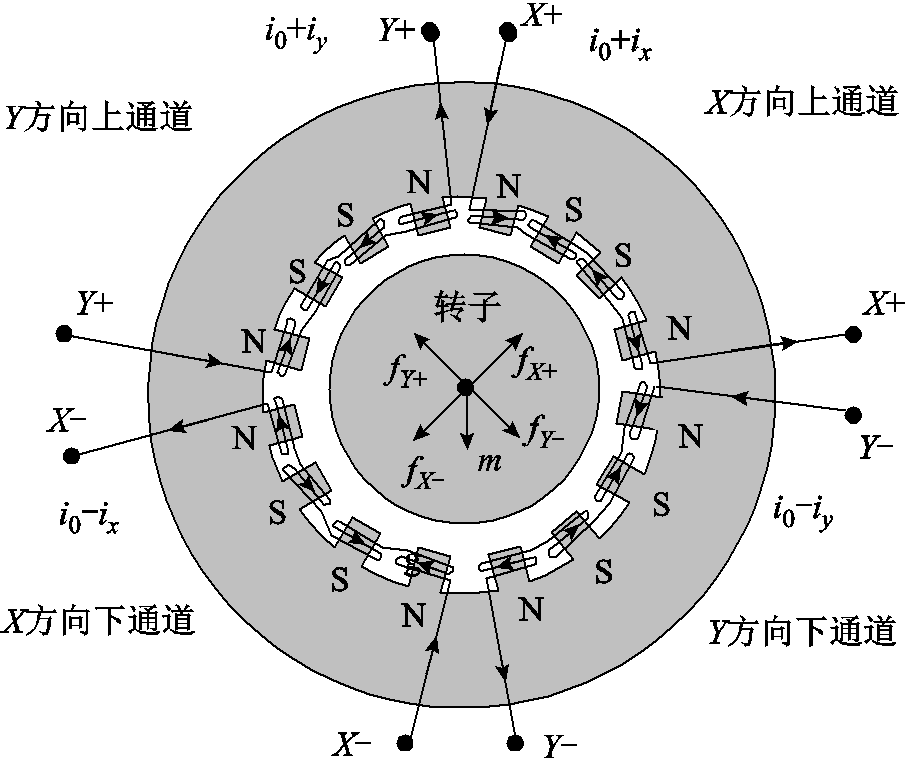
图1 16极磁轴承径向线圈分布示意图
Fig.1 Radial coil distribution diagram of 16 pole magnetic bearing
忽略铁磁材料饱和与漏磁,气隙磁通密度为

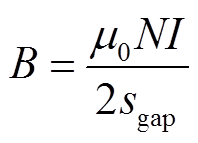 (2)
(2)
式中,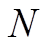 为线圈匝数;
为线圈匝数;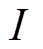 为线圈电流;
为线圈电流;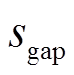 为气隙长度。综合式(1)和式(2)可得
为气隙长度。综合式(1)和式(2)可得

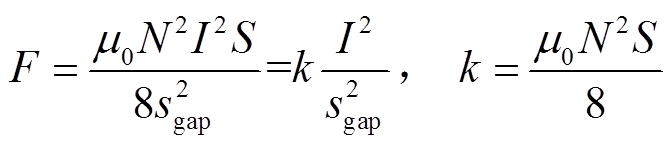 (3)
(3)
磁轴承结构参数确定后k为常数。
图1线圈采用差动控制,即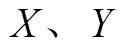 方向上、下执行器电流分别为偏置电流加减控制电流,转子在X方向上偏离平衡位置位移为x,转子在X方向的电磁合力
方向上、下执行器电流分别为偏置电流加减控制电流,转子在X方向上偏离平衡位置位移为x,转子在X方向的电磁合力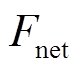 在平衡位置处对位移、电流求一阶泰勒展开可得到电流刚度
在平衡位置处对位移、电流求一阶泰勒展开可得到电流刚度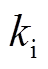 、位移刚度
、位移刚度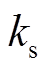 为
为
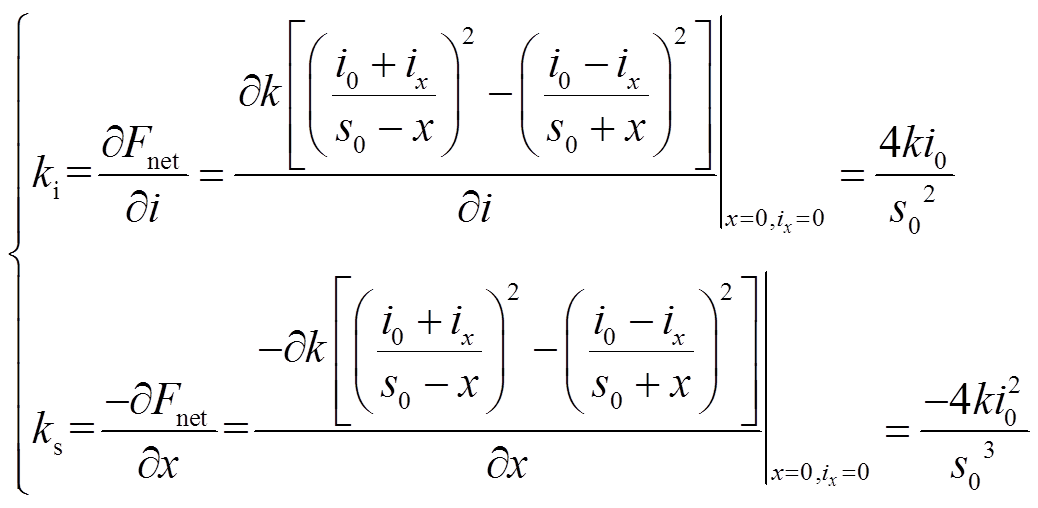 (4)
(4)
式中,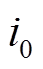 为偏置电流;
为偏置电流;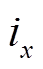 为X方向控制电流;
为X方向控制电流;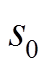 为转子在平衡位置时的电磁气隙。
为转子在平衡位置时的电磁气隙。
磁轴承系统控制架构采用最为典型的分散PID+双闭环系统,其中内环为电流环,外环为位移环。由于内环带宽通常远大于外环,故本文暂忽略电流内环的动态特性。这时,对于采用分散PID进行位移外环控制的磁轴承,每个自由度的控制电流可以表示为
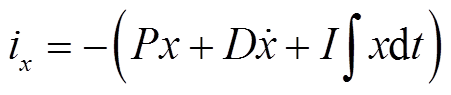 (5)
(5)
式中,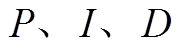 分别为比例、积分、微分参数。将式(5)代入式(4)得
分别为比例、积分、微分参数。将式(5)代入式(4)得
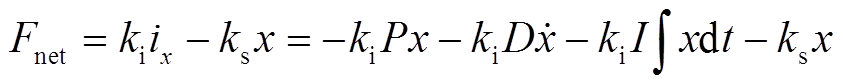 (6)
(6)
本文针对采用两个径向轴承和一个轴向轴承的5自由度磁悬浮轴承-转子系统开展研究。由于轴径向耦合较小,故仅分析径向控制自由度。当磁轴承在采用分散PID控制且转子没有与保护轴承碰撞时,径向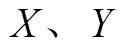 方向之间仅有陀螺效应带来的耦合,而对于细长型转子来说这种耦合效应较弱,本文分析时暂不考虑。以图2为例,假设转子右侧X方向某执行器故障,本文只考虑转子在
方向之间仅有陀螺效应带来的耦合,而对于细长型转子来说这种耦合效应较弱,本文分析时暂不考虑。以图2为例,假设转子右侧X方向某执行器故障,本文只考虑转子在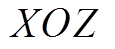 平面的两自由度运动,其中
平面的两自由度运动,其中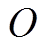 为转子在平衡位置时的质心位置;
为转子在平衡位置时的质心位置;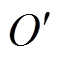 为转子当前质心位置;
为转子当前质心位置;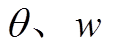 分别为转子在XOZ平面内绕质心逆时针旋转的角度、角速度;
分别为转子在XOZ平面内绕质心逆时针旋转的角度、角速度;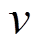 为质心运动速度;
为质心运动速度;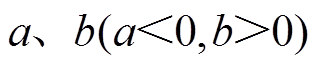 为转子质心到左右侧径向磁轴承的位移;
为转子质心到左右侧径向磁轴承的位移;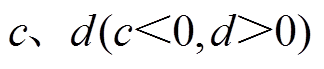 为转子质心到左右侧位移传感器的位移;
为转子质心到左右侧位移传感器的位移;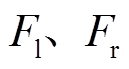 为左右侧的电磁合力。转子惯性主轴的偏心会使转子质心处受到一个随转子转动的不平衡力,
为左右侧的电磁合力。转子惯性主轴的偏心会使转子质心处受到一个随转子转动的不平衡力,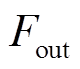 为重力与不平衡力的合力在X方向的分力;
为重力与不平衡力的合力在X方向的分力;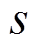 为质心在X方向的位移;
为质心在X方向的位移;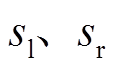 为传感器处转子位移;
为传感器处转子位移;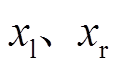 为电磁铁处转子位移。
为电磁铁处转子位移。
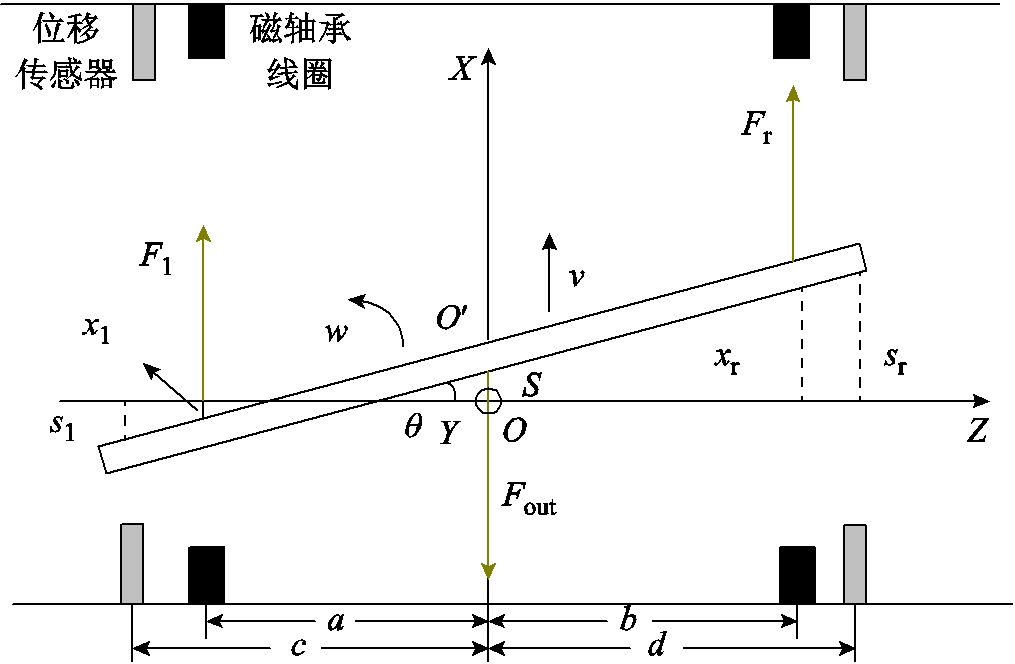
图2 转子在XOZ平面受力示意图
Fig.2 Force diagram of rotor in XOZ plane
忽略不平衡力的影响,则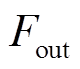 等于转子重力mg在X方向的分力
等于转子重力mg在X方向的分力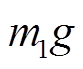 ,其中g为重力加速度,质心处的转矩
,其中g为重力加速度,质心处的转矩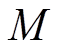 与力
与力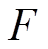 为
为
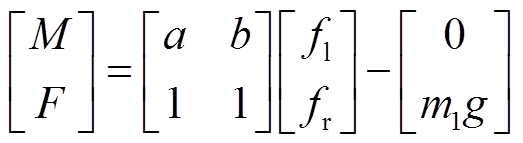 (7)
(7)
稳态时转子力系平衡,由式(7)有
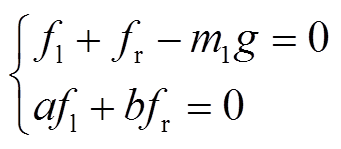 (8)
(8)
可得
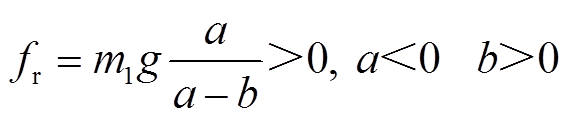 (9)
(9)
右侧下执行器故障后,转子达到稳态时右侧上执行器产生电磁力等于故障前差动线圈产生的电磁合力,由式(3)有
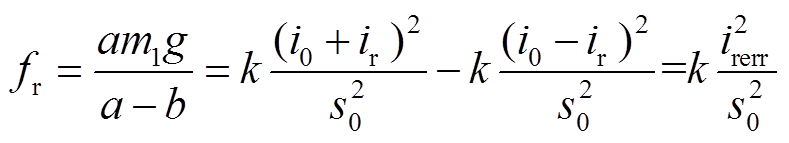 (10)
(10)
式中,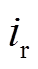 为故障前右侧稳态控制电流;
为故障前右侧稳态控制电流;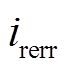 为故障右侧稳态执行器电流;
为故障右侧稳态执行器电流;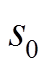 为转子在平衡位置时转子两侧电磁气隙。
为转子在平衡位置时转子两侧电磁气隙。
化简得
 (11)
(11)
由于故障后上执行器稳态电流比正常稳态电流小,转子能够达到力系平衡。
由于采用PID控制时积分环节在稳态下对电流影响与比例、微分环节相比较小,在分析稳定性时可以忽略,则式(6)可表示为
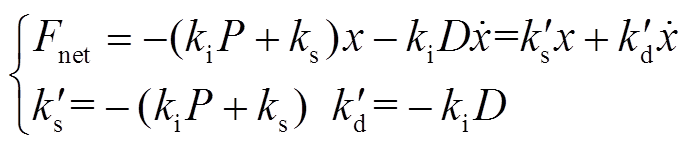 (12)
(12)
式中,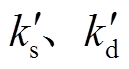 分别为等效刚度系数、等效阻尼系数。由于转子重力与静态控制电流产生的电磁力平衡,转子所受合力即为
分别为等效刚度系数、等效阻尼系数。由于转子重力与静态控制电流产生的电磁力平衡,转子所受合力即为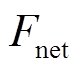 ,故有
,故有

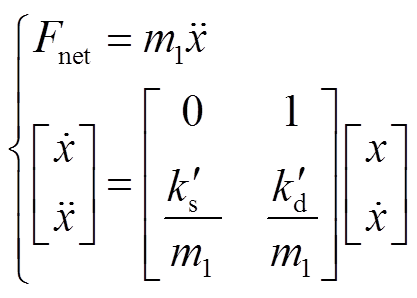 (13)
(13)
上述状态空间方程对应的特征根 为
为
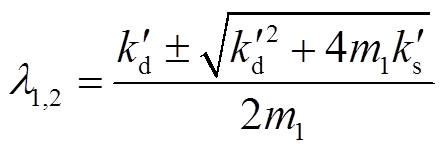 (14)
(14)
根据状态空间方程的稳定性判据,由于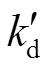 为负,当
为负,当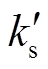 小于0时系统稳定。对于一个经过动平衡后的磁轴承-转子系统,在整个转速范围内,转子运动位移与电磁气隙相比往往较小,故可同样用一阶泰勒展开的方法求出单个上线圈电磁力
小于0时系统稳定。对于一个经过动平衡后的磁轴承-转子系统,在整个转速范围内,转子运动位移与电磁气隙相比往往较小,故可同样用一阶泰勒展开的方法求出单个上线圈电磁力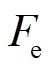 在平衡位置对应的位移刚度
在平衡位置对应的位移刚度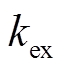 、电流刚度
、电流刚度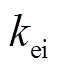 。
。
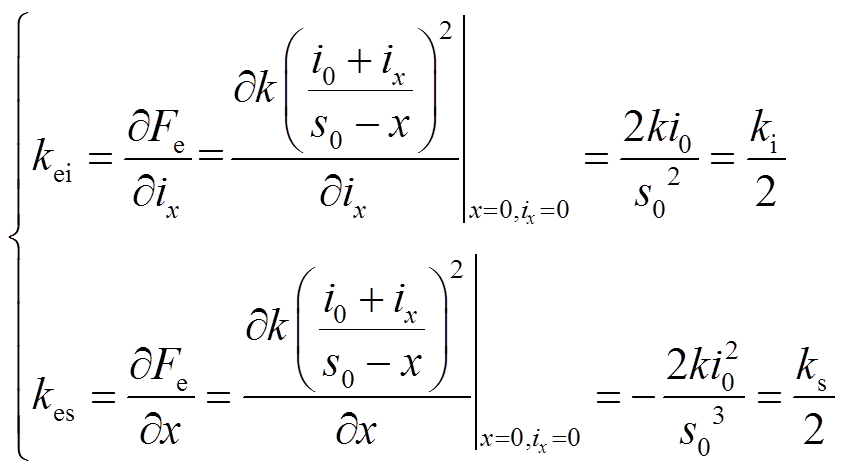 (15)
(15)
此时电磁力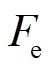 可以表示为
可以表示为
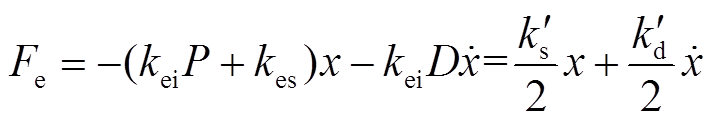 (16)
(16)
可见故障后,等效刚度与等效阻尼值均减小为正常时的一半,故障自由度位移幅值会增大,但两个特征根仍分布在极坐标左半平面,满足系统稳定条件,故障后系统仍能保持稳定。
对于径向4自由度系统,以右侧X方向下执行器故障为例,由于转子X、Y方向运动解耦,故障后Y方向仍保持稳定;左侧X方向刚度与阻尼系数不变,稳定后该自由度承受的重力分量不变,仍保持稳定,右侧X方向也仍能保持稳定,所以故障后转子最终仍能在径向上达到稳定状态。
实际情况下,上、下执行器都有可能发生故障。当发生上执行器故障后,由于该自由度电磁力无法提供向上的电磁力与重力平衡,只能通过布置冗余线圈的方法实现容错控制,以维持转子悬浮;对于下执行器故障,则有可能在不改变原有系统硬件结构的基础上,通过容错控制算法维持转子悬浮,并对动态响应过程进行优化,本文针对下执行器故障的容错控制算法进行设计。
以图2为例,假设X方向右侧下执行器发生失效故障。由于θ很小,可以认为式(17)成立。
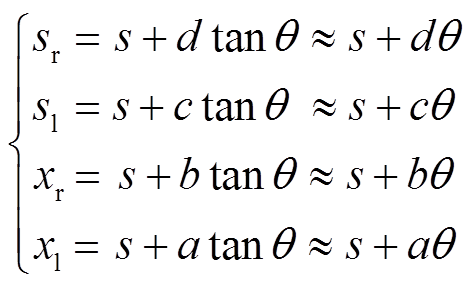 (17)
(17)
定义控制系统启动时刻为0时刻。转子在故障时刻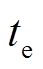 前已在平衡位置稳定悬浮,即
前已在平衡位置稳定悬浮,即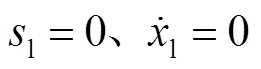 ,由式(6)得到
,由式(6)得到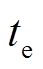 时刻左侧电磁合力
时刻左侧电磁合力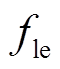 为
为
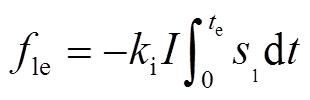 (18)
(18)
故障后短时间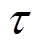 内积分环节对控制电流变化的影响可以忽略,此时左侧电磁合力
内积分环节对控制电流变化的影响可以忽略,此时左侧电磁合力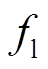 为
为
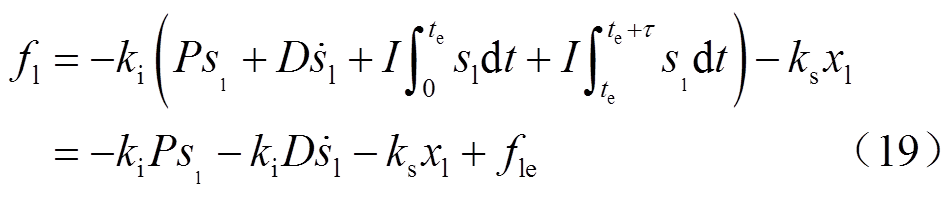
由式(6)、式(7)、式(17)~式(19)可以得到如式(20)所示的质心变量的状态空间方程。
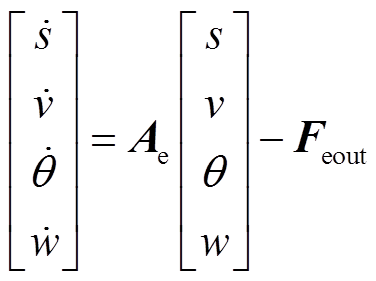 (20)
(20)
其中

式中,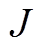 为转子绕Y轴的转动惯量。在已知磁轴承系统参数、右侧电磁力的情况下,通过该方程可以得到质心各变量随时间变化的函数。
为转子绕Y轴的转动惯量。在已知磁轴承系统参数、右侧电磁力的情况下,通过该方程可以得到质心各变量随时间变化的函数。
理想情况下,上、下两个执行器的电流和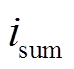 在正常状态下的值为
在正常状态下的值为
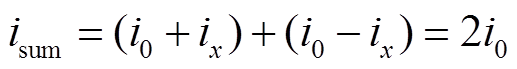
 (21)
(21)
当发生单个执行器失效故障后,故障通道的电流会迅速下降,转子在该自由度上会向非故障方向运动,导致故障自由度的正常通道电流也会迅速减小,此时差动的两个执行器的电流和将迅速小于两倍的偏置电流。通过设置故障诊断阈值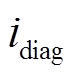 ,可得到执行器故障的诊断结果
,可得到执行器故障的诊断结果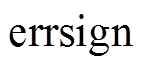 为
为
 (22)
(22)
通过电流和变化只能判断故障执行器所在自由度,还需通过执行器电流变化斜率识别出故障执行器。某执行器通道断路后,线圈电流通过续流二极管构成故障通道电路如图3所示,图中各电气量关系满足
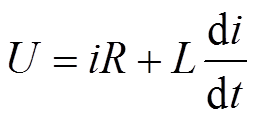 (23)
(23)
式中,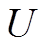 为充电时的直流母线电压,故障时为0;
为充电时的直流母线电压,故障时为0;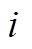 为线圈与续流二极管构成的通路电流;L为电路电感;
为线圈与续流二极管构成的通路电流;L为电路电感;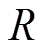 为线圈电阻。若故障时刻
为线圈电阻。若故障时刻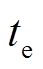 对应通道电流
对应通道电流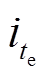 ,则
,则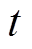 时刻电流
时刻电流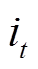 为
为
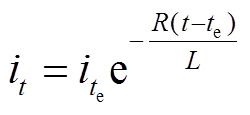 (24)
(24)
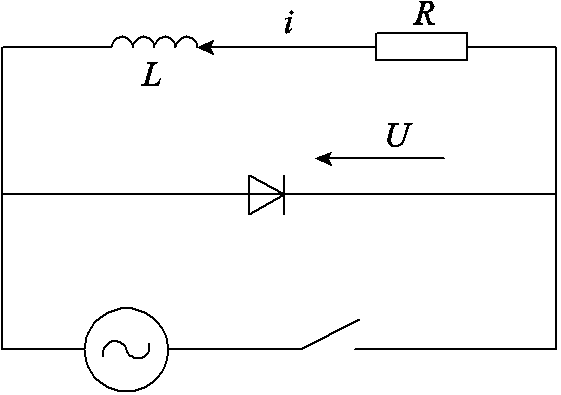
图3 故障通道电路
Fig.3 Fault channel circuit
一般可认为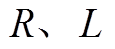 的值在短时间内为常数,则故障初期故障通道电流变化率与
的值在短时间内为常数,则故障初期故障通道电流变化率与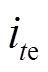 的值无关。正常通道电流在开关管导通时上升,在关断时以续流方式下降,因此故障通道电流下降速度为最快电流下降速度,通过判断执行器电流下降斜率是否超过故障电流下降斜率
的值无关。正常通道电流在开关管导通时上升,在关断时以续流方式下降,因此故障通道电流下降速度为最快电流下降速度,通过判断执行器电流下降斜率是否超过故障电流下降斜率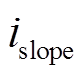 可判断执行器是否故障。
可判断执行器是否故障。
为确定故障诊断阈值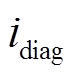 ,需要分析差动电流和与
,需要分析差动电流和与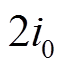 偏差最大值,该偏差主要由两部分组成。第一部分偏差由稳态时的电流纹波带来,以磁轴承常用的三电平脉宽调制功放为例[22],其纹波大小
偏差最大值,该偏差主要由两部分组成。第一部分偏差由稳态时的电流纹波带来,以磁轴承常用的三电平脉宽调制功放为例[22],其纹波大小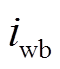 约为
约为
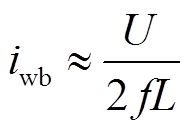 (25)
(25)
式中,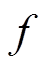 为开关频率。差动线圈电流和与
为开关频率。差动线圈电流和与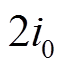 的偏差最大为
的偏差最大为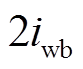 。
。
第二部分是转子运动过程中,上、下功放电流变化速度不同带来的影响。对应的差动上、下线圈电流及电流和变化如图4所示。
假设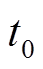 时刻上、下线圈电流为
时刻上、下线圈电流为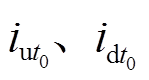 ,上下执行器通路的电阻、电感均为
,上下执行器通路的电阻、电感均为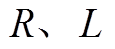 ,转子运动过程中,假设上线圈电流通过直流母线电压充电增大,在
,转子运动过程中,假设上线圈电流通过直流母线电压充电增大,在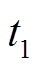 时刻的电流
时刻的电流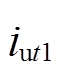 为
为
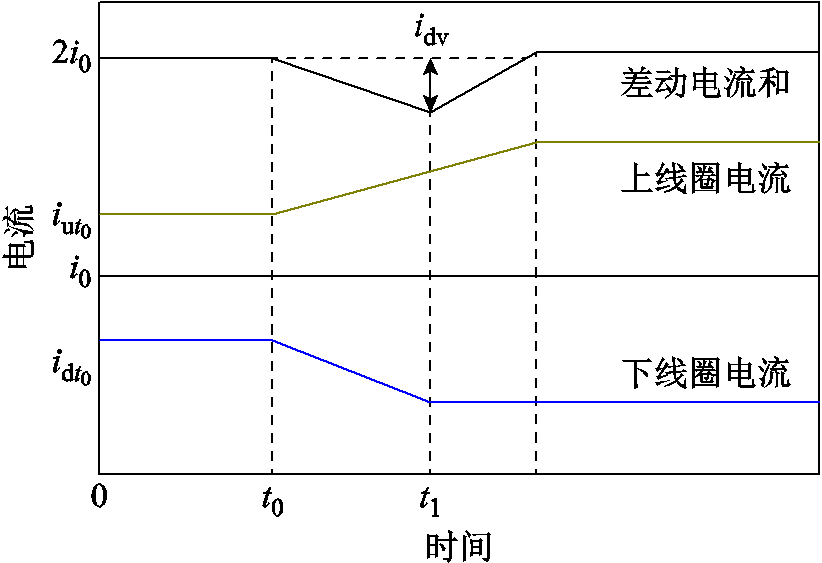
图4 差动线圈电流变化
Fig.4 Current changes on differentid coils
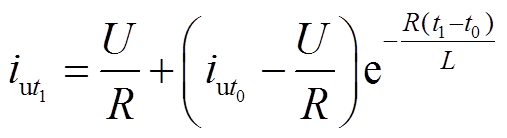 (26)
(26)
式中,充电时的直流母线电压U通过开关管的占空比进行控制。下线圈电流值因二极管续流减小,在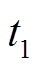 时刻的电流
时刻的电流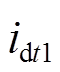 为
为
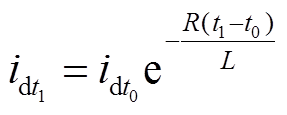 (27)
(27)
转子在稳态下受到冲击后电流变化幅值最大的情况为上线圈电流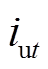 变为0,下线圈电流
变为0,下线圈电流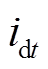 变为
变为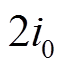 ,在此过程中,差动电流和与
,在此过程中,差动电流和与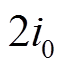 的最大偏差幅值
的最大偏差幅值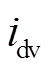 为
为
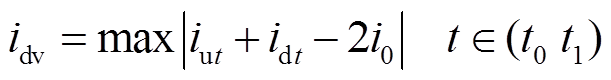 (28)
(28)
将两种差动电流和的偏差相加得到理论上的最大偏差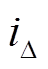 为
为
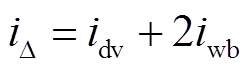 (29)
(29)
考虑到不同执行器支路电阻、电感差异,在决定故障判断阈值时留有一定的裕量,取
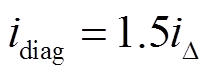 (30)
(30)
控制板上电过程中各自由度两个执行器电流和从0逐渐增大,此过程中errsign=1,为防止误判,电流稳定且errsign=0(正常)后的errsign=1(故障)信号才会触发容错控制,整体的故障识别流程如图5所示。
以右侧为故障侧为例,故障后转子右侧在电磁力与重力的向上合力作用下有向上运动趋势,上线圈电流随之减小,产生的电磁力也随之减小。当PID参数选取合适时,能够避免转子与保护轴承发生碰撞,但该参数往往不适用于稳态下的悬浮控制,且对转子最大幅值抑制效果有限,故需要提出新的方法对故障后的瞬态过程进行优化控制。
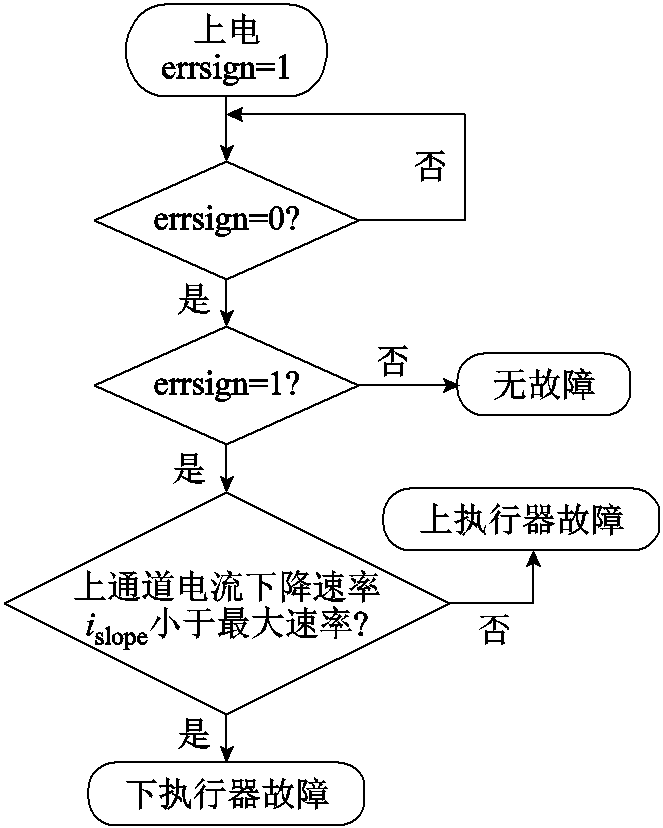
图5 单个执行器故障诊断流程
Fig.5 The flow chart of diagnosis of single actuator fault
本文考虑使用时间最优控制使转子最快回到平衡位置。首先判断磁轴承-转子系统的能控性,根据式(20)中的状态空间方程,得到系统的能控性判别矩阵Re为
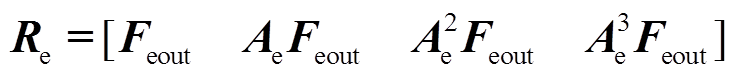 (31)
(31)
对于设计好的磁轴承参数,可满足秩rank(Re)=4即满秩,说明系统各变量完全可控,各个变量能够在有限时间内从任意初始状态回到0状态。对于这样的正常系统,根据最优控制理论,其时间最优控制就是Bang-Bang控制[23]。
Bang-Bang控制的特点是在控制过程中,控制量总选择控制区间的边界值,以实现时间最优。考虑故障侧上执行器电流,将电流为0A作为零电磁力控制方式;将电流为最大允许电流作为最大电磁力控制方式,分别对应故障后右侧的电磁力为0与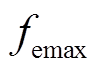 。假设故障识别时转子状态如图2所示,右侧零电磁力控制能够最有效地抑制右侧位移幅值向上继续增大,最大电磁力控制能使右侧在接近平衡位置时减速,以使位移、速度同时为0。
。假设故障识别时转子状态如图2所示,右侧零电磁力控制能够最有效地抑制右侧位移幅值向上继续增大,最大电磁力控制能使右侧在接近平衡位置时减速,以使位移、速度同时为0。
Bang-Bang控制的控制切换点可以通过相平面法来分析。相平面的横坐标为故障侧位移,纵坐标为故障侧速度,如图6所示。从式(20)的数值解可以得到速度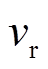 与位移
与位移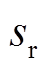 的微分关系如式(32)所示,由于
的微分关系如式(32)所示,由于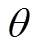 很小,约等于号成立。
很小,约等于号成立。
故障诊断时刻故障侧位移、速度可能在相平面的任何象限,以转子故障端在零电磁力控制和最大电磁力控制下回到相平面原点的轨迹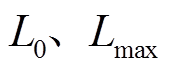 为界,将相平面分成边界下的A区(图中阴影区域)和边界上的B区。以故障诊断时刻故障自由度状态位于B区为例:首先采用零电磁力控制,运动轨迹对应图中
为界,将相平面分成边界下的A区(图中阴影区域)和边界上的B区。以故障诊断时刻故障自由度状态位于B区为例:首先采用零电磁力控制,运动轨迹对应图中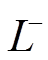 段,当运动到与
段,当运动到与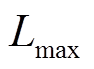 相交,改为最大电磁力控制,并沿
相交,改为最大电磁力控制,并沿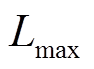 段回到相平面原点。
段回到相平面原点。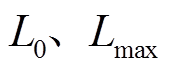 段轨迹可以通过反向求解得到:用欧拉离散法将式(20)变换为式(33),其中状态变量及下标
段轨迹可以通过反向求解得到:用欧拉离散法将式(20)变换为式(33),其中状态变量及下标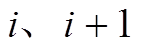 表示该状态在第
表示该状态在第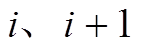 步的值,右侧电磁合力取零电磁力或最大电磁力,从某初始状态开始运动并在经过n步后到达相平面0点,当步长取得足够小,可以证明约等于号成立,从第n步反推即可得到两种控制下的轨迹。
步的值,右侧电磁合力取零电磁力或最大电磁力,从某初始状态开始运动并在经过n步后到达相平面0点,当步长取得足够小,可以证明约等于号成立,从第n步反推即可得到两种控制下的轨迹。
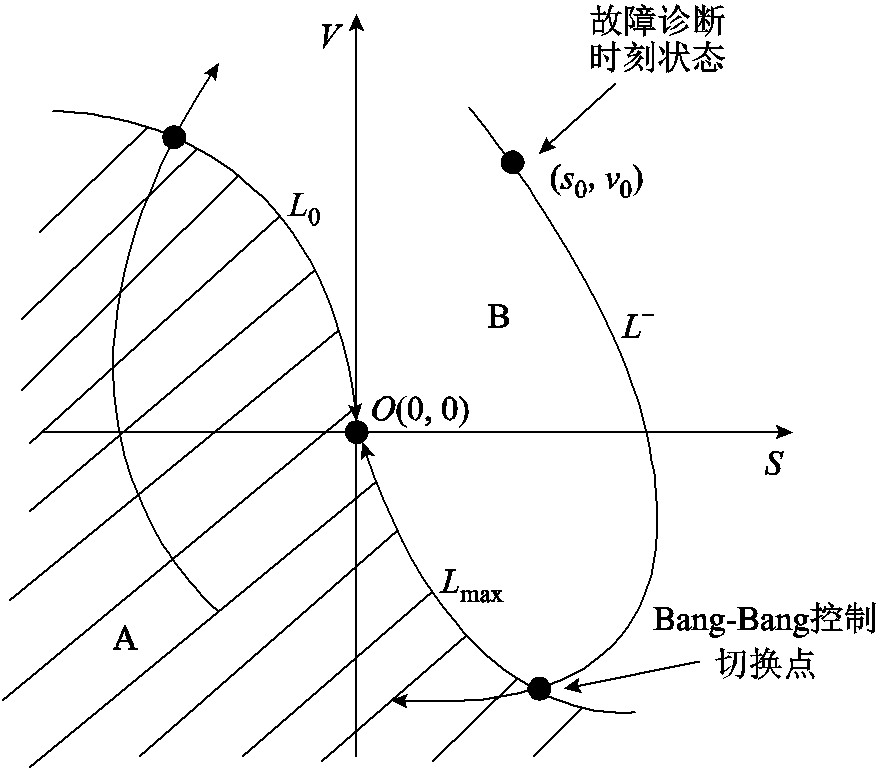
图6 Bang-Bang控制的相平面轨迹
Fig.6 Phase plane trajectory of Bang-Bang control
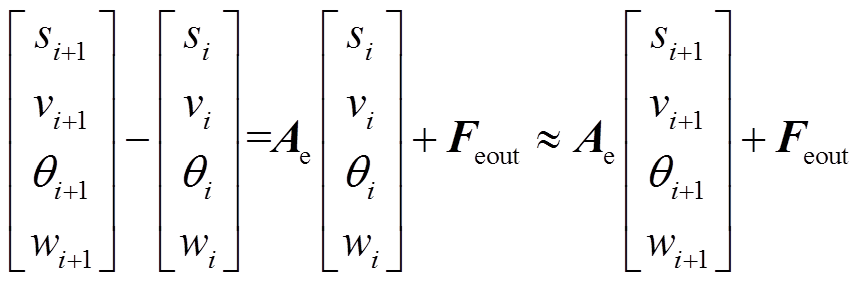 (33)
(33)
故障后,首先根据故障自由度位移、速度判断当前所处于相平面区域,并采用相应的电磁力控制方式,运动到与边界线相交时切换到另一种电磁力控制方式,并最终回到相平面原点。因此,采用Bang-Bang控制能最大限度地避免碰撞,使故障侧最快回到平衡位置且速度为0。
但根据Bang-Bang控制的特点,两种控制模式下的频繁切换会导致转子在平衡位置附近高频振荡。为避免该振荡,容错控制结束后控制方法应切换回PID控制。
假设转子在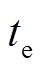 时刻达到正常稳态并发生故障,在
时刻达到正常稳态并发生故障,在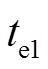 时刻达到故障稳态,由于控制方式在故障前后转子稳定时均为PID控制,忽略外部干扰,两时刻位移的微分项与比例项均为0。根据式(5)可得两个时刻的控制电流值
时刻达到故障稳态,由于控制方式在故障前后转子稳定时均为PID控制,忽略外部干扰,两时刻位移的微分项与比例项均为0。根据式(5)可得两个时刻的控制电流值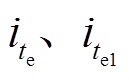 满足式(34)。
满足式(34)。
 (34)
(34)
式中,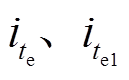 为定值,积分参数
为定值,积分参数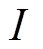 为定值,故位移积分也为定值。若容错控制抑制了位移的向上运动幅值,故障侧恢复至平衡位置所需时间会更长。这就带来减小故障自由度幅值与加快恢复速度的矛盾。
为定值,故位移积分也为定值。若容错控制抑制了位移的向上运动幅值,故障侧恢复至平衡位置所需时间会更长。这就带来减小故障自由度幅值与加快恢复速度的矛盾。
为解决该矛盾,本文采用前馈控制的思路:当转子在Bang-Bang控制下回到平衡位置时,通过前馈控制使故障侧电流值直接变为故障后的稳态电流值,此时故障侧电流将不再需要通过位移积分来达到稳态,转子将能够快速达到PID控制下的稳定。整个容错控制算法的流程如图7所示。

图7 Bang-Bang+前馈控制算法流程
Fig.7 The flow chart of Bang-Bang + feedforward control algorithm
故障后达到稳态时故障自由度上执行器产生电磁力等于故障前差动线圈产生的电磁合力,由式(10)有
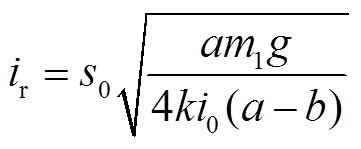 (35)
(35)
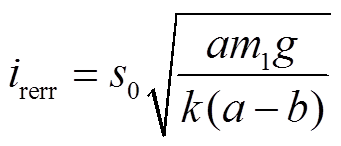 (36)
(36)
假设故障侧在Bang-Bang控制下回到平衡位置,且速度为0时的时刻为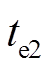 ,由于Bang-Bang控制能够使故障侧状态快速回到相平面原点,即
,由于Bang-Bang控制能够使故障侧状态快速回到相平面原点,即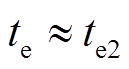 ,由式(34)可知
,由式(34)可知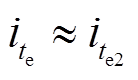 。为使Bang-Bang控制结束后故障侧上执行器电流迅速达到故障稳定电流,电流前馈值
。为使Bang-Bang控制结束后故障侧上执行器电流迅速达到故障稳定电流,电流前馈值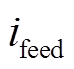 应为
应为
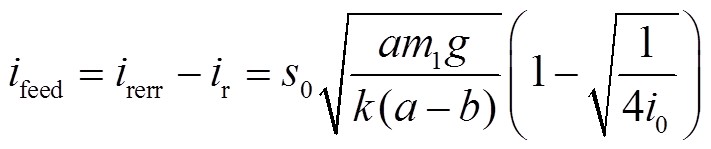 (37)
(37)
基于式(20)建立磁轴承的仿真模型,模型框图如图8所示,模型参数见表1。
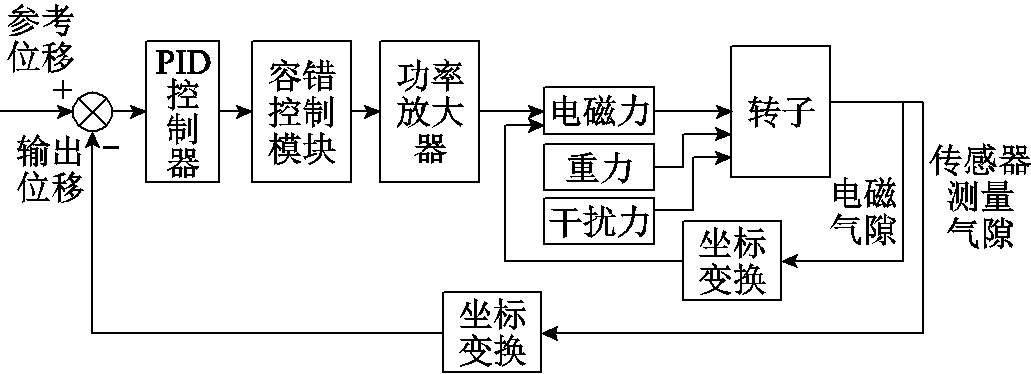
图8 仿真模型框图
Fig.8 Simulation model
表1 模型参数
Tab.1 Model parameter

参数数值参数数值 -0.3450.39 0.375 -0.415929 0.430 503100 15120 9.810
将表1的参数值代入式(20)计算可以分别得到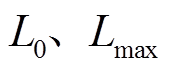 的轨迹方程,其中位移单位为
的轨迹方程,其中位移单位为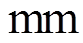 ,速度单位为
,速度单位为 ,对轨迹进行二阶拟合得到
,对轨迹进行二阶拟合得到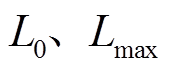 的轨迹方程
的轨迹方程
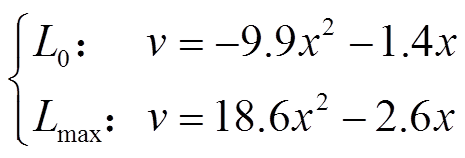 (38)
(38)
根据式(20)的状态空间方程数值解得到的有无容错控制的故障自由度位移如图9所示。
可以看出,无容错控制下的转子故障侧位移能在平衡位置稳定,但会与保护轴承碰撞并持续一段时间后缓慢回到平衡位置。采用本文所提容错控制策略能大大减小故障侧最大位移幅值,并缩短恢复稳定所需时间。
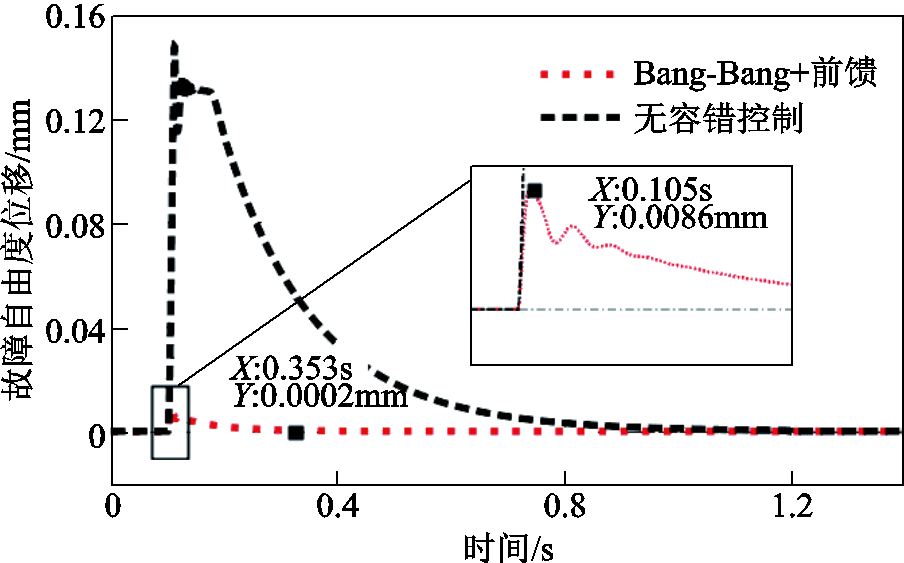
图9 故障自由度位移仿真结果
Fig.9 Simulation results of fault DOF displacement
本文所用的实验平台如图10所示,拖动电机的额定转速为6500r/min,磁轴承保护气隙为0.15mm,其余实验平台参数与表1中参数相同。

图10 实验平台
Fig.10 Testing platform
为模拟执行器故障,设置使能信号,默认情况下值为1,使能后值为0,将开关管PWM信号与该值进行与运算后对开关管进行控制,如图11所示。默认情况下该支路正常工作,使能故障信号后,模拟开路故障。
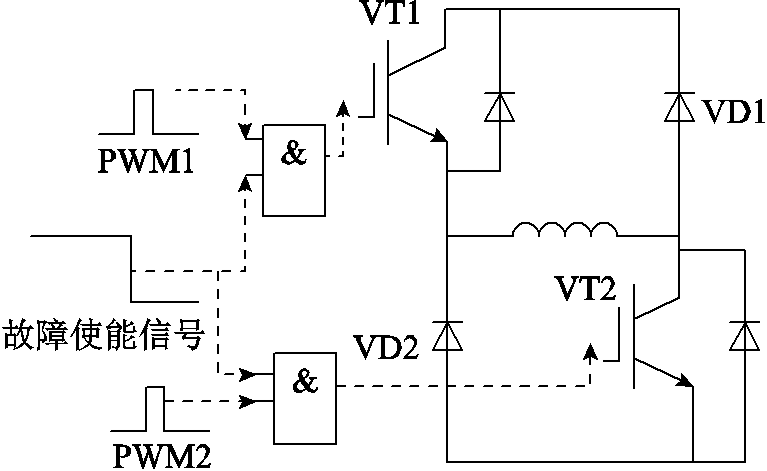
图11 开关功放故障控制
Fig.11 Fault control of switch power amplifier
为验证该算法在转子旋转情况下发生故障的容错控制性能,本文进行了转子转速在1000~6500r/min区间的容错控制实验。实验得到的转子在静止悬浮状态以及在6 500r/min转速发生下执行器故障后有无容错控制时故障自由度位移对比如图12所示。
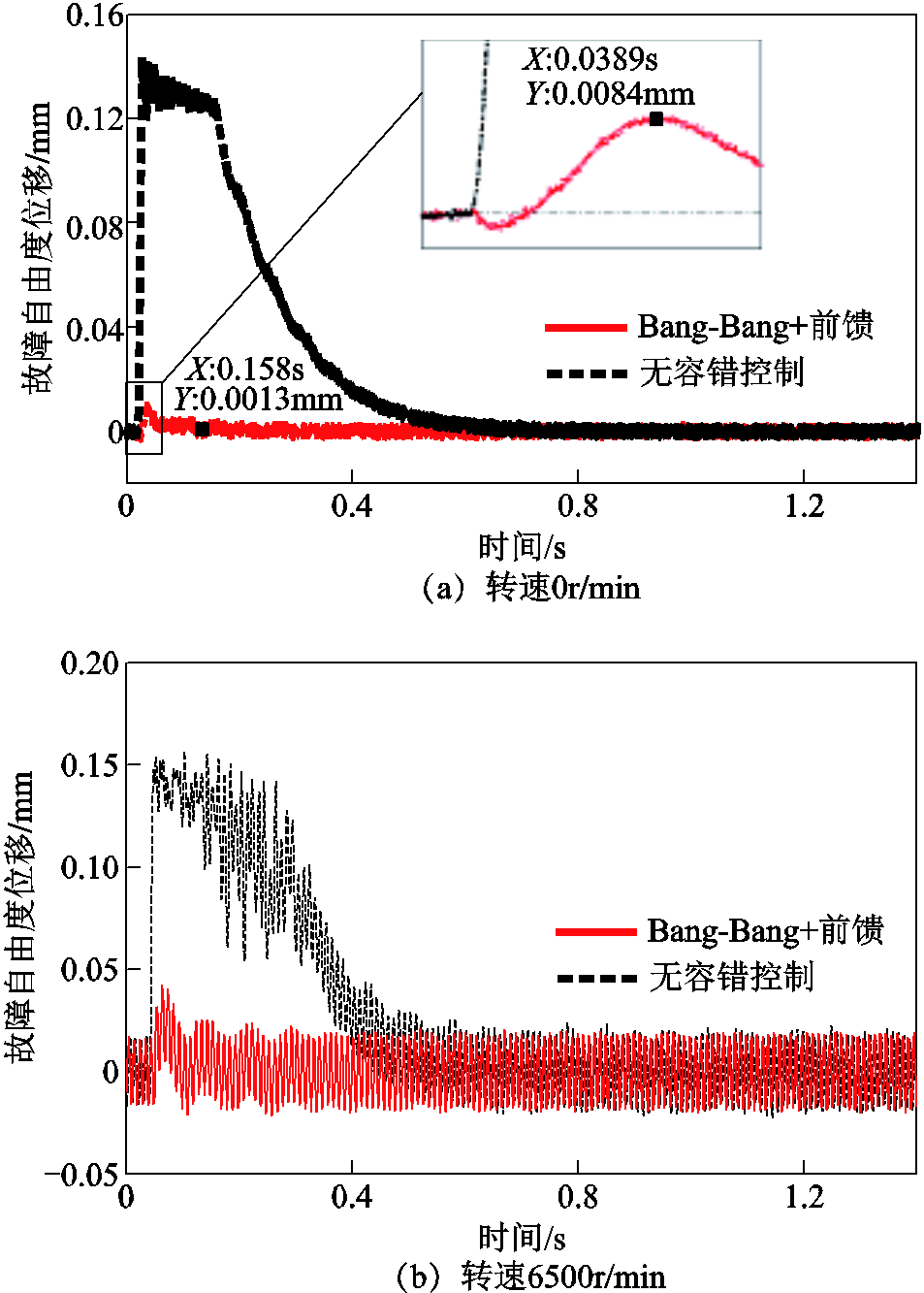
图12 故障自由度位移实验结果
Fig.12 Experimental results of fault DOF displacement
实验结果表明,该容错控制算法能够在故障发生后0.2s内使转子回到平衡位置,且最大位移幅值不超过0.04mm。由于位移传感器的测量值以离散的数字信号形式传到控制板,故不能将位移是否等于0作为Bang-Bang控制是否结束的判断标准,实际算法是在位移小于一个很小的负值后进行前馈控制,并转换到PID控制。
实验得到的转子在静止悬浮状态,以及在 6500r/min转速下故障自由度上执行器电流在故障前后的变化如图13所示。从局部图上可以看出Bang-Bang控制能加快故障侧上执行器电流下降速度,从而使故障侧电磁合力快速下降;前馈控制在位移达到切换条件后使电流直接达到故障稳定电流附近,减少转子恢复至稳态所需时间。可以看出尽管前馈控制值已通过实验校正,但考虑到各种外部干扰以及非理想因素,实际仍难以直接将电流值准确控制到故障稳态电流值。
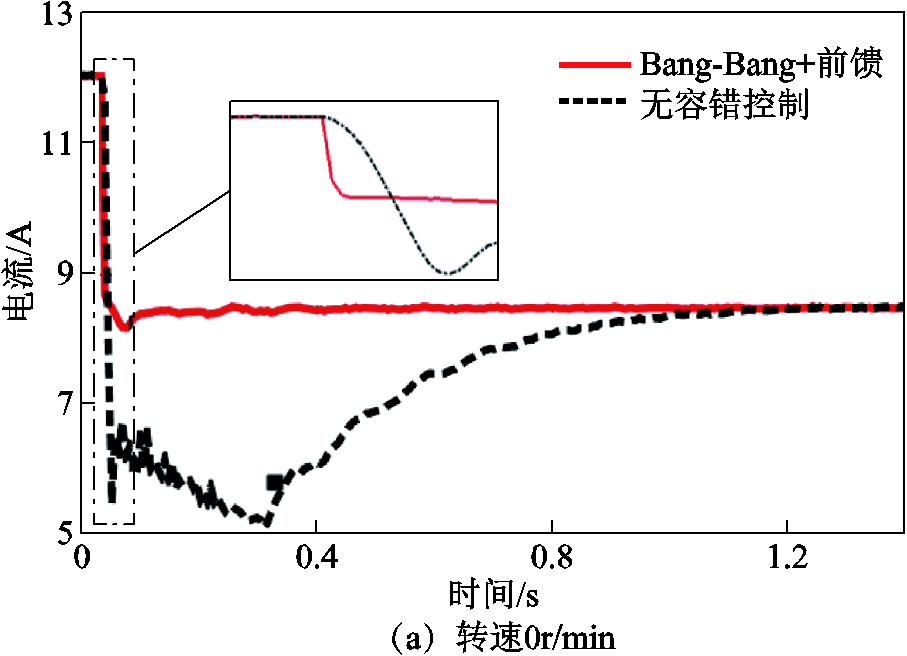
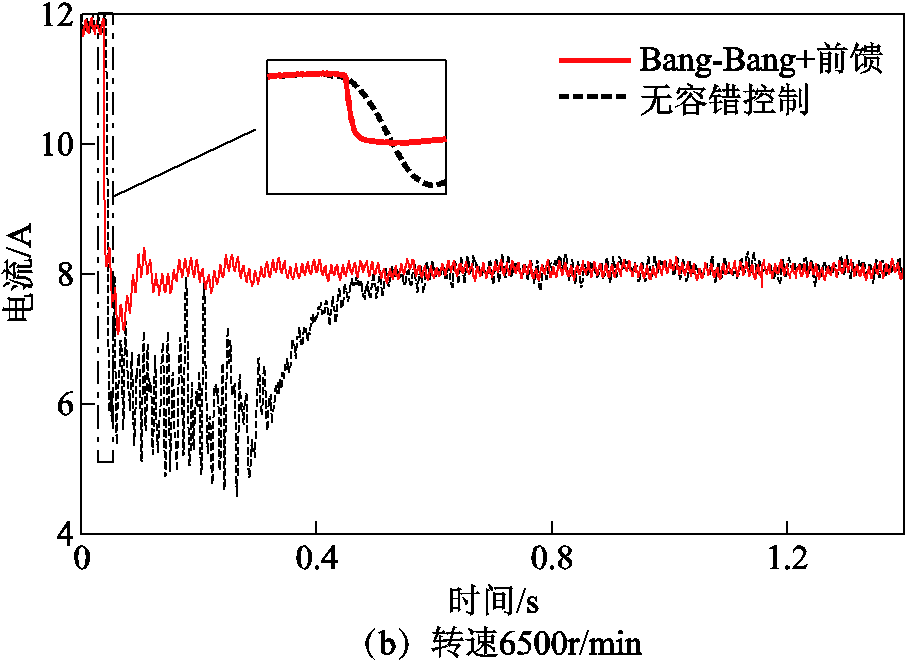
图13 故障自由度上执行器电流
Fig.13 Actuator current of fault DOF
在转速为2 000r/min、4 000r/min、6 500r/min时对应的故障自由度位移曲线如图14所示。
进一步以额定转速6 500r/min为例,给出故障前后径向4自由度位移变化曲线,如图15所示。故障自由度为右侧X方向,由于故障自由度位移刚度与电流刚度发生变化,两侧X方向位移幅值变化较大。两侧Y方向位移幅值有变化但变化很小,且在故障后的动态过程中没有变化,证明前述关于X、Y方向位移在故障后的动态过程中解耦的简化成立。从图15可以看出,当故障自由度位移达到稳态后各个自由度位移均达到稳态,故可以从故障自由度位移是否达到稳态判断转子是否达到稳态。
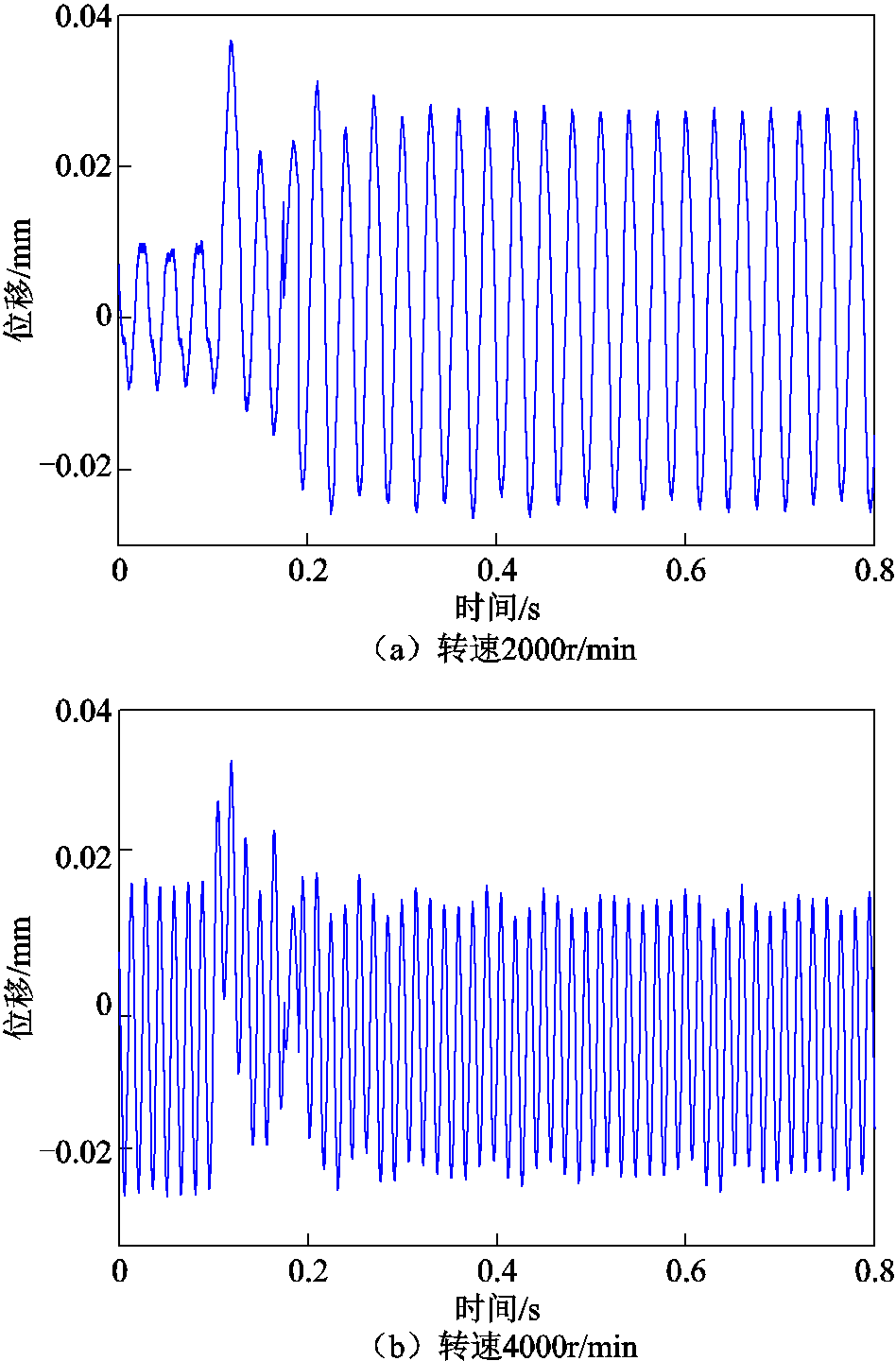
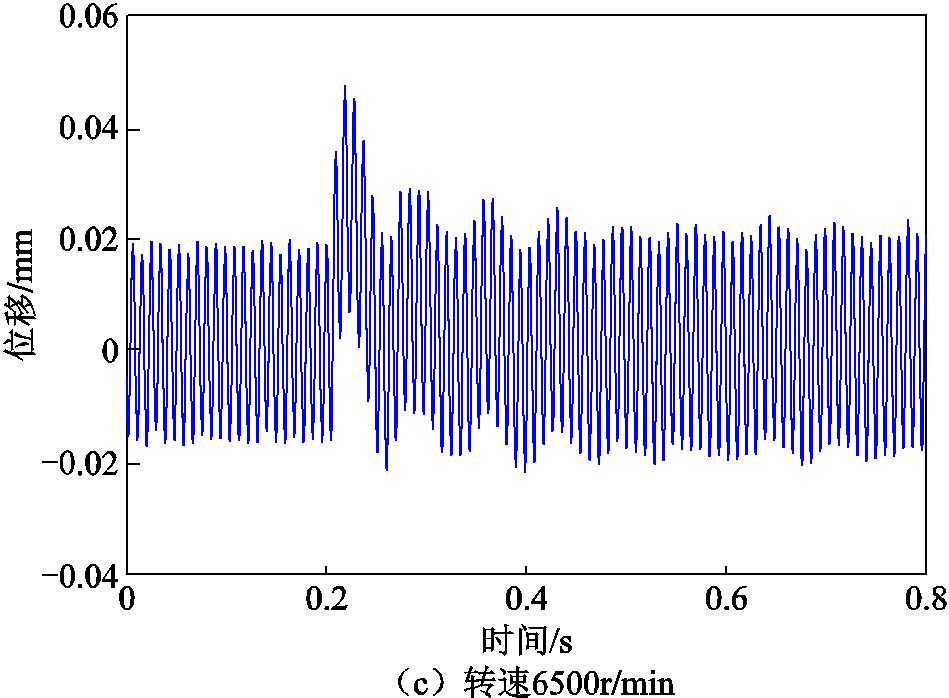
图14 不同转下故障自由度位移
Fig.14 Displacement of fault DOF under different rotating rate
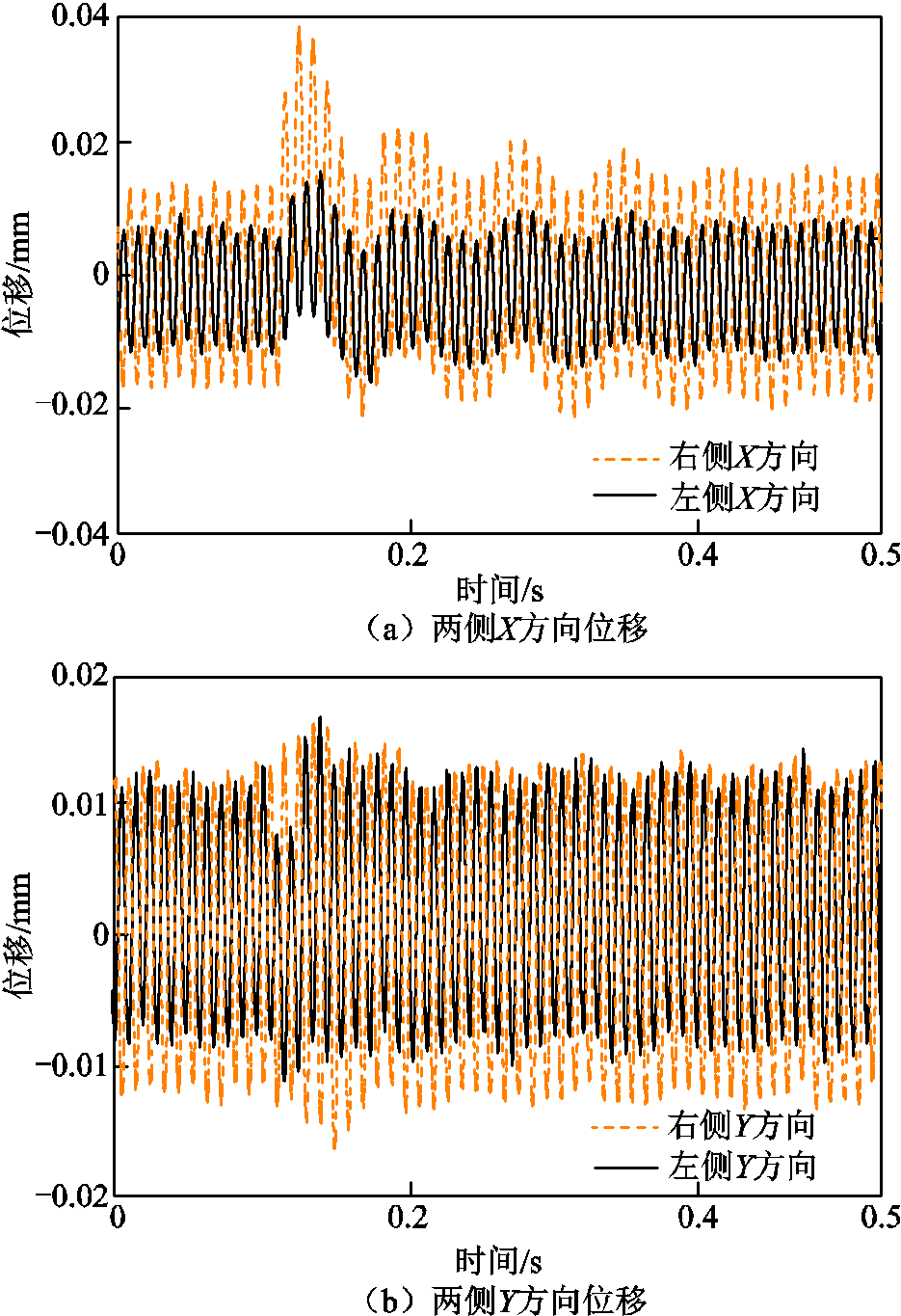
图15 径向4自由度位移
Fig.15 Displacement of radial 4-DOF
为测量故障后的瞬态过程中碰撞或电磁力变化对定子加速度的影响,在径向磁轴承的定子上沿四个线圈方向布置加速度传感器(量程为10m/s2),在转速为2 000r/min、4 000r/min、6 500r/min下定子径向4自由度加速度在故障前后变化如图16所示。可以看出,在没有容错控制时,故障后转子与保护轴承的碰撞导致定子在故障自由度加速度幅值增大,且持续时间约为0.3s;采用本文设计的容错控制方法后,故障后定子加速度变化仅因电磁力的快速变化发生很小的抖动,且持续时间不到0.03s。
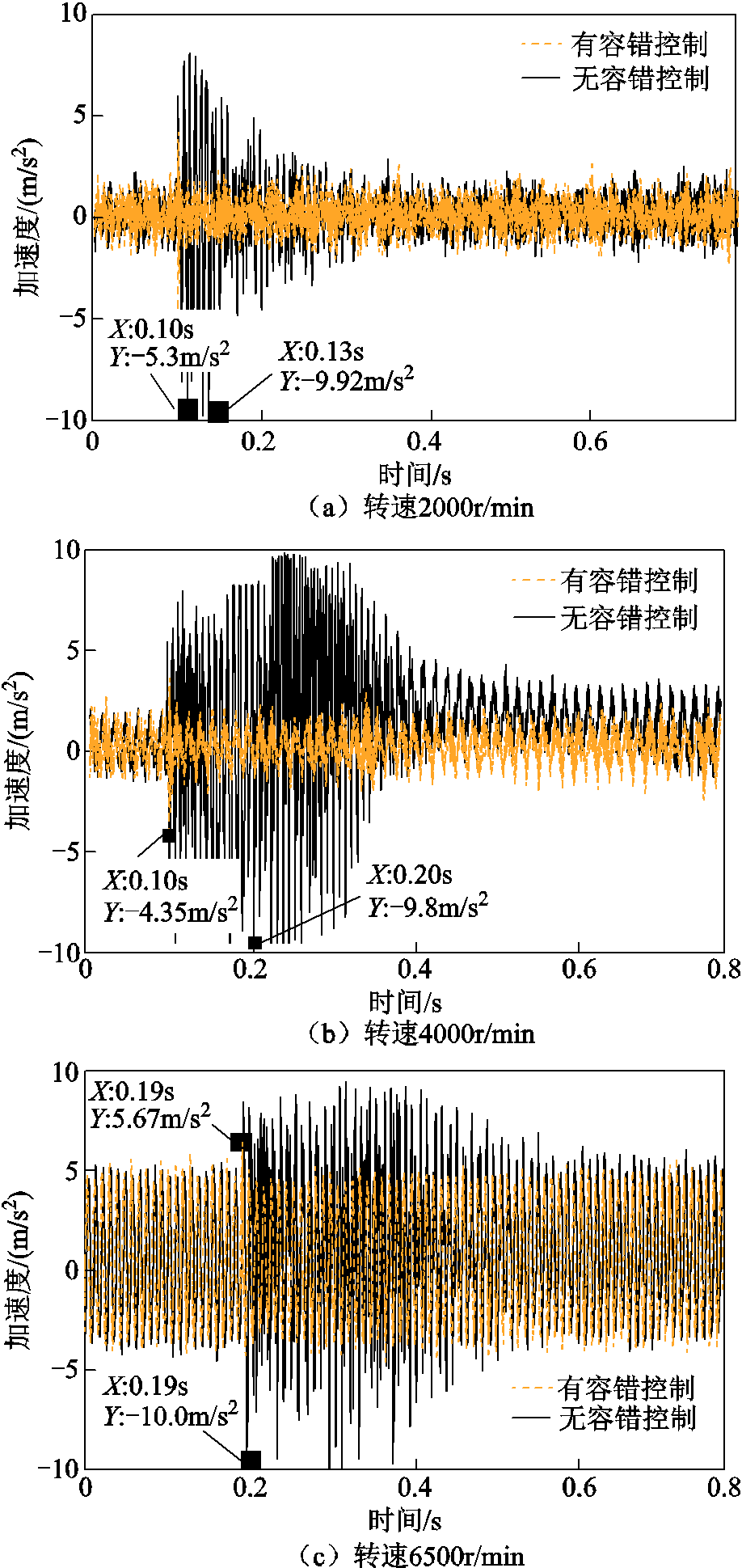
图16 有无容错控制下定子加速度对比
Fig.16 Comparison of stator acceleration with and without fault-tolerant control
全转速范围内故障自由度位移在故障前后的稳态幅值,以及有无容错控制时的位移峰值对比如图17所示。可知,全转速范围内采用本文所提容错控制器算法后均有效避免了定转子碰撞。故障后振动稳态振动幅值在3 000r/min以上小于故障前,这是由于该转速已高于转子刚体平动模态,且故障后轴承等效刚度降低所致。
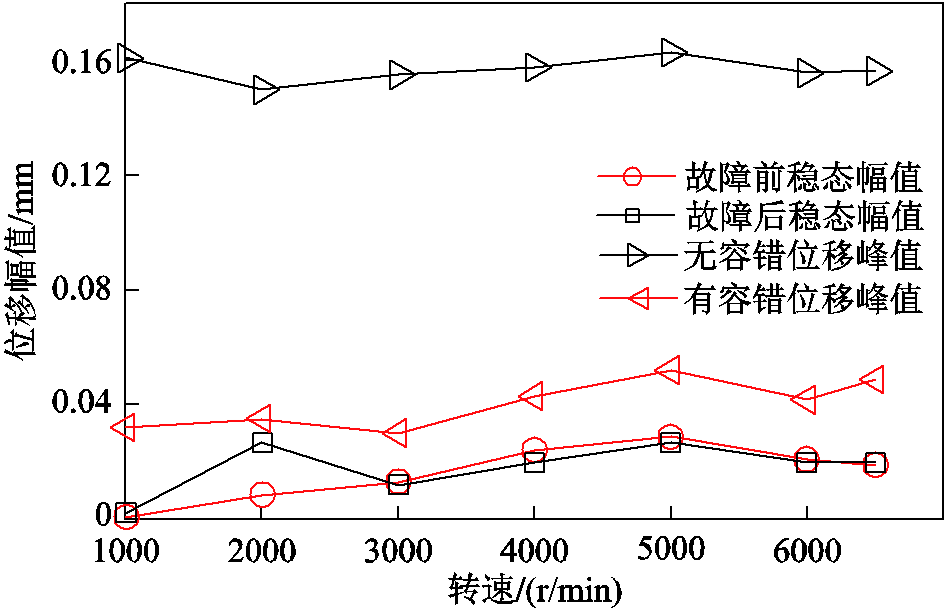
图17 故障前后、有无容错控制故障自由度位移幅值
Fig.17 Fault DOF displacement value before and after the fault, with and without fault tolerance control
从上述实验结果可以看出在该容错控制器的控制下,在全转速范围内故障自由度的最大位移幅值与正常工作时的转子振动幅值相比不超过0.04mm,转子在0.2s内恢复至稳态悬浮;定子加速度变化不大且在0.03s内恢复至稳态值,说明该控制策略能够有效防止故障后的碰撞,并大大减少转子恢复至稳态所需时间。
现有的磁轴承执行器故障容错控制均需要在磁轴承典型结构上增加硬件或改变开关管拓扑,这将降低磁轴承功率密度,或降低直流母线电压利用率。为在不改变传统磁轴承硬件结构和功放拓扑的基础上实现执行器故障的容错控制,本文设计了基于Bang-Bang控制+前馈控制的容错控制器,仿真与实验结果表明:
1)故障侧上执行器电流采用Bang-Bang控制后下降速度加快,故障侧电磁合力下降速度加快,故障侧最大位移幅值被有效抑制;Bang-Bang控制结束后对故障侧上执行器电流的前馈控制加快了故障侧恢复至稳定速度。
2)当故障侧位移达到稳态时,另三个径向自由度位移也达到稳态,故可由故障自由度状态判断转子是否稳定。
3)故障后,该容错控制器能在全转速范围内有效防止转子与保护轴承碰撞,提高转子运行稳定性及保护轴承使用寿命:故障侧最大位移幅值与正常状态转子轴振幅值相比不超过0.04mm,且转子在0.2s内以PID控制方式恢复至稳态悬浮,定子加速度变化不大且在0.03s内恢复至稳态值。
参考文献
[1] 李万杰, 张国民, 王新文, 等. 飞轮储能系统用超导电磁混合磁悬浮轴承设计[J]. 电工技术学报, 2020, 35(增刊1): 10-18.
Li Wanjie, Zhang Guomin, Wang Xinwen, et al. Integration design of high-temperature superconducting bearing and electromagnetic thrust bearing for flywheel energy storage system[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 10-18.
[2] 宗鸣, 吴桐, 王大朋. 高速电机用混合式径向磁轴承前馈解耦控制[J]. 电工技术学报, 2015, 30(14): 539-544.
Zong Ming, Wu Tong, Wang Dapeng. Feed-forward compensation decoupling control for hybrid radial magnetic bearing used in high speed electric machine[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 539-544.
[3] 巩磊, 杨智, 祝长生. 主动电磁轴承-刚性转子系统加速响应的鲁棒性[J]. 电工技术学报, 2021, 36(2): 268-281.
Gong Lei, Yang Zhi, Zhu Changsheng. Acceleration responses robustness of active magnetic bearings-rigid rotor system[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 268-281.
[4] 周天豪, 陈磊, 祝长生, 等. 基于自适应变步长最小均方算法的磁悬浮高速电机不平衡补偿[J]. 电工技术学报, 2020, 35(9): 1900-1911.
Zhou Tianhao, Chen Lei, Zhu Changsheng, et al. Unbalance compensation for magnetically levitated high-speed motors based on adaptive variable step size least mean square algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1900-1911.
[5] 李志, 苏振中, 胡靖华, 等. 磁轴承复合位移传感设计与实验研究[J]. 电工技术学报, 2021, 36(7): 1425-1433.
Li Zhi, Su Zhenzhong, Hu Jinghua, et al. Design and experimental research of magnetic bearing compound displacement sensor[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1425-1433.
[6] 黄威, 邓智泉, 李克翔, 等. 一种磁悬浮轴承支承刚性转子现场动平衡方法[J]. 电工技术学报, 2020, 35(22): 4636-4646.
Huang Wei, Deng Zhiquan, Li Kexiang, et al. A filed dynamic balancing method for rigid rotor supported by magnetic bearings[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4636-4646.
[7] Chand S, Reddy A S, Agarwal P K. Application of artificial neural networks for the fault detection and diagnosis of active magnetic bearings[J]. International Journal of Mechatronics and Automation, 2018, 6(2/3): 130.
[8] 张利胜, 王坤, 郑世强. 磁轴承用新型自感位移传感器设计与实验研究[J]. 仪器仪表学报, 2018, 39(1): 100-109.
Zhang Lisheng, Wang Kun, Zheng Shiqiang. Design and experimental study of a novel self-inductance displacement sensor for active magnetic bearings[J]. Chinese Journal of Scientific Instrument, 2018, 39(1): 100-109.
[9] 李田. 磁悬浮轴承的容错控制系统研究[D]. 武汉: 华中科技大学, 2019.
[10] Storace A, Sood D, Lyons J, et al. Integration of magnetic bearings in the design of advanced gas turbine engines[J]. Journal of Engineering for Gas Turbines and Power, 1994, 1(4): 435-449.
[11] Maslen E H, Meeker D C. Fault tolerance of magnetic bearings by generalized bias current linearization[J]. IEEE Transactions on Magnetics, 1995, 31(3): 2304-2314.
[12] Na U J. Fault tolerance of homopolar magnetic bearings[J]. Journal of Sound and Vibration, 2004, 272(3/4/5): 495-511.
[13] Schroder P, Chipperfield A J, Fleming P J, et al. Fault tolerant control of active magnetic bearings[C]//IEEE International Symposium on Industrial Electronics, Pretoria, 1995: 573-578.
[14] Noh M D, Cho S R, Kyung J H, et al. Design and implementation of a fault-tolerant magnetic bearing system for turbo-molecular vacuum pump[J]. IEEE/ASME Transactions on Mechatronics, 2005, 10(6): 626-631.
[15] Wang Xiaoguang, Liu Qian, Hu Yefa, et al. Research on redundancy of weak coupling radial magnetic bearing[C]//14th International Symposium on Magnetic Bearings, Linz, 2014: 19-24.
[16] Meeker D, Maslen E. A parametric solution to the generalized bias linearization problem[J]. Actuators, 2020, 9(1): 14.
[17] Cheng Xin, Liu Han, Song Shao, et al. Reconfiguration of tightly-coupled redundant supporting structure in active magnetic bearings under the failures of electromagnetic actuators[J]. International Journal of Applied Electromagnetics and Mechanics, 2017, 54(3): 1-12.
[18] Cheng Xin, Deng Shuai, Cheng Baixin, et al. Design and implementation of a fault-tolerant magnetic bearing control system combined with a novel fault-diagnosis of actuators[J]. IEEE Access, 9: 2454-2465.
[19] Cheng Xin, Cheng Baixin, Lu Meiqian, et al. An online fault-diagnosis of electromagnetic actuator based on variation characteristics of load current[J]. Automatika, 2020, 61(1): 11-20.
[20] Jiang Dong, Li Tian, Hu Zaidong, et al. Novel topologies of power electronics converter as active magnetic bearing drive[J]. IEEE Transactions on Industrial Electronics, 2020, 67(2): 950-959.
[21] Nagi F H, Inayat-Hussain J I, Ahmed S K. Fuzzy Bang-Bang relay control of a single-axis active magnetic bearing system[J]. Simulation Modelling Practice and Theory, 2009, 17(10): 1734-1747.
[22] 张亮, 房建成. 电磁轴承脉宽调制型开关功放的实现及电流纹波分析[J]. 电工技术学报, 2007, 22(3): 13-20.
Zhang Liang, Fang Jiancheng. Analysis of current ripple and implementation of pulse width modulation switching power amplifiers for active magnetic bearing[J]. Transactions of China Electrotechnical Society, 2007, 22(3): 13-20.
[23] 胡寿松, 王执铨, 胡维礼. 最优控制理论与系统[M]. 3版. 北京: 科学出版社, 2017.
Abstract Failure of single lower actuator of magnetic bearing (MB) can easily lead to collision between suspended rotor and auxiliary bearing, which affects the operation stability, even leads to the instability of the suspension system and endangers the safe operation. Existing fault-tolerant control methods for actuators generally require adding magnetic poles and power amplifiers or changing the topology of power amplifiers. Adding hardware increases both the design cost of MB and the volume of the entire system. In order to overcome the above defects, a fault-tolerant control strategy based on Bang-Bang + feedforward is proposed in this paper, in which radial MB for horizontal rotating equipment is studied. The fault-tolerant control of single lower actuator failure is realized without changing the hardware architecture of MB.
Firstly, a two-degree-of-freedom (DOF) rotor dynamics model is established and proved to be a normal system in general, and the time optimal control to a normal system is Bang-Bang control. Then, the phase plane analysis method is used to fit the rotor motion curve and obtain the equation for calculating the Bang-Bang control switching point. After switching back to PID control, current feed-forward control is further used to make the rotor stable quickly. The feed-forward value is calculated from the rotor dynamic equation. Meanwhile, the method of actuator fault diagnosis is analyzed in this paper. The fluctuation in the sum of upper and lower actuator current under normal conditions can be decomposed into two parts, the ripple caused by the pulse width modulation and the current variation deviation of coils during rotor motion, thus the diagnosis threshold is determined. Finally, the effectiveness of the fault-tolerant control strategy is verified by simulation and tests.
The Bang-Bang control can suppress the maximum displacement amplitude of the rotor with lower actuator failure, but it will lead to high frequency oscillation. In order to avoid the oscillation, the control method should be switched back to PID control after the Bang-Bang control, while PID control can only change the value of steady-state current by displacement integration, which means rotor cannot restore stability quickly. Therefore, feedforward control is neededto change the value quickly. Experiments show when the lower actuator failure occurs without fault-tolerant control, the rotor and auxiliary bearing will collide. The maximum displacement of the rotor will reach 0.13 mm, the stator acceleration peak reaches 10 m/s2 and continues for about 0.3s before returning to stability. After adopting the proposed fault-tolerant controller, the maximum displacement amplitude in fault freedom exceed the normal vibration amplitude lees than 0.04 mm and the rotor can recover to steady suspension in 0.2 s. Because there is no collision, the stator acceleration does not change significantly.
The following conclusions can be drawn through simulation analysis and experiments: ①Bang-Bang control can effectively suppress the maximum displacement amplitude of rotor and feedforward control can accelerate rotor stability after a single lower actuator failure. ② When the fault DOF reaches stable, the other three DOFs also reach steady state, so the rotor stability can be judged by the state of fault DOF. ③ After the failure of the lower actuator, the fault-tolerant controller can effectively prevent the collision between the rotor and auxiliary bearing in full speed range. Improving the stability of the rotor and the service life of the auxiliary bearing, the maximum displacement amplitude of the fault side exceed the normal vibration amplitude lees than 0.04mm and the rotor can recover to the steady suspension in 0.2s. the stator acceleration changes little and recover to stability within 0.03s.
Keywords:Magnetic bearing, actuator failure, fault tolerant control, Bang-Bang control, feedforward control
DOI:DOI:10.19595/j.cnki.1000-6753.tces.210784
中图分类号:TM355
刘 奇 男,1995年生,硕士,研究方向为磁轴承及其容错控制。E-mail:1159591124@qq.com
苏振中 男,1989 年生,副研究员,硕士生导师, 研究方向为磁悬浮技术、电力集成技术。 E-mail:suayst@163.com(通信作者)
国家自然科学基金资助项目(51707201,51690181,51825703)。
收稿日期 2021-06-01
改稿日期 2021-09-29
(编辑 赫蕾)