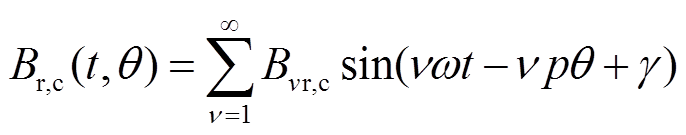（1）
摘要 随着永磁电机朝着高效化和轻质化方向发展，其功率密度和转速越来越高，使得绕组交流铜耗增加，从而导致电机局部过热、效率降低。该文以永磁电机为研究对象，着重研究绕组涡流损耗的产生机理及计算方法，提出基于快速有限元的绕组涡流损耗半解析算法。首先，介绍借助快速有限元提取槽漏磁的方法，并构建导体排布模型；其次，推导了导体涡流损耗的低频和高频解析计算方法，并通过搭建基于Matlab和开源有限元软件FEMM的仿真平台将提出的半解析方法予以实现，并与传统商用有限元软件仿真结果进行对比；最后，通过实验进一步验证了其准确性。结果表明，该方法的计算速度提高了近100倍，在较大频率范围内误差小于5%。
关键词：永磁电机 绕组涡流损耗 导体排布模型 快速有限元 半解析算法
近年来，电机系统正朝着高速化、轻量化的方向发展，在电力电子技术和稀土材料快速发展的背景下，永磁电机正逐渐成为新一轮电气化进程的主角。然而，随着永磁电机功率密度和转速的提升，电机高频交流效应越发显著[1-3]，造成绕组交流铜耗增加，不仅降低了电机效率，还会引起电机过热，危及电机安全运行。因此，准确且快速地评估绕组交流铜耗成为永磁电机，特别是高功率密度、高转速和高负载电机研发的重要一环[4-6]。
永磁电机的交流铜耗可分解为环流损耗、涡流损耗及直流铜耗三部分[7]。对于多根导线并绕的绕组，由于各导体所处的磁场环境不同，感生电动势存在差异，并绕导线间会形成环流[8]，引起环流损耗。此外，槽漏磁和高频交流电会产生邻近效应和趋肤效应，使得导体电流密度分布不均[9]，产生涡流损耗。为了分析和抑制交流铜耗，需要对其进行精确计算，现有的计算方法主要有解析法、有限元法和半解析法。
解析法以槽漏磁和损耗的解析计算为基础，求解快速，但通常需要进行模型简化和问题假设，因此计算精度不高。P. L. Dowell等提出的一种经典一维解析模型[10-12]广泛应用于高频变压器的交流铜耗计算，该模型假设铁心磁导率无穷大，并假设槽内漏磁场为平行磁场且平行于槽底，用方导线等效圆导线，但只能满足一定频率下的解析精度。C. R. Sullivan和P. Mellor等[13-14]通过假设导体内部的磁场稳定不变，利用微积分求解导体涡流损耗，但该解析法只适用于开口槽电机，对于半闭口槽电机，由于其齿槽效应，槽开口处漏磁并不平行于槽底，给解析计算的精确性带来挑战。L. J. Wu等[15-16]利用子域模型分析了多种槽形尺寸下电机槽内漏磁场的求解方法，其考虑到由于槽开口而导致的槽漏磁场畸变，在一定程度上具有较高的精度，但忽略了铁心饱和的影响。
考虑到铁心饱和、开槽效应等因素，通常采用有限元法求解交流铜耗，此时就必须对槽内所有导体建模，但是对于导体随机排布的漆包散线绕组电机，其建模过程复杂，网格剖分密集，极大地增加了计算量，因此有限元法不太适合大规模的设计优化。针对该问题，A. Lehikoinen和A. Arkkio等[17-18]将圆导线拟合为近似多边形，优化网格剖分形式，在不重要的圆弧外面上减少网格剖分，相比商业有限元软件，大大减少了网格数量，从而加快了交流铜耗的计算。
解析法计算快速，但忽略了电机的饱和效应，槽漏磁计算不准确，降低了涡流损耗的求解精度；而有限元法计算准确，但网格密集，求解十分耗时。因此综合两种方法的优缺点，将有限元法与解析法相结合的半解析法成为研究热点[19-21]，其主要思想是先利用有限元计算准确的槽漏磁，再代入损耗解析式求解，既保证了求解精度，又能显著提高求解速度。
利用半解析法计算绕组涡流损耗仍需要借助有限元，花费大量计算时间，并且传统的涡流损耗解析计算基于低频的假设，存在局限性。本文以散线永磁电机为研究对象，重点对绕组涡流损耗的计算方法进行研究，提出了一种高效计算永磁电机绕组涡流损耗的高频半解析算法，并融入快速有限元的思想，根据1/6电周期静磁场解重构槽漏磁数据，大大减少了有限元计算时间；通过搭建Matlab和FEMM（finite element method magnetics）联合仿真平台实现该方法，并与商用有限元软件Maxwell的仿真结果进行对比；最后通过实验验证该方法的可行性。
永磁电机的饱和特性会使定子槽内形成漏磁场，引起槽内导体电流密度的不均匀分布，形成涡流，从而产生涡流损耗。因此，掌握槽漏磁分布规律和槽漏磁谐波成分是半解析算法计算绕组涡流损耗的基础。由于无法脱离有限元，本文提出了基于快速有限元的槽漏磁计算方法，以提高半解析算法的效率。
正弦波电流调节的三相永磁电机的电路和磁路具有时空对称性[22-23]，根据这一性质不仅能得到电机的最简仿真模型，还可以用1/6电周期的静磁场解重构出全周期的磁场数据。
电机定子上某点的径向磁通密度Br和切向磁通密度Bc的时空分布可表示为
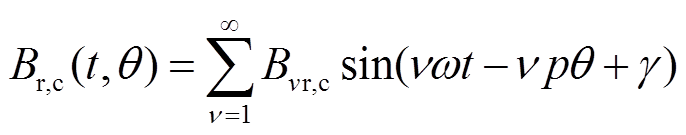（1）
式中，n为谐波次数；w为电角速度；t为时间；p为转子极对数；q为转子位置角；g为相位。同时，永磁电机中的转子位置角、转子机械角速度Ω和电角速度满足关系
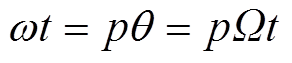（2）
因此，结合磁通密度时空分布表达式可得
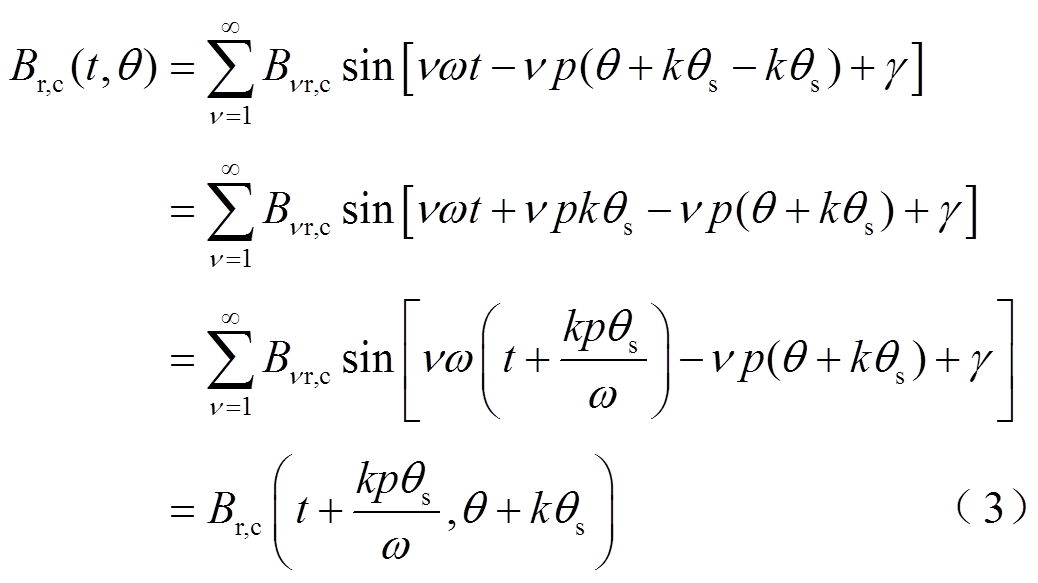
式中，qs为槽距角；k为整数，取决于永磁电机的拓扑结构和绕组类型。考虑周期性和对称性，式（3）可拓展为
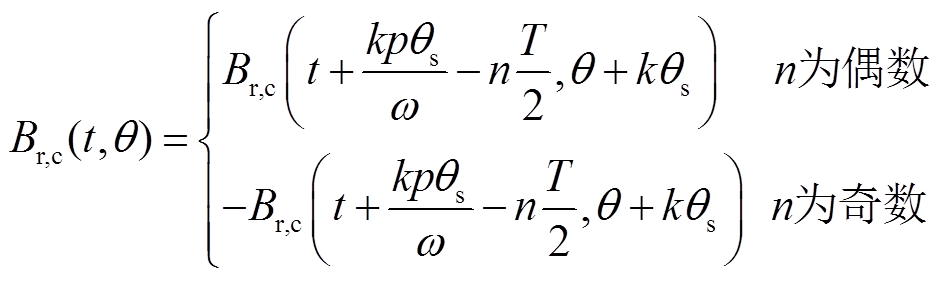（4）
式中，n为整数；T为电周期。可以发现，磁通密度分布的时空对称性为永磁电机快速有限元提供了理论支撑，从而能快速评估电机性能，加快电机设计和优化过程。
以12槽10极的表贴式永磁（Surface Permanent Magnet, SPM）电机为例说明快速有限元计算槽漏磁的方法，其拓扑结构如图1所示。
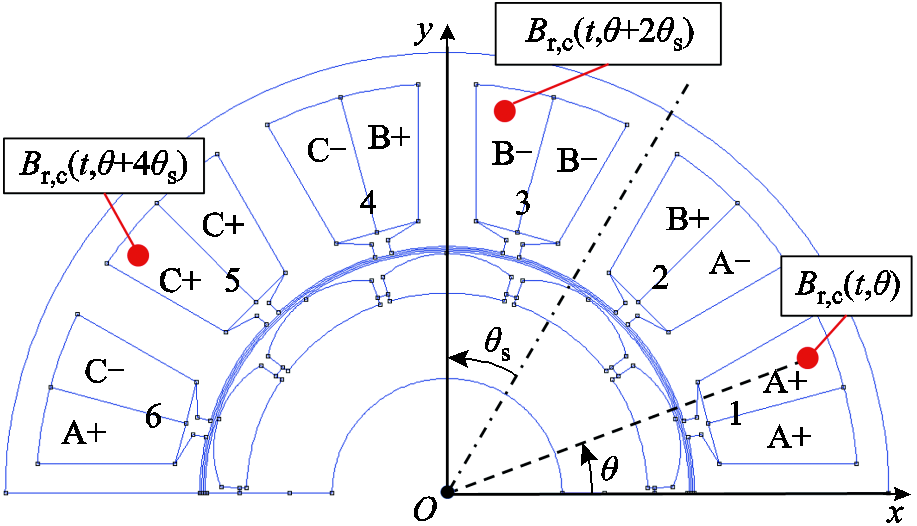
图1 SPM电机拓扑结构
Fig.1 Topology of surface permanent magnet machine
定子槽沿着逆时针方向依次编号1～6。1、3、5号槽内两个线圈边磁动势同相，幅值为2NIm，称为同相槽，其中N为线圈匝数，Im为线圈电流幅值；而2、4、6号槽内两个线圈边磁动势互差60°，幅值为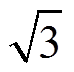
NIm，称为异相槽。因此该电机具有交替出现的两种槽类型，故k取2的整数倍，于是定子上某点的磁通密度可以表示为
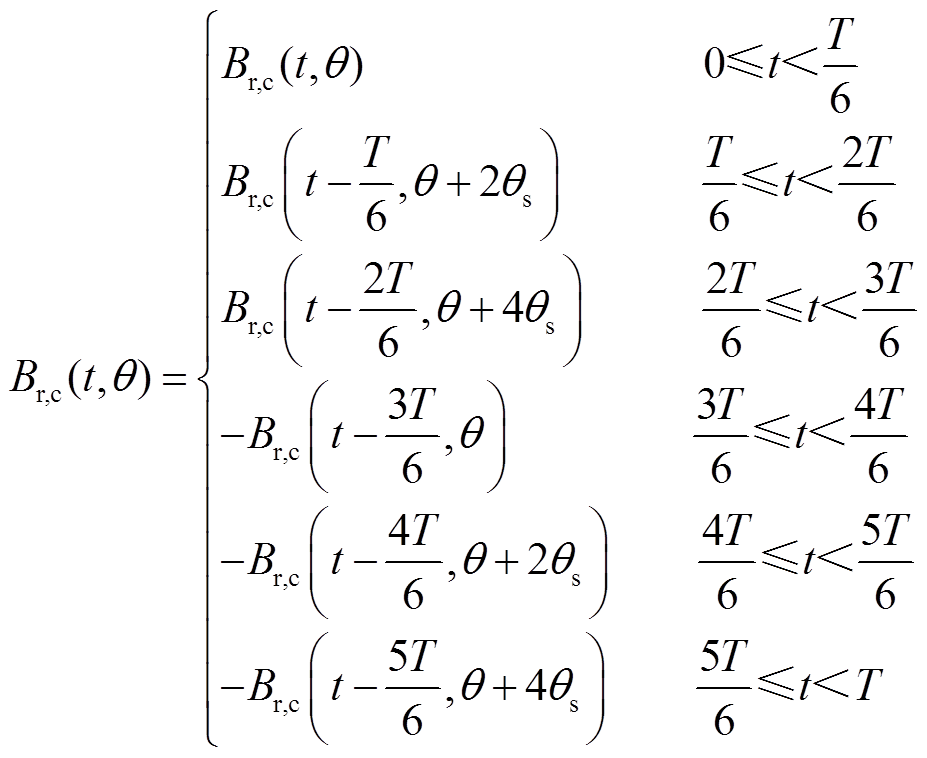（5）
显然，只要通过有限元求解0～1/6电周期的静磁场，就能得到整个周期的解，而传统有限元需要求解整个周期的静磁场，计算量显著增加。因此，若要获得1号槽某点的全周期漏磁波形，只需要提取1号、3号和5号槽漏磁的1/6电周期数据，即可根据式（5）重构出来。图2是1号槽某点的漏磁重构波形，该点位置见图1标注。
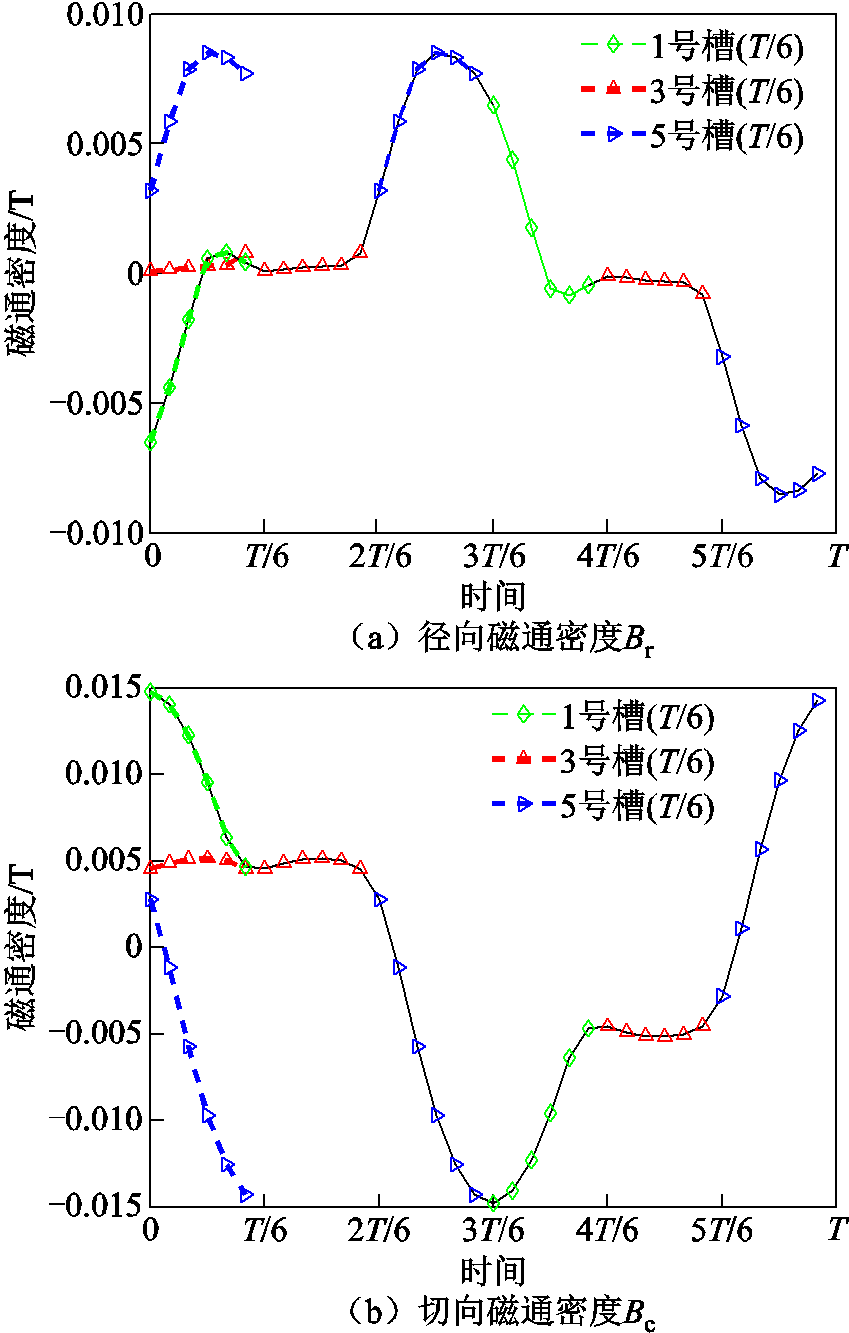
图2 1号槽某点漏磁磁通密度重构波形
Fig. 2 Reconstruction of magnetic flux leakage density waveform at a point of slot 1
以A相线圈为例，其两个线圈边分别位于同相槽和异相槽（如1号槽A+和2号槽A-），传统有限元和快速有限元计算的结果如图3所示，两者波形一致，重构效果十分理想，这说明了快速有限元的准确性。上述方法同样适用于其他永磁电机拓扑的槽漏磁计算。
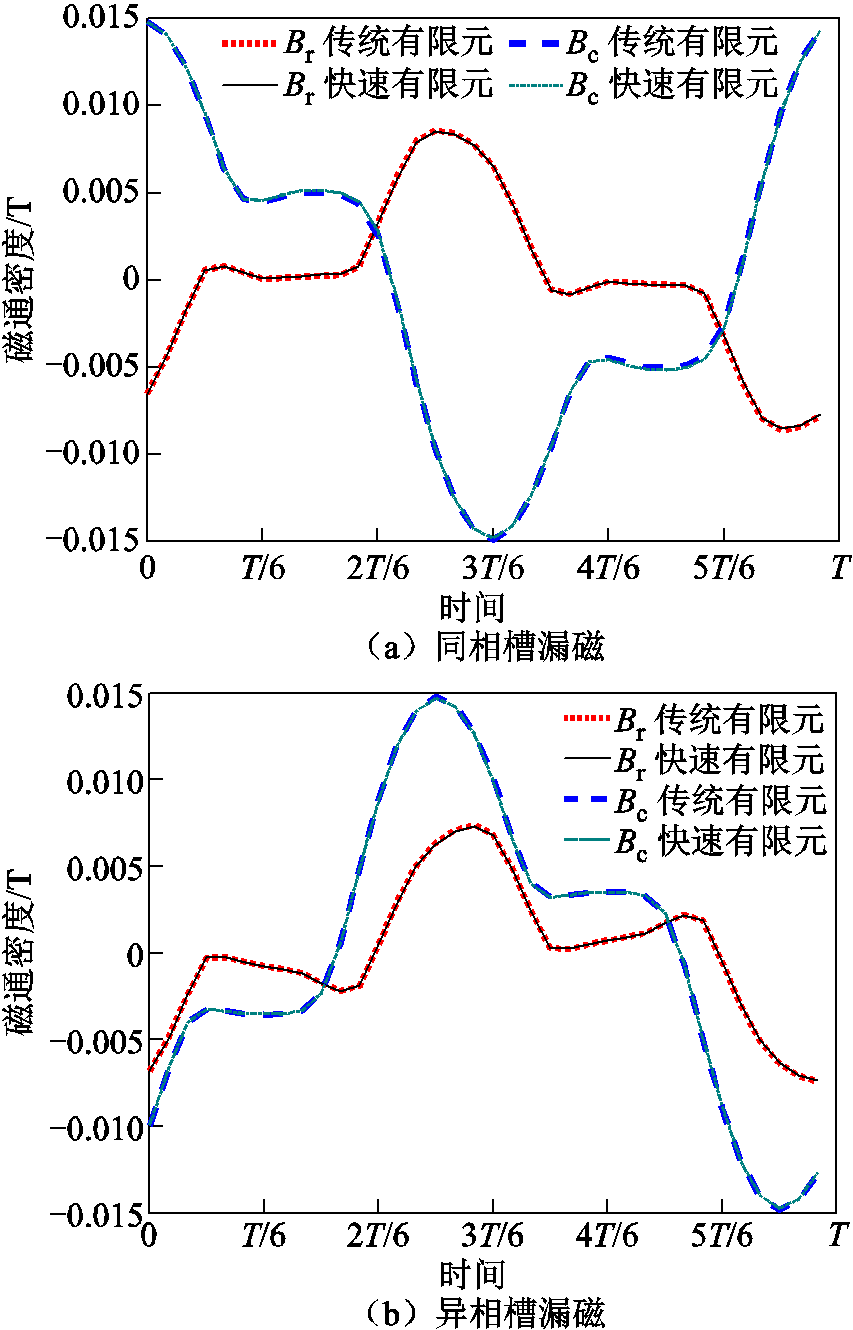
图3 两种有限元求解A相线圈槽漏磁波形
Fig.3 Two finite element methods for solving magnetic flux leakage density of A phase coil slot
永磁电机绕组涡流损耗取决于各导体所处的漏磁环境，与导体位置密切相关，但在实际电机绕线过程中，导体排布没有规律。本文按照最密堆积方式模拟槽内导体的排布，并且考虑间距。导体最密堆积示意图如图4所示，一个堆积单元由铜导体、绝缘层和导线间距构成。
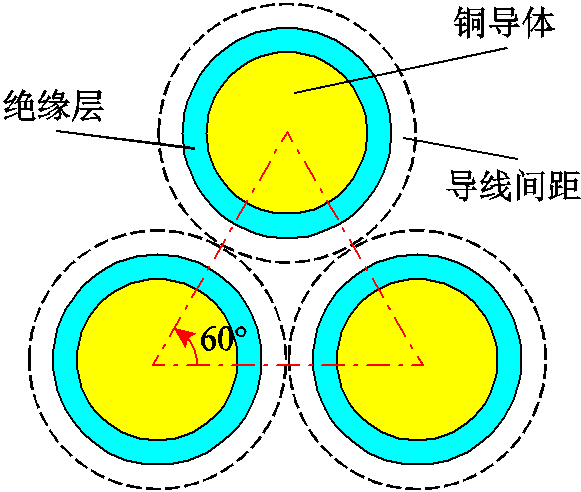
图4 导体最密堆积示意图
Fig.4 Schematic diagram of the most densely packed conductors
以紧靠槽边的槽底导体为基准导体，沿着槽边从槽底向槽口排布，并逐列排开，按照上述规则在Matlab与FEMM仿真平台中编程，自动计算导体的位置坐标。需要说明的是，半解析计算绕组涡流损耗并不需要对实际导体建模，仅需借助导体排布模型计算导体坐标，从而提取该点槽漏磁供解析计算。1号槽和2号槽的A相线圈导体排布示意图如图5所示。
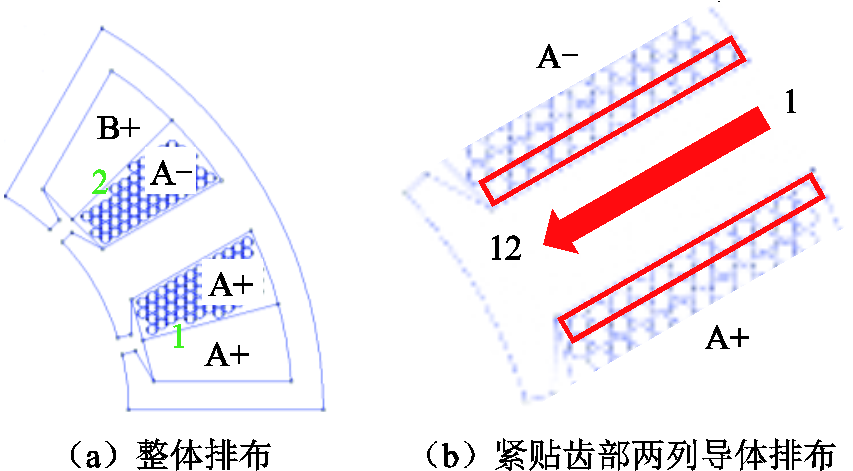
图5 A相线圈导体排布示意图
Fig.5 Schematic diagram of A-phase coil conductor arrangement
考察图5中紧贴齿部的两列导体，导体从槽底至槽口依次编号1～12，各导体所受槽漏磁各次谐波成分如图6所示，主要存在基波和3次谐波。由于同相槽的磁动势较大，其各次谐波磁通密度幅值大于异相槽，会引起损耗差异。因此需分别计算两种槽内的涡流损耗，再计算绕组的涡流损耗。此外，由于开槽的影响，槽漏磁大小呈现从槽底向槽口递增的趋势，导致靠近槽口处的导体涡流损耗较大，再加上槽口散热困难，极易成为绕组热点。
图6 槽漏磁谐波成分
Fig.6 Harmonic component of slot magnetic leakage flux density
采用有限元法求解绕组涡流损耗需要对导体建模，细化网格，从而使得计算量庞大、花费时间长，但有限元法在处理铁心饱和等复杂电磁环境时的准确度高，因此将有限元计算与解析计算结合，即采用半解析法求解绕组涡流损耗，其基本原理在于先用有限元模型计算得到槽漏磁数据，然后代入解析模型中求出绕组涡流损耗。所提出的半解析计算模型基于上述快速有限元方法，从而能更加快速地计算出绕组涡流损耗。
此外，由于解析模型中所需要的电磁参数为槽漏磁的磁通密度，而实际槽内漏磁场远大于单根导体感应出的磁场[24]，因此可认为导体涡流对槽漏磁没有影响。故在有限元模型中无需画出槽内导体，从而将传统的有限元模型分解为一般有限元磁场模型和导体排布模型，避免了密集网格的剖分，极大地减少了计算量。通过导体排布模型确定导体位置，在有限元计算结果的基础上提取导体圆心坐标的磁通密度，作为整个导体所受外加磁场的平均值，代入解析式即可求解槽漏磁引起的涡流损耗。
以单根无限长直导体为研究对象，其半径为r0，建立柱坐标系下的模型，如图7所示。对其施加幅值为B0的平行磁场，其角频率为w。
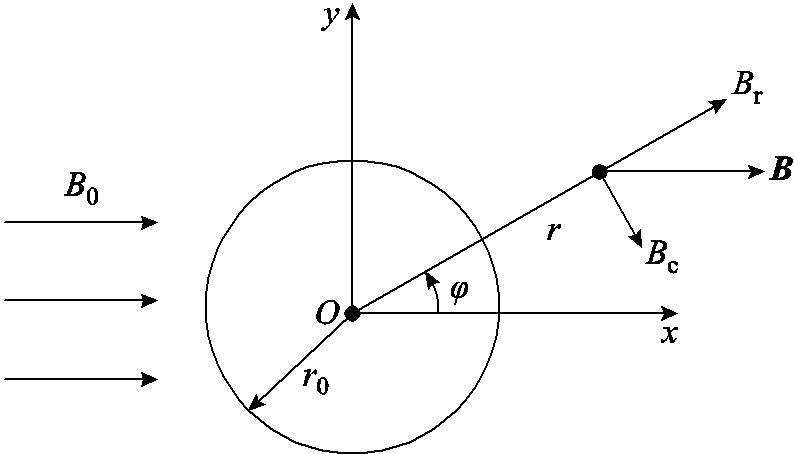
图7 涡流场二维解析模型
Fig.7 2D analytic model of eddy current field
在导体本身无电流通过的情况下，当磁场频率较低时，可认为某一时刻导体内部磁场处处相等，此时单根导体平均涡流损耗为[14,22]
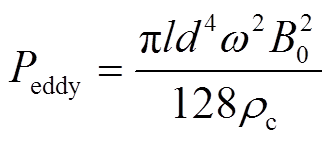（6）
式中，l、d和ρc分别为导体长度、直径和电阻率。该方法基于频率较低的假设，称为涡流损耗的低频解析法。
高频磁场下导体磁通密度云图如图8所示。当导体外加磁场频率升高时，导体内涡流去磁效应明显，导体内部磁场不再处处相等，磁通密度由内向外逐渐增大，低频损耗解析计算模型失效，因此需要研究考虑退磁作用的高频涡流损耗解析计算公式。
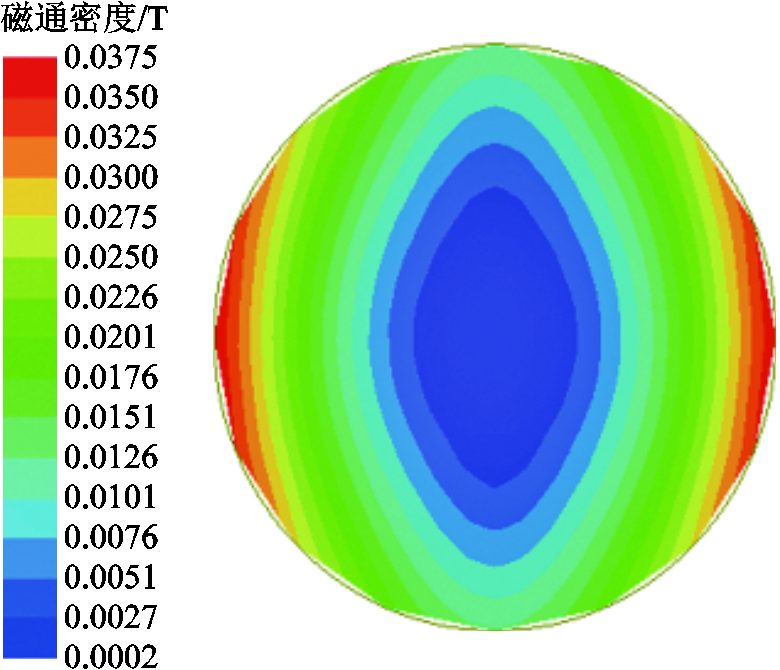
图8 高频磁场下导体磁通密度
Fig.8 Magnetic flux density contour of conductor under high frequency magnetic field
引入磁矢量A，B=
×A，A仅含有z轴分量，因此考虑二维解法。根据麦克斯韦方程组，可以得到空间中磁矢量在柱坐标系下满足的方程为[25]
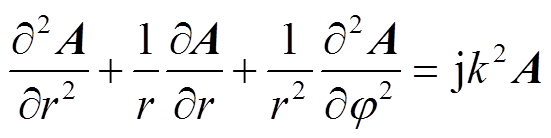（7）
式中，k2=wgm，g和m为求解区域的电导率和磁导率，由于其在导体内外不同，因此需分别对导体内和导体外求解。
对于导体内部，其磁矢量可设为
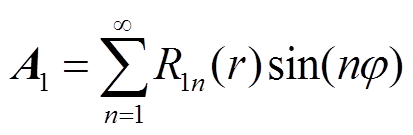（8）
式中，R1n为距离导体圆心r处磁矢量的n次谐波幅值，将其分量代入方程式（7）可得
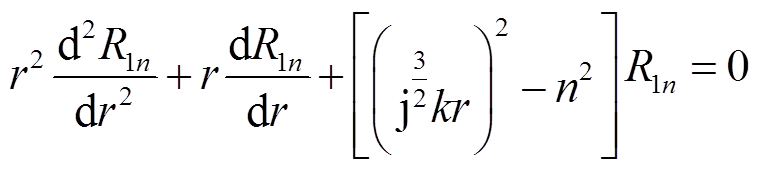（9）
该微分方程称为贝塞尔方程，其通解可表示为
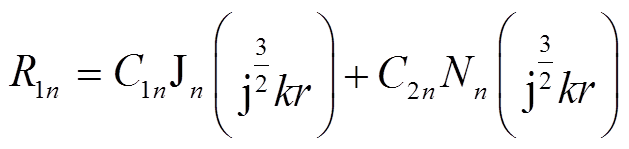（10）
式中，Jn(·)为n阶第一类贝塞尔函数；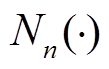
为n阶第二类贝塞尔函数；C1n和C2n为两个常系数，由于在r=0处磁矢量存在有限值，故C2n=0。因此可得导体内部磁矢量的通解为
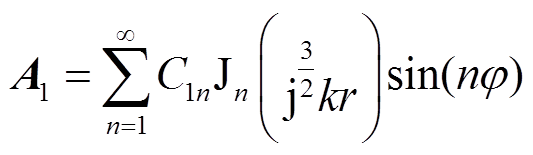（11）
根据磁矢量与磁通密度的关系，可得到径向和切向的磁通密度为
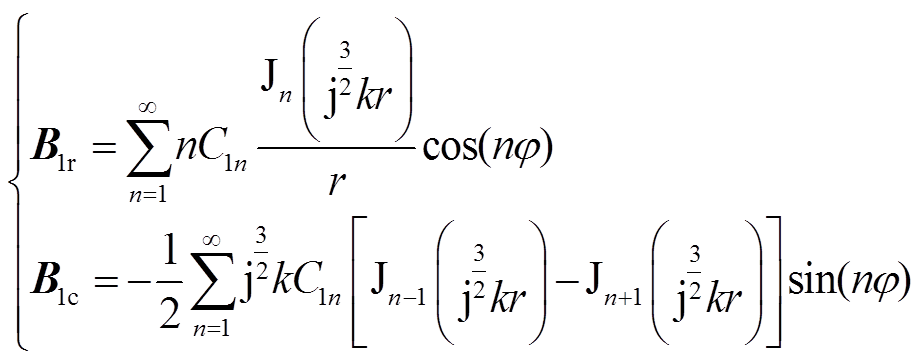（12）
同理，可得到导体外部区域磁矢量通解为
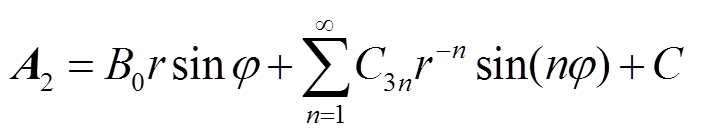（13）
式中，C3n为常系数；C为常数。则磁通密度径向和切向分量为
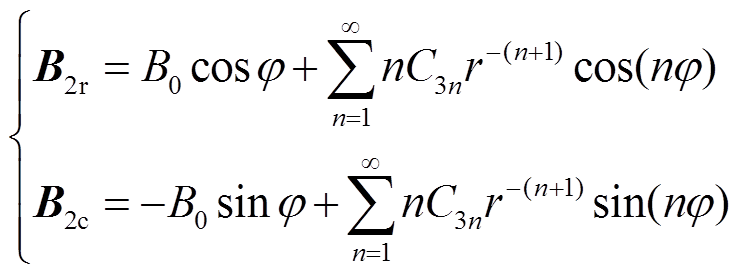（14）
由于磁场在导体与空气的接触面上连续，故在r=r0处满足介质交界面条件
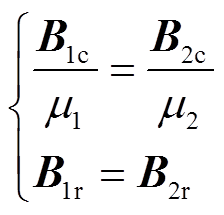（15）
式中，μ1和μ2分别为导体内外区域磁导率，由于导体内外磁导率几乎相同，可认为均等于真空磁导率μ0。将磁通密度通解代入交界面条件，可以发现n的取值只能为1，从而解得
（16）
故导体区域的磁矢量为
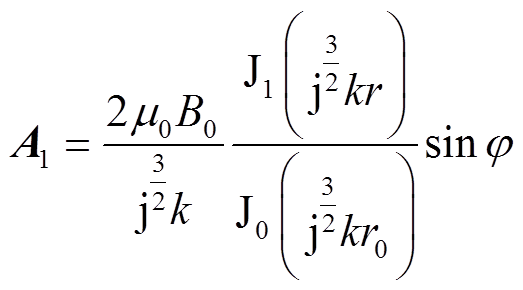（17）
根据电磁场基本方程及坡印廷定理可得导体内涡流损耗为
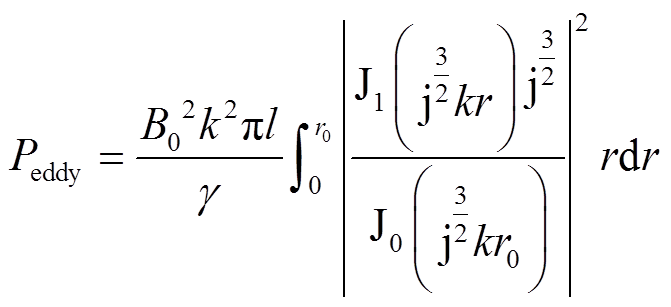（18）
因此，在得到槽漏磁数据的基础上，通过快速傅里叶变换（Fast Fourier Transform, FFT），分解出磁通密度的各次谐波分量，分别作用到导体上，再根据上述解析式算出各次谐波引起的涡流损耗，最后相加即可得到槽漏磁作用下导体的涡流损耗。
前文推导了导体在不通电流的情况下，槽漏磁作用引起的涡流损耗。实际上电机工作时导体通以交变电流，交变电流会在导体中产生交变磁场，导致电流集中在导体表面，称为趋肤效应，这会使得导体等效电阻增加[26]，产生附加的涡流损耗。考虑单根长直导体，通入正弦电流İ，没有外加磁场的作用，根据磁准静态场方程可得
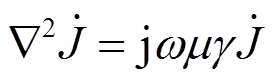（19）
式中，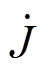
为沿着导体径向的电流密度。根据式（19）和上文推导可解出其分布为
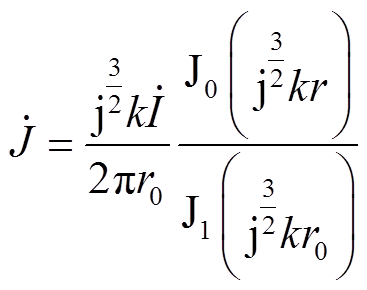（20）
根据麦克斯韦方程与坡印亭定理，可推导出交流阻抗为
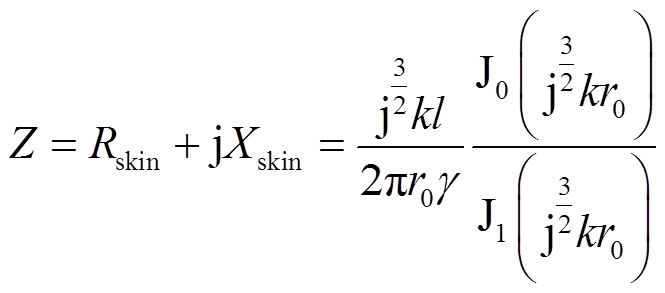（21）
式中，Rskin和Xskin分别为趋肤效应作用下的交流电阻和交流电抗。因此，由趋肤效应引起的涡流损耗为
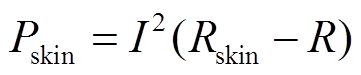（22）
式中，R为导体直流电阻。导体直流铜耗为
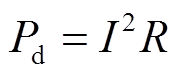（23）
根据前文的推导可知，趋肤效应引起的涡流损耗Pskin与槽漏磁引起的涡流损耗Peddy共同构成了导体的涡流损耗Pec，因此电机有效部分的总涡流损耗为
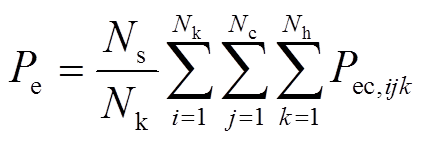（24）
式中，Ns为永磁电机槽数；Nk为电机槽类型个数；Nc为槽内导体数；Nh为槽漏磁谐波最高次数；Pec, ijk为i号槽中，j号导体在k次槽漏磁谐波作用下产生的涡流损耗。因此，对于导线无并绕的永磁电机而言，绕组没有环流损耗，故有效部分的交流铜耗为
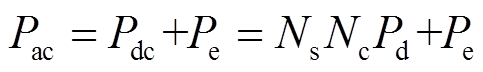（25）
若考虑电机的端部，则电机总直流铜耗修正为
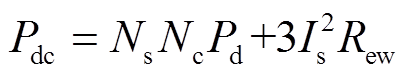（26）
式中，Is为定子电流有效值；Rew为端部绕组相电阻。由于电机端部漏磁较小，可忽略由漏磁引起的涡流损耗，认为仅存在由趋肤效应引起的涡流损耗，故电机总交流铜耗修正为
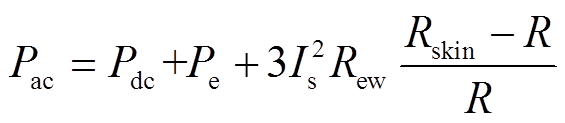（27）
本文通过搭建Matlab与FEMM的联合仿真平台来实现上述基于快速有限元的绕组涡流损耗半解析计算，并与商用有限元软件Maxwell的仿真结果进行对比分析。所研究的对象为一台12槽10极的表贴式永磁电机，其主要参数见表1。
表1 永磁电机主要参数
Tab.1 Main parameters of permanent magnet machine
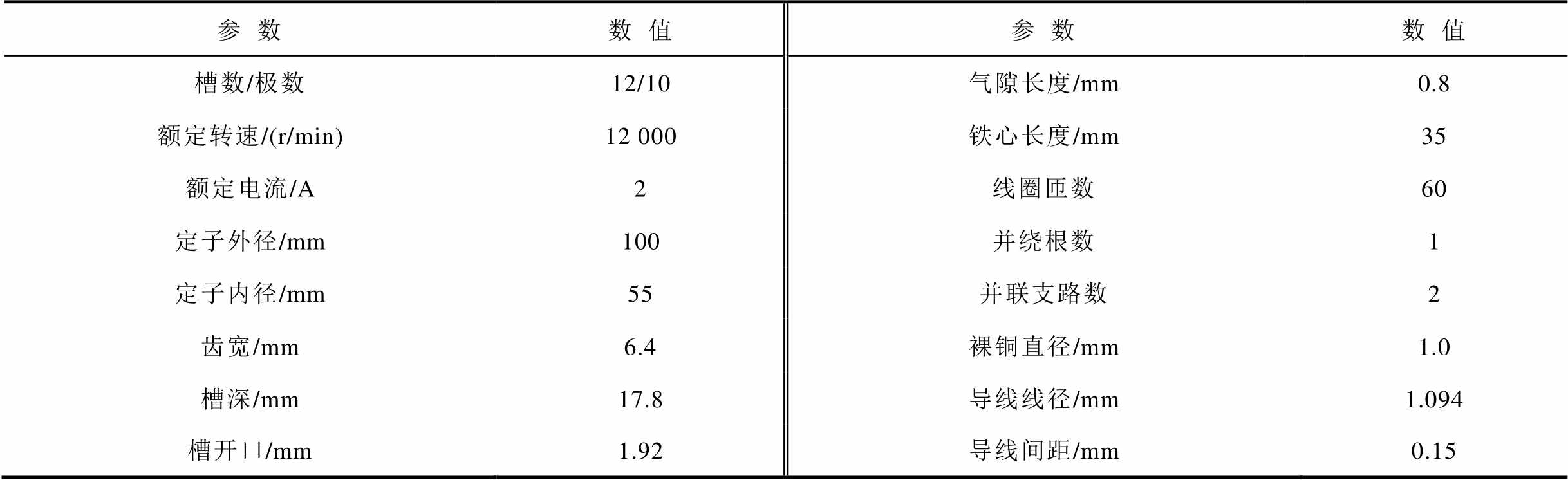
参数数值参数数值 槽数/极数12/10气隙长度/mm0.8 额定转速/(r/min)12 000铁心长度/mm35 额定电流/A2线圈匝数60 定子外径/mm100并绕根数1 定子内径/mm55并联支路数2 齿宽/mm6.4裸铜直径/mm1.0 槽深/mm17.8导线线径/mm1.094 槽开口/mm1.92导线间距/mm0.15
开源有限元软件FEMM能够对电磁场问题进行有限元仿真，其最大的优点在于与Matlab交互性强，可针对所处理问题自由编程，其联合仿真平台如图9所示。所开发的程序内置了快速有限元计算绕组涡流损耗的半解析方法，并对所有参数都进行了参数化。对任意散线电机，从电机建模、材料设置、激励设置及边界条件设置等前处理，到导体坐标计算、槽漏磁提取及损耗计算等后处理均自动实现，极大地节省了时间，为电机设计和优化提供了便利，程序具有一定的通用性。
图9 Matlab与FEMM联合仿真平台
Fig.9 Simulation platform based on Matlab and FEMM
图10给出了电机交流铜耗的计算流程。首先利用Matlab和FEMM仿真平台构建电机的一般有限元模型（不含导体），并进行1/6电周期静磁场有限元仿真；接着按照导体排布模型计算导体圆心坐标，提取槽漏磁并进行重构；然后对重构的槽漏磁进行FFT，求出基波和谐波涡流损耗，与趋肤效应引起的涡流损耗和直流铜耗相加，得到电机的交流铜耗。因此，电机交流铜耗包括涡流损耗Pe和直流铜耗Pdc，而涡流损耗又分为由槽漏磁引起的涡流损耗Pe1和趋肤效应引起的涡流损耗Pe2，为避免损耗分离的过程，下文通过计算交流等效电阻与直流等效电阻之比（Rac/Rdc）来表征涡流损耗的大小，其值与Pac/Pdc相同。
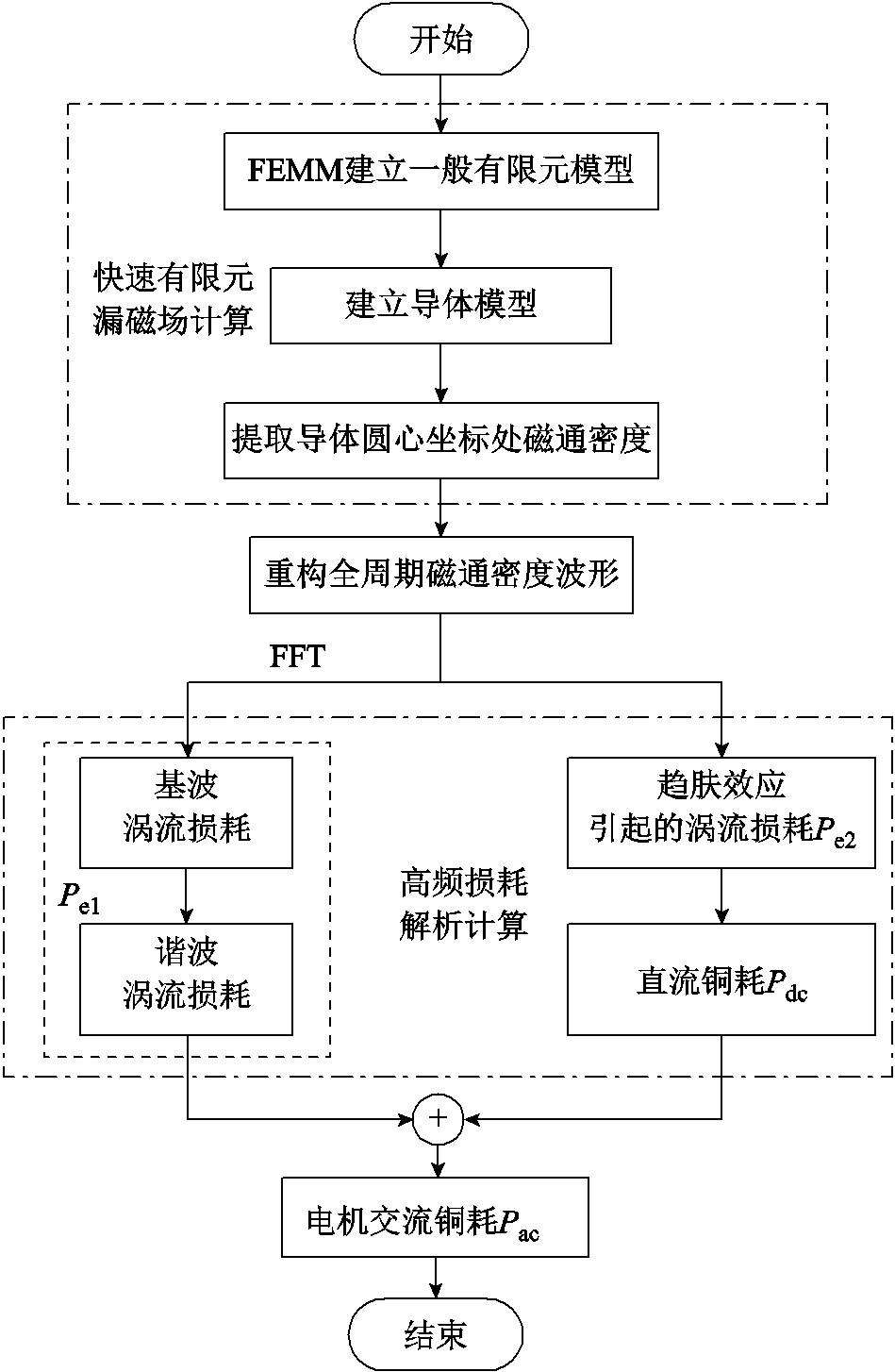
图10 绕组涡流损耗计算流程
Fig.10 Flow chart of winding eddy current loss calculation
为验证所提计算方法的快速性与准确性，借助商用有限元软件Maxwell求解绕组涡流损耗进行对比，只考虑永磁电机的有效部分，其求解模型如图11所示。
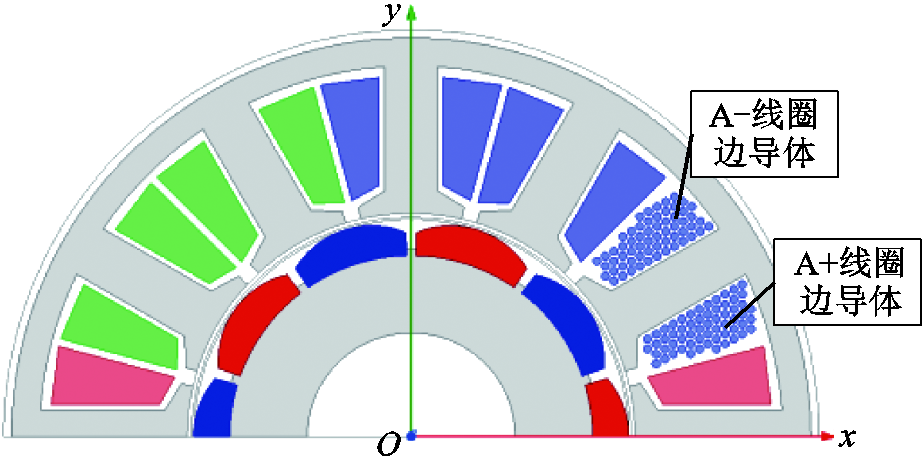
图11 基于Maxwell的交流铜耗求解模型
Fig.11 Solving model of AC copper loss based on Maxwell
对比在2A电流下，低频解析法、高频解析法和Maxwell仿真的Rac/Rdc计算结果，如图12所示。低频解析法在频率小于10kHz时与有限元结果接近，此时涡流磁场去磁作用小，导体内的磁场趋于恒稳；但随着频率的升高，结果逐渐偏大，此时导体内产生的涡流变大，去磁作用明显，磁场分布不均匀，不再符合低频解析算法的假设。而高频解析算法不仅在低频时与有限元结果吻合，当频率达到50kHz时，误差仍保持在5%以内。该方法从电磁场基本方程出发，更好地描述了导体内磁场的分布，克服了低频解析算法的局限性，这说明了考虑退磁作用的高频损耗解析计算的精确性。
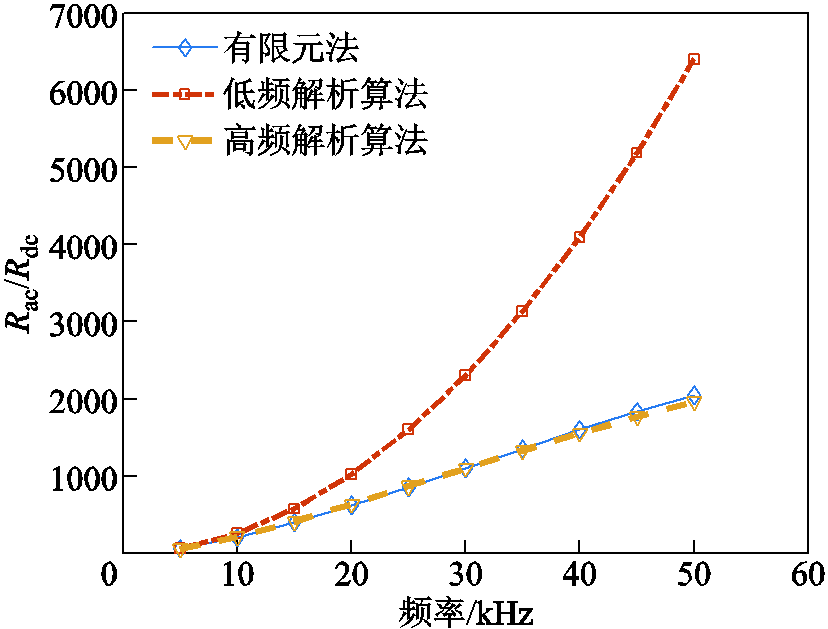
图12 不同频率下，Rac/Rdc计算结果对比
Fig.12 Comparison of Rac/Rdc calculation results under different frequencies
电机不同负载状态下，有限元法与半解析法的Rac/Rdc计算结果对比如图13所示。首先，半解析法与有限元法在低频域计算结果趋于一致，但在高频情况下，低频解析法不再准确，而高频解析法仍与有限元结果贴近。其次，在频率保持不变的前提下，随着负载的增加，Rac/Rdc逐渐减小，这是因为铁心的饱和特性使槽漏磁磁通密度幅值逐渐饱和，涡流损耗趋于极限，而直流铜耗与电流平方成比例增加，因此造成交流铜耗与直流铜耗的比值降低。
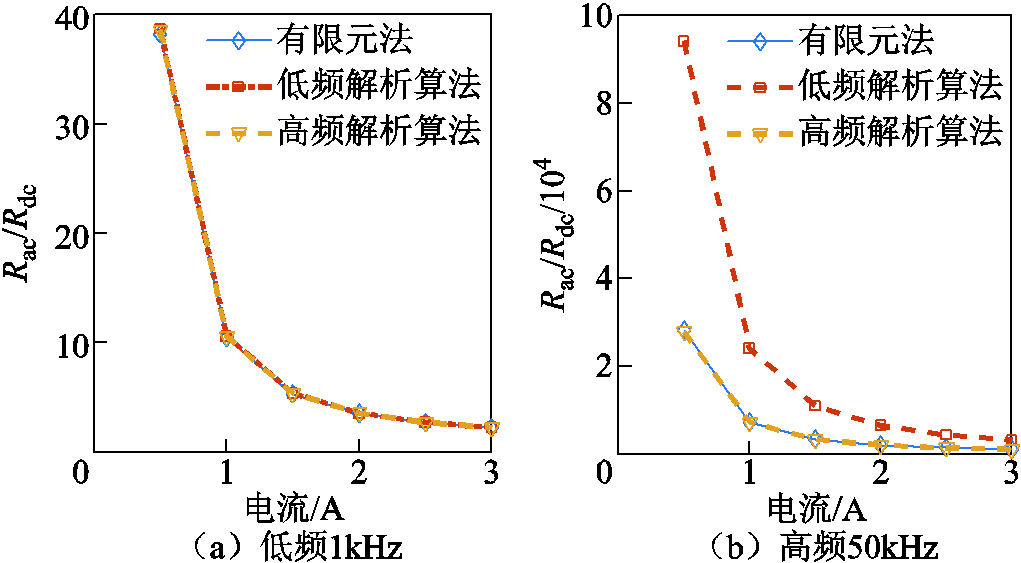
图13 不同负载下，Rac/Rdc计算结果对比
Fig.13 Comparison of Rac/Rdc calculation results under different loads
表2列出了电流为2A时，通过高频解析算法计算电机铜耗的组成部分。对于所研究的电机，在50kHz的频率范围内，由趋肤效应引起的涡流损耗数值极小，可以忽略不计，因此可认为绕组铜耗仅存在槽漏磁引起的涡流损耗和直流铜耗。
表2 交流铜耗组成
Tab.2 Composition of AC copper loss
组成部分低频（1kHz）高频（50kHz） 涡流损耗Pe1/W3.012 321.57 涡流损耗Pe2/W7.51×10-50.17 直流铜耗Pdc/W1.181.18 交流铜耗Pac/W4.192 321.73
此外，所提出的半解析法在计算过程中就已经分别计算出各导体和各槽的损耗，这对预测电机绕组的热点是极其有利的。借助半解析法计算不同槽型的涡流损耗对比如图14所示，可见同相槽涡流损耗较大，同相槽与异相槽的涡流损耗两者平均比值为1.155，约为两槽磁动势幅值之比。
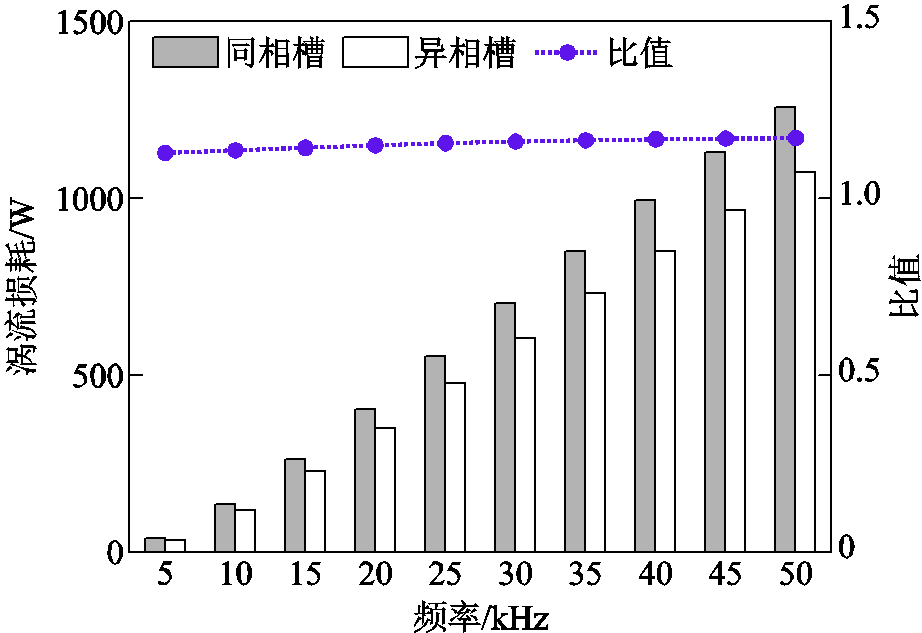
图14 不同槽型的涡流损耗对比
Fig.14 Comparison of eddy current loss of different slot types
表3对比了基于快速有限元的半解析法（低频、高频）、线性有限元法和传统有限元法计算绕组涡流损耗的速度和准确度。计算均在同一台个人计算机上运行，处理器为Intel(R) Core(TM) i7—7700 CPU@3.60GHz，RAM为12G。由表3可知，线性有限元法计算很快，但由于没有考虑电机饱和的影响，导致计算误差大；传统有限元法计算最为准确，但密集的导体网格极大增加了计算时间；而基于快速有限元的半解析法将计算速度提高了近100倍，且高频解析法无论在低频还是高频均具有相当小的误差，其快速性和准确性为电机设计和优化提供了良好的保障。
表3 不同方法的计算性能比较
Tab.3 Comparison of calculation performance of different methods
求解方法耗时/s误差(%) 低频(1kHz)高频(50kHz) 低频解析法10.91.05212.67 高频解析法11.80.833.84 线性有限元1.964.683.7 传统有限元1 160——
实验中为方便分离出绕组铜耗，仅对电机定子进行实验，而实际槽内漏磁还会受到转子侧影响，且一般解析法计算往往忽略了转子侧的影响[27]，为此，有必要研究转子侧对绕组涡流损耗的影响。求解依然借助上述所提出的半解析法。
仍选取图5中紧贴齿部的两列导体为研究对象，施加2A额定电流时，带转子和不带转子时导体所受漏磁场的对比如图15所示。对于所研究的永磁电机，不论是同相槽还是异相槽，带转子时槽漏磁均较大，这是因为转子永磁体也会产生一部分的漏磁，因此忽略转子所求出的绕组涡流损耗偏小，可见一般解析法的不足。而基于快速有限元的半解析算法借助了有限元，能更真实地获取槽漏磁数据，很好地克服了解析法的缺点。
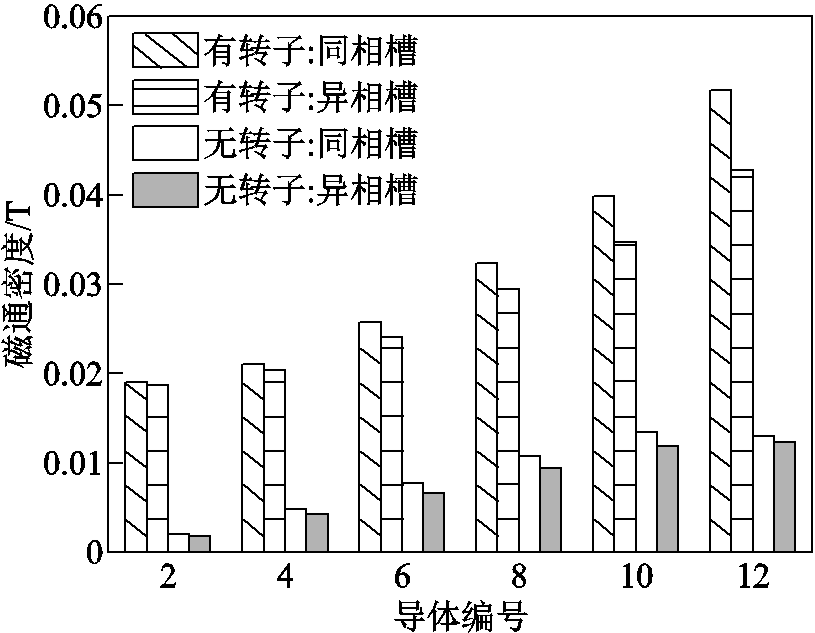
图15 转子对槽漏磁磁通密度的影响
Fig.15 The influence of the rotor on the magnetic flux leakage density of the slot
不同频率下有转子和无转子两种情况下计算的Rac/Rdc曲线（不考虑端部）如图16所示。受转子的影响，绕组涡流损耗增加，且随着频率的升高，两者的差距呈指数上升，可见转子对绕组涡流损耗的影响很大，忽略转子求解的做法不可取。所提出的半解析法基于有限元仿真结果，因而具有很高的保真度。
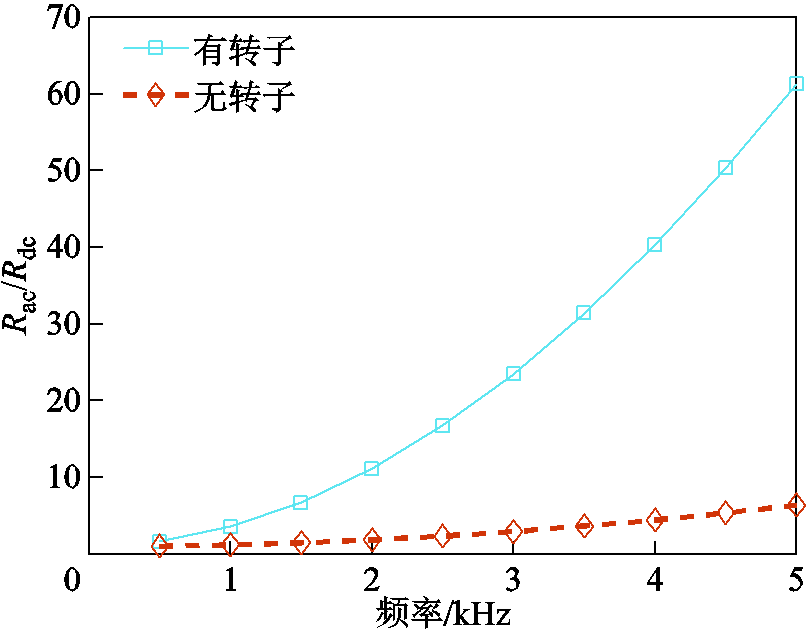
图16 有转子与无转子计算结果对比
Fig.16 Comparison of calculation results with and without the rotor
电机在实际运行过程中采用逆变器供电，逆变器开关会引入高频电流谐波，在绕组上产生显著的涡流损耗，因此十分有必要对这部分损耗进行估算。本文所采用的逆变器直流母线电压为540V，开关频率为20kHz，额定工况下的仿真电流波形和谐波分析如图17所示，除了基波电流外，主要还存在一次开关边带谐波与二次开关边带谐波。
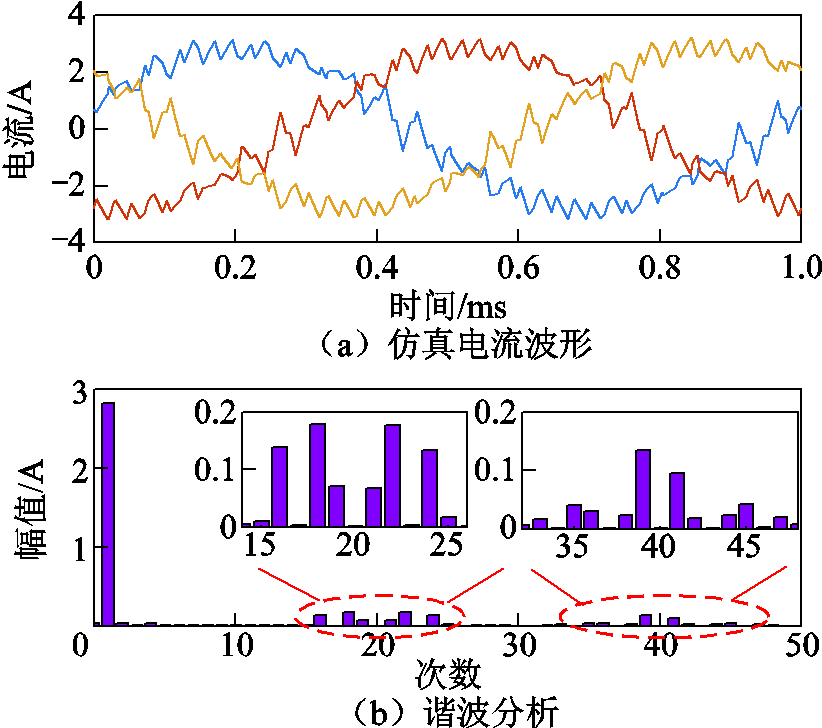
图17 逆变器供电时的仿真电流波形及其谐波分析
Fig.17 Simulated current waveform and its harmonic analysis under inverter power supply
为验证逆变器供电下所提半解析计算方法的有效性，将半解析计算与有限元仿真的结果进行对比。首先注入电流基波分量，通过半解析计算得到基波损耗；然后在磁饱和主要由基波引起的假设基础上，在每一基波计算时间步冻结磁导率，分别注入不同频率电流，计算出槽漏磁，并代入解析式求解出各次谐波损耗；最后与基波损耗相加得到绕组总损耗。该方法能够计算绕组损耗来源。逆变器供电时不同方法计算的绕组损耗如图18所示。可以发现，逆变器开关引起的谐波涡流损耗占比较大，这在电机设计过程中不容忽视。高频解析法与有限元仿真的结果十分吻合，误差仅为0.8%；而低频解析法计算的总损耗高出了21.2%，显著高估了高频电流谐波尤其是二次开关边带谐波引起的损耗。
图18 逆变器供电时不同方法计算的绕组损耗
Fig.18 Winding copper loss calculated by different methods under inverter power supply
在实验中，利用能量守恒原理分离交流铜耗。实验去除了电机转子，由电源向定子线圈供电，此时输入功率应等于线圈的总铜耗和定子铁耗之和。传统意义上交流铜耗的测量往往忽略了定子铁心相关参数对铁耗和交流铜耗的影响，给准确测量交流铜耗带来严峻的挑战。为保证实验中所测得的交流铜耗精度，需分别进行铁磁材料特性测量实验和交流铜耗测量实验。
铁磁材料的特性主要包括铁心的磁通密度-磁场强度（B-H）特性曲线和有关铁耗的损耗密度-磁通密度（P-B）曲线，这是计算定子铁耗的依据。文中电机所采用的铁磁材料牌号为10JNEX900，厚度为0.1mm。
借助空载变压器原理测量，得到不同频率下铁磁材料的特性曲线，如图19和图20所示。可见损耗随着磁通密度及频率的上升而增加，由于测量仪器的限制，最大频率为10kHz。将所测曲线导入有限元软件即可计算电机的定子铁耗。
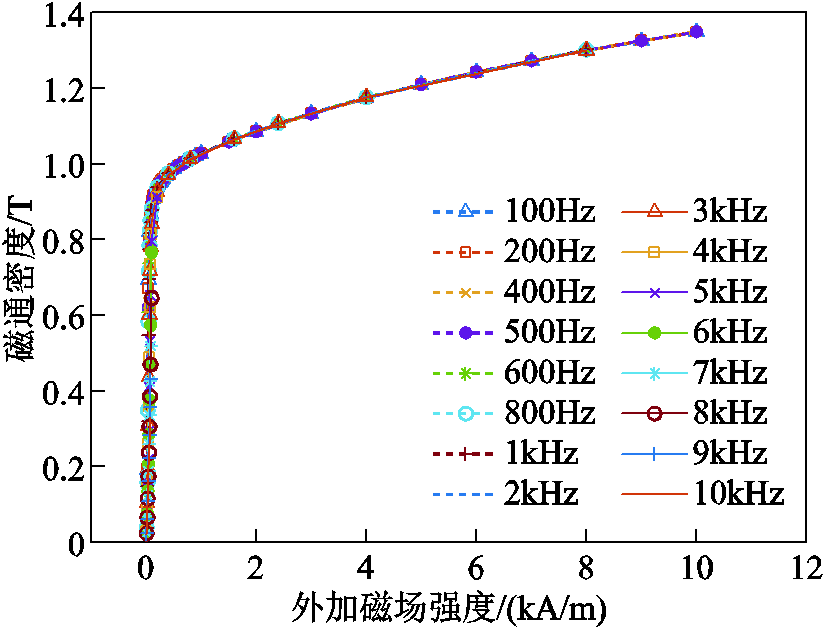
图19 所测铁磁材料的B-H特性曲线
Fig.19 B-H curves of the measured ferromagnetic material
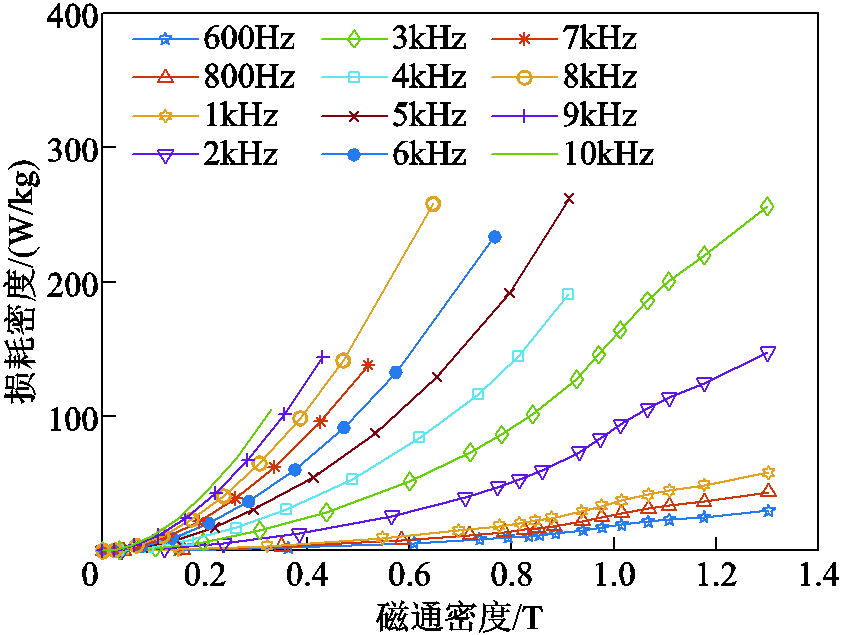
图20 所测铁磁材料的P-B特性曲线
Fig.20 P-B curves of the measured ferromagnetic material
交流铜耗测量实验平台如图21所示，实验环境温度为30℃。电机采用2A正弦电流供电，交流电源所能提供的最高频率为5kHz，由功率分析仪测量损耗。
图21 交流铜耗测量实验平台
Fig.21 Experimental platform for AC copper loss measurement
永磁电机的损耗构成复杂且难以分离，尤其是转子风摩损耗、磁钢损耗等相关参数难以测量，影响因素过多，因此去除转子，只对定子部分进行实验研究，这样电机损耗仅由定子铁耗和交流铜耗构成，易于分离。相应地，在FEMM和Matlab平台中仅保留定子仿真模型。此外，实际电机存在绕组端部，而半解析算法仅针对电机有效部分，由于端部漏磁较小，故可以忽略由漏磁引起的涡流损耗。结合前文仿真分析，在50kHz以内，趋肤效应引起的涡流损耗极小，因此可认为端部仅存在直流铜耗。通过高精度微欧计测量电机的相电阻，再减去有效部分的电阻得到端部电阻，从而可算出端部直流铜耗，结合2.3节的推导公式修正得到电机最终的直流铜耗Pdc和交流铜耗Pac。
受实验室交流电源（ITECH 7625）输出条件的限制，仅能测得5kHz范围内的交流铜耗，以Rac/Rdc形式表示，如图22所示。由图22可知，实验结果与半解析计算结果十分吻合，误差均在5%以内。由于频率并不高，高频去磁效应并不显著，低频解析法与高频解析法的计算结果并无太大差别。为进一步说明高频解析法的有效性，采用精密LCR表（KEYSIGHT E4980AL）测量绕组高频电阻来进行对比，结果如图23所示。在50kHz范围内，高频解析法计算结果与LCR表的测量值吻合，误差大都在5%以内，在50kHz时误差最大，为6.9%；而低频解析法计算误差随着频率上升快速放大，与前文仿真部分的结论一致。不过LCR表的测量值始终略高于高频解析法的计算结果，误差来源主要有以下两点：①LCR表通过注入高频电流测量高频电阻，铁心中不可避免地会产生涡流，LCR表的测量结果包含了铁心引起的阻抗，导致所测绕组高频电阻偏大；②实际电机槽内的导体排布随机性很强，与仿真所建立的导体位置模型存在差别。
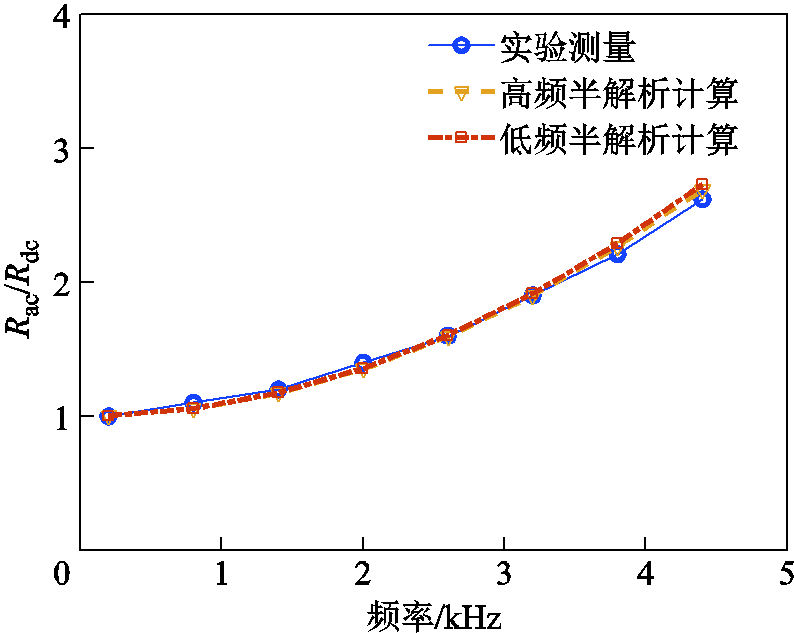
图22 通过交流铜耗对比半解析的计算与实验结果
Fig.22 Result comparison of semi-analytical and experimental by copper loss
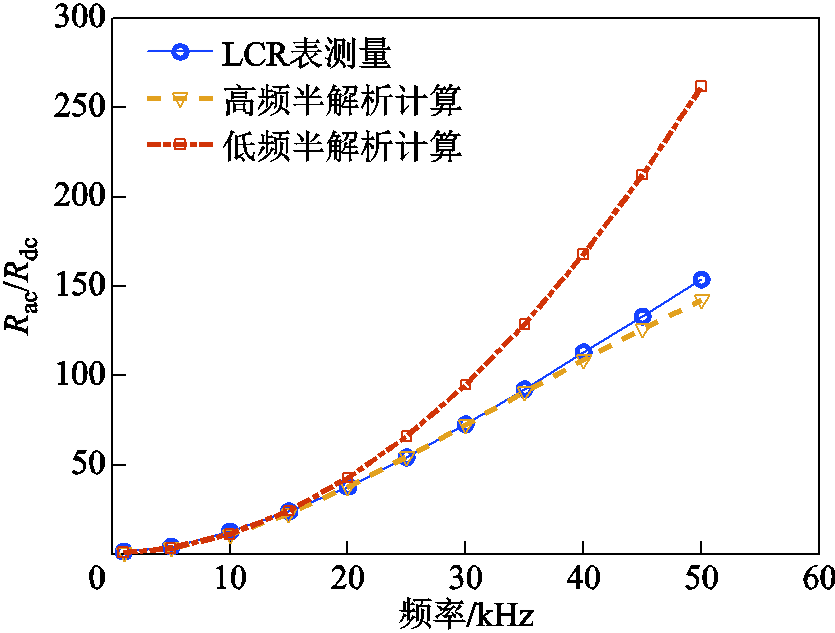
图23 通过高频电阻对比半解析的计算与实验结果
Fig.23 Result comparison of semi-analytical and experimental by high-frequency resistance
本文以散线绕制的永磁电机为研究对象，提出基于快速有限元绕组涡流损耗的半解析计算方法，针对有限元计算涡流损耗的不足，将传统的有限元模型分解为一般有限元模型和导体位置模型，并借助于快速有限元的思想快速提取槽漏磁数据为解析算法服务，大大减少了有限元仿真时间。根据涡流损耗的产生机理，文中揭示了导体涡流损耗一般低频解析式的局限性，对高频情况下考虑涡流去磁效应的导体涡流损耗进行了解析推导。最后通过搭建基于FEMM和Matlab仿真平台来实现上述方法，并采用实验对所提出的方法进行了验证。本文主要结论如下：
1）与Maxwell仿真对比分析发现，低频解析算法仅适用于10kHz以内，而高频解析算法在50kHz时仍具有足够高的精度，并通过实验进一步验证了高频解析算法的准确性，在较大频率范围内误差低于5%。
2）相较于传统有限元计算电机绕组涡流损耗，基于快速有限元的半解析算法将计算速度提高了近100倍，对电机设计和优化具有很大的应用价值。
3）半解析算法能计算出不同槽类型的涡流损耗，同相槽的涡流损耗大于异相槽的，两者比值约等于槽磁动势之比。
4）电机饱和与转子侧对绕组涡流损耗的影响较大，一般解析法不考虑上述因素，而所提出的半解析算法基于快速有限元，具有高保真度。
虽然本文提出的绕组涡流损耗半解析算法计算高效，但仍存在一些不足。一方面，本文研究的绕组无并绕导线，对于并绕导线绕组，还需要研究环流损耗的算法；另一方面，对于成型绕组的涡流损耗高效计算也是一项课题，上述问题将作为后续研究永磁电机交流铜耗的重点。
参考文献
[1] 唐任远. 现代永磁电机: 理论与设计[M]. 北京: 机械工业出版社, 1997.
[2] 孔晓光, 王凤翔, 邢军强. 高速永磁电机的损耗计算与温度场分析[J]. 电工技术学报, 2012, 27(9): 166-173.
Kong Xiaoguang, Wang Fengxiang, Xing Junqiang. Losses calculation and temperature field analysis of high speed permanent magnet machines[J]. Transactionsof China Electrotechnical Society, 2012, 27(9): 166-173.
[3] 张凤阁, 杜光辉, 王天煜, 等. 高速电机发展与设计综述[J]. 电工技术学报, 2016, 31(7): 1-18.
Zhang Fengge, Du Guanghui, Wang Tianyu, et al. Review on development and design of high speed machines[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 1-18.
[4] Al-Timimy A, Giangrande P, Degano M, et al. Design and losses analysis of a high power density machine for flooded pump applications[J]. IEEE Transactions on Industry Applications, 2018, 54(4): 3260-3270.
[5] 刘毓希, 李立毅, 曹继伟, 等. 短时高过载永磁同步电机电磁热研究[J]. 电工技术学报, 2019, 34(11): 2296-2305.
Liu Yuxi, Li Liyi, Cao Jiwei, et al. Electromagnetic thermal analysis for short-term high-overload permanent magnet synchronous motor[J]. Tran-sactions of China Electrotechnical Society, 2019, 34(11): 2296-2305.
[6] 王雨婷, 张卓然, 于立, 等. 低压大电流双凸极无刷直流发电机电枢绕组股线环流的抑制方法[J]. 电工技术学报, 2018, 33(2): 275-283.
Wang Yuting, Zhang Zhuoran, Yu Li, et al. Strand circulating current suppression method in armature windings of low voltage high current doubly salient brushless DC generator[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 275-283.
[7] Soualmi A, Dubas F, Depernet D, et al. Study of copper losses in the stator windings and PM eddy-current losses for PM synchronous machines taking into account influence of PWM harmonics[C]//2012 15th International Conference on Electrical Machines and Systems (ICEMS), Sapporo, Japan, 2012: 1-5.
[8] van der Geest M, Polinder H, Ferreira J A, et al. Current sharing analysis of parallel strands in low-voltage high-speed machines[J]. IEEE Transactions on Industrial Electronics, 2014, 61(6): 3064-3070.
[9] Liu Jingyi, Fan Xinggang, Li Dawei, et al. Minimization of AC copper loss in permanent magnet machines by transposed coil connection[J]. IEEE Transactions on Industry Applications, 2021, 57(3): 2460-2470.
[10] Dowell P L. Effects of eddy currents in transformer windings[J]. Proceedings of the Institution of Electrical Engineers, 1966, 113(8): 1387-1394.
[11] Robert F. A theoretical discussion about the layer copper factor used in winding losses calculation[J]. IEEE Transactions on Magnetics, 2002, 38(5): 3177-3179.
[12] 旷建军. 平面变压器PCB板绕组的损耗分析、计算与设计优化[D]. 福州: 福州大学, 2002.
[13] Sullivan C R. Computationally efficient winding loss calculation with multiple windings, arbitrary waveforms, and two-dimensional or three-dimensional field geometry[J]. IEEE Transactions on Power Electronics, 2001, 16(1): 142-150.
[14] Mellor P, Wrobel R, Simpson N. AC losses in high frequency electrical machine windings formed from large section conductors[C]//2014 IEEE Energy Conversion Congress and Exposition(ECCE), Pittsburgh, PA, USA, 2014: 5563-5570.
[15] Wu L J, Zhu Z Q. Simplified analytical model and investigation of open-circuit AC winding loss of permanent-magnet machines[J]. IEEE Transactions on Industrial Electronics, 2014, 61(9): 4990-4999.
[16] Wu L J, Zhu Z Q, Staton D, et al. Analytical model of eddy current loss in windings of permanent-magnet machines accounting for load[J]. IEEE Transactions on Magnetics, 2012, 48(7): 2138-2151.
[17] Lehikoinen A, Arkkio A, Belahcen A. Reduced basis finite element modeling of electrical machines with multiconductor windings[J]. IEEE Transactions on Industry Applications, 2017, 53(5): 4252-4259.
[18] Lehikoinen A, Arkkio A. Efficient finite-element computation of circulating currents in thin parallel strands[J]. IEEE Transactions on Magnetics, 2016, 52(3): 1-4.
[19] Hajji T E, Hlioui S, Louf F, et al. Hybrid model for AC losses in high speed PMSM for arbitrary flux density waveforms[C]//2020 International Conference on Electrical Machines (ICEM), Gothenburg, Sweden, 2020: 2426-2432.
[20] Roth C, Birnkammer F, Gerling D. Analytical model for AC loss calculation applied to parallel conductors in electrical machines[C]// 2018Ⅷ International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 2018: 1088-1094.
[21] Fatemi A, Ionel D M, Demerdash N A O, et al. Computationally efficient strand eddy current loss calculation in electric machines[J]. IEEE Transactions on Industry Applications, 2019, 55(4): 3479-3489.
[22] 朱洒, 卢智鹏, 王卫东, 等. 基于CE-FEA和小信号分析快速计算逆变器供电下聚磁式场调制电机中永磁体涡流损耗[J]. 电工技术学报, 2020, 35(5): 963-971.
Zhu Sa, Lu Zhipeng, Wang Weidong, et al. Fast calculation of PM eddy current loss in FCFMPM machine under PWM VSI supply based on CE-FEA and small-signal analysis[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 963-971.
[23] Ionel D M, Popescu M. Ultrafast finite-element analysis of brushless PM machines based on space–time transformations[J]. IEEE Transactions on Industry Applications, 2011, 47(2): 744-753.
[24] Tang Xu, Sullivan C R. Stranded wire with uninsulated strands as a low-cost alternative to Litz wire[C]//IEEE 34th Annual Conference on Power Electronics Specialist, Acapulco, Mexico, 2003: 289-295.
[25] Lammeraner J, Stafl M. Eddy currents[M]. Prague: Publishers of Technical Literature Press, 1966.
[26] 冯慈璋, 马西奎. 工程电磁场导论[M]. 北京: 高等教育出版社, 2000.
[27] 许欣, 邓智泉, 张忠明, 等. 高速电机定子单槽绕组交流损耗近似解析建模及验证[J]. 中国电机工程学报, 2021, 41(12): 4306-4316.
Xu Xin, Deng Zhiquan, Zhang Zhongming, et al. Approximate analytical modeling and verification of AC loss in stator single slot windings of high speed motor[J]. Proceedings of the CSEE, 2021, 41(12): 4306-4316.
Abstract Winding eddy current loss is the main component of AC copper loss of permanent magnet machines, and its estimation is an important step in machine design. In the traditional design process, the estimation of winding eddy current loss is generally based on 2D finite element method (FEM) simulation, but it is inevitable to model the conductors and divide them into dense meshes, which will take a lot of computing time. Another method is analytical calculation. Although this method is not time-consuming, the nonlinear characteristic of the ferromagnetic material cannot be considered, and it will result in low calculation accuracy. To achieve a balance between calculation speed and accuracy, this paper studies the generation mechanism of winding eddy current loss of permanent magnet machines, and proposes a semi-analytical algorithm to calculate the winding eddy current loss. On the one hand, the analytical algorithm only depends on slot magnetic leakage flux density, so it is not necessary to establish the conductor model in the FEM model. To further reduce the time cost, the fast FEM is used to extract and reconstruct the slot magnetic leakage flux density. On the other hand, the slot magnetic leakage flux density obtained by FEM has high fidelity, and the analytical algorithm considering high-frequency demagnetization effect in conductor is applied, thus improving the calculation accuracy of winding eddy current loss.
Firstly, the reconstruction algorithm of slot magnetic flux leakage is derived based on the fast FEM theory and the slot/pole configuration of the permanent magnet machine, and the conductor layout model is established to obtain the conductor coordinates. Secondly, the machine FE model without conductors is established, and 1/6 electrical period simulation is carried out. The slot magnetic leakage flux density is extracted based on conductor coordinate, and the entire electrical period slot magnetic leakage flux density is reconstructed. Finally, fast Fourier transform (FFT) is performed for the slot magnetic leakage flux density, and each harmonic magnetic flux density is substituted into the high-frequency analytical algorithm to solve eddy current loss. The total winding eddy current losses can be obtained by summing the losses caused by all harmonic magnetic densities of all conductors.
The proposed semi-analytical method based on fast FEM is implemented by established simulation platform based on Matlab and open source finite element software FEMM, and a 12-slot, 10-pole surface permanent magnet machine was used to verify the proposed method. Firstly, compared with the simulation results obtained by traditional commercial finite element software, the calculation speed of the proposed method is improved by nearly 100 times, and the errors are less than 4% within 50kHz. Secondly, the effectiveness of proposed method is verified through experiments, to separate the winding eddy current loss conveniently, only the stator is used for experimental research. The winding eddy current loss below 5kHz is separated by directly measuring the input power, while the eddy current loss above 5kHz is indirectly characterized by measuring the Rac/Rdc by LCR meter due to the limit of the highest frequency (5kHz) output of the sinusoidal power supply device. The experimental results show that the error of winding eddy current loss calculated by proposed method is generally within 5%, and the maximum error is 6.9% at 50kHz.
The semi-analytical method based on fast FEM proposed in this paper only focuses on the efficient calculation of winding eddy current loss. For multi-stranded winding, it is necessary to study the efficient calculation method of circulating current loss in the future. In addition, the proposed method is only applicable to the machine with cylindrical winding, and the efficient calculation method of hair-pin winding eddy current loss remains to be studied.
keywords：Permanent magnet machine, winding eddy current loss, conductor layout model, fast finite element method, semi-analytical algorithm
DOI:10.19595/j.cnki.1000-6753.tces.211603
中图分类号：TM351
曹龙飞 男，1998年生，硕士研究生，研究方向为高功率密度永磁电机设计与热分析。E-mail：longfeic@hust.edu.cn
范兴纲 男，1992年生，博士，讲师，研究方向为永磁电机设计及电机电磁热流体多物理场分析。E-mail：xinggangfan@hust.edu.cn（通信作者）
国家自然科学基金资助项目（52007069）。
收稿日期 2021-10-10
改稿日期 2022-05-07
（编辑 李冰）