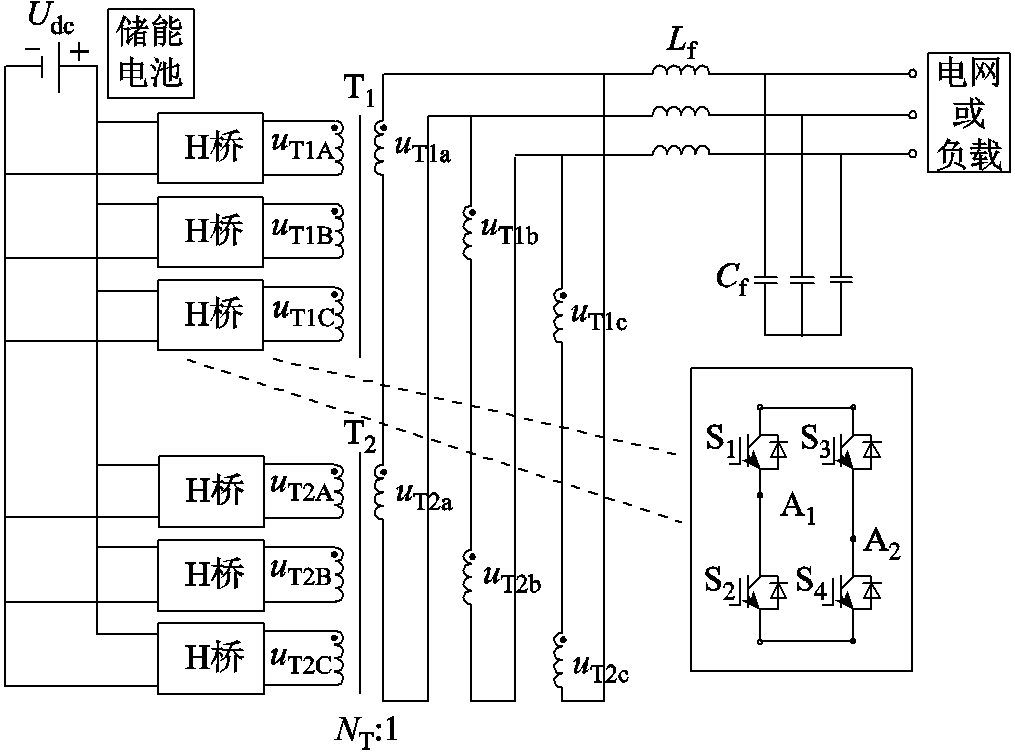
图1 新型级联H桥组合式逆变电源拓扑
Fig. 1 Topology diagram of new cascaded H-bridge combined inverter power supply
摘要 针对一种宽输入电压范围双向逆变电源,可采用磁集成方法提高其功率密度。与传统三相平面叠铁心变压器相比,立体卷铁心变压器具有磁路对称、重量轻等优势,该文拟开展PWM非正弦激励下考虑漏感频变特性的立体卷铁心变压器建模相关研究。首先,基于Foster频变磁阻模型,提出一种考虑漏感频变特性的立体卷铁心变压器模型,通过全局优化算法计算模型参数;其次,针对级联H桥组合式DC-AC拓扑的典型工作点,分析了PWM非正弦激励的谐波特征,重点关注不同H桥之间各次谐波的相对相位关系,给出简化等效电路;最后搭建逆变电源试验平台,开展了稳态和动态试验,验证了模型的准确性。
关键词:立体卷铁心 双重傅里叶分析 漏电感 频变特性 磁路模型
在新能源[1]、船舶[2]、机车等独立电力系统中,储能电池接入双向隔离型DC-AC变换器的直流侧电压波动范围大,交流侧电能质量、功率密度要求高。一种新型级联H桥[3-4]组合式逆变电源拓扑如图1所示,主电路主要包含6个H桥功率单元、三相变压器(T1、T2)、输出LC滤波器(Lf、Cf)等元器件,其中Lf为变压器漏感。记第一组H桥输出的一次电压分别为UT1A、UT1B、UT1C,对应二次电压为UT1a、UT1b、UT1c;第二组H桥输出的一次电压分别为UT2A、UT2B、UT2C,对应二次电压为UT2a、UT2b、UT2c。该拓扑的主要优点包括直流侧电压范围宽、交流侧电能质量高、功率密度高。拓扑中每个H桥采用单极倍频调制,每相两个H桥之间载波移相。载波移相PWM调制的双H桥级联拓扑能够显著提高谐波频率,降低输出滤波电感值,进而可引入磁集成技术以提高功率密度。本文磁集成体现在两个方面:①铁心磁路集成;②滤波电感集成至隔离变压器漏感。组合式隔离变压器铁心磁集成设计思路如图2所示。

图1 新型级联H桥组合式逆变电源拓扑
Fig. 1 Topology diagram of new cascaded H-bridge combined inverter power supply
由于PWM非正弦激励谐波含量丰富,需考虑变压器漏感频变特性。目前,考虑绕组阻抗频变特性的变压器等效模型主要有集中参数电路模型、分布参数电路模型、混合参数电路模型和Foster模型,多应用于系统级电磁暂态仿真。
1)集中参数电路模型。将变压器线圈划分为若干单元,如图3所示[5],每个单元用集中电容C1、C2和C3、电感L、电阻R及代表匝间损耗的等效电导G表示。集中参数电路模型的频率适用范围有限,不适合宽频建模且系统级建模稳定性不强。
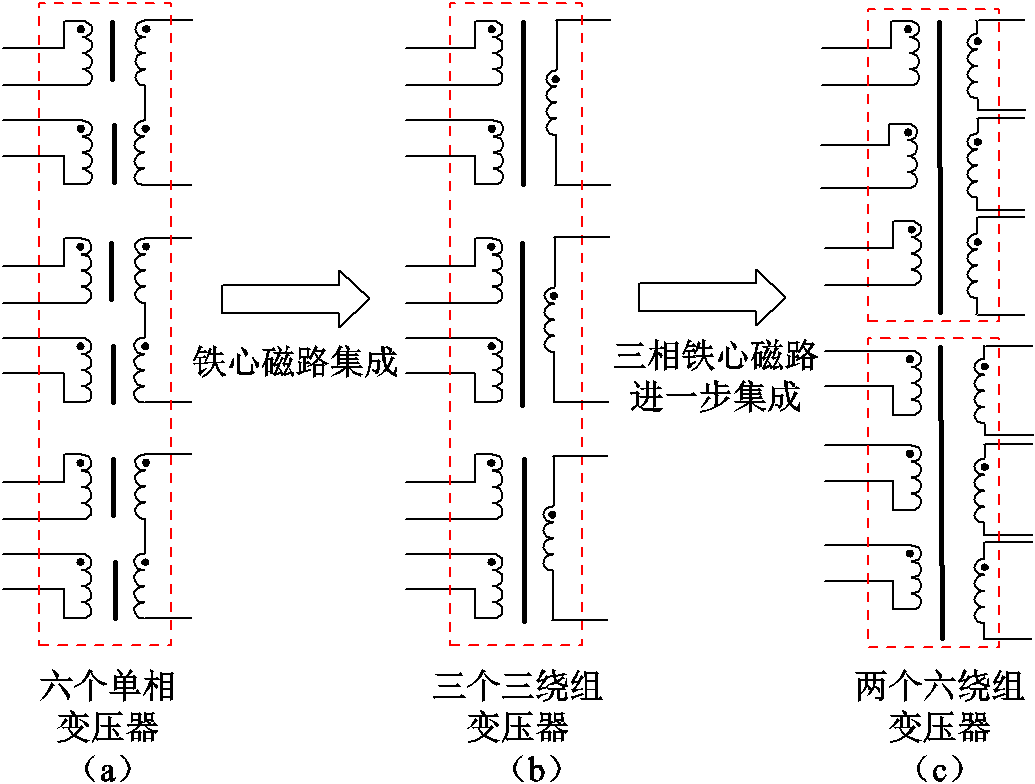
图2 组合式隔离变压器铁心磁集成设计思路
Fig. 2 Magnetic integration design of combined isolation transformer core
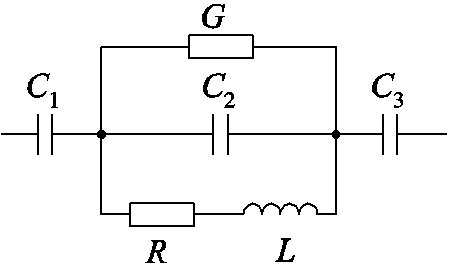
图3 集中参数电路模型
Fig. 3 Lumped parameter circuit model
2)分布参数电路模型。通常在高频范围内描述系统的响应特性。主要分为以下两类:①变压器绕组的多导体传输线模型[6]。该模型将变压器绕组的每一匝看作一根传输线,具有更高的仿真精度。②变压器绕组的分数阶传输线模型[7]。文献[7]建立了考虑绕组和油纸介电常数频变特性的油浸式变压器绕组的分数阶传输线模型。常用求解方法包括矢量匹配和递归卷积结合法、时域有限差分法、时域有限元(Finite Element Method, FEM)法、分数阶法,不足之处是求解过程复杂。
3)混合参数电路模型。主要分为两类:一类是采用集中参数模型与分布参数模型相混合的方式;一类是对绕组不同部分采用不同的单元进行剖分,以降低模型规模和计算量[8]。不足之处是混合参数模型求解方程时易出现病态解。
4)Foster模型。通常指的是由阻抗(或导纳)方程展开成包含角频率w的分式,再使用电阻、电感并联或串联电路拟合上述分式。Foster模型可以通过角频率w将阻抗频域的频变特性转化到时域的计算过程中,数值计算稳定,适用性强。通常分为并联Foster模型和串联Foster模型,图4所示为三阶Foster模型。文献[9]分析了涡流效应对于变压器绕组损耗的影响,并提出了以电阻、电感元件进行串并联组合来拟合绕组电气参数频率变化特性的Foster电路。文献[10]指出Foster模型忽略了位移电流,因此它只适用于低于绕组第一谐振频率以下的范围。
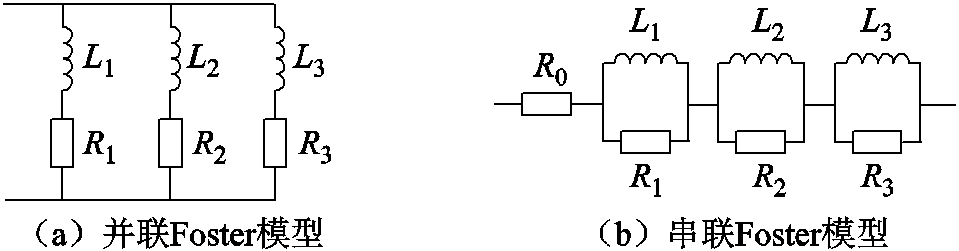
图4 三阶Foster模型
Fig.4 Third-order Foster model
与传统三相平面叠铁心变压器相比,立体卷铁心变压器具有磁路对称、重量轻等优势,其典型结构如图5所示。在考虑漏感频变特性的立体卷铁心变压器建模方面,目前未见文献报道。文献[11]建立了1MVA立体卷铁心干式配电变压器三维FEM仿真模型,进行了铁耗计算。文献[12]建立了简化单柱二维电磁场模型,分析了绕组漏磁。
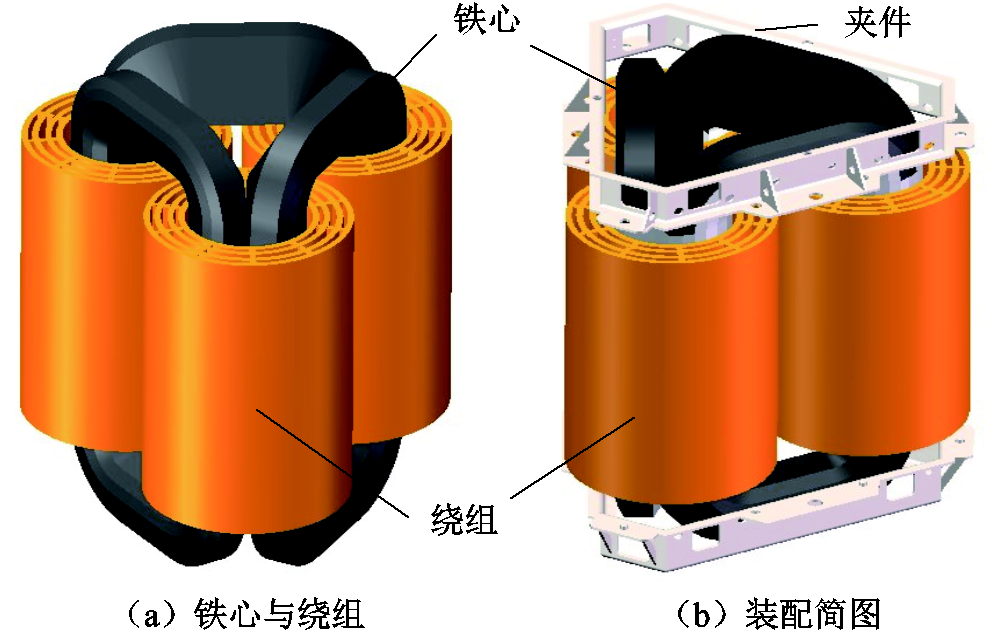
图5 立体卷铁心变压器结构
Fig. 5 3D wound core transformer
本文首先提出一种考虑绕组频变特性与耦合关系的立体卷铁心变压器频变漏感磁路模型;然后针对图1所示新型级联H桥组合式逆变电源拓扑,开展了一次电压谐波分析;最后搭建64kV·A逆变电源试验平台,通过试验验证模型准确性。
立体卷铁心变压器频变漏感磁路模型如图6所示,其中RL为零序磁阻模块,铁心主磁通磁阻RmAB、RmBC、RmCA采用B-H曲线拟合铁心饱和特性,漏磁路磁阻采用频变磁阻模块Rn,根据电磁对偶原理,将电路模型中频变漏感转换为磁路模型中对应的漏磁路频变磁阻。
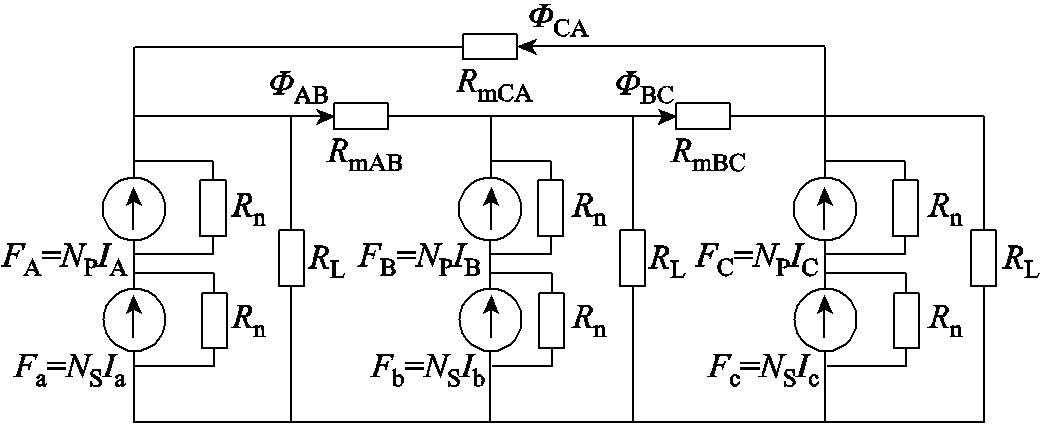
图6 立体卷铁心变压器频变漏感磁路模型原理示意图
Fig. 6 Schematic diagram of the frequency-dependent leakage inductance magnetic circuit model of 3D wound core transformer
变压器中不在铁心区域范围内的磁通均可以算作漏磁通,主要是指仅与一个绕组交链且主要通过空气或油而闭合的那部分磁通。漏磁通存储能量,该效应可以用与绕组串联的集中参数——漏感Ls来体现[13]。P. L. Dowell于1966年提出由于绕组受到自身磁场和邻近绕组产生磁场的作用,会在绕组中产生涡流,使绕组漏感随频率而变化[14]。
本文针对立体卷铁心变压器的结构特征,平行于铁心窗口,沿等边三角形展开为FEM二维等效模型,同时设置周期性边界条件,如图7所示。二维等效建模时维持电压比NT、磁路横截面积A和磁路长度L不变,保持铁心和绕组主体结构不变。基于图7所示建立的立体卷铁心变压器FEM二维等效模型,开展变压器漏感在不同频率下的涡流场计算。
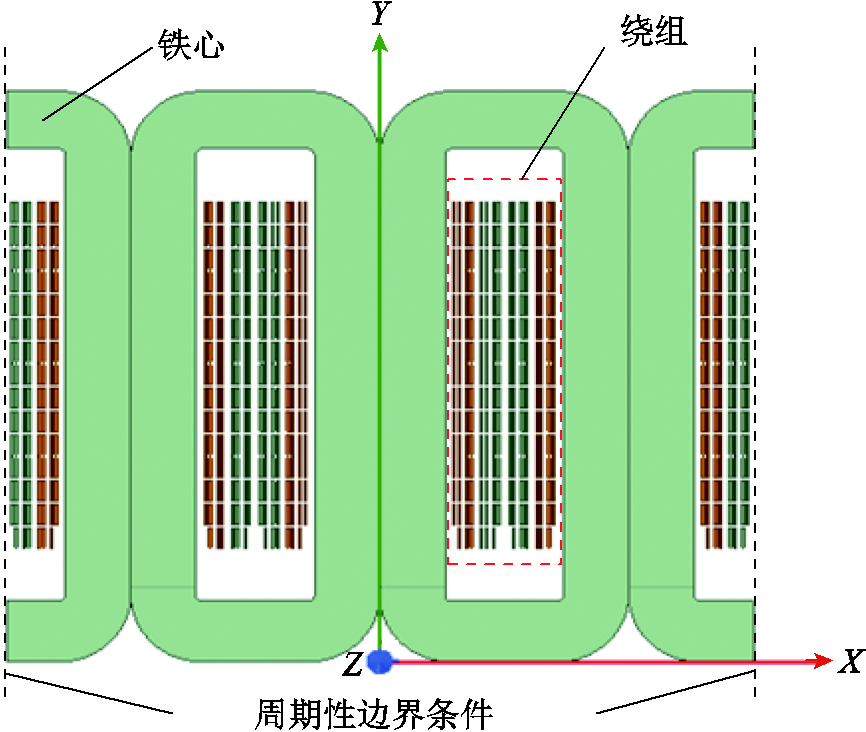
图7 立体卷铁心变压器二维等效模型
Fig. 7 Two-dimensional equivalent model of 3D wound core transformer
根据立体卷铁心变压器FEM二维等效模型仿真计算漏感Ls,漏感值平均分配到一次、二次侧,按照电磁对偶原理,利用式(1)计算对应的磁阻。
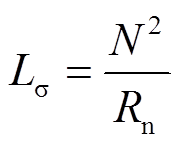 (1)
(1)
式中,N为对应绕组匝数。
频变磁阻模块Rn由固定磁阻模块Rn1与Foster频变磁阻模块Rn2并联组成,即
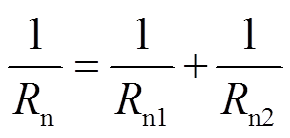 (2)
(2)
式中,固定磁阻Rn1对应漏感的固定部分;Foster频变磁阻模块Rn2对应漏感的频变部分。根据电磁对偶原理,在磁路法中磁动势对应电压,磁通量对应电流,频变磁阻对应电阻,故利用一阶Foster模型中的电阻部分拟合频变磁阻,并使一阶Foster模型中的电感部分数量级远小于电阻部分,使其可以忽略。
一阶Foster模型阻抗Z为
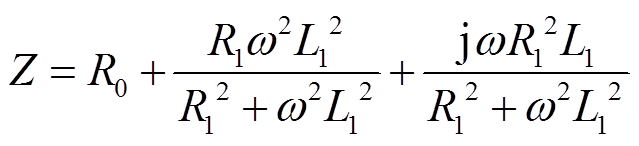 (3)
(3)
根据电力系统电磁暂态计算理论[15],电感L可以表示为一个等效电阻Requ=2L/Dt与历史电流源ihist(t-Dt)并联的电路,如图8所示。
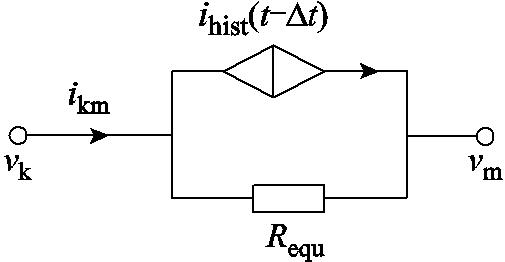
图8 电感暂态解的等效电阻电路
Fig. 8 Equivalent resistance circuit for transient solution of inductance
暂态解的精确微分方程式为
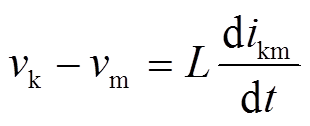 (4)
(4)
式中,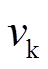 、
、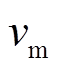 为节点电压;
为节点电压;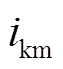 为支路电流。
为支路电流。
将式(4)用近似的中心差分方程式代替,即
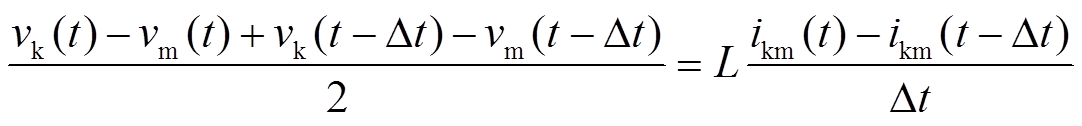 (5)
(5)
由式(5)得
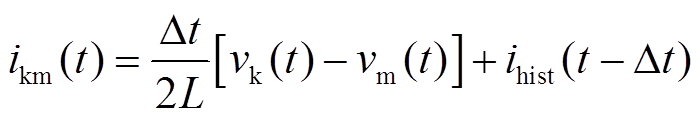 (6)
(6)
式中,历史电流源histi(t-Dt)可以从前一时间步的解中算出。
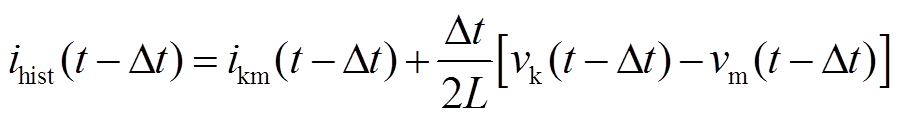 (7)
(7)
根据以上电路暂态分析过程与一阶Foster模型,在磁路模型中自定义频变磁阻模块Rn2,其原理图如图9所示。图中,F1、F2、F3为磁动势,Rm1、Rm2为磁阻;Rm_equ1为等效磁阻;F1hist(t-Dt)为历史磁通源。
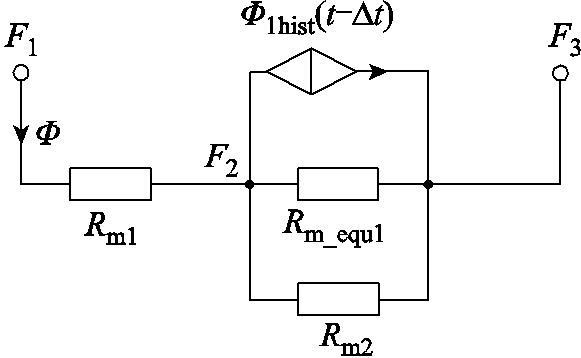
图9 自定义频变磁阻模块原理图
Fig. 9 Schematic diagram of custom frequency-dependent magnetoresistance module
根据磁路的基尔霍夫第一定律,对于有n个节点的磁路,可得
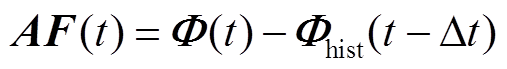 (8)
(8)
式中,A为系数矩阵。
对图9所示磁路网络,令F3=0为磁动势参考点,Dt为仿真步长,可得
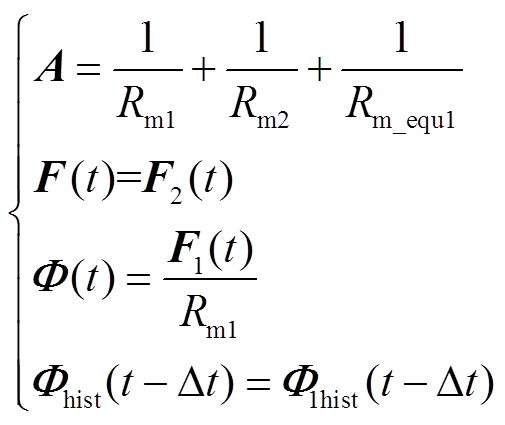 (9)
(9)
一阶Foster模型使用全局优化(Global Search, GS)算法拟合频变磁阻值。GS算法是一种全局最优算法,通过多次局部寻优对比,返回目标函数全局的最小值和对应的参数[16-17]。引入频变磁阻Rn2的方均根误差RMSE作为GS算法的目标函数,将Foster模型三个参数的辨识问题转换为寻找目标函数全局最小值的优化问题。目标函数为
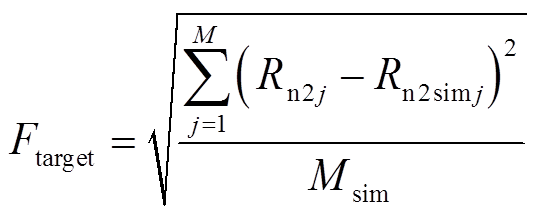 (10)
(10)
式中,Rn2simj为第j个频变磁阻拟合值;Msim为采样个数。
拟合得到一阶Foster模型R0、R1、L1三个参数值,其与自定义频变磁阻模块中Rm1、Rm2、Rm_equ1三个参数值具有以下对应关系:
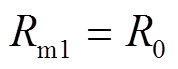 (11)
(11)
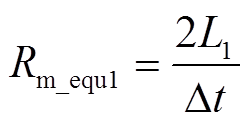 (12)
(12)
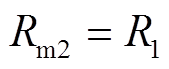 (13)
(13)
二次绕组开路时,一次绕组施加零序电压分量激励,此时变压器零序阻抗与铁心结构密切相关,工程中通过经验公式很难获得准确数值[18]。立体卷铁心变压器三维模型如图10所示,图中显示了零序磁通路径,通过三维FEM仿真计算零序阻抗。
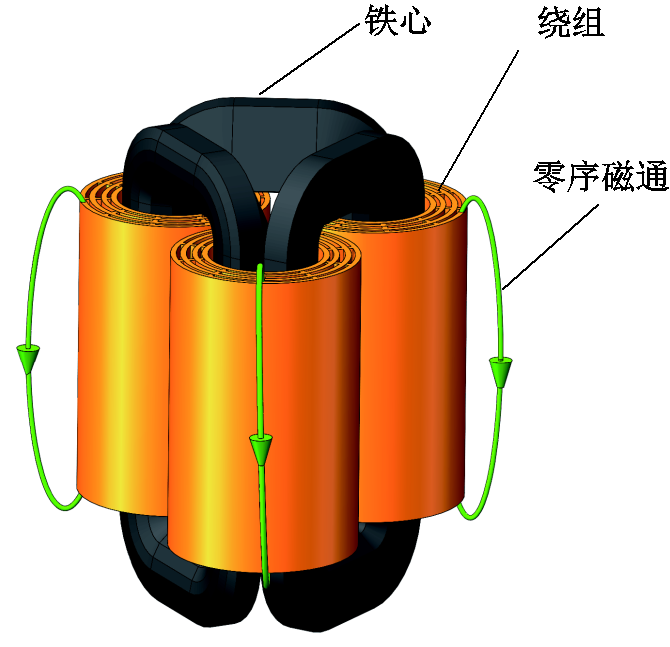
图10 立体卷铁心变压器三维模型
Fig. 10 Three-dimensional model of 3D wound core transformer
逆变电源A相两组H桥级联等效电路如图11所示。载波移相PWM调制方法等效原理如图12所示。根据多电平载波移相原理,uc1为第一组H桥A1和A2所在桥臂的载波;uc2为第二组H桥A3和A4所在桥臂的载波;ur1为A1和A3所在左桥臂的调制波;ur2为A2和A4所在右桥臂的调制波;ur1和ur2相位互差180°。
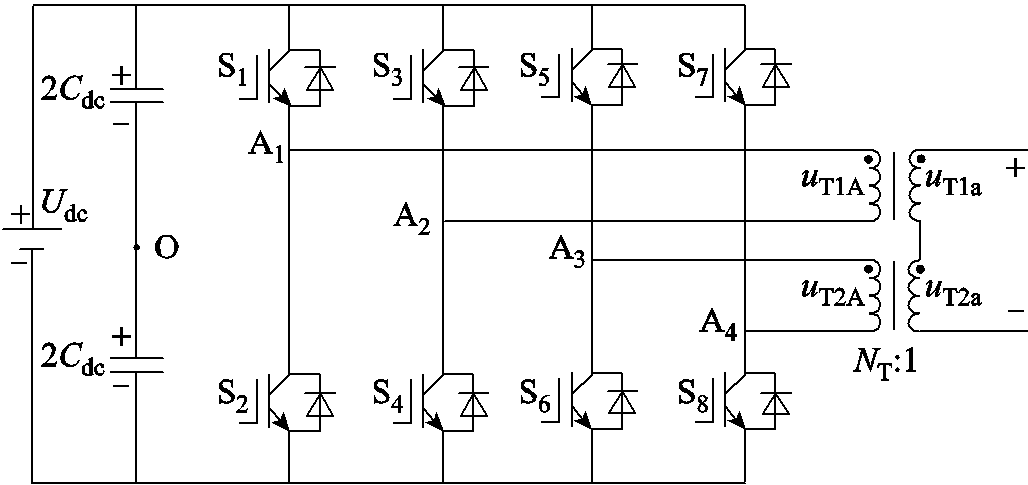
图11 两组H桥载波移相等效电路
Fig. 11 Equivalent circuit of two groups carrier phase shift H-bridge
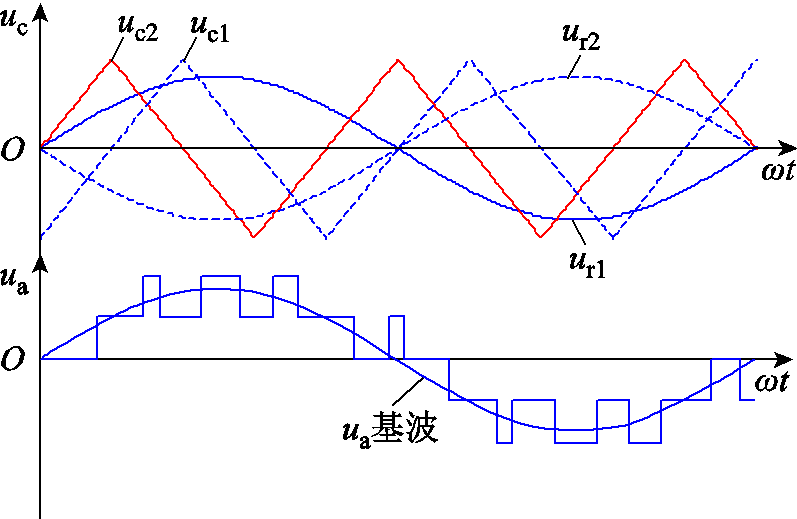
图12 载波移相PWM调制方法等效原理图
Fig. 12 Equivalent schematic diagram of carrier phase-shifting PWM modulation method
载波移相PWM调制的特征是多谐波叠加,频谱分量比较丰富[19],主要包含基频与倍数开关频率边频带,需要分类讨论。
2.2.1 不考虑死区影响
由图12可知第一组H桥输出电压uT1A的双重傅里叶级数表达式[20]为
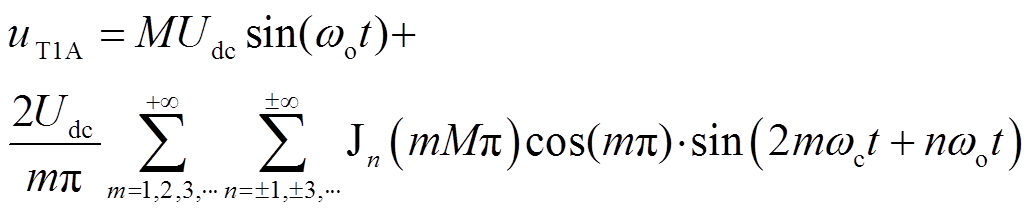 (14)
(14)
式中,M为调制比;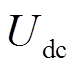 为直流母线电压;wo为调制波角频率;wc为载波角频率;m为相对于载波的谐波次数;n为相对于调制波的谐波次数;
为直流母线电压;wo为调制波角频率;wc为载波角频率;m为相对于载波的谐波次数;n为相对于调制波的谐波次数;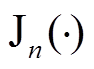 为n阶贝塞尔函数。
为n阶贝塞尔函数。
第二组H桥输出电压uT2A的双重傅里叶级数表达式为
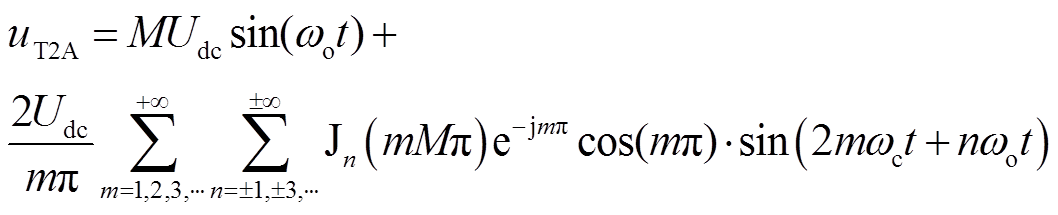 (15)
(15)
变压器T1和T2的电压比均为NT,根据图4可得,变压器二次侧的电压ua为
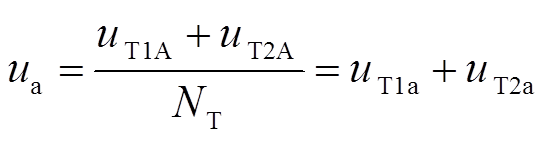 (16)
(16)
将式(14)、式(15)代入式(16)可得
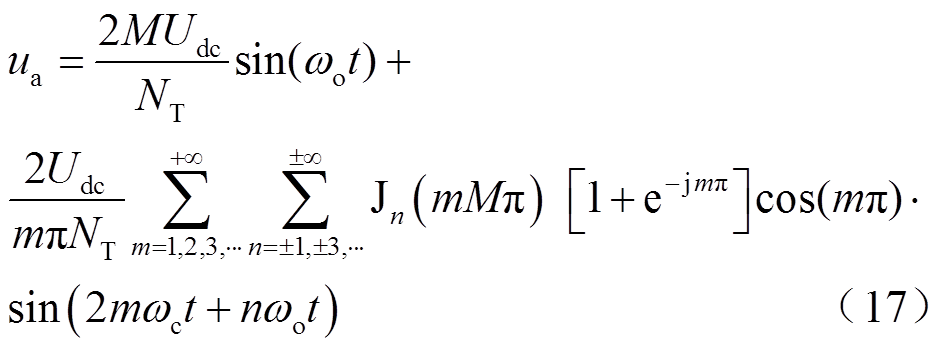
式(17)即为在图12所示载波移相PWM调制下,组合式三相二重化逆变电源A相输出电压ua的表达式。由式(17)可知谐波主要集中于2倍载波频率附近。以下通过典型案例说明六个H桥的主要谐波幅值及相位关系。取典型值Udc为400V,调制比M为0.693,调制波频率fo为50Hz,载波频率fc为6.5kHz。
载波移相PWM调制下一次电压谐波分量主要包含两倍载波频率(13kHz)和四倍载波频率(26kHz)边频带谐波。不考虑死区影响的PWM电压激励谐波特征如图13所示。
第一组与第二组H桥输出的一次电压基频分量具有对称性,如图13a所示。基频谐波分量激励时,空载工况下等效电路如图14所示。
13kHz边频带如图13b所示,可知第一组与第二组H桥输出的各次谐波分量幅值相同,相位相差180°,在逆变电源中两台变压器二次侧串联叠加后可以抵消,不产生谐波电流。图13b中,13 050Hz零序谐波分量激励时,空载工况等效电路如图15所示。图中Zm0为零序阻抗,L1s=L2s=Ls/2,逆变电源中两台变压器二次侧三角形联结,零序电流无法输出到滤波电容,故图中开关Q2为开断;又因为两组H桥输出的每相电压相位相差180°,故在二次侧不产生电流,相当于二次侧开路,则图中开关Q1为开断。由于立体卷铁心变压器存在磁通的零序通路,故一次电流不为0。本文将此类仅在一次侧产生谐波电流的零序分量称为零序谐波分量(一、二组可抵消)。
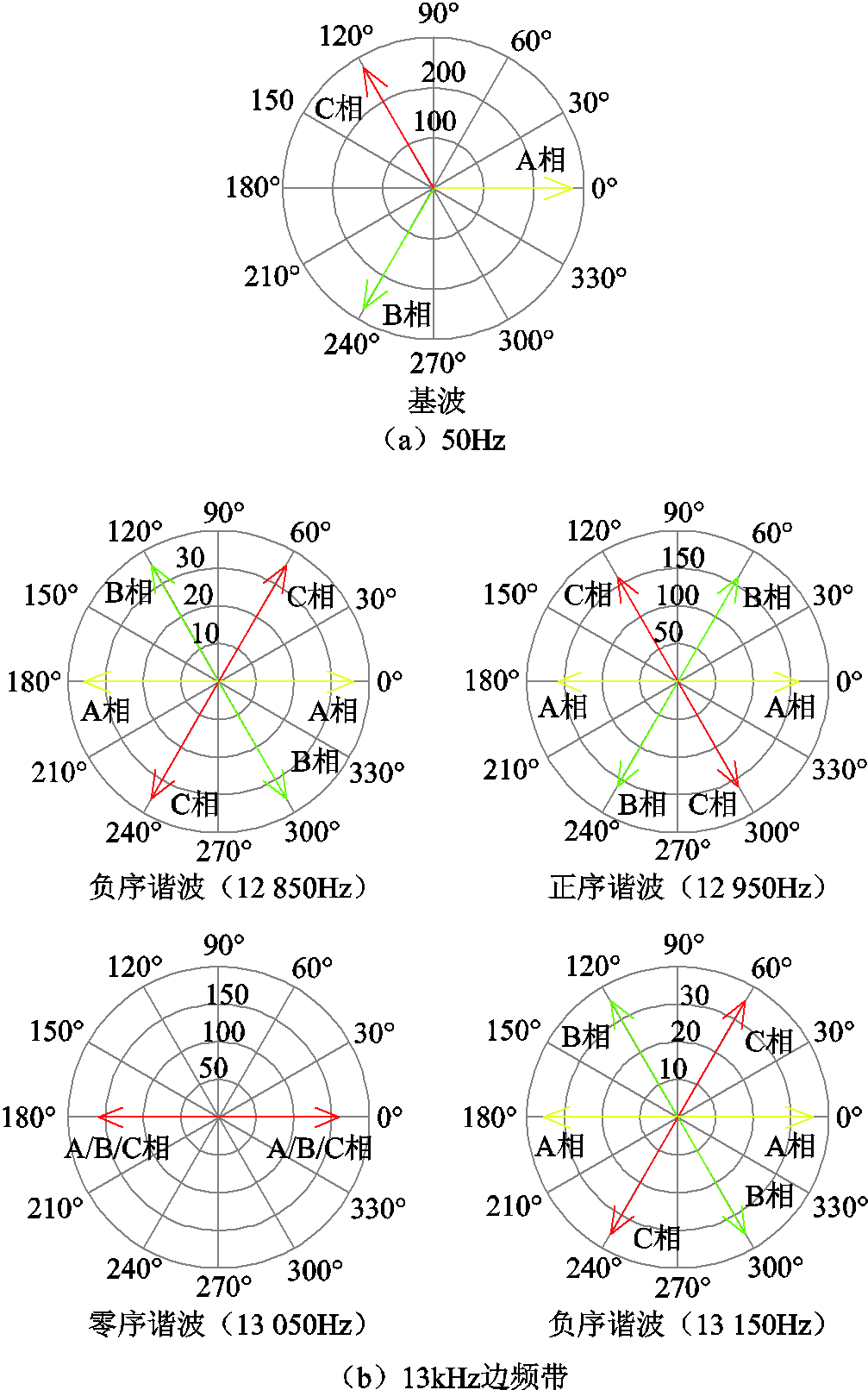
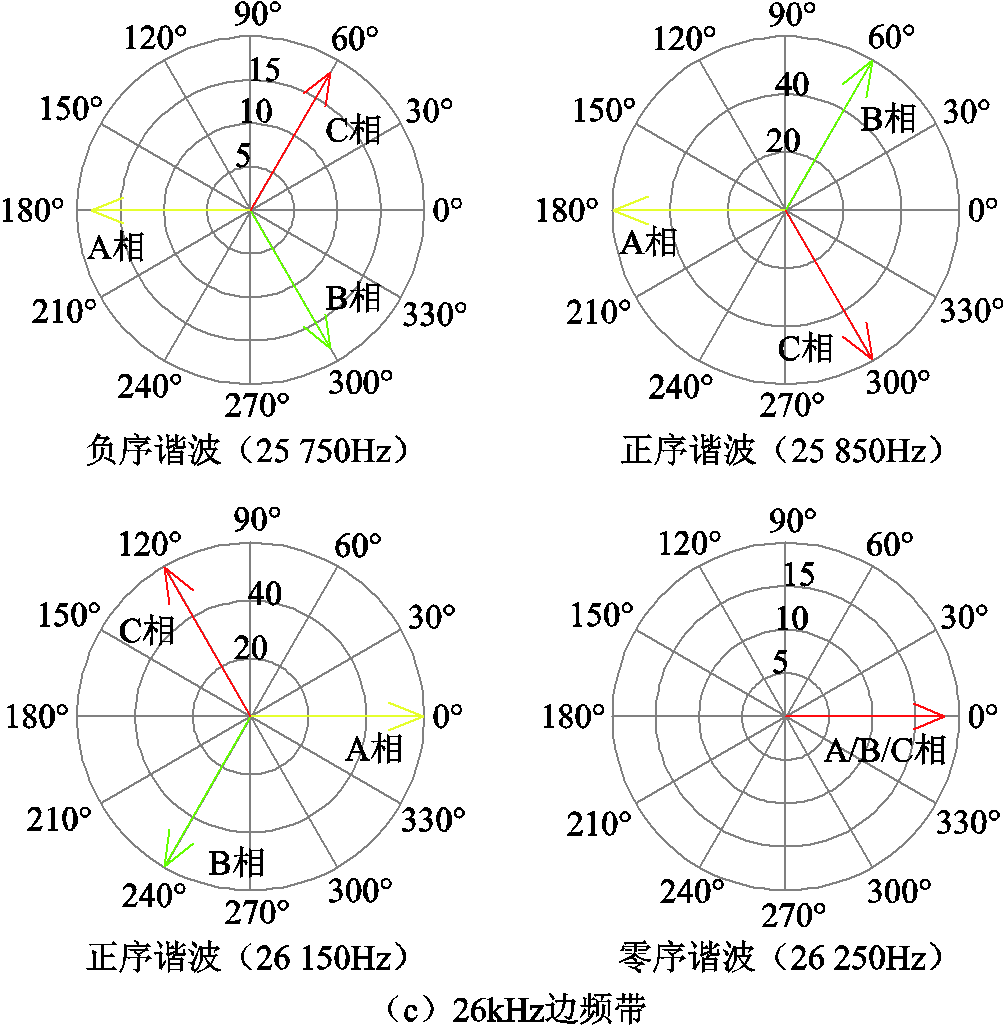
图13 不考虑死区影响的PWM非正弦激励谐波特征
Fig. 13 Harmonic characteristics of PWM non-sinusoidal excitation without considering the influence of dead zone
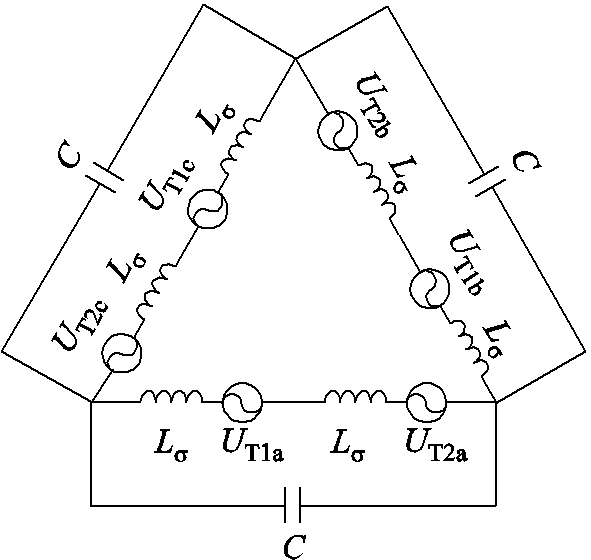
图14 正序、负序分量激励下等效电路
Fig. 14 Equivalent circuit under positive sequence or negative sequence component excitation
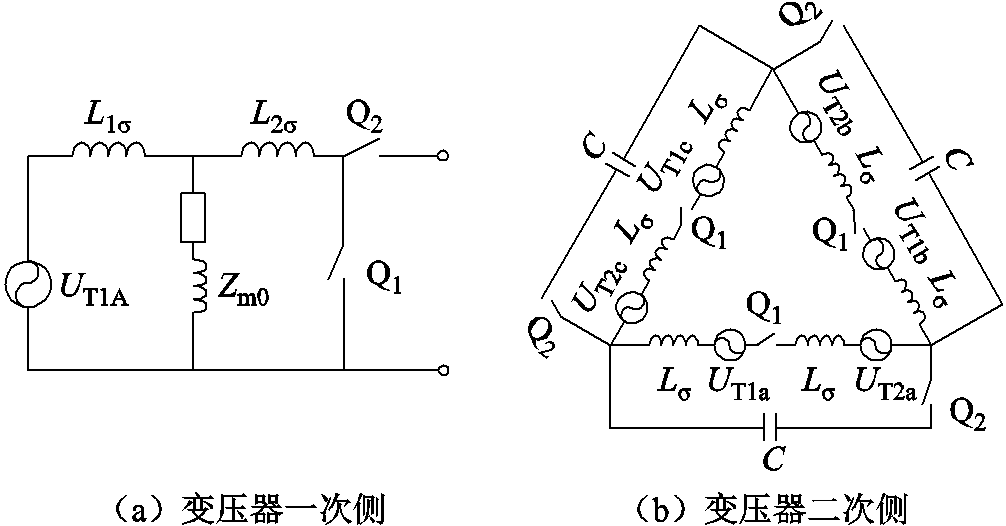
图15 零序谐波分量(一、二组可抵消)激励下等效电路
Fig. 15 Equivalent circuit under excitation of zero sequence harmonic components (one and two groups can be offseted)
26kHz边频带如图13c所示,可知第一组与第二组H桥输出的26kHz边频带分量幅值、相位相同,在逆变电源中两台变压器二次侧串联叠加后不可抵消。其正序、负序谐波分量激励时,空载工况下滤波电容的阻抗远小于漏感的阻抗,等效电路如图14所示。26 250Hz零序谐波分量激励时,6个H桥的谐波分量幅值、相位相同,两台变压器在二次侧串联后每相的26 250Hz零序谐波分量分别叠加,等效电路如图16所示。逆变电源空载工况下变压器二次侧三角形联结,零序电流无法输出到滤波电容,故图中开关Q2为开断;又因两台变压器每相相位相同,故零序电流可以在三角形内部流通,图中开关Q1为闭合。但由于26 250Hz激励时阻抗较大,因此产生的零序电流分量很小,可以忽略。本文将此类在一次侧与二次侧都产生谐波电流的零序分量称为零序谐波分量(一、二组不可抵消)。

图16 零序谐波分量(一、二组不可抵消)激励下等效电路
Fig.16 Equivalent circuit diagram under excitation of zero sequence harmonic components (one and two groups can not be offseted)
2.2.2 考虑死区影响
为了避免载波移相PWM调制拓扑中H桥同桥臂上下两只开关管同时导通,需要设置开关死区时间Dt[21],本文拓扑采用单边不对称方式设置死区,即开关管按时关断,延迟Dt开通。在感性负载时,H桥反并联二极管续流会引起输出电压波形发生畸变。
如图11所示,记uA1O为第一组H桥左半桥与直流电源电压中点“O”之间的电压,uA2O为第一组H桥右半桥与直流电源电压中点“O”之间的电压,u′A1O、u′A2O为设置死区时无反并联二极管续流的电压,u″A1O、u″A2O为反并联二极管续流引起的误差。
以u′A1O的相位为基准[20],得
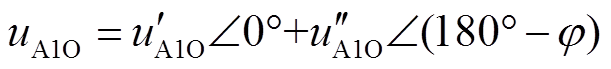 (18)
(18)
式中,j为功率因数角。
uA1O的双重傅里叶级数表达式[20]为
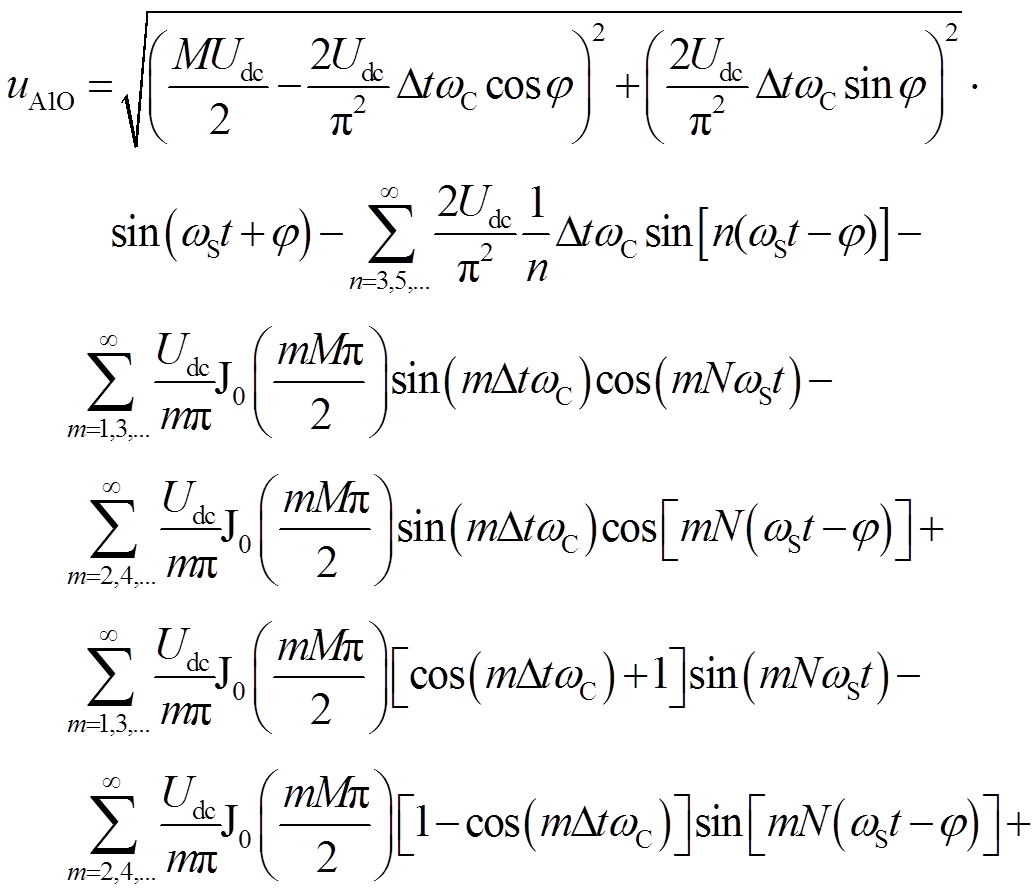 (19)
(19)
由1.1节可知,uA2O的载波与uA1O的载波相同,uA2O的调制波与uA1O的调制波相位相差180°,以u′A1O的相位为基准,故得
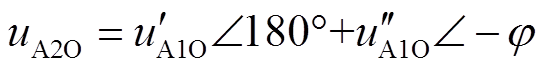 (20)
(20)
考虑死区影响的第一组H桥输出电压uA为
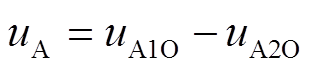 (21)
(21)
为了便于分析考虑死区影响的六个H桥输出电压谐波特征,利用数值仿真方法开展谐波分析,如图17所示。与图13对比可知,考虑死区影响前后,基频相位关系不变,13kHz、26kHz边频带的相对相位关系不变。考虑死区影响后出现150Hz零序分量,属于零序谐波分量(一、二组不可抵消)。
在负载工况下,变压器二次侧三角形联结,H桥反并联二极管续流会引起输出电压波形发生畸变。考虑死区影响前后PWM电压激励谐波幅值的对比如图18所示,可知,死区导致PWM电压激励基波幅值与倍数开关频率边频带谐波幅值略微减小。考虑死区影响后6个H桥产生的150Hz零序谐波分量(一、二组不可抵消)幅值、相位相同,两台变压器在二次侧串联后每相的150Hz零序谐波分量分别叠加,等效电路如图16所示。
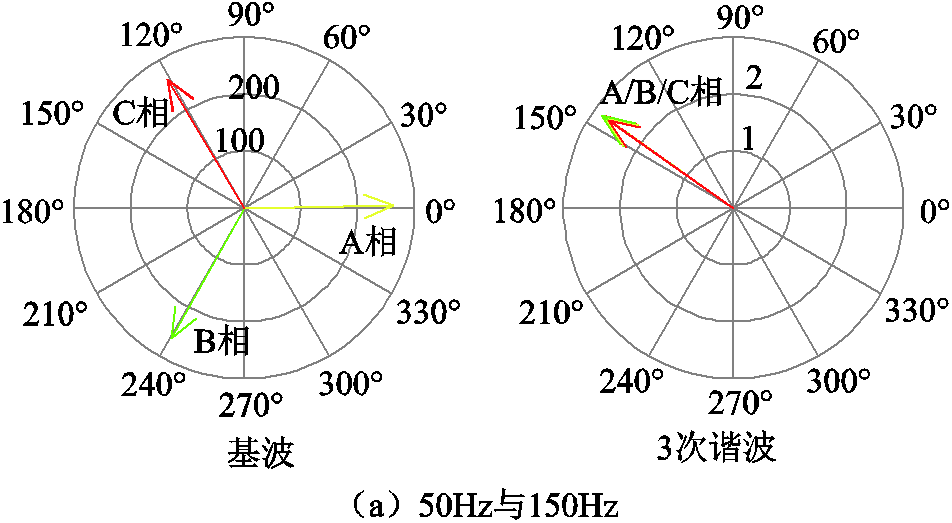
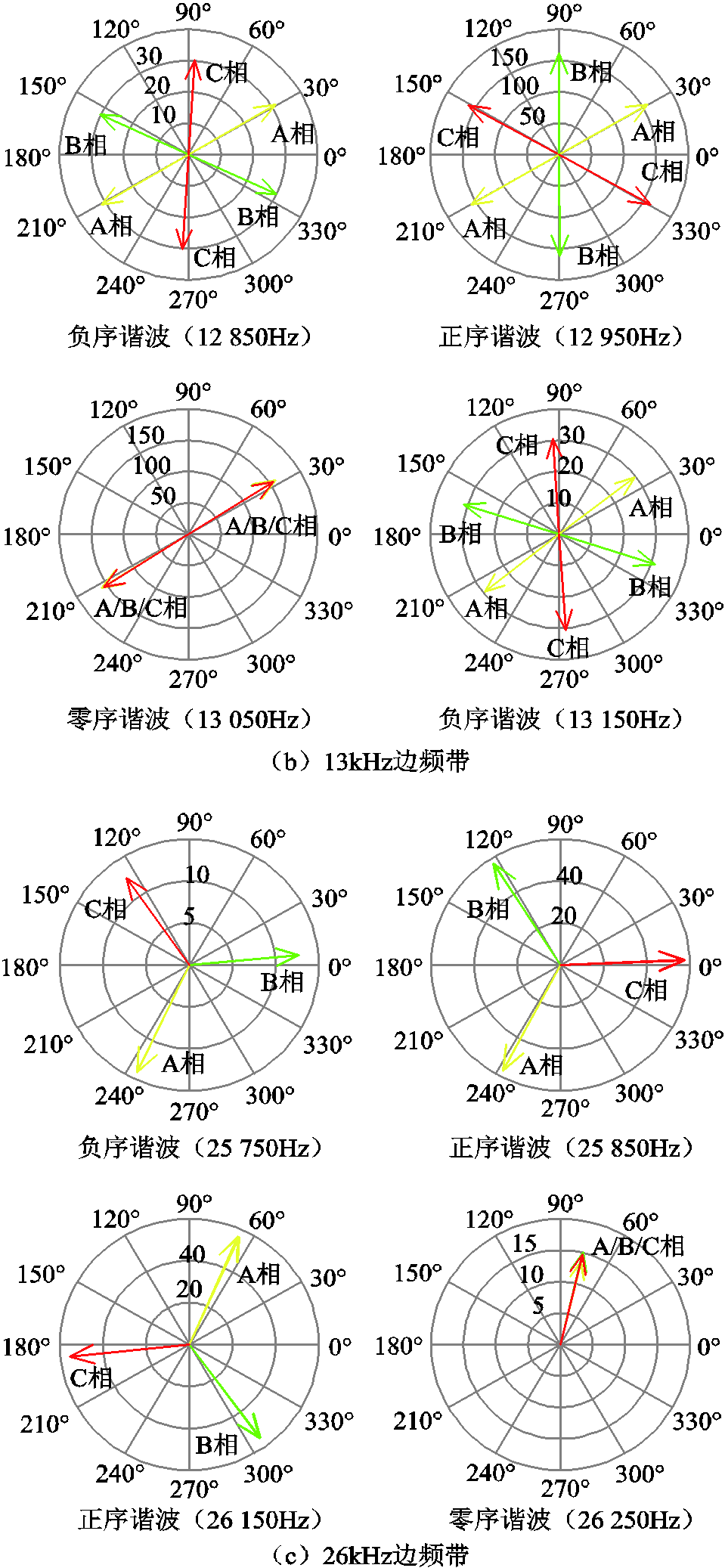
图17 考虑死区影响的PWM非正弦激励谐波特征
Fig. 17 Harmonic characteristics of PWM non-sinusoidal excitation considering the influence of dead zone
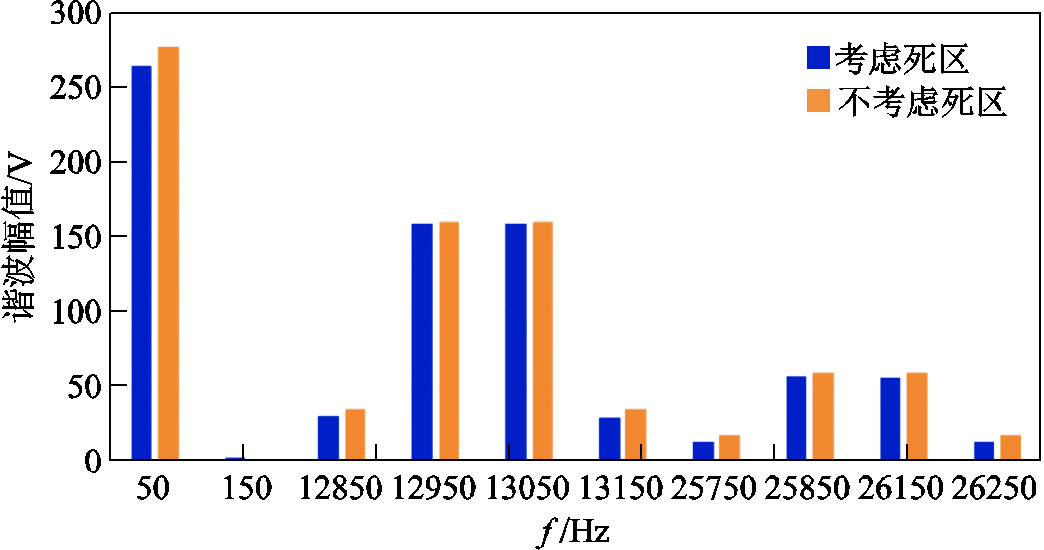
图18 考虑死区影响前后PWM非正弦激励谐波幅值对比
Fig. 18 Comparison of PWM non-sinusoidal excitation harmonic amplitude before and after considering the influence of dead zone
负载工况下,死区引起的150Hz零序分量会在一次、二次绕组中产生相应的谐波电流。由于150Hz激励时阻抗较小(主要为一、二次绕组漏感),因此将产生明显的零序电流分量。
空载工况下,开关器件电流较小,反并联二极管续流的同时,由于开关器件小电流时关断时间延长[22],死区的影响可忽略,因此空载时变压器绕组无150Hz谐波电流分量。
根据上述谐波分析,各次谐波分量可分为正序、负序、零序(一、二组可抵消)、零序(一、二组不可抵消)四类,需在变压器建模中相应考虑。
根据图1中的拓扑结构,将两个变压器频变漏感磁路模型二次侧每相串联后再连接成三角形,搭建逆变电源系统级电路仿真。同时利用立体卷铁心变压器固定漏感磁路模型搭建逆变电源系统级电路仿真做对比。
建立某64kV·A逆变电源试验平台如图19所示,其中立体卷铁心变压器样机参数见表1。主要测量设备为泰克DD0405HB示波器、泰克P5210A(1 000:1)电压探头、CWT15B(2mV/A)电流探头。试验内容包括空载稳态工况、负载稳态工况和动态工况三部分。

图19 试验平台
Fig. 19 Experimental platform
表1 立体卷铁心变压器样机基本参数
Tab. 1 Basic parameters of 3D wound core transformer prototype

参数数值 容量/(kV·A)32 电压比1:1 一次绕组匝数59 一次侧额定电压/ V200 一次侧额定电流/ A53.33
根据立体卷铁心变压器FEM二维等效模型仿真得出漏感Ls,然后计算对应的Foster频变磁阻Rn2,使用GS全局最优算法辨识一阶Foster模型中R0、R1、L1三个参数,初始值和优化值参考表2。GS优化算法拟合出的频变磁阻与FEM仿真计算的频变磁阻对比如图20所示。可以看出,GS优化算法拟合的频变磁阻与FEM计算值基本吻合,可以有效反映磁阻随频率的变化特性。
表2 一阶Foster模型初始值和优化值
Tab. 2 Initial and optimized values of the first-order Foster model

参数R0/WR1/WL1/H 初始值1004000.001 55 GS优化值145.593 9480.987 80.004 47
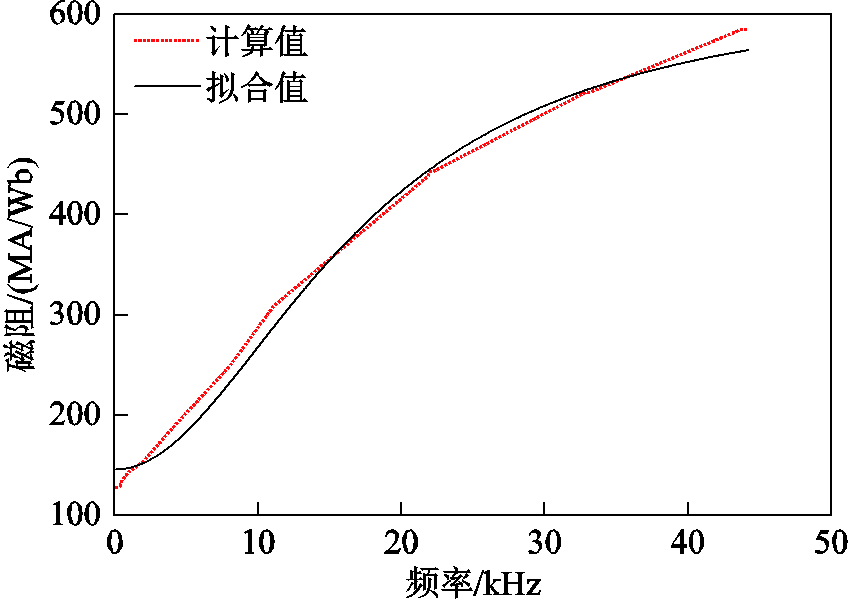
图20 GS算法拟合与仿真计算的频变磁阻对比
Fig.20 Comparison of frequency-dependent magnetoresistance between GS algorithm and simulation calculation
根据图6立体卷铁心变压器频变漏感磁路模型原理示意图,建立立体卷铁心变压器频变漏感磁路模型,设置单极倍频SPWM非正弦激励,添加给立体卷铁心变压器频变漏感磁路模型,验证立体卷铁心变压器频变漏感磁路模型漏感的频变特性,其等效电路如图21所示。图中NA、NB、NC分别表示A、B、C三相的一次绕组,Na、Nb、Nc表示二次绕组,UPA表示单相电压激励。
图22所示为立体卷铁心变压器频变漏感磁路模型时域仿真后得到的单相绕组漏感与FEM二维等效模型计算值、试验值的对比。与试验值对比,FEM二维等效模型漏感计算值相对误差不大于2.81%,立体卷铁心变压器频变漏感磁路模型漏感时域仿真值相对误差不大于9.15%。
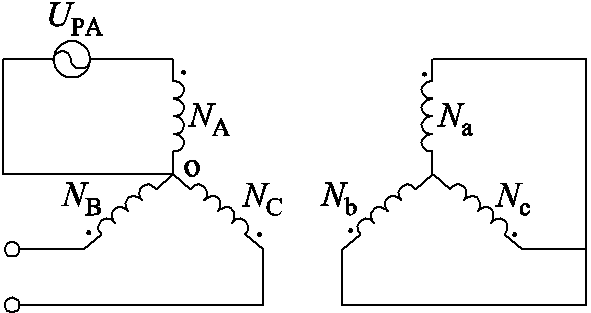
图21 单相SPWM非正弦激励短路工况等效电路
Fig. 21 Equivalent circuit of short-circuit condition under single-phase SPWM non-sinusoidal excitation
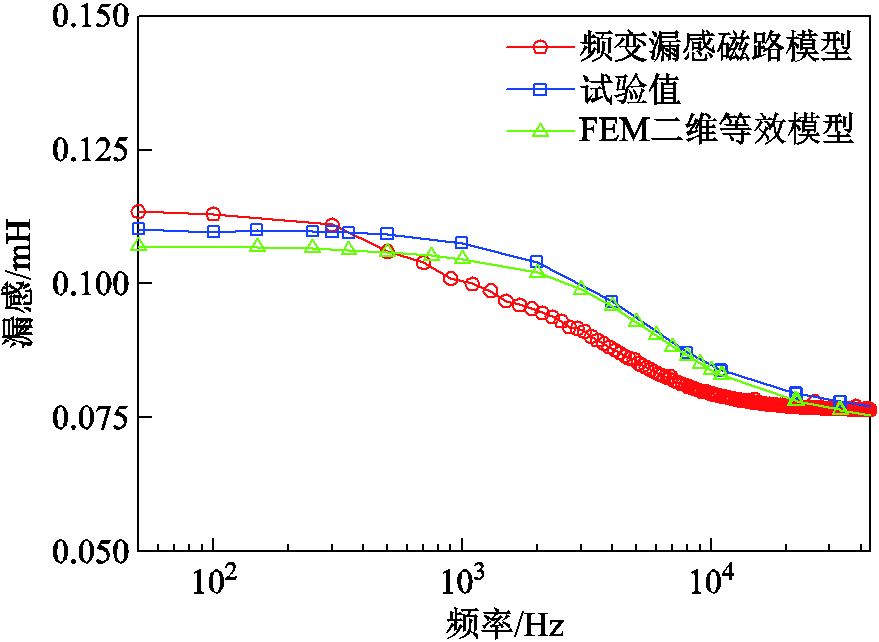
图22 立体卷铁心变压器漏感试验值与FEM计算值、时域仿真值对比
Fig.22 Comparison of leakage inductance experimental value with FEMcalculation and time domain simulation value of 3D wound core transformer
逆变电源空载稳态工况下立体卷铁心变压器一次电流试验值与频变漏感磁路模型、固定漏感磁路模型对比如图23所示,具体数值对比见表3与图24。
与试验值对比,在空载稳态工况下,固定漏感磁路模型、频变漏感磁路模型一次电流基频分量幅值一致,倍数开关频率边频带的主要谐波分量频变漏感磁路模型比固定漏感磁路模型更贴近实际,其中13 050Hz谐波幅值与试验值相对误差由28.12%下降至8.34%,26 150Hz谐波幅值与试验值相对误差由18.87%下降至1.91%。
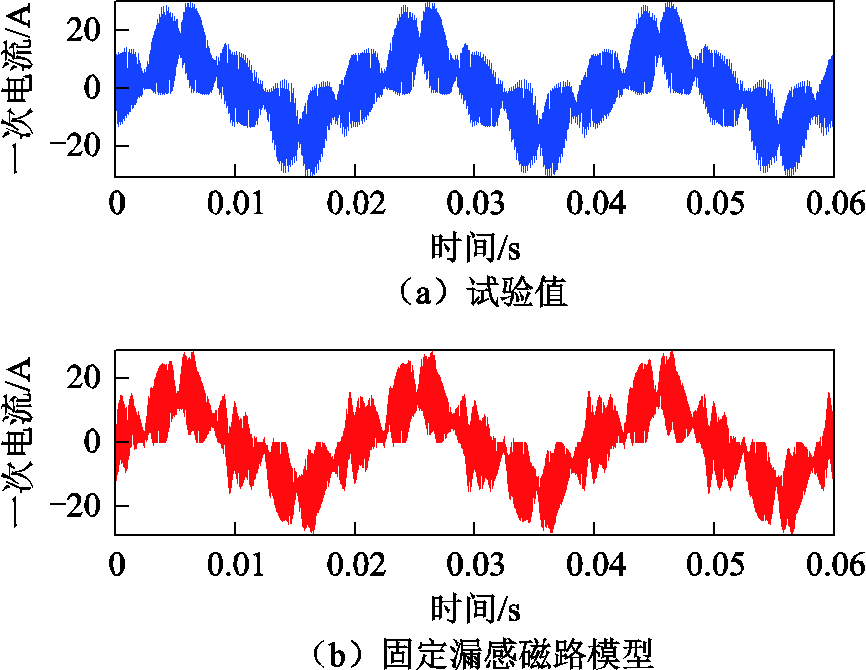
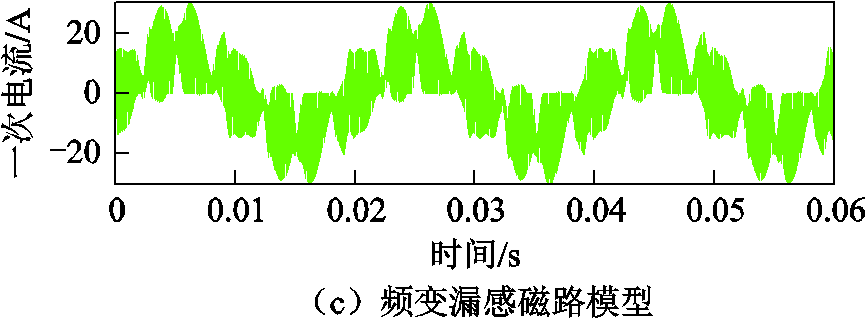
图23 空载稳态工况一次电流试验值与磁路模型仿真结果对比
Fig.23 Comparison of primary current experimental value and simulation values ofmagnetic circuit models under no-load steady-state condition
表3 空载稳态工况一次电流谐波频谱对比
Tab. 3 Comparison of primary current harmonic spectrum under no-load steady-state condition
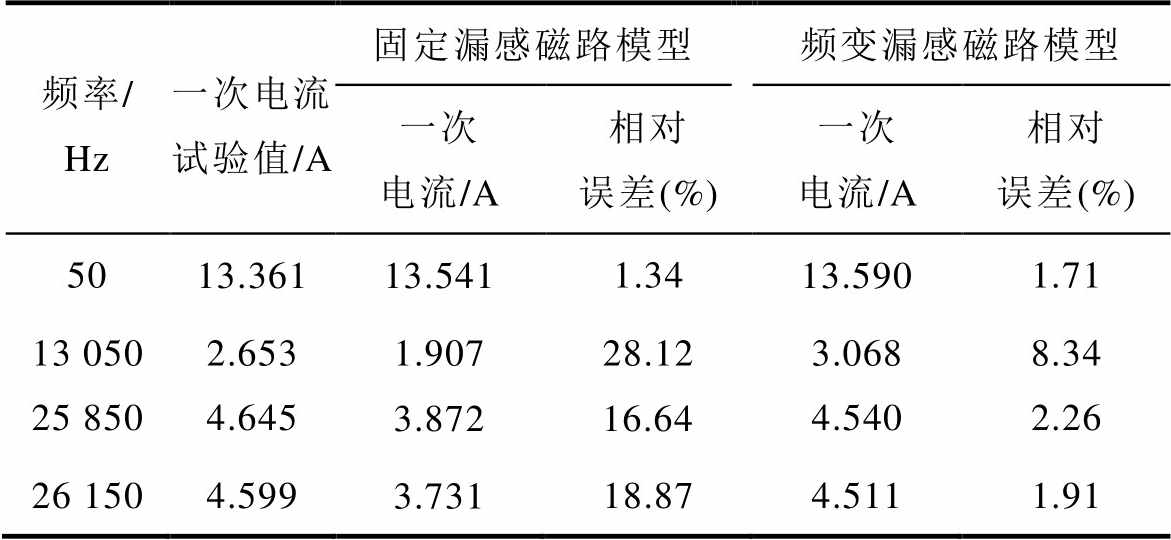
频率/Hz一次电流试验值/A固定漏感磁路模型频变漏感磁路模型 一次电流/A相对误差(%)一次电流/A相对误差(%) 5013.36113.5411.3413.5901.71 13 0502.6531.90728.123.0688.34 25 8504.6453.87216.644.5402.26 26 1504.5993.73118.874.5111.91
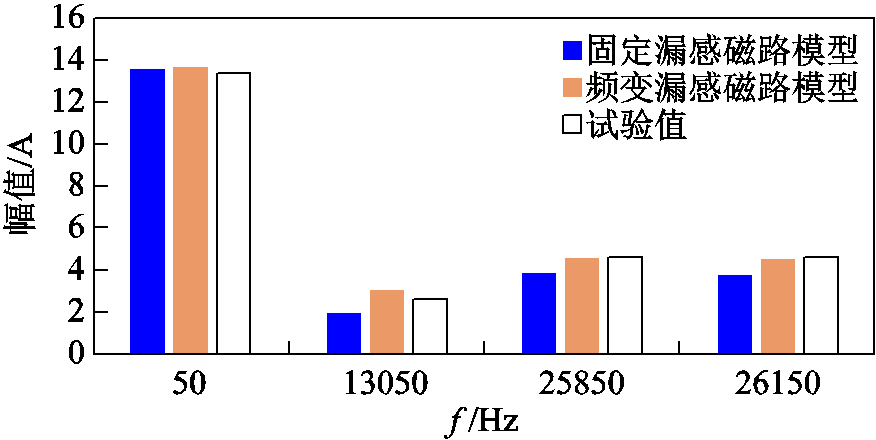
图24 空载稳态工况一次电流谐波频谱对比
Fig.24 Comparison of primary current harmonic spectrum under no-load steady-state condition
在85%额定负载稳态工况下立体卷铁心变压器一次电流试验值与频变漏感磁路模型、固定漏感磁路模型仿真值对比如图25所示,具体数值对比见表4与图26。
与试验值对比,在85%额定负载稳态工况下,固定漏感磁路模型和频变漏感磁路模型一次电流基频分量幅值一致,倍数开关频率边频带的主要谐波分量频变漏感磁路模型比固定漏感磁路模型更贴近实际,其中13 050Hz谐波幅值与试验值相对误差由37.26%下降至3.27%,26 150Hz谐波幅值与试验值相对误差由22.83%下降至6.01%。在逆变电源负载稳态工况下,一次电流出现明显的3次零序分量。
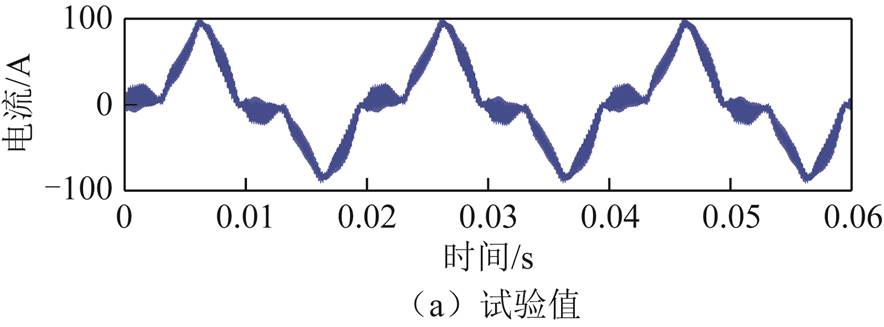
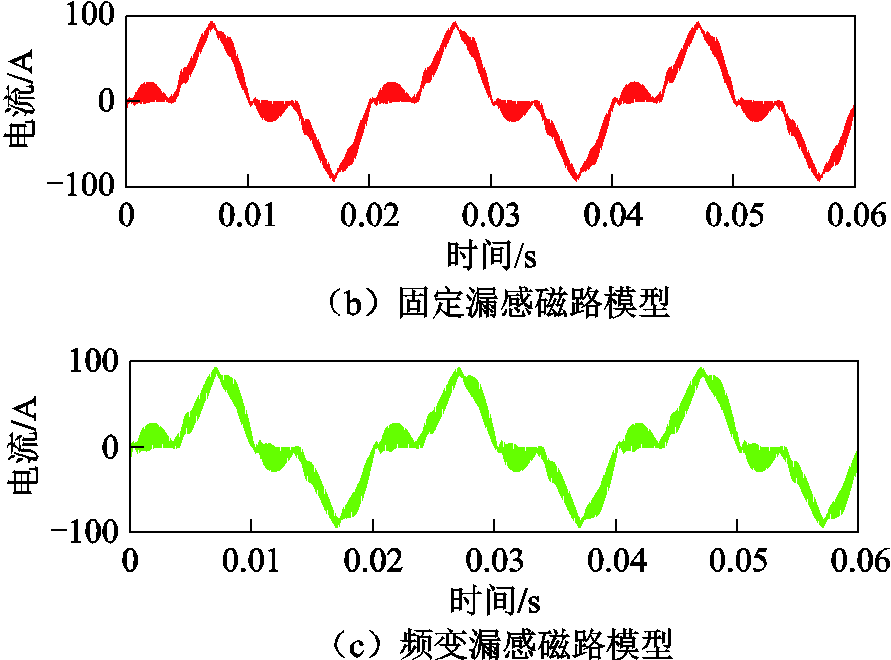
图25 负载稳态工况一次电流试验值与两种磁路模型仿真值结果对比
Fig.25 Comparison of primary current experimental value and simulation values of two magnetic circuit models under load steady-state condition
表4 负载稳态工况一次电流谐波频谱对比
Tab.4 Comparison of primary current harmonic spectrum under load steady-state condition

频率/Hz一次电流试验值/A固定漏感磁路模型频变漏感磁路模型 一次电流/A相对误差(%)一次电流/A相对误差(%) 5058.43058.0500.6558.3800.09 15023.87026.40110.6025.7407.83 13 0502.7831.74637.262.8743.27 25 8504.9143.87221.204.7553.24 26 1504.7263.64722.834.4426.01
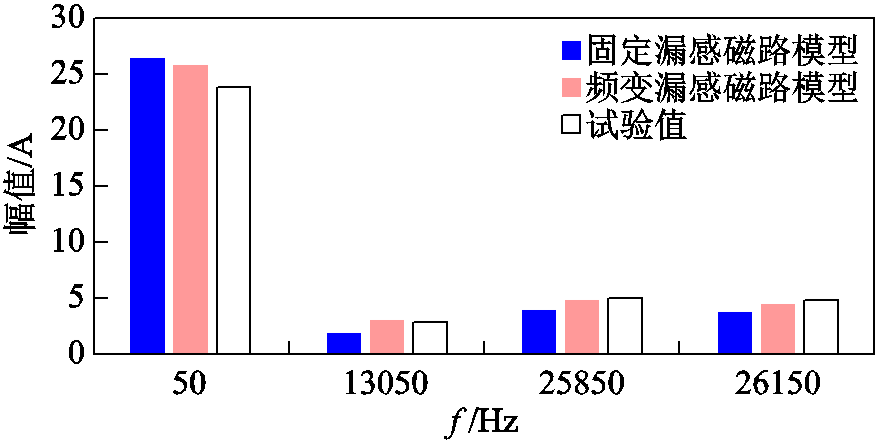
图26 负载稳态工况一次电流谐波频谱对比
Fig.26 Comparison of primary current harmonic spectrum underload steady-state condition
空载与负载稳态工况一次电压试验值谐波频谱对比如图27所示,由图可知,空载与负载稳态工况下一次电压基波分量、13kHz边频带、26kHz边频带的谐波分量幅值相差不大,主要区别在于负载稳态工况下一次电压出现明显的3次谐波分量。此试验结果验证了2.2节谐波分析的正确性。
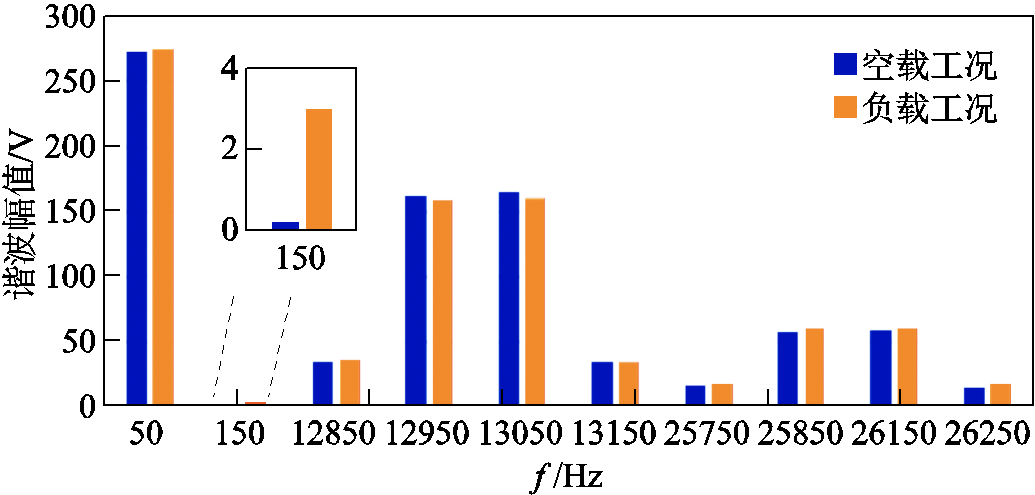
图27 空载与负载稳态工况一次电压试验值谐波频谱对比
Fig. 27 Comparison of experimentalprimary voltage harmonic spectrum under no-load and load steady-state condition
30%负载突加至两倍限流,一次电流试验值与频变漏感磁路模型仿真值对比如图28所示。
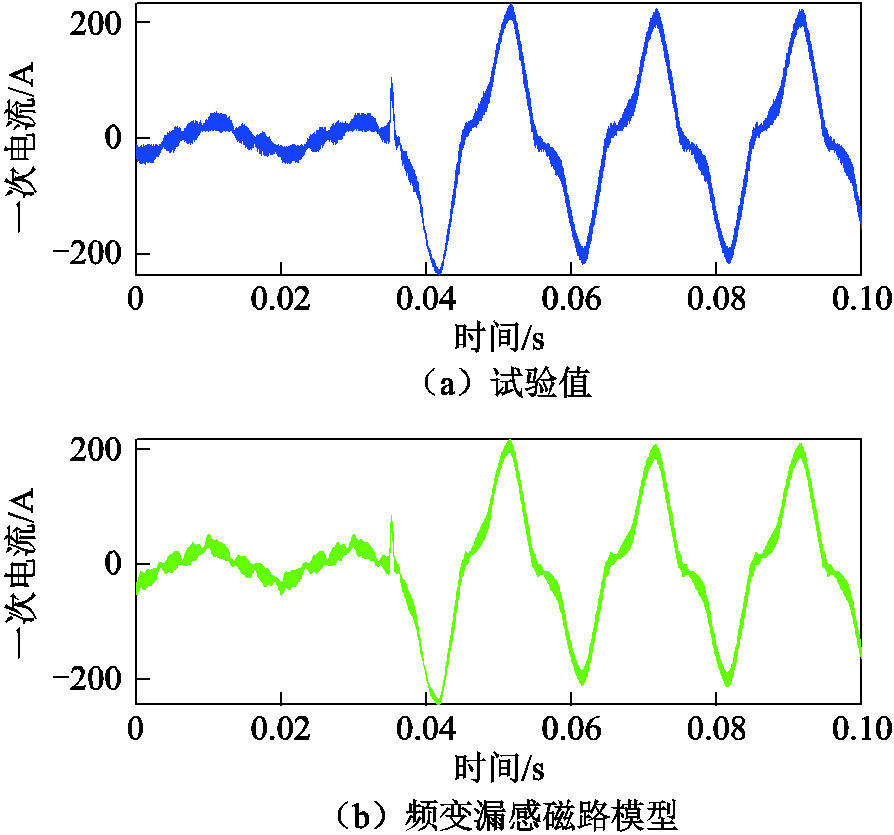
图28 动态工况一次电流试验值与频变漏感磁路模型仿真值对比
Fig.28 Comparison of primary current experimental value and simulation value of the frequency-dependent leakage inductance magnetic circuit model under dynamic condition
突加至两倍限流后频变漏感磁路模型计算得到的一次电流暂态峰值为217.51A,试验暂态峰值为231.30A,相对误差为5.96%。突加负载稳态后频变漏感磁路模型一次电流幅值为209.81A,一次电流试验值幅值为223.30A,相对误差为6.05%。验证了频变漏感磁路模型在动态工况下的准确性。
1)对于本文所述级联H桥组合式DC-AC拓扑,两台变压器二次侧串联后进行三角形联结,各次谐波分量可分为正序、负序、零序(一、二组可抵消)和零序(一、二组不可抵消)四类。
2)在逆变电源负载工况下,变压器二次侧三角形联结,死区引起的150Hz零序分量会在一次、二次绕组中产生相应的谐波电流。在空载工况下,反并联二极管续流的同时,由于开关器件小电流时关断时间延长,死区影响可忽略,空载时变压器绕组无150Hz谐波电流分量。
3)在逆变电源空载稳态工况和负载稳态工况下,固定漏感磁路模型和频变漏感磁路模型一次电流基频分量幅值一致,倍数开关频率边频带的主要谐波分量频变漏感磁路模型精度比固定漏感磁路模型高。
4)在动态工况下,频变漏感磁路模型一次电流暂态峰值与试验暂态峰值相对误差为5.96%,验证了频变漏感磁路模型在动态工况下的准确性。
5)本文模型可用于PWM非正弦激励下立体卷铁心变压器的暂态工作特性分析,为立体卷铁心变压器在电力电子电能变换领域的应用提供技术支撑,后续拟开展载波移相PWM非正弦激励下立体卷铁心变压器直流偏磁的研究。
参考文献
[1] 施静容, 李勇, 贺悝, 等. 一种提升交直流混合微电网动态特性的综合惯量控制方法[J]. 电工技术学报, 2020, 35(2): 337-345.
Shi Jingrong, Li Yong, He Li, et al.A comprehensive inertia control method for improving the dynamic characteristics of hybrid AC-DC microgrid[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 337-345.
[2] 刘计龙, 朱志超, 肖飞, 等. 一种面向舰船综合电力系统的模块化三端口直流变换器[J]. 电工技术学报, 2020, 35(19): 4085-4096.
Liu Jilong, Zhu Zhichao, Xiao Fei, et al. A modular three-port DC-DC converter for vessel integrated power system[J]. Transactions of China Electro-technical Society, 2020, 35(19): 4085-4096.
[3] 叶满园, 任威, 李宋, 等. 基于控制载波自由度的级联H桥逆变器改进型PWM技术[J]. 电工技术学报, 2021, 36(14): 3010-3021.
Ye Manyuan, Ren Wei, Li Song, et al. Improved PWM technology of cascaded H-bridge inverter based on control of carrier degree of freedom[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 3010-3021.
[4] 陈仲, 孙健博, 许亚明, 等. 采用输出周期脉冲循环的级联H桥型逆变器功率均衡方法[J]. 电工技术学报, 2020, 35(4): 827-838.
Chen Zhong, Sun Jianbo, Xu Yaming, et al. Power balance method of cascaded H-bridge inverter based on pulse circulation in output period[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 827-838.
[5] Miki A, Hosoya T, Okuyama K. A calculation method for impulse voltage distribution and transferred voltage in transformer windings[J]. IEEE Transactions on Power Apparatus and Systems, 1978, PAS-97(3): 930-939.
[6] 赵淳, 阮羚, 阮江军, 等. 基于多导体传输线模型的变压器绕组电压分布求解[J]. 变压器, 2009, 46(7): 31-34, 60.
Zhao Chun, Ruan Ling, Ruan Jiangjun, et al. Solution for voltage distribution in transformer winding based on model of multi-conductor transmission line[J]. Transformer, 2009, 46(7): 31-34, 60.
[7] 梁贵书, 王雁超. 考虑频变参数的油浸式变压器绕组分数阶传输线模型[J]. 电工技术学报, 2016, 31(17): 178-186.
Liang Guishu, Wang Yanchao. Fractional transmission line model of oil-immersed transformer winding considering frequency-dependent parameters[J]. Transactions of China Electrotechnical Society, 2016, 31(17): 178-186.
[8] 陈伟根, 胡金星, 杜林, 等. 基于准静态电磁场的变压器线圈中特快速暂态仿真建模[J]. 电网技术, 2005, 29(23): 56-61.
Chen Weigen, Hu Jinxing, Du Lin, et al. Modeling of transformer winding for very fast transient voltage simulation based on quasi-stationary electromagnetic field[J]. Power System Technology, 2005, 29(23): 56-61.
[9] de Leon F, Semlyen A. Time domain modeling of eddy current effects for transformer transients[J]. IEEE Transactions on Power Delivery, 1993, 8(1): 271-280.
[10] Martinez J A, Mork B A. Transformer modeling for low- and mid-frequency transients - a review[J]. IEEE Transactions on Power Delivery, 2005, 20(2): 1625-1632.
[11] Upadhyay G, Singh A, Seth S K, et al. FEM based no-load loss calculation of triangular wound core transformer[C]//2016 IEEE 1st International Con-ference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 2016: 1-4.
[12] 郑黎明. 油浸式立体卷铁心变压器的优化设计研究[D]. 广州: 华南理工大学, 2013.
[13] 陈彬, 李琳, 赵志斌. 一种考虑频变特性的大容量高频变压器漏电感解析计算方法[J]. 中国电机工程学报, 2017, 37(13): 3928-3937.
Chen Bin, Li Lin, Zhao Zhibin. An analytical calculation method of leakage inductance in high-power high-frequency transformers considering frequency-dependence characteristics[J]. Proceedings of the CSEE, 2017, 37(13): 3928-3937.
[14] Dowell P L. Effects of eddy currents in transformer windings[J]. Proceedings of the Institution of Electrical Engineers, 1966, 113(8): 1387-1394.
[15] Dommel H W, 著. 电力系统电磁暂态计算理论[M]. 李永庄, 等译. 北京: 水利电力出版社, 1991.
[16] 范学鑫, 彭方成, 王瑞田, 等. 大容量变流器DCM模式下带逆变器级联系统静态稳定性分析[J]. 海军工程大学学报, 2020, 32(3): 18-25.
Fan Xuexin, Peng Fangcheng, Wang Ruitian, et al. Static stability analysis of cascaded system with high-capacity converter and inverter in DCM[J]. Journal of Naval University of Engineering, 2020, 32(3): 18-25.
[17] 陈龙, 易琼洋, 贲彤, 等. 全局优化算法在Preisach磁滞模型参数辨识问题中的应用与性能对比[J]. 电工技术学报, 2021, 36(12): 2585-2593, 2606.
Chen Long, Yi Qiongyang, Ben Tong, et al. Application and performance comparison of global optimization algorithms in the parameter identification problems of the Preisach hysteresis model[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2585-2593, 2606.
[18] 郭健, 林鹤云, 徐子宏, 等. 三相三柱变压器零序阻抗的场路耦合计算与分析[J]. 电工技术学报, 2009, 24(3): 80-85.
Guo Jian, Lin Heyun, Xu Zihong, et al. Calculation and analysis of zero-sequence impedance of three-phase and three limbs transformer based on field circuit coupled method[J]. Transactions of China Electrotechnical Society, 2009, 24(3): 80-85.
[19] 陈轶涵, 郭鸿浩, 陈家伟. 基于载波移相控制的模块化串并联逆变器非理想条件谐波特性分析[J]. 电工技术学报, 2020, 35(8): 1690-1704.
Chen Yihan, Guo Honghao, Chen Jiawei. Analysis of harmonic characteristics in non-ideal conditions of modular series/parallel inverter based on carrier phase shift control[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1690-1704.
[20] 刘凤君. 现代逆变技术及应用[M]. 北京: 电子工业出版社, 2006.
[21] 陈杰, 章新颖, 闫震宇, 等. 基于虚拟阻抗的逆变器死区补偿及谐波电流抑制分析[J]. 电工技术学报, 2021, 36(8): 1671-1680.
Chen Jie, Zhang Xinying, Yan Zhenyu, et al. Dead-time effect and background grid-voltage harmonic suppression methods for inverters with virtual impedance control[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1671-1680.
[22] 罗毅飞, 刘宾礼, 汪波, 等. IGBT开关机理对逆变器死区时间的影响[J]. 电机与控制学报, 2014, 18(5): 62-68, 75.
Luo Yifei, Liu Binli, Wang Bo, et al. The influence of IGBT switching mechanism on the dead-time of inverters[J]. Electric Machines and Control, 2014, 18(5): 62-68, 75.
(编辑 李冰)
Abstract For a bidirectional inverter power supply with a wide input voltage range, the magnetic integration method can be used to increase the power density. Magnetic integration is used in two aspects: ①core magnetic circuit integration; ②filter inductor integration to isolate transformer leakage inductance. Compared with the traditional three-phase planar laminated core transformer, the 3D wound core transformer has the advantages of a symmetrical magnetic circuit and light weight. Due to the rich harmonic of PWM excitation, the frequency-dependent characteristics of the leakage inductance of the 3D wound core transformer need to be considered. This article intends to carry out related research on the modeling of the 3D wound core transformer considering the frequency-dependent characteristic of the leakage inductance under PWM non-sinusoidal excitation.
First, according to the principle of electromagnetic correspondence, the frequency-dependent leakage inductance in the circuit model was converted to the corresponding frequency-dependent reluctance in the magnetic circuit model. Based on the Foster frequency-dependent reluctance model, a 3D wound core transformer model considering the frequency-dependent characteristic of leakage inductance was proposed, and the model parameters were calculated by a global optimization algorithm.
Secondly, according to the cascaded H-bridge combined DC-AC topology, the harmonic characteristics of PWM non-sinusoidal excitation were analyzed, focusing on the relative phase relationship of the harmonics between different H-bridges. The two transformers were triangularly connected in series on the secondary side, and the various harmonic components between different H-bridges on the primary side could be divided into four categories: positive sequence, negative sequence, zero sequence (one and two groups can cancel), and zero sequence (one and two groups cannot cancel). The dead zone led to a slight reduction of fundamental amplitude and the harmonic amplitude of the multiplier switching-frequency sideband under the PWM voltage excitation. Under load conditions, the 150Hz zero-sequence component caused by the dead zone generated the corresponding harmonic currents in the primary and secondary windings. Since the impedance at 150Hz excitation was small (mainly the leakage inductance of the primary and secondary windings), a significant zero-sequence current component would be generated. Under no-load conditions, the switching current was small, and the anti-parallel diode renewed, so the switching shutdown time was extended, the dead-zone effect could be ignored, and transformer winding didn’t contain 150Hz harmonic current components.
Finally, an inverter power experimental platform was built, and steady-state and dynamic experiments were carried out to verify the accuracy of the model. Under the no-load steady-state condition and load steady-state condition of the inverter power supply, compared with the simulation results of the fixed leakage inductance magnetic circuit model, the fundamental frequency component of the primary current of the frequency-dependent leakage inductance magnetic circuit model had the same amplitude, and the simulation results of the main harmonic components of the multiplier switching-frequency sideband had higher accuracy. Under dynamic conditions, the relative error of the transient peak value of the primary current between the frequency-dependent leakage inductance magnetic circuit model and the experiment was 5.96%, which verified the accuracy of the frequency-dependent leakage inductance magnetic circuit model under dynamic conditions.
The frequency-dependent leakage inductance magnetic circuit model can be used to analyze the transient operating characteristics of the 3D wound core transformer under PWM non-sinusoidal excitation, and provide technical support for the application of the 3D wound core transformer in the field of power electronic conversion.
keywords:3D wound core, double-Fourier analysis, leakage inductance, frequency-dependent characteristic, magnetic circuit model
DOI:10.19595/j.cnki.1000-6753.tces.210966
中图分类号:TM401
范学鑫 男,1977年生,副研究员,研究方向为电力电子与电力传动。E-mail:fxxdldz@163.com
王瑞田 男,1987年生,副研究员,研究方向为电力电子与电力传动。E-mail:wangrt4321@163.com(通信作者)
中国博士后基金第64批面上项目(2018M643866)和国家自然科学基金(51707200,51907199)资助。
收稿日期 2021-06-30
改稿日期 2021-09-03
(编辑 李冰)