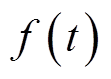分解为
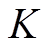个模态分量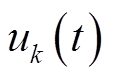
；其次，通过希尔伯特变换得到各模态分量包络信号；再次，在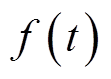与各模态分量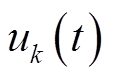之和相等的约束条件下，将包络信号与预估中心频率混合，即摘要 针对电力变压器油中溶解气体浓度序列非线性、非平稳特性影响预测精度问题，该文基于黏菌算法（SMA）和变分模态分解（VMD）构成黏菌算法优化的变分模态分解（SMA-VMD），结合门控循环单元（GRU）组成分解-预测-重构的变压器油中溶解气体含量预测模型。首先，采用差分法提取原始序列趋势项；然后利用SMA-VMD对剩余序列进行分解，得到一组平稳的模态分量；之后通过GRU对分解所得各模态分量分别进行预测；最后对预测结果进行重构。该研究通过对变压器油中溶解气体H2进行仿真实验，并与另外五种预测模型对比，得出SMA-VMD-GRU模型预测结果平均绝对百分比误差为0.36%，方均根误差为1.76mL/L，有效地提高了变压器油中溶解气体含量含量预测精度。通过对变压器油中溶解气体成分CH4、CO、总烃进行仿真实验，证明了该研究所提预测模型的有效性。
关键词：差分法 黏菌算法 变分模态分解 油中溶解气体预测 门控循环单元
变压器作为电力系统的关键枢纽设备，其安全稳定运行是优质电能正常供应的必要基础[1]。变压器主要采用油纸绝缘结构，在变压器运行过程中，油纸绝缘材料受热应力、电应力、催化剂等因素的影响，会逐渐老化分解，在油中产生少量的溶解气体（H2、CH4、C2H6、C2H2、C2H4、CO、CO2等）[2]。油中溶解气体分析（Dissolved Gas Analysis, DGA）技术依据气体组分含量、比值、相对百分比的变化，能够有效地发现变压器内部潜在故障，追踪故障发展趋势[2-5]。因此，油中溶解气体含量预测有着重要的意义[6-7]。
变压器油中溶解气体所测数据一般为时间序列[8]。目前，变压器油中溶解气体预测研究方法一般有统计预测与机器学习的智能预测。统计预测主要为灰色理论[8]和卡尔曼滤波[9]等预测方法，这类预测模型所得预测结果对实验数据分布依赖性较大，即非线性拟合能力有限。机器学习智能预测主要是指利用机器学习方法构建预测模型，包括支持向量机[10]、随机森林[11]等。机器学习在处理非线性问题时有着明显的优势[9,11]，但是传统的机器学习模型在预测过程中没有考虑其数据在时间上的联系，因此对时间序列数据预测存在一定的不足。近些年，由于人工智能飞速发展，相应的深度学习模型也被很多国内外学者应用到变压器油中溶解气体含量预测中。文献[12]利用深度学习模型中的长短期记忆神经网络（Long Short-Term Memory, LSTM）模型对变压器油中溶解气体含量进行预测，且从实验中可以看出在变压器溶解气体含量预测方面，深度学习模型预测效果相较于传统机器学习预测结果精度更高，且能更准确预测变化趋势。文献[13]利用深度信念网络（Deep Recurrent BeliefNetwork, DRBN）模型对油中溶解气体进行预测，很好地解决了时序数据时移特征所带来的预测误差问题。文献[14]利用元启式优化算法与深度神经网络相结合的思想，提出基于粒子群优化长短期记忆网络的组合预测模型，有效地解决了由于LSTM在预测过程中因参数较多而无法确定其最优参数所导致的预测精度误差较大的问题。文献[15]考虑到在预测油中溶解气体含量时其他变量带来的影响，提出在预测模型中添加注意力机制的方法，有效地提高了预测精度。文献[16]在参数优化的预测模型中添加注意力机制，提出的预测模型有效解决了环境温度、湿度及其他溶解气体等多变量影响预测精度的问题。以上变压器油中溶解气体预测方法有效地提高了气体含量预测精度，但以增加多变量注意力机制权重来提高气体预测精度，对多变量历史数据采集的准确性要求很高，没有考虑到当多变量历史数据采集出现误差时，反而会给变压器油中溶解气体含量预测精度带来误差，且不可能将所有的变量都考虑到。另外，变压器油中溶解气体序列由于其他变量及自身历史含量的影响，存在非线性、非平稳特性，上述方法没有考虑其对模型预测精度产生的影响，使得上述方法在进一步提升油中溶解气体含量预测精度上受到限制。
因此，既需要考虑多变量对预测精度的影响效果，也需要对气体含量序列进行平稳化处理。通过对原始序列进行分解，可以将多变量对气体含量变化产生的影响及自身含量变化规律等多种成分分解为一组规律性较强的平稳序列。目前对序列分解的手段多种多样，例如文献[17]中的小波分解、文献[18]中的经验模态分解（Empirical Mode Decomposition, EMD）、文献[19]中的变分模态分解（Variational Mode Decomposition, VMD）等。其中，小波分解方法由于较难确定分解层数和小波基，从而导致模型效果的不确定性。经验模态分解往往会出现严重的模态混叠而导致分解效果不佳，影响预测精度[20]。文献[21]是在EMD分解的基础上增加白噪声来抑制其模态混叠，但是会造成模型计算量大且所得模态分量超过真实序列量。文献[19]中的VMD方法是一种自适应滤波器，能够解决EMD在分解过程中所存在的问题，但VMD在处理同时包含趋势项与波动项的序列时，会将趋势项误分解为周期项，从而影响预测精度，并且其参数的确定对分解结果至关重要[19]。
鉴于上述分析，本文首先采用差分法[22]对油中溶解气体序列进行提取趋势预处理；其次，基于黏菌算法（Slime Mold Algorithm, SMA）与VMD方法构造SMA-VMD序列分解模型，将去趋势化预处理后的油中溶解气体序列分解为平稳、周期性强的模态分量；再次，对分解所得各模态分量分别建立预测模型，由于门控循环单元（Gate Recurrent Unit, GRU）相较于LSTM具有参数量少、训练速度快、预测精度高等优点[23-24]，所以本研究以GRU为变压器油中溶解气体含量预测模型，并基于以上方法，提出了基于SMA-VMD-GRU的油中溶解气体含量组合预测模型；最后，分别与LSTM、GRU、EMD-LSTM、EMD-GRU、SMA-VMD-LSTM五种预测模型进行对比仿真实验[18,25-26]，验证SMA-VMD-GRU模型的有效性。
变分模态分解的实质是将输入序列分解为K个具有中心频率的有限带宽，主要包括构造变分问题及其变分问题的求解[27-28]。
1.1.1 变分问题的构造
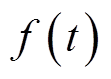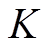首先，将原始序列分解为个模态分量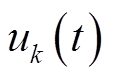；其次，通过希尔伯特变换得到各模态分量包络信号；再次，在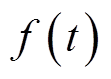与各模态分量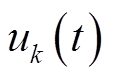之和相等的约束条件下，将包络信号与预估中心频率混合，即
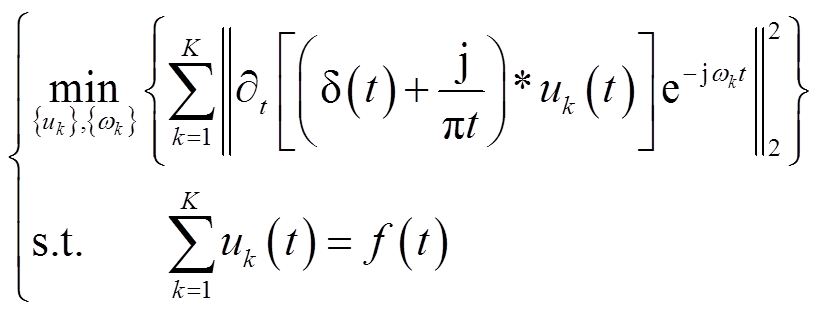（1）
式中，
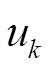(t)为第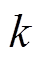
个模态函数；
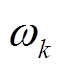为第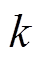个模态函数的中心频率；
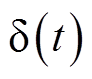为冲激函数；
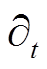为对
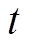求偏导数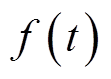；为原信号；
为卷积运算。
1.1.2 变分问题的求解
为将上述问题转换为无约束变分问题，给上述变分问题引入拉格朗日乘子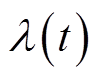
和二次惩罚因子
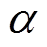，如式（2）所示。
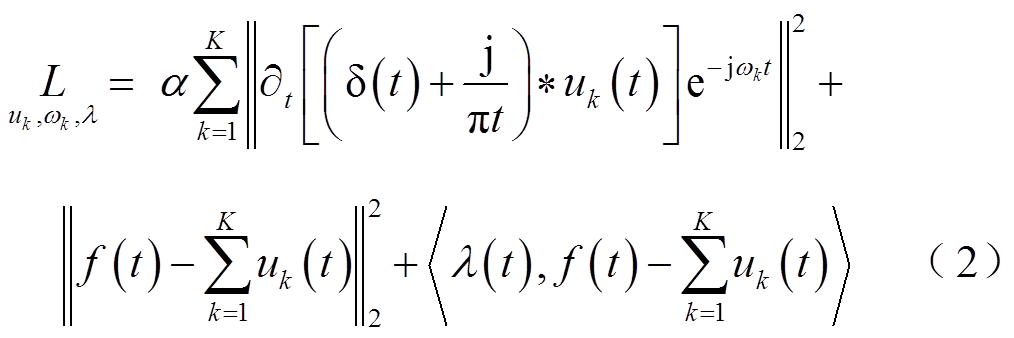
式中，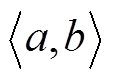
表示变量a与b求内积。
采用交替方向乘子法求取式（2）的鞍点，求得式（1）最优的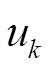及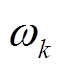。具体步骤如下：
（1）初始化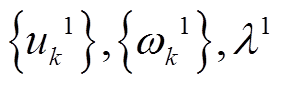
，初始VMD迭代次数
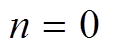。设置循环过程，令n=n+1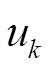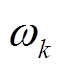，、和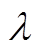
依次根据式（3）～式（5）进行更新。
（2）在非负频率区间内，更新。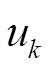
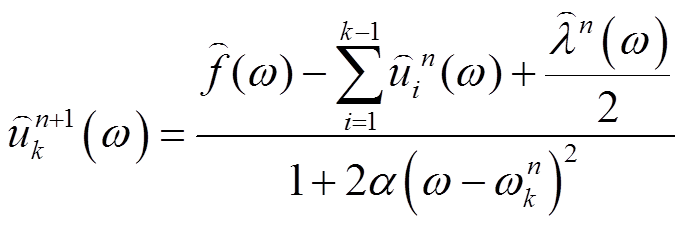（3）
式中，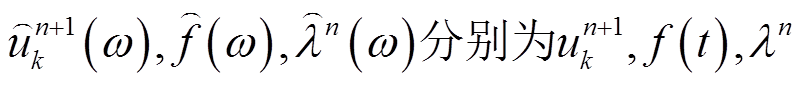
所对应的傅里叶变换。
（3）更新。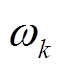
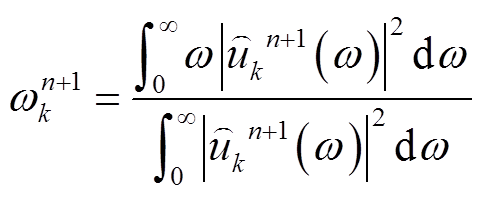（4）
（4）在非负频率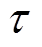
区间，更新
。
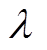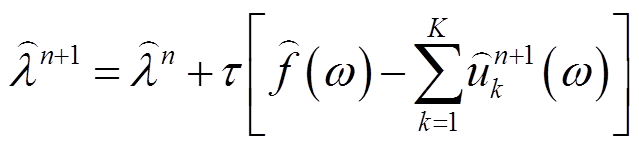（5）
（5）对于给定判定精度ε＞0，有
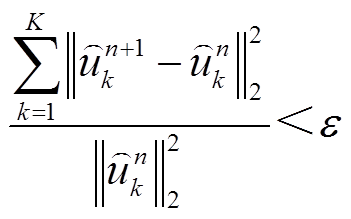（6）
（6）满足式（6）则停止迭代，否则返回步骤（2）。
黏菌算法是Li Shimin等于2020年提出的一种元启式优化算法[29]，其思想是根据黏菌多头绒泡菌在寻找食物过程中发生的一连串的动作和身体变化来构建数学模型。从文献[30]可以看出该算法在解决实际寻找最优解问题时能够快速收敛并求解。因为黏菌算法相较于常用的算法优化算法（Arithmetic Opthmetic Algorithm, AOA）、海洋捕食者算法（Marine Predators Algorithm, MPA）、樽海鞘优化算法（Salp Swarm Algorithm, SSA）等具有更优的精度和稳定性，寻优能力强[30]，所以本研究选择SMA对VMD进行优化。
神经网络模型由许多神经元组成，GRU神经元的内部结构如图1所示。
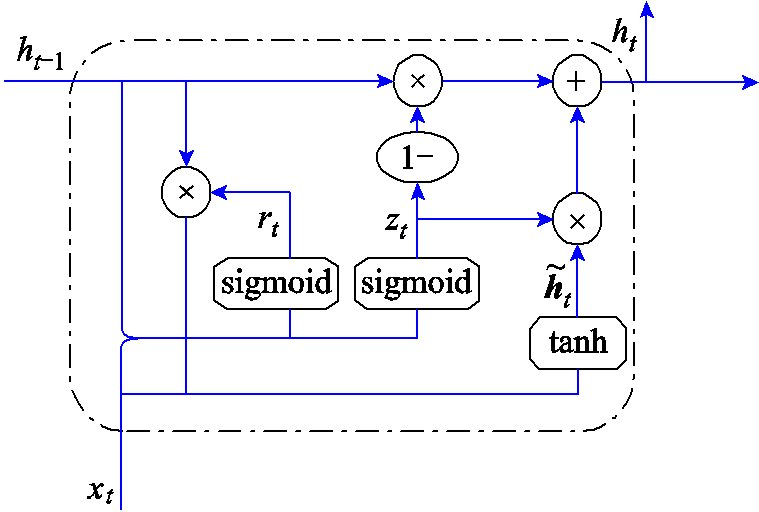
图1 GRU神经元内部结构
Fig.1 Internal structure of GRU neuron
GRU神经元由以下几个部分组成：
（1）两个输入，分别为
，分别代表上一时刻的神经元输出与上一层神经元输出。
（2）两个门，分别为更新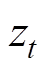门
和重置门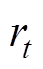
。
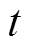时刻更新门和重置门使用sigmoid函数进行激活，即
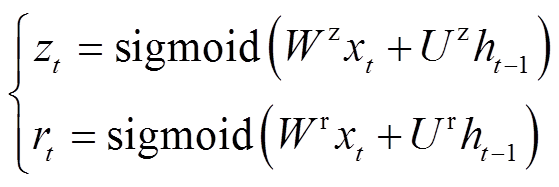（7）
式中，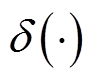
为sigmoid函数；
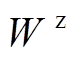和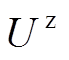
为更新门的权重；
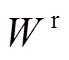和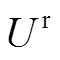
为重置门的权重。
（3）一个状态，即t时刻神经元的内部状态，可以表达为
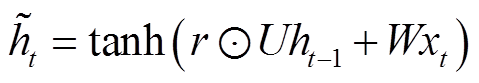（8）
式中，U和W为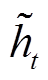
的权重；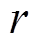
为重置门状态；
表示Hadamard乘积。
（4）一个输出，即为最终输出，可以表达为
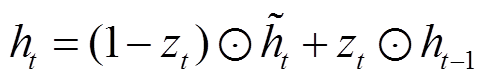（9）
文献[31]使用控制变量法讨论了VMD参数选取对分解结果的影响，说明了分解数K与惩罚因子a对分解结果有较大的影响，因此，有必要研究K与a的优化取值方法。其他参数则选取经验值。
本文采用信号排列熵[31-32]与能量追踪法[33]作为适应度函数的构造原理。排列熵可以很好地反映时间序列的变化规律，而且序列排列熵能很好地评估时间序列的复杂程度；而能量追踪法能够很好地体现各子序列与原始时间序列的关系。
对各固有模态函数（Intrinsic Mode Function, IMF）分量进行相空间重构得到矩阵X。构造向量Xj为
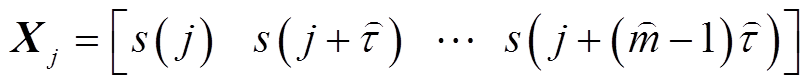（10）
式中，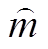
为嵌入维数；
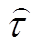为延时；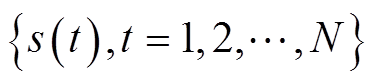
为分量时间序列；
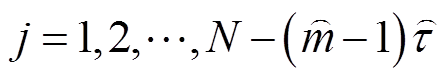。其中，相空间重构嵌入维数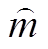与延时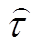分别使用假近邻算法与自相关法计算[34]。
将重构向量Xj作为X的行向量，即可得到一个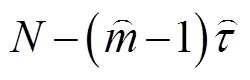
行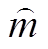，列的重构矩阵X。将矩阵X每一行中的元素重新进行升序排列得到
（11）
式中，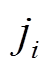
为升序排列后的新向量中的每个数值在未升序排列之前原始向量中的位置信息。
此时矩阵X每一行均可得到一组符号序列矩阵，有
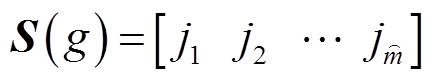（12）
式中，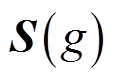
为只含位置信息的符号矩阵，
，
。
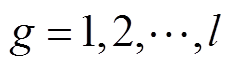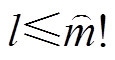计算各符号序列概率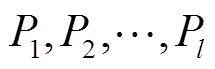
，再通过Shannon熵计算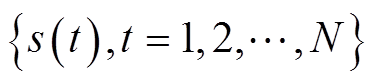的排列熵为
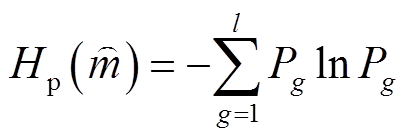（13）
将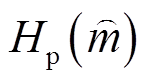
进行归一化处理，得到
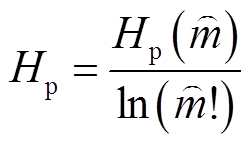（14）
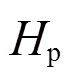越大，说明时间序列越随机，反之亦然。
通过式（13）及式（14）计算各模态分量的排列熵值，表示为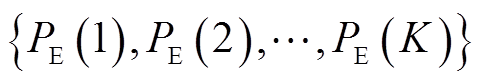
。根据能量追踪法可知，当原始信号达到分解最优时，各IMF分量满足正交性，即原始信号的能量与各分量能量之和相等。基于此，本文借助能量追踪法思想，以各分量占原始信号的能量份额为权值，然后将各IMF排列熵值进行加权求和。
令原始序列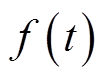
的能量为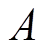
,分量能量为
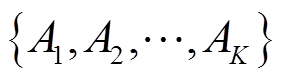，令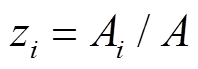
，则适应度函数为
（15）
以各分解分量的排列熵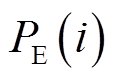
进行加权求和的值最小为优化目标函数，采用SMA对VMD参数组
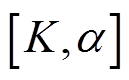的值进行寻优。
SMA对VMD进行参数寻优的步骤见文献[29]，寻优流程如图2所示。
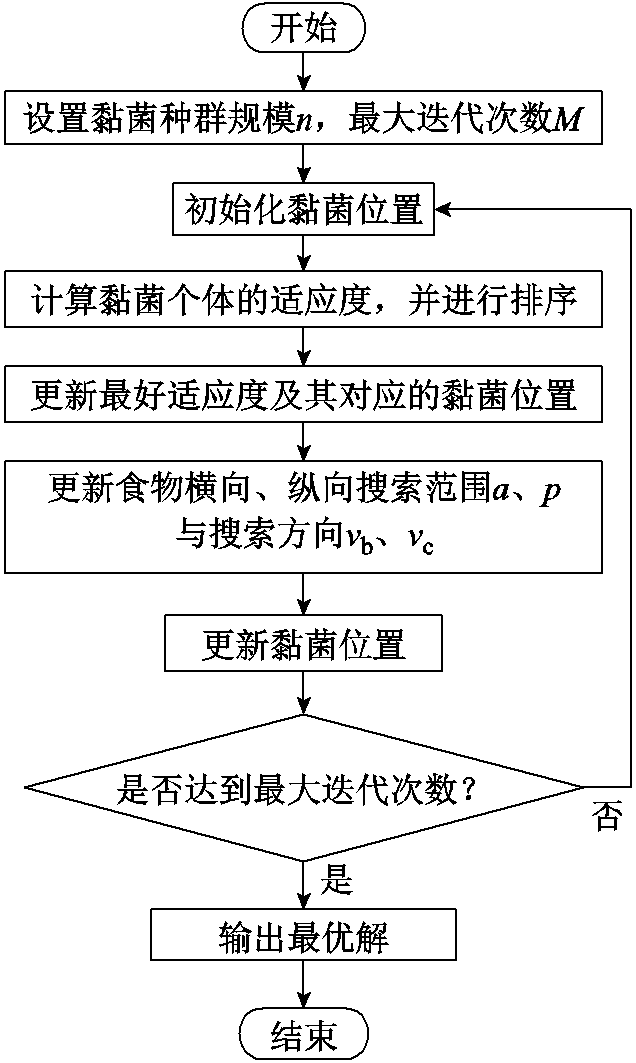
图2 SMA寻优流程
Fig.2 Flow chart of SMA method
SMA-VMD-GRU预测模型流程如图3所示。
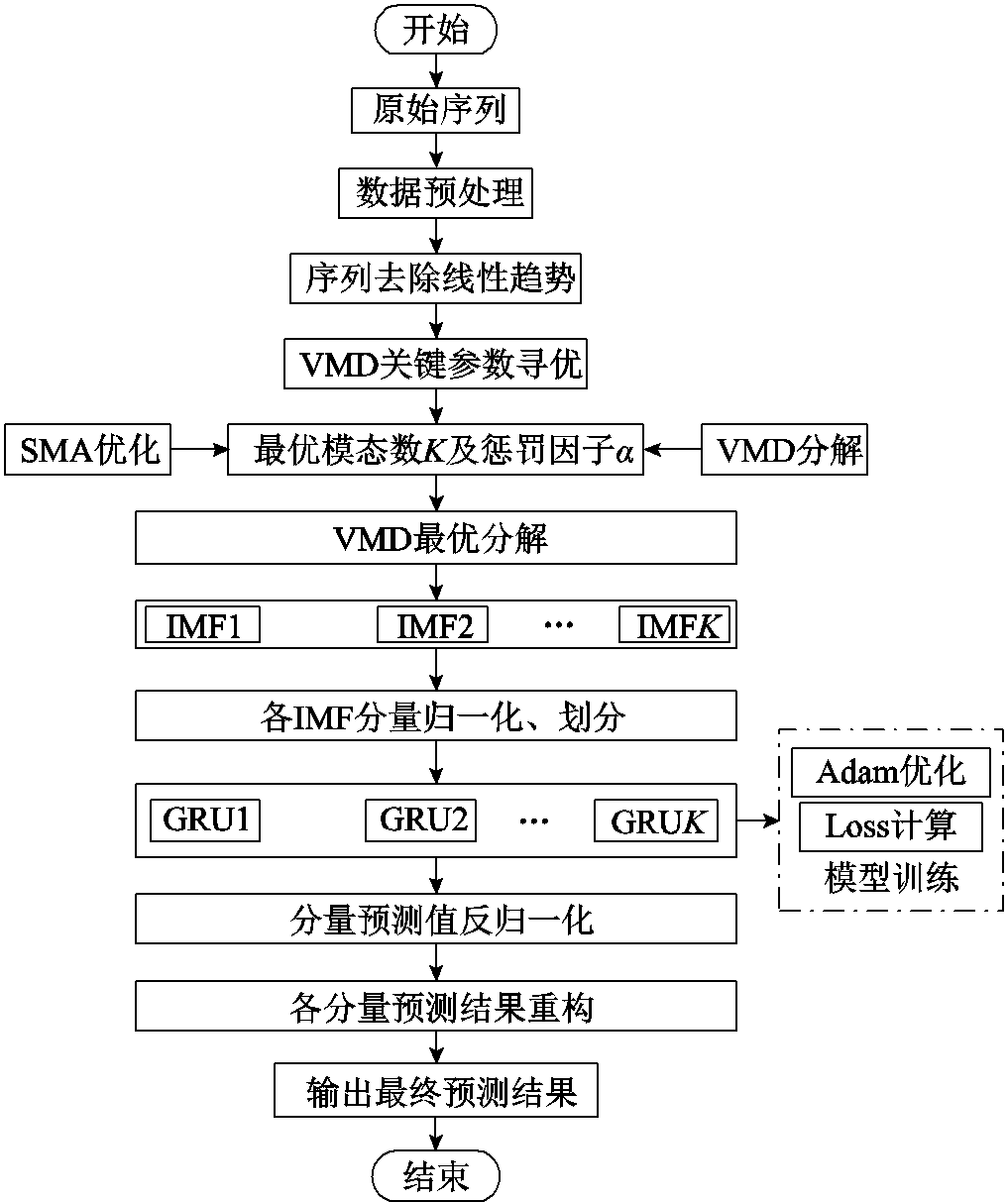
图3 SMA-VMD-GRU预测模型流程
Fig.3 Forecasting flow chart of the SMA-VMD-GRU model
本文油中溶解气体预测模型分为四个步骤：
（1）首先，对原始序列进行去除病态值等预处理，处理方法见文献[32,35-36]；其次，使用差分法[28]对序列进行去趋势化处理。
（2）使用SMA对VMD进行参数自适应寻优，接着使用最优化VMD对去趋势序列进行分解得到频段不同的各模态分量。
（3）归一化分解数据后，对各分量分别建立GRU预测模型，并选用Adam优化器更新网络参数。
（4）反归一化预测分量，重构各分量预测结果，输出最终预测结果。
为了定量分析在采样点数为n时所得到的预测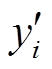值
与真实值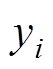
，本文选用平均绝对百分比误差（Mean Absolute Percentage Error, MAPE）与方均根误差（Root Mean Squared Error, RMSE）作为预测模型评价指标，计算公式分别为
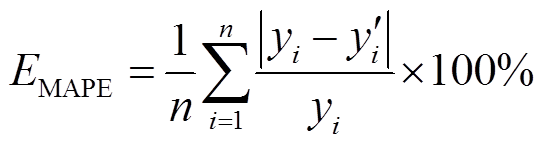（16）
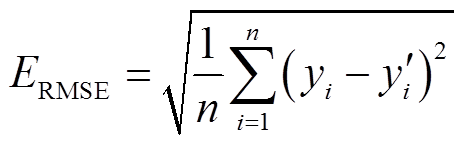（17）
本文选用重庆市某220kV在运变压器2020年7月23日～2021年10月5日在线采集的450组溶解气体时序数据作为实验数据，时序数据为等间隔采样，采样周期为1天。其中，将单一气体含量前390天数据作为预测模型训练集，后60天数据作为预测模型测试集，即训练好的模型使用前10天历史数据预测第11天气体含量，再结合第2天～第10天数据与上一步预测所得的第11天数据来预测第12天的含量，依此类推，将会得到第11天～第60天的预测数据，即未来50天气体含量预测数据。选用Keras框架构建预测模型，对比实验预测模型与本文所提SMA-VMD-GRU预测模型均设计为80-100-1双隐藏层结构，即双隐藏层神经元分别设定为80个与100个，并包含1个输出。训练过程中选用Adam优化更新模型参数，迭代周期设定为100，学习率设定为0.001。本文以H2含量为例对所提模型进行对比分析。H2含量序列曲线如图4所示。
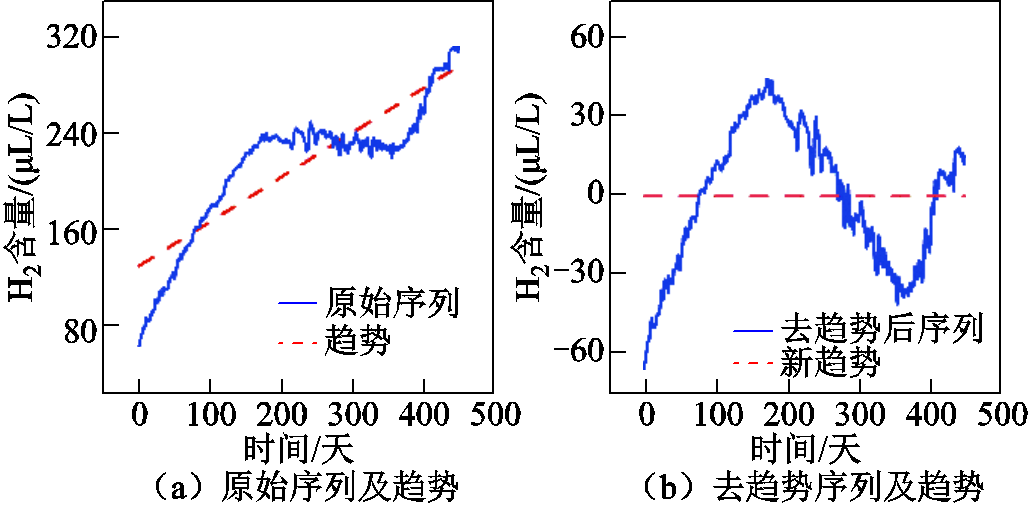
图4 H2含量序列曲线
Fig.4 Sequence of H2 concentration
首先，直接利用差分法对序列进行去趋势化处理，图4a为含趋势项原始H2含量序列，图4b为去趋势后H2含量变化曲线。
其次，将SMA优化算法初始种群数量设为30，迭代次数为50次，进而得到最小适应度值PEW为0.265 963，最优K值为7，a值为1 572。其所对应的SMA迭代曲线与最优值所对应的分解模态中心频率分别如图5a和图5b所示。由图5b可以看出，使用最优参数分解H2序列得到的各模态分量中心频率没有出现混叠现象。
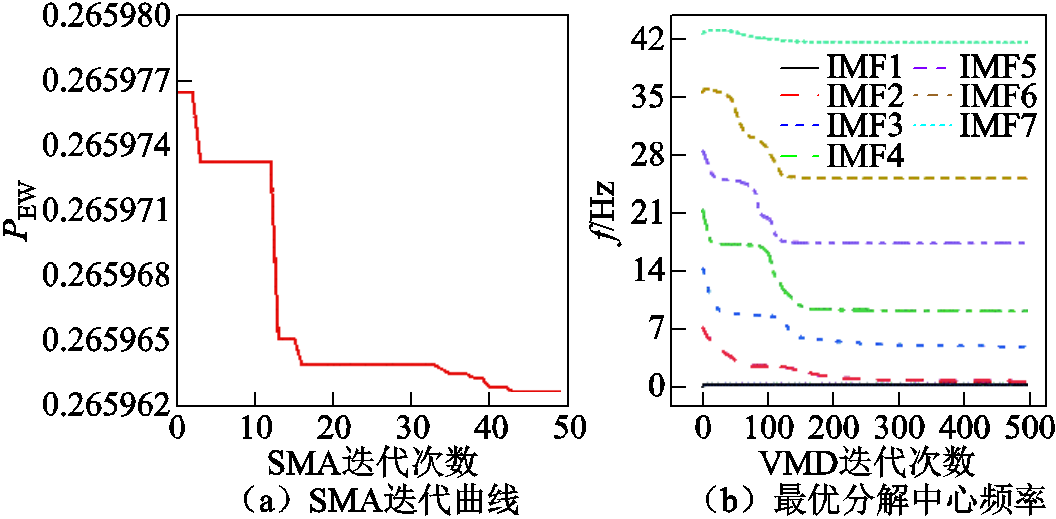
图5 SMA迭代曲线与最优分解中心频率
Fig.5 SMA iteration curve and optimal decomposition center frequency
最后，将最优分解后的子序列进行预测。
使用GRU和LSTM方法的两组单一预测模型预测结果如图6所示，预测误差见表1。由表1可得，GRU模型的预测结果MAPE为2.03%，RMSE为43.30mL/L，相较于LSTM模型分别降低了0.30%和6.66mL/L。结合图6可以得出，GRU模型在解决变压器油中溶解气体含量预测问题时相较于LSTM预测模型更优。
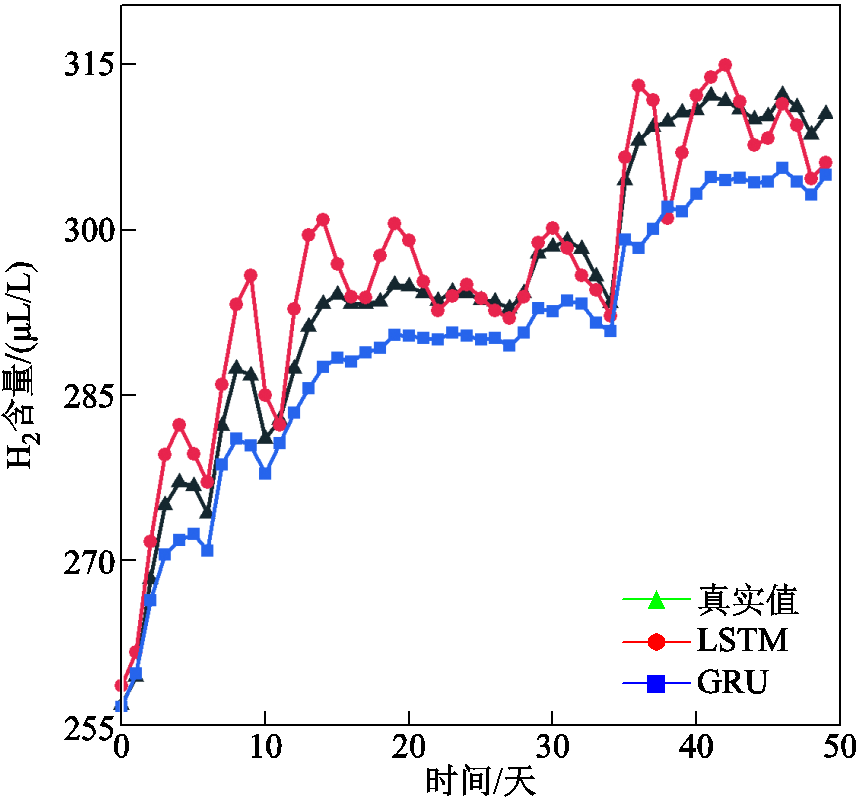
图6 单一模型预测结果对比
Fig.6 Comparison of prediction results of single model
表1 GRU与LSTM预测误差对比
Tab.1 Comparison of GRU and LSTM prediction errors
模型MAPE(%)RMSE/(mL/L) LSTM2.3349.96 GRU2.0343.30
LSTM和GRU模型的网络总参数、可训练参数及运行时间见表2。GRU预测模型总参数和可训练参数都为74 621，相比于LSTM预测模型参数量减少了24120，在运行时间上可以看出GRU模型运行时间为9.71s，而LSTM模型为11.18s。基于此，从考虑变压器油中溶解气体含量预测时效性角度出发，GRU也更加具有优势。
表2 GRU与LSTM性能对比
Tab.2 Performance comparison between GRU and LSTM
模型总参数可训练参数运行时间/s LSTM98 74198 74111.18 GRU74 62174 6219.71
EMD对序列分解后的效果如图7所示，SMA-VMD对序列分解后的效果如图8所示。其中图7a和图8a为所对应的IMF，图7b和图8b代表各自的IMF频谱图。图9为GRU对SMA-VMD分解分量预测效果图。本文将LSTM、GRU分别与EMD、SMA-VMD结合，组成四种预测模型，对H2含量的预测结果如图10所示。
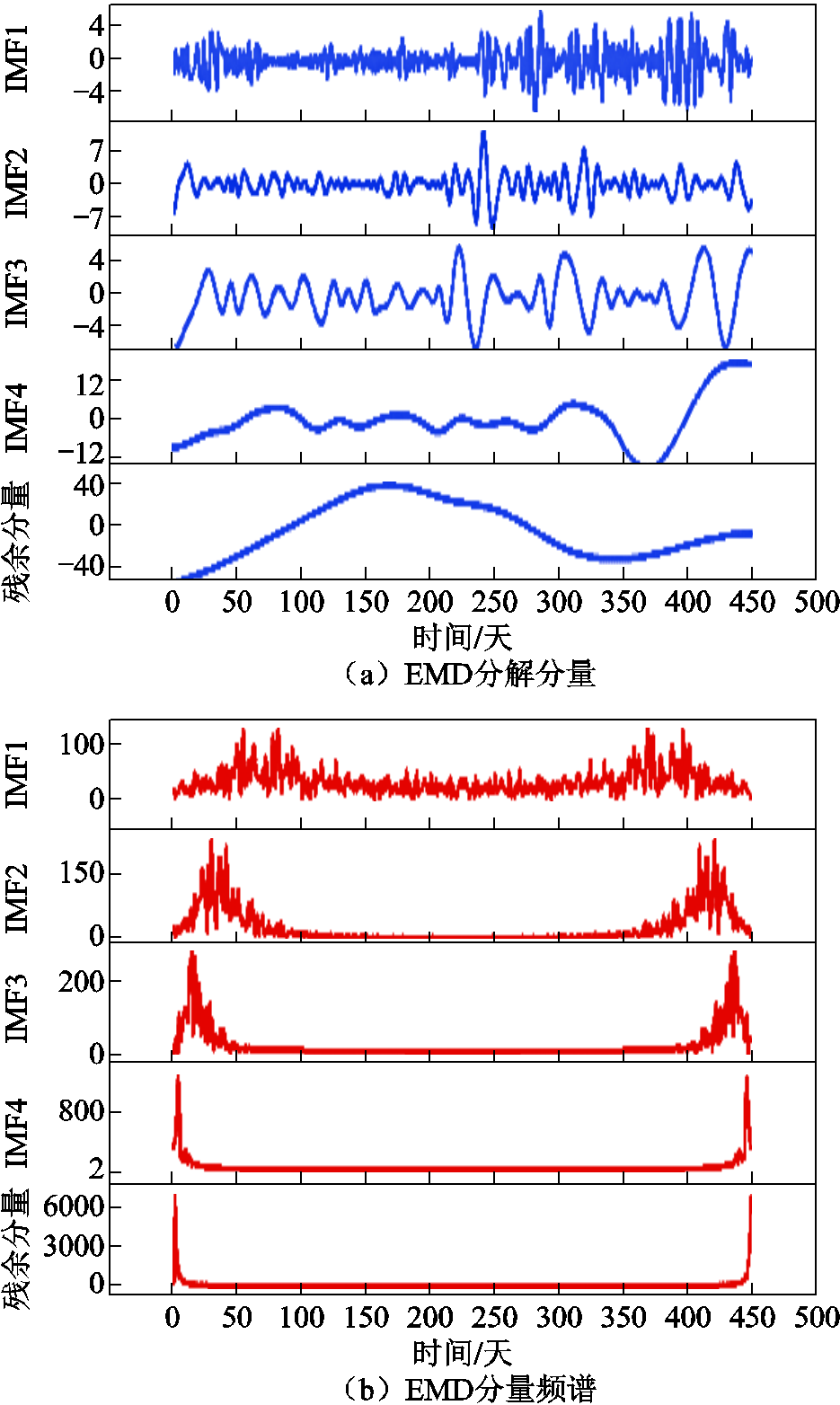
图7 EMD分解分量与频谱
Fig.7 EMD decomposition component and spectrum
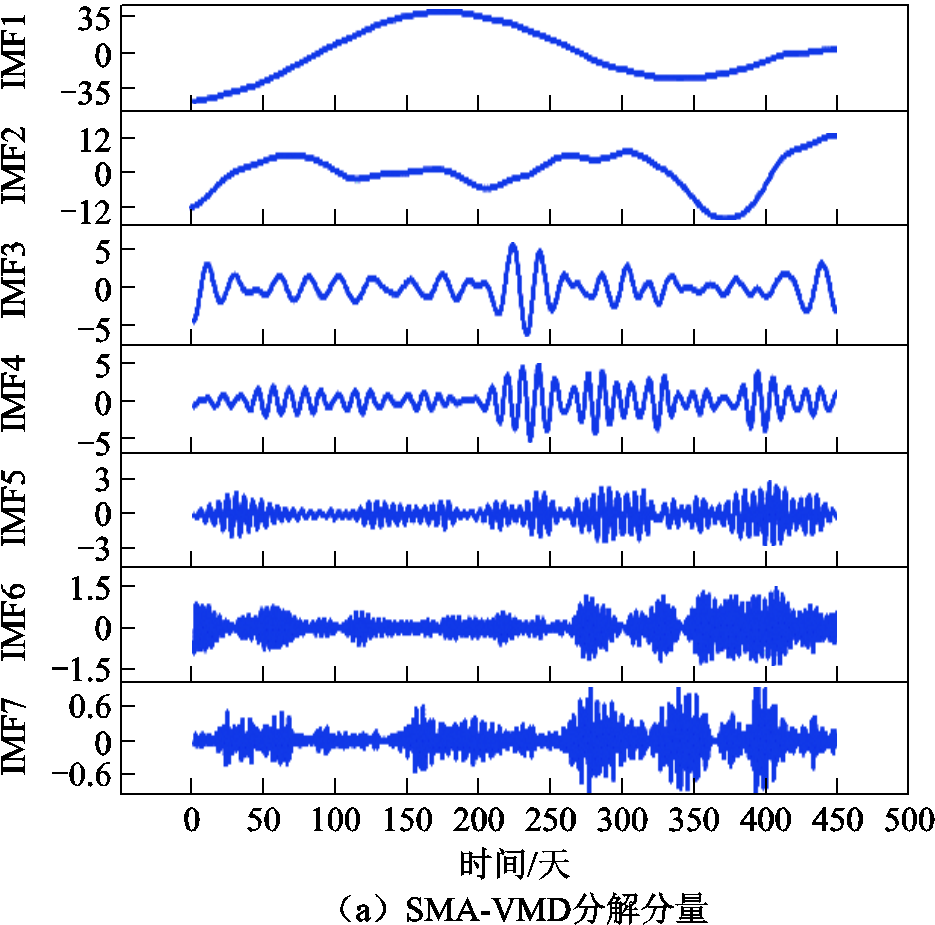
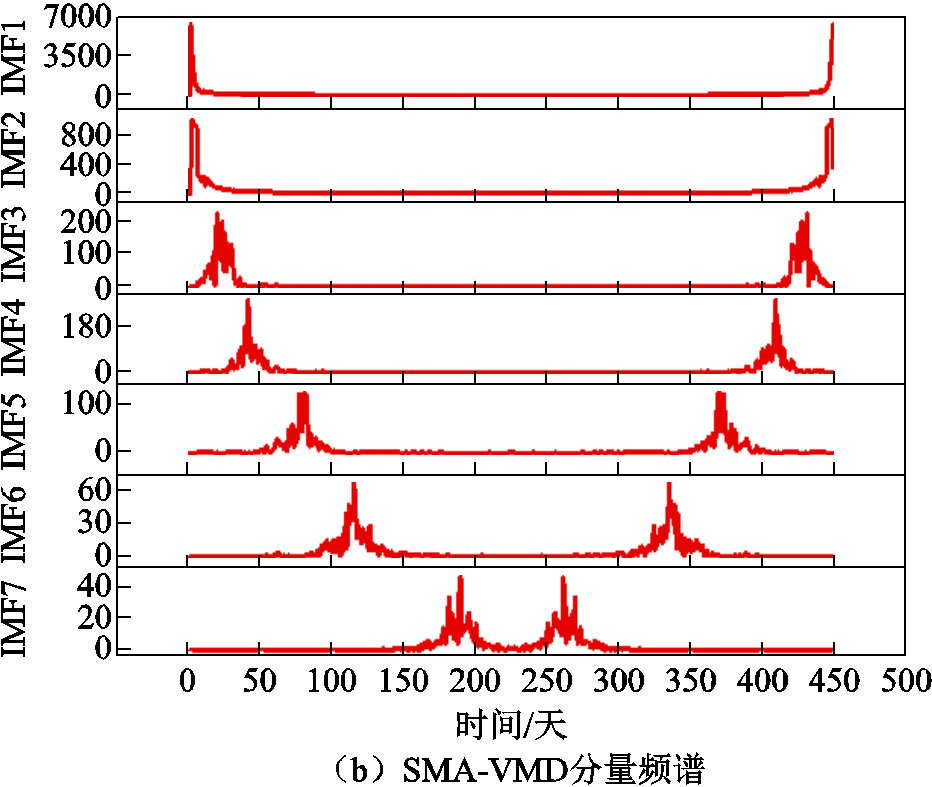
图8 SMA-VMD最优分解分量与频谱
Fig.8 SMA-VMD optimal decomposition components and spectrum
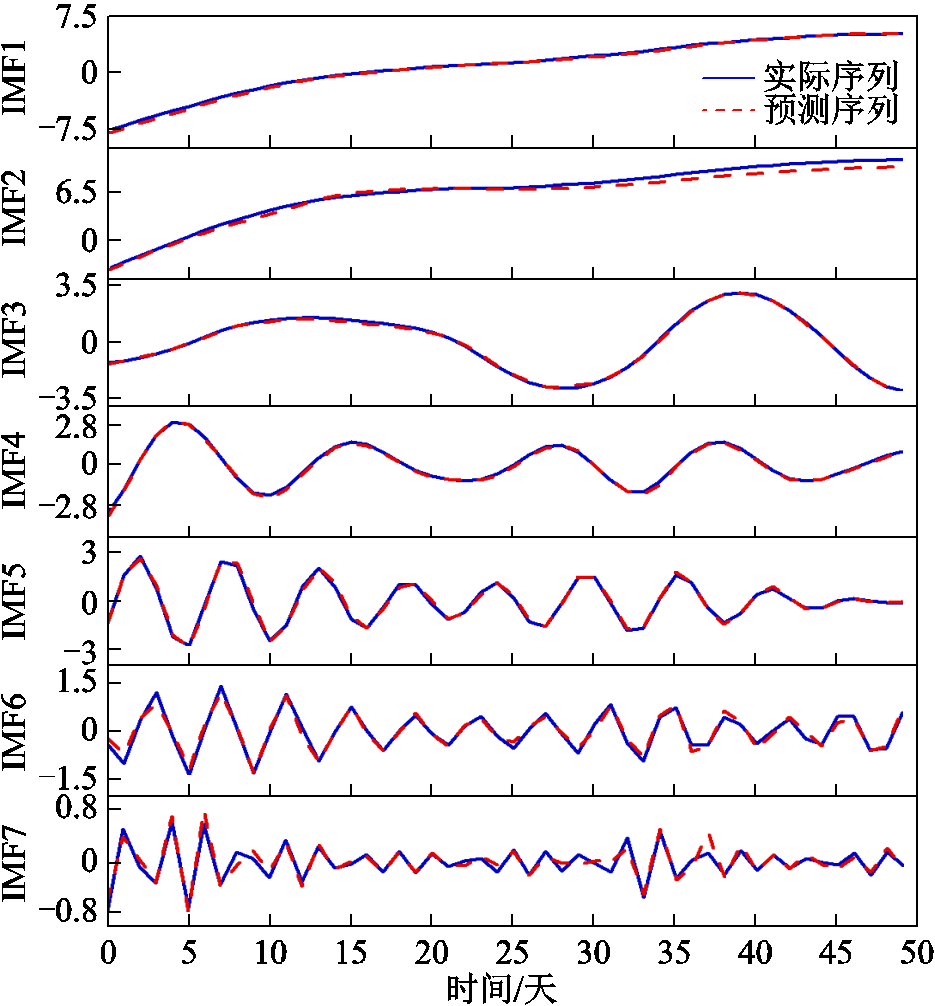
图9 SMA-VMD-GRU分量预测结果
Fig.9 Component prediction results of SMA-VMD-GRU
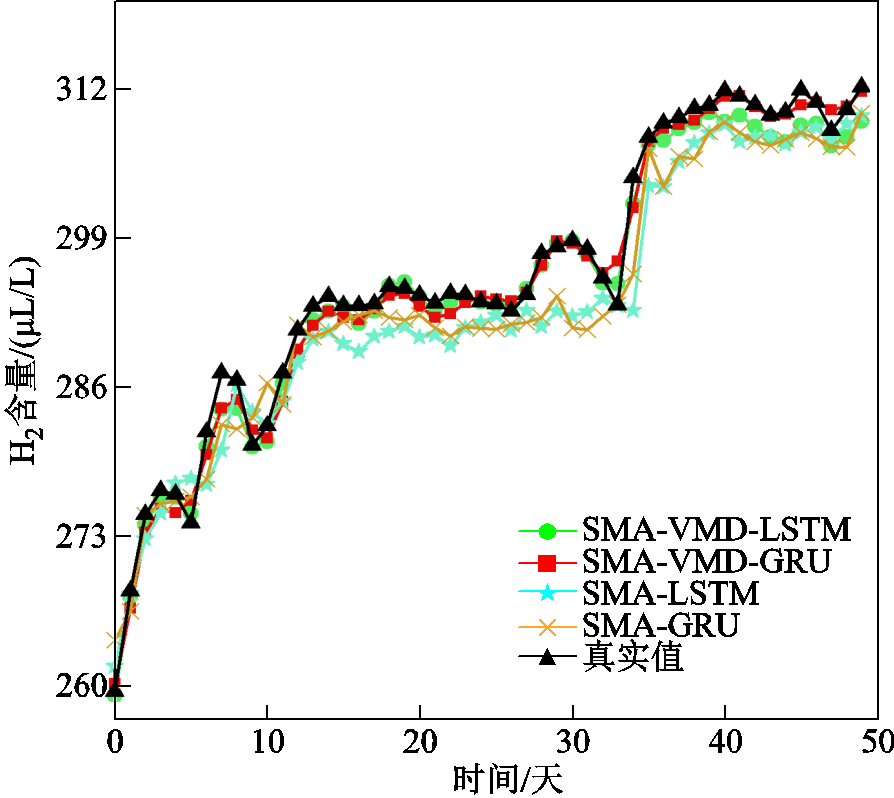
图10 组合模型预测结果对比
Fig.10 Comparison of prediction results of combined models
组合预测模型对油中H2含量的预测误差见表3。表1中LSTM与GRU预测结果MAPE分别为2.33%与2.03%，而表3中EMD-LSTM组合预测模型的MAPE最大为1.35%。再结合图10和图6可以明显看出，含有模态分解的变压器油中溶解气体含量组合预测模型相比单一预测模型对变压器油中溶解气体H2预测效果更加贴近真实值。
表3 组合预测模型预测误差对比
Tab.3 Comparison of combined prediction models
模型MAPE(%)RMSE/(mL/L) SMA-VMD-GRU0.361.76 EMD-GRU1.0513.72 SMA-VMD-LSTM0.777.83 EMD-LSTM1.3524.83
由图7a与图8a可以看出，通过模态分解的手段将原始含量序列分解为平稳的低频高幅成分与规律性较强的高频低幅成分，很好地将变压器油中溶解气体序列中所包含的环境温度、湿度等多变量影响因素及自身变化规律信息进行了提取，有效地解决了因其他变量采集误差影响变压器油中溶解气体预测精度的问题。
由图7b中可以看出EMD分解出现了严重的模态混叠，而从图8b可看出SMA-VMD分解得到的各IMF基本没有出现频谱混叠现象。此外，从图8a中后3个IMF分量看出分解得到的高频分量的变化更加规律。可以得出，SMA-VMD相较于EMD性能较优，并且从图9分量预测结果图可以看出GRU能对平稳的低频高幅分量和规律性较强的高频低幅分量进行较好的预测，解决了变压器油中溶解气体含量非线性、非平稳特性以及多变量影响预测精度问题。
表3则定量地评价了四种组合预测模型，EMD-LSTM和EMD-GRU两组基于EMD的组合预测模型的MAPE分别为1.35%与1.05%，相较于SMA-VMD-LSTM和SMA-VMD-GRU两组基于VMD的组合预测模型的MAPE分别增加0.58%与0.69%。其中，SMA-VMD-GRU组合预测模型的MAPE与RMSE分别为0.36%与1.76mL/L，相较于其他三组组合预测模型预测误差最小。根据图10的最终预测结果所示，SMA-VMD-GRU模型在预测含有非线性、非平稳特性的变压器油中溶解气体含量时，相较于未含模态分解的模型与分解较差模型都有较优的拟合效果。
本文以3.2节所使用变压器中另外三种油中溶解气体CH4、CO、总烃含量为例，验证所提SMA-VMD-GRU组合预测模型的有效性。验证实验中训练集与测试集划分、模型构建框架、模型结构设计、参数更新方法、学习率设定均与3.2节中H2实验相同。
CH4、CO、总烃含量原始序列曲线如图11所示，并对去趋势预处理后的序列进行分解。
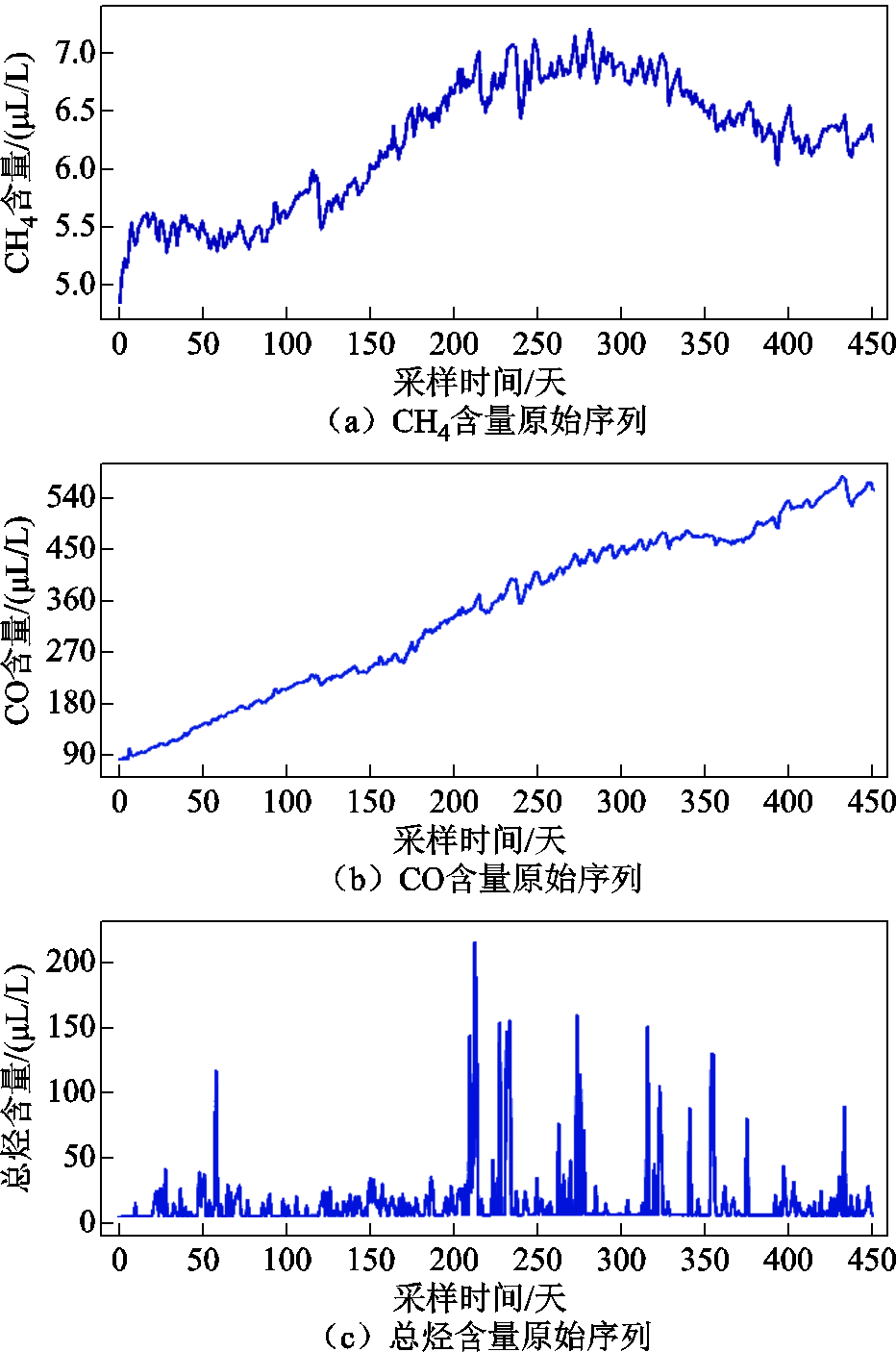
图11 三种气体原始序列曲线
Fig.11 Curves of three gas primordial sequences
首先，利用SMA优化算法对三种序列进行VMD分解参数寻优，SMA初始种群数量设为30，迭代次数为50次，进而得到最小适应度值PEW、最优K值、a值见表4。三种序列寻优所对应的SMA迭代曲线与最优值所对应分解模态中心频率分别如图12、图13所示。由图13可以看出，使用最优参数分解CH4、CO、总烃三种油中溶解气体含量序列得到的各模态分量中心频率没有出现混叠现象。
表4 SMA-GRU寻优参数
Tab.4 Optimization parameters of SMA-GRU
参数CH4CO总烃 寻优PEW值0.2827520.2915860.037922 最优K值657 最优a值18441265169
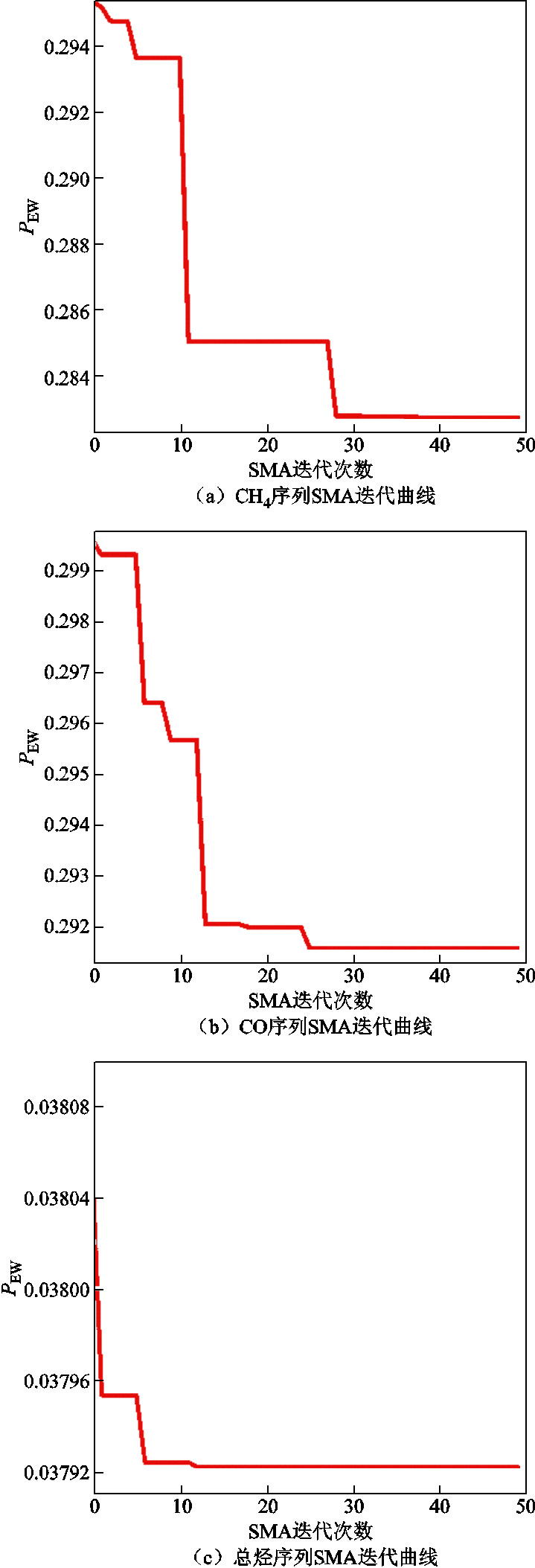
图12 三种气体SMA迭代曲线
Fig.12 SMA iteration curves for three gases
CH4、CO和总烃含量分解分量预测结果分别如图14、图15和图16所示。
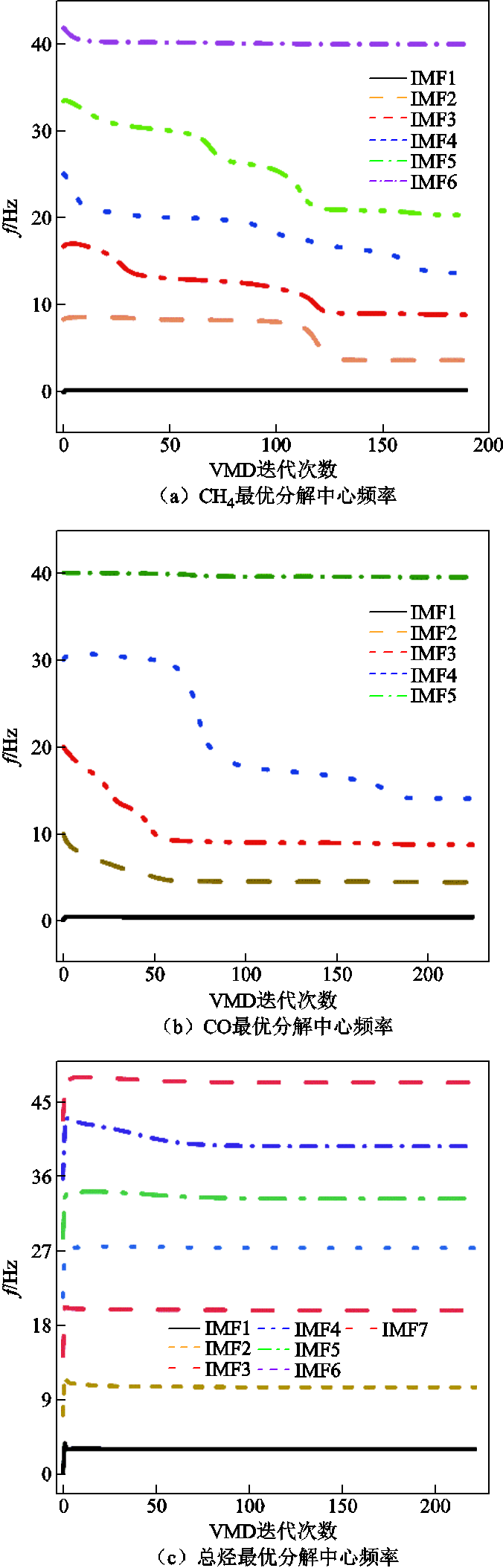
图13 三种气体最优SMA-VMD分解中心频率
Fig.13 Optimal SMA-VMD decomposition center frequency for three gases
图14a、图15a、图16a分别为CH4、CO、总烃序列最优SMA-VMD分解图。可以看出，相较于图11中含有非线性、非平稳特性的三种油中溶解气体原始序列，三组分解序列已平稳化且周期性较强。
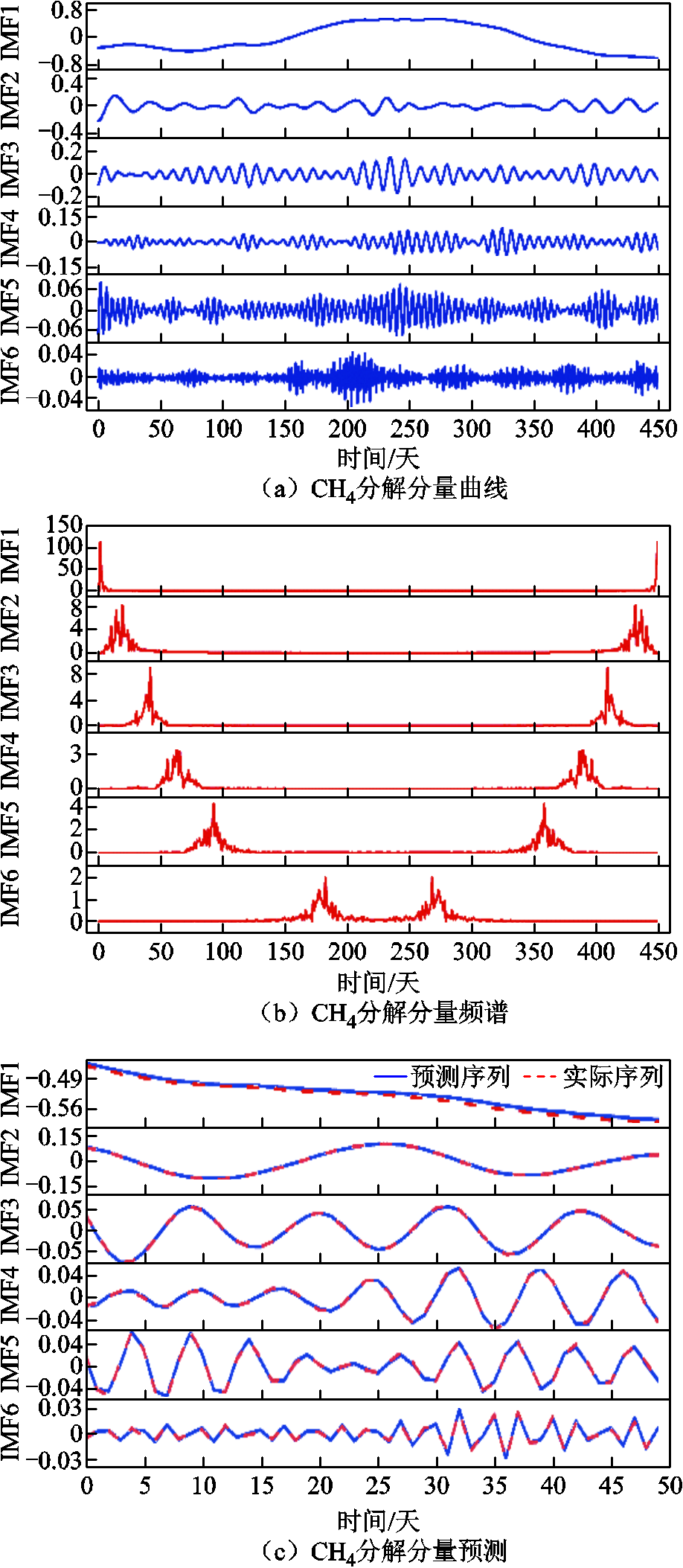
图14 CH4最优分解与分量预测
Fig.14 CH4 optimal decomposition and component prediction
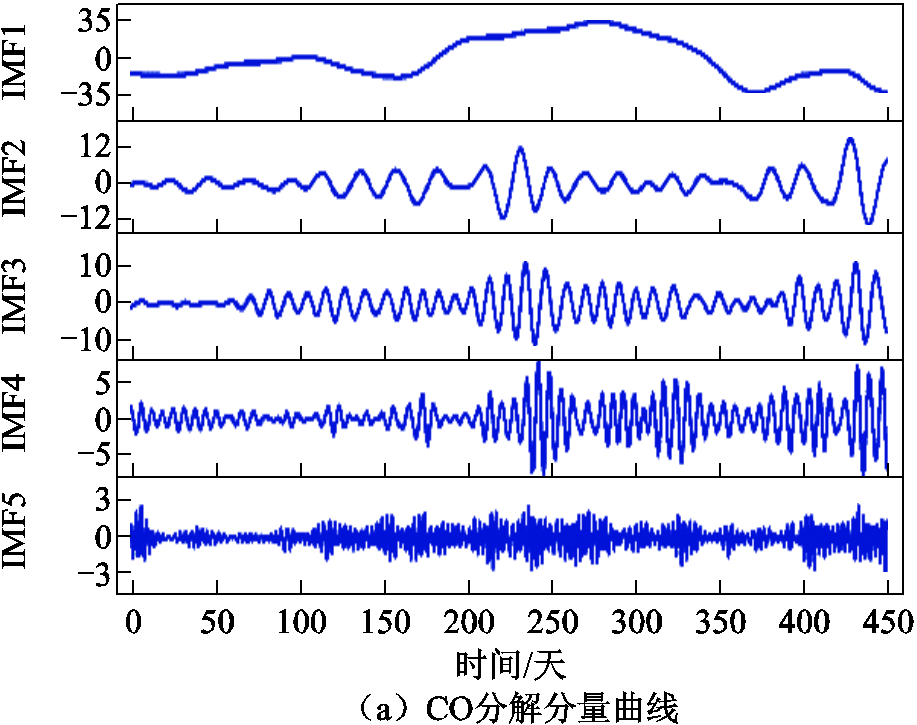
图15 CO最优分解与分量预测
Fig.15 CO optimal decomposition and component prediction
图14c、图15c、图16c分别为三组分解分量预测结果拟合图。从预测效果可以看出，对于平稳化且周期性较强的序列，预测效果较佳，证明了分解得到的平稳化序列的可预测性。
综上所述，证明了本文中所提预测模型分解部分对油中溶解气体含量序列的有效性。
三种气体分解序列预测结果重构后得到的最终预测结果如图17所示，预测误差见表5。表5中三种气体预测的MAPE仅为0.29%、0.15%、4.99%，RMSE仅为0.02mL/L、1.13mL/L、0.50mL/L，结合图17，证明了本研究所提SMA-VMD-GRU组合预测模型对变压器油中溶解气体含量预测的有效性。
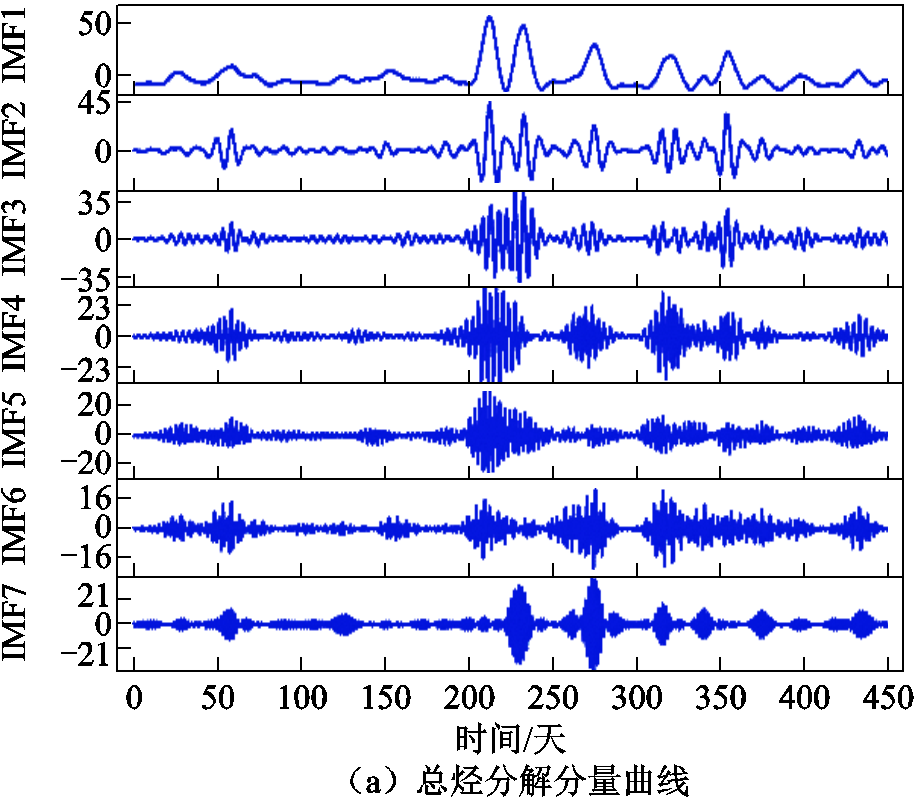
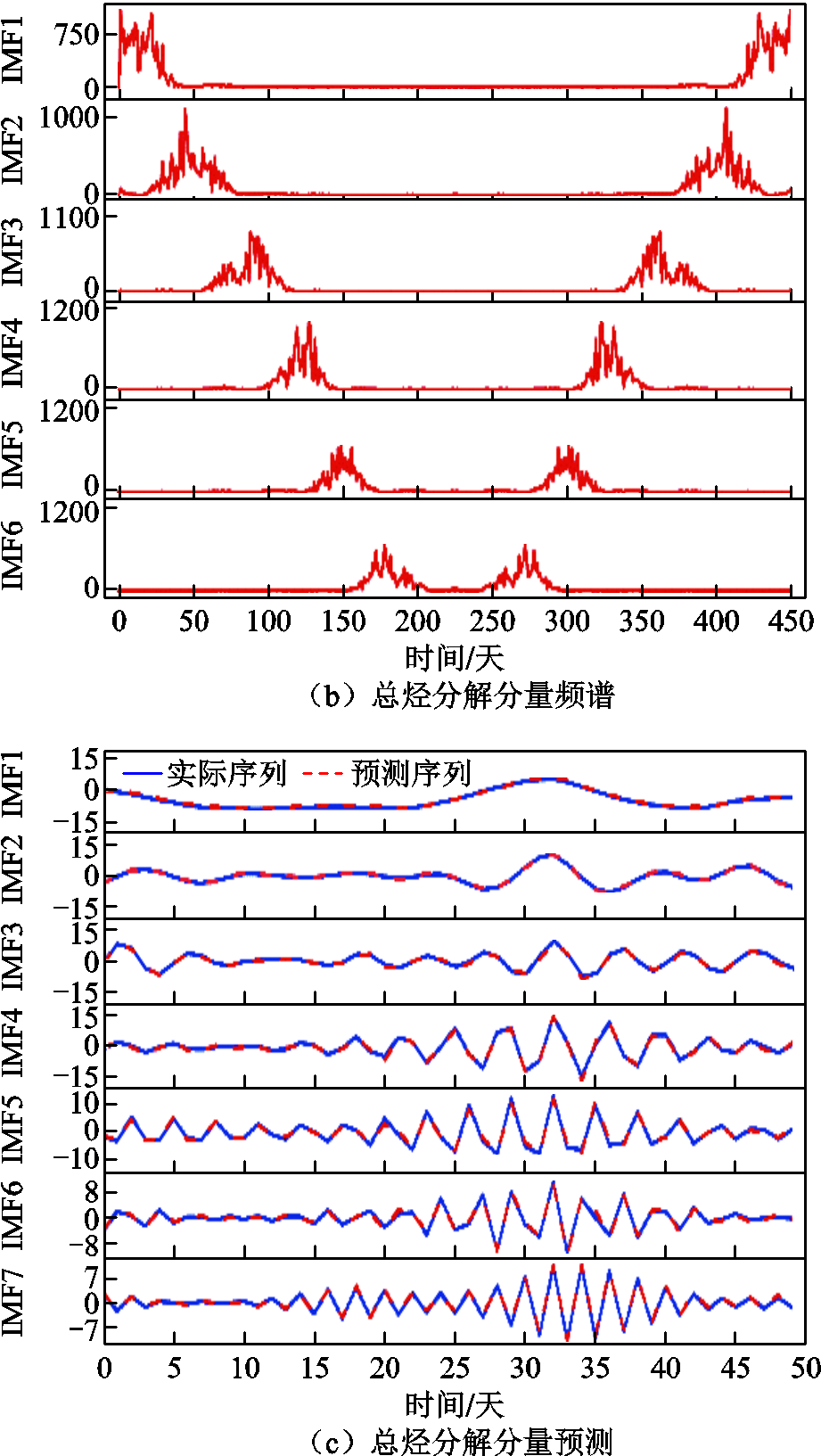
图16 总烃最优分解与分量预测
Fig.16 Optimal decomposition and component prediction of total hydrocarbons
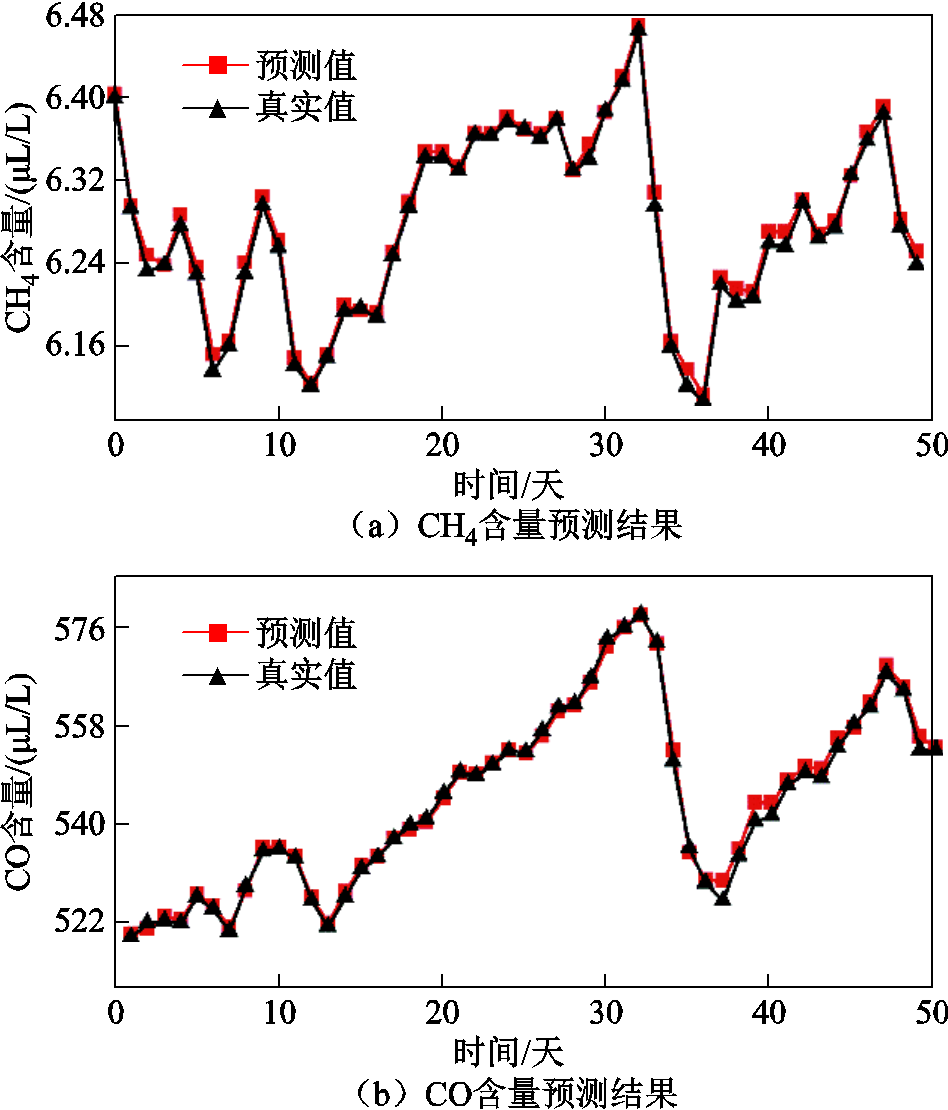
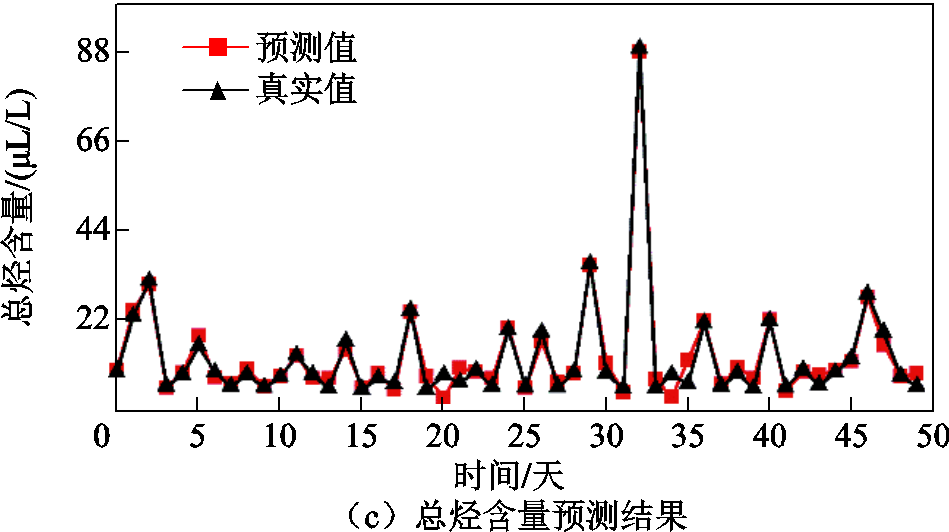
图17 三种气体预测结果
Fig.17 Prediction results of three gases
表5 SMA-VMD-GRU组合预测模型预测误差
Tab.5 Prediction accuracy of SMA-VMD-GRU combined prediction mode
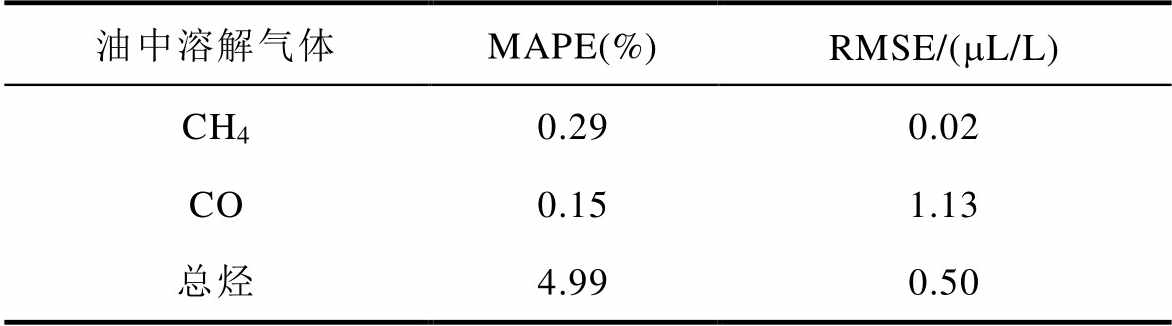
油中溶解气体MAPE(%)RMSE/(mL/L) CH40.290.02 CO0.151.13 总烃4.990.50
本文针对变压器油中溶解气体含量序列非线性、非平稳特性影响预测精度问题，提出了一种SMA-VMD结合GRU的变压器油中溶解气体组合预测模型，实验结果表明：
1）使用差分法对序列趋势项提取，有效地解决了VMD无法准确提取趋势项的不足。再通过SMA优化后的VMD分解处理后的序列，可以将复杂的油中溶解气体序列分解，成为一组平稳的、周期性强的模态分量，有效地解决了原始序列非线性、非平稳特性对预测精度的影响。
2）在变压器油中溶解气体预测中，GRU网络相比LSTM网络收敛速度更快。因此，GRU网络比LSTM更加具有优势。在前期通过差分法与SMA-VMD提升序列可预测性的前提下，进一步将油中溶解气体含量预测精度提高，有助于变压器前期故障诊断。
3）通过对变压器油中溶解气体中多种气体含量进行仿真预测实验，证明了本研究所提基于SMA-VMD-GRU的变压器油中溶解气体含量预测模型的有效性。
参考文献
[1] 梁得亮, 柳轶彬, 寇鹏, 等. 智能配电变压器发展趋势分析[J]. 电力系统自动化, 2020, 44(7): 1-14.
Liang Deliang, Liu Yibin, Kou Peng, et al. Analysis of development trend for intelligent distribution transformer[J]. Automation of Electric Power Systems, 2020, 44(7): 1-14.
[2] 李恩文, 王力农, 宋斌, 等. 基于改进模糊聚类算法的变压器油色谱分析[J]. 电工技术学报, 2018, 33(19): 4594-4602.
Li Enwen, Wang Linong, Song Bin, et al. Analysis of transformer oil chromatography based on improved fuzzy clustering algorithm[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4594-4602.
[3] 国家能源局. DL/T 573—2021 电力变压器检修导则[S]. 北京: 中国电力出版社, 2021.
[4] 国家能源局. DL/T 722—2014 变压器油中溶解气体分析和判断导则[S]. 北京: 中国电力出版社, 2015.
[5] 张燕, 方瑞明. 基于油中溶解气体动态网络标志物模型的变压器缺陷预警与辨识[J]. 电工技术学报, 2020, 35(9): 2032-2041.
Zhang Yan, Fang Ruiming. Fault detection and identification of transformer based on dynamical network marker model of dissolved gas in oil[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2032-2041.
[6] 江秀臣, 盛戈皞. 电力设备状态大数据分析的研究和应用[J]. 高电压技术, 2018, 44(4): 1041-1050.
Jiang Xiuchen, Sheng Gehao. Research and application of big data analysis of power equipment condition[J]. High Voltage Engineering, 2018, 44(4): 1041-1050.
[7] 蒲天骄, 乔骥, 韩笑, 等. 人工智能技术在电力设备运维检修中的研究及应用[J]. 高电压技术, 2020, 46(2): 369-383.
Pu Tianjiao, Qiao Ji, Han Xiao, et al. Research and application of artificial intelligence in operation and maintenance for power equipment[J]. High Voltage Engineering, 2020, 46(2): 369-383.
[8] Liu Chang, Zhang Hongzhi, Xie Zhicheng, et al. Combined forecasting method of dissolved gases concentration and its application in condition-based maintenance[J]. IEEE Transactions on Power Delivery, 2019, 34(4): 1269-1279.
[9] 修春波, 任晓, 李艳晴, 等. 基于卡尔曼滤波的风速序列短期预测方法[J]. 电工技术学报, 2014, 29(2): 253-259.
Xiu Chunbo, Ren Xiao, Li Yanqing, et al. Short-term prediction method of wind speed series based on Kalman filtering fusion[J]. Transactions of China Electrotechnical Society, 2014, 29(2): 253-259.
[10] 张婷婷, 于明, 李宾, 等. 基于Wavelet降噪和支持向量机的锂离子电池容量预测研究[J]. 电工技术学报, 2020, 35(14): 3126-3136.
Zhang Tingting, Yu Ming, Li Bin, et al. Capacity prediction of lithium-ion batteries based on Wavelet noise reduction and support vector machine[J]. Transactions of China Electrotechnical Society, 2020, 35(14): 3126-3136.
[11] 徐肖伟, 李鹤健, 于虹, 等. 基于随机森林的变压器油中溶解气体浓度预测[J]. 电子测量技术, 2020, 43(3): 66-70.
Xu Xiaowei, Li Hejian, Yu Hong, et al. Concentration prediction of dissolved gases in transformer oil based on random forest[J]. Electronic Measurement Technology, 2020, 43(3): 66-70.
[12] 代杰杰, 宋辉, 盛戈皞, 等. 采用LSTM网络的电力变压器运行状态预测方法研究[J]. 高电压技术, 2018, 44(4): 1099-1106.
Dai Jiejie, Song Hui, Sheng Gehao, et al. Prediction method for power transformer running state based on LSTM network[J]. High Voltage Engineering, 2018, 44(4): 1099-1106.
[13] Qi Bo, Wang Yiming, Zhang Peng, et al. A novel deep recurrent belief network model for trend prediction of transformer DGA data[J]. IEEE Access, 2019, 7: 80069-80078.
[14] 刘可真, 苟家萁, 骆钊, 等. 基于粒子群优化-长短期记忆网络模型的变压器油中溶解气体浓度预测方法[J]. 电网技术, 2020, 44(7): 2778-2785.
Liu Kezhen, Gou Jiaqi, Luo Zhao, et al. Prediction of dissolved gas concentration in transformer oil based on PSO-LSTM model[J]. Power System Technology, 2020, 44(7): 2778-2785.
[15] 崔宇, 侯慧娟, 胥明凯, 等. 基于双重注意力机制的变压器油中溶解气体预测模型[J]. 中国电机工程学报, 2020, 40(1): 338-347, 400.
Cui Yu, Hou Huijuan, Xu Mingkai, et al. A prediction method for dissolved gas in power transformer oil based on dual-stage attention mechanism[J]. Proceedings of the CSEE, 2020, 40(1): 338-347, 400.
[16] 刘展程, 王爽, 唐波. 基于SSA-BiGRU-Attention模型的变压器油中溶解气体含量预测[J]. 高电压技术, 2022, 48(8): 2972-2981.
Liu Zhancheng, Wang Shuang, Tang Bo. Prediction of dissolved gas content in transformer oil based on SSA-BiGRU-attention model[J]. High Voltage Engineering, 2022, 48(8): 2972-2981.
[17] 马星河, 张登奎. 基于改进经验小波变换的高压电缆局部放电噪声抑制研究[J]. 电工技术学报, 2021, 36(增刊1): 353-361.
Ma Xinghe, Zhang Dengkui. Research on suppression of partial discharge noise of high voltage cable based on improved empirical wavelet transform[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 353-361.
[18] 林琳, 陈志英. 基于粗糙集神经网络和振动信号的高压断路器机械故障诊断[J]. 电工技术学报, 2020, 35(增刊1): 277-283.
Lin Lin, Chen Zhiying. Mechanical fault diagnosis of high voltage circuit breakers based on rough set neural networks and vibration signals[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 277-283.
[19] Dragomiretskiy K, Zosso D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.
[20] 叶林, 刘鹏. 基于经验模态分解和支持向量机的短期风电功率组合预测模型[J]. 中国电机工程学报, 2011, 31(31): 102-108.
Ye Lin, Liu Peng. Combined model based on EMD-SVM for short-term wind power prediction[J]. Proceedings of the CSEE, 2011, 31(31): 102-108.
[21] Wu Zhaohua, Huang N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.
[22] 曹奇, 岳东杰, 高永攀, 等. 基于非平稳时间序列的不同趋势项提取方法对比研究[J]. 大地测量与地球动力学, 2013, 33(6): 150-154.
Cao Qi, Yue Dongjie, Gao Yongpan, et al. Contrast study on various methods extracting trend extraction based on non-stationary time series[J]. Journal of Geodesy and Geodynamics, 2013, 33(6): 150-154.
[23] 杨茂, 白玉莹. 基于多位置NWP和门控循环单元的风电功率超短期预测[J]. 电力系统自动化, 2021, 45(1): 177-183.
Yang Mao, Bai Yuying. Ultra-short-term prediction of wind power based on multi-location numerical weather prediction and gated recurrent unit[J]. Automation of Electric Power Systems, 2021, 45(1): 177-183.
[24] 李超然, 肖飞, 樊亚翔, 等. 基于门控循环单元神经网络和Huber-M估计鲁棒卡尔曼滤波融合方法的锂离子电池荷电状态估算方法[J]. 电工技术学报, 2020, 35(9): 2051-2062.
Li Chaoran, Xiao Fei, Fan Yaxiang, et al. A hybrid approach to lithium-ion battery SOC estimation based on recurrent neural network with gated recurrent unit and Huber-M robust Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2051-2062.
[25] 王科, 苟家萁, 彭晶, 等. 基于LSTM网络的变压器油中溶解气体浓度预测[J]. 电子测量技术, 2020, 43(4): 81-87.
Wang Ke, Gou Jiaqi, Peng Jing, et al. Prediction of dissolved gas concentration in transformer oil based on LSTM network[J]. Electronic Measurement Technology, 2020, 43(4): 81-87.
[26] 卫永鹏, 苏益辉, 王胜利, 等. 基于改进门控循环单元的变压器油中气体浓度预测[J]. 电气技术, 2022, 23(2): 55-60.
Wei Yongpeng, Su Yihui, Wang Shengli, et al. Prediction of gas concentration in transformer oil based on improved gated recurrent unit[J]. Electrical Engineering, 2022, 23(2): 55-60.
[27] Ali M, Khan A, Rehman N U. Hybrid multiscale wind speed forecasting based on variational mode decomposition[J]. International Transactions on Electrical Energy Systems, 2018, 28(1): e2466.
[28] 陈强伟, 蔡文皓, 牛春光, 等. 基于VMD的APF谐波检测算法[J]. 电力科学与技术学报, 2018, 33(1): 120-124.
Chen Qiangwei, Cai Wenhao, Niu Chunguang, et al. A APF harmonics detection method based on VMD[J]. Journal of Electric Power Science and Technology, 2018, 33(1): 120-124.
[29] Li Shimin, Chen Huiling, Wang Mingjing, et al. Slime mould algorithm: a new method for stochastic optimization[J]. Future Generation Computer Systems, 2020, 111: 300-323.
[30] Gürses D, Bureerat S, Sait S M, et al. Comparison of the arithmetic optimization algorithm, the slime mold optimization algorithm, the marine predators algorithm, the salp swarm algorithm for real-world engineering applications[J]. Materials Testing, 2021, 63(5): 448-452.
[31] 李青, 张新燕, 马天娇, 等. 基于ECBO-VMD-WKELM的风电功率超短期多步预测[J]. 电网技术, 2021, 45(8): 3070-3080.
Li Qing, Zhang Xinyan, Ma Tianjiao, et al. Multi-step ahead ultra-short term forecasting of wind power based on ECBO-VMD-WKELM[J]. Power System Technology, 2021, 45(8): 3070-3080.
[32] 刘树鑫, 宋健, 刘洋, 等. 交流接触器触头系统运动分析及故障诊断研究[J]. 电工技术学报, 2021, 36(增刊2): 477-486.
Liu Shuxin, Song Jian, Liu Yang, et al. Research on motion analysis and fault diagnosis of contact system of AC contactor[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 477-486.
[33] 李舒适, 王丰华, 耿俊秋, 等. 基于优化VMD的高压断路器机械状态检测[J]. 电力自动化设备, 2018, 38(11): 148-154.
Li Shushi, Wang Fenghua, Geng Junqiu, et al. Mechanical state detection of high voltage circuit breaker based on optimized VMD algorithm[J]. Electric Power Automation Equipment, 2018, 38(11): 148-154.
[34] Zhang Lijun, Zhang Bin, He Fei, et al. Impact analyzing based on new method of phase space reconstruction[C]//2013 IEEE International Conference on Mechatronics and Automation, Takamatsu, Japan, 2013: 587-592.
[35] 向玲, 邓泽奇, 赵玥. 基于LPF-VMD和KELM的风速多步预测模型[J]. 电网技术, 2019, 43(12): 4461-4467.
Xiang Ling, Deng Zeqi, Zhao Yue. Multi-step wind speed prediction model based on LPF-VMD and KELM[J]. Power System Technology, 2019, 43(12): 4461-4467.
[36] He Jiangbiao, Yang Qichen, Wang Zheng. On-line fault diagnosis and fault-tolerant operation of modular multilevel converters—a comprehensive review[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(4): 360-372.
Abstract Dissolved gas analysis (DGA) in transformer oil is the most effective and convenient method for fault diagnosis of oil-immersed transformers. However, DGA only analyzes the real-time content of dissolved gases in transformer oil. Therefore, how to use effective historical data to accurately predict the content of dissolved gas in transformer oil for a period of time in the future is of great significance for transformer early fault diagnosis.
The content of dissolved gas in transformer oil is affected by external factors such as temperature and its own content, which will lead to nonlinear and non-stationary characteristics of the gas content sequence, leading to errors in the prediction accuracy. Aiming at the problem that the nonlinear and non-stationary characteristics of dissolved gas concentration series in power transformer oil affect the prediction accuracy, a prediction model of dissolved gas concentration in power transformer oil is proposed based on slime mold algorithm (SMA) to optimize the variated mode decomposition (VMD) and combined with gating cycle unit (GRU).
First, the preprocessed original sequence is detrended by the difference method. Secondly, based on the slime mold algorithm and the variational mode decomposition, a variational mode decomposition optimized by the slime mold algorithm is constructed, and the detrending sequence is decomposed into a set of stationary and regular mode components. Thirdly, the GRU with better prediction performance is used to predict the modal components obtained by decomposition. Finally, the final prediction result is obtained by superposition reconstruction.
The simulation results of 450 days historical data of an oil-carrying immersed transformer show that the absolute percentage error and root mean square error of the proposed prediction model for the H2 content of dissolved gas in transformer oil in the next 50 days are 0.36% and 1.76mL/L, respectively. Compared with the prediction model composed of empirical mode decomposition (EMD) and long short-term memory neural network (LSTM), the SMA-VMD-GRU prediction model proposed in this study has the smallest error. And the same method was used to predict the dissolved gas CH4, CO and total hydrocarbon content in the same transformer oil. The absolute percentage error of the three gas prediction results was 0.29%, 0.15% and 4.99%, respectively, and the root mean square error was 0.02mL/L, 1.13mL/L and 0.50mL/L, respectively. The effectiveness of the proposed prediction model based on SMA-VMD-GRU was verified.
Through simulation analysis, the following conclusions can be drawn: ①Using the difference method to extract the sequence trend term effectively solves the deficiency of VMD that cannot accurately extract the trend term. Then, through VMD decomposition after SMA optimization, the complex dissolved gas sequence in oil can be decomposed into a group of stable and periodic mode components, which effectively solves the problem of the influence of nonlinear and non-stationary characteristics of the original sequence on the prediction accuracy. ②In the prediction of dissolved gas in transformer oil, the GRU network converges faster than the LSTM network. Therefore, GRU network has more advantages than LSTM. On the premise that the differential method and VMD lifting sequence can be predicted in the early stage, the prediction accuracy of dissolved gas concentration in oil is further improved, which is helpful to the early fault diagnosis of transformers. ③The effectiveness of the prediction model of dissolved gas content in transformer oil based on SMA-VMD-GRU is proved by simulation and prediction experiments of various gas concentrations in dissolved gas in transformer oil.
Keywords: Difference method, slime mold algorithm, variational modal decomposition, dissolved gas in oil prediction, gate recurrent unit
DOI:10.19595/j.cnki.1000-6753.tces.221085
中图分类号：TM411
杨童亮 男，1996年生，硕士研究生，研究方向为电力设备状态监测与故障诊断。E-mail：Yang__TL@163.com
谢菊芳 女，1975年生，博士，副教授，硕士生导师，研究方向为电力系统自动化、电力设备状态监测与故障诊断。E-mail：375464831@qq.com（通信作者）
国家自然科学基金资助项目（51977179）。
收稿日期 2022-06-10
改稿日期 2022-08-11
（编辑 李冰）