图1 光伏机组P-U特性曲线
Fig.1 P-U characteristics of PV generation system
摘要 大规模光伏机组并网导致电力系统面临惯性下降与调频能力不足的问题。现有的有功备用方案虽然可以满足一次调频的需求，但难以提供惯量支撑，且弃光运行会影响发电效益。为此，提出一种储能辅助光伏机组实现虚拟惯量和一次调频的协调控制策略，在保证光伏发电效益的同时能够减少一半的储能容量。所提策略通过光伏变功率跟踪响应频率上扰、储能装置响应频率下扰的方式进行一次调频，并控制储能装置为系统提供惯量支撑。构建数学模型揭示由锁相环测量频率变化率（RoCoF）引发惯性功率跌落的本质原因，据此提出了运用一阶高通环节对频率变化率测量值进行修正的方法，以提升虚拟惯量控制效果。通过微电网算例仿真对比分析了有功备用控制和所提协调控制的频率调节效果，结果表明协调控制策略性能更优。
关键词：变功率跟踪 储能装置 协调控制 频率调节 光伏发电 锁相环
从2015年底至今，我国光伏和风机的装机容量一直位居世界首位，并仍呈现增长趋势[1]。根据国家能源局数据，截至2020年底，我国光伏并网发电装机容量累计达到2.53亿kW（占总装机容量的12%）。到2030年，风电、太阳能发电总装机容量将达到12亿kW以上[2]。未来利用太阳能发电将会成为主流能源利用形式，然而已投运光伏机组普遍采用最大功率点跟踪（Maximum Power Point Tracking, MPPT）算法，使其无法参与系统的一次调频且缺乏传统发电机的惯量阻尼特性，电力系统更容易受到功率波动和系统故障的影响[3-4]。针对该问题，部分新能源高渗透国家/地区已明确要求新能源发电机组必须具备一定的参与电网调频能力[5]。我国《电力系统网源协调技术规范》（DL/T1870—2018）中已明确了“新能源一次调频技术”相关要求。新能源（风电场、光伏发电站）通过保留有功备用或配置储能设备，并利用相应的有功控制系统来实现一次调频功能。要求并网运行时一次调频功能始终投入并确保正常运行。
配置电池或超容储能方案具有可控性强的特点，不仅可以参与一次调频，还可以提供快速的惯量功率支援来抑制系统频率快速波动；能够多模式和多场景运行，尤其适用于离网模式和夜间场景[6-9]。目前，针对光伏机组配置储能装置的方案已有较多研究，分为光储一体化并网结构[10-13]和光伏、储能独立并网结构[8, 14-16]，其在国内的示范工程中均有应用[17]。但在应用实践中仍然存在一些问题，如配套测试规范的量化指标不清晰、关键参数的整定、储能单元的配置以及调频效果方面还有待优化与提升[17]。
有功备用方案需要为参与调频预留一定的备用容量。该方案的初衷是解决配置储能方案的造价和维护成本较为昂贵的问题，而且部分地区的光伏电站还存在“弃光”现象，但有功备用方案降低了光伏发电效益。文献[18-21]针对有功备用控制研究了变功率点跟踪（Variable Power Point Tracking, VPPT）算法的实现。文献[22]提出在不依赖储能装置的情况下，将光伏电源通过虚拟同步机（Virtual Synchronous Generator, VSG）技术与电网相连，并验证了其在离网和并网模式下的有效性。文献[4-5, 23]研究了通过有功备用控制实现光伏为电网提供惯量支撑和一次调频的方法。文献[24]针对有功备用方案进行了快速一次调频的现场试验。需要指出的是，受限于功率跟踪算法的步长和秒级响应速度[24]，有功备用方案能够达到的惯量支撑效果较弱，且难以在实际工程中实施。
上述文献对配置储能方案和有功备用方案分别进行了研究和验证。基于场景及需求，这两种方案有效结合亦或是其他方案，最终寻求更经济更有效的应用方案是大规模新能源机组参与电网调频亟待解决的问题之一[17]。针对两种方案的比较，文献[25]从平抑光伏并网功率波动的需求出发，通过电价对比分析表明配置电池储能与减载运行相配合是最经济的方案。文献[26]针对双馈风电机组参与一次调频的需求，探索了配置储能和变功率跟踪方案的结合，提出一种双馈风电机组和超级电容储能的协调控制策略，进行技术性和经济性两方面的论证，结果表明协调控制方案优于预留 10%备用容量的方案。然而，针对光伏机组参与一次调频和惯量支撑的场景及需求，变功率跟踪与储能相结合的控制方案鲜有报道，有待探索储能提升光伏机组调频效果的协调控制策略。
为改善调频效果，在一次调频控制基础上，增加的基于频率变化率（Rate of Change of Frequency，RoCoF）反馈的虚拟惯量控制也被广泛采用。但由于突加负荷扰动下锁相环（Phase Locked Loop, PLL）或锁频环（Frequency Locked Loop, FLL）难以精确测量实际的频率变化率响应[27]，虚拟惯量控制效果欠佳。当前，针对频率变化率难以准确测量的原因和改进方法的研究并没有得到足够重视。为了提高惯量支撑控制效果，文献[27]放弃锁相环，而直接通过通信的方式获取虚拟同步机的内禀角频率和频率变化率，进而用作光储单元虚拟惯量控制环节的输入信号。这种方式依赖高带宽通信，不适用于分布式和分散式结构微电网。文献[28]提出一种自适应机制，可以提高相位大范围跳变情况下锁相环相位角和频率响应的动态性能。但负荷突变伴随的相位角变化量较小，此时文献[28]的自适应锁相环无法改善频率测量性能。因此，有必要研究突加负荷扰动下频率变化率难以准确测量的原因和改进方法。
为了增强调频能力，本文提出一种储能辅助光伏机组惯量支撑和一次调频的光储协调控制策略。该策略在无频率扰动时光伏运行在最大功率点处，当频率升高时通过VPPT减少光伏出力，当频率降低时由备用的储能装置提供调频功率。为提升惯量支撑效果，针对锁相环难以精确测量实际频率及频率变化率的问题，进行了分析和改进。所研究内容对于大规模光伏发电系统的技术升级和改造具有一定的参考意义。
有功备用控制以光伏机组的输出特性曲线为基础。光伏机组的稳定运行区域为右侧区域，而左侧区域为不稳定区域[4, 23]。光伏机组的P-U特性曲线如图1所示，A点为光伏机组在减载率为d%的有功备用点，输出功率为PA；M点为光伏机组正常运行时的最大功率点，输出功率为PM。根据国标《虚拟同步机技术总则》可知[29]：系统频率下降/上升期间，光伏虚拟同步机应增加/减少有功输出，有功出力可调节量的最大值至少为10%PN，PN为额定功率。因此将减载率d%定为10%，PB为光伏机组在频率上升期间的功率最低点。
图1 光伏机组P-U特性曲线
Fig.1 P-U characteristics of PV generation system
为使光伏系统参与一次调频，引入具有下垂特性的一次调频控制环节，有功备用控制框如图2所示[3]。系统初始时首先以MPPT算法运行在最大功率点PM；之后切换成有功备用算法，根据最大功率点PM可求得减载后运行点。
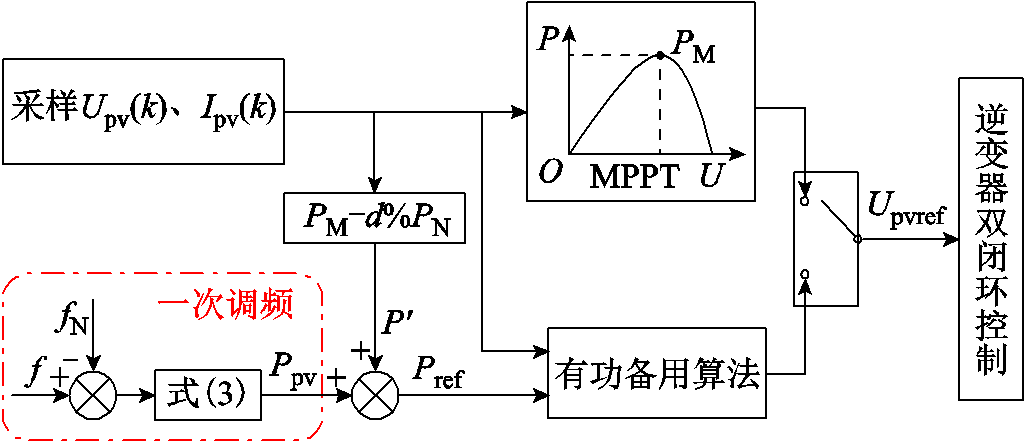
图2 有功备用控制框图
Fig.2 Control block diagram in active-power reserve mode
由图2可知，有功备用模式下功率参考为
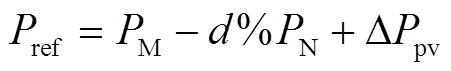（1）
式中，Pref为光伏的参考功率值。
无频率扰动时光伏机组运行在有功备用点；当检测到频率偏差大于±0.033 Hz的死区[30]时一次调频环路发生作用，引起的光伏出力偏差为
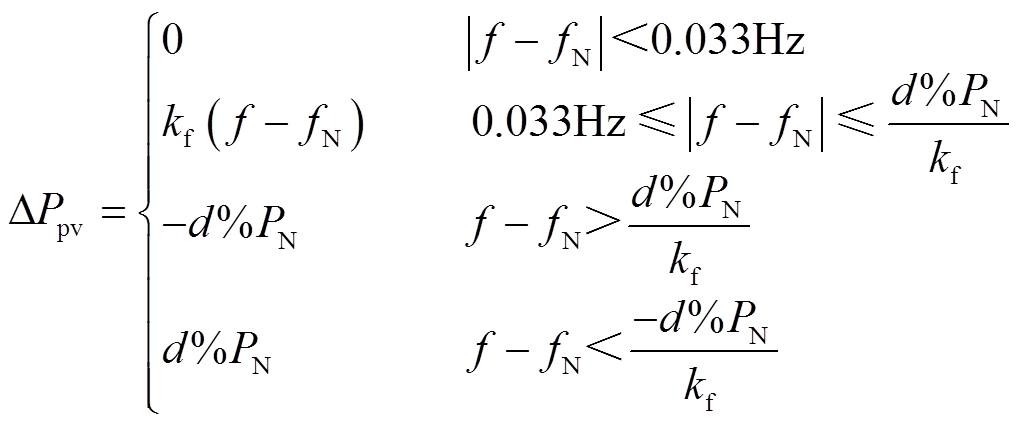（2）
式中，kf为一次调频系数；f为电网实际频率；fN为额定频率。
由于系统不断地在MPPT控制和有功备用控制之间切换运行，控制模式切换频繁[4]，易影响系统的稳定性。而且当网侧出现频率升高导致的出力减小时，光伏直流电压进一步增大，易达到限值。为此，需要进一步探索最大功率跟踪算法在正常工作时的最大化发电效益，即将变功率跟踪与超级电容储能结合的模式。
采用VPPT算法与超级电容储能结合的工作模式，在系统正常工作时，以MPPT算法运行在点M；当频率升高时，VPPT算法启动，使光伏系统由M点开始运行至右侧区域。
根据网侧频率波动判断扰动类型，Δf = f-fN。当Δf＞0.033Hz时，系统负荷减小或频率升高；Δf＜-0.033Hz时，系统负荷增加或频率降低；|Δf |≤0.033Hz时，系统无扰动。根据不同扰动情况采用不同的控制模式。无扰动的情况下光伏系统运行在MPPT模式。
频率升高时的一次调频策略：若频率偏高并大于0.033 Hz的一次调频死区，则一次调频控制启动，并得到功率参考值ΔPpv为
（3）
根据式（3），进一步得到频率偏高时光伏的参考功率值Pref为
（4）
采用图3的VPPT算法实现目标值Pref的跟踪。
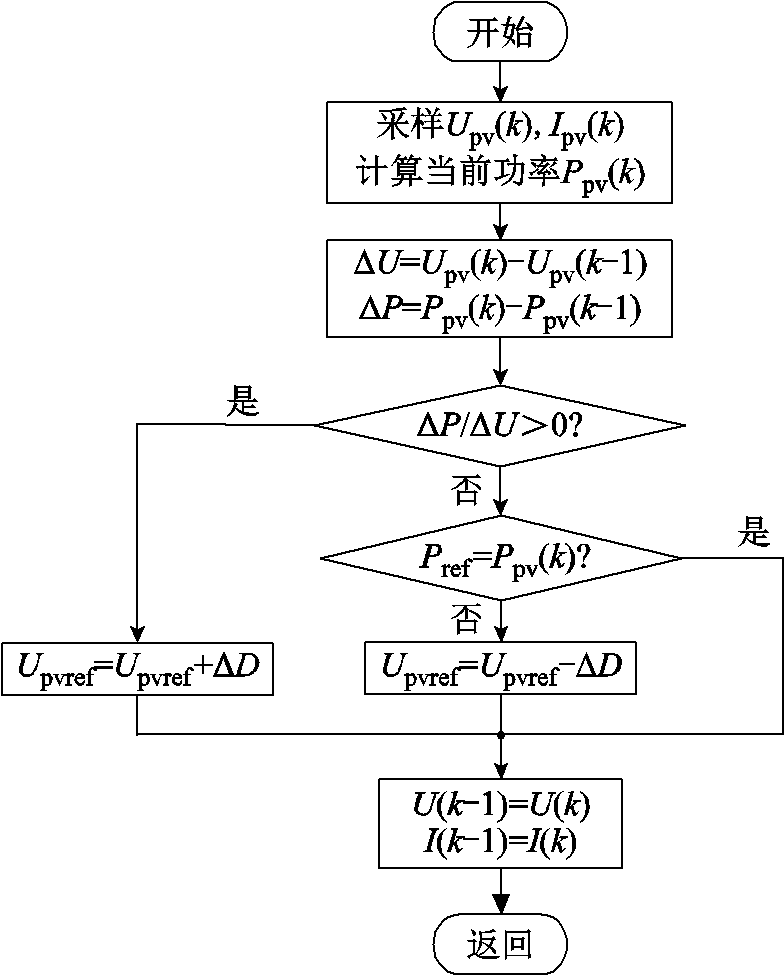
图3 变功率跟踪算法流程
Fig.3 Flow chart of VPPT algorithm
在频率降低时，由于光伏系统已经运行在最大功率点，无可用的调频容量，因此需要配置储能装置。光伏系统储能配置如图4所示，储能装置经过双向DC-DC变换器与光伏直流侧母线电容相连接。为防止过充或过放，储能系统一般对SOC值进行约束[31]，则有
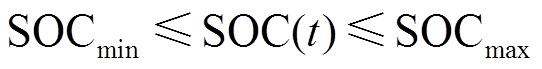（5）
式中，SOCmin和SOCmax为限值。在无扰动的情况下，储能系统进行恒功率充电（Pscref = Psc0）以使SOC保持在SOCmax。当发生频率扰动后，超级电容储能系统根据一次调频功率和惯量支撑功率参考值之和进行充放电，即Pscref=ΔPsc1+ΔPsc2，其中一次调频功率参考值ΔPsc1如式（6）所示，惯量支撑功率的参考值ΔPsc2见第2.3节。放电过程中如果SOC(t)≤ SOCmin则停止放电，充电过程中如果SOC(t)＞SOCmax则停止充电。
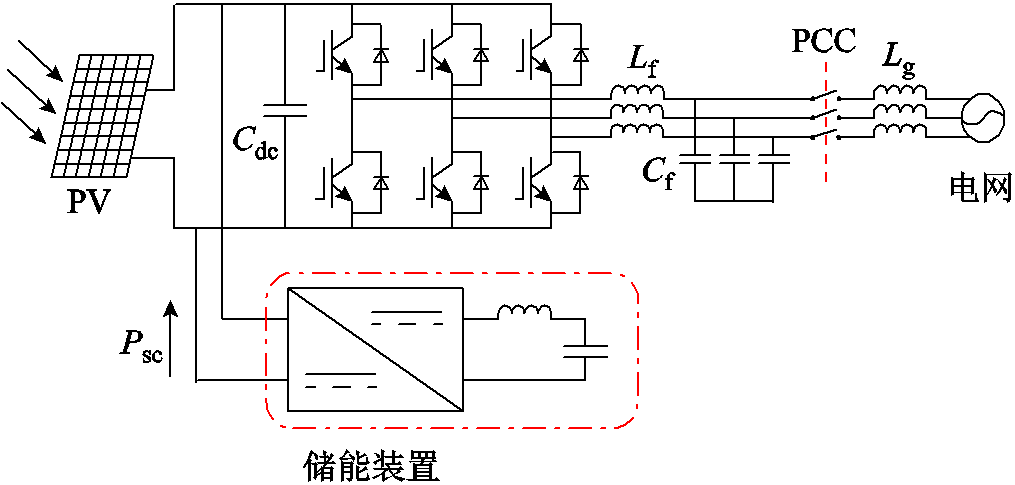
图4 光伏系统储能配置
Fig.4 Storage configuration for PV generation system
（6）
储能装置除参与一次调频过程以外还可以提供快速的惯量功率支撑。通常采用频率微分反馈进行惯量支撑控制，其参考值ΔPsc2为[32]
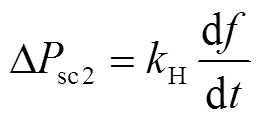（7）
式中，kH为虚拟惯量系数。扰动过程中电网频率的变化率df/dt可由PLL或FLL实时测量和记录[32]。
根据相关标准[29]的容量配置方法参见文献[26]。以容量为500kW的集中式光伏逆变器为例，光伏系统配置10%PN的储能备用，储能参与惯量调频和一次调频的时间为30s，则储能容量We为50kW× 30s。综合考虑超级电容器组的成本和放电效率问题，采用160V×12F 超级电容器2串5并共10组作为光伏机组的储能装置，其最低工作电压Umin为16.8V，最高工作电压Umax为320V，其放电效率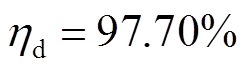
。
综上所述，基于变功率跟踪和储能单元协调控制的光储系统调频控制框图和流程如图5所示。
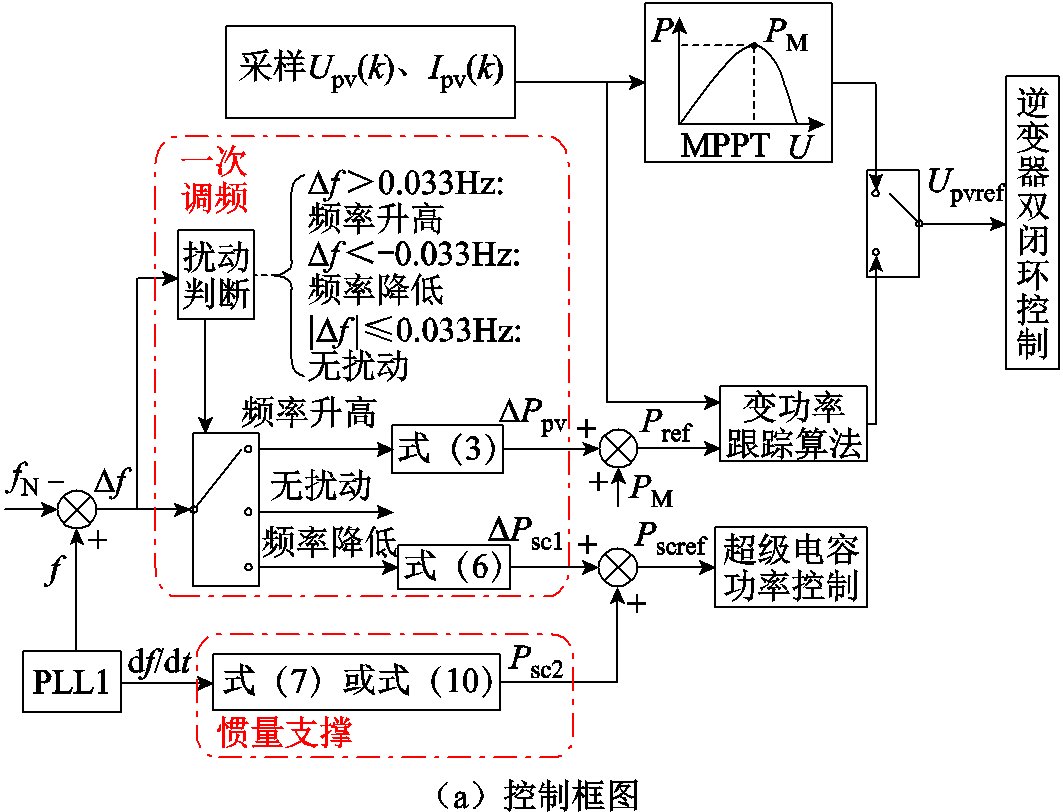
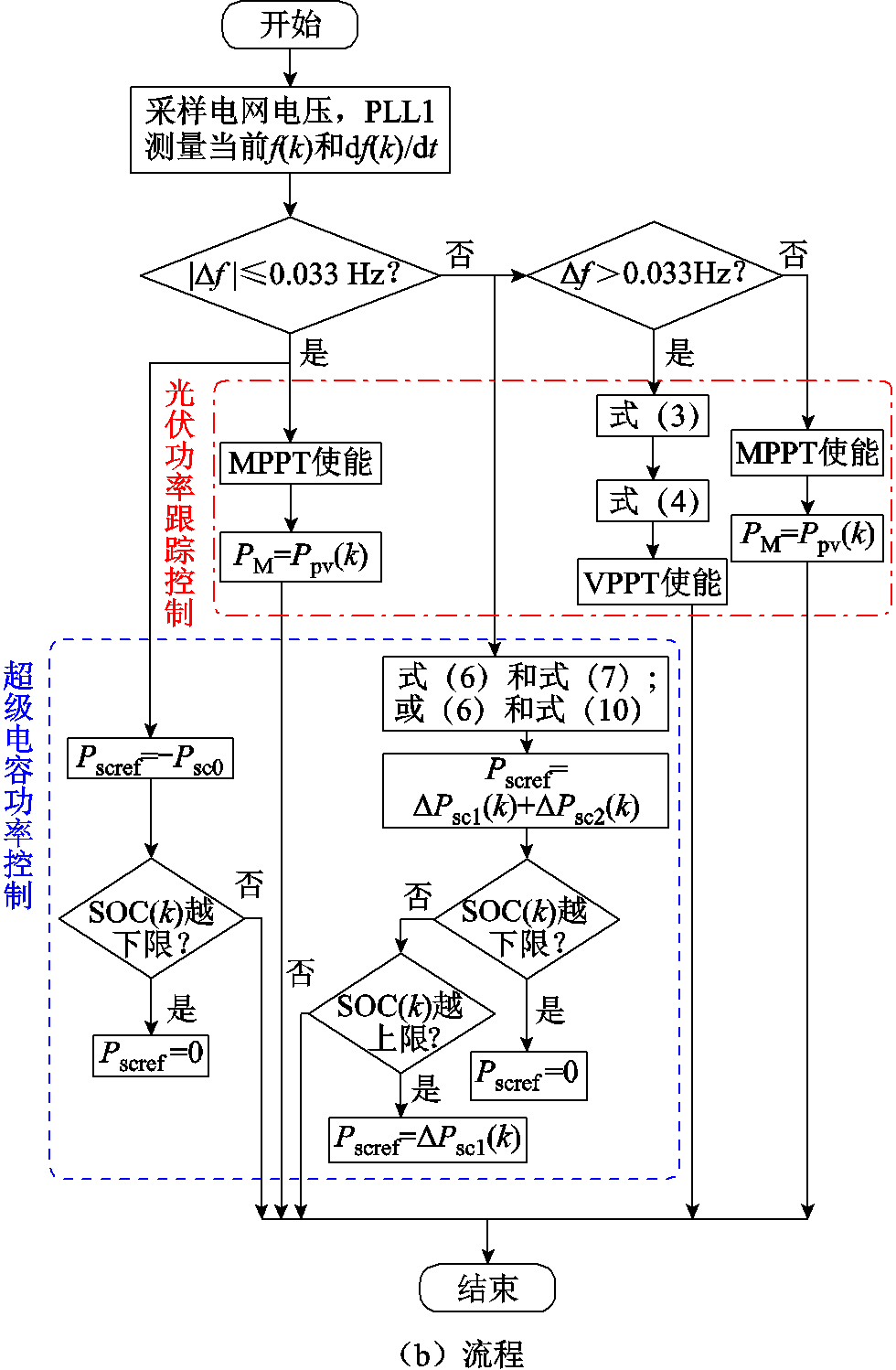
图5 变功率跟踪和超级电容储能的协调控制
Fig.5 Coordinated control of VPPT and supercapacitor energy storage
两种调频方案的技术经济性对比见表1。可知采用有功备用的调频方案虽然仅改造控制系统，但其频率上扰的调节深度小，且光照不充足工况下（如光伏出力低于20%PN）需切回MPPT模式而无法参与调频；相比之下，配置储能装置方案的频率上扰调节深度大，光照不充足工况适用性强，并且由于超级电容储能装置参与调频过程，光储系统能够快速地提供惯量支撑功率，技术性更加完备。
表1 两种应用模式技术经济性对比
Tab.1 Technical and economic comparison of the two application modes
应用模式实施复杂度调频深度惯量支撑效果适用工况经济性 预留10%pu备用容量仅改造控制系统频率上扰调节深度小一般光照充足年均损失6万元/（MV·A） 配置10%pu容量的储能装置改造控制系统和增设装置频率上扰调节深度大较好光照充足和不充足年均投资3.2万元/（MV·A）
尽管式（7）的虚拟惯量控制方案已被广泛采用，但由于负荷突变时PLL或FLL难以精确测量实际频率变化率[28]，式（7）的方案控制效果欠佳。有必要研究频率变化率精准测量方法。
以两种典型锁相环为例，结构如图6a、图6b所示[33-34]。PLL1和PLL2的区别是环路滤波器的差异。PLL1和PLL2的环路滤波器分别为一阶惯性环节和PI（比例-积分）环节，如式（8）所示。两种锁相环的线性化模型如图6c所示。图中，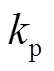
为比例系数，ki为积分系数，Tf为滤波时间常数。
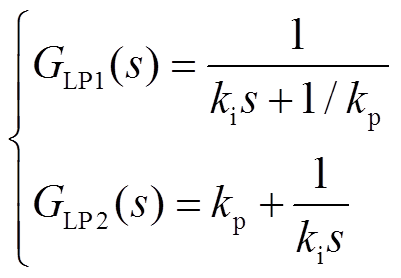（8）
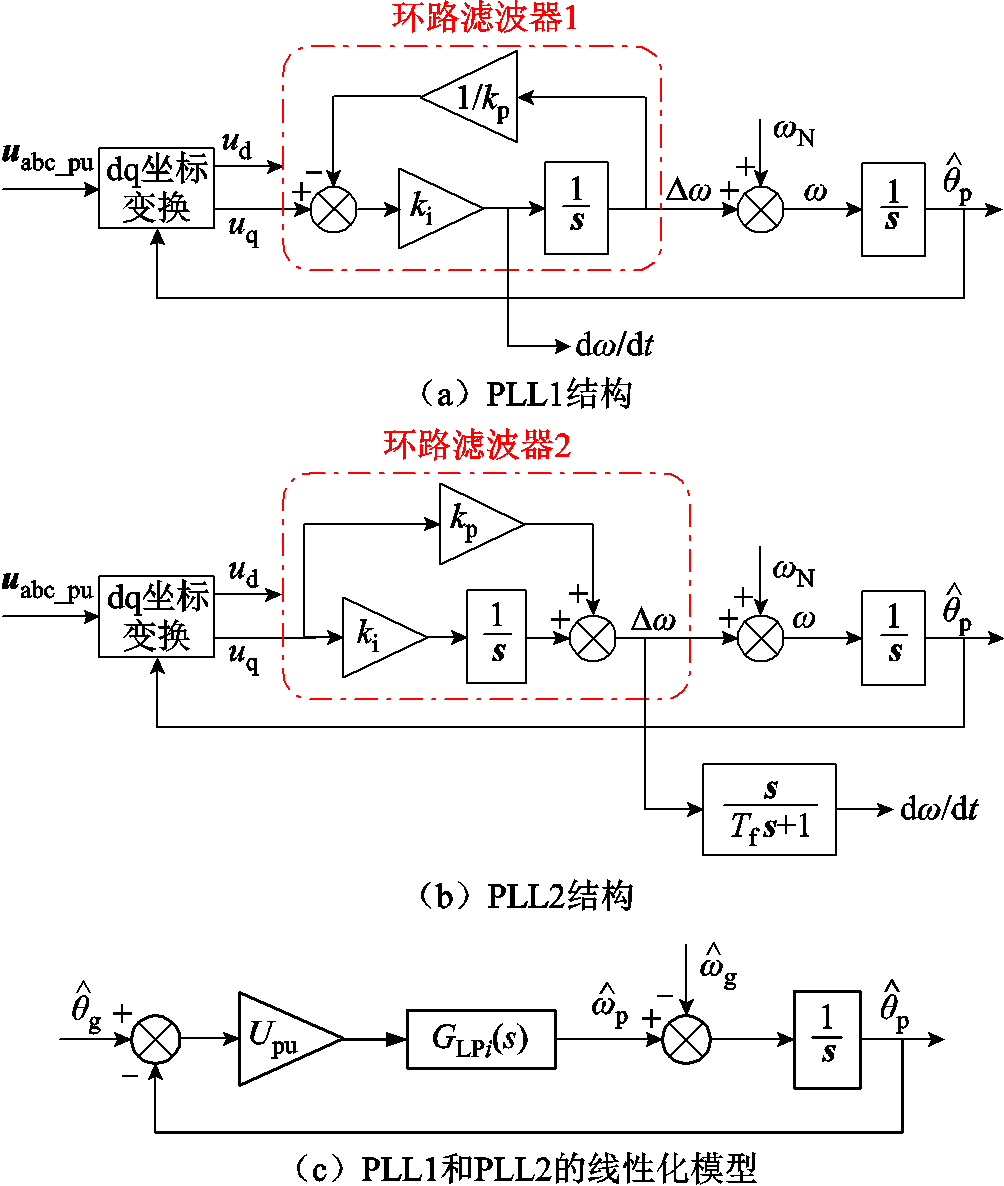
图6 两种PLL结构及其线性化模型
Fig.6 Two kinds of phase-locked loops and their linearization models
算例系统如图7所示。为便于对锁相环的动态特性进行剖析，暂不考虑同步发电机的接入，分别建立单机和双机并联系统的线性化模型。
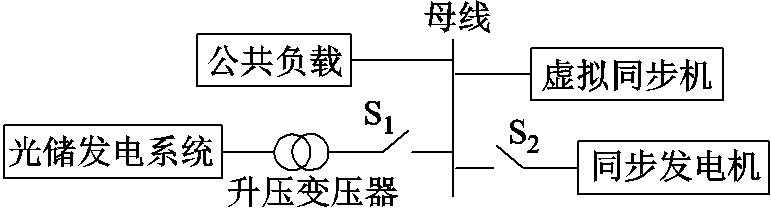
图7 仿真系统
Fig.7 Simulation system
首先以虚拟同步机[35]和负载构成的单机系统来测试两种锁相环在有功负载突加情形下的动态响应。单机系统频率响应的传递函数为
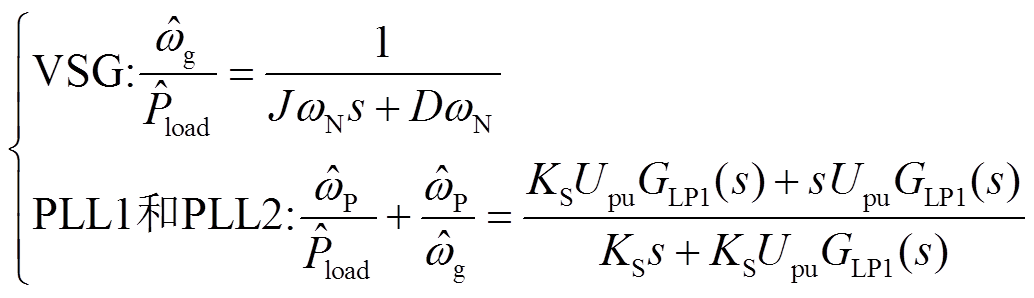（9）
式中，Pload为负载有功功率；KS为同步系数；上标“^”表示小扰动量。频率变化率响应的传递函数为频率响应传递函数乘以s算子。频率及频率变化率的仿真测量结果和线性化模型的响应如图8所示，参数见附表1。对比可知：PLL2的频率和频率变化率均会突变，动态性能较差，而PLL1的频率和频率变化率的测量准确度较高；但在扰动初始阶段，PLL1和PLL2频率变化率的测量结果都存在一个振荡波动。
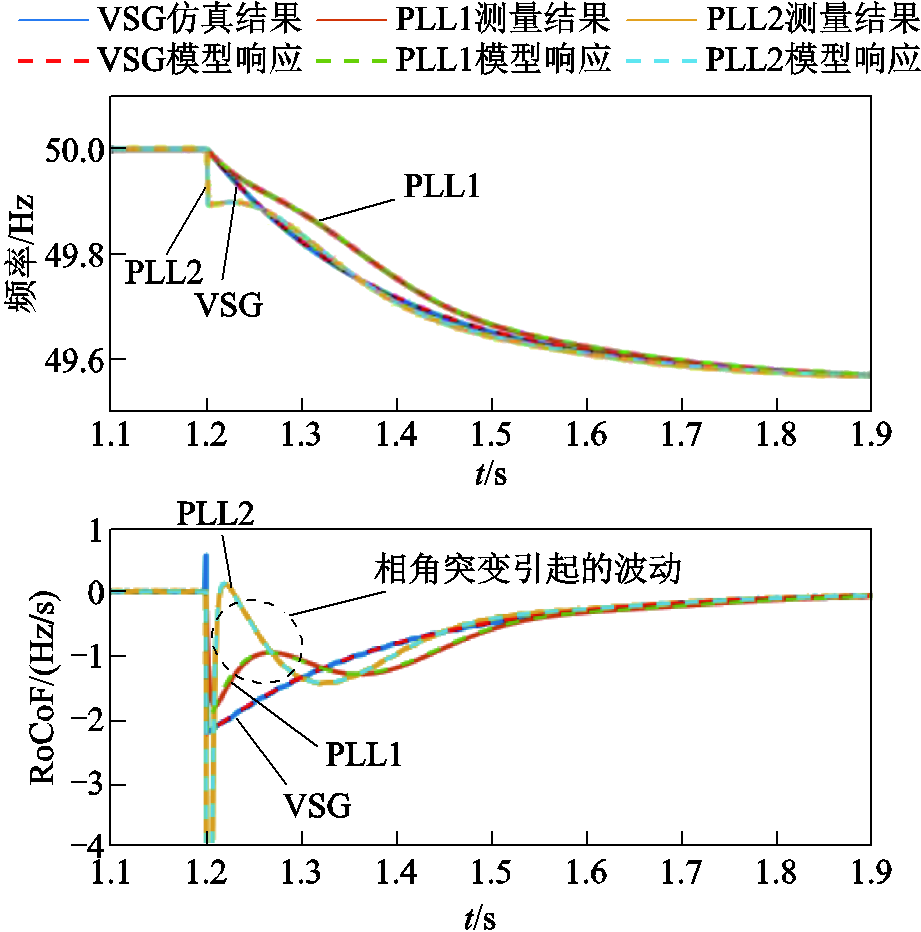
图8 单机系统PLL1和PLL2的测量结果及模型响应
Fig.8 Measurement results and model response of PLL1 and PLL2 for single-machine system
突加功率扰动下PLL难以精确测量实际频率及频率变化率的原因是：功率扰动下实际系统会出现相位突变和频率变化这两个过程；PLL测量的频率及频率变化率由这两个过程引起，其中相位突变会使频率及频率变化率难以准确测量，特别是使得频率变化率的测量结果出现振荡波动。
进一步地，构建光储单元和虚拟同步机并联系统功率频率响应的线性化模型，如图9所示，其中光储单元采用式（6）和式（7）的一次调频和惯量支撑控制方案，频率由PLL1测量。并联系统的仿真测量结果和线性化模型的响应如图10所示，两类响应保持一致，表明所构建的线性化模型能够准确描述算例系统的动态特性。对比图8和图10可知，光储单元的接入主要是减小了稳态频率偏差，由相位突变引起的一个PLL1频率变化率的振荡波动仍然存在于扰动初始阶段。对应地，这可能导致储能系统提供的惯量支撑功率出现回落/跌落现象，弱化惯量控制效果。
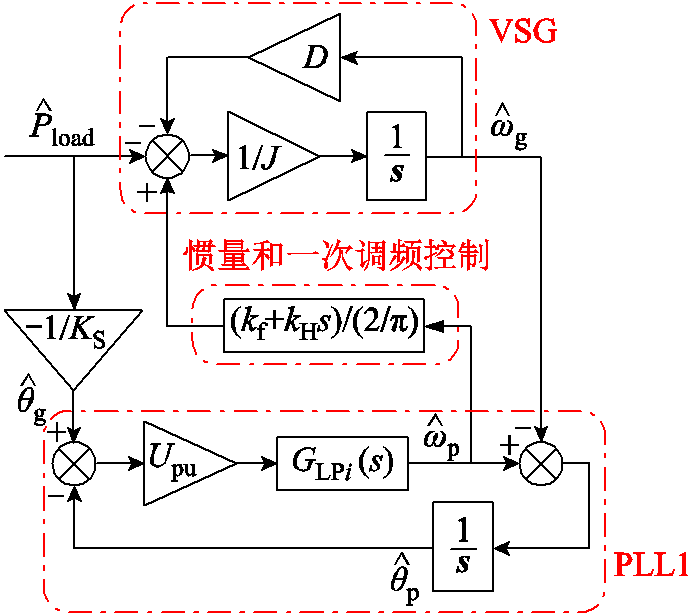
图9 光储单元和虚拟同步机并联系统的小信号模型
Fig.9 Small signal model of the parallel system of PV-storage unit and virtual synchronous generator
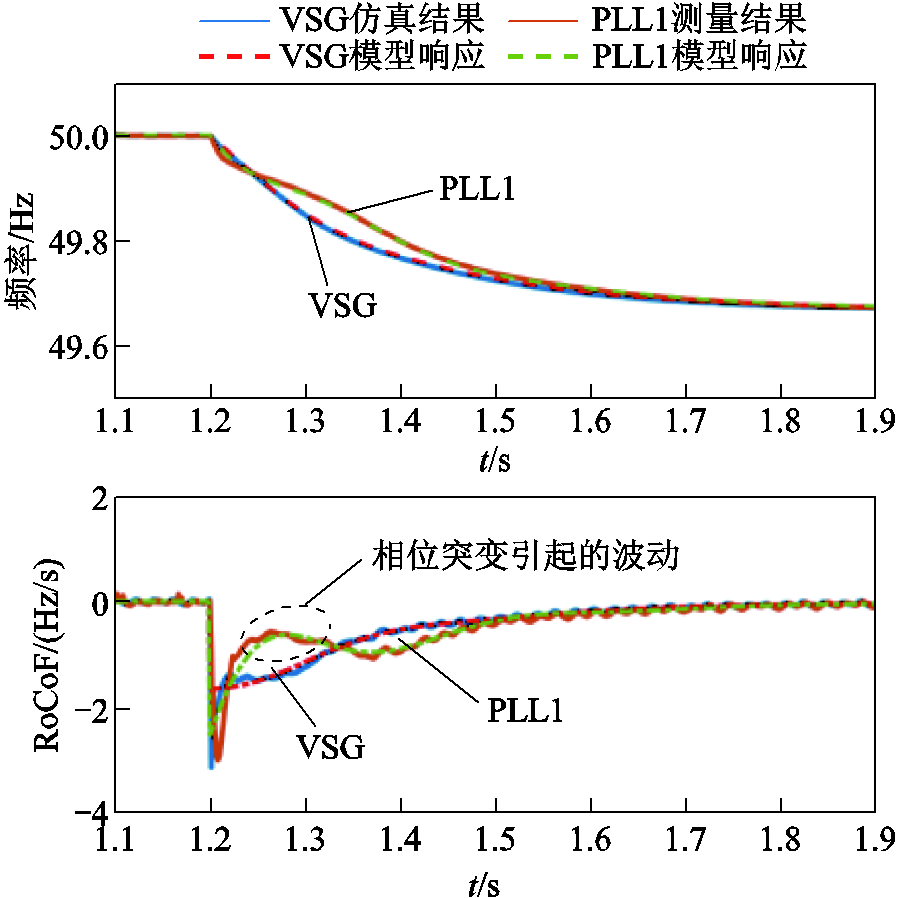
图10 并联系统仿真测量结果和模型响应
Fig.10 Simulation results and linearized model response for the parallel system
为此，提出对PLL1频率变化率的测量进行修正。具体方法是：当PLL1测量的RoCoF大于限值
并达到最大值Rmax后，选择一阶高通环节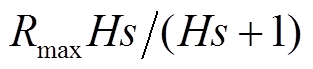
的响应作为频率变化率的测量值；当RoCoF小于限值或未达到最大值Rmax时，直接选择RoCoF作为频率变化率的测量值。PLL1频率变化率的测量结果及修正后的测量结果如图11所示，可见修正后的测量值能够近似表征实际系统的频率变化率，避免了测量结果出现振荡波动的情况。
运用修正的频率变化率测量结果进行惯量功率参考值ΔPsc2的计算。当RoCoF大于限值并达到最大值Rmax后，通过一阶高通环节
计算参考值ΔPsc2；当RoCoF小于限值或未达到最大值Rmax时，通过式（7）计算参考值ΔPsc2。计算公式为
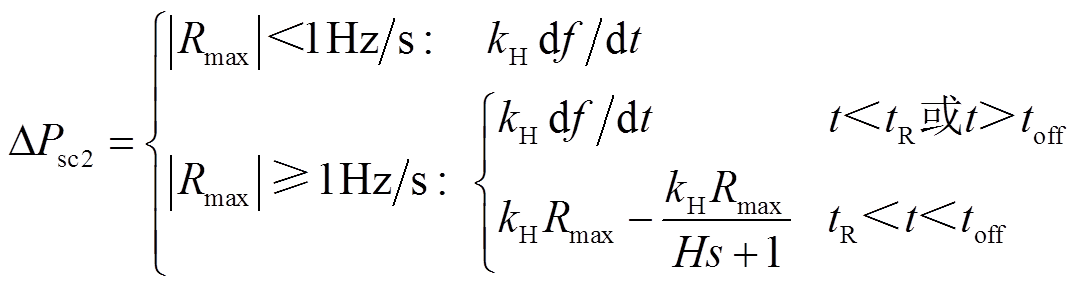（10）
式中，tR为RoCoF达到最大值Rmax的时刻；toff为退出一阶高通环节控制指令的时刻，具体见图11的坐标标注。在RoCoF较小时（设为0.1）结束一阶高通环节控制，重新切回频率微分环节控制。
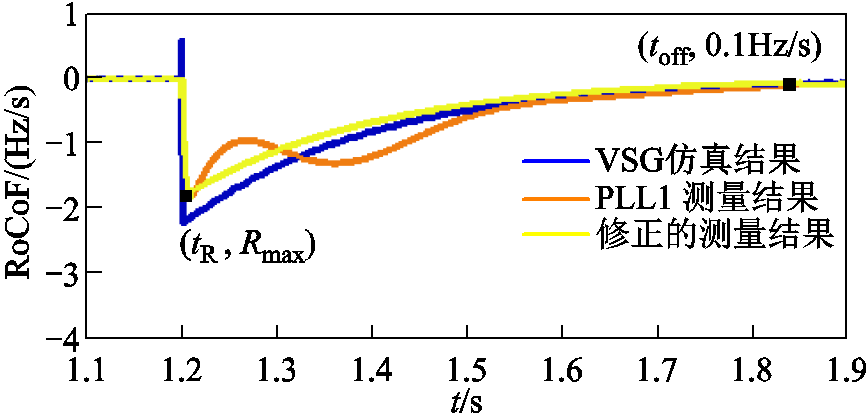
图11 PLL1频率变化率的测量结果及修正后的测量结果
Fig.11 Measurement results of RoCoF and the corrected measurement results for PLL1
4.1.1 参数设置
1）根据调频深度Δfmax和光储系统总调频容量来确定一次调频系数kf和虚拟惯量系数kH。设光储系统总调频容量占额定容量的10%，虚拟惯性功率和一次调频功率之和，也即总调频功率的大小不应超过10%PN。再取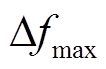
= ±0.5 Hz，代入式（11）可确定两个参数值。
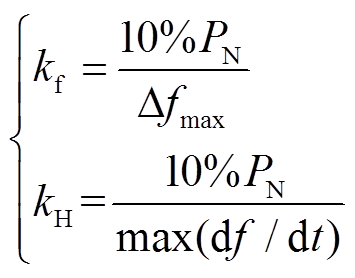（11）
2）在电网频率降低的小扰动下，功率和频率的频域关系为
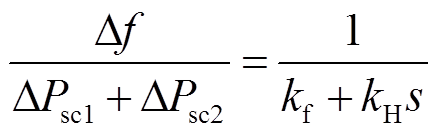（12）
根据式（12），为提升惯量控制性能，应取一阶高通环节的时间常数H≥kH/kf。
3）RoCoF限值是根据所研究系统的惯量水平和负荷扰动大小DPload确定的。算例系统的总惯量为Jå，算例系统界定的扰动功率为DPload_def，则近似计算可得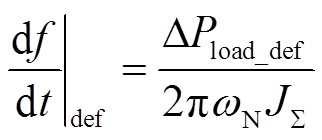
。RoCoF的限值即为
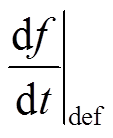。文中同步发电机和虚拟同步机的总惯量为Jå=76.6 kg·m2，负荷扰动界定值为150kW，可得
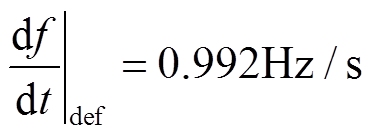，因此限值设置为1Hz/s。当扰动大于界定的负荷扰动值时，RoCoF达到限值，此时对锁相环的RoCoF测量值进行修正来提高光储单元的惯量支撑能力。
4）初始状态光照强度为850W/m2,温度25℃保持不变，超级电容初始电压为300V。同步发电机及其调速器和励磁控制器参数见文献[35]。其他光储系统仿真参数见附表1，表中kH= -12 500，其等效惯量为JPV= -kH/(2πwN)= 6.33 kg·m2。
4.1.2 工况设置：
闭合图7的算例系统中开关S1和S2，用500kV×A电压源型VSG和1MV×A同步发电机模拟弱电网。光伏系统容量为3MV×A，包含6个光储发电单元。为验证光储系统协调控制方案的各项性能，对四种调频方案进行比较，分别为：方案1，不参与调频的方案/MPPT模式；方案2，有功备用方式的一次调频；方案3，储能和VPPT协调控制的惯量支撑与一次调频，惯量功率计算公式为式（7）；方案4，储能和VPPT协调控制的惯量支撑与一次调频，惯量功率计算公式为式（10）。
四种方案的仿真结果如图12所示，仿真情形见表2。图12中展示了直流侧电压、光储系统总输出有功功率、VSG频率的波形。
表2 仿真情形
Tab.2 Simulation cases
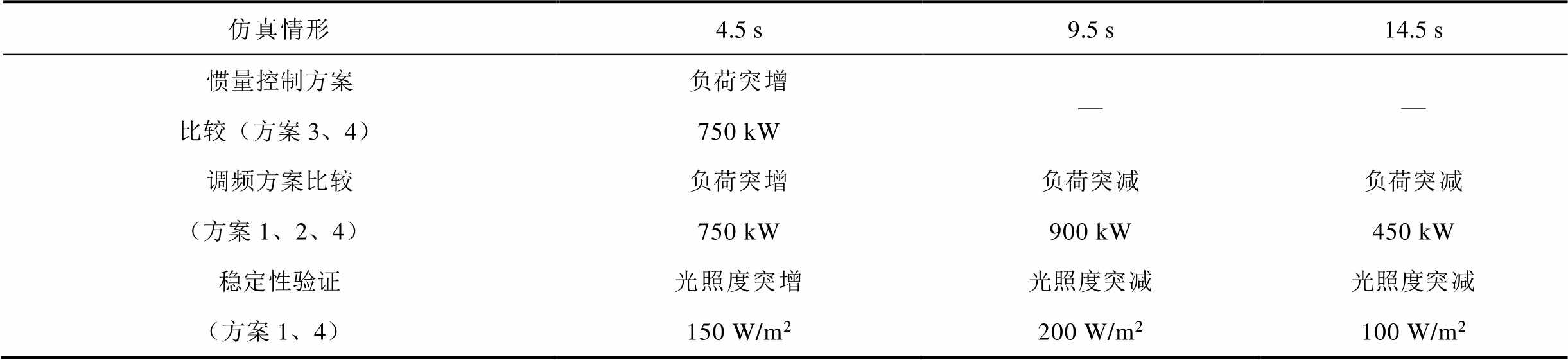
仿真情形4.5 s9.5 s14.5 s 惯量控制方案比较（方案3、4）负荷突增750 kW—— 调频方案比较（方案1、2、4）负荷突增750 kW负荷突减900 kW负荷突减450 kW 稳定性验证（方案1、4）光照度突增150 W/m2光照度突减200 W/m2光照度突减100 W/m2
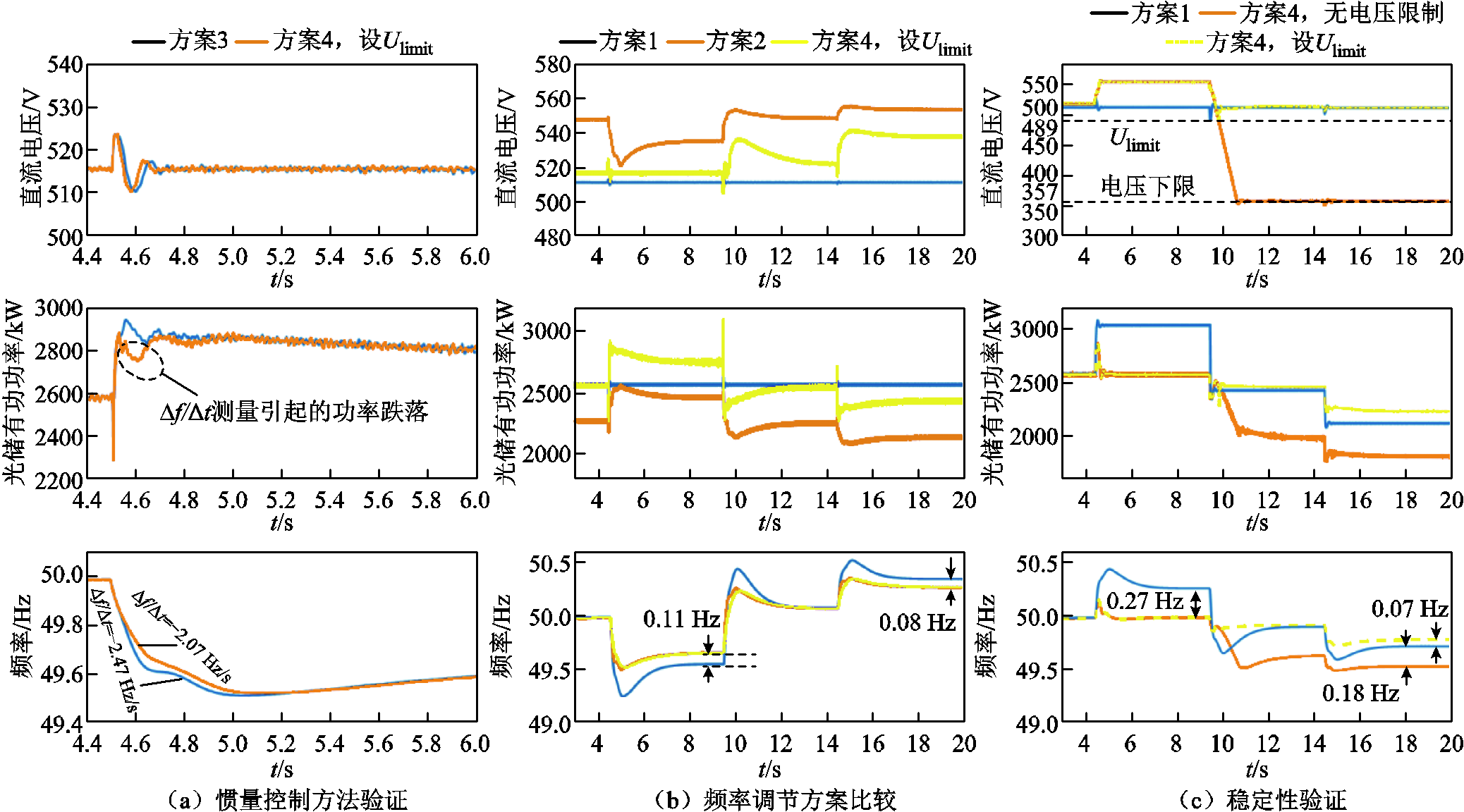
图12 不同工况下的仿真结果
Fig.12 Simulation results under different operating conditions
为验证本文提出的PLL1频率变化率测量的修正方法，图13中比较了PLL1测量结果和修正后测量结果的误差，图中RoCoF测量误差为测量结果与仿真结果的差值。可见，修正后测量值的误差较小。进而对式（7）和式（10）这两种惯量控制方式进行对比，如图12a所示。可知，采用式（7）时，负荷突增后的0.2s内会出现由df/dt测量引起的功率跌落，导致储能单元不能够有效地提供惯量支撑功率。而采用式（10）能够避免出现功率跌落状况，储能单元能够有效地提供惯量支撑功率来减小频率变化率，扰动后0.15s内的平均频率变化率由2.47Hz/s降至2.07Hz/s。
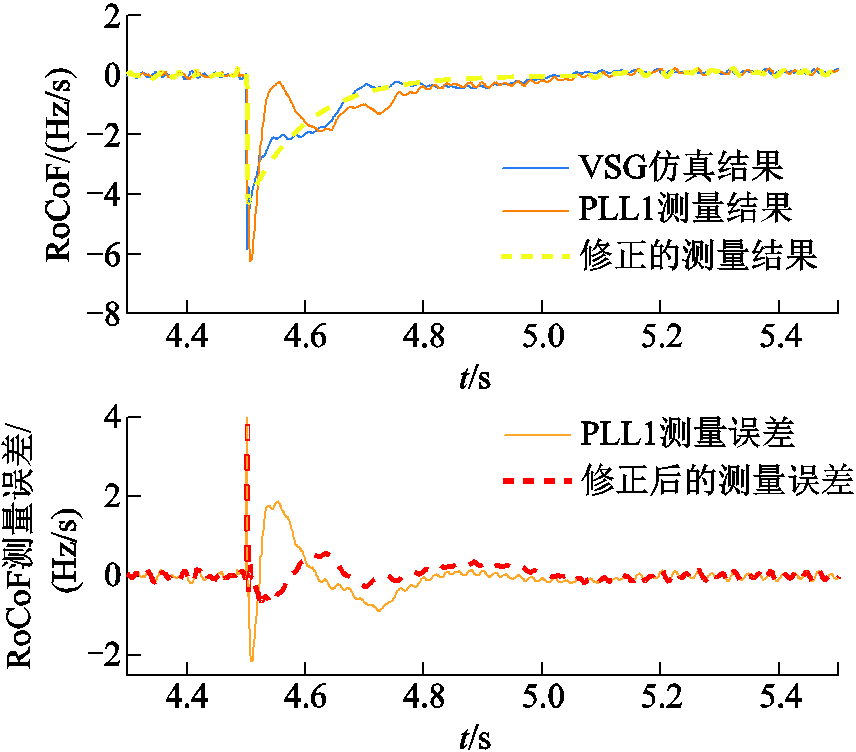
图13 频率变化率测量结果的对比
Fig.13 Comparison of measurement results of RoCoF
负荷突变的工况设置见表2，调频方案1、2、4的仿真结果如图12b所示。方案4控制下储能单元的波形如图14所示。可见，方案2随着负荷增加/减小，直流电压减小/增加，通过有功备用算法进行一次调频。虽然有功备用方案中也可以加入惯量控制环节[23]，但由于有功备用跟踪算法的响应速度慢于超级电容储能系统，其减小频率变化速率的效果弱于光储系统协调控制方案4。方案4在负荷突增时，储能单元处于放电状态，同时提供惯量支撑功率和一次调频功率；而在负荷突减时，储能单元处于充电状态并通过吸收较少的电量来提供惯量支撑，由光伏系统通过VPPT的方式进行一次调频。
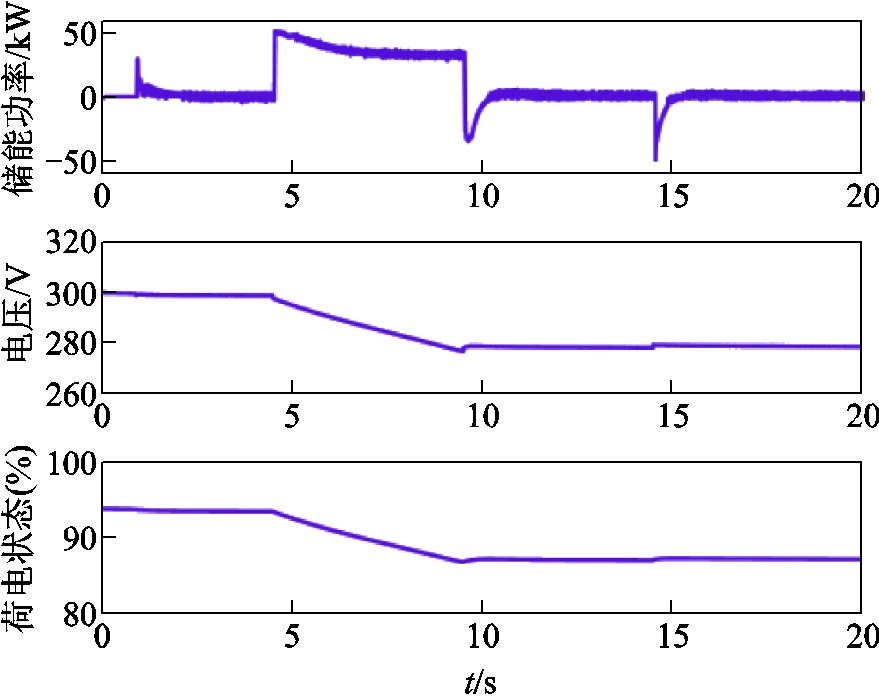
图14 方案4在负荷突变情形下储能单元的波形
Fig.14 Waveforms of energy storage unit in cases of load increase and decrease for control scheme 4
对比三种方案，方案2、4均能够减小稳态频率偏差，但只有方案4能够减小负荷扰动后0.1s内的频率变化速率，起到抑制频率快速波动的效果。
在光照强度突变的情形下对所提光储协调控制策略的稳定性进行仿真验证。光照强度突变时光伏单元可能运行到左半平面（不稳定区域），恶化系统的频率响应。为此，设置最低运行电压为低于最大功率点电压20V的电压值[23]，即Ulimit=UM-20V。当实时采集的直流电压小于Ulimit时光伏系统控制模式即刻由VPPT模式切换回MPPT模式。
光照强度突变的工况设置见表2，方案1、无Ulimit的方案4、设置Ulimit的方案4的仿真结果如图12c所示。光伏系统的PV特性曲线及实际运行轨迹如图15所示，图15a为方案1，图15b为方案4且不设置Ulimit，图15c为方案4且设置Ulimit= UM-20V。方案1在光照强度突变工况下，光伏单元始终稳定在最大功率点处，运行轨迹为多段线M1M2M3M4。方案4在光照强度突变工况下，无Ulimit限制时，光伏单元的运行轨迹为多段线A1A2A3A4M3A5A6A7；有Ulimit限制时，光伏单元的运行轨迹为多段线A1A2A3A4M3A8M3M4。可见，方案4在光照强度突增时不会引起不稳定，光伏单元始终运行在右半平面（稳定区域），并且系统频率能够无偏差地稳定在50Hz。而光照强度突减会引起不稳定，光伏单元的运行轨迹会从右半平面经最大功率点M3后进入左半平面。
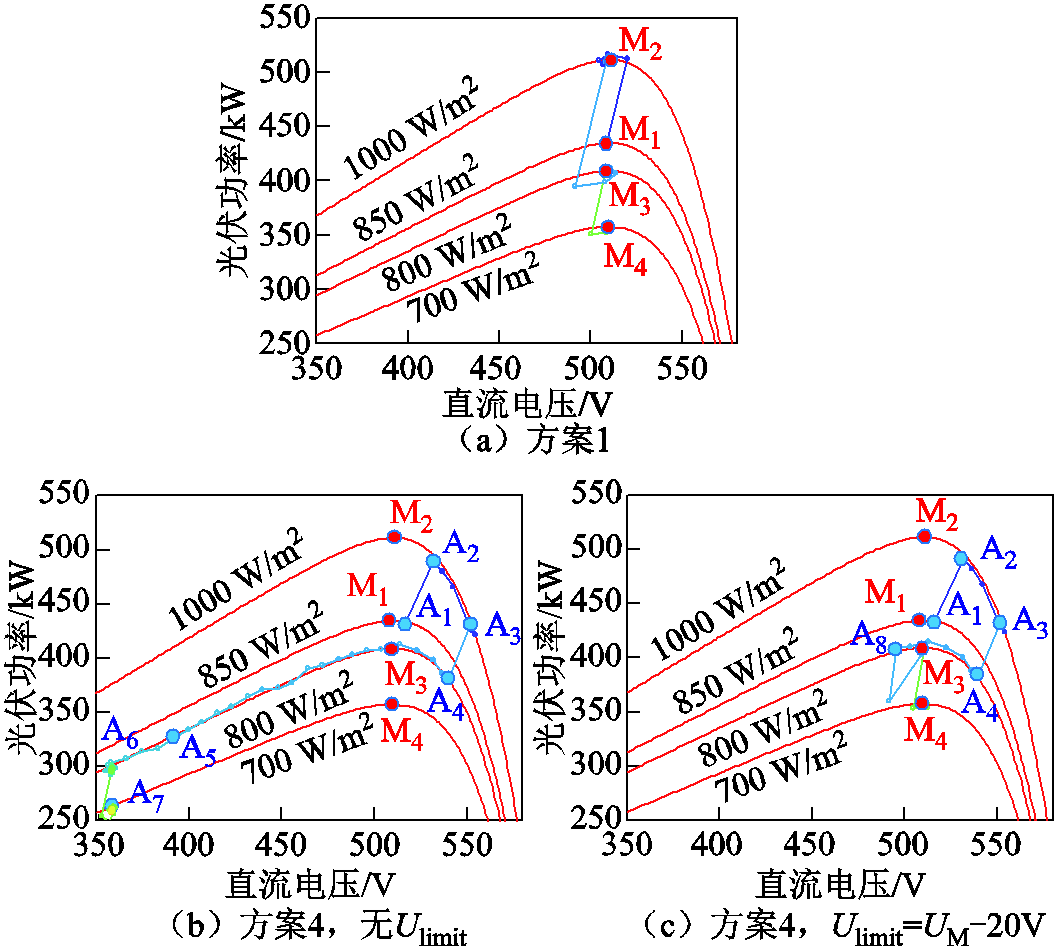
图15 光伏单元的P-U特性曲线及运行轨迹
Fig.15 P-U characteristic curves and operation trajectory diagrams of PV generation unit
无Ulimit限制时，光照度突减后光伏系统最终稳定运行在电压下限357V处（点A7)。由于光伏输出功率急剧减小，系统频率跌落严重，相比方案1稳态频率偏差增大了0.18Hz （见图12c中标注）。
设置Ulimit限制时，光照强度突减导致光伏系统运行至Ulimit=489V处（点A8）后，控制模式即刻切换为MPPT模式，最终稳定运行在最大功率点M4处。由于储能单元提供了一次调频功率，相比方案1稳态频率偏差减小了0.07Hz。
由于直流侧电容的缓冲作用，图12中相比于负荷突变工况，光照强度突变时方案1和4的频率变化均较慢，即频率变化率较小。并且由于储能单元提供了惯量支撑功率，方案4的频率变化率小于方案1。
进一步设置负荷和光照强度随机波动的工况，如图16a所示，仿真结果如图16b和图16c所示。可见，在30s之前方案4具有向上和向下的调频能力，相比于方案1能够减小随机波动下的频率偏差和频率变化率峰值。在31.5s时光照度大幅减小导致方案4由VPPT模式切换为MPPT模式；32.1 s之后方案4不再输出向下的一次调频功率，但仍然由储能单元提供惯量功率和向上的一次调频功率，也体现出一定的调频效果。因此，源荷随机波动时的仿真结果充分验证了所提方案4的有效性。
图16 源荷随机波动时的仿真结果
Fig.16 Simulation results when light intensity and load power are randomly fluctuating
本文提出了一种超级电容储能辅助光伏机组惯量支撑和一次调频的光储协调控制策略。通过与有功备用控制的比较，表明所提协调控制策略为优选方案。主要结论如下：
1）所提控制策略不仅能够减小准稳态频率的正/负偏差，而且能够抑制频率的快速波动。同时，其通过VPPT模式和MPPT模式的切换能够保证在光照强度突减后光伏机组不会运行到P-U曲线的左侧不稳定区域。
2）构建的频率响应模型能够准确描述光储系统的功频动态特性。锁相环难以准确测量RoCoF是由突加负荷扰动下实际节点电压相位发生突变导致的。所提改进的RoCoF测量方法能够使测量值更接近于实际值，避免了由锁相环直接测量引起的惯量支撑功率回落/跌落现象。
3）与有功备用控制相比，所提控制策略在取得相同一次调频效果的同时具有更好的惯量支撑效果，且配置储能的年均投资仅为预留备用容量损失的一半。
附表1 仿真参数
App.Tab.1 Simulation parameters
参数数值 光伏单元额定容量PN /kW额定直流电压/V直流电压运行范围/V额定交流电压/V额定频率fN/Hz滤波电感Lf/mH滤波电容Cf/mF直流侧电容Cdc/mF一次调频系数kf/(Hz·W-1)500480357～580250500.065.165.1-1´105 最低电压Ulimit/VUmpp-20
（续）
参数数值 减载率d(%)10 直流电压环PI(pu)2, 80 电流环PI(pu)0.3, 20 PLL参数比例系数kp, 积分系数ki, 滤波时间常数Tf (pu)25, 509, 0.003 储能单元容量/kW50 惯量系数kH/(W·s·Hz-1)-1.25´104 惯性时间系数H/s0.2 一次调频系数kf/(Hz·W-1)-1´105 VSG[35]惯量系数J /(kg·m2)56.3 阻尼系数DP /(N·m·s·rad-1)286.4 电压下垂系数Dq /(var·V-1)3 711 无功环节参数K/(var·rad)27 980 同步系数KS /(W/rad)8.00´106 线路阻抗/W0.237+j0.408 同步发电机容量/kW1 000 惯量系数20.3 阻尼系数0 调差系数Rw (pu)0.017 69 调速器增益Kw (pu)50
参考文献
[1] 刘辉, 葛俊, 巩宇, 等. 风电场参与电网一次调频最优方案选择与风储协调控制策略研究[J]. 全球能源互联网, 2019, 2(1): 44-52.
Liu Hui, Ge Jun, Gong Yu, et al. Wind farm participation in grid primary frequency optimization scheme selection and wind storage coordination control strategy research[J]. Global Energy Internet, 2019, 2(1): 44-52.
[2] 习近平. 在气候雄心峰会上的讲话[Z].中华人民共和国国务院公报, 2020(35): 7.
[3] 颜湘武, 吕佳伟, 贾焦心, 等. 双级式有功备用光伏虚拟同步机控制策略[J]. 电力系统保护与控制, 2020, 48(15): 61-68.
Yan Xiangwu, Lü Jiawei, Jia Jiaoxin, et al. Two-stage active standby photovoltaic virtual synchronous machine control strategy[J]. Power System Protection and Control, 2020, 48(15): 61-68.
[4] 张海峥, 张兴, 李明, 等. 基于变步长功率跟踪的有功备用式PV-VSG控制策略[J]. 电力系统自动化, 2019, 43(5): 92-104.
Zhang Haizheng, Zhang Xing, Li Ming, et al. Control strategy of PV-VSG in active power reserve mode based on power tracking with variable step[J]. Automation of Electric Power Systems, 2019, 43(5): 92-104.
[5] 钟诚, 周顺康, 严干贵, 等. 基于变减载率的光伏发电参与电网调频控制策略[J]. 电工技术学报, 2019, 34(5): 1013-1024.
Zhong Cheng, Zhou Shunkang, Yan Gangui, et al. A new frequency regulation control strategy for photovoltaic power plant based on variable power reserve level control[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 1013-1024.
[6] Papadopoulos A M. Renewable energies and storage in small insular systems: potential, perspectives and a case study[J]. Renewable Energy, 2019, 149(2020): 103-114.
[7] Perdana Y S, Muyeen S M, Al-Durra A, et al. Direct connection of supercapacitor–battery hybrid storage system to the grid-tied photovoltaic system[J]. IEEE Transactions on Sustainable Energy, 2019, 10(3): 1370- 1379.
[8] 马伟, 王玮, 吴学智, 等. 平抑光伏并网功率波动的混合储能系统优化调度策略[J].电力系统自动化, 2019, 43(3): 58-66.
Ma Wei, Wang Wei, Wu Xuezhi, et al. Optimal dispatching strategy of hybrid energy storage system for smoothing power fluctuation caused by grid-connected photovoltaic[J]. Automation of Electric Power Systems, 2019, 43(3): 58-66.
[9] 张纯江，董杰，刘君，等. 蓄电池与超级电容混合储能系统的控制策略[J]. 电工技术学报, 2014, 29(4): 334- 340.
Zhang Chunjiang, Dong Jie, Liu Jun, et al. A control strategy for battery-ultracapacitor hybrid energy storage system[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 334-340.
[10] 曾正, 邵伟华, 冉立, 等. 虚拟同步发电机的模型及储能单元优化配置[J]. 电力系统自动化, 2015, 39(13): 22-31.
Zeng Zheng, Shao Weihua, Ran Li, et al. Mathematical model and strategic energy storage of virtual synchronous generators[J]. Automation of Electric Power Systems, 2015, 39(13): 22-31.
[11] 涂春鸣, 兰征, 肖凡, 等. 具备同步电机特性的级联型光伏发电系统[J]. 中国电机工程学报, 2017, 37(2): 433-444.
Tu Chunming, Lan Zheng, Xiao Fan, et al. Study on cascaded H-bridge photovoltaic power systems with synchronous generator characteristics[J]. Proceedings of the CSEE, 2017, 37(2): 433-444.
[12] 高建瑞, 李国杰, 汪可友, 等. 考虑储能充放电功率限制的并网光储虚拟同步机控制[J]. 电力系统自动化, 2020, 44(4): 134-141.
Gao Jianrui, Li Guojie, Wang Keyou, et al. Control of grid-connected PV-battery virtual synchronous machine considering battery charging/discharging power limit[J]. Automation of Electric Power Systems, 2020, 44(4): 134-141.
[13] 温烨婷, 戴瑜兴, 毕大强, 等. 一种电网友好型光储分布式电源控制策略[J]. 中国电机工程学报, 2017, 37(2): 464-475.
Wen Yeting, Dai Yuxing, Bi Daqiang, et al. A grid friendly PV/BESS distributed generation control strategy [J]. Proceedings of the CSEE, 2017, 37(2): 464-475.
[14] 巩宇, 李娜, 刘喜梅. 考虑弃光损失的并网光伏电站储能容量配置方法[J]. 华北电力技术, 2017(10): 33-37.
Gong Yu, Li Na, Liu Ximei. Configuration method for capacity of energy storage in PV station considering wind power curtailment[J]. North China Electric Power, 2017(10): 33-37.
[15] 陈文倩, 辛小南, 程志平. 基于虚拟同步发电机的光储并网发电控制技术[J]. 电工技术学报, 2018, 33(增刊2): 538-545.
Chen Wenqian, Xin Xiaonan, Cheng Zhiping. Control of grid-connected of photovoltaic system with storage based on virtual synchronous generator[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 538-545.
[16] 王振雄, 易皓, 卓放, 等. 应用于光伏微网的一种虚拟同步发电机结构及其动态性能分析[J]. 中国电机工程学报, 2017, 37(2): 444-454.
Wang Zhenxiong, Yi Hao, Zhuo Fang, et al. A hardware structure of virtual synchronous generator in photovoltaic microgrid and its dynamic performance analysis[J]. Proceedings of the CSEE, 2017, 37(2): 444-454.
[17] 刘国宇, 蔺圣杰, 吴鸣, 等. 虚拟同步机示范工程综述[J]. 供用电, 2019, 36(4): 37-42.
Liu Guoyu, Lin Shengjie, Wu Ming, et al. Summary of virtual synchronous machine technology demonstration project[J]. Distribution & Utilization, 2019, 36(4): 37-42.
[18] Tafti H D, Konstantinou G, Townsend C D, et al. Extended functionalities of photovoltaic systems with flexible power point tracking: recent advances[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 9342-9356.
[19] Tafti H D, Sangwongwanich A, Yang Y, et al. An adaptive control scheme for flexible power point tracking in photovoltaic systems[J]. IEEE Transactions on Power Electronics, 2019, 34(6): 5451-5463.
[20] Sangwongwanich A, Yang Y, Sera D, et al. Delta power control strategy for multistring grid-connected PV inverters[J]. IEEE Transactions on Industry Applications, 2017, 53(4): 3862-3870.
[21] Sangwongwanich A, Yang Y, Blaabjerg F. A sensorless power reserve control strategy for two-stage grid-connected PV systems[J]. IEEE Transactions on Power Electronics, 2017, 32(11): 8559-8569.
[22] 郑天文, 陈来军, 刘炜, 等. 考虑源端动态特性的光伏虚拟同步机多模式运行控制[J]. 中国电机工程学报, 2017, 37(2): 454-464.
Zheng Tianwen, Chen Laijun, Liu Wei, et al. Multimode operation control for photovoltaic virtual synchronous generator considering the dynamic characteristics of primary source[J]. Proceedings of the CSEE, 2017, 37(2): 454-464.
[23] 张海峥, 张兴, 李明, 等. 一种有功备用式光伏虚拟同步控制策略[J]. 电网技术, 2019, 43(2): 514-520.
Zhang Haizheng, Zhang Xing, Li Ming, et al. A photovoltaic virtual synchronous generator control strategy based on active power reserve[J]. Power System Technology, 2019, 43(2): 514-520.
[24] 王淑超, 孙光辉, 俞诚生, 等. 光伏发电系统级快速功率调控技术及其应用[J]. 中国电机工程学报, 2018, 38(21): 6254-6263.
Wang Shuchao, Sun Guanghui, Yu Chengsheng, et al. Photovoltaic power generation system level rapid power control technology and its application[J]. Proceedings of the CSEE, 2018, 38(21): 6254-6263.
[25] Omran W A, Kazerani M, Salama M M A. Investigation of methods for reduction of power fluctuations generated from large grid-connected photovoltaic systems[J]. IEEE Transactions on Energy Conversion, 2011, 26(1): 318-327.
[26] 颜湘武, 宋子君, 崔森, 等. 基于变功率点跟踪和超级电容器储能协调控制的双馈风电机组一次调频策略[J]. 电工技术学报, 2020, 35(3): 530-541.
Yan Xiangwu, Song Zijun, Cui Sen, et al. Primary frequency regulation strategy of doubly-fed wind turbine based on variable power point tracking and supercapacitor energy storage[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 530-541.
[27] Bose U, Chattopadhyay S K, Chakraborty C. A novel method of frequency regulation in microgrid[J]. IEEE Transactions on Industry Applications, 2019, 55(1): 111-121.
[28] Ghartemani M K, Khajehoddin S A, Jain P K, et al. Problems of startup and phase jumps in PLL systems[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 1830-1838.
[29] 赵婷, 吕志鹏, 刘国宇, 等. 虚拟同步机技术系列标准解读[J]. 供用电, 2019, 36(4): 13-17, 36.
Zhao Ting, Lü Zhipeng, Liu Guoyu, et al. Interpretation of virtual synchronous machine technology series standards[J]. Distribution & Utilization, 2019, 36(4): 13-17, 36.
[30] 马智慧, 李欣然, 谭庄熙, 等. 考虑储能调频死区的一次调频控制方法[J]. 电工技术学报, 2019, 34(10): 2102-2115.
Ma Zhihui, Li Xinran, Tan Zhuangxi, et al. Integrated control of primary frequency regulation considering dead band of energy storage[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2102-2115.
[31] 季宇, 熊雄, 寇凌峰, 等. 基于经济运行模型的储能系统投资效益分析[J]. 电力系统保护与控制, 2020, 48(4): 143-150.
Ji Yu, Xiong Xiong, Kou Lingfeng, et al. Analysis of energy storage system investment benefit based on economic operation model[J]. Power System Protection and Control, 2020, 48(4): 143-150.
[32] Fang Jingyang, Zhang Ruiqi, Li Hongchang, et al. Frequency derivative-based inertia enhancement by grid-connected power converters with a frequency-locked-loop[J]. IEEE Transactions on Smart Grid, 2019, 10(5): 4918-4927.
[33] He Wei, Yuan Xiaoming, Hu Jiabing. Inertia provision and estimation of PLL-based DFIG wind turbines[J]. IEEE Transactions on Power Systems, 2017, 32(1): 510-521.
[34] 张涛, 陈亮. 电荷泵锁相环环路滤波器参数设计与分析[J]. 现代电子技术, 2008, 31(9): 87-90.
Zhang Tao, Chen Liang. Parameter′s design and analysis of the charge pump phase-locked loop′s loop filter[J]. Modern Electronics Technique, 2008, 31(9): 87-90.
[35] Dong Shuan, Chen Yu Christine. A method to directly compute synchronverter parameters for desired dynamic response[J]. IEEE Transactions on Energy Conversion, 2018, 33(2): 814-825.
Fast Frequency Regulation Strategy of PV Power System Assisted by Energy Storage Based on Improved Measurement Method of RoCoF
Abstract Large-scale photovoltaic (PV) grid-connected power generation causes a power system to face the problem of inertia decline and insufficient frequency regulation capability. Although the current scheme of active power reserve (APR) can meet the needs participating in primary frequency regulation, it is difficult to provide inertia support and the operation of abandoned solar energy will affect generation benefits. Accordingly, a coordinated control strategy of virtual inertia and primary frequency regulation for energy-storage assisted PV system is proposed. The proposed strategy reduces energy storage capacity by half without losing power generation benefits. The primary frequency regulation is accomplished by the means that variable power point tracking (VPPT) responses frequency’s up disturbance and energy storage equipment responses frequency’s down disturbance. Moreover, energy storage device is used for inertia support control. The essential reason of inertia-power sag caused by the measurement of rate of change of frequency (RoCoF) is revealed through mathematical modeling, and a method to correct the measurement value of RoCoF by the first-order high-pass link is proposed to improve the inertia control effect. The control effects of the proposed strategy and the APR strategy are compared and analyzed in simulation example of microgrid. The results show that the coordinated strategy has better performance.
Keywords：Variable power point tracking, energy storage device, coordinated control, frequency regulation, photovoltaic power generation, phaselocked loop(PLL)
DOI:10.19595/j.cnki.1000-6753.tces.210610
中图分类号：TM732
国网河北省电力公司科技项目（SGHEDK00JYJS2100145）和北京市自然科学基金项目（3212037）资助。
收稿日期 2021-04-29
改稿日期 2021-07-12
贾焦心 男，1991年生，博士，讲师，研究方向为微电网运行及接口变换器控制、新能源发电系统建模和控制。E-mail：jiajx33@163.com
颜湘武 男，1965年生，教授，博士生导师，研究方向为新能源电力系统分析与控制、现代电力变换、新型储能与节能技术。E-mail：xiangwuy@ncepu.edu.cn（通信作者）
（编辑 郭丽军）