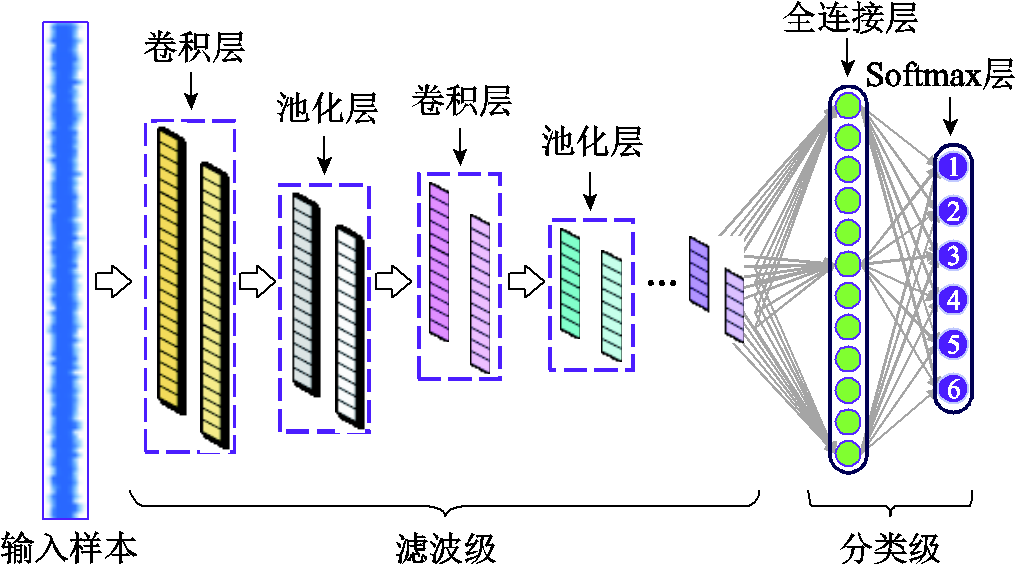
图1 一维卷积神经网络结构图
Fig.1 The structure diagram of 1D CNN
摘要 针对机电作动器的传统故障诊断方法依赖于人工特征提取和工程经验的问题,该文提出一种基于一维卷积神经网络(1DCNN)的智能故障诊断方法。相较于传统故障诊断算法中特征提取和分类的分开处理,该方法将两者合二为一、共同进行。首先,利用重叠采样对直驱型机电作动器的正常信号和故障信号进行预处理来获取数据样本;然后将样本输入到设计的一维卷积神经网络模型中,通过多层数据变换得到有效的特征表示,从而建立原始数据端与运行状态端之间的映射关系,实现机电作动器端到端的故障诊断。实验结果表明,该方法可以有效地诊断出机电作动器的故障,且故障识别率可以达到98%左右。另外,该方法在不同白噪声下仍可以保持较高的故障识别率,具有比较好的鲁棒性和泛化能力。
关键词:直驱型机电作动器 一维卷积神经网络 故障诊断 深度学习
随着高密度伺服电动机、电力电子和数字控制技术的发展,电力作动系统以其质量轻、成本低、效率高、可靠性高及便于维护等优点被广泛认可。因此在航空、航天和航海等很多领域,电力作动系统正在逐步取代传统的液压作动系统[1]。机电作动器作为电力作动系统的一种典型代表,广泛应用于现代飞行控制系统,来控制飞机舵面,从而改变飞机的飞行姿态和轨迹,其健康状态对于飞机的飞行状态和安全至关重要。因此,准确及时地诊断、预测机电作动器的实时状况,对保障飞机安全运行和经济维护具有重要意义。
目前,机电作动器故障时的故障诊断方法主要可以分为基于模型[2-4]和基于数据驱动[5-9]两类方法。其中,基于模型的故障诊断方法通常需要建立精确的系统模型,但模型的确定性也决定了其通用性较差;而基于数据驱动的故障诊断方法,无需精确的数学模型,但要求有比较完备的数据集。随着互联网技术的发展和智能制造水平的提高,社会的数据量和数据面呈指数式增长,使基于数据驱动的故障诊断方法得到更广泛的应用。
随着人工智能的不断兴起和蓬勃发展,机器学习成为了数据驱动下故障诊断的主流方法之一。机器学习的故障诊断通常包括特征提取、特征降维和故障分类三个部分。由于现实中采集到的原始数据存在大量的冗余信息和噪声,难以直接处理,因此通常需要先对原始数据进行特征提取来获取与故障相关的特征,如小波包变换(Wavelet Packet Transform,WPT)[6-7]、快速傅里叶变换(Fast Fourior Transfermation, FFT)[8]、统计特征[9]以及经验模态分解[10-11]等常见的特征提取方法;然后对上一步提取后的特征进行降维,剔除冗余和无用的特征,常用方法有主成分分析[12-13]、核主元分析[14]和流形学习[14]等;最后将得到的有效故障特征进行故障分类,其中比较有代表的分类器有BP神经网[15]、自组织映射(Self-Organizing Maps,SOM)神经网络[7]、支持向量机(Support Vector Machine,SVM)[9,12]以及概率神经网络(Probabilistic Neural Network,PNN)[13]等。上述方法可以看作是不同的特征提取器与分类器的相互组合,虽然取得了较为不错的效果,但也存在两个主要问题:一是特征提取作为故障诊断的重要一环,但操作时往往依赖人工设计和一定的工程经验;二是特征提取和故障分类虽然形式上组合,但两个过程实质上是先后单独进行的,因此当设备或装置变化时,难以保证二者组合的最优性,即无法保证智能故障诊断算法的通用性,同时这种分段进行的组合方式也难以保证诊断的实时性。
而近年来,由于训练资源的大幅增加和计算能力的快速发展,深度学习逐渐成为智能故障诊断领域中的新秀。文献[16]介绍了当前四种主流的深度学习模型,实现了四种主流深度学习模型在故障诊断中的应用。文献[17-19]把卷积神经网络(Convolutional Neural Network,CNN)应用到滚动轴承的故障诊断;文献[20-22]分别把CNN应用到了绝缘子状态检测、直流交联聚乙烯电缆局部放电模式识别和低压万能式断路器附件故障诊断;文献[23-24]则分别利用CNN对风电场风速与锂离子电池容量进行预测和估算,且均达到了不错的效果。CNN的概念最早可以追溯到Hubel等对猫脑视觉皮层研究中提出的感受野,后经过Fukushima、LeCun等的研究工作,现在已经成为深度学习的经典算法之一,并广泛应用于计算机视觉[25]、语音识别[26]以及自然语言处理[27]等领域。CNN是一种前馈式多层监督学习神经网络,通常由卷积层、激活层、池化层、全连接层4个部分构成。其中,卷积层利用卷积核对输入信号进行特征提取,激活层用来提高网络的非线性特性,池化层对卷积层产生的特征图进行维度约简,最后全连接层对高维特征进行具体的分类操作。与普通神经网络相比,卷积层具有局部连接和权值共享的特性,这有利于减少卷积层的训练参数,在一定程度上降低了网络的复杂度和计算量[16]。
针对目前机电作动器诊断依赖人工特征提取和工程经验以及浅层学习模型特征提取能力不足的问题,本文将一维卷积神经网络结构引入机电作动器故障诊断中,直接以作动器输出的原始信号作为网络输入,把特征提取和分类合二为一,实现端到端的智能故障诊断。首先是获取和处理数据,其次优选参数进行网络模型构建,然后通过实验对模型进行验证,最后将所提方法与其他算法对比验证,并进行鲁棒性测试。实验结果表明,本文算法可以有效地实现机电作动器的故障诊断。
根据网络输入数据的不同,CNN又可以分为一维、二维和三维CNN,分别用于一维数据、图像和视频的处理。由于本文研究的机电作动器的输出信号为一维数据,符合一维CNN的数据输入要求,因此构建了1DCNN的网络结构,依据功能的不同可以分为滤波级和分类级两个部分,如图1所示。其中,滤波级包含卷积层和池化层,用于提取输入样本的特征;分类级由全连接和Softmax层组成,用来对学习到的特征进行分类。

图1 一维卷积神经网络结构图
Fig.1 The structure diagram of 1D CNN
虽然CNN被称为卷积神经网络,不过在实际操作中通常并不使用卷积运算,而是使用相关运算,图2所示为一维卷积层运算示例。图中卷积核尺寸为3×1,并以固定步幅遍历输入,每次与被卷区域对应的数值相乘、再作和,得到一个logits值,然后卷积核移动1个步幅,重复以上操作,直到卷积核遍历完输入的所有区域。假设第l层是卷积层,则该层的一维卷积运算式为

图2 一维卷积层运算示例
Fig.2 The example of 1D convolutional layer operation
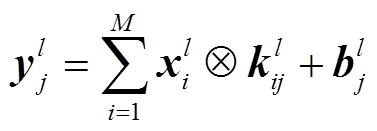 (1)
(1)
式中,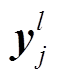 为l层的第j个卷积计算后得到的向量;
为l层的第j个卷积计算后得到的向量;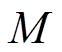 为输入特征向量的个数;
为输入特征向量的个数;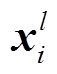 为
为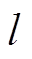 层的第
层的第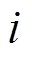 个输入特征向量;
个输入特征向量; 表示相关运算;
表示相关运算;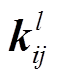 为
为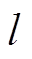 层与第
层与第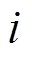 个输入特征向量进行卷积的第
个输入特征向量进行卷积的第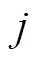 个卷积核;
个卷积核;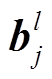 为l层的第j个偏置向量。
为l层的第j个偏置向量。
卷积层属于隐藏层,卷积运算之后通常会利用激活函数对每一个卷积输出的logits值进行非线性映射变换,来增加网络模型的非线性特性。考虑到收敛速度和过拟合问题,本文采用修正线性单元(Rectified Linear Unit,ReLU)作为隐含层激活函数,该激活函数无梯度耗散问题,比Sigmoid函数有更快的收敛速度,同时可以提高网络的稀疏性,有效防止过拟合问题。ReLU定义为
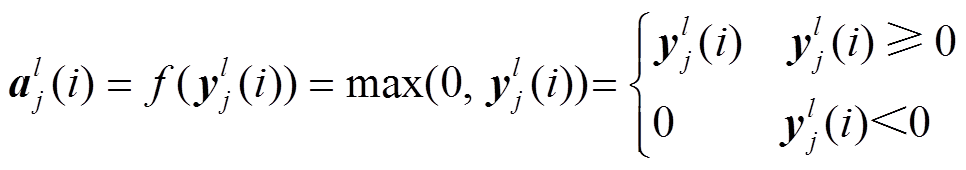 (2)
(2)
式中,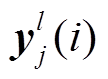 为l层的第j个卷积运算后的第i个输出;
为l层的第j个卷积运算后的第i个输出;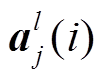 为
为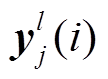 的激活值。
的激活值。
经ReLU激活后,为了增加模型的稀疏性和提高网络训练速度,利用池化层对卷积层所学习到的特征维度约简。常用池化操作主要有最大池化和均值池化,前者以局部接受域的最大值作为输出,后者以局部接受域的均值作为输出。本文采用最大池化进行下采样,具体的最大池化操作示例如图3所示,图中池化窗口为2×1,并以步幅2移动,遍历输入。第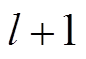 层是池化层,则该层池化计算式为
层是池化层,则该层池化计算式为
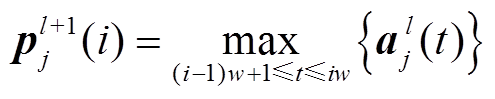 (3)
(3)
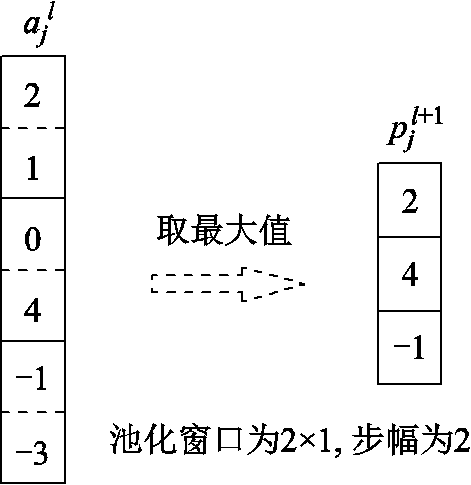
图3 最大池化操作示例
Fig.3 The example of maximum pooling operation
式中,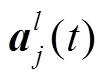 为l层中第j个特征向量的第t个神经元的激活值;
为l层中第j个特征向量的第t个神经元的激活值; 为池化区域的宽度;
为池化区域的宽度;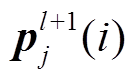 为
为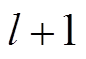 层神经元对应的池化结果。
层神经元对应的池化结果。
分类层由一个全连接隐含层和一个Softmax层组成,其中全连接层把前面池化层的输出展平为一维特征向量,并首尾全连接,隐含层的激活函数为ReLU;Softmax是Logistic回归的推广,主要用于多分类问题。假设类别标签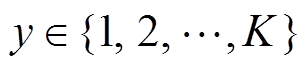 ,给定一个样本x,则样本x属于类别
,给定一个样本x,则样本x属于类别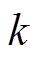 的概率为
的概率为
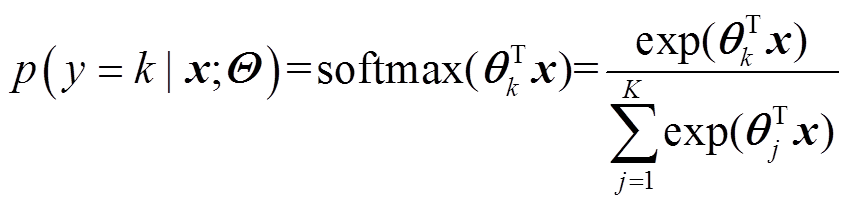 (4)
(4)
式中, 为Softmax回归模型中所有训练参数,
为Softmax回归模型中所有训练参数,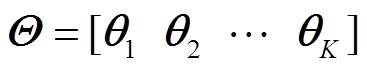 ;
;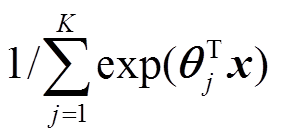 为归一化函数。
为归一化函数。
为了使模型的输出与预期值达到一致,需要衡量输出与预期值之间的距离,而衡量这个距离的函数便是损失函数。损失函数有很多种,不过当处理多分类问题时,通常会采用交叉熵损失函数,其数学表达式为
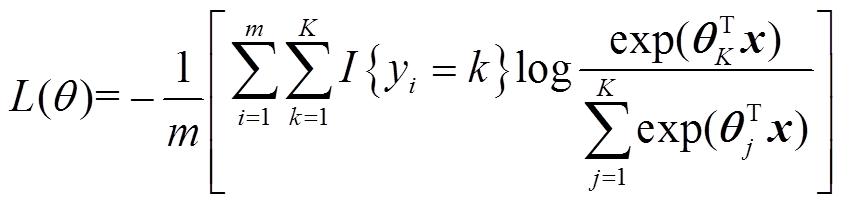 (5)
(5)
式中,m为样本个数或者输入的批量大小;I{·}为指标函数,当{·}值为真时,指标函数值为1,否则指标函数值为0。
为了使模型的损失函数值达到最小,就需要对神经网络进行权值优化调整,并由优化器利用反向传播算法来完成,数学描述为
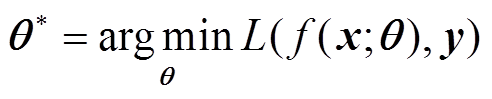 (6)
(6)
式中,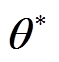 为模型的最优参数;
为模型的最优参数;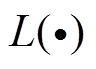 为损失函数;
为损失函数;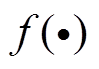 和y分别为模型的输出值和目标值。
和y分别为模型的输出值和目标值。
首先获取机电作动器输出的电磁转矩信号,并对信号数据做归一化处理得到数据集,然后再将数据集划分为训练集、验证集和测试集。其中训练集用来训练网络,验证集用来进行模型选择,测试集用来测试模型的泛化能力,流程如图4所示。
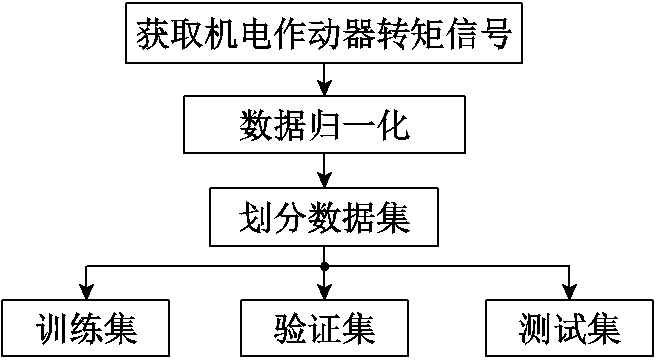
图4 信号数据的获取和处理流程
Fig.4 Signal data acquisition and processing flow
1DCNN的故障诊断算法的流程总体上可以分为训练过程和测试过程两个阶段,如图5所示。在模型训练过程中,首先初始化神经网络的参数;然后是网络的前向传播,即经过交替的卷积层和池化层、全连接和Softmax层后计算得到网络的误差,并判断误差是否达到要求,若不满足,则利用优化算法使误差反向传播来更新网络的参数,直到网络误差或者迭代次数到达设定要求;最终检验验证集精度是否达到要求,若满足要求,则保存网络模型,若不满足,则重新配置网络的超参数,并重复以上操作。在模型的测试阶段,将已训练好的1DCNN模型对测试集进行诊断,直接输出故障诊断的结果。

图5 基于1DCNN的故障诊断流程图
Fig.5 Fault diagnosis flow chart based on 1DCNN
机电作动器根据驱动方式的不同主要分为以下两种形式:带齿轮减速机构的滚珠丝杠机电作动器和直驱型滚珠丝杠机电作动器。直驱型机电作动器去掉了齿轮减速的机构,将滚珠丝杠副与电机直接集成在一起从而使结构简单、提高了效率[28]。
机电作动器是一种位置伺服控制系统,广泛用于军事、交通、航天、工业等领域,通过控制电动机的运行来驱动负载运动,实现目标的位置控制。本文所述的直驱式机电作动器系统主要由控制器、功率变换电路、电机本体、滚珠丝杠、负载和反馈元件(电流传感器、旋转变压器和线性可变差动变压器)组成,其结构如图6所示。其中,功率变换器采用四相不对称半桥电路;电机采用了具有一定容错能力的开关磁阻电机(Switched Reluctance Motor, SRM)。当直驱型机电作动器工作时,控制器通过处理飞行指令以及反馈的传感器信号来控制功率变换器,并由功率变换器产生的开关信号控制电机转动,然后滚珠丝杠副将转子的旋转运动转化为直线运动,从而驱动飞机操纵面的摆动。整个过程中,由传感器将实时测量的位置、速度和电流信息反馈给控制器,从而形成闭环控制。根据机电作动器的组成结构和原理,采用位置、速度和电流的三闭环作为控制策略,最终搭建了直驱型机电作动器模型。
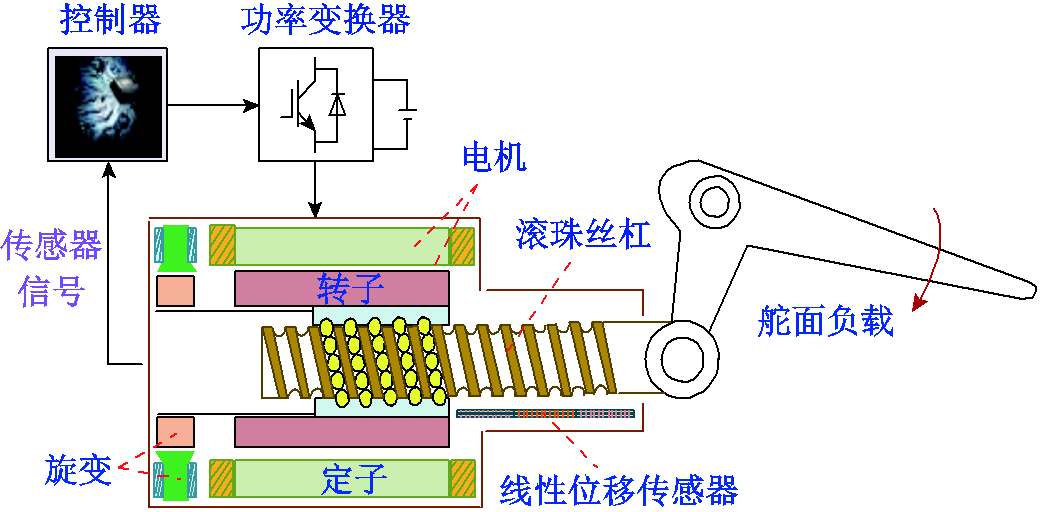
图6 直驱式机电作动器结构
Fig.6 The structural diagram of direct-drive electromechanical actuator
机电作动器的故障按照不同的标准可分为多个种类,但不管依据哪个标准,总体来看主要包括电机故障、控制器故障、功率模块故障、传动机构故障和传感器故障,同时每类故障又可以具体细分,如电机故障又包括绕组短路、绕组开路等。本文对机电作动器故障发生的频率、影响程度以及故障表现的相似度这三个因素进行综合考虑,选择电机绕组匝间短路、轴承卡死、电机损伤、功率管开路和传感器偏差五个故障进行研究。
1)绕组匝间短路故障发生时,短路匝所在定子极绕组的磁通变化,故障相等效阻抗降低、相电流增大,电机各相对称性遭到破坏,电磁转矩会依据故障程度的不同而变化。具体的故障模型可以参考文献[29]。
2)轴承卡死故障发生时,系统的输出会固定在某个位置,不再响应输入指令,其数学描述为
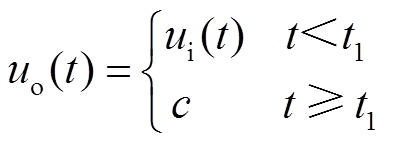 (7)
(7)
式中,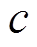 为故障发生时卡死的位置,是一个常值;
为故障发生时卡死的位置,是一个常值;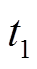 为故障发生时刻。
为故障发生时刻。
3)电机损伤故障发生时,电机驱动负载的能力将达不到预期的效果,其数学描述为
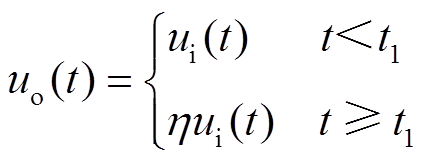 (8)
(8)
式中,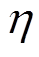 为增益系数且
为增益系数且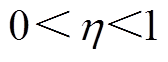 。当
。当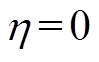 时,效果相当于电机卡死在零偏位置;
时,效果相当于电机卡死在零偏位置;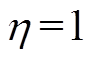 时,电机正常工作,没有故障发生。
时,电机正常工作,没有故障发生。
4)某相功率管开路故障发生时,该相电流和输出转矩变为零,系统进入缺相运行状态,导致系统输出转矩品质恶化,带载能力下降[29]。
5)传感器偏差故障发生时,系统输出会与给定值之间存在恒定偏差,其数学描述为
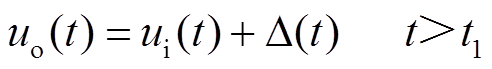 (9)
(9)
式中,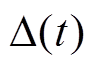 为偏差,且其导数恒为0。
为偏差,且其导数恒为0。
基于对电机绕组匝间短路、轴承卡死、电机损伤、功率管开路和传感器偏差五类故障的分析,对已经搭建好的机电作动器模型进行故障注入。通过预先设置模型的故障发生时间、故障性质及故障程度,以电磁转矩Te作为输出,然后仿真获得机电作动器正常输出信号和五类故障信号。采样频率为20kHz,采样时间为20s,采样点数为400000。为了在有限数据样本内可以包含更多周期的信号,对输出信号进行降采样1/2处理,然后剪去作动器起动过程的数据点,最后得到的采样点数为180000。为了便于训练卷积神经网络,对每段信号x均做归一化处理,其数学描述为
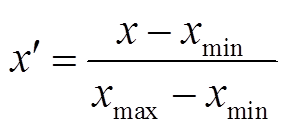 (10)
(10)
数据规模的大小是深度学习成功的重要因素,通常来说,网络模型的训练样本越多,其泛化能力越强。因此,在深度学习模型训练过程中,经常会采用数据扩增技术,即在没有实质性的数据增加的情况下,让有限的数据产生等价于更多数据的价值。数据扩增方法有很多,同时根据不同的任务会有所区别。如在计算机视觉领域,常采用裁剪、翻转和旋转、图像变换等方法。考虑到机电作动器的输出是一维序列信号,本文采用重叠采样的方法达到数据扩增的目的,采样方式如图7所示。
以一定的重叠比例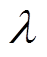 ,对机电作动器不同状态下输出的信号进行分割,得到训练集、验证集和测试集,具体的实现方法如下[17]。
,对机电作动器不同状态下输出的信号进行分割,得到训练集、验证集和测试集,具体的实现方法如下[17]。
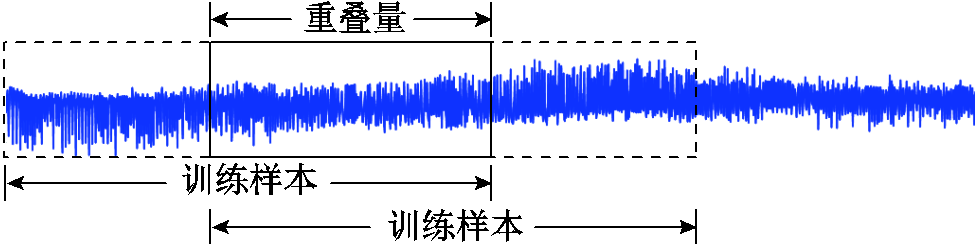
图7 数据扩增方式
Fig.7 The method data augmentation
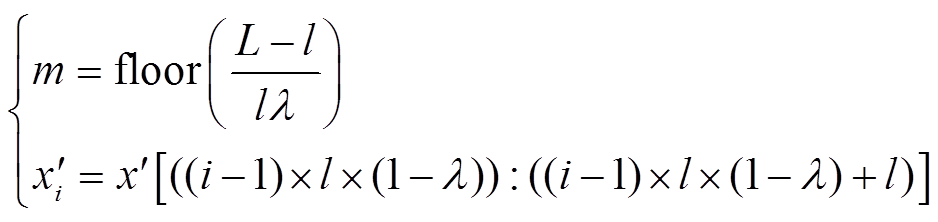 (11)
(11)
式中,m为每段信号的最大可分割样本数量;floor(·)为向下取整函数L为每段信号的长度;l为设置的样本长度;λ为重叠率;xi’为分割后的第i个数据样本,i∈[1,m];x’为归一化后的信号。
本文设置样本长度l=4096,以1/3的重叠率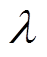 对
对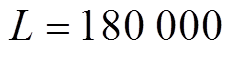 的信号进行分割实现样本集扩增,得到6144个样本。每种状态随机选择800个样本作为训练样本,200个样本用来模型验证,24个样本用于泛化性测试,具体样本信息见表1。
的信号进行分割实现样本集扩增,得到6144个样本。每种状态随机选择800个样本作为训练样本,200个样本用来模型验证,24个样本用于泛化性测试,具体样本信息见表1。
表1 实验样本组成
Tab.1 The composition of experimental samples
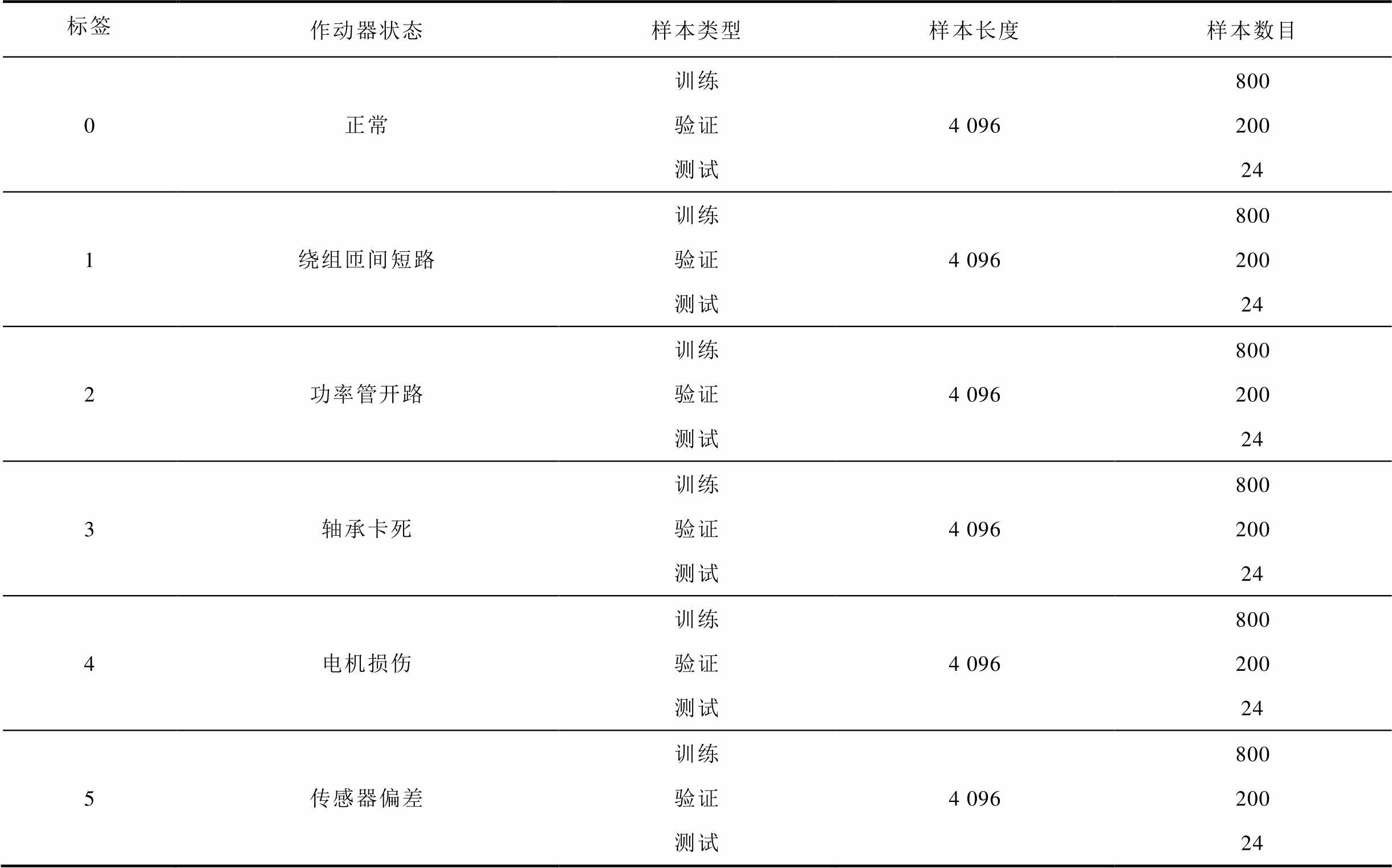
标签作动器状态样本类型样本长度样本数目 0正常训练验证测试4 09680020024 1绕组匝间短路训练验证测试4 09680020024 2功率管开路训练验证测试4 09680020024 3轴承卡死训练验证测试4 09680020024 4电机损伤训练验证测试4 09680020024 5传感器偏差训练验证测试4 09680020024
构建深度学习模型时,选择合适的超参数对模型的性能至关重要。如利用CNN做故障诊断时,网络的卷积层数、卷积层的卷积核数目及大小、优化器类型及其学习率、每批量处理样本的数目等对故障诊断准确性都有很大的影响。因此,本文针对1DCNN模型需要着重考虑的几个超参数进行实验,选择能够使模型的性能相对较优的参数值。
3.2.1 优化器类型
考虑到随机梯度下降(Stochastic Gradient Descent,SGD)在参数众多的深度网络中很可能陷入局部最优点,而RMSprop、Adam和Adadelta是三种自适应学习率的优化算法,可以加快损失函数的收敛,避免陷入局部最优点。因此本文以RMSprop、Adam和Adadelta三种优化器作为备选,并以SGD为参照。每个优化器分别进行10次实验,并以训练集、验证集和测试集的平均正确率作为评价指标,实验结果见表2。
表2 不同优化器对模型诊断准确率的影响
Tab.2 The effect of different optimizers on the diagnostic accuracy of the model

优化器类型平均准确率(%) 训练集验证集测试集 SGD88.6688.6086.54 RMSprop98.8798.5298.52 Adam 99.1098.7598.91 Adadelta99.5098.8198.94
从表2中可以看出,优化器采用Adadelta时,模型的平均准确率最高;其次为Adam,且它的实验结果与Adadelta仅有微小的差距;模型采用RMSprop的平均准确率较Adadelta和Adam有1%左右的差距,而使用SGD得到的实验结果最差。因此,本文选择Adadelta作为模型的优化器。
3.2.2 卷积层数及卷积核数目
在CNN中,可以通过增加网络的卷积层数和卷积核数目来获得更高的准确率,但过多的卷积层数和卷积核数目可能会因模型的训练参数大量增加而导致模型过拟合,同时模型的训练时间和计算成本也会增加。因此,构建CNN结构时需要兼顾高准确率和训练时间,本文先通过实验来确定卷积层数量,然后在卷积层数确定的基础上选择更优的卷积核数目。
1)卷积层数量
设计三种网络结构,卷积层数分别2、3和4层,对应的卷积核数目分别为(32、64)、(32、32、64)和(32、32、64、64),其余配置均相同,来考察不同卷积层数目对模型诊断性能的影响,重复进行5次实验,并以训练集、验证集和测试集的平均正确率作为评价指标,实验结果见表3。
表3 不同卷积层数对模型诊断准确率的影响
Tab.3 The effect of the number of convolutional layers on the diagnostic accuracy of the model

卷积层数量平均准确率(%) 训练集验证集测试集 299.6390.2591.31 399.3598.8999.03 499.1098.9299.17
从表3可见,随着卷积层数的增加,模型在验证集和测试集上的平均正确率在上升,且当卷积层数为3层和4层时的正确率明显高于卷积层数为2层的结果;因卷积层数为3层时模型的正确率已经可以达到99%左右,所以卷积层数增加到4层时模型的提升空间不大,即该层对诊断模型的贡献度不高,所以本文选择3个卷积层。
2)卷积核数目
在确定卷积层数为3层的前提下,考察不同卷积核配置方式对模型诊断性能的影响。设置模型的训练次数Epochs为100次,重复进行5次实验,并以训练集、验证集和测试集的平均正确率以及训练时间作为评价指标,实验结果见表4。
表4 不同卷积核数目对模型诊断准确率的影响
Tab.4 The effect of the number of different convolution kernels on the diagnostic accuracy of the model

卷积核数目平均准确率(%)平均训练时间/s 训练集验证集测试集 (8, 16, 32)89.0288.8387.66145 (16, 32, 64)99.0698.5498.75240 (32, 32, 64)99.1398.8398.89300 (32, 64, 64)99.2698.8698.61320 (32, 64, 128)99.2998.7598.89400
3.2.3 批量大小
深度学习通常有较大的训练样本,所以模型训练时往往会将训练样本分成多个批量,实现对网络参数的更新,而不同的批量大小(Batch-size)对于模型的故障识别准确率又有较大影响。因此本文分别取不同的Batch-size重复进行5次实验,设置模型的训练次数Epochs为100次,然后以数据集上的平均正确率以及训练时间作为评价指标,实验结果见表5。
由表5可见批量规模(Batch-size)为32时,模型在验证集和测试集上的平均正确率最高,但其平均训练时间较长;而Batch-size为64时的平均正确率稍次于前者,但训练时间明显小于前者,因此综合考虑后选择Batch-size为64。
表5 不同批量大小对模型诊断准确率的影响
Tab.5 The effect of different batch sizes on the diagnostic accuracy of the model
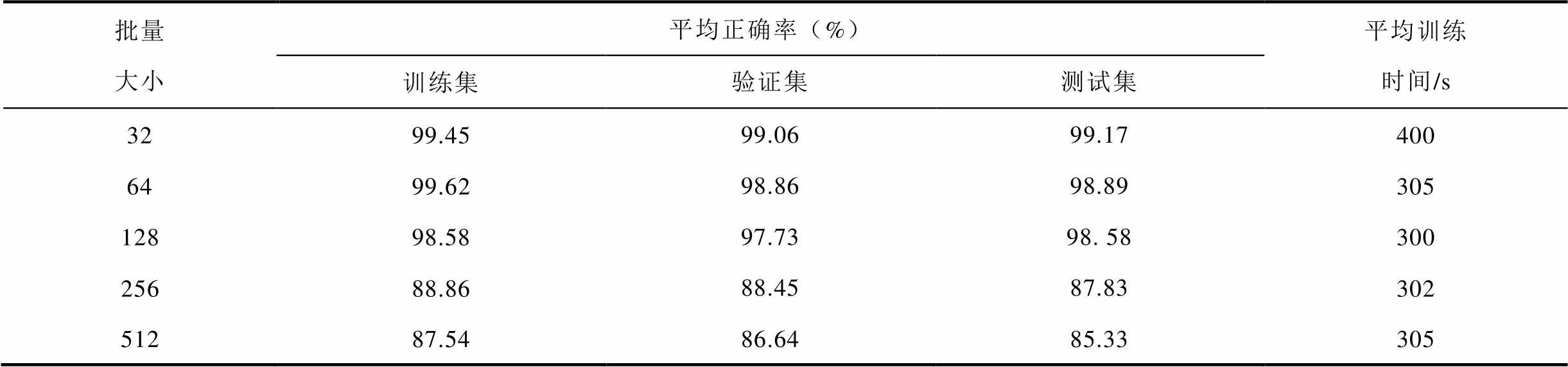
批量大小平均正确率(%)平均训练时间/s 训练集验证集测试集 3299.4599.0699.17400 6499.6298.8698.89305 12898.5897.7398. 58300 25688.8688.4587.83302 51287.5486.6485.33305
综合以上实验结果,最终建立一维卷积神经网络故障诊断模型,优化器为Adadelta,批量大小为64,具体超参数见表6。
表6 一维卷积神经网络模型超参数
Tab.6 The hyperparameters of the 1D CNN model
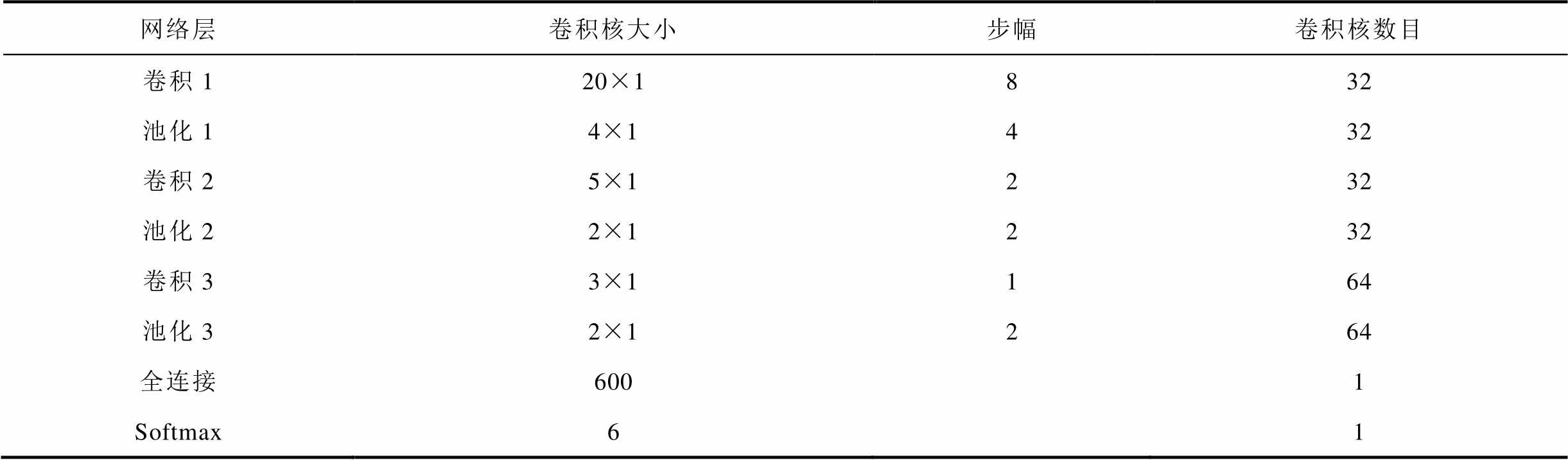
网络层卷积核大小步幅卷积核数目 卷积120×1832 池化14×1432 卷积25×1232 池化22×1232 卷积33×1164 池化32×1264 全连接6001 Softmax61
本文使用的深度学习框架是由谷歌工程师François Chollet开发的Keras,并以TensorFlow作为后端引擎,所用计算机的处理器为Intel(R) Core(TM) i5-9500 CPU @3.00GHz,内存为16GB,利用Python在Keras环境下搭建了一维卷积神经网络模型。然后利用搭建好的网络模型对训练集进行训练,并使用验证集进行验证。为防止模型发生过拟合,在每个池化层以及全连接层后使用Dropout机制,且每个池化层后的丢弃率为0.2,全连接层后的丢弃率0.5;同时为减少网络内部协变量转移,提高网络的训练效率以及增强模型的泛化能力,在卷积层卷积操作后进行批标准化处理。
1)先设定Epochs为300,即用训练集训练模型300次,得到的训练集与验证集的损失函数值和准确率如图8所示。从图8中可以看出,模型的损失函数值和准确率在训练次数40~50附近有较大的振荡,不过随后逐渐趋向稳定;当训练次数为100时,模型在训练集上的准确率已经稳定在99%左右,而在验证集上的准确率可以达到98.5%左右,已经能够满足故障诊断的要求,因此本文以100作为模型的训练次数。
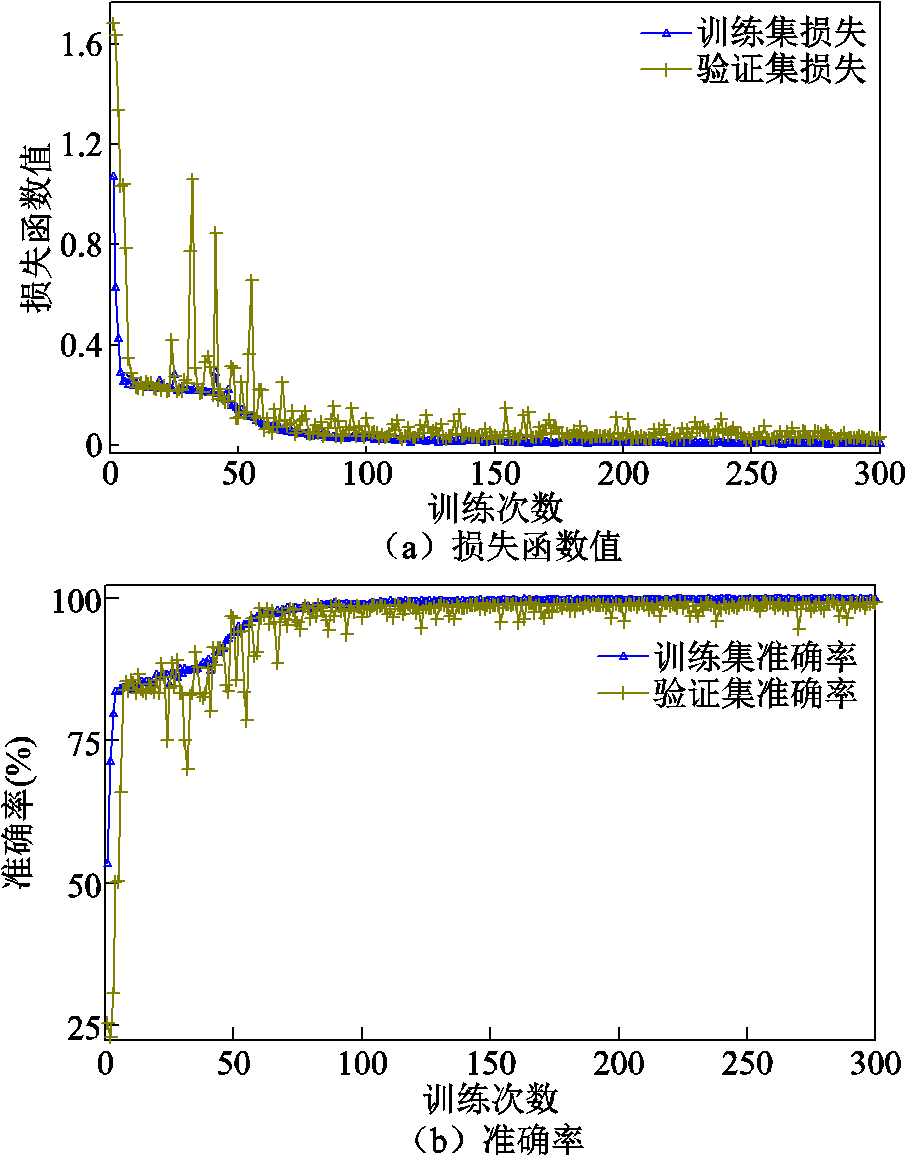
图8 训练集与验证集的损失函数值和准确率
Fig.8 The loss function value and accuracy of training set and validation set
2)由于每次训练时卷积神经网络的初值是随机的,为了验证实验结果的可靠性,重复以上操作10次,得到的实验结果如图9所示。
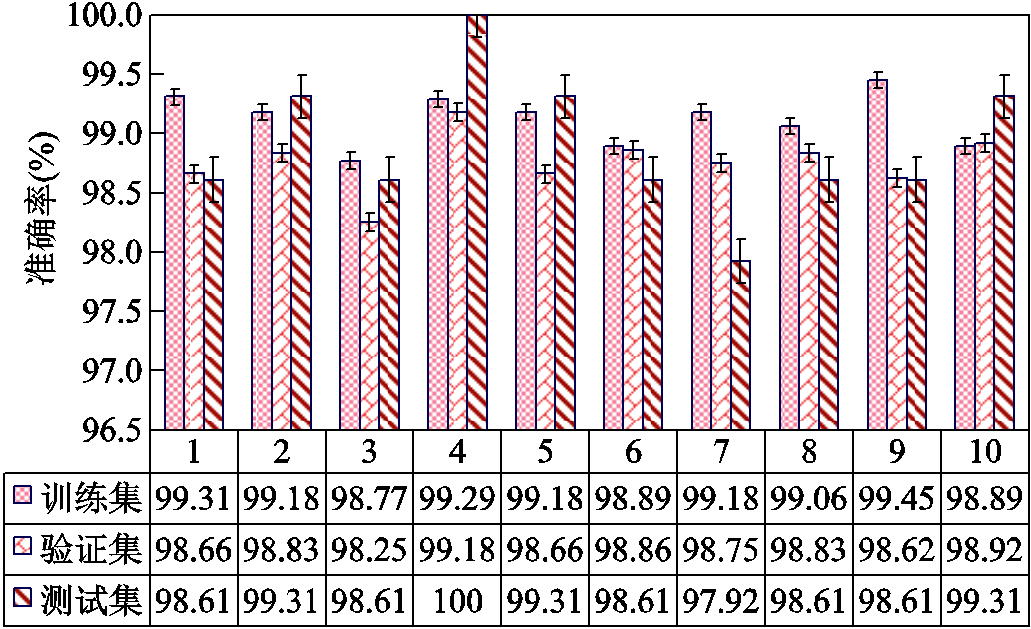
图9 1DCNN诊断模型在数据集上的准确率
Fig.9 The accuracy of 1DCNN diagnostic model on the data set
从图9中可以看出,本文构建的模型在验证集和测试集上的诊断准确率均不低于98%,表明1DCNN可以直接作用于原始信号,并能有效地诊断出机电作动器的故障。此外,虽然模型训练时间较长,但构建的模型通常是先经过离线训练,然后再用于在线故障诊断,所以训练时间的长短并不会影响故障诊断系统的性能,关键在于在线故障诊断所耗的时长。而本文中,如果将测试样本输入已经训练好的网络模型,则每次诊断所需的平均时间约为30ms,因此能够满足实时诊断的需要。对于功率管开路和绕组匝间短路两类故障,可以在确定发生故障的前提下,再根据各相电流传感器的值来具体到某一相或某几相出现故障。
为进一步考察模型对测试集的各个类别的诊断结果,本文引入混淆矩阵对实验结果进行量化分析,来清楚地反映机电作动器每种状态的诊断正确率和误判率,以及真实类别被误判为何种类别等信息,测试集诊断结果的混淆矩阵如图10所示。x、y轴上数字0~5分别为真实标签和预测结果,代表了机电作动器的六种不同状态,具体可参照表1。从图10可以看出,除传感器偏差(标签为5)故障中有4%被误判为正常状态外,其余五种状态类型都达到了100%的诊断精度,表明本文算法对机电作动器故障具有较高的诊断准确率。
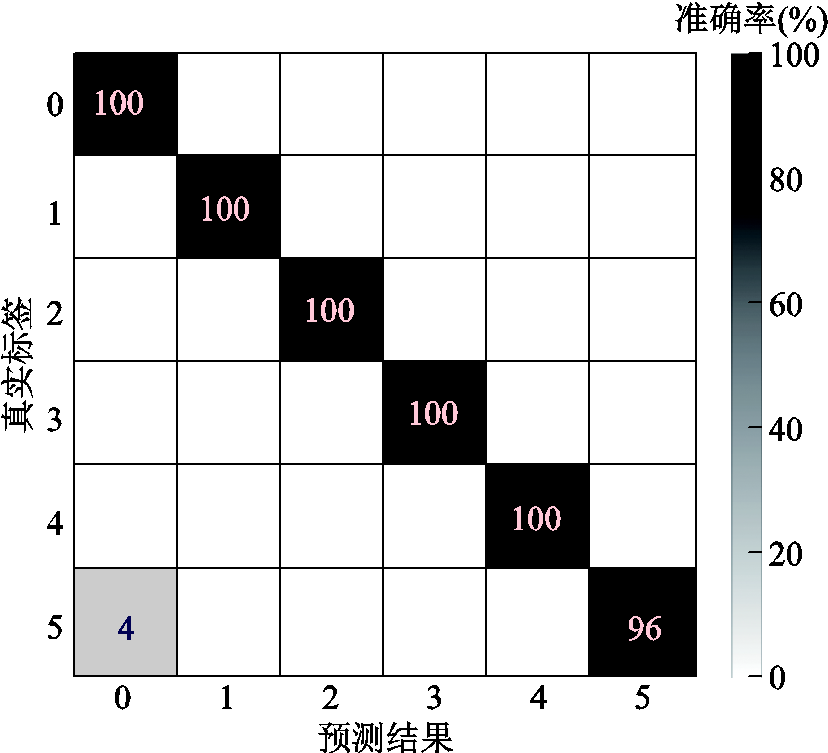
图10 测试集诊断结果的混淆矩阵
Fig.10 The confusion matrix of the diagnostic results of test set
为验证本文故障诊断算法的有效性,将所提方法与SVM、极限学习机(Extreme Learning Machine,ELM)、PNN和深度神经网络(Deep Neural Network,DNN)四种算法进行对比验证。其中,本文故障诊断算法的输入为4096个采样点的原始数据样本;SVM、PNN、ELM和DNN四种算法的输入分为两种形式:第一种为4096个采样点的原始数据样本;第二种采用WPT和时域统计特征(Time-domain Statistical Features,TSF)两种人工特征提取的方法对原始数据进行特征提取,分别把得到的特征向量作为输入样本。每种算法均重复进行8次实验,且每次实验时训练样本量为4800,并从验证集中随机选择144个作为测试样本。
1)各算法的输入均采用第一种形式,即不事先经过特征提取,测试样本的诊断结果如图11所示。从图11中可以看出,由于PNN、ELM和SVM均为浅层结构,从原始数据中直接进行特征提取的能力不足,不能为分类操作提供有效的特征,所以诊断准确率都比较低;而DNN虽然是深层网络,但其并不具备CNN那样比较强大的特征提取能力,因此其诊断准确率较本文算法有一定的差距。
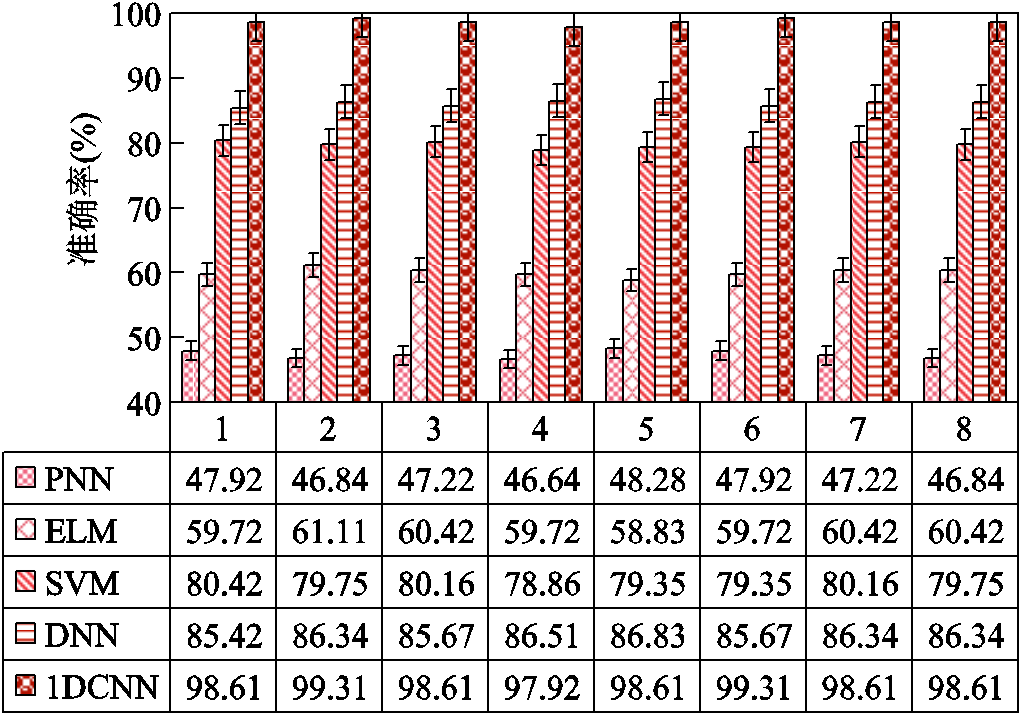
图11 各算法在测试样本的诊断结果
Fig.11 The diagnosis results of each algorithm on test samples
2)本文算法的输入仍采取第一种形式,其余四种算法的输入为第二种形式,测试样本的诊断结果如图12所示。从图12中可以看出,当PNN、ELM、SVM和DNN的输入为第二种形式时,由于事先经过人工特征提取,为分类器提供了更有效和更有区分度的特征,所以这四种算法的诊断准确率均有所上升,并可以达到90%左右,但较本文算法仍然有一定的差距,由此可见本文算法的有效性和优越性。
为进一步凸显本文算法对不同类别特征的学习能力,利用流形学习中t-SNE[30]降维技术,将WPT和TSF两种人工特征提取方法作用于原始数据后得到的特征以及1DCNN最后一个隐含层的特征均约简成二维,并与原始数据的t-SNE的表达进行可视化对比。以验证集作为原始输入,实验结果如图13所示。图13a为原始数据的分布结果,由于原始信号本身存在的冗余性,导致几个类别之间难以区分。图13b和图13c分别为经人工特征提取后得到的样本分布结果,可以看出除类别0和类别5的样本分布存在大面积重叠外,其他类别都可以较好的区别,但类别3没有很好的聚拢。图13d为1DCNN特征学习后的样本分布结果,可以看出各个类别的样本均聚拢在一定的区域,每个类别之间都有比较明显的区分,因此本文算法的故障识别率相对很高。
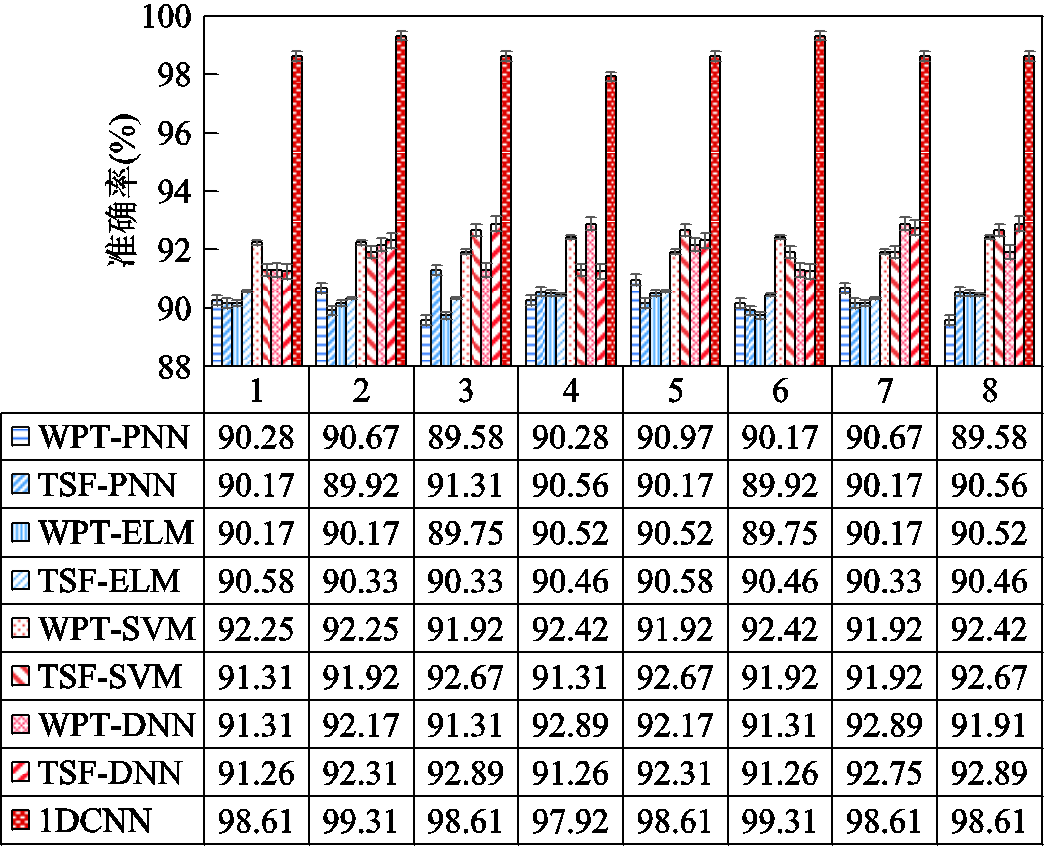
图12 各算法在测试样本的诊断结果
Fig.12 The diagnosis results of each algorithm on test samples
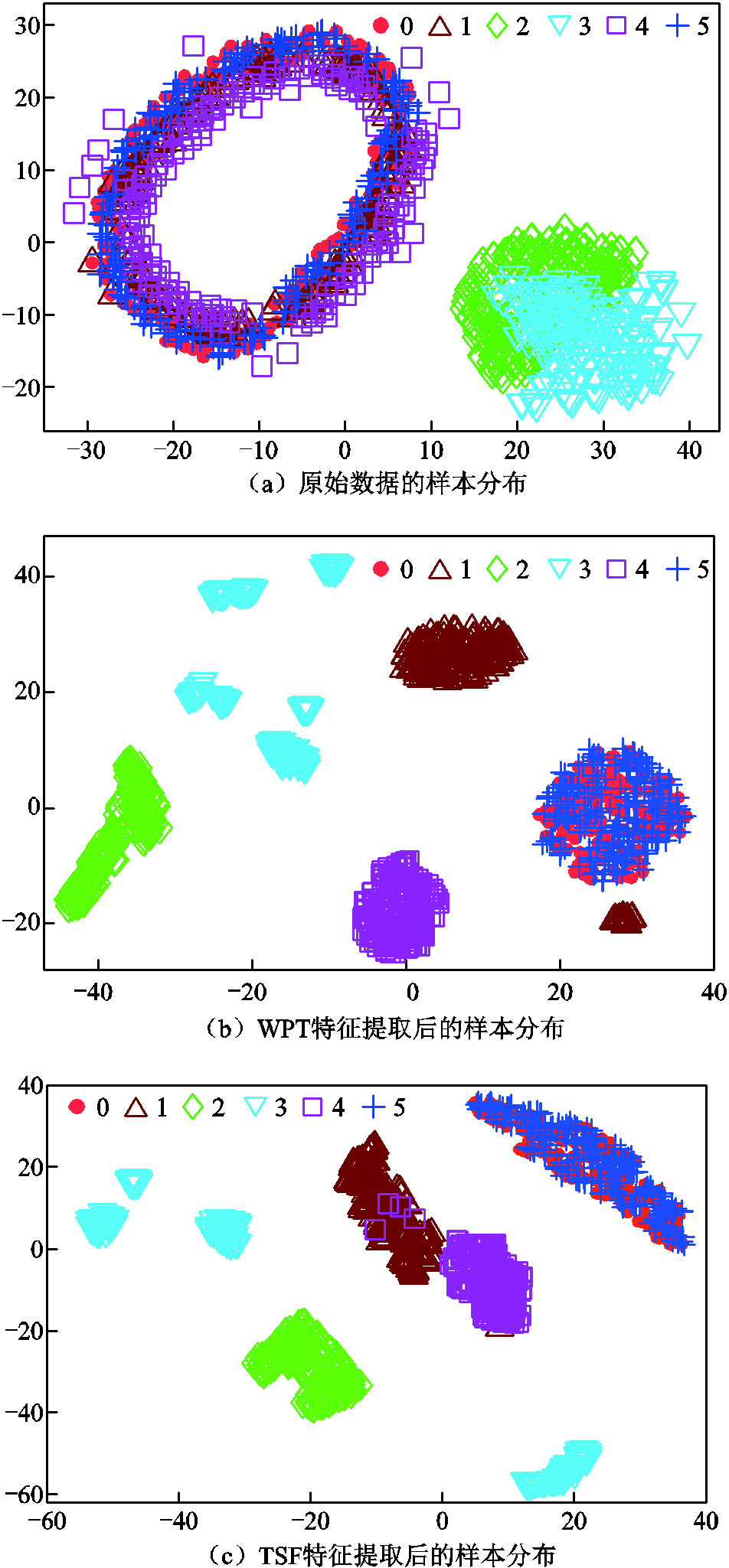
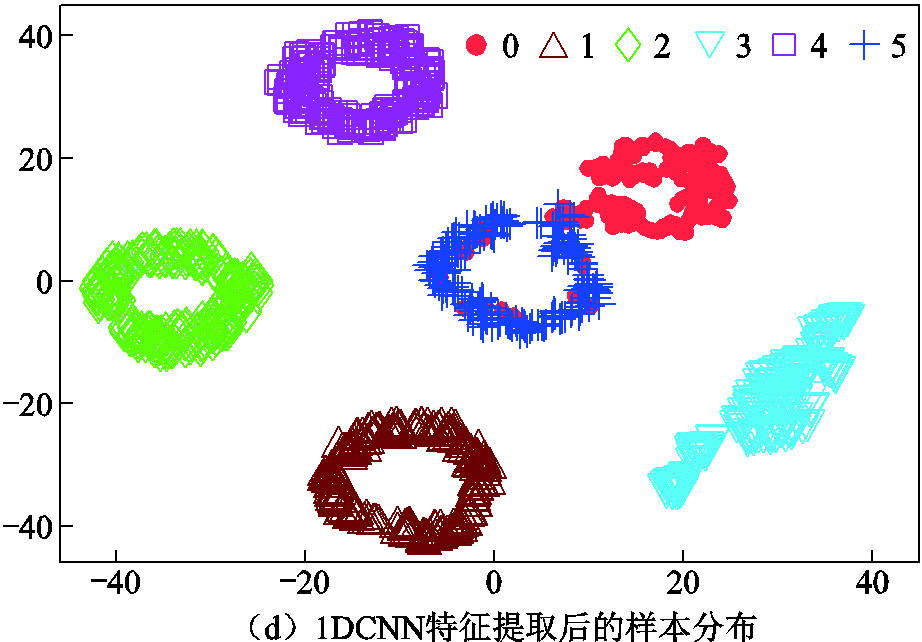
图13 不同方法下特征学习的可视化图
Fig.13 Visualizations of feature learning in different ways
在实际情况中,由于外界干扰噪声的存在,机电作动器输出的信号必然包含一定的噪声。为了验证本文算法的鲁棒性和泛化能力,考察其在含有噪声信号上的识别率,对划分好的测试集分别添加5%、10%、15%和20%的高斯白噪声,并各自作为一个测试集进行实验验证。每个测试集重复进行5次实验,实验结果见表7。
表7 不同高斯白噪声下测试样本的诊断结果
Tab.7 The diagnostic results of test samples under different white noise conditions
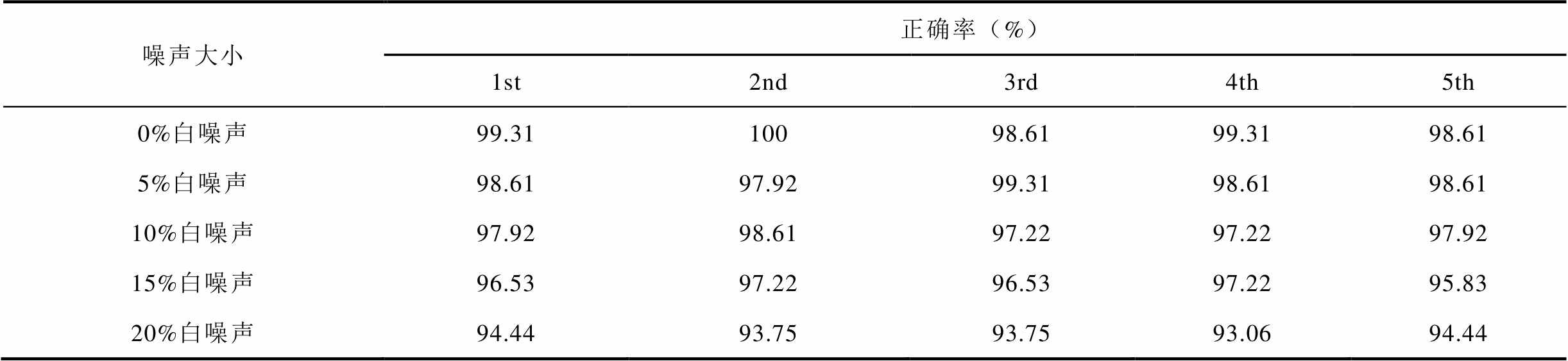
噪声大小正确率(%) 1st2nd3rd4th5th 0%白噪声99.3110098.6199.3198.61 5%白噪声98.6197.9299.3198.6198.61 10%白噪声97.9298.6197.2297.2297.92 15%白噪声96.5397.2296.5397.2295.83 20%白噪声94.4493.7593.7593.0694.44
由表7可见,随着高斯白噪声比例的增加,网络模型的诊断准确率呈下降趋势,但在包含20%白噪声的情况下,其仍然保持了较高的准确率,表明本文算法具有比较好的鲁棒性和泛化能力。另外,当外界噪声很大时可以通过适当地增加第一层卷积的卷积核大小以及网络的深度来提高网络模型的抗噪能力。
本文针对传统故障诊断方法依赖人工特征提取和专家知识的问题,提出了一种基于一维卷积神经网络的机电作动器故障诊断方法。通过对搭建的机电作动器模型仿真得到的数据进行故障诊断,验证了该方法的有效性,并得出以下结论:
1)相比于传统故障诊断方法,本文方法不需要人工特征提取,可以直接作用于原始信号并自适应地提取对诊断有益的特征,同时具有很高的故障诊断准确率。
2)本方法直接以原始数据作为模型输入,把特征提取和分类合二为一,并具有很短的诊断时间,可以真正实现端到端的智能故障诊断,因此具有更好的可操作性和通用性,有利于实现在线监测和快速智能诊断的应用。
3)该方法的泛化能力和鲁棒性较强,在较大噪声的情况下,仍然可以保持较高的诊断准确率。
参考文献
[1] Li Jianming, Yu Zhiyuan, Huang Yuping, et al. A review of electromechanical actuation system for more electric aircraft[C]//IEEE International Conference on Aircraft Utility Systems(AUS), Beijing, China, 2016: 490-497.
[2] 柳志娟, 李清, 柳先辉, 等. 基于强跟踪多模型估计器的作动器故障诊断[J]. 清华大学学报(自然科学版), 2012, 52(5): 642-647.
Liu Zhijuan, Li Qing, Liu Xianhui, et al. Actuator fault diagnosis based on a strong-tracking multiple model estimator[J]. Journal of Tsinghua University (Science & Technology), 2012, 52(5): 642-647.
[3] 王剑, 曹宇燕, 李婷, 等. 基于代数模型的机电作动器Vague动态故障树分析[J]. 西北工业大学学报, 2015, 33(6): 977-983.
Wang Jian, Cao Yuyan, Li Ting, et al. A method for analyzing Vague dynamic fault tree of electro- mechanical actuator based on algebraic model[J]. Journal of Northwestern Polytechnical University, 2015, 33(6): 977-983.
[4] 宋玉琴, 章卫国, 刘小雄. 基于RBF神经网络观测器飞控系统故障诊断[J]. 计算机仿真, 2010, 27(3): 85-88, 93.
Song Yuqin, Zhang Weiguo, Liu Xiaoxiong. Fault diagnosis based on RBF neural network observer in flight control system[J]. Computer Simulation, 2010, 27(3): 85-88, 93.
[5] Ruiz-Carcel C, Starr A. Data-based detection and diagnosis of faults in linear actuators[J]. IEEE Transactions on Instrumentation and Measurement, 2018, 67(9): 2035-2047.
[6] 王淑娟, 陈博, 赵国良. 基于小波包变换预处理的模拟电路故障诊断方法[J]. 电工技术学报, 2003, 18(4): 118-122.
Wang Shujuan, Chen Bo, Zhao Guoliang. Analog circuit fault diagnosis based on wavelet packet preconditioning[J]. Transactions of China Electrotechnical Society, 2003, 18(4): 118-122.
[7] 田瑶瑶, 张惠娟, 杨忠, 等. 基于小波包和SOM 神经网络的电作动器故障诊断[J]. 应用科技, 2018, 45(1): 1-6.
Tian Yaoyao, Zhang Huijuan, Yang Zhong, et al. Fault diagnosis of electromechanical actuator based on wavelet packet and SOM neural network[J]. Applied Science and Technology, 2018, 45(1): 1-6.
[8] Rai V K, Mohanty A R. Bearing fault diagnosis using FFT of intrinsic mode functions in Hilbert-Huang transform[J]. Mechanical Systems and Signal Processing, 2007, 21(6): 2607-2615.
[9] Delgado M, García A, Ortega J A, et al. Multidimensional intelligent diagnosis system based on support vector machine classifier[C]//IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 2011: 2124-2131.
[10] 陈宗祥, 陈明星, 焦民胜, 等. 基于改进EMD和双谱分析的电机轴承故障诊断实现[J]. 电机与控制学报, 2018, 22(5): 78-83.
Chen Zongxiang, Chen Mingxing, Jiao Minsheng, et al. Fault diagnosis of motor bearings using modified empirical mode decomposition and bi-spectrum[J]. Electric Machines and Control, 2018, 22(5): 78-83.
[11] 刘俊, 王占林, 付永领, 等. 基于EEMD分解的直驱式机电作动器故障诊断[J]. 北京航空航天大学学报, 2012, 38(12): 1567-1571.
Liu Jun, Wang Zhanlin, Fu Yongling, et al. Fault diagnosis of direct-driven electromechanical actuator based on ensemble empirical mode decomposition[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(12): 1567-1571.
[12] Wang Xingjian, Zhao Jian, Wang Shaoping, et al. Fault diagnosis of electromechanical actuator based on principal component analysis and support vector machine[C]//CSAA/IET International Conference on Aircraft Utility Systems (AUS), Guiyang, China, 2018: 1467-1471.
[13] Liu Hongmei, Jing Jiayao, Ma Jian. Fault diagnosis of electromechanical actuator based on VMD multifractal detrended fluctuation analysis and PNN [J]. Complexity, 2018(2): 1-11.
[14] 刘永斌. 基于非线性信号分析的滚动轴承状态监测诊断研究[D]. 合肥: 中国科学技术大学, 2011.
[15] Chen Juan, Wang Liyang. Electromechanical actuator modeling and its application in fault diagnosis[C]// International Conference on Mechanical, Electronic and Information Technology, Shanghai, China, 2018: 223-228.
[16] 姜洪开, 邵海东, 李兴球. 基于深度学习的飞行器智能故障诊断方法[J]. 机械工程学报, 2019, 55(7): 27-34.
Jiang Hongkai, Shao Haidong, Li Xingqiu. Deep learning theory with application in intelligent fault diagnosis of aircraft[J]. Journal of Mechanical Engineering, 2019, 55(7): 27-34.
[17] 曲建岭, 余路, 袁涛, 等. 基于一维卷积神经网络的滚动轴承自适应故障诊断算法[J]. 仪器仪表学报, 2018, 39(7): 134-143.
Qu Jianling, Yu Lu, Yuan Tao, et al. Adaptive fault diagnosis algorithm for rolling bearings based on one-dimensional convolutional neural network[J]. Chinese Journal of Scientific Instrument, 2018, 39(7): 134-143.
[18] Zhang Wei, Peng Gaoliang, Li Chuanhao, et al. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals[J]. Sensors, 2017, 17(2): 425.
[19] 肖雄, 王健翔, 张勇军, 等. 一种用于轴承故障诊断的二维卷积神经网络优化方法[J]. 中国电机工程学报, 2019, 39(15): 4558-4568.
Xiao Xiong, Wang Jianxiang, Zhang Yongjun, et al. A two-dimensional convolutional neural network optimization method for bearing fault diagnosis[J]. Proceedings of the CSEE, 2019, 39(15): 4558-4568.
[20] 张倩, 王建平, 李帷韬. 基于反馈机制的卷积神经网络绝缘子状态检测方法[J]. 电工技术学报, 2019, 34(16): 3311-3321.
Zhang Qian, Wang Jianping, Li Weitao. Insulator state detection of convolutional neural networks based on feedback mechanism[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3311-3321.
[21] 朱煜峰, 许永鹏, 陈孝信, 等. 基于卷积神经网络的直流XLPE电缆局部放电模式识别技术[J]. 电工技术学报, 2020, 35(3): 659-668.
Zhu Yufeng, Xu Yongpeng, Chen Xiaoxin, et al. Pattern recognition of partial discharges in DC XLPE cables based on convolutional neural network[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 659-668.
[22] 孙曙光, 李勤, 杜太行, 等. 基于一维卷积神经网络的低压万能式断路器附件故障诊断[J]. 电工技术学报, 2020, 35(12): 2562-2573.
Sun Shuguang, Li Qin, Du Taihang, et al. Fault diagnosis of accessories for the low voltage conventionalcircuit breaker based on one-dimensional convolutional neural network[J]. Transactions of China Electrote-chnical Society, 2020, 35(12): 2562-2573.
[23] 王晨, 寇鹏. 基于卷积神经网络和简单循环单元集成模型的风电场内多风机风速预测[J]. 电工技术学报, 2020, 35(13): 2723-2735.
Wang Chen, Kou Peng. Wind speed forecasts of multiple wind turbines in a wind farm based on integration model built by convolutional neural network and simple recurrent unit[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2723-2735.
[24] 李超然, 肖飞, 樊亚翔, 等. 基于卷积神经网络的锂离子电池SOH估算[J]. 电工技术学报, 2020, 35(19): 4106-4119.
Li Chaoran, Xiao Fei, Fan Yaxiang, et al. An approach to Lithium-ion battery SOH estimation based on convolutional neural network[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4106-4119.
[25] Krizhevsky A, Sutskever I, Hinton G E. Image Net classification with deep convolutional neural networks[J].Communications of the ACM, 2017, 60(6): 84-90.
[26] Hinton G, Deng Li, Yu Dong, et al. Deep neural networks for acoustic modeling in speech recognition: the shared views of four research groups[J]. IEEE Signal Processing Magazine, 2012, 29(6): 82-97.
[27] Kim Y. Convolutional neural networks for sentence classification[J]. arXiv Preprint, 2014.
[28] 付永领, 刘和松, 庞尧, 等. 机载直驱式机电作动器的伺服控制器设计研究[J]. 测控技术, 2010, 29(7): 36-40.
Fu Yongling, Liu Hesong, Pang Yao, et al. Design of controller for airborne direct drive electro-mechanical actuators[J]. Measurement & Control Technology, 2010, 29(7): 36-40.
[29] 卢胜利. 开关磁阻电机系统的故障诊断方法研究[D].徐州:中国矿业大学, 2010.
[30] Maaten L, Hinton G. Visualizing data using t-SNE[J]. Journal of Machine Learning Research, 2008, 9(2): 2579-2605.
Fault Diagnosis of Electromechanical Actuators Based on One-Dimensional Convolutional Neural Network
Abstract To address the problem that traditional fault diagnosis methods of electromechanical actuators largely depend on artificial feature extraction and engineering experience, this paper proposes an intelligent fault diagnosis method based on one dimensional convolutional neural network (1DCNN). Compared with the separation of feature extraction and classification in the traditional fault diagnosis algorithm, the proposed method combines the two into one. Firstly, the normal signals and fault signals of direct-driven electromechanical actuators are preprocessed by overlapping sampling to acquire data samples. Subsequently, the obtained samples are fed into the designed one-dimensional convolutional neural network model, and the effective feature representation is acquired through multi-layer data transformation, thereby establishing a mapping relationship between the raw data and operating state and achieving end-to-end fault diagnosisof electromechanical actuators. The experimental results demonstrate that the proposed algorithm can effectively diagnose the fault of the electromechanical actuator, and the fault recognition accuracy can reach about 98%. In addition, the proposed method can still maintain a high fault recognition accuracy under different white noise conditions, which shows that it has good robustness and generalization performance.
keywords:Direct-drive electromechanical actuator, one-dimensional convolutional neural network, fault diagnosis, deep learning
DOI:10.19595/j.cnki.1000-6753.tces.L90390
中图分类号:TM307.1; TP206.3
国家自然科学基金项目(51877172)、中央高校基本科研业务费专项资金项目(1191329824)和陕西省自然科学基础研究计划青年项目(2019JQ-458)资助。
收稿日期 2020-07-11
改稿日期 2020-09-15
李世晓 男,1996年生,硕士研究生,研究方向为电气设备状态监测和故障诊断。E-mail:lishixiao925@stu.xjtu.edu.cn
杜锦华 女,1984年生,副教授,博士生导师,研究方向为电机设计及其驱动研究。E-mail:jinhuadu@mail.xjtu.edu.cn(通信作者)
(编辑 郭丽军)