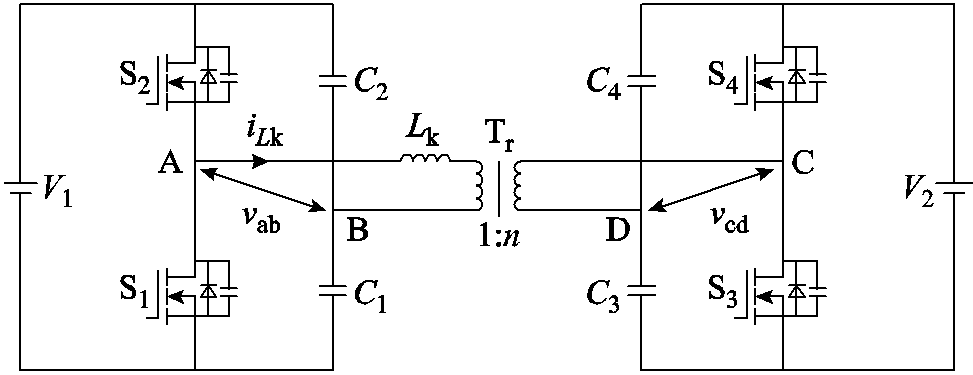
图1 DAHB 电路原理图
Fig.1 Circuit schematic of DAHB
摘要 为减小双主动半桥直流变换器（DAHB）在传统双重移相（DPS）调制下轻载区较大的功率损耗，该文提出一种基于强化学习（RL）的DPS调制效率优化方案（QDPS）。该方案使用Q-learning算法作为一种RL的典型算法，通过对智能体进行离线训练，得到优化后的调制策略QDPS。该策略能够为DAHB直流变换器提供最优的移相角，有效减小变换器在轻载区的功率损耗。与现有的单移相控制策略和双重移相控制策略相比，QDPS移相控制策略能够有效提高变换器的运行效率，改善变换器的性能。最后，通过Matlab/Simulink仿真验证了所提出优化方案的有效性。
关键词：双重移相控制 双主动半桥直流变换器 强化学习 Q-learning 效率
随着太阳能和风能发电等绿色可再生能源装机容量的快速增长，双向多端口直流变换器的利用受到了更广泛的关注[1]。双主动半桥（Dual-Active-Half-Bridge, DAHB）直流变换器由于具有许多优点，除了能实现能量的双向流动之外[2-3]，还包括高功率密度、高电压传输比、易于实现软开关等，逐渐成为此类应用的研究热点[4-5]，在新能源汽车、电力电子变压器、可再生能源发电等场合有着重要的应用[6-7]。
与双主动全桥直流变换器（Dual-Active-Bridge, DAB）相同，调节DAHB直流变换器中功率流的方法[8-9]有单移相（Single-Phase-Shift, SPS）控制和双重移相（Dual-Phase-Shift, DPS）控制[10]等。SPS控制简单，易实现，而且可以在有效电压转换比为1时实现在整个功率范围内的零电压开通（Zero Voltage Switching, ZVS）操作[11]。但这种控制方式在应用中存在两大限制，一方面SPS控制仅当有效电压转换比为1时，才可以在整个功率范围内进行ZVS操作；另一方面，SPS控制会导致电路电流应力增大、无功环流增加，从而导致变换器的效率降低[12]。
鉴于上述局限性，文献[13-14]中提出了几种直流变换器调制技术，文献[15-16]中提出了几种改进电路拓扑的方法，达到了拓宽软开关实现的功率范围，减少变换器损耗的目的。文献[17]分析了SPS控制的局限性，提出了基于DPS的控制策略，用以减小变换器的无功环流和电流应力。该控制策略在两侧半桥外移相的基础上，都以相同的占空比（非0.5）驱动半桥开关管导通，通过优化两自由度的取值来达到所需的优化目标[18]。但采用DPS控制的DAHB直流变换器的优化目标的实现过程存在复杂的计算，同时也存在轻载区功率损耗较高，变换器效率较低的问题[19]。
近年来，人工智能技术的快速发展改变了过去的传统控制策略。例如，文献[20]中提出了一种利用神经网络的优化控制，可用于减小DAB直流转换器的无功功率。但是，这种神经网络的利用受到耗时长、过拟合等问题的限制。随着强化学习的快速发展，它已被广泛应用于控制问题的优化[21-22]。作为机器学习的一个重要分支，强化学习区别于深度学习中的有监督学习和无监督学习，主要通过试错与环境交互改进控制策略，进行自主学习和在线学习。强化学习的原理受到大脑学习本质的启发，模拟动物学习行为过程中大脑的学习过程，通过智能体与环境条件相互作用获得之前状态数据，自主进行动作选择，并生成控制策略，进行多次训练，使智能体具有自主学习能力。
强化学习的基本学习机制表明，它可以在没有环境模型的情况下接受和处理动态环境中的不完整和不确定的信息，产生最佳策略，选择最佳动作。作为最常用的代表性强化学习方法之一，Q-learning算法近年来引起了越来越多的关注[23]。Q-learning是强化学习算法中value-based的算法[24]，与其他强化学习算法相比，Q-learning算法中Q函数简单，可以在智能体与动态环境[25]交互时在线使用，采用试错的方法寻找最优的行为策略。结合本文中DAHB直流变换器DPS控制策略的分析，该算法非常适合为其寻找最优控制量。
因此，本文分析DAHB直流变换器在DPS控制下的工作特性和存在问题，提出一种基于强化学习中Q-learning算法的DPS（Q-learning Dual-Phase-Shift, QDPS）调制效率优化方案，成功地规避了传统方案中选择最优运行方式的繁琐过程并达到了减小变换器的功率损耗的目的。
本文对DAHB直流变换器的控制策略进行详细研究，提出一种基于强化学习的DAHB直流变换器的效率优化方案。该方案将为DAHB直流变换器寻找最佳控制变量，减小变换器在轻载条件下的功率损耗，改善变换器在轻载条件下的效率特性。本文首先介绍了DPS控制的工作原理，然后给出了DPS控制下DAHB直流变换器的模态和损耗分析，再结合强化学习中的Q-learning算法，设计了算法的状态、动作空间和奖励函数，并设置训练参数，完成训练过程，得到效率优化方案。最后，搭建仿真模型，并通过Matlab/Simulink仿真验证了方案的有效性。
DAHB的电路工作原理如图1所示，两个高频半桥通过中间的高频变压器连接。V1和V2分别为变压器两侧直流电压，vab和vcd分别为两侧半桥直流电压，S1～S4为开关管，C1～C4为半桥均压电容。变压器的电压比为1:n，Lk为变压器折算到一次侧的漏感和外部串联电感之和，iLk为流过Lk的电流。一次侧半桥（S1,S2）与低压直流端口（V1）接口连接，而二次侧半桥（S3,S4）与高压直流端口（V2）连接。
DPS控制下，DAHB直流变换器的工作波形如图2所示，T为一个开关周期，D1为一次侧开关管的导通占空比，D2为两侧半桥之间的移相比。
图1 DAHB 电路原理图
Fig.1 Circuit schematic of DAHB
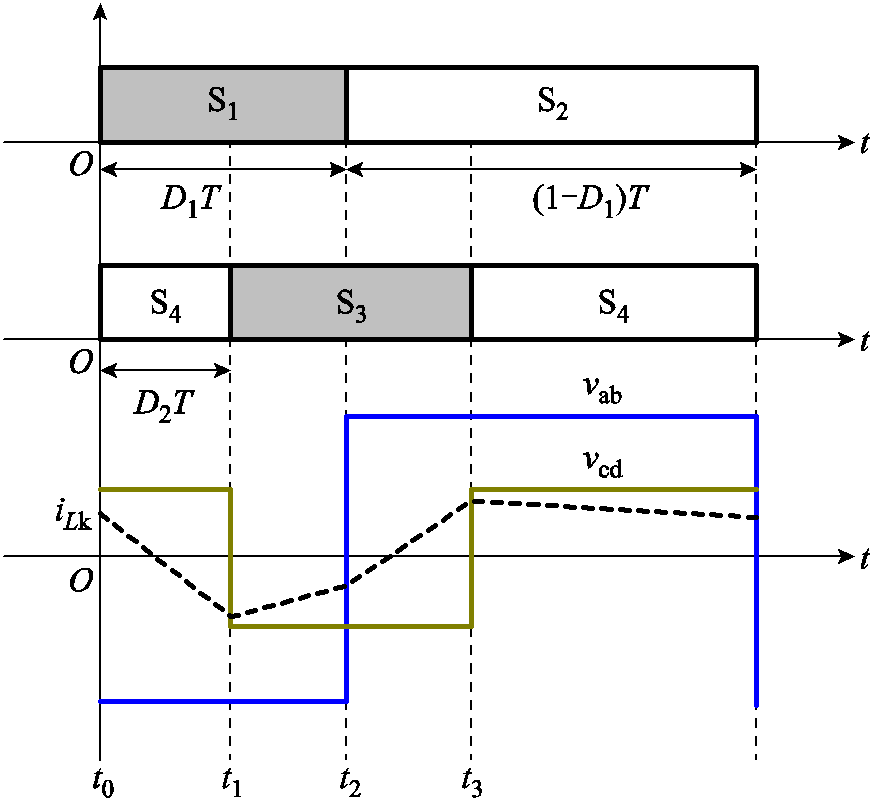
图2 DAHB在DPS控制下的工作波形
Fig.2 Operating waveforms of DAHB with DPS control
从图2中可以看出，流经Lk的电流iLk的波形是分段线性的，具有四个部分。假设其斜率分别k1、k2、k3、k4，Lk在t0、t1、t2、t3时刻的电流值分别为i0、i1、i2、i3。根据C1和C2的电荷平衡，可以求得各个时刻流经Lk的电流值大小，即各个开关管开通时刻的电流值为
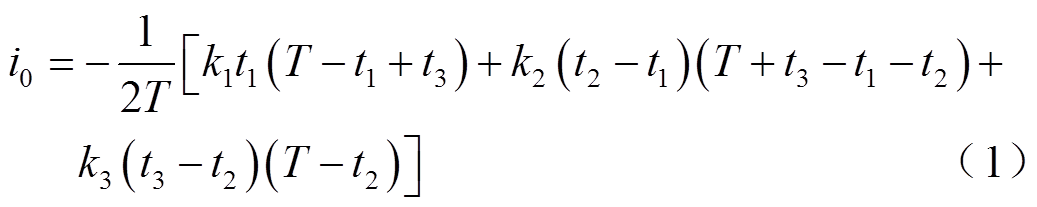
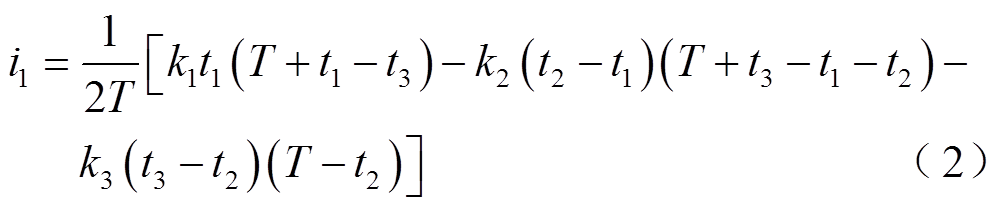
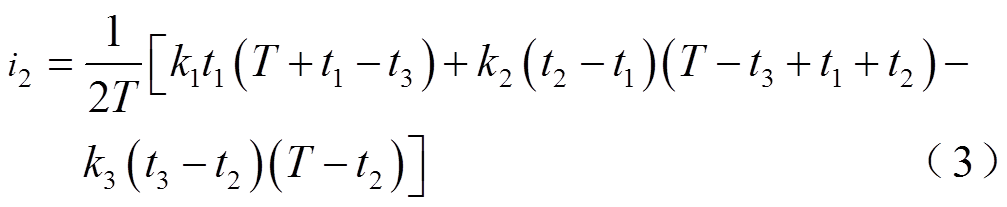
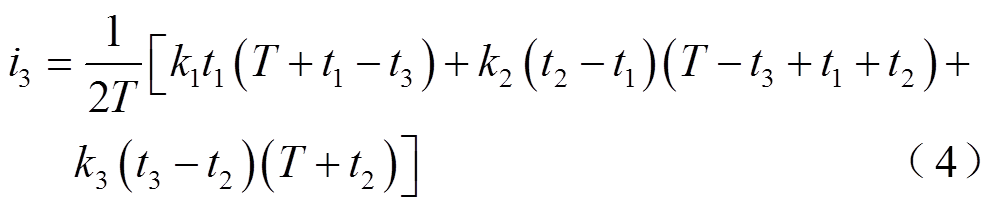
开关管的开通时刻为
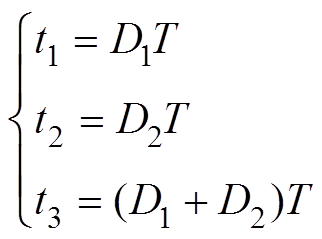（5）
D1和D2的取值范围分别为0＜D1＜1，0＜D2＜1。
根据D1和D2的不同取值，可以将DPS控制DAHB直流变换器的工作模态分为6个。每个模态下的操作约束见表1。根据各个模态的约束条件，给出DAHB直流变换器在DPS控制下各个模态的工作波形如图3所示。
表1 模态操作约束
Tab.1 Mode operational constraints
模态模态约束 模态一D1＜0.5, D2＜D1 模态二D1＜0.5, D1＜D2＜1-D1 模态三D1＜0.5, 1-D1＜D2 模态四0.5＜D1, D2＜1-D1 模态五0.5＜D1, 1-D1＜D2＜D1 模态六0.5＜D1, D1＜D2
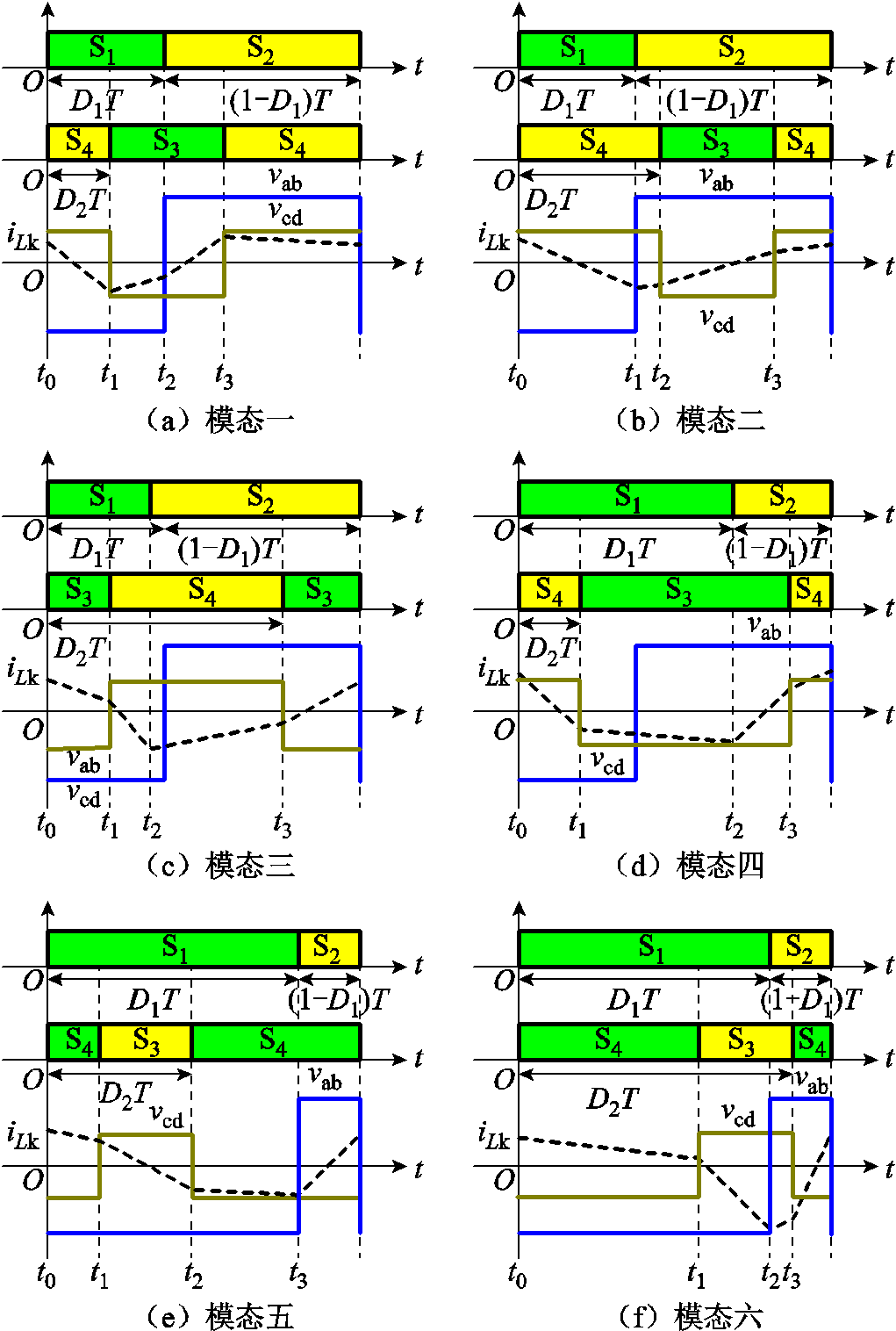
图3 DPS控制下各个模态的工作波形
Fig.3 Operating waveforms of each mode with DPS control
变换器在每一个开关周期的平均输出有功功率为
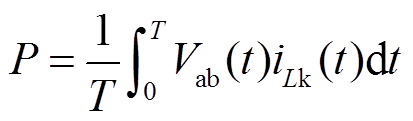（6）
电感电流有效值为
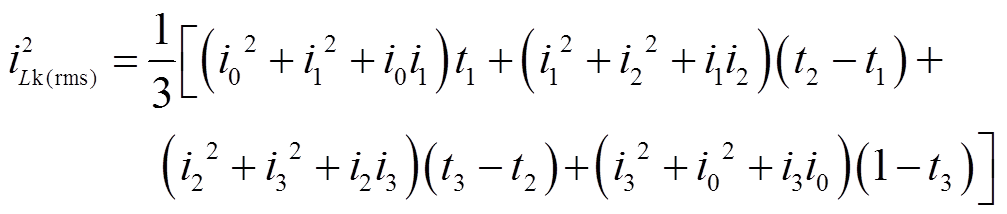（7）
以模态一为例，DAHB直流变换器在一个周期内的平均输出有功功率为
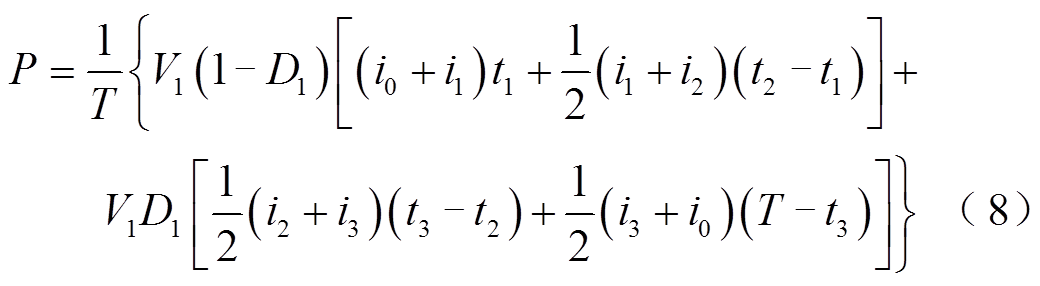
此外，变换器的最大传输功率为
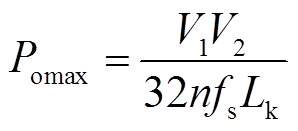（9）
式中，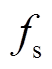
为开关管开关频率。
DAHB直流变换器中通常包含四种功率损耗：开关管损耗PS、磁性元件损耗PM、电容损耗PC和未知损耗PU[26]。具体来说，开关管损耗PS可以分为导通损耗PC_S、开关损耗PSw_S和门极驱动损耗PGat_S。磁性元件损耗PM集中在变压器Tr和串联电感器Lk、包括铜损PCop_M和铁损PCor_M。此外，未知损耗PU主要包含与磁性设备和电源开关模块有关的随温度变化的铜损和传导损耗。由于PU在所有功率损耗PA中占比很少，为简化理论分析，常选择忽略这部分损耗。
由此，得到整个DAHB变换器所有损耗PA的表达式为
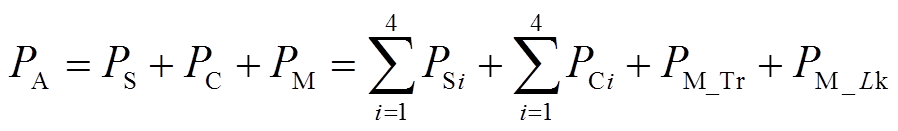（10）
式中，PSi为四个开关管（S1～S4）中的损耗；PM_Tr和PM_Lk分别为变压器和电感Lk中的磁性元件损耗；PCi为电容C1～C4损耗。损耗分类见附表1[27-29]。
Q-learning是一种用于机器学习的强化学习算法，它的优势是可以在无需环境模型和调整的情况下，处理随机转换和奖励的问题。本文在Q-learning算法中，将学习的经验记录在Q值表中，根据该Q值表获得最佳行动策略。具体来说，Q值表由不同状态的转移概率组成，该算法将基于最大值行为选择，直接选择具有最高Q值的行为。因此，Q-learning算法非常适合用于本文中快速寻求DAHB直流变换器的最佳控制变量（D1和D2），从而获得DAHB在整个工作范围内的最小功耗。下面将基于Q-learning算法构造状态空间以及动作空间，给出奖赏函数的定义和Q值更新公式，实现对DAHB直流变换器的最优控制量D1和D2的快速求解。
Q-learning算法中有三个要素，分别是状态、动作和奖励。在DAHB直流变换器中，参考输入量由输入电压V1、输出电压V2和传输功率Po组成。对于参考输入量V1、V2和Po，当前输入条件下的功率损耗PA由当前移相角D1和D2确定。因此，在Q-learning算法中定义状态空间为s，即
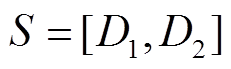（11）
状态s的变化由当前动作a决定。根据当前状态s，可通过策略π获得最佳新状态。由于当前状态s由D1和D2确定，因此可以通过更改D1、D2的值来获得下一个状态s'。此外，状态s的值应根据传输功率和移相角之间的灵敏度来量化，故将Di空间定义为
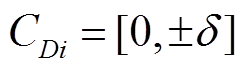（12）
式中，δ为状态s的量化量。D1和D2的增量∆Di应满足约束
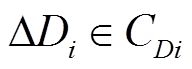（13）
因此，定义动作空间为
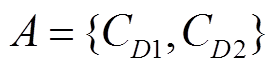（14）
在Q-learning算法中定义奖励函数为
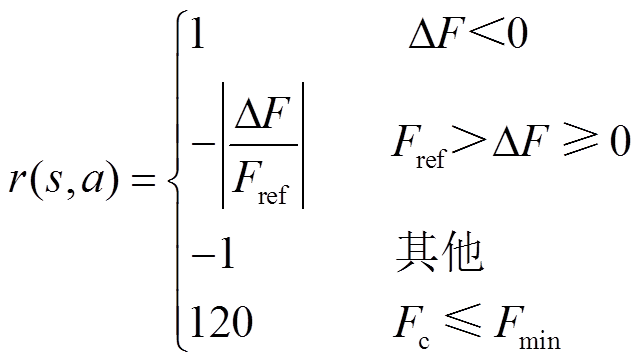（15）
式中，F为最小功率误差和最小功率损耗的目标函数；Fc为当前状态下的目标函数F的值；Fref为目标函数F的参考值，且Fref＞0；Fmin为目标函数F的最小值；ΔF为两个相邻状态之间目标函数F的差，即
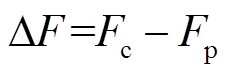（16）
式中，Fp为目标函数F在之前状态的值。
可以通过目标函数F来评估DAHB直流变换器的性能，F值越小，则说明变换器性能越好。
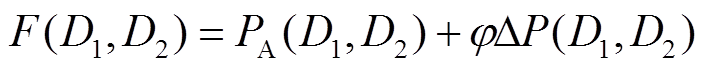（17）
式中，PA(D1, D2)为功率损耗函数；ΔP(D1, D2)为功率误差函数；φ为惩罚因子。由于非线性等式约束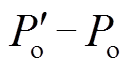
很难在Q-learning算法中直接使用，因此定义功率误差函数为ΔP，即
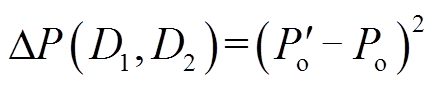（18）
式中，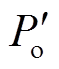
为在训练过程中的传输功率；Po为预期的传输功率。
ΔF＞0表示当前状态下目标函数F的值大于先前状态，该动作将导致负向奖励；ΔF＜0意味着在动作a之后目标函数F的值减小，该动作将导致正向奖励。一旦目标函数F的值小于或等于目标函数Fmin的最小值，则给出较大的奖励值，这表明DAHB直流变换器已从初始状态达到最佳状态。
Q-learning算法的主要目的是在DAHB直流变换器的整个工作范围内寻找最优的控制策略，即寻找最优的D1和D2，以获得最小的功率损耗。优化方案在完成状态空间、动作空间创建并设置奖励函数之后，进行Q值更新和动作选择。Q-learning算法作为一种增量动态规划算法，学习的最佳策略是逐步确定的。对于策略π，Q值的计算方法为
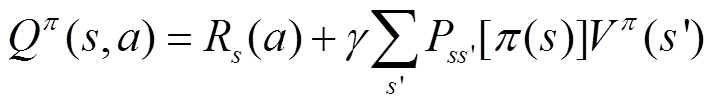（19）
式中，Rs(a)为状态s的奖励平均值；Pss'[π(s)]为在策略π下的状态转移概率；Vπ(s')为在状态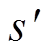
下遵循策略π获得的期望值。在学习过程之后，Vπ(s)的值将收敛到V*(s)，将其定义为
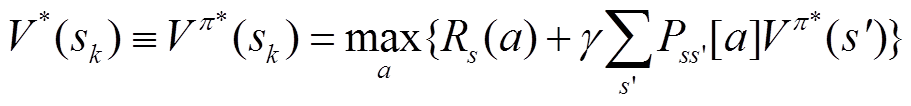（20）
式中，k为迭代次数。实际上，通常可以将Q-learning算法的主体的状态转换过程建模为马尔可夫决策过程（Markov Decision Processes, MDP）。因此，Q值的更新公式可以表示为
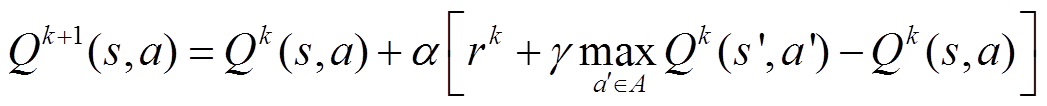（21）
式中，α为学习率；γ为折扣因子；Qk(s,a)为在状态s和动作a下的Q值。Q-learning算法的关键参数见表2。
表2 Q-learning算法关键参数
Tab.2 Critical parameters of the Q-learning algorithm
参数数值 惩罚因子φ1.0 学习速率α1.0 折扣因子γ0.8 状态量δ10-3 F的参考值Fref20 最大训练时长NT106 步长Ni2 500 先前状态中F最小值Fmin120 基于e-greedy的探索次数M103
为了获得DAHB直流变换器的最佳效率。本文采用
-greedy方法进行行为选择，在选择过程中，尽可能地探索更多的策略，并保存每种策略中的最优的功率损耗状态。经过N次的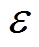-greedy方法学习后，选择N次训练中得到的最小目标函数值Fmin作为状态更新中的参数，然后利用Q值最大的方法进行行为选择继续进行训练，直到Q-learning算法学习得到的策略收敛。
本文的DAHB直流变换器的工作范围见表3，其中输入电压V1范围为40～60V，输出电压V2保持在200V，传输功率P0范围为0～375W。分别设置V1和P0的间隔为0.5V和0.5W，若采用类似文献[20]中提出的启发式算法，每次在操作环境（V1、V2和P0）改变时都需要完成30 791个优化过程[30]，将面临计算复杂度增加的问题。本文提出的基于强化学习的双主动半桥直流变换器的效率优化方案无需如此复杂的优化过程。在完成Q-learning算法的训练过程之后，将训练结果存储在查找表中。查找表中的输入为当前操作环境，包括输入电压V1、输出电压V2和传输功率P0。查找表中的输出为当前状态的动作策略响应。此外，分别设置V1和P0的间隔为0.5V和0.5W，以合理控制精度和查询表的大小。实际上，当检测到操作环境时，将首先对其进行量化，然后直接从此查找表中找到相应的动作策略（D1和D2）。如果在查找表中找不到量化的操作环境，则选择与当前操作环境最接近的值，直接找到相应的动作策略（D1和D2），这种方法类似于文献[25, 31]中的方法。与使用启发式算法相比使用Q-learning算法的双主动半桥直流变换器的效率优化方案，解决了其计算复杂度增加的问题，并可在不同的操作环境下获得优化策略。
经过训练，Q-learning算法结合传统DAHB直流变换器的DPS移相控制，得到了DAHB直流变换器最佳控制变量D1和D2，构成QDPS控制策略。该策略将为DAHB直流变换器提供最佳移相角，使得变换器的功率损耗最小。
本文在Matlab/Simulink中搭建了DAHB直流变换器的仿真模型，参数设置见表2。输出电压V2控制为200V，输入电压V1可变，来模拟端口电压变化的情况。电压传输比随V1变化而变化，用以验证DAHB直流变换器在不同电压传输比下的特性。通过仿真模型测得DAHB直流变换器的电流峰值和电流有效值等参数，并结合附表1计算出变换器的损耗。
不同运行条件下得到的训练移相角D1和D2如图4所示，本节使用搭建的仿真模型对所提出的QDPS控制策略的性能进行评估。
图4 不同运行条件下的训练移相角
Fig.4 Curves of the phase-shift angles under different operation conditions after training.
图5为V1=50V，V2=200V，传输功率为125W时，DAHB直流变换器分别在DPS和QDPS调制策略下的工作波形。观察得到，在QDPS调制策略下变换器电感电流峰值相比DPS调制策略明显减小，测量得到其绝对值从DPS调制下的36.60A降低为QDPS调制下的24.66A。
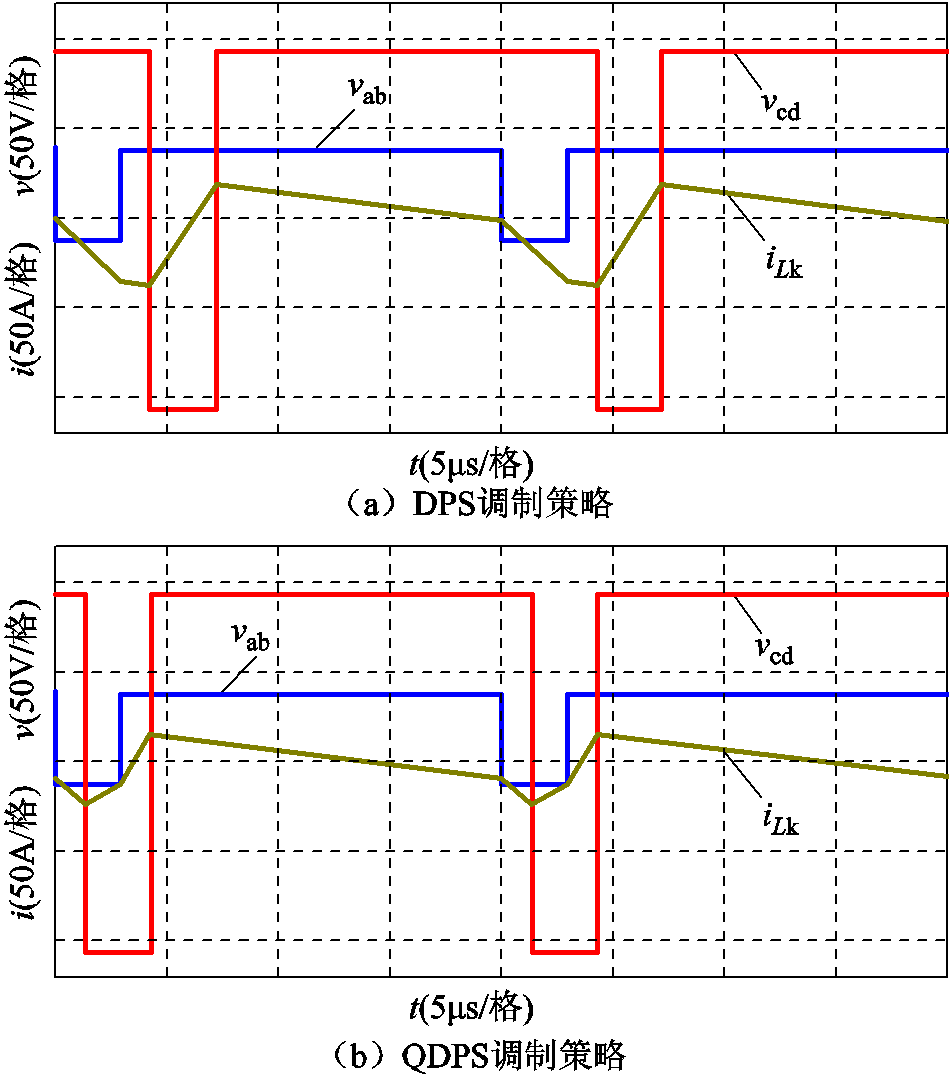
图5 V1=50V, V2=200V, Po=125 W时DAHB的工作波形
Fig.5 Operating waveforms of DAHB at V1=50V, V2=200V, Po=125W
图6给出了在不同电压传输比条件下，DAHB直流变换器电感电流有效值与传输功率的关系曲线。从图6中可以看出，在整个轻载功率范围内，QDPS调制策略下的电感电流有效值在不同电压传输比的情况下都明显小于SPS调制和DPS调制下对应的电感电流有效值。
图7给出了在传输功率为125W时，DAHB直流变换器工作在不同电压传输比下的损耗和效率特性曲线。可以看出，变换器处于低功率段时，在不同的电压传输比下QDPS调制策略同SPS和DPS调制策略相比，能够显著降低变换器功率损耗PA，明显提高变换器效率。测量得到，相较于SPS调制策略，QDPS调制策略，将DAHB直流变换器效率最高提升了21.06%；相较于DPS调制策略，QDPS调制策略，将DAHB直流变换器效率最高提升了15.66%。
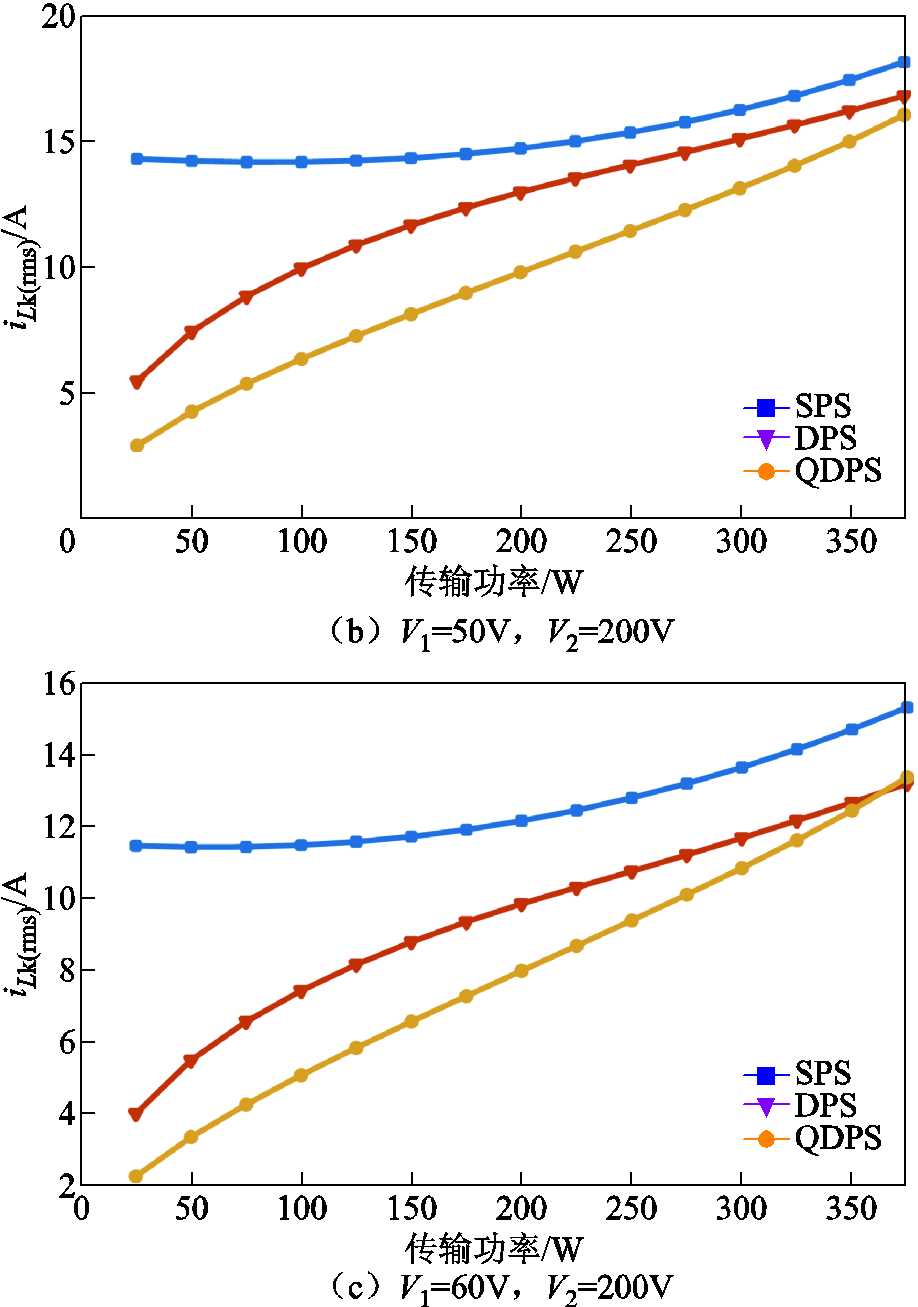
图6 电感电流有效值与传输功率的关系曲线
Fig.6 RMS current of inductor with transmission power
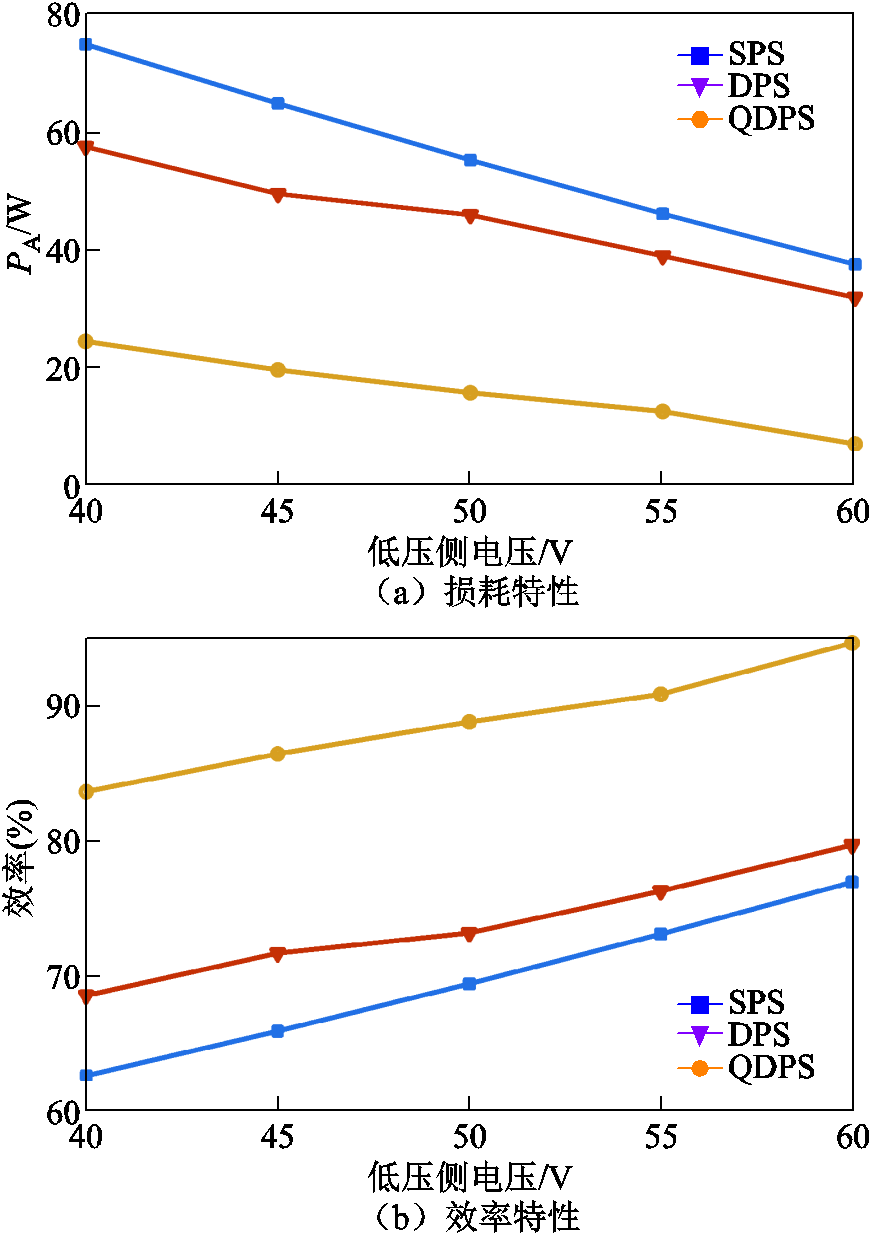
图7 传输功率为125W时DAHB的损耗和效率特性
Fig.7 Loss and efficiency characteristics of DAHB at Po=125W
图8给出了在传输功率为350W时，DAHB直流变换器工作在不同电压传输比下的损耗和效率特性曲线。可以看出，变换器处于重载条件下时，在不同的电压传输比下QDPS调制策略同SPS和DPS调制策略相比，能够降低变换器功率损耗PA，提高变换器效率。测量得到，QDPS调制策略相较于SPS调制策略，将DAHB直流变换器效率最高提升了3.31%；相较于DPS调制策略，将DAHB直流变换器效率最高提升了5.06%。
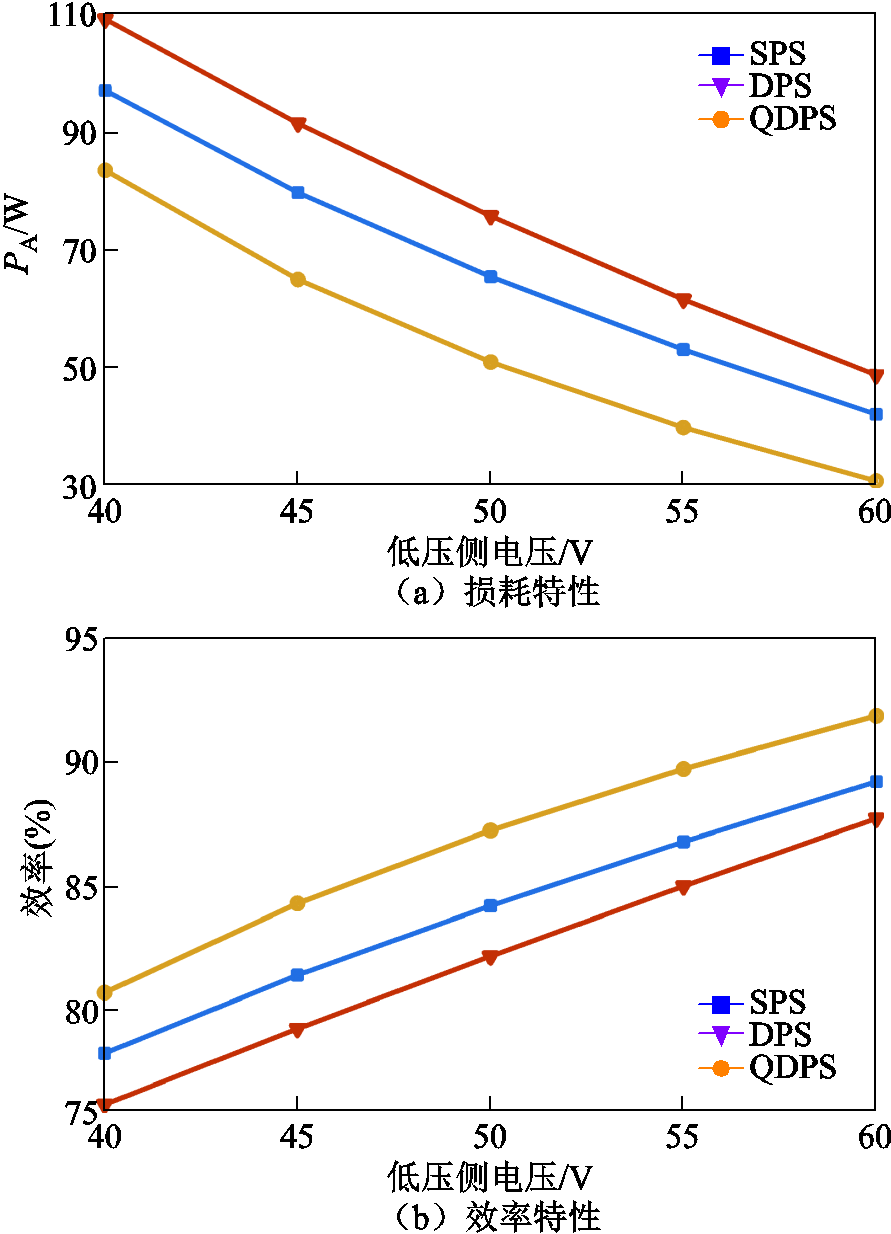
图8 传输功率为350W时DAHB的损耗和效率特性
Fig.8 Loss and efficiency characteristics of DAHB at Po=350W
DAHB直流变换器工作在V1=50V、V2=200V时的损耗和效率特性如图9所示。可以看出，在当前条件下，相比传统的SPS和DPS调制策略，QDPS调制策略在整个功率范围内都能表现出更好的效率特性。当传输功率为125W时，QDPS调制下的变换器效率相较于SPS调制下的69.33%和DPS调制下的73.10%提升至88.76%。
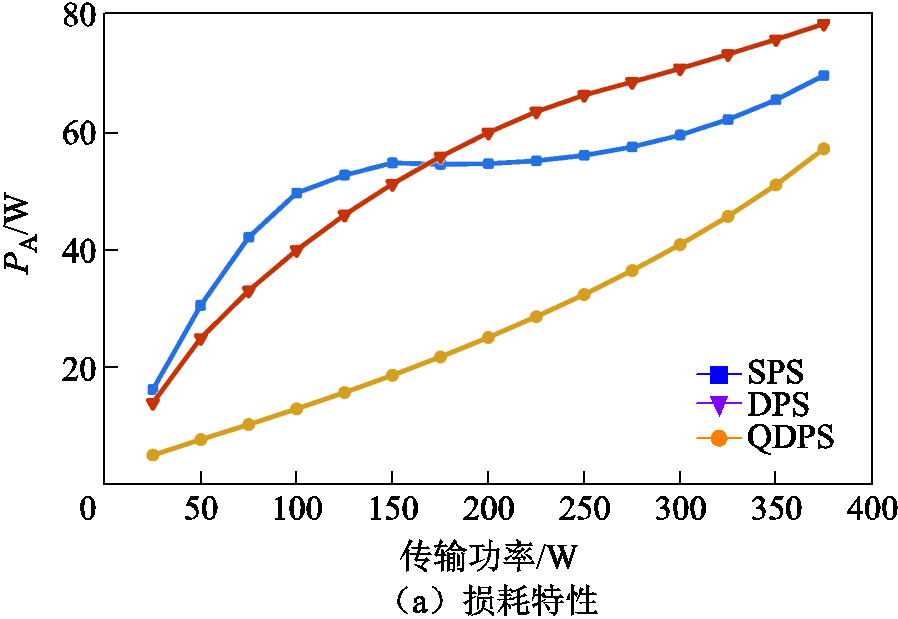
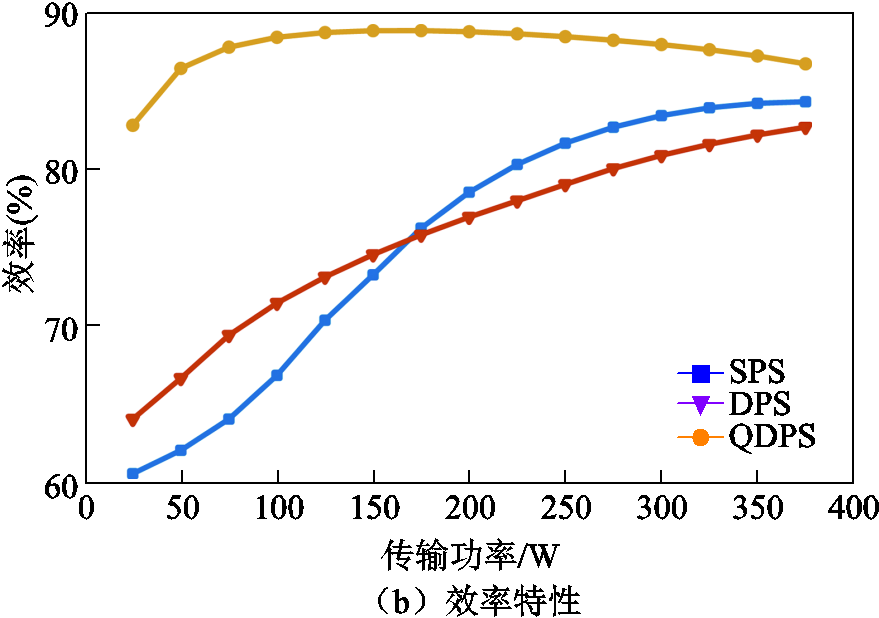
图9 V1=50V，V2=200V时DAHB的损耗和效率特性
Fig.9 Loss and efficiency characteristics of DAHB at V1=50V，V2=200V
本文提出了一种基于强化学习的双主动半桥直流变换器的效率优化方案，能够改善变换器在轻载条件下的效率特性。该方案利用Q-learning算法为DAHB直流变换器寻找最佳的调制策略，文中重点描述了如何使用Q-learning算法为DAHB选取最优控制量，并使用Matlab/Simulink仿真给出了SPS、DPS和QDPS三种调制策略在不同运行条件下的性能比较。结果表明，在QDPS调制策略下，DAHB直流变换器在全功率范围内的功率损耗均小于SPS和DPS调制策略下得到的最优值，从而提高了变换器的功率传输效率，且在轻载条件下的改善尤为明显，验证了所提出效率优化方案的有效性和正确性。
附表1 损耗分类
App.Tab.1 The classification of the power losses
损耗类型公式 开关管损耗PS导通损耗PC_S 开关损耗PSw_S 门极驱动损耗PGat_S 磁性元件损耗PM铜损PCop_M 铁损PCor_M 电容损耗PC电容损耗Pcap
参考文献
[1] ZhangXing, WangMingda, ZhaoTao, et al. Topological comparison and analysis of medium-voltage and high-power direct-linked PV inverter[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(4): 327-334.
[2] 杨博, 葛琼璇, 赵鲁, 等. 基于输入串联输出并联的双向全桥串联谐振DC-DC变换器系统控制策略研究[J]. 电工技术学报, 2020, 35(12): 2574-2584.
Yang Bo, Ge Qiongxuan, Zhao Lu, et al. Control strategy of dual bridge series resonant DC-DC converter system based on input series output parallel connection[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2574-2584.
[3] 黄先进, 赵鹃, 游小杰. 一种基于输入串联输出并联移相全桥变换器的改进交错控制方法[J]. 电工技术学报, 2020, 35(增刊1): 81-90.
Huang Xianjin, Zhao Juan, You Xiaojie. An improved interleaved control method based on input-series output-parallel phase-shifted full-bridge converter[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 81-90.
[4] Chan Y P, Loo K H, Yaqoob M, et al. A structurally reconfigurable resonant dual-active-bridge converter and modulation method to achieve full-range soft-switching and enhanced light-load efficiency[J]. IEEE Transactions on Power Electronics, 2019, 34(5): 4195-4207.
[5] Li Haoyu, Zhao Lei, Xu Chuanyu, et al. A dual half-bridge phase-shifted converter with wide ZVZCS switching range[J]. IEEE Transactions on Power Electronics, 2018, 33(4): 2976-2985.
[6] 陈红坤, 夏方舟, 袁栋, 等. 直流配电网中含光伏的电动汽车快速充电站优化配置方案[J]. 电力系统自动化, 2020, 44(16): 53-60.
Chen Hongkun, Xia Fangzhou, Yuan Dong, et al. Optimal configuration scheme of fast electric vehicle charging station with photovoltaic in DC distribution network[J]. Automation of Electric Power Systems, 2020, 44(16): 53-60.
[7] Pan Xuewei, Rathore A K. Novel bidirectional snubberless naturally commutated soft-switching current-fed full-bridge isolated DC/DC converter for fuel cell vehicles[J]. IEEE Transactions on Industrial Electronics, 2014, 61(5): 2307-2315.
[8] 赵彪, 宋强, 刘文华, 等. 用于柔性直流配电的高频链直流固态变压器[J]. 中国电机工程学报, 2014, 34(25): 4295-4303.
Zhao Biao, Song Qiang, Liu Wenhua, et al. High-frequency-link DC solid state transformers for flexible dc distribution[J]. Proceedings of the CSEE, 2014, 34(25): 4295-4303.
[9] Inoue S, Akagi H. A bidirectional isolated DC-DC converter as a core circuit of the next-generation medium-voltage power conversion system[J]. IEEE Transactions on Power Electronics, 2007, 22(2): 535-542.
[10] 曾进辉, 孙志峰, 雷敏, 等. 双重移相控制的双主动全桥变换器全局电流应力分析及优化控制策略[J]. 电工技术学报, 2019, 34(12): 2507-2518.
Zeng Jinhui, Sun Zhifeng, Lei Min, et al. Global current stress analysis and optimal control strategy of dual-active full bridge converter based on dual phase shift control[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2507-2518.
[11] Kheraluwala M N, Gascoigne R W, Divan D M, et al. Performance characterization of a high-power dual active bridge DC-to-DC converter[J]. IEEE Transactions on Industry Applications, 1992, 28(6): 1294-1301.
[12] 林雪凤, 许建平, 周翔. 谐振软开关耦合电感高增益DC-DC变换器[J]. 电工技术学报, 2019, 34(4): 747-755.
Lin Xuefeng, Xu Jianping, Zhou Xiang. Soft-switched high step-up DC-DC converter with coupled inductor of resonance[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 747-755.
[13] Oggier G G, Garcla G O, Oliva A R. Switching control strategy to minimize dual active bridge converter losses[J]. IEEE Transactions on Power Electronics, 2009, 24(7): 1826-1838.
[14] Chakraborty S, Chattopadhyay S. Minimum-RMS- current operation of asymmetric dual active half-bridge converters with and without ZVS[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5132-5145.
[15] Kojima K, Tsuruta Y, Kawamura A. Proposal of dual active bridge converter with auxiliary circuit for multiple pulse width modulation[C]//2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 2016: 1-8.
[16] 周国华, 范先焱, 许多, 等. 具有宽范围输入和高效率的改进型LLC谐振变换器[J]. 电机与控制学报, 2020, 24(10): 9-18.
Zhou Guohua, Fan Xianyan, Xu Duo, et al. Improved LLC resonant converter with wide range input and high efficiency[J]. Electric Machines and Control, 2020, 24(10): 9-18.
[17] Tong Anping, Hang Lijun, Li Guojie, et al. Modeling and analysis of a dual-active-bridge-isolated bidirectional DC/DC converter to minimize RMS current with whole operating range[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 5302-5316.
[18] 安峰, 杨柯欣, 王嵩, 等. 基于模型前馈的双有源全桥DC-DC变换器电流应力优化方法[J]. 电工技术学报, 2019, 34(14): 2946-2956.
An Feng, Yang Kexin, Wang Song, et al. Current stress optimized scheme with model-based feedforward for dual-active-bridge DC-DC converters[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 2946-2956.
[19] 杨超, 许海平, 张祖之, 等. PWM与移相结合控制下的混合三电平隔离型双向DC-DC最小回流功率控制研究[J]. 电工技术学报, 2019, 34(15): 3186-3197.
Yang Chao, Xu Haiping, Zhang Zuzhi, et al. Global minimum peak current control of the three level isolated half-bridge bi-directional DC-DC converters with PWM-phase-shifting control[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3186-3197.
[20] Harrye Y A, Ahmed K H, Aboushady A A. Reactive power minimization of dual active bridge DC/DC converter with triple phase shift control using neural network[C]//2014 International Conference on Renewable Energy Research and Application (ICRERA), Milwaukee, WI, USA, 2014: 566-571.
[21] Munos R, Stepleton T, Harutyunyan A, et al. Safe and efficient off-policy reinforcement learning[C]// Proceedings of the 30th International Conference on Neural Information Processing Systems (NIPS), Barcelona, SPAIN, 2016: 1054-1062.
[22] Fu Jian, He Haibo, Zhou Xinmin. Adaptive learning and control for MIMO system based on adaptive dynamic programming[J]. IEEE Transactions on Neural Networks, 2011, 22(7): 1133-1148.
[23] Wei Qinglai, Lewis F L, Sun Qiuye, et al. Discrete-time deterministic Q-learning: a novel convergence analysis[J]. IEEE Transactions on Cybernetics, 2017, 47(5): 1224-1237.
[24] Jang B, Kim M, Harerimana G, et al. Q-learning algorithms: a comprehensive classification and applications[J]. IEEE Access, 2019, 7: 133653-133667.
[25] Wei Qinglai, Liu Derong, Shi Guang. A novel dual iterative Q-learning method for optimal battery management in smart residential environments[J]. IEEE Transactions on Industrial Electronics, 2015, 62(4): 2509-2518.
[26] Akagi H, Yamagishi T, Tan N M L, et al. Power-loss breakdown of a 750-V 100-kW 20-kHz bidirectional isolated DC-DC converter using SiC-MOSFET/SBD dual modules[J]. IEEE Transactions on Industry Applications, 2015, 51(1): 420-428.
[27] Ji Baojian, Wang Jianhua, Zhao Jianfeng. High-efficiency single-phase transformerless PV H6 inverter with hybrid modulation method[J]. IEEE Transactions on Industrial Electronics, 2013, 60(5): 2104-2115.
[28] Shih L C, Liu Yihua, Chiu H J. A novel hybrid mode control for phase-shift full bridge converter featuring high efficiency over a full load range[J]. IEEE Transactions on Power Electronics, 2018, 34(3): 2794-2804.
[29] Liu Bochen, Davari P, Blaabjerg F. An optimized control scheme for reducing conduction and switching losses in dual active bridge converters[C]//2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 2018: 622-629.
[30] Xiong Rui, Cao Jiayi, Yu Quanqing. Reinforcement learning-based real-time power management for hybrid energy storage system in the plug-in hybrid electric vehicle[J]. Applied Energy, 2018, 211(1): 538-548.
[31] Jiang Yi, Fan Jialu, Chai Tianyou, et al. Tracking control for linear discrete-time networked control systems with unknown dynamics and dropout[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(10): 4607-4620.
Efficiency Optimization Scheme of Dual-Active-Half-Bridge DC-DC Converter Based on Reinforcement Learning
Abstract Aiming to optimize the modulation efficiency of the dual-active-half-bridge (DAHB) DC-DC converter under traditional dual-phase-shift (DPS) modulation in the light load region with large power loss, a DPS modulation efficiency optimization scheme (QDPS) based on reinforcement learning (RL) is proposed in this paper. Using the Q-learning algorithm as a typical RL algorithm, the scheme obtains the optimized modulation strategy QDPS through offline training of the agent, which can provide the optimal phase shift angle for the DAHB DC-DC converter and effectively reduce the power loss of the converter in the light load region. Compared with the existing single-phase-shift and dual-phase-shift control strategy, the QDPS phase shift control strategy can effectively increase the operating efficiency and improve the performance of the converter. Finally, Matlab/Simulink simulation verifies the effectiveness of the proposed optimization scheme.
keywords：Dual-phase-shift control, dual-active-half-bridge DC-DC converter, reinforcement learning, Q-learning, efficiency
DOI: 10.19595/j.cnki.1000-6753.tces.L90399
中图分类号：TM46
四川省科技计划（杰出青年科技人才）资助项目（2020JDJQ0037）。
收稿日期 2020-07-11
改稿日期 2020-11-11
胡 广 男，1995年生，硕士，研究方向为双有源桥DC-DC变换器。E-mail：1006150682@qq.com
胡维昊 男，1982年生，教授，博士生导师, 研究方向为人工智能在电力系统中的应用、可再生能源发电技术。E-mail：whu@uestc.edu.cn（通信作者）
（编辑 郭丽军）