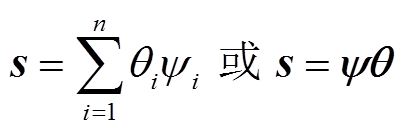（1）
摘要 该文引入压缩感知理论，有效降低了IGBT状态监测系统的采样频率。对功率半导体器件而言，各种电气参数的准确测量是保障其状态监测系统预测精度的重要基础，其中关断峰值电压作为判别IGBT老化状态的重要参数之一，其获取方式严重依赖于高速率采样单元。为了大幅度降低信号采集过程所需的数据量，引入压缩感知理论对信号进行压缩采样和重构。由于关断电压波形在时域下不具备显著的稀疏性，为此引入傅里叶基和离散小波基对信号进行稀疏表示，并讨论其在不同变换基下的稀疏性。此外为了便于压缩感知理论实际工程的实现，对比分析不同观测矩阵下信号的重构精度。最后通过仿真和数据分析，证明了压缩感知理论应用于基于关断峰值电压的状态监测系统的可行性和准确性。
关键词：绝缘栅双极型晶体管 状态监测 压缩感知 稀疏基
绝缘栅双极型晶体管（Insulated Gate Bipolar Transistor, IGBT）具有高电压耐受和高功率密度的特点，因此被广泛应用于交流电机驱动、可再生能源发电、电能传输等多个工业场合[1]。随着宽禁带材料的引入和融合，IGBT器件得以进一步提升功率密度和效率，并由此大幅度拓宽应用场景[2]。不过，由于长期暴露于大幅度变化的温度应力和湿度应力下，IGBT成为了电力电子系统最容易失效的器件之一[3]。根据工业调查显示[4]，IGBT模块应为过去20年间发生在电力电子系统中的20%以上的故障负责。因此，提高IGBT器件的可靠性对满足电力电子系统在安全性、成本和可用性方面的严格要求至关重要[5]。
国内外学者对IGBT的失效机理展开了大量的研究[6-7]，并将其大致分为芯片失效和封装失效两种类型。其中，芯片失效主要源于电气过应力、热激活等偶发原因；而封装失效则和设备的老化机制息息相关，其表现形式包括键合线断裂和焊料疲劳等[8]。通常情况下，设备的老化失效会引起相应的电气参数发生迁移，由此便诞生了一系列针对IGBT寿命预测的状态监测系统。常见的用于指示设备状态的电气参数包括集电极-发射极通态电压VCE,on[9]、栅极阈值电压VGE,on[10]和模块热阻Rth[11]，分别对应着功率器件的键合线脱落、门极氧化降解和焊料疲劳的失效类型。此外，米勒平台持续时间tGP[12]、开通关断时延ton、toff[13]和关断峰值电压Vpeak,off[14]等暂态特性参量也被证明与功率器件的老化过程有关，因此也被应用到状态监测和寿命预测方案中。
不过，尽管研究老化过程中电气参数迁移规律的文献层出不穷，真正投入实际工程应用中的状态监测方案种类却非常单一[15]。现有的文献中，几乎只有基于通态电压VCE,on的状态监测方案被应用到实际工程中。其他电气参数的在线监测难以实现的原因：一方面是诸如栅极电压VGE,on和模块热阻Rth等参数的测量需要在原系统中嵌入额外的传感器，带来额外成本的同时可能会引入寄生参数，从而恶化原系统的效率和可靠性[16]；另一方面，诸如米勒平台持续时间tGP和开通关断时延ton、toff等暂态特性的测量需要有极高的采样频率，通常情况下高于100MHz，这无疑给采样单元和储存芯片提出了极高的要求[17]。虽然可以采用峰值检测电路和时间测量电路等模拟元件完成关断峰值电压、米勒平台时间等参数的测量，但是在绝大数情况下完整记录电压电流暂态波形对设备的状态监测具有更大的意义。
为此，为了获取功率器件的暂态特性，并缓解状态监测系统对高速率采样单元的依赖，本文引入了压缩感知理论以求大幅度降低采样频率。事实上，自从压缩感知理论由陶哲轩等科学家改进以来，许多从事电气工作的学者就广泛探讨了其在本领域应用的可能性。文献[18]通过将一维信号映射到二维空间，实现了暂态和短时电能质量扰动信号的压缩采样和重构。文献[19]针对电能质量信号主要分布在低频域的特点，改进了观测矩阵并由此获得了更好的信号重构质量。文献[20]结合坐标变换，进一步缩小了信号采集的数据量和重构结果的误差。
上述文献采用压缩感知的对象均为电能质量信号，它们的特点是在频域上的稀疏性。然而，功率器件的开关电压波形无论是在时域还是频域上均没有显著的稀疏性。为此，文献[21]引入了小波稀疏基对开断电压信号进行了稀疏变换，并结合正交匹配追踪（Orthogonal Matching Pursuit, OMP）法高精度重构了原始信号。然而高斯随机观测矩阵的使用导致其结果存在不确定性，且硬件实现困难，需要有大量的储存空间。
本文在文献[21]的基础上，对比分析了不同观测矩阵下信号的重构质量，通过引入重构效果固定的确定性观测矩阵，为压缩感知在状态监测中的工程实现奠定了基础。本文首先介绍了压缩感知的基本原理，并分析不同观测矩阵的特点；然后说明了以IGBT关断峰值电压作为器件的老化指示量的依据，并研究了其在不同变换基下的稀疏性。最后通过仿真证明了所述方法的可行性。
Nyquist采样定理指出，只有在采样频率大于信号最高频率的2倍时，才能完整地获取原始信号的所有信息。对于功率器件高速开断过程的电压波形而言，这无疑给采样系统带来了极大的挑战。Candes等于2006年提出，如果信号本身在某个变换域可以稀疏表示，那么就能够以极大的概率从少量的采样点中重构出原始信号的大部分信息[22]。这就是压缩感知（Compressed Sensing, CS）的核心思想。它为大幅度降低信号采集过程中的采样率、传输量和储存量创造了可能。
压缩感知的前提是长度为n的信号s(sÎRn)在某正交空间ψ下可以稀疏表示为
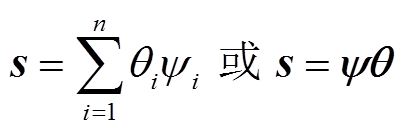（1）
式中，系数矩阵θ仅包含极少大系数。若θ中非零值个数K远小于信号长度n，则信号s为K-稀疏。
在信号稀疏的基础上，取与原正交空间ψ（又称稀疏基矩阵）不相关的观测矩阵ΦÎRm×n，可以获取m(m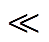
n)维测量值为
（2）
至此，完成了信号的压缩采样部分。然后根据m维测量值y重构出n维原始信号s，也就是求解l0最优化问题，即
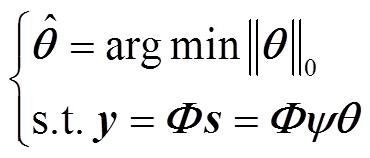（3）
其可以被转换为凸优化问题以便于求解，即
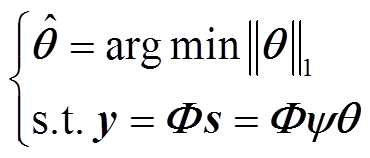（4）
常见的求解算法有正交匹配追踪和最小全变分（Total Variation, TV）的共轭梯度法。此后根据
（5）
就可以获取原始信号的重构值。
根据以上分析，应用压缩感知算法的关键包括寻找合适的稀疏基矩阵ψ以获取原始信号的稀疏表示和寻找合适的观测矩阵Φ以降低测量频率并提高重构精度。由于信号的稀疏表示与其本身的性质有关，通常情况下ψ的选择较为单一。而观测矩阵则有所不同，在满足一定条件的前提下，许多矩阵可以被用作观测矩阵。
要想准确地重构原始信号，其采集过程的数据量m不可以无限制地缩小。在合适的重构精度下尽可能地缩小数据量m，和观测矩阵的选择有很大关系。此外，观测矩阵的选择也并不随意，首先前提是满足约束等距特性（Restricted Isometric Property, RIP），即
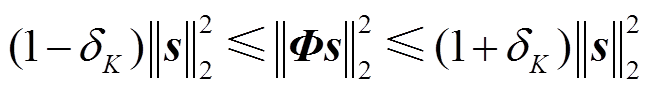（6）
式中，δKÎ(0,1)，称之为RIP常数。
观测矩阵可以分为随机矩阵和确定性矩阵两种类型。其中随机矩阵的典型是高斯测量矩阵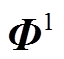
（矩阵中的元素独立服从正态分布）和伯努利矩阵
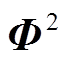（矩阵中的元素独立服从伯努利分布），矩阵中的元素分别为
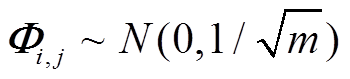（7）
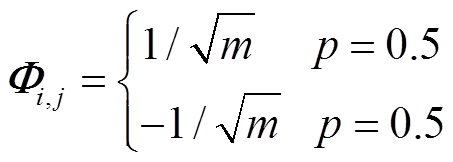（8）
随机观测矩阵的优点在于能够在较低的压缩比（定义为m/n）下获取较高的重构准确率，理论证明只需采样长度m≥cKlog(n/K)，就能够以较高概率重构原始信号。不过，随机观测矩阵的缺点却限制了其广泛的应用[23-24]。一方面，随机观测矩阵将会引起重构结果的不确定性，为保障高成功率通常要被迫提高采样维度m；另一方面，随机采样的硬件实现异常困难，矩阵元素需要大量储存空间。一些学者尝试用确定性随机序列进行解决，但是随之引起重构准确率和成功率的降低。
为了解决观测矩阵的工程实现问题，许多学者引出了与随机矩阵相对的确定性矩阵，常见的有部分哈达玛矩阵、托普利兹矩阵和循环矩阵。它们在构造的过程中虽然要随机选取，不过在系统和构造参数确定后也会随之固定。它们的特点在于信号的重构结果不确定性小，且所需储存空间小、易于硬件实现。以托普利兹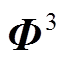矩阵
和循环矩阵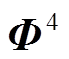
为例，一般形式分别为
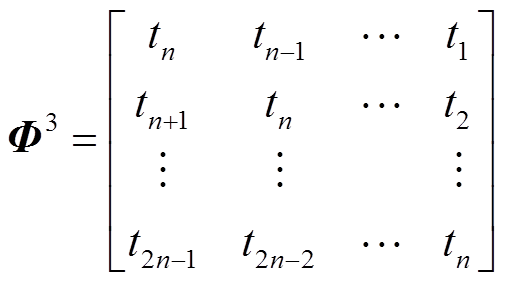（9）
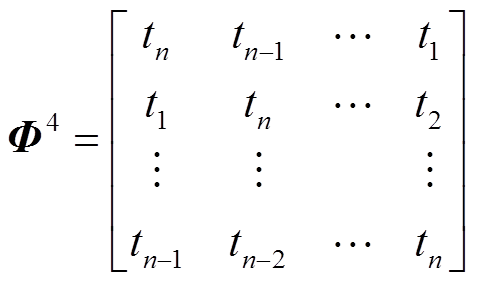（10）
在构造过程中，首先需要生成一个n维随机向量u，然后经过m次循环构造剩余m-1行向量，最后归一化处理获取观测矩阵Φ。整个矩阵的构造依赖于循环位移，也就非常容易通过硬件实现。为了推动压缩采样的工程实现，本文对比了几种常见观测矩阵下的信号重构效果，从而为工程实现提供参考。
除了观测矩阵的合理选择外，压缩感知应用的另一个关键是采样信号的稀疏表示。由于本文选取关断峰值电压作为表征IGBT状态的电气参数，因此完整地重构出关断电压波形就是压缩感知的首要目标。为此本节分析了关断电压波形的稀疏表示方法。另外，还分析了关断峰值电压受其他因素的影响规律。
IGBT模块的封装结构及其等效电路分别如图1和图2所示。由于IGBT的封装采用了多层具有不同热膨胀系数的金属材料，导致各层结构在温度波动下发生相对位移，最终出现键合线断裂或焊料层空洞等影响设备正常运行的老化现象。
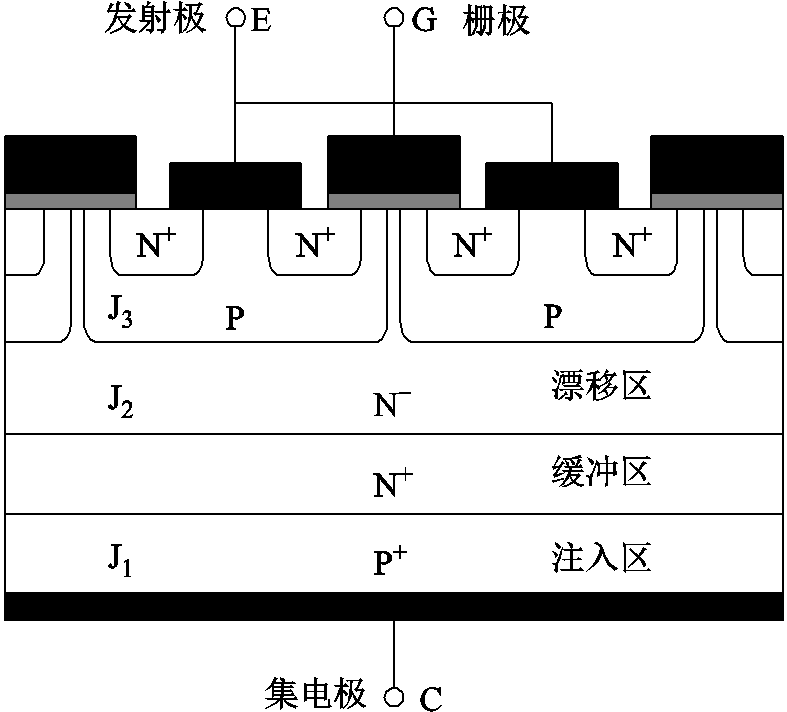
图1 IGBT的封装结构
Fig.1 Package structure of IGBT
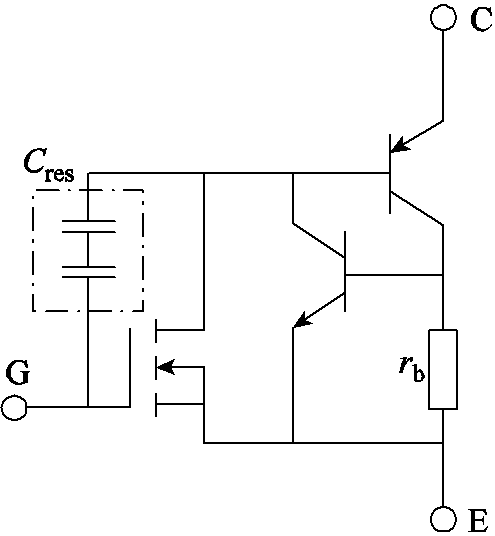
图2 IGBT的等效电路
Fig.2 Equivalent circuit of IGBT
常规方法监测通态电压VCE,on和模块热阻Rth揭示键合线断裂或焊料层空洞。不过这两种失效现象通常是长期累积磨损的突发表征，因此VCE,on和Rth会在寿命终点出现突变，无法借助这两个参数进行线性寿命预测，提前预警的时间受到了限制。
对比而言，IGBT的动态特性体现在开通延迟时间、关断峰值电压等参数，通常会在设备老化的过程中同步变化。由于各层材料的相对位移，导致模块的电容电感等分布参数发生变化，由此引起动态特性发生同步迁移。这也是本文选取关断峰值电压作为监测信号的原因。IGBT关断过程的电压电流波形如图3所示，图中，VCE(t)为集射极电压；IC(t)为集电极电流。
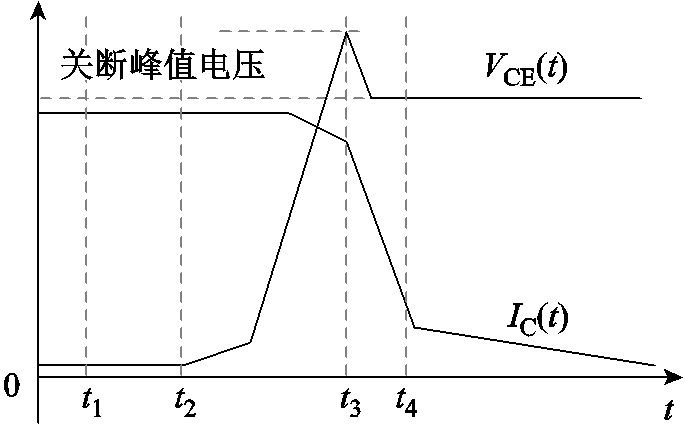
图3 IGBT开通关断过程电压电流波形
Fig.3 Voltage and current waveforms during turn-off
很明显，由于关断过程的电压信号中包含有多个非零值，其在时域上不属于稀疏信号；另外由于其波形接近于方波，导致其在频域上也存在多个分量，因此在傅里叶变换下也不能较好地进行稀疏表示。图4给出了关断电压的傅里叶频域投影，可以看出，信号该域下有多个不为零的分量。
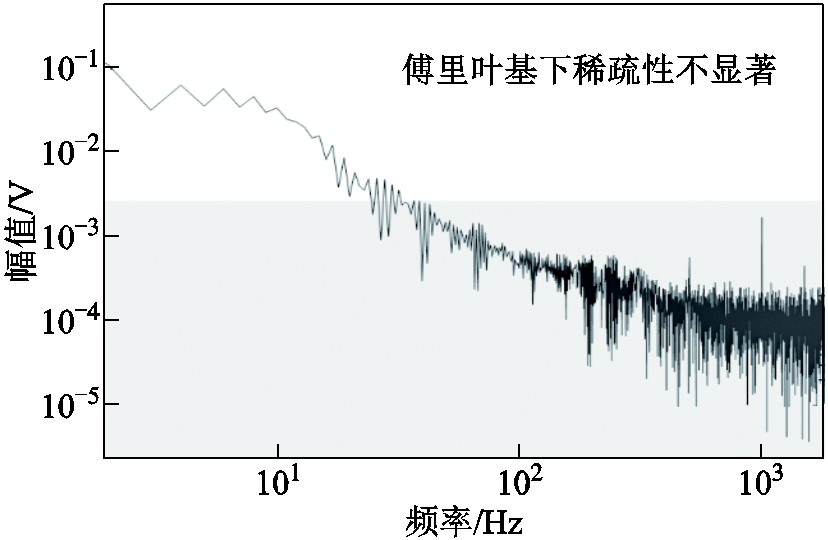
图4 关断电压波形在傅里叶基下的投影
Fig.4 Projection of turn off voltage waveforms on Fourier sparse basis
但是，信号的频率主要集中在低频区域，这为小波基下的稀疏表示提供了可能。小波变换可以将关断电压信号按照频率分为许多子区间，并在指定区间内提供优质的频率和时间分辨率。由于关断电压的频域分量主要集中在低频区域，这使得其在小波基下表现出稀疏的特点。图5给出了关断电压在小波稀疏基下的投影，可以看出，小波基下不为零的分量个数较少。
图5 关断电压在小波稀疏基下的投影
Fig.5 Projection of turn off voltage waveform on wavelet sparse basis
根据上述分析，可以选用小波变换稀疏基对关断电压信号进行稀疏表示。借助不同的母小波下的离散小波变换，就可以构建出n×n维小波稀疏基ψ。由于不同的母小波下效果类似，本文选取的母小波为Symlets小波族小波，序号为8。
通过合理选择稀疏矩阵和观测矩阵，就可以在低采样率下重构出原始的关断电压波形，从而进一步提取出关断峰值电压。根据文献[14]的实验结果可知，关断峰值电压在IGBT老化的过程中将会有小幅度的降低，因此可以将其作为设备老化的判定依据。不过，除了设备的老化影响外，诸如负载电压、通态电流等外界因素也会影响到关断峰值电压的大小。要想将关断峰值电压作为设备老化的指示量，必须要研究其他因素的影响机制。为此本文结合PSpice仿真软件，研究了集电极-发射极稳态电压、驱动电阻以及驱动电感对设备关断过程电压变化规律的影响。
图6和图7分别给出了不同外界因素下IGBT器件的关断波形。从图6中可以看出，稳态电压直接影响到器件的关断时间和关断峰值电压，越大的稳态电压引起越长的关断时间和越高的关断峰值电压。当稳态电压波动程度大于IGBT器件在整个寿命范围内关断峰值电压变化程度时，即使获取到精确的关断电压波形，也难以判断IGBT器件的寿命状态。不过幸运的是，实际场景中稳态电压的波动通常较小，不需要对关断峰值电压进行补偿[17]。
图6 不同集电极-发射极电压下的关断电压波形
Fig.6 Turn-off waveforms under different VCE
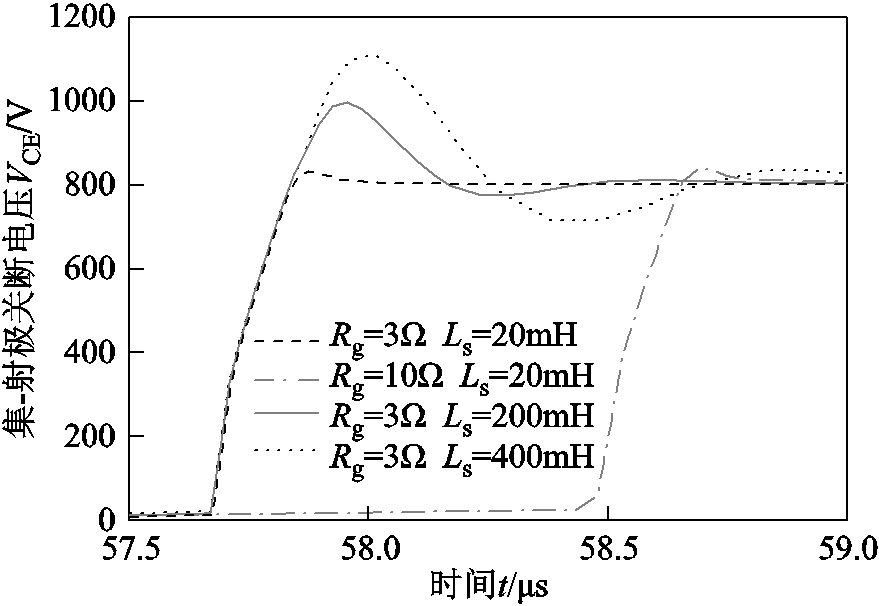
图7 不同驱动条件下的关断电压波形
Fig.7 Turn-off waveforms under different driving conditions
此外，驱动电阻和电感值的变化也会影响到IGBT器件的关断特性。从图7中可以看出，驱动电阻增大会导致驱动信号与器件动作间的延时增加，不过此时器件关断时长和关断峰值电压的变化较小。相反地，驱动电感值的变化对关断特性的影响较大，不合理的电感值会导致峰值电压过大且引起波形发生振荡。不过，通常情况下电感值发生漂移的幅度较小，且几乎不受温度和老化的影响。因此实际中，当驱动电阻和电感值确定后，关断峰值电压所受的影响较小。
另外，通态电流和环境温度也会对关断峰值电压有所影响。文献[17]利用线性拟合找出了通态电流和关断峰值电压的关系，并用其对峰值电压进行补偿。综上所述，即使IGBT的关断电压特性受到除设备老化外其他各种因素的影响。但由于实际应用中诸如驱动电阻、电感类的参量变化较小，稳态电压通常可以得到有效控制，通态电流和环境温度的影响可以通过拟合的函数关系进行补偿，因此选用关断峰值电压作为IGBT寿命状态的判定依据完全可行。本文针对IGBT状态监测的重点关注问题为关断峰值电压能否使用压缩感应进行完美重构。
为了验证所述压缩感知理论在重构关断峰值电压时的准确度，本文借助NASA PcoE研究中心的IGBT加速寿命实验数据进行了验证，并对比分析了不同稀疏矩阵和观测矩阵下的重构质量。
为研究IGBT的失效机理，NASA建立了IGBT的加速寿命实验台[14]。通过往门极注入固定占空比的方波信号，迫使器件产生大幅度的温度波动。监测器件壳温的变化，当器件出现闩锁效应时，温度持续上升，此时终止实验并判定IGBT失效，其他相关的实验参数见表1。
第一组加速实验共持续41 752次，直至IGBT不能可靠开通关断。在实验过程中，考虑到采样率过高且储存空间有限，每进行100次功率循环才记录一次开关过程的暂态波形，包括门极信号、栅极电压、集电极-发射极电压波形等，从中可以计算出分断过程的关断电压峰值。为了便于观察，绘制出几次典型分断过程的集电极-发射极电压暂态波形如图8所示，从图中可以看出，随着循环次数的增加，关断峰值电压逐渐减小，且在加速实验的初期，便能呈现出明显的变化趋势。
表1 IGBT加速实验参数
Tab.1 The parameters of acceleration experiment of IGBT
参数数值（型号） IGBT器件IRG4BC30KD 额定电压Vrate/V600 额定电流Irate/A15 负载电阻Rload/Ω0.2 负载电压Vsupply/V0～4 门极电压Vgate/V10 门极信号占空比D(%)40 开关频率fswitch/Hz10 000 采样频率fsamp/GHz1
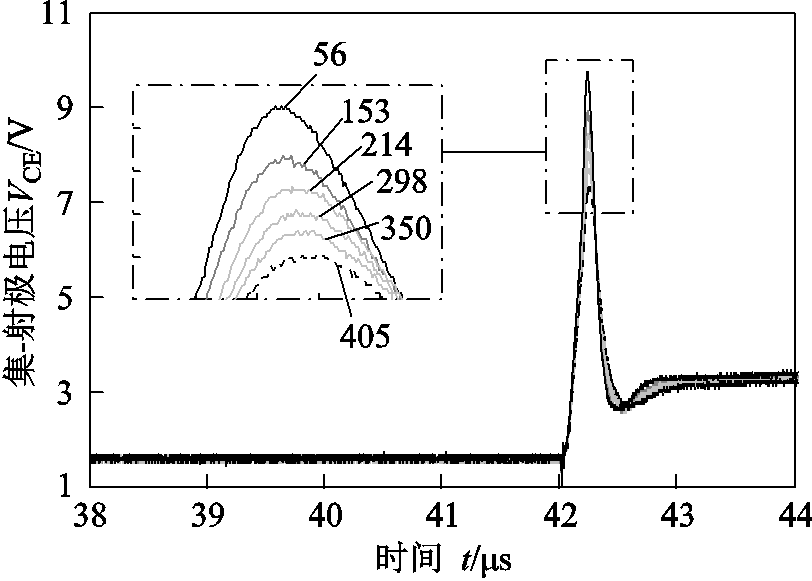
图8 IGBT分断过程电压暂态波形
Fig.8 Transient voltage waveforms during IGBT switching
另外，结合418组暂态波形，可以计算出整个寿命区间内关断峰值电压的变化趋势，如图9所示。从图中可以看出，不同于VCE,on和Rth在失效前的突变，关断峰值电压Vpeak,off在整个寿命范围内几乎都呈现出较为一致的线性变化，且幅值变化范围接近3.5V。这对在IGBT寿命初期判定设备剩余使用时长具有非常重要的意义。
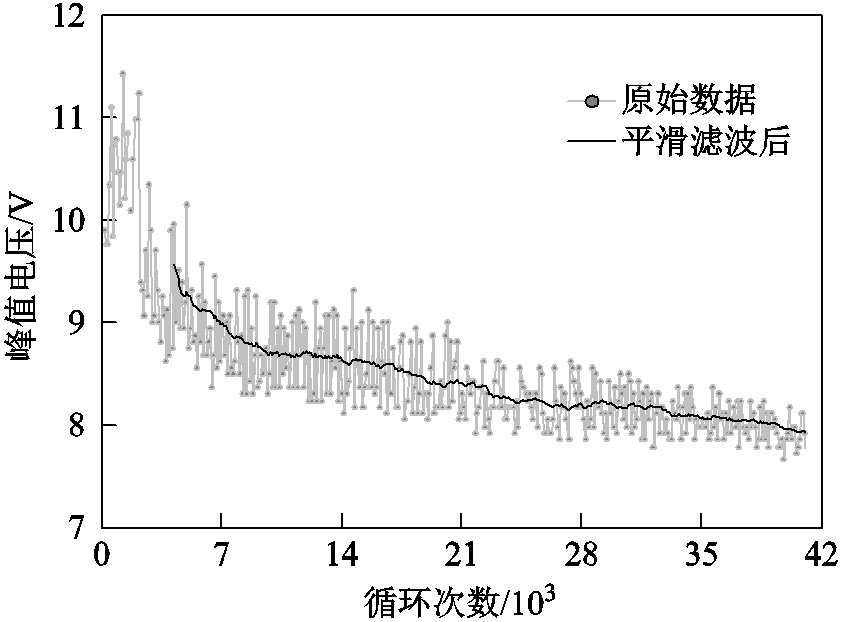
图9 关断峰值电压全寿命周期变化规律
Fig.9 Variation of turn off peak voltage in whole lifetime
在初步分析完加速实验数据后，选择第100组暂态关断电压波形验证压缩感知算法的可行性。本节首先讨论了不同稀疏基下重构信号的精度问题。从该组暂态数据中提取出包含关断尖峰在内的4 096个采样点，然后分别采用傅里叶稀疏基和小波稀疏基对信号进行压缩。另外两组实验对象均采用高斯测量矩阵和正交匹配追踪重构算法。
图10和图11分别给出了观测数据维度m=100以及m=200下的重构波形。需要注意的是，当压缩比过低时，重构的成功率接近100%，图11给出的为该压缩比下某次成功重构的图像。此外由于原始信号在不同稀疏基下稀疏度不同（见2.1节分析），则两者采用正交匹配算法的迭代次数也有所不同，傅里叶稀疏基下算法的迭代次数远大于小波稀疏基。
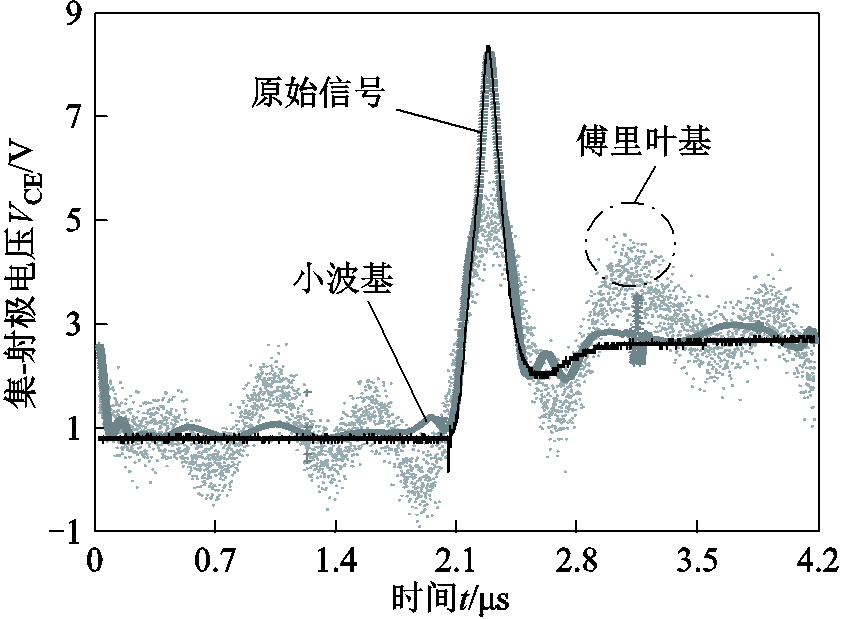
图10 m=100时关断电压在不同稀疏基下的重构信号波形
Fig.10 Reconstruction waveforms of turn-off voltage under different sparse bases when m=100
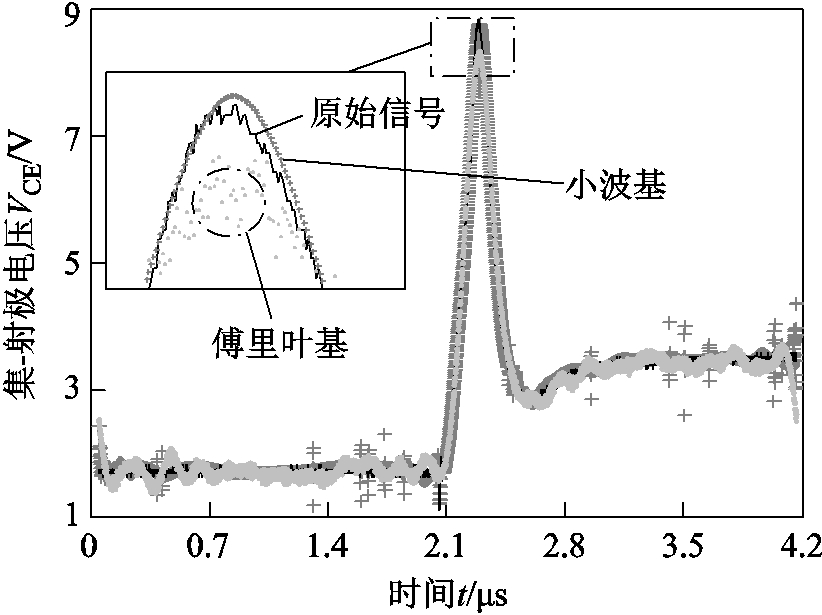
图11 m=200时关断电压在不同稀疏基下的重构信号波形
Fig.11 Reconstruction waveforms of turn-off voltage under different sparse bases when m=200
从图10和图11中可以看出，虽然傅里叶基下压缩感知能够重构出原信号的大多数低频分量，但由于电压尖峰部分所涉及的频率分量过多，难以得到完美的重构。虽然当采集信号维度m上升时，能够还原的频率分量增多，信号的重构峰值越来越接近原始峰值。此时所需的观测矩阵的维度和迭代次数也同时增大，造成了计算时长的提升和信号压缩比的降低。
而在小波稀疏基下信号的峰值能够得到较为完美的重构，虽然在信号的平坦部分会出现个别的重构误差，但并不影响对电压波形的尖峰部分的完美复原，这足够求解关断峰值电压来判断IGBT的寿命状态。综合以上分析可知，小波稀疏基更能满足低观测维度高重构精度的要求。
随着稀疏基的选定，进一步提高信号重构质量的关键变成了观测矩阵的选择。为了获取更为优质的观测矩阵，以获得较低的压缩比和较高的重构质量，同时便于工程实现。本节对比分析了部分哈达玛矩阵、托普利兹矩阵和循环矩阵三种观测矩阵下信号的重构质量。定义定量评价信号重构质量的参数重构误差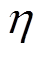
为
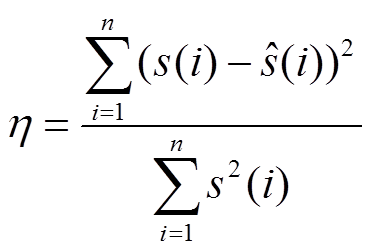（11）
式中，s(i)为原始信号；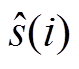
为重构信号。
首先分析了不同观测矩阵对信号压缩比的要求，选择稀疏基为小波基，绘制出不同观测矩阵下重构误差与压缩比的关系如图12所示。由于压缩比较低时，信号重构的成功率并不为1，因此为获取准确的重构误差，图12所示为多次计算的平均值。当重构误差η＜0.05时，认为信号完美重构。
图12 关断电压在不同观测矩阵下的重构误差
Fig.12 Reconstruction error of turn-off voltage under different observation matrices
从图12中可以看出，相比另外两种观测矩阵而言，部分哈达玛矩阵可以在更小的压缩比（约0.024）下重构原始信号，不过其工程实现也相对复杂。对于另外两种观测矩阵而言，也能在非常低的压缩比（分别为0.026和0.034）下重构出原始信号。借用这几种观测矩阵可以将原始的1GS/s的采样率降为30MS/s左右，极大地减轻了采样系统和储存系统的负担。在实际中可以采用更为简单的循环矩阵以便于实际工程实现。
另外，由于本文以关断峰值电压作为主要的监测对象，定义峰值重构误差为
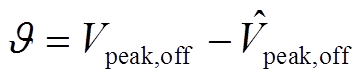（12）
式中，
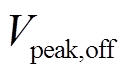和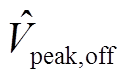
分别为原始和重构电压峰值。
为验证压缩感知算法的可重复性，在不同压缩比和不同观测矩阵下分别重复50次仿真计算，获取峰值重构误差平均值如图13所示。从图13中可以看出，在测量长度m=150时，托普利兹和循环矩阵下出现较大的离群值，影响到了峰值电压的重构精度，不过50次重复实验中，托普利兹仅出现2次，循环矩阵仅出现1次，且离群值远大于正常值，容易剔除。当测量长度m=200时，离群值的出现频率降低且对结果的影响大幅度降低。该组实验证明了压缩感知的可重复性和重构准确度。
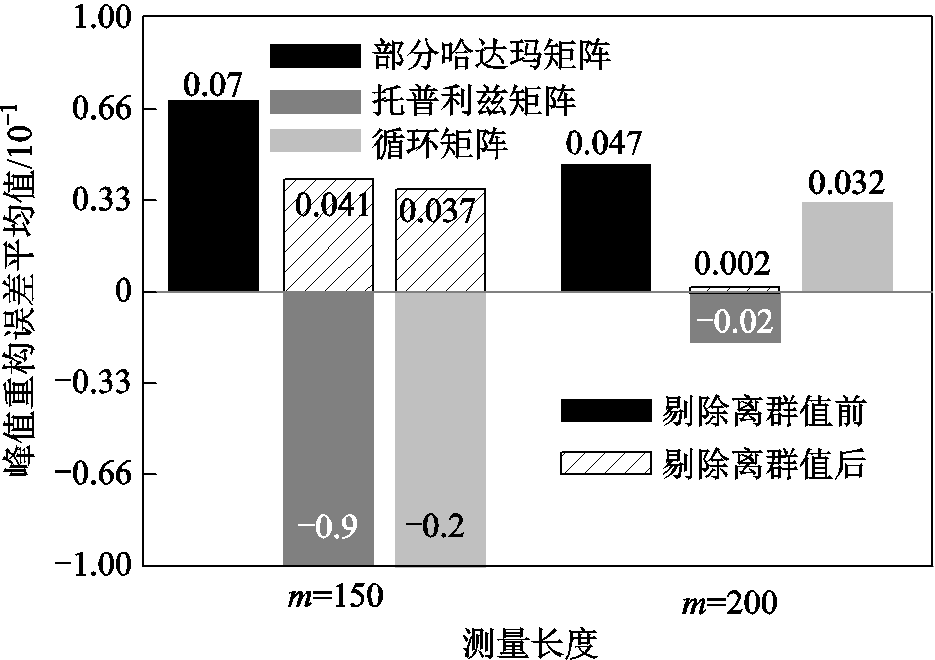
图13 电压峰值重构误差
Fig.13 Voltage peak reconstruction error
最后，本文采用小波基作为稀疏基，托普利兹矩阵作为观测矩阵，正交匹配追踪作为重构算法计算了压缩比为200/4 096时，418组暂态电压波形的重构峰值电压，绘制结果如图14所示。结果表明，重构后的峰值电压呈现出原始信号一致的下降趋势，因此压缩感知可以用于基于关断峰值电压的IGBT状态监测方案中。
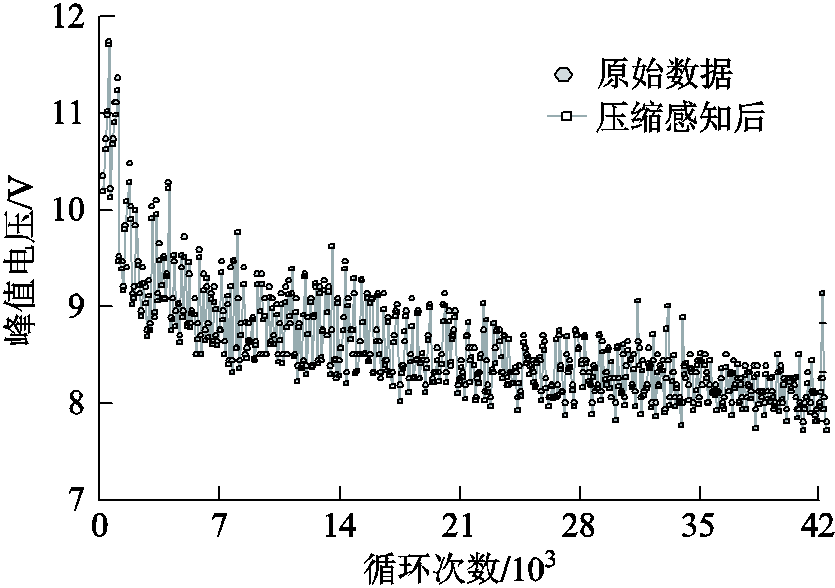
图14 重构峰值电压变化规律
Fig.14 The change rule of reconstructed peak voltage
本文采用压缩感知算法有效降低了IGBT状态监测系统的采样频率。通过分析IGBT关断电压在不同变换基下的稀疏性，合理选择小波变换基作为稀疏矩阵。对比了不同观测矩阵下电压信号的重构精度，提出可以采用确定性观测矩阵完成峰值电压的重构，为压缩感知的工程实现奠定了基本。本文的研究证明了压缩感知算法在降低基于关断峰值电压的IGBT状态监测系统的采样频率时的有效性。
参考文献
[1] Falck J, Felgemacher C, Rojko A, et al. Reliability of power electronic systems: an industry perspective[J]. IEEE Industrial Electronics Magazine, 2018, 12(2): 24-35.
[2] Millan J, Godignon P, Perpina X, et al. A survey of wide bandgap power semiconductor devices[J]. IEEE Transactions on Power Electronics, 2014, 29(5): 2155-2163.
[3] 陈民铀, 高兵, 杨帆, 等. 基于电-热-机械应力多物理场的IGBT焊料层健康状态研究[J]. 电工技术学报, 2015, 30(20): 252-260.
Chen Minyou, Gao Bing, Yang Fan, et al. Healthy evaluation on IGBT solder based on electro-thermal-mechanical analysis[J]. Transactions of China Electrotechnical Society, 2015, 30(20): 252-260.
[4] Wang Huai, Liserre M, Blaabjerg F. Toward reliable power electronics: challenges, design tools, and opportunities[J]. Industrial Electronics Magazine IEEE, 2013, 7(2): 17-26.
[5] Choi U M, Blaabjerg F, 
S, et al. Reliability improvement of power converters by means of condition monitoring of IGBT modules[J]. IEEE Transactions on Power Electronics, 2017, 32(10): 7990-7997.
[6] Yang Shaoyong, Xiang Dawei, Bryant A, et al. Condition monitoring for device reliability in power electronic converters: a review[J]. IEEE Transactions on Power Electronics, 2010, 25(11): 2734-2752.
[7] 李亚萍, 周雒维, 孙鹏菊, 等. 基于特定集电极电流下饱和压降的IGBT模块老化失效状态监测方法[J]. 电工技术学报, 2018, 33(14): 3202-3212.
Li Yaping, Zhou Luowei, Sun Pengju, et al. Condition monitoring for IGBT module aging failure on VCE(on) under certain IC conditions[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3202-3212.
[8] 赖伟. 计及低强度热载荷疲劳累积效应的IGBT功率器件寿命模型研究[D]. 重庆: 重庆大学, 2016.
[9] 王学梅, 张波, 吴海平. 基于失效物理的功率器件疲劳失效机理[J]. 电工技术学报, 2019, 34(4): 717-727.
Wang Xuemei, Zhang Bo, Wu Haiping. A review of fatigue mechanism of power devices based on physics-of-failure[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 717-727.
[10] Mandeya R, Chen Cuili, Pickert V, et al. Gate-emitter pre-threshold voltage as a health sensitive parameter for IGBT chip failure monitoring in high voltage multichip IGBT power modules[J]. IEEE Transactions on Power Electronics, 2019, 34(9): 9158-9169.
[11] 陈民铀, 陈一高, 高兵, 等. 考虑老化进程对热参数影响的IGBT模块寿命评估[J]. 中国电机工程学报, 2017, 37(18): 5427-5436, 5542.
Chen Minyou, Chen Yigao, Gao Bing, et al. Lifetime estimation of IGBT module considering influence of aging process on thermal parameters[J]. Proceedings of the CSEE, 2017, 37(18): 5427-5436, 5542.
[12] Liu Jingcun, Zhang Guogang, Chen Qian, et al. Insitu condition monitoring of IGBTs based on the miller plateau duration[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 769-782.
[13] Brown D W, Abbas M, Ginart A, et al. Turn-off time as an early indicator of insulated gate bipolar transistor latch-up[J]. IEEE Transactions on Power Electronics, 2012, 27(2): 479-489.
[14] Sonnenfeld G, Goebel K, Celaya J R. An agile accelerated aging, characterization and scenario simulation system for gate controlled power transistors[C]//IEEE Autotestcon, Salt Lake City, UT, USA, 2008: 208-215.
[15] Hanif A, Yu Yuechuan, DeVoto D, et al. A comprehensive review toward the state-of-the-art in failure and lifetime predictions of power electronic devices[J]. IEEE Transactions on Power Electronics, 2019, 34(5): 4729-4746.
[16] Wang Ye, Ma Mingyao, Yuan Kexiang, et al. A plug-and-play condition monitoring system for IGBT module bonding wires[C]//IEEE International Power Electronics and Application Conference and Exposition, Shenzhen, China, 2018: 1-5.
[17] Wuest F, Trampert S, Sehr F, et al. Integrated condition monitoring by measuring the delay of gate turn-off[C]//European Microelectronics and Packaging Conference & Exhibition, Pisa, Italy, 2019.
[18] 王学伟, 王琳, 苗桂君, 等. 暂态和短时电能质量扰动信号压缩采样与重构方法[J]. 电网技术, 2012, 36(3): 191-196.
Wang Xuewei, Wang Lin, Miao Guijun, et al. An approach for compressive sampling and reconstruction of transient and short-time power quality disturbance signals[J]. Power System Technology, 2012, 36(3): 191-196.
[19] 田霄, 贺建军, 喻寿益. 基于压缩感知理论的谐波畸变电压信号采集方法研究[J]. 电工电能新技术, 2014, 33(11): 61-64, 69.
Tian Xiao, He Jianjun, Yu Shouyi. Study on harmonic distortion of voltage signal acquisition method based on compressed sensing theory[J]. Advanced Technology of Electrical Engineering and Energy, 2014, 33(11): 61-64, 69.
[20] 董唯光, 张晓东, 郭俊锋, 等. 基于坐标变换的风电变流器电压信号CS压缩方法[J]. 电子测量与仪器学报, 2016, 30(12): 1818-1827.
Dong Weiguang, Zhang Xiaodong, Guo Junfeng, et al. Compressed sensing compression method for wind power converter voltage signal based on coordinate transformation[J]. Journal of Electronic Measurement and Instrument, 2016, 30(12): 1818-1827.
[21] Li Hao, Xiang Dawei, Yang Xingwu, et al. Compressed sensing method for IGBT high-speed switching time on-line monitoring[J]. IEEE Transactions on Industrial Electronics, 2018, 66(4): 1.
[22] 姜媛媛. 电力电子电路故障诊断及预测关键技术研究[D]. 南京: 南京航空航天大学, 2018.
[23] 王侠, 王开, 王青云, 等. 压缩感知中的确定性随机观测矩阵构造[J]. 信号处理, 2014, 30(4): 436-442.
Wang Xia, Wang Kai, Wang Qingyun, et al. Deterministic random measurement matrices construction for compressed sensing[J]. Journal of Signal Processing, 2014, 30(4): 436-442.
[24] 李臻, 罗林根, 盛戈皞, 等. 基于压缩感知的特高频局部放电定位法[J]. 电工技术学报, 2018, 33(1): 202-208.
Li Zhen, Luo Lingen, Sheng Gehao, et al. Ultrahigh frequency partial discharge localization methodology based on compressed sensing[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 202-208.
Application of Compressed Sensing Method in Condition Monitoring of Insulated Gate Bipolar Transistor
Abstract In this paper, the compressed sensing theory was introduced to effectively reduce the sampling frequency of IGBT condition monitoring system. For power semiconductor devices, accurate measurement of various electrical parameters is an important basis to ensure the prediction accuracy of the condition monitoring system. Turn-off peak voltage is one of the important parameters to judge the aging state of IGBT, and its acquisition method relies heavily on the high-speed sampling unit. In order to greatly reduce the amount of data needed in the process of signal acquisition, compressed sensing theory was introduced to compress sampling and reconstruction of signals. Since the turn off voltage waveform has no significant sparsity in time domain, Fourier basis and discrete wavelet basis were introduced to represent the signal sparsely, and their sparsity under different transform bases was discussed. In addition, in order to facilitate the practical engineering implementation of compressed sensing theory, the reconstruction accuracy of signals under different observation matrices was compared and analyzed. Finally, through simulation experiments and data analysis, the feasibility and accuracy of applying compressed sensing theory to the condition monitoring system based on turn off peak voltage were verified.
keywords：Insulated gate bipolar transistor, condition monitoring, compressed sensing, sparse basis
DOI:10.19595/j.cnki.1000-6753.tces.L90353
中图分类号：TP277
中央高校基本科研业务费专项资金资助项目(2018YJS163)。
收稿日期 2020-07-09
改稿日期 2020-11-22
李 庭 男，1994年生，博士研究生，研究方向为功率器件的在线监测和寿命预测。E-mail：18117010@bjtu.edu.cn
陈 杰 男，1986年生，副教授，博士生导师，研究方向为电力电子及电力传动。E-mail：jiechen@bjtu.edu.cn（通信作者）
（编辑 陈诚）