0 引言
目前,照明损耗约占全球能源损耗的25%[1]。因发光二极管(Light-Emitting Diodes, LED)具有寿命长、能效高和绿色环保等优点,已然成为新一代照明光源。由于LED本身不能直接与交流源相连,因此需要整流器作为中间环节;但要求恒功率输出以避免LED频闪[2]。为满足要求,无源解耦方案因拓扑简单、无需额外控制而被广泛应用[3-4]。然而,在无源解耦方案中,额定功率为100W的变换器需要匹配2 650μF的电容才可将电压纹波控制在2V[5]。上述方案明显有悖于变换器小型化设计理念。
鉴于此,文献[6-7]通过在输入电流中注入3、5次谐波以降低电流峰值与平均值比,从而达到对整流器的输入电流进行重塑,降低对母线电容的依赖。但是随着注入谐波的增加,电流严重失真,功率因数(Power Factor, PF)不再满足电气标准。对此,文献[8]提出一种基于负载模块的控制策略。但是,为消除输出侧功率二倍工频脉动,多路负载必须选择性通断,这导致LED负载冗余度较高。因此,与改进控制策略相比,优化现有拓扑具有功率因数高、所需电容值小等优势。现有功率解耦拓扑可分为独立解耦电路和集成解耦电路,两者能量传递路径如图1所示,第三端口用以缓冲脉动功率Pde。详言之,文献[9-12]提出一类具有独立解耦电路的单相电流源变换器;其中,H桥电路、Flyback电路和Buck- Boost电路分别用作功率缓冲单元。此类变换器有利于辅助电路(功率解耦单元)和主电路调制方案及控制策略的单独设计,并减少了输出要求强加的操作限制。另外,文献[13-14]提出将一个对称的半桥电路和两个相同的薄膜电容相结合以吸收脉动功率,其实质为通过拓扑推演使得两个薄膜电容的输出电压呈现幅值相同、相位互补的正弦波,此类变换器具有对称性好、结构简单和易于加工等优势。
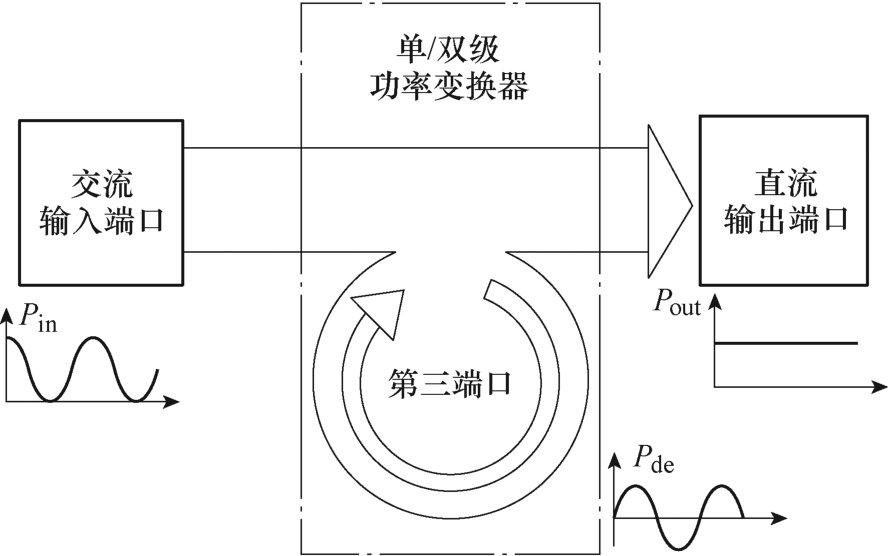
图1 能量传递路径
Fig.1 Energy transfer path
同时,文献[15-16]在输出端口并联双向DC-DC变换器用于吸收纹波电流的交流分量,如图2a所示[15]。通过计算可得功率损耗为
式中,Pin为输入功率;ηPFC和ηbi分别为PFC变换器和双向DC-DC变换器的效率。
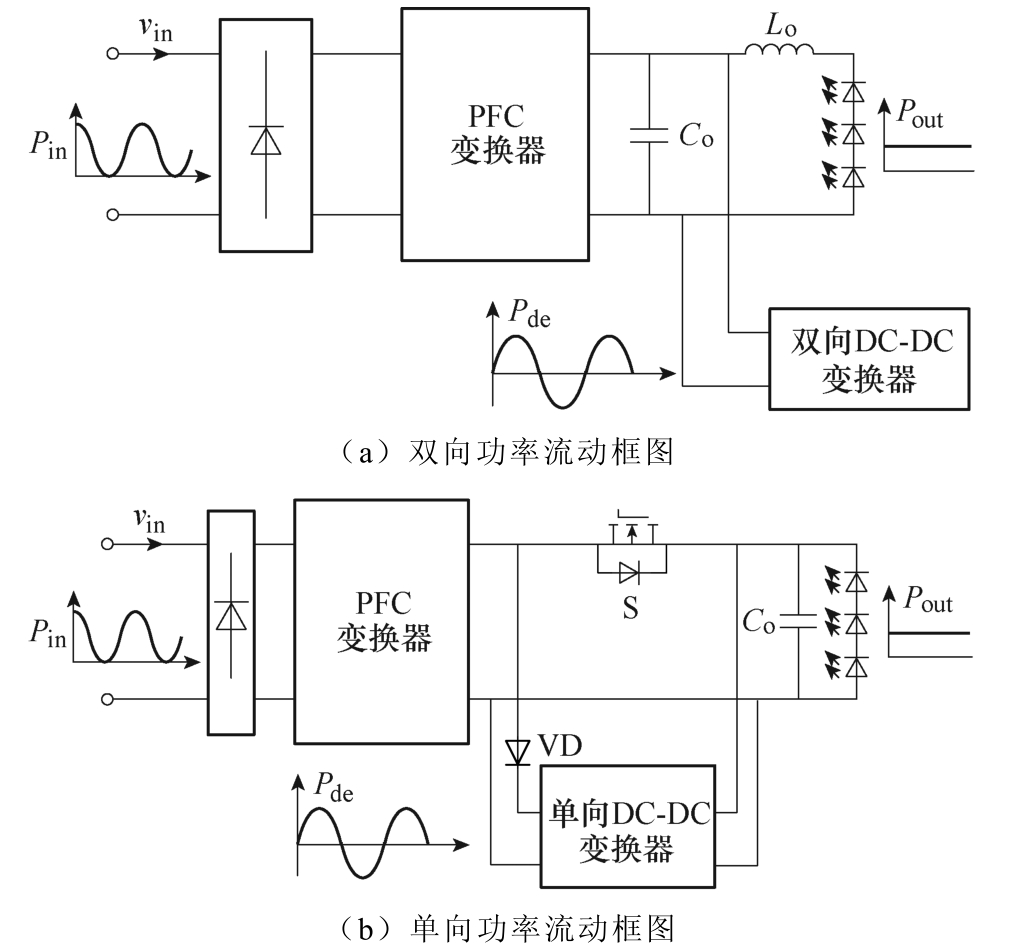
图2 能量流动方向
Fig.2 Direction of energy flow
同理,文献[17-18]提出一种单向功率解耦电路,脉动功率仅由DC-DC变换器处理一次,与双向变换器相比,效率更高,如图2b所示。通过计算可得功率损耗为
式中,PS/D为开关管和二极管的损耗功率。
但是上述方案均存在较多的不理想因素,如器件冗余度高和能量多级传递等问题。
因此,设计一类结构更加紧凑的新型拓扑显得尤为重要。鉴于此,文献[19-22]通过器件分时复用或共用的方式,实现了AC-DC变换器(主电路)和DC-DC变换器(解耦电路)功率器件部分或完全集成。文献[23]仅利用一个二极管和一个MOS管完成了功率解耦。但由于电路的不对称性,前、后端产生的磁通不能完全抵消,因此在低压侧造成了额外的损耗。此外,电感作为非理想储能元件,损耗较大,并且较低的功率密度与轻量化设计冲 突[23-24]。因此,去除或尽量避免电路中存在的大量磁性器件为另一热点问题。
为此,本文提出了一种具有功率解耦和自动功率因数校正能力的新型单级整流器。该拓扑具有元器件数量少、功率密度大、效率高和成本低等优点,值得注意的是,升压电感和解耦电感处于特殊位置,为后续磁集成设计提供有利条件。
1 拓扑结构分析
图3为本文所提电路拓扑,由VDr1、VDr2、Q1、Q2、LM1和电磁干扰(Electromagnetic Interference, EMI)滤波电流构成的功率因数校正(Power Factor Correction, PFC)单元和Q1、Q2、Sa1、Sa2、VDa、CD及LM1、LM2构成的解耦单元两部分构成。值得注意的是,所提整流器工作在不连续导通模式(Dis- continuous Conduction Mode, DCM)。
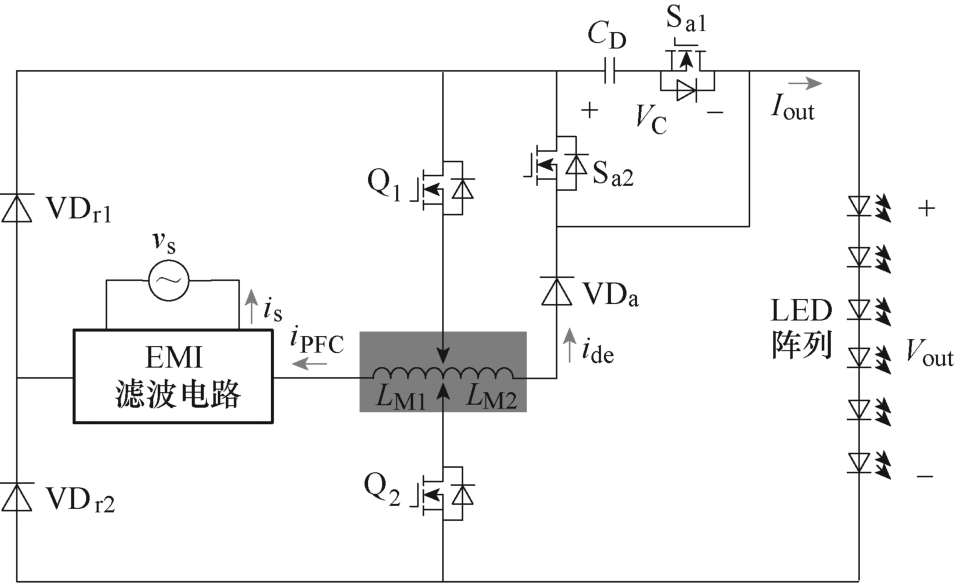
图3 本文所提电路拓扑
Fig.3 Proposed circuit topology
该拓扑:①基于复用原理,实现了功率器件的共享,同时解耦电感用于输出滤波,提高了电路的整体效率;②采用脉冲驱动方式,消除了传统电路中承受大电压应力的输出电容,提高了电路的功率密度;③开关器件Sa1和Sa2的峰值电压始终受解耦电容VC钳位,具有较低的电压应力,元器件选型更广、成本更低;④处于特殊位置的电感LM1和LM2(见图3中阴影部分)为磁集成提供了有利条件,为进一步降低磁损提供了可能。
2 工作原理分析
图4为一个工频周期内的开关状态,GQ1、GQ2和GS1、GS2分别为开关管Q1、Q2和S1、S2的触发脉冲;iPFC和is分别为流经电感LM1和网侧的电流。本文将其工作原理分为充电和放电两种模式。简言之,当输入功率Pin高于输出功率Pout时为模态Ⅱ,冗余能量Pin−Pout存储在解耦电容CD中;当输入功率Pin低于输出功率Pout时为模态Ⅰ,解耦电容CD通过谐振方式将能量释放至解耦电感LM2中,以弥补功率赤字(|Pin−Pout|)。
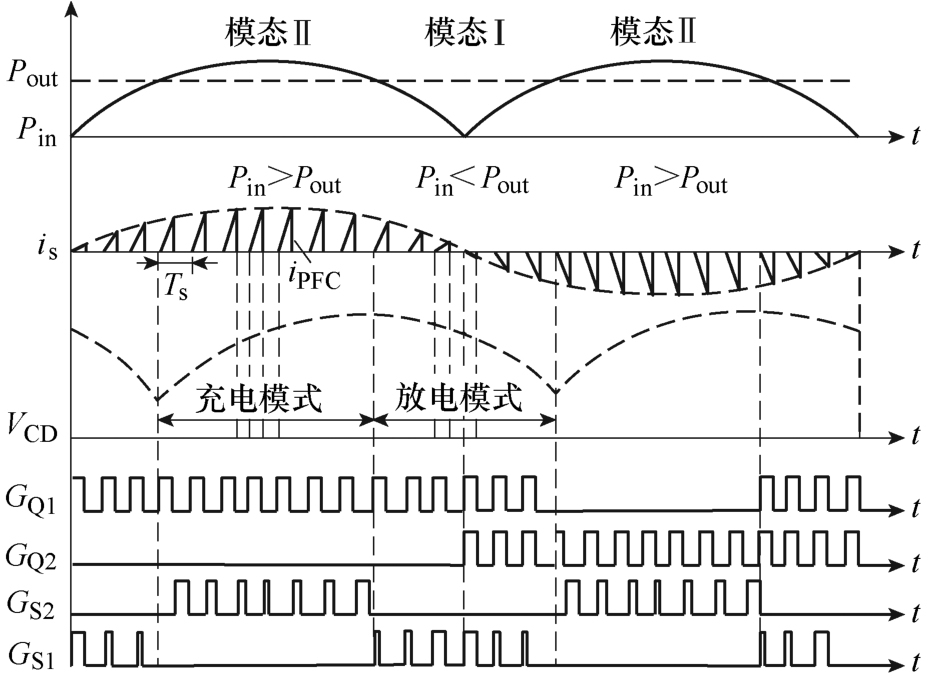
图4 图3的关键波形
Fig.4 Key waveforms for Fig.3
为便于分析,做出以下假设:
(1)开关周期Ts远小于工频周期T,因此每个开关周期中,输入电压vs可以视为常量。
(2)忽略开关管死区时间。
(3)PF=1。此外,模态Ⅰ和Ⅱ根据开关状态均可分为3个工作模式,电流波形及驱动信号在模态Ⅰ和模态Ⅱ如图5所示。
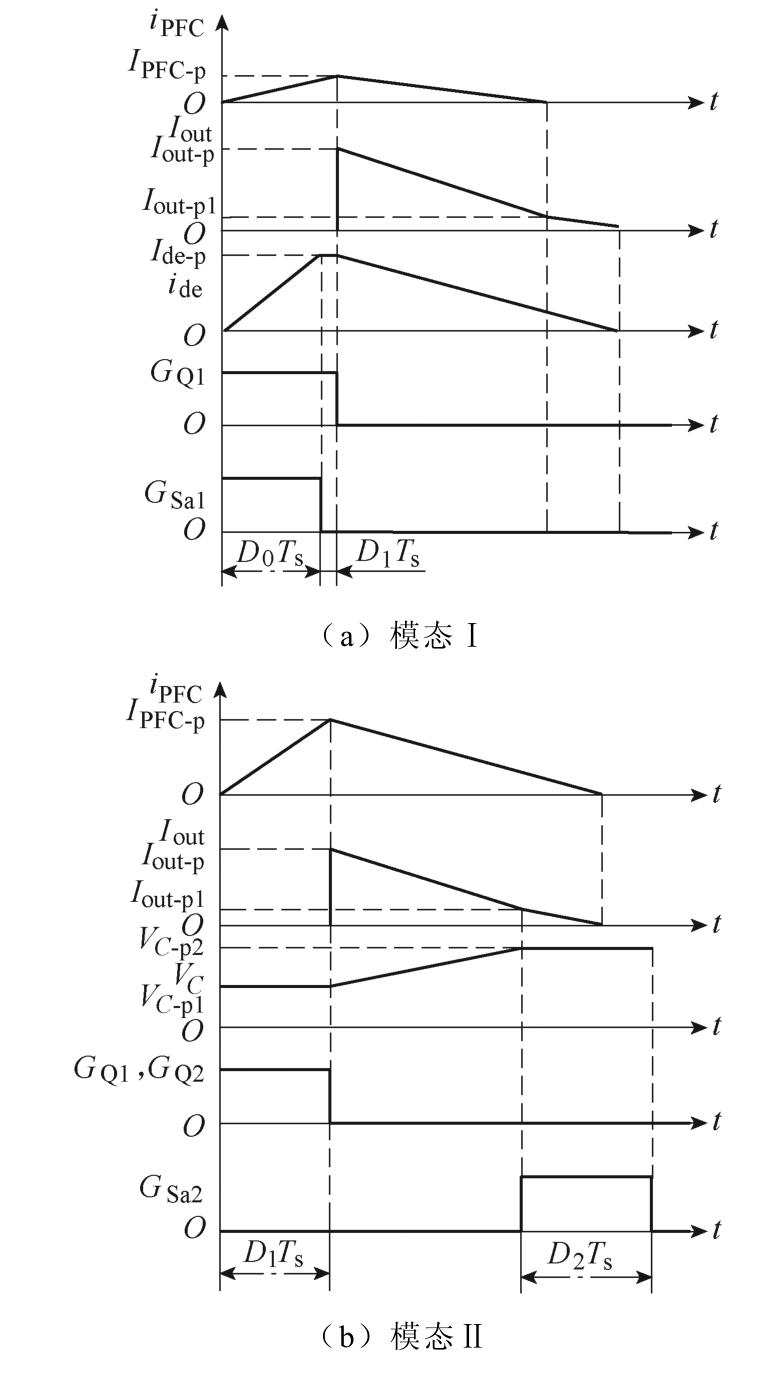
图5 电流波形及驱动信号在模态Ⅰ和模态Ⅱ
Fig.5 Current waveforms and driving signals under mode Ⅰ and mode Ⅱ
2.1 模态Ⅰ
模态Ⅰ时,各关键点电流和驱动信号波形如图5a所示。在该模态:①能量从网侧传递至电感LM1,同时解耦电容CD释放能量至电感LM2;②LM1和LM2同时给负载供电;③由于DCM运行,等待下一个开关周期。值得注意的是,由于输入电压vs极性,三种模式均有两种情况。
模式1:模态Ⅰ中工作模式1等效电路如图6所示,该阶段开始,开关管Q1、Q2触发导通。此时vs、二极管VDr1、VDr2和电感LM1形成闭合回路。网侧馈电至电感LM1,电流iLM1线性增加。同时,解耦电容CD、开关管Q1、Sa1和二极管VDa形成另一回路,解耦电容CD给电感LM2充电,电流iLM2增加。当Q1、Q2关闭时,电流iPFC达到峰值IPFC-p。
式中,ω为工频角频率;D1为Q1、Q2的占空比。
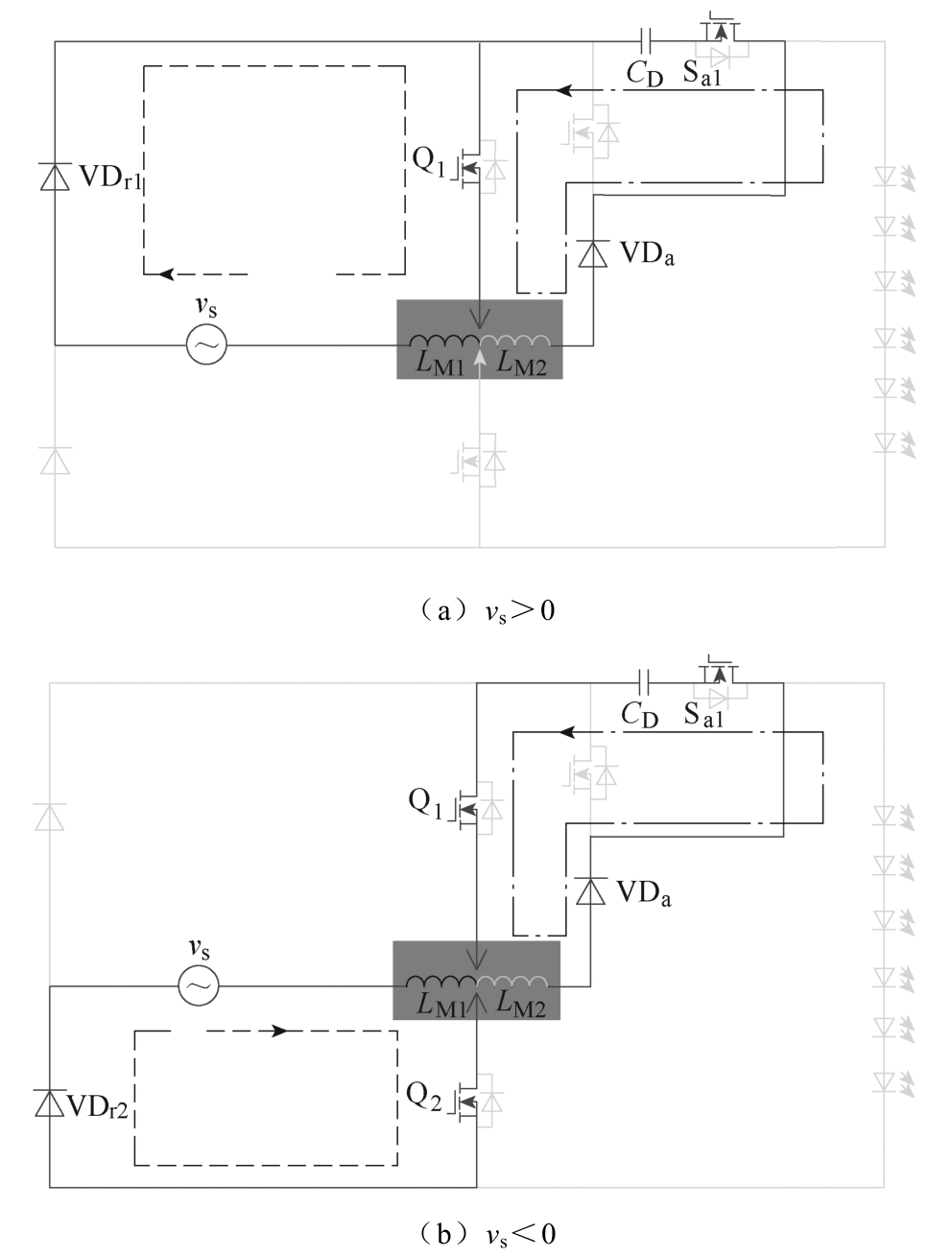
图6 模态Ⅰ中工作模式1等效电路
Fig.6 Equivalent circuit for period 1 in mode Ⅰ
同理,电流ide的峰值Ide-p可表示为
式中,D0为Sa1的占空比;VC-av为解耦电容CD两端的平均电压。
模式2:模态Ⅰ中工作模式2等效电路如图7所示,该阶段Q1、Q2处于关断状态。此时,Q2反并联二极管和VDa为电流ide提供续流通道;此外,Sa2导通,LM1向负载放电,可得所需输出电流的峰值为
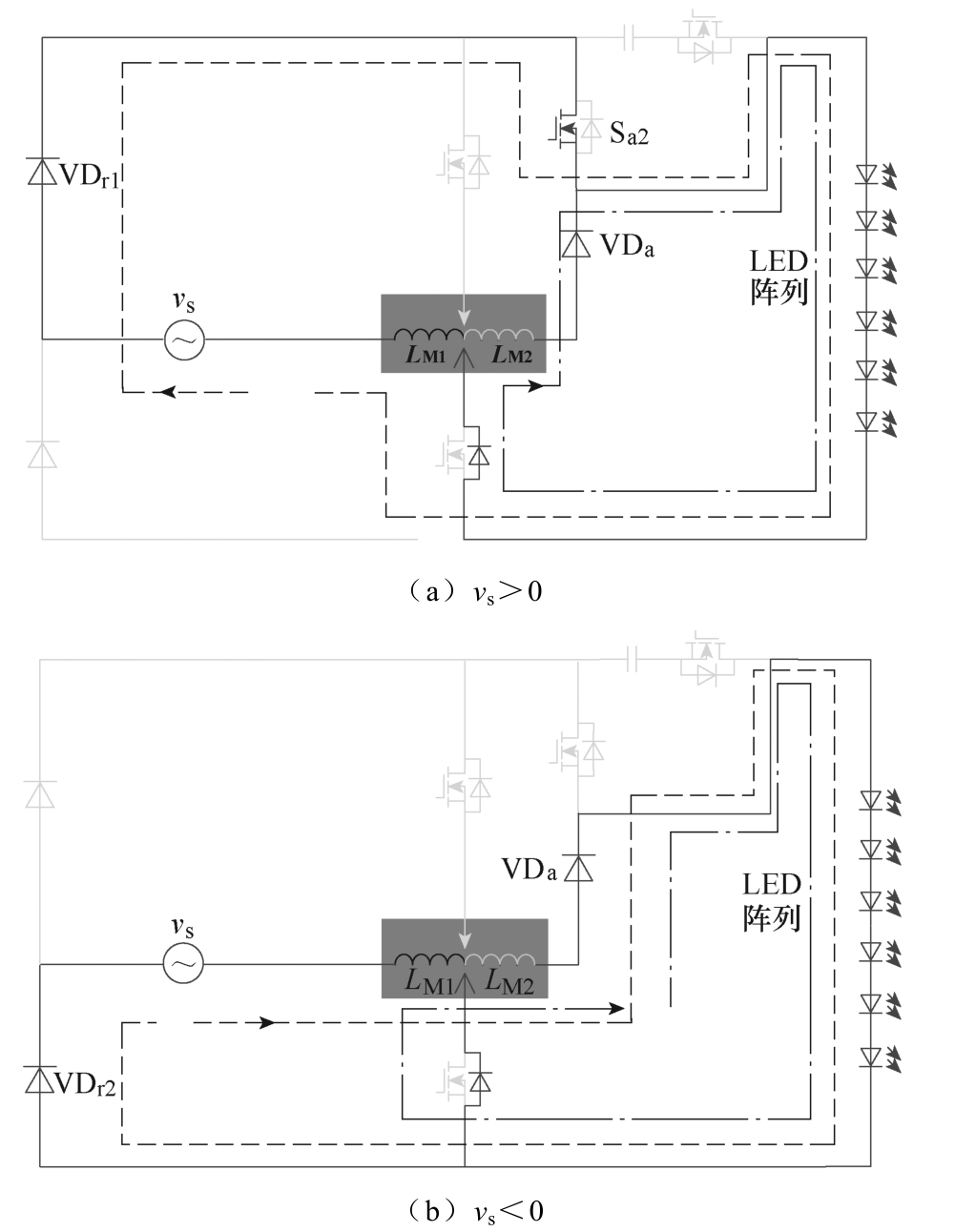
图7 模态Ⅰ中工作模式2等效电路
Fig.7 Equivalent circuit for period 2 in mode Ⅰ
因此,负载消耗的能量为
将式(3)和式(4)代入式(6)消去中间变量IPFC-p、Ide-p可知,D0Ts控制解耦电容CD释放能量,以弥补输入、输出瞬时功率不均衡造成的赤字,保证恒功率输出。
模式3:该阶段,所有开关管均处于关断状态,LM1能量完全释放;此时,无电流回路。因此,不再给出等效电路。
2.2 模态Ⅱ
模态Ⅱ下解耦电容电压和驱动信号波形如图5b所示。该模态:①能量从网侧存储至电感LM1;②LM1放电至解耦电容CD和负载;③负载到达所需电流值时,短路解耦电容。
模式1:与模态Ⅰ模式1类似,在此不再赘述。
模式2:此阶段,开关管Q1、Q2关闭,其续流二极管为CD和LM1提供电流路径,模态Ⅱ中工作模式2等效电路如图8所示。此时网侧输入功率可分解为输出功率Pout和脉动功率Pde两部分,则解耦电容获得的瞬时能量ΔEde为
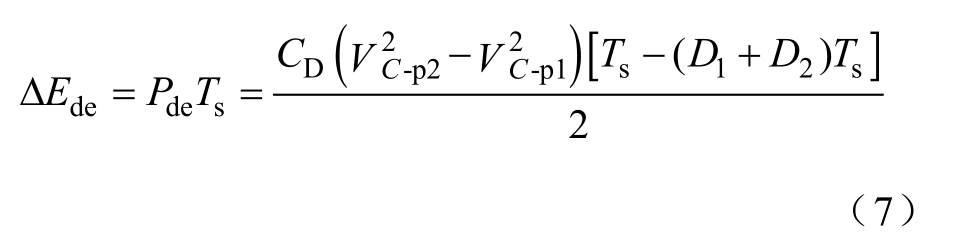
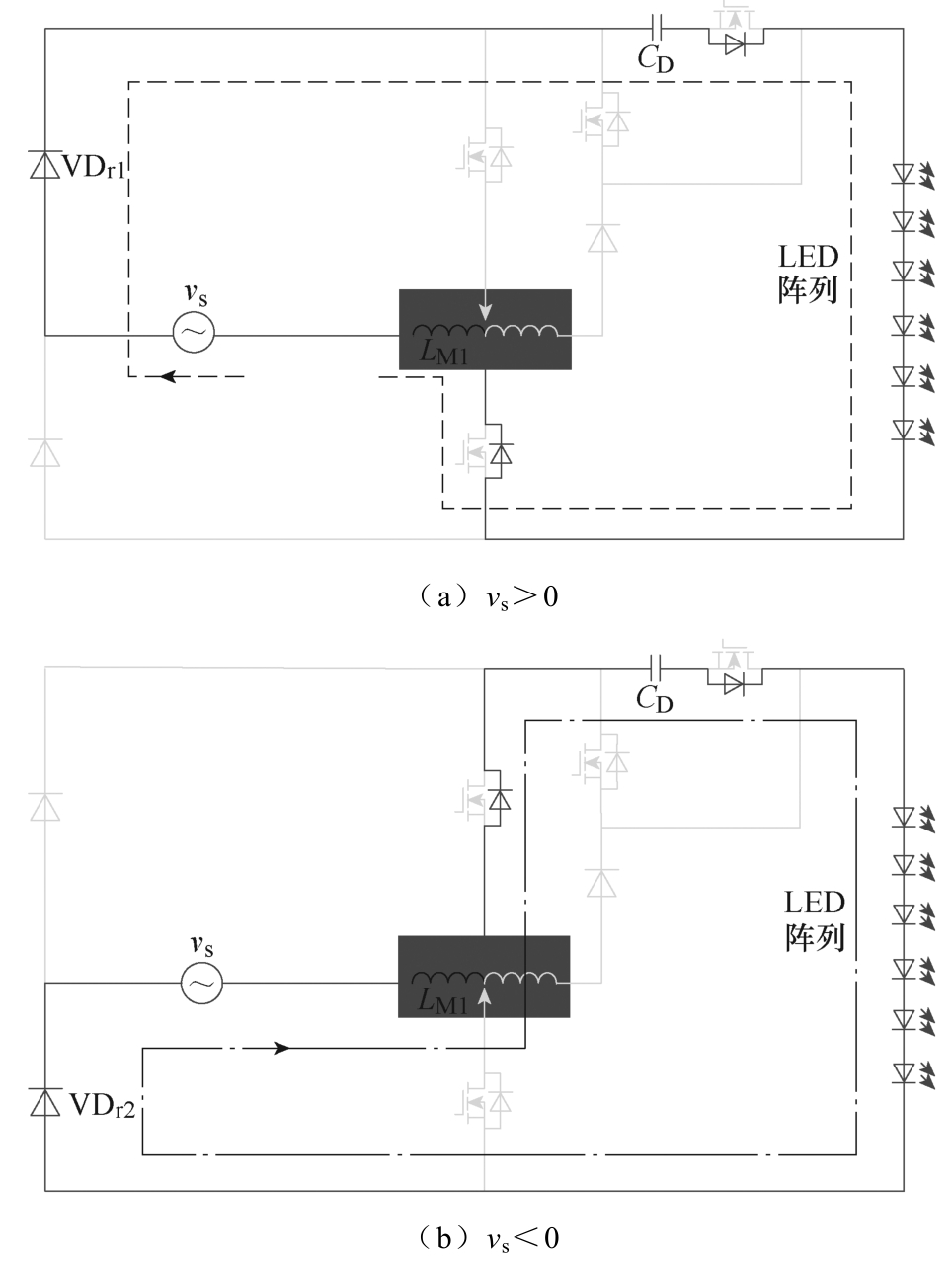
图8 模态Ⅱ中工作模式2等效电路
Fig.8 Equivalent circuit for period 2 in mode Ⅱ
同理,此阶段负载侧获得的能量为
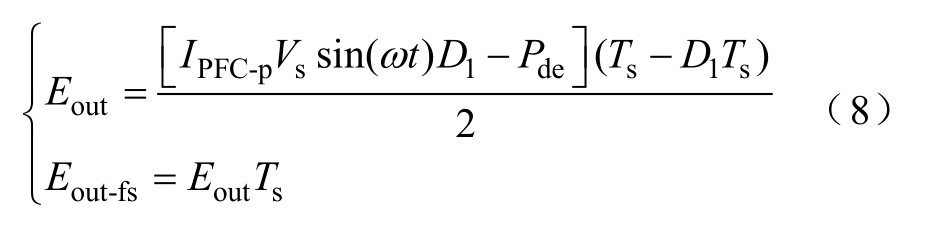
式中,Eout-fs为负载一个开关周期Ts内消耗的能量。
联立式(3)、式(7)和式(8)可知,输入功率存在的脉动功率通过控制变量D2Ts即开关管S2导通时间,可保证恒功率输出。
模式3:与模态Ⅰ模式3类似,模态Ⅱ中工作模式3等效电路如图9所示,将不再赘述。
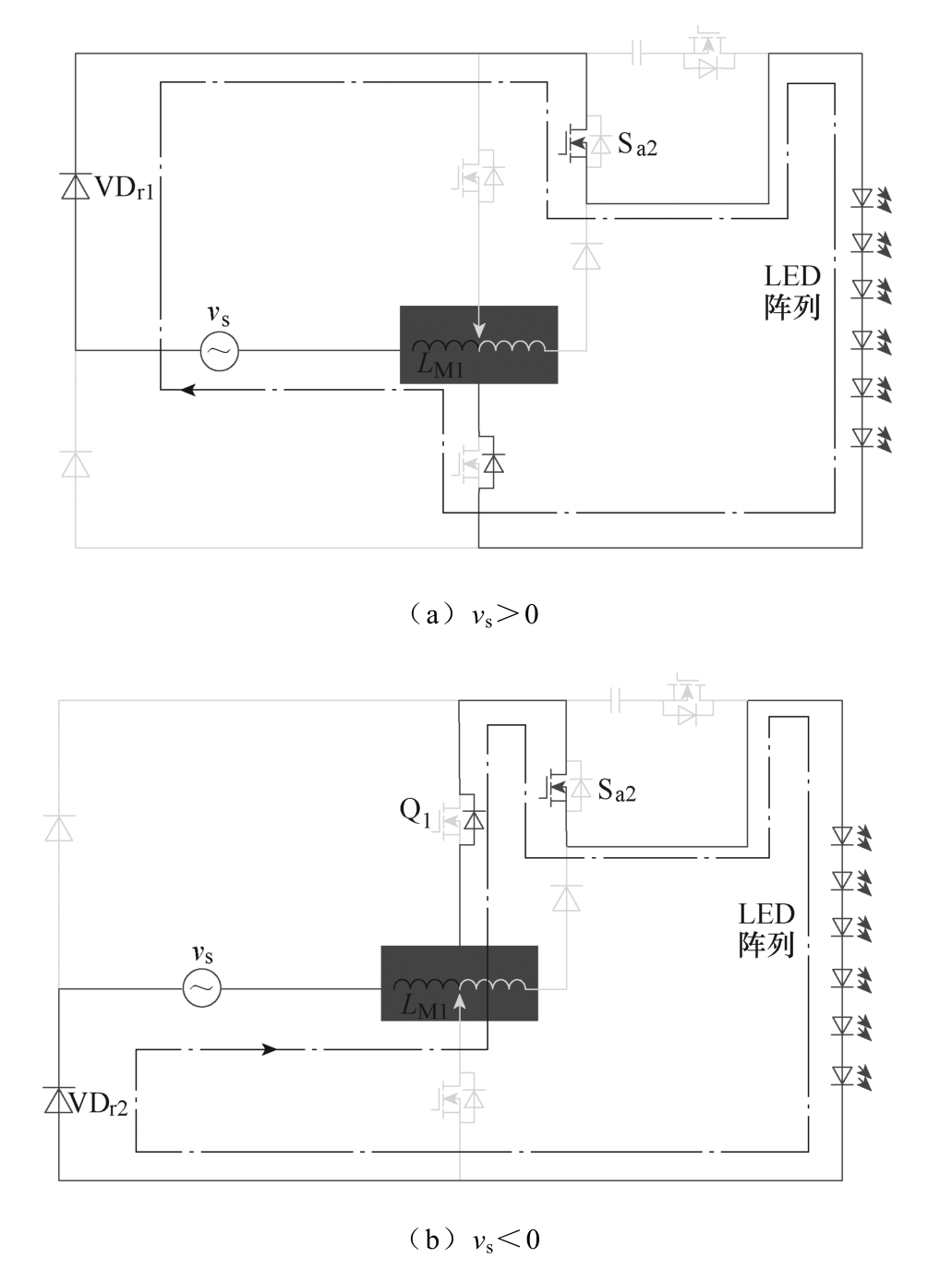
图9 模态Ⅱ中工作模式3等效电路
Fig.9 Equivalent circuit for period 3 in mode Ⅱ
3 设计考虑
3.1 功率器件选择
根据模态分析可知,Q1、Q2和VDr1、VDr2承受的电压应力高于其他功率器件,Vs为输入电压vs峰值。考虑到解耦电容CD钳位,Q1、Q2和VDr1、VDr2承受的电压应力明显降低,因此可选择电压应力较低的器件型号。表1列出了在vs>0的情况下VDr1、VDr2、Q1、Q2、VDa、Sa1和Sa2额定电压。
表1 器件的额定电压
Tab.1 Voltage ratings for devices
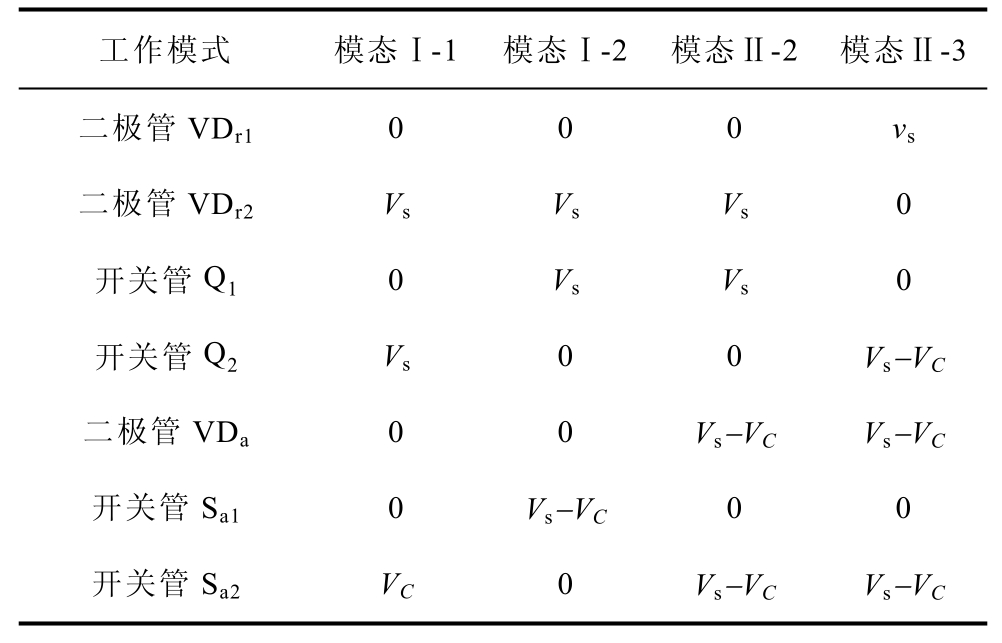
工作模式 模态Ⅰ-1 模态Ⅰ-2 模态Ⅱ-2 模态Ⅱ-3二极管VDr1 0 0 0 vs二极管VDr2 Vs Vs Vs 0 开关管Q1 0 Vs Vs 0 开关管Q2 Vs 0 0 Vs−VC二极管VDa 0 0 Vs−VC Vs−VC开关管Sa1 0 Vs−VC 0 0 开关管Sa2 VC 0 Vs−VC Vs−VC
3.2 解耦电容设计
解耦电容在半个工频周期内完成一次充放电,如图4所示。因此,通过对此时间段积分可得解耦电容的能量变化量为
同时,ΔEde也可以表示为
式中,VC-max和VC-min分别为VC的峰值和谷值。
瞬时输入功率Pin(t)包括两倍工频的脉动功率,可分解为
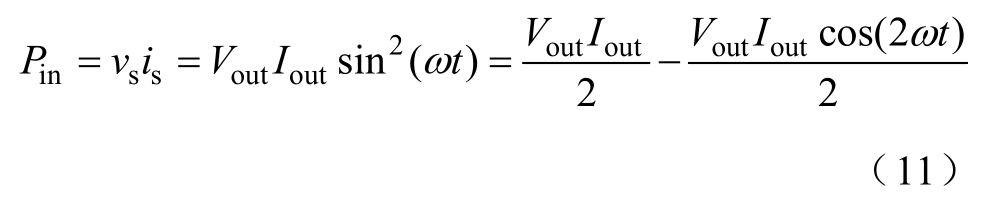
联立式(9)~式(11)可得,所需解耦电容及其电压应力分别为
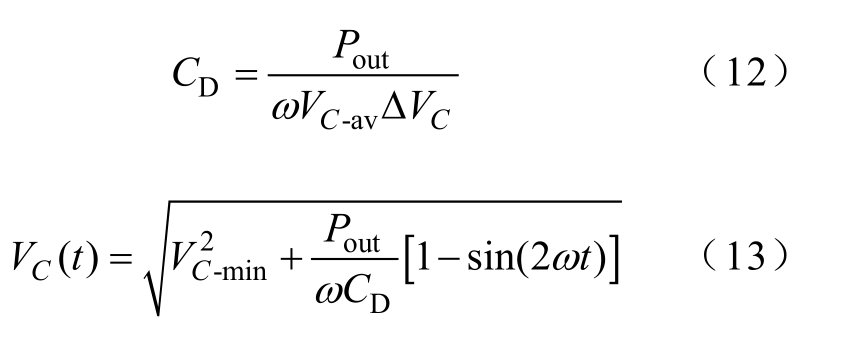
其中
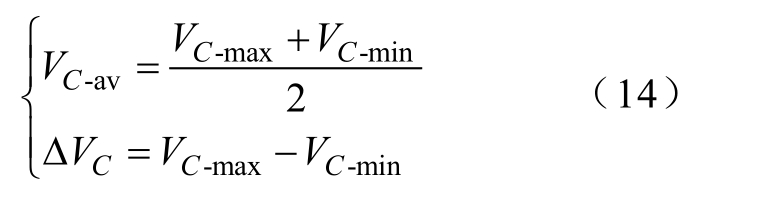
此外,电压纹波比Kr可表示为
因此,所需电容可表示为
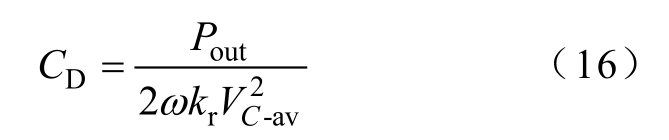
同理,所需电感可表示为
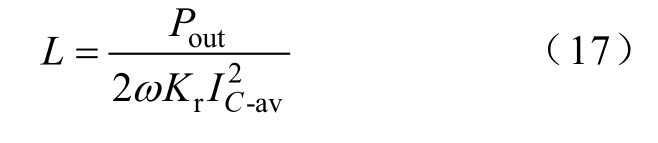
假设Pout=100W,Kr=2%,通过式(16)和式(17)计算可得,传统降压型和升压型变换器的解耦元件参数如图10所示。
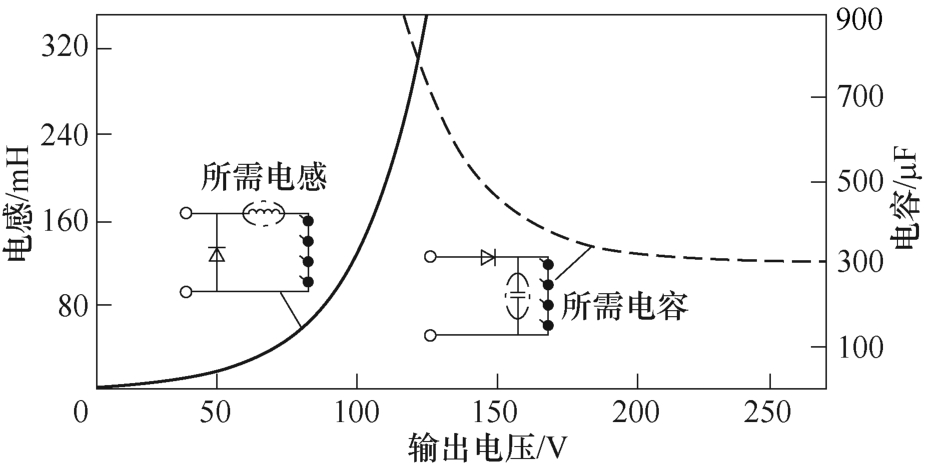
图10 无源解耦电路所需元件参数
Fig.10 Reference value of components required for passive decoupling circuit
从图10可以看出,由于无源器件的纹波受Vout的纹波率影响,所需值较大。其结果为Vout=140V时,所需的电容值约为500μF。因此,电解电容成为必要元件。图11给出了在相同条件下所提变换器的所需电容。上述分析可知,解耦单元通过控制单元调制开关管Sa1和Sa2的占空比,将脉动功率转移至解耦电容。因此,二倍工频的脉动纹波不会影响输出电压,大大降低了对母线电容的依赖。
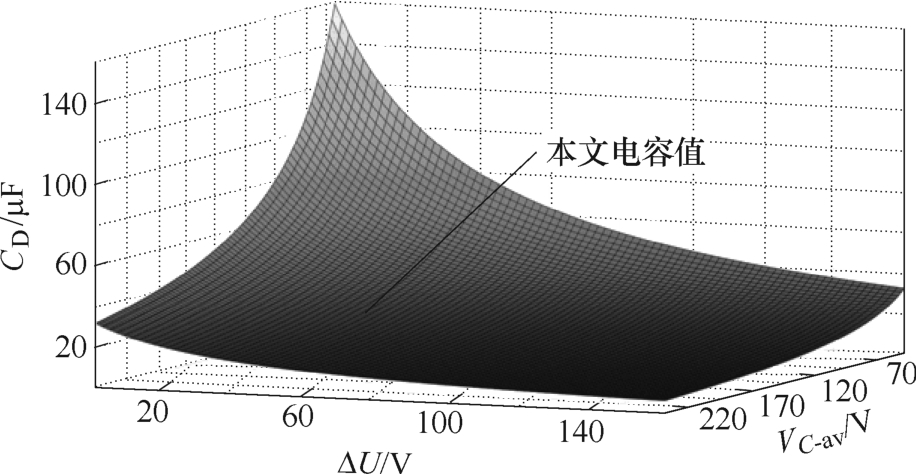
图11 解耦电容电压与纹波的关系
Fig.11 Relationship between decoupling capacitor voltage and ripple
3.3 电感设计
图12为电感LM1、LM2在DCM下的工作状态;本节以模态Ⅱ模式2为例进行分析。其中,Ton-Q1、Ton-Q2和Toff-Q1、Toff-Q2、Ton-Sa1和Toff-Sa1分别是Q1、Q2和Sa1的开通和关断时间。
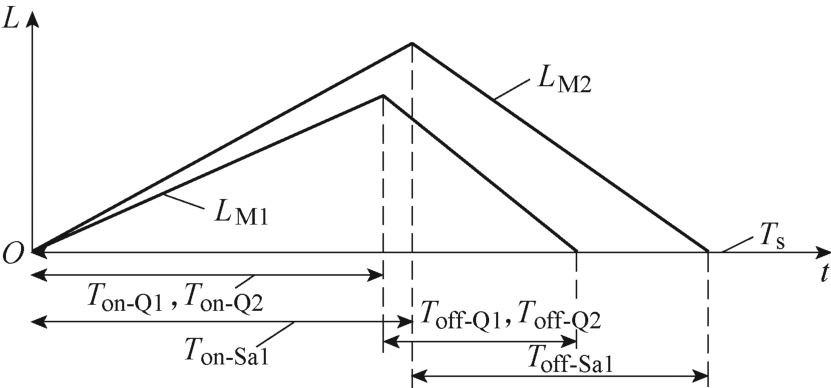
图12 一个开关周期内LMI1和LMI2的波形
Fig.12 Waveforms of LMI1 and LMI2under one switching-period
为了简化分析,将K定义为分配比率,且必须大于0.5[17],其数学表达式为
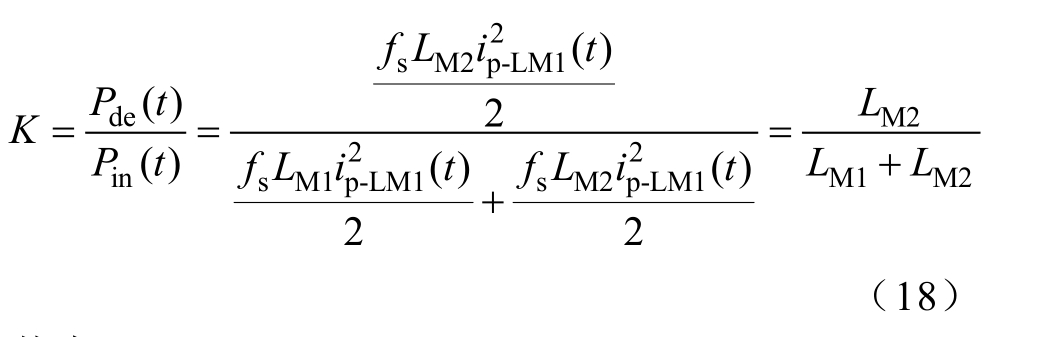
其中
由图12可知,LM1和LM2必须在一个开关周期内完成放电,那么Ton-Q1、Ton-Q2、Toff-Q1、Toff-Q2、Ton-Sa1和Toff-Sa1需满足
其中
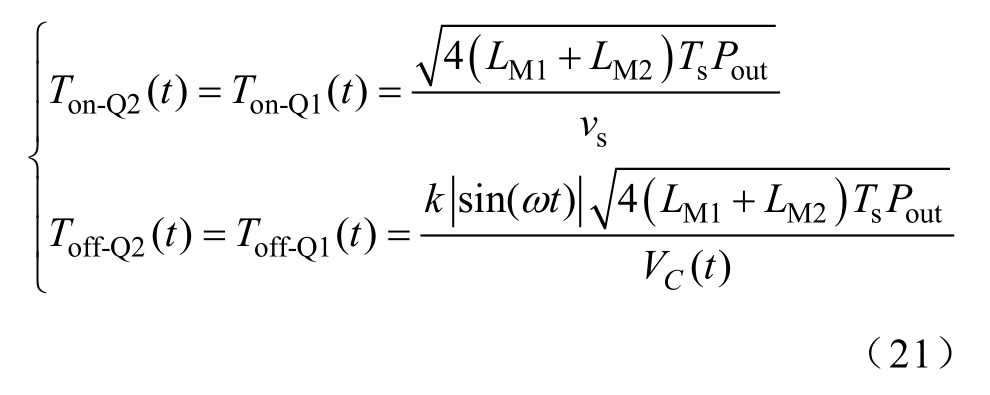
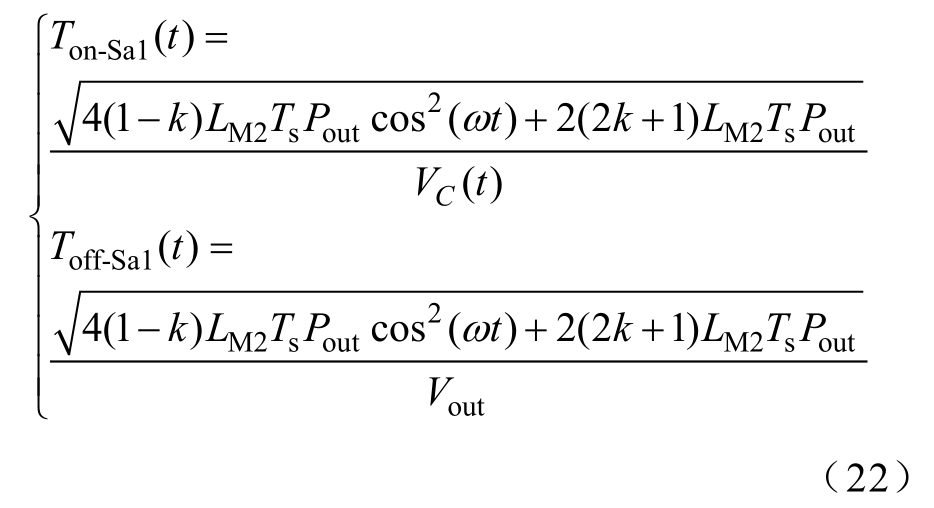
因此,在DCM运行下,LM1和LM2需满足
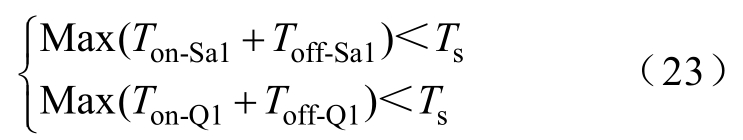
其中
考虑到输入电压和负载的变化,应降低Max(Ton-Sa1+Toff-Sa1)以预留一定的安全裕度。由式(4)可知,大的电感值可有效降低Sa1的电流应力;但这将意味着电路体积和成本增加。因此,本文最终选取解耦电感值为550μF。
3.4 控制策略
图13a给出了所提变换器的控制单元。实现功率解耦的关键是输入参考电流IPFC-ref和输出参考电流Iout-ref,即输出电流跟踪Iout-ref,输入电流跟踪IPFC-ref。此外,由于网侧存在一定失真,为获得良好的输入电流,锁相环(Phase Locked Loop, PLL)对输入电流进行锁相。输出参考电流Iout-ref为给定值;输入参考电流IPFC-ref为跟随时间变化的变量。
理论分析中为方便计算,假设输出功率等于输入功率。但实际中,变换器会存在不同损耗,如导通损耗、磁损耗和开关损耗。因此,Pout小于理论值。鉴于此,本次控制单元中增设一个电压控制回路以保持解耦电压稳定,且该回路旨在补偿系统中存在的额外损失。
传统方案往往对输入电流、输出电流和母线电容电压均需采样再比较,形成多PI控制,导致系统较为复杂,响应较慢。本文所提控制单元采用峰值电流控制法,只需检测vs和VC,进而比较IPFC-ref、Iout-ref和vs判断电路的工作模式,从而产生相应的PWM脉冲,简单易行、便于操作。具体而言,峰值电流控制框图中提供了两个参考值IPFC-ref、Iout-ref和1个采样电压vs,如图13b所示。其中,F1和F2为通过式(3)和式(4)得到的D0和D1的电流参考系数。对瞬时脉动功率进行处理后,使Pin和Pout符合图4理论波形。
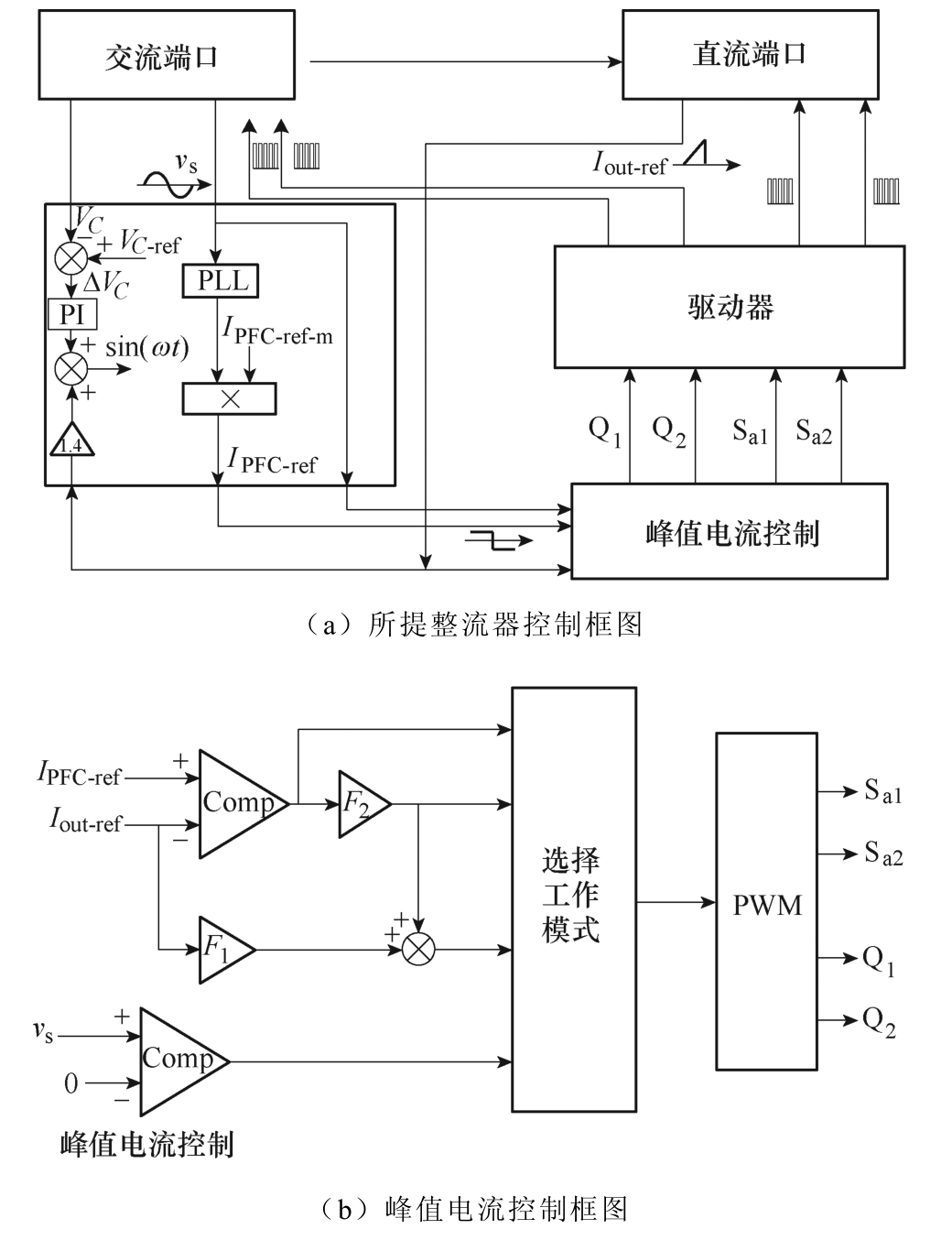
图13 控制电路结构
Fig.13 Structure of control circuit
4 实验结果
为验证所提变换器的正确性,本文搭建了110W的实验样机,如图14所示。其中,Cree XR-E系列LED作为负载。实验器件参数详见表2。

图14 实验样机
Fig.14 Experimental prototype
表2 器件参数
Tab.2 Component parameters
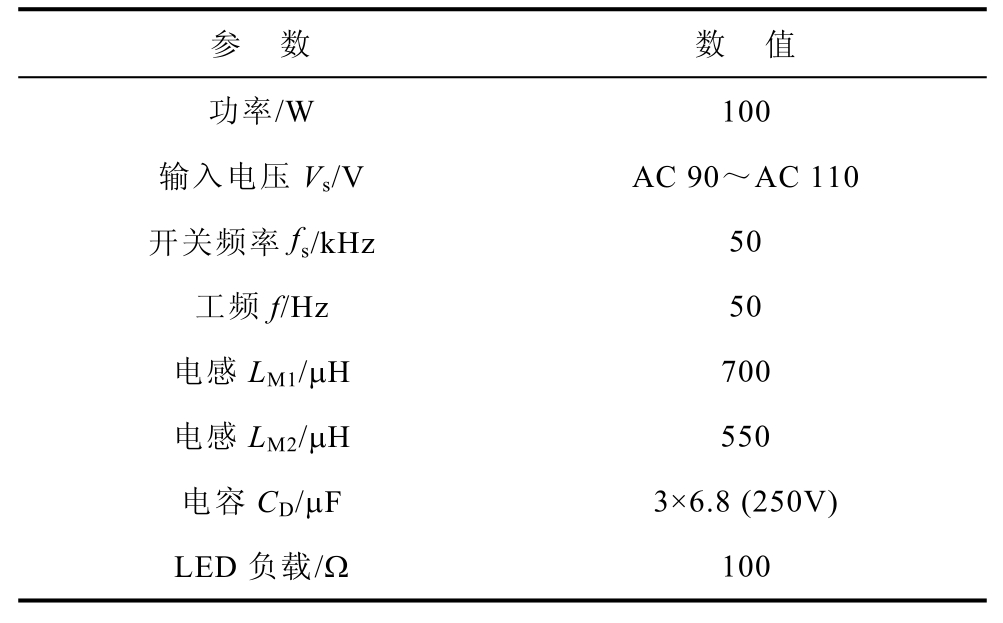
参 数 数 值 功率/W 100 输入电压Vs/V AC 90~AC 110 开关频率fs/kHz 50 工频f/Hz 50 电感LM1/μH 700 电感LM2/μH 550 电容CD/μF 3×6.8 (250V) LED负载/Ω 100
图15为输入电压有效值为90V和110V时,is和iPFC的实验波形。结果表明,PF分别为0.977和0.983,符合电气标准。此外,更详尽的PF实测数据将在下文呈现。图15a表明LM1工作在DCM,验证了参数选取的正确性,消除了整流二极管的反向恢复时间。
图16给出了不同输入电压等级下解耦电容VC的实验波形。结果表明,解耦电容电压VC具有两个特征:①低电压应力(约100V);②大电压纹波率(约38%)。由式(15)可知,较大的纹波比可有效降低母线电容值,为薄膜电容替换电解电容提供了可能。此外,解耦电容CD的钳位作用,保证了开关管Sa1和Sa2较低的导通损耗。
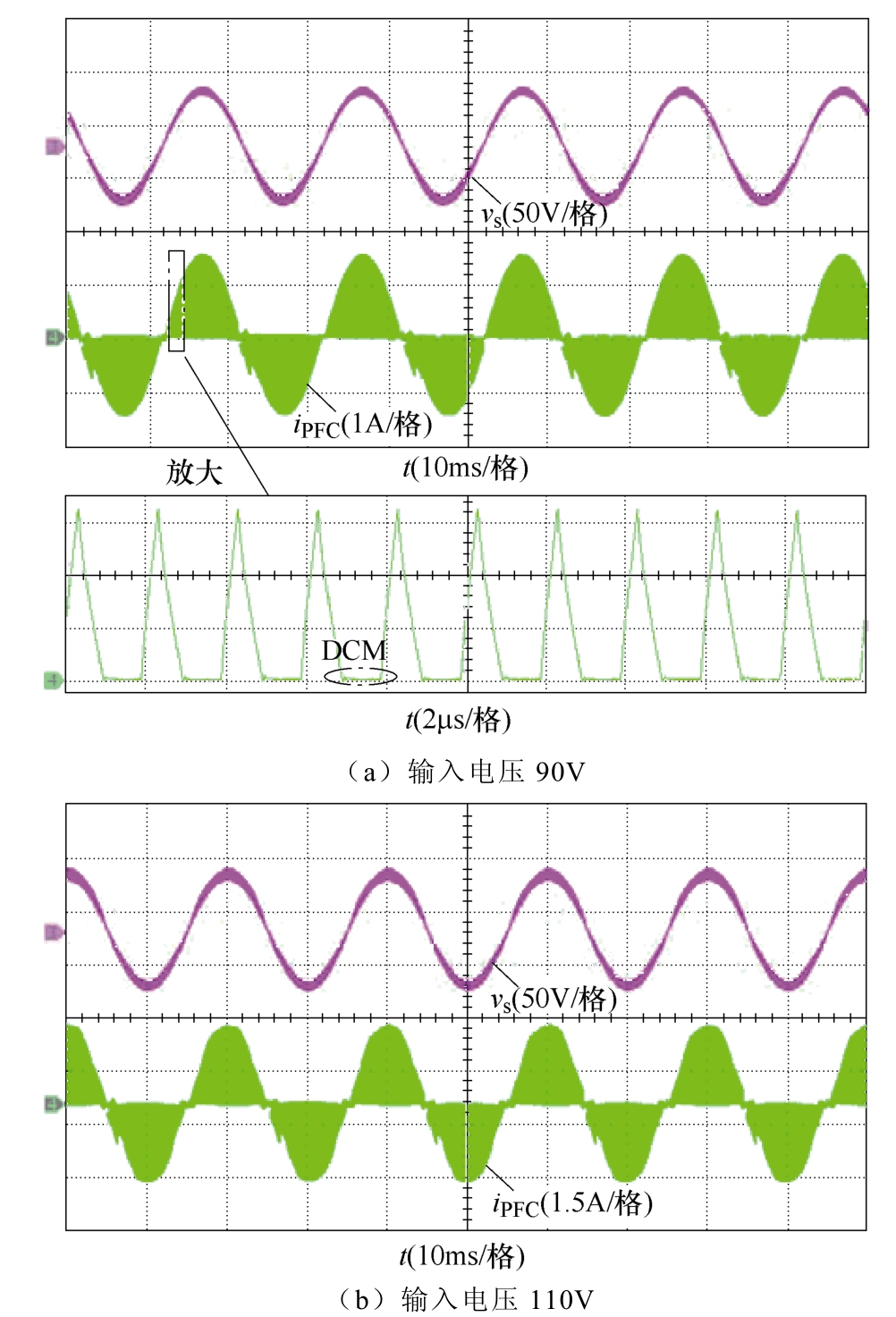
图15 is和iPFC的实验波形
Fig.15 Key experimental waveforms of is and iPFC
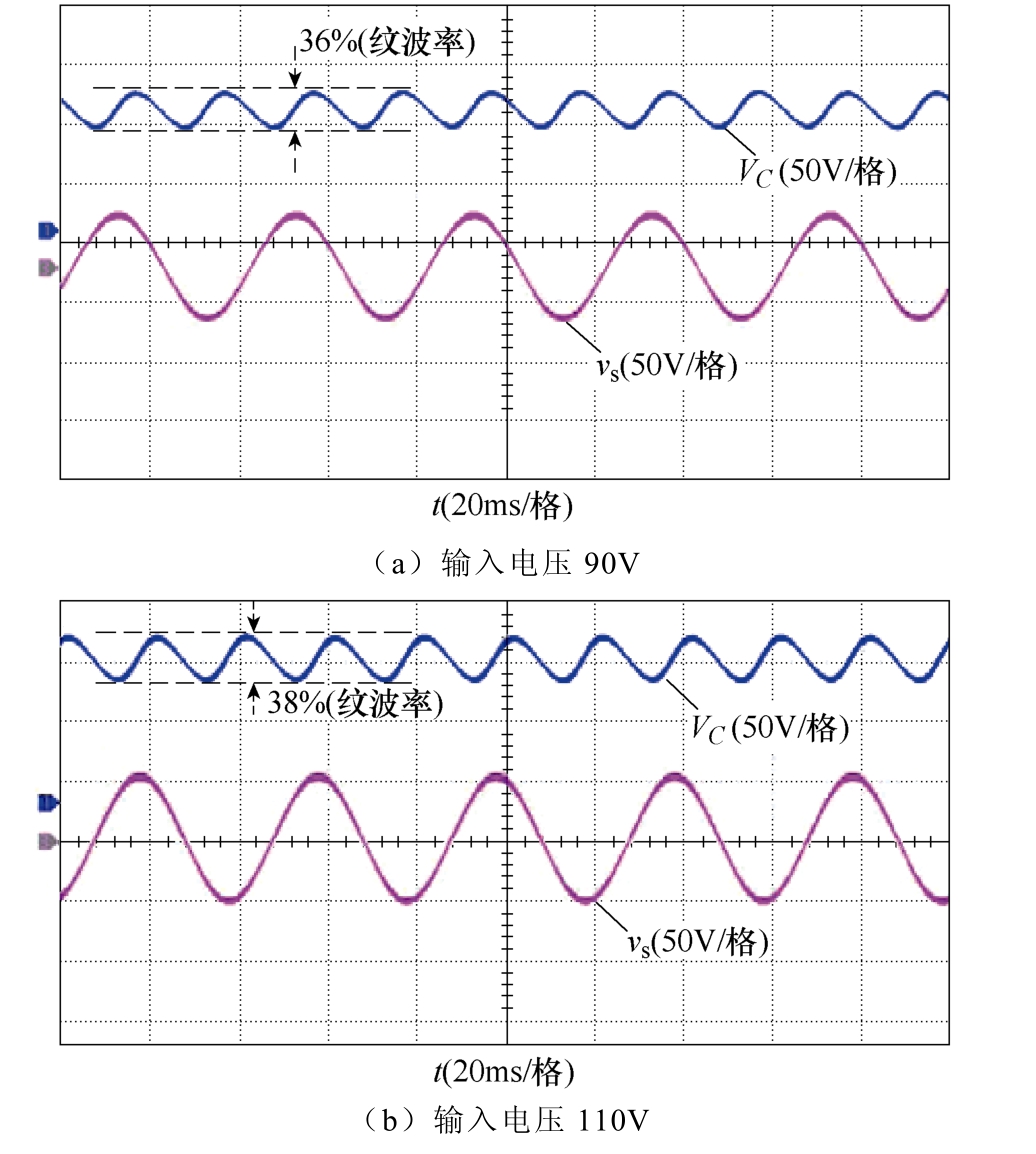
图16 VC实验波形
Fig.16 Key experimental waveforms of VC
为满足照明要求,亮度调节是必要的。图17a和图17b为输入电压有效值为90V、Q1、Q2的占空比为0.25和0.35时输出电流波形。其实验结果在占空比为0.25下,纹波约为112mA,占平均输出电流的10.2%;在占空比为0.35下,纹波为平均输出电流的9.3%。实验结果表明,较于相似工作14.1%的纹波率[25],本文电路具有输出电流质量更佳和无闪烁的驱动特性。此外,图17c给出了快速动态响应和平滑调光过程。

图17 输出电流波形
Fig.17 Waveforms of output current
图18给出了开关管的驱动信号波形。可以看出,当Pin>Pout时,Sa2导通,VC增加,CD充电;反之,亦然。结果表明,Q1分时复用于调光和功率解耦,并且解耦电路中不存在能量的双向流动,与理论分析一致。
图19为损耗分布和效率曲线。从图19a可以看出,磁性器件和二极管产生的损耗占比较高。但是,由于两个电感在电路中特殊位置使得未来的工作中可考虑磁集成技术以减少磁性器件的损耗。从图19b可以看出,与其他单向变换器相比,当功率从90W变化至130W时,所提整流器始终保持较高的传递效率,其数值均高于89.8%,并且在100W时达到最大92.5%。
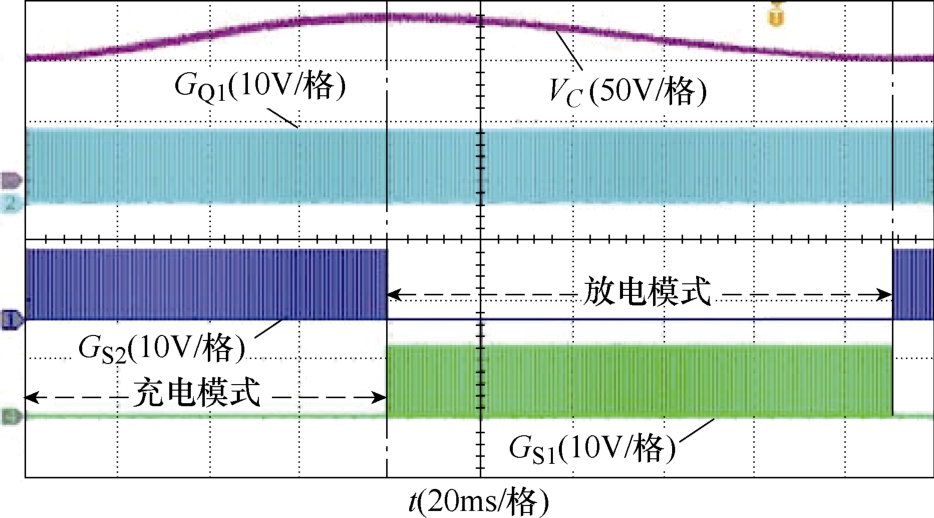
图18 开关管的驱动信号
Fig.18 Driving signal of each switch
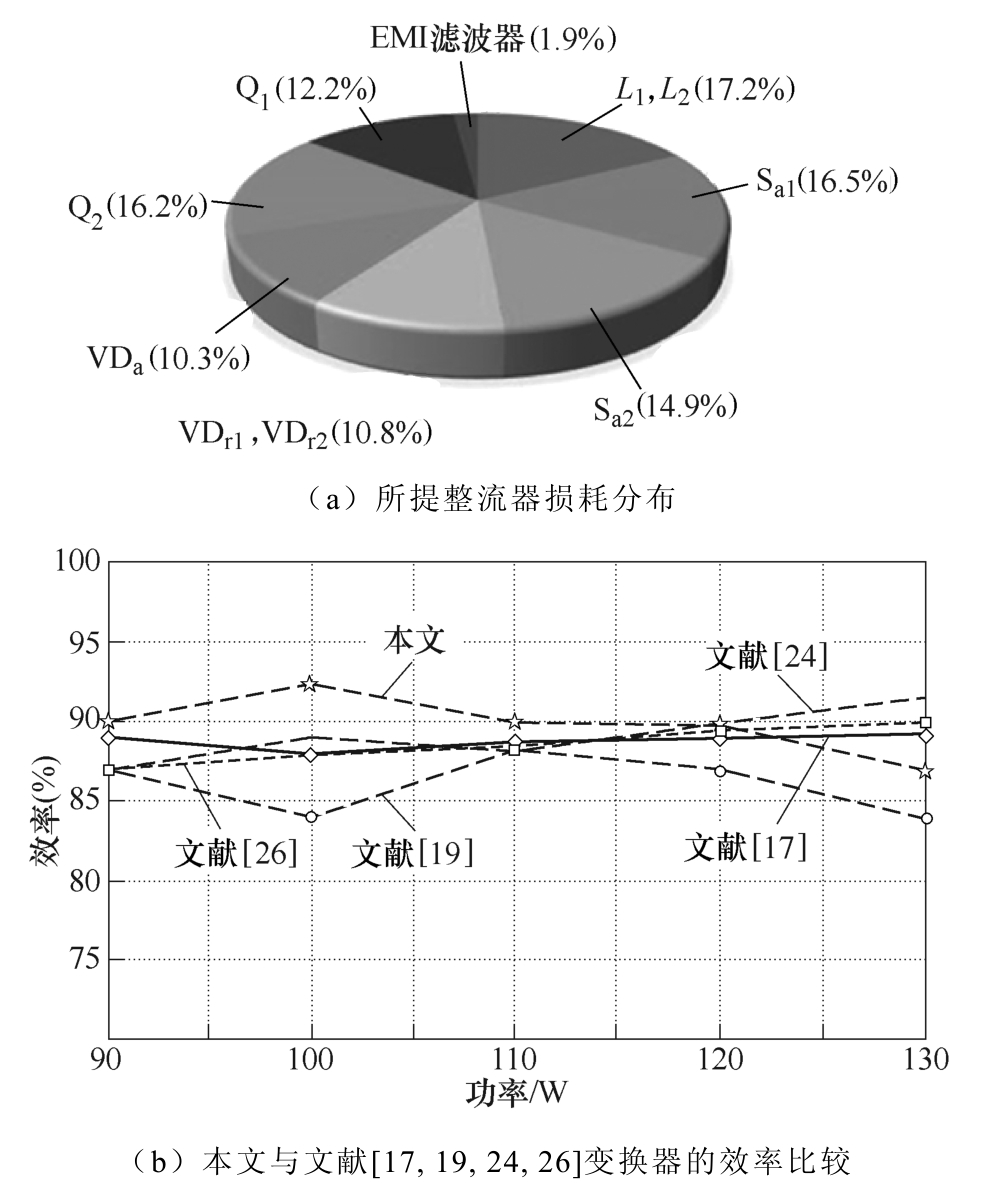
图19 损耗分析和效率曲线
Fig.19 Loss analysis and efficiency curves
图20给出了性能分析结果,包括满载情况下输入电流谐波含量、功率因数和总谐波畸变率(Total Harmonic Distortion, THD)的测量结果。图20a表明,所有电流谐波含量均满足IEC−61000−3−2 ClassC要求;图20b的结果表明,0.976的功率因数远远满足Energy Star的要求。此外,输入电压有效值在90~110V的范围内,其输入电流的THD均小于7.2%。由此表明,LED负载可与本文所提整流器实现较好的结合。
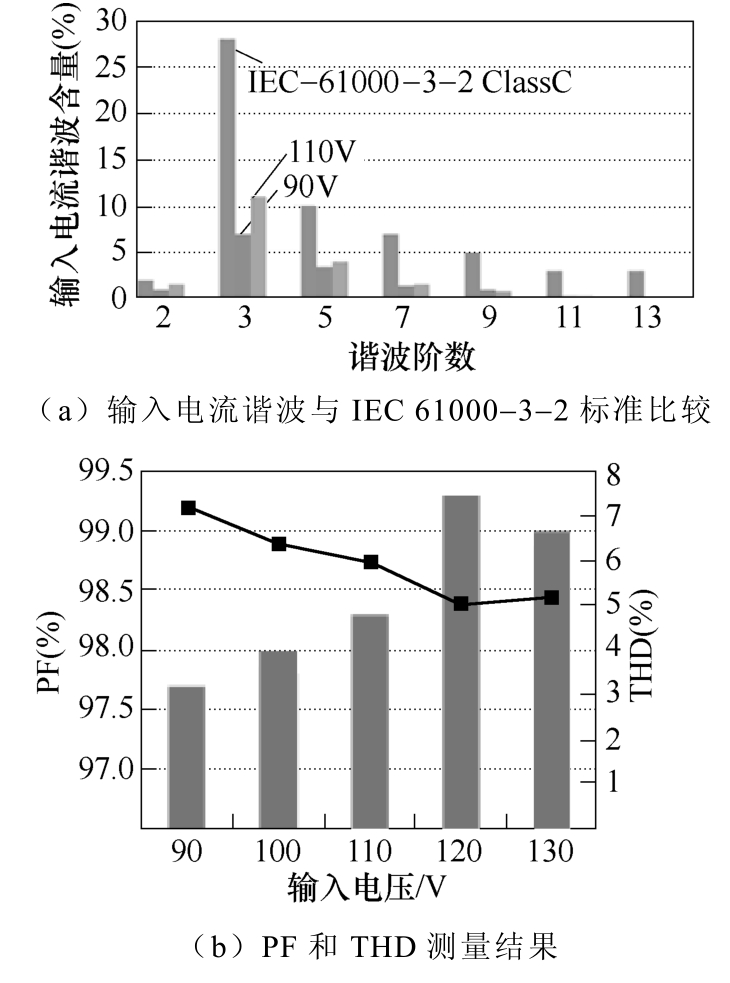
图20 性能分析
Fig.20 Performance analysis
5 结论
对于传统AC-DC LED驱动器而言,通常需要较大的电解电容平衡功率脉动,不仅限制了系统的整体寿命,而且影响了其轻量化的发展。此外,尽管Boost电路在PFC方面具有出色的性能,但导致大量元器件承受高电压应力,从而增加了导通损耗。现有方案器件冗余度高,同时控制回路较为复杂。鉴于此,本文提出了一种新型三端口整流器,消除电解电容的同时,还具有以下优点:
1)采用3×6.8μF/250V的薄膜电容替代电解电容;并且解耦电容的钳位作用使得开关管Sa1和Sa2导通损耗明显降低。
2)器件分时复用完成了单元间整合,消除了冗余器件。详言之,桥臂Sa1和Sa2不仅用于功率因数校正单元,同时用于功率解耦单元。此外,功率因数均高于0.975,符合相关要求。
3)通过改变驱动模式,消除了传统电路中承受高压应力的输出电容,效率得到了进一步提高。
最后,实验结果表明,本文介绍的整流器在消除对电解电容的依赖方面具有优势,并且拥有良好的输出电流质量,满足了LED无频闪的要求,不会造成视觉疲劳。
[1] 田涵雷, 刘俊峰, 曾君, 等. 基于可控开关电容的定频谐振式多路LED均流驱动器[J]. 电工技术学报, 2019, 34(2): 88-97.
Tian Hanlei, Liu Junfeng, Zeng Jun, et al. Fixed frequency resonant multi-channel LED current sharing driver based on controllable switched capacitor[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 88-97.
[2] Liu Junfeng, Tian Hanlei, Zeng Jun. Multi-channel LED driver based on switched-controlled capacitor with constant frequency control[J]. IET Power Elec- tronics, 2018, 11(12): 1991-1999.
[3] 王立乔, 李占一, 刘乐, 等. 一种无电解电容单级Buck-Boost逆变器[J]. 电工技术学报, 2019, 34(20): 129-139.
Wang Liqiao, Li Zhanyi, Liu Le, et al. A single-stage Buck-Boost inverter without electrolytic capacitor[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 129-139.
[4] 魏星, 朱信舜, 袁宇波, 等. 级联型电力电子变压器分级解耦控制[J]. 电力系统自动化, 2021, 45(8): 194-199.
Wei Xing, Zhu Xinshun, Yuan Yubo, et al. Hierarchi- cal decoupling control of cascaded power electronic transformers[J]. Automation of Electric Power Systems, 2021, 45(8): 194-199.
[5] 梁国壮, 田涵雷, 王子园, 等. 一种单级无桥式高功率因数无电解电容AC-DC LED驱动器[J]. 电工技术学报, 2019, 34(16): 3396-3407.
Liang Guozhuang, Tian Hanlei, Wang Ziyuan, et al. A single-stage AC-DC LED driver without bridge and high power factor and electrolytic capacitor[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3396-3407.
[6] Wang Beibei, Ruan Xinbo, Kai Yao, et al. A method of reducing the peak-to-average ratio of LED current for electrolytic capacitor-less AC-DC drivers[J]. IEEE Transactions on Power Electronics, 2010, 25(3): 592-601.
[7] 杨洋, 阮新波, 叶志红. 无电解电容AC/DC LED驱动电源中减小输出电流脉动的前馈控制策略[J]. 中国电机工程学报, 2013, 33(21): 18-25.
Yang Yang, Ruan Xinbo, Ye Zhihong. Feed forward control strategy for reducing output current ripple in AC/DC led driving power supply without electrolytic capacitor[J]. Proceedings of the CSEE, 2013, 33(21): 18-25.
[8] Ma Hongbo, Feng Quanyuan, Yu Wensong, et al. A novel valley-fill SEPIC-derived power supply without electrolytic capacitor for LED lighting application[J]. IEEE Transactions on Power Electronics, 2012, 27(6): 3057-3071.
[9] 王立乔, 王海旭, 崔舒敏, 等. 串联型功率解耦型无电解电容PFC电路[J]. 中国电机工程学报, 2019, 39(17): 5195-5204. Wang Liqiao, Wang Haixu, Cui Shumin, et al. Series power decoupling PFC circuit without electrolytic capacitor[J]. Proceedings of the CSEE, 2019, 39(17): 5195-5204.
[10] Pierquet B, Perreault D. A single-phase photovoltaic inverter topology with a series connected power buffer[J]. IEEE Transactions on Power Electronics, 2013, 28(10): 4603-4611.
[11] Qiu Yajie, Wang Laili, Wang Hongliang, et al. Bipolar ripple cancellation method to achieve single- stage electrolytic-capacitor-less high-power LED driver[J]. IEEE Journal of Emerging&Selected Topics in Power Electronics, 2015, 3(3): 698-713.
[12] Wang Yijie, Hu Xihong, Guan Yueshi, et al. A single-stage LED driver based on half-bridge CLCL resonant converter and Buck-Boost circuit[J]. IEEE Journal of Emerging&Selected Topics in Power Elec- tronics, 2019, 7(1): 196-208.
[13] Liu Yanfei, Fang Peng. Energy channeling LED driver technology to achieve flicker-free operation with true single stage power factor correction[J]. IEEE Transactions on Power Electronics, 2017, 32(5): 3892-3907.
[14] Tang Yi, Frede Blaabjerg, Poh Chiang Loh, et al. Decoupling of fluctuating power in single-phase systems through a symmetrical half-bridge circuit[J]. IEEE Transactions on Power Electronics, 2015, 30(4): 1855-1865.
[15] Fang Peng, Sheng Bo, Samuel Webb, et al. LED driver achieves electrolytic capacitor-less and flicker- free operation with an energy buffer unit[J]. IEEE Transactions on Power Electronics, 2019, 34(7): 6777-6793.
[16] Hyun Kim, Moon Chul, Sungwoo Kim, et al. An AC-DC LED driver with a two-parallel inverted buck topology for reducing the light flicker in lighting applications to low-risk levels[J]. IEEE Transactions on Power Electronics, 2017, 32(5): 3879-3891.
[17] Dong Hanjing, Xie Xiaogao, Jiang Lei, et al. An electrolytic capacitor-less high power factor LED driver based on a “one-and-a-half stage” forward flyback topology[J]. IEEE Transactions on Power Electronics, 2018, 33(2): 1572-1584.
[18] Fang Peng, Sam Webb, Liu Yanfei, et al. Single-stage LED driver achieves electrolytic capacitor-less and flicker-free operation with unidirectional current compensator[J]. IEEE Transactions on Power Elec- tronics, 2019, 34(7): 6760-6776.
[19] Shan Zhenyu, Chen Xiaomei, Jatskevich Juri, et al. An AC-DC LED driver with an additional active rectifier and a unidirectional auxiliary circuit for ac power ripple isolation[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 685-699.
[20] 曾君, 刘锋, 刘俊峰. 一种单极式多模态宽范围输入电压无电解电容LED驱动器[J]. 中国电机工程学报, 2020, 40(8): 2628-2637.
Zeng Jun, Liu Feng, Liu Junfeng. A unipolar multimode wide range input voltage LED driver with- out electrolytic capacitor[J]. Proceedings of the CSEE, 2020, 40(8): 2628-2637.
[21] Wang Fei, Li Lin, Zhong Yuexu, et al. Flyback-based three-port topologies of electrolytic capacitor-less LED drivers[J]. IEEE Transactions on Industrial Elec- tronics, 2017, 64(7): 5818-5827.
[22] Lam John, Praveen Jain. A high power factor, electrolytic capacitor-less AC-input LED driver topo- logy with high frequency pulsating output current[J]. IEEE Transactions on Power Electronics, 2015, 30(2): 943-955.
[23] Fang Peng, Liu Yanfei. Energy channelling LED driver technology to achieve flicker-free operation with true single stage power factor correction[J]. IEEE Transactions on Power Electronics, 2017, 32(5): 3892-3907.
[24] Li Huan, Li Sinan, Xiao Weidong. Single-phase LED driver with reduced power processing and power decoupling[J]. IEEE Transactions on Power Elec- tronics, 2020, 36(4): 4540-4548.
[25] 张超, 胡鑫, 朱孝勇, 等. 基于微升压功率解耦电路的无电解电容驱动系统研究[J]. 电工技术学报, 2019, 34(16): 3322-3332.
Zhang Chao, Hu Xin, Zhu Xiaoyong, et al. Research on non electrolytic capacitor drive system based on micro boost power decoupling circuit[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3322-3332.
[26] Li Sinan, Qi Wenlong, Wu Jiayang, et al. Minimum active switch requirements for single-phase PFC rectifiers without electrolytic capacitors[J]. IEEE Transactions on Power Electronics, 2019, 34(6): 5524-5536.